parent function assignment

Parent Functions And Their Graphs

Lessons with videos, examples and solutions to help PreCalculus students learn how about parent functions and their graphs.

Related Pages More Graphs And PreCalculus Lessons Graphs Of Functions

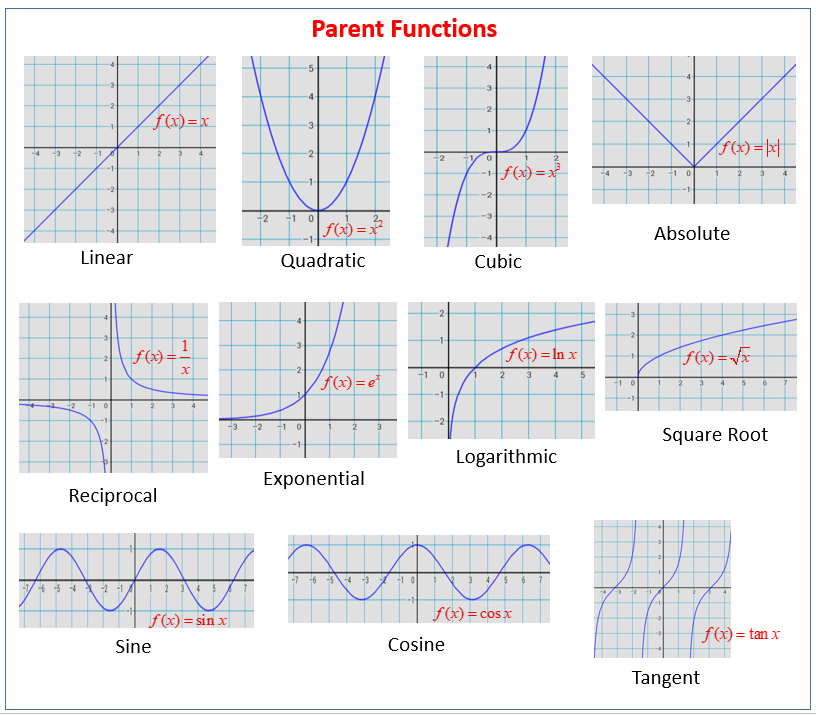
The following figures show the graphs of parent functions: linear, quadratic, cubic, absolute, reciprocal, exponential, logarithmic, square root, sine, cosine, tangent. Scroll down the page for more examples and solutions.

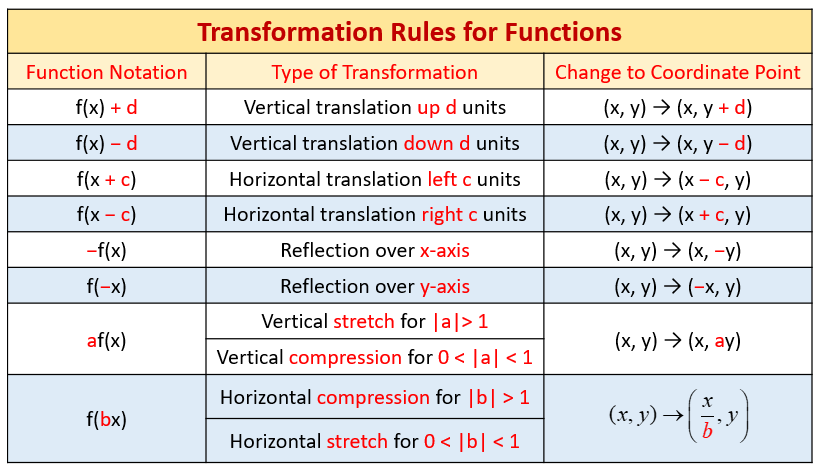
The following table shows the transformation rules for functions. Scroll down the page for examples and solutions on how to use the transformation rules.

Parent Functions And Their Graphs - How To Graph Elementary Functions?

In math, we often encounter certain elementary functions. These elementary functions include rational functions, exponential functions, basic polynomials, absolute values and the square root function. It is important to recognize the graphs of elementary functions, and to be able to graph them ourselves. This will be especially useful when doing transformations.

Basic Graphs That Every Algebra Student Should Know

Basic graphs that are useful to know for any math student taking algebra or higher. y = mx + b (linear function) y = x 2 (quadratic) y = x 3 (cubic) y = x 5 y = |x| (absolute) y = √x (square root) y = 1/x (reciprocal) y = 1/x 2 y = log b (x) for b > 1 y = a x for a > 1 (exponential) y = a x for 0 < a < 1

The Graphs Of Six Basic Functions That You Should Know

f(x) = x f(x) = x 2 f(x) = x 3 f(x) = √x f(x) = cube root(x) f(x) = |x|

7 Parent Functions With Equations, Graphs, Domain, Range And Asymptotes

y = x y = x 2 y = √x y = x 3 y = 1/x y = 1/x 2 y = |x|

Exploring Properties Of Parent Functions

In math, every function can be classified as a member of a family. Each member of a family of functions is related to its simpler, or most basic, function sharing the same characteristics. This function is called the parent function.

This lesson discusses some of the basic characteristics of linear, quadratic, square root, absolute value and reciprocal functions.

Transformations Of Parent Functions

Learn how to shift graphs up, down, left, and right by looking at their equations.

Vertical Shifts: f(x) + c moves up, f(x) - c moves down.

Horizontal Shifts: f(x + c) moves left, f(x - c) moves right.

Transforming Graphs And Equations Of Parent Functions

Looking at some parent functions and using the idea of translating functions to draw graphs and write equations.

Here is a list of topics:

• F(x) functions and transformations
• Horizontal Shift - Left and Right Units
• Vertical Shift - Units Up and Down
• Reflection about the x-axis, y-axis, and origin
• Inverse function f-1(x)
• Domain and Range - X and Y Values
• Horizontal and Vertical Asymptotes
• End Behavior - Left and Right Side
• Linear Functions: y=x
• Parabolas and Quadratic Functions: y=x 2
• Polynomial Functions - Cubic Functions: y=x 3
• Absolute Value Functions
• Cube Root Functions
• Square Root and Radical Functions
• Rational Functions y = 1/x - Vertical and Horizontal Asymptotes
• Exponential Functions: y=e x
• Logarithmic Functions - Log and Natural Log Functions y=lnx
• Trigonometric Functions - sine, cosine, and tangent - sin cos tan
• Inverse Trigonometric Functions y = sin -1 x cos -1 (x) and tan -1 (x)

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 9: Transformations of functions

About this unit.

We can think graphs of absolute value and quadratic functions as transformations of the parent functions |x| and x². Importantly, we can extend this idea to include transformations of any function whatsoever! This fascinating concept allows us to graph many other types of functions, like square/cube root, exponential and logarithmic functions.

Shifting functions

• Shifting functions introduction (Opens a modal)
• Shifting functions examples (Opens a modal)
• Graphing shifted functions (Opens a modal)
• Shift functions Get 3 of 4 questions to level up!

Reflecting functions

• Reflecting functions introduction (Opens a modal)
• Reflecting functions: examples (Opens a modal)
• Reflect functions Get 3 of 4 questions to level up!

Symmetry of functions

• Function symmetry introduction (Opens a modal)
• Even and odd functions: Graphs (Opens a modal)
• Even and odd functions: Tables (Opens a modal)
• Even and odd functions: Equations (Opens a modal)
• Even and odd functions: Find the mistake (Opens a modal)
• Symmetry of polynomials (Opens a modal)
• Even and odd functions: Graphs and tables Get 3 of 4 questions to level up!
• Even & odd functions: Equations Get 3 of 4 questions to level up!

Scaling functions

• Scaling functions introduction (Opens a modal)
• Scaling functions vertically: examples (Opens a modal)
• Scaling functions horizontally: examples (Opens a modal)
• Identifying horizontal squash from graph (Opens a modal)
• Scale functions vertically Get 3 of 4 questions to level up!
• Scale functions horizontally Get 3 of 4 questions to level up!

Putting it all together

• Identifying function transformations (Opens a modal)
• Identify function transformations Get 3 of 4 questions to level up!

Graphs of square and cube root functions

• Graphing square and cube root functions (Opens a modal)
• Radical functions & their graphs (Opens a modal)
• Graphs of square and cube root functions Get 3 of 4 questions to level up!

Graphs of exponential functions

• Transforming exponential graphs (Opens a modal)
• Transforming exponential graphs (example 2) (Opens a modal)
• Graphing exponential functions (Opens a modal)
• Graphs of exponential functions Get 3 of 4 questions to level up!

Graphs of logarithmic functions

• Graphical relationship between 2ˣ and log₂(x) (Opens a modal)
• Graphing logarithmic functions (example 1) (Opens a modal)
• Graphing logarithmic functions (example 2) (Opens a modal)
• Transformations of functions: FAQ (Opens a modal)
• Graphs of logarithmic functions Get 3 of 4 questions to level up!

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Parent Functions – Types, Properties & Examples

JUMP TO TOPIC

Parent function definition

Constant functions, linear functions, quadratic functions, cubic functions, absolute value functions, radical functions, exponential functions, logarithmic functions, reciprocal functions, practice questions, open problems, open problem solutions, parent functions – types, properties & examples.

A parent function represents a family of functions’ simplest form.

This definition perfectly summarizes what parent functions are. We use parent functions to guide us in graphing functions that are found in the same family. In this article, we will:

• Review all the unique parent functions (you might have already encountered some before).
• Learn how to identify the parent function that a function belongs to.

Being able to identify and graph functions using their parent functions can help us understand functions more, so what are we waiting for?

What is a parent function?

Now that we understand how important it is for us to master the different types of parent functions let’s first start to understand what parent functions are and how their families of functions are affected by their properties.

Parent functions are the simplest form of a given family of functions . A family of functions is a group of functions that share the same highest degree and, consequently, the same shape for their graphs .

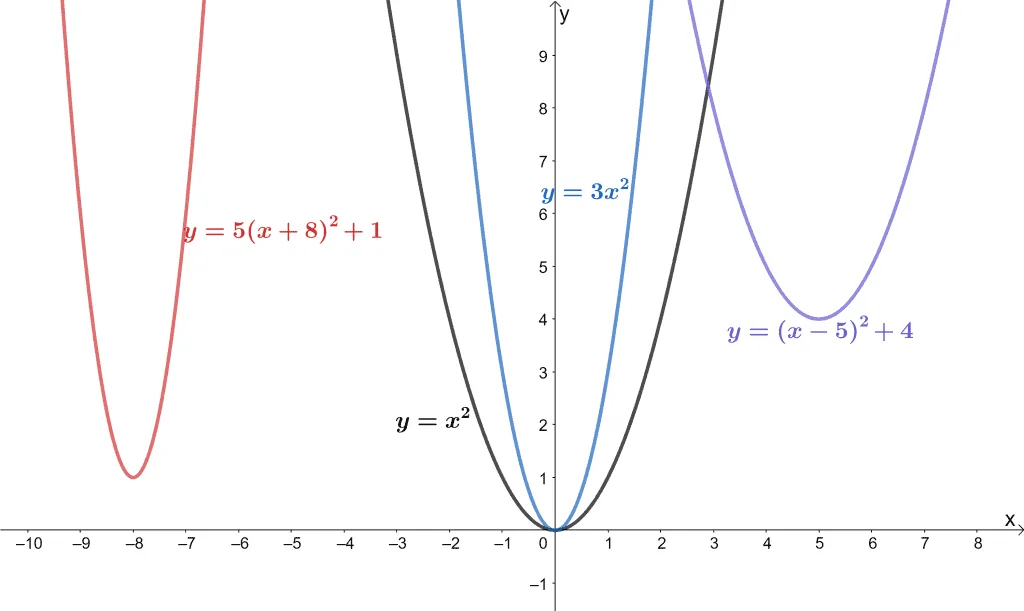
The graph above shows four graphs that exhibit the U-shaped graph we call the parabola. Since they all share the same highest degree of two and the same shape, we can group them as one family of function. Can you guess which family do they belong to?

These four are all quadratic functions, and their simplest form would be y = x 2 . Hence, the parent function for this family is y = x 2 .

Since parent functions are the simplest form of a given group of functions, they can immediately give you an idea of how a given function from the same family would look like.

What are the different types of parent functions?

It’s now time to refresh our knowledge about functions and also learn about new functions. As we have mentioned, familiarizing ourselves with the known parent functions will help us understand and graph functions better and faster.

Why don’t we start with the ones that we might already have learned in the past?

The first four parent functions involve polynomials with increasing degrees. Let’s observe how their graphs behave and take note of the respective parent functions’ domain and range.

Constant functions are functions that are defined by their respective constant, c. All constant functions will have a horizontal line as its graph and contain only a constant as its term.

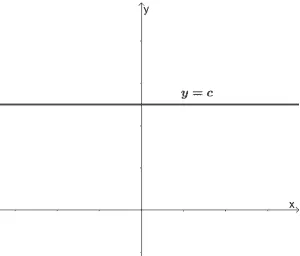
All constant functions will have all real numbers as its domain and y = c as its range. They also each have a y-intercept at (0, c).

An object’s motion when it is at rest is a good example of a constant function.

Linear functions have x as the term with the highest degree and a general form of y = a + bx. All linear functions have a straight line as a graph .

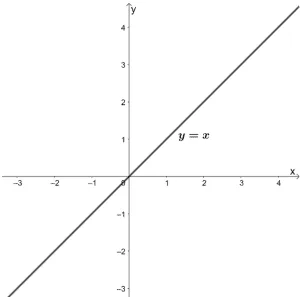
The parent function of linear functions is y = x, and it passes through the origin. The domain and range of all linear functions are all real numbers .

These functions represent relationships between two objects that are linearly proportional to each other.

Quadratic functions are functions with 2 as its highest degree . All quadratic functions return a parabola as their graph . As discussed in the previous section, quadratic functions have y = x 2 as their parent function .

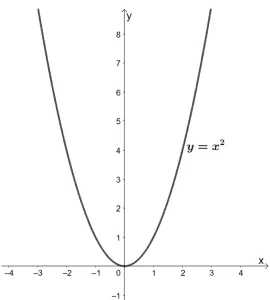
The vertex of the parent function y = x 2 lies on the origin. It also has a domain of all real numbers and a range of [0, ∞) . Observe that this function increases when x is positive and decreases while x is negative .

A good application of quadratic functions is projectile motion. We can observe an object’s projectile motion by graphing the quadratic function that represents it.

Let’s move on to the parent function of polynomials with 3 as its highest degree . Cubic functions share a parent function of y = x 3 . This function is increasing throughout its domain .

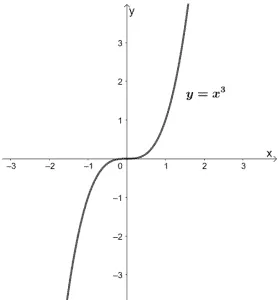
As with the two previous parent functions, the graph of y = x 3 also passes through the origin. Its domain and range are both (-∞, ∞) or all real numbers as well.

The parent function of absolute value functions is y = |x| . As shown from the parent function’s graph, absolute value functions are expected to return V-shaped graphs .

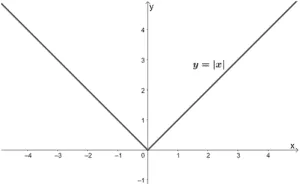
The vertex of y = |x| is found at the origin as well. Since it extends on both ends of the x-axis, y= |x| has a domain at (-∞, ∞).  Absolute values can never be negative, so the parent function has a range of [0, ∞) .

We use absolute value functions to highlight that a function’s value must always be positive.

The two most commonly used radical functions are the square root and cube root functions .

The parent function of a square root function is y = √x . Its graph shows that both its x and y values can never be negative.

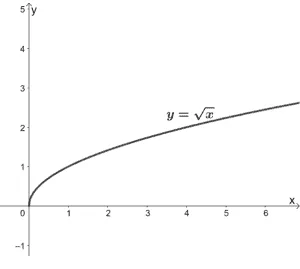
This means that the domain and range of y = √x are both [0, ∞ ) . The starting point or vertex of the parent function is also found at the origin . The parent function y = √x is also increasing throughout its domain .

Let’s now study the parent function of cube root functions. Similar to the square root function, its parent function is expressed as y = ∛ x .

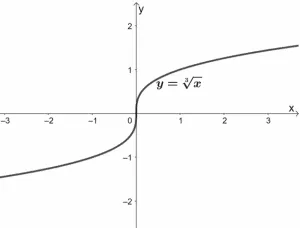
The graph shows that the parent function has a domain and range of (-∞, ∞) . We can also see that y = ∛x is increasing throughout its domain .

Exponential functions are functions that have algebraic expressions in their exponent. Their parent function can be expressed as y = b x , where b can be any nonzero constant. The parent function graph, y = e x , is shown below, and from it, we can see that it will never be equal to 0 .

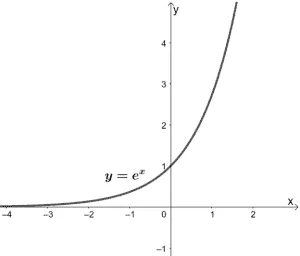
And when x = 0, y passing through the y-axis at y = 1. We can also see that the parent function is never found below the y-axis, so its range is (0, ∞ ). Its domain, however, can be all real numbers . We can also see that this function is increasing throughout its domain.

One of the most common applications of exponential functions is modeling population growth and compound interest.

Logarithmic functions are the inverse functions of exponential functions. Its parent function can be expressed as y = log b x , where b is a nonzero positive constant. Let’s observe the graph when b = 2 .

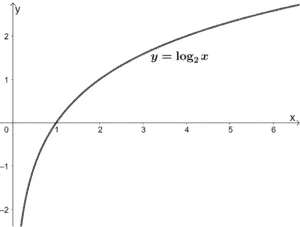
Like the exponential function, we can see that x can never be less than or equal to zero for y = log 2 x. Hence, its domain is (0,∞) .  Its range, however, contains all real numbers . We can also see that this function is increasing throughout its domain.

We use logarithmic functions to model natural phenomena such as an earthquake’s magnitude. We also apply it when calculating the half-life decay rate in physics and chemistry.

Reciprocal functions are functions that contain a constant numerator and x as its denominator. Its parent function is y = 1/x .

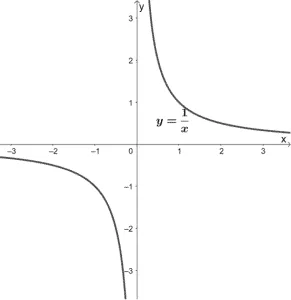
As can be seen from its graph, both x and y can never be equal to zero. This means that its domain and range are (-∞, 0) U (0, ∞) . We can also see that the function is decreasing throughout its domain .

There are many other parent functions throughout our journey with functions and graphs, but these eight parent functions are that of the most commonly used and discussed functions .

You can even summarize what you’ve learned so far by creating a table showing all the parent functions’ properties.

How to find the parent function?

What if we’re given a function or its graph, and we need to identify its parent function? We can do this by remembering each function’s important properties and identifying which of the parent graphs we’ve discussed match the one that’s given.

Here are some guide questions that can help us:

• What is the function’s highest degree?
• Does it contain a square root or cube root?
• Is the function found at the exponent or denominator?
• Is the function’s graph decreasing or increasing?
• What is the function’s domain or range?

If we can answer some of these questions by inspection, we will be able to deduce our options and eventually identify the parent function.

Let’s try f(x) = 5(x – 1) 2 . We can see that the highest degree of f(x) is 2 , so we know that this function is a quadratic function. Hence, its parent function is y = x 2 .

Why don’t we graph f(x) and confirm our answer as well?

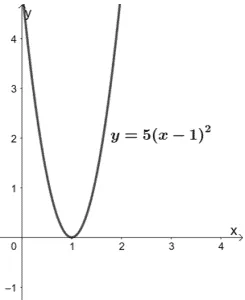
From the graph, we can see that it forms a parabola, confirming that its parent function is y = x 2 .

Review the first few sections of this article and your own notes, then let’s try out some questions to check our knowledge on parent functions.

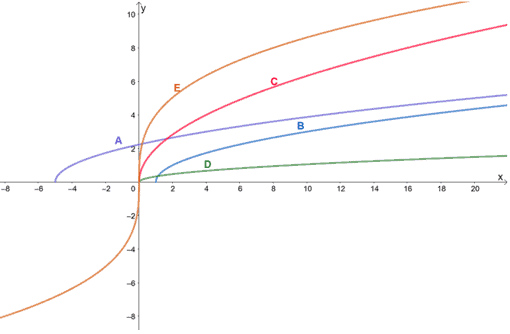
Graphs of the five functions are shown below. Which of the following functions do not belong to the given family of functions?

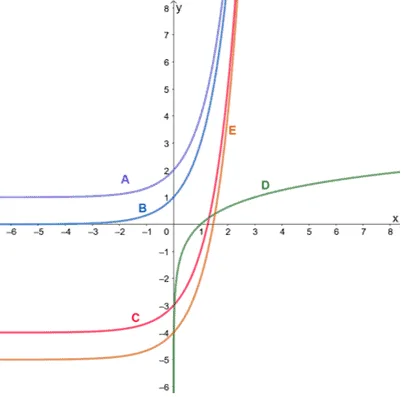
The functions represented by graphs A, B, C, and E share a similar shape but are either translated upward or downward. In fact, these functions represent a family of exponential functions . This means that they also all share a common parent function:  y=b x .

On the other hand, the graph of D represents a logarithmic function, so D does not belong to the group of exponential functions.

Which of the following functions do not belong to the given family of functions?

• y = -2x 2 + 3x – 1
• y = x(3x 2 )
• y = (x – 1)(x + 1)

The function y = 5x 2 has the highest degree of two, so it is a quadratic function. This means that its parent function is y = x 2 . The same goes for y = -2x 2 + 3x – 1. From this, we can confirm that we’re looking at a family of quadratic functions.

Applying the difference of perfect squares on the fourth option, we have y = x 2 – 1. This is also a quadratic function. That leaves us with the third option.

When expanded, y = x(3x 2 ) becomes y = 3x 3, and this shows that it has 3 as its highest degree. Hence, it can’t be part of the given family of functions.

  Identify the parent function of the following functions based on their graphs. Define each function’s domain and range as well.

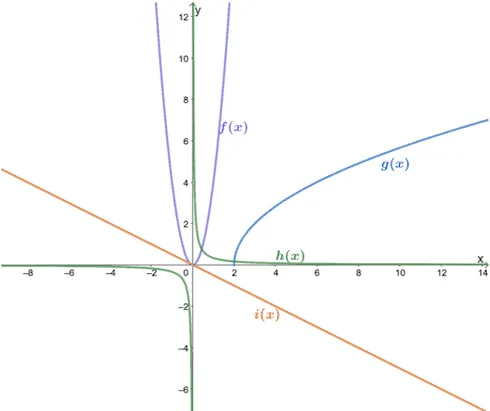
Let’s start with f(x). We can see that it has a parabola for its graph, so we can say that f(x) is a quadratic function .

• This means that f(x) has a parent function of y = x 2 .
• The graph extends on both sides of x, so it has a domain of (-∞, ∞) .
• The parabola never goes below the x-axis, so it has a range of [0,∞) .

Based on the graph, we can see that the x and y values of g(x) will never be negative. They also show an increasing curve that resembles the graph of a square root function .

• Hence, the parent function of g(x) is y = √x .
• The graph extends to the right side of x and is never less than 2, so it has a domain of [2, ∞) .

The h(x) graph shows that their x and y values will never be equal to 0. The symmetric curves also look like the graph of reciprocal functions.

• This means that h(x) has a parent function of y = 1/x.
• As long as the x and y are never equal to zero, h(x) is still valid, so it has both a domain and range of (-∞, ∞) .

The straight lines representing i(x) tells that it is a linear function.

• It has a parent function of y = x.
• The graph extends on both sides of x and y, so it has a domain and range of (-∞, ∞) .

Identify the parent function of the following functions.

• f(x) = x 3 – 2x + 1
• g(x) = 3√x + 1
• h(x) = 4/ x
• i(x) = e x + 1
• The highest degree of f(x) is 3, so it’s a cubic function. This means that it has a parent function of y = x 3 .
• The function g(x) has a radical expression, 3√x. Since it has a term with a square root, the function is a square root function and has a parent function of y = √x.
• We can see that x is found at the denominator for h(x), so it is reciprocal. Hence, its parent function is y = 1/x .
• The function’s exponents contain x, so this alone tells us that i(x) is an exponential function. Hence, its parent function can be expressed as y = b x , where b is a constant. For the case of i(x), we have y = e x as its parent function.

1. Describe the difference between $f(x) = -5(x – 1)^2$ and its parent function. What is the domain and range of $f(x)$?

2. Let $a$ and $b$ be two nonzero constants. Describe the difference between $g(x) = ax + b$ and its parent function. What is the domain and range of $g(x)$?

1. The parent function of $f(x)$ is $y = x^2$. This means that $f(x)$ has been transformed as follow:

• Translated one unit to the right.
• Reflected over the $x$-axis.
• Compressed by a scale factor of $5$.

The domain of $f(x)$ will be all real numbers while its range is all real numbers less than or equal to zero.

2. The function, $g(x) = ax + b$, has a parent function of $y =x$. This means that it differs by the following transformations:

• Stretched by a factor of $a$ when $a$ is a fraction or compressed by a factor of $a$ greater than $1$.
• Translated $b$ units upward if $b$ is positive or $b$ units downward if $b$ is negative.

The domain and range of $f(x)$ are all real numbers.

Images/mathematical drawings are created with GeoGebra.

Previous Lesson  |  Main Page | Next Lesson

• All Courses
• 4th Grade Math Blog
• 5th Grade Math Blog
• 6th Grade Math Blog
• PreAlgebra Blog (Grades 7-8)
• Algebra 1 Blog
• Geometry Blog
• Algebra 2 & Trig Blog
• PreCalculus Blog
• Curriculum Maps

Resources for Math Teachers

• Teacher Forums

1-5 Parent Functions and Transformations

Here are the sample resources for Pre-Calculus Lesson 1-5 Parent Functions and Transformations.

BELL WORK 1-5 Bell Work SE - Parent Functions and Transformations   (PDF) 1-5 Bell Work - Parent Functions and Transformations   (PDF) 1-5 Bell Work - Parent Functions and Transformations   (Doc) HOMEWORK ASSIGNMENT 1-5 Assignment SE- Parent Functions and Transformations   (PDF) 1-5 Assignment - Parent Functions and Transformations   (PDF) 1-5 Assignment - Parent Functions and Transformations   (Doc) POWER POINT PRESENTATION 1-5 Slide Show - Parent Functions and Transformations   (PPT) 1-5 Slide Show - Parent Functions and Transformations   (PDF) ONLINE ACTIVITIES 1-5 Online Activites - Parent Functions and Transformations   (PDF) 1-5 Online Activites - Parent Functions and Transformations   (Doc) LESSON PLAN 1-5 Lesson Plan - Parent Functions and Transformations   (PDF) 1-5 Lesson Plan - Parent Functions and Transformations   (Doc) GUIDED NOTES 1-5 Guided Notes SE - Parent Functions and Transformations   (PDF) 1-5 Guided Notes SE - Parent Functions and Transformations   (Doc) 1-5 Guided Notes TE - Parent Functions and Transformations   (PDF) 1-5 Guided Notes TE - Parent Functions and Transformations   (Doc) EXIT QUIZ 1-5 Exit Quiz SE- Parent Functions and Transformations   (PDF) 1-5 Exit Quiz - Parent Functions and Transformations   (PDF) 1-5 Exit Quiz - Parent Functions and Transformations   (Doc)

If you are ready to Join the Math Teacher Coach Membership Click the Button Below:

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.4: Graphs of Logarithmic Functions

• Last updated
• Save as PDF
• Page ID 34905

Learning Objectives

• Graph basic logarithmic functions and transformations of those functions
• Algebraically find the domain and vertical asymptote of a logarithmic function
• Find an equation of a logarithmic function given its graph

In a previous section, it was shown how creating a graphical representation of an exponential model provides some insight in predicting future events. Logarithmic graphs provide similar insight but in reverse because every logarithmic function is the inverse of an exponential function. This section illustrates how logarithm functions can be graphed, and for what values a logarithmic function is defined.

Graphs  of Basic Logarithmic Functions

To graph a logarithmic function \(y=log_{b}(x)\), it is easiest to convert the equation to its exponential form, \(x=b^{y}\). Generally, when graphing a function, various \(x\)-values are chosen and each is used to calculate the corresponding \(y\)-value. In contrast, for this method, it is the \(y\)-values that are chosen and the corresponding \(x\)-values that are then calculated.

Example \(\PageIndex{1}\)

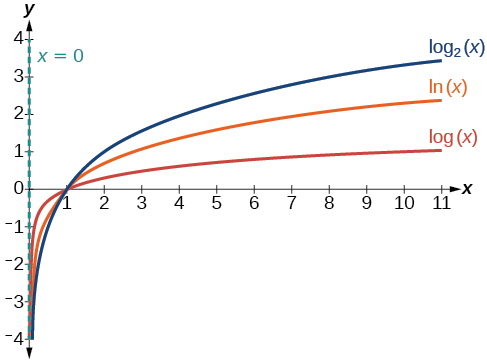
The graphs of \(y=\log _{2} (x), y=\log _{3} (x)\), and \(y=\log _{5} (x)\) (all log functions with \(b>1\)), are similar in shape and also:

• All graphs contains the key point \((  {\color{Cerulean}{1}} ,0)\) because \(0=log_{b}(  {\color{Cerulean}{1}}  )  \) means \(b^{0}=( {\color{Cerulean}{1}})\) which is true for any \(b\).
• All graphs contains the key point \((  {\color{Cerulean}{b}}  ,1)\) because \(1=\log _{b} (  {\color{Cerulean}{b}}  )\) means \(b^{1}=(  {\color{Cerulean}{b}}  )\) which is true for any \(b\).
• All graphs contain the key point \(\left(  {\color{Cerulean}{\frac{1}{b}}}  ,-1\right)\) because \(-1=\log _{b}(   {\color{Cerulean}{\frac{1}{b}}}  )\) means \(b^{-1}=(  {\color{Cerulean}{\frac{1}{b}}} )\), which is true for any \(b\).
• All graphs approach the \(y\)-axis very closely but never touch it. This line \(x=0\), the \(y\)-axis, is a vertical asymptote.
• The graphs never touch the \(y\)-axis so the domain is all positive numbers, written \((0,∞)\) in interval notation.
• All the graphs have the same range - the set of all real numbers, written in interval notation as \((−∞,∞)\).

Our next example looks at the graph of \(y=\log_{b}(x)\) when \(0<b<1\).

Example \(\PageIndex{2}\)

The graphs of \(y=\log _{\frac{1}{2}} (x), y=\log _{\frac{1}{3}} (x)\) and \(y=\log _{\frac{1}{4}} (x)\) are similar. 

• The graphs of all have the same basic shape. This is because all the log functions have a fractional base \(0<b<1\).
• All graphs contain the vertical asymptote \(x=0\) and key points \((1,0),\: (b, 1),\: \left(\frac{1}{b},-1\right)\), just like when \(b>1\).
• The domain and range are also the same as when \(b>1\). The domain is \((0,∞)\), the range is \((−∞,∞)\) and the \(y\)-axis is the vertical asymptote.

We summarize these properties in the chart below.  

CHARACTERISTICS OF THE GRAPH OF THE PARENT FUNCTION, \(f(x) = log_b(x)\)

For any real number \(x\) and constant \(b>0\), \(b≠1\), we can see the following characteristics in the graph of \(f(x)={\log}_b(x)\):

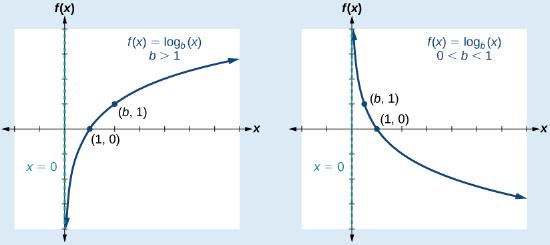
• vertical asymptote: \(x=0\)
• key points: \(x\) - intercept: \((1,0)\),  \((b,1)\) and \( \left(\tfrac{1}{b},-1\right) \)
• \(y\)-intercept: none
• domain: \((0,\infty)\)
• range: \((−\infty,\infty)\) 
• increasing if \(b>1\)
• decreasing if \(0<b<1\)

The family of logarithmic functions includes the parent function \(y={\log}_b(x)\) along with all its transformations: shifts, stretches, compressions, and reflections. When graphing transformations, we always begin with graphing the parent function \(y={\log}_b(x)\).  Below is a summary of how to graph parent log functions.

How to: Graph the parent logarithmic function \(f(x)={\log}_b(x)\).

• Draw and label the vertical asymptote, \(x=0\).
• Plot the keypoints: the \(x\) - intercept, \((1,0)\),  \((b,1)\), and \( \left( \tfrac{1}{b},-1 \right) \)
• Obtain additional points if they are needed by rewriting \(f(x)=\log_b{x}\) in exponential form as \(b^y=x\). Choose small \(y\) values (like 2, 3 and -1), calculate the corresponding value for \(x\), and plot the point on the graph.
• Draw a smooth curve through the points.
• State the domain, \((0,\infty)\), the range, \((−\infty,\infty)\), and the vertical asymptote, \(x=0\).

Graph Transformations of Logarithmic Functions

Transformations of logarithmic graphs behave similarly to those of other parent functions. We can shift, stretch, compress, and reflect the parent function \(y={\log}_b(x)\) without loss of basic shape. The general outline of the process appears below. Then illustrations of each type of transformation are described in detail. Finally, a summary of the steps involved in graphing a function with multiple transformations appears at the end of this section.

• Determine the parent function of \(f(x)\) and graph the parent function \(y={\log}_b(x) \) and its asymptote.
• Identify the transformations on the graph of \(y\) needed to obtain the graph of \(f(x)\).
• Use transformations to graph \(f(x)\) and its asymptote.

Vertical Shifts 

When a constant \(d\) is added to the parent function \(f(x)={\log}_b(x)\), the result is a vertical shift \(d\) units in the direction of the sign on \(d\). To visualize vertical shifts, we can observe the general graph of the parent function \(f(x)={\log}_b(x)\) alongside the shift up, \(g(x)={\log}_b(x)+d\) and the shift down, \(h(x)={\log}_b(x)−d\). 

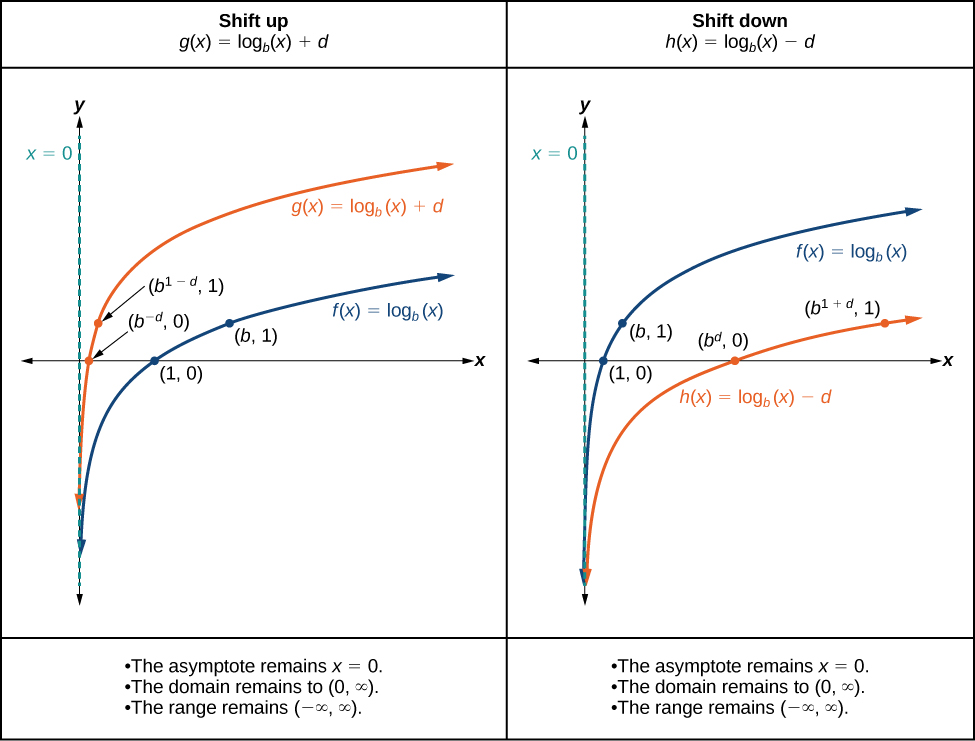
VERTICAL SHIFTS OF THE PARENT FUNCTION \(y = \log_b(x)\)

For any constant \(d\), the function \(f(x)={\log}_b(x)+d\)

• shifts the parent function \(y={\log}_b(x)\) up \(d\) units if \(d>0\).
• shifts the parent function \(y={\log}_b(x)\) down \(d\) units if \(d<0\).

The new \(y\) coordinates are equal to  \(y + d\).

Example \(\PageIndex{4}\): Graph a Vertical Shift of the Parent Function \(y = \log_b(x)\)

Sketch a graph of \(f(x)={\log}_3(x)−2\) alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

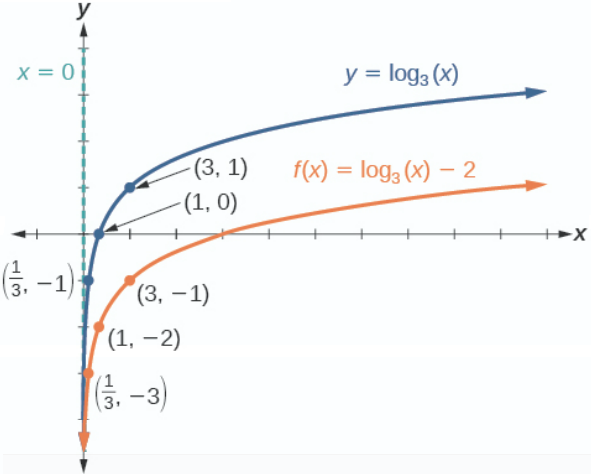
Step 2. Transformation on the graph of \(y\) needed to obtain the graph of \(f(x)\) is: shift down 2 units.

Step 3. Shifting down 2 units means the new \(y\) coordinates are found by subtracting \(2\) from the old \(y\) coordinates. Therefore,

• The vertical asymptote for the translated function \(f\) is still \(x=0\).
• The key points for the translated function \(f\) are \((1,−2)\), \((3,−1)\), and \(\left(\frac{1}{3},−3\right)\). Additional points are \( 9, 0)\) and \( 27,1) \).

The domain is \((0,\infty)\), the range is \((−\infty,\infty)\),and the vertical asymptote is \(x=0\).

Sketch a graph of \(f(x)={\log}_2(x)+2\) alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

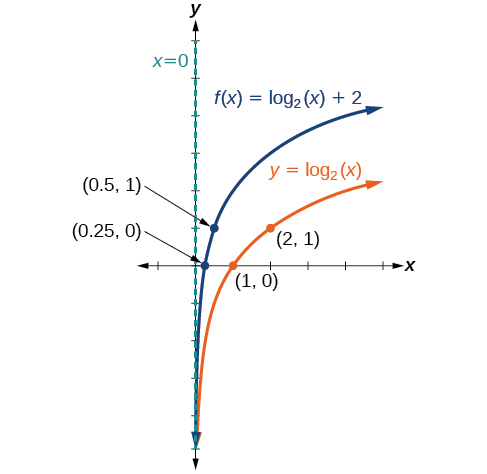
The domain is \((0,\infty)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\).

Horizontal Shifts 

When a constant \(c\) is added to the input of the parent function \(f(x)={\log}_b(x)\), the result is a horizontal shift \(c\) units in the opposite direction of the sign on \(c\). To visualize horizontal shifts, we can observe the general graph of the parent function \(f(x)={\log}_b(x)\) and for \(c>0\) alongside the shift left, \(g(x)={\log}_b(x+c)\), and the shift right, \(h(x)={\log}_b(x−c)\). See Figure \(\PageIndex{5}\).

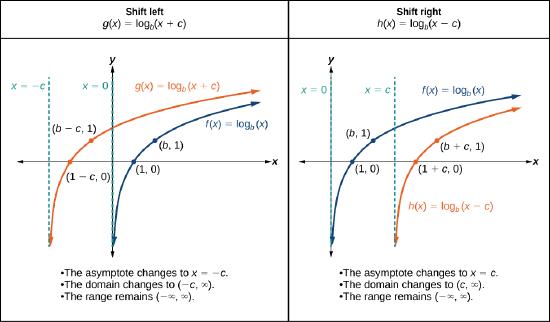
HORIZONTAL SHIFTS OF THE PARENT FUNCTION \(y = \log_b(x)\)

For any constant \(c\), the function \(f(x)={\log}_b(x+c)\)

• shifts the parent function \(y={\log}_b(x)\) left \(c\) units if \(c>0\).
• shifts the parent function \(y={\log}_b(x)\) right \(c\) units if \(c<0\).

The new \(x\) coordinates are equal to \(x - c\). 

Example \(\PageIndex{5}\): Graph a Horizontal Shift of the Parent Function \(y = \log_b(x)\)

Sketch the horizontal shift \(f(x)={\log}_3(x−2)\) alongside its parent function. Include the key points and asymptotes on the graph. State the domain, range, and asymptote.

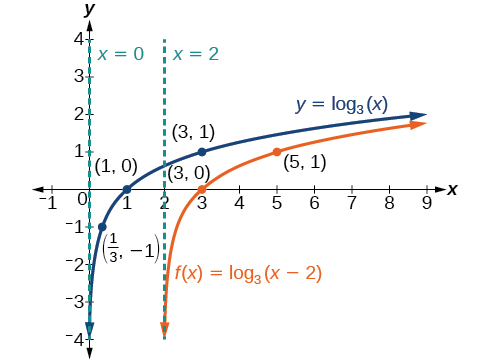
Step 2. Transformation on the graph of \(y\) needed to obtain the graph of \(f(x)\) is: shift right 2 units.

Step 3. Shifting right 2 units means the new \(x\) coordinates are found by adding \(2\) to the old \(x\) coordinates. Therefore,

• The vertical asymptote for the translated function \(f\) is \(x=0+2)\) or \(x=2\).
• The key points for the translated function \(f\) are \((3,0)\), \((5,1)\), and \(\left(\frac{7}{3},−1\right)\).

The domain is \((2,\infty)\), the range is \((−\infty,\infty)\),and the vertical asymptote is \(x=2\).

Sketch a graph of \(f(x)={\log}_3(x+4)\) alongside its parent function. Include the key points and asymptotes on the graph. State the domain, range, and asymptote.

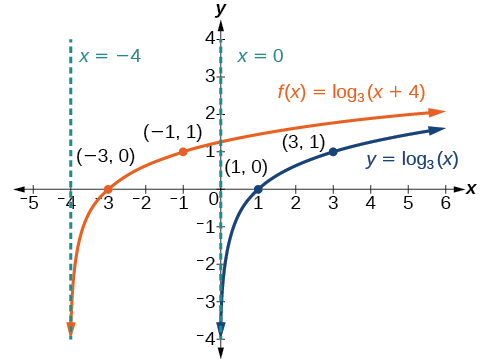
The domain is \((−4,\infty)\), the range \((−\infty,\infty)\), and the asymptote \(x=–4\).

Reflections 

When the parent function \(f(x)={\log}_b(x)\) is multiplied by \(−1\),the result is a reflection about the \(x\)-axis. When the input is multiplied by \(−1\), the result is a reflection about the \(y\)-axis. To visualize reflections, we restrict \(b>1\), and observe the general graph of the parent function \(f(x)={\log}_b(x)\) alongside the reflection about the \(x\)-axis, \(g(x)=−{\log}_b(x)\) and the reflection about the \(y\)-axis, \(h(x)={\log}_b(−x)\).

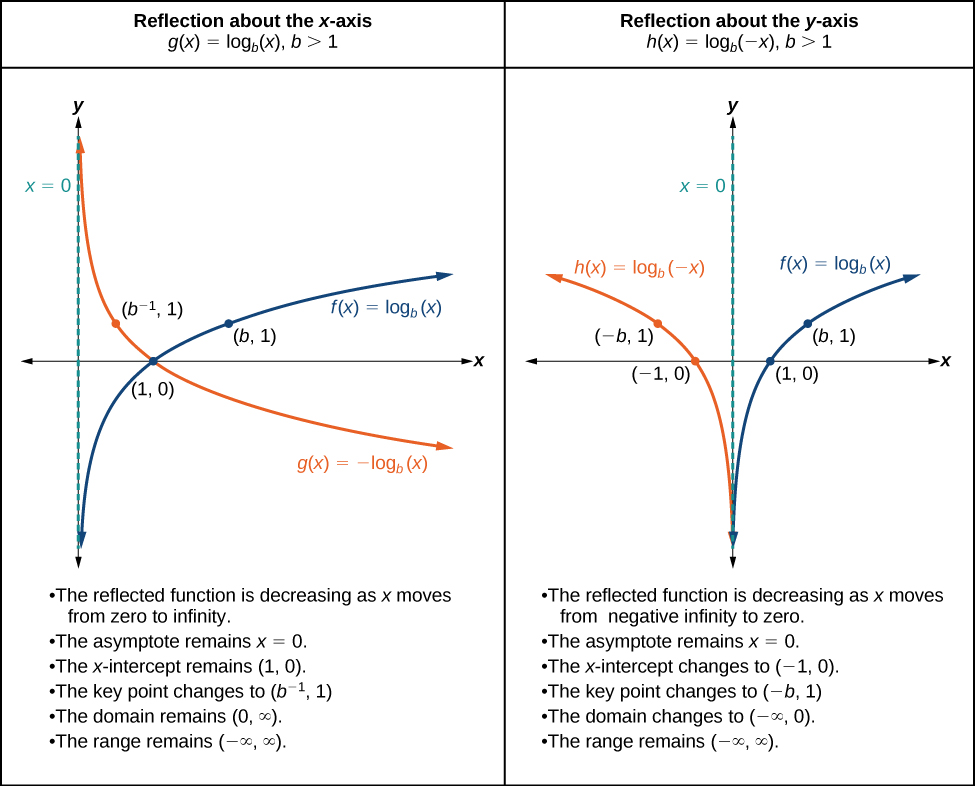
REFLECTIONS OF THE PARENT FUNCTION \(y = log_b(x)\)

\(f(x)=−{\log}_b(x) \;\;\; \)reflects the parent function about the \(x\)-axis. Domain, range and vertical asymptote are unchanged.

\(f(x)={\log}_b(−x) \;\;\; \)reflects the parent function about the \(y\)-axis. Domain is changed.

Example \(\PageIndex{6}\): Graphing a Reflection of a Logarithmic Function

Sketch a graph of \(f(x)=\log(−x)\) alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

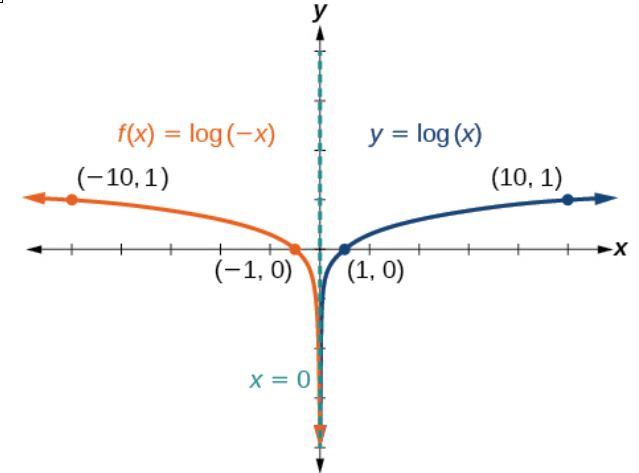
Step 2. Transformation on the graph of \(y\) needed to obtain the graph of \(f(x)\) is: reflection of the parent graph about the \(y\) - axis.

Step 3. The reflection about the \(y\)-axis is accomplished by multiplying all the \(x\)-coordinates by −1. Therefore,

• The vertical asymptote for the translated function \(f\) remains \(x=0\).
• The key points for the translated function \(f\) are \(\left(-\frac{1}{10},−1\right)\), \((-1,0)\), and \((-10,1)\).

The domain is \((−\infty,0)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\).

Graph \(f(x)=−\log(−x)\). State the domain, range, and asymptote.

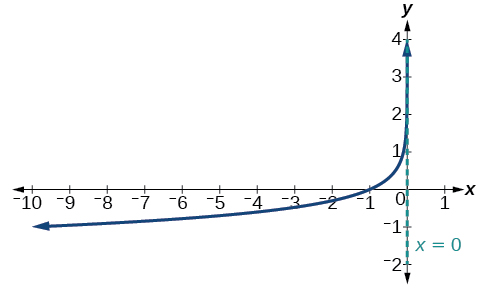
The domain is \((−\infty,0)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\).

Vertical Stretches and Compressions

When the parent function \(f(x)={\log}_b(x)\) is multiplied by a constant \(a>0\), the result is a vertical stretch or compression of the original graph. To visualize stretches and compressions, we set \(a>1\) and observe the general graph of the parent function \(f(x)={\log}_b(x)\) alongside the vertical stretch, \(g(x)=a{\log}_b(x)\) and the vertical compression, \(h(x)=\dfrac{1}{a}{\log}_b(x)\). 

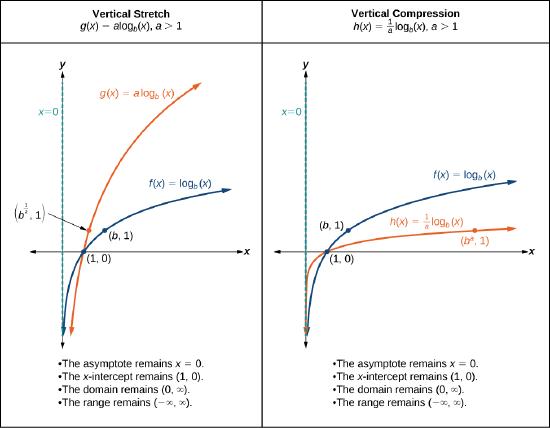
VERTICAL STRETCHES AND COMPRESSIONS OF THE PARENT FUNCTION \(y = log_b(x)\)

For any constant \(a \ne 0\), the function \(f(x)=a{\log}_b(x)\)

• stretches the parent function \(y={\log}_b(x)\) vertically by a factor of \(a\) if \(|a|>1\).
• compresses the parent function \(y={\log}_b(x)\) vertically by a factor of \(a\) if \(0<|a|<1\).

The new \(y\) coordinates are equal to \( ay \). (This would also include vertical reflection if present).

Example \(\PageIndex{7}\): Graph a Stretch or Compression of the Parent Function \(y = log_b(x)\)

Sketch a graph of \(f(x)=2{\log}_4(x)\) alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

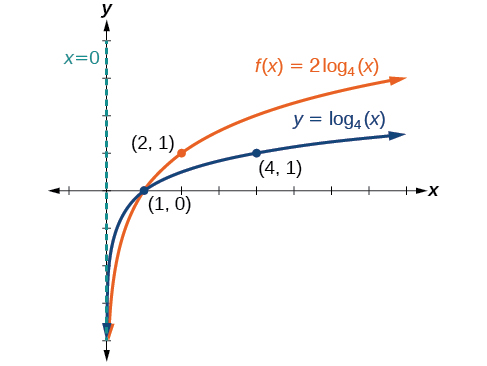
Step 2. Transformation on the graph of \(y\) needed to obtain the graph of \(f(x)\) is: stretch the function \(f(x)={\log}_4(x)\) by a factor of \(2\).

Step 3. A vertical stretch by a factor of \(2\)  means the new \(y\) coordinates are found by multiplying the \(y\) coordinates by \(2\). Therefore,

• The key points for the translated function \(f\) are \(\left(\frac{1}{4},−2\right)\), \((1,0)\), and \((4,2)\).

The domain is \((0, \infty)\), the range is \((−\infty, \infty)\), and the vertical asymptote is \(x=0\).

Sketch a graph of \(f(x)=\dfrac{1}{2}{\log}_4(x)\) alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

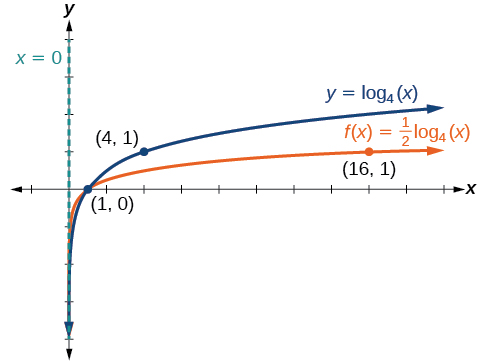
The domain is \((0,\infty)\), the range is \((−\infty,\infty),\) and the vertical asymptote is \(x=0\).

Horizontal Stretches and Compressions

When the input of the parent function \(f(x)={\log}_b(x)\) is multiplied by \(m\), the result is a stretch or compression of the original graph. To visualize horizontal stretches and compressions, compare the graph of the parent function \(f(x)={\log}_b(x)\) with the graph of \(g(x)={\log}_b(mx)\). If \( f(p) = {\log}_b(p) = q\), then in order to obtain the same \(y\) value for \(g\), the argument in \(g\) must be equal to that of \(f\). Therefore, the argument on \(g\) must be \(\frac{p}{m} \) because then \(g(\frac{p}{m} ={\log}_b(m \frac{p}{m} ) = {\log}_b(p) = q\). Thus in order for \(g\) to have the same output value as \(f\), the input to \(g\) must be the original input value to \(f\), multiplied by the factor \( \frac{1}{m}\) .

For any constant \(m \ne 0\), the function \(f(x)={\log}_b(mx)\)

• compresses the parent function \(y={\log}_b(x)\) vertically by a factor of  \( \frac{1}{m}\) if \(|m|>1\).
• stretches the parent function \(y={\log}_b(x)\) vertically by a factor of \( \frac{1}{m}\) if \(0<|m|<1\).

The new \(x\) coordinates are equal to \(  \frac{1}{m} x \). (This would also include horizontal reflection if present).

Example \(\PageIndex{8}\): Graph a Stretch or Compression of the Parent Function \(y = log_b(x)\)

Sketch a graph of \(f(x)={\log}_2(4x)\) alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

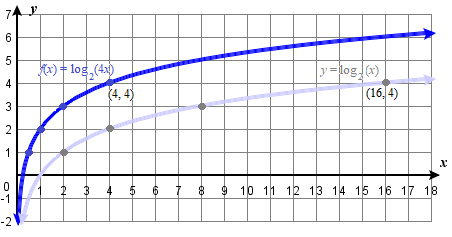
Step 2. Transformation on the graph of \(y\) needed to obtain the graph of \(f(x)\) is: horizontally shrink the function \(f(x)={\log}_2(x)\) by a factor of \(\frac{1}{4}\).

Step 3. A vertical stretch by a factor of \(\frac{1}{4}\)  means the new \(x\) coordinates are found by multiplying the \(x\) coordinates by \(\frac{1}{4}\). Therefore,

• The key points for the translated function \(f\) are \(\left(\frac{1}{4},0 \right)\), \((1,2)\), and \((4,4)\).

Sketch a graph of \(f(x)={\log}_2(\dfrac{1}{4}x)\) alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

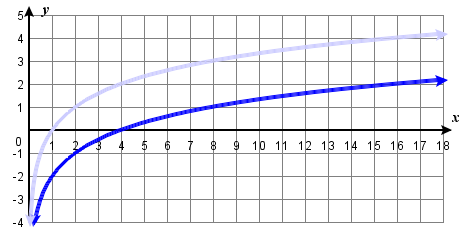
Transformation: \( x \rightarrow 4x. \) Some key points of graph of \(f\) include \( (4, 0 )\), \((8, 1)\), and \((16, 2)\). The domain is \((0,\infty)\), the range is \((−\infty,\infty),\) and the vertical asymptote is \(x=0\).

Combine a Horizontal Shift and a Vertical Stretch

Example \(\PageIndex{9}\): Combine a Shift and a Stretch

Sketch a graph of \(f(x)=5{\log}(x+2)\). State the domain, range, and asymptote.

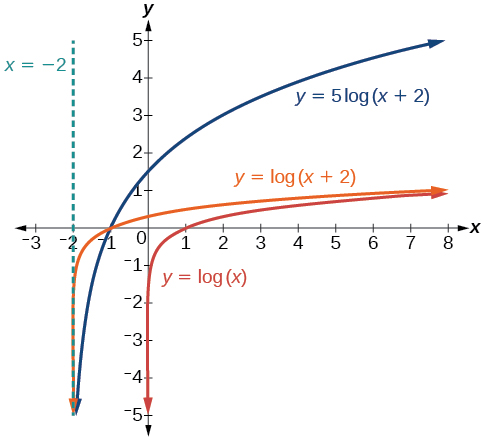
Step 2. Transformations on the graph of \(y\) needed to obtain the graph of \(f(x)\) are: move left \(2\) units (subtract 2 from all the \(x\)-coordinates), then vertically stretch by a factor of \(5\) (multiply all \(y\)-coordinates by 5). (Since these two transformations operate perpendicularly to each other, the order they are done does not matter, but it is a good idea to do all transformations in a prescribed order in order to establish a routine that will always work).

Step 3. 1.  \(x \rightarrow x-2\),     2.  \(y \rightarrow 5y\). Therefore,

• The vertical asymptote for the translated function \(f\) will be shifted to \(x=−2\).
• The key points for the translated function \(f\) are \(\left( -1\frac{9}{10},−5\right)\), \((-1,0)\), and \((8,5)\).

The domain is \((−2,\infty)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=−2\).

Sketch a graph of the function \(f(x)=3{\log}(x−2)+1\). State the domain, range, and asymptote.

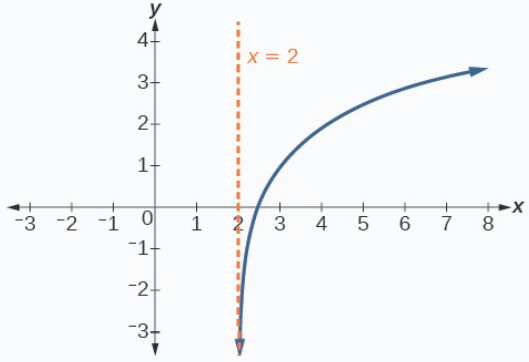
The domain is \((2,\infty)\), the range is \((−\infty,\infty),\) and the vertical asymptote is \(x=2\).

Summary of Transformations of the Logarithmic Function

Now that we have worked with each type of translation for the logarithmic function, we can summarize how to graph logarithmic functions that have undergone multiple transformations of their parent function.

Transformations of the parent logarithmic function, \(y={\log}_b(x)\), have the form \(f(x)=a{\log}_b(mx+c)+d\) 

• FIRST , shift horizontally to the left \(c\) units if \(c>0\) or to the right if \(c<0\).
• Then, if the coefficient of \(x\) is negative, the graph of the parent function is reflected about the y -axis.
• If \(m \ne 1 \) then the graph if stretched or shrunk horizontally by a factor of \( \frac{1}{m} \).
• If \(p\) is the \(x\)-coordinate of a point on the parent graph, then its new value is \(\frac{(p−c)}{m}\) 
• If the function has the form \(f(x)=a{\log}_b(m(x+c))+d\) then do the stretching or reflecting FIRST , and then the horizontal shift.
• stretched vertically by a factor of \(|a|\) if \(|a|>0\).
• compressed vertically by a factor of \(|a|\) if \(0<|a|<1\).
• reflected about the \(x\) - axis when \(a<0\).
• LAST , shift vertically up \(d\) units if \(d>0\) or down if \(d<0\).
• If \(p\) is the \(y\)-coordinate of a point on the parent graph, then its new value is \(ap+d\)
• If the coefficient of \(x\) was positive, the domain is \((−c, \infty)\), and the vertical asymptote is \(x=−c\).
• If the coefficient of \(x\) was negative, the domain is \((−\infty, c)\), and the vertical asymptote is \(x=c\).

Find the Domain and Asymptote of a Logarithmic Function

Previously, the domain and vertical asymptote were determined by graphing a logarithmic function. It is also possible to determine the domain and vertical asymptote of any logarithmic function algebraically. Here we will take a look at the domain (the set of input values) for which the logarithmic function is defined, and its vertical asymptote.

Recall that the exponential function is defined as \(y=b^x\) for any real number \(x\) and constant \(b>0\), \(b≠1\), where

• The domain of \(y\) is \((−\infty,\infty)\).
• The range of \(y\) is \((0,\infty)\).

In the last section we learned that the logarithmic function \(y={\log}_b(x)\) is the inverse of the exponential function \(y=b^x\). So, as inverse functions:

• The domain of \(y={\log}_b(x)\) is the range of \(y=b^x\): \((0,\infty)\).
• The range of \(y={\log}_b(x)\) is the domain of \(y=b^x\): \((−\infty,\infty)\).

When exponential functions are graphed, certain transformations can change the range of \(y=b^x\). Similarly, applying transformations to the parent function \(y={\log}_b(x)\) can change the domain . When finding the domain of a logarithmic function, therefore, it is important to remember that the domain consists only of positive real numbers . That is, the argument of the logarithmic function must be greater than zero .

For example, consider \(f(x)={\log}_4(2x−3)\). This function is defined for any values of \(x\) such that the argument, in this case \(2x−3\),is greater than zero. To find the domain, we set up an inequality and solve for \(x\):

\[\begin{align*} 2x-3&> 0 &&\qquad \text {Show the argument greater than zero}\\ 2x&> 3 &&\qquad \text{Add 3} \\ x&> 1.5 &&\qquad \text{Divide by 2} \\ \end{align*}\]

In interval notation, the domain of \(f(x)={\log}_4(2x−3)\) is \((1.5,\infty)\).

• Set up an inequality showing the argument greater than zero.
• Solve for \(x\).
• Write the domain in interval notation.

 The location of the asymptote of a logarithmic equation is always at the boundary of its domain .  Therefore the vertical asymptote of a logarithmic function can be obtained by setting its argument to zero and solving for \(x\).

• Set up an inequality showing the argument of the logarithmic function equal to zero.
• The result is the equation for the logarithmic function's vertical asymptote.

Example \(\PageIndex{10}\): Identifying the Domain of a Logarithmic Shift

What is the domain of \(f(x)={\log}_2(x+3)\)? 

The logarithmic function is defined only when the input is positive, so this function is defined when \(x+3>0\). Solving this inequality,

\[\begin{align*} x+3&> 0 &&\qquad \text{The input must be positive}\\ x&> -3 &&\qquad \text{Subtract 3} \end{align*}\]

The domain of \(f(x)={\log}_2(x+3)\) is \((−3,\infty)\). The vertical asymptote is \(x = −3 \)

What is the domain of \(f(x)={\log}_5(x−2)+1\)?  

Domain is \((2,\infty)\). The vertical asymptote is \(x = 2\).

Example \(\PageIndex{11}\): Identifying the Domain of a Logarithmic Shift and Reflection

What is the domain of \(f(x)=\log(5−2x)\)? What is the equation for its vertical asymptote?

The logarithmic function is defined only when the input is positive, so this function is defined when \(5–2x>0\). Solving this inequality,

\[\begin{align*} 5-2x&> 0 &&\qquad \text{The input must be positive}\\ -2x&> -5 &&\qquad \text{Subtract 5}\\ x&< \dfrac{5}{2} &&\qquad \text{Divide by -2 and switch the inequality} \end{align*}\]

The domain of \(f(x)=\log(5−2x)\) is \(\left(–\infty,\dfrac{5}{2}\right)\). The vertical asymptote is \(x = \dfrac{5}{2} \).

What is the domain of \(f(x)=\log(x−5)+2\)? What is the equation for its vertical asymptote?

\((5,\infty)\) The vertical asymptote is \(x = 5\).

Example \(\PageIndex{12}\): Finding the Vertical Asymptote of a Logarithm Graph

What is the vertical asymptote of \(f(x)=−2{\log}_3(x+4)+5\)?

The vertical asymptote is at \(x=−4\).

The coefficient, the base, and the upward translation do not affect the asymptote. The shift of the curve \(4\) units to the left shifts the vertical asymptote to\(x=−4\).

What is the vertical asymptote of \(f(x)=3+\ln(x−1)\)?

Find the Equation of a Logarithmic Function given its Graph

In the discussion of transformations, a factor that contributes to horizontal stretching or shrinking was included. However, it is always possible to construct an equivalent equation for a transformation of a logarithmic equation that does not have a horizontal stretching of shrinking component to it. Therefore, when constructing an equation that corresponds to a graph, it is safe to assume the general logarithmic equation to be found is of the form  \(f(x)=a{\log}_b(x+c)+d\) or  \(f(x)=a{\log}_b(-x+c)+d\). 

Example \(\PageIndex{13}\): Finding the Equation from a Graph

Find a possible equation for the common logarithmic function graphed below.

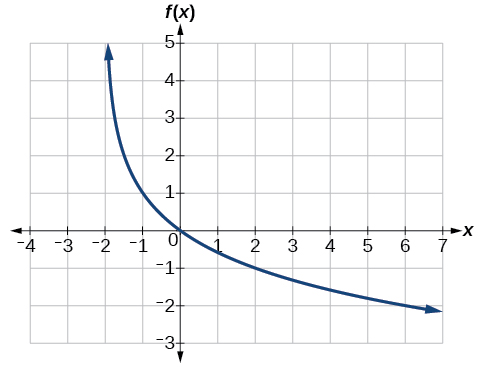
Two slightly different approaches will be givene here. The general form of the common logarithmic function is \( f(x)=a{\log} ( \pm x+c)+d\), or if a base \(B\) logarithm is used instead, the general form would be \( f(x)=a{\log_B} ( \pm x+c)+d\). 

This graph has a vertical asymptote at \(x=–2\) and has not been horizontally reflected. Therefore the argument of the logarithmic function must be \( (x+2) \).  The graph has been vertically reflected so we know the parameter \(a\) is negative. We do not know yet the vertical shift or the vertical stretch. Thus, so far we know that the equation will have form:

\(f(x)=−a\log(x+2)+d\) or \(f(x)=−a\log_B(x+2)+d\)

Method 1 . In this approach, the general form of the function used will be \(f(x)=−a\log_B(x+2)+d\).

Recall that \(\log_B(1) = 0 \). Therefore, when \(x+2=1\) (or when \(x=-1\)), then \(y=d\). From the graph we see that when \(x=-1\), \(y = 1\). Therefore \(d=1\). Now the equation looks like 

\(f(x)=−a\log_B(x+2)+1\).

Recall that \(\log_B(B) = 1 \). Therefore, when \(x+2 = B\), \(y = -a+1\). Another point observed to be on the graph is  \((2,–1)\). Substituting these values for \(x\) and \(y\) in this pair of equations, we can get values for \(B\) and \(a\): \(2+2 = B\) and \(-1 = -a+1\). Thus \(B=4\) and \(a=2\), and the final form of the equation is obtained:

\(f(x)=-2{\log}_4(x+2)+1\).

Method 2 . In this approach, the general form of the function used will be \(f(x)=−a\log(x+2)+d\) instead.

It appears the graph passes through the points \((–1,1)\) and \((2,–1)\). Substituting \((–1,1)\),

\[\begin{align*} 1&= -a\log(-1+2)+d &&\qquad \text{Substitute} (-1,1)\\ 1&= -a\log(1)+d &&\qquad \text{Arithmetic}\\ 1&= d &&\qquad \text{Because }\log(1)= 0 \end{align*}\]

Thus the equation now looks like \(f(x)=−a\log(x+2)+1\). Next, substituting in \((2,–1)\),

\[\begin{align*} -1&= -a\log(2+2)+1 &&\qquad \text{Substitute} (2,-1)\\ -2&= -a\log(4) &&\qquad \text{Arithmetic}\\ a&= \dfrac{2}{\log(4)} &&\qquad \text{Solve for a} \end{align*}\]

Now the equation is \(f(x)=–\dfrac{2}{\log(4)}\log(x+2)+1\). Furthermore, \( \dfrac{\log(x+2)}{\log(4)} = {\log}_4(x+2) \) by The Change of Base Formula, so the equation can be written as \(f(x)=-2{\log}_4(x+2)+1\). 

We can verify this answer by calculating various values of our \(f(x)\) and comparing with corresponding points on the graph.

Give the equation of the natural logarithm graphed below. 

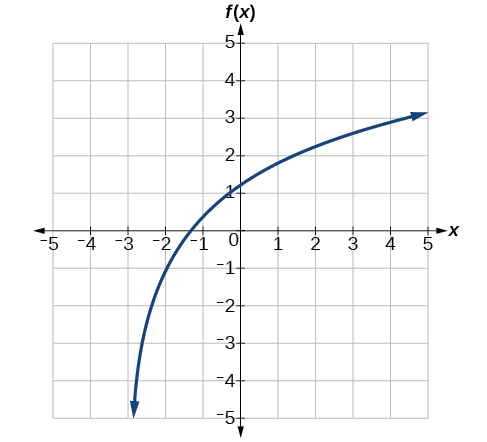
\(f(x)=2\ln(x+3)−1\)

Key Equations

General Form for the Transformation of the Parent Logarithmic Function \(f(x)={\log}_b(x) \) is \(f(x)=a{\log}_b( \pm x+c)+d\)

Key Concepts

• Landmarks on the graph of the parent function \(f(x)={\log}_b(x)\)  are: vertical asymptote \(x=0\), and keypoints \(x\) - intercept \((1,0)\),  \((b,1)\), and \( \left( \tfrac{1}{b},-1 \right) \). Domain is \((0,\infty)\) and range is \((−\infty,\infty)\). The function is increasing if \(b>1\); the function is decreasing if \(0<b<1\).  
• The equation \(f(x)={\log}_b(x+c)\) shifts the parent function \(y={\log}_b(x)\) horizontally: left \(c\) units if \(c>0\), right \(c\) units if \(c<0\).   
• The equation \(f(x)={\log}_b(x)+d\) shifts the parent function \(y={\log}_b(x)\) vertically: up \(d\) units if \(d>0\), down \(d\) units if \(d<0\).
• stretches the parent function \(y={\log}_b(x)\) vertically by a factor of \(a\) if \(|a|>1\).
• compresses the parent function \(y={\log}_b(x)\) vertically by a factor of \(a\) if \(|a|<\)1  
• The equation \(f(x)=−{\log}_b(x)\) represents a reflection of the parent function about the x- axis. The equation \(f(x)={\log}_b(−x)\) represents a reflection of the parent function about the y- axis.
• To find the domain of a logarithmic function, set up an inequality showing the argument greater than zero, and solve for \(x\).  The vertical asymptote, \(x=v\) is along the border of this domain.
• The general equation \(f(x)=a{\log}_b( \pm x+c)+d\) can be used to write the equation of a logarithmic function given its graph. 

3.6 Absolute Value Functions

Learning objectives.

In this section, you will:

• Graph an absolute value function.
• Solve an absolute value equation.

Until the 1920s, the so-called spiral nebulae were believed to be clouds of dust and gas in our own galaxy, some tens of thousands of light years away. Then, astronomer Edwin Hubble proved that these objects are galaxies in their own right, at distances of millions of light years. Today, astronomers can detect galaxies that are billions of light years away. Distances in the universe can be measured in all directions. As such, it is useful to consider distance as an absolute value function. In this section, we will continue our investigation of absolute value functions .

Understanding Absolute Value

Recall that in its basic form f ( x ) = | x | , f ( x ) = | x | , the absolute value function is one of our toolkit functions. The absolute value function is commonly thought of as providing the distance the number is from zero on a number line. Algebraically, for whatever the input value is, the output is the value without regard to sign. Knowing this, we can use absolute value functions to solve some kinds of real-world problems.

Absolute Value Function

The absolute value function can be defined as a piecewise function

Using Absolute Value to Determine Resistance

Electrical parts, such as resistors and capacitors, come with specified values of their operating parameters: resistance, capacitance, etc. However, due to imprecision in manufacturing, the actual values of these parameters vary somewhat from piece to piece, even when they are supposed to be the same. The best that manufacturers can do is to try to guarantee that the variations will stay within a specified range, often ±1%, ± 5%, ±1%, ± 5%, or ± 10% . ± 10% .

Suppose we have a resistor rated at 680 ohms, ± 5 % . ± 5 % . Use the absolute value function to express the range of possible values of the actual resistance.

We can find that 5% of 680 ohms is 34 ohms. The absolute value of the difference between the actual and nominal resistance should not exceed the stated variability, so, with the resistance R R in ohms,

Students who score within 20 points of 80 will pass a test. Write this as a distance from 80 using absolute value notation.

Graphing an Absolute Value Function

The most significant feature of the absolute value graph is the corner point at which the graph changes direction. This point is shown at the origin in Figure 2 .

Figure 3 shows the graph of y = 2 | x – 3 | + 4. y = 2 | x – 3 | + 4. The graph of y = | x | y = | x | has been shifted right 3 units, vertically stretched by a factor of 2, and shifted up 4 units. This means that the corner point is located at ( 3 , 4 ) ( 3 , 4 ) for this transformed function.

Writing an Equation for an Absolute Value Function Given a Graph

Write an equation for the function graphed in Figure 4 .

The basic absolute value function changes direction at the origin, so this graph has been shifted to the right 3 units and down 2 units from the basic toolkit function. See Figure 5 .

We also notice that the graph appears vertically stretched, because the width of the final graph on a horizontal line is not equal to 2 times the vertical distance from the corner to this line, as it would be for an unstretched absolute value function. Instead, the width is equal to 1 times the vertical distance as shown in Figure 6 .

From this information we can write the equation

Note that these equations are algebraically equivalent—the stretch for an absolute value function can be written interchangeably as a vertical or horizontal stretch or compression. Note also that if the vertical stretch factor is negative, there is also a reflection about the x-axis.

If we couldn’t observe the stretch of the function from the graphs, could we algebraically determine it?

Yes. If we are unable to determine the stretch based on the width of the graph, we can solve for the stretch factor by putting in a known pair of values for x x and f ( x ) . f ( x ) .

Now substituting in the point (1, 2)

Write the equation for the absolute value function that is horizontally shifted left 2 units, is vertically reflected, and vertically shifted up 3 units.

Do the graphs of absolute value functions always intersect the vertical axis? The horizontal axis?

Yes, they always intersect the vertical axis. The graph of an absolute value function will intersect the vertical axis when the input is zero.

No, they do not always intersect the horizontal axis. The graph may or may not intersect the horizontal axis, depending on how the graph has been shifted and reflected. It is possible for the absolute value function to intersect the horizontal axis at zero, one, or two points (see Figure 7 ).

Solving an Absolute Value Equation

In Other Type of Equations , we touched on the concepts of absolute value equations. Now that we understand a little more about their graphs, we can take another look at these types of equations. Now that we can graph an absolute value function, we will learn how to solve an absolute value equation. To solve an equation such as 8 = | 2 x − 6 | , 8 = | 2 x − 6 | , we notice that the absolute value will be equal to 8 if the quantity inside the absolute value is 8 or -8. This leads to two different equations we can solve independently.

Knowing how to solve problems involving absolute value functions is useful. For example, we may need to identify numbers or points on a line that are at a specified distance from a given reference point.

An absolute value equation is an equation in which the unknown variable appears in absolute value bars. For example,

Solutions to Absolute Value Equations

For real numbers A A and B B , an equation of the form | A | = B , | A | = B , with B ≥ 0 , B ≥ 0 , will have solutions when A = B A = B or A = − B . A = − B . If B < 0 , B < 0 , the equation | A | = B | A | = B has no solution.

Given the formula for an absolute value function, find the horizontal intercepts of its graph .

• Isolate the absolute value term.
• Use | A | = B | A | = B to write A = B A = B or −A = B , −A = B , assuming B > 0. B > 0.
• Solve for x . x .

Finding the Zeros of an Absolute Value Function

For the function f ( x ) = | 4 x + 1 | − 7 , f ( x ) = | 4 x + 1 | − 7 , find the values of x x such that f ( x ) = 0. f ( x ) = 0.

The function outputs 0 when x = 3 2 x = 3 2 or x = − 2. x = − 2. See Figure 8 .

For the function f ( x ) = | 2 x − 1 | − 3 , f ( x ) = | 2 x − 1 | − 3 , find the values of x x such that f ( x ) = 0. f ( x ) = 0.

Should we always expect two answers when solving | A | = B ? | A | = B ?

No. We may find one, two, or even no answers. For example, there is no solution to 2 + | 3 x − 5 | = 1. 2 + | 3 x − 5 | = 1.

Access these online resources for additional instruction and practice with absolute value.

• Graphing Absolute Value Functions
• Graphing Absolute Value Functions 2

3.6 Section Exercises

How do you solve an absolute value equation?

How can you tell whether an absolute value function has two x -intercepts without graphing the function?

When solving an absolute value function, the isolated absolute value term is equal to a negative number. What does that tell you about the graph of the absolute value function?

How can you use the graph of an absolute value function to determine the x -values for which the function values are negative?

Describe all numbers x x that are at a distance of 4 from the number 8. Express this set of numbers using absolute value notation.

Describe all numbers x x that are at a distance of 1 2 1 2 from the number −4. Express this set of numbers using absolute value notation.

Describe the situation in which the distance that point x x is from 10 is at least 15 units. Express this set of numbers using absolute value notation.

Find all function values f ( x ) f ( x ) such that the distance from f ( x ) f ( x ) to the value 8 is less than 0.03 units. Express this set of numbers using absolute value notation.

For the following exercises, find the x - and y -intercepts of the graphs of each function.

f ( x ) = 4 | x − 3 | + 4 f ( x ) = 4 | x − 3 | + 4

f ( x ) = − 3 | x − 2 | − 1 f ( x ) = − 3 | x − 2 | − 1

f ( x ) = − 2 | x + 1 | + 6 f ( x ) = − 2 | x + 1 | + 6

f ( x ) = − 5 | x + 2 | + 15 f ( x ) = − 5 | x + 2 | + 15

f ( x ) = 2 | x − 1 | − 6 f ( x ) = 2 | x − 1 | − 6

f ( x ) = | − 2 x + 1 | − 13 f ( x ) = | − 2 x + 1 | − 13

f ( x ) = − | x − 9 | + 16 f ( x ) = − | x − 9 | + 16

For the following exercises, graph the absolute value function. Plot at least five points by hand for each graph.

y = | x − 1 | y = | x − 1 |

y = | x + 1 | y = | x + 1 |

y = | x | + 1 y = | x | + 1

For the following exercises, graph the given functions by hand.

y = | x | − 2 y = | x | − 2

y = − | x | y = − | x |

y = − | x | − 2 y = − | x | − 2

y = − | x − 3 | − 2 y = − | x − 3 | − 2

f ( x ) = − | x − 1 | − 2 f ( x ) = − | x − 1 | − 2

f ( x ) = − | x + 3 | + 4 f ( x ) = − | x + 3 | + 4

f ( x ) = 2 | x + 3 | + 1 f ( x ) = 2 | x + 3 | + 1

f ( x ) = 3 | x − 2 | + 3 f ( x ) = 3 | x − 2 | + 3

f ( x ) = | 2 x − 4 | − 3 f ( x ) = | 2 x − 4 | − 3

f ( x ) = | 3 x + 9 | + 2 f ( x ) = | 3 x + 9 | + 2

f ( x ) = − | x − 1 | − 3 f ( x ) = − | x − 1 | − 3

f ( x ) = − | x + 4 | − 3 f ( x ) = − | x + 4 | − 3

f ( x ) = 1 2 | x + 4 | − 3 f ( x ) = 1 2 | x + 4 | − 3

Use a graphing utility to graph f ( x ) = 10 | x − 2 | f ( x ) = 10 | x − 2 | on the viewing window [ 0 , 4 ] . [ 0 , 4 ] . Identify the corresponding range. Show the graph.

Use a graphing utility to graph f ( x ) = − 100 | x | + 100 f ( x ) = − 100 | x | + 100 on the viewing window [ − 5 , 5 ] . [ − 5 , 5 ] . Identify the corresponding range. Show the graph.

For the following exercises, graph each function using a graphing utility. Specify the viewing window.

f ( x ) = − 0.1 | 0.1 ( 0.2 − x ) | + 0.3 f ( x ) = − 0.1 | 0.1 ( 0.2 − x ) | + 0.3

f ( x ) = 4 × 10 9 | x − ( 5 × 10 9 ) | + 2 × 10 9 f ( x ) = 4 × 10 9 | x − ( 5 × 10 9 ) | + 2 × 10 9

For the following exercises, solve the inequality.

If possible, find all values of a a such that there are no x - x - intercepts for f ( x ) = 2 | x + 1 | + a . f ( x ) = 2 | x + 1 | + a .

If possible, find all values of a a such that there are no y y -intercepts for f ( x ) = 2 | x + 1 | + a . f ( x ) = 2 | x + 1 | + a .

Real-World Applications

Cities A and B are on the same east-west line. Assume that city A is located at the origin. If the distance from city A to city B is at least 100 miles and x x represents the distance from city B to city A, express this using absolute value notation.

The true proportion p p of people who give a favorable rating to Congress is 8% with a margin of error of 1.5%. Describe this statement using an absolute value equation.

Students who score within 18 points of the number 82 will pass a particular test. Write this statement using absolute value notation and use the variable x x for the score.

A machinist must produce a bearing that is within 0.01 inches of the correct diameter of 5.0 inches. Using x x as the diameter of the bearing, write this statement using absolute value notation.

The tolerance for a ball bearing is 0.01. If the true diameter of the bearing is to be 2.0 inches and the measured value of the diameter is x x inches, express the tolerance using absolute value notation.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra-2e/pages/3-6-absolute-value-functions

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.