mathia problem solving with rational numbers

• World Languages
• English Language Arts
• Computer Science
• Help Center

Getting Started: MATHia for Educators

In this article we cover the absolute basics of MATHia, to get you started. We've outlined your first three weeks using the software, as well as included teaching stategies to get you started on the right foot. 

Download a copy of MATHia Resources for Educators

materials to send home

• MATHia Student User Links
• Using Carnegie Learning textbooks & MATHia? Click here to download the parent letter to send home with students.
• Only using MATHia?  Click here to download the parent letter to send home with students.

Your First Three Weeks with the Software Solution

Teacher and student responsibilities during lab time.

View and share these math lab learning logs with your students.

As you start off the year, you'll want to set expectations for students should be completing in MATHia. Watch the video to find out more.

MATH LAB CLASS DAILY SCHEDULE

Customer and tech support.

We'll be in touch soon.

Let's work together to put better learning within reach for your students.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.5: Rational Numbers

• Last updated
• Save as PDF
• Page ID 129525

Learning Objectives

After completing this section, you should be able to:

• Define and identify numbers that are rational.
• Simplify rational numbers and express in lowest terms.
• Add and subtract rational numbers.
• Convert between improper fractions and mixed numbers.
• Convert rational numbers between decimal and fraction form.
• Multiply and divide rational numbers.
• Apply the order of operations to rational numbers to simplify expressions.
• Apply density property of rational numbers.
• Solve problems involving rational numbers.
• Use fractions to convert between units.
• Define and apply percent.
• Solve problems using percent.

We are often presented with percentages or fractions to explain how much of a population has a certain feature. For example, the 6-year graduation rate of college students at public institutions is 57.6%, or 72/125. That fraction may be unsettling. But without the context, the percentage is hard to judge. So how does that compare to private institutions? There, the 6-year graduation rate is 65.4%, or 327/500. Comparing the percentages is straightforward, but the fractions are harder to interpret due to different denominators. For more context, historical data could be found. One study reported that the 6-year graduation rate in 1995 was 56.4%. Comparing that historical number to the recent 6-year graduation rate at public institutions of 57.6% shows that there hasn't been much change in that rate.

Defining and Identifying Numbers That Are Rational

A rational number (called rational since it is a ratio) is just a fraction where the numerator is an integer and the denominator is a non-zero integer. As simple as that is, they can be represented in many ways. It should be noted here that any integer is a rational number. An integer, n n , written as a fraction of two integers is n 1 n 1 .

In its most basic representation, a rational number is an integer divided by a non-zero integer, such as 3 12 Figure 3.21). Similarly, if in a group of 20 people, 5 are wearing hats, then 5 20 Figure 3.22).

Another representation of rational numbers is as a mixed number, such as 2 5 8 Figure 3.23). This represents a whole number (2 in this case), plus a fraction (the 5 8 5 8 ).

Rational numbers may also be expressed in decimal form; for instance, as 1.34. When 1.34 is written, the decimal part, 0.34, represents the fraction 34 100 34 100 , and the number 1.34 is equal to 1 34 100 1 34 100 . However, not all decimal representations are rational numbers.

A number written in decimal form where there is a last decimal digit (after a given decimal digit, all following decimal digits are 0) is a terminating decimal , as in 1.34 above. Alternately, any decimal numeral that, after a finite number of decimal digits, has digits equal to 0 for all digits following the last non-zero digit.

All numbers that can be expressed as a terminating decimal are rational. This comes from what the decimal represents. The decimal part is the fraction of the decimal part divided by the appropriate power of 10. That power of 10 is the number of decimal digits present, as for 0.34, with two decimal digits, being equal to 34 100 34 100 .

Another form that is a rational number is a decimal that repeats a pattern, such as 67.1313… When a rational number is expressed in decimal form and the decimal is a repeated pattern, we use special notation to designate the part that repeats. For example, if we have the repeating decimal 4.3636…, we write this as 4. 36 ¯ 4. 36 ¯ . The bar over the 36 indicates that the 36 repeats forever.

If the decimal representation of a number does not terminate or form a repeating decimal, that number is not a rational number.

One class of numbers that is not rational is the square roots of integers or rational numbers that are not perfect squares , such as 10 10 and 25 6 25 6 . More generally, the number b b is the square root of the number a a if a = b 2 a = b 2 . The notation for this is b = a b = a , where the symbol is the square root sign. An integer perfect square is any integer that can be written as the square of another integer. A rational perfect square is any rational number that can be written as a fraction of two integers that are perfect squares.

Sometimes you may be able to identify a perfect square from memory. Another process that may be used is to factor the number into the product of an integer with itself. Or a calculator (such as Desmos) may be used to find the square root of the number. If the calculator yields an integer, the original number was a perfect square.

Using Desmos to Find the Square Root of a Number

When Desmos is used, there is a tab at the bottom of the screen that opens the keyboard for Desmos. The keyboard is shown below. On the keyboard (Figure 3.24) is the square root symbol ( ) ( ) . To find the square root of a number, click the square root key, and then type the number. Desmos will automatically display the value of the square root as you enter the number.

Example 3.51

Identifying perfect squares.

Which of the following are perfect squares?

• We could attempt to find the perfect square by factoring. Writing all the factor pairs of 45 results in 1 × 45 , 3 × 15 1 × 45 , 3 × 15 , and 5 × 9 5 × 9 . None of the pairs is a square, so 45 is not a perfect square. Using a calculator to find the square root of 45, we obtain 6.708 (rounded to three decimal places). Since this was not an integer, the original number was not a perfect square.
• We could attempt to find the perfect square by factoring. Writing all the factor pairs of 144 results in 1 × 144 , 2 × 72 , 3 × 48 , 6 × 24 , 8 × 18 1 × 144 , 2 × 72 , 3 × 48 , 6 × 24 , 8 × 18 , and 12 × 12 12 × 12 . Since the last pair is an integer multiplied by itself, 144 is a perfect square. Alternately, using Desmos to find the square root of 144, we obtain 12. Since the square root of 144 is an integer, 144 is a perfect square.

Your Turn 3.51

Introduction to Fractions

Example 3.52

Identifying rational numbers.

Determine which of the following are rational numbers:

• 4.556 4.556
• 3 1 5 3 1 5
• 41 17 41 17
• 5 . 64 ¯ 5 . 64 ¯
• Since 73 is not a perfect square, its square root is not a rational number. This can also be seen when a calculator is used. Entering 73 73 into a calculator results in 8.544003745317 (and then more decimal values after that). There is no repeated pattern, so this is not a rational number.
• Since 4.556 is a decimal that terminates, this is a rational number.
• 3 1 5 3 1 5 is a mixed number, so it is a rational number.
• 41 17 41 17 is an integer divided by an integer, so it is a rational number.
• 5.646464... 5.646464... is a decimal that repeats a pattern, so it is a rational number.

Your Turn 3.52

Simplifying rational numbers and expressing in lowest terms.

A rational number is one way to express the division of two integers. As such, there may be multiple ways to express the same value with different rational numbers. For instance, 4 5 4 5 and 12 15 12 15 are the same value. If we enter them into a calculator, they both equal 0.8. Another way to understand this is to consider what it looks like in a figure when two fractions are equal.

In Figure 3.25, we see that 3 5 3 5 of the rectangle and 9 15 9 15 of the rectangle are equal areas.

They are the same proportion of the area of the rectangle. The left rectangle has 5 pieces, three of which are shaded. The right rectangle has 15 pieces, 9 of which are shaded. Each of the pieces of the left rectangle was divided equally into three pieces. This was a multiplication. The numerator describing the left rectangle was 3 but it becomes 3 × 3 3 × 3 , or 9, as each piece was divided into three. Similarly, the denominator describing the left rectangle was 5, but became 5 × 3 5 × 3 , or 15, as each piece was divided into 3. The fractions 3 5 3 5 and 9 15 9 15 are equivalent because they represent the same portion (often loosely referred to as equal).

This understanding of equivalent fractions is very useful for conceptualization, but it isn’t practical, in general, for determining when two fractions are equivalent. Generally, to determine if the two fractions a b a b and c d c d are equivalent, we check to see that a × d = b × c a × d = b × c . If those two products are equal, then the fractions are equal also.

Example 3.53

Determining if two fractions are equivalent.

Determine if 12 30 12 30 and 14 35 14 35 are equivalent fractions.

Applying the definition, a = 12 , b = 30 , c = 14 a = 12 , b = 30 , c = 14 and d = 35 d = 35 . So a × d = 12 × 35 = 420 a × d = 12 × 35 = 420 . Also, b × c = 30 × 14 = 420 b × c = 30 × 14 = 420 . Since these values are equal, the fractions are equivalent.

Your Turn 3.53

That a × d = b × c a × d = b × c indicates the fractions a b a b and c d c d are equivalent is due to some algebra. One property of natural numbers, integers, and rational numbers (also irrational numbers) is that for any three numbers a , b , a , b , and c c with c ≠ 0 c ≠ 0 , if a = b a = b , then a / c = b / c a / c = b / c . In other words, when two numbers are equal, then dividing both numbers by the same non-zero number, the two newly obtained numbers are also equal. We can apply that to a × d a × d and b × c b × c , to show that a b a b and c d c d are equivalent if a × d = b × c a × d = b × c .

If a × d = b × c a × d = b × c , and c ≠ 0 , d ≠ 0 c ≠ 0 , d ≠ 0 , we can divide both sides by and obtain the following: a × d c = b × c c a × d c = b × c c . We can divide out the c c on the right-hand side of the equation, resulting in a × d c = b a × d c = b . Similarly, we can divide both sides of the equation by d d and obtain the following: a × d c × d = b d a × d c × d = b d . We can divide out d d the on the left-hand side of the equation, resulting in a c = b d a c = b d . So, the rational numbers a c a c and b d b d are equivalent when a × d = b × c a × d = b × c .

Equivalent Fractions

Recall that a common divisor or common factor of a set of integers is one that divides all the numbers of the set of numbers being considered. In a fraction, when the numerator and denominator have a common divisor, that common divisor can be divided out . This is often called canceling the common factors or, more colloquially, as canceling .

To show this, consider the fraction 36 63 36 63 . The numerator and denominator have the common factor 3. We can rewrite the fraction as 36 63 = 12 × 3 21 × 3 36 63 = 12 × 3 21 × 3 . The common divisor 3 is then divided out, or canceled, and we can write the fraction as 12 × 3 21 × 3 = 12 21 12 × 3 21 × 3 = 12 21 . The 3s have been crossed out to indicate they have been divided out. The process of dividing out two factors is also referred to as reducing the fraction .

If the numerator and denominator have no common positive divisors other than 1, then the rational number is in lowest terms .

The process of dividing out common divisors of the numerator and denominator of a fraction is called reducing the fraction .

One way to reduce a fraction to lowest terms is to determine the GCD of the numerator and denominator and divide out the GCD. Another way is to divide out common divisors until the numerator and denominator have no more common factors.

Example 3.54

Reducing Fractions to Lowest Terms

Express the following rational numbers in lowest terms:

• 36 48 36 48
• 100 250 100 250
• 51 136 51 136

Step 1: We can then rewrite the numerator and denominator by factoring 12 from both.

36 48 = 12 × 3 12 × 4 36 48 = 12 × 3 12 × 4

Step 2: We can now divide out the 12s from the numerator and denominator.

36 48 = 12 × 3 12 × 4 = 3 4 36 48 = 12 × 3 12 × 4 = 3 4

So, when 36 48 36 48 is reduced to lowest terms, the result is 3 4 3 4 .

Alternately, you could identify a common factor, divide out that common factor, and repeat the process until the remaining fraction is in lowest terms.

Step 1: You may notice that 4 is a common factor of 36 and 48.

Step 2: Divide out the 4, as in 36 48 = 4 × 9 4 × 12 = 4 × 9 4 × 12 = 9 12 36 48 = 4 × 9 4 × 12 = 4 × 9 4 × 12 = 9 12 .

Step 3: Examining the 9 and 12, you identify 3 as a common factor and divide out the 3, as in 9 12 = 3 × 3 3 × 4 = 3 4 9 12 = 3 × 3 3 × 4 = 3 4 . The 3 and 4 have no common positive factors other than 1, so it is in lowest terms.

Step 2: We can then rewrite the numerator and denominator by factoring 50 from both.

100 250 = 50 × 2 50 × 5 100 250 = 50 × 2 50 × 5 .

Step 3: We can now divide out the 50s from the numerator and denominator.

100 250 = 50 × 2 50 × 5 = 2 5 100 250 = 50 × 2 50 × 5 = 2 5

So, when 100 250 100 250 is reduced to lowest terms, the result is 2 5 2 5 .

Step 2: We can then rewrite the numerator and denominator by factoring 17 from both.

51 136 = 17 × 3 17 × 8 51 136 = 17 × 3 17 × 8

Step 3: We can now divide out the 17s from the numerator and denominator.

51 136 = 17 × 3 17 × 8 = 3 8 51 136 = 17 × 3 17 × 8 = 3 8

So, when 51 136 51 136 is reduced to lowest terms, the result is 3 8 3 8 .

Your Turn 3.54

Using desmos to find lowest terms.

Desmos is a free online calculator . Desmos supports reducing fractions to lowest terms. When a fraction is entered, Desmos immediately calculates the decimal representation of the fraction. However, to the left of the fraction, there is a button that, when clicked, shows the fraction in reduced form.

Using Desmos to Reduce a Fraction

Adding and Subtracting Rational Numbers

Adding or subtracting rational numbers can be done with a calculator, which often returns a decimal representation, or by finding a common denominator for the rational numbers being added or subtracted.

Using Desmos to Add Rational Numbers in Fractional Form

To create a fraction in Desmos, enter the numerator, then use the division key (/) on your keyboard, and then enter the denominator. The fraction is then entered. Then click the right arrow key to exit the denominator of the fraction. Next, enter the arithmetic operation (+ or –). Then enter the next fraction. The answer is displayed dynamically (calculates as you enter). To change the Desmos result from decimal form to fractional form, use the fraction button (Figure 3.26) on the left of the line that contains the calculation:

Example 3.55

Adding rational numbers using desmos.

Calculate 23 42 + 9 56 23 42 + 9 56 using Desmos.

Enter 23 42 + 9 56 23 42 + 9 56 in Desmos. The result is displayed as 0.70833333333 0.70833333333 (which is 0.708 3 ¯ 0.708 3 ¯ ). Clicking the fraction button to the left on the calculation line yields 17 24 17 24 .

Your Turn 3.55

Performing addition and subtraction without a calculator may be more involved. When the two rational numbers have a common denominator, then adding or subtracting the two numbers is straightforward. Add or subtract the numerators, and then place that value in the numerator and the common denominator in the denominator. Symbolically, we write this as a c ± b c = a ± b c Figure 3.27, which shows 3 20 + 4 20 = 7 20 3 20 + 4 20 = 7 20 .

It is customary to then write the result in lowest terms.

If c c is a non-zero integer, then a c ± b c = a ± b c a c ± b c = a ± b c .

Example 3.56

Adding rational numbers with the same denominator.

Calculate 13 28 + 7 28 13 28 + 7 28 .

Since the rational numbers have the same denominator, we perform the addition of the numerators, 13 + 7 13 + 7 , and then place the result in the numerator and the common denominator, 28, in the denominator. 13 28 + 7 28 = 13 + 7 28 = 20 28 13 28 + 7 28 = 13 + 7 28 = 20 28

Once we have that result, reduce to lowest terms, which gives 20 28 = 4 × 5 4 × 7 = 4 × 5 4 × 7 = 5 7 20 28 = 4 × 5 4 × 7 = 4 × 5 4 × 7 = 5 7 .

Your Turn 3.56

Example 3.57, subtracting rational numbers with the same denominator.

Calculate 45 136 − 17 136 45 136 − 17 136 .

Since the rational numbers have the same denominator, we perform the subtraction of the numerators, 45 − 17 45 − 17 , and then place the result in the numerator and the common denominator, 136, in the denominator. 45 136 − 17 136 − 45 − 17 136 = 28 136 45 136 − 17 136 − 45 − 17 136 = 28 136

Once we have that result, reduce to lowest terms, this gives 28 136 = 4 × 7 4 × 34 = 4 × 7 4 × 34 = 7 34 28 136 = 4 × 7 4 × 34 = 4 × 7 4 × 34 = 7 34 .

Your Turn 3.57

When the rational numbers do not have common denominators, then we have to transform the rational numbers so that they do have common denominators. The common denominator that reduces work later in the problem is the LCM of the numerator and denominator. When adding or subtracting the rational numbers a b a b and c d c d , we perform the following steps.

Step 1: Find LCM ( b , d ) LCM ( b , d ) .

Step 2: Calculate n = LCM ( b , d ) b n = LCM ( b , d ) b and m = L C M ( b , d ) d m = L C M ( b , d ) d .

Step 3: Multiply the numerator and denominator of a b a b by n n , yielding a × n b × n a × n b × n .

Step 4: Multiply the numerator and denominator of c d c d by m m , yielding c × m d × m c × m d × m .

Step 5: Add or subtract the rational numbers from Steps 3 and 4, since they now have the common denominators.

You should be aware that the common denominator is LCM ( b , d ) LCM ( b , d ) . For the first denominator, we have b × n = b × L C M ( b , d ) b = L C M ( b , d ) b × n = b × L C M ( b , d ) b = L C M ( b , d ) , since we multiply and divide LCM ( b , d ) LCM ( b , d ) by the same number. For the same reason, d × m = d × L C M ( b , d ) b = L C M ( b , d ) d × m = d × L C M ( b , d ) b = L C M ( b , d ) .

Example 3.58

Adding rational numbers with unequal denominators.

Calculate 11 18 + 2 15 11 18 + 2 15 .

The denominators of the fractions are 18 and 15, so we label b = 18 b = 18 and d = 15 d = 15 .

Step 1: Find LCM(18,15). This is 90.

Step 2 : Calculate n n and m m . n = 90 18 = 5 n = 90 18 = 5 and m = 90 15 = 6 m = 90 15 = 6 .

Step 3: Multiplying the numerator and denominator of 11 18 11 18 by n = 5 n = 5 yields 11 × 5 18 × 5 = 55 90 11 × 5 18 × 5 = 55 90 .

Step 4: Multiply the numerator and denominator of 2 15 2 15 by m = 6 m = 6 yields 2 × 6 15 × 6 = 12 90 2 × 6 15 × 6 = 12 90 .

Step 5: Now we add the values from Steps 3 and 4: 55 90 + 12 90 = 67 90 55 90 + 12 90 = 67 90 .

This is in lowest terms, so we have found that 11 18 + 2 15 = 67 90 11 18 + 2 15 = 67 90 .

Your Turn 3.58

Example 3.59, subtracting rational numbers with unequal denominators.

Calculate 14 25 − 9 70 14 25 − 9 70 .

The denominators of the fractions are 25 and 70, so we label b = 25 b = 25 and d = 70 d = 70 .

Step 1: Find LCM(25,70). This is 350.

Step 2: Calculate n n and m m : n = 350 25 = 14 n = 350 25 = 14 and m = 350 70 = 5 m = 350 70 = 5 .

Step 3: Multiplying the numerator and denominator of 14 25 14 25 by n = 14 n = 14 yields 14 × 14 25 × 14 = 196 350 14 × 14 25 × 14 = 196 350 .

Step 4: Multiplying the numerator and denominator of 9 70 9 70 by m = 5 m = 5 yields 9 × 5 70 × 5 = 45 350 9 × 5 70 × 5 = 45 350 .

Step 5: Now we subtract the value from Step 4 from the value in Step 3: 196 350 − 45 350 = 151 350 196 350 − 45 350 = 151 350 .

This is in lowest terms, so we have found that 14 25 − 9 70 = 151 350 14 25 − 9 70 = 151 350 .

Your Turn 3.59

Adding and Subtracting Fractions with Different Denominators

Converting Between Improper Fractions and Mixed Numbers

One way to visualize a fraction is as parts of a whole, as in 5 12 5 12 of a pizza. But when the numerator is larger than the denominator, as in 23 12 23 12 , then the idea of parts of a whole seems not to make sense. Such a fraction is an improper fraction. That kind of fraction could be written as an integer plus a fraction, which is a mixed number . The fraction 23 12 23 12 rewritten as a mixed number would be 1 11 12 1 11 12 . Arithmetically, 1 11 12 1 11 12 is equivalent to 1 + 11 12 1 + 11 12 , which is read as “one and 11 twelfths.”

Improper fractions can be rewritten as mixed numbers using division and remainders. To find the mixed number representation of an improper fraction, divide the numerator by the denominator. The quotient is the integer part, and the remainder becomes the numerator of the remaining fraction.

Example 3.60

Rewriting an improper fraction as a mixed number.

Rewrite 48 13 48 13 as a mixed number.

When 48 is divided by 13, the result is 3 with a remainder of 9. So, we can rewrite 48 13 48 13 as 3 9 13 3 9 13 .

Your Turn 3.60

Converting an Improper Fraction to a Mixed Number Using Desmos

Similarly, we can convert a mixed number into an improper fraction. To do so, first convert the whole number part to a fraction by writing the whole number as itself divided by 1, and then add the two fractions.

Alternately, we can multiply the whole number part and the denominator of the fractional part. Next, add that product to the numerator. Finally, express the number as that product divided by the denominator.

Example 3.61

Rewriting a mixed number as an improper fraction.

Rewrite 5 4 9 5 4 9 as an improper fraction.

Step 1: Multiply the integer part, 5, by the denominator, 9, which gives 5 × 9 = 45 5 × 9 = 45 .

Step 2: Add that product to the numerator, which gives 45 + 4 = 49 45 + 4 = 49 .

Step 3: Write the number as the sum, 49, divided by the denominator, 9, which gives 49 9 49 9 .

Your Turn 3.61

Using desmos to rewrite a mixed number as an improper fraction.

Desmos can be used to convert from a mixed number to an improper fraction. To do so, we use the idea that a mixed number, such as 5 6 11 5 6 11 , is another way to represent 5 + 6 11 5 + 6 11 . If 5 + 6 11 5 + 6 11 is entered in Desmos, the result is the decimal form of the number. However, clicking the fraction button to the left will convert the decimal to an improper fraction, 61 11 61 11 . As an added bonus, Desmos will automatically reduce the fraction to lowest terms.

Converting Rational Numbers Between Decimal and Fraction Forms

Understanding what decimals represent is needed before addressing conversions between the fractional form of a number and its decimal form , or writing a number in decimal notation . The decimal number 4.557 is equal to 4 557 1,000 4 557 1,000 . The decimal portion, .557, is 557 divided by 1,000. To write any decimal portion of a number expressed as a terminating decimal, divide the decimal number by 10 raised to the power equal to the number of decimal digits. Since there were three decimal digits in 4.557, we divided 557 by 10 3 = 1000 10 3 = 1000 .

Decimal representations may be very long. It is convenient to round off the decimal form of the number to a certain number of decimal digits. To round off the decimal form of a number to n n (decimal) digits, examine the ( n + 1 n + 1 )st decimal digit. If that digit is 0, 1, 2, 3, or 4, the number is rounded off by writing the number to the n n th decimal digit and no further. If the ( n + 1 n + 1 )st decimal digit is 5, 6, 7, 8, or 9, the number is rounded off by writing the number to the n n th digit, then replacing the n n th digit by one more than the n n th digit.

Example 3.62

Rounding off a number in decimal form to three digits.

Round 5.67849 to three decimal digits.

The third decimal digit is 8. The digit following the 8 is 4. When the digit is 4, we write the number only to the third digit. So, 5.67849 rounded off to three decimal places is 5.678.

Your Turn 3.62

Example 3.63, rounding off a number in decimal form to four digits.

Round 45.11475 to four decimal digits.

The fourth decimal digit is 7. The digit following the 7 is 5. When the digit is 5, we write the number only to the fourth decimal digit, 45.1147. We then replace the fourth decimal digit by one more than the fourth digit, which yields 45.1148. So, 45.11475 rounded off to four decimal places is 45.1148.

Your Turn 3.63

To convert a rational number in fraction form to decimal form, use your calculator to perform the division.

Example 3.64

Converting a rational number in fraction form into decimal form.

Convert 47 25 47 25 into decimal form.

Using a calculator to divide 47 by 25, the result is 1.88.

Your Turn 3.64

Converting a terminating decimal to the fractional form may be done in the following way:

Step 1: Count the number of digits in the decimal part of the number, labeled n n .

Step 2: Raise 10 to the n n th power.

Step 3: Rewrite the number without the decimal.

Step 4: The fractional form is the number from Step 3 divided by the result from Step 2.

This process works due to what decimals represent and how we work with mixed numbers. For example, we could convert the number 7.4536 to fractional from. The decimal part of the number, the .4536 part of 7.4536, has four digits. By the definition of decimal notation, the decimal portion represents 4,536 10 4 = 4,536 10,000 4,536 10 4 = 4,536 10,000 . The decimal number 7.4536 is equal to the improper fraction 7 4,536 10,000 7 4,536 10,000 . Adding those to fractions yields 74,536 10,000 74,536 10,000 .

Example 3.65

Converting from decimal form to fraction form with terminating decimals.

Convert 3.2117 to fraction form.

Step 1: There are four digits after the decimal point, so n = 4 n = 4 .

Step 2: Raise 10 to the fourth power, 10 4 = 10,000 10 4 = 10,000 .

Step 3: When we remove the decimal point, we have 32,117.

Step 4: The fraction has as its numerator the result from Step 3 and as its denominator the result of Step 2, which is the fraction 32,117 10,000 32,117 10,000 .

Your Turn 3.65

The process is different when converting from the decimal form of a rational number into fraction form when the decimal form is a repeating decimal. This process is not covered in this text.

Multiplying and Dividing Rational Numbers

Multiplying rational numbers is less complicated than adding or subtracting rational numbers, as there is no need to find common denominators. To multiply rational numbers, multiply the numerators, then multiply the denominators, and write the numerator product divided by the denominator product. Symbolically, a b × c d = a × c b × d a b × c d = a × c b × d . As always, rational numbers should be reduced to lowest terms.

If b b and d d are non-zero integers, then a b × c d = a × c b × d a b × c d = a × c b × d .

Example 3.66

Multiplying rational numbers.

Calculate 12 25 × 10 21 12 25 × 10 21 .

Multiply the numerators and place that in the numerator, and then multiply the denominators and place that in the denominator.

12 25 × 10 21 = 12 × 10 25 × 21 = 120 525 12 25 × 10 21 = 12 × 10 25 × 21 = 120 525

This is not in lowest terms, so this needs to be reduced. The GCD of 120 and 525 is 15.

120 525 = 15 × 8 15 × 35 = 8 35 120 525 = 15 × 8 15 × 35 = 8 35

Your Turn 3.66

Multiplying Fractions

As with multiplication, division of rational numbers can be done using a calculator.

Example 3.67

Dividing decimals with a calculator.

Calculate 3.45 ÷ 2.341 using a calculator. Round to three decimal places if necessary.

Using a calculator, we obtain 1.473729175565997. Rounding to three decimal places we have 1.474.

Your Turn 3.67

Before discussing division of fractions without a calculator, we should look at the reciprocal of a number. The reciprocal of a number is 1 divided by the number. For a fraction, the reciprocal is the fraction formed by switching the numerator and denominator. For the fraction a b a b , the reciprocal is b a b a . An important feature for a number and its reciprocal is that their product is 1.

When dividing two fractions by hand, find the reciprocal of the divisor (the number that is being divided into the other number). Next, replace the divisor by its reciprocal and change the division into multiplication. Then, perform the multiplication. Symbolically, b a ÷ c d = a b × d c = a × d b × c b a ÷ c d = a b × d c = a × d b × c . As before, reduce to lowest terms.

If b , c b , c and d d are non-zero integers, then b a ÷ c d = a b × d c = a × d b × c b a ÷ c d = a b × d c = a × d b × c .

Example 3.68

Dividing rational numbers.

• Calculate 4 21 ÷ 6 35 4 21 ÷ 6 35 .
• Calculate 1 8 ÷ 5 28 1 8 ÷ 5 28 .

Step 2: Multiply the first fraction by that reciprocal.

4 21 ÷ 6 35 = 4 21 × 35 6 = 140 126 4 21 ÷ 6 35 = 4 21 × 35 6 = 140 126

The answer, 140 126 140 126 is not in lowest terms. The GCD of 140 and 126 is 14. Factoring and canceling gives 140 126 = 14 × 10 14 × 9 = 10 9 140 126 = 14 × 10 14 × 9 = 10 9 .

Step 2: Multiply the first fraction by that reciprocal: 1 8 ÷ 5 28 = 1 8 × 28 5 = 28 40 1 8 ÷ 5 28 = 1 8 × 28 5 = 28 40

The answer, 28 40 28 40 , is not in lowest reduced form. The GCD of 28 and 40 is 4. Factoring and canceling gives 28 40 = 4 × 7 4 × 10 = 7 10 28 40 = 4 × 7 4 × 10 = 7 10 .

Your Turn 3.68

Dividing Fractions

Applying the Order of Operations to Simplify Expressions

The order of operations for rational numbers is the same as for integers, as discussed in Order of Operations. The order of operations makes it easier for anyone to correctly calculate and represent. The order follows the well-known acronym PEMDAS:

The first step in calculating using the order of operations is to perform operations inside the parentheses. Moving down the list, next perform all exponent operations moving from left to right. Next (left to right once more), perform all multiplications and divisions. Finally, perform the additions and subtractions.

Example 3.69

Applying the order of operations with rational numbers.

Correctly apply the rules for the order of operations to accurately compute ( 5 7 − 2 7 ) × 2 3 ( 5 7 − 2 7 ) × 2 3 .

Step 1: To calculate this, perform all calculations within the parentheses before other operations.

( 5 7 − 2 7 ) × 2 3 = ( 3 7 ) × 2 3 ( 5 7 − 2 7 ) × 2 3 = ( 3 7 ) × 2 3

Step 2: Since all parentheses have been cleared, we move left to right, and compute all the exponents next.

( 3 7 ) × 2 3 = ( 3 7 ) × 8 ( 3 7 ) × 2 3 = ( 3 7 ) × 8

Step 3: Now, perform all multiplications and divisions, moving left to right.

( 3 7 ) × 8 = 24 7 ( 3 7 ) × 8 = 24 7

Your Turn 3.69

Example 3.70.

Correctly apply the rules for the order of operations to accurately compute 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 .

To calculate this, perform all calculations within the parentheses before other operations. Evaluate the innermost parentheses first. We can work separate parentheses expressions at the same time.

Step 1: The innermost parentheses contain 2 3 + 5 2 3 + 5 . Calculate that first, dividing after finding the common denominator.

4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 1 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 15 3 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 1 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 15 3 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2

Step 2: Calculate the exponent in the parentheses, ( 5 9 ) 2 ( 5 9 ) 2 .

4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2 = 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2 = 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2

Step 3: Subtract inside the parentheses is done, using a common denominator.

4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 × 27 3 × 27 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 459 81 ) ) 2 4 + 2 3 ÷ ( ( − 434 81 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 × 27 3 × 27 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 459 81 ) ) 2 4 + 2 3 ÷ ( ( − 434 81 ) ) 2

Step 4: At this point, evaluate the exponent and divide.

4 + 2 3 ÷ ( ( − 434 81 ) ) 2 4 + 2 3 ÷ ( 188,356 6,561 ) = 4 + 2 3 × ( 6,561 188,356 ) = 4 + 2,187 94,178 4 + 2 3 ÷ ( ( − 434 81 ) ) 2 4 + 2 3 ÷ ( 188,356 6,561 ) = 4 + 2 3 × ( 6,561 188,356 ) = 4 + 2,187 94,178

Step 5: Add.

4 + 2,187 94,178 = 378,899 94,178 4 + 2,187 94,178 = 378,899 94,178

Had this been done on a calculator, the decimal form of the answer would be 4.0232 (rounded to four decimal places).

Your Turn 3.70

Order of Operations Using Fractions

Applying the Density Property of Rational Numbers

Between any two rational numbers, there is another rational number. This is called the density property of the rational numbers.

Finding a rational number between any two rational numbers is very straightforward.

Step 1: Add the two rational numbers.

Step 2: Divide that result by 2.

The result is always a rational number. This follows what we know about rational numbers. If two fractions are added, then the result is a fraction. Also, when a fraction is divided by a fraction (and 2 is a fraction), then we get another fraction. This two-step process will give a rational number, provided the first two numbers were rational.

Example 3.71

Demonstrate the density property of rational numbers by finding a rational number between 4 11 4 11 and 7 12 7 12 .

To find a rational number between 4 11 4 11 and 7 12 7 12 :

Step 1: Add the fractions.

4 11 + 7 12 = 4 × 12 11 × 12 + 7 × 11 12 × 11 = 48 132 + 77 132 = 125 132 4 11 + 7 12 = 4 × 12 11 × 12 + 7 × 11 12 × 11 = 48 132 + 77 132 = 125 132

Step 2: Divide the result by 2. Recall that to divide by 2, you multiply by the reciprocal of 2. The reciprocal of 2 is 1 2 1 2 , as seen below.

125 132 ÷ 2 = 125 132 × 1 2 = 125 264 125 132 ÷ 2 = 125 132 × 1 2 = 125 264

So, one rational number between 4 11 4 11 and 7 12 7 12 is 125 264 125 264 .

We could check that the number we found is between the other two by finding the decimal representation of the numbers. Using a calculator, the decimal representations of the rational numbers are 0.363636…, 0.473484848…, and 0.5833333…. Here it is clear that 125 264 125 264 is between 4 11 4 11 and 7 12 7 12 .

Your Turn 3.71

Solving problems involving rational numbers.

Rational numbers are used in many situations, sometimes to express a portion of a whole, other times as an expression of a ratio between two quantities. For the sciences, converting between units is done using rational numbers, as when converting between gallons and cubic inches. In chemistry, mixing a solution with a given concentration of a chemical per unit volume can be solved with rational numbers. In demographics, rational numbers are used to describe the distribution of the population. In dietetics, rational numbers are used to express the appropriate amount of a given ingredient to include in a recipe. As discussed, the application of rational numbers crosses many disciplines.

Example 3.72

Mixing soil for vegetables.

James is mixing soil for a raised garden, in which he plans to grow a variety of vegetables. For the soil to be suitable, he determines that 2 5 2 5 of the soil can be topsoil, but 2 5 2 5 needs to be peat moss and 1 5 1 5 has to be compost. To fill the raised garden bed with 60 cubic feet of soil, how much of each component does James need to use?

In this example, we know the proportion of each component to mix, and we know the total amount of the mix we need. In this kind of situation, we need to determine the appropriate amount of each component to include in the mixture. For each component of the mixture, multiply 60 cubic feet, which is the total volume of the mixture we want, by the fraction required of the component.

Step 1: The required fraction of topsoil is 2 5 2 5 , so James needs 60 × 2 5 60 × 2 5 cubic feet of topsoil. Performing the multiplication, James needs 60 × 2 5 = 120 5 = 24 60 × 2 5 = 120 5 = 24 (found by treating the fraction as division, and 120 divided by 5 is 24) cubic feet of topsoil.

Step 2: The required fraction of peat moss is also 2 5 2 5 , so he also needs 60 × 2 5 60 × 2 5 cubic feet, or 60 × 2 5 = 120 5 = 24 60 × 2 5 = 120 5 = 24 cubic feet of peat moss.

Step 3: The required fraction of compost is 1 5 1 5 . For the compost, he needs 60 × 1 5 = 60 5 = 12 60 × 1 5 = 60 5 = 12 cubic feet.

Your Turn 3.72

Example 3.73, determining the number of specialty pizzas.

At Bella’s Pizza, one-third of the pizzas that are ordered are one of their specialty varieties. If there are 273 pizzas ordered, how many were specialty pizzas?

One-third of the whole are specialty pizzas, so we need one-third of 273, which gives 1 3 × 273 = 273 3 = 91 1 3 × 273 = 273 3 = 91 , found by dividing 273 by 3. So, 91 of the pizzas that were ordered were specialty pizzas.

Your Turn 3.73

Finding a Fraction of a Total

Using Fractions to Convert Between Units

A common application of fractions is called unit conversion , or converting units , which is the process of changing from the units used in making a measurement to different units of measurement.

For instance, 1 inch is (approximately) equal to 2.54 cm. To convert between units, the two equivalent values are made into a fraction. To convert from the first type of unit to the second type, the fraction has the second unit as the numerator, and the first unit as the denominator.

From the inches and centimeters example, to change from inches to centimeters, we use the fraction 2.54 cm 1 in 2.54 cm 1 in . If, on the other hand, we wanted to convert from centimeters to inches, we’d use the fraction 1 in 2.54 cm 1 in 2.54 cm . This fraction is multiplied by the number of units of the type you are converting from , which means the units of the denominator are the same as the units being multiplied.

Example 3.74

Converting liters to gallons.

It is known that 1 liter (L) is 0.264172 gallons (gal). Use this to convert 14 liters into gallons.

We know that 1 liter = 0.264172 gal. Since we are converting from liters, when we create the fraction we use, make sure the liter part of the equivalence is in the denominator. So, to convert the 14 liters to gallons, we multiply 14 by 1 gal 0.264172 gal / 1 liter 1 gal 0.264172 gal / 1 liter . Notice the gallon part is in the numerator since we’re converting to gallons, and the liter part is in the denominator since we are converting from liters. Performing this and rounding to three decimal places, we find that 14 liters is 14 liter × 0.264172 gal 1 liter = 3.69841 gal 14 liter × 0.264172 gal 1 liter = 3.69841 gal .

Your Turn 3.74

Example 3.75, converting centimeters to inches.

It is known that 1 inch is 2.54 centimeters. Use this to convert 100 centimeters into inches.

We know that 1 inch = 2.54 cm. Since we are converting from centimeters, when we create the fraction we use, make sure the centimeter part of the equivalence is in the denominator, 1 in 2.54 cm 1 in 2.54 cm . To convert the 100 cm to inches, multiply 100 by 1 in 2.54 cm 1 in 2.54 cm . Notice the inch part is in the numerator since we’re converting to inches, and the centimeter part is in the denominator since we are converting from centimeters. Performing this and rounding to three decimal places, we obtain 100 cm × 1 in 2.54 cm = 39.370 in 100 cm × 1 in 2.54 cm = 39.370 in . This means 100 cm equals 39.370 in.

Your Turn 3.75

Converting Units

Defining and Applying Percent

A percent is a specific rational number and is literally per 100. n n percent, denoted n n %, is the fraction n 100 n 100 .

Example 3.76

Rewriting a percentage as a fraction.

Rewrite the following as fractions:

• Using the definition and n = 31 n = 31 , 31% in fraction form is 31 100 31 100 .
• Using the definition and n = 93 n = 93 , 93% in fraction form is 93 100 93 100 .

Your Turn 3.76

Example 3.77, rewriting a percentage as a decimal.

Rewrite the following percentages in decimal form:

• Using the definition and n = 54 n = 54 , 54% in fraction form is 54 100 54 100 . Dividing a number by 100 moves the decimal two places to the left; 54% in decimal form is then 0.54.
• Using the definition and n = 83 n = 83 , 83% in fraction form is 83 100 83 100 . Dividing a number by 100 moves the decimal two places to the left; 83% in decimal form is then 0.83.

Your Turn 3.77

You should notice that you can simply move the decimal two places to the left without using the fractional definition of percent.

Percent is used to indicate a fraction of a total. If we want to find 30% of 90, we would perform a multiplication, with 30% written in either decimal form or fractional form. The 90 is the total , 30 is the percentage , and 27 (which is 0.30 × 90 0.30 × 90 ) is the percentage of the total .

n % n % of x x items is n 100 × x n 100 × x . The x x is referred to as the total , the n n is referred to as the percent or percentage , and the value obtained from n 100 × x n 100 × x is the part of the total and is also referred to as the percentage of the total .

Example 3.78

Finding a percentage of a total.

• Determine 40% of 300.
• Determine 64% of 190.
• The total is 300, and the percentage is 40. Using the decimal form of 40% and multiplying we obtain 0.40 × 300 = 120 0.40 × 300 = 120 .
• The total is 190, and the percentage is 64. Using the decimal form of 64% and multiplying we obtain 0.64 × 190 = 121.6 0.64 × 190 = 121.6 .

Your Turn 3.78

In the previous situation, we knew the total and we found the percentage of the total. It may be that we know the percentage of the total, and we know the percent, but we don't know the total. To find the total if we know the percentage the percentage of the total, use the following formula.

If we know that n n % of the total is x x , then the total is 100 × x n 100 × x n .

Example 3.79

Finding the total when the percentage and percentage of the total are known.

• What is the total if 28% of the total is 140?
• What is the total if 6% of the total is 91?
• 28 is the percentage, so n = 28 n = 28 . 28% of the total is 140, so x = 140 x = 140 . Using those we find that the total was 100 × 140 28 = 500 100 × 140 28 = 500 .
• 6 is the percentage, so n = 6 n = 6 . 6% of the total is 91, so x = 91 x = 91 . Using those we find that the total was 100 × 91 6 = 1,516.6 100 × 91 6 = 1,516.6 .

Your Turn 3.79

The percentage can be found if the total and the percentage of the total is known. If you know the total, and the percentage of the total, first divide the part by the total. Move the decimal two places to the right and append the symbol %. The percentage may be found using the following formula.

The percentage, n n , of b b that is a a is a b × 100 % a b × 100 % .

Example 3.80

Finding the percentage when the total and percentage of the total are known.

Find the percentage in the following:

• Total is 300, percentage of the total is 60.
• Total is 440, percentage of the total is 176.
• The total is 300; the percentage of the total is 60. Calculating yields 0.2. Moving the decimal two places to the right gives 20. Appending the percentage to this number results in 20%. So, 60 is 20% of 300.
• The total is 440; the percentage of the total is 176. Calculating yields 0.4. Moving the decimal two places to the right gives 40. Appending the percentage to this number results in 40%. So, 176 is 40% of 440.

Your Turn 3.80

Solve problems using percent.

In the media, in research, and in casual conversation percentages are used frequently to express proportions. Understanding how to use percent is vital to consuming media and understanding numbers. Solving problems using percentages comes down to identifying which of the three components of a percentage you are given, the total, the percentage, or the percentage of the total. If you have two of those components, you can find the third using the methods outlined previously.

Example 3.81

Percentage of students who are sleep deprived.

A study revealed that 70% of students suffer from sleep deprivation, defined to be sleeping less than 8 hours per night. If the survey had 400 participants, how many of those participants had less than 8 hours of sleep per night?

The percentage of interest is 70%. The total number of students is 400. With that, we can find how many were in the percentage of the total, or, how many were sleep deprived. Applying the formula from above, the number who were sleep deprived was 0.70 × 400 = 280 0.70 × 400 = 280 ; 280 students on the study were sleep deprived.

Your Turn 3.81

Example 3.82, amazon prime subscribers.

There are 126 million users who are U.S. Amazon Prime subscribers. If there are 328.2 million residents in the United States, what percentage of U.S. residents are Amazon Prime subscribers?

We are asked to find the percentage. To do so, we divide the percentage of the total, which is 126 million, by the total, which is 328.2 million. Performing this division and rounding to three decimal places yields 126 328.2 = 0.384 126 328.2 = 0.384 . The decimal is moved to the right by two places, and a % sign is appended to the end. Doing this shows us that 38.4% of U.S. residents are Amazon Prime subscribers.

Your Turn 3.82

Example 3.83.

Evander plays on the basketball team at their university and 73% of the athletes at their university receive some sort of scholarship for attending. If they know 219 of the student-athletes receive some sort of scholarship, how many student-athletes are at the university?

We need to find the total number of student-athletes at Evander’s university.

Step 1: Identify what we know. We know the percentage of students who receive some sort of scholarship, 73%. We also know the number of athletes that form the part of the whole, or 219 student-athletes.

Step 2: To find the total number of student-athletes, use 100 × x n 100 × x n , with x = 219 x = 219 and n = 73 n = 73 . Calculating with those values yields 100 × 219 73 = 300 100 × 219 73 = 300 .

So, there are 300 total student-athletes at Evander’s university

Your Turn 3.83

Check your understanding, section 3.4 exercises.

• Studying and going to class?
• Not sleeping?
• Determine the markup in dollars.
• The markup is what percent of the original cost? Round the percentage to one decimal place.
• Calculate the markup on the item, in dollars.
• What is the price for which Wegmans sells the item? This is the price Wegmans paid, plus the markup.
• Suppose Wegmans then offers a 25% discount on the sale price of the item (found in part b). In dollars, how much is the discount?
• Determine the price of the item after the discount (this is the sales price of the item minus the discount). Round to two decimal places.
• Is the new price after the markup and discount equal to the price Wegmans paid for the item? Explain.
• The original price was $150. After the 50% discount, what is the price of the item?
• The coupon is applied to the discount price. The coupon is for 25%. Find 25% of the sale price (found in part a).
• Find the price after applying the coupon (this is the value from part a minus the value from part b).
• The total amount saved on the item is the original price after all the discounts. Determine the total amount saved by subtracting the final price paid (part c) from the original price of the item.
• Determine the effective discount percentage, which is the total amount saved divided by the original price of the item.
• Was the effective discount percentage equal to 75%, which would be the 50% plus the 25%? Explain.

Solving Rational Equations · Examples

Listen up, fraction fans! In today’s lesson, you will learn and practice solving rational equations. As you will see, these are any equation involving a fraction, also known as a rational number in math talk!

By the end, you will know the difference between rational and irrational numbers and have two tricks for solving rational equations.

You could even tackle one of the tricky challenges to form a rational equation using the Pythagorean theorem , or to simplify an expression involving some radicals!

What is a Rational Equation? How to Solve Rational Equations Step 1: Eliminate the Denominators Step 2: Simplify the Equation Step 3: Solve the Equation Step 4: Check Solutions Practice & Challenges Question 1 Question 2 Challenge 1 Challenge 2 Worksheet To Sum Up (Pun Intended!)

What is a Rational Equation?

A rational equation is simply an equation involving a rational number.

A ratio -nal number can be written as a ratio of two integers – an irratio -nal number cannot.

Most of the numbers you know and love such as \(\Large\frac{2}{7}\), \(\Large\frac{1}{2}\) and \(-\Large\frac{20817}{43}\) are rational. Some common irrational numbers are π, \(\sqrt{2}\) and Euler’s number, e. These cannot be written as a fraction of integers.

Numberphile has an interesting video about All the Numbers , which categorizes number types, including rational and irrational numbers .

Technically speaking, basic equations like x+2=5 are rational because each term is a rational number. However, the rational equations you will solve today won’t be so easy!

An example of what you will more likely see in an exam is something like this:

Each term is shown as a fraction.

Rational equations can also include radicals:

Or other operations such as division:

Luckily, the technique you learn now will work for every type of rational equation!

How to Solve Rational Equations

The method to solve these equations is pretty much the same for every type of rational equation. You’ll see questions of varying difficulty in this lesson; don’t be afraid to tackle the challenges later on!

Step 1: The Denominator Elimination Round!

First, you need to deal with the elephant in the room: what should you do with the denominators!?

Solving rational equations is just like solving any other equation once you complete this step.

If it’s a simple case, where you have one fraction being equal to one other fraction, you can cross multiply .

Multiply both sides by the values of both denominators. In this example, both sides are multiplied by 3, then 5.

The 3 cancels with the left denominator and the 5 cancels with the right denominator, leaving you with 5(x+4)=3×2.

See why it’s called cross multiplying?

The product of the left denominator and right numerator equals the product of the right denominator and left numerator !

The more general way to deal with the denominators is to find their lowest common multiple (LCM) . This is the smallest number which all denominators divide neatly, leaving no remainder.

If you cannot find the LCM by inspection – if you cannot “just see it” – you need to factor every denominator like you would with a polynomial.

If you have more than one constant term, you may need to find their prime factors.

The LCM is the smallest combination of each denominator’s factors.

You’ll now see a worked example to illustrate!

Remember, you can only cross multiply when each side has only one fraction, so in this case, your first step is to find the LCM.

The only factors of 3x you know for certain are 3 and x. The only factor you know of x is just x, and 4 is a constant so you can use it as it is.

Write down each denominator’s polynomial factors into rows, with similar terms lined up in the same column.

You need to include both 3 and 4 because neither is a factor of the other. You don’t need both copies of x because x is a factor of itself! So the LCM is 12x.

You might find another example of finding the LCM with the same technique helpful.

You’re now ready to eliminate the denominators by multiplying both sides by the LCM.

Step 2: Simplify the Equation

Multiply each term by the LCM. Continuing from the last example, you have:

You now have a regular equation with no fractions, which should be familiar ground!

Step 3: Solve the Equation

Solving rational equations usually produces a simple polynomial equation. Hopefully, you’ve solved lots of these before!

You could complete the square, factor the terms by inspection, or use the quadratic formula.

This example can be solved by factoring the polynomial, having found that x+2 and x+4 are factors.

You could also solve the equation by completing the square:

Or by using the quadratic formula with a=1, b=6 and c=8:

Each way of solving the simplified rational equation is valid, but you will find that some are quicker than others!

Step 4: Check Every Solution

It is important to check that your solutions are complete, meaning you’ve found all of them and that they don’t give any weird numbers when substituted into the original equation.

In the worked example, you were left with a quadratic equation and found two distinct roots.

Quadratic equations either have two distinct solutions, one repeated solution, or no real solution so the solution x=-2 or x=-4 is complete.

You must be careful that none of the rational terms in the original equation have a zero in the denominator.

Do this by going back to the beginning and substituting your answers into the denominators!

The denominators in the worked example are 3x, x, and 4. Replacing x with -2 or -4 doesn’t give you zero in any of them, so you’re safe here!

A solution that gives a zero-denominator is not allowed. That’s because dividing by zero is “illegal” in math!

Any number divided by zero gives an error on a calculator. Ever wondered why that is?

This is your time to shine – try solving rational equations for yourself and, if you’re feeling confident, tackle the challenges too.

As they say, practice makes perfect! Use the worked example for guidance if you get stuck.

Find x in the following rational equation:

The equation is two equal fractions so you can cross-multiply. You could also simplify \(\Large\frac{15}{3}\normalsize\) to 5, but this does not change the final answer.

Each term is divisible by 9. Simplify the equation by dividing both sides by 9:

This form is called the difference of two squares because it can be factored like this:

So the solution is x=±3.

These must be all the solutions because quadratic equations have a maximum of two distinct real roots.

Neither denominator in the original rational equation has an x term, so substituting any value for x makes no difference to their values – there is no chance of them being zero!

This means the solutions x=3 and x=-3 are valid.

Solve the following rational equation:

There are three fractions so you cannot cross-multiply.

See that the second denominator is the difference of two squares?

Multiply each term by the LCM and simplify.

So its solution is -5, right?… STOP RIGHT THERE! Don’t forget, we can’t divide by zero!

If you put x=±5 into the original equation, at least one of the denominators is always zero, so the original equation has no solutions.

Challenge 1

Can you spot the mistake in the following example? Hint: there has been some cheating with radicals!

If you need a refresher on radicals , check out our lesson on multiplying them. That will get you on the right track!

The mistake is that radicals cannot be subtracted like normal terms.

Instead, you must square both sides of the equation to remove the radical. Similar terms can then be combined as usual.

Still confused? You can find lots of interactive questions on Lumen Learning . Radicals often pop up in rational equations, so getting comfortable with radicals is super helpful for exam success!

Challenge 2

Find the value of x, by using the Pythagorean theorem on the following right-angled triangle:

If you need a refresher on the Pythagorean theorem or are interested in the man himself, check out our lesson. Do the worksheets and you’ll be acing triangle questions in no time !

The Pythagorean theorem states that:

Where c is the length of the hypotenuse, and a and b are the other side lengths.

This gives the rational equation:

Simplifying, you find:

The LCM is 36 so the denominators are removed by dividing each term by this:

It’s always fun when different areas of math link together!

To Sum Up (Pun Intended!)

In today’s lesson on solving rational equations, you first saw the difference between rational and irrational numbers.

Rational numbers are “nice” because they can be written as a fraction of integers. Remember that all integers are rational because they can be written with a denominator of 1!

Irrational numbers are a little more abstract. They include weird but incredibly beautiful numbers like π and e, which cannot be written as a fraction of integers.

Rational equations are solved by eliminating the denominator in every term, then simplifying and solving as normal.

Denominators can be removed by cross-multiplication if there is only one fraction on either side or by finding the LCM if the equation is more complicated.

Don’t be shy, leave a comment below if you have any questions or need help!

Still curious about rational numbers, or eager for an extra challenge? Check out our lesson on the rational root theorem , which combines algebra and equation solving.

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 5: Rational number arithmetic

Lesson 1: interpreting negative numbers.

• Missing numbers on the number line examples (Opens a modal)
• Comparing rational numbers (Opens a modal)
• Missing numbers on the number line Get 3 of 4 questions to level up!
• Order rational numbers Get 3 of 4 questions to level up!

Lesson 2: Changing temperatures

• Signs of sums on a number line (Opens a modal)
• Adding negative numbers review (Opens a modal)
• Adding negative numbers Get 5 of 7 questions to level up!

Lesson 3: Changing elevation

• Adding negative numbers on the number line (Opens a modal)
• Number equations & number lines (Opens a modal)
• Adding fractions with different signs (Opens a modal)
• Signs of sums Get 5 of 7 questions to level up!
• Adding negative numbers on the number line Get 5 of 7 questions to level up!
• Number equations & number lines Get 3 of 4 questions to level up!

Lesson 4: Money and debts

• Rational number word problem: checking account (Opens a modal)

Lesson 5: Representing subtraction

• Adding the opposite with number lines (Opens a modal)
• Subtracting negative numbers review (Opens a modal)
• Understand subtraction as adding the opposite Get 3 of 4 questions to level up!
• Subtracting negative numbers Get 5 of 7 questions to level up!

Lesson 6: Subtracting rational numbers

• Graphing negative number addition and subtraction expressions (Opens a modal)
• Interpreting numeric expressions example (Opens a modal)
• Absolute value as distance between numbers (Opens a modal)
• Interpret negative number addition and subtraction expressions Get 3 of 4 questions to level up!
• Adding & subtracting negative fractions Get 5 of 7 questions to level up!
• Absolute value to find distance Get 5 of 7 questions to level up!
• Adding & subtracting rational numbers Get 3 of 4 questions to level up!

Lessons 1-6: Extra practice

• Adding integers: find the missing value (Opens a modal)
• Subtracting integers: find the missing value (Opens a modal)
• Associative and commutative properties of addition with negatives (Opens a modal)
• Equivalent expressions with negative numbers (Opens a modal)
• Adding & subtracting negative numbers Get 5 of 7 questions to level up!
• Addition & subtraction: find the missing value Get 3 of 4 questions to level up!
• Commutative and associative properties of addition with integers Get 3 of 4 questions to level up!
• Equivalent expressions with negative numbers Get 3 of 4 questions to level up!

Lesson 7: Adding and subtracting to solve problems

• Interpreting negative number statements (Opens a modal)
• Negative number word problem: Alaska (Opens a modal)
• Interpreting negative number statements Get 3 of 4 questions to level up!
• Negative number addition and subtraction: word problems Get 3 of 4 questions to level up!

Lesson 9: Multiplying rational numbers

• Multiplying a positive and a negative number (Opens a modal)
• Multiplying two negative numbers (Opens a modal)
• Why a negative times a negative makes sense (Opens a modal)
• Why a negative times a negative is a positive (Opens a modal)
• Multiplying negative numbers review (Opens a modal)
• Multiplying negative numbers Get 3 of 4 questions to level up!

Lesson 10: Multiply!

• Multiplying positive and negative fractions (Opens a modal)
• Multiplying positive and negative fractions Get 3 of 4 questions to level up!

Lesson 11: Dividing rational numbers

• Dividing positive and negative numbers (Opens a modal)
• Dividing negative numbers review (Opens a modal)
• Dividing negative fractions (Opens a modal)
• Dividing negative numbers Get 3 of 4 questions to level up!
• Dividing positive and negative fractions Get 3 of 4 questions to level up!
• Dividing mixed numbers with negatives Get 3 of 4 questions to level up!

Lesson 12: Negative rates

• Interpreting multiplication & division of negative numbers (Opens a modal)
• Multiplying & dividing negative numbers word problems Get 3 of 4 questions to level up!

Lesson 13: Expressions with rational numbers

• Substitution with negative numbers (Opens a modal)
• Ordering expressions (Opens a modal)
• Negative signs in fractions (Opens a modal)
• Expressions with rational numbers (Opens a modal)
• Substitution with negative numbers Get 5 of 7 questions to level up!
• Ordering negative number expressions Get 3 of 4 questions to level up!
• Negative signs in fractions Get 3 of 4 questions to level up!
• Signs of expressions Get 5 of 7 questions to level up!

Lesson 14: Solving problems with rational numbers

• Intro to order of operations (Opens a modal)
• Order of operations with rational numbers (Opens a modal)
• Rational number word problem: cab (Opens a modal)
• Order of operations with negative numbers Get 5 of 7 questions to level up!
• Rational number word problems Get 3 of 4 questions to level up!

Lesson 15: Solving equations with rational numbers

• No videos or articles available in this lesson
• One-step equations with negatives (add & subtract) Get 5 of 7 questions to level up!
• One-step equations with negatives (multiply & divide) Get 5 of 7 questions to level up!

SOLVING PROBLEMS WITH RATIONAL NUMBERS

In this section, we will learn how to solve problems with rational numbers.

A number that is expressed in the form a/b is called as rational number.

Here, both "a" and "b" are integers and also b  ≠ 0. 

Problem 1 : 

The area of a rectangular sandbox is 56 2/3 square feet. The length of the  sandbox is 8 1/2 feet. What is the width ?

We know the formula to find area of the rectangle.

That is, 

Area of the rectangle  =  length x width 

Plug the known values area and length and solve for the unknown value width.

56 2/3  =  8 1/2 x width 

170/3  =  17/2 x width

(170/3) x (2/17)  =  width

20/3  =  width

6 2/3  =  width

Therefore, the width of the rectangle is 6 2/3 feet.

Problem 2 : 

Mr. Webster is buying carpet for an exercise  room where the basement of the room is in the shape of rectangle. The length and width of the room are 18 2/5 feet and  12 1/2 feet respectively. Find the total cost of the carpet, if the price of the carpet is $3 per square feet ?

To know the total cost of the carpet, first we have to know the area of the basement.

Area of the basement  =  length x width

=  18 2/5 x 12 1/2

=  (92/5) x (25/2)

=  46 x 5

=  230 square feet

So, we need 230 square feet of carpet.

The cost each square feet of carpet  =  $3

Then, the cost of 230 square ft of carpet is

=  3 x 230

=  $690

Therefore,  the total cost of the carpet is $690.

Problem 3 : 

Problem 4 : 

David is cooking enough lentils for lentil barley soup and lentil salad. The  lentil barley soup recipe calls for 3/ 4 cup of dried lentils. The lentil salad  recipe calls for 1 1/ 2 cups of dried lentils. David has a 1/ 8 -cup scoop. How many  scoops of dried lentils will David need to have enough for the soup and  the salad?

David needs 3/ 4 cup of dried lentils for soup and 1 1/ 2 cups for salad.

Total amount dried lentils that David need is

=  (3/4) + (1 1/2)

=  3/4 + 3/2

=   3/4 + 6/4

=  (3+6) / 4

=  9/4

David needs 9/4 cups  of dried lentils for both the soup and the salad.

To find how many 1/8 -cup scoops he needs, divide the total amount of dried  lentils into groups of 1/8.

Then, we have 

=  9/4 ÷ 1/8

=  9/4 x 8/1

=  9 x 2

Hence, David will need 18 scoops of dried lentils to have enough for both the lentil  barley soup and the lentil salad.

Problem 5 :

If the numerator of a fraction is increased by 2 and the denominator by 1, it becomes 1. In case, the numerator is decreased by 4 and the denominator by 2, it becomes 1/2. Find the fraction. 

Let "x/y" be the required fraction. 

"If the numerator is increased by 2 and the denominator by 1, the fraction becomes 1"

From the above information, we have (x+2) / (y+1) = 1

(x + 2) / (y + 1)  =  1

x + 2  =  y + 1

x - y = -1 ----(1)

"In case the numerator is decreased by 4 and the denominator by 2, the fraction becomes 1/2"

From the above information, we have

(x - 4) / (y - 2)  =  1 / 2

2(x - 4)  =  y - 2

2x - y  =  6 ----(1)

Solving (1) and (2), we get

x  =  7 and y  =  8

x / y  =  7 / 8 

So, the required fraction is 7/8.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

Complex Plane

Apr 14, 24 07:56 AM

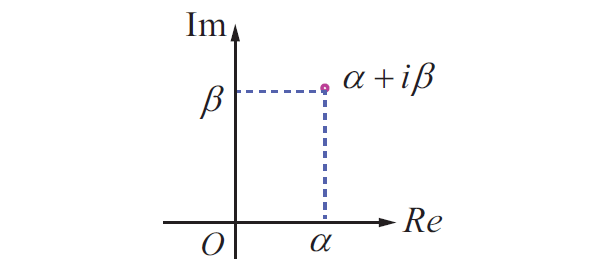
Real Analysis

Apr 14, 24 02:50 AM

Study Guides > College Algebra

Solving a rational equation, example 3: solving a rational equation.

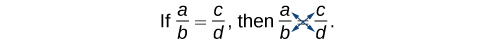
A General Note: Rational Equations

How to: given a rational equation, solve it..

• Factor all denominators in the equation.
• Find and exclude values that set each denominator equal to zero.
• Find the LCD.
• Multiply the whole equation by the LCD. If the LCD is correct, there will be no denominators left.
• Solve the remaining equation.
• Make sure to check solutions back in the original equations to avoid a solution producing zero in a denominator

Example 4: Solving a Rational Equation without Factoring

Example 5: solving a rational equation by factoring the denominator, example 6: solving rational equations with a binomial in the denominator.

• [latex]\frac{3}{x - 6}=\frac{5}{x}[/latex]
• [latex]\frac{x}{x - 3}=\frac{5}{x - 3}-\frac{1}{2}[/latex]
• [latex]\frac{x}{x - 2}=\frac{5}{x - 2}-\frac{1}{2}[/latex]
• The denominators [latex]x[/latex] and [latex]x - 6[/latex] have nothing in common. Therefore, the LCD is the product [latex]x\left(x - 6\right)[/latex]. However, for this problem, we can cross-multiply. [latex]\begin{array}{l}\frac{3}{x - 6}=\frac{5}{x}\hfill \\ 3x=5\left(x - 6\right)\text{Distribute}.\hfill \\ 3x=5x - 30\hfill \\ -2x=-30\hfill \\ x=15\hfill \end{array}[/latex] The solution is [latex]x=15[/latex]. The excluded values are [latex]x=6[/latex] and [latex]x=0[/latex].
• The LCD is [latex]2\left(x - 3\right)[/latex]. Multiply both sides of the equation by [latex]2\left(x - 3\right)[/latex]. [latex]\begin{array}{l}2\left(x - 3\right)\left[\frac{x}{x - 3}\right]\hfill&=\left[\frac{5}{x - 3}-\frac{1}{2}\right]2\left(x - 3\right)\hfill \\ \frac{2\cancel{\left(x - 3\right)}x}{\cancel{x - 3}}\hfill&=\frac{2\cancel{\left(x - 3\right)}5}{\cancel{x - 3}}-\frac{\cancel{2}\left(x - 3\right)}{\cancel{2}}\hfill \\ 2x\hfill&=10-\left(x - 3\right)\hfill \\ 2x\hfill&=10-x+3\hfill \\ 2x\hfill&=13-x\hfill \\ 3x\hfill&=13\hfill \\ x\hfill&=\frac{13}{3}\hfill \end{array}[/latex] The solution is [latex]x=\frac{13}{3}[/latex]. The excluded value is [latex]x=3[/latex].
• The least common denominator is [latex]2\left(x - 2\right)[/latex]. Multiply both sides of the equation by [latex]x\left(x - 2\right)[/latex]. [latex]\begin{array}{l}2\left(x - 2\right)\left[\frac{x}{x - 2}\right]=\left[\frac{5}{x - 2}-\frac{1}{2}\right]2\left(x - 2\right)\hfill \\ 2x=10-\left(x - 2\right)\hfill \\ 2x=12-x\hfill \\ 3x=12\hfill \\ x=4\hfill \end{array}[/latex] The solution is [latex]x=4[/latex]. The excluded value is [latex]x=2[/latex].

Example 7: Solving a Rational Equation with Factored Denominators and Stating Excluded Values

Licenses & attributions, cc licensed content, specific attribution.

• College Algebra. Provided by: OpenStax Authored by: OpenStax College Algebra. Located at: https://cnx.org/contents/ [email protected] :1/Preface. License: CC BY: Attribution .

Please add a message.

Message received. Thanks for the feedback.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 8: Rational Expressions

8.7 Solving Rational Equations

When solving equations that are made up of rational expressions, we use the same strategy we used to solve complex fractions, where the easiest solution involved multiplying by the LCD to remove the fractions. Consider the following examples.

Example 8.7.1

Solve the following:

[latex]\dfrac{2x}{3}-\dfrac{5}{6}=\dfrac{3}{4}[/latex]

For these three fractions, the LCD is 12. Therefore, multiply all parts of the equation by 12:

[latex]12\left(\dfrac{2x}{3}-\dfrac{5}{6}\right)=\left(\dfrac{3}{4}\right)12[/latex]

This reduces the rational equation to:

[latex]4(2x)-2(5)=3(3)[/latex]

Multiplying this out yields:

[latex]8x - 10 = 9[/latex]

Now isolate and solve for [latex]x[/latex]:

[latex]\begin{array}{rrrrr} 8x&-&10&=&9 \\ &+&10&&+10 \\ \hline &&8x&=&19 \\ \\ &&x&=&\dfrac{19}{8} \end{array}[/latex]

Example 8.7.2

[latex]\dfrac{x}{x+2}+\dfrac{1}{x+1}=\dfrac{5}{(x+1)(x+2)}[/latex]

For these three fractions, the LCD is [latex](x + 1)(x + 2)[/latex]. Therefore, multiply all parts of the equation by [latex](x + 1)(x + 2)[/latex]:

[latex](x+1)(x+2)\left(\dfrac{x}{x+2}+\dfrac{1}{x+1}\right)=\left(\dfrac{5}{(x+1)(x+2)}\right)(x+1)(x+2)[/latex]

[latex]x(x + 1) + 1(x + 2) = 5[/latex]

[latex]x^2 + x + x + 2 = 5[/latex]

Which reduces to:

[latex]x^2 + 2x + 2 = 5[/latex]

Now subtract 5 from both sides of the equation to turn this into an equation that can be easily factored:

[latex]\begin{array}{rrrrrrr} x^2&+&2x&+&2&=&5 \\ &&&-&5&&-5 \\ \hline x^2&+&2x&-&3&=&0 \end{array}[/latex]

This equation factors to:

[latex](x + 3)(x - 1) = 0[/latex]

The solutions are:

[latex]x = -3 \text{ and }1[/latex]

Solve each rational equation.

• [latex]3x-\dfrac{1}{2}-\dfrac{1}{x}=0[/latex]
• [latex]x+1=\dfrac{4}{x+1}[/latex]
• [latex]x+\dfrac{20}{x-4}=\dfrac{5x}{x-4}-2[/latex]
• [latex]\dfrac{x^2+6}{x-1}+\dfrac{x-2}{x-1}=2x[/latex]
• [latex]x+\dfrac{6}{x-3}=\dfrac{2x}{x-3}[/latex]
• [latex]\dfrac{x-4}{x-1}=\dfrac{12}{3-x}+1[/latex]
• [latex]\dfrac{3m}{2m-5}-\dfrac{7}{3m+1}=\dfrac{3}{2}[/latex]
• [latex]\dfrac{4-x}{1-x}=\dfrac{12}{3-x}[/latex]
• [latex]\dfrac{7}{y-3}-\dfrac{1}{2}=\dfrac{y-2}{y-4}[/latex]
• [latex]\dfrac{1}{x+2}+\dfrac{1}{x-2}=\dfrac{3x+8}{x^2-4}[/latex]
• [latex]\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}=\dfrac{5}{6}[/latex]
• [latex]\dfrac{x-2}{x+3}-\dfrac{1}{x-2}=\dfrac{1}{x^2+x-6}[/latex]
• [latex]\dfrac{x}{x-1}-\dfrac{2}{x+1}=\dfrac{4x^2}{x^2-1}[/latex]
• [latex]\dfrac{2x}{x+2}+\dfrac{2}{x-4}=\dfrac{3x}{x^2-2x-8}[/latex]
• [latex]\dfrac{2x}{x+1}-\dfrac{3}{x+5}=\dfrac{-8x^2}{x^2+6x+5}[/latex]

Answer Key 8.7

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Rational Functions

Solve applied problems involving rational functions.

In Example 2, we shifted a toolkit function in a way that resulted in the function [latex]f\left(x\right)=\frac{3x+7}{x+2}[/latex]. This is an example of a rational function. A rational function is a function that can be written as the quotient of two polynomial functions. Many real-world problems require us to find the ratio of two polynomial functions. Problems involving rates and concentrations often involve rational functions.

A General Note: Rational Function

A rational function is a function that can be written as the quotient of two polynomial functions [latex]P\left(x\right) \text{and} Q\left(x\right)[/latex].

Example 3: Solving an Applied Problem Involving a Rational Function

A large mixing tank currently contains 100 gallons of water into which 5 pounds of sugar have been mixed. A tap will open pouring 10 gallons per minute of water into the tank at the same time sugar is poured into the tank at a rate of 1 pound per minute. Find the concentration (pounds per gallon) of sugar in the tank after 12 minutes. Is that a greater concentration than at the beginning?

Let t  be the number of minutes since the tap opened. Since the water increases at 10 gallons per minute, and the sugar increases at 1 pound per minute, these are constant rates of change. This tells us the amount of water in the tank is changing linearly, as is the amount of sugar in the tank. We can write an equation independently for each:

The concentration, C , will be the ratio of pounds of sugar to gallons of water

The concentration after 12 minutes is given by evaluating [latex]C\left(t\right)[/latex] at [latex]t=\text{ }12[/latex].

This means the concentration is 17 pounds of sugar to 220 gallons of water.

At the beginning, the concentration is

Since [latex]\frac{17}{220}\approx 0.08>\frac{1}{20}=0.05[/latex], the concentration is greater after 12 minutes than at the beginning.

Analysis of the Solution

To find the horizontal asymptote, divide the leading coefficient in the numerator by the leading coefficient in the denominator:

Notice the horizontal asymptote is [latex]y=\text{ }0.1[/latex]. This means the concentration, C , the ratio of pounds of sugar to gallons of water, will approach 0.1 in the long term.

There are 1,200 freshmen and 1,500 sophomores at a prep rally at noon. After 12 p.m., 20 freshmen arrive at the rally every five minutes while 15 sophomores leave the rally. Find the ratio of freshmen to sophomores at 1 p.m.

• Precalculus. Authored by : Jay Abramson, et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download For Free at : http://cnx.org/contents/[email protected].

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

Precalculus : Solve and Graph Rational Inequalities

Study concepts, example questions & explanations for precalculus, all precalculus resources, example questions, example question #1 : solving polynomial and rational inequalities.

Solve the inequality. 

Then find the common denominator and simplify 

Next, factor out the numerator 

The solutions are 

Thus, the solution to the inequality is  

Example Question #2 : Solving Polynomial And Rational Inequalities

Solve and graph:

1) Multiply both sides of the equation by the common denominator of the fractions:

2) Simplify:

3) For standard notation, and the fact that inequalities can be read backwards:

     For interval notation:

Example Question #3 : Solving Polynomial And Rational Inequalities

Graph the rational expression,

4) The funtion y is exists over the allowed x-intervals:

One approach for solving the inequality: 

Another approach for solving the inequality:

Example Question #4 : Solve And Graph Rational Inequalities

Which of the following best describes the statement:

The undefined points of rational functions are vertical asymptotes.

The statement is always true

The statement is always false

The statement is true in some cases and false in others

Example Question #5 : Solve And Graph Rational Inequalities

Which of the following is a graph of the function:

We begin by finding the zeros of the equation using the numerator.

Example Question #6 : Solve And Graph Rational Inequalities

Determine the zeros of the following function and the points where the function will be undefined.

Example Question #1 : Solve And Graph Rational Inequalities

Example Question #8 : Solve And Graph Rational Inequalities

We will first begin by solving for the zeros and undefined points of the inequality.  We solve for the zeros by setting the numerator equal to zero.

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&