example of problem solving in newton's second law of motion

Gurumuda Networks

Newton’s second law of motion – problems and solutions

Solved problems in Newton’s laws of motion – Newton’s second law of motion 

1. A 1 kg object accelerated at a constant 5 m/s 2 . Estimate the net force needed to accelerate the object.

Mass (m) = 1 kg

Acceleration (a) = 5 m/s 2

Wanted : net force (∑F)

We use Newton’s second law to get the net force.

∑ F = (1 kg)(5 m/s 2 ) = 5 kg m/s 2 = 5 Newton

2. Mass of an object = 1 kg, net force ∑F = 2 Newton. Determine the magnitude and direction of the object’s acceleration….

Net force (∑F) = 2 Newton

Wanted : The magnitude and direction of the acceleration (a)

a = 2 m/s 2

The direction of the acceleration = the direction of the net force (∑F)

3. Object’s mass = 2 kg, F 1 = 5 Newton, F 2 = 3 Newton. The magnitude and direction of the acceleration is…

Mass (m) = 2 kg

F 1 = 5 Newton

F 2 = 3 Newton

net force :

∑ F = F 1 – F 2 = 5 – 3 = 2 Newton

The magnitude of the acceleration :

a = 1 m/s 2

Direction of the acceleration = direction of the net force = direction of F 1

4. Object’s mass = 2 kg, F 1 = 10 Newton, F 2 = 1 Newton. The magnitude and direction of the acceleration is…

F 2 = 1 Newton

F 1 = 10 Newton

F 1x = F 1 cos 60 o = (10)(0.5) = 5 Newton

Net force :

∑ F = F 1x – F 2 = 5 – 1 = 4 Newton

Direction of the acceleration = direction of the net force = direction of F 1x

5. F 1 = 10 Newton, F 2 = 1 Newton, m 1 = 1 kg, m 2 = 2 kg. The magnitude and direction of the acceleration is…

Mass 1 (m 1 ) = 1 kg

Mass 2 (m 2 ) = 2 kg

The net force :

∑ F = F 1 – F 2 = 10 – 1 = 9 Newton

a = ∑F / (m 1 + m 2 )

a = 9 / (1 + 2)

a = 3 m/s 2

The direction of the acceleration = the direction of the net force = direction of F 1

A 40-kg block accelerated by a force of 200 N. Acceleration of the block is 3 m/ s 2 . Determine the magnitude of friction force experienced by the block.

Mass (m) = 40 kg

Force (F) = 200 N

Acceleration (a) = 3 m/s 2

Wanted: Friction force (F g )

The equation of Newton’s second law of motion

∑ F = net force, m = mass, a = acceleration

The direction of force F rightward, the direction of friction force leftward (the direction of friction force is opposite with the direction of object’s motion).

Choose rightward as positive and leftward as negative.

F – F g = m a

200 – F g = (40)(3)

200 – F g = 120

F g = 200 – 120

F g = 80 Newton

The correct answer is D.

7. Block A with a mass of 100-gram place above block B with a mass of 300 gram, and then block b pushed with a force of 5 N vertically upward. Determine the normal force exerted by block B on block A.

Force (F) = 5 Newton

Mass of block A (m A ) = 100 gram = 0.1 kg

Mass of block B (m B ) = 300 gram = 0.3 kg

Acceleration of gravity (g) = 10 m/s 2

Weight of block A (w A ) = (0.1 kg)(10 m/s 2 ) = 1 kg m/s 2 = 1 Newton

Weight of block B (w B ) = (0.3 kg)(10 m/s 2 ) = 3 kg m/s 2 = 3 Newton

Wanted : Normal force exerted by block B to block A

F = push force (act on block B)

w A = weight of block A (act on block A)

w B = weight of block B (act on block B)

N A = normal force exerted by block B on block A (Act on block A)

N A ’ = normal force exerted by block A on block B (Act on block B)

Apply Newton’s second law of motion on both blocks :

F – w A – w B + N A – N A ’ = (m A + m B ) a

N A and N A ’ are action-reaction forces that have the same magnitude but opposite in direction so eliminated from the equation.

F – w A – w B = (m A + m B ) a

5 – 1 – 3 = (0.1 + 0.3) a

5 – 4 = (0.4) a

1 = (0.4) a

a = 1 / 0.4

a = 2.5 m/s 2

Apply Newton’s second law of motion on block A :

N A – w A = m A a

N A – 1 = (0.1)(2.5)

N A – 1 = 0.25

N A = 1 + 0.25

N A = 1.25 Newton

The correct answer is B.

8. An object with weight of 4 N supported by a cord and pulley. A force of 2 N acts on the block and one end of the cord pulled by a force of 9 N. Determine the net force acts on object X.

B. 4 N downward

C. 9 N upward

D. 9 N downward

Weight of X (w X ) = 4 Newton

Pull force (F x ) = 2 Newton

Tension force (F T ) = 9 Newton

Wanted: Net force acts on object X

Vertically upward forces that act on object X :

The tension force has the same magnitude in all part of the cord. So the tension force is 9 N.

Vertically downward forces that act on object X :

There are two forces that act on object X and both forces are vertically downward, the horizontal component of weight w x and the horizontal component of force F x .

Net force act on the object X :

F T – w X – F x = 9 – 4 – 2 = 9 – 6 = 3

The net force act on the object X is 3 Newton, vertically upward.

The correct answer is A.

9. An object initially at rest on a smooth horizontal surface. A force of 16 N acts on the object so the object accelerated at 2 m/s 2 . If the same object at rest on a rough horizontal surface so the friction force acts on the object is 2 N, then determine the acceleration of the object if the same force of 16 N acts on the object.

A. 1.75 m/s 2

B. 1.50 m/s 2

C. 1.00 m/s 2

D. 0.88 m/s 2

Force (F) = 16 Newton = 16 kg m/s 2

Acceleration (a) = 2 m/s 2

Friction force (F fric ) = 2 Newton = 2 kg m/s 2

Wanted : Object’s acceleration ?

Smooth horizontal surface (no friction force) :

Mass of object is 8 kilogram.

Rough horizontal surface (there is a friction force) :

F – F fric = m a

16 – 2 = 8 a

a = 1.75 m/s 2

Object’s acceleration is 1.75 m/s 2 .

10. Tom and Andrew push an object on the smooth floor. Tom push the object with a force of 5.70 N. If the mass of the object is 2.00 kg and acceleration experienced by the object is 2.00 ms -2 , then determine the magnitude and direction of force act by Tom.

A. 1.70 N and its direction is opposite with force acted by Andre.w

B. 1.70 N and its direction same as force acted by Andrew

C. 2.30 N and its direction is opposite with force acted by Andrew.

D. 2.30 N and its direction same as force acted by Andrew.

Push force acted by Andrew (F 1 ) = 5.70 Newton

Mass of object (m) = 2.00 kg

Acceleration (a) = 2.00 m/s 2

Wanted : Magnitude and direction of force acted by Tom (F 2 ) ?

Apply Newton’s second law of motion :

F 1 + F 2 = m a

5.70 + F 2 = (2)(2)

5.70 + F 2 = 4

F 2 = 4 – 5.70

F 2 = – 1.7 Newton

Minus sign indicated that (F 2 ) is opposite with push force act by Andrew (F 1 ).

11. If the mass of the block is the same, which figure shows the smallest acceleration?

Net force A :

ΣF = 4 N + 2 N – 3 N = 6 N – 3 N = 3 Newton, leftward

Net force B :

ΣF = 2 N + 3 N – 4 N = 5 N – 4 N = 1 Newton, rightward

Net force C :

ΣF = 4 N + 3 N – 2 N = 7 N – 2 N = 5 Newton, rightward

Net force D :

ΣF = 3 N + 4 N + 2 N = 9 Newton, rightward

The equation of Newton’s second law :

a = acceleration, ΣF = net force, m = mass

Based on the above formula, the acceleration (a) is directly proportional to the net force (ΣF) and inversely proportional to mass (m). If the mass of an object is the same, the greater the resultant force, the greater the acceleration or the smaller the resultant force, the smaller the acceleration. Based on the above calculation, the smallest net force is 1 Newton so the acceleration is also smallest.

12. Some forces act on an object with a mass of 20 kg, as shown in the figure below.

Determine the object’s acceleration.

Mass of object (m) = 20 kg

Net force (ΣF) = 25 N + 30 N – 15 N = 40 N

Wanted: Acceleration of an object

Object’s acceleration calculated using the equation of Newton’s second law :

a = ΣF / m = 40 N / 20 kg = 2 N/kg = 2 m/s 2

13. Which statements below describes Newton’s third law?

(1) Passengers pushed forward when the bus braked suddenly

(2) B ooks on paper are not falling when the paper is pulled quickly

(3) When playing skateboard when the foot pushes the ground back then the skateboard will slide forward

(4) O ars pushed backward, boats moving forward

(1) Newton’s first law

(2) Newton’s first law

(3) Newton’s third law

(4) Newton’s third law

[wpdm_package id=’470′]

• Mass and weight
• Normal force
• Newton’s second law of motion
• Friction force
• Motion on the horizontal surface without friction force
• The motion of two bodies with the same acceleration on the rough horizontal surface with the friction force
• Motion on the inclined plane without friction force
• Motion on the rough inclined plane with the friction force
• Motion in an elevator
• The motion of bodies connected by cord and pulley
• Two bodies with the same magnitude of accelerations
• Rounding a flat curve – dynamics of circular motion
• Rounding a banked curve – dynamics of circular motion
• Uniform motion in a horizontal circle
• Centripetal force in uniform circular motion

Share this:

Leave a comment cancel reply.

You must be logged in to post a comment.

This site uses Akismet to reduce spam. Learn how your comment data is processed .

Discover more from Physics

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

Newton Second Law of Motion Example Problems with Answers

Newton's 2nd law of motion involves force, mass and acceleration of an object. It is the acceleration of an object produced by an action or force which is directly proportional to the magnitude of the net force in the same direction and inversely proportional to the object mass. Calculate net force, mass and acceleration of an object by referring the below Newton second law of motion example problems with answers.

Newton 2nd Law of Motion Problems with Solutions

Let us consider the problem: A 15 kg object moving to the west with an acceleration of 10m/s 2 . What is the net force acting on an object?

We can calculate Force, Mass and Acceleration using the given formula.

Newton's Second Law of Motion Formulae:

Substituting the values in the above given formula,

Net Force (F net )= 15 x 10 = 150 N Therefore, the value of Net force = 150 N

Refer the newton 2nd law of motion problems with solutions: A softball has a mass of 1.5 kg and hits the catcher's glove with a force of 30 N? What is the acceleration of the softball?

Substituting the values in the above given formula, Acceleration = 30 / 1.5 = 20 m/s 2 Therefore, the value of Acceleration is 20 m/s 2

Refer the problem with solution: What is the mass of a truck if it produces a force of 15000 N while accelerating at a rate of 6 m/s 2 ?

Substituting the values in the above given formula, Mass = 15000 / 6 = 2500 kg Therefore, the value of Mass is 2500 kg

Related Examples:

• Potential Energy Examples
• Young's Modulus Calculation Examples
• Kinetic Energy Example
• Force Examples
• Work Physics Problems With Solutions
• Difference Quotient Examples

Calculators and Converters

• Classical Physics

Ask a Question

Top calculators, popular calculators.

• Derivative Calculator
• Inverse of Matrix Calculator
• Compound Interest Calculator
• Pregnancy Calculator Online

Top Categories

6 Applications of Newton’s Laws

6.1 Solving Problems with Newton’s Laws

Learning objectives.

By the end of the section, you will be able to:

• Apply problem-solving techniques to solve for quantities in more complex systems of forces
• Use concepts from kinematics to solve problems using Newton’s laws of motion
• Solve more complex equilibrium problems
• Solve more complex acceleration problems
• Apply calculus to more advanced dynamics problems

Success in problem solving is necessary to understand and apply physical principles. We developed a pattern of analyzing and setting up the solutions to problems involving Newton’s laws in Newton’s Laws of Motion ; in this chapter, we continue to discuss these strategies and apply a step-by-step process.

Problem-Solving Strategies

We follow here the basics of problem solving presented earlier in this text, but we emphasize specific strategies that are useful in applying Newton’s laws of motion . Once you identify the physical principles involved in the problem and determine that they include Newton’s laws of motion, you can apply these steps to find a solution. These techniques also reinforce concepts that are useful in many other areas of physics. Many problem-solving strategies are stated outright in the worked examples, so the following techniques should reinforce skills you have already begun to develop.

Problem-Solving Strategy: Applying Newton’s Laws of Motion

• Identify the physical principles involved by listing the givens and the quantities to be calculated.
• Sketch the situation, using arrows to represent all forces.
• Determine the system of interest. The result is a free-body diagram that is essential to solving the problem.
• Apply Newton’s second law to solve the problem. If necessary, apply appropriate kinematic equations from the chapter on motion along a straight line.
• Check the solution to see whether it is reasonable.

Let’s apply this problem-solving strategy to the challenge of lifting a grand piano into a second-story apartment. Once we have determined that Newton’s laws of motion are involved (if the problem involves forces), it is particularly important to draw a careful sketch of the situation. Such a sketch is shown in Figure (a). Then, as in Figure (b), we can represent all forces with arrows. Whenever sufficient information exists, it is best to label these arrows carefully and make the length and direction of each correspond to the represented force.

As with most problems, we next need to identify what needs to be determined and what is known or can be inferred from the problem as stated, that is, make a list of knowns and unknowns. It is particularly crucial to identify the system of interest, since Newton’s second law involves only external forces. We can then determine which forces are external and which are internal, a necessary step to employ Newton’s second law. (See Figure (c).) Newton’s third law may be used to identify whether forces are exerted between components of a system (internal) or between the system and something outside (external). As illustrated in Newton’s Laws of Motion , the system of interest depends on the question we need to answer. Only forces are shown in free-body diagrams, not acceleration or velocity. We have drawn several free-body diagrams in previous worked examples. Figure (c) shows a free-body diagram for the system of interest. Note that no internal forces are shown in a free-body diagram.

Once a free-body diagram is drawn, we apply Newton’s second law. This is done in Figure (d) for a particular situation. In general, once external forces are clearly identified in free-body diagrams, it should be a straightforward task to put them into equation form and solve for the unknown, as done in all previous examples. If the problem is one-dimensional—that is, if all forces are parallel—then the forces can be handled algebraically. If the problem is two-dimensional, then it must be broken down into a pair of one-dimensional problems. We do this by projecting the force vectors onto a set of axes chosen for convenience. As seen in previous examples, the choice of axes can simplify the problem. For example, when an incline is involved, a set of axes with one axis parallel to the incline and one perpendicular to it is most convenient. It is almost always convenient to make one axis parallel to the direction of motion, if this is known. Generally, just write Newton’s second law in components along the different directions. Then, you have the following equations:

(If, for example, the system is accelerating horizontally, then you can then set [latex]{a}_{y}=0.[/latex]) We need this information to determine unknown forces acting on a system.

As always, we must check the solution. In some cases, it is easy to tell whether the solution is reasonable. For example, it is reasonable to find that friction causes an object to slide down an incline more slowly than when no friction exists. In practice, intuition develops gradually through problem solving; with experience, it becomes progressively easier to judge whether an answer is reasonable. Another way to check a solution is to check the units. If we are solving for force and end up with units of millimeters per second, then we have made a mistake.

There are many interesting applications of Newton’s laws of motion, a few more of which are presented in this section. These serve also to illustrate some further subtleties of physics and to help build problem-solving skills. We look first at problems involving particle equilibrium, which make use of Newton’s first law, and then consider particle acceleration, which involves Newton’s second law.

Particle Equilibrium

Recall that a particle in equilibrium is one for which the external forces are balanced. Static equilibrium involves objects at rest, and dynamic equilibrium involves objects in motion without acceleration, but it is important to remember that these conditions are relative. For example, an object may be at rest when viewed from our frame of reference, but the same object would appear to be in motion when viewed by someone moving at a constant velocity. We now make use of the knowledge attained in Newton’s Laws of Motion , regarding the different types of forces and the use of free-body diagrams, to solve additional problems in particle equilibrium .

Different Tensions at Different Angles

Consider the traffic light (mass of 15.0 kg) suspended from two wires as shown in Figure . Find the tension in each wire, neglecting the masses of the wires.

The system of interest is the traffic light, and its free-body diagram is shown in Figure (c). The three forces involved are not parallel, and so they must be projected onto a coordinate system. The most convenient coordinate system has one axis vertical and one horizontal, and the vector projections on it are shown in Figure (d). There are two unknowns in this problem ([latex]{T}_{1}[/latex] and [latex]{T}_{2}[/latex]), so two equations are needed to find them. These two equations come from applying Newton’s second law along the vertical and horizontal axes, noting that the net external force is zero along each axis because acceleration is zero.

First consider the horizontal or x -axis:

Thus, as you might expect,

This gives us the following relationship:

Note that [latex]{T}_{1}[/latex] and [latex]{T}_{2}[/latex] are not equal in this case because the angles on either side are not equal. It is reasonable that [latex]{T}_{2}[/latex] ends up being greater than [latex]{T}_{1}[/latex] because it is exerted more vertically than [latex]{T}_{1}.[/latex]

Now consider the force components along the vertical or y -axis:

This implies

Substituting the expressions for the vertical components gives

There are two unknowns in this equation, but substituting the expression for [latex]{T}_{2}[/latex] in terms of [latex]{T}_{1}[/latex] reduces this to one equation with one unknown:

which yields

Solving this last equation gives the magnitude of [latex]{T}_{1}[/latex] to be

Finally, we find the magnitude of [latex]{T}_{2}[/latex] by using the relationship between them, [latex]{T}_{2}=1.225{T}_{1}[/latex], found above. Thus we obtain

Significance

Both tensions would be larger if both wires were more horizontal, and they will be equal if and only if the angles on either side are the same (as they were in the earlier example of a tightrope walker in Newton’s Laws of Motion .

Particle Acceleration

We have given a variety of examples of particles in equilibrium. We now turn our attention to particle acceleration problems, which are the result of a nonzero net force. Refer again to the steps given at the beginning of this section, and notice how they are applied to the following examples.

Drag Force on a Barge

Two tugboats push on a barge at different angles ( Figure ). The first tugboat exerts a force of [latex]2.7\times {10}^{5}\,\text{N}[/latex] in the x -direction, and the second tugboat exerts a force of [latex]3.6\times {10}^{5}\,\text{N}[/latex] in the y -direction. The mass of the barge is [latex]5.0\times {10}^{6}\,\text{kg}[/latex] and its acceleration is observed to be [latex]7.5\times {10}^{-2}\,{\text{m/s}}^{2}[/latex] in the direction shown. What is the drag force of the water on the barge resisting the motion? ( Note: Drag force is a frictional force exerted by fluids, such as air or water. The drag force opposes the motion of the object. Since the barge is flat bottomed, we can assume that the drag force is in the direction opposite of motion of the barge.)

The directions and magnitudes of acceleration and the applied forces are given in Figure (a). We define the total force of the tugboats on the barge as [latex]{\mathbf{\overset{\to }{F}}}_{\text{app}}[/latex] so that

The drag of the water [latex]{\mathbf{\overset{\to }{F}}}_{\text{D}}[/latex] is in the direction opposite to the direction of motion of the boat; this force thus works against [latex]{\mathbf{\overset{\to }{F}}}_{\text{app}},[/latex] as shown in the free-body diagram in Figure (b). The system of interest here is the barge, since the forces on it are given as well as its acceleration. Because the applied forces are perpendicular, the x – and y -axes are in the same direction as [latex]{\mathbf{\overset{\to }{F}}}_{1}[/latex] and [latex]{\mathbf{\overset{\to }{F}}}_{2}.[/latex] The problem quickly becomes a one-dimensional problem along the direction of [latex]{\mathbf{\overset{\to }{F}}}_{\text{app}}[/latex], since friction is in the direction opposite to [latex]{\mathbf{\overset{\to }{F}}}_{\text{app}}.[/latex] Our strategy is to find the magnitude and direction of the net applied force [latex]{\mathbf{\overset{\to }{F}}}_{\text{app}}[/latex] and then apply Newton’s second law to solve for the drag force [latex]{\mathbf{\overset{\to }{F}}}_{\text{D}}.[/latex]

Since [latex]{F}_{x}[/latex] and [latex]{F}_{y}[/latex] are perpendicular, we can find the magnitude and direction of [latex]{\mathbf{\overset{\to }{F}}}_{\text{app}}[/latex] directly. First, the resultant magnitude is given by the Pythagorean theorem:

The angle is given by

From Newton’s first law, we know this is the same direction as the acceleration. We also know that [latex]{\mathbf{\overset{\to }{F}}}_{\text{D}}[/latex] is in the opposite direction of [latex]{\mathbf{\overset{\to }{F}}}_{\text{app}},[/latex] since it acts to slow down the acceleration. Therefore, the net external force is in the same direction as [latex]{\mathbf{\overset{\to }{F}}}_{\text{app}},[/latex] but its magnitude is slightly less than [latex]{\mathbf{\overset{\to }{F}}}_{\text{app}}.[/latex] The problem is now one-dimensional. From the free-body diagram, we can see that

However, Newton’s second law states that

This can be solved for the magnitude of the drag force of the water [latex]{F}_{\text{D}}[/latex] in terms of known quantities:

Substituting known values gives

The direction of [latex]{\mathbf{\overset{\to }{F}}}_{\text{D}}[/latex] has already been determined to be in the direction opposite to [latex]{\mathbf{\overset{\to }{F}}}_{\text{app}},[/latex] or at an angle of [latex]53^\circ[/latex] south of west.

The numbers used in this example are reasonable for a moderately large barge. It is certainly difficult to obtain larger accelerations with tugboats, and small speeds are desirable to avoid running the barge into the docks. Drag is relatively small for a well-designed hull at low speeds, consistent with the answer to this example, where [latex]{F}_{\text{D}}[/latex] is less than 1/600th of the weight of the ship.

In Newton’s Laws of Motion , we discussed the normal force , which is a contact force that acts normal to the surface so that an object does not have an acceleration perpendicular to the surface. The bathroom scale is an excellent example of a normal force acting on a body. It provides a quantitative reading of how much it must push upward to support the weight of an object. But can you predict what you would see on the dial of a bathroom scale if you stood on it during an elevator ride? Will you see a value greater than your weight when the elevator starts up? What about when the elevator moves upward at a constant speed? Take a guess before reading the next example.

What Does the Bathroom Scale Read in an Elevator?

Figure shows a 75.0-kg man (weight of about 165 lb.) standing on a bathroom scale in an elevator. Calculate the scale reading: (a) if the elevator accelerates upward at a rate of [latex]1.20\,{\text{m/s}}^{2},[/latex] and (b) if the elevator moves upward at a constant speed of 1 m/s.

If the scale at rest is accurate, its reading equals [latex]{\mathbf{\overset{\to }{F}}}_{\text{p}}[/latex], the magnitude of the force the person exerts downward on it. Figure (a) shows the numerous forces acting on the elevator, scale, and person. It makes this one-dimensional problem look much more formidable than if the person is chosen to be the system of interest and a free-body diagram is drawn, as in Figure (b). Analysis of the free-body diagram using Newton’s laws can produce answers to both Figure (a) and (b) of this example, as well as some other questions that might arise. The only forces acting on the person are his weight [latex]\mathbf{\overset{\to }{w}}[/latex] and the upward force of the scale [latex]{\mathbf{\overset{\to }{F}}}_{\text{s}}.[/latex] According to Newton’s third law, [latex]{\mathbf{\overset{\to }{F}}}_{\text{p}}[/latex] and [latex]{\mathbf{\overset{\to }{F}}}_{\text{s}}[/latex] are equal in magnitude and opposite in direction, so that we need to find [latex]{F}_{\text{s}}[/latex] in order to find what the scale reads. We can do this, as usual, by applying Newton’s second law,

From the free-body diagram, we see that [latex]{\mathbf{\overset{\to }{F}}}_{\text{net}}={\mathbf{\overset{\to }{F}}}_{s}-\mathbf{\overset{\to }{w}},[/latex] so we have

Solving for [latex]{F}_{s}[/latex] gives us an equation with only one unknown:

or, because [latex]w=mg,[/latex] simply

No assumptions were made about the acceleration, so this solution should be valid for a variety of accelerations in addition to those in this situation. ( Note: We are considering the case when the elevator is accelerating upward. If the elevator is accelerating downward, Newton’s second law becomes [latex]{F}_{s}-w=\text{−}ma.[/latex])

which gives

The scale reading in Figure (a) is about 185 lb. What would the scale have read if he were stationary? Since his acceleration would be zero, the force of the scale would be equal to his weight:

Thus, the scale reading in the elevator is greater than his 735-N (165-lb.) weight. This means that the scale is pushing up on the person with a force greater than his weight, as it must in order to accelerate him upward. Clearly, the greater the acceleration of the elevator, the greater the scale reading, consistent with what you feel in rapidly accelerating versus slowly accelerating elevators. In Figure (b), the scale reading is 735 N, which equals the person’s weight. This is the case whenever the elevator has a constant velocity—moving up, moving down, or stationary.

Check Your Understanding

Now calculate the scale reading when the elevator accelerates downward at a rate of [latex]1.20\,{\text{m/s}}^{2}.[/latex]

[latex]{F}_{\text{s}}=645\,\text{N}[/latex]

The solution to the previous example also applies to an elevator accelerating downward, as mentioned. When an elevator accelerates downward, a is negative, and the scale reading is less than the weight of the person. If a constant downward velocity is reached, the scale reading again becomes equal to the person’s weight. If the elevator is in free fall and accelerating downward at g , then the scale reading is zero and the person appears to be weightless.

Two Attached Blocks

Figure shows a block of mass [latex]{m}_{1}[/latex] on a frictionless, horizontal surface. It is pulled by a light string that passes over a frictionless and massless pulley. The other end of the string is connected to a block of mass [latex]{m}_{2}.[/latex] Find the acceleration of the blocks and the tension in the string in terms of [latex]{m}_{1},{m}_{2},\,\text{and}\,g.[/latex]

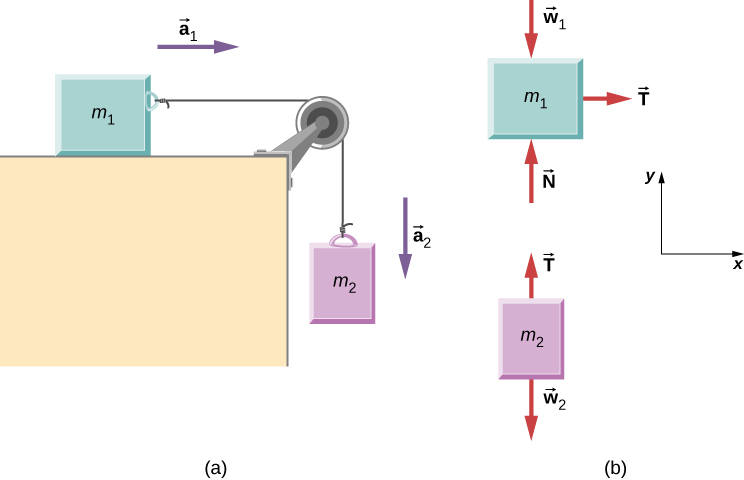
We draw a free-body diagram for each mass separately, as shown in Figure . Then we analyze each one to find the required unknowns. The forces on block 1 are the gravitational force, the contact force of the surface, and the tension in the string. Block 2 is subjected to the gravitational force and the string tension. Newton’s second law applies to each, so we write two vector equations:

For block 1: [latex]\mathbf{\overset{\to }{T}}+{\mathbf{\overset{\to }{w}}}_{1}+\mathbf{\overset{\to }{N}}={m}_{1}{\mathbf{\overset{\to }{a}}}_{1}[/latex]

For block 2: [latex]\mathbf{\overset{\to }{T}}+{\mathbf{\overset{\to }{w}}}_{2}={m}_{2}{\mathbf{\overset{\to }{a}}}_{2}.[/latex]

Notice that [latex]\mathbf{\overset{\to }{T}}[/latex] is the same for both blocks. Since the string and the pulley have negligible mass, and since there is no friction in the pulley, the tension is the same throughout the string. We can now write component equations for each block. All forces are either horizontal or vertical, so we can use the same horizontal/vertical coordinate system for both objects

The component equations follow from the vector equations above. We see that block 1 has the vertical forces balanced, so we ignore them and write an equation relating the x -components. There are no horizontal forces on block 2, so only the y -equation is written. We obtain these results:

When block 1 moves to the right, block 2 travels an equal distance downward; thus, [latex]{a}_{1x}=\text{−}{a}_{2y}.[/latex] Writing the common acceleration of the blocks as [latex]a={a}_{1x}=\text{−}{a}_{2y},[/latex] we now have

From these two equations, we can express a and T in terms of the masses [latex]{m}_{1}\,\text{and}\,{m}_{2},\,\text{and}\,g:[/latex]

Notice that the tension in the string is less than the weight of the block hanging from the end of it. A common error in problems like this is to set [latex]T={m}_{2}g.[/latex] You can see from the free-body diagram of block 2 that cannot be correct if the block is accelerating.

Calculate the acceleration of the system, and the tension in the string, when the masses are [latex]{m}_{1}=5.00\,\text{kg}[/latex] and [latex]{m}_{2}=3.00\,\text{kg}.[/latex]

[latex]a=3.68\,{\text{m/s}}^{2},[/latex] [latex]T=18.4\,\text{N}[/latex]

Atwood Machine

A classic problem in physics, similar to the one we just solved, is that of the Atwood machine , which consists of a rope running over a pulley, with two objects of different mass attached. It is particularly useful in understanding the connection between force and motion. In Figure , [latex]{m}_{1}=2.00\,\text{kg}[/latex] and [latex]{m}_{2}=4.00\,\text{kg}\text{.}[/latex] Consider the pulley to be frictionless. (a) If [latex]{m}_{2}[/latex] is released, what will its acceleration be? (b) What is the tension in the string?

We draw a free-body diagram for each mass separately, as shown in the figure. Then we analyze each diagram to find the required unknowns. This may involve the solution of simultaneous equations. It is also important to note the similarity with the previous example. As block 2 accelerates with acceleration [latex]{a}_{2}[/latex] in the downward direction, block 1 accelerates upward with acceleration [latex]{a}_{1}[/latex]. Thus, [latex]a={a}_{1}=\text{−}{a}_{2}.[/latex]

(The negative sign in front of [latex]{m}_{2}a[/latex] indicates that [latex]{m}_{2}[/latex] accelerates downward; both blocks accelerate at the same rate, but in opposite directions.) Solve the two equations simultaneously (subtract them) and the result is

Solving for a :

• Observing the first block, we see that [latex]\begin{array}{c}T-{m}_{1}g={m}_{1}a\hfill \\ T={m}_{1}(g+a)=(2\,\text{kg})(9.8\,{\text{m/s}}^{2}+3.27\,{\text{m/s}}^{2})=26.1\,\text{N}\text{.}\hfill \end{array}[/latex]

The result for the acceleration given in the solution can be interpreted as the ratio of the unbalanced force on the system, [latex]({m}_{2}-{m}_{1})g[/latex], to the total mass of the system, [latex]{m}_{1}+{m}_{2}[/latex]. We can also use the Atwood machine to measure local gravitational field strength.

Determine a general formula in terms of [latex]{m}_{1},{m}_{2}[/latex] and g for calculating the tension in the string for the Atwood machine shown above.

[latex]T=\frac{2{m}_{1}{m}_{2}}{{m}_{1}+{m}_{2}}g[/latex] (This is found by substituting the equation for acceleration in Figure (a), into the equation for tension in Figure (b).)

Newton’s Laws of Motion and Kinematics

Physics is most interesting and most powerful when applied to general situations that involve more than a narrow set of physical principles. Newton’s laws of motion can also be integrated with other concepts that have been discussed previously in this text to solve problems of motion. For example, forces produce accelerations, a topic of kinematics , and hence the relevance of earlier chapters.

When approaching problems that involve various types of forces, acceleration, velocity, and/or position, listing the givens and the quantities to be calculated will allow you to identify the principles involved. Then, you can refer to the chapters that deal with a particular topic and solve the problem using strategies outlined in the text. The following worked example illustrates how the problem-solving strategy given earlier in this chapter, as well as strategies presented in other chapters, is applied to an integrated concept problem.

What Force Must a Soccer Player Exert to Reach Top Speed?

A soccer player starts at rest and accelerates forward, reaching a velocity of 8.00 m/s in 2.50 s. (a) What is her average acceleration? (b) What average force does the ground exert forward on the runner so that she achieves this acceleration? The player’s mass is 70.0 kg, and air resistance is negligible.

To find the answers to this problem, we use the problem-solving strategy given earlier in this chapter. The solutions to each part of the example illustrate how to apply specific problem-solving steps. In this case, we do not need to use all of the steps. We simply identify the physical principles, and thus the knowns and unknowns; apply Newton’s second law; and check to see whether the answer is reasonable.

Substituting the known values yields

Substituting the known values of m and a gives

This is a reasonable result: The acceleration is attainable for an athlete in good condition. The force is about 50 pounds, a reasonable average force.

This example illustrates how to apply problem-solving strategies to situations that include topics from different chapters. The first step is to identify the physical principles, the knowns, and the unknowns involved in the problem. The second step is to solve for the unknown, in this case using Newton’s second law. Finally, we check our answer to ensure it is reasonable. These techniques for integrated concept problems will be useful in applications of physics outside of a physics course, such as in your profession, in other science disciplines, and in everyday life.

The soccer player stops after completing the play described above, but now notices that the ball is in position to be stolen. If she now experiences a force of 126 N to attempt to steal the ball, which is 2.00 m away from her, how long will it take her to get to the ball?

What Force Acts on a Model Helicopter?

A 1.50-kg model helicopter has a velocity of [latex]5.00\mathbf{\hat{j}}\,\text{m/s}[/latex] at [latex]t=0.[/latex] It is accelerated at a constant rate for two seconds (2.00 s) after which it has a velocity of [latex](6.00\mathbf{\hat{i}}+12.00\mathbf{\hat{j}})\text{m/s}\text{.}[/latex] What is the magnitude of the resultant force acting on the helicopter during this time interval?

We can easily set up a coordinate system in which the x -axis [latex](\mathbf{\hat{i}}[/latex] direction) is horizontal, and the y -axis [latex](\mathbf{\hat{j}}[/latex] direction) is vertical. We know that [latex]\Delta t=2.00s[/latex] and [latex](6.00\mathbf{\hat{i}}+12.00\mathbf{\hat{j}}\,\text{m/s})-(5.00\mathbf{\hat{j}}\,\text{m/s}).[/latex] From this, we can calculate the acceleration by the definition; we can then apply Newton’s second law.

The magnitude of the force is now easily found:

The original problem was stated in terms of [latex]\mathbf{\hat{i}}-\mathbf{\hat{j}}[/latex] vector components, so we used vector methods. Compare this example with the previous example.

Find the direction of the resultant for the 1.50-kg model helicopter.

49.4 degrees

Baggage Tractor

Figure (a) shows a baggage tractor pulling luggage carts from an airplane. The tractor has mass 650.0 kg, while cart A has mass 250.0 kg and cart B has mass 150.0 kg. The driving force acting for a brief period of time accelerates the system from rest and acts for 3.00 s. (a) If this driving force is given by [latex]F=(820.0t)\,\text{N,}[/latex] find the speed after 3.00 seconds. (b) What is the horizontal force acting on the connecting cable between the tractor and cart A at this instant?

A free-body diagram shows the driving force of the tractor, which gives the system its acceleration. We only need to consider motion in the horizontal direction. The vertical forces balance each other and it is not necessary to consider them. For part b, we make use of a free-body diagram of the tractor alone to determine the force between it and cart A. This exposes the coupling force [latex]\mathbf{\overset{\to }{T}},[/latex] which is our objective.

Since acceleration is a function of time, we can determine the velocity of the tractor by using [latex]a=\frac{dv}{dt}[/latex] with the initial condition that [latex]{v}_{0}=0[/latex] at [latex]t=0.[/latex] We integrate from [latex]t=0[/latex] to [latex]t=3\text{:}[/latex]

• Refer to the free-body diagram in Figure (b). [latex]\begin{array}{ccc}\hfill \sum {F}_{x}& =\hfill & {m}_{\text{tractor}}{a}_{x}\hfill \\ \hfill 820.0t-T& =\hfill & {m}_{\text{tractor}}(0.7805)t\hfill \\ \hfill (820.0)(3.00)-T& =\hfill & (650.0)(0.7805)(3.00)\hfill \\ \hfill T& =\hfill & 938\,\text{N}.\hfill \end{array}[/latex]

Since the force varies with time, we must use calculus to solve this problem. Notice how the total mass of the system was important in solving Figure (a), whereas only the mass of the truck (since it supplied the force) was of use in Figure (b).

Recall that [latex]v=\frac{ds}{dt}[/latex] and [latex]a=\frac{dv}{dt}[/latex]. If acceleration is a function of time, we can use the calculus forms developed in Motion Along a Straight Line , as shown in this example. However, sometimes acceleration is a function of displacement. In this case, we can derive an important result from these calculus relations. Solving for dt in each, we have [latex]dt=\frac{ds}{v}[/latex] and [latex]dt=\frac{dv}{a}.[/latex] Now, equating these expressions, we have [latex]\frac{ds}{v}=\frac{dv}{a}.[/latex] We can rearrange this to obtain [latex]{a}^{}ds={v}^{}dv.[/latex]

Motion of a Projectile Fired Vertically

A 10.0-kg mortar shell is fired vertically upward from the ground, with an initial velocity of 50.0 m/s (see Figure ). Determine the maximum height it will travel if atmospheric resistance is measured as [latex]{F}_{\text{D}}=(0.0100{v}^{2})\,\text{N,}[/latex] where v is the speed at any instant.

The known force on the mortar shell can be related to its acceleration using the equations of motion. Kinematics can then be used to relate the mortar shell’s acceleration to its position.

Initially, [latex]{y}_{0}=0[/latex] and [latex]{v}_{0}=50.0\,\text{m/s}\text{.}[/latex] At the maximum height [latex]y=h,v=0.[/latex] The free-body diagram shows [latex]{F}_{\text{D}}[/latex] to act downward, because it slows the upward motion of the mortar shell. Thus, we can write

The acceleration depends on v and is therefore variable. Since [latex]a=f(v)\text{,}[/latex] we can relate a to v using the rearrangement described above,

We replace ds with dy because we are dealing with the vertical direction,

We now separate the variables ( v ’s and dv ’s on one side; dy on the other):

Thus, [latex]h=114\,\text{m}\text{.}[/latex]

Notice the need to apply calculus since the force is not constant, which also means that acceleration is not constant. To make matters worse, the force depends on v (not t ), and so we must use the trick explained prior to the example. The answer for the height indicates a lower elevation if there were air resistance. We will deal with the effects of air resistance and other drag forces in greater detail in Drag Force and Terminal Speed .

If atmospheric resistance is neglected, find the maximum height for the mortar shell. Is calculus required for this solution?

Explore the forces at work in this simulation when you try to push a filing cabinet. Create an applied force and see the resulting frictional force and total force acting on the cabinet. Charts show the forces, position, velocity, and acceleration vs. time. View a free-body diagram of all the forces (including gravitational and normal forces).

• Newton’s laws of motion can be applied in numerous situations to solve motion problems.
• Some problems contain multiple force vectors acting in different directions on an object. Be sure to draw diagrams, resolve all force vectors into horizontal and vertical components, and draw a free-body diagram. Always analyze the direction in which an object accelerates so that you can determine whether [latex]{F}_{\text{net}}=ma[/latex] or [latex]{F}_{\text{net}}=0.[/latex]
• The normal force on an object is not always equal in magnitude to the weight of the object. If an object is accelerating vertically, the normal force is less than or greater than the weight of the object. Also, if the object is on an inclined plane, the normal force is always less than the full weight of the object.
• Some problems contain several physical quantities, such as forces, acceleration, velocity, or position. You can apply concepts from kinematics and dynamics to solve these problems.

Conceptual Questions

To simulate the apparent weightlessness of space orbit, astronauts are trained in the hold of a cargo aircraft that is accelerating downward at g . Why do they appear to be weightless, as measured by standing on a bathroom scale, in this accelerated frame of reference? Is there any difference between their apparent weightlessness in orbit and in the aircraft?

The scale is in free fall along with the astronauts, so the reading on the scale would be 0. There is no difference in the apparent weightlessness; in the aircraft and in orbit, free fall is occurring.

A 30.0-kg girl in a swing is pushed to one side and held at rest by a horizontal force [latex]\mathbf{\overset{\to }{F}}[/latex] so that the swing ropes are [latex]30.0^\circ[/latex] with respect to the vertical. (a) Calculate the tension in each of the two ropes supporting the swing under these conditions. (b) Calculate the magnitude of [latex]\mathbf{\overset{\to }{F}}.[/latex]

a. 170 N; b. 170 N

Find the tension in each of the three cables supporting the traffic light if it weighs 2.00 × 10 2 N.

Three forces act on an object, considered to be a particle, which moves with constant velocity [latex]v=(3\mathbf{\hat{i}}-2\mathbf{\hat{j}})\,\text{m/s}\text{.}[/latex] Two of the forces are [latex]{\mathbf{\overset{\to }{F}}}_{1}=(3\mathbf{\hat{i}}+5\mathbf{\hat{j}}-6\mathbf{\hat{k}})\,\text{N}[/latex] and [latex]{\mathbf{\overset{\to }{F}}}_{2}=(4\mathbf{\hat{i}}-7\mathbf{\hat{j}}+2\mathbf{\hat{k}})\,\text{N}\text{.}[/latex] Find the third force.

[latex]{\mathbf{\overset{\to }{F}}}_{3}=(-7\mathbf{\hat{i}}+2\mathbf{\hat{j}}+4\mathbf{\hat{k}})\,\text{N}[/latex]

A flea jumps by exerting a force of [latex]1.20\times {10}^{-5}\,\text{N}[/latex] straight down on the ground. A breeze blowing on the flea parallel to the ground exerts a force of [latex]0.500\times {10}^{-6}\,\text{N}[/latex] on the flea while the flea is still in contact with the ground. Find the direction and magnitude of the acceleration of the flea if its mass is [latex]6.00\times {10}^{-7}\,\text{kg}[/latex]. Do not neglect the gravitational force.

Two muscles in the back of the leg pull upward on the Achilles tendon, as shown below. (These muscles are called the medial and lateral heads of the gastrocnemius muscle.) Find the magnitude and direction of the total force on the Achilles tendon. What type of movement could be caused by this force?

After a mishap, a 76.0-kg circus performer clings to a trapeze, which is being pulled to the side by another circus artist, as shown here. Calculate the tension in the two ropes if the person is momentarily motionless. Include a free-body diagram in your solution.

A 35.0-kg dolphin decelerates from 12.0 to 7.50 m/s in 2.30 s to join another dolphin in play. What average force was exerted to slow the first dolphin if it was moving horizontally? (The gravitational force is balanced by the buoyant force of the water.)

When starting a foot race, a 70.0-kg sprinter exerts an average force of 650 N backward on the ground for 0.800 s. (a) What is his final speed? (b) How far does he travel?

A large rocket has a mass of [latex]2.00\times {10}^{6}\,\text{kg}[/latex] at takeoff, and its engines produce a thrust of [latex]3.50\times {10}^{7}\,\text{N}.[/latex] (a) Find its initial acceleration if it takes off vertically. (b) How long does it take to reach a velocity of 120 km/h straight up, assuming constant mass and thrust?

a. [latex]7.70\,{\text{m/s}}^{2}[/latex]; b. 4.33 s

A basketball player jumps straight up for a ball. To do this, he lowers his body 0.300 m and then accelerates through this distance by forcefully straightening his legs. This player leaves the floor with a vertical velocity sufficient to carry him 0.900 m above the floor. (a) Calculate his velocity when he leaves the floor. (b) Calculate his acceleration while he is straightening his legs. He goes from zero to the velocity found in (a) in a distance of 0.300 m. (c) Calculate the force he exerts on the floor to do this, given that his mass is 110.0 kg.

A 2.50-kg fireworks shell is fired straight up from a mortar and reaches a height of 110.0 m. (a) Neglecting air resistance (a poor assumption, but we will make it for this example), calculate the shell’s velocity when it leaves the mortar. (b) The mortar itself is a tube 0.450 m long. Calculate the average acceleration of the shell in the tube as it goes from zero to the velocity found in (a). (c) What is the average force on the shell in the mortar? Express your answer in newtons and as a ratio to the weight of the shell.

a. 46.4 m/s; b. [latex]2.40\times {10}^{3}\,{\text{m/s}}^{2}\text{;}[/latex] c. 5.99 × 10 3 N; ratio of 245

A 0.500-kg potato is fired at an angle of [latex]80.0^\circ[/latex] above the horizontal from a PVC pipe used as a “potato gun” and reaches a height of 110.0 m. (a) Neglecting air resistance, calculate the potato’s velocity when it leaves the gun. (b) The gun itself is a tube 0.450 m long. Calculate the average acceleration of the potato in the tube as it goes from zero to the velocity found in (a). (c) What is the average force on the potato in the gun? Express your answer in newtons and as a ratio to the weight of the potato.

An elevator filled with passengers has a mass of [latex]1.70\times {10}^{3}\,\text{kg}[/latex]. (a) The elevator accelerates upward from rest at a rate of [latex]1.20\,{\text{m/s}}^{2}[/latex] for 1.50 s. Calculate the tension in the cable supporting the elevator. (b) The elevator continues upward at constant velocity for 8.50 s. What is the tension in the cable during this time? (c) The elevator decelerates at a rate of [latex]0.600\,{\text{m/s}}^{2}[/latex] for 3.00 s. What is the tension in the cable during deceleration? (d) How high has the elevator moved above its original starting point, and what is its final velocity?

a. [latex]1.87\times {10}^{4}\,\text{N;}[/latex] b. [latex]1.67\times {10}^{4}\,\text{N;}[/latex] c. [latex]1.56\times {10}^{4}\,\text{N;}[/latex] d. 19.4 m, 0 m/s

A 20.0-g ball hangs from the roof of a freight car by a string. When the freight car begins to move, the string makes an angle of [latex]35.0^\circ[/latex] with the vertical. (a) What is the acceleration of the freight car? (b) What is the tension in the string?

A student’s backpack, full of textbooks, is hung from a spring scale attached to the ceiling of an elevator. When the elevator is accelerating downward at [latex]3.8\,{\text{m/s}}^{2}[/latex], the scale reads 60 N. (a) What is the mass of the backpack? (b) What does the scale read if the elevator moves upward while slowing down at a rate [latex]3.8\,{\text{m/s}}^{2}[/latex]? (c) What does the scale read if the elevator moves upward at constant velocity? (d) If the elevator had no brakes and the cable supporting it were to break loose so that the elevator could fall freely, what would the spring scale read?

a. 10 kg; b. 90 N; c. 98 N; d. 0

A service elevator takes a load of garbage, mass 10.0 kg, from a floor of a skyscraper under construction, down to ground level, accelerating downward at a rate of [latex]1.2\,{\text{m/s}}^{2}[/latex]. Find the magnitude of the force the garbage exerts on the floor of the service elevator?

A roller coaster car starts from rest at the top of a track 30.0 m long and inclined at [latex]20.0^\circ[/latex] to the horizontal. Assume that friction can be ignored. (a) What is the acceleration of the car? (b) How much time elapses before it reaches the bottom of the track?

a. [latex]3.35\,{\text{m/s}}^{2}[/latex]; b. 4.2 s

The device shown below is the Atwood’s machine considered in Figure . Assuming that the masses of the string and the frictionless pulley are negligible, (a) find an equation for the acceleration of the two blocks; (b) find an equation for the tension in the string; and (c) find both the acceleration and tension when block 1 has mass 2.00 kg and block 2 has mass 4.00 kg.

Two blocks are connected by a massless rope as shown below. The mass of the block on the table is 4.0 kg and the hanging mass is 1.0 kg. The table and the pulley are frictionless. (a) Find the acceleration of the system. (b) Find the tension in the rope. (c) Find the speed with which the hanging mass hits the floor if it starts from rest and is initially located 1.0 m from the floor.

Shown below are two carts connected by a cord that passes over a small frictionless pulley. Each cart rolls freely with negligible friction. Calculate the acceleration of the carts and the tension in the cord.

A 2.00 kg block (mass 1) and a 4.00 kg block (mass 2) are connected by a light string as shown; the inclination of the ramp is [latex]40.0^\circ[/latex]. Friction is negligible. What is (a) the acceleration of each block and (b) the tension in the string?

6.1 Solving Problems with Newton’s Laws Copyright © 2016 by OpenStax. All Rights Reserved.

Share This Book

4.3 Newton’s Second Law of Motion: Concept of a System

Learning objectives.

By the end of this section, you will be able to:

• Define net force, external force, and system.
• Understand Newton’s second law of motion.
• Apply Newton’s second law to determine the weight of an object.

Newton’s second law of motion is closely related to Newton’s first law of motion. It mathematically states the cause and effect relationship between force and changes in motion. Newton’s second law of motion is more quantitative and is used extensively to calculate what happens in situations involving a force. Before we can write down Newton’s second law as a simple equation giving the exact relationship of force, mass, and acceleration, we need to sharpen some ideas that have already been mentioned.

First, what do we mean by a change in motion? The answer is that a change in motion is equivalent to a change in velocity. A change in velocity means, by definition, that there is an acceleration . Newton’s first law says that a net external force causes a change in motion; thus, we see that a net external force causes acceleration .

Another question immediately arises. What do we mean by an external force? An intuitive notion of external is correct—an external force acts from outside the system (object or collection of objects) of interest. For example, in Figure 4.5 (a) the system of interest is the wagon plus the child in it. The two forces exerted by the other children are external forces. An internal force acts between elements of the system. Again looking at Figure 4.5 (a), the force the child in the wagon exerts to hang onto the wagon is an internal force between elements of the system of interest. Only external forces affect the motion of a system, according to Newton’s first law. (The internal forces actually cancel, as we shall see in the next section.) You must define the boundaries of the system before you can determine which forces are external . Sometimes the system is obvious, whereas other times identifying the boundaries of a system is more subtle. The concept of a system is fundamental to many areas of physics, as is the correct application of Newton’s laws. This concept will be revisited many times on our journey through physics.

Now, it seems reasonable that acceleration should be directly proportional to and in the same direction as the net (total) external force acting on a system. This assumption has been verified experimentally and is illustrated in Figure 4.5 . In part (a), a smaller force causes a smaller acceleration than the larger force illustrated in part (c). For completeness, the vertical forces are also shown; they are assumed to cancel since there is no acceleration in the vertical direction. The vertical forces are the weight w w and the support of the ground N N , and the horizontal force f f represents the force of friction. These will be discussed in more detail in later sections. For now, we will define friction as a force that opposes the motion past each other of objects that are touching. Figure 4.5 (b) shows how vectors representing the external forces add together to produce a net force, F net F net .

To obtain an equation for Newton’s second law, we first write the relationship of acceleration and net external force as the proportionality

where the symbol ∝ ∝ means “proportional to,” and F net F net is the net external force . (The net external force is the vector sum of all external forces and can be determined graphically, using the head-to-tail method, or analytically, using components. The techniques are the same as for the addition of other vectors, and are covered in Two-Dimensional Kinematics .) This proportionality states what we have said in words— acceleration is directly proportional to the net external force . Once the system of interest is chosen, it is important to identify the external forces and ignore the internal ones. It is a tremendous simplification not to have to consider the numerous internal forces acting between objects within the system, such as muscular forces within the child’s body, let alone the myriad of forces between atoms in the objects, but by doing so, we can easily solve some very complex problems with only minimal error due to our simplification

Now, it also seems reasonable that acceleration should be inversely proportional to the mass of the system. In other words, the larger the mass (the inertia), the smaller the acceleration produced by a given force. And indeed, as illustrated in Figure 4.6 , the same net external force applied to a car produces a much smaller acceleration than when applied to a basketball. The proportionality is written as

where m m is the mass of the system. Experiments have shown that acceleration is exactly inversely proportional to mass, just as it is exactly linearly proportional to the net external force.

It has been found that the acceleration of an object depends only on the net external force and the mass of the object. Combining the two proportionalities just given yields Newton's second law of motion.

Newton’s Second Law of Motion

The acceleration of a system is directly proportional to and in the same direction as the net external force acting on the system, and inversely proportional to its mass.

In equation form, Newton’s second law of motion is

This is often written in the more familiar form

When only the magnitude of force and acceleration are considered, this equation is simply

Although these last two equations are really the same, the first gives more insight into what Newton’s second law means. The law is a cause and effect relationship among three quantities that is not simply based on their definitions. The validity of the second law is completely based on experimental verification.

Units of Force

F net = m a F net = m a is used to define the units of force in terms of the three basic units for mass, length, and time. The SI unit of force is called the newton (abbreviated N) and is the force needed to accelerate a 1-kg system at the rate of 1 m/s 2 1 m/s 2 . That is, since F net = m a F net = m a ,

While almost the entire world uses the newton for the unit of force, in the United States the most familiar unit of force is the pound (lb), where 1 N = 0.225 lb.

Weight and the Gravitational Force

When an object is dropped, it accelerates toward the center of Earth. Newton’s second law states that a net force on an object is responsible for its acceleration. If air resistance is negligible, the net force on a falling object is the gravitational force, commonly called its weight w w . Weight can be denoted as a vector w w because it has a direction; down is, by definition, the direction of gravity, and hence weight is a downward force. The magnitude of weight is denoted as w w . Galileo was instrumental in showing that, in the absence of air resistance, all objects fall with the same acceleration g g . Using Galileo’s result and Newton’s second law, we can derive an equation for weight.

Consider an object with mass m m falling downward toward Earth. It experiences only the downward force of gravity, which has magnitude w w . Newton’s second law states that the magnitude of the net external force on an object is F net = ma F net = ma .

Since the object experiences only the downward force of gravity, F net = w F net = w . We know that the acceleration of an object due to gravity is g g , or a = g a = g . Substituting these into Newton’s second law gives

This is the equation for weight —the gravitational force on a mass m m :

Since g = 9.80 m/s 2 g = 9.80 m/s 2 on Earth, the weight of a 1.0 kg object on Earth is 9.8 N, as we see:

Recall that g g can take a positive or negative value, depending on the positive direction in the coordinate system. Be sure to take this into consideration when solving problems with weight.

When the net external force on an object is its weight, we say that it is in free-fall . That is, the only force acting on the object is the force of gravity. In the real world, when objects fall downward toward Earth, they are never truly in free-fall because there is always some upward force from the air acting on the object.

The acceleration due to gravity g g varies slightly over the surface of Earth, so that the weight of an object depends on location and is not an intrinsic property of the object. Weight varies dramatically if one leaves Earth’s surface. On the Moon, for example, the acceleration due to gravity is only 1.625 m/s 2 1.625 m/s 2 . A 1.0-kg mass thus has a weight of 9.8 N on Earth and only about 1.7 N on the Moon.

The broadest definition of weight in this sense is that the weight of an object is the gravitational force on it from the nearest large body , such as Earth, the Moon, the Sun, and so on. This is the most common and useful definition of weight in physics. It differs dramatically, however, from the definition of weight used by NASA and the popular media in relation to space travel and exploration. When they speak of “weightlessness” and “microgravity,” they are really referring to the phenomenon we call “free-fall” in physics. We shall use the above definition of weight, and we will make careful distinctions between free-fall and actual weightlessness.

It is important to be aware that weight and mass are very different physical quantities, although they are closely related. Mass is the quantity of matter (how much “stuff”) and does not vary in classical physics, whereas weight is the gravitational force and does vary depending on gravity. It is tempting to equate the two, since most of our examples take place on Earth, where the weight of an object only varies a little with the location of the object. Furthermore, the terms mass and weight are used interchangeably in everyday language; for example, our medical records often show our “weight” in kilograms, but never in the correct units of newtons.

Common Misconceptions: Mass vs. Weight

Mass and weight are often used interchangeably in everyday language. However, in science, these terms are distinctly different from one another. Mass is a measure of how much matter is in an object. The typical measure of mass is the kilogram (or the “slug” in English units). Weight, on the other hand, is a measure of the force of gravity acting on an object. Weight is equal to the mass of an object ( m m ) multiplied by the acceleration due to gravity ( g g ). Like any other force, weight is measured in terms of newtons (or pounds in English units).

Assuming the mass of an object is kept intact, it will remain the same, regardless of its location. However, because weight depends on the acceleration due to gravity, the weight of an object can change when the object enters into a region with stronger or weaker gravity. For example, the acceleration due to gravity on the Moon is 1.625 m/s 2 1.625 m/s 2 (which is much less than the acceleration due to gravity on Earth, 9.80 m/s 2 9.80 m/s 2 ). If you measured your weight on Earth and then measured your weight on the Moon, you would find that you “weigh” much less, even though you do not look any skinnier. This is because the force of gravity is weaker on the Moon. In fact, when people say that they are “losing weight,” they really mean that they are losing “mass” (which in turn causes them to weigh less).

Take-Home Experiment: Mass and Weight

What do bathroom scales measure? When you stand on a bathroom scale, what happens to the scale? It depresses slightly. The scale contains springs that compress in proportion to your weight—similar to rubber bands expanding when pulled. The springs provide a measure of your weight (for an object which is not accelerating). This is a force in newtons (or pounds). In most countries, the measurement is divided by 9.80 to give a reading in mass units of kilograms. The scale measures weight but is calibrated to provide information about mass. While standing on a bathroom scale, push down on a table next to you. What happens to the reading? Why? Would your scale measure the same “mass” on Earth as on the Moon?

Example 4.1

What acceleration can a person produce when pushing a lawn mower.

Suppose that the net external force (push minus friction) exerted on a lawn mower is 51 N (about 11 lb) parallel to the ground. The mass of the mower is 24 kg. What is its acceleration?

Since F net F net and m m are given, the acceleration can be calculated directly from Newton’s second law as stated in F net = m a F net = m a .

The magnitude of the acceleration a a is a = F net m a = F net m . Entering known values gives

Substituting the units kg ⋅ m/s 2 kg ⋅ m/s 2 for N yields

The direction of the acceleration is the same direction as that of the net force, which is parallel to the ground. There is no information given in this example about the individual external forces acting on the system, but we can say something about their relative magnitudes. For example, the force exerted by the person pushing the mower must be greater than the friction opposing the motion (since we know the mower moves forward), and the vertical forces must cancel if there is to be no acceleration in the vertical direction (the mower is moving only horizontally). The acceleration found is small enough to be reasonable for a person pushing a mower. Such an effort would not last too long because the person’s top speed would soon be reached.

Example 4.2

What rocket thrust accelerates this sled.

Prior to space flights carrying astronauts, rocket sleds were used to test aircraft, missile equipment, and physiological effects on human subjects at high speeds. They consisted of a platform that was mounted on one or two rails and propelled by several rockets. Calculate the magnitude of force exerted by each rocket, called its thrust T T , for the four-rocket propulsion system shown in Figure 4.8 . The sled’s initial acceleration is 49 m/s 2 , 49 m/s 2 , the mass of the system is 2100 kg, and the force of friction opposing the motion is known to be 650 N.

Although there are forces acting vertically and horizontally, we assume the vertical forces cancel since there is no vertical acceleration. This leaves us with only horizontal forces and a simpler one-dimensional problem. Directions are indicated with plus or minus signs, with right taken as the positive direction. See the free-body diagram in the figure.

Since acceleration, mass, and the force of friction are given, we start with Newton’s second law and look for ways to find the thrust of the engines. Since we have defined the direction of the force and acceleration as acting “to the right,” we need to consider only the magnitudes of these quantities in the calculations. Hence we begin with

where F net F net is the net force along the horizontal direction. We can see from Figure 4.8 that the engine thrusts add, while friction opposes the thrust. In equation form, the net external force is

Substituting this into Newton’s second law gives

Using a little algebra, we solve for the total thrust 4 T :

Substituting known values yields

So the total thrust is

and the individual thrusts are

The numbers are quite large, so the result might surprise you. Experiments such as this were performed in the early 1960s to test the limits of human endurance and the setup designed to protect human subjects in jet fighter emergency ejections. Speeds of 1000 km/h were obtained, with accelerations of 45 g g 's. (Recall that g g , the acceleration due to gravity, is 9 . 80 m/s 2 9 . 80 m/s 2 . When we say that an acceleration is 45 g g 's, it is 45 × 9 . 80 m/s 2 45 × 9 . 80 m/s 2 , which is approximately 440 m/s 2 440 m/s 2 .) While living subjects are not used any more, land speeds of 10,000 km/h have been obtained with rocket sleds. In this example, as in the preceding one, the system of interest is obvious. We will see in later examples that choosing the system of interest is crucial—and the choice is not always obvious.

Newton’s second law of motion is more than a definition; it is a relationship among acceleration, force, and mass. It can help us make predictions. Each of those physical quantities can be defined independently, so the second law tells us something basic and universal about nature. The next section introduces the third and final law of motion.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: College Physics 2e
• Publication date: Jul 13, 2022
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units
• Section URL: https://openstax.org/books/college-physics-2e/pages/4-3-newtons-second-law-of-motion-concept-of-a-system

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Applications of Newton’s Laws

Solving Problems with Newton’s Laws

Learning objectives.

By the end of the section, you will be able to:

• Apply problem-solving techniques to solve for quantities in more complex systems of forces
• Use concepts from kinematics to solve problems using Newton’s laws of motion
• Solve more complex equilibrium problems
• Solve more complex acceleration problems
• Apply calculus to more advanced dynamics problems

Success in problem solving is necessary to understand and apply physical principles. We developed a pattern of analyzing and setting up the solutions to problems involving Newton’s laws in Newton’s Laws of Motion ; in this chapter, we continue to discuss these strategies and apply a step-by-step process.

Problem-Solving Strategies

We follow here the basics of problem solving presented earlier in this text, but we emphasize specific strategies that are useful in applying Newton’s laws of motion . Once you identify the physical principles involved in the problem and determine that they include Newton’s laws of motion, you can apply these steps to find a solution. These techniques also reinforce concepts that are useful in many other areas of physics. Many problem-solving strategies are stated outright in the worked examples, so the following techniques should reinforce skills you have already begun to develop.

• Identify the physical principles involved by listing the givens and the quantities to be calculated.
• Sketch the situation, using arrows to represent all forces.
• Determine the system of interest. The result is a free-body diagram that is essential to solving the problem.
• Apply Newton’s second law to solve the problem. If necessary, apply appropriate kinematic equations from the chapter on motion along a straight line.
• Check the solution to see whether it is reasonable.

Let’s apply this problem-solving strategy to the challenge of lifting a grand piano into a second-story apartment. Once we have determined that Newton’s laws of motion are involved (if the problem involves forces), it is particularly important to draw a careful sketch of the situation. Such a sketch is shown in (Figure) (a). Then, as in (Figure) (b), we can represent all forces with arrows. Whenever sufficient information exists, it is best to label these arrows carefully and make the length and direction of each correspond to the represented force.

As with most problems, we next need to identify what needs to be determined and what is known or can be inferred from the problem as stated, that is, make a list of knowns and unknowns. It is particularly crucial to identify the system of interest, since Newton’s second law involves only external forces. We can then determine which forces are external and which are internal, a necessary step to employ Newton’s second law. (See (Figure) (c).) Newton’s third law may be used to identify whether forces are exerted between components of a system (internal) or between the system and something outside (external). As illustrated in Newton’s Laws of Motion , the system of interest depends on the question we need to answer. Only forces are shown in free-body diagrams, not acceleration or velocity. We have drawn several free-body diagrams in previous worked examples. (Figure) (c) shows a free-body diagram for the system of interest. Note that no internal forces are shown in a free-body diagram.

Once a free-body diagram is drawn, we apply Newton’s second law. This is done in (Figure) (d) for a particular situation. In general, once external forces are clearly identified in free-body diagrams, it should be a straightforward task to put them into equation form and solve for the unknown, as done in all previous examples. If the problem is one-dimensional—that is, if all forces are parallel—then the forces can be handled algebraically. If the problem is two-dimensional, then it must be broken down into a pair of one-dimensional problems. We do this by projecting the force vectors onto a set of axes chosen for convenience. As seen in previous examples, the choice of axes can simplify the problem. For example, when an incline is involved, a set of axes with one axis parallel to the incline and one perpendicular to it is most convenient. It is almost always convenient to make one axis parallel to the direction of motion, if this is known. Generally, just write Newton’s second law in components along the different directions. Then, you have the following equations:

As always, we must check the solution. In some cases, it is easy to tell whether the solution is reasonable. For example, it is reasonable to find that friction causes an object to slide down an incline more slowly than when no friction exists. In practice, intuition develops gradually through problem solving; with experience, it becomes progressively easier to judge whether an answer is reasonable. Another way to check a solution is to check the units. If we are solving for force and end up with units of millimeters per second, then we have made a mistake.

There are many interesting applications of Newton’s laws of motion, a few more of which are presented in this section. These serve also to illustrate some further subtleties of physics and to help build problem-solving skills. We look first at problems involving particle equilibrium, which make use of Newton’s first law, and then consider particle acceleration, which involves Newton’s second law.

Particle Equilibrium

Recall that a particle in equilibrium is one for which the external forces are balanced. Static equilibrium involves objects at rest, and dynamic equilibrium involves objects in motion without acceleration, but it is important to remember that these conditions are relative. For example, an object may be at rest when viewed from our frame of reference, but the same object would appear to be in motion when viewed by someone moving at a constant velocity. We now make use of the knowledge attained in Newton’s Laws of Motion , regarding the different types of forces and the use of free-body diagrams, to solve additional problems in particle equilibrium .

Different Tensions at Different Angles Consider the traffic light (mass of 15.0 kg) suspended from two wires as shown in (Figure) . Find the tension in each wire, neglecting the masses of the wires.

Solution First consider the horizontal or x -axis:

Thus, as you might expect,

This gives us the following relationship:

Now consider the force components along the vertical or y -axis:

This implies

Substituting the expressions for the vertical components gives

which yields

Significance Both tensions would be larger if both wires were more horizontal, and they will be equal if and only if the angles on either side are the same (as they were in the earlier example of a tightrope walker in Newton’s Laws of Motion .

Particle Acceleration

We have given a variety of examples of particles in equilibrium. We now turn our attention to particle acceleration problems, which are the result of a nonzero net force. Refer again to the steps given at the beginning of this section, and notice how they are applied to the following examples.

The angle is given by

However, Newton’s second law states that

Substituting known values gives

In Newton’s Laws of Motion , we discussed the normal force , which is a contact force that acts normal to the surface so that an object does not have an acceleration perpendicular to the surface. The bathroom scale is an excellent example of a normal force acting on a body. It provides a quantitative reading of how much it must push upward to support the weight of an object. But can you predict what you would see on the dial of a bathroom scale if you stood on it during an elevator ride? Will you see a value greater than your weight when the elevator starts up? What about when the elevator moves upward at a constant speed? Take a guess before reading the next example.

which gives

Significance The scale reading in (Figure) (a) is about 185 lb. What would the scale have read if he were stationary? Since his acceleration would be zero, the force of the scale would be equal to his weight:

Thus, the scale reading in the elevator is greater than his 735-N (165-lb.) weight. This means that the scale is pushing up on the person with a force greater than his weight, as it must in order to accelerate him upward. Clearly, the greater the acceleration of the elevator, the greater the scale reading, consistent with what you feel in rapidly accelerating versus slowly accelerating elevators. In (Figure) (b), the scale reading is 735 N, which equals the person’s weight. This is the case whenever the elevator has a constant velocity—moving up, moving down, or stationary.

The solution to the previous example also applies to an elevator accelerating downward, as mentioned. When an elevator accelerates downward, a is negative, and the scale reading is less than the weight of the person. If a constant downward velocity is reached, the scale reading again becomes equal to the person’s weight. If the elevator is in free fall and accelerating downward at g , then the scale reading is zero and the person appears to be weightless.

Strategy We draw a free-body diagram for each mass separately, as shown in (Figure) . Then we analyze each one to find the required unknowns. The forces on block 1 are the gravitational force, the contact force of the surface, and the tension in the string. Block 2 is subjected to the gravitational force and the string tension. Newton’s second law applies to each, so we write two vector equations:

Solution The component equations follow from the vector equations above. We see that block 1 has the vertical forces balanced, so we ignore them and write an equation relating the x -components. There are no horizontal forces on block 2, so only the y -equation is written. We obtain these results:

Solving for a :

Newton’s Laws of Motion and Kinematics

Physics is most interesting and most powerful when applied to general situations that involve more than a narrow set of physical principles. Newton’s laws of motion can also be integrated with other concepts that have been discussed previously in this text to solve problems of motion. For example, forces produce accelerations, a topic of kinematics , and hence the relevance of earlier chapters.

When approaching problems that involve various types of forces, acceleration, velocity, and/or position, listing the givens and the quantities to be calculated will allow you to identify the principles involved. Then, you can refer to the chapters that deal with a particular topic and solve the problem using strategies outlined in the text. The following worked example illustrates how the problem-solving strategy given earlier in this chapter, as well as strategies presented in other chapters, is applied to an integrated concept problem.

What Force Must a Soccer Player Exert to Reach Top Speed? A soccer player starts at rest and accelerates forward, reaching a velocity of 8.00 m/s in 2.50 s. (a) What is her average acceleration? (b) What average force does the ground exert forward on the runner so that she achieves this acceleration? The player’s mass is 70.0 kg, and air resistance is negligible.

Strategy To find the answers to this problem, we use the problem-solving strategy given earlier in this chapter. The solutions to each part of the example illustrate how to apply specific problem-solving steps. In this case, we do not need to use all of the steps. We simply identify the physical principles, and thus the knowns and unknowns; apply Newton’s second law; and check to see whether the answer is reasonable.

Substituting the known values yields

Substituting the known values of m and a gives

This is a reasonable result: The acceleration is attainable for an athlete in good condition. The force is about 50 pounds, a reasonable average force.

Significance This example illustrates how to apply problem-solving strategies to situations that include topics from different chapters. The first step is to identify the physical principles, the knowns, and the unknowns involved in the problem. The second step is to solve for the unknown, in this case using Newton’s second law. Finally, we check our answer to ensure it is reasonable. These techniques for integrated concept problems will be useful in applications of physics outside of a physics course, such as in your profession, in other science disciplines, and in everyday life.

Check Your Understanding The soccer player stops after completing the play described above, but now notices that the ball is in position to be stolen. If she now experiences a force of 126 N to attempt to steal the ball, which is 2.00 m away from her, how long will it take her to get to the ball?

Solution We have

The magnitude of the force is now easily found:

Check Your Understanding Find the direction of the resultant for the 1.50-kg model helicopter.

49.4 degrees

Significance Since the force varies with time, we must use calculus to solve this problem. Notice how the total mass of the system was important in solving (Figure) (a), whereas only the mass of the truck (since it supplied the force) was of use in (Figure) (b).

Strategy The known force on the mortar shell can be related to its acceleration using the equations of motion. Kinematics can then be used to relate the mortar shell’s acceleration to its position.

We replace ds with dy because we are dealing with the vertical direction,

We now separate the variables ( v ’s and dv ’s on one side; dy on the other):

Significance Notice the need to apply calculus since the force is not constant, which also means that acceleration is not constant. To make matters worse, the force depends on v (not t ), and so we must use the trick explained prior to the example. The answer for the height indicates a lower elevation if there were air resistance. We will deal with the effects of air resistance and other drag forces in greater detail in Drag Force and Terminal Speed .

Check Your Understanding If atmospheric resistance is neglected, find the maximum height for the mortar shell. Is calculus required for this solution?

Explore the forces at work in this simulation when you try to push a filing cabinet. Create an applied force and see the resulting frictional force and total force acting on the cabinet. Charts show the forces, position, velocity, and acceleration vs. time. View a free-body diagram of all the forces (including gravitational and normal forces).

• Newton’s laws of motion can be applied in numerous situations to solve motion problems.

• The normal force on an object is not always equal in magnitude to the weight of the object. If an object is accelerating vertically, the normal force is less than or greater than the weight of the object. Also, if the object is on an inclined plane, the normal force is always less than the full weight of the object.
• Some problems contain several physical quantities, such as forces, acceleration, velocity, or position. You can apply concepts from kinematics and dynamics to solve these problems.

Conceptual Questions

To simulate the apparent weightlessness of space orbit, astronauts are trained in the hold of a cargo aircraft that is accelerating downward at g . Why do they appear to be weightless, as measured by standing on a bathroom scale, in this accelerated frame of reference? Is there any difference between their apparent weightlessness in orbit and in the aircraft?

The scale is in free fall along with the astronauts, so the reading on the scale would be 0. There is no difference in the apparent weightlessness; in the aircraft and in orbit, free fall is occurring.

a. 170 N; b. 170 N

Find the tension in each of the three cables supporting the traffic light if it weighs 2.00 × 10 2 N.

Two muscles in the back of the leg pull upward on the Achilles tendon, as shown below. (These muscles are called the medial and lateral heads of the gastrocnemius muscle.) Find the magnitude and direction of the total force on the Achilles tendon. What type of movement could be caused by this force?

376 N pointing up (along the dashed line in the figure); the force is used to raise the heel of the foot.

After a mishap, a 76.0-kg circus performer clings to a trapeze, which is being pulled to the side by another circus artist, as shown here. Calculate the tension in the two ropes if the person is momentarily motionless. Include a free-body diagram in your solution.

A 35.0-kg dolphin decelerates from 12.0 to 7.50 m/s in 2.30 s to join another dolphin in play. What average force was exerted to slow the first dolphin if it was moving horizontally? (The gravitational force is balanced by the buoyant force of the water.)

When starting a foot race, a 70.0-kg sprinter exerts an average force of 650 N backward on the ground for 0.800 s. (a) What is his final speed? (b) How far does he travel?

A basketball player jumps straight up for a ball. To do this, he lowers his body 0.300 m and then accelerates through this distance by forcefully straightening his legs. This player leaves the floor with a vertical velocity sufficient to carry him 0.900 m above the floor. (a) Calculate his velocity when he leaves the floor. (b) Calculate his acceleration while he is straightening his legs. He goes from zero to the velocity found in (a) in a distance of 0.300 m. (c) Calculate the force he exerts on the floor to do this, given that his mass is 110.0 kg.

A 2.50-kg fireworks shell is fired straight up from a mortar and reaches a height of 110.0 m. (a) Neglecting air resistance (a poor assumption, but we will make it for this example), calculate the shell’s velocity when it leaves the mortar. (b) The mortar itself is a tube 0.450 m long. Calculate the average acceleration of the shell in the tube as it goes from zero to the velocity found in (a). (c) What is the average force on the shell in the mortar? Express your answer in newtons and as a ratio to the weight of the shell.

a. 10 kg; b. 90 N; c. 98 N; d. 0

The device shown below is the Atwood’s machine considered in (Figure) . Assuming that the masses of the string and the frictionless pulley are negligible, (a) find an equation for the acceleration of the two blocks; (b) find an equation for the tension in the string; and (c) find both the acceleration and tension when block 1 has mass 2.00 kg and block 2 has mass 4.00 kg.

Two blocks are connected by a massless rope as shown below. The mass of the block on the table is 4.0 kg and the hanging mass is 1.0 kg. The table and the pulley are frictionless. (a) Find the acceleration of the system. (b) Find the tension in the rope. (c) Find the speed with which the hanging mass hits the floor if it starts from rest and is initially located 1.0 m from the floor.

Shown below are two carts connected by a cord that passes over a small frictionless pulley. Each cart rolls freely with negligible friction. Calculate the acceleration of the carts and the tension in the cord.

Solving Problems with Newton’s Laws Copyright © 2016 by cnxuniphysics. All Rights Reserved.

• TPC and eLearning
• Read Watch Interact
• What's NEW at TPC?
• Practice Review Test
• Teacher-Tools
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Classes (Version 2)
• Student Progress Edit
• Task Properties
• Export Student Progress
• Task, Activities, and Scores
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Intermolecular Forces Preview
• Melting Points and Boiling Points Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Gaining Teacher Access
• Tasks and Classes
• Tasks - Classic
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Task Tracker Directions
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Stoichiometry
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• Solutions Guide
• Solutions Guide Digital Download
• Motion in One Dimension
• Work, Energy and Power
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the CD
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Classes (Legacy Version)
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law

Newton's Second Law - Revisited

• Newton's Second Law - Revisited
• Amusement Park Physics
• Analyzing Circular Movements in Athletics

Newton's second law states that the acceleration of an object is directly proportional to the net force acting upon the object and inversely proportional to the mass of the object. The law is often expressed in the form of the following two equations.

Newton's Second Law and a Force Analysis

In this Lesson, we will use Unit 2 principles (free-body diagrams, Newton's second law equation, etc.) and circular motion concepts in order to analyze a variety of physical situations involving the motion of objects in circles or along curved paths. The mathematical equations discussed in Lesson 1 and the concept of a centripetal force requirement will be applied in order to analyze roller coasters and other amusement park rides and various athletic movements .

CIrcular Motion in a Horizontal Plane

To illustrate how circular motion principles can be combined with Newton's second law to analyze a physical situation, consider a car moving in a horizontal circle on a level surface. The diagram below depicts the car on the left side of the circle.

Now consider the following two problems pertaining to this physical scenario of the car making a turn on a horizontal surface.

Sample problem #1 provides kinematic information (v and R) and requests the value of an individual force. As such the solution of the problem will demand that the acceleration and the net force first be determined; then the individual force value can be found by use of the free-body diagram. Sample problem #2 provides information about the individual force values (or at least information that allows for the determination of the individual force values) and requests the value of the maximum speed of the car. As such, its solution will demand that individual force values be used to determine the net force and acceleration; then the acceleration can be used to determine the maximum speed of the car. The two problems will be solved using the same general principles. Yet because the given and requested information is different in each, the solution method will be slightly different.

The known information and requested information in sample problem #1 is:

The mass of the object can be used to determine the force of gravity acting in the downward direction. Use the equation

where g is 9.8 m/s/s. Knowing that there is no vertical acceleration of the car, it can be concluded that the vertical forces balance each other. Thus, F grav = F norm = 9261 N . This allows us to determine two of the three forces identified in the free-body diagram. Only the friction force remains unknown.

Since the force of friction is the only horizontal force, it must be equal to the net force acting upon the object. So if the net force can be determined, then the friction force is known. To determine the net force, the mass and the kinematic information (speed and radius) must be substituted into the following equation:

Substituting the given values yields a net force of 3780 Newton. Thus, the force of friction is 3780 N .

Finally the coefficient of friction (μ) can be determined using the equation that relates the coefficient of friction to the force of friction and the normal force.

Substituting 3780 N for F frict and 9261 N for F norm yields a coefficient of friction of 0.408 .

Once again, the problem begins by identifying the known and requested information. The known information and requested information in the sample problem #2 is:

The mass of the car can be used to determine the force of gravity acting in the downward direction. Use the equation

where g is 9.8 m/s/s. Knowing that there is no vertical acceleration of the car, it can be concluded that the vertical forces balance each other. Thus, F grav = F norm = 9261 N . Since the coefficient of friction (μ) is given, the force of friction can be determined using the following equation:

This allows us to determine all three forces identified in the free-body diagram.

The net force acting upon any object is the vector sum of all individual forces acting upon that object. So if all individual force values are known (as is the case here), the net force can be calculated. The vertical forces add to 0 N. Since the force of friction is the only horizontal force, it must be equal to the net force acting upon the object. Thus, F net = 7872 N .

Once the net force is determined, the acceleration can be quickly calculated using the following equation.

Substituting the given values yields an acceleration of 8.33 m/s/s . Finally, the speed at which the car could travel around the turn can be calculated using the equation for centripetal acceleration:

Substituting the known values for a and R into this equation and solving algebraically yields a maximum speed of 17.1 m/s .

Developing the Proper Problem-Solving Approach

Each of the two sample problems above was solved using the same basic problem-solving approach. The approach can be summarized as follows.

The method prescribed above will serve you well as you approach circular motion problems. However, one caution is in order. Every physics problem differs from the previous problem. As such, there is no magic formula for solving every one. Using an appropriate approach to solving such problems (which involves constructing a FBD, identifying known information, identifying the requested information, and using available equations) will never eliminate the need to think, analyze and problem-solve . For this reason, make an effort to develop an appropriate approach to every problem; yet always engage your critical analysis skills in the process of the solution. If physics problems were a mere matter of following a foolproof, 5-step formula or using some memorized algorithm, then we wouldn't call them "problems."

We Would Like to Suggest ...

Check Your Understanding

Use your understanding of Newton's second law and circular motion principles to determine the unknown values in the following practice problems. Click the button to check your answers.

1. A 1.50-kg bucket of water is tied by a rope and whirled in a circle with a radius of 1.00 m. At the top of the circular loop, the speed of the bucket is 4.00 m/s. Determine the acceleration, the net force and the individual force values when the bucket is at the top of the circular loop.

a = ________ m/s/s

F net = _________ N

F grav = m • g = 14.7 N (g is 9.8 m/s/s)

a = v 2 / R = (4 • F grav )/1 = 16 m/s/s

F net = m • a = 1.5 kg •16 m/s/s = 24 N, down

F net = F grav + F tens , so

F tens = F net - F grav

F tens = 24 N - 14.7 N = 9.3 N

2. A 1.50-kg bucket of water is tied by a rope and whirled in a circle with a radius of 1.00 m. At the bottom of the circular loop, the speed of the bucket is 6.00 m/s. Determine the acceleration, the net force and the individual force values when the bucket is at the bottom of the circular loop.

a = v 2 / R = (6 2 ) / 1

a = 36 m/s/s

F net = m • a = 1.5 kg • 36 m/s/s

F net = 54 N, up

F net = F tens - F grav , so

F tens = F net + F grav

F tens = 54 N +14.7 N = 68.7 N

• Gravity is More Than a Name

• Reflection of Light
• Equations of Motion
• Wave Theory
• Electromagnetic Induction
• Physics Notes Class 8
• Physics Notes Class 9
• Physics Notes Class 10
• Physics Notes Class 11
• Physics Notes Class 12
• List of Physics Scientists and Their Inventions
• How to Calculate Moment Of Inertia?
• Wave Particle Duality
• Acceleration-Time Graphs
• Introduction to Aeromodelling
• Laws of Motion Numericals
• Some Systems executing Simple Harmonic Motion
• AC Voltage Applied to a Capacitor
• Power in AC Circuit
• Alternating Current
• AC Voltage Applied to an Inductor
• Difference between Electric Field and Magnetic Field
• Motion of a Charged Particle in a Magnetic Field
• Interaction of Forces
• Change in State of Motion
• Refraction of Light through Glass Slab
• Work - Definition, Formula, Types of Work, Sample Problems
• Increasing and Reducing Friction
• Fluid Friction

Applications of Newton’s Second Law

Newton’s 2nd Law has several practical applications, such as car safety engineering and sports performance. Engineers can design safer vehicles by applying it to understand how impacts weaken cars. The Utilization of Newton’s Second Law of Motion provides athletes with the means to optimize their movements, as seen in sprinting and basketball. Through our understanding of these real-life scenarios, we acquire a deeper and more thorough understanding of the significance of the second law of Newton in our daily lives and technology.

What are Applications of Newton’s Second Law of Motion?

Newton’s second law of motion states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. It is given as F= ma. This law describes the relationship between force, mass, and acceleration for objects subject to external forces. It implies that the greater the force applied to an object, the greater its acceleration will be, assuming the mass remains constant. Some real-life applications of Newton’s 2nd Law are given below:

In Automotive Industry

In the automotive industry, Newton’s Second Law is responsible for the design and implementation of safety measures like airbags and seat highs. In a scenario such as a crash where the vehicles have to suddenly stop due to collisions or abrupt braking, passengers feel a pretty rapid and sharp decrease in velocity. Newton’s Second Law states that this deceleration is basically what results in a very powerful force applied to the people in the car. The airbags are activated to minimize the force of this impact by drawing out the collision duration, thus decreasing the violence against the car passengers. Another way restraints work, like seat belts do, is they distribute the impact force upon larger parts of the body and prevent more serious injuries.

Rocket Propulsion

Newton’s Second Law also finds remarkable applications in rocket places and spacecraft propulsion. On a legal point, “For every action, there exists a reaction, which is equal, and opposite” is one of the laws. During the rocket propelling, hot gases get expelled through the rocket’s nozzle and this push them in a single direction but the rocket moves in the opposite direction. Because of the engines, rockets can exhaust mass completely, which on top of achieving high speeds helps them escape the gravitational pull of the Earth. This makes possible space exploration and placing satellites in space.

Sports Performance and Equipment Design

To improve performance and tailor athletic gear to optimal conditions, modern athletes and sport equipment designers apply Newton’s Second Law. As an example, a baseball bat being struck may cause the ball to fly in either direction or travel far. Through appreciating the correlation of force, mass, and acceleration, athletes realize more the perfect technique. Furthermore, hardware like golf clubs, tennis racquets, and bicycles are made to follow these tenets, so that they can comprehensively function and provide the best output.

Check, Newton’s Laws of Motion | Formula, Examples and Questions

Real-Life Experiments of Newton’s 2nd Law

Some of the real life experiments using Newton’s second law of motion are discussed below:

Experiment 1: Car Collision

Materials: Two cars of different masses, crash test barrier.

• Perform two tests by impacting two cars with a barrier from the opposite direction.
• Make a mass table of the cars and speeds prior to the collision.

Explanation:

• Newton’s Second Law: F = ma (Force = Mass × Acceleration).
• Once a car accelerates or decelerates quickly, the inertia of the car’s mass comes into play and leads to force during a car crash just like it was an impact of another object.
• Even car mass or the intensity of speed causes stronger forces that are proportional to the intensity in the acceleration equation F=ma.

Experiment 2: Football Kick

Materials: Football, kicker.

• Make a player, who kicks a football, have different force and kicking in different directions.
• By measuring the distance and speed the ball to moves after each kick.
• Whenever you kick a ball football, the forces are what determines the velocity and range of its travel.
• A greater (stronger) kick (more force) causes the ball to accelerate more quickly, perhaps going further and more quickly.

Experiment 3: Driving a Car

Materials: Car, ignition system.

• Start the car’s engine and speed up.
• Watch and calculate the car’s speed and acceleration.
• When an automobile increases its speed, the engine strives to move it forward with a certain force.
• The amount of acceleration is the product of force exerted by the engine and the mass of the car. The larger the car is, the higher the force needed is to make it with the same speed, and F = ma describes the force.

In conclusion, Newton’s Second Law, which consists of a straightforward and powerful mathematical formula, has a wide range of applications in our daily life. Ranging from making roads safer to taking us into the space, its uses are multiple and diverse. Through comprehending the law, we achieve deeper knowledge of the motion laws, which, in turn, enables us to innovate, create and move around the world with higher accuracy and effectiveness.

Also, Check

• Real Life Applications of Pascal’s Law
• Real Life Applications of Avogadro Law
• Real Life Applications of Hooke’s Law

FAQs on Real-life Applications of Newton’s 2nd Law

What is a key role of newton’s 2nd law of motion in our lives everyday.

The theory of Newton’s Second Law allows us to understand and solve problems related to forces affecting the motion of objects, it also helps us to design safety features, improve sports equipment and much more.

How does the Newton’s Second Law differ from the other laws of motion?

Newton’s Second Law with the First and Third Laws constitutes the foundation of classical mechanics. The First Law treats the inertia while the Third Law with action and reaction. The Second Law determines how force influences acceleration.

Can Newton’s Second Law be used for linear or non-linear systems?

Yes, with some adaptations. It is primarily designed for ways of linear motion but can be used through mathematical techniques. Yet, there is the need to factor in more complicated systems as well.

What will occur when there is zero net force acting on an object?

According to Newton’s First Law, the object is at rest or it is moving with the same speed.

Is the idea of Newton’s Second Law valid for bigger items only?

No, it is valid for all sizes of objects. However, for extremely microscopic objects quantum mechanics comes into effect.

Please Login to comment...

Similar reads.

• Real Life Application
• School Learning
• School Physics
• What are Tiktok AI Avatars?
• Poe Introduces A Price-per-message Revenue Model For AI Bot Creators
• Truecaller For Web Now Available For Android Users In India
• Google Introduces New AI-powered Vids App
• 30 OOPs Interview Questions and Answers (2024)

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.8: Drawing Free-Body Diagrams

• Last updated
• Save as PDF
• Page ID 94561

Learning Objectives

• Explain the rules for drawing a free-body diagram
• Construct free-body diagrams for different situations

The first step in describing and analyzing most phenomena in physics involves the careful drawing of a free-body diagram. Free-body diagrams have been used in examples throughout this chapter. Remember that a free-body diagram must only include the external forces acting on the body of interest. Once we have drawn an accurate free-body diagram, we can apply Newton’s first law if the body is in equilibrium (balanced forces; that is, \(F_{net} = 0\)) or Newton’s second law if the body is accelerating (unbalanced force; that is, \(F_{net} \neq 0\)).

In Forces , we gave a brief problem-solving strategy to help you understand free-body diagrams. Here, we add some details to the strategy that will help you in constructing these diagrams.

Problem-Solving Strategy: Constructing Free-Body Diagrams

Observe the following rules when constructing a free-body diagram:

• Draw the object under consideration; it does not have to be artistic. At first, you may want to draw a circle around the object of interest to be sure you focus on labeling the forces acting on the object. If you are treating the object as a particle (no size or shape and no rotation), represent the object as a point. We often place this point at the origin of an xy-coordinate system.
• Include all forces that act on the object, representing these forces as vectors. Consider the types of forces described in Common Forces —normal force, friction, tension, and spring force—as well as weight and applied force. Do not include the net force on the object. With the exception of gravity, all of the forces we have discussed require direct contact with the object. However, forces that the object exerts on its environment must not be included. We never include both forces of an action-reaction pair.
• Convert the free-body diagram into a more detailed diagram showing the x- and y-components of a given force (this is often helpful when solving a problem using Newton’s first or second law). In this case, place a squiggly line through the original vector to show that it is no longer in play—it has been replaced by its x- and y-components.
• If there are two or more objects, or bodies, in the problem, draw a separate free-body diagram for each object.

Note : If there is acceleration, we do not directly include it in the free-body diagram; however, it may help to indicate acceleration outside the free-body diagram. You can label it in a different color to indicate that it is separate from the free-body diagram.

Let’s apply the problem-solving strategy in drawing a free-body diagram for a sled. In Figure \(\PageIndex{1a}\), a sled is pulled by force \(\vec{P}\) at an angle of 30°. In part (b), we show a free-body diagram for this situation, as described by steps 1 and 2 of the problem-solving strategy. In part (c), we show all forces in terms of their x- and y-components, in keeping with step 3.

Example \(\PageIndex{1}\): Two Blocks on an Inclined Plane

Construct the free-body diagram for object A and object B in Figure \(\PageIndex{1}\).

We follow the four steps listed in the problem-solving strategy.

We start by creating a diagram for the first object of interest. In Figure \(\PageIndex{2a}\), object A is isolated (circled) and represented by a dot.

We now include any force that acts on the body. Here, no applied force is present. The weight of the object acts as a force pointing vertically downward, and the presence of the cord indicates a force of tension pointing away from the object. Object A has one interface and hence experiences a normal force, directed away from the interface. The source of this force is object B, and this normal force is labeled accordingly. Since object B has a tendency to slide down, object A has a tendency to slide up with respect to the interface, so the friction f BA is directed downward parallel to the inclined plane.

As noted in step 4 of the problem-solving strategy, we then construct the free-body diagram in Figure 5.32(b) using the same approach. Object B experiences two normal forces and two friction forces due to the presence of two contact surfaces. The interface with the inclined plane exerts external forces of N B and f B , and the interface with object B exerts the normal force N AB and friction f AB ; N AB is directed away from object B, and f AB is opposing the tendency of the relative motion of object B with respect to object A.

Significance

The object under consideration in each part of this problem was circled in gray. When you are first learning how to draw free-body diagrams, you will find it helpful to circle the object before deciding what forces are acting on that particular object. This focuses your attention, preventing you from considering forces that are not acting on the body

Example \(\PageIndex{2}\): Two Blocks in Contact

A force is applied to two blocks in contact, as shown.

Draw a free-body diagram for each block. Be sure to consider Newton’s third law at the interface where the two blocks touch.

\(\vec{A}_{21}\) is the action force of block 2 on block 1. \(\vec{A}_{12}\) is the reaction force of block 1 on block 2. We use these free-body diagrams in Applications of Newton’s Laws .

Example \(\PageIndex{3}\): Block on the Table (Coupled Blocks)

A block rests on the table, as shown. A light rope is attached to it and runs over a pulley. The other end of the rope is attached to a second block. The two blocks are said to be coupled. Block m 2 exerts a force due to its weight, which causes the system (two blocks and a string) to accelerate.

We assume that the string has no mass so that we do not have to consider it as a separate object. Draw a free-body diagram for each block.

Each block accelerates (notice the labels shown for \(\vec{a}_{1}\) and \(\vec{a}_{2}\)); however, assuming the string remains taut, they accelerate at the same rate. Thus, we have |\(\vec{a}_{1}\)| = |\(\vec{a}_{2}\)|. If we were to continue solving the problem, we could simply call the acceleration \(\vec{a}\). Also, we use two free-body diagrams because we are usually finding tension T, which may require us to use a system of two equations in this type of problem. The tension is the same on both m 1 and m 2 .

Exercise \(\PageIndex{1}\)

• Draw the free-body diagram for the situation shown.
• Redraw it showing components; use x-axes parallel to the two ramps.

View this simulation to predict, qualitatively, how an external force will affect the speed and direction of an object’s motion. Explain the effects with the help of a free-body diagram. Use free-body diagrams to draw position, velocity, acceleration, and force graphs, and vice versa. Explain how the graphs relate to one another. Given a scenario or a graph, sketch all four graphs.