problem solving strategy guess and check

Fun teaching resources & tips to help you teach math with confidence

Math Strategies: Solving Problems Using Guess and Check

Welcome to the last post in my series on problem solving strategies ! There are so many different ways to approach math word problems, but it’s important that we share these various methods with kids so that they can be equipped to tackle them. This week I’m explaining a strategy that doesn’t sound overly mathematical , but can be extremely useful when done properly: solving problems using guess and check ! As with the other strategies I’ve discussed, it’s important to help kids understand how to use this method so that they are not randomly pulling answers out of their head and wasting time .

–>Pssst! Do your kids need help making sense of and solving word problems? You might like this set of editable word problem solving templates ! Use these with any grade level, for any type of word problem :

Guess & Check Math Strategy: 

You may hear the name of this strategy and think, “Guess? Isn’t the whole point of math instruction to teach kids to solve problems so that they’re no longer merely guessing ??”

While it is certainly true that we don’t want kids to simply guess random answers for every math problem they ever encounter, there are instances when educated guesses are important, valid and useful.

For instance, learning and understanding how to accurately estimate is an important mathematical skill. A good estimate, however, is not just a random guess. It takes effort and logic to formulate an estimate that makes sense and is (hopefully) close to the correct answer. (For fun and easy estimation practice, try this Mummy Math activity ! )

Similarly, solving problems using guess and check is a process that requires logic and an understanding of the question so that it can be done in a way that is organized and time saving.

So what does guess and check mean? To be more specific, this strategy should be called, “Guess, Check and Revise.”

The basic structure of the strategy looks like this:

• Form an educated guess
• Check your solution to see if it works and solves the problem
• If not, revise your guess based on whether it is too high or too low

This is a useful strategy when you’re given the total and you’re asked to find the kinds or number of things making up the total.

Or when the question asks for the value of two or more different kinds of things .

For instance, you might be asked how many girls and how many boys are in the class, or how many cats and how many dogs a pet owner has.

When guess and check seems like an appropriate strategy for a word problem, it will be helpful and necessary to then organize the information in a table or list to keep track of the different guesses.

This provides a visual of the important information, and will also help ensure that subsequent guesses are logical and not random .

Using the Guess and Check Strategy:

To begin, students should make a guess using what they know from the problem. This first guess can be anything at all, so long as it follows the criteria given. Then, once a guess is made, students can begin to make more educated guesses based on how close they are to the correct answer.

For example, if their initial guess gives a total that is too high, they need to choose smaller numbers for their next guess.

Likewise, if their guess gives a total that is too low, they need to choose larger numbers.

The most important thing for students to understand when using this method is that after their initial guess, they should work towards getting closer to the correct answer by making logical changes to their guess. They should not be choosing random numbers anymore!

Here’s an example to consider:

In Ms. Brown’s class, there are 24 students. There are 6 more girls than boys. How many boys and girls are there?

Because we know the class total (24), and we’re asked to find more than one value (number of boys and number of girls), we can solve this using the guess and check method .

To organize the question, we can form a table with boys, girls and the total. Because we know there are 6 more girls than boys, we can guess a number for the boys, and then calculate the girls and the total from there.

With an initial guess of 12 boys, we see that there would be 18 girls, giving a total class size of 30. The total, however, should only be 24, which means our guess was too high . Knowing this, the number of boys is revised and the total recalculated .

Lowering the number of boys to 10 would mean there are 16 girls, which gives a class total of 26. This is still just a little bit too high, so we can once again revise the guess to 9 boys. If there are 9 boys, that would mean there are 15 girls, which gives a class total of 24.

Therefore, the solution is 9 boys and 15 girls.

This is a fairly simple example, and likely you will have students who can solve this problem without writing out a table and forming multiple guesses. But for students who struggle with math , this problem may seem overwhelming and complicated.

By giving them a starting point and helping them learn to make more educated guesses , you can equip them to not only solve word problems, but feel more confident in tackling them.

This is also a good strategy because it helps kids see that it’s ok to make mistakes and that we shouldn’t expect to get the right answer on the first try, but rather, we should expect to make mistakes and use our mistake to learn and find the right answer.

What do you think? Do you use or teach this strategy to students? Do you find it helpful?

And of course, don’t miss the rest of the problem solving strategy series:

• Problem Solve by Solving an Easier Problem
• Problem Solve by Drawing a Picture
• Problem Solve by Working Backwards
• Problem Solve by Making a List
• Problem Solve by Finding a Pattern

My strategy was usually more “guess and hope for the best”. Yours sounds much wiser, lol! Thanks for sharing at the Thoughtful Spot!

Haha!! Yes, I think that’s what most people think of when they hear, “Guess and Check!” Hope this was helpful, 🙂

How exactly do you do this?

Sorry, your way was amazing…but I’m still confused:(

I’m so sorry you’re confused. Can you explain what part you don’t understand so I can try and make it clearer? The object is to make a reasonable guess, and then adjust your guess based on if your answer is too high or too low (try to be logical rather than random).

Nicely explained post and a different logic for solving problems “Guess and check”, I don’t know that how much helpful it is but I’m sure that your idea will help to change the thinking of readers. Thanks for sharing a different kind of idea for problem solving.

Comments are closed.

Similar Posts

Weekly Math Freebie Round Up!

Weekly Math Freebies Round-Up!

Race to Pi: Simple and Fun Pi Day Card Game

Exploring Surface Area of Pyramids and Cones!

Redbird Mathematics Online Math Program Review

Find more resources to help make math engaging, join 165k+ parents & teachers.

Who learn new tips and strategies, as well as receive engaging resources to make math fun!

• Privacy Policy

Math Time Doesn't Have to End in Tears

Join 165,000+ parents and teachers who learn new tips and strategies, as well as receive engaging resources to make math fun. Plus, receive my guide, "5 Games You Can Play Today to Make Math Fun," as my free gift to get you started!

Learn the Guess and Check Method

What is the guess and check math strategy.

The Guess and Check Math strategy is one of the first few Math Heuristics that is introduced to Primary 3 students. Although some students may switch to more advanced techniques like the Assumption method in Primary 4, mastering this method is still going to be useful to those who don’t in their upper primary years. The main idea behind the Guess and Check method is to guess the answer to a problem and then check if the answer fits the given scenario. If it doesn’t, we’ll adjust our guess accordingly until all conditions are met.

Here’s what we’re going to cover:

• How does the Guess and check method work
• Examples of guess and check questions
• How to identify guess and check questions
• How to part 1: Building the guess and check table
• How to part 2: How to do the guess and check method

How does the Guess and Check Method work?

The Guess and Check problem solving strategy is a fairly easy way of solving problems. Think of it as a 3-step-approach:

1. Guess –> 2. Check –> 3. Repeat if needed

While we are guessing the numbers, we’ll need to learn how to make smart guesses. Knowing how to do that helps us minimize the number of guessing, making the process more efficient. We’ll see how to do that in a while.

Back to top

Examples of Guess and Check Questions

Here are some samples of how Guess and Check Math Questions can look like. Can you figure out what they have in common?

Primary 3 and 4 Math:

There are 15 cats and birds in a park. There are 42 legs altogether.

How many cats are there?

Primary 5 and 6 Math: Jay did 20 Math questions during his math practice. He received 5 marks for every correct answer and he got 2 marks deducted for every wrong answer. If Jay earned 35 experience points in total, how many questions did he answer wrongly?

How do we identify questions that use the Guess and Check Method?

If you looked carefully, both problems that you see above has a total that’s made up of 2 kinds of items. on top of that, we also have some information about each item and we need to find the number of one of those items. Let’s use the lower primary math problem as an example and go through the Guess and Check method step by step.

Part A: How to build the Guess and Check table the right way

Before we start guessing and checking, it’s always a good habit to build a guess and check table so that we know exactly what to look out for and keep things organised.

Step 1: List the 2 items that is in the question

The first thing that we’ll want to do is to build our guess and check table is to think about what we want to solve for. This is the answer that we are going to guess and it goes into our first column. In our case, it’s going to be the number of cats. Next, we’ll list the number of the second item, which happens to be the number of birds as shown below:

Step 2: List the common thing that the 2 items have

What do the cats and birds have in common? Legs. So the number of cats’ legs and the number of birds’ legs go into another 2 columns.

Step 3: Add in what we need to check 

Time to think about the relationship between the columns and how they help us check if the answer that we have guessed is correct. For our answer to be right, the total number of legs that we have has to add up to 42 and the way that we calculate this is to add the number of cats’ legs to the number of birds’ legs. Let’s add another column to include the total number of legs and because we are going to use this to check of our guess is correct, we are going to add in another special column called “Check” to help us keep track of our progress.

Is the Guess and Check Table really necessary?

When we are busy making guesses, it is easy to lose track of the numbers that we have tried along with their calculations. That’s where a guess and check table can really come in handy. Not only does a guess and check table help us organize our guesses in a neat visual way, it also prevents us from making careless mistakes.

How to use the Guess and Check method efficiently

As you might have guessed, guessing and checking comes with a lot of hits and misses. Here’s the trick to keep our guesses to a minimal and make the guess and check method work better!

Step 1: Start with the middle number as your first guess

In our example, since we have 15 pets,  half of 15 would be approximately 7 or 8 (not 7.5 because we can’t have half a pet). Let’s pick 7 as our guess.

Step 2: Filling up our guess and check table from left to right

Once we have our guess, it’s time to work through the columns of our guess and check table and decide if our guess is correct. If we had 7 cats and each puppy has 4 legs, we are going to have 7 x 4 cats’ legs = 28 cats’ legs. To find the number of birds, let’s subtract 7 from the total of 15 pets. This gives us 8 birds. 8 birds are going to have 8 x 2 birds’ legs, 16 legs in all. Let’s check the total number of legs we have against what is given in the problem. When we add 28 and 16, we are going to get a total of 44 legs. However, this is more than the 42 legs that we are given in the problem. Let’s make a note of that under the “Check” column.

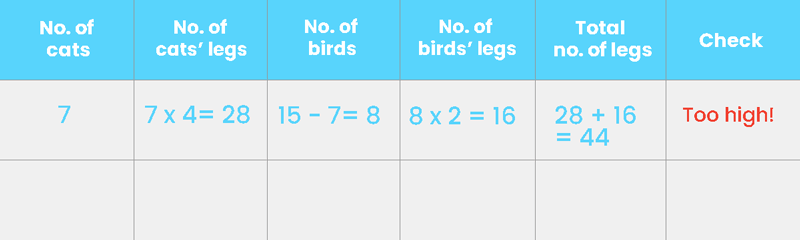
Step 3: Adjust our guess accordingly and check again

The next thing that we’ll want to do is to estimate how far our guess is to our target, and make a better guess. Comparing our guess which resulted in 44 legs against the 42 legs that we want, we can tell that our guess is very close. Since we want to reduce the number of legs, should we increase or decrease our second guess? Because the cats have more legs than birds and we want fewer legs, we’ll need to lower what we’ve guessed. When we work systematically across our guess and check table, this happens to be the answer that we are looking for!

All it takes for us to get the correct answer are 2 guesses, and this definitely didn’t happen by chance. When we made the first guess, it gave us some information about how far we are from the answer. This helped us make a better guess the second time. As you can see, we are making logical guesses instead of just guessing random numbers and trying our luck.

And that’s how you do the Guess and Check method!

Using the Guess and Check method is good when you are dealing with smaller numbers which are easier to work with. However, it does take practice to improve the accuracy of your guesses and some children may take a longer time to do the calculations in between, giving room to possible careless mistakes. If you are looking for a faster alternative that involves fewer steps, you might want to check out the Assumption Method and see if that works better for you.

Need more examples?

Check out how this Math video on how to use the guess and check method to solve a Primary 3 question.

Like what you see? Subscribe to our Youtube channel for more Practicle Singapore Math videos!

Practicle is an online gamified Singapore Math adaptive learning platform that helps primary school children master Math through understanding and fun.

• EAF Certification
• Privacy policy
• Terms of use
• Math heuristics guide
• Math problem sum guide

© 2024 Practicle. All Rights Reserved,

• A.I. Math Tutor
• Math Vision: Our video tutorials

Question: Amy and Judy sold 12 show tickets altogether. Amy sold 2 more tickets than Judy. How many tickets did each girl sell? Strategy: 1) UNDERSTAND: What do you need to find? You need to know that 12 tickets were sold in all. You also need to know that Amy sold 2 more tickets than Judy. 2) PLAN: How can you solve the problem? You can guess and check to find two numbers with a sum of 12 and a difference of 2. If your first guess does not work, try two different numbers. 3) SOLVE: First Guess: Amy = 8 tickets Judy = 4 tickets Check 8 + 4 = 12 8 - 4 = 4 ( Amy sold 4 more tickets) These numbers do not work! Second Guess: Amy = 7 tickets Judy = 5 tickets Check 7 + 5 = 12 7- 5 = 2 ( Amy sold 2 more tickets) These numbers do work! Amy sold 7 tickets and Judy sold 5 tickets.

Math Problem Solving Strategies

In these lessons, we will learn some math problem solving strategies for example, Verbal Model (or Logical Reasoning), Algebraic Model, Block Model (or Singapore Math), Guess & Check Model and Find a Pattern Model.

Related Pages Solving Word Problems Using Block Models Heuristic Approach to Problem-Solving Algebra Lessons

Problem Solving Strategies

The strategies used in solving word problems:

• What do you know?
• What do you need to know?
• Draw a diagram/picture

Solution Strategies Label Variables Verbal Model or Logical Reasoning Algebraic Model - Translate Verbal Model to Algebraic Model Solve and Check.

Solving Word Problems

Step 1: Identify (What is being asked?) Step 2: Strategize Step 3: Write the equation(s) Step 4: Answer the question Step 5: Check

Problem Solving Strategy: Guess And Check

Using the guess and check problem solving strategy to help solve math word problems.

Example: Jamie spent $40 for an outfit. She paid for the items using $10, $5 and $1 bills. If she gave the clerk 10 bills in all, how many of each bill did she use?

Problem Solving : Make A Table And Look For A Pattern

• Identify - What is the question?
• Plan - What strategy will I use to solve the problem?
• Solve - Carry out your plan.
• Verify - Does my answer make sense?

Example: Marcus ran a lemonade stand for 5 days. On the first day, he made $5. Every day after that he made $2 more than the previous day. How much money did Marcus made in all after 5 days?

Find A Pattern Model (Intermediate)

In this lesson, we will look at some intermediate examples of Find a Pattern method of problem-solving strategy.

Example: The figure shows a series of rectangles where each rectangle is bounded by 10 dots. a) How many dots are required for 7 rectangles? b) If the figure has 73 dots, how many rectangles would there be?

a) The number of dots required for 7 rectangles is 52.

b) If the figure has 73 dots, there would be 10 rectangles.

Example: Each triangle in the figure below has 3 dots. Study the pattern and find the number of dots for 7 layers of triangles.

The number of dots for 7 layers of triangles is 36.

Example: The table below shows numbers placed into groups I, II, III, IV, V and VI. In which groups would the following numbers belong? a) 25 b) 46 c) 269

Solution: The pattern is: The remainder when the number is divided by 6 determines the group. a) 25 ÷ 6 = 4 remainder 1 (Group I) b) 46 ÷ 6 = 7 remainder 4 (Group IV) c) 269 ÷ 6 = 44 remainder 5 (Group V)

Example: The following figures were formed using matchsticks.

a) Based on the above series of figures, complete the table below.

b) How many triangles are there if the figure in the series has 9 squares?

c) How many matchsticks would be used in the figure in the series with 11 squares?

b) The pattern is +2 for each additional square.   18 + 2 = 20   If the figure in the series has 9 squares, there would be 20 triangles.

c) The pattern is + 7 for each additional square   61 + (3 x 7) = 82   If the figure in the series has 11 squares, there would be 82 matchsticks.

Example: Seven ex-schoolmates had a gathering. Each one of them shook hands with all others once. How many handshakes were there?

Total = 6 + 5 + 4 + 3 + 2 + 1 = 21 handshakes.

The following video shows more examples of using problem solving strategies and models. Question 1: Approximate your average speed given some information Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern. Find the number of seats in the last row. Question 3: You are hanging three pictures in the wall of your home that is 16 feet wide. The width of your pictures are 2, 3 and 4 feet. You want space between your pictures to be the same and the space to the left and right to be 6 inches more than between the pictures. How would you place the pictures?

The following are some other examples of problem solving strategies.

Explore it/Act it/Try it (EAT) Method (Basic) Explore it/Act it/Try it (EAT) Method (Intermediate) Explore it/Act it/Try it (EAT) Method (Advanced)

Finding A Pattern (Basic) Finding A Pattern (Intermediate) Finding A Pattern (Advanced)

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Problem-Solving Strategies

There are many different ways to solve a math problem, and equipping students with problem-solving strategies is just as important as teaching computation and algorithms. Problem-solving strategies help students visualize the problem or present the given information in a way that can lead them to the solution. Solving word problems using strategies works great as a number talks activity and helps to revise many skills.

Problem-solving strategies

1. create a diagram/picture, 2. guess and check., 3. make a table or a list., 4. logical reasoning., 5. find a pattern, 6. work backward, 1. create a diagram/draw a picture.

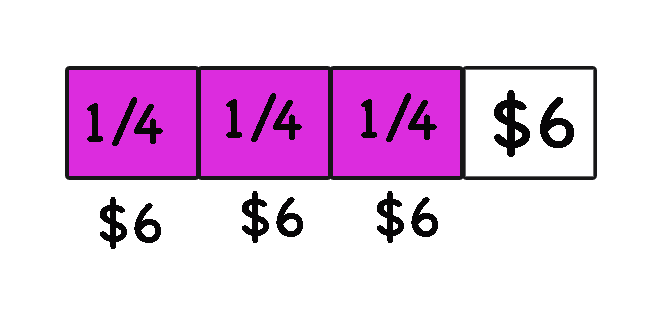
Creating a diagram helps students visualize the problem and reach the solution. A diagram can be a picture with labels, or a representation of the problem with objects that can be manipulated. Role-playing and acting out the problem like a story can help get to the solution.

Alice spent 3/4 of her babysitting money on comic books. She is left with $6. How much money did she make from babysitting?

2. Guess and check

Teach students the same strategy research mathematicians use.

With this strategy, students solve problems by making a reasonable guess depending on the information given. Then they check to see if the answer is correct and they improve it accordingly.  By repeating this process, a student can arrive at a correct answer that has been checked. It is recommended that the students keep a record of their guesses by making a chart, a table or a list. This is a flexible strategy that works for many types of problems. When students are stuck, guessing and checking helps them start and explore the problem. However, there is a trap. Exactly because it is such a simple strategy to use, some students find it difficult to consider other strategies. As problems get more complicated, other strategies become more important and more effective.

Find two numbers that have sum 11 and product 24.

Try/guess  5 and 6  the product is 30 too high

  adjust  to 4 and 7 with product 28 still high

  adjust  again 3 and 8 product 24

3. Make a table or a list

Carefully organize the information on a table or list according to the problem information. It might be a table of numbers, a table with ticks and crosses to solve a logic problem or a list of possible answers. Seeing the given information sorted out on a table or a list will help find patterns and lead to the correct solution.

To make sure you are listing all the information correctly read the problem carefully.

Find the common factors of 24, 30 and 18

Logical reasoning is the process of using logical, systemic steps to arrive at a conclusion based on given facts and mathematic principles. Read and understand the problem. Then find the information that helps you start solving the problem. Continue with each piece of information and write possible answers.

Thomas, Helen, Bill, and Mary have cats that are black, brown, white, or gray. The cats’ names are Buddy, Lucky, Fifi, and Moo. Buddy is brown. Thoma’s cat, Lucky, is not gray. Helen’s cat is white but is not named Moo. The gray cat belongs to Bill. Which cat belongs to each student, and what is its color?

A table or list is useful in solving logic problems.

Since Lucky is not gray it can be black or brown. However, Buddy is brown so Lucky has to be black.

Buddy is brown so it cannot be Helen’s cat. Helen’s cat cannot be Moo, Buddy or Lucky, so it is Fifi.

Therefore, Moo is Bill’s cat and Buddy is Mary’s cat.

5. Find a pattern.

Finding a pattern is a strategy in which students look for patterns in the given information in order to solve the problem. When the problem consists of data like numbers or events that are repeated then it can be solved using the “find a pattern” problem-solving strategy. Data can be organized in a table or a list to reveal the pattern and help discover the “rule” of the pattern.

 The “rule” can then be used to find the answer to the question and complete the table/list.

Shannon’s Pizzeria made 5 pizzas on Sunday, 10 pizzas on Monday, 20 pizzas on Tuesday, and 40 pizzas on Wednesday. If this pattern continues, how many pizzas will the pizzeria make on Saturday?

6. Working backward

Problems that can be solved with this strategy are the ones that  list a series of events or a sequence of steps .

In this strategy, the students must start with the solution and work back to the beginning. Each operation must be reversed to get back to the beginning. So if working forwards requires addition, when students work backward they will need to subtract. And if they multiply working forwards, they must divide when working backward.

Mom bought a box of candy. Mary took 5 of them, Nick took 4 of them and 31 were given out on Halloween night. The next morning they found 8 pieces of candy in the box. How many candy pieces were in the box when mom bought it.

For this problem, we know that the final number of candy was 8, so if we work backward to “put back” the candy that was taken from the box we can reach the number of candy pieces that were in the box, to begin with.

The candy was taken away so we will normally subtract them. However, to get back to the original number of candy we need to work backward and do the opposite, which is to add them.

8 candy pieces were left + the 31 given out + plus the ones Mary took + the ones Nick took

8+31+5+4= 48   Answer: The box came with 48 pieces of candy.

Selecting the best strategy for a problem comes with practice and often problems will require the use of more than one strategies.

Print and digital activities

I have created a collection of print and digital activity cards and worksheets with word problems (print and google slides) to solve using the strategies above. The collection includes 70 problems (5 challenge ones) and their solution s and explanations.

sample below

How to use the activity cards

Allow the students to use manipulatives to solve the problems. (counters, shapes, lego blocks, Cuisenaire blocks, base 10 blocks, clocks) They can use manipulatives to create a picture and visualize the problem. They can use counters for the guess and check strategy. Discuss which strategy/strategies are better for solving each problem. Discuss the different ways. Use the activities as warm-ups, number talks, initiate discussions, group work, challenge, escape rooms, and more.

Ask your students to write their own problems using the problems in this resource, and more, as examples. Start with a simple type. Students learn a lot when trying to compose a problem. They can share the problem with their partner or the whole class. Make a collection of problems to share with another class.

For the google slides the students can use text boxes to explain their thinking with words, add shapes and lines to create diagrams, and add (insert) tables and diagrams.

Many of the problems can be solved faster by using algebraic expressions. However, since I created this resource for grades 4 and up I chose to show simple conceptual ways of solving the problems using the strategies above. You can suggest different ways of solving the problems based on the grade level.

Find the free and premium versions of the resource below. The premium version includes 70 problems (challenge problems included) and their solutions

There are 2 versions of the resource

70 google slides with explanations + 70 printable task cards

70 google slides with explanations + 11 worksheets