introduction to quadratic functions assignment quizlet

5.1 Quadratic Functions

Learning objectives.

In this section, you will:

• Recognize characteristics of parabolas.
• Understand how the graph of a parabola is related to its quadratic function.
• Determine a quadratic function’s minimum or maximum value.
• Solve problems involving a quadratic function’s minimum or maximum value.

Curved antennas, such as the ones shown in Figure 1 , are commonly used to focus microwaves and radio waves to transmit television and telephone signals, as well as satellite and spacecraft communication. The cross-section of the antenna is in the shape of a parabola, which can be described by a quadratic function.

In this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion. Working with quadratic functions can be less complex than working with higher degree functions, so they provide a good opportunity for a detailed study of function behavior.

Recognizing Characteristics of Parabolas

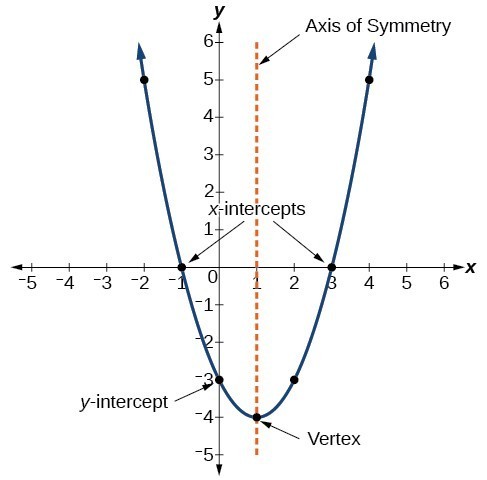
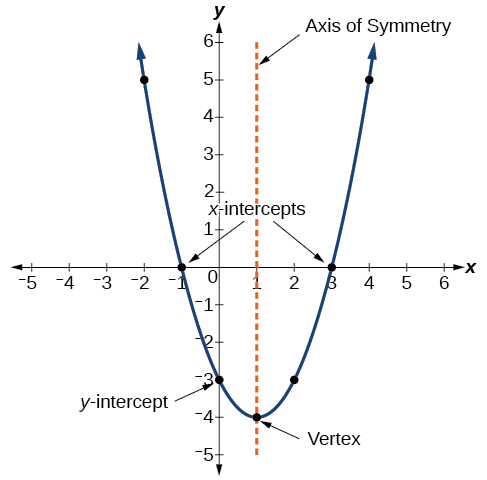
The graph of a quadratic function is a U-shaped curve called a parabola . One important feature of the graph is that it has an extreme point, called the vertex . If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value . In either case, the vertex is a turning point on the graph. The graph is also symmetric with a vertical line drawn through the vertex, called the axis of symmetry . These features are illustrated in Figure 2 .

The y -intercept is the point at which the parabola crosses the y -axis. The x -intercepts are the points at which the parabola crosses the x -axis. If they exist, the x -intercepts represent the zeros , or roots , of the quadratic function, the values of x x at which y = 0. y = 0.

Identifying the Characteristics of a Parabola

Determine the vertex, axis of symmetry, zeros, and y - y - intercept of the parabola shown in Figure 3 .

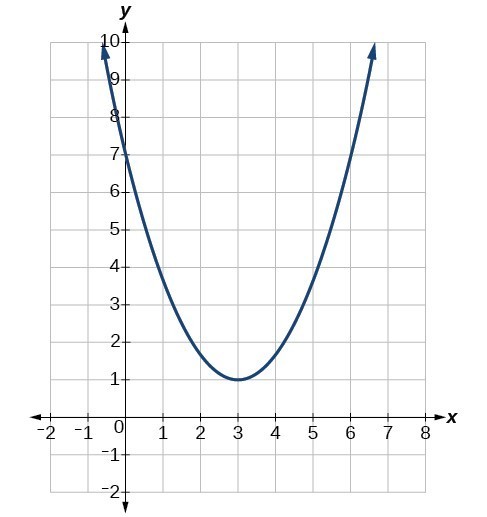
The vertex is the turning point of the graph. We can see that the vertex is at ( 3 , 1 ) . ( 3 , 1 ) . Because this parabola opens upward, the axis of symmetry is the vertical line that intersects the parabola at the vertex. So the axis of symmetry is x = 3. x = 3. This parabola does not cross the x - x - axis, so it has no zeros. It crosses the y - y - axis at ( 0 , 7 ) ( 0 , 7 ) so this is the y -intercept.

Understanding How the Graphs of Parabolas are Related to Their Quadratic Functions

The general form of a quadratic function presents the function in the form

where a , b , a , b , and c c are real numbers and a ≠ 0. a ≠ 0. If a > 0 , a > 0 , the parabola opens upward. If a < 0 , a < 0 , the parabola opens downward. We can use the general form of a parabola to find the equation for the axis of symmetry.

The axis of symmetry is defined by x = − b 2 a . x = − b 2 a . If we use the quadratic formula, x = − b ± b 2 − 4 a c 2 a , x = − b ± b 2 − 4 a c 2 a , to solve a x 2 + b x + c = 0 a x 2 + b x + c = 0 for the x - x - intercepts, or zeros, we find the value of x x halfway between them is always x = − b 2 a , x = − b 2 a , the equation for the axis of symmetry.

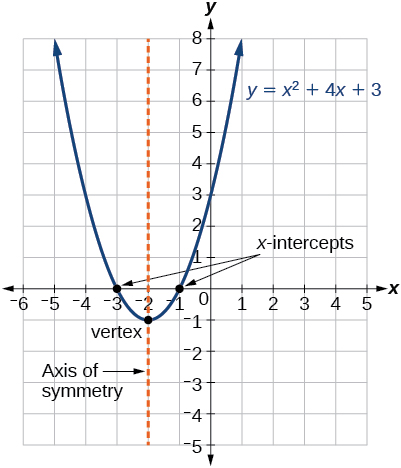
Figure 4 represents the graph of the quadratic function written in general form as y = x 2 + 4 x + 3. y = x 2 + 4 x + 3. In this form, a = 1 , b = 4 , a = 1 , b = 4 , and c = 3. c = 3. Because a > 0 , a > 0 , the parabola opens upward. The axis of symmetry is x = − 4 2 ( 1 ) = −2. x = − 4 2 ( 1 ) = −2. This also makes sense because we can see from the graph that the vertical line x = −2 x = −2 divides the graph in half. The vertex always occurs along the axis of symmetry. For a parabola that opens upward, the vertex occurs at the lowest point on the graph, in this instance, ( −2 , −1 ) . ( −2 , −1 ) . The x - x - intercepts, those points where the parabola crosses the x - x - axis, occur at ( −3 , 0 ) ( −3 , 0 ) and ( −1 , 0 ) . ( −1 , 0 ) .

The standard form of a quadratic function presents the function in the form

where ( h , k ) ( h , k ) is the vertex. Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function .

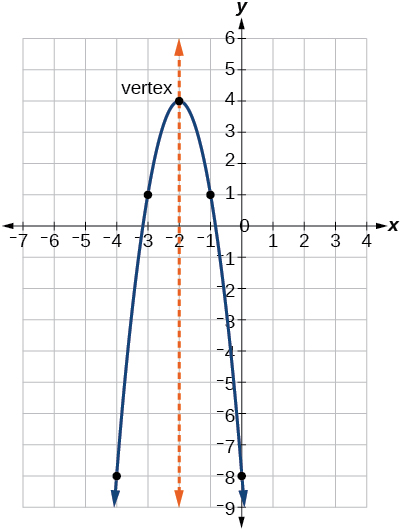
As with the general form, if a > 0 , a > 0 , the parabola opens upward and the vertex is a minimum. If a < 0 , a < 0 , the parabola opens downward, and the vertex is a maximum. Figure 5 represents the graph of the quadratic function written in standard form as y = −3 ( x + 2 ) 2 + 4. y = −3 ( x + 2 ) 2 + 4. Since x – h = x + 2 x – h = x + 2 in this example, h = –2. h = –2. In this form, a = −3 , h = −2 , a = −3 , h = −2 , and k = 4. k = 4. Because a < 0 , a < 0 , the parabola opens downward. The vertex is at ( − 2 , 4 ) . ( − 2 , 4 ) .

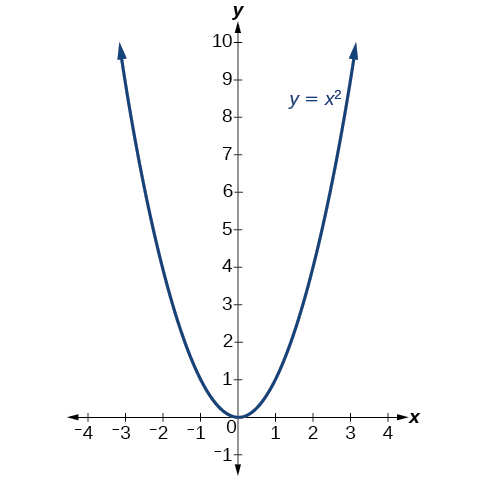
The standard form is useful for determining how the graph is transformed from the graph of y = x 2 . y = x 2 . Figure 6 is the graph of this basic function.

If k > 0 , k > 0 , the graph shifts upward, whereas if k < 0 , k < 0 , the graph shifts downward. In Figure 5 , k > 0 , k > 0 , so the graph is shifted 4 units upward. If h > 0 , h > 0 , the graph shifts toward the right and if h < 0 , h < 0 , the graph shifts to the left. In Figure 5 , h < 0 , h < 0 , so the graph is shifted 2 units to the left. The magnitude of a a indicates the stretch of the graph. If | a | > 1 , | a | > 1 , the point associated with a particular x - x - value shifts farther from the x- axis, so the graph appears to become narrower, and there is a vertical stretch. But if | a | < 1 , | a | < 1 , the point associated with a particular x - x - value shifts closer to the x- axis, so the graph appears to become wider, but in fact there is a vertical compression. In Figure 5 , | a | > 1 , | a | > 1 , so the graph becomes narrower.

The standard form and the general form are equivalent methods of describing the same function. We can see this by expanding out the general form and setting it equal to the standard form.

For the linear terms to be equal, the coefficients must be equal.

This is the axis of symmetry we defined earlier. Setting the constant terms equal:

In practice, though, it is usually easier to remember that k is the output value of the function when the input is h , h , so f ( h ) = k . f ( h ) = k .

Forms of Quadratic Functions

A quadratic function is a polynomial function of degree two. The graph of a quadratic function is a parabola.

The general form of a quadratic function is f ( x ) = a x 2 + b x + c f ( x ) = a x 2 + b x + c where a , b , a , b , and c c are real numbers and a ≠ 0. a ≠ 0.

The standard form of a quadratic function is f ( x ) = a ( x − h ) 2 + k f ( x ) = a ( x − h ) 2 + k where a ≠ 0. a ≠ 0.

The vertex ( h , k ) ( h , k ) is located at

Given a graph of a quadratic function, write the equation of the function in general form.

• Identify the horizontal shift of the parabola; this value is h . h . Identify the vertical shift of the parabola; this value is k . k .
• Substitute the values of the horizontal and vertical shift for h h and k . k . in the function f ( x ) = a ( x – h ) 2 + k . f ( x ) = a ( x – h ) 2 + k .
• Substitute the values of any point, other than the vertex, on the graph of the parabola for x x and f ( x ) . f ( x ) .
• Solve for the stretch factor, | a | . | a | .
• Expand and simplify to write in general form.

Writing the Equation of a Quadratic Function from the Graph

Write an equation for the quadratic function g g in Figure 7 as a transformation of f ( x ) = x 2 , f ( x ) = x 2 , and then expand the formula, and simplify terms to write the equation in general form.

We can see the graph of g is the graph of f ( x ) = x 2 f ( x ) = x 2 shifted to the left 2 and down 3, giving a formula in the form g ( x ) = a ( x − ( −2 ) ) 2 − 3 = a ( x + 2 ) 2 – 3. g ( x ) = a ( x − ( −2 ) ) 2 − 3 = a ( x + 2 ) 2 – 3.

Substituting the coordinates of a point on the curve, such as ( 0 , −1 ) , ( 0 , −1 ) , we can solve for the stretch factor.

In standard form, the algebraic model for this graph is ( g ) x = 1 2 ( x + 2 ) 2 – 3. ( g ) x = 1 2 ( x + 2 ) 2 – 3.

To write this in general polynomial form, we can expand the formula and simplify terms.

Notice that the horizontal and vertical shifts of the basic graph of the quadratic function determine the location of the vertex of the parabola; the vertex is unaffected by stretches and compressions.

We can check our work using the table feature on a graphing utility. First enter Y1 = 1 2 ( x + 2 ) 2 − 3. Y1 = 1 2 ( x + 2 ) 2 − 3. Next, select TBLSET, TBLSET, then use TblStart = – 6 TblStart = – 6 and Δ Tbl = 2, Δ Tbl = 2, and select TABLE . TABLE . See Table 1 .

The ordered pairs in the table correspond to points on the graph.

A coordinate grid has been superimposed over the quadratic path of a basketball in Figure 8 . Assume that the point (–4, 7) is the highest point of the basketball’s trajectory. Find an equation for the path of the ball. Does the shooter make the basket?

Given a quadratic function in general form, find the vertex of the parabola.

• Identify a ,   b ,   and   c . a ,   b ,   and   c .
• Find h , h , the x -coordinate of the vertex, by substituting a a and b b into h = – b 2 a . h = – b 2 a .
• Find k , k , the y -coordinate of the vertex, by evaluating k = f ( h ) = f ( − b 2 a ) . k = f ( h ) = f ( − b 2 a ) .

Finding the Vertex of a Quadratic Function

Find the vertex of the quadratic function f ( x ) = 2 x 2 – 6 x + 7. f ( x ) = 2 x 2 – 6 x + 7. Rewrite the quadratic in standard form (vertex form).

The horizontal coordinate of the vertex will be at h = − b 2 a = − −6 2 ( 2 ) = 6 4 = 3 2 The vertical coordinate of the vertex will be at k = f ( h ) = f ( 3 2 ) = 2 ( 3 2 ) 2 − 6 ( 3 2 ) + 7 = 5 2 The horizontal coordinate of the vertex will be at h = − b 2 a = − −6 2 ( 2 ) = 6 4 = 3 2 The vertical coordinate of the vertex will be at k = f ( h ) = f ( 3 2 ) = 2 ( 3 2 ) 2 − 6 ( 3 2 ) + 7 = 5 2

Rewriting into standard form, the stretch factor will be the same as the a a in the original quadratic. First, find the horizontal coordinate of the vertex. Then find the vertical coordinate of the vertex. Substitute the values into standard form, using the " a a " from the general form.

The standard form of a quadratic function prior to writing the function then becomes the following:

One reason we may want to identify the vertex of the parabola is that this point will inform us where the maximum or minimum value of the output occurs, k , k , and where it occurs, x . x .

Given the equation g ( x ) = 13 + x 2 − 6 x , g ( x ) = 13 + x 2 − 6 x , write the equation in general form and then in standard form.

Finding the Domain and Range of a Quadratic Function

Any number can be the input value of a quadratic function. Therefore, the domain of any quadratic function is all real numbers. Because parabolas have a maximum or a minimum point, the range is restricted. Since the vertex of a parabola will be either a maximum or a minimum, the range will consist of all y -values greater than or equal to the y -coordinate at the turning point or less than or equal to the y -coordinate at the turning point, depending on whether the parabola opens up or down.

Domain and Range of a Quadratic Function

The domain of any quadratic function is all real numbers unless the context of the function presents some restrictions.

The range of a quadratic function written in general form f ( x ) = a x 2 + b x + c f ( x ) = a x 2 + b x + c with a positive a a value is f ( x ) ≥ f ( − b 2 a ) , f ( x ) ≥ f ( − b 2 a ) , or [ f ( − b 2 a ) , ∞ ) ; [ f ( − b 2 a ) , ∞ ) ; the range of a quadratic function written in general form with a negative a a value is f ( x ) ≤ f ( − b 2 a ) , f ( x ) ≤ f ( − b 2 a ) , or ( − ∞ , f ( − b 2 a ) ] . ( − ∞ , f ( − b 2 a ) ] .

The range of a quadratic function written in standard form f ( x ) = a ( x − h ) 2 + k f ( x ) = a ( x − h ) 2 + k with a positive a a value is f ( x ) ≥ k ; f ( x ) ≥ k ; the range of a quadratic function written in standard form with a negative a a value is f ( x ) ≤ k . f ( x ) ≤ k .

Given a quadratic function, find the domain and range.

• Identify the domain of any quadratic function as all real numbers.
• Determine whether a a is positive or negative. If a a is positive, the parabola has a minimum. If a a is negative, the parabola has a maximum.
• Determine the maximum or minimum value of the parabola, k . k .
• If the parabola has a minimum, the range is given by f ( x ) ≥ k , f ( x ) ≥ k , or [ k , ∞ ) . [ k , ∞ ) . If the parabola has a maximum, the range is given by f ( x ) ≤ k , f ( x ) ≤ k , or ( − ∞ , k ] . ( − ∞ , k ] .

Find the domain and range of f ( x ) = − 5 x 2 + 9 x − 1. f ( x ) = − 5 x 2 + 9 x − 1.

As with any quadratic function, the domain is all real numbers.

Because a a is negative, the parabola opens downward and has a maximum value. We need to determine the maximum value. We can begin by finding the x - x - value of the vertex.

The maximum value is given by f ( h ) . f ( h ) .

The range is f ( x ) ≤ 61 20 , f ( x ) ≤ 61 20 , or ( − ∞ , 61 20 ] . ( − ∞ , 61 20 ] .

Find the domain and range of f ( x ) = 2 ( x − 4 7 ) 2 + 8 11 . f ( x ) = 2 ( x − 4 7 ) 2 + 8 11 .

Determining the Maximum and Minimum Values of Quadratic Functions

The output of the quadratic function at the vertex is the maximum or minimum value of the function, depending on the orientation of the parabola . We can see the maximum and minimum values in Figure 9 .

There are many real-world scenarios that involve finding the maximum or minimum value of a quadratic function, such as applications involving area and revenue.

Finding the Maximum Value of a Quadratic Function

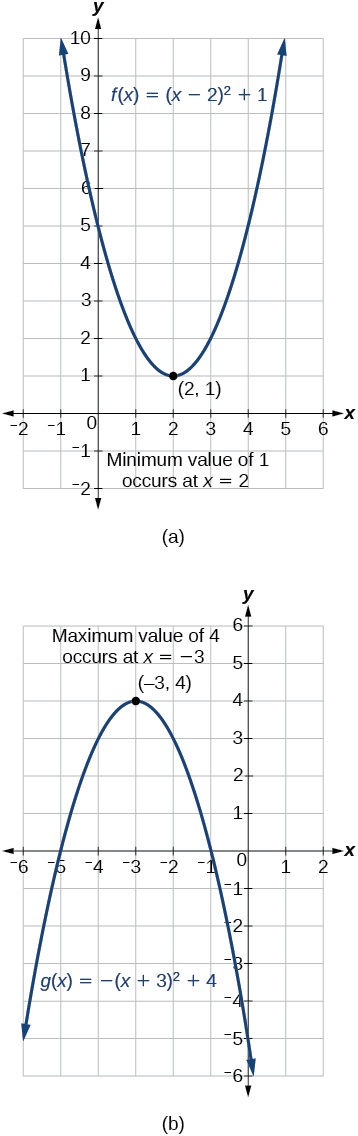
A backyard farmer wants to enclose a rectangular space for a new garden within her fenced backyard. She has purchased 80 feet of wire fencing to enclose three sides, and she will use a section of the backyard fence as the fourth side.

• ⓐ Find a formula for the area enclosed by the fence if the sides of fencing perpendicular to the existing fence have length L . L .
• ⓑ What dimensions should she make her garden to maximize the enclosed area?

Let’s use a diagram such as Figure 10 to record the given information. It is also helpful to introduce a temporary variable, W , W , to represent the width of the garden and the length of the fence section parallel to the backyard fence.

Now we are ready to write an equation for the area the fence encloses. We know the area of a rectangle is length multiplied by width, so

This formula represents the area of the fence in terms of the variable length L . L . The function, written in general form, is

• ⓑ The quadratic has a negative leading coefficient, so the graph will open downward, and the vertex will be the maximum value for the area. In finding the vertex, we must be careful because the equation is not written in standard polynomial form with decreasing powers. This is why we rewrote the function in general form above. Since a a is the coefficient of the squared term, a = −2 , b = 80 , a = −2 , b = 80 , and c = 0. c = 0.

To find the vertex:

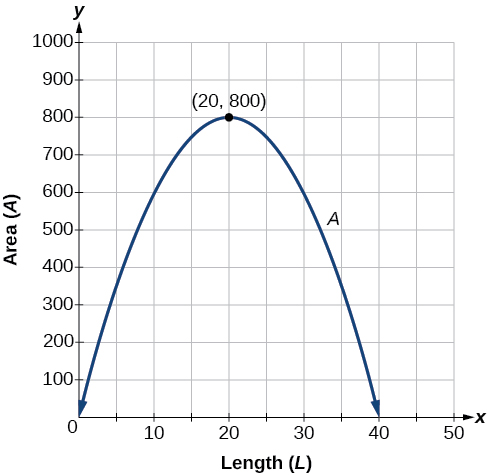
The maximum value of the function is an area of 800 square feet, which occurs when L = 20 L = 20 feet. When the shorter sides are 20 feet, there is 40 feet of fencing left for the longer side. To maximize the area, she should enclose the garden so the two shorter sides have length 20 feet and the longer side parallel to the existing fence has length 40 feet.

This problem also could be solved by graphing the quadratic function. We can see where the maximum area occurs on a graph of the quadratic function in Figure 11 .

Given an application involving revenue, use a quadratic equation to find the maximum.

• Write a quadratic equation for a revenue function.
• Find the vertex of the quadratic equation.
• Determine the y -value of the vertex.

Finding Maximum Revenue

The unit price of an item affects its supply and demand. That is, if the unit price goes up, the demand for the item will usually decrease. For example, a local newspaper currently has 84,000 subscribers at a quarterly charge of $30. Market research has suggested that if the owners raise the price to $32, they would lose 5,000 subscribers. Assuming that subscriptions are linearly related to the price, what price should the newspaper charge for a quarterly subscription to maximize their revenue?

Revenue is the amount of money a company brings in. In this case, the revenue can be found by multiplying the price per subscription times the number of subscribers, or quantity. We can introduce variables, p p for price per subscription and Q Q for quantity, giving us the equation Revenue = p Q . Revenue = p Q .

Because the number of subscribers changes with the price, we need to find a relationship between the variables. We know that currently p = 30 p = 30 and Q = 84,000. Q = 84,000. We also know that if the price rises to $32, the newspaper would lose 5,000 subscribers, giving a second pair of values, p = 32 p = 32 and Q = 79,000. Q = 79,000. From this we can find a linear equation relating the two quantities. The slope will be

This tells us the paper will lose 2,500 subscribers for each dollar they raise the price. We can then solve for the y -intercept.

This gives us the linear equation Q = −2,500 p + 159,000 Q = −2,500 p + 159,000 relating cost and subscribers. We now return to our revenue equation.

We now have a quadratic function for revenue as a function of the subscription charge. To find the price that will maximize revenue for the newspaper, we can find the vertex.

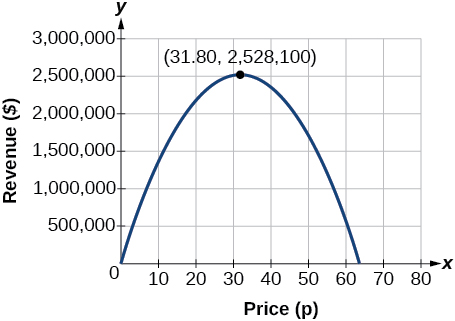
The model tells us that the maximum revenue will occur if the newspaper charges $31.80 for a subscription. To find what the maximum revenue is, we evaluate the revenue function.

This could also be solved by graphing the quadratic as in Figure 12 . We can see the maximum revenue on a graph of the quadratic function.

Finding the x - and y -Intercepts of a Quadratic Function

Much as we did in the application problems above, we also need to find intercepts of quadratic equations for graphing parabolas. Recall that we find the y - y - intercept of a quadratic by evaluating the function at an input of zero, and we find the x - x - intercepts at locations where the output is zero. Notice in Figure 13 that the number of x - x - intercepts can vary depending upon the location of the graph.

Given a quadratic function f ( x ) , f ( x ) , find the y - y - and x -intercepts.

• Evaluate f ( 0 ) f ( 0 ) to find the y -intercept.
• Solve the quadratic equation f ( x ) = 0 f ( x ) = 0 to find the x -intercepts.

Finding the y - and x -Intercepts of a Parabola

Find the y - and x -intercepts of the quadratic f ( x ) = 3 x 2 + 5 x − 2. f ( x ) = 3 x 2 + 5 x − 2.

We find the y -intercept by evaluating f ( 0 ) . f ( 0 ) .

So the y -intercept is at ( 0 , −2 ) . ( 0 , −2 ) .

For the x -intercepts, we find all solutions of f ( x ) = 0. f ( x ) = 0.

In this case, the quadratic can be factored easily, providing the simplest method for solution.

So the x -intercepts are at ( 1 3 , 0 ) ( 1 3 , 0 ) and ( − 2 , 0 ) . ( − 2 , 0 ) .

By graphing the function, we can confirm that the graph crosses the y -axis at ( 0 , −2 ) . ( 0 , −2 ) . We can also confirm that the graph crosses the x -axis at ( 1 3 , 0 ) ( 1 3 , 0 ) and ( −2 , 0 ) . ( −2 , 0 ) . See Figure 14

Rewriting Quadratics in Standard Form

In Example 7 , the quadratic was easily solved by factoring. However, there are many quadratics that cannot be factored. We can solve these quadratics by first rewriting them in standard form.

Given a quadratic function, find the x - x - intercepts by rewriting in standard form .

• Substitute a a and b b into h = − b 2 a . h = − b 2 a .
• Substitute x = h x = h into the general form of the quadratic function to find k . k .
• Rewrite the quadratic in standard form using h h and k . k .
• Solve for when the output of the function will be zero to find the x - x - intercepts.

Finding the x -Intercepts of a Parabola

Find the x - x - intercepts of the quadratic function f ( x ) = 2 x 2 + 4 x − 4. f ( x ) = 2 x 2 + 4 x − 4.

We begin by solving for when the output will be zero.

Because the quadratic is not easily factorable in this case, we solve for the intercepts by first rewriting the quadratic in standard form.

We know that a = 2. a = 2. Then we solve for h h and k . k .

So now we can rewrite in standard form.

We can now solve for when the output will be zero.

The graph has x -intercepts at ( −1 − 3 , 0 ) ( −1 − 3 , 0 ) and ( −1 + 3 , 0 ) . ( −1 + 3 , 0 ) .

We can check our work by graphing the given function on a graphing utility and observing the x - x - intercepts. See Figure 15 .

We could have achieved the same results using the quadratic formula. Identify a = 2 , b = 4 a = 2 , b = 4 and c = −4. c = −4.

So the x -intercepts occur at ( − 1 − 3 , 0 ) ( − 1 − 3 , 0 ) and ( − 1 + 3 , 0 ) . ( − 1 + 3 , 0 ) .

In a Try It , we found the standard and general form for the function g ( x ) = 13 + x 2 − 6 x . g ( x ) = 13 + x 2 − 6 x . Now find the y - and x -intercepts (if any).

Applying the Vertex and x -Intercepts of a Parabola

A ball is thrown upward from the top of a 40 foot high building at a speed of 80 feet per second. The ball’s height above ground can be modeled by the equation H ( t ) = − 16 t 2 + 80 t + 40. H ( t ) = − 16 t 2 + 80 t + 40.

• ⓐ When does the ball reach the maximum height?
• ⓑ What is the maximum height of the ball?
• ⓒ When does the ball hit the ground?

The ball reaches a maximum height after 2.5 seconds.

The ball reaches a maximum height of 140 feet.

We use the quadratic formula.

Because the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions.

The second answer is outside the reasonable domain of our model, so we conclude the ball will hit the ground after about 5.458 seconds. See Figure 16 .

Note that the graph does not represent the physical path of the ball upward and downward. Keep the quantities on each axis in mind while interpreting the graph.

A rock is thrown upward from the top of a 112-foot high cliff overlooking the ocean at a speed of 96 feet per second. The rock’s height above ocean can be modeled by the equation H ( t ) = −16 t 2 + 96 t + 112. H ( t ) = −16 t 2 + 96 t + 112.

• ⓐ When does the rock reach the maximum height?
• ⓑ What is the maximum height of the rock?
• ⓒ When does the rock hit the ocean?

Access these online resources for additional instruction and practice with quadratic equations.

• Graphing Quadratic Functions in General Form
• Graphing Quadratic Functions in Standard Form
• Quadratic Function Review
• Characteristics of a Quadratic Function

5.1 Section Exercises

Explain the advantage of writing a quadratic function in standard form.

How can the vertex of a parabola be used in solving real-world problems?

Explain why the condition of a ≠ 0 a ≠ 0 is imposed in the definition of the quadratic function.

What is another name for the standard form of a quadratic function?

What two algebraic methods can be used to find the horizontal intercepts of a quadratic function?

For the following exercises, rewrite the quadratic functions in standard form and give the vertex.

f ( x ) = x 2 − 12 x + 32 f ( x ) = x 2 − 12 x + 32

g ( x ) = x 2 + 2 x − 3 g ( x ) = x 2 + 2 x − 3

f ( x ) = x 2 − x f ( x ) = x 2 − x

f ( x ) = x 2 + 5 x − 2 f ( x ) = x 2 + 5 x − 2

h ( x ) = 2 x 2 + 8 x − 10 h ( x ) = 2 x 2 + 8 x − 10

k ( x ) = 3 x 2 − 6 x − 9 k ( x ) = 3 x 2 − 6 x − 9

f ( x ) = 2 x 2 − 6 x f ( x ) = 2 x 2 − 6 x

f ( x ) = 3 x 2 − 5 x − 1 f ( x ) = 3 x 2 − 5 x − 1

For the following exercises, determine whether there is a minimum or maximum value to each quadratic function. Find the value and the axis of symmetry.

y ( x ) = 2 x 2 + 10 x + 12 y ( x ) = 2 x 2 + 10 x + 12

f ( x ) = 2 x 2 − 10 x + 4 f ( x ) = 2 x 2 − 10 x + 4

f ( x ) = − x 2 + 4 x + 3 f ( x ) = − x 2 + 4 x + 3

f ( x ) = 4 x 2 + x − 1 f ( x ) = 4 x 2 + x − 1

h ( t ) = −4 t 2 + 6 t − 1 h ( t ) = −4 t 2 + 6 t − 1

f ( x ) = 1 2 x 2 + 3 x + 1 f ( x ) = 1 2 x 2 + 3 x + 1

f ( x ) = − 1 3 x 2 − 2 x + 3 f ( x ) = − 1 3 x 2 − 2 x + 3

For the following exercises, determine the domain and range of the quadratic function.

f ( x ) = ( x − 3 ) 2 + 2 f ( x ) = ( x − 3 ) 2 + 2

f ( x ) = −2 ( x + 3 ) 2 − 6 f ( x ) = −2 ( x + 3 ) 2 − 6

f ( x ) = x 2 + 6 x + 4 f ( x ) = x 2 + 6 x + 4

f ( x ) = 2 x 2 − 4 x + 2 f ( x ) = 2 x 2 − 4 x + 2

For the following exercises, use the vertex ( h , k ) ( h , k ) and a point on the graph ( x , y ) ( x , y ) to find the general form of the equation of the quadratic function.

( h , k ) = ( 2 , 0 ) , ( x , y ) = ( 4 , 4 ) ( h , k ) = ( 2 , 0 ) , ( x , y ) = ( 4 , 4 )

( h , k ) = ( −2 , −1 ) , ( x , y ) = ( −4 , 3 ) ( h , k ) = ( −2 , −1 ) , ( x , y ) = ( −4 , 3 )

( h , k ) = ( 0 , 1 ) , ( x , y ) = ( 2 , 5 ) ( h , k ) = ( 0 , 1 ) , ( x , y ) = ( 2 , 5 )

( h , k ) = ( 2 , 3 ) , ( x , y ) = ( 5 , 12 ) ( h , k ) = ( 2 , 3 ) , ( x , y ) = ( 5 , 12 )

( h , k ) = ( − 5 , 3 ) , ( x , y ) = ( 2 , 9 ) ( h , k ) = ( − 5 , 3 ) , ( x , y ) = ( 2 , 9 )

( h , k ) = ( 3 , 2 ) , ( x , y ) = ( 10 , 1 ) ( h , k ) = ( 3 , 2 ) , ( x , y ) = ( 10 , 1 )

( h , k ) = ( 0 , 1 ) , ( x , y ) = ( 1 , 0 ) ( h , k ) = ( 0 , 1 ) , ( x , y ) = ( 1 , 0 )

( h , k ) = ( 1 , 0 ) , ( x , y ) = ( 0 , 1 ) ( h , k ) = ( 1 , 0 ) , ( x , y ) = ( 0 , 1 )

For the following exercises, sketch a graph of the quadratic function and give the vertex, axis of symmetry, and intercepts.

f ( x ) = x 2 − 2 x f ( x ) = x 2 − 2 x

f ( x ) = x 2 − 6 x − 1 f ( x ) = x 2 − 6 x − 1

f ( x ) = x 2 − 5 x − 6 f ( x ) = x 2 − 5 x − 6

f ( x ) = x 2 − 7 x + 3 f ( x ) = x 2 − 7 x + 3

f ( x ) = −2 x 2 + 5 x − 8 f ( x ) = −2 x 2 + 5 x − 8

f ( x ) = 4 x 2 − 12 x − 3 f ( x ) = 4 x 2 − 12 x − 3

For the following exercises, write the equation for the graphed quadratic function.

For the following exercises, use the table of values that represent points on the graph of a quadratic function. By determining the vertex and axis of symmetry, find the general form of the equation of the quadratic function.

For the following exercises, use a calculator to find the answer.

Graph on the same set of axes the functions f ( x ) = x 2 f ( x ) = x 2 , f ( x ) = 2 x 2 f ( x ) = 2 x 2 , and f ( x ) = 1 3 x 2 f ( x ) = 1 3 x 2 .

What appears to be the effect of changing the coefficient?

Graph on the same set of axes f ( x ) = x 2 , f ( x ) = x 2 + 2 f ( x ) = x 2 , f ( x ) = x 2 + 2 and f ( x ) = x 2 , f ( x ) = x 2 + 5 f ( x ) = x 2 , f ( x ) = x 2 + 5 and f ( x ) = x 2 − 3. f ( x ) = x 2 − 3. What appears to be the effect of adding a constant?

Graph on the same set of axes f ( x ) = x 2 , f ( x ) = ( x − 2 ) 2 , f ( x − 3 ) 2 f ( x ) = x 2 , f ( x ) = ( x − 2 ) 2 , f ( x − 3 ) 2 , and f ( x ) = ( x + 4 ) 2 . f ( x ) = ( x + 4 ) 2 .

What appears to be the effect of adding or subtracting those numbers?

The path of an object projected at a 45 degree angle with initial velocity of 80 feet per second is given by the function h ( x ) = − 32 ( 80 ) 2 x 2 + x h ( x ) = − 32 ( 80 ) 2 x 2 + x where x x is the horizontal distance traveled and h ( x ) h ( x ) is the height in feet. Use the TRACE feature of your calculator to determine the height of the object when it has traveled 100 feet away horizontally.

A suspension bridge can be modeled by the quadratic function h ( x ) = .0001 x 2 h ( x ) = .0001 x 2 with −2000 ≤ x ≤ 2000 −2000 ≤ x ≤ 2000 where | x | | x | is the number of feet from the center and h ( x ) h ( x ) is height in feet. Use the TRACE feature of your calculator to estimate how far from the center does the bridge have a height of 100 feet.

For the following exercises, use the vertex of the graph of the quadratic function and the direction the graph opens to find the domain and range of the function.

Vertex ( 1 , −2 ) , ( 1 , −2 ) , opens up.

Vertex ( −1 , 2 ) ( −1 , 2 ) opens down.

Vertex ( −5 , 11 ) , ( −5 , 11 ) , opens down.

Vertex ( −100 , 100 ) , ( −100 , 100 ) , opens up.

For the following exercises, write the equation of the quadratic function that contains the given point and has the same shape as the given function.

Contains ( 1 , 1 ) ( 1 , 1 ) and has shape of f ( x ) = 2 x 2 . f ( x ) = 2 x 2 . Vertex is on the y - y - axis.

Contains ( −1 , 4 ) ( −1 , 4 ) and has the shape of f ( x ) = 2 x 2 . f ( x ) = 2 x 2 . Vertex is on the y - y - axis.

Contains ( 2 , 3 ) ( 2 , 3 ) and has the shape of f ( x ) = 3 x 2 . f ( x ) = 3 x 2 . Vertex is on the y - y - axis.

Contains ( 1 , −3 ) ( 1 , −3 ) and has the shape of f ( x ) = − x 2 . f ( x ) = − x 2 . Vertex is on the y - y - axis.

Contains ( 4 , 3 ) ( 4 , 3 ) and has the shape of f ( x ) = 5 x 2 . f ( x ) = 5 x 2 . Vertex is on the y - y - axis.

Contains ( 1 , −6 ) ( 1 , −6 ) has the shape of f ( x ) = 3 x 2 . f ( x ) = 3 x 2 . Vertex has x-coordinate of −1. −1.

Real-World Applications

Find the dimensions of the rectangular dog park producing the greatest enclosed area given 200 feet of fencing.

Find the dimensions of the rectangular dog park split into 2 pens of the same size producing the greatest possible enclosed area given 300 feet of fencing.

Find the dimensions of the rectangular dog park producing the greatest enclosed area split into 3 sections of the same size given 500 feet of fencing.

Among all of the pairs of numbers whose sum is 6, find the pair with the largest product. What is the product?

Among all of the pairs of numbers whose difference is 12, find the pair with the smallest product. What is the product?

Suppose that the price per unit in dollars of a cell phone production is modeled by p = $ 45 − 0.0125 x , p = $ 45 − 0.0125 x , where x x is in thousands of phones produced, and the revenue represented by thousands of dollars is R = x ⋅ p . R = x ⋅ p . Find the production level that will maximize revenue.

A rocket is launched in the air. Its height, in meters above sea level, as a function of time, in seconds, is given by h ( t ) = −4.9 t 2 + 229 t + 234. h ( t ) = −4.9 t 2 + 229 t + 234. Find the maximum height the rocket attains.

A ball is thrown in the air from the top of a building. Its height, in meters above ground, as a function of time, in seconds, is given by h ( t ) = − 4.9 t 2 + 24 t + 8. h ( t ) = − 4.9 t 2 + 24 t + 8. How long does it take to reach maximum height?

A soccer stadium holds 62,000 spectators. With a ticket price of $11, the average attendance has been 26,000. When the price dropped to $9, the average attendance rose to 31,000. Assuming that attendance is linearly related to ticket price, what ticket price would maximize revenue?

A farmer finds that if she plants 75 trees per acre, each tree will yield 20 bushels of fruit. She estimates that for each additional tree planted per acre, the yield of each tree will decrease by 3 bushels. How many trees should she plant per acre to maximize her harvest?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra-2e/pages/5-1-quadratic-functions

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 14

• Quiz 1 Quadratic functions & equations

Introduction to Quadratics

Note the other Quadratics section that follow: Solving Quadratics by Factoring and Completing the Square , Quadratic Inequalities , and  Quadratic Applications.

Quadratics and the Parabola

One special type of polynomial equation that you’ll work with a lot is a Quadratic Equation , (also known as a Quadratic Function , if it meets the requirements of being a function ).

A quadratic is a polynomial that has an $ \boldsymbol{{x}^{2}}$ in it; it’s as simple as that. The degree of quadratic polynomials is two , since the highest power (exponent) of $ x$ is two . The quadratic curve is called a parabola . Technically, the parabola is the actual picture of the graph (shaped like a “$ \bigcup $”), and the quadratic is the equation that represent the points on the parabola. But a lot of times we hear the words “quadratic” and “parabola” used interchangeably.

This is interesting: if you were to create a chart with the $ x$’s and $ y$’s with a quadratic equation, if the $ x$’s are all spaced evenly apart, the second difference (the differences of the differences) of the $ y$’s are equal. (A linear equation has the first differences equal, as we saw earlier). For example, for $ y={{x}^{2}}$,

It seems like every math book talks about quadratics with either a thrown ball or rocket ship example. I’d like to change things up a bit and talk about a bride throwing her bouquet behind her – going up in the air and coming back down to be caught. We’ll look more at this specific example below.

For the purposes of this section, we will only deal with “ vertical parabolas ” in quadratics, that either go up or back down (like our bouquet), or they go down and then back up. (Actually, they can go sideways, too, as we’ll see in the Conics section , but these are not functions). Thus, these quadratics either have a maximum point, or a minimum point; whatever this point is, it’s called the vertex .

The basic (parent) function for a quadratic is $ y={{x}^{2}}$, where the vertex is $ (0,0)$ and the parabola faces up. There are many different forms of the transformed function (which we’ll talk about in the Parent Functions and Transformation section ), as shown below. (The “sideways” parabolas are in the form $ x={{y}^{2}}$; these are not functions, since they don’t meet the vertical line test).

Below are the three basic equations for a parabola; Standard Form , Vertex Form , and Factored (Intercept) Form . They all tell us different things about the parabola. Do you see why they are called what they are called?

Here are some examples of parabolas in standard form, with their characteristics:

Graphing Quadratics (Parabolas)

Parent function.

Before we talk specifically about the Vertex and Factored forms of quadratics, let’s graph the simplest form of a parabola, $ y={{x}^{2}}$, using a t-chart .

Note that parabolas have symmetry ; it is a mirror image of itself across the vertical line that contains the vertex ; this line is called the line of symmetry ( LOS) , or axis of symmetry ( AOS ). In this case, our LOS is $ x=0$. Do you see how the LOS is always “$ x=x \text{ value of the vertex point}$” for these “up and down” parabolas?

You’ll probably be asked to get the domain (all the possible $ x$-values) and range (all the possible $ y$-values) when you graph parabolas. Remember to use your pencil to check the domain and range like we did here in the Algebraic Functions section .

For the parent function $ y={{x}^{2}}$, the domain is $ \left( {-\infty ,\infty } \right)$ ,  or all real numbers, since these types of parabolas go up and out to the sides forever (this is true for every vertical parabola). However, the range is just $ \left[ {0,\infty } \right)$, since the parabola has a vertex at $ (0,0$) and the $ y$-values never get below 0 .

Here’s our first graph:

Domain:  $ \left( {-\infty ,\infty } \right)$

Range: $ \left[ {0,\infty } \right)$

Graphing with Vertex Form

It’s very important to find out how to get the vertex of a parabola, since that you way can get the line of symmetry ( LOS) and graph it more easily. As we saw earlier, one of the forms of a quadratic equation is what we call vertex form . If we get the equation in that form, we can get the vertex easily:

With this equation, the vertex is the point $ (h,k)$. In the example above, the vertex is $ (-2,1)$. The LOS is $ x=-2$, and the vertex is a minimum , since there is no negative sign before the 3 . Note that we have to be a little careful with the signs in this equation and remember that this equation is the same as $ y=3{{(x-(-2))}^{2}}+(-1)$, and that’s why the vertex is $ (-2,-1)$.

Let’s graph the equation  $ y=3{{(x+2)}^{2}}-1$ . Since the $ y$ -intercept is when $ x=0$, we can easily solve for it: $ y$-intercept is $ y=3{{(0+2)}^{2}}-1=3{{(2)}^{2}}-1=12-1=11$; the point is $ (0,11)$.

We can graph the vertex and the $ y$-intercept, and then do a quick t-chart to find some of the other values. The graph is shifted down 1 , over to the left 2 , and a little skinnier than the graph of $ y={{x}^{2}}$. We’ll talk about these transformations of graphs later in the Parent Graphs and Transformations section.

The domain of this graph is still all real numbers, yet the range is $ \left[ {-1,\infty } \right)$ ; this is because the $ y$-part of the vertex is  –1 , so that is the lowest point of the range. Here is the graph:

        Domain: $ \left( {-\infty ,\infty } \right)$

        Range: $ \left[ {-1,\infty } \right)$

One more thing to mention: we call points of a parabola that are directly opposite each other (over the  LOS ) a  point of reflection , or  reflection point . For example, the  reflection point of $ (0,11)$ is $ (-4,11)$. See how both points are equidistant from $ x=-2$?

Also note that sometimes the equation is almost in vertex form; it might look something like $ \displaystyle y=-2{{\left( \frac{1}{2}x+2 \right)}^{2}}-3$, and we can do some algebra to change it into $ \displaystyle y=-2{{\left( {\frac{1}{2}\left( {x+4} \right)} \right)}^{2}}-3=-2{{\left( {\frac{1}{2}} \right)}^{2}}{{\left( {x+4} \right)}^{2}}-3=-2\left( {\frac{1}{4}} \right){{\left( {x+4} \right)}^{2}}-3=-\frac{1}{2}{{\left( {x+4} \right)}^{2}}-3$, so the vertex is $ (-4,3)$.

Graphing with Standard Form

When the equation is given in standard form , it’s useful to know the formulas below to get the vertex and $ y$ -intercept . (We can also Complete the Square to go from Standard Form to Vertex Form , which we learn how to do here in the Solving Quadratics by Factoring and Completing the Square section .)

Once you graph the vertex and know which direction the parabola points, you can either graph the $ y$-intercept, or other points close to the vertex to graph the actual graph.

Graphing with Factored (Intercept) Form

With factored , or intercept form , we automatically have the $ x$-intercept(s), so we can graph those right away. Then, when we get the $ x$-intercepts, we can take the average (the point right in the middle) to get the Line of Symmetry ( LOS ). Then, to get the vertex , we can plug in the line of symmetry $ x$-point in the original equation to get the $ y$.

Here is an example:

Standard Form to Vertex Form

Let’s look at some examples where we get the vertex from a standard form equation. Remember that when the coefficient of $ {{x}^{2}}$ is positive, the parabola faces up, and when the coefficient is negative, it faces down.

Let’s graph the last equation above $ y=-{{x}^{2}}+4x+3$ , where the $ y$-intercept is $ (0,3)$. and the vertex is $ (2,7)$. The t-chart includes other points.

Range:  $ \left( {-\infty ,7} \right]$

Example Real-Life Quadratic Application

Let’s make the $ x$- axis be the time (in seconds) and the $ y$- axis  the height of the bouquet at that time (in feet).

Note : The $ x$-axis is time, not a distance; sometimes parabolas represent the distance on the $ x$-axis and the height on the $ y$-axis, and the shapes are similar. Height versus distance would be the actual path or trajectory of the bouquet, whereas this graph is the height versus the time .)

Let’s say, hypothetically speaking, that the trajectory of the bouquet (the height  it takes in the air, per a certain amount of time ) can be modeled by the equation below. We can also call this the “ projectile ” of the bouquet (usually in math books, they talk about trajectories of rockets or balls):

$ f(t)=-16{{t}^{2}}+20t+5$      Remember function n otation ? If not go back and review here in the Algebraic Functions section .

Why the parabolic shape? Think about it; if you were to throw something up in the air, it doesn’t keep going; it makes a curve and comes backs down. This is because of gravity.

Just for some history and a tiny bit of physics : The Italian scientist Galileo discovered the parabolic trajectory of projectiles in the early 17 th century. Neglecting air friction, the $ -16{{t}^{2}}$ represents the gravity of of an object in feet per second per second (actually the $ 16$ is half the force of gravity). The constant ( $ 5$  feet, in our example) represents the height $ h$ at which the object is thrown at the beginning, and the $ 20$ in the $ 20t$ represents the initial velocity $ {{v}_{0}}$ vertically upward, feet per second, or how fast the object is thrown up in the air. Thus, we have $ f(t)=-16{{t}^{2}}+{{v}_{0}}t+h$  for these applications.

Let’s figure out how high the bouquet goes, when it hits this highest point, and when it hits the ground, assuming it is not caught .

To get the highest point of the bouquet, we need to get the vertex, which will be at a maximum , since we have a negative coefficient before the $ {{x}^{2}}$. Since our quadratic equation is in standard form, let’s use our cool $ \displaystyle \left( {-\frac{b}{{2a}},\,\,f\left( {-\frac{b}{{2a}}} \right)} \right)$ trick to obtain the vertex (highest point), and $ y$-intercept to graph our equation:

The highest point is at ( .625 seconds, 11.25 feet). Our $ y$-intercept is $ (0,5)$.

Here’s what the graph looks like. Note that even though this may look like the path of the bouquet (distance of the bouquet from where it was thrown), we are actually graphing the  height of the bouquet per   time .

Note that we’ll see this type of application, as well as more applications in the Quadratic Applications section .

Solving for Roots with Quadratics

Many times we want to know where the quadratic hits the $ \boldsymbol{x}$ – axis (for example, to find out where the bouquet in our example hits the ground) ; these are called “$ \boldsymbol {x}$ -intercepts “, “ zeroes “, or “ roots ” of the quadratic equation. This is how we “ solve ” quadratic equations; we set them to 0 (like we do with linear equations!). Quadratics can have one or two roots , and when they never hit the $ \boldsymbol{x}$ -axis the roots are “imaginary”; we’ll address them later in the Imaginary (Non-Real) and Complex Numbers section.

Again, as we saw above, when the quadratic is in factored form , we can get the $ x$-intercepts by setting each factor to 0 and solving. We will learn about other ways to solve quadratic equations in the Solving Quadratics by Factoring and Completing the Square section .

Quadratic Formula (Quadratic Equation) for Solving Roots

When a quadratic equation is not in factored form, we can put in in standard form and use the Quadratic Equation to solve for the roots. It looks complicated, but it’s not too bad, once you get the hang of it. The nice thing about the Quadratic Formula is that it can be used with any quadratic, even those without actual $ x$-intercepts, in which case they will be imaginary (see examples here in the Imaginary (Non-Real) and Complex Numbers section ).

The $ \pm$ means that, since we typically have two solutions, unless the vertex is on the $ x$-axis, in which case we have one solution. We need to find one solution using a “$ +$” in that part of the equation, and one using a “$ -$” there. Here’s an example:

The Quadratic Formula is a very important thing to remember; you may even learn a song to help you remember it! You may sing it to “Pop Goes the Weasel”: “$ x$ equals negative $ b$, plus or minus the square root, of $ b$ squared minus $ 4ac$, all over $ 2a$”.

Now let’s get the roots by using the complete quadratic equation for our bouquet-throwing equation. These roots are a little more complicated, since they aren’t rational ; which means they actually go on and on “forever”. We’ll find the answers to the thousandths place ( 3 decimal places after the decimal point). This is one we couldn’t have factored!

Which of the roots do we want when we are getting the time the bouquet hits the ground? Since time can’t be nevative, we want the positive one ! Many times in math application, we need to “throw away” some or all of the answers.

The bouquet hit the ground approximately 1.464 seconds after the bride threw it up in the air. (Note that this is a time, not a distance; sometimes parabolas represent the distance on the $ x$-axis and the height on the $ y$-axis, and the shapes are similar.)

Note that, from above, $ \displaystyle \text{ }\frac{{5-3\sqrt{5}}}{8}\text{ and }\frac{{5+3\sqrt{5}}}{8}$ (also written as $ \displaystyle \frac{5}{8}-\frac{{3\sqrt{5}}}{8}\text{ and }\frac{5}{8}+\frac{{3\sqrt{5}}}{8}$) are called conjugates or radical conjugates , since they are identical, except for the change in signs in the middle of the real terms and the irrational terms. When we have an irrational value for roots, the conjugate  is also a root. As other examples, if $ \displaystyle 3+\sqrt{{17}}$ is a root, then $ \displaystyle 3-\sqrt{{17}}$ is also a root; if $ \sqrt{2}$ is a root, then $ -\sqrt{2}$ is also a root.

Let’s ask one more question, and you can see the result on the graph below. How high will be bouquet be after 1 second, and is it on its way up, or its way down?

At one second, we can plug in “ 1 ” for the $ t$, since the $ t$-axis (this is usually what we call the $ x$-axis) is time. We have:

$ \begin{array}{c}f(t)=-16{{t}^{2}}+20t+5\,\\f(1)=-16{{(1)}^{2}}+20(1)+5=-16+20+5=9\end{array}$

This means at 1 second, the bouquet is 9 feet off the ground. Look at the graph below; at 1 second, it’s after the time when it was at its highest, so the bouquet is on its way down. We can also see that the time of 1 second is later than the time of the highest point (vertex) at .625 seconds to know that it’s on its way down.

Using the Discriminant to Determine Types of Solutions

It turns out that what’s under the radicand in the Quadratic Equation, which is $ \displaystyle {{b}^{2}}-4ac$ for the equation $ a{{x}^{2}}+bx+c=0$, happens to be very important; so important, that’s it’s given the name “ the discriminant.” It helps us to discriminate between the type and number of $ \boldsymbol{x}$ – intercepts , or “ real roots ” that we’ll get from that equation.

Note that we use the word “ real ” to indicate that the root isn’t imaginary . In fact, only real roots have $ \boldsymbol{x}$ – intercepts , as shown:

Using the Graphing Calculator to Find the Vertex and Solve Quadratics

We can use the graphing calculator to graph the quadratic, and also find the vertex (which is the minimum or maximum), the roots, $ y$-intercept, and any values on the graph. Some teachers will let you use it during tests! If you need a quick introduction to the graphing calculator, read the Introduction to the Graphing Calculator section first. (I’m using the TI-84 Plus CE calculator.)

NOTE: If at any time the graphing calculator gets “stuck” (blinking line in top right of screen), simply turn the calculator OFF (2 nd ON ), and then back ON again.

To find the Vertex of a quadratic equation using a graphing calculator:

You can find the $ \boldsymbol{x}$ – intercepts , or roots of a quadratic (or any polynomial) equation as follows. Note that when the parabola doesn’t cross the $ x$-axis, and thus there are no real solutions, you’ll get an error in your calculator when you try to find the zeros.

We can also use the calculator to get any $ y$-value for $ x$, the $ \boldsymbol{y}$ -intercept , and see a table of the $ x,y$-values:

There’s one more really neat thing we can do with the calculator; we can check the answers we get from the Quadratic Formula – even if they are quite complicated. To do this, we’ll store the answers we get in a variable $ x$ in the calculator, and then type in the quadratic to see if we used the Quadratic Formula correctly (the quadratic should be 0 ).

Quadratic Transformations

We will learn about transforming parent functions here in the Parent Functions and Transformations section , but transforming quadratics isn’t that difficult for horizontal parabolas.

The parent function for quadratics is $ \boldsymbol{{x}^{2}}$ with a vertex at $ (0,0)$. We can see most easily see a quadratic transformation by putting the quadratic into vertex form , and plotting the new vertex. When the vertex is other than $ (0, 0)$, we have a horizontal and/or vertical shift of the parent function. When there is no vertical or horizontal stretch , we go over 1 (on each side of the vertex, since the function is symmetrical) and either up or down 1 to get the points close to the vertex. When the parabola is “upside down”, there is a negative before the term with the $ {x}^{2}$.

Thus, for the transformed function $ y=a{{\left( {x-h} \right)}^{2}}+k$, $ (h,k)$ is the vertex, and “$ a$” is a vertical stretch. (If “$ a$” isn’t 1 , go over 1 or back 1 , but then go up or down the value of “$ a$”). If the “$ a$” is negative, do the same with a flipped (facing down) graph. Then you can plug in other values of “$ x$” close to the axis of symmetry, to get the new values for “$ y$”. (For a horizontal stretch , such as $ y={{\left( {b\left( {x-h} \right)} \right)}^{2}}+k$, go up 1 or down 1 from the vertex, and then go over and back the value of “$ \displaystyle \frac{1}{b}$”).

Here are some examples; we can also do these transformations with t-charts like we do here in the Parent Functions and Transformations section :

Here are other types of problems you may see:

Quadratic Regression

We learned about regression here in the Scatterplots, Correlation, and Regression section ; let’s find a Quadratic Regression .

Model the following data set using the graphing calculator.

Enter the data and perform regression in the calculator.

Study Guides > College Algebra

Graphs of quadratic functions.

Characteristics of Parabolas

Example: Identifying the Characteristics of a Parabola

Answer: The vertex is the turning point of the graph. We can see that the vertex is at (3, 1). Because this parabola opens upward, the axis of symmetry is the vertical line that intersects the parabola at the vertex. So the axis of symmetry is x  = 3. This parabola does not cross the x -axis, so it has no zeros. It crosses the y -axis at (0, 7) so this is the y -intercept.

Equations of Quadratic Functions

[latex]f\left(x\right)=a{x}^{2}+bx+c[/latex]

[latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex]

Given a quadratic function in general form, find the vertex of the parabola.

[latex]f(x)=ax^2+bx+c[/latex]

• Identify a ,  b , and  c .
• Find h , the x -coordinate of the vertex, by substituting a and b  into [latex]h=-\frac{b}{2a}[/latex].
• Find k , the y -coordinate of the vertex, by evaluating [latex]k=f\left(h\right)=f\left(-\frac{b}{2a}\right)[/latex]

Example: Finding the Vertex of a Quadratic Function

[latex]\begin{array}{c}h=-\frac{b}{2a}\hfill \\ \text{ }=-\frac{-6}{2\left(2\right)}\hfill \\ \text{ }=\frac{6}{4}\hfill \\ \text{ }=\frac{3}{2}\hfill \end{array}[/latex]

[latex]\begin{array}{c}k=f\left(h\right)\hfill \\ \text{ }=f\left(\frac{3}{2}\right)\hfill \\ \text{ }=2{\left(\frac{3}{2}\right)}^{2}-6\left(\frac{3}{2}\right)+7\hfill \\ \text{ }=\frac{5}{2}\hfill \end{array}[/latex]

[latex]\begin{array}{c}f\left(x\right)=a{x}^{2}+bx+c\hfill \\ f\left(x\right)=2{x}^{2}-6x+7\hfill \end{array}[/latex]

[latex]f\left(x\right)=2{\left(x-\frac{3}{2}\right)}^{2}+\frac{5}{2}[/latex]

Answer: [latex]g\left(x\right)={x}^{2}-6x+13[/latex] in general form; [latex]g\left(x\right)={\left(x - 3\right)}^{2}+4[/latex] in standard form

Finding the Domain and Range of a Quadratic Function

A general note: domain and range of a quadratic function, how to: given a quadratic function, find the domain and range..

• Identify the domain of any quadratic function as all real numbers.
• Determine whether a  is positive or negative. If a  is positive, the parabola has a minimum. If a  is negative, the parabola has a maximum.
• Determine the maximum or minimum value of the parabola, k .
• If the parabola has a minimum, the range is given by [latex]f\left(x\right)\ge k[/latex], or [latex]\left[k,\infty \right)[/latex]. If the parabola has a maximum, the range is given by [latex]f\left(x\right)\le k[/latex], or [latex]\left(-\infty ,k\right][/latex].

Example: Finding the Domain and Range of a Quadratic Function

[latex]\begin{array}{c}h=-\frac{b}{2a}\hfill \\ \text{ }=-\frac{9}{2\left(-5\right)}\hfill \\ \text{ }=\frac{9}{10}\hfill \end{array}[/latex]

[latex]\begin{array}{c}f\left(\frac{9}{10}\right)=5{\left(\frac{9}{10}\right)}^{2}+9\left(\frac{9}{10}\right)-1\hfill \\ \text{ }=\frac{61}{20}\hfill \end{array}[/latex]

Answer: The domain is all real numbers. The range is [latex]f\left(x\right)\ge \frac{8}{11}[/latex], or [latex]\left[\frac{8}{11},\infty \right)[/latex].

Transformations of Quadratic Functions

[latex]\begin{array}{c}a{\left(x-h\right)}^{2}+k=a{x}^{2}+bx+c\hfill \\ a{x}^{2}-2ahx+\left(a{h}^{2}+k\right)=a{x}^{2}+bx+c\hfill \end{array}[/latex]

[latex]-2ah=b,\text{ so }h=-\frac{b}{2a}[/latex].

[latex]\begin{array}{c}a{h}^{2}+k=c\hfill \\ \text{ }k=c-a{h}^{2}\hfill \\ \text{ }=c-a-{\left(\frac{b}{2a}\right)}^{2}\hfill \\ \text{ }=c-\frac{{b}^{2}}{4a}\hfill \end{array}[/latex]

A General Note: Forms of Quadratic Functions

[latex]h=-\frac{b}{2a},\text{ }k=f\left(h\right)=f\left(\frac{-b}{2a}\right)[/latex].

How To: Given a graph of a quadratic function, write the equation of the function in general form.

• Identify the horizontal shift of the parabola; this value is h . Identify the vertical shift of the parabola; this value is k .
• Substitute the values of the horizontal and vertical shift for h  and k . in the function [latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex].
• Substitute the values of any point, other than the vertex, on the graph of the parabola for x  and [latex]f\left(x\right)[/latex].
• Solve for the stretch factor, | a |.
• If the parabola opens up, [latex]a>0[/latex]. If the parabola opens down, [latex]a<0[/latex] since this means the graph was reflected about the x -axis.
• Expand and simplify to write in general form.

Example: Writing the Equation of a Quadratic Function from the Graph

[latex]\begin{array}{c}-1=a{\left(0+2\right)}^{2}-3\hfill \\ \text{ }2=4a\hfill \\ \text{ }a=\frac{1}{2}\hfill \end{array}[/latex]

[latex]\begin{array}{c}g\left(x\right)=\frac{1}{2}{\left(x+2\right)}^{2}-3\hfill \\ \text{ }=\frac{1}{2}\left(x+2\right)\left(x+2\right)-3\hfill \\ \text{ }=\frac{1}{2}\left({x}^{2}+4x+4\right)-3\hfill \\ \text{ }=\frac{1}{2}{x}^{2}+2x+2 - 3\hfill \\ \text{ }=\frac{1}{2}{x}^{2}+2x - 1\hfill \end{array}[/latex]

Analysis of the Solution

Answer: The path passes through the origin and has vertex at [latex]\left(-4,\text{ }7\right)[/latex], so [latex]\left(h\right)x=-\frac{7}{16}{\left(x+4\right)}^{2}+7[/latex]. To make the shot, [latex]h\left(-7.5\right)[/latex] would need to be about 4 but [latex]h\left(-7.5\right)\approx 1.64[/latex]; he doesn’t make it.

Key Equations

Key concepts.

• A polynomial function of degree two is called a quadratic function.
• The graph of a quadratic function is a parabola. A parabola is a U-shaped curve that can open either up or down.
• The axis of symmetry is the vertical line passing through the vertex.
• Quadratic functions are often written in general form. Standard or vertex form is useful to easily identify the vertex of a parabola. Either form can be written from a graph.
• The vertex can be found from an equation representing a quadratic function.
• The domain of a quadratic function is all real numbers. The range varies with the function.

Licenses & Attributions

Cc licensed content, original.

• Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution .

CC licensed content, Shared previously

• College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution . License terms: Download for free at http://cnx.org/contents/ [email protected] .
• Question ID 120303, 120300. Authored by: Lumen Learning. License: CC BY: Attribution . License terms: IMathAS Community License CC-BY + GPL.

Please add a message.

Message received. Thanks for the feedback.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.7: Modeling with Quadratic Functions

• Last updated
• Save as PDF
• Page ID 93930

Learning Objectives

• Recognize characteristics of parabolas
• Understand how the graph of a parabola is related to its quadratic function
• Solve problems involving a quadratic function’s minimum or maximum value

in order to apply mathematical modeling to solve real-world applications.

Curved antennas, such as the ones shown in Figure \(\PageIndex{1}\), are commonly used to focus microwaves and radio waves to transmit television and telephone signals, as well as satellite and spacecraft communication. The cross-section of the antenna is in the shape of a parabola, which can be described by a quadratic function.

In this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion. Working with quadratic functions can be less complex than working with higher degree functions, so they provide a good opportunity for a detailed study of function behavior.

Recognizing Characteristics of Parabolas

The graph of a quadratic function is a U-shaped curve called a parabola. One important feature of the graph is that it has an extreme point, called the vertex . If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value . In either case, the vertex is a turning point on the graph. The graph is also symmetric with a vertical line drawn through the vertex, called the axis of symmetry . These features are illustrated in Figure \(\PageIndex{2}\).

The y-intercept is the point at which the parabola crosses the \(y\)-axis. The x-intercepts are the points at which the parabola crosses the \(x\)-axis. If they exist, the x-intercepts represent the zeros , or roots , of the quadratic function, the values of \(x\) at which \(y=0\).

Example \(\PageIndex{1}\): Identifying the Characteristics of a Parabola

Determine the vertex, axis of symmetry, zeros, and y-intercept of the parabola shown in Figure \(\PageIndex{3}\).

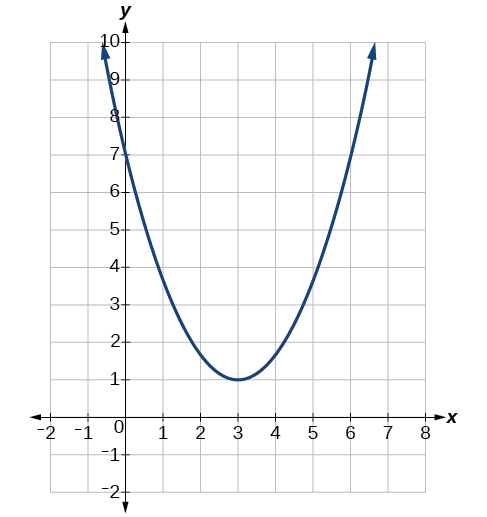
The vertex is the turning point of the graph. We can see that the vertex is at \((3,1)\). Because this parabola opens upward, the axis of symmetry is the vertical line that intersects the parabola at the vertex. So the axis of symmetry is \(x=3\). This parabola does not cross the x-axis, so it has no zeros. It crosses the \(y\)-axis at \((0,7)\) so this is the y-intercept.

Understanding How the Graphs of Parabolas are Related to Their Quadratic Functions

The general form of a quadratic function presents the function in the form

\[f(x)=ax^2+bx+c\]

where \(a\), \(b\), and \(c\) are real numbers and \(a{\neq}0\). If \(a>0\), the parabola opens upward. If \(a<0\), the parabola opens downward. We can use the general form of a parabola to find the equation for the axis of symmetry.

The axis of symmetry is defined by \(x=−\frac{b}{2a}\). If we use the quadratic formula, \(x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}\), to solve \(ax^2+bx+c=0\) for the x-intercepts, or zeros, we find the value of \(x\) halfway between them is always \(x=−\frac{b}{2a}\), the equation for the axis of symmetry.

Figure \(\PageIndex{4}\) represents the graph of the quadratic function written in general form as \(y=x^2+4x+3\). In this form, \(a=1\), \(b=4\), and \(c=3\). Because \(a>0\), the parabola opens upward. The axis of symmetry is \(x=−\frac{4}{2(1)}=−2\). This also makes sense because we can see from the graph that the vertical line \(x=−2\) divides the graph in half. The vertex always occurs along the axis of symmetry. For a parabola that opens upward, the vertex occurs at the lowest point on the graph, in this instance, \((−2,−1)\). The x-intercepts, those points where the parabola crosses the x-axis, occur at \((−3,0)\) and \((−1,0)\).

The standard form of a quadratic function presents the function in the form

\[f(x)=a(x−h)^2+k\]

where \((h, k)\) is the vertex. Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function .

As with the general form, if \(a>0\), the parabola opens upward and the vertex is a minimum. If \(a<0\), the parabola opens downward, and the vertex is a maximum. Figure \(\PageIndex{5}\) represents the graph of the quadratic function written in standard form as \(y=−3(x+2)^2+4\). Since \(x–h=x+2\) in this example, \(h=–2\). In this form, \(a=−3\), \(h=−2\), and \(k=4\). Because \(a<0\), the parabola opens downward. The vertex is at \((−2, 4)\).

The standard form is useful for determining how the graph is transformed from the graph of \(y=x^2\). Figure \(\PageIndex{6}\) is the graph of this basic function.

If \(k>0\), the graph shifts upward, whereas if \(k<0\), the graph shifts downward. In Figure \(\PageIndex{5}\), \(k>0\), so the graph is shifted 4 units upward. If \(h>0\), the graph shifts toward the right and if \(h<0\), the graph shifts to the left. In Figure \(\PageIndex{5}\), \(h<0\), so the graph is shifted 2 units to the left. The magnitude of \(a\) indicates the stretch of the graph. If \(|a|>1\), the point associated with a particular x-value shifts farther from the x-axis, so the graph appears to become narrower, and there is a vertical stretch. But if \(|a|<1\), the point associated with a particular x-value shifts closer to the x-axis, so the graph appears to become wider, but in fact there is a vertical compression. In Figure \(\PageIndex{5}\), \(|a|>1\), so the graph becomes narrower.

The standard form and the general form are equivalent methods of describing the same function. We can see this by expanding out the general form and setting it equal to the standard form.

\[\begin{align*} a(x−h)^2+k &= ax^2+bx+c \\[4pt] ax^2−2ahx+(ah^2+k)&=ax^2+bx+c \end{align*} \]

For the linear terms to be equal, the coefficients must be equal.

\[–2ah=b \text{, so } h=−\dfrac{b}{2a}. \nonumber\]

This is the axis of symmetry we defined earlier. Setting the constant terms equal:

\[\begin{align*} ah^2+k&=c \\ k&=c−ah^2 \\ &=c−a−\Big(\dfrac{b}{2a}\Big)^2 \\ &=c−\dfrac{b^2}{4a} \end{align*}\]

In practice, though, it is usually easier to remember that \(k\) is the output value of the function when the input is \(h\), so \(f(h)=k\).

Definitions: Forms of Quadratic Functions

A quadratic function is a function of degree two. The graph of a quadratic function is a parabola.

• The general form of a quadratic function is \(f(x)=ax^2+bx+c\) where \(a\), \(b\), and \(c\) are real numbers and \(a{\neq}0\).
• The standard form of a quadratic function is \(f(x)=a(x−h)^2+k\).
• The vertex \((h,k)\) is located at \[h=–\dfrac{b}{2a},\;k=f(h)=f(\dfrac{−b}{2a}).\]

HOWTO: Write a quadratic function in a general form

Given a graph of a quadratic function, write the equation of the function in general form.

• Identify the horizontal shift of the parabola; this value is \(h\). Identify the vertical shift of the parabola; this value is \(k\).
• Substitute the values of the horizontal and vertical shift for \(h\) and \(k\). in the function \(f(x)=a(x–h)^2+k\).
• Substitute the values of any point, other than the vertex, on the graph of the parabola for \(x\) and \(f(x)\).
• Solve for the stretch factor, \(|a|\).
• If the parabola opens up, \(a>0\). If the parabola opens down, \(a<0\) since this means the graph was reflected about the x-axis.
• Expand and simplify to write in general form.

Example \(\PageIndex{2}\): Writing the Equation of a Quadratic Function from the Graph

Write an equation for the quadratic function \(g\) in Figure \(\PageIndex{7}\) as a transformation of \(f(x)=x^2\), and then expand the formula, and simplify terms to write the equation in general form.

We can see the graph of \(g\) is the graph of \(f(x)=x^2\) shifted to the left 2 and down 3, giving a formula in the form \(g(x)=a(x+2)^2–3\).

Substituting the coordinates of a point on the curve, such as \((0,−1)\), we can solve for the stretch factor.

\[\begin{align} −1&=a(0+2)^2−3 \\ 2&=4a \\ a&=\dfrac{1}{2} \end{align}\]

In standard form, the algebraic model for this graph is \(g(x)=\dfrac{1}{2}(x+2)^2–3\).

To write this in general polynomial form, we can expand the formula and simplify terms.

\[\begin{align} g(x)&=\dfrac{1}{2}(x+2)^2−3 \\ &=\dfrac{1}{2}(x+2)(x+2)−3 \\ &=\dfrac{1}{2}(x^2+4x+4)−3 \\ &=\dfrac{1}{2}x^2+2x+2−3 \\ &=\dfrac{1}{2}x^2+2x−1 \end{align}\]

Notice that the horizontal and vertical shifts of the basic graph of the quadratic function determine the location of the vertex of the parabola; the vertex is unaffected by stretches and compressions.

We can check our work using the table feature on a graphing utility. First enter \(\mathrm{Y1=\dfrac{1}{2}(x+2)^2−3}\). Next, select \(\mathrm{TBLSET}\), then use \(\mathrm{TblStart=–6}\) and \(\mathrm{ΔTbl = 2}\), and select \(\mathrm{TABLE}\). See Table \(\PageIndex{1}\)

The ordered pairs in the table correspond to points on the graph.

Exercise \(\PageIndex{2}\)

A coordinate grid has been superimposed over the quadratic path of a basketball in Figure \(\PageIndex{8}\). Find an equation for the path of the ball. Does the shooter make the basket?

Figure \(\PageIndex{8}\): Stop motioned picture of a boy throwing a basketball into a hoop to show the parabolic curve it makes. (credit: modification of work by Dan Meyer)

The path passes through the origin and has vertex at \((−4, 7)\), so \(h(x)=–\frac{7}{16}(x+4)^2+7\). To make the shot, \(h(−7.5)\) would need to be about 4 but \(h(–7.5){\approx}1.64\); he doesn’t make it.

• Identify \(a\), \(b\), and \(c\).
• Find \(h\), the x-coordinate of the vertex, by substituting \(a\) and \(b\) into \(h=–\frac{b}{2a}\).
• Find \(k\), the y-coordinate of the vertex, by evaluating \(k=f(h)=f\Big(−\frac{b}{2a}\Big)\).

Example \(\PageIndex{3}\): Finding the Vertex of a Quadratic Function

Find the vertex of the quadratic function \(f(x)=2x^2–6x+7\). Rewrite the quadratic in standard form (vertex form).

The horizontal coordinate of the vertex will be at

\[\begin{align} h&=–\dfrac{b}{2a} \\ &=-\dfrac{-6}{2(2)} \\ &=\dfrac{6}{4} \\ &=\dfrac{3}{2}\end{align}\]

The vertical coordinate of the vertex will be at

\[\begin{align} k&=f(h) \\ &=f\Big(\dfrac{3}{2}\Big) \\ &=2\Big(\dfrac{3}{2}\Big)^2−6\Big(\dfrac{3}{2}\Big)+7 \\ &=\dfrac{5}{2} \end{align}\]

Rewriting into standard form, the stretch factor will be the same as the \(a\) in the original quadratic.

\[f(x)=ax^2+bx+c \\ f(x)=2x^2−6x+7\]

Using the vertex to determine the shifts,

\[f(x)=2\Big(x–\dfrac{3}{2}\Big)^2+\dfrac{5}{2}\]

One reason we may want to identify the vertex of the parabola is that this point will inform us what the maximum or minimum value of the function is, \((k)\),and where it occurs, \((h)\).

Exercise \(\PageIndex{3}\)

Given the equation \(g(x)=13+x^2−6x\), write the equation in general form and then in standard form.

\(g(x)=x^2−6x+13\) in general form; \(g(x)=(x−3)^2+4\) in standard form.

Determining the Maximum and Minimum Values of Quadratic Functions

The output of the quadratic function at the vertex is the maximum or minimum value of the function, depending on the orientation of the parabola . We can see the maximum and minimum values in Figure \(\PageIndex{9}\).

There are many real-world scenarios that involve finding the maximum or minimum value of a quadratic function, such as applications involving area and revenue.

Example \(\PageIndex{5}\): Finding the Maximum Value of a Quadratic Function

A backyard farmer wants to enclose a rectangular space for a new garden within her fenced backyard. She has purchased 80 feet of wire fencing to enclose three sides, and she will use a section of the backyard fence as the fourth side.

• Find a formula for the area enclosed by the fence if the sides of fencing perpendicular to the existing fence have length \(L\).
• What dimensions should she make her garden to maximize the enclosed area?

Let’s use a diagram such as Figure \(\PageIndex{10}\) to record the given information. It is also helpful to introduce a temporary variable, \(W\), to represent the width of the garden and the length of the fence section parallel to the backyard fence.

a. We know we have only 80 feet of fence available, and \(L+W+L=80\), or more simply, \(2L+W=80\). This allows us to represent the width, \(W\), in terms of \(L\).

\[W=80−2L\]

Now we are ready to write an equation for the area the fence encloses. We know the area of a rectangle is length multiplied by width, so

\[\begin{align} A&=LW=L(80−2L) \\ A(L)&=80L−2L^2 \end{align}\]

This formula represents the area of the fence in terms of the variable length \(L\). The function, written in general form, is

\[A(L)=−2L^2+80L\].

The quadratic has a negative leading coefficient, so the graph will open downward, and the vertex will be the maximum value for the area. In finding the vertex, we must be careful because the equation is not written in standard polynomial form with decreasing powers. This is why we rewrote the function in general form above. Since \(a\) is the coefficient of the squared term, \(a=−2\), \(b=80\), and \(c=0\).

To find the vertex:

\[\begin{align} h& =−\dfrac{80}{2(−2)} &k&=A(20) \\ &=20 & \text{and} \;\;\;\; &=80(20)−2(20)^2 \\ &&&=800 \end{align}\]

The maximum value of the function is an area of 800 square feet, which occurs when \(L=20\) feet. When the shorter sides are 20 feet, there is 40 feet of fencing left for the longer side. To maximize the area, she should enclose the garden so the two shorter sides have length 20 feet and the longer side parallel to the existing fence has length 40 feet.

This problem also could be solved by graphing the quadratic function. We can see where the maximum area occurs on a graph of the quadratic function in Figure \(\PageIndex{11}\).

• Write a quadratic equation for revenue.
• Find the vertex of the quadratic equation.
• Determine the y-value of the vertex.

Example \(\PageIndex{6}\): Finding Maximum Revenue

The unit price of an item affects its supply and demand. That is, if the unit price goes up, the demand for the item will usually decrease. For example, a local newspaper currently has 84,000 subscribers at a quarterly charge of $30. Market research has suggested that if the owners raise the price to $32, they would lose 5,000 subscribers. Assuming that subscriptions are linearly related to the price, what price should the newspaper charge for a quarterly subscription to maximize their revenue?

Revenue is the amount of money a company brings in. In this case, the revenue can be found by multiplying the price per subscription times the number of subscribers, or quantity. We can introduce variables, \(p\) for price per subscription and \(Q\) for quantity, giving us the equation \(\text{Revenue}=pQ\).

Because the number of subscribers changes with the price, we need to find a relationship between the variables. We know that currently \(p=30\) and \(Q=84,000\). We also know that if the price rises to $32, the newspaper would lose 5,000 subscribers, giving a second pair of values, \(p=32\) and \(Q=79,000\). From this we can find a linear equation relating the two quantities. The slope will be

\[\begin{align} m&=\dfrac{79,000−84,000}{32−30} \\ &=−\dfrac{5,000}{2} \\ &=−2,500 \end{align}\]

This tells us the paper will lose 2,500 subscribers for each dollar they raise the price. We can then solve for the y-intercept.

\[\begin{align} Q&=−2500p+b &\text{Substitute in the point $Q=84,000$ and $p=30$} \\ 84,000&=−2500(30)+b &\text{Solve for $b$} \\ b&=159,000 \end{align}\]

This gives us the linear equation \(Q=−2,500p+159,000\) relating cost and subscribers. We now return to our revenue equation.

\[\begin{align} \text{Revenue}&=pQ \\ \text{Revenue}&=p(−2,500p+159,000) \\ \text{Revenue}&=−2,500p^2+159,000p \end{align}\]

We now have a quadratic function for revenue as a function of the subscription charge. To find the price that will maximize revenue for the newspaper, we can find the vertex.

\[\begin{align} h&=−\dfrac{159,000}{2(−2,500)} \\ &=31.8 \end{align}\]

The model tells us that the maximum revenue will occur if the newspaper charges $31.80 for a subscription. To find what the maximum revenue is, we evaluate the revenue function.

\[\begin{align} \text{maximum revenue}&=−2,500(31.8)^2+159,000(31.8) \\ &=2,528,100 \end{align}\]

This could also be solved by graphing the quadratic as in Figure \(\PageIndex{12}\). We can see the maximum revenue on a graph of the quadratic function.

Example \(\PageIndex{10}\): Applying the Vertex and x-Intercepts of a Parabola

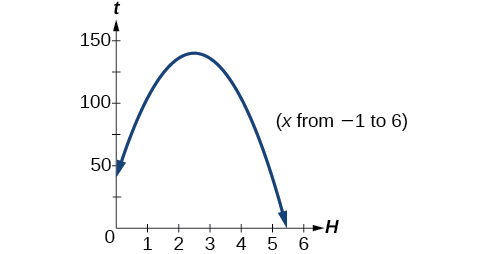
A ball is thrown upward from the top of a 40 foot high building at a speed of 80 feet per second. The ball’s height above ground can be modeled by the equation \(H(t)=−16t^2+80t+40\).

When does the ball reach the maximum height? What is the maximum height of the ball? When does the ball hit the ground?

The ball reaches the maximum height at the vertex of the parabola. \[\begin{align} h &= −\dfrac{80}{2(−16)} \\ &=\dfrac{80}{32} \\ &=\dfrac{5}{2} \\ & =2.5 \end{align}\]

The ball reaches a maximum height after 2.5 seconds.

To find the maximum height, find the y-coordinate of the vertex of the parabola. \[\begin{align} k &=H(−\dfrac{b}{2a}) \\ &=H(2.5) \\ &=−16(2.5)^2+80(2.5)+40 \\ &=140 \end{align}\]

The ball reaches a maximum height of 140 feet.

To find when the ball hits the ground, we need to determine when the height is zero, \(H(t)=0\).

We use the quadratic formula.

\[\begin{align} t & =\dfrac{−80±\sqrt{80^2−4(−16)(40)}}{2(−16)} \\ & = \dfrac{−80±\sqrt{8960}}{−32} \end{align} \]

Because the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions.

\[t=\dfrac{−80-\sqrt{8960}}{−32} ≈5.458 \text{ or }t=\dfrac{−80+\sqrt{8960}}{−32} ≈−0.458 \]

The second answer is outside the reasonable domain of our model, so we conclude the ball will hit the ground after about 5.458 seconds. See Figure \(\PageIndex{16}\).

Example \(\PageIndex{11}\): Using Technology to Find the Best Fit Quadratic Model

A ball is thrown into the air, and the following data is collected where x represents the time in seconds after the ball is thrown up and y represents the height in meters of the ball. We can use desmos to create a quadratic model that fits the given data.

On desmos, type the data into a table with the x-values in the first column and the y-values in the second column. Then, to tell desmos to compute a quadratic model, type in y 1 ~ a x 1 2 + b x 1 + c. You will get a result that looks like this:

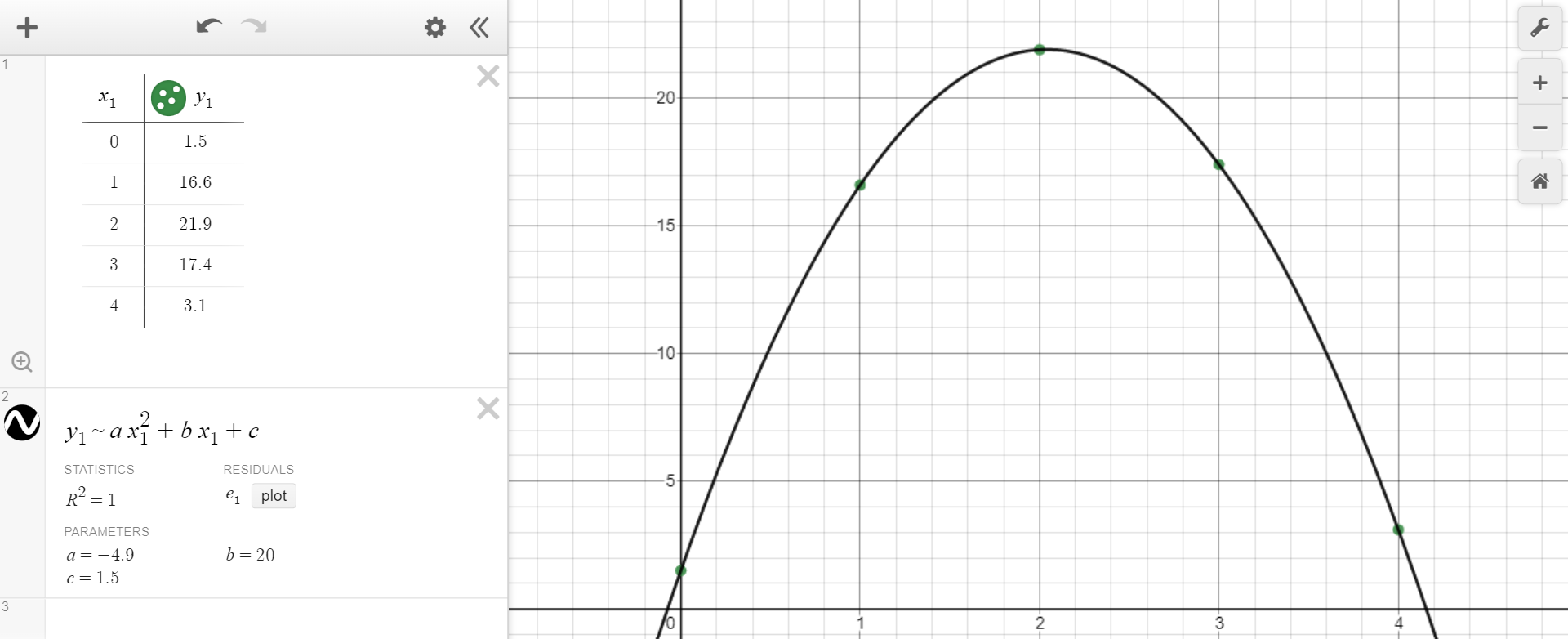
You can go to this problem in desmos by clicking https://www.desmos.com/calculator/u8ytorpnhk . Looking at the results, the quadratic model that fits the data is \[y = -4.9 x^2 + 20 x + 1.5\]