An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
- My Bibliography
- Collections
- Citation manager

Save citation to file
Email citation, add to collections.
- Create a new collection
- Add to an existing collection
Add to My Bibliography
Your saved search, create a file for external citation management software, your rss feed.
- Search in PubMed
- Search in NLM Catalog
- Add to Search
Biostatistics 101: data presentation
Affiliation.
- 1 Clinical trials and Epidemiology Research Unit, 226 Outram Road, Blk A #02-02, Singapore 169039. [email protected]
- PMID: 14560857
PubMed Disclaimer
Similar articles
- Biostatistical approaches to reducing the number of animals used in biomedical research. Puopolo M. Puopolo M. Ann Ist Super Sanita. 2004;40(2):157-63. Ann Ist Super Sanita. 2004. PMID: 15536265 Review.
- Multivariate tests of means in independent groups designs. Effects of covariance heterogeneity and nonnormality. Lix LM, Keselman HJ. Lix LM, et al. Eval Health Prof. 2004 Mar;27(1):45-69. doi: 10.1177/0163278703261213. Eval Health Prof. 2004. PMID: 14994559
- [Presentation of statistical date, 1--Tables: more complicated than anticipated]. Ostermann R, Wilhelm AF, Wolf-Ostermann K. Ostermann R, et al. Pflege Z. 2004 Jan;57(1):18-21. Pflege Z. 2004. PMID: 14768162 German. No abstract available.
- Bootstraps and jackknives: new, computer-intensive statistical tools that require no mathematical theories. Fiellin DA, Feinstein AR. Fiellin DA, et al. J Investig Med. 1998 Feb;46(2):22-6. J Investig Med. 1998. PMID: 9549224 Review. No abstract available.
- The new biostatistics of resampling. Simon JL, Bruce P. Simon JL, et al. MD Comput. 1995 Mar-Apr;12(2):115-21, 141. MD Comput. 1995. PMID: 7700123
- Monounsaturated fat-rich diet reduces body adiposity in women with obesity, but does not influence energy expenditure and substrate oxidation: a parallel randomized controlled clinical trial. Lopes MCODS, Kaippert VC, Crovesy L, de Carvalho DP, Rosado EL. Lopes MCODS, et al. Eur J Clin Nutr. 2024 Apr;78(4):335-343. doi: 10.1038/s41430-024-01401-3. Epub 2024 Jan 12. Eur J Clin Nutr. 2024. PMID: 38216647 Clinical Trial.
- Multivariate indicators of disease severity in COVID-19. Bean J, Kuri-Cervantes L, Pennella M, Betts MR, Meyer NJ, Hassan WM. Bean J, et al. Sci Rep. 2023 Mar 29;13(1):5145. doi: 10.1038/s41598-023-31683-9. Sci Rep. 2023. PMID: 36991002 Free PMC article.
- Count data models for outpatient health services utilisation. Abu Bakar NS, Ab Hamid J, Mohd Nor Sham MSJ, Sham MN, Jailani AS. Abu Bakar NS, et al. BMC Med Res Methodol. 2022 Oct 5;22(1):261. doi: 10.1186/s12874-022-01733-3. BMC Med Res Methodol. 2022. PMID: 36199028 Free PMC article.
- PAIN IN POST-POLIO SYNDROME: A SEPARATE PAIN ENTITY? Boshuis EC, Melin E, Borg K. Boshuis EC, et al. J Rehabil Med Clin Commun. 2022 Jan 22;5:1000077. doi: 10.2340/20030711-1000077. eCollection 2022. J Rehabil Med Clin Commun. 2022. PMID: 35173911 Free PMC article.
- Virtual learning during the COVID-19 pandemic: What are the barriers and how to overcome them? Khobragade SY, Soe HHK, Khobragade YS, Abas ALB. Khobragade SY, et al. J Educ Health Promot. 2021 Sep 30;10:360. doi: 10.4103/jehp.jehp_1422_20. eCollection 2021. J Educ Health Promot. 2021. PMID: 34761046 Free PMC article.
- Search in MeSH
- Citation Manager
NCBI Literature Resources
MeSH PMC Bookshelf Disclaimer
The PubMed wordmark and PubMed logo are registered trademarks of the U.S. Department of Health and Human Services (HHS). Unauthorized use of these marks is strictly prohibited.
Basic Concepts for Biostatistics
Lisa Sullivan, PhD, Professor of Biostatistics, Boston University School of Public Health

Introduction
Biostatistics is the application of statistical principles to questions and problems in medicine, public health or biology. One can imagine that it might be of interest to characterize a given population (e.g., adults in Boston or all children in the United States) with respect to the proportion of subjects who are overweight or the proportion who have asthma, and it would also be important to estimate the magnitude of these problems over time or perhaps in different locations. In other circumstances in would be important to make comparisons among groups of subjects in order to determine whether certain behaviors (e.g., smoking, exercise, etc.) are associated with a greater risk of certain health outcomes. It would, of course, be impossible to answer all such questions by collecting information (data) from all subjects in the populations of interest. A more realistic approach is to study samples or subsets of a population. The discipline of biostatistics provides tools and techniques for collecting data and then summarizing, analyzing, and interpreting it. If the samples one takes are representative of the population of interest, they will provide good estimates regarding the population overall. Consequently, in biostatistics one analyzes samples in order to make inferences about the population. This module introduces fundamental concepts and definitions for biostatistics.
Learning Objectives
After completing this module, the student will be able to:
- Define and distinguish between populations and samples.
- Define and distinguish between population parameters and sample statistics.
- Compute a sample mean, sample variance, and sample standard deviation.
- Compute a population mean, population variance, and population standard deviation.
- Explain what is meant by statistical inference.
-----------
Population Parameters versus Sample Statistics
As noted in the Introduction, a fundamental task of biostatistics is to analyze samples in order to make inferences about the population from which the samples were drawn . To illustrate this, consider the population of Massachusetts in 2010, which consisted of 6,547,629 persons. One characteristic (or variable) of potential interest might be the diastolic blood pressure of the population. There are a number of ways of reporting and analyzing this, which will be considered in the module on Summarizing Data. However, for the time being, we will focus on the mean diastolic blood pressure of all people living in Massachusetts. It is obviously not feasible to measure and record blood pressures for of all the residents, but one could take samples of the population in order estimate the population's mean diastolic blood pressure.

Despite the simplicity of this example, it raises a series of concepts and terms that need to be defined. The terms population , subjects , sample , variable , and data elements are defined in the tabbed activity below.
It is possible to select many samples from a given population, and we will see in other learning modules that there are several methods that can be used for selecting subjects from a population into a sample. The simple example above shows three small samples that were drawn to estimate the mean diastolic blood pressure of Massachusetts residents, although it doesn't specify how the samples were drawn. Note also that each of the samples provided a different estimate of the mean value for the population, and none of the estimates was the same as the actual mean for the overall population (78 mm Hg in this hypothetical example). In reality, one generally doesn't know the true mean values of the characteristics of the population, which is of course why we are trying to estimate them from samples. Consequently, it is important to define and distinguish between:
- population size versus sample size
- parameter versus sample statistic.
Sample Statistics
In order to illustrate the computation of sample statistics, we selected a small subset (n=10) of participants in the Framingham Heart Study. The data values for these ten individuals are shown in the table below. The rightmost column contains the body mass index (BMI) computed using the height and weight measurements. We will come back to this example in the module on Summarizing Data, but it provides a useful illustration of some of the terms that have been introduced and will also serve to illustrate the computation of some sample statistics.
Data Values for a Small Sample
| Participant ID | Systolic Blood Pressure | Diastolic Blood Pressure | Total Serum Cholesterol | Weight | Height | Body Mass Index |
|---|---|---|---|---|---|---|
| 1 | 141 | 76 | 199 | 138 | 63.00 | 24.4 |
| 2 | 119 | 64 | 150 | 183 | 69.75 | 26.4 |
| 3 | 122 | 62 | 227 | 153 | 65.75 | 24.9 |
| 4 | 127 | 81 | 227 | 178 | 70.00 | 25.5 |
| 5 | 125 | 70 | 163 | 161 | 70.50 | 22.8 |
| 6 | 123 | 72 | 210 | 206 | 70.00 | 29.6 |
| 7 | 105 | 81 | 205 | 235 | 72.00 | 31.9 |
| 8 | 113 | 63 | 275 | 151 | 60.75 | 28.8 |
| 9 | 106 | 67 | 208 | 213 | 69.00 | 31.5 |
| 10 | 131 | 77 | 159 | 142 | 61.00 | 26.8 |
The first summary statistic that is important to report is the sample size. In this example the sample size is n=10. Because this sample is small (n=10), it is easy to summarize the sample by inspecting the observed values, for example, by listing the diastolic blood pressures in ascending order:
62 63 64 67 70 72 76 77 81 81
Simple inspection of this small sample gives us a sense of the center of the observed diastolic pressures and also gives us a sense of how much variability there is. However, for a large sample, inspection of the individual data values does not provide a meaningful summary, and summary statistics are necessary. The two key components of a useful summary for a continuous variable are:
- a description of the center or 'average' of the data (i.e., what is a typical value?) and
- an indication of the variability in the data.
Sample Mean
There are several statistics that describe the center of the data, but for now we will focus on the sample mean, which is computed by summing all of the values for a particular variable in the sample and dividing by the sample size. For the sample of diastolic blood pressures in the table above, the sample mean is computed as follows:
To simplify the formulas for sample statistics (and for population parameters), we usually denote the variable of interest as "X". X is simply a placeholder for the variable being analyzed. Here X=diastolic blood pressure.
The general formula for the sample mean is:
The X with the bar over it represents the sample mean, and it is read as "X bar". The Σ indicates summation (i.e., sum of the X's or sum of the diastolic blood pressures in this example).
When reporting summary statistics for a continuous variable, the convention is to report one more decimal place than the number of decimal places measured. Systolic and diastolic blood pressures, total serum cholesterol and weight were measured to the nearest integer, therefore the summary statistics are reported to the nearest tenth place. Height was measured to the nearest quarter inch (hundredths place), therefore the summary statistics are reported to the nearest thousandths place. Body mass index was computed to the nearest tenths place, summary statistics are reported to the nearest hundredths place.
Sample Variance and Standard Deviation
If there are no extreme or outlying values of the variable, the mean is the most appropriate summary of a typical value, and to summarize variability in the data we specifically estimate the variability in the sample around the sample mean. If all of the observed values in a sample are close to the sample mean, the standard deviation will be small (i.e., close to zero), and if the observed values vary widely around the sample mean, the standard deviation will be large. If all of the values in the sample are identical, the sample standard deviation will be zero.
When discussing the sample mean, we found that the sample mean for diastolic blood pressure = 71.3. The table below shows each of the observed values along with its respective deviation from the sample mean.
Table - Diastolic Blood Pressures and Deviations from the Sample Mean
| X=Diastolic Blood Pressure | Deviation from the Mean |
|---|---|
| 76 | 4.7 |
| 64 | -7.3 |
| 62 | -9.3 |
| 81 | 9.7 |
| 70 | -1.3 |
| 72 | 0.7 |
| 81 | 9.7 |
| 63 | -8.3 |
| 67 | -4.3 |
| 77 | 5.7 |
|
|
|
The deviations from the mean reflect how far each individual's diastolic blood pressure is from the mean diastolic blood pressure. The first participant's diastolic blood pressure is 4.7 units above the mean while the second participant's diastolic blood pressure is 7.3 units below the mean. What we need is a summary of these deviations from the mean, in particular a measure of how far, on average, each participant is from the mean diastolic blood pressure. If we compute the mean of the deviations by summing the deviations and dividing by the sample size we run into a problem. The sum of the deviations from the mean is zero. This will always be the case as it is a property of the sample mean, i.e., the sum of the deviations below the mean will always equal the sum of the deviations above the mean. However, the goal is to capture the magnitude of these deviations in a summary measure. To address this problem of the deviations summing to zero, we could take absolute values or square each deviation from the mean. Both methods would address the problem. The more popular method to summarize the deviations from the mean involves squaring the deviations (absolute values are difficult in mathematical proofs). The table below displays each of the observed values, the respective deviations from the sample mean and the squared deviations from the mean.
|
|
|
|
| 76 | 4.7 | 22.09 |
| 64 | -7.3 | 53.29 |
| 62 | -9.3 | 86.49 |
| 81 | 9.7 | 94.09 |
| 70 | -1.3 | 1.69 |
| 72 | 0.7 | 0.49 |
| 81 | 9.7 | 94.09 |
| 63 | -8.3 | 68.89 |
| 67 | -4.3 | 18.49 |
| 77 | 5.7 | 32.49 |
|
|
|
|
The squared deviations are interpreted as follows. The first participant's squared deviation is 22.09 meaning that his/her diastolic blood pressure is 22.09 units squared from the mean diastolic blood pressure, and the second participant's diastolic blood pressure is 53.29 units squared from the mean diastolic blood pressure. A quantity that is often used to measure variability in a sample is called the sample variance, and it is essentially the mean of the squared deviations. The sample variance is denoted s 2 and is computed as follows:
| Why do we divided by (n-1) instead of n? The sample variance is not actually the mean of the squared deviations, because we divide by (n-1) instead of n. In statistical inference (described in detail in another module) we make generalizations or estimates of population parameters based on sample statistics. If we were to compute the sample variance by taking the mean of the squared deviations and dividing by n we would consistently underestimate the true population variance. Dividing by (n-1) produces a better estimate of the population variance. The sample variance is nonetheless usually interpreted as the average squared deviation from the mean. |
In this sample of n=10 diastolic blood pressures, the sample variance is s 2 = 472.10/9 = 52.46. Thus, on average diastolic blood pressures are 52.46 units squared from the mean diastolic blood pressure. Because of the squaring, the variance is not particularly interpretable. The more common measure of variability in a sample is the sample standard deviation, defined as the square root of the sample variance:

A sample of 10 women seeking prenatal care at Boston Medical center agree to participate in a study to assess the quality of prenatal care. At the time of study enrollment, you the study coordinator, collected background characteristics on each of the moms including their age (in years).The data are shown below:
24 18 28 32 26 21 22 43 27 29

A sample of 12 men have been recruited into a study on the risk factors for cardiovascular disease. The following data are HDL cholesterol levels (mg/dL) at study enrollment:
50 45 67 82 44 51 64 105 56 60 74 68

Population Parameters
The previous page outlined the sample statistics for diastolic blood pressure measurement in our sample. If we had diastolic blood pressure measurements for all subjects in the population, we could also calculate the population parameters as follows:
Population Mean
Typically, a population mean is designated by the lower case Greek letter µ (pronounced 'mu'), and the formula is as follows:
where "N" is the populations size.
Population Variance and Standard Deviation
Statistical inference.
We usually don't have information about all of the subjects in a population of interest, so we take samples from the population in order to make inferences about unknown population parameters .
An obvious concern would be how good a given sample's statistics are in estimating the characteristics of the population from which it was drawn. There are many factors that influence diastolic blood pressure levels, such as age, body weight, fitness, and heredity.
We would ideally like the sample to be representative of the population . Intuitively, it would seem preferable to have a random sample , meaning that all subjects in the population have an equal chance of being selected into the sample; this would minimize systematic errors caused by biased sampling.
In addition, it is also intuitive that small samples might not be representative of the population just by chance, and large samples are less likely to be affected by "the luck of the draw"; this would reduce so-called random error. Since we often rely on a single sample to estimate population parameters, we never actually know how good our estimates are. However, one can use sampling methods that reduce bias, and the degree of random error in a given sample can be estimated in order to get a sense of the precision of our estimates.
- Corpus ID: 9321583
Biostatistics 101: data presentation.
- Published in Singapore medical journal 2003
Figures and Tables from this paper
76 Citations
Biostatistics 201: linear regression analysis., statistics for dental researchers: descriptive statistics, are you a p-value worshipper, psychometric properties of the five-digit test in patients with stroke, multivariate indicators of disease severity in covid-19, evaluating the impact of coronavirus disease on burnout among healthcare workers using maslach burnout inventory tool: a systematic review, investigation of the effect of covid-19 infection on sperm dna fragmentation, virtual learning during the covid-19 pandemic: what are the barriers and how to overcome them, development of a computerized digit vigilance test and validation in patients with stroke., estimating regression to the mean and true effects of an intervention in a four-wave panel study., 9 references, randomised controlled trials (rcts)--sample size: the magic number, biostatistics: a methodology for the health sciences, practical statistics for medical research, an introduction to medical statistics, medical statistics − a commonsense approach, cartoon guide to statistics, statistics further from scratch: for health care professionals, basic and clinical biostatistics, principles of biostatistics, related papers.
Showing 1 through 3 of 0 Related Papers
Alison's New App is now available on iOS and Android! Download Now
Do you represent a business or organization that would like to train and upskill their employees?
If yes, check out Alison’s Free LMS here!
header.all_certificate_courses
Personal development, sales & marketing, engineering & construction, teaching & academics.
Become an Alison Affiliate in one click, and start earning money by sharing any page on the Alison website.
- Change Language

Understanding Data Representation and Plotting in Biostatistics
This free online course includes:.
- Hours of Learning
- CPD Accreditation
- Final Assessment
Rate This Course & Get Better Recommendations!
Thanks for your review, in this free course, you will learn how to.
Biostatisticians play a unique role in protecting public health and improving people's lives. This course discusses the significance of plotting data to visualise variation or demonstrate relationships between variables. It begins by describing how statistics are used in data gathering, organisation, analysis, and interpretation. You will learn about various types of statistical studies as well as the process of selecting pre-arranged observations from a population in the form of a sample. In addition, you will also understand the importance of biostatistics in the development, implementation, and application of statistical methods in medical research. The concepts of descriptive and inferential statistics are then discussed. You explore the process of describing and making predictions from data. Additionally, the methods for summarising the characteristics of a data set in order to draw meaningful conclusions using statistical techniques are explained. Following that, you study the methods for calculating the values of the same and different units.
The next section deals with the main differences and the process of arithmetic and geometric calculation. Learn how to calculate the range, absolute mean, and standard deviation. In addition, you will study the process of determining the spread of data points from the centre using measures of variability. Following that, the procedure for calculating the standard error of the mean (SEM) is described. Discover the method of determining the deviations from the mean. You will also learn how to use the Z-score to calculate the chance of a score falling into a normal distribution and how to compare two scores from different normal distributions. Go on to see how to graphically display numerical group data based on quartiles using box plots. You will also discover how to use a box plot to show the form of distribution, as well as its central value and variability.
Finally, the concepts of moments, as well as the skewness of statistical distribution, are described. You will comprehend the significance of moments in studying a distribution's central tendency, dispersion, skewness, and kurtosis. Next, the process of using ‘skewness’ to measure the symmetry of distribution is explained. Discover how the variation of the distribution from the normal distribution can be measured by the skewness. Following that, you will explore how to use kurtosis to determine whether data is heavy-tailed or light-tailed in comparison to a normal distribution. In addition, you will learn how kurtosis helps in comprehending where the most information is hiding and how to analyse outliers in a given data set. Lastly, the course shows how to use the R programming language to perform a variety of statistical tasks such as data cleaning, analysis, and visualisation. It will help you understand how each form of data is processed, saved, and displayed within a device, as well as the implications for how it is used.
All Alison courses are free to enrol study and complete. To successfully complete this course and become an Alison Graduate, you need to achieve 80% or higher in each course assessment. Once you have completed this course, you have the option to acquire an official Diploma, which is a great way to share your achievement with the world.
Your Alison is:
- Ideal for sharing with potential employers
- Great for your CV, professional social media profiles and job applications.
- An indication of your commitment to continuously learn, upskill & achieve high results.
- An incentive for you to continue empowering yourself through lifelong learning.
Alison offers 3 types of Diplomas for completed Diploma courses:
- Digital : a downloadable in PDF format immediately available to you when you complete your purchase.
- : a physical version of your officially branded and security-marked , posted to you with FREE shipping.
- Framed : a physical version of your officially branded and security marked in a stylish frame, posted to you with FREE shipping.

All s are available to purchase through the Alison Shop . For more information on purchasing Alison , please visit our FAQs . If you decide not to purchase your Alison , you can still demonstrate your achievement by sharing your Learner Record or Learner Achievement Verification, both of which are accessible from your Account Settings . For more details on our pricing, please visit our Pricing Page
Knowledge & Skills You Will Learn
Complete this cpd accredited course & get your certificate , certify your skills, stand out from the crowd, advance in your career.

Learner Reviews & Feedback For Understanding Data Representation and Plotting in Biostatistics
Want to create a customised learning path for your team.
Our dedicated Learning Advisors are here to help you curate a customised learning path tailored to your organisation's needs and goals.
Explore Careers Related To This Course
Not sure where to begin or even what you want to do.
Discover the career most suitable for you and get started in the field with a step-by-step plan.
About Your Alison Course Publisher
- alison stats, more free online courses by this publisher, learners who took this course also enrolled in, explore subjects related to this course.
Join our community of 40 million+ learners, upskill with CPD UK accredited courses, explore career development tools and psychometrics - all for free.
- Reset password form here
Basic Concepts, Organizing, and Displaying Data
- First Online: 16 June 2018
Cite this chapter

- M. Ataharul Islam 3 &
- Abdullah Al-Shiha 4
3751 Accesses
- The original version of this chapter was revised: The explanation related to Table 1.5. has been corrected. The correction to this chapter is available at https://doi.org/10.1007/978-981-10-8627-4_12
This chapter introducesbiostatistics as a discipline that deals with designing studies, analyzingdata , and developing new statistical techniques to address the problems in the fields of life sciences. This includes collection, organization, summarization, and analysis of data in the fields of biological, health, and medical sciences including other life sciences. One major objective of a biostatistician is to find the values that summarize the basic facts from the sample data and to makeinference about the representativeness of the estimates using the sample data to make inference about the correspondingpopulation characteristics. The basic concepts are discussed along with examples and sources of data, levels ofmeasurement , and types of variables. Various methods of organizing and displaying data are discussed for both ungrouped andgrouped data . The construction of table is discussed in details. This chapter includes methods of constructing frequency bar chart, dot plot, pie chart,histogram ,frequency polygon , andogive . In addition, the construction ofstem-and-leaf display is discussed in details. All these are illustrated with examples. As the raw materials ofstatistics aredata , a brief section on designing of sample surveys including planning of a survey and major components is introduced in order to provide some background about collection of data.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or Ebook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Available as EPUB and PDF
- Compact, lightweight edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
- Durable hardcover edition
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Change history
04 september 2020, author information, authors and affiliations.
ISRT, University of Dhaka, Dhaka, Bangladesh
M. Ataharul Islam
Department of Statistics and Operations Research, College of Science, King Saud University, Riyadh, Saudi Arabia
Abdullah Al-Shiha
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to M. Ataharul Islam .
Rights and permissions
Reprints and permissions
Copyright information
© 2018 Springer Nature Singapore Pte Ltd.
About this chapter
Islam, M.A., Al-Shiha, A. (2018). Basic Concepts, Organizing, and Displaying Data. In: Foundations of Biostatistics. Springer, Singapore. https://doi.org/10.1007/978-981-10-8627-4_1
Download citation
DOI : https://doi.org/10.1007/978-981-10-8627-4_1
Published : 16 June 2018
Publisher Name : Springer, Singapore
Print ISBN : 978-981-10-8626-7
Online ISBN : 978-981-10-8627-4
eBook Packages : Mathematics and Statistics Mathematics and Statistics (R0)
Share this chapter
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research

Associate Director Biostatistics
About the role.
Our Development Team is guided by our purpose: to reimagine medicine to improve and extend people’s lives.
To do this, we are optimizing and strengthening our processes and ways of working. We are investing in new technologies and building specific therapeutic areas and platform depth and capabilities – all to bring our medicines to patients even faster.
We are seeking key talent, like you, to join us and help give people with disease and their families a brighter future to look forward to.
Apply today and welcome to where we thrive together!
The Role:
We are seeking a highly skilled and motivated individual to join our team as Associate Director of Biostatistics . Y ou will be required to influence and drive the statistical strategy / innovation directly taking part in cross-functional collaboration and decision making for program(s) across (pre/early/full) clinical development and/or medical affairs. You will have p roven experience in supporting complex clinical trials and leading strategy through collaborations with partners across the drug development organization.
This role may be in Early Development, Preclinical or Global Medical Affairs
Key responsibilities :
Responsible for all statistical tasks on assigned clinical trials , with a high level of independence seeking peer input/review as required . Responsible for protocol development in alignment with the clinical development plan, developing statistical analysis plan, and leading study- and indication-level reporting activities.
Contribute to planning and execution of exploratory analyses, innovative analyses related to publications and pricing & reimbursement / submission and/or PK, PK/PD analyses, exploratory biomarker and diagnostic analyses, and statistical consultation. Initiate, drive, and implement novel methods and innovative trial designs and dose-finding strategies in alignment with the Lead Statistician.
Independently lead interactions with external review boards/ethics committees, external consultants, and other external parties with oversight as appropriate . Represent Novartis in statistical discussions at external congresses, conferences, scientific meetings.
Represent the Biostatistics & Pharmacometrics Line Function on cross-functional teams for the assigned trials. Responsible for functional alignment and ensuring line function awareness throughout the trials.
Collaborate with other line functions. Explain statistical concepts in an easily understandable way to non-statisticians and provide adequate statistical justifications and interpretation of analysis results for actions/decisions/statements, when required .
Establish and maintain collaborative relationships and effective communication s within the C linical T rial T eam and Biostatistics & Pharmacometrics team.
Independent oversight of Biostatistics resources and deliverables for assigned trials.
Ensure all Biostatistics deliverables for assigned clinical trials and/or non-clinical related activities are delivered in a timely manner with the highest level of quality.
Your Experience:
MS Statistics with 10+ years’ work experience or PhD (in Statistics or equivalent) with 6years + work experience
Fluent in English with strong communication and presentation skills, with the ability to articulate complex concepts to diverse audiences.
Effective utilization of innovative statistics and quantitative analytics to influence assigned program team decisions and support department to deliver objectives .
Proven knowledge and expertise in statistics and its application to clinical trials. Depending on the assignment, may require proven expertise in pharmacokinetics, exposure-response modelling, exploratory biomarker, diagnostic analyses, applied Bayesian statistics, or data exploration skills. Demonstrated excellence in use of statistical software packages (e.g. SAS, R). Strong knowledge of drug development and Health Authority guidelines. Experience independently leading a multidisciplinary team to achieve team objectives . Expert skills to facilitate and maximize the contribution of quantitative team. Hands-on experience in leading the interface to regulatory agencies/leading the early clinical development campaign.
Experience in providing statistical expertise to support submission activities, including documents, meetings with and responses to Health Authorities, pricing agencies and drug development activities, as required .
Strong understanding of Franchise/Therapeutic Area and / or regulatory activities in at least one disease area .
Expert scientific leadership skills demonstrated in facilitating and optimizing the clinical development strategy.
Strong track record for global scientific leadership in the development and evaluation of modern program/trial design methodologies.
Demonstrated strong skills in building partnerships and collaborations. Ability to mentor for up to 8 associates.
This role offers hybrid working, requiring 3 days per week or 12 days per month in our London Office.
Why Novartis: Helping people with disease and their families takes more than innovative science. It takes a community of smart, passionate people like you. Collaborating, supporting, and inspiring each other. Combining to achieve breakthroughs that change patients’ lives. Ready to create a brighter future together? https://www.novartis.com/about/strategy/people-and-culture
Commitment to Diversity & Inclusion :
Novartis is committed to building an outstanding, inclusive work environment and diverse team’s representative of the patients and communities we serve.
Join our Novartis Network:
Not the right Novartis role for you? Sign up to our talent community to stay connected and learn about suitable career opportunities as soon as they come up: https://talentnetwork.novartis.com/network
Why Novartis: Helping people with disease and their families takes more than innovative science. It takes a community of smart, passionate people like you. Collaborating, supporting and inspiring each other. Combining to achieve breakthroughs that change patients’ lives. Ready to create a brighter future together? https://www.novartis.com/about/strategy/people-and-culture
Join our Novartis Network: Not the right Novartis role for you? Sign up to our talent community to stay connected and learn about suitable career opportunities as soon as they come up: https://talentnetwork.novartis.com/network

An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- Indian J Pharmacol
- v.44(4); Jul-Aug 2012
Basic biostatistics for post-graduate students
Ganesh n. dakhale.
Department of Pharmacology, Indira Gandhi Govt. Medical College, Nagpur - 440 018, Maharashtra, India

Sachin K. Hiware
Abhijit t. shinde, mohini s. mahatme.
Statistical methods are important to draw valid conclusions from the obtained data. This article provides background information related to fundamental methods and techniques in biostatistics for the use of postgraduate students. Main focus is given to types of data, measurement of central variations and basic tests, which are useful for analysis of different types of observations. Few parameters like normal distribution, calculation of sample size, level of significance, null hypothesis, indices of variability, and different test are explained in detail by giving suitable examples. Using these guidelines, we are confident enough that postgraduate students will be able to classify distribution of data along with application of proper test. Information is also given regarding various free software programs and websites useful for calculations of statistics. Thus, postgraduate students will be benefitted in both ways whether they opt for academics or for industry.
Introduction
Statistics is basically a way of thinking about data that are variable. This article deals with basic biostatistical concepts and their application to enable postgraduate medical and allied science students to analyze and interpret their study data and to critically interpret published literature. Acquiring such skills currently forms an integral part of their postgraduate training. It has been commonly seen that most postgraduate students have an inherent apprehension and prefer staying away from biostatistics, except for memorizing some information that helps them through their postgraduate examination. Self-motivation for effective learning and application of statistics is lacking.
Statistics implies both, data and statistical methods. It can be considered as an art as well as science. Statistics can neither prove not disprove anything. It is just a tool. Statistics without scientific application has no roots. Thus, statistics may be defined as the discipline concerned with the treatment of numerical data derived from group of individuals. These individuals may be human beings, animals, or other organisms. Biostatistics is a branch of statistics applied to biological or medical sciences. Biostatistics covers applications and contributions not only from health, medicines and, nutrition but also from fields such as genetics, biology, epidemiology, and many others.[ 1 ] Biostatistics mainly consists of various steps like generation of hypothesis, collection of data, and application of statistical analysis. To begin with, readers should know about the data obtained during the experiment, its distribution, and its analysis to draw a valid conclusion from the experiment.
Statistical method has two major branches mainly descriptive and inferential. Descriptive statistics explain the distribution of population measurements by providing types of data, estimates of central tendency (mean, mode and median), and measures of variability (standard deviation, correlation coefficient), whereas inferential statistics is used to express the level of certainty about estimates and includes hypothesis testing, standard error of mean, and confidence interval.
Types of Data
Observations recorded during research constitute data. There are three types of data i.e. nominal, ordinal, and interval data. Statistical methods for analysis mainly depend on type of data. Generally, data show picture of the variability and central tendency. Therefore, it is very important to understand the types of data.
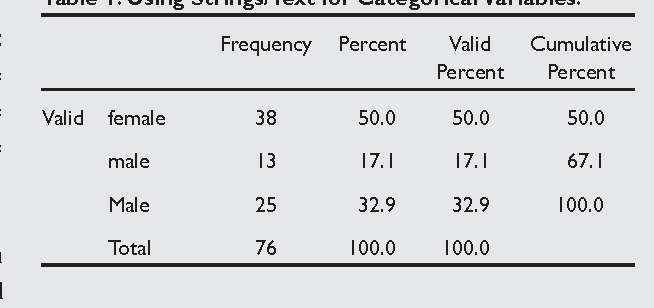
1) Nominal data: This is synonymous with categorical data where data is simply assigned “names” or categories based on the presence or absence of certain attributes/characteristics without any ranking between the categories.[ 2 ] For example, patients are categorized by gender as males or females; by religion as Hindu, Muslim, or Christian. It also includes binominal data, which refers to two possible outcomes. For example, outcome of cancer may be death or survival, drug therapy with drug ‘X’ will show improvement or no improvement at all.
2) Ordinal data: It is also called as ordered, categorical, or graded data. Generally, this type of data is expressed as scores or ranks. There is a natural order among categories, and they can be ranked or arranged in order.[ 2 ] For example, pain may be classified as mild, moderate, and severe. Since there is an order between the three grades of pain, this type of data is called as ordinal. To indicate the intensity of pain, it may also be expressed as scores (mild = 1, moderate = 2, severe = 3). Hence, data can be arranged in an order and rank.
3) Interval data: This type of data is characterized by an equal and definite interval between two measurements. For example, weight is expressed as 20, 21, 22, 23, 24 kg. The interval between 20 and 21 is same as that between 23 and 24. Interval type of data can be either continuous or discrete. A continuous variable can take any value within a given range. For example: hemoglobin (Hb) level may be taken as 11.3, 12.6, 13.4 gm % while a discrete variable is usually assigned integer values i.e. does not have fractional values. For example, blood pressure values are generally discrete variables or number of cigarettes smoked per day by a person.
Sometimes, certain data may be converted from one form to another form to reduce skewness and make it to follow the normal distribution. For example, drug doses are converted to their log values and plotted in dose response curve to obtain a straight line so that analysis becomes easy.[ 3 ] Data can be transformed by taking the logarithm, square root, or reciprocal. Logarithmic conversion is the most common data transformation used in medical research.
Measures of Central Tendencies
Mean, median, and mode are the three measures of central tendencies. Mean is the common measure of central tendency, most widely used in calculations of averages. It is least affected by sampling fluctuations. The mean of a number of individual values (X) is always nearer the true value of the individual value itself. Mean shows less variation than that of individual values, hence they give confidence in using them. It is calculated by adding up the individual values (Σx) and dividing the sum by number of items (n). Suppose height of 7 children's is 60, 70, 80, 90, 90, 100, and 110 cms. Addition of height of 7 children is 600 cm, so mean(X) = Σx/n=600/7=85.71.
Median is an average, which is obtained by getting middle values of a set of data arranged or ordered from lowest to the highest (or vice versa ). In this process, 50% of the population has the value smaller than and 50% of samples have the value larger than median. It is used for scores and ranks. Median is a better indicator of central value when one or more of the lowest or the highest observations are wide apart or are not evenly distributed. Median in case of even number of observations is taken arbitrary as an average of two middle values, and in case of odd number, the central value forms the median. In above example, median would be 90. Mode is the most frequent value, or it is the point of maximum concentration. Most fashionable number, which occurred repeatedly, contributes mode in a distribution of quantitative data . In above example, mode is 90. Mode is used when the values are widely varying and is rarely used in medical studies. For skewed distribution or samples where there is wide variation, mode, and median are useful.
Even after calculating the mean, it is necessary to have some index of variability among the data. Range or the lowest and the highest values can be given, but this is not very useful if one of these extreme values is far off from the rest. At the same time, it does not tell how the observations are scattered around the mean. Therefore, following indices of variability play a key role in biostatistics.
Standard Deviation
In addition to the mean, the degree of variability of responses has to be indicated since the same mean may be obtained from different sets of values. Standard deviation (SD) describes the variability of the observation about the mean.[ 4 ] To describe the scatter of the population, most useful measure of variability is SD. Summary measures of variability of individuals (mean, median, and mode) are further needed to be tested for reliability of statistics based on samples from population variability of individual.
To calculate the SD, we need its square called variance. Variance is the average square deviation around the mean and is calculated by Variance = Σ(x-x-) 2/n OR Σ(x-x-) 2/n-1, now SD = √variance. SD helps us to predict how far the given value is away from the mean, and therefore, we can predict the coverage of values. SD is more appropriate only if data are normally distributed. If individual observations are clustered around sample mean (M) and are scattered evenly around it, the SD helps to calculate a range that will include a given percentage of observation. For example, if N ≥ 30, the range M ± 2(SD) will include 95% of observation and the range M ± 3(SD) will include 99% of observation. If observations are widely dispersed, central values are less representative of data, hence variance is taken. While reporting mean and SD, better way of representation is ‘mean (SD)’ rather than ‘mean ± SD’ to minimize confusion with confidence interval.[ 5 , 6 ]
Correlation Coefficient
Correlation is relationship between two variables. It is used to measure the degree of linear relationship between two continuous variables.[ 7 ] It is represented by ‘r’. In Chi-square test, we do not get the degree of association, but we can know whether they are dependent or independent of each other. Correlation may be due to some direct relationship between two variables. This also may be due to some inherent factors common to both variables. The correlation is expressed in terms of coefficient. The correlation coefficient values are always between -1 and +1. If the variables are not correlated, then correlation coefficient is zero. The maximum value of 1 is obtained if there is a straight line in scatter plot and considered as perfect positive correlation. The association is positive if the values of x-axis and y-axis tend to be high or low together. On the contrary, the association is negative i.e. -1 if the high y axis values tends to go with low values of x axis and considered as perfect negative correlation. Larger the correlation coefficient, stronger is the association. A weak correlation may be statistically significant if the numbers of observation are large. Correlation between the two variables does not necessarily suggest the cause and effect relationship. It indicates the strength of association for any data in comparable terms as for example, correlation between height and weight, age and height, weight loss and poverty, parity and birth weight, socioeconomic status and hemoglobin. While performing these tests, it requires x and y variables to be normally distributed. It is generally used to form hypothesis and to suggest areas of future research.
Types of Distribution
Though this universe is full of uncertainty and variability, a large set of experimental/biological observations always tend towards a normal distribution. This unique behavior of data is the key to entire inferential statistics. There are two types of distribution.
1) Gaussian /normal distribution
If data is symmetrically distributed on both sides of mean and form a bell-shaped curve in frequency distribution plot, the distribution of data is called normal or Gaussian. The noted statistician professor Gauss developed this, and therefore, it was named after him. The normal curve describes the ideal distribution of continuous values i.e. heart rate, blood sugar level and Hb % level. Whether our data is normally distributed or not, can be checked by putting our raw data of study directly into computer software and applying distribution test. Statistical treatment of data can generate a number of useful measurements, the most important of which are mean and standard deviation of mean. In an ideal Gaussian distribution, the values lying between the points 1 SD below and 1 SD above the mean value (i.e. ± 1 SD) will include 68.27% of all values. The range, mean ± 2 SD includes approximately 95% of values distributed about this mean, excluding 2.5% above and 2.5% below the range [ Figure 1 ]. In ideal distribution of the values; the mean, mode, and median are equal within population under study.[ 8 ] Even if distribution in original population is far from normal, the distribution of sample averages tend to become normal as size of sample increases. This is the single most important reason for the curve of normal distribution. Various methods of analysis are available to make assumptions about normality, including ‘t’ test and analysis of variance (ANOVA). In normal distribution, skew is zero. If the difference (mean–median) is positive, the curve is positively skewed and if it is (mean–median) negative, the curve is negatively skewed, and therefore, measure of central tendency differs [ Figure 1 ]

Diagram showing normal distribution curve with negative and positive skew μ = Mean, σ = Standard deviation
2) Non-Gaussian (non-normal) distribution
If the data is skewed on one side, then the distribution is non-normal. It may be binominal distribution or Poisson distribution. In binominal distribution, event can have only one of two possible outcomes such as yes/no, positive/negative, survival/death, and smokers/non-smokers. When distribution of data is non-Gaussian, different test like Wilcoxon, Mann-Whitney, Kruskal-Wallis, and Friedman test can be applied depending on nature of data.
Standard Error of Mean
Since we study some points or events (sample) to draw conclusions about all patients or population and use the sample mean (M) as an estimate of the population mean (M 1 ), we need to know how far M can vary from M 1 if repeated samples of size N are taken. A measure of this variability is provided by Standard error of mean (SEM), which is calculated as (SEM = SD/√n). SEM is always less than SD. What SD is to the sample, the SEM is to the population mean.
Applications of Standard Error of Mean:
Applications of SEM include:
- 1) To determine whether a sample is drawn from same population or not when it's mean is known.
Mean fasting blood sugar + 2 SEM = 90 + (2 × 0.56) = 91.12 while
Mean fasting blood sugar - 2 SEM = 90 - (2 × 0.56) = 88.88
So, confidence limits of fasting blood sugar of lawyer's population are 88.88 to 91.12 mg %. If mean fasting blood sugar of another lawyer is 80, we can say that, he is not from the same population.
Confidence Interval (CI) OR (Fiducial limits)
Confidence limits are two extremes of a measurement within which 95% observations would lie. These describe the limits within which 95% of the mean values if determined in similar experiments are likely to fall. The value of ‘t’ corresponding to a probability of 0.05 for the appropriate degree of freedom is read from the table of distribution. By multiplying this value with the standard error, the 95% confidence limits for the mean are obtained as per formula below.
Lower confidence limit = mean - (t 0.05 × SEM)
Upper confidence limit = mean + (t 0.05 × SEM)
If n > 30, the interval M ± 2(SEM) will include M with a probability of 95% and the interval M ± 2.8(SEM) will include M with probability of 99%. These intervals are, therefore, called the 95% and 99% confidence intervals, respectively.[ 9 ] The important difference between the ‘p’ value and confidence interval is that confidence interval represents clinical significance, whereas ‘p’ value indicates statistical significance. Therefore, in many clinical studies, confidence interval is preferred instead of ‘p’ value,[ 4 ] and some journals specifically ask for these values.
Various medical journals use mean and SEM to describe variability within the sample. The SEM is a measure of precision for estimated population mean, whereas SD is a measure of data variability around mean of a sample of population. Hence, SEM is not a descriptive statistics and should not be used as such.[ 10 ] Correct use of SEM would be only to indicate precision of estimated mean of population.
Null Hypothesis
The primary object of statistical analysis is to find out whether the effect produced by a compound under study is genuine and is not due to chance. Hence, the analysis usually attaches a test of statistical significance. First step in such a test is to state the null hypothesis. In null hypothesis (statistical hypothesis), we make assumption that there exist no differences between the two groups. Alternative hypothesis (research hypothesis) states that there is a difference between two groups. For example, a new drug ‘A’ is claimed to have analgesic activity and we want to test it with the placebo. In this study, the null hypothesis would be ‘drug A is not better than the placebo.’ Alternative hypothesis would be ‘there is a difference between new drug ‘A’ and placebo.’ When the null hypothesis is accepted, the difference between the two groups is not significant. It means, both samples were drawn from single population, and the difference obtained between two groups was due to chance. If alternative hypothesis is proved i.e. null hypothesis is rejected, then the difference between two groups is statistically significant. A difference between drug ‘A’ and placebo group, which would have arisen by chance is less than five percent of the cases, that is less than 1 in 20 times is considered as statistically significant ( P < 0.05). In any experimental procedure, there is possibility of occurring two errors.
1) Type I Error (False positive)
This is also known as α error. It is the probability of finding a difference; when no such difference actually exists, which results in the acceptance of an inactive compound as an active compound. Such an error, which is not unusual, may be tolerated because in subsequent trials, the compound will reveal itself as inactive and thus finally rejected.[ 11 ] For example, we proved in our trial that new drug ‘A’ has an analgesic action and accepted as an analgesic. If we commit type I error in this experiment, then subsequent trial on this compound will automatically reject our claim that drug ‘A’ is having analgesic action and later on drug ‘A’ will be thrown out of market. Type I error is actually fixed in advance by choice of the level of significance employed in test.[ 12 ] It may be noted that type I error can be made small by changing the level of significance and by increasing the size of sample.
2) Type II Error (False negative)
This is also called as β error. It is the probability of inability to detect the difference when it actually exists, thus resulting in the rejection of an active compound as an inactive. This error is more serious than type I error because once we labeled the compound as inactive, there is possibility that nobody will try it again. Thus, an active compound will be lost.[ 11 ] This type of error can be minimized by taking larger sample and by employing sufficient dose of the compound under trial. For example, we claim that drug ‘A’ is not having analgesic activity after suitable trial. Therefore, drug ‘A’ will not be tried by any other researcher for its analgesic activity and thus drug ‘A’, in spite of having analgesic activity, will be lost just because of our type II error. Hence, researcher should be very careful while reporting type II error.
Level of Significance
If the probability ( P ) of an event or outcome is high, we say it is not rare or not uncommon. But, if the P is low, we say it is rare or uncommon. In biostatistics, a rare event or outcome is called significant, whereas a non-rare event is called non-significant. The ‘ P ’ value at which we regard an event or outcomes as enough to be regarded as significant is called the significance level.[ 2 ] In medical research, most commonly P value less than 0.05 or 5% is considered as significant level . However, on justifiable grounds, we may adopt a different standard like P < 0.01 or 1%. Whenever possible, it is better to give actual P values instead of P < 0.05.[ 13 ] Even if we have found the true value or population value from sample, we cannot be confident as we are dealing with a part of population only; howsoever big the sample may be. We would be wrong in 5% cases only if we place the population value within 95% confidence limits. Significant or insignificant indicates whether a value is likely or unlikely to occur by chance. ‘ P ’ indicates probability of relative frequency of occurrence of the difference by chance.
Sometimes, when we analyze the data, one value is very extreme from the others. Such value is referred as outliers. This could be due to two reasons. Firstly, the value obtained may be due to chance; in that case, we should keep that value in final analysis as the value is from the same distribution. Secondly, it may be due to mistake. Causes may be listed as typographical or measurement errors. In such cases, these values should be deleted, to avoid invalid results.
One-tailed and Two-tailed Test
When comparing two groups of continuous data, the null hypothesis is that there is no real difference between the groups (A and B). The alternative hypothesis is that there is a real difference between the groups. This difference could be in either direction e.g. A > B or A < B. When there is some sure way to know in advance that the difference could only be in one direction e.g. A > B and when a good ground considers only one possibility, the test is called one-tailed test. Whenever we consider both the possibilities, the test of significance is known as a two-tailed test. For example, when we know that English boys are taller than Indian boys, the result will lie at one end that is one tail distribution, hence one tail test is used. When we are not absolutely sure of the direction of difference, which is usual, it is always better to use two-tailed test.[ 14 ] For example, a new drug ‘X’ is supposed to have an antihypertensive activity, and we want to compare it with atenolol. In this case, as we don’t know exact direction of effect of drug ‘X’, so one should prefer two-tailed test. When you want to know the action of particular drug is different from that of another, but the direction is not specific, always use two-tailed test. At present, most of the journals use two-sided P values as a standard norm in biomedical research.[ 15 ]
Importance of Sample Size Determination
Sample is a fraction of the universe. Studying the universe is the best parameter. But, when it is possible to achieve the same result by taking fraction of the universe, a sample is taken. Applying this, we are saving time, manpower, cost, and at the same time, increasing efficiency. Hence, an adequate sample size is of prime importance in biomedical studies. If sample size is too small, it will not give us valid results, and validity in such a case is questionable, and therefore, whole study will be a waste. Furthermore, large sample requires more cost and manpower. It is a misuse of money to enroll more subjects than required. A good small sample is much better than a bad large sample. Hence, appropriate sample size will be ethical to produce precise results.
Factors Influencing Sample Size Include
- 1) Prevalence of particular event or characteristics- If the prevalence is high, small sample can be taken and vice versa . If prevalence is not known, then it can be obtained by a pilot study.
- 2) Probability level considered for accuracy of estimate- If we need more safeguard about conclusions on data, we need a larger sample. Hence, the size of sample would be larger when the safeguard is 99% than when it is only 95%. If only a small difference is expected and if we need to detect even that small difference, then we need a large sample.
- 3) Availability of money, material, and manpower.
- 4) Time bound study curtails the sample size as routinely observed with dissertation work in post graduate courses.
Sample Size Determination and Variance Estimate
To calculate sample size, the formula requires the knowledge of standard deviation or variance, but the population variance is unknown. Therefore, standard deviation has to be estimated. Frequently used sources for estimation of standard deviation are:
- A pilot[ 16 ] or preliminary sample may be drawn from the population, and the variance computed from the sample may be used as an estimate of standard deviation. Observations used in pilot sample may be counted as a part of the final sample.[ 17 ]
- Estimates of standard deviation may be accessible from the previous or similar studies,[ 17 ] but sometimes, they may not be correct.
Calculation of Sample Size
Calculation of sample size plays a key role while doing any research. Before calculation of sample size, following five points are to be considered very carefully. First of all, we have to assess the minimum expected difference between the groups. Then, we have to find out standard deviation of variables. Different methods for determination of standard deviation have already been discussed previously. Now, set the level of significance (alpha level, generally set at P < 0.05) and Power of study (1-beta = 80%). After deciding all these parameters, we have to select the formula from computer programs to obtain the sample size. Various softwares are available free of cost for calculation of sample size and power of study. Lastly, appropriate allowances are given for non-compliance and dropouts, and this will be the final sample size for each group in study. We will work on two examples to understand sample size calculation.
- a) The mean (SD) diastolic blood pressure of hypertensive patient after enalapril therapy is found to be 88(8). It is claimed that telmisartan is better than enalapril, and a trial is to be conducted to find out the truth. By our convenience, suppose we take minimum expected difference between the two groups is 6 at significance level of 0.05 with 80% power. Results will be analyzed by unpaired ‘t’ test. In this case, minimum expected difference is 6, SD is 8 from previous study, alpha level is 0.05, and power of study is 80%. After putting all these values in computer program, sample size comes out to be 29. If we take allowance to non-compliance and dropout to be 4, then final sample size for each group would be 33.
- b) The mean hemoglobin (SD) of newborn is observed to be 10.5 (1.4) in pregnant mother of low socioeconomic group. It was decided to carry out a study to decide whether iron and folic acid supplementation would increase hemoglobin level of newborn. There will be two groups, one with supplementation and other without supplementation. Minimum difference expected between the two groups is taken as 1.0 with 0.05 level of significance and power as 90%. In this example, SD is 1.4 with minimum difference 1.0. After keeping these values in computer-based formula, sample size comes out to be 42 and with allowance of 10%, final sample size would be 46 in each group.
Power of Study
It is a probability that study will reveal a difference between the groups if the difference actually exists. A more powerful study is required to pick up the higher chances of existing differences. Power is calculated by subtracting the beta error from 1. Hence, power is (1-Beta). Power of study is very important while calculation of sample size. Power of study can be calculated after completion of study called as posteriori power calculation. This is very important to know whether study had enough power to pick up the difference if it existed. Any study to be scientifically sound should have at least 80% power. If power of study is less than 80% and the difference between groups is not significant, then we can say that difference between groups could not be detected, rather than no difference between the groups. In this case, power of study is too low to pick up the exiting difference. It means probability of missing the difference is high and hence the study could have missed to detect the difference. If we increase the power of study, then sample size also increases. It is always better to decide power of study at initial level of research.
How to Choose an Appropriate Statistical Test
There are number of tests in biostatistics, but choice mainly depends on characteristics and type of analysis of data. Sometimes, we need to find out the difference between means or medians or association between the variables. Number of groups used in a study may vary; therefore, study design also varies. Hence, in such situation, we will have to make the decision which is more precise while selecting the appropriate test. Inappropriate test will lead to invalid conclusions. Statistical tests can be divided into parametric and non-parametric tests. If variables follow normal distribution, data can be subjected to parametric test, and for non-Gaussian distribution, we should apply non-parametric test. Statistical test should be decided at the start of the study. Following are the different parametric test used in analysis of various types of data.
1) Student's ‘t’ Test
Mr. W. S. Gosset, a civil service statistician, introduced ‘t’ distribution of small samples and published his work under the pseudonym ‘Student.’ This is one of the most widely used tests in pharmacological investigations, involving the use of small samples. The ‘t’ test is always applied for analysis when the number of sample is 30 or less. It is usually applicable for graded data like blood sugar level, body weight, height etc. If sample size is more than 30, ‘Z’ test is applied. There are two types of ‘t’ test, paired and unpaired.
When to apply paired and unpaired
- a) When comparison has to be made between two measurements in the same subjects after two consecutive treatments, paired ‘t’ test is used. For example, when we want to compare effect of drug A (i.e. decrease blood sugar) before start of treatment (baseline) and after 1 month of treatment with drug A.
- b) When comparison is made between two measurements in two different groups, unpaired ‘t’ test is used. For example, when we compare the effects of drug A and B (i.e. mean change in blood sugar) after one month from baseline in both groups, unpaired ‘t’ test’ is applicable.
When we want to compare two sets of unpaired or paired data, the student's ‘t’ test is applied. However, when there are 3 or more sets of data to analyze, we need the help of well-designed and multi-talented method called as analysis of variance (ANOVA). This test compares multiple groups at one time.[ 18 ] In ANOVA, we draw assumption that each sample is randomly drawn from the normal population, and also they have same variance as that of population. There are two types of ANOVA.
A) One way ANOVA
It compares three or more unmatched groups when the data are categorized in one way. For example, we may compare a control group with three different doses of aspirin in rats. Here, there are four unmatched group of rats. Therefore, we should apply one way ANOVA. We should choose repeated measures ANOVA test when the trial uses matched subjects. For example, effect of supplementation of vitamin C in each subject before, during, and after the treatment. Matching should not be based on the variable you are com paring. For example, if you are comparing blood pressures in two groups, it is better to match based on age or other variables, but it should not be to match based on blood pressure. The term repeated measures applies strictly when you give treatments repeatedly to one subjects. ANOVA works well even if the distribution is only approximately Gaussian. Therefore, these tests are used routinely in many field of science. The P value is calculated from the ANOVA table.
B) Two way ANOVA
Also called two factors ANOVA, determines how a response is affected by two factors. For example, you might measure a response to three different drugs in both men and women. This is a complicated test. Therefore, we think that for postgraduates, this test may not be so useful.
Importance of post hoc test
Post tests are the modification of ‘t’ test. They account for multiple comparisons, as well as for the fact that the comparison are interrelated. ANOVA only directs whether there is significant difference between the various groups or not. If the results are significant, ANOVA does not tell us at what point the difference between various groups subsist. But, post test is capable to pinpoint the exact difference between the different groups of comparison. Therefore, post tests are very useful as far as statistics is concerned. There are five types of post- hoc test namely; Dunnett's, Turkey, Newman-Keuls, Bonferroni, and test for linear trend between mean and column number.[ 18 ]
How to select a post test?
- I) Select Dunnett's post-hoc test if one column represents control group and we wish to compare all other columns to that control column but not to each other.
- II) Select the test for linear trend if the columns are arranged in a natural order (i.e. dose or time) and we want to test whether there is a trend so that values increases (or decreases) as you move from left to right across the columns.
- III) Select Bonferroni, Turkey's, or Newman's test if we want to compare all pairs of columns.
Following are the non-parametric tests used for analysis of different types of data.
1) Chi-square test
The Chi-square test is a non-parametric test of proportions. This test is not based on any assumption or distribution of any variable. This test, though different, follows a specific distribution known as Chi-square distribution, which is very useful in research. It is most commonly used when data are in frequencies such as number of responses in two or more categories. This test involves the calculations of a quantity called Chi-square (x 2 ) from Greek letter ‘Chi’(x) and pronounced as ‘Kye.’ It was developed by Karl Pearson.
Applications
- a) Test of proportion: This test is used to find the significance of difference in two or more than two proportions.
- b) Test of association: The test of association between two events in binomial or multinomial samples is the most important application of the test in statistical methods. It measures the probabilities of association between two discrete attributes. Two events can often be studied for their association such as smoking and cancer, treatment and outcome of disease, level of cholesterol and coronary heart disease. In these cases, there are two possibilities, either they influence or affect each other or they do not. In other words, you can say that they are dependent or independent of each other. Thus, the test measures the probability ( P ) or relative frequency of association due to chance and also if two events are associated or dependent on each other. Varieties used are generally dichotomous e.g. improved / not improved. If data are not in that format, investigator can transform data into dichotomous data by specifying above and below limit. Multinomial sample is also useful to find out association between two discrete attributes. For example, to test the association between numbers of cigarettes equal to 10, 11- 20, 21-30, and more than 30 smoked per day and the incidence of lung cancer. Since, the table presents joint occurrence of two sets of events, the treatment and outcome of disease, it is called contingency table (Con- together, tangle- to touch).
How to prepare 2 × 2 table
When there are only two samples, each divided into two classes, it is called as four cell or 2 × 2 contingency table. In contingency table, we need to enter the actual number of subjects in each category. We cannot enter fractions or percentage or mean. Most contingency tables have two rows (two groups) and two columns (two possible outcomes). The top row usually represents exposure to a risk factor or treatment, and bottom row is mainly for control. The outcome is entered as column on the right side with the positive outcome as the first column and the negative outcome as the second column. A particular subject or patient can be only in one column but not in both. The following table explains it in more detail:

Even if sample size is small (< 30), this test is used by using Yates correction, but frequency in each cell should not be less than 5.[ 19 ] Though, Chi-square test tells an association between two events or characters, it does not measure the strength of association. This is the limitation of this test. It only indicates the probability ( P ) of occurrence of association by chance. Yate's correction is not applicable to tables larger than 2 X 2. When total number of items in 2 X 2 table is less than 40 or number in any cell is less than 5, Fischer's test is more reliable than the Chi-square test.[ 20 ]
2) Wilcoxon-Matched-Pairs Signed-Ranks Test
This is a non-parametric test. This test is used when data are not normally distributed in a paired design. It is also called Wilcoxon-Matched Pair test. It analyses only the difference between the paired measurements for each subject. If P value is small, we can reject the idea that the difference is coincidence and conclude that the populations have different medians.
3) Mann-Whitney test
It is a Student's ‘t’ test performed on ranks. For large numbers, it is almost as sensitive as Student's ‘t’ test. For small numbers with unknown distribution, this test is more sensitive than Student's ‘t’ test. This test is generally used when two unpaired groups are to be compared and the scale is ordinal (i.e. ranks and scores), which are not normally distributed.
4) Friedman test
This is a non-parametric test, which compares three or more paired groups. In this, we have to rank the values in each row from low to high. The goal of using a matched test is to control experimental variability between subjects, thus increasing the power of the test.
5) Kruskal-Wallis test
It is a non-parametric test, which compares three or more unpaired groups. Non-parametric tests are less powerful than parametric tests. Generally, P values tend to be higher, making it harder to detect real differences. Therefore, first of all, try to transform the data. Sometimes, simple transformation will convert non-Gaussian data to a Gaussian distribution. Non-parametric test is considered only if outcome variable is in rank or scale with only a few categories [ Table 1 ]. In this case, population is far from Gaussian or one or few values are off scale, too high, or too low to measure.
Summary of statistical tests applied for different types of data

Common problems faced by researcher in any trial and how to address them
Whenever any researcher thinks of any experimental or clinical trial, number of queries arises before him/her. To explain some common difficulties, we will take one example and try to solve it. Suppose, we want to perform a clinical trial on effect of supplementation of vitamin C on blood glucose level in patients of type II diabetes mellitus on metformin. Two groups of patients will be involved. One group will receive vitamin C and other placebo.
a) How much should be the sample size?
In such trial, first problem is to find out the sample size. As discussed earlier, sample size can be calculated if we have S.D, minimum expected difference, alpha level, and power of study. S.D. can be taken from the previous study. If the previous study report is not reliable, you can do pilot study on few patients and from that you will get S.D. Minimum expected difference can be decided by investigator, so that the difference would be clinically important. In this case, Vitamin C being an antioxidant, we will take difference between the two groups in blood sugar level to be 15. Minimum level of significance may be taken as 0.05 or with reliable ground we can increase it, and lastly, power of study is taken as 80% or you may increase power of study up to 95%, but in both the situations, sample size will be increased accordingly. After putting all the values in computer software program, we will get sample size for each group.
b) Which test should I apply?
After calculating sample size, next question is to apply suitable statistical test. We can apply parametric or non-parametric test. If data are normally distributed, we should use parametric test otherwise apply non-parametric test. In this trial, we are measuring blood sugar level in both groups after 0, 6, 12 weeks, and if data are normally distributed, then we can apply repeated measure ANOVA in both the groups followed by Turkey's post-hoc test if we want to compare all pairs of column with each other and Dunnet's post-hoc for comparing 0 with 6 or 12 weeks observations only. If we want to see whether supplementation of vitamin C has any effect on blood glucose level as compared to placebo, then we will have to consider change from baseline i.e. from 0 to 12 weeks in both groups and apply unpaired ‘t’ with two-tailed test as directions of result is non-specific. If we are comparing effects only after 12 weeks, then paired ‘t’ test can be applied for intra-group comparison and unpaired ‘t’ test for inter-group comparison. If we want to find out any difference between basic demographic data regarding gender ratio in each group, we will have to apply Chi-square test.
c) Is there any correlation between the variable?
To see whether there is any correlation between age and blood sugar level or gender and blood sugar level, we will apply Spearman or Pearson correlation coefficient test, depending on Gaussian or non-Gaussian distribution of data. If you answer all these questions before start of the trial, it becomes painless to conduct research efficiently.
Softwares for Biostatistics
Statistical computations are now made very feasible owing to availability of computers and suitable software programs. Now a days, computers are mostly used for performing various statistical tests as it is very tedious to perform it manually. Commonly used software's are MS Office Excel, Graph Pad Prism, SPSS, NCSS, Instant, Dataplot, Sigmastat, Graph Pad Instat, Sysstat, Genstat, MINITAB, SAS, STATA, and Sigma Graph Pad. Free website for statistical softwares are www.statistics.com , http://biostat.mc.vanderbilt.edu/wiki/Main/PowerSampleSize .
Statistical methods are necessary to draw valid conclusion from the data. The postgraduate students should be aware of different types of data, measures of central tendencies, and different tests commonly used in biostatistics, so that they would be able to apply these tests and analyze the data themselves. This article provides a background information, and an attempt is made to highlight the basic principles of statistical techniques and methods for the use of postgraduate students.
Acknowledgement
The authors gratefully acknowledge to Dr. Suparna Chatterjee, Associate Professor, Pharmacology, IPGMER, Kolkata for the helpful discussion and input while preparing this article.
Source of Support: Nil.
Conflict of Interest: None declared.
Data Analyst (underfill option)
The University of Michigan Health System is home to multiple Collaborative Quality Initiatives (CQIs) coordinating centers which seek to address some of the most common, complex, and costly areas of surgical and medical care. With funding from Blue Cross Blue Shield of Michigan (BCBSM), the CQIs work collaboratively with health care providers throughout Michigan to collect data to a centralized registry. The data are analyzed and shared to identify processes that lead to improved delivery of care and outcomes, and guide quality improvement interventions.
The Inspiring Health Advances in Lung Care INHALE CQI is a recently established CQI focused on addressing lung health in patients with Asthma and COPD. The ultimate goal is to partner all CQIs with communities across the state to ensure all patients have access to social health interventions needed for optimal care and health outcomes.
Each CQI is organized and facilitated by a Coordinating Center, led by Program Directors and Co-directors (physicians and nurses), and a Program Manager. A CQIs staffing typically includes Quality Improvement (QI) coordinators, project managers, and analysts. The current role is for a novel CQI that will interface with all other existing CQIs as well as community partners across the state.
Role Summary: The INHALE Data Analyst will perform data management, statistical programming, analysis and reporting using large administrative claims and clinical extracts.
Mission Statement
Michigan Medicine improves the health of patients, populations and communities through excellence in education, patient care, community service, research and technology development, and through leadership activities in Michigan, nationally and internationally. Our mission is guided by our Strategic Principles and has three critical components; patient care, education and research that together enhance our contribution to society.
Responsibilities*
This position involves a wide range of tasks including claims and clinical data management, provider participation and performance tracking for value-based reimbursement supporting quality improvement. Under the direction of the INHALE program directors and in collaboration with the CQI population health data hub, the position involves providing independent and collaborative analytic support for the INHALE CQI.
Responsibilities include but are not limited to:
Data Analysis:
- Extract, transform, and merge raw data from various data sources into usable forms and construct datasets.
- Write, test, and implement programs using SAS or other statistical software to analyze incoming data for accuracy
- Design and prepare standard automated and ad hoc reports for participating provider organizations
- Work closely with the INHALE team and the data hub to develop new quality measures and dashboard views.
- Work closely with the INHALE team to summarize, interpret, and present results in written, tabular, and visual formats. Apply a broad knowledge of measurement, analysis, ROI, and performance improvement to implement QI and other projects throughout the collaborative, facilitating the adoption and implementation of best practices.
- Document processes and data sources and make recommendations for improvements.
- Harmonize data with previously collected data or aggregate disparate data sources for analysis and reporting.
Data Reporting:
- Respond to questions, data needs, and ad-hoc requests from CQI participants.
- Prepare standard reports for BCBSM detailing provider and practice participation.
- Independently document quality assurance operations performed in final reports and provide basic documentation on datasets.
- Document procedures for future reference and make recommendations for data analysis process improvements.
Behavioral & Work Environment Expectations:
- Identify and act on current priorities while maintaining flexibility and openness to changes.
- Bring a participatory and constructive approach to problem solving.
- Consider impact of work on internal and external audiences and be mindful of project timelines, staff needs across projects.
- Be approachable, responsive, and accessible, acting as a support and resource for others.
- Proactively share knowledge to keep team members informed and work to overcome obstacles and seek resolutions with others.
- Move between leader and follower roles within projects.
Required Qualifications*
Senior Level:
- Bachelor's degree in Statistics, Biostatics, Public Health, Computer Science, Informatics, or related field or appropriate job experience.
- At least 5 years of professional experience in SAS programing and analysis (or other similar statistical software such as Stata or R) required for placement at the senior level
Intermediate Level:
- At least 3 years of professional experience in SAS programing and analysis (or other similar statistical software such as Stata or R) required for placement at the intermediate level
- Strong, demonstrable programming skills and experience with relational databases, complex data structure, and linkages between data sources
- Experience with Microsoft Excel and PowerPoint for the development of presentation materials
- Proven ability to write clear and concise technical documentation, summaries of various methodologies, and descriptions of statistical results
- Excellent communication, both oral and written in English language, and interpersonal skills are essential
- Ability to prioritize, organize, and efficiently work on multiple projects at the same time
- Working knowledge of epidemiologic concepts and methodology
- Experience working with International Classification Diagnosis and Procedures (ICD 10) codes, National Drug Codes (NDC), Current Procedural Terminology (CPT) and Healthcare Common Procedure Coding System (HCPCS) codes.
- Experience with real world healthcare claims data, such as Blue Cross/Blue Shield, MarketScan, Optum, Medicare, Medicaid, and/or Electronic Medical Record Databases
Desired Qualifications*
- Master's degree in Statistics, Biostatistics, Public Health, Informatics, Computer Science, or related field.
- Experience with additional statistical software and reporting tools (e.g. Tableau) and/or the ability and willingness to learn as necessary.
Underfill Statement
This position may be underfilled at a lower classification depending on the qualifications of the selected candidate.
Additional Information
Note: Examples of your SAS or other statistical code, reports, or other work product may be requested.
Background Screening
Michigan Medicine conducts background screening and pre-employment drug testing on job candidates upon acceptance of a contingent job offer and may use a third party administrator to conduct background screenings. Background screenings are performed in compliance with the Fair Credit Report Act. Pre-employment drug testing applies to all selected candidates, including new or additional faculty and staff appointments, as well as transfers from other U-M campuses.
Application Deadline
Job openings are posted for a minimum of seven calendar days. The review and selection process may begin as early as the eighth day after posting. This opening may be removed from posting boards and filled anytime after the minimum posting period has ended.
U-M EEO/AA Statement
The University of Michigan is an equal opportunity/affirmative action employer.
Associate Director, Biostatistics
Job Posting for Associate Director, Biostatistics at Vera Therapeutics, Inc.
Vera Therapeutics (Nasdaq: VERA), is a late-stage biotechnology company focused on developing treatments for serious immunological diseases. Vera’s mission is to advance treatments that target the source of immunologic diseases in order to change the standard of care for patients. Vera’s lead product candidate is atacicept, a fusion protein self-administered as a subcutaneous injection once weekly that blocks both B lymphocyte stimulator (BLyS) and a proliferation inducing ligand (APRIL), which stimulate B cells and plasma cells to produce autoantibodies contributing to certain autoimmune diseases, including IgA nephropathy (IgAN), also known as Berger’s disease and lupus nephritis. In addition, Vera is evaluating additional diseases where the reduction of autoantibodies by atacicept may prove medically useful. Vera is also developing MAU868, a monoclonal antibody designed to neutralize infection with BK Virus, a polyomavirus that can have devastating consequences in certain settings such as kidney transplant. For more information please visit: www.veratx.com.
Our values are the cornerstone of our culture. Our values inspire us every day and guide everything we do—from how we hire great people, to advancing our mission together, to achieving our ultimate goal to improve medical treatment for patients suffering from immunological diseases.
Position Summary:
The Associate Director, Biostatistics is a member of a cross-functional product development team and contributes to trial design, protocol development, analysis planning, interpretation of results, and preparation of regulatory submissions. Reporting to the Vice President, Biostatistics, this position will also contribute to biostatistics infrastructure development to support long-term department goals.
Responsibilities:
- Contributes to the design of scientifically sound clinical trials, including the selection of study population/sample size/endpoints to address study objectives.
- Authors/reviews protocol, statistical analysis plan, clinical study reports, publications, and product level documents.
- Acts as the primary contact and able to act as the lead project biostatistician for all biostatistics related activities outsourced to CROs and other external vendors.
- Works collaboratively with vendors, Clinical Research, Drug Safety, Regulatory Affairs, Clinical Operation, and Project Management teams to meet project deliverables and timelines for statistical data analysis and reporting.
- Presents summary data and analyses results in an effective manner.
- Provides statistical support and provide scientifically rigorous statistical expertise in addressing health authority requests, publications, presentations, and other public release of information.
- Manages multiple studies to ensure consistency and adherence to standards within a therapeutic area.
- Responsible for complying with all company processes and SOPs.
Qualifications:
- PhD (5 years) or MS (8 years) in statistics or biostatistics or related scientific field with experience in clinical trials in the pharmaceutical or biotechnology industry.
- Proficiency in scientific computing/programming (SAS or R) and implementation of advanced statistical analysis, data manipulation, graphing, and simulation.
- Excellent communication skills with the ability to deliver difficult or complex messages and provide feedback with both tact and diplomacy
- Expertise in statistical/clinical trials methodology as it relates to clinical development and ability to apply to relevant clinical development framework that will significantly advance the teams’ capabilities and performance.
- Good understanding of regulatory landscape and experience with participating in regulatory interactions.
- Able to identify opportunities for strategic cross-functional collaborations that can carry significant impact to the business.
- Proven project management skills with the ability to plan, organize, and prioritize multiple work assignments.
Vera Therapeutics Inc. is an equal opportunity employer.
Vera Therapeutics is committed to fair and equitable compensation practices, and we strive to provide employees with total compensation packages that are market competitive. For this role, the anticipated base pay range is $197,000 - $215,000. The exact base pay offered for this role will depend on various factors, including but not limited to the candidate’s geography, qualifications, skills, and experience.
At Vera, base pay is only one part of your total compensation package. The successful candidate will be eligible for an annual performance incentive bonus, new hire equity, and ongoing performance-based equity. Vera Therapeutics also offers various benefits offerings, including, but not limited to, medical, dental, and vision insurance, 401k match, flexible time off, and a number of paid holidays.
COVID-19 Policy
Vera’s top priority is the health and safety of our employees, their families and the communities where they live and work. As part of our commitment to health and safety, we require all U.S. employees to be fully vaccinated against COVID-19. If your role at Vera requires you to work or otherwise be on Vera’s premises, full or part-time, we require our employees to comply with Vera’s mandatory COVID-19 vaccination policy (currently requiring full vaccination). Anyone unable to be vaccinated, either because of a sincerely held religious belief or a medical condition or disability that prevents them from being vaccinated, may request a reasonable accommodation with Human Resources. Your employment is also subject to ongoing compliance with the mandatory vaccination policy and all other Vera policies, as they may be modified from time to time, at the sole discretion of Vera.
Notice to Recruiters/Staffing Agencies
Recruiters and staffing agencies should not contact Vera Therapeutics through this page. All recruitment vendors (search firms, recruitment agencies, and staffing companies) are prohibited from contacting our hiring manager(s), executive team members, or employees.
We require that all recruiters and staffing agencies have a fully executed, formal written agreement on file. Vera Therapeutics’ receipt or acceptance of an unsolicited resume submitted by a vendor organization to this website or employee does not constitute an actual or implied contract between Vera Therapeutics and such organization and will be considered unsolicited and Vera Therapeutics will not be responsible for related fees.
Apply for this job
Receive alerts for other Associate Director, Biostatistics job openings
Report this Job
Salary.com Estimation for Associate Director, Biostatistics in Brisbane, CA
$156,776 - $207,211
For Employer
Looking to price a job for your company?
Sign up to receive alerts about other jobs that are on the Associate Director, Biostatistics career path.
Click the checkbox next to the jobs that you are interested in.
Sign up to receive alerts about other jobs with skills like those required for the Associate Director, Biostatistics .
BI Analytics/Reporting Tools Skill
- Sustainability Manager Income Estimation: $114,769 - $168,759
- Database Report Writer IV Income Estimation: $119,776 - $164,250
Capacity Management Skill
- Enterprise Infrastructure Director Income Estimation: $213,605 - $289,033
- Systems Architecture Director Income Estimation: $224,714 - $282,482
Job openings at Vera Therapeutics, Inc.
Not the job you're looking for here are some other associate director, biostatistics jobs in the brisbane, ca area that may be a better fit., we don't have any other associate director, biostatistics jobs in the brisbane, ca area right now..
Cytokinetics , South San Francisco, CA
Cargo Therapeutics , San Mateo, CA

IMAGES
VIDEO
COMMENTS
The measures of central tendency give us an indication of the typical score in a sample. Another important descriptive statistics to be presented for quantitative data is its variability - the spread of the data scores.
The document provides an overview of different types of data and methods for presenting data. It discusses qualitative vs quantitative data, primary vs secondary data, and different ways to present data visually including bar charts, histograms, frequency polygons, scatter diagrams, line diagrams and pie charts. Guidelines are provided for tabular presentation of data to make it clear, concise ...
Josée Dupuis, PhD, Professor of Biostatistics, Boston University School of Public Health
In this article, the techniques of data and information presentation in textual, tabular, and graphical forms are introduced. Text is the principal method for explaining findings, outlining trends, and providing contextual information. A table is best suited for representing individual information and represents both quantitative and ...
Statistical presentation of data is key to understanding patterns and drawing inferences about biomedical phenomena. In this article, we provide an overview of basic statistical considerations for data analysis. Assessment of whether tested parameters are distributed normally is important to decide whether to employ parametric or non-parametric data analyses. The nature of variables ...
What IS biostatistics? A process that converts data into useful information, whereby practitioners. form a question of interest, collect and summarize data, and interpret the results. STA 102: Introduction to Biostatistics. Department of Statistical Science, Duke University.
This book introduces the open source R software language that can be implemented in biostatistics for data organization, statistical analysis, and graphical presentation.
Through real-world datasets, this book shows the reader how to work with material in biostatistics using the open source software R. These include tools that are critical to dealing with missing data, which is a pressing scientific issue for those engaged in biostatistics. Readers will be equipped to run analyses and make graphical presentations based on the sample dataset and their own data ...
1 Clinical trials and Epidemiology Research Unit, 226 Outram Road, Blk A #02-02, Singapore 169039. [email protected] Biostatistics 101: data presentation
Request PDF | On Jan 1, 2014, Thomas W. MacFarland published Introduction to Data Analysis and Graphical Presentation in Biostatistics with R: Statistics in the Large | Find, read and cite all the ...
The discipline of biostatistics provides tools and techniques for collecting data and then summarizing, analyzing, and interpreting it. If the samples one takes are representative of the population of interest, they will provide good estimates regarding the population overall. Consequently, in biostatistics one analyzes samples in order to make ...
It is important to understand the different types of data and their mutual interconversion. Biostatistics begins with descriptive statistics that implies summarizing a collection of data from a sample or population. Categorical data are described in terms of percentages or proportions.
Baek, Jonggyu, "Introduction to Biostatistics - Lecture 1: Introduction and Descriptive Statistics" (2019). PEER Liberia Project. 10.
Presentation of the collected data. Analysis and interpretation of the results. Making decisions on the basis of such analysis Therefore, when different statistical methods are applied in biological, medical and public health data they constitute the discipline of biostatistics.
Generally, the steps involved in biostatistics are data collection, data preparation, data presentation, data analysis, and interpretation of results. In data analysis, various tools are involved.
Biostatistics 101: data presentation. Y. Chan. Published in Singapore medical journal 2003. Biology. TLDR. This article will discuss how to present the collected data and the forthcoming write-ups will highlight on the appropriate statistical tests to be applied. Expand.
Biostatistics refers to the application of statistical techniques to biologic data collected prospectively and/or retrospectively. Briefly speaking, statistics plays a key role in all phases of a research project starting from the design stage and continuing through the monitoring, data collection, data analysis and interpretation of the ...
Osmosis Introductory Biostatistics high-yield notes offers clear overviews with striking illustrations, tables, and diagrams. Make learning more manageable.
Biostatistics. This document provides an overview of biostatistics. It defines biostatistics and discusses topics like data collection, presentation through tables and charts, measures of central tendency and dispersion, sampling, tests of significance, and applications of biostatistics in various medical fields. The document aims to introduce ...
This course demonstrates how to use statistical techniques to summarize the characteristics of a data set to draw meaningful conclusions. Study the various methods for presenting information in the form of charts and graphs. Discover how to use R programming for statistical analysis, graphical representation, and data reporting.
A working definition of biostatistics states biostatistics as the discipline that deals with the collection, organization, summarization, and analysis of data in the fields of biological, health, and medical sciences including other life sciences.
Study with Quizlet and memorize flashcards containing terms like Biostatistics, Descriptive, Inferential and more.
Ensure all Biostatistics deliverables for assigned clinical trials and/or non-clinical related activities are delivered in a timely manner with the highest level of quality. ... with 6years + work experience Fluent in English with strong communication and presentation skills, with the ability to articulate complex concepts to diverse audiences ...
This article provides background information related to fundamental methods and techniques in biostatistics for the use of postgraduate students. Main focus is given to types of data, measurement of central variations and basic tests, which are useful for analysis of different types of observations. Few parameters like normal distribution ...
The INHALE Data Analyst will perform data management, statistical programming, analysis and reporting using large administrative claims and clinical extracts. ... Experience with Microsoft Excel and PowerPoint for the development of presentation materials; ... Master's degree in Statistics, Biostatistics, Public Health, Informatics, Computer ...
Presents summary data and analyses results in an effective manner. Provides statistical support and provide scientifically rigorous statistical expertise in addressing health authority requests, publications, presentations, and other public release of information.