

Common Problem-Solving Models & How to Use Them
Problem – solving models are step-by-step processes that provide a framework for addressing challenges. Problems arise in every facet of life. From work. to home. to friends and family, problems and conflicts can make life difficult and interfere with our physical and mental well-being. Understanding how to approach problems when they arise and implementing problem-solving techniques can make the journey through a problem less onerous on ourselves and those around us.
By building a structured problem-solving process, you can begin to build muscle memory by repeatedly practicing the same approach, and eventually, you may even begin to find yourself solving complex problems . Building a problem-solving model for each of the situations where you may encounter a problem can give you a path forward, even when the most difficult of problems arise.
This article will explore the concept of problem-solving models and dive into examples of such models and how to use them. It will also outline the benefits of implementing a problem-solving model in each area of life and why these problem-solving methods can have a large impact on your overall well-being. The goal of this article is to help you identify effective problem-solving strategies and develop critical thinking to generate solutions for any problem that comes your way.
Problem-Solving Model Defined
The first step in creating a problem-solving plan is to understand what we mean when we say problem-solving models. A problem-solving model is a step-by-step process that helps a team identify and effectively solve problems that they may encounter. This problem-solving approach gives the team the muscle memory and guide to address a conflict and resolve disputes quickly and effectively.
There are common problem-solving models that many teams have implemented, but there is also the freedom to shape a method to fit the needs of a specific situation. These models often rely on various problem-solving techniques to identify the root cause of the issue and find the best solution. This article will explore some common problem-solving models as well as general problem-solving techniques to help a team engage with and solve problems effectively.
Benefits of Implementing Problem-Solving Models
Before we discuss the exact models for problem-solving, it can be helpful to discuss why problem-solving models are beneficial in the first place. There are a variety of benefits to having a plan in place when a problem arises, but a few important benefits are listed below.
Guide Posts
When a team encounters a problem and has a guide for how to approach and solve the problem, it can be a relief to know that they have a process to fall back on when the issue cannot be resolved quickly from the beginning. A problem-solving strategy will serve as a guide for the parties to know which steps to take next and how to identify the appropriate solution.
It can also clarify when the issue needs to stay within the team, and when the issue needs to be escalated to someone in a position with more authority. It can also help the entire team solve complex problems without creating an issue out of the way the team solves the problem. It gives the team a blueprint to work from and encourages them to find a good solution.
Creative Solutions That Last
When the team or family has a way to fall back on to solve a problem, it takes some of the pressure off of coming up with the process and allows the parties to focus on identifying the relevant information and coming up with various potential solutions to the issue. By using a problem-solving method, the parties can come up with different solutions and find common ground with the best solution. This can be stifled if the team is too focused on figuring out how to solve the problem.
Additionally, the solutions that the parties come up with through problem-solving tools will often address the root cause of the issue and stop the team from having to revisit the same problem over and over again. This can lead to overall productivity and well-being and help the team continue to output quality work. By encouraging collaboration and creativity, a problem-solving technique will often keep solving problems between the parties moving forward and possibly even address them before they show up.
Common Models to Use in the Problem-Solving Process
Several models can be applied to a complex problem and create possible solutions. These range from common and straightforward to creative and in-depth to identify the most effective ways to solve a problem. This section will discuss and break down the problem-solving models that are most frequently used.
Standard Problem-Solving Process
When you search for a problem-solving technique, chances are you will find the standard model for saving problems. This model identifies and uses several important steps that will often be used in other models as well, so it can be helpful to begin the model-building process with an understanding of this model as a base. Other models often draw from this process and adapt one or more of the steps to help create additional options. Each of these steps works to accomplish a specific goal in furtherance of a solution.
Define the Problem
The first step in addressing a problem is to create a clear definition of the issue at hand. This will often require the team to communicate openly and honestly to place parameters around the issue. As the team defines the problem, it will be clear what needs to be solved and what pieces of the conflict are ancillary to the major issue. It helps to find the root causes of the issue and begin a process to address that rather than the symptoms of the problem. The team can also create a problem statement, which outlines the parameters of the problem and what needs to be fixed.
In addition to open and honest communication, other techniques can help to identify the root cause and define the problem. This includes a thorough review of the processes and steps that are currently used in the task and whether any of those steps are directly or indirectly causing the problem.
This includes reviewing how tasks are done, how communication is shared, and the current partners and team members that work together to identify if any of those are part of the issue. It is also the time to identify if some of the easy fixes or new tools would solve the problem and what the impact would be.
It is also important to gain a wide understanding of the problem from all of the people involved. Many people will have opinions on what is going on, but it is also important to understand the facts over the opinions that are affecting the problem. This can also help you identify if the problem is arising from a boundary or standard that is not being met or honored. By gathering data and understanding the source of the problem, the process of solving it can begin.
Generate Solutions
The next step in the basic process is to generate possible solutions to the problem. At this step, it is less important to evaluate how each of the options will play out and how they may change the process and more important to identify solutions that could address the issue. This includes solutions that support the goals of the team and the task, and the team can also identify short and long-term solutions.
The team should work to brainstorm as many viable solutions as possible to give them the best options to consider moving forward. They cannot pick the first solution that is proposed and consider it a successful problem-solving process.
Evaluate and Select
After a few good options have been identified, the next step is to evaluate the options and pick the most viable option that also supports the goals of the team or organization. This includes looking at each of the possible solutions and determining how they would either encourage or hinder the goals and standards of the team. These should evaluated without bias toward the solution proposed or the person putting forward the solution. Additionally, the team should consider both actual outcomes that have happened in the past and predicted instances that may occur if the solution is chosen.
Each solution should be evaluated by considering if the solution would solve the current problem without causing additional issues, the willingness of the team to buy in and implement the solution, and the actual ability of the team to implement the solution.
Participation and honesty from all team members will make the process go more smoothly and ensure that the best option for everyone involved is selected. Once the team picks the option they would like to use for the specific problem, they should clearly define what the solution is and how it should be implemented. There should also be a strategy for how to evaluate the effectiveness of the solution.
Implement the Solution and Follow Up
Once a solution is chosen, a team will often assume that the work of solving problems is complete. However, the final step in the basic model is an important step to determine if the matter is resolved or if additional options are needed. After the solution has been implemented by the team, the members of the team must provide feedback and identify any potential obstacles that may have been missed in the decision-making process.
This encourages long-term solutions for the problem and helps the team to continue to move forward with their work. It also gives the team a sense of ownership and an example of how to evaluate an idea in the future.
If the solution is not working the way that it should, the team will often need to adapt the option, or they may get to the point where they scrap the option and attempt another. Solving a problem is not always a linear process, and encouraging reform and change within the process will help the team find the answer to the issues that they face.
GROW Method
Another method that is similar to the standard method is the G.R.O.W. method. This method has very similar steps to the standard method, but the catchiness of the acronym helps a team approach the problem from the same angle each time and work through the method quickly.
The first step in the method is to identify a goal, which is what the “g” stands for in “grow.” To establish a goal, the team will need to look at the issues that they are facing and identify what they would like to accomplish and solve through the problem-solving process. The team will likely participate in conversations that identify the issues that they are facing and what they need to resolve.
The next step is to establish the current reality that the group is facing. This helps them to determine where they currently are and what needs to be done to move them forward. This can help the group establish a baseline for where they started and what they would like to change.
The next step is to find any obstacles that may be blocking the group from achieving their goal. This is where the main crux of the issues that the group is facing will come out. This is also helpful in giving the group a chance to find ways around these obstacles and toward a solution.
Way Forward
After identifying the obstacles and potential ways to avoid them, the group will then need to pick the best way to move forward and approach their goal together. Here, they will need to create steps to move forward with that goal.
Divide and Conquer
Another common problem-solving method is the divide-and-conquer method. Here, instead of the entire team working through each step of the process as a large group, they split up the issue into smaller problems that can be solved and have individual members or small groups work through the smaller problems. Once each group is satisfied with the solution to the problem, they present it to the larger group to consider along with the other options.
This process can be helpful if there is a large team attempting to solve a large and complex problem. It is also beneficial because it can be used in teams with smaller, specialized teams within it because it allows each smaller group to focus on what they know best.
However, it does encourage the parties to shy away from collaboration on the overall issue, and the different solutions that each proposes may not be possible when combined and implemented.
For this reason, it is best to use this solution when approaching complex problems with large teams and the ability to combine several problem-solving methods into one.
Six Thinking Hats
The Six Thinking Hats theory is a concept designed for a team with a lot of differing conflict styles and problem-solving techniques. This method was developed to help sort through the various techniques that people may use and help a team find a solution that works for everyone involved. It helps to organize thinking and lead the conversation to the best possible solution.
Within this system, there are six different “hats” that identify with the various aspects of the decision-making process: the overall process, idea generation, intuition and emotions, values, information gathering, and caution or critical thinking. The group agrees to participate in the process by agreeing on which of the hats the group is wearing at a given moment. This helps set parameters and expectations around what the group is attempting to achieve at any moment.
This system is particularly good in a group with different conflict styles or where people have a hard time collecting and organizing their thoughts. It can be incredibly beneficial for complex problems with many moving parts. It can also help groups identify how each of the smaller sections relates to the big picture and help create new ideas to answer the overall problem.
However, it can derail if the group focuses too heavily or for too long on one of the “hats.” The group should ensure that they have a facilitator to guide them through the process and ensure that each idea and section is considered adequately.
Trial and Error
The trial and error process takes over the evaluation and selection process and instead chooses to try out each of the alternatives to determine what the best option would be. It allows the team to gather data on each of the options and how they apply practically. It also provides the ability for the team to have an example of each possible answer to help a decision-maker determine what the best option is.
Problem-solving methods that focus on trial and error can be helpful when a team has a simple problem or a lot of time to test potential solutions, gather data, and determine an answer to the issue.
It can also be helpful when the team has a sense of the best guess for a solution but wants to test it out to determine if the data supports that option, or if they have several viable options and would like to identify the best one. However, it can be incredibly time-consuming to test each of the options and evaluate how they went. Time can often be saved by evaluating each option and selecting the best to test.
Other Problem-Solving Skills
In addition to the methods outlined above, other problem-solving skills can be used regardless of the model that is used. These techniques can round out the problem-solving process and help address either specific steps in the overall method or alter the step in some way to help it fit a specific situation.
Ask Good Questions
One of the best ways to work through any of the problem-solving models is to ask good questions. This will help the group find the issue at the heart of the problem and address that issue rather than the symptoms. The best questions will also help the group find viable solutions and pick the solution that the group can use to move forward. The more creative the questions , the more likely that they will produce innovative solutions.
Take a Step Back
Occasionally, paying attention to a problem too much can give the group tunnel vision and harm the overall processes that the group is using. Other times, the focus can lead to escalations in conflict. When this happens, it can be helpful to set aside the problem and give the group time to calm down. Once they have a chance to reconsider the options and how they apply, they can approach the issue with a new sense of purpose and determination. This can lead to additional creative solutions that may help the group find a new way forward.
Final Thoughts
Problem-solving can be a daunting part of life. However, with a good problem-solving method and the right techniques, problems can be addressed well and quickly. Applying some of these options outlined in this article can give you a head start in solving your next problem and any others that arise.
To learn more about problem-solving models, problem-solving activities, and more, contact ADR Times !
Must-read Articles:

- Recent Posts

- Understanding the Benefits of Caucus Mediation - May 3, 2024
- When Does an Informal Agreement Become a Binding Contract? - May 2, 2024
- How Much Do Mediators Make? An Overview - April 30, 2024
- Search Menu
- Browse content in Arts and Humanities
- Browse content in Archaeology
- Anglo-Saxon and Medieval Archaeology
- Archaeological Methodology and Techniques
- Archaeology by Region
- Archaeology of Religion
- Archaeology of Trade and Exchange
- Biblical Archaeology
- Contemporary and Public Archaeology
- Environmental Archaeology
- Historical Archaeology
- History and Theory of Archaeology
- Industrial Archaeology
- Landscape Archaeology
- Mortuary Archaeology
- Prehistoric Archaeology
- Underwater Archaeology
- Urban Archaeology
- Zooarchaeology
- Browse content in Architecture
- Architectural Structure and Design
- History of Architecture
- Residential and Domestic Buildings
- Theory of Architecture
- Browse content in Art
- Art Subjects and Themes
- History of Art
- Industrial and Commercial Art
- Theory of Art
- Biographical Studies
- Byzantine Studies
- Browse content in Classical Studies
- Classical History
- Classical Philosophy
- Classical Mythology
- Classical Literature
- Classical Reception
- Classical Art and Architecture
- Classical Oratory and Rhetoric
- Greek and Roman Papyrology
- Greek and Roman Epigraphy
- Greek and Roman Law
- Greek and Roman Archaeology
- Late Antiquity
- Religion in the Ancient World
- Digital Humanities
- Browse content in History
- Colonialism and Imperialism
- Diplomatic History
- Environmental History
- Genealogy, Heraldry, Names, and Honours
- Genocide and Ethnic Cleansing
- Historical Geography
- History by Period
- History of Emotions
- History of Agriculture
- History of Education
- History of Gender and Sexuality
- Industrial History
- Intellectual History
- International History
- Labour History
- Legal and Constitutional History
- Local and Family History
- Maritime History
- Military History
- National Liberation and Post-Colonialism
- Oral History
- Political History
- Public History
- Regional and National History
- Revolutions and Rebellions
- Slavery and Abolition of Slavery
- Social and Cultural History
- Theory, Methods, and Historiography
- Urban History
- World History
- Browse content in Language Teaching and Learning
- Language Learning (Specific Skills)
- Language Teaching Theory and Methods
- Browse content in Linguistics
- Applied Linguistics
- Cognitive Linguistics
- Computational Linguistics
- Forensic Linguistics
- Grammar, Syntax and Morphology
- Historical and Diachronic Linguistics
- History of English
- Language Evolution
- Language Reference
- Language Acquisition
- Language Variation
- Language Families
- Lexicography
- Linguistic Anthropology
- Linguistic Theories
- Linguistic Typology
- Phonetics and Phonology
- Psycholinguistics
- Sociolinguistics
- Translation and Interpretation
- Writing Systems
- Browse content in Literature
- Bibliography
- Children's Literature Studies
- Literary Studies (Romanticism)
- Literary Studies (American)
- Literary Studies (Asian)
- Literary Studies (European)
- Literary Studies (Eco-criticism)
- Literary Studies (Modernism)
- Literary Studies - World
- Literary Studies (1500 to 1800)
- Literary Studies (19th Century)
- Literary Studies (20th Century onwards)
- Literary Studies (African American Literature)
- Literary Studies (British and Irish)
- Literary Studies (Early and Medieval)
- Literary Studies (Fiction, Novelists, and Prose Writers)
- Literary Studies (Gender Studies)
- Literary Studies (Graphic Novels)
- Literary Studies (History of the Book)
- Literary Studies (Plays and Playwrights)
- Literary Studies (Poetry and Poets)
- Literary Studies (Postcolonial Literature)
- Literary Studies (Queer Studies)
- Literary Studies (Science Fiction)
- Literary Studies (Travel Literature)
- Literary Studies (War Literature)
- Literary Studies (Women's Writing)
- Literary Theory and Cultural Studies
- Mythology and Folklore
- Shakespeare Studies and Criticism
- Browse content in Media Studies
- Browse content in Music
- Applied Music
- Dance and Music
- Ethics in Music
- Ethnomusicology
- Gender and Sexuality in Music
- Medicine and Music
- Music Cultures
- Music and Media
- Music and Religion
- Music and Culture
- Music Education and Pedagogy
- Music Theory and Analysis
- Musical Scores, Lyrics, and Libretti
- Musical Structures, Styles, and Techniques
- Musicology and Music History
- Performance Practice and Studies
- Race and Ethnicity in Music
- Sound Studies
- Browse content in Performing Arts
- Browse content in Philosophy
- Aesthetics and Philosophy of Art
- Epistemology
- Feminist Philosophy
- History of Western Philosophy
- Metaphysics
- Moral Philosophy
- Non-Western Philosophy
- Philosophy of Language
- Philosophy of Mind
- Philosophy of Perception
- Philosophy of Science
- Philosophy of Action
- Philosophy of Law
- Philosophy of Religion
- Philosophy of Mathematics and Logic
- Practical Ethics
- Social and Political Philosophy
- Browse content in Religion
- Biblical Studies
- Christianity
- East Asian Religions
- History of Religion
- Judaism and Jewish Studies
- Qumran Studies
- Religion and Education
- Religion and Health
- Religion and Politics
- Religion and Science
- Religion and Law
- Religion and Art, Literature, and Music
- Religious Studies
- Browse content in Society and Culture
- Cookery, Food, and Drink
- Cultural Studies
- Customs and Traditions
- Ethical Issues and Debates
- Hobbies, Games, Arts and Crafts
- Lifestyle, Home, and Garden
- Natural world, Country Life, and Pets
- Popular Beliefs and Controversial Knowledge
- Sports and Outdoor Recreation
- Technology and Society
- Travel and Holiday
- Visual Culture
- Browse content in Law
- Arbitration
- Browse content in Company and Commercial Law
- Commercial Law
- Company Law
- Browse content in Comparative Law
- Systems of Law
- Competition Law
- Browse content in Constitutional and Administrative Law
- Government Powers
- Judicial Review
- Local Government Law
- Military and Defence Law
- Parliamentary and Legislative Practice
- Construction Law
- Contract Law
- Browse content in Criminal Law
- Criminal Procedure
- Criminal Evidence Law
- Sentencing and Punishment
- Employment and Labour Law
- Environment and Energy Law
- Browse content in Financial Law
- Banking Law
- Insolvency Law
- History of Law
- Human Rights and Immigration
- Intellectual Property Law
- Browse content in International Law
- Private International Law and Conflict of Laws
- Public International Law
- IT and Communications Law
- Jurisprudence and Philosophy of Law
- Law and Politics
- Law and Society
- Browse content in Legal System and Practice
- Courts and Procedure
- Legal Skills and Practice
- Primary Sources of Law
- Regulation of Legal Profession
- Medical and Healthcare Law
- Browse content in Policing
- Criminal Investigation and Detection
- Police and Security Services
- Police Procedure and Law
- Police Regional Planning
- Browse content in Property Law
- Personal Property Law
- Study and Revision
- Terrorism and National Security Law
- Browse content in Trusts Law
- Wills and Probate or Succession
- Browse content in Medicine and Health
- Browse content in Allied Health Professions
- Arts Therapies
- Clinical Science
- Dietetics and Nutrition
- Occupational Therapy
- Operating Department Practice
- Physiotherapy
- Radiography
- Speech and Language Therapy
- Browse content in Anaesthetics
- General Anaesthesia
- Neuroanaesthesia
- Clinical Neuroscience
- Browse content in Clinical Medicine
- Acute Medicine
- Cardiovascular Medicine
- Clinical Genetics
- Clinical Pharmacology and Therapeutics
- Dermatology
- Endocrinology and Diabetes
- Gastroenterology
- Genito-urinary Medicine
- Geriatric Medicine
- Infectious Diseases
- Medical Toxicology
- Medical Oncology
- Pain Medicine
- Palliative Medicine
- Rehabilitation Medicine
- Respiratory Medicine and Pulmonology
- Rheumatology
- Sleep Medicine
- Sports and Exercise Medicine
- Community Medical Services
- Critical Care
- Emergency Medicine
- Forensic Medicine
- Haematology
- History of Medicine
- Browse content in Medical Skills
- Clinical Skills
- Communication Skills
- Nursing Skills
- Surgical Skills
- Browse content in Medical Dentistry
- Oral and Maxillofacial Surgery
- Paediatric Dentistry
- Restorative Dentistry and Orthodontics
- Surgical Dentistry
- Medical Ethics
- Medical Statistics and Methodology
- Browse content in Neurology
- Clinical Neurophysiology
- Neuropathology
- Nursing Studies
- Browse content in Obstetrics and Gynaecology
- Gynaecology
- Occupational Medicine
- Ophthalmology
- Otolaryngology (ENT)
- Browse content in Paediatrics
- Neonatology
- Browse content in Pathology
- Chemical Pathology
- Clinical Cytogenetics and Molecular Genetics
- Histopathology
- Medical Microbiology and Virology
- Patient Education and Information
- Browse content in Pharmacology
- Psychopharmacology
- Browse content in Popular Health
- Caring for Others
- Complementary and Alternative Medicine
- Self-help and Personal Development
- Browse content in Preclinical Medicine
- Cell Biology
- Molecular Biology and Genetics
- Reproduction, Growth and Development
- Primary Care
- Professional Development in Medicine
- Browse content in Psychiatry
- Addiction Medicine
- Child and Adolescent Psychiatry
- Forensic Psychiatry
- Learning Disabilities
- Old Age Psychiatry
- Psychotherapy
- Browse content in Public Health and Epidemiology
- Epidemiology
- Public Health
- Browse content in Radiology
- Clinical Radiology
- Interventional Radiology
- Nuclear Medicine
- Radiation Oncology
- Reproductive Medicine
- Browse content in Surgery
- Cardiothoracic Surgery
- Gastro-intestinal and Colorectal Surgery
- General Surgery
- Neurosurgery
- Paediatric Surgery
- Peri-operative Care
- Plastic and Reconstructive Surgery
- Surgical Oncology
- Transplant Surgery
- Trauma and Orthopaedic Surgery
- Vascular Surgery
- Browse content in Science and Mathematics
- Browse content in Biological Sciences
- Aquatic Biology
- Biochemistry
- Bioinformatics and Computational Biology
- Developmental Biology
- Ecology and Conservation
- Evolutionary Biology
- Genetics and Genomics
- Microbiology
- Molecular and Cell Biology
- Natural History
- Plant Sciences and Forestry
- Research Methods in Life Sciences
- Structural Biology
- Systems Biology
- Zoology and Animal Sciences
- Browse content in Chemistry
- Analytical Chemistry
- Computational Chemistry
- Crystallography
- Environmental Chemistry
- Industrial Chemistry
- Inorganic Chemistry
- Materials Chemistry
- Medicinal Chemistry
- Mineralogy and Gems
- Organic Chemistry
- Physical Chemistry
- Polymer Chemistry
- Study and Communication Skills in Chemistry
- Theoretical Chemistry
- Browse content in Computer Science
- Artificial Intelligence
- Computer Architecture and Logic Design
- Game Studies
- Human-Computer Interaction
- Mathematical Theory of Computation
- Programming Languages
- Software Engineering
- Systems Analysis and Design
- Virtual Reality
- Browse content in Computing
- Business Applications
- Computer Security
- Computer Games
- Computer Networking and Communications
- Digital Lifestyle
- Graphical and Digital Media Applications
- Operating Systems
- Browse content in Earth Sciences and Geography
- Atmospheric Sciences
- Environmental Geography
- Geology and the Lithosphere
- Maps and Map-making
- Meteorology and Climatology
- Oceanography and Hydrology
- Palaeontology
- Physical Geography and Topography
- Regional Geography
- Soil Science
- Urban Geography
- Browse content in Engineering and Technology
- Agriculture and Farming
- Biological Engineering
- Civil Engineering, Surveying, and Building
- Electronics and Communications Engineering
- Energy Technology
- Engineering (General)
- Environmental Science, Engineering, and Technology
- History of Engineering and Technology
- Mechanical Engineering and Materials
- Technology of Industrial Chemistry
- Transport Technology and Trades
- Browse content in Environmental Science
- Applied Ecology (Environmental Science)
- Conservation of the Environment (Environmental Science)
- Environmental Sustainability
- Environmentalist Thought and Ideology (Environmental Science)
- Management of Land and Natural Resources (Environmental Science)
- Natural Disasters (Environmental Science)
- Nuclear Issues (Environmental Science)
- Pollution and Threats to the Environment (Environmental Science)
- Social Impact of Environmental Issues (Environmental Science)
- History of Science and Technology
- Browse content in Materials Science
- Ceramics and Glasses
- Composite Materials
- Metals, Alloying, and Corrosion
- Nanotechnology
- Browse content in Mathematics
- Applied Mathematics
- Biomathematics and Statistics
- History of Mathematics
- Mathematical Education
- Mathematical Finance
- Mathematical Analysis
- Numerical and Computational Mathematics
- Probability and Statistics
- Pure Mathematics
- Browse content in Neuroscience
- Cognition and Behavioural Neuroscience
- Development of the Nervous System
- Disorders of the Nervous System
- History of Neuroscience
- Invertebrate Neurobiology
- Molecular and Cellular Systems
- Neuroendocrinology and Autonomic Nervous System
- Neuroscientific Techniques
- Sensory and Motor Systems
- Browse content in Physics
- Astronomy and Astrophysics
- Atomic, Molecular, and Optical Physics
- Biological and Medical Physics
- Classical Mechanics
- Computational Physics
- Condensed Matter Physics
- Electromagnetism, Optics, and Acoustics
- History of Physics
- Mathematical and Statistical Physics
- Measurement Science
- Nuclear Physics
- Particles and Fields
- Plasma Physics
- Quantum Physics
- Relativity and Gravitation
- Semiconductor and Mesoscopic Physics
- Browse content in Psychology
- Affective Sciences
- Clinical Psychology
- Cognitive Psychology
- Cognitive Neuroscience
- Criminal and Forensic Psychology
- Developmental Psychology
- Educational Psychology
- Evolutionary Psychology
- Health Psychology
- History and Systems in Psychology
- Music Psychology
- Neuropsychology
- Organizational Psychology
- Psychological Assessment and Testing
- Psychology of Human-Technology Interaction
- Psychology Professional Development and Training
- Research Methods in Psychology
- Social Psychology
- Browse content in Social Sciences
- Browse content in Anthropology
- Anthropology of Religion
- Human Evolution
- Medical Anthropology
- Physical Anthropology
- Regional Anthropology
- Social and Cultural Anthropology
- Theory and Practice of Anthropology
- Browse content in Business and Management
- Business Ethics
- Business Strategy
- Business History
- Business and Technology
- Business and Government
- Business and the Environment
- Comparative Management
- Corporate Governance
- Corporate Social Responsibility
- Entrepreneurship
- Health Management
- Human Resource Management
- Industrial and Employment Relations
- Industry Studies
- Information and Communication Technologies
- International Business
- Knowledge Management
- Management and Management Techniques
- Operations Management
- Organizational Theory and Behaviour
- Pensions and Pension Management
- Public and Nonprofit Management
- Strategic Management
- Supply Chain Management
- Browse content in Criminology and Criminal Justice
- Criminal Justice
- Criminology
- Forms of Crime
- International and Comparative Criminology
- Youth Violence and Juvenile Justice
- Development Studies
- Browse content in Economics
- Agricultural, Environmental, and Natural Resource Economics
- Asian Economics
- Behavioural Finance
- Behavioural Economics and Neuroeconomics
- Econometrics and Mathematical Economics
- Economic History
- Economic Systems
- Economic Methodology
- Economic Development and Growth
- Financial Markets
- Financial Institutions and Services
- General Economics and Teaching
- Health, Education, and Welfare
- History of Economic Thought
- International Economics
- Labour and Demographic Economics
- Law and Economics
- Macroeconomics and Monetary Economics
- Microeconomics
- Public Economics
- Urban, Rural, and Regional Economics
- Welfare Economics
- Browse content in Education
- Adult Education and Continuous Learning
- Care and Counselling of Students
- Early Childhood and Elementary Education
- Educational Equipment and Technology
- Educational Strategies and Policy
- Higher and Further Education
- Organization and Management of Education
- Philosophy and Theory of Education
- Schools Studies
- Secondary Education
- Teaching of a Specific Subject
- Teaching of Specific Groups and Special Educational Needs
- Teaching Skills and Techniques
- Browse content in Environment
- Applied Ecology (Social Science)
- Climate Change
- Conservation of the Environment (Social Science)
- Environmentalist Thought and Ideology (Social Science)
- Natural Disasters (Environment)
- Social Impact of Environmental Issues (Social Science)
- Browse content in Human Geography
- Cultural Geography
- Economic Geography
- Political Geography
- Browse content in Interdisciplinary Studies
- Communication Studies
- Museums, Libraries, and Information Sciences
- Browse content in Politics
- African Politics
- Asian Politics
- Chinese Politics
- Comparative Politics
- Conflict Politics
- Elections and Electoral Studies
- Environmental Politics
- European Union
- Foreign Policy
- Gender and Politics
- Human Rights and Politics
- Indian Politics
- International Relations
- International Organization (Politics)
- International Political Economy
- Irish Politics
- Latin American Politics
- Middle Eastern Politics
- Political Behaviour
- Political Economy
- Political Institutions
- Political Methodology
- Political Communication
- Political Philosophy
- Political Sociology
- Political Theory
- Politics and Law
- Public Policy
- Public Administration
- Quantitative Political Methodology
- Regional Political Studies
- Russian Politics
- Security Studies
- State and Local Government
- UK Politics
- US Politics
- Browse content in Regional and Area Studies
- African Studies
- Asian Studies
- East Asian Studies
- Japanese Studies
- Latin American Studies
- Middle Eastern Studies
- Native American Studies
- Scottish Studies
- Browse content in Research and Information
- Research Methods
- Browse content in Social Work
- Addictions and Substance Misuse
- Adoption and Fostering
- Care of the Elderly
- Child and Adolescent Social Work
- Couple and Family Social Work
- Developmental and Physical Disabilities Social Work
- Direct Practice and Clinical Social Work
- Emergency Services
- Human Behaviour and the Social Environment
- International and Global Issues in Social Work
- Mental and Behavioural Health
- Social Justice and Human Rights
- Social Policy and Advocacy
- Social Work and Crime and Justice
- Social Work Macro Practice
- Social Work Practice Settings
- Social Work Research and Evidence-based Practice
- Welfare and Benefit Systems
- Browse content in Sociology
- Childhood Studies
- Community Development
- Comparative and Historical Sociology
- Economic Sociology
- Gender and Sexuality
- Gerontology and Ageing
- Health, Illness, and Medicine
- Marriage and the Family
- Migration Studies
- Occupations, Professions, and Work
- Organizations
- Population and Demography
- Race and Ethnicity
- Social Theory
- Social Movements and Social Change
- Social Research and Statistics
- Social Stratification, Inequality, and Mobility
- Sociology of Religion
- Sociology of Education
- Sport and Leisure
- Urban and Rural Studies
- Browse content in Warfare and Defence
- Defence Strategy, Planning, and Research
- Land Forces and Warfare
- Military Administration
- Military Life and Institutions
- Naval Forces and Warfare
- Other Warfare and Defence Issues
- Peace Studies and Conflict Resolution
- Weapons and Equipment

- < Previous chapter
- Next chapter >
48 Problem Solving
Department of Psychological and Brain Sciences, University of California, Santa Barbara
- Published: 03 June 2013
- Cite Icon Cite
- Permissions Icon Permissions
Problem solving refers to cognitive processing directed at achieving a goal when the problem solver does not initially know a solution method. A problem exists when someone has a goal but does not know how to achieve it. Problems can be classified as routine or nonroutine, and as well defined or ill defined. The major cognitive processes in problem solving are representing, planning, executing, and monitoring. The major kinds of knowledge required for problem solving are facts, concepts, procedures, strategies, and beliefs. Classic theoretical approaches to the study of problem solving are associationism, Gestalt, and information processing. Current issues and suggested future issues include decision making, intelligence and creativity, teaching of thinking skills, expert problem solving, analogical reasoning, mathematical and scientific thinking, everyday thinking, and the cognitive neuroscience of problem solving. Common themes concern the domain specificity of problem solving and a focus on problem solving in authentic contexts.
The study of problem solving begins with defining problem solving, problem, and problem types. This introduction to problem solving is rounded out with an examination of cognitive processes in problem solving, the role of knowledge in problem solving, and historical approaches to the study of problem solving.
Definition of Problem Solving
Problem solving refers to cognitive processing directed at achieving a goal for which the problem solver does not initially know a solution method. This definition consists of four major elements (Mayer, 1992 ; Mayer & Wittrock, 2006 ):
Cognitive —Problem solving occurs within the problem solver’s cognitive system and can only be inferred indirectly from the problem solver’s behavior (including biological changes, introspections, and actions during problem solving). Process —Problem solving involves mental computations in which some operation is applied to a mental representation, sometimes resulting in the creation of a new mental representation. Directed —Problem solving is aimed at achieving a goal. Personal —Problem solving depends on the existing knowledge of the problem solver so that what is a problem for one problem solver may not be a problem for someone who already knows a solution method.
The definition is broad enough to include a wide array of cognitive activities such as deciding which apartment to rent, figuring out how to use a cell phone interface, playing a game of chess, making a medical diagnosis, finding the answer to an arithmetic word problem, or writing a chapter for a handbook. Problem solving is pervasive in human life and is crucial for human survival. Although this chapter focuses on problem solving in humans, problem solving also occurs in nonhuman animals and in intelligent machines.
How is problem solving related to other forms of high-level cognition processing, such as thinking and reasoning? Thinking refers to cognitive processing in individuals but includes both directed thinking (which corresponds to the definition of problem solving) and undirected thinking such as daydreaming (which does not correspond to the definition of problem solving). Thus, problem solving is a type of thinking (i.e., directed thinking).
Reasoning refers to problem solving within specific classes of problems, such as deductive reasoning or inductive reasoning. In deductive reasoning, the reasoner is given premises and must derive a conclusion by applying the rules of logic. For example, given that “A is greater than B” and “B is greater than C,” a reasoner can conclude that “A is greater than C.” In inductive reasoning, the reasoner is given (or has experienced) a collection of examples or instances and must infer a rule. For example, given that X, C, and V are in the “yes” group and x, c, and v are in the “no” group, the reasoning may conclude that B is in “yes” group because it is in uppercase format. Thus, reasoning is a type of problem solving.
Definition of Problem
A problem occurs when someone has a goal but does not know to achieve it. This definition is consistent with how the Gestalt psychologist Karl Duncker ( 1945 , p. 1) defined a problem in his classic monograph, On Problem Solving : “A problem arises when a living creature has a goal but does not know how this goal is to be reached.” However, today researchers recognize that the definition should be extended to include problem solving by intelligent machines. This definition can be clarified using an information processing approach by noting that a problem occurs when a situation is in the given state, the problem solver wants the situation to be in the goal state, and there is no obvious way to move from the given state to the goal state (Newell & Simon, 1972 ). Accordingly, the three main elements in describing a problem are the given state (i.e., the current state of the situation), the goal state (i.e., the desired state of the situation), and the set of allowable operators (i.e., the actions the problem solver is allowed to take). The definition of “problem” is broad enough to include the situation confronting a physician who wishes to make a diagnosis on the basis of preliminary tests and a patient examination, as well as a beginning physics student trying to solve a complex physics problem.
Types of Problems
It is customary in the problem-solving literature to make a distinction between routine and nonroutine problems. Routine problems are problems that are so familiar to the problem solver that the problem solver knows a solution method. For example, for most adults, “What is 365 divided by 12?” is a routine problem because they already know the procedure for long division. Nonroutine problems are so unfamiliar to the problem solver that the problem solver does not know a solution method. For example, figuring out the best way to set up a funding campaign for a nonprofit charity is a nonroutine problem for most volunteers. Technically, routine problems do not meet the definition of problem because the problem solver has a goal but knows how to achieve it. Much research on problem solving has focused on routine problems, although most interesting problems in life are nonroutine.
Another customary distinction is between well-defined and ill-defined problems. Well-defined problems have a clearly specified given state, goal state, and legal operators. Examples include arithmetic computation problems or games such as checkers or tic-tac-toe. Ill-defined problems have a poorly specified given state, goal state, or legal operators, or a combination of poorly defined features. Examples include solving the problem of global warming or finding a life partner. Although, ill-defined problems are more challenging, much research in problem solving has focused on well-defined problems.
Cognitive Processes in Problem Solving
The process of problem solving can be broken down into two main phases: problem representation , in which the problem solver builds a mental representation of the problem situation, and problem solution , in which the problem solver works to produce a solution. The major subprocess in problem representation is representing , which involves building a situation model —that is, a mental representation of the situation described in the problem. The major subprocesses in problem solution are planning , which involves devising a plan for how to solve the problem; executing , which involves carrying out the plan; and monitoring , which involves evaluating and adjusting one’s problem solving.
For example, given an arithmetic word problem such as “Alice has three marbles. Sarah has two more marbles than Alice. How many marbles does Sarah have?” the process of representing involves building a situation model in which Alice has a set of marbles, there is set of marbles for the difference between the two girls, and Sarah has a set of marbles that consists of Alice’s marbles and the difference set. In the planning process, the problem solver sets a goal of adding 3 and 2. In the executing process, the problem solver carries out the computation, yielding an answer of 5. In the monitoring process, the problem solver looks over what was done and concludes that 5 is a reasonable answer. In most complex problem-solving episodes, the four cognitive processes may not occur in linear order, but rather may interact with one another. Although some research focuses mainly on the execution process, problem solvers may tend to have more difficulty with the processes of representing, planning, and monitoring.
Knowledge for Problem Solving
An important theme in problem-solving research is that problem-solving proficiency on any task depends on the learner’s knowledge (Anderson et al., 2001 ; Mayer, 1992 ). Five kinds of knowledge are as follows:
Facts —factual knowledge about the characteristics of elements in the world, such as “Sacramento is the capital of California” Concepts —conceptual knowledge, including categories, schemas, or models, such as knowing the difference between plants and animals or knowing how a battery works Procedures —procedural knowledge of step-by-step processes, such as how to carry out long-division computations Strategies —strategic knowledge of general methods such as breaking a problem into parts or thinking of a related problem Beliefs —attitudinal knowledge about how one’s cognitive processing works such as thinking, “I’m good at this”
Although some research focuses mainly on the role of facts and procedures in problem solving, complex problem solving also depends on the problem solver’s concepts, strategies, and beliefs (Mayer, 1992 ).
Historical Approaches to Problem Solving
Psychological research on problem solving began in the early 1900s, as an outgrowth of mental philosophy (Humphrey, 1963 ; Mandler & Mandler, 1964 ). Throughout the 20th century four theoretical approaches developed: early conceptions, associationism, Gestalt psychology, and information processing.
Early Conceptions
The start of psychology as a science can be set at 1879—the year Wilhelm Wundt opened the first world’s psychology laboratory in Leipzig, Germany, and sought to train the world’s first cohort of experimental psychologists. Instead of relying solely on philosophical speculations about how the human mind works, Wundt sought to apply the methods of experimental science to issues addressed in mental philosophy. His theoretical approach became structuralism —the analysis of consciousness into its basic elements.
Wundt’s main contribution to the study of problem solving, however, was to call for its banishment. According to Wundt, complex cognitive processing was too complicated to be studied by experimental methods, so “nothing can be discovered in such experiments” (Wundt, 1911/1973 ). Despite his admonishments, however, a group of his former students began studying thinking mainly in Wurzburg, Germany. Using the method of introspection, subjects were asked to describe their thought process as they solved word association problems, such as finding the superordinate of “newspaper” (e.g., an answer is “publication”). Although the Wurzburg group—as they came to be called—did not produce a new theoretical approach, they found empirical evidence that challenged some of the key assumptions of mental philosophy. For example, Aristotle had proclaimed that all thinking involves mental imagery, but the Wurzburg group was able to find empirical evidence for imageless thought .
Associationism
The first major theoretical approach to take hold in the scientific study of problem solving was associationism —the idea that the cognitive representations in the mind consist of ideas and links between them and that cognitive processing in the mind involves following a chain of associations from one idea to the next (Mandler & Mandler, 1964 ; Mayer, 1992 ). For example, in a classic study, E. L. Thorndike ( 1911 ) placed a hungry cat in what he called a puzzle box—a wooden crate in which pulling a loop of string that hung from overhead would open a trap door to allow the cat to escape to a bowl of food outside the crate. Thorndike placed the cat in the puzzle box once a day for several weeks. On the first day, the cat engaged in many extraneous behaviors such as pouncing against the wall, pushing its paws through the slats, and meowing, but on successive days the number of extraneous behaviors tended to decrease. Overall, the time required to get out of the puzzle box decreased over the course of the experiment, indicating the cat was learning how to escape.
Thorndike’s explanation for how the cat learned to solve the puzzle box problem is based on an associationist view: The cat begins with a habit family hierarchy —a set of potential responses (e.g., pouncing, thrusting, meowing, etc.) all associated with the same stimulus (i.e., being hungry and confined) and ordered in terms of strength of association. When placed in the puzzle box, the cat executes its strongest response (e.g., perhaps pouncing against the wall), but when it fails, the strength of the association is weakened, and so on for each unsuccessful action. Eventually, the cat gets down to what was initially a weak response—waving its paw in the air—but when that response leads to accidentally pulling the string and getting out, it is strengthened. Over the course of many trials, the ineffective responses become weak and the successful response becomes strong. Thorndike refers to this process as the law of effect : Responses that lead to dissatisfaction become less associated with the situation and responses that lead to satisfaction become more associated with the situation. According to Thorndike’s associationist view, solving a problem is simply a matter of trial and error and accidental success. A major challenge to assocationist theory concerns the nature of transfer—that is, where does a problem solver find a creative solution that has never been performed before? Associationist conceptions of cognition can be seen in current research, including neural networks, connectionist models, and parallel distributed processing models (Rogers & McClelland, 2004 ).
Gestalt Psychology
The Gestalt approach to problem solving developed in the 1930s and 1940s as a counterbalance to the associationist approach. According to the Gestalt approach, cognitive representations consist of coherent structures (rather than individual associations) and the cognitive process of problem solving involves building a coherent structure (rather than strengthening and weakening of associations). For example, in a classic study, Kohler ( 1925 ) placed a hungry ape in a play yard that contained several empty shipping crates and a banana attached overhead but out of reach. Based on observing the ape in this situation, Kohler noted that the ape did not randomly try responses until one worked—as suggested by Thorndike’s associationist view. Instead, the ape stood under the banana, looked up at it, looked at the crates, and then in a flash of insight stacked the crates under the bananas as a ladder, and walked up the steps in order to reach the banana.
According to Kohler, the ape experienced a sudden visual reorganization in which the elements in the situation fit together in a way to solve the problem; that is, the crates could become a ladder that reduces the distance to the banana. Kohler referred to the underlying mechanism as insight —literally seeing into the structure of the situation. A major challenge of Gestalt theory is its lack of precision; for example, naming a process (i.e., insight) is not the same as explaining how it works. Gestalt conceptions can be seen in modern research on mental models and schemas (Gentner & Stevens, 1983 ).
Information Processing
The information processing approach to problem solving developed in the 1960s and 1970s and was based on the influence of the computer metaphor—the idea that humans are processors of information (Mayer, 2009 ). According to the information processing approach, problem solving involves a series of mental computations—each of which consists of applying a process to a mental representation (such as comparing two elements to determine whether they differ).
In their classic book, Human Problem Solving , Newell and Simon ( 1972 ) proposed that problem solving involved a problem space and search heuristics . A problem space is a mental representation of the initial state of the problem, the goal state of the problem, and all possible intervening states (based on applying allowable operators). Search heuristics are strategies for moving through the problem space from the given to the goal state. Newell and Simon focused on means-ends analysis , in which the problem solver continually sets goals and finds moves to accomplish goals.
Newell and Simon used computer simulation as a research method to test their conception of human problem solving. First, they asked human problem solvers to think aloud as they solved various problems such as logic problems, chess, and cryptarithmetic problems. Then, based on an information processing analysis, Newell and Simon created computer programs that solved these problems. In comparing the solution behavior of humans and computers, they found high similarity, suggesting that the computer programs were solving problems using the same thought processes as humans.
An important advantage of the information processing approach is that problem solving can be described with great clarity—as a computer program. An important limitation of the information processing approach is that it is most useful for describing problem solving for well-defined problems rather than ill-defined problems. The information processing conception of cognition lives on as a keystone of today’s cognitive science (Mayer, 2009 ).
Classic Issues in Problem Solving
Three classic issues in research on problem solving concern the nature of transfer (suggested by the associationist approach), the nature of insight (suggested by the Gestalt approach), and the role of problem-solving heuristics (suggested by the information processing approach).
Transfer refers to the effects of prior learning on new learning (or new problem solving). Positive transfer occurs when learning A helps someone learn B. Negative transfer occurs when learning A hinders someone from learning B. Neutral transfer occurs when learning A has no effect on learning B. Positive transfer is a central goal of education, but research shows that people often do not transfer what they learned to solving problems in new contexts (Mayer, 1992 ; Singley & Anderson, 1989 ).
Three conceptions of the mechanisms underlying transfer are specific transfer , general transfer , and specific transfer of general principles . Specific transfer refers to the idea that learning A will help someone learn B only if A and B have specific elements in common. For example, learning Spanish may help someone learn Latin because some of the vocabulary words are similar and the verb conjugation rules are similar. General transfer refers to the idea that learning A can help someone learn B even they have nothing specifically in common but A helps improve the learner’s mind in general. For example, learning Latin may help people learn “proper habits of mind” so they are better able to learn completely unrelated subjects as well. Specific transfer of general principles is the idea that learning A will help someone learn B if the same general principle or solution method is required for both even if the specific elements are different.
In a classic study, Thorndike and Woodworth ( 1901 ) found that students who learned Latin did not subsequently learn bookkeeping any better than students who had not learned Latin. They interpreted this finding as evidence for specific transfer—learning A did not transfer to learning B because A and B did not have specific elements in common. Modern research on problem-solving transfer continues to show that people often do not demonstrate general transfer (Mayer, 1992 ). However, it is possible to teach people a general strategy for solving a problem, so that when they see a new problem in a different context they are able to apply the strategy to the new problem (Judd, 1908 ; Mayer, 2008 )—so there is also research support for the idea of specific transfer of general principles.
Insight refers to a change in a problem solver’s mind from not knowing how to solve a problem to knowing how to solve it (Mayer, 1995 ; Metcalfe & Wiebe, 1987 ). In short, where does the idea for a creative solution come from? A central goal of problem-solving research is to determine the mechanisms underlying insight.
The search for insight has led to five major (but not mutually exclusive) explanatory mechanisms—insight as completing a schema, insight as suddenly reorganizing visual information, insight as reformulation of a problem, insight as removing mental blocks, and insight as finding a problem analog (Mayer, 1995 ). Completing a schema is exemplified in a study by Selz (Fridja & de Groot, 1982 ), in which people were asked to think aloud as they solved word association problems such as “What is the superordinate for newspaper?” To solve the problem, people sometimes thought of a coordinate, such as “magazine,” and then searched for a superordinate category that subsumed both terms, such as “publication.” According to Selz, finding a solution involved building a schema that consisted of a superordinate and two subordinate categories.
Reorganizing visual information is reflected in Kohler’s ( 1925 ) study described in a previous section in which a hungry ape figured out how to stack boxes as a ladder to reach a banana hanging above. According to Kohler, the ape looked around the yard and found the solution in a flash of insight by mentally seeing how the parts could be rearranged to accomplish the goal.
Reformulating a problem is reflected in a classic study by Duncker ( 1945 ) in which people are asked to think aloud as they solve the tumor problem—how can you destroy a tumor in a patient without destroying surrounding healthy tissue by using rays that at sufficient intensity will destroy any tissue in their path? In analyzing the thinking-aloud protocols—that is, transcripts of what the problem solvers said—Duncker concluded that people reformulated the goal in various ways (e.g., avoid contact with healthy tissue, immunize healthy tissue, have ray be weak in healthy tissue) until they hit upon a productive formulation that led to the solution (i.e., concentrating many weak rays on the tumor).
Removing mental blocks is reflected in classic studies by Duncker ( 1945 ) in which solving a problem involved thinking of a novel use for an object, and by Luchins ( 1942 ) in which solving a problem involved not using a procedure that had worked well on previous problems. Finding a problem analog is reflected in classic research by Wertheimer ( 1959 ) in which learning to find the area of a parallelogram is supported by the insight that one could cut off the triangle on one side and place it on the other side to form a rectangle—so a parallelogram is really a rectangle in disguise. The search for insight along each of these five lines continues in current problem-solving research.
Heuristics are problem-solving strategies, that is, general approaches to how to solve problems. Newell and Simon ( 1972 ) suggested three general problem-solving heuristics for moving from a given state to a goal state: random trial and error , hill climbing , and means-ends analysis . Random trial and error involves randomly selecting a legal move and applying it to create a new problem state, and repeating that process until the goal state is reached. Random trial and error may work for simple problems but is not efficient for complex ones. Hill climbing involves selecting the legal move that moves the problem solver closer to the goal state. Hill climbing will not work for problems in which the problem solver must take a move that temporarily moves away from the goal as is required in many problems.
Means-ends analysis involves creating goals and seeking moves that can accomplish the goal. If a goal cannot be directly accomplished, a subgoal is created to remove one or more obstacles. Newell and Simon ( 1972 ) successfully used means-ends analysis as the search heuristic in a computer program aimed at general problem solving, that is, solving a diverse collection of problems. However, people may also use specific heuristics that are designed to work for specific problem-solving situations (Gigerenzer, Todd, & ABC Research Group, 1999 ; Kahneman & Tversky, 1984 ).
Current and Future Issues in Problem Solving
Eight current issues in problem solving involve decision making, intelligence and creativity, teaching of thinking skills, expert problem solving, analogical reasoning, mathematical and scientific problem solving, everyday thinking, and the cognitive neuroscience of problem solving.
Decision Making
Decision making refers to the cognitive processing involved in choosing between two or more alternatives (Baron, 2000 ; Markman & Medin, 2002 ). For example, a decision-making task may involve choosing between getting $240 for sure or having a 25% change of getting $1000. According to economic theories such as expected value theory, people should chose the second option, which is worth $250 (i.e., .25 x $1000) rather than the first option, which is worth $240 (1.00 x $240), but psychological research shows that most people prefer the first option (Kahneman & Tversky, 1984 ).
Research on decision making has generated three classes of theories (Markman & Medin, 2002 ): descriptive theories, such as prospect theory (Kahneman & Tversky), which are based on the ideas that people prefer to overweight the cost of a loss and tend to overestimate small probabilities; heuristic theories, which are based on the idea that people use a collection of short-cut strategies such as the availability heuristic (Gigerenzer et al., 1999 ; Kahneman & Tversky, 2000 ); and constructive theories, such as mental accounting (Kahneman & Tversky, 2000 ), in which people build a narrative to justify their choices to themselves. Future research is needed to examine decision making in more realistic settings.
Intelligence and Creativity
Although researchers do not have complete consensus on the definition of intelligence (Sternberg, 1990 ), it is reasonable to view intelligence as the ability to learn or adapt to new situations. Fluid intelligence refers to the potential to solve problems without any relevant knowledge, whereas crystallized intelligence refers to the potential to solve problems based on relevant prior knowledge (Sternberg & Gregorenko, 2003 ). As people gain more experience in a field, their problem-solving performance depends more on crystallized intelligence (i.e., domain knowledge) than on fluid intelligence (i.e., general ability) (Sternberg & Gregorenko, 2003 ). The ability to monitor and manage one’s cognitive processing during problem solving—which can be called metacognition —is an important aspect of intelligence (Sternberg, 1990 ). Research is needed to pinpoint the knowledge that is needed to support intelligent performance on problem-solving tasks.
Creativity refers to the ability to generate ideas that are original (i.e., other people do not think of the same idea) and functional (i.e., the idea works; Sternberg, 1999 ). Creativity is often measured using tests of divergent thinking —that is, generating as many solutions as possible for a problem (Guilford, 1967 ). For example, the uses test asks people to list as many uses as they can think of for a brick. Creativity is different from intelligence, and it is at the heart of creative problem solving—generating a novel solution to a problem that the problem solver has never seen before. An important research question concerns whether creative problem solving depends on specific knowledge or creativity ability in general.
Teaching of Thinking Skills
How can people learn to be better problem solvers? Mayer ( 2008 ) proposes four questions concerning teaching of thinking skills:
What to teach —Successful programs attempt to teach small component skills (such as how to generate and evaluate hypotheses) rather than improve the mind as a single monolithic skill (Covington, Crutchfield, Davies, & Olton, 1974 ). How to teach —Successful programs focus on modeling the process of problem solving rather than solely reinforcing the product of problem solving (Bloom & Broder, 1950 ). Where to teach —Successful programs teach problem-solving skills within the specific context they will be used rather than within a general course on how to solve problems (Nickerson, 1999 ). When to teach —Successful programs teaching higher order skills early rather than waiting until lower order skills are completely mastered (Tharp & Gallimore, 1988 ).
Overall, research on teaching of thinking skills points to the domain specificity of problem solving; that is, successful problem solving depends on the problem solver having domain knowledge that is relevant to the problem-solving task.
Expert Problem Solving
Research on expertise is concerned with differences between how experts and novices solve problems (Ericsson, Feltovich, & Hoffman, 2006 ). Expertise can be defined in terms of time (e.g., 10 years of concentrated experience in a field), performance (e.g., earning a perfect score on an assessment), or recognition (e.g., receiving a Nobel Prize or becoming Grand Master in chess). For example, in classic research conducted in the 1940s, de Groot ( 1965 ) found that chess experts did not have better general memory than chess novices, but they did have better domain-specific memory for the arrangement of chess pieces on the board. Chase and Simon ( 1973 ) replicated this result in a better controlled experiment. An explanation is that experts have developed schemas that allow them to chunk collections of pieces into a single configuration.
In another landmark study, Larkin et al. ( 1980 ) compared how experts (e.g., physics professors) and novices (e.g., first-year physics students) solved textbook physics problems about motion. Experts tended to work forward from the given information to the goal, whereas novices tended to work backward from the goal to the givens using a means-ends analysis strategy. Experts tended to store their knowledge in an integrated way, whereas novices tended to store their knowledge in isolated fragments. In another study, Chi, Feltovich, and Glaser ( 1981 ) found that experts tended to focus on the underlying physics concepts (such as conservation of energy), whereas novices tended to focus on the surface features of the problem (such as inclined planes or springs). Overall, research on expertise is useful in pinpointing what experts know that is different from what novices know. An important theme is that experts rely on domain-specific knowledge rather than solely general cognitive ability.
Analogical Reasoning
Analogical reasoning occurs when people solve one problem by using their knowledge about another problem (Holyoak, 2005 ). For example, suppose a problem solver learns how to solve a problem in one context using one solution method and then is given a problem in another context that requires the same solution method. In this case, the problem solver must recognize that the new problem has structural similarity to the old problem (i.e., it may be solved by the same method), even though they do not have surface similarity (i.e., the cover stories are different). Three steps in analogical reasoning are recognizing —seeing that a new problem is similar to a previously solved problem; abstracting —finding the general method used to solve the old problem; and mapping —using that general method to solve the new problem.
Research on analogical reasoning shows that people often do not recognize that a new problem can be solved by the same method as a previously solved problem (Holyoak, 2005 ). However, research also shows that successful analogical transfer to a new problem is more likely when the problem solver has experience with two old problems that have the same underlying structural features (i.e., they are solved by the same principle) but different surface features (i.e., they have different cover stories) (Holyoak, 2005 ). This finding is consistent with the idea of specific transfer of general principles as described in the section on “Transfer.”
Mathematical and Scientific Problem Solving
Research on mathematical problem solving suggests that five kinds of knowledge are needed to solve arithmetic word problems (Mayer, 2008 ):
Factual knowledge —knowledge about the characteristics of problem elements, such as knowing that there are 100 cents in a dollar Schematic knowledge —knowledge of problem types, such as being able to recognize time-rate-distance problems Strategic knowledge —knowledge of general methods, such as how to break a problem into parts Procedural knowledge —knowledge of processes, such as how to carry our arithmetic operations Attitudinal knowledge —beliefs about one’s mathematical problem-solving ability, such as thinking, “I am good at this”
People generally possess adequate procedural knowledge but may have difficulty in solving mathematics problems because they lack factual, schematic, strategic, or attitudinal knowledge (Mayer, 2008 ). Research is needed to pinpoint the role of domain knowledge in mathematical problem solving.
Research on scientific problem solving shows that people harbor misconceptions, such as believing that a force is needed to keep an object in motion (McCloskey, 1983 ). Learning to solve science problems involves conceptual change, in which the problem solver comes to recognize that previous conceptions are wrong (Mayer, 2008 ). Students can be taught to engage in scientific reasoning such as hypothesis testing through direct instruction in how to control for variables (Chen & Klahr, 1999 ). A central theme of research on scientific problem solving concerns the role of domain knowledge.
Everyday Thinking
Everyday thinking refers to problem solving in the context of one’s life outside of school. For example, children who are street vendors tend to use different procedures for solving arithmetic problems when they are working on the streets than when they are in school (Nunes, Schlieman, & Carraher, 1993 ). This line of research highlights the role of situated cognition —the idea that thinking always is shaped by the physical and social context in which it occurs (Robbins & Aydede, 2009 ). Research is needed to determine how people solve problems in authentic contexts.
Cognitive Neuroscience of Problem Solving
The cognitive neuroscience of problem solving is concerned with the brain activity that occurs during problem solving. For example, using fMRI brain imaging methodology, Goel ( 2005 ) found that people used the language areas of the brain to solve logical reasoning problems presented in sentences (e.g., “All dogs are pets…”) and used the spatial areas of the brain to solve logical reasoning problems presented in abstract letters (e.g., “All D are P…”). Cognitive neuroscience holds the potential to make unique contributions to the study of problem solving.
Problem solving has always been a topic at the fringe of cognitive psychology—too complicated to study intensively but too important to completely ignore. Problem solving—especially in realistic environments—is messy in comparison to studying elementary processes in cognition. The field remains fragmented in the sense that topics such as decision making, reasoning, intelligence, expertise, mathematical problem solving, everyday thinking, and the like are considered to be separate topics, each with its own separate literature. Yet some recurring themes are the role of domain-specific knowledge in problem solving and the advantages of studying problem solving in authentic contexts.
Future Directions
Some important issues for future research include the three classic issues examined in this chapter—the nature of problem-solving transfer (i.e., How are people able to use what they know about previous problem solving to help them in new problem solving?), the nature of insight (e.g., What is the mechanism by which a creative solution is constructed?), and heuristics (e.g., What are some teachable strategies for problem solving?). In addition, future research in problem solving should continue to pinpoint the role of domain-specific knowledge in problem solving, the nature of cognitive ability in problem solving, how to help people develop proficiency in solving problems, and how to provide aids for problem solving.
Anderson L. W. , Krathwohl D. R. , Airasian P. W. , Cruikshank K. A. , Mayer R. E. , Pintrich P. R. , Raths, J., & Wittrock M. C. ( 2001 ). A taxonomy for learning, teaching, and assessing: A revision of Bloom’s taxonomy of educational objectives. New York : Longman.
Baron J. ( 2000 ). Thinking and deciding (3rd ed.). New York : Cambridge University Press.
Google Scholar
Google Preview
Bloom B. S. , & Broder B. J. ( 1950 ). Problem-solving processes of college students: An exploratory investigation. Chicago : University of Chicago Press.
Chase W. G. , & Simon H. A. ( 1973 ). Perception in chess. Cognitive Psychology, 4, 55–81.
Chen Z. , & Klahr D. ( 1999 ). All other things being equal: Acquisition and transfer of the control of variable strategy . Child Development, 70, 1098–1120.
Chi M. T. H. , Feltovich P. J. , & Glaser R. ( 1981 ). Categorization and representation of physics problems by experts and novices. Cognitive Science, 5, 121–152.
Covington M. V. , Crutchfield R. S. , Davies L. B. , & Olton R. M. ( 1974 ). The productive thinking program. Columbus, OH : Merrill.
de Groot A. D. ( 1965 ). Thought and choice in chess. The Hague, The Netherlands : Mouton.
Duncker K. ( 1945 ). On problem solving. Psychological Monographs, 58 (3) (Whole No. 270).
Ericsson K. A. , Feltovich P. J. , & Hoffman R. R. (Eds.). ( 2006 ). The Cambridge handbook of expertise and expert performance. New York : Cambridge University Press.
Fridja N. H. , & de Groot A. D. ( 1982 ). Otto Selz: His contribution to psychology. The Hague, The Netherlands : Mouton.
Gentner D. , & Stevens A. L. (Eds.). ( 1983 ). Mental models. Hillsdale, NJ : Erlbaum.
Gigerenzer G. , Todd P. M. , & ABC Research Group (Eds.). ( 1999 ). Simple heuristics that make us smart. Oxford, England : Oxford University Press.
Goel V. ( 2005 ). Cognitive neuroscience of deductive reasoning. In K. J. Holyoak & R. G. Morrison (Eds.), The Cambridge handbook of thinking and reasoning (pp. 475–492). New York : Cambridge University Press.
Guilford J. P. ( 1967 ). The nature of human intelligence. New York : McGraw-Hill.
Holyoak K. J. ( 2005 ). Analogy. In K. J. Holyoak & R. G. Morrison (Eds.), The Cambridge handbook of thinking and reasoning (pp. 117–142). New York : Cambridge University Press.
Humphrey G. ( 1963 ). Thinking: An introduction to experimental psychology. New York : Wiley.
Judd C. H. ( 1908 ). The relation of special training and general intelligence. Educational Review, 36, 28–42.
Kahneman D. , & Tversky A. ( 1984 ). Choices, values, and frames. American Psychologist, 39, 341–350.
Kahneman D. , & Tversky A. (Eds.). ( 2000 ). Choices, values, and frames. New York : Cambridge University Press.
Kohler W. ( 1925 ). The mentality of apes. New York : Liveright.
Larkin J. H. , McDermott J. , Simon D. P. , & Simon H. A. ( 1980 ). Expert and novice performance in solving physics problems. Science, 208, 1335–1342.
Luchins A. ( 1942 ). Mechanization in problem solving. Psychological Monographs, 54 (6) (Whole No. 248).
Mandler J. M. , & Mandler G. ( 1964 ). Thinking from associationism to Gestalt. New York : Wiley.
Markman A. B. , & Medin D. L. ( 2002 ). Decision making. In D. Medin (Ed.), Stevens’ handbook of experimental psychology, Vol. 2. Memory and cognitive processes (2nd ed., pp. 413–466). New York : Wiley.
Mayer R. E. ( 1992 ). Thinking, problem solving, cognition (2nd ed). New York : Freeman.
Mayer R. E. ( 1995 ). The search for insight: Grappling with Gestalt psychology’s unanswered questions. In R. J. Sternberg & J. E. Davidson (Eds.), The nature of insight (pp. 3–32). Cambridge, MA : MIT Press.
Mayer R. E. ( 2008 ). Learning and instruction. Upper Saddle River, NJ : Merrill Prentice Hall.
Mayer R. E. ( 2009 ). Information processing. In T. L. Good (Ed.), 21st century education: A reference handbook (pp. 168–174). Thousand Oaks, CA : Sage.
Mayer R. E. , & Wittrock M. C. ( 2006 ). Problem solving. In P. A. Alexander & P. H. Winne (Eds.), Handbook of educational psychology (2nd ed., pp. 287–304). Mahwah, NJ : Erlbaum.
McCloskey M. ( 1983 ). Intuitive physics. Scientific American, 248 (4), 122–130.
Metcalfe J. , & Wiebe D. ( 1987 ). Intuition in insight and non-insight problem solving. Memory and Cognition, 15, 238–246.
Newell A. , & Simon H. A. ( 1972 ). Human problem solving. Englewood Cliffs, NJ : Prentice-Hall.
Nickerson R. S. ( 1999 ). Enhancing creativity. In R. J. Sternberg (Ed.), Handbook of creativity (pp. 392–430). New York : Cambridge University Press.
Nunes T. , Schliemann A. D. , & Carraher D. W , ( 1993 ). Street mathematics and school mathematics. Cambridge, England : Cambridge University Press.
Robbins P. , & Aydede M. (Eds.). ( 2009 ). The Cambridge handbook of situated cognition. New York : Cambridge University Press.
Rogers T. T. , & McClelland J. L. ( 2004 ). Semantic cognition: A parallel distributed processing approach. Cambridge, MA : MIT Press.
Singley M. K. , & Anderson J. R. ( 1989 ). The transfer of cognitive skill. Cambridge, MA : Harvard University Press.
Sternberg R. J. ( 1990 ). Metaphors of mind: Conceptions of the nature of intelligence. New York : Cambridge University Press.
Sternberg R. J. ( 1999 ). Handbook of creativity. New York : Cambridge University Press.
Sternberg R. J. , & Gregorenko E. L. (Eds.). ( 2003 ). The psychology of abilities, competencies, and expertise. New York : Cambridge University Press.
Tharp R. G. , & Gallimore R. ( 1988 ). Rousing minds to life: Teaching, learning, and schooling in social context. New York : Cambridge University Press.
Thorndike E. L. ( 1911 ). Animal intelligence. New York: Hafner.
Thorndike E. L. , & Woodworth R. S. ( 1901 ). The influence of improvement in one mental function upon the efficiency of other functions. Psychological Review, 8, 247–261.
Wertheimer M. ( 1959 ). Productive thinking. New York : Harper and Collins.
Wundt W. ( 1973 ). An introduction to experimental psychology. New York : Arno Press. (Original work published in 1911).
Further Reading
Baron, J. ( 2008 ). Thinking and deciding (4th ed). New York: Cambridge University Press.
Duncker, K. ( 1945 ). On problem solving. Psychological Monographs , 58(3) (Whole No. 270).
Holyoak, K. J. , & Morrison, R. G. ( 2005 ). The Cambridge handbook of thinking and reasoning . New York: Cambridge University Press.
Mayer, R. E. , & Wittrock, M. C. ( 2006 ). Problem solving. In P. A. Alexander & P. H. Winne (Eds.), Handbook of educational psychology (2nd ed., pp. 287–304). Mahwah, NJ: Erlbaum.
Sternberg, R. J. , & Ben-Zeev, T. ( 2001 ). Complex cognition: The psychology of human thought . New York: Oxford University Press.
Weisberg, R. W. ( 2006 ). Creativity . New York: Wiley.
- About Oxford Academic
- Publish journals with us
- University press partners
- What we publish
- New features
- Open access
- Institutional account management
- Rights and permissions
- Get help with access
- Accessibility
- Advertising
- Media enquiries
- Oxford University Press
- Oxford Languages
- University of Oxford
Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide
- Copyright © 2024 Oxford University Press
- Cookie settings
- Cookie policy
- Privacy policy
- Legal notice
This Feature Is Available To Subscribers Only
Sign In or Create an Account
This PDF is available to Subscribers Only
For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

What is Problem Solving? (Steps, Techniques, Examples)
By Status.net Editorial Team on May 7, 2023 — 5 minutes to read
What Is Problem Solving?
Definition and importance.
Problem solving is the process of finding solutions to obstacles or challenges you encounter in your life or work. It is a crucial skill that allows you to tackle complex situations, adapt to changes, and overcome difficulties with ease. Mastering this ability will contribute to both your personal and professional growth, leading to more successful outcomes and better decision-making.
Problem-Solving Steps
The problem-solving process typically includes the following steps:
- Identify the issue : Recognize the problem that needs to be solved.
- Analyze the situation : Examine the issue in depth, gather all relevant information, and consider any limitations or constraints that may be present.
- Generate potential solutions : Brainstorm a list of possible solutions to the issue, without immediately judging or evaluating them.
- Evaluate options : Weigh the pros and cons of each potential solution, considering factors such as feasibility, effectiveness, and potential risks.
- Select the best solution : Choose the option that best addresses the problem and aligns with your objectives.
- Implement the solution : Put the selected solution into action and monitor the results to ensure it resolves the issue.
- Review and learn : Reflect on the problem-solving process, identify any improvements or adjustments that can be made, and apply these learnings to future situations.
Defining the Problem
To start tackling a problem, first, identify and understand it. Analyzing the issue thoroughly helps to clarify its scope and nature. Ask questions to gather information and consider the problem from various angles. Some strategies to define the problem include:
- Brainstorming with others
- Asking the 5 Ws and 1 H (Who, What, When, Where, Why, and How)
- Analyzing cause and effect
- Creating a problem statement
Generating Solutions
Once the problem is clearly understood, brainstorm possible solutions. Think creatively and keep an open mind, as well as considering lessons from past experiences. Consider:
- Creating a list of potential ideas to solve the problem
- Grouping and categorizing similar solutions
- Prioritizing potential solutions based on feasibility, cost, and resources required
- Involving others to share diverse opinions and inputs
Evaluating and Selecting Solutions
Evaluate each potential solution, weighing its pros and cons. To facilitate decision-making, use techniques such as:
- SWOT analysis (Strengths, Weaknesses, Opportunities, Threats)
- Decision-making matrices
- Pros and cons lists
- Risk assessments
After evaluating, choose the most suitable solution based on effectiveness, cost, and time constraints.
Implementing and Monitoring the Solution
Implement the chosen solution and monitor its progress. Key actions include:
- Communicating the solution to relevant parties
- Setting timelines and milestones
- Assigning tasks and responsibilities
- Monitoring the solution and making adjustments as necessary
- Evaluating the effectiveness of the solution after implementation
Utilize feedback from stakeholders and consider potential improvements. Remember that problem-solving is an ongoing process that can always be refined and enhanced.
Problem-Solving Techniques
During each step, you may find it helpful to utilize various problem-solving techniques, such as:
- Brainstorming : A free-flowing, open-minded session where ideas are generated and listed without judgment, to encourage creativity and innovative thinking.
- Root cause analysis : A method that explores the underlying causes of a problem to find the most effective solution rather than addressing superficial symptoms.
- SWOT analysis : A tool used to evaluate the strengths, weaknesses, opportunities, and threats related to a problem or decision, providing a comprehensive view of the situation.
- Mind mapping : A visual technique that uses diagrams to organize and connect ideas, helping to identify patterns, relationships, and possible solutions.
Brainstorming
When facing a problem, start by conducting a brainstorming session. Gather your team and encourage an open discussion where everyone contributes ideas, no matter how outlandish they may seem. This helps you:
- Generate a diverse range of solutions
- Encourage all team members to participate
- Foster creative thinking
When brainstorming, remember to:
- Reserve judgment until the session is over
- Encourage wild ideas
- Combine and improve upon ideas
Root Cause Analysis
For effective problem-solving, identifying the root cause of the issue at hand is crucial. Try these methods:
- 5 Whys : Ask “why” five times to get to the underlying cause.
- Fishbone Diagram : Create a diagram representing the problem and break it down into categories of potential causes.
- Pareto Analysis : Determine the few most significant causes underlying the majority of problems.
SWOT Analysis
SWOT analysis helps you examine the Strengths, Weaknesses, Opportunities, and Threats related to your problem. To perform a SWOT analysis:
- List your problem’s strengths, such as relevant resources or strong partnerships.
- Identify its weaknesses, such as knowledge gaps or limited resources.
- Explore opportunities, like trends or new technologies, that could help solve the problem.
- Recognize potential threats, like competition or regulatory barriers.
SWOT analysis aids in understanding the internal and external factors affecting the problem, which can help guide your solution.
Mind Mapping
A mind map is a visual representation of your problem and potential solutions. It enables you to organize information in a structured and intuitive manner. To create a mind map:
- Write the problem in the center of a blank page.
- Draw branches from the central problem to related sub-problems or contributing factors.
- Add more branches to represent potential solutions or further ideas.
Mind mapping allows you to visually see connections between ideas and promotes creativity in problem-solving.
Examples of Problem Solving in Various Contexts
In the business world, you might encounter problems related to finances, operations, or communication. Applying problem-solving skills in these situations could look like:
- Identifying areas of improvement in your company’s financial performance and implementing cost-saving measures
- Resolving internal conflicts among team members by listening and understanding different perspectives, then proposing and negotiating solutions
- Streamlining a process for better productivity by removing redundancies, automating tasks, or re-allocating resources
In educational contexts, problem-solving can be seen in various aspects, such as:
- Addressing a gap in students’ understanding by employing diverse teaching methods to cater to different learning styles
- Developing a strategy for successful time management to balance academic responsibilities and extracurricular activities
- Seeking resources and support to provide equal opportunities for learners with special needs or disabilities
Everyday life is full of challenges that require problem-solving skills. Some examples include:
- Overcoming a personal obstacle, such as improving your fitness level, by establishing achievable goals, measuring progress, and adjusting your approach accordingly
- Navigating a new environment or city by researching your surroundings, asking for directions, or using technology like GPS to guide you
- Dealing with a sudden change, like a change in your work schedule, by assessing the situation, identifying potential impacts, and adapting your plans to accommodate the change.
- How to Resolve Employee Conflict at Work [Steps, Tips, Examples]
- How to Write Inspiring Core Values? 5 Steps with Examples
- 30 Employee Feedback Examples (Positive & Negative)

How it works
For Business
Join Mind Tools
Article • 8 min read
The FOCUS Model
A simple, efficient problem-solving approach.
By the Mind Tools Content Team

Are your business processes perfect, or could you improve them?
In an ever-changing world, nothing stays perfect for long. To stay ahead of your competitors, you need to be able to refine your processes on an ongoing basis, so that your services remain efficient and your customers stay happy.
This article looks the FOCUS Model – a simple quality-improvement tool that helps you do this.
About the Model
The FOCUS Model, which was created by the Hospital Corporation of America (HCA), is a structured approach to Total Quality Management (TQM) , and it is widely used in the health care industry.
The model is helpful because it uses a team-based approach to problem solving and to business-process improvement, and this makes it particularly useful for solving cross-departmental process issues. Also, it encourages people to rely on objective data rather than on personal opinions, and this improves the quality of the outcome.
It has five steps:
- F ind the problem.
- O rganize a team.
- C larify the problem.
- U nderstand the problem.
- S elect a solution.
Applying the FOCUS Model
Follow the steps below to apply the FOCUS Model in your organization.
Step 1: Find the Problem
The first step is to identify a process that needs to be improved. Process improvements often follow the Pareto Principle , where 80 percent of issues come from 20 percent of problems. This is why identifying and solving one real problem can significantly improve your business, if you find the right problem to solve.
According to a popular analogy, identifying problems is like harvesting apples. At first, this is easy – you can pick apples up from the ground and from the lower branches of the tree. But the more fruit you collect, the harder it becomes. Eventually, the remaining fruit is all out of reach, and you need to use a ladder to reach the topmost branches.
Start with a simple problem to get the team up to speed with the FOCUS method. Then, when confidence is high, turn your attention to more complex processes.
If the problem isn't obvious, use these questions to identify possible issues:
- What would our customers want us to improve?
- How can we improve quality ?
- What processes don't work as efficiently as they could?
- Where do we experience bottlenecks in our processes?
- What do our competitors or comparators do that we could do?
- What frustrates and irritates our team?
- What might happen in the future that could become a problem for us?
If you have several problems that need attention, list them all and use Pareto Analysis , Decision Matrix Analysis , or Paired Comparison Analysis to decide which problem to address first. (If you try to address too much in one go, you'll overload team members and cause unnecessary stress.)
Step 2: Organize a Team
Your next step is to assemble a team to address the problem.
Where possible, bring together team members from a range of disciplines – this will give you a broad range of skills, perspectives, and experience to draw on.
Select team members who are familiar with the issue or process in hand, and who have a stake in its resolution. Enthusiasm for the project will be greatest if people volunteer for it, so emphasize how individuals will benefit from being involved.
If your first choice of team member isn't available, try to appoint someone close to them, or have another team member use tools like Perceptual Positioning and Rolestorming to see the issue from their point of view.
Keep in mind that a diverse team is more likely to find a creative solution than a group of people with the same outlook.
Step 3: Clarify the Problem
Before the team can begin to solve the problem, you need to define it clearly and concisely.
According to " Total Quality Management for Hospital Nutrition Services ," a key text on the FOCUS Model, an enthusiastic team may be keen to attack an "elephant-sized" problem, but the key to success is to break it down into "sushi-sized" pieces that can be analyzed and solved more easily.
Use the Drill Down technique to break big problems down into their component parts. You can also use the 5 Whys Technique , Cause and Effect Analysis , and Root Cause Analysis to get to the bottom of a problem.
Record the details in a problem statement, which will then serve as the focal point for the rest of the exercise ( CATWOE can help you do this effectively.) Focus on factual events and measurable conditions such as:
- Who does the problem affect?
- What has happened?
- Where is it occurring?
- When does it happen?
The problem statement must be objective, so avoid relying on personal opinions, gut feelings, and emotions. Also, be on guard against "factoids" – statements that appear to be facts, but that are really opinions that have come to be accepted as fact.
Step 4: Understand the Problem
Once the problem statement has been completed, members of the team gather data about the problem to understand it more fully.
Dedicate plenty of time to this stage, as this is where you will identify the fundamental steps in the process that, when changed, will bring about the biggest improvement.
Consider what you know about the problem. Has anyone else tried to fix a similar problem before? If so, what happened, and what can you learn from this?
Use a Flow Chart or Swim Lane Diagram to organize and visualize each step; this can help you discover the stage at which the problem is happening. And try to identify any bottlenecks or failures in the process that could be causing problems.
As you develop your understanding, potential solutions to the problem may become apparent. Beware of jumping to "obvious" conclusions – these could overlook important parts of the problem, and could create a whole new process that fails to solve the problem.
Generate as many possible solutions as you can through normal structured thinking, brainstorming , reverse brainstorming , and Provocation . Don't criticize ideas initially – just come up with lots of possible ideas to explore.
Step 5: Select a Solution
The final stage in the process is to select a solution.
Use appropriate decision-making techniques to select the most viable option. Decision Trees , Paired Comparison Analysis , and Decision Matrix Analysis are all useful tools for evaluating your options.
Once you've selected an idea, use tools such as Risk Analysis , "What If" Analysis , and the Futures Wheel to think about the possible consequences of moving ahead, and make a well-considered go/no-go decision to decide whether or not you should run the project.
People commonly use the FOCUS Model in conjunction with the Plan-Do-Check-Act cycle. Use this approach to implement your solutions in a controlled way.
The FOCUS Model is a simple quality-improvement tool commonly used in the health care industry. You can use it to improve any process, but it is particularly useful for processes that span different departments.
The five steps in FOCUS are as follows:
People often use the FOCUS Model in conjunction with the Plan-Do-Check-Act cycle, which allows teams to implement their solution in a controlled way.
Bataldan, P. (1992). 'Building Knowledge for Improvement: an Introductory Guide to the Use of FOCUS-PDCA,' Nashville: TN Quality Resource Group, Hospital Corporation of America.
Schiller, M., Miller-Kovach, M., and Miller-Kovach, K. (1994). 'Total Quality Management for Hospital Nutrition Services,' Aspen Publishers Inc. Available here .
You've accessed 1 of your 2 free resources.
Get unlimited access
Discover more content
Book Insights
Stolen Focus: Why You Can’t Pay Attention
By Johann Hari
Active Listening
Hear What People are Really Saying
Add comment
Comments (0)
Be the first to comment!

Get 30% off your first year of Mind Tools
Great teams begin with empowered leaders. Our tools and resources offer the support to let you flourish into leadership. Join today!
Sign-up to our newsletter
Subscribing to the Mind Tools newsletter will keep you up-to-date with our latest updates and newest resources.
Subscribe now
Business Skills
Personal Development
Leadership and Management
Member Extras
Most Popular
Latest Updates

Tips for Dealing with Customers Effectively

Pain Points Podcast - Procrastination
Mind Tools Store
About Mind Tools Content
Discover something new today
Pain points podcast - starting a new job.
How to Hit the Ground Running!
Ten Dos and Don'ts of Career Conversations
How to talk to team members about their career aspirations.
How Emotionally Intelligent Are You?
Boosting Your People Skills
Self-Assessment
What's Your Leadership Style?
Learn About the Strengths and Weaknesses of the Way You Like to Lead
Recommended for you
Delayed decision making.
With Frank Partnoy
Expert Interviews
Business Operations and Process Management
Strategy Tools
Customer Service
Business Ethics and Values
Handling Information and Data
Project Management
Knowledge Management
Self-Development and Goal Setting
Time Management
Presentation Skills
Learning Skills
Career Skills
Communication Skills
Negotiation, Persuasion and Influence
Working With Others
Difficult Conversations
Creativity Tools
Self-Management
Work-Life Balance
Stress Management and Wellbeing
Coaching and Mentoring
Change Management
Team Management
Managing Conflict
Delegation and Empowerment
Performance Management
Leadership Skills
Developing Your Team
Talent Management
Problem Solving
Decision Making
Member Podcast

Critical & Creative Thinking - OER & More Resources: IDEAL problem solving
- Self evaluation
- Creating goals
- Creating personal mission statement
- Creative Thinking
- Problem Solving
- IDEAL problem solving
- CRITICAL THINKING
- Critical Thinking Tips
- Logic Terms
- Logic Traps
- Free OER Textbooks
- More Thinking: OER
- Ethics - OER Textbooks
- Evidence-Based Critical Thinking
- BELIEFS & BIAS
- Limits of Perception
- Reality & Assumptions
- Stereotypes & Race
- MAKING YOUR CASE
- Argument (OER)
- Inductive Arguments
- Information Literacy: Be Savvy about your Sources
- Persuasive Speaking (OER)
- Philosophy & Thinking
- WiPhi Philosophy Project
- Browse All Guides
VM: I had to inter-library loan this item to read the original content. This is highly cited throughout literature, so I wanted to have a good grasp on what it covered. Here are my notes and commentary:
- Full text From TNtech.edu: "Ideal Problem Solver, 2 ed." (c) 1984, 1993 more... less... Thanks to Center for Assessment & Improvement of Learning - Reports & Publications"
- Full text from ERIC: The IDEAL Workplace: Strategies for Improving Learning, Problem Solving, and Creativity
- Show your support: The Ideal Problem Solver: A Guide to Improving Thinking, Learning, and Creativity Second Edition
The reason you should learn the IDEAL method is so you don't need to avoid problems. The more know about and practice problem solving, the easier it gets. It is learnable skill. It also prompts you to look for problems and solutions instead of just doing things the same old way.
Improvement of problem solving skills.
Model for analyzing the processes that underlie effective problem solving.
IDEAL Model for improving problem solving (Verbatim copy of Fig 2.1; p.12)
I = Identifying the problem.
D = Define and represent the problem.
E = Explore possible strategies.
A = Act on the strategies.
L = Look back and evaluate the effects of your activities.
ELABORATION:
I = Identifying that there is a problem that, once described as a problem, may be solved or improved.
D = Define and represent the problem. Draw it instead of trying to imagine it.
E = Explore possible strategies & alternative approaches or viewpoints.
General strategies: Break problem down into small simple problems. Working a problem backwards. Build scale model Try simulation experiment, with smaller or simpler sets.
A = Act on the strategies. Try, then reflect or recall. Actively try learning strategy.
L = Look back and evaluate the effects of your activities. Look at results of learning strategy used: Does it work to allow full recall?
"Many students make the mistake of assuming that they have "learned" adequately if the information seems to make sense as they read it in a textbook or hear it in a lecture." (p. 23" Must use or practice, recall, or paraphrase - in order to evaluate effectiveness of learning.
Math: Do example problems before looking at solution to practice concepts. Look at solution to see where you went wrong (or not).
Don't let the test be the first time you evaluate your understanding of material
Problem identification and definition.
Proof of concept - act/look/evaluate.
To find an answer to a problem, you can dig deeper, or dig somewhere else.
Question assumptions about limits The old - think outside the box- strategy.
When memorizing, know what you need to remember Definitions? Concepts? Graphs? Dates? each teacher has different priorities...ask them what to focus on
Ways to solve problem of learning new information.
Techniques for improving memory.
Short term meomory
Long term memory
Remembering people's names
Studying for an essay test.
Using cues to retrieve information. For example, you can remember IDEAL first and that will help you reconstruct the idea of how to solve problems.
Some strategies for remembering information:
Make a story full of memorable images.
Funny obnoxious "vivid images" or "mental pictures" are more memorabl e. (Ex: random words in a list, passwords, people's names. Banana vomit haunts me.)
Rehearse over and over - over learn. (Ex: Memorizing a phone number 867-5309 )
Rehearse words in groups - chunking. (Ex: Memorizing a part in a play, poems, pledges, short stories.)
Organize words into conceptual categories - Look for unifying relationships. (Recall, order not important. Ex: Shopping list, points in an essay.)
Look for similarities and coincidences in the words themselves. (Ex: How many words have e's, or 2 syllables, or have pun-ishing homonyms)
The feet that use the manual transmission car pedals are, from left to right: C ( L eft-foot) utch , the B( R ight-foot) ake , and the A ccelerato ( R ight-foot)
Does order mimic alphabetical order? The manual transmission car pedals are, from left to right, the C lutch, the B rake, and the A ccelerator )
Use Acronyms I dentify D efine E xplore A ct L ook
Acronym- easily remembered word: FACE

Acrostic- easily remembered phrase: E very G ood B oy D eserves F udge
- Modified image source: Commons.wikimedia.org
Don't waste time studying what you already know
Image - Name Strategy:
What is unique about the person? What is unique about their name?
Find a relationship between the two.
Other Pairing Strategies:
method of loci: arranging words to be remembered in association with familiar location or path .
Peg-word method: arranging words to be remembered in association with number order or alphabet letter order .
Strategies to comprehend new information.
more difficult than
Strategies to memorize new information.
Learning with understanding - comprehending new information.
Knowledge of CORE CONCEPTS in a field SIMPLIFIES problem solving.
Ways to approach a problem of learning information that seems to be arbitrary:
Over-learn: rehearse the facts until they are mastered. 2+2=4
Find relationships between images or words that are memorable: story telling, silmilarieties, vivid images, pegging, etc.
When a concept seems unclear, learn more about it.
Memory- can be of seemingly arbitrary words or numbers: ROTE (Ex. Facts and relationships) appearance
Comprehension - is understanding significance or relationships or function
Novices often forced to memorize information until they learn enough (related concepts and context) to understand it.
The mere memorization of information rarely provides useful conceptual tools that enable one to solve new problems later on. (p. 61,69)
Taking notes will not necessarily lead to effective recall prompts. How do you know when you understand material? Self-test by trying to explain material to another person.That will expose gaps in understanding.
Recall answers or solve problems out of order to be sure you know which concepts to apply and why.
Look at mistakes made as soon as possible, and learn where you went wrong.
Uses of information require more or less precision in understanding, depending on context. (A pilot must know more about an airplane than a passenger.)
Evaluation basics: evaluate factual claims look for flaws in logic question assumptions that form the basis of the argument
Correlation does not necessarily prove cause and effect.
Importance of being able to criticize ideas and generate alternatives.
Strategies for effective criticism.
Strategies for formulating creative solutions.
Finding/understanding implicit assumptions that hamper brainstorming.
Strategies for making implicit assumptions explicit.
"The uncreative mind can spot wrong answers, but it takes a creative mnd to spot wrong questions ." Emphasis added. - Anthony Jay, (p.93)
Making implicit assumptions explicit: look for inconsistencies question assumptions make predictions analyze worst case get feedback & criticism from others
Increase generation of novel ideas: break down problem into smaller parts analyze properties on a simpler level use analogies use brainstorming give it a rest, sleep on it don't be in a hurry, let ideas incubate: talk to others, read, keep the problem in the back of your mind try to communicate your ideas as clearly as possible, preferably in writing. attempting to write or teach an idea can function as a discovery technique
Strategies for Effective Communication
What we are trying to accomplish (goal)
Evaluating communication fro effectiveness:
Identify and Define: Have you given audience basis to understand different points of view about a topic? Different problem definitions can lead to different solutions. Did you Explore pros and cons of different strategies? Did you take Action and then Look at consequences? Did you organize your content into main points that are easy to identify and remeber?
Did you use analogies and background information to put facts into context?
Did you make sure your facts were accurate and did you avoid making assumptions?Always check for logical fallacies and inconsistencies. Did you include information that is novel and useful, instead of just regurgitating what everyone already knows?
After you communicate, get feedback and evaluate your strategies. Look for effects, and learn from your mistakes. (p. 117)
Identify and Define what (problem) you want to communicate, with respect to your audience and your goals. Explore strategies for communicating your ideas.Act - based on your strategies. Look at effects.
Summaries of Useful Attitudes and Strategies: Anybody can use the IDEAL system to improve their problem solving skills.
Related Resources:
- Teaching The IDEAL Problem-Solving Method To Diverse Learners Written by: Amy Sippl
- ~[123]~: Mar 13, 2024 3:04 PM
- ~[124]~: https://library.fvtc.edu/Thinking
About Us • Contact Us • FVTC Terms of Service • Sitemap FVTC Mission, Vision, Values & Purposes • FVTC Privacy Statement • FVTC Library Services Accessibility Statement DISCLAIMER: Any commercial mentions on our website are for instructional purposes only. Our guides are not a substitute for professional legal or medical advice. Fox Valley Technical College • Library Services • 1825 N. Bluemound Drive • Room G113 Appleton, WI 54912-2277 • United States • (920) 735-5653 © 2024 • Fox Valley Technical College • All Rights Reserved.
The https://library.fvtc.edu/ pages are hosted by SpringShare. Springshare Privacy Policy.
- Bipolar Disorder
- Therapy Center
- When To See a Therapist
- Types of Therapy
- Best Online Therapy
- Best Couples Therapy
- Best Family Therapy
- Managing Stress
- Sleep and Dreaming
- Understanding Emotions
- Self-Improvement
- Healthy Relationships
- Student Resources
- Personality Types
- Guided Meditations
- Verywell Mind Insights
- 2024 Verywell Mind 25
- Mental Health in the Classroom
- Editorial Process
- Meet Our Review Board
- Crisis Support
Problem-Solving Strategies and Obstacles
Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."
:max_bytes(150000):strip_icc():format(webp)/IMG_9791-89504ab694d54b66bbd72cb84ffb860e.jpg)
Sean is a fact-checker and researcher with experience in sociology, field research, and data analytics.
:max_bytes(150000):strip_icc():format(webp)/Sean-Blackburn-1000-a8b2229366944421bc4b2f2ba26a1003.jpg)
JGI / Jamie Grill / Getty Images
- Application
- Improvement
From deciding what to eat for dinner to considering whether it's the right time to buy a house, problem-solving is a large part of our daily lives. Learn some of the problem-solving strategies that exist and how to use them in real life, along with ways to overcome obstacles that are making it harder to resolve the issues you face.
What Is Problem-Solving?
In cognitive psychology , the term 'problem-solving' refers to the mental process that people go through to discover, analyze, and solve problems.
A problem exists when there is a goal that we want to achieve but the process by which we will achieve it is not obvious to us. Put another way, there is something that we want to occur in our life, yet we are not immediately certain how to make it happen.
Maybe you want a better relationship with your spouse or another family member but you're not sure how to improve it. Or you want to start a business but are unsure what steps to take. Problem-solving helps you figure out how to achieve these desires.
The problem-solving process involves:
- Discovery of the problem
- Deciding to tackle the issue
- Seeking to understand the problem more fully
- Researching available options or solutions
- Taking action to resolve the issue
Before problem-solving can occur, it is important to first understand the exact nature of the problem itself. If your understanding of the issue is faulty, your attempts to resolve it will also be incorrect or flawed.
Problem-Solving Mental Processes
Several mental processes are at work during problem-solving. Among them are:
- Perceptually recognizing the problem
- Representing the problem in memory
- Considering relevant information that applies to the problem
- Identifying different aspects of the problem
- Labeling and describing the problem
Problem-Solving Strategies
There are many ways to go about solving a problem. Some of these strategies might be used on their own, or you may decide to employ multiple approaches when working to figure out and fix a problem.
An algorithm is a step-by-step procedure that, by following certain "rules" produces a solution. Algorithms are commonly used in mathematics to solve division or multiplication problems. But they can be used in other fields as well.
In psychology, algorithms can be used to help identify individuals with a greater risk of mental health issues. For instance, research suggests that certain algorithms might help us recognize children with an elevated risk of suicide or self-harm.
One benefit of algorithms is that they guarantee an accurate answer. However, they aren't always the best approach to problem-solving, in part because detecting patterns can be incredibly time-consuming.
There are also concerns when machine learning is involved—also known as artificial intelligence (AI)—such as whether they can accurately predict human behaviors.
Heuristics are shortcut strategies that people can use to solve a problem at hand. These "rule of thumb" approaches allow you to simplify complex problems, reducing the total number of possible solutions to a more manageable set.
If you find yourself sitting in a traffic jam, for example, you may quickly consider other routes, taking one to get moving once again. When shopping for a new car, you might think back to a prior experience when negotiating got you a lower price, then employ the same tactics.
While heuristics may be helpful when facing smaller issues, major decisions shouldn't necessarily be made using a shortcut approach. Heuristics also don't guarantee an effective solution, such as when trying to drive around a traffic jam only to find yourself on an equally crowded route.
Trial and Error
A trial-and-error approach to problem-solving involves trying a number of potential solutions to a particular issue, then ruling out those that do not work. If you're not sure whether to buy a shirt in blue or green, for instance, you may try on each before deciding which one to purchase.
This can be a good strategy to use if you have a limited number of solutions available. But if there are many different choices available, narrowing down the possible options using another problem-solving technique can be helpful before attempting trial and error.
In some cases, the solution to a problem can appear as a sudden insight. You are facing an issue in a relationship or your career when, out of nowhere, the solution appears in your mind and you know exactly what to do.
Insight can occur when the problem in front of you is similar to an issue that you've dealt with in the past. Although, you may not recognize what is occurring since the underlying mental processes that lead to insight often happen outside of conscious awareness .
Research indicates that insight is most likely to occur during times when you are alone—such as when going on a walk by yourself, when you're in the shower, or when lying in bed after waking up.
How to Apply Problem-Solving Strategies in Real Life
If you're facing a problem, you can implement one or more of these strategies to find a potential solution. Here's how to use them in real life:
- Create a flow chart . If you have time, you can take advantage of the algorithm approach to problem-solving by sitting down and making a flow chart of each potential solution, its consequences, and what happens next.
- Recall your past experiences . When a problem needs to be solved fairly quickly, heuristics may be a better approach. Think back to when you faced a similar issue, then use your knowledge and experience to choose the best option possible.
- Start trying potential solutions . If your options are limited, start trying them one by one to see which solution is best for achieving your desired goal. If a particular solution doesn't work, move on to the next.
- Take some time alone . Since insight is often achieved when you're alone, carve out time to be by yourself for a while. The answer to your problem may come to you, seemingly out of the blue, if you spend some time away from others.
Obstacles to Problem-Solving
Problem-solving is not a flawless process as there are a number of obstacles that can interfere with our ability to solve a problem quickly and efficiently. These obstacles include:
- Assumptions: When dealing with a problem, people can make assumptions about the constraints and obstacles that prevent certain solutions. Thus, they may not even try some potential options.
- Functional fixedness : This term refers to the tendency to view problems only in their customary manner. Functional fixedness prevents people from fully seeing all of the different options that might be available to find a solution.
- Irrelevant or misleading information: When trying to solve a problem, it's important to distinguish between information that is relevant to the issue and irrelevant data that can lead to faulty solutions. The more complex the problem, the easier it is to focus on misleading or irrelevant information.
- Mental set: A mental set is a tendency to only use solutions that have worked in the past rather than looking for alternative ideas. A mental set can work as a heuristic, making it a useful problem-solving tool. However, mental sets can also lead to inflexibility, making it more difficult to find effective solutions.
How to Improve Your Problem-Solving Skills
In the end, if your goal is to become a better problem-solver, it's helpful to remember that this is a process. Thus, if you want to improve your problem-solving skills, following these steps can help lead you to your solution:
- Recognize that a problem exists . If you are facing a problem, there are generally signs. For instance, if you have a mental illness , you may experience excessive fear or sadness, mood changes, and changes in sleeping or eating habits. Recognizing these signs can help you realize that an issue exists.
- Decide to solve the problem . Make a conscious decision to solve the issue at hand. Commit to yourself that you will go through the steps necessary to find a solution.
- Seek to fully understand the issue . Analyze the problem you face, looking at it from all sides. If your problem is relationship-related, for instance, ask yourself how the other person may be interpreting the issue. You might also consider how your actions might be contributing to the situation.
- Research potential options . Using the problem-solving strategies mentioned, research potential solutions. Make a list of options, then consider each one individually. What are some pros and cons of taking the available routes? What would you need to do to make them happen?
- Take action . Select the best solution possible and take action. Action is one of the steps required for change . So, go through the motions needed to resolve the issue.
- Try another option, if needed . If the solution you chose didn't work, don't give up. Either go through the problem-solving process again or simply try another option.
You can find a way to solve your problems as long as you keep working toward this goal—even if the best solution is simply to let go because no other good solution exists.
Sarathy V. Real world problem-solving . Front Hum Neurosci . 2018;12:261. doi:10.3389/fnhum.2018.00261
Dunbar K. Problem solving . A Companion to Cognitive Science . 2017. doi:10.1002/9781405164535.ch20
Stewart SL, Celebre A, Hirdes JP, Poss JW. Risk of suicide and self-harm in kids: The development of an algorithm to identify high-risk individuals within the children's mental health system . Child Psychiat Human Develop . 2020;51:913-924. doi:10.1007/s10578-020-00968-9
Rosenbusch H, Soldner F, Evans AM, Zeelenberg M. Supervised machine learning methods in psychology: A practical introduction with annotated R code . Soc Personal Psychol Compass . 2021;15(2):e12579. doi:10.1111/spc3.12579
Mishra S. Decision-making under risk: Integrating perspectives from biology, economics, and psychology . Personal Soc Psychol Rev . 2014;18(3):280-307. doi:10.1177/1088868314530517
Csikszentmihalyi M, Sawyer K. Creative insight: The social dimension of a solitary moment . In: The Systems Model of Creativity . 2015:73-98. doi:10.1007/978-94-017-9085-7_7
Chrysikou EG, Motyka K, Nigro C, Yang SI, Thompson-Schill SL. Functional fixedness in creative thinking tasks depends on stimulus modality . Psychol Aesthet Creat Arts . 2016;10(4):425‐435. doi:10.1037/aca0000050
Huang F, Tang S, Hu Z. Unconditional perseveration of the short-term mental set in chunk decomposition . Front Psychol . 2018;9:2568. doi:10.3389/fpsyg.2018.02568
National Alliance on Mental Illness. Warning signs and symptoms .
Mayer RE. Thinking, problem solving, cognition, 2nd ed .
Schooler JW, Ohlsson S, Brooks K. Thoughts beyond words: When language overshadows insight. J Experiment Psychol: General . 1993;122:166-183. doi:10.1037/0096-3445.2.166
By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."
35 problem-solving techniques and methods for solving complex problems

Design your next session with SessionLab
Join the 150,000+ facilitators using SessionLab.
Recommended Articles
A step-by-step guide to planning a workshop, how to create an unforgettable training session in 8 simple steps, 47 useful online tools for workshop planning and meeting facilitation.
All teams and organizations encounter challenges as they grow. There are problems that might occur for teams when it comes to miscommunication or resolving business-critical issues . You may face challenges around growth , design , user engagement, and even team culture and happiness. In short, problem-solving techniques should be part of every team’s skillset.
Problem-solving methods are primarily designed to help a group or team through a process of first identifying problems and challenges , ideating possible solutions , and then evaluating the most suitable .
Finding effective solutions to complex problems isn’t easy, but by using the right process and techniques, you can help your team be more efficient in the process.
So how do you develop strategies that are engaging, and empower your team to solve problems effectively?
In this blog post, we share a series of problem-solving tools you can use in your next workshop or team meeting. You’ll also find some tips for facilitating the process and how to enable others to solve complex problems.
Let’s get started!
How do you identify problems?
How do you identify the right solution.
- Tips for more effective problem-solving
Complete problem-solving methods
- Problem-solving techniques to identify and analyze problems
- Problem-solving techniques for developing solutions
Problem-solving warm-up activities
Closing activities for a problem-solving process.
Before you can move towards finding the right solution for a given problem, you first need to identify and define the problem you wish to solve.
Here, you want to clearly articulate what the problem is and allow your group to do the same. Remember that everyone in a group is likely to have differing perspectives and alignment is necessary in order to help the group move forward.
Identifying a problem accurately also requires that all members of a group are able to contribute their views in an open and safe manner. It can be scary for people to stand up and contribute, especially if the problems or challenges are emotive or personal in nature. Be sure to try and create a psychologically safe space for these kinds of discussions.
Remember that problem analysis and further discussion are also important. Not taking the time to fully analyze and discuss a challenge can result in the development of solutions that are not fit for purpose or do not address the underlying issue.
Successfully identifying and then analyzing a problem means facilitating a group through activities designed to help them clearly and honestly articulate their thoughts and produce usable insight.
With this data, you might then produce a problem statement that clearly describes the problem you wish to be addressed and also state the goal of any process you undertake to tackle this issue.
Finding solutions is the end goal of any process. Complex organizational challenges can only be solved with an appropriate solution but discovering them requires using the right problem-solving tool.
After you’ve explored a problem and discussed ideas, you need to help a team discuss and choose the right solution. Consensus tools and methods such as those below help a group explore possible solutions before then voting for the best. They’re a great way to tap into the collective intelligence of the group for great results!
Remember that the process is often iterative. Great problem solvers often roadtest a viable solution in a measured way to see what works too. While you might not get the right solution on your first try, the methods below help teams land on the most likely to succeed solution while also holding space for improvement.
Every effective problem solving process begins with an agenda . A well-structured workshop is one of the best methods for successfully guiding a group from exploring a problem to implementing a solution.
In SessionLab, it’s easy to go from an idea to a complete agenda . Start by dragging and dropping your core problem solving activities into place . Add timings, breaks and necessary materials before sharing your agenda with your colleagues.
The resulting agenda will be your guide to an effective and productive problem solving session that will also help you stay organized on the day!
Tips for more effective problem solving
Problem-solving activities are only one part of the puzzle. While a great method can help unlock your team’s ability to solve problems, without a thoughtful approach and strong facilitation the solutions may not be fit for purpose.
Let’s take a look at some problem-solving tips you can apply to any process to help it be a success!
Clearly define the problem
Jumping straight to solutions can be tempting, though without first clearly articulating a problem, the solution might not be the right one. Many of the problem-solving activities below include sections where the problem is explored and clearly defined before moving on.
This is a vital part of the problem-solving process and taking the time to fully define an issue can save time and effort later. A clear definition helps identify irrelevant information and it also ensures that your team sets off on the right track.
Don’t jump to conclusions
It’s easy for groups to exhibit cognitive bias or have preconceived ideas about both problems and potential solutions. Be sure to back up any problem statements or potential solutions with facts, research, and adequate forethought.
The best techniques ask participants to be methodical and challenge preconceived notions. Make sure you give the group enough time and space to collect relevant information and consider the problem in a new way. By approaching the process with a clear, rational mindset, you’ll often find that better solutions are more forthcoming.
Try different approaches
Problems come in all shapes and sizes and so too should the methods you use to solve them. If you find that one approach isn’t yielding results and your team isn’t finding different solutions, try mixing it up. You’ll be surprised at how using a new creative activity can unblock your team and generate great solutions.
Don’t take it personally
Depending on the nature of your team or organizational problems, it’s easy for conversations to get heated. While it’s good for participants to be engaged in the discussions, ensure that emotions don’t run too high and that blame isn’t thrown around while finding solutions.
You’re all in it together, and even if your team or area is seeing problems, that isn’t necessarily a disparagement of you personally. Using facilitation skills to manage group dynamics is one effective method of helping conversations be more constructive.
Get the right people in the room
Your problem-solving method is often only as effective as the group using it. Getting the right people on the job and managing the number of people present is important too!
If the group is too small, you may not get enough different perspectives to effectively solve a problem. If the group is too large, you can go round and round during the ideation stages.
Creating the right group makeup is also important in ensuring you have the necessary expertise and skillset to both identify and follow up on potential solutions. Carefully consider who to include at each stage to help ensure your problem-solving method is followed and positioned for success.
Document everything
The best solutions can take refinement, iteration, and reflection to come out. Get into a habit of documenting your process in order to keep all the learnings from the session and to allow ideas to mature and develop. Many of the methods below involve the creation of documents or shared resources. Be sure to keep and share these so everyone can benefit from the work done!
Bring a facilitator
Facilitation is all about making group processes easier. With a subject as potentially emotive and important as problem-solving, having an impartial third party in the form of a facilitator can make all the difference in finding great solutions and keeping the process moving. Consider bringing a facilitator to your problem-solving session to get better results and generate meaningful solutions!
Develop your problem-solving skills
It takes time and practice to be an effective problem solver. While some roles or participants might more naturally gravitate towards problem-solving, it can take development and planning to help everyone create better solutions.
You might develop a training program, run a problem-solving workshop or simply ask your team to practice using the techniques below. Check out our post on problem-solving skills to see how you and your group can develop the right mental process and be more resilient to issues too!
Design a great agenda
Workshops are a great format for solving problems. With the right approach, you can focus a group and help them find the solutions to their own problems. But designing a process can be time-consuming and finding the right activities can be difficult.
Check out our workshop planning guide to level-up your agenda design and start running more effective workshops. Need inspiration? Check out templates designed by expert facilitators to help you kickstart your process!
In this section, we’ll look at in-depth problem-solving methods that provide a complete end-to-end process for developing effective solutions. These will help guide your team from the discovery and definition of a problem through to delivering the right solution.
If you’re looking for an all-encompassing method or problem-solving model, these processes are a great place to start. They’ll ask your team to challenge preconceived ideas and adopt a mindset for solving problems more effectively.
- Six Thinking Hats
- Lightning Decision Jam
- Problem Definition Process
- Discovery & Action Dialogue
Design Sprint 2.0
- Open Space Technology
1. Six Thinking Hats
Individual approaches to solving a problem can be very different based on what team or role an individual holds. It can be easy for existing biases or perspectives to find their way into the mix, or for internal politics to direct a conversation.
Six Thinking Hats is a classic method for identifying the problems that need to be solved and enables your team to consider them from different angles, whether that is by focusing on facts and data, creative solutions, or by considering why a particular solution might not work.
Like all problem-solving frameworks, Six Thinking Hats is effective at helping teams remove roadblocks from a conversation or discussion and come to terms with all the aspects necessary to solve complex problems.
2. Lightning Decision Jam
Featured courtesy of Jonathan Courtney of AJ&Smart Berlin, Lightning Decision Jam is one of those strategies that should be in every facilitation toolbox. Exploring problems and finding solutions is often creative in nature, though as with any creative process, there is the potential to lose focus and get lost.
Unstructured discussions might get you there in the end, but it’s much more effective to use a method that creates a clear process and team focus.
In Lightning Decision Jam, participants are invited to begin by writing challenges, concerns, or mistakes on post-its without discussing them before then being invited by the moderator to present them to the group.
From there, the team vote on which problems to solve and are guided through steps that will allow them to reframe those problems, create solutions and then decide what to execute on.
By deciding the problems that need to be solved as a team before moving on, this group process is great for ensuring the whole team is aligned and can take ownership over the next stages.
Lightning Decision Jam (LDJ) #action #decision making #problem solving #issue analysis #innovation #design #remote-friendly The problem with anything that requires creative thinking is that it’s easy to get lost—lose focus and fall into the trap of having useless, open-ended, unstructured discussions. Here’s the most effective solution I’ve found: Replace all open, unstructured discussion with a clear process. What to use this exercise for: Anything which requires a group of people to make decisions, solve problems or discuss challenges. It’s always good to frame an LDJ session with a broad topic, here are some examples: The conversion flow of our checkout Our internal design process How we organise events Keeping up with our competition Improving sales flow
3. Problem Definition Process
While problems can be complex, the problem-solving methods you use to identify and solve those problems can often be simple in design.
By taking the time to truly identify and define a problem before asking the group to reframe the challenge as an opportunity, this method is a great way to enable change.
Begin by identifying a focus question and exploring the ways in which it manifests before splitting into five teams who will each consider the problem using a different method: escape, reversal, exaggeration, distortion or wishful. Teams develop a problem objective and create ideas in line with their method before then feeding them back to the group.
This method is great for enabling in-depth discussions while also creating space for finding creative solutions too!
Problem Definition #problem solving #idea generation #creativity #online #remote-friendly A problem solving technique to define a problem, challenge or opportunity and to generate ideas.
4. The 5 Whys
Sometimes, a group needs to go further with their strategies and analyze the root cause at the heart of organizational issues. An RCA or root cause analysis is the process of identifying what is at the heart of business problems or recurring challenges.
The 5 Whys is a simple and effective method of helping a group go find the root cause of any problem or challenge and conduct analysis that will deliver results.
By beginning with the creation of a problem statement and going through five stages to refine it, The 5 Whys provides everything you need to truly discover the cause of an issue.
The 5 Whys #hyperisland #innovation This simple and powerful method is useful for getting to the core of a problem or challenge. As the title suggests, the group defines a problems, then asks the question “why” five times, often using the resulting explanation as a starting point for creative problem solving.
5. World Cafe
World Cafe is a simple but powerful facilitation technique to help bigger groups to focus their energy and attention on solving complex problems.
World Cafe enables this approach by creating a relaxed atmosphere where participants are able to self-organize and explore topics relevant and important to them which are themed around a central problem-solving purpose. Create the right atmosphere by modeling your space after a cafe and after guiding the group through the method, let them take the lead!
Making problem-solving a part of your organization’s culture in the long term can be a difficult undertaking. More approachable formats like World Cafe can be especially effective in bringing people unfamiliar with workshops into the fold.
World Cafe #hyperisland #innovation #issue analysis World Café is a simple yet powerful method, originated by Juanita Brown, for enabling meaningful conversations driven completely by participants and the topics that are relevant and important to them. Facilitators create a cafe-style space and provide simple guidelines. Participants then self-organize and explore a set of relevant topics or questions for conversation.
6. Discovery & Action Dialogue (DAD)
One of the best approaches is to create a safe space for a group to share and discover practices and behaviors that can help them find their own solutions.
With DAD, you can help a group choose which problems they wish to solve and which approaches they will take to do so. It’s great at helping remove resistance to change and can help get buy-in at every level too!
This process of enabling frontline ownership is great in ensuring follow-through and is one of the methods you will want in your toolbox as a facilitator.
Discovery & Action Dialogue (DAD) #idea generation #liberating structures #action #issue analysis #remote-friendly DADs make it easy for a group or community to discover practices and behaviors that enable some individuals (without access to special resources and facing the same constraints) to find better solutions than their peers to common problems. These are called positive deviant (PD) behaviors and practices. DADs make it possible for people in the group, unit, or community to discover by themselves these PD practices. DADs also create favorable conditions for stimulating participants’ creativity in spaces where they can feel safe to invent new and more effective practices. Resistance to change evaporates as participants are unleashed to choose freely which practices they will adopt or try and which problems they will tackle. DADs make it possible to achieve frontline ownership of solutions.
7. Design Sprint 2.0
Want to see how a team can solve big problems and move forward with prototyping and testing solutions in a few days? The Design Sprint 2.0 template from Jake Knapp, author of Sprint, is a complete agenda for a with proven results.
Developing the right agenda can involve difficult but necessary planning. Ensuring all the correct steps are followed can also be stressful or time-consuming depending on your level of experience.
Use this complete 4-day workshop template if you are finding there is no obvious solution to your challenge and want to focus your team around a specific problem that might require a shortcut to launching a minimum viable product or waiting for the organization-wide implementation of a solution.
8. Open space technology
Open space technology- developed by Harrison Owen – creates a space where large groups are invited to take ownership of their problem solving and lead individual sessions. Open space technology is a great format when you have a great deal of expertise and insight in the room and want to allow for different takes and approaches on a particular theme or problem you need to be solved.
Start by bringing your participants together to align around a central theme and focus their efforts. Explain the ground rules to help guide the problem-solving process and then invite members to identify any issue connecting to the central theme that they are interested in and are prepared to take responsibility for.
Once participants have decided on their approach to the core theme, they write their issue on a piece of paper, announce it to the group, pick a session time and place, and post the paper on the wall. As the wall fills up with sessions, the group is then invited to join the sessions that interest them the most and which they can contribute to, then you’re ready to begin!
Everyone joins the problem-solving group they’ve signed up to, record the discussion and if appropriate, findings can then be shared with the rest of the group afterward.
Open Space Technology #action plan #idea generation #problem solving #issue analysis #large group #online #remote-friendly Open Space is a methodology for large groups to create their agenda discerning important topics for discussion, suitable for conferences, community gatherings and whole system facilitation
Techniques to identify and analyze problems
Using a problem-solving method to help a team identify and analyze a problem can be a quick and effective addition to any workshop or meeting.
While further actions are always necessary, you can generate momentum and alignment easily, and these activities are a great place to get started.
We’ve put together this list of techniques to help you and your team with problem identification, analysis, and discussion that sets the foundation for developing effective solutions.
Let’s take a look!
- The Creativity Dice
- Fishbone Analysis
- Problem Tree
- SWOT Analysis
- Agreement-Certainty Matrix
- The Journalistic Six
- LEGO Challenge
- What, So What, Now What?
- Journalists
Individual and group perspectives are incredibly important, but what happens if people are set in their minds and need a change of perspective in order to approach a problem more effectively?
Flip It is a method we love because it is both simple to understand and run, and allows groups to understand how their perspectives and biases are formed.
Participants in Flip It are first invited to consider concerns, issues, or problems from a perspective of fear and write them on a flip chart. Then, the group is asked to consider those same issues from a perspective of hope and flip their understanding.
No problem and solution is free from existing bias and by changing perspectives with Flip It, you can then develop a problem solving model quickly and effectively.
Flip It! #gamestorming #problem solving #action Often, a change in a problem or situation comes simply from a change in our perspectives. Flip It! is a quick game designed to show players that perspectives are made, not born.
10. The Creativity Dice
One of the most useful problem solving skills you can teach your team is of approaching challenges with creativity, flexibility, and openness. Games like The Creativity Dice allow teams to overcome the potential hurdle of too much linear thinking and approach the process with a sense of fun and speed.
In The Creativity Dice, participants are organized around a topic and roll a dice to determine what they will work on for a period of 3 minutes at a time. They might roll a 3 and work on investigating factual information on the chosen topic. They might roll a 1 and work on identifying the specific goals, standards, or criteria for the session.
Encouraging rapid work and iteration while asking participants to be flexible are great skills to cultivate. Having a stage for idea incubation in this game is also important. Moments of pause can help ensure the ideas that are put forward are the most suitable.
The Creativity Dice #creativity #problem solving #thiagi #issue analysis Too much linear thinking is hazardous to creative problem solving. To be creative, you should approach the problem (or the opportunity) from different points of view. You should leave a thought hanging in mid-air and move to another. This skipping around prevents premature closure and lets your brain incubate one line of thought while you consciously pursue another.
11. Fishbone Analysis
Organizational or team challenges are rarely simple, and it’s important to remember that one problem can be an indication of something that goes deeper and may require further consideration to be solved.
Fishbone Analysis helps groups to dig deeper and understand the origins of a problem. It’s a great example of a root cause analysis method that is simple for everyone on a team to get their head around.
Participants in this activity are asked to annotate a diagram of a fish, first adding the problem or issue to be worked on at the head of a fish before then brainstorming the root causes of the problem and adding them as bones on the fish.
Using abstractions such as a diagram of a fish can really help a team break out of their regular thinking and develop a creative approach.
Fishbone Analysis #problem solving ##root cause analysis #decision making #online facilitation A process to help identify and understand the origins of problems, issues or observations.
12. Problem Tree
Encouraging visual thinking can be an essential part of many strategies. By simply reframing and clarifying problems, a group can move towards developing a problem solving model that works for them.
In Problem Tree, groups are asked to first brainstorm a list of problems – these can be design problems, team problems or larger business problems – and then organize them into a hierarchy. The hierarchy could be from most important to least important or abstract to practical, though the key thing with problem solving games that involve this aspect is that your group has some way of managing and sorting all the issues that are raised.
Once you have a list of problems that need to be solved and have organized them accordingly, you’re then well-positioned for the next problem solving steps.
Problem tree #define intentions #create #design #issue analysis A problem tree is a tool to clarify the hierarchy of problems addressed by the team within a design project; it represents high level problems or related sublevel problems.
13. SWOT Analysis
Chances are you’ve heard of the SWOT Analysis before. This problem-solving method focuses on identifying strengths, weaknesses, opportunities, and threats is a tried and tested method for both individuals and teams.
Start by creating a desired end state or outcome and bare this in mind – any process solving model is made more effective by knowing what you are moving towards. Create a quadrant made up of the four categories of a SWOT analysis and ask participants to generate ideas based on each of those quadrants.
Once you have those ideas assembled in their quadrants, cluster them together based on their affinity with other ideas. These clusters are then used to facilitate group conversations and move things forward.
SWOT analysis #gamestorming #problem solving #action #meeting facilitation The SWOT Analysis is a long-standing technique of looking at what we have, with respect to the desired end state, as well as what we could improve on. It gives us an opportunity to gauge approaching opportunities and dangers, and assess the seriousness of the conditions that affect our future. When we understand those conditions, we can influence what comes next.
14. Agreement-Certainty Matrix
Not every problem-solving approach is right for every challenge, and deciding on the right method for the challenge at hand is a key part of being an effective team.
The Agreement Certainty matrix helps teams align on the nature of the challenges facing them. By sorting problems from simple to chaotic, your team can understand what methods are suitable for each problem and what they can do to ensure effective results.
If you are already using Liberating Structures techniques as part of your problem-solving strategy, the Agreement-Certainty Matrix can be an invaluable addition to your process. We’ve found it particularly if you are having issues with recurring problems in your organization and want to go deeper in understanding the root cause.
Agreement-Certainty Matrix #issue analysis #liberating structures #problem solving You can help individuals or groups avoid the frequent mistake of trying to solve a problem with methods that are not adapted to the nature of their challenge. The combination of two questions makes it possible to easily sort challenges into four categories: simple, complicated, complex , and chaotic . A problem is simple when it can be solved reliably with practices that are easy to duplicate. It is complicated when experts are required to devise a sophisticated solution that will yield the desired results predictably. A problem is complex when there are several valid ways to proceed but outcomes are not predictable in detail. Chaotic is when the context is too turbulent to identify a path forward. A loose analogy may be used to describe these differences: simple is like following a recipe, complicated like sending a rocket to the moon, complex like raising a child, and chaotic is like the game “Pin the Tail on the Donkey.” The Liberating Structures Matching Matrix in Chapter 5 can be used as the first step to clarify the nature of a challenge and avoid the mismatches between problems and solutions that are frequently at the root of chronic, recurring problems.
Organizing and charting a team’s progress can be important in ensuring its success. SQUID (Sequential Question and Insight Diagram) is a great model that allows a team to effectively switch between giving questions and answers and develop the skills they need to stay on track throughout the process.
Begin with two different colored sticky notes – one for questions and one for answers – and with your central topic (the head of the squid) on the board. Ask the group to first come up with a series of questions connected to their best guess of how to approach the topic. Ask the group to come up with answers to those questions, fix them to the board and connect them with a line. After some discussion, go back to question mode by responding to the generated answers or other points on the board.
It’s rewarding to see a diagram grow throughout the exercise, and a completed SQUID can provide a visual resource for future effort and as an example for other teams.
SQUID #gamestorming #project planning #issue analysis #problem solving When exploring an information space, it’s important for a group to know where they are at any given time. By using SQUID, a group charts out the territory as they go and can navigate accordingly. SQUID stands for Sequential Question and Insight Diagram.
16. Speed Boat
To continue with our nautical theme, Speed Boat is a short and sweet activity that can help a team quickly identify what employees, clients or service users might have a problem with and analyze what might be standing in the way of achieving a solution.
Methods that allow for a group to make observations, have insights and obtain those eureka moments quickly are invaluable when trying to solve complex problems.
In Speed Boat, the approach is to first consider what anchors and challenges might be holding an organization (or boat) back. Bonus points if you are able to identify any sharks in the water and develop ideas that can also deal with competitors!
Speed Boat #gamestorming #problem solving #action Speedboat is a short and sweet way to identify what your employees or clients don’t like about your product/service or what’s standing in the way of a desired goal.
17. The Journalistic Six
Some of the most effective ways of solving problems is by encouraging teams to be more inclusive and diverse in their thinking.
Based on the six key questions journalism students are taught to answer in articles and news stories, The Journalistic Six helps create teams to see the whole picture. By using who, what, when, where, why, and how to facilitate the conversation and encourage creative thinking, your team can make sure that the problem identification and problem analysis stages of the are covered exhaustively and thoughtfully. Reporter’s notebook and dictaphone optional.
The Journalistic Six – Who What When Where Why How #idea generation #issue analysis #problem solving #online #creative thinking #remote-friendly A questioning method for generating, explaining, investigating ideas.
18. LEGO Challenge
Now for an activity that is a little out of the (toy) box. LEGO Serious Play is a facilitation methodology that can be used to improve creative thinking and problem-solving skills.
The LEGO Challenge includes giving each member of the team an assignment that is hidden from the rest of the group while they create a structure without speaking.
What the LEGO challenge brings to the table is a fun working example of working with stakeholders who might not be on the same page to solve problems. Also, it’s LEGO! Who doesn’t love LEGO!
LEGO Challenge #hyperisland #team A team-building activity in which groups must work together to build a structure out of LEGO, but each individual has a secret “assignment” which makes the collaborative process more challenging. It emphasizes group communication, leadership dynamics, conflict, cooperation, patience and problem solving strategy.

19. What, So What, Now What?
If not carefully managed, the problem identification and problem analysis stages of the problem-solving process can actually create more problems and misunderstandings.
The What, So What, Now What? problem-solving activity is designed to help collect insights and move forward while also eliminating the possibility of disagreement when it comes to identifying, clarifying, and analyzing organizational or work problems.
Facilitation is all about bringing groups together so that might work on a shared goal and the best problem-solving strategies ensure that teams are aligned in purpose, if not initially in opinion or insight.
Throughout the three steps of this game, you give everyone on a team to reflect on a problem by asking what happened, why it is important, and what actions should then be taken.
This can be a great activity for bringing our individual perceptions about a problem or challenge and contextualizing it in a larger group setting. This is one of the most important problem-solving skills you can bring to your organization.
W³ – What, So What, Now What? #issue analysis #innovation #liberating structures You can help groups reflect on a shared experience in a way that builds understanding and spurs coordinated action while avoiding unproductive conflict. It is possible for every voice to be heard while simultaneously sifting for insights and shaping new direction. Progressing in stages makes this practical—from collecting facts about What Happened to making sense of these facts with So What and finally to what actions logically follow with Now What . The shared progression eliminates most of the misunderstandings that otherwise fuel disagreements about what to do. Voila!
20. Journalists
Problem analysis can be one of the most important and decisive stages of all problem-solving tools. Sometimes, a team can become bogged down in the details and are unable to move forward.
Journalists is an activity that can avoid a group from getting stuck in the problem identification or problem analysis stages of the process.
In Journalists, the group is invited to draft the front page of a fictional newspaper and figure out what stories deserve to be on the cover and what headlines those stories will have. By reframing how your problems and challenges are approached, you can help a team move productively through the process and be better prepared for the steps to follow.
Journalists #vision #big picture #issue analysis #remote-friendly This is an exercise to use when the group gets stuck in details and struggles to see the big picture. Also good for defining a vision.
Problem-solving techniques for developing solutions
The success of any problem-solving process can be measured by the solutions it produces. After you’ve defined the issue, explored existing ideas, and ideated, it’s time to narrow down to the correct solution.
Use these problem-solving techniques when you want to help your team find consensus, compare possible solutions, and move towards taking action on a particular problem.
- Improved Solutions
- Four-Step Sketch
- 15% Solutions
- How-Now-Wow matrix
- Impact Effort Matrix
21. Mindspin
Brainstorming is part of the bread and butter of the problem-solving process and all problem-solving strategies benefit from getting ideas out and challenging a team to generate solutions quickly.
With Mindspin, participants are encouraged not only to generate ideas but to do so under time constraints and by slamming down cards and passing them on. By doing multiple rounds, your team can begin with a free generation of possible solutions before moving on to developing those solutions and encouraging further ideation.
This is one of our favorite problem-solving activities and can be great for keeping the energy up throughout the workshop. Remember the importance of helping people become engaged in the process – energizing problem-solving techniques like Mindspin can help ensure your team stays engaged and happy, even when the problems they’re coming together to solve are complex.
MindSpin #teampedia #idea generation #problem solving #action A fast and loud method to enhance brainstorming within a team. Since this activity has more than round ideas that are repetitive can be ruled out leaving more creative and innovative answers to the challenge.
22. Improved Solutions
After a team has successfully identified a problem and come up with a few solutions, it can be tempting to call the work of the problem-solving process complete. That said, the first solution is not necessarily the best, and by including a further review and reflection activity into your problem-solving model, you can ensure your group reaches the best possible result.
One of a number of problem-solving games from Thiagi Group, Improved Solutions helps you go the extra mile and develop suggested solutions with close consideration and peer review. By supporting the discussion of several problems at once and by shifting team roles throughout, this problem-solving technique is a dynamic way of finding the best solution.
Improved Solutions #creativity #thiagi #problem solving #action #team You can improve any solution by objectively reviewing its strengths and weaknesses and making suitable adjustments. In this creativity framegame, you improve the solutions to several problems. To maintain objective detachment, you deal with a different problem during each of six rounds and assume different roles (problem owner, consultant, basher, booster, enhancer, and evaluator) during each round. At the conclusion of the activity, each player ends up with two solutions to her problem.
23. Four Step Sketch
Creative thinking and visual ideation does not need to be confined to the opening stages of your problem-solving strategies. Exercises that include sketching and prototyping on paper can be effective at the solution finding and development stage of the process, and can be great for keeping a team engaged.
By going from simple notes to a crazy 8s round that involves rapidly sketching 8 variations on their ideas before then producing a final solution sketch, the group is able to iterate quickly and visually. Problem-solving techniques like Four-Step Sketch are great if you have a group of different thinkers and want to change things up from a more textual or discussion-based approach.
Four-Step Sketch #design sprint #innovation #idea generation #remote-friendly The four-step sketch is an exercise that helps people to create well-formed concepts through a structured process that includes: Review key information Start design work on paper, Consider multiple variations , Create a detailed solution . This exercise is preceded by a set of other activities allowing the group to clarify the challenge they want to solve. See how the Four Step Sketch exercise fits into a Design Sprint
24. 15% Solutions
Some problems are simpler than others and with the right problem-solving activities, you can empower people to take immediate actions that can help create organizational change.
Part of the liberating structures toolkit, 15% solutions is a problem-solving technique that focuses on finding and implementing solutions quickly. A process of iterating and making small changes quickly can help generate momentum and an appetite for solving complex problems.
Problem-solving strategies can live and die on whether people are onboard. Getting some quick wins is a great way of getting people behind the process.
It can be extremely empowering for a team to realize that problem-solving techniques can be deployed quickly and easily and delineate between things they can positively impact and those things they cannot change.
15% Solutions #action #liberating structures #remote-friendly You can reveal the actions, however small, that everyone can do immediately. At a minimum, these will create momentum, and that may make a BIG difference. 15% Solutions show that there is no reason to wait around, feel powerless, or fearful. They help people pick it up a level. They get individuals and the group to focus on what is within their discretion instead of what they cannot change. With a very simple question, you can flip the conversation to what can be done and find solutions to big problems that are often distributed widely in places not known in advance. Shifting a few grains of sand may trigger a landslide and change the whole landscape.
25. How-Now-Wow Matrix
The problem-solving process is often creative, as complex problems usually require a change of thinking and creative response in order to find the best solutions. While it’s common for the first stages to encourage creative thinking, groups can often gravitate to familiar solutions when it comes to the end of the process.
When selecting solutions, you don’t want to lose your creative energy! The How-Now-Wow Matrix from Gamestorming is a great problem-solving activity that enables a group to stay creative and think out of the box when it comes to selecting the right solution for a given problem.
Problem-solving techniques that encourage creative thinking and the ideation and selection of new solutions can be the most effective in organisational change. Give the How-Now-Wow Matrix a go, and not just for how pleasant it is to say out loud.
How-Now-Wow Matrix #gamestorming #idea generation #remote-friendly When people want to develop new ideas, they most often think out of the box in the brainstorming or divergent phase. However, when it comes to convergence, people often end up picking ideas that are most familiar to them. This is called a ‘creative paradox’ or a ‘creadox’. The How-Now-Wow matrix is an idea selection tool that breaks the creadox by forcing people to weigh each idea on 2 parameters.
26. Impact and Effort Matrix
All problem-solving techniques hope to not only find solutions to a given problem or challenge but to find the best solution. When it comes to finding a solution, groups are invited to put on their decision-making hats and really think about how a proposed idea would work in practice.
The Impact and Effort Matrix is one of the problem-solving techniques that fall into this camp, empowering participants to first generate ideas and then categorize them into a 2×2 matrix based on impact and effort.
Activities that invite critical thinking while remaining simple are invaluable. Use the Impact and Effort Matrix to move from ideation and towards evaluating potential solutions before then committing to them.
Impact and Effort Matrix #gamestorming #decision making #action #remote-friendly In this decision-making exercise, possible actions are mapped based on two factors: effort required to implement and potential impact. Categorizing ideas along these lines is a useful technique in decision making, as it obliges contributors to balance and evaluate suggested actions before committing to them.
27. Dotmocracy
If you’ve followed each of the problem-solving steps with your group successfully, you should move towards the end of your process with heaps of possible solutions developed with a specific problem in mind. But how do you help a group go from ideation to putting a solution into action?
Dotmocracy – or Dot Voting -is a tried and tested method of helping a team in the problem-solving process make decisions and put actions in place with a degree of oversight and consensus.
One of the problem-solving techniques that should be in every facilitator’s toolbox, Dot Voting is fast and effective and can help identify the most popular and best solutions and help bring a group to a decision effectively.
Dotmocracy #action #decision making #group prioritization #hyperisland #remote-friendly Dotmocracy is a simple method for group prioritization or decision-making. It is not an activity on its own, but a method to use in processes where prioritization or decision-making is the aim. The method supports a group to quickly see which options are most popular or relevant. The options or ideas are written on post-its and stuck up on a wall for the whole group to see. Each person votes for the options they think are the strongest, and that information is used to inform a decision.
All facilitators know that warm-ups and icebreakers are useful for any workshop or group process. Problem-solving workshops are no different.
Use these problem-solving techniques to warm up a group and prepare them for the rest of the process. Activating your group by tapping into some of the top problem-solving skills can be one of the best ways to see great outcomes from your session.
- Check-in/Check-out
- Doodling Together
- Show and Tell
- Constellations
- Draw a Tree
28. Check-in / Check-out
Solid processes are planned from beginning to end, and the best facilitators know that setting the tone and establishing a safe, open environment can be integral to a successful problem-solving process.
Check-in / Check-out is a great way to begin and/or bookend a problem-solving workshop. Checking in to a session emphasizes that everyone will be seen, heard, and expected to contribute.
If you are running a series of meetings, setting a consistent pattern of checking in and checking out can really help your team get into a groove. We recommend this opening-closing activity for small to medium-sized groups though it can work with large groups if they’re disciplined!
Check-in / Check-out #team #opening #closing #hyperisland #remote-friendly Either checking-in or checking-out is a simple way for a team to open or close a process, symbolically and in a collaborative way. Checking-in/out invites each member in a group to be present, seen and heard, and to express a reflection or a feeling. Checking-in emphasizes presence, focus and group commitment; checking-out emphasizes reflection and symbolic closure.
29. Doodling Together
Thinking creatively and not being afraid to make suggestions are important problem-solving skills for any group or team, and warming up by encouraging these behaviors is a great way to start.
Doodling Together is one of our favorite creative ice breaker games – it’s quick, effective, and fun and can make all following problem-solving steps easier by encouraging a group to collaborate visually. By passing cards and adding additional items as they go, the workshop group gets into a groove of co-creation and idea development that is crucial to finding solutions to problems.
Doodling Together #collaboration #creativity #teamwork #fun #team #visual methods #energiser #icebreaker #remote-friendly Create wild, weird and often funny postcards together & establish a group’s creative confidence.
30. Show and Tell
You might remember some version of Show and Tell from being a kid in school and it’s a great problem-solving activity to kick off a session.
Asking participants to prepare a little something before a workshop by bringing an object for show and tell can help them warm up before the session has even begun! Games that include a physical object can also help encourage early engagement before moving onto more big-picture thinking.
By asking your participants to tell stories about why they chose to bring a particular item to the group, you can help teams see things from new perspectives and see both differences and similarities in the way they approach a topic. Great groundwork for approaching a problem-solving process as a team!
Show and Tell #gamestorming #action #opening #meeting facilitation Show and Tell taps into the power of metaphors to reveal players’ underlying assumptions and associations around a topic The aim of the game is to get a deeper understanding of stakeholders’ perspectives on anything—a new project, an organizational restructuring, a shift in the company’s vision or team dynamic.
31. Constellations
Who doesn’t love stars? Constellations is a great warm-up activity for any workshop as it gets people up off their feet, energized, and ready to engage in new ways with established topics. It’s also great for showing existing beliefs, biases, and patterns that can come into play as part of your session.
Using warm-up games that help build trust and connection while also allowing for non-verbal responses can be great for easing people into the problem-solving process and encouraging engagement from everyone in the group. Constellations is great in large spaces that allow for movement and is definitely a practical exercise to allow the group to see patterns that are otherwise invisible.
Constellations #trust #connection #opening #coaching #patterns #system Individuals express their response to a statement or idea by standing closer or further from a central object. Used with teams to reveal system, hidden patterns, perspectives.
32. Draw a Tree
Problem-solving games that help raise group awareness through a central, unifying metaphor can be effective ways to warm-up a group in any problem-solving model.
Draw a Tree is a simple warm-up activity you can use in any group and which can provide a quick jolt of energy. Start by asking your participants to draw a tree in just 45 seconds – they can choose whether it will be abstract or realistic.
Once the timer is up, ask the group how many people included the roots of the tree and use this as a means to discuss how we can ignore important parts of any system simply because they are not visible.
All problem-solving strategies are made more effective by thinking of problems critically and by exposing things that may not normally come to light. Warm-up games like Draw a Tree are great in that they quickly demonstrate some key problem-solving skills in an accessible and effective way.
Draw a Tree #thiagi #opening #perspectives #remote-friendly With this game you can raise awarness about being more mindful, and aware of the environment we live in.
Each step of the problem-solving workshop benefits from an intelligent deployment of activities, games, and techniques. Bringing your session to an effective close helps ensure that solutions are followed through on and that you also celebrate what has been achieved.
Here are some problem-solving activities you can use to effectively close a workshop or meeting and ensure the great work you’ve done can continue afterward.
- One Breath Feedback
- Who What When Matrix
- Response Cards
How do I conclude a problem-solving process?
All good things must come to an end. With the bulk of the work done, it can be tempting to conclude your workshop swiftly and without a moment to debrief and align. This can be problematic in that it doesn’t allow your team to fully process the results or reflect on the process.
At the end of an effective session, your team will have gone through a process that, while productive, can be exhausting. It’s important to give your group a moment to take a breath, ensure that they are clear on future actions, and provide short feedback before leaving the space.
The primary purpose of any problem-solving method is to generate solutions and then implement them. Be sure to take the opportunity to ensure everyone is aligned and ready to effectively implement the solutions you produced in the workshop.
Remember that every process can be improved and by giving a short moment to collect feedback in the session, you can further refine your problem-solving methods and see further success in the future too.
33. One Breath Feedback
Maintaining attention and focus during the closing stages of a problem-solving workshop can be tricky and so being concise when giving feedback can be important. It’s easy to incur “death by feedback” should some team members go on for too long sharing their perspectives in a quick feedback round.
One Breath Feedback is a great closing activity for workshops. You give everyone an opportunity to provide feedback on what they’ve done but only in the space of a single breath. This keeps feedback short and to the point and means that everyone is encouraged to provide the most important piece of feedback to them.
One breath feedback #closing #feedback #action This is a feedback round in just one breath that excels in maintaining attention: each participants is able to speak during just one breath … for most people that’s around 20 to 25 seconds … unless of course you’ve been a deep sea diver in which case you’ll be able to do it for longer.
34. Who What When Matrix
Matrices feature as part of many effective problem-solving strategies and with good reason. They are easily recognizable, simple to use, and generate results.
The Who What When Matrix is a great tool to use when closing your problem-solving session by attributing a who, what and when to the actions and solutions you have decided upon. The resulting matrix is a simple, easy-to-follow way of ensuring your team can move forward.
Great solutions can’t be enacted without action and ownership. Your problem-solving process should include a stage for allocating tasks to individuals or teams and creating a realistic timeframe for those solutions to be implemented or checked out. Use this method to keep the solution implementation process clear and simple for all involved.
Who/What/When Matrix #gamestorming #action #project planning With Who/What/When matrix, you can connect people with clear actions they have defined and have committed to.
35. Response cards
Group discussion can comprise the bulk of most problem-solving activities and by the end of the process, you might find that your team is talked out!
Providing a means for your team to give feedback with short written notes can ensure everyone is head and can contribute without the need to stand up and talk. Depending on the needs of the group, giving an alternative can help ensure everyone can contribute to your problem-solving model in the way that makes the most sense for them.
Response Cards is a great way to close a workshop if you are looking for a gentle warm-down and want to get some swift discussion around some of the feedback that is raised.
Response Cards #debriefing #closing #structured sharing #questions and answers #thiagi #action It can be hard to involve everyone during a closing of a session. Some might stay in the background or get unheard because of louder participants. However, with the use of Response Cards, everyone will be involved in providing feedback or clarify questions at the end of a session.
Save time and effort discovering the right solutions
A structured problem solving process is a surefire way of solving tough problems, discovering creative solutions and driving organizational change. But how can you design for successful outcomes?
With SessionLab, it’s easy to design engaging workshops that deliver results. Drag, drop and reorder blocks to build your agenda. When you make changes or update your agenda, your session timing adjusts automatically , saving you time on manual adjustments.
Collaborating with stakeholders or clients? Share your agenda with a single click and collaborate in real-time. No more sending documents back and forth over email.
Explore how to use SessionLab to design effective problem solving workshops or watch this five minute video to see the planner in action!

Over to you
The problem-solving process can often be as complicated and multifaceted as the problems they are set-up to solve. With the right problem-solving techniques and a mix of creative exercises designed to guide discussion and generate purposeful ideas, we hope we’ve given you the tools to find the best solutions as simply and easily as possible.
Is there a problem-solving technique that you are missing here? Do you have a favorite activity or method you use when facilitating? Let us know in the comments below, we’d love to hear from you!
thank you very much for these excellent techniques
Certainly wonderful article, very detailed. Shared!
Your list of techniques for problem solving can be helpfully extended by adding TRIZ to the list of techniques. TRIZ has 40 problem solving techniques derived from methods inventros and patent holders used to get new patents. About 10-12 are general approaches. many organization sponsor classes in TRIZ that are used to solve business problems or general organiztational problems. You can take a look at TRIZ and dwonload a free internet booklet to see if you feel it shound be included per your selection process.
Leave a Comment Cancel reply
Your email address will not be published. Required fields are marked *
Going from a mere idea to a workshop that delivers results for your clients can feel like a daunting task. In this piece, we will shine a light on all the work behind the scenes and help you learn how to plan a workshop from start to finish. On a good day, facilitation can feel like effortless magic, but that is mostly the result of backstage work, foresight, and a lot of careful planning. Read on to learn a step-by-step approach to breaking the process of planning a workshop into small, manageable chunks. The flow starts with the first meeting with a client to define the purposes of a workshop.…

How does learning work? A clever 9-year-old once told me: “I know I am learning something new when I am surprised.” The science of adult learning tells us that, in order to learn new skills (which, unsurprisingly, is harder for adults to do than kids) grown-ups need to first get into a specific headspace. In a business, this approach is often employed in a training session where employees learn new skills or work on professional development. But how do you ensure your training is effective? In this guide, we'll explore how to create an effective training session plan and run engaging training sessions. As team leader, project manager, or consultant,…

Effective online tools are a necessity for smooth and engaging virtual workshops and meetings. But how do you choose the right ones? Do you sometimes feel that the good old pen and paper or MS Office toolkit and email leaves you struggling to stay on top of managing and delivering your workshop? Fortunately, there are plenty of online tools to make your life easier when you need to facilitate a meeting and lead workshops. In this post, we’ll share our favorite online tools you can use to make your job as a facilitator easier. In fact, there are plenty of free online workshop tools and meeting facilitation software you can…
Design your next workshop with SessionLab
Join the 150,000 facilitators using SessionLab
Sign up for free

- Meet Our Team
- Discover The LSA Difference
- Coaching Process
- Core Values
What is Executive Functioning?
- Understanding the EF Ripple Effect
- For Daily Life
- ND-Friendly Tools
- Executive Functioning Assessment
- Executive Functioning Meal Plan
- Executive Functioning 101 Resource Hub
- Executive Functioning IEP Goal Resource Hub
- How To Make Stuff More EF Friendly
Teaching the IDEAL Problem-Solving Method to Diverse Learners
Written by:
Amy Sippl
Filed under: EF 101 Series , Executive Functioning , Problem Solving
Published: January 21, 2021
Last Reviewed: April 10, 2023
READING TIME: ~ minutes
We may assume that teens and young adults come equipped with a strong sense of approaching difficult or uncertain situations. For many of the individuals we work with, problem-solving needs to be practiced and developed in the same way as academic and social skills. The IDEAL Problem Solving Method is one option to teach problem-solving to diverse learners.
What is problem-solving?
Problem-solving is the capacity to identify and describe a problem and generate solutions to fix it .
Problem-solving involves other executive functioning behaviors as well, including attentional control, planning , and task initiation . Individuals might use time management , emotional control, or organization skills to solve problems as well. Over time, learners can observe their behavior, use working memory , and self-monitor behaviors to influence how we solve future issues.
Why are problem-solving strategies important?
Not all diverse learners develop adequate problem-solving. Learners with a history of behavioral and learning challenges may not always use good problem-solving skills to manage stressful situations. Some students use challenging behaviors like talking back, arguing, property destruction, and aggression when presented with challenging tasks. Others might shut down, check out, or struggle to follow directions when encountering new or unknown situations.
Without a step-by-step model for problem-solving , including identifying a problem and choosing a replacement behavior to solve it, many of our children and students use challenging behaviors instead. The IDEAL Problem-Solving Method is one option to teach diverse learners to better approach difficult situations.
IDEAL Problem-Solving Method
In 1984, Bransford and Stein published one of the most popular and well-regarded problem-solving methods. It’s used both in industry and in education to help various learners establish a problem, generate solutions, and move forward quickly and efficiently. By teaching your learner each step of the IDEAL model, you can provide them with a set of steps to approach a problem with confidence.
The IDEAL Problem-Solving Method includes:

I – Identify the problem.
There’s no real way to create a solution to a problem unless you first know the scope of the problem. Encourage your learner to identify the issue in their own words. Outline the facts and the unknowns. Foster an environment where your learner is praised and supported for identifying and taking on new problems.
Examples of identifying problems:
- “I have a math quiz next week and don’t know how to do the problems.”
- “I can’t access my distance learning course website.”
- “The trash needs to be taken out, and I can’t find any trash bags.”
D – Define an outcome
The second step in the IDEAL problem-solving process is to define an outcome or goal for problem-solving. Multiple people can agree that a problem exists but have very different ideas on goals or outcomes. By deciding on an outlined objective first, it can speed up the process of identifying solutions.
Defining outcomes and goals may be a difficult step for some diverse learners. The results don’t need to be complicated, but just clear for everyone involved.
Examples of defining outcomes:
- “I want to do well on my math quiz.”
- “I get access to the course website.”
- “The trash gets taken out before the trash pickup day tomorrow.”
E – Explore possible strategies.
Once you have an outcome, encourage your learner to brainstorm possible strategies. All possible solutions should be on the table during this stage, so encourage learners to make lists, use sticky notes, or voice memos to record any ideas. If your learner struggles with creative idea generation, help them develop a plan of resources for who they might consult in the exploration stage.
Examples of possible strategies to solve a problem:
- “I review the textbook; I ask for math help from a friend; I look up the problems online; I email my teacher.”
- “I email my teacher for the course access; I ask for help from a classmate; I try to reset my password.”
- “I use something else for a trash bag; I place an online order for bags; I take the trash out without a bag; I ask a neighbor for a bag; I go shopping for trash bags.”
A – Anticipate Outcomes & Act
Once we generate a list of strategies, the next step in the IDEAL problem-solving model recommends that you review the potential steps and decide which one is the best option to use first. Helping learners to evaluate the pros and cons of action steps can take practice. Ask questions like, “What might happen if you take this step?” or “Does that step make you feel good about moving forward or uncertain?”
After evaluating the outcomes, the next step is to take action. Encourage your learner to move forward even if they may not know the full result of taking action. Support doing something, even if it might not be the same strategy, you might take to solve a problem or the ‘best’ solution.
L – Look and Learn
The final step in the IDEAL problem-solving model is to look and learn from an attempt to solve a problem. Many parents and teachers forget this critical step in helping diverse learners to stop and reflect when problem-solving goes well and doesn’t go well. Helping our students and children learn from experience can make problem-solving more efficient and effective in the future. Ask questions like “How did that go?” and “What do you think you’ll do differently next time?”
Examples of Look and Learn statements:
- “I didn’t learn the problems from looking at the textbook, but it did help to call a friend. I’ll start there next time.”
- “When I didn’t have access to the course website, resetting my password worked.”
- “I ran out of trash bags because I forgot to put them on the shopping list . I’ll buy an extra box of trash bags to have them on hand, so I don’t run out next time.”
Practice Problem-Solving
For ideas on common problems, download our deck of problem-solving practice cards. Set aside time to practice, role-play, give feedback, and rehearse again if needed.
How to teach the IDEAL problem-solving method
Top businesses and corporations spend thousands of dollars on training teams to implement problem-solving strategies like the IDEAL method. Employees practice and role-play common problems in the workplace . Coaches give supportive feedback until everyone feels confident in each of the steps.
Teachers and parents can use the same process to help students and children use the IDEAL problem-solving method. Set aside time to review common problems or social scenarios your learner might encounter. Practice using the IDEAL method when emotions and tensions aren’t running as high. Allow your learner to ask questions, work through problems, and receive feedback and praise for creating logical action plans.
Further Reading
- Bransford, J., and Stein, B., “The Ideal Problem Solver” (1993). Centers for Teaching and Technology – Book Library . 46. https://digitalcommons.georgiasouthern.edu/ct2-library/4
- Executive Functioning 101: Planning Skills
- Executive Functioning: Task Initiation
- Executive Functioning Skills by Age: What to Expect
- Kern, L., George, M. P., & Weist, M. D. (2016). Supporting students with emotional and behavioral problems. Baltimore, MD: Paul H. Brookes.
About The Author
Amy Sippl is a Minnesota-based Board Certified Behavior Analyst (BCBA) and freelance content developer specializing in helping individuals with autism and their families reach their best possible outcomes. Amy earned her Master's Degree in Applied Behavior Analysis from St. Cloud State University and also holds undergraduate degrees in Psychology and Family Social Science from University of Minnesota – Twin Cities. Amy has worked with children with autism and related developmental disabilities for over a decade in both in-home and clinical settings. Her content focuses on parents, educators, and professionals in the world of autism—emphasizing simple strategies and tips to maximize success. To see more of her work visit amysippl.com .
Related Posts
6 effective strategies for getting organized in the new year, how brain dumping can improve executive functioning in diverse learners, time blindness & adhd: what you need to know, hyperfixations & adhd: what you need to know, time management skills: long-term supports & strategies for diverse learners.
Life Skills Advocate is a participant in the Amazon Services LLC Associates Program, an affiliate advertising program designed to provide a means for sites to earn advertising fees by advertising and linking to Amazon.com. Some of the links in this post may be Amazon.com affiliate links, which means if you make a purchase, Life Skills Advocate will earn a commission. However, we only promote products we actually use or those which have been vetted by the greater community of families and professionals who support individuals with diverse learning needs.
Session expired
Please log in again. The login page will open in a new tab. After logging in you can close it and return to this page.
- Business Essentials
- Leadership & Management
- Credential of Leadership, Impact, and Management in Business (CLIMB)
- Entrepreneurship & Innovation
- Digital Transformation
- Finance & Accounting
- Business in Society
- For Organizations
- Support Portal
- Media Coverage
- Founding Donors
- Leadership Team

- Harvard Business School →
- HBS Online →
- Business Insights →
Business Insights
Harvard Business School Online's Business Insights Blog provides the career insights you need to achieve your goals and gain confidence in your business skills.
- Career Development
- Communication
- Decision-Making
- Earning Your MBA
- Negotiation
- News & Events
- Productivity
- Staff Spotlight
- Student Profiles
- Work-Life Balance
- AI Essentials for Business
- Alternative Investments
- Business Analytics
- Business Strategy
- Business and Climate Change
- Design Thinking and Innovation
- Digital Marketing Strategy
- Disruptive Strategy
- Economics for Managers
- Entrepreneurship Essentials
- Financial Accounting
- Global Business
- Launching Tech Ventures
- Leadership Principles
- Leadership, Ethics, and Corporate Accountability
- Leading with Finance
- Management Essentials
- Negotiation Mastery
- Organizational Leadership
- Power and Influence for Positive Impact
- Strategy Execution
- Sustainable Business Strategy
- Sustainable Investing
- Winning with Digital Platforms
What Is Creative Problem-Solving & Why Is It Important?

- 01 Feb 2022
One of the biggest hindrances to innovation is complacency—it can be more comfortable to do what you know than venture into the unknown. Business leaders can overcome this barrier by mobilizing creative team members and providing space to innovate.
There are several tools you can use to encourage creativity in the workplace. Creative problem-solving is one of them, which facilitates the development of innovative solutions to difficult problems.
Here’s an overview of creative problem-solving and why it’s important in business.
Access your free e-book today.
What Is Creative Problem-Solving?
Research is necessary when solving a problem. But there are situations where a problem’s specific cause is difficult to pinpoint. This can occur when there’s not enough time to narrow down the problem’s source or there are differing opinions about its root cause.
In such cases, you can use creative problem-solving , which allows you to explore potential solutions regardless of whether a problem has been defined.
Creative problem-solving is less structured than other innovation processes and encourages exploring open-ended solutions. It also focuses on developing new perspectives and fostering creativity in the workplace . Its benefits include:
- Finding creative solutions to complex problems : User research can insufficiently illustrate a situation’s complexity. While other innovation processes rely on this information, creative problem-solving can yield solutions without it.
- Adapting to change : Business is constantly changing, and business leaders need to adapt. Creative problem-solving helps overcome unforeseen challenges and find solutions to unconventional problems.
- Fueling innovation and growth : In addition to solutions, creative problem-solving can spark innovative ideas that drive company growth. These ideas can lead to new product lines, services, or a modified operations structure that improves efficiency.

Creative problem-solving is traditionally based on the following key principles :
1. Balance Divergent and Convergent Thinking
Creative problem-solving uses two primary tools to find solutions: divergence and convergence. Divergence generates ideas in response to a problem, while convergence narrows them down to a shortlist. It balances these two practices and turns ideas into concrete solutions.
2. Reframe Problems as Questions
By framing problems as questions, you shift from focusing on obstacles to solutions. This provides the freedom to brainstorm potential ideas.
3. Defer Judgment of Ideas
When brainstorming, it can be natural to reject or accept ideas right away. Yet, immediate judgments interfere with the idea generation process. Even ideas that seem implausible can turn into outstanding innovations upon further exploration and development.
4. Focus on "Yes, And" Instead of "No, But"
Using negative words like "no" discourages creative thinking. Instead, use positive language to build and maintain an environment that fosters the development of creative and innovative ideas.
Creative Problem-Solving and Design Thinking
Whereas creative problem-solving facilitates developing innovative ideas through a less structured workflow, design thinking takes a far more organized approach.
Design thinking is a human-centered, solutions-based process that fosters the ideation and development of solutions. In the online course Design Thinking and Innovation , Harvard Business School Dean Srikant Datar leverages a four-phase framework to explain design thinking.
The four stages are:

- Clarify: The clarification stage allows you to empathize with the user and identify problems. Observations and insights are informed by thorough research. Findings are then reframed as problem statements or questions.
- Ideate: Ideation is the process of coming up with innovative ideas. The divergence of ideas involved with creative problem-solving is a major focus.
- Develop: In the development stage, ideas evolve into experiments and tests. Ideas converge and are explored through prototyping and open critique.
- Implement: Implementation involves continuing to test and experiment to refine the solution and encourage its adoption.
Creative problem-solving primarily operates in the ideate phase of design thinking but can be applied to others. This is because design thinking is an iterative process that moves between the stages as ideas are generated and pursued. This is normal and encouraged, as innovation requires exploring multiple ideas.
Creative Problem-Solving Tools
While there are many useful tools in the creative problem-solving process, here are three you should know:
Creating a Problem Story
One way to innovate is by creating a story about a problem to understand how it affects users and what solutions best fit their needs. Here are the steps you need to take to use this tool properly.
1. Identify a UDP
Create a problem story to identify the undesired phenomena (UDP). For example, consider a company that produces printers that overheat. In this case, the UDP is "our printers overheat."
2. Move Forward in Time
To move forward in time, ask: “Why is this a problem?” For example, minor damage could be one result of the machines overheating. In more extreme cases, printers may catch fire. Don't be afraid to create multiple problem stories if you think of more than one UDP.
3. Move Backward in Time
To move backward in time, ask: “What caused this UDP?” If you can't identify the root problem, think about what typically causes the UDP to occur. For the overheating printers, overuse could be a cause.
Following the three-step framework above helps illustrate a clear problem story:
- The printer is overused.
- The printer overheats.
- The printer breaks down.
You can extend the problem story in either direction if you think of additional cause-and-effect relationships.
4. Break the Chains
By this point, you’ll have multiple UDP storylines. Take two that are similar and focus on breaking the chains connecting them. This can be accomplished through inversion or neutralization.
- Inversion: Inversion changes the relationship between two UDPs so the cause is the same but the effect is the opposite. For example, if the UDP is "the more X happens, the more likely Y is to happen," inversion changes the equation to "the more X happens, the less likely Y is to happen." Using the printer example, inversion would consider: "What if the more a printer is used, the less likely it’s going to overheat?" Innovation requires an open mind. Just because a solution initially seems unlikely doesn't mean it can't be pursued further or spark additional ideas.
- Neutralization: Neutralization completely eliminates the cause-and-effect relationship between X and Y. This changes the above equation to "the more or less X happens has no effect on Y." In the case of the printers, neutralization would rephrase the relationship to "the more or less a printer is used has no effect on whether it overheats."
Even if creating a problem story doesn't provide a solution, it can offer useful context to users’ problems and additional ideas to be explored. Given that divergence is one of the fundamental practices of creative problem-solving, it’s a good idea to incorporate it into each tool you use.
Brainstorming
Brainstorming is a tool that can be highly effective when guided by the iterative qualities of the design thinking process. It involves openly discussing and debating ideas and topics in a group setting. This facilitates idea generation and exploration as different team members consider the same concept from multiple perspectives.
Hosting brainstorming sessions can result in problems, such as groupthink or social loafing. To combat this, leverage a three-step brainstorming method involving divergence and convergence :
- Have each group member come up with as many ideas as possible and write them down to ensure the brainstorming session is productive.
- Continue the divergence of ideas by collectively sharing and exploring each idea as a group. The goal is to create a setting where new ideas are inspired by open discussion.
- Begin the convergence of ideas by narrowing them down to a few explorable options. There’s no "right number of ideas." Don't be afraid to consider exploring all of them, as long as you have the resources to do so.
Alternate Worlds
The alternate worlds tool is an empathetic approach to creative problem-solving. It encourages you to consider how someone in another world would approach your situation.
For example, if you’re concerned that the printers you produce overheat and catch fire, consider how a different industry would approach the problem. How would an automotive expert solve it? How would a firefighter?
Be creative as you consider and research alternate worlds. The purpose is not to nail down a solution right away but to continue the ideation process through diverging and exploring ideas.

Continue Developing Your Skills
Whether you’re an entrepreneur, marketer, or business leader, learning the ropes of design thinking can be an effective way to build your skills and foster creativity and innovation in any setting.
If you're ready to develop your design thinking and creative problem-solving skills, explore Design Thinking and Innovation , one of our online entrepreneurship and innovation courses. If you aren't sure which course is the right fit, download our free course flowchart to determine which best aligns with your goals.

About the Author

- What is Problem-Oriented Policing?
- History of Problem-Oriented Policing
- Key Elements of POP
The SARA Model
- The Problem Analysis Triangle
- Situational Crime Prevention
- 25 Techniques
- Links to Other POP Friendly Sites
- About POP en Español
A commonly used problem-solving method is the SARA model (Scanning, Analysis, Response and Assessment). The SARA model contains the following elements:
- Identifying recurring problems of concern to the public and the police.
- Identifying the consequences of the problem for the community and the police.
- Prioritizing those problems.
- Developing broad goals.
- Confirming that the problems exist.
- Determining how frequently the problem occurs and how long it has been taking place.
- Selecting problems for closer examination.
- Identifying and understanding the events and conditions that precede and accompany the problem.
- Identifying relevant data to be collected.
- Researching what is known about the problem type.
- Taking inventory of how the problem is currently addressed and the strengths and limitations of the current response.
- Narrowing the scope of the problem as specifically as possible.
- Identifying a variety of resources that may be of assistance in developing a deeper understanding of the problem.
- Developing a working hypothesis about why the problem is occurring.
- Brainstorming for new interventions.
- Searching for what other communities with similar problems have done.
- Choosing among the alternative interventions.
- Outlining a response plan and identifying responsible parties.
- Stating the specific objectives for the response plan.
- Carrying out the planned activities.
Assessment:
- Determining whether the plan was implemented (a process evaluation).
- Collecting pre and postresponse qualitative and quantitative data.
- Determining whether broad goals and specific objectives were attained.
- Identifying any new strategies needed to augment the original plan.
- Conducting ongoing assessment to ensure continued effectiveness.
- Get Posts Sent via Email
- Contributors
- Most Popular
- Most Commented
- Lean Comedy
- Podcast Home
- Browse Episodes
- Episode Collections
- Podcast Home & Subscribe
- Lean Whiskey
- My Favorite Mistake
- Practicing Lean
- Toyota Kata Podcast
- Featured Videos
- YouTube Channel
- Via MarkGraban.com
- About Mark Graban
- About the Blog
- What is “Lean”?
- Standardized Work
- Privacy Tools
- Healthcare Improvement
- Lean-Focused Blogs
- Lean Healthcare Blogs
- Other Blogs
- Lean Resources
- Contact Form
- Get Posts via Email
- Mark’s Newsletter

Do We Need Another Share in the See, Solve, Share Model of Continuous Improvement?
I love Steve Spear ‘s emphasis on a Toyota-based Lean model of:
“See, Solve, Share”
See problems, solve problems, and share problems. That's the ideal, and it's powerful where it exists.
At Toyota, and companies like it, there's an understanding that speaking up about problems leads to a constructive response from leaders.
That's not always true at other companies that are starting or attempting their “Lean Journey.” The
The Psychological Safety that might be taken for granted at Toyota must be actively cultivated in a company before continuous improvement can really take root, let alone take off.
I think the model could also be stated as:
“See, Share, Solve, Share”
Because we cannot solve a problem that isn't shared.
Often, the assumption seems to be, “We need to help employees see problems and waste.”
Oh, they see the problems. Or at least most of them.
I think the necessary starting point needs to be, “We need to help employees feel safe to speak up and share problems.”
Or we could say:
“See, Speak Up, Solve, Share.”
What are your thoughts and experiences related to this? Please post a comment below or join the LinkedIn discussion on this topic .
Maria Mentzer, who works with Spear, wrote :
“I love the added share/speak up after see! It appropriately emphasizes the power of a collective see-solve-share learning & improvement dynamic depends on collectively seeing problems. Collectively seeing can only be realized if people share what they see, which requires an environment that appreciates such sharing and management systems that helps make the sharing easier across the organization. None of that will happen until people are treated in such a way that it is safe, encouraged, and even celebrated to be raising ones hand when one don't have the answer. Rather than, like most of us are trained to do from an early age, raising our hands only when we have the answer.”

Get New Posts Sent To You
Check your inbox or spam folder to confirm your subscription.
RELATED ARTICLES MORE FROM AUTHOR
Uncovering Root Causes: Beyond the Conference Room – The Lean Approach to Problem Solving
Rewriting the Management Gospel: Lessons from Hayes, Abernathy, and the Frontlines of Industry
Ryan McCormack’s Operational Excellence Mixtape: April 19, 2024
Leave a reply cancel reply.
Save my name, email, and website in this browser for the next time I comment.
Yes, email me about new posts, daily!
This site uses Akismet to reduce spam. Learn how your comment data is processed .
EVEN MORE NEWS
Japan Study Trips: A Voyage of Leadership Discovery with Katie Anderson
Uncovering Root Causes: Beyond the Conference Room – The Lean Approach...
Ryan McCormack’s Operational Excellence Mixtape: May 3, 2024
Popular category.
- Interviews 494
- Mixtape 138
- Lean Whiskey 45
- Lean Blog Interviews
- Lean Blog Audio
- Privacy Policy

How it works
Transform your enterprise with the scalable mindsets, skills, & behavior change that drive performance.
Explore how BetterUp connects to your core business systems.
We pair AI with the latest in human-centered coaching to drive powerful, lasting learning and behavior change.
Build leaders that accelerate team performance and engagement.
Unlock performance potential at scale with AI-powered curated growth journeys.
Build resilience, well-being and agility to drive performance across your entire enterprise.
Transform your business, starting with your sales leaders.
Unlock business impact from the top with executive coaching.
Foster a culture of inclusion and belonging.
Accelerate the performance and potential of your agencies and employees.
See how innovative organizations use BetterUp to build a thriving workforce.
Discover how BetterUp measurably impacts key business outcomes for organizations like yours.
A demo is the first step to transforming your business. Meet with us to develop a plan for attaining your goals.

- What is coaching?
Learn how 1:1 coaching works, who its for, and if it's right for you.
Accelerate your personal and professional growth with the expert guidance of a BetterUp Coach.
Types of Coaching
Navigate career transitions, accelerate your professional growth, and achieve your career goals with expert coaching.
Enhance your communication skills for better personal and professional relationships, with tailored coaching that focuses on your needs.
Find balance, resilience, and well-being in all areas of your life with holistic coaching designed to empower you.
Discover your perfect match : Take our 5-minute assessment and let us pair you with one of our top Coaches tailored just for you.

Research, expert insights, and resources to develop courageous leaders within your organization.
Best practices, research, and tools to fuel individual and business growth.
View on-demand BetterUp events and learn about upcoming live discussions.
The latest insights and ideas for building a high-performing workplace.
- BetterUp Briefing
The online magazine that helps you understand tomorrow's workforce trends, today.
Innovative research featured in peer-reviewed journals, press, and more.
Founded in 2022 to deepen the understanding of the intersection of well-being, purpose, and performance
We're on a mission to help everyone live with clarity, purpose, and passion.
Join us and create impactful change.
Read the buzz about BetterUp.
Meet the leadership that's passionate about empowering your workforce.

For Business
For Individuals
GROW model for coaching: achieve goals and boost performance

Jump to section
What is the GROW model for coaching?
Benefits of using the grow model, applying the grow model in coaching , beyond the coaching session: using grow in everyday life, watching your success with the grow model for coaching.
The GROW model for coaching is a framework used by coaches and managers to guide individuals and teams toward achieving their goals and unlocking their full potential. This model provides a step-by-step approach to coaching conversations, making them more focused and effective.
If you’re looking for a solution-focused coaching model for yourself or clients that produces results, the GROW model may be a great fit.
The GROW coaching model was designed to transcend the impact of traditional coaching models. Sir John Whitmore first developed GROW coaching in the late 1980s. He expanded on his ideas in his 1992 book, Coaching For Performance , which was originally meant to serve as a guide for both coaches and managers.
Whitmore worked closely with two other individuals to build what is now known as the GROW model. Performance coaching expert and speaker Alan Fine, with contributing author Graham Alexander, built on Sir John Whitmore's GROW model image. Together, the three created a coaching framework that has improved the lives of many.
GROW is an acronym with each part symbolizing one of the four steps of the GROW coaching model:
O bstacles or O ptions
W ay forward or W ill
Using the GROW model for coaching helps leaders and team members increase performance. It can also help you succeed in personal development.
Following the GROW model coaching plan can yield several benefits. You can follow the GROW model yourself or with the support of a professional coach. These benefits include increased productivity and improved self-esteem .
The GROW model can also create a more positive workplace environment by increasing your engagement. GROW coaching for performance improvement can help those trying to awaken their human potential .
The GROW model was designed to be multifunctional and work for various objectives:
- A senior leader onboarding a new leader
- A nutrition coach helping clients stay motivated to lose weight
- A business mentor aiming to improve their mentoring sessions
- A manager wanting higher productivity within their team
- A career advisor helping clients explore job options
- A tennis coach teaching players to increase performance outcomes
- An online peer tutoring group seeking study improvements
A randomized control study found that even virtual GROW sessions improved subjective well-being . Below, we’ll examine some of this coaching model’s benefits and then discuss exactly how to apply this framework.
Improved clarity and focus on goals
Learning how to focus on your goals can be challenging with all of life’s distractions. The GROW coaching model encourages you to keep your goals at the forefront of your mind.
One way you can focus better is by including steps toward your goals in your daily schedule . By doing something small for your goals every day, you’re prioritizing your future.
The GROW model is also a perfect tool for any mindset coach who wants to help their clients stay on track. Coaches can use it to help others find purpose and clarify the goals they value most.
Enhanced self-awareness and problem-solving skills
Developing self-awareness is a key component of the GROW coaching model. With each coaching session, you can learn more about yourself.
Maybe you’ve been job-hopping because you need more intellectual challenges in your career field . Or maybe you’ve put off chasing your goals because you struggle with imposter syndrome . With the right coaching skills , you can learn to address underlying obstacles and move in the right direction.
The GROW model also improves problem-solving strategies . As a result, you learn how to form your own conclusions and think independently.
Increased motivation and commitment
It’s easy to get excited about initial goal-setting and coaching sessions. Yet staying committed to them is far more difficult. Coaching conversations using the GROW model encourage you to stick to your objectives.
Coaches provide motivation and inspiration through difficult times. Throughout your coaching journey, you’ll discuss each session’s goal and your overall progress. Having either a coaching team or an individual coach by your side can be uplifting and build motivation.
Boosted empowerment and ownership of personal growth
Taking ownership of your personal development isn’t always easy. The GROW model makes taking accountability feel natural and turns transitions into transformation . Coaches empower you and help you improve your self-determination .
To take ownership of personal growth, acknowledge your responsibilities outside of coaching sessions. This ownership is required to make the most of the GROW model. Adopting a coaching mindset means realizing that your future and success are in your own hands.

Qualities that make a great coach include innovating and finding what works best for clients. Executive coaches can use GROW model coaching to enhance engagement in coaching sessions. Leadership coaches, business coaches, and other coaching professionals can use the GROW model as well.
GROW can be applied to each session goal with a client to generate more effective results. Using individual or team development plans, here’s how coaches and coaches can jointly execute this model.
1. Setting SMART goals
It’s essential that goal-setting is done correctly. SMART goals are an integral part of the GROW coaching model framework. SMART is an acronym that stands for specific, measurable, achievable, relevant, and time-bound. The SMART goal model is more effective because it takes the ambiguity out of setting goals.
If you haven’t determined your goals yet, you can work out your ideas during a coaching session. The goals you set will be the basis of your coaching process moving forward.
2. Exploring current reality
The reality phase of the GROW process involves examining your current strengths, challenges, and obstacles. Collectively, these things are known as your “current reality.”
During your coaching session, your coach will likely ask several GROW model questions. When you answer questions about your current reality, your coach can better understand how to help you.
Your coach’s GROW model questions may be similar to these examples:
- What are the greatest obstacles you need to overcome?
- What prompted you to seek out GROW model performance coaching?
- If you’ve tried another coaching model before, what elements were lacking?
- Which coaching leadership style do you thrive under?
- How do you cope with stress and anxiety caused by challenges?
- What are the benefits of achieving your goals?
- What actions are you taking right now to achieve your goals?
- Where can you go for support?
These are also excellent questions to ask yourself. Looking inward prompts you to think about how to achieve a new reality.
3. Generating options and solutions
Developing your problem-solving skills is necessary for overcoming problems. Work with your coach to brainstorm ideas and set a session goal to think of solutions to potential obstacles.
In this phase, you’ll come up with ways to utilize your strengths and resources. Thinking about this will result in options and possibilities for you moving forward. It’s helpful to have alternative plans for roadblocks that may come up.
Creativity is one of the most important GROW coaching skills for a reason. Unique challenges call for unique innovations. Challenge yourself to think creatively and solve problems from a new perspective.
4. Developing a will to act or a way forward
Will or way forward is the final step of the GROW process. When you envision the way forward, you make your dreams more than a concept. Instead, they become a possibility within reach. This final step ultimately determines the success of the process.
Willpower is the internal drive that ensures you stick to your plans. The GROW model increases willpower by having you put a voice to your actions. Rather than just saying “I want to,” your mentality switches to “I will.”
Your personal development can be fueled by action planning and commitment strategies. An action plan consists of feasible steps to achieve your goal.
Wrap up your coaching sessions by stating how you’ll execute your action plan. Having a coach helps you stick to your word and follow through.
GROW coaching ideology isn’t exclusive to coaching sessions. You can apply the GROW model to other areas of life.
Applying GROW to different areas
The best thing about knowledge is that it’s easily transferable. For example, the GROW model encourages better communication skills. Increased communication skills can lead to improved relationships.
The GROW process can also be used to achieve personal goals , including health goals and financial goals . You can even use the GROW coaching model to beat your high score in a game or to learn a new language. Whatever your goals may be, you can use GROW coaching tools to achieve them.
Self-coaching techniques using the GROW framework
By internalizing the coaching mindset, you can take matters into your own hands and coach yourself using the GROW framework. Self-coaching requires self-reflection and deep thinking about your goals and values. You’ll also need to be highly aware of your strengths and weaknesses .
As long as you have self-motivation , self-coaching can work. Use the GROW model to ask yourself coaching questions and stick to your action plan. You can start journaling to keep track of your milestones and obstacles. Measuring success and progress is essential for staying on the right path.
Building self-discipline and accountability for goal achievement
One of the most important things taught by the GROW model is how to hold yourself accountable for your life and current reality. As you achieve personal growth, you may naturally assume more responsibility for your life. Accountability also means learning from your mistakes and making better decisions in the future.
For instance, if you fail to achieve your goal, you must examine why. What caused your procrastination ? Do you need to overcome fear of failure or address a lack of motivation ?
Make a list of things you can change to achieve your goal next time. The GROW coaching process can teach you the lasting discipline you need to do better in the future.
The GROW model for coaching delivers transformative results. From improved productivity to better self-esteem, its benefits are evident. It’s also inspired many to change their lives.
To spark change in your life, consider connecting with certified coaches who use the GROW model in their coaching framework. By signing up for 1:1 coaching sessions, you’re committing to working on self-improvement . Over time, you can better yourself as well as your team members.
Mikayla Balk
Mikayla Balk is a content writer focusing on emotional wellness and mental health. She’s previously written for True. Women’s Health and Behavioral Health of New York. Her passions include mental health advocacy, travel, animals, and nature photography. Mikayla holds a B.A. in Writing and Philosophy from Grand Valley State University.
5 coaching frameworks to develop your team
Can you get an internship after college yes, and here’s how, 10 examples of principles that can guide your approach to work, 15 career goals examples to inspire you to set your own, how to break bad habits: 7 tips to succeed, learn types of gestures and their meanings to improve your communication, the secret to developing managers that help your business thrive, how performance reviews can reinforce gender bias: 5 steps to avoid it, the ultimate guide to motivating a team — and why it matters, stay connected with betterup, get our newsletter, event invites, plus product insights and research..
3100 E 5th Street, Suite 350 Austin, TX 78702
- Platform Overview
- Integrations
- Powered by AI
- BetterUp Lead
- BetterUp Manage™
- BetterUp Care™
- Sales Performance
- Diversity & Inclusion
- Case Studies
- Why BetterUp?
- About Coaching
- Find your Coach
- Career Coaching
- Communication Coaching
- Life Coaching
- News and Press
- Leadership Team
- Become a BetterUp Coach
- BetterUp Labs
- Center for Purpose & Performance
- Leadership Training
- Business Coaching
- Contact Support
- Contact Sales
- Privacy Policy
- Acceptable Use Policy
- Trust & Security
- Cookie Preferences
Help | Advanced Search
Computer Science > Machine Learning
Title: characterizing the accuracy - efficiency trade-off of low-rank decomposition in language models.
Abstract: Large language models (LLMs) have emerged and presented their general problem-solving capabilities with one model. However, the model size has increased dramatically with billions of parameters to enable such broad problem-solving capabilities. In addition, due to the dominance of matrix-matrix and matrix-vector multiplications in LLMs, the compute-to-model size ratio is significantly lower than that of CNNs. This shift pushes LLMs from a computation-bound regime to a memory-bound regime. Therefore, optimizing the memory footprint and traffic is an important optimization direction for LLMs today. Model compression methods such as quantization and parameter pruning have been actively explored for achieving the memory footprint and traffic optimization. However, the accuracy-efficiency trade-off of rank pruning for LLMs is not well-understood yet. Therefore, we characterize the accuracy-efficiency trade-off of a low-rank decomposition method, specifically Tucker decomposition, on recent language models, including an open-source LLM, Llama 2. We formalize the low-rank decomposition design space and show that the decomposition design space is enormous (e.g., O($2^{37}$) for Llama2-7B). To navigate such a vast design space, we formulate the design space and perform thorough case studies of accuracy-efficiency trade-offs using six widely used LLM benchmarks on BERT and Llama 2 models. Our results show that we can achieve a 9\% model size reduction with minimal accuracy drops, which range from 4\%p to 10\%p, depending on the difficulty of the benchmark, without any retraining to recover accuracy after decomposition. The results show that low-rank decomposition can be a promising direction for LLM-based applications that require real-time service in scale (e.g., AI agent assist and real-time coding assistant), where the latency is as important as the model accuracy.
Submission history
Access paper:.
- HTML (experimental)
- Other Formats
References & Citations
- Google Scholar
- Semantic Scholar
BibTeX formatted citation
Bibliographic and Citation Tools
Code, data and media associated with this article, recommenders and search tools.
- Institution
arXivLabs: experimental projects with community collaborators
arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.
Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .
New discrete-time zeroing neural network for solving time-dependent linear equation with boundary constraint
- Open access
- Published: 13 May 2024
- Volume 57 , article number 140 , ( 2024 )
Cite this article
You have full access to this open access article

- Naimeng Cang 1 ,
- Feng Qiu 1 ,
- Shan Xue 1 , 2 ,
- Zehua Jia 1 ,
- Dongsheng Guo 1 ,
- Zhijun Zhang 3 &
- Weibing Li 4
Recently, continuous- and discrete-time models of a zeroing neural network (ZNN) have been developed to provide online solutions for the time-dependent linear equation (TDLE) with boundary constraint. This paper presents a novel approach to address the bound-constrained TDLE (BCTDLE) problem by proposing a new discrete-time ZNN (DTZNN) model. The proposed DTZNN model is designed using the Taylor difference formula to discretize the previous continuous-time ZNNN (CTZNN) model. Theoretical analysis indicates the computational property of the proposed DTZNN model, and numerical results further demonstrate its validity. The applicability of the proposed DTZNN model is finally confirmed via its application to the motion planning of a PUMA560 robotic arm.
Avoid common mistakes on your manuscript.
1 Introduction
Linear and nonlinear equations are fundamental mathematical tools that play essential roles in several industrial applications, such as robot path planning, image recognition, and signal processing (Zhao 2013 ; Tsiligianni et al. 2015 ; Zhang and Jin 2017 ; Li et al. 2019 ). Extensive work has been conducted on solving linear and nonlinear equations, typically using numerical algorithms (Sharma 2005 ; Neta et al. 2014 ; Abdelmalek 1977 ; Donoho et al. 2012 ; Zeng et al. 2014 ; Spedicato et al. 2000 ; Morigi and Sgallari 2001 ) and neurodynamic methods (Kumar 2022a , b ; Kumar 2023 ; Cichocki et al. 1992 ; Xia et al. 1999 ; Liang and Tso 2002 ). Among the numerical algorithms, direct methods and iterative methods are mainly used. In Abdelmalek ( 1977 ), the minimum \(L_{\infty }\) solution of the linear equation was first proposed. In Donoho et al. ( 2012 ), the sparse approximate solution of the linear equation was obtained by using the stagewise orthogonal matching pursuit algorithm. Many iterative algorithms have also been developed to bring solutions to the linear equation, such as adaptive iterative thresholding algorithms (Zeng et al. 2014 ), abstraction algorithms (Spedicato et al. 2000 ), and regularizing Lanczos iterative algorithms (Morigi and Sgallari 2001 ). However, these numerical algorithms may encounter challenges such as the accumulation of numerical errors, slow convergence rates, and low stability (Zhang et al. 2013 ).
In recent years, neural network models have garnered widespread attention for addressing modeling and control problems in both linear and nonlinear dynamic systems (Zhang et al. 2018 ; Li et al. 2019 ; Xiao et al. 2020 ; Liao et al. 2024 ; Kumar 2022a , b ; Kumar 2023 ). Particularly, the introduction of novel neural network models such as the Lyapunov-stability-based context-layered recurrent pi-sigma neural network (CLRPSNN) (Kumar 2022a ), the memory recurrent Elman neural network (MRENN) (Kumar 2022b ), and the higher-order recurrent neural network (HORNN) (Kumar 2023 ) have provided new approaches for solving the identification and control problems of nonlinear dynamic systems. The CLRPSNN model effectively addresses the issue of nonlinear system identification by introducing an additional layer of context nodes, demonstrating significant performance advantages in simulation results. However, stability has always been a crucial consideration in the design of neural network models. The MRENN and HORNN models innovate in stability design, ensuring stability and convergence of the models by combining Lyapunov stability criteria and recursive learning rate schemes. This emphasis on stability makes these models more reliable and practical when dealing with nonlinear dynamic systems.
Similar to numerical algorithms, neurodynamic methods also significantly improve the efficiency of solving the linear equation. Cichocki et al. ( 1992 ) proposed different recurrent neural networks (RNNs) to address the linear equation with an inequality constraint. Xia et al. ( 1999 ) designed an RNN model that can converge faster and provide more accurate solutions to the linear equation with an inequality constraint. The discrete-time form of such an RNN model was further deduced by Liang and Tso ( 2002 ). It is worth noting that these studies are based on the assumption of time-invariant when solving linear equations. However, many systems in practical engineering applications are always time-varying. Therefore, directly applying these methods to solve time-varying linear equations may yield poor results. Moreover, the mathematical domain of the variables involved in a linear equation must be set during the solution process (Zhang et al. 2018 ; Park et al. 1998 ). For example, it is assumed that many robotic arms can lead to task failure or even damage if the physical constraints of the joints are exceeded. Thus, appropriate methods must be investigated to ensure that joint angle, velocity, and/or acceleration are within the proper mathematical intervals (Guo et al. 2018 ; Zhang et al. 2013 ). In other words, solving time-varying underdetermined linear equations with boundary constraint is of importance in practical engineering applications.
In many industrial applications, there is a high demand for the real-time performance of linear equation, making them time-dependent. Existing studies are less concerned with methods for solving time-dependent linear equation (TDLE) with boundary constraint. To solve a given time-dependent problem, a representative RNN was presented and refined by Zhang and Guo ( 2015 ); Zhang and Yi ( 2011 ); Zhang et al. ( 2012 , 2015 ). The main idea of this model was to define the error control equation and then derive the RNN (depicted in an ordinary equation) so that the computational error can converge globally and eventually become 0, hence the name zeroing neural network (ZNN). Focusing on solving the bound-constrained TDLE (BCTDLE), Xu et al. ( 2019a ) developed the continuous-time ZNN (CTZNN) model, which they successfully employed to solve time-varying linear equations and inequality systems (Xu et al. 2019b ). Sun and Liu ( 2020 ) designed a novel noise-resistant CTZNN model for solving time-varying Lyapunov equations. However, directly implementing the CTZNN model into hardware in practical engineering applications is challenging.
Therefore, for the purpose of possible hardware implementation, researchers discretize the CTZNN model using difference equations. The traditional numerical differentiation algorithm for discretizing continuous systems is typically implemented using the Euler difference formula. Specifically, in Guo and Zhang ( 2012 ), a one-step iteration description of the DTZNN model is proposed for dynamic matrix inversion. The simulation results show that this model has an error mode of \(O({{\varepsilon }^{2}})\) , that is, when the sampling interval \(\varepsilon\) decreases by a factor of 10, the steady-state calculation error (SSCE) decreases by a factor of 100. Unlike the traditional Euler difference formula, in Guo et al. ( 2017 ), a new Taylor-type difference rule is constructed. For the approximation of first-order derivatives, this rule has been proven to have a smaller SSCE than the Euler difference rule and possesses an error mode of \(O({{\varepsilon }^{3}})\) , that is, when the sampling interval \(\varepsilon\) decreases by a factor of 10, the SSCE decreases by a factor of 1000. Using the new Taylor difference rule, researchers have successively developed Taylor difference formulas with the error modes \(O({{\varepsilon }^{4}})\) and \(O({{\varepsilon }^{5}})\) . Specifically, Huang et al. ( 2022 ) developed a Taylor difference formula with an error mode of \(O({{\varepsilon }^{4}})\) to solve time-variant underdetermined nonlinear systems under bound constraint. Different from the proposed DTZNN model in this paper, their model focuses on solving nonlinear systems and may not necessarily be applicable to linear equations, whereas DTZNN model proposed in this paper exhibits superior accuracy. Cai et al. ( 2021 ) also discretized the CTZNN model based on Taylor series expansion. However, their model mainly focuses on solving a time-varying system of linear equation and inequality, and does not consider boundary constraint. A recent study (Ma and Guo 2021 ) showed that the DTZNN model can effectively solve the BCTDLE with an SSCE of the order \(O(\varepsilon ^{4})\) , where \(\varepsilon\) is the sampling distance.
Following but differing from the previous work (Ma and Guo 2021 ), this paper establishes a new DTZNN model that can effectively solve the TDLE with boundary constraint. The validity of such a model is supported by both theoretical and numerical results. Considering the importance of robotic arms in industrial applications (Xu et al. 2019a ; Ma and Guo 2021 ; Zhang et al. 2019 ), this paper further applies the proposed DTZNN model to the PUMA560 robotic arm to demonstrate the applicability of the model. The primary contributions of this paper can be summarized as follows:
The new DTZNN model, which has not been previously reported, is studied to solve the TDLE with boundary constraint. Notably, the proposed model is clearly different from the previous DTZNN model (Ma and Guo 2021 ), and achieves better performance on computing and solving the BCTDLE.
Theoretical analysis denotes the computational characteristic of the proposed DTZNN model, and numerical results verify its validity. More importantly, these results show that the DTZNN calculation error at steady state is of order \(O(\varepsilon ^{5})\) . This is the first time that a computing model with \(O(\varepsilon ^{5})\) mode is presented to solve the BCTDLE.
The proposed DTZNN model is utilized for robotic arms by solving the linear kinematic equation that involves joint physical constraint. Simulation results using the PUMA560 robotic arm with different examples demonstrate the effectiveness and practicality of the proposed DTZNN model.
The upcoming sections of this paper are structured as follows. Section 2 presents the problem statement and the ZNN models for the TDLE with boundary constraint. Section 3 describes the proposed DTZNN composition and theoretical analysis. Section 4 provides numerical validation experiments with the proposed DTZNN model. Section 5 shows the applicability of the DTZNN model to robotic arms with joint constraints. Section 6 concludes this paper.
2 Preliminary
This section outlines the problem to address the TDLE with boundary constraint. To probe the matter further, the continuous- and discrete-time models of ZNN are shown as basis.
2.1 Problem statement
The TDLE with boundary constraint considered in this paper is formulated as follows (Lu et al. 2019 ; Xu et al. 2019a ):
where matrix \(G(t)\in R^{m\times n}\) (with \(m<n\) ) is time-dependent and full-rank, vector \(h(t)\in R^{m}\) is time-dependent and smooth, vector \(x(t)\in R^n\) is unknown and must be obtained by solving ( 1 ), and \(x^\pm\) is the bounds of x ( t ). This paper aims to find a viable x ( t ) that satisfies both the linear equation and the boundary constraint outlined in ( 1 ).
As shown in Xu et al. ( 2019b ), solving the BCTDLE ( 1 ) can be transformed into finding the solution of the system as follows:
with \(U=[-I;I]\in R^{2n\times n}\) , \(\vartheta =[-x^{-};x^{+}]\in R^{2n}\) , and \(V(t)=\text {diag}\{y_{1}(t),\cdots ,y_{2n}(t)\}\in R^{2n\times 2n}\) . \(I\in R^{n\times n}\) is the identity matrix, and y ( t ) is an unknown vector that must still be determined when solving ( 2 ). The matrix–vector form of ( 2 ) is then expressed as follows:
with \(Q(t)\in R^{(m+2n)\times (3n)}\) , \(w\left( t\right) \in R^{(3n)}\) , and \(r(t)\in R^{(m+2n)}\) being
In this way, solving the BCTDLE ( 1 ) is equivalent to solving the matrix–vector equation presented in ( 3 ) for \(t\geqslant 0\) .
2.2 CTZNN model
In this subsection, to solve the BCTDLE ( 1 ), following the ZNN design principle (Xu et al. 2019b ), the error equation \(e(t)\in R^{(m+2n)}\) is defined by
Then, a decay exponent formula is introduced to achieve the convergence of e ( t ) to 0 (Xu et al. 2019b ), and the resultant CTZNN model is derived and formulated as follows (Lu et al. 2019 ):
where vectors \(\dot{w}(t)\) and \(\dot{r}(t)\) denote the time derivatives of \(w\left( t\right)\) and \(r\left( t\right)\) , respectively, and matrices \(P(t)\in R^{(m+2n)\times (3n)}\) and \(M(t)\in R^{(m+2n)\times (3n)}\) are
with \(P^+(t)\in R^{(3n)\times (m+2n)}\) being the right pseudoinverse matrix of P ( t ). The following theoretical conclusion regarding the CTZNN model ( 5 ) is given and proved in Xu et al. ( 2019b ).
When considering a solvable BCTDLE ( 1 ), the CTZNN model ( 5 ) can produce an exact time-dependent solution of ( 1 ).
2.3 DTZNN model
The study of discrete-time models of ZNN is of practical interest because of hardware implementation and development of numerical algorithms (Guo et al. 2017 ; Mathews and Fink 2004 ). The widely-used method for deriving a discrete-time model is by using the Euler difference formula (Mathews and Fink 2004 ), which is given by
where \({w}_k={w}(t_k=k\varepsilon )\) , \(\varepsilon =t_{k+1}-t_k\) represents the sampling interval, \(k=0,1,2,\ldots\) is the number of iterations, and \(O(\varepsilon )\) is the truncation error.
Evidently, the discretization of the CTZNN model ( 5 ) via Euler difference formula ( 6 ) yields the following expression:
where \(P_k^+=P^+(t_k=k\varepsilon )\) , \(Q_k=Q(t_k=k\varepsilon )\) , \(M_k=M(t_k=k\varepsilon )\) , \({\dot{r}}_k={\dot{r}}(t_k=k\varepsilon )\) , \(r_k=r(t_k=k\varepsilon )\) , and \(\mu =\lambda \varepsilon >0\) is the step size.
By eliminating \(O(\varepsilon ^2)\) from ( 7 ), the following DTZNN model to solve the BCTDLE ( 1 ) is derived below:
In relation to the DTZNN model ( 7 ), it is a variation law with an \(O(\varepsilon ^2)\) error form. That is, when the sampling interval \(\varepsilon\) is reduced by a factor of 10, the stationary error is reduced by a factor of 100. Such a DTZNN model may not satisfy the high-precision requirement in practice. Thus, a new DTZNN model with better performance on computing and solving the BCTDLE ( 1 ) is proposed in this paper.
3 New DTZNN model
In this section, on the basis of the Taylor difference formula (Cai et al. 2021 ), the new DTZNN model is developed to solve the BCTDLE ( 1 ). Theoretical analysis is also provided to denote the computational characteristic of the proposed DTZNN model.
3.1 Model formulation
The approximation of a first order derivative via Taylor series expansion has been the subject of numerous studies (Zhang et al. 2019 ). In the previous study (Cai et al. 2021 ), the Taylor difference formula that has higher accuracy and lower steady-state error than the conventional Euler difference formula ( 6 ) has been constructed.
The following Taylor difference formula (Cai et al. 2021 ) is shown to approximate the first order derivative:
with \(k=6,7,8,\cdots\) and \(f(\cdot )\) being the objective function.
To discretize the CTZNN model ( 5 ) using the above Taylor difference formula ( 9 ), the following vector form of ( 9 ) is presented for the approximation of \(\dot{w}_{k}\) :
By applying the Taylor difference formula ( 10 ) to the discretization of the CTZNN model ( 5 ), the discrete-time expression is given by
By eliminating \(O(\varepsilon ^5)\) from ( 11 ), the DTZNN model proposed in this paper to solve the BCTDLE ( 1 ) is expressed as follows:
Regarding the proposed DTZNN model ( 12 ), it requires seven initial states (i.e., \(w_0\) , \(w_1\) , \(w_2\) , \(w_3\) , \(w_4\) , \(w_5\) and \(w_6\) ) to activate the iterative computation. Thus, given an initial value \(w_0\) , the rest are found by the DTZNN model ( 8 ) and are computed as follows:
The procedure of the proposed DTZNN model ( 12 ) to solve the BCTDLE problem ( 1 ) is as follows:
Initialization: Given the time duration T , sampling gap \(\varepsilon\) , step size \(\mu\) , constraint boundary \(\left[ -{{x}^{-}},{{x}^{+}} \right]\) . Initialize \({{t}_{0}}\) , \({{w}_{0}}\) , \({{G}_{0}}\) , \({{\dot{G}}_{0}}\) , \({{h}_{0}}\) , and \({{\dot{h}}_{0}}\) . Receive \(P_{0}^{+}\) , \({{r}_{0}}\) , \({{\dot{r}}_{0}}\) , \({{Q}_{0}}\) and \({{M}_{0}}\) . Compute \({{\left\| {{e}_{0}} \right\| }_{2}}={{\left\| {{Q}_{0}}{{w}_{0}}-{{r}_{0}} \right\| }_{2}}\) .
First Loop (with \(k = 0, 1, 2, 3, 4, 5\) ): Compute \({{w}_{k+1}}\) through ( 8 ). Receive \(P_{_{k+1}}^{+}\) , \({{r}_{_{k+1}}}\) , \({{\dot{r}}_{_{k+1}}}\) , \({{Q}_{_{k+1}}}\) and \({{M}_{_{k+1}}}\) . Compute \({{\left\| {{e}_{_{k+1}}} \right\| }_{2}}={{\left\| {{Q}_{_{k+1}}}{{w}_{_{k+1}}}-{{r}_{_{k+1}}} \right\| }_{2}}\) .
Second Loop (with \(k = 6, \ldots {}\) , int \((T) / \varepsilon )\) ): Compute \({{w}_{k+1}}\) through ( 12 ). Receive \(P_{_{k+1}}^{+}\) , \({{r}_{_{k+1}}}\) , \({{\dot{r}}_{_{k+1}}}\) , \({{Q}_{_{k+1}}}\) and \({{M}_{_{k+1}}}\) . Compute \({{\left\| {{e}_{_{k+1}}} \right\| }_{2}}={{\left\| {{Q}_{_{k+1}}}{{w}_{_{k+1}}}-{{r}_{_{k+1}}} \right\| }_{2}}\) .
Output: Save \({{w}_{k}}\) and \({{\left\| {{e}_{_{k}}} \right\| }_{2}}={{\left\| {{Q}_{_{k}}}{{w}_{_{k}}}-{{r}_{_{k}}} \right\| }_{2}}\) , and plot figures.
An important criterion for measuring the performance of numerical algorithms is computational complexity. For ( 12 ), the overall computational complexity is \(O((m+2n)\times (3n))\) (with \(m<n\in R\) ). Thus, the proposed DTZNN model ( 12 ) has low computational complexity, i.e., \(O(n^2)\) .
3.2 Theoretical analysis
In this subsection, the computational characteristic of the proposed DTZNN model ( 12 ) is analyzed and proved theoretically.
The proposed DTZNN model ( 12 ) is characterized by zero stability and consistency, and thus has convergence property.
By analyzing the characteristic polynomial, it has been determined that the proposed DTZNN model in Equation ( 12 ) exhibits zero stability (Guo et al. 2018 ). Then, from the derivation of ( 12 ), its truncation error is \(O({\varepsilon }^5)\) , reflecting its consistency. Referring to the findings of Griffiths and Higham ( 2010 ), the zero stability and consistency are essential for the convergence of the proposed DTZNN model ( 12 ). With that, the proof is now fully established. \(\square\)
The proposed DTZNN model ( 12 ) can produce a precise time-dependent solution of the solvable BCTDLE ( 1 ).
By following Lemma 3 , the solution \(w_k\) computed by the proposed DTZNN model ( 12 ) can converge to a theoretical solution \(w_k^*=w^*(t_k=k\varepsilon )\) of ( 3 ). Mathematically, \(w_k\rightarrow w_k^*\) if k is large enough (Huang et al. 2022 ). By virtue of \(Q_kw_k-r_k=0\) and the given definitions of \(Q_k\) and \(r_k\) , the following equation can be deduced:
\(\square\)
Knowing that \(V_{k} y_{k} \ge 0, U=[-I; I] \in R^{2 n \times n}, \text{ and } \vartheta =\left[ -x^{-}; x^{+}\right] \in R^{n \times n}\) , ( 13 ) is reformulated as stated below:
( 14 ) indicates that, when k is large enough, the DTZNN model ( 12 ) has \(x_k\rightarrow x_k^*(t_k=k\varepsilon )\) for the BCTDLE ( 1 ) to hold. This statement further shows that the proposed DTZNN model ( 12 ) can offer a precise time-dependent solution of the solvable BCTDLE ( 1 ). With that, the proof is now fully established. \(\square\)
Considering the BCTDLE ( 1 ) is solved by the proposed DTZNN model ( 12 ), the SSCE varies in the mode of \(O({\varepsilon }^5)\) .
Based on the error function ( 4 ), the SSCE of ( 12 ) is given by
According to Lemmas 3 and 4 , \(w_k=w_k^*+O({\varepsilon }^{5})\) with a large enough k . Then, the following result on the SSCE of ( 12 ) is obtained:
\(\square\) which means that the DTZNN calculation error at steady state is of order \(O(\varepsilon ^{5})\) . Therefore, considering the BCTDLE ( 1 ) is solved by the proposed DTZNN model ( 12 ), the SSCE varies in the mode of \(O({\varepsilon }^5)\) . With that, the proof is now fully established. \(\square\)
To summarize, Lemmas 3 – 5 provide theoretical guarantees that the proposed DTZNN model ( 12 ) can effectively solve the BCTDLE ( 1 ).
Numerical results for the previous DTZNN model ( 16 ) with \(\varepsilon =0.01\) and \(\mu =0.1\) to solve the BCTDLE ( 1 )
Numerical results for the proposed DTZNN model ( 12 ) with \(\varepsilon =0.01\) and \(\mu =0.1\) to solve the BCTDLE ( 1 )
4 Numerical verification and comparison
This section showcases numerical simulations to verify the superiority and effectiveness of the proposed DTZNN model ( 12 ) in solving the BCTDLE ( 1 ). Notably, the recent research (Guo et al. 2017 ) indicates that the DTZNN model via Taylor difference formula can outperform the DTZNN model ( 8 ) via Euler difference formula. Thus, this section only offers the comparative numerical results of using the proposed DTZNN model ( 12 ) and the previous DTZNN model in Guo et al. ( 2017 ). For convenience, the previous DTZNN model in Guo et al. ( 2017 ) is expressed as follows:
These simulations are also performed via MATLAB R2021b on a digital computer equipped with an AMD Ryzen 7 5800 H processor with Radeon Graphics @3.20 GHz, 32 GB of memory, and Windows 10 OS.
4.1 Model comparison
In this subsection, numerical simulation comparative experiments are conducted using the following example to demonstrate the effectiveness and superiority of the proposed DTZNN model ( 12 ) in solving BCTDLE ( 1 ). In the ensuing numerical experiments, the DTZNN models ( 12 ) and ( 16 ) are used to solve the BCTDLE ( 1 ) with the following coefficients:
The relevant numerical results are provided in Figs. 1 , 2 , 3 , 4 and Table 1 .
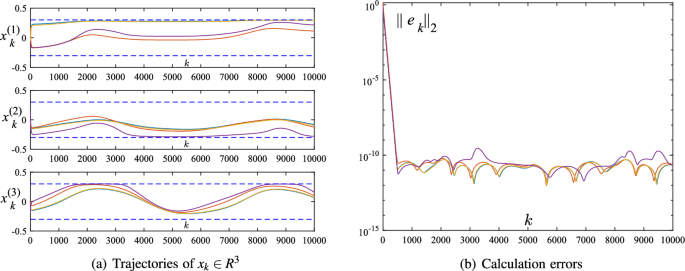
Numerical results for the previous DTZNN model ( 16 ) with \(\varepsilon =0.001\) and \(\mu =0.1\) to solve the BCTDLE ( 1 )
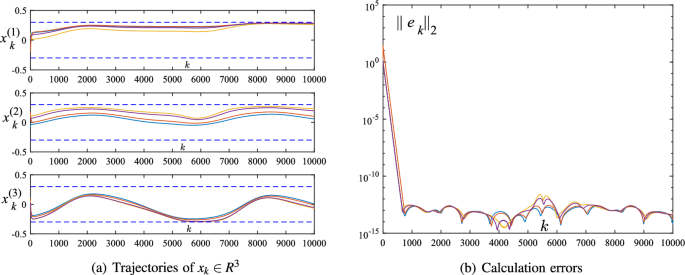
Numerical results for the proposed DTZNN model ( 12 ) with \(\varepsilon =0.001\) and \(\mu =0.1\) to solve the BCTDLE ( 1 )
Figure 1 presents the simulation results of the previous DTZNN model ( 16 ) using \(\varepsilon =0.01\) and \(\mu =0.1\) and four different initial values to solve the BCTDLE ( 1 ), where \(x_k^{(i)}(i=1,2,3)\) indicates the i th element of the feasible solution vector \(x_k\) of ( 1 ). In Fig. 1 a, the trajectories of \(x_k\) are time-dependent, and the changing values are within the constraint boundary \([x^-,x^+]\) . These results mean that the exact solution of ( 1 ) can be obtained by applying the previous DTZNN model ( 16 ). In Fig. 1 b, the calculation errors \(\Vert e_{k}\Vert _{2}\) of ( 16 ) converge, and the SSCEs are in the order of \({10}^{-6}\) . According to these results, the previous DTZNN model ( 16 ) can effectively solve the BCTDLE ( 1 ).
Figure 2 presents the simulation results of the proposed DTZNN model ( 12 ) using \(\varepsilon =0.01\) and \(\mu =0.1\) and four different initial values to solve the BCTDLE ( 1 ). In Fig. 2 a, the trajectories of \(x_k\) are time-dependent as well and numerically bounded (or say, they satisfy \(x_k\in [x^-,x^+]\) ). In Fig. 2 b, the calculation errors of ( 12 ) demonstrate convergence, with the SSCE values reaching the order of \({10}^{-8}\) . These findings provide strong evidence for the validity of ( 12 ) in solving ( 1 ). More importantly, comparing the results in Figs. 1 b and 2 b, the SSCE of the proposed model ( 12 ) is 100 times smaller than that of the previous model ( 16 ). This comparison indicates that ( 12 ) has smaller errors and higher accuracy than ( 16 ). Therefore, the proposed DTZNN model ( 12 ) offers greater advantages than the previous DTZNN model ( 16 ) in solving the TDLE with boundary constraint, i.e., ( 1 ).
By reducing the sampling interval \(\varepsilon\) by a factor of 10 and repeating the above numerical experiments, the corresponding results of using the DTZNN models ( 16 ) and ( 12 ) are shown in Figs. 3 and 4 , respectively. In such two figures, as computed by ( 16 ) or ( 12 ), the trajectories of \(x_k\) are time-dependent and satisfy \(x_k\in [x^-,x^+]\) . The related computational errors converge with the SSCE being small enough. These simulation results verify again the effectiveness of the DTZNN models ( 16 ) and ( 12 ) in solving the BCTDLE ( 1 ). In particular, comparing Figs. 3 b and 4 b, the SSCEs of ( 16 ) and ( 12 ) for solving ( 1 ) are \({10}^{-{10}}\) and \({10}^{-{13}}\) orders of magnitude, respectively. The latter is about 1000 times smaller than the former. Therefore, the proposed DTZNN model ( 12 ) can be more advantageous than the previous DTZNN model ( 16 ) in solving the BCTDLE ( 1 ).
For further investigation, the SSCEs of the DTZNN models ( 16 ) and ( 12 ) are compared and validated using different values of \(\varepsilon\) and \(\mu\) , with a fixed initial state of \(w_0=0.2\) and the same sampling time. The detailed data are provided in Table 1 , which demonstrates that the proposed model ( 12 ) is computationally better than the previous model ( 16 ). These results also verify that the calculation error variation mode of ( 12 ) is \(O(\varepsilon ^5)\) . Specifically, when \(\varepsilon =0.001\) , the SSCE can reach the order of \({10}^{-14}\) . In addition to this, the performance of the proposed DTZNN model ( 12 ) on computing and solving ( 1 ) can be improved by decreasing the sampling interval \(\varepsilon\) or increasing \(\mu\) in the appropriate range.
Overall, the simulation results presented in Figs. 1 , 2 , 3 , 4 and Table 1 confirm the superiority and efficacy of the proposed DTZNN model ( 12 ) in solving the BCTDLE ( 1 ) in comparison with the previous DTZNN model ( 16 ).
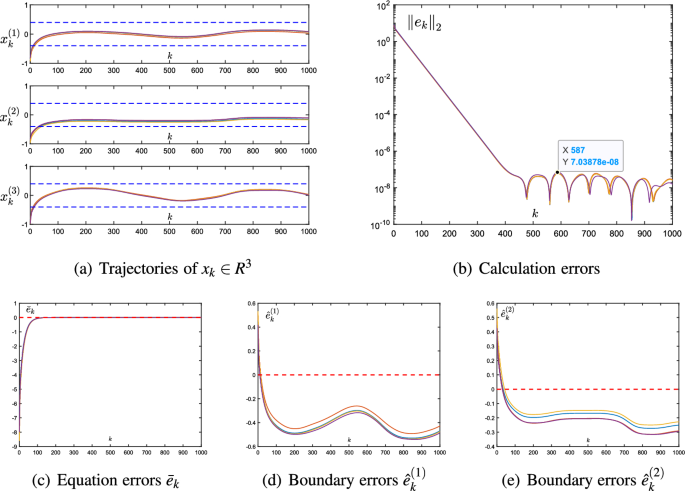
Calculation errors for the proposed DTZNN model ( 12 ) with different \(\varepsilon\) and \(\mu\) to solve the BCTDLE ( 1 )
4.2 Influence of \(\varepsilon\) and \(\mu\)
In the previous section, the effectiveness and superiority of the proposed DTZNN model ( 12 ) in solving the BCTDLE problem are demonstrated through simulation comparisons. The proposed DTZNN model ( 12 ), it has two adjustable parameters (i.e., \(\varepsilon\) and \(\mu\) ). Since different values of \(\varepsilon\) and \(\mu\) can have an effect on the solution effectiveness, this section delves into the influence of these two adjustable parameters on the proposed DTZNN model ( 12 ) using a new example. The time period for the simulation is set to \(T = 10\) s. The coefficient matrix and the constraint boundary of the BCTDLE ( 1 ) to be solved are given as follows:
To better demonstrate the effectiveness of the proposed DTZNN model ( 12 ) in solving BCTDLE ( 1 ), two additional computational errors are introduced: the equation error \({{\bar{e}}_{k}}=G(t)x(t)-h(t)\) and the constraint boundary error \({{\hat{e}}_{k}}=Ux(t)-\vartheta\) .
Figure 5 a clearly illustrates that the feasible solution of the BCTDLE ( 1 ) under the influence of the proposed DTZNN ( 12 ) model, undergoes rapid convergence from an initially out-of-boundary state and reaches the boundary constraint range. This result clearly validates the effectiveness and convergence properties of the proposed DTZNN model ( 12 ). Figure 5 b indicates that when the iteration count k is sufficiently large, the SSCE \({\left\| {{e}_{k}} \right\| }_{2}\) converges, and the maximum value is in the smaller order of magnitude of \({{10}^{-8}}\) after stabilization. This outcome suggests that the proposed DTZNN model ( 12 ) can effectively solve BCTDLE ( 1 ). From Fig. 5 c, it can be seen that with increasing iteration count k and after reaching stability, the equation error \({{\bar{e}}_{k}}\) converges to 0. The trend of the variation in \({\hat{e}}_{k}\) in Fig. 5 d and e also illustrates that under the influence of the proposed DTZNN model ( 12 ), \({x}_{k}\) transitions from initially exceeding the boundary to returning within the boundary constraint range. Therefore, in Fig. 5 a, \({x}_{k}\) is the exact solution of BCTDLE ( 1 ), confirming that the proposed DTZNN model ( 12 ) can effectively solve BCTDLE ( 1 ).
The above simulation results are obtained with the sampling interval \(\varepsilon = 0.01\) . To showcase the high precision characteristics of the proposed DTZNN model ( 12 ) and highlight the impact of the sampling interval on the solution effectiveness, the sampling interval is further reduced to \(\varepsilon = 0.001\) , while keeping other parameters constant. The relevant simulation results for solving BCTDLE ( 1 ) are presented below.
Figures 6 a, d, and e reveal that even with four different initial values exceeding the boundary constraints, \({x}_{^{k}}\) can rapidly converge within the boundary constraint range under the influence of the proposed DTZNN model ( 12 ). Comparing Fig. 5 b with Fig. 6 b, it is also noticeable that as the sampling interval \(\varepsilon\) decreases, the computational performance improves. Specifically, \((9.35241\times {{10}^{-13}})/(7.03878\times {{10}^{-8}})\approx 1.32870\times {{10}^{-5}}\) , indicating that the proposed DTZNN model ( 12 ) follows an \(O({{\varepsilon }^{5}})\) error model, that is, as the sampling interval \(\varepsilon\) is reduced by a factor of 10, the SSCE can be reduced by a factor of 100000. Therefore, it is possible to appropriately decrease the value of \(\varepsilon\) based on practical requirements to enhance computational accuracy and obtain more precise time-varying solutions.
In addition to the sampling interval \(\varepsilon\) , the proposed DTZNN model ( 12 ) has another adjustable parameter, \(\mu\) . To further explore the influnce of the two parameters on the proposed DTZNN model ( 12 ), six sets of simulation experiments are conducted. From Fig. 7 a, c, and e, it can be observed that with the sampling interval \(\varepsilon = 0.01\) , the SSCEs of the proposed DTZNN model ( 12 ) for solving BCTDLE ( 1 ) decreases as the step size \(\mu\) increases. This similar conclusion can be obtained from Fig. 7 b, d, and f. While the impact of increasing \(\mu\) on the SSCE is not as pronounced as decreasing \(\varepsilon\) , in practical situations, the sampling interval cannot be made arbitrarily small owing to some constraints. Therefore, when adjusting the sampling interval to the minimum achievable under practical conditions, increasing \(\mu\) can be employed to further reduce the SSCE and enhance precision.
By comparing the simulation results between the left and right of Fig. 7 , it can be observed that, with the step size \(\mu\) held constant, as the sampling interval \(\varepsilon\) decreases from 0.01 to 0.001, the SSCEs reduce from the order of \({10}^{-8}\) to \({10}^{-13}\) . This magnitude reduction once again confirms that the proposed DTZNN model ( 12 ) exhibits an error model of \(O({{\varepsilon }^{5}})\) . Therefore, the numerical simulation results above strongly demonstrate the effectiveness and superiority of the proposed DTZNN model ( 12 ) in solving BCTDLE ( 1 ).
It is worth noting that the main difference in this section compared to the previous one lies in the fact that the initial values exceed the boundary constraint. Therefore, the comparison of simulation results show that while keeping the sampling interval \(\varepsilon\) and the step size \(\mu\) constant, the SSCE in this section is reduced by a factor of 10 compared to the previous section. However, both sections still keep an \(O({{\varepsilon }^{5}})\) error model. Such a phenomenon occurs not only in the proposed DTZNN model ( 12 ) but also in the previous DTZNN model ( 16 ), where model accuracy is sacrificed to ensure regression to within the boundary constraint. However, the proposed DTZNN model has smaller calculation errors and demonstrates greater fault tolerance, thus making it more widely applicable in practical engineering scenarios.
5 DTZNN application to robotics
This section presents the application of the proposed DTZNN model ( 12 ) to the robotic arms with joint physical constraints to demonstrate the applicability of the model.
5.1 Motion planning of robotic arms
The motion planning of a robotic arm involves generating the joint trajectory \(\theta (t)\in R^n\) in real-time to accurately follow the desired Cartesian path \(r(t)\in R^m\) of the end-effector (Li et al. 2019 ).
In particular, taking into consideration the feedback and joint limits, the motion planning of robotic arms is achieved by efficiently solving the TDLE with boundary constraints as follows (Xu et al. 2019b ):
The above equation involves several key variables, including Jacobian matrix \(J(\theta (t))\in R^{m\times n}\) , joint velocity \(\dot{\theta }(t)\in R^n\) , time derivative of r ( t ) denoted as \(\dot{r}(t)\in R^m\) , the feedback parameter \(k>0\in R\) , and the differentiable nonlinear mapping function \(\phi (\cdot )\) . In addition, \(\theta ^\pm\) and \({\dot{\theta }}^\pm\) represent the limits of \(\theta (t)\) and \(\dot{\theta }(t)\) , respectively.
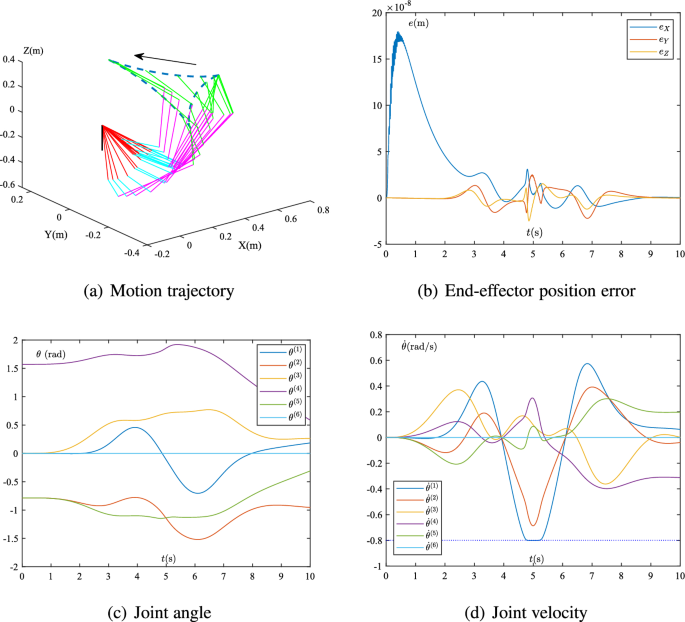
Simulation results of the motion planning scheme ( 19 ) with \(\varepsilon =0.01\) and \(\mu =0.1\) for PUMA560 robotic arm tracking the tricuspid path
It follows from (Zhang et al. 2004 ) that the boundary constraints in ( 17 ) are unified as
with \(\rho >0\in R\) . Then, the following reformulation of ( 17 ) is further obtained:
with \(\delta ^{-}=\max \{\rho (\theta ^{-}-\theta ), \dot{\theta }^{-}\}\) and \(\delta ^{+}=\min \{\rho (\theta ^{+}-\theta ), \dot{\theta }^{+}\}\) . At this point, solving ( 18 ) is the same as solving the BCTDLE ( 1 ), with the correlation coefficients as follows:
Moreover, the following augmented coefficient matrices and vectors are presented:
Therefore, the proposed DTZNN model ( 12 ) for the BCTDLE ( 1 ) can be introduced to solve ( 18 ) and ( 17 ), where \(w_k=[{\dot{\theta }}_k;y_k] \in R^{3n}\) . Notably, the Taylor difference formula ( 10 ) is also employed to calculate the joint angle \(\theta _k=\theta \left( t_k=k\varepsilon \right)\) at every instance. On the basis of ( 12 ), the following detailed formulation for realizing the motion planning of robotic arms with joint physical constraints is provided:
Hereafter, ( 19 ) is called the new motion planing scheme for physically-constrained robotic arms. With regard to such a motion planning scheme ( 19 ), seven initial values must still be determined to start the iterative computation. Similarly, given the initial joint angle \(\theta _{0}\) and \(w_{0}\) , the rest is obtained via the following iterative computation:
where \(i=0,1,\ldots ,6\) .
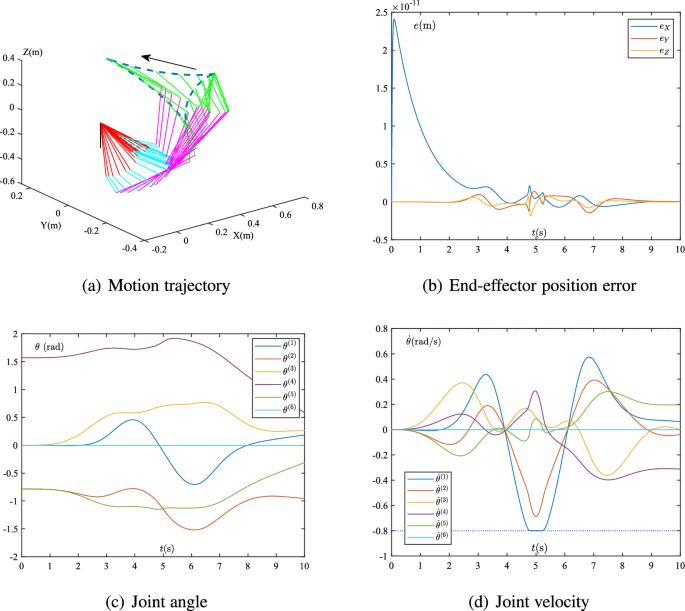
Simulation results of the motion planning scheme ( 19 ) with \(\varepsilon =0.001\) and \(\mu =0.1\) for PUMA560 robotic arm tracking the tricuspid path
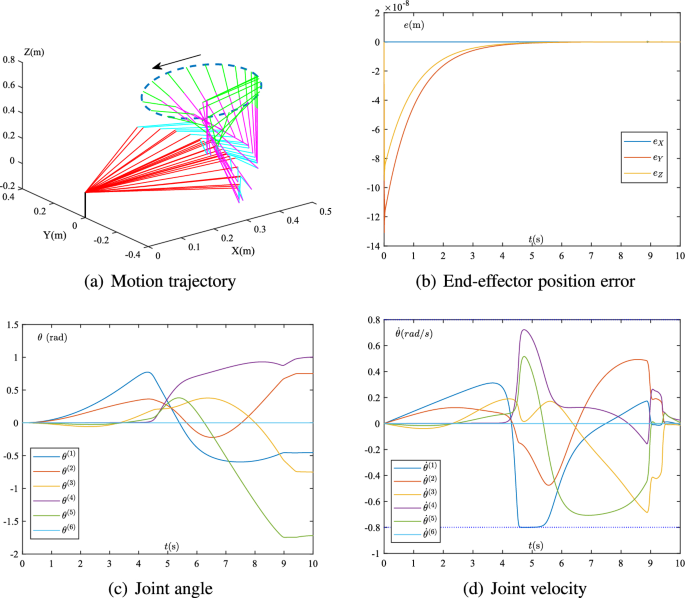
Simulation results of the motion planning scheme ( 19 ) with \(\varepsilon =0.01\) and \(\mu =0.1\) for PUMA560 robotic arm tracking the circular path
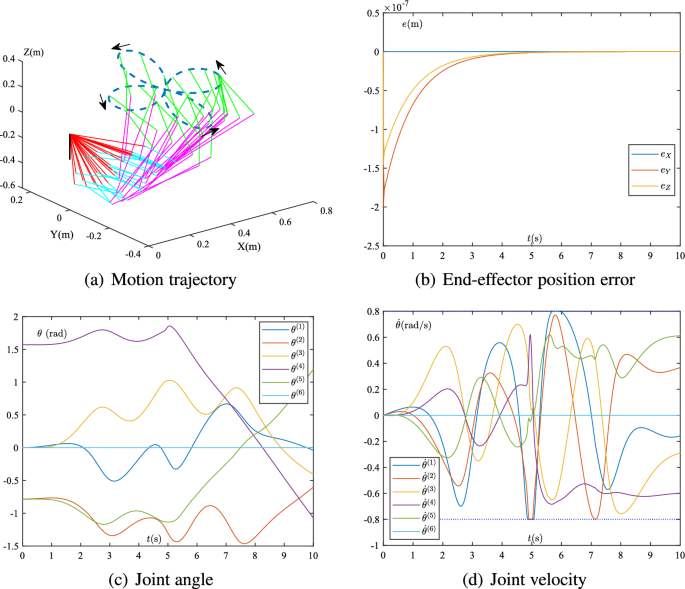
Simulation results of the motion planning scheme ( 19 ) with \(\varepsilon =0.01\) and \(\mu =0.1\) for PUMA560 robotic arm tracking the Rhodonea path
5.2 Simulation verification
To demonstrate the effectiveness of the new motion planning scheme ( 19 ), simulations are conducted using the PUMA560 robotic arm for a set desired path [i.e., the tricuspid path ( 20 ), circular path ( 21 ), and Rhodonea path ( 22 )]. In this way, the validity and practicality of the proposed DTZNN model ( 12 ) is thus confirmed.
In these simulations, the limits of the PUMA560 robotic arm are defined as
The desired end-effector position vectors for the tricuspid path, circular path, and Rhodonea path are respectively designed as
where \(\phi =2\pi {{\sin }^{2}}({\pi t}/{2T})\) , time \(t\in [0,T]\) , the parameter \(\alpha\) is constant, and r is the radius of the desired path. In addition, \(i_{x_0}\) , \(i_{y_0}\) and \(i_{z_0}\) respectively denote the X-axis, Y-axis and Z-axis components of the initial position vector of the end-effector.
To better show the simulation effect, the PUMA560 end-effector path tracking periods are all set to \(T=10s\) , and the initial joint configuration is set to \(\theta _0=[0;0;0;0;0;0]\) rad. The related simulation results are depicted in Figs. 8 , 9 , 10 , 11 , where \(t\in \left\{ 0,\varepsilon ,2\varepsilon ,\ldots ,10\right\}\) , \(e=\phi (\theta \left( t\right) )-r\left( t\right) \in R^3\) , and \({\dot{\theta }}^{(i)}\) and \(\theta ^{(i)} (i=1,2,\cdots ,6)\) represent the i th element of \(\dot{\theta }(t)\) and \(\theta (t)\) .
Figure 8 presents the results of the new motion planning scheme ( 19 ) with \(\varepsilon =0.01\) and \(\mu =0.1\) for the PUMA560 robotic arm tracking the tricuspid path. In Figs. 8 a and b, it can be observed that the PUMA560 end-effector trajectory closely follows the desired tricuspid path, and the maximum positioning error is \({6.11775\times 10}^{-7}\) m. In particular, Fig. 8 c denotes that the value of joint angle \(\theta\) calculated by ( 19 ) remains within its limits. In Fig. 8 d, the joint velocity \(\dot{\theta }\) stays within the limits even after the lower limit is reached. That is, \({\dot{\theta }}^-\le \dot{\theta }(t)\le {\dot{\theta }}^+\) and \(\theta ^-\le \theta (t)\le \theta ^+\) are satisfied. These simulation results demonstrate that the new scheme ( 19 ) can effectively implement the motion planning of the PUMA560 robotic arm in the presence of joint physical constraints and further verify the practical application of the proposed DTZNN model ( 12 ).
To further present the high accuracy characteristics of the new motion planning scheme ( 19 ), the simulation is repeated with the sampling interval \(\varepsilon\) reduced by a factor of 10 (i.e., from \(\varepsilon =0.01\) to \(\varepsilon =0.001\) ) and the rest of the condition parameters unchanged. The first two subfigures of Fig. 8 show that the PUMA560 end-effector successfully tracks the desired path again, with the maximum error is \({1.34149\times 10}^{-11}\) m. The rest of the subfigures of Figs. 8 c and d denote that joint angle \(\theta\) and joint velocity \(\dot{\theta }\) also satisfy \({\dot{\theta }}^-\le \dot{\theta }(t)\le {\dot{\theta }}^+\) and \(\theta ^-\le \theta (t)\le \theta ^+\) , respectively, thus demonstrating the effectiveness of the new motion planning scheme ( 19 ). Notably, the PUMA560 end-effector positioning error decreases by a factor of 10,000 as the sampling interval \(\varepsilon\) decreases, that is, \({(1.34149\times 10}^{-11})/{(6.11775\times 10}^{-7})\approx 2.19278\times {10}^{-5}\) . This finding underscores the importance of the sampling interval \(\varepsilon\) for the new motion planning scheme ( 19 ) and reflects an \(O(\varepsilon ^5)\) error variation pattern. Therefore, in practical applications, \(\varepsilon\) in the new motion planning scheme ( 19 ) should be set small enough to ensure the high planning accuracy required for robotic arms.
For further investigation, the tracking path of the PUMA560 end-effector is set to a circular path and a Rhodonea path for the new motion planning scheme ( 19 ) with \(\varepsilon =0.001\) and \(\mu =0.1\) . Figures 10 and 11 show the corresponding simulation results, which fully demonstrate the validity of the new motion planning scheme ( 19 ). In particular, the end-effector tracking trajectory closely follows the desired path, and the corresponding maximum error is of the order of \({10}^{-10}\) m or \({10}^{-11}\) m. Joint velocity \(\dot{\theta }\) and the joint angle \(\theta\) obtained through the new scheme ( 19 ) also remain within their respective limits, ensuring that they satisfy the conditions \({\dot{\theta }}^-\le \dot{\theta }(t)\le {\dot{\theta }}^+\) and \(\theta ^-\le \theta (t)\le \theta ^+\) , respectively.
In summary, the simulation results provided in Figs. 8 , 9 , 10 , 11 confirm the validity of the new motion planning scheme ( 19 ) for the PUMA560 robotic arm. Furthermore, these results underscore the effectiveness and practicality of the proposed DTZNN model ( 12 ).
6 Conclusion
In this paper, utilizing the Taylor difference formula ( 9 ) to discretize the CTZNN model ( 5 ), the new DTZNN model ( 12 ) is proposed and studied to address the BCTDLE ( 1 ). Theoretical analysis demonstrates that the proposed DTZNN model ( 12 ) has convergence property and can generate the exact time-dependent solution of ( 1 ). Numerical results indicate the validity and superiority of the proposed DTZNN model ( 12 ) and further point to the SSCE variation being of the \(O(\varepsilon ^5)\) mode. Such a DTZNN model is finally applied to robotic arms, and the related new motion planning scheme ( 19 ) is derived. Simulation results obtained from the PUMA560 robotic arm denote the validity and reliability of the new motion planning scheme ( 19 ) for different desired path tracking examples. The applicability of the proposed DTZNN model ( 12 ) is confirmed as well.
One future research directions involves utilizing the proposed DTZNN model ( 12 ) to solve the BCTDLE ( 1 ) in a noisy environment. Another direction is to explore the application of the proposed DTZNN model ( 12 ) in other tasks of redundant robot manipulators, such as repetitive motions and obstacle avoidance. As a continuation of this paper, further efforts will focus on designing and selecting different activation functions to enhance the robustness of the proposed DTZNN model ( 12 ).
Code or data availability
The code or data were available in this manuscript.
Abdelmalek NN (1977) Minimum L ∞ solution of underdetermined systems of linear equations. J Approx Theory 20(1):57–69
Article MathSciNet Google Scholar
Cichocki A, Ramirez-Angulo J, Unbehauen R (1992) Architectures for analog VLSI implementation of neural networks for solving linear equations with inequality constraints. Proc IEEE Int Symp Circuits Syst 3:1529–1532
Google Scholar
Donoho DL, Tsaig Y, Drori I, Starck JL (2012) Sarse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit. IEEE Trans Inf Theory 58(2):1094–1121
Article Google Scholar
Griffiths DF, Higham DJ (2010) Numerical methods for ordinary differential equations initial value problems. Springer, London
Book Google Scholar
Guo D, Zhang Y (2012) Zhang neural network, Getz-Marsden dynamic system, and discrete-time algorithms for time-varying matrix inversion with application to robots’ kinematic control. Neurocomputing 97:22–32
Guo D, Nie Z, Yan L (2017) Novel discrete-time Zhang neural network for time-varying matrix inversion. IEEE Trans Syst Man Cybern: Syst 47(8):2301–2310
Guo D, Li K, Liao B (2018) Bi-criteria minimization with MWVN-INAM type for motion planning and control of redundant robot manipulators. Robotica 36(5):655–675
Guo D, Xu F, Li Z, Nie Z, Shao H (2018) Design, verification, and application of new discrete-time recurrent neural network for dynamic nonlinear equations solving. IEEE Trans Ind Informat 14(9):3936–3945
Huang S, Ma Z, Yu S, Han Y (2022) New discrete-time zeroing neural network for solving time-variant underdetermined nonlinear systems under bound constraint. Neurocomputing 487:214–227
Kumar R (2022) A Lyapunov-stability-based context-layered recurrent pi-sigma neural network for the identification of nonlinear systems. Appl Soft Comput 122:108836
Kumar R (2022) Memory recurrent Elman neural network-based identification of time-delayed nonlinear dynamical system. IEEE Trans Syst Man Cybern: Syst 53(2):753–762
Kumar R (2023) Double internal loop higher-order recurrent neural network-based adaptive control of the nonlinear dynamical system. Soft Comput 27:17313–17331
Li S, Jin L, Mirza MA (2019) Kinematic control of redundant robot arms using neural networks. Wiley, Hoboken
Li W, Xiao L, Liao B (2019) A finite-time convergent and noise-rejection recurrent neural network and its discretization for dynamic nonlinear equations solving. IEEE Trans Cybern 50(7):3195–3207
Liang XB, Tso SK (2002) Improved upper bound on step-size parameters of discrete-time recurrent neural networks for linear inequality and equation system. IEEE Trans Circuits Syst I Fundam Theory Appl 49(5):695–698
Liao B, Han L, Cao X, Li S, Li J (2024) Double integral?enhanced Zeroing neural network with linear noise rejection for time? Varying matrix inverse. CAAI Trans Intell Technol 9(1):197–210
Lu H, Jin L, Luo X, Liao B, Guo D, Xiao L (2019) RNN for solving perturbed time-varying underdetermined linear system with double bound limits on residual errors and state variables. IEEE Trans Indus Inf 15(11):5931–5942
Ma Z, Guo D (2021) Discrete-time recurrent neural network for solving bound-constrained time-varying underdetermined linear system. IEEE Trans Ind Informat 17(6):3869–3878
Mathews JH, Fink KD (2004) Numerical methods using MATLAB, 4th edn. Prentice-Hall, Upper Saddle River
Morigi S, Sgallari F (2001) A regularizing L-curve Lanczos method for underdetermined linear systems. Appl Math Comput 121(1):55–73
MathSciNet Google Scholar
Neta B, Chun C, Scott M (2014) Basins of attraction for optimal eighth order methods to find simple roots of nonlinear equations. Appl Math Comput 227:567–592
Park K, Chang P, Kim S (1998) The enhanced compact QP method for redundant manipulators using practical inequality constraints. Proc IEEE Int Conf Robot Autom 1:107–114
Sharma JR (2005) A composite third order Newton–Steffensen method for solving nonlinear equations. Appl Math Comput 169(1):242–246
Spedicato E, Xia Z, Zhang L (2000) ABS algorithms for linear equations and optimization. J Comput Appl Math 124(1/2):155–170
Sun M, Liu J (2020) A novel noise-tolerant Zhang neural network for time-varying Lyapunov equation. Adv Diff Equ 1:1–15
Tsiligianni E, Kondi LP, Katsaggelos AK (2015) Preconditioning for underdetermined linear systems with sparse solutions. IEEE Signal Process Lett 22(9):1239–1243
Xia Y, Wang J, Hung DL (1999) Recurrent neural networks for solving linear inequalities and equations. IEEE Trans Circuits Syst I: Fundam Theory Appl 46(4):452–462
Xiao L, Dai J, Lu R, Li S, Li J, Wang S (2020) Design and comprehensive analysis of a noise-tolerant ZNN model with limited-time convergence for time-dependent nonlinear minimization. IEEE Trans Neural Netw Learn Syst 31(12):5339–5348
Xu F, Li Z, Nie Z, Shao H, Guo D (2019) New recurrent neural network for online solution of time-dependent underdetermined linear system with bound constraint. IEEE Trans Ind Informat 15(4):2167–2176
Xu F, Li Z, Nie Z, Shao H, Guo D (2019) Zeroing neural network for solving time-varying linear equation and inequality systems. IEEE Trans Neural Netw Learn Syst 30(8):2346–2357
Zeng J, Lin S, Xu Z (2014) Sparse solution of underdetermined linear equations via adaptively iterative thresholding. Signal Process 97:152–161
Zhang Y, Guo D (2015) Zhang functions and various models. Springer, Germany
Zhang Y, Jin L (2017) Robot manipulator redundancy resolution. Wiley, Hoboken
Zhang Y, Yi C (2011) Zhang neural networks and neural-dynamic method. Nova, New York
Zhang Y, Ge SS, Lee TH (2004) A unified quadratic-programming-based dynamical system approach to joint torque optimization of physically constrained redundant manipulators. IEEE Trans on Syst Man Cybern 34(5):2126–2132
Zhang Y, Li W, Guo D, Ke Z (2013) Different Zhang functions leading to different ZNN models illustrated via time-varying matrix square roots finding. Expert Syst Appl 40(11):4393–4403
Zhang Y, Wang Y, Jin L (2013) Different ZFs leading to various ZNN models illustrated via online solution of time-varying underdetermined systems of linear equations with robotic application. Lect Notes Comput Sci 7952:481–488
Zhang Z, Zheng L, Li L, Deng X, Xiao L, Huang G (2018) A new finite-time varying-parameter convergent-differential neural-network for solving nonlinear and nonconvex optimization problems. Neurocomputing 319:74–83
Zhang Y, Li S, Gui J, Luo X (2018) Velocity-level control with compliance to acceleration-level constraints: a novel scheme for manipulator redundancy resolution. IEEE Trans Ind Informat 14(3):921–930
Zhang Y, Yang M, Huang H, Xiao M, Hu H (2019) New discrete solution model for solving future different-level linear inequality and equality with robot manipulator control. IEEE Trans Ind Informat 15(4):1975–1984
Zhao YB (2013) New and improved conditions for uniqueness of sparsest solutions of underdetermined linear systems. Appl Math Comput 224:58–73
Zhang Y, Shi Y, Xiao L, Mu B (2012) Convergence and stability results of Zhang neural network solving systems of time-varying nonlinear equations. Proc 8th Int Conf Natural Comput 143–147
Zhang Y, Qiu H, Peng C, Shi Y, Tan H (2015) Simply and effectively proved square characteristics of discrete-time zd solving systems of time-varying nonlinear equations. Proc IEEE Int Conf Robot Autom 1457–1462
Cai J, Feng Q, Guo D (2021) New discrete-time zeroing neural network for solving time-varying system of linear equation and inequality. Proc 33rd Chinese Control Decision Conf 3806–3811
Download references
Acknowledgements
The authors would like to thank the editors and reviewers for their time and effort in evaluating this paper and for the constructive comments for the improvement of its presentation and quality.
This work is partly supported by Scientific Research Fund of Hainan University under Grant (KYQD(ZR)23025), Shenzhen Science and Technology Program under Grant (JCYJ20230807093513027), the National Science and Technology Major Project (Grant No. 2022ZD0119900), Shanghai Science and Technology program (Grant No. 22015810300), Hainan Province Science and Technology Special Fund (Grant No. ZDYF2024GXJS003), the Hainan Provincial Natural Science Foundation of China (Grant No. 620QN284), National Natural Science Foundation (Grant Nos. 61976096 and 62373157), and National High-Level Talents Special Support Program (Youth Talent of Technological Innovation of Ten-Thousands Talents Program) (Grant No. C7220060).
Author information
Authors and affiliations.
School of Information and Communication Engineering, Hainan University, Haikou, China
Naimeng Cang, Feng Qiu, Shan Xue, Zehua Jia & Dongsheng Guo
School of System Design and Intelligent Manufacturing, South China University of Technology, Shenzhen, China
School of Automation Science and Engineering, South China University of Technology, Guangzhou, China
Zhijun Zhang
School of Computer Science and Engineering, Sun Yat-sen University, Guangzhou, China
You can also search for this author in PubMed Google Scholar
Contributions
All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Naimeng Cang, Dongsheng Guo and Shan Xue. The first draft of the manuscript was written by Naimeng Cang and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Correspondence to Dongsheng Guo .
Ethics declarations
Conflict of interest.
The authors have no relevant financial or non-financial interests to disclose
Ethical approval
This paper does not contain any studies with human participants or animals performed by any of the authors.
Consent to participate
Informed consent was obtained from all individual participants included in the study.
Consent for publication
The authors affirm that human research participants provided informed consent for publication of the images in all figures.
Additional information
Publisher's note.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .
Reprints and permissions
About this article
Cang, N., Qiu, F., Xue, S. et al. New discrete-time zeroing neural network for solving time-dependent linear equation with boundary constraint. Artif Intell Rev 57 , 140 (2024). https://doi.org/10.1007/s10462-024-10746-x
Download citation
Accepted : 06 March 2024
Published : 13 May 2024
DOI : https://doi.org/10.1007/s10462-024-10746-x
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Discrete-time zeroing neural network
- Time-dependent linear equation
- Boundary constraint
- Taylor difference formula
- Robotic arm
- Find a journal
- Publish with us
- Track your research

IMAGES
VIDEO
COMMENTS
Here is a six-step process to follow when using a problem-solving model: 1. Define the problem. First, determine the problem that your team needs to solve. During this step, teams may encourage open and honest communication so everyone feels comfortable sharing their thoughts and concerns.
Identify the people, information (data), and things needed to resolve the problem. Step. Description. Step 3: Select an Alternative. After you have evaluated each alternative, select the alternative that comes closest to solving the problem with the most advantages and fewest disadvantages.
1. Define the problem. Diagnose the situation so that your focus is on the problem, not just its symptoms. Helpful problem-solving techniques include using flowcharts to identify the expected steps of a process and cause-and-effect diagrams to define and analyze root causes.. The sections below help explain key problem-solving steps.
Problem solving is the process of finding solutions to complex or challenging issues. It involves various skills, such as creativity, logic, analysis, and decision making. This article on Wikipedia provides an overview of different problem solving methods, models, techniques, and applications in various domains.
Structured problem solving strategies can be used to address almost any complex challenge in business or public policy. ... Classic problem solving often gravitates toward a model; design thinking migrates toward a prototype. Rather than writing a big deck with all my supporting evidence, they'll bring an example, a thing, and that feels ...
What is the Six Step Problem-Solving Model? It is a collaborative and systematic approach to addressing problems. Instead of tackling issues haphazardly, this model encourages a sequential process ...
The Problem-Solving Process. Problem-solving is an important part of planning and decision-making. The process has much in common with the decision-making process, and in the case of complex decisions, can form part of the process itself. We face and solve problems every day, in a variety of guises and of differing complexity.
The first step in creating a problem-solving plan is to understand what we mean when we say problem-solving models. A problem-solving model is a step-by-step process that helps a team identify and effectively solve problems that they may encounter. This problem-solving approach gives the team the muscle memory and guide to address a conflict ...
Problem solving refers to cognitive processing directed at achieving a goal when the problem solver does not initially know a solution method. A problem exists when someone has a goal but does not know how to achieve it. Problems can be classified as routine or nonroutine, and as well defined or ill defined.
The McKinsey guide to problem solving. Become a better problem solver with insights and advice from leaders around the world on topics including developing a problem-solving mindset, solving problems in uncertain times, problem solving with AI, and much more.
Problem solving is the process of articulating solutions to problems. Problems have two critical attributes. First, a problem is an unknown in some context. That is, there is a situation in which there is something that is unknown (the difference between a goal state and a current state). Those situations vary from algorithmic math problems to ...
Problem-solving is a mental process that involves discovering, analyzing, and solving problems. The ultimate goal of problem-solving is to overcome obstacles and find a solution that best resolves the issue. The best strategy for solving a problem depends largely on the unique situation. In some cases, people are better off learning everything ...
The problem-solving process typically includes the following steps: Identify the issue: Recognize the problem that needs to be solved. Analyze the situation: Examine the issue in depth, gather all relevant information, and consider any limitations or constraints that may be present. Generate potential solutions: Brainstorm a list of possible ...
In insight problem-solving, the cognitive processes that help you solve a problem happen outside your conscious awareness. 4. Working backward. Working backward is a problem-solving approach often ...
The model is helpful because it uses a team-based approach to problem solving and to business-process improvement, and this makes it particularly useful for solving cross-departmental process issues. Also, it encourages people to rely on objective data rather than on personal opinions, and this improves the quality of the outcome. It has five ...
IDEAL Model for improving problem solving (Verbatim copy of Fig 2.1; p.12) I = Identifying the problem. D = Define and represent the problem. ... Knowledge of CORE CONCEPTS in a field SIMPLIFIES problem solving. Ways to approach a problem of learning information that seems to be arbitrary: Over-learn: rehearse the facts until they are mastered. ...
Problem-solving is a vital skill for coping with various challenges in life. This webpage explains the different strategies and obstacles that can affect how you solve problems, and offers tips on how to improve your problem-solving skills. Learn how to identify, analyze, and overcome problems with Verywell Mind.
The 8D problem solving model establishes a permanent corrective action based on statistical analysis of the problem and focuses on the origin of the problem by determining its root causes. Although it originally comprised eight stages, or disciplines, the eight disciplines system was later augmented by an initial planning stage.
Problem-solving games that help raise group awareness through a central, unifying metaphor can be effective ways to warm-up a group in any problem-solving model. Draw a Tree is a simple warm-up activity you can use in any group and which can provide a quick jolt of energy.
Problem-solving is the capacity to identify and describe a problem and generate solutions to fix it. Problem-solving involves other executive functioning behaviors as well, including attentional control, planning, and task initiation. Individuals might use time management, emotional control, or organization skills to solve problems as well.
In this chapter we (a) review the early development of the problem-solving model for social work practice; (b) discuss the later development of the problem solving model in terms of its extension to and further elaboration by generalist models of social work practice; (c) provide an overview of how the problem-solving model allows for the integration of the scientific and artistic elements of ...
Problem solving models are used to address the many challenges that arise in the workplace. While many people regularly solve problems, there are a range of different approaches that can be used to find a solution. Complex challenges for teams, working groups and boards etc., are usually solved
Creative problem-solving primarily operates in the ideate phase of design thinking but can be applied to others. This is because design thinking is an iterative process that moves between the stages as ideas are generated and pursued. This is normal and encouraged, as innovation requires exploring multiple ideas.
The SARA Model. A commonly used problem-solving method is the SARA model (Scanning, Analysis, Response and Assessment). The SARA model contains the following elements: Scanning: Identifying recurring problems of concern to the public and the police. Identifying the consequences of the problem for the community and the police. Prioritizing those ...
I love Steve Spear's emphasis on a Toyota-based Lean model of: "See, Solve, Share" See problems, solve problems, and share problems. That's the ideal, and it's powerful where it exists. At Toyota, and companies like it, there's an understanding that speaking up about problems leads to a constructive response from leaders.
The GROW model is also a perfect tool for any mindset coach who wants to help their clients stay on track. Coaches can use it to help others find purpose and clarify the goals they value most. Enhanced self-awareness and problem-solving skills. Developing self-awareness is a key component of the GROW coaching model. With each coaching session ...
Large language models (LLMs) have emerged and presented their general problem-solving capabilities with one model. However, the model size has increased dramatically with billions of parameters to enable such broad problem-solving capabilities. In addition, due to the dominance of matrix-matrix and matrix-vector multiplications in LLMs, the compute-to-model size ratio is significantly lower ...
Computational thinking skill is a new framework that belongs to the hybrid modes of thinking. This study aims to explore the effect of the problem-solving laboratory and gender in practicing computational thinking skills. Learning media is pursued by designing experimental-based learning using smartphone sensors. A smartphone sensor was used to facilitate students to measure physical ...
Recently, continuous- and discrete-time models of a zeroing neural network (ZNN) have been developed to provide online solutions for the time-dependent linear equation (TDLE) with boundary constraint. This paper presents a novel approach to address the bound-constrained TDLE (BCTDLE) problem by proposing a new discrete-time ZNN (DTZNN) model. The proposed DTZNN model is designed using the ...
Recent advancements in Large Language Models (LLMs) like ChatGPT and Copilot have led to their integration into various educational domains, including software development education. Regular use of LLMs in the learning process is still not well-researched; thus, this paper intends to fill this gap. The paper explores the nuanced impact of informal LLM usage on undergraduate students ...