problem solving education maths

• Our Mission

6 Tips for Teaching Math Problem-Solving Skills

Solving word problems is tougher than computing with numbers, but elementary teachers can guide students to do the deep thinking involved.

A growing concern with students is the ability to problem-solve, especially with complex, multistep problems. Data shows that students struggle more when solving word problems than they do with computation , and so problem-solving should be considered separately from computation. Why?

Consider this. When we’re on the way to a new destination and we plug in our location to a map on our phone, it tells us what lane to be in and takes us around any detours or collisions, sometimes even buzzing our watch to remind us to turn. When I experience this as a driver, I don’t have to do the thinking. I can think about what I’m going to cook for dinner, not paying much attention to my surroundings other than to follow those directions. If I were to be asked to go there again, I wouldn’t be able to remember, and I would again seek help.

If we can switch to giving students strategies that require them to think instead of giving them too much support throughout the journey to the answer, we may be able to give them the ability to learn the skills to read a map and have several ways to get there.

Here are six ways we can start letting students do this thinking so that they can go through rigorous problem-solving again and again, paving their own way to the solution. 

1. Link problem-solving to reading

When we can remind students that they already have many comprehension skills and strategies they can easily use in math problem-solving, it can ease the anxiety surrounding the math problem. For example, providing them with strategies to practice, such as visualizing, acting out the problem with math tools like counters or base 10 blocks, drawing a quick sketch of the problem, retelling the story in their own words, etc., can really help them to utilize the skills they already have to make the task less daunting.

We can break these skills into specific short lessons so students have a bank of strategies to try on their own. Here's an example of an anchor chart that they can use for visualizing . Breaking up comprehension into specific skills can increase student independence and help teachers to be much more targeted in their problem-solving instruction. This allows students to build confidence and break down the barriers between reading and math to see they already have so many strengths that are transferable to all problems.

2. Avoid boxing students into choosing a specific operation

It can be so tempting to tell students to look for certain words that might mean a certain operation. This might even be thoroughly successful in kindergarten and first grade, but just like when our map tells us where to go, that limits students from becoming deep thinkers. It also expires once they get into the upper grades, where those words could be in a problem multiple times, creating more confusion when students are trying to follow a rule that may not exist in every problem.

We can encourage a variety of ways to solve problems instead of choosing the operation first. In first grade, a problem might say, “Joceline has 13 stuffed animals and Jordan has 17. How many more does Jordan have?” Some students might choose to subtract, but a lot of students might just count to find the amount in between. If we tell them that “how many more” means to subtract, we’re taking the thinking out of the problem altogether, allowing them to go on autopilot without truly solving the problem or using their comprehension skills to visualize it. 

3. Revisit ‘representation’

The word “representation” can be misleading. It seems like something to do after the process of solving. When students think they have to go straight to solving, they may not realize that they need a step in between to be able to support their understanding of what’s actually happening in the problem first.

Using an anchor chart like one of these ( lower grade , upper grade ) can help students to choose a representation that most closely matches what they’re visualizing in their mind. Once they sketch it out, it can give them a clearer picture of different ways they could solve the problem.

Think about this problem: “Varush went on a trip with his family to his grandmother’s house. It was 710 miles away. On the way there, three people took turns driving. His mom drove 214 miles. His dad drove 358 miles. His older sister drove the rest. How many miles did his sister drive?”

If we were to show this student the anchor chart, they would probably choose a number line or a strip diagram to help them understand what’s happening.

If we tell students they must always draw base 10 blocks in a place value chart, that doesn’t necessarily match the concept of this problem. When we ask students to match our way of thinking, we rob them of critical thinking practice and sometimes confuse them in the process. 

4. Give time to process

Sometimes as educators, we can feel rushed to get to everyone and everything that’s required. When solving a complex problem, students need time to just sit with a problem and wrestle with it, maybe even leaving it and coming back to it after a period of time.

This might mean we need to give them fewer problems but go deeper with those problems we give them. We can also speed up processing time when we allow for collaboration and talk time with peers on problem-solving tasks. 

5. Ask questions that let Students do the thinking

Questions or prompts during problem-solving should be very open-ended to promote thinking. Telling a student to reread the problem or to think about what tools or resources would help them solve it is a way to get them to try something new but not take over their thinking.

These skills are also transferable across content, and students will be reminded, “Good readers and mathematicians reread.” 

6. Spiral concepts so students frequently use problem-solving skills

When students don’t have to switch gears in between concepts, they’re not truly using deep problem-solving skills. They already kind of know what operation it might be or that it’s something they have at the forefront of their mind from recent learning. Being intentional within their learning stations and assessments about having a variety of rigorous problem-solving skills will refine their critical thinking abilities while building more and more resilience throughout the school year as they retain content learning in the process. 

Problem-solving skills are so abstract, and it can be tough to pinpoint exactly what students need. Sometimes we have to go slow to go fast. Slowing down and helping students have tools when they get stuck and enabling them to be critical thinkers will prepare them for life and allow them multiple ways to get to their own destination.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5 Teaching Mathematics Through Problem Solving

Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem  in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems  includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving  focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a  neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method

should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning

involves teaching a skill so that a student can later solve a story problem

when we teach students how to problem solve

teaching mathematics content through real contexts, problems, situations, and models

a mathematical activity where everyone in the group can begin and then work on at their own level of engagement

20 seconds to 2 minutes for students to make sense of questions

Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Learn by   .css-1v0lc0l{color:var(--chakra-colors-blue-500);} doing

Guided interactive problem solving that’s effective and fun. Master concepts in 15 minutes a day.

Data Analysis

Computer Science

Programming & AI

Science & Engineering

Join over 10 million people learning on Brilliant

Over 50,000 5-star reviews on iOS App Store and Google Play

Master concepts in 15 minutes a day

Whether you’re a complete beginner or ready to dive into machine learning and beyond, Brilliant makes it easy to level up fast with fun, bite-sized lessons.

Effective, hands-on learning

Visual, interactive lessons make concepts feel intuitive — so even complex ideas just click. Our real-time feedback and simple explanations make learning efficient.

Learn at your level

Students and professionals alike can hone dormant skills or learn new ones. Progress through lessons and challenges tailored to your level. Designed for ages 13 to 113.

Guided bite-sized lessons

We make it easy to stay on track, see your progress, and build your problem-solving skills one concept at a time.

Stay motivated

Form a real learning habit with fun content that’s always well-paced, game-like progress tracking, and friendly reminders.

Guided courses for every journey

Courses in   .css-1vg6q84{font-weight:700;} foundational math.

Solving Equations

Understanding Graphs

Geometry Fundamentals

Systems of Equations

Functions & Quadratics

Calculus in a Nutshell

All of our 70+ courses are crafted by award-winning teachers, researchers, and professionals from:

10K+ Ratings

60K+ Ratings

© 2024 Brilliant Worldwide, Inc., Brilliant and the Brilliant Logo are trademarks of Brilliant Worldwide, Inc.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Module 1: Problem Solving Strategies

• Last updated
• Save as PDF
• Page ID 10352

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.

Pólya’s How to Solve It

George Pólya was a great champion in the field of teaching effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985.1

1. Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

First, you have to understand the problem.

After understanding, then make a plan.

Carry out the plan.

Look back on your work. How could it be better?

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

Problem Solving Strategy 1 (Guess and Test)

Make a guess and test to see if it satisfies the demands of the problem. If it doesn't, alter the guess appropriately and check again. Keep doing this until you find a solution.

Mr. Jones has a total of 25 chickens and cows on his farm. How many of each does he have if all together there are 76 feet?

Step 1: Understanding the problem

We are given in the problem that there are 25 chickens and cows.

All together there are 76 feet.

Chickens have 2 feet and cows have 4 feet.

We are trying to determine how many cows and how many chickens Mr. Jones has on his farm.

Step 2: Devise a plan

Going to use Guess and test along with making a tab

Many times the strategy below is used with guess and test.

Make a table and look for a pattern:

Procedure: Make a table reflecting the data in the problem. If done in an orderly way, such a table will often reveal patterns and relationships that suggest how the problem can be solved.

Step 3: Carry out the plan:

Notice we are going in the wrong direction! The total number of feet is decreasing!

Better! The total number of feet are increasing!

Step 4: Looking back:

Check: 12 + 13 = 25 heads

24 + 52 = 76 feet.

We have found the solution to this problem. I could use this strategy when there are a limited number of possible answers and when two items are the same but they have one characteristic that is different.

Videos to watch:

1. Click on this link to see an example of “Guess and Test”

http://www.mathstories.com/strategies.htm

2. Click on this link to see another example of Guess and Test.

http://www.mathinaction.org/problem-solving-strategies.html

Check in question 1:

Place the digits 8, 10, 11, 12, and 13 in the circles to make the sums across and vertically equal 31. (5 points)

Check in question 2:

Old McDonald has 250 chickens and goats in the barnyard. Altogether there are 760 feet . How many of each animal does he have? Make sure you use Polya’s 4 problem solving steps. (12 points)

Problem Solving Strategy 2 (Draw a Picture). Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric thinking visually can help!

Videos to watch demonstrating how to use "Draw a Picture".

1. Click on this link to see an example of “Draw a Picture”

2. Click on this link to see another example of Draw a Picture.

Problem Solving Strategy 3 ( Using a variable to find the sum of a sequence.)

Gauss's strategy for sequences.

last term = fixed number ( n -1) + first term

The fix number is the the amount each term is increasing or decreasing by. "n" is the number of terms you have. You can use this formula to find the last term in the sequence or the number of terms you have in a sequence.

Ex: 2, 5, 8, ... Find the 200th term.

Last term = 3(200-1) +2

Last term is 599.

To find the sum of a sequence: sum = [(first term + last term) (number of terms)]/ 2

Sum = (2 + 599) (200) then divide by 2

Sum = 60,100

Check in question 3: (10 points)

Find the 320 th term of 7, 10, 13, 16 …

Then find the sum of the first 320 terms.

Problem Solving Strategy 4 (Working Backwards)

This is considered a strategy in many schools. If you are given an answer, and the steps that were taken to arrive at that answer, you should be able to determine the starting point.

Videos to watch demonstrating of “Working Backwards”

https://www.youtube.com/watch?v=5FFWTsMEeJw

Karen is thinking of a number. If you double it, and subtract 7, you obtain 11. What is Karen’s number?

1. We start with 11 and work backwards.

2. The opposite of subtraction is addition. We will add 7 to 11. We are now at 18.

3. The opposite of doubling something is dividing by 2. 18/2 = 9

4. This should be our answer. Looking back:

9 x 2 = 18 -7 = 11

5. We have the right answer.

Check in question 4:

Christina is thinking of a number.

If you multiply her number by 93, add 6, and divide by 3, you obtain 436. What is her number? Solve this problem by working backwards. (5 points)

Problem Solving Strategy 5 (Looking for a Pattern)

Definition: A sequence is a pattern involving an ordered arrangement of numbers.

We first need to find a pattern.

Ask yourself as you search for a pattern – are the numbers growing steadily larger? Steadily smaller? How is each number related?

Example 1: 1, 4, 7, 10, 13…

Find the next 2 numbers. The pattern is each number is increasing by 3. The next two numbers would be 16 and 19.

Example 2: 1, 4, 9, 16 … find the next 2 numbers. It looks like each successive number is increase by the next odd number. 1 + 3 = 4.

So the next number would be

25 + 11 = 36

Example 3: 10, 7, 4, 1, -2… find the next 2 numbers.

In this sequence, the numbers are decreasing by 3. So the next 2 numbers would be -2 -3 = -5

-5 – 3 = -8

Example 4: 1, 2, 4, 8 … find the next two numbers.

This example is a little bit harder. The numbers are increasing but not by a constant. Maybe a factor?

So each number is being multiplied by 2.

16 x 2 = 32

1. Click on this link to see an example of “Looking for a Pattern”

2. Click on this link to see another example of Looking for a Pattern.

Problem Solving Strategy 6 (Make a List)

Example 1 : Can perfect squares end in a 2 or a 3?

List all the squares of the numbers 1 to 20.

1 4 9 16 25 36 49 64 81 100 121 144 169 196 225 256 289 324 361 400.

Now look at the number in the ones digits. Notice they are 0, 1, 4, 5, 6, or 9. Notice none of the perfect squares end in 2, 3, 7, or 8. This list suggests that perfect squares cannot end in a 2, 3, 7 or 8.

How many different amounts of money can you have in your pocket if you have only three coins including only dimes and quarters?

Quarter’s dimes

0 3 30 cents

1 2 45 cents

2 1 60 cents

3 0 75 cents

Videos demonstrating "Make a List"

Check in question 5:

How many ways can you make change for 23 cents using only pennies, nickels, and dimes? (10 points)

Problem Solving Strategy 7 (Solve a Simpler Problem)

Geometric Sequences:

How would we find the nth term?

Solve a simpler problem:

1, 3, 9, 27.

1. To get from 1 to 3 what did we do?

2. To get from 3 to 9 what did we do?

Let’s set up a table:

Term Number what did we do

Looking back: How would you find the nth term?

Find the 10 th term of the above sequence.

Let L = the tenth term

Problem Solving Strategy 8 (Process of Elimination)

This strategy can be used when there is only one possible solution.

I’m thinking of a number.

The number is odd.

It is more than 1 but less than 100.

It is greater than 20.

It is less than 5 times 7.

The sum of the digits is 7.

It is evenly divisible by 5.

a. We know it is an odd number between 1 and 100.

b. It is greater than 20 but less than 35

21, 23, 25, 27, 29, 31, 33, 35. These are the possibilities.

c. The sum of the digits is 7

21 (2+1=3) No 23 (2+3 = 5) No 25 (2 + 5= 7) Yes Using the same process we see there are no other numbers that meet this criteria. Also we notice 25 is divisible by 5. By using the strategy elimination, we have found our answer.

Check in question 6: (8 points)

Jose is thinking of a number.

The number is not odd.

The sum of the digits is divisible by 2.

The number is a multiple of 11.

It is greater than 5 times 4.

It is a multiple of 6

It is less than 7 times 8 +23

What is the number?

Click on this link for a quick review of the problem solving strategies.

https://garyhall.org.uk/maths-problem-solving-strategies.html

Featured Topics

Featured series.

A series of random questions answered by Harvard experts.

Explore the Gazette

Read the latest.

One way to help big groups of students? Volunteer tutors.

Footnote leads to exploration of start of for-profit prisons in N.Y.

Should NATO step up role in Russia-Ukraine war?

“Teachers should teach math in a way that encourages students to engage in sense-making and not merely to memorize or internalize exactly what the teacher says or does,” says Jon R. Star.

Kris Snibbe/Harvard Staff Photographer

One way is the wrong way to do math. Here’s the right way.

Harvard Staff Writer

Research by Ed School psychologist reinforces case for stressing multiple problem-solving paths over memorization

There’s never just one way to solve a math problem, says Jon R. Star , a psychologist and professor of education at the Harvard Graduate School of Education. With researchers from Vanderbilt University, Star found that teaching students multiple ways to solve math problems instead of using a single method improves teaching and learning. In an interview with the Gazette, Star, a former math teacher, outlined the research and explained how anyone, with the right instruction, can develop a knack for numbers.

Jon R. Star

GAZETTE: What is the most common misconception about math learning?

STAR: That you’re either a math person or you’re not a math person — that some people are just born with math smarts, and they can do math, and other people are just not, and there’s not much you can do about it.

GAZETTE: What does science say about the process of learning math?

STAR: One thing we know from psychology about the learning process is that the act of reaching into your brain, grabbing some knowledge, pulling it out, chewing on it, talking about it, and putting it back helps you learn. Psychologists call this elaborative encoding. The more times you can do that process — putting knowledge in, getting it out, elaborating on it, putting it back in — the more you will have learned, remembered, and understood the material. We’re trying to get math teachers to help students engage in that process of elaborative encoding.

GAZETTE: How did you learn math yourself?

STAR: Learning math should involve some sense-making. It’s necessary that we listen to what our teacher tells us about the math and try to make sense of it in our minds. Math learning is not about pouring the words directly from the teacher’s mouth into the students’ ears and brains. That’s not the way it works. I think that’s how I learned math. But that’s not how I hope students learn math and that’s not how I hope teachers think about the teaching of math. Teachers should teach math in a way that encourages students to engage in sense-making and not merely to memorize or internalize exactly what the teacher says or does.

GAZETTE: Tell us about the teaching method described in the research.

STAR: One of the strategies that some teachers may use when teaching math is to show students how to solve problems and expect that the student is going to end up using the same method that the teacher showed. But there are many ways to solve math problems; there’s never just one way.

The strategy we developed asks that teachers compare two ways for solving a problem, side by side, and that they follow an instructional routine to lead a discussion to help students understand the difference between the two methods. That discussion is really the heart of this routine because it is fundamentally about sharing reasoning: Teachers ask students to explain why a strategy works, and students must dig into their heads and try to say what they understand. And listening to other people’s reasoning reinforces the process of learning.

GAZETTE: Why is this strategy an improvement over just learning a single method?

STAR: We think that learning multiple strategies for solving problems deepens students’ understanding of the content. There is a direct benefit to learning through comparing multiple methods, but there are also other types of benefits to students’ motivation. In this process, students come to see math a little differently — not just as a set of problems, each of which has exactly one way to solve it that you must memorize, but rather, as a terrain where there are always decisions to be made and multiple strategies that one might need to justify or debate. Because that is what math is.

For teachers, this can also be empowering because they are interested in increasing their students’ understanding, and we’ve given them a set of tools that can help them do that and potentially make the class more interesting as well. It’s important to note, too, that this approach is not something that we invented. In this case, what we’re asking teachers to do is something that they do a little bit of already. Every high school math teacher, for certain topics, is teaching students multiple strategies. It’s built into the curriculum. All that we’re saying is, first, you should do it more because it’s a good thing, and second, when you do it, this is a certain way that we found to be especially effective, both in terms of the visual materials and the pedagogy. It’s not a big stretch for most teachers. Conversations around ways to teach math for the past 30 or 40 years, and perhaps longer, have been emphasizing the use of multiple strategies.

GAZETTE: What are the potential challenges for math teachers to put this in practice?

STAR: If we want teachers to introduce students to multiple ways to solve problems, we must recognize that that is a lot of information for students and teachers. There is a concern that there could be information overload, and that’s very legitimate. Also, a well-intentioned teacher might take our strategy too far. A teacher might say something like, “Well, if comparing two strategies is good, then why don’t I compare three or four or five?” Not that that’s impossible to do well. But the visual materials you would have to design to help students manage that information overload are quite challenging. We don’t recommend that.

Share this article

You might like.

Research finds low-cost, online program yields significant results

Historian traces 19th-century murder case that brought together historical figures, helped shape American thinking on race, violence, incarceration

National security analysts outline stakes ahead of July summit

When should Harvard speak out?

Institutional Voice Working Group provides a roadmap in new report

Women who follow Mediterranean diet live longer

Large study shows benefits against cancer, cardiovascular mortality, also identifies likely biological drivers of better health

Had a bad experience meditating? You're not alone.

Altered states of consciousness through yoga, mindfulness more common than thought and mostly beneficial, study finds — though clinicians ill-equipped to help those who struggle

• Open access
• Published: 19 December 2019

Problematizing teaching and learning mathematics as “given” in STEM education

• Yeping Li 1 &
• Alan H. Schoenfeld 2  

International Journal of STEM Education volume  6 , Article number:  44 ( 2019 ) Cite this article

109k Accesses

85 Citations

25 Altmetric

Metrics details

Mathematics is fundamental for many professions, especially science, technology, and engineering. Yet, mathematics is often perceived as difficult and many students leave disciplines in science, technology, engineering, and mathematics (STEM) as a result, closing doors to scientific, engineering, and technological careers. In this editorial, we argue that how mathematics is traditionally viewed as “given” or “fixed” for students’ expected acquisition alienates many students and needs to be problematized. We propose an alternative approach to changes in mathematics education and show how the alternative also applies to STEM education.

Introduction

Mathematics is commonly perceived to be difficult (e.g., Fritz et al. 2019 ). Moreover, many believe “it is ok—not everyone can be good at math” (Rattan et al. 2012 ). With such perceptions, many students stop studying mathematics soon after it is no longer required of them. Giving up learning mathematics may seem acceptable to those who see mathematics as “optional,” but it is deeply problematic for society as a whole. Mathematics is a gateway to many scientific and technological fields. Leaving it limits students’ opportunities to learn a range of important subjects, thus limiting their future job opportunities and depriving society of a potential pool of quantitatively literate citizens. This situation needs to be changed, especially as we prepare students for the continuously increasing demand for quantitative and computational literacy over the twenty-first century (e.g., Committee on STEM Education 2018 ).

The goal of this editorial is to re-frame issues of change in mathematics education, with connections to science, technology, engineering, and mathematics (STEM) education. We are hardly the first to call for such changes; the history of mathematics and philosophy has seen ongoing changes in conceptualization of the discipline, and there have been numerous changes in the past century alone (Schoenfeld 2001 ). Yet changes in practice of how mathematics is viewed, taught, and learned have fallen far short of espoused aspirations. While there has been an increased focus on the processes and practices of mathematics (e.g., problem solving) over the past half century, the vast majority of the emphasis is still on what content should be presented to students. It is thus not surprising that significant progress has not been made.

We propose a two-fold reframing. The first shift is to re-emphasize the nature of mathematics—indeed, all of STEM—as a sense-making activity. Mathematics is typically conceptualized and presented as a body of content to be learned and processes to be engaged in, which can be seen in both the NCTM Standards volumes and the Common Core Standards. Alternatively, we believe that all of the mathematics studied in K-12 can be viewed as the codification of experiences of both making sense and sense making through various practices including problem solving, reasoning, communicating, and mathematical modeling, and that students can and should experience it that way. Indeed, much of the inductive part of mathematics has been lost, and the deductive part is often presented as rote procedures rather than a form of sense making. If we arrange for students to have the right experiences, the formal mathematics can serve to organize and systematize those experiences.

The second shift is suggested by the first, with specific attention to classroom instruction. Whether mathematics or STEM, the main focus of most instruction has been on the content and practices of the discipline, and what the teacher should do in order to make it accessible to students. Instead, we urge that the main focus should be on the student’s experience of the discipline – on the affordances the environment provides the student for disciplinary sense making. We will introduce the Teaching for Robust Understanding (TRU) Framework, which can be used to problematize instruction and guide needed reframing. The first dimension of TRU (The Discipline) focuses on the re-framing discussed above: is the content conceptualized as something rich and connected that can be experienced and codified in meaningful ways? The second dimension (Cognitive Demand) examines opportunities students have to do that kind of sense-making and codification. The third (Equitable Access to Content) examines who has such opportunities: is there equitable access to the core ideas? Dimension 4 (Agency, Ownership, and Identity) asks, do students encounter the discipline in ways that enable them to see themselves as sense makers, building both agency and positive disciplinary identities? Finally, dimension 5 (Formative Assessment) asks, does instruction routinely use formative assessment, allowing student thinking to become public so that instruction can be adjusted accordingly?

We begin with a historical background, briefly discussing different views regarding the nature of mathematics. We then problematize traditional approaches to mathematics teaching and learning. Finally, we discuss possible changes in the context of STEM education.

Knowing the background: the development of conceptions about the nature of mathematics

The scholarly understanding of the nature of mathematics has evolved over its long history (e.g., Devlin 2012 ; Dossey 1992 ). Explicit discussions regarding the nature of mathematics took place among Greek mathematicians from 500 BC to 300 AD (see, https://en.wikipedia.org/wiki/Greek_mathematics ). In contrast to the primarily utilitarian approaches that preceded them, the Greeks pioneered the study of mathematics for its own sake and pursued the development and use of generalized mathematical theories and proofs, especially in geometry and measurement (Boyer 1991 ). Different perspectives about the nature of mathematics were gradually developed during that time. Plato perceived the study of mathematics as pursuing the truth that exists in external world beyond people’s mind. Mathematics was treated as a body of knowledge, in the ideal forms, that exists on its own, which human’s mind may or may not sense. Aristotle, Plato’s student, believed that mathematicians constructed mathematical ideas as a result of the idealization of their experience with objects (Dossey 1992 ). In this perspective, Aristotle emphasized logical reasoning and empirical realization of mathematical objects that are accessible to the human senses. The two schools of thought that evolved from Plato’s and Aristotle’s contrasting conceptions of the nature of mathematics have had important implications for the ensuing development of mathematics as a discipline, and for mathematics education.

Several more schools of thought were developed as mathematicians tackled new problems in mathematics (Dossey 1992 ). Davis and Hersh ( 1980 ) provides an entertaining and informative account of these developments. Three major schools of thought in the early 1900s dealt with paradoxes in the real number system and the theory of sets: (1) logicism, as an outgrowth of the Platonic school, accepts the external existence of mathematics and emphasizes the form rather than the interpretation in a specific setting; (2) intuitionism, as influenced by Aristotle’s ideas, only accepts the mathematics to be developed from the natural numbers forward via “valid” patterns of mental reasoning (not empirical realization in Aristotle’s thought); and (3) formalism, also aligned with Aristotle’s ideas, builds mathematics upon the formal axiomatic structures to free mathematics from contradictions. These three schools of thought are similar in that they view the contents of mathematics as products , but they differ in whether products are viewed as pre-existing or created through experience. The development of these three schools of thought illustrates that the view of mathematics as products has its long history in mathematics.

With the gradual development of school mathematics since 1900s (Stanic and Kilpatrick 1992 ), the conception of the nature of mathematics has increasingly received attention from mathematics educators. Which notion of mathematics mathematics education adopts and uses has a direct and strong impact on the way of school mathematics being presented and approached in education. Although the history of school mathematics is relatively short in comparison with mathematics itself, we can find ample examples about the influence of different views of mathematics on curriculum and classroom instruction in the USA and other education systems (e.g., Dossey et al. 2016 ; Li and Lappan 2014 ; Li, Silver, and Li 2014 ; Stanic and Kilpatrick 1992 ). For instance, the “New Math” movement of 1950s and 1960s used the formalism school of thought as the core of reform efforts. The content was presented in a structural format, using the set theoretic language and conceptions. But the result was not a successful progression toward a school mathematics that is best for students and teachers (e.g., Kline 1973 ). Alternatively, Dossey ( 1992 ), in his review of the nature of mathematics, identified and selected scholars’ works and ideas applicable to both professional mathematicians and mathematics educators (e.g., Davis and Hersh 1980 ; Hersh 1986 ; Tymoczko 1986 ). Those scholars' ideas rested on what professional mathematicians do, not what mathematicians think about what mathematics is. Dossey ( 1992 ) specifically cited Hersh ( 1986 ) to emphasize mathematics is about ideas and should be accepted as a human activity, not strictly governed by any one school of thought.

Devlin ( 2000 ) argued that mathematics is not a single entity but has four different faces: (1) computation, formal reasoning, and problem solving; (2) a way of knowing; (3) a creative medium; and (4) applications. Further, he contended school mathematics typically focuses on the first face, makes some reference to the fourth face, but pays almost no attention to the other two faces. His conception of mathematics assembles ideas from the history of mathematics and observes mathematical activities occurring across different settings.

Our brief review shows that the nature of mathematics can be understood as having different faces, rather than being governed by any single school of thought. At the same time, the ideas of Plato and Aristotle continue to influence the ways that mathematicians, mathematics educators, and the general public perceive mathematics. Despite nearly a half century of process-oriented research (see below), let alone Pólya’s work on problem solving, mathematics is still perceived of largely as products —a body of knowledge as highlighted in the three schools (logicist, intuitionist, formalist) of thought, rather than ideas that call for active thinking and creation. The evolving conceptions about the nature of mathematics in history suggests there is room for us to decide how mathematics can be perceived, rather than being bounded by a pre-occupied notion of mathematics as “given” or “fixed.” Each and every learner can experience mathematics through different practices and “own” mathematics as a human activity.

Problematizing what is important for students to learn in and through mathematics

The evolving conceptions about the nature of mathematics suggest that choices exist when deciding what and how to teach and learn mathematics but they do not specify what and how to make the choice. Decisions require articulating options for conceptions of what is important for students to learn in and through mathematics and evaluating the advantages and drawbacks for the students for each option.

According to Stanic and Kilpatrick ( 1992 ), the history of school mathematics curricula presents two important and real changes over the years: one is at the turn of the twentieth century when school mathematics was reformed as a unified and applied curriculum to accommodate dramatically increased student populations from diverse backgrounds, and the other is the “New Math” movement of the 1950s and 1960s, intended to integrate modern mathematics into school curriculum. The perceived failure of the “New Math” movement led to the “Back to Basics” movement in the 1970s, followed by “Problem Solving” in the 1980s, and then the Curriculum Standards movement in the 1990s and after. The history shows school mathematics curricula have emphasized teaching and learning mathematical knowledge and skills, together with problem solving and some applications of mathematics, a picture that is consistent with what Devlin ( 2000 ) refers to as the 1st face and some reference to the 4th face of mathematics.

Therefore, although there have been reforms in mathematics curriculum and instruction, there are hardly real changes in how mathematics is conceptualized and presented in school education in the USA (Stanic and Kilpatrick 1992 ) and other education systems (e.g., Leung and Li 2010 ; Li and Lappan 2014 ). The dominant conception remains mathematics as products , frequently referring to a body of static knowledge and skills that need to be learned and acquired (Fisher 1990 ). This continues to be largely the case in practice, despite advances in conceptualization (see below).

It should be noted that conceptualizing mathematics as “a body of knowledge and skills” is not wrong, especially with such a long history of knowledge creation and accumulation in mathematics, but it is not adequate for school mathematics nowadays. The set of concepts and procedures, after years of development, exceeds what could be covered in any school curricula. Moreover, this body of knowledge and skills keeps growing, as the product of human intelligence and scholarship in mathematics. Devlin ( 2012 ) pointed out that school mathematics mainly covers what was developed in the Greek mathematics, plus just two further advances from the seventh century: calculus and probability theory. It is no wonder if someone questions the value of learning such a small set of knowledge and skills developed more than a thousand years ago. Meanwhile, this body of knowledge and skills are often abstract, static, and “foreign” to many students and teachers who learned to perceive mathematics as an external entity in existence (Plato’s notion) rather than Aristotelian emphasis on experimentation (Cooney 1987 ). It is thus not surprising for so many students and teachers to claim that mathematics is difficult (e.g., Fritz et al. 2019 ) and “it is ok—not everyone can be good at math” (Rattan et al. 2012 ).

What can be made meaningful should be critically important to those who want to (or need to) learn and teach mathematics. In fact, there is significant evidence that students often try to make sense of mathematics that is “presented” or “given” to them, although they made numerous errors that can be decoded to study their thinking (e.g., Ashlock 2010 ). Indeed, misconceptions are best thought of not as errors that need to be “fixed,” but as plausible abstractions on the basis of what students have learned—i.e., attempts at sense-making (Smith et al. 1993 ). Conceiving mathematics as about “ideas,” we can help students to play, own, experience, and think about some key ideas just like what they do in many other activities, such as game play (Gee 2005 ). Definitions of concepts and formal languages and procedures can be postponed until students are ready to consider why and how they are needed. Mathematics should be taken and accepted as a human activity (Dossey 1992 ), and developing students’ mathematical thinking (about ideas) should be emphasized in learning mathematics itself (Devlin 2012 ) and in STEM (Li et al. 2019a ).

Along with the shift from products to ideas in mathematics, scholars have already focused on how people work with ideas in mathematics. Elaborated in detail by Schoenfeld ( in press ), the revolution began with George Pólya (1887–1985) who had a fundamental interest in having students learn and understand content via problem solving. For Pólya, mathematics was about inquiry, sense making, and understanding how and why mathematical ideas (instead of content as products) fit together the way they do. The call for problem solving in the 1980s in the USA was (at least partially) inspired by Pólya’s ideas after a decade of “back to basics” in the 1970s. It has been recognized since that the practices of mathematics (including problem solving) are every bit as important as the content itself, and the two shouldn’t be separated. In the follow-up standards movement, the content and practices have been the “warp and weave” of the fabric doing mathematics, as articulated in Principles and Standards for School Standards (NCTM 2000 ). There were five content standards and five process standards (i.e., problem solving, reasoning, connecting, communicating, representing). It is widely acknowledged, also in the Common Core State Standards in the USA (CCSSI 2010 ), that both content and processes/practices are essential and they form the base for next steps.

Problematizing how mathematics is taught and learned, with connections to STEM education

How the ways that mathematics is often taught cause concerns.

Conceiving mathematics as a body of facts and procedures to be “mastered” has been long-standing in mathematics education practice, and it often results in students’ learning by rote memorization. For example, Schoenfeld ( 1988 ) provided a detailed account of the disasters of a “well-taught” mathematics course, documenting a 10th-grade geometry class taught by a confident and experienced teacher. The teacher taught and managed his class well, and his students also did well on standardized examinations, which focused on content and procedures. At the same time, however, Schoenfeld pointed out that the students developed counterproductive views of mathematics. Although the students developed some level of proficiency in content and procedures, they gained (or were reinforced in) the kinds of beliefs about mathematics as being fragmented and disconnected. Schoenfeld argued that the course led students to develop a robust and counterproductive set of beliefs about the nature of geometry.

Seeking possible origins about students’ counterproductive beliefs about mathematics from mathematics instruction motivated Schoenfeld’s study (Schoenfeld 1988 ). Such an intuitive motivation is also evident in other studies. Keitel ( 2006 ) compared the lessons of two teachers (T1 and T2) in Germany who taught their classes very differently. T1 regularly taught the class emphasizing routine individual practice and memorization of specific algebraic rules. T1 emphasized the importance of such practices for test taking, and the students followed his instruction. Even when T1 one day introduced a non-routine problem that connects algebra and geometry, the overwhelming emphasis on mastering routines and algorithms seemed to overshadow in dealing such a non-routine problem. In contrast, T2’s teaching emphasized students’ initiatives and collaboration, although T2 also used formal routine tasks. At the end, students in T2’s class reported positively about their experience, enjoyed working together, and appreciated the opportunities of thinking mathematically. Studies by Schoenfeld ( 1988 ) and Keitel ( 2006 ) indicate how students’ experience in mathematics classes influences their perceptions of mathematics and also imply the importance of learning about teachers’ perceptions of mathematics that likely guide their instructional practice (Cooney 1987 ).

Rattan et al. ( 2012 ) found that teachers with different perceptions of mathematics teach differently. Specifically, Rattan et al. looked at these teachers holding an entity (fixed) theory of mathematics intelligence (G1) versus incremental theory (G2). Through their studies, Rattan and colleagues found that G1 teachers more readily judged students to have low ability, comforted students for low mathematical ability, and used “kind” strategies (e.g., assigning less homework) unlikely to promote their engagement with the field than G2 teachers. Students who received comfort-oriented feedback perceived their teachers’ entity theory and low expectations and reported lowered motivation and expectations for their own performance. The results suggest how teachers’ inadequate perceptions of mathematics and beliefs about the nature of students’ mathematical intelligence contributed to low achievement, diminished self-esteem and viewed mathematics is only a set of static facts and procedures. Further, the results suggest that how mathematics is taught influences more than students’ proficiency with mathematics content in a class. Sun ( 2018 ) made a similar argument after synthesizing existing literature and analyzing classroom observation data.

Based on the 2012 US national survey of science and mathematics education conducted by Horizon Research, Banilower et al. ( 2013 ) reported that a vast majority of mathematics teachers, from 81% at the high school level to 90% at the elementary level, believe that students should be given definitions of new vocabulary at the beginning of instruction on a mathematical idea. Also, many teachers believe that they should explain an idea to students before having them consider evidence for it and that hands-on activities should be used primarily to reinforce ideas students have already learned. The report suggests many teachers emphasized pedagogical practices of “give” and “present,” perhaps influenced by conceptions of mathematics that are more Platonic than Aristotelian, similar to what was reported about teachers’ practices more than two decades ago (Cooney 1987 ).

How to change?

Given that the evidence demonstrates a compelling case for changing how mathematics is taught, we turn our attention to suggesting how to realize this transformation. Changing how mathematics is taught and learned is not a new endeavor for both mathematics educators and mathematicians (e.g., Li, Silver, and Li 2014 ; Schoenfeld in press ). For example, the “Moore Method,” developed and used by Robert Lee Moore (a famous topologist) in the early twentieth century, shifted instruction from teacher-centered lecturing to student-centered mathematical development (Coppin et al. 2009 ). In its purest form, students were presented with mathematical definitions and asked to develop and/or prove theorems from them after class, without reading mathematics books or using other resources. When students returned to the class, they were asked to prove a theorem. As a result, students developed the mathematics themselves, instead of the instructor presenting the proofs and doing the mathematics for students. The method has had its own success in producing many great mathematicians; however, the high-pressure environment also drowned many students who might have been successful otherwise (Schoenfeld in press ).

Although the “Moore Method” was used primarily in advanced mathematics courses at the post-secondary level, it illustrates how a different conception of mathematics led to a different instructional approach in which students developed mathematics. However, it might be the opposite end of a spectrum, in comparison to approaches that present mathematics to students in accommodating and easy-to-digest ways that can be as much easy as possible. Neither extreme is a good option for K-12 students. Again, it becomes important for us to consider options that can support the value of learning mathematics.

Our discussion in the previous section highlights the importance of taking mathematics as a human activity, ensuring it is meaningful to students, and developing students’ mathematical thinking about ideas, rather than simply absorbing a set of static and disconnected knowledge and skills. We call for a shift in teaching mathematics based on Platonic conceptions to approaches based on more of Aristotelian conceptions. In essence, Plato emphasized ideal forms of mathematical objects, perhaps inaccessible through people’s sense making efforts. As a result, learners lack ownership of the ideal forms of mathematical objects, because mathematical objects cannot and should not be created by human reasoning. In contrast, Aristotle emphasized that mathematical objects are developed through logic reasoning and empirical realization. In other words, mathematical objects exist only when they can be sensed and verified by people's efforts. This differs from Plato’s passive perspective, highlights human ownership of mathematical ideas and encourages people to make mathematics make sense, termed as making sense by McCallum ( 2018 ). Aristotelian conceptions view mathematics as objects that learners can actively develop and structure as mathematically meaningful, which is more in line with what research mathematicians do. McCallum ( 2018 ) argued that both sense-making and making-sense stances are needed for a complete view of mathematics and learning, recognizing that not attending to both stances carries risks. “Just as it is a risk of the sense-making stance that the mathematics gets ignored, it is a risk of the making-sense stance that the sense-maker gets ignored.” (McCallum 2018 ).

In addition, there is the issue of personal identity: if students come to avoid mathematics because they are uncomfortable with it (in fact, mathematics anxiety has become a widespread problem for all ages across the globe, see Luttenberger et al. 2018 ) then mathematics instruction has failed them, regardless of test scores.

In the following, we discuss sense-making and making-sense stances first with specific examples from mathematics. Then, we discuss connections to STEM education.

Sense making is much more than the acquisition of knowledge and skills

Sense making has long been emphasized in mathematics education community. William A. Brownell is a well-known, early 20 th century scholar who advocated the value of sense making in the learning of mathematics. For example, Brownell ( 1945 ) discussed how arithmetic can and should be taught and learned not only as procedures, but also as a meaningful system of thinking. He shared many examples like the following division,

Brownell suggested to ask questions: what does the 5 of 576 mean? Why must 57 be the first partial dividend? Do you actually divide 8 into 57, or into 57…’s? etc., instead of simply letting students memorize how to carry out the procedure. What Brownell advocated has been commonly accepted and emphasized in mathematics education nowadays as sense making (e.g., Schoenfeld 1992 ).

There can be different ways of sense making of the same computation. As an example, the sense making process for the above long division can come out with mental math as: I am looking to see how close I can get to 570 with multiples of 80; 7 multiples of 80 gives me 560, which is close. Of course, given base 10 notation, that’s the same as 8 multiples of 70, which is why the 7 goes over the 57. And when I subtract 560, there are 16 left over, so that’s another 2 8 s. Such a sense-making process also works, as finding the answer (quotient, k ) of 576 ÷ 8 is the same operation as to find k that satisfies 576 = k × 8. In mathematics, division and multiplication are alternate but equivalent ways of doing the same operation.

To help students build numerical reasoning and make sense of computations, many teachers use number talks in their classrooms for students to practice and share these mental math and computation strategies (e.g., Parrish 2011 ). In fact, new terms are being created and used in mathematics education about sense making, such as number sense (e.g., Sowder 1992 ) and symbol sense (Arcavi, 1994 ). Some instructional programs, such as Cognitively Guided Instruction (see, e.g., Carpenter et al., 1997 , 1998 ), make sense making the core of instructional activities. We argue that such activities should be more widely adopted.

Making sense makes the other side of mathematical practice visible, and values idea development and ownership

The making-sense stance, as termed by McCallum ( 2018 ), is not commonly practiced as it is pertinent to expert mathematician’s practices. Where sense making (as discussed previously) emphasizes the process of making sense of what is being learned, making sense emphasizes the process of making mathematics make sense. Making sense highlights the importance for students to experience mathematics through creating, designing, developing, and connecting mathematical ideas. As an example, for the above division computation, 8 \( \overline{\Big)576\ } \) , students may wonder why the division procedure is performed from left to right, which is different from the other operations (addition, subtraction, and multiplication) that are all performed from right to left. In fact, students can be encouraged to explore if the division can also be performed from right to left (i.e., starting from the one’s place). They may discover, with possible support from the teacher, that the division can be done in this way. However, once the division is moved to the high-value places, it will require the process to go back down to the low-value places for completion. In other words, the division process starting from the low-value place would require repeated processes of returning to the low-value places; as a result, it is inefficient. As mathematical procedure is designed to improve efficiency, the division procedure is thus set to be carried out from the high-value place to low-value place (i.e., from left to right). Students who work this out experience mathematics more deeply than the sense-making described by Brownell ( 1945 ).

There are plenty of making-sense opportunities in classroom instruction. For example, kindergarten children are often given opportunities to play with manipulatives like cube trains and snub cubes, to explore and learn about patterns, numbers, and measurement through various connections. The recording of such activities typically results in numerical expressions or operations of these connections. In addition, such activities can also serve as a context to encourage students to design and create a way of “recording” these connections directly with a drawing line next to the connected train cubes. Such a design activity will help students to develop the concept of a number line that includes the original/starting point, unit, and direction (i.e., making mathematics make sense), instead of introducing the number line to students as a mathematical concept being “given” years later.

Learning how to provide students with opportunities to develop mathematics may occur with experience. Huang et al. ( 2010 ) found that expert and novice teachers in China both valued students’ mastering of mathematical knowledge and skills and their development in mathematical thinking methods and abilities. However, novice teachers were particularly concerned about the effectiveness of their guidance, in contrast to expert teachers who emphasized the development of students’ mathematical thinking and higher-order thinking abilities and properly dealing with important and difficult content points. The results suggest that teachers’ perceptions and pedagogical practices can change and improve over time. However, it may be worth asking if support for teacher development would accelerate the process.

Connecting changes in mathematics and STEM education

Although it is commonly acknowledged that mathematics is foundational to STEM, mathematics is being related to STEM education at a distance in practice and also in scholarship development (English 2016 , see additional notes at the end of this editorial). Holding the conception of mathematics as products does not support integrating mathematics with other STEM disciplines, as mathematics can be perceived simply as a set of tools for these disciplines. At the same time, mathematics and science have often proceeded along parallel tracks, with mathematics focused on “problem solving” while science has focused on “inquiry.” To better connect mathematics and other disciplines in STEM, we should focus on ideas and thinking development in mathematics (Li et al. 2019a ), unifying instruction from the student perspective (the Teaching for Robust Understanding framework, discussed below).

Emphasizing both sense making and making sense in mathematics education opens opportunities for connections with similar practices in other STEM disciplines. For example, sense making is very much emphasized in science education (Hogan 2019 ; Kapon 2017 ; Odden and Russ 2019 ), often combined with reflections in engineering (Kilgore et al. 2013 ; Turns et al. 2014 ), and also in the context of using technology (e.g., Antonietti and Cantoia 2000 ; Dick and Hollebrands 2011 ). Science is fundamentally about discovery and understanding of the natural world. This notion provides a natural link to mathematical modeling (e.g., Burkhardt 1981 ). Beyond that, in science education, sense making places a heavy focus on the construction and evaluation of explanation (Kapon 2017 ), and can even be defined as a process of constructing an explanation to resolve a perceived gap or conflict in knowledge (Odden and Russ 2019 ). Design and making play vital roles in engineering and technology education (Dym et al., 2005 ), as is student reflection on these experiences (e.g., Turns et al. 2014 ). Indeed, STEM disciplines share the same conceptual process of sense making as learners, individually or in a group, actively engage with the natural or man-made world, explore it, and then develop, test, refine, and use ideas together with specific explanation. If mathematics was conceived as an “empirical” discipline, connections with other STEM disciplines would be strengthened. In philosophical terms, Lakatos ( 1976 ) made similar claims Footnote 1 .

Similar to the emphasis on sense making placed in the Mathematics Curriculum Standards (e.g., NCTM, 1989 , 2000 ), Next Generation Science Standards (NGSS Lead States 2013 ) prompted a shift in science education away from simply knowing science content and procedures to practicing and using science, together with engineering, to make sense of the world and create the future. In a review, Fitzgerald and Palincsar ( 2019 ) concluded sense making is a productive lens for investigating and characterizing great teaching across multiple disciplines.

Mathematics has stronger linkages to creation and design than traditionally imagined. Therefore, its connections to engineering and technology could be much stronger. However, the deep-rooted conception of mathematics as products has traditionally discouraged students and teachers from considering and valuing design and design thinking (Li et al. 2019b ). Conceiving mathematics as making sense should help promote conceptual changes in mathematical practice to value idea generation and design activity. Connections generated from such a shift will support teaching and learning not only in individual STEM disciplines, but also in integrated STEM education.

At the same time, although STEM education as a commonly recognized field does not have a long history (Li 2014 , 2018a ), its rapid development can help introduce ideas for exploring how mathematics can be taught and learned. For example, the concept of projects is common in engineering professional practice, and the project-based learning (PjBL) as an instructional approach is a key component in some engineering programs (e.g., Berger 2016 ; de los Ríos et al. 2010 ; Mills and Treagust 2003 ). de los Ríos et al. ( 2010 ) highlighted three main advantages of PjBL: (1) development in technical, personal, and contextual competences; (2) students’ engagement with real problems from professional contexts; and (3) collaborative learning facilitated through the integration of teaching and research. Such advantages are important for students’ learning of mathematics and are aligned well with efforts to develop 21 st century skills, including problem solving, communication, collaboration, and critical thinking.

Design-based learning (DBL) is another instructional approach commonly used in engineering and technology fields. Gómez Puente et al. ( 2013 ) conducted a sampled review and concluded that DBL projects consist of open-ended, hands-on, authentic, and multidisciplinary design tasks. Teachers using DBL facilitate both the process for students to gain domain-specific knowledge and thinking activities to generate innovative solutions. Such features could be adapted for mathematics education, especially integrated STEM education, in concert with design and design thinking. In addition to a few examples discussed above about making sense in mathematics, there is a growing body of publications developed by and for mathematics teachers with specific examples of investigations, design projects, and instructional activities associated with STEM (Li et al. 2019b ).

A framework for helping students to gain important experiences in and through mathematics, as connected to other disciplines in STEM

For observing and evaluating classroom instruction in general and mathematics classroom instruction in specific, there are several widely used frameworks and rubrics available. However, a trial use of selected frameworks with sampled mathematics classroom instruction episodes suggested their disagreements on what counts as high-quality instruction, especially with aspects on disciplinary thinking being valued and relevant classroom practices (Schoenfeld et al. 2018 ). The results suggest the importance of choice making, when we consider a framework in discussing and evaluating teaching practices.

Our discussion above highlights the importance of shifting away from viewing mathematics simply as a set of static knowledge and skills, to focusing on ideas and thinking development in teaching and learning mathematics. Further discussion of several aspects of changes specifies the needs of developing and using practices associated with sense making, making sense, and connecting mathematics and STEM education for changes.

To support effective mathematics instruction, we propose the use of the Teaching for Robust Understanding (TRU) framework to help characterize powerful learning environments. With the conception of mathematics as “empirical” and a focus on students’ experience, then the focus of instruction should also be changed. We argue that shift is from instruction conceived as “what should the teacher do” to instruction conceived as “what mathematical experiences should students have in order for them to develop into powerful thinkers?” It is the shift in the frame of TRU that makes it so powerful and pertinent for all these proposed changes. Moreover, TRU only uses a small number of actionable dimensions after distilling the literature on teaching for robust or powerful understanding. That makes TRU a practical mechanism for problematizing instruction.

Figure 1 presents the TRU Math framework that identifies five key dimensions along which powerful classroom environments can be characterized: the mathematics; cognitive demand; equitable access; agency, ownership, and identity; and formative assessment. These five dimensions were distilled from an extensive literature review, thus capturing what the literature considers to be essential. They were tested against classroom videotapes and data on student performance, and the results indicated that classrooms that did well on the TRU dimensions produced students who did correspondingly well on tests of mathematical knowledge, thinking, and problem solving (e.g., Schoenfeld 2014 , 2019 ). In brief, the argument regarding the importance of the five dimensions of TRU Math is as follows. First, the quality of the mathematics discussed (dimension 1) is critical. What individual students learn is unlikely to be richer than what they experience in the classroom. Whether individual students’ understanding rises to the level of what is discussed/presented in the classroom depends on other factors, which are captured in the remaining four dimensions. For example, you surely have had the experience, at a lecture, of hearing beautiful content presented, and then not being able to do any of the assigned problems! The remaining four dimensions capture aspects needed to support the development of all students with respect to sense making, making sense, ownership, and feedback loop. Dimension 2: Cognitive Demand. Are students engaged in sense making and making sense? Are they engaged in “productive struggle”? Dimension 3: Equitable Access. Are all students fully engaged with the central content and practices of the domain so that every student can profit from it? Dimension 4: Agency, Ownership, and Identity. Do all students have opportunities to develop idea ownership and mathematical agency? Dimension 5: Formative Assessment. Are students encouraged and supported to share their thinking with a meaningful feedback loop for instructional adjustment and improvement?

The TRU Mathematics Framework: The five dimensions of powerful mathematics classrooms

The first key point about TRU is that students learn more in classrooms that are powerful along the five TRU dimensions. Second, the shift of attention from the teacher to the environment is fundamentally important. The key question is not “Is the teacher doing particular things to support learning?”; instead, it is, “Are students experiencing instruction so that it is conducive to their growth as mathematical thinkers and learners?” Third, the framework is not prescriptive; it respects teacher autonomy. There are many ways to be an excellent teacher. The question is, Does the learning environment created by the teacher provide each student rich opportunities along the five dimensions of the framework? Specifically, in describing the dimensions of powerful instruction, the framework serves to problematize instruction. Asking “how am I doing along each dimension; how can I improve?” can lead to richer instruction without prescribing or imposing a particular style or particular norms on teachers.

Extending to STEM education

Now, we suggest the following. If you teach biology, chemistry, physics, engineering, or any other STEM field, replace “mathematics” in Fig. 1 with your discipline. The first dimension is about rich content and practices in your field. And the remaining four dimensions are about necessary aspects of your students’ classroom engagement with the discipline. Practices associated with sense making, making sense, and STEM education are all be reflected in these five dimensions, with central attention on students’ experience in such classroom environments. Although the TRU framework was originally developed for characterizing effective mathematics classroom environments, it has been carefully framed in a way that is applicable to many different disciplines (Schoenfeld 2014 ). Our discussion above already specified why sense making, making sense, and specific instructional approaches like PjBL and DBL are shared across disciplines in STEM education. Thus, the TRU framework is applicable to other STEM disciplines. The natural analogue of the TRU framework for any field is given in Fig. 2 .

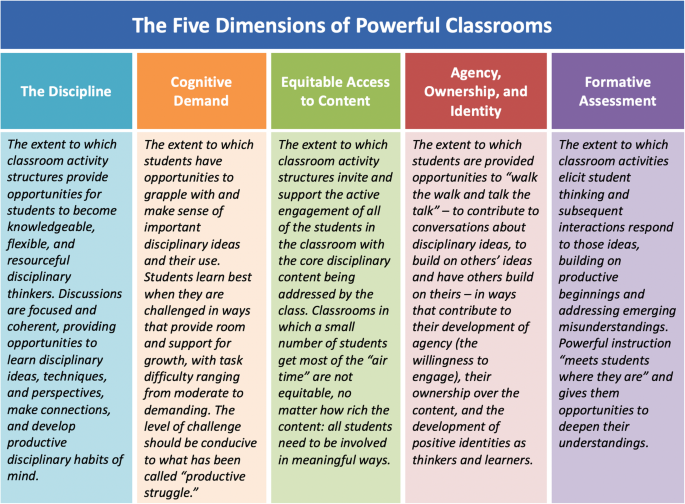
The domain-general version of the TRU framework

Both the San Francisco Unified School District and the Chicago Public Schools adopted the TRU Math framework and found results within mathematics sufficiently promising that they expanded their efforts to all subject areas for professional development and instruction, using the domain-general TRU framework. Work is still in its early stages. Current efforts might be best conceptualized as a laboratory for exploration rather than a promissory note for improvement across all different disciplines. It will take time to accumulate data to show effectiveness. For further information about the domain-general TRU framework and tools for professional development are available at the TRU framework website, https://truframework.org/

Finally, as a framework, TRU is not a set of specific tools or guidelines, although it can be used to guide their development. To help lead our discussion to something more practical, we can use the framework to check and identify aspects that are typically under-emphasized and move them to center stage in order to improve classroom instruction. Specifically, the following is a list of sample under-emphasized norms and practices that can be identified (Schoenfeld in press ).

Establishing a climate of inquiry, in which mathematics is experienced as a discipline of exploration and sense making.

Developing students’ ownership of ideas through the process of developing, sharing, refining, and using ideas; concepts and language can come later.

Focusing on big ideas, and not losing the forest for the trees.

Making student thinking central to classroom discourse.

Ensuring that classroom discourse is respectful and inviting.

Where to start? Begin by problematizing teaching and the nature of learning environments

Here we start by stipulating that STEM disciplines as practiced, are living, breathing fields of inquiry. Knowledge is important; ideas are important; practices are important. The list given above applied to all STEM disciplines, not just mathematics.

The issue, then, is developing teacher capacity to craft environments that have the properties described immediately above. Here we share some thoughts, and the topic itself can well be discussed extensively in another paper. To make changes in teaching, it should start with assessing and changing teaching practice itself (Hiebert and Morris 2012 ). Opening up teachers’ perceptions of teaching practices should not be done by telling teachers what to do!—the same rules of learning apply to teachers as they apply to students. Learning environments for teachers should offer teachers the same opportunities for rich engagement, challenge, equitable access, and ownership as we hope students will experience (Schoenfeld 2015 ). Working together with teachers to study and reflect on their teaching practices in light of the TRU framework, we can help teachers to find out what their students are experiencing and why changes are needed. The framework can also help guide teachers to learn what changes would be needed, and to try out changes to learn how their students’ learning may differ. It is this iterative and concrete process that can hopefully help shift participating teachers’ perceptions of mathematics. Many tools for problematizing teaching are available at the TRU web site (see https://truframework.org/ ). If teachers can work together with a focus on selected lessons like what teachers often do in China, the process would help form a school-based learning community that can contribute to not only participating teachers’ practice change but also their expertise improvement (Huang et al. 2011 ; Li and Huang 2013 ).

As reported before (Li 2018b ), publications in the International Journal of STEM Education show a mix of individual-disciplinary and multidisciplinary education in STEM over the past several years. Although one journal’s publications are limited in its scope of providing a picture about the scholarship development related to mathematics and STEM education, it can allow us to get a sense of related development.

If taking a closer look at the journal’s publications over the past three years from 2016 to 2018, we found that the number of articles published with a clear focus on mathematics is relatively small: three (out of 21) in 2016, six (out of 34) in 2017, and five (out of 56) in 2018. At the same time, we should point out that these publications from 2016 to 2018 seem to reflect a trend, over these three years, of moving toward issues that can go beyond mathematics itself, as what was noted before (Li 2018b ). Specifically, for these three articles published in 2016, they are all about mathematics education at either elementary school (Ding 2016 ; Zhao et al. 2016 ) or university levels (Schoenfeld et al. 2016 ). Out of the six published in 2017, three are on mathematics education (Hagman et al. 2017 ; Keller et al. 2017 ; Ulrich and Wilkins 2017 ) and the other three on either teacher professional development (Borko et al. 2017 ; Jacobs et al. 2017 ) or connection with engineering (Jehopio and Wesonga 2017 ). For the five published in 2018, two are on mathematics education (Beumann and Wegner 2018 ; Wilkins and Norton 2018 ) and the other three have close association with other disciplines in STEM (Blotnicky et al. 2018 ; Hayward and Laursen 2018 ; Nye et al. 2018 ). This trend likely reflects a growing interest, with close connection to mathematics, in both mathematics education community and a broader STEM education community of developing and sharing multidisciplinary and interdisciplinary scholarship.

Availability of data and materials

Not applicable

Interestingly, Lakatos was advised by both Popper and Pólya—his ideas being in some ways a unification of Pólya’s emphasis on mathematics as an empirical discipline and Popper’s reflections on the nature of the scientific endeavor.

Antonietti, A., & Cantoia, M. (2000). To see a painting versus to walk in a painting: An experiment on sense-making through virtual reality. Computers & Education, 34 , 213–223.

Article   Google Scholar  

Arcavi, A. (1994). Symbol sense: Informal sense-making in formal mathematics. For the Learning of Mathematics, 14 (3), 24–35.

Google Scholar  

Ashlock, R. B. (2010). Error patterns in computation (Tenth Edition) . Boston, MA: Allyn & Bacon.

Banilower, E. R., Smith, P. S., Weiss, I. R., Malzahn, K. A., Campbell, K. M., et al. (2013). Report of the 2012 national survey of science and mathematics education. Horizon Research, Chapel Hill, NC. Retrieved from http://www.nnstoy.org/download/stem/2012%20NSSME%20Full%20Report.pdf

Berger, C. (2016). Engineering is perfect for K-5 project-based learning. Engineering is Elementary (EiE) Blog, https://blog.eie.org/engineering-is-perfect-for-k-5-project-based-learning

Beumann, S. & Wegner, S.-A. (2018). An outlook on self-assessment of homework assignments in higher mathematics education. International Journal of STEM Education, 5 :55. https://doi.org/10.1186/s40594-018-0146-z

Blotnicky, K. A., Franz-Odendaal, T., French, F., & Joy, P. (2018). A study of the correlation between STEM career knowledge, mathematics self-efficacy, career interests, and career activities on the likelihood of pursuing a STEM career among middle school students. International Journal of STEM Education, 5 :22. https://doi.org/10.1186/s40594-018-0118-3

Borko, H., Carlson, J., Mangram, C., Anderson, R., Fong, A., Million, S., Mozenter, S., & Villa, A. M. (2017). The role of video-based discussion in model for preparing professional development leaders. International Journal of STEM Education, 4 :29. https://doi.org/10.1186/s40594-017-0090-3

Boyer, C. B. (1991). A history of mathematics (2nd ed.) . New York: Wiley.

Brownell, W. A. (1945). When is arithmetic meaningful? The Journal of Educational Research, 38 (7), 481–498.

Burkhardt, H. (1981). The real world and mathematics . Glasgow: Blackie, reissued Nottingham: Shell Centre Publications.

Carpenter, T., Fennema, E., & Franke, M. (1997). Cognitively guided instruction: A knowledge base for reform in primary mathematics instruction. Elementary School Journal, 97 , 3–20.

Carpenter, T., Franke, M., Jacobs, V. R., & Fennema, E. (1998). A longitudinal study of invention and understanding in children’s multidigit addition and subtraction. Journal for Research in Mathematics Education, 29 (1), 3–20.

Committee on STEM Education, National Science & Technology Council, the White House (2018). Charting a course for success: America’s strategy for STEM education . Washington, DC. https://www.whitehouse.gov/wp-content/uploads/2018/12/STEM-Education-Strategic-Plan-2018.pdf Retrieved on 18 January, 2019.

Common Core State Standards Initiative (CCSSI). (2010). Common core state standards for mathematics . Retrieved from http://www.corestandards.org/Math/Practice

Cooney, T (1987). The issue of reform: What have we learned from yesteryear? In Mathematical Sciences Education Board, The teacher of mathematics: Issues for today and tomorrow (pp. 17-35). Washington, DC: National Academy Press.

Coppin, C. A., Mahavier, W. T., May, E. L., & Parker, E. (2009). The Moore Method . Washington, DC: Mathematical Association of America.

Davis, P., & Hersh, R. (1980). The mathematical experience . Boston: Birkhauser.

de los Ríos, I., Cazorla, A., Díaz-Puente, J. M., & Yagüe, J. L. (2010). Project–based learning in engineering higher education: Two decades of teaching competences in real environments. Procedia Social and Behavioral Sciences, 2 , 1368–1378.

Devlin, K. (2000). The four faces of mathematics. In M. J. Burke & F. R. Curcio (Eds.), Learning Mathematics for a New Century: 2000 Yearbook of the National Council of Teachers of Mathematics (pp. 16–27). Reston, VA: NCTM.

Devlin, K. (2012). Introduction to mathematical thinking. Stanford, CA: The author.

Dick, T. P., & Hollebrands, K. F. (2011). Focus on high school mathematics: Technology to support reasoning and sense making . Reston, VA: NCTM.

Ding, M. (2016). Developing preservice elementary teachers’ specialized content knowledge: The case of associative property. International Journal of STEM Education, 3 , 9 https://doi.org/10.1186/s40594-016-0041-4 .

Dossey, J. A. (1992). The nature of mathematics: Its role and its influence. In D. Grouws (Ed.), Handbook for Research on Mathematics Teaching and Learning (pp. 39–48). New York: MacMillan.

Dossey, J. A., McCrone, S. S., & Halvorsen, K. T. (2016). Mathematics education in the United States 2016: A capsule summary fact book . Reston, VA: The National Council of Teachers of Mathematics.

Dym, C. L., Agogino, A. M., Eris, O., Frey, D. D., & Leifer, L. J. (2005). Engineering design thinking, teaching, and learning. Journal of Engineering Education, 94 (1), 103–120.

English, L. D. (2016). STEM education K-12: Perspectives on integration. International Journal of STEM Education, 3:3, https://doi.org/10.1186/s40594-016-0036-1

Fisher, C. (1990). The research agenda project as prologue. Journal for Research in Mathematics Education, 21 , 81–89.

Fitzgerald, M. S., & Palincsar, A. S. (2019). Teaching practices that support student sensemaking across grades and disciplines: A conceptual review. Review of Research in Education, 43 , 227–248.

Fritz, A., Haase, V. G., & Rasanen, P. (Eds.). (2019). International handbook of mathematical learning difficulties . Cham, Switzerland: Springer.

Gee, J. P. (2005). What would a state of the art instructional video game look like? Innovate: Journal of Online Education, 1 (6) Retrieved from https://nsuworks.nova.edu/innovate/vol1/iss6/1 .

Gómez Puente, S. M., van Eijck, M., & Jochems, W. (2013). A sampled literature review of design-based learning approaches: A search for key characteristics. International Journal of Technology and Design Education . https://doi.org/10.1007/s10798-012-9212-x .

Hagman, J. E., Johnson, E., & Fosdick, B. K. (2017). Factors contributing to students and instructors experiencing a lack of time in college calculus. International Journal of STEM Education, 4 , 12 https://doi.org/10.1186/s40594-017-0070-7 .

Hayward, C. N. & Laursen, S. L. (2018). Supporting instructional change in mathematics: Using social network analysis to understand online support processes following professional development workshops. International Journal of STEM Education, 5 :28. https://doi.org/10.1186/s40594-018-0120-9

Hersh, R. (1986). Some proposals for reviving the philosophy of mathematics . In T. Tymoczko (Ed.), New directions in the philosophy of mathematics (pp. 9–28). Boston: Birkhauser.

Hiebert, J., & Morris, A. K. (2012). Teaching, rather than teachers, as a path toward improving classroom instruction. Journal of Teacher Education, 63 (2), 92–102.

Hogan, M. (2019). Sense-making is the core of NGSS. In Illuminate education blog, https://www.illuminateed.com/blog/2019/03/sense-making-is-the-core-of-ngss/ Accessed 15 Oct 2019.

Huang, R., Li, Y., & He, X. (2010). What constitutes effective mathematics instruction: A comparison of Chinese expert and novice teachers’ views. Canadian Journal of Science, Mathematics and Technology Education, 10 (4), 293-306. https://doi.org/10.1080/14926156.2010.524965

Huang, R., Li, Y., Zhang, J., & Li, X. (2011). Improving teachers’ expertise in mathematics instruction through exemplary lesson development. ZDM – The International Journal on Mathematics Education, 43 (6-7), 805–817.

Jacobs, J., Seago, N., & Koellner, K. (2017). Preparing facilitators to use and adapt mathematics professional development materials productively. International Journal of STEM Education, 4 , 30 https://doi.org/10.1186/s40594-017-0089-9 .

Jehopio, P. J., & Wesonga, R. (2017). Polytechnic engineering mathematics: assessing its relevance to the productivity of industries in Uganda. International Journal of STEM Education, 4 , 16 https://doi.org/10.1186/s40594-017-0078-z .

Kapon, S. (2017). Unpacking sensemaking. Science Education, 101 (1), 165–198.

Keitel, C. (2006). ‘Setting a task’ in German schools: Different frames for different ambitions. In D. Clarke, C. Keitel, & Y. Shimizu (Eds.), Mathematics classrooms in 12 countries: The insiders’ perspective (pp. 37–58). Rotterdam Netherlands: Sense Publishers.

Keller, R. E., Johnson, E., & DeShong, S. (2017). A structural equation model looking at student’s participatory behavior and their success in Calculus I. International Journal of STEM Education, 4 , 24 https://doi.org/10.1186/s40594-017-0093-0 .

Kilgore, D., Sattler, B., & Turns, J. (2013). From fragmentation to continuity: Engineering students making sense of experience through the development of a professional portfolio. Studies in Higher Education, 38 (6), 807–826.

Kline, M. (1973). Why Johnny can’t add: The failure of new math . New York: St. Martin’s.

Lakatos, I. (1976). Proofs and refutations: The logic of mathematical discovery . Cambridge, England: Cambridge University Press.

Book   Google Scholar  

Leung, F. K. S., & Li, Y. (Eds.). (2010). Reforms and issues in school mathematics in East Asia – Sharing and understanding mathematics education policies and practices . Rotterdam, Netherlands: Sense Publishers.

Li, Y. (2014). International Journal of STEM Education – A platform to promote STEM education and research worldwide. International Journal of STEM Education, 1 , 1 https://doi.org/10.1186/2196-7822-1-1 .

Li, Y. (2018a). Journal for STEM Education Research – Promoting the development of interdisciplinary research in STEM education. Journal for STEM Education Research, 1 (1-2), 1–6 https://doi.org/10.1007/s41979-018-0009-z .

Li, Y. (2018b). Four years of development as a gathering place for international researcher and readers in STEM education. International Journal of STEM Education, 5 , 54 https://doi.org/10.1186/s40594-018-0153-0 .

Li, Y., & Huang, R. (Eds.). (2013). How Chinese teach mathematics and improve teaching . New York: Routledge.

Li, Y., & Lappan, G. (Eds.). (2014). Mathematics curriculum in school education . Dordrecht: Springer.

Li, Y., Schoenfeld, A. H., diSessa, A. A., Grasser, A. C., Benson, L. C., English, L. D., & Duschl, R. A. (2019a). On thinking and STEM education. Journal for STEM Education Research, 2 (1), 1–13. https://doi.org/10.1007/s41979-019-00014-x .

Li, Y., Schoenfeld, A. H., diSessa, A. A., Grasser, A. C., Benson, L. C., English, L. D., & Duschl, R. A. (2019b). Design and design thinking in STEM education. Journal for STEM Education Research, 2 (2), 93-104. https://doi.org/10.1007/s41979-019-00020-z .

Li, Y., Silver, E. A., & Li, S. (Eds.). (2014). Transforming mathematics instruction: Multiple approaches and practices . Cham, Switzerland: Springer.

Luttenberger, S., Wimmer, S., & Paechter, M. (2018). Spotlight on math anxiety. Psychology Research and Behavior Management, 11 , 311–322.

McCallum, W. (2018). Sense-making and making sense. https://blogs.ams.org/matheducation/2018/12/05/sense-making-and-making-sense/ Retrieved on October 1, 2019.

Mills, J. E. & Treagust, D. F. (2003). Engineering education – Is problem-based or project-based learning the answer? Australasian Journal of Engineering Education , https://www.researchgate.net/profile/Nathan_Scott2/publication/238670687_AUSTRALASIAN_JOURNAL_OF_ENGINEERING_EDUCATION_Co-Editors/links/0deec53a08c7553c37000000.pdf Retrieved on October 15, 2019.

National Council of Teachers of Mathematics (NCTM). (1989). Curriculum and evaluation standards for school mathematics . Reston, VA: NCTM.

National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics . Reston, VA: NCTM.

NGSS Lead States. (2013). Next generation science standards: For states, by states . Washington, DC: National Academies Press.

Nye, B., Pavlik Jr., P. I., Windsor, A., Olney, A. M., Hajeer, M., & Hu, X. (2018). SKOPE-IT (Shareable Knowledge Objects as Portable Intelligent Tutors): Overlaying natural language tutoring on an adaptive learning system for mathematics. International Journal of STEM Education, 5 , 12 https://doi.org/10.1186/s40594-018-0109-4 .

Odden, T. O. B., & Russ, R. S. (2019). Defining sensemaking: Bringing clarity to a fragmented theoretical construct. Science Education, 103 , 187–205.

Parrish, S. D. (2011). Number talks build numberical reasoning. Teaching Children Mathematics, 18 (3), 198–206.

Rattan, A., Good, C., & Dweck, C. S. (2012). “It’s ok – Not everyone can be good at math”: Instructors with an entity theory comfort (and demotivate) students. Journal of Experimental Social Psychology . https://doi.org/10.1016/j.jesp.2011.12.012 .

Schoenfeld, A. H. (1988). When good teaching leads to bad results: The disasters of “well-taught” mathematics courses. Educational Psychologist, 23 (2), 145–166.

Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense-making in mathematics. In D. Grouws (Ed.), Handbook for Research on Mathematics Teaching and Learning (pp. 334–370). New York: MacMillan.

Schoenfeld, A. H. (2001). Mathematics education in the 20th century. In L. Corno (Ed.), Education across a century: The centennial volume (100th Yearbook of the National Society for the Study of Education) (pp. 239–278). Chicago, IL: National Society for the Study of Education.

Schoenfeld, A. H. (2014). What makes for powerful classrooms, and how can we support teachers in creating them? A story of research and practice, productively interwined. Educational Researcher, 43 (8), 404–412. https://doi.org/10.3102/0013189X1455 .

Schoenfeld, A. H. (2015). Thoughts on scale. ZDM, the International Journal of Mathematics Education, 47 , 161–169. https://doi.org/10.1007/s11858-014-0662-3 .

Schoenfeld, A. H. (2019). Reframing teacher knowledge: A research and development agenda. ZDM – The International Journal on Mathematics Education . https://doi.org/10.1007/s11858-019-01057-5

Schoenfeld, A. H. (in press). Mathematical practices, in theory and practice. ZDM – The International Journal on Mathematics Education .

Schoenfeld, A. H., Floden, R., El Chidiac, F., Gillingham, D., Fink, H., Hu, S., Sayavedra, A., Weltman, A., & Zarkh, A. (2018). On classroom observations. Journal for STEM Educ Res, 1 (1-2), 34–59 https://doi.org/10.1007/s41979-018-0001-7 .

Schoenfeld, A. H., Thomas, M., & Barton, B. (2016). On understanding and improving the teaching of university mathematics. International Journal of STEM Education, 3 , 4 https://doi.org/10.1186/s40594-016-0038-z .

Smith, J., diSessa, A., & Roschelle, J. (1993). Misconceptions reconceived: A constructivist analysis of knowledge in transition. Journal of the Learning Sciences, 3 (2), 115–163.

Sowder, J. (1992). Estimation and number sense. In D. Grouws (Ed.), Handbook for research on mathematics teaching and learning (pp. 371–389). New York: MacMillan.

Stanic, G. M. A., & Kilpatrick, J. (1992). Mathematics curriculum reform in the United States: A historical perspective. International Journal of Educational Research, 17 (5), 407–417.

Sun, K. L. (2018). The role of mathematics teaching in fostering student growth mindset. Journal for Research in Mathematics Education, 49 (3), 330–355.

Turns, J. A., Sattler, B., Yasuhara, K., Borgford-Parnell, J. L., & Atman, C. J. (2014). Integrating reflection into engineering education. Proceedings of 2014 American Society of Engineering Education Annual Conference , Paper ID #9230.

Tymoczko, T. (1986). New directions in the philosophy of mathematics . Boston: Birkhauser.

Ulrich, C., & Wilkins, J. L. M. (2017). Using written work to investigate stages in sixth-grade students’ construction and coordination of units. International Journal of STEM Education, 4 , 23 https://doi.org/10.1186/s40594-017-0085-0 .

Wilkins, J. L. M., & Norton, A. (2018). Learning progression toward a measurement concept of fractions. International Journal of STEM Education, 5 , 27 https://doi.org/10.1186/s40594-018-0119-2 .

Zhao, X., Van den Heuvel-Panhuizen, M., & Veldhuis, M. (2016). Teachers’ use of classroom assessment techniques in primary mathematics education – An explorative study with six Chinese teachers. International Journal of STEM Education, 3 , 19 https://doi.org/10.1186/s40594-016-0051-2 .

Download references

Acknowledgments

Many thanks to Jeffrey E. Froyd for his careful review and detailed comments on an earlier version of this editorial that help improve its readability and clarity. Thanks also go to Marius Jung for his valuable feedback.

Author information

Authors and affiliations.

Texas A&M University, College Station, TX, 77843-4232, USA

University of California at Berkeley, Berkeley, CA, USA

Alan H. Schoenfeld

You can also search for this author in PubMed   Google Scholar

Contributions

Both authors contributed ideas to conceptualize this article. YL took the lead in developing and drafting the article, and AHS reviewed drafts and contributed to revisions. Both authors read and approved the final manuscript.

Corresponding author

Correspondence to Yeping Li .

Ethics declarations

Competing interests.

The authors declare that they have no competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License ( http://creativecommons.org/licenses/by/4.0/ ), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Reprints and permissions

About this article

Cite this article.

Li, Y., Schoenfeld, A.H. Problematizing teaching and learning mathematics as “given” in STEM education. IJ STEM Ed 6 , 44 (2019). https://doi.org/10.1186/s40594-019-0197-9

Download citation

Received : 15 November 2019

Accepted : 19 November 2019

Published : 19 December 2019

DOI : https://doi.org/10.1186/s40594-019-0197-9

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Design-based learning
• Making sense
• Mathematics
• Project-based learning
• Sense making
• STEM education

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Published 2016 Revised 2019

Mathematical Problem Solving in the Early Years: Developing Opportunities, Strategies and Confidence

• familiar contexts
• meaningful purposes
• mathematical complexity.

• which they understand - in familiar contexts,
• where the outcomes matter to them - even if imaginary,
• where they have control of the process,
• involving mathematics with which they are confident.
• taking some from one doll and giving to another, in several moves,
• starting again and dealing, either in ones or twos,
• taking two from each original doll and giving to the new doll,
• collecting the biscuits and crumbling them into a heap, then sharing out handfuls of crumbs.

• brute force: trying to hammer bits so that they fit,
• local correction: adjusting one part, often creating a different problem,
• dismantling: starting all over again,
• holistic review: considering multiple relations or simultaneous adjustments e.g. repairing by insertion and reversal.
• getting a feel for the problem, looking at it holistically, checking they have understood e.g. talking it through or asking questions;
• planning, preparing and predicting outcomes e.g. gathering blocks together before building;
• monitoring progress towards the goal e.g. checking that the bears will fit the houses;
• being systematic, trying possibilities methodically without repetition, rather than at random, e.g. separating shapes tried from those not tried in a puzzle;
• trying alternative approaches and evaluating strategies e.g. trying different positions for shapes;
• refining and improving solutions e.g. solving a puzzle again in fewer moves (Gifford, 2005: 153).
• Getting to grips:     What are we trying to do?    
• Connecting to previous experience:  Have we done anything like this before?
• Planning:      What do we need?
• Considering alternative methods:   Is there another way?
• Monitoring progress:    How does it look so far?
• Evaluating solutions:    Does it work?  How can we check?  Could we make it even better?

• Construction - finding shapes which fit together or balance
• Pattern-making - creating a rule to create a repeating pattern
• Shape pictures - selecting shapes with properties to represent something
• Puzzles - finding ways of fitting shapes to fit a puzzle
• Role-play areas - working out how much to pay in a shop
• Measuring tools - finding out how different kinds of scales work
• Nesting, posting, ordering - especially if they are not obvious
• Robots - e.g. beebots: directing and making routes
• preparing, getting the right number e.g. scissors, paper for creative activities
• sharing equal amounts e.g. at snack time
• tidying up, checking nothing is lost
• gardening and cooking  e.g. working out how many bulbs to plant where, measuring amounts in a recipe using scales or jugs
• games, developing rules, variations and scoring
• PE: organising in groups, timing and recording

• Decision making - what shall we call the new guinea pig?
• Parties, picnics and trips e.g. how much lemonade shall we make?
• Design Projects - the role play area, new outdoor gardens or circuits
• Hiding games - feely bags with shapes, the 'Box' game
• Story problems - e.g. unfair sharing, with remainders and fractions, making things to fit giants or fairies

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 1: Algebra foundations

Unit 2: solving equations & inequalities, unit 3: working with units, unit 4: linear equations & graphs, unit 5: forms of linear equations, unit 6: systems of equations, unit 7: inequalities (systems & graphs), unit 8: functions, unit 9: sequences, unit 10: absolute value & piecewise functions, unit 11: exponents & radicals, unit 12: exponential growth & decay, unit 13: quadratics: multiplying & factoring, unit 14: quadratic functions & equations, unit 15: irrational numbers, unit 16: creativity in algebra.

Top 10 Challenges to Teaching Math and Science Using Real Problems

• Share article

Nine in ten educators believe that using a problem-solving approach to teaching math and science can be motivating for students, according to an EdWeek Research Center survey.

But that doesn’t mean it’s easy.

Teachers perceive lack of time as a big hurdle. In fact, a third of educators—35 percent—worry that teaching math or science through real-world problems—rather than focusing on procedures—eats up too many precious instructional minutes.

Other challenges: About another third of educators said they weren’t given sufficient professional development in how to teach using a real-world problem-solving approach. Nearly a third say reading and writing take priority over STEM, leaving little bandwidth for this kind of instruction. About a quarter say that it’s tough to find instructional materials that embrace a problem-solving perspective.

Nearly one in five cited teachers’ lack of confidence in their own problem solving, the belief that this approach isn’t compatible with standardized tests, low parent support, and the belief that student behavior is so poor that this approach would not be feasible.

The nationally representative survey included 1,183 district leaders, school leaders, and teachers, and was conducted from March 27 to April 14. (Note: The chart below lists 11 challenges because the last two on the list—dealing with teacher preparation and student behavior—received the exact percentage of responses.)

Trying to incorporate a problem-solving approach to tackling math can require rethinking long-held beliefs about how students learn, said Elham Kazemi, a professor in the teacher education program at the University of Washington.

Most teachers were taught math using a procedural perspective when they were in school. While Kazemi believes that approach has merit, she advocates for exposing students to both types of instruction.

Many educators have “grown up around a particular model of thinking of teaching and learning as the teacher in the front of the room, imparting knowledge, showing kids how to do things,” Kazemi said.

To be sure, some teachers have figured out how to incorporate some real-world problem solving alongside more traditional methods. But it can be tough for their colleagues to learn from them because “teachers don’t have a lot of time to collaborate with one another and see each other teach,” Kazemi said.

What’s more, there are limited instructional materials emphasizing problem solving, Kazemi said.

Though that’s changing, many of the resources available have “reinforced the idea that the teacher demonstrates solutions for kids,” Kazemi said.

Molly Daley, a regional math coordinator for Education Service District 112, which serves about 30 districts near Vancouver, Wash., has heard teachers raise concerns that teaching math from a problem-solving perspective takes too long—particularly given the pressure to get through all the material students will need to perform well on state tests.

Daley believes, however, that being taught to think about math in a deeper way will help students tackle math questions on state assessments that may look different from what they’ve seen before.

“It’s myth that it’s possible to cover everything that will be on the test,” as it will appear, she said. “There’s actually no way to make sure that kids have seen every single possible thing the way it will show up. That’s kind of a losing proposition.”

But rushing through the material in a purely procedural way may actually be counterproductive, she said.

Teachers don’t want kids to “sit down at the test and say, ‘I haven’t seen this and therefore I can’t do it,’” Daley said. “I think a lot of times teachers can unintentionally foster that because they’re so urgently trying to cover everything. That’s where the kind of mindless [teaching] approaches come in.”

Teachers may think to themselves: “’OK, I’m gonna make this as simple as possible, make sure everyone knows how to follow the steps and then when they see it, they can follow it,” Daley said.

But that strategy might “take away their students’ confidence that they can figure out what to do when they don’t know what to do, which is really what you want them to be thinking when they go to approach a test,” Daley said.

Data analysis for this article was provided by the EdWeek Research Center. Learn more about the center’s work.

Sign Up for EdWeek Update

Edweek top school jobs.

Sign Up & Sign In

• Skip to main content
• Skip to primary sidebar
• Skip to footer

Additional menu

Khan Academy Blog

Free Math Worksheets — Over 100k free practice problems on Khan Academy

Looking for free math worksheets.

You’ve found something even better!

That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!

Just choose your grade level or topic to get access to 100% free practice questions:

Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.

• Trigonometry

Statistics and probability

High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.

• Addition and subtraction
• Place value (tens and hundreds)
• Addition and subtraction within 20
• Addition and subtraction within 100
• Addition and subtraction within 1000
• Measurement and data
• Counting and place value
• Measurement and geometry
• Place value
• Measurement, data, and geometry
• Add and subtract within 20
• Add and subtract within 100
• Add and subtract within 1,000
• Money and time
• Measurement
• Intro to multiplication
• 1-digit multiplication
• Addition, subtraction, and estimation
• Intro to division
• Understand fractions
• Equivalent fractions and comparing fractions
• More with multiplication and division
• Arithmetic patterns and problem solving
• Quadrilaterals
• Represent and interpret data
• Multiply by 1-digit numbers
• Multiply by 2-digit numbers
• Factors, multiples and patterns
• Add and subtract fractions
• Multiply fractions
• Understand decimals
• Plane figures
• Measuring angles
• Area and perimeter
• Units of measurement
• Decimal place value
• Add decimals
• Subtract decimals
• Multi-digit multiplication and division
• Divide fractions
• Multiply decimals
• Divide decimals
• Powers of ten
• Coordinate plane
• Algebraic thinking
• Converting units of measure
• Properties of shapes
• Ratios, rates, & percentages
• Arithmetic operations
• Negative numbers
• Properties of numbers
• Variables & expressions
• Equations & inequalities introduction
• Data and statistics
• Negative numbers: addition and subtraction
• Negative numbers: multiplication and division
• Fractions, decimals, & percentages
• Rates & proportional relationships
• Expressions, equations, & inequalities
• Numbers and operations
• Solving equations with one unknown
• Linear equations and functions
• Systems of equations
• Geometric transformations
• Data and modeling
• Volume and surface area
• Pythagorean theorem
• Transformations, congruence, and similarity
• Arithmetic properties
• Factors and multiples
• Reading and interpreting data
• Negative numbers and coordinate plane
• Ratios, rates, proportions
• Equations, expressions, and inequalities
• Exponents, radicals, and scientific notation
• Foundations
• Algebraic expressions
• Linear equations and inequalities
• Graphing lines and slope
• Expressions with exponents
• Quadratics and polynomials
• Equations and geometry
• Algebra foundations
• Solving equations & inequalities
• Working with units
• Linear equations & graphs
• Forms of linear equations
• Inequalities (systems & graphs)
• Absolute value & piecewise functions
• Exponents & radicals
• Exponential growth & decay
• Quadratics: Multiplying & factoring
• Quadratic functions & equations
• Irrational numbers
• Performing transformations
• Transformation properties and proofs
• Right triangles & trigonometry
• Non-right triangles & trigonometry (Advanced)
• Analytic geometry
• Conic sections
• Solid geometry
• Polynomial arithmetic
• Complex numbers
• Polynomial factorization
• Polynomial division
• Polynomial graphs
• Rational exponents and radicals
• Exponential models
• Transformations of functions
• Rational functions
• Trigonometric functions
• Non-right triangles & trigonometry
• Trigonometric equations and identities
• Analyzing categorical data
• Displaying and comparing quantitative data
• Summarizing quantitative data
• Modeling data distributions
• Exploring bivariate numerical data
• Study design
• Probability
• Counting, permutations, and combinations
• Random variables
• Sampling distributions
• Confidence intervals
• Significance tests (hypothesis testing)
• Two-sample inference for the difference between groups
• Inference for categorical data (chi-square tests)
• Advanced regression (inference and transforming)
• Analysis of variance (ANOVA)
• Scatterplots
• Data distributions
• Two-way tables
• Binomial probability
• Normal distributions
• Displaying and describing quantitative data
• Inference comparing two groups or populations
• Chi-square tests for categorical data
• More on regression
• Prepare for the 2020 AP®︎ Statistics Exam
• AP®︎ Statistics Standards mappings
• Polynomials
• Composite functions
• Probability and combinatorics
• Limits and continuity
• Derivatives: definition and basic rules
• Derivatives: chain rule and other advanced topics
• Applications of derivatives
• Analyzing functions
• Parametric equations, polar coordinates, and vector-valued functions
• Applications of integrals
• Differentiation: definition and basic derivative rules
• Differentiation: composite, implicit, and inverse functions
• Contextual applications of differentiation
• Applying derivatives to analyze functions
• Integration and accumulation of change
• Applications of integration
• AP Calculus AB solved free response questions from past exams
• AP®︎ Calculus AB Standards mappings
• Infinite sequences and series
• AP Calculus BC solved exams
• AP®︎ Calculus BC Standards mappings
• Integrals review
• Integration techniques
• Thinking about multivariable functions
• Derivatives of multivariable functions
• Applications of multivariable derivatives
• Integrating multivariable functions
• Green’s, Stokes’, and the divergence theorems
• First order differential equations
• Second order linear equations
• Laplace transform
• Vectors and spaces
• Matrix transformations
• Alternate coordinate systems (bases)

Frequently Asked Questions about Khan Academy and Math Worksheets

Why is khan academy even better than traditional math worksheets.

Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.

What do Khan Academy’s interactive math worksheets look like?

Here’s an example:

What are teachers saying about Khan Academy’s interactive math worksheets?

“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”

Is Khan Academy free?

Khan Academy’s practice questions are 100% free—with no ads or subscriptions.

What do Khan Academy’s interactive math worksheets cover?

Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.

Is Khan Academy a company?

Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.

Want to get even more out of Khan Academy?

Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.

Get Khanmigo

The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo. 

For learners     For teachers     For parents

• Open supplemental data
• Reference Manager
• Simple TEXT file

People also looked at

Original research article, mathematical problem-solving through cooperative learning—the importance of peer acceptance and friendships.

• 1 Department of Education, Uppsala University, Uppsala, Sweden
• 2 Department of Education, Culture and Communication, Malardalen University, Vasteras, Sweden
• 3 School of Natural Sciences, Technology and Environmental Studies, Sodertorn University, Huddinge, Sweden
• 4 Faculty of Education, Gothenburg University, Gothenburg, Sweden

Mathematical problem-solving constitutes an important area of mathematics instruction, and there is a need for research on instructional approaches supporting student learning in this area. This study aims to contribute to previous research by studying the effects of an instructional approach of cooperative learning on students’ mathematical problem-solving in heterogeneous classrooms in grade five, in which students with special needs are educated alongside with their peers. The intervention combined a cooperative learning approach with instruction in problem-solving strategies including mathematical models of multiplication/division, proportionality, and geometry. The teachers in the experimental group received training in cooperative learning and mathematical problem-solving, and implemented the intervention for 15 weeks. The teachers in the control group received training in mathematical problem-solving and provided instruction as they would usually. Students (269 in the intervention and 312 in the control group) participated in tests of mathematical problem-solving in the areas of multiplication/division, proportionality, and geometry before and after the intervention. The results revealed significant effects of the intervention on student performance in overall problem-solving and problem-solving in geometry. The students who received higher scores on social acceptance and friendships for the pre-test also received higher scores on the selected tests of mathematical problem-solving. Thus, the cooperative learning approach may lead to gains in mathematical problem-solving in heterogeneous classrooms, but social acceptance and friendships may also greatly impact students’ results.

Introduction

The research on instruction in mathematical problem-solving has progressed considerably during recent decades. Yet, there is still a need to advance our knowledge on how teachers can support their students in carrying out this complex activity ( Lester and Cai, 2016 ). Results from the Program for International Student Assessment (PISA) show that only 53% of students from the participating countries could solve problems requiring more than direct inference and using representations from different information sources ( OECD, 2019 ). In addition, OECD (2019) reported a large variation in achievement with regard to students’ diverse backgrounds. Thus, there is a need for instructional approaches to promote students’ problem-solving in mathematics, especially in heterogeneous classrooms in which students with diverse backgrounds and needs are educated together. Small group instructional approaches have been suggested as important to promote learning of low-achieving students and students with special needs ( Kunsch et al., 2007 ). One such approach is cooperative learning (CL), which involves structured collaboration in heterogeneous groups, guided by five principles to enhance group cohesion ( Johnson et al., 1993 ; Johnson et al., 2009 ; Gillies, 2016 ). While CL has been well-researched in whole classroom approaches ( Capar and Tarim, 2015 ), few studies of the approach exist with regard to students with special educational needs (SEN; McMaster and Fuchs, 2002 ). This study contributes to previous research by studying the effects of the CL approach on students’ mathematical problem-solving in heterogeneous classrooms, in which students with special needs are educated alongside with their peers.

Group collaboration through the CL approach is structured in accordance with five principles of collaboration: positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing ( Johnson et al., 1993 ). First, the group tasks need to be structured so that all group members feel dependent on each other in the completion of the task, thus promoting positive interdependence. Second, for individual accountability, the teacher needs to assure that each group member feels responsible for his or her share of work, by providing opportunities for individual reports or evaluations. Third, the students need explicit instruction in social skills that are necessary for collaboration. Fourth, the tasks and seat arrangements should be designed to promote interaction among group members. Fifth, time needs to be allocated to group processing, through which group members can evaluate their collaborative work to plan future actions. Using these principles for cooperation leads to gains in mathematics, according to Capar and Tarim (2015) , who conducted a meta-analysis on studies of cooperative learning and mathematics, and found an increase of .59 on students’ mathematics achievement scores in general. However, the number of reviewed studies was limited, and researchers suggested a need for more research. In the current study, we focused on the effect of CL approach in a specific area of mathematics: problem-solving.

Mathematical problem-solving is a central area of mathematics instruction, constituting an important part of preparing students to function in modern society ( Gravemeijer et al., 2017 ). In fact, problem-solving instruction creates opportunities for students to apply their knowledge of mathematical concepts, integrate and connect isolated pieces of mathematical knowledge, and attain a deeper conceptual understanding of mathematics as a subject ( Lester and Cai, 2016 ). Some researchers suggest that mathematics itself is a science of problem-solving and of developing theories and methods for problem-solving ( Hamilton, 2007 ; Davydov, 2008 ).

Problem-solving processes have been studied from different perspectives ( Lesh and Zawojewski, 2007 ). Problem-solving heuristics Pólya, (1948) has largely influenced our perceptions of problem-solving, including four principles: understanding the problem, devising a plan, carrying out the plan, and looking back and reflecting upon the suggested solution. Schoenfield, (2016) suggested the use of specific problem-solving strategies for different types of problems, which take into consideration metacognitive processes and students’ beliefs about problem-solving. Further, models and modelling perspectives on mathematics ( Lesh and Doerr, 2003 ; Lesh and Zawojewski, 2007 ) emphasize the importance of engaging students in model-eliciting activities in which problem situations are interpreted mathematically, as students make connections between problem information and knowledge of mathematical operations, patterns, and rules ( Mousoulides et al., 2010 ; Stohlmann and Albarracín, 2016 ).

Not all students, however, find it easy to solve complex mathematical problems. Students may experience difficulties in identifying solution-relevant elements in a problem or visualizing appropriate solution to a problem situation. Furthermore, students may need help recognizing the underlying model in problems. For example, in two studies by Degrande et al. (2016) , students in grades four to six were presented with mathematical problems in the context of proportional reasoning. The authors found that the students, when presented with a word problem, could not identify an underlying model, but rather focused on superficial characteristics of the problem. Although the students in the study showed more success when presented with a problem formulated in symbols, the authors pointed out a need for activities that help students distinguish between different proportional problem types. Furthermore, students exhibiting specific learning difficulties may need additional support in both general problem-solving strategies ( Lein et al., 2020 ; Montague et al., 2014 ) and specific strategies pertaining to underlying models in problems. The CL intervention in the present study focused on supporting students in problem-solving, through instruction in problem-solving principles ( Pólya, 1948 ), specifically applied to three models of mathematical problem-solving—multiplication/division, geometry, and proportionality.

Students’ problem-solving may be enhanced through participation in small group discussions. In a small group setting, all the students have the opportunity to explain their solutions, clarify their thinking, and enhance understanding of a problem at hand ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ). In fact, small group instruction promotes students’ learning in mathematics by providing students with opportunities to use language for reasoning and conceptual understanding ( Mercer and Sams, 2006 ), to exchange different representations of the problem at hand ( Fujita et al., 2019 ), and to become aware of and understand groupmates’ perspectives in thinking ( Kazak et al., 2015 ). These opportunities for learning are created through dialogic spaces characterized by openness to each other’s perspectives and solutions to mathematical problems ( Wegerif, 2011 ).

However, group collaboration is not only associated with positive experiences. In fact, studies show that some students may not be given equal opportunities to voice their opinions, due to academic status differences ( Langer-Osuna, 2016 ). Indeed, problem-solvers struggling with complex tasks may experience negative emotions, leading to uncertainty of not knowing the definite answer, which places demands on peer support ( Jordan and McDaniel, 2014 ; Hannula, 2015 ). Thus, especially in heterogeneous groups, students may need additional support to promote group interaction. Therefore, in this study, we used a cooperative learning approach, which, in contrast to collaborative learning approaches, puts greater focus on supporting group cohesion through instruction in social skills and time for reflection on group work ( Davidson and Major, 2014 ).

Although cooperative learning approach is intended to promote cohesion and peer acceptance in heterogeneous groups ( Rzoska and Ward, 1991 ), previous studies indicate that challenges in group dynamics may lead to unequal participation ( Mulryan, 1992 ; Cohen, 1994 ). Peer-learning behaviours may impact students’ problem-solving ( Hwang and Hu, 2013 ) and working in groups with peers who are seen as friends may enhance students’ motivation to learn mathematics ( Deacon and Edwards, 2012 ). With the importance of peer support in mind, this study set out to investigate whether the results of the intervention using the CL approach are associated with students’ peer acceptance and friendships.

The Present Study

In previous research, the CL approach has shown to be a promising approach in teaching and learning mathematics ( Capar and Tarim, 2015 ), but fewer studies have been conducted in whole-class approaches in general and students with SEN in particular ( McMaster and Fuchs, 2002 ). This study aims to contribute to previous research by investigating the effect of CL intervention on students’ mathematical problem-solving in grade 5. With regard to the complexity of mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach in this study was combined with problem-solving principles pertaining to three underlying models of problem-solving—multiplication/division, geometry, and proportionality. Furthermore, considering the importance of peer support in problem-solving in small groups ( Mulryan, 1992 ; Cohen, 1994 ; Hwang and Hu, 2013 ), the study investigated how peer acceptance and friendships were associated with the effect of the CL approach on students’ problem-solving abilities. The study aimed to find answers to the following research questions:

a) What is the effect of CL approach on students’ problem-solving in mathematics?

b) Are social acceptance and friendship associated with the effect of CL on students’ problem-solving in mathematics?

Participants

The participants were 958 students in grade 5 and their teachers. According to power analyses prior to the start of the study, 1,020 students and 51 classes were required, with an expected effect size of 0.30 and power of 80%, provided that there are 20 students per class and intraclass correlation is 0.10. An invitation to participate in the project was sent to teachers in five municipalities via e-mail. Furthermore, the information was posted on the website of Uppsala university and distributed via Facebook interest groups. As shown in Figure 1 , teachers of 1,165 students agreed to participate in the study, but informed consent was obtained only for 958 students (463 in the intervention and 495 in the control group). Further attrition occurred at pre- and post-measurement, resulting in 581 students’ tests as a basis for analyses (269 in the intervention and 312 in the control group). Fewer students (n = 493) were finally included in the analyses of the association of students’ social acceptance and friendships and the effect of CL on students’ mathematical problem-solving (219 in the intervention and 274 in the control group). The reasons for attrition included teacher drop out due to sick leave or personal circumstances (two teachers in the control group and five teachers in the intervention group). Furthermore, some students were sick on the day of data collection and some teachers did not send the test results to the researchers.

FIGURE 1 . Flow chart for participants included in data collection and data analysis.

As seen in Table 1 , classes in both intervention and control groups included 27 students on average. For 75% of the classes, there were 33–36% of students with SEN. In Sweden, no formal medical diagnosis is required for the identification of students with SEN. It is teachers and school welfare teams who decide students’ need for extra adaptations or special support ( Swedish National Educational Agency, 2014 ). The information on individual students’ type of SEN could not be obtained due to regulations on the protection of information about individuals ( SFS 2009 ). Therefore, the information on the number of students with SEN on class level was obtained through teacher reports.

TABLE 1 . Background characteristics of classes and teachers in intervention and control groups.

Intervention

The intervention using the CL approach lasted for 15 weeks and the teachers worked with the CL approach three to four lessons per week. First, the teachers participated in two-days training on the CL approach, using an especially elaborated CL manual ( Klang et al., 2018 ). The training focused on the five principles of the CL approach (positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing). Following the training, the teachers introduced the CL approach in their classes and focused on group-building activities for 7 weeks. Then, 2 days of training were provided to teachers, in which the CL approach was embedded in activities in mathematical problem-solving and reading comprehension. Educational materials containing mathematical problems in the areas of multiplication and division, geometry, and proportionality were distributed to the teachers ( Karlsson and Kilborn, 2018a ). In addition to the specific problems, adapted for the CL approach, the educational materials contained guidance for the teachers, in which problem-solving principles ( Pólya, 1948 ) were presented as steps in problem-solving. Following the training, the teachers applied the CL approach in mathematical problem-solving lessons for 8 weeks.

Solving a problem is a matter of goal-oriented reasoning, starting from the understanding of the problem to devising its solution by using known mathematical models. This presupposes that the current problem is chosen from a known context ( Stillman et al., 2008 ; Zawojewski, 2010 ). This differs from the problem-solving of the textbooks, which is based on an aim to train already known formulas and procedures ( Hamilton, 2007 ). Moreover, it is important that students learn modelling according to their current abilities and conditions ( Russel, 1991 ).

In order to create similar conditions in the experiment group and the control group, the teachers were supposed to use the same educational material ( Karlsson and Kilborn, 2018a ; Karlsson and Kilborn, 2018b ), written in light of the specified view of problem-solving. The educational material is divided into three areas—multiplication/division, geometry, and proportionality—and begins with a short teachers’ guide, where a view of problem solving is presented, which is based on the work of Polya (1948) and Lester and Cai (2016) . The tasks are constructed in such a way that conceptual knowledge was in focus, not formulas and procedural knowledge.

Implementation of the Intervention

To ensure the implementation of the intervention, the researchers visited each teachers’ classroom twice during the two phases of the intervention period, as described above. During each visit, the researchers observed the lesson, using a checklist comprising the five principles of the CL approach. After the lesson, the researchers gave written and oral feedback to each teacher. As seen in Table 1 , in 18 of the 23 classes, the teachers implemented the intervention in accordance with the principles of CL. In addition, the teachers were asked to report on the use of the CL approach in their teaching and the use of problem-solving activities embedding CL during the intervention period. As shown in Table 1 , teachers in only 11 of 23 classes reported using the CL approach and problem-solving activities embedded in the CL approach at least once a week.

Control Group

The teachers in the control group received 2 days of instruction in enhancing students’ problem-solving and reading comprehension. The teachers were also supported with educational materials including mathematical problems Karlsson and Kilborn (2018b) and problem-solving principles ( Pólya, 1948 ). However, none of the activities during training or in educational materials included the CL approach. As seen in Table 1 , only 10 of 25 teachers reported devoting at least one lesson per week to mathematical problem-solving.

Tests of Mathematical Problem-Solving

Tests of mathematical problem-solving were administered before and after the intervention, which lasted for 15 weeks. The tests were focused on the models of multiplication/division, geometry, and proportionality. The three models were chosen based on the syllabus of the subject of mathematics in grades 4 to 6 in the Swedish National Curriculum ( Swedish National Educational Agency, 2018 ). In addition, the intention was to create a variation of types of problems to solve. For each of these three models, there were two tests, a pre-test and a post-test. Each test contained three tasks with increasing difficulty ( Supplementary Appendix SA ).

The tests of multiplication and division (Ma1) were chosen from different contexts and began with a one-step problem, while the following two tasks were multi-step problems. Concerning multiplication, many students in grade 5 still understand multiplication as repeated addition, causing significant problems, as this conception is not applicable to multiplication beyond natural numbers ( Verschaffel et al., 2007 ). This might be a hindrance in developing multiplicative reasoning ( Barmby et al., 2009 ). The multi-step problems in this study were constructed to support the students in multiplicative reasoning.

Concerning the geometry tests (Ma2), it was important to consider a paradigm shift concerning geometry in education that occurred in the mid-20th century, when strict Euclidean geometry gave way to other aspects of geometry like symmetry, transformation, and patterns. van Hiele (1986) prepared a new taxonomy for geometry in five steps, from a visual to a logical level. Therefore, in the tests there was a focus on properties of quadrangles and triangles, and how to determine areas by reorganising figures into new patterns. This means that structure was more important than formulas.

The construction of tests of proportionality (M3) was more complicated. Firstly, tasks on proportionality can be found in many different contexts, such as prescriptions, scales, speeds, discounts, interest, etc. Secondly, the mathematical model is complex and requires good knowledge of rational numbers and ratios ( Lesh et al., 1988 ). It also requires a developed view of multiplication, useful in operations with real numbers, not only as repeated addition, an operation limited to natural numbers ( Lybeck, 1981 ; Degrande et al., 2016 ). A linear structure of multiplication as repeated addition leads to limitations in terms of generalization and development of the concept of multiplication. This became evident in a study carried out in a Swedish context ( Karlsson and Kilborn, 2018c ). Proportionality can be expressed as a/b = c/d or as a/b = k. The latter can also be expressed as a = b∙k, where k is a constant that determines the relationship between a and b. Common examples of k are speed (km/h), scale, and interest (%). An important pre-knowledge in order to deal with proportions is to master fractions as equivalence classes like 1/3 = 2/6 = 3/9 = 4/12 = 5/15 = 6/18 = 7/21 = 8/24 … ( Karlsson and Kilborn, 2020 ). It was important to take all these aspects into account when constructing and assessing the solutions of the tasks.

The tests were graded by an experienced teacher of mathematics (4 th author) and two students in their final year of teacher training. Prior to grading, acceptable levels of inter-rater reliability were achieved by independent rating of students’ solutions and discussions in which differences between the graders were resolved. Each student response was to be assigned one point when it contained a correct answer and two points when the student provided argumentation for the correct answer and elaborated on explanation of his or her solution. The assessment was thus based on quality aspects with a focus on conceptual knowledge. As each subtest contained three questions, it generated three student solutions. So, scores for each subtest ranged from 0 to 6 points and for the total scores from 0 to 18 points. To ascertain that pre- and post-tests were equivalent in degree of difficulty, the tests were administered to an additional sample of 169 students in grade 5. Test for each model was conducted separately, as students participated in pre- and post-test for each model during the same lesson. The order of tests was switched for half of the students in order to avoid the effect of the order in which the pre- and post-tests were presented. Correlation between students’ performance on pre- and post-test was .39 ( p < 0.000) for tests of multiplication/division; .48 ( p < 0.000) for tests of geometry; and .56 ( p < 0.000) for tests of proportionality. Thus, the degree of difficulty may have differed between pre- and post-test.

Measures of Peer Acceptance and Friendships

To investigate students’ peer acceptance and friendships, peer nominations rated pre- and post-intervention were used. Students were asked to nominate peers who they preferred to work in groups with and who they preferred to be friends with. Negative peer nominations were avoided due to ethical considerations raised by teachers and parents ( Child and Nind, 2013 ). Unlimited nominations were used, as these are considered to have high ecological validity ( Cillessen and Marks, 2017 ). Peer nominations were used as a measure of social acceptance, and reciprocated nominations were used as a measure of friendship. The number of nominations for each student were aggregated and divided by the number of nominators to create a proportion of nominations for each student ( Velásquez et al., 2013 ).

Statistical Analyses

Multilevel regression analyses were conducted in R, lme4 package Bates et al. (2015) to account for nestedness in the data. Students’ classroom belonging was considered as a level 2 variable. First, we used a model in which students’ results on tests of problem-solving were studied as a function of time (pre- and post) and group belonging (intervention and control group). Second, the same model was applied to subgroups of students who performed above and below median at pre-test, to explore whether the CL intervention had a differential effect on student performance. In this second model, the results for subgroups of students could not be obtained for geometry tests for subgroup below median and for tests of proportionality for subgroup above median. A possible reason for this must have been the skewed distribution of the students in these subgroups. Therefore, another model was applied that investigated students’ performances in math at both pre- and post-test as a function of group belonging. Third, the students’ scores on social acceptance and friendships were added as an interaction term to the first model. In our previous study, students’ social acceptance changed as a result of the same CL intervention ( Klang et al., 2020 ).

The assumptions for the multilevel regression were assured during the analyses ( Snijders and Bosker, 2012 ). The assumption of normality of residuals were met, as controlled by visual inspection of quantile-quantile plots. For subgroups, however, the plotted residuals deviated somewhat from the straight line. The number of outliers, which had a studentized residual value greater than ±3, varied from 0 to 5, but none of the outliers had a Cook’s distance value larger than 1. The assumption of multicollinearity was met, as the variance inflation factors (VIF) did not exceed a value of 10. Before the analyses, the cases with missing data were deleted listwise.

What Is the Effect of the CL Approach on Students’ Problem-Solving in Mathematics?

As seen in the regression coefficients in Table 2 , the CL intervention had a significant effect on students’ mathematical problem-solving total scores and students’ scores in problem solving in geometry (Ma2). Judging by mean values, students in the intervention group appeared to have low scores on problem-solving in geometry but reached the levels of problem-solving of the control group by the end of the intervention. The intervention did not have a significant effect on students’ performance in problem-solving related to models of multiplication/division and proportionality.

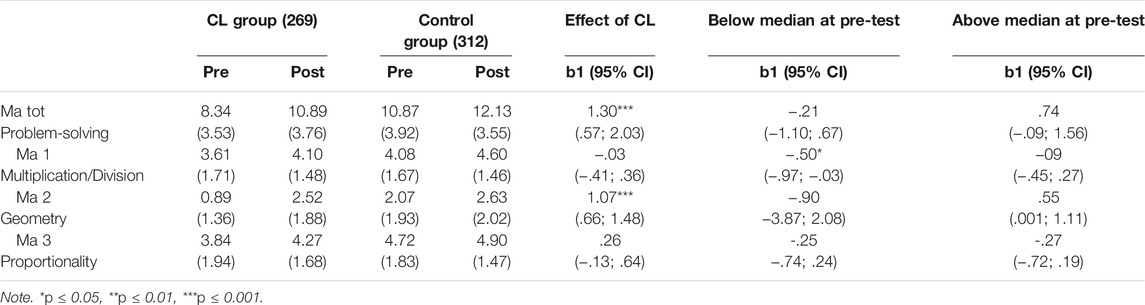
TABLE 2 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving.

The question is, however, whether CL intervention affected students with different pre-test scores differently. Table 2 includes the regression coefficients for subgroups of students who performed below and above median at pre-test. As seen in the table, the CL approach did not have a significant effect on students’ problem-solving, when the sample was divided into these subgroups. A small negative effect was found for intervention group in comparison to control group, but confidence intervals (CI) for the effect indicate that it was not significant.

Is Social Acceptance and Friendships Associated With the Effect of CL on Students’ Problem-Solving in Mathematics?

As seen in Table 3 , students’ peer acceptance and friendship at pre-test were significantly associated with the effect of the CL approach on students’ mathematical problem-solving scores. Changes in students’ peer acceptance and friendships were not significantly associated with the effect of the CL approach on students’ mathematical problem-solving. Consequently, it can be concluded that being nominated by one’s peers and having friends at the start of the intervention may be an important factor when participation in group work, structured in accordance with the CL approach, leads to gains in mathematical problem-solving.

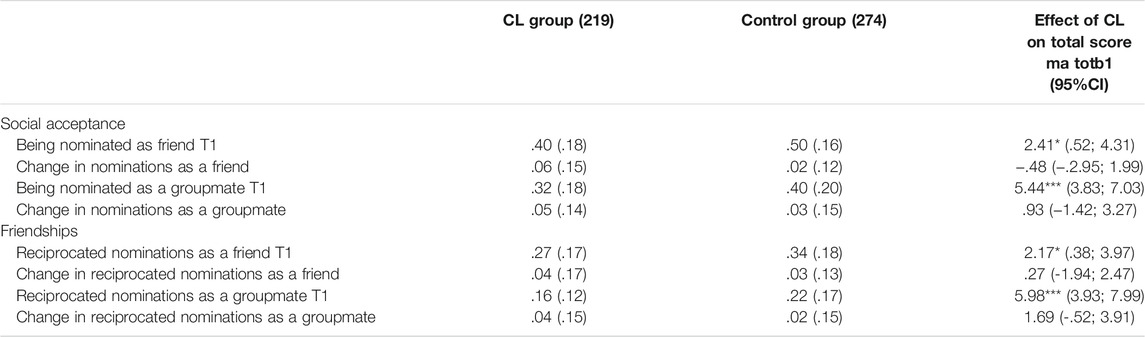
TABLE 3 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving, including scores of social acceptance and friendship in the model.

In light of the limited number of studies on the effects of CL on students’ problem-solving in whole classrooms ( Capar and Tarim, 2015 ), and for students with SEN in particular ( McMaster and Fuchs, 2002 ), this study sought to investigate whether the CL approach embedded in problem-solving activities has an effect on students’ problem-solving in heterogeneous classrooms. The need for the study was justified by the challenge of providing equitable mathematics instruction to heterogeneous student populations ( OECD, 2019 ). Small group instructional approaches as CL are considered as promising approaches in this regard ( Kunsch et al., 2007 ). The results showed a significant effect of the CL approach on students’ problem-solving in geometry and total problem-solving scores. In addition, with regard to the importance of peer support in problem-solving ( Deacon and Edwards, 2012 ; Hwang and Hu, 2013 ), the study explored whether the effect of CL on students’ problem-solving was associated with students’ social acceptance and friendships. The results showed that students’ peer acceptance and friendships at pre-test were significantly associated with the effect of the CL approach, while change in students’ peer acceptance and friendships from pre- to post-test was not.

The results of the study confirm previous research on the effect of the CL approach on students’ mathematical achievement ( Capar and Tarim, 2015 ). The specific contribution of the study is that it was conducted in classrooms, 75% of which were composed of 33–36% of students with SEN. Thus, while a previous review revealed inconclusive findings on the effects of CL on student achievement ( McMaster and Fuchs, 2002 ), the current study adds to the evidence of the effect of the CL approach in heterogeneous classrooms, in which students with special needs are educated alongside with their peers. In a small group setting, the students have opportunities to discuss their ideas of solutions to the problem at hand, providing explanations and clarifications, thus enhancing their understanding of problem-solving ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ).

In this study, in accordance with previous research on mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach was combined with training in problem-solving principles Pólya (1948) and educational materials, providing support in instruction in underlying mathematical models. The intention of the study was to provide evidence for the effectiveness of the CL approach above instruction in problem-solving, as problem-solving materials were accessible to teachers of both the intervention and control groups. However, due to implementation challenges, not all teachers in the intervention and control groups reported using educational materials and training as expected. Thus, it is not possible to draw conclusions of the effectiveness of the CL approach alone. However, in everyday classroom instruction it may be difficult to separate the content of instruction from the activities that are used to mediate this content ( Doerr and Tripp, 1999 ; Gravemeijer, 1999 ).

Furthermore, for successful instruction in mathematical problem-solving, scaffolding for content needs to be combined with scaffolding for dialogue ( Kazak et al., 2015 ). From a dialogical perspective ( Wegerif, 2011 ), students may need scaffolding in new ways of thinking, involving questioning their understandings and providing arguments for their solutions, in order to create dialogic spaces in which different solutions are voiced and negotiated. In this study, small group instruction through CL approach aimed to support discussions in small groups, but the study relies solely on quantitative measures of students’ mathematical performance. Video-recordings of students’ discussions may have yielded important insights into the dialogic relationships that arose in group discussions.

Despite the positive findings of the CL approach on students’ problem-solving, it is important to note that the intervention did not have an effect on students’ problem-solving pertaining to models of multiplication/division and proportionality. Although CL is assumed to be a promising instructional approach, the number of studies on its effect on students’ mathematical achievement is still limited ( Capar and Tarim, 2015 ). Thus, further research is needed on how CL intervention can be designed to promote students’ problem-solving in other areas of mathematics.

The results of this study show that the effect of the CL intervention on students’ problem-solving was associated with students’ initial scores of social acceptance and friendships. Thus, it is possible to assume that students who were popular among their classmates and had friends at the start of the intervention also made greater gains in mathematical problem-solving as a result of the CL intervention. This finding is in line with Deacon and Edwards’ study of the importance of friendships for students’ motivation to learn mathematics in small groups ( Deacon and Edwards, 2012 ). However, the effect of the CL intervention was not associated with change in students’ social acceptance and friendship scores. These results indicate that students who were nominated by a greater number of students and who received a greater number of friends did not benefit to a great extent from the CL intervention. With regard to previously reported inequalities in cooperation in heterogeneous groups ( Cohen, 1994 ; Mulryan, 1992 ; Langer Osuna, 2016 ) and the importance of peer behaviours for problem-solving ( Hwang and Hu, 2013 ), teachers should consider creating inclusive norms and supportive peer relationships when using the CL approach. The demands of solving complex problems may create negative emotions and uncertainty ( Hannula, 2015 ; Jordan and McDaniel, 2014 ), and peer support may be essential in such situations.

Limitations

The conclusions from the study must be interpreted with caution, due to a number of limitations. First, due to the regulation of protection of individuals ( SFS 2009 ), the researchers could not get information on type of SEN for individual students, which limited the possibilities of the study for investigating the effects of the CL approach for these students. Second, not all teachers in the intervention group implemented the CL approach embedded in problem-solving activities and not all teachers in the control group reported using educational materials on problem-solving. The insufficient levels of implementation pose a significant challenge to the internal validity of the study. Third, the additional investigation to explore the equivalence in difficulty between pre- and post-test, including 169 students, revealed weak to moderate correlation in students’ performance scores, which may indicate challenges to the internal validity of the study.

Implications

The results of the study have some implications for practice. Based on the results of the significant effect of the CL intervention on students’ problem-solving, the CL approach appears to be a promising instructional approach in promoting students’ problem-solving. However, as the results of the CL approach were not significant for all subtests of problem-solving, and due to insufficient levels of implementation, it is not possible to conclude on the importance of the CL intervention for students’ problem-solving. Furthermore, it appears to be important to create opportunities for peer contacts and friendships when the CL approach is used in mathematical problem-solving activities.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by the Uppsala Ethical Regional Committee, Dnr. 2017/372. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author Contributions

NiK was responsible for the project, and participated in data collection and data analyses. NaK and WK were responsible for intervention with special focus on the educational materials and tests in mathematical problem-solving. PE participated in the planning of the study and the data analyses, including coordinating analyses of students’ tests. MK participated in the designing and planning the study as well as data collection and data analyses.

The project was funded by the Swedish Research Council under Grant 2016-04,679.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to express our gratitude to teachers who participated in the project.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2021.710296/full#supplementary-material

Barmby, P., Harries, T., Higgins, S., and Suggate, J. (2009). The array representation and primary children's understanding and reasoning in multiplication. Educ. Stud. Math. 70 (3), 217–241. doi:10.1007/s10649-008-914510.1007/s10649-008-9145-1

CrossRef Full Text | Google Scholar

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting Linear Mixed-Effects Models Usinglme4. J. Stat. Soft. 67 (1), 1–48. doi:10.18637/jss.v067.i01

Capar, G., and Tarim, K. (2015). Efficacy of the cooperative learning method on mathematics achievement and attitude: A meta-analysis research. Educ. Sci-theor Pract. 15 (2), 553–559. doi:10.12738/estp.2015.2.2098

Child, S., and Nind, M. (2013). Sociometric methods and difference: A force for good - or yet more harm. Disabil. Soc. 28 (7), 1012–1023. doi:10.1080/09687599.2012.741517

Cillessen, A. H. N., and Marks, P. E. L. (2017). Methodological choices in peer nomination research. New Dir. Child Adolesc. Dev. 2017, 21–44. doi:10.1002/cad.20206

PubMed Abstract | CrossRef Full Text | Google Scholar

Clarke, B., Cheeseman, J., and Clarke, D. (2006). The mathematical knowledge and understanding young children bring to school. Math. Ed. Res. J. 18 (1), 78–102. doi:10.1007/bf03217430

Cohen, E. G. (1994). Restructuring the classroom: Conditions for productive small groups. Rev. Educ. Res. 64 (1), 1–35. doi:10.3102/00346543064001001

Davidson, N., and Major, C. H. (2014). Boundary crossings: Cooperative learning, collaborative learning, and problem-based learning. J. Excell. Coll. Teach. 25 (3-4), 7.

Google Scholar

Davydov, V. V. (2008). Problems of developmental instructions. A Theoretical and experimental psychological study . New York: Nova Science Publishers, Inc .

Deacon, D., and Edwards, J. (2012). Influences of friendship groupings on motivation for mathematics learning in secondary classrooms. Proc. Br. Soc. Res. into Learn. Math. 32 (2), 22–27.

Degrande, T., Verschaffel, L., and van Dooren, W. (2016). “Proportional word problem solving through a modeling lens: a half-empty or half-full glass?,” in Posing and Solving Mathematical Problems, Research in Mathematics Education . Editor P. Felmer.

Doerr, H. M., and Tripp, J. S. (1999). Understanding how students develop mathematical models. Math. Thinking Learn. 1 (3), 231–254. doi:10.1207/s15327833mtl0103_3

Fujita, T., Doney, J., and Wegerif, R. (2019). Students' collaborative decision-making processes in defining and classifying quadrilaterals: a semiotic/dialogic approach. Educ. Stud. Math. 101 (3), 341–356. doi:10.1007/s10649-019-09892-9

Gillies, R. (2016). Cooperative learning: Review of research and practice. Ajte 41 (3), 39–54. doi:10.14221/ajte.2016v41n3.3

Gravemeijer, K. (1999). How Emergent Models May Foster the Constitution of Formal Mathematics. Math. Thinking Learn. 1 (2), 155–177. doi:10.1207/s15327833mtl0102_4

Gravemeijer, K., Stephan, M., Julie, C., Lin, F.-L., and Ohtani, M. (2017). What mathematics education may prepare students for the society of the future? Int. J. Sci. Math. Educ. 15 (S1), 105–123. doi:10.1007/s10763-017-9814-6

Hamilton, E. (2007). “What changes are needed in the kind of problem-solving situations where mathematical thinking is needed beyond school?,” in Foundations for the Future in Mathematics Education . Editors R. Lesh, E. Hamilton, and Kaput (Mahwah, NJ: Lawrence Erlbaum ), 1–6.

Hannula, M. S. (2015). “Emotions in problem solving,” in Selected Regular Lectures from the 12 th International Congress on Mathematical Education . Editor S. J. Cho. doi:10.1007/978-3-319-17187-6_16

Hwang, W.-Y., and Hu, S.-S. (2013). Analysis of peer learning behaviors using multiple representations in virtual reality and their impacts on geometry problem solving. Comput. Edu. 62, 308–319. doi:10.1016/j.compedu.2012.10.005

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (2009). Circle of Learning: Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (1993). Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Jordan, M. E., and McDaniel, R. R. (2014). Managing uncertainty during collaborative problem solving in elementary school teams: The role of peer influence in robotics engineering activity. J. Learn. Sci. 23 (4), 490–536. doi:10.1080/10508406.2014.896254

Karlsson, N., and Kilborn, W. (2018a). Inclusion through learning in group: tasks for problem-solving. [Inkludering genom lärande i grupp: uppgifter för problemlösning] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2018c). It's enough if they understand it. A study of teachers 'and students' perceptions of multiplication and the multiplication table [Det räcker om de förstår den. En studie av lärares och elevers uppfattningar om multiplikation och multiplikationstabellen]. Södertörn Stud. Higher Educ. , 175.

Karlsson, N., and Kilborn, W. (2018b). Tasks for problem-solving in mathematics. [Uppgifter för problemlösning i matematik] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2020). “Teacher’s and student’s perception of rational numbers,” in Interim Proceedings of the 44 th Conference of the International Group for the Psychology of Mathematics Education , Interim Vol., Research Reports . Editors M. Inprasitha, N. Changsri, and N. Boonsena (Khon Kaen, Thailand: PME ), 291–297.

Kazak, S., Wegerif, R., and Fujita, T. (2015). Combining scaffolding for content and scaffolding for dialogue to support conceptual breakthroughs in understanding probability. ZDM Math. Edu. 47 (7), 1269–1283. doi:10.1007/s11858-015-0720-5

Klang, N., Olsson, I., Wilder, J., Lindqvist, G., Fohlin, N., and Nilholm, C. (2020). A cooperative learning intervention to promote social inclusion in heterogeneous classrooms. Front. Psychol. 11, 586489. doi:10.3389/fpsyg.2020.586489

Klang, N., Fohlin, N., and Stoddard, M. (2018). Inclusion through learning in group: cooperative learning [Inkludering genom lärande i grupp: kooperativt lärande] . Uppsala: Uppsala University .

Kunsch, C. A., Jitendra, A. K., and Sood, S. (2007). The effects of peer-mediated instruction in mathematics for students with learning problems: A research synthesis. Learn. Disabil Res Pract 22 (1), 1–12. doi:10.1111/j.1540-5826.2007.00226.x

Langer-Osuna, J. M. (2016). The social construction of authority among peers and its implications for collaborative mathematics problem solving. Math. Thinking Learn. 18 (2), 107–124. doi:10.1080/10986065.2016.1148529

Lein, A. E., Jitendra, A. K., and Harwell, M. R. (2020). Effectiveness of mathematical word problem solving interventions for students with learning disabilities and/or mathematics difficulties: A meta-analysis. J. Educ. Psychol. 112 (7), 1388–1408. doi:10.1037/edu0000453

Lesh, R., and Doerr, H. (2003). Beyond Constructivism: Models and Modeling Perspectives on Mathematics Problem Solving, Learning and Teaching . Mahwah, NJ: Erlbaum .

Lesh, R., Post, T., and Behr, M. (1988). “Proportional reasoning,” in Number Concepts and Operations in the Middle Grades . Editors J. Hiebert, and M. Behr (Hillsdale, N.J.: Lawrence Erlbaum Associates ), 93–118.

Lesh, R., and Zawojewski, (2007). “Problem solving and modeling,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor L. F. K. Lester (Charlotte, NC: Information Age Pub ), vol. 2.

Lester, F. K., and Cai, J. (2016). “Can mathematical problem solving be taught? Preliminary answers from 30 years of research,” in Posing and Solving Mathematical Problems. Research in Mathematics Education .

Lybeck, L. (1981). “Archimedes in the classroom. [Arkimedes i klassen],” in Göteborg Studies in Educational Sciences (Göteborg: Acta Universitatis Gotoburgensis ), 37.

McMaster, K. N., and Fuchs, D. (2002). Effects of Cooperative Learning on the Academic Achievement of Students with Learning Disabilities: An Update of Tateyama-Sniezek's Review. Learn. Disabil Res Pract 17 (2), 107–117. doi:10.1111/1540-5826.00037

Mercer, N., and Sams, C. (2006). Teaching children how to use language to solve maths problems. Lang. Edu. 20 (6), 507–528. doi:10.2167/le678.0

Montague, M., Krawec, J., Enders, C., and Dietz, S. (2014). The effects of cognitive strategy instruction on math problem solving of middle-school students of varying ability. J. Educ. Psychol. 106 (2), 469–481. doi:10.1037/a0035176

Mousoulides, N., Pittalis, M., Christou, C., and Stiraman, B. (2010). “Tracing students’ modeling processes in school,” in Modeling Students’ Mathematical Modeling Competencies . Editor R. Lesh (Berlin, Germany: Springer Science+Business Media ). doi:10.1007/978-1-4419-0561-1_10

Mulryan, C. M. (1992). Student passivity during cooperative small groups in mathematics. J. Educ. Res. 85 (5), 261–273. doi:10.1080/00220671.1992.9941126

OECD (2019). PISA 2018 Results (Volume I): What Students Know and Can Do . Paris: OECD Publishing . doi:10.1787/5f07c754-en

CrossRef Full Text

Pólya, G. (1948). How to Solve it: A New Aspect of Mathematical Method . Princeton, N.J.: Princeton University Press .

Russel, S. J. (1991). “Counting noses and scary things: Children construct their ideas about data,” in Proceedings of the Third International Conference on the Teaching of Statistics . Editor I. D. Vere-Jones (Dunedin, NZ: University of Otago ), 141–164., s.

Rzoska, K. M., and Ward, C. (1991). The effects of cooperative and competitive learning methods on the mathematics achievement, attitudes toward school, self-concepts and friendship choices of Maori, Pakeha and Samoan Children. New Zealand J. Psychol. 20 (1), 17–24.

Schoenfeld, A. H. (2016). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics (reprint). J. Edu. 196 (2), 1–38. doi:10.1177/002205741619600202

SFS 2009:400. Offentlighets- och sekretesslag. [Law on Publicity and confidentiality] . Retrieved from https://www.riksdagen.se/sv/dokument-lagar/dokument/svensk-forfattningssamling/offentlighets--och-sekretesslag-2009400_sfs-2009-400 on the 14th of October .

Snijders, T. A. B., and Bosker, R. J. (2012). Multilevel Analysis. An Introduction to Basic and Advanced Multilevel Modeling . 2nd Ed. London: SAGE .

Stillman, G., Brown, J., and Galbraith, P. (2008). Research into the teaching and learning of applications and modelling in Australasia. In H. Forgasz, A. Barkatas, A. Bishop, B. Clarke, S. Keast, W. Seah, and P. Sullivan (red.), Research in Mathematics Education in Australasiae , 2004-2007 , p.141–164. Rotterdam: Sense Publishers .doi:10.1163/9789087905019_009

Stohlmann, M. S., and Albarracín, L. (2016). What is known about elementary grades mathematical modelling. Edu. Res. Int. 2016, 1–9. doi:10.1155/2016/5240683

Swedish National Educational Agency (2014). Support measures in education – on leadership and incentives, extra adaptations and special support [Stödinsatser I utbildningen – om ledning och stimulans, extra anpassningar och särskilt stöd] . Stockholm: Swedish National Agency of Education .

Swedish National Educational Agency (2018). Syllabus for the subject of mathematics in compulsory school . Retrieved from https://www.skolverket.se/undervisning/grundskolan/laroplan-och-kursplaner-for-grundskolan/laroplan-lgr11-for-grundskolan-samt-for-forskoleklassen-och-fritidshemmet?url=-996270488%2Fcompulsorycw%2Fjsp%2Fsubject.htm%3FsubjectCode%3DGRGRMAT01%26tos%3Dgr&sv.url=12.5dfee44715d35a5cdfa219f ( on the 32nd of July, 2021).

van Hiele, P. (1986). Structure and Insight. A Theory of Mathematics Education . London: Academic Press .

Velásquez, A. M., Bukowski, W. M., and Saldarriaga, L. M. (2013). Adjusting for Group Size Effects in Peer Nomination Data. Soc. Dev. 22 (4), a–n. doi:10.1111/sode.12029

Verschaffel, L., Greer, B., and De Corte, E. (2007). “Whole number concepts and operations,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor F. K. Lester (Charlotte, NC: Information Age Pub ), 557–628.

Webb, N. M., and Mastergeorge, A. (2003). Promoting effective helping behavior in peer-directed groups. Int. J. Educ. Res. 39 (1), 73–97. doi:10.1016/S0883-0355(03)00074-0

Wegerif, R. (2011). “Theories of Learning and Studies of Instructional Practice,” in Theories of learning and studies of instructional Practice. Explorations in the learning sciences, instructional systems and Performance technologies . Editor T. Koschmann (Berlin, Germany: Springer ). doi:10.1007/978-1-4419-7582-9

Yackel, E., Cobb, P., and Wood, T. (1991). Small-group interactions as a source of learning opportunities in second-grade mathematics. J. Res. Math. Edu. 22 (5), 390–408. doi:10.2307/749187

Zawojewski, J. (2010). Problem Solving versus Modeling. In R. Lesch, P. Galbraith, C. R. Haines, and A. Hurford (red.), Modelling student’s mathematical modelling competencies: ICTMA , p. 237–243. New York, NY: Springer .doi:10.1007/978-1-4419-0561-1_20

Keywords: cooperative learning, mathematical problem-solving, intervention, heterogeneous classrooms, hierarchical linear regression analysis

Citation: Klang N, Karlsson N, Kilborn W, Eriksson P and Karlberg M (2021) Mathematical Problem-Solving Through Cooperative Learning—The Importance of Peer Acceptance and Friendships. Front. Educ. 6:710296. doi: 10.3389/feduc.2021.710296

Received: 15 May 2021; Accepted: 09 August 2021; Published: 24 August 2021.

Reviewed by:

Copyright © 2021 Klang, Karlsson, Kilborn, Eriksson and Karlberg. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Nina Klang, [email protected]

• Grades 6-12
• School Leaders

NEW: Classroom Clean-Up/Set-Up Email Course! 🧽

30 Thought-Provoking Math Puzzles for Middle Schoolers

Critical thinking, trial and error, and pure logic abound.

Tired of your tried-and-true math routine? Chances are if you’re feeling the itch to incorporate new activities into your math time, your students are as well. Mixing it up in math class can bring fresh perspectives to stale concepts or standards, and your students will enjoy stretching their brains in different ways with these middle school math puzzles. Critical thinking, trial and error, and pure logic abound in these 30 though-provoking puzzles. Get ready to reignite your middle schoolers’ excitement for math!

(Just a heads up, WeAreTeachers may collect a share of sales from the links on this page. We only recommend items our team loves!)

Sudoku is way more than just an activity to pass the time on long-haul flights. This math puzzle is actually a fantastic problem-solving activity for middle schoolers. Kick-starting your typical math class with a Sudoku puzzle will have your students thinking critically, practicing trial and error, and looking at math in a totally different way. Plus, you can differentiate by providing Easy, Medium, and Difficult puzzles.

Learn more: Sodoku Puzzles To Print

2. 5 Pirates Puzzle

Ahoy and shiver me timbers! This logic puzzle is perfect for a small-group activity to get your middle schoolers working together to solve the conundrum of how pirates plan to share treasure among themselves. Multiple scenarios will play out in this puzzle, so scaffolding with problem-solving strategies is a must.

Learn more:  5 Pirates Puzzles/Math Is Fun

3. Fives Challenge Puzzle

This puzzle is perfect for reviewing addition, multiplication, division, and subtraction and would be a great activity to do when gearing up to teach order of operations. Students could work in pairs or small groups to riddle out each target number.

Learn more:  Fives Challenge Puzzle/Math = Love

4. Beehive Puzzle

Perfect for a station during math rotation or for a rainy-day recess activity, this logic puzzle involves creating a beehive shape without having any squares of the same color touching each other. Students can practice trial and error as well as problem-solving.

Learn more:  Beehive Puzzle/Math = Love

5. Guess My Number

Guess My Number is just as much a riddle as it is a math puzzle. Students use their number sense to determine the number in question. As an extension activity, students can come up with their own clues and trade them with a classmate to solve.

Learn more:  Guess My Number/Education.com

6. Math Riddles

Perfect for a morning warmup, these middle school math puzzles activate all kinds of math knowledge. You can poll the class and have them show their work before clicking to reveal the correct answer. This site even has more challenging puzzles if your middle schoolers fly through the easier ones.

Learn more:  Math Riddles/Get Riddles

My seventh graders loved playing this puzzle as an early-finisher activity. Though the idea is simple (move the tiles until two of the same numbers touch), it’s actually great for recognizing exponents and also for thinking strategically.

Learn more:  2048/Prodigy

8. Magic Squares

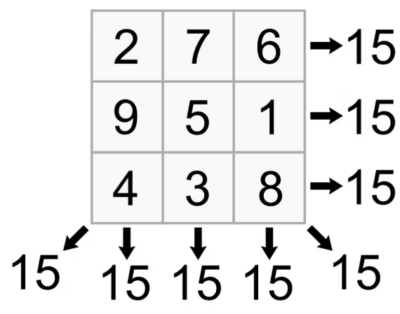
Magic Squares have been around for thousands of years, and they come in all shapes and sizes. The 3×3 grid is a great size to introduce to your students and then work up to larger and more complex grids. You can even bring this puzzle off the paper and have your students write the grid out in sidewalk chalk, or write the numbers on water bottle caps to make a fun tactile activity.

Learn more:  Magic Squares/Prodigy

9. Impossible Domino Bridge

Using dominoes to build a seemingly impossible bridge is a perfect activity for the first day or week of a new school year. Your students can work together in small groups and get to know one another as they attempt to construct the bridge that looks like it could turn into a game of Jenga at any moment.

Learn more:  Impossible Domino Bridge/Math = Love

10. Math Picture Puzzles

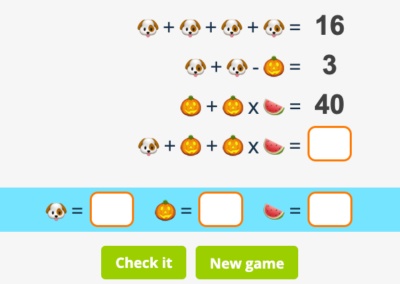
Your students communicate through emojis anyway, so why not get math involved? This self-checking site allows them to work independently (on the honor system) and also choose between three levels of difficulty. Students can take this idea to the next level, create their own emojis, and arrange them in number sentences for their classmates to solve.

Learn more: Picture Puzzles/MathEasily.com

11. What Is the Weight?

Sometimes you just need a quick resource to get your students working on solving a math puzzle. This puzzle comes from an app, so you can have it downloaded on your students’ iPads or tablets. Middle schoolers will focus on determining the weights of different animals, which is good practice for estimating and working with customary/metric units of measurement.

Learn more: Brain Teasers/Mental Up

12. Colorku

Math doesn’t always have to be just about numbers. This board game uses colors and patterns to focus on analyzing sequences, and would be great to have on hand for those rainy-day recesses as well as for inclusion in a math station. Further, Colorku can be used as a calm-down tool or even a fidget tool.

Buy it: Colorku at Amazon

13. Rubik’s Cube

Rubik’s Cubes made a major comeback in popularity when I taught fifth grade. My students would happily sit together at recess to race each other to see who could solve the cube faster. Though entertaining, Rubik’s Cubes are also suited to teach students about growth mindset, spacial awareness, and 3D space.

Buy it: Rubik’s Cube at Amazon

14. SafeCracker

Though this puzzle looks like something out of an Indiana Jones quest, it’s actually a tactilely engaging tool that will delight even your most resistant math learners. The goal is to align the wheel into columns where the sum adds up to 40. You might need to get more than one of these middle school math puzzles for your classroom.

Buy it: SafeCracker at Amazon

15. “T” Brain Teaser Puzzle

In addition to sparking structural design creativity, this boxed wooden puzzle challenges middle schoolers to engage in trial and error as they work at fitting 50+ pieces into a cube. Much of math is learning how to persevere through tricky problems or procedures, and this puzzle definitely fosters that.

Buy it: T Brain Teaser at Amazon

16. Multistep Equation Puzzle

Solve-and-sort puzzles add flair to repeatedly solving different variations of a math problem for practice. In this free puzzle, students will need to not only solve the equations with variables on both sides, they will also need to sort the problem based on if their solution is positive or negative in order to uncover the secret word.

Get it: Solve-and-Sort Puzzle/Teachers Pay Teachers

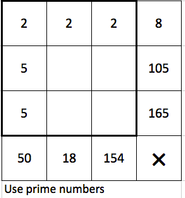
In this variation of a classic Sudoku puzzle, students practice critical thinking and exercise their knowledge of how the four math operations work. The best thing about these types of puzzles is that the differentiation potential is endless. Students can solve smaller puzzles with addition, or use only prime numbers in a more complex multiplication problem.

Learn more: Yohaku

18. Jigmaze

One of the Standards for Mathematical Practices is perseverance, and all teachers know that this is a tough one to instill in students, even more so if students are struggling in foundational skills. This type of puzzle can be used to strengthen perseverance as students physically arrange and rearrange pieces of a broken maze.

Learn more: Jigmaze/Math = Love

19. Flexagons

Flexagons, octaflexagons, and dodecaflexagons (say that one 10 times fast!) are a mathematical take on traditional origami. Through constructing these paper creations, your students will get exposure to geometrical terms such as faces ,  equilateral triangles , and all manner of types of 3D shapes.

Get it: Flexagons/Medium

20. Möbius Strip

Though the high-level mathematical equation may be well above your students’ heads (and mine too, if I’m being honest), the STEAM-centered concept of a Möbius strip can be a fun one to explore and create (no need to go into cosines and conversational belts). Middle school math puzzles for the win!

Get it for free: Make a Möbius/STEAMsational

In this complex-looking puzzle, the goal is for the sum of each vertical or horizontal line to match the number given at the beginning of the row or column. This site comes with a great explanation on exactly what that means and how to achieve it. A Kakuro puzzle would be a great “learn as you go” activity for students where they really must pay close attention to the instructions to be able to understand the goal.

Learn more: Kakuro/Braingle

22. Number Searches

This school district’s site has tons of grade-specific number puzzles that would be perfect for when you need to be out of the classroom and have a substitute teacher. They are ready to be printed and contain easy explanations for your students. Check out the number searches, patterns, and 3D riddles.

Learn more: Number Searches/Cranbury School District

23. Two Truths and One Lie

The tried-and-true icebreaker used at many a staff meeting and the first week of school, Two Truths and One Lie can also be used to review and practice tons of mathematical concepts. These middle school math puzzles cover concepts such as negative numbers, fractions, and a ton more.

Buy it: Two Truths & One Lie Math Edition at Amazon

24. Adding Integers Puzzle

The objective of this cuttable resource is for students to solve the integer problem and match up expressions that end up having the same sum. The multiple size options are great for differentiation or to make this independent activity into a small-group collaborative activity.

Buy it: Adding Integers at Teachers Pay Teachers

25. Perfect Square Roots

For upper middle school students, this square-roots puzzle helps with the recognition of perfect square roots. Rather than simply memorizing the perfect square roots, students work to identify and spell out the specific square root and ensure that it fits within the crossword. In this way, the puzzle is self-checking as well.

Buy it: Square Roots Crossword at Teachers Pay Teachers

26. Factor Tree Challenge

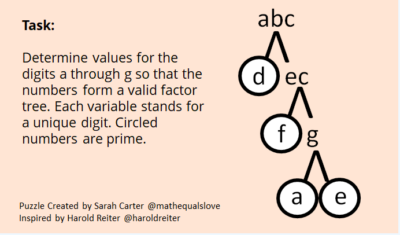
Factor trees are an effective way to visually show students the factors of numbers. Trees allow a chain of multiple factors, so you can start with a large number and end up with “branches” that show all of the factors. Once your middle schoolers are familiar with this concept, have them explore this self-checking challenge (and many others as well) that will test their knowledge of abstract factors.

Learn more: Prime Challenges/Transum

27. Ludicross

Another take on Sudoku, Ludicross is interactive in that students can drag and drop the number into position with the goal of making the sum of the numbers in both diagonals the same. Like several of the other puzzles mentioned in this list, students can take this number puzzle to the next level by creating their own and swapping with a classmate to solve.

Learn more: Ludicross/Transum

28. Interactive Mobiles

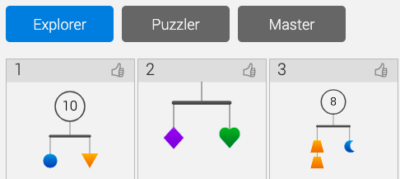
These colorfully shaped mobiles are a unique way for students to make pattern associations. Because these puzzles are self-paced, students can begin with a simple puzzle and work their way up to complex mobiles with three or more shapes.

Try it: Mobiles/SolveMe Puzzles

29. Deleting Sheep

This logic puzzle is a doozy! The objective is to remove only two numbers in each row with the result being that each horizontal and vertical line equals 30. Trial and error and problem-solving skills abound in this puzzle, and it will keep your middle schoolers engaged for quite some time.

Get it: Deleting Sheep/Dover Publications

30. Pips Puzzle

Have any spare decks of cards lying around your classroom? This inexpensive item provides a different take on a Magic Square. Students can work in small groups, and maybe you can ignite a little class competition to see which groups can complete the challenge the fastest.

Buy it: Pips Puzzle/Math = Love

Looking for more engaging math resources? Try these Magical Math Puzzles and Number Tricks To Wow Your Students .

Plus, get all the latest teaching tips and tricks when you sign up for our free newsletters .

You Might Also Like

35 Math Brain Teasers To Puzzle Even Your Smartest Students

When does 9 + 5 = 2? Continue Reading

Copyright © 2024. All rights reserved. 5335 Gate Parkway, Jacksonville, FL 32256

• Skip to content
• Skip to search
• Staff portal (Inside the department)
• Student portal
• Key links for students

Other users

• Forgot password

Notifications

{{item.title}}, my essentials, ask for help, contact edconnect, directory a to z, how to guides, maths trains brains, five games to have fun with maths in years 7 and 8.

These games will help enrich your child's reasoning and problem-solving skills as they enhance their knowledge of how numbers work, quantifying collections, patterning, algebra and probability. Help your child expand their mathematical skills using these five fun games.

Prime Climb

A colourful board game for ages 10 and up, Prime Climb combines strategy and luck as players battle to be the first to land both pawns in the 101 circle at the centre of the game board.

By rolling dice and choosing which operation you’d like to use, players can bump their opponent’s pawns off the board in this exciting race to 101!

A classic game, chess is steeped in opportunities to deepen mathematical skills and understanding. Players take turns moving one chess piece at a time until one player is able to capture their opponent's king

A great game to develop mathematical reasoning and patient problem solving, chess promotes your child’s understanding of concepts such as position, angles and probability.

Does your child like codebreaking? They may enjoy Mastermind, where they can pit themselves against an opponent and use deduction to unlock a secret code recorded in coloured pegs on a board.

Fun fact: Mind lends itself to strategy, mathematical reasoning and algebra, with mathematicians studying the game since the late 1970s to come up with elegant and efficient solutions.

Monopoly isn’t just a great family board game, it can also be a great experience to enrich an understanding of working with money. Players have to budget, invest and explore the value of acquiring assets - in a fun, risk-free way!

By applying skills and understanding in position, probability and patterning, players can give themselves a competitive edge.

Cribbage is a classic game that can lead to some amazing battles. The game is based on scoring points by collecting particular combinations of cards. Each card is given a numerical value, with the players aiming to keep the sum of the cards at 31 or lower. The first player to reach 121 points wins.

Aside from the opportunity to develop their understanding of operations and quantifying collections, Cribbage can help your teen enhance their problem-solving skills and mathematical reasoning. It also requires relatively little equipment to play - just a deck of cards and a cribbage board for keeping score, which your teen can make.

Explore more

• Share full article

Advertisement

Supported by

The Algebra Problem: How Middle School Math Became a National Flashpoint

Top students can benefit greatly by being offered the subject early. But many districts offer few Black and Latino eighth graders a chance to study it.

By Troy Closson

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system. Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly four in five poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class. San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’s administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12 percent of Black and Latino eighth graders do, compared with roughly 24 percent of white pupils, a federal report found .

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research . A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Mass., the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside of school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, Mr. de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80 percent from 60 percent. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s current schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won both support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Mr. Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Mr. Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100 percent, yes,” he added. “That was not something that I could live with.”

Troy Closson reports on K-12 schools in New York City for The Times. More about Troy Closson

May 31, 2024

10 min read

Math Can Help Solve Social Justice Problems

Mathematicians are working on ways to use their field to tackle major social issues, such as social inequality and the need for gender equity

By Rachel Crowell & Nature magazine

MicroStockHub/Getty Images

When Carrie Diaz Eaton trained as a mathematician, they didn’t expect their career to involve social-justice research. Growing up in Providence, Rhode Island, Diaz Eaton first saw social justice in action when their father, who’s from Peru, helped other Spanish-speaking immigrants to settle in the United States.

But it would be decades before Diaz Eaton would forge a professional path to use their mathematical expertise to study social-justice issues. Eventually, after years of moving around for education and training, that journey brought them back to Providence, where they collaborated with the Woonasquatucket River Watershed Council on projects focused on preserving the local environment of the river’s drainage basin, and bolstering resources for the surrounding, often underserved communities.

By “thinking like a mathematician” and leaning on data analysis, data science and visualization skills, they found that their expertise was needed in surprising ways, says Diaz Eaton, who is now executive director of the Institute for a Racially Just, Inclusive, and Open STEM Education at Bates College in Lewiston, Maine.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

For example, the council identified a need to help local people to better connect with community resources. “Even though health care and education don’t seem to fall under the purview of a watershed council, these are all interrelated issues,” Diaz Eaton says. Air pollution can contribute to asthma attacks, for example. In one project, Diaz Eaton and their collaborators built a quiz to help community members to choose the right health-care option, depending on the nature of their illness or injury, immigration status and health-insurance coverage.

“One of the things that makes us mathematicians, is our skills in logic and the questioning of assumptions”, and creating that quiz “was an example of logic at play”, requiring a logic map of cases and all of the possible branches of decision-making to make an effective quiz, they say.

Maths might seem an unlikely bedfellow for social-justice research. But applying the rigour of the field is turning out to be a promising approach for identifying, and sometimes even implementing, fruitful solutions for social problems.

Mathematicians can experience first-hand the messiness and complexity — and satisfaction — of applying maths to problems that affect people and their communities. Trying to work out how to help people access much-needed resources, reduce violence in communities or boost gender equity requires different technical skills, ways of thinking and professional collaborations compared with breaking new ground in pure maths. Even for an applied mathematician like Diaz Eaton, transitioning to working on social-justice applications brings fresh challenges.

Mathematicians say that social-justice research is difficult yet fulfilling — these projects are worth taking on because of their tremendous potential for creating real-world solutions for people and the planet.

Data-driven research

Mathematicians are digging into issues that range from social inequality and health-care access to racial profiling and predictive policing. However, the scope of their research is limited by their access to the data, says Omayra Ortega, an applied mathematician and mathematical epidemiologist at Sonoma State University in Rohnert Park, California. “There has to be that measured information,” Ortega says.

Fortunately, data for social issues abound. “Our society is collecting data at a ridiculous pace,” Ortega notes. Her mathematical epidemiology work has examined which factors affect vaccine uptake in different communities. Her work has found, for example, that, in five years, a national rotavirus-vaccine programme in Egypt would reduce disease burden enough that the cost saving would offset 76% of the costs of the vaccine. “Whenever we’re talking about the distribution of resources, there’s that question of social justice: who gets the resources?” she says.

Lily Khadjavi’s journey with social-justice research began with an intriguing data set.

About 15 years ago, Khadjavi, a mathematician at Loyola Marymount University in Los Angeles, California, was “on the hunt for real-world data” for an undergraduate statistics class she was teaching. She wanted data that the students could crunch to “look at new information and pose their own questions”. She realized that Los Angeles Police Department (LAPD) traffic-stop data fit that description.

At that time, every time that LAPD officers stopped pedestrians or pulled over drivers, they were required to report stop data. Those data included “the perceived race or ethnicity of the person they had stopped”, Khadjavi notes.

When the students analysed the data, the results were memorable. “That was the first time I heard students do a computation absolutely correctly and then audibly gasp at their results,” she says. The data showed that one in every 5 or 6 police stops of Black male drivers resulted in a vehicle search — a rate that was more than triple the national average, which was about one out of every 20 stops for drivers of any race or ethnicity, says Khadjavi.

Her decision to incorporate that policing data into her class was a pivotal moment in Khadjavi’s career — it led to a key publication and years of building expertise in using maths to study racial profiling and police practice. She sits on California’s Racial Identity and Profiling Advisory Board , which makes policy recommendations to state and local agencies on how to eliminate racial profiling in law enforcement.

In 2023, she was awarded the Association for Women in Mathematics’ inaugural Mary & Alfie Gray Award for Social Justice, named after a mathematician couple who championed human rights and equity in maths and government.

Sometimes, gaining access to data is a matter of networking. One of Khadjavi’s colleagues shared Khadjavi’s pivotal article with specialists at the American Civil Liberties Union. In turn, these specialists shared key data obtained through public-records requests with Khadjavi and her colleague. “Getting access to that data really changed what we could analyse,” Khadjavi says. “[It] allowed us to shine a light on the experiences of civilians and police in hundreds of thousands of stops made every year in Los Angeles.”

The data-intensive nature of this research can be an adjustment for some mathematicians, requiring them to develop new skills and approach problems differently. Such was the case for Tian An Wong, a mathematician at the University of Michigan-Dearborn who trained in number theory and representation theory.

In 2020, Wong wanted to know more about the controversial issue of mathematicians collaborating with the police, which involves, in many cases, using mathematical modelling and data analysis to support policing activities. Some mathematicians were protesting about the practice as part of a larger wave of protests around systemic racism , following the killing of George Floyd by police in Minneapolis, Minnesota. Wong’s research led them to a technique called predictive policing, which Wong describes as “the use of historical crime and other data to predict where future crime will occur, and [to] allocate policing resources based on those predictions”.

Wong wanted to know whether the tactics that mathematicians use to support police work could instead be used to critique it. But first, they needed to gain some additional statistics and data analysis skills. To do so, Wong took an online introductory statistics course, re-familiarized themself with the Python programming language, and connected with colleagues trained in statistical methods. They also got used to reading research papers across several disciplines.

Currently, Wong applies those skills to investigating the policing effectiveness of a technology that automatically locates gunshots by sound. That technology has been deployed in parts of Detroit, Michigan, where community members and organizations have raised concerns about its multimillion-dollar cost and about whether such police surveillance makes a difference to public safety.

Getting the lay of the land

For some mathematicians, social-justice work is a natural extension of their career trajectories. “My choice of mathematical epidemiology was also partially born out of out of my love for social justice,” Ortega says. Mathematical epidemiologists apply maths to study disease occurrence in specific populations and how to mitigate disease spread. When Ortega’s PhD adviser mentioned that she could study the uptake of a then-new rotovirus vaccine in the mid-2000s, she was hooked.

Mathematicians, who decide to jump into studying social-justice issues anew, must do their homework and dedicate time to consider how best to collaborate with colleagues of diverse backgrounds.

Jonathan Dawes, an applied mathematician at the University of Bath, UK, investigates links between the United Nations’ Sustainable Development Goals (SDGs) and their associated target actions. Adopted in 2015, the SDGs are “a universal call to action to end poverty, protect the planet, and ensure that by 2030 all people enjoy peace and prosperity,” according to the United Nations , and each one has a number of targets.

“As a global agenda, it’s an invitation to everybody to get involved,” says Dawes. From a mathematical perspective, analysing connections in the complex system of SDGs “is a nice level of problem,” Dawes says. “You’ve got 17 Sustainable Development Goals. Between them, they have 169 targets. [That’s] an amount of data that isn’t very large in big-data terms, but just big enough that it’s quite hard to hold all of it in your head.”

Dawes’ interest in the SDGs was piqued when he read a 2015 review that focused on how making progress on individual goals could affect progress on the entire set. For instance, if progress is made on the goal to end poverty how does that affect progress on the goal to achieve quality education for all, as well as the other 15 SDGs?

“If there’s a network and you can put some numbers on the strengths and signs of the edges, then you’ve got a mathematized version of the problem,” Dawes says. Some of his results describe how the properties of the network change if one or more of the links is perturbed, much like an ecological food web. His work aims to identify hierarchies in the SDG networks, pinpointing which SDGs should be prioritized for the health of the entire system.

As Dawes dug into the SDGs, he realized that he needed to expand what he was reading to include different journals, including publications that were “written in very different ways”. That involved “trying to learn a new language”, he explains. He also kept up to date with the output of researchers and organizations doing important SDG-related work, such as the International Institute for Applied Systems Analysis in Laxenburg, Austria, and the Stockholm Environment Institute.

Dawes’ research showed that interactions between the SDGs mean that “there are lots of positive reinforcing effects between poverty, hunger, health care, education, gender equity and so on.” So, “it’s possible to lift all of those up” when progress is made on even one of the goals. With one exception: managing and protecting the oceans. Making progress on some of the other SDGs could, in some cases, stall progress for, or even harm, life below water.

Collaboration care

Because social-justice projects are often inherently cross-disciplinary, mathematicians studying social justice say it’s key in those cases to work with community leaders, activists or community members affected by the issues.

Getting acquainted with these stakeholders might not always feel comfortable or natural. For instance, when Dawes started his SDG research, he realized that he was entering a field in which researchers already knew each other, followed each other’s work and had decades of experience. “There’s a sense of being like an uninvited guest at a party,” Dawes says. He became more comfortable after talking with other researchers, who showed a genuine interest in what he brought to the discussion, and when his work was accepted by the field’s journals. Over time, he realized “the interdisciplinary space was big enough for all of us to contribute to”.

Even when mathematicians have been invited to join a team of social-justice researchers, they still must take care, because first impressions can set the tone.

Michael Small is an applied mathematician and director of the Data Institute at the University of Western Australia in Perth. For much of his career, Small focused on the behaviour of complex systems, or those with many simple interacting parts, and dynamical systems theory, which addresses physical and mechanical problems.

But when a former vice-chancellor at the university asked him whether he would meet with a group of psychiatrists and psychologists to discuss their research on mental health and suicide in young people, it transformed his research. After considering the potential social impact of better understanding the causes and risks of suicide in teenagers and younger children, and thinking about how the problem meshed well with his research in complex systems and ‘non-linear dynamics’, Small agreed to collaborate with the group.

The project has required Small to see beyond the numbers. For the children’s families, the young people are much more than a single data point. “If I go into the room [of mental-health professionals] just talking about mathematics, mathematics, mathematics, and how this is good because we can prove this really cool theorem, then I’m sure I will get push back,” he says. Instead, he notes, it’s important to be open to insights and potential solutions from other fields. Listening before talking can go a long way.

Small’s collaborative mindset has led him to other mental-health projects, such as the Transforming Indigenous Mental Health and Wellbeing project to establish culturally sensitive mental-health support for Indigenous Australians.

Career considerations

Mathematicians who engage in social-justice projects say that helping to create real-world change can be tremendously gratifying. Small wants “to work on problems that I think can do good” in the world. Spending time pursuing them “makes sense both as a technical challenge [and] as a social choice”, he says.

However, pursuing this line of maths research is not without career hurdles. “It can be very difficult to get [these kinds of] results published,” Small says. Although his university supports, and encourages, his mental-health research, most of his publications are related to his standard mathematics research. As such, he sees “a need for balance” between the two lines of research, because a paucity of publications can be a career deal breaker.

Diaz Eaton says that mathematicians pursuing social-justice research could experience varying degrees of support from their universities. “I’ve seen places where the work is supported, but it doesn’t count for tenure [or] it won’t help you on the job market,” they say.

Finding out whether social-justice research will be supported “is about having some really open and transparent conversations. Are the people who are going to write your recommendation letters going to see that work as scholarship?” Diaz Eaton notes.

All things considered, mathematicians should not feel daunted by wading into solving the world’s messy problems, Khadjavi says: “I would like people to follow their passions. It’s okay to start small.”

This article is reproduced with permission and was first published on May 22, 2024 .

Advertisement

Research on early childhood mathematics teaching and learning

• Survey Paper
• Open access
• Published: 23 June 2020
• Volume 52 , pages 607–619, ( 2020 )

Cite this article

You have full access to this open access article

• Camilla Björklund   ORCID: orcid.org/0000-0001-5436-537X 1 ,
• Marja van den Heuvel-Panhuizen 2 , 3 &
• Angelika Kullberg 1  

64k Accesses

26 Citations

4 Altmetric

Explore all metrics

This paper reports an overview of contemporary research on early childhood mathematics teaching and learning presented at recent mathematics education research conferences and papers included in the special issue (2020–4) of ZDM Mathematics Education . The research covers the broad spectrum of educational research focusing on different content and methods in teaching and learning mathematics among the youngest children in the educational systems. Particular focus in this paper is directed to what lessons can be drawn from teaching interventions in early childhood, what facilitates children’s mathematical learning and development, and what mathematical key concepts can be observed in children. Together, these themes offer a coherent view of the complexity of researching mathematical teaching and learning in early childhood, but the research also brings this field forward by adding new knowledge that extends our understanding of aspects of mathematics education and research in this area, in the dynamic context of early childhood. This knowledge is important for future research and for the development of educational practices.

Similar content being viewed by others

Evolution and Revolution in Artificial Intelligence in Education

Teaching with digital technology

Mathematics and interdisciplinary STEM education: recent developments and future directions

Avoid common mistakes on your manuscript.

1 Introduction

Early childhood mathematics education is a rich field of study and practice that includes the provision of stimulating activities and learning environments, organized and orchestrated by teachers, care-takers and other professionals with the aim of offering young children experiences that extend their knowledge and development of mathematical concepts and skills. Generally, early childhood mathematics education involves children aged 3–6 years, but in many countries even the youngest toddlers go to early childhood centres. Therefore, contemporary research on early mathematics education focuses on children from birth until they enter formal schooling in the first grade. To develop this field of research, a strong foundation of theory and methodology is necessary, along with consideration of the practical settings of young children’s learning as well as the societal needs and relevant educational policy frameworks. Moreover, from a didactical perspective, it also requires consideration of the essence of the mathematics to be taught to young children.

High-quality research grounded in theory is necessary for all areas of mathematics education, in order to move forward and contribute to the generation of new knowledge from which the educational practice can benefit. Since there is much evidence that later development in mathematics is laid in the early years (e.g., Duncan et al. 2007 ; Krajewski and Schneider 2009 ; Levine et al. 2010 ), such high-quality research is especially critical for early childhood mathematics education. Research involving young children entails certain challenges that cannot simply be solved by adopting research designs that are used with older students. The aim of gaining deep knowledge of how young children’s mathematical understanding can be fostered places high demands on research methods. As early as 40 years ago, Donaldson ( 1978 ) stated that children act differently in their everyday situations than they do in experiment situations, and this has been confirmed by many others since then. Thus, gaining knowledge about teaching and learning mathematics in the early years requires research that is conducted in various learning environments and that acknowledges that these learning environments are complex, multifaceted, and dynamic.

Research in mathematics education is a relatively recent scientific discipline beginning in the last century (Kilpatrick 2014 ). Investigating young children’s mathematical learning and teaching became part of this discipline much later. Early childhood mathematics has long been the research field of developmental psychology and cognitive sciences. From the studies of mental abilities and thinking in mathematical problem-solving carried out in these disciplines, we have gained knowledge about the influence of working memory and attention span (e.g., Ashcraft et al. 1992 ; Passolunghi and Costa 2016 ; Stipek and Valentino 2015 ), as well as about the role of innate abilities of numerical awareness in children’s mathematical performance (e.g., Butterworth 2005 ; Wynn 1998 ). Yet, these studies lack a deeper investigation of the mathematics that is performed and how it is developed by children. Neither do such investigations address why certain mathematical competencies are important or why some activities stimulate their development and others do not. Contrary to psychological research, mathematics education research has a didactic perspective, which means that it is linked to the perspective of the learning child, the teaching teacher, and the environment offering learning opportunities in which the teaching and learning take place. Above all, didactic research distinguishes itself from psychological research because it deals explicitly with the question of what the mathematics is in early childhood activities, both within and outside formal education.

2 A brief overview of the current field of early mathematics education research

As shown by the many publications on teaching and learning of mathematics in early childhood that have been released in the past few years, this area of mathematics education research has increasingly become a mature discipline. The same is reflected by the special interest groups, working groups, and research fora dedicated to mathematics education in the early years. No self-respecting conference today can afford not to pay attention to the area of early mathematics, and there are now also communities and conferences that focus exclusively on early childhood mathematics education. All these communities and conferences are the epicentres where the latest developments in this field are brought together. To set the scene for research on early childhood mathematics teaching and learning, without it being complete, we first provide a brief overview of recently presented and discussed early mathematics education research. As an orientation point for this overview, we used what has recently been presented by researchers at three international meetings.

2.1 CERME 11 thematic working group (TWG) on early years mathematics

A conference that already has a considerable track record for including early childhood mathematics as a fixed part of its programme is the biennial conference of the European Society for Research in Mathematics Education (ERME). This conference started in 2009 with a Thematic Working Group (TWG) on Early Years Mathematics. Since then, the number of participants in this group has grown consistently. In 2019, this TWG (that is, TWG13) consisted not only of European researchers but also attracted participants from Canada, Japan, and Malawi. The most dominant theme presented there involved studies of children’s emerging number knowledge. Many of these presentations were traditional in design, including giving children tasks that had to be solved both individually when the children were interviewed and when they worked in groups in a classroom setting. Based on these studies, researchers formulated descriptions of the children’s knowledge. Sometimes, learning trajectories could be generated from these empirical observations. However, within this TWG several examples of studies with more innovative designs and research settings were also presented, including different modes of exploring and expressing numbers, which can extend our knowledge of early childhood mathematics education. An example of such research is Bjørnebye’s ( 2019 ) study, in which a dice game including elements of multiple representations and embodiment of counting strategies opened up the possibility of observing how children’s actions and responses reflect their understanding. Other studies investigated how affordances of manipulatives and applications encouraged children to develop new ways of thinking about numbers either by working in a digital environment (Bakos and Sinclair 2019 ) or by using their fingers to represent numbers (Lüken 2019 ; Björklund and Runesson Kempe 2019 ).

A characteristic of the research community gathered at CERME11 TWG13 is that the participants generally had in common an interest in better understanding the mathematical thinking of the child. Therefore, it was considered crucial that research establish clues for how to recognize mathematical thinking in the early years. For this purpose, Sprenger and Benz ( 2019 ) used eye-tracking data, as this platform was considered to contribute to the analysis of children’s perception of structure in the process of determining quantities. Yet, what Sprenger and Benz discovered is that data from technological devices still need to be interpreted, and that other expressions of children’s perceptions and reasoning are necessary assets for drawing valid conclusions.

A further important issue that was present at CERME11 TWG13 was related to teaching practice. Specifically, several presentations addressed the questions of how mathematics education should be orchestrated in early childhood education and what opportunities to learn should be offered to children. For example, Breive ( 2019 ) investigated the link between inquiry-based education and open-ended problem-solving, and the role of the teacher in orchestrating such conditions for mathematical exploration. In her paper, Breive described the teachers’ behaviour in terms of the degrees of freedom offered to the children with respect to their actions related to the mathematical content and context. Based on the data she collected, Breive concluded that teachers’ ways of acting, and the accompanying learning opportunities, should be given more attention within early mathematics education research. Similarly, Vogler ( 2019 ), who observed teacher–child group interactions, concluded that so-called indirect learning (which can be found as a common approach in many preschool settings) may induce an obstacle to learning mathematics embedded in activities if there is not a mutual understanding of what learning content is the aim of the activity. In line with these two studies, other researchers who focused on teachers’ interactions with children also highlighted critical issues for educational practice and supported further research inquiries.

Another source for learning about the latest developments in early childhood mathematics education research is the POEM conferences (Mathematics education perspective on early mathematics learning between the poles of instruction and construction). The latest conference, POEM4, was held in 2018. The presentations published in the conference proceedings (Carlsen et al. 2020 ) all, in one way or another, reflect the question “In what way—and how much—should children be ‘educated’ in mathematics before entering primary school?” This was also the recurring question in the discussions between the participating scholars. Among the contributions, three themes stood out: children’s mathematical reasoning, early mathematics teaching, and parents’ role in children’s mathematical development. There was a strong interest in children’s reasoning abilities and strategies in problem-solving. For example, Tsamir et al. ( 2020 ) investigated how children express their understanding of patterning. For this purpose, the researchers provided preschoolers with patterns to be copied and compared, while observing their strategies. Children’s strategy use was also observed in relation to play situations. Bjørnebye and Sigurjonsson ( 2020 ) observed them in teacher-led outdoor games, while Lossius and Lundhaug ( 2020 ) observed child-initiated play activities. Some researchers used their observations of children’s encounters with mathematical content for theoretical discussions on how to understand children’s meaning-making, for example by taking the semiotic mediation perspective (e.g., Bartolini Bussi 2020 ) or through the lens of attentional processes (Verschaffel et al. 2020 ).

With respect to early mathematics teaching, at POEM4 it was discussed that teachers’ educational work largely concerns how to empower children in the learning process, assuming that children have agency in their learning (Radford 2020 ). Some of the presented studies (e.g., Palmér and Björklund 2020 ) specifically chose children's perspectives and problematized how seriation was made a content for learning in a children’s story. They showed how different manipulatives and tools used in teaching have different implications for what is made possible for the children to learn. A critical but essential notion was expressed by Tzekaki ( 2020 ), who underlined that whether children act and think mathematically and learn mathematical concepts depends on what is defined to be mathematical thinking and acting. In line with this perspective, Keuch and Brandt ( 2020 ) and Bruns et al. ( 2020 ) also raised the issue that teachers’ and student teachers’ knowledge of mathematics in early childhood education affects their readiness to exploit the content in ways that facilitate children’s mathematical learning.

The issue of the knowledge of mathematics in early childhood was also addressed in papers on the role of parents in children’s learning of mathematics. Parents are recognized as young children’s first educators, contributing to their mathematical understanding and skills. One example of this research focus is Lembrér’s ( 2020 ) study. In order to know what experiences children bring with them into preschool education and thus might inform their encounter with mathematics, she investigated what parents value in the mathematics activities in which their children are engaged at home.

2.3 ICME-13 monograph “Contemporary research and perspectives on early childhood mathematics education”

The ICME-13 Monograph “Contemporary research and perspectives on early childhood mathematics education” (Elia et al. 2018 ) is the third source for becoming informed about the state of the art in the field of teaching and learning mathematics in early childhood. This book, which has its foundations in the ICME-13 (International Congress on Mathematical Education) Topic Study Group 1 (TSG1) “Early childhood mathematics education” held in 2016, contains chapters on a broad range of topics grouped into five key themes: pattern and structure, number sense, embodied action and context, technology, and early childhood educators’ professional issues and education.

Within these themes, the domain-overarching theme of pattern and structure played a prominent role. As Mulligan and Mitchelmore ( 2018 ) showed in a series of studies, children’s awareness of mathematical structures turned out to be crucial for acquiring mathematical competence. Particularly children’s structuring skills were found to be critical to developing coherent mathematical concepts and relationships. These findings are in line with Lüken and Kampmann’s ( 2018 ) intervention study with first graders, in which 5 months of explicit teaching of pattern and structure during regular mathematics lessons resulted in significant differences between pre- and post-test arithmetic achievement scores in the intervention group. Moreover, the intervention was most beneficial to the low-achieving children.

The research within the theme number sense examined a large variety of different aspects of number development. For example, there was a study about children’s enumeration skills when making lists for designating and representing collections of objects (Dorier and Coutat 2016 ). Also, attention was paid to the use of numerical finger gestures and other bodily-based communication in order to facilitate the learning process (Rinvold 2016 ), children’s spontaneous focusing on numerosity (SFON) (Rathé et al. 2018 ; Bojorque et al. 2018 ), and the link between writing skills and number development (Adenegan 2016 ). Furthermore, an exploration of children’s ability to operate with numbers revealed that 5-year-olds were able to solve multiplication and division problems when they were presented in familiar contexts (Young-Loveridge and Bicknell 2016 ).

In the theme embodied action and context , Karsli’s ( 2016 ) video-ethnographic research in a pre-kindergarten classroom showed that young children’s hand and body movements hold rich potential for engaging them in mathematics, and underlined the importance of early childhood teachers’ attention to the embodied ways in which children engage with mathematics, with potential for creating teachable moments. Other studies investigated children’s engagement in the context of play. In Henschen’s ( 2016 ) study free play was examined, while Nakken et al. ( 2016 ) compared free with guided play, of which the latter resulted in the children exhibiting deeper mathematical thinking, and engagement with more specific mathematical concepts. Anderson and Anderson ( 2018 ) broadened the scope by investigating children’s learning of mathematics in their home environment. Thom’s ( 2018 ) and Elia’s ( 2018 ) research on geometrical and spatial thinking in early childhood offered further insights into the crucial role of the body and other semiotic resources (language, drawings, and artefacts) by which young children develop and communicate spatial-geometrical thinking. A general conclusion within this theme was that the limited ways in which young children are invited to engage with geometrical, spatial, and measurement concepts undervalue the embodied, gestural, in-context nature of their mathematical thinking.

The theme technology specifically addressed the integration of technology into early childhood mathematics teaching and learning both at school and at home. The focus was mostly on touch-screen tablet-based applications. Because this new technology significantly differs from the traditional physical aid materials, professional development is needed to help educators identify and implement effective uses of these applications. To learn more about the role of the educator (teacher or parent) in the child’s interaction with the software, Baccaglini-Frank ( 2018 ) carried out an analysis of student-software-teacher relations, revealing how the teacher’s goal of helping the children experience success actually limited their development of numerical abilities. The use of technology also opened a window to a new perspective in early childhood mathematics, namely by exposing young children to advanced mathematics such as understanding symmetric transformation (Fletcher and Ginsburg 2016 ) and dealing with large numbers (also in symbolic form) and ordinality (Sinclair 2018 ).

In the theme early childhood educators’ professional issues and education , Cooke and Bruns ( 2018 ) provided a comprehensive overview of the various contributions in TSG1, for which they proposed to distinguish conditions at three levels that influence opportunities for young children to develop mathematical understanding and skills. At the macro level, curricula provide a framework (aims, content to learn, and activities) for mathematics teaching and learning in early childhood, with varying views. Several papers mentioned the tensions regarding new curricula and frameworks that may impose mathematical content rather than allowing the child to develop understanding of mathematical concepts through play. At the meso level, with focus on the teachers’ competence, all involved papers agreed as to the importance that the teacher possess a fundamental understanding of mathematics as the basis for high-quality early mathematics education. However, different studies used different conceptualizations and instruments to measure teachers’ mathematical competence. The micro level refers to the mathematics educational programmes and materials, as well as to the required training for teachers to develop their ability to effectively select and implement such programmes that address children’s mathematical needs (Fritz-Stratmann et al. 2016 ).

In sum, the common themes that stand out from the three international meetings are children’s learning through play, and concerns regarding how to apply content-focused teaching, with or without technology. We found that a great deal of the research is on children’s mathematical thinking and learning, including two main areas concerning children’s emerging number knowledge and children’s learning of patterns. It is noteworthy that in both areas, how children perceive structure or how they manifest structuring abilities were analysed in several of the studies. There were also a number of studies that focused on how finger patterns, gestures, or bodily-based communication may facilitate children’s learning of numbers.

Children’s learning through free or guided play is also a main issue that was discussed. Teachers’ guiding interaction with children in play was shown to contribute more to deeper mathematical thinking and engagement with specific mathematical content. How teaching affects children’s learning opportunities in preschool was furthermore of great concern in several of the studies. A conclusion drawn from this research is that teachers’ ways of acting and the learning opportunities created for children should be given more attention. In what way, and how much, children should be educated before entering primary school remains a central issue.

3 The contributions of this special issue

In this special issue of ZDM Mathematics Education (Issue 2020–4), contemporary research on early childhood mathematics teaching and learning is discussed by researchers from all over the world. The initiative emanated from the 42nd PME conference in Umeå, Sweden (July 2018), where we had the opportunity to organize a Research Forum in which researchers involved in the field of early childhood mathematics education gathered to present and discuss theoretical and methodological challenges and outcomes of studies on learning and teaching arithmetic skills in early years (Björklund et al. 2018 ; Van den Heuvel-Panhuizen 2018 ). The conclusion of the Research Forum was that early childhood mathematics education research is key, but that more efforts are needed to bring together the state of the art within this field as a foundation for moving early childhood mathematics education research forward. This special issue again provides a window into the contemporary field of research on early childhood mathematics teaching and learning. To discuss what this special issue adds to this field and reflect on the challenges that lie ahead for research on early childhood mathematics education, in the next section we synthesize the themes that emerge from the 15 papers included in this special issue. Each theme highlights the papers’ shared knowledge and contributions to research methods. Many papers are related to several themes, but for our discussion we chose those papers that predominantly belong to a particular theme. In total, we identified three recurring themes: the early interventions and their effects, the facilitating factors for learning and development, and the mathematical key concepts that can be observed in children. Together, these themes bring to the fore aspects that are essential for understanding the learning and teaching of mathematics in the early years.

3.1 What lessons can be drawn from interventions?

Research shows that children’s development of mathematical skills and knowledge is often influenced by socio-economic and curricular factors, and by social interaction in both short- and long-term perspectives (Pruden et al. 2011 ). Thus, there is a raised awareness of the impact early childhood education may have on reducing differences in conditions for learning and on increasing and securing equal opportunities for a good foundation in learning for all children. Based on their meta study of early mathematics education research, Duncan et al. ( 2007 ) stated that early intervention counts and numerous references to the same study indicate that this is an important standpoint in research. Why else indulge in the challenging task of researching learning among the youngest in our education systems, if one does not believe that efforts made through teaching are significant for children’s wellbeing and lifelong learning path?

Research on teaching and learning mathematics often shares a common research design in which interventions are implemented (designed, conducted, and the outcomes assessed) with the aim of finding ways to improve teaching practice for the benefit of the learning child, and often to reduce socio-economic inequality. Intervention studies can be objects of research in different ways, focusing on the children’s learning outcomes or the teaching practices. Nevertheless, the goal is to enhance learning through improved teaching. In the papers in this special issue we find efforts to implement well-designed interventions, explicitly focusing on how to teach. Some implement and analyse fine-grained differences in (teaching) actions and the effects on children’s attention to certain content (Paliwal and Baroody 2020 ; Mulligan et al. 2020 ), while others study the effects of attentiveness to children’s experiences and knowledge and the related choices of tasks (Clements et al. 2020 ; Grando and Lopes 2020 ). Nevertheless, essential to studying intervention success or failure is how learning outcomes are measured and interpreted, which is also an important aspect of early childhood mathematics education research (Li et al. 2020 ).

How teaching is framed to present mathematical content to young children, in order for it to be meaningful to them, and in order to be attentive to children’s experiences and knowledge, is investigated and discussed by Grando and Lopes ( 2020 ). Through narratives provided by early childhood teachers, they find insights into how teachers chose to frame the subjects of statistics and probability in ways that engaged children and were responsive to the children’s own experiences, rather than using materials provided by textbooks. Unconventional teaching methods whereby teachers turned their mathematics classroom into a space of creative insubordination are discussed in this paper in relation to the opportunities they offer children to become equipped with critical thinking. The authors argue that the specific content—statistics and probability—demands problematizing activities and experimentation with uncertain outcomes of problems in order to develop probabilistic thinking. This study highlights an essential issue in didactical research: that the content to be taught is not indifferent to how the teaching is designed. The study particularly raises concerns that the design of teaching cannot be random but rather has to be linked to the educational environment and the students attending that particular environment. Consequently, the generalizability of intervention programmes and teaching methods has to be taken into serious consideration if they are to be implemented in different educational settings.

Clements et al. ( 2020 ) set out to investigate the efficacy of implementing an intervention programme in which instructions and progression are grounded in a research-based learning trajectory. Even though the programme itself had previously been found to have positive outcomes for preschool children’s mathematics learning, the goal of the current study was to investigate how to teach in the most successful way. For this purpose, the authors used the same programme but adapted the choices of the tasks’ difficulty level to the children’s current knowledge levels. How to teach was then related to what to teach individual children. Results indicate that skipping difficulty levels to shorten the steps to the learning goals was not successful. This thorough investigation of teaching by adapting the complexity of the content to the child’s ability to learn best what is intended draws attention to the delicate work of teaching in early childhood education. The study supports child-centred approaches that are sensitive to the individual needs and potential of the child, while simultaneously aiming for the learning goals set by the curriculum.

While Clements et al. investigated the effects of an intervention programme covering broader numerical knowledge, Paliwal and Baroody ( 2020 ) aimed to investigate what conditions for learning the cardinality principle are most effective and how subitizing abilities impact on cardinality knowledge achievement. Their efforts were directed towards a fine-grained analysis of how to teach this aspect of the number concept, and what learning processes different approaches elicit in children. What stands out in their study is that they used a highly advanced research design, which allowed them to examine the effects of different ways of directing children’s attention to seeing numbers’ cardinality. In their paper, they point out the importance of directing children’s attention to various ways of seeing numbers’ cardinality, as follows: as a constructing act by adding units to get a number; as an act starting from naming the whole set with a counting word and then differentiating the added units by counting; and a third condition, attending only to single units in a counting act. Thus, their intervention was designed with explicit rigour as to what was made possible for the children to experience, and their investigation concerned the learning outcomes of the different conditions. While this attention in Paliwal and Baroody’s study to the different conditions can at first glance be considered subtle and far from the instruction children encounter in their mathematics education, the study offers insight into the importance of teachers’ awareness of their way of directing children’s attention to certain meanings of the content.

In another paper focusing on the effects of an intervention programme, Mulligan et al. ( 2020 ) analysed children’s written answers to pattern tasks in order to identify differences and changes in their structural awareness. They found a positive effect on the children’s development of awareness of mathematical pattern and structure (AMPS), and showed how the levels changed as an effect of a 37-week intervention programme. Mulligan et al. add to the field of early childhood mathematics knowledge of a particular ability (structural awareness), how it can be identified among young children, and also how the ability changes over a prolonged period of time (during an intervention), which may provide insight into what children actually learn while taking part in an intervention programme.

Children’s learning is of course at the centre of attention in intervention studies, and Li et al. ( 2020 ) pay explicit attention to how to interpret results from a pre- and post-diagnostic test. In their study, Li et al. investigated the development of mathematics problem-solving skills among kindergarteners by analysing their responses to a cognitive diagnostic test. As in most large-scale analyses, it can be shown in quantitative terms how children develop in producing correct answers that indicate growth in knowledge within certain domains that are tested for. However, Li et al. take a step further in their inquiry and illustrate how two children who scored similarly on the cognitive diagnostic test before an intervention had made different progress during the intervention period. Li et al. suggest that the reason for this difference may lie in how children understand and approach tasks, indicating different understanding even though similar answers are produced. Quantitative measures alone do not reveal such differences. The study thus shows the significance of paying attention to how children reason in order to solve a task. Based on their study, Li et al. recommend that children’s learning outcomes from participating in interventions be seen in the light of how the effects of interventions are measured, as it is observed that some developed skills do not endure over time and similar outcomes among children may conceal different learning paths.

3.2 What facilitates children’s learning and development?

Today, it is undisputed that the development of mathematical skills and the teaching of emerging skills in the early years are essential for mathematics education and developmental progress in the long term (Aunio and Niemivirta 2010 ; Duncan et al. 2007 ; Krajewski and Schneider 2009 ). However, in contrast to this perspective, a recent overview of the long-term effects of preschool mathematics education and interventions (Watts et al. 2018 ) challenges this almost taken-for-granted assumption, as most early interventions have a substantial fadeout effect. Thus, there is a need to revisit our current knowledge of teaching and learning, and scrutinize what seems to make a difference. Some of the papers in the special issue particularly consider this issue in their efforts to ascertain what facilitates children’s mathematical learning and development, and focus on influential aspects found in play settings (Reikerås 2020 ; Tirosh et al. 2020 ), verbal communication in teaching practices (Hundeland et al. 2020 ), and the home numeracy environment (Rathé et al. 2020 ).

Hundeland et al. ( 2020 ) raise the question of how children learn to use and understand the canonical language of mathematics, and study this aspect in terms of mathematical discourses taking place in kindergarten teaching sessions. They take a sociocultural stance (see Vygotsky 1987 ), seeing communication as the link between internal communication (thinking) and external communication (interaction). Therefore, children’s opportunities to contribute ideas and arguments are vital for their (mathematical) learning processes. Earlier research has also shown that care-takers’ talk influences not only children’s vocabulary but also, for instance, their spatial problem-solving (Pruden et al. 2011 ). The deeper knowledge that the study by Hundeland et al. ( 2020 ) provides regarding the quantity and quality of mathematical talk in which children are involved, offers us better opportunities also to organize supportive and stimulating conditions for knowledge growth.

What differs in the study by Hundeland et al. compared to most others with similar research questions is their focus on the kind of interaction that the mathematical discourse induces, which, based on the chosen sociocultural theoretical framework, should be crucial for positive learning outcomes. However, what they study and compare is the impact on the mathematical discourse that a certain in-service training has. This places mathematics in the spotlight of mathematics education research. While psychological and cognitive research provides us with important knowledge of mental processes and developmental advancement, studies like the one by Hundeland et al. have a clear direction towards understanding, and not least improving, the conditions for children’s learning and development, either by implementing teachers’ professional development or through curriculum improvements.

It is commonly agreed that young children’s learning is often situated in play. In a large-scale observation study, Reikerås ( 2020 ) conducted a thorough examination of the kind of play in which toddlers engage, for the purpose of learning how play skills may be related to early mathematical skills. It was found that competencies that allow the child to be active in solitary and parallel play, as well as children’s ability to initiate and remain in a play activity, correlated positively with the toddlers’ mathematical skills. The kind of play skills that showed the highest correlation with mathematical skills was their competence to interact in play. General social play skills thus seem to have an impact on mathematical learning, but Reikerås’ study cannot reveal how these are connected or any causal effects. An effort to better understand the interaction going on in toddlers’ play is made by Tirosh et al. ( 2020 ), investigating the challenges toddlers may face as they practise one-to-one correspondence in a playful context, and how different individuals participate in the playful mathematical context. Here, interaction and social skills become one issue with an impact on the learning opportunities arising in the play.

In many cases, the messy context of children’s play is a methodological challenge. It is not possible to control influencing variables to the same extent as in an experimental design. On the other hand, findings from the messy settings are more likely to bring to the fore aspects that were not anticipated, which raises new questions for research and theory development. Design research supports this kind of knowledge contribution, as several cycles are conducted, each developed based on insights from the previous cycle. These cycles adhere to children’s initiatives such as practising one-to-one correspondence in a setting the table task by putting one spoon inside each cup instead of placing one spoon beside each cup (see Tirosh et al. 2020 ); thus, the child is expressing an understanding of the concept, but is expressing it differently than how the task suggests. This highlights the importance of directing attention to instructions used in research studies, and particularly to the language of mathematics and the spatial aspects of props used in a task, related to the possibilities involved as young children interpret and execute a task.

Children take part in cultural life, where today numerical aspects are an inevitable part of the everyday environment. Nevertheless, there are differences in the extent to which children attend to these aspects, and consequently in how they learn the meaning of numbers, graphical representations of numbers, and how to use numbers. A common assumption is that home numeracy environment is a strong factor (LeFevre et al. 2009 ; Skwarchuk et al. 2014 ), which is reflected not least in the abundance of studies regarding socio-cultural background and demographic factors as a pre-cursor for learning progress. Rathé et al. ( 2020 ) put the common assumption to the test—that home environment has an influence on children’s progress in mathematical development—by comparing young children’s tendency to focus spontaneously on numeracy and numerical symbols in their home numeracy environment. Concerning this specific directionality to numbers, which is assumed to have an impact on children’s arithmetic skills in later years (see McMullen et al. 2015 ), based on their study they propose that the home numeracy environment does not seem to have any significant impact.

3.3 What mathematical key concepts can be observed in children?

A great deal of research in the field of early childhood mathematics education studies what mathematics children understand and how this understanding evolves. This knowledge is crucial in designing teaching that contributes to more advanced thinking and problem-solving strategies that support conceptual growth. Therefore, children’s utterances and how they act are the centre of interest for many researchers. Also, in this special issue, much attention is paid to the mathematical key concepts that can be attributed to children’s thinking, resulting in papers addressing children’s understanding of similarity in mathematical objects (Palmér and Van Bommel 2020 ), their understanding and use of structures (Sprenger and Bentz 2020 ; Kullberg and Björklund 2020 ), their understanding of the concept of cardinality and ordinality (Askew and Venkat 2020 ), and the underlying structure of their quantitative competencies (Van den Heuvel-Panhuizen and Elia 2020 ).

Children’s expressions, and how they are allowed to express themselves, are critical for our understanding of the learning of mathematics. Children’s problem posing is one aspect that can tell us about their understanding of mathematics (Cai et al. 2015 ). In the special issue, this is particularly addressed in the paper by Palmér and Van Bommel ( 2020 ), who investigated children’s understanding of similarity in mathematical objects. They analysed how children themselves created tasks in three-dimensional geometry that were similar to a previous problem-solving task they had worked on. It is suggested that this finding sheds light on the children’s interpretation of the specific mathematical features of the original task.

How children perceive structure has been shown to play an important role in how they, for example, determine a number of objects or solve an arithmetic problem (Ellemor-Collins and Wright 2009 ; Resnick 1983 ). In line with these earlier studies, Sprenger and Bentz ( 2020 ) investigated how 5-year-olds perceive structures in visually presented sets. By having the children determine the number of eggs in a 10-egg box while using an eye-tracking device (and recording the children’s utterances and gestures), they were able to analyse the children’s gaze when determining the cardinality of the set, and thereby gain insight into the process of perception. The eye-tracking data showed, for example, that many of the children were able to see structures (e.g. 4 + 1 or 3 + 2) and use them to determine a quantity without having to count all the objects. The authors argue that children’s ability to perceive structures in sets and use them to determine cardinality is central for their further arithmetic learning, as how children perceive sets (e.g., as individual objects, as a composite whole, or in structured part-whole relations) affects the strategies they use for solving arithmetic tasks.

Similar ideas are found in the study by Kullberg and Björklund ( 2020 ), who studied 5-year-olds’ use of finger patterns to structure number relations while solving an arithmetic problem. They identified two major ways of structuring the task: only structuring, and counting and structuring. In the group that both structured using their fingers and counted on some fingers, some ways were found to be more powerful. Children who solved the arithmetic task (3 + _ = 8) by creating a finger pattern of eight raised fingers and simultaneously identifying (‘seeing’) the missing part (5) on two hands (3 + (2 + 3) = 8) were more successful in solving arithmetic tasks, even in a later follow-up assessment. It is suggested that a possible reason for this later success is that these children were able to see numbers as parts included in other numbers, which has been found in earlier research (Resnick 1983 ) to be important for developing arithmetic skills.

Baccaglini-Frank et al. ( 2020 ) also argue that the appropriate use of fingers can contribute to developing children’s number sense. They studied how 4-year-olds interacted (verbally and using finger patterns) when using the application TouchCounts. The app combines multi-touch with audile, visual, and symbolic representation, and several solution strategies are possible, affording the simultaneous experience of, for example, finger patterns on the screen, with the number both seen and spoken. In their paper the authors emphasize how multimodal affordances may encourage children to use different strategies in response to different tasks, and thus experience a broad range of abilities related to number sense, including both cardinality and ordinality.

Askew and Venkat ( 2020 ) examined children’s understanding of the concept of cardinality and ordinality in connection with their awareness of additive and multiplicative number relations. To investigate this topic, first graders (6- and 7-year-olds) in South Africa were asked to position the numerals 1–9 on a bounded 0–10 number line. The children were able to do this in the correct order, with the fewest errors at the upper and lower ends of the number range. Furthermore, evidence was found that awareness of ordinality and that of cardinality develop alongside each other. However, the logarithmic scale, predicted in earlier research, which is considered to indicate a multiplicative structuring of number relationships, was not confirmed in the South African data. Instead, when the numerals grew larger the intervals became more stretched out rather than compressed. In fact, the children’s responses were closer to the linear model, which is considered to indicate an additive structuring of number relationships. Also, the use of unit sizes that did not take into account the length of the number line, together with the underestimation of the position of 5 on the 0–10 line, offered limited evidence of the children’s awareness of the multiplicative structure of the cardinality of numbers. More research is needed to disclose the deep interconnections between children’s understanding of cardinality and ordinality, and their understanding of multiplicative and additive number relations.

Another effort to unravel the complex nature of children’s early number understanding was carried out by Van den Heuvel-Panhuizen and Elia ( 2020 ), investigating the structure of the quantitative competence repertoire of kindergartners. Based on a literature review, they arrived at a model consisting of two constituent parts: quantification (the ability to connect a number to a given collection of objects) and quantitative reasoning (the ability to think and operate with quantities). Quantification was split up into counting and subitizing, and quantitative reasoning into additive and multiplicative reasoning. Although this model is partly in line with models found in earlier research, it also extends previously developed models by including multiplicative reasoning. Data were collected in the Netherlands and Cyprus. A series of confirmatory factor analyses showed that the hypothesized four-factor model fitted the empirical data of the Netherlands, but not those of Cyprus, which clearly challenges the model’s generalizability. A comparison of the component performances in the Dutch sample revealed that, in accordance with other studies, the lowest scores were found for multiplicative reasoning and that the competence of subitizing seems to develop before counting. This was partly confirmed by a statistical implicative analysis at item level. Although this analysis resulted in different implicative chains in the two countries, in both samples the multiplicative reasoning and conceptual subitizing items were found at the top of the chain and the counting and perceptual subitizing items at the end. Also, more research is necessary here, particularly concerning the generalizability of the model to other countries.

4 Future directions for research on early mathematics teaching and learning

After the Research Forum at PME42 we concluded that to move early childhood mathematics education research forward, more efforts are needed to bring together the state of the art within this field. Thus, we proposed a special issue on the theme Research on early childhood mathematics teaching and learning for the purpose of opening up further discussion and inquiry. In this article, the 15 papers included in the special issue are synthesized and discussed in terms of their contribution to the current field of research in early mathematics teaching and learning along with recent research presented at international mathematics education research conferences. Naturally, these do not cover the worldwide field of research, but they at least give a general idea of the current research interests and challenges.

All the papers in this special issue address aspects of early mathematics education and its underlying theories and research methodologies. They share common interests and challenges concerning how to gain knowledge of the youngest children’s mathematical development, and they identify prosperous teaching approaches. Our appeal to researchers participating in the special issue was to cover the broad span of mathematical ideas that are relevant in early childhood education. Nevertheless, we see a strong direction towards research on the learning and teaching of number concepts and basic arithmetic. This is in line with Alpaslan and Erden ( 2015 ) review of early mathematics research published in 2000–2013 in high-ranked scientific journals in the field of mathematics education, in which the most frequently reported research topics were number systems and arithmetic. The same trend is also found in the research addressed in the latest meetings of ICME, ERME, and POEM. We believe further research should widen this scope, and consider and investigate mathematical topics that are currently less highlighted. There is a need for deeper insight into what mathematics means to young children, and also how the foundations can be laid for the domains of spatial and geometric thinking and measurement, as well as for the domains of structures and patterns, data handling, problem-solving and mathematical reasoning.

Moving an educational field forward, however, is not solely based in covering a broad field of content. To strengthen the field, we need to scrutinize the research designs and methods that are used and the knowledge that is generated. Here, new technologies may open up opportunities for designing tools for investigating children’s competencies. However, this initiative goes beyond choosing digital tools or concrete building blocks; it concerns children’s opportunities to express themselves within different environments and make use of tools and manipulatives that may reveal new insights into their competencies and open up for innovative research questions to be posed. What is made available to experience surely has an impact on children’s expressions of knowledge. And expressions in both words and gestures are important keys here to interpreting the youngest children’s knowledge and skills. We can see this in the recent ICME, ERME, and POEM meetings’ presentation of a large variety of research designs and in the papers of this special issue. Many innovative research designs have been developed that allow thorough investigation of children’s mathematical competence and understanding. What we see, for example, is that subtle differences in expression (e.g. gaze, finger use, or ways of posing questions) reveal new and important insights for developing knowledge of children’s mathematical learning. These innovations in methodology allow for the thorough investigation of key features of learning mathematics that go beyond the broad content areas and highlight how mathematical aspects such as cardinality, ordinality, and number structure are experienced by children. Several of the papers in the special issue particularly attend to these aspects, and do so by creating and using new methodologies and technologies.

The consensus in the field of early mathematics education, reflected in the papers and conference presentations, is strong concerning the impact of early interventions on children’s opportunities to thrive as mathematics learners. From longitudinal studies, we know that early knowledge and skills seem to follow through the child’s development; that is, weak mathematical skills in early childhood years are likely to predict weak mathematics performance in later school years (Reikerås and Salomonsen 2019 ; Hannula-Sormunen et al. 2015 ). This means that early intervention and knowledge of how to offer all children a good start for their mathematical learning are essential to the field of early childhood mathematics education. However, it cannot be assumed that simply participating in education, whether it is framed as free or guided play or problem-solving, or stimulating interactive environments, will result in successful learning outcomes, even though most interventions do have a positive impact and most children develop their knowledge to some extent (Wang et al. 2016 ). Common research objectives, therefore, concern intervention implementation, and analyses of children’s learning outcomes from participating in differently designed activities. These studies are of high importance, as they connect the teaching to the learning and provide insights into what seem to be key aspects in the teaching practice. Nevertheless, researching interventions is delicate work, and it is essential to maintain scientific rigor in the design and analysis. Because early childhood education most often takes place in dynamic settings, the conditions under which children learn vary greatly. This diversity is observed in many studies in which children’s engagement in play, both self-initiated and guided, is used as data for analysing their mathematics competencies and learning of mathematics. This phenomenon means that the conditions offered to explore mathematical concepts and principles should be critically examined, along with how learning from interventions is measured and valued. There is a need to determine what works, what seems critical, and what aspects serve as particular challenges. In research, also special attention has to be given to the nature of the teaching practices. What we learn from intervention studies, both those included in the special issue and those in other contemporary research, is the importance of situating research in the current field of knowledge and the context in which the research is conducted. Each study broadens the picture of the teaching–learning relationship, which is by no means one-directional. There are many aspects to consider that potentially influence this relationship, and all of them cannot be included in one study alone.

Early childhood mathematics education research often attends to the opportunities and conditions that are offered for learning. There is no doubt that children’s activities and interaction with others, already from an early age, offer many opportunities to learn mathematical concepts and basic principles, but our ability to discern what children actually learn from the mathematical learning environments offered to them places high demands on the interpretation process. How to understand the processes going on in play and interaction, and what impacts the children’s learning outcomes—what is made possible to learn—often remains an unsolved issue, as the interaction between teacher and children is dynamic, and particularly as play is multidirectional in nature. Studies of interaction in both formal and informal contexts are nevertheless important, as they are conducted in the complex of social and cultural settings that do influence, through norms and individuals’ experiences, what is possible for children to learn.

Adenegan, K. E. (2016). An investigation into the writing and computational skills of school pupils of age 3–6: Implications for early childhood numeracy. In Paper presented at the 13th International Congress on Mathematical Education, Hamburg, Germany .

Alpaslan, Z. G., & Erden, F. T. (2015). The status of early childhood mathematics education research in the last decade. In CERME9—Ninth Congress of the European Society for Research in Mathematics Education (pp. 1933–1939). Charles University in Prague, Faculty of Education; ERME, Feb 2015, Prague, Czech Republic.

Anderson, A., & Anderson, J. (2018). Math-in-context: The types of math preschoolers ‘do’ at home. In I. Elia, J. Mulligan, A. Anderson, A. Baccaglini-Frank, & C. Benz (Eds.), Contemporary research and perspectives on early childhood mathematics education (pp. 183–202). Cham: Springer Nature.

Chapter   Google Scholar  

Ashcraft, M. H., Donley, R., Halas, M. A., & Vakali, M. (1992). Working memory, automaticity and problem difficulty. In J. I. D. Campbell (Ed.), The nature and origins of mathematical skills, advances in psychology, vol. 91 (pp. 301–329). Amsterdam: North-Holland.

Askew, M., & Venkat, H. (2020). Deconstructing South African Grade 1 learners’ awareness of number in terms of cardinality, ordinality and relational understandings. ZDM . https://doi.org/10.1007/s11858-020-01132-2 . (This issue) .

Article   Google Scholar  

Aunio, P., & Niemivirta, M. (2010). Predicting children’s mathematical performance in grade one by early numeracy. Learning and Individual Differences, 20 (5), 427–435.

Baccaglini-Frank, A. (2018). What schemes do preschoolers’ develop when using multi-touch applications to foster number sense (and why)? In I. Elia, J. Mulligan, A. Anderson, A. Baccaglini-Frank, & C. Benz (Eds.), Contemporary research and perspectives on early childhood mathematics education (pp. 223–243). Cham: Springer Nature.

Baccaglini-Frank, A., Carotenuto, G., & Sinclair, N. (2020). Eliciting preschoolers’ number abilities using open, multi-touch environments. ZDM . https://doi.org/10.1007/s11858-020-01144-y . (This issue) .

Bakos, S., & Sinclair, N. (2019). Pips (times) Pods: Dancing towards multiplicative thinking. In Eleventh Congress of the European Society for Research in Mathematics Education (CERME11) , Utrecht University, Feb 2019, Utrecht, Netherlands.

Bartolini Bussi, M. G. (2020). Early years mathematics: Semiotic and cultural mediation. In M. Carlsen, I. Erfjord, & P. S. Hundeland (Eds.), Mathematics education in the early years. Results from the POEM4 conference, 2018 (pp. 1–21). Berlin: Springer.

Google Scholar  

Björklund, C., Kullberg, A., Runesson Kempe, A., Reis, M., Clements, D., Sarama, J., Levenson, E., Barkai, R., Tirosh, D., Tsamir, P., Askew, M., Venkat, H., & Hannula-Sormunen, M. (2018). Learning and teaching of arithmetic skills in early years. (Research Forum). In E. Bergqvist, M. Österholm, C. Granberg & L. Sumpter (Eds.), Proceedings of the 42nd Conference of the International Group for the Psychology of Mathematics Education (vol. 1) (pp. 125–155). Umeå, Sweden: PME.

Björklund, C., & Runesson Kempe, U. (2019). Framework for analysing children’s ways of experiencing numbers. In Eleventh Congress of the European Society for Research in Mathematics Education (CERME11) , Utrecht University, Feb 2019, Utrecht, Netherlands.

Bjørnebye, M. (2019). Pre-schoolers’ ability to synchronise multiple representations of numerosity in embodiment of a counting-on-strategy. In Eleventh Congress of the European Society for Research in Mathematics Education (CERME11) , Utrecht University, Feb 2019, Utrecht, Netherlands.

Bjørnebye, M., & Sigurjonsson, T. (2020). Young children’s cross-domain mapping of numerosity in path navigation. In M. Carlsen, I. Erfjord, & P. S. Hundeland (Eds.), Mathematics education in the early years. Results from the POEM4 conference, 2018 (pp. 109–126). Cham: Springer.

Bojorque, G., Torbeyns, J., Hannula-Sormunen, M. M., Van Nijlen, D., & Verschaffel, L. (2018). Ecuadorian kindergartners’ spontaneous focusing on numerosity development: Contribution of numerical abilities and quality of mathematics education. In I. Elia, J. Mulligan, A. Anderson, A. Baccaglini-Frank, & C. Benz (Eds.), Contemporary research and perspectives on early childhood mathematics education (pp. 69–86). Cham: Springer Nature.

Breive, S. (2019). Kindergarten teachers’ orchestration of mathematical learning activities: The balance between freedom and structure. In Eleventh Congress of the European Society for Research in Mathematics Education (CERME11) , Utrecht University, Feb 2019, Utrecht, Netherlands.

Bruns, J., Carlsen, M., Eichen, L., Erfjord, I., & Hundeland, P. S. (2020). Situational perception in mathematics (SPiM)—Results of a cross-country study in Austria and Norway. In M. Carlsen, I. Erfjord, & P. S. Hundeland (Eds.), Mathematics education in the early years. Results from the POEM4 conference, 2018 (pp. 317–332). Cham: Springer.

Butterworth, B. (2005). The development of arithmetical abilities. Journal of Child Psychology and Psychiatry, 46 (1), 3–18. https://doi.org/10.1111/j.1469-7610.2005.00374.x .

Cai, J., Hwang, C., Jiang, C., & Silber, S. (2015). Problem-posing research in mathematics education: Some answered questions and unanswered questions. In F. M. Singer, N. F. Ellerton, & J. Cai (Eds.), Mathematical problem posing: From research to effective practice (pp. 3–34). New York: Springer.

Carlsen, M., Erfjord, I., & Hundeland, P. S. (Eds.). (2020). Mathematics education in the early years. Results from the POEM4 conference, 2018 . Berlin: Springer.

Clements, D. H., Sarama, J., Baroody, A. J., & Joswick, C. (2020). Efficacy of a learning trajectory approach compared to a teach-to-target approach for addition and subtraction. ZDM . https://doi.org/10.1007/s11858-019-01122-z . (This issue) .

Cooke, A., & Bruns, J. (2018). Early childhood educators’ issues and perspectives in mathematics education. In I. Elia, J. Mulligan, A. Anderson, A. Baccaglini-Frank, & C. Benz (Eds.), Contemporary research and perspectives on early childhood mathematics education (pp. 267–289). Cham: Springer Nature.

Donaldson, M. (1978). Children's minds . Glasgow: Fontana/Collins.

Dorier, J. L., & Coutat, S. (2016). Conceptualizing order in early school. In Paper presented at the 13th International Congress on Mathematical Education, Hamburg, Germany .

Duncan, G. J., Dowsett, C. J., Claessens, A., Magnuson, K., Huston, A. C., Klebanov, P., et al. (2007). School readiness and later achievement. Developmental Psychology, 43 (6), 1428–1446. https://doi.org/10.1037/0012-1649.43.6.1428 .

Elia, I. (2018). Observing the use of gestures in young children’s geometric thinking. In I. Elia, J. Mulligan, A. Anderson, A. Baccaglini-Frank, & C. Benz (Eds.), Contemporary research and perspectives on early childhood mathematics education (pp. 159–182). Cham: Springer Nature.

Elia, I., Mulligan, J., Anderson, A., Baccaglini-Frank, A., & Benz, C. (Eds.). (2018). Contemporary research and perspectives on early childhood mathematics education. ICME-13 monographs . Cham: Springer Nature.

Ellemor-Collins, D., & Wright, R. (2009). Structuring numbers 1–20: Developing facile addition and subtraction. Mathematics Education Research Journal, 21 (2), 50–75.

Fletcher, N., & Ginsburg, H. (2016). Teaching symmetry in the early childhood classroom: Using software to facilitate discourse and promote understanding of symmetric transformations. In Paper presented at the 13th International Congress on Mathematical Education, Hamburg, Germany .

Fritz-Stratmann, A., Ehlert, M., & Herzog, A. (2016). From thought to reality— Implementation of an in-school mathematics training in South Africa. In Paper presented at the 13th International Congress on Mathematical Education, Hamburg, Germany .

Grando, R. C., & Lopes, C. E. (2020). Creative insubordination of teachers proposing statistics and probability problems to children. ZDM . https://doi.org/10.1007/s11858-020-01166-6 . (This issue) .

Hannula-Sormunen, M. M., Lehtinen, E., & Räsänen, P. (2015). Preschool children’s spontaneous focusing on numerosity, subitizing, and counting skills as predictors of their mathematical performance seven years later at school. Mathematical Thinking and Learning, 17 (2–3), 155–177. https://doi.org/10.1080/10986065.2015.1016814 .

Henschen, E. (2016). Mathematical content of play activities in kindergarten, exemplified on blockplay activities. In Poster presented at the 13th International Congress on Mathematical Education, Hamburg, Germany .

Hundeland, P. S., Carlsen, M., & Erfjord, I. (2020). Qualities of mathematical discourses in Kindergartens. ZDM . https://doi.org/10.1007/s11858-020-01146-w . (This issue) .

Karsli, E. (2016). Young children’s embodied mathematical practices in a pre-K classroom. In Paper presented at the 13th International Congress on Mathematical Education, Hamburg, Germany .

Keuch, S., & Brandt, B. (2020). ‘You are already bigger than the giraffe!’ The use of adjectives in measurement activities in Kindergarten. In M. Carlsen, I. Erfjord, & P. S. Hundeland (Eds.), Mathematics education in the early years. Results from the POEM4 conference, 2018 (pp. 369–384). Cham: Springer.

Kilpatrick, J. (2014). History of research in mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education . Dordrecht: Springer. https://doi.org/10.1007/978-94-007-4978-8_71

Krajewski, K., & Schneider, W. (2009). Early development of quantity to number-word linkage as a precursor of mathematical school achievement and mathematical difficulties: Findings from a four-year longitudinal study. Learning and Instruction, 19 (6), 513–526.

Kullberg, A., & Björklund, C. (2020). Preschoolers’ different ways of structuring part-part-whole relations with finger patterns when solving an arithmetic task. ZDM . https://doi.org/10.1007/s11858-019-01119-8 . (This issue) .

LeFevre, J.-A., Skwarchuk, S.-L., Smith-Chant, B. L., Fast, L., Kamawar, D., & Bisanz, J. (2009). Home numeracy experiences and children’s math performance in the early school years. Canadian Journal of Behavioural Science, 41 , 55–66. https://doi.org/10.1037/a0014532 .

Lembrér, D. (2020). Parents’ valuing of mathematics for young children. In M. Carlsen, I. Erfjord, & P. S. Hundeland (Eds.), Mathematics education in the early years. Results from the POEM4 conference, 2018 (pp. 403–420). Cham: Springer.

Levine, S., Suriyakham, L. W., Rowe, M., Huttenlocher, J., & Gunderson, E. (2010). What counts in the development of young children’s number knowledge? Developmental Psychology, 46 (5), 1309–1319.

Li, L., Zhou, X., Gao, X., & Tu, D. (2020). The development and influencing factors of Kindergarteners’ mathematics problem solving based on cognitive diagnosis assessment. ZDM . https://doi.org/10.1007/s11858-020-01153-x . (This issue) .

Lossius, M., & Lundhaug, T. (2020). Mathematical problem-solving visualised in outdoor activities. In M. Carlsen, I. Erfjord, & P. S. Hundeland (Eds.), Mathematics education in the early years. Results from the POEM4 conference, 2018 (pp. 127–141). Cham: Springer.

Lüken, M. (2019). Using finger patterns—The case of communicating age. In Eleventh Congress of the European Society for Research in Mathematics Education (CERME11) , Utrecht University, Feb 2019, Utrecht, Netherlands.

Lüken, M., & Kampmann, R. (2018). The influence of fostering children’s patterning abilities on their arithmetic skills in Grade 1. In I. Elia, J. Mulligan, A. Anderson, A. Baccaglini-Frank, & C. Benz (Eds.), Contemporary research and perspectives on early childhood mathematics education (pp. 55–66). Cham: Springer Nature.

McMullen, J., Hannula-Sormunen, M. M., & Lehtinen, E. (2015). Preschool spontaneous focusing on numerosity predicts rational number conceptual knowledge 6 years later. ZDM, 47 (5), 813–824. https://doi.org/10.1007/s11858-015-0669-4 .

Mulligan, J. T., & Mitchelmore, M. C. (2018). Promoting early mathematical structural development through an integrated assessment and pedagogical program. In I. Elia, J. Mulligan, A. Anderson, A. Baccaglini-Frank, & C. Benz (Eds.), Contemporary research and perspectives on early childhood mathematics education (pp. 17–33). Cham: Springer Nature.

Mulligan, J., Oslington, G., & English, L. (2020). Supporting early mathematical development through a ‘pattern and structure’ intervention program. ZDM . https://doi.org/10.1007/s11858-020-01147-9 . (This issue) .

Nakken, A., Grimeland, Y., Nergard, B., & Thiel, O. (2016). Young children’s play in a mathematics room. In Poster presented at the 13th International Congress on Mathematical Education, Hamburg, Germany .

Paliwal, V., & Baroody, A. J. (2020). Cardinality principle understanding: The role of focusing on the subitizing ability. ZDM . https://doi.org/10.1007/s11858-020-01150-0 . (This issue) .

Palmér, H., & Björklund, C. (2020). Preschoolers’ ways of using fingers in numerical reasoning. In M. Carlsen, I. Erfjord, & P. S. Hundeland (Eds.), Mathematics education in the early years. Results from the POEM4 conference, 2018 (pp. 93–107). Cham: Springer.

Palmér, H., & Van Bommel, J. (2020). Young students posing problem-solving tasks: What does posing a similar task imply to students? ZDM . https://doi.org/10.1007/s11858-020-01129-x . (This issue) .

Passolunghi, M. C., & Costa, H. M. (2016). Working memory and early numeracy training in preschool children. Child Neuropsychology, 22 (1), 81–98.

Pruden, S., Levine, S., & Huttenlocher, J. (2011). Children’s spatial thinking: does talk about the spatial world matter? Developmental Science, 14 (6), 1417–1430.

Radford, L. (2020). Play and the production of subjectivities in preschool. In M. Carlsen, I. Erfjord, & P. S. Hundeland (Eds.), Mathematics education in the early years. Results from the POEM4 conference, 2018 (pp. 43–60). Cham: Springer.

Rathé, S., Torbeyns, J., De Smedt, B., Hannula-Sormunen, M. M., & Verschaffel, L. (2018). Kindergartners’ spontaneous focus on number during picture book reading. In I. Elia, J. Mulligan, A. Anderson, A. Baccaglini-Frank, & C. Benz (Eds.), Contemporary research and perspectives on early childhood mathematics education (pp. 87–99). Cham: Springer Nature.

Rathé, S., Torbeyns, J., De Smedt, B., & Verschaffel, L. (2020). Are children’s spontaneous number focusing tendencies related to their home numeracy environment? ZDM . https://doi.org/10.1007/s11858-020-01127-z . (This issue) .

Reikerås, E. (2020). Relations between play skills and mathematical skills in toddlers. ZDM . https://doi.org/10.1007/s11858-020-01141-1 . (This issue) .

Reikerås, E., & Salomonsen, T. (2019). Weak mathematical skills at an early age: Persistent or temporary? Children with weak mathematical skills and their development from toddlers to preschoolers. Early Child Development and Care, 189 (4), 670–682. https://doi.org/10.1080/03004430.2017.1337753 .

Resnick, L. B. (1983). A developmental theory of number understanding. In H. Ginsburg (Ed.), The development of mathematical thinking (pp. 109–151). New York: Academic Press.

Rinvold, A. R. (2016). The difficulty of learning the three first numerosities. In Poster presented at the 13th International Congress on Mathematical Education, Hamburg, Germany .

Sinclair, N. (2018). Time, immersion and articulation: Digital technology for early childhood mathematics. In I. Elia, J. Mulligan, A. Anderson, A. Baccaglini-Frank, & C. Benz (Eds.), Contemporary research and perspectives on early childhood mathematics education (pp. 205–221). Cham: Springer Nature.

Skwarchuk, S.-L., Sowinski, C., & LeFevre, J.-A. (2014). Formal and informal home learning activities in relation to children’s early numeracy and literacy skills: The development of a home numeracy model. Journal of Experimental Child Psychology, 121 , 63–84. https://doi.org/10.1016/j.jecp.2013.11.006 .

Sprenger, P., & Bentz, C. (2020). Children’s perception of structures when determining cardinality of sets: Results of an eye-tracking study with five-year-old children. ZDM . https://doi.org/10.1007/s11858-020-01137-x . (This issue) .

Sprenger, P., & Benz, C. (2019). Perceiving and using structures in sets—The contribution of eye-tracking in a three-level evaluation process. In Eleventh Congress of the European Society for Research in Mathematics Education (CERME11) , Utrecht University, Feb 2019, Utrecht, Netherlands.

Stipek, D., & Valentino, R. A. (2015). Early childhood memory and attention as predictors of academic growth trajectories. Journal of Educational Psychology, 107 (3), 771–788. https://doi.org/10.1037/edu0000004 .

Thom, J. S. (2018). (Re)(con)figuring space: Three children’s geometric reasonings. In I. Elia, J. Mulligan, A. Anderson, A. Baccaglini-Frank, & C. Benz (Eds.), Contemporary research and perspectives on early childhood mathematics education (pp. 131–158). Cham: Springer Nature.

Tirosh, D., Tsamir, P., Levenson, E. S., & Barkai, R. (2020). Setting the table with toddlers: A playful context for engaging in one-to-one correspondence. ZDM . https://doi.org/10.1007/s11858-019-01126-9 . (This issue) .

Tsamir, P., Tirosh, D., Barkai, R., & Levenson, E. (2020). Copying and comparing repeating patterns: Children’s strategies and descriptions. In M. Carlsen, I. Erfjord, & P. S. Hundeland (Eds.), Mathematics education in the early years. Results from the POEM4 conference, 2018 (pp. 63–78). Cham: Springer.

Tzekaki, M. (2020). Mathematical activity in early childhood and the role of generalization. In M. Carlsen, I. Erfjord, & P. S. Hundeland (Eds.), Mathematics education in the early years. Results from the POEM4 conference, 2018 (pp. 301–313). Cham: Springer.

Van den Heuvel-Panhuizen, M. (2018). Theories, methodologies, results in early arithmetic research. In Presented at PME 42, in Research Forum: Learning and teaching of arithmetic skills in early years , Umeå, Sweden, 3–8 July, 2018.

Van den Heuvel-Panhuizen, M., & Elia, I. (2020). Mapping kindergartners’ quantitative competence. ZDM . https://doi.org/10.1007/s11858-020-01138-w . (This issue) .

Verschaffel, L., Rathé, S., Wijns, N., Degrande, T., Van Dooren, W., De Smedt, B., et al. (2020). Young children’s early mathematical competencies: The role of mathematical focusing tendencies. In M. Carlsen, I. Erfjord, & P. S. Hundeland (Eds.), Mathematics education in the early years. Results from the POEM4 conference, 2018 (pp. 23–42). Cham: Springer.

Vogler, A-M. (2019). Chances and obstacles of ‘indirect’ learning processes in situations with preschool teachers. In Eleventh congress of the European Society for Research in Mathematics Education (CERME11) , Utrecht University, Feb 2019, Utrecht, Netherlands.

Vygotsky, L. S. (1987). The collected works of L.S. Vygotsky, Vol. 1: Problems of general psychology, including the volume Thinking and Speech. Edited by R. W. Rieber and A. S. Carton; translated by N. Minick. New York: Plenum.

Wang, A., Firmender, J., Power, J., & Byrnes, J. (2016). Understanding the program effectiveness of early mathematics interventions for prekindergarten and kindergarten environments: A meta-analytic review. Early Education and Development, 27 (5), 692–713.

Watts, T. W., Duncan, G. J., Clements, D. H., & Sarama, J. (2018). What is the long-run impact of learning mathematics during preschool? Child Development, 89 (2), 539–555. https://doi.org/10.1111/cdev.12713 .

Wynn, K. (1998). Numerical competence in infants. In C. Donlan (Ed.), The development of mathematical skills . Hove: Psychology Press.

Young-Loveridge, J., & Bicknell, B. (2016). Tens awareness: A framework for early place value learning. In Poster presented at the 13th International Congress on Mathematical Education, Hamburg, Germany .

Download references

Acknowledgements

Open access funding provided by University of Gothenburg.

Author information

Authors and affiliations.

University of Gothenburg, Gothenburg, Sweden

Camilla Björklund & Angelika Kullberg

Utrecht University, Utrecht, The Netherlands

Marja van den Heuvel-Panhuizen

Nord University, Bodø, Norway

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Camilla Björklund .

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Björklund, C., van den Heuvel-Panhuizen, M. & Kullberg, A. Research on early childhood mathematics teaching and learning. ZDM Mathematics Education 52 , 607–619 (2020). https://doi.org/10.1007/s11858-020-01177-3

Download citation

Accepted : 18 June 2020

Published : 23 June 2020

Issue Date : August 2020

DOI : https://doi.org/10.1007/s11858-020-01177-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Find a journal
• Publish with us
• Track your research

Robotics for Kids: The Future With AI and Robotics Education

R obotics for kids is an exciting and engaging way to introduce children to the world of technology, engineering, and programming. By getting into this interactive field, kids can develop essential skills such as creativity, problem-solving, and coding. It’s never too early for kids to explore their curiosity for robotics, as various robotic toys and kits cater to different ages and interests.

Science, technology, engineering, and math (STEM) focused and clever robotic toys help kids understand the science behind circuits and motion and inspire them to take on more challenging projects in the future. 

The Foundations of Robotics

When teaching kids about robotics, understanding the basics is the first part. Robotics is an exciting field combining STEM elements.

Let’s start with the core components that make up robotics:

• Mechanical Engineering : This aspect deals with robot design, construction, and operation. It involves understanding materials, structures, and mechanisms that enable robots to perform various tasks, such as moving, grabbing, and interacting with objects.
• Electrical Engineering : In this area, kids learn about electronic circuits and components that power robotic systems. They’ll explore topics such as voltage, current, and resistance, helping them grasp how electrical signals control a robot’s movements and functions.
• Computer Programming : At the heart of a robot lies its ‘brain’ – a computer or microcontroller that processes information and sends commands to its mechanical and electrical components. Kids can create code that brings a robot to life by learning programming languages like Scratch or Python.

With these components covered, kids can create robots, experimenting with other designs and functions. 

Getting Started With Robotics

For beginners, it’s good to start with a simple design and building projects, like creating a bristlebot, a tiny robot made from a toothbrush head, a battery, and a small motor. This simple project introduces the basic concepts of robot design and encourages hands-on learning.

When explaining robotics to kids, maintain a casual tone and keep explanations relatable and straightforward. Encourage creativity, problem-solving, and critical thinking as crucial skills for thriving in robotics.

Choosing a Starter Robotics Kit

Consider investing in a starter robotics kit to make the initial jump enjoyable. Here are some popular options for various age groups:

• LEGO Education WeDo 2.0
• Dash Robot by Wonder Workshop
• mBot by Makeblock
• LEGO Mindstorms EV3

These kits typically come with clear instructions, software, and all the necessary components to build a functional robot. They offer a learning experience with simple, well-guided projects to help kids familiarize themselves with coding, electronics, and mechanics.

Considerations and Challenges in Robotics for Kids

While robotics offers kids an exciting gateway into technology and innovation, it will have some challenges and other considerations. 

Firstly, the cost can be a significant factor; not all families can easily access expensive robotics kits or resources. It’s vital to explore cost-effective alternatives or seek out community programs that provide access to robotics education. Robot kits have a wide price range, from beginner to more complex, so there is a right fit for every family. 

Additionally, supervision is crucial, especially for younger children. Working with electronic components and programming requires guidance to ensure safety and practical learning. 

Moreover, the learning curve varies from child to child. Some may grasp concepts quickly, while others need more time and patience. Recognizing these challenges helps us approach robotics education for children in a more supportive way, ensuring that every child can explore and learn at their own pace.

No More Eye-Rolling: 14 Family Movies That Please Both Kids and Parents

Digging deeper into robotics.

For kids, programming is vital in helping them understand how to give robots the intelligence and capabilities to perform the desired tasks. Kids can start by learning block-based programming languages like Scratch, which provide an easy way to grasp coding concepts without syntax complexity.

Children can explore more advanced programming languages like Python and Java as they progress. Python is a versatile language favored by many for its readability and ease of use. In contrast, Java, though more complex, is widely used in various industries and provides a solid foundation for further learning.

This is a list of programming languages that can be used in robotics:

• Scratch (block-based)

The Science Behind Robotics

Understanding science will help kids to comprehend robotics fully. The science behind robotics involves various fields, such as artificial intelligence (AI), machine learning, and mechanical engineering. By grasping these concepts, kids can further enhance their robotic creations and make them more advanced and efficient.

AI and machine learning, in particular, have been instrumental in making robots more adept at mimicking human behavior and learning from their environments. These technologies allow robots to analyze large data sets and draw new insights, enabling them to adapt and grow over time.

For instance, comparing AI, machine learning, and robotics can be as follows:

• Key Focus: Simulating human intelligence in machines
• Application in Robotics: Decision-making and pattern recognition
• Key Focus: Algorithms that learn from data and improve over time
• Application in Robotics: Autonomously adapting to new scenarios
• Key Focus: Design, construction, and operation of robots
• Application in Robotics: Physical implementation of AI and machine learning concepts

Taking Robotics to the Next Level

For kids who have already mastered the basics of robotics, various advanced projects can help them further deepen their understanding. By participating in more complex projects, they’ll enhance crucial skills like problem-solving, coding, and engineering .

Some advanced project ideas include:

• Walking robots : Designing a robot that can walk using servo motors, microcontrollers, and sensors
• Remote-controlled robots : Building a robot that can be controlled wirelessly through a smartphone or a custom remote control
• Autonomous robots : Creating a self-driving robot that can navigate using different sensors, like ultrasonic or infrared

These projects provide a great learning experience and allow kids to showcase their creations to the community by sharing videos, participating in online forums, and entering robotics competitions.

Robotics in Real-Life Applications

Robotics isn’t just a fun hobby – it’s a growing field with a wide range of real-life applications that have the potential to make an immense impact. Here are some examples of where robotics is playing a vital role:

• Self-driving cars : Companies like Tesla and Waymo are working on fully autonomous vehicles that rely on advanced robotics and artificial intelligence. Introducing kids to robotics can increase their interest in the technology powering these cars.
• Manufacturing : Robotics is transforming the manufacturing industry by automating tasks, improving efficiency, and reducing the risk of human injuries. Familiarizing kids with robotics can prepare them for career opportunities.
• NASA : Robotics is playing a significant role in space exploration, too. NASA uses robots like the Mars rovers to collect and analyze data from other planets, helping scientists learn more about our solar system.

Taking robotics to the next level helps kids hone their skills and exposes them to the vast possibilities of applying their knowledge to real-life scenarios. 

The Future of Robotics

In the coming years, we anticipate many breakthroughs in robotics and AI technology, leading to the development of more advanced and user-friendly robots. These innovations will significantly impact people’s everyday lives, including kids, who will grow up surrounded by technology and automation.

Children should be introduced to robotics at a young age or whenever they show interest in how things work. Encouraging kids to study topics related to robotics, AI, and technology will equip them with the necessary skills and spark their curiosity and creativity. 

Here are some aspects kids can focus on:

• Coding : Learning to code helps build a strong foundation for understanding and interacting with robots and AI systems
• STEM education : Science, Technology, Engineering, and Mathematics are essential fields that contribute to advancing robotics and AI
• Problem-solving : Developing critical thinking and problem-solving skills will enable kids to adapt to and understand the complexities of future technology

Integrating robots and AI will play a significant role in various sectors, such as education, healthcare, and transportation. 

For kids, this might translate into classrooms becoming more interactive with AI-driven teaching assistants that can customize learning experiences. Additionally, robotic toys could engage and stimulate creativity while teaching programming and other skills. There would also be a greater emphasis on technologically driven extracurricular activities, including robotic clubs and competitions.

As we wrap up, it’s clear that robotics isn’t just an excellent hobby for kids; it’s a window into a future filled with exciting possibilities. It’s more than just coding and gears; it sparks curiosity, builds problem-solving skills, and opens doors to creativity. 

There are hurdles like cost and the need for guidance, but these are small compared to the enormous benefits. By giving kids a head start in robotics, we’re not just keeping them busy with a fun activity. We’re preparing them for a world where technology is everywhere. And who knows? Today’s kids tinkering with robots could lead to the next big tech revolution.

27 Skills Millennials Learned in the 90s That Are Irrelevant Today