coordinate geometry problem solving questions

Coordinate Geometry Questions

The coordinate geometry questions are given here, along with answers, to help students understand the concept easily. The chapter coordinate geometry has been included in Class 9 and 10. The Class 9 coordinate geometry chapter includes a basic introduction to coordinate geometry, how to locate the points in a coordinate plane and the equality of two points on a coordinate system. In Class 10, the coordinate geometry chapter deals with finding the distance between two points, section formula and area of a triangle whose vertices are given in the form of coordinate points, etc. In this article, you will get some important questions on coordinate geometry, as per the latest NCERT curriculum.

What is Coordinate Geometry?

Coordinate geometry is one of the important branches of Mathematics in which the position of a point in a plane is described using coordinates. Hence, the plane is called the Cartesian system or Cartesian plane.

Learn: Coordinate geometry

Coordinate Geometry Questions and Answers

1. What is the name of horizontal and vertical lines drawn to determine the position of any point in the Cartesian plane?

As we know, to locate the position of an object or a point in a plane (Cartesian or coordinate plane), we require two perpendicular lines. One of them is horizontal, and the other is vertical. The horizontal line is the x-axis, and the vertical line is the y-axis.

2. Without plotting the points, indicate the quadrant in which they will lie, if

(i) ordinate is 3 and abscissa is –5

(ii) abscissa is –3 and ordinate is – 5

(iii) ordinate is 3 and abscissa is 5

Here, the x-coordinate is -5, and the y-coordinate is 3.

The point = (-5, 3), i.e. (-, +)

Hence, the point lies in quadrant II.

Here, the x-coordinate is -3, and the y-coordinate is -5.

The point = (-3, -5), i.e. (-, -)

Hence, the point lies in quadrant III.

Here, the x-coordinate is 5, and the y-coordinate is 3.

The point = (5, 3), i.e. (+, +)

Hence, the point lies in quadrant I.

3. Find the coordinates of the point

(i) which lies on both the x and y axes.

(ii) whose ordinate is -6, and which lies on the y-axis.

(iii) whose abscissa is 4, and which lies on the x-axis.

(i) The point which lies on both x and y-axes is the origin whose coordinates are (0, 0).

(ii) Given that the ordinate is –6, the point lies on the y-axis.

So, the x-coordinate will be zero.

Therefore, the point is (0, -6).

(iii) Given that the abscissa is 4, the point lies on the x-axis.

So, the y-coordinate will be zero.

Therefore, the point is (4, 0).

4. A point lies on the x-axis at a distance of 8 units from the y-axis. What are its coordinates? What will be the coordinates if it lies on the y-axis at a distance of –8 units from the x-axis?

Given that the point lies on the x-axis at a distance of 8 units from the y-axis.

That means the point lies in the positive direction of the x-axis, and its y-coordinate is 0.

So, its coordinates are (8, 0).

If the point lies on the y-axis at a distance of –8 units from the x-axis, its x-coordinate must be 0, and the point lies in the negative direction of the y-axis.

So its coordinates are (0, -8).

5. Find the distance between two points, A(–1, 2) and B(3, 2).

Let the given points be:

A(-1, 2) = (x 1 , y 1 )

B(3, 2) = (x 2 , y 2 )

Using the distance formula,

Distance between A and B is:

Therefore, the distance between two points, A(–1, 2) and B(3, 2) is 4 units.

6. Find the value of a, if the distance between the points P(–3, –14) and Q(a, –5) is 9 units.

P(-3, -14) = (x 1 , y 1 )

Q(a, -5) = (x 2 , y 2 )

√[(a + 3) 2 + 81] = 9 {from the given}

Squaring on both sides,

(a + 3) 2 + 81 = 81

(a + 3) 2 = 0

7. Find the coordinates of the point which divides the line segment joining the points (4, – 3) and (8, 5) in the ratio 3 : 1 internally.

Let P(x, y) be the required point.

From the given,

(4, -3) = (x 1 , y 1 )

(8, 5) = (x 2 , y 2 )

Using the section formula, we get;

x = [3(8) + 1(4)]/(3 + 1) = (24 + 4)/4 = 28/4 = 7

y = [3(5) + 1(-3)]/(3 + 1) = (15 – 3)/4 = 12/4 = 3

Therefore, (7, 3) is the required point.

8. If the mid-point of the line segment joining the points A(3, 4) and B(k, 6) is P(x, y) and x + y – 10 = 0, find the value of k.

Given that the mid-point of the line segment joining the points A(3, 4) and B(k, 6) is P(x, y).

Using the mid-point formula,

x = (3 + k)/2

y = (4 + 6)/2

y = 10/2 = 5

x + y – 10 = 0

Substituting y = 5 in this equation, we get;

(3 + k)/2 = 5

k = 10 – 3 = 7

Therefore, k = 7.

9. Find the area of a triangle whose vertices are (1, –1), (–4, 6) and (–3, –5).

A(1,-1) = (x 1 , y 1 )

B(-4, 6) = (x 2 , y 2 )

C(-3, -5) = (x 3 , y 3 )

The area of the triangle formed by the points (x 1 , y 1 ), (x 2 , y 2 ) and (x 3 , y 3 ) is the numerical value of the expression 1/2 |x 1 (y 2 – y 3 ) + x 2 (y 3 – y 1 ) + x 3 (y 1 – y 2 )|.

Now, the area of triangle ABC = (1/2)|1(6 + 5) – 4(-5 + 1) -3(-1 – 6)|

= (1/2) |11 – 4(-4) – 3(-7)|

= (1/2) |11 + 16 + 21|

= (1/2) × 48

Therefore, the area of the triangle is 24 square units.

10. Find the value of m if the points (5, 1), (–2, –3) and (8, 2m ) are collinear.

A(5, 1) = (x 1 , y 1 )

B(-2, -3) = (x 2 , y 2 )

C(8, 2m) = (x 3 , y 3 )

We know that the area of the triangle formed by collinear points is 0.

So, the area of triangle ABC = 0

⇒ (1/2) |5(-3 – 2m) – 2(2m – 1) + 8(1 + 3)| = 0

⇒ |5(-3 – 2m) – 2(2m – 1) + 8(4)| = 0

⇒ |-15 – 10m – 4m + 2 + 32| = 0

⇒ |-14m + 19| = 0

⇒ -14m + 19 = 0

⇒ m = 19/14

Video Lesson on Coordinate Geometry Toughest Problems

Practice Questions

Solve the following coordinate geometry problems.

• Taking 0.5 cm as 1 unit, plot the following points on the graph paper :
• A (1, 3), B (– 3, – 1), C (1, – 4), D (– 2, 3), E (0, – 8), F (1, 0)
• Find a point that is equidistant from points A (–5, 4) and B (–1, 6)? How many such points are there?
• If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
• The points A (2, 9), B (a, 5) and C (5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ∆ABC.
• Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, – 3) and B is (1, 4).

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Coordinate plane

Here you will learn about a coordinate plane, including the general form of a coordinate plane, plotting coordinates on different axes, and determining the coordinates of a point.

Students will first learn about coordinate planes as part of the number system in 6th grade.

What is a coordinate plane?

A coordinate plane is formed when a vertical number line overlaps a horizontal number line, forming a 2 dimensional gridded surface. It can also be called a coordinate grid.

The horizontal number line is called the \textbf{x} -axis and the vertical number line is called the \textbf{y} -axis . They intersect at the origin , (0,0).

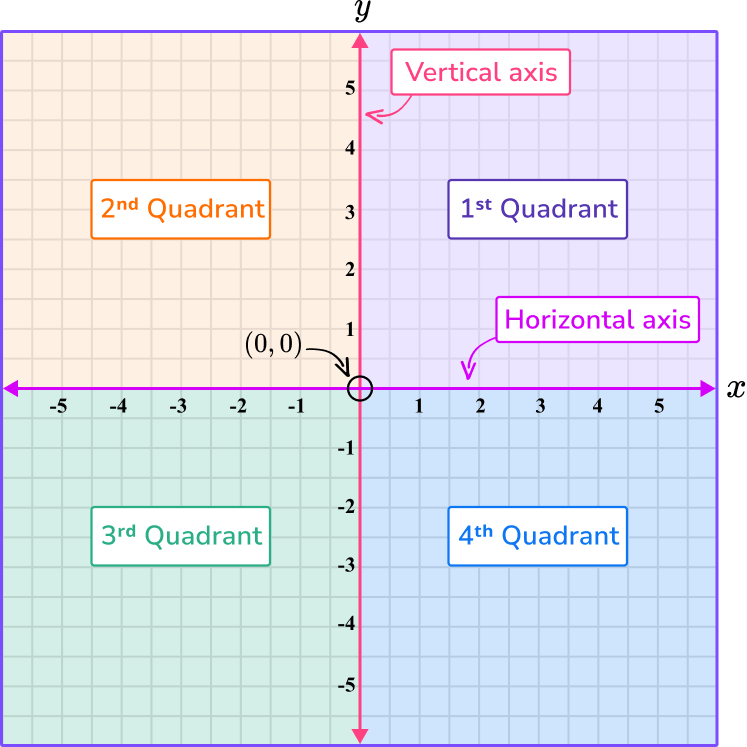
In a coordinate plane there are four quadrants. The values on the x and y axes are different in each quadrant :

Note, it is also common for the names of the quadrants to be written with Roman numerals (I, II, III, IV).

Each axis has a scale . The scale must increase in equal amounts , but the scale does not have to be the same for both axes.

For example,

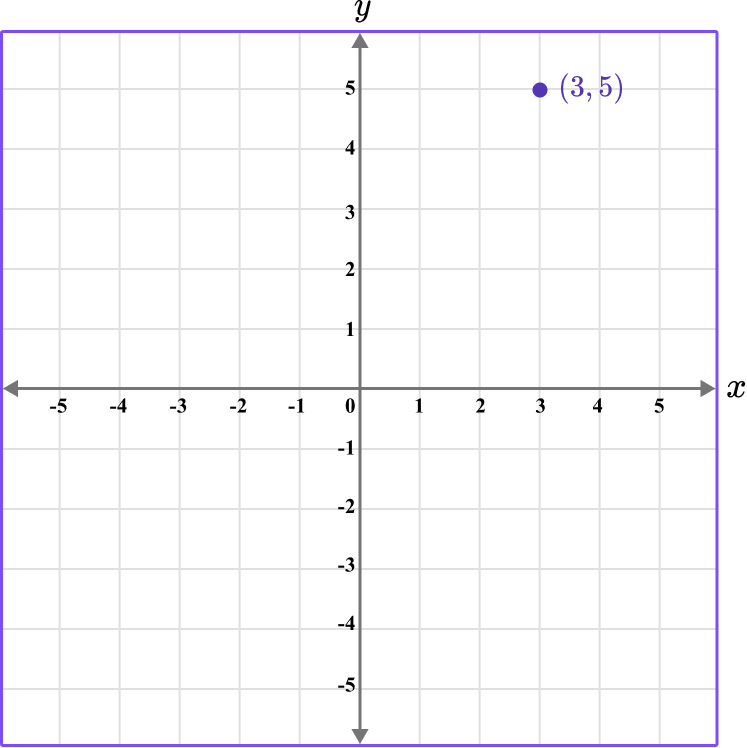
Coordinates are used to determine location on the coordinate plane.

A coordinate is written as (x,y), where the value for the x -coordinate represents the horizontal position of the coordinate, the value for the y -coordinate represents the vertical position of the coordinate and they are enclosed with parentheses.

These can also be referred to as ordered pairs.

For example, the coordinate (3,5) has a horizontal position of 3, and a vertical position of 5.

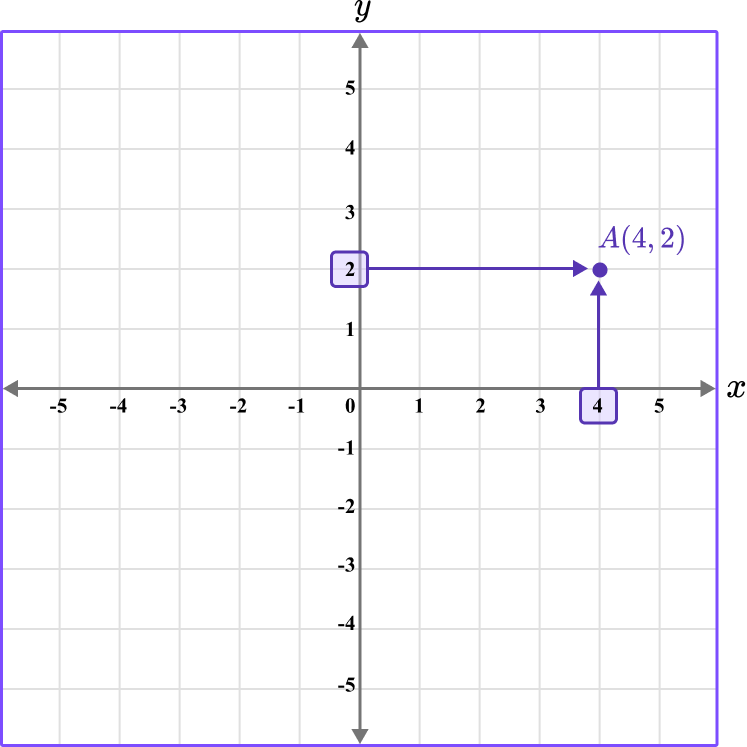
Besides locating the position of a coordinate, you can also plot coordinates within all four quadrants.

To do this, determine the horizontal and vertical position of the coordinate on the axes, and follow these values until the two values meet.

Draw the point A \, (4,2).

To draw the point, locate 4 on the x -axis, and then 2 on the y -axis. Follow the straight lines from these points to the coordinate A \, (4,2).

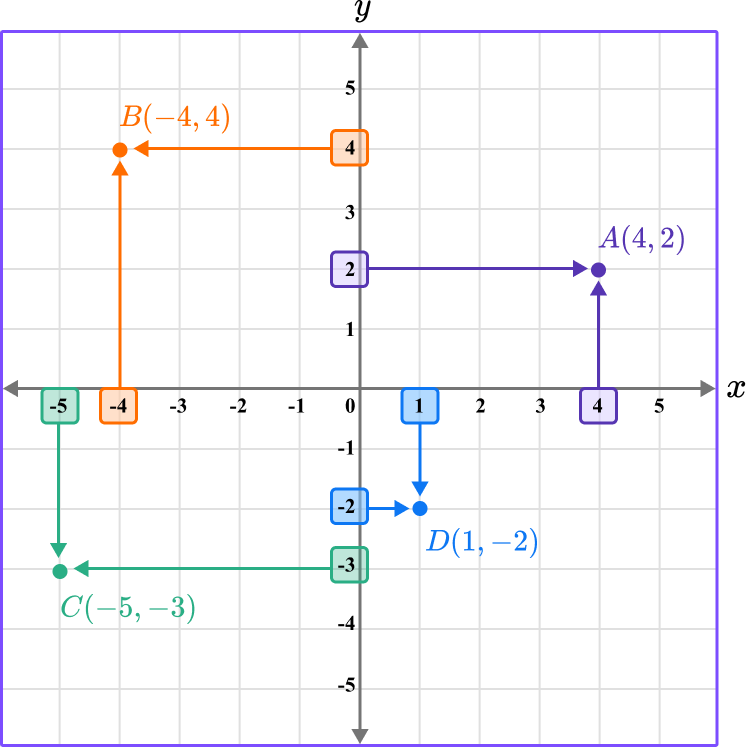
Note, to give a coordinate a specific name, label it as a point by using a capital letter.

Repeating this process by plotting points B \, (-4,4), \, C \, (-5,-3), and D \, (1,-2)…

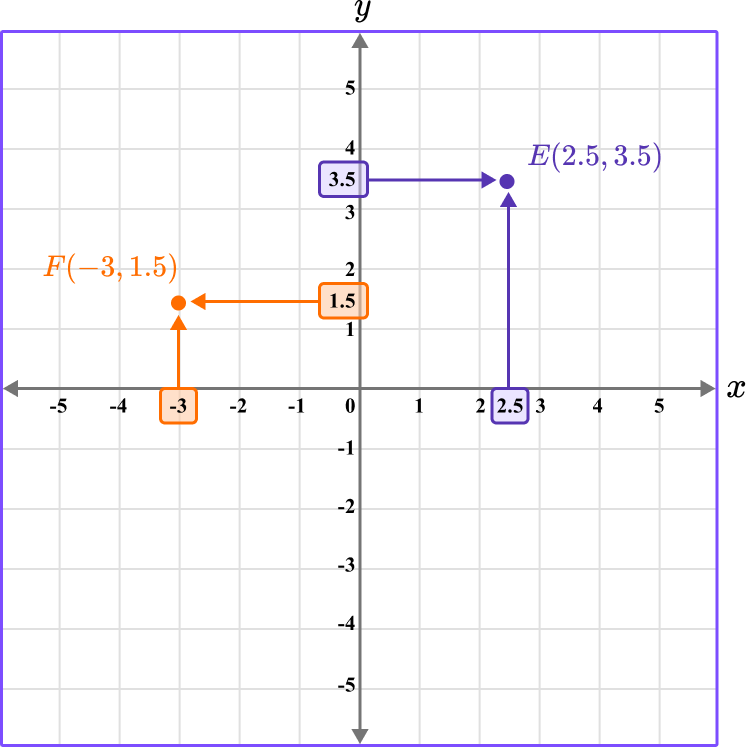
Note that coordinates can have decimal values. It is common to only see integer coordinates that lie on a grid line, however, you can also plot coordinates that have a decimal value, such as E \, (2.5, 3.5) and F \, (-3, 1.5).

These would lie within or on the edge of a grid square.

[FREE] Math Worksheets

Use these quizzes to check your students’ understanding of math. Contains series of worksheets designed by math experts to identify areas of strength and support!

Common Core State Standards

How does this relate to 6th grade math?

• Grade 6 – The Number System (6.NS.C.8) Solve real-world and mathematical problems by graphing points in all four quadrants of the coordinate plane. Include use of coordinates and absolute value to find distances between points with the same first coordinate or the same second coordinate.

How to plot on a coordinate plane

In order to plot on a coordinate plane:

Determine the horizontal position of the coordinate (the value of \textbf{x} ).

Determine the vertical position of the coordinate (the value of \textbf{y} ).

Follow the gridlines until the two values meet and draw a point.

Coordinate plane examples

Example 1: plot a coordinate.

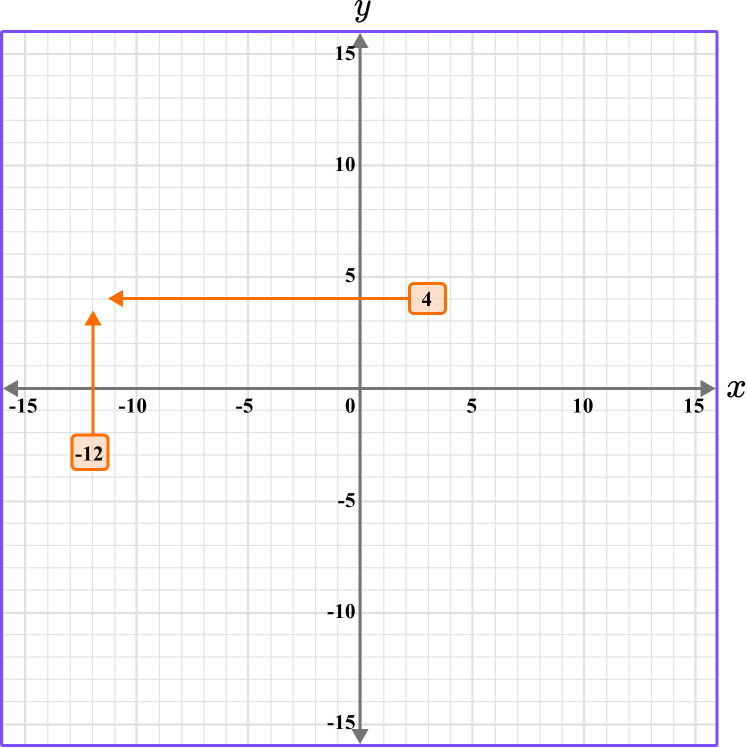
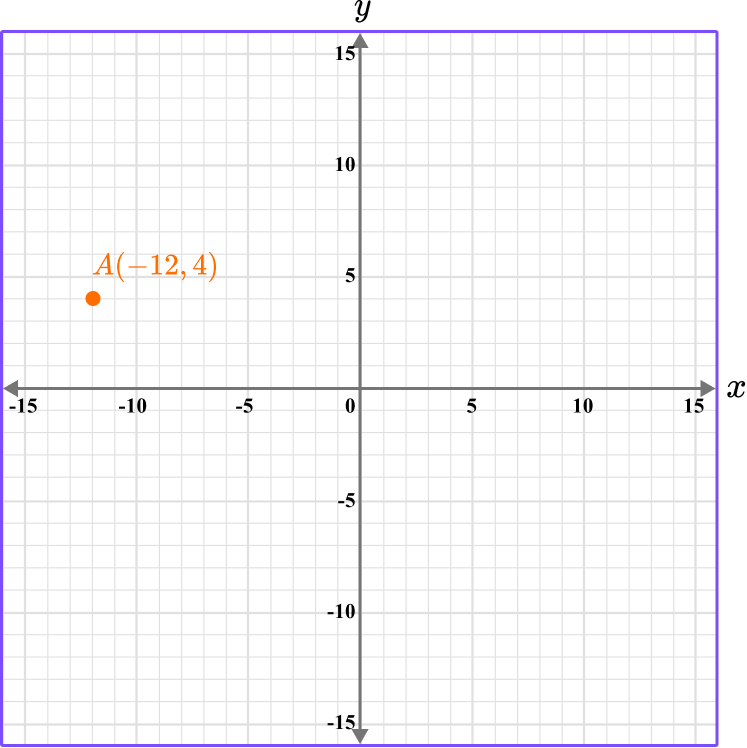
Plot the coordinate A \, (-12, 4).

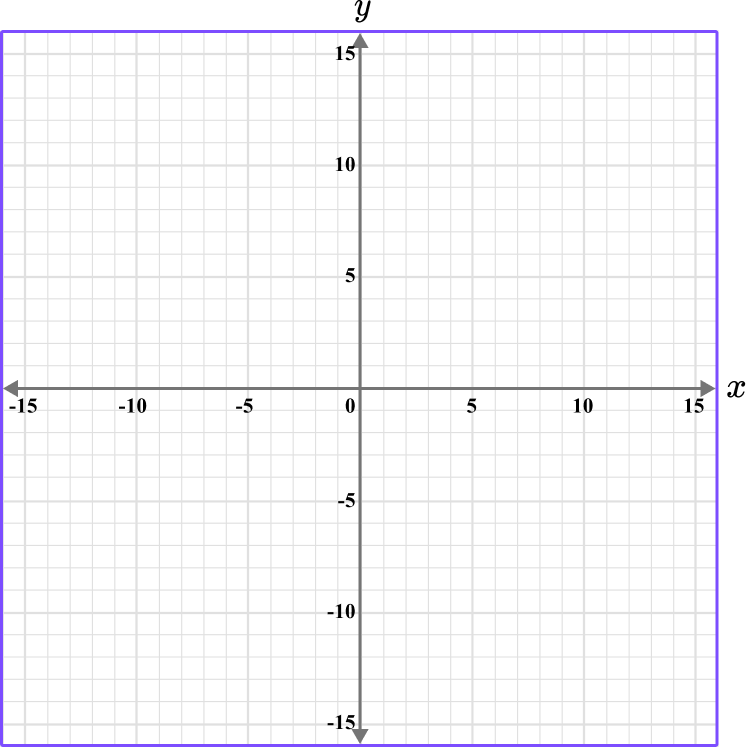
The x value is -12, so locate -12 on the x -axis. The scale is 1, so -12 is two gridlines after -10.

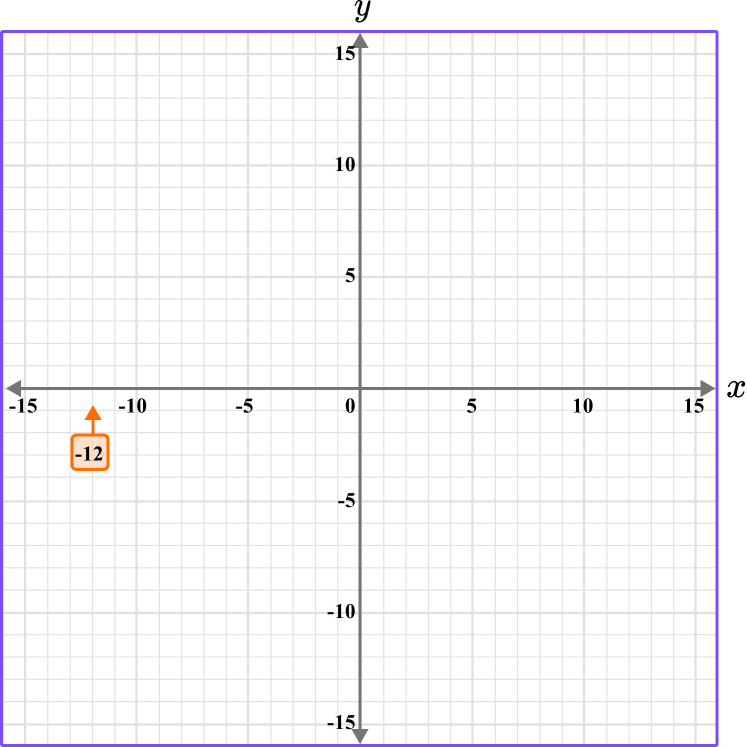
2 Determine the vertical position of the coordinate (the value of \textbf{y} ).

The y value is 4, so locate 4 on the y -axis. The scale is 1, so 4 is one gridline before 5.

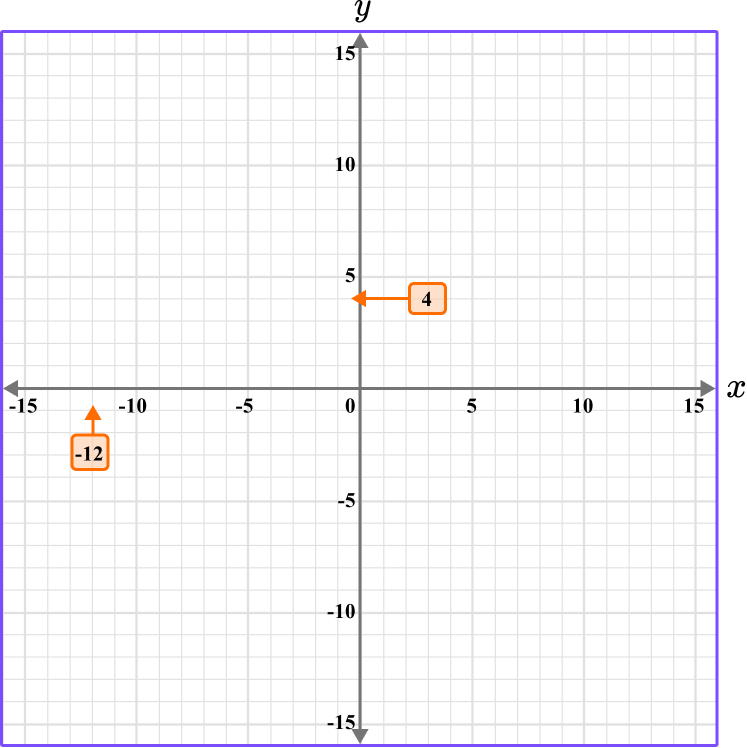
3 Follow the gridlines until the two values meet and draw a point.

Following the gridlines…

This gives us the final solution.

Example 2: plot a coordinate

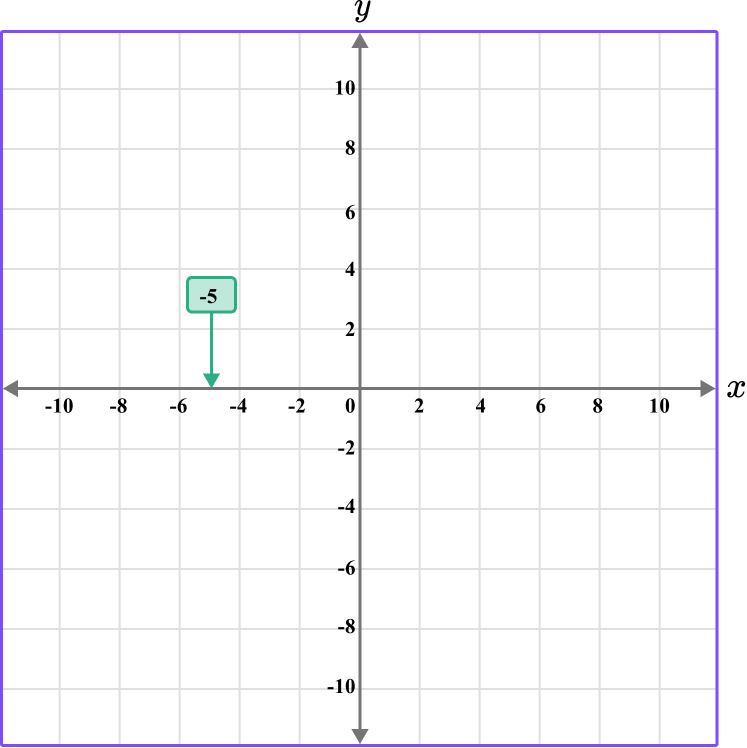
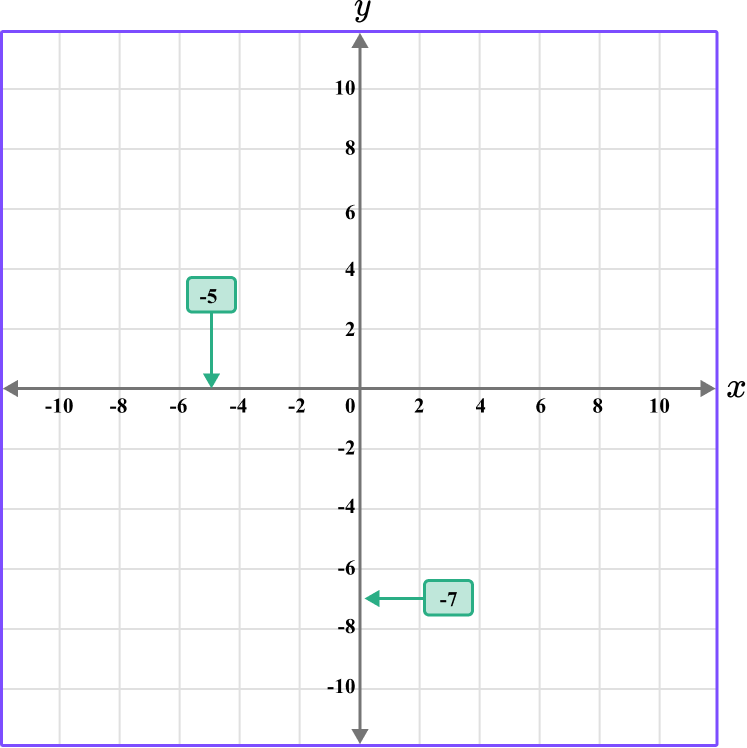
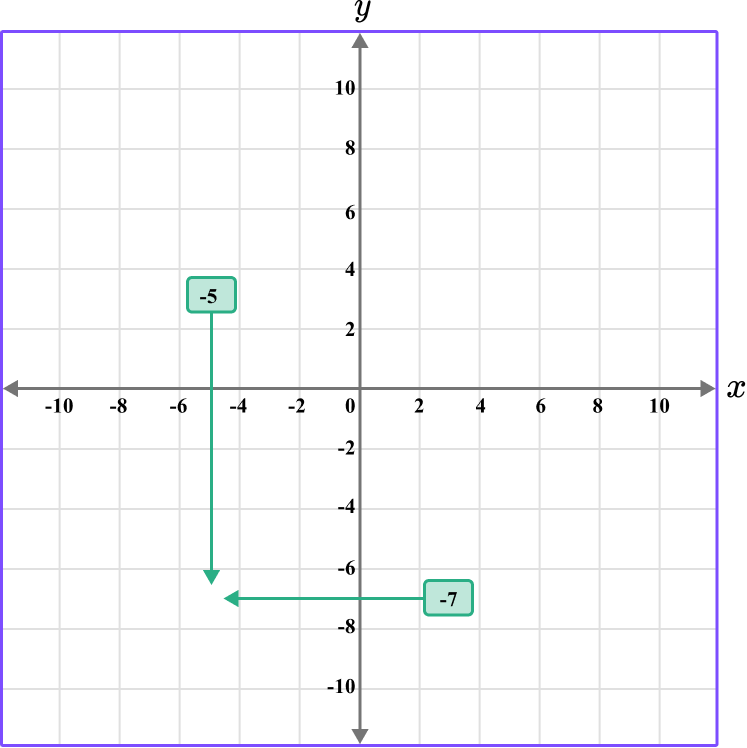
Plot the coordinate H \, (-5, -7).

The x value is -5, so locate -5 on the x -axis. The scale is 2, so -5 is between -4 and -6.

The y value is -7, so locate -7 on the y -axis. The scale is 2, so -7 is between -6 and -8.

Following between the gridlines…

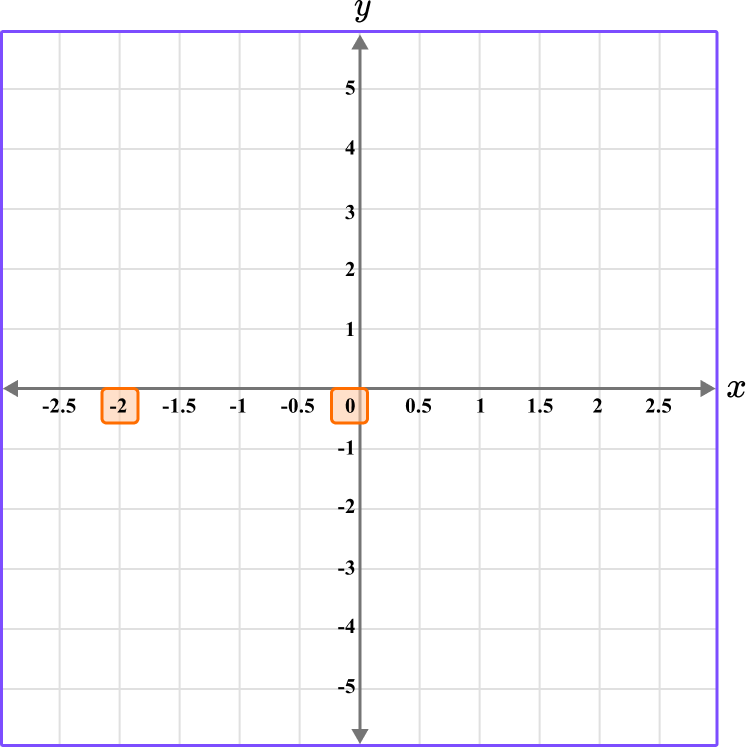
Example 3: plot a coordinate on the x -axis

Plot the coordinate B \, (-2,0).

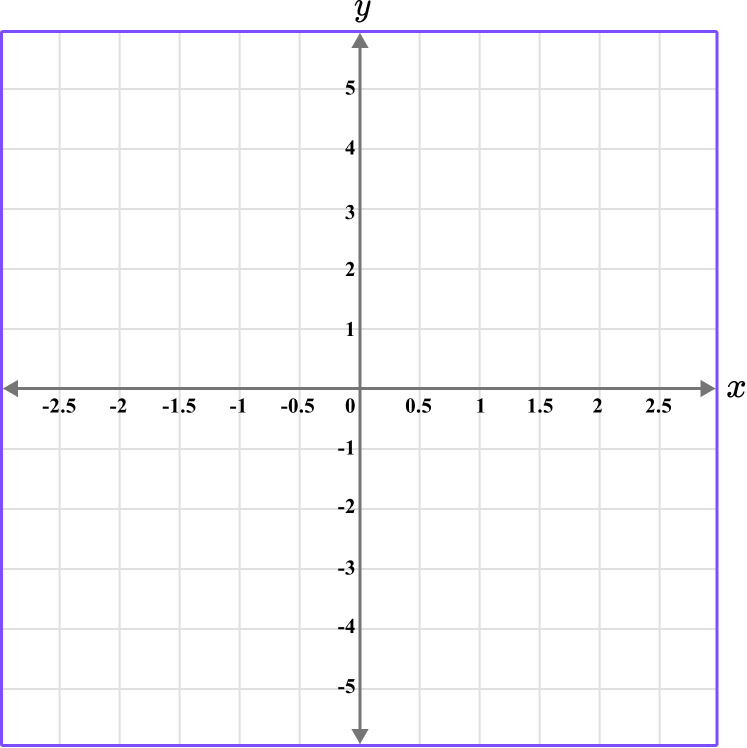
The x value is -2, so locate -2 on the x -axis.

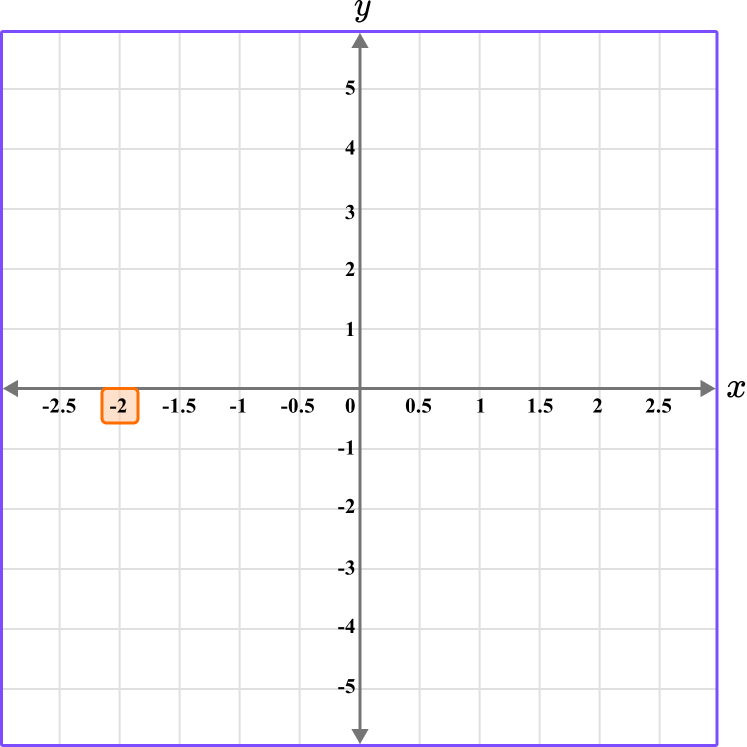
The y value is 0, so locate 0 on the y -axis.

Example 4: plot a coordinate on the y -axis

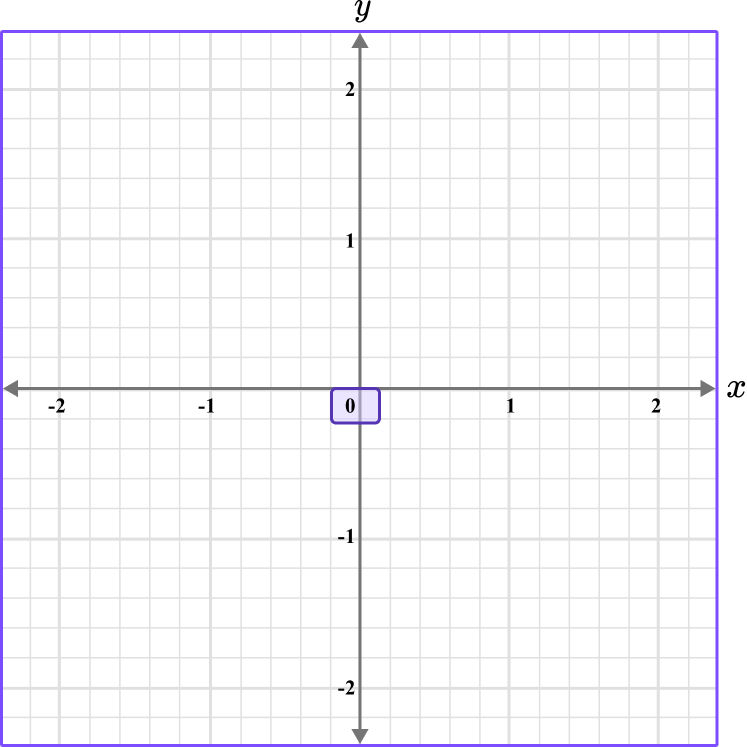
Plot the coordinate C \, (0,0.4).

The x value is 0, so locate 0 on the x -axis.

The y value is 0.4, so locate 0.4 on the y -axis. The scale is 0.2, so 0.4 is two gridlines above 0.

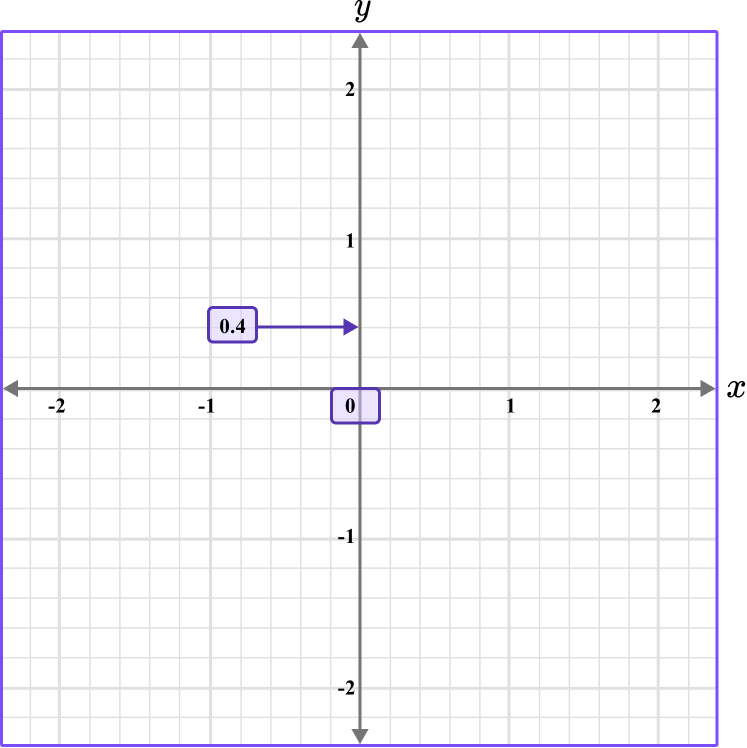
Example 5: plotting two coordinates

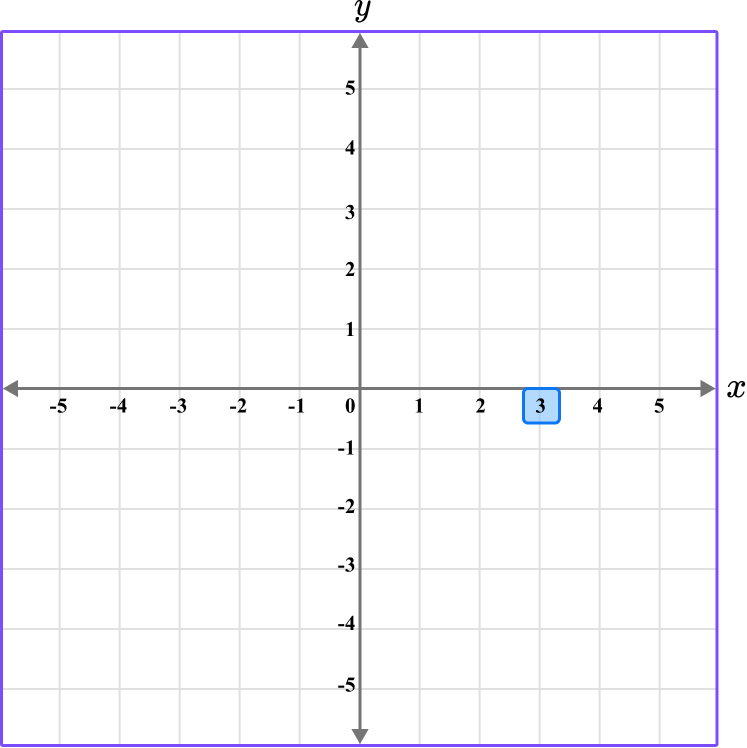
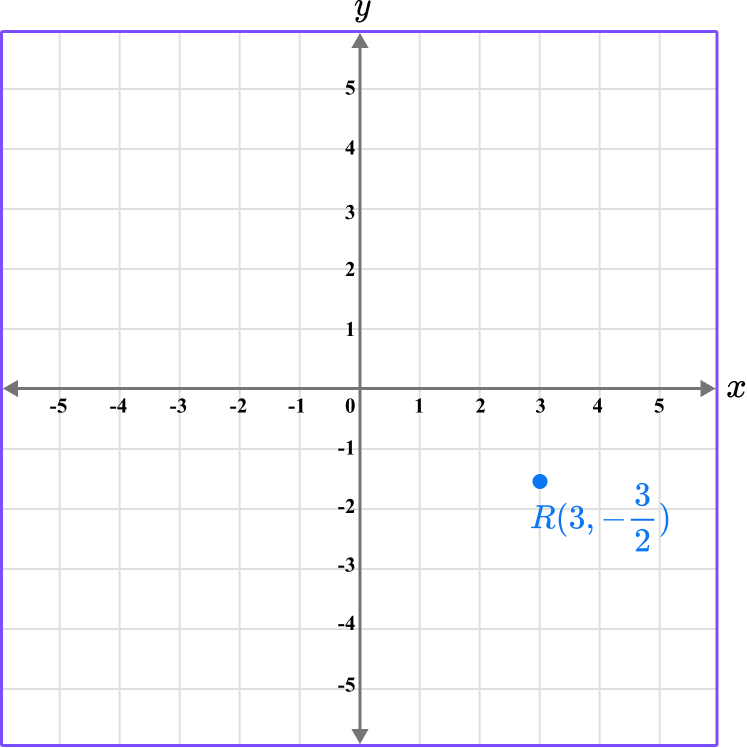
Plot the coordinates R \left(3,- \, \cfrac{3}{2} \, \right) and Q \left(\cfrac{5}{2},- \, 5 \right).

Since there are two coordinates, plot each point one at a time.

The x value of the point R is 3, so locate 3 on the x -axis.

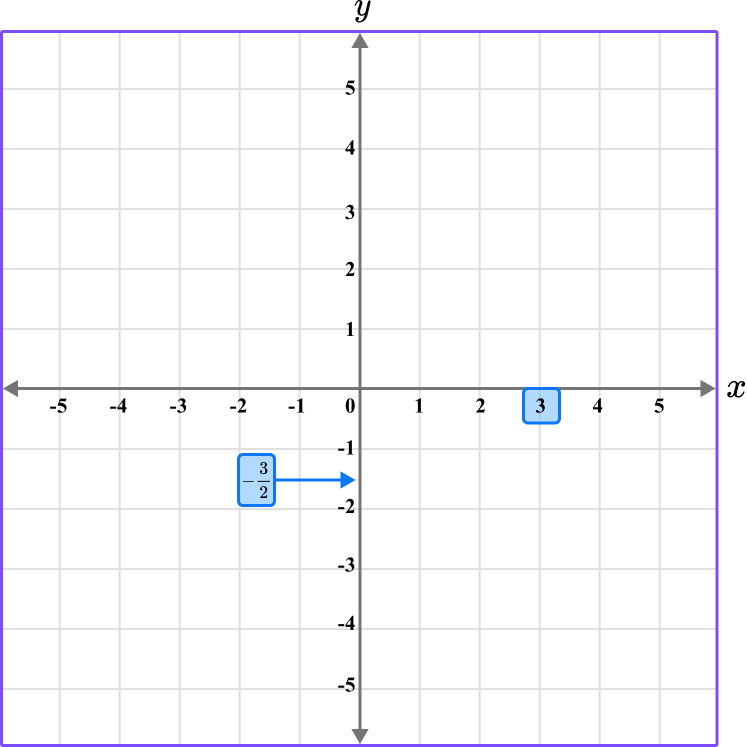
The y value of the point R is -\cfrac{3}{2} \, , so locate -\cfrac{3}{2} \, on the y -axis.

Since -\cfrac{3}{2}= -1 \, \cfrac{1}{2} \, , it is in between -1 and -2.

Following the gridlines (and between them)…

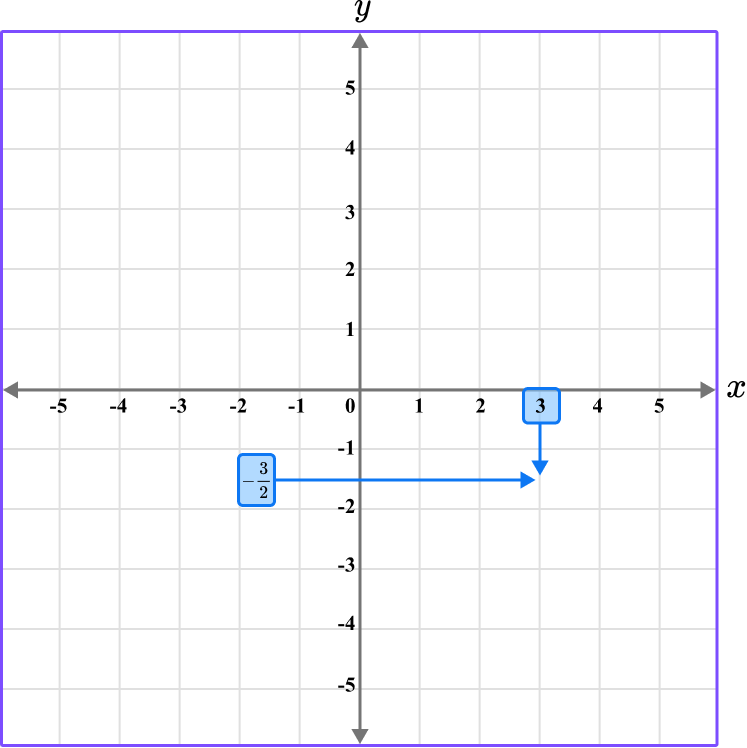
The point R is located here.

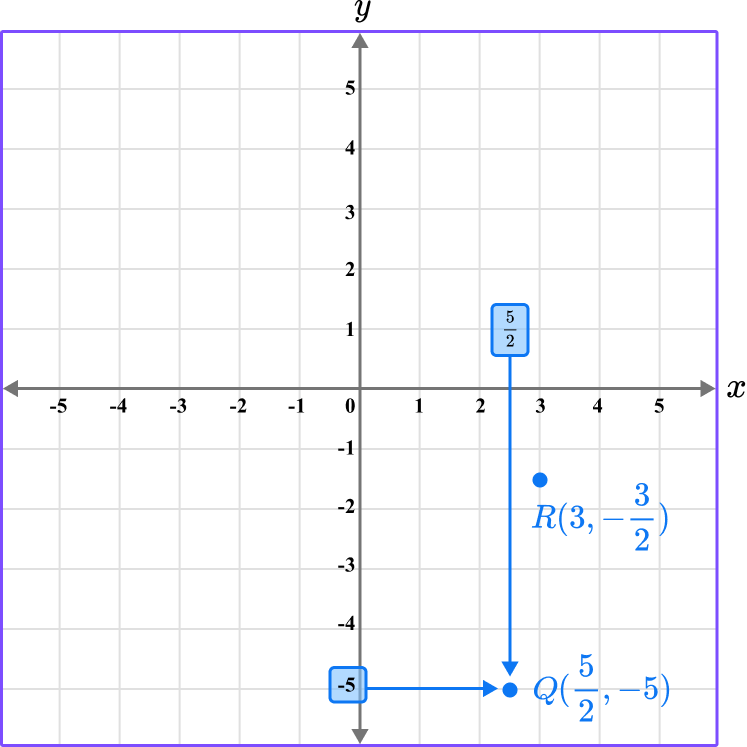
Repeat this process for the point Q \left(\cfrac{5}{2},- \, 5 \right).

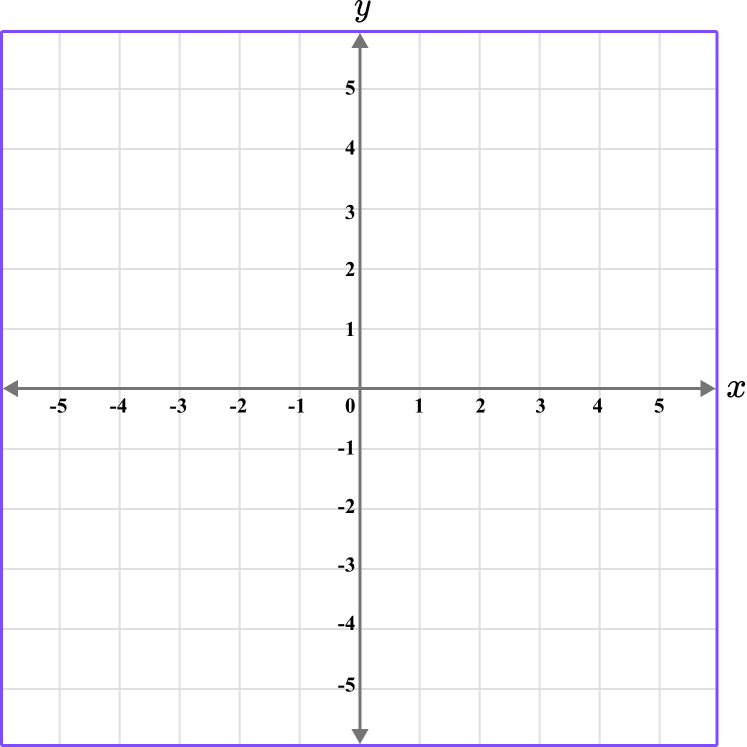
Example 6: plotting coordinates in three quadrants

Plot the coordinates D \, (-1,-3), \, E \, (-1,5) , and F\, (3,-2) on the set of axes below.

Since there are three coordinates, plot each point one at a time.

The x value of the point D is -1, so locate -1 on the x -axis.

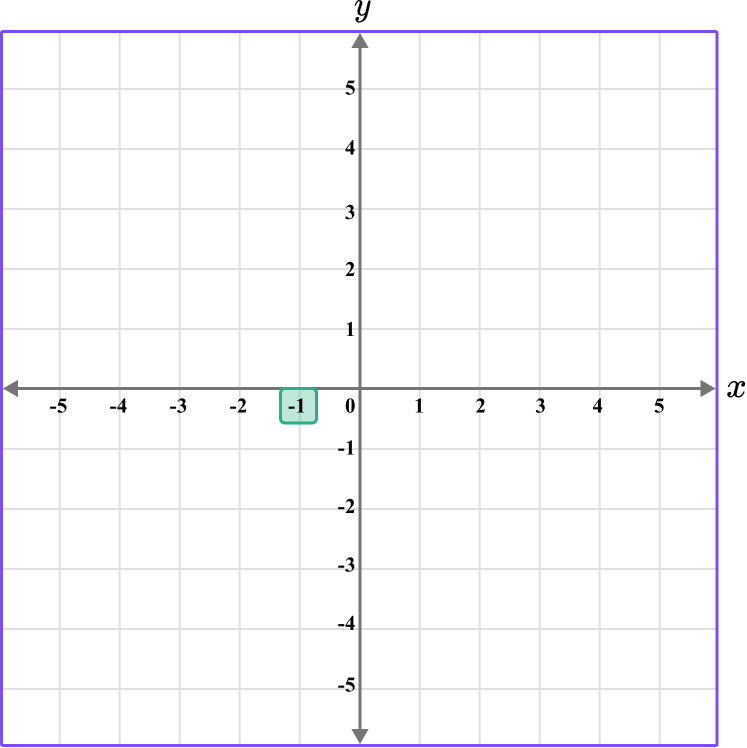
The y value of the point D is -3, so locate -3 on the y -axis.

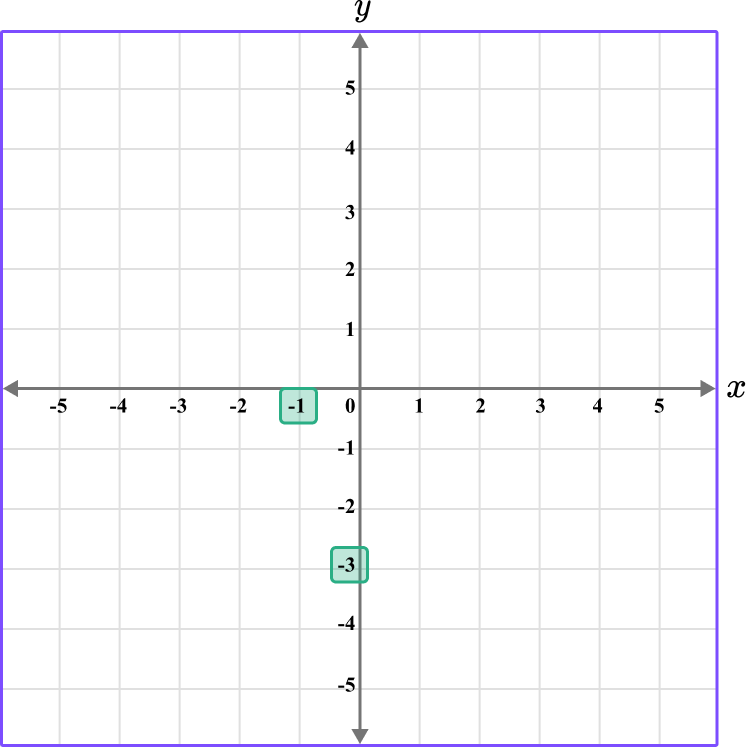
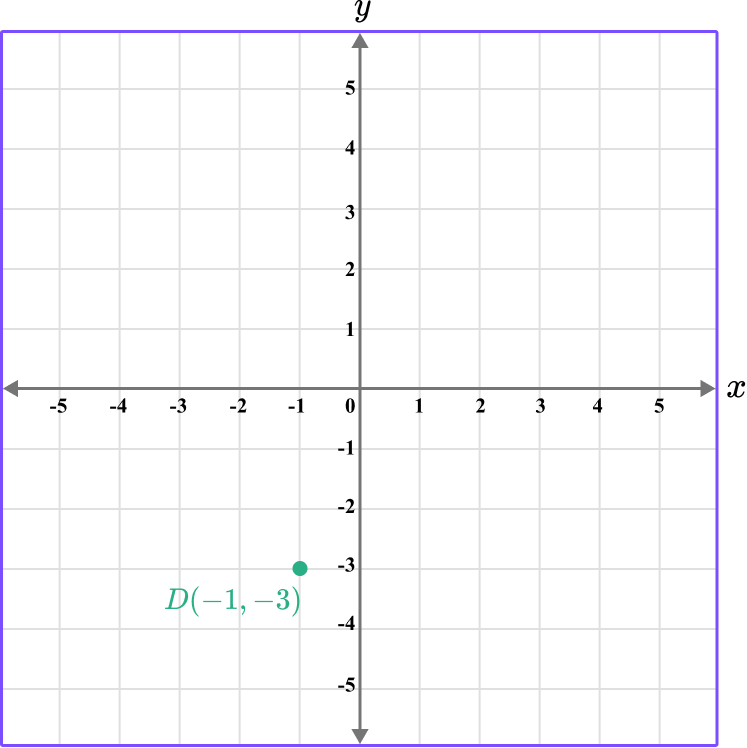
The point D is located here.

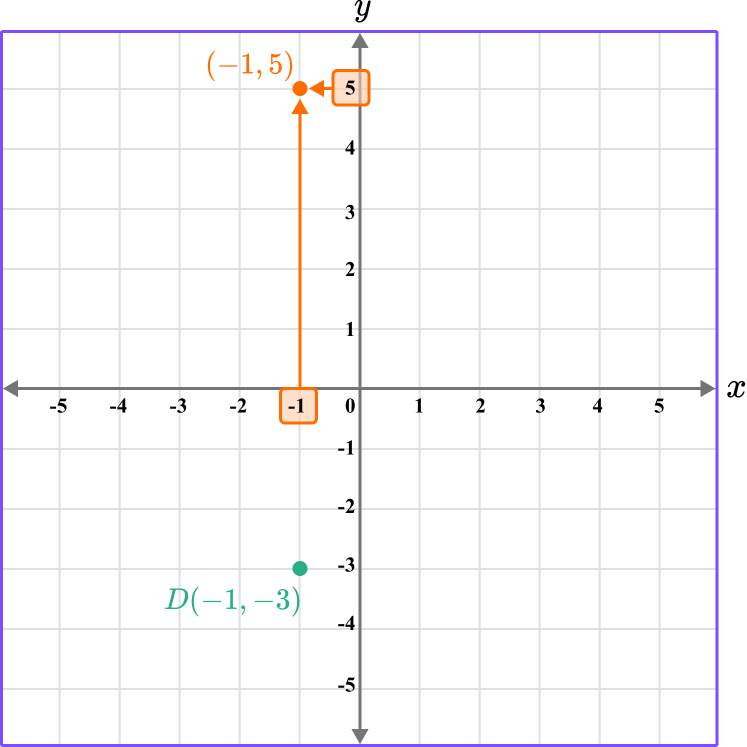
Repeat this process for the point E…

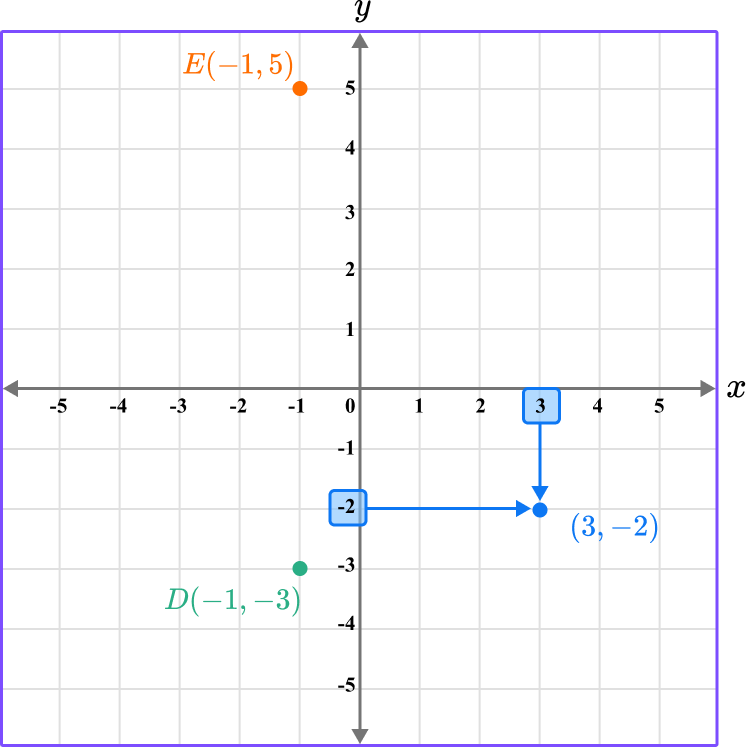
Repeating the process for the point F…

Teaching tips for the coordinate plane

• Worksheets play an important role when students are learning to plot on a coordinate plane, but they are not the only option. There are digital coordinate planes available where students can easily change the scale and explore grids with very small or very large scales that would be harder to represent on paper. You can also utilize a tiled floor or wall to create a physical version of the coordinate plane within the classroom.
• Coordinate planes have so many real life uses, and students understand them best with repeated use. To make the repeated practice more engaging, give students the opportunity to create and use a coordinate plane to solve a real world problem. It could be physical, for example, using string and stakes to create a grid in the school garden for proper plant distances. Or using a program to code a video game that requires students to indicate the position of the characters and items in each frame of the game.

Easy mistakes to make

• Mixing up the values in the coordinate It is important to remember that the first number is x and represents the horizontal axis. The second number is y and represents the vertical axis. Confusing these, in most cases, will affect the location of the coordinate.
• Forgetting the values between the gridlines Each axis is created by a number line, which has infinite rational values on it. If a coordinate lies between gridlines, rather than on a gridline, a smaller ratio of the scale can be used to find the exact position. Continuing to use the original scale or guessing, will lead to an incorrect answer.
• Not using parentheses and a comma The parentheses and the comma are required when writing a coordinate. Coordinates can be incorrectly written as 3,2 without the parentheses, this is just a list of numbers; (3,2) is a coordinate.

Related coordinate plane lessons

• Interpreting graphs
• x and y axis
• Graph transformations
• Plot points on a graph
• Independent and dependent variables

Practice coordinate plane questions

1. What is the coordinate shown below?

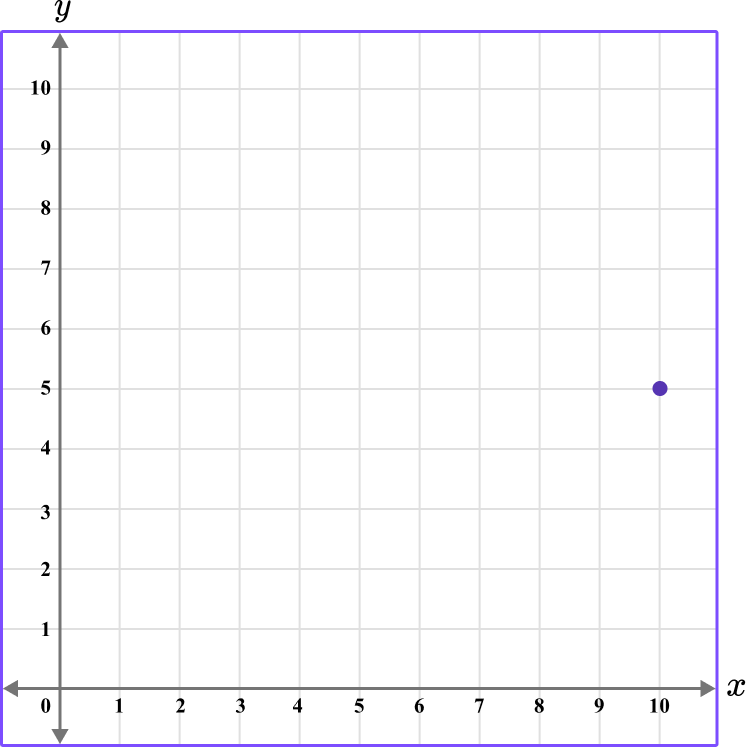
The first value is along the x axis and the second value is along the y axis.

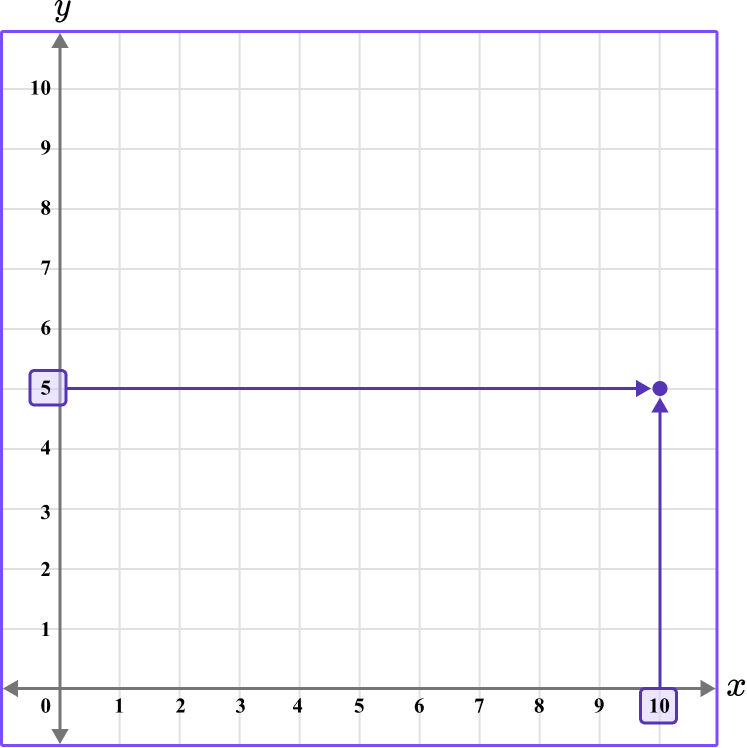
The x value of the coordinate is 10.

The y value of the coordinate is 5.

The coordinate is written as (10,5).

2. What is the coordinate shown below?

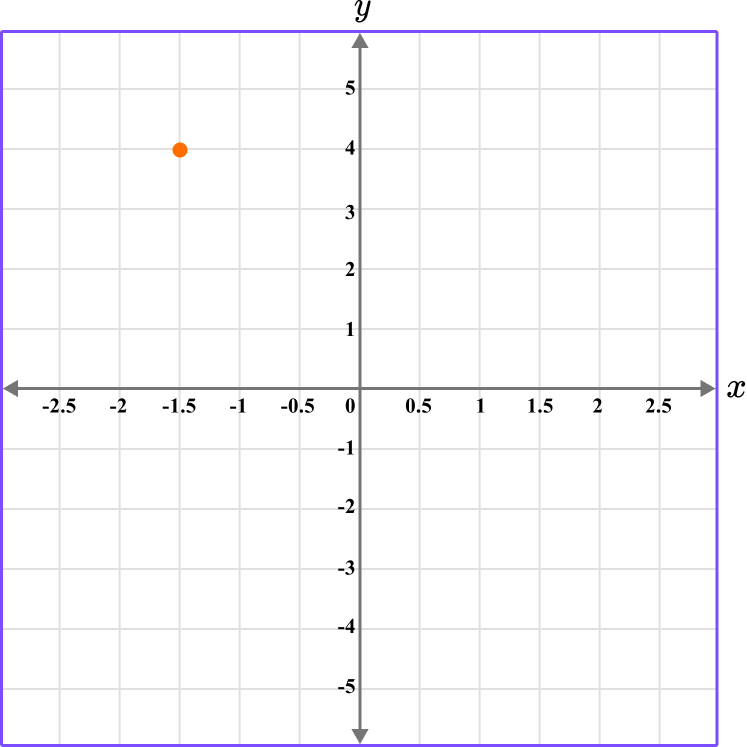
The coordinate is written as (-1.5,4).

3. Which diagram correctly shows the location of the point (2.5,4.5)?

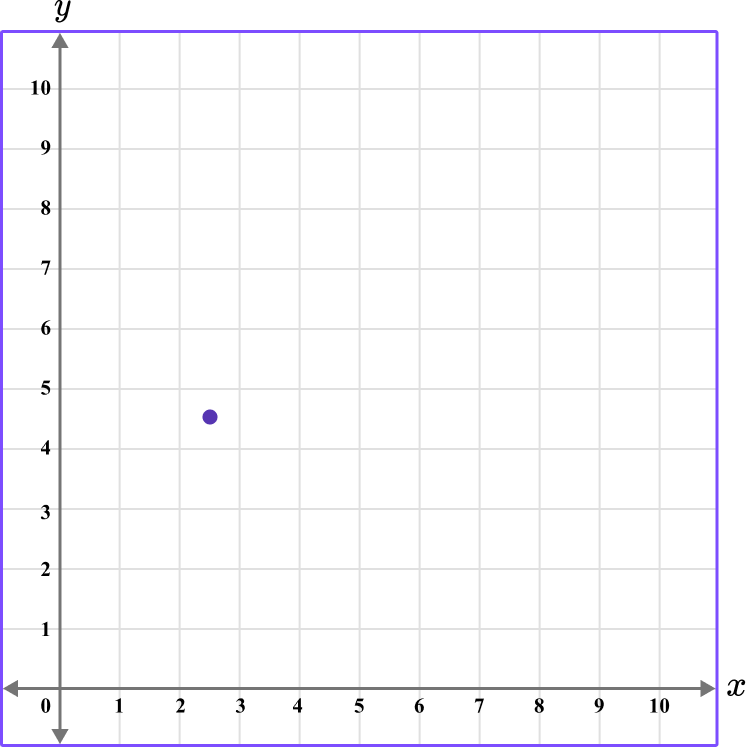
This graph shows the coordinate (2.5,4.5).

4. Which diagram correctly shows the location of the point A \, (-3,-1)?

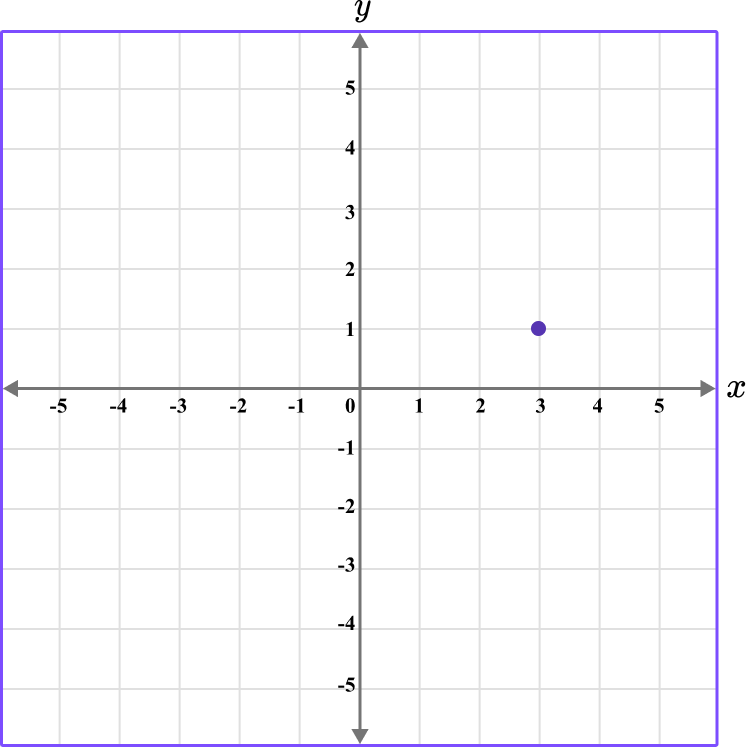
This graph shows the coordinate (-3,-1).

5. What is the coordinate shown below?

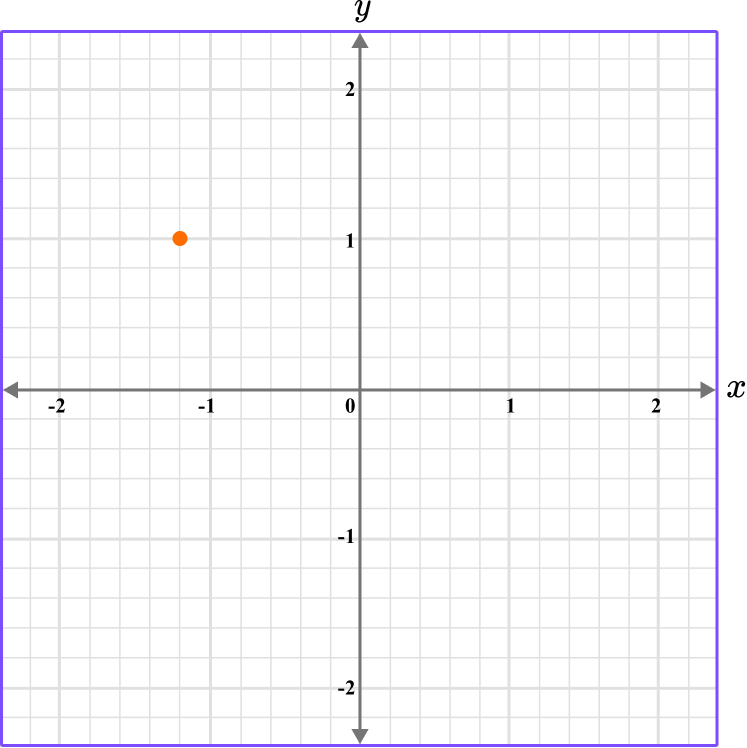
The scale for the x and y axes is 0.2.

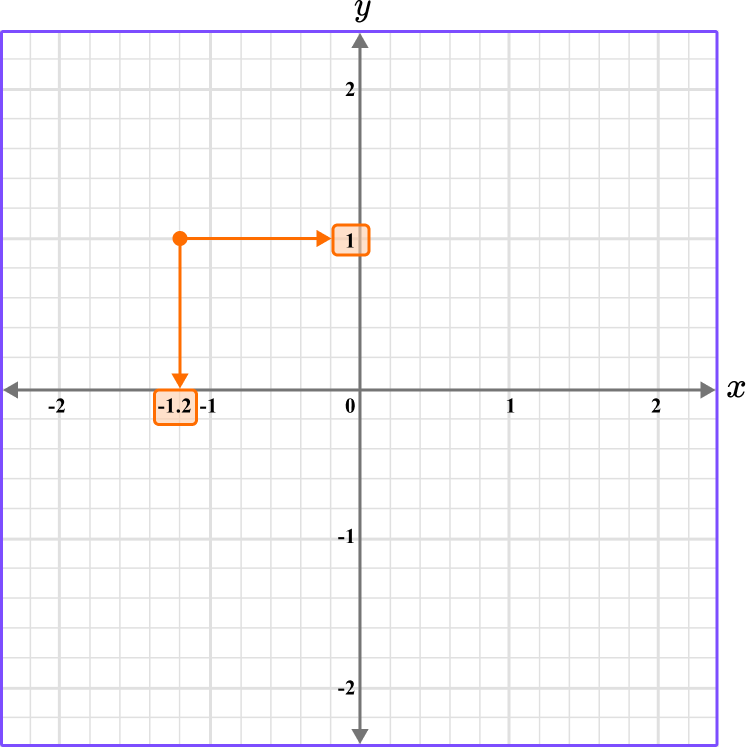
This graph shows the coordinate (-1.2,1).

6. What is the coordinate shown below?

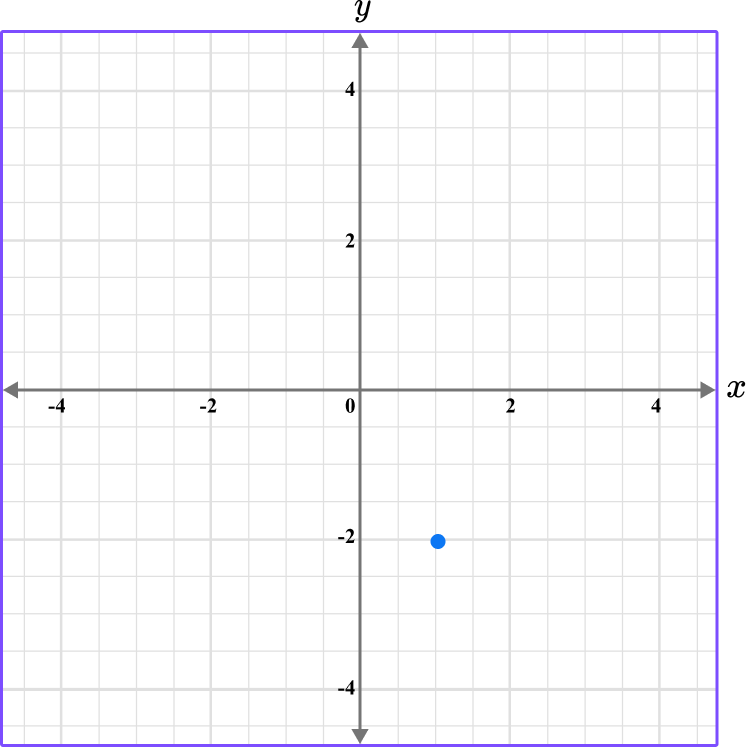
The scale for the x and y axes is 0.5.

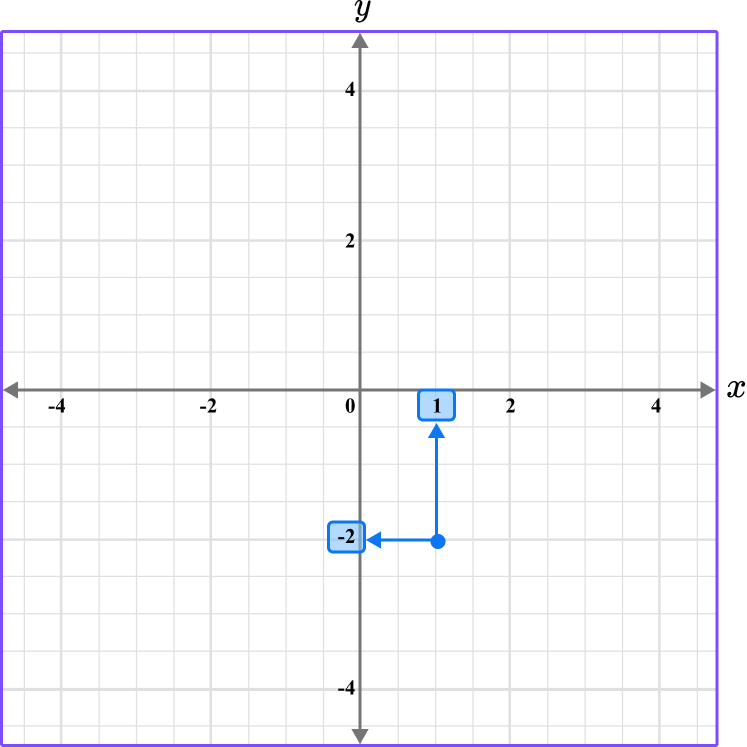
This graph shows the coordinate (1,-2).

Coordinate plane FAQs

This is the same as a coordinate plane. This name refers to the French mathematician Rene Descartes who is credited with incorporating the use of the coordinate plane into mathematics.

Coordinate planes have many uses in the real world and come up extensively in upper level math topics like geometry, algebra, and statistics.

The next lessons are

• Types of graphs
• Graphing linear equations
• Rate of change

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

C1 Coordinate Geometry

Revision Notes

• Testimonial
• Web Stories

Learning Home

Not Now! Will rate later

• Co-ordinate Geometry: Practice Questions

• Co-ordinate Geometry: Theory & Formulas
• Co-ordinate Geometry: Solved Examples

Most Popular Articles - PS

Time and Work Concepts

Time and Work Formula and Solved Problems

Time and Work Problems (Easy)

Time and Work Problems (Difficult)

Problems on Ages Practice Problems : Level 02

Chain Rule : Theory & Concepts

Chain Rule Solved Examples

Chain Rule Practice Problems: Level 01

Chain Rule Practice Problems : Level 02

Problems on Numbers System : Level 02

Download our app.

• Learn on-the-go
• Unlimited Prep Resources
• Better Learning Experience
• Personalized Guidance

Get More Out of Your Exam Preparation - Try Our App!

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

SAT Math : Coordinate Geometry

Study concepts, example questions & explanations for sat math, all sat math resources, example questions, example question #1 : parallel lines.

Which of the following is the equation of a line that is parallel to the line 4 x –  y = 22 and passes through the origin?

4 x + 8 y = 0

4 x  –  y = 0

y  – 4 x = 22

(1/4) x + y = 0

We start by rearranging the equation into the form y = mx + b (where m is the slope and b is the y intercept); y = 4 x  – 22 Now we know the slope is 4 and so the equation we are looking for must have the m = 4 because the lines are parallel. We are also told that the equation must pass through the origin; this means that b = 0.

In 4 x  – y = 0 we can rearrange to get y = 4 x . This fulfills both requirements.

Example Question #1 : Coordinate Geometry

What line is parallel to 2x + 5y = 6 through (5, 3)?

y = –2/3x + 3

y = –2/5x + 5

y = 5/2x + 3

y = 5/3x – 5

y = 3/5x – 2

The given equation is in standard form and needs to be converted to slope-intercept form which gives y = –2/5x + 6/5. The parallel line will have a slope of –2/5 (the same slope as the old line). The slope and the given point are substituted back into the slope-intercept form to yield y = –2/5x +5.

Example Question #3 : Coordinate Geometry

There is a line defined by the equation below:

Parallel lines have the same slope. Solve for the slope in the first line by converting the equation to slope-intercept form.

3x + 4y = 12

4y = – 3x + 12

y = – (3/4)x + 3

slope = – 3/4

We know that the second line will also have a slope of – 3/4, and we are given the point (1,2). We can set up an equation in slope-intercept form and use these values to solve for the y-intercept.

2 = – 3/4(1) + b

2 = – 3/4 + b

b = 2 + 3/4 = 2.75

Plug the y-intercept back into the equation to get our final answer.

y = – (3/4)x + 2.75

Example Question #5 : Coordinate Geometry

To solve, we will need to find the slope of the line. We know that it is parallel to the line given by the equation, meaning that the two lines will have equal slopes. Find the slope of the given line by converting the equation to slope-intercept form.

Example Question #6 : Coordinate Geometry

Start by converting the original equation to slop-intercept form.

Plug the y-intercept into the slope-intercept equation to get the final answer.

Example Question #1 : How To Find The Equation Of A Parallel Line

Converting the given line to slope-intercept form we get the following equation:

Use the y-intercept in the slope-intercept equation to find the final answer.

Example Question #9 : Coordinate Geometry

Normal 0 false false false EN-US X-NONE X-NONE MicrosoftInternetExplorer4

None of the answers are correct

If the line through the points (5, –3) and (–2,  p ) is parallel to the line  y  = –2 x  – 3, what is the value of  p  ?

Since the lines are parallel, the slopes must be the same. Therefore, (p+3) divided by ( – 2 – 5) must equal – 2. 11 is the only choice that makes that equation true. This can be solved by setting up the equation and solving for p, or by plugging in the other answer choices for p. 

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

3D Coordinates Practice Questions

Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

• Share full article

For more audio journalism and storytelling, download New York Times Audio , a new iOS app available for news subscribers.

• May 23, 2024   •   34:24 I.C.C. Prosecutor Requests Warrants for Israeli and Hamas Leaders
• May 22, 2024   •   23:20 Biden’s Open War on Hidden Fees
• May 21, 2024   •   24:14 The Crypto Comeback
• May 20, 2024   •   31:51 Was the 401(k) a Mistake?
• May 19, 2024   •   33:23 The Sunday Read: ‘Why Did This Guy Put a Song About Me on Spotify?’
• May 17, 2024   •   51:10 The Campus Protesters Explain Themselves
• May 16, 2024   •   30:47 The Make-or-Break Testimony of Michael Cohen
• May 15, 2024   •   27:03 The Possible Collapse of the U.S. Home Insurance System
• May 14, 2024   •   35:20 Voters Want Change. In Our Poll, They See It in Trump.
• May 13, 2024   •   27:46 How Biden Adopted Trump’s Trade War With China
• May 10, 2024   •   27:42 Stormy Daniels Takes the Stand
• May 9, 2024   •   34:42 One Strongman, One Billion Voters, and the Future of India

The Sunday Read: ‘Why Did This Guy Put a Song About Me on Spotify?’

The answer involves a remarkable — and lucrative, and ridiculous — scheme to game the way we find music today..

By Brett Martin

Read by Eric Jason Martin

Produced by Adrienne Hurst and Aaron Esposito

Narration produced by Tanya Pérez and Krish Seenivasan

Edited by John Woo

Original music by Aaron Esposito

Engineered by Sophia Lanman and Devin Murphy

Listen and follow The Daily Apple Podcasts | Spotify

Have you heard the song “Brett Martin, You a Nice Man, Yes”?

Probably not. On Spotify, “Brett Martin, You a Nice Man, Yes” has not yet accumulated enough streams to even register a tally. Even Brett Martin, a contributing writer for The New York Times Magazine and the titular Nice Man, didn’t hear the 1 minute 14 second song until last summer, a full 11 years after it was uploaded by an artist credited as Papa Razzi and the Photogs.

When Martin stumbled on “Brett Martin, You a Nice Man, Yes,” he naturally assumed it was about a different, more famous Brett Martin: perhaps Brett Martin, the left-handed reliever who until recently played for the Texas Rangers; or Brett Martin, the legendary Australian squash player; or even Clara Brett Martin, the Canadian who in 1897 became the British Empire’s first female lawyer. Only when the singer began referencing details of stories that he made for public radio’s “This American Life” almost 20 years ago did he realize the song was actually about him. The song ended, “I really like you/Will you be my friend?/Will you call me on the phone?” Then it gave a phone number, with a New Hampshire area code.

So, he called.

There are a lot of ways to listen to ‘The Daily.’ Here’s how.

We want to hear from you. Tune in, and tell us what you think. Email us at [email protected] . Follow Michael Barbaro on X: @mikiebarb . And if you’re interested in advertising with The Daily, write to us at [email protected] .

Additional production for The Sunday Read was contributed by Isabella Anderson, Anna Diamond, Sarah Diamond, Elena Hecht, Emma Kehlbeck, Tanya Pérez, Frannie Carr Toth and Krish Seenivasan.

Advertisement