case study on kinematics class 11

CBSE Expert

CBSE Case Study Questions Class 11 Physics PDF Download

Are you a Class 11 Physics student looking to enhance your understanding and prepare effectively for your exams? Look no further! In this comprehensive guide, we present a curated collection of CBSE Case Study Questions Class 11 Physics that will help you grasp the core concepts of Physics while reinforcing your problem-solving skills.

CBSE 11th Standard CBSE Physics question papers, important notes, study materials, Previous Year Questions, Syllabus, and exam patterns. Free 11th Standard CBSE Physics books and syllabus online. Important keywords, Case Study Questions, and Solutions.

Class 11 Physics Case Study Questions

CBSE Class 11 Physics question paper will have case study questions too. These case-based questions will be objective type in nature. So, Class 11 Physics students must prepare themselves for such questions. First of all, you should study NCERT Textbooks line by line, and then you should practice as many questions as possible.

Chapter-wise Solved Case Study Questions for Class 11 Physics

• Chapter 1: Physical World
• Chapter 2: Units and Measurements
• Chapter 3: Motion in a Straight Line
• Chapter 4: Motion in a Plane
• Chapter 5: Laws of Motion
• Chapter 6: Work, Energy, and Power
• Chapter 7: System of Particles and Rotational Motion
• Chapter 8: Gravitation
• Chapter 9: Mechanical Properties of Solids
• Chapter 10: Mechanical Properties of Fluids
• Chapter 11: Thermal Properties of Matter
• Chapter 12: Thermodynamics
• Chapter 13: Kinetic Theory
• Chapter 14: Oscillations
• Chapter 15: Waves

Class 11 students should go through important Case Study problems for Physics before the exams. This will help them to understand the type of Case Study questions that can be asked in Grade 11 Physics examinations. Our expert faculty for standard 11 Physics have designed these questions based on the trend of questions that have been asked in last year’s exams. The solutions have been designed in a manner to help the grade 11 students understand the concepts and also easy-to-learn solutions.

Class 11 Books for Boards

Why Case Study Questions Matter

Case study questions are an invaluable resource for Class 11 Physics students. Unlike traditional textbook exercises, these questions simulate real-life scenarios, challenging students to apply theoretical knowledge to practical situations. This approach fosters critical thinking and helps students build a deep understanding of the subject matter.

Let’s delve into the different topics covered in this collection of case study questions:

1. Motion and Gravitation

In this section, we explore questions related to motion, velocity, acceleration, and the force of gravity. These questions are designed to test your grasp of the fundamental principles governing motion and gravitation.

2. Work, Energy, and Power

This set of questions delves into the concepts of work, energy, and power. You will encounter scenarios that require you to calculate work done, potential and kinetic energy, and power in various contexts.

3. Mechanical Properties of Solids and Fluids

This section presents case study questions about the mechanical properties of solids and fluids. From stress and strain calculations to understanding the behavior of fluids in different situations, these questions cover a wide range of applications.

4. Thermodynamics

Thermodynamics can be a challenging topic, but fear not! This part of the guide offers case study questions that will clarify the laws of thermodynamics, heat transfer, and thermal expansion, among other concepts.

5. Oscillations and Waves

Get ready to explore questions related to oscillations, simple harmonic motion, and wave characteristics. These questions will deepen your understanding of wave propagation and the behavior of oscillatory systems.

6. Kinetic Theory and Laws of Motion

Kinetic theory and the laws of motion can be complex, but with our case study questions, you’ll find yourself mastering these topics effortlessly.

Discover a wide array of questions dealing with light, lenses, and mirrors. This section will improve your problem-solving skills in optics and enhance your ability to analyze optical phenomena.

8. Electrical Effects of Current

Electricity and circuits are fundamental to physics. The case study questions in this section will challenge you to apply Ohm’s law, Kirchhoff’s laws, and other principles in various electrical circuits.

9. Magnetic Effects of Current

Delve into the fascinating world of magnets and magnetic fields. This set of questions will strengthen your understanding of magnetic effects and their applications.

10. Electromagnetic Induction

The final section covers electromagnetic induction, Faraday’s law, and Lenz’s law. You’ll be presented with scenarios that test your ability to predict induced electromotive forces and analyze electromagnetic phenomena.

In conclusion, mastering Class 11 Physics requires a thorough understanding of fundamental concepts and their practical applications. The case study questions provided in this guide will undoubtedly assist you in achieving a deeper comprehension of the subject.

Remember, practice is key! Regularly attempt these case study questions to strengthen your problem-solving abilities and boost your confidence for the exams. Happy studying, and may you excel in your Physics journey!

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Download India's best Exam Preparation App Now.

Key Features

• Revision Notes
• Important Questions
• Previous Years Questions
• Case-Based Questions
• Assertion and Reason Questions

No thanks, I’m not interested!

Kinematics Class 11 Physics | Notes

Kinematics:.

The branch of physics which deals with the study of motion as the function of time is known as kinematics. It does not give any information about force that causes it to move.

An object is said to be in rest if it does not changes its position with respect to a reference point.

An object is said to be in motion if it changes its position with respect to a reference point.

Motion in straight line

The total length of actual path moved by an object from its initial position to final position is known as distance. It is a scalar quantity.

The distance of a moving body can be never be zero. Its unit is metre (m).

Displacement:

The shortest distance between any two points in specified direction. (i.e. initial to final) is known as displacement. It is vector quantity and denoted by ($\overrightarrow{S}$)

The displacement of a moving body may be zero. Its unit is metre (m).

Note: The ratio of distance to magnitude of displacement is greater than or equal to 1

Q. An object moves 3.5 times around a circular path of radius 100m. Calculate its total distance and total displacement. 

Radius, r = 100 m

Distance, S = 2$\pi $r × n = 2×$\frac{\text{22}}{\text{7}}$×100×3.5 = 2200m

Displacement, ($\overrightarrow{S}$) = 2r = 2×100= 200m

Q. A car is moving on a circular track of radius 70m. Find the distance and displacement made when the car reaches to opposite end of the track.

Radius, r = 70m.

Distance, S = $\frac{\text{2 }\!\!\pi\!\!\text{ }\text{r}}{\text{2}}$

= $\frac{\text{22}}{\text{7}}$×70

Displacement, ($\overrightarrow{S}$)= 2r

It is defined as the rate of change of distance with respect to time.

Mathematically, speed= $\frac{\text{distance(s)}}{\text{time(t)}}$

Its unit is ms –1 . It is a scalar quantity.

Types of Speed:

(i) Average speed:

It is defined as the ratio of total distance covered to the total time taken.

Mathematically, average speed = $\frac{\text{total distance}}{\text{total time}}$

Avg. speed = $\frac{\text{total distance}}{\text{total time}}$ = $\frac{{{\text{S}}_{\text{1}}}\text{+}{{\text{S}}_{\text{2}}}\text{+}{{\text{S}}_{\text{3}}}}{{{\text{t}}_{\text{1}}}\text{+}{{\text{t}}_{\text{2}}}\text{+}{{\text{t}}_{\text{3}}}}$= $\frac{\sum S}{\sum t}$

(ii) Uniform speed:

The speed of an object is said to be uniform if it covers equal distances in equal interval of time. 

(iii) Non-uniform speed:

The speed of an object is said to be non-uniform if it covers unequal distances in equal interval of time.

(iv) Instantaneous speed:

The speed of an object calculated for very small interval of time is called instantaneous speed.

Mathematically, V ins =  $\underset{\Delta t\to 0}{\mathop{\lim }}\,\text{ }\frac{\Delta s}{\Delta t}$

The rate of change of displacement with respect to time is known as velocity.

Mathematically, Velocity = $\frac{\text{displacement}}{\text{time}}$

It’s unit is ms –1 . It is a vector quantity.

Types of velocity:

(i) average velocity:.

It is defined as the ratio of total displacement covered to total time taken.

Mathematically, average velocity = $\frac{\text{total displacement}}{\text{total time}}$                                                        

(ii) Uniform velocity:

The velocity of an object is said to be uniform if it covers equal displacements in equal interval of time.

(iii) Non-uniform velocity:

The velocity of an object is said to be non-uniform if it covers unequal displacements in equal interval of time.

(iv) Instantaneous velocity:

The velocity of an object calculated for very small interval of time is called instantaneous velocity.

Mathematically, $\overrightarrow{{{V}_{ins}}}$= $\underset{\Delta t\to 0}{\mathop{\lim }}\,\text{ }\frac{\overrightarrow{\Delta s}}{\Delta t}$=$\frac{\overrightarrow{ds}}{dt}$

Note: (i) If time is equally divided then the average speed is V =  $\frac{{{\text{v}}_{\text{1}}}\text{+}{{\text{v}}_{\text{2}}}}{\text{2}}$

         (ii) If distance is equally divided, then the average speed is     V =  $\frac{\text{2}{{\text{v}}_{\text{1}}}{{\text{v}}_{\text{2}}}}{{{\text{v}}_{\text{1}}}\text{+}{{\text{v}}_{\text{2}}}}$

         (iii) For uniform motion i.e. constant velocity, $\overrightarrow{{{V}_{avg}}}$=  $\overrightarrow{{{V}_{ins}}}$

Facts about uniform velocity:

(i)         The object always moves in a straight line and in the same direction.

(ii)        The magnitude of velocity is equal to speed.

(iii)       The average velocity is equal to instantaneous velocity.

(iv)       Since velocity is constant, acceleration is zero and hence net force (resultant force) is also zero.

Acceleration and retardation (or deceleration):

The rate of change of velocity with respect to time is known as acceleration. It is denoted by ‘a’ and given by

                                     a = $\frac{v-u}{t}$    i.e. v = u+at

It is a vector quantity retardation. The negative value of acceleration is called retardation (or deceleration).

For uniform velocity, acceleration is zero.

Equations related to uniform acceleration.

1.      v = u+at

2.      S = ut + $\frac{1}{2}$at 2

3.      V 2 = u 2 + 2as

Types of acceleration

(a) Average acceleration,

$\overrightarrow{{{a}_{avg}}}$= $\frac{\overrightarrow{\Delta v}}{\Delta t}$

(b) Instantaneous acceleration,

$\overrightarrow{{{a}_{ins}}}$= $\underset{\Delta t\to 0}{\mathop{\lim }}\,\text{ }\frac{\overrightarrow{\Delta v}}{\Delta t}$=$\frac{\overrightarrow{dv}}{dt}$

Graphical treatment:

(i)         displacement- time graph for uniform motion.

(i.e. velocity, V = constant and acceleration, a = 0)

Slope = $\frac{BC}{AC}$ = velocity

(ii)        Displacement- time graph for non-uniform motion

Slope at P = $\frac{BC}{AC}$= Velocity at point P

(iii)       Velocity – time graph for uniform motion

(iv) Velocity – time graph for constant acceleration (for u = 0)

(v) Velocity – time graph for constant acceleration (for u > 0)

(vi) Velocity – time graph for non-uniform acceleration.

Slope at P = $\frac{BC}{AC}$ = acceleration at point P

Displacement-time graph (s-t graph):

 Fig: Displacement-time graph for uniform motion

Let us consider a body initially at S o is moving with constant velocity for time ‘t’ where it covers distance ‘S’. Let this motion is represented by line AB in a s-t graph.

Draw BM perpendicular to t-axis and AN perpendicular to BM.

OA = MN = S o

OM = AN = t

BN = BM – MN = S – S o

Slope of S-t graph  = Slope of line AB

=  $\frac{BN}{AN}$

= $\frac{S-{{S}_{o}}}{t}$ = velocity         

$\therefore $  Slope of S-t graph = Velocity of a body

Physical significance of s-t graph

• The slope of (s-t) graph gives velocity   i.e.$\overrightarrow{V}$= $\frac{\overrightarrow{\Delta s}}{\Delta t}$
• It gives position of a body at any instant.
• It gives distance covered by a body in any interval of time.  

(i) Derivation of   S = S o + vt for a body moving with constant velocity by graphical method.

We have, Slope of S-t graph = velocity

Slope of line AB = V

  $\frac{BN}{AN}$ = V

$\frac{S-{{S}_{o}}}{t}$ = v

$\therefore $ S = S o + vt ……….is the required expression for displacement.

Velocity-time graph (v-t graph):

Let us consider a body moving initially with velocity ‘u’ is accelerated for time ‘t’ and velocity increases to ‘v’. Let this motion is represented by line AB in v-t graph.

Draw perpendicular BM to t-axis AN perpendicular to BM.

OA = MN = u

BN = BM – MN = v -u

Slope of v-t graph = slope of line AB

= $\frac{BN}{AN}$  =  $\frac{v-u}{t}$ = a

$\therefore $ Slope of v-t graph  = acceleration

Also, Area of v-t graph with t- axis = Area of trapezium OABM

= Area of rectangle OANM + Area of triangle ABN

= OA× OM + $\frac{1}{2}$ AN ×BN

=  ut + $\frac{1}{2}$ t × at =  displacement (S)

$\therefore $ Area of v-t graph with t- axis = displacement (S)

Physical significance of v-t graph are

• The slope of (v – t) graph gives acceleration   i.e.$\overrightarrow{a}$= $\frac{\overrightarrow{\Delta v}}{\Delta t}$
• The area under (v – t) graph with time – axis gives displacement .
• It gives velocity at any instant of time.

Kinematical equations by graphical method:

(i) Derive v = u + at for a body with constant acceleration by graphical method.

Draw perpendicular BM to t-axis and AN perpendicular to BM.

Slope of v-t graph = acceleration

i.e. slope of line AB = a

Or,    $\frac{BN}{AN}$ = a

Or,   $\frac{v-u}{t}$ = a

$\therefore $ v = u + at  ………This is the required expression.

(ii) Derivation of S = ut + $\frac{\text{1}}{\text{2}}$ at 2 for a uniformly accelerating body by graphical method.

Or, BN = at

Now, Area of v-t graph with t- axis = distance

Or, Area of trapezium OABM = S

Or, Area of rectangle OANM + Area of triangle ABN = S

Or, OA× OM + $\frac{1}{2}$ AN ×BN = S

Or, ut + $\frac{1}{2}$ t × at = S

$\therefore $ S = ut + $\frac{\text{1}}{\text{2}}$ at 2 ………This is the required expression.

(iii)  Derivation of  v 2 = u 2 + 2as for a uniformly accelerating body by graphical method.

BN = BM – MN = v – u

i.e, slope of line AB = a

Or, $\frac{BN}{AN}$ = a

Or, AN = $\frac{v-u}{a}$ ………………. (i)

i.e, Area of trapezium OABM = S

Or, $\frac{1}{2}$ (OA + BM) × AN = S

Or, $\frac{1}{2}$ ( u + v)  $\frac{v-u}{a}$ = S

Or, $\frac{{{v}^{2}}-{{u}^{2}}}{2a}$ = S                 

Or, v 2 – u 2 = 2as

$\therefore $ v 2 = u 2 + 2as ………..This is the required expression.

Distance covered by a body in n th second ( S n th formula):

The distance covered by a body in the interval of ‘n’ sec and (n-1) sec is called S n th formula.

It is given by S n th = S n – S n-1

i.e, S n th   = u + $\frac{a}{2}$ (2n – 1)

Derivation:

Let us consider a body moving initially with velocity ‘u’ is accelerated to distances S n and S n-1 in ‘n’ sec and (n-1) sec respectively.

As we know,    S = ut + $\frac{1}{2}$ at 2

So,    S n = u × n + $\frac{1}{2}$ an 2 ……………..(i)

and   S n-1 = u(n-1) + $\frac{1}{2}$ a(n-1) 2 ……………….(ii)

Now, distance covered in n th second = S n – S n-1

Or,       S n th   = un + $\frac{1}{2}$ an 2 – [u(n-1) + $\frac{1}{2}$ a(n-1) 2 )]

Or,       S n th = un + $\frac{1}{2}$ an 2 – [un-u + $\frac{1}{2}$ a(n 2 – 2n+1)]

Or,       S n th = un + $\frac{1}{2}$ an 2 – [un – u + $\frac{1}{2}$ an 2 – an +$\frac{1}{2}$ a]

Or,       S n th = un + $\frac{1}{2}$ an 2 – un + u – $\frac{1}{2}$ an 2 + an – $\frac{1}{2}$ a

Or,      S n th = u + a( n- $\frac{1}{2}$ )

$\therefore $ S n th = u + $\frac{\text{a}}{\text{2}}$ (2n – 1)…………………is the required expression.

Projectile: 

An object which is thrown in space and falls under the action of gravity alone is known as projectile. We neglect air resistance during the projectile motion. The path followed by projectile is known as trajectory.

Examples of projectile:

i. A stone thrown into space.

ii. A ball thrown towards a player in a playground. 

iii. A bomb dropped from an airplane.

Assumptions for the study of projectile motion 

1. The acceleration along y–axis is only considered, i.e. the projected object falls under the action of gravity alone.

2. The acceleration along x–axis is zero (a x = 0). The horizontal velocity does not change at all throughout the projectile motion, i.e. u x = V x  

3. Air resistance is neglected.

Case I: When an object is projected making an angle ‘$\theta $’ with the horizontal.

Let us consider an object projected from ground with an initial speed ‘u’ making an angle ‘$\theta $’ with horizontal (ground) as shown in figure.

Resolving the initial velocity ‘u’ into its rectangular components, we get, 

u x = u cos$\theta $ and u y = u sin$\theta $ along horizontal and vertical direction respectively.

1. Path of the projectile:

Let S x = x and S y = y be the components of displacement along horizontal and vertical direction respectively at any point.

We know, S = ut + $\frac{1}{2}$at 2 …………(i)

Taking horizontal component, equation (i) becomes,

 S x = u x t + $\frac{1}{2}$a x t 2  

Or, x = u cos$\theta $.t    $\because $ a x = 0

Or, t = $\frac{x}{u\cos \theta }$………….(ii)

Taking vertical component, equation (i) becomes,

 S y = u y t + $\frac{1}{2}$a y t 2  

Or, y = u sin$\theta $$\frac{x}{u\cos \theta }$ + $\frac{1}{2}$(–g) ${{\left( \frac{x}{u\cos \theta } \right)}^{2}}$

Or, y = tan$\theta $.x – $\frac{g}{2{{u}^{2}}{{\cos }^{2}}\theta }$x 2

This equation is of the parabolic form y = ax + bx 2 ,

where, a = tan$\theta $ and b = $\frac{-g}{2{{u}^{2}}{{\cos }^{2}}\theta }$

2. Maximum Height (H max ):

It is the maximum vertical displacement attained by the projectile.

We know, v 2 = u 2 + 2as ….(iii)

Taking vertical component, equation (iii) becomes,

v y 2 = u y 2 + 2 a y s y

For maximum height, s y = H max and v y = 0

$\therefore $ 0 = u 2 sin 2 $\theta $ + 2 (-g) H max

Or, 2 g H max = u 2 sin 2 $\theta $

$\therefore $ H max = $\frac{{{u}^{2}}si{{n}^{2}}\theta }{2g}$ 

This is the required expression for maximum height.

3. Time of flight (T):

It is the total time spent by projectile in air.

We know, S = ut + $\frac{1}{2}$at 2 …………(iv)

Taking vertical component, equation (iv) becomes,

For time of flight (total time), t = T and S y = 0

Or, 0 = u sin$\theta $. T + $\frac{1}{2}$(–g) T 2

Or, $\frac{1}{2}$g T 2 = u sin$\theta $. T

$\therefore $T = $\frac{2u\sin \theta }{g}$

This is the required expression for time of flight.

Time to reach the greatest height / time of ascend (t asc ) / time of descend (t des ):

T 1/2 = t asc = t des =  $\frac{T}{2}$= $\frac{u\sin \theta }{g}$

4. Horizontal Range (R):

It is the total horizontal distance covered by the projectile.

We know, S = ut + $\frac{1}{2}$at 2 …………(v)

Taking horizontal component, equation (v) becomes,

Or, S x = u x t + a x t 2  

Or, S x = u cos$\theta $. t $\because $ a x = 0

For horizontal range (total horizontal displacement), S x = R and t = T, then 

R = u cos$\theta $.T

Or, R = u cos$\theta $.$\frac{2u\sin \theta }{g}$

 $\therefore $ R = $\frac{{{u}^{2}}\sin 2\theta }{g}$

This is the required expression for horizontal range.

Condition for maximum horizontal range (R max ):

We have, R = $\frac{{{u}^{2}}\sin 2\theta }{g}$

For maximum value of R, $\operatorname{sin}2\theta $ must be maximum.

i.e. $\operatorname{sin}2\theta $ = 1

Or, $\operatorname{sin}2\theta $ = Sin90 o

$\therefore $ $\theta $ = 45 o

The horizontal range is maximum for$\theta $ = 45 o .

5. Velocity of the projectile at any instant:

Let $\overrightarrow{V}$ be the velocity of the projectile at any instant. Let ‘V x ’ and ‘V y ’ be the components of velocity $\overrightarrow{V}$along x-axis and y-axis respectively and ‘$\alpha $’ be the angle made by the velocity with the horizontal.

We have V = u + at   ……. (vi)

Taking horizontal component, equation (vi) becomes,

V x = u x + a x t  

Or, V x = ucos$\theta $  {$\because $ a x = 0} 

Similarly taking vertical component, equation (vi) becomes,

V y = u y + a y t  

Or, V y = usin$\theta $ – gt 

Now, magnitude of velocity 

V = $\sqrt{{{V}_{x}}^{2}+{{V}_{y}}^{2}}$= $\sqrt{{{u}^{2}}{{\cos }^{2}}\theta +{{\left( u\sin \theta -gt \right)}^{2}}}$

Or, V =$\sqrt{{{u}^{2}}{{\cos }^{2}}\theta +{{\left( u\sin \theta -gt \right)}^{2}}}$

and direction, $\tan \alpha $= $\frac{{{V}_{y}}}{{{V}_{x}}}$

Or, $\alpha $= tan –1 $\left( \frac{usin~\theta gt}{u\cos \theta } \right)$

For the velocity with which the projectile hits the ground, we replace the time ‘t’ by time of flight ‘T’ and angle ($\alpha $) by the striking angle ($\beta $)  then magnitude and direction become

Magnitude, V =$\sqrt{{{u}^{2}}{{\cos }^{2}}\theta +{{\left( u\sin \theta -gT \right)}^{2}}}$

and direction, $\beta $= tan -1 $\left( \frac{usin~\theta gT}{u\cos \theta } \right)$

6. Two angles of projection for same horizontal range:

For the angle of projection ‘$\theta $’, the horizontal range is given by,

R 1 = $\frac{{{u}^{2}}\sin 2\theta }{g}$

Again, for the angle of projection (90 –$\theta $), the horizontal range is given by

R 2 = $\frac{{{u}^{2}}\sin 2(90-\theta )}{g}$  

=  $\frac{{{u}^{2}}\sin (180-2\theta )}{g}$

=  $\frac{{{u}^{2}}\sin 2\theta }{g}$

From above equations

Hence, two angles of projection for the same horizontal range are $\theta $ and (90 –$\theta $ ).

Case II: When an object is projected horizontally from height (h) above the ground.

Let us consider an object projected horizontally from a height ‘h’ above the ground with initial velocity ‘u’. Here angle made by initial velocity with horizontal is zero (i.e. $\theta $= 0). In projectile motion, vertical velocity changes continuously but the horizontal velocity remains constant throughout the motion because the acceleration due to gravity doesn’t act in horizontal direction. Let ‘V x ’ and ‘V y ’ be the rectangular components of velocity ‘V’ after time ‘t’, u y = usin0 o = 0.

1. Path of the projectile: 

Let S x = x and S y = y be two rectangular components of displacement along horizontal and vertical direction respectively at any point.

Or, x = u cos$\theta $.t    {$\because $ a x = 0}

Or, x = u cos0 o .t      {$\because $$\theta $   = 0}

Or, t = $\frac{x}{u}$………….(ii)

Or, y = u sin$\theta $.t + $\frac{1}{2}$.g ${{\left( \frac{x}{u} \right)}^{2}}$

Or, y = u sin0 o .t +$\frac{g}{2{{u}^{2}}}$x 2

Or, y = $\frac{g}{2{{u}^{2}}}$x 2

This equation is of the parabolic form y = ax 2 ,

where, a = $\frac{g}{2{{u}^{2}}}$

2. Time of flight / time to reach the ground (T):

The total time of a projectile spent in air is known as time of flight. When the projectile reaches the ground.

We know, S = ut + $\frac{1}{2}$at 2 …………(iii)

For total time, S y = h and t = T

Or, h = u sin0 o .t +$\frac{1}{2}$g T 2

Or, h = $\frac{1}{2}$g T 2  

This is the required expression for height. 

From above equation

T 2 = $\frac{2h}{g}$

$\therefore $T = $\sqrt{\frac{2h}{g}}$

This is required expression for time of flight.

3. Horizontal Range (R):

Taking horizontal component, equation (iv) becomes,

 S x = u x t + $\frac{1}{2}$a x t 2 

S x = u x t {$\because $ a x = 0}

For horizontal range (total horizontal displacement) S x = R and t = T

Or, R = u cos0 o .T      {$\because $$\theta $   = 0}

Or, R = u  $\sqrt{\frac{2h}{g}}$

4. Velocity with which the projectile hits the ground.

Let $\overrightarrow{V}$ be the velocity of the projectile at any instant. Let ‘V x ’ and ‘V y ’ be the rectangular components of velocity $\overrightarrow{V}$along x-axis and y-axis respectively and ‘$\alpha $’ be the angle made by the velocity with the horizontal.

We have, V = u + at  …….  (v)

Or, V x = ucos$\theta $  {$\because $ a x = 0}

 Or, V x = ucos0 o = u 

Similarly taking vertical component, equation (v) becomes,

Or, V y = usin$\theta $ + gt 

Or, V y = gt {$\because $$\theta $= 0 o }

V = $\sqrt{{{V}_{x}}^{2}+{{V}_{y}}^{2}}$= $\sqrt{{{u}^{2}}+{{g}^{2}}{{t}^{2}}}$

Or, V =  $\sqrt{{{u}^{2}}+{{g}^{2}}{{t}^{2}}}$

And direction, $\tan \alpha $= $\frac{{{V}_{y}}}{{{V}_{x}}}$

Or, $\alpha $= tan –1 $\left( \frac{gt}{u} \right)$

For the velocity with which the projectile hits the ground, we replace the time ‘t’ by time of flight ‘T’ and angle ($\alpha $) by the striking angle ($\beta $) then magnitude and direction becomes

Magnitude, V =$\sqrt{{{u}^{2}}+{{g}^{2}}{{T}^{2}}}$

And direction, $\beta $= tan –1 $\left( \frac{gT}{u} \right)$

Crossing of River:

Let, width of river = AB

Velocity of flow of river = V R

Velocity of swimmer in still water = V S  

1. For shortest route: 

(a) Direction:

Sin$\theta $ = $\frac{p}{h}$= ,

$\theta $ = sin –1$\left( \frac{{{V}_{R}}}{{{V}_{S}}} \right)$

(b) Velocity along AB, V AB = Vs cos$\theta $

(c) Time to cross the river (t) = $\frac{AB}{Vscos\theta }$

2. For least time to cross the river:

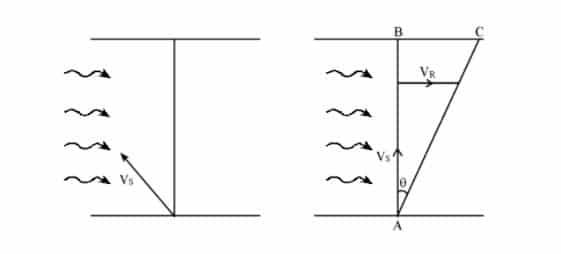
We have, 

Time to cross the river, t = $\frac{AB}{{{V}_{s}}cos\theta }$

For t min , cos$\theta $ = max m  

i.e. cos$\theta $ = 1

Or, cos$\theta $ =  cos0 o

Or, $\theta $ = 0 o

Then, t min = $\frac{AB}{{{V}_{S}}}$

From fig (ii), 

Tan$\theta $ = $\frac{{{V}_{R}}}{{{V}_{s}}}$= $\frac{BC}{AB}$

Distance apart from opposite end

BC = $\frac{{{V}_{R}}}{{{V}_{s}}}$AB

$\therefore $Distance apart from the opposite end (BC) = $\frac{{{V}_{R}}}{{{V}_{s}}}$× width of river {OR, BC Tan$\theta $ × width of river} 

When a swimmer is swimming in river (Downstream or Upstream):

Let V S be the velocity of swimmer in still water and V R   be the velocity of flow of river.

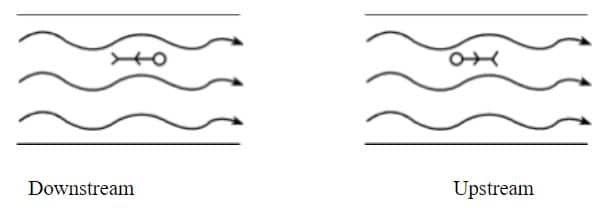
V total = V S + V R V total = V S – V R

In downstream resultant velocity increases while in upstream it decreases.

Relative velocity:

The rate of change of displacement of an object with respect to another object when both are in motion is known as relative velocity of one object w.r.t. another object.

The relative velocity of ‘A’ w.r.t. ‘B’ is 

  $\overrightarrow{{{V}_{AB}}}$=$\overrightarrow{{{V}_{A}}}$ –$\overrightarrow{{{V}_{B}}}$

Let us consider two objects A and B moving with velocities at $\overrightarrow{{{V}_{A}}}$and $\overrightarrow{{{V}_{B}}}$an angle ‘$\theta $’. To find the relative velocity of ‘A’ w.r.t. ‘B’, the velocity of ‘B’ is supposed to be zero. For this, draw a negative vector of  $\overrightarrow{{{V}_{B}}}$ and complete a parallelogram as shown in figure.

The resultant of $\overrightarrow{{{V}_{A}}}$and –$\overrightarrow{{{V}_{B}}}$gives the relative velocity of ‘A’ w.r.t. ‘B’ i.e. $\overrightarrow{{{V}_{AB}}}$

In fig, ‘β’ is the dir n of$\overrightarrow{R}$ (=$\overrightarrow{{{V}_{AB}}}$) with $\overrightarrow{{{V}_{A}}}$

Now, the magnitude of $\overrightarrow{{{V}_{AB}}}$is 

V AB =$\sqrt{{{V}_{A}}^{2}+2{{V}_{A}}{{V}_{B}}\cos (180-\theta )+{{V}_{B}}^{2}}$

= $\sqrt{{{V}_{A}}^{2}-2{{V}_{A}}{{V}_{B}}\cos \theta +{{V}_{B}}^{2}}$

the direction of $\overrightarrow{{{V}_{AB}}}$ with $\overrightarrow{{{V}_{A}}}$is

α = tan –1 $\left( \frac{{{V}_{B}}\sin (180-\theta )}{{{V}_{A}}+{{V}_{B}}\cos (180-\theta )} \right)$

α = tan –1 $\left( \frac{{{V}_{B}}\sin \theta }{{{V}_{A}}-{{V}_{B}}\cos \theta } \right)$

Special Cases :

(i) When two objects are moving in the same direction i.e. $\theta $=0° then,

V AB = $\sqrt{{{V}_{A}}^{2}-2{{V}_{A}}{{V}_{B}}\cos {{0}^{o}}+{{V}_{B}}^{2}}$

  = $\sqrt{{{V}_{A}}^{2}-2{{V}_{A}}{{V}_{B}}+{{V}_{B}}^{2}}$

= $\sqrt{{{({{V}_{A}}-{{V}_{B}})}^{2}}}$

$\therefore $V AB = V A –V B

(ii)  When two objects are moving in opposite direction i.e. $\theta $=180° then, 

V AB = $\sqrt{{{V}_{A}}^{2}-2{{V}_{A}}{{V}_{B}}\cos {{180}^{o}}+{{V}_{B}}^{2}}$

= $\sqrt{{{V}_{A}}^{2}+2{{V}_{A}}{{V}_{B}}+{{V}_{B}}^{2}}$

= $\sqrt{{{({{V}_{A}}+{{V}_{B}})}^{2}}}$

$\therefore $V AB = V A +V B

(iii) When two objects are moving perpendicular to each direction i.e. $\theta $=90°then, 

V AB = $\sqrt{{{V}_{A}}^{2}-2{{V}_{A}}{{V}_{B}}cos90{}^\circ +{{V}_{B}}2}$

$\therefore $V AB = $\sqrt{{{V}_{A}}^{2}+{{V}_{B}}^{2}}$

(iv) When two objects are moving with same magnitude velocities:

Let,$\left| \overrightarrow{{{V}_{A}}} \right|$= $\left| \overrightarrow{{{V}_{B}}} \right|$ = V 

then, 

V AB =$\sqrt{{{V}_{A}}^{2}-2{{V}_{A}}{{V}_{B}}\cos \theta +{{V}_{B}}^{2}}$

= $\sqrt{{{V}^{2}}-2{{V}^{2}}\cos \theta +{{V}^{2}}}$

= $\sqrt{2{{V}^{2}}-2{{V}^{2}}cos\theta }$

= $\sqrt{2{{V}^{2}}(1-\theta cos)}$

= $\sqrt{2{{V}^{2}}.2si{{n}^{2}}\frac{\theta }{2}}$

$\therefore $V AB = 2Vsin$\frac{\theta }{2}$

Examples of Relative Velocity:

1. The front windscreen of a moving car gets wet in rain while the behind screen remains dry.

2. Rain drops hitting the side of windows of a car in motion often leave diagonal streaks.

3. Person has to incline the umbrella forward with vertical while running in rain. etc.

Q. The front windscreen of a moving car gets wet in rain while the behind screen remains dry. Why?

This is due to the relative velocity of rain with respect to the car. 

Let $\overrightarrow{{{V}_{C}}}$ the velocity of the car along the horizontal direction and $\overrightarrow{{{V}_{R}}}$ be the velocity of rain vertically downward. From the above figure, the resultant of $\overrightarrow{{{V}_{R}}}$and –$\overrightarrow{{{V}_{C}}}$gives the relative velocity of rain with respect to the car as shown in the figure above.

Here, Tan$\theta $ = $\frac{p}{b}$= $\frac{AY}{OY}$= $\frac{{{V}_{C}}}{{{V}_{R}}}$

$\therefore $ $\theta $= tan –1 $\left( \frac{{{V}_{C}}}{{{V}_{R}}} \right)$

So, the raindrop strikes the front windscreen making an angle $\theta $= tan –1$\left( \frac{{{V}_{C}}}{{{V}_{R}}} \right)$ with vertical direction. Thus, the front windscreen of a moving car gets wet in rain while behind the screen remains dry.

Numerical Problems ( Kinematics)

Take acceleration due to gravity, g = 10 ms –2

Q.1 A car travelling with a speed of 15m/s is braked and it slows down with uniform retardation. It covers a distance of 88 m as its velocity reduces to 7m/s. If the car continues to slow down with the same rate, after what further distance will it be brought to rest?  Ans: 24.5 m

Q.2 A body falls freely from the top of a tower and during the last second of its fall, it falls through 25m. Find the height of tower.   Ans: 45 m

Q.3 An object is dropped from the top of the tower of height 156.8 m. and at the same time another object is   thrown vertically upward with the velocity of 78.1 m/s from   the foot of the tower, when and where the object meet?            Ans: 2 sec. and 20 m below from top

Q.4 An object is dropped from the top of the tower of height 100m and after 2 sec another object is thrown vertically upward with velocity 25 m/s from the foot of the tower. When and where the objects meet?

Ans: after 3 sec of 1 st object dropped, 45m below the top.

Q.5 A swimmer’s speed along the river (down-stream) is 20 km/h and can swim up-stream at 8 km/h. Calculate the velocity of the stream and the swimmer’s possible speed in still water.          Ans: 14 km/hr, 6 km/hr

Q.6 A swimmer’s speed along the river is 20 kmph and up-stream is 8 kmph. Calculate the velocity of the stream and the swimmer’s possible speed in still water.     Ans: 14 km/hr, 6 krnihr

Q.7 A man wishes to swim across a river 600m wide. If he can swim at the rate of 4km/h in still water and the river flows at 2km/h. Then in what direction must he swim to reach a point exactly opposite to the starting point and when will he reach it?         Ans: 120° with water and 10.4 min

Q.8 A projectile is fired from ground level with a velocity 500 ms -1 at 30 o to the horizontal. Find the horizontal range, the greatest height and the time to reach the greatest height.     Ans:  21651m, 3125m, 25 sec

Q.9 A baseball is thrown towards a player with an initial velocity 20 ms -1 at 45 o with the horizontal. At the moment, the ball is thrown the player is 50 m from the thrower. At what is speed and in what direction must he run to catch the ball at the same height at which it is released?          Ans: 3.5 ms -1 towards the thrower

Q.10 A body is projected upwards making an angle $\theta $ with the horizontal with a velocity of 300 m/s. Find the value of $\theta $ so that the horizontal range will be maximum. Find its range and time of flight.  Ans: 45°, 9000 m

Q.11 A stone on the top of a vertical cliff is kicked horizontally so that its initial velocity is 9 ms -1 . If the cliff is 200 m high, calculate

(i) taken by the stone to reach the ground.

(ii) How far from the bottom of the cliff, the stone will hit the ground?       Ans: (i) 6.32 sec (ii) 56.92 m

Q.12 A stone on the edge of a vertical cliff is kicked so that its initial velocity is 9 m/s horizontally. If the cliff is 200m high, calculate: i. time taken by stone to reach the ground. ii. How far from the cliff the stone will hit the ground?                  Ans: (i) 6.32 sec (ii) 56.92 m

Q.13 A bullet is fired with a velocity of 100 m/s from the ground at an angle of 60° with the horizontal. Calculate the horizontal range covered by the bullet. Also calculate the maximum height attained.                Ans: 866m; 375 m

Q.14 A projectile is fired from the ground level with velocity 150 m/s at 30° to the horizontal. Find its   horizontal range. What will be the least speed with which it can.be projected to achieve the same horizontal range?       Ans: 1949 m, 140 m/s

Q.15 A projectile is fired from the ground level with velocity of 500 m/s at 30° to horizon. Find the horizontal range, and greatest vertical height to which it rises. What is   the least speed with which it could be projected in order to   achieve the same horizontal range? [g = 10 N kg -1 ]     Ans: 21651 m, 3125 m, 464 ms -1

Q.16 A body is projected horizontally from the top of   a tower 100 m high with a velocity of 9.8 ms -1 . Find the velocity with which it hits the ground.      Ans: 45.82 m/s at 77.9°

Q.17 A batter hits a baseball so that it leaves the bat with an initial speed 37m/s at an angle of 53°. Find the position of the ball and the magnitude and direction of its velocity after 2 seconds. Treat the baseball as a projectile.         Ans: 24.23 m/sec, 23.21°

Q.18 A stone is projected horizontally with 20m/s from top of a tall building. Calculate its position and velocity after 3 sec neglecting the air resistance.        Ans: 36 m/sec; 56.3°

Q.19 A projectile is launched with an initial velocity of 30 m/s at an angle of 60° above the horizontal. Calculate the magnitude and direction of its velocity 5s after launch. Ans: 28.3 m/s and 58° C from horizontal

Q.20 An airplane is flying with a velocity of 90 m/s at an angle of 23.0° above the horizontal. When the plane is 114 m directly above a dog that is standing on level ground, a suitcase drops out of luggage compartment far from the dog will the suitcase land? You can ignore it resistance.            Ans: 778.7 m from dog

Q.21 To a cyclist riding due west with a speed of 4 m/s, a wind appears to blow from south west. The wind appears to blow from south to a man, running at 2ms -1 in the same direction. What is the actual velocity of the wind?  Ans: 2$\sqrt2$ ms -1 from south east

Q.22 To a person going due east in a car with a velocity 25 km/hr, a train appear to move due north with a velocity of 25$\sqrt3$ km/hr. What is the actual velocity and direction of motion of train?

Ans: 50 km/hr along a direction 30° east of north.

Q.23 Two ships A and B are moving in a sea. If A moves with uniform velocity of 8 kmhr –1 due east B moves with uniform velocity 6 kmhr –1 due south. Calculate the relative velocity of ship A with respect to ship B.

Also Read: Vector Notes Class 11

14 thoughts on “Kinematics Class 11 Physics | Notes”

Excellent Notes, just a complete concept on kinematics. Thanks for your hard work!

Thank you very much for this. I really really need this one. again thank you.

very helpful

yes very helpful

thank u very much this too much helpful

Thanks alot sir

These notes are really very helpful all the topics are covered loved them thankyou

THANK YOU SO MUCH. THIS WAS EXACTLY WHAT I WAS LOOKING FOR.

Great Notes. Motion in a plane is also required . Kindly help ..

Thankyou AJ sir for this notes it helped me a lot 🙂

Nice sir 🙏🏾🙏🏾🙏🏾🙏🏾🙏🏾🙏🏾🙏🏾 God bless you लेकिन भगवान करे कि जो आपने notes बनाएं हैं वो एक एक question syllabus में हो।

Great note . Best teacher of uniglobe SS college AJ sir. Thank you very helpful note.

Excellent explanation

This notes were amazing👍

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Kinematics - Physics For Class 11 - Class 11 - Notes, Videos & Tests

Part of the course, kinematics study material.

Notes for Kinematics - Physics For Class 11 | Class 11

Online test for kinematics - physics for class 11 | class 11, other chapters in physics for class 11, top courses for class 11.

Importance of Kinematics Class 11

Kinematics notes free pdf download, important questions for kinematics, kinematics practice questions, welcome back, create your account for free.

Forgot Password

Unattempted tests, change country, practice & revise.

• Book Solutions
• State Boards

Class 11 Physics Case Study Question

Case study question class 11 physics (cbse / ncert board).

Class 11 Physics Case Study Question and Answer: CBSE / NCERT Board Class 11 Physics Case Study Question prepared by expert Physics Teacher. Students can learn Case Based Question / Paragraph Type Question for NCERT Class 11 Physics.

There are total 15 chapter Physical World, Units and Measurement, Motion in a Straight Line, Motion in a Plane, Laws of Motion, Work, Energy and Power, Systems of Particles and Rotational Motion, Gravitation, Mechanical Properties of Solids, Mechanical Properties of Fluids, Thermal Properties of Matter, Thermodynamics, Kinetic Theory, Oscillations, Waves.

For any problem during learning any Case or any doubts please comment us. We are always ready to help You.

CBSE Class 11 Physics Case Study Question

• Chapter 1 Physical World,
• Chapter 2 Units and Measurement,
• Chapter 3 Motion in a Straight Line,
• Chapter 4 Motion in a Plane,
• Chapter 5 Laws of Motion
• Chapter 6 Work, Energy and Power,
• Chapter 7 Systems of Particles and Rotational Motion,
• Chapter 8 Gravitation,
• Chapter 9 Mechanical Properties of Solids,
• Chapter 10 Mechanical Properties of Fluids,
• Chapter 11 Thermal Properties of Matter,
• Chapter 12 Thermodynamics,
• Chapter 13 Kinetic Theory,
• Chapter 14 Oscillations,
• Chapter 15 Waves

What is Case Study Question?

Ans. At case Study there will one paragraph and on the basis of that concept some question will made. Students have to solve that question.

How many marks will have at case based question?

Most of time 5 questions will made from each case. There will 1 or 2 marks for each question.

Ye case study download kaise hyonge.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

We have a strong team of experienced Teachers who are here to solve all your exam preparation doubts

Rs aggarwal class 5 solutions chapter 11, 2025 solved icse specimen paper class 10 english paper 1, sikkim scert class 4 evs chapter 2 games we play solution, sikkim scert class 4 evs chapter 1 changing families solution.

Sign in to your account

Username or Email Address

Remember Me

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Class 11 Physics (India)

Unit 1: physical world, unit 2: units and measurement, unit 3: basic math concepts for physics (prerequisite), unit 4: differentiation for physics (prerequisite), unit 5: integration for physics (prerequisite), unit 6: motion in a straight line, unit 7: vectors (prerequisite), unit 8: motion in a plane, unit 9: laws of motion, unit 10: work, energy and power, unit 11: system of particles and rotational motion, unit 12: gravitation, unit 13: mechanical properties of solids, unit 14: mechanical properties of fluid, unit 15: thermal properties of matter, unit 16: thermodynamics, unit 17: kinetic theory, unit 18: oscillations, unit 19: waves.

Important Questions of Kinematics | Class 11

• Post author: Vikas Sir (Vikas Meel - IIT Delhi)
• Post published: June 9, 2021
• Post category: Chapter Wise Approach
• Post comments: 0 Comments

In JEE Main paper, you can expect up to 2 questions from ‘Kinematics’ while in JEE Advanced (IIT JEE) you can expect up to 1 question. It is generally considered to be a scoring topic, if you can master the different types questions that have been or could be asked in JEE Main and JEE Advanced papers on Kinematics. So here in this blog, we would examine all different types of questions asked on this topic and will highlight the Important Questions of Kinematics Class 11 topic. 

A rating of 5 stars means that you should have that question mastered, so make sure that you practice similar questions on AceJEE platform and do listen to the explanation video on that question type by Vikas Sir where he covers all the basics, step by step approach along with a solved problem from latest JEE Main / Advanced papers. A rating of 3 stars means that there is a good chance that questions might be asked on that question type as well based on previous 3 year question papers and a rating of 1 means we have not seen the focus on that question type in last 3 to 5 years but that does not mean that you should ignore that question type as examiners do tend to move around between the question types.

So let’s begin with a quick overview of one dimensional motion

Kinematics | One Dimensional Motion

For a body moving along one dimension, say $x$, 

• it’s displacement $\Delta x$ is defined as final position minus initial position i.e. $x_f – $ $x_i$ which may be positive or may be negative and may or may not be equal to the distance travelled in going from $x_i$ to $x_f$
• it’s average speed is defined as $=\cfrac{Total \ Distance}{Time \ Duration}$ or distance travelled in 1 sec and may or may NOT be same as average velocity ($\cfrac{Net \ Displacement}{Time \ Duration}$)
• it’s instantaneous velocity is $\cfrac{ds}{dt}$, i.e. small displacement $ds$ in small time duration $dt$ at time $t$. Note instantaneous speed = magnitude of instantaneous velocity
• it’s two independent equations of motion for constant acceleration are given by $v =$ $u +$ $at$, $\Delta x =$ $ut+$ $\cfrac{1}{2} at^2$, where you have 5 variables $u$, $v$, $\Delta x$, $a$, and $t$, which means you can only solve for 2 unknown variables or you must be given information on other 3 variables.
• Alternate form of above equations are $v^2 =$ $u^2 +$ $2a \Delta x$, no $t$ involved here (more commonly used), $\Delta x =$ $vt -$ $\cfrac{1}{2} at^2$, no $u$ involved here and $\Delta x =$ $(\cfrac{v+u}{2})t$

Now let’s take a look at different types of questions asked in JEE Main and JEE Advanced on one dimensional motion

Important Questions | One Dimensional Motion

In JEE Advanced we have not seen many questions over last 5 to 10 years but in JEE Mains 2020 and 2021, we saw an equal spread of questions between 1D (one dimensional) Motion and 2D (two dimensional) Motion (including vectors) 

So here we will look at questions involving variable acceleration and questions involving constant acceleration

Variable Acceleration

There are 5 different types of questions you can expect in JEE Main or JEE Advanced on 1D Motion involving variable acceleration

Questions Type 1/40 : Given position $x(t)$ or velocity $v(t)$ or acceleration, $a(t)$ of a particle, you will be asked to determine information about the other two kinematic variables. For example,

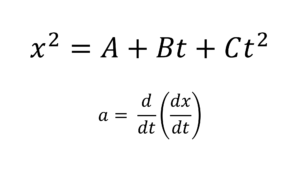
Question Type 2/40 : Given information on speed, $v$, vs time, $t$ graph, you will be asked to determine some information about particle’s position or acceleration (average or instantaneous). For example,

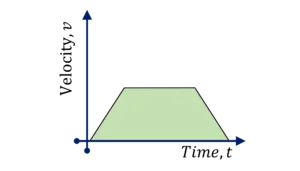
Question Type 3/40 : Given acceleration $a$ as a function of time $t$, determine speed, $v$ as a function of time $t$ and further you might be asked to determine parameters such as maximum speed in the given time duration. For example,

Question Type 4/40 : Given acceleration $a$, as a function of position, $x$, determine velocity $v$ as a function of position $x$. For example,

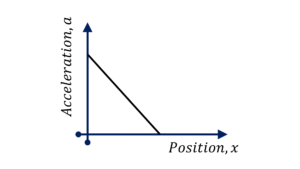
Question Type 5/40 : Given acceleration $a$ of a particle as a function of its velocity $v$, determine the velocity or position of the particle at some time $t$. For example,

Constant Acceleration

Questions on 1D Motion with particle under constant acceleration can be divided into the following 4 question types.

Question Type 6/40 : Simpler application | For a particle under constant acceleration, determine the unknown using two independent kinematic equations $v=$ $u+$ $at$, $x=$ $ut+$ $\cfrac{1}{2} a t^2$. For example,

Question Type 7/40 : 1D Motion with constant acceleration without change in direction of motion. Here the information on 3 of the 5 kinematic variables ($v$, $u$, $a$, $t$ and displacement $s$) is given at three points along the particle’s path (instead of initial and final points only). Use  $v=$ $u+$ $at$, $x=$ $ut+$ $\cfrac{1}{2} a t^2$. Note that sometimes $v^2 +$ $u^2 +$ $2as$, comes in handy when information is not given on time $t$. For example,

Question Type 8/40 :  1D Motion with constant acceleration but particle’s initial velocity is in opposite direction to its acceleration which means that the particle would undergo change in direction during its motion. In such situations, the distance and displacement will not be equal if the time duration of interest includes the moment when particle changes direction. Here you might be given position $x$ as an algebraic function of time $t$ ($x=A +$ $Bt + Ct^2$ – constant acceleration) and you might be asked to determine the distance traveled. In such questions check for signs of velocity and acceleration at time $t = 0$ and if the signs are opposite, note that displacement will not be same as distance, if the particle has zero velocity at some time $t$ in the duration of interest. For example,

Question Type 9/40 : 1D Motion with different acceleration for different segments of the journey. Here you need to make sure that you write your kinematic equations for constant acceleration,  $v=$ $u+$ $at$, $x=$ $ut+$ $\cfrac{1}{2} a t^2$, separately for the two segments and then solve for the unknown. For example,

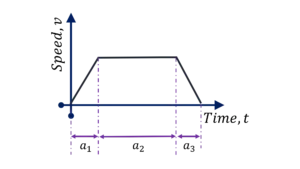
Vectors are physical quantities which have a magnitude as well as a direction and they obey laws of vector algebra. Please refer to the lecture video for detailed understanding of vectors. But make sure that you are comfortable with graphical representation and treatment of vectors as well as treatment of vectors in unit vector notation ($\overrightarrow{a} =$ $a_x \hat{i} +$ $a_y \hat{j} +$ $a_z \hat{k}$).

And note that vectors can be multiplied in two different ways, a scalar/dot product or a cross/vector product

Scalar/Dot product: $\overrightarrow{A}.\overrightarrow{B}=$ $AB \cos \theta=$ $A_x B_x+$ $A_y B_y+$ $A_z B_z$

Vector/Cross Product: $\overrightarrow{A} \times \overrightarrow{B}=$ $AB \sin \theta \hat{n}=$ $(A_y B_z – A_z B_y)$ $\hat{i}-$ $(A_x B_z – A_z B_x)$ $\hat{j}+$ $(A_x B_y – A_y B_x)$ $\hat{k}$

Now let’s take a look at different types of questions asked in JEE Main and JEE Advanced on vectors.

Important Questions of Kinematics Class 11 | Vectors

Question Type 10/40 : Given coordinates of two points, find the vector joining those two points. For example,

Question Type 11/40 : Find angle between two vectors given some relation between the two vectors. Here the two vector algebra operations that come in handy are (1) $\overrightarrow{A}.\overrightarrow{B}=$ $AB \cos \theta$ (2) $|\overrightarrow{A}+\overrightarrow{B}|^2=$ $(\overrightarrow{A}+\overrightarrow{B}).(\overrightarrow{A}+\overrightarrow{B})$

For example,

Question Type 12/40 : Questions involving use of vector algebra with vectors either given in unit vector notation or in graphical representation. For example,

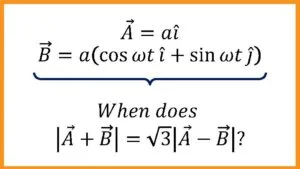
Two Dimensional Motion

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.

Kinematics Class 11 Important Questions | Two Dimensional Motion

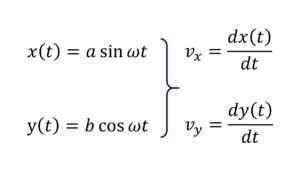
Question Type 13/40 : For a particle moving along $x$ and $y$, given $x(t)$ and $y(t)$ i.e. given $x$ and $y$ as a function of time $t$, determine it’s velocity or acceleration vector at some time $t$ or determine it’s trajectory (which is nothing but equation relating $x$ and $y$, without $t$ in it). For example,

Question Type 14/40 : For a group of particles that are symmetrically placed and moving towards each other at constant speed, determine the time it will taken for them to meet/collide. For example,

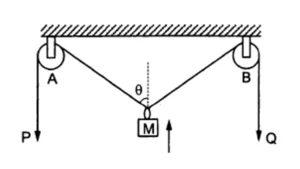
Question Type 15/40 : Establish motion of connected objects. For example,

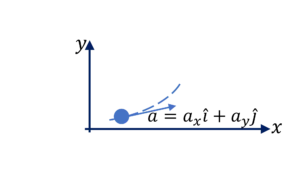
Question Type 16/40 : Given that a particle is under constant acceleration with the 2D/3D acceleration vector given in unit vector notation $\overrightarrow{a}=$ $a_x \hat{i} +$ $a_y \hat{j} +$ $a_z \hat{k}$, determine velocity vector, $\overrightarrow{v}$ or position vector $\overrightarrow{r}$ at time $t$. For example:

One Dimensional Motion

Projectile Motion ( Sign up for Free for question types on projectile motion)

Relative Velocity ( Sign up for Free for question types on relative velocity)

You Might Also Like

Pulley Problems IIT JEE | JEE Main

Motion of Connected Bodies | JEE Advanced Practice Questions

Projectile Motion Examples

Leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

• Physics Important Questions
• Class 11 Physics

CBSE Important Questions for Class 11 Physics

CBSE Important Questions for Class 11 Physics provide you with excellent strategies to prepare for the Physics examination. Questions can be framed from any corner of the book or outside the textbook for the final exams. Thus, you need advanced knowledge rather than practising only through textbooks. This page provides you with CBSE Important Questions Class 11 with medium to advance level Physics questions, helping you to become well-prepared for the competitive examinations.

CBSE Class 11 Physics Important Questions

Important questions for Class 11 Physics are framed according to the NCERT syllabus. Students can click the link below to access the chapter-wise important questions of CBSE Class 11 Physics.

The repeatedly asked questions and the questions of high priority according to the syllabus are provided with answers, at BYJU’S for free. Thus, CBSE Important Questions are essential in building clear concepts and excelling in the Class 11 examination. It plays a major role in helping students face exams confidently and achieve good grades.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

thank you sir

This is very useful for me I’m really thank you so much sir

Thankuu so much It really helps me a lot to score higher in annual exams.

Thank you sir

This site is very helpful to me thanks

MY FULL EXAM PAPER WAS BASED ON THESE QUESTIONS AND I GOT 720/720 THANK YOU BYJU’S I AM A PROUD BYJUITE!!

thanks to all byjus sir and mam

very usefulls sir thank you

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Class 11 Physics Case Study Questions Chapter 2 Units and Measurements

• Post author: studyrate
• Post published:
• Post category: Class 11
• Post comments: 0 Comments

In Class 11 Final Exams there will be Case studies and Passage Based Questions will be asked, So practice these types of questions. Study Rate is always there to help you. Free PDF Downloads of CBSE Class 11 Physics Chapter 2 Case Study and Passage-Based Questions with Answers were Prepared Based on the Latest Exam Pattern. Students can solve Class 11 Physics Case Study Questions Units and Measurements  to know their preparation level.

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

In CBSE Class 11 Physics Paper, There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

Units and Measurements Case Study Questions With Answers

Here, we have provided case-based/passage-based questions for Class 11 Physics  Chapter 2 Units and Measurements

Case Study/Passage-Based Questions

Case Study 1: The rules for determining the uncertainty or error in the measured quantity in arithmetic operations can be understood from the following examples.

a.)  If the length and breadth of a thin rectangular sheet are measured, using a meter scale as 16.2 cm and, 10.1 cm respectively, there are three significant figures in each measurement. It means that the length L may be written as L = 16.2 ± 0.1 cm   = 16.2 cm ± 0.6 %.

Similarly, the breadth b may be written as b = 10.1 ± 0.1 cm = 10.1 cm ± 1 %

Then, the error of the product of two (or more) experimental values, using the combination of errors rule, will be L*b = 163.62 cm2 + 1.6% = 163.62 + 2.6 cm2

This leads us to quote the final result as L*b = 164 + 3 cm 2 . Here 3 cm 2  is the uncertainty or error in the estimation of the area of the rectangular sheet.

b.)  If a set of experimental data is specified to n significant figures a result obtained by combining the data will also be valid to n significant figures. However, if data are subtracted, the number of significant figures can be reduced. For example, 12.9 g – 7.06 g, both specified to three significant figures, cannot properly be evaluated as 5.84 g but only as 5.8 g, as uncertainties in subtraction or addition combine in a different fashion (smallest number of decimal places rather than the number of significant figures in any of the number added or subtracted).

c.)  The relative error of a value of a number specified to significant figures depends not only on n but also on the number itself. For example, the accuracy in the measurement of mass 1.02 g is ± 0.01 g whereas another measurement of 9.89 g is also accurate to ± 0.01 g. The relative error in 1.02 g is

= (± 0.01/1.02) × 100 % = ± 1%

Similarly, the relative error in 9.89 g is = (± 0.01/9.89) × 100 % = ± 0.1 %

Finally, remember that intermediate results in a multi-step computation should be calculated to one more significant figure in every measurement than the number of digits in the least precise measurement.

d.)  The nature of a physical quantity is described by its dimensions. All the physical quantities represented by derived units can be expressed in terms of some combination of seven fundamental or base quantities. We shall call these base quantities the seven dimensions of the physical world, which are denoted with square brackets [ ]. Thus, length has the dimension [L], mass [M], time [T], electric current [A], thermodynamic temperature [K], luminous intensity [cd], and amount of substance [mol]. The dimensions of a physical quantity are the powers (or exponents) to which the base quantities are raised to represent that quantity. Note that using the square brackets [ ] around a quantity means that we are dealing with ‘the dimensions of’ the quantity. In mechanics, all the physical quantities can be written in terms of the dimensions [L], [M], and [T]. For example, the volume occupied by an object is expressed as the product of length, breadth, and height, or three lengths. Hence the dimensions of volume are [L] × [L] × [L] = [L 3 ].

When measuring the length and breadth of a rectangular sheet as 16.2 cm and 10.1 cm respectively, what is the uncertainty in the length? a) 0.6% b) 0.1% c) 1% d) 0.6 cm

Answer: a) 0.6%

In the calculation of the area of a rectangular sheet, the final result is expressed as 164 + 3 cm². What does the 3 cm² represent? a) The length of the rectangular sheet b) The breadth of the rectangular sheet c) The uncertainty or error in the estimation d) The percentage error in the calculation

Answer: c) The uncertainty or error in the estimation

When dealing with subtraction of numbers like 12.9 g – 7.06 g, how should the result be properly evaluated? a) 5.84 g b) 5.8 g c) 5.9 g d) 6.0 g

Answer: b) 5.8 g

Which of the following accurately represents the relative error in the measurement of 9.89 g? a) ± 1% b) ± 0.1% c) ± 0.01% d) ± 0.9%

Answer: b) ± 0.1%

In a multi-step computation, intermediate results should be calculated to how many more significant figures than the least precise measurement? a) Two more significant figures b) One more significant figure c) The same number of significant figures d) Three more significant figures

Answer: b) One more significant figure

Which of the following represents the dimensions of volume? a) [L] b) [L^2] c) [L3] d) [L * M * T]

Answer: c) [L3]

How many fundamental or base quantities are used to express all physical quantities in derived units? a) Five b) Six c) Seven d) Eight

Answer: c) Seven

Case Study 2: Measurement of Physical Quantity : All engineering phenomena deal with definite and measured quantities and so depend on the making of the measurement. We must be clear and precise in making these measurements. To make a measurement, the magnitude of the physical quantity (unknown) is compared. The record of a measurement consists of three parts, i.e. the dimension of the quantity, the unit which represents a standard quantity, and a number which is the ratio of the measured quantity to the standard quantity.

(i) A device which is used for measurement of length to an accuracy of about 10 -5 m, is (a) screw gauge (b) spherometer (c) vernier calipers (d) Either (a) or (b)

Answer: (d) Either (a) or (b)

(ii) Which of the technique is not used for measuring time intervals? (a) Electrical oscillator (b) Atomic clock (c) Spring oscillator (d) Decay of elementary particles

Answer: (c) Spring oscillator

(iii) The mean length of an object is 5 cm. Which of the following measurements is most accurate? (a) 4.9 cm (b) 4.805 cm (c) 5.25 cm (d) 5.4 cm

Answer: (a) 4.9 cm

(iv) If the length of rectangle l = 10.5 cm, breadth b = 2.1 cm and minimum possible measurement by scale = 0.1 cm, then the area is (a) 22.0 cm 2 (b) 21.0 cm 2 (c) 22.5 cm 2 (d) 21.5 cm 2

Answer: (a) 22.0 cm2

(v) Age of the universe is about 10 10  yr, whereas the mankind has existed for 10 6  yr. For how many seconds would the man have existed, if age of universe were 1 day? (a) 9.2 s (b) 10.2 s (c) 8.6 s (d) 10.5 s

Answer: (c) 8.6 s

Hope the information shed above regarding Case Study and Passage Based Questions for Class 11 Physics Chapter 2 Units and Measurements with Answers Pdf free download has been useful to an extent. If you have any other queries about CBSE Class 11 Physics Units and Measurements Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible. By Team Study Rate

You Might Also Like

Class 11 chemistry: case study of chapter 8 redox reactions pdf download, mcq questions class 11 english snapshots chapter 5 mother’s day with answers, mcq questions class 11 business studies chapter 6 social responsibilities of business and business ethics with answers, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

This site uses Akismet to reduce spam. Learn how your comment data is processed .

The Topper Combo Flashcards

• Contains the Latest NCERT in just 350 flashcards.
• Colourful and Interactive
• Summarised Important reactions according to the latest PYQs of NEET(UG) and JEE

No thanks, I’m not interested!

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Questions on Kinematics (Class 11 Physics)

• Last modified on: 3 years ago
• Reading Time: 6 Minutes
• If a particle is accelerating, it is either speeding up or speeding down. Do you agree with this statement?
• Two balls of different masses are thrown vertically upwards with the same speed. They pass through the point of projection in their downward motion with the same speed. Do you agree with this statement?
• Is the vertical height taken by a long jumper important while taking the jump?
• A woman standing on the edge of a cliff throws a ball straight up with a speed of 8 km/h and then throws another ball straight down with a speed of 8 km/h from the same position. What is the ratio of the speeds with which the balls hit the ground ?
• Find the average velocity during the time of flight, if a particle is projected with v at an angle θ with horizontal plane.
• Establish the relation x(t) = v(0)t + (1/2) at^2 by calculus method.
• Derive the velocity–time relationship by (i) calculus method, (ii) graphical method.
• A stone is thrown upwards from the top of a tower 85 m high. It reaches the ground in 5 second. Calculate (i) the greatest height above the ground, (ii) the velocity with which it reaches the ground and (iii) the time taken to reach the maximum height. (Given: g = 10 m/s^2.)
• A car starts from rest and accelerates uniformly for 10 s to a velocity of 8 m/s. It then runs at a constant velocity and is finally brought to rest in 64 m with a constant retardation. The total distance covered by the car is 584 m. Find the values of acceleration, retardation and total time taken.
• Prove that there are two times for which a projectile travels the same vertical distance. Also prove that the sum of the two times is equal to the time of flight.
• No, not always. In case of uniform circular motion, the particle is accelerating but its speed is neither decreasing nor increasing, only direction of velocity changes.
• This is true as motion under gravity is independent of mass of the body and so the body comes back to the point of projection with the same speed.
• Yes, because for the longest jump the player should throw himself at an angle of 45 degree wrt horizontal. The vertical height required for this purpose should be u2/4g, where u is velocity of throw. If the vertical height is different from u2/4g then the angle will be different from 45 degree and the horizontal distance covered also will be less.
• 1 : 1, both the balls will hit the ground with the same speed.

8. h = 3.2 m, v = 42 m/s, t = 0.8 sec.

9. 0.8 m/s2, 0.5 m/s2 and 86 sec.

Download CBSE Books

Exam Special Series:

• Sample Question Paper for CBSE Class 10 Science (for 2024)
• Sample Question Paper for CBSE Class 10 Maths (for 2024)
• CBSE Most Repeated Questions for Class 10 Science Board Exams
• CBSE Important Diagram Based Questions Class 10 Physics Board Exams
• CBSE Important Numericals Class 10 Physics Board Exams
• CBSE Practical Based Questions for Class 10 Science Board Exams
• CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
• Sample Question Papers for CBSE Class 12 Physics (for 2024)
• Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
• Sample Question Papers for CBSE Class 12 Maths (for 2024)
• Sample Question Papers for CBSE Class 12 Biology (for 2024)
• CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
• Master Organic Conversions CBSE Class 12 Chemistry Board Exams
• CBSE Important Numericals Class 12 Physics Board Exams
• CBSE Important Definitions Class 12 Physics Board Exams
• CBSE Important Laws & Principles Class 12 Physics Board Exams
• 10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
• ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
• ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
• ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
• ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
• ICSE Important Functions and Locations Based Questions Class 10 Biology
• ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Leave a Reply Cancel reply

Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

• Active page

Kinematics of Class 11

Motion that occurs solely under the influence of gravity is called free fall.

In the absence of air resistance all falling bodies have the same acceleration due to gravity, regardless of their sizes or shapes.

The value of the acceleration due to gravity depends on both latitude and altitude. It is approximately 9.8 m/s 2

The equations of kinematics may be modified as

Example 7.8

A ball thrown up from the ground reaches a maximum height of 20 m. Find

(a) its initial velocity

(b) the time taken to reach the highest point

(c) its velocity just before hitting the ground

(d) its displacement between 0.5 and 2.5 s

(e) the time at which it is 15 m above the ground.

(b) Given:v 0 = 20 m/s

Either Equation (7.9)(7.11) would lead to t. Since equation (7.11) involves a quadratic it is quicker to use equation (7.9)

0 = 20 −t

Thus t = 2 s

(c) Given: y0= 0; y = 0; vo=20 m/s

Unknownv = ?; t = ?

From equation (7.12) we have

Thus, v ± v 0. At the single point yv 0 −v 0

(d) To find the displacement, Δyy 2 −y 1 , we need equation (7.11);

y 1 −

y 2 −

Hence Δy

(e) Given: y = 15 m; y0 = 0; v0 = 20 m/s

Unknown: t = ?

Since equations (7.9), (7.10) and (7.12) also contain the other unknown, we use equation (7.11)

15 = 0 + 20t−t2

The solutions of the quadratic equations are

Example 7.9

A ball is thrown upward with an initial velocity of 10 m/s from a rooftop 40 m high. Find

(a) its velocity on hitting the ground.

(b) the time of flight

(c) the maximum height

(d) the time to return to roof level

(e) the time it is 15 m below the rooftop.

−30 = 10 −t

which gives t = 4 s. If v were unknown we could use equation (7.11)

0 = 40 +10t−t2

(c) At the maximum height v = 0, so from equation (7.12)

0 = (10) 2 −10) (y−

(d) At the roof level, the final position is y(7.11)

40 = 40 + 10t−t 2

Therefore, tt

(e) Again from equation (7.11), with y

25 = 40 + 10t−t 2

After solving, we get t

Example 7.10

Two balls are thrown towards each other, ball A at 20 m/s upward from the ground, and two second later ball B at 10 m/s downward from a roof 30 m high.

(a) Where and when do they meet

(b) What are their velocities on impact?

They meet when yA= yB. This condition immediately leads to t = 3 s. Substituting into either yAor By = 15 m

(b) Since t = 3 s, we have vA= 20 + (−10) (3) = −10 m/s

and vB= −10 + (−10) (3−2) =−20 m/s. Notice that A is already moving downward when it collides with B.

• Circular Motion
• Projectile Motion
• Motion In One Dimension
• Graphical Interpretation of Displacement, Velocity And Acceleration
• Motion With Constant Acceleration
• Motion In Two Dimensions
• Relative Velocity
• solved question

Talk to Our counsellor

Case study questions on kinematics class 11

Mycbseguide: a true saviour for many students.

myCBSEguide has been a true saviour for many students who struggle to find resources elsewhere. It is a reliable source of information and provides students with everything they need to excel in their academics. myCBSEguide has helped many students score high marks in their exams and has been a valuable resource for their studies. Teachers recommend myCBSEguide to all CBSE students. And best of all, it’s available 24/7, so you can study at your own pace, anytime, anywhere. So why wait? Get started today and see the difference myCBSEguide can make to your studies.

Related Posts

Which of the following allows different operating systems to coexist on the same physical computer?

What is being defined as the degree to which something is related or useful to what is happening or being talked about?

Which of the following is NOT a pathway in the oxidation of glucose

Juan is the person employees go to when knowledge of a topic was needed. juan holds ________ power.

Which of the following is not a standard mounting dimension for an electric motor? select one:

Which set of characteristics will produce the smallest value for the estimated standard error?

Is a program that assesses and reports information about various computer resources and devices.

How much energy is needed to move one electron through a potential difference of 1.0 102 volts

Includes procedures and techniques that are designed to protect a computer from intentional theft

How to write notes for a speech

What brand of castor oil is best for hair?

What are control charts based on?

Vscode No server install found in WSL, needs x64

How do you get to Motion settings on iPhone?

How long is a furlong in horse?

Replace the underlined word with the correct form

How many spinach plants per person

Bread clip in wallet when traveling

What aisle is heavy cream on?

How do you play Roblox on a Chromebook without downloading it

• Advertising

LATEST NEWS

How fast does hair grow per day.

• Privacy Policy
• Terms of Services
• Cookie Policy
• Knowledge Base
• Remove a question

myCBSEguide

• Mathematics
• Class 11 Mathematics Case...

Class 11 Mathematics Case Study Questions

Table of Contents

myCBSEguide App

Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.

If you’re seeking a comprehensive and dependable study resource with Class 11 mathematics case study questions for CBSE, myCBSEguide is the place to be. It has a wide range of study notes, case study questions, previous year question papers, and practice questions to help you ace your examinations. Furthermore, it is routinely updated to bring you up to speed with the newest CBSE syllabus. So, why delay? Begin your path to success with myCBSEguide now!

The rationale behind teaching Mathematics

The general rationale to teach Mathematics at the senior secondary level is to assist students:

• In knowledge acquisition and cognitive understanding of basic ideas, words, principles, symbols, and mastery of underlying processes and abilities, notably through motivation and visualization.
• To experience the flow of arguments while demonstrating a point or addressing an issue.
• To use the information and skills gained to address issues using several methods wherever possible.
• To cultivate a good mentality in order to think, evaluate, and explain coherently.
• To spark interest in the subject by taking part in relevant tournaments.
• To familiarise pupils with many areas of mathematics utilized in daily life.
• To pique students’ interest in studying mathematics as a discipline.

Case studies in Class 11 Mathematics

A case study in mathematics is a comprehensive examination of a specific mathematical topic or scenario. Case studies are frequently used to investigate the link between theory and practise, as well as the connections between different fields of mathematics. A case study will frequently focus on a specific topic or circumstance and will investigate it using a range of methodologies. These approaches may incorporate algebraic, geometric, and/or statistical analysis.

Sample Class 11 Mathematics case study questions

When it comes to preparing for Class 11 Mathematics, one of the best things Class 11 Mathematics students can do is to look at some Class 11 Mathematics sample case study questions. Class 11 Mathematics sample case study questions will give you a good idea of the types of Class 11 Mathematics sample case study questions that will be asked in the exam and help you to prepare more effectively.

Looking at sample questions is also a good way to identify any areas of weakness in your knowledge. If you find that you struggle with a particular topic, you can then focus your revision on that area.

myCBSEguide offers ample Class 11 Mathematics case study questions, so there is no excuse. With a little bit of preparation, Class 11 Mathematics students can boost their chances of getting the grade they deserve.

Some samples of Class 11 Mathematics case study questions are as follows:

Class 11 Mathematics case study question 1

• 9 km and 13 km
• 9.8 km and 13.8 km
• 9.5 km and 13.5 km
• 10 km and 14 km
• x  ≤   −1913
• x <  −1613
• −1613  < x <  −1913
• There are no solution.
• y  ≤   12 x+2
• y >  12 x+2
• y  ≥   12 x+2
• y <  12 x+2

Answer Key:

• (b) 9.8 km and 13.8 km
• (a) −1913   ≤  x 
• (b)  y >  12 x+2
• (d) (-5, 5)

Class 11 Mathematics case study question 2

• 2 C 1 × 13 C 10
• 2 C 1 × 10 C 13
• 1 C 2 × 13 C 10
• 2 C 10 × 13 C 10
• 6 C 2​ × 3 C 4   × 11 C 5 ​
• 6 C 2​ × 3 C 4   × 11 C 5
• 6 C 2​ × 3 C 5 × 11 C 4 ​
• 6 C 2 ​  ×   3 C 1 ​  × 11 C 5 ​
• (b) (13) 4  ways
• (c) 2860 ways.

Class 11 Mathematics case study question 3

Read the Case study given below and attempt any 4 sub parts: Father of Ashok is a builder, He planned a 12 story building in Gurgaon sector 5. For this, he bought a plot of 500 square yards at the rate of Rs 1000 /yard². The builder planned ground floor of 5 m height, first floor of 4.75 m and so on each floor is 0.25 m less than its previous floor.

Class 11 Mathematics case study question 4

Read the Case study given below and attempt any 4 sub parts: villages of Shanu and Arun’s are 50km apart and are situated on Delhi Agra highway as shown in the following picture. Another highway YY’ crosses Agra Delhi highway at O(0,0). A small local road PQ crosses both the highways at pints A and B such that OA=10 km and OB =12 km. Also, the villages of Barun and Jeetu are on the smaller high way YY’. Barun’s village B is 12km from O and that of Jeetu is 15 km from O.

Now answer the following questions:

• 5x + 6y = 60
• 6x + 5y = 60
• (a) (10, 0)
• (b) 6x + 5y = 60
• (b) 60/√ 61 km
• (d) 2√61 km

A peek at the Class 11 Mathematics curriculum

The Mathematics Syllabus has evolved over time in response to the subject’s expansion and developing societal requirements. The Senior Secondary stage serves as a springboard for students to pursue higher academic education in Mathematics or professional subjects such as Engineering, Physical and Biological Science, Commerce, or Computer Applications. The current updated curriculum has been prepared in compliance with the National Curriculum Framework 2005 and the instructions provided by the Focus Group on Teaching Mathematics 2005 in order to satisfy the rising demands of all student groups. Greater focus has been placed on the application of various principles by motivating the themes from real-life events and other subject areas.

Class 11 Mathematics (Code No. 041)

Design of Class 11 Mathematics exam paper

CBSE Class 11 mathematics question paper is designed to assess students’ understanding of the subject’s essential concepts. Class 11 mathematics question paper will assess their problem-solving and analytical abilities. Before beginning their test preparations, students in Class 11 maths should properly review the question paper format. This will assist Class 11 mathematics students in better understanding the paper and achieving optimum scores. Refer to the Class 11 Mathematics question paper design provided.

 Class 11 Mathematics Question Paper Design

• No chapter-wise weightage. Care to be taken to cover all the chapters.
• Suitable internal variations may be made for generating various templates keeping the overall weightage to different forms of questions and typology of questions the same.  

Choice(s): There will be no overall choice in the question paper. However, 33% of internal choices will be given in all the sections.

  Prescribed Books:

• Mathematics Textbook for Class XI, NCERT Publications
• Mathematics Exemplar Problem for Class XI, Published by NCERT
• Mathematics Lab Manual class XI, published by NCERT

myCBSEguide guarantees LHS=RHS

With myCBSEguide it will always be LHS=RHS, Hence Proved!

myCBSEguide is a prominent streaming resource for students studying for CBSE examinations. The site offers extensive study material, practice papers, case study questions, online examinations, and other resources at the push of a click. myCBSEguide also has a mobile app for learning on the move. There’s no excuse not to try myCBSEguide with so much convenience and simplicity of access! Hence Proved!

Test Generator

Create question paper PDF and online tests with your own name & logo in minutes.

Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes

Related Posts

• Competency Based Learning in CBSE Schools
• Class 11 Physical Education Case Study Questions
• Class 11 Sociology Case Study Questions
• Class 12 Applied Mathematics Case Study Questions
• Class 11 Applied Mathematics Case Study Questions
• Class 11 Biology Case Study Questions
• Class 12 Physical Education Case Study Questions
• Class 12 Computer Science Case Study Questions

1 thought on “Class 11 Mathematics Case Study Questions”

teri meri meri teri prem kahani hai muskil dolabjo main sayana hop jaye ek ladka aur ek ladki ki prem kahani hai muskil

Leave a Comment

Save my name, email, and website in this browser for the next time I comment.