non directional hypothesis symbol

Statistics Made Easy

What is a Directional Hypothesis? (Definition & Examples)

A statistical hypothesis is an assumption about a population parameter . For example, we may assume that the mean height of a male in the U.S. is 70 inches.

The assumption about the height is the statistical hypothesis and the true mean height of a male in the U.S. is the population parameter .

To test whether a statistical hypothesis about a population parameter is true, we obtain a random sample from the population and perform a hypothesis test on the sample data.

Whenever we perform a hypothesis test, we always write down a null and alternative hypothesis:

• Null Hypothesis (H 0 ): The sample data occurs purely from chance.
• Alternative Hypothesis (H A ): The sample data is influenced by some non-random cause.

A hypothesis test can either contain a directional hypothesis or a non-directional hypothesis:

• Directional hypothesis: The alternative hypothesis contains the less than (“<“) or greater than (“>”) sign. This indicates that we’re testing whether or not there is a positive or negative effect.
• Non-directional hypothesis: The alternative hypothesis contains the not equal (“≠”) sign. This indicates that we’re testing whether or not there is some effect, without specifying the direction of the effect.

Note that directional hypothesis tests are also called “one-tailed” tests and non-directional hypothesis tests are also called “two-tailed” tests.

Check out the following examples to gain a better understanding of directional vs. non-directional hypothesis tests.

Example 1: Baseball Programs

A baseball coach believes a certain 4-week program will increase the mean hitting percentage of his players, which is currently 0.285.

To test this, he measures the hitting percentage of each of his players before and after participating in the program.

He then performs a hypothesis test using the following hypotheses:

• H 0 : μ = .285 (the program will have no effect on the mean hitting percentage)
• H A : μ > .285 (the program will cause mean hitting percentage to increase)

This is an example of a directional hypothesis because the alternative hypothesis contains the greater than “>” sign. The coach believes that the program will influence the mean hitting percentage of his players in a positive direction.

Example 2: Plant Growth

A biologist believes that a certain pesticide will cause plants to grow less during a one-month period than they normally do, which is currently 10 inches.

To test this, she applies the pesticide to each of the plants in her laboratory for one month.

She then performs a hypothesis test using the following hypotheses:

• H 0 : μ = 10 inches (the pesticide will have no effect on the mean plant growth)
• H A : μ < 10 inches (the pesticide will cause mean plant growth to decrease)

This is also an example of a directional hypothesis because the alternative hypothesis contains the less than “<” sign. The biologist believes that the pesticide will influence the mean plant growth in a negative direction.

Example 3: Studying Technique

A professor believes that a certain studying technique will influence the mean score that her students receive on a certain exam, but she’s unsure if it will increase or decrease the mean score, which is currently 82.

To test this, she lets each student use the studying technique for one month leading up to the exam and then administers the same exam to each of the students.

• H 0 : μ = 82 (the studying technique will have no effect on the mean exam score)
• H A : μ ≠ 82 (the studying technique will cause the mean exam score to be different than 82)

This is an example of a non-directional hypothesis because the alternative hypothesis contains the not equal “≠” sign. The professor believes that the studying technique will influence the mean exam score, but doesn’t specify whether it will cause the mean score to increase or decrease.

Additional Resources

Introduction to Hypothesis Testing Introduction to the One Sample t-test Introduction to the Two Sample t-test Introduction to the Paired Samples t-test

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

Module 9: Hypothesis Testing With One Sample

Null and alternative hypotheses, learning outcomes.

• Describe hypothesis testing in general and in practice

The actual test begins by considering two  hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make adecision. There are two options for a  decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in  H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

H a : p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40

• H 0 : p = 0.40
• H a : p > 0.40

Concept Review

In a  hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

H 0 and H a are contradictory.

• OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License

Research Hypothesis In Psychology: Types, & Examples

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A research hypothesis, in its plural form “hypotheses,” is a specific, testable prediction about the anticipated results of a study, established at its outset. It is a key component of the scientific method .

Hypotheses connect theory to data and guide the research process towards expanding scientific understanding

Some key points about hypotheses:

• A hypothesis expresses an expected pattern or relationship. It connects the variables under investigation.
• It is stated in clear, precise terms before any data collection or analysis occurs. This makes the hypothesis testable.
• A hypothesis must be falsifiable. It should be possible, even if unlikely in practice, to collect data that disconfirms rather than supports the hypothesis.
• Hypotheses guide research. Scientists design studies to explicitly evaluate hypotheses about how nature works.
• For a hypothesis to be valid, it must be testable against empirical evidence. The evidence can then confirm or disprove the testable predictions.
• Hypotheses are informed by background knowledge and observation, but go beyond what is already known to propose an explanation of how or why something occurs.

Predictions typically arise from a thorough knowledge of the research literature, curiosity about real-world problems or implications, and integrating this to advance theory. They build on existing literature while providing new insight.

Types of Research Hypotheses

Alternative hypothesis.

The research hypothesis is often called the alternative or experimental hypothesis in experimental research.

It typically suggests a potential relationship between two key variables: the independent variable, which the researcher manipulates, and the dependent variable, which is measured based on those changes.

The alternative hypothesis states a relationship exists between the two variables being studied (one variable affects the other).

A hypothesis is a testable statement or prediction about the relationship between two or more variables. It is a key component of the scientific method. Some key points about hypotheses:

• Important hypotheses lead to predictions that can be tested empirically. The evidence can then confirm or disprove the testable predictions.

In summary, a hypothesis is a precise, testable statement of what researchers expect to happen in a study and why. Hypotheses connect theory to data and guide the research process towards expanding scientific understanding.

An experimental hypothesis predicts what change(s) will occur in the dependent variable when the independent variable is manipulated.

It states that the results are not due to chance and are significant in supporting the theory being investigated.

The alternative hypothesis can be directional, indicating a specific direction of the effect, or non-directional, suggesting a difference without specifying its nature. It’s what researchers aim to support or demonstrate through their study.

Null Hypothesis

The null hypothesis states no relationship exists between the two variables being studied (one variable does not affect the other). There will be no changes in the dependent variable due to manipulating the independent variable.

It states results are due to chance and are not significant in supporting the idea being investigated.

The null hypothesis, positing no effect or relationship, is a foundational contrast to the research hypothesis in scientific inquiry. It establishes a baseline for statistical testing, promoting objectivity by initiating research from a neutral stance.

Many statistical methods are tailored to test the null hypothesis, determining the likelihood of observed results if no true effect exists.

This dual-hypothesis approach provides clarity, ensuring that research intentions are explicit, and fosters consistency across scientific studies, enhancing the standardization and interpretability of research outcomes.

Nondirectional Hypothesis

A non-directional hypothesis, also known as a two-tailed hypothesis, predicts that there is a difference or relationship between two variables but does not specify the direction of this relationship.

It merely indicates that a change or effect will occur without predicting which group will have higher or lower values.

For example, “There is a difference in performance between Group A and Group B” is a non-directional hypothesis.

Directional Hypothesis

A directional (one-tailed) hypothesis predicts the nature of the effect of the independent variable on the dependent variable. It predicts in which direction the change will take place. (i.e., greater, smaller, less, more)

It specifies whether one variable is greater, lesser, or different from another, rather than just indicating that there’s a difference without specifying its nature.

For example, “Exercise increases weight loss” is a directional hypothesis.

Falsifiability

The Falsification Principle, proposed by Karl Popper , is a way of demarcating science from non-science. It suggests that for a theory or hypothesis to be considered scientific, it must be testable and irrefutable.

Falsifiability emphasizes that scientific claims shouldn’t just be confirmable but should also have the potential to be proven wrong.

It means that there should exist some potential evidence or experiment that could prove the proposition false.

However many confirming instances exist for a theory, it only takes one counter observation to falsify it. For example, the hypothesis that “all swans are white,” can be falsified by observing a black swan.

For Popper, science should attempt to disprove a theory rather than attempt to continually provide evidence to support a research hypothesis.

Can a Hypothesis be Proven?

Hypotheses make probabilistic predictions. They state the expected outcome if a particular relationship exists. However, a study result supporting a hypothesis does not definitively prove it is true.

All studies have limitations. There may be unknown confounding factors or issues that limit the certainty of conclusions. Additional studies may yield different results.

In science, hypotheses can realistically only be supported with some degree of confidence, not proven. The process of science is to incrementally accumulate evidence for and against hypothesized relationships in an ongoing pursuit of better models and explanations that best fit the empirical data. But hypotheses remain open to revision and rejection if that is where the evidence leads.

• Disproving a hypothesis is definitive. Solid disconfirmatory evidence will falsify a hypothesis and require altering or discarding it based on the evidence.
• However, confirming evidence is always open to revision. Other explanations may account for the same results, and additional or contradictory evidence may emerge over time.

We can never 100% prove the alternative hypothesis. Instead, we see if we can disprove, or reject the null hypothesis.

If we reject the null hypothesis, this doesn’t mean that our alternative hypothesis is correct but does support the alternative/experimental hypothesis.

Upon analysis of the results, an alternative hypothesis can be rejected or supported, but it can never be proven to be correct. We must avoid any reference to results proving a theory as this implies 100% certainty, and there is always a chance that evidence may exist which could refute a theory.

How to Write a Hypothesis

• Identify variables . The researcher manipulates the independent variable and the dependent variable is the measured outcome.
• Operationalized the variables being investigated . Operationalization of a hypothesis refers to the process of making the variables physically measurable or testable, e.g. if you are about to study aggression, you might count the number of punches given by participants.
• Decide on a direction for your prediction . If there is evidence in the literature to support a specific effect of the independent variable on the dependent variable, write a directional (one-tailed) hypothesis. If there are limited or ambiguous findings in the literature regarding the effect of the independent variable on the dependent variable, write a non-directional (two-tailed) hypothesis.
• Make it Testable : Ensure your hypothesis can be tested through experimentation or observation. It should be possible to prove it false (principle of falsifiability).
• Clear & concise language . A strong hypothesis is concise (typically one to two sentences long), and formulated using clear and straightforward language, ensuring it’s easily understood and testable.

Consider a hypothesis many teachers might subscribe to: students work better on Monday morning than on Friday afternoon (IV=Day, DV= Standard of work).

Now, if we decide to study this by giving the same group of students a lesson on a Monday morning and a Friday afternoon and then measuring their immediate recall of the material covered in each session, we would end up with the following:

• The alternative hypothesis states that students will recall significantly more information on a Monday morning than on a Friday afternoon.
• The null hypothesis states that there will be no significant difference in the amount recalled on a Monday morning compared to a Friday afternoon. Any difference will be due to chance or confounding factors.

More Examples

• Memory : Participants exposed to classical music during study sessions will recall more items from a list than those who studied in silence.
• Social Psychology : Individuals who frequently engage in social media use will report higher levels of perceived social isolation compared to those who use it infrequently.
• Developmental Psychology : Children who engage in regular imaginative play have better problem-solving skills than those who don’t.
• Clinical Psychology : Cognitive-behavioral therapy will be more effective in reducing symptoms of anxiety over a 6-month period compared to traditional talk therapy.
• Cognitive Psychology : Individuals who multitask between various electronic devices will have shorter attention spans on focused tasks than those who single-task.
• Health Psychology : Patients who practice mindfulness meditation will experience lower levels of chronic pain compared to those who don’t meditate.
• Organizational Psychology : Employees in open-plan offices will report higher levels of stress than those in private offices.
• Behavioral Psychology : Rats rewarded with food after pressing a lever will press it more frequently than rats who receive no reward.

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

8.1.2 - Hypothesis Testing

A hypothesis test for a proportion is used when you are comparing one group to a known or hypothesized population proportion value. In other words, you have one sample with one categorical variable. The hypothesized value of the population proportion is symbolized by \(p_0\) because this is the value in the null hypothesis (\(H_0\)).

If \(np_0 \ge 10\) and \(n(1-p_0) \ge 10\) then the distribution of sample proportions is approximately normal and can be estimated using the normal distribution. That sampling distribution will have a mean of \(p_0\) and a standard deviation (i.e., standard error) of \(\sqrt{\frac{p_0 (1-p_0)}{n}}\)

Recall that the standard normal distribution is also known as the z distribution. Thus, this is known as a "single sample proportion z test" or "one sample proportion z test." 

If \(np_0 < 10\) or \(n(1-p_0) < 10\) then the distribution of sample proportions follows a binomial distribution. We will not be conducting this test by hand in this course, however you will learn how this can be conducted using Minitab using the exact method.

8.1.2.1 - Normal Approximation Method Formulas

Here we will be using the five step hypothesis testing procedure to compare the proportion in one random sample to a specified population proportion using the normal approximation method.

In order to use the normal approximation method, the assumption is that both \(n p_0 \geq 10\) and \(n (1-p_0) \geq 10\). Recall that \(p_0\) is the population proportion in the null hypothesis.

Where \(p_0\) is the hypothesized population proportion that you are comparing your sample to.

When using the normal approximation method we will be using a z test statistic. The z test statistic tells us how far our sample proportion is from the hypothesized population proportion in standard error units. Note that this formula follows the basic structure of a test statistic that you learned in the last lesson:

\(test\;statistic=\dfrac{sample\;statistic-null\;parameter}{standard\;error}\)

\(\widehat{p}\) = sample proportion \(p_{0}\) = hypothesize population proportion \(n\) = sample size

Given that the null hypothesis is true, the p value is the probability that a randomly selected sample of n would have a sample proportion as different, or more different, than the one in our sample, in the direction of the alternative hypothesis. We can find the p value by mapping the test statistic from step 2 onto the z distribution. 

Note that p-values are also symbolized by \(p\). Do not confuse this with the population proportion which shares the same symbol.

We can look up the \(p\)-value using Minitab by constructing the sampling distribution.  Because we are using the normal approximation here, we have a \(z\) test statistic that we can map onto the \(z\) distribution. Recall, the z distribution is a normal distribution with a mean of 0 and standard deviation of 1. If we are conducting a one-tailed (i.e., right- or left-tailed) test, we look up the area of the sampling distribution that is beyond our test statistic. If we are conducting a two-tailed (i.e., non-directional) test there is one additional step: we need to multiple the area by two to take into account the possibility of being in the right or left tail. 

We can decide between the null and alternative hypotheses by examining our p-value. If \(p \leq \alpha\) reject the null hypothesis. If \(p>\alpha\) fail to reject the null hypothesis. Unless stated otherwise, assume that \(\alpha=.05\).

When we reject the null hypothesis our results are said to be statistically significant.

Based on our decision in step 4, we will write a sentence or two concerning our decision in relation to the original research question.

8.1.2.1.1 - Video Example: Male Babies

8.1.2.1.2 - Example: Handedness

Research Question : Are more than 80% of American's right handed?

In a sample of 100 Americans, 87 were right handed.

\(np_0 = 100(0.80)=80\)

\(n(1-p_0) = 100 (1-0.80) = 20\)

Both \(np_0\) and \(n(1-p_0)\) are at least 10 so we can use the normal approximation method. 

This is a right-tailed test because we want to know if the proportion is greater than 0.80.

\(H_{0}\colon p=0.80\) \(H_{a}\colon p>0.80\)

\(z=\dfrac{\widehat{p}- p_0 }{\sqrt{\frac{p_0 (1- p_0)}{n}}}\)

\(\widehat{p}=\dfrac{87}{100}=0.87\), \(p_{0}=0.80\), \(n=100\)

\(z= \dfrac{\widehat{p}- p_0 }{\sqrt{\frac{p_0 (1- p_0)}{n}}}= \dfrac{0.87-0.80}{\sqrt{\frac{0.80 (1-0.80)}{100}}}=1.75\)

Our \(z\) test statistic is 1.75.

This is a right-tailed test so we need to find the area to the right of the test statistic, \(z=1.75\), on the z distribution.

Using Minitab , we find the probability \(P(z\geq1.75)=0.0400592\) which may be rounded to \(p\; value=0.0401\).

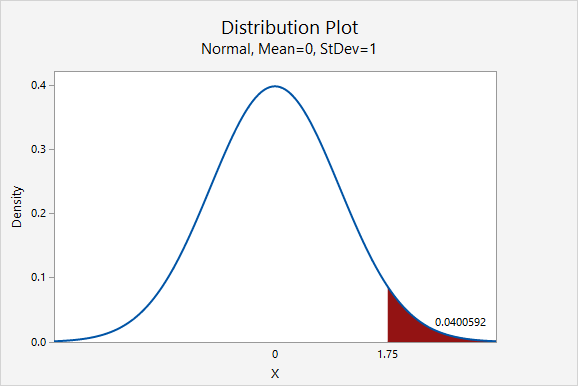
\(p\leq .05\), therefore our decision is to reject the null hypothesis

Yes, there is statistical evidence to state that more than 80% of all Americans are right handed.

8.1.2.1.3 - Example: Ice Cream

Research Question : Is the percentage of Creamery customers who prefer chocolate ice cream over vanilla less than 80%?

In a sample of 50 customers 60% preferred chocolate over vanilla.

\(np_0 = 50(0.80) = 40\)

\(n(1-p_0)=50(1-0.80) = 10\)

Both \(np_0\) and \(n(1-p_0)\) are at least 10. We can use the normal approximation method.

This is a left-tailed test because we want to know if the proportion is less than 0.80.

\(H_{0}\colon p=0.80\) \(H_{a}\colon p<0.80\)

\(\widehat{p}=0.60\), \(p_{0}=0.80\), \(n=50\)

\(z= \dfrac{\widehat{p}- p_0 }{\sqrt{\frac{p_0 (1- p_0)}{n}}}= \dfrac{0.60-0.80}{\sqrt{\frac{0.80 (1-0.80)}{50}}}=-3.536\)

Our \(z\) test statistic is -3.536.

This is a left-tailed test so we need to find the area to the right of our test statistic, \(z=-3.536\).

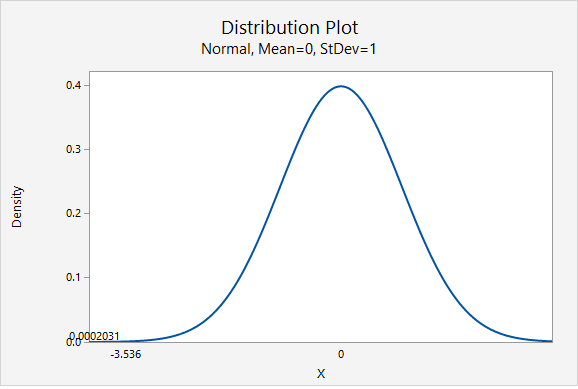
From the Minitab output above, the p-value is 0.0002031

\(p \leq.05\), therefore our decision is to reject the null hypothesis.

Yes, there is evidence that the percentage of all Creamery customers who prefer chocolate ice cream over vanilla is less than 80%.

8.1.2.1.4 - Example: Overweight Citizens

According to the Center for Disease Control (CDC), the percent of adults 20 years of age and over in the United States who are overweight is 69.0% (see  http://www.cdc.gov/nchs/fastats/obesity-overweight.htm ). One city’s council wants to know if the proportion of overweight citizens in their city is different from this known national proportion. They take a random sample of 150 adults 20 years of age or older in their city and find that 98 are classified as overweight. Let’s use the five step hypothesis testing procedure to determine if there is evidence that the proportion in this city is different from the known national proportion.

\(np_0 =150 (0.690)=103.5 \)

\(n (1-p_0) =150 (1-0.690)=46.5\)

Both \(n p_0\) and \(n (1-p_0)\) are at least 10, this assumption has been met.

Research question: Is this city’s proportion of overweight individuals different from 0.690?

This is a non-directional test because our question states that we are looking for a differences as opposed to a specific direction. This will be a two-tailed test.

\(H_{0}\colon p=0.690\) \(H_{a}\colon p\neq 0.690\)

\(\widehat{p}=\dfrac{98}{150}=.653\)

\( z =\dfrac{0.653- 0.690 }{\sqrt{\frac{0.690 (1- 0.690)}{150}}} = -0.980 \)

Our test statistic is \(z=-0.980\)

This is a non-directional (i.e., two-tailed) test, so we need to find the area under the z distribution that is more extreme than \(z=-0.980\).

In Minitab, we find the proportion of a normal curve beyond \(\pm0.980\):

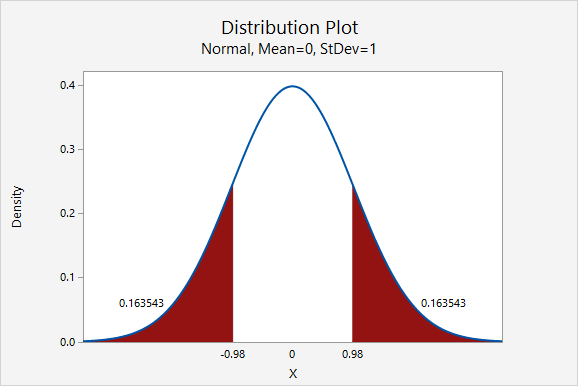
\(p-value=0.163543+0.163543=0.327086\)

\(p>\alpha\), therefore we fail to reject the null hypothesis

There is not sufficient evidence to state that the proportion of citizens of this city who are overweight is different from the national proportion of 0.690.

8.1.2.2 - Minitab: Hypothesis Tests for One Proportion

A hypothesis test for one proportion can be conducted in Minitab. This can be done using raw data or summarized data.

• If you have a data file with every individual's observation, then you have  raw data .
• If you do not have each individual observation, but rather have the sample size and number of successes in the sample, then you have summarized data.

The next two pages will show you how to use Minitab to conduct this analysis using either raw data or summarized data .

Note that the default method for constructing the sampling distribution in Minitab is to use the exact method.  If \(np_0 \geq 10\) and \(n(1-p_0) \geq 10\) then you will need to change this to the normal approximation method.  This must be done manually.  Minitab will use the method that you select, it will not check assumptions for you!

8.1.2.2.1 - Minitab: 1 Proportion z Test, Raw Data

If you have data in a Minitab worksheet, then you have what we call "raw data."  This is in contrast to "summarized data" which you'll see on the next page.

In order to use the normal approximation method both \(np_0 \geq 10\) and \(n(1-p_0) \geq 10\). Before we can conduct our hypothesis test we must check this assumption to determine if the normal approximation method or exact method should be used. This must be checked manually.  Minitab will not check assumptions for you.

In the example below, we want to know if there is evidence that the proportion of students who are male is different from 0.50.

\(n=226\) and \(p_0=0.50\)

\(np_0 = 226(0.50)=113\) and \(n(1-p_0) = 226(1-0.50)=113\)

Both \(np_0 \geq 10\) and \(n(1-p_0) \geq 10\) so we can use the normal approximation method. 

Minitab ®  – Conducting a One Sample Proportion z Test: Raw Data

Research question:  Is the proportion of students who are male different from 0.50?

• class_survey.mpx
• In Minitab, select Stat > Basic Statistics > 1 Proportion
• Select One or more samples, each in a column from the dropdown
• Double-click the variable  Biological Sex  to insert it into the box
• Check the box next to  Perform hypothesis test and enter  0.50  in the  Hypothesized proportion  box
• Select Options
• Use the default  Alternative hypothesis  setting of  Proportion ≠ hypothesized proportion value 
• Use the default  Confidence level  of 95
• Select  Normal approximation method
• Click OK and OK

The result should be the following output:

Event: Biological Sex = Male p: proportion where Biological Sex = Male Normal approximation is used for this analysis.

Summary of Results

We could summarize these results using the five-step hypothesis testing procedure:

\(np_0 = 226(0.50)=113\) and \(n(1-p_0) = 226(1-0.50)=113\) therefore the normal approximation method will be used.

 \(H_0\colon p = 0.50\)

 \(H_a\colon p \ne 0.50\)

From the Minitab output, \(z\) = -1.86

From the Minitab output, \(p\) = 0.0625

\(p > \alpha\), fail to reject the null hypothesis

There is NOT enough evidence that the proportion of all students in the population who are male is different from 0.50.

8.1.2.2.2 - Minitab: 1 Sample Proportion z test, Summary Data

Example: overweight.

The following example uses a scenario in which we want to know if the proportion of college women who think they are overweight is less than 40%. We collect data from a random sample of 129 college women and 37 said that they think they are overweight.

First, we should check assumptions to determine if the normal approximation method or exact method should be used:

\(np_0=129(0.40)=51.6\) and \(n(1-p_0)=129(1-0.40)=77.4\) both values are at least 10 so we can use the normal approximation method.

Minitab ®  – Performing a One Proportion z Test with Summarized Data

To perform a one sample proportion  z  test with summarized data in Minitab:

• Select Summarized data from the dropdown
• For number of events, add 37 and for number of trials add 129.
• Check the box next to  Perform hypothesis test and enter  0.40  in the  Hypothesized proportion  box
• Use the default  Alternative hypothesis  setting of  Proportion < hypothesized proportion value 

Event: Event proportion Normal approximation is used for this analysis.

\(H_0\colon p = 0.40\)

\(H_a\colon p < 0.40\)

From output, \(z\) = -2.62

From output, \(p\) = 0.004

\(p \leq \alpha\), reject the null hypothesis

There is evidence that the proportion of women in the population who think they are overweight is less than 40%.

8.1.2.2.2.1 - Minitab Example: Normal Approx. Method

Example: gym membership.

Research question:  Are less than 50% of all individuals with a membership at one gym female?

A simple random sample of 60 individuals with a membership at one gym was collected. Each individual's biological sex was recorded. There were 24 females. 

First we have to check the assumptions:

  np = 60 (0.50) = 30

  n(1-p) = 60(1-0.50) = 30

The assumptions are met to use the normal approximation method.

• For number of events, add 24 and for number of trials add 60.

\(np_0=60(0.50)=30\) and \(n(1-p_0)=60(1-0.50)=30\) both values are at least 10 so we can use the normal approximation method.

\(H_0\colon p = 0.50\)

\(H_a\colon p < 0.50\)

From output, \(z\) = -1.55

From output, \(p\) = 0.061

\(p \geq \alpha\), fail to reject the null hypothesis

There is not enough evidence to support the alternative that the proportion of women memberships at this gym is less than 50%.

Directional and non-directional hypothesis: A Comprehensive Guide

Karolina Konopka

Customer support manager

In the world of research and statistical analysis, hypotheses play a crucial role in formulating and testing scientific claims. Understanding the differences between directional and non-directional hypothesis is essential for designing sound experiments and drawing accurate conclusions. Whether you’re a student, researcher, or simply curious about the foundations of hypothesis testing, this guide will equip you with the knowledge and tools to navigate this fundamental aspect of scientific inquiry.

Understanding Directional Hypothesis

Understanding directional hypotheses is crucial for conducting hypothesis-driven research, as they guide the selection of appropriate statistical tests and aid in the interpretation of results. By incorporating directional hypotheses, researchers can make more precise predictions, contribute to scientific knowledge, and advance their fields of study.

Definition of directional hypothesis

Directional hypotheses, also known as one-tailed hypotheses, are statements in research that make specific predictions about the direction of a relationship or difference between variables. Unlike non-directional hypotheses, which simply state that there is a relationship or difference without specifying its direction, directional hypotheses provide a focused and precise expectation.

A directional hypothesis predicts either a positive or negative relationship between variables or predicts that one group will perform better than another. It asserts a specific direction of effect or outcome. For example, a directional hypothesis could state that “increased exposure to sunlight will lead to an improvement in mood” or “participants who receive the experimental treatment will exhibit higher levels of cognitive performance compared to the control group.”

Directional hypotheses are formulated based on existing theory, prior research, or logical reasoning, and they guide the researcher’s expectations and analysis. They allow for more targeted predictions and enable researchers to test specific hypotheses using appropriate statistical tests.

The role of directional hypothesis in research

Directional hypotheses also play a significant role in research surveys. Let’s explore their role specifically in the context of survey research:

• Objective-driven surveys : Directional hypotheses help align survey research with specific objectives. By formulating directional hypotheses, researchers can focus on gathering data that directly addresses the predicted relationship or difference between variables of interest.
• Question design and measurement : Directional hypotheses guide the design of survey question types and the selection of appropriate measurement scales. They ensure that the questions are tailored to capture the specific aspects related to the predicted direction, enabling researchers to obtain more targeted and relevant data from survey respondents.
• Data analysis and interpretation : Directional hypotheses assist in data analysis by directing researchers towards appropriate statistical tests and methods. Researchers can analyze the survey data to specifically test the predicted relationship or difference, enhancing the accuracy and reliability of their findings. The results can then be interpreted within the context of the directional hypothesis, providing more meaningful insights.
• Practical implications and decision-making : Directional hypotheses in surveys often have practical implications. When the predicted relationship or difference is confirmed, it informs decision-making processes, program development, or interventions. The survey findings based on directional hypotheses can guide organizations, policymakers, or practitioners in making informed choices to achieve desired outcomes.
• Replication and further research : Directional hypotheses in survey research contribute to the replication and extension of studies. Researchers can replicate the survey with different populations or contexts to assess the generalizability of the predicted relationships. Furthermore, if the directional hypothesis is supported, it encourages further research to explore underlying mechanisms or boundary conditions.

By incorporating directional hypotheses in survey research, researchers can align their objectives, design effective surveys, conduct focused data analysis, and derive practical insights. They provide a framework for organizing survey research and contribute to the accumulation of knowledge in the field.

Examples of research questions for directional hypothesis

Here are some examples of research questions that lend themselves to directional hypotheses:

• Does increased daily exercise lead to a decrease in body weight among sedentary adults?
• Is there a positive relationship between study hours and academic performance among college students?
• Does exposure to violent video games result in an increase in aggressive behavior among adolescents?
• Does the implementation of a mindfulness-based intervention lead to a reduction in stress levels among working professionals?
• Is there a difference in customer satisfaction between Product A and Product B, with Product A expected to have higher satisfaction ratings?
• Does the use of social media influence self-esteem levels, with higher social media usage associated with lower self-esteem?
• Is there a negative relationship between job satisfaction and employee turnover, indicating that lower job satisfaction leads to higher turnover rates?
• Does the administration of a specific medication result in a decrease in symptoms among individuals with a particular medical condition?
• Does increased access to early childhood education lead to improved cognitive development in preschool-aged children?
• Is there a difference in purchase intention between advertisements with celebrity endorsements and advertisements without, with celebrity endorsements expected to have a higher impact?

These research questions generate specific predictions about the direction of the relationship or difference between variables and can be tested using appropriate research methods and statistical analyses.

Definition of non-directional hypothesis

Non-directional hypotheses, also known as two-tailed hypotheses, are statements in research that indicate the presence of a relationship or difference between variables without specifying the direction of the effect. Instead of making predictions about the specific direction of the relationship or difference, non-directional hypotheses simply state that there is an association or distinction between the variables of interest.

Non-directional hypotheses are often used when there is no prior theoretical basis or clear expectation about the direction of the relationship. They leave the possibility open for either a positive or negative relationship, or for both groups to differ in some way without specifying which group will perform better or worse.

Advantages and utility of non-directional hypothesis

Non-directional hypotheses in survey s offer several advantages and utilities, providing flexibility and comprehensive analysis of survey data. Here are some of the key advantages and utilities of using non-directional hypotheses in surveys:

• Exploration of Relationships : Non-directional hypotheses allow researchers to explore and examine relationships between variables without assuming a specific direction. This is particularly useful in surveys where the relationship between variables may not be well-known or there may be conflicting evidence regarding the direction of the effect.
• Flexibility in Question Design : With non-directional hypotheses, survey questions can be designed to measure the relationship between variables without being biased towards a particular outcome. This flexibility allows researchers to collect data and analyze the results more objectively.
• Open to Unexpected Findings : Non-directional hypotheses enable researchers to be open to unexpected or surprising findings in survey data. By not committing to a specific direction of the effect, researchers can identify and explore relationships that may not have been initially anticipated, leading to new insights and discoveries.
• Comprehensive Analysis : Non-directional hypotheses promote comprehensive analysis of survey data by considering the possibility of an effect in either direction. Researchers can assess the magnitude and significance of relationships without limiting their analysis to only one possible outcome.
• S tatistical Validity : Non-directional hypotheses in surveys allow for the use of two-tailed statistical tests, which provide a more conservative and robust assessment of significance. Two-tailed tests consider both positive and negative deviations from the null hypothesis, ensuring accurate and reliable statistical analysis of survey data.
• Exploratory Research : Non-directional hypotheses are particularly useful in exploratory research, where the goal is to gather initial insights and generate hypotheses. Surveys with non-directional hypotheses can help researchers explore various relationships and identify patterns that can guide further research or hypothesis development.

It is worth noting that the choice between directional and non-directional hypotheses in surveys depends on the research objectives, existing knowledge, and the specific variables being investigated. Researchers should carefully consider the advantages and limitations of each approach and select the one that aligns best with their research goals and survey design.

• Share with others
• Twitter Twitter Icon
• LinkedIn LinkedIn Icon

Related posts

How to implement nps surveys: a step-by-step guide, 15 best website survey questions to ask your visitors, how to write a good survey introduction, 7 best ai survey generators, multiple choice questions: types, examples & samples, how to make a gdpr compliant survey, get answers today.

• No credit card required
• No time limit on Free plan

You can modify this template in every possible way.

All templates work great on every device.

Live revision! Join us for our free exam revision livestreams Watch now →

Reference Library

Collections

• See what's new
• All Resources
• Student Resources
• Assessment Resources
• Teaching Resources
• CPD Courses
• Livestreams

Study notes, videos, interactive activities and more!

Psychology news, insights and enrichment

Currated collections of free resources

Browse resources by topic

• All Psychology Resources

Resource Selections

Currated lists of resources

Non-Directional Hypothesis

A non-directional hypothesis is a two-tailed hypothesis that does not predict the direction of the difference or relationship (e.g. girls and boys are different in terms of helpfulness).

• Share on Facebook
• Share on Twitter
• Share by Email

Research Methods: MCQ Revision Test 1 for AQA A Level Psychology

Topic Videos

Example Answers for Research Methods: A Level Psychology, Paper 2, June 2018 (AQA)

Exam Support

Example Answer for Question 14 Paper 2: AS Psychology, June 2017 (AQA)

Model answer for question 11 paper 2: as psychology, june 2016 (aqa), a level psychology topic quiz - research methods.

Quizzes & Activities

Our subjects

• › Criminology
• › Economics
• › Geography
• › Health & Social Care
• › Psychology
• › Sociology
• › Teaching & learning resources
• › Student revision workshops
• › Online student courses
• › CPD for teachers
• › Livestreams
• › Teaching jobs

Boston House, 214 High Street, Boston Spa, West Yorkshire, LS23 6AD Tel: 01937 848885

• › Contact us
• › Terms of use
• › Privacy & cookies

© 2002-2024 Tutor2u Limited. Company Reg no: 04489574. VAT reg no 816865400.

psychologyrocks

Hypotheses; directional and non-directional, what is the difference between an experimental and an alternative hypothesis.

Nothing much! If the study is a laboratory experiment then we can call the hypothesis “an experimental hypothesis”, where we make a prediction about how the IV causes an effect on the DV. If we have a non-experimental design, i.e. we are not able to manipulate the IV as in a natural or quasi-experiment , or if some other research method has been used, then we call it an “alternativehypothesis”, alternative to the null.

Directional hypothesis: A directional (or one tailed hypothesis) states which way you think the results are going to go, for example in an experimental study we might say…”Participants who have been deprived of sleep for 24 hours will have more cold symptoms in the following week after exposure to a virus than participants who have not been sleep deprived”; the hypothesis compares the two groups/conditions and states which one will ….have more/less, be quicker/slower, etc.

If we had a correlational study, the directional hypothesis would state whether we expect a positive or a negative correlation, we are stating how the two variables will be related to each other, e.g. there will be a positive correlation between the number of stressful life events experienced in the last year and the number of coughs and colds suffered, whereby the more life events you have suffered the more coughs and cold you will have had”. The directional hypothesis can also state a negative correlation, e.g. the higher the number of face-book friends, the lower the life satisfaction score “

Non-directional hypothesis: A non-directional (or two tailed hypothesis) simply states that there will be a difference between the two groups/conditions but does not say which will be greater/smaller, quicker/slower etc. Using our example above we would say “There will be a difference between the number of cold symptoms experienced in the following week after exposure to a virus for those participants who have been sleep deprived for 24 hours compared with those who have not been sleep deprived for 24 hours.”

When the study is correlational, we simply state that variables will be correlated but do not state whether the relationship will be positive or negative, e.g. there will be a significant correlation between variable A and variable B.

Null hypothesis The null hypothesis states that the alternative or experimental hypothesis is NOT the case, if your experimental hypothesis was directional you would say…

Participants who have been deprived of sleep for 24 hours will NOT have more cold symptoms in the following week after exposure to a virus than participants who have not been sleep deprived and any difference that does arise will be due to chance alone.

or with a directional correlational hypothesis….

There will NOT be a positive correlation between the number of stress life events experienced in the last year and the number of coughs and colds suffered, whereby the more life events you have suffered the more coughs and cold you will have had”

With a non-directional or  two tailed hypothesis…

There will be NO difference between the number of cold symptoms experienced in the following week after exposure to a virus for those participants who have been sleep deprived for 24 hours compared with those who have not been sleep deprived for 24 hours.

or for a correlational …

there will be NO correlation between variable A and variable B.

When it comes to conducting an inferential stats test, if you have a directional hypothesis , you must do a one tailed test to find out whether your observed value is significant. If you have a non-directional hypothesis , you must do a two tailed test .

Exam Techniques/Advice

• Remember, a decent hypothesis will contain two variables, in the case of an experimental hypothesis there will be an IV and a DV; in a correlational hypothesis there will be two co-variables
• both variables need to be fully operationalised to score the marks, that is you need to be very clear and specific about what you mean by your IV and your DV; if someone wanted to repeat your study, they should be able to look at your hypothesis and know exactly what to change between the two groups/conditions and exactly what to measure (including any units/explanation of rating scales etc, e.g. “where 1 is low and 7 is high”)
• double check the question, did it ask for a directional or non-directional hypothesis?
• if you were asked for a null hypothesis, make sure you always include the phrase “and any difference/correlation (is your study experimental or correlational?) that does arise will be due to chance alone”

Practice Questions:

• Mr Faraz wants to compare the levels of attendance between his psychology group and those of Mr Simon, who teaches a different psychology group. Which of the following is a suitable directional (one tailed) hypothesis for Mr Faraz’s investigation?

A There will be a difference in the levels of attendance between the two psychology groups.

B Students’ level of attendance will be higher in Mr Faraz’s group than Mr Simon’s group.

C Any difference in the levels of attendance between the two psychology groups is due to chance.

D The level of attendance of the students will depend upon who is teaching the groups.

2. Tracy works for the local council. The council is thinking about reducing the number of people it employs to pick up litter from the street. Tracy has been asked to carry out a study to see if having the streets cleaned at less regular intervals will affect the amount of litter the public will drop. She studies a street to compare how much litter is dropped at two different times, once when it has just been cleaned and once after it has not been cleaned for a month.

Write a fully operationalised non-directional (two-tailed) hypothesis for Tracy’s study. (2)

3. Jamila is conducting a practical investigation to look at gender differences in carrying out visuo-spatial tasks. She decides to give males and females a jigsaw puzzle and will time them to see who completes it the fastest. She uses a random sample of pupils from a local school to get her participants.

(a) Write a fully operationalised directional (one tailed) hypothesis for Jamila’s study. (2) (b) Outline one strength and one weakness of the random sampling method. You may refer to Jamila’s use of this type of sampling in your answer. (4)

4. Which of the following is a non-directional (two tailed) hypothesis?

A There is a difference in driving ability with men being better drivers than women

B Women are better at concentrating on more than one thing at a time than men

C Women spend more time doing the cooking and cleaning than men

D There is a difference in the number of men and women who participate in sports

Revision Activity

writing-hypotheses-revision-sheet

Quizizz link for teachers: https://quizizz.com/admin/quiz/5bf03f51add785001bc5a09e

Share this:

• Already have a WordPress.com account? Log in now.
• Subscribe Subscribed
• Copy shortlink
• Report this content
• View post in Reader
• Manage subscriptions
• Collapse this bar

Directional vs Non-Directional Hypothesis: Difference Between Them

In statistics, a directional hypothesis, also known as a one-tailed hypothesis, is a type of hypothesis that predicts the direction of the relationship between variables or the direction of the difference between groups.

The introduction of a directional hypothesis in a research study provides an overview of the specific prediction being made about the relationship between variables or the difference between groups. It sets the stage for the research question and outlines the expected direction of the findings. The introduction typically includes the following elements:

Research Context: Begin by introducing the general topic or research area that the study is focused on. Provide background information and highlight the significance of the research question.

Research Question: Clearly state the specific research question that the study aims to answer. This question should be directly related to the variables being investigated.

Previous Research: Summarize relevant literature or previous studies that have explored similar or related topics. This helps establish the existing knowledge base and provides a rationale for the hypothesis.

Hypothesis Statement: Present the directional hypothesis clearly and concisely. State the predicted relationship between variables or the expected difference between groups. For example, if studying the impact of a new teaching method on student performance, a directional hypothesis could be, “Students who receive the new teaching method will demonstrate higher test scores compared to students who receive the traditional teaching method.”

Justification: Provide a logical explanation for the directional hypothesis based on the existing literature or theoretical framework. Discuss any previous findings, theories, or empirical evidence that support the predicted direction of the relationship or difference.

Objectives: Outline the specific objectives or aims of the study, which should align with the research question and hypothesis. These objectives help guide the research process and provide a clear focus for the study.

By including these elements in the introduction of a research study, the directional hypothesis is introduced effectively, providing a clear and justified prediction about the expected outcome of the research.

When formulating a directional hypothesis, researchers make a specific prediction about the expected relationship or difference between variables. They specify whether they expect an increase or decrease in the dependent variable, or whether one group will score higher or lower than another group

What is Directional Hypothesis?

With a correlational study, a directional hypothesis states that there is a positive (or negative) correlation between two variables. When a hypothesis states the direction of the results, it is referred to as a directional (one-tailed) hypothesis; this is because it states that the results go in one direction.

Definition :

A directional hypothesis is a one-tailed hypothesis that states the direction of the difference or relationship (e.g. boys are more helpful than girls).

Research Question: Does exercise have a positive impact on mood?

Directional Hypothesis: Engaging in regular exercise will result in an increase in positive mood compared to a sedentary lifestyle.

In this example, the directional hypothesis predicts that regular exercise will have a specific effect on mood, specifically leading to an increase in positive mood. The researcher expects that individuals who engage in regular exercise will experience improvements in their overall mood compared to individuals who lead a sedentary lifestyle.

It’s important to note that this is just one example, and directional hypotheses can be formulated in various research areas and contexts. The key is to make a specific prediction about the direction of the relationship or difference between variables based on prior knowledge or theoretical considerations.

Advantages of Directional Hypothesis

There are several advantages to using a directional hypothesis in research studies. Here are a few key benefits:

Specific Prediction:

A directional hypothesis allows researchers to make a specific prediction about the expected relationship or difference between variables. This provides a clear focus for the study and helps guide the research process. It also allows for more precise interpretation of the results.

Testable and Refutable:

Directional hypotheses can be tested and either supported or refuted by empirical evidence. Researchers can design their study and select appropriate statistical tests to specifically examine the predicted direction of the relationship or difference. This enhances the rigor and validity of the research.

Efficiency and Resource Allocation:

By making a specific prediction, researchers can allocate their resources more efficiently. They can focus on collecting data and conducting analyses that directly test the directional hypothesis, rather than exploring all possible directions or relationships. This can save time, effort, and resources.

Theory Development:

Directional hypotheses contribute to the development of theories and scientific knowledge. When a directional hypothesis is supported by empirical evidence, it provides support for existing theories or helps generate new theories. This advancement in knowledge can guide future research and understanding in the field.

Practical Applications:

Directional hypotheses can have practical implications and applications. If a hypothesis predicts a specific direction of change, such as the effectiveness of a treatment or intervention, it can inform decision-making and guide practical applications in fields such as medicine, psychology, or education.

Enhanced Communication:

Directional hypotheses facilitate clearer communication of research findings. When researchers have made specific predictions about the direction of the relationship or difference, they can effectively communicate their results to both academic and non-academic audiences. This promotes better understanding and application of the research outcomes.

It’s important to note that while directional hypotheses offer advantages, they also require stronger evidence to support them compared to non-directional hypotheses. Researchers should carefully consider the research context, existing literature, and theoretical considerations before formulating a directional hypothesis.

Disadvantages of Directional Hypothesis

While directional hypotheses have their advantages, there are also some potential disadvantages to consider:

Risk of Type I Error:

Directional hypotheses increase the risk of committing a Type I error, also known as a false positive. By focusing on a specific predicted direction, researchers may overlook the possibility of an opposite or null effect. If the actual relationship or difference does not align with the predicted direction, researchers may incorrectly conclude that there is no effect when, in fact, there may be.

Narrow Focus:

Directional hypotheses restrict the scope of investigation to a specific predicted direction. This narrow focus may overlook other potential relationships, nuances, or alternative explanations. Researchers may miss valuable insights or unexpected findings by excluding other possibilities from consideration.

Limited Generalizability:

Directional hypotheses may limit the generalizability of findings. If the study supports the predicted direction, the results may only apply to the specific context and conditions outlined in the hypothesis. Generalizing the findings to different populations, settings, or variables may require further research.

Biased Interpretation:

Directional hypotheses can introduce bias in the interpretation of results. Researchers may be inclined to selectively focus on evidence that supports the predicted direction while downplaying or ignoring contradictory evidence. This can hinder objectivity and lead to biased conclusions.

Increased Sample Size Requirements:

Directional hypotheses often require larger sample sizes compared to non-directional hypotheses. This is because statistical power needs to be sufficient to detect the predicted direction with a reasonable level of confidence. Larger samples can be more time-consuming and resource-intensive to obtain.

Reduced Flexibility:

Directional hypotheses limit flexibility in data analysis and statistical testing. Researchers may feel compelled to use specific statistical tests or analytical approaches that align with the predicted direction, potentially overlooking alternative methods that may be more appropriate or informative.

It’s important to weigh these disadvantages against the specific research context and objectives when deciding whether to use a directional hypothesis. In some cases, a non-directional hypothesis may be more suitable, allowing for a more exploratory and comprehensive investigation of the research question.

Non-Directional Hypothesis:

A non-directional hypothesis, also known as a two-tailed hypothesis, is a type of hypothesis that does not specify the direction of the relationship between variables or the difference between groups. Instead of predicting a specific direction, a non-directional hypothesis suggests that there will be a significant relationship or difference, without indicating whether it will be positive or negative, higher or lower, etc.

The introduction of a non-directional hypothesis in a research study provides an overview of the general prediction being made about the relationship between variables or the difference between groups, without specifying the direction. It sets the stage for the research question and outlines the expectation of a significant relationship or difference. The introduction typically includes the following elements:

Research Context:

Begin by introducing the general topic or research area that the study is focused on. Provide background information and highlight the significance of the research question.

Research Question:

Clearly state the specific research question that the study aims to answer. This question should be directly related to the variables being investigated.

Previous Research:

Summarize relevant literature or previous studies that have explored similar or related topics. This helps establish the existing knowledge base and provides a rationale for the hypothesis.

Hypothesis Statement:

Present the non-directional hypothesis clearly and concisely. State that there is an expected relationship or difference between variables or groups without specifying the direction. For example, if studying the relationship between socioeconomic status and academic achievement, a non-directional hypothesis could be, “There is a significant relationship between socioeconomic status and academic achievement.”

Justification:

Provide a logical explanation for the non-directional hypothesis based on the existing literature or theoretical framework. Discuss any previous findings, theories, or empirical evidence that support the notion of a relationship or difference between the variables or groups.

Objectives:

Outline the specific objectives or aims of the study, which should align with the research question and hypothesis. These objectives help guide the research process and provide a clear focus for the study.

By including these elements in the introduction of a research study, the non-directional hypothesis is introduced effectively, indicating the expectation of a significant relationship or difference without specifying the direction

What is Non-directional hypothesis?

In a non-directional hypothesis, researchers acknowledge that there may be an effect or relationship between variables but do not make a specific prediction about the direction of that effect. This allows for a more exploratory approach to data analysis and interpretation

If a hypothesis does not state a direction but simply says that one factor affects another, or that there is an association or correlation between two variables then it is called a non-directional (two-tailed) hypothesis.

Research Question: Is there a relationship between social media usage and self-esteem?

Non-Directional Hypothesis: There is a significant relationship between social media usage and self-esteem.

In this example, the non-directional hypothesis suggests that there is a relationship between social media usage and self-esteem without specifying whether higher social media usage is associated with higher or lower self-esteem. The hypothesis acknowledges the possibility of an effect but does not make a specific prediction about the direction of that effect.

It’s important to note that this is just one example, and non-directional hypotheses can be formulated in various research areas and contexts. The key is to indicate the expectation of a significant relationship or difference without specifying the direction, allowing for a more exploratory approach to data analysis and interpretation.

Advantages of Non-directional hypothesis

Non-directional hypotheses, also known as two-tailed hypotheses, offer several advantages in research studies. Here are some of the key advantages:

Flexibility in Data Analysis:

Non-directional hypotheses allow for flexibility in data analysis. Researchers are not constrained by a specific predicted direction and can explore the relationship or difference in various ways. This flexibility enables a more comprehensive examination of the data, considering both positive and negative associations or differences.

Objective and Open-Minded Approach:

Non-directional hypotheses promote an objective and open-minded approach to research. Researchers do not have preconceived notions about the direction of the relationship or difference, which helps mitigate biases in data interpretation. They can objectively analyze the data without being influenced by their initial expectations.

Comprehensive Understanding:

By not specifying the direction, non-directional hypotheses facilitate a comprehensive understanding of the relationship or difference being investigated. Researchers can explore and consider all possible outcomes, leading to a more nuanced interpretation of the findings. This broader perspective can provide deeper insights into the research question.

Greater Sensitivity:

Non-directional hypotheses can be more sensitive to detecting unexpected or surprising relationships or differences. Researchers are not solely focused on confirming a specific predicted direction, but rather on uncovering any significant association or difference. This increased sensitivity allows for the identification of novel patterns and relationships that may have been overlooked with a directional hypothesis.

Replication and Generalizability:

Non-directional hypotheses support replication studies and enhance the generalizability of findings. By not restricting the investigation to a specific predicted direction, the results can be more applicable to different populations, contexts, or conditions. This broader applicability strengthens the validity and reliability of the research.

Hypothesis Generation:

Non-directional hypotheses can serve as a foundation for generating new hypotheses and research questions. Significant findings without a specific predicted direction can lead to further investigations and the formulation of more focused directional hypotheses in subsequent studies.

It’s important to consider the specific research context and objectives when deciding between a directional or non-directional hypothesis. Non-directional hypotheses are particularly useful when researchers are exploring new areas or when there is limited existing knowledge about the relationship or difference being studied.

Disadvantages of Non-directional hypothesis

Non-directional hypotheses have their advantages, there are also some potential disadvantages to consider:

Lack of Specificity: Non-directional hypotheses do not provide a specific prediction about the direction of the relationship or difference between variables. This lack of specificity may limit the interpretability and practical implications of the findings. Stakeholders may desire clear guidance on the expected direction of the effect.

Non-directional hypotheses often require larger sample sizes compared to directional hypotheses. This is because statistical power needs to be sufficient to detect any significant relationship or difference, regardless of the direction. Obtaining larger samples can be more time-consuming, resource-intensive, and costly.

Reduced Precision:

By not specifying the direction, non-directional hypotheses may result in less precise findings. Researchers may obtain statistically significant results indicating a relationship or difference, but the lack of direction may hinder their ability to understand the practical implications or mechanism behind the effect.

Potential for Post-hoc Interpretation:

Non-directional hypotheses can increase the risk of post-hoc interpretation of results. Researchers may be tempted to selectively interpret and highlight only the significant findings that support their preconceived notions or expectations, leading to biased interpretations.

Limited Theoretical Guidance:

Non-directional hypotheses may lack theoretical guidance in terms of understanding the underlying mechanisms or causal pathways. Without a specific predicted direction, it can be challenging to develop a comprehensive theoretical framework to explain the relationship or difference being studied.

Potential Missed Opportunities:

Non-directional hypotheses may limit the exploration of specific directions or subgroups within the data. By not focusing on a specific direction, researchers may miss important nuances or interactions that could contribute to a deeper understanding of the phenomenon under investigation.

It’s important to carefully consider the research question, available literature, and research objectives when deciding whether to use a non-directional hypothesis. Depending on the context and goals of the study, a non-directional hypothesis may be appropriate, but researchers should also be aware of the potential limitations and address them accordingly in their research design and interpretation of results.

Difference between directional and non-directional hypothesis

the main difference between a directional hypothesis and a non-directional hypothesis lies in the specificity of the prediction made about the relationship between variables or the difference between groups.

Directional Hypothesis:

A directional hypothesis, also known as a one-tailed hypothesis, makes a specific prediction about the direction of the relationship or difference. It states the expected outcome, whether it is a positive or negative relationship, a higher or lower value, an increase or decrease, etc. The directional hypothesis guides the research in a focused manner, specifying the direction to be tested.

Example: “Students who receive tutoring will demonstrate higher test scores compared to students who do not receive tutoring.”

A non-directional hypothesis, also known as a two-tailed hypothesis, does not specify the direction of the relationship or difference. It acknowledges the possibility of a relationship or difference between variables without predicting a specific direction. The non-directional hypothesis allows for exploration and analysis of both positive and negative associations or differences.

Example: “There is a significant relationship between sleep quality and academic performance.”

In summary, a directional hypothesis makes a specific prediction about the direction of the relationship or difference, while a non-directional hypothesis suggests a relationship or difference without specifying the direction. The choice between the two depends on the research question, existing literature, and the researcher’s objectives. Directional hypotheses provide a focused prediction, while non-directional hypotheses allow for more exploratory analysis.

When to use Directional Hypothesis?

A directional hypothesis is appropriate to use in specific situations where researchers have a clear theoretical or empirical basis for predicting the direction of the relationship or difference between variables. Here are some scenarios where a directional hypothesis is commonly employed:

Prior Research and Theoretical Framework: When previous studies, existing theories, or established empirical evidence strongly suggest a specific direction of the relationship or difference, a directional hypothesis can be formulated. Researchers can build upon the existing knowledge base and make a focused prediction based on this prior information.

Cause-and-Effect Relationships: In studies aiming to establish cause-and-effect relationships, directional hypotheses are often used. When there is a clear theoretical understanding of the causal relationship between variables, researchers can predict the expected direction of the effect based on the proposed mechanism.

Specific Research Objectives: If the research study has specific objectives that require a clear prediction about the direction, a directional hypothesis can be appropriate. For instance, if the aim is to test the effectiveness of a particular intervention or treatment, a directional hypothesis can guide the evaluation by predicting the expected positive or negative outcome.

Practical Applications: Directional hypotheses are useful when the research findings have direct practical implications. For example, in fields such as medicine, psychology, or education, researchers may formulate directional hypotheses to predict the effects of certain interventions or treatments on patient outcomes or educational achievement.

Hypothesis-Testing Approach: Researchers who adopt a hypothesis-testing approach, where they aim to confirm or disconfirm specific predictions, often use directional hypotheses. This approach involves formulating a specific hypothesis and conducting statistical tests to determine whether the data support or refute the predicted direction of the relationship or difference.

When to use non directional hypothesis?

A non-directional hypothesis, also known as a two-tailed hypothesis, is appropriate to use in several situations where researchers do not have a specific prediction about the direction of the relationship or difference between variables. Here are some scenarios where a non-directional hypothesis is commonly employed:

Exploratory Research:

When the research aims to explore a new area or investigate a relationship that has limited prior research or theoretical guidance, a non-directional hypothesis is often used. It allows researchers to gather initial data and insights without being constrained by a specific predicted direction.

Preliminary Studies:

Non-directional hypotheses are useful in preliminary or pilot studies that seek to gather preliminary evidence and generate hypotheses for further investigation. By using a non-directional hypothesis, researchers can gather initial data to inform the development of more specific hypotheses in subsequent studies.

Neutral Expectations:

If researchers have no theoretical or empirical basis to predict the direction of the relationship or difference, a non-directional hypothesis is appropriate. This may occur in situations where there is a lack of prior research, conflicting findings, or inconclusive evidence to support a specific direction.

Comparative Studies:

In studies where the objective is to compare two or more groups or conditions, a non-directional hypothesis is commonly used. The focus is on determining whether a significant difference exists, without making specific predictions about which group or condition will have higher or lower values.

Data-Driven Approach:

When researchers adopt a data-driven or exploratory approach to analysis, non-directional hypotheses are preferred. Instead of testing specific predictions, the aim is to explore the data, identify patterns, and generate hypotheses based on the observed relationships or differences.

Hypothesis-Generating Studies:

Non-directional hypotheses are often used in studies aimed at generating new hypotheses and research questions. By exploring associations or differences without specifying the direction, researchers can identify potential relationships or factors that can serve as a basis for future research.

Strategies to improve directional and non-directional hypothesis

To improve the quality of both directional and non-directional hypotheses, researchers can employ various strategies. Here are some strategies to enhance the formulation of hypotheses:

Strategies to Improve Directional Hypotheses:

Review existing literature:.

Conduct a thorough review of relevant literature to identify previous research findings, theories, and empirical evidence related to the variables of interest. This will help inform and support the formulation of a specific directional hypothesis based on existing knowledge.

Develop a Theoretical Framework:

Build a theoretical framework that outlines the expected causal relationship between variables. The theoretical framework should provide a clear rationale for predicting the direction of the relationship based on established theories or concepts.

Conduct Pilot Studies:

Conducting pilot studies or preliminary research can provide valuable insights and data to inform the formulation of a directional hypothesis. Initial findings can help researchers identify patterns or relationships that support a specific predicted direction.

Seek Expert Input:

Seek input from experts or colleagues in the field who have expertise in the area of study. Discuss the research question and hypothesis with them to obtain valuable insights, perspectives, and feedback that can help refine and improve the directional hypothesis.

Clearly Define Variables:

Clearly define and operationalize the variables in the hypothesis to ensure precision and clarity. This will help avoid ambiguity and ensure that the hypothesis is testable and measurable.

Strategies to Improve Non-Directional Hypotheses:

Preliminary exploration:.

Conduct initial exploratory research to gather preliminary data and insights on the relationship or difference between variables. This can provide a foundation for formulating a non-directional hypothesis based on observed patterns or trends.

Analyze Existing Data:

Analyze existing datasets to identify potential relationships or differences. Exploratory data analysis techniques such as data visualization , descriptive statistics, and correlation analysis can help uncover initial insights that can guide the formulation of a non-directional hypothesis.

Use Exploratory Research Designs:

Employ exploratory research designs such as qualitative studies, case studies, or grounded theory approaches. These designs allow researchers to gather rich data and explore relationships or differences without preconceived notions about the direction.

Consider Alternative Explanations:

When formulating a non-directional hypothesis, consider alternative explanations or potential factors that may influence the relationship or difference between variables. This can help ensure a comprehensive and nuanced understanding of the phenomenon under investigation.

Refine Based on Initial Findings:

Refine the non-directional hypothesis based on initial findings and observations from exploratory analyses. These findings can guide the formulation of more specific hypotheses in subsequent studies or inform the direction of further research.

In conclusion, both directional and non-directional hypotheses have their merits and are valuable in different research contexts.

 Here’s a summary of the key points regarding directional and non-directional hypotheses:

• A directional hypothesis makes a specific prediction about the direction of the relationship or difference between variables.
• It is appropriate when there is a clear theoretical or empirical basis for predicting the direction.
• Directional hypotheses provide a focused approach, guiding the research towards confirming or refuting a specific predicted direction.
• They are useful in studies where cause-and-effect relationships are being examined or when specific practical implications are desired.
• Directional hypotheses require careful consideration of prior research, theoretical frameworks, and available evidence.
• A non-directional hypothesis does not specify the direction of the relationship or difference between variables.
• It is employed when there is limited prior knowledge, conflicting findings, or a desire for exploratory analysis.
• Non-directional hypotheses allow for flexibility and open-mindedness in exploring the data, considering both positive and negative associations or differences.
• They are suitable for preliminary studies, exploratory research, or when the research question does not have a clear predicted direction.
• Non-directional hypotheses are beneficial for generating new hypotheses, replication studies, and enhancing generalizability.

In both cases, it is essential to ensure that hypotheses are clear, testable, and aligned with the research objectives. Researchers should also be open to revising and refining hypotheses based on the findings and feedback obtained during the research process. The choice between a directional and non-directional hypothesis depends on factors such as the research question, available literature, theoretical frameworks, and the specific objectives of the study. Researchers should carefully consider these factors to determine the most appropriate type of hypothesis to use in their research

Related posts:

• Best Chart to Show Trends Over Time: How to Visualize your Data with respect to Time
• What is a Waterfall Chart and its Importance in Data Visualization
• Context Diagram is Essential for a Business Analyst to Define System Context
• Close-Ended Questionnaires: Types, Examples (Pros and Cons)
• How can I Hide and Unhide rows in Excel?

How much did you enjoy this article?

Related articles

Qlik vs Tableau: Which one is better?

Qlik vs Tableau: Choose the Best Analytics Tool. Elevate Your Data Insights for Informed Decisions. Compare Now!

Google Forms vs. SurveyMonkey: Which one is better?

Google Forms vs. SurveyMonkey: Choose the Best Survey Tool. Enhance Data Collection for Informed Insights. Compare and Decide!

Lucidchart vs. Miro: Which one is better?

Deciding between Lucidchart and Miro depends on your specific needs, preferences, and the nature of your projects. Both platforms have their strengths and are well-regarded in their respective areas. 

Looker vs Data Studio: Which one is better?

"Looker" and "Data Studio" are both popular business intelligence and data visualization tools, but they have different features, capabilities, and use cases.

Power BI vs. Domo: Which one is better?

Power BI and Domo are powerful business intelligence (BI) tools offering data visualization, analytics, and reporting capabilities. However, they differ in features, pricing, user interface, and target audience. Let's compare some critical aspects of Power BI and Domo:

Directional vs. Non-Directional Hypothesis in Research

In the world of research and statistical analysis, formulating hypotheses is a crucial step in the scientific process. Hypotheses guide researchers in making predictions and testing relationships between variables. When it comes to hypotheses, there are two main types: directional and non-directional.

In this blog post, we will explore the differences between Directional vs. Non-Directional Hypothesis in Research and their implications in research.

• Table of Contents

Directional Hypothesis

A directional hypothesis, also known as a one-tailed hypothesis, is formulated with a specific predicted direction of the relationship between variables. It indicates an expectation of the relationship being either positive or negative.

The directional hypothesis is often used when there is prior knowledge or theoretical reasoning supporting the predicted direction of the relationship. It allows researchers to make more specific predictions and draw conclusions based on the expected direction of the effect.

Example of Directional Hypothesis

For example, a directional hypothesis might state that “increased physical activity will lead to a decrease in body weight.” Here, the researcher expects a negative relationship between physical activity and body weight.

Advantages of Directional Hypothesis

• Specific predictions: Directional hypotheses provide a clear prediction of the expected relationship between variables, allowing for a focused investigation.
• Increased statistical power: By focusing on one direction of the relationship, researchers can allocate more statistical power to that specific direction, increasing the chances of detecting a significant effect if it exists.

Non-Directional Hypothesis

A non-directional hypothesis, also known as a two-tailed hypothesis, does not make a specific prediction about the direction of the relationship between variables. Instead, it states that there is a relationship, but without indicating whether it will be positive or negative.

Non-directional hypotheses are often used when there is insufficient prior knowledge or theoretical basis to predict the direction of the relationship. It allows for a more exploratory approach, where the researcher is open to discovering the nature of the relationship through data analysis .

Read More: Internal Validity vs External Validity | Examples

Example of Non-Directional Hypothesis

For example, a non-directional hypothesis might state that “there is a relationship between caffeine consumption and reaction time.” Here, the researcher expects a relationship between the variables but does not specify the direction.

Read More: Population vs Sample | Examples

Advantages of Non-Directional Hypothesis:

• Flexibility: Non-directional hypotheses provide flexibility in exploring relationships between variables without preconceived notions about the direction of the effect.
• Open to unexpected findings : By not specifying the direction, researchers remain open to unexpected results or alternative explanations that may emerge during the analysis.

Difference Between Directional and Non-Directional Hypotheses

Choosing Between Directional and Non-Directional Hypotheses: The choice between a directional and non-directional hypothesis depends on the research question, existing knowledge, and theoretical background. Here are a few considerations for selecting the appropriate type of hypothesis:

• Prior research: If previous studies have established a clear direction of the relationship, a directional hypothesis may be more appropriate.
• Theoretical reasoning: If there is a strong theoretical foundation supporting a specific direction, a directional hypothesis can provide a focused investigation.
• Exploratory nature: If the research question is exploratory or lacks prior knowledge, a non-directional hypothesis allows for a more open-ended investigation.

Read More: Reliability vs Validity | Examples

• Directional vs. Non-Directional Hypothesis

Formulating hypotheses is an essential step in the research process, guiding researchers in testing relationships between variables.

Directional hypotheses offer specific predictions about the expected direction of the relationship, whereas non-directional hypotheses allow for more exploratory investigations without preconceived notions of the direction.

The choice between these types of hypotheses depends on the research question, prior knowledge, and theoretical background.

By understanding the distinctions between directional and non-directional hypotheses, researchers can effectively formulate hypotheses that align with their research goals and contribute to the advancement of scientific knowledge.

Remember, hypotheses serve as a roadmap for research, and regardless of their type, they play a crucial role in scientific inquiry and the pursuit of knowledge.

Other articles

Please read through some of our other articles with examples and explanations if you’d like to learn more about research methodology.

Comparision

• Basic and Applied Research
• Cross-Sectional vs Longitudinal Studies
• Survey vs Questionnaire
• Open Ended vs Closed Ended Questions
• Experimental and Non-Experimental Research
• Inductive vs Deductive Approach
• Null and Alternative Hypothesis
• Reliability vs Validity
• Population vs Sample
• Conceptual Framework and Theoretical Framework
• Bibliography and Reference
• Stratified vs Cluster Sampling
• Sampling Error vs Sampling Bias
• Internal Validity vs External Validity
• Full-Scale, Laboratory-Scale and Pilot-Scale Studies
• Plagiarism and Paraphrasing
• Research Methodology Vs. Research Method
• Mediator and Moderator
• Type I vs Type II error
• Descriptive and Inferential Statistics
• Microsoft Excel and SPSS
• Parametric and Non-Parametric Test
• Independent vs. Dependent Variable – MIM Learnovate
• Research Article and Research Paper
• Proposition and Hypothesis
• Principal Component Analysis and Partial Least Squares
• Academic Research vs Industry Research
• Clinical Research vs Lab Research
• Research Lab and Hospital Lab
• Thesis Statement and Research Question
• Quantitative Researchers vs. Quantitative Traders
• Premise, Hypothesis and Supposition
• Survey Vs Experiment
• Hypothesis and Theory
• Independent vs. Dependent Variable
• APA vs. MLA
• Ghost Authorship vs. Gift Authorship
• Research Methods
• Quantitative Research
• Qualitative Research
• Case Study Research
• Survey Research
• Conclusive Research
• Descriptive Research
• Cross-Sectional Research
• Theoretical Framework
• Conceptual Framework
• Triangulation
• Grounded Theory
• Quasi-Experimental Design
• Mixed Method
• Correlational Research
• Randomized Controlled Trial
• Stratified Sampling
• Ethnography
• Ghost Authorship
• Secondary Data Collection
• Primary Data Collection
• Ex-Post-Facto
•   Dissertation Topic
• Thesis Statement
• Research Proposal
• Research Questions
• Research Problem
• Research Gap
• Types of Research Gaps
• Operationalization of Variables
• Literature Review
• Research Hypothesis
• Questionnaire
• Reliability
• Measurement of Scale
• Sampling Techniques
• Acknowledgements
• PLS-SEM model
• Principal Components Analysis
• Multivariate Analysis
• Friedman Test
• Chi-Square Test (Χ²)
• Effect Size

Related Posts

Survey sampling: what it is, types & tips, cluster sampling | method and examples, who is a good peer reviewer, peer review | types of peer review, ethics in research: safeguarding integrity and credibility, advantages and disadvantages of snowball sampling, exploring qualitative researcher skills: what they are and how to develop them, difference between quota sampling and stratified sampling, how effective laboratory design impacts health, safety, and productivity, why is laboratory safety important in research, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

Directional Hypothesis: Definition and 10 Examples

A directional hypothesis refers to a type of hypothesis used in statistical testing that predicts a particular direction of the expected relationship between two variables.

In simpler terms, a directional hypothesis is an educated, specific guess about the direction of an outcome—whether an increase, decrease, or a proclaimed difference in variable sets.

For example, in a study investigating the effects of sleep deprivation on cognitive performance, a directional hypothesis might state that as sleep deprivation (Independent Variable) increases, cognitive performance (Dependent Variable) decreases (Killgore, 2010). Such a hypothesis offers a clear, directional relationship whereby a specific increase or decrease is anticipated.

Global warming provides another notable example of a directional hypothesis. A researcher might hypothesize that as carbon dioxide (CO2) levels increase, global temperatures also increase (Thompson, 2010). In this instance, the hypothesis clearly articulates an upward trend for both variables. 

In any given circumstance, it’s imperative that a directional hypothesis is grounded on solid evidence. For instance, the CO2 and global temperature relationship is based on substantial scientific evidence, and not on a random guess or mere speculation (Florides & Christodoulides, 2009).

Directional vs Non-Directional vs Null Hypotheses

A directional hypothesis is generally contrasted to a non-directional hypothesis. Here’s how they compare:

• Directional hypothesis: A directional hypothesis provides a perspective of the expected relationship between variables, predicting the direction of that relationship (either positive, negative, or a specific difference). 
• Non-directional hypothesis: A non-directional hypothesis denotes the possibility of a relationship between two variables ( the independent and dependent variables ), although this hypothesis does not venture a prediction as to the direction of this relationship (Ali & Bhaskar, 2016). For example, a non-directional hypothesis might state that there exists a relationship between a person’s diet (independent variable) and their mood (dependent variable), without indicating whether improvement in diet enhances mood positively or negatively. Overall, the choice between a directional or non-directional hypothesis depends on the known or anticipated link between the variables under consideration in research studies.

Another very important type of hypothesis that we need to know about is a null hypothesis :

• Null hypothesis : The null hypothesis stands as a universality—the hypothesis that there is no observed effect in the population under study, meaning there is no association between variables (or that the differences are down to chance). For instance, a null hypothesis could be constructed around the idea that changing diet (independent variable) has no discernible effect on a person’s mood (dependent variable) (Yan & Su, 2016). This proposition is the one that we aim to disprove in an experiment.

While directional and non-directional hypotheses involve some integrated expectations about the outcomes (either distinct direction or a vague relationship), a null hypothesis operates on the premise of negating such relationships or effects.

The null hypotheses is typically proposed to be negated or disproved by statistical tests, paving way for the acceptance of an alternate hypothesis (either directional or non-directional).

Directional Hypothesis Examples

1. exercise and heart health.

Research suggests that as regular physical exercise (independent variable) increases, the risk of heart disease (dependent variable) decreases (Jakicic, Davis, Rogers, King, Marcus, Helsel, Rickman, Wahed, Belle, 2016). In this example, a directional hypothesis anticipates that the more individuals maintain routine workouts, the lesser would be their odds of developing heart-related disorders. This assumption is based on the underlying fact that routine exercise can help reduce harmful cholesterol levels, regulate blood pressure, and bring about overall health benefits. Thus, a direction – a decrease in heart disease – is expected in relation with an increase in exercise. 

2. Screen Time and Sleep Quality

Another classic instance of a directional hypothesis can be seen in the relationship between the independent variable, screen time (especially before bed), and the dependent variable, sleep quality. This hypothesis predicts that as screen time before bed increases, sleep quality decreases (Chang, Aeschbach, Duffy, Czeisler, 2015). The reasoning behind this hypothesis is the disruptive effect of artificial light (especially blue light from screens) on melatonin production, a hormone needed to regulate sleep. As individuals spend more time exposed to screens before bed, it is predictably hypothesized that their sleep quality worsens. 

3. Job Satisfaction and Employee Turnover

A typical scenario in organizational behavior research posits that as job satisfaction (independent variable) increases, the rate of employee turnover (dependent variable) decreases (Cheng, Jiang, & Riley, 2017). This directional hypothesis emphasizes that an increased level of job satisfaction would lead to a reduced rate of employees leaving the company. The theoretical basis for this hypothesis is that satisfied employees often tend to be more committed to the organization and are less likely to seek employment elsewhere, thus reducing turnover rates.

4. Healthy Eating and Body Weight

Healthy eating, as the independent variable, is commonly thought to influence body weight, the dependent variable, in a positive way. For example, the hypothesis might state that as consumption of healthy foods increases, an individual’s body weight decreases (Framson, Kristal, Schenk, Littman, Zeliadt, & Benitez, 2009). This projection is based on the premise that healthier foods, such as fruits and vegetables, are generally lower in calories than junk food, assisting in weight management.

5. Sun Exposure and Skin Health

The association between sun exposure (independent variable) and skin health (dependent variable) allows for a definitive hypothesis declaring that as sun exposure increases, the risk of skin damage or skin cancer increases (Whiteman, Whiteman, & Green, 2001). The premise aligns with the understanding that overexposure to the sun’s ultraviolet rays can deteriorate skin health, leading to conditions like sunburn or, in extreme cases, skin cancer.

6. Study Hours and Academic Performance

A regularly assessed relationship in academia suggests that as the number of study hours (independent variable) rises, so too does academic performance (dependent variable) (Nonis, Hudson, Logan, Ford, 2013). The hypothesis proposes a positive correlation , with an increase in study time expected to contribute to enhanced academic outcomes.

7. Screen Time and Eye Strain

It’s commonly hypothesized that as screen time (independent variable) increases, the likelihood of experiencing eye strain (dependent variable) also increases (Sheppard & Wolffsohn, 2018). This is based on the idea that prolonged engagement with digital screens—computers, tablets, or mobile phones—can cause discomfort or fatigue in the eyes, attributing to symptoms of eye strain.

8. Physical Activity and Stress Levels

In the sphere of mental health, it’s often proposed that as physical activity (independent variable) increases, levels of stress (dependent variable) decrease (Stonerock, Hoffman, Smith, Blumenthal, 2015). Regular exercise is known to stimulate the production of endorphins, the body’s natural mood elevators, helping to alleviate stress.

9. Water Consumption and Kidney Health

A common health-related hypothesis might predict that as water consumption (independent variable) increases, the risk of kidney stones (dependent variable) decreases (Curhan, Willett, Knight, & Stampfer, 2004). Here, an increase in water intake is inferred to reduce the risk of kidney stones by diluting the substances that lead to stone formation.

10. Traffic Noise and Sleep Quality

In urban planning research, it’s often supposed that as traffic noise (independent variable) increases, sleep quality (dependent variable) decreases (Muzet, 2007). Increased noise levels, particularly during the night, can result in sleep disruptions, thus, leading to poor sleep quality.

11. Sugar Consumption and Dental Health

In the field of dental health, an example might be stating as one’s sugar consumption (independent variable) increases, dental health (dependent variable) decreases (Sheiham, & James, 2014). This stems from the fact that sugar is a major factor in tooth decay, and increased consumption of sugary foods or drinks leads to a decline in dental health due to the high likelihood of cavities.

See 15 More Examples of Hypotheses Here

A directional hypothesis plays a critical role in research, paving the way for specific predicted outcomes based on the relationship between two variables. These hypotheses clearly illuminate the expected direction—the increase or decrease—of an effect. From predicting the impacts of healthy eating on body weight to forecasting the influence of screen time on sleep quality, directional hypotheses allow for targeted and strategic examination of phenomena. In essence, directional hypotheses provide the crucial path for inquiry, shaping the trajectory of research studies and ultimately aiding in the generation of insightful, relevant findings.

Ali, S., & Bhaskar, S. (2016). Basic statistical tools in research and data analysis. Indian Journal of Anaesthesia, 60 (9), 662-669. doi: https://doi.org/10.4103%2F0019-5049.190623  

Chang, A. M., Aeschbach, D., Duffy, J. F., & Czeisler, C. A. (2015). Evening use of light-emitting eReaders negatively affects sleep, circadian timing, and next-morning alertness. Proceeding of the National Academy of Sciences, 112 (4), 1232-1237. doi: https://doi.org/10.1073/pnas.1418490112  

Cheng, G. H. L., Jiang, D., & Riley, J. H. (2017). Organizational commitment and intrinsic motivation of regular and contractual primary school teachers in China. New Psychology, 19 (3), 316-326. Doi: https://doi.org/10.4103%2F2249-4863.184631  

Curhan, G. C., Willett, W. C., Knight, E. L., & Stampfer, M. J. (2004). Dietary factors and the risk of incident kidney stones in younger women: Nurses’ Health Study II. Archives of Internal Medicine, 164 (8), 885–891.

Florides, G. A., & Christodoulides, P. (2009). Global warming and carbon dioxide through sciences. Environment international , 35 (2), 390-401. doi: https://doi.org/10.1016/j.envint.2008.07.007

Framson, C., Kristal, A. R., Schenk, J. M., Littman, A. J., Zeliadt, S., & Benitez, D. (2009). Development and validation of the mindful eating questionnaire. Journal of the American Dietetic Association, 109 (8), 1439-1444. doi: https://doi.org/10.1016/j.jada.2009.05.006  

Jakicic, J. M., Davis, K. K., Rogers, R. J., King, W. C., Marcus, M. D., Helsel, D., … & Belle, S. H. (2016). Effect of wearable technology combined with a lifestyle intervention on long-term weight loss: The IDEA randomized clinical trial. JAMA, 316 (11), 1161-1171.

Khan, S., & Iqbal, N. (2013). Study of the relationship between study habits and academic achievement of students: A case of SPSS model. Higher Education Studies, 3 (1), 14-26.

Killgore, W. D. (2010). Effects of sleep deprivation on cognition. Progress in brain research , 185 , 105-129. doi: https://doi.org/10.1016/B978-0-444-53702-7.00007-5  

Marczinski, C. A., & Fillmore, M. T. (2014). Dissociative antagonistic effects of caffeine on alcohol-induced impairment of behavioral control. Experimental and Clinical Psychopharmacology, 22 (4), 298–311. doi: https://psycnet.apa.org/doi/10.1037/1064-1297.11.3.228  

Muzet, A. (2007). Environmental Noise, Sleep and Health. Sleep Medicine Reviews, 11 (2), 135-142. doi: https://doi.org/10.1016/j.smrv.2006.09.001  

Nonis, S. A., Hudson, G. I., Logan, L. B., & Ford, C. W. (2013). Influence of perceived control over time on college students’ stress and stress-related outcomes. Research in Higher Education, 54 (5), 536-552. doi: https://doi.org/10.1023/A:1018753706925  

Sheiham, A., & James, W. P. (2014). A new understanding of the relationship between sugars, dental caries and fluoride use: implications for limits on sugars consumption. Public health nutrition, 17 (10), 2176-2184. Doi: https://doi.org/10.1017/S136898001400113X  

Sheppard, A. L., & Wolffsohn, J. S. (2018). Digital eye strain: prevalence, measurement and amelioration. BMJ open ophthalmology , 3 (1), e000146. doi: http://dx.doi.org/10.1136/bmjophth-2018-000146

Stonerock, G. L., Hoffman, B. M., Smith, P. J., & Blumenthal, J. A. (2015). Exercise as Treatment for Anxiety: Systematic Review and Analysis. Annals of Behavioral Medicine, 49 (4), 542–556. doi: https://doi.org/10.1007/s12160-014-9685-9  

Thompson, L. G. (2010). Climate change: The evidence and our options. The Behavior Analyst , 33 , 153-170. Doi: https://doi.org/10.1007/BF03392211  

Whiteman, D. C., Whiteman, C. A., & Green, A. C. (2001). Childhood sun exposure as a risk factor for melanoma: a systematic review of epidemiologic studies. Cancer Causes & Control, 12 (1), 69-82. doi: https://doi.org/10.1023/A:1008980919928

Yan, X., & Su, X. (2009). Linear regression analysis: theory and computing . New Jersey: World Scientific.

Chris Drew (PhD)

Dr. Chris Drew is the founder of the Helpful Professor. He holds a PhD in education and has published over 20 articles in scholarly journals. He is the former editor of the Journal of Learning Development in Higher Education. [Image Descriptor: Photo of Chris]

• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ Social-Emotional Learning (Definition, Examples, Pros & Cons)
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ What is Educational Psychology?
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ What is IQ? (Intelligence Quotient)
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ 5 Top Tips for Succeeding at University

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.5.1: Critical Values

• Last updated
• Save as PDF
• Page ID 22071

• Michelle Oja
• Taft College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Okay, this whole chapter is full of complex theoretical ideas. Critical values and null hypothesis significance testing is a TOUGH concept to get. Here's another description of critical values, p-values, and significance. Everyone learns differently, so hopefully this slightly different explanation will help understand the prior section.

We understand that we need a research hypothesis that predicts the relationship between two groups on an measured outcome (DV), and that each research hypothesis has a null hypothesis that says that there is no relationship between the two groups on the measured outcome (the means of the DV are similar). If we reject the null hypothesis (which says that the means are similar), we are saying that the means are different; this may or may not be in the direction that we predicted in the research hypothesis so we may or may not support the research hypothesis. If we retain (fail to reject) the null hypothesis, we are saying that the means are similar and then we cannot support the research hypothesis. Got it?

But how do we decide again to retain or reject the null hypothesis? We compare a calculated statistic (there are many, depending on your variables, that we'll cover for the rest of this textbook) to a critical value from a table. The table uses probability (p-values) to tell us what calculated values are so extreme to be absolutely unlikely.

Critical Regions and Critical Values

The critical region of any test corresponds to those values of the test statistic that would lead us to reject null hypothesis (which is why the critical region is also sometimes called the rejection region). How do we find this critical region? Well, let’s consider what we know:

• The test statistic should be very big or very small (extreme) in order to reject the null hypothesis.
• If α=.05 (α is "alpha," and is just another notation for probability; we'll talk about it more in the section on errors), the critical region must cover 5% of a Standard Normal Distribution.

It’s only important to make sure you understand this last point when you are dealing with non-directional hypotheses (which we will only do for Confidence Intervals). The critical region corresponds to those values of the test statistic for which we would reject the null hypothesis, and the Standard Normal Distribution describes the probability that we would obtain a particular value if the null hypothesis (that the means are similar) were actually true. Now, let’s suppose that we chose a critical region that covers 20% of the Standard Normal Distribution, and suppose that the null hypothesis is actually true. What would be the probability of incorrectly rejecting the null (saying that there is a difference between the means when there really isn't a difference)? The answer is 20%. And therefore, we would have built a test that had an α level of 0.2. If we want α=.05, the critical region only covers 5% of the Standard Normal Distribution.

Huh? Let's draw that out. Figure \(\PageIndex{1}\) shows the critical region associated with a non-directional hypothesis test (also called a "two-sided test" because the calculated value might be in either tail of the distribution). Figure \(\PageIndex{1}\) itself shows the sampling distribution of X (the scores we got). The grey bars correspond to those values for which we would retain the null hypothesis. The blue (dark) bars show the critical region: those values for which we would reject the null. In this example, the research hypothesis was non-directional, so the critical region covers both tails of the distribution. To ensure an α level of .05, we need to ensure that each of the two regions encompasses 2.5% of the sampling distribution.

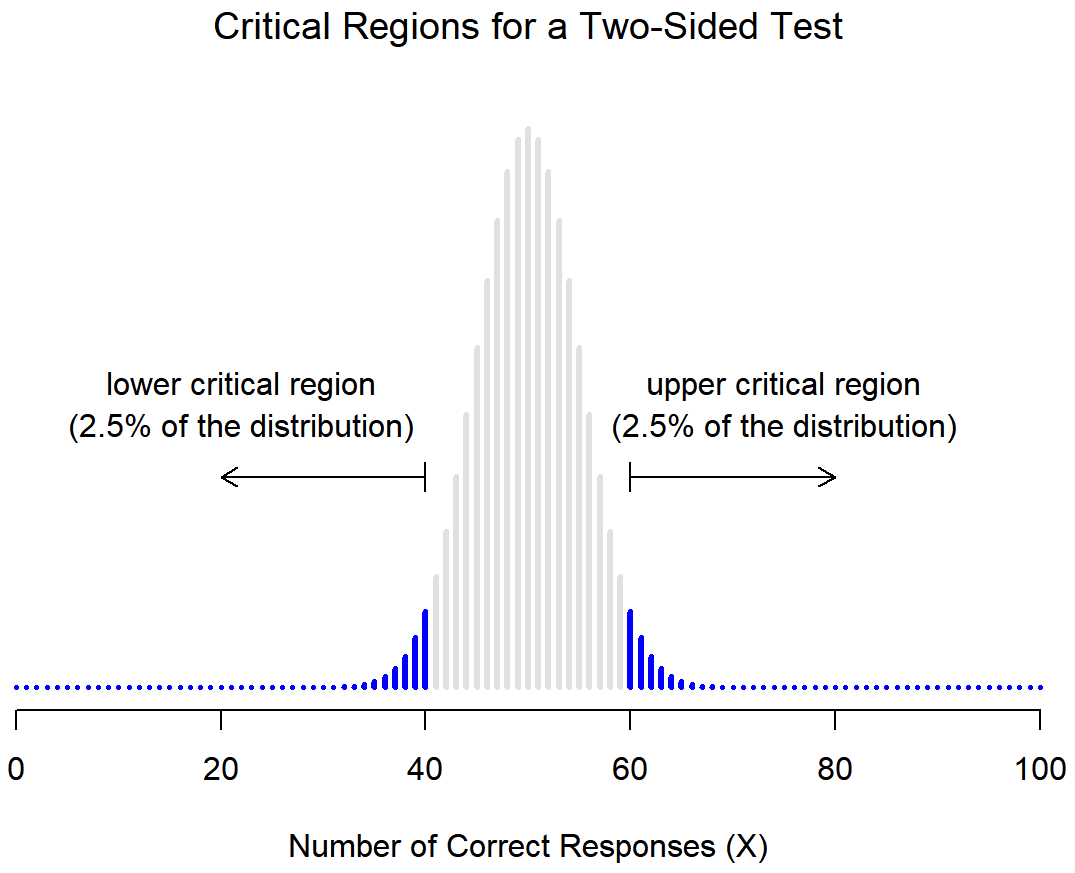
Our critical region consists of the most extreme values , known as the tails of the distribution.

At this point, our hypothesis test is essentially complete: (1) we choose an α level (e.g., α=.05, (2) come up with some test statistic (more on this step later) that does a good job (in some meaningful sense) of comparing the null hypothesis to the research hypothesis, (3) calculate the critical region that produces an appropriate α level, and then (4) calculate the value of the test statistic for the real data and then compare it to the critical values to make our decision. If we reject the null hypothesis, we say that the test has produced a significant result.

A note on statistical “significance”

Like other occult techniques of divination, the statistical method has a private jargon deliberately contrived to obscure its methods from non-practitioners. – Attributed to G. O. Ashley*

A very brief digression is in order at this point, regarding the word “significant”. The concept of statistical significance is actually a very simple one, but has a very unfortunate name. If the data allow us to reject the null hypothesis, we say that “the result is statistically significant ”, which is often shortened to “the result is significant”. This terminology is rather old, and dates back to a time when “significant” just meant something like “indicated”, rather than its modern meaning, which is much closer to “important”. As a result, a lot of modern readers get very confused when they start learning statistics, because they think that a “significant result” must be an important one. It doesn’t mean that at all. All that “statistically significant” means is that the data allowed us to reject a null hypothesis. Whether or not the result is actually important in the real world is a very different question, and depends on all sorts of other things.

Directional and Non-Directional Hypotheses

There’s one more thing to point out about the hypothesis test that we’ve just constructed. In statistical language, this is an example of a non-directional hypothesis, also known as a two-sided test. It’s called this because the alternative hypothesis covers the area on both “sides” of the null hypothesis, and as a consequence the critical region of the test covers both tails of the sampling distribution (2.5% on either side if α=.05), as illustrated earlier in Figure \(\PageIndex{1}\).

However, that’s not the only possibility, and not the situation that we'll be using with our directional research hypotheses (the ones that predict which group will have a higher mean). A directional research hypothesis would only cover the possibility that p>.5, and as a consequence the null hypothesis now becomes p≤.5. When this happens, we have what’s called a one-sided test , and when this happens the critical region only covers one tail of the sampling distribution. This is illustrated in Figure \(\PageIndex{2}\). In this case, we would only reject the null hypothesis for large values of of our test statistic (values that are more extreme but only in one direction). As a consequence, the critical region only covers the upper tail of the sampling distribution; specifically the upper 5% of the distribution. Contrast this to the two-sided version earlier in Figure \(\PageIndex{1}\).

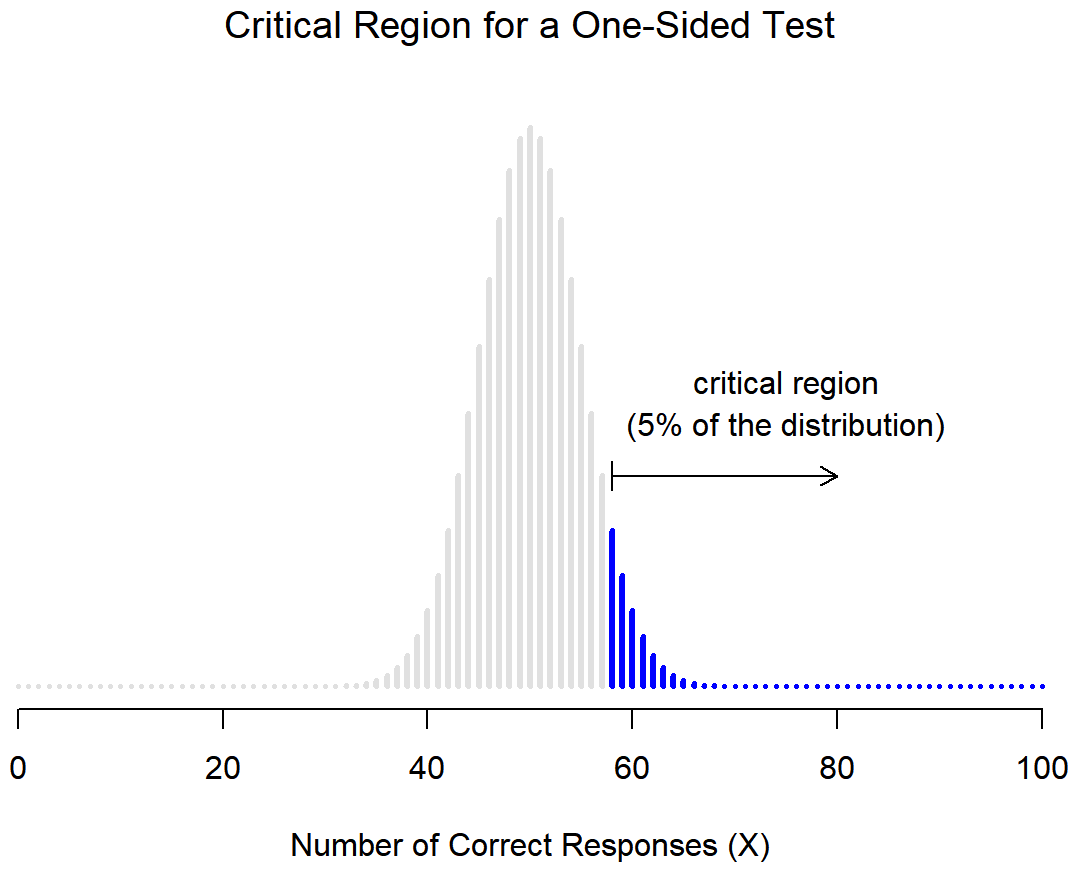
Clear as mud? Let's try one more way to describe how research hypotheses, null hypotheses, p-values, and null hypothesis significance testing work.

*The internet seems fairly convinced that Ashley said this, though I can’t for the life of me find anyone willing to give a source for the claim.

Contributors and Attributions

• Danielle Navarro ( University of New South Wales )

Dr. MO ( Taft College )

Directional vs Non-Directional Hypothesis – Collect Feedback More Effectively 

To conduct a perfect survey, you should know the basics of good research . That’s why in Startquestion we would like to share with you our knowledge about basic terms connected to online surveys and feedback gathering . Knowing the basis you can create surveys and conduct research in more effective ways and thanks to this get meaningful feedback from your customers, employees, and users. That’s enough for the introduction – let’s get to work. This time we will tell you about the hypothesis .

What is a Hypothesis?

A Hypothesis can be described as a theoretical statement built upon some evidence so that it can be tested as if it is true or false. In other words, a hypothesis is a speculation or an idea, based on insufficient evidence that allows it further analysis and experimentation.  

The purpose of a hypothetical statement is to work like a prediction based on studied research and to provide some estimated results before it ha happens in a real position. There can be more than one hypothesis statement involved in a research study, where you need to question and explore different aspects of a proposed research topic. Before putting your research into directional vs non-directional hypotheses, let’s have some basic knowledge.

Most often, a hypothesis describes a relation between two or more variables. It includes:

An Independent variable – One that is controlled by the researcher

Dependent Variable – The variable that the researcher observes in association with the Independent variable.

Try one of the best survey tools for free!

Start trial period without any credit card or subscription. Easily conduct your research and gather feedback via link, social media, email, and more.

Create first survey

No credit card required · Cancel any time · GDRP Compilant

How to write an effective Hypothesis?

To write an effective hypothesis follow these essential steps.

• Inquire a Question

The very first step in writing an effective hypothesis is raising a question. Outline the research question very carefully keeping your research purpose in mind. Build it in a precise and targeted way. Here you must be clear about the research question vs hypothesis. A research question is the very beginning point of writing an effective hypothesis.

Do Literature Review

Once you are done with constructing your research question, you can start the literature review. A literature review is a collection of preliminary research studies done on the same or relevant topics. There is a diversified range of literature reviews. The most common ones are academic journals but it is not confined to that. It can be anything including your research, data collection, and observation.

At this point, you can build a conceptual framework. It can be defined as a visual representation of the estimated relationship between two variables subjected to research.

Frame an Answer

After a collection of literature reviews, you can find ways how to answer the question. Expect this stage as a point where you will be able to make a stand upon what you believe might have the exact outcome of your research. You must formulate this answer statement clearly and concisely.

Build a Hypothesis

At this point, you can firmly build your hypothesis. By now, you knew the answer to your question so make a hypothesis that includes:

• Applicable Variables                     
• Particular Group being Studied (Who/What)
• Probable Outcome of the Experiment

Remember, your hypothesis is a calculated assumption, it has to be constructed as a sentence, not a question. This is where research question vs hypothesis starts making sense.

Refine a Hypothesis

Make necessary amendments to the constructed hypothesis keeping in mind that it has to be targeted and provable. Moreover, you might encounter certain circumstances where you will be studying the difference between one or more groups. It can be correlational research. In such instances, you must have to testify the relationships that you believe you will find in the subject variables and through this research.

Build Null Hypothesis

Certain research studies require some statistical investigation to perform a data collection. Whenever applying any scientific method to construct a hypothesis, you must have adequate knowledge of the Null Hypothesis and an Alternative hypothesis.

Null Hypothesis: 

A null Hypothesis denotes that there is no statistical relationship between the subject variables. It is applicable for a single group of variables or two groups of variables. A Null Hypothesis is denoted as an H0. This is the type of hypothesis that the researcher tries to invalidate. Some of the examples of null hypotheses are:

–        Hyperactivity is not associated with eating sugar.

–        All roses have an equal amount of petals.

–        A person’s preference for a dress is not linked to its color.

Alternative Hypothesis: 

An alternative hypothesis is a statement that is simply inverse or opposite of the null hypothesis and denoted as H1. Simply saying, it is an alternative statement for the null hypothesis. The same examples will go this way as an alternative hypothesis:

–        Hyperactivity is associated with eating sugar.

–        All roses do not have an equal amount of petals.

–        A person’s preference for a dress is linked to its color.

Start your research right now: use professional survey templates

• Brand Awareness Survey
• Survey for the thesis
• Website Evaluation Survey

See more templates

Types of Hypothesis

Apart from null and alternative hypotheses, research hypotheses can be categorized into different types. Let’s have a look at them:

Simple Hypothesis:

This type of hypothesis is used to state a relationship between a particular independent variable and only a dependent variable.

Complex Hypothesis:

A statement that states the relationship between two or more independent variables and two or more dependent variables, is termed a complex hypothesis.

Associative and Causal Hypothesis:

This type of hypothesis involves predicting that there is a point of interdependency between two variables. It says that any kind of change in one variable will cause a change in the other one.  Similarly, a casual hypothesis says that a change in the dependent variable is due to some variations in the independent variable.

Directional vs non-directional hypothesis

Directional hypothesis:.

A hypothesis that is built upon a certain directional relationship between two variables and constructed upon an already existing theory, is called a directional hypothesis. To understand more about what is directional hypothesis here is an example, Girls perform better than boys (‘better than’ shows the direction predicted)

Non-directional Hypothesis:

It involves an open-ended non-directional hypothesis that predicts that the independent variable will influence the dependent variable; however, the nature or direction of a relationship between two subject variables is not defined or clear.

For Example, there will be a difference in the performance of girls & boys (Not defining what kind of difference)

As a professional, we suggest you apply a non-directional alternative hypothesis when you are not sure of the direction of the relationship. Maybe you’re observing potential gender differences on some psychological test, but you don’t know whether men or women would have the higher ratio. Normally, this would say that you are lacking practical knowledge about the proposed variables. A directional test should be more common for tests. 

Author: Ula Kamburov-Niepewna

Updated: 18 November 2022

12 Post Event Survey Questions to Ask

After your meticulously planned event concludes, there’s one crucial step left: gathering feedback. Post-event surveys are invaluable tools for understanding attendee experiences, identifying areas for improvement, and maintaining attendee satisfaction.

Yes or No Questions in Online Surveys

This article will discuss the benefits of using yes or no questions, explore common examples, and provide practical tips for using them effectively in your surveys.

How to Write Good Survey Questions

In this comprehensive guide, we will explore the impact of poorly designed survey questions, offer tips for crafting excellent and unbiased questionnaires, and provide examples of valid survey questions.

• Math Article

Null Hypothesis

In mathematics, Statistics deals with the study of research and surveys on the numerical data. For taking surveys, we have to define the hypothesis. Generally, there are two types of hypothesis. One is a null hypothesis, and another is an alternative hypothesis .

In probability and statistics, the null hypothesis is a comprehensive statement or default status that there is zero happening or nothing happening. For example, there is no connection among groups or no association between two measured events. It is generally assumed here that the hypothesis is true until any other proof has been brought into the light to deny the hypothesis. Let us learn more here with definition, symbol, principle, types and example, in this article.

Table of contents:

• Comparison with Alternative Hypothesis

Null Hypothesis Definition

The null hypothesis is a kind of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data. This hypothesis is either rejected or not rejected based on the viability of the given population or sample . In other words, the null hypothesis is a hypothesis in which the sample observations results from the chance. It is said to be a statement in which the surveyors wants to examine the data. It is denoted by H 0 .

Null Hypothesis Symbol

In statistics, the null hypothesis is usually denoted by letter H with subscript ‘0’ (zero), such that H 0 . It is pronounced as H-null or H-zero or H-nought. At the same time, the alternative hypothesis expresses the observations determined by the non-random cause. It is represented by H 1 or H a .

Null Hypothesis Principle

The principle followed for null hypothesis testing is, collecting the data and determining the chances of a given set of data during the study on some random sample, assuming that the null hypothesis is true. In case if the given data does not face the expected null hypothesis, then the outcome will be quite weaker, and they conclude by saying that the given set of data does not provide strong evidence against the null hypothesis because of insufficient evidence. Finally, the researchers tend to reject that.

Null Hypothesis Formula

Here, the hypothesis test formulas are given below for reference.

The formula for the null hypothesis is:

H 0 :  p = p 0

The formula for the alternative hypothesis is:

H a = p >p 0 , < p 0 ≠ p 0

The formula for the test static is:

Remember that,  p 0  is the null hypothesis and p – hat is the sample proportion.

Also, read:

Types of Null Hypothesis

There are different types of hypothesis. They are:

Simple Hypothesis

It completely specifies the population distribution. In this method, the sampling distribution is the function of the sample size.

Composite Hypothesis

The composite hypothesis is one that does not completely specify the population distribution.

Exact Hypothesis

Exact hypothesis defines the exact value of the parameter. For example μ= 50

Inexact Hypothesis

This type of hypothesis does not define the exact value of the parameter. But it denotes a specific range or interval. For example 45< μ <60

Null Hypothesis Rejection

Sometimes the null hypothesis is rejected too. If this hypothesis is rejected means, that research could be invalid. Many researchers will neglect this hypothesis as it is merely opposite to the alternate hypothesis. It is a better practice to create a hypothesis and test it. The goal of researchers is not to reject the hypothesis. But it is evident that a perfect statistical model is always associated with the failure to reject the null hypothesis.

How do you Find the Null Hypothesis?

The null hypothesis says there is no correlation between the measured event (the dependent variable) and the independent variable. We don’t have to believe that the null hypothesis is true to test it. On the contrast, you will possibly assume that there is a connection between a set of variables ( dependent and independent).

When is Null Hypothesis Rejected?

The null hypothesis is rejected using the P-value approach. If the P-value is less than or equal to the α, there should be a rejection of the null hypothesis in favour of the alternate hypothesis. In case, if P-value is greater than α, the null hypothesis is not rejected.

Null Hypothesis and Alternative Hypothesis

Now, let us discuss the difference between the null hypothesis and the alternative hypothesis.

Null Hypothesis Examples

Here, some of the examples of the null hypothesis are given below. Go through the below ones to understand the concept of the null hypothesis in a better way.

If a medicine reduces the risk of cardiac stroke, then the null hypothesis should be “the medicine does not reduce the chance of cardiac stroke”. This testing can be performed by the administration of a drug to a certain group of people in a controlled way. If the survey shows that there is a significant change in the people, then the hypothesis is rejected.

Few more examples are:

1). Are there is 100% chance of getting affected by dengue?

Ans: There could be chances of getting affected by dengue but not 100%.

2). Do teenagers are using mobile phones more than grown-ups to access the internet?

Ans: Age has no limit on using mobile phones to access the internet.

3). Does having apple daily will not cause fever?

Ans: Having apple daily does not assure of not having fever, but increases the immunity to fight against such diseases.

4). Do the children more good in doing mathematical calculations than grown-ups?

Ans: Age has no effect on Mathematical skills.

In many common applications, the choice of the null hypothesis is not automated, but the testing and calculations may be automated. Also, the choice of the null hypothesis is completely based on previous experiences and inconsistent advice. The choice can be more complicated and based on the variety of applications and the diversity of the objectives. 

The main limitation for the choice of the null hypothesis is that the hypothesis suggested by the data is based on the reasoning which proves nothing. It means that if some hypothesis provides a summary of the data set, then there would be no value in the testing of the hypothesis on the particular set of data. 

Frequently Asked Questions on Null Hypothesis

What is meant by the null hypothesis.

In Statistics, a null hypothesis is a type of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data.

What are the benefits of hypothesis testing?

Hypothesis testing is defined as a form of inferential statistics, which allows making conclusions from the entire population based on the sample representative.

When a null hypothesis is accepted and rejected?

The null hypothesis is either accepted or rejected in terms of the given data. If P-value is less than α, then the null hypothesis is rejected in favor of the alternative hypothesis, and if the P-value is greater than α, then the null hypothesis is accepted in favor of the alternative hypothesis.

Why is the null hypothesis important?

The importance of the null hypothesis is that it provides an approximate description of the phenomena of the given data. It allows the investigators to directly test the relational statement in a research study.

How to accept or reject the null hypothesis in the chi-square test?

If the result of the chi-square test is bigger than the critical value in the table, then the data does not fit the model, which represents the rejection of the null hypothesis.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.