hypothesis testing in nursing

The P value: What it really means

As nurses, we must administer nursing care based on the best available scientific evidence. But for many nurses, critical appraisal, the process used to determine the best available evidence, can seem intimidating. To make critical appraisal more approachable, let’s examine the P value and make sure we know what it is and what it isn’t.

Defining P value

The P value is the probability that the results of a study are caused by chance alone. To better understand this definition, consider the role of chance.

The concept of chance is illustrated with every flip of a coin. The true probability of obtaining heads in any single flip is 0.5, meaning that heads would come up in half of the flips and tails would come up in half of the flips. But if you were to flip a coin 10 times, you likely would not obtain heads five times and tails five times. You’d be more likely to see a seven-to-three split or a six-to-four split. Chance is responsible for this variation in results.

Just as chance plays a role in determining the flip of a coin, it plays a role in the sampling of a population for a scientific study. When subjects are selected, chance may produce an unequal distribution of a characteristic that can affect the outcome of the study. Statistical inquiry and the P value are designed to help us determine just how large a role chance plays in study results. We begin a study with the assumption that there will be no difference between the experimental and control groups. This assumption is called the null hypothesis. When the results of the study indicate that there is a difference, the P value helps us determine the likelihood that the difference is attributed to chance.

Competing hypotheses

In every study, researchers put forth two kinds of hypotheses: the research or alternative hypothesis and the null hypothesis. The research hypothesis reflects what the researchers hope to show—that there is a difference between the experimental group and the control group. The null hypothesis directly competes with the research hypothesis. It states that there is no difference between the experimental group and the control group.

It may seem logical that researchers would test the research hypothesis—that is, that they would test what they hope to prove. But the probability theory requires that they test the null hypothesis instead. To support the research hypothesis, the data must contradict the null hypothesis. By demonstrating a difference between the two groups, the data contradict the null hypothesis.

Testing the null hypothesis

Now that you know why we test the null hypothesis, let’s look at how we test the null hypothesis.

After formulating the null and research hypotheses, researchers decide on a test statistic they can use to determine whether to accept or reject the null hypothesis. They also propose a fixed-level P value. The fixed level P value is often set at .05 and serves as the value against which the test-generated P value must be compared. (See Why .05?)

A comparison of the two P values determines whether the null hypothesis is rejected or accepted. If the P value associated with the test statistic is less than the fixed-level P value, the null hypothesis is rejected because there’s a statistically significant difference between the two groups. If the P value associated with the test statistic is greater than the fixed-level P value, the null hypothesis is accepted because there’s no statistically significant difference between the groups.

The decision to use .05 as the threshold in testing the null hypothesis is completely arbitrary. The researchers credited with establishing this threshold warned against strictly adhering to it.

Remember that warning when appraising a study in which the test statistic is greater than .05. The savvy reader will consider other important measurements, including effect size, confidence intervals, and power analyses when deciding whether to accept or reject scientific findings that could influence nursing practice.

Real-world hypothesis testing

How does this play out in real life? Let’s assume that you and a nurse colleague are conducting a study to find out if patients who receive backrubs fall asleep faster than patients who do not receive backrubs.

1. State your null and research hypotheses

Your null hypothesis will be that there will be no difference in the average amount of time it takes patients in each group to fall asleep. Your research hypothesis will be that patients who receive backrubs fall asleep, on average, faster than those who do not receive backrubs. You will be testing the null hypothesis in hopes of supporting your research hypothesis.

2. Propose a fixed-level P value

Although you can choose any value as your fixed-level P value, you and your research colleague decide you’ll stay with the conventional .05. If you were testing a new medical product or a new drug, you would choose a much smaller P value (perhaps as small as .0001). That’s because you would want to be as sure as possible that any difference you see between groups is attributed to the new product or drug and not to chance. A fixed-level P value of .0001 would mean that the difference between the groups was attributed to chance only 1 time out of 10,000. For a study on backrubs, however, .05 seems appropriate.

3. Conduct hypothesis testing to calculate a probability value

You and your research colleague agree that a randomized controlled study will help you best achieve your research goals, and you design the process accordingly. After consenting to participate in the study, patients are randomized to one of two groups:

• the experimental group that receives the intervention—the backrub group
• the control group—the non-backrub group.

After several nights of measuring the number of minutes it takes each participant to fall asleep, you and your research colleague find that on average, the backrub group takes 19 minutes to fall asleep and the non-backrub group takes 24 minutes to fall asleep.

Now the question is: Would you have the same results if you conducted the study using two different groups of people? That is, what role did chance play in helping the backrub group fall asleep 5 minutes faster than the non-backrub group? To answer this, you and your colleague will use an independent samples t-test to calculate a probability value.

An independent samples t-test is a kind of hypothesis test that compares the mean values of two groups (backrub and non-backrub) on a given variable (time to fall asleep).

Hypothesis testing is really nothing more than testing the null hypothesis. In this case, the null hypothesis is that the amount of time needed to fall asleep is the same for the experimental group and the control group. The hypothesis test addresses this question: If there’s really no difference between the groups, what is the probability of observing a difference of 5 minutes or more, say 10 minutes or 15 minutes?

We can define the P value as the probability that the observed time difference resulted from chance. Some find it easier to understand the P value when they think of it in relationship to error. In this case, the P value is defined as the probability of committing a Type 1 error. (Type 1 error occurs when a true null hypothesis is incorrectly rejected.)

4. Compare and interpret the P value

Early on in your study, you and your colleague selected a fixed-level P value of .05, meaning that you were willing to accept that 5% of the time, your results might be caused by chance. Also, you used an independent samples t-test to arrive at a probability value that will help you determine the role chance played in obtaining your results. Let’s assume, for the sake of this example, that the probability value generated by the independent samples t-test is .01 (P = .01). Because this P value associated with the test statistic is less than the fixed-level statistic (.01 < .05), you can reject the null hypothesis. By doing so, you declare that there is a statistically significant difference between the experimental and control groups. (See Putting the P value in context.)

In effect, you’re saying that the chance of observing a difference of 5 minutes or more, when in fact there is no difference, is less than 5 in 100. If the P value associated with the test statistic would have been greater than .05, then you would accept the null hypothesis, which would mean that there is no statistically significant difference between the control and experimental groups. Accepting the null hypothesis would mean that a difference of 5 minutes or more between the two groups would occur more than 5 times in 100.

Putting the P value in context

Although the P value helps you interpret study results, keep in mind that many factors can influence the P value—and your decision to accept or reject the null hypothesis. These factors include the following:

• Insufficient power. The study may not have been designed appropriately to detect an effect of the independent variable on the dependent variable. Therefore, a change may have occurred without your knowing it, causing you to incorrectly reject your hypothesis.
• Unreliable measures. Instruments that don’t meet consistency or reliability standards may have been used to measure a particular phenomenon.
• Threats to internal validity. Various biases, such as selection of patients, regression, history, and testing bias, may unduly influence study outcomes.

A decision to accept or reject study findings should focus not only on P value but also on other metrics including the following:

• Confidence intervals (an estimated range of values with a high probability of including the true population value of a given parameter)
• Effect size (a value that measures the magnitude of a treatment effect)

Remember, P value tells you only whether a difference exists between groups. It doesn’t tell you the magnitude of the difference.

5. Communicate your findings

The final step in hypothesis testing is communicating your findings. When sharing research findings (hypotheses) in writing or discussion, understand that they are statements of relationships or differences in populations. Your findings are not proved or disproved. Scientific findings are always subject to change. But each study leads to better understanding and, ideally, better outcomes for patients.

Key concepts

The P value isn’t the only concept you need to understand to analyze research findings. But it is a very important one. And chances are that understanding the P value will make it easier to understand other key analytical concepts.

Selected references

Burns N, Grove S: The Practice of Nursing Research: Conduct, Critique, and Utilization. 5th ed. Philadelphia: WB Saunders; 2004.

Glaser DN: The controversy of significance testing: misconceptions and alternatives. Am J Crit Care. 1999;8(5):291-296.

Kenneth J. Rempher, PhD, RN, MBA, CCRN, APRN,BC, is Director, Professional Nursing Practice at Sinai Hospital of Baltimore (Md.). Kathleen Urquico, BSN, RN, is a Direct Care Nurse in the Rubin Institute of Advanced Orthopedics at Sinai Hospital of Baltimore.

NurseLine Newsletter

• First Name *
• Last Name *
• Hidden Referrer

*By submitting your e-mail, you are opting in to receiving information from Healthcom Media and Affiliates. The details, including your email address/mobile number, may be used to keep you informed about future products and services.

Test Your Knowledge

Recent posts.

Interpreting statistical significance in nursing research

Introduction to qualitative nursing research

Navigating statistics for successful project implementation

Nurse research and the institutional review board

Research 101: Descriptive statistics

Research 101: Forest plots

Understanding confidence intervals helps you make better clinical decisions

Differentiating statistical significance and clinical significance

Differentiating research, evidence-based practice, and quality improvement

Are you confident about confidence intervals?

Making sense of statistical power

• Physician Physician Board Reviews Physician Associate Board Reviews CME Lifetime CME Free CME
• Student USMLE Step 1 USMLE Step 2 USMLE Step 3 COMLEX Level 1 COMLEX Level 2 COMLEX Level 3 96 Medical School Exams Student Resource Center NCLEX - RN NCLEX - LPN/LVN/PN 24 Nursing Exams
• Nurse Practitioner APRN/NP Board Reviews CNS Certification Reviews CE - Nurse Practitioner FREE CE
• Nurse RN Certification Reviews CE - Nurse FREE CE
• Pharmacist Pharmacy Board Exam Prep CE - Pharmacist
• Allied Allied Health Exam Prep Dentist Exams CE - Social Worker CE - Dentist
• Point of Care
• Free CME/CE

Hypothesis Testing, P Values, Confidence Intervals, and Significance

Definition/introduction.

Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting these findings, which may affect the adequate application of the data.

Issues of Concern

Register for free and read the full article, learn more about a subscription to statpearls point-of-care.

Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. Therefore, an overview of these concepts is provided to allow medical professionals to use their expertise to determine if results are reported sufficiently and if the study outcomes are clinically appropriate to be applied in healthcare practice.

Hypothesis Testing

Investigators conducting studies need research questions and hypotheses to guide analyses. Starting with broad research questions (RQs), investigators then identify a gap in current clinical practice or research. Any research problem or statement is grounded in a better understanding of relationships between two or more variables. For this article, we will use the following research question example:

Research Question: Is Drug 23 an effective treatment for Disease A?

Research questions do not directly imply specific guesses or predictions; we must formulate research hypotheses. A hypothesis is a predetermined declaration regarding the research question in which the investigator(s) makes a precise, educated guess about a study outcome. This is sometimes called the alternative hypothesis and ultimately allows the researcher to take a stance based on experience or insight from medical literature. An example of a hypothesis is below.

Research Hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.

The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis.

Researchers should be aware of journal recommendations when considering how to report p values, and manuscripts should remain internally consistent.

Regarding p values, as the number of individuals enrolled in a study (the sample size) increases, the likelihood of finding a statistically significant effect increases. With very large sample sizes, the p-value can be very low significant differences in the reduction of symptoms for Disease A between Drug 23 and Drug 22. The null hypothesis is deemed true until a study presents significant data to support rejecting the null hypothesis. Based on the results, the investigators will either reject the null hypothesis (if they found significant differences or associations) or fail to reject the null hypothesis (they could not provide proof that there were significant differences or associations).

To test a hypothesis, researchers obtain data on a representative sample to determine whether to reject or fail to reject a null hypothesis. In most research studies, it is not feasible to obtain data for an entire population. Using a sampling procedure allows for statistical inference, though this involves a certain possibility of error. [1]  When determining whether to reject or fail to reject the null hypothesis, mistakes can be made: Type I and Type II errors. Though it is impossible to ensure that these errors have not occurred, researchers should limit the possibilities of these faults. [2]

Significance

Significance is a term to describe the substantive importance of medical research. Statistical significance is the likelihood of results due to chance. [3]  Healthcare providers should always delineate statistical significance from clinical significance, a common error when reviewing biomedical research. [4]  When conceptualizing findings reported as either significant or not significant, healthcare providers should not simply accept researchers' results or conclusions without considering the clinical significance. Healthcare professionals should consider the clinical importance of findings and understand both p values and confidence intervals so they do not have to rely on the researchers to determine the level of significance. [5]  One criterion often used to determine statistical significance is the utilization of p values.

P values are used in research to determine whether the sample estimate is significantly different from a hypothesized value. The p-value is the probability that the observed effect within the study would have occurred by chance if, in reality, there was no true effect. Conventionally, data yielding a p<0.05 or p<0.01 is considered statistically significant. While some have debated that the 0.05 level should be lowered, it is still universally practiced. [6]  Hypothesis testing allows us to determine the size of the effect.

An example of findings reported with p values are below:

Statement: Drug 23 reduced patients' symptoms compared to Drug 22. Patients who received Drug 23 (n=100) were 2.1 times less likely than patients who received Drug 22 (n = 100) to experience symptoms of Disease A, p<0.05.

Statement:Individuals who were prescribed Drug 23 experienced fewer symptoms (M = 1.3, SD = 0.7) compared to individuals who were prescribed Drug 22 (M = 5.3, SD = 1.9). This finding was statistically significant, p= 0.02.

For either statement, if the threshold had been set at 0.05, the null hypothesis (that there was no relationship) should be rejected, and we should conclude significant differences. Noticeably, as can be seen in the two statements above, some researchers will report findings with < or > and others will provide an exact p-value (0.000001) but never zero [6] . When examining research, readers should understand how p values are reported. The best practice is to report all p values for all variables within a study design, rather than only providing p values for variables with significant findings. [7]  The inclusion of all p values provides evidence for study validity and limits suspicion for selective reporting/data mining.  

While researchers have historically used p values, experts who find p values problematic encourage the use of confidence intervals. [8] . P-values alone do not allow us to understand the size or the extent of the differences or associations. [3]  In March 2016, the American Statistical Association (ASA) released a statement on p values, noting that scientific decision-making and conclusions should not be based on a fixed p-value threshold (e.g., 0.05). They recommend focusing on the significance of results in the context of study design, quality of measurements, and validity of data. Ultimately, the ASA statement noted that in isolation, a p-value does not provide strong evidence. [9]

When conceptualizing clinical work, healthcare professionals should consider p values with a concurrent appraisal study design validity. For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study [7] . The p-value debate has smoldered since the 1950s [10] , and replacement with confidence intervals has been suggested since the 1980s. [11]

Confidence Intervals

A confidence interval provides a range of values within given confidence (e.g., 95%), including the accurate value of the statistical constraint within a targeted population. [12]  Most research uses a 95% CI, but investigators can set any level (e.g., 90% CI, 99% CI). [13]  A CI provides a range with the lower bound and upper bound limits of a difference or association that would be plausible for a population. [14]  Therefore, a CI of 95% indicates that if a study were to be carried out 100 times, the range would contain the true value in 95, [15]  confidence intervals provide more evidence regarding the precision of an estimate compared to p-values. [6]

In consideration of the similar research example provided above, one could make the following statement with 95% CI:

Statement: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22; there was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

It is important to note that the width of the CI is affected by the standard error and the sample size; reducing a study sample number will result in less precision of the CI (increase the width). [14]  A larger width indicates a smaller sample size or a larger variability. [16]  A researcher would want to increase the precision of the CI. For example, a 95% CI of 1.43 – 1.47 is much more precise than the one provided in the example above. In research and clinical practice, CIs provide valuable information on whether the interval includes or excludes any clinically significant values. [14]

Null values are sometimes used for differences with CI (zero for differential comparisons and 1 for ratios). However, CIs provide more information than that. [15]  Consider this example: A hospital implements a new protocol that reduced wait time for patients in the emergency department by an average of 25 minutes (95% CI: -2.5 – 41 minutes). Because the range crosses zero, implementing this protocol in different populations could result in longer wait times; however, the range is much higher on the positive side. Thus, while the p-value used to detect statistical significance for this may result in "not significant" findings, individuals should examine this range, consider the study design, and weigh whether or not it is still worth piloting in their workplace.

Similarly to p-values, 95% CIs cannot control for researchers' errors (e.g., study bias or improper data analysis). [14]  In consideration of whether to report p-values or CIs, researchers should examine journal preferences. When in doubt, reporting both may be beneficial. [13]  An example is below:

Reporting both: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22, p = 0.009. There was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

Clinical Significance

Recall that clinical significance and statistical significance are two different concepts. Healthcare providers should remember that a study with statistically significant differences and large sample size may be of no interest to clinicians, whereas a study with smaller sample size and statistically non-significant results could impact clinical practice. [14]  Additionally, as previously mentioned, a non-significant finding may reflect the study design itself rather than relationships between variables.

Healthcare providers using evidence-based medicine to inform practice should use clinical judgment to determine the practical importance of studies through careful evaluation of the design, sample size, power, likelihood of type I and type II errors, data analysis, and reporting of statistical findings (p values, 95% CI or both). [4]  Interestingly, some experts have called for "statistically significant" or "not significant" to be excluded from work as statistical significance never has and will never be equivalent to clinical significance. [17]

The decision on what is clinically significant can be challenging, depending on the providers' experience and especially the severity of the disease. Providers should use their knowledge and experiences to determine the meaningfulness of study results and make inferences based not only on significant or insignificant results by researchers but through their understanding of study limitations and practical implications.

Nursing, Allied Health, and Interprofessional Team Interventions

All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts in this chapter. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care. 

Jones M, Gebski V, Onslow M, Packman A. Statistical power in stuttering research: a tutorial. Journal of speech, language, and hearing research : JSLHR. 2002 Apr:45(2):243-55     [PubMed PMID: 12003508]

Sedgwick P. Pitfalls of statistical hypothesis testing: type I and type II errors. BMJ (Clinical research ed.). 2014 Jul 3:349():g4287. doi: 10.1136/bmj.g4287. Epub 2014 Jul 3     [PubMed PMID: 24994622]

Fethney J. Statistical and clinical significance, and how to use confidence intervals to help interpret both. Australian critical care : official journal of the Confederation of Australian Critical Care Nurses. 2010 May:23(2):93-7. doi: 10.1016/j.aucc.2010.03.001. Epub 2010 Mar 29     [PubMed PMID: 20347326]

Hayat MJ. Understanding statistical significance. Nursing research. 2010 May-Jun:59(3):219-23. doi: 10.1097/NNR.0b013e3181dbb2cc. Epub     [PubMed PMID: 20445438]

Ferrill MJ, Brown DA, Kyle JA. Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. Journal of pharmacy practice. 2010 Aug:23(4):344-51. doi: 10.1177/0897190009358774. Epub 2010 Apr 13     [PubMed PMID: 21507834]

Infanger D, Schmidt-Trucksäss A. P value functions: An underused method to present research results and to promote quantitative reasoning. Statistics in medicine. 2019 Sep 20:38(21):4189-4197. doi: 10.1002/sim.8293. Epub 2019 Jul 3     [PubMed PMID: 31270842]

Dorey F. Statistics in brief: Interpretation and use of p values: all p values are not equal. Clinical orthopaedics and related research. 2011 Nov:469(11):3259-61. doi: 10.1007/s11999-011-2053-1. Epub     [PubMed PMID: 21918804]

Liu XS. Implications of statistical power for confidence intervals. The British journal of mathematical and statistical psychology. 2012 Nov:65(3):427-37. doi: 10.1111/j.2044-8317.2011.02035.x. Epub 2011 Oct 25     [PubMed PMID: 22026811]

Tijssen JG, Kolm P. Demystifying the New Statistical Recommendations: The Use and Reporting of p Values. Journal of the American College of Cardiology. 2016 Jul 12:68(2):231-3. doi: 10.1016/j.jacc.2016.05.026. Epub     [PubMed PMID: 27386779]

Spanos A. Recurring controversies about P values and confidence intervals revisited. Ecology. 2014 Mar:95(3):645-51     [PubMed PMID: 24804448]

Freire APCF, Elkins MR, Ramos EMC, Moseley AM. Use of 95% confidence intervals in the reporting of between-group differences in randomized controlled trials: analysis of a representative sample of 200 physical therapy trials. Brazilian journal of physical therapy. 2019 Jul-Aug:23(4):302-310. doi: 10.1016/j.bjpt.2018.10.004. Epub 2018 Oct 16     [PubMed PMID: 30366845]

Dorey FJ. In brief: statistics in brief: Confidence intervals: what is the real result in the target population? Clinical orthopaedics and related research. 2010 Nov:468(11):3137-8. doi: 10.1007/s11999-010-1407-4. Epub     [PubMed PMID: 20532716]

Porcher R. Reporting results of orthopaedic research: confidence intervals and p values. Clinical orthopaedics and related research. 2009 Oct:467(10):2736-7. doi: 10.1007/s11999-009-0952-1. Epub 2009 Jun 30     [PubMed PMID: 19565303]

Gardner MJ, Altman DG. Confidence intervals rather than P values: estimation rather than hypothesis testing. British medical journal (Clinical research ed.). 1986 Mar 15:292(6522):746-50     [PubMed PMID: 3082422]

Cooper RJ, Wears RL, Schriger DL. Reporting research results: recommendations for improving communication. Annals of emergency medicine. 2003 Apr:41(4):561-4     [PubMed PMID: 12658257]

Doll H, Carney S. Statistical approaches to uncertainty: P values and confidence intervals unpacked. Equine veterinary journal. 2007 May:39(3):275-6     [PubMed PMID: 17520981]

Colquhoun D. The reproducibility of research and the misinterpretation of p-values. Royal Society open science. 2017 Dec:4(12):171085. doi: 10.1098/rsos.171085. Epub 2017 Dec 6     [PubMed PMID: 29308247]

Use the mouse wheel to zoom in and out, click and drag to pan the image

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• v.19(7); 2019 Jul

Hypothesis tests

Associated data.

• • Hypothesis tests are used to assess whether a difference between two samples represents a real difference between the populations from which the samples were taken.
• • A null hypothesis of ‘no difference’ is taken as a starting point, and we calculate the probability that both sets of data came from the same population. This probability is expressed as a p -value.
• • When the null hypothesis is false, p- values tend to be small. When the null hypothesis is true, any p- value is equally likely.

Learning objectives

By reading this article, you should be able to:

• • Explain why hypothesis testing is used.
• • Use a table to determine which hypothesis test should be used for a particular situation.
• • Interpret a p- value.

A hypothesis test is a procedure used in statistics to assess whether a particular viewpoint is likely to be true. They follow a strict protocol, and they generate a ‘ p- value’, on the basis of which a decision is made about the truth of the hypothesis under investigation. All of the routine statistical ‘tests’ used in research— t- tests, χ 2 tests, Mann–Whitney tests, etc.—are all hypothesis tests, and in spite of their differences they are all used in essentially the same way. But why do we use them at all?

Comparing the heights of two individuals is easy: we can measure their height in a standardised way and compare them. When we want to compare the heights of two small well-defined groups (for example two groups of children), we need to use a summary statistic that we can calculate for each group. Such summaries (means, medians, etc.) form the basis of descriptive statistics, and are well described elsewhere. 1 However, a problem arises when we try to compare very large groups or populations: it may be impractical or even impossible to take a measurement from everyone in the population, and by the time you do so, the population itself will have changed. A similar problem arises when we try to describe the effects of drugs—for example by how much on average does a particular vasopressor increase MAP?

To solve this problem, we use random samples to estimate values for populations. By convention, the values we calculate from samples are referred to as statistics and denoted by Latin letters ( x ¯ for sample mean; SD for sample standard deviation) while the unknown population values are called parameters , and denoted by Greek letters (μ for population mean, σ for population standard deviation).

Inferential statistics describes the methods we use to estimate population parameters from random samples; how we can quantify the level of inaccuracy in a sample statistic; and how we can go on to use these estimates to compare populations.

Sampling error

There are many reasons why a sample may give an inaccurate picture of the population it represents: it may be biased, it may not be big enough, and it may not be truly random. However, even if we have been careful to avoid these pitfalls, there is an inherent difference between the sample and the population at large. To illustrate this, let us imagine that the actual average height of males in London is 174 cm. If I were to sample 100 male Londoners and take a mean of their heights, I would be very unlikely to get exactly 174 cm. Furthermore, if somebody else were to perform the same exercise, it would be unlikely that they would get the same answer as I did. The sample mean is different each time it is taken, and the way it differs from the actual mean of the population is described by the standard error of the mean (standard error, or SEM ). The standard error is larger if there is a lot of variation in the population, and becomes smaller as the sample size increases. It is calculated thus:

where SD is the sample standard deviation, and n is the sample size.

As errors are normally distributed, we can use this to estimate a 95% confidence interval on our sample mean as follows:

We can interpret this as meaning ‘We are 95% confident that the actual mean is within this range.’

Some confusion arises at this point between the SD and the standard error. The SD is a measure of variation in the sample. The range x ¯ ± ( 1.96 × SD ) will normally contain 95% of all your data. It can be used to illustrate the spread of the data and shows what values are likely. In contrast, standard error tells you about the precision of the mean and is used to calculate confidence intervals.

One straightforward way to compare two samples is to use confidence intervals. If we calculate the mean height of two groups and find that the 95% confidence intervals do not overlap, this can be taken as evidence of a difference between the two means. This method of statistical inference is reasonably intuitive and can be used in many situations. 2 Many journals, however, prefer to report inferential statistics using p -values.

Inference testing using a null hypothesis

In 1925, the British statistician R.A. Fisher described a technique for comparing groups using a null hypothesis , a method which has dominated statistical comparison ever since. The technique itself is rather straightforward, but often gets lost in the mechanics of how it is done. To illustrate, imagine we want to compare the HR of two different groups of people. We take a random sample from each group, which we call our data. Then:

• (i) Assume that both samples came from the same group. This is our ‘null hypothesis’.
• (ii) Calculate the probability that an experiment would give us these data, assuming that the null hypothesis is true. We express this probability as a p- value, a number between 0 and 1, where 0 is ‘impossible’ and 1 is ‘certain’.
• (iii) If the probability of the data is low, we reject the null hypothesis and conclude that there must be a difference between the two groups.

Formally, we can define a p- value as ‘the probability of finding the observed result or a more extreme result, if the null hypothesis were true.’ Standard practice is to set a cut-off at p <0.05 (this cut-off is termed the alpha value). If the null hypothesis were true, a result such as this would only occur 5% of the time or less; this in turn would indicate that the null hypothesis itself is unlikely. Fisher described the process as follows: ‘Set a low standard of significance at the 5 per cent point, and ignore entirely all results which fail to reach this level. A scientific fact should be regarded as experimentally established only if a properly designed experiment rarely fails to give this level of significance.’ 3 This probably remains the most succinct description of the procedure.

A question which often arises at this point is ‘Why do we use a null hypothesis?’ The simple answer is that it is easy: we can readily describe what we would expect of our data under a null hypothesis, we know how data would behave, and we can readily work out the probability of getting the result that we did. It therefore makes a very simple starting point for our probability assessment. All probabilities require a set of starting conditions, in much the same way that measuring the distance to London needs a starting point. The null hypothesis can be thought of as an easy place to put the start of your ruler.

If a null hypothesis is rejected, an alternate hypothesis must be adopted in its place. The null and alternate hypotheses must be mutually exclusive, but must also between them describe all situations. If a null hypothesis is ‘no difference exists’ then the alternate should be simply ‘a difference exists’.

Hypothesis testing in practice

The components of a hypothesis test can be readily described using the acronym GOST: identify the Groups you wish to compare; define the Outcome to be measured; collect and Summarise the data; then evaluate the likelihood of the null hypothesis, using a Test statistic .

When considering groups, think first about how many. Is there just one group being compared against an audit standard, or are you comparing one group with another? Some studies may wish to compare more than two groups. Another situation may involve a single group measured at different points in time, for example before or after a particular treatment. In this situation each participant is compared with themselves, and this is often referred to as a ‘paired’ or a ‘repeated measures’ design. It is possible to combine these types of groups—for example a researcher may measure arterial BP on a number of different occasions in five different groups of patients. Such studies can be difficult, both to analyse and interpret.

In other studies we may want to see how a continuous variable (such as age or height) affects the outcomes. These techniques involve regression analysis, and are beyond the scope of this article.

The outcome measures are the data being collected. This may be a continuous measure, such as temperature or BMI, or it may be a categorical measure, such as ASA status or surgical specialty. Often, inexperienced researchers will strive to collect lots of outcome measures in an attempt to find something that differs between the groups of interest; if this is done, a ‘primary outcome measure’ should be identified before the research begins. In addition, the results of any hypothesis tests will need to be corrected for multiple measures.

The summary and the test statistic will be defined by the type of data that have been collected. The test statistic is calculated then transformed into a p- value using tables or software. It is worth looking at two common tests in a little more detail: the χ 2 test, and the t -test.

Categorical data: the χ 2 test

The χ 2 test of independence is a test for comparing categorical outcomes in two or more groups. For example, a number of trials have compared surgical site infections in patients who have been given different concentrations of oxygen perioperatively. In the PROXI trial, 4 685 patients received oxygen 80%, and 701 patients received oxygen 30%. In the 80% group there were 131 infections, while in the 30% group there were 141 infections. In this study, the groups were oxygen 80% and oxygen 30%, and the outcome measure was the presence of a surgical site infection.

The summary is a table ( Table 1 ), and the hypothesis test compares this table (the ‘observed’ table) with the table that would be expected if the proportion of infections in each group was the same (the ‘expected’ table). The test statistic is χ 2 , from which a p- value is calculated. In this instance the p -value is 0.64, which means that results like this would occur 64% of the time if the null hypothesis were true. We thus have no evidence to reject the null hypothesis; the observed difference probably results from sampling variation rather than from an inherent difference between the two groups.

Table 1

Summary of the results of the PROXI trial. Figures are numbers of patients.

Continuous data: the t- test

The t- test is a statistical method for comparing means, and is one of the most widely used hypothesis tests. Imagine a study where we try to see if there is a difference in the onset time of a new neuromuscular blocking agent compared with suxamethonium. We could enlist 100 volunteers, give them a general anaesthetic, and randomise 50 of them to receive the new drug and 50 of them to receive suxamethonium. We then time how long it takes (in seconds) to have ideal intubation conditions, as measured by a quantitative nerve stimulator. Our data are therefore a list of times. In this case, the groups are ‘new drug’ and suxamethonium, and the outcome is time, measured in seconds. This can be summarised by using means; the hypothesis test will compare the means of the two groups, using a p- value calculated from a ‘ t statistic’. Hopefully it is becoming obvious at this point that the test statistic is usually identified by a letter, and this letter is often cited in the name of the test.

The t -test comes in a number of guises, depending on the comparison being made. A single sample can be compared with a standard (Is the BMI of school leavers in this town different from the national average?); two samples can be compared with each other, as in the example above; or the same study subjects can be measured at two different times. The latter case is referred to as a paired t- test, because each participant provides a pair of measurements—such as in a pre- or postintervention study.

A large number of methods for testing hypotheses exist; the commonest ones and their uses are described in Table 2 . In each case, the test can be described by detailing the groups being compared ( Table 2 , columns) the outcome measures (rows), the summary, and the test statistic. The decision to use a particular test or method should be made during the planning stages of a trial or experiment. At this stage, an estimate needs to be made of how many test subjects will be needed. Such calculations are described in detail elsewhere. 5

Table 2

The principle types of hypothesis test. Tests comparing more than two samples can indicate that one group differs from the others, but will not identify which. Subsequent ‘post hoc’ testing is required if a difference is found.

Controversies surrounding hypothesis testing

Although hypothesis tests have been the basis of modern science since the middle of the 20th century, they have been plagued by misconceptions from the outset; this has led to what has been described as a crisis in science in the last few years: some journals have gone so far as to ban p -value s outright. 6 This is not because of any flaw in the concept of a p -value, but because of a lack of understanding of what they mean.

Possibly the most pervasive misunderstanding is the belief that the p- value is the chance that the null hypothesis is true, or that the p- value represents the frequency with which you will be wrong if you reject the null hypothesis (i.e. claim to have found a difference). This interpretation has frequently made it into the literature, and is a very easy trap to fall into when discussing hypothesis tests. To avoid this, it is important to remember that the p- value is telling us something about our sample , not about the null hypothesis. Put in simple terms, we would like to know the probability that the null hypothesis is true, given our data. The p- value tells us the probability of getting these data if the null hypothesis were true, which is not the same thing. This fallacy is referred to as ‘flipping the conditional’; the probability of an outcome under certain conditions is not the same as the probability of those conditions given that the outcome has happened.

A useful example is to imagine a magic trick in which you select a card from a normal deck of 52 cards, and the performer reveals your chosen card in a surprising manner. If the performer were relying purely on chance, this would only happen on average once in every 52 attempts. On the basis of this, we conclude that it is unlikely that the magician is simply relying on chance. Although simple, we have just performed an entire hypothesis test. We have declared a null hypothesis (the performer was relying on chance); we have even calculated a p -value (1 in 52, ≈0.02); and on the basis of this low p- value we have rejected our null hypothesis. We would, however, be wrong to suggest that there is a probability of 0.02 that the performer is relying on chance—that is not what our figure of 0.02 is telling us.

To explore this further we can create two populations, and watch what happens when we use simulation to take repeated samples to compare these populations. Computers allow us to do this repeatedly, and to see what p- value s are generated (see Supplementary online material). 7 Fig 1 illustrates the results of 100,000 simulated t -tests, generated in two set of circumstances. In Fig 1 a , we have a situation in which there is a difference between the two populations. The p- value s cluster below the 0.05 cut-off, although there is a small proportion with p >0.05. Interestingly, the proportion of comparisons where p <0.05 is 0.8 or 80%, which is the power of the study (the sample size was specifically calculated to give a power of 80%).

The p- value s generated when 100,000 t -tests are used to compare two samples taken from defined populations. ( a ) The populations have a difference and the p- value s are mostly significant. ( b ) The samples were taken from the same population (i.e. the null hypothesis is true) and the p- value s are distributed uniformly.

Figure 1 b depicts the situation where repeated samples are taken from the same parent population (i.e. the null hypothesis is true). Somewhat surprisingly, all p- value s occur with equal frequency, with p <0.05 occurring exactly 5% of the time. Thus, when the null hypothesis is true, a type I error will occur with a frequency equal to the alpha significance cut-off.

Figure 1 highlights the underlying problem: when presented with a p -value <0.05, is it possible with no further information, to determine whether you are looking at something from Fig 1 a or Fig 1 b ?

Finally, it cannot be stressed enough that although hypothesis testing identifies whether or not a difference is likely, it is up to us as clinicians to decide whether or not a statistically significant difference is also significant clinically.

Hypothesis testing: what next?

As mentioned above, some have suggested moving away from p -values, but it is not entirely clear what we should use instead. Some sources have advocated focussing more on effect size; however, without a measure of significance we have merely returned to our original problem: how do we know that our difference is not just a result of sampling variation?

One solution is to use Bayesian statistics. Up until very recently, these techniques have been considered both too difficult and not sufficiently rigorous. However, recent advances in computing have led to the development of Bayesian equivalents of a number of standard hypothesis tests. 8 These generate a ‘Bayes Factor’ (BF), which tells us how more (or less) likely the alternative hypothesis is after our experiment. A BF of 1.0 indicates that the likelihood of the alternate hypothesis has not changed. A BF of 10 indicates that the alternate hypothesis is 10 times more likely than we originally thought. A number of classifications for BF exist; greater than 10 can be considered ‘strong evidence’, while BF greater than 100 can be classed as ‘decisive’.

Figures such as the BF can be quoted in conjunction with the traditional p- value, but it remains to be seen whether they will become mainstream.

Declaration of interest

The author declares that they have no conflict of interest.

The associated MCQs (to support CME/CPD activity) will be accessible at www.bjaed.org/cme/home by subscribers to BJA Education .

Jason Walker FRCA FRSS BSc (Hons) Math Stat is a consultant anaesthetist at Ysbyty Gwynedd Hospital, Bangor, Wales, and an honorary senior lecturer at Bangor University. He is vice chair of his local research ethics committee, and an examiner for the Primary FRCA.

Matrix codes: 1A03, 2A04, 3J03

Supplementary data to this article can be found online at https://doi.org/10.1016/j.bjae.2019.03.006 .

Supplementary material

The following is the Supplementary data to this article:

Fastest Nurse Insight Engine

• MEDICAL ASSISSTANT
• Abdominal Key
• Anesthesia Key
• Basicmedical Key
• Otolaryngology & Ophthalmology
• Musculoskeletal Key
• Obstetric, Gynecology and Pediatric
• Oncology & Hematology
• Plastic Surgery & Dermatology
• Clinical Dentistry
• Radiology Key
• Thoracic Key
• Veterinary Medicine
• Gold Membership

Hypothesis testing: selection and use of statistical tests

20 Hypothesis testing selection and use of statistical tests Chapter Contents Introduction  The logic of hypothesis testing  Steps in hypothesis testing  Illustrations of hypothesis testing  The relationship between descriptive and inferential statistics  Selection of the appropriate inferential test  The χ 2 test  χ 2 and contingency tables  Statistical packages  Summary  Introduction Hypotheses are statements about the association between variables as pertaining to a specific person or population. For example, ‘penicillin is an effective treatment for pneumonia’ or ‘obesity is a risk factor for heart disease’. Hypotheses addressing the state of populations are tested using sample data. Inferences are conclusions based on data using samples and are therefore always open to the possibility of error. In this chapter we will examine the use of inferential statistics for establishing the probable truth of hypotheses, as tested through sample data. Inferential statistics are based on applied probability theory and entail the use of statistical tests. There are numerous statistical tests available that are used in a similar fashion to analyse clinical data. That is, all statistical tests involve setting up the relevant hypotheses, H 0 and H A , and then, on the basis of the appropriate inferential statistics, computing the probability of the sample statistics obtained occurring by chance alone. We are not going to attempt to examine all statistical tests in this introductory book. These are described in various statistics textbooks or in data analysis manuals. Rather, in this chapter we will examine the criteria used for selecting tests appropriate for the analysis of the data obtained in specific investigations. To illustrate the use of statistical tests we will examine the use of the chi-square test (χ 2 ). This is a statistical test commonly employed to analyse categorical data. Finally, we will briefly examine the uses of the Statistical Package for Social Sciences™ (SPSS) for data analysis in general. The aims of this chapter are to: 1.  Discuss the criteria by which a statistical test is selected for analysing the data for a specific study. 2.  Demonstrate the use of the χ 2 test for analysing nominal scale data. 3.  Explain how statistical packages are used for quantitative data analysis. The logic of hypothesis testing Hypothesis testing is the process of deciding using statistics whether the findings of an investigation reflect chance or real effects at a given level of probability or certainty. If the results seem to not represent chance effects, then we say that the results are statistically significant. That is, when we say that our results are statistically significant we mean that the patterns or differences seen in the sample data are likely to be generalizable to the wider population from our study sample. The mathematical procedures for hypothesis testing are based on the application of probability theory and sampling, as discussed previously. Because of the probabilistic nature of the process, decision errors in hypothesis testing cannot be entirely eliminated. However, the procedures outlined in this chapter enable us to specify the probability level at which we can claim that the data obtained in an investigation support experimental hypotheses. This procedure is fundamental for determining the statistical significance of the data as well as being relevant to the logic of clinical decision making. Steps in hypothesis testing The following steps are conventionally followed in hypothesis testing: 1.  State the alternative hypothesis (H A ), which is the based on the research hypothesis. The H A asserts that the results are ‘real’ or ‘significant’, i.e. that the independent variable influenced the dependent variable, or that there is a real difference among groups. The important point here is that H A is a statement concerning the population. A real or significant effect means that the results in the sample data can be generalized to the population. 2.  State the null hypothesis (H 0 ), which is the logical opposite of the H A . The H 0 claims that any differences in the data were just due to chance: that the independent variable had no effect on the dependent variable, or that any difference among groups is due to random effects. In other words, if the H 0 is retained, differences or patterns seen in the sample data should not be generalized to the population. 3.  Set the decision level, α (alpha). There are two mutually exclusive hypotheses (H A and H 0 ) competing to explain the results of an investigation. Hypothesis testing, or statistical decision making, involves establishing the probability of H 0 being true. If this probability is very small, we are in a position to reject the H 0 . You might ask ‘How small should the probability (α) be for rejecting H 0 ?’ By convention, we use the probability of α = 0.05. If the H 0 being true is less than 0.05, we can reject H 0 . We can choose an α of 0.05, but not more, That is, by convention among researchers, results are not characterized as significant if p > 0.05. 4.  Calculate the probability of H 0 being true. That is, we assume that H 0 is true and calculate the probability of the outcome of the investigation being due to chance alone, i.e. due to random effects. We must use an appropriate sampling distribution for this calculation. 5.  Make a decision concerning H 0 . The following decision rule is used. If the probability of H 0 being true is less than α, then we reject H 0 at the level of significance set by α. However, if the probability of H 0 is greater than α, then we must retain H 0 . In other words, if: a.  p (H 0 is true) ≤ α, reject H 0 b.  p (H 0 is true) > α, retain H 0 It follows that if we reject H 0 we are in a position to accept H A , its logical alternative. If p ≤ 0.05 then we reject H 0 , and decide that H A is probably true. Illustrations of hypothesis testing One of the simplest forms of gambling is betting on the fall of a coin. Let us play a little game. We, the authors, will toss a coin. If it comes out heads (H) you will give us ≤1; if it comes out tails (T) we will give you ≤1. To make things interesting, let us have 10 tosses. The results are: Oh dear, you seem to have lost. Never mind, we were just lucky, so send along your cheque for ≤10. Are you a little hesitant? Are you saying that we ‘fixed’ the game? There is a systematic procedure for demonstrating the probable truth of your allegations: 1.  We can state two competing hypotheses concerning the outcome of the game: a.  the authors fixed the game; that is, the outcome did not reflect the fair throwing of a coin. Let us call this statement the ‘alternative hypothesis’, H A . In effect, the H A claims that the sample of 10 heads came from a population other than P (probability of heads) = Q (probability of tails) = 0.5 b.  the authors did not fix the game; that is, the outcome is due to the tossing of a fair coin. Let us call this statement the ‘null hypothesis’, or H 0 . H 0 suggests that the sample of 10 heads was a random sample from a population where P = Q = 0.5. 2.  It can be shown that the probability of tossing 10 consecutive heads with a fair coin is actually p = 0.001, as discussed previously (see Ch. 19). That is, the probability of obtaining such a sample from a population where P = Q = 0.5 is extremely low. 3.  Now we can decide between H 0 and H A . It was shown that the probability of H 0 being true was p = 0.001 (1 in a 1000). Therefore, in the balance of probabilities, we can reject it as being true and accept H A , which is the logical alternative. In other words, it is likely that the game was fixed and no ≤10 cheque needed to be posted. The probability of calculating the truth of H 0 depended on the number of tosses ( n = the sample size). For instance, the probability of obtaining heads every times with five coin tosses is shown in Table 19.4 . As the sample size ( n ) becomes larger, the probability for which it is possible to reject H 0 becomes smaller. With only a few tosses we really cannot be sure if the game is fixed or not: without sufficient information it becomes hard to reject H 0 at a reasonable level of probability. A question emerges: ‘What is a reasonable level of probability for rejecting H 0 ?’ As we shall see, there are conventions for specifying these probabilities. One way to proceed, however, is to set the appropriate probability for rejecting H 0 on the basis of the implications of erroneous decisions. Obviously, any decision made on a probabilistic basis might be in error. Two types of decision errors are identified in statistics as type I and type II errors . A type I error involves mistakenly rejecting H 0 , while a type II error involves mistakenly retaining the H 0 . Researchers can make mistakes about the truth or falsity of hypotheses using sample research data. Statistical method does not provide a guarantee against making a mistake, but it is the most rigorous way of making these decisions. In the above example, a type I error would involve deciding that the outcome was not due to chance when in fact it was. The practical outcome of this would be to falsely accuse the authors of fixing the game. A type II error would represent the decision that the outcome was due to chance, when in fact it was due to a ‘fix’. The practical outcome of this would be to send your hard-earned ≤10 to a couple of crooks. Clearly, in a situation like this, a type II error would be more odious than a type I error, and you would set a fairly high probability for rejecting H 0 . However, if you were gambling with a villain, who had a loaded revolver handy, you would tend to set a very low probability for rejecting H 0 . We will examine these ideas more formally in subsequent parts of this chapter. Let us look at another example. A rehabilitation therapist has devised an exercise program which is expected to reduce the time taken for people to leave hospital following orthopaedic surgery. Previous records show that the recovery time for patients had been µ = 30 days, with σ = 8 days. A sample of 64 patients were treated with the exercise program, and their mean recovery time was found to be = 24 days. Do these results show that patients who had the treatment recovered significantly faster than previous patients? We can apply the steps for hypothesis testing to make our decision. 1.  State H A : ‘The exercise program reduces the time taken for patients to recover from orthopaedic surgery’. That is, the researcher claims that the independent variable (the treatment) has a ‘real’ or ‘generalizable’ effect on the dependent variable (time to recover). 2.  State H 0 : ‘The exercise program does not reduce the time taken for patients to recover from orthopaedic surgery’. That is, the statement claims that the independent variable has no effect on the dependent variable. The statement implies that the treated sample with = 24, and n = 64 is in fact a random sample from the population µ = 30, σ = 8. Any difference between and µ can be attributed to sampling error. 3.  The decision level, α, is set before the results are analysed. The probability of α depends on how certain the investigator wants to be that the results show real differences. If he set α = 0.01, then the probability of falsely rejecting a true H 0 is less than or equal to 0.01 (1/100). If he set α = 0.05, then the probability of falsely rejecting a true H 0 is less than or equal to 0.05 or (1/20). That is, the smaller the α, the more confident the researcher is that the results support the alternative hypothesis. We also call α the level of significance. The smaller the α, the more significant the findings for a study, if we can reject H 0 . In this case, say that the researcher sets α = 0.01. (Note: by convention, α should not be greater than 0.05.) 4.  Calculate the probability of H 0 being true. As stated above, H 0 implies that the sample with = 24 is a random sample from the population with µ = 30, σ = 8. How probable is it that this statement is true? To calculate this probability, we must generate an appropriate sampling distribution. As we have seen in Chapter 17 , the sampling distribution of the mean will enable us to calculate the probability of obtaining a sample mean of = 24 or more extreme from a population with known parameters. As shown in Figure 20.1 , we can calculate the probability of drawing a sample mean of = 24 or less. Using the table of normal curves (Appendix A), as outlined previously, we find that the probability of randomly selecting a sample mean of = 24 (or less) is extremely small. In terms of our table, which only shows the exact probability of up to z = 4.00, we can see that the present probability is less than 0.00003. Therefore, the probability that H 0 is true is less than 0.00003. Figure 20.1 Sampling distribution of means. Sample size = 64, population mean = 30, standard deviation = 8. 5.  Make a decision. We have set α = 0.01. The calculated probability was less than 0.0001. Clearly, the calculated probability is far less than α, indicating that the difference is unlikely to be due to chance. Therefore, the investigator can reject the statement that H 0 is true and accept H A , that patients in general treated with the exercise program recover earlier than the population of untreated patients. The relationship between descriptive and inferential statistics As we have seen in the previous chapters, statistics may be classified as descriptive or inferential. Descriptive statistics describe the characteristics of data and are concerned with issues such as ‘What is the average length of hospitalization of a group of patients?’ Inferential statistics are used to address issues such as whether the differences in average lengths of hospitalization of patients in two groups are significantly different statistically. Thus, descriptive statistics describe aspects of the data such as the frequencies of scores, and the average or the range of values for samples, whereas inferential statistics enables researchers to decide (infer) whether differences between groups or relationships between variables represent persistent and reproducible trends in the populations. In Section 5 we saw that the selection of appropriate descriptive statistics depends on the type of data being described. For example, in a variable such as incomes of patients, the best statistics to represent the typical income would be the mean and/or the median. If you had a millionaire in the group of patients, the mean statistic might give a distorted impression of the central tendency. In this situation the median statistic would be the most appropriate one to use. The mode is most commonly used when the data being described are categorical data. For example, if in a questionnaire respondents were asked to indicate their sex and 65% said they were male and 35% said they were female, then ‘male’ is the modal response. It is quite unusual to use the mode only with data that are not nominal. As a rule, the scale of measurement used to obtain the data and its distribution determine which descriptive statistics are selected. In the same way, the appropriate inferential statistics are determined by the characteristics of the data being analysed. For example, where the mean is the appropriate descriptive statistic, the inferential statistics will determine if the differences between the means are statistically significant. In the case of ordinal data, the appropriate inferential statistics will make it possible to decide if either the medians or the rank orders are significantly different. With nominal data, the appropriate inferential statistic will decide if proportions of cases falling into specific categories are significantly different. Thus, when the data have been adequately described, the appropriate inferential statistic will follow logically. However, when selecting an appropriate statistical test, the design of the investigation must also be taken into account.

Share this:

• Click to share on Twitter (Opens in new window)
• Click to share on Facebook (Opens in new window)

Related posts:

• Surveys and quasi-experimental designs
• 11:Questionnaires
• Effect size and the interpretation of evidence
• Standard scores and normal distributions

Stay updated, free articles. Join our Telegram channel

Comments are closed for this page.

Full access? Get Clinical Tree

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

6.6 - confidence intervals & hypothesis testing.

Confidence intervals and hypothesis tests are similar in that they are both inferential methods that rely on an approximated sampling distribution. Confidence intervals use data from a sample to estimate a population parameter. Hypothesis tests use data from a sample to test a specified hypothesis. Hypothesis testing requires that we have a hypothesized parameter. 

The simulation methods used to construct bootstrap distributions and randomization distributions are similar. One primary difference is a bootstrap distribution is centered on the observed sample statistic while a randomization distribution is centered on the value in the null hypothesis. 

In Lesson 4, we learned confidence intervals contain a range of reasonable estimates of the population parameter. All of the confidence intervals we constructed in this course were two-tailed. These two-tailed confidence intervals go hand-in-hand with the two-tailed hypothesis tests we learned in Lesson 5. The conclusion drawn from a two-tailed confidence interval is usually the same as the conclusion drawn from a two-tailed hypothesis test. In other words, if the the 95% confidence interval contains the hypothesized parameter, then a hypothesis test at the 0.05 \(\alpha\) level will almost always fail to reject the null hypothesis. If the 95% confidence interval does not contain the hypothesize parameter, then a hypothesis test at the 0.05 \(\alpha\) level will almost always reject the null hypothesis.

Example: Mean Section  

This example uses the Body Temperature dataset built in to StatKey for constructing a  bootstrap confidence interval and conducting a randomization test . 

Let's start by constructing a 95% confidence interval using the percentile method in StatKey:

The 95% confidence interval for the mean body temperature in the population is [98.044, 98.474].

Now, what if we want to know if there is enough evidence that the mean body temperature is different from 98.6 degrees? We can conduct a hypothesis test. Because 98.6 is not contained within the 95% confidence interval, it is not a reasonable estimate of the population mean. We should expect to have a p value less than 0.05 and to reject the null hypothesis.

\(H_0: \mu=98.6\)

\(H_a: \mu \ne 98.6\)

\(p = 2*0.00080=0.00160\)

\(p \leq 0.05\), reject the null hypothesis

There is evidence that the population mean is different from 98.6 degrees. 

Selecting the Appropriate Procedure Section  

The decision of whether to use a confidence interval or a hypothesis test depends on the research question. If we want to estimate a population parameter, we use a confidence interval. If we are given a specific population parameter (i.e., hypothesized value), and want to determine the likelihood that a population with that parameter would produce a sample as different as our sample, we use a hypothesis test. Below are a few examples of selecting the appropriate procedure. 

Example: Cheese Consumption Section  

Research question: How much cheese (in pounds) does an average American adult consume annually? 

What is the appropriate inferential procedure? 

Cheese consumption, in pounds, is a quantitative variable. We have one group: American adults. We are not given a specific value to test, so the appropriate procedure here is a  confidence interval for a single mean .

Example: Age Section  

Research question:  Is the average age in the population of all STAT 200 students greater than 30 years?

There is one group: STAT 200 students. The variable of interest is age in years, which is quantitative. The research question includes a specific population parameter to test: 30 years. The appropriate procedure is a  hypothesis test for a single mean .

Try it! Section  

For each research question, identify the variables, the parameter of interest and decide on the the appropriate inferential procedure.

Research question:  How strong is the correlation between height (in inches) and weight (in pounds) in American teenagers?

There are two variables of interest: (1) height in inches and (2) weight in pounds. Both are quantitative variables. The parameter of interest is the correlation between these two variables.

We are not given a specific correlation to test. We are being asked to estimate the strength of the correlation. The appropriate procedure here is a  confidence interval for a correlation . 

Research question:  Are the majority of registered voters planning to vote in the next presidential election?

The parameter that is being tested here is a single proportion. We have one group: registered voters. "The majority" would be more than 50%, or p>0.50. This is a specific parameter that we are testing. The appropriate procedure here is a  hypothesis test for a single proportion .

Research question:  On average, are STAT 200 students younger than STAT 500 students?

We have two independent groups: STAT 200 students and STAT 500 students. We are comparing them in terms of average (i.e., mean) age.

If STAT 200 students are younger than STAT 500 students, that translates to \(\mu_{200}<\mu_{500}\) which is an alternative hypothesis. This could also be written as \(\mu_{200}-\mu_{500}<0\), where 0 is a specific population parameter that we are testing. 

The appropriate procedure here is a  hypothesis test for the difference in two means .

Research question:  On average, how much taller are adult male giraffes compared to adult female giraffes?

There are two groups: males and females. The response variable is height, which is quantitative. We are not given a specific parameter to test, instead we are asked to estimate "how much" taller males are than females. The appropriate procedure is a  confidence interval for the difference in two means .

Research question:  Are STAT 500 students more likely than STAT 200 students to be employed full-time?

There are two independent groups: STAT 500 students and STAT 200 students. The response variable is full-time employment status which is categorical with two levels: yes/no.

If STAT 500 students are more likely than STAT 200 students to be employed full-time, that translates to \(p_{500}>p_{200}\) which is an alternative hypothesis. This could also be written as \(p_{500}-p_{200}>0\), where 0 is a specific parameter that we are testing. The appropriate procedure is a  hypothesis test for the difference in two proportions.

Research question:  Is there is a relationship between outdoor temperature (in Fahrenheit) and coffee sales (in cups per day)?

There are two variables here: (1) temperature in Fahrenheit and (2) cups of coffee sold in a day. Both variables are quantitative. The parameter of interest is the correlation between these two variables.

If there is a relationship between the variables, that means that the correlation is different from zero. This is a specific parameter that we are testing. The appropriate procedure is a  hypothesis test for a correlation . 

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 31289

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

CO-6: Apply basic concepts of probability, random variation, and commonly used statistical probability distributions.

Learning Objectives

LO 6.26: Outline the logic and process of hypothesis testing.

LO 6.27: Explain what the p-value is and how it is used to draw conclusions.

Video: Hypothesis Testing (8:43)

Introduction

We are in the middle of the part of the course that has to do with inference for one variable.

So far, we talked about point estimation and learned how interval estimation enhances it by quantifying the magnitude of the estimation error (with a certain level of confidence) in the form of the margin of error. The result is the confidence interval — an interval that, with a certain confidence, we believe captures the unknown parameter.

We are now moving to the other kind of inference, hypothesis testing . We say that hypothesis testing is “the other kind” because, unlike the inferential methods we presented so far, where the goal was estimating the unknown parameter, the idea, logic and goal of hypothesis testing are quite different.

In the first two parts of this section we will discuss the idea behind hypothesis testing, explain how it works, and introduce new terminology that emerges in this form of inference. The final two parts will be more specific and will discuss hypothesis testing for the population proportion ( p ) and the population mean ( μ, mu).

If this is your first statistics course, you will need to spend considerable time on this topic as there are many new ideas. Many students find this process and its logic difficult to understand in the beginning.

In this section, we will use the hypothesis test for a population proportion to motivate our understanding of the process. We will conduct these tests manually. For all future hypothesis test procedures, including problems involving means, we will use software to obtain the results and focus on interpreting them in the context of our scenario.

General Idea and Logic of Hypothesis Testing

The purpose of this section is to gradually build your understanding about how statistical hypothesis testing works. We start by explaining the general logic behind the process of hypothesis testing. Once we are confident that you understand this logic, we will add some more details and terminology.

To start our discussion about the idea behind statistical hypothesis testing, consider the following example:

A case of suspected cheating on an exam is brought in front of the disciplinary committee at a certain university.

There are two opposing claims in this case:

• The student’s claim: I did not cheat on the exam.
• The instructor’s claim: The student did cheat on the exam.

Adhering to the principle “innocent until proven guilty,” the committee asks the instructor for evidence to support his claim. The instructor explains that the exam had two versions, and shows the committee members that on three separate exam questions, the student used in his solution numbers that were given in the other version of the exam.

The committee members all agree that it would be extremely unlikely to get evidence like that if the student’s claim of not cheating had been true. In other words, the committee members all agree that the instructor brought forward strong enough evidence to reject the student’s claim, and conclude that the student did cheat on the exam.

What does this example have to do with statistics?

While it is true that this story seems unrelated to statistics, it captures all the elements of hypothesis testing and the logic behind it. Before you read on to understand why, it would be useful to read the example again. Please do so now.

Statistical hypothesis testing is defined as:

• Assessing evidence provided by the data against the null claim (the claim which is to be assumed true unless enough evidence exists to reject it).

Here is how the process of statistical hypothesis testing works:

• We have two claims about what is going on in the population. Let’s call them claim 1 (this will be the null claim or hypothesis) and claim 2 (this will be the alternative) . Much like the story above, where the student’s claim is challenged by the instructor’s claim, the null claim 1 is challenged by the alternative claim 2. (For us, these claims are usually about the value of population parameter(s) or about the existence or nonexistence of a relationship between two variables in the population).
• We choose a sample, collect relevant data and summarize them (this is similar to the instructor collecting evidence from the student’s exam). For statistical tests, this step will also involve checking any conditions or assumptions.
• We figure out how likely it is to observe data like the data we obtained, if claim 1 is true. (Note that the wording “how likely …” implies that this step requires some kind of probability calculation). In the story, the committee members assessed how likely it is to observe evidence such as the instructor provided, had the student’s claim of not cheating been true.
• If, after assuming claim 1 is true, we find that it would be extremely unlikely to observe data as strong as ours or stronger in favor of claim 2, then we have strong evidence against claim 1, and we reject it in favor of claim 2. Later we will see this corresponds to a small p-value.
• If, after assuming claim 1 is true, we find that observing data as strong as ours or stronger in favor of claim 2 is NOT VERY UNLIKELY , then we do not have enough evidence against claim 1, and therefore we cannot reject it in favor of claim 2. Later we will see this corresponds to a p-value which is not small.

In our story, the committee decided that it would be extremely unlikely to find the evidence that the instructor provided had the student’s claim of not cheating been true. In other words, the members felt that it is extremely unlikely that it is just a coincidence (random chance) that the student used the numbers from the other version of the exam on three separate problems. The committee members therefore decided to reject the student’s claim and concluded that the student had, indeed, cheated on the exam. (Wouldn’t you conclude the same?)

Hopefully this example helped you understand the logic behind hypothesis testing.

Interactive Applet: Reasoning of a Statistical Test

To strengthen your understanding of the process of hypothesis testing and the logic behind it, let’s look at three statistical examples.

A recent study estimated that 20% of all college students in the United States smoke. The head of Health Services at Goodheart University (GU) suspects that the proportion of smokers may be lower at GU. In hopes of confirming her claim, the head of Health Services chooses a random sample of 400 Goodheart students, and finds that 70 of them are smokers.

Let’s analyze this example using the 4 steps outlined above:

• claim 1: The proportion of smokers at Goodheart is 0.20.
• claim 2: The proportion of smokers at Goodheart is less than 0.20.

Claim 1 basically says “nothing special goes on at Goodheart University; the proportion of smokers there is no different from the proportion in the entire country.” This claim is challenged by the head of Health Services, who suspects that the proportion of smokers at Goodheart is lower.

• Choosing a sample and collecting data: A sample of n = 400 was chosen, and summarizing the data revealed that the sample proportion of smokers is p -hat = 70/400 = 0.175.While it is true that 0.175 is less than 0.20, it is not clear whether this is strong enough evidence against claim 1. We must account for sampling variation.
• Assessment of evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves: How surprising is it to get a sample proportion as low as p -hat = 0.175 (or lower), assuming claim 1 is true? In other words, we need to find how likely it is that in a random sample of size n = 400 taken from a population where the proportion of smokers is p = 0.20 we’ll get a sample proportion as low as p -hat = 0.175 (or lower).It turns out that the probability that we’ll get a sample proportion as low as p -hat = 0.175 (or lower) in such a sample is roughly 0.106 (do not worry about how this was calculated at this point – however, if you think about it hopefully you can see that the key is the sampling distribution of p -hat).
• Conclusion: Well, we found that if claim 1 were true there is a probability of 0.106 of observing data like that observed or more extreme. Now you have to decide …Do you think that a probability of 0.106 makes our data rare enough (surprising enough) under claim 1 so that the fact that we did observe it is enough evidence to reject claim 1? Or do you feel that a probability of 0.106 means that data like we observed are not very likely when claim 1 is true, but they are not unlikely enough to conclude that getting such data is sufficient evidence to reject claim 1. Basically, this is your decision. However, it would be nice to have some kind of guideline about what is generally considered surprising enough.

A certain prescription allergy medicine is supposed to contain an average of 245 parts per million (ppm) of a certain chemical. If the concentration is higher than 245 ppm, the drug will likely cause unpleasant side effects, and if the concentration is below 245 ppm, the drug may be ineffective. The manufacturer wants to check whether the mean concentration in a large shipment is the required 245 ppm or not. To this end, a random sample of 64 portions from the large shipment is tested, and it is found that the sample mean concentration is 250 ppm with a sample standard deviation of 12 ppm.

• Claim 1: The mean concentration in the shipment is the required 245 ppm.
• Claim 2: The mean concentration in the shipment is not the required 245 ppm.

Note that again, claim 1 basically says: “There is nothing unusual about this shipment, the mean concentration is the required 245 ppm.” This claim is challenged by the manufacturer, who wants to check whether that is, indeed, the case or not.

• Choosing a sample and collecting data: A sample of n = 64 portions is chosen and after summarizing the data it is found that the sample mean concentration is x-bar = 250 and the sample standard deviation is s = 12.Is the fact that x-bar = 250 is different from 245 strong enough evidence to reject claim 1 and conclude that the mean concentration in the whole shipment is not the required 245? In other words, do the data provide strong enough evidence to reject claim 1?
• Assessing the evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves the following question: If the mean concentration in the whole shipment were really the required 245 ppm (i.e., if claim 1 were true), how surprising would it be to observe a sample of 64 portions where the sample mean concentration is off by 5 ppm or more (as we did)? It turns out that it would be extremely unlikely to get such a result if the mean concentration were really the required 245. There is only a probability of 0.0007 (i.e., 7 in 10,000) of that happening. (Do not worry about how this was calculated at this point, but again, the key will be the sampling distribution.)
• Making conclusions: Here, it is pretty clear that a sample like the one we observed or more extreme is VERY rare (or extremely unlikely) if the mean concentration in the shipment were really the required 245 ppm. The fact that we did observe such a sample therefore provides strong evidence against claim 1, so we reject it and conclude with very little doubt that the mean concentration in the shipment is not the required 245 ppm.

Do you think that you’re getting it? Let’s make sure, and look at another example.

Is there a relationship between gender and combined scores (Math + Verbal) on the SAT exam?

Following a report on the College Board website, which showed that in 2003, males scored generally higher than females on the SAT exam, an educational researcher wanted to check whether this was also the case in her school district. The researcher chose random samples of 150 males and 150 females from her school district, collected data on their SAT performance and found the following:

Again, let’s see how the process of hypothesis testing works for this example:

• Claim 1: Performance on the SAT is not related to gender (males and females score the same).
• Claim 2: Performance on the SAT is related to gender – males score higher.

Note that again, claim 1 basically says: “There is nothing going on between the variables SAT and gender.” Claim 2 represents what the researcher wants to check, or suspects might actually be the case.

• Choosing a sample and collecting data: Data were collected and summarized as given above. Is the fact that the sample mean score of males (1,025) is higher than the sample mean score of females (1,010) by 15 points strong enough information to reject claim 1 and conclude that in this researcher’s school district, males score higher on the SAT than females?
• Assessment of evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves: If SAT scores are in fact not related to gender (claim 1 is true), how likely is it to get data like the data we observed, in which the difference between the males’ average and females’ average score is as high as 15 points or higher? It turns out that the probability of observing such a sample result if SAT score is not related to gender is approximately 0.29 (Again, do not worry about how this was calculated at this point).
• Conclusion: Here, we have an example where observing a sample like the one we observed or more extreme is definitely not surprising (roughly 30% chance) if claim 1 were true (i.e., if indeed there is no difference in SAT scores between males and females). We therefore conclude that our data does not provide enough evidence for rejecting claim 1.
• “The data provide enough evidence to reject claim 1 and accept claim 2”; or
• “The data do not provide enough evidence to reject claim 1.”

In particular, note that in the second type of conclusion we did not say: “ I accept claim 1 ,” but only “ I don’t have enough evidence to reject claim 1 .” We will come back to this issue later, but this is a good place to make you aware of this subtle difference.

Hopefully by now, you understand the logic behind the statistical hypothesis testing process. Here is a summary:

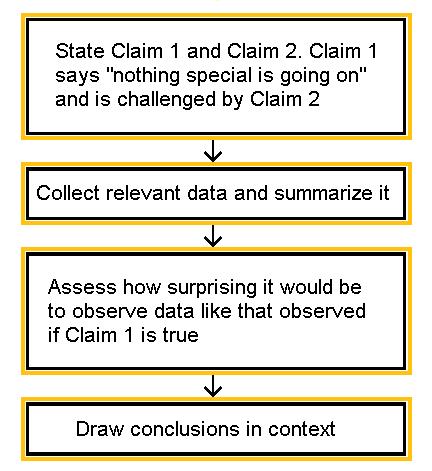
Learn by Doing: Logic of Hypothesis Testing

Did I Get This?: Logic of Hypothesis Testing

Steps in Hypothesis Testing

Video: Steps in Hypothesis Testing (16:02)

Now that we understand the general idea of how statistical hypothesis testing works, let’s go back to each of the steps and delve slightly deeper, getting more details and learning some terminology.

Hypothesis Testing Step 1: State the Hypotheses

In all three examples, our aim is to decide between two opposing points of view, Claim 1 and Claim 2. In hypothesis testing, Claim 1 is called the null hypothesis (denoted “ Ho “), and Claim 2 plays the role of the alternative hypothesis (denoted “ Ha “). As we saw in the three examples, the null hypothesis suggests nothing special is going on; in other words, there is no change from the status quo, no difference from the traditional state of affairs, no relationship. In contrast, the alternative hypothesis disagrees with this, stating that something is going on, or there is a change from the status quo, or there is a difference from the traditional state of affairs. The alternative hypothesis, Ha, usually represents what we want to check or what we suspect is really going on.

Let’s go back to our three examples and apply the new notation:

In example 1:

• Ho: The proportion of smokers at GU is 0.20.
• Ha: The proportion of smokers at GU is less than 0.20.

In example 2:

• Ho: The mean concentration in the shipment is the required 245 ppm.
• Ha: The mean concentration in the shipment is not the required 245 ppm.

In example 3:

• Ho: Performance on the SAT is not related to gender (males and females score the same).
• Ha: Performance on the SAT is related to gender – males score higher.

Learn by Doing: State the Hypotheses

Did I Get This?: State the Hypotheses

Hypothesis Testing Step 2: Collect Data, Check Conditions and Summarize Data

This step is pretty obvious. This is what inference is all about. You look at sampled data in order to draw conclusions about the entire population. In the case of hypothesis testing, based on the data, you draw conclusions about whether or not there is enough evidence to reject Ho.

There is, however, one detail that we would like to add here. In this step we collect data and summarize it. Go back and look at the second step in our three examples. Note that in order to summarize the data we used simple sample statistics such as the sample proportion ( p -hat), sample mean (x-bar) and the sample standard deviation (s).

In practice, you go a step further and use these sample statistics to summarize the data with what’s called a test statistic . We are not going to go into any details right now, but we will discuss test statistics when we go through the specific tests.

This step will also involve checking any conditions or assumptions required to use the test.

Hypothesis Testing Step 3: Assess the Evidence

As we saw, this is the step where we calculate how likely is it to get data like that observed (or more extreme) when Ho is true. In a sense, this is the heart of the process, since we draw our conclusions based on this probability.

• If this probability is very small (see example 2), then that means that it would be very surprising to get data like that observed (or more extreme) if Ho were true. The fact that we did observe such data is therefore evidence against Ho, and we should reject it.
• On the other hand, if this probability is not very small (see example 3) this means that observing data like that observed (or more extreme) is not very surprising if Ho were true. The fact that we observed such data does not provide evidence against Ho. This crucial probability, therefore, has a special name. It is called the p-value of the test.

In our three examples, the p-values were given to you (and you were reassured that you didn’t need to worry about how these were derived yet):

• Example 1: p-value = 0.106
• Example 2: p-value = 0.0007
• Example 3: p-value = 0.29

Obviously, the smaller the p-value, the more surprising it is to get data like ours (or more extreme) when Ho is true, and therefore, the stronger the evidence the data provide against Ho.

Looking at the three p-values of our three examples, we see that the data that we observed in example 2 provide the strongest evidence against the null hypothesis, followed by example 1, while the data in example 3 provides the least evidence against Ho.

• Right now we will not go into specific details about p-value calculations, but just mention that since the p-value is the probability of getting data like those observed (or more extreme) when Ho is true, it would make sense that the calculation of the p-value will be based on the data summary, which, as we mentioned, is the test statistic. Indeed, this is the case. In practice, we will mostly use software to provide the p-value for us.

Hypothesis Testing Step 4: Making Conclusions

Since our statistical conclusion is based on how small the p-value is, or in other words, how surprising our data are when Ho is true, it would be nice to have some kind of guideline or cutoff that will help determine how small the p-value must be, or how “rare” (unlikely) our data must be when Ho is true, for us to conclude that we have enough evidence to reject Ho.

This cutoff exists, and because it is so important, it has a special name. It is called the significance level of the test and is usually denoted by the Greek letter α (alpha). The most commonly used significance level is α (alpha) = 0.05 (or 5%). This means that:

• if the p-value < α (alpha) (usually 0.05), then the data we obtained is considered to be “rare (or surprising) enough” under the assumption that Ho is true, and we say that the data provide statistically significant evidence against Ho, so we reject Ho and thus accept Ha.
• if the p-value > α (alpha)(usually 0.05), then our data are not considered to be “surprising enough” under the assumption that Ho is true, and we say that our data do not provide enough evidence to reject Ho (or, equivalently, that the data do not provide enough evidence to accept Ha).

Now that we have a cutoff to use, here are the appropriate conclusions for each of our examples based upon the p-values we were given.

In Example 1:

• Using our cutoff of 0.05, we fail to reject Ho.
• Conclusion : There IS NOT enough evidence that the proportion of smokers at GU is less than 0.20
• Still we should consider: Does the evidence seen in the data provide any practical evidence towards our alternative hypothesis?

In Example 2:

• Using our cutoff of 0.05, we reject Ho.
• Conclusion : There IS enough evidence that the mean concentration in the shipment is not the required 245 ppm.

In Example 3:

• Conclusion : There IS NOT enough evidence that males score higher on average than females on the SAT.

Notice that all of the above conclusions are written in terms of the alternative hypothesis and are given in the context of the situation. In no situation have we claimed the null hypothesis is true. Be very careful of this and other issues discussed in the following comments.

• Although the significance level provides a good guideline for drawing our conclusions, it should not be treated as an incontrovertible truth. There is a lot of room for personal interpretation. What if your p-value is 0.052? You might want to stick to the rules and say “0.052 > 0.05 and therefore I don’t have enough evidence to reject Ho”, but you might decide that 0.052 is small enough for you to believe that Ho should be rejected. It should be noted that scientific journals do consider 0.05 to be the cutoff point for which any p-value below the cutoff indicates enough evidence against Ho, and any p-value above it, or even equal to it , indicates there is not enough evidence against Ho. Although a p-value between 0.05 and 0.10 is often reported as marginally statistically significant.
• It is important to draw your conclusions in context . It is never enough to say: “p-value = …, and therefore I have enough evidence to reject Ho at the 0.05 significance level.” You should always word your conclusion in terms of the data. Although we will use the terminology of “rejecting Ho” or “failing to reject Ho” – this is mostly due to the fact that we are instructing you in these concepts. In practice, this language is rarely used. We also suggest writing your conclusion in terms of the alternative hypothesis.Is there or is there not enough evidence that the alternative hypothesis is true?
• Let’s go back to the issue of the nature of the two types of conclusions that I can make.
• Either I reject Ho (when the p-value is smaller than the significance level)
• or I cannot reject Ho (when the p-value is larger than the significance level).

As we mentioned earlier, note that the second conclusion does not imply that I accept Ho, but just that I don’t have enough evidence to reject it. Saying (by mistake) “I don’t have enough evidence to reject Ho so I accept it” indicates that the data provide evidence that Ho is true, which is not necessarily the case . Consider the following slightly artificial yet effective example:

An employer claims to subscribe to an “equal opportunity” policy, not hiring men any more often than women for managerial positions. Is this credible? You’re not sure, so you want to test the following two hypotheses:

• Ho: The proportion of male managers hired is 0.5
• Ha: The proportion of male managers hired is more than 0.5

Data: You choose at random three of the new managers who were hired in the last 5 years and find that all 3 are men.

Assessing Evidence: If the proportion of male managers hired is really 0.5 (Ho is true), then the probability that the random selection of three managers will yield three males is therefore 0.5 * 0.5 * 0.5 = 0.125. This is the p-value (using the multiplication rule for independent events).

Conclusion: Using 0.05 as the significance level, you conclude that since the p-value = 0.125 > 0.05, the fact that the three randomly selected managers were all males is not enough evidence to reject the employer’s claim of subscribing to an equal opportunity policy (Ho).

However, the data (all three selected are males) definitely does NOT provide evidence to accept the employer’s claim (Ho).

Learn By Doing: Using p-values

Did I Get This?: Using p-values

Comment about wording: Another common wording in scientific journals is:

• “The results are statistically significant” – when the p-value < α (alpha).
• “The results are not statistically significant” – when the p-value > α (alpha).

Often you will see significance levels reported with additional description to indicate the degree of statistical significance. A general guideline (although not required in our course) is:

• If 0.01 ≤ p-value < 0.05, then the results are (statistically) significant .
• If 0.001 ≤ p-value < 0.01, then the results are highly statistically significant .
• If p-value < 0.001, then the results are very highly statistically significant .
• If p-value > 0.05, then the results are not statistically significant (NS).
• If 0.05 ≤ p-value < 0.10, then the results are marginally statistically significant .

Let’s summarize

We learned quite a lot about hypothesis testing. We learned the logic behind it, what the key elements are, and what types of conclusions we can and cannot draw in hypothesis testing. Here is a quick recap:

Video: Hypothesis Testing Overview (2:20)

Here are a few more activities if you need some additional practice.

Did I Get This?: Hypothesis Testing Overview

• Notice that the p-value is an example of a conditional probability . We calculate the probability of obtaining results like those of our data (or more extreme) GIVEN the null hypothesis is true. We could write P(Obtaining results like ours or more extreme | Ho is True).
• We could write P(Obtaining a test statistic as or more extreme than ours | Ho is True).
• In this case we are asking “Assuming the null hypothesis is true, how rare is it to observe something as or more extreme than what I have found in my data?”
• If after assuming the null hypothesis is true, what we have found in our data is extremely rare (small p-value), this provides evidence to reject our assumption that Ho is true in favor of Ha.
• The p-value can also be thought of as the probability, assuming the null hypothesis is true, that the result we have seen is solely due to random error (or random chance). We have already seen that statistics from samples collected from a population vary. There is random error or random chance involved when we sample from populations.

In this setting, if the p-value is very small, this implies, assuming the null hypothesis is true, that it is extremely unlikely that the results we have obtained would have happened due to random error alone, and thus our assumption (Ho) is rejected in favor of the alternative hypothesis (Ha).

• It is EXTREMELY important that you find a definition of the p-value which makes sense to you. New students often need to contemplate this idea repeatedly through a variety of examples and explanations before becoming comfortable with this idea. It is one of the two most important concepts in statistics (the other being confidence intervals).
• We infer that the alternative hypothesis is true ONLY by rejecting the null hypothesis.
• A statistically significant result is one that has a very low probability of occurring if the null hypothesis is true.
• Results which are statistically significant may or may not have practical significance and vice versa.

Error and Power

LO 6.28: Define a Type I and Type II error in general and in the context of specific scenarios.

LO 6.29: Explain the concept of the power of a statistical test including the relationship between power, sample size, and effect size.

Video: Errors and Power (12:03)

Type I and Type II Errors in Hypothesis Tests

We have not yet discussed the fact that we are not guaranteed to make the correct decision by this process of hypothesis testing. Maybe you are beginning to see that there is always some level of uncertainty in statistics.

Let’s think about what we know already and define the possible errors we can make in hypothesis testing. When we conduct a hypothesis test, we choose one of two possible conclusions based upon our data.

If the p-value is smaller than your pre-specified significance level (α, alpha), you reject the null hypothesis and either

• You have made the correct decision since the null hypothesis is false
• You have made an error ( Type I ) and rejected Ho when in fact Ho is true (your data happened to be a RARE EVENT under Ho)

If the p-value is greater than (or equal to) your chosen significance level (α, alpha), you fail to reject the null hypothesis and either

• You have made the correct decision since the null hypothesis is true
• You have made an error ( Type II ) and failed to reject Ho when in fact Ho is false (the alternative hypothesis, Ha, is true)

The following summarizes the four possible results which can be obtained from a hypothesis test. Notice the rows represent the decision made in the hypothesis test and the columns represent the (usually unknown) truth in reality.

Although the truth is unknown in practice – or we would not be conducting the test – we know it must be the case that either the null hypothesis is true or the null hypothesis is false. It is also the case that either decision we make in a hypothesis test can result in an incorrect conclusion!

A TYPE I Error occurs when we Reject Ho when, in fact, Ho is True. In this case, we mistakenly reject a true null hypothesis.

• P(TYPE I Error) = P(Reject Ho | Ho is True) = α = alpha = Significance Level

A TYPE II Error occurs when we fail to Reject Ho when, in fact, Ho is False. In this case we fail to reject a false null hypothesis.

P(TYPE II Error) = P(Fail to Reject Ho | Ho is False) = β = beta

When our significance level is 5%, we are saying that we will allow ourselves to make a Type I error less than 5% of the time. In the long run, if we repeat the process, 5% of the time we will find a p-value < 0.05 when in fact the null hypothesis was true.

In this case, our data represent a rare occurrence which is unlikely to happen but is still possible. For example, suppose we toss a coin 10 times and obtain 10 heads, this is unlikely for a fair coin but not impossible. We might conclude the coin is unfair when in fact we simply saw a very rare event for this fair coin.

Our testing procedure CONTROLS for the Type I error when we set a pre-determined value for the significance level.

Notice that these probabilities are conditional probabilities. This is one more reason why conditional probability is an important concept in statistics.

Unfortunately, calculating the probability of a Type II error requires us to know the truth about the population. In practice we can only calculate this probability using a series of “what if” calculations which depend upon the type of problem.

Comment: As you initially read through the examples below, focus on the broad concepts instead of the small details. It is not important to understand how to calculate these values yourself at this point.

• Try to understand the pictures we present. Which pictures represent an assumed null hypothesis and which represent an alternative?
• It may be useful to come back to this page (and the activities here) after you have reviewed the rest of the section on hypothesis testing and have worked a few problems yourself.

Interactive Applet: Statistical Significance

Here are two examples of using an older version of this applet. It looks slightly different but the same settings and options are available in the version above.

In both cases we will consider IQ scores.

Our null hypothesis is that the true mean is 100. Assume the standard deviation is 16 and we will specify a significance level of 5%.

In this example we will specify that the true mean is indeed 100 so that the null hypothesis is true. Most of the time (95%), when we generate a sample, we should fail to reject the null hypothesis since the null hypothesis is indeed true.

Here is one sample that results in a correct decision:

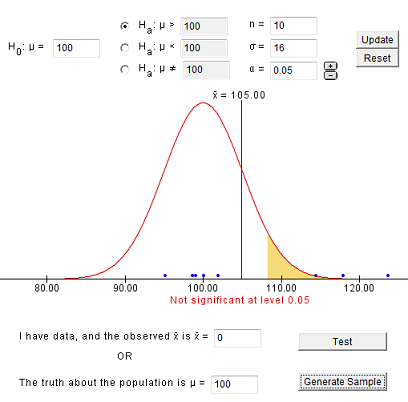
In the sample above, we obtain an x-bar of 105, which is drawn on the distribution which assumes μ (mu) = 100 (the null hypothesis is true). Notice the sample is shown as blue dots along the x-axis and the shaded region shows for which values of x-bar we would reject the null hypothesis. In other words, we would reject Ho whenever the x-bar falls in the shaded region.

Enter the same values and generate samples until you obtain a Type I error (you falsely reject the null hypothesis). You should see something like this:

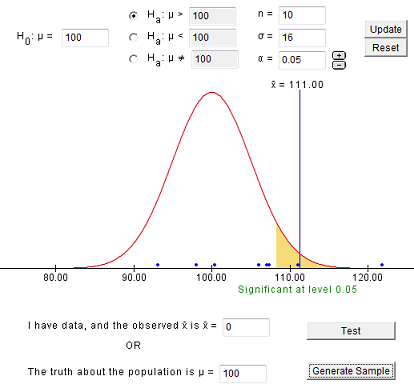
If you were to generate 100 samples, you should have around 5% where you rejected Ho. These would be samples which would result in a Type I error.

The previous example illustrates a correct decision and a Type I error when the null hypothesis is true. The next example illustrates a correct decision and Type II error when the null hypothesis is false. In this case, we must specify the true population mean.

Let’s suppose we are sampling from an honors program and that the true mean IQ for this population is 110. We do not know the probability of a Type II error without more detailed calculations.

Let’s start with a sample which results in a correct decision.

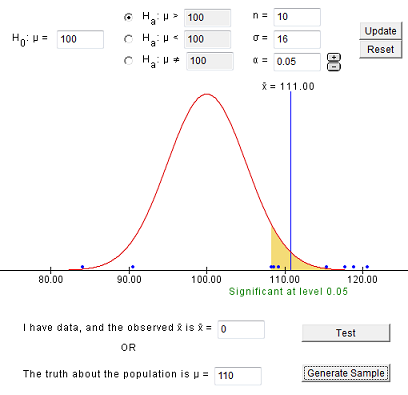
In the sample above, we obtain an x-bar of 111, which is drawn on the distribution which assumes μ (mu) = 100 (the null hypothesis is true).

Enter the same values and generate samples until you obtain a Type II error (you fail to reject the null hypothesis). You should see something like this:

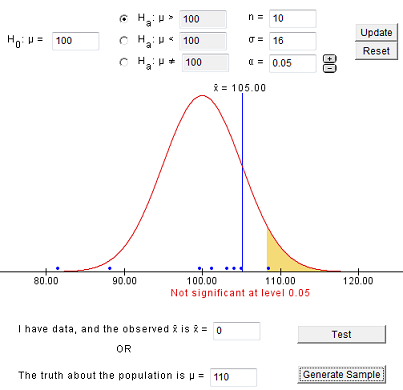
You should notice that in this case (when Ho is false), it is easier to obtain an incorrect decision (a Type II error) than it was in the case where Ho is true. If you generate 100 samples, you can approximate the probability of a Type II error.

We can find the probability of a Type II error by visualizing both the assumed distribution and the true distribution together. The image below is adapted from an applet we will use when we discuss the power of a statistical test.

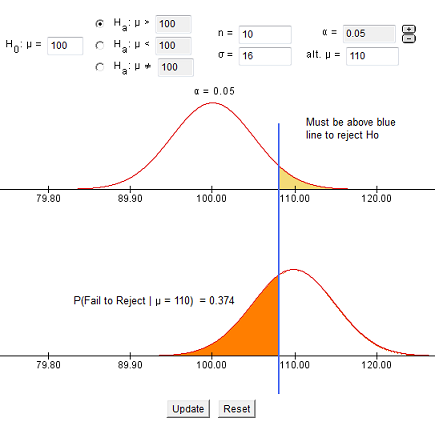
There is a 37.4% chance that, in the long run, we will make a Type II error and fail to reject the null hypothesis when in fact the true mean IQ is 110 in the population from which we sample our 10 individuals.

Can you visualize what will happen if the true population mean is really 115 or 108? When will the Type II error increase? When will it decrease? We will look at this idea again when we discuss the concept of power in hypothesis tests.

• It is important to note that there is a trade-off between the probability of a Type I and a Type II error. If we decrease the probability of one of these errors, the probability of the other will increase! The practical result of this is that if we require stronger evidence to reject the null hypothesis (smaller significance level = probability of a Type I error), we will increase the chance that we will be unable to reject the null hypothesis when in fact Ho is false (increases the probability of a Type II error).
• When α (alpha) = 0.05 we obtained a Type II error probability of 0.374 = β = beta

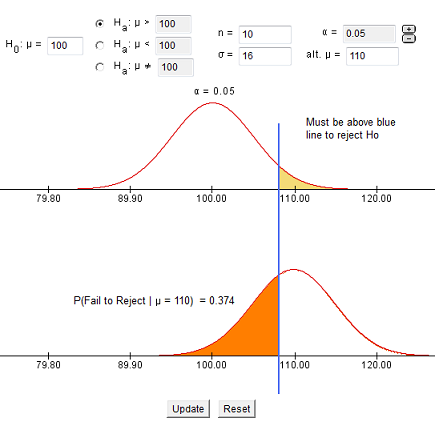
• When α (alpha) = 0.01 (smaller than before) we obtain a Type II error probability of 0.644 = β = beta (larger than before)

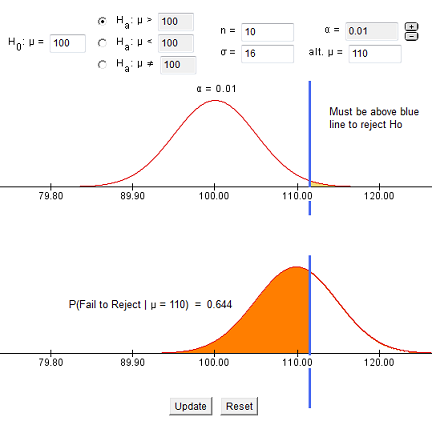
• As the blue line in the picture moves farther right, the significance level (α, alpha) is decreasing and the Type II error probability is increasing.
• As the blue line in the picture moves farther left, the significance level (α, alpha) is increasing and the Type II error probability is decreasing

Let’s return to our very first example and define these two errors in context.

• Ho = The student’s claim: I did not cheat on the exam.
• Ha = The instructor’s claim: The student did cheat on the exam.

Adhering to the principle “innocent until proven guilty,” the committee asks the instructor for evidence to support his claim.

There are four possible outcomes of this process. There are two possible correct decisions:

• The student did cheat on the exam and the instructor brings enough evidence to reject Ho and conclude the student did cheat on the exam. This is a CORRECT decision!
• The student did not cheat on the exam and the instructor fails to provide enough evidence that the student did cheat on the exam. This is a CORRECT decision!

Both the correct decisions and the possible errors are fairly easy to understand but with the errors, you must be careful to identify and define the two types correctly.

TYPE I Error: Reject Ho when Ho is True

• The student did not cheat on the exam but the instructor brings enough evidence to reject Ho and conclude the student cheated on the exam. This is a Type I Error.

TYPE II Error: Fail to Reject Ho when Ho is False

• The student did cheat on the exam but the instructor fails to provide enough evidence that the student cheated on the exam. This is a Type II Error.

In most situations, including this one, it is more “acceptable” to have a Type II error than a Type I error. Although allowing a student who cheats to go unpunished might be considered a very bad problem, punishing a student for something he or she did not do is usually considered to be a more severe error. This is one reason we control for our Type I error in the process of hypothesis testing.

Did I Get This?: Type I and Type II Errors (in context)

• The probabilities of Type I and Type II errors are closely related to the concepts of sensitivity and specificity that we discussed previously. Consider the following hypotheses:

Ho: The individual does not have diabetes (status quo, nothing special happening)

Ha: The individual does have diabetes (something is going on here)

In this setting:

When someone tests positive for diabetes we would reject the null hypothesis and conclude the person has diabetes (we may or may not be correct!).

When someone tests negative for diabetes we would fail to reject the null hypothesis so that we fail to conclude the person has diabetes (we may or may not be correct!)

Let’s take it one step further:

Sensitivity = P(Test + | Have Disease) which in this setting equals P(Reject Ho | Ho is False) = 1 – P(Fail to Reject Ho | Ho is False) = 1 – β = 1 – beta

Specificity = P(Test – | No Disease) which in this setting equals P(Fail to Reject Ho | Ho is True) = 1 – P(Reject Ho | Ho is True) = 1 – α = 1 – alpha

Notice that sensitivity and specificity relate to the probability of making a correct decision whereas α (alpha) and β (beta) relate to the probability of making an incorrect decision.

Usually α (alpha) = 0.05 so that the specificity listed above is 0.95 or 95%.

Next, we will see that the sensitivity listed above is the power of the hypothesis test!

Reasons for a Type I Error in Practice

Assuming that you have obtained a quality sample:

• The reason for a Type I error is random chance.
• When a Type I error occurs, our observed data represented a rare event which indicated evidence in favor of the alternative hypothesis even though the null hypothesis was actually true.

Reasons for a Type II Error in Practice

Again, assuming that you have obtained a quality sample, now we have a few possibilities depending upon the true difference that exists.

• The sample size is too small to detect an important difference. This is the worst case, you should have obtained a larger sample. In this situation, you may notice that the effect seen in the sample seems PRACTICALLY significant and yet the p-value is not small enough to reject the null hypothesis.
• The sample size is reasonable for the important difference but the true difference (which might be somewhat meaningful or interesting) is smaller than your test was capable of detecting. This is tolerable as you were not interested in being able to detect this difference when you began your study. In this situation, you may notice that the effect seen in the sample seems to have some potential for practical significance.
• The sample size is more than adequate, the difference that was not detected is meaningless in practice. This is not a problem at all and is in effect a “correct decision” since the difference you did not detect would have no practical meaning.
• Note: We will discuss the idea of practical significance later in more detail.

Power of a Hypothesis Test

It is often the case that we truly wish to prove the alternative hypothesis. It is reasonable that we would be interested in the probability of correctly rejecting the null hypothesis. In other words, the probability of rejecting the null hypothesis, when in fact the null hypothesis is false. This can also be thought of as the probability of being able to detect a (pre-specified) difference of interest to the researcher.

Let’s begin with a realistic example of how power can be described in a study.

In a clinical trial to study two medications for weight loss, we have an 80% chance to detect a difference in the weight loss between the two medications of 10 pounds. In other words, the power of the hypothesis test we will conduct is 80%.

In other words, if one medication comes from a population with an average weight loss of 25 pounds and the other comes from a population with an average weight loss of 15 pounds, we will have an 80% chance to detect that difference using the sample we have in our trial.

If we were to repeat this trial many times, 80% of the time we will be able to reject the null hypothesis (that there is no difference between the medications) and 20% of the time we will fail to reject the null hypothesis (and make a Type II error!).

The difference of 10 pounds in the previous example, is often called the effect size . The measure of the effect differs depending on the particular test you are conducting but is always some measure related to the true effect in the population. In this example, it is the difference between two population means.

Recall the definition of a Type II error:

Notice that P(Reject Ho | Ho is False) = 1 – P(Fail to Reject Ho | Ho is False) = 1 – β = 1- beta.

The POWER of a hypothesis test is the probability of rejecting the null hypothesis when the null hypothesis is false . This can also be stated as the probability of correctly rejecting the null hypothesis .

POWER = P(Reject Ho | Ho is False) = 1 – β = 1 – beta

Power is the test’s ability to correctly reject the null hypothesis. A test with high power has a good chance of being able to detect the difference of interest to us, if it exists .

As we mentioned on the bottom of the previous page, this can be thought of as the sensitivity of the hypothesis test if you imagine Ho = No disease and Ha = Disease.

Factors Affecting the Power of a Hypothesis Test

The power of a hypothesis test is affected by numerous quantities (similar to the margin of error in a confidence interval).

Assume that the null hypothesis is false for a given hypothesis test. All else being equal, we have the following:

• Larger samples result in a greater chance to reject the null hypothesis which means an increase in the power of the hypothesis test.
• If the effect size is larger, it will become easier for us to detect. This results in a greater chance to reject the null hypothesis which means an increase in the power of the hypothesis test. The effect size varies for each test and is usually closely related to the difference between the hypothesized value and the true value of the parameter under study.
• From the relationship between the probability of a Type I and a Type II error (as α (alpha) decreases, β (beta) increases), we can see that as α (alpha) decreases, Power = 1 – β = 1 – beta also decreases.
• There are other mathematical ways to change the power of a hypothesis test, such as changing the population standard deviation; however, these are not quantities that we can usually control so we will not discuss them here.

In practice, we specify a significance level and a desired power to detect a difference which will have practical meaning to us and this determines the sample size required for the experiment or study.

For most grants involving statistical analysis, power calculations must be completed to illustrate that the study will have a reasonable chance to detect an important effect. Otherwise, the money spent on the study could be wasted. The goal is usually to have a power close to 80%.

For example, if there is only a 5% chance to detect an important difference between two treatments in a clinical trial, this would result in a waste of time, effort, and money on the study since, when the alternative hypothesis is true, the chance a treatment effect can be found is very small.

• In order to calculate the power of a hypothesis test, we must specify the “truth.” As we mentioned previously when discussing Type II errors, in practice we can only calculate this probability using a series of “what if” calculations which depend upon the type of problem.

The following activity involves working with an interactive applet to study power more carefully.

Learn by Doing: Power of Hypothesis Tests

The following reading is an excellent discussion about Type I and Type II errors.

(Optional) Outside Reading: A Good Discussion of Power (≈ 2500 words)

We will not be asking you to perform power calculations manually. You may be asked to use online calculators and applets. Most statistical software packages offer some ability to complete power calculations. There are also many online calculators for power and sample size on the internet, for example, Russ Lenth’s power and sample-size page .

Proportions (Introduction & Step 1)

CO-4: Distinguish among different measurement scales, choose the appropriate descriptive and inferential statistical methods based on these distinctions, and interpret the results.

LO 4.33: In a given context, distinguish between situations involving a population proportion and a population mean and specify the correct null and alternative hypothesis for the scenario.

LO 4.34: Carry out a complete hypothesis test for a population proportion by hand.

Video: Proportions (Introduction & Step 1) (7:18)

Now that we understand the process of hypothesis testing and the logic behind it, we are ready to start learning about specific statistical tests (also known as significance tests).

The first test we are going to learn is the test about the population proportion (p).

This test is widely known as the “z-test for the population proportion (p).”

We will understand later where the “z-test” part is coming from.

This will be the only type of problem you will complete entirely “by-hand” in this course. Our goal is to use this example to give you the tools you need to understand how this process works. After working a few problems, you should review the earlier material again. You will likely need to review the terminology and concepts a few times before you fully understand the process.

In reality, you will often be conducting more complex statistical tests and allowing software to provide the p-value. In these settings it will be important to know what test to apply for a given situation and to be able to explain the results in context.

Review: Types of Variables

When we conduct a test about a population proportion, we are working with a categorical variable. Later in the course, after we have learned a variety of hypothesis tests, we will need to be able to identify which test is appropriate for which situation. Identifying the variable as categorical or quantitative is an important component of choosing an appropriate hypothesis test.

Learn by Doing: Review Types of Variables

One Sample Z-Test for a Population Proportion

In this part of our discussion on hypothesis testing, we will go into details that we did not go into before. More specifically, we will use this test to introduce the idea of a test statistic , and details about how p-values are calculated .

Let’s start by introducing the three examples, which will be the leading examples in our discussion. Each example is followed by a figure illustrating the information provided, as well as the question of interest.

A machine is known to produce 20% defective products, and is therefore sent for repair. After the machine is repaired, 400 products produced by the machine are chosen at random and 64 of them are found to be defective. Do the data provide enough evidence that the proportion of defective products produced by the machine (p) has been reduced as a result of the repair?

The following figure displays the information, as well as the question of interest:

The question of interest helps us formulate the null and alternative hypotheses in terms of p, the proportion of defective products produced by the machine following the repair:

• Ho: p = 0.20 (No change; the repair did not help).
• Ha: p < 0.20 (The repair was effective at reducing the proportion of defective parts).

There are rumors that students at a certain liberal arts college are more inclined to use drugs than U.S. college students in general. Suppose that in a simple random sample of 100 students from the college, 19 admitted to marijuana use. Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) is higher than the national proportion, which is 0.157? (This number is reported by the Harvard School of Public Health.)

Again, the following figure displays the information as well as the question of interest:

As before, we can formulate the null and alternative hypotheses in terms of p, the proportion of students in the college who use marijuana:

• Ho: p = 0.157 (same as among all college students in the country).
• Ha: p > 0.157 (higher than the national figure).

Polls on certain topics are conducted routinely in order to monitor changes in the public’s opinions over time. One such topic is the death penalty. In 2003 a poll estimated that 64% of U.S. adults support the death penalty for a person convicted of murder. In a more recent poll, 675 out of 1,000 U.S. adults chosen at random were in favor of the death penalty for convicted murderers. Do the results of this poll provide evidence that the proportion of U.S. adults who support the death penalty for convicted murderers (p) changed between 2003 and the later poll?

Here is a figure that displays the information, as well as the question of interest:

Again, we can formulate the null and alternative hypotheses in term of p, the proportion of U.S. adults who support the death penalty for convicted murderers.

• Ho: p = 0.64 (No change from 2003).
• Ha: p ≠ 0.64 (Some change since 2003).

Learn by Doing: Proportions (Overview)

Did I Get This?: Proportions ( Overview )

Recall that there are basically 4 steps in the process of hypothesis testing:

• STEP 1: State the appropriate null and alternative hypotheses, Ho and Ha.
• STEP 2: Obtain a random sample, collect relevant data, and check whether the data meet the conditions under which the test can be used . If the conditions are met, summarize the data using a test statistic.
• STEP 3: Find the p-value of the test.
• STEP 4: Based on the p-value, decide whether or not the results are statistically significant and draw your conclusions in context.
• Note: In practice, we should always consider the practical significance of the results as well as the statistical significance.

We are now going to go through these steps as they apply to the hypothesis testing for the population proportion p. It should be noted that even though the details will be specific to this particular test, some of the ideas that we will add apply to hypothesis testing in general.

Step 1. Stating the Hypotheses

Here again are the three set of hypotheses that are being tested in each of our three examples:

Has the proportion of defective products been reduced as a result of the repair?

Is the proportion of marijuana users in the college higher than the national figure?

Did the proportion of U.S. adults who support the death penalty change between 2003 and a later poll?

The null hypothesis always takes the form:

• Ho: p = some value

and the alternative hypothesis takes one of the following three forms:

• Ha: p < that value (like in example 1) or
• Ha: p > that value (like in example 2) or
• Ha: p ≠ that value (like in example 3).

Note that it was quite clear from the context which form of the alternative hypothesis would be appropriate. The value that is specified in the null hypothesis is called the null value , and is generally denoted by p 0 . We can say, therefore, that in general the null hypothesis about the population proportion (p) would take the form:

• Ho: p = p 0

We write Ho: p = p 0 to say that we are making the hypothesis that the population proportion has the value of p 0 . In other words, p is the unknown population proportion and p 0 is the number we think p might be for the given situation.

The alternative hypothesis takes one of the following three forms (depending on the context):

Ha: p < p 0 (one-sided)

Ha: p > p 0 (one-sided)

Ha: p ≠ p 0 (two-sided)

The first two possible forms of the alternatives (where the = sign in Ho is challenged by < or >) are called one-sided alternatives , and the third form of alternative (where the = sign in Ho is challenged by ≠) is called a two-sided alternative. To understand the intuition behind these names let’s go back to our examples.

Example 3 (death penalty) is a case where we have a two-sided alternative:

In this case, in order to reject Ho and accept Ha we will need to get a sample proportion of death penalty supporters which is very different from 0.64 in either direction, either much larger or much smaller than 0.64.

In example 2 (marijuana use) we have a one-sided alternative:

Here, in order to reject Ho and accept Ha we will need to get a sample proportion of marijuana users which is much higher than 0.157.

Similarly, in example 1 (defective products), where we are testing:

in order to reject Ho and accept Ha, we will need to get a sample proportion of defective products which is much smaller than 0.20.

Learn by Doing: State Hypotheses (Proportions)

Did I Get This?: State Hypotheses (Proportions)

Proportions (Step 2)

Video: Proportions (Step 2) (12:38)

Step 2. Collect Data, Check Conditions, and Summarize Data

After the hypotheses have been stated, the next step is to obtain a sample (on which the inference will be based), collect relevant data , and summarize them.

It is extremely important that our sample is representative of the population about which we want to draw conclusions. This is ensured when the sample is chosen at random. Beyond the practical issue of ensuring representativeness, choosing a random sample has theoretical importance that we will mention later.

In the case of hypothesis testing for the population proportion (p), we will collect data on the relevant categorical variable from the individuals in the sample and start by calculating the sample proportion p-hat (the natural quantity to calculate when the parameter of interest is p).

Let’s go back to our three examples and add this step to our figures.

As we mentioned earlier without going into details, when we summarize the data in hypothesis testing, we go a step beyond calculating the sample statistic and summarize the data with a test statistic . Every test has a test statistic, which to some degree captures the essence of the test. In fact, the p-value, which so far we have looked upon as “the king” (in the sense that everything is determined by it), is actually determined by (or derived from) the test statistic. We will now introduce the test statistic.

The test statistic is a measure of how far the sample proportion p-hat is from the null value p 0 , the value that the null hypothesis claims is the value of p. In other words, since p-hat is what the data estimates p to be, the test statistic can be viewed as a measure of the “distance” between what the data tells us about p and what the null hypothesis claims p to be.

Let’s use our examples to understand this:

The parameter of interest is p, the proportion of defective products following the repair.

The data estimate p to be p-hat = 0.16

The null hypothesis claims that p = 0.20

The data are therefore 0.04 (or 4 percentage points) below the null hypothesis value.

It is hard to evaluate whether this difference of 4% in defective products is enough evidence to say that the repair was effective at reducing the proportion of defective products, but clearly, the larger the difference, the more evidence it is against the null hypothesis. So if, for example, our sample proportion of defective products had been, say, 0.10 instead of 0.16, then I think you would all agree that cutting the proportion of defective products in half (from 20% to 10%) would be extremely strong evidence that the repair was effective at reducing the proportion of defective products.

The parameter of interest is p, the proportion of students in a college who use marijuana.

The data estimate p to be p-hat = 0.19

The null hypothesis claims that p = 0.157

The data are therefore 0.033 (or 3.3. percentage points) above the null hypothesis value.

The parameter of interest is p, the proportion of U.S. adults who support the death penalty for convicted murderers.

The data estimate p to be p-hat = 0.675

The null hypothesis claims that p = 0.64

There is a difference of 0.035 (or 3.5. percentage points) between the data and the null hypothesis value.

The problem with looking only at the difference between the sample proportion, p-hat, and the null value, p 0 is that we have not taken into account the variability of our estimator p-hat which, as we know from our study of sampling distributions, depends on the sample size.

For this reason, the test statistic cannot simply be the difference between p-hat and p 0 , but must be some form of that formula that accounts for the sample size. In other words, we need to somehow standardize the difference so that comparison between different situations will be possible. We are very close to revealing the test statistic, but before we construct it, let’s be reminded of the following two facts from probability:

Fact 1: When we take a random sample of size n from a population with population proportion p, then

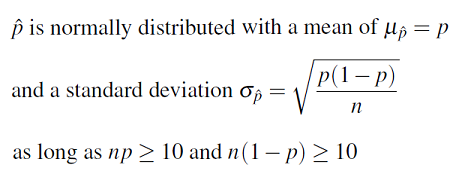
Fact 2: The z-score of any normal value (a value that comes from a normal distribution) is calculated by finding the difference between the value and the mean and then dividing that difference by the standard deviation (of the normal distribution associated with the value). The z-score represents how many standard deviations below or above the mean the value is.

Thus, our test statistic should be a measure of how far the sample proportion p-hat is from the null value p 0 relative to the variation of p-hat (as measured by the standard error of p-hat).

Recall that the standard error is the standard deviation of the sampling distribution for a given statistic. For p-hat, we know the following:

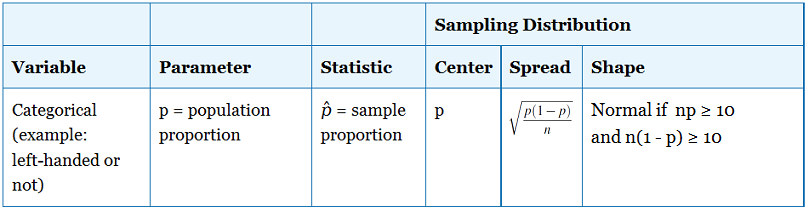
To find the p-value, we will need to determine how surprising our value is assuming the null hypothesis is true. We already have the tools needed for this process from our study of sampling distributions as represented in the table above.

If we assume the null hypothesis is true, we can specify that the center of the distribution of all possible values of p-hat from samples of size 400 would be 0.20 (our null value).

We can calculate the standard error, assuming p = 0.20 as

\(\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}=\sqrt{\dfrac{0.2(1-0.2)}{400}}=0.02\)

The following picture represents the sampling distribution of all possible values of p-hat of samples of size 400, assuming the true proportion p is 0.20 and our other requirements for the sampling distribution to be normal are met (we will review these during the next step).

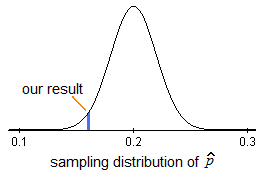
In order to calculate probabilities for the picture above, we would need to find the z-score associated with our result.

This z-score is the test statistic ! In this example, the numerator of our z-score is the difference between p-hat (0.16) and null value (0.20) which we found earlier to be -0.04. The denominator of our z-score is the standard error calculated above (0.02) and thus quickly we find the z-score, our test statistic, to be -2.

The sample proportion based upon this data is 2 standard errors below the null value.

Hopefully you now understand more about the reasons we need probability in statistics!!

Now we will formalize the definition and look at our remaining examples before moving on to the next step, which will be to determine if a normal distribution applies and calculate the p-value.

Test Statistic for Hypothesis Tests for One Proportion is:

\(z=\dfrac{\hat{p}-p_{0}}{\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}}\)

It represents the difference between the sample proportion and the null value, measured in standard deviations (standard error of p-hat).

The picture above is a representation of the sampling distribution of p-hat assuming p = p 0 . In other words, this is a model of how p-hat behaves if we are drawing random samples from a population for which Ho is true.

Notice the center of the sampling distribution is at p 0 , which is the hypothesized proportion given in the null hypothesis (Ho: p = p 0 .) We could also mark the axis in standard error units,

\(\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}\)

For example, if our null hypothesis claims that the proportion of U.S. adults supporting the death penalty is 0.64, then the sampling distribution is drawn as if the null is true. We draw a normal distribution centered at 0.64 (p 0 ) with a standard error dependent on sample size,

\(\sqrt{\dfrac{0.64(1-0.64)}{n}}\).

Important Comment:

• Note that under the assumption that Ho is true (and if the conditions for the sampling distribution to be normal are satisfied) the test statistic follows a N(0,1) (standard normal) distribution. Another way to say the same thing which is quite common is: “The null distribution of the test statistic is N(0,1).”

By “null distribution,” we mean the distribution under the assumption that Ho is true. As we’ll see and stress again later, the null distribution of the test statistic is what the calculation of the p-value is based on.

Let’s go back to our remaining two examples and find the test statistic in each case:

Since the null hypothesis is Ho: p = 0.157, the standardized (z) score of p-hat = 0.19 is

\(z=\dfrac{0.19-0.157}{\sqrt{\dfrac{0.157(1-0.157)}{100}}} \approx 0.91\)

This is the value of the test statistic for this example.

We interpret this to mean that, assuming that Ho is true, the sample proportion p-hat = 0.19 is 0.91 standard errors above the null value (0.157).

Since the null hypothesis is Ho: p = 0.64, the standardized (z) score of p-hat = 0.675 is

\(z=\dfrac{0.675-0.64}{\sqrt{\dfrac{0.64(1-0.64)}{1000}}} \approx 2.31\)

We interpret this to mean that, assuming that Ho is true, the sample proportion p-hat = 0.675 is 2.31 standard errors above the null value (0.64).

Learn by Doing: Proportions (Step 2)

Comments about the Test Statistic:

• We mentioned earlier that to some degree, the test statistic captures the essence of the test. In this case, the test statistic measures the difference between p-hat and p 0 in standard errors. This is exactly what this test is about. Get data, and look at the discrepancy between what the data estimates p to be (represented by p-hat) and what Ho claims about p (represented by p 0 ).
• You can think about this test statistic as a measure of evidence in the data against Ho. The larger the test statistic, the “further the data are from Ho” and therefore the more evidence the data provide against Ho.

Learn by Doing: Proportions (Step 2) Understanding the Test Statistic

Did I Get This?: Proportions (Step 2)

• It should now be clear why this test is commonly known as the z-test for the population proportion . The name comes from the fact that it is based on a test statistic that is a z-score.
• Recall fact 1 that we used for constructing the z-test statistic. Here is part of it again:

When we take a random sample of size n from a population with population proportion p 0 , the possible values of the sample proportion p-hat ( when certain conditions are met ) have approximately a normal distribution with a mean of p 0 … and a standard deviation of

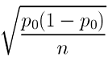
This result provides the theoretical justification for constructing the test statistic the way we did, and therefore the assumptions under which this result holds (in bold, above) are the conditions that our data need to satisfy so that we can use this test. These two conditions are:

i. The sample has to be random.

ii. The conditions under which the sampling distribution of p-hat is normal are met. In other words:

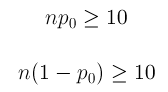
• Here we will pause to say more about condition (i.) above, the need for a random sample. In the Probability Unit we discussed sampling plans based on probability (such as a simple random sample, cluster, or stratified sampling) that produce a non-biased sample, which can be safely used in order to make inferences about a population. We noted in the Probability Unit that, in practice, other (non-random) sampling techniques are sometimes used when random sampling is not feasible. It is important though, when these techniques are used, to be aware of the type of bias that they introduce, and thus the limitations of the conclusions that can be drawn from them. For our purpose here, we will focus on one such practice, the situation in which a sample is not really chosen randomly, but in the context of the categorical variable that is being studied, the sample is regarded as random. For example, say that you are interested in the proportion of students at a certain college who suffer from seasonal allergies. For that purpose, the students in a large engineering class could be considered as a random sample, since there is nothing about being in an engineering class that makes you more or less likely to suffer from seasonal allergies. Technically, the engineering class is a convenience sample, but it is treated as a random sample in the context of this categorical variable. On the other hand, if you are interested in the proportion of students in the college who have math anxiety, then the class of engineering students clearly could not possibly be viewed as a random sample, since engineering students probably have a much lower incidence of math anxiety than the college population overall.

Learn by Doing: Proportions (Step 2) Valid or Invalid Sampling?

Let’s check the conditions in our three examples.

i. The 400 products were chosen at random.

ii. n = 400, p 0 = 0.2 and therefore:

\(n p_{0}=400(0.2)=80 \geq 10\)

\(n\left(1-p_{0}\right)=400(1-0.2)=320 \geq 10\)

i. The 100 students were chosen at random.

ii. n = 100, p 0 = 0.157 and therefore:

\begin{gathered} n p_{0}=100(0.157)=15.7 \geq 10 \\ n\left(1-p_{0}\right)=100(1-0.157)=84.3 \geq 10 \end{gathered}

i. The 1000 adults were chosen at random.

ii. n = 1000, p 0 = 0.64 and therefore:

\begin{gathered} n p_{0}=1000(0.64)=640 \geq 10 \\ n\left(1-p_{0}\right)=1000(1-0.64)=360 \geq 10 \end{gathered}

Learn by Doing: Proportions (Step 2) Verify Conditions

Checking that our data satisfy the conditions under which the test can be reliably used is a very important part of the hypothesis testing process. Be sure to consider this for every hypothesis test you conduct in this course and certainly in practice.

The Four Steps in Hypothesis Testing

With respect to the z-test, the population proportion that we are currently discussing we have:

Step 1: Completed

Step 2: Completed

Step 3: This is what we will work on next.

Proportions (Step 3)

Video: Proportions (Step 3) (14:46)

Calculators and Tables

Step 3. Finding the P-value of the Test

So far we’ve talked about the p-value at the intuitive level: understanding what it is (or what it measures) and how we use it to draw conclusions about the statistical significance of our results. We will now go more deeply into how the p-value is calculated.

It should be mentioned that eventually we will rely on technology to calculate the p-value for us (as well as the test statistic), but in order to make intelligent use of the output, it is important to first understand the details, and only then let the computer do the calculations for us. Again, our goal is to use this simple example to give you the tools you need to understand the process entirely. Let’s start.

Recall that so far we have said that the p-value is the probability of obtaining data like those observed assuming that Ho is true. Like the test statistic, the p-value is, therefore, a measure of the evidence against Ho. In the case of the test statistic, the larger it is in magnitude (positive or negative), the further p-hat is from p 0 , the more evidence we have against Ho. In the case of the p-value , it is the opposite; the smaller it is, the more unlikely it is to get data like those observed when Ho is true, the more evidence it is against Ho . One can actually draw conclusions in hypothesis testing just using the test statistic, and as we’ll see the p-value is, in a sense, just another way of looking at the test statistic. The reason that we actually take the extra step in this course and derive the p-value from the test statistic is that even though in this case (the test about the population proportion) and some other tests, the value of the test statistic has a very clear and intuitive interpretation, there are some tests where its value is not as easy to interpret. On the other hand, the p-value keeps its intuitive appeal across all statistical tests.

How is the p-value calculated?

Intuitively, the p-value is the probability of observing data like those observed assuming that Ho is true. Let’s be a bit more formal:

• Since this is a probability question about the data , it makes sense that the calculation will involve the data summary, the test statistic.
• What do we mean by “like” those observed? By “like” we mean “as extreme or even more extreme.”

Putting it all together, we get that in general:

The p-value is the probability of observing a test statistic as extreme as that observed (or even more extreme) assuming that the null hypothesis is true.

By “extreme” we mean extreme in the direction(s) of the alternative hypothesis.

Specifically , for the z-test for the population proportion:

• If the alternative hypothesis is Ha: p < p 0 (less than) , then “extreme” means small or less than , and the p-value is: The probability of observing a test statistic as small as that observed or smaller if the null hypothesis is true.
• If the alternative hypothesis is Ha: p > p 0 (greater than) , then “extreme” means large or greater than , and the p-value is: The probability of observing a test statistic as large as that observed or larger if the null hypothesis is true.
• If the alternative is Ha: p ≠ p 0 (different from) , then “extreme” means extreme in either direction either small or large (i.e., large in magnitude) or just different from , and the p-value therefore is: The probability of observing a test statistic as large in magnitude as that observed or larger if the null hypothesis is true.(Examples: If z = -2.5: p-value = probability of observing a test statistic as small as -2.5 or smaller or as large as 2.5 or larger. If z = 1.5: p-value = probability of observing a test statistic as large as 1.5 or larger, or as small as -1.5 or smaller.)

OK, hopefully that makes (some) sense. But how do we actually calculate it?

Recall the important comment from our discussion about our test statistic,

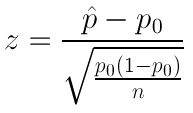
which said that when the null hypothesis is true (i.e., when p = p 0 ), the possible values of our test statistic follow a standard normal (N(0,1), denoted by Z) distribution. Therefore, the p-value calculations (which assume that Ho is true) are simply standard normal distribution calculations for the 3 possible alternative hypotheses.

Alternative Hypothesis is “Less Than”

The probability of observing a test statistic as small as that observed or smaller , assuming that the values of the test statistic follow a standard normal distribution. We will now represent this probability in symbols and also using the normal distribution.

Looking at the shaded region, you can see why this is often referred to as a left-tailed test. We shaded to the left of the test statistic, since less than is to the left.

Alternative Hypothesis is “Greater Than”

The probability of observing a test statistic as large as that observed or larger , assuming that the values of the test statistic follow a standard normal distribution. Again, we will represent this probability in symbols and using the normal distribution

Looking at the shaded region, you can see why this is often referred to as a right-tailed test. We shaded to the right of the test statistic, since greater than is to the right.

Alternative Hypothesis is “Not Equal To”

The probability of observing a test statistic which is as large in magnitude as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution.

This is often referred to as a two-tailed test, since we shaded in both directions.

Next, we will apply this to our three examples. But first, work through the following activities, which should help your understanding.

Learn by Doing: Proportions (Step 3)

Did I Get This?: Proportions (Step 3)

The p-value in this case is:

• The probability of observing a test statistic as small as -2 or smaller, assuming that Ho is true.

OR (recalling what the test statistic actually means in this case),

• The probability of observing a sample proportion that is 2 standard deviations or more below the null value (p 0 = 0.20), assuming that p 0 is the true population proportion.

OR, more specifically,

• The probability of observing a sample proportion of 0.16 or lower in a random sample of size 400, when the true population proportion is p 0 =0.20

In either case, the p-value is found as shown in the following figure:

To find P(Z ≤ -2) we can either use the calculator or table we learned to use in the probability unit for normal random variables. Eventually, after we understand the details, we will use software to run the test for us and the output will give us all the information we need. The p-value that the statistical software provides for this specific example is 0.023. The p-value tells us that it is pretty unlikely (probability of 0.023) to get data like those observed (test statistic of -2 or less) assuming that Ho is true.

• The probability of observing a test statistic as large as 0.91 or larger, assuming that Ho is true.
• The probability of observing a sample proportion that is 0.91 standard deviations or more above the null value (p 0 = 0.157), assuming that p 0 is the true population proportion.
• The probability of observing a sample proportion of 0.19 or higher in a random sample of size 100, when the true population proportion is p 0 =0.157

Again, at this point we can either use the calculator or table to find that the p-value is 0.182, this is P(Z ≥ 0.91).

The p-value tells us that it is not very surprising (probability of 0.182) to get data like those observed (which yield a test statistic of 0.91 or higher) assuming that the null hypothesis is true.

• The probability of observing a test statistic as large as 2.31 (or larger) or as small as -2.31 (or smaller), assuming that Ho is true.
• The probability of observing a sample proportion that is 2.31 standard deviations or more away from the null value (p 0 = 0.64), assuming that p 0 is the true population proportion.
• The probability of observing a sample proportion as different as 0.675 is from 0.64, or even more different (i.e. as high as 0.675 or higher or as low as 0.605 or lower) in a random sample of size 1,000, when the true population proportion is p 0 = 0.64

Again, at this point we can either use the calculator or table to find that the p-value is 0.021, this is P(Z ≤ -2.31) + P(Z ≥ 2.31) = 2*P(Z ≥ |2.31|)

The p-value tells us that it is pretty unlikely (probability of 0.021) to get data like those observed (test statistic as high as 2.31 or higher or as low as -2.31 or lower) assuming that Ho is true.

• We’ve just seen that finding p-values involves probability calculations about the value of the test statistic assuming that Ho is true. In this case, when Ho is true, the values of the test statistic follow a standard normal distribution (i.e., the sampling distribution of the test statistic when the null hypothesis is true is N(0,1)). Therefore, p-values correspond to areas (probabilities) under the standard normal curve.

Similarly, in any test , p-values are found using the sampling distribution of the test statistic when the null hypothesis is true (also known as the “null distribution” of the test statistic). In this case, it was relatively easy to argue that the null distribution of our test statistic is N(0,1). As we’ll see, in other tests, other distributions come up (like the t-distribution and the F-distribution), which we will just mention briefly, and rely heavily on the output of our statistical package for obtaining the p-values.

We’ve just completed our discussion about the p-value, and how it is calculated both in general and more specifically for the z-test for the population proportion. Let’s go back to the four-step process of hypothesis testing and see what we’ve covered and what still needs to be discussed.

With respect to the z-test the population proportion:

Step 3: Completed

Step 4. This is what we will work on next.

Learn by Doing: Proportions (Step 3) Understanding P-values

Proportions (Step 4 & Summary)

Video: Proportions (Step 4 & Summary) (4:30)

Step 4. Drawing Conclusions Based on the P-Value

This last part of the four-step process of hypothesis testing is the same across all statistical tests, and actually, we’ve already said basically everything there is to say about it, but it can’t hurt to say it again.

The p-value is a measure of how much evidence the data present against Ho. The smaller the p-value, the more evidence the data present against Ho.

We already mentioned that what determines what constitutes enough evidence against Ho is the significance level (α, alpha), a cutoff point below which the p-value is considered small enough to reject Ho in favor of Ha. The most commonly used significance level is 0.05.

• Conclusion: There IS enough evidence that Ha is True
• Conclusion: There IS NOT enough evidence that Ha is True

Where instead of Ha is True , we write what this means in the words of the problem, in other words, in the context of the current scenario.

It is important to mention again that this step has essentially two sub-steps:

(i) Based on the p-value, determine whether or not the results are statistically significant (i.e., the data present enough evidence to reject Ho).

(ii) State your conclusions in the context of the problem.

Note: We always still must consider whether the results have any practical significance, particularly if they are statistically significant as a statistically significant result which has not practical use is essentially meaningless!

Let’s go back to our three examples and draw conclusions.

We found that the p-value for this test was 0.023.

Since 0.023 is small (in particular, 0.023 < 0.05), the data provide enough evidence to reject Ho.

Conclusion:

• There IS enough evidence that the proportion of defective products is less than 20% after the repair .

The following figure is the complete story of this example, and includes all the steps we went through, starting from stating the hypotheses and ending with our conclusions:

We found that the p-value for this test was 0.182.

Since .182 is not small (in particular, 0.182 > 0.05), the data do not provide enough evidence to reject Ho.

• There IS NOT enough evidence that the proportion of students at the college who use marijuana is higher than the national figure.

Here is the complete story of this example:

Learn by Doing: Learn by Doing – Proportions (Step 4)

We found that the p-value for this test was 0.021.

Since 0.021 is small (in particular, 0.021 < 0.05), the data provide enough evidence to reject Ho

• There IS enough evidence that the proportion of adults who support the death penalty for convicted murderers has changed since 2003.

Did I Get This?: Proportions (Step 4)

Many Students Wonder: Hypothesis Testing for the Population Proportion

Many students wonder why 5% is often selected as the significance level in hypothesis testing, and why 1% is the next most typical level. This is largely due to just convenience and tradition.

When Ronald Fisher (one of the founders of modern statistics) published one of his tables, he used a mathematically convenient scale that included 5% and 1%. Later, these same 5% and 1% levels were used by other people, in part just because Fisher was so highly esteemed. But mostly these are arbitrary levels.

The idea of selecting some sort of relatively small cutoff was historically important in the development of statistics; but it’s important to remember that there is really a continuous range of increasing confidence towards the alternative hypothesis, not a single all-or-nothing value. There isn’t much meaningful difference, for instance, between a p-value of .049 or .051, and it would be foolish to declare one case definitely a “real” effect and to declare the other case definitely a “random” effect. In either case, the study results were roughly 5% likely by chance if there’s no actual effect.

Whether such a p-value is sufficient for us to reject a particular null hypothesis ultimately depends on the risk of making the wrong decision, and the extent to which the hypothesized effect might contradict our prior experience or previous studies.

Let’s Summarize!!

We have now completed going through the four steps of hypothesis testing, and in particular we learned how they are applied to the z-test for the population proportion. Here is a brief summary:

Step 1: State the hypotheses

State the null hypothesis:

State the alternative hypothesis:

where the choice of the appropriate alternative (out of the three) is usually quite clear from the context of the problem. If you feel it is not clear, it is most likely a two-sided problem. Students are usually good at recognizing the “more than” and “less than” terminology but differences can sometimes be more difficult to spot, sometimes this is because you have preconceived ideas of how you think it should be! Use only the information given in the problem.

Step 2: Obtain data, check conditions, and summarize data

Obtain data from a sample and:

(i) Check whether the data satisfy the conditions which allow you to use this test.

random sample (or at least a sample that can be considered random in context)

the conditions under which the sampling distribution of p-hat is normal are met

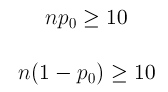
(ii) Calculate the sample proportion p-hat, and summarize the data using the test statistic:

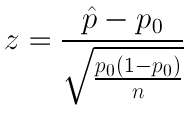
( Recall: This standardized test statistic represents how many standard deviations above or below p 0 our sample proportion p-hat is.)

Step 3: Find the p-value of the test by using the test statistic as follows

IMPORTANT FACT: In all future tests, we will rely on software to obtain the p-value.

When the alternative hypothesis is “less than” the probability of observing a test statistic as small as that observed or smaller , assuming that the values of the test statistic follow a standard normal distribution. We will now represent this probability in symbols and also using the normal distribution.

When the alternative hypothesis is “greater than” the probability of observing a test statistic as large as that observed or larger , assuming that the values of the test statistic follow a standard normal distribution. Again, we will represent this probability in symbols and using the normal distribution

When the alternative hypothesis is “not equal to” the probability of observing a test statistic which is as large in magnitude as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution.

Step 4: Conclusion

Reach a conclusion first regarding the statistical significance of the results, and then determine what it means in the context of the problem.

If p-value ≤ 0.05 then WE REJECT Ho Conclusion: There IS enough evidence that Ha is True

If p-value > 0.05 then WE FAIL TO REJECT Ho Conclusion: There IS NOT enough evidence that Ha is True

Recall that: If the p-value is small (in particular, smaller than the significance level, which is usually 0.05), the results are statistically significant (in the sense that there is a statistically significant difference between what was observed in the sample and what was claimed in Ho), and so we reject Ho.

If the p-value is not small, we do not have enough statistical evidence to reject Ho, and so we continue to believe that Ho may be true. ( Remember: In hypothesis testing we never “accept” Ho ).

Finally, in practice, we should always consider the practical significance of the results as well as the statistical significance.

Learn by Doing: Z-Test for a Population Proportion

What’s next?

Before we move on to the next test, we are going to use the z-test for proportions to bring up and illustrate a few more very important issues regarding hypothesis testing. This might also be a good time to review the concepts of Type I error, Type II error, and Power before continuing on.

More about Hypothesis Testing

CO-1: Describe the roles biostatistics serves in the discipline of public health.

LO 1.11: Recognize the distinction between statistical significance and practical significance.

LO 6.30: Use a confidence interval to determine the correct conclusion to the associated two-sided hypothesis test.

Video: More about Hypothesis Testing (18:25)

The issues regarding hypothesis testing that we will discuss are:

• The effect of sample size on hypothesis testing.
• Statistical significance vs. practical importance.
• Hypothesis testing and confidence intervals—how are they related?

Let’s begin.

1. The Effect of Sample Size on Hypothesis Testing

We have already seen the effect that the sample size has on inference, when we discussed point and interval estimation for the population mean (μ, mu) and population proportion (p). Intuitively …

Larger sample sizes give us more information to pin down the true nature of the population. We can therefore expect the sample mean and sample proportion obtained from a larger sample to be closer to the population mean and proportion, respectively. As a result, for the same level of confidence, we can report a smaller margin of error, and get a narrower confidence interval. What we’ve seen, then, is that larger sample size gives a boost to how much we trust our sample results.

In hypothesis testing, larger sample sizes have a similar effect. We have also discussed that the power of our test increases when the sample size increases, all else remaining the same. This means, we have a better chance to detect the difference between the true value and the null value for larger samples.

The following two examples will illustrate that a larger sample size provides more convincing evidence (the test has greater power), and how the evidence manifests itself in hypothesis testing. Let’s go back to our example 2 (marijuana use at a certain liberal arts college).

We do not have enough evidence to conclude that the proportion of students at the college who use marijuana is higher than the national figure.

Now, let’s increase the sample size.

There are rumors that students in a certain liberal arts college are more inclined to use drugs than U.S. college students in general. Suppose that in a simple random sample of 400 students from the college, 76 admitted to marijuana use . Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) is higher than the national proportion, which is 0.157? (Reported by the Harvard School of Public Health).

Our results here are statistically significant . In other words, in example 2* the data provide enough evidence to reject Ho.

• Conclusion: There is enough evidence that the proportion of marijuana users at the college is higher than among all U.S. students.

What do we learn from this?

We see that sample results that are based on a larger sample carry more weight (have greater power).

In example 2, we saw that a sample proportion of 0.19 based on a sample of size of 100 was not enough evidence that the proportion of marijuana users in the college is higher than 0.157. Recall, from our general overview of hypothesis testing, that this conclusion (not having enough evidence to reject the null hypothesis) doesn’t mean the null hypothesis is necessarily true (so, we never “accept” the null); it only means that the particular study didn’t yield sufficient evidence to reject the null. It might be that the sample size was simply too small to detect a statistically significant difference.

However, in example 2*, we saw that when the sample proportion of 0.19 is obtained from a sample of size 400, it carries much more weight, and in particular, provides enough evidence that the proportion of marijuana users in the college is higher than 0.157 (the national figure). In this case, the sample size of 400 was large enough to detect a statistically significant difference.

The following activity will allow you to practice the ideas and terminology used in hypothesis testing when a result is not statistically significant.

Learn by Doing: Interpreting Non-significant Results

2. Statistical significance vs. practical importance.

Now, we will address the issue of statistical significance versus practical importance (which also involves issues of sample size).

The following activity will let you explore the effect of the sample size on the statistical significance of the results yourself, and more importantly will discuss issue 2: Statistical significance vs. practical importance.

Important Fact: In general, with a sufficiently large sample size you can make any result that has very little practical importance statistically significant! A large sample size alone does NOT make a “good” study!!

This suggests that when interpreting the results of a test, you should always think not only about the statistical significance of the results but also about their practical importance.

Learn by Doing: Statistical vs. Practical Significance

3. Hypothesis Testing and Confidence Intervals

The last topic we want to discuss is the relationship between hypothesis testing and confidence intervals. Even though the flavor of these two forms of inference is different (confidence intervals estimate a parameter, and hypothesis testing assesses the evidence in the data against one claim and in favor of another), there is a strong link between them.

We will explain this link (using the z-test and confidence interval for the population proportion), and then explain how confidence intervals can be used after a test has been carried out.

Recall that a confidence interval gives us a set of plausible values for the unknown population parameter. We may therefore examine a confidence interval to informally decide if a proposed value of population proportion seems plausible.

For example, if a 95% confidence interval for p, the proportion of all U.S. adults already familiar with Viagra in May 1998, was (0.61, 0.67), then it seems clear that we should be able to reject a claim that only 50% of all U.S. adults were familiar with the drug, since based on the confidence interval, 0.50 is not one of the plausible values for p.

In fact, the information provided by a confidence interval can be formally related to the information provided by a hypothesis test. ( Comment: The relationship is more straightforward for two-sided alternatives, and so we will not present results for the one-sided cases.)

Suppose we want to carry out the two-sided test:

• Ha: p ≠ p 0

using a significance level of 0.05.

An alternative way to perform this test is to find a 95% confidence interval for p and check:

• If p 0 falls outside the confidence interval, reject Ho.
• If p 0 falls inside the confidence interval, do not reject Ho.

In other words,

• If p 0 is not one of the plausible values for p, we reject Ho.
• If p 0 is a plausible value for p, we cannot reject Ho.

( Comment: Similarly, the results of a test using a significance level of 0.01 can be related to the 99% confidence interval.)

Let’s look at an example:

Recall example 3, where we wanted to know whether the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, when it was 0.64.

We are testing:

and as the figure reminds us, we took a sample of 1,000 U.S. adults, and the data told us that 675 supported the death penalty for convicted murderers (p-hat = 0.675).

A 95% confidence interval for p, the proportion of all U.S. adults who support the death penalty, is:

\(0.675 \pm 1.96 \sqrt{\dfrac{0.675(1-0.675)}{1000}} \approx 0.675 \pm 0.029=(0.646,0.704)\)

Since the 95% confidence interval for p does not include 0.64 as a plausible value for p, we can reject Ho and conclude (as we did before) that there is enough evidence that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003.

You and your roommate are arguing about whose turn it is to clean the apartment. Your roommate suggests that you settle this by tossing a coin and takes one out of a locked box he has on the shelf. Suspecting that the coin might not be fair, you decide to test it first. You toss the coin 80 times, thinking to yourself that if, indeed, the coin is fair, you should get around 40 heads. Instead you get 48 heads. You are puzzled. You are not sure whether getting 48 heads out of 80 is enough evidence to conclude that the coin is unbalanced, or whether this a result that could have happened just by chance when the coin is fair.

Statistics can help you answer this question.

Let p be the true proportion (probability) of heads. We want to test whether the coin is fair or not.

• Ho: p = 0.5 (the coin is fair).
• Ha: p ≠ 0.5 (the coin is not fair).

The data we have are that out of n = 80 tosses, we got 48 heads, or that the sample proportion of heads is p-hat = 48/80 = 0.6.

A 95% confidence interval for p, the true proportion of heads for this coin, is:

\(0.6 \pm 1.96 \sqrt{\dfrac{0.6(1-0.6)}{80}} \approx 0.6 \pm 0.11=(0.49,0.71)\)

Since in this case 0.5 is one of the plausible values for p, we cannot reject Ho. In other words, the data do not provide enough evidence to conclude that the coin is not fair.

The context of the last example is a good opportunity to bring up an important point that was discussed earlier.

Even though we use 0.05 as a cutoff to guide our decision about whether the results are statistically significant, we should not treat it as inviolable and we should always add our own judgment. Let’s look at the last example again.

It turns out that the p-value of this test is 0.0734. In other words, it is maybe not extremely unlikely, but it is quite unlikely (probability of 0.0734) that when you toss a fair coin 80 times you’ll get a sample proportion of heads of 48/80 = 0.6 (or even more extreme). It is true that using the 0.05 significance level (cutoff), 0.0734 is not considered small enough to conclude that the coin is not fair. However, if you really don’t want to clean the apartment, the p-value might be small enough for you to ask your roommate to use a different coin, or to provide one yourself!

Did I Get This?: Connection between Confidence Intervals and Hypothesis Tests

Did I Get This?: Hypothesis Tests for Proportions (Extra Practice)

Here is our final point on this subject:

When the data provide enough evidence to reject Ho, we can conclude (depending on the alternative hypothesis) that the population proportion is either less than, greater than, or not equal to the null value p 0 . However, we do not get a more informative statement about its actual value. It might be of interest, then, to follow the test with a 95% confidence interval that will give us more insight into the actual value of p.

In our example 3,

we concluded that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, when it was 0.64. It is probably of interest not only to know that the proportion has changed, but also to estimate what it has changed to. We’ve calculated the 95% confidence interval for p on the previous page and found that it is (0.646, 0.704).

We can combine our conclusions from the test and the confidence interval and say:

Data provide evidence that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, and we are 95% confident that it is now between 0.646 and 0.704. (i.e. between 64.6% and 70.4%).

Let’s look at our example 1 to see how a confidence interval following a test might be insightful in a different way.

Here is a summary of example 1:

We conclude that as a result of the repair, the proportion of defective products has been reduced to below 0.20 (which was the proportion prior to the repair). It is probably of great interest to the company not only to know that the proportion of defective has been reduced, but also estimate what it has been reduced to, to get a better sense of how effective the repair was. A 95% confidence interval for p in this case is:

\(0.16 \pm 1.96 \sqrt{\dfrac{0.16(1-0.16)}{400}} \approx 0.16 \pm 0.036=(0.124,0.196)\)

We can therefore say that the data provide evidence that the proportion of defective products has been reduced, and we are 95% confident that it has been reduced to somewhere between 12.4% and 19.6%. This is very useful information, since it tells us that even though the results were significant (i.e., the repair reduced the number of defective products), the repair might not have been effective enough, if it managed to reduce the number of defective products only to the range provided by the confidence interval. This, of course, ties back in to the idea of statistical significance vs. practical importance that we discussed earlier. Even though the results are statistically significant (Ho was rejected), practically speaking, the repair might still be considered ineffective.

Learn by Doing: Hypothesis Tests and Confidence Intervals

Even though this portion of the current section is about the z-test for population proportion, it is loaded with very important ideas that apply to hypothesis testing in general. We’ve already summarized the details that are specific to the z-test for proportions, so the purpose of this summary is to highlight the general ideas.

The process of hypothesis testing has four steps :

I. Stating the null and alternative hypotheses (Ho and Ha).

II. Obtaining a random sample (or at least one that can be considered random) and collecting data. Using the data:

Check that the conditions under which the test can be reliably used are met.

Summarize the data using a test statistic.

• The test statistic is a measure of the evidence in the data against Ho. The larger the test statistic is in magnitude, the more evidence the data present against Ho.

III. Finding the p-value of the test. The p-value is the probability of getting data like those observed (or even more extreme) assuming that the null hypothesis is true, and is calculated using the null distribution of the test statistic. The p-value is a measure of the evidence against Ho. The smaller the p-value, the more evidence the data present against Ho.

IV. Making conclusions.

Conclusions about the statistical significance of the results:

If the p-value is small, the data present enough evidence to reject Ho (and accept Ha).

If the p-value is not small, the data do not provide enough evidence to reject Ho.

To help guide our decision, we use the significance level as a cutoff for what is considered a small p-value. The significance cutoff is usually set at 0.05.

Conclusions should then be provided in the context of the problem.

Additional Important Ideas about Hypothesis Testing

• Results that are based on a larger sample carry more weight, and therefore as the sample size increases, results become more statistically significant.
• Even a very small and practically unimportant effect becomes statistically significant with a large enough sample size. The distinction between statistical significance and practical importance should therefore always be considered.
• Confidence intervals can be used in order to carry out two-sided tests (95% confidence for the 0.05 significance level). If the null value is not included in the confidence interval (i.e., is not one of the plausible values for the parameter), we have enough evidence to reject Ho. Otherwise, we cannot reject Ho.
• If the results are statistically significant, it might be of interest to follow up the tests with a confidence interval in order to get insight into the actual value of the parameter of interest.
• It is important to be aware that there are two types of errors in hypothesis testing ( Type I and Type II ) and that the power of a statistical test is an important measure of how likely we are to be able to detect a difference of interest to us in a particular problem.

Means (All Steps)

NOTE: Beginning on this page, the Learn By Doing and Did I Get This activities are presented as interactive PDF files. The interactivity may not work on mobile devices or with certain PDF viewers. Use an official ADOBE product such as ADOBE READER .

If you have any issues with the Learn By Doing or Did I Get This interactive PDF files, you can view all of the questions and answers presented on this page in this document:

• QUESTION/Answer (SPOILER ALERT!)

Tests About μ (mu) When σ (sigma) is Unknown – The t-test for a Population Mean

The t-distribution.

Video: Means (All Steps) (13:11)

So far we have talked about the logic behind hypothesis testing and then illustrated how this process proceeds in practice, using the z-test for the population proportion (p).

We are now moving on to discuss testing for the population mean (μ, mu), which is the parameter of interest when the variable of interest is quantitative.

A few comments about the structure of this section:

• The basic groundwork for carrying out hypothesis tests has already been laid in our general discussion and in our presentation of tests about proportions.

Therefore we can easily modify the four steps to carry out tests about means instead, without going into all of the details again.

We will use this approach for all future tests so be sure to go back to the discussion in general and for proportions to review the concepts in more detail.

• In our discussion about confidence intervals for the population mean, we made the distinction between whether the population standard deviation, σ (sigma) was known or if we needed to estimate this value using the sample standard deviation, s .

In this section, we will only discuss the second case as in most realistic settings we do not know the population standard deviation .

In this case we need to use the t- distribution instead of the standard normal distribution for the probability aspects of confidence intervals (choosing table values) and hypothesis tests (finding p-values).

• Although we will discuss some theoretical or conceptual details for some of the analyses we will learn, from this point on we will rely on software to conduct tests and calculate confidence intervals for us , while we focus on understanding which methods are used for which situations and what the results say in context.

If you are interested in more information about the z-test, where we assume the population standard deviation σ (sigma) is known, you can review the Carnegie Mellon Open Learning Statistics Course (you will need to click “ENTER COURSE”).

Like any other tests, the t- test for the population mean follows the four-step process:

• STEP 1: Stating the hypotheses H o and H a .
• STEP 2: Collecting relevant data, checking that the data satisfy the conditions which allow us to use this test, and summarizing the data using a test statistic.
• STEP 3: Finding the p-value of the test, the probability of obtaining data as extreme as those collected (or even more extreme, in the direction of the alternative hypothesis), assuming that the null hypothesis is true. In other words, how likely is it that the only reason for getting data like those observed is sampling variability (and not because H o is not true)?
• STEP 4: Drawing conclusions, assessing the statistical significance of the results based on the p-value, and stating our conclusions in context. (Do we or don’t we have evidence to reject H o and accept H a ?)
• Note: In practice, we should also always consider the practical significance of the results as well as the statistical significance.

We will now go through the four steps specifically for the t- test for the population mean and apply them to our two examples.

Only in a few cases is it reasonable to assume that the population standard deviation, σ (sigma), is known and so we will not cover hypothesis tests in this case. We discussed both cases for confidence intervals so that we could still calculate some confidence intervals by hand.

For this and all future tests we will rely on software to obtain our summary statistics, test statistics, and p-values for us.

The case where σ (sigma) is unknown is much more common in practice. What can we use to replace σ (sigma)? If you don’t know the population standard deviation, the best you can do is find the sample standard deviation, s, and use it instead of σ (sigma). (Note that this is exactly what we did when we discussed confidence intervals).

Is that it? Can we just use s instead of σ (sigma), and the rest is the same as the previous case? Unfortunately, it’s not that simple, but not very complicated either.

Here, when we use the sample standard deviation, s, as our estimate of σ (sigma) we can no longer use a normal distribution to find the cutoff for confidence intervals or the p-values for hypothesis tests.

Instead we must use the t- distribution (with n-1 degrees of freedom) to obtain the p-value for this test.

We discussed this issue for confidence intervals. We will talk more about the t- distribution after we discuss the details of this test for those who are interested in learning more.

It isn’t really necessary for us to understand this distribution but it is important that we use the correct distributions in practice via our software.

We will wait until UNIT 4B to look at how to accomplish this test in the software. For now focus on understanding the process and drawing the correct conclusions from the p-values given.

Now let’s go through the four steps in conducting the t- test for the population mean.

The null and alternative hypotheses for the t- test for the population mean (μ, mu) have exactly the same structure as the hypotheses for z-test for the population proportion (p):

The null hypothesis has the form:

• Ho: μ = μ 0 (mu = mu_zero)

(where μ 0 (mu_zero) is often called the null value)

• Ha: μ < μ 0 (mu < mu_zero) (one-sided)
• Ha: μ > μ 0 (mu > mu_zero) (one-sided)
• Ha: μ ≠ μ 0 (mu ≠ mu_zero) (two-sided)

where the choice of the appropriate alternative (out of the three) is usually quite clear from the context of the problem.

If you feel it is not clear, it is most likely a two-sided problem. Students are usually good at recognizing the “more than” and “less than” terminology but differences can sometimes be more difficult to spot, sometimes this is because you have preconceived ideas of how you think it should be! You also cannot use the information from the sample to help you determine the hypothesis. We would not know our data when we originally asked the question.

Now try it yourself. Here are a few exercises on stating the hypotheses for tests for a population mean.

Learn by Doing: State the Hypotheses for a test for a population mean

Here are a few more activities for practice.

Did I Get This?: State the Hypotheses for a test for a population mean

When setting up hypotheses, be sure to use only the information in the research question. We cannot use our sample data to help us set up our hypotheses.

For this test, it is still important to correctly choose the alternative hypothesis as “less than”, “greater than”, or “different” although generally in practice two-sample tests are used.

Obtain data from a sample:

• In this step we would obtain data from a sample. This is not something we do much of in courses but it is done very often in practice!

Check the conditions:

• Then we check the conditions under which this test (the t- test for one population mean) can be safely carried out – which are:
• The sample is random (or at least can be considered random in context).
• We are in one of the three situations marked with a green check mark in the following table (which ensure that x-bar is at least approximately normal and the test statistic using the sample standard deviation, s, is therefore a t- distribution with n-1 degrees of freedom – proving this is beyond the scope of this course):
• For large samples, we don’t need to check for normality in the population . We can rely on the sample size as the basis for the validity of using this test.
• For small samples , we need to have data from a normal population in order for the p-values and confidence intervals to be valid.

In practice, for small samples, it can be very difficult to determine if the population is normal. Here is a simulation to give you a better understanding of the difficulties.

Video: Simulations – Are Samples from a Normal Population? (4:58)

Now try it yourself with a few activities.

Learn by Doing: Checking Conditions for Hypothesis Testing for the Population Mean

• It is always a good idea to look at the data and get a sense of their pattern regardless of whether you actually need to do it in order to assess whether the conditions are met.
• This idea of looking at the data is relevant to all tests in general. In the next module—inference for relationships—conducting exploratory data analysis before inference will be an integral part of the process.

Here are a few more problems for extra practice.

Did I Get This?: Checking Conditions for Hypothesis Testing for the Population Mean

When setting up hypotheses, be sure to use only the information in the res

Calculate Test Statistic

Assuming that the conditions are met, we calculate the sample mean x-bar and the sample standard deviation, s (which estimates σ (sigma)), and summarize the data with a test statistic.

The test statistic for the t -test for the population mean is:

\(t=\dfrac{\bar{x} - \mu_0}{s/ \sqrt{n}}\)

Recall that such a standardized test statistic represents how many standard deviations above or below μ 0 (mu_zero) our sample mean x-bar is.

Therefore our test statistic is a measure of how different our data are from what is claimed in the null hypothesis. This is an idea that we mentioned in the previous test as well.

Again we will rely on the p-value to determine how unusual our data would be if the null hypothesis is true.

As we mentioned, the test statistic in the t -test for a population mean does not follow a standard normal distribution. Rather, it follows another bell-shaped distribution called the t- distribution.

We will present the details of this distribution at the end for those interested but for now we will work on the process of the test.

Here are a few important facts.

• In statistical language we say that the null distribution of our test statistic is the t- distribution with (n-1) degrees of freedom. In other words, when Ho is true (i.e., when μ = μ 0 (mu = mu_zero)), our test statistic has a t- distribution with (n-1) d.f., and this is the distribution under which we find p-values.
• For a large sample size (n), the null distribution of the test statistic is approximately Z, so whether we use t (n – 1) or Z to calculate the p-values does not make a big difference. However, software will use the t -distribution regardless of the sample size and so will we.

Although we will not calculate p-values by hand for this test, we can still easily calculate the test statistic.

Try it yourself:

Learn by Doing: Calculate the Test Statistic for a Test for a Population Mean

From this point in this course and certainly in practice we will allow the software to calculate our test statistics and we will use the p-values provided to draw our conclusions.

We will use software to obtain the p-value for this (and all future) tests but here are the images illustrating how the p-value is calculated in each of the three cases corresponding to the three choices for our alternative hypothesis.

Note that due to the symmetry of the t distribution, for a given value of the test statistic t, the p-value for the two-sided test is twice as large as the p-value of either of the one-sided tests. The same thing happens when p-values are calculated under the t distribution as when they are calculated under the Z distribution.

We will show some examples of p-values obtained from software in our examples. For now let’s continue our summary of the steps.

As usual, based on the p-value (and some significance level of choice) we assess the statistical significance of results, and draw our conclusions in context.

To review what we have said before:

If p-value ≤ 0.05 then WE REJECT Ho

If p-value > 0.05 then WE FAIL TO REJECT Ho

This step has essentially two sub-steps:

We are now ready to look at two examples.

A certain prescription medicine is supposed to contain an average of 250 parts per million (ppm) of a certain chemical. If the concentration is higher than this, the drug may cause harmful side effects; if it is lower, the drug may be ineffective.

The manufacturer runs a check to see if the mean concentration in a large shipment conforms to the target level of 250 ppm or not.

A simple random sample of 100 portions is tested, and the sample mean concentration is found to be 247 ppm with a sample standard deviation of 12 ppm.

Here is a figure that represents this example:

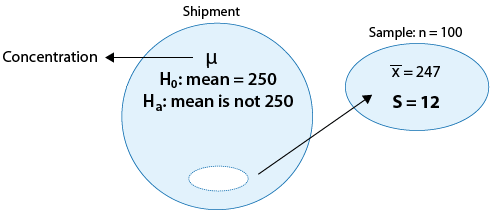
1. The hypotheses being tested are:

• Ha: μ ≠ μ 0 (mu ≠ mu_zero)
• Where μ = population mean part per million of the chemical in the entire shipment

2. The conditions that allow us to use the t-test are met since:

• The sample is random
• The sample size is large enough for the Central Limit Theorem to apply and ensure the normality of x-bar. We do not need normality of the population in order to be able to conduct this test for the population mean. We are in the 2 nd column in the table below.
• The test statistic is:

\(t=\dfrac{\bar{x}-\mu_{0}}{s / \sqrt{n}}=\dfrac{247-250}{12 / \sqrt{100}}=-2.5\)

• The data (represented by the sample mean) are 2.5 standard errors below the null value.

3. Finding the p-value.

• To find the p-value we use statistical software, and we calculate a p-value of 0.014.

4. Conclusions:

• The p-value is small (.014) indicating that at the 5% significance level, the results are significant.
• We reject the null hypothesis.
• There is enough evidence to conclude that the mean concentration in entire shipment is not the required 250 ppm.
• It is difficult to comment on the practical significance of this result without more understanding of the practical considerations of this problem.

Here is a summary:

• The 95% confidence interval for μ (mu) can be used here in the same way as for proportions to conduct the two-sided test (checking whether the null value falls inside or outside the confidence interval) or following a t- test where Ho was rejected to get insight into the value of μ (mu).
• We find the 95% confidence interval to be (244.619, 249.381) . Since 250 is not in the interval we know we would reject our null hypothesis that μ (mu) = 250. The confidence interval gives additional information. By accounting for estimation error, it estimates that the population mean is likely to be between 244.62 and 249.38. This is lower than the target concentration and that information might help determine the seriousness and appropriate course of action in this situation.

In most situations in practice we use TWO-SIDED HYPOTHESIS TESTS, followed by confidence intervals to gain more insight.

For completeness in covering one sample t-tests for a population mean, we still cover all three possible alternative hypotheses here HOWEVER, this will be the last test for which we will do so.

A research study measured the pulse rates of 57 college men and found a mean pulse rate of 70 beats per minute with a standard deviation of 9.85 beats per minute.

Researchers want to know if the mean pulse rate for all college men is different from the current standard of 72 beats per minute.

• The hypotheses being tested are:
• Ho: μ = 72
• Ha: μ ≠ 72
• Where μ = population mean heart rate among college men
• The conditions that allow us to use the t- test are met since:
• The sample is random.
• The sample size is large (n = 57) so we do not need normality of the population in order to be able to conduct this test for the population mean. We are in the 2 nd column in the table below.

\(t=\dfrac{\bar{x}-\mu}{s / \sqrt{n}}=\dfrac{70-72}{9.85 / \sqrt{57}}=-1.53\)

• The data (represented by the sample mean) are 1.53 estimated standard errors below the null value.
• Recall that in general the p-value is calculated under the null distribution of the test statistic, which, in the t- test case, is t (n-1). In our case, in which n = 57, the p-value is calculated under the t (56) distribution. Using statistical software, we find that the p-value is 0.132 .
• Here is how we calculated the p-value. http://homepage.stat.uiowa.edu/~mbognar/applets/t.html .

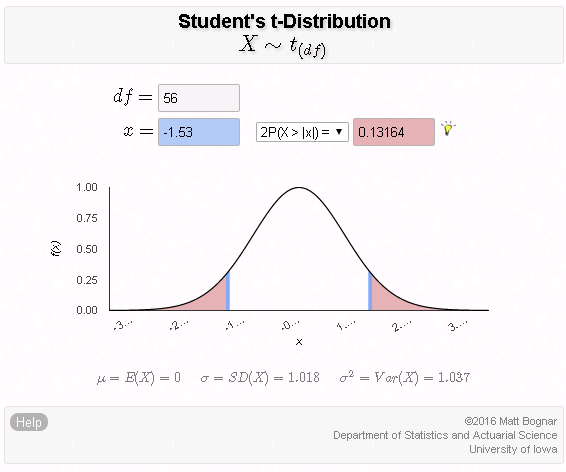
4. Making conclusions.

• The p-value (0.132) is not small, indicating that the results are not significant.
• We fail to reject the null hypothesis.
• There is not enough evidence to conclude that the mean pulse rate for all college men is different from the current standard of 72 beats per minute.
• The results from this sample do not appear to have any practical significance either with a mean pulse rate of 70, this is very similar to the hypothesized value, relative to the variation expected in pulse rates.

Now try a few yourself.

Learn by Doing: Hypothesis Testing for the Population Mean

From this point in this course and certainly in practice we will allow the software to calculate our test statistic and p-value and we will use the p-values provided to draw our conclusions.

That concludes our discussion of hypothesis tests in Unit 4A.

In the next unit we will continue to use both confidence intervals and hypothesis test to investigate the relationship between two variables in the cases we covered in Unit 1 on exploratory data analysis – we will look at Case CQ, Case CC, and Case QQ.

Before moving on, we will discuss the details about the t- distribution as a general object.

We have seen that variables can be visually modeled by many different sorts of shapes, and we call these shapes distributions. Several distributions arise so frequently that they have been given special names, and they have been studied mathematically.

So far in the course, the only one we’ve named, for continuous quantitative variables, is the normal distribution, but there are others. One of them is called the t- distribution.

The t- distribution is another bell-shaped (unimodal and symmetric) distribution, like the normal distribution; and the center of the t- distribution is standardized at zero, like the center of the standard normal distribution.

Like all distributions that are used as probability models, the normal and the t- distribution are both scaled, so the total area under each of them is 1.

So how is the t-distribution fundamentally different from the normal distribution?

• The spread .

The following picture illustrates the fundamental difference between the normal distribution and the t-distribution:

Here we have an image which illustrates the fundamental difference between the normal distribution and the t- distribution:

You can see in the picture that the t- distribution has slightly less area near the expected central value than the normal distribution does, and you can see that the t distribution has correspondingly more area in the “tails” than the normal distribution does. (It’s often said that the t- distribution has “fatter tails” or “heavier tails” than the normal distribution.)

This reflects the fact that the t- distribution has a larger spread than the normal distribution. The same total area of 1 is spread out over a slightly wider range on the t- distribution, making it a bit lower near the center compared to the normal distribution, and giving the t- distribution slightly more probability in the ‘tails’ compared to the normal distribution.

Therefore, the t- distribution ends up being the appropriate model in certain cases where there is more variability than would be predicted by the normal distribution. One of these cases is stock values, which have more variability (or “volatility,” to use the economic term) than would be predicted by the normal distribution.

There’s actually an entire family of t- distributions. They all have similar formulas (but the math is beyond the scope of this introductory course in statistics), and they all have slightly “fatter tails” than the normal distribution. But some are closer to normal than others.

The t- distributions that have higher “degrees of freedom” are closer to normal (degrees of freedom is a mathematical concept that we won’t study in this course, beyond merely mentioning it here). So, there’s a t- distribution “with one degree of freedom,” another t- distribution “with 2 degrees of freedom” which is slightly closer to normal, another t- distribution “with 3 degrees of freedom” which is a bit closer to normal than the previous ones, and so on.

The following picture illustrates this idea with just a couple of t- distributions (note that “degrees of freedom” is abbreviated “d.f.” on the picture):

The test statistic for our t-test for one population mean is a t -score which follows a t- distribution with (n – 1) degrees of freedom. Recall that each t- distribution is indexed according to “degrees of freedom.” Notice that, in the context of a test for a mean, the degrees of freedom depend on the sample size in the study.

Remember that we said that higher degrees of freedom indicate that the t- distribution is closer to normal. So in the context of a test for the mean, the larger the sample size , the higher the degrees of freedom, and the closer the t- distribution is to a normal z distribution .

As a result, in the context of a test for a mean, the effect of the t- distribution is most important for a study with a relatively small sample size .

We are now done introducing the t-distribution. What are implications of all of this?

• The null distribution of our t-test statistic is the t-distribution with (n-1) d.f. In other words, when Ho is true (i.e., when μ = μ 0 (mu = mu_zero)), our test statistic has a t-distribution with (n-1) d.f., and this is the distribution under which we find p-values.
• For a large sample size (n), the null distribution of the test statistic is approximately Z, so whether we use t(n – 1) or Z to calculate the p-values does not make a big difference.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 12: Significance tests (hypothesis testing)

About this unit.

Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values to make conclusions about hypotheses.

The idea of significance tests

• Simple hypothesis testing (Opens a modal)
• Idea behind hypothesis testing (Opens a modal)
• Examples of null and alternative hypotheses (Opens a modal)
• P-values and significance tests (Opens a modal)
• Comparing P-values to different significance levels (Opens a modal)
• Estimating a P-value from a simulation (Opens a modal)
• Using P-values to make conclusions (Opens a modal)
• Simple hypothesis testing Get 3 of 4 questions to level up!
• Writing null and alternative hypotheses Get 3 of 4 questions to level up!
• Estimating P-values from simulations Get 3 of 4 questions to level up!

Error probabilities and power

• Introduction to Type I and Type II errors (Opens a modal)
• Type 1 errors (Opens a modal)
• Examples identifying Type I and Type II errors (Opens a modal)
• Introduction to power in significance tests (Opens a modal)
• Examples thinking about power in significance tests (Opens a modal)
• Consequences of errors and significance (Opens a modal)
• Type I vs Type II error Get 3 of 4 questions to level up!
• Error probabilities and power Get 3 of 4 questions to level up!

Tests about a population proportion

• Constructing hypotheses for a significance test about a proportion (Opens a modal)
• Conditions for a z test about a proportion (Opens a modal)
• Reference: Conditions for inference on a proportion (Opens a modal)
• Calculating a z statistic in a test about a proportion (Opens a modal)
• Calculating a P-value given a z statistic (Opens a modal)
• Making conclusions in a test about a proportion (Opens a modal)
• Writing hypotheses for a test about a proportion Get 3 of 4 questions to level up!
• Conditions for a z test about a proportion Get 3 of 4 questions to level up!
• Calculating the test statistic in a z test for a proportion Get 3 of 4 questions to level up!
• Calculating the P-value in a z test for a proportion Get 3 of 4 questions to level up!
• Making conclusions in a z test for a proportion Get 3 of 4 questions to level up!

Tests about a population mean

• Writing hypotheses for a significance test about a mean (Opens a modal)
• Conditions for a t test about a mean (Opens a modal)
• Reference: Conditions for inference on a mean (Opens a modal)
• When to use z or t statistics in significance tests (Opens a modal)
• Example calculating t statistic for a test about a mean (Opens a modal)
• Using TI calculator for P-value from t statistic (Opens a modal)
• Using a table to estimate P-value from t statistic (Opens a modal)
• Comparing P-value from t statistic to significance level (Opens a modal)
• Free response example: Significance test for a mean (Opens a modal)
• Writing hypotheses for a test about a mean Get 3 of 4 questions to level up!
• Conditions for a t test about a mean Get 3 of 4 questions to level up!
• Calculating the test statistic in a t test for a mean Get 3 of 4 questions to level up!
• Calculating the P-value in a t test for a mean Get 3 of 4 questions to level up!
• Making conclusions in a t test for a mean Get 3 of 4 questions to level up!

More significance testing videos

• Hypothesis testing and p-values (Opens a modal)
• One-tailed and two-tailed tests (Opens a modal)
• Z-statistics vs. T-statistics (Opens a modal)
• Small sample hypothesis test (Opens a modal)
• Large sample proportion hypothesis testing (Opens a modal)

Hypothesis testing

• PMID: 8900794
• DOI: 10.1097/00002800-199607000-00009

Hypothesis testing is the process of making a choice between two conflicting hypotheses. The null hypothesis, H0, is a statistical proposition stating that there is no significant difference between a hypothesized value of a population parameter and its value estimated from a sample drawn from that population. The alternative hypothesis, H1 or Ha, is a statistical proposition stating that there is a significant difference between a hypothesized value of a population parameter and its estimated value. When the null hypothesis is tested, a decision is either correct or incorrect. An incorrect decision can be made in two ways: We can reject the null hypothesis when it is true (Type I error) or we can fail to reject the null hypothesis when it is false (Type II error). The probability of making Type I and Type II errors is designated by alpha and beta, respectively. The smallest observed significance level for which the null hypothesis would be rejected is referred to as the p-value. The p-value only has meaning as a measure of confidence when the decision is to reject the null hypothesis. It has no meaning when the decision is that the null hypothesis is true.

• Data Interpretation, Statistical*
• Nursing Research
• Reproducibility of Results

Statistics Made Easy

4 Examples of Hypothesis Testing in Real Life

In statistics, hypothesis tests are used to test whether or not some hypothesis about a population parameter is true.

To perform a hypothesis test in the real world, researchers will obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:

• Null Hypothesis (H 0 ): The sample data occurs purely from chance.
• Alternative Hypothesis (H A ): The sample data is influenced by some non-random cause.

If the p-value of the hypothesis test is less than some significance level (e.g. α = .05), then we can reject the null hypothesis and conclude that we have sufficient evidence to say that the alternative hypothesis is true.

The following examples provide several situations where hypothesis tests are used in the real world.

Example 1: Biology

Hypothesis tests are often used in biology to determine whether some new treatment, fertilizer, pesticide, chemical, etc. causes increased growth, stamina, immunity, etc. in plants or animals.

For example, suppose a biologist believes that a certain fertilizer will cause plants to grow more during a one-month period than they normally do, which is currently 20 inches. To test this, she applies the fertilizer to each of the plants in her laboratory for one month.

She then performs a hypothesis test using the following hypotheses:

• H 0 : μ = 20 inches (the fertilizer will have no effect on the mean plant growth)
• H A : μ > 20 inches (the fertilizer will cause mean plant growth to increase)

If the p-value of the test is less than some significance level (e.g. α = .05), then she can reject the null hypothesis and conclude that the fertilizer leads to increased plant growth.

Example 2: Clinical Trials

Hypothesis tests are often used in clinical trials to determine whether some new treatment, drug, procedure, etc. causes improved outcomes in patients.

For example, suppose a doctor believes that a new drug is able to reduce blood pressure in obese patients. To test this, he may measure the blood pressure of 40 patients before and after using the new drug for one month.

He then performs a hypothesis test using the following hypotheses:

• H 0 : μ after = μ before (the mean blood pressure is the same before and after using the drug)
• H A : μ after < μ before (the mean blood pressure is less after using the drug)

If the p-value of the test is less than some significance level (e.g. α = .05), then he can reject the null hypothesis and conclude that the new drug leads to reduced blood pressure.

Example 3: Advertising Spend

Hypothesis tests are often used in business to determine whether or not some new advertising campaign, marketing technique, etc. causes increased sales.

For example, suppose a company believes that spending more money on digital advertising leads to increased sales. To test this, the company may increase money spent on digital advertising during a two-month period and collect data to see if overall sales have increased.

They may perform a hypothesis test using the following hypotheses:

• H 0 : μ after = μ before (the mean sales is the same before and after spending more on advertising)
• H A : μ after > μ before (the mean sales increased after spending more on advertising)

If the p-value of the test is less than some significance level (e.g. α = .05), then the company can reject the null hypothesis and conclude that increased digital advertising leads to increased sales.

Example 4: Manufacturing

Hypothesis tests are also used often in manufacturing plants to determine if some new process, technique, method, etc. causes a change in the number of defective products produced.

For example, suppose a certain manufacturing plant wants to test whether or not some new method changes the number of defective widgets produced per month, which is currently 250. To test this, they may measure the mean number of defective widgets produced before and after using the new method for one month.

They can then perform a hypothesis test using the following hypotheses:

• H 0 : μ after = μ before (the mean number of defective widgets is the same before and after using the new method)
• H A : μ after ≠ μ before (the mean number of defective widgets produced is different before and after using the new method)

If the p-value of the test is less than some significance level (e.g. α = .05), then the plant can reject the null hypothesis and conclude that the new method leads to a change in the number of defective widgets produced per month.

Additional Resources

Introduction to Hypothesis Testing Introduction to the One Sample t-test Introduction to the Two Sample t-test Introduction to the Paired Samples t-test

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

• Open access
• Published: 21 May 2024

The mediating effects of self-efficacy and study engagement on the relationship between specialty identity and career maturity of Chinese nursing students: a cross-sectional study

• Yanjia Liu 1 , 2 ,
• Mei Chan Chong 2 ,
• Yanhong Han 1 ,
• Hui Wang 3 &
• Lijuan Xiong 1  

BMC Nursing volume  23 , Article number:  339 ( 2024 ) Cite this article

151 Accesses

Metrics details

Career maturity is a crucial indicator of career preparedness and unpreparedness can cause the turnover of new nurses. Considerable empirical work demonstrates the potential associations between specialty identity, self-efficacy, study engagement, and career maturity. This study aimed to explore the mediation role of self-efficacy and study engagement on the relationships between specialty identity and career maturity among Chinese nursing students.

Four hundred twenty-six Chinese nursing students were recruited between September 11 and October 30, 2022. The online survey was conducted following the CHERRIES checklist. Electronic questionnaires assessed their perceived specialty identity, self-efficacy, study engagement, and career maturity. The descriptive analysis, Harman single-factor analysis, Pearson correlation tests, structural equation modeling, and the bootstrap method were employed in data analysis.

Bivariate correlation analysis identified a positive correlation between specialty identity, self-efficacy, study engagement, and career maturity ( r  = 0.276–0.440, P  < 0.001). Self-efficacy and study engagement partially mediated the relationship between specialty identity and career maturity. Self-efficacy and study engagement played a chain mediating role between specialty identity and career maturity.

Conclusions

The underlying mechanism can explain the relationships between specialty identity and career maturity: a direct predictor and an indirect effect through self-efficacy and study engagement. Policymakers and educators should emphasize the importance of specialty identity and provide tailored strategies for improving care maturity depending on nursing students’ specialty identity, self-efficacy, study engagement in the early stages of career development.

Peer Review reports

Introduction

The media visibility obtained by nursing during the COVID-19 pandemic has made the public aware of nurses’ role in promoting and maintaining health [ 1 ]. As the social environment becomes more conducive to nursing career development, adequate awareness and preparedness for nursing careers are driving nursing students to adapt to and be satisfied with their careers [ 2 , 3 ].

Career maturity is a crucial indicator of career preparedness [ 4 ], which is defined as the readiness to make age-appropriate career decisions with adequate information and accomplish career development-related tasks [ 5 ]. Unpreparedness and difficulties in taking on the nurse’s role were the main reasons newly graduated nursing students left nursing in their first years [ 6 ]. The turnover rate for new nurses in their first year of employment can reach as high as 69%, with a range of 12.10–69% [ 6 , 7 , 8 , 9 ]. In addition, new nurses who experienced higher levels of career maturity were also less likely to leave the profession [ 10 ]. Therefore, more research focusing on career maturity should re-engage nursing educators and managers and support the development of customized programs in the early stage of career development.

Specialty identity as a predictor to career maturity

Super’s theory emphasizes that career development is a lifelong activity closely related to individual maturity and experiences [ 11 ]. It encompasses the development of behaviors and professional identity [ 12 ]. Work values, including professional identity, are crucial for career development and can influence career maturity [ 13 ]. professional identity significantly correlates with high school students’ career maturity [ 14 ]. Additionally, specialty identity appears as a part of professional identity in studies worldwide [ 15 ]. To clarify this concept in student groups, specialty identity is defined as the emotional acceptance and recognition of learners based on their understanding of the specialty being studied, accompanied by positive external behaviors and an inner sense of satisfaction [ 15 ]. Therefore, this study proposes Hypothesis 1: specialty identity significantly predicts career maturity among Chinese nursing students.

The mediating effect of self-efficacy between specialty identity and career maturity

Self-efficacy and career maturity are positively related [ 16 , 17 ]. According to social cognitive theory, self-efficacy is a belief in a person’s ability to achieve their goal [ 18 ]. Regarding career maturity, self-efficacy could be an internal driver for students to dedicate themselves to the fields they have chosen [ 16 ]. Students with high self-efficacy can improve their professionalism and self-confidence, thereby achieving high degrees of career maturity [ 16 ]. Further, professional identity is found to be significantly correlated with self-efficacy [ 19 , 20 ]. Yao et al. [ 21 ] found that self-efficacy mediated between professional identity and self-reported competence among nursing students. Thus, this study poses Hypothesis 2: Self-efficacy is the mediating variable affecting specialty identity and career maturity among Chinese nursing students.

The mediating effect of study engagement between specialty identity and career maturity

Study engagement is a vital variable related to academic performance, achievement, persistence, and retention, which refers to a positive psychological process including attention, energy and effort in learning [ 22 , 23 ]. Astin’s theory of student involvement emphasizes that the significant environmental factors that can influence their engagement entail students’ backgrounds, such as residence, experiences, and academic involvement [ 24 ]. A significant correlation exists between study engagement and career maturity [ 25 ]. Moreover, Liu et al. [ 26 ] report that professional identity is positively correlated with study engagement, and the mediating role of study engagement in professional identity and career adaptability is significant. Based on the above evidence, this study posits Hypothesis 3: study engagement is the mediating variable affecting specialty identity and career maturity among Chinese nursing students.

The chain mediating effect of self-efficacy and study engagement between specialty identity and career maturity

Based on the aforementioned information, self-efficacy and study engagement may play a single mediating role between specialty identity and career maturity. However, the relationship between self-efficacy and study engagement remains to be clarified. In addition, whether these variables play a chain mediating effect between specialty identity and career maturity must be explored. Previous research has shown that self-efficacy positively correlates with study engagement [ 27 , 28 ]. The relationship between specialty identity and career maturity may be influenced by self-efficacy in the first place and by study engagement in the second. Therefore, this study proposes Hypothesis 4: Chain mediation describes the relationship among the four variables.

Overall, this study explores the relationship between specialty identity and career maturity. It also examines the potential mediation model of specialty identity, self-efficacy, and career maturity, the potential mediation model of specialty identity, study engagement, and career maturity, and the potential chain mediation of the four variables using mediation analysis.

This cross-sectional online survey was conducted among nursing students between September 11 and October 30, 2022. This online survey was designed, disseminated and conducted following the Checklist for Reporting Results of Internet E-Surveys (CHERRIES) [ 29 ] (see in the Supplement File 1 ). The online questionnaire entailed demographic sheet and four instruments with different question styles (single choice and Likert scales).

Variables and data collection instruments

Sociodemographic variables.

Sex (female, male), Higher education institution type (university, college), and Degree (diploma, bachelor’s).

• Specialty identity

The College Student Specialty Identity Scale (CSSIS) developed by Qin [ 15 ], was used to measure medical students’ specialty identity [ 30 ]. It is a 23-item scale with four subscales (cognitive, emotional, behavioral, and appropriateness). Students scored each item on a five-point Likert scale (1–5: strongly disagree to strongly agree). In Qin’s study, it had good reliability (α = 0.955) [ 15 ]. In the present study, Cronbach’s α was 0.949.

• Study engagement

Study engagement was assessed using the Utrecht Work Engagement Scale-Student (UWES-S) [ 31 ]. Schaufeli et al. [ 32 ] developed the UWES and revised its items to measure students’ study engagement. Li & Huang [ 31 ] introduced UWES-S, translated it into Chinese, and validated it among undergraduate students. The UWES-S comprises 17 items grouped into three subscales (vigor, dedication, and absorption) and uses a 7-point scale (0 = never, to 7 = always). The cumulative scores range from 0 to 102, with higher scores indicating greater study engagement. The internal consistency using Cronbach’s alpha was 0.919 [ 31 ]. In this study, Cronbach’s α = 0.956.

• Self-efficacy

This study used the Chinese version of the General Self-Efficacy Scale to assess self-efficacy [ 33 ]. Schwarzer et al. [ 34 ] developed the original version. It was adapted to the context of China and validated by Wang et al. [ 33 ]. It is a 10-item scale with a 4-point Likert scale (from completely incorrect to completely correct). Cronbach’s alpha was 0.871 in Wang et al.’s study [ 33 ]. In this study, Cronbach’s α = 0.899.

• Career maturity

Career maturity was measured using the validated Chinese version of the career maturity scale [ 35 ]. The original version developed by Lee [ 36 ] was translated into Chinese by Zhang et al. [ 35 ]. The instrument entails 34 items broken down into six subscales: career decisiveness (CD), career confidence (CC), career independence (CI), career value (CV), relational dependence (RD), and career reference (CR). A 5-point Likert scale, ranging from strongly disagree to strongly agree, was adopted. The range of total scores was 34–170, with higher values indicating higher levels of career maturity. Its reliability coefficient was 0.86, as measured using Cronbach’s alpha [ 35 ]. In this sample, Cronbach’s α = 0.900.

Participants and data collection procedure

This study was conducted at five higher education institutions in Hubei province, China. The target population, full-time nursing students, were surveyed using convenience sampling. The suggested minimum sample size based on Monte Carlo simulations studies was adopted [ 37 ], and the minimum and maximum sample sizes for structural equation models were 200 and 460 respectively [ 38 ]. The final sample size in the design stage was 250–575, accommodating a possible dropout rate of 20%.

For data collection, we uploaded the integrated questionnaires on Wenjuanxing ( https://www.wjx.cn/ , Acquired NO.168,902,709). This website offers the most popular and convenient tool for anonymous data collection and collecting data anonymously extraction. One investigator from each university or college was invited to collect the data. All investigators held master’s degrees and understood the critical points for questionnaire collection well. Simple training was conducted before questionnaire distribution. Each nursing student can review and change their answers if necessary, but they were provided only one chance to submit the online questionnaires. The individual IP address can be yielded after submissions and provided for verification. Finally, 560 questionnaires were administered. After double-checking and eliminating invalid questionnaires, 426 valid questionnaires were extracted, yielding an effective response rate of 76.07%.

Data analysis

After completing the descriptive analysis, Harman single-factor analysis was performed to assess the common method bias, and Pearson correlations were calculated in SPSS Version 26.0. Subsequently, structural equation modeling was validated, and the chain-mediation effect was examined using the bootstrap method in AMOS Version 23.0 with 5000 samples. The significance level was set at 0.05.

Ethical considerations

This study was approved by the Ethics Committee of Jingmen No. 2 People’s Hospital, affiliated to Jingchu University of Technology (Approval No.2020002-1). All students provided verbal consent to participate in the study and voluntarily completed and submitted the questionnaire.

Harman single-factor analysis

The self-reported nature of the data meant the possibility of common method bias [ 39 ]. The Harman single-factor analysis showed that the eigenvalues of the five common factors were greater than 1. The first common factor explained 35.50% of the variance, which is lower than the recommended threshold of 50% [ 40 ]. Therefore, no common method bias was detected.

Descriptive statistics and correlation analysis

The sociodemographic variables were as follows: female ( n  = 370, 86.85%), male ( n  = 56, 13.15%); university ( n  = 322, 75.59%), college ( n  = 104, 24.41%); freshmen ( n  = 101, 23.71%), sophomores ( n  = 166, 38.97%), juniors ( n  = 127, 29.81%), seniors ( n  = 32, 7.51%); Urban areas ( n  = 151, 35.45%), Rural areas ( n  = 275, 64.55%). The age of nursing students range from 18 to 25 (mean = 19.89, SD=1.27 ) (see Table  1 ).

Table  2 shows the mean scores of the four key variables were 80.40 ± 21.66, 57.56 ± 16.04, 26.23 ± 9.37, and 113.42 ± 31.61. Positive correlations were found between the key variables: specialty identity and study engagement ( r  = 0.276), specialty identity and self-efficacy ( r  = 0.319), specialty identity and career maturity ( r  = 0.300), study engagement and self-efficacy ( r  = 0.420), study engagement and career maturity ( r  = 0.319), and self-efficacy and career maturity ( r  = 0.440) (each p  < 0.001).

The chain-mediation effect analysis

A chain-mediation structural model was constructed with specialty identity as the independent variable, career maturity as the dependent variable, and self-efficacy and study engagement as the mediating variables. The model fitting results showed that χ 2 /df = 2.965, the comparative fit index = 0.963, the Tucker-Lewis index = 0.958, and the root mean square error of approximation = 0.068, indicating good model fit. The chain-mediation effect model diagram of specialty identity, self-efficacy, study engagement, and career maturity of nursing students is shown in Fig.  1 .

The chain mediation effect model diagram of specialty identity, self-efficacy, study engagement, and career maturity of nursing students

The bootstrapping method found that the 95% confidence interval (95% CI) of the chain-mediation path from specialty identity to career maturity was [0.002, 0.054], which did not include 0, indicating significance. Thus, two possible mediation effects were detected: the mediating roles of self-efficacy in the relationship between specialty identity and career maturity and of study engagement in the relationship between specialty identity and career maturity, both of which were significant with a 95% CI (see Table  3 ).

This study explored the relationships between specialty identity, self-efficacy, study engagement, and career maturity and demonstrated the mediation models in Chinese nursing students. The finding identified a positive correlation between specialty identity and career maturity, and specialty identity can influence career maturity in three ways: self-efficacy, study engagement, and self-efficacy → study engagement, supporting the four Hypotheses. Despite this study did not validate the potential confounders such as career resilience [ 20 ], career adaptability [ 26 ], and resource management [ 29 ], the findings may improve our understanding of the underlying mechanism of these four variables and provide meaningful ideas for taking measures to improve nursing students’ career maturity.

In this study, the findings revealed a positive correlation between specialty identity and career maturity, indicating that specialty identity could significantly predict career maturity in nursing students, which is consistent with previous studies [ 14 , 41 ]. However, most nursing students enrolled in nursing school with insufficient specialty identity owing to poor nursing image and a lack of acknowledgment of career growth [ 42 ], meaning their unpreparedness for learning nursing and career development. Specialty identity is an emotional foundation of career maturity, and it can serve as a powerful psychological adjustment when it comes to nursing students’ specialty or job selection. Therefore, the importance of specialty identity on career maturity should be valued by nurse educators and clinical mentors, and further studies should specifically develop and conduct the education program to verify the roles of specialty identity in the early stage of career development. For example, an innovative course about the power of nursing including embracing the healer’s art course, seed talk and reflection exercises was found to connect the nursing students’ values to their specialty identity, and facilitate their professional formation and the development of nursing practice [ 43 ].

The first pathway confirmed was the mediating role of self-efficacy in the relationship between specialty identity and career maturity, aligning with its mediating effect on professional identity and career maturity in a previous study [ 41 ]. When nursing students perceive higher levels of specialty identity, they may have a stronger sense of self-efficacy and achieve greater career maturity. This finding is consistent with the Knowledge–Attitude–Belief–Practice model [ 44 ]. For nursing students, specialty identity and self-efficacy can support attitudes and beliefs about learning nursing specialties [ 21 ] and play the role of internal driving strength in the chase for a feasible professional study plan and career plan. As a result, career maturity could be a feedback indicator for learning behaviors and career preparedness.

This study also verified the mediating effect of study engagement on specialty identity and career maturity. This finding is consistent with a mediation analysis confirming the mediating role of study engagement between professional identity and career maturity among pre-service kindergarten teachers [ 25 ]. This result also supports the predictive impact of study engagement on the beneficial development of careers [ 26 , 45 ]. The mediating effect of study engagement revealed that if nursing students perceive high levels of specialty identity, they might have greater study engagement, achieve more knowledge and skills related to the nursing specialty, and possess high degrees of career maturity to adapt to the nursing profession. However, this study identified the study engagement had a limited mediating effect with a low effect size. The possible reason is that nursing is a specialized and complex discipline, which requires lifelong learning as health needs change and medical technology advances. In a short period, study engagement can improve nursing knowledge and skills, which is conducive to career preparedness, but high levels of career maturity are the result of long-term study engagement especially since this career needs continued education or continued career development [ 46 ].

Additionally, these findings supported the assertion that the chain relationship between self-efficacy and study engagement mediates the relationship between specialty identity and career maturity. The indirect effect of the pathway, including self-efficacy, was greater than that of the chain pathway and the pathway, including a single study engagement. Higher specialty identity could yield higher self-efficacy [ 19 , 20 ], and higher self-efficacy is related to greater study engagement [ 27 , 28 ]. Thus, nursing students with higher specialty identity might have higher self-efficacy and greater study engagement, which leads to higher career maturity. This model also revealed that increased self-efficacy might contribute to nursing students’ high study engagement levels. When nursing students have a sense of high self-efficacy, their learning behaviors become more effective. They are more willing to devote themselves to learning, thus producing higher study engagement. Despite some studies have demonstrated the effect of interventions such as career planning group counseling [ 47 ] and self-reflection-focused career course [ 48 ] on nursing students’ career maturity, what we found in this study provide theoretical foundation for the development and implementation of multifaceted interventions to improve nursing students career maturity and career development. Furthermore, further attention should be given to the interdisciplinary collaborations, such as positive psychology and nursing education, that can be contribute to explore novel perspectives and approaches to studying career maturity.

This study had some limitations. First, the cross-sectional design without a longitudinal method fails to explore the changes in psychological variables over time, which might restrict the temporal and causal inference. Therefore, scholars should focus on exploring the trajectory changes of these variables, notably the mutability of these psychological features, in the further studies, and the longitudinal and sustained interventions like tutor systems and peer learning should be strongly encouraged. Second, the nursing students were selected from five schools in Hubei province, China, which might limit the generalizability to all Chinese nursing students. As there are disparities in the curriculum systems of different schools, the results could be impacted by cognitive errors caused by teaching philosophy and training purposes. Therefore, the potential influencing factors should be considered and other mediators excluding self-efficacy and study engagement also should be explored in further studies. Third, selection bias may arise from the application of convenience sampling. Therefore, scholars could employ probability sampling methods like random stratified sampling to recruit nursing students. Finally, since all instruments were self-reported, the true feelings of these nursing students were not captured or tracked. From this, the research designs to deepen the understanding of the mechanisms underlying nursing students’ career development, such as mixed-method study and qualitative study, should be considered.

A correlational and mediation analysis was used to examine the relationships between four variables. Specialty identity could be a predictive factor for nursing students’ career maturity. Most importantly, specialty identity can indirectly influence career maturity among nursing students through the mediating effect of self-efficacy, study engagement, and the chain mediating effect of self-efficacy and study engagement, supporting career-related theories. Policymakers and educators should focus on the value of specialty identity to promote nursing students’ career development. Specialty identity may be conducive to stimulating students with a strong sense of self-efficacy and robust study engagement. Nursing students with high self-efficacy and study engagement may perceive greater career maturity. Thus, scholars and educators should be encouraged to provide tailored career guidance programs and practical interventions to enhance nursing students’ career maturity in the early stage of career development.

Data availability

The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.

Fawaz M, Anshasi H, Samaha A. Nurses at the Front line of COVID-19: roles,responsibilities, risks, and rights. Am J Trop Med Hyg. 2020;103(4):1341–2. https://doi.org/10.4269/ajtmh.20-0650 .

Article   CAS   PubMed   PubMed Central   Google Scholar  

Kim J, Shin S. Development of the nursing practice readiness scale for new graduate nurses: a methodological study. Nurse Educ Pract. 2022;59:103298. https://doi.org/10.1016/j.nepr.2022.103298 .

Article   PubMed   Google Scholar  

Zhang J, Shields L, Ma B, et al. The clinical learning environment, supervision and future intention to work as a nurse in nursing students: a cross-sectional and descriptive study. BMC Med Educ. 2022;22(1):548. https://doi.org/10.1186/s12909-022-03609-y .

Article   PubMed   PubMed Central   Google Scholar  

Lee I, Heok JW, Rojewski, Roger B. Hill. Classifying Korean adolescents’ career preparedness. Int J Educ Vocat Guid. 2013;13:25–45. https://doi.org/10.1007/s10775-012-9236-5 .

Article   Google Scholar  

Savickas ML. Career maturity: the construct and its measurement. Vocat Guid Q. 1984;32(4):222–31. https://doi.org/10.1002/j.2164-585X.1984.tb01585.x .

Casey K, Fink R, Jaynes C, Campbell L, Cook P, Wilson V. Readiness for practice: the senior practicum experience. J Nurs Educ. 2011;50(11):646–52. https://doi.org/10.3928/01484834-20110817-03 .

Chen SF, Fang YW, Wang MH, Wang TF. Effects of an Adaptive Education Program on the Learning, Mental Health and Work intentions of New Graduate nurses. Int J Environ Res Public Health. 2021;18(11):5891. https://doi.org/10.3390/ijerph181158915 . Published 2021 May 31.

Kovner CT, Brewer CS, Fatehi F, Jun J. What does nurse turnover rate mean and what is the rate? [published correction appears in Policy Polit Nurs Pract. 2017;18(4):216–217]. Policy Polit Nurs Pract. 2014;15(3–4):64–71. https://doi.org/10.1177/1527154414547953 .

Zhang YP, Huang X, Xu SY, Xu CJ, Feng XQ, Jin JF. Can a one-on-one mentorship program reduce the turnover rate of new graduate nurses in China? A longitudinal study. Nurse Educ Pract. 2019;40:102616. https://doi.org/10.1016/j.nepr.2019.08.010 .

Kawai K, Yamazaki Y. The effects of pre-entry career maturity and support networks in workplace on newcomers’ mental health. J Occup Health. 2006;48(6):451–61. https://doi.org/10.1539/joh.48.451 .

Super DE. A life-span, life-space approach to career development, edited by D Brown, L Brooks & Associates. Career choice and development: Applying contemporary theories to practice.1990.2nd edition. San Francisco: Jossey-Bass.

Schreuder AMG, Coetzee M, Careers. An organisational perspective. 2011. 4th edition. Cape Town: Juta.

Langley R, Du Toit R, Herbst DL. Manual for the career development questionnaire. Pretoria: Human Sciences Research Council. 1992; 157:373–422.

Dipeolu A, Deutch S, Hargrave S, Storlie CA. Developmentally relevant Career constructs: response patterns of youth with ADHD and LDs. Can J Career Dev. 2019;18(1):45–55.

Google Scholar  

Qin P. B.The characteristics and correlation study of college students’ specialty identity [Chinese]. Master thesis: Southwest University.2009.

Purwandika R, Ayriza Y. The influence of self-efficacy on career maturity of high school students in pacitan regency. In2nd International Seminar on Guidance and Counseling 2019 (ISGC 2019) 2020; (pp. 93–7). Atlantis.

Singh PK, Shukla RP. Relationship between career maturity and self-efficacy among male and female senior secondary students. MIER J Educational Stud Trends Practices. 2015 Nov;10:164–79. https://doi.org/10.52634/mier/2015/v5/i2/1486 .

Bandura A. On the functional properties of perceived self-efficacy revisited. J Manag. 2012;38(1):9–44.

Mei XX, Wang HY, Wu XN, Wu JY, Lu YZ, Ye ZJ. Self-Efficacy and Professional Identity among freshmen nursing students: a latent Profile and Moderated Mediation Analysis. Front Psychol. 2022;13:779986. https://doi.org/10.3389/fpsyg.2022.779986 .

Zhou Y, Chen S, Deng X, Wang S, Shi L. Self-efficacy and career resilience: the mediating role of professional identity and work passion in kindergarten teachers. J Psychol Afr. 2023;33(2):165–70. https://doi.org/10.1080/14330237.2023.2207052 .

Yao X, Yu L, Shen Y, Kang Z, Wang X. The role of self-efficacy in mediating between professional identity and self-reported competence among nursing students in the internship period: a quantitative study. Nurse Educ Pract. 2021;57:103252. https://doi.org/10.1016/j.nepr.2021.103252 .

Bond M, Buntins K, Bedenlier S, Zawacki-Richter O, Kerres M. Mapping research in student engagement and educational technology in higher education: a systematic evidence map. Int J Educational Technol High Educ. 2020;17(1):1–30. https://doi.org/10.1186/s41239-019-0176-8 .

Schaufeli WB, Martinez IM, Pinto AM, Salanova M, Bakker AB. Burnout and engagement in university students: a cross-national study. J Cross-Cult Psychol. 2002;33(5):464–81.

Astin AW. Student involvement: a developmental theory for higher education. InCollege student development and academic life, 2014 (pp. 251–62). Routledge.

Zhang L, Chen M, Zeng X, Wang X. The relationship between professional identity and career maturity among pre-service kindergarten teachers: the mediating effect of learning engagement. Open J Social Sci. 2018;6(6):167–86. https://doi.org/10.4236/jss.2018.66016 .

Liu X, Ji X, Zhang Y, Gao W. Professional Identity and Career adaptability among Chinese Engineering students: the Mediating Role of Learning Engagement. Behav Sci (Basel). 2023;13(6):480. https://doi.org/10.3390/bs13060480 .

Wu H, Li S, Zheng J, Guo J. Medical students’ motivation and academic performance: the mediating roles of self-efficacy and learning engagement. Med Educ Online. 2020;25(1):1742964. https://doi.org/10.1080/10872981.2020.1742964 .

Eysenbach G. Improving the quality of web surveys: the Checklist for reporting results of internet E-Surveys (CHERRIES). J Med Internet Res. 2004;6(3):e34. https://doi.org/10.2196/jmir.6.3.e34 .

Heo H, Bonk CJ, Doo MY. Influences of depression, self-efficacy, and resource management on learning engagement in blended learning during COVID-19. Internet High Educ. 2022;54:100856. https://doi.org/10.1016/j.iheduc.2022.100856 .

Zhang X, Sun B, Tian Z, et al. Relationship between honesty-credit, specialty identity, career identity, and willingness to fulfill the contract among rural-oriented tuition-waived medical students of China: a cross-sectional study. Front Public Health. 2023;11:1089625. https://doi.org/10.3389/fpubh.2023.1089625 .

Li X, Huang R. A revise of the UWES-S of Chinese college samples. Psychol Res. 2010;3(1):84–8.

Schaufeli WB, Salanova M, González-Romá V, Bakker AB. The measurement of engagement and burnout: a two sample confirmatory factor analytic approach. J Happiness Stud. 2002;3:71–92.

Wang CK, Hu ZF, Liu Y. Reliability and validity of General self-efficacy scale. Chin J Appl Psychol. 2001;7(1):37–40. https://doi.org/10.396 9/j.issn.1006-6020.2001.01.007. (in Chinese).

Schwarzer R, Mueller J, Greenglass E. Assessment of perceived general self-efficacy on the internet: data collection in cyberspace. Anxiety Stress Coping. 1999;12(2):145–61.

Zhang ZY, Rong Y, Guan YJ. Reliability and validity of Career Maturity Scale for Chinese College Students. J Southwest Normal Univ (Humanities Social Sci Edition). 2006;32(5):1–6. (in Chinese).

Lee KH. A cross-cultural study of the career maturity of Korean and United States high school students. J Career Dev. 2001;28(1):43–57. https://doi.org/10.1023/A:1011189931409 .

Kyriazos TA. Applied psychometrics: sample size and sample power considerations in factor analysis (EFA, CFA) and SEM in general. Psychology. 2018;9(08):2207. https://doi.org/10.4236/psych.2018.98126 .

Wolf EJ, Harrington KM, Clark SL, Miller MW. Sample size requirements for structural equation models: an evaluation of power, bias, and solution propriety. Educ Psychol Meas. 2013;73(6):913–34.

Jordan PJ, Troth AC. Common method bias in applied settings: the dilemma of researching in organizations. Aust J Manage. 2020;45(1):3–14. https://doi.org/10.1177/0312896219871976 .

Duong CD. Psychological distress related to Covid-19 in healthy public (CORPD): a statistical method for assessing the validation of scale. MethodsX. 2022;9:101645. https://doi.org/10.1016/j.mex.2022.101645 .

Kornspan AS, Etzel EF. The relationship of demographic and Psychological Variables to Career Maturity of Junior College Student-Athletes. J Coll Student Dev. 2001;42(2):122–32.

Kandil F, El Seesy N, Banakhar M. Factors affecting students’ preference for nursing education and their intent to leave: a cross-sectional study. Open Nurs J. 2021;15(1):1–8. https://doi.org/10.2174/187443460211501000 .

WHO. Knowledge, Attitudes, and Practices (KAP) Surveys during Cholera Vaccination Campaigns: Guidance for Oral Cholera Vaccine Stockpile Campaigns. [(accessed on 15 July 2023)]. Available online: https://www.who.int/publications/m/item/knowledge-attitudes-and-practices-(kap)-surveys-during-cholera-vaccination-campaigns-guidance-for-oral-cholera-vaccine-stockpile-campaigns .

Peng MY, Yue X. Enhancing Career decision status of socioeconomically disadvantaged students through Learning Engagement: perspective of SOR Model. Front Psychol. 2022;13:778928. https://doi.org/10.3389/fpsyg.2022.778928 .

Day L, Ziehm SR, Jessup MA, Amedro P, Dawson-Rose C, Derouin A, Kennedy BB, Manahan S, Parish AL, Remen RN. The power of nursing: an innovative course in values clarification and self-discovery. J Prof Nurs. 2017;33(4):267–70. https://doi.org/10.1016/j.profnurs.2017.01.005 .

Mlambo M, Silén C, McGrath C. Lifelong learning and nurses’ continuing professional development, a metasynthesis of the literature. BMC Nurs. 2021;20(1):62. https://doi.org/10.1186/s12912-021-00579-2 .

Xie WY, Yang XL, Cai YM, Mo W, Shen ZM, Li YH, Zhou BF, Li YL. Evaluation of career planning group counseling and its effectiveness for intern male nursing students. BMC Med Educ. 2023;17(1):34. https://doi.org/10.1186/s12909-022-03981-9 .

Kim JH, Shin HS. Effects of self-reflection-focused career course on career search efficacy, career maturity, and career adaptability in nursing students: a mixed methods study. J Prof Nurs. 2020;36(5):395–403. https://doi.org/10.1016/j.profnurs.2020.03.003

Download references

Acknowledgements

We greatly appreciate the support of all nursing students from five schools in Hubei province for their voluntary participation in this study.

Not applicable.

Author information

Authors and affiliations.

Department of Nursing, Wuhan Union Hospital, Tongji Medical College, Huazhong University of Science and Technology, Wuhan, China

Yanjia Liu, Yanhong Han & Lijuan Xiong

Department of Nursing Science, Faculty of Medicine, Universiti Malaya, Kuala Lumpur, Malaysia

Yanjia Liu & Mei Chan Chong

Department of Medicine, Jingchu University of Technology, Jingmen, Hubei, China

You can also search for this author in PubMed   Google Scholar

Contributions

Study design: XLJ, CMC, HYH; Data collection and analysis: WH, LYJ; Manuscript preparation: LYJ, HYH. All authors reviewed the manuscript.

Corresponding author

Correspondence to Lijuan Xiong .

Ethics declarations

Ethics approval and consent to participate.

This study has been approved by the Ethical Review Committee of Jingmen No.2 People’s Hospital, affiliated with Jingchu University of Technology (Approval No.2022002-1). All methods were performed in accordance with the relevant guidelines and regulations. Informed consent was obtained from all subjects involved in the study.

Consent for publication

Not application.

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary Material 1

Rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Liu, Y., Chong, M.C., Han, Y. et al. The mediating effects of self-efficacy and study engagement on the relationship between specialty identity and career maturity of Chinese nursing students: a cross-sectional study. BMC Nurs 23 , 339 (2024). https://doi.org/10.1186/s12912-024-02002-y

Download citation

Received : 13 December 2023

Accepted : 08 May 2024

Published : 21 May 2024

DOI : https://doi.org/10.1186/s12912-024-02002-y

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Nursing students
• Mediating effect

BMC Nursing

ISSN: 1472-6955

• General enquiries: [email protected]