math skills research questions

251+ Math Research Topics [2024 Updated]

Mathematics, often dubbed as the language of the universe, holds immense significance in shaping our understanding of the world around us. It’s not just about crunching numbers or solving equations; it’s about unraveling mysteries, making predictions, and creating innovative solutions to complex problems. In this blog, we embark on a journey into the realm of math research topics, exploring various branches of mathematics and their real-world applications.

How Do You Write A Math Research Topic?

Writing a math research topic involves several steps to ensure clarity, relevance, and feasibility. Here’s a guide to help you craft a compelling math research topic:

• Identify Your Interests: Start by exploring areas of mathematics that interest you. Whether it’s pure mathematics, applied mathematics, or interdisciplinary topics, choose a field that aligns with your passion and expertise.
• Narrow Down Your Focus: Mathematics is a broad field, so it’s essential to narrow down your focus to a specific area or problem. Consider the scope of your research and choose a topic that is manageable within your resources and time frame.
• Review Existing Literature: Conduct a thorough literature review to understand the current state of research in your chosen area. Identify gaps, controversies, or unanswered questions that could form the basis of your research topic.
• Formulate a Research Question: Based on your exploration and literature review, formulate a clear and concise research question. Your research question should be specific, measurable, achievable, relevant, and time-bound (SMART).
• Consider Feasibility: Assess the feasibility of your research topic in terms of available resources, data availability, and research methodologies. Ensure that your topic is realistic and achievable within the constraints of your project.
• Consult with Experts: Seek feedback from mentors, advisors, or experts in the field to validate your research topic and refine your ideas. Their insights can help you identify potential challenges and opportunities for improvement.
• Refine and Iterate: Refine your research topic based on feedback and further reflection. Iterate on your ideas to ensure clarity, coherence, and relevance to the broader context of mathematics research.
• Craft a Title: Once you have finalized your research topic, craft a compelling title that succinctly summarizes the essence of your research. Your title should be descriptive, engaging, and reflective of the key themes of your study.
• Write a Research Proposal: Develop a comprehensive research proposal outlining the background, objectives, methodology, and expected outcomes of your research. Your research proposal should provide a clear roadmap for your study and justify the significance of your research topic.

By following these steps, you can effectively write a math research topic that is well-defined, relevant, and poised to make a meaningful contribution to the field of mathematics.

251+ Math Research Topics: Beginners To Advanced

• Prime Number Distribution in Arithmetic Progressions
• Diophantine Equations and their Solutions
• Applications of Modular Arithmetic in Cryptography
• The Riemann Hypothesis and its Implications
• Graph Theory: Exploring Connectivity and Coloring Problems
• Knot Theory: Unraveling the Mathematics of Knots and Links
• Fractal Geometry: Understanding Self-Similarity and Dimensionality
• Differential Equations: Modeling Physical Phenomena and Dynamical Systems
• Chaos Theory: Investigating Deterministic Chaos and Strange Attractors
• Combinatorial Optimization: Algorithms for Solving Optimization Problems
• Computational Complexity: Analyzing the Complexity of Algorithms
• Game Theory: Mathematical Models of Strategic Interactions
• Number Theory: Exploring Properties of Integers and Primes
• Algebraic Topology: Studying Topological Invariants and Homotopy Theory
• Analytic Number Theory: Investigating Properties of Prime Numbers
• Algebraic Geometry: Geometry Arising from Algebraic Equations
• Galois Theory: Understanding Field Extensions and Solvability of Equations
• Representation Theory: Studying Symmetry in Linear Spaces
• Harmonic Analysis: Analyzing Functions on Groups and Manifolds
• Mathematical Logic: Foundations of Mathematics and Formal Systems
• Set Theory: Exploring Infinite Sets and Cardinal Numbers
• Real Analysis: Rigorous Study of Real Numbers and Functions
• Complex Analysis: Analytic Functions and Complex Integration
• Measure Theory: Foundations of Lebesgue Integration and Probability
• Topological Groups: Investigating Topological Structures on Groups
• Lie Groups and Lie Algebras: Geometry of Continuous Symmetry
• Differential Geometry: Curvature and Topology of Smooth Manifolds
• Algebraic Combinatorics: Enumerative and Algebraic Aspects of Combinatorics
• Ramsey Theory: Investigating Structure in Large Discrete Structures
• Analytic Geometry: Studying Geometry Using Analytic Methods
• Hyperbolic Geometry: Non-Euclidean Geometry of Curved Spaces
• Nonlinear Dynamics: Chaos, Bifurcations, and Strange Attractors
• Homological Algebra: Studying Homology and Cohomology of Algebraic Structures
• Topological Vector Spaces: Vector Spaces with Topological Structure
• Representation Theory of Finite Groups: Decomposition of Group Representations
• Category Theory: Abstract Structures and Universal Properties
• Operator Theory: Spectral Theory and Functional Analysis of Operators
• Algebraic Number Theory: Study of Algebraic Structures in Number Fields
• Cryptanalysis: Breaking Cryptographic Systems Using Mathematical Methods
• Discrete Mathematics: Combinatorics, Graph Theory, and Number Theory
• Mathematical Biology: Modeling Biological Systems Using Mathematical Tools
• Population Dynamics: Mathematical Models of Population Growth and Interaction
• Epidemiology: Mathematical Modeling of Disease Spread and Control
• Mathematical Ecology: Dynamics of Ecological Systems and Food Webs
• Evolutionary Game Theory: Evolutionary Dynamics and Strategic Behavior
• Mathematical Neuroscience: Modeling Brain Dynamics and Neural Networks
• Mathematical Physics: Mathematical Models in Physical Sciences
• Quantum Mechanics: Foundations and Applications of Quantum Theory
• Statistical Mechanics: Statistical Methods in Physics and Thermodynamics
• Fluid Dynamics: Modeling Flow of Fluids Using Partial Differential Equations
• Mathematical Finance: Stochastic Models in Finance and Risk Management
• Option Pricing Models: Black-Scholes Model and Beyond
• Portfolio Optimization: Maximizing Returns and Minimizing Risk
• Stochastic Calculus: Calculus of Stochastic Processes and Itô Calculus
• Financial Time Series Analysis: Modeling and Forecasting Financial Data
• Operations Research: Optimization of Decision-Making Processes
• Linear Programming: Optimization Problems with Linear Constraints
• Integer Programming: Optimization Problems with Integer Solutions
• Network Flow Optimization: Modeling and Solving Flow Network Problems
• Combinatorial Game Theory: Analysis of Games with Perfect Information
• Algorithmic Game Theory: Computational Aspects of Game-Theoretic Problems
• Fair Division: Methods for Fairly Allocating Resources Among Parties
• Auction Theory: Modeling Auction Mechanisms and Bidding Strategies
• Voting Theory: Mathematical Models of Voting Systems and Social Choice
• Social Network Analysis: Mathematical Analysis of Social Networks
• Algorithm Analysis: Complexity Analysis of Algorithms and Data Structures
• Machine Learning: Statistical Learning Algorithms and Data Mining
• Deep Learning: Neural Network Models with Multiple Layers
• Reinforcement Learning: Learning by Interaction and Feedback
• Natural Language Processing: Statistical and Computational Analysis of Language
• Computer Vision: Mathematical Models for Image Analysis and Recognition
• Computational Geometry: Algorithms for Geometric Problems
• Symbolic Computation: Manipulation of Mathematical Expressions
• Numerical Analysis: Algorithms for Solving Numerical Problems
• Finite Element Method: Numerical Solution of Partial Differential Equations
• Monte Carlo Methods: Statistical Simulation Techniques
• High-Performance Computing: Parallel and Distributed Computing Techniques
• Quantum Computing: Quantum Algorithms and Quantum Information Theory
• Quantum Information Theory: Study of Quantum Communication and Computation
• Quantum Error Correction: Methods for Protecting Quantum Information from Errors
• Topological Quantum Computing: Using Topological Properties for Quantum Computation
• Quantum Algorithms: Efficient Algorithms for Quantum Computers
• Quantum Cryptography: Secure Communication Using Quantum Key Distribution
• Topological Data Analysis: Analyzing Shape and Structure of Data Sets
• Persistent Homology: Topological Invariants for Data Analysis
• Mapper Algorithm: Method for Visualization and Analysis of High-Dimensional Data
• Algebraic Statistics: Statistical Methods Based on Algebraic Geometry
• Tropical Geometry: Geometric Methods for Studying Polynomial Equations
• Model Theory: Study of Mathematical Structures and Their Interpretations
• Descriptive Set Theory: Study of Borel and Analytic Sets
• Ergodic Theory: Study of Measure-Preserving Transformations
• Combinatorial Number Theory: Intersection of Combinatorics and Number Theory
• Additive Combinatorics: Study of Additive Properties of Sets
• Arithmetic Geometry: Interplay Between Number Theory and Algebraic Geometry
• Proof Theory: Study of Formal Proofs and Logical Inference
• Reverse Mathematics: Study of Logical Strength of Mathematical Theorems
• Nonstandard Analysis: Alternative Approach to Analysis Using Infinitesimals
• Computable Analysis: Study of Computable Functions and Real Numbers
• Graph Theory: Study of Graphs and Networks
• Random Graphs: Probabilistic Models of Graphs and Connectivity
• Spectral Graph Theory: Analysis of Graphs Using Eigenvalues and Eigenvectors
• Algebraic Graph Theory: Study of Algebraic Structures in Graphs
• Metric Geometry: Study of Geometric Structures Using Metrics
• Geometric Measure Theory: Study of Measures on Geometric Spaces
• Discrete Differential Geometry: Study of Differential Geometry on Discrete Spaces
• Algebraic Coding Theory: Study of Error-Correcting Codes
• Information Theory: Study of Information and Communication
• Coding Theory: Study of Error-Correcting Codes
• Cryptography: Study of Secure Communication and Encryption
• Finite Fields: Study of Fields with Finite Number of Elements
• Elliptic Curves: Study of Curves Defined by Cubic Equations
• Hyperelliptic Curves: Study of Curves Defined by Higher-Degree Equations
• Modular Forms: Analytic Functions with Certain Transformation Properties
• L-functions: Analytic Functions Associated with Number Theory
• Zeta Functions: Analytic Functions with Special Properties
• Analytic Number Theory: Study of Number Theoretic Functions Using Analysis
• Dirichlet Series: Analytic Functions Represented by Infinite Series
• Euler Products: Product Representations of Analytic Functions
• Arithmetic Dynamics: Study of Iterative Processes on Algebraic Structures
• Dynamics of Rational Maps: Study of Dynamical Systems Defined by Rational Functions
• Julia Sets: Fractal Sets Associated with Dynamical Systems
• Mandelbrot Set: Fractal Set Associated with Iterations of Complex Quadratic Polynomials
• Arithmetic Geometry: Study of Algebraic Geometry Over Number Fields
• Diophantine Geometry: Study of Solutions of Diophantine Equations Using Geometry
• Arithmetic of Elliptic Curves: Study of Elliptic Curves Over Number Fields
• Rational Points on Curves: Study of Rational Solutions of Algebraic Equations
• Galois Representations: Study of Representations of Galois Groups
• Automorphic Forms: Analytic Functions with Certain Transformation Properties
• L-functions: Analytic Functions Associated with Automorphic Forms
• Selberg Trace Formula: Tool for Studying Spectral Theory and Automorphic Forms
• Langlands Program: Program to Unify Number Theory and Representation Theory
• Hodge Theory: Study of Harmonic Forms on Complex Manifolds
• Riemann Surfaces: One-dimensional Complex Manifolds
• Shimura Varieties: Algebraic Varieties Associated with Automorphic Forms
• Modular Curves: Algebraic Curves Associated with Modular Forms
• Hyperbolic Manifolds: Manifolds with Constant Negative Curvature
• Teichmüller Theory: Study of Moduli Spaces of Riemann Surfaces
• Mirror Symmetry: Duality Between Calabi-Yau Manifolds
• Kähler Geometry: Study of Hermitian Manifolds with Special Symmetries
• Algebraic Groups: Linear Algebraic Groups and Their Representations
• Lie Algebras: Study of Algebraic Structures Arising from Lie Groups
• Representation Theory of Lie Algebras: Study of Representations of Lie Algebras
• Quantum Groups: Deformation of Lie Groups and Lie Algebras
• Algebraic Topology: Study of Topological Spaces Using Algebraic Methods
• Homotopy Theory: Study of Continuous Deformations of Spaces
• Homology Theory: Study of Algebraic Invariants of Topological Spaces
• Cohomology Theory: Study of Dual Concepts to Homology Theory
• Singular Homology: Homology Theory Defined Using Simplicial Complexes
• Sheaf Theory: Study of Sheaves and Their Cohomology
• Differential Forms: Study of Multilinear Differential Forms
• De Rham Cohomology: Cohomology Theory Defined Using Differential Forms
• Morse Theory: Study of Critical Points of Smooth Functions
• Symplectic Geometry: Study of Symplectic Manifolds and Their Geometry
• Floer Homology: Study of Symplectic Manifolds Using Pseudoholomorphic Curves
• Gromov-Witten Invariants: Invariants of Symplectic Manifolds Associated with Pseudoholomorphic Curves
• Mirror Symmetry: Duality Between Symplectic and Complex Geometry
• Calabi-Yau Manifolds: Ricci-Flat Complex Manifolds
• Moduli Spaces: Spaces Parameterizing Geometric Objects
• Donaldson-Thomas Invariants: Invariants Counting Sheaves on Calabi-Yau Manifolds
• Algebraic K-Theory: Study of Algebraic Invariants of Rings and Modules
• Homological Algebra: Study of Homology and Cohomology of Algebraic Structures
• Derived Categories: Categories Arising from Homological Algebra
• Stable Homotopy Theory: Homotopy Theory with Stable Homotopy Groups
• Model Categories: Categories with Certain Homotopical Properties
• Higher Category Theory: Study of Higher Categories and Homotopy Theory
• Higher Topos Theory: Study of Higher Categorical Structures
• Higher Algebra: Study of Higher Categorical Structures in Algebra
• Higher Algebraic Geometry: Study of Higher Categorical Structures in Algebraic Geometry
• Higher Representation Theory: Study of Higher Categorical Structures in Representation Theory
• Higher Category Theory: Study of Higher Categorical Structures
• Homotopical Algebra: Study of Algebraic Structures in Homotopy Theory
• Homotopical Groups: Study of Groups with Homotopical Structure
• Homotopical Categories: Study of Categories with Homotopical Structure
• Homotopy Groups: Algebraic Invariants of Topological Spaces
• Homotopy Type Theory: Study of Foundations of Mathematics Using Homotopy Theory

In conclusion, the world of mathematics is vast and multifaceted, offering endless opportunities for exploration and discovery. Whether delving into the abstract realms of pure mathematics or applying mathematical principles to solve real-world problems, mathematicians play a vital role in advancing human knowledge and shaping the future of our world.

By embracing diverse math research topics and interdisciplinary collaborations, we can unlock new possibilities and harness the power of mathematics to address the challenges of today and tomorrow. So, let’s embark on this journey together as we unravel the mysteries of numbers and explore the boundless horizons of mathematical inquiry.

Related Posts

Step by Step Guide on The Best Way to Finance Car

The Best Way on How to Get Fund For Business to Grow it Efficiently

Leave a comment cancel reply.

Your email address will not be published. Required fields are marked *

• Math Careers

Search form

• MAA Centennial
• Spotlight: Archives of American Mathematics
• MAA Officers
• MAA to the Power of New
• Council and Committees
• MAA Code of Conduct
• Policy on Conflict of Interest
• Statement about Conflict of Interest
• Recording or Broadcasting of MAA Events
• Policy for Establishing Endowments and Funds
• Avoiding Implicit Bias
• Copyright Agreement
• Principal Investigator's Manual
• Planned Giving
• The Icosahedron Society
• Our Partners
• Advertise with MAA
• Employment Opportunities
• Staff Directory
• 2022 Impact Report
• In Memoriam
• Membership Categories
• Become a Member
• Membership Renewal
• MERCER Insurance
• MAA Member Directories
• New Member Benefits
• The American Mathematical Monthly
• Mathematics Magazine
• The College Mathematics Journal
• How to Cite
• Communications in Visual Mathematics
• About Convergence
• What's in Convergence?
• Convergence Articles
• Mathematical Treasures
• Portrait Gallery
• Paul R. Halmos Photograph Collection
• Other Images
• Critics Corner
• Problems from Another Time
• Conference Calendar
• Guidelines for Convergence Authors
• Math Horizons
• Submissions to MAA Periodicals
• Guide for Referees
• Scatterplot
• Math Values
• MAA Book Series
• MAA Press (an imprint of the AMS)
• MAA Library Recommendations
• Additional Sources for Math Book Reviews
• About MAA Reviews
• Mathematical Communication
• Information for Libraries
• Author Resources
• MAA MathFest
• Proposal and Abstract Deadlines
• MAA Policies
• Invited Paper Session Proposals
• Contributed Paper Session Proposals
• Panel, Poster, Town Hall, and Workshop Proposals
• Minicourse Proposals
• MAA Section Meetings
• Virtual Programming
• Joint Mathematics Meetings
• Calendar of Events
• MathFest Programs Archive
• MathFest Abstract Archive
• Historical Speakers
• Information for School Administrators
• Information for Students and Parents
• Registration
• Getting Started with the AMC
• AMC Policies
• AMC Administration Policies
• Important AMC Dates
• Competition Locations
• Invitational Competitions
• Putnam Competition Archive
• AMC International
• Curriculum Inspirations
• Sliffe Award
• MAA K-12 Benefits
• Mailing List Requests
• Statistics & Awards
• Submit an NSF Proposal with MAA
• MAA Distinguished Lecture Series
• Common Vision
• CUPM Curriculum Guide
• Instructional Practices Guide
• Möbius MAA Placement Test Suite
• META Math Webinar May 2020
• Progress through Calculus
• Survey and Reports
• "Camp" of Mathematical Queeries
• DMEG Awardees
• National Research Experience for Undergraduates Program (NREUP)
• Neff Outreach Fund Awardees
• Tensor SUMMA Grants
• Tensor Women & Mathematics Grants
• Grantee Highlight Stories
• "Best Practices" Statements
• CoMInDS Summer Workshop 2023
• MAA Travel Grants for Project ACCCESS
• 2024 Summer Workshops
• Minority Serving Institutions Leadership Summit
• Previous Workshops
• Frequently Asked Questions
• Course Resources
• Industrial Math Case Studies
• Participating Faculty
• 2020 PIC Math Student Showcase
• Previous PIC Math Workshops on Data Science
• Dates and Locations
• Past Programs
• Leadership Team
• Support Project NExT
• Section NExT
• Section Officers Meeting History
• Preparations for Section Meetings
• Bylaws Template
• Editor Lectures Program
• MAA Section Lecturer Series
• Officer Election Support
• Section Awards
• Section Liaison Programs
• Section Visitors Program
• Expense Reimbursement
• Guidelines for Bylaw Revisions
• Guidelines for Local Arrangement Chair and/or Committee
• Guidelines for Section Webmasters
• MAA Logo Guidelines
• MAA Section Email Policy
• Section Newsletter Guidelines
• Statement on Federal Tax ID and 501(c)3 Status
• Communication Support
• Guidelines for the Section Secretary and Treasurer
• Legal & Liability Support for Section Officers
• Section Marketing Services
• Section in a Box
• Subventions and Section Finances
• Web Services
• Joining a SIGMAA
• Forming a SIGMAA
• History of SIGMAA
• SIGMAA Officer Handbook
• MAA Connect
• Meetings and Conferences for Students
• Opportunities to Present
• Information and Resources
• MAA Undergraduate Student Poster Session
• Undergraduate Research Resources
• MathFest Student Paper Sessions
• Research Experiences for Undergraduates
• Student Poster Session FAQs
• High School
• A Graduate School Primer
• Reading List
• Student Chapters
• Awards Booklets
• Carl B. Allendoerfer Awards
• Regulations Governing the Association's Award of The Chauvenet Prize
• Trevor Evans Awards
• Paul R. Halmos - Lester R. Ford Awards
• Merten M. Hasse Prize
• George Pólya Awards
• David P. Robbins Prize
• Beckenbach Book Prize
• Euler Book Prize
• Daniel Solow Author’s Award
• Henry L. Alder Award
• Deborah and Franklin Tepper Haimo Award
• Certificate of Merit
• Gung and Hu Distinguished Service
• JPBM Communications Award
• Meritorious Service
• MAA Award for Inclusivity
• T. Christine Stevens Award
• Dolciani Award Guidelines
• Morgan Prize Information
• Selden Award Eligibility and Guidelines for Nomination
• Selden Award Nomination Form
• AMS-MAA-SIAM Gerald and Judith Porter Public Lecture
• Etta Zuber Falconer
• Hedrick Lectures
• James R. C. Leitzel Lecture
• Pólya Lecturer Information
• Putnam Competition Individual and Team Winners
• D. E. Shaw Group AMC 8 Awards & Certificates
• Maryam Mirzakhani AMC 10 A Awards & Certificates
• Two Sigma AMC 10 B Awards & Certificates
• Jane Street AMC 12 A Awards & Certificates
• Akamai AMC 12 B Awards & Certificates
• High School Teachers
• MAA Social Media

You are here

Research sampler: research questions, research questions.

>From time-to-time, new entries will be added and old entries annotated (but not altered).

Entries are speculative. They have not appeared in refereed publications and should not be regarded as, in any way, describing "facts."

• Proof, Validation, and Trains of Thought , September 19, 2000.

Dummy View - NOT TO BE DELETED

• MAA History
• Policies and Procedures
• Support MAA
• Member Discount Programs
• Periodicals
• MAA Reviews
• Propose a Session
• MathFest Archive
• Putnam Competition
• AMC Resources
• Curriculum Resources
• Outreach Initiatives
• Professional Development
• Communities

Connect with MAA

Mathematical Association of America P: (800) 331-1622 F: (240) 396-5647 Email: [email protected]

Copyright © 2024

• Terms of Use
• Privacy Policy
• Mobile Version

Advertisement

Posing Researchable Questions in Mathematics and Science Education: Purposefully Questioning the Questions for Investigation

• Published: 07 April 2020
• Volume 18 , pages 1–7, ( 2020 )

Cite this article

• Jinfa Cai 1 &
• Rachel Mamlok-Naaman 2  

5550 Accesses

8 Citations

2 Altmetric

Explore all metrics

A Correction to this article was published on 15 May 2020

This article has been updated

Avoid common mistakes on your manuscript.

Perhaps the most obvious example is the set of 23 influential mathematical problems posed by David Hilbert that inspired a great deal of progress in the discipline of mathematics (Hilbert, 1901 -1902). Einstein and Infeld ( 1938 ) claimed that “to raise new questions, new possibilities, to regard old problems from a new angle, requires creative imagination and marks real advance in science” (p. 95). Both Cantor and Klamkin recommended that, in mathematics, the art of posing a question be held as high or higher in value than solving it. Similarly, in the history of science, formulating precise, answerable questions not only advances new discoveries but also gives scientists intellectual excitement (Kennedy, 2005 ; Mosteller, 1980 ).

In research related to mathematics and science education, there is no shortage of evidence for the impact of posing important and researchable questions: Posing new, researchable questions marks real advances in mathematics and science education (Cai et al., 2019a ). Although research in mathematics and science education begins with researchable questions, only recently have researchers begun to purposefully and systematically discuss the nature of researchable questions. To conduct research, we must have researchable questions, but what defines a researchable question? What are the sources of researchable questions? How can we purposefully discuss researchable questions?

This special issue marks effort for the field’s discussion of researchable questions. As the field of mathematics and science education matures, it is necessary to reflect on the field at such a metalevel (Inglis & Foster, 2018 ). Although the authors in this special issue discuss researchable questions from different angles, they all refer to researchable questions as those that can be investigated empirically. For any empirical study, one can discuss its design, its conduct, and how it can be written up for publication. Therefore, researchable questions in mathematics and science education can be discussed with respect to study design, the conduct of research, and the dissemination of that research.

Even though there are many lines of inquiry that we can explore with respect to researchable questions, each exploring the topic from a different angle, we have decided to focus on the following three aspects to introduce this special issue: (1) criteria for selecting researchable questions, (2) sources of researchable questions, and (3) alignment of researchable questions with the conceptual framework as well as appropriate research methods.

Criteria for Selecting Researchable Questions

It is clear that not all researchable questions are worth the effort to investigate. According to Cai et al. ( 2020 ), of all researchable questions in mathematics and science education, priority is given to those that are significant. Research questions are significant if they can advance the fields’ knowledge and understanding about the teaching and learning of science and mathematics. Through an analysis of peer reviews for a research journal, Cai et al. ( 2020 ) provide a window into the field’s frontiers related to significant researchable questions. In an earlier article, Cai et al. ( 2019a ) argued that

The significance of a research question cannot be determined just by reading it. Rather, its significance stands in relation to the knowledge of the field. The justification for the research question itself—why it is a significant question to investigate—must therefore be made clear through an explicit argument that ties the research question to what is and is not already known. (p. 118)

In their analysis, Cai et al. ( 2020 ) provide evidence that many reviews that highlighted issues with the research questions in rejected manuscripts specifically called for authors to make an argument to motivate the research questions, whereas none of the manuscripts that were ultimately accepted (pending revisions) received this kind of comment. Cai et al. ( 2020 ) provide a framework not only for analyzing peer reviews about research questions but also for how to communicate researchable questions in journal manuscript preparations.

Whereas Cai and his colleagues, as editors of a journal, discuss significant research questions from the perspective of peer review and publication, King, Ochsendorf, Solomon, and Sloane ( 2020 ), as program directors at the Directorate for Education and Human Resources at the U.S. National Science Foundation (NSF), discuss fundable research questions for research in mathematics and science education. King et al. ( 2020 ) situate their discussion of fundable research questions in the context of writing successful educational research grant proposals. For them, fundable research questions must be transformative and significant with specific and clear constructs. In addition, they present examples of STEM education research questions from different types of research (Institute of Education Sciences [IES] & NSF, 2013 ) and how the questions themselves direct specific design choices, methodologies, measures, study samples, and analytical models as well as how they can reflect the disciplinary orientations of the researchers.

Hjalmarson and Baker ( 2020 ) take a quite different approach to discussing researchable questions for teacher professional development. They argue for the need to include mathematics specialists (e.g. mathematics coaches or mathematics teacher leaders) for studying teacher learning and development. To Hjalmarson and Baker ( 2020 ), researchable questions related to teacher professional learning should be selected by including mathematics specialists because of their role in connecting research and practice.

Sanchez ( 2020 ) discuss, in particular, the importance of replication studies in mathematics and the kinds of researchable questions that would be productive to explore within this category. With the increased acknowledgement of the importance of replication studies (Cai et al., 2018 ), Sanchez Aguilar has provided a useful typology of fundamental questions that can guide a replication study in mathematics (and science) education.

Schoenfeld ( 2020 ) is very direct in suggesting that researchable questions must advance the field and that these research questions must be meaningful and generative: “What is meant by meaningful is that the answer to the questions posed should matter to either practice or theory in some important way. What is meant by generative is that working on the problem, whether it is ‘solved’ or not, is likely to provide valuable insights” (pp. XX). Schoenfeld calls for researchers to establish research programs—that is, one not only selects meaningful research questions to investigate but also continues in that area of research to produce ongoing insights and further meaningful questions.

Stylianides and Stylianides ( 2020 ) argue that, collectively, researchers can and need to pose new researchable questions. The new researchable questions are worth investigating if they reflect the field’s growing understanding of the web of potentially influential factors surrounding the investigation of a particular area. The argument that Stylianides and Stylianides ( 2020 ) use is very similar to Schoenfeld’s ( 2020 ) generative criteria, but Stylianides and Stylianides ( 2020 ) explicitly emphasize the collective nature of the field’s growing understanding of a particular phenomenon.

Sources of Researchable Questions

Research questions in science and mathematics education arise from multiple sources, including problems of practice, extensions of theory, and lacunae in existing areas of research. Therefore, through a research question’s connections to prior research, it should be clear how answering the question extends the field’s knowledge (Cai et al., 2019a ). Across the papers in this special issue lies a common theme that researchable questions arise from understanding the area under study. Cai et al. ( 2020 ) take the position that the significance of researchable questions must be justified in the context of prior research. In particular, reviewers of manuscripts submitted for publication will evaluate if the study is adequately motivated. In fact, posing significant researchable questions is an iterative process beginning with some broader, general sense of an idea which is potentially fruitful and leading, eventually, to a well-specified, stated research question (Cai et al., 2019a ). Similarly, King et al. ( 2020 ) argue that fundable research questions should be grounded in prior research and make explicit connections to what is known or not known in the given area of study.

Sanchez ( 2020 ) suggest that it is time for the field of mathematics and science education research to seriously consider replication studies. Researchable questions related to replication studies might arise from the examination of the following two questions: (1) Do the results of the original study hold true beyond the context in which it was developed? (2) Are there alternative ways to study and explain an identified phenomenon or finding? Similarly, Hjalmarson and Baker ( 2020 ) specifically suggest two needs related to mathematics specialists in studies of professional development that drive researchable questions: (1) defining practices and hidden players involved in systematic school change and (2) identifying the unit of analysis and scaling up professional development.

Schoenfeld ( 2020 ) uses various examples to illustrate the origin of researchable questions. One of his (perhaps most familiar) examples is his decade-long research on mathematical problem solving. He elaborates on how answering one specific research question leads to another and another. In the context of research on mathematical proof, Stylianides and Stylianides ( 2020 ) also illustrate how researchable questions arise from existing research in the area leading to new researchable questions in the dynamic process of educational research. The arguments and examples in both Schoenfeld ( 2020 ) and Stylianides and Stylianides ( 2020 ) are quite powerful in the sense that this source of researchable questions facilitates the accumulation of knowledge for the given areas of study.

A related source of researchable questions is not discussed in this set of papers—unexpected findings. A potentially powerful source of research questions is the discovery of an unexpected finding when conducting research (Cai et al., 2019b ). Many important advances in scientific research have their origins in serendipitous, unexpected findings. Researchers are often faced with unexpected and perhaps surprising results, even when they have developed a carefully crafted theoretical framework, posed research questions tightly connected to this framework, presented hypotheses about expected outcomes, and selected methods that should help answer the research questions. Indeed, unexpected findings can be the most interesting and valuable products of the study and a source of further researchable questions (Cai et al., 2019b ).

Of course, researchable questions can also arise from established scholars in a given field—those who are most familiar with the scope of the research that has been done. For example, in 2005, in celebrating the 125th anniversary of the publication of Science ’s first issue, the journal invited researchers from around the world to propose the 125 most important research questions in the scientific enterprise (Kennedy, 2005 ). A list of unanswered questions like this is a great source for researchable questions in science, just as the 23 great questions in mathematics by Hilbert ( 1901 -1902) spurred the field for decades. In mathematics and science education, one can look to research handbooks and compendiums. These volumes often include lists of unanswered research questions in the hopes of prompting further research in various areas (e.g. Cai, 2017 ; Clements, Bishop, Keitel, Kilpatrick, & Leung, 2013 ; Talbot-Smith, 2013 ).

Alignment of Researchable Questions with the Conceptual Framework and Appropriate Research Methods

Cai et al. ( 2020 ) and King et al. ( 2020 ) explicitly discuss the alignment of researchable questions with the conceptual framework and appropriate research methods. In writing journal publications or grant proposals, it is extremely important to justify the significance of the researchable questions based on the chosen theoretical framework and then determine robust methods to answer the research questions. According to Cai et al. ( 2019a ), justification for the significance of the research questions depends on a theoretical framework: “The theoretical framework shapes the researcher’s conception of the phenomenon of interest, provides insight into it, and defines the kinds of questions that can be asked about it” (p. 119). It is true that the notion of a theoretical framework can remain somewhat mysterious and confusing for researchers. However, it is clear that the theoretical framework links research questions to existing knowledge, thus helping to establish their significance; provides guidance and justification for methodological choices; and provides support for the coherence that is needed between research questions, methods, results, and interpretations of findings (Cai & Hwang, 2019 ; Cai et al., 2019c ).

Analyzing reviews for a research journal in mathematics education, Cai et al. ( 2020 ) found that the reviewers wanted manuscripts to be explicit about how the research questions, the theoretical framework, the methods, and the findings were connected. Even for manuscripts that were accepted (pending revisions), making explicit connections across all parts of the manuscript was a challenging proposition. Thus, in preparing manuscripts for publication, it is essential to communicate the significance of a study by developing a coherent chain of justification connecting researchable questions, the theoretical framework, and the research methods chosen to address the research questions.

The Long Journey Has Just Begun with a First Step

As the field of mathematics and science education matures, there is a need to take a step back and reflect on what has been done so that the field can continue to grow. This special issue represents a first step by reflecting on the posing of significant researchable questions to advance research in mathematics and science education. Such reflection is useful and necessary not only for the design of studies but also for the writing of research reports for publication. Most importantly, working on significant researchable questions cannot only contribute to theory generation about the teaching and learning of mathematics and science but also contribute to improving the impact of research on practice in mathematics and science classrooms.

To conclude, we want to draw readers’ attention to a parallel between this reflection on research in our field and a line of research that investigates the development of school students’ problem-posing and questioning skills in mathematics and science (Blonder, Rapp, Mamlok-Naaman, & Hofstein, 2015 ; Cai, Hwang, Jiang, & Silber, 2015 ; Cuccio-Schirripa & Steiner, 2000 ; Hofstein, Navon, Kipnis, & Mamlok-Naaman, 2005 ; Silver, 1994 ; Singer, Ellerton, & Cai, 2015 ). Posing researchable questions is critical for advancing research in mathematics and science education. Similarly, providing students opportunities to pose problems is critical for the development of their thinking and learning. With the first step in this journey made, perhaps we can dream of something bigger further on down the road.

Change history

15 may 2020.

The original version of this article unfortunately contains correction.

Blonder, R., Rapp, S., Mamlok-Naaman, R., & Hofstein, A. (2015). Questioning behavior of students in the inquiry chemistry laboratory: Differences between sectors and genders in the Israeli context. International Journal of Science and Mathematics Education, 13 (4), 705–732.

Google Scholar  

Cai, J. (Ed.). (2017). Compendium for research in mathematics education . Reston, VA: National Council for Teachers of Mathematics.

Cai, J., & Hwang, S. (2019). Constructing and employing theoretical frameworks in (mathematics) education research. For the Learning of Mathematics, 39 (3), 45–47.

Cai, J., Hwang, S., Hiebert, J., Hohensee, C., Morris, A., & Robison, V. (2020). Communicating the significance of research questions: Insights from peer review at a flagship journal. International Journal of Science and Mathematics Education . https://doi.org/10.1007/s10763-020-10073-x .

Cai, J., Hwang, S., Jiang, C., & Silber, S. (2015). Problem posing research in mathematics: Some answered and unanswered questions. In F. M. Singer, N. Ellerton, & J. Cai (Eds.), Mathematical problem posing: From research to effective practice (pp. 3–34). New York, NY: Springer.

Cai, J., Morris, A., Hohensee, C., Hwang, S., Robison, V., Cirillo, M., . . . Hiebert, J. (2019a). Posing significant research questions. Journal for Research in Mathematics Education , 50 (2), 114120. https://doi.org/10.5951/jresematheduc.50.2.0114 .

Cai, J., Morris, A., Hohensee, C., Hwang, S., Robison, V., Cirillo, M., . . . Hiebert, J. (2019b). So what? Justifying conclusions and interpretations of data. Journal for Research in Mathematics Education , 50 (5), 470477. https://doi.org/10.5951/jresematheduc.50.5.0470 .

Cai, J., Morris, A., Hohensee, C., Hwang, S., Robison, V., Cirillo, M., . . . Hiebert, J. (2019c). Theoretical framing as justifying. Journal for Research in Mathematics Education , 50 (3), 218224. https://doi.org/10.5951/jresematheduc.50.3.0218 .

Cai, J., Morris, A., Hohensee, C., Hwang, S., Robison, V., & Hiebert, J. (2018). The role of replication studies in educational research. Journal for Research in Mathematics Education, 49 (1), 2–8. https://doi.org/10.5951/jresematheduc.49.1.0002 .

Clements, M. A., Bishop, A., Keitel, C., Kilpatrick, J., & Leung, K. S. F. (Eds.). (2013). Third international handbook of mathematics education research . New York, NY: Springer.

Cuccio-Schirripa, S., & Steiner, H. E. (2000). Enhancement and analysis of science question level for middle school students. Journal of Research in Science Teaching, 37 , 210–224.

Einstein, A., & Infeld, L. (1938). The evolution of physics: The growth of ideas from early concepts to relativity and quanta . Cambridge, England: Cambridge University Press.

Hilbert, D. (1901-1902). Mathematical problems. Bulletin of the American Mathematical Society , 8 , 437–479.

Hjalmarson, M. A., & Baker, C. K. (2020). Mathematics specialists as the hidden players in professional development: Researchable questions and methodological considerations. International Journal of Science and Mathematics Education . https://doi.org/10.1007/s10763-020-10077-7 .

Hofstein, A., Navon, O., Kipnis, M., & Mamlok-Naaman, R. (2005). Developing students ability to ask more and better questions resulting from inquiry-type chemistry laboratories. Journal of Research in Science Teaching, 42 , 791–806.

Inglis, M., & Foster, C. (2018). Five decades of mathematics education research. Journal for Research in Mathematics Education, 49 (4), 462–500.

Institute of Education Sciences & National Science Foundation. (2013). Common guidelines for education research and development . Washington, DC: Authors.

Kennedy, D. (2005). Editorial. Science, 310 (5749), 787. https://doi.org/10.1126/science.310.5749.787b .

King, K., Ochsendorf, R. J., Solomon, G. E. A., & Sloane, F. C. (2020). Posing fundable questions in mathematics and science education. International Journal of Science and Mathematics Education . https://doi.org/10.1007/s10763-020-10088-4 .

Mosteller, F. (1980). The next 100 years of science. Science, 209 (4452), 21–23. https://doi.org/10.1126/science.7280662 .

Sanchez, M. (2020). Replication studies in mathematics education: What kind of questions would be productive to explore? International Journal of Science and Mathematics Education . https://doi.org/10.1007/s10763-020-10069-7 .

Schoenfeld, A. (2020). On meaningful, researchable, and generative questions. International Journal of Science and Mathematics Education . https://doi.org/10.1007/s10763-020-10068-8 .

Silver, E. A. (1994). On mathematical problem posing. For the Learning of Mathematics, 14 (1), 19–28.

Singer, F. M., Ellerton, N., & Cai, J. (2015). Mathematical problem posing: From research to effective practice . New York, NY: Springer.

Stylianides, G. J., & Stylianides, A. J. (2020). Posing new researchable questions as a dynamic process in educational research. International Journal of Science and Mathematics Education . https://doi.org/10.1007/s10763-020-10067-9 .

Talbot-Smith, M. (2013). Handbook of research on science education . Waltham, Massachusetts, Focal Press.

Download references

Author information

Authors and affiliations.

University of Delaware, Newark, DE, USA

Weizmann Institute of Science, Rehovot, Israel

Rachel Mamlok-Naaman

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Jinfa Cai .

Rights and permissions

Reprints and permissions

About this article

Cai, J., Mamlok-Naaman, R. Posing Researchable Questions in Mathematics and Science Education: Purposefully Questioning the Questions for Investigation. Int J of Sci and Math Educ 18 (Suppl 1), 1–7 (2020). https://doi.org/10.1007/s10763-020-10079-5

Download citation

Published : 07 April 2020

Issue Date : May 2020

DOI : https://doi.org/10.1007/s10763-020-10079-5

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Find a journal
• Publish with us
• Track your research

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 18 July 2023

Fostering twenty-first century skills among primary school students through math project-based learning

• Nadia Rehman   ORCID: orcid.org/0000-0002-4172-625X 1 ,
• Wenlan Zhang 1 ,
• Amir Mahmood 1 ,
• Muhammad Zeeshan Fareed 2 &
• Samia Batool 3  

Humanities and Social Sciences Communications volume  10 , Article number:  424 ( 2023 ) Cite this article

5257 Accesses

5 Citations

2 Altmetric

Metrics details

• Development studies

In today’s modern world, students must be equipped with twenty-first century skills, particularly those related to solving real-life problems, to ensure competitiveness in the current global economy. The present study employed project-based learning (PBL) as an instructional tool for teaching math at the primary level. A convergent mixed-methods approach was adopted to determine whether the PBL approach has improved students’ twenty-first century skills, including collaborative, problem-solving, and critical thinking skills. Thirty-five students of the experimental group were treated with PBL, while 35 students of the control were treated with the traditional teaching method. ANCOVA test for “critical thinking skills” showed a significant difference between the experimental and control group ( F  = 104.833, p  = 0.000 < 0.05). For collaborative skills, results also showed a significant difference between the two groups ( F  = 32.335, p  = 0.000 < 0.05). For problem-solving skills, the mean value of experimental (25.54) and control group (16.94) showed a high difference after the intervention. The t -value (8.284) and the p value ( p  = 0.000) also showed a highly significant difference. Observations of the classroom also revealed the favorable effects of employing PBL. PBL activities boosted the level of collaboration and problem-solving skills among students. Students could advance their collaboration abilities, including promoting one another’s viewpoints, speaking out when necessary, listening to one another, and participating in thoughtful discussions. During the PBL project, students’ active participation and effective collaboration were observed, significantly contributing to its success.

Similar content being viewed by others

A meta-analysis to gauge the impact of pedagogies employed in mixed-ability high school biology classrooms

The effectiveness of collaborative problem solving in promoting students’ critical thinking: A meta-analysis based on empirical literature

Secondary school students’ attitude towards mathematics word problems

Introduction.

Learners of the twenty-first century need to equip with the core knowledge and necessary skills to perform in various situations to succeed. There are many different educational philosophies, each of which contains essential elements for human development (Parrado-Martínez and Sánchez-Andjar 2020 ). In 2017, Alif Ailaan published a report entitled “Powering Pakistan for the 21st -Century,” highlighting the dismal state of math and science education nationwide. Report data showed that, on average, fourth graders earned 433 out of 1000 points in math on the National Education Assessment System exam. The survey concluded that students performed exceptionally poorly in mathematics and geometry (Ailaan 2017 ). Most students in public schools are not actively involved in their education because of the teacher-centered nature of the classroom. In teachers’ eyes, students’ knowledge, passions, and individuality are irrelevant (Rehman et al. 2021 ).

The National Education Policy of 2009 states that teachers should adapt their teaching methods according to the need of the students and situation. The National Curriculum for 2006 also emphasizes a significant shift in the teacher’s role, from information transmitter to classroom environment maker, to assist students in gaining a sound knowledge of mathematical topics. Several factors affect how effectively the math curriculum is put into practice. These factors include the school setting, student demographics, and instructional resources (Mazana et al. 2018 ). Teachers must adopt cutting-edge practices to ensure their students are well-equipped for the twenty-first century. Using ICT, these novel methods may assist teachers in honing these abilities and adapting instruction to meet the moment’s needs (Muthukrishnan et al. 2022 ).

PBL and twenty-first century skills

In the twenty-first century, cognitive abilities are an unquestionably reliable measure of a student’s success (Saduakassova et al. 2023 ). Students of this generation need to be aware of how the world is changing and prepare themselves with the skills necessary for a more challenging way of life (Wongdaeng and Hajihama 2018 ). Students need to be able to engage in critical thinking to survive in this competitive era. It will enable them to take the initiative and devise meaningful solutions to emerging problems (Suwastini et al. 2021 ). Students need to have strong communication skills and the ability to work effectively with others to succeed in today’s world when networking is essential to one’s career (Akcanca 2020 ). Students must have an imaginative and creative mindset to keep up with the rapid advances. The terms “communication”, “cooperation”, “creativity”, “problem-solving skill”, and “innovation skills” are often referred to as “the 4Cs” that PBL supports; in the present study, the author only focused on the three skills, collaborative, critical thinking and problem-solving that has more influence in math learning (Almazroui 2023 , pp. 125–136).

Educational professionals have recognized the importance of the 4Cs to student success. They have proposed that PBL as an instructional design can improve students’ mastery of the 4Cs (Kurniahtunnisa and Wowor 2023 ). According to Moghaddas and Khoshsaligheh ( 2019 ), PBL is a teaching strategy that falls under the constructivist approach and centers on having students participate in a series of research-oriented activities that require their collaborative actions to achieve the goal. By participating in these activities and interacting with others, students’ critical thinking, communication, collaboration, and creative abilities can be enhanced (Papanastasiou et al. 2019 ).

There are several problems with Pakistan’s educational system, including a lack of funds, inefficient program execution, and poor management and instruction (Shah Bukhari et al. 2022 ). As a result, most of our educational institutions continue employing more conventional instruction modes. Math is the most powerful tool for acquiring knowledge that exists in the world (Sithole et al. 2017 ). Math is the discipline in the scientific world that focuses on developing individuals’ perceptual and cognitive abilities. History shows that every ancient civilization placed a high value on mastering arithmetic. History also shows that every ancient civilization greatly valued becoming proficient in arithmetic (Alsaad et al. 2023 ). Students who are not good at math struggle academically due to their lack of enthusiasm for studying the subject since they either do not find it interesting or challenging. Children lose interest in understanding complex concepts such as algebra, arithmetic, or geometry at a young age when teachers force them to learn without focusing on the twenty-first century skills (Abramovich et al. 2019 ). The present study investigates the impact of PBL on students’ twenty-first century skills, including problem-solving, critical thinking, and collaborative skills.

Reasons for implementing project-based learning in math

One of the main reasons for implementing PBL in math is to address the low math scores of Pakistani students, as reported by TIMSS 2019 and Alif Ailaan reports ( 2017 ). Finland has improved its ranking in PISA by implementing PBL in its education system, which has helped to promote student-centered learning, collaboration, and problem-solving skills and to develop a deep understanding of the subjects studied, resulting in improved academic performance. PBL can help students to develop a deeper understanding of mathematical concepts and skills through hands-on, real-world problem-solving activities. For technology-deprived classrooms, PBL effectively engages students in active learning experiences, such as group projects and case studies. Technology integration is impossible in many public schools due to a lack of access to basic infrastructure such as electricity and internet connectivity. Implementing PBL in math can promote student motivation, collaboration, and creativity, essential for developing twenty-first century skills and preparing students for future careers. PBL can shift the focus from teacher-centered instruction to student-centered learning, allowing students to take ownership of their learning and develop critical thinking skills.

Research question

Q1. Is there any statistically significant difference in the students’ collaborative skills between the experimental and the control group?

Q2. Is there any statistically significant difference in the students’ problem-solving skills between the experimental and the control group?

Q3. Is there any statistically significant difference in the students’ critical thinking skills between the experimental and the control group?

Q4. How do students collaborate with group members during classroom project learning?

Literature review

Pbl and collaborative skills.

Collaborative learning (CL) is a fundamental component of the twenty-first century skills. It involves students collaborating to exchange ideas, solve an issue, or achieve a common objective (O’Grady-Jones and Grant 2023 ). In math education, CL’s popularity skyrocketed in the 1980s, but it has continued to develop since then (Simon 2020 ). The educational strategy known as collaborative learning tries to improve students’ education by having them work on projects together in groups (Vogel et al. 2016 ). This method encourages students to construct their meaning from various sources of knowledge rather than relying solely on memorizing facts and figures. To complete a wide range of class projects and assignments, students work together in small groups to better grasp complex ideas and concepts (Roldán Roa et al. 2020 ). Primary factors determining the efficacy of collaborative work are students’ level of involvement in the learning process and teachers’ readiness to evaluate project outputs (Kaendler et al. 2015 ).

In PBL, students are encouraged to work in groups of two or more pairs or classes to discover common ground, develop ideas, define concepts, or generate an end product (Rizkiyah et al. 2020 ). Students attentively follow the teacher’s instructions and diligently interpret and apply their understanding of the course material, demonstrating their grasp through study and application (Qureshi et al. 2021 ). The usage of CL has brought about a profound shift away from the old classroom atmosphere centered on the teacher delivering lectures. The ways of taking notes, listening to a lecture, and simply observing may only partially disappear in a classroom setting, emphasizing collaboration. However, they coexist with other strategies for promoting active learning and student conversation regarding the course content (Kollar et al. 2014 ). Teachers who employ interactive teaching methods perceive themselves not merely as transmitters of expert knowledge to students but, more significantly, as mentors or coaches facilitating a mature learning process. They see their role as expert designers of the cognitive experiences their students engagement. This shift in perspective allows them to engage students better in the learning process (Lim et al. 2023 ).

Recent research has shown that both meaning and behavior influence the process of learning. During collaborative learning activities, the students are encouraged to overcome challenging obstacles. Immersive learning activities often begin with topics in which students must supply particular facts and perspectives (Almazroui 2023 ). Contrarily, traditional classrooms typically initiate by providing information and concepts before transitioning into a practical application (Markula and Aksela 2022 ). In this setting, teachers expect students to quickly evolve from their roles as preliminary researchers, dealing with questions and answers or problems and solutions, to becoming competent experts. It requires them to employ higher-order thinking and problem-solving strategies (Brown et al. 1989 ). Despite the term “collaborative learning” being widely applied across various fields and disciplines, it still needs universal approval. Though many may still need to grasp the concept fully, certain commonalities tend to emerge (Qureshi et al. 2021 ). In the twenty-first century, there was a rise in working together. Because the focus has shifted from individual actions to group efforts and from the individual to society, it is more vital than ever for people to think about and collaborate on significant issues (Laal et al. 2012 ).

PBL and problem-solving skills

Project-based learning is an approach to education in which students demonstrate mastery of a topic by developing and presenting their solutions to real-world problems (Chiang and Lee 2016 ). In the planning stage, students must evaluate the needs for product development, identify issues with current products, and modify these products based on the principle of creative problem-solving. PBL can benefit students’ knowledge, skills, attitudes, and creativity in problem-solving capacities (Andanawarih et al. 2019 ). However, unlike conventional teaching methods, project-based education can be challenging to put into practice. Tee ( 2018 ) stated that students must communicate effectively to ensure the success of project-based learning projects. The students struggled through the project planning phase to apply the concept of creative problem-solving, which is essential when building a product (Artama et al. 2023 ). Therefore, educators are encouraged to craft a guide for innovative problem-solving by harnessing student-generated product concepts. However, the current student knowledge and abilities level can challenge the effective implementation of project-based learning (DeCoito and Briona 2023 ). Students are to fault for this since they need more practice solving problems or participating in project-based learning. The students’ incapacity to apply strategies for overcoming creative obstacles while learning contributes to the low quality of their work (Kiong et al. 2022 ). Therefore, it is essential to emphasize the use of creative problem-solving strategies in PBL to provide students with the means to finish the projects associated with each chapter with relative ease and better prepare them for higher education (Devanda and Elizar 2023 ).

PBL and critical thinking skills

In addition to content knowledge, PBL fosters skills like critical thinking, creativity, lifetime learning, communication, teamwork, flexibility, and self-evaluation (Artama et al. 2023 ). Creating science and mathematics curricula aims to train students to think more critically. Analytical and critical thinking is examining data, making inferences, articulating ideas, and assessing claims. However, the student’s critical thinking skills are still formative (Mutakinati et al. 2018 ). For this reason, schools must implement programs that help students develop their abilities in areas like creativity and critical thinking, which are in high demand in the modern workplace. Project-based learning is an effective method of teaching and learning in the contemporary era. This approach in the education sector offers equal treatment of real-world issues. At the outset of each lecture, students examine problems from the real world, which are then recast as problems for them to solve in pairs or small groups (Pan et al. 2023 ).

Critical thinking is an essential life skill. Future success requires students to have strong communication and critical thinking skills. Critical thinking is analyzing and evaluating one’s thinking to make constructive changes. Nadeak and Naibaho ( 2020 ) identified six levels of critical thinking: unreflective thinker, challenged thinker, novice, practicing thinker, advanced practitioner, and master. When we talk about “critical thinking”, we are talking about the ability to analyze information, evaluate its relevance, and comprehend problems. Analyzing, evaluating, reasoning, and reflecting are part of the process (Rati et al. 2017 ).

The Paul–Elder Framework for critical thinking defines critical thinking as a self-reflective and disciplined process involving constant self-monitoring and correction. This framework encourages an analytical approach to personal thought processes to enhance them. The unreflective thinker, the challenged thinker, the novice thinker, the experienced thinker, the expert thinker, and the master thinker are the six stages of critical thinking (Paul and Elder 2008 ). According to Paul and Elder ( 2008 ), there are eight parts to a thinking process: an objective, a set of questions, a body of data, a set of interpretations and interferences, a set of ideas, a set of assumptions, some potential outcomes, and a point of view (Fig. 1 ). The intellectual standards outline the criteria for good critical thinking (Mutakinati et al. 2018 ).

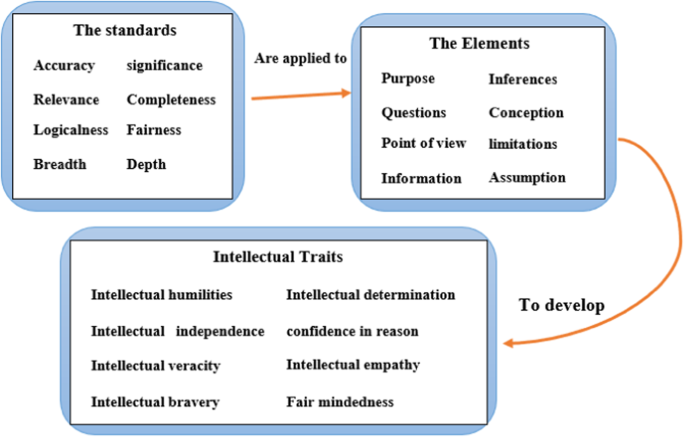
The author made this figure based on the framework provided by Paul and Elder ( 2008 ).

Math education incorporates many skills, including self-awareness, the ability to plan and organize learning, and the capacity to think critically. The assessment of students determines the accuracy, credibility, and relevance (or applicability) of the provided materials. Critical thinking and mathematics are deeply intertwined; one must integrate both to understand the discipline truly. Every child must learn and practice arithmetic and logic. Therefore, any program that teaches critical thinking should incorporate strategies that cater to diverse student populations (Holmes and Hwang 2016 ).

Previous studies on PBL

PBL has gained recognition worldwide as an alternative approach to traditional teacher-centered education, emphasizing hands-on, collaborative, and inquiry-based learning activities (Yang et al. 2021 ). Previous studies have shown that PBL can effectively promote student learning, engagement, and achievement across various subjects, including math and science. For example, a study by Paryanto et al. ( 2023 ) found that PBL improved student achievement and attitudes toward learning in engineering education.

However, some studies have also criticized the effectiveness of PBL in specific contexts, highlighting the challenges of implementing PBL and potential limitations. For instance, a study by Loyens et al. ( 2023 ) found that PBL had a limited impact on students’ cognitive and metacognitive skills in medical education. The authors suggested that the lack of clear guidelines and support for PBL implementation and the complex and dynamic nature of medical education may have contributed to these results (Saqr and López-Pernas 2023 ). Furthermore, some researchers have argued that the effectiveness of PBL may depend on various factors, such as the level of student readiness, teacher training and support, curriculum alignment, and assessment methods. For example, a study by Jincheng and Chayanuvat ( 2020 ) found that PBL is more effective when integrated into a comprehensive curriculum reform program than used as a stand-alone intervention. Additionally, the authors emphasized the importance of aligning PBL with clear learning objectives, providing appropriate scaffolding and support, and using valid and reliable assessments to measure student learning (Szalay et al. 2023 ). While PBL has shown promise as a practical approach to teaching and learning, its implementation and effectiveness may depend on various factors, and caution should be exercised in its application (Jincheng and Chayanuvat 2020 ).

Constructivist theory

The social constructivist approach is consistent with project-based learning since it stresses students’ involvement in the learning process through group work and instructor guidance (Huang et al. 2022 ). Therefore, educators should foster classroom environments where students can take charge of their learning. Students in project-based learning classes are encouraged to participate actively in their education and develop critical transferable skills while working on real-world projects (Le et al. 2023 ). Interpersonal learning occurs when individuals participate in groups, share information, and work together to overcome obstacles (Dolmans 2019 ). Students develop essential life skills in groups where they take full responsibility for their education (Harden 2018 ). Students’ ability to think creatively and fill the gap between their knowledge and talents is aided by acquiring these new life skills. It highlights the significance of PBL, which brings transformative experiences, facilitates long-term knowledge retention, and nurtures students’ commitment to an inclusive and participatory society (Mielikäinen 2022 ).

In addition, the multiple intelligence theory developed by Howard Gardner fits well with the approach taken in project-based education (Owens and Hite 2022 ). Gardner highlighted that all humans possess eight types of intelligence, each manifested in a unique set of skills and abilities, and he discriminated between these types in the context of students. Due to these differences, teaching and learning styles vary. By incorporating a wide range of activities, project-based courses may effectively accommodate students with a wide range of learning preferences (Radkowitsch et al. 2022 ).

The experiential learning theory (ELT) developed by Kolb ( 1984 ) served as the theoretical foundation for PBL (Sevgül and Yavuzcan 2022 ). The ELT works well with the principles of PBL, and it proposes that young children have an innate interest in the scientific method and want to know how the things they meet in their everyday lives function. Sevgül and Yavuzcan ( 2022 ) argued that children are naturally curious and continually engaged in meaningful interactions with the world around them. They learn to think critically and solve difficulties by interacting with one another. Consultation with adults, peers, and educators promotes collaborative learning. Like experience, growth is a continuous process, with each step having its distinct logic and psychology that prime the learner for the next level (Rajabzadeh et al. 2022 ). The principles of PBL exemplify Kolb’s ELT due to their emphasis on fostering a learning environment that resonates with students and a real-world audience. Students must provide classroom activities that enable them to benefit from real-world applications and cultivate meaningful relationships with their peers. Students gain a sense of belonging to something greater than themselves when they work together toward a common objective (Sevgül and Yavuzcan 2022 ). The study focused on understanding how learning occurs in PBL, and Kolb’s ELT provided a framework for doing so based on meaningful and authentic experiences. Students can only engage in meaningful learning if they can build on their existing knowledge and participate in projects with personal and global significance (Erstad and Voogt 2018 ).

Methodology

In the present study, the researcher adopted a convergent mixed-methods approach to determine if the problem-based learning (PBL) method has enhanced students’ twenty-first century skills, including collaboration, problem-solving, and critical thinking. A quasi-experimental design was used for the quantitative part, and a non-equivalent control group pre-test-post-test design was employed. This design remains prevalent in educational research (Cohen et al. 2017 ). For the qualitative part, students were observed during intervention using the collaborative framework to understand the students’ involvement during their project work. Students in 5th grade were selected as the object of the study, one section (35 students) was selected as an experimental, and others (35 students) were selected as a control group. The experimental group was treated with PBL intervention, while the control group was treated with the traditional teaching method. Random sampling was not possible due to fix schedule of the school. It was a 6-week project, and the detail of the PBL project is provided in Table 1 . In the control group, teachers implemented the same content traditionally. Before and after the intervention, collaborative, critical thinking, and problem-solving were measured in both groups of students.

Instruments

The researcher adopted a collaborative scale Tibi ( 2015 ) developed to answer the research questions. This scale was used to evaluate the students in the control and experimental groups to see how well they could work together (see Table 2 ). The questionnaire consisted of 37 five-point Likert-style statements. To assess problem-solving skills math test was designed, which contains twenty items. To measure the students’ creative and critical skills, the researcher adopted Gelerstein et al. ( 2016 ), Yoon ( 2017 ), Sumarni and Kadarwati ( 2020 ) open-ended questionnaire. The study collected data using a critical thinking skills test comprising ten problems. These problems measured sub-skills, including interpretation, analysis, evaluation, inference, explanation, and self-regulation. Table 1 presents the instruments used for this critical thinking test.

Ventista ( 2018 ) also used this questionnaire in his study. The scale’s reliability was determined to be 0.76 using the Cronbach alpha test. In conclusion, higher-order cognitive skills emerged from metacognitive processes (Coskun 2018 ). This finding agreed with prior work published by Sumarni and Kadarwati ( 2020 ) on developing test items to gauge students’ creative abilities. The critical thinking instrument used in this research exhibited high validity and reliability, making it possible to assess students’ critical and creative thinking skills in the context of math.

The math test was designed to check how well students can solve problems. This test uses content from three chapters of a 5th-grade math teacher’s guide to see their improvement. The test consisted of 20 questions and aimed to gauge fifth-grade students’ problem-solving abilities in angle measurement and geometry. The test consists of ten questions related to each category. The first ten questions measured students’ problem-solving skills related to angle measurement, while the second set measured their geometry-related skills. Test questions are crafted carefully to assess the students’ understanding of these concepts and their ability to apply them to real-world scenarios. The test was administered to the students, and the results were analyzed to determine their proficiency in problem-solving skills related to these topics (see Table 2 ).

The study utilized the “ITEMAN” tool to perform item analysis on these data (Ramadhan et al. 2019 , pp. 743–751). The results showed that the difficulty index might range from 0.33 to 0.85, and the discrimination index may range from 0.31 to 0.82. According to the findings of Susanto and Retnawati ( 2016 ), We considered an item to be of generally high quality if its difficulty index ranged from 0.31 to 0.89 and had a discrimination value of at least 0.22.

The classroom observations tool served as a source for gathering qualitative data. Before the observational activities, participants received information about the researcher’s intentions. The study utilized a collaborative framework tool to monitor students’ behavior and engagement in the experimental classroom. Before initiating data collection, the instrument underwent a validation process.

Stages of the experiment

Before the intervention, homogeneity of the 5th-grade math students was established. Both groups were randomly allocated as the 5-B experimental and 5-A as the control group. Before the intervention, we examined all the experimental and control variables, including collaborative, critical thinking, and problem-solving skills.

Before the intervention, twenty-first century skills were measured as a pre-test from both groups.

In the experimental group, PBL was used as an instructional tool for delivering math content. Different lesson plans and modules are prepared concerning the “Measurements of angels, geometry, and decimal concept”. A control group was treated with a traditional method with the same content (see Table 3 ).

Lesson schedule (6 weeks, 5 h weekly, for 30 class hours), lesson plans, and modules were designed before intervention. Lessons planning followed Math Core standards.

Before the intervention, AV aids were prepared for classroom activities. Students worked in the classroom in groups of six girls (five groups) in each session.

For assessment, teachers used worksheets and projects at the end of the session and followed the operational stages mentioned by “Buck Institute” Kaptan and Korkmaz ( 2000 ).

After the intervention, both groups implemented the “math attitude, creativity, and problem-solving test” as a post-test.

During the project work, experimental group students were observed to assess their engagement and collaboration with peers and groups.

PBL project implementation

A hands-on project.

During this procedure, the students worked on creating a new product. They discuss and present an actual model.

For the present study, students constructed a project after 4 weeks of lessons and presented it at the end of the experiment. All group members participated and presented their work to the class (see Fig. 2 ).

Students’ group activity in PBL in the classroom.

Driving questions

During this procedure, students strive to provide a solution to an open-ended question. For the present study, the instructor prepares different open-ended questions for students to answer. The best part was that every member was participating. Every classroom consists of average, below-average, and high achievers. PBL encouraged every category student to get participated in project-making.

Q1. Identifying Right, Obtuse, and Acute Angles?

Q2. Name the marked angle.

(a) Name the vertex of the angle.

(b) Name the arms of the angle

Q3. Classify the following angles into acute, obtuse, right, and reflex angles:

(i) 35°(ii) 185°(iii) 90°(iv) 92°(v) 260°

Q4. Observe the given figure with a protractor and give the measure of each of the angles.

New information

As a result of participating in this process, students acquire new mathematical information. This task also helped students to review previously learned knowledge. For the present study, the teacher introduces the new concept with examples, like percentages, discounts, and real value.

Student-driven elements

The teacher performs indirectly as a facilitator while the students direct their learning. Throughout the lesson, the teacher acted as a facilitator, and it was the first time for students to learn math with different teaching strategies; so, at every step researcher and the trainer acted as a facilitator and provided a zone of proximal development (ZPD), throughout their learning process.

Realistic goals and outcomes

Students work on a realistic project, and it has some objectives. It is appropriate both for the age of the students and aligned with course standards. PBL is appropriate for primary-grade students; PBL helps them strengthen their foundation and make concepts more precise and practical.

Application to the real world

The mathematical concepts involved things that learners might encounter outside the classroom. All the essential elements are followed rigorously (see Table 4 ).

The effect of PBL improving students’ collaborative skills

The study uses one-way ANCOVA for the pre-and post-test on the experimental and control groups to check the effectiveness of PBL in improving the 5th-grade students’ collaborative skills. Before proceeding to a one-way analysis of covariance, a homogeneity of variance test analysis is performed to ensure the data aligns with the fundamental premise of ANCOVA (see Table 5 ).

Levene’s test result, shown in Table 5 , demonstrates no difference between the experimental and control groups before the intervention ( F  = 0.806, p  = 0.0373 > 0.05). The data analysis aligns with the primary hypothesis of ANCOVA. That means that the two groups’ variations are identical to one another. Therefore, the two samples originate from populations with the same variance.

Table 6 represents a result of one-way ANCOVA for the students about collaborative skills. Results show a significant difference between the experimental and control groups ( F  = 253.564, p  = 0.000 < 0.05). This indicates that PBL activities impact the fifth-grade students’ collaborative skills during project learning. Students in the intervention group developed collaborative skills during the math project compared to the control group students.

The effect of PBL improving students’ critical thinking skills

One-way, ANCOVA compares the pre-and post-test results of the “critical thinking skills” of the treatment and control groups for the fifth-grade math students. In determining whether the data are consistent with the fundamental premise of ANCOVA, a homogeneity of variance test analysis is performed before a one-way analysis of covariance (see Table 7 ).

Table 7 represents a result of Levene’s test, which revealed no significant difference between the two groups ( F  = 3.711, p  = 0.58 > 0.05). The fundamental premise of ANCOVA applies once the data analysis is complete.

Table 8 represents the result of one-way ANCOVA for the students’ “critical thinking skills”. Results showed a significant difference between the treatment and control groups ( F  = 23.281, p  = 0.000 < 0.05). The intervention group’s critical thinking skills improved compared to control group students. PBL helps the students to develop twenty-first century skills and involve them in critical thinking during their project learning.

The effect of PBL improving students’ problem-solving skills

Problem-solving skills.

An accomplishment exam was developed to evaluate students’ problem-solving skills in math. This test required students to respond to 10 questions (20 marks) chosen and crafted according to the math curriculum’s standards-based learning objectives (SLO). Before and after the experiment, the test was given to students of both groups to know the difference.

Table 9 represents the mean scores of the experimental and control group students’ problem-solving test results. The mean value of the experimental group before the intervention was 12.46, and after the intervention was (25.54). While the pre-mean value of the control group was (11.80) and after was (16.94). The data reveals an increase in the mean value for both groups. However, the experimental group, which received instruction through the PBL method, exhibited a more substantial increase than the group taught math using the traditional method. The p value also shows that before the intervention, the p value was ( p  = 0.421), which is greater than 0.05, which means there was no significant difference between the experimental and control group. While after the intervention, the p value ( p  = 0.00) shows that there is a significant difference.

To check the difference in the mean scores between the control and experimental group before and after the experiment, an independent sample t -test was applied.

Table 10 represents the result of the independent sample t -test; the mean value of the experimental group (12.46) and the control group (11.80) shows a minor difference in both groups before the intervention. The t -value (0.809) and the p value ( p  = 4.22) also show no significant difference. The results of this table show that group of experimental group and control group performed the same on achievement and problem-solving skills before the intervention; there was no significant difference between experimental and control group students. The p value ( p  = 4.22) is more significant than 0.005. That specified no significant difference between the experimental and control groups before the treatment.

Table 11 represents the result of the independent sample t -test; the mean value of the experimental group (25.54) and the control group (16.94) show a high difference in both groups after intervention. The t -value (8.284) and the p value ( p  = 0.000) also show a highly significant difference. This table shows that the experimental group performed better on problem-solving skills than the control group, which was not treated with PBL. PBL as an instructional tool was suggested as one of the best teachings for teaching math at the primary level. Cohen’s d value of 1.82 specified a big difference between the group treated with the PBL instruction method and those treated through traditional teaching methodology.

Paired sample t -test was applied to check the difference between the pre-and post-scores of the experimental and control group.

Table 12 shows the results of paired sample t -test. Paired sample t -test is applied to the pre-post-test of the experimental and control group to know the difference before and after the intervention. The mean value of the scores showed that there were highly significantly different. As the p value is smaller than 0.05 ( p  = 0.005), the probability value is highly significant, and there is a difference in the mean scores of the experimental group. PBL helps the students develop more problem-solving skills than the control group. On the other hand, the mean value of the control group’s scores showed a minor difference, and the p value is more significant than 0.05, which means that the traditional method did not significantly affect the students’ problem-solving skills.

Qualitative analysis

All experimental group members were observed using a collaborative scale framework during project work. Students were observed under the project’s four themes: individual accountability, social skills, and group processing. This method is widely used in social sciences (Pleşan 2021 ). The instructor divided the students into seven groups (five girls in each group) with varying abilities and potential. The students were able to acquire various skills in these diverse groups to enhance them as well as intragroup interpersonal interactions. Classroom observations were conducted several times a week over 6 weeks. The study utilizes two inductive and deductive reasoning cycles during the coding process (Ridder 2014 ). Four themes were generated from the observational data: student group work, a student, shared duties, the interdependence of the student’s work and their decision-making

Students’ group work

During the PBL, students collaborated in groups from the project planning stage to creating the product and project presentation. Students collaborated in groups to discuss statistical applications in their classrooms throughout the project preparation stage. Then, they discuss further the project’s title, description, and objectives, the project’s implementation steps, the project schedule, and each group member’s responsibilities. Additionally, observations revealed that students leveraged social media platforms, such as WhatsApp group chats, for discussions outside school hours.

Students shared responsibilities

Each group assigned its members a task and set a deadline, ensuring students appropriately shared duties. Therefore, the students were expected to finish the related activities before the due date. When it was their chance to speak on what they had discovered about angles, how they are measured, and how these angles differ from one another, the students were sharing responsibility. This circumstance demonstrated that each group member must collaborate to develop their awareness of many aspects and apply them to their project. Additionally, each student took part in constructing the presentation of their work on hard copy paper and outlining the presentation materials for their project presentation in front of the entire class. The project tasks involved cutting paper, measuring angels, and sketching various shapes with various angles and were shared among the pupils to produce the final items.

The students made decisions regarding the theme of the project, the activities they would undertake, the project’s timeline, individual roles within the group, the final product, and the materials and tools required for the project. They also determined the most effective method to present their project results to others. When making substantial judgments about the project’s topic, process, and output, students always hold an initial conversation to address individual ideas collectively. To influence the choice, the students bargained their thoughts. The observation revealed that the student gained confidence in her ability to voice her opinions during the group assignment. When students encountered divergent viewpoints among group members regarding the process of making important decisions, they conducted voting and arrived at a consensus opinion.

Additionally, the researcher discovered that one student needed help developing the project’s product, particularly the finished item. The student expressed concern about the final product’s adornment, which she feared would be overdone and lower its esthetic worth. These data demonstrate that the student and her team were making crucial design decisions that impacted the result.

Students’ interdependent work

From the observations, it is clear that the task required each group member to create a unique set of presentation materials on angles, which were to be assembled into a cohesive presentation on stiff chart paper. Therefore, if any group member does not complete their tasks in time, it may cause a delay in the final presentation chart’s completion. This circumstance demonstrated the interdependence of the student’s contributions to the PBL. The researcher observed and documented students’ collaborative efforts in a project-based learning environment, and the following are excerpts from these observations. In addition, each group member was assigned to prepare and bring the tools and supplies required to complete the project. The manufacturing process is improved if one team member gets the necessary tools or materials. That demonstrated how student effort is interdependent and dramatically impacts the project. This requirement enables students to comprehend and be conscious of the significance of their part in completing the project. Students were able to apply the concept of an angel to everyday problems through the completion of their mathematics project. In this project, students worked in small groups to gather and describe the data using their knowledge and observations. Subsequently, they transformed the angles into visual representations. The student’s final projects, displayed in the counseling room, the students’ club room, and the school wall magazine, served as references for significant school statistics.

The findings above conclude that applying PBL in mathematics enhances students’ teamwork skills. When students share responsibility equitably, make crucial decisions, and produce an interdependent project product, they attain level 5 according to the criteria for twenty-first century students’ collaboration skills.

The present study’s findings contribute to the growing body of literature on PBL and its potential for promoting students’ twenty-first century skills, particularly in Math education. The results showed that students who received PBL instruction developed collaborative, critical thinking, and problem-solving skills, as measured by various assessment tools, including questionnaires, tests, and classroom observations. These skills are essential for preparing students for the complex challenges of the twenty-first century, such as global competition, technological advancements, and social and environmental issues. It aligns with previous research highlighting the benefits of PBL for promoting critical and creative thinking (Darling-Hammond et al. 2020 ). However, students in Pakistani government schools need to become more accustomed to engaging in critical thinking while solving arithmetic problems, as reported by the TIMSS study. That is a big challenge for teachers seeking to improve math and Science Education (Ahmad et al. 2022 ).

The study sheds light on implementing PBL activities in classrooms and how they can enhance students’ critical thinking, problem-solving, and collaborative abilities. This finding can help teachers reevaluate how students gain from participating in PBL activities and restructure their instructional approaches to achieve student-centered learning. The study’s results are consistent with previous research, suggesting that PBL can help students build collaborative skills through group projects (Chistyakov et al. 2023 ). Collaboration abilities are crucial for success in today’s interconnected working environment and global culture. PBL is one educational activity that can help students build these skills, as it demands that students collaborate in small groups to solve problems and produce products. PBL is an ideal method for teaching mathematics at the primary level. It helps students recognize the relationships between different mathematical concepts and develop a conceptual understanding of the subject. It can help students identify partial order in the collection of mathematical notions, an essential aspect of mathematical concept development.

However, it is essential to note that the effectiveness of PBL may depend on various factors, such as teacher training and support, curriculum alignment, assessment methods, and student readiness. For instance, Loyens et al. ( 2023 ) research revealed that PBL minimally influences students’ cognitive and metacognitive abilities within medical education. The researchers posited that the absence of well-defined guidelines and assistance for PBL implementation might have yielded these findings in conjunction with medical education’s intricate and ever-changing landscape. Furthermore, implementing PBL may require significant time, resources, and training for teachers and students, posing challenges in specific educational contexts. Therefore, further research is needed to explore the effectiveness and feasibility of PBL across different subjects, grade levels, and cultural contexts and identify the optimal conditions for its implementation.

In conclusion, this study provides empirical evidence of the potential benefits of PBL for promoting twenty-first century skills in math education, including collaboration, critical thinking, and problem-solving. The findings underscore the importance of student-centered, inquiry-based, and authentic learning experiences that can prepare students for the complex challenges of the twenty-first century. The study’s results inform the development of practical pedagogical approaches that promote student learning and engagement and contribute to the ongoing dialog on educational reform and innovation.

This study has a unique contribution to the context of the Pakistani educational landscape. While the literature is abundant with studies on the benefits of project-based learning (PBL), this study specifically addresses the implementation and effectiveness of PBL in teaching mathematics to 5th-grade students in Pakistan. By providing detailed insights into the local context, including the cultural, social, and educational factors that may influence the adoption and outcomes of PBL, we have enriched the understanding of PBL’s applicability and potential benefits in diverse settings. Furthermore, the interpretation of our results highlights the development of twenty-first century skills, collaborative abilities, problem-solving aptitude, and creative thinking skills among the participating students, demonstrating the value of PBL as an instructional tool within the Pakistani context. This original contribution advances the global understanding of PBL’s effectiveness. It offers practical implications for educators and policymakers in Pakistan seeking innovative ways to improve learning outcomes and foster essential skills in their students. Moreover, in Pakistani public schools where technology integration is not feasible, PBL can be an effective alternative for math teaching by utilizing low-tech resources such as manipulatives, posters, and group activities. Teachers can create engaging and collaborative problem-solving experiences for students, fostering critical thinking skills even in technology-deprived classrooms.

Data availability

The data supporting this study’s findings are available on request from the corresponding author. These data are part of a large project, and only a portion is available for the following reasons: (1) Some participants in the study requested complete anonymity, which restricts the availability of specific datasets to protect their privacy and confidentiality. We have taken all necessary steps to ensure no personal or identifiable information is included in the available data. (2) Additionally, some of the data are reserved for future publication. It ensures the integrity of ongoing analyses and prevents potential overlap in research findings. We understand the importance of data availability in promoting transparency, reproducibility, and open science, and we commit to making as much of the data available as possible within these constraints. Data are available at https://doi.org/10.7910/DVN/YJY0FI and accessed with the author’s permission.

Abramovich S, Grinshpan AZ, Milligan DL (2019) Teaching mathematics through concept motivation and action learning. Educ Res Int 2019:1–13

Article   Google Scholar  

Ahmad S, Rodrigues S, Muzaffar Bhutta S (2022) Pakistan’s first ever participation in international large-scale assessment (TIMSS): critique and implications. J Educ Educ Dev 9(2):191–210

Ailaan A (2017) Pakistan district education ranking 2017, vol 66. Alif Ailaan, Islamabad

Akcanca N (2020) 21st century skills: the predictive role of attitudes regarding STEM education and problem-based learning. Int J Progress Educ 16(5):443–458

Almazroui KM (2023) Project-based learning for 21st-century skills: an overview and case study of moral education in the UAE. Soc Stud 114(3):125–136

Alsaad AA, Mansor ZBD, Ghazali HB (2023) The effect of TQM practices on job satisfaction in higher education institutes. A systematic literature review from the last two decades. J Optim Ind Eng 16(1):75–87

Google Scholar  

Andanawarih M, Diana S, Amprasto A (2019) The implementation of authentic assessment through project-based learning to improve student’s problem solving ability and concept mastery of environmental pollution topic. J Phys Conf Ser 1157:022116

Artama KKJ, Budasi IG, Ratminingsih NM (2023) Promoting the 21st century skills using project-based learning. Lang Cir J Lang Lit 17(2):325–332

Brown JS, Collins A, Duguid P (1989) Situated cognition and the culture of learning. Educ Res 18(1):32–42

Chiang CL, Lee H (2016) The effect of project-based learning on learning motivation and problem-solving ability of vocational high school students. Int J Inf Educ Technol 6(9):709–712

Chistyakov AA, Zhdanov SP, Avdeeva EL, Dyadichenko EA, Kunitsyna ML, Yagudina RI (2023) Exploring the characteristics and effectiveness of project-based learning for science and STEAM education. Eurasia J Math Sci Technol Educ 19(5):em2256

Cohen L, Manion L, Morrison K (2017) Research methods in education, 8th edn. Routledge

Coskun Y (2018) A study on metacognitive thinking skills of university students. J Educ Train Stud 6(3):38–46

Article   MathSciNet   Google Scholar  

Darling-Hammond L, Flook L, Cook-Harvey C, Barron B, Osher D (2020) Implications for educational practice of the science of learning and development. Appl Dev Sci 24(2):97–140

DeCoito I, Briona LK (2023) Fostering an entrepreneurial mindset through project-based learning and digital technologies in STEM teacher education. In: Kaya-Capocci S, Peters-Burton E, (eds.), Enhancing entrepreneurial mindsets through STEM education. Springer International Publishing, Cham, p 195–222

Devanda B, Elizar E (2023) The effectiveness of the STEM project based learning approach in physics learning to improve scientific work skills of high school students. Int J Hum Educ Soc Sci 2(4):1219–1226

Dolmans DHJM (2019) How theory and design-based research can mature PBL practice and research. Adv Health Sci Educ Theory Pract 24(5):879–891

Article   PubMed   PubMed Central   Google Scholar  

Erstad O, Voogt J (2018) The twenty-first century curriculum: issues and challenges. In: Voogt J, Knezek G, Christensen R, Lai KW (eds) Springer international handbooks of education. Springer, Cham. p 19–36

Gelerstein D, Río RD, Nussbaum M, Chiuminatto P, López X (2016) Designing and implementing a test for measuring critical thinking in primary school. Think Skills Creat 20:40–49

Harden RM (2018) Ten key features of the future medical school—not an impossible dream. Med Teach 40(10):1010–1015

Article   PubMed   Google Scholar  

Holmes V-L, Hwang Y (2016) Exploring the effects of project-based learning in secondary mathematics education. J Educ Res 109(5):449–463

Huang W, London JS, Perry LA (2022) Project-based learning promotes students’ perceived relevance in an engineering statistics course: a comparison of learning in synchronous and online learning environments. J Stat Data Sci Educ 00(0):1–9

Jincheng J, Chayanuvat A (2020) The effects of project-based learning on Chinese vocabulary learning achievement of secondary three Thai students. Walailak J Learn Innov 6(2):133–164

Kaendler C, Wiedmann M, Rummel N, Spada H (2015) Teacher competencies for the implementation of collaborative learning in the classroom: a framework and research review. Educ Psychol Rev 27(3):505–536

Kaptan F, Korkmaz H (2000) Fen öğretiminde tümel (portfolio) değerlendirme. Hacettepe Üniversitesi Eğitim Fakültesi Dergisi 19(19):212–219

Kiong TT, Rusly NSM, Abd Hamid RI, Swaran SCK, Hanapi Z (2022) Inventive problem-solving in project-based learning on design and technology: a needs analysis for module development. Asian J Univ Educ 18(1):271–278

Kolb B (1984) Functions of the frontal cortex of the rat: a comparative review. Brain Res Rev 8(1):65–98

Kollar I, Ufer S, Reichersdorfer E, Vogel F, Fischer F, Reiss K (2014) Effects of collaboration scripts and heuristic worked examples on the acquisition of mathematical argumentation skills of teacher students with different levels of prior achievement. Learn Instr 32:22–36

Kurniahtunnisa K, Wowor EC (2023) Development of STEM-project based learning devices to train 4C skills of students. Bioeduca J Biol Educ 5(1):66–78

Laal M, Laal M, Kermanshahi ZK (2012) 21st century learning; learning in collaboration. Procedia Soc Behav Sci 47:1696–1701

Le HC, Nguyen VH, Nguyen TL (2023) Integrated STEM approaches and associated outcomes of K-12 student learning: a systematic review. Educ Sci 13(3):297

Lim SW, Jawawi R, Jaidin JH, Roslan R (2023) Learning history through project-based learning. J Educ Learn (EduLearn) 17(1):67–75

Loyens SM, Van Meerten JE, Schaap L, Wijnia L (2023) Situating higher-order, critical, and critical-analytic thinking in problem-and project-based learning environments: a systematic review. Educ Psychol Rev 35(2):39

Markula A, Aksela M (2022) The key characteristics of project-based learning: how teachers implement projects in K-12 science education. Discip Interdiscip Sci Educ Res 4(1):1–17

Article   ADS   Google Scholar  

Mazana MY, Montero CS, Casmir RO (2018) Investigating students’ attitude towards learning mathematics. Int Electron J Math Educ 14(1):207–231

Mielikäinen M (2022) Towards blended learning: stakeholders’ perspectives on a project-based integrated curriculum in ICT engineering education. Ind High Educ 36(1):74–85

Moghaddas M, Khoshsaligheh M (2019) Implementing project-based learning in a Persian translation class: a mixed-methods study. Interpret Transl Train 13(2):190–209

Mutakinati L, Anwari I, Kumano Y (2018) Analysis of Students’ critical thinking skill of middle school through STEM education project-based learning. J Pendidik IPA Indones 7(1):54–65

Muthukrishnan P, Choo KA, Kam NKBMZ, Omar II SMKP, Sipitang S, Singh MP (2022) Preservice teachers’ motivation and adoption of 21st-century skills. Comput Assist Lang Learn 23(4):205–218

Nadeak B, Naibaho L (2020) The effectiveness of problem-based learning on students’ critical thinking. J Din Pendidik 13(1):1–7

O’Grady-Jones M, Grant MM (2023) Ready coder one: collaborative game design-based learning on gifted fourth graders’ 21st century skills. Gift Child Today 46(2):84–107

Owens AD, Hite RL (2022) Enhancing student communication competencies in STEM using virtual global collaboration project based learning. Res Sci Technol Educ 40(1):76–102

Pan AJ, Lai CF, Kuo HC (2023) Investigating the impact of a possibility-thinking integrated project-based learning history course on high school students’ creativity, learning motivation, and history knowledge. Think Skills Creat 47:101214

Papanastasiou G, Drigas A, Skianis C, Lytras M, Papanastasiou E (2019) Virtual and augmented reality effects on K-12, higher and tertiary education students’ twenty-first century skills. Virtual Real 23:425–436

Parrado-Martínez P, Sánchez-Andújar S (2020) Development of competences in postgraduate studies of finance: A project-based learning (PBL) case study. Int Rev Econ Educ 35:100192

Paryanto P, Munadi S, Purnomo W, Nugraha RN, Altandi SA, Pamungkas A, Cahyani PA (2023) Implementation of project-based learning model to improve employability skills and student achievement. In: AIP conference proceedings, vol. 2671, No. 1. AIP Publishing. Yogyakarta, Indonesia

Paul R, Elder L (2008) Critical thinking: strategies for improving student learning. Part II. J Dev Educ 32(2):34–35

Pleşan NC (2021) The method of observing the student’s behavior in the educational environment. MATEC Web Conf 342:11009

Qureshi MA, Khaskheli A, Qureshi JA, Raza SA, Yousufi SQ (2021) Factors affecting students’ learning performance through collaborative learning and engagement. Interact Learn Environ 1–21

Radkowitsch A, Sailer M, Fischer MR, Schmidmaier R, Fischer F (2022) Diagnosing collaboratively: a theoretical model and a simulation-based learning environment. In: Fischer F, Opitz A (eds); Learning to diagnose with simulations: teacher education and medical education. Springer Nature, p 123–141

Rajabzadeh AR, Mehrtash M, Srinivasan S (2022) Multidisciplinary problem-based learning (MPBL) approach in undergraduate programs. In: New realities, mobile systems and applications: proceedings of the 14th IMCL conference. Springer International Publishing, Cham, p 454–463

Ramadhan S, Mardapi D, Prasetyo ZK, Utomo HB (2019) The development of an instrument to measure the higher order thinking skill in physics. Eur J Educ Res 8(3):743–751

Rati NW, Kusmaryatni N, Rediani N (2017) Model pembelajaran berbasis proyek, kreativitas dan hasil belajar mahasiswa. J Pendidik Indones 6(1):60–71

Rehman N, Zhang W, Mahmood A, Alam F (2021) Teaching physics with interactive computer simulation at secondary level. Cad Educ Tecnol Soc 14(1):127–141

Ridder HG (2014) Book Review: Qualitative data analysis. A methods sourcebook, vol. 28. Sage publications, London, England, p 485–487

Rizkiyah Z, Hariyadi S, Novenda I (2020) The influence of project based learning models on science technology, engineering and mathematics approach to collaborative skills and learning results of student. ScienceEdu 3(1):1–6

Roldán Roa E, Roldán Roa É, Chounta IA (2020) Learning music and math, together as one: towards a collaborative approach for practicing math skills with music. In: Collaboration technologies and social computing: 26th international conference, CollabTech 2020, Tartu, Estonia, September 8–11, 2020, proceedings 26. Springer International Publishing, p 143–156

Saduakassova A, Shynarbek N, Sagyndyk N (2023) Students’ perception towards project-based learning in enhancing 21st century skills in mathematics classes. Scientific Collection «InterConf» 150:159–170

Saqr M, López-Pernas S (2023) The temporal dynamics of online problem-based learning: why and when sequence matters. Int J Comput Support Collab Learn 18(1):11–37

Sevgül Ö, Yavuzcan HG (2022) Learning and evaluation in the design studio. Gazi Univ J Sci Part B Art Humanit Des Plan 10(1):43–53

Shah Bukhari SKU, Said H, Gul R, Ibna Seraj PM (2022) Barriers to sustainability at Pakistan public universities and the way forward. Int J Sustain High Educ 23(4):865–886

Simon MA (2020) Reconstructing mathematics pedagogy from a constructivist perspective. J Res Math Educ 26(2):114–145

Sithole A, Chiyaka ET, McCarthy P, Mupinga DM, Bucklein BK, Kibirige J (2017) Student attraction, persistence and retention in STEM programs: successes and continuing challenges. High Educ Stud 7(1):46–59

Sumarni W, Kadarwati S (2020) Ethno-stem project-based learning: its impact to critical and creative thinking skills. J Pendidik IPA Indones 9(1):11–21

Susanto E, Retnawati H (2016) PBL characterizes mathematics learning tools to develop HOTS for high school students. J Ris Pend Math 3(2):189–197

Suwastini NKA, Puspawati NWN, Adnyani NLPS, Dantes GR, Rusnalasari ZD (2021) Problem-based learning and 21st-century skills: are they compatible?. EduLite J English Educ Lit Cult 6(2):326–340

Szalay L, Tóth Z, Borbás R, Füzesi I (2023) Scaffolding of experimental design skills. Chem Educ Res Pract 24(2):599–623

Tee WJ (2018). Project-based learning for building work and life skills in line with TGC and purpose learning. In: Tang SF, Lim CL (eds); Preparing the next generation of teachers for 21st century education. IGI Global, p 109–125. https://www.igi-global.com/book/preparing-next-generation-teachers-21st/182585#table-of-contents

Tibi MH (2015) Technologies in education. In: Encyclopedia of education and human development, vol 10. Champaign, Illinois, USA by Common Ground Publishing LLC, p 201–238

Ventista OM (2018) Multi-trait multi-method matrices for the validation of creativity and critical thinking assessments for secondary school students in England and Greece. Int J Assess Tool Educ 5(1):15–32

Vogel F, Kollar I, Ufer S, Reichersdorfer E, Reiss K, Fischer F (2016) Developing argumentation skills in mathematics through computer-supported collaborative learning: the role of transactivity. Instr Sci 44:477–500

Wongdaeng M, Hajihama S (2018) Perceptions of project-based learning on promoting 21st century skills and learning motivation in a Thai EFL setting. J Stud English Lang 13(2):158–190

Yang D, Skelcher S, Gao F (2021) An investigation of teacher experiences in learning the project-based learning approach. J Educ Learn (EduLearn) 15(4):490–504

Yoon CH (2017) A validation study of the Torrance Tests of Creative Thinking with a sample of Korean elementary school students. Think Skills Creat 26:38–50

Download references

Author information

Authors and affiliations.

School of Education, Shaanxi Normal University, Xi’an, China

Nadia Rehman, Wenlan Zhang & Amir Mahmood

Xian Jiaotong University, Xi’an, China

Muhammad Zeeshan Fareed

Sichuan University, Chengdu, China

Samia Batool

You can also search for this author in PubMed   Google Scholar

Contributions

NR: made significant contributions to the conception and design of the study, writing, data collection, analysis, and interpretation. WZ: provided valuable insights into the theoretical framework conceptualization, resources, supervision, validation, and proofreading. AM: writing, review, and editing. MZF: actively participated in the manuscript revising for scientific accuracy and ensuring clarity in the “Methodology” section. SB: review and editing. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Nadia Rehman .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Ethical approval

This study received ethics approval “SNNU-ETH-2023-Ed1045” from the Institutional Ethical Board (IEB) of Shaanxi Normal University. The research team adhered to the ethical guidelines and principles set forth by Shaanxi Normal University throughout the study to ensure the responsible and respectful treatment of all participants involved.

Informed consent

In this study, all participants provided their informed consent in written form. Additionally, the ethics committee reviewed and approved the need for consent.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Authorship letter, grammarly report, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Rehman, N., Zhang, W., Mahmood, A. et al. Fostering twenty-first century skills among primary school students through math project-based learning. Humanit Soc Sci Commun 10 , 424 (2023). https://doi.org/10.1057/s41599-023-01914-5

Download citation

Received : 02 February 2023

Accepted : 30 June 2023

Published : 18 July 2023

DOI : https://doi.org/10.1057/s41599-023-01914-5

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

• Libraries Home
• Research Guides

Mathematics Resources

• Research Skills
• ACCUPLACER Math Skills

Research Mindset

Steps in research, keyword & subject searching, limits or filters, evaluate information.

• Articles (Databases)
• ArcherSearch
• Books & Ebooks
• Math Education
• Citation & Writing Help

Develop a research mindset. Understand research as a process of asking questions and exploring. 

The quality of your research depends largely on the questions you ask. Practice asking a lot of them. Adopt the mindset of an explorer or investigator. What qualities and characteristics do successful explorers and investigators have?  Develop a plan; where will you start?  As you begin to explore, you will discover that research can be messy. Expect and welcome twists and turns, keep an open mind, and keep asking questions throughout the process. Use many different kinds of search tools and resources, and conduct many different kinds of searches. 

Research takes time and patience; it can also be fun and has value.

Developing your research skills will enable you to identify a problem, collect informational resources that can help address the problem, evaluate these resources for quality and relevance, and come up with an effective solution to a problem. Research skills develop critical thinking and equip you to write better research papers and craft better speeches. You will also improve problem solving skills required to tackle issues in your personal life and in the workplace. 

Follow these steps.

Keep an open mind. You may need to refine your topic, ask new questions, and repeat steps as you go along.

Identify and define your topic. Put your research topic into a question such as, "What is the debate surrounding vaccination refusal?" Now you can identify the main concepts and keywords, including alternate terms, for your topic.

Background reading will deepen your understanding and vocabulary around the topic, which will help you identify search terms and develop an effective research question. Subject encyclopedias (in print or in Credo Reference)   are excellent resources. 

Use ArcherSearch or the library catalog to find books . 

Use ArcherSearch or individual databases to find articles from magazines, journals and newspapers . Choose appropriate databases for your topic.

Search for credible website resources. Try the librarian-recommended websites on this guide.

Always evaluate what you find. Consider timeliness, relevance, authority, accuracy, and purpose.

Cite your sources . Citing gives proper credit to the authors of materials you use and allows your professors to verify your conclusions. 

Keyword Searching

Keyword searching is used by internet search engines, databases, and the library catalog. Keep in mind that the search will find matches for specific words, not concepts. The default in the library catalog (and most databases) is find results that include every word in your search. Think of this as using AND between the words: 

• algebra AND problem AND solving
• algebra problem solving
• calculus AND applications

The two searches above are the same, and will find all books in the library catalog that have all three words in the description of the book. 

If you want to find a specific phrase, with the words next to each other in order, use double quotation marks around the phrase:

• "math anxiety" 

You might want to broaden your search to include synonyms or other related words. To find either of two words or phrases, use OR between them:

• math* OR arithmetic

You can also use truncation to search for different forms of a word. The asterisk * is used in the library catalog and many databases for this. 

• math* AND "word problems"

In the above searches, math*  will find the words math, mathematics, mathematical, mathematician, maths,  etc. 

When combining searches, use parentheses () around different parts of the search, as in the examples above. 

Subject Heading Searching

Think of subject headings as labels or tags that someone has used to identify the subject of a book or article. The subject headings are standardized so that only one term is used for a specific subject.  You can search directly by subject, or click on a subject heading in the description of a book you find by keyword searching. Instead of a list of search results, you'll get a list of subject headings to choose from.  Here are a few examples:

• Algebra (view related LC Subject Heading and subheadings)
• Algebras, Linear
• Business Mathematics
• Geometry (and subheadings)
• Mathematics (view related LC Subject Heading and subheadings)
• Mathematics -- Popular works
• Mathematics -- Problems, exercises, etc.
• Trigonometry

Use the filters or limits to see just a subset of your search results. Depending on the tool you are using, search limits may show up in the left margin, at the top of the results, or below the search box. 

Date limits are especially useful to filter out older, outdated material. You can usually choose a preset limit such as "current 5 years," or set a custom range of publication dates. 

Scholarly/Peer-Reviewed Journals

This will limit to only journals that publish articles that have undergone a rigorous peer-review process. These are usually articles that report on a specific study, analysis, experiment, or other piece of the research. Some scholarly/peer-reviewed articles are systematic reviews  which survey a wide range of published peer-reviewed articles to give an overview of the current state of knowledge on the topic.

The Subject limit will help you narrow your results by subject terms. These are like tags or labels; they indicate that the book, article, or other source focuses on the subject of interest. Without this limit, you may find items that include your search words but are not about your topic. Keep in mind that different databases may use different subject terms.  

The Full-text limit is already applied for most searches. It is very useful to filter out articles where you only have access to a citation or a description of an article, not the full the full article. Unless you are required to find everything out there is published on a given subject, this limit should be applied every time you search. If you do find resources that are not full text but would be useful to you, STLCC Libraries may be able provide them. See the Borrowing from Other Libraries page for details and the form for requests. 

• Borrowing from Other Libraries

Evaluating the information you find, whether in print or digital format, is an essential aspect of doing research.

Learn to think critically about the source of information and the information within each source by using the Evaluate Your Sources guide. 

• Evaluate Your Sources STLCC Libraries
• << Previous: ACCUPLACER Math Skills
• Next: Articles (Databases) >>
• Last Updated: Dec 20, 2023 11:38 AM
• URL: https://guides.stlcc.edu/math

• Future Students
• Current Students
• Faculty/Staff

News and Media

• News & Media Home
• Research Stories
• School's In
• In the Media

You are here

Research shows the best ways to learn math.

Students learn math best when they approach the subject as something they enjoy. Speed pressure, timed testing and blind memorization pose high hurdles in the pursuit of math, according to Jo Boaler, professor of mathematics education  at Stanford Graduate School of Education and lead author on a new working paper called "Fluency Without Fear."

"There is a common and damaging misconception in mathematics – the idea that strong math students are fast math students," said Boaler, also cofounder of YouCubed at Stanford, which aims to inspire and empower math educators by making accessible in the most practical way the latest research on math learning.

Fortunately, said Boaler , the new national curriculum standards known as the Common Core Standards for K-12 schools de-emphasize the rote memorization of math facts. Maths facts are fundamental assumptions about math, such as the times tables (2 x 2 = 4), for example. Still, the expectation of rote memorization continues in classrooms and households across the United States.

While research shows that knowledge of math facts is important, Boaler said the best way for students to know math facts is by using them regularly and developing understanding of numerical relations. Memorization, speed and test pressure can be damaging, she added.

Number sense is critical

On the other hand, people with "number sense" are those who can use numbers flexibly, she said. For example, when asked to solve the problem of 7 x 8, someone with number sense may have memorized 56, but they would also be able to use a strategy such as working out 10 x 7 and subtracting two 7s (70-14).

"They would not have to rely on a distant memory," Boaler wrote in the paper.

In fact, in one research project the investigators found that the high-achieving students actually used number sense, rather than rote memory, and the low-achieving students did not.

The conclusion was that the low achievers are often low achievers not because they know less but because they don't use numbers flexibly.

"They have been set on the wrong path, often from an early age, of trying to memorize methods instead of interacting with numbers flexibly," she wrote. Number sense is the foundation for all higher-level mathematics, she noted.

Role of the brain

Boaler said that some students will be slower when memorizing, but still possess exceptional mathematics potential.

"Math facts are a very small part of mathematics, but unfortunately students who don't memorize math facts well often come to believe that they can never be successful with math and turn away from the subject," she said.

Prior research found that students who memorized more easily were not higher achieving – in fact, they did not have what the researchers described as more "math ability" or higher IQ scores. Using an MRI scanner, the only brain differences the researchers found were in a brain region called the hippocampus, which is the area in the brain responsible for memorizing facts – the working memory section.

But according to Boaler, when students are stressed – such as when they are solving math questions under time pressure – the working memory becomes blocked and the students cannot as easily recall the math facts they had previously studied. This particularly occurs among higher achieving students and female students, she said.

Some estimates suggest that at least a third of students experience extreme stress or "math anxiety" when they take a timed test, no matter their level of achievement. "When we put students through this anxiety-provoking experience, we lose students from mathematics," she said.

Math treated differently

Boaler contrasts the common approach to teaching math with that of teaching English. In English, a student reads and understands novels or poetry, without needing to memorize the meanings of words through testing. They learn words by using them in many different situations – talking, reading and writing.

"No English student would say or think that learning about English is about the fast memorization and fast recall of words," she added.

Strategies, activities

In the paper, coauthored by Cathy Williams, cofounder of YouCubed, and Amanda Confer, a Stanford graduate student in education, the scholars provide activities for teachers and parents that help students learn math facts at the same time as developing number sense. These include number talks, addition and multiplication activities, and math cards.

Importantly, Boaler said, these activities include a focus on the visual representation of number facts. When students connect visual and symbolic representations of numbers, they are using different pathways in the brain, which deepens their learning, as shown by recent brain research.

"Math fluency" is often misinterpreted, with an over-emphasis on speed and memorization, she said. "I work with a lot of mathematicians, and one thing I notice about them is that they are not particularly fast with numbers; in fact some of them are rather slow. This is not a bad thing; they are slow because they think deeply and carefully about mathematics."

She quotes the famous French mathematician, Laurent Schwartz. He wrote in his autobiography that he often felt stupid in school, as he was one of the slowest math thinkers in class.

Math anxiety and fear play a big role in students dropping out of mathematics, said Boaler.

"When we emphasize memorization and testing in the name of fluency we are harming children, we are risking the future of our ever-quantitative society and we are threatening the discipline of mathematics," she said. "We have the research knowledge we need to change this and to enable all children to be powerful mathematics learners. Now is the time to use it."

More Stories

⟵ Go to all Research Stories

Get the Educator

Subscribe to our monthly newsletter.

Stanford Graduate School of Education

482 Galvez Mall Stanford, CA 94305-3096 Tel: (650) 723-2109

• Contact Admissions
• GSE Leadership
• Site Feedback
• Web Accessibility
• Career Resources
• Faculty Open Positions
• Explore Courses
• Academic Calendar
• Office of the Registrar
• Cubberley Library
• StanfordWho
• StanfordYou

Improving lives through learning

• Stanford Home
• Maps & Directions
• Search Stanford
• Emergency Info
• Terms of Use
• Non-Discrimination
• Accessibility

© Stanford University , Stanford , California 94305 .

all the numbers are changing, but what doesn't change is the relationship between x and y: y is always one more than twice x. That is, y=2x+1. Finding what doesn't change "tames" the situation. So, you have tamed this problem! Yay. And if you want a fancy mathematical name for things that don’t vary, we call these things "invariants." The number of messed-up recruits is invariant, even though they are all wiggling back and forth, trying to figure out which way is right!

3) Encourage generalizations

So, of course, the next question that comes to my mind is how to generalize what you’ve already discovered: there are 15 ways that 2 mistakes can be arranged in a line of 6 recruits. What about a different number of mistakes? Or a different number of recruits? Is there some way to predict? Or, alternatively, is there some way to predict how these 15 ways of making mistakes will play out as the recruits try to settle themselves down? Which direction interests you?

4) Inquire about reasoning and rigor

The students were looking at the number of ways the recruits could line up with 2 out of n faced the wrong way: Anyway, I had a question of my own. It looks like the number of possibilities increases pretty fast, as the number of recruits increases. For example, I counted 15 possibilities in your last set (the line of six). What I wonder is this: when the numbers get that large, how you can possibly know that you've found all the possibilities? (For example, I noticed that >>>><< is missing.) The question "How do I know I've counted 'em all?" is actually quite a big deal in mathematics, as mathematicians are often called upon to find ways of counting things that nobody has ever listed (exactly like the example you are working on).

The students responded by finding a pattern for generating the lineups in a meaningful order: The way that we can prove that we have all the possibilities is that we can just add the number of places that the second wrong person could be in. For example, if 2 are wrong in a line of 6, then the first one doesn’t move and you count the space in which the second one can move in. So for the line of six, it would be 5+4+3+2+1=15. That is the way to make sure that we have all the ways. Thanks so much for giving challenges. We enjoyed thinking!

5) Work towards proof

a) The group wrote the following: When we found out that 6 recruits had 15 different starting arrangements, we needed more information. We needed to figure out how many starting positions are there for a different number of recruits.

By drawing out the arrangements for 5 recruits and 7 recruits we found out that the number of starting arrangements for the recruit number before plus that recruit number before it would equal the number of starting arrangements for that number of recruits.

We also found out that if you divide the starting arrangements by the number of recruits there is a pattern.

To which the mentor replied: Wow! I don't think (in all the years I've been hanging around mathematics) I've ever seen anyone describe this particular pattern before! Really nice! If you already knew me, you'd be able to predict what I'm about to ask, but you don't, so I have to ask it: "But why?" That is, why is this pattern (the 6, 10, 15, 21, 28…) the pattern that you find for this circumstance (two recruits wrong in lines of lengths, 4, 5, 6, 7, 8…)? Answering that—explaining why you should get those numbers and why the pattern must continue for longer lines—is doing the kind of thing that mathematics is really about.

b) Responding to students studying a circular variation of raw recruits that never settled down: This is a really interesting conclusion! How can you show that it will always continue forever and that it doesn’t matter what the original arrangement was? Have you got a reason or did you try all the cases or…? I look forward to hearing more from you.

6) Distinguish between examples and reasons

a) You have very thoroughly dealt with finding the answer to the problem you posed—it really does seem, as you put it, "safe to say" how many there will be. Is there a way that you can show that that pattern must continue? I guess I’d look for some reason why adding the new recruit adds exactly the number of additional cases that you predict. If you could say how the addition of one new recruit depends on how long the line already is, you’d have a complete proof. Want to give that a try?

b) A student, working on Amida Kuji and having provided an example, wrote the following as part of a proof: In like manner, to be given each relationship of objects in an arrangement, you can generate the arrangement itself, for no two different arrangements can have the same object relationships. The mentor response points out the gap and offers ways to structure the process of extrapolating from the specific to the general: This statement is the same as your conjecture, but this is not a proof. You repeat your claim and suggest that the example serves as a model for a proof. If that is so, it is up to you to make the connections explicit. How might you prove that a set of ordered pairs, one per pair of objects forces a unique arrangement for the entire list? Try thinking about a given object (e.g., C) and what each of its ordered pairs tells us? Try to generalize from your example. What must be true for the set of ordered pairs? Are all sets of n C2 ordered pairs legal? How many sets of n C2 ordered pairs are there? Do they all lead to a particular arrangement? Your answers to these questions should help you work toward a proof of your conjecture.

9) Encourage extensions

What you’ve done—finding the pattern, but far more important, finding the explanation (and stating it so clearly)—is really great! (Perhaps I should say "finding and stating explanations like this is real mathematics"!) Yet it almost sounded as if you put it down at the very end, when you concluded "making our project mostly an interesting coincidence." This is a truly nice piece of work!

The question, now, is "What next?" You really have completely solved the problem you set out to solve: found the answer, and proved that you’re right!

I began looking back at the examples you gave, and noticed patterns in them that I had never seen before. At first, I started coloring parts red, because they just "stuck out" as noticeable and I wanted to see them better. Then, it occurred to me that I was coloring the recruits that were back-to-back, and that maybe I should be paying attention to the ones who were facing each other, as they were "where the action was," so I started coloring them pink. (In one case, I recopied your example to do the pinks.) To be honest, I’m not sure what I’m looking for, but there was such a clear pattern of the "action spot" moving around that I thought it might tell me something new. Anything come to your minds?

10) Build a Mathematical Community

I just went back to another paper and then came back to yours to look again. There's another pattern in the table. Add the recruits and the corresponding starting arrangements (for example, add 6 and 15) and you get the next number of starting arrangements. I don't know whether this, or your 1.5, 2, 2.5, 3, 3.5… pattern will help you find out why 6, 10, 15… make sense as answers, but they might. Maybe you can work with [your classmates] who made the other observation to try to develop a complete understanding of the problem.

11) Highlight Connections

Your rule—the (n-1)+(n-2)+(n-3)+… +3+2+1 part—is interesting all by itself, as it counts the number of dots in a triangle of dots. See how?

12) Wrap Up

This is really a very nice and complete piece of work: you've stated a problem, found a solution, and given a proof (complete explanation of why that solution must be correct). To wrap it up and give it the polish of a good piece of mathematical research, I'd suggest two things.

The first thing is to extend the idea to account for all but two mistakes and the (slightly trivial) one mistake and all but one mistake. (If you felt like looking at 3 and all but 3, that'd be nice, too, but it's more work—though not a ton—and the ones that I suggested are really not more work.)

The second thing I'd suggest is to write it all up in a way that would be understandable by someone who did not know the problem or your class: clear statement of the problem, the solution, what you did to get the solution, and the proof.

I look forward to seeing your masterpiece!

Advice for Keeping a Formal Mathematics Research Logbook

As part of your mathematics research experience, you will keep a mathematics research logbook. In this logbook, keep a record of everything you do and everything you read that relates to this work. Write down questions that you have as you are reading or working on the project. Experiment. Make conjectures. Try to prove your conjectures. Your journal will become a record of your entire mathematics research experience. Don’t worry if your writing is not always perfect. Often journal pages look rough, with notes to yourself, false starts, and partial solutions. However, be sure that you can read your own notes later and try to organize your writing in ways that will facilitate your thinking. Your logbook will serve as a record of where you are in your work at any moment and will be an invaluable tool when you write reports about your research.

Ideally, your mathematics research logbook should have pre-numbered pages. You can often find numbered graph paper science logs at office supply stores. If you can not find a notebook that has the pages already numbered, then the first thing you should do is go through the entire book putting numbers on each page using pen.

• Date each entry.

• Work in pen.

• Don’t erase or white out mistakes. Instead, draw a single line through what you would like ignored. There are many reasons for using this approach:

– Your notebook will look a lot nicer if it doesn’t have scribbled messes in it.

– You can still see what you wrote at a later date if you decide that it wasn’t a mistake after all.

– It is sometimes useful to be able to go back and see where you ran into difficulties.

– You’ll be able to go back and see if you already tried something so you won’t spend time trying that same approach again if it didn’t work.

• When you do research using existing sources, be sure to list the bibliographic information at the start of each section of notes you take. It is a lot easier to write down the citation while it is in front of you than it is to try to find it at a later date.

• Never tear a page out of your notebook. The idea is to keep a record of everything you have done. One reason for pre-numbering the pages is to show that nothing has been removed.

• If you find an interesting article or picture that you would like to include in your notebook, you can staple or tape it onto a page.

Advice for Keeping a Loose-Leaf Mathematics Research Logbook

Get yourself a good loose-leaf binder, some lined paper for notes, some graph paper for graphs and some blank paper for pictures and diagrams. Be sure to keep everything that is related to your project in your binder.

– Your notebook will look a lot nicer if it does not have scribbled messes in it.

• Be sure to keep everything related to your project. The idea is to keep a record of everything you have done.

• If you find an interesting article or picture that you would like to include in your notebook, punch holes in it and insert it in an appropriate section in your binder.

Making Mathematics Home | Mathematics Projects | Students | Teachers | Mentors | Parents | Hard Math Café |

• Write my thesis
• Thesis writers
• Buy thesis papers
• Bachelor thesis
• Master's thesis
• Thesis editing services
• Thesis proofreading services
• Buy a thesis online
• Write my dissertation
• Dissertation proposal help
• Pay for dissertation
• Custom dissertation
• Dissertation help online
• Buy dissertation online
• Cheap dissertation
• Dissertation editing services
• Write my research paper
• Buy research paper online
• Pay for research paper
• Research paper help
• Order research paper
• Custom research paper
• Cheap research paper
• Research papers for sale
• Thesis subjects
• How It Works

181 Mathematics Research Topics From PhD Experts

If you are reading this blog post, it means you are looking for some exceptional math research topics. You want them to be original, unique even. If you manage to find topics like this, you can be sure your professor will give you a top grade (if you write a decent paper, that is). The good news is that you have arrived at just the right place – at the right time. We have just finished updating our list of topics, so you will find plenty of original ideas right on this page. All our topics are 100 percent free to use as you see fit. You can reword them and you don’t need to give us any credit.

And remember: if you need assistance from a professional, don’t hesitate to reach out to us. We are not just the best place for math research topics for high school students; we are also the number one choice for students looking for top-notch research paper writing services.

Our Newest Research Topics in Math

We know you probably want the best and most recent research topics in math. You want your paper to stand out from all the rest. After all, this is the best way to get some bonus points from your professor. On top of this, finding some great topics for your next paper makes it easier for you to write the essay. As long as you know at least something about the topic, you’ll find that writing a great paper or buy phd thesis isn’t as difficult as you previously thought.

So, without further ado, here are the 181 brand new topics for your next math research paper:

Cool Math Topics to Research

Are you looking for some cool math topics to research? We have a list of original topics for your right here. Pick the one you like and start writing now:

• Roll two dice and calculate a probability
• Discuss ancient Greek mathematics
• Is math really important in school?
• Discuss the binomial theorem
• The math behind encryption
• Game theory and its real-life applications
• Analyze the Bernoulli scheme
• What are holomorphic functions and how do they work?
• Describe big numbers
• Solving the Tower of Hanoi problem

Undergraduate Math Research Topics

If you are an undergraduate looking for some research topics for your next math paper, you will surely appreciate our list of interesting undergraduate math research topics:

• Methods to count discrete objects
• The origins of Greek symbols in mathematics
• Methods to solve simultaneous equations
• Real-world applications of the theorem of Pythagoras
• Discuss the limits of diffusion
• Use math to analyze the abortion data in the UK over the last 100 years
• Discuss the Knot theory
• Analyze predictive models (take meteorology as an example)
• In-depth analysis of the Monte Carlo methods for inverse problems
• Squares vs. rectangles (compare and contrast)

Number Theory Topics to Research

Interested in writing about number theory? It is not an easy subject to discuss, we know. However, we are sure you will appreciate these number theory topics:

• Discuss the greatest common divisor
• Explain the extended Euclidean algorithm
• What are RSA numbers?
• Discuss Bézout’s lemma
• In-depth analysis of the square-free polynomial
• Discuss the Stern-Brocot tree
• Analyze Fermat’s little theorem
• What is a discrete logarithm?
• Gauss’s lemma in number theory
• Analyze the Pentagonal number theorem

Math Research Topics for High School

High school students shouldn’t be too worried about their math papers because we have some unique, and quite interesting, math research topics for high school right here:

• Discuss Brun’s constant
• An in-depth look at the Brahmagupta–Fibonacci identity
• What is derivative algebra?
• Describe the Symmetric Boolean function
• Discuss orders of approximation in limits
• Solving Regiomontanus’ angle maximization problem
• What is a Quadratic integral?
• Define and describe complementary angles
• Analyze the incircle and excircles of a triangle
• Analyze the Bolyai–Gerwien theorem in geometry
• Math in our everyday life

Complex Math Topics

If you want to give some complex math topics a try, we have the best examples below. Remember, these topics should only be attempted by students who are proficient in mathematics:

• Mathematics and its appliance in Artificial Intelligence
• Try to solve an unsolved problem in math
• Discuss Kolmogorov’s zero-one law
• What is a discrete random variable?
• Analyze the Hewitt–Savage zero-one law
• What is a transferable belief model?
• Discuss 3 major mathematical theorems
• Describe and analyze the Dempster-Shafer theory
• An in-depth analysis of a continuous stochastic process
• Identify and analyze Gauss-Markov processes

Easy Math Research Paper Topics

Perhaps you don’t want to spend too much time working on your next research paper. Who can blame you? Check out these easy math research paper topics:

• Define the hyperbola
• Do we need to use a calculator during math class?
• The binomial theorem and its real-world applications
• What is a parabola in geometry?
• How do you calculate the slope of a curve?
• Define the Jacobian matrix
• Solving matrix problems effectively
• Why do we need differential equations?
• Should math be mandatory in all schools?
• What is a Hessian matrix?

Logic Topics to Research

We have some interesting logical topics for research papers. These are perfect for students interested in writing about math logic. Pick one right now:

• Discuss the reductio ad absurdum approach
• Discuss Boolean algebra
• What is consistency proof?
• Analyze Trakhtenbrot’s theorem (the finite model theory)
• Discuss the Gödel completeness theorem
• An in-depth analysis of Morley’s categoricity theorem
• How does the Back-and-forth method work?
• Discuss the Ehrenfeucht–Fraïssé game technique
• Discuss Aleph numbers (Aleph-null and Aleph-one)
• Solving the Suslin problem

Algebra Topics for a Research Paper

Would you like to write about an algebra topic? No problem, our seasoned writers have compiled a list of the best algebra topics for a research paper:

• Discuss the differential equation
• Analyze the Jacobson density theorem
• The 4 properties of a binary operation in algebra
• Analyze the unary operator in depth
• Analyze the Abel–Ruffini theorem
• Epimorphisms vs. monomorphisms: compare and contrast
• Discuss the Morita duality in algebraic structures
• Idempotent vs. nilpotent in Ring theory
• Discuss the Artin-Wedderburn theorem
• What is a commutative ring in algebra?
• Analyze and describe the Noetherian ring

Math Education Research Topics

There is nothing wrong with writing about math education, especially if your professor did not give you writing prompts. Here are some very nice math education research topics:

• What are the goals a mathematics professor should have?
• What is math anxiety in the classroom?
• Teaching math in UK schools: the difficulties
• Computer programming or math in high school?
• Is math education in Europe at a high enough level?
• Common Core Standards and their effects on math education
• Culture and math education in Africa
• What is dyscalculia and how does it manifest itself?
• When was algebra first thought in schools?
• Math education in the United States versus the United Kingdom

Computability Theory Topics to Research

Writing about computability theory can be a very interesting adventure. Give it a try! Here are some of our most interesting computability theory topics to research:

• What is a multiplication table?
• Analyze the Scholz conjecture
• Explain exponentiating by squaring
• Analyze the Myhill-Nerode theorem
• What is a tree automaton?
• Compare and contrast the Pushdown automaton and the Büchi automaton
• Discuss the Markov algorithm
• What is a Turing machine?
• Analyze the post correspondence problem
• Discuss the linear speedup theorem
• Discuss the Boolean satisfiability problem

Interesting Math Research Topics

We know you want topics that are interesting and relatively easy to write about. This is why we have a separate list of our most interesting math research topics:

• What is two-element Boolean algebra?
• The life of Gauss
• The life of Isaac Newton
• What is an orthodiagonal quadrilateral?
• Tessellation in Euclidean plane geometry
• Describe a hyperboloid in 3D geometry
• What is a sphericon?
• Discuss the peculiarities of Borel’s paradox
• Analyze the De Finetti theorem in statistics
• What are Martingales?
• The basics of stochastic calculus

Applied Math Research Topics

Interested in writing about applied mathematics? Our team managed to create a list of awesome applied math research topics from scratch for you:

• Discuss Newton’s laws of motion
• Analyze the perpendicular axes rule
• How is a Galilean transformation done?
• The conservation of energy and its applications
• Discuss Liouville’s theorem in Hamiltonian mechanics
• Analyze the quantum field theory
• Discuss the main components of the Lorentz symmetry
• An in-depth look at the uncertainty principle

Geometry Topics for a Research Paper

Geometry can be a very captivating subject, especially when you know plenty about it. Check out our list of geometry topics for a research paper and pick the best one today:

• Most useful trigonometry functions in math
• The life of Archimedes and his achievements
• Trigonometry in computer graphics
• Using Vincenty’s formulae in geodesy
• Define and describe the Heronian tetrahedron
• The math behind the parabolic microphone
• Discuss the Japanese theorem for concyclic polygons
• Analyze Euler’s theorem in geometry

Math Research Topics for Middle School

Yes, even middle school children can write about mathematics. We have some original math research topics for middle school right here:

• Finding critical points in a graph
• The basics of calculus
• What makes a graph ultrahomogeneous?
• How do you calculate the area of different shapes?
• What contributions did Euclid have to the field of mathematics?
• What is Diophantine geometry?
• What makes a graph regular?
• Analyze a full binary tree

Math Research Topics for College Students

As you’ve probably already figured out, college students should pick topics that are a bit more complex. We have some of the best math research topics for college students right here:

• What are extremal problems and how do you solve them?
• Discuss an unsolvable math problem
• How can supercomputers solve complex mathematical problems?
• An in-depth analysis of fractals
• Discuss the Boruvka’s algorithm (related to the minimum spanning tree)
• Discuss the Lorentz–FitzGerald contraction hypothesis in relativity
• An in-depth look at Einstein’s field equation
• The math behind computer vision and object recognition

Calculus Topics for a Research Paper

Let’s face it: calculus is not a very difficult field. So, why don’t you pick one of our excellent calculus topics for a research paper and start writing your essay right away:

• When do we need to apply the L’Hôpital rule?
• Discuss the Leibniz integral rule
• Calculus in ancient Egypt
• Discuss and analyze linear approximations
• The applications of calculus in real life
• The many uses of Stokes’ theorem
• Discuss the Borel regular measure
• An in-depth analysis of Lebesgue’s monotone convergence theorem

Simple Math Research Paper Topics for High School

This is the place where you can find some pretty simple topics if you are a high school student. Check out our simple math research paper topics for high school:

• The life and work of the famous Pierre de Fermat
• What are limits and why are they useful in calculus?
• Explain the concept of congruency
• The life and work of the famous Jakob Bernoulli
• Analyze the rhombicosidodecahedron and its applications
• Calculus and the Egyptian pyramids
• The life and work of the famous Jean d’Alembert
• Discuss the hyperplane arrangement in combinatorial computational geometry
• The smallest enclosing sphere method in combinatorics

Business Math Topics

If you want to surprise your professor, why don’t you write about business math? We have some exceptional topics that nobody has thought about right here:

• Is paying a loan with another loan a good approach?
• Discuss the major causes of a stock market crash
• Best debt amortization methods in the US
• How do bank loans work in the UK?
• Calculating interest rates the easy way
• Discuss the pros and cons of annuities
• Basic business math skills everyone should possess
• Business math in United States schools
• Analyze the discount factor

Probability and Statistics Topics for Research

Probability and statistics are not easy fields. However, you can impress your professor with one of our unique probability and statistics topics for research:

• What is the autoregressive conditional duration?
• Applying the ANOVA method to ranks
• Discuss the practical applications of the Bates distribution
• Explain the principle of maximum entropy
• Discuss Skorokhod’s representation theorem in random variables
• What is the Factorial moment in the Theory of Probability?
• Compare and contrast Cochran’s C test and his Q test
• Analyze the De Moivre-Laplace theorem
• What is a negative probability?

Need Help With Research Paper?

We offer the absolute best high school and college research paper writing service on the Internet. When you need any kind of research paper help, our experienced ENL writers and professional editors are here to help. With years of experience under their belts, our experts can get your research paper done in as little as 3 hours.

Getting cheap online help with research papers has never been easier. College students should just get in touch with us and tell us what they need. We will assign them our most affordable and experienced math writer in minutes, even during the night. We are the best-rated online writing company on the Internet because we always deliver high-quality academic content at the most competitive prices. Give us a try today!

Leave a Reply Cancel reply

share this!

April 29, 2024

This article has been reviewed according to Science X's editorial process and policies . Editors have highlighted the following attributes while ensuring the content's credibility:

fact-checked

trusted source

Intervention based on science of reading and math boosts comprehension and word problem-solving skills

by University of Kansas

New research from the University of Kansas has found that an intervention based on the science of reading and math effectively helped English learners boost their comprehension, visualize and synthesize information, and make connections that significantly improved their math performance.

The intervention , performed for 30 minutes twice a week for 10 weeks with 66 third-grade English language learners who displayed math learning difficulties, improved students' performance when compared to students who received general instruction. This indicates that emphasizing cognitive concepts involved in the science of reading and math are key to helping students improve, according to researchers.

"Word problem-solving is influenced by both the science of reading and the science of math. Key components include number sense, decoding, language comprehension and working memory. Utilizing direct and explicit teaching methods enhances understanding and enables students to effectively connect these skills to solve math problems . This integrated approach ensures that students are equipped with necessary tools to navigate both the linguistic and numerical demands of word problems," said Michael Orosco, professor of educational psychology at KU and lead author of the study.

The intervention incorporates comprehension strategy instruction in both reading and math, focusing and decoding, phonological awareness, vocabulary development, inferential thinking, contextualized learning and numeracy.

"It is proving to be one of the most effective evidence-based practices available for this growing population," Orosco said.

The study, co-written with Deborah Reed of the University of Tennessee, was published in the journal Learning Disabilities Research and Practice .

For the research, trained tutors implemented the intervention, developed by Orosco and colleagues based on cognitive and culturally responsive research conducted over a span of 20 years. One example of an intervention session tested in the study included a script in which a tutor examined a word problem explaining that a person made a quesadilla for his friend Mario and gave him one-fourth of it, then asked students to determine how much remained.

The tutor first asked students if they remembered a class session in which they made quesadillas and what shape they were, and demonstrated concepts by drawing a circle on the board, dividing it into four equal pieces, having students repeat terms like numerator and denominator. The tutor explains that when a question asks how much is left, subtraction is required. The students also collaborated with peers to practice using important vocabulary in sentences. The approach both helps students learn and understand mathematical concepts while being culturally responsive.

"Word problems are complex because they require translating words into mathematical equations, and this involves integrating the science of reading and math through language concepts and differentiated instruction," Orosco said. "We have not extensively tested these approaches with this group of children. However, we are establishing an evidence-based framework that aids them in developing background knowledge and connecting it to their cultural contexts."

Orosco, director of KU's Center for Culturally Responsive Educational Neuroscience, emphasized the critical role of language in word problems, highlighting the importance of using culturally familiar terms. For instance, substituting "pastry" for "quesadilla" could significantly affect comprehension for students from diverse backgrounds. Failure to grasp the initial scenario could impede subsequent problem-solving efforts.

The study proved effective in improving students' problem-solving abilities, despite covariates including an individual's basic calculation skills, fluid intelligence and reading comprehension scores. That finding is key, as while ideally all students would begin on equal footing and there would be few variations in a classroom, in reality, covariates exist and are commonplace.

The study had trained tutors deliver the intervention, and its effectiveness should be further tested with working teachers, the authors wrote. Orosco said professional development to help teachers gain the skills is necessary, and it is vital for teacher preparation programs to train future teachers with such skills as well. And helping students at the elementary level is necessary to help ensure success in future higher-level math classes such as algebra.

The research builds on Orosco and colleagues' work in understanding and improving math instruction for English learners. Future work will continue to examine the role of cognitive functions such as working memory and brain science, as well as potential integration of artificial intelligence in teaching math.

"Comprehension strategy instruction helps students make connections, ask questions, visualize, synthesize and monitor their thinking about word problems," Orosco and Reed wrote. "Finally, applying comprehension strategy instruction supports ELs in integrating their reading, language and math cognition…. Focusing on relevant language in word problems and providing collaborative support significantly improved students' solution accuracy."

Provided by University of Kansas

Explore further

Feedback to editors

Earthquakes are moving northeast in Midland Basin of Texas, scientists find

5 hours ago

New black hole visualization takes viewers beyond the brink

6 hours ago

Research team develops fast-track process for genetic improvement of plant traits

Boeing's first Starliner mission with humans set for historic Space Coast launch tonight

Researchers develop a nanoparticle that can penetrate the blood-brain barrier

Geologists, biologists unearth the atomic fingerprints of cancer

Listening to giants: The search for the elusive Antarctic blue whale

8 hours ago

Bee body mass, pathogens and local climate influence heat tolerance

Astronomers observe elusive stellar light surrounding ancient quasars

9 hours ago

Engineers solve 'catalysis vs corrosion' mystery in electrochemical ozone production

Relevant physicsforums posts, physics instructor minimum education to teach community college.

13 hours ago

Studying "Useful" vs. "Useless" Stuff in School

Apr 30, 2024

Why are Physicists so informal with mathematics?

Apr 29, 2024

Plagiarism & ChatGPT: Is Cheating with AI the New Normal?

Apr 28, 2024

Digital oscilloscope for high school use

Apr 25, 2024

Motivating high school Physics students with Popcorn Physics

Apr 3, 2024

More from STEM Educators and Teaching

Related Stories

Study shows program improves teaching skills, students' word problem–solving

Jun 14, 2022

Study shows approach can help English learners improve at math word problems

Jun 19, 2018

Study examines role of working memory, cognitive functions in English learners learning to write

Oct 17, 2023

Cognitive study shows lack of bilingual education adversely affects English language learners' writing skills

Oct 14, 2021

How vocabulary breadth and depth influence bilingual reading comprehension

Aug 21, 2023

Study validates the simple view of reading for enhancing second and foreign language learners' experience

Aug 17, 2023

Recommended for you

Investigation reveals varied impact of preschool programs on long-term school success

May 2, 2024

Training of brain processes makes reading more efficient

Apr 18, 2024

Researchers find lower grades given to students with surnames that come later in alphabetical order

Apr 17, 2024

Earth, the sun and a bike wheel: Why your high-school textbook was wrong about the shape of Earth's orbit

Apr 8, 2024

Touchibo, a robot that fosters inclusion in education through touch

Apr 5, 2024

More than money, family and community bonds prep teens for college success: Study

Let us know if there is a problem with our content.

Use this form if you have come across a typo, inaccuracy or would like to send an edit request for the content on this page. For general inquiries, please use our contact form . For general feedback, use the public comments section below (please adhere to guidelines ).

Please select the most appropriate category to facilitate processing of your request

Thank you for taking time to provide your feedback to the editors.

Your feedback is important to us. However, we do not guarantee individual replies due to the high volume of messages.

E-mail the story

Your email address is used only to let the recipient know who sent the email. Neither your address nor the recipient's address will be used for any other purpose. The information you enter will appear in your e-mail message and is not retained by Phys.org in any form.

Newsletter sign up

Get weekly and/or daily updates delivered to your inbox. You can unsubscribe at any time and we'll never share your details to third parties.

More information Privacy policy

Donate and enjoy an ad-free experience

We keep our content available to everyone. Consider supporting Science X's mission by getting a premium account.

E-mail newsletter

You are using an outdated browser. Upgrade your browser today or install Google Chrome Frame to better experience this site.

• Professional learning

Teach. Learn. Grow.

Teach. learn. grow. the education blog.

Summer learning loss: What we know and what we’re learning

Concerns about students losing ground academically during summer break go back at least a century, with early evidence suggesting that summer contributed to large disparities in students’ outcomes. This narrative spurred expansion of a variety of summer programs and interventions aimed at stemming summer learning loss.

However, in the last five years, there has been a spirited debate about two long-standing questions about students’ summers: 1) the degree to which test scores actually drop during the summer and 2) the degree to which summer break contributes to educational inequities. A new layer to this conversation is the response to the learning disruptions caused by the COVID-19 pandemic. School leaders and policymakers have used the summer break as a potential time for academic recovery. Summer programs have emerged as one of the most popular recovery strategies offered by school districts, with an estimated $5.8 billion of ESSER funds expected to be spent on summer programs by September 2024.

With more focus on the impact of summer on students’ learning and the potential to extend the school year, it is essential for educators, policymakers, and families to have an up-to-date understanding of the impact of summer breaks on students’ learning patterns. In this post, we aim to highlight what is known about summer learning loss by quickly summarizing recent research and posing some questions that remain unanswered about the role of summers on students’ learning.

Students’ test scores flatten or drop during the summer

While our initial understanding of summer learning loss dates back to studies conducted in the 70s and 80s , a recent collection of studies in the last six years provides a fresh look at students’ learning across summers using four modern assessments ( ECLS-K direct cognitive tests , MAP® Growth™, Star, and i-Ready) with large national (though not typically nationally representative) samples. See “School’s out: The role of summers in understanding achievement disparities,” “When does inequality grow? School, summer, and achievement gaps,” “Evidence of ‘summer learning loss’ on the i-Ready diagnostic assessment,” “Findings on summer learning loss often fail to replicate, even in recent data,” and “Inequality in reading and math skills forms mainly before kindergarten: A replication, and partial correction, of ‘Are schools the great equalizer?’”

Figure 1 compares the test score patterns across four different studies. Three important patterns stand out:

• On average, test scores flatten or drop during the summer , with larger drops typically in math than reading.
• Studies using test scores from ECLS-K:2011 show that student learning slows down but does not drop over the summers after kindergarten and first grade. However, research using interim and diagnostic assessments ( MAP Growth , Star, and i-Ready ) has found far larger summer drops across a range of grade levels.
• Given the sizable differences in the magnitude of test score drops across tests, it remains uncertain whether summer slide should be considered a trivial issue or a serious educational challenge.

Figure 1. Comparison of summer slide estimates across datasets

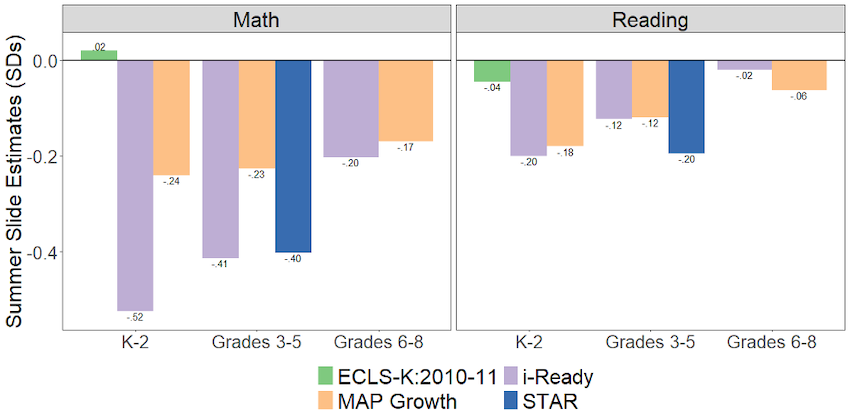
Note: All estimates are reported as the total average summer test score change in standard deviation (SD) units relative to the prior spring test score. Whenever possible, we report the estimate that adjusted scores for time in school prior/after testing in the fall and spring. Sources: Author calculations based on data reported in ECLS-K:20210-11 , MAP Growth , i-Ready , and Star .  

Who is most likely to show summer learning loss.

While all three diagnostic assessments show some degree of summer slide in grades 3–8 on average, the research community lacks consensus about whether summers disproportionately impact certain students. Paul von Hippel and colleagues have pointed out that whether and how much summers contribute to educational inequalities (across students of different income levels, races, ethnicities, and genders) depends on the test used to study students’ learning patterns. Nonetheless, we can present a few key patterns from this line of research:

• Learning rates are more variable during the summer than during the school year. See “School’s out: The role of summers in understanding achievement disparities,”   “When does inequality grow? School, summer, and achievement gaps,”  and  “Inequality in reading and math skills forms mainly before kindergarten: A replication, and partial correction, of ‘Are schools the great equalizer?’”
• Gaps between students attending low- and high-poverty schools do not consistently widen during the summer. See “Is summer learning loss real, and does it widen test score gaps by family income?”  and  “Is summer learning loss real?”
• Test score differences between Black and white students hold steady or narrow during the summer. See “Do test score gaps grow before, during, or between the school years? Measurement artifacts and what we know in spite of them”  and  “When does inequality grow? School, summer, and achievement gaps,” though results can be sensitive to the metric and test used. See also  “Black-white summer learning gaps: Interpreting the variability of estimates across representations” and “Findings on summer learning loss often fail to replicate, even in recent data.”
• The field cannot really explain why differences in students’ summer learning occur. See “Rethinking summer slide: The more you gain, the more you lose”  and  “Inequality in reading and math skills forms mainly before kindergarten: A replication, and partial correction, of ‘Are schools the great equalizer?’”

Planning effective summer programming

It is clear across recent studies that summer is a particularly variable time for students. Summer break is also increasingly a time in which districts are offering a range of academic offerings.

During summer 2022, an estimated 90% of school districts offered summer programs with an academic focus. However, evidence on the effectiveness of academic summer programs during and after the COVID-19 pandemic is limited. One study of eight summer programs in summer 2022 found a small positive impact on math test scores (0.03 SD), but not on reading. The improvements in math were largely driven by elementary students compared to middle schoolers. However, the effectiveness of these programs remained consistent across student groups, including race/ethnicity, poverty, and English learner status.

It is crucial to recognize the challenges associated with scaling up summer programs. In the districts studied, only 13% of students participated in the summer programs , which only lasted for an average of three to four weeks. Prior research indicates that for summer programs to yield measurable academic benefits, they should run at least five weeks with at least three hours of instruction a day. Additionally, getting students to regularly attend summer programs remains a significant hurdle. To address this issue, districts should actively recruit families to participate and offer a mix of academic instruction and engaging extracurricular activities. By adopting these strategies, districts can maximize the effectiveness of their summer programs and better support student learning during the break.

If you’re interested in learning more about effective summer programs, we encourage you to read the following:

• “Effective summer programming: What educators and policymakers should know”
• “Investing in successful summer programs: A review of evidence under the Every Student Succeeds Act”
• “Analysis: Summer learning is more popular than ever. How to make sure your district’s program is effective”
• “The impact of summer learning programs on low-income children’s mathematics achievement: A meta-analysis”
• “The effects of summer reading on low-income children’s literacy achievement from kindergarten to grade 8: A meta-analysis of classroom and home interventions”

Recommended for you

From the pages of  Literacy Today : How to boost reading achievement using dyslexia research

NWEA research snapshot: Insights on academic recovery strategies

How AI can improve digital accessibility in math

White Paper

Worth the investment: Why research and innovation matter for improving outcomes for all kids

Making sound, student-focused decisions amid constant change can feel impossible. Partnering with a research-based assessment provider can help.

Read the white paper

STAY CURRENT by subscribing to our newsletter

You are now signed up to receive our newsletter containing the latest news, blogs, and resources from nwea..

APPLY NOW   --> REQUEST INFO

Apply Today

Ready to apply to Penn LPS Online? Apply Now

Learn more about Penn LPS Online

Request More Information

The liberal arts math revolution: how math is more than just numbers

Whether we know it or not, math is integrated into many aspects of our daily lives. This article answers the question, “What is liberal arts math?” and explores how math concepts are incorporated into other core disciplines. Learn how liberal arts math can help you build your analytical, critical, and problem-solving skills and help you prepare for a variety of career paths.

What is liberal arts math?

Liberal arts math typically includes a comprehensive interdisciplinary approach, meaning courses are designed to align with other foundational subjects to build the mathematical know-how to solve real-world issues.

For example, liberal arts math courses can help you develop skills in quantitative reasoning, statistics, sampling bias, and exponential growth, which can be applied to disciplines including economics, political science, psychology, and social sciences.

Common topics in liberal arts math include applied statistics, linear algebra, logic and probability, geometry, game theory, philosophy of math, problem-solving, and everyday applications for mathematics.

Liberal arts math vs. traditional math

Traditional mathematics tends to focus on standard math sequences or calculations that are taught in isolation. For instance, when you were a child, you may have relied on memorization to learn your multiplication tables.

On the other hand, the goal of liberal arts math is to increase your understanding of mathematical basics and develop high-order reasoning skills that you can apply in practical contexts.

For instance, in MTHS 2000: Mathematics All Around You at Penn LPS Online, you’ll learn how math and logic provide the framework for everything—from quickly calculating a discount in your head to writing a story or presenting a persuasive argument in court.

Is math for liberal arts easy?

Easy is a relative term. If you find traditional mathematics easy, then you’ll likely feel the same way about liberal arts math. Conversely, if you struggle with traditional math, the same may be true with math designed for liberal arts students—although likely to a lesser extent.

That’s because rather than focusing strictly on numbers, concepts, equations, or calculations, liberal arts math incorporates real-world learning scenarios that draw from other disciplines. To that end, the concepts you learn in MTHS 3000: Linear Algebra are critical to the study of fields such as physics, chemistry, economics, computer science, and data science.

Liberal arts math concepts

Once you discover how frequently mathematical models are featured in other liberal arts disciplines, you’ll likely gain a greater understanding of why math is called “the language of the universe.”

Math and art

The connection between math and art can be seen throughout history. Pre-Columbian cultures demonstrated knowledge of geometric patterns in many of their aesthetic artifacts. Early and High Renaissance artists also used mathematical concepts, such as perspective and symmetry, to make their paintings and sculptures appear more realistic.

Examples of well-known art and artists that showcase mathematic principles include:

• The Parthenon: Phidias used the golden ratio (1.618) in his designs for sculptures in this grand architectural feat of Antiquity.
• Vitruvian Man and Mona Lisa: Leonardo Da Vinci used math to calculate the ideal proportions of the human body for the Vitruvian Man, which was drawn within geometric shapes. He also utilized the golden ratio to create proportions for the face, head, and neck of the Mona Lisa.
• Abstract modernist artwork: Bauhaus artist Wassily Kandinsky used mathematical forms like concentric circles, triangles, and open and closed lines in his paintings. Although it may not be readily apparent, abstract expressionist Jackson Pollock used the repetition of the geometric model of fractals in his work.

Math and literature

You may be surprised to learn that the underlying structure, pattern, and uniformity of math can also be found in literature. This makes sense when you stop to think about it, given that good writing relies on the same types of arrangement and form inherent to successful math equations.

There are metaphors related to cycloids (or mathematical curves) in Herman Melville’s Moby-Dick . Other famous authors such as James Joyce and Leo Tolstoy include references to geometry and calculus in their respective works. And, interestingly, Julio Cortazar encourages readers to traverse the maze of chapters in the novel  Hopscotch by picking a linear or non-linear structure of reading, which changes the story’s perspective.

Principles of algebra (or formulas) also prescribe the number of syllables that define different forms of poetry including:

• “Fib” poems, based on the Fibonacci sequence in math (1,1,2,3, 5, 8, 13, 21)
• Haikus, which include three lines with a total of 17 syllables
• Sonnets, which have 14 lines with 10 syllables per line
• Cinquain verses of five lines that don’t rhyme  

Math and philosophy

Not only does a branch of philosophy called metaphysics rely on advanced math concepts to help us understand the universe, the philosophy of mathematics is also a distinct area of study. The philosophy of math is a branch of epistemology, which is the investigation of how humans know things.

This philosophy is focused on cognition, including determining how mathematical knowledge fits into the wider scheme of things. Mathematics philosophers also question how we can refer to or know of mathematical objects if they don’t have causes or effects.

Four schools of thought in the philosophy of math include:

• Logicism: Supposes that mathematical truths are logical truths
• Intuitionism: Argues that math is a creation of the mind
• Formalism: Reduces math and logic to rules for manipulating formulas without reference to meaning
• Predicativism: Supposes that math should be restricted to the study of objects that can be quantified predicatively

Math as a language

As the most fundamental type of logic possible, mathematics is routinely referred to as “the language of science” and “the language of the universe.” Generally, to be considered a language, there must be vocabulary, syntax, grammar, narrative, and people who use and comprehend it.

Math meets these criteria as a universal language whose symbols and organizations comprise equations that are recognized and understood worldwide. Additionally, mathematicians, scientists, educators, and others use math to communicate both real-world and abstract concepts.

The importance of liberal arts math

Without a basic understanding of math, it would be difficult to function effectively in the world. Math is involved in everything from baking and telling time to setting and keeping a budget and filing your taxes.

If you wish to attend college, not only do you need to meet the necessary math prerequisites, but math skills are also critical to doing well on standardized tests such as the SAT, ACT, GRE, GMAT, and LSAT.

Read on to explore other ways that math can be beneficial to your ability to thrive.

Critical thinking and problem-solving skills

Did you know that reading and solving arithmetic problems has been shown to improve brain health and cognitive function? Starting with word problems in elementary school, math forms the groundwork to help students develop critical thinking and problem-solving skills with real-world applications.

Later in life, a strong understanding of algorithms and other math concepts provides the basis for analytical and logical reasoning skills that are essential to finding solutions to personal, professional, and academic issues. This may include navigating an argument, preparing a work presentation, or authoring a persuasive essay.

Creativity and innovation

Flexible thinking and creativity spur innovation. Research shows that math training can enhance investigative skills, resourcefulness, and creativity. Creativity involves combining ideas that have no obvious relationship to develop new forms of expression or unique solutions to problems. Mathematicians routinely use existing knowledge to find new connections within the mathematical world that can be used to address real-world issues. For example, statistics and probability are utilized to make predictions for scenarios involving financial markets, climate change and weather patterns, or the spread of disease and viruses (such as with COVID-19).

Preparation for a wide range of careers

Building a strong foundation in math can also help prepare students for their future career paths, whether they are related to math or not.

Math courses are typically included in the general education requirements for most bachelor’s degree programs. The ability to identify and analyze patterns and use logic, critical thinking, and problem-solving skills are valued in industries including business, healthcare, marketing, finance, psychology, social sciences, manufacturing, and more.

There are also many jobs that rely heavily on math concepts such as scientists, architects, and accountants. Examples of in-demand STEM roles and their predicted job growth rates by 2031 include:

• Data scientists (36%)
• Information security analysts (35%)
• Logisticians (28%)
• Statisticians (33%)
• Web developers (30%)

Explore the future of liberal arts math at Penn LPS Online

Interested in combining the analytical tools of data science with a practical understanding of the social sciences? Read more about the Data Analytics and Social Sciences concentration for the Bachelor of Applied Arts and Sciences (BAAS) degree at Penn LPS Online.

In this program, you’ll develop statistical and data programming skills to solve everyday issues, learn how to make and communicate data-driven decisions, and customize your credential with Ivy League courses in organizational anthropology, global and area studies, leadership, and other social sciences.

Develop the expertise to:

• Implement and analyze surveys and basic regression models
• Understand predictive modeling and machine learning
• Create experiments and A/B tests to solve real-world problems
• Obtain skills in statistical programming and data analysis in R
• Use visualization to make complex information more accessible
• Develop rhetorical strategies to effectively persuade audiences

If you haven’t already, apply to Penn LPS Online today, and enroll in the Data Analytics and Social Sciences concentration for the BAAS degree . You can also register for individual classes or view our course guide to see what’s available in any upcoming term.