a guide to problem solving chemistry answer key

Solutions for Holt Chemistry 1st

R.thomas myers, keith oldham,savatore tocci, get access to all of the answers and step-by-step video explanations to this book and 5,000+ more. try numerade free., the science of chemistry.

Matter and Energy

Atoms and Moles

The periodic table, lons and lonic compounds.

Covalent Compounds

The mole and chemical composition.

Chemical Equations and Reactions

Stoichiometry, causes of change, states of matter and intermolecular forces, chemical equilibrium, acids and bases, reaction rates, oxidation, reduction, and electrochemistry, nuclear chemistry, carbon and organic compounds, biological chemistry.

97% of Numerade Students Report Better Grades

Create an account to get free access

Log in to watch this video ...and 100,000,000 more!

One example for NH 3 as a conjugate acid: NH 2 − + H + ⟶ NH 3 ; NH 2 − + H + ⟶ NH 3 ; as a conjugate base: NH 4 + ( a q ) + OH − ( a q ) ⟶ NH 3 ( a q ) + H 2 O ( l ) NH 4 + ( a q ) + OH − ( a q ) ⟶ NH 3 ( a q ) + H 2 O ( l )

(a) H 3 O + ( a q ) ⟶ H + ( a q ) + H 2 O ( l ) ; H 3 O + ( a q ) ⟶ H + ( a q ) + H 2 O ( l ) ; (b) HCl ( aq ) ⟶ H + ( a q ) + Cl − ( a q ) ; HCl ( aq ) ⟶ H + ( a q ) + Cl − ( a q ) ; (c) NH 3 ( a q ) ⟶ H + ( a q ) + NH 2 − ( a q ) ; NH 3 ( a q ) ⟶ H + ( a q ) + NH 2 − ( a q ) ; (d) CH 3 CO 2 H ( a q ) ⟶ H + ( a q ) + CH 3 CO 2 − ( a q ) ; CH 3 CO 2 H ( a q ) ⟶ H + ( a q ) + CH 3 CO 2 − ( a q ) ; (e) NH 4 + ( a q ) ⟶ H + ( a q ) + NH 3 ( a q ) ; NH 4 + ( a q ) ⟶ H + ( a q ) + NH 3 ( a q ) ; (f) HSO 4 − ( a q ) ⟶ H + ( a q ) + SO 4 2− ( a q ) HSO 4 − ( a q ) ⟶ H + ( a q ) + SO 4 2− ( a q )

(a) H 2 O ( l ) + H + ( a q ) ⟶ H 3 O + ( a q ) ; H 2 O ( l ) + H + ( a q ) ⟶ H 3 O + ( a q ) ; (b) OH − ( a q ) + H + ( a q ) ⟶ H 2 O ( l ) ; OH − ( a q ) + H + ( a q ) ⟶ H 2 O ( l ) ; (c) NH 3 ( a q ) + H + ( a q ) ⟶ NH 4 + ( a q ) ; NH 3 ( a q ) + H + ( a q ) ⟶ NH 4 + ( a q ) ; (d) CN − ( a q ) + H + ( a q ) ⟶ HCN ( a q ) ; CN − ( a q ) + H + ( a q ) ⟶ HCN ( a q ) ; (e) S 2− ( a q ) + H + ( a q ) ⟶ HS − ( a q ) ; S 2− ( a q ) + H + ( a q ) ⟶ HS − ( a q ) ; (f) H 2 PO 4 − ( a q ) + H + ( a q ) ⟶ H 3 PO 4 ( a q ) H 2 PO 4 − ( a q ) + H + ( a q ) ⟶ H 3 PO 4 ( a q )

(a) H 2 O, O 2− ; (b) H 3 O + , OH − ; (c) H 2 CO 3 , CO 3 2− ; CO 3 2− ; (d) NH 4 + , NH 4 + , NH 2 − ; NH 2 − ; (e) H 2 SO 4 , SO 4 2− ; SO 4 2− ; (f) H 3 O 2 + , H 3 O 2 + , HO 2 − ; HO 2 − ; (g) H 2 S; S 2− ; (h) H 6 N 2 2+ , H 6 N 2 2+ , H 4 N 2

The labels are Brønsted-Lowry acid = BA; its conjugate base = CB; Brønsted-Lowry base = BB; its conjugate acid = CA. (a) HNO 3 (BA), H 2 O(BB), H 3 O + (CA), NO 3 − ( CB ) ; NO 3 − ( CB ) ; (b) CN − (BB), H 2 O(BA), HCN(CA), OH − (CB); (c) H 2 SO 4 (BA), Cl − (BB), HCl(CA), HSO 4 − ( CB ) ; HSO 4 − ( CB ) ; (d) HSO 4 − ( BA ) , HSO 4 − ( BA ) , OH − (BB), SO 4 2− SO 4 2− (CB), H 2 O(CA); (e) O 2− (BB), H 2 O(BA) OH − (CB and CA); (f) [Cu(H 2 O) 3 (OH)] + (BB), [Al(H 2 O) 6 ] 3+ (BA), [Cu(H 2 O) 4 ] 2+ (CA), [Al(H 2 O) 5 (OH)] 2+ (CB); (g) H 2 S(BA), NH 2 − ( BB ) , NH 2 − ( BB ) , HS − (CB), NH 3 (CA)

Amphiprotic species may either gain or lose a proton in a chemical reaction, thus acting as a base or an acid. An example is H 2 O. As an acid: H 2 O ( a q ) + NH 3 ( a q ) ⇌ NH 4 + ( a q ) + OH − ( a q ) . H 2 O ( a q ) + NH 3 ( a q ) ⇌ NH 4 + ( a q ) + OH − ( a q ) . As a base: H 2 O ( a q ) + HCl ( a q ) ⇌ H 3 O + ( a q ) + Cl − ( a q ) H 2 O ( a q ) + HCl ( a q ) ⇌ H 3 O + ( a q ) + Cl − ( a q )

amphiprotic: (a) NH 3 + H 3 O + ⟶ NH 4 OH + H 2 O , NH 3 + H 3 O + ⟶ NH 4 OH + H 2 O , NH 3 + OCH 3 − ⟶ NH 2 − + CH 3 OH ; NH 3 + OCH 3 − ⟶ NH 2 − + CH 3 OH ; (b) HPO 4 2− + OH − ⟶ PO 4 3− + H 2 O , HPO 4 2− + OH − ⟶ PO 4 3− + H 2 O , HPO 4 2− + HClO 4 ⟶ H 2 PO 4 − + ClO 4 − ; HPO 4 2− + HClO 4 ⟶ H 2 PO 4 − + ClO 4 − ; not amphiprotic: (c) Br − ; (d) NH 4 + ; NH 4 + ; (e) AsO 4 3− AsO 4 3−

In a neutral solution [H 3 O + ] = [OH − ]. At 40 °C, [H 3 O + ] = [OH − ] = (2.910 −14 ) 1/2 = 1.7 × × 10 −7 .

x = 3.051 × × 10 −7 M = [H 3 O + ] = [OH − ] pH = −log3.051 × × 10 −7 = −(−6.5156) = 6.5156 pOH = pH = 6.5156

(a) pH = 3.587; pOH = 10.413; (b) pH = 0.68; pOH = 13.32; (c) pOH = 3.85; pH = 10.15; (d) pH = −0.40; pOH = 14.4

[H 3 O + ] = 3.0 × × 10 −7 M ; [OH − ] = 3.3 × × 10 −8 M

[H 3 O + ] = 1 × × 10 −2 M ; [OH − ] = 1 × × 10 −12 M

[OH − ] = 3.1 × × 10 −12 M

The salt ionizes in solution, but the anion slightly reacts with water to form the weak acid. This reaction also forms OH − , which causes the solution to be basic.

[H 2 O] > [CH 3 CO 2 H] > [ H 3 O + ] [ H 3 O + ] ≈ [ CH 3 CO 2 − ] [ CH 3 CO 2 − ] > [OH − ]

The oxidation state of the sulfur in H 2 SO 4 is greater than the oxidation state of the sulfur in H 2 SO 3 .

Mg ( OH ) 2 ( s ) + 2HCl ( a q ) ⟶ Mg 2+ ( a q ) + 2 Cl − ( a q ) + 2H 2 O ( l ) BB BA CB CA Mg ( OH ) 2 ( s ) + 2HCl ( a q ) ⟶ Mg 2+ ( a q ) + 2 Cl − ( a q ) + 2H 2 O ( l ) BB BA CB CA

K a = 2.3 × 10 −11 K a = 2.3 × 10 −11

The stronger base or stronger acid is the one with the larger K b or K a , respectively. In these two examples, they are (CH 3 ) 2 NH and CH 3 NH 3 + . CH 3 NH 3 + .

triethylamine.

(a) HSO 4 − ; HSO 4 − ; higher electronegativity of the central ion. (b) H 2 O; NH 3 is a base and water is neutral, or decide on the basis of K a values. (c) HI; PH 3 is weaker than HCl; HCl is weaker than HI. Thus, PH 3 is weaker than HI. (d) PH 3 ; in binary compounds of hydrogen with nonmetals, the acidity increases for the element lower in a group. (e) HBr; in a period, the acidity increases from left to right; in a group, it increases from top to bottom. Br is to the left and below S, so HBr is the stronger acid.

(a) NaHSeO 3 < NaHSO 3 < NaHSO 4 ; in polyoxy acids, the more electronegative central element—S, in this case—forms the stronger acid. The larger number of oxygen atoms on the central atom (giving it a higher oxidation state) also creates a greater release of hydrogen atoms, resulting in a stronger acid. As a salt, the acidity increases in the same manner. (b) ClO 2 − < BrO 2 − < IO 2 − ; ClO 2 − < BrO 2 − < IO 2 − ; the basicity of the anions in a series of acids will be the opposite of the acidity in their oxyacids. The acidity increases as the electronegativity of the central atom increases. Cl is more electronegative than Br, and I is the least electronegative of the three. (c) HOI < HOBr < HOCl; in a series of the same form of oxyacids, the acidity increases as the electronegativity of the central atom increases. Cl is more electronegative than Br, and I is the least electronegative of the three. (d) HOCl < HOClO < HOClO 2 < HOClO 3 ; in a series of oxyacids of the same central element, the acidity increases as the number of oxygen atoms increases (or as the oxidation state of the central atom increases). (e) HTe − < HS − << PH 2 − < NH 2 − ; HTe − < HS − << PH 2 − < NH 2 − ; PH 2 − PH 2 − and NH 2 − NH 2 − are anions of weak bases, so they act as strong bases toward H + . HTe − HTe − and HS − are anions of weak acids, so they have less basic character. In a periodic group, the more electronegative element has the more basic anion. (f) BrO 4 − < BrO 3 − < BrO 2 − < BrO − ; BrO 4 − < BrO 3 − < BrO 2 − < BrO − ; with a larger number of oxygen atoms (that is, as the oxidation state of the central ion increases), the corresponding acid becomes more acidic and the anion consequently less basic.

[ H 2 O ] > [ C 6 H 4 OH ( CO 2 H ) ] > [H + ] 0 > [C 6 H 4 OH ( CO 2 ) − ] ≫ [ C 6 H 4 O ( CO 2 H ) − ] > [ OH − ] [ H 2 O ] > [ C 6 H 4 OH ( CO 2 H ) ] > [H + ] 0 > [C 6 H 4 OH ( CO 2 ) − ] ≫ [ C 6 H 4 O ( CO 2 H ) − ] > [ OH − ]

Strong electrolytes are 100% ionized, and, as long as the component ions are neither weak acids nor weak bases, the ionic species present result from the dissociation of the strong electrolyte. Equilibrium calculations are necessary when one (or more) of the ions is a weak acid or a weak base.

1. Assume that the change in initial concentration of the acid as the equilibrium is established can be neglected, so this concentration can be assumed constant and equal to the initial value of the total acid concentration. 2. Assume we can neglect the contribution of water to the equilibrium concentration of H 3 O + .

(b) The addition of HCl

(a) Adding HCl will add H 3 O + ions, which will then react with the OH − ions, lowering their concentration. The equilibrium will shift to the right, increasing the concentration of HNO 2 , and decreasing the concentration of NO 2 − NO 2 − ions. (b) Adding HNO 2 increases the concentration of HNO 2 and shifts the equilibrium to the left, increasing the concentration of NO 2 − NO 2 − ions and decreasing the concentration of OH − ions. (c) Adding NaOH adds OH − ions, which shifts the equilibrium to the left, increasing the concentration of NO 2 − NO 2 − ions and decreasing the concentrations of HNO 2 . (d) Adding NaCl has no effect on the concentrations of the ions. (e) Adding KNO 2 adds NO 2 − NO 2 − ions and shifts the equilibrium to the right, increasing the HNO 2 and OH − ion concentrations.

This is a case in which the solution contains a mixture of acids of different ionization strengths. In solution, the HCO 2 H exists primarily as HCO 2 H molecules because the ionization of the weak acid is suppressed by the strong acid. Therefore, the HCO 2 H contributes a negligible amount of hydronium ions to the solution. The stronger acid, HCl, is the dominant producer of hydronium ions because it is completely ionized. In such a solution, the stronger acid determines the concentration of hydronium ions, and the ionization of the weaker acid is fixed by the [H 3 O + ] produced by the stronger acid.

(a) K b = 1.8 × 10 −5 ; K b = 1.8 × 10 −5 ; (b) K a = 4.5 × 10 −4 ; K a = 4.5 × 10 −4 ; (c) K b = 7.4 × 10 −5 ; K b = 7.4 × 10 −5 ; (d) K a = 5.6 × 10 −10 K a = 5.6 × 10 −10

K a = 1.2 × 10 −2 K a = 1.2 × 10 −2

(a) K b = 4.3 × 10 −12 ; K b = 4.3 × 10 −12 ; (b) K a = 1.6 × 10 −8 ; K a = 1.6 × 10 −8 ; (c) K b = 5.9 × 10 −7 ; K b = 5.9 × 10 −7 ; (d) K b = 4.2 × 10 −3 ; K b = 4.2 × 10 −3 ; (e) K b = 2.3 × 10 −3 ; K b = 2.3 × 10 −3 ; (f) K b = 6.3 × 10 −13 K b = 6.3 × 10 −13

(a) is the correct statement.

[H 3 O + ] = 7.5 × × 10 −3 M [HNO 2 ] = 0.127 [OH − ] = 1.3 × × 10 −12 M [BrO − ] = 4.5 × × 10 −8 M [HBrO] = 0.120 M

[OH − ] = [ NO 4 + ] [ NO 4 + ] = 0.0014 M [NH 3 ] = 0.144 M [H 3 O + ] = 6.9 × × 10 −12 M [ C 6 H 5 NH 3 + ] [ C 6 H 5 NH 3 + ] = 3.9 × × 10 −8 M [C 6 H 5 NH 2 ] = 0.100 M

(a) [ H 3 O + ] [ ClO − ] [ HClO ] = ( x ) ( x ) ( 0.0092 − x ) ≈ ( x ) ( x ) 0.0092 = 2.9 × 10 −8 [ H 3 O + ] [ ClO − ] [ HClO ] = ( x ) ( x ) ( 0.0092 − x ) ≈ ( x ) ( x ) 0.0092 = 2.9 × 10 −8 Solving for x gives 1.63 × × 10 −5 M . This value is less than 5% of 0.0092, so the assumption that it can be neglected is valid. Thus, the concentrations of solute species at equilibrium are: [H 3 O + ] = [ClO] = 5.8 × × 10 −5 M [HClO] = 0.00092 M [OH − ] = 6.1 × × 10 −10 M ; (b) [ C 6 H 5 NH 3 + ] [ OH − ] [ C 6 H 5 NH 2 ] = ( x ) ( x ) ( 0.0784 − x ) ≈ ( x ) ( x ) 0.0784 = 4.3 × 10 −10 [ C 6 H 5 NH 3 + ] [ OH − ] [ C 6 H 5 NH 2 ] = ( x ) ( x ) ( 0.0784 − x ) ≈ ( x ) ( x ) 0.0784 = 4.3 × 10 −10 Solving for x gives 5.81 × × 10 −6 M . This value is less than 5% of 0.0784, so the assumption that it can be neglected is valid. Thus, the concentrations of solute species at equilibrium are: [ CH 3 CO 2 − ] [ CH 3 CO 2 − ] = [OH − ] = 5.8 × × 10 −6 M [C 6 H 5 NH 2 ] = 0.00784 [H 3 O + ] = 1.7 × × 10 −9 M ; (c) [ H 3 O + ] [ CN − ] [ HCN ] = ( x ) ( x ) ( 0.0810 − x ) ≈ ( x ) ( x ) 0.0810 = 4.9 × 10 −10 [ H 3 O + ] [ CN − ] [ HCN ] = ( x ) ( x ) ( 0.0810 − x ) ≈ ( x ) ( x ) 0.0810 = 4.9 × 10 −10 Solving for x gives 6.30 × × 10 −6 M . This value is less than 5% of 0.0810, so the assumption that it can be neglected is valid. Thus, the concentrations of solute species at equilibrium are: [H 3 O + ] = [CN − ] = 6.3 × × 10 −6 M [HCN] = 0.0810 M [OH − ] = 1.6 × × 10 −9 M ; (d) [ ( CH 3 ) 3 NH + ] [ OH − ] [ ( CH 3 ) 3 N ] = ( x ) ( x ) ( 0.11 − x ) ≈ ( x ) ( x ) 0.11 = 6.3 × 10 −5 [ ( CH 3 ) 3 NH + ] [ OH − ] [ ( CH 3 ) 3 N ] = ( x ) ( x ) ( 0.11 − x ) ≈ ( x ) ( x ) 0.11 = 6.3 × 10 −5 Solving for x gives 2.63 × × 10 −3 M . This value is less than 5% of 0.11, so the assumption that it can be neglected is valid. Thus, the concentrations of solute species at equilibrium are: [(CH 3 ) 3 NH + ] = [OH − ] = 2.6 × × 10 −3 M [(CH 3 ) 3 N] = 0.11 M [H 3 O + ] = 3.8 × × 10 −12 M ; (e) [ Fe ( H 2 O ) 5 ( OH ) + ] [ H 3 O + ] [ Fe ( H 2 O ) 6 2+ ] = ( x ) ( x ) ( 0.120 − x ) ≈ ( x ) ( x ) 0.120 = 1.6 × 10 −7 [ Fe ( H 2 O ) 5 ( OH ) + ] [ H 3 O + ] [ Fe ( H 2 O ) 6 2+ ] = ( x ) ( x ) ( 0.120 − x ) ≈ ( x ) ( x ) 0.120 = 1.6 × 10 −7 Solving for x gives 1.39 × × 10 −4 M . This value is less than 5% of 0.120, so the assumption that it can be neglected is valid. Thus, the concentrations of solute species at equilibrium are: [Fe(H 2 O) 5 (OH) + ] = [H 3 O + ] = 1.4 × × 10 −4 M [ Fe ( H 2 O ) 6 2+ ] [ Fe ( H 2 O ) 6 2+ ] = 0.120 M [OH − ] = 7.2 × × 10 −11 M

[C 10 H 14 N 2 ] = 0.049 M [C 10 H 14 N 2 H + ] = 1.9 × × 10 −4 M [ C 10 H 14 N 2 H 2 2+ ] [ C 10 H 14 N 2 H 2 2+ ] = 1.4 × × 10 −11 M [OH − ] = 1.9 × × 10 −4 M [H 3 O + ] = 5.3 × × 10 −11 M

K b = 1.77 × 10 −5 K b = 1.77 × 10 −5

(a) acidic; (b) basic; (c) acidic; (d) neutral

[H 3 O + ] and [ HCO 3 − ] [ HCO 3 − ] are practically equal

[C 6 H 4 (CO 2 H) 2 ] 7.2 × × 10 −3 M , [C 6 H 4 (CO 2 H)(CO 2 ) − ] = [H 3 O + ] 2.8 × × 10 −3 M , [ C 6 H 4 ( CO 2 ) 2 2− ] [ C 6 H 4 ( CO 2 ) 2 2− ] 3.9 × × 10 −6 M , [OH − ] 3.6 × × 10 −12 M

(a) K a2 = 1.5 × 10 −11 ; K a2 = 1.5 × 10 −11 ; (b) K b = 4.3 × 10 −12 ; K b = 4.3 × 10 −12 ; (c) [ Te 2− ] [ H 3 O + ] [ HTe − ] = ( x ) ( 0.0141 + x ) ( 0.0141 − x ) ≈ ( x ) ( 0.0141 ) 0.0141 = 1.5 × 10 −11 [ Te 2− ] [ H 3 O + ] [ HTe − ] = ( x ) ( 0.0141 + x ) ( 0.0141 − x ) ≈ ( x ) ( 0.0141 ) 0.0141 = 1.5 × 10 −11 Solving for x gives 1.5 × × 10 −11 M . Therefore, compared with 0.014 M , this value is negligible (1.1 × × 10 −7 %).

Excess H 3 O + is removed primarily by the reaction: H 3 O + ( a q ) + H 2 PO 4 − ( a q ) ⟶ H 3 PO 4 ( a q ) + H 2 O ( l ) H 3 O + ( a q ) + H 2 PO 4 − ( a q ) ⟶ H 3 PO 4 ( a q ) + H 2 O ( l ) Excess base is removed by the reaction: OH − ( a q ) + H 3 PO 4 ( a q ) ⟶ H 2 PO 4 − ( a q ) + H 2 O ( l ) OH − ( a q ) + H 3 PO 4 ( a q ) ⟶ H 2 PO 4 − ( a q ) + H 2 O ( l )

[H 3 O + ] = 1.5 × × 10 −4 M

[OH − ] = 4.2 × × 10 −4 M

[NH 4 NO 3 ] = 0.36 M

(a) The added HCl will increase the concentration of H 3 O + slightly, which will react with CH 3 CO 2 − CH 3 CO 2 − and produce CH 3 CO 2 H in the process. Thus, [ CH 3 CO 2 − ] [ CH 3 CO 2 − ] decreases and [CH 3 CO 2 H] increases. (b) The added KCH 3 CO 2 will increase the concentration of [ CH 3 CO 2 − ] [ CH 3 CO 2 − ] which will react with H 3 O + and produce CH 3 CO 2 H in the process. Thus, [H 3 O + ] decreases slightly and [CH 3 CO 2 H] increases. (c) The added NaCl will have no effect on the concentration of the ions. (d) The added KOH will produce OH − ions, which will react with the H 3 O + , thus reducing [H 3 O + ]. Some additional CH 3 CO 2 H will dissociate, producing [ CH 3 CO 2 − ] [ CH 3 CO 2 − ] ions in the process. Thus, [CH 3 CO 2 H] decreases slightly and [ CH 3 CO 2 − ] [ CH 3 CO 2 − ] increases. (e) The added CH 3 CO 2 H will increase its concentration, causing more of it to dissociate and producing more [ CH 3 CO 2 − ] [ CH 3 CO 2 − ] and H 3 O + in the process. Thus, [H 3 O + ] increases slightly and [ CH 3 CO 2 − ] [ CH 3 CO 2 − ] increases.

37 g (0.27 mol)

(a) pH = 5.222; (b) The solution is acidic. (c) pH = 5.221

To prepare the best buffer for a weak acid HA and its salt, the ratio [ H 3 O + ] K a [ H 3 O + ] K a should be as close to 1 as possible for effective buffer action. The [H 3 O + ] concentration in a buffer of pH 3.1 is [H 3 O + ] = 10 −3.1 = 7.94 × × 10 −4 M We can now solve for K a of the best acid as follows: [ H 3 O + ] K a = 1 K a = [ H 3 O + ] 1 = 7.94 × 10 −4 [ H 3 O + ] K a = 1 K a = [ H 3 O + ] 1 = 7.94 × 10 −4 In Table 14.2 , the acid with the closest K a to 7.94 × × 10 −4 is HF, with a K a of 7.2 × × 10 −4 .

For buffers with pHs > 7, you should use a weak base and its salt. The most effective buffer will have a ratio [ OH − ] K b [ OH − ] K b that is as close to 1 as possible. The pOH of the buffer is 14.00 − 10.65 = 3.35. Therefore, [OH − ] is [OH − ] = 10 −pOH = 10 −3.35 = 4.467 × × 10 −4 M . We can now solve for K b of the best base as follows: [ OH − ] K b = 1 [ OH − ] K b = 1 K b = [OH − ] = 4.47 × × 10 −4 In Table 14.3 , the base with the closest K b to 4.47 × × 10 −4 is CH 3 NH 2 , with a K b = 4.4 × × 10 −4 .

The molar mass of sodium saccharide is 205.169 g/mol. Using the abbreviations HA for saccharin and NaA for sodium saccharide the number of moles of NaA in the solution is: 9.75 × × 10 −6 mol The pKa for [HA] is 1.68, so [HA] = 6.2 × 19 –9 6.2 × 19 –9 M . Thus, [A–] (saccharin ions) is 3.90 × 10 –5 3.90 × 10 –5 M . Thus, [A − ](saccarin ions) is 3.90 × × 10 −5 M

At the equivalence point in the titration of a weak base with a strong acid, the resulting solution is slightly acidic due to the presence of the conjugate acid. Thus, pick an indicator that changes color in the acidic range and brackets the pH at the equivalence point. Methyl orange is a good example.

In an acid solution, the only source of OH − ions is water. We use K w to calculate the concentration. If the contribution from water was neglected, the concentration of OH − would be zero.

(a) pH = 2.50; (b) pH = 4.01; (c) pH = 5.60; (d) pH = 8.35; (e) pH = 11.08

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/chemistry/pages/1-introduction

• Authors: Paul Flowers, William R. Robinson, PhD, Richard Langley, Klaus Theopold
• Publisher/website: OpenStax
• Book title: Chemistry
• Publication date: Mar 11, 2015
• Location: Houston, Texas
• Book URL: https://openstax.org/books/chemistry/pages/1-introduction
• Section URL: https://openstax.org/books/chemistry/pages/chapter-14

© Feb 15, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• Science Notes Posts
• Contact Science Notes
• Todd Helmenstine Biography
• Anne Helmenstine Biography
• Free Printable Periodic Tables (PDF and PNG)
• Periodic Table Wallpapers
• Interactive Periodic Table
• Periodic Table Posters
• How to Grow Crystals
• Chemistry Projects
• Fire and Flames Projects
• Holiday Science

Chemistry Problems With Answers

• Physics Problems
• Unit Conversion Example Problems
• Chemistry Worksheets
• Biology Worksheets
• Periodic Table Worksheets
• Physical Science Worksheets
• Science Lab Worksheets
• My Amazon Books

Use chemistry problems as a tool for mastering chemistry concepts. Some of these examples show using formulas while others include lists of examples.

Acids, Bases, and pH Chemistry Problems

Learn about acids and bases. See how to calculate pH, pOH, K a , K b , pK a , and pK b .

• Practice calculating pH.
• Get example pH, pK a , pK b , K a , and K b calculations.
• Get examples of amphoterism.

Atomic Structure Problems

Learn about atomic mass, the Bohr model, and the part of the atom.

• Practice identifying atomic number, mass number, and atomic mass.
• Get examples showing ways to find atomic mass.
• Use Avogadro’s number and find the mass of a single atom .
• Review the Bohr model of the atom.
• Find the number of valence electrons of an element’s atom.

Chemical Bonds

Learn how to use electronegativity to determine whether atoms form ionic or covalent bonds. See chemistry problems drawing Lewis structures.

• Identify ionic and covalent bonds.
• Learn about ionic compounds and get examples.
• Practice identifying ionic compounds.
• Get examples of binary compounds.
• Learn about covalent compounds and their properties.
• See how to assign oxidation numbers.
• Practice drawing Lewis structures.
• Practice calculating bond energy.

Chemical Equations

Practice writing and balancing chemical equations.

• Learn the steps of balancing equations.
• Practice balancing chemical equations (practice quiz).
• Get examples finding theoretical yield.
• Practice calculating percent yield.
• Learn to recognize decomposition reactions.
• Practice recognizing synthesis reactions.
• Practice recognizing single replacement reactions.
• Recognize double replacement reactions.
• Find the mole ratio between chemical species in an equation.

Concentration and Solutions

Learn how to calculate concentration and explore chemistry problems that affect chemical concentration, including freezing point depression, boiling point elevation, and vapor pressure elevation.

• Get example concentration calculations in several units.
• Practice calculating normality (N).
• Practice calculating molality (m).
• Explore example molarity (M) calculations.
• Get examples of colligative properties of solutions.
• See the definition and examples of saturated solutions.
• See the definition and examples of unsaturated solutions.
• Get examples of miscible and immiscible liquids.

Error Calculations

Learn about the types of error and see worked chemistry example problems.

• See how to calculate percent.
• Practice absolute and relative error calculations.
• See how to calculate percent error.
• See how to find standard deviation.
• Calculate mean, median, and mode.
• Review the difference between accuracy and precision.

Equilibrium Chemistry Problems

Learn about Le Chatelier’s principle, reaction rates, and equilibrium.

• Solve activation energy chemistry problems.
• Review factors that affect reaction rate.
• Practice calculating the van’t Hoff factor.

Practice chemistry problems using the gas laws, including Raoult’s law, Graham’s law, Boyle’s law, Charles’ law, and Dalton’s law of partial pressures.

• Calculate vapor pressure.
• Solve Avogadro’s law problems.
• Practice Boyle’s law problems.
• See Charles’ law example problems.
• Solve combined gas law problems.
• Solve Gay-Lussac’s law problems.

Some chemistry problems ask you identify examples of states of matter and types of mixtures. While there are any chemical formulas to know, it’s still nice to have lists of examples.

• Practice density calculations.
• Identify intensive and extensive properties of matter.
• See examples of intrinsic and extrinsic properties of matter.
• Get the definition and examples of solids.
• Get the definition and examples of gases.
• See the definition and examples of liquids.
• Learn what melting point is and get a list of values for different substances.
• Get the azeotrope definition and see examples.
• See how to calculate specific volume of a gas.
• Get examples of physical properties of matter.
• Get examples of chemical properties of matter.
• Review the states of matter.

Molecular Structure Chemistry Problems

See chemistry problems writing chemical formulas. See examples of monatomic and diatomic elements.

• Practice empirical and molecular formula problems.
• Practice simplest formula problems.
• See how to calculate molecular mass.
• Get examples of the monatomic elements.
• See examples of binary compounds.
• Calculate the number of atoms and molecules in a drop of water.

Nomenclature

Practice chemistry problems naming ionic compounds, hydrocarbons, and covalent compounds.

• Practice naming covalent compounds.
• Learn hydrocarbon prefixes in organic chemistry.

Nuclear Chemistry

These chemistry problems involve isotopes, nuclear symbols, half-life, radioactive decay, fission, fusion.

• Review the types of radioactive decay.

Periodic Table

Learn how to use a periodic table and explore periodic table trends.

• Know the trends in the periodic table.
• Review how to use a periodic table.
• Explore the difference between atomic and ionic radius and see their trends on the periodic table.

Physical Chemistry

Explore thermochemistry and physical chemistry, including enthalpy, entropy, heat of fusion, and heat of vaporization.

• Practice heat of vaporization chemistry problems.
• Practice heat of fusion chemistry problems.
• Calculate heat required to turn ice into steam.
• Practice calculating specific heat.
• Get examples of potential energy.
• Get examples of kinetic energy.
• See example activation energy calculations.

Spectroscopy and Quantum Chemistry Problems

See chemistry problems involving the interaction between light and matter.

• Calculate wavelength from frequency or frequency from wavelength.

Stoichiometry Chemistry Problems

Practice chemistry problems balancing formulas for mass and charge. Learn about reactants and products.

• Get example mole ratio problems.
• Calculate percent yield.
• Learn how to assign oxidation numbers.
• Get the definition and examples of reactants in chemistry.
• Get the definition and examples of products in chemical reactions.

Unit Conversions

There are some many examples of unit conversions that they have their own separate page!

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Chemistry library

Course: chemistry library   >   unit 3.

• Chemical reactions introduction
• Balancing chemical equations
• Balancing more complex chemical equations
• Visually understanding balancing chemical equations
• Balancing another combustion reaction
• Balancing chemical equation with substitution

Balancing chemical equations 1

• Your answer should be
• an integer, like 6 ‍  
• an exact decimal, like 0.75 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.10: Problem Solving - Unit Conversions and Estimating Answers

• Last updated
• Save as PDF
• Page ID 86586

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Convert a value reported in one unit to a corresponding value in a different unit.

The ability to convert from one unit to another is an important skill. For example, a nurse with 50 mg aspirin tablets who must administer 0.2 g of aspirin to a patient needs to know that 0.2 g equals 200 mg, so 4 tablets are needed. Fortunately, there is a simple way to convert from one unit to another.

Conversion Factors

If you learned the SI units and prefixes described previously, then you know that 1 cm is 1/100th of a meter.

\[ 1\; \rm{cm} = \dfrac{1}{100} \; \rm{m} \nonumber \]

\[100\; \rm{cm} = 1\; \rm{m} \nonumber \]

Suppose we divide both sides of the equation by 1 m (both the number and the unit):

\[\mathrm{\dfrac{100\:cm}{1\:m}=\dfrac{1\:m}{1\:m}} \nonumber \]

As long as we perform the same operation on both sides of the equals sign, the expression remains an equality. Look at the right side of the equation; it now has the same quantity in the numerator (the top) as it has in the denominator (the bottom). Any fraction that has the same quantity in the numerator and the denominator has a value of 1:

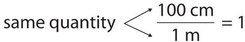
We know that 100 cm is 1 m, so we have the same quantity on the top and the bottom of our fraction, although it is expressed in different units. A fraction that has equivalent quantities in the numerator and the denominator but expressed in different units is called a conversion factor .

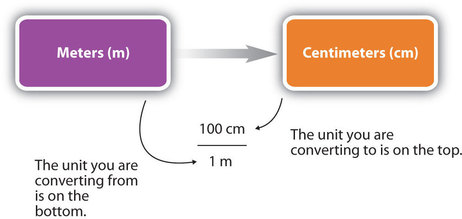
Here is a simple example. How many centimeters are there in 3.55 m? Perhaps you can determine the answer in your head. If there are 100 cm in every meter, then 3.55 m equals 355 cm. To solve the problem more formally with a conversion factor, we first write the quantity we are given, 3.55 m. Then we multiply this quantity by a conversion factor, which is the same as multiplying it by 1. We can write 1 as \(\mathrm{\frac{100\:cm}{1\:m}}\) and multiply:

\[ 3.55 \; \rm{m} \times \dfrac{100 \; \rm{cm}}{1\; \rm{m}} \nonumber \]

The 3.55 m can be thought of as a fraction with a 1 in the denominator. Because m, the abbreviation for meters, occurs in both the numerator and the denominator of our expression, they cancel out:

\[\dfrac{3.55 \; \cancel{\rm{m}}}{ 1} \times \dfrac{100 \; \rm{cm}}{1 \; \cancel{\rm{m}}} \nonumber \]

The final step is to perform the calculation that remains once the units have been canceled:

\[ \dfrac{3.55}{1} \times \dfrac{100 \; \rm{cm}}{1} = 355 \; \rm{cm} \label{Ex1} \]

In the final answer, we omit the 1 in the denominator. Thus, by a more formal procedure, we find that 3.55 m equals 355 cm. A generalized description of this process is as follows:

\[\text{quantity (in old units)} \times \text{conversion factor} = \text{quantity (in new units)} \nonumber \]

You may be wondering why we use a seemingly complicated procedure for a straightforward conversion. In later studies, the conversion problems you will encounter will not always be so simple . If you can master the technique of applying conversion factors, you will be able to solve a large variety of problems.

In the previous example (Equation \ref{Ex1}), we used the fraction \(\frac{100 \; \rm{cm}}{1 \; \rm{m}}\) as a conversion factor. Does the conversion factor \(\frac{1 \; \rm m}{100 \; \rm{cm}}\) also equal 1? Yes, it does; it has the same quantity in the numerator as in the denominator (except that they are expressed in different units). Why did we not use that conversion factor? If we had used the second conversion factor, the original unit would not have canceled, and the result would have been meaningless. Here is what we would have gotten:

\[ 3.55 \; \rm{m} \times \dfrac{1\; \rm{m}}{100 \; \rm{cm}} = 0.0355 \dfrac{\rm{m}^2}{\rm{cm}} \nonumber \]

For the answer to be meaningful, we have to construct the conversion factor in a form that causes the original unit to cancel out . Figure \(\PageIndex{1}\) shows a concept map for constructing a proper conversion.

Significant Figures in Conversions

How do conversion factors affect the determination of significant figures? Numbers in conversion factors based on prefix changes, such as kilograms to grams, are not considered in the determination of significant figures in a calculation because the numbers in such conversion factors are exact. Exact numbers are defined or counted numbers, not measured numbers, and can be considered as having an infinite number of significant figures. (In other words, 1 kg is exactly 1,000 g, by the definition of kilo-.) Counted numbers are also exact. If there are 16 students in a classroom, the number 16 is exact. In contrast, conversion factors that come from measurements (such as density, as we will see shortly) or are approximations have a limited number of significant figures and should be considered in determining the significant figures of the final answer.

Example \(\PageIndex{1}\)

• The average volume of blood in an adult male is 4.7 L. What is this volume in milliliters?
• A hummingbird can flap its wings once in 18 ms. How many seconds are in 18 ms?
• We start with what we are given, 4.7 L. We want to change the unit from liters to milliliters. There are 1,000 mL in 1 L. From this relationship, we can construct two conversion factors:

\[ \dfrac{1\; \rm{L}}{1,000\; \rm{mL}} \; \text{ or } \; \dfrac{1,000 \; \rm{mL}}{1\; \rm{L}} \nonumber \]

We use the conversion factor that will cancel out the original unit, liters, and introduce the unit we are converting to, which is milliliters. The conversion factor that does this is the one on the right.

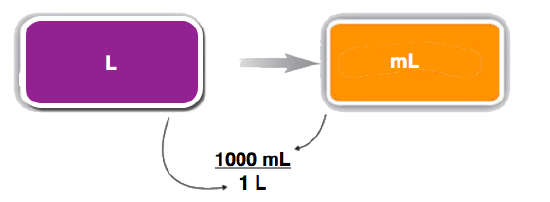
\[ 4.7 \cancel{\rm{L}} \times \dfrac{1,000 \; \rm{mL}}{1\; \cancel{\rm{L}}} = 4,700\; \rm{mL} \nonumber \]

Because the numbers in the conversion factor are exact, we do not consider them when determining the number of significant figures in the final answer. Thus, we report two significant figures in the final answer.

• We can construct two conversion factors from the relationships between milliseconds and seconds:

\[ \dfrac{1,000 \; \rm{ms}}{1\; \rm{s}} \; \text{ or } \; \dfrac{1\; \rm{s}}{1,000 \; \rm{ms}} \nonumber \]

To convert 18 ms to seconds, we choose the conversion factor that will cancel out milliseconds and introduce seconds. The conversion factor on the right is the appropriate one. We set up the conversion as follows:

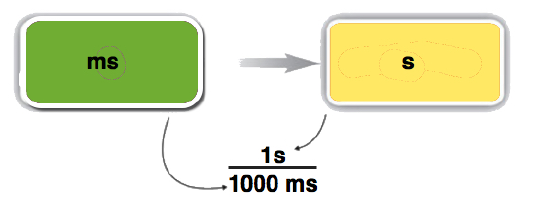
\[ 18 \; \cancel{\rm{ms}} \times \dfrac{1\; \rm{s}}{1,000 \; \cancel{\rm{ms}}} = 0.018\; \rm{s} \nonumber \]

The conversion factor’s numerical values do not affect our determination of the number of significant figures in the final answer.

Exercise \(\PageIndex{1}\)

Perform each conversion.

• 101,000 ns to seconds
• 32.08 kg to grams

\[ 101,000 \cancel{\rm{ns}} \times \dfrac{1\; \rm{s}}{1,000,000,000\; \cancel{\rm{ns}}} = 0.000101\; \rm{s} \nonumber \]

\[ 32.08 \cancel{\rm{kg}} \times \dfrac{1,000 \; \rm{g}}{1\; \cancel{\rm{kg}}} = 32,080\; \rm{g} \nonumber \]

Conversion Factors From Different Units

Conversion factors can also be constructed for converting between different kinds of units. For example, density can be used to convert between the mass and the volume of a substance. Consider mercury, which is a liquid at room temperature and has a density of 13.6 g/mL. The density tells us that 13.6 g of mercury have a volume of 1 mL. We can write that relationship as follows:

13.6 g mercury = 1 mL mercury

This relationship can be used to construct two conversion factors:

\[\mathrm{\dfrac{13.6\:g}{1\:mL}\:and\:\dfrac{1\:mL}{13.6\:g}} \nonumber \]

Which one do we use? It depends, as usual, on the units we need to cancel and introduce. For example, suppose we want to know the mass of 16 mL of mercury. We would use the conversion factor that has milliliters on the bottom (so that the milliliter unit cancels) and grams on top so that our final answer has a unit of mass:

\[ \begin{align*} \mathrm{16\:\cancel{mL}\times\dfrac{13.6\:g}{1\:\cancel{mL}}} &= \mathrm{217.6\:g} \\[4pt] &\approx \mathrm{220\:g} \end{align*} \nonumber \]

In the last step, we limit our final answer to two significant figures because the volume quantity has only two significant figures; the 1 in the volume unit is considered an exact number, so it does not affect the number of significant figures. The other conversion factor would be useful if we were given a mass and asked to find volume, as the following example illustrates.

Density can be used as a conversion factor between mass and volume.

Example \(\PageIndex{2}\): Mercury Thermometer

A mercury thermometer for measuring a patient’s temperature contains 0.750 g of mercury. What is the volume of this mass of mercury?

Because we are starting with grams, we want to use the conversion factor that has grams in the denominator. The gram unit will cancel algebraically, and milliliters will be introduced in the numerator.

\[ \begin{align*} 0.750 \; \cancel{\rm{g}} \times \dfrac{1\; \rm{mL}}{13.6 \; \cancel{\rm{g}}} &= 0.055147 \ldots \; \rm{mL} \\[4pt] &\approx 0.0551\; \rm{mL} \end{align*} \nonumber \]

We have limited the final answer to three significant figures.

Exercise \(\PageIndex{2}\)

What is the volume of 100.0 g of air if its density is 1.3 g/L?

\[100.0 \cancel{\rm{g}} \times \dfrac{1\; \rm{L}}{1.3\; \cancel{\rm{g}}} = 76.92307692\; \rm{L} ≈ 77 L \nonumber \]

Because the density (1.3 g/L) has only 2 significant figures, we are rounding off the final answer to 2 significant figures.

Problem Solving With Multiple Conversions

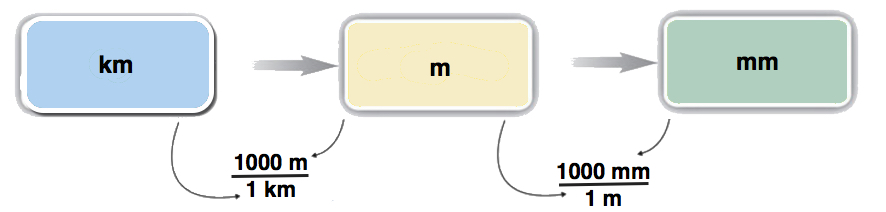
Sometimes you will have to perform more than one conversion to obtain the desired unit. For example, suppose you want to convert 54.7 km into millimeters. You can either memorize the relationship between kilometers and millimeters, or you can do the conversion in two steps. Most people prefer to convert in steps.

To do a stepwise conversion, we first convert the given amount to the base unit. In this example, the base unit is meters. We know that there are 1,000 m in 1 km:

\[ 54.7\; \cancel{\rm{km}} \times \dfrac{1,000 \; \rm{m}}{1\; \cancel{\rm{km}}} = 54,700\; \rm{m} \nonumber \]

Then we take the result (54,700 m) and convert it to millimeters, remembering that there are \(1,000\; \rm{mm}\) for every \(1\; \rm{m}\):

\[ \begin{align*} 54,700 \; \cancel{\rm{m}} \times \dfrac{1,000 \; \rm{mm}}{1\; \cancel{\rm{m}}} &= 54,700,000 \; \rm{mm} \\[4pt] &= 5.47 \times 10^7\; \rm{mm} \end{align*} \nonumber \]

We have expressed the final answer in scientific notation.

As a shortcut, both steps in the conversion can be combined into a single, multistep expression:

Concept Map

Calculation

\[ \begin{align*} 54.7\; \cancel{\rm{km}} \times \dfrac{1,000 \; \cancel{\rm{m}}}{1\; \cancel{\rm{km}}} \times \dfrac{1,000 \; \rm{mm}}{1\; \cancel{\rm{m}}} &= 54,700,000 \; \rm{mm} \\[4pt] &= 5.47 \times 10^7\; \rm{mm} \end{align*} \nonumber \]

In each step, the previous unit is canceled and the next unit in the sequence is produced, each successive unit canceling out until only the unit needed in the answer is left.

Either method—one step at a time or all the steps together—is acceptable. If you do all the steps together, the restriction for the proper number of significant figures should be done after the last step. As long as the math is performed correctly, you should get the same answer no matter which method you use.

Example \(\PageIndex{3}\)

Convert 58.2 ms to megaseconds in one multistep calculation.

First, convert the given unit (ms) to the base unit—in this case, seconds—and then convert seconds to the final unit, megaseconds:

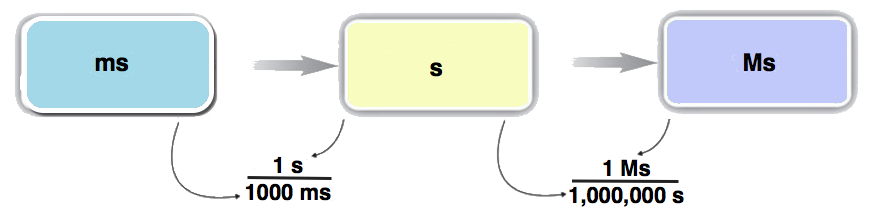
\[ \begin{align*} 58.2 \; \cancel{\rm{ms}} \times \dfrac{\cancel{1 \rm{s}}}{1,000\; \cancel{\rm{ms}}} \times \dfrac{1\; \rm{Ms}}{1,000,000\; \cancel{ \rm{s}}} &=0.0000000582\; \rm{Ms} \\[4pt] &= 5.82 \times 10^{-8}\; \rm{Ms} \end{align*} \nonumber \]

Neither conversion factor affects the number of significant figures in the final answer.

Exercise \(\PageIndex{3}\)

Convert 43.007 mg to kilograms in one multistep calculation.

\[ \begin{align*} 43.007 \; \cancel{\rm{mg}} \times \dfrac{\cancel{1 \rm{g}}}{1,000\; \cancel{\rm{mg}}} \times \dfrac{1\; \rm{kg}}{1,000\; \cancel{ \rm{g}}} &=0.000043007\; \rm{kg} \\[4pt] &= 4.3007 \times 10^{-5}\; \rm{kg} \end{align*} \nonumber \].

Career Focus: Pharmacist

A pharmacist dispenses drugs that have been prescribed by a doctor. Although that may sound straightforward, pharmacists in the United States must hold a doctorate in pharmacy and be licensed by the state in which they work. Most pharmacy programs require four years of education in a specialty pharmacy school.

Pharmacists must know a lot of chemistry and biology so they can understand the effects that drugs (which are chemicals, after all) have on the body. Pharmacists can advise physicians on the selection, dosage, interactions, and side effects of drugs. They can also advise patients on the proper use of their medications, including when and how to take specific drugs properly. Pharmacists can be found in drugstores, hospitals, and other medical facilities.

Curiously, an outdated name for pharmacist is chemist , which was used when pharmacists formerly did a lot of drug preparation, or compounding . In modern times, pharmacists rarely compound their own drugs, but their knowledge of the sciences, including chemistry, helps them provide valuable services in support of everyone’s health.

Key Takeaway

• A unit can be converted to another unit of the same type with a conversion factor.

Concept Review Exercises

• How do you determine which quantity in a conversion factor goes in the denominator of the fraction?
• State the guidelines for determining significant figures when using a conversion factor.
• Write a concept map (a plan) for how you would convert \(1.0 \times 10^{12}\) nano liters (nL) to kilo liters (kL).
• The unit you want to cancel from the numerator goes in the denominator of the conversion factor.
• Exact numbers that appear in many conversion factors do not affect the number of significant figures; otherwise, the normal rules of multiplication and division for significant figures apply.
• Concept Map: Convert the given (nanoliters, nL) to liters; then convert liters to kiloliters.