z test in hypothesis testing

Z-Test for Statistical Hypothesis Testing Explained

The Z-test is a statistical hypothesis test used to determine where the distribution of the test statistic we are measuring, like the mean , is part of the normal distribution .

There are multiple types of Z-tests, however, we’ll focus on the easiest and most well known one, the one sample mean test. This is used to determine if the difference between the mean of a sample and the mean of a population is statistically significant.

What Is a Z-Test?

A Z-test is a type of statistical hypothesis test where the test-statistic follows a normal distribution.  

The name Z-test comes from the Z-score of the normal distribution. This is a measure of how many standard deviations away a raw score or sample statistics is from the populations’ mean.

Z-tests are the most common statistical tests conducted in fields such as healthcare and data science . Therefore, it’s an essential concept to understand.

Requirements for a Z-Test

In order to conduct a Z-test, your statistics need to meet a few requirements, including:

• A Sample size that’s greater than 30. This is because we want to ensure our sample mean comes from a distribution that is normal. As stated by the c entral limit theorem , any distribution can be approximated as normally distributed if it contains more than 30 data points.
• The standard deviation and mean of the population is known .
• The sample data is collected/acquired randomly .

More on Data Science:   What Is Bootstrapping Statistics?

Z-Test Steps

There are four steps to complete a Z-test. Let’s examine each one.

4 Steps to a Z-Test

• State the null hypothesis.
• State the alternate hypothesis.
• Choose your critical value.
• Calculate your Z-test statistics. 

1. State the Null Hypothesis

The first step in a Z-test is to state the null hypothesis, H_0 . This what you believe to be true from the population, which could be the mean of the population, μ_0 :

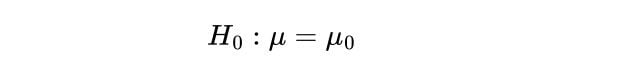
2. State the Alternate Hypothesis

Next, state the alternate hypothesis, H_1 . This is what you observe from your sample. If the sample mean is different from the population’s mean, then we say the mean is not equal to μ_0:

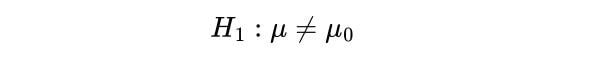
3. Choose Your Critical Value

Then, choose your critical value, α , which determines whether you accept or reject the null hypothesis. Typically for a Z-test we would use a statistical significance of 5 percent which is z = +/- 1.96 standard deviations from the population’s mean in the normal distribution:

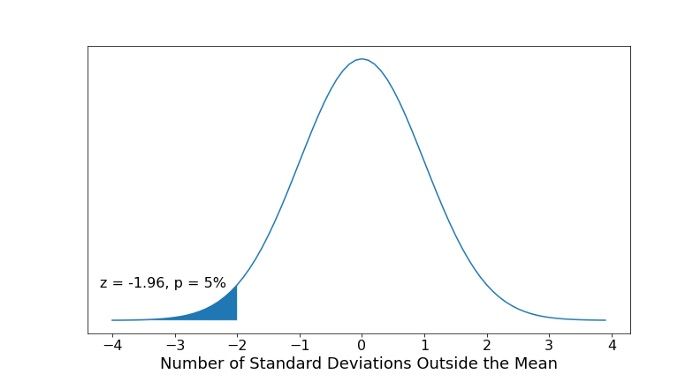
This critical value is based on confidence intervals.

4. Calculate Your Z-Test Statistic

Compute the Z-test Statistic using the sample mean, μ_1 , the population mean, μ_0 , the number of data points in the sample, n and the population’s standard deviation, σ :

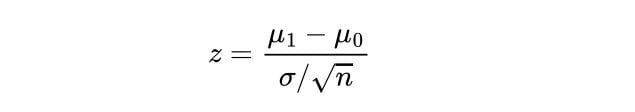
If the test statistic is greater (or lower depending on the test we are conducting) than the critical value, then the alternate hypothesis is true because the sample’s mean is statistically significant enough from the population mean.

Another way to think about this is if the sample mean is so far away from the population mean, the alternate hypothesis has to be true or the sample is a complete anomaly.

More on Data Science: Basic Probability Theory and Statistics Terms to Know

Z-Test Example

Let’s go through an example to fully understand the one-sample mean Z-test.

A school says that its pupils are, on average, smarter than other schools. It takes a sample of 50 students whose average IQ measures to be 110. The population, or the rest of the schools, has an average IQ of 100 and standard deviation of 20. Is the school’s claim correct?

The null and alternate hypotheses are:

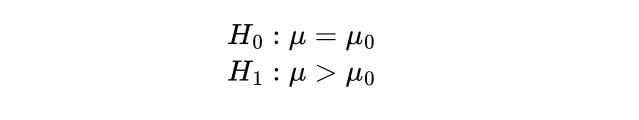
Where we are saying that our sample, the school, has a higher mean IQ than the population mean.

Now, this is what’s called a right-sided, one-tailed test as our sample mean is greater than the population’s mean. So, choosing a critical value of 5 percent, which equals a Z-score of 1.96 , we can only reject the null hypothesis if our Z-test statistic is greater than 1.96.

If the school claimed its students’ IQs were an average of 90, then we would use a left-tailed test, as shown in the figure above. We would then only reject the null hypothesis if our Z-test statistic is less than -1.96.

Computing our Z-test statistic, we see:

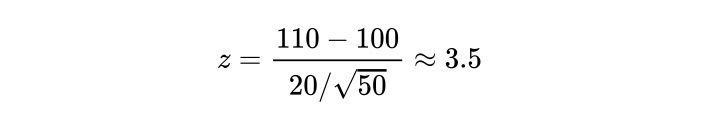
Therefore, we have sufficient evidence to reject the null hypothesis, and the school’s claim is right.

Hope you enjoyed this article on Z-tests. In this post, we only addressed the most simple case, the one-sample mean test. However, there are other types of tests, but they all follow the same process just with some small nuances.  

Built In’s expert contributor network publishes thoughtful, solutions-oriented stories written by innovative tech professionals. It is the tech industry’s definitive destination for sharing compelling, first-person accounts of problem-solving on the road to innovation.

Great Companies Need Great People. That's Where We Come In.

10 Chapter 10: Hypothesis Testing with Z

Setting up the hypotheses.

When setting up the hypotheses with z, the parameter is associated with a sample mean (in the previous chapter examples the parameters for the null used 0). Using z is an occasion in which the null hypothesis is a value other than 0. For example, if we are working with mothers in the U.S. whose children are at risk of low birth weight, we can use 7.47 pounds, the average birth weight in the US, as our null value and test for differences against that. For now, we will focus on testing a value of a single mean against what we expect from the population.

Using birthweight as an example, our null hypothesis takes the form: H 0 : μ = 7.47 Notice that we are testing the value for μ, the population parameter, NOT the sample statistic ̅X (or M). We are referring to the data right now in raw form (we have not standardized it using z yet). Again, using inferential statistics, we are interested in understanding the population, drawing from our sample observations. For the research question, we have a mean value from the sample to use, we have specific data is – it is observed and used as a comparison for a set point.

As mentioned earlier, the alternative hypothesis is simply the reverse of the null hypothesis, and there are three options, depending on where we expect the difference to lie. We will set the criteria for rejecting the null hypothesis based on the directionality (greater than, less than, or not equal to) of the alternative.

If we expect our obtained sample mean to be above or below the null hypothesis value (knowing which direction), we set a directional hypothesis. O ur alternative hypothesis takes the form based on the research question itself. In our example with birthweight, this could be presented as H A : μ > 7.47 or H A : μ < 7.47. 

Note that we should only use a directional hypothesis if we have a good reason, based on prior observations or research, to suspect a particular direction. When we do not know the direction, such as when we are entering a new area of research, we use a non-directional alternative hypothesis. In our birthweight example, this could be set as H A : μ ≠ 7.47

In working with data for this course we will need to set a critical value of the test statistic for alpha (α) for use of test statistic tables in the back of the book. This is determining the critical rejection region that has a set critical value based on α.

Determining Critical Value from α

We set alpha (α) before collecting data in order to determine whether or not we should reject the null hypothesis. We set this value beforehand to avoid biasing ourselves by viewing our results and then determining what criteria we should use.

When a research hypothesis predicts an effect but does not predict a direction for the effect, it is called a non-directional hypothesis . To test the significance of a non-directional hypothesis, we have to consider the possibility that the sample could be extreme at either tail of the comparison distribution. We call this a two-tailed test .

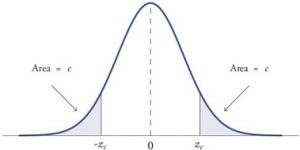
Figure 1. showing a 2-tail test for non-directional hypothesis for z for area C is the critical rejection region.

When a research hypothesis predicts a direction for the effect, it is called a directional hypothesis . To test the significance of a directional hypothesis, we have to consider the possibility that the sample could be extreme at one-tail of the comparison distribution. We call this a one-tailed test .

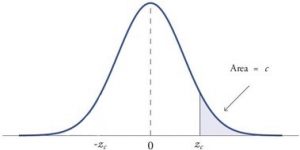
Figure 2. showing a 1-tail test for a directional hypothesis (predicting an increase) for z for area C is the critical rejection region.

Determining Cutoff Scores with Two-Tailed Tests

Typically we specify an α level before analyzing the data. If the data analysis results in a probability value below the α level, then the null hypothesis is rejected; if it is not, then the null hypothesis is not rejected. In other words, if our data produce values that meet or exceed this threshold, then we have sufficient evidence to reject the null hypothesis ; if not, we fail to reject the null (we never “accept” the null). According to this perspective, if a result is significant, then it does not matter how significant it is. Moreover, if it is not significant, then it does not matter how close to being significant it is. Therefore, if the 0.05 level is being used, then probability values of 0.049 and 0.001 are treated identically. Similarly, probability values of 0.06 and 0.34 are treated identically. Note we will discuss ways to address effect size (which is related to this challenge of NHST).

When setting the probability value, there is a special complication in a two-tailed test. We have to divide the significance percentage between the two tails. For example, with a 5% significance level, we reject the null hypothesis only if the sample is so extreme that it is in either the top 2.5% or the bottom 2.5% of the comparison distribution. This keeps the overall level of significance at a total of 5%. A one-tailed test does have such an extreme value but with a one-tailed test only one side of the distribution is considered.

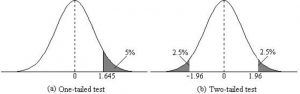
Figure 3. Critical value differences in one and two-tail tests. Photo Credit

Let’s re view th e set critical values for Z.

We discussed z-scores and probability in chapter 8.  If we revisit the z-score for 5% and 1%, we can identify the critical regions for the critical rejection areas from the unit standard normal table.

• A two-tailed test at the 5% level has a critical boundary Z score of +1.96 and -1.96
• A one-tailed test at the 5% level has a critical boundary Z score of +1.64 or -1.64
• A two-tailed test at the 1% level has a critical boundary Z score of +2.58 and -2.58
• A one-tailed test at the 1% level has a critical boundary Z score of +2.33 or -2.33.

Review: Critical values, p-values, and significance level

There are two criteria we use to assess whether our data meet the thresholds established by our chosen significance level, and they both have to do with our discussions of probability and distributions. Recall that probability refers to the likelihood of an event, given some situation or set of conditions. In hypothesis testing, that situation is the assumption that the null hypothesis value is the correct value, or that there is no effec t. The value laid out in H 0 is our condition under which we interpret our results. To reject this assumption, and thereby reject the null hypothesis, we need results that would be very unlikely if the null was true.

Now recall that values of z which fall in the tails of the standard normal distribution represent unlikely values. That is, the proportion of the area under the curve as or more extreme than z is very small as we get into the tails of the distribution. Our significance level corresponds to the area under the tail that is exactly equal to α: if we use our normal criterion of α = .05, then 5% of the area under the curve becomes what we call the rejection region (also called the critical region) of the distribution. This is illustrated in Figure 4.

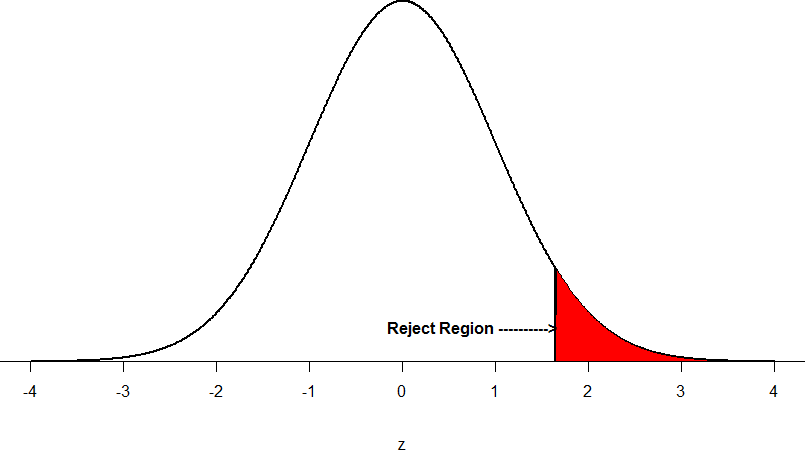
Figure 4: The rejection region for a one-tailed test

The shaded rejection region takes us 5% of the area under the curve. Any result which falls in that region is sufficient evidence to reject the null hypothesis.

The rejection region is bounded by a specific z-value, as is any area under the curve. In hypothesis testing, the value corresponding to a specific rejection region is called the critical value, z crit (“z-crit”) or z* (hence the other name “critical region”). Finding the critical value works exactly the same as finding the z-score corresponding to any area under the curve like we did in Unit 1. If we go to the normal table, we will find that the z-score corresponding to 5% of the area under the curve is equal to 1.645 (z = 1.64 corresponds to 0.0405 and z = 1.65 corresponds to 0.0495, so .05 is exactly in between them) if we go to the right and -1.645 if we go to the left. The direction must be determined by your alternative hypothesis, and drawing then shading the distribution is helpful for keeping directionality straight.

Suppose, however, that we want to do a non-directional test. We need to put the critical region in both tails, but we don’t want to increase the overall size of the rejection region (for reasons we will see later). To do this, we simply split it in half so that an equal proportion of the area under the curve falls in each tail’s rejection region. For α = .05, this means 2.5% of the area is in each tail, which, based on the z-table, corresponds to critical values of z* = ±1.96. This is shown in Figure 5.

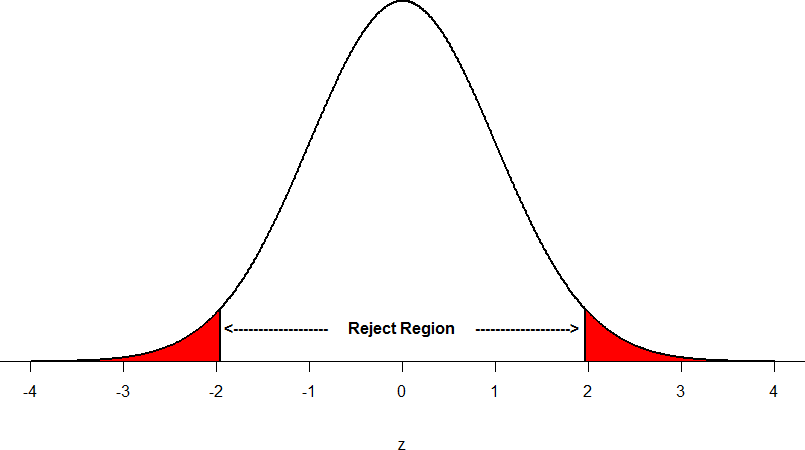
Figure 5: Two-tailed rejection region

Thus, any z-score falling outside ±1.96 (greater than 1.96 in absolute value) falls in the rejection region. When we use z-scores in this way, the obtained value of z (sometimes called z-obtained) is something known as a test statistic, which is simply an inferential statistic used to test a null hypothesis.

Calculate the test statistic: Z

Now that we understand setting up the hypothesis and determining the outcome, let’s examine hypothesis testing with z!  The next step is to carry out the study and get the actual results for our sample. Central to hypothesis test is comparison of the population and sample means. To make our calculation and determine where the sample is in the hypothesized distribution we calculate the Z for the sample data.

Make a decision

To decide whether to reject the null hypothesis, we compare our sample’s Z score to the Z score that marks our critical boundary. If our sample Z score falls inside the rejection region of the comparison distribution (is greater than the z-score critical boundary) we reject the null hypothesis.

The formula for our z- statistic has not changed:

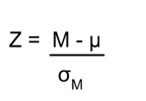
To formally test our hypothesis, we compare our obtained z-statistic to our critical z-value. If z obt > z crit , that means it falls in the rejection region (to see why, draw a line for z = 2.5 on Figure 1 or Figure 2) and so we reject H 0 . If z obt < z crit , we fail to reject. Remember that as z gets larger, the corresponding area under the curve beyond z gets smaller. Thus, the proportion, or p-value, will be smaller than the area for α, and if the area is smaller, the probability gets smaller. Specifically, the probability of obtaining that result, or a more extreme result, under the condition that the null hypothesis is true gets smaller.

Conversely, if we fail to reject, we know that the proportion will be larger than α because the z-statistic will not be as far into the tail. This is illustrated for a one- tailed test in Figure 6.

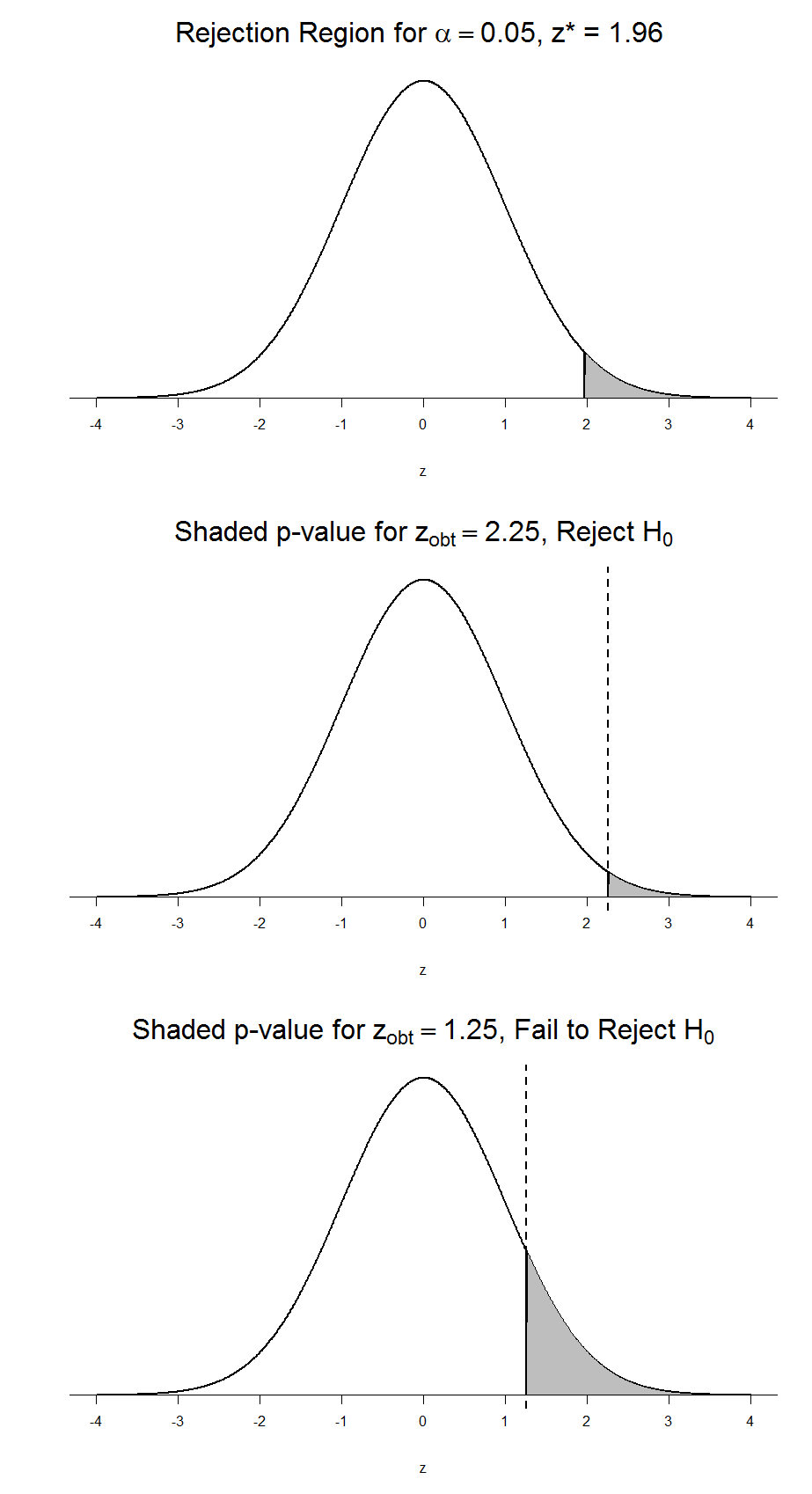
Figure 6. Relation between α, z obt , and p

When the null hypothesis is rejected, the effect is said to be statistically significant . Do not confuse statistical significance with practical significance. A small effect can be highly significant if the sample size is large enough.

Why does the word “significant” in the phrase “statistically significant” mean something so different from other uses of the word? Interestingly, this is because the meaning of “significant” in everyday language has changed. It turns out that when the procedures for hypothesis testing were developed, something was “significant” if it signified something. Thus, finding that an effect is statistically significant signifies that the effect is real and not due to chance. Over the years, the meaning of “significant” changed, leading to the potential misinterpretation.

Review: Steps of the Hypothesis Testing Process

The process of testing hypotheses follows a simple four-step procedure. This process will be what we use for the remained of the textbook and course, and though the hypothesis and statistics we use will change, this process will not.

Step 1: State the Hypotheses

Your hypotheses are the first thing you need to lay out. Otherwise, there is nothing to test! You have to state the null hypothesis (which is what we test) and the alternative hypothesis (which is what we expect). These should be stated mathematically as they were presented above AND in words, explaining in normal English what each one means in terms of the research question.

Step 2: Find the Critical Values

Next, we formally lay out the criteria we will use to test our hypotheses. There are two pieces of information that inform our critical values: α, which determines how much of the area under the curve composes our rejection region, and the directionality of the test, which determines where the region will be.

Step 3: Compute the Test Statistic

Once we have our hypotheses and the standards we use to test them, we can collect data and calculate our test statistic, in this case z . This step is where the vast majority of differences in future chapters will arise: different tests used for different data are calculated in different ways, but the way we use and interpret them remains the same.

Step 4: Make the Decision

Finally, once we have our obtained test statistic, we can compare it to our critical value and decide whether we should reject or fail to reject the null hypothesis. When we do this, we must interpret the decision in relation to our research question, stating what we concluded, what we based our conclusion on, and the specific statistics we obtained.

Example: Movie Popcorn

Let’s see how hypothesis testing works in action by working through an example. Say that a movie theater owner likes to keep a very close eye on how much popcorn goes into each bag sold, so he knows that the average bag has 8 cups of popcorn and that this varies a little bit, about half a cup. That is, the known population mean is μ = 8.00 and the known population standard deviation is σ =0.50. The owner wants to make sure that the newest employee is filling bags correctly, so over the course of a week he randomly assesses 25 bags filled by the employee to test for a difference (n = 25). He doesn’t want bags overfilled or under filled, so he looks for differences in both directions. This scenario has all of the information we need to begin our hypothesis testing procedure.

Our manager is looking for a difference in the mean cups of popcorn bags compared to the population mean of 8. We will need both a null and an alternative hypothesis written both mathematically and in words. We’ll always start with the null hypothesis:

H 0 : There is no difference in the cups of popcorn bags from this employee H 0 : μ = 8.00

Notice that we phrase the hypothesis in terms of the population parameter μ, which in this case would be the true average cups of bags filled by the new employee.

Our assumption of no difference, the null hypothesis, is that this mean is exactly

the same as the known population mean value we want it to match, 8.00. Now let’s do the alternative:

H A : There is a difference in the cups of popcorn bags from this employee H A : μ ≠ 8.00

In this case, we don’t know if the bags will be too full or not full enough, so we do a two-tailed alternative hypothesis that there is a difference.

Our critical values are based on two things: the directionality of the test and the level of significance. We decided in step 1 that a two-tailed test is the appropriate directionality. We were given no information about the level of significance, so we assume that α = 0.05 is what we will use. As stated earlier in the chapter, the critical values for a two-tailed z-test at α = 0.05 are z* = ±1.96. This will be the criteria we use to test our hypothesis. We can now draw out our distribution so we can visualize the rejection region and make sure it makes sense

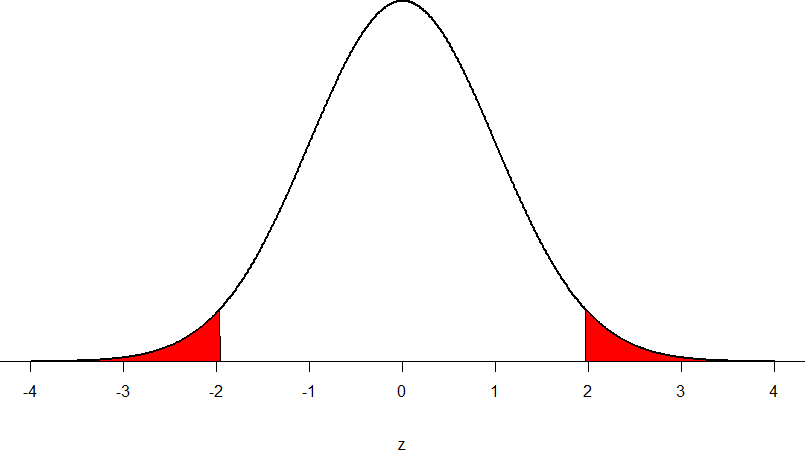
Figure 7: Rejection region for z* = ±1.96

Step 3: Calculate the Test Statistic

Now we come to our formal calculations. Let’s say that the manager collects data and finds that the average cups of this employee’s popcorn bags is ̅X = 7.75 cups. We can now plug this value, along with the values presented in the original problem, into our equation for z:

So our test statistic is z = -2.50, which we can draw onto our rejection region distribution:

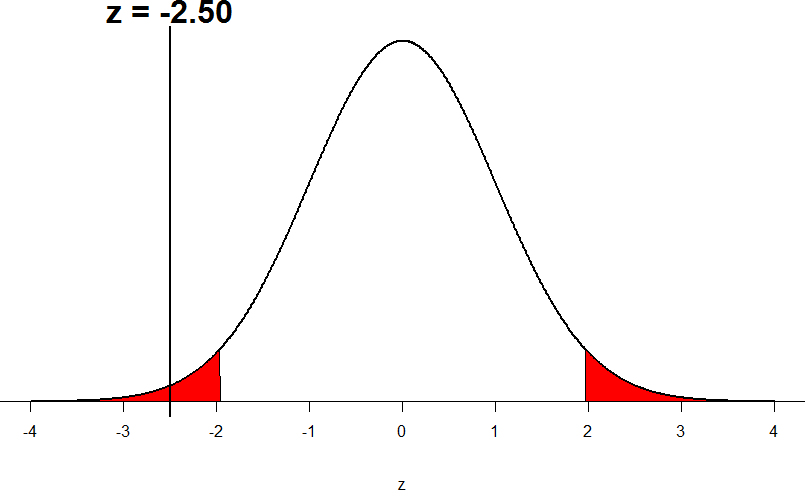
Figure 8: Test statistic location

Looking at Figure 5, we can see that our obtained z-statistic falls in the rejection region. We can also directly compare it to our critical value: in terms of absolute value, -2.50 > -1.96, so we reject the null hypothesis. We can now write our conclusion:

When we write our conclusion, we write out the words to communicate what it actually means, but we also include the average sample size we calculated (the exact location doesn’t matter, just somewhere that flows naturally and makes sense) and the z-statistic and p-value. We don’t know the exact p-value, but we do know that because we rejected the null, it must be less than α.

Effect Size

When we reject the null hypothesis, we are stating that the difference we found was statistically significant, but we have mentioned several times that this tells us nothing about practical significance. To get an idea of the actual size of what we found, we can compute a new statistic called an effect size. Effect sizes give us an idea of how large, important, or meaningful a statistically significant effect is.

For mean differences like we calculated here, our effect size is Cohen’s d :

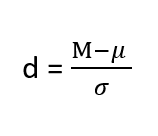
Effect sizes are incredibly useful and provide important information and clarification that overcomes some of the weakness of hypothesis testing. Whenever you find a significant result, you should always calculate an effect size

Table 1. Interpretation of Cohen’s d

Example: Office Temperature

Let’s do another example to solidify our understanding. Let’s say that the office building you work in is supposed to be kept at 74 degree Fahrenheit but is allowed

to vary by 1 degree in either direction. You suspect that, as a cost saving measure, the temperature was secretly set higher. You set up a formal way to test your hypothesis.

You start by laying out the null hypothesis:

H 0 : There is no difference in the average building temperature H 0 : μ = 74

Next you state the alternative hypothesis. You have reason to suspect a specific direction of change, so you make a one-tailed test:

H A : The average building temperature is higher than claimed H A : μ > 74

Now that you have everything set up, you spend one week collecting temperature data:

You calculate the average of these scores to be 𝑋̅ = 76.6 degrees. You use this to calculate the test statistic, using μ = 74 (the supposed average temperature), σ = 1.00 (how much the temperature should vary), and n = 5 (how many data points you collected):

z = 76.60 − 74.00 = 2.60    = 5.78

          1.00/√5            0.45

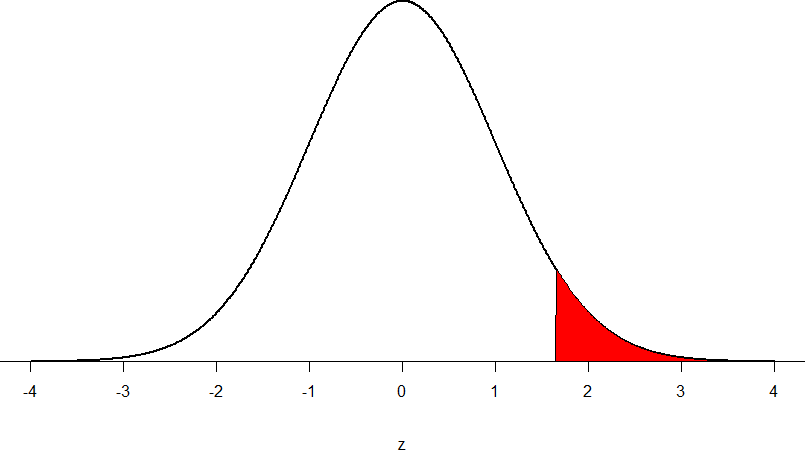
This value falls so far into the tail that it cannot even be plotted on the distribution!

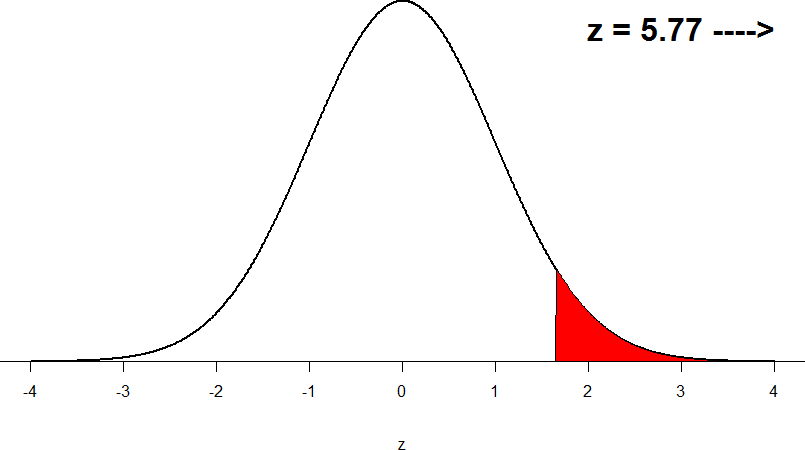
Figure 7: Obtained z-statistic

You compare your obtained z-statistic, z = 5.77, to the critical value, z* = 1.645, and find that z > z*. Therefore you reject the null hypothesis, concluding: Based on 5 observations, the average temperature (𝑋̅ = 76.6 degrees) is statistically significantly higher than it is supposed to be, z = 5.77, p < .05.

d = (76.60-74.00)/ 1= 2.60

The effect size you calculate is definitely large, meaning someone has some explaining to do!

Example: Different Significance Level

First, let’s take a look at an example phrased in generic terms, rather than in the context of a specific research question, to see the individual pieces one more time. This time, however, we will use a stricter significance level, α = 0.01, to test the hypothesis.

We will use 60 as an arbitrary null hypothesis value: H 0 : The average score does not differ from the population H 0 : μ = 50

We will assume a two-tailed test: H A : The average score does differ H A : μ ≠ 50

We have seen the critical values for z-tests at α = 0.05 levels of significance several times. To find the values for α = 0.01, we will go to the standard normal table and find the z-score cutting of 0.005 (0.01 divided by 2 for a two-tailed test) of the area in the tail, which is z crit * = ±2.575. Notice that this cutoff is much higher than it was for α = 0.05. This is because we need much less of the area in the tail, so we need to go very far out to find the cutoff. As a result, this will require a much larger effect or much larger sample size in order to reject the null hypothesis.

We can now calculate our test statistic.  The average of 10 scores is M = 60.40 with a µ = 60. We will use σ = 10 as our known population standard deviation. From this information, we calculate our z-statistic as:

Our obtained z-statistic, z = 0.13, is very small. It is much less than our critical value of 2.575. Thus, this time, we fail to reject the null hypothesis. Our conclusion would look something like:

Notice two things about the end of the conclusion. First, we wrote that p is greater than instead of p is less than, like we did in the previous two examples. This is because we failed to reject the null hypothesis. We don’t know exactly what the p- value is, but we know it must be larger than the α level we used to test our hypothesis. Second, we used 0.01 instead of the usual 0.05, because this time we tested at a different level. The number you compare to the p-value should always be the significance level you test at. Because we did not detect a statistically significant effect, we do not need to calculate an effect size. Note: some statisticians will suggest to always calculate effects size as a possibility of Type II error. Although insignificant, calculating d = (60.4-60)/10 = .04 which suggests no effect (and not a possibility of Type II error).

Review Considerations in Hypothesis Testing

Errors in hypothesis testing.

Keep in mind that rejecting the null hypothesis is not an all-or-nothing decision. The Type I error rate is affected by the α level: the lower the α level the lower the Type I error rate. It might seem that α is the probability of a Type I error. However, this is not correct. Instead, α is the probability of a Type I error given that the null hypothesis is true. If the null hypothesis is false, then it is impossible to make a Type I error. The second type of error that can be made in significance testing is failing to reject a false null hypothesis. This kind of error is called a Type II error.

Statistical Power

The statistical power of a research design is the probability of rejecting the null hypothesis given the sample size and expected relationship strength. Statistical power is the complement of the probability of committing a Type II error. Clearly, researchers should be interested in the power of their research designs if they want to avoid making Type II errors. In particular, they should make sure their research design has adequate power before collecting data. A common guideline is that a power of .80 is adequate. This means that there is an 80% chance of rejecting the null hypothesis for the expected relationship strength.

Given that statistical power depends primarily on relationship strength and sample size, there are essentially two steps you can take to increase statistical power: increase the strength of the relationship or increase the sample size. Increasing the strength of the relationship can sometimes be accomplished by using a stronger manipulation or by more carefully controlling extraneous variables to reduce the amount of noise in the data (e.g., by using a within-subjects design rather than a between-subjects design). The usual strategy, however, is to increase the sample size. For any expected relationship strength, there will always be some sample large enough to achieve adequate power.

Inferential statistics uses data from a sample of individuals to reach conclusions about the whole population. The degree to which our inferences are valid depends upon how we selected the sample (sampling technique) and the characteristics (parameters) of population data. Statistical analyses assume that sample(s) and population(s) meet certain conditions called statistical assumptions.

It is easy to check assumptions when using statistical software and it is important as a researcher to check for violations; if violations of statistical assumptions are not appropriately addressed then results may be interpreted incorrectly.

Learning Objectives

Having read the chapter, students should be able to:

• Conduct a hypothesis test using a z-score statistics, locating critical region, and make a statistical decision including.
• Explain the purpose of measuring effect size and power, and be able to compute Cohen’s d.

Exercises – Ch. 10

• List the main steps for hypothesis testing with the z-statistic. When and why do you calculate an effect size?
• z = 1.99, two-tailed test at α = 0.05
• z = 1.99, two-tailed test at α = 0.01
• z = 1.99, one-tailed test at α = 0.05
• You are part of a trivia team and have tracked your team’s performance since you started playing, so you know that your scores are normally distributed with μ = 78 and σ = 12. Recently, a new person joined the team, and you think the scores have gotten better. Use hypothesis testing to see if the average score has improved based on the following 8 weeks’ worth of score data: 82, 74, 62, 68, 79, 94, 90, 81, 80.
• A study examines self-esteem and depression in teenagers.  A sample of 25 teens with a low self-esteem are given the Beck Depression Inventory.  The average score for the group is 20.9.  For the general population, the average score is 18.3 with σ = 12.  Use a two-tail test with α = 0.05 to examine whether teenagers with low self-esteem show significant differences in depression.
• You get hired as a server at a local restaurant, and the manager tells you that servers’ tips are $42 on average but vary about $12 (μ = 42, σ = 12). You decide to track your tips to see if you make a different amount, but because this is your first job as a server, you don’t know if you will make more or less in tips. After working 16 shifts, you find that your average nightly amount is $44.50 from tips. Test for a difference between this value and the population mean at the α = 0.05 level of significance.

Answers to Odd- Numbered Exercises – Ch. 10

1. List hypotheses. Determine critical region. Calculate z.  Compare z to critical region. Draw Conclusion.  We calculate an effect size when we find a statistically significant result to see if our result is practically meaningful or important

5. Step 1: H 0 : μ = 42 “My average tips does not differ from other servers”, H A : μ ≠ 42 “My average tips do differ from others”

Introduction to Statistics for Psychology Copyright © 2021 by Alisa Beyer is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Approximate Hypothesis Tests: the z Test and the t Test

This chapter presents two common tests of the hypothesis that a population mean equals a particular value and of the hypothesis that two population means are equal: the z test and the t test. These tests are approximate : They are based on approximations to the probability distribution of the test statistic when the null hypothesis is true, so their significance levels are not exactly what they claim to be. If the sample size is reasonably large and the population from which the sample is drawn has a nearly normal distribution —a notion defined in this chapter—the nominal significance levels of the tests are close to their actual significance levels. If these conditions are not met, the significance levels of the approximate tests can differ substantially from their nominal values. The z test is based on the normal approximation ; the t test is based on Student's t curve, which approximates some probability histograms better than the normal curve does. The chapter also presents the deep connection between hypothesis tests and confidence intervals, and shows how to compute approximate confidence intervals for the population mean of nearly normal populations using Student's t -curve.

where \(\phi\) is the pooled sample percentage of the two samples. The estimate of \(SE(\phi^{t-c})\) under the null hypothesis is

\[ se = s^*\times(1/n_t + 1/n_c)^{1/2}, \]

where \(n_t\) and \(n_c\) are the sizes of the two samples. If the null hypothesis is true, the Z statistic,

\[ Z=\phi^{t-c}/se, \]

is the original test statistic \(\phi^{t-c}\) in approximately standard units , and Z has a probability histogram that is approximated well by the normal curve , which allowed us to select the rejection region for the approximate test.

This strategy—transforming a test statistic approximately to standard units under the assumption that the null hypothesisis true, and then using the normal approximation to determine the rejection region for the test—works to construct approximate hypothesis tests in many other situations, too. The resulting hypothesis test is called a z test. Suppose that we are testing a null hypothesis using a test statistic \(X\) , and the following conditions hold:

• We have a probability model for how the observations arise, assuming the null hypothesis is true. Typically, the model is that under the null hypothesis, the data are like random draws with or without replacement from a box of numbered tickets.
• Under the null hypothesis, the test statistic \(X\) , converted to standard units, has a probability histogram that can be approximated well by the normal curve.
• Under the null hypothesis, we can find the expected value of the test statistic, \(E(X)\) .
• Under the null hypothesis, either we can find the SE of the test statistic, \(SE(X)\) , or we can estimate \(SE(X)\) accurately enough to ignore the error of the estimate of the SE. Let se denote either the exact SE of \(X\) under the null hypothesis, or the estimated value of \(SE(X)\) under the null hypothesis.

Then, under the null hypothesis, the probability histogram of the Z statistic

\[ Z = (X-E(X))/se \]

is approximated well by the normal curve, and we can use the normal approximation to select the rejection region for the test using \(Z\) as the test statistic. If the null hypothesis is true,

\[ P(Z < z_a) \approx a \]

\[ P(Z > z_{1-a} ) \approx a, \]

\[ P(|Z| > z_{1-a/2} ) \approx a. \]

These three approximations yield three different z tests of the hypothesis that \(\mu = \mu_0\) at approximate significance level \(a\) :

• Reject the null hypothesis whenever \(Z (left-tail z test)
• Reject the null hypothesis whenever \(Z > z_{1-a}\) (right-tail z test)
• Reject the null hypothesis whenever \(|Z|> z_{1-a/2}\) (two-tail z test)

The word "tail" refers to the tails of the normal curve: In a left-tail test, the probability of a Type I error is approximately the area of the left tail of the normal curve, from minus infinity to \(z_a\) . In a right-tail test, the probability of a Type I error is approximately the area of the right tail of the normal curve, from \(z_{1-a}\) to infinity. In a two-tail test, the probability of a Type I error is approximately the sum of the areas of both tails of the normal curve, the left tail from minus infinity to \(z_{a/2}\) and the right tail from \(z_{1-a/2}\) to infinity. All three of these tests are called z tests. The observed value of Z is called the z score .

Which of these three tests, if any, should one use? The answer depends on the probability distribution of Z when the alternative hypothesis is true. As a rule of thumb, if, under the alternative hypothesis, \(E(Z) , use the left-tail test. If, under the alternative hypothesis, \(E(Z) > 0\) , use the right-tail test. If, under the alternative hypothesis, it is possible that \(E(Z) and it is possible that \(E(Z) > 0\) , use the two-tail test. If, under the alternative hypothesis, \(E(Z) = 0\) , consult a statistician. Generally (but not always), this rule of thumb selects the test with the most power for a given significance level.

P values for z tests

Each of the three z tests gives us a family of procedures for testing the null hypothesis at any (approximate) significance level \(a\) between 0 and 100%—we just use the appropriate quantile of the normal curve. This makes it particularly easy to find the P value for a z test. Recall that the P value is the smallest significance level for which we would reject the null hypothesis, among a family of tests of the null hypothesis at different significance levels.

Suppose the z score (the observed value of \(Z\) ) is \(x\) . In a left-tail test, the P value is the area under the normal curve to the left of \(x\) : Had we chosen the significance level \(a\) so that \(z_a=x\) , we would have rejected the null hypothesis, but we would not have rejected it for any smaller value of \(a\) , because for all smaller values of \(a\) , \(z_a . Similarly, for a right-tail z test, the P value is the area under the normal curve to the right of \(x\) : If \(x=z_{1-a}\) we would reject the null hypothesis at approximate significance level \(a\) , but not at smaller significance levels. For a two-tail z test, the P value is the sum of the area under the normal curve to the left of \(-|x|\) and the area under the normal curve to the right of \(|x|\) .

Finding P values and specifying the rejection region for the z test involves the probability distribution of \(Z\) under the assumption that the null hypothesis is true. Rarely is the alternative hypothesis sufficiently detailed to specify the probability distribution of \(Z\) completely, but often the alternative does help us choose intelligently among left-tail, right-tail, and two-tail z tests. This is perhaps the most important issue in deciding which hypothesis to take as the null hypothesis and which as the alternative: We calculate the significance level under the null hypothesis, and that calculation must be tractable.

However, to construct a z test, we need to know the expected value and SE of the test statistic under the null hypothesis. Usually it is easy to determine the expected value, but often the SE must be estimated from the data. Later in this chapter we shall see what to do if the SE cannot be estimated accurately, but the shape of the distribution of the numbers in the population is known. The next section develops z tests for the population percentage and mean, and for the difference between two population means.

Examples of z tests

The central limit theorem assures us that the probability histogram of the sample mean of random draws with replacement from a box of tickets—transformed to standard units—can be approximated increasingly well by a normal curve as the number of draws increases. In the previous section, we learned that the probability histogram of a sum or difference of independent sample means of draws with replacement also can be approximated increasingly well by a normal curve as the two sample sizes increase. We shall use these facts to derive z tests for population means and percentages and differences of population means and percentages.

z Test for a Population Percentage

Suppose we have a population of \(N\) units of which \(G\) are labeled "1" and the rest are labeled "0." Let \(p = G/N\) be the population percentage. Consider testing the null hypothesis that \(p = p_0\) against the alternative hypothesis that \(p \ne p_0\) , using a random sample of \(n\) units drawn with replacement. (We could assume instead that \(N >> n\) and allow the draws to be without replacement.)

Under the null hypothesis, the sample percentage

\[ \phi = \frac{\mbox{# tickets labeled "1" in the sample}}{n} \]

has expected value \(E(\phi) = p_0\) and standard error

\[ SE(\phi) = \sqrt{\frac{p_0 \times (1 - p_0)}{n}}. \]

Let \(Z\) be \(\phi\) transformed to standard units :

\[ Z = (\phi - p_0)/SE(\phi). \]

Provided \(n\) is large and \(p_0\) is not too close to zero or 100% (say \(n \times p > 30\) and \(n \times (1-p) > 30)\) , the probability histogram of \(Z\) will be approximated reasonably well by the normal curve, and we can use it as the Z statistic in a z test. For example, if we reject the null hypothesis when \(|Z| > 1.96\) , the significance level of the test will be about 95%.

z Test for a Population Mean

The approach in the previous subsection applies, mutatis mutandis , to testing the hypothesis that the population mean equals a given value, even when the population contains numbers other than just 0 and 1. However, in contrast to the hypothesis that the population percentage equals a given value, the null hypothesis that a more general population mean equals a given value does not specify the SD of the population, which poses difficulties that are surmountable (by approximation and estimation) if the sample size is large enough. (There are also nonparametric methods that can be used.)

Consider testing the null hypothesis that the population mean \(\mu\) is equal to a specific null value \(\mu_0\) , against the alternative hypothesis that \(\mu , on the basis of a random sample with replacement of size \(n\) . Recall that the sample mean \(M\) of \(n\) random draws with or without replacement from a box of numbered tickets is an unbiased estimator of the population mean \(\mu\) : If

\[ M = \frac{\mbox{sum of sample values}}{n}, \]

\[ E(M) = \mu = \frac{\mbox{sum of population values}}{N}, \]

where \(N\) is the size of the population. The population mean determines the expected value of the sample mean. The SE of the sample mean of a random sample with replacement is

\[ \frac{SD(\mbox{box})}{\sqrt{n}}, \]

where SD(box) is the SD of the list of all the numbers in the box, and \(n\) is the sample size. As a special case, the sample percentage \phi of \(n\) independent random draws from a 0-1 box is an unbiased estimator of the population percentage p , with SE equal to

\[ \sqrt{\frac{p\times(1-p)}{n}}. \]

In testing the null hypothesis that a population percentage \(p\) equals \(p_0\) , the null hypothesis specifies not only the expected value of the sample percentage \phi, it automatically specifies the SE of the sample percentage as well, because the SD of the values in a 0-1 box is determined by the population percentage \(p\) :

\[ SD(box) = \sqrt{p\times(1-p)}. \]

The null hypothesis thus gives us all the information we need to standardize the sample percentage under the null hypothesis. In contrast, the SD of the values in a box of tickets labeled with arbitrary numbers bears no particular relation to the mean of the values, so the null hypothesis that the population mean \(\mu\) of a box of tickets labeled with arbitrary numbers equals a specific value \(\mu_0\) determines the expected value of the sample mean, but not the standard error of the sample mean. To standardize the sample mean to construct a z test for the value of a population mean, we need to estimate the SE of the sample mean under the null hypothesis. When the sample size is large, the sample standard deviation s> is likely to be close to the SD of the population, and

\[ se=\frac{s}{\sqrt{n}} \]

is likely to be an accurate estimate of \(SE(M)\) . The central limit theorem tells us that when the sample size \(n\) is large, the probability histogram of the sample mean, converted to standard units, is approximated well by the normal curve. Under the null hypothesis,

\[ E(M) = \mu_0, \]

and thus when \(n\) is large

\[ Z = \frac{M-\mu_0}{s/\sqrt{n}} \]

has expected value zero, and its probability histogram is approximated well by the normal curve, so we can use \(Z\) as the Z statistic in a z test. If the alternative hypothesis is true, the expected value of \(Z\) could be either greater than zero or less than zero, so it is appropriate to use a two-tail z test. If the alternative hypothesis is \(\mu > \mu_0\) , then under the alternative hypothesis, the expected value of \(Z\) is greater than zero, and it is appropriate to use a right-tail z test. If the alternative hypothesis is \(\mu , then under the alternative hypothesis, the expected value of \(Z\) is less than zero, and it is appropriate to use a left-tail z test.

z Test for a Difference of Population Means

Consider the problem of testing the hypothesis that two population means are equal, using random samples from the two populations. Different sampling designs lead to different hypothesis testing procedures. In this section, we consider two kinds of random samples from the two populations: paired samples and independent samples , and construct z tests appropriate for each.

Paired Samples

Consider a population of \(N\) individuals, each of whom is labeled with two numbers. For example, the \(N\) individuals might be a group of doctors, and the two numbers that label each doctor might be the annual payments to the doctor by an HMO under the terms of the current contract and under the terms of a proposed revision of the contract. Let the two numbers associated with individual \(i\) be \(c_i\) and \(t_i\) . (Think of \(c\) as control and \(t\) as treatment . In this example, control is the current contract, and treatment is the proposed contract.) Let \(\mu_c\) be the population mean of the \(N\) values

\[ \{c_1, c_2, \ldots, c_N \}, \]

and let \(\mu_t\) be the population mean of the \(N\) values

\[ \{t_1, t_2, \ldots, t_N\}. \]

Suppose we want to test the null hypothesis that

\[ \mu = \mu_t - \mu_c = \mu_0 \]

against the alternative hypothesis that \(\mu . With \(\mu_0=\$0\) , this null hypothesis is that the average annual payment to doctors under the proposed revision would be the same as the average payment under the current contract, and the alternative is that on average doctors would be paid less under the new contract than under the current contract. With \(\mu_0=-\$5,000\) , this null hypothesis is that the proposed contract would save the HMO an average of $5,000 per doctor, compared with the current contract; the alternative is that under the proposed contract, the HMO would save even more than that. With \(\mu_0=\$1,000\) , this null hypothesis is that doctors would be paid an average of $1,000 more per year under the new contract than under the old one; the alternative hypothesis is that on average doctors would be paid less than an additional $1,000 per year under the new contract—perhaps even less than they are paid under the current contract. For the remainder of this example, we shall take \(\mu_0=\$1,000\) .

The data on which we shall base the test are observations of both \(c_i\) and \(t_i\) for a sample of \(n\) individuals chosen at random with replacement from the population of \(N\) individuals (or a simple random sample of size \(n ): We select \(n\) doctors at random from the \(N\) doctors under contract to the HMO, record the current annual payments to them, and calculate what the payments to them would be under the terms of the new contract. This is called a paired sample , because the samples from the population of control values and from the population of treatment values come in pairs: one value for control and one for treatment for each individual in the sample. Testing the hypothesis that the difference between two population means is equal to \(\mu_0\) using a paired sample is just the problem of testing the hypothesis that the population mean \(\mu\) of the set of differences

\[ d_i = t_i - c_i, \;\; i= 1, 2, \ldots, N, \]

is equal to \(\mu_0\) . Denote the \(n\) (random) observed values of \(c_i\) and \(t_i\) by \(\{C_1, C_2, \ldots, C_n\}\) and \(\{T_1, T_2, \ldots, T_n \}\) , respectively. The sample mean \(M\) of the differences between the observed values of \(t_i\) and \(c_i\) is the difference of the two sample means:

\[ M = \frac{(T_1-C_1)+(T_2-C_2) + \cdots + (T_n-C_n)}{n} = \frac{T_1+T_2+ \cdots + T_n}{n} - \frac{C_1+C_2+ \cdots + C_n}{n} \]

\[ = (\mbox{sample mean of observed values of } t_i) - (\mbox{sample mean of observed values of } c_i). \]

\(M\) is an unbiased estimator of \(\mu\) , and if n is large, the normal approximation to its probability histogram will be accurate. The SE of \(M\) is the population standard deviation of the \(N\) values \(\{d_1, d_2, \ldots, d_N\}\) , which we shall denote \(SD_d\) , divided by the square root of the sample size, \(n^{1/2}\) . Let \(sd\) denote the sample standard deviation of the \(n\) observed differences \((T_i - C_i), \;\; i=1, 2, \ldots, n\) :

\[ sd = \sqrt{\frac{(T_1-C_1-M)^2 + (T_2-C_2-M)^2 + \cdots + (T_n-C_n-M)^2}{n-1}} \]

(recall that \(M\) is the sample mean of the observed differences). If the sample size \(n\) is large, sd is very likely to be close to SD( d ), and so, under the null hypothesis,

\[ Z = \frac{M-\mu_0}{sd/n^{1/2}} \]

has expected value zero, and when \(n\) is large the probability histogram of \(Z\) can be approximated well by the normal curve. Thus we can use \(Z\) as the Z statistic in a z test of the null hypothesis that \(\mu=\mu_0\) . Under the alternative hypothesis that \(\mu (doctors on the average are paid less than an additional $1,000 per year under the new contract), the expected value of \(Z\) is less than zero, so we should use a left-tail z test. Under the alternative hypothesis \(\mu\ne\mu_0\) (on average, the difference in average annual payments to doctors is not an increase of $1,000, but some other number instead), the expected value of \(Z\) could be positive or negative, so we would use a two-tail z test. Under the alternative hypothesis that \(\mu>\mu_0\) (on average, under the new contract, doctors are paid more than an additional $1,000 per year), the expected value of \(Z\) would be greater than zero, so we should use a right-tail z test.

Independent Samples

Consider two separate populations of numbers, with population means \(\mu_t\) and \(\mu_c\) , respectively. Let \(\mu=\mu_t-\mu_c\) be the difference between the two population means. We would like to test the null hypothesis that \(\mu=\mu_0\) against the alternative hypothesis that \(\mu>0\) . For example, let \(\mu_t\) be the average annual payment by an HMO to doctors in the Los Angeles area, and let \(\mu_c\) be the average annual payment by the same HMO to doctors in the San Francisco area. Then the null hypothesis with \(\mu_0=0\) is that the HMO pays doctors in the two regions the same amount annually, on average; the alternative hypothesis is that the average annual payment by the HMO to doctors differs between the two areas. Suppose we draw a random sample of size \(n_t\) with replacement from the first population, and independently draw a random sample of size \(n_c\) with replacement from the second population. Let \(M_t\) and \(M_c\) be the sample means of the two samples, respectively, and let

\[ M = M_t - M_c \]

be the difference between the two sample means. Because the expected value of \(M_t\) is \(\mu_t\) and the expected value of \(M_c\) is \(\mu_c\) , the expected value of \(M\) is

\[ E(M) = E(M_t - M_c) = E(M_t) - E(M_c) = \mu_t - \mu_c = \mu. \]

Because the two random samples are independent , \(M_t\) and \(-M_c\) are independent random variables, and the SE of their sum is

\[ SE(M) = (SE^2(M_t) + SE^2(M_c))^{1/2}. \]

Let \(s_t\) and \(s_c\) be the sample standard deviations of the two samples, respectively. If \(n_t\) and \(n_c\) are both very large, the two sample standard deviations are likely to be close to the standard deviations of the corresponding populations, and so \(s_t/n_t^{1/2}\) is likely to be close to \(SE(M_t)\) , and \(s_c/n_c^{1/2}\) is likely to be close to \(SE(M_c)\) . Therefore, the pooled estimate of the standard error

\[ se_\mbox{diff} = ( (s_t/n_t^{1/2})^2 + (s_c/n_c^{1/2})^2)^{1/2} = \sqrt{ s_t^2/n_t + s_c^2/n_c} \]

is likely to be close to \(SE(M)\) . Under the null hypothesis, the statistic

\[ Z = \frac{M - \mu_0}{se_\mbox{diff}} = \frac{M_1 - M_2 - \mu_0}{\sqrt{ s_t^2/n_t + s_c^2/n_c}} \]

has expected value zero and its probability histogram is approximated well by the normal curve, so we can use it as the Z statistic in a z test.

Under the alternative hypothesis

\[ \mu = \mu_t - \mu_c > \mu_0, \]

the expected value of \(Z\) is greater than zero, so it is appropriate to use a right-tail z test.

If the alternative hypothesis were \(\mu \ne \mu_0\) , under the alternative the expected value of \(Z\) could be greater than zero or less than zero, so it would be appropriate to use a two-tail z test. If the alternative hypothesis were \(\mu , under the alternative the expected value of \(Z\) would be less than zero, so it would be appropriate to use a left-tail z test.

The following exercises check that you can compute the z test for a population mean or a difference of population means. The exercises are dynamic: the data will tend to change when you reload the page.

For the nominal significance level of the z test for a population mean to be approximately correct, the sample size typically must be large. When the sample size is small, two factors limit the accuracy of the z test: the normal approximation to the probability distribution of the sample mean can be poor, and the sample standard deviation can be an inaccurate estimate of the population standard deviation, so se is not an accurate estimate of the SE of the test statistic Z . For nearly normal populations , defined in the next subsection, the probability distribution of the sample mean is nearly normal even when the sample size is small, and the uncertainty of the sample standard deviation as an estimate of the population standard deviation can be accounted for by using a curve that is broader than the normal curve to approximate the probability distribution of the (approximately) standardized test statistic. The broader curve is Student's t curve . Student's t curve depends on the sample size: The smaller the sample size, the more spread out the curve.

Nearly Normally Distributed Populations

A list of numbers is nearly normally distributed if the fraction of values in any range is close to the area under the normal curve for the corresponding range of standard units—that is, if the list has mean \(\mu\) and standard deviation SD, and for every pair of values \(a < b\) ,

\[ \mbox{ the fraction of numbers in the list between } a \mbox{ and } b \approx \mbox{the area under the normal curve between } (a - \mu)/SD \mbox{ and } (b - \mu)/SD. \]

A list is nearly normally distributed if the normal curve is a good approximation to the histogram of the list transformed to standard units. The histogram of a list that is approximately normally distributed is (nearly) symmetric about some point, and is (nearly) bell-shaped.

No finite population can be exactly normally distributed, because the area under the normal curve between every two distinct values is strictly positive—no matter how large or small the values nor how close together they are. No population that contains only a finite number of distinct values can be exactly normally distributed, for the same reason. In particular, populations that contain only zeros and ones are not approximately normally distributed, so results for the sample mean of samples drawn from nearly normally distributed populations need not apply to the sample percentage of samples drawn from 0-1 boxes. Such results will be more accurate for the sample percentage when the population percentage is close to 50% than when the population percentage is close to 0% or 100%, because then the histogram of population values is more nearly symmetric.

Suppose a population is nearly normally distributed. Then a histogram of the population is approximately symmetric about the mean of the population. The fraction of numbers in the population within ±1 SD of the mean of the population is about 68%, the fraction of numbers within ±2 SD of the mean of the population is about 95%, and the fraction of numbers in the population within ±3 SD of the mean of the population is about 99.7%.

The following exercises check that you understand what it means for a list to be nearly normally distributed. The exercises are dynamic: the data tend to change when you reload the page.

Student's t -curve

Student's t curve is similar to the normal curve, but broader. It is positive, has a single maximum, and is symmetric about zero. The total area under Student's t curve is 100%. Student's t curve approximates some probability histograms more accurately than the normal curve does. There are actually infinitely many Student t curves, one for each positive integer value of the degrees of freedom. As the degrees of freedom increases, the difference between Student's t curve and the normal curve decreases.

Consider a population of \(N\) units labeled with numbers. Let \(\mu\) denote the population mean of the \(N\) numbers, and let SD denote the population standard deviation of the \(N\) numbers. Let \(M\) denote the sample mean of a random sample of size \(n\) drawn with replacement from a population, and let s> denote the sample standard deviation of the sample. The expected value of \(M\) is \(\mu\) , and the SE of \(M\) is \(SD/n^{1/2}\) . Let

\[ Z = (M - \mu)/(SD/n^{1/2}). \]

Then the expected value of \(Z\) is zero, the SE of \(Z\) is 1, and if \(n\) is large enough, the normal curve is a good approximation to the probability histogram of \(Z\) . The closer to normal the distribution of values in the population is, the smaller \(n\) needs to be for the normal curve to be a good approximation to the distribution of \(Z\) . Consider the statistic

\[ T = \frac{M - \mu}{s/n^{1/2}}, \]

which replaces SD by its estimated value (the sample standard deviation \(s\) ). If \(n\) is large enough, \(s\) is very likely to be close to SD, so \(T\) will be close to \(Z\) ; the normal curve will be a good approximation to the probability histogram of \(T\) ; and we can use \(T\) as the Z statistic in a z test of hypotheses about \(\mu\) .

For many populations, when the sample size is small—say less than 25, but the accuracy depends on the population—the normal curve is not a good approximation to the probability histogram of \(T\) . For nearly normally distributed populations, when the sample size is intermediate—say 25–100, but again this depends on the population—the normal curve is a good approximation to the probability histogram of \(Z\) , but not to the probability histogram of \(T\) , because of the variability of the sample standard deviation s> from sample to sample, which tends to broaden the probability distribution of \(T\) (i.e., to make \(SE(T)>1\) ).

When you first load this page, the degrees of freedom will be set to 25, and the region from -1.96 to 1.96 will be hilighted. The area under the normal curve between ±1.96 is 95%, but for Student's t curve with 25 degrees of freedom, the area is about 93.9%: Student's t curve with d.f.=25 is broader than the normal curve. Increase the degrees of freedom to 200; you will see that the Student t curve gets slightly narrower, and the area under the curve between ±1.96 is about 94.9%.

We define quantiles of Student t curves in the same way we defined quantiles of the normal curve: For any number a between 0 and 100%, the a quantile of Student's t curve with \(d.f.=d\) , \(t_{d,a}\) , is the unique value such that the area under the Student t curve with d degrees of freedom from minus infinity to \(t_{d,a}\) is equal to \(a\) . For example, \(t_{d,0.5} = 0\) for all values of \(d\) . Generally, the value of \(t_{d,a}\) depends on the degrees of freedom \(d\) . The probability calculator allows you to find quantiles of Student's t curve.

t test for the Mean of a Nearly Normally Distributed Population

We can use Student's t curve to construct approximate tests of hypotheses about the population mean \(\mu\) when the population standard deviation is unknown, for intermediate values of the sample size \(n\) . The approach is directly analogous to the z test, but instead of using a quantile of the normal curve, we use the corresponding quantile of Student's t curve (with the appropriate number of degrees of freedom). However, for the test to be accurate when \(n\) is small or intermediate, the distribution of values in the population must be nearly normal for the test to have approximately its nominal level. This is a somewhat bizarre restriction: It may require a very large sample to detect that the population is not nearly normal—but if the sample is very large, we can use the z test instead of the t test, so we don't need to rely as much on the assumption. It is my opinion that the t test is over-taught and overused—because its assumptions are not verifiable in the situations where it is potentially useful.

Consider testing the null hypothesis that \(\mu=\mu_0\) using the sample mean \(M\) and sample standard deviation s> of a random sample of size \(n\) drawn with replacement from a population that is known to have a nearly normal distribution. Define

\[ T = \frac{M - \mu_0}{s/n^{1/2}}. \]

Under the null hypothesis, if \(n\) is not too small, Student's t curve with \(n-1\) degrees of freedom will be an accurate approximation to the probability histogram of \(T\) , so

\[ P(T < t_{n-1,a}), \]

\[ P(T > t_{n-1,1-a}), \]

\[ P(|T| > t_{n-1,1-a/2}) \]

all are approximately equal to \(a\) . As we saw earlier in this chapter for the Z statistic, these three approximations give three tests of the null hypothesis \(\mu=\mu_0\) at approximate significance level \(a\) —a left-tail t test, a right-tail t test, and a two-tail t test:

• Reject the null hypothesis if \(T (left-tail)
• Reject the null hypothesis if \(T > t_{n-1,1-a}\) (right-tail)
• Reject the null hypothesis if \(|T| > t_{n-1,1-a/2}\) (two-tail)

To decide which t test to use, we can apply the same rule of thumb we used for the z test:

• Use a left-tail t test if, under the alternative hypothesis, the expected value of \(T\) is less than zero.
• Use a right-tail t test if, under the alternative hypothesis, the expected value of \(T\) is greater than zero.
• Use a two-tail t test if, under the alternative hypothesis, the expected value of \(T\) is not zero, but could be less than or greater than zero.
• Consult a statistician for a more appropriate test if, under the alternative hypothesis, the expected value of \(T\) is zero.

P-values for t tests are computed in much the same way as P-values for z tests. Let t be the observed value of \(T\) (the t score). In a left-tail t test, the P-value is the area under Student's t curve with \(n-1\) degrees of freedom, from minus infinity to \(t\) . In a right-tail t test, the P-value is the area under Student's t curve with \(n-1\) degrees of freedom, from \(t\) to infinity. In a two-tail t test, the P-value is the total area under Student's t curve with \(n-1\) degrees of freedom between minus infinity and \(-|t|\) and between \(|t|\) and infinity.

There are versions of the t test for comparing two means, as well. Just like for the z test, the method depends on how the samples from the two populations are drawn. For example, if the two samples are paired (if we are sampling individuals labeled with two numbers and for each individual in the sample, we observe both numbers), we may base the t test on the sample mean of the paired differences and the sample standard deviation of the paired differences. Let \(\mu_1\) and \(\mu_2\) be the means of the two populations, and let

\[ \mu = \mu_1 - \mu_2. \]

The \(T\) statistic to test the null hypothesis that \(\mu=\mu_0\) is

\[ T = \frac{(\mbox{sample mean of differences}) - \mu_0 }{(\mbox{sample standard deviation of differences})/n^{1/2}}, \]

and the appropriate curve to use to find the rejection region for the test is Student's t curve with \(n-1\) degrees of freedom, where \(n\) is the number of individuals (differences) in the sample.

Two-sample t tests for a difference of means using independent samples depend on additional assumptions, such as equality of the two population standard deviations; we shall not present such tests here. The following exercises check your ability to compute t tests. The exercises are dynamic: the data tend to change when you reload the page.

Hypothesis Tests and Confidence Intervals

There is a deep connection between hypothesis tests about parameters, and confidence intervals for parameters. If we have a procedure for constructing a level \(100\% \times (1-a)\) confidence interval for a parameter \(\mu\) , then the following rule is a two-sided significance level \(a\) test of the null hypothesis that \(\mu = \mu_0\) :

reject the null hypothesis if the confidence interval does not contain \(\mu_0\).

Similarly, suppose we have an hypothesis-testing procedure that lets us test the null hypothesis that \(\mu=\mu_0\) for any value of \(\mu_0\) , at significance level \(a\) . Define

\(A\) = (all values of \(\mu_0\) for which we would not reject the null hypothesis that \(\mu = \mu_0\)).

Then \(A\) is a \(100\% \times (1-a)\) confidence set for \(\mu\) :

\[ P( A \mbox{ contains the true value of } \mu ) = 100\% \times (1-a). \]

(A confidence set is a generalization of the idea of a confidence interval: a \(1-a\) confidence set for the parameter \(\mu\) is a random set that has probability \(1-a\) of containing \(\mu\) . As is the case with confidence intervals, the probability makes sense only before collecting the data.) The set \(A\) might or might not be an interval, depending on the nature of the test. If one starts with a two-tail z test or two-tail t test, one ends up with a confidence interval rather than a more general confidence set.

Confidence Intervals Using Student's t curve

The t test lets us test the hypothesis that the population mean \(\mu\) is equal to \(\mu_0\) at approximate significance level a using a random sample with replacement of size n from a population with a nearly normal distribution. If the sample size n is small, the actual significance level is likely to differ considerably from the nominal significance level. Consider a two-sided t test of the hypothesis \(\mu=\mu_0\) at significance level \(a\) . If the sample mean is \(M\) and the sample standard deviation is \(s\) , we would not reject the null hypothesis at significance level \(a\) if

\[ \frac{|M-\mu_0|}{s/n^{1/2}} \le t_{n-1,1-a/2}. \]

We rearrange this inequality:

\[ -t_{n-1,1-a/2} \le \frac{M-\mu_0}{s/n^{1/2}} \le t_{n-1,1-a/2} \]

\[ -t_{n-1,1-a/2} \times s/n^{1/2} \le M - \mu_0 \le t_{n-1,1-a/2} \times s/n^{1/2} \]

\[ -M - t_{n-1,1-a/2} \times s/n^{1/2} \le - \mu_0 \le -M + t_{n-1,1-a/2} \times s/n^{1/2} \]

\[ M + t_{n-1,1-a/2} \times s/n^{1/2} \le \mu_0 \le M - t_{n-1,1-a/2} \times s/n^{1/2} \]

That is, we would not reject the hypothesis \(\mu = \mu_0\) provided \(\mu_0\) is in the interval

\[ [M - t_{n-1,1-a/2} \times s/n^{1/2}, M + t_{n-1,1-a/2} \times s/n^{1/2}]. \]

Therefore, that interval is a \(100\%-a\) confidence interval for \(\mu\) :

\[ P([M - t_{n-1,1-a/2} \times s/n^{1/2}, M + t_{n-1,1-a/2} \times s/n^{1/2}] \mbox{ contains } \mu) \approx 1-a. \]

The following exercise checks that you can use Student's t curve to construct a confidence interval for a population mean. The exercise is dynamic: the data tend to change when you reload the page.

In hypothesis testing, a Z statistic is a random variable whose probability histogram is approximated well by the normal curve if the null hypothesis is correct: If the null hypothesis is true, the expected value of a Z statistic is zero, the SE of a Z statistic is approximately 1, and the probability that a Z statistic is between \(a\) and \(b\) is approximately the area under the normal curve between \(a\) and \(b\) . Suppose that the random variable \(Z\) is a Z statistic. If, under the alternative hypothesis, \(E(Z) , the appropriate z test to test the null hypothesis at approximate significance level \(a\) is the left-tailed z test: Reject the null hypothesis if \(Z , where \(z_a\) is the \(a\) quantile of the normal curve. If, under the alternative hypothesis, \(E(Z)>0\) , the appropriate z test to test the null hypothesis at approximate significance level \(a\) is the right-tailed z test: Reject the null hypothesis if \(Z>z_{1-a}\) . If, under the alternative hypothesis, \(E(Z)\ne 0 \) but could be greater than 0 or less than 0, the appropriate z test to test the null hypothesis at approximate significance level \(a\) is the two-tailed z test: reject the null hypothesis if \(|Z|>z_{1-a/2}\) . If, under the alternative hypothesis, \(E(Z)=0\) , a z test probably is not appropriate—consult a statistician. The exact significance levels of these tests differ from \(a\) by an amount that depends on how closely the normal curve approximates the probability histogram of \(Z\) .

Z statistics often are constructed from other statistics by transforming approximately to standard units, which requires knowing the expected value and SE of the original statistic on the assumption that the null hypothesis is true. Let \(X\) be a test statistic; let \(E(X)\) be the expected value of \(X\) if the null hypothesis is true, and let \(se\) be approximately equal to the SE of \(X\) if the null hypothesis is true. If \(X\) is a sample sum of a large random sample with replacement, a sample mean of a large random sample with replacement, or a sum or difference of independent sample means of large samples with replacement,

\[ Z = \frac{X-E(X)}{se} \]

is a Z statistic.

Consider testing the null hypothesis that a population percentage \(p\) is equal to the value \(p_0\) on the basis of the sample percentage \phi of a random sample of size \(n\) with replacement. Under the null hypothesis, \(E(\phi)=p_0\) and

\[ SE(\phi) = \sqrt{\frac{p_0\times(1-p_0)}{n}}, \]

and if \(n\) is sufficiently large (say \(n \times p > 30\) and \(n \times (1-p)>30\) , but this depends on the desired accuracy), the normal approximation to

\[ Z = \frac{\phi-p_0}{\sqrt{(p_0 \times (1-p_0))/n}} \]

will be reasonably accurate, so \(Z\) can be used as the Z statistic in a z test of the null hypothesis \(p=p_0\) .

Consider testing the null hypothesis that a population mean \(\mu\) is equal to the value \(\mu_0\) , on the basis of the sample mean \(M\) of a random sample of size \(n\) with replacement. Let \(s\) denote the sample standard deviation. Under the null hypothesis, \(E(M)=\mu_0\) , and if \(n\) is large,

\[ SE(M)=SD/n^{1/2} \approx s/n^{1/2}, \]

and the normal approximation to

\[ Z = \frac{M-\mu_0}{s/n^{1/2}} \]

will be reasonably accurate, so \(Z\) can be used as the Z statistic in a z test of the null hypothesis \(\mu=\mu_0\) .

Consider a population of \(N\) individuals, each labeled with two numbers. The \(i\) th individual is labeled with the numbers \(c_i\) and \(t_i\) , \(i=1, 2, \ldots, N\) . Let \(\mu_c\) be the population mean of the \(N\) values \(\{c_1, \ldots, c_N\}\) and let \(\mu_t\) be the population mean of the \(N\) values \(\{t_1, \ldots, t_N \}\) . Let \(\mu=\mu_t-\mu_c\) be the difference between the two population means. Consider testing the null hypothesis that \(\mu=\mu_0\) on the basis of a paired random sample of size \(n\) with replacement from the population: that is, a random sample of size \(n\) is drawn with replacement from the population, and for each individual \(i\) in the sample, \(c_i\) and \(t_i\) are observed. This is equivalent to testing the hypothesis that the population mean of the \(N\) values \(\{(t_1-c_1), \ldots, (t_N-c_N)\}\) is equal to \(\mu_0\) , on the basis of the random sample of size \(n\) drawn with replacement from those \(N\) values. Let \(M_t\) be the sample mean of the \(n\) observed values of \(t_i\) and let \(M_c\) be the sample mean of the \(n\) observed values of \(c_i\) . Let \(sd\) denote the sample standard deviation of the \(n\) observed differences \(\{(t_i-c_i)\}\) . Under the null hypothesis, the expected value of \(M_t-M_c\) is \(\mu_0\) , and if \(n\) is large,

\[ SE(M_t-M_c) \approx sd/n^{1/2}, \]

and the normal approximation to the probability histogram of

\[ Z = \frac{M_t-M_c-\mu_0}{sd/n^{1/2}} \]

will be reasonably accurate, so \(Z\) can be used as the Z statistic in a z test of the null hypothesis that \(\mu_t-\mu_c=\mu_0\) .

Consider testing the hypothesis that the difference ( \(\mu_t-\mu_c\) ) between two population means, \(\mu_c\) and \(\mu_t\) , is equal to \(\mu_0\) , on the basis of the difference ( \(M_t-M_c\) ) between the sample mean \(M_c\) of a random sample of size \(n_c\) with replacement from the first population and the sample mean \(M_t\) of an independent random sample of size \(n_t\) with replacement from the second population. Let \(s_c\) denote the sample standard deviation of the sample of size \(n_c\) from the first population and let \(s_t\) denote the sample standard deviation of the sample of size \(n_t\) from the second population. If the null hypothesis is true,

\[ E(M_t-M_c)=\mu_0, \]

and if \(n_c\) and \(n_t\) are both large,

\[ SE(M_t-M_c) \approx \sqrt{s_t^2/n_t + s_c^2/n_c} \]

\[ Z = \frac{M_t-M_c-\mu_0}{\sqrt{s_t^2/n_t + s_c^2/n_c}} \]

A list of numbers is nearly normally distributed if the fraction of numbers between any pair of values, \(a , is approximately equal to the area under the normal curve between \((a-\mu)/SD\) and \((b-\mu)/SD\) , where \(\mu\) is the mean of the list and SD is the standard deviation of the list.

Student's t curve with \(d\) degrees of freedom is symmetric about 0, has a single bump centered at 0, and is broader and flatter than the normal curve. The total area under Student's t curve is 1, no matter what \(d\) is; as \(d\) increases, Student's t curve gets narrower, its peak gets higher, and it becomes closer and closer to the normal curve.

Let \(M\) be the sample mean of a random sample of size \(n\) with replacement from a population with mean \(\mu\) and a nearly normal distribution, and let \(s\) be the sample standard deviation of the random sample. For moderate values of \(n\) ( \(n or so), Student's t curve approximates the probability histogram of \((M-\mu)/(s/n^{1/2})\) better than the normal curve does, which can lead to an approximate hypothesis test about \(\mu\) that is more accurate than the z test.

Consider testing the null hypothesis that the mean \(\mu\) of a population with a nearly normal distribution is equal to \(\mu_0\) from a random sample of size \(n\) with replacement. Let

\[ T=\frac{M-\mu_0}{s/n^{1/2}}, \]

where \(M\) is the sample mean and \(s\) is the sample standard deviation. The tests that reject the null hypothesis if \(T (left-tail t test), if \(T>t_{n-1,1-a}\) (right-tail t test), or if \(|T|>t_{n-1,1-a/2}\) (two-tail t test) all have approximate significance level \(a\) . How close the nominal significance level \(a\) is to the true significance level depends on the distribution of the numbers in the population, the sample size \(n\) , and \(a\) . The same rule of thumb for selecting whether to use a left, right, or two-tailed z test (or not to use a z test at all) works to select whether to use a left, right, or two-tailed t test: If, under the alternative hypothesis, \(E(T) , use a left-tail test. If, under the alternative hypothesis, \(E(T) > 0 \) , use a right-tail test. If, under the alternative hypothesis, \(E(T)\) could be less than zero or greater than zero, use a two-tail test. If, under the alternative hypothesis, \(E(T) = 0 \) , consult an expert. Because the t test differs from the z test only when the sample size is small, and from a small sample it is not possible to tell whether the population has a nearly normal distribution, the t test should be used with caution.

A \(1-a\) confidence set for a parameter \(\mu\) is like a \(1-a\) confidence interval for a parameter \(\mu\) : It is a random set of values that has probability \(1-a\) of containing the true value of \(\mu\) . The difference is that the set need not be an interval.

There is a deep duality between hypothesis tests about a parameter \(\mu\) and confidence sets for \(\mu\) . Given a procedure for constructing a \(1-a\) confidence set for \(\mu\) , the rule reject the null hypothesis that \(\mu=\mu_0\) if the confidence set does not contain \(\mu\) is a significance level \(a\) test of the null hypothesis that \(\mu=\mu_0\) . Conversely, given a family of significance level \(a\) hypothesis tests that allow one to test the hypothesis that \(\mu=\mu_0\) for any value of \(\mu_0\) , the set of all values \(\mu_0\) for which the test does not reject the null hypothesis that \(\mu=\mu_0\) is a \(1-a\) confidence set for \(\mu\) .

• alternative hypothesis
• central limit theorem
• confidence interval
• confidence set
• expected value
• independent
• independent random variable
• mutatis mutandis
• nearly normal distribution
• normal approximation
• normal curve
• null hypothesis
• pooled bootstrap estimate of the population SD
• pooled bootstrap estimate of the SE
• population mean
• population percentage
• population standard deviation
• probability
• probability distribution
• probability histogram
• random sample
• random variable
• rejection region
• sample mean
• sample percentage
• sample size
• sample standard deviation
• significance level
• simple random sample
• standard deviation (SD)
• standard error (SE)
• standard unit
• Student's t curve
• test statistic
• two-tailed test
• Type I error
• Z statistic

Introduction to Statistics and Data Analysis

6 hypothesis testing: the z-test.

We’ve all had the experience of standing at a crosswalk waiting staring at a pedestrian traffic light showing the little red man. You’re waiting for the little green man so you can cross. After a little while you’re still waiting and there aren’t any cars around. You might think ‘this light is really taking a long time’, but you continue waiting. Minutes pass and there’s still no little green man. At some point you come to the conclusion that the light is broken and you’ll never see that little green man. You cross on the little red man when it’s clear.

You may not have known this but you just conducted a hypothesis test. When you arrived at the crosswalk, you assumed that the light was functioning properly, although you will always entertain the possibility that it’s broken. In terms of hypothesis testing, your ‘null hypothesis’ is that the light is working and your ‘alternative hypothesis’ is that it’s broken. As time passes, it seems less and less likely that light is working properly. Eventually, the probability of the light working given how long you’ve been waiting becomes so low that you reject the null hypothesis in favor of the alternative hypothesis.

This sort of reasoning is the backbone of hypothesis testing and inferential statistics. It’s also the point in the course where we turn the corner from descriptive statistics to inferential statistics. Rather than describing our data in terms of means and plots, we will now start using our data to make inferences, or generalizations, about the population that our samples are drawn from. In this course we’ll focus on standard hypothesis testing where we set up a null hypothesis and determine the probability of our observed data under the assumption that the null hypothesis is true (the much maligned p-value). If this probability is small enough, then we conclude that our data suggests that the null hypothesis is false, so we reject it.

In this chapter, we’ll introduce hypothesis testing with examples from a ‘z-test’, when we’re comparing a single mean to what we’d expect from a population with known mean and standard deviation. In this case, we can convert our observed mean into a z-score for the standard normal distribution. Hence the name z-test.

It’s time to introduce the hypothesis test flow chart . It’s pretty self explanatory, even if you’re not familiar with all of these hypothesis tests. The z-test is (1) based on means, (2) with only one mean, and (3) where we know \(\sigma\) , the standard deviation of the population. Here’s how to find the z-test in the flow chart:

6.1 Women’s height example

Let’s work with the example from the end of the last chapter where we started with the fact that the heights of US women has a mean of 63 and a standard deviation of 2.5 inches. We calculated that the average height of the 122 women in Psych 315 is 64.7 inches. We then used the central limit theorem and calculated the probability of a random sample 122 heights from this population having a mean of 64.7 or greater is 2.4868996^{-14}. This is a very, very small number.

Here’s how we do it using R:

Let’s think of our sample as a random sample of UW psychology students, which is a reasonable assumption since all psychology students have to take a statistics class. What does this sample say about the psychology students that are women at UW compared to the US population? It could be that these psychology students at UW have the same mean and standard deviation as the US population, but our sample just happens to have an unusual number of tall women, but we calculated that the probability of this happening is really low. Instead, it makes more sense that the population that we’re drawing from has a mean that’s greater than the US population mean. Notice that we’re making a conclusion about the whole population of women psychology students based on our one sample.

Using the terminology of hypothesis testing, we first assumed the null hypothesis that UW women psych students have the same mean (and standard deviation) as the US population. The null hypothesis is written as:

\[ H_{0}: \mu = 63 \] In this example, our alternative hypothesis is that the mean of our population is larger than the mean of null hypothesis population. We write this as:

\[ H_{A}: \mu > 63 \]

Next, after obtaining a random sample and calculate the mean, we calculate the probability of drawing a mean this large (or larger) from the null hypothesis distribution.

If this probability is low enough, we reject the null hypothesis in favor of the alternative hypothesis. When our probability allows us to reject the null hypothesis, we say that our observed results are ‘statistically significant’.

In statistics terms, we never say we ‘accept that alternative hypothesis’ as true. All we can say is that we don’t think the null hypothesis is true. I know it’s subtle, but in science can never prove that a hypothesis is true or not. There’s always the possibility that we just happened to grab an unusual sample from the null hypothesis distribution.

6.2 The hated p<.05

The probability that we obtain our observed mean or greater given that the null hypothesis is true is called the p-value. How improbable is improbable enough to reject the null hypothesis? The p-value for our example above on women’s heights is astronomically low, so it’s clear that we should reject \(H_{0}\) .

The p-value that’s on the border of rejection is called the alpha ( \(\alpha\) ) value. We reject \(H_{0}\) when our p-value is less than \(\alpha\) .

You probably know that the most common value of alpha is \(\alpha = .05\) .

The first publication of this value dates back to Sir Ronald Fisher, in his seminal 1925 book Statistical Methods for Research Workers where he states:

“It is convenient to take this point as a limit in judging whether a deviation is considered significant or not. Deviations exceeding twice the standard deviation are thus formally regarded as significant.” (p. 47)

If you read the chapter on the normal distribution, then you should know that 95% of the area under the normal distribution lies within \(\pm\) two standard deviations of the mean. So the probability of obtaining a sample that exceeds two standard deviations from the mean (in either direction) is .05.

6.3 IQ example

Let’s do an example using IQ scores. IQ scores are normalized to have a mean of 100 and a standard deviation of 15 points. Because they’re normalized, they are a rare example of a population which has a known mean and standard deviation. In the next chapter we’ll discuss the t-test, which is used in the more common situation when we don’t know the population standard deviation.

Suppose you have the suspicion that graduate students have higher IQ’s than the general population. You have enough time to go and measure the IQ’s of 25 randomly sampled grad students and obtain a mean of 105. Is this difference between our this observed mean and 100 statistically significant using an alpha value of \(\alpha = 0.05\) ?

Here the null hypothesis is:

\[ H_{0}: \mu = 100\]

And the alternative hypothesis is:

\[ H_{A}: \mu > 100 \]

We know that the parameters for the null hypothesis are:

\[ \mu = 100 \] and \[ \sigma = 15 \]

From this, we can calculate the probability of observing our mean of 105 or higher using the central limit theorem and what we know about the normal distribution:

\[ \sigma_{\bar{x}} = \frac{\sigma_{x}}{\sqrt{n}} = \frac{15}{\sqrt{25}} = 3 \] From this, we can calculate the probability of our observed mean using R’s ‘pnorm’ function. Here’s how to do the whole thing in R.

Since our p-value of 0.0478 is (just barely) less than our chosen value of \(\alpha = 0.05\) as our criterion, we reject \(H_{0}\) for this (contrived) example and conclude that our observed mean of 105 is significantly greater than 100, so our study suggests that the average graduate student has a higher IQ than the overall population.

You should feel uncomfortable making such a hard, binary decision for such a borderline case. After all, if we had chosen our second favorite value of alpha, \(\alpha = .01\) , we would have failed to reject \(H_{0}\) . This discomfort is a primary reason why statisticians are moving away from this discrete decision making process. Later on we’ll discuss where things are going, including reporting effect sizes, and using confidence intervals.

6.4 Alpha values vs. critical values

Using R’s qnorm function, we can find the z-score for which only 5% of the area lies above:

So the probability of a randomly sampled z-score exceeding 1.644854 is less than 5%. It follows that if we convert our observed mean into z-score values, we will reject \(H_{0}\) if and only if our z-score is greater than 1.644854. This value is called the ‘critical value’ because it lies on the boundary between rejecting and failing to reject \(H_{0}\) .

In our last example, the z-score for our observed mean is:

\[ z = \frac{X-\mu}{\frac{\sigma}{\sqrt{n}}} = \frac{105 - 100}{3} = 1.67 \] Our z-score is just barely greater than the critical value of 1.644854, which makes sense because our p-value is just barely less than 0.05.

Sometimes you’ll see textbooks will compare critical values to observed scores for the decision making process in hypothesis testing. This dates back to days were computers were less available and we had to rely on tables instead. There wasn’t enough space in a book to hold complete tables which prohibited the ability to look up a p-value for any observed value. Instead only critical values for specific values of alpha were included. If you look at really old papers, you’ll see statistics reported as \(p<.05\) or \(p<.01\) instead of actual p-values for this reason.

It may help to visualize the relationship between p-values, alpha values and critical values like this:

The red shaded region is the upper 5% of the standard normal distribution which starts at the critical value of z=1.644854. This is sometimes called the ‘rejection region’. The blue vertical line is drawn at our observed value of z=1.67. You can see that the red line falls just inside the rejection region, so we Reject \(H_{0}\) !

6.5 One vs. two-tailed tests

Recall that our alternative hypothesis was to reject if our mean IQ was significantly greater than the null hypothesis mean: \(H_{A}: \mu > 100\) . This implies that the situation where \(\mu < 100\) is never even in consideration, which is weird. In science, we’re trying to understand the true state of the world. Although we have a hunch that grad student IQ’s are higher than average, there is always the possibility that they are lower than average. If our sample came up with an IQ well below 100, we’d simply fail to reject \(H_{0}\) and move on. This feels like throwing out important information.

The test we just ran is called a ‘one-tailed’ test because we only reject \(H_{0}\) if our results fall in one of the two tails of the population distribution.

Instead, it might make more sense to reject \(H_{0}\) if we get either an unusually large or small score. This means we need two critical values - one above and one below zero. At first thought you might think we just duplicate our critical value from a one-tailed test to the other side. But will double the area of the rejection region. That’s not a good thing because if \(H_{0}\) is true, there’s actually a \(2\alpha\) probability that we’ll draw a score in the rejection region.

Instead, we divide the area into two tails, each containing an area of \(\frac{\alpha}{2}\) . For \(\alpha\) = 0.05, we can find the critical value of z with qnorm:

So with a two-tailed test at \(\alpha = 0.05\) we reject \(H_{0}\) if our observed z-score is either above z = 1.96 or less than -1.96. This is that value around 2 that Sir Ronald Fischer was talking about!

Here’s what the critical regions and observed value of z looks like for our example with a two-tailed test:

You can see that splitting the area of \(\alpha = 0.05\) into two halves increased the critical value in the positive direction from 1.64 to 1.96, making it harder to reject \(H_{0}\) . For our example, this changes our decision: our observed value of z = 1.67 no longer falls into the rejection region, so now we fail to reject \(H_{0}\) .

If we now fail to reject \(H_{0}\) , what about the p-value? Remember, for a one-tailed test, p = \(\alpha\) if our observed z-score lands right on the critical value of z. The same is true for a two-tailed test. But the z-score moved so that the area above that score is \(\frac{\alpha}{2}\) . So for a two-tailed test, in order to have a p-value of \(\alpha\) when our z-score lands right on the critical value, we need to double p-value hat we’d get for a one-tailed test.

For our example, the p-value for the one tailed test was \(p=0.0478\) . So if we use a two-tailed test, our p-value is \((2)(0.0478) = 0.0956\) . This value is greater than \(\alpha\) = 0.05, which makes sense because we just showed above that we fail to reject \(H_{0}\) with a two tailed test.

Which is the right test, one-tailed or two-tailed? Ideally, as scientists, we should be agnostic about the results of our experiment. But in reality, we all know that the results are more interesting if they are statistically significant. So you can imagine that for this example, given a choice between one and two-tailed, we’d choose a one-tailed test so that we can reject \(H_{0}\) .

There are two problems with this. First, we should never adjust our choice of hypothesis test after we observe the data. That would be an example of ‘p-hacking’, a topic we’ll discuss later. Second, most statisticians these days strongly recommend against one-tailed tests. The only reason for a one-tailed test is if there is no logical or physical possibility for a population mean to fall below the null hypothesis mean.

• Search Search Please fill out this field.

What Is a Z-Test?

Understanding z-tests, one-sample z-test example.

• Z-Test FAQs

The Bottom Line

• Corporate Finance
• Financial Analysis

Z-Test Definition: Its Uses in Statistics Simply Explained With Example

James Chen, CMT is an expert trader, investment adviser, and global market strategist.

Investopedia / Julie Bang

A z-test is a statistical test used to determine whether two population means are different when the variances are known and the sample size is large. It can also be used to compare one mean to a hypothesized value.

The data must approximately fit a normal distribution , otherwise the test doesn't work. Parameters such as variance and standard deviation should be calculated for a z-test to be performed.

Key Takeaways

• A z-test is a statistical test to determine whether two population means are different or to compare one mean to a hypothesized value when the variances are known and the sample size is large.
• A z-test is a hypothesis test for data that follows a normal distribution. 
• A z-statistic, or z-score, is a number representing the result from the z-test.
• Z-tests are closely related to t-tests, but t-tests are best performed when an experiment has a small sample size.
• Z-tests assume the standard deviation is known, while t-tests assume it is unknown.

The z-test is also a hypothesis test in which the z-statistic follows a normal distribution. The z-test is best used for greater-than-30 samples because, under the central limit theorem , as the number of samples gets larger, the samples are considered to be approximately normally distributed.

When conducting a z-test, the null and alternative hypotheses, and alpha level should be stated. The z-score , also called a test statistic, should be calculated, and the results and conclusion stated. A z-statistic, or z-score, is a number representing how many standard deviations above or below the mean population a score derived from a z-test is.

Examples of tests that can be conducted as z-tests include a one-sample location test, a two-sample location test, a paired difference test, and a maximum likelihood estimate. Z-tests are closely related to t-tests, but t-tests are best performed when an experiment has a small sample size. Also, t-tests assume the standard deviation is unknown, while z-tests assume it is known. If the standard deviation of the population is unknown, the assumption of the sample variance equaling the population variance is made.

Assume an investor wishes to test whether the average daily return of a stock is greater than 3%. A simple random sample of 50 returns is calculated and has an average of 2%. Assume the standard deviation of the returns is 2.5%. Therefore, the null hypothesis is when the average, or mean, is equal to 3%.

Conversely, the alternative hypothesis is whether the mean return is greater or less than 3%. Assume an alpha of 0.05% is selected with a two-tailed test . Consequently, there is 0.025% of the samples in each tail, and the alpha has a critical value of 1.96 or -1.96. If the value of z is greater than 1.96 or less than -1.96, the null hypothesis is rejected.

The value for z is calculated by subtracting the value of the average daily return selected for the test, or 3% in this case, from the observed average of the samples. Next, divide the resulting value by the standard deviation divided by the square root of the number of observed values.

Therefore, the test statistic is:

(0.02 - 0.03) ÷ (0.025 ÷ √ 50) = -2.83

The investor rejects the null hypothesis since z is less than -1.96 and concludes that the average daily return is less than 3%.

What's the Difference Between a T-Test and Z-Test?

Z-tests are closely related to t-tests, but t-tests are best performed when the data consists of a small sample size, i.e., less than 30. Also, t-tests assume the standard deviation is unknown, while z-tests assume it is known.

When Should You Use a Z-Test?

If the standard deviation of the population is known and the sample size is greater than or equal to 30, the z-test can be used. Regardless of the sample size, if the population standard deviation is unknown, a t-test should be used instead.

What Is a Z-Score?

A z-score, or z-statistic, is a number representing how many standard deviations above or below the mean population the score derived from a z-test is. Essentially, it is a numerical measurement that describes a value's relationship to the mean of a group of values. If a z-score is 0, it indicates that the data point's score is identical to the mean score. A z-score of 1.0 would indicate a value that is one standard deviation from the mean. Z-scores may be positive or negative, with a positive value indicating the score is above the mean and a negative score indicating it is below the mean.

What Is Central Limit Theorem (CLT)?

In the study of probability theory, the central limit theorem (CLT) states that the distribution of sample approximates a normal distribution (also known as a “bell curve”) as the sample size becomes larger, assuming that all samples are identical in size, and regardless of the population distribution shape. Sample sizes equal to or greater than 30 are considered sufficient for the CLT to predict the characteristics of a population accurately. The z-test's fidelity relies on the CLT holding.

A z-test is used in hypothesis testing to evaluate whether a finding or association is statistically significant or not. In particular, it tests whether two means are the same (the null hypothesis). A z-test can only be used if the population standard deviation is known and the sample size is 30 data points or larger. Otherwise, a t-test should be employed.

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

• Prompt Library
• DS/AI Trends
• Stats Tools
• Interview Questions
• Generative AI
• Machine Learning
• Deep Learning

Z-tests for Hypothesis testing: Formula & Examples

Z-tests are statistical hypothesis testing techniques that are used to determine whether the null hypothesis relating to comparing sample means or proportions with that of population at a given significance level can be rejected or otherwise based on the z-statistics or z-score. As a data scientist , you must get a good understanding of the z-tests and its applications to test the hypothesis for your statistical models. In this blog post, we will discuss an overview of different types of z-tests and related concepts with the help of examples. You may want to check my post on hypothesis testing titled – Hypothesis testing explained with examples

Table of Contents

What are Z-tests & Z-statistics?

Z-tests can be defined as statistical hypothesis testing techniques that are used to quantify the hypothesis testing related to claim made about the population parameters such as mean and proportion. Z-test uses the sample data to test the hypothesis about the population parameters (mean or proportion). There are different types of Z-tests which are used to estimate the population mean or proportion, or, perform hypotheses testing related to samples’ means or proportions.

Different types of Z-tests 

There are following different types of Z-tests which are used to perform different types of hypothesis testing.  

• One-sample Z-test for means
• Two-sample Z-test for means
• One sample Z-test for proportion
• Two sample Z-test for proportions

Four variables are involved in the Z-test for performing hypothesis testing for different scenarios. They are as follows:

• An independent variable that is called the “sample” and assumed to be normally distributed;
• A dependent variable that is known as the test statistic (Z) and calculated based on sample data
• Different types of Z-test that can be used for performing hypothesis testing
• A significance level or “alpha” is usually set at 0.05 but can take the values such as 0.01, 0.05, 0.1

When to use Z-test – Explained with examples

The following are different scenarios when Z-test can be used:

• Compare the sample or a single group with that of the population with respect to the parameter, mean. This is called as one-sample Z-test for means. For example, whether the student of a particular school has been scoring marks in Mathematics which is statistically significant than the other schools. This can also be thought of as a hypothesis test to check whether the sample belongs to the population or otherwise.
• Compare two groups with respect to the population parameter, mean. This is called as two-samples Z-test for means. For example, you want to compare class X students from different schools and determine if students of one school are better than others based on their score of Mathematics.
• Compare hypothesized proportion of the population to that of population theoritical proportion. For example, whether the unemployment rate of a given state is different than the well-established rate for the ccountry
• Compare the proportion of one population with the proportion of othe rproportion. For example, whether the efficacy rate of vaccination in two different population are statistically significant or otherwise.

Z-test Interview Questions 

Here is a list of a few interview questions you may expect in your data scientists interview:

• What is Z-test?
• What is Z-statistics or Z-score?
• When to use Z-test vs other tests such as T-test or Chi-square test?
• What is Z-distribution?
• What is the difference between Z-distribution and T-distribution?
• What is sampling distribution?
• What are different types of Z-tests?
• Explain different types of Z-tests with the help of real-world examples?
• What’s the difference two samples Z-test for means and two-samples Z-test for proportions? Explain with one example each.
• As data scientists, give some scenarios when you would like to use Z-test when building machine learning models?

Recent Posts

• Feature Selection vs Feature Extraction: Machine Learning - May 2, 2024
• Model Selection by Evaluating Bias & Variance: Example - May 2, 2024
• Bias-Variance Trade-off in Machine Learning: Examples - May 1, 2024

Ajitesh Kumar

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

• Search for:
• Excellence Awaits: IITs, NITs & IIITs Journey

ChatGPT Prompts (250+)

• Generate Design Ideas for App
• Expand Feature Set of App
• Create a User Journey Map for App
• Generate Visual Design Ideas for App
• Generate a List of Competitors for App
• Feature Selection vs Feature Extraction: Machine Learning
• Model Selection by Evaluating Bias & Variance: Example
• Bias-Variance Trade-off in Machine Learning: Examples
• Mean Squared Error vs Cross Entropy Loss Function
• Cross Entropy Loss Explained with Python Examples

Data Science / AI Trends

• • Prepend any arxiv.org link with talk2 to load the paper into a responsive chat application
• • Custom LLM and AI Agents (RAG) On Structured + Unstructured Data - AI Brain For Your Organization
• • Guides, papers, lecture, notebooks and resources for prompt engineering
• • Common tricks to make LLMs efficient and stable
• • Machine learning in finance

Free Online Tools

• Create Scatter Plots Online for your Excel Data
• Histogram / Frequency Distribution Creation Tool
• Online Pie Chart Maker Tool
• Z-test vs T-test Decision Tool
• Independent samples t-test calculator

Recent Comments

I found it very helpful. However the differences are not too understandable for me

Very Nice Explaination. Thankyiu very much,

in your case E respresent Member or Oraganization which include on e or more peers?

Such a informative post. Keep it up

Thank you....for your support. you given a good solution for me.

• Practice Mathematical Algorithm
• Mathematical Algorithms
• Pythagorean Triplet
• Fibonacci Number
• Euclidean Algorithm
• LCM of Array
• GCD of Array
• Binomial Coefficient
• Catalan Numbers
• Sieve of Eratosthenes
• Euler Totient Function
• Modular Exponentiation
• Modular Multiplicative Inverse
• Stein's Algorithm
• Juggler Sequence
• Chinese Remainder Theorem
• Quiz on Fibonacci Numbers
• Machine Learning Mathematics

Linear Algebra and Matrix

• Scalar and Vector
• Python Program to Add Two Matrices
• Python program to multiply two matrices
• Vector Operations
• Product of Vectors
• Scalar Product of Vectors
• Dot and Cross Products on Vectors
• Transpose a matrix in Single line in Python
• Transpose of a Matrix
• Adjoint and Inverse of a Matrix
• How to inverse a matrix using NumPy
• Determinant of a Matrix
• Program to find Normal and Trace of a matrix
• Data Science | Solving Linear Equations
• Data Science - Solving Linear Equations with Python
• System of Linear Equations
• System of Linear Equations in three variables using Cramer's Rule
• Eigenvalues
• Applications of Eigenvalues and Eigenvectors
• How to compute the eigenvalues and right eigenvectors of a given square array using NumPY?

Statistics for Machine Learning

• Descriptive Statistic
• Measures of Central Tendency
• Measures of Dispersion | Types, Formula and Examples
• Mean, Variance and Standard Deviation
• Calculate the average, variance and standard deviation in Python using NumPy
• Random Variables
• Difference between Parametric and Non-Parametric Methods
• Probability Distribution
• Confidence Interval
• Mathematics | Covariance and Correlation
• Program to find correlation coefficient
• Robust Correlation
• Normal Probability Plot
• Quantile Quantile plots
• True Error vs Sample Error
• Bias-Variance Trade Off - Machine Learning
• Understanding Hypothesis Testing
• Paired T-Test - A Detailed Overview
• P-value in Machine Learning
• F-Test in Statistics
• Residual Leverage Plot (Regression Diagnostic)
• Difference between Null and Alternate Hypothesis
• Mann and Whitney U test
• Wilcoxon Signed Rank Test
• Kruskal Wallis Test
• Friedman Test
• Mathematics | Probability

Probability and Probability Distributions

• Mathematics - Law of Total Probability
• Bayes's Theorem for Conditional Probability
• Mathematics | Probability Distributions Set 1 (Uniform Distribution)
• Mathematics | Probability Distributions Set 4 (Binomial Distribution)
• Mathematics | Probability Distributions Set 5 (Poisson Distribution)
• Uniform Distribution Formula
• Mathematics | Probability Distributions Set 2 (Exponential Distribution)
• Mathematics | Probability Distributions Set 3 (Normal Distribution)
• Mathematics | Beta Distribution Model
• Gamma Distribution Model in Mathematics
• Chi-Square Test for Feature Selection - Mathematical Explanation
• Student's t-distribution in Statistics
• Python - Central Limit Theorem
• Mathematics | Limits, Continuity and Differentiability
• Implicit Differentiation

Calculus for Machine Learning

• Engineering Mathematics - Partial Derivatives
• Advanced Differentiation
• How to find Gradient of a Function using Python?
• Optimization techniques for Gradient Descent
• Higher Order Derivatives
• Taylor Series
• Application of Derivative - Maxima and Minima | Mathematics
• Absolute Minima and Maxima
• Optimization for Data Science
• Unconstrained Multivariate Optimization
• Lagrange Multipliers
• Lagrange's Interpolation
• Linear Regression in Machine learning
• Ordinary Least Squares (OLS) using statsmodels

Regression in Machine Learning

Different tests are used in statistics to compare distinct samples or groups and make conclusions about populations. These tests, also referred to as statistical tests, concentrate on examining the probability or possibility of acquiring the observed data under particular premises or hypotheses. They offer a framework for evaluating the evidence for or against a given hypothesis. 

A statistical test starts with the formulation of a null hypothesis (H0) and an alternative hypothesis (Ha). The alternative hypothesis proposes a particular link or effect, whereas the null hypothesis reflects the default assumption and often states no effect or no difference.

The p-value indicates the likelihood of observing the data or more extreme results assuming the null hypothesis is true. Researchers compare the calculated p-value to a predetermined significance level, often denoted as α, to make a decision regarding the null hypothesis. If the p-value is smaller than α, the results are considered statistically significant, leading to the rejection of the null hypothesis in favor of the alternative hypothesis.

The p-value is calculated using a variety of statistical tests, including the Z-test, T-test , Chi-squared test , ANOVA , Z-test , and F-test , among others. In this article, we will focus on explaining the Z-test.

What is Z-Test?

Z-test is a statistical test that is used to determine whether the mean of a sample is significantly different from a known population mean when the population standard deviation is known. It is particularly useful when the sample size is large (>30).

Z-test can also be defined as a statistical method that is used to determine whether the distribution of the test statistics can be approximated using the normal distribution or not. It is the method to determine whether two sample means are approximately the same or different when their variance is known and the sample size is large (should be >= 30).

The Z-test compares the difference between the sample mean and the population means by considering the standard deviation of the sampling distribution. The resulting Z-score represents the number of standard deviations that the sample mean deviates from the population mean. This Z-Score is also known as Z-Statistics, and can be formulated as:

The average family annual income in India is 200k, with a standard deviation of 5k, and the average family annual income in Delhi is 300k.

Then Z-Score for Delhi will be.

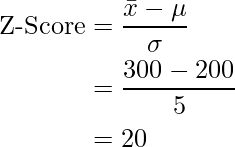
This indicates that the average family’s annual income in Delhi is 20 standard deviations above the mean of the population (India).

When to Use Z-test:

• The sample size should be greater than 30. Otherwise, we should use the t-test.
• Samples should be drawn at random from the population.
• The standard deviation of the population should be known.
• Samples that are drawn from the population should be independent of each other.
• The data should be normally distributed , however, for a large sample size, it is assumed to have a normal distribution because central limit theorem

Hypothesis Testing

A hypothesis is an educated guess/claim about a particular property of an object. Hypothesis testing is a way to validate the claim of an experiment.

• Null Hypothesis: The null hypothesis is a statement that the value of a population parameter (such as proportion, mean, or standard deviation) is equal to some claimed value. We either reject or fail to reject the null hypothesis. The null hypothesis is denoted by H 0 .
• Alternate Hypothesis: The alternative hypothesis is the statement that the parameter has a value that is different from the claimed value. It is denoted by H A .

Level of significance: It means the degree of significance in which we accept or reject the null hypothesis. Since in most of the experiments 100% accuracy is not possible for accepting or rejecting a hypothesis, we, therefore, select a level of significance. It is denoted by alpha (∝).

Steps to perform Z-test:

• First, identify the null and alternate hypotheses.
• Determine the level of significance (∝).
• Find the critical value of z in the z-test using

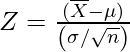
• n: sample size.
• Now compare with the hypothesis and decide whether to reject or not reject the null hypothesis

Type of Z-test

• Left-tailed Test: In this test, our region of rejection is located to the extreme left of the distribution. Here our null hypothesis is that the claimed value is less than or equal to the mean population value.

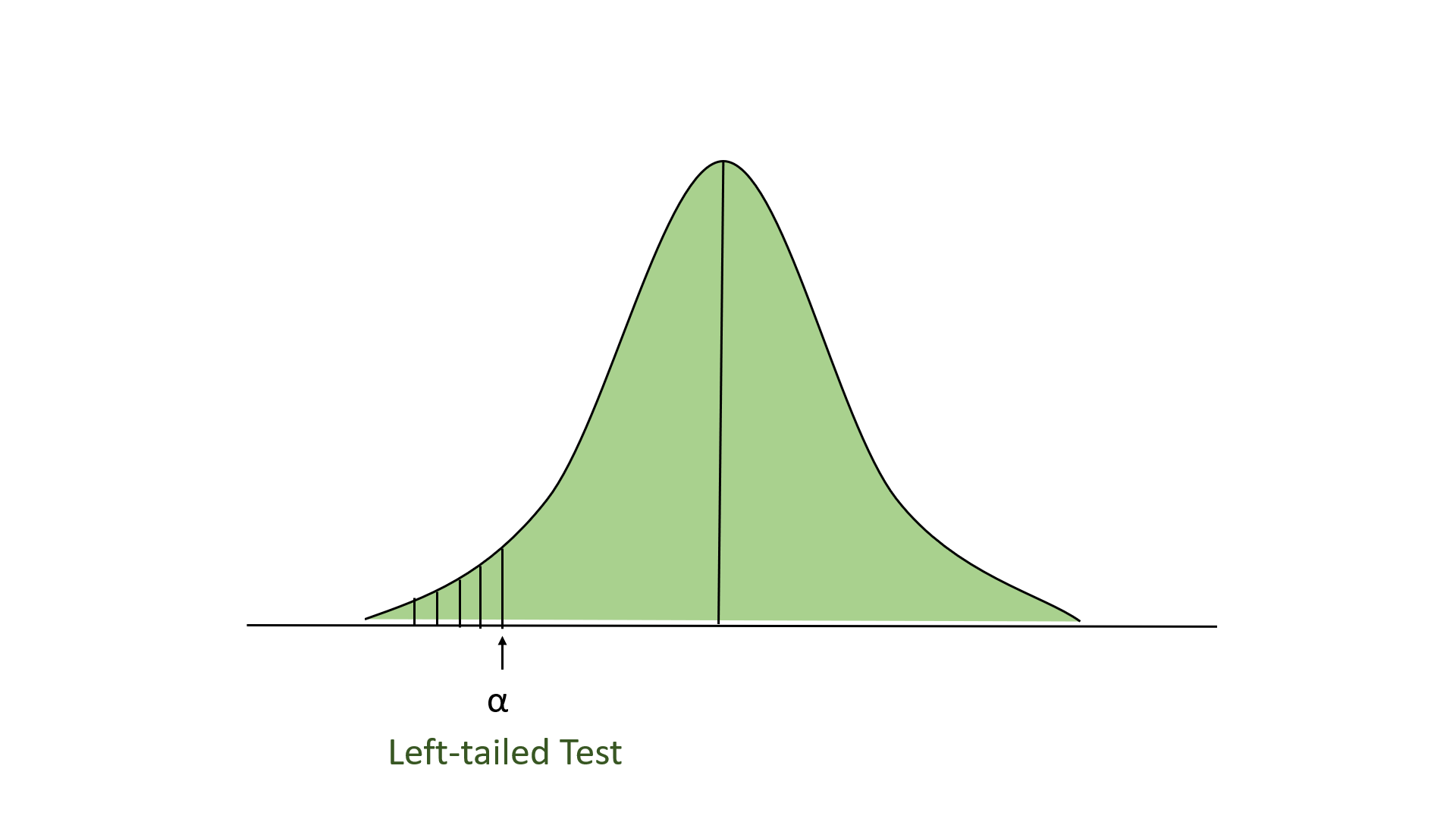
• Right-tailed Test: In this test, our region of rejection is located to the extreme right of the distribution. Here our null hypothesis is that the claimed value is less than or equal to the mean population value.

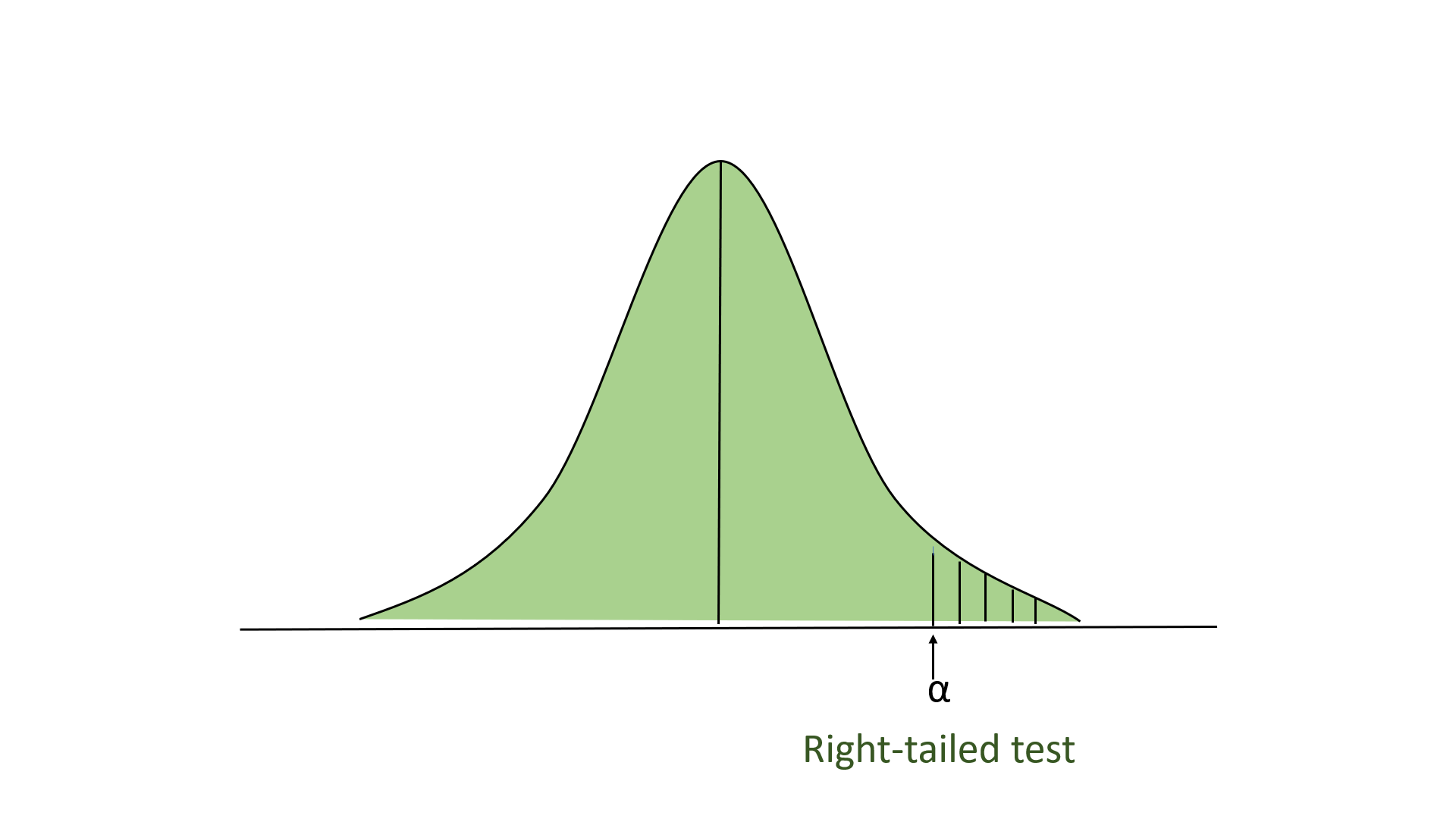
• Two-tailed test: In this test, our region of rejection is located to both extremes of the distribution. Here our null hypothesis is that the claimed value is equal to the mean population value.

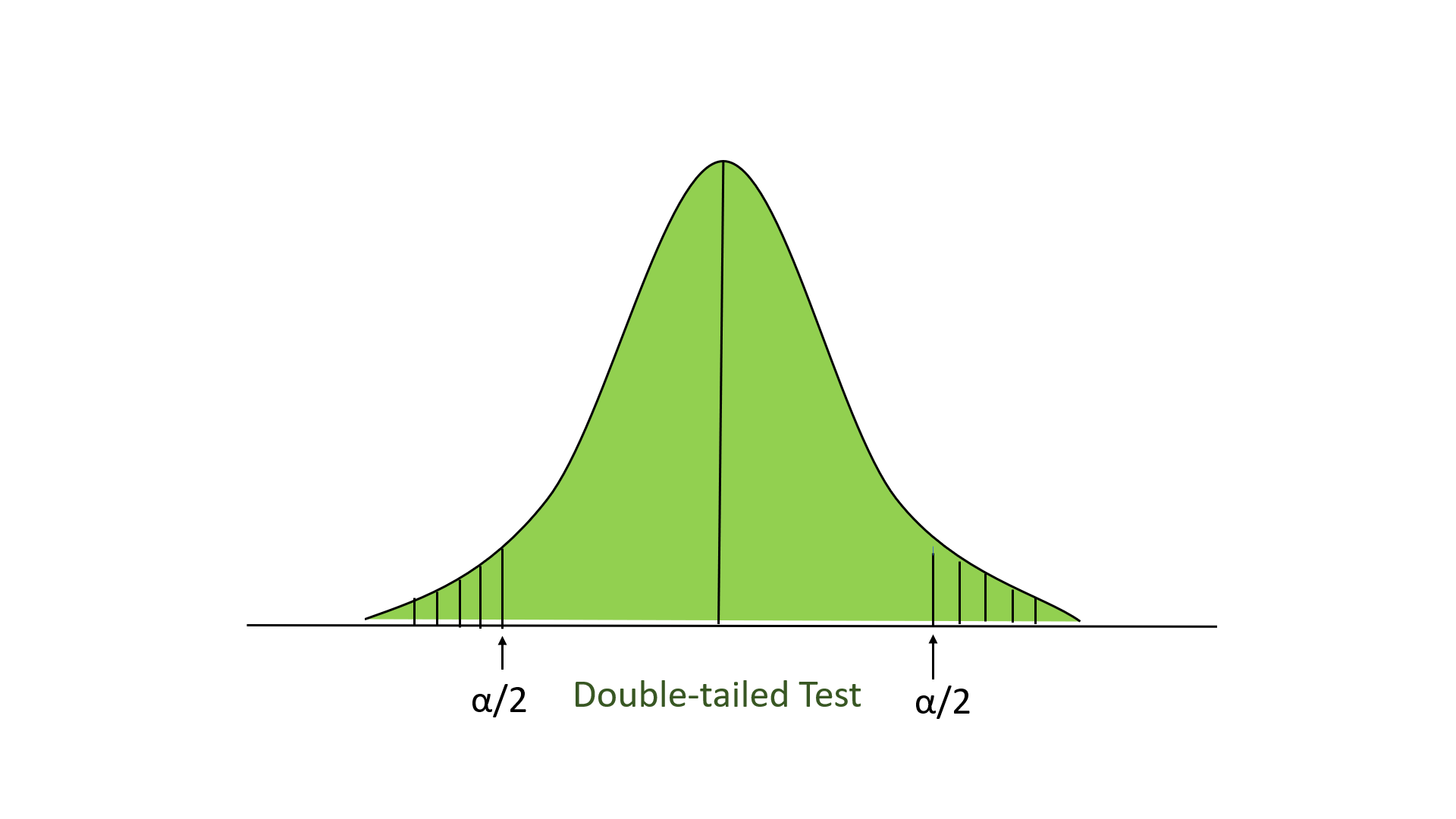
Below is an example of performing the z-test:

Example One-Tailed Test:

 A school claimed that the students who study that are more intelligent than the average school. On calculating the IQ scores of 50 students, the average turns out to be 110. The mean of the population IQ is 100 and the standard deviation is 15. State whether the claim of the principal is right or not at a 5% significance level.

• Now, we look up to the z-table. For the value of ∝=0.05, the z-score for the right-tailed test is 1.645.
• Here 4.71 >1.645, so we reject the null hypothesis. 
• If the z-test statistics are less than the z-score, then we will not reject the null hypothesis.

Code Implementations

Two-sampled z-test:.

In this test, we have provided 2 normally distributed and independent populations, and we have drawn samples at random from both populations. Here, we consider u 1 and u 2 to be the population mean, and X 1 and X 2 to be the observed sample mean. Here, our null hypothesis could be like this:

and alternative hypothesis

and the formula for calculating the z-test score:

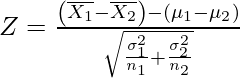
There are two groups of students preparing for a competition: Group A and Group B. Group A has studied offline classes, while Group B has studied online classes. After the examination, the score of each student comes. Now we want to determine whether the online or offline classes are better.

Group A: Sample size = 50, Sample mean = 75, Sample standard deviation = 10 Group B: Sample size = 60, Sample mean = 80, Sample standard deviation = 12

Assuming a 5% significance level, perform a two-sample z-test to determine if there is a significant difference between the online and offline classes.

Step 1: Null & Alternate Hypothesis

Step 2: Significance Label

Step 3: Z-Score

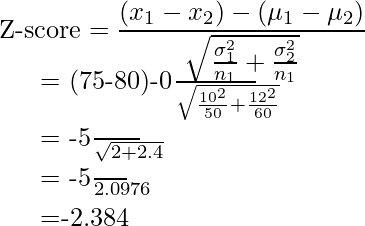
Step 4: Check to Critical Z-Score value in the Z-Table for apha/2 = 0.025

•  Critical Z-Score = 1.96

Step 5: Compare with the absolute Z-Score value

• absolute(Z-Score) > Critical Z-Score
• Reject the null hypothesis. There is a significant difference between the online and offline classes.

Type 1 error and Type II error:

• Type I error: Type 1 error has occurred when we reject the null hypothesis, even when the hypothesis is true. This error is denoted by alpha.
• Type II error: Type II error occurred when we didn’t reject the null hypothesis, even when the hypothesis is false. This error is denoted by beta.

Please Login to comment...

Similar reads.

• Engineering Mathematics
• Machine Learning
• Mathematical

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

• z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
• t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
• \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

• One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
• Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

• One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
• Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

\(H_{0}\): The population parameter is ≤ some value

\(H_{1}\): The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

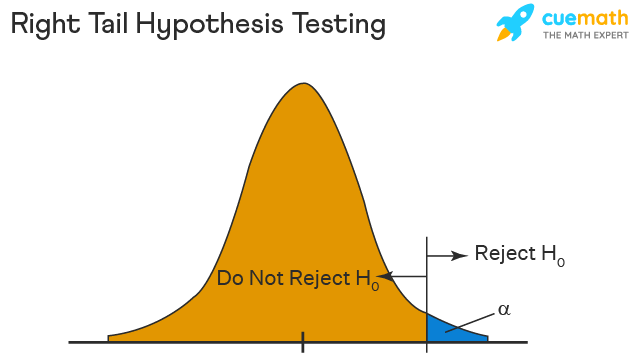
Left Tailed Hypothesis Testing

The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

\(H_{0}\): The population parameter is ≥ some value

\(H_{1}\): The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

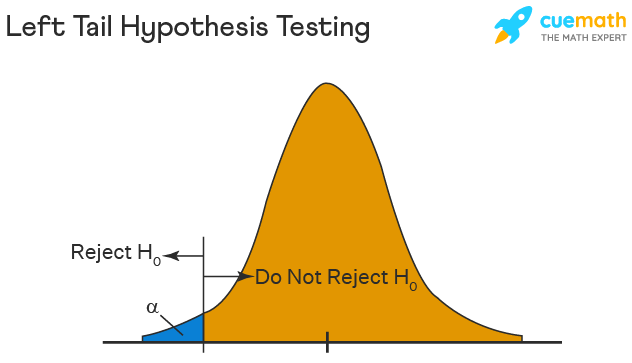
Two Tailed Hypothesis Testing

In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

\(H_{0}\): the population parameter = some value

\(H_{1}\): the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

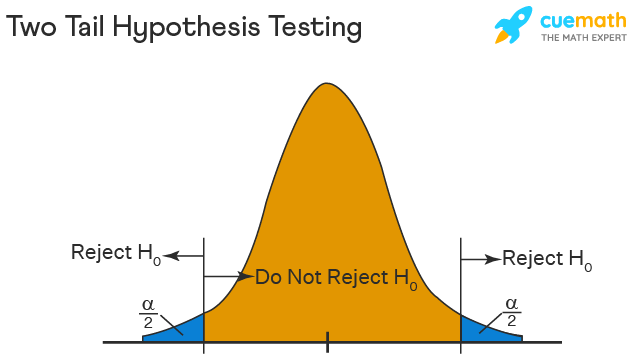
Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

• Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
• Step 2: Set up the alternative hypothesis.
• Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
• Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
• Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.

Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.

Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.

1 - \(\alpha\) = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).

\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15

z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Related Articles:

• Probability and Statistics
• Data Handling

Important Notes on Hypothesis Testing

• Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
• It involves the setting up of a null hypothesis and an alternate hypothesis.
• There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
• Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

• Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
• Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
• Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.

Statistics Made Easy

Two Sample Z-Test: Definition, Formula, and Example

A  two sample z-test is used to test whether two population means are equal.

This test assumes that the standard deviation of each population is known.

This tutorial explains the following:

• The formula to perform a two sample z-test.
• The assumptions of a two sample z-test.
• An example of how to perform a two sample z-test.

Let’s jump in!

Two Sample Z-Test: Formula

A two sample z-test uses the following null and alternative hypotheses:

• H 0 :  μ 1 = μ 2 (the two population means are equal)
• H A :  μ 1 ≠ μ 2 (the two population means are not equal)

We use the following formula to calculate the z test statistic:

• z = ( x 1 – x 2 ) / √ σ 1 2 /n 1 + σ 2 2 /n 2 )
• x 1 , x 2 : sample means
• σ 1 , σ 2 : population standard deviations
• n 1 , n 2 : sample sizes

If the p-value that corresponds to the z test statistic is less than your chosen significance level (common choices are 0.10, 0.05, and 0.01) then you can reject the null hypothesis .

Two Sample Z-Test: Assumptions

For the results of a two sample z-test to be valid, the following assumptions should be met:

• The data from each population are continuous (not discrete).
• Each sample is a simple random sample from the population of interest.
• The data in each population is approximately normally distributed .
• The population standard deviations are known.

Two Sample Z-Test : Example

Suppose the IQ levels among individuals in two different cities are known to be normally distributed each with population standard deviations of 15.

A scientist wants to know if the mean IQ level between individuals in city A and city B are different, so she selects a simple random sample of  20 individuals from each city and records their IQ levels.

To test this, she will perform a two sample z-test at significance level α = 0.05 using the following steps:

Step 1: Gather the sample data.

Suppose she collects two simple random samples with the following information:

•   x 1  (sample 1 mean IQ) = 100.65
• n 1 (sample 1 size) = 20
• x 2 (sample 2 mean IQ) = 108.8
• n 2 (sample 2 size) = 20

Step 2: Define the hypotheses.

She will perform the two sample z-test with the following hypotheses:

Step 3: Calculate the z test statistic.

The z test statistic is calculated as:

• z = (100.65-108.8) / √ 15 2 /20 + 15 2 /20)

Step 4: Calculate the p-value of the z test statistic.

According to the Z Score to P Value Calculator , the two-tailed p-value associated with z = -1.718 is 0.0858 .

Step 5: Draw a conclusion.

Since the p-value (0.0858) is not less than the significance level (.05), the scientist will fail to reject the null hypothesis.

There is not sufficient evidence to say that the mean IQ level is different between the two populations.

Note:  You can also perform this entire two sample z-test by using the Two Sample Z-Test Calculator .

Additional Resources

The following tutorials explain how to perform a two sample z-test using different statistical software:

How to Perform Z-Tests in Excel How to Perform Z-Tests in R How to Perform Z-Tests in Python

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

One Reply to “Two Sample Z-Test: Definition, Formula, and Example”

I’m a 200 Level Statistics Student. And this has really helped me.

God bless you Soo much.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *