null hypothesis examples in business

• Business Essentials
• Leadership & Management
• Credential of Leadership, Impact, and Management in Business (CLIMB)
• Entrepreneurship & Innovation
• Digital Transformation
• Finance & Accounting
• Business in Society
• For Organizations
• Support Portal
• Media Coverage
• Founding Donors
• Leadership Team

• Harvard Business School →
• HBS Online →
• Business Insights →

Business Insights

Harvard Business School Online's Business Insights Blog provides the career insights you need to achieve your goals and gain confidence in your business skills.

• Career Development
• Communication
• Decision-Making
• Earning Your MBA
• Negotiation
• News & Events
• Productivity
• Staff Spotlight
• Student Profiles
• Work-Life Balance
• AI Essentials for Business
• Alternative Investments
• Business Analytics
• Business Strategy
• Business and Climate Change
• Design Thinking and Innovation
• Digital Marketing Strategy
• Disruptive Strategy
• Economics for Managers
• Entrepreneurship Essentials
• Financial Accounting
• Global Business
• Launching Tech Ventures
• Leadership Principles
• Leadership, Ethics, and Corporate Accountability
• Leading with Finance
• Management Essentials
• Negotiation Mastery
• Organizational Leadership
• Power and Influence for Positive Impact
• Strategy Execution
• Sustainable Business Strategy
• Sustainable Investing
• Winning with Digital Platforms

A Beginner’s Guide to Hypothesis Testing in Business

• 30 Mar 2021

Becoming a more data-driven decision-maker can bring several benefits to your organization, enabling you to identify new opportunities to pursue and threats to abate. Rather than allowing subjective thinking to guide your business strategy, backing your decisions with data can empower your company to become more innovative and, ultimately, profitable.

If you’re new to data-driven decision-making, you might be wondering how data translates into business strategy. The answer lies in generating a hypothesis and verifying or rejecting it based on what various forms of data tell you.

Below is a look at hypothesis testing and the role it plays in helping businesses become more data-driven.

Access your free e-book today.

What Is Hypothesis Testing?

To understand what hypothesis testing is, it’s important first to understand what a hypothesis is.

A hypothesis or hypothesis statement seeks to explain why something has happened, or what might happen, under certain conditions. It can also be used to understand how different variables relate to each other. Hypotheses are often written as if-then statements; for example, “If this happens, then this will happen.”

Hypothesis testing , then, is a statistical means of testing an assumption stated in a hypothesis. While the specific methodology leveraged depends on the nature of the hypothesis and data available, hypothesis testing typically uses sample data to extrapolate insights about a larger population.

Hypothesis Testing in Business

When it comes to data-driven decision-making, there’s a certain amount of risk that can mislead a professional. This could be due to flawed thinking or observations, incomplete or inaccurate data , or the presence of unknown variables. The danger in this is that, if major strategic decisions are made based on flawed insights, it can lead to wasted resources, missed opportunities, and catastrophic outcomes.

The real value of hypothesis testing in business is that it allows professionals to test their theories and assumptions before putting them into action. This essentially allows an organization to verify its analysis is correct before committing resources to implement a broader strategy.

As one example, consider a company that wishes to launch a new marketing campaign to revitalize sales during a slow period. Doing so could be an incredibly expensive endeavor, depending on the campaign’s size and complexity. The company, therefore, may wish to test the campaign on a smaller scale to understand how it will perform.

In this example, the hypothesis that’s being tested would fall along the lines of: “If the company launches a new marketing campaign, then it will translate into an increase in sales.” It may even be possible to quantify how much of a lift in sales the company expects to see from the effort. Pending the results of the pilot campaign, the business would then know whether it makes sense to roll it out more broadly.

Related: 9 Fundamental Data Science Skills for Business Professionals

Key Considerations for Hypothesis Testing

1. alternative hypothesis and null hypothesis.

In hypothesis testing, the hypothesis that’s being tested is known as the alternative hypothesis . Often, it’s expressed as a correlation or statistical relationship between variables. The null hypothesis , on the other hand, is a statement that’s meant to show there’s no statistical relationship between the variables being tested. It’s typically the exact opposite of whatever is stated in the alternative hypothesis.

For example, consider a company’s leadership team that historically and reliably sees $12 million in monthly revenue. They want to understand if reducing the price of their services will attract more customers and, in turn, increase revenue.

In this case, the alternative hypothesis may take the form of a statement such as: “If we reduce the price of our flagship service by five percent, then we’ll see an increase in sales and realize revenues greater than $12 million in the next month.”

The null hypothesis, on the other hand, would indicate that revenues wouldn’t increase from the base of $12 million, or might even decrease.

Check out the video below about the difference between an alternative and a null hypothesis, and subscribe to our YouTube channel for more explainer content.

2. Significance Level and P-Value

Statistically speaking, if you were to run the same scenario 100 times, you’d likely receive somewhat different results each time. If you were to plot these results in a distribution plot, you’d see the most likely outcome is at the tallest point in the graph, with less likely outcomes falling to the right and left of that point.

With this in mind, imagine you’ve completed your hypothesis test and have your results, which indicate there may be a correlation between the variables you were testing. To understand your results' significance, you’ll need to identify a p-value for the test, which helps note how confident you are in the test results.

In statistics, the p-value depicts the probability that, assuming the null hypothesis is correct, you might still observe results that are at least as extreme as the results of your hypothesis test. The smaller the p-value, the more likely the alternative hypothesis is correct, and the greater the significance of your results.

3. One-Sided vs. Two-Sided Testing

When it’s time to test your hypothesis, it’s important to leverage the correct testing method. The two most common hypothesis testing methods are one-sided and two-sided tests , or one-tailed and two-tailed tests, respectively.

Typically, you’d leverage a one-sided test when you have a strong conviction about the direction of change you expect to see due to your hypothesis test. You’d leverage a two-sided test when you’re less confident in the direction of change.

4. Sampling

To perform hypothesis testing in the first place, you need to collect a sample of data to be analyzed. Depending on the question you’re seeking to answer or investigate, you might collect samples through surveys, observational studies, or experiments.

A survey involves asking a series of questions to a random population sample and recording self-reported responses.

Observational studies involve a researcher observing a sample population and collecting data as it occurs naturally, without intervention.

Finally, an experiment involves dividing a sample into multiple groups, one of which acts as the control group. For each non-control group, the variable being studied is manipulated to determine how the data collected differs from that of the control group.

Learn How to Perform Hypothesis Testing

Hypothesis testing is a complex process involving different moving pieces that can allow an organization to effectively leverage its data and inform strategic decisions.

If you’re interested in better understanding hypothesis testing and the role it can play within your organization, one option is to complete a course that focuses on the process. Doing so can lay the statistical and analytical foundation you need to succeed.

Do you want to learn more about hypothesis testing? Explore Business Analytics —one of our online business essentials courses —and download our Beginner’s Guide to Data & Analytics .

About the Author

Null Hypothesis Examples

ThoughtCo / Hilary Allison

• Scientific Method
• Chemical Laws
• Periodic Table
• Projects & Experiments
• Biochemistry
• Physical Chemistry
• Medical Chemistry
• Chemistry In Everyday Life
• Famous Chemists
• Activities for Kids
• Abbreviations & Acronyms
• Weather & Climate
• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

In statistical analysis, the null hypothesis assumes there is no meaningful relationship between two variables. Testing the null hypothesis can tell you whether your results are due to the effect of manipulating ​a dependent variable or due to chance. It's often used in conjunction with an alternative hypothesis, which assumes there is, in fact, a relationship between two variables.

The null hypothesis is among the easiest hypothesis to test using statistical analysis, making it perhaps the most valuable hypothesis for the scientific method. By evaluating a null hypothesis in addition to another hypothesis, researchers can support their conclusions with a higher level of confidence. Below are examples of how you might formulate a null hypothesis to fit certain questions.

What Is the Null Hypothesis?

The null hypothesis states there is no relationship between the measured phenomenon (the dependent variable ) and the independent variable , which is the variable an experimenter typically controls or changes. You do not​ need to believe that the null hypothesis is true to test it. On the contrary, you will likely suspect there is a relationship between a set of variables. One way to prove that this is the case is to reject the null hypothesis. Rejecting a hypothesis does not mean an experiment was "bad" or that it didn't produce results. In fact, it is often one of the first steps toward further inquiry.

To distinguish it from other hypotheses , the null hypothesis is written as ​ H 0  (which is read as “H-nought,” "H-null," or "H-zero"). A significance test is used to determine the likelihood that the results supporting the null hypothesis are not due to chance. A confidence level of 95% or 99% is common. Keep in mind, even if the confidence level is high, there is still a small chance the null hypothesis is not true, perhaps because the experimenter did not account for a critical factor or because of chance. This is one reason why it's important to repeat experiments.

Examples of the Null Hypothesis

To write a null hypothesis, first start by asking a question. Rephrase that question in a form that assumes no relationship between the variables. In other words, assume a treatment has no effect. Write your hypothesis in a way that reflects this.

Other Types of Hypotheses

In addition to the null hypothesis, the alternative hypothesis is also a staple in traditional significance tests . It's essentially the opposite of the null hypothesis because it assumes the claim in question is true. For the first item in the table above, for example, an alternative hypothesis might be "Age does have an effect on mathematical ability."

Key Takeaways

• In hypothesis testing, the null hypothesis assumes no relationship between two variables, providing a baseline for statistical analysis.
• Rejecting the null hypothesis suggests there is evidence of a relationship between variables.
• By formulating a null hypothesis, researchers can systematically test assumptions and draw more reliable conclusions from their experiments.
• What 'Fail to Reject' Means in a Hypothesis Test
• What Is a Hypothesis? (Science)
• Null Hypothesis Definition and Examples
• What Are the Elements of a Good Hypothesis?
• Scientific Method Vocabulary Terms
• Definition of a Hypothesis
• Six Steps of the Scientific Method
• What Is the Difference Between Alpha and P-Values?
• Hypothesis Test for the Difference of Two Population Proportions
• Understanding Simple vs Controlled Experiments
• Null Hypothesis and Alternative Hypothesis
• What Are Examples of a Hypothesis?
• What It Means When a Variable Is Spurious
• Hypothesis Test Example
• How to Conduct a Hypothesis Test
• What Is a P-Value?

Hypothesis Testing in Business Analytics – A Beginner’s Guide

Introduction  

Organizations must understand how their decisions can impact the business in this data-driven age. Hypothesis testing enables organizations to analyze and examine their decisions’ causes and effects before making important management decisions. Based on research by the Harvard Business School Online, prior to making any decision, organizations like to explore the advantages of hypothesis testing and the investigation of decisions in a proper “laboratory” setting. By performing such tests, organizations can be more confident with their decisions. Read on to learn all about hypothesis testing , o ne of the essential concepts in Business Analytics.  

What Is Hypothesis Testing?  

To learn about hypothesis testing, it is crucial that you first understand what the term hypothesis is.   

A hypothesis statement or hypothesis tries to explain why something happened or what may happen under specific conditions. A hypothesis can also help understand how various variables are connected to each other. These are generally compiled as if-then statements; for example, “If something specific were to happen, then a specific condition will come true and vice versa.” Thus, the hypothesis is an arithmetical method of testing a hypothesis or an assumption that has been stated in the hypothesis.  

Turning into a decision-maker who is driven by data can add several advantages to an organization, such as allowing one to recognize new opportunities to follow and reducing the number of threats. In analytics, a hypothesis is nothing but an assumption or a supposition made about a specific population parameter, such as any measurement or quantity about the population that is set and that can be used as a value to the distribution variable. General examples of parameters used in hypothesis testing are variance and mean. In simpler words, hypothesis testing in business analytics is a method that helps researchers, scientists, or anyone for that matter, test the legitimacy or the authenticity of their hypotheses or claims about real-life or real-world events.  

To understand the example of hypothesis testing in business analytics, consider a restaurant owner interested in learning how adding extra house sauce to their chicken burgers can impact customer satisfaction. Or, you could also consider a social media marketing organization. A hypothesis test can be set up to explain how an increase in labor impacts productivity. Thus, hypothesis testing aims to discover the connection between two or more than two variables in the experimental setting.  

How Does Hypothesis Testing Work?  

Generally, each research begins with a hypothesis; the investigator makes a certain claim and experiments to prove that the claim is false or true. For example, if you claim that students drinking milk before class accomplish tasks better than those who do not, then this is a kind of hypothesis that can be refuted or confirmed using an experiment. There are different kinds of hypotheses. They are:  

• Simple Hypothesis : Simple hypothesis, also known as a basic hypothesis, proposes that an independent variable is accountable for the corresponding dependent variable. In simpler words, the occurrence of independent variable results in the existence of the dependent variable. Generally, simple hypotheses are thought of as true and they create a causal relationship between the two variables. One example of a simple hypothesis is smoking cigarettes daily leads to cancer.  
• Complex Hypothesis : This type of hypothesis is also termed a modal. It holds for the relationship between two variables that are independent and result in a dependent variable. This means that the amalgamation of independent variables results in the dependent variables. An example of this kind of hypothesis can be “adults who don’t drink and smoke are less likely to have liver-related problems.  
• Null Hypothesis : A null hypothesis is created when a researcher thinks that there is no connection between the variables that are being observed. An example of this kind of hypothesis can be “A student’s performance is not impacted if they drink tea or coffee before classes.  
• Alternative Hypothesis : If a researcher wants to disapprove of a null hypothesis, then the researcher has to develop an opposite assumption—known as an alternative hypothesis. For example, beginning your day with tea instead of coffee can keep you more alert.  
• Logical Hypothesis: A proposed explanation supported by scant data is called a logical hypothesis. Generally, you wish to test your hypotheses or postulations by converting a logical hypothesis into an empirical hypothesis. For example, waking early helps one to have a productive day.  
• Empirical Hypothesis : This type of hypothesis is based on real evidence, evidence that is verifiable by observation as opposed to something that is correct in theory or by some kind of reckoning or logic. This kind of hypothesis depends on various variables that can result in specific outcomes. For example, individuals eating more fish can run faster than those eating meat.   
• Statistical Hypothesis : This kind of hypothesis is most common in systematic investigations that involve a huge target audience. For example, in Louisiana, 45% of students have middle-income parents.  

Four Steps of Hypothesis Testing  

There are four main steps in hypothesis testing in business analytics :  

Step 1: State the Null and Alternate Hypothesis  

After the initial research hypothesis, it is essential to restate it as a null (Ho) hypothesis and an alternate (Ha) hypothesis so that it can be tested mathematically.  

Step 2: Collate Data  

For a test to be valid, it is essential to do some sampling and collate data in a manner designed to test the hypothesis. If your data are not representative, then statistical inferences cannot be made about the population you are trying to analyze.  

Step 3: Perform a Statistical Test  

Various statistical tests are present, but all of them depend on the contrast of within-group variance (how to spread out the data in a group) against between-group variance (how dissimilar the groups are from one another).  

Step 4: Decide to Reject or Accept Your Null Hypothesis  

Based on the result of your statistical test, you need to decide whether you want to accept or reject your null hypothesis.  

Hypothesis Testing in Business   

When we talk about data-driven decision-making, a specific amount of risk can deceive a professional. This could result from flawed observations or thinking inaccurate or incomplete information , or unknown variables. The threat over here is that if key strategic decisions are made on incorrect insights, it can lead to catastrophic outcomes for an organization. The actual importance of hypothesis testing is that it enables professionals to analyze their assumptions and theories before putting them into action. This enables an organization to confirm the accuracy of its analysis before making key decisions.  

Key Considerations for Hypothesis Testing  

Let us look at the following key considerations of hypothesis testing:  

• Alternative Hypothesis and Null Hypothesis : If a researcher wants to disapprove of a null hypothesis, then the researcher has to develop an opposite assumption—known as an alternative hypothesis. A null hypothesis is created when a researcher thinks that there is no connection between the variables that are being observed.  
• Significance Level and P-Value : The statistical significance level is generally expressed as a p-value that lies between 0 and 1. The lesser the p-value, the more it suggests that you reject the null hypothesis. A p-value of less than 0.05 (generally ≤ 0.05) is significant statistically.  
• One-Sided vs. Two-Sided Testing : One-sided tests suggest the possibility of an effect in a single direction only. Two-sided tests test for the likelihood of the effect in two directions—negative and positive. One-sided tests comprise more statistical power to identify an effect in a single direction than a two-sided test with the same significance level and design.   
• Sampling: For hypothesis testing , you are required to collate a sample of data that has to be examined. In hypothesis testing, an analyst can test a statistical sample with the aim of providing proof of the credibility of the null hypothesis. Statistical analysts can test a hypothesis by examining and measuring a random sample of the population that is being examined.  

Real-World Example of Hypothesis Testing  

The following two examples give a glimpse of the various situations in which hypothesis testing is used in real-world scenarios.  

Example: BioSciences  

Hypothesis tests are frequently used in biological sciences. For example, consider that a biologist is sure that a certain kind of fertilizer will lead to better growth of plants which is at present 10 inches. To test this, the fertilizer is sprayed on the plants in the laboratory for a month. A hypothesis test is then done using the following:  

• H0: μ = 10 inches (the fertilizer has no effect on the plant growth)  
• HA: μ > 10 inches (the fertilizer leads to an increase in plant growth)  

Suppose the p-value is lesser than the significance level (e.g., α = .04). In that case, the null hypothesis can be rejected, and it can be concluded that the fertilizer results in increased plant growth.  

Example: Clinical Trials  

Consider an example where a doctor feels that a new medicine can decrease blood sugar in patients. To confirm this, he can measure the sugar of 20 diabetic patients prior to and after administering the new drug for a month. A hypothesis test is then done using the following:  

• H0: μafter = μbefore (the blood sugar is the same as before and after administering the new drug)  
• HA: μafter < μbefore (the blood sugar is less after the drug)  

If the p-value is less than the significance level (e.g., α = .04), then the null hypothesis can be rejected, and it can be proven that the new drug leads to reduced blood sugar.  

Conclusion  

Now you are aware of the need for hypotheses in Business Analytics . A hypothesis is not just an assumption— it has to be based on prior knowledge and theories. It also needs to be, which means that you can accept or reject it using scientific research methods (such as observations, experiments, and statistical data analysis). Most genuine Hypothesis testing programs teach you how to use hypothesis testing in real-world scenarios. If you are interested in getting a certificate degree in Integrated Program In Business Analytics , UNext Jigsaw is highly recommended.

Fill in the details to know more

PEOPLE ALSO READ

Related Articles

Understanding the Staffing Pyramid!

May 15, 2023

From The Eyes Of Emerging Technologies: IPL Through The Ages

April 29, 2023

Understanding HR Terminologies!

April 24, 2023

How Does HR Work in an Organization?

A Brief Overview: Measurement Maturity Model!

April 20, 2023

HR Analytics: Use Cases and Examples

What Are SOC and NOC In Cyber Security? What’s the Difference?

February 27, 2023

Fundamentals of Confidence Interval in Statistics!

February 26, 2023

A Brief Introduction to Cyber Security Analytics

Cyber Safe Behaviour In Banking Systems

February 17, 2023

Everything Best Of Analytics for 2023: 7 Must Read Articles!

December 26, 2022

Best of 2022: 5 Most Popular Cybersecurity Blogs Of The Year

December 22, 2022

10 Reasons Why Business Analytics Is Important In Digital Age

February 28, 2023

Bivariate Analysis: Beginners Guide | UNext

November 18, 2022

Everything You Need to Know About Hypothesis Tests: Chi-Square

November 17, 2022

Everything You Need to Know About Hypothesis Tests: Chi-Square, ANOVA

November 15, 2022

Are you ready to build your own career?

Query? Ask Us

Enter Your Details ×

A Beginner’s Guide to Hypothesis Testing in Business Analytics

• December 5, 2023
• Analytics , Statistics

Hypothesis testing is a statistical method used to make decisions about a population based on a sample. It helps business analysts draw conclusions about business metrics and make data-driven decisions. This beginner’s guide will provide an introduction to hypothesis testing and how it is applied in business analytics.

What is a Hypothesis?

A hypothesis is an assumption about a population parameter. It is a tentative statement that proposes a possible relationship between two or more variables.

In statistical terms, a hypothesis is an assertion or conjecture about one or more populations. For example, a business hypothesis could be –

“Our social media advertising results in an increase in sales.”

“Customer ratings of our product have decreased this month compared to last month.”

A hypothesis can be:

• Null hypothesis (H0) – a statement that there is no difference or no effect.
• Alternative hypothesis (H1) – a claim about the population that is contradictory to H0.

Hypothesis testing evaluates two mutually exclusive statements (H0 and H1) to determine which statement is best supported by the sample data.

Why Hypothesis Testing is Important in Business

Hypothesis testing allows business analysts to make statistical inferences about a business problem. It is an objective data-driven approach to:

• Evaluate business metrics against a target value. For example – is the current customer satisfaction score significantly lower than our target of 85%?
• Compare business metrics across time periods or categories. For example – has website conversion rate increased this month compared to last month?
• Quantify the impact of business initiatives. For example – did the email marketing campaign result in a significant increase in sales?

Some key benefits of hypothesis testing in business analytics:

• Supports data-driven decision making with statistical evidence.
• Helps save costs by making decisions backed by data insights.
• Enables measurement of success for business initiatives like marketing campaigns, new product launches etc.
• Provides a structured framework for business metric analysis.
• Reduces the influence of individual biases in decision making.

By incorporating hypothesis testing in data analysis, businesses can make sound decisions that are supported by statistical evidence.

Steps in Hypothesis Testing

Hypothesis testing involves the following five steps:

1. State the Hypotheses

This involves stating the null and alternate hypotheses. The hypotheses are stated in a way that they are mutually exclusive – if one is true, the other must be false.

Null hypothesis (H0) – represents the status quo, states that there is no effect or no difference.

Alternative hypothesis (H1) – states that there is an effect or a difference.

For example –

H0: The average customer rating this month is the same as last month.

H1: The average customer rating this month is lower than last month.

2. Choose the Significance Level

The significance level (α) is the probability of rejecting H0 when it is actually true. It is the maximum risk we are willing to take in making an incorrect decision.

Typical values are 0.10, 0.05 or 0.01. A lower α indicates lower risk tolerance. For example α = 0.05 indicates only a 5% risk of concluding there is a difference when actually there is none.

3. Select the Sample and Collect Data

The sample should be representative of the population. Data is collected relevant to the hypotheses – for example, customer ratings this month and last month.

4. Analyze the Sample Data

An appropriate statistical test is applied to analyze the sample data. Common tests used are t-tests, z-tests, ANOVA, chi-square etc. The test provides a test statistic that can be compared against critical values to determine statistical significance.

5. Make a Decision

If the test statistic falls in the rejection region, we reject H0 in favor of H1. Otherwise, we fail to reject H0 and conclude there is not enough evidence against it.

The key question is – “Is the sample data unlikely, assuming H0 is true?” If yes, we reject H0.

Types of Hypothesis Tests

There are two main types of hypothesis tests:

1. Parametric Tests

These tests make assumptions about the shape or parameters of the population distribution.

Some examples are:

• Z-test – Tests a population mean when population standard deviation is known.
• T-test – Tests a population mean when standard deviation is unknown.
• F-test – Compares variances from two normal populations.
• ANOVA – Compares means of two or more populations.

Parametric tests are more powerful as they make use of the distribution characteristics. But the assumptions need to hold true for valid results.

2. Non-parametric Tests

These tests make no assumptions about the exact distribution of the population. They are based on either ranks or frequencies.

• Chi-square test – Tests if two categorical variables are related.
• Mann-Whitney U test – Compares medians from two independent groups.
• Wilcoxon signed-rank test – Compares paired observations or repeated measurements.
• Kruskal Wallis test – Compares medians from two or more groups.

Non-parametric tests are distribution-free but less powerful than parametric tests. They can be used when assumptions of parametric tests are violated.

The choice of statistical test depends on the hypotheses, data type and other factors.

One-tailed and Two-tailed Hypothesis Tests

Hypothesis tests can be one-tailed or two-tailed:

• One-tailed test – When H1 specifies a direction. For example: H0: μ = 10 H1: μ > 10 (or μ < 10)
• Two-tailed test – When H1 simply states ≠, not a specific direction. For example: H0: μ = 10 H1: μ ≠ 10

One-tailed tests have greater power to detect an effect in the specified direction. But we need prior knowledge on the direction of effect for using them.

Two-tailed tests do not assume any direction and are more conservative. They are used when we have no clear prior expectation on the directionality.

Interpreting Hypothesis Test Results

Hypothesis testing results can be interpreted based on:

• p-value – Probability of obtaining sample results if H0 is true. Small p-value (< α) indicates significant evidence against H0.
• Confidence intervals – Range of likely values for the population parameter. If it does not contain the H0 value, we reject H0.
• Test statistic – Standardized value computed from sample data. Compared against critical values to determine statistical significance.
• Effect size – Quantifies the magnitude or size of effect. Important for interpreting practical significance.

Hypothesis testing indicates whether an effect exists or not. Measures like effect size and confidence intervals provide additional insights on the observed effect.

Common Errors in Hypothesis Testing

Some common errors to watch out for:

• Having unclear, ambiguous hypotheses.
• Choosing an inappropriate significance level α.
• Using the wrong statistical test for data analysis.
• Interpreting a non-significant result as proof of no effect. Absence of evidence is not evidence of absence.
• Concluding practical significance from statistical significance. Small p-values don’t always imply practical business impact.
• Multiple testing without adjustment leading to elevated Type I errors.
• Stopping data collection prematurely when a significant result is obtained.
• Overlooking effect sizes, confidence intervals while focusing solely on p-values.

Proper application of hypothesis testing methodology minimizes such errors and improves decision making.

Real-world Example of Hypothesis Testing

Let’s take an example of using hypothesis testing in business analytics:

A retailer wants to test if launching a new ecommerce website has resulted in increased online sales.

The retailer gathers weekly sales data before and after the website launch:

H0: Launching the new website did not increase the average weekly online sales

H1: Launching the new website increased the average weekly online sales

Significance level is chosen as 0.05. Appropriate parametric / non-parametric test is selected based on data. Test results show that the p-value is 0.01, which is less than 0.05.

Therefore, we reject the null hypothesis and conclude that the new website launch has resulted in significantly increased online sales at the 5% significance level.

The analyst also computes a 95% confidence interval for the difference in sales before and after website launch. The retailer uses these insights to make data-backed decisions on marketing budget allocation between traditional and digital channels.

Hypothesis testing provides a formal process for making statistical decisions using sample data. It helps assess business metrics against benchmarks, quantify impact of initiatives and compare performance across time periods or segments. By embedding hypothesis testing in analytics, businesses can derive actionable insights for data-driven decision making.

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base
• Null and Alternative Hypotheses | Definitions & Examples

Null and Alternative Hypotheses | Definitions & Examples

Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

• Null hypothesis (H 0 ): There’s no effect in the population .
• Alternative hypothesis (H A ): There’s an effect in the population.

The effect is usually the effect of the independent variable on the dependent variable .

Table of contents

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.

Null and alternative hypotheses are similar in some ways:

• They’re both answers to the research question
• They both make claims about the population
• They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

• Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
• Alternative hypothesis (H A ): Independent variable affects dependent variable .

Test-specific

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 6 May 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/

Is this article helpful?

Shaun Turney

Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.1: Null and Alternative Hypotheses

• Last updated
• Save as PDF
• Page ID 23459

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

\(H_0\): The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.

\(H_a\): The alternative hypothesis: It is a claim about the population that is contradictory to \(H_0\) and what we conclude when we reject \(H_0\). This is usually what the researcher is trying to prove.

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject \(H_0\)" if the sample information favors the alternative hypothesis or "do not reject \(H_0\)" or "decline to reject \(H_0\)" if the sample information is insufficient to reject the null hypothesis.

\(H_{0}\) always has a symbol with an equal in it. \(H_{a}\) never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example \(\PageIndex{1}\)

• \(H_{0}\): No more than 30% of the registered voters in Santa Clara County voted in the primary election. \(p \leq 30\)
• \(H_{a}\): More than 30% of the registered voters in Santa Clara County voted in the primary election. \(p > 30\)

Exercise \(\PageIndex{1}\)

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

• \(H_{0}\): The drug reduces cholesterol by 25%. \(p = 0.25\)
• \(H_{a}\): The drug does not reduce cholesterol by 25%. \(p \neq 0.25\)

Example \(\PageIndex{2}\)

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

• \(H_{0}: \mu = 2.0\)
• \(H_{a}: \mu \neq 2.0\)

Exercise \(\PageIndex{2}\)

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol \((=, \neq, \geq, <, \leq, >)\) for the null and alternative hypotheses.

• \(H_{0}: \mu \_ 66\)
• \(H_{a}: \mu \_ 66\)
• \(H_{0}: \mu = 66\)
• \(H_{a}: \mu \neq 66\)

Example \(\PageIndex{3}\)

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

• \(H_{0}: \mu \geq 5\)
• \(H_{a}: \mu < 5\)

Exercise \(\PageIndex{3}\)

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• \(H_{0}: \mu \_ 45\)
• \(H_{a}: \mu \_ 45\)
• \(H_{0}: \mu \geq 45\)
• \(H_{a}: \mu < 45\)

Example \(\PageIndex{4}\)

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

• \(H_{0}: p \leq 0.066\)
• \(H_{a}: p > 0.066\)

Exercise \(\PageIndex{4}\)

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (\(=, \neq, \geq, <, \leq, >\)) for the null and alternative hypotheses.

• \(H_{0}: p \_ 0.40\)
• \(H_{a}: p \_ 0.40\)
• \(H_{0}: p = 0.40\)
• \(H_{a}: p > 0.40\)

COLLABORATIVE EXERCISE

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:

• Evaluate the null hypothesis , typically denoted with \(H_{0}\). The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality \((=, \leq \text{or} \geq)\)
• Always write the alternative hypothesis , typically denoted with \(H_{a}\) or \(H_{1}\), using less than, greater than, or not equals symbols, i.e., \((\neq, >, \text{or} <)\).
• If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis.
• Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

\(H_{0}\) and \(H_{a}\) are contradictory.

• If \(\alpha \leq p\)-value, then do not reject \(H_{0}\).
• If\(\alpha > p\)-value, then reject \(H_{0}\).

\(\alpha\) is preconceived. Its value is set before the hypothesis test starts. The \(p\)-value is calculated from the data.References

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm .

If you still have questions or prefer to get help directly from an agent, please submit a request. We’ll get back to you as soon as possible.

Please fill out the contact form below and we will reply as soon as possible.

• Economics, Finance, & Analytics
• Research, Quantitative Analysis, & Decision Science

Null Hypothesis - Explained

What is the null hypothesis.

Written by Jason Gordon

Updated at April 22nd, 2024

• Marketing, Advertising, Sales & PR Principles of Marketing Sales Advertising Public Relations SEO, Social Media, Direct Marketing
• Accounting, Taxation, and Reporting Managerial & Financial Accounting & Reporting Business Taxation
• Professionalism & Career Development
• Law, Transactions, & Risk Management Government, Legal System, Administrative Law, & Constitutional Law Legal Disputes - Civil & Criminal Law Agency Law HR, Employment, Labor, & Discrimination Business Entities, Corporate Governance & Ownership Business Transactions, Antitrust, & Securities Law Real Estate, Personal, & Intellectual Property Commercial Law: Contract, Payments, Security Interests, & Bankruptcy Consumer Protection Insurance & Risk Management Immigration Law Environmental Protection Law Inheritance, Estates, and Trusts
• Business Management & Operations Operations, Project, & Supply Chain Management Strategy, Entrepreneurship, & Innovation Business Ethics & Social Responsibility Global Business, International Law & Relations Business Communications & Negotiation Management, Leadership, & Organizational Behavior
• Economics, Finance, & Analytics Economic Analysis & Monetary Policy Research, Quantitative Analysis, & Decision Science Investments, Trading, and Financial Markets Banking, Lending, and Credit Industry Business Finance, Personal Finance, and Valuation Principles

A null hypothesis refers to a kind of statistical hypothesis that signifies the absence of statistical significance for a group of specific observations. It showcases that there is not any variation involved between variables. Or, it can state that one variable is similar to its mean. It is considered to be accurate until an alternative hypothesis proves it wrong. For instance, in case, the hypothesis test is conducted in such a manner that the alternative hypothesis showcases a difference between the population parameter and the claimed amount. Hence, the population means cook time is not equivalent to 12 minutes. Instead, it tends to be different, either more or less than the given value. In case, the null hypothesis is true, or the hypothesis test says that the population mean tends to be 12 minutes, then it will automatically lead to the elimination of the alternative hypothesis, and vice-versa. 

Key Points to Remember

• A null hypothesis refers to a statistical approach that involves no statistical relation in the group of said observations.
• The null hypothesis is created against an alternative hypothesis with an objective to display no existing variations between variables. In other words, it says that there is no difference between the mean and a variable.
• Hypothesis testing, by using a certain confidence level, lets a statistical model to either accept or neglect a null hypothesis.

How is the Null Hypothesis Used? 

Null hypothesis is also referred to as the conjecture. It is based on the belief that odds are responsible for creating any sort of difference or variations in a given set of variables. In contrast to the null hypothesis, there exists another hypothesis known as alternative hypothesis. The null hypothesis refers to the first claim that the value of the population mean tends to be equal to the claim value. For instance, a particular pasta brand takes 12 minutes on an average to cook well. Hence, the null hypothesis for this assumption would be: The population mean is equivalent to 12 minutes. In case, there is a rejection of the null hypothesis, the alternative hypothesis would be accepted in return. A statistical model can accept or reject a null hypothesis falling in a specific confidence interval by using hypothesis testing. This test involves four steps which are:

• First of all, the statistician should state null and alternate hypothesis, out of which only one would be accurate.
• The second step is to create an analysis strategy in order to evaluate the information.
• The third step is to implement the plan or strategy created in the second step, and do sample data analysis.
• The last step is to compare the results, and find out which hypothesis, null or alternate, needs to be accepted.

Statisticians are more keen to reject or eliminate the null hypothesis for eliminating at least one variable.

Examples of setting up a null hypothesis

Lets take this example. As per a college principal, the students secured 7/10 marks on an average in tests. For this hypothesis test, we took a sample size of 30 students from the total population of 300 students in the school. We ascertained the sample mean, and compared the calculated mean with the population mean, and then take decision about the hypothesis. In another example, a specific mutual fund offers an annual rate of return of 8%. Lets say that this mutual fund has been operating for a period of 20 years. We took a random sample of mutual funds returns received per year for 5 years, and then determine its average or mean. The next step is to strike a comparison with the sample mean calculated for 5 years, and the population mean for coming to a conclusion. Generally, the reported number is referred to as the hypothesis, and assumed to be right. For the aforementioned instances, hypothesis will be:

• For the first example, students secure a score of 7 out of 10 in school exams.
• For the second example, the yearly rate of return for the mutual fund is 8%.

The above two statements which form the null hypothesis are assumed to be correct. It is similar to the court proceedings where an accused is presumed to be non-guilty until the other party presents evidence against him, and proves him guilty. Similarly, the first stage of hypothesis testing is to create a null hypothesis, and determine if this presumption is right or wrong. The null hypothesis is tested for ensuring its validity and reliability. Any data that is in contrast to the null hypothesis is stored in alternate hypothesis. Hence, the alternate hypothesis for the above two instances would be:

• The average score of school students is not equal to 7.
• The yearly rate of return on mutual funds is not equal to 8% p.a.

Therefore, it is right to say that the alternate hypothesis is exactly the opposite of the null hypothesis.

Hypothesis Testing for Investments

Considering an instance from financial markets, lets suppose that Mr. A believes that his investment strategy would offer more returns on an average as compared to merely purchasing and holding a stock. As per the null hypothesis, two average returns dont show any difference or variations. Mr. A needs to agree to this hypothesis until he proves it wrong. For doing so, he needs to consider using different tests. Hence, the alternate hypothesis would show that the investment strategy offers more average rate of return as compared to a basic buy-and-hold investment strategy. Analysts use the p-value for knowing the mathematical importance of the outcomes. If the p-value is either equal to or lower than 0.5, it shows a big evidence that is not in favor of the null hypothesis. In case, Mr. A uses any of the tests, and finds out that there is a significant level of difference in his returns and the buy-and-hold returns, then he can agree to the alternate hypothesis and reject the null hypothesis.

Related Articles

• Sampling Distribution - Explained
• Histogram - Explained
• Predictive Analytics - Explained
• Law of Large Numbers - Explained

• Search Search Please fill out this field.

What Is Hypothesis Testing?

Step 1: define the hypothesis, step 2: set the criteria, step 3: calculate the statistic, step 4: reach a conclusion, types of errors, the bottom line.

• Trading Skills
• Trading Basic Education

Hypothesis Testing in Finance: Concept and Examples

Charlene Rhinehart is a CPA , CFE, chair of an Illinois CPA Society committee, and has a degree in accounting and finance from DePaul University.

Your investment advisor proposes you a monthly income investment plan that promises a variable return each month. You will invest in it only if you are assured of an average $180 monthly income. Your advisor also tells you that for the past 300 months, the scheme had investment returns with an average value of $190 and a standard deviation of $75. Should you invest in this scheme? Hypothesis testing comes to the aid for such decision-making.

Key Takeaways

• Hypothesis testing is a mathematical tool for confirming a financial or business claim or idea.
• Hypothesis testing is useful for investors trying to decide what to invest in and whether the instrument is likely to provide a satisfactory return.
• Despite the existence of different methodologies of hypothesis testing, the same four steps are used: define the hypothesis, set the criteria, calculate the statistic, and reach a conclusion.
• This mathematical model, like most statistical tools and models, has limitations and is prone to certain errors, necessitating investors also considering other models in conjunction with this one

Hypothesis or significance testing is a mathematical model for testing a claim, idea or hypothesis about a parameter of interest in a given population set, using data measured in a sample set. Calculations are performed on selected samples to gather more decisive information about the characteristics of the entire population, which enables a systematic way to test claims or ideas about the entire dataset.

Here is a simple example: A school principal reports that students in their school score an average of 7 out of 10 in exams. To test this “hypothesis,” we record marks of say 30 students (sample) from the entire student population of the school (say 300) and calculate the mean of that sample. We can then compare the (calculated) sample mean to the (reported) population mean and attempt to confirm the hypothesis.

To take another example, the annual return of a particular mutual fund is 8%. Assume that mutual fund has been in existence for 20 years. We take a random sample of annual returns of the mutual fund for, say, five years (sample) and calculate its mean. We then compare the (calculated) sample mean to the (claimed) population mean to verify the hypothesis.

This article assumes readers' familiarity with concepts of a normal distribution table, formula, p-value and related basics of statistics.

Different methodologies exist for hypothesis testing, but the same four basic steps are involved:

Usually, the reported value (or the claim statistics) is stated as the hypothesis and presumed to be true. For the above examples, the hypothesis will be:

• Example A: Students in the school score an average of 7 out of 10 in exams.
• Example B: The annual return of the mutual fund is 8% per annum.

This stated description constitutes the “ Null Hypothesis (H 0 ) ” and is  assumed  to be true – the way a defendant in a jury trial is presumed innocent until proven guilty by the evidence presented in court. Similarly, hypothesis testing starts by stating and assuming a “ null hypothesis ,” and then the process determines whether the assumption is likely to be true or false.

The important point to note is that we are testing the null hypothesis because there is an element of doubt about its validity. Whatever information that is against the stated null hypothesis is captured in the  Alternative Hypothesis (H 1 ).  For the above examples, the alternative hypothesis will be:

• Students score an average that is not equal to 7.
• The annual return of the mutual fund is not equal to 8% per annum.

In other words, the alternative hypothesis is a direct contradiction of the null hypothesis.

As in a trial, the jury assumes the defendant's innocence (null hypothesis). The prosecutor has to prove otherwise (alternative hypothesis). Similarly, the researcher has to prove that the null hypothesis is either true or false. If the prosecutor fails to prove the alternative hypothesis, the jury has to let the defendant go (basing the decision on the null hypothesis). Similarly, if the researcher fails to prove an alternative hypothesis (or simply does nothing), then the null hypothesis is assumed to be true.

The decision-making criteria have to be based on certain parameters of datasets.

The decision-making criteria have to be based on certain parameters of datasets and this is where the connection to normal distribution comes into the picture.

As per the standard statistics postulate  about sampling distribution , “For any sample size n, the sampling distribution of X̅ is normal if the population X from which the sample is drawn is normally distributed.” Hence, the probabilities of all other possible sample mean that one could select are normally distributed.

For e.g., determine if the average daily return, of any stock listed on XYZ stock market , around New Year's Day is greater than 2%.

H 0 : Null Hypothesis: mean = 2%

H 1 : Alternative Hypothesis: mean > 2% (this is what we want to prove)

Take the sample (say of 50 stocks out of total 500) and compute the mean of the sample.

For a normal distribution, 95% of the values lie within two standard deviations of the population mean. Hence, this normal distribution and central limit assumption for the sample dataset allows us to establish 5% as a significance level. It makes sense as, under this assumption, there is less than a 5% probability (100-95) of getting outliers that are beyond two standard deviations from the population mean. Depending upon the nature of datasets, other significance levels can be taken at 1%, 5% or 10%. For financial calculations (including behavioral finance), 5% is the generally accepted limit. If we find any calculations that go beyond the usual two standard deviations, then we have a strong case of outliers to reject the null hypothesis.  

Graphically, it is represented as follows:

In the above example, if the mean of the sample is much larger than 2% (say 3.5%), then we reject the null hypothesis. The alternative hypothesis (mean >2%) is accepted, which confirms that the average daily return of the stocks is indeed above 2%.

However, if the mean of the sample is not likely to be significantly greater than 2% (and remains at, say, around 2.2%), then we CANNOT reject the null hypothesis. The challenge comes on how to decide on such close range cases. To make a conclusion from selected samples and results, a level of significance is to be determined, which enables a conclusion to be made about the null hypothesis. The alternative hypothesis enables establishing the level of significance or the "critical value” concept for deciding on such close range cases.

According to the textbook standard definition , “A critical value is a cutoff value that defines the boundaries beyond which less than 5% of sample means can be obtained if the null hypothesis is true. Sample means obtained beyond a critical value will result in a decision to reject the null hypothesis."   In the above example, if we have defined the critical value as 2.1%, and the calculated mean comes to 2.2%, then we reject the null hypothesis. A critical value establishes a clear demarcation about acceptance or rejection.

This step involves calculating the required figure(s), known as test statistics (like mean, z-score , p-value , etc.), for the selected sample. (We'll get to these in a later section.)

With the computed value(s), decide on the null hypothesis. If the probability of getting a sample mean is less than 5%, then the conclusion is to reject the null hypothesis. Otherwise, accept and retain the null hypothesis.

There can be four possible outcomes in sample-based decision-making, with regard to the correct applicability to the entire population:

The “Correct” cases are the ones where the decisions taken on the samples are truly applicable to the entire population. The cases of errors arise when one decides to retain (or reject) the null hypothesis based on the sample calculations, but that decision does not really apply for the entire population. These cases constitute Type 1 ( alpha ) and Type 2 ( beta ) errors, as indicated in the table above.

Selecting the correct critical value allows eliminating the type-1 alpha errors or limiting them to an acceptable range.

Alpha denotes the error on the level of significance and is determined by the researcher. To maintain the standard 5% significance or confidence level for probability calculations, this is retained at 5%.

According to the applicable decision-making benchmarks and definitions:

• “This (alpha) criterion is usually set at 0.05 (a = 0.05), and we compare the alpha level to the p-value. When the probability of a Type I error is less than 5% (p < 0.05), we decide to reject the null hypothesis; otherwise, we retain the null hypothesis.”  
• The technical term used for this probability is the p-value . It is defined as “the probability of obtaining a sample outcome, given that the value stated in the null hypothesis is true. The p-value for obtaining a sample outcome is compared to the level of significance."  
• A Type II error, or beta error, is defined as the probability of incorrectly retaining the null hypothesis, when in fact it is not applicable to the entire population.  

A few more examples will demonstrate this and other calculations.

A monthly income investment scheme exists that promises variable monthly returns. An investor will invest in it only if they are assured of an average $180 monthly income. The investor has a sample of 300 months’ returns which has a mean of $190 and a standard deviation of $75. Should they invest in this scheme?

Let’s set up the problem. The investor will invest in the scheme if they are assured of the investor's desired $180 average return.

H 0 : Null Hypothesis: mean = 180

H 1 : Alternative Hypothesis: mean > 180

Method 1: Critical Value Approach

Identify a critical value X L for the sample mean, which is large enough to reject the null hypothesis – i.e. reject the null hypothesis if the sample mean >= critical value X L

P (identify a Type I alpha error) = P(reject H 0  given that H 0  is true),

This would be achieved when the sample mean exceeds the critical limits.

= P (given that H 0  is true) = alpha

Graphically, it appears as follows:

Taking alpha = 0.05 (i.e. 5% significance level), Z 0.05  = 1.645 (from the Z-table or normal distribution table)

           = > X L  = 180 +1.645*(75/sqrt(300)) = 187.12

Since the sample mean (190) is greater than the critical value (187.12), the null hypothesis is rejected, and the conclusion is that the average monthly return is indeed greater than $180, so the investor can consider investing in this scheme.

Method 2: Using Standardized Test Statistics

One can also use standardized value z.

Test Statistic, Z = (sample mean – population mean) / (std-dev / sqrt (no. of samples).

Then, the rejection region becomes the following:

Z= (190 – 180) / (75 / sqrt (300)) = 2.309

Our rejection region at 5% significance level is Z> Z 0.05  = 1.645.

Since Z= 2.309 is greater than 1.645, the null hypothesis can be rejected with a similar conclusion mentioned above.

Method 3: P-value Calculation

We aim to identify P (sample mean >= 190, when mean = 180).

= P (Z >= (190- 180) / (75 / sqrt (300))

= P (Z >= 2.309) = 0.0084 = 0.84%

The following table to infer p-value calculations concludes that there is confirmed evidence of average monthly returns being higher than 180:

A new stockbroker (XYZ) claims that their brokerage fees are lower than that of your current stock broker's (ABC). Data available from an independent research firm indicates that the mean and std-dev of all ABC broker clients are $18 and $6, respectively.

A sample of 100 clients of ABC is taken and brokerage charges are calculated with the new rates of XYZ broker. If the mean of the sample is $18.75 and std-dev is the same ($6), can any inference be made about the difference in the average brokerage bill between ABC and XYZ broker?

H 0 : Null Hypothesis: mean = 18

H 1 : Alternative Hypothesis: mean <> 18 (This is what we want to prove.)

Rejection region: Z <= - Z 2.5  and Z>=Z 2.5  (assuming 5% significance level, split 2.5 each on either side).

Z = (sample mean – mean) / (std-dev / sqrt (no. of samples))

= (18.75 – 18) / (6/(sqrt(100)) = 1.25

This calculated Z value falls between the two limits defined by:

- Z 2.5  = -1.96 and Z 2.5  = 1.96.

This concludes that there is insufficient evidence to infer that there is any difference between the rates of your existing broker and the new broker.

Alternatively, The p-value = P(Z< -1.25)+P(Z >1.25)

= 2 * 0.1056 = 0.2112 = 21.12% which is greater than 0.05 or 5%, leading to the same conclusion.

Graphically, it is represented by the following:

Criticism Points for the Hypothetical Testing Method:

• A statistical method based on assumptions
• Error-prone as detailed in terms of alpha and beta errors
• Interpretation of p-value can be ambiguous, leading to confusing results

Hypothesis testing allows a mathematical model to validate a claim or idea with a certain confidence level. However, like the majority of statistical tools and models, it is bound by a few limitations. The use of this model for making financial decisions should be considered with a critical eye, keeping all dependencies in mind. Alternate methods like  Bayesian Inference are also worth exploring for similar analysis.

Sage Publications. " Introduction to Hypothesis Testing ," Page 13.

Sage Publications. " Introduction to Hypothesis Testing ," Page 11.

Sage Publications. " Introduction to Hypothesis Testing ," Page 7.

Sage Publications. " Introduction to Hypothesis Testing ," Pages 10-11.

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.5: Full Hypothesis Test Examples

• Last updated
• Save as PDF
• Page ID 79055

Tests on Means

Example \(\PageIndex{1}\)

Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle.

His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles. Frank bought Jeffrey a new pair of expensive goggles and timed Jeffrey for 15 25-yard freestyle swims . For the 15 swims, Jeffrey's mean time was 16 seconds , with a standard deviation of 0.8 seconds . Frank thought that the goggles helped Jeffrey to swim faster than the 16.43 seconds. Conduct a hypothesis test using test statistics and \(p\)-values with a preset \(\alpha = 0.05\).

Set up the Hypothesis Test:

Since the problem is about a mean, this is a test of a single population mean .

Set the null and alternative hypothesis:

In this case there is an implied challenge or claim. This is that the goggles will reduce the swimming time. The effect of this is to set the hypothesis as a one-tailed test. The claim will always be in the alternative hypothesis because the burden of proof always lies with the alternative. Remember that the status quo must be defeated with a high degree of confidence, in this case 95% confidence. The null and alternative hypotheses are thus:

\(H_0: \mu \geq 16.43\)  \(H_a: \mu < 16.43\)

For Jeffrey to swim faster, his time should be less than 16.43 seconds. The "<" tells you this is left-tailed.

Determine the distribution needed:

Random variable: \(\overline x\) = the mean time to swim the 25-yard freestyle.

Distribution for the test statistic:

The sample size is less than 30 and we do not know the population standard deviation so this is a t -test. The proper formula is: \(t_{obs}=\frac{\overline{x}-\mu_{0}}{s / \sqrt{n}}\)

\(\mu_ 0 = 16.43\) comes from \(H_0\) and not the data. \(\overline x = 16\), \(s = 0.8\), and \(n = 15\).

Our step 2, setting the level of confidence, has already been determined by the problem, \(\alpha\) of .05 corresponds to a 95% confidence level. It is worth thinking about the meaning of this choice. The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on average, in 16.43 seconds or more. (Reject the null hypothesis when the null hypothesis is true.) For this case the only concern with a Type I error would seem to be that Jeffrey’s dad may fail to bet on his son’s victory because he does not have appropriate confidence in the effect of the goggles.

To find the critical value we need to select the appropriate test statistic. We have concluded that this is a t -test on the basis of the sample size and that we are interested in a population mean. We can now draw the graph of the t -distribution and mark the critical value. For this problem the degrees of freedom are n-1, or 14. Looking up 14 degrees of freedom at the 0.05 column of the t -table we find 1.761. This is the critical value and we can put this on our graph.

Step 3 is the calculation of the test statistic using the formula we have selected. We find that the observed test statistic is -2.08, meaning that the sample mean is 2.08 standard errors below the hypothesized mean of 16.43.

\[t_{obs}=\frac{\overline{x}-\mu_{0}}{s / \sqrt{n}}=\frac{16-16.43}{.8 / \sqrt{15}}=-2.08\nonumber\]

Figure \(\PageIndex{1}\)

Step 4 has us compare the test statistic and the critical value and mark these on the graph. We see that the test statistic is in the tail and thus we move to step 4 and reach a conclusion. The probability that an average time of 16 minutes could come from a distribution with a population mean of 16.43 minutes is too unlikely to have occurred under the null hypothesis. We reject the null.

Step 5 has us state our conclusions first formally and then less formally. A formal conclusion would be stated as: “With a 95% level of confidence we reject the null hypothesis that the swimming time with goggles comes from a distribution with a population mean time of 16.43 minutes.” Less formally, “With 95% confidence, we believe that the goggles improved swimming speed".

If we wished to use the \(p\)-value system of reaching a conclusion we would calculate the statistic and take the additional step to find the probability of being 2.08 standard errors from the mean on a t -distribution. The \(p\)-value interval is (.025, .05), that we get by looking up the one-tailed probabilities associated with the closest t -scores (1.761 and 2.145) to the observed test statistic (-2.08) in the relevant df row of 14 in the t -table. Comparing this interval to the significance level of .05 we see that we reject the null. The \(p\)-value has been put on the graph as the shaded area beyond -2.08 and it shows that it is smaller than the hatched area which is the \(\alpha\) level of 0.05. Both methods reach the same conclusion that we reject the null hypothesis.

Exercise \(\PageIndex{1}\)

The mean throwing distance of a football for Marco, a high school freshman quarterback, is 40 yards, with a standard deviation of two yards. The team coach tells Marco to adjust his grip to get more distance. The coach records the distances for 20 throws. For the 20 throws, Marco’s mean distance was 45 yards. The coach thought the different grip helped Marco throw farther than 40 yards. Conduct a hypothesis test using a preset \(\alpha = 0.05\). Assume the throw distances for footballs are normal.

First, determine what type of test this is, set up the hypothesis test, find the \(p\)-value, sketch the graph, and state your conclusion.

Example \(\PageIndex{2}\)

Jane has just begun her new job as on the sales force of a very competitive company. In a sample of 16 sales calls it was found that she closed the contract for an average value of 108 dollars with a standard deviation of 12 dollars. Company policy requires that new members of the sales force must exceed an average of $100 per contract during the trial employment period. Can we conclude that Jane has met this requirement at the significance level of 5%?

• \(H_0: \mu \leq 100\) \(H_a: \mu > 100\) The null and alternative hypothesis are for the parameter \(\mu\) because the number of dollars of the contracts is a continuous random variable. Also, this is a one-tailed test because the company has only an interested if the number of dollars per contact is below a particular number not "too high" a number. This can be thought of as making a claim that the requirement is being met and thus the claim is in the alternative hypothesis.
• Test statistic: \(t_{obs}=\frac{\overline{x}-\mu_{0}}{\frac{s}{\sqrt{n}}}=\frac{108-100}{\left(\frac{12}{\sqrt{16}}\right)}=2.67\)
• Critical value: \(t_\alpha=1.753\) with \(n-1\) degrees of freedom = 15

The test statistic is a Student's t because the sample size is below 100; therefore, we cannot use the normal distribution. Comparing the observed value of the test statistic and the critical value of t at a 5% significance level, we see that the observed value is in the tail of the distribution. Thus, we conclude that 108 dollars per contract is significantly larger than the hypothesized value of 100 and thus we must reject the null hypothesis. There is evidence that Jane's performance meets company standards.

Figure \(\PageIndex{2}\)

Exercise \(\PageIndex{2}\)

It is believed that a stock price for a particular company will grow at a rate of $5 per week with a standard deviation of $1. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows: $4, $3, $2, $3, $1, $7, $2, $1, $1, $2. Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, state your conclusion, and identify the Type I and Type II errors.

Example \(\PageIndex{3}\)

A manufacturer of salad dressings uses machines to dispense liquid ingredients into bottles that move along a filling line. The machine that dispenses salad dressings is working properly when 8 ounces are dispensed. Suppose that the average amount dispensed in a particular sample of 35 bottles is 7.91 ounces with a variance of 0.03 ounces squared, \(s^2\). Is there evidence that the machine should be stopped and production wait for repairs? The lost production from a shutdown is potentially so great that management feels that the level of confidence in the analysis should be 99%.

Again we will follow the steps in our analysis of this problem.

STEP 1 : Set the null and alternative hypothesis.

The random variable is the quantity of fluid placed in the bottles. This is a continuous random variable and the parameter we are interested in is the mean. Our hypothesis therefore is about the mean. In this case we are concerned that the machine is not filling properly. From what we are told it does not matter if the machine is over-filling or under-filling, both seem to be an equally bad error. This tells us that this is a two-tailed test: if the machine is malfunctioning it will be shutdown regardless if it is from over-filling or under-filling. The null and alternative hypotheses are thus:

\[H_0:\mu=8\nonumber\]

\[Ha:\mu \neq 8\nonumber\]

STEP 2 : Decide the level of significance and draw the graph showing the critical value.

This problem has already set the level of confidence at 99%. The decision seems an appropriate one and shows the thought process when setting the significance level. Management wants to be very certain, as certain as probability will allow, that they are not shutting down a machine that is not in need of repair. To draw the distribution and the critical value, we need to know which distribution to use. Because the sample size is under 100, the appropriate distribution is the t -distribution and the relevant critical value is 2.750 from the t -table at 0.005 column and 30 degrees of freedom (closest available row to our actual 34 df here). We need to draw the graph and mark these points.

STEP 3 : Calculate sample parameters and the test statistic.

The sample parameters are provided, the sample mean is 7.91 and the sample variance is .03 and the sample size is 35. We need to note that the sample variance was provided, not the sample standard deviation, which is what we need for the formula. Remembering that the standard deviation is simply the square root of the variance, we therefore know the sample standard deviation, \(s\), is 0.173. With this information we can calculate the test statistic as -3.07, and mark it on the graph.

\[t_{obs}=\frac{\overline{x}-\mu_{0}}{s / \sqrt{n}}=\frac{7.91-8}{\cdot 173 / \sqrt{35}}=-3.07\nonumber\]

STEP 4 : Compare test statistic and the critical values.

Now we compare the test statistic and the critical value by placing the test statistic on the graph. The test statistic is in the tail, decidedly greater than the critical value of 2.750. We note that even the very small difference between the hypothesized value and the sample value is still a large number of standard errors. The sample mean is only 0.08 ounces different from the required level of 8 ounces, but it is 3+ standard errors away from the required 8 ounces, and thus we reject the null hypothesis.

STEP 5 : Reach a conclusion.

Three standard errors of a test statistic will guarantee that the test will fail. The probability that anything is beyond three standard errors of a hypothesized null value - given a large enough sample size - is close to zero. Looking at the closest t -scores in df =30 row in the t -table, we get the \(p\)-value interval of (.01, .002) after doubling the one-tailed probabilities of .005 and .001. Our formal conclusion would be “At a 99% level of confidence, we reject the null hypothesis that the sample mean came from a distribution with a mean of 8 ounces”. Or less formally, and getting to the point, “At a 99% level of confidence, we conclude that the machine is under-filling the bottles and is in need of repair”.

Hypothesis Test for Proportions

Just as there were confidence intervals for proportions, or more formally, the population parameter \(P\), there is the ability to test hypotheses concerning \(P\).

The estimated value (point estimate) for \(P\) is \(P^{\prime}\) where \(P^{\prime} = x/n\), \(x\) is the number of observations in the category of interest in the sample and \(n\) is the sample size.

When you perform a hypothesis test of a population proportion \(P\), you take a random sample from the population. To ensure normality of the distribution, sampling must be random and the total sample size must be greater than 100. There is no distribution that can correct for this small sample bias and thus if these conditions are not met we simply cannot test the hypothesis with the data available at that time. We met this condition when we were first estimating confidence intervals for \(P\).

Again, we begin with the modified standardizing formula:

\[z=\frac{P^{\prime}-P}{\sqrt{\frac{P(1-P)}{n}}}\nonumber\]

Substituting \(P_0\), the hypothesized value of \(P\), we have:

\[z_{obs}=\frac{P^{\prime}-P_{0}}{\sqrt{\frac{P_{0} (1-P_{0})}{n}}}\nonumber\]

This is the test statistic for testing hypothesized values of \(P\), where the null and alternative hypotheses take one of the following forms:

Table \(\PageIndex{1}\)

The decision rule stated above applies here also: if the calculated value of \(z_{obs}\) shows that the sample proportion is "too many" standard errors from the hypothesized proportion, the null hypothesis is rejected. The decision as to what is "too many" is pre-determined by the analyst depending on the level of significance required in the test.

Example \(\PageIndex{4}\)

The mortgage department of a large bank is interested in the nature of loans of first-time borrowers. This information will be used to tailor their marketing strategy. They believe that 50% of first-time borrowers take out smaller loans than other borrowers. They perform a hypothesis test to determine if the percentage is different from 50% . They sample 101 first-time borrowers and find 54 of these loans are smaller that the other borrowers. For the hypothesis test, they choose a 5% level of significance.

\(H_0: P = 0.50\)  \(H_a: P \neq 0.50\)

The words "is different from" tell you this is a two-tailed test. The Type I and Type II errors are as follows: The Type I error is to conclude that the proportion of borrowers is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true). The Type II error is there is not enough evidence to conclude that the proportion of first time borrowers differs from 50% when, in fact, the proportion does differ from 50%. (You fail to reject the null hypothesis when the null hypothesis is false.)

STEP 2 : Decide the level of significance and draw the graph showing the critical value

The level of confidence has been set by the problem at 95%. Because this is two-tailed test one-half of the \(\alpha\) value will be in the upper tail and one-half in the lower tail as shown on the graph. The critical value for the normal distribution at the 95% level of confidence is 1.96. This can easily be found on the Student’s t -table at the very bottom at infinite degrees of freedom remembering that at infinity the t -distribution is the normal distribution. Of course, the value can also be found on the standard normal table but you have go looking for the tail probability, \(\alpha\)/2, inside the body of the table and then read out to the sides and top for the number of standard errors.

Figure \(\PageIndex{3}\)

STEP 3 : Calculate the sample parameters and critical value of the test statistic.

The test statistic is a normal distribution, \(z\), for testing proportions and is:

\[z=\frac{P^{\prime}-P_{0}}{\sqrt{\frac{P_{0} (1-P_{0})}{n}}}=\frac{.53-.50}{\sqrt{\frac{.5(.5)}{101}}}=0.60\nonumber\]

For this case, the sample of 101 found 54 first-time borrowers were different from other borrowers. The sample proportion, \(P^{\prime} = 54/101= 0.53\) The test question, therefore, is : “Is 0.53 significantly different from 0.50?” Putting these values into the formula for the test statistic we find that 0.53 is only 0.60 standard errors away from 0.50. This is barely off of the mean of the standard normal distribution of zero. There is virtually no difference from the sample proportion and the hypothesized proportion in terms of standard errors.

STEP 4 : Compare the test statistic and the critical value.

The observed value is well within the critical values of \(\pm 1.96\) standard errors and thus we cannot reject the null hypothesis. To reject the null hypothesis we need significant evidence of difference between the hypothesized value and the sample value. In this case the sample value is very nearly the same as the hypothesized value measured in terms of standard errors.

The formal conclusion would be “At a 95% level of confidence we cannot reject the null hypothesis that 50% of first-time borrowers have the same size loans as other borrowers”. Less formally, we would say that “There is no evidence that one-half of first-time borrowers are significantly different in loan size from other borrowers”. Notice the length to which the conclusion goes to include all of the conditions that are attached to the conclusion. Statisticians, for all the criticism they receive, are careful to be very specific even when this seems trivial. Statisticians cannot say more than they know and the data constrain the conclusion to be within the metes and bounds of the data.

Exercise \(\PageIndex{3}\)

A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 104 students and 89 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.

Example \(\PageIndex{5}\)

Suppose a consumer group suspects that the proportion of households that have three or more cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test using 90% confidence. Their marketing people survey 150 households with the result that 43 of the households have three or more cell phones.

Here is an abbreviated version of the system to solve hypothesis tests applied to a test on a proportions.

\[H_0 : P = 0.3 \nonumber\]

\[H_a : P \neq 0.3 \nonumber\]

\[n = 150\nonumber\]

\[P^{\prime}=\frac{x}{n}=\frac{43}{150}=0.287\nonumber\]

\[z_{obs}=\frac{P^{\prime}-P_{0}}{\sqrt{\frac{P_{0} (1-P_{0})}{n}}}=\frac{0.287-0.3}{\sqrt{\frac{.3(.7)}{150}}}=0.347\nonumber\]

At a confidence level of 90% we cannot reject the null hypothesis that the consumer group is correct.

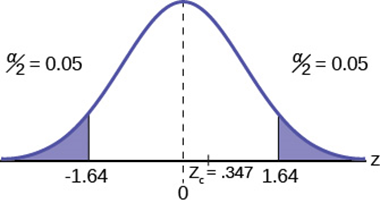
Figure \(\PageIndex{4}\)

Example \(\PageIndex{6}\)

In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.

We need to conduct a hypothesis test on the claimed cancer rate. Our hypotheses will be:

If we commit a Type I error, we are essentially accepting an incorrect claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.

9.4 Full Hypothesis Test Examples

Tests on means, example 9.8.

Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle, with a standard deviation of 0.8 seconds . His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles. Frank bought Jeffrey a new pair of expensive goggles and timed Jeffrey for 15 25-yard freestyle swims . For the 15 swims, Jeffrey's mean time was 16 seconds. Frank thought that the goggles helped Jeffrey to swim faster than the 16.43 seconds. Conduct a hypothesis test using a preset α = 0.05.

Set up the Hypothesis Test:

Since the problem is about a mean, this is a test of a single population mean .

Set the null and alternative hypothesis:

In this case there is an implied challenge or claim. This is that the goggles will reduce the swimming time. The effect of this is to set the hypothesis as a one-tailed test. The claim will always be in the alternative hypothesis because the burden of proof always lies with the alternative. Remember that the status quo must be defeated with a high degree of confidence, in this case 95 % confidence. The null and alternative hypotheses are thus:

H 0 : μ ≥ 16.43   H a : μ < 16.43

For Jeffrey to swim faster, his time will be less than 16.43 seconds. The "<" tells you this is left-tailed.

Determine the distribution needed:

Random variable: X ¯ X ¯ = the mean time to swim the 25-yard freestyle.

Distribution for the test statistic:

The sample size is less than 30 and we do not know the population standard deviation so this is a t-test. and the proper formula is: t c = X ¯ - μ 0 σ / n t c = X ¯ - μ 0 σ / n

μ 0 = 16.43 comes from H 0 and not the data. X ¯ X ¯ = 16. s = 0.8, and n = 15.

Our step 2, setting the level of significance, has already been determined by the problem, .05 for a 95 % significance level. It is worth thinking about the meaning of this choice. The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on average, in 16.43 seconds. (Reject the null hypothesis when the null hypothesis is true.) For this case the only concern with a Type I error would seem to be that Jeffery’s dad may fail to bet on his son’s victory because he does not have appropriate confidence in the effect of the goggles.

To find the critical value we need to select the appropriate test statistic. We have concluded that this is a t-test on the basis of the sample size and that we are interested in a population mean. We can now draw the graph of the t-distribution and mark the critical value. For this problem the degrees of freedom are n-1, or 14. Looking up 14 degrees of freedom at the 0.05 column of the t-table we find 1.761. This is the critical value and we can put this on our graph.

Step 3 is the calculation of the test statistic using the formula we have selected. We find that the calculated test statistic is 2.08, meaning that the sample mean is 2.08 standard deviations away from the hypothesized mean of 16.43.

Step 4 has us compare the test statistic and the critical value and mark these on the graph. We see that the test statistic is in the tail and thus we move to step 4 and reach a conclusion. The probability that an average time of 16 minutes could come from a distribution with a population mean of 16.43 minutes is too unlikely for us to accept the null hypothesis. We cannot accept the null.

Step 5 has us state our conclusions first formally and then less formally. A formal conclusion would be stated as: “With a 95% level of significance we cannot accept the null hypothesis that the swimming time with goggles comes from a distribution with a population mean time of 16.43 minutes.” Less formally, “With 95% significance we believe that the goggles improves swimming speed”

If we wished to use the p-value system of reaching a conclusion we would calculate the statistic and take the additional step to find the probability of being 2.08 standard deviations from the mean on a t-distribution. This value is .0187. Comparing this to the α-level of .05 we see that we cannot accept the null. The p-value has been put on the graph as the shaded area beyond -2.08 and it shows that it is smaller than the hatched area which is the alpha level of 0.05. Both methods reach the same conclusion that we cannot accept the null hypothesis.

The mean throwing distance of a football for Marco, a high school freshman quarterback, is 40 yards, with a standard deviation of two yards. The team coach tells Marco to adjust his grip to get more distance. The coach records the distances for 20 throws. For the 20 throws, Marco’s mean distance was 45 yards. The coach thought the different grip helped Marco throw farther than 40 yards. Conduct a hypothesis test using a preset α = 0.05. Assume the throw distances for footballs are normal.

First, determine what type of test this is, set up the hypothesis test, find the p -value, sketch the graph, and state your conclusion.

Example 9.9

Jane has just begun her new job as on the sales force of a very competitive company. In a sample of 16 sales calls it was found that she closed the contract for an average value of 108 dollars with a standard deviation of 12 dollars. Test at 5% significance that the population mean is at least 100 dollars against the alternative that it is less than 100 dollars. Company policy requires that new members of the sales force must exceed an average of $100 per contract during the trial employment period. Can we conclude that Jane has met this requirement at the significance level of 95%?

• H 0 : µ ≤ 100 H a : µ > 100 The null and alternative hypothesis are for the parameter µ because the number of dollars of the contracts is a continuous random variable. Also, this is a one-tailed test because the company has only an interested if the number of dollars per contact is below a particular number not "too high" a number. This can be thought of as making a claim that the requirement is being met and thus the claim is in the alternative hypothesis.
• Test statistic: t c = x ¯ − µ 0 s n = 108 − 100 ( 12 16 ) = 2.67 t c = x ¯ − µ 0 s n = 108 − 100 ( 12 16 ) = 2.67
• Critical value: t a = 1.753 t a = 1.753 with n-1 degrees of freedom= 15

The test statistic is a Student's t because the sample size is below 30; therefore, we cannot use the normal distribution. Comparing the calculated value of the test statistic and the critical value of t t ( t a ) ( t a ) at a 5% significance level, we see that the calculated value is in the tail of the distribution. Thus, we conclude that 108 dollars per contract is significantly larger than the hypothesized value of 100 and thus we cannot accept the null hypothesis. There is evidence that supports Jane's performance meets company standards.

It is believed that a stock price for a particular company will grow at a rate of $5 per week with a standard deviation of $1. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows: $4, $3, $2, $3, $1, $7, $2, $1, $1, $2. Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, state your conclusion, and identify the Type I errors.

Example 9.10

A manufacturer of salad dressings uses machines to dispense liquid ingredients into bottles that move along a filling line. The machine that dispenses salad dressings is working properly when 8 ounces are dispensed. Suppose that the average amount dispensed in a particular sample of 35 bottles is 7.91 ounces with a variance of 0.03 ounces squared, s 2 s 2 . Is there evidence that the machine should be stopped and production wait for repairs? The lost production from a shutdown is potentially so great that management feels that the level of significance in the analysis should be 99%.

Again we will follow the steps in our analysis of this problem.

STEP 1 : Set the Null and Alternative Hypothesis. The random variable is the quantity of fluid placed in the bottles. This is a continuous random variable and the parameter we are interested in is the mean. Our hypothesis therefore is about the mean. In this case we are concerned that the machine is not filling properly. From what we are told it does not matter if the machine is over-filling or under-filling, both seem to be an equally bad error. This tells us that this is a two-tailed test: if the machine is malfunctioning it will be shutdown regardless if it is from over-filling or under-filling. The null and alternative hypotheses are thus:

STEP 2 : Decide the level of significance and draw the graph showing the critical value.

This problem has already set the level of significance at 99%. The decision seems an appropriate one and shows the thought process when setting the significance level. Management wants to be very certain, as certain as probability will allow, that they are not shutting down a machine that is not in need of repair. To draw the distribution and the critical value, we need to know which distribution to use. Because this is a continuous random variable and we are interested in the mean, and the sample size is greater than 30, the appropriate distribution is the normal distribution and the relevant critical value is 2.575 from the normal table or the t-table at 0.005 column and infinite degrees of freedom. We draw the graph and mark these points.

STEP 3 : Calculate sample parameters and the test statistic. The sample parameters are provided, the sample mean is 7.91 and the sample variance is .03 and the sample size is 35. We need to note that the sample variance was provided not the sample standard deviation, which is what we need for the formula. Remembering that the standard deviation is simply the square root of the variance, we therefore know the sample standard deviation, s, is 0.173. With this information we calculate the test statistic as -3.07, and mark it on the graph.

STEP 4 : Compare test statistic and the critical values Now we compare the test statistic and the critical value by placing the test statistic on the graph. We see that the test statistic is in the tail, decidedly greater than the critical value of 2.575. We note that even the very small difference between the hypothesized value and the sample value is still a large number of standard deviations. The sample mean is only 0.08 ounces different from the required level of 8 ounces, but it is 3 plus standard deviations away and thus we cannot accept the null hypothesis.

STEP 5 : Reach a Conclusion

Three standard deviations of a test statistic will guarantee that the test will fail. The probability that anything is within three standard deviations is almost zero. Actually it is 0.0026 on the normal distribution, which is certainly almost zero in a practical sense. Our formal conclusion would be “ At a 99% level of significance we cannot accept the hypothesis that the sample mean came from a distribution with a mean of 8 ounces” Or less formally, and getting to the point, “At a 99% level of significance we conclude that the machine is under filling the bottles and is in need of repair”.

Hypothesis Test for Proportions

Just as there were confidence intervals for proportions, or more formally, the population parameter p of the binomial distribution, there is the ability to test hypotheses concerning p .

The population parameter for the binomial is p . The estimated value (point estimate) for p is p′ where p′ = x/n , x is the number of successes in the sample and n is the sample size.

When you perform a hypothesis test of a population proportion p , you take a simple random sample from the population. The conditions for a binomial distribution must be met, which are: there are a certain number n of independent trials meaning random sampling, the outcomes of any trial are binary, success or failure, and each trial has the same probability of a success p . The shape of the binomial distribution needs to be similar to the shape of the normal distribution. To ensure this, the quantities np′ and nq′ must both be greater than five ( np′ > 5 and nq′ > 5). In this case the binomial distribution of a sample (estimated) proportion can be approximated by the normal distribution with μ = np μ = np and σ = npq σ = npq . Remember that q = 1 – p q = 1 – p . There is no distribution that can correct for this small sample bias and thus if these conditions are not met we simply cannot test the hypothesis with the data available at that time. We met this condition when we first were estimating confidence intervals for p .

Again, we begin with the standardizing formula modified because this is the distribution of a binomial.

Substituting p 0 p 0 , the hypothesized value of p , we have:

This is the test statistic for testing hypothesized values of p , where the null and alternative hypotheses take one of the following forms:

The decision rule stated above applies here also: if the calculated value of Z c shows that the sample proportion is "too many" standard deviations from the hypothesized proportion, the null hypothesis cannot be accepted. The decision as to what is "too many" is pre-determined by the analyst depending on the level of significance required in the test.

Example 9.11

The mortgage department of a large bank is interested in the nature of loans of first-time borrowers. This information will be used to tailor their marketing strategy. They believe that 50% of first-time borrowers take out smaller loans than other borrowers. They perform a hypothesis test to determine if the percentage is the same or different from 50% . They sample 100 first-time borrowers and find 53 of these loans are smaller that the other borrowers. For the hypothesis test, they choose a 5% level of significance.

STEP 1 : Set the null and alternative hypothesis.

H 0 : p = 0.50   H a : p ≠ 0.50

The words "is the same or different from" tell you this is a two-tailed test. The Type I and Type II errors are as follows: The Type I error is to conclude that the proportion of borrowers is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true). The Type II error is there is not enough evidence to conclude that the proportion of first time borrowers differs from 50% when, in fact, the proportion does differ from 50%. (You fail to reject the null hypothesis when the null hypothesis is false.)

STEP 2 : Decide the level of significance and draw the graph showing the critical value

The level of significance has been set by the problem at the 95% level. Because this is two-tailed test one-half of the alpha value will be in the upper tail and one-half in the lower tail as shown on the graph. The critical value for the normal distribution at the 95% level of confidence is 1.96. This can easily be found on the student’s t-table at the very bottom at infinite degrees of freedom remembering that at infinity the t-distribution is the normal distribution. Of course the value can also be found on the normal table but you have go looking for one-half of 95 (0.475) inside the body of the table and then read out to the sides and top for the number of standard deviations.

STEP 3 : Calculate the sample parameters and critical value of the test statistic.

The test statistic is a normal distribution, Z, for testing proportions and is:

For this case, the sample of 100 found 53 first-time borrowers were different from other borrowers. The sample proportion, p′ = 53/100= 0.53 The test question, therefore, is : “Is 0.53 significantly different from .50?” Putting these values into the formula for the test statistic we find that 0.53 is only 0.60 standard deviations away from .50. This is barely off of the mean of the standard normal distribution of zero. There is virtually no difference from the sample proportion and the hypothesized proportion in terms of standard deviations.

STEP 4 : Compare the test statistic and the critical value.

The calculated value is well within the critical values of ± 1.96 standard deviations and thus we cannot reject the null hypothesis. To reject the null hypothesis we need significant evident of difference between the hypothesized value and the sample value. In this case the sample value is very nearly the same as the hypothesized value measured in terms of standard deviations.

STEP 5 : Reach a conclusion

The formal conclusion would be “At a 95% level of significance we cannot reject the null hypothesis that 50% of first-time borrowers have the same size loans as other borrowers”. Less formally we would say that “There is no evidence that one-half of first-time borrowers are significantly different in loan size from other borrowers”. Notice the length to which the conclusion goes to include all of the conditions that are attached to the conclusion. Statisticians for all the criticism they receive, are careful to be very specific even when this seems trivial. Statisticians cannot say more than they know and the data constrain the conclusion to be within the metes and bounds of the data.

Try It 9.11

A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.

Example 9.12

Suppose a consumer group suspects that the proportion of households that have three or more cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test. Their marketing people survey 150 households with the result that 43 of the households have three or more cell phones.

Here is an abbreviate version of the system to solve hypothesis tests applied to a test on a proportions.

Example 9.13

The National Institute of Standards and Technology provides exact data on conductivity properties of materials. Following are conductivity measurements for 11 randomly selected pieces of a particular type of glass.

1.11; 1.07; 1.11; 1.07; 1.12; 1.08; .98; .98 1.02; .95; .95 Is there convincing evidence that the average conductivity of this type of glass is greater than one? Use a significance level of 0.05.

Let’s follow a four-step process to answer this statistical question.

• H 0 : μ ≤ 1
• H a : μ > 1
• Plan : We are testing a sample mean without a known population standard deviation with less than 30 observations. Therefore, we need to use a Student's-t distribution. Assume the underlying population is normal.
• Do the calculations and draw the graph .
• State the Conclusions : We cannot accept the null hypothesis. It is reasonable to state that the data supports the claim that the average conductivity level is greater than one.

Example 9.14

In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.

• H 0 : p ≤ 0.00034
• H a : p > 0.00034

If we commit a Type I error, we are essentially accepting a false claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.

• We will be testing a sample proportion with x = 172 and n = 420,019. The sample is sufficiently large because we have np' = 420,019(0.00034) = 142.8, nq' = 420,019(0.99966) = 419,876.2, two independent outcomes, and a fixed probability of success p' = 0.00034. Thus we will be able to generalize our results to the population.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/introductory-business-statistics/pages/1-introduction

• Authors: Alexander Holmes, Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Introductory Business Statistics
• Publication date: Nov 29, 2017
• Location: Houston, Texas
• Book URL: https://openstax.org/books/introductory-business-statistics/pages/1-introduction
• Section URL: https://openstax.org/books/introductory-business-statistics/pages/9-4-full-hypothesis-test-examples

© Jun 23, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Statistics Made Easy

4 Examples of Hypothesis Testing in Real Life

In statistics, hypothesis tests are used to test whether or not some hypothesis about a population parameter is true.

To perform a hypothesis test in the real world, researchers will obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:

• Null Hypothesis (H 0 ): The sample data occurs purely from chance.
• Alternative Hypothesis (H A ): The sample data is influenced by some non-random cause.

If the p-value of the hypothesis test is less than some significance level (e.g. α = .05), then we can reject the null hypothesis and conclude that we have sufficient evidence to say that the alternative hypothesis is true.

The following examples provide several situations where hypothesis tests are used in the real world.

Example 1: Biology

Hypothesis tests are often used in biology to determine whether some new treatment, fertilizer, pesticide, chemical, etc. causes increased growth, stamina, immunity, etc. in plants or animals.

For example, suppose a biologist believes that a certain fertilizer will cause plants to grow more during a one-month period than they normally do, which is currently 20 inches. To test this, she applies the fertilizer to each of the plants in her laboratory for one month.

She then performs a hypothesis test using the following hypotheses:

• H 0 : μ = 20 inches (the fertilizer will have no effect on the mean plant growth)
• H A : μ > 20 inches (the fertilizer will cause mean plant growth to increase)

If the p-value of the test is less than some significance level (e.g. α = .05), then she can reject the null hypothesis and conclude that the fertilizer leads to increased plant growth.

Example 2: Clinical Trials

Hypothesis tests are often used in clinical trials to determine whether some new treatment, drug, procedure, etc. causes improved outcomes in patients.

For example, suppose a doctor believes that a new drug is able to reduce blood pressure in obese patients. To test this, he may measure the blood pressure of 40 patients before and after using the new drug for one month.

He then performs a hypothesis test using the following hypotheses:

• H 0 : μ after = μ before (the mean blood pressure is the same before and after using the drug)
• H A : μ after < μ before (the mean blood pressure is less after using the drug)

If the p-value of the test is less than some significance level (e.g. α = .05), then he can reject the null hypothesis and conclude that the new drug leads to reduced blood pressure.

Example 3: Advertising Spend

Hypothesis tests are often used in business to determine whether or not some new advertising campaign, marketing technique, etc. causes increased sales.

For example, suppose a company believes that spending more money on digital advertising leads to increased sales. To test this, the company may increase money spent on digital advertising during a two-month period and collect data to see if overall sales have increased.

They may perform a hypothesis test using the following hypotheses:

• H 0 : μ after = μ before (the mean sales is the same before and after spending more on advertising)
• H A : μ after > μ before (the mean sales increased after spending more on advertising)

If the p-value of the test is less than some significance level (e.g. α = .05), then the company can reject the null hypothesis and conclude that increased digital advertising leads to increased sales.

Example 4: Manufacturing

Hypothesis tests are also used often in manufacturing plants to determine if some new process, technique, method, etc. causes a change in the number of defective products produced.

For example, suppose a certain manufacturing plant wants to test whether or not some new method changes the number of defective widgets produced per month, which is currently 250. To test this, they may measure the mean number of defective widgets produced before and after using the new method for one month.

They can then perform a hypothesis test using the following hypotheses:

• H 0 : μ after = μ before (the mean number of defective widgets is the same before and after using the new method)
• H A : μ after ≠ μ before (the mean number of defective widgets produced is different before and after using the new method)

If the p-value of the test is less than some significance level (e.g. α = .05), then the plant can reject the null hypothesis and conclude that the new method leads to a change in the number of defective widgets produced per month.

Additional Resources

Introduction to Hypothesis Testing Introduction to the One Sample t-test Introduction to the Two Sample t-test Introduction to the Paired Samples t-test

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

I have read and agree to the terms & conditions

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes

Null Hypothesis

• Hypothesis Testing Formula
• SQLite IS NULL
• MySQL NOT NULL Constraint
• Real-life Applications of Hypothesis Testing
• Null in JavaScript
• SQL NOT NULL Constraint
• Null Cipher
• Hypothesis in Machine Learning
• Understanding Hypothesis Testing
• Difference between Null and Alternate Hypothesis
• Hypothesis Testing in R Programming
• SQL | NULL functions
• Kotlin Null Safety
• PHP | is_null() Function
• MySQL | NULLIF( ) Function
• Null-Coalescing Operator in C#
• Nullity of a Matrix

Null Hypothesis , often denoted as H 0, is a foundational concept in statistical hypothesis testing. It represents an assumption that no significant difference, effect, or relationship exists between variables within a population. It serves as a baseline assumption, positing no observed change or effect occurring. The null is t he truth or falsity of an idea in analysis.

In this article, we will discuss the null hypothesis in detail, along with some solved examples and questions on the null hypothesis.

Table of Content

What is Null Hypothesis?

Null hypothesis symbol, formula of null hypothesis, types of null hypothesis, null hypothesis examples, principle of null hypothesis, how do you find null hypothesis, null hypothesis in statistics, null hypothesis and alternative hypothesis, null hypothesis and alternative hypothesis examples, null hypothesis – practice problems.

Null Hypothesis in statistical analysis suggests the absence of statistical significance within a specific set of observed data. Hypothesis testing, using sample data, evaluates the validity of this hypothesis. Commonly denoted as H 0 or simply “null,” it plays an important role in quantitative analysis, examining theories related to markets, investment strategies, or economies to determine their validity.

Null Hypothesis Meaning

Null Hypothesis represents a default position, often suggesting no effect or difference, against which researchers compare their experimental results. The Null Hypothesis, often denoted as H 0 asserts a default assumption in statistical analysis. It posits no significant difference or effect, serving as a baseline for comparison in hypothesis testing.

The null Hypothesis is represented as H 0 , the Null Hypothesis symbolizes the absence of a measurable effect or difference in the variables under examination.

Certainly, a simple example would be asserting that the mean score of a group is equal to a specified value like stating that the average IQ of a population is 100.

The Null Hypothesis is typically formulated as a statement of equality or absence of a specific parameter in the population being studied. It provides a clear and testable prediction for comparison with the alternative hypothesis. The formulation of the Null Hypothesis typically follows a concise structure, stating the equality or absence of a specific parameter in the population.

Mean Comparison (Two-sample t-test)

H 0 : μ 1 = μ 2

This asserts that there is no significant difference between the means of two populations or groups.

Proportion Comparison

H 0 : p 1 − p 2 = 0

This suggests no significant difference in proportions between two populations or conditions.

Equality in Variance (F-test in ANOVA)

H 0 : σ 1 = σ 2

This states that there’s no significant difference in variances between groups or populations.

Independence (Chi-square Test of Independence):

H 0 : Variables are independent

This asserts that there’s no association or relationship between categorical variables.

Null Hypotheses vary including simple and composite forms, each tailored to the complexity of the research question. Understanding these types is pivotal for effective hypothesis testing.

Equality Null Hypothesis (Simple Null Hypothesis)

The Equality Null Hypothesis, also known as the Simple Null Hypothesis, is a fundamental concept in statistical hypothesis testing that assumes no difference, effect or relationship between groups, conditions or populations being compared.

Non-Inferiority Null Hypothesis

In some studies, the focus might be on demonstrating that a new treatment or method is not significantly worse than the standard or existing one.

Superiority Null Hypothesis

The concept of a superiority null hypothesis comes into play when a study aims to demonstrate that a new treatment, method, or intervention is significantly better than an existing or standard one.

Independence Null Hypothesis

In certain statistical tests, such as chi-square tests for independence, the null hypothesis assumes no association or independence between categorical variables.

Homogeneity Null Hypothesis

In tests like ANOVA (Analysis of Variance), the null hypothesis suggests that there’s no difference in population means across different groups.

• Medicine: Null Hypothesis: “No significant difference exists in blood pressure levels between patients given the experimental drug versus those given a placebo.”
• Education: Null Hypothesis: “There’s no significant variation in test scores between students using a new teaching method and those using traditional teaching.”
• Economics: Null Hypothesis: “There’s no significant change in consumer spending pre- and post-implementation of a new taxation policy.”
• Environmental Science: Null Hypothesis: “There’s no substantial difference in pollution levels before and after a water treatment plant’s establishment.”

The principle of the null hypothesis is a fundamental concept in statistical hypothesis testing. It involves making an assumption about the population parameter or the absence of an effect or relationship between variables.

In essence, the null hypothesis (H 0 ) proposes that there is no significant difference, effect, or relationship between variables. It serves as a starting point or a default assumption that there is no real change, no effect or no difference between groups or conditions.

The null hypothesis is usually formulated to be tested against an alternative hypothesis (H 1 or H [Tex]\alpha [/Tex] ) which suggests that there is an effect, difference or relationship present in the population.

Null Hypothesis Rejection

Rejecting the Null Hypothesis occurs when statistical evidence suggests a significant departure from the assumed baseline. It implies that there is enough evidence to support the alternative hypothesis, indicating a meaningful effect or difference. Null Hypothesis rejection occurs when statistical evidence suggests a deviation from the assumed baseline, prompting a reconsideration of the initial hypothesis.

Identifying the Null Hypothesis involves defining the status quotient, asserting no effect and formulating a statement suitable for statistical analysis.

When is Null Hypothesis Rejected?

The Null Hypothesis is rejected when statistical tests indicate a significant departure from the expected outcome, leading to the consideration of alternative hypotheses. It occurs when statistical evidence suggests a deviation from the assumed baseline, prompting a reconsideration of the initial hypothesis.

In statistical hypothesis testing, researchers begin by stating the null hypothesis, often based on theoretical considerations or previous research. The null hypothesis is then tested against an alternative hypothesis (Ha), which represents the researcher’s claim or the hypothesis they seek to support.

The process of hypothesis testing involves collecting sample data and using statistical methods to assess the likelihood of observing the data if the null hypothesis were true. This assessment is typically done by calculating a test statistic, which measures the difference between the observed data and what would be expected under the null hypothesis.

In the realm of hypothesis testing, the null hypothesis (H 0 ) and alternative hypothesis (H₁ or Ha) play critical roles. The null hypothesis generally assumes no difference, effect, or relationship between variables, suggesting that any observed change or effect is due to random chance. Its counterpart, the alternative hypothesis, asserts the presence of a significant difference, effect, or relationship between variables, challenging the null hypothesis. These hypotheses are formulated based on the research question and guide statistical analyses.

Difference Between Null Hypothesis and Alternative Hypothesis

The null hypothesis (H 0 ) serves as the baseline assumption in statistical testing, suggesting no significant effect, relationship, or difference within the data. It often proposes that any observed change or correlation is merely due to chance or random variation. Conversely, the alternative hypothesis (H 1 or Ha) contradicts the null hypothesis, positing the existence of a genuine effect, relationship or difference in the data. It represents the researcher’s intended focus, seeking to provide evidence against the null hypothesis and support for a specific outcome or theory. These hypotheses form the crux of hypothesis testing, guiding the assessment of data to draw conclusions about the population being studied.

Let’s envision a scenario where a researcher aims to examine the impact of a new medication on reducing blood pressure among patients. In this context:

Null Hypothesis (H 0 ): “The new medication does not produce a significant effect in reducing blood pressure levels among patients.”

Alternative Hypothesis (H 1 or Ha): “The new medication yields a significant effect in reducing blood pressure levels among patients.”

The null hypothesis implies that any observed alterations in blood pressure subsequent to the medication’s administration are a result of random fluctuations rather than a consequence of the medication itself. Conversely, the alternative hypothesis contends that the medication does indeed generate a meaningful alteration in blood pressure levels, distinct from what might naturally occur or by random chance.

People Also Read:

Mathematics Maths Formulas Probability and Statistics

Example 1: A researcher claims that the average time students spend on homework is 2 hours per night.

Null Hypothesis (H 0 ): The average time students spend on homework is equal to 2 hours per night. Data: A random sample of 30 students has an average homework time of 1.8 hours with a standard deviation of 0.5 hours. Test Statistic and Decision: Using a t-test, if the calculated t-statistic falls within the acceptance region, we fail to reject the null hypothesis. If it falls in the rejection region, we reject the null hypothesis. Conclusion: Based on the statistical analysis, we fail to reject the null hypothesis, suggesting that there is not enough evidence to dispute the claim of the average homework time being 2 hours per night.

Example 2: A company asserts that the error rate in its production process is less than 1%.

Null Hypothesis (H 0 ): The error rate in the production process is 1% or higher. Data: A sample of 500 products shows an error rate of 0.8%. Test Statistic and Decision: Using a z-test, if the calculated z-statistic falls within the acceptance region, we fail to reject the null hypothesis. If it falls in the rejection region, we reject the null hypothesis. Conclusion: The statistical analysis supports rejecting the null hypothesis, indicating that there is enough evidence to dispute the company’s claim of an error rate of 1% or higher.

Q1. A researcher claims that the average time spent by students on homework is less than 2 hours per day. Formulate the null hypothesis for this claim?

Q2. A manufacturing company states that their new machine produces widgets with a defect rate of less than 5%. Write the null hypothesis to test this claim?

Q3. An educational institute believes that their online course completion rate is at least 60%. Develop the null hypothesis to validate this assertion?

Q4. A restaurant claims that the waiting time for customers during peak hours is not more than 15 minutes. Formulate the null hypothesis for this claim?

Q5. A study suggests that the mean weight loss after following a specific diet plan for a month is more than 8 pounds. Construct the null hypothesis to evaluate this statement?

Summary – Null Hypothesis and Alternative Hypothesis

The null hypothesis (H 0 ) and alternative hypothesis (H a ) are fundamental concepts in statistical hypothesis testing. The null hypothesis represents the default assumption, stating that there is no significant effect, difference, or relationship between variables. It serves as the baseline against which the alternative hypothesis is tested. In contrast, the alternative hypothesis represents the researcher’s hypothesis or the claim to be tested, suggesting that there is a significant effect, difference, or relationship between variables. The relationship between the null and alternative hypotheses is such that they are complementary, and statistical tests are conducted to determine whether the evidence from the data is strong enough to reject the null hypothesis in favor of the alternative hypothesis. This decision is based on the strength of the evidence and the chosen level of significance. Ultimately, the choice between the null and alternative hypotheses depends on the specific research question and the direction of the effect being investigated.

FAQs on Null Hypothesis

What does null hypothesis stands for.

The null hypothesis, denoted as H 0 ​, is a fundamental concept in statistics used for hypothesis testing. It represents the statement that there is no effect or no difference, and it is the hypothesis that the researcher typically aims to provide evidence against.

How to Form a Null Hypothesis?

A null hypothesis is formed based on the assumption that there is no significant difference or effect between the groups being compared or no association between variables being tested. It often involves stating that there is no relationship, no change, or no effect in the population being studied.

When Do we reject the Null Hypothesis?

In statistical hypothesis testing, if the p-value (the probability of obtaining the observed results) is lower than the chosen significance level (commonly 0.05), we reject the null hypothesis. This suggests that the data provides enough evidence to refute the assumption made in the null hypothesis.

What is a Null Hypothesis in Research?

In research, the null hypothesis represents the default assumption or position that there is no significant difference or effect. Researchers often try to test this hypothesis by collecting data and performing statistical analyses to see if the observed results contradict the assumption.

What Are Alternative and Null Hypotheses?

The null hypothesis (H0) is the default assumption that there is no significant difference or effect. The alternative hypothesis (H1 or Ha) is the opposite, suggesting there is a significant difference, effect or relationship.

What Does it Mean to Reject the Null Hypothesis?

Rejecting the null hypothesis implies that there is enough evidence in the data to support the alternative hypothesis. In simpler terms, it suggests that there might be a significant difference, effect or relationship between the groups or variables being studied.

How to Find Null Hypothesis?

Formulating a null hypothesis often involves considering the research question and assuming that no difference or effect exists. It should be a statement that can be tested through data collection and statistical analysis, typically stating no relationship or no change between variables or groups.

How is Null Hypothesis denoted?

The null hypothesis is commonly symbolized as H 0 in statistical notation.

What is the Purpose of the Null hypothesis in Statistical Analysis?

The null hypothesis serves as a starting point for hypothesis testing, enabling researchers to assess if there’s enough evidence to reject it in favor of an alternative hypothesis.

What happens if we Reject the Null hypothesis?

Rejecting the null hypothesis implies that there is sufficient evidence to support an alternative hypothesis, suggesting a significant effect or relationship between variables.

What are Test for Null Hypothesis?

Various statistical tests, such as t-tests or chi-square tests, are employed to evaluate the validity of the Null Hypothesis in different scenarios.

Please Login to comment...

Similar reads.

• Geeks Premier League 2023
• Math-Concepts
• Geeks Premier League
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?