research model meaning

• Link to facebook
• Link to linkedin
• Link to twitter
• Link to youtube
• Writing Tips

The Four Types of Research Paradigms: A Comprehensive Guide

5-minute read

• 22nd January 2023

In this guide, you’ll learn all about the four research paradigms and how to choose the right one for your research.

Introduction to Research Paradigms

A paradigm is a system of beliefs, ideas, values, or habits that form the basis for a way of thinking about the world. Therefore, a research paradigm is an approach, model, or framework from which to conduct research. The research paradigm helps you to form a research philosophy, which in turn informs your research methodology.

Your research methodology is essentially the “how” of your research – how you design your study to not only accomplish your research’s aims and objectives but also to ensure your results are reliable and valid. Choosing the correct research paradigm is crucial because it provides a logical structure for conducting your research and improves the quality of your work, assuming it’s followed correctly.

Three Pillars: Ontology, Epistemology, and Methodology

Before we jump into the four types of research paradigms, we need to consider the three pillars of a research paradigm.

Ontology addresses the question, “What is reality?” It’s the study of being. This pillar is about finding out what you seek to research. What do you aim to examine?

Epistemology is the study of knowledge. It asks, “How is knowledge gathered and from what sources?”

Methodology involves the system in which you choose to investigate, measure, and analyze your research’s aims and objectives. It answers the “how” questions.

Let’s now take a look at the different research paradigms.

1.   Positivist Research Paradigm

The positivist research paradigm assumes that there is one objective reality, and people can know this reality and accurately describe and explain it. Positivists rely on their observations through their senses to gain knowledge of their surroundings.

In this singular objective reality, researchers can compare their claims and ascertain the truth. This means researchers are limited to data collection and interpretations from an objective viewpoint. As a result, positivists usually use quantitative methodologies in their research (e.g., statistics, social surveys, and structured questionnaires).

This research paradigm is mostly used in natural sciences, physical sciences, or whenever large sample sizes are being used.

2.   Interpretivist Research Paradigm

Interpretivists believe that different people in society experience and understand reality in different ways – while there may be only “one” reality, everyone interprets it according to their own view. They also believe that all research is influenced and shaped by researchers’ worldviews and theories.

As a result, interpretivists use qualitative methods and techniques to conduct their research. This includes interviews, focus groups, observations of a phenomenon, or collecting documentation on a phenomenon (e.g., newspaper articles, reports, or information from websites).

3.   Critical Theory Research Paradigm

The critical theory paradigm asserts that social science can never be 100% objective or value-free. This paradigm is focused on enacting social change through scientific investigation. Critical theorists question knowledge and procedures and acknowledge how power is used (or abused) in the phenomena or systems they’re investigating.

Find this useful?

Subscribe to our newsletter and get writing tips from our editors straight to your inbox.

Researchers using this paradigm are more often than not aiming to create a more just, egalitarian society in which individual and collective freedoms are secure. Both quantitative and qualitative methods can be used with this paradigm.

4.   Constructivist Research Paradigm

Constructivism asserts that reality is a construct of our minds ; therefore, reality is subjective. Constructivists believe that all knowledge comes from our experiences and reflections on those experiences and oppose the idea that there is a single methodology to generate knowledge.

This paradigm is mostly associated with qualitative research approaches due to its focus on experiences and subjectivity. The researcher focuses on participants’ experiences as well as their own.

Choosing the Right Research Paradigm for Your Study

Once you have a comprehensive understanding of each paradigm, you’re faced with a big question: which paradigm should you choose? The answer to this will set the course of your research and determine its success, findings, and results.

To start, you need to identify your research problem, research objectives , and hypothesis . This will help you to establish what you want to accomplish or understand from your research and the path you need to take to achieve this.

You can begin this process by asking yourself some questions:

• What is the nature of your research problem (i.e., quantitative or qualitative)?
• How can you acquire the knowledge you need and communicate it to others? For example, is this knowledge already available in other forms (e.g., documents) and do you need to gain it by gathering or observing other people’s experiences or by experiencing it personally?
• What is the nature of the reality that you want to study? Is it objective or subjective?

Depending on the problem and objective, other questions may arise during this process that lead you to a suitable paradigm. Ultimately, you must be able to state, explain, and justify the research paradigm you select for your research and be prepared to include this in your dissertation’s methodology and design section.

Using Two Paradigms

If the nature of your research problem and objectives involves both quantitative and qualitative aspects, then you might consider using two paradigms or a mixed methods approach . In this, one paradigm is used to frame the qualitative aspects of the study and another for the quantitative aspects. This is acceptable, although you will be tasked with explaining your rationale for using both of these paradigms in your research.

Choosing the right research paradigm for your research can seem like an insurmountable task. It requires you to:

●  Have a comprehensive understanding of the paradigms,

●  Identify your research problem, objectives, and hypothesis, and

●  Be able to state, explain, and justify the paradigm you select in your methodology and design section.

Although conducting your research and putting your dissertation together is no easy task, proofreading it can be! Our experts are here to make your writing shine. Your first 500 words are free !

Share this article:

Post A New Comment

Got content that needs a quick turnaround? Let us polish your work. Explore our editorial business services.

Free email newsletter template.

Promoting a brand means sharing valuable insights to connect more deeply with your audience, and...

6-minute read

How to Write a Nonprofit Grant Proposal

If you’re seeking funding to support your charitable endeavors as a nonprofit organization, you’ll need...

9-minute read

How to Use Infographics to Boost Your Presentation

Is your content getting noticed? Capturing and maintaining an audience’s attention is a challenge when...

8-minute read

Why Interactive PDFs Are Better for Engagement

Are you looking to enhance engagement and captivate your audience through your professional documents? Interactive...

7-minute read

Seven Key Strategies for Voice Search Optimization

Voice search optimization is rapidly shaping the digital landscape, requiring content professionals to adapt their...

4-minute read

Five Creative Ways to Showcase Your Digital Portfolio

Are you a creative freelancer looking to make a lasting impression on potential clients or...

Make sure your writing is the best it can be with our expert English proofreading and editing.

What is a Model? 5 Essential Components

In the research and statistics context, what does the term model mean? This article defines what is a model, poses guide questions on how to create one, lists steps on how to construct a model and provides simple examples to clarify points arising from those questions.

One of the interesting things that I particularly like in statistics is the prospect of being able to predict an outcome (referred to as the independent variable) from a set of factors (referred to as the independent variables). A multiple regression equation or a model derived from a set of interrelated variables achieves this end.

The usefulness of a model is determined by how well it can predict the behavior of dependent variables from a set of independent variables.

To clarify the concept, I will describe here an example of a research activity that aimed to develop a multiple regression model from both secondary and primary data sources.

What is a Model?

Before going into a detailed discussion on what is a model, it is always good practice to define what we mean here by a model.

A model, in research and statistics, is a representation of reality using variables that somehow relate with each other. I italicize the word “somehow” here being reminded of the possibility of a correlation between variables when in fact there is no logical connection between them.

A Classic Example of Nonsensical Correlation

A classic example given to illustrate nonsensical correlation is the high correlation between length of hair and height. They found out in a study that if a person has short hair, that person is tall and vice versa.

Actually, the conclusion of that study is spurious because there is no real correlation between length of hair and height. It so happened that men usually have short hair while women have long hair. Men are taller than women. The true variable behind what really determines height is the sex or gender of the individual, not the length of hair.

The model is only an approximation of the likely outcome of things because there will always be errors involved in building it. This is the reason scientists adopt a five percent error (p=0.05) as a standard in making conclusions from statistical computations. There is no such thing as absolute certainty in predicting the probability of a phenomenon.

Things Needed to Construct A Model

In developing a multiple regression model which will be fully described here, you will need to have a clear idea of:

• What is your intention or reason in constructing the model?
• What is the time frame and unit of your analysis?
• What has been done so far in line with the model that you intend to construct?
• What variables would you like to include in your model?
• How would you ensure your model has predictive value?

These questions will guide you towards developing a model that will help you achieve your goal. I explain the expected answers to the above questions. I provide examples to further clarify the points.

1. Purpose in Constructing the Model

Why would you like to have a model in the first place? What would you like to get from it? The objectives of your research, therefore, should be clear enough so that you can derive full benefit from it.

Here, I sought to develop a model. The main purpose is to determine the predictors of the number of published papers produced by the faculty in the university. The major question, therefore, is:

“What are the crucial factors that will motivate the faculty members to engage in research and publish research papers?”

Once the research director of the university, I figured out that the best way to increase the number of research publications is to zero in on those variables that really matter. There are so many variables that will influence the turnout of publications, but which ones do really matter?

A certain number of research publications is required each year, so what should the interventions be to reach those targets? There is a need to identify the reasons for the failure of the faculty members to publish research papers to rectify the problem.

2. Time Frame and Unit of Analysis

You should have a specific time frame on which you should base your analysis from.

There are many considerations in selecting the time frame of the analysis but of foremost importance is the availability of data. For established universities with consistent data collection fields, this poses no problem. But for struggling universities without an established database, it will be much more challenging.

Why do I say consistent data collection fields? If you want to see trends, then the same data must be collected in a series through time.

What do I mean by this?

In the particular case I mentioned, i.e., number of publications, one of the suspected predictors is the time spent by the faculty in administrative work. In a 40-hour work week, how much time do they spend in designated posts such as unit head, department head, or dean? This variable which is a unit of analysis , therefore, should be consistently monitored every semester, for many years for correlation with the number of publications.

How many years should these data be collected?

From what I collect, peer-reviewed publications can be produced normally from two to three years. Hence, the study must cover at least three years of data to log the number of publications produced. That is, if no systematic data collection ensued to supply the study’s data needs.

If data was systematically collected, you can backtrack and get data for as long as you want. It is even possible to compare publication performance before and after implementation of a research policy in the university.

3. Literature Review

You might be guilty of “reinventing the wheel” if you did not take time to review published literature on your specific research concern. Reinventing the wheel means you duplicate the work of others. It is possible that other researchers have already satisfactorily studied the area you are trying to clarify issues on. For this reason, an exhaustive review of literature will enhance the quality and predictive value of your model.

For the model I attempted to make on the number of publications made by the faculty, I bumped on a summary of the predictors made by Bland et al . [1] based on a considerable number of published papers. Below is the model they prepared to sum up the findings.

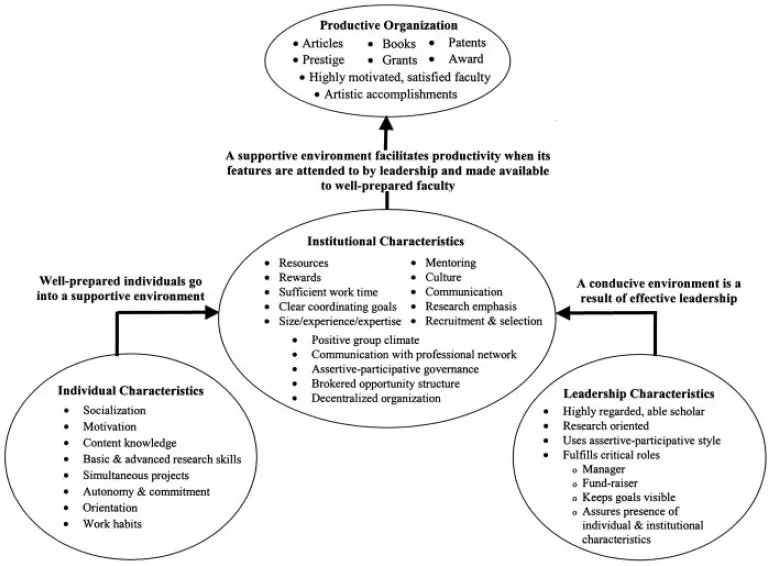
Bland and colleagues found that three major areas determine research productivity namely,

1) the individual’s characteristics,

2) institutional characteristics, and

3) leadership characteristics.

This just means that you cannot just threaten the faculty with the so-called publish and perish policy if the required institutional resources are absent and/or leadership quality is poor.

4. Select the Variables for Study

The model given by Bland and colleagues in the figure above is still too general to allow statistical analysis to take place.

For example, in individual characteristics, how can socialization as a variable be measured? How about motivation ?

This requires you to further delve on literature on how to properly measure socialization and motivation, among other variables you are interested in. The dependent variable I reflected productivity in a recent study I conducted with students is the number of total publications , whether these are peer-reviewed.

5. Ensuring the Predictive Value of the Model

The predictive value of a model depends on influence of a set of predictor variables on the dependent variable. How do you determine influence of these variables?

In Bland’s model, we may include all the variables associated with those concepts identified in analyzing data. But of course, this will be costly and time-consuming as there are a lot of variables to consider. Besides, the greater the number of variables you included in your analysis, the more samples you will need to get a good correlation between the predictor variables and the dependent variable .

Stevens [2] recommends a nominal number of 15 cases for one predictor variable. This means that if you want to study 10 variables, you will need at least 150 cases to make your multiple regression model valid in some sense. But of course, the more samples you have, the greater the certainty in predicting outcomes.

Once you have decided on the number of variables you intend to incorporate in your multiple regression model, you will then be able to input your data on a spreadsheet or a statistical software such as SPSS, Statistica, or related software applications. The software application will automatically produce the results for you.

The next concern is how to interpret the results of a model such as the results of a multiple regression analysis . I will consider this topic in my upcoming posts.

A model is only as good as the data used to create it. You must therefore make sure that your data is accurate and reliable for better predictive outcomes.

• Bland, C.J., Center, B.A., Finstad, D.A., Risbey, K.R., and J. G. Staples. (2005). A Theoretical, Practical, Predictive Model of Faculty and Department Research Productivity.  Academic Medicine , Vol. 80, No. 3, 225-237.
• Stevens, J. 2002. Applied multivariate statistics for the social sciences, 3rd ed . New Jersey: Lawrence Erlbaum Publishers. p. 72.

Updated May 6, 2022 © P. A. Regoniel

Related Posts

Five weaknesses of the survey method, how to write the abstract.

Analyzing Data in Qualitative Research

About the author, patrick regoniel.

Dr. Regoniel, a faculty member of the graduate school, served as consultant to various environmental research and development projects covering issues and concerns on climate change, coral reef resources and management, economic valuation of environmental and natural resources, mining, and waste management and pollution. He has extensive experience on applied statistics, systems modelling and analysis, an avid practitioner of LaTeX, and a multidisciplinary web developer. He leverages pioneering AI-powered content creation tools to produce unique and comprehensive articles in this website.

NOTIFICATIONS

Scientific modelling.

• + Create new collection

In science, a model is a representation of an idea, an object or even a process or a system that is used to describe and explain phenomena that cannot be experienced directly. Models are central to what scientists do, both in their research as well as when communicating their explanations.

Models are a mentally visual way of linking theory with experiment, and they guide research by being simplified representations of an imagined reality that enable predictions to be developed and tested by experiment.

Why scientists use models

Models have a variety of uses – from providing a way of explaining complex data to presenting as a hypothesis. There may be more than one model proposed by scientists to explain or predict what might happen in particular circumstances. Often scientists will argue about the ‘rightness’ of their model, and in the process, the model will evolve or be rejected. Consequently, models are central to the process of knowledge-building in science and demonstrate how science knowledge is tentative.

Think about a model showing the Earth – a globe. Until 2005, globes were always an artist’s representation of what we thought the planet looked like. (In 2005, the first globe using satellite pictures from NASA was produced.) The first known globe to be made (in 150BC) was not very accurate. The globe was constructed in Greece so perhaps only showed a small amount of land in Europe, and it wouldn’t have had Australia, China or New Zealand on it! As the amount of knowledge has built up over hundreds of years, the model has improved until, by the time a globe made from real images was produced, there was no noticeable difference between the representation and the real thing.

Building a model

Scientists start with a small amount of data and build up a better and better representation of the phenomena they are explaining or using for prediction as time goes on. These days, many models are likely to be mathematical and are run on computers, rather than being a visual representation, but the principle is the same.

Using models for predicting

In some situations, models are developed by scientists to try and predict things. The best examples are climate models and climate change. Humans don’t know the full effect they are having on the planet, but we do know a lot about carbon cycles, water cycles and weather. Using this information and an understanding of how these cycles interact, scientists are trying to figure out what might happen. Models further rely on the work of scientists to collect quality data to feed into the models. To learn more about work to collate data for models, look at the Argo Project and the work being done to collect large-scale temperature and salinity data to understand what role the ocean plays in climate and climate change.

For example, they can use data to predict what the climate might be like in 20 years if we keep producing carbon dioxide at current rates – what might happen if we produce more carbon dioxide and what would happen if we produce less. The results are used to inform politicians about what could happen to the climate and what can be changed.

Another common use of models is in management of fisheries. Fishing and selling fish to export markets is an important industry for many countries including New Zealand (worth $1.4 billion dollars in 2009). However, overfishing is a real risk and can cause fishing grounds to collapse. Scientists use information about fish life cycles, breeding patterns, weather, coastal currents and habitats to predict how many fish can be taken from a particular area before the population is reduced below the point where it can’t recover.

Models can also be used when field experiments are too expensive or dangerous, such as models used to predict how fire spreads in road tunnels and how a fire might develop in a building .

How do we know if a model works?

Models are often used to make very important decisions, for example, reducing the amount of fish that can be taken from an area might send a company out of business or prevent a fisher from having a career that has been in their family for generations.

The costs associated with combating climate change are almost unimaginable, so it’s important that the models are right, but often it is a case of using the best information available to date. Models need to be continually tested to see if the data used provides useful information. A question scientists can ask of a model is: Does it fit the data that we know?

For climate change, this is a bit difficult. It might fit what we know now, but do we know enough? One way to test a climate change model is to run it backwards. Can it accurately predict what has already happened? Scientists can measure what has happened in the past, so if the model fits the data, it is thought to be a little more trustworthy. If it doesn’t fit, it’s time to do some more work.

This process of comparing model predictions with observable data is known as ‘ground-truthing’. For fisheries management, ground-truthing involves going out and taking samples of fish at different areas. If there are not as many fish in the region as the model predicts, it is time to do some more work.

Learn more about ground truthing in Satellites measure sea ice thickness . Here scientists are validating sateliite data on ice thickness in Antarctica so the data can be used to model how the Earth’s climate, sea temperature and sea levels may be changing.

Nature of science

Models have always been important in science and continue to be used to test hypotheses and predict information. Often they are not accurate because the scientists may not have all the data. It is important that scientists test their models and be willing to improve them as new data comes to light. Model-building can take time – an accurate globe took more than 2,000 years to create – hopefully, an accurate model for climate change will take significantly less time.

Useful links

An example of a scientific model on YouTube.

See our newsletters here .

Would you like to take a short survey?

This survey will open in a new tab and you can fill it out after your visit to the site.

Modeling in Scientific Research: Simplifying a system to make predictions

by Anne E. Egger, Ph.D., Anthony Carpi, Ph.D.

Listen to this reading

Did you know that scientific models can help us peer inside the tiniest atom or examine the entire universe in a single glance? Models allow scientists to study things too small to see, and begin to understand things too complex to imagine.

Modeling involves developing physical, conceptual, or computer-based representations of systems.

Scientists build models to replicate systems in the real world through simplification, to perform an experiment that cannot be done in the real world, or to assemble several known ideas into a coherent whole to build and test hypotheses.

Computer modeling is a relatively new scientific research method, but it is based on the same principles as physical and conceptual modeling.

LEGO ® bricks have been a staple of the toy world since they were first manufactured in Denmark in 1953. The interlocking plastic bricks can be assembled into an endless variety of objects (see Figure 1). Some kids (and even many adults) are interested in building the perfect model – finding the bricks of the right color, shape, and size, and assembling them into a replica of a familiar object in the real world, like a castle, the space shuttle , or London Bridge. Others focus on using the object they build – moving LEGO knights in and out of the castle shown in Figure 1, for example, or enacting a space shuttle mission to Mars. Still others may have no particular end product in mind when they start snapping bricks together and just want to see what they can do with the pieces they have.

Figure 1 : On the left, individual LEGO® bricks. On the right, a model of a NASA space center built with LEGO bricks.

On the most basic level, scientists use models in much the same way that people play with LEGO bricks. Scientific models may or may not be physical entities, but scientists build them for the same variety of reasons: to replicate systems in the real world through simplification, to perform an experiment that cannot be done in the real world, or to assemble several known ideas into a coherent whole to build and test hypotheses .

• Types of models: Physical, conceptual, mathematical

At the St. Anthony Falls Laboratory at the University of Minnesota, a group of engineers and geologists have built a room-sized physical replica of a river delta to model a real one like the Mississippi River delta in the Gulf of Mexico (Paola et al., 2001). These researchers have successfully incorporated into their model the key processes that control river deltas (like the variability of water flow, the deposition of sediments transported by the river, and the compaction and subsidence of the coastline under the pressure of constant sediment additions) in order to better understand how those processes interact. With their physical model, they can mimic the general setting of the Mississippi River delta and then do things they can't do in the real world, like take a slice through the resulting sedimentary deposits to analyze the layers within the sediments. Or they can experiment with changing parameters like sea level and sedimentary input to see how those changes affect deposition of sediments within the delta, the same way you might "experiment" with the placement of the knights in your LEGO castle.

Figure 2 : A photograph of the St. Anthony Falls lab river delta model, showing the experimental setup with pink-tinted water flowing over sediments. Image courtesy the National Center for Earth-Surface Dynamics Data Repository http://www.nced.umn.edu [accessed September, 2008]

Not all models used in scientific research are physical models. Some are conceptual, and involve assembling all of the known components of a system into a coherent whole. This is a little like building an abstract sculpture out of LEGO bricks rather than building a castle. For example, over the past several hundred years, scientists have developed a series of models for the structure of an atom . The earliest known model of the atom compared it to a billiard ball, reflecting what scientists knew at the time – they were the smallest piece of an element that maintained the properties of that element. Despite the fact that this was a purely conceptual model, it could be used to predict some of the behavior that atoms exhibit. However, it did not explain all of the properties of atoms accurately. With the discovery of subatomic particles like the proton and electron , the physicist Ernest Rutherford proposed a "solar system" model of the atom, in which electrons orbited around a nucleus that included protons (see our Atomic Theory I: The Early Days module for more information). While the Rutherford model is useful for understanding basic properties of atoms, it eventually proved insufficient to explain all of the behavior of atoms. The current quantum model of the atom depicts electrons not as pure particles, but as having the properties of both particles and waves , and these electrons are located in specific probability density clouds around the atom's nucleus.

Both physical and conceptual models continue to be important components of scientific research . In addition, many scientists now build models mathematically through computer programming. These computer-based models serve many of the same purposes as physical models, but are determined entirely by mathematical relationships between variables that are defined numerically. The mathematical relationships are kind of like individual LEGO bricks: They are basic building blocks that can be assembled in many different ways. In this case, the building blocks are fundamental concepts and theories like the mathematical description of turbulent flow in a liquid , the law of conservation of energy, or the laws of thermodynamics, which can be assembled into a wide variety of models for, say, the flow of contaminants released into a groundwater reservoir or for global climate change.

Comprehension Checkpoint

• Modeling as a scientific research method

Whether developing a conceptual model like the atomic model, a physical model like a miniature river delta , or a computer model like a global climate model, the first step is to define the system that is to be modeled and the goals for the model. "System" is a generic term that can apply to something very small (like a single atom), something very large (like the Earth's atmosphere), or something in between, like the distribution of nutrients in a local stream. So defining the system generally involves drawing the boundaries (literally or figuratively) around what you want to model, and then determining the key variables and the relationships between those variables.

Though this initial step may seem straightforward, it can be quite complicated. Inevitably, there are many more variables within a system than can be realistically included in a model , so scientists need to simplify. To do this, they make assumptions about which variables are most important. In building a physical model of a river delta , for example, the scientists made the assumption that biological processes like burrowing clams were not important to the large-scale structure of the delta, even though they are clearly a component of the real system.

Determining where simplification is appropriate takes a detailed understanding of the real system – and in fact, sometimes models are used to help determine exactly which aspects of the system can be simplified. For example, the scientists who built the model of the river delta did not incorporate burrowing clams into their model because they knew from experience that they would not affect the overall layering of sediments within the delta. On the other hand, they were aware that vegetation strongly affects the shape of the river channel (and thus the distribution of sediments), and therefore conducted an experiment to determine the nature of the relationship between vegetation density and river channel shape (Gran & Paola, 2001).

Figure 3: Dalton's ball and hook model for the atom.

Once a model is built (either in concept, physical space, or in a computer), it can be tested using a given set of conditions. The results of these tests can then be compared against reality in order to validate the model. In other words, how well does the model do at matching what we see in the real world? In the physical model of delta sediments , the scientists who built the model looked for features like the layering of sand that they have seen in the real world. If the model shows something really different than what the scientists expect, the relationships between variables may need to be redefined or the scientists may have oversimplified the system . Then the model is revised, improved, tested again, and compared to observations again in an ongoing, iterative process . For example, the conceptual "billiard ball" model of the atom used in the early 1800s worked for some aspects of the behavior of gases, but when that hypothesis was tested for chemical reactions , it didn't do a good job of explaining how they occur – billiard balls do not normally interact with one another. John Dalton envisioned a revision of the model in which he added "hooks" to the billiard ball model to account for the fact that atoms could join together in reactions , as conceptualized in Figure 3.

While conceptual and physical models have long been a component of all scientific disciplines, computer-based modeling is a more recent development, and one that is frequently misunderstood. Computer models are based on exactly the same principles as conceptual and physical models, however, and they take advantage of relatively recent advances in computing power to mimic real systems .

• The beginning of computer modeling: Numerical weather prediction

In the late 19 th century, Vilhelm Bjerknes , a Norwegian mathematician and physicist, became interested in deriving equations that govern the large-scale motion of air in the atmosphere . Importantly, he recognized that circulation was the result not just of thermodynamic properties (like the tendency of hot air to rise), but of hydrodynamic properties as well, which describe the behavior of fluid flow. Through his work, he developed an equation that described the physical processes involved in atmospheric circulation, which he published in 1897. The complexity of the equation reflected the complexity of the atmosphere, and Bjerknes was able to use it to describe why weather fronts develop and move.

• Using calculations predictively

Bjerknes had another vision for his mathematical work, however: He wanted to predict the weather. The goal of weather prediction, he realized, is not to know the paths of individual air molecules over time, but to provide the public with "average values over large areas and long periods of time." Because his equation was based on physical principles , he saw that by entering the present values of atmospheric variables like air pressure and temperature, he could solve it to predict the air pressure and temperature at some time in the future. In 1904, Bjerknes published a short paper describing what he called "the principle of predictive meteorology", (Bjerknes, 1904) (see the Research links for the entire paper). In it, he says:

Based upon the observations that have been made, the initial state of the atmosphere is represented by a number of charts which give the distribution of seven variables from level to level in the atmosphere. With these charts as the starting point, new charts of a similar kind are to be drawn, which represent the new state from hour to hour.

In other words, Bjerknes envisioned drawing a series of weather charts for the future based on using known quantities and physical principles . He proposed that solving the complex equation could be made more manageable by breaking it down into a series of smaller, sequential calculations, where the results of one calculation are used as input for the next. As a simple example, imagine predicting traffic patterns in your neighborhood. You start by drawing a map of your neighborhood showing the location, speed, and direction of every car within a square mile. Using these parameters , you then calculate where all of those cars are one minute later. Then again after a second minute. Your calculations will likely look pretty good after the first minute. After the second, third, and fourth minutes, however, they begin to become less accurate. Other factors you had not included in your calculations begin to exert an influence, like where the person driving the car wants to go, the right- or left-hand turns that they make, delays at traffic lights and stop signs, and how many new drivers have entered the roads.

Trying to include all of this information simultaneously would be mathematically difficult, so, as proposed by Bjerknes, the problem can be solved with sequential calculations. To do this, you would take the first step as described above: Use location, speed, and direction to calculate where all the cars are after one minute. Next, you would use the information on right- and left-hand turn frequency to calculate changes in direction, and then you would use information on traffic light delays and new traffic to calculate changes in speed. After these three steps are done, you would solve your first equation again for the second minute time sequence, using location, speed, and direction to calculate where the cars are after the second minute. Though it would certainly be rather tiresome to do by hand, this series of sequential calculations would provide a manageable way to estimate traffic patterns over time.

Although this method made calculations tedious, Bjerknes imagined "no intractable mathematical difficulties" with predicting the weather. The method he proposed (but never used himself) became known as numerical weather prediction, and it represents one of the first approaches towards numerical modeling of a complex, dynamic system .

• Advancing weather calculations

Bjerknes' challenge for numerical weather prediction was taken up sixteen years later in 1922 by the English scientist Lewis Fry Richardson . Richardson related seven differential equations that built on Bjerknes' atmospheric circulation equation to include additional atmospheric processes. One of Richardson's great contributions to mathematical modeling was to solve the equations for boxes within a grid; he divided the atmosphere over Germany into 25 squares that corresponded with available weather station data (see Figure 4) and then divided the atmosphere into five layers, creating a three-dimensional grid of 125 boxes. This was the first use of a technique that is now standard in many types of modeling. For each box, he calculated each of nine variables in seven equations for a single time step of three hours. This was not a simple sequential calculation, however, since the values in each box depended on the values in the adjacent boxes, in part because the air in each box does not simply stay there – it moves from box to box.

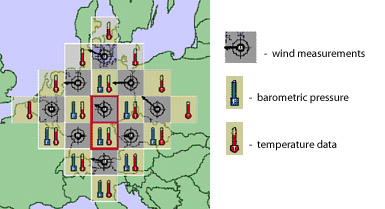
Figure 4: Data for Richardson's forecast included measurements of winds, barometric pressure and temperature. Initial data were recorded in 25 squares, each 200 kilometers on a side, but conditions were forecast only for the two central squares outlined in red.

Richardson's attempt to make a six-hour forecast took him nearly six weeks of work with pencil and paper and was considered an utter failure, as it resulted in calculated barometric pressures that exceeded any historically measured value (Dalmedico, 2001). Probably influenced by Bjerknes, Richardson attributed the failure to inaccurate input data , whose errors were magnified through successive calculations (see more about error propagation in our Uncertainty, Error, and Confidence module).

Figure 5: Norwegian stamp bearing an image of Vilhelm Bjerknes

In addition to his concerns about inaccurate input parameters , Richardson realized that weather prediction was limited in large part by the speed at which individuals could calculate by hand. He thus envisioned a "forecast factory," in which thousands of people would each complete one small part of the necessary calculations for rapid weather forecasting.

• First computer for weather prediction

Richardson's vision became reality in a sense with the birth of the computer, which was able to do calculations far faster and with fewer errors than humans. The computer used for the first one-day weather prediction in 1950, nicknamed ENIAC (Electronic Numerical Integrator and Computer), was 8 feet tall, 3 feet wide, and 100 feet long – a behemoth by modern standards, but it was so much faster than Richardson's hand calculations that by 1955, meteorologists were using it to make forecasts twice a day (Weart, 2003). Over time, the accuracy of the forecasts increased as better data became available over the entire globe through radar technology and, eventually, satellites.

The process of numerical weather prediction developed by Bjerknes and Richardson laid the foundation not only for modern meteorology , but for computer-based mathematical modeling as we know it today. In fact, after Bjerknes died in 1951, the Norwegian government recognized the importance of his contributions to the science of meteorology by issuing a stamp bearing his portrait in 1962 (Figure 5).

• Modeling in practice: The development of global climate models

The desire to model Earth's climate on a long-term, global scale grew naturally out of numerical weather prediction. The goal was to use equations to describe atmospheric circulation in order to understand not just tomorrow's weather, but large-scale patterns in global climate, including dynamic features like the jet stream and major climatic shifts over time like ice ages. Initially, scientists were hindered in the development of valid models by three things: a lack of data from the more inaccessible components of the system like the upper atmosphere , the sheer complexity of a system that involved so many interacting components, and limited computing powers. Unexpectedly, World War II helped solve one problem as the newly-developed technology of high altitude aircraft offered a window into the upper atmosphere (see our Technology module for more information on the development of aircraft). The jet stream, now a familiar feature of the weather broadcast on the news, was in fact first documented by American bombers flying westward to Japan.

As a result, global atmospheric models began to feel more within reach. In the early 1950s, Norman Phillips, a meteorologist at Princeton University, built a mathematical model of the atmosphere based on fundamental thermodynamic equations (Phillips, 1956). He defined 26 variables related through 47 equations, which described things like evaporation from Earth's surface , the rotation of the Earth, and the change in air pressure with temperature. In the model, each of the 26 variables was calculated in each square of a 16 x 17 grid that represented a piece of the northern hemisphere. The grid represented an extremely simple landscape – it had no continents or oceans, no mountain ranges or topography at all. This was not because Phillips thought it was an accurate representation of reality, but because it simplified the calculations. He started his model with the atmosphere "at rest," with no predetermined air movement, and with yearly averages of input parameters like air temperature.

Phillips ran the model through 26 simulated day-night cycles by using the same kind of sequential calculations Bjerknes proposed. Within only one "day," a pattern in atmospheric pressure developed that strongly resembled the typical weather systems of the portion of the northern hemisphere he was modeling (see Figure 6). In other words, despite the simplicity of the model, Phillips was able to reproduce key features of atmospheric circulation , showing that the topography of the Earth was not of primary importance in atmospheric circulation. His work laid the foundation for an entire subdiscipline within climate science: development and refinement of General Circulation Models (GCMs).

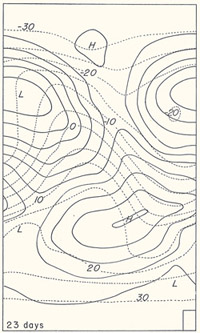
Figure 6: A model result from Phillips' 1956 paper. The box in the lower right shows the size of a grid cell. The solid lines represent the elevation of the 1000 millibar pressure, so the H and L represent areas of high and low pressure, respectively. The dashed lines represent lines of constant temperature, indicating a decreasing temperature at higher latitudes. This is the 23 rd simulated day.

By the 1980s, computing power had increased to the point where modelers could incorporate the distribution of oceans and continents into their models . In 1991, the eruption of Mt. Pinatubo in the Philippines provided a natural experiment: How would the addition of a significant volume of sulfuric acid , carbon dioxide, and volcanic ash affect global climate? In the aftermath of the eruption, descriptive methods (see our Description in Scientific Research module) were used to document its effect on global climate: Worldwide measurements of sulfuric acid and other components were taken, along with the usual air temperature measurements. Scientists could see that the large eruption had affected climate , and they quantified the extent to which it had done so. This provided a perfect test for the GCMs . Given the inputs from the eruption, could they accurately reproduce the effects that descriptive research had shown? Within a few years, scientists had demonstrated that GCMs could indeed reproduce the climatic effects induced by the eruption, and confidence in the abilities of GCMs to provide reasonable scenarios for future climate change grew. The validity of these models has been further substantiated by their ability to simulate past events, like ice ages, and the agreement of many different models on the range of possibilities for warming in the future, one of which is shown in Figure 7.

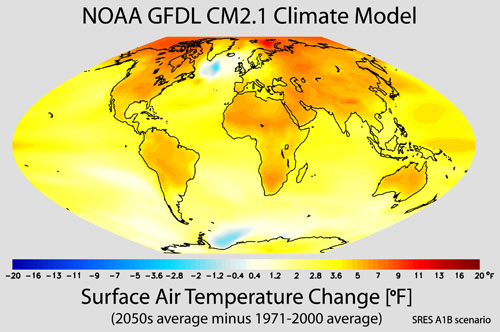
Figure 7: Projected change in annual mean surface air temperature from the late 20th century (1971-2000 average) to the middle 21st century (2051-2060 average). Image courtesy NOAA Geophysical Fluid Dynamics Laboratory.

• Limitations and misconceptions of models

The widespread use of modeling has also led to widespread misconceptions about models , particularly with respect to their ability to predict. Some models are widely used for prediction, such as weather and streamflow forecasts, yet we know that weather forecasts are often wrong. Modeling still cannot predict exactly what will happen to the Earth's climate , but it can help us see the range of possibilities with a given set of changes. For example, many scientists have modeled what might happen to average global temperatures if the concentration of carbon dioxide (CO 2 ) in the atmosphere is doubled from pre-industrial levels (pre-1950); though individual models differ in exact output, they all fall in the range of an increase of 2-6° C (IPCC, 2007).

All models are also limited by the availability of data from the real system . As the amount of data from a system increases, so will the accuracy of the model. For climate modeling, that is why scientists continue to gather data about climate in the geologic past and monitor things like ocean temperatures with satellites – all those data help define parameters within the model. The same is true of physical and conceptual models, too, well-illustrated by the evolution of our model of the atom as our knowledge about subatomic particles increased.

• Modeling in modern practice

The various types of modeling play important roles in virtually every scientific discipline, from ecology to analytical chemistry and from population dynamics to geology. Physical models such as the river delta take advantage of cutting edge technology to integrate multiple large-scale processes. As computer processing speed and power have increased, so has the ability to run models on them. From the room-sized ENIAC in the 1950s to the closet-sized Cray supercomputer in the 1980s to today's laptop, processing speed has increased over a million-fold, allowing scientists to run models on their own computers rather than booking time on one of only a few supercomputers in the world. Our conceptual models continue to evolve, and one of the more recent theories in theoretical physics digs even deeper into the structure of the atom to propose that what we once thought were the most fundamental particles – quarks – are in fact composed of vibrating filaments, or strings. String theory is a complex conceptual model that may help explain gravitational force in a way that has not been done before. Modeling has also moved out of the realm of science into recreation, and many computer games like SimCity® involve both conceptual modeling (answering the question, "What would it be like to run a city?") and computer modeling, using the same kinds of equations that are used model traffic flow patterns in real cities. The accessibility of modeling as a research method allows it to be easily combined with other scientific research methods, and scientists often incorporate modeling into experimental, descriptive, and comparative studies.

Table of Contents

Activate glossary term highlighting to easily identify key terms within the module. Once highlighted, you can click on these terms to view their definitions.

Activate NGSS annotations to easily identify NGSS standards within the module. Once highlighted, you can click on them to view these standards.

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, automatically generate references for free.

• Knowledge Base
• Methodology

Research Design | Step-by-Step Guide with Examples

Published on 5 May 2022 by Shona McCombes . Revised on 20 March 2023.

A research design is a strategy for answering your research question  using empirical data. Creating a research design means making decisions about:

• Your overall aims and approach
• The type of research design you’ll use
• Your sampling methods or criteria for selecting subjects
• Your data collection methods
• The procedures you’ll follow to collect data
• Your data analysis methods

A well-planned research design helps ensure that your methods match your research aims and that you use the right kind of analysis for your data.

Table of contents

Step 1: consider your aims and approach, step 2: choose a type of research design, step 3: identify your population and sampling method, step 4: choose your data collection methods, step 5: plan your data collection procedures, step 6: decide on your data analysis strategies, frequently asked questions.

• Introduction

Before you can start designing your research, you should already have a clear idea of the research question you want to investigate.

There are many different ways you could go about answering this question. Your research design choices should be driven by your aims and priorities – start by thinking carefully about what you want to achieve.

The first choice you need to make is whether you’ll take a qualitative or quantitative approach.

Qualitative research designs tend to be more flexible and inductive , allowing you to adjust your approach based on what you find throughout the research process.

Quantitative research designs tend to be more fixed and deductive , with variables and hypotheses clearly defined in advance of data collection.

It’s also possible to use a mixed methods design that integrates aspects of both approaches. By combining qualitative and quantitative insights, you can gain a more complete picture of the problem you’re studying and strengthen the credibility of your conclusions.

Practical and ethical considerations when designing research

As well as scientific considerations, you need to think practically when designing your research. If your research involves people or animals, you also need to consider research ethics .

• How much time do you have to collect data and write up the research?
• Will you be able to gain access to the data you need (e.g., by travelling to a specific location or contacting specific people)?
• Do you have the necessary research skills (e.g., statistical analysis or interview techniques)?
• Will you need ethical approval ?

At each stage of the research design process, make sure that your choices are practically feasible.

Prevent plagiarism, run a free check.

Within both qualitative and quantitative approaches, there are several types of research design to choose from. Each type provides a framework for the overall shape of your research.

Types of quantitative research designs

Quantitative designs can be split into four main types. Experimental and   quasi-experimental designs allow you to test cause-and-effect relationships, while descriptive and correlational designs allow you to measure variables and describe relationships between them.

With descriptive and correlational designs, you can get a clear picture of characteristics, trends, and relationships as they exist in the real world. However, you can’t draw conclusions about cause and effect (because correlation doesn’t imply causation ).

Experiments are the strongest way to test cause-and-effect relationships without the risk of other variables influencing the results. However, their controlled conditions may not always reflect how things work in the real world. They’re often also more difficult and expensive to implement.

Types of qualitative research designs

Qualitative designs are less strictly defined. This approach is about gaining a rich, detailed understanding of a specific context or phenomenon, and you can often be more creative and flexible in designing your research.

The table below shows some common types of qualitative design. They often have similar approaches in terms of data collection, but focus on different aspects when analysing the data.

Your research design should clearly define who or what your research will focus on, and how you’ll go about choosing your participants or subjects.

In research, a population is the entire group that you want to draw conclusions about, while a sample is the smaller group of individuals you’ll actually collect data from.

Defining the population

A population can be made up of anything you want to study – plants, animals, organisations, texts, countries, etc. In the social sciences, it most often refers to a group of people.

For example, will you focus on people from a specific demographic, region, or background? Are you interested in people with a certain job or medical condition, or users of a particular product?

The more precisely you define your population, the easier it will be to gather a representative sample.

Sampling methods

Even with a narrowly defined population, it’s rarely possible to collect data from every individual. Instead, you’ll collect data from a sample.

To select a sample, there are two main approaches: probability sampling and non-probability sampling . The sampling method you use affects how confidently you can generalise your results to the population as a whole.

Probability sampling is the most statistically valid option, but it’s often difficult to achieve unless you’re dealing with a very small and accessible population.

For practical reasons, many studies use non-probability sampling, but it’s important to be aware of the limitations and carefully consider potential biases. You should always make an effort to gather a sample that’s as representative as possible of the population.

Case selection in qualitative research

In some types of qualitative designs, sampling may not be relevant.

For example, in an ethnography or a case study, your aim is to deeply understand a specific context, not to generalise to a population. Instead of sampling, you may simply aim to collect as much data as possible about the context you are studying.

In these types of design, you still have to carefully consider your choice of case or community. You should have a clear rationale for why this particular case is suitable for answering your research question.

For example, you might choose a case study that reveals an unusual or neglected aspect of your research problem, or you might choose several very similar or very different cases in order to compare them.

Data collection methods are ways of directly measuring variables and gathering information. They allow you to gain first-hand knowledge and original insights into your research problem.

You can choose just one data collection method, or use several methods in the same study.

Survey methods

Surveys allow you to collect data about opinions, behaviours, experiences, and characteristics by asking people directly. There are two main survey methods to choose from: questionnaires and interviews.

Observation methods

Observations allow you to collect data unobtrusively, observing characteristics, behaviours, or social interactions without relying on self-reporting.

Observations may be conducted in real time, taking notes as you observe, or you might make audiovisual recordings for later analysis. They can be qualitative or quantitative.

Other methods of data collection

There are many other ways you might collect data depending on your field and topic.

If you’re not sure which methods will work best for your research design, try reading some papers in your field to see what data collection methods they used.

Secondary data

If you don’t have the time or resources to collect data from the population you’re interested in, you can also choose to use secondary data that other researchers already collected – for example, datasets from government surveys or previous studies on your topic.

With this raw data, you can do your own analysis to answer new research questions that weren’t addressed by the original study.

Using secondary data can expand the scope of your research, as you may be able to access much larger and more varied samples than you could collect yourself.

However, it also means you don’t have any control over which variables to measure or how to measure them, so the conclusions you can draw may be limited.

As well as deciding on your methods, you need to plan exactly how you’ll use these methods to collect data that’s consistent, accurate, and unbiased.

Planning systematic procedures is especially important in quantitative research, where you need to precisely define your variables and ensure your measurements are reliable and valid.

Operationalisation

Some variables, like height or age, are easily measured. But often you’ll be dealing with more abstract concepts, like satisfaction, anxiety, or competence. Operationalisation means turning these fuzzy ideas into measurable indicators.

If you’re using observations , which events or actions will you count?

If you’re using surveys , which questions will you ask and what range of responses will be offered?

You may also choose to use or adapt existing materials designed to measure the concept you’re interested in – for example, questionnaires or inventories whose reliability and validity has already been established.

Reliability and validity

Reliability means your results can be consistently reproduced , while validity means that you’re actually measuring the concept you’re interested in.

For valid and reliable results, your measurement materials should be thoroughly researched and carefully designed. Plan your procedures to make sure you carry out the same steps in the same way for each participant.

If you’re developing a new questionnaire or other instrument to measure a specific concept, running a pilot study allows you to check its validity and reliability in advance.

Sampling procedures

As well as choosing an appropriate sampling method, you need a concrete plan for how you’ll actually contact and recruit your selected sample.

That means making decisions about things like:

• How many participants do you need for an adequate sample size?
• What inclusion and exclusion criteria will you use to identify eligible participants?
• How will you contact your sample – by mail, online, by phone, or in person?

If you’re using a probability sampling method, it’s important that everyone who is randomly selected actually participates in the study. How will you ensure a high response rate?

If you’re using a non-probability method, how will you avoid bias and ensure a representative sample?

Data management

It’s also important to create a data management plan for organising and storing your data.

Will you need to transcribe interviews or perform data entry for observations? You should anonymise and safeguard any sensitive data, and make sure it’s backed up regularly.

Keeping your data well organised will save time when it comes to analysing them. It can also help other researchers validate and add to your findings.

On their own, raw data can’t answer your research question. The last step of designing your research is planning how you’ll analyse the data.

Quantitative data analysis

In quantitative research, you’ll most likely use some form of statistical analysis . With statistics, you can summarise your sample data, make estimates, and test hypotheses.

Using descriptive statistics , you can summarise your sample data in terms of:

• The distribution of the data (e.g., the frequency of each score on a test)
• The central tendency of the data (e.g., the mean to describe the average score)
• The variability of the data (e.g., the standard deviation to describe how spread out the scores are)

The specific calculations you can do depend on the level of measurement of your variables.

Using inferential statistics , you can:

• Make estimates about the population based on your sample data.
• Test hypotheses about a relationship between variables.

Regression and correlation tests look for associations between two or more variables, while comparison tests (such as t tests and ANOVAs ) look for differences in the outcomes of different groups.

Your choice of statistical test depends on various aspects of your research design, including the types of variables you’re dealing with and the distribution of your data.

Qualitative data analysis

In qualitative research, your data will usually be very dense with information and ideas. Instead of summing it up in numbers, you’ll need to comb through the data in detail, interpret its meanings, identify patterns, and extract the parts that are most relevant to your research question.

Two of the most common approaches to doing this are thematic analysis and discourse analysis .

There are many other ways of analysing qualitative data depending on the aims of your research. To get a sense of potential approaches, try reading some qualitative research papers in your field.

A sample is a subset of individuals from a larger population. Sampling means selecting the group that you will actually collect data from in your research.

For example, if you are researching the opinions of students in your university, you could survey a sample of 100 students.

Statistical sampling allows you to test a hypothesis about the characteristics of a population. There are various sampling methods you can use to ensure that your sample is representative of the population as a whole.

Operationalisation means turning abstract conceptual ideas into measurable observations.

For example, the concept of social anxiety isn’t directly observable, but it can be operationally defined in terms of self-rating scores, behavioural avoidance of crowded places, or physical anxiety symptoms in social situations.

Before collecting data , it’s important to consider how you will operationalise the variables that you want to measure.

The research methods you use depend on the type of data you need to answer your research question .

• If you want to measure something or test a hypothesis , use quantitative methods . If you want to explore ideas, thoughts, and meanings, use qualitative methods .
• If you want to analyse a large amount of readily available data, use secondary data. If you want data specific to your purposes with control over how they are generated, collect primary data.
• If you want to establish cause-and-effect relationships between variables , use experimental methods. If you want to understand the characteristics of a research subject, use descriptive methods.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

McCombes, S. (2023, March 20). Research Design | Step-by-Step Guide with Examples. Scribbr. Retrieved 1 November 2024, from https://www.scribbr.co.uk/research-methods/research-design/

Is this article helpful?

Shona McCombes

Overview of the Research Process

• First Online: 01 January 2012

Cite this chapter

• Phyllis G. Supino EdD 3  

6480 Accesses

2 Citations

1 Altmetric

Research is a rigorous problem-solving process whose ultimate goal is the discovery of new knowledge. Research may include the description of a new phenomenon, definition of a new relationship, development of a new model, or application of an existing principle or procedure to a new context. Research is systematic, logical, empirical, reductive, replicable and transmittable, and generalizable. Research can be classified according to a variety of dimensions: basic, applied, or translational; hypothesis generating or hypothesis testing; retrospective or prospective; longitudinal or cross-sectional; observational or experimental; and quantitative or qualitative. The ultimate success of a research project is heavily dependent on adequate planning.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime
• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

Research: Meaning and Purpose

The Roadmap to Research: Fundamentals of a Multifaceted Research Process

Research Questions and Research Design

Calvert J, Martin BR (2001) Changing conceptions of basic research? Brighton, England: Background document for the Workshop on Policy Relevance and Measurement of Basic Research, Oslo, 29–30 Oct 2001. Brighton, England: SPRU.

Google Scholar  

Leedy PD. Practical research. Planning and design. 6th ed. Upper Saddle River: Prentice Hall; 1997.

Tuckman BW. Conducting educational research. 3rd ed. New York: Harcourt Brace Jovanovich; 1972.

Tanenbaum SJ. Knowing and acting in medical practice. The epistemological policies of outcomes research. J Health Polit Policy Law. 1994;19:27–44.

Article   PubMed   CAS   Google Scholar  

Richardson WS. We should overcome the barriers to evidence-based clinical diagnosis! J Clin Epidemiol. 2007;60:217–27.

Article   PubMed   Google Scholar  

MacCorquodale K, Meehl PE. On a distinction between hypothetical constructs and intervening variables. Psych Rev. 1948;55:95–107.

Article   CAS   Google Scholar  

The National Commission for the Protection of Human Subjects of Biomedical and Behavioral Research: The Belmont Report: Ethical principles and guidelines for the protection of human subjects of research. Washington: DHEW Publication No. (OS) 78–0012, Appendix I, DHEW Publication No. (OS) 78–0013, Appendix II, DHEW Publication (OS) 780014; 1978.

Coryn CLS. The fundamental characteristics of research. J Multidisciplinary Eval. 2006;3:124–33.

Smith NL, Brandon PR. Fundamental issues in evaluation. New York: Guilford; 2008.

Committee on Criteria for Federal Support of Research and Development, National Academy of Sciences, National Academy of Engineering, Institute of Medicine, National Research Council. Allocating federal funds for science and technology. Washington, DC: The National Academies; 1995.

Busse R, Fleming I. A critical look at cardiovascular translational research. Am J Physiol Heart Circ Physiol. 1999;277:H1655–60.

CAS   Google Scholar  

Schuster DP, Powers WJ. Translational and experimental clinical research. Philadelphia: Lippincott, Williams & Williams; 2005.

Woolf SH. The meaning of translational research and why it matters. JAMA. 2008;299:211–21.

Robertson D, Williams GH. Clinical and translational science: principles of human research. London: Elsevier; 2009.

Goldblatt EM, Lee WH. From bench to bedside: the growing use of translational research in cancer medicine. Am J Transl Res. 2010;2:1–18.

PubMed   Google Scholar  

Milloy SJ. Science without sense: the risky business of public health research. In: Chapter 5, Mining for statistical associations. Cato Institute. 2009. http://www.junkscience.com/news/sws/sws-chapter5.html . Retrieved 29 Oct 2009.

Gawande A. The cancer-cluster myth. The New Yorker, 8 Feb 1999, p. 34–37.

Kerlinger F. [Chapter 2: problems and hypotheses]. In: Foundations of behavioral research 3rd edn. Orlando: Harcourt, Brace; 1986.

Ioannidis JP. Why most published research findings are false. PLoS Med. 2005;2:e124. Epub 2005 Aug 30.

Andersen B. Methodological errors in medical research. Oxford: Blackwell Scientific Publications; 1990.

DeAngelis C. An introduction to clinical research. New York: Oxford University Press; 1990.

Hennekens CH, Buring JE. Epidemiology in medicine. 1st ed. Boston: Little Brown; 1987.

Jekel JF. Epidemiology, biostatistics, and preventive medicine. 3rd ed. Philadelphia: Saunders Elsevier; 2007.

Hess DR. Retrospective studies and chart reviews. Respir Care. 2004;49:1171–4.

Wissow L, Pascoe J. Types of research models and methods (chapter four). In: An introduction to clinical research. New York: Oxford University Press; 1990.

Bacchieri A, Della Cioppa G. Fundamentals of clinical research: bridging medicine, statistics and operations. Milan: Springer; 2007.

Wood MJ, Ross-Kerr JC. Basic steps in planning nursing research. From question to proposal. 6th ed. Boston: Jones and Barlett; 2005.

DeVita VT, Lawrence TS, Rosenberg SA, Weinberg RA, DePinho RA. Cancer. Principles and practice of oncology, vol. 1. Philadelphia: Wolters Klewer/Lippincott Williams & Wilkins; 2008.

Portney LG, Watkins MP. Foundations of clinical research. Applications to practice. 2nd ed. Upper Saddle River: Prentice Hall Health; 2000.

Marks RG. Designing a research project. The basics of biomedical research methodology. Belmont: Lifetime Learning Publications: A division of Wadsworth; 1982.

Easterbrook PJ, Berlin JA, Gopalan R, Matthews DR. Publication bias in clinical research. Lancet. 1991;337:867–72.

Download references

Author information

Authors and affiliations.

Department of Medicine, College of Medicine, SUNY Downstate Medical Center, 450 Clarkson Avenue, 1199, Brooklyn, NY, 11203, USA

Phyllis G. Supino EdD

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Phyllis G. Supino EdD .

Editor information

Editors and affiliations.

, Cardiovascular Medicine, SUNY Downstate Medical Center, Clarkson Avenue, box 1199 450, Brooklyn, 11203, USA

Phyllis G. Supino

, Cardiovascualr Medicine, SUNY Downstate Medical Center, Clarkson Avenue 450, Brooklyn, 11203, USA

Jeffrey S. Borer

Rights and permissions

Reprints and permissions

Copyright information

© 2012 Springer Science+Business Media, LLC

About this chapter

Supino, P.G. (2012). Overview of the Research Process. In: Supino, P., Borer, J. (eds) Principles of Research Methodology. Springer, New York, NY. https://doi.org/10.1007/978-1-4614-3360-6_1

Download citation

DOI : https://doi.org/10.1007/978-1-4614-3360-6_1

Published : 18 April 2012

Publisher Name : Springer, New York, NY

Print ISBN : 978-1-4614-3359-0

Online ISBN : 978-1-4614-3360-6

eBook Packages : Medicine Medicine (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research