problem solving maths examples

• Prodigy Math
• Prodigy English

From our blog

• Is a Premium Membership Worth It?
• Promote a Growth Mindset
• Help Your Child Who's Struggling with Math
• Parent's Guide to Prodigy
• Assessments
• Math Curriculum Coverage
• English Curriculum Coverage
• Game Portal

120 Math Word Problems To Challenge Students Grades 1 to 8

Written by Marcus Guido

Hey teachers! 👋

Use Prodigy to spark a love for math in your students – including when solving word problems!

• Teaching Tools
• Subtraction
• Multiplication
• Mixed operations
• Ordering and number sense
• Comparing and sequencing
• Physical measurement
• Ratios and percentages
• Probability and data relationships

You sit at your desk, ready to put a math quiz, test or activity together. The questions flow onto the document until you hit a section for word problems.

A jolt of creativity would help. But it doesn’t come.

Whether you’re a 3rd grade teacher or an 8th grade teacher preparing students for high school, translating math concepts into real world examples can certainly be a challenge.

This resource is your jolt of creativity. It provides examples and templates of math word problems for 1st to 8th grade classes.

There are 120 examples in total.

The list of examples is supplemented by tips to create engaging and challenging math word problems.

120 Math word problems, categorized by skill

Addition word problems.

Best for: 1st grade, 2nd grade

1. Adding to 10: Ariel was playing basketball. 1 of her shots went in the hoop. 2 of her shots did not go in the hoop. How many shots were there in total?

2. Adding to 20: Adrianna has 10 pieces of gum to share with her friends. There wasn’t enough gum for all her friends, so she went to the store to get 3 more pieces of gum. How many pieces of gum does Adrianna have now?

3. Adding to 100: Adrianna has 10 pieces of gum to share with her friends. There wasn’t enough gum for all her friends, so she went to the store and got 70 pieces of strawberry gum and 10 pieces of bubble gum. How many pieces of gum does Adrianna have now?

4. Adding Slightly over 100: The restaurant has 175 normal chairs and 20 chairs for babies. How many chairs does the restaurant have in total?

5. Adding to 1,000: How many cookies did you sell if you sold 320 chocolate cookies and 270 vanilla cookies?

6. Adding to and over 10,000: The hobby store normally sells 10,576 trading cards per month. In June, the hobby store sold 15,498 more trading cards than normal. In total, how many trading cards did the hobby store sell in June?

7. Adding 3 Numbers: Billy had 2 books at home. He went to the library to take out 2 more books. He then bought 1 book. How many books does Billy have now?

8. Adding 3 Numbers to and over 100: Ashley bought a big bag of candy. The bag had 102 blue candies, 100 red candies and 94 green candies. How many candies were there in total?

Subtraction word problems

Best for: 1st grade, second grade

9. Subtracting to 10: There were 3 pizzas in total at the pizza shop. A customer bought 1 pizza. How many pizzas are left?

10. Subtracting to 20: Your friend said she had 11 stickers. When you helped her clean her desk, she only had a total of 10 stickers. How many stickers are missing?

11. Subtracting to 100: Adrianna has 100 pieces of gum to share with her friends. When she went to the park, she shared 10 pieces of strawberry gum. When she left the park, Adrianna shared another 10 pieces of bubble gum. How many pieces of gum does Adrianna have now?

Practice math word problems with Prodigy Math

Join millions of teachers using Prodigy to make learning fun and differentiate instruction as they answer in-game questions, including math word problems from 1st to 8th grade!

12. Subtracting Slightly over 100: Your team scored a total of 123 points. 67 points were scored in the first half. How many were scored in the second half?

13. Subtracting to 1,000: Nathan has a big ant farm. He decided to sell some of his ants. He started with 965 ants. He sold 213. How many ants does he have now?

14. Subtracting to and over 10,000: The hobby store normally sells 10,576 trading cards per month. In July, the hobby store sold a total of 20,777 trading cards. How many more trading cards did the hobby store sell in July compared with a normal month?

15. Subtracting 3 Numbers: Charlene had a pack of 35 pencil crayons. She gave 6 to her friend Theresa. She gave 3 to her friend Mandy. How many pencil crayons does Charlene have left?

16. Subtracting 3 Numbers to and over 100: Ashley bought a big bag of candy to share with her friends. In total, there were 296 candies. She gave 105 candies to Marissa. She also gave 86 candies to Kayla. How many candies were left?

Multiplication word problems

Best for: 2nd grade, 3rd grade

17. Multiplying 1-Digit Integers: Adrianna needs to cut a pan of brownies into pieces. She cuts 6 even columns and 3 even rows into the pan. How many brownies does she have?

18. Multiplying 2-Digit Integers: A movie theatre has 25 rows of seats with 20 seats in each row. How many seats are there in total?

19. Multiplying Integers Ending with 0: A clothing company has 4 different kinds of sweatshirts. Each year, the company makes 60,000 of each kind of sweatshirt. How many sweatshirts does the company make each year?

20. Multiplying 3 Integers: A bricklayer stacks bricks in 2 rows, with 10 bricks in each row. On top of each row, there is a stack of 6 bricks. How many bricks are there in total?

21. Multiplying 4 Integers: Cayley earns $5 an hour by delivering newspapers. She delivers newspapers 3 days each week, for 4 hours at a time. After delivering newspapers for 8 weeks, how much money will Cayley earn?

Division word problems

Best for: 3rd grade, 4th grade, 5th grade

22. Dividing 1-Digit Integers: If you have 4 pieces of candy split evenly into 2 bags, how many pieces of candy are in each bag?

23. Dividing 2-Digit Integers: If you have 80 tickets for the fair and each ride costs 5 tickets, how many rides can you go on?

24. Dividing Numbers Ending with 0: The school has $20,000 to buy new computer equipment. If each piece of equipment costs $50, how many pieces can the school buy in total?

25. Dividing 3 Integers: Melissa buys 2 packs of tennis balls for $12 in total. All together, there are 6 tennis balls. How much does 1 pack of tennis balls cost? How much does 1 tennis ball cost?

26. Interpreting Remainders: An Italian restaurant receives a shipment of 86 veal cutlets. If it takes 3 cutlets to make a dish, how many cutlets will the restaurant have left over after making as many dishes as possible?

Mixed operations word problems

27. Mixing Addition and Subtraction: There are 235 books in a library. On Monday, 123 books are taken out. On Tuesday, 56 books are brought back. How many books are there now?

28. Mixing Multiplication and Division: There is a group of 10 people who are ordering pizza. If each person gets 2 slices and each pizza has 4 slices, how many pizzas should they order?

29. Mixing Multiplication, Addition and Subtraction: Lana has 2 bags with 2 marbles in each bag. Markus has 2 bags with 3 marbles in each bag. How many more marbles does Markus have?

30. Mixing Division, Addition and Subtraction: Lana has 3 bags with the same amount of marbles in them, totaling 12 marbles. Markus has 3 bags with the same amount of marbles in them, totaling 18 marbles. How many more marbles does Markus have in each bag?

Ordering and number sense word problems

31. Counting to Preview Multiplication: There are 2 chalkboards in your classroom. If each chalkboard needs 2 pieces of chalk, how many pieces do you need in total?

32. Counting to Preview Division: There are 3 chalkboards in your classroom. Each chalkboard has 2 pieces of chalk. This means there are 6 pieces of chalk in total. If you take 1 piece of chalk away from each chalkboard, how many will there be in total?

33. Composing Numbers: What number is 6 tens and 10 ones?

34. Guessing Numbers: I have a 7 in the tens place. I have an even number in the ones place. I am lower than 74. What number am I?

35. Finding the Order: In the hockey game, Mitchell scored more points than William but fewer points than Auston. Who scored the most points? Who scored the fewest points?

Fractions word problems

Best for: 3rd grade, 4th grade, 5th grade, 6th grade

36. Finding Fractions of a Group: Julia went to 10 houses on her street for Halloween. 5 of the houses gave her a chocolate bar. What fraction of houses on Julia’s street gave her a chocolate bar?

37. Finding Unit Fractions: Heather is painting a portrait of her best friend, Lisa. To make it easier, she divides the portrait into 6 equal parts. What fraction represents each part of the portrait?

38. Adding Fractions with Like Denominators: Noah walks ⅓ of a kilometre to school each day. He also walks ⅓ of a kilometre to get home after school. How many kilometres does he walk in total?

39. Subtracting Fractions with Like Denominators: Last week, Whitney counted the number of juice boxes she had for school lunches. She had ⅗ of a case. This week, it’s down to ⅕ of a case. How much of the case did Whitney drink?

40. Adding Whole Numbers and Fractions with Like Denominators: At lunchtime, an ice cream parlor served 6 ¼ scoops of chocolate ice cream, 5 ¾ scoops of vanilla and 2 ¾ scoops of strawberry. How many scoops of ice cream did the parlor serve in total?

41. Subtracting Whole Numbers and Fractions with Like Denominators: For a party, Jaime had 5 ⅓ bottles of cola for her friends to drink. She drank ⅓ of a bottle herself. Her friends drank 3 ⅓. How many bottles of cola does Jaime have left?

42. Adding Fractions with Unlike Denominators: Kevin completed ½ of an assignment at school. When he was home that evening, he completed ⅚ of another assignment. How many assignments did Kevin complete?

43. Subtracting Fractions with Unlike Denominators: Packing school lunches for her kids, Patty used ⅞ of a package of ham. She also used ½ of a package of turkey. How much more ham than turkey did Patty use?

44. Multiplying Fractions: During gym class on Wednesday, the students ran for ¼ of a kilometre. On Thursday, they ran ½ as many kilometres as on Wednesday. How many kilometres did the students run on Thursday? Write your answer as a fraction.

45. Dividing Fractions: A clothing manufacturer uses ⅕ of a bottle of colour dye to make one pair of pants. The manufacturer used ⅘ of a bottle yesterday. How many pairs of pants did the manufacturer make?

46. Multiplying Fractions with Whole Numbers: Mark drank ⅚ of a carton of milk this week. Frank drank 7 times more milk than Mark. How many cartons of milk did Frank drink? Write your answer as a fraction, or as a whole or mixed number.

Decimals word problems

Best for: 4th grade, 5th grade

47. Adding Decimals: You have 2.6 grams of yogurt in your bowl and you add another spoonful of 1.3 grams. How much yogurt do you have in total?

48. Subtracting Decimals: Gemma had 25.75 grams of frosting to make a cake. She decided to use only 15.5 grams of the frosting. How much frosting does Gemma have left?

49. Multiplying Decimals with Whole Numbers: Marshall walks a total of 0.9 kilometres to and from school each day. After 4 days, how many kilometres will he have walked?

50. Dividing Decimals by Whole Numbers: To make the Leaning Tower of Pisa from spaghetti, Mrs. Robinson bought 2.5 kilograms of spaghetti. Her students were able to make 10 leaning towers in total. How many kilograms of spaghetti does it take to make 1 leaning tower?

51. Mixing Addition and Subtraction of Decimals: Rocco has 1.5 litres of orange soda and 2.25 litres of grape soda in his fridge. Antonio has 1.15 litres of orange soda and 0.62 litres of grape soda. How much more soda does Rocco have than Angelo?

52. Mixing Multiplication and Division of Decimals: 4 days a week, Laura practices martial arts for 1.5 hours. Considering a week is 7 days, what is her average practice time per day each week?

Comparing and sequencing word problems

Best for: Kindergarten, 1st grade, 2nd grade

53. Comparing 1-Digit Integers: You have 3 apples and your friend has 5 apples. Who has more?

54. Comparing 2-Digit Integers: You have 50 candies and your friend has 75 candies. Who has more?

55. Comparing Different Variables: There are 5 basketballs on the playground. There are 7 footballs on the playground. Are there more basketballs or footballs?

56. Sequencing 1-Digit Integers: Erik has 0 stickers. Every day he gets 1 more sticker. How many days until he gets 3 stickers?

57. Skip-Counting by Odd Numbers: Natalie began at 5. She skip-counted by fives. Could she have said the number 20?

58. Skip-Counting by Even Numbers: Natasha began at 0. She skip-counted by eights. Could she have said the number 36?

59. Sequencing 2-Digit Numbers: Each month, Jeremy adds the same number of cards to his baseball card collection. In January, he had 36. 48 in February. 60 in March. How many baseball cards will Jeremy have in April?

Time word problems

66. Converting Hours into Minutes: Jeremy helped his mom for 1 hour. For how many minutes was he helping her?

69. Adding Time: If you wake up at 7:00 a.m. and it takes you 1 hour and 30 minutes to get ready and walk to school, at what time will you get to school?

70. Subtracting Time: If a train departs at 2:00 p.m. and arrives at 4:00 p.m., how long were passengers on the train for?

71. Finding Start and End Times: Rebecca left her dad’s store to go home at twenty to seven in the evening. Forty minutes later, she was home. What time was it when she arrived home?

Money word problems

Best for: 1st grade, 2nd grade, 3rd grade, 4th grade, 5th grade

60. Adding Money: Thomas and Matthew are saving up money to buy a video game together. Thomas has saved $30. Matthew has saved $35. How much money have they saved up together in total?

61. Subtracting Money: Thomas has $80 saved up. He uses his money to buy a video game. The video game costs $67. How much money does he have left?

62. Multiplying Money: Tim gets $5 for delivering the paper. How much money will he have after delivering the paper 3 times?

63. Dividing Money: Robert spent $184.59 to buy 3 hockey sticks. If each hockey stick was the same price, how much did 1 cost?

64. Adding Money with Decimals: You went to the store and bought gum for $1.25 and a sucker for $0.50. How much was your total?

65. Subtracting Money with Decimals: You went to the store with $5.50. You bought gum for $1.25, a chocolate bar for $1.15 and a sucker for $0.50. How much money do you have left?

67. Applying Proportional Relationships to Money: Jakob wants to invite 20 friends to his birthday, which will cost his parents $250. If he decides to invite 15 friends instead, how much money will it cost his parents? Assume the relationship is directly proportional.

68. Applying Percentages to Money: Retta put $100.00 in a bank account that gains 20% interest annually. How much interest will be accumulated in 1 year? And if she makes no withdrawals, how much money will be in the account after 1 year?

Physical measurement word problems

Best for: 1st grade, 2nd grade, 3rd grade, 4th grade

72. Comparing Measurements: Cassandra’s ruler is 22 centimetres long. April’s ruler is 30 centimetres long. How many centimetres longer is April’s ruler?

73. Contextualizing Measurements: Picture a school bus. Which unit of measurement would best describe the length of the bus? Centimetres, metres or kilometres?

74. Adding Measurements: Micha’s dad wants to try to save money on gas, so he has been tracking how much he uses. Last year, Micha’s dad used 100 litres of gas. This year, her dad used 90 litres of gas. How much gas did he use in total for the two years?

75. Subtracting Measurements: Micha’s dad wants to try to save money on gas, so he has been tracking how much he uses. Over the past two years, Micha’s dad used 200 litres of gas. This year, he used 100 litres of gas. How much gas did he use last year?

76. Multiplying Volume and Mass: Kiera wants to make sure she has strong bones, so she drinks 2 litres of milk every week. After 3 weeks, how many litres of milk will Kiera drink?

77. Dividing Volume and Mass: Lillian is doing some gardening, so she bought 1 kilogram of soil. She wants to spread the soil evenly between her 2 plants. How much will each plant get?

78. Converting Mass: Inger goes to the grocery store and buys 3 squashes that each weigh 500 grams. How many kilograms of squash did Inger buy?

79. Converting Volume: Shad has a lemonade stand and sold 20 cups of lemonade. Each cup was 500 millilitres. How many litres did Shad sell in total?

80. Converting Length: Stacy and Milda are comparing their heights. Stacy is 1.5 meters tall. Milda is 10 centimetres taller than Stacy. What is Milda’s height in centimetres?

81. Understanding Distance and Direction: A bus leaves the school to take students on a field trip. The bus travels 10 kilometres south, 10 kilometres west, another 5 kilometres south and 15 kilometres north. To return to the school, in which direction does the bus have to travel? How many kilometres must it travel in that direction?

Ratios and percentages word problems

Best for: 4th grade, 5th grade, 6th grade

82. Finding a Missing Number: The ratio of Jenny’s trophies to Meredith’s trophies is 7:4. Jenny has 28 trophies. How many does Meredith have?

83. Finding Missing Numbers: The ratio of Jenny’s trophies to Meredith’s trophies is 7:4. The difference between the numbers is 12. What are the numbers?

84. Comparing Ratios: The school’s junior band has 10 saxophone players and 20 trumpet players. The school’s senior band has 18 saxophone players and 29 trumpet players. Which band has the higher ratio of trumpet to saxophone players?

85. Determining Percentages: Mary surveyed students in her school to find out what their favourite sports were. Out of 1,200 students, 455 said hockey was their favourite sport. What percentage of students said hockey was their favourite sport?

86. Determining Percent of Change: A decade ago, Oakville’s population was 67,624 people. Now, it is 190% larger. What is Oakville’s current population?

87. Determining Percents of Numbers: At the ice skate rental stand, 60% of 120 skates are for boys. If the rest of the skates are for girls, how many are there?

88. Calculating Averages: For 4 weeks, William volunteered as a helper for swimming classes. The first week, he volunteered for 8 hours. He volunteered for 12 hours in the second week, and another 12 hours in the third week. The fourth week, he volunteered for 9 hours. For how many hours did he volunteer per week, on average?

Probability and data relationships word problems

Best for: 4th grade, 5th grade, 6th grade, 7th grade

89. Understanding the Premise of Probability: John wants to know his class’s favourite TV show, so he surveys all of the boys. Will the sample be representative or biased?

90. Understanding Tangible Probability: The faces on a fair number die are labelled 1, 2, 3, 4, 5 and 6. You roll the die 12 times. How many times should you expect to roll a 1?

91. Exploring Complementary Events: The numbers 1 to 50 are in a hat. If the probability of drawing an even number is 25/50, what is the probability of NOT drawing an even number? Express this probability as a fraction.

92. Exploring Experimental Probability: A pizza shop has recently sold 15 pizzas. 5 of those pizzas were pepperoni. Answering with a fraction, what is the experimental probability that he next pizza will be pepperoni?

93. Introducing Data Relationships: Maurita and Felice each take 4 tests. Here are the results of Maurita’s 4 tests: 4, 4, 4, 4. Here are the results for 3 of Felice’s 4 tests: 3, 3, 3. If Maurita’s mean for the 4 tests is 1 point higher than Felice’s, what’s the score of Felice’s 4th test?

94. Introducing Proportional Relationships: Store A is selling 7 pounds of bananas for $7.00. Store B is selling 3 pounds of bananas for $6.00. Which store has the better deal?

95. Writing Equations for Proportional Relationships: Lionel loves soccer, but has trouble motivating himself to practice. So, he incentivizes himself through video games. There is a proportional relationship between the amount of drills Lionel completes, in x , and for how many hours he plays video games, in y . When Lionel completes 10 drills, he plays video games for 30 minutes. Write the equation for the relationship between x and y .

Geometry word problems

Best for: 4th grade, 5th grade, 6th grade, 7th grade, 8th grade

96. Introducing Perimeter:  The theatre has 4 chairs in a row. There are 5 rows. Using rows as your unit of measurement, what is the perimeter?

97. Introducing Area: The theatre has 4 chairs in a row. There are 5 rows. How many chairs are there in total?

98. Introducing Volume: Aaron wants to know how much candy his container can hold. The container is 20 centimetres tall, 10 centimetres long and 10 centimetres wide. What is the container’s volume?

99. Understanding 2D Shapes: Kevin draws a shape with 4 equal sides. What shape did he draw?

100. Finding the Perimeter of 2D Shapes: Mitchell wrote his homework questions on a piece of square paper. Each side of the paper is 8 centimetres. What is the perimeter?

101. Determining the Area of 2D Shapes: A single trading card is 9 centimetres long by 6 centimetres wide. What is its area?

102. Understanding 3D Shapes: Martha draws a shape that has 6 square faces. What shape did she draw?

103. Determining the Surface Area of 3D Shapes: What is the surface area of a cube that has a width of 2cm, height of 2 cm and length of 2 cm?

104. Determining the Volume of 3D Shapes: Aaron’s candy container is 20 centimetres tall, 10 centimetres long and 10 centimetres wide. Bruce’s container is 25 centimetres tall, 9 centimetres long and 9 centimetres wide. Find the volume of each container. Based on volume, whose container can hold more candy?

105. Identifying Right-Angled Triangles: A triangle has the following side lengths: 3 cm, 4 cm and 5 cm. Is this triangle a right-angled triangle?

106. Identifying Equilateral Triangles: A triangle has the following side lengths: 4 cm, 4 cm and 4 cm. What kind of triangle is it?

107. Identifying Isosceles Triangles: A triangle has the following side lengths: 4 cm, 5 cm and 5 cm. What kind of triangle is it?

108. Identifying Scalene Triangles: A triangle has the following side lengths: 4 cm, 5 cm and 6 cm. What kind of triangle is it?

109. Finding the Perimeter of Triangles: Luigi built a tent in the shape of an equilateral triangle. The perimeter is 21 metres. What is the length of each of the tent’s sides?

110. Determining the Area of Triangles: What is the area of a triangle with a base of 2 units and a height of 3 units?

111. Applying Pythagorean Theorem: A right triangle has one non-hypotenuse side length of 3 inches and the hypotenuse measures 5 inches. What is the length of the other non-hypotenuse side?

112. Finding a Circle’s Diameter: Jasmin bought a new round backpack. Its area is 370 square centimetres. What is the round backpack’s diameter?

113. Finding a Circle's Area: Captain America’s circular shield has a diameter of 76.2 centimetres. What is the area of his shield?

114. Finding a Circle’s Radius: Skylar lives on a farm, where his dad keeps a circular corn maze. The corn maze has a diameter of 2 kilometres. What is the maze’s radius?

Variables word problems

Best for: 6th grade, 7th grade, 8th grade

115. Identifying Independent and Dependent Variables: Victoria is baking muffins for her class. The number of muffins she makes is based on how many classmates she has. For this equation, m is the number of muffins and c is the number of classmates. Which variable is independent and which variable is dependent?

116. Writing Variable Expressions for Addition: Last soccer season, Trish scored g goals. Alexa scored 4 more goals than Trish. Write an expression that shows how many goals Alexa scored.

117. Writing Variable Expressions for Subtraction: Elizabeth eats a healthy, balanced breakfast b times a week. Madison sometimes skips breakfast. In total, Madison eats 3 fewer breakfasts a week than Elizabeth. Write an expression that shows how many times a week Madison eats breakfast.

118. Writing Variable Expressions for Multiplication: Last hockey season, Jack scored g goals. Patrik scored twice as many goals than Jack. Write an expression that shows how many goals Patrik scored.

119. Writing Variable Expressions for Division: Amanda has c chocolate bars. She wants to distribute the chocolate bars evenly among 3 friends. Write an expression that shows how many chocolate bars 1 of her friends will receive.

120. Solving Two-Variable Equations: This equation shows how the amount Lucas earns from his after-school job depends on how many hours he works: e = 12h . The variable h represents how many hours he works. The variable e represents how much money he earns. How much money will Lucas earn after working for 6 hours?

How to easily make your own math word problems & word problems worksheets

Armed with 120 examples to spark ideas, making your own math word problems can engage your students and ensure alignment with lessons. Do:

• Link to Student Interests:  By framing your word problems with student interests, you’ll likely grab attention. For example, if most of your class loves American football, a measurement problem could involve the throwing distance of a famous quarterback.
• Make Questions Topical:  Writing a word problem that reflects current events or issues can engage students by giving them a clear, tangible way to apply their knowledge.
• Include Student Names:  Naming a question’s characters after your students is an easy way make subject matter relatable, helping them work through the problem.
• Be Explicit:  Repeating keywords distills the question, helping students focus on the core problem.
• Test Reading Comprehension:  Flowery word choice and long sentences can hide a question’s key elements. Instead, use concise phrasing and grade-level vocabulary.
• Focus on Similar Interests:  Framing too many questions with related interests -- such as football and basketball -- can alienate or disengage some students.
• Feature Red Herrings:  Including unnecessary information introduces another problem-solving element, overwhelming many elementary students.

A key to differentiated instruction , word problems that students can relate to and contextualize will capture interest more than generic and abstract ones.

Final thoughts about math word problems

You’ll likely get the most out of this resource by using the problems as templates, slightly modifying them by applying the above tips. In doing so, they’ll be more relevant to -- and engaging for -- your students.

Regardless, having 120 curriculum-aligned math word problems at your fingertips should help you deliver skill-building challenges and thought-provoking assessments.

The result?

A greater understanding of how your students process content and demonstrate understanding, informing your ongoing teaching approach.

• Skip to main content
• Skip to primary sidebar
• Skip to footer

Additional menu

Khan Academy Blog

Free Math Worksheets — Over 100k free practice problems on Khan Academy

Looking for free math worksheets.

You’ve found something even better!

That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!

Just choose your grade level or topic to get access to 100% free practice questions:

Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.

• Trigonometry

Statistics and probability

High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.

• Addition and subtraction
• Place value (tens and hundreds)
• Addition and subtraction within 20
• Addition and subtraction within 100
• Addition and subtraction within 1000
• Measurement and data
• Counting and place value
• Measurement and geometry
• Place value
• Measurement, data, and geometry
• Add and subtract within 20
• Add and subtract within 100
• Add and subtract within 1,000
• Money and time
• Measurement
• Intro to multiplication
• 1-digit multiplication
• Addition, subtraction, and estimation
• Intro to division
• Understand fractions
• Equivalent fractions and comparing fractions
• More with multiplication and division
• Arithmetic patterns and problem solving
• Quadrilaterals
• Represent and interpret data
• Multiply by 1-digit numbers
• Multiply by 2-digit numbers
• Factors, multiples and patterns
• Add and subtract fractions
• Multiply fractions
• Understand decimals
• Plane figures
• Measuring angles
• Area and perimeter
• Units of measurement
• Decimal place value
• Add decimals
• Subtract decimals
• Multi-digit multiplication and division
• Divide fractions
• Multiply decimals
• Divide decimals
• Powers of ten
• Coordinate plane
• Algebraic thinking
• Converting units of measure
• Properties of shapes
• Ratios, rates, & percentages
• Arithmetic operations
• Negative numbers
• Properties of numbers
• Variables & expressions
• Equations & inequalities introduction
• Data and statistics
• Negative numbers: addition and subtraction
• Negative numbers: multiplication and division
• Fractions, decimals, & percentages
• Rates & proportional relationships
• Expressions, equations, & inequalities
• Numbers and operations
• Solving equations with one unknown
• Linear equations and functions
• Systems of equations
• Geometric transformations
• Data and modeling
• Volume and surface area
• Pythagorean theorem
• Transformations, congruence, and similarity
• Arithmetic properties
• Factors and multiples
• Reading and interpreting data
• Negative numbers and coordinate plane
• Ratios, rates, proportions
• Equations, expressions, and inequalities
• Exponents, radicals, and scientific notation
• Foundations
• Algebraic expressions
• Linear equations and inequalities
• Graphing lines and slope
• Expressions with exponents
• Quadratics and polynomials
• Equations and geometry
• Algebra foundations
• Solving equations & inequalities
• Working with units
• Linear equations & graphs
• Forms of linear equations
• Inequalities (systems & graphs)
• Absolute value & piecewise functions
• Exponents & radicals
• Exponential growth & decay
• Quadratics: Multiplying & factoring
• Quadratic functions & equations
• Irrational numbers
• Performing transformations
• Transformation properties and proofs
• Right triangles & trigonometry
• Non-right triangles & trigonometry (Advanced)
• Analytic geometry
• Conic sections
• Solid geometry
• Polynomial arithmetic
• Complex numbers
• Polynomial factorization
• Polynomial division
• Polynomial graphs
• Rational exponents and radicals
• Exponential models
• Transformations of functions
• Rational functions
• Trigonometric functions
• Non-right triangles & trigonometry
• Trigonometric equations and identities
• Analyzing categorical data
• Displaying and comparing quantitative data
• Summarizing quantitative data
• Modeling data distributions
• Exploring bivariate numerical data
• Study design
• Probability
• Counting, permutations, and combinations
• Random variables
• Sampling distributions
• Confidence intervals
• Significance tests (hypothesis testing)
• Two-sample inference for the difference between groups
• Inference for categorical data (chi-square tests)
• Advanced regression (inference and transforming)
• Analysis of variance (ANOVA)
• Scatterplots
• Data distributions
• Two-way tables
• Binomial probability
• Normal distributions
• Displaying and describing quantitative data
• Inference comparing two groups or populations
• Chi-square tests for categorical data
• More on regression
• Prepare for the 2020 AP®︎ Statistics Exam
• AP®︎ Statistics Standards mappings
• Polynomials
• Composite functions
• Probability and combinatorics
• Limits and continuity
• Derivatives: definition and basic rules
• Derivatives: chain rule and other advanced topics
• Applications of derivatives
• Analyzing functions
• Parametric equations, polar coordinates, and vector-valued functions
• Applications of integrals
• Differentiation: definition and basic derivative rules
• Differentiation: composite, implicit, and inverse functions
• Contextual applications of differentiation
• Applying derivatives to analyze functions
• Integration and accumulation of change
• Applications of integration
• AP Calculus AB solved free response questions from past exams
• AP®︎ Calculus AB Standards mappings
• Infinite sequences and series
• AP Calculus BC solved exams
• AP®︎ Calculus BC Standards mappings
• Integrals review
• Integration techniques
• Thinking about multivariable functions
• Derivatives of multivariable functions
• Applications of multivariable derivatives
• Integrating multivariable functions
• Green’s, Stokes’, and the divergence theorems
• First order differential equations
• Second order linear equations
• Laplace transform
• Vectors and spaces
• Matrix transformations
• Alternate coordinate systems (bases)

Frequently Asked Questions about Khan Academy and Math Worksheets

Why is khan academy even better than traditional math worksheets.

Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.

What do Khan Academy’s interactive math worksheets look like?

Here’s an example:

What are teachers saying about Khan Academy’s interactive math worksheets?

“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”

Is Khan Academy free?

Khan Academy’s practice questions are 100% free—with no ads or subscriptions.

What do Khan Academy’s interactive math worksheets cover?

Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.

Is Khan Academy a company?

Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.

Want to get even more out of Khan Academy?

Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.

Get Khanmigo

The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo. 

For learners     For teachers     For parents

Math Problem Solving Strategies

In these lessons, we will learn some math problem solving strategies for example, Verbal Model (or Logical Reasoning), Algebraic Model, Block Model (or Singapore Math), Guess & Check Model and Find a Pattern Model.

Related Pages Solving Word Problems Using Block Models Heuristic Approach to Problem-Solving Algebra Lessons

Problem Solving Strategies

The strategies used in solving word problems:

• What do you know?
• What do you need to know?
• Draw a diagram/picture

Solution Strategies Label Variables Verbal Model or Logical Reasoning Algebraic Model - Translate Verbal Model to Algebraic Model Solve and Check.

Solving Word Problems

Step 1: Identify (What is being asked?) Step 2: Strategize Step 3: Write the equation(s) Step 4: Answer the question Step 5: Check

Problem Solving Strategy: Guess And Check

Using the guess and check problem solving strategy to help solve math word problems.

Example: Jamie spent $40 for an outfit. She paid for the items using $10, $5 and $1 bills. If she gave the clerk 10 bills in all, how many of each bill did she use?

Problem Solving : Make A Table And Look For A Pattern

• Identify - What is the question?
• Plan - What strategy will I use to solve the problem?
• Solve - Carry out your plan.
• Verify - Does my answer make sense?

Example: Marcus ran a lemonade stand for 5 days. On the first day, he made $5. Every day after that he made $2 more than the previous day. How much money did Marcus made in all after 5 days?

Find A Pattern Model (Intermediate)

In this lesson, we will look at some intermediate examples of Find a Pattern method of problem-solving strategy.

Example: The figure shows a series of rectangles where each rectangle is bounded by 10 dots. a) How many dots are required for 7 rectangles? b) If the figure has 73 dots, how many rectangles would there be?

a) The number of dots required for 7 rectangles is 52.

b) If the figure has 73 dots, there would be 10 rectangles.

Example: Each triangle in the figure below has 3 dots. Study the pattern and find the number of dots for 7 layers of triangles.

The number of dots for 7 layers of triangles is 36.

Example: The table below shows numbers placed into groups I, II, III, IV, V and VI. In which groups would the following numbers belong? a) 25 b) 46 c) 269

Solution: The pattern is: The remainder when the number is divided by 6 determines the group. a) 25 ÷ 6 = 4 remainder 1 (Group I) b) 46 ÷ 6 = 7 remainder 4 (Group IV) c) 269 ÷ 6 = 44 remainder 5 (Group V)

Example: The following figures were formed using matchsticks.

a) Based on the above series of figures, complete the table below.

b) How many triangles are there if the figure in the series has 9 squares?

c) How many matchsticks would be used in the figure in the series with 11 squares?

b) The pattern is +2 for each additional square.   18 + 2 = 20   If the figure in the series has 9 squares, there would be 20 triangles.

c) The pattern is + 7 for each additional square   61 + (3 x 7) = 82   If the figure in the series has 11 squares, there would be 82 matchsticks.

Example: Seven ex-schoolmates had a gathering. Each one of them shook hands with all others once. How many handshakes were there?

Total = 6 + 5 + 4 + 3 + 2 + 1 = 21 handshakes.

The following video shows more examples of using problem solving strategies and models. Question 1: Approximate your average speed given some information Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern. Find the number of seats in the last row. Question 3: You are hanging three pictures in the wall of your home that is 16 feet wide. The width of your pictures are 2, 3 and 4 feet. You want space between your pictures to be the same and the space to the left and right to be 6 inches more than between the pictures. How would you place the pictures?

The following are some other examples of problem solving strategies.

Explore it/Act it/Try it (EAT) Method (Basic) Explore it/Act it/Try it (EAT) Method (Intermediate) Explore it/Act it/Try it (EAT) Method (Advanced)

Finding A Pattern (Basic) Finding A Pattern (Intermediate) Finding A Pattern (Advanced)

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Problem Solving in Mathematics

• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade

The main reason for learning about math is to become a better problem solver in all aspects of life. Many problems are multistep and require some type of systematic approach. There are a couple of things you need to do when solving problems. Ask yourself exactly what type of information is being asked for: Is it one of addition, subtraction, multiplication , or division? Then determine all the information that is being given to you in the question.

Mathematician George Pólya’s book, “ How to Solve It: A New Aspect of Mathematical Method ,” written in 1957, is a great guide to have on hand. The ideas below, which provide you with general steps or strategies to solve math problems, are similar to those expressed in Pólya’s book and should help you untangle even the most complicated math problem.

Use Established Procedures

Learning how to solve problems in mathematics is knowing what to look for. Math problems often require established procedures and knowing what procedure to apply. To create procedures, you have to be familiar with the problem situation and be able to collect the appropriate information, identify a strategy or strategies, and use the strategy appropriately.

Problem-solving requires practice. When deciding on methods or procedures to use to solve problems, the first thing you will do is look for clues, which is one of the most important skills in solving problems in mathematics. If you begin to solve problems by looking for clue words, you will find that these words often indicate an operation.

Look for Clue Words

Think of yourself as a math detective. The first thing to do when you encounter a math problem is to look for clue words. This is one of the most important skills you can develop. If you begin to solve problems by looking for clue words, you will find that those words often indicate an operation.

Common clue words for addition  problems:

Common clue words for  subtraction  problems:

• How much more

Common clue words for multiplication problems:

Common clue words for division problems:

Although clue words will vary a bit from problem to problem, you'll soon learn to recognize which words mean what in order to perform the correct operation.

Read the Problem Carefully

This, of course, means looking for clue words as outlined in the previous section. Once you’ve identified your clue words, highlight or underline them. This will let you know what kind of problem you’re dealing with. Then do the following:

• Ask yourself if you've seen a problem similar to this one. If so, what is similar about it?
• What did you need to do in that instance?
• What facts are you given about this problem?
• What facts do you still need to find out about this problem?

Develop a Plan and Review Your Work

Based on what you discovered by reading the problem carefully and identifying similar problems you’ve encountered before, you can then:

• Define your problem-solving strategy or strategies. This might mean identifying patterns, using known formulas, using sketches, and even guessing and checking.
• If your strategy doesn't work, it may lead you to an ah-ha moment and to a strategy that does work.

If it seems like you’ve solved the problem, ask yourself the following:

• Does your solution seem probable?
• Does it answer the initial question?
• Did you answer using the language in the question?
• Did you answer using the same units?

If you feel confident that the answer is “yes” to all questions, consider your problem solved.

Tips and Hints

Some key questions to consider as you approach the problem may be:

• What are the keywords in the problem?
• Do I need a data visual, such as a diagram, list, table, chart, or graph?
• Is there a formula or equation that I'll need? If so, which one?
• Will I need to use a calculator? Is there a pattern I can use or follow?

Read the problem carefully, and decide on a method to solve the problem. Once you've finished working the problem, check your work and ensure that your answer makes sense and that you've used the same terms and or units in your answer.

• 2nd Grade Math Word Problems
• The Horse Problem: A Math Challenge
• 2020-21 Common Application Essay Option 4—Solving a Problem
• How to Use Math Journals in Class
• The Frayer Model for Math
• Algorithms in Mathematics and Beyond
• "Grandpa's Rubik's Cube"—Sample Common Application Essay, Option #4
• Math Stumper: Use Two Squares to Make Separate Pens for Nine Pigs
• Critical Thinking Definition, Skills, and Examples
• College Interview Tips: "Tell Me About a Challenge You Overcame"
• Graphic Organizers in Math
• Christmas Word Problem Worksheets
• Solving Problems Involving Distance, Rate, and Time
• Innovative Ways to Teach Math
• Study Tips for Math Homework and Math Tests
• How to Do Algebra Word Problems

• Math Article

Algebra Problems

Algebra problems are not only based on algebraic expressions but also on various types of equations in Maths where a quantity or variable is unknown to us. Many of us are familiar with the word problem, but are we aware of the fact and problems related to variables and constants? When we say 5 it means a number but what if we say x=5 or 5y or something like that?

This is where algebra came into existence algebra is that branch of mathematics which not only deals with numbers but also variable and alphabets. The versatility of Algebra is very deep and very conceptual, all the non-numeric character represents variable and numeric as constants. Let us solve some problems based algebra with solutions which will cover the syllabus for class 6, 7, 8. Below are some of the examples of algebraic expressions .

For example.

Algebra Word Problems deal with real-time situations and solutions which can be solved using algebra.

Basic Algebra Identities

• (a + b) 2  = a 2 + b 2 + 2ab
• (a – b) 2 = a 2  + b 2 – 2ab
• a 2 – b 2 = (a + b)(a – b)
• a 2 + b 2 = (a + b) 2 – 2ab = (a – b) 2 + 2ab
• a 3 + b 3 = (a + b)(a 2 – ab + b 2 )
• a 3 – b 3 = (a – b)(a 2 + ab + b 2 )
• (a + b) 3 = a 3 + 3ab(a + b) + b 3
• (a – b) 3 = a 3 – 3ab(a – b) – b 3

Algebra problems With Solutions

Example 1: Solve, (x-1) 2 = [4√(x-4)] 2 Solution: x 2 -2x+1 = 16(x-4)

x 2 -2x+1 = 16x-64

x 2 -18x+65 = 0

(x-13) (x-5) = 0

Hence, x = 13 and x = 5.

Algebra Problems for Class 6

In class 6, students will be introduced with an algebra concept. Here, you will learn how the unknown values are represented in terms of variables.  The given expression can be solved only if we know the value of unknown variable. Let us see some examples.

Example: Solve, 4x + 5 when, x = 3.

Solution: Given, 4x + 5

Now putting the value of x=3, we get;

4 (3) + 5 = 12 + 5 = 17.

Example: Give expressions for the following cases:

(i) 12 added to 2x

(ii) 6 multiplied by y

(iii) 25 subtracted from z

(iv) 17 times of m 

(i) 12 + 2x

Algebra Problems for Class 7

In class 7, students will deal with algebraic expressions like x+y, xy, 32x 2 -12y 2 , etc. There are different kinds of the terminology used in case algebraic equations such as;

• Coefficient

Let us understand these terms with an example. Suppose 4x + 5y is an algebraic expression, then 4x and 5y are the terms. Since here the variables used are x and y, therefore, x and y are the factors of 4x + 5y. And the numerical factor attached to the variables are the coefficient such as 4 and 5 are the coefficient of x and y in the given expression.

Any expression with one or more terms is called a polynomial. Specifically, a one-term expression is called a monomial; a two-term expression is called a binomial, and a three-term expression is called a trinomial.

Terms which have the same algebraic factors are like terms . Terms which have different algebraic factors are unlike terms . Thus, terms 4xy and – 3xy are like terms; but terms 4xy and – 3x are not like terms.

Example: Add 3x + 5x

Solution: Since 3x and 5x have the same algebraic factors, hence, they are like terms and can be added by their coefficient.

3x + 5x = 8x

Example: Collect like terms and simplify the expression: 12x 2 – 9x + 5x – 4x 2 – 7x + 10.

Solution: 12x 2 – 9x + 5x – 4x 2 – 7x + 10

= (12 – 4)x 2 – 9x + 5x – 7x + 10

=  8x 2 – 11x + 10

Algebra Problems for Class 8

Here, students will deal with algebraic identities. See the examples.

Example: Solve (2x+y) 2

Solution: Using the identity: (a+b) 2  = a 2 + b 2 + 2 ab, we get;

(2x+y) = (2x) 2 + y 2 + 2.2x.y = 4x 2 + y 2 + 4xy

Example: Solve (99) 2 using algebraic identity.

Solution: We can write, 99 = 100 -1

Therefore, (100 – 1 ) 2

= 100 2 + 1 2 – 2 x 100 x 1  [By identity: (a -b) 2 = a 2 + b 2 – 2ab

= 10000 + 1 – 200

Algebra Word Problems

Question 1: There are 47 boys in the class. This is three more than four times the number of girls. How many girls are there in the class?

Solution: Let the number of girls be x

As per the given statement,

4 x + 3 = 47

4x = 47 – 3

Question 2: The sum of two consecutive numbers is 41. What are the numbers?

Solution: Let one of the numbers be x.

Then the other number will x+1

Now, as per the given questions,

x + x + 1 = 41

2x + 1 = 41

So, the first number is 20 and second number is 20+1 = 21

Linear Algebra Problems

There are various methods For Solving the Linear Equations

• Cross multiplication method
• Replacement method or Substitution method
• Hit and trial method

There are Variety of different Algebra problem present and are solved depending upon their functionality and state. For example, a linear equation problem can’t be solved using a quadratic equation formula and vice verse for, e.g., x+x/2=7 then solve for x is an equation in one variable for x which can be satisfied by only one value of x. Whereas x 2 +5x+6 is a quadratic equation which is satisfied for two values of x the domain of algebra is huge and vast so for more information. Visit BYJU’S. where different techniques are explained different algebra problem.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 1: Algebra foundations

Unit 2: solving equations & inequalities, unit 3: working with units, unit 4: linear equations & graphs, unit 5: forms of linear equations, unit 6: systems of equations, unit 7: inequalities (systems & graphs), unit 8: functions, unit 9: sequences, unit 10: absolute value & piecewise functions, unit 11: exponents & radicals, unit 12: exponential growth & decay, unit 13: quadratics: multiplying & factoring, unit 14: quadratic functions & equations, unit 15: irrational numbers, unit 16: creativity in algebra.

Solving Equations

What is an equation.

An equation says that two things are equal. It will have an equals sign "=" like this:

That equations says:

what is on the left (x − 2)  equals  what is on the right (4)

So an equation is like a statement " this equals that "

What is a Solution?

A Solution is a value we can put in place of a variable (such as x ) that makes the equation true .

Example: x − 2 = 4

When we put 6 in place of x we get:

which is true

So x = 6 is a solution.

How about other values for x ?

• For x=5 we get "5−2=4" which is not true , so x=5 is not a solution .
• For x=9 we get "9−2=4" which is not true , so x=9 is not a solution .

In this case x = 6 is the only solution.

You might like to practice solving some animated equations .

More Than One Solution

There can be more than one solution.

Example: (x−3)(x−2) = 0

When x is 3 we get:

(3−3)(3−2) = 0 × 1 = 0

And when x is 2 we get:

(2−3)(2−2) = (−1) × 0 = 0

which is also true

So the solutions are:

x = 3 , or x = 2

When we gather all solutions together it is called a Solution Set

The above solution set is: {2, 3}

Solutions Everywhere!

Some equations are true for all allowed values and are then called Identities

Example: sin(−θ) = −sin(θ) is one of the Trigonometric Identities

Let's try θ = 30°:

sin(−30°) = −0.5 and

−sin(30°) = −0.5

So it is true for θ = 30°

Let's try θ = 90°:

sin(−90°) = −1 and

−sin(90°) = −1

So it is also true for θ = 90°

Is it true for all values of θ ? Try some values for yourself!

How to Solve an Equation

There is no "one perfect way" to solve all equations.

A Useful Goal

But we often get success when our goal is to end up with:

x = something

In other words, we want to move everything except "x" (or whatever name the variable has) over to the right hand side.

Example: Solve 3x−6 = 9

Now we have x = something ,

and a short calculation reveals that x = 5

Like a Puzzle

In fact, solving an equation is just like solving a puzzle. And like puzzles, there are things we can (and cannot) do.

Here are some things we can do:

• Add or Subtract the same value from both sides
• Clear out any fractions by Multiplying every term by the bottom parts
• Divide every term by the same nonzero value
• Combine Like Terms
• Expanding (the opposite of factoring) may also help
• Recognizing a pattern, such as the difference of squares
• Sometimes we can apply a function to both sides (e.g. square both sides)

Example: Solve √(x/2) = 3

And the more "tricks" and techniques you learn the better you will get.

Special Equations

There are special ways of solving some types of equations. Learn how to ...

• solve Quadratic Equations
• solve Radical Equations
• solve Equations with Sine, Cosine and Tangent

Check Your Solutions

You should always check that your "solution" really is a solution.

How To Check

Take the solution(s) and put them in the original equation to see if they really work.

Example: solve for x:

2x x − 3 + 3 = 6 x − 3     (x≠3)

We have said x≠3 to avoid a division by zero.

Let's multiply through by (x − 3) :

2x + 3(x−3) = 6

Bring the 6 to the left:

2x + 3(x−3) − 6 = 0

Expand and solve:

2x + 3x − 9 − 6 = 0

5x − 15 = 0

5(x − 3) = 0

Which can be solved by having x=3

Let us check x=3 using the original question:

2 × 3 3 − 3 + 3  =   6 3 − 3

Hang On: 3 − 3 = 0 That means dividing by Zero!

And anyway, we said at the top that x≠3 , so ...

x = 3 does not actually work, and so:

There is No Solution!

That was interesting ... we thought we had found a solution, but when we looked back at the question we found it wasn't allowed!

This gives us a moral lesson:

"Solving" only gives us possible solutions, they need to be checked!

• Note down where an expression is not defined (due to a division by zero, the square root of a negative number, or some other reason)
• Show all the steps , so it can be checked later (by you or someone else)

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5 Teaching Mathematics Through Problem Solving

Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem  in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems  includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving  focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a  neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method

should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning

involves teaching a skill so that a student can later solve a story problem

when we teach students how to problem solve

teaching mathematics content through real contexts, problems, situations, and models

a mathematical activity where everyone in the group can begin and then work on at their own level of engagement

20 seconds to 2 minutes for students to make sense of questions

Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• Knowledge Base
• Math for kids

10 Strategies for Problem Solving in Math

Created: May 19, 2022

Last updated: January 6, 2024

When faced with problem-solving, children often get stuck. Word puzzles and math questions with an unknown variable, like x, usually confuse them. Therefore, this article discusses math strategies and how your students may use them since instructors often have to lead students through this problem-solving maze.

What Are Problem Solving Strategies in Math?

If you want to fix a problem, you need a solid plan. Math strategies for problem solving are ways of tackling math in a way that guarantees better outcomes. These strategies simplify math for kids so that less time is spent figuring out the problem. Both those new to mathematics and those more knowledgeable about the subject may benefit from these methods.

There are several methods to apply problem-solving procedures in math, and each strategy is different. While none of these methods failsafe, they may help your student become a better problem solver, particularly when paired with practice and examples. The more math problems kids tackle, the more math problem solving skills they acquire, and practice is the key.

Strategies for Problem-solving in Math

Even if a student is not a math wiz, a suitable solution to mathematical problems in math may help them discover answers. There is no one best method for helping students solve arithmetic problems, but the following ten approaches have shown to be very effective.

Understand the Problem

Understanding the nature of math problems is a prerequisite to solving them. They need to specify what kind of issue it is ( fraction problem , word problem, quadratic equation, etc.). Searching for keywords in the math problem, revisiting similar questions, or consulting the internet are all great ways to strengthen their grasp of the material. This step keeps the pupil on track.

Math for Kids

Guess and Check

One of the time-intensive strategies for resolving mathematical problems is the guess and check method. In this approach, students keep guessing until they get the answer right.

After assuming how to solve a math issue, students should reintroduce that assumption to check for correctness. While the approach may appear cumbersome, it is typically successful in revealing patterns in a child’s thought process.

Work It Out

Encourage pupils to record their thinking process as they go through a math problem. Since this technique requires an initial comprehension of the topic, it serves as a self-monitoring method for mathematics students. If they immediately start solving the problem, they risk making mistakes.

Students may keep track of their ideas and fix their math problems as they go along using this method. A youngster may still need you to explain their methods of solving the arithmetic questions on the extra page. This confirmation stage etches the steps they took to solve the problem in their minds.

Work Backwards

In mathematics, a fresh perspective is sometimes the key to a successful solution. Young people need to know that the ability to recreate math problems is valuable in many professional fields, including project management and engineering.

Students may better prepare for difficulties in real-world circumstances by using the “Work Backwards” technique. The end product may be used as a start-off point to identify the underlying issue.

In most cases, a visual representation of a math problem may help youngsters understand it better. Some of the most helpful math tactics for kids include having them play out the issue and picture how to solve it.

One way to visualize a workout is to use a blank piece of paper to draw a picture or make tally marks. Students might also use a marker and a whiteboard to draw as they demonstrate the technique before writing it down.

Find a Pattern

Kids who use pattern recognition techniques can better grasp math concepts and retain formulae. The most remarkable technique for problem solving in mathematics is to help students see patterns in math problems by instructing them how to extract and list relevant details. This method may be used by students when learning shapes and other topics that need repetition.

Students may use this strategy to spot patterns and fill in the blanks. Over time, this strategy will help kids answer math problems quickly.

When faced with a math word problem, it might be helpful to ask, “What are some possible solutions to this issue?” It encourages you to give the problem more thought, develop creative solutions, and prevent you from being stuck in a rut. So, tell the pupils to think about the math problems and not just go with the first solution that comes to mind.

Draw a Picture or Diagram

Drawing a picture of a math problem can help kids understand how to solve it, just like picturing it can help them see it. Shapes or numbers could be used to show the forms to keep things easy. Kids might learn how to use dots or letters to show the parts of a pattern or graph if you teach them.

Charts and graphs can be useful even when math isn’t involved. Kids can draw pictures of the ideas they read about to help them remember them after they’ve learned them. The plan for how to solve the mathematical problem will help kids understand what the problem is and how to solve it.

Trial and Error Method

The trial and error method may be one of the most common problem solving strategies for kids to figure out how to solve problems. But how well this strategy is used will determine how well it works. Students have a hard time figuring out math questions if they don’t have clear formulas or instructions.

They have a better chance of getting the correct answer, though, if they first make a list of possible answers based on rules they already know and then try each one. Don’t be too quick to tell kids they shouldn’t learn by making mistakes.

Review Answers with Peers

It’s fun to work on your math skills with friends by reviewing the answers to math questions together. If different students have different ideas about how to solve the same problem, get them to share their thoughts with the class.

During class time, kids’ ways of working might be compared. Then, students can make their points stronger by fixing these problems.

Check out the Printable Math Worksheets for Your Kids!

There are different ways to solve problems that can affect how fast and well students do on math tests. That’s why they need to learn the best ways to do things. If students follow the steps in this piece, they will have better experiences with solving math questions.

Jessica is a a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.

After-School Math Program

• Boost Math Skills After School!
• Join our Math Program, Ideal for Students in Grades 1-8!

Kid’s grade

After-School Math Program Boost Your Child's Math Abilities! Ideal for 1st-8th Graders, Perfectly Synced with School Curriculum!

Related posts

August 25, 2023

How to Classify Quadrilaterals: Brighterly Guide for Kids

When studying geometry, one essential skill is the ability to classify quadrilaterals. Quadrilaterals — those shapes with four sides — are as much a part of a child’s world as the games they play and the stories they read. Imagine a world where every tile on the floor, every window frame, and every board screen […]

May 19, 2022

13 Successful Teaching Strategies

Teaching children is a complex process because they require more attention than an adult person. You may need to employ different teaching strategies when teaching kids. But what are teaching strategies? Teaching strategies are the methods to ensure your kids or students learn efficiently. But not all strategies yield similarly, and if the one you […]

April 29, 2022

How to Use an Abacus?

Have you ever quickly done math with an abacus? Aside from being useful, the tool has also been shown to be fun and instructive. You will learn about abacus math and how to use one in this article. Specifically, you will learn addition, subtraction, multiplication, division, and figuring out percentages. We will show you how […]

We use cookies to help give you the best service possible. If you continue to use the website we will understand that you consent to the Terms and Conditions. These cookies are safe and secure. We will not share your history logs with third parties. Learn More

• Our Mission

6 Tips for Teaching Math Problem-Solving Skills

Solving word problems is tougher than computing with numbers, but elementary teachers can guide students to do the deep thinking involved.

A growing concern with students is the ability to problem-solve, especially with complex, multistep problems. Data shows that students struggle more when solving word problems than they do with computation , and so problem-solving should be considered separately from computation. Why?

Consider this. When we’re on the way to a new destination and we plug in our location to a map on our phone, it tells us what lane to be in and takes us around any detours or collisions, sometimes even buzzing our watch to remind us to turn. When I experience this as a driver, I don’t have to do the thinking. I can think about what I’m going to cook for dinner, not paying much attention to my surroundings other than to follow those directions. If I were to be asked to go there again, I wouldn’t be able to remember, and I would again seek help.

If we can switch to giving students strategies that require them to think instead of giving them too much support throughout the journey to the answer, we may be able to give them the ability to learn the skills to read a map and have several ways to get there.

Here are six ways we can start letting students do this thinking so that they can go through rigorous problem-solving again and again, paving their own way to the solution. 

1. Link problem-solving to reading

When we can remind students that they already have many comprehension skills and strategies they can easily use in math problem-solving, it can ease the anxiety surrounding the math problem. For example, providing them with strategies to practice, such as visualizing, acting out the problem with math tools like counters or base 10 blocks, drawing a quick sketch of the problem, retelling the story in their own words, etc., can really help them to utilize the skills they already have to make the task less daunting.

We can break these skills into specific short lessons so students have a bank of strategies to try on their own. Here's an example of an anchor chart that they can use for visualizing . Breaking up comprehension into specific skills can increase student independence and help teachers to be much more targeted in their problem-solving instruction. This allows students to build confidence and break down the barriers between reading and math to see they already have so many strengths that are transferable to all problems.

2. Avoid boxing students into choosing a specific operation

It can be so tempting to tell students to look for certain words that might mean a certain operation. This might even be thoroughly successful in kindergarten and first grade, but just like when our map tells us where to go, that limits students from becoming deep thinkers. It also expires once they get into the upper grades, where those words could be in a problem multiple times, creating more confusion when students are trying to follow a rule that may not exist in every problem.

We can encourage a variety of ways to solve problems instead of choosing the operation first. In first grade, a problem might say, “Joceline has 13 stuffed animals and Jordan has 17. How many more does Jordan have?” Some students might choose to subtract, but a lot of students might just count to find the amount in between. If we tell them that “how many more” means to subtract, we’re taking the thinking out of the problem altogether, allowing them to go on autopilot without truly solving the problem or using their comprehension skills to visualize it. 

3. Revisit ‘representation’

The word “representation” can be misleading. It seems like something to do after the process of solving. When students think they have to go straight to solving, they may not realize that they need a step in between to be able to support their understanding of what’s actually happening in the problem first.

Using an anchor chart like one of these ( lower grade , upper grade ) can help students to choose a representation that most closely matches what they’re visualizing in their mind. Once they sketch it out, it can give them a clearer picture of different ways they could solve the problem.

Think about this problem: “Varush went on a trip with his family to his grandmother’s house. It was 710 miles away. On the way there, three people took turns driving. His mom drove 214 miles. His dad drove 358 miles. His older sister drove the rest. How many miles did his sister drive?”

If we were to show this student the anchor chart, they would probably choose a number line or a strip diagram to help them understand what’s happening.

If we tell students they must always draw base 10 blocks in a place value chart, that doesn’t necessarily match the concept of this problem. When we ask students to match our way of thinking, we rob them of critical thinking practice and sometimes confuse them in the process. 

4. Give time to process

Sometimes as educators, we can feel rushed to get to everyone and everything that’s required. When solving a complex problem, students need time to just sit with a problem and wrestle with it, maybe even leaving it and coming back to it after a period of time.

This might mean we need to give them fewer problems but go deeper with those problems we give them. We can also speed up processing time when we allow for collaboration and talk time with peers on problem-solving tasks. 

5. Ask questions that let Students do the thinking

Questions or prompts during problem-solving should be very open-ended to promote thinking. Telling a student to reread the problem or to think about what tools or resources would help them solve it is a way to get them to try something new but not take over their thinking.

These skills are also transferable across content, and students will be reminded, “Good readers and mathematicians reread.” 

6. Spiral concepts so students frequently use problem-solving skills

When students don’t have to switch gears in between concepts, they’re not truly using deep problem-solving skills. They already kind of know what operation it might be or that it’s something they have at the forefront of their mind from recent learning. Being intentional within their learning stations and assessments about having a variety of rigorous problem-solving skills will refine their critical thinking abilities while building more and more resilience throughout the school year as they retain content learning in the process. 

Problem-solving skills are so abstract, and it can be tough to pinpoint exactly what students need. Sometimes we have to go slow to go fast. Slowing down and helping students have tools when they get stuck and enabling them to be critical thinkers will prepare them for life and allow them multiple ways to get to their own destination.

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

In order to access this I need to be confident with:

Ratio problem solving

Here you will learn about ratio problem solving, including how to set up and solve problems. You will also look at real life ratio word problems.

Students will first learn about ratio problem solving as part of ratio and proportion in 6 th grade and 7 th grade.

What is ratio problem solving?

Ratio problem solving is a collection of ratio and proportion word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem.

A ratio is a relationship between two or more quantities. They are usually written in the form a : b where a and b are two quantities. When problem solving with a ratio, the key facts that you need to know are:

• What is the ratio involved?
• What order are the quantities in the ratio?
• What is the total amount / what is the part of the total amount known?
• What are you trying to calculate ?

As with all problem solving, there is not one unique method to solve a problem. However, this does not mean that there aren’t similarities between different problems that you can use to help you find an answer.

The key to any problem solving is being able to draw from prior knowledge and use the correct piece of information to allow you to get to the next step and then the solution.

Let’s look at a couple of methods you can use when given certain pieces of information.

When solving ratio word problems, it is very important that you are able to use ratios. This includes being able to use ratio notation.

For example, Charlie and David share some sweets in the ratio of 3 : 5. This means that for every 3 sweets Charlie gets, David receives 5 sweets.

Charlie and David share 40 sweets, how many sweets do they each get?

You use the ratio to divide 40 sweets into 8 equal parts.

40 \div 8=5

Then you multiply each part of the ratio by 5.

3\times 5:5\times 5=15 : 25

This means that Charlie will get 15 sweets and David will get 25 sweets.

There can be ratio word problems involving different operations and types of numbers.

Here are some examples of different types of ratio word problems:

Common Core State Standards

How does this relate to 6 th and 7 th grade math?

• Grade 6 – Ratios and Proportional Relationships (6.RP.A.3) Use ratio and rate reasoning to solve real-world and mathematical problems, for example, by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
• Grade 7 – Ratio and Proportional Relationships (7.RP.A.2) Recognize and represent proportional relationships between quantities.

How to do ratio problem solving

In order to solve problems including ratios:

Identify key information within the question.

Know what you are trying to calculate.

Use prior knowledge to structure a solution.

[FREE] Ratio Check for Understanding Quiz (Grade 6 and 7)

Use this quiz to check your 6th and 7th grade students’ understanding of ratios. 10+ questions with answers covering a range of 6th and 7th grade ratio topics to identify areas of strength and support!

Ratio problem solving examples

Example 1: part:part ratio.

Within a school, the total number of students who have school lunches to packed lunches is 5 : 7. If 465 students have a school lunch, how many students have a packed lunch?

Within a school, the number of students who have school lunches to packed lunches is \textbf{5 : 7} . If \textbf{465} students have a school lunch, how many students have a packed lunch?

Here you can see that the ratio is 5 : 7, where the first part of the ratio represents school lunches (S) and the second part of the ratio represents packed lunches (P).

You could write this as:

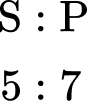
Where the letter above each part of the ratio links to the question.

You know that 465 students have school lunch.

2 Know what you are trying to calculate.

From the question, you need to calculate the number of students that have a packed lunch, so you can now write a ratio below the ratio 5 : 7 that shows that you have 465 students who have school lunches, and p students who have a packed lunch.

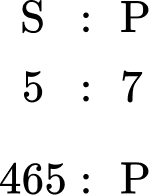
You need to find the value of p.

3 Use prior knowledge to structure a solution.

You are looking for an equivalent ratio to 5 : 7. So you need to calculate the multiplier.

You do this by dividing the known values on the same side of the ratio by each other.

465\div 5 = 93

This means to create an equivalent ratio, you can multiply both sides by 93.

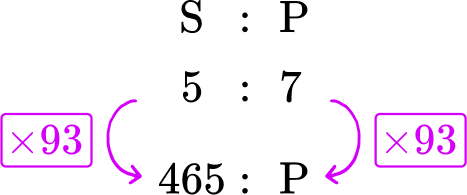
So the value of p is equal to 7 \times 93=651.

There are 651 students that have a packed lunch.

Example 2: unit conversions

The table below shows the currency conversions on one day.

Use the table above to convert £520 \; (GBP) to Euros € \; (EUR).

Use the table above to convert \bf{￡520} \textbf{ (GBP)} to Euros \textbf{€ } \textbf{(EUR)}.

The two values in the table that are important are \text{GBP} and EUR. Writing this as a ratio, you can state,

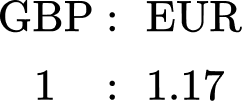
You know that you have £520.

You need to convert GBP to EUR and so you are looking for an equivalent ratio with GBP=£520 and EUR=E.

To get from 1 to 520, you multiply by 520 and so to calculate the number of Euros for £520, you need to multiply 1.17 by 520.

1.17 \times 520=608.4

So £520=€608.40.

Example 3: writing a ratio 1 : n

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the 500 \, ml of concentrated plant food must be diluted into 2 \, l of water. Express the ratio of plant food to water, respectively, in the ratio 1 : n.

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the \bf{500 \, ml} of concentrated plant food must be diluted into \bf{2 \, l} of water. Express the ratio of plant food to water respectively as a ratio in the form 1 : n.

Using the information in the question, you can now state the ratio of plant food to water as 500 \, ml : 2 \, l. As you can convert liters into milliliters, you could convert 2 \, l into milliliters by multiplying it by 1000.

2 \, l=2000 \, ml

So you can also express the ratio as 500 : 2000 which will help you in later steps.

You want to simplify the ratio 500 : 2000 into the form 1:n.

You need to find an equivalent ratio where the first part of the ratio is equal to 1. You can only do this by dividing both parts of the ratio by 500 (as 500 \div 500=1 ).

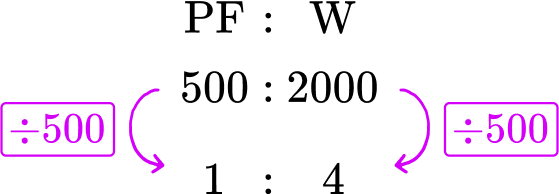
So the ratio of plant food to water in the form 1 : n is 1 : 4.

Example 4: forming and solving an equation

Three siblings, Josh, Kieran and Luke, receive an allowance each week proportional to their age. Kieran is 3 years older than Josh. Luke is twice Josh’s age. If Josh receives \$ 8 allowance, how much money do the three siblings receive in total?

Three siblings, Josh, Kieran and Luke, receive an allowance each week proportional to their ages. Kieran is \bf{3} years older than Josh. Luke is twice Josh’s age. If Luke receives \bf{\$ 8} allowance, how much money do the three siblings receive in total?

You can represent the ages of the three siblings as a ratio. Taking Josh as x years old, Kieran would therefore be x+3 years old, and Luke would be 2x years old. As a ratio, you have:

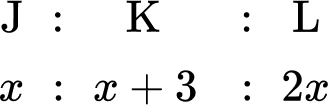
You also know that Luke receives \$ 8.

You want to calculate the total amount of allowance for the three siblings.

You need to find the value of x first. As Luke receives \$ 8, you can state the equation 2x=8 and so x=4.

Now you know the value of x, you can substitute this value into the other parts of the ratio to obtain how much money the siblings each receive.

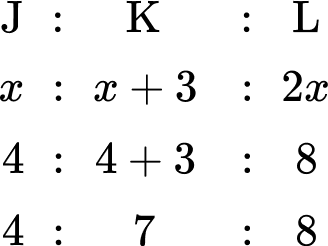
The total amount of allowance is therefore 4+7+8=\$ 19.

Example 5: simplifying ratios

Below is a bar chart showing the results for the colors of counters in a bag.

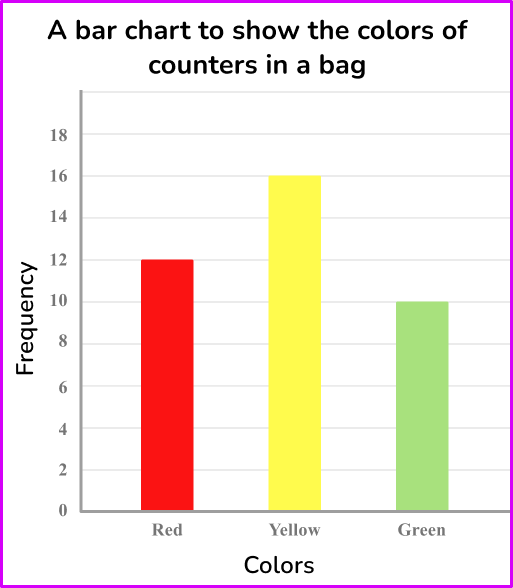
Express this data as a ratio in its simplest form.

From the bar chart, you can read the frequencies to create the ratio.

You need to simplify this ratio.

To simplify a ratio, you need to find the highest common factor of all the parts of the ratio. By listing the factors of each number, you can quickly see that the highest common factor is 2.

\begin{aligned} & 12 = 1, {\color{red}2}, 3, 4, 6, 12 \\\\ & 16 = 1, {\color{red}2}, 4, 8, 16 \\\\ & 10 = 1, {\color{red}2}, 5, 10 \end{aligned}

HCF(12,16,10) = 2

Dividing all the parts of the ratio by 2, you get

Our solution is 6 : 8 : 5.

Example 6: combining two ratios

Glass is made from silica, lime and soda. The ratio of silica to lime is 15 : 2. The ratio of silica to soda is 5 : 1. State the ratio of silica:lime:soda.

Glass is made from silica, lime and soda. The ratio of silica to lime is \bf{15 : 2}. The ratio of silica to soda is \bf{5 : 1}. State the ratio of silica:lime:soda.

You know the two ratios

You are trying to find the ratio of all 3 components: silica, lime and soda.

Using equivalent ratios you can say that the ratio of Silica:Soda is equivalent to 15 : 3 by multiplying the ratio by 3.

You now have the same amount of silica in both ratios and so you can now combine them to get the ratio 15 : 2 : 3.

Example 7: using bar modeling

India and Beau share some popcorn in the ratio of 5 : 2. If India has 75 \, g more popcorn than Beau, what was the original quantity?

India and Beau share some popcorn in the ratio of \bf{5 : 2} . If India has \bf{75 \, g} more popcorn than Beau, what was the original quantity?

You know that the initial ratio is 5 : 2 and that India has three more parts than Beau.

You want to find the original quantity.

Drawing a bar model of this problem, you have:

Where India has 5 equal shares, and Beau has 2 equal shares.

Each share is the same value and so if you can find out this value, you can then find the total quantity.

From the question, India’s share is 75 \, g more than Beau’s share so you can write this on the bar model.

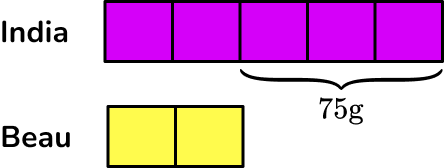
You can find the value of one share by working out 75 \div 3=25 \, g.

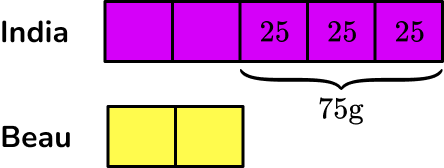
You can fill in each share to be 25 \, g.

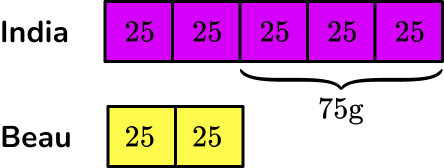
Adding up each share, you get

India=5 \times 25=125 \, g

Beau=2 \times 25=50 \, g

The total amount of popcorn was 125+50=175 \, g.

Teaching tips for ratio problem solving

• Continue to remind students that when solving ratio word problems, it’s important to identify the quantities being compared and express the ratio in its simplest form.
• Create practice problems for students using the information in your classroom. For example, ask students to find the ratio of boys to the ratio of girls using the total number of students in your classroom, then the school.
• To find more practice questions, utilize educational websites and apps instead of worksheets. Some of these may also provide tutorials for struggling students. These can also be helpful for test prep as they are more engaging for students.
• Use a variety of numbers in your ratio word problems – whole numbers, fractions, decimals, and mixed numbers – to give students a variety of practice.
• Provide students with a step-by-step process for problem solving, like the one shown above, that can be applied to every ratio word problem.

Easy mistakes to make

• Mixing units Make sure that all the units in the ratio are the same. For example, in example 6, all the units in the ratio were in milliliters. You did not mix ml and l in the ratio.
• Writing ratios in the wrong order For example, the number of dogs to cats is given as the ratio 12 : 13 but the solution is written as 13 : 12.

• Counting the number of parts in the ratio, not the total number of shares For example, the ratio 5 : 4 has 9 shares, and 2 parts. This is because the ratio contains 2 numbers but the sum of these parts (the number of shares) is 5+4=9. You need to find the value per share, so you need to use the 9 shares in your next line of working.
• Ratios of the form \bf{1 : \textbf{n}} The assumption can be incorrectly made that n must be greater than 1, but n can be any number, including a decimal.

Related ratio lessons

• Unit rate math
• Simplifying ratios
• Ratio to fraction
• How to calculate exchange rates
• Ratio to percent
• How to write a ratio
• Dividing ratios
• How to find the unit rate
• Ratio scale
• Constant of proportionality

Practice ratio problem solving questions

1. An online shop sells board games and computer games. The ratio of board games to the total number of games sold in one month is 3 : 8. What is the ratio of board games to computer games?

8-3=5 computer games sold for every 3 board games.

2. The ratio of prime numbers to non-prime numbers from 1-200 is 45 : 155. Express this as a ratio in the form 1 : n.

You need to simplify the ratio so that the first number is 1. That means you need to divide each number in the ratio by 45.

45 \div 45=1

155\div{45}=3\cfrac{4}{9}

3. During one month, the weather was recorded into 3 categories: sunshine, cloud and rain. The ratio of sunshine to cloud was 2 : 3 and the ratio of cloud to rain was 9 : 11. State the ratio that compares sunshine:cloud:rain for the month.

3 \times S : C=6 : 9

4. The angles in a triangle are written as the ratio x : 2x : 3x. Calculate the size of each angle.

You should know that the 3 angles in a triangle always equal 180^{\circ}.

\begin{aligned} & x+2 x+3 x=180 \\\\ & 6 x=180 \\\\ & x=30^{\circ} \\\\ & 2 x=60^{\circ} \\\\ & 3 x=90^{\circ} \end{aligned}

5. A clothing company has a sale on tops, dresses and shoes. \cfrac{1}{3} of sales were for tops, \cfrac{1}{5} of sales were for dresses, and the rest were for shoes. Write a ratio of tops to dresses to shoes sold in its simplest form.

\cfrac{1}{3}+\cfrac{1}{5}=\cfrac{5+3}{15}=\cfrac{8}{15}

1-\cfrac{8}{15}=\cfrac{7}{15}

6. The volume of gas is directly proportional to the temperature (in degrees Kelvin). A balloon contains 2.75 \, l of gas and has a temperature of 18^{\circ}K. What is the volume of gas if the temperature increases to 45^{\circ}K?

The given ratio in the word problem is 2. 75 \mathrm{~L}: 18^{\circ} \mathrm{K}

Divide 45 by 18 to see the relationship between the two temperatures.

45 \div 18=2.5

45 is 2.5 times greater than 18. So we multiply 2.75 by 2.5 to get the amount of gas.

2.75 \times 2.5=6.875 \mathrm{~l}

Ratio problem solving FAQs

A ratio is a comparison of two or more quantities. It shows how much one quantity is related to another.

A recipe calls for 2 cups of flour and 1 cup of sugar. What is the ratio of flour to sugar? (2 : 1)

In middle school ( 7 th grade and 8 th grade), students transition from understanding basic ratios to working with more complex and real-life applications of ratios and proportions. They gain a deeper understanding of how ratios relate to different mathematical concepts, making them more prepared for higher-level math topics in high school.

The next lessons are

• Converting fractions, decimals and percentages

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.6: Problem Solving Strategies

• Last updated
• Save as PDF
• Page ID 132869

• Michelle Manes
• University of Hawaii

Think back to the first problem in this chapter, the ABC Problem. What did you do to solve it? Even if you did not figure it out completely by yourself, you probably worked towards a solution and figured out some things that did not work.

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solve them), you learn strategies and techniques that can be useful. But no single strategy works every time.

How to Solve It

George Pólya was a great champion in the field of teaching  effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, How to Solve it . Pólya died at the age 98 in 1985. [1]

George Pólya, circa 1973

• Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY 2.0 ( http://creativecommons.org/licenses/by/2.0 )], via Wikimedia Commons ↵

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

• First, you have to understand the problem.
• After understanding, then make a plan.
• Carry out the plan.
• Look back on your work. How could it be better?

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

We have already seen one problem solving strategy, which we call “Wishful Thinking.” Do not be afraid to change the problem! Ask yourself “what if” questions:

• What if the picture was different?
• What if the numbers were simpler?
• What if I just made up some numbers?

You need to be sure to go back to the original problem at the end, but wishful thinking can be a powerful strategy for getting started.

This brings us to the most important problem solving strategy of all:

A Problem Solving Strategy: Try Something!

If you are really trying to solve a problem, the whole point is that you do not know what to do right out of the starting gate. You need to just try something! Put pencil to paper (or stylus to screen or chalk to board or whatever!) and try something. This is often an important step in understanding the problem; just mess around with it a bit to understand the situation and figure out what is going on.

Note that being "good at mathematics" is not about doing things right the first time. It is about figuring things out. Practice being okay with having done something incorrectly. Try to avoid using an eraser and just lightly cross out incorrect work (do not black out the entire thing). This way if it turns out that you did something useful, you still have that work to reference! If what you tried first does not work, try something else! Play around with the problem until you have a feel for what is going on.

Last week, Alex borrowed money from several of his friends. He finally got paid at work, so he brought cash to school to pay back his debts. First he saw Brianna, and he gave her 1/4 of the money he had brought to school. Then Alex saw Chris and gave him 1/3 of what was left after paying Brianna. Finally, Alex saw David and gave him 1/2 of the remaining money. Who got the most money from Alex?

Think/Pair/Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner if possible (even if you have not solved it). What did you try? What did you figure out about the problem? This problem lends itself to two particular strategies. Did you try either of these as you worked on the problem? If not, read about the strategy and then try it out before watching the solution.

A Problem Solving Strategy: Draw a Picture

Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric, like this one, thinking visually can help! Can you represent something in the situation by a picture?

Draw a square to represent all of Alex’s money. Then shade 1/4 of the square — that’s what he gave away to Brianna. How can the picture help you finish the problem?

After you have worked on the problem yourself using this strategy (or if you are completely stuck), you can watch someone else’s solution.

A Problem Solving Strategy: Make Up Numbers

Part of what makes this problem difficult is that it is about money, but there are no numbers given. That means the numbers must not be important. So just make them up!

Try this: Assume (that is, pretend) Alex had some specific amount of money when he showed up at school, say $100. Then figure out how much he gives to each person.

Or try working backward: suppose Alex has some specific amount left at the end, say $10. Since he gave David half of what he had before seeing David, that means he had $20 before running into David. Now, work backwards and figure out how much each person got.

Watch the solution only after you tried this strategy for yourself.

If you use the “Make Up Numbers” strategy, it is really important to remember what the original problem was asking! You do not want to answer something like “Everyone got $10.” That is not true in the original problem; that is an artifact of the numbers you made up. So after you work everything out, be sure to re-read the problem and answer what was asked!

(Squares on a Chess Board)

How many squares, of any possible size, are on a 8 × 8 chess board? (The answer is not 64... It’s a lot bigger!)

Remember Pólya’s first step is to understand the problem. If you are not sure what is being asked, or why the answer is not just 64, be sure to ask someone!

Think / Pair / Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner if possible (even if you have not solved it). What did you try? What did you figure out about the problem, even if you have not solved it completely?

Most people want to draw a picture for this problem, but even with the picture it can be hard to know if you have found the correct answer. The numbers get big, and it can be hard to keep track of your work. Your goal at the end is to be absolutely positive that you found the right answer. Instead of asking the teacher, “Is this right?”, you should be ready to justify it and say, “Here’s my answer, and here is how I got it.”

A Problem Solving Strategy: Try a Simpler Problem

Pólya suggested this strategy: “If you can’t solve a problem, then there is an easier problem you can solve: find it.” He also said, “If you cannot solve the proposed problem, try to solve first some related problem. Could you imagine a more accessible related problem?” In this case, an 8 × 8 chess board is pretty big. Can you solve the problem for smaller boards? Like 1 × 1? 2 × 2? 3 × 3?

The ultimate goal is to solve the original problem. But working with smaller boards might give you some insight and help you devise your plan (that is Pólya’s step (2)).

A Problem Solving Strategy: Work Systematically

If you are working on simpler problems, it is useful to keep track of what you have figured out and what changes as the problem gets more complicated.

For example, in this problem you might keep track of how many 1 × 1 squares are on each board, how many 2 × 2 squares on are each board, how many 3 × 3 squares are on each board, and so on. You could keep track of the information in a table:

A Problem Solving Strategy: Use Manipulatives to Help You Investigate

Sometimes even drawing a picture may not be enough to help you investigate a problem. Having actual materials that you move around can sometimes help a lot!

For example, in this problem it can be difficult to keep track of which squares you have already counted. You might want to cut out 1 × 1 squares, 2 × 2 squares, 3 × 3 squares, and so on. You can actually move the smaller squares across the chess board in a systematic way, making sure that you count everything once and do not count anything twice.

A Problem Solving Strategy: Look for and Explain Patterns

Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand! It would be much more appealing to find a pattern in the smaller boards and then extend that pattern to solve the problem for a 100 × 100 chess board just with a calculation.

If you have not done so already, extend the table above all the way to an 8 × 8 chess board, filling in all the rows and columns. Use your table to find the total number of squares in an 8 × 8 chess board. Then:

• Describe all of the patterns you see in the table. If possible, actually describe these to a friend.
• Explain and justify any of the patterns you see (if possible, actually do this with a friend). If you don't have a partner to work with, imagine they asked you, "How can you be sure the patterns will continue?"
• Expand this to find what calculation(s) you would perform to find the total number of squares on a 100 × 100 chess board.

(We will come back to this question soon. So if you are not sure right now how to explain and justify the patterns you found, that is OK.)

(Broken Clock)

This clock has been broken into three pieces. If you add the numbers in each piece, the sums are consecutive numbers. ( Consecutive numbers are whole numbers that appear one after the other, such as 1, 2, 3, 4 or 13, 14, 15.)

Can you break another clock into a different number of pieces so that the sums are consecutive numbers? Assume that each piece has at least two numbers and that no number is damaged (e.g. 12 isn’t split into two digits 1 and 2).

Remember that your first step is to understand the problem. Work out what is going on here. What are the sums of the numbers on each piece? Are they consecutive?

After you have worked on the problem on your own for a while, talk through your ideas with a partner if possible (even if you have not solved it). What did you try? What progress have you made?

A Problem Solving Strategy: Find the Math, Remove the Context

Sometimes the problem has a lot of details in it that are unimportant, or at least unimportant for getting started. The goal is to find the underlying math problem, then come back to the original question and see if you can solve it using the math.

In this case, worrying about the clock and exactly how the pieces break is less important than worrying about finding consecutive numbers that sum to the correct total. Ask yourself:

• What is the sum of all the numbers on the clock’s face?
• Can I find two consecutive numbers that give the correct sum? Or four consecutive numbers? Or some other amount?
• How do I know when I am done? When should I stop looking?

Of course, solving the question about consecutive numbers is not the same as solving the original problem. You have to go back and see if the clock can actually break apart so that each piece gives you one of those consecutive numbers. Maybe you can solve the math problem, but it does not translate into solving the clock problem.

A Problem Solving Strategy: Check Your Assumptions

When solving problems, it is easy to limit your thinking by adding extra assumptions that are not in the problem. Be sure you ask yourself: Am I constraining my thinking too much?

In the clock problem, because the first solution has the clock broken radially (all three pieces meet at the center, so it looks like slicing a pie), many people assume that is how the clock must break. But the problem does not require the clock to break radially. It might break into pieces like this:

Were you assuming the clock would break in a specific way? Try to solve the problem now, if you have not already.

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations

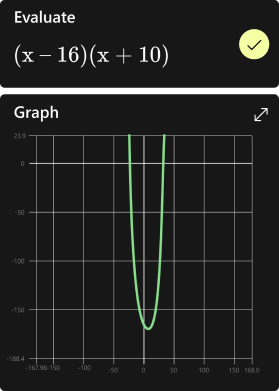
Graph your math problems

Practice, practice, practice

Get math help in your language

• For a new problem, you will need to begin a new live expert session.
• You can contact support with any questions regarding your current subscription.
• You will be able to enter math problems once our session is over.
• I am only able to help with one math problem per session. Which problem would you like to work on?
• Does that make sense?
• I am currently working on this problem.
• Are you still there?
• It appears we may have a connection issue. I will end the session - please reconnect if you still need assistance.
• Let me take a look...
• Can you please send an image of the problem you are seeing in your book or homework?
• If you click on "Tap to view steps..." you will see the steps are now numbered. Which step # do you have a question on?
• Please make sure you are in the correct subject. To change subjects, please exit out of this live expert session and select the appropriate subject from the menu located in the upper left corner of the Mathway screen.
• What are you trying to do with this input?
• While we cover a very wide range of problems, we are currently unable to assist with this specific problem. I spoke with my team and we will make note of this for future training. Is there a different problem you would like further assistance with?
• Mathway currently does not support this subject. We are more than happy to answer any math specific question you may have about this problem.
• Mathway currently does not support Ask an Expert Live in Chemistry. If this is what you were looking for, please contact support.
• Mathway currently only computes linear regressions.
• We are here to assist you with your math questions. You will need to get assistance from your school if you are having problems entering the answers into your online assignment.
• Have a great day!
• Hope that helps!
• You're welcome!
• Per our terms of use, Mathway's live experts will not knowingly provide solutions to students while they are taking a test or quiz.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• SUGGESTED TOPICS
• The Magazine
• Newsletters
• Managing Yourself
• Managing Teams
• Work-life Balance
• The Big Idea
• Data & Visuals
• Reading Lists
• Case Selections
• HBR Learning
• Topic Feeds
• Account Settings
• Email Preferences

Share Podcast

Do You Understand the Problem You’re Trying to Solve?

To solve tough problems at work, first ask these questions.

• Apple Podcasts
• Google Podcasts

Problem solving skills are invaluable in any job. But all too often, we jump to find solutions to a problem without taking time to really understand the dilemma we face, according to Thomas Wedell-Wedellsborg , an expert in innovation and the author of the book, What’s Your Problem?: To Solve Your Toughest Problems, Change the Problems You Solve .

In this episode, you’ll learn how to reframe tough problems by asking questions that reveal all the factors and assumptions that contribute to the situation. You’ll also learn why searching for just one root cause can be misleading.

Key episode topics include: leadership, decision making and problem solving, power and influence, business management.

HBR On Leadership curates the best case studies and conversations with the world’s top business and management experts, to help you unlock the best in those around you. New episodes every week.

• Listen to the original HBR IdeaCast episode: The Secret to Better Problem Solving (2016)
• Find more episodes of HBR IdeaCast
• Discover 100 years of Harvard Business Review articles, case studies, podcasts, and more at HBR.org .

HANNAH BATES: Welcome to HBR on Leadership , case studies and conversations with the world’s top business and management experts, hand-selected to help you unlock the best in those around you.

Problem solving skills are invaluable in any job. But even the most experienced among us can fall into the trap of solving the wrong problem.

Thomas Wedell-Wedellsborg says that all too often, we jump to find solutions to a problem – without taking time to really understand what we’re facing.

He’s an expert in innovation, and he’s the author of the book, What’s Your Problem?: To Solve Your Toughest Problems, Change the Problems You Solve .

  In this episode, you’ll learn how to reframe tough problems, by asking questions that reveal all the factors and assumptions that contribute to the situation. You’ll also learn why searching for one root cause can be misleading. And you’ll learn how to use experimentation and rapid prototyping as problem-solving tools.

This episode originally aired on HBR IdeaCast in December 2016. Here it is.

SARAH GREEN CARMICHAEL: Welcome to the HBR IdeaCast from Harvard Business Review. I’m Sarah Green Carmichael.

Problem solving is popular. People put it on their resumes. Managers believe they excel at it. Companies count it as a key proficiency. We solve customers’ problems.

The problem is we often solve the wrong problems. Albert Einstein and Peter Drucker alike have discussed the difficulty of effective diagnosis. There are great frameworks for getting teams to attack true problems, but they’re often hard to do daily and on the fly. That’s where our guest comes in.

Thomas Wedell-Wedellsborg is a consultant who helps companies and managers reframe their problems so they can come up with an effective solution faster. He asks the question “Are You Solving The Right Problems?” in the January-February 2017 issue of Harvard Business Review. Thomas, thank you so much for coming on the HBR IdeaCast .

THOMAS WEDELL-WEDELLSBORG: Thanks for inviting me.

SARAH GREEN CARMICHAEL: So, I thought maybe we could start by talking about the problem of talking about problem reframing. What is that exactly?

THOMAS WEDELL-WEDELLSBORG: Basically, when people face a problem, they tend to jump into solution mode to rapidly, and very often that means that they don’t really understand, necessarily, the problem they’re trying to solve. And so, reframing is really a– at heart, it’s a method that helps you avoid that by taking a second to go in and ask two questions, basically saying, first of all, wait. What is the problem we’re trying to solve? And then crucially asking, is there a different way to think about what the problem actually is?

SARAH GREEN CARMICHAEL: So, I feel like so often when this comes up in meetings, you know, someone says that, and maybe they throw out the Einstein quote about you spend an hour of problem solving, you spend 55 minutes to find the problem. And then everyone else in the room kind of gets irritated. So, maybe just give us an example of maybe how this would work in practice in a way that would not, sort of, set people’s teeth on edge, like oh, here Sarah goes again, reframing the whole problem instead of just solving it.

THOMAS WEDELL-WEDELLSBORG: I mean, you’re bringing up something that’s, I think is crucial, which is to create legitimacy for the method. So, one of the reasons why I put out the article is to give people a tool to say actually, this thing is still important, and we need to do it. But I think the really critical thing in order to make this work in a meeting is actually to learn how to do it fast, because if you have the idea that you need to spend 30 minutes in a meeting delving deeply into the problem, I mean, that’s going to be uphill for most problems. So, the critical thing here is really to try to make it a practice you can implement very, very rapidly.

There’s an example that I would suggest memorizing. This is the example that I use to explain very rapidly what it is. And it’s basically, I call it the slow elevator problem. You imagine that you are the owner of an office building, and that your tenants are complaining that the elevator’s slow.

Now, if you take that problem framing for granted, you’re going to start thinking creatively around how do we make the elevator faster. Do we install a new motor? Do we have to buy a new lift somewhere?

The thing is, though, if you ask people who actually work with facilities management, well, they’re going to have a different solution for you, which is put up a mirror next to the elevator. That’s what happens is, of course, that people go oh, I’m busy. I’m busy. I’m– oh, a mirror. Oh, that’s beautiful.

And then they forget time. What’s interesting about that example is that the idea with a mirror is actually a solution to a different problem than the one you first proposed. And so, the whole idea here is once you get good at using reframing, you can quickly identify other aspects of the problem that might be much better to try to solve than the original one you found. It’s not necessarily that the first one is wrong. It’s just that there might be better problems out there to attack that we can, means we can do things much faster, cheaper, or better.

SARAH GREEN CARMICHAEL: So, in that example, I can understand how A, it’s probably expensive to make the elevator faster, so it’s much cheaper just to put up a mirror. And B, maybe the real problem people are actually feeling, even though they’re not articulating it right, is like, I hate waiting for the elevator. But if you let them sort of fix their hair or check their teeth, they’re suddenly distracted and don’t notice.

But if you have, this is sort of a pedestrian example, but say you have a roommate or a spouse who doesn’t clean up the kitchen. Facing that problem and not having your elegant solution already there to highlight the contrast between the perceived problem and the real problem, how would you take a problem like that and attack it using this method so that you can see what some of the other options might be?

THOMAS WEDELL-WEDELLSBORG: Right. So, I mean, let’s say it’s you who have that problem. I would go in and say, first of all, what would you say the problem is? Like, if you were to describe your view of the problem, what would that be?

SARAH GREEN CARMICHAEL: I hate cleaning the kitchen, and I want someone else to clean it up.

THOMAS WEDELL-WEDELLSBORG: OK. So, my first observation, you know, that somebody else might not necessarily be your spouse. So, already there, there’s an inbuilt assumption in your question around oh, it has to be my husband who does the cleaning. So, it might actually be worth, already there to say, is that really the only problem you have? That you hate cleaning the kitchen, and you want to avoid it? Or might there be something around, as well, getting a better relationship in terms of how you solve problems in general or establishing a better way to handle small problems when dealing with your spouse?

SARAH GREEN CARMICHAEL: Or maybe, now that I’m thinking that, maybe the problem is that you just can’t find the stuff in the kitchen when you need to find it.

THOMAS WEDELL-WEDELLSBORG: Right, and so that’s an example of a reframing, that actually why is it a problem that the kitchen is not clean? Is it only because you hate the act of cleaning, or does it actually mean that it just takes you a lot longer and gets a lot messier to actually use the kitchen, which is a different problem. The way you describe this problem now, is there anything that’s missing from that description?

SARAH GREEN CARMICHAEL: That is a really good question.

THOMAS WEDELL-WEDELLSBORG: Other, basically asking other factors that we are not talking about right now, and I say those because people tend to, when given a problem, they tend to delve deeper into the detail. What often is missing is actually an element outside of the initial description of the problem that might be really relevant to what’s going on. Like, why does the kitchen get messy in the first place? Is it something about the way you use it or your cooking habits? Is it because the neighbor’s kids, kind of, use it all the time?

There might, very often, there might be issues that you’re not really thinking about when you first describe the problem that actually has a big effect on it.

SARAH GREEN CARMICHAEL: I think at this point it would be helpful to maybe get another business example, and I’m wondering if you could tell us the story of the dog adoption problem.

THOMAS WEDELL-WEDELLSBORG: Yeah. This is a big problem in the US. If you work in the shelter industry, basically because dogs are so popular, more than 3 million dogs every year enter a shelter, and currently only about half of those actually find a new home and get adopted. And so, this is a problem that has persisted. It’s been, like, a structural problem for decades in this space. In the last three years, where people found new ways to address it.

So a woman called Lori Weise who runs a rescue organization in South LA, and she actually went in and challenged the very idea of what we were trying to do. She said, no, no. The problem we’re trying to solve is not about how to get more people to adopt dogs. It is about keeping the dogs with their first family so they never enter the shelter system in the first place.

In 2013, she started what’s called a Shelter Intervention Program that basically works like this. If a family comes and wants to hand over their dog, these are called owner surrenders. It’s about 30% of all dogs that come into a shelter. All they would do is go up and ask, if you could, would you like to keep your animal? And if they said yes, they would try to fix whatever helped them fix the problem, but that made them turn over this.

And sometimes that might be that they moved into a new building. The landlord required a deposit, and they simply didn’t have the money to put down a deposit. Or the dog might need a $10 rabies shot, but they didn’t know how to get access to a vet.

And so, by instigating that program, just in the first year, she took her, basically the amount of dollars they spent per animal they helped went from something like $85 down to around $60. Just an immediate impact, and her program now is being rolled out, is being supported by the ASPCA, which is one of the big animal welfare stations, and it’s being rolled out to various other places.

And I think what really struck me with that example was this was not dependent on having the internet. This was not, oh, we needed to have everybody mobile before we could come up with this. This, conceivably, we could have done 20 years ago. Only, it only happened when somebody, like in this case Lori, went in and actually rethought what the problem they were trying to solve was in the first place.

SARAH GREEN CARMICHAEL: So, what I also think is so interesting about that example is that when you talk about it, it doesn’t sound like the kind of thing that would have been thought of through other kinds of problem solving methods. There wasn’t necessarily an After Action Review or a 5 Whys exercise or a Six Sigma type intervention. I don’t want to throw those other methods under the bus, but how can you get such powerful results with such a very simple way of thinking about something?

THOMAS WEDELL-WEDELLSBORG: That was something that struck me as well. This, in a way, reframing and the idea of the problem diagnosis is important is something we’ve known for a long, long time. And we’ve actually have built some tools to help out. If you worked with us professionally, you are familiar with, like, Six Sigma, TRIZ, and so on. You mentioned 5 Whys. A root cause analysis is another one that a lot of people are familiar with.

Those are our good tools, and they’re definitely better than nothing. But what I notice when I work with the companies applying those was those tools tend to make you dig deeper into the first understanding of the problem we have. If it’s the elevator example, people start asking, well, is that the cable strength, or is the capacity of the elevator? That they kind of get caught by the details.

That, in a way, is a bad way to work on problems because it really assumes that there’s like a, you can almost hear it, a root cause. That you have to dig down and find the one true problem, and everything else was just symptoms. That’s a bad way to think about problems because problems tend to be multicausal.

There tend to be lots of causes or levers you can potentially press to address a problem. And if you think there’s only one, if that’s the right problem, that’s actually a dangerous way. And so I think that’s why, that this is a method I’ve worked with over the last five years, trying to basically refine how to make people better at this, and the key tends to be this thing about shifting out and saying, is there a totally different way of thinking about the problem versus getting too caught up in the mechanistic details of what happens.

SARAH GREEN CARMICHAEL: What about experimentation? Because that’s another method that’s become really popular with the rise of Lean Startup and lots of other innovation methodologies. Why wouldn’t it have worked to, say, experiment with many different types of fixing the dog adoption problem, and then just pick the one that works the best?

THOMAS WEDELL-WEDELLSBORG: You could say in the dog space, that’s what’s been going on. I mean, there is, in this industry and a lot of, it’s largely volunteer driven. People have experimented, and they found different ways of trying to cope. And that has definitely made the problem better. So, I wouldn’t say that experimentation is bad, quite the contrary. Rapid prototyping, quickly putting something out into the world and learning from it, that’s a fantastic way to learn more and to move forward.

My point is, though, that I feel we’ve come to rely too much on that. There’s like, if you look at the start up space, the wisdom is now just to put something quickly into the market, and then if it doesn’t work, pivot and just do more stuff. What reframing really is, I think of it as the cognitive counterpoint to prototyping. So, this is really a way of seeing very quickly, like not just working on the solution, but also working on our understanding of the problem and trying to see is there a different way to think about that.

If you only stick with experimentation, again, you tend to sometimes stay too much in the same space trying minute variations of something instead of taking a step back and saying, wait a minute. What is this telling us about what the real issue is?

SARAH GREEN CARMICHAEL: So, to go back to something that we touched on earlier, when we were talking about the completely hypothetical example of a spouse who does not clean the kitchen–

THOMAS WEDELL-WEDELLSBORG: Completely, completely hypothetical.

SARAH GREEN CARMICHAEL: Yes. For the record, my husband is a great kitchen cleaner.

You started asking me some questions that I could see immediately were helping me rethink that problem. Is that kind of the key, just having a checklist of questions to ask yourself? How do you really start to put this into practice?

THOMAS WEDELL-WEDELLSBORG: I think there are two steps in that. The first one is just to make yourself better at the method. Yes, you should kind of work with a checklist. In the article, I kind of outlined seven practices that you can use to do this.

But importantly, I would say you have to consider that as, basically, a set of training wheels. I think there’s a big, big danger in getting caught in a checklist. This is something I work with.

My co-author Paddy Miller, it’s one of his insights. That if you start giving people a checklist for things like this, they start following it. And that’s actually a problem, because what you really want them to do is start challenging their thinking.

So the way to handle this is to get some practice using it. Do use the checklist initially, but then try to step away from it and try to see if you can organically make– it’s almost a habit of mind. When you run into a colleague in the hallway and she has a problem and you have five minutes, like, delving in and just starting asking some of those questions and using your intuition to say, wait, how is she talking about this problem? And is there a question or two I can ask her about the problem that can help her rethink it?

SARAH GREEN CARMICHAEL: Well, that is also just a very different approach, because I think in that situation, most of us can’t go 30 seconds without jumping in and offering solutions.

THOMAS WEDELL-WEDELLSBORG: Very true. The drive toward solutions is very strong. And to be clear, I mean, there’s nothing wrong with that if the solutions work. So, many problems are just solved by oh, you know, oh, here’s the way to do that. Great.

But this is really a powerful method for those problems where either it’s something we’ve been banging our heads against tons of times without making progress, or when you need to come up with a really creative solution. When you’re facing a competitor with a much bigger budget, and you know, if you solve the same problem later, you’re not going to win. So, that basic idea of taking that approach to problems can often help you move forward in a different way than just like, oh, I have a solution.

I would say there’s also, there’s some interesting psychological stuff going on, right? Where you may have tried this, but if somebody tries to serve up a solution to a problem I have, I’m often resistant towards them. Kind if like, no, no, no, no, no, no. That solution is not going to work in my world. Whereas if you get them to discuss and analyze what the problem really is, you might actually dig something up.

Let’s go back to the kitchen example. One powerful question is just to say, what’s your own part in creating this problem? It’s very often, like, people, they describe problems as if it’s something that’s inflicted upon them from the external world, and they are innocent bystanders in that.

SARAH GREEN CARMICHAEL: Right, or crazy customers with unreasonable demands.

THOMAS WEDELL-WEDELLSBORG: Exactly, right. I don’t think I’ve ever met an agency or consultancy that didn’t, like, gossip about their customers. Oh, my god, they’re horrible. That, you know, classic thing, why don’t they want to take more risk? Well, risk is bad.

It’s their business that’s on the line, not the consultancy’s, right? So, absolutely, that’s one of the things when you step into a different mindset and kind of, wait. Oh yeah, maybe I actually am part of creating this problem in a sense, as well. That tends to open some new doors for you to move forward, in a way, with stuff that you may have been struggling with for years.

SARAH GREEN CARMICHAEL: So, we’ve surfaced a couple of questions that are useful. I’m curious to know, what are some of the other questions that you find yourself asking in these situations, given that you have made this sort of mental habit that you do? What are the questions that people seem to find really useful?

THOMAS WEDELL-WEDELLSBORG: One easy one is just to ask if there are any positive exceptions to the problem. So, was there day where your kitchen was actually spotlessly clean? And then asking, what was different about that day? Like, what happened there that didn’t happen the other days? That can very often point people towards a factor that they hadn’t considered previously.

SARAH GREEN CARMICHAEL: We got take-out.

THOMAS WEDELL-WEDELLSBORG: S,o that is your solution. Take-out from [INAUDIBLE]. That might have other problems.

Another good question, and this is a little bit more high level. It’s actually more making an observation about labeling how that person thinks about the problem. And what I mean with that is, we have problem categories in our head. So, if I say, let’s say that you describe a problem to me and say, well, we have a really great product and are, it’s much better than our previous product, but people aren’t buying it. I think we need to put more marketing dollars into this.

Now you can go in and say, that’s interesting. This sounds like you’re thinking of this as a communications problem. Is there a different way of thinking about that? Because you can almost tell how, when the second you say communications, there are some ideas about how do you solve a communications problem. Typically with more communication.

And what you might do is go in and suggest, well, have you considered that it might be, say, an incentive problem? Are there incentives on behalf of the purchasing manager at your clients that are obstructing you? Might there be incentive issues with your own sales force that makes them want to sell the old product instead of the new one?

So literally, just identifying what type of problem does this person think about, and is there different potential way of thinking about it? Might it be an emotional problem, a timing problem, an expectations management problem? Thinking about what label of what type of problem that person is kind of thinking as it of.

SARAH GREEN CARMICHAEL: That’s really interesting, too, because I think so many of us get requests for advice that we’re really not qualified to give. So, maybe the next time that happens, instead of muddying my way through, I will just ask some of those questions that we talked about instead.

THOMAS WEDELL-WEDELLSBORG: That sounds like a good idea.

SARAH GREEN CARMICHAEL: So, Thomas, this has really helped me reframe the way I think about a couple of problems in my own life, and I’m just wondering. I know you do this professionally, but is there a problem in your life that thinking this way has helped you solve?

THOMAS WEDELL-WEDELLSBORG: I’ve, of course, I’ve been swallowing my own medicine on this, too, and I think I have, well, maybe two different examples, and in one case somebody else did the reframing for me. But in one case, when I was younger, I often kind of struggled a little bit. I mean, this is my teenage years, kind of hanging out with my parents. I thought they were pretty annoying people. That’s not really fair, because they’re quite wonderful, but that’s what life is when you’re a teenager.

And one of the things that struck me, suddenly, and this was kind of the positive exception was, there was actually an evening where we really had a good time, and there wasn’t a conflict. And the core thing was, I wasn’t just seeing them in their old house where I grew up. It was, actually, we were at a restaurant. And it suddenly struck me that so much of the sometimes, kind of, a little bit, you love them but they’re annoying kind of dynamic, is tied to the place, is tied to the setting you are in.

And of course, if– you know, I live abroad now, if I visit my parents and I stay in my old bedroom, you know, my mother comes in and wants to wake me up in the morning. Stuff like that, right? And it just struck me so, so clearly that it’s– when I change this setting, if I go out and have dinner with them at a different place, that the dynamic, just that dynamic disappears.

SARAH GREEN CARMICHAEL: Well, Thomas, this has been really, really helpful. Thank you for talking with me today.

THOMAS WEDELL-WEDELLSBORG: Thank you, Sarah.  

HANNAH BATES: That was Thomas Wedell-Wedellsborg in conversation with Sarah Green Carmichael on the HBR IdeaCast. He’s an expert in problem solving and innovation, and he’s the author of the book, What’s Your Problem?: To Solve Your Toughest Problems, Change the Problems You Solve .

We’ll be back next Wednesday with another hand-picked conversation about leadership from the Harvard Business Review. If you found this episode helpful, share it with your friends and colleagues, and follow our show on Apple Podcasts, Spotify, or wherever you get your podcasts. While you’re there, be sure to leave us a review.

We’re a production of Harvard Business Review. If you want more podcasts, articles, case studies, books, and videos like this, find it all at HBR dot org.

This episode was produced by Anne Saini, and me, Hannah Bates. Ian Fox is our editor. Music by Coma Media. Special thanks to Maureen Hoch, Adi Ignatius, Karen Player, Ramsey Khabbaz, Nicole Smith, Anne Bartholomew, and you – our listener.

See you next week.

• Subscribe On:

Latest in this series

This article is about leadership.

• Decision making and problem solving
• Power and influence
• Business management

Partner Center

The math problem that took nearly a century to solve: Secret to Ramsey numbers

Mathematicians unlock the secret to ramsey numbers.

We've all been there: staring at a math test with a problem that seems impossible to solve. What if finding the solution to a problem took almost a century? For mathematicians who dabble in Ramsey theory, this is very much the case. In fact, little progress had been made in solving Ramsey problems since the 1930s.

Now, University of California San Diego researchers Jacques Verstraete and Sam Mattheus have found the answer to r(4,t), a longstanding Ramsey problem that has perplexed the math world for decades.

What was Ramsey's problem, anyway?

In mathematical parlance, a graph is a series of points and the lines in between those points. Ramsey theory suggests that if the graph is large enough, you're guaranteed to find some kind of order within it -- either a set of points with no lines between them or a set of points with all possible lines between them (these sets are called "cliques"). This is written as r(s,t) where s are the points with lines and t are the points without lines.

To those of us who don't deal in graph theory, the most well-known Ramsey problem, r(3,3), is sometimes called "the theorem on friends and strangers" and is explained by way of a party: in a group of six people, you will find at least three people who all know each other or three people who all don't know each other. The answer to r(3,3) is six.

"It's a fact of nature, an absolute truth," Verstraete states. "It doesn't matter what the situation is or which six people you pick -- you will find three people who all know each other or three people who all don't know each other. You may be able to find more, but you are guaranteed that there will be at least three in one clique or the other."

What happened after mathematicians found that r(3,3) = 6? Naturally, they wanted to know r(4,4), r(5,5), and r(4,t) where the number of points that are not connected is variable. The solution to r(4,4) is 18 and is proved using a theorem created by Paul Erdös and George Szekeres in the 1930s.

Currently r(5,5) is still unknown.

A good problem fights back

Why is something so simple to state so hard to solve? It turns out to be more complicated than it appears. Let's say you knew the solution to r(5,5) was somewhere between 40-50. If you started with 45 points, there would be more than 10 234 graphs to consider!

"Because these numbers are so notoriously difficult to find, mathematicians look for estimations," Verstraete explained. "This is what Sam and I have achieved in our recent work. How do we find not the exact answer, but the best estimates for what these Ramsey numbers might be?"

Math students learn about Ramsey problems early on, so r(4,t) has been on Verstraete's radar for most of his professional career. In fact, he first saw the problem in print in Erdös on Graphs: His Legacy of Unsolved Problems, written by two UC San Diego professors, Fan Chung and the late Ron Graham. The problem is a conjecture from Erdös, who offered $250 to the first person who could solve it.

"Many people have thought about r(4,t) -- it's been an open problem for over 90 years," Verstraete said. "But it wasn't something that was at the forefront of my research. Everybody knows it's hard and everyone's tried to figure it out, so unless you have a new idea, you're not likely to get anywhere."

Then about four years ago, Verstraete was working on a different Ramsey problem with a mathematician at the University of Illinois-Chicago, Dhruv Mubayi. Together they discovered that pseudorandom graphs could advance the current knowledge on these old problems.

In 1937, Erdös discovered that using random graphs could give good lower bounds on Ramsey problems. What Verstraete and Mubayi discovered was that sampling from pseudo random graphs frequently gives better bounds on Ramsey numbers than random graphs. These bounds -- upper and lower limits on the possible answer -- tightened the range of estimations they could make. In other words, they were getting closer to the truth.

In 2019, to the delight of the math world, Verstraete and Mubayi used pseudorandom graphs to solve r(3,t). However, Verstraete struggled to build a pseudorandom graph that could help solve r(4,t).

He began pulling in different areas of math outside of combinatorics, including finite geometry, algebra and probability. Eventually he joined forces with Mattheus, a postdoctoral scholar in his group whose background was in finite geometry.

"It turned out that the pseudorandom graph we needed could be found in finite geometry," Verstraete stated. "Sam was the perfect person to come along and help build what we needed."

Once they had the pseudorandom graph in place, they still had to puzzle out several pieces of math. It took almost a year, but eventually they realized they had a solution: r(4,t) is close to a cubic function of t . If you want a party where there will always be four people who all know each other or t people who all don't know each other, you will need roughly t 3 people present. There is a small asterisk (actually an o) because, remember, this is an estimate, not an exact answer. But t 3 is very close to the exact answer.

The findings are currently under review with the Annals of Mathematics .

"It really did take us years to solve," Verstraete stated. "And there were many times where we were stuck and wondered if we'd be able to solve it at all. But one should never give up, no matter how long it takes."

Verstraete emphasizes the importance of perseverance -- something he reminds his students of often. "If you find that the problem is hard and you're stuck, that means it's a good problem. Fan Chung said a good problem fights back. You can't expect it just to reveal itself."

Verstraete knows such dogged determination is well-rewarded: "I got a call from Fan saying she owes me $250."

• Mathematics
• Math Puzzles
• Mathematical Modeling
• Educational Technology
• Computer Modeling
• Distributed Computing
• Quantum computer
• Knot theory
• Massively multiplayer online game
• Supercomputer
• Algebraic geometry
• John von Neumann
• Scientific method

Story Source:

Materials provided by University of California - San Diego . Original written by Michelle Franklin. Note: Content may be edited for style and length.

Journal Reference :

• Sam Mattheus, Jacques Verstraete. The asymptotics of r(4,t) . Annals of Mathematics , 2024; 199 (2) DOI: 10.4007/annals.2024.199.2.8

Cite This Page :

Explore More

• Drug Development Made Easier
• RNA That Doesn't Age
• 'Rainbow' Detected On an Exoplanet
• Spears and Throwing Sticks 300,000 Years Old
• High Carbon Impact of Tourism at Yellowstone
• Extreme Starburst Galaxy
• Asthma: Disease May Be Stoppable
• Stellar Collisions and Zombie-Like Survivors
• Tiny Robot Swarms Inspired by Herd Mentality
• How the Brain Regulates Emotions

Trending Topics

Strange & offbeat.