hypothesis testing approach

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

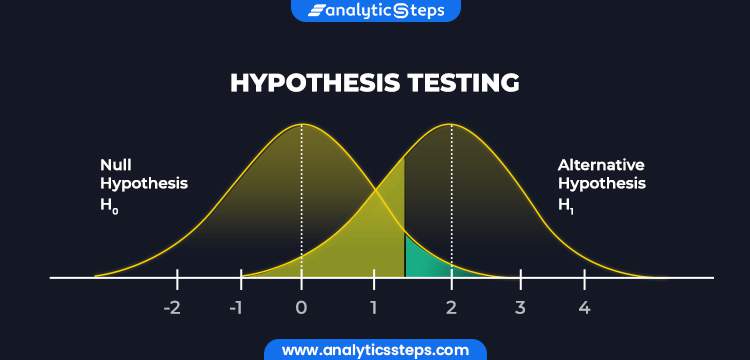
1.4: Basic Concepts of Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 1715

• John H. McDonald
• University of Delaware

Learning Objectives

• One of the main goals of statistical hypothesis testing is to estimate the \(P\) value, which is the probability of obtaining the observed results, or something more extreme, if the null hypothesis were true. If the observed results are unlikely under the null hypothesis, reject the null hypothesis.
• Alternatives to this "frequentist" approach to statistics include Bayesian statistics and estimation of effect sizes and confidence intervals.

Introduction

There are different ways of doing statistics. The technique used by the vast majority of biologists, and the technique that most of this handbook describes, is sometimes called "frequentist" or "classical" statistics. It involves testing a null hypothesis by comparing the data you observe in your experiment with the predictions of a null hypothesis. You estimate what the probability would be of obtaining the observed results, or something more extreme, if the null hypothesis were true. If this estimated probability (the \(P\) value) is small enough (below the significance value), then you conclude that it is unlikely that the null hypothesis is true; you reject the null hypothesis and accept an alternative hypothesis.

Many statisticians harshly criticize frequentist statistics, but their criticisms haven't had much effect on the way most biologists do statistics. Here I will outline some of the key concepts used in frequentist statistics, then briefly describe some of the alternatives.

Null Hypothesis

The null hypothesis is a statement that you want to test. In general, the null hypothesis is that things are the same as each other, or the same as a theoretical expectation. For example, if you measure the size of the feet of male and female chickens, the null hypothesis could be that the average foot size in male chickens is the same as the average foot size in female chickens. If you count the number of male and female chickens born to a set of hens, the null hypothesis could be that the ratio of males to females is equal to a theoretical expectation of a \(1:1\) ratio.

The alternative hypothesis is that things are different from each other, or different from a theoretical expectation.

For example, one alternative hypothesis would be that male chickens have a different average foot size than female chickens; another would be that the sex ratio is different from \(1:1\).

Usually, the null hypothesis is boring and the alternative hypothesis is interesting. For example, let's say you feed chocolate to a bunch of chickens, then look at the sex ratio in their offspring. If you get more females than males, it would be a tremendously exciting discovery: it would be a fundamental discovery about the mechanism of sex determination, female chickens are more valuable than male chickens in egg-laying breeds, and you'd be able to publish your result in Science or Nature . Lots of people have spent a lot of time and money trying to change the sex ratio in chickens, and if you're successful, you'll be rich and famous. But if the chocolate doesn't change the sex ratio, it would be an extremely boring result, and you'd have a hard time getting it published in the Eastern Delaware Journal of Chickenology . It's therefore tempting to look for patterns in your data that support the exciting alternative hypothesis. For example, you might look at \(48\) offspring of chocolate-fed chickens and see \(31\) females and only \(17\) males. This looks promising, but before you get all happy and start buying formal wear for the Nobel Prize ceremony, you need to ask "What's the probability of getting a deviation from the null expectation that large, just by chance, if the boring null hypothesis is really true?" Only when that probability is low can you reject the null hypothesis. The goal of statistical hypothesis testing is to estimate the probability of getting your observed results under the null hypothesis.

Biological vs. Statistical Null Hypotheses

It is important to distinguish between biological null and alternative hypotheses and statistical null and alternative hypotheses. "Sexual selection by females has caused male chickens to evolve bigger feet than females" is a biological alternative hypothesis; it says something about biological processes, in this case sexual selection. "Male chickens have a different average foot size than females" is a statistical alternative hypothesis; it says something about the numbers, but nothing about what caused those numbers to be different. The biological null and alternative hypotheses are the first that you should think of, as they describe something interesting about biology; they are two possible answers to the biological question you are interested in ("What affects foot size in chickens?"). The statistical null and alternative hypotheses are statements about the data that should follow from the biological hypotheses: if sexual selection favors bigger feet in male chickens (a biological hypothesis), then the average foot size in male chickens should be larger than the average in females (a statistical hypothesis). If you reject the statistical null hypothesis, you then have to decide whether that's enough evidence that you can reject your biological null hypothesis. For example, if you don't find a significant difference in foot size between male and female chickens, you could conclude "There is no significant evidence that sexual selection has caused male chickens to have bigger feet." If you do find a statistically significant difference in foot size, that might not be enough for you to conclude that sexual selection caused the bigger feet; it might be that males eat more, or that the bigger feet are a developmental byproduct of the roosters' combs, or that males run around more and the exercise makes their feet bigger. When there are multiple biological interpretations of a statistical result, you need to think of additional experiments to test the different possibilities.

Testing the Null Hypothesis

The primary goal of a statistical test is to determine whether an observed data set is so different from what you would expect under the null hypothesis that you should reject the null hypothesis. For example, let's say you are studying sex determination in chickens. For breeds of chickens that are bred to lay lots of eggs, female chicks are more valuable than male chicks, so if you could figure out a way to manipulate the sex ratio, you could make a lot of chicken farmers very happy. You've fed chocolate to a bunch of female chickens (in birds, unlike mammals, the female parent determines the sex of the offspring), and you get \(25\) female chicks and \(23\) male chicks. Anyone would look at those numbers and see that they could easily result from chance; there would be no reason to reject the null hypothesis of a \(1:1\) ratio of females to males. If you got \(47\) females and \(1\) male, most people would look at those numbers and see that they would be extremely unlikely to happen due to luck, if the null hypothesis were true; you would reject the null hypothesis and conclude that chocolate really changed the sex ratio. However, what if you had \(31\) females and \(17\) males? That's definitely more females than males, but is it really so unlikely to occur due to chance that you can reject the null hypothesis? To answer that, you need more than common sense, you need to calculate the probability of getting a deviation that large due to chance.

In the figure above, I used the BINOMDIST function of Excel to calculate the probability of getting each possible number of males, from \(0\) to \(48\), under the null hypothesis that \(0.5\) are male. As you can see, the probability of getting \(17\) males out of \(48\) total chickens is about \(0.015\). That seems like a pretty small probability, doesn't it? However, that's the probability of getting exactly \(17\) males. What you want to know is the probability of getting \(17\) or fewer males. If you were going to accept \(17\) males as evidence that the sex ratio was biased, you would also have accepted \(16\), or \(15\), or \(14\),… males as evidence for a biased sex ratio. You therefore need to add together the probabilities of all these outcomes. The probability of getting \(17\) or fewer males out of \(48\), under the null hypothesis, is \(0.030\). That means that if you had an infinite number of chickens, half males and half females, and you took a bunch of random samples of \(48\) chickens, \(3.0\%\) of the samples would have \(17\) or fewer males.

This number, \(0.030\), is the \(P\) value. It is defined as the probability of getting the observed result, or a more extreme result, if the null hypothesis is true. So "\(P=0.030\)" is a shorthand way of saying "The probability of getting \(17\) or fewer male chickens out of \(48\) total chickens, IF the null hypothesis is true that \(50\%\) of chickens are male, is \(0.030\)."

False Positives vs. False Negatives

After you do a statistical test, you are either going to reject or accept the null hypothesis. Rejecting the null hypothesis means that you conclude that the null hypothesis is not true; in our chicken sex example, you would conclude that the true proportion of male chicks, if you gave chocolate to an infinite number of chicken mothers, would be less than \(50\%\).

When you reject a null hypothesis, there's a chance that you're making a mistake. The null hypothesis might really be true, and it may be that your experimental results deviate from the null hypothesis purely as a result of chance. In a sample of \(48\) chickens, it's possible to get \(17\) male chickens purely by chance; it's even possible (although extremely unlikely) to get \(0\) male and \(48\) female chickens purely by chance, even though the true proportion is \(50\%\) males. This is why we never say we "prove" something in science; there's always a chance, however miniscule, that our data are fooling us and deviate from the null hypothesis purely due to chance. When your data fool you into rejecting the null hypothesis even though it's true, it's called a "false positive," or a "Type I error." So another way of defining the \(P\) value is the probability of getting a false positive like the one you've observed, if the null hypothesis is true.

Another way your data can fool you is when you don't reject the null hypothesis, even though it's not true. If the true proportion of female chicks is \(51\%\), the null hypothesis of a \(50\%\) proportion is not true, but you're unlikely to get a significant difference from the null hypothesis unless you have a huge sample size. Failing to reject the null hypothesis, even though it's not true, is a "false negative" or "Type II error." This is why we never say that our data shows the null hypothesis to be true; all we can say is that we haven't rejected the null hypothesis.

Significance Levels

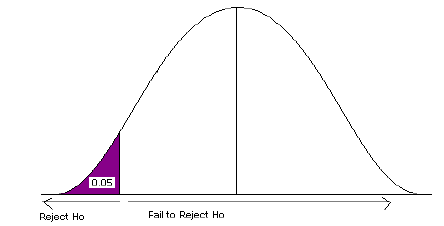
Does a probability of \(0.030\) mean that you should reject the null hypothesis, and conclude that chocolate really caused a change in the sex ratio? The convention in most biological research is to use a significance level of \(0.05\). This means that if the \(P\) value is less than \(0.05\), you reject the null hypothesis; if \(P\) is greater than or equal to \(0.05\), you don't reject the null hypothesis. There is nothing mathematically magic about \(0.05\), it was chosen rather arbitrarily during the early days of statistics; people could have agreed upon \(0.04\), or \(0.025\), or \(0.071\) as the conventional significance level.

The significance level (also known as the "critical value" or "alpha") you should use depends on the costs of different kinds of errors. With a significance level of \(0.05\), you have a \(5\%\) chance of rejecting the null hypothesis, even if it is true. If you try \(100\) different treatments on your chickens, and none of them really change the sex ratio, \(5\%\) of your experiments will give you data that are significantly different from a \(1:1\) sex ratio, just by chance. In other words, \(5\%\) of your experiments will give you a false positive. If you use a higher significance level than the conventional \(0.05\), such as \(0.10\), you will increase your chance of a false positive to \(0.10\) (therefore increasing your chance of an embarrassingly wrong conclusion), but you will also decrease your chance of a false negative (increasing your chance of detecting a subtle effect). If you use a lower significance level than the conventional \(0.05\), such as \(0.01\), you decrease your chance of an embarrassing false positive, but you also make it less likely that you'll detect a real deviation from the null hypothesis if there is one.

The relative costs of false positives and false negatives, and thus the best \(P\) value to use, will be different for different experiments. If you are screening a bunch of potential sex-ratio-changing treatments and get a false positive, it wouldn't be a big deal; you'd just run a few more tests on that treatment until you were convinced the initial result was a false positive. The cost of a false negative, however, would be that you would miss out on a tremendously valuable discovery. You might therefore set your significance value to \(0.10\) or more for your initial tests. On the other hand, once your sex-ratio-changing treatment is undergoing final trials before being sold to farmers, a false positive could be very expensive; you'd want to be very confident that it really worked. Otherwise, if you sell the chicken farmers a sex-ratio treatment that turns out to not really work (it was a false positive), they'll sue the pants off of you. Therefore, you might want to set your significance level to \(0.01\), or even lower, for your final tests.

The significance level you choose should also depend on how likely you think it is that your alternative hypothesis will be true, a prediction that you make before you do the experiment. This is the foundation of Bayesian statistics, as explained below.

You must choose your significance level before you collect the data, of course. If you choose to use a different significance level than the conventional \(0.05\), people will be skeptical; you must be able to justify your choice. Throughout this handbook, I will always use \(P< 0.05\) as the significance level. If you are doing an experiment where the cost of a false positive is a lot greater or smaller than the cost of a false negative, or an experiment where you think it is unlikely that the alternative hypothesis will be true, you should consider using a different significance level.

One-tailed vs. Two-tailed Probabilities

The probability that was calculated above, \(0.030\), is the probability of getting \(17\) or fewer males out of \(48\). It would be significant, using the conventional \(P< 0.05\)criterion. However, what about the probability of getting \(17\) or fewer females? If your null hypothesis is "The proportion of males is \(17\) or more" and your alternative hypothesis is "The proportion of males is less than \(0.5\)," then you would use the \(P=0.03\) value found by adding the probabilities of getting \(17\) or fewer males. This is called a one-tailed probability, because you are adding the probabilities in only one tail of the distribution shown in the figure. However, if your null hypothesis is "The proportion of males is \(0.5\)", then your alternative hypothesis is "The proportion of males is different from \(0.5\)." In that case, you should add the probability of getting \(17\) or fewer females to the probability of getting \(17\) or fewer males. This is called a two-tailed probability. If you do that with the chicken result, you get \(P=0.06\), which is not quite significant.

You should decide whether to use the one-tailed or two-tailed probability before you collect your data, of course. A one-tailed probability is more powerful, in the sense of having a lower chance of false negatives, but you should only use a one-tailed probability if you really, truly have a firm prediction about which direction of deviation you would consider interesting. In the chicken example, you might be tempted to use a one-tailed probability, because you're only looking for treatments that decrease the proportion of worthless male chickens. But if you accidentally found a treatment that produced \(87\%\) male chickens, would you really publish the result as "The treatment did not cause a significant decrease in the proportion of male chickens"? I hope not. You'd realize that this unexpected result, even though it wasn't what you and your farmer friends wanted, would be very interesting to other people; by leading to discoveries about the fundamental biology of sex-determination in chickens, in might even help you produce more female chickens someday. Any time a deviation in either direction would be interesting, you should use the two-tailed probability. In addition, people are skeptical of one-tailed probabilities, especially if a one-tailed probability is significant and a two-tailed probability would not be significant (as in our chocolate-eating chicken example). Unless you provide a very convincing explanation, people may think you decided to use the one-tailed probability after you saw that the two-tailed probability wasn't quite significant, which would be cheating. It may be easier to always use two-tailed probabilities. For this handbook, I will always use two-tailed probabilities, unless I make it very clear that only one direction of deviation from the null hypothesis would be interesting.

Reporting your results

In the olden days, when people looked up \(P\) values in printed tables, they would report the results of a statistical test as "\(P< 0.05\)", "\(P< 0.01\)", "\(P>0.10\)", etc. Nowadays, almost all computer statistics programs give the exact \(P\) value resulting from a statistical test, such as \(P=0.029\), and that's what you should report in your publications. You will conclude that the results are either significant or they're not significant; they either reject the null hypothesis (if \(P\) is below your pre-determined significance level) or don't reject the null hypothesis (if \(P\) is above your significance level). But other people will want to know if your results are "strongly" significant (\(P\) much less than \(0.05\)), which will give them more confidence in your results than if they were "barely" significant (\(P=0.043\), for example). In addition, other researchers will need the exact \(P\) value if they want to combine your results with others into a meta-analysis.

Computer statistics programs can give somewhat inaccurate \(P\) values when they are very small. Once your \(P\) values get very small, you can just say "\(P< 0.00001\)" or some other impressively small number. You should also give either your raw data, or the test statistic and degrees of freedom, in case anyone wants to calculate your exact \(P\) value.

Effect Sizes and Confidence Intervals

A fairly common criticism of the hypothesis-testing approach to statistics is that the null hypothesis will always be false, if you have a big enough sample size. In the chicken-feet example, critics would argue that if you had an infinite sample size, it is impossible that male chickens would have exactly the same average foot size as female chickens. Therefore, since you know before doing the experiment that the null hypothesis is false, there's no point in testing it.

This criticism only applies to two-tailed tests, where the null hypothesis is "Things are exactly the same" and the alternative is "Things are different." Presumably these critics think it would be okay to do a one-tailed test with a null hypothesis like "Foot length of male chickens is the same as, or less than, that of females," because the null hypothesis that male chickens have smaller feet than females could be true. So if you're worried about this issue, you could think of a two-tailed test, where the null hypothesis is that things are the same, as shorthand for doing two one-tailed tests. A significant rejection of the null hypothesis in a two-tailed test would then be the equivalent of rejecting one of the two one-tailed null hypotheses.

A related criticism is that a significant rejection of a null hypothesis might not be biologically meaningful, if the difference is too small to matter. For example, in the chicken-sex experiment, having a treatment that produced \(49.9\%\) male chicks might be significantly different from \(50\%\), but it wouldn't be enough to make farmers want to buy your treatment. These critics say you should estimate the effect size and put a confidence interval on it, not estimate a \(P\) value. So the goal of your chicken-sex experiment should not be to say "Chocolate gives a proportion of males that is significantly less than \(50\%\) ((\(P=0.015\))" but to say "Chocolate produced \(36.1\%\) males with a \(95\%\) confidence interval of \(25.9\%\) to \(47.4\%\)." For the chicken-feet experiment, you would say something like "The difference between males and females in mean foot size is \(2.45mm\), with a confidence interval on the difference of \(\pm 1.98mm\)."

Estimating effect sizes and confidence intervals is a useful way to summarize your results, and it should usually be part of your data analysis; you'll often want to include confidence intervals in a graph. However, there are a lot of experiments where the goal is to decide a yes/no question, not estimate a number. In the initial tests of chocolate on chicken sex ratio, the goal would be to decide between "It changed the sex ratio" and "It didn't seem to change the sex ratio." Any change in sex ratio that is large enough that you could detect it would be interesting and worth follow-up experiments. While it's true that the difference between \(49.9\%\) and \(50\%\) might not be worth pursuing, you wouldn't do an experiment on enough chickens to detect a difference that small.

Often, the people who claim to avoid hypothesis testing will say something like "the \(95\%\) confidence interval of \(25.9\%\) to \(47.4\%\) does not include \(50\%\), so we conclude that the plant extract significantly changed the sex ratio." This is a clumsy and roundabout form of hypothesis testing, and they might as well admit it and report the \(P\) value.

Bayesian statistics

Another alternative to frequentist statistics is Bayesian statistics. A key difference is that Bayesian statistics requires specifying your best guess of the probability of each possible value of the parameter to be estimated, before the experiment is done. This is known as the "prior probability." So for your chicken-sex experiment, you're trying to estimate the "true" proportion of male chickens that would be born, if you had an infinite number of chickens. You would have to specify how likely you thought it was that the true proportion of male chickens was \(50\%\), or \(51\%\), or \(52\%\), or \(47.3\%\), etc. You would then look at the results of your experiment and use the information to calculate new probabilities that the true proportion of male chickens was \(50\%\), or \(51\%\), or \(52\%\), or \(47.3\%\), etc. (the posterior distribution).

I'll confess that I don't really understand Bayesian statistics, and I apologize for not explaining it well. In particular, I don't understand how people are supposed to come up with a prior distribution for the kinds of experiments that most biologists do. With the exception of systematics, where Bayesian estimation of phylogenies is quite popular and seems to make sense, I haven't seen many research biologists using Bayesian statistics for routine data analysis of simple laboratory experiments. This means that even if the cult-like adherents of Bayesian statistics convinced you that they were right, you would have a difficult time explaining your results to your biologist peers. Statistics is a method of conveying information, and if you're speaking a different language than the people you're talking to, you won't convey much information. So I'll stick with traditional frequentist statistics for this handbook.

Having said that, there's one key concept from Bayesian statistics that is important for all users of statistics to understand. To illustrate it, imagine that you are testing extracts from \(1000\) different tropical plants, trying to find something that will kill beetle larvae. The reality (which you don't know) is that \(500\) of the extracts kill beetle larvae, and \(500\) don't. You do the \(1000\) experiments and do the \(1000\) frequentist statistical tests, and you use the traditional significance level of \(P< 0.05\). The \(500\) plant extracts that really work all give you \(P< 0.05\); these are the true positives. Of the \(500\) extracts that don't work, \(5\%\) of them give you \(P< 0.05\) by chance (this is the meaning of the \(P\) value, after all), so you have \(25\) false positives. So you end up with \(525\) plant extracts that gave you a \(P\) value less than \(0.05\). You'll have to do further experiments to figure out which are the \(25\) false positives and which are the \(500\) true positives, but that's not so bad, since you know that most of them will turn out to be true positives.

Now imagine that you are testing those extracts from \(1000\) different tropical plants to try to find one that will make hair grow. The reality (which you don't know) is that one of the extracts makes hair grow, and the other \(999\) don't. You do the \(1000\) experiments and do the \(1000\) frequentist statistical tests, and you use the traditional significance level of \(P< 0.05\). The one plant extract that really works gives you P <0.05; this is the true positive. But of the \(999\) extracts that don't work, \(5\%\) of them give you \(P< 0.05\) by chance, so you have about \(50\) false positives. You end up with \(51\) \(P\) values less than \(0.05\), but almost all of them are false positives.

Now instead of testing \(1000\) plant extracts, imagine that you are testing just one. If you are testing it to see if it kills beetle larvae, you know (based on everything you know about plant and beetle biology) there's a pretty good chance it will work, so you can be pretty sure that a \(P\) value less than \(0.05\) is a true positive. But if you are testing that one plant extract to see if it grows hair, which you know is very unlikely (based on everything you know about plants and hair), a \(P\) value less than \(0.05\) is almost certainly a false positive. In other words, if you expect that the null hypothesis is probably true, a statistically significant result is probably a false positive. This is sad; the most exciting, amazing, unexpected results in your experiments are probably just your data trying to make you jump to ridiculous conclusions. You should require a much lower \(P\) value to reject a null hypothesis that you think is probably true.

A Bayesian would insist that you put in numbers just how likely you think the null hypothesis and various values of the alternative hypothesis are, before you do the experiment, and I'm not sure how that is supposed to work in practice for most experimental biology. But the general concept is a valuable one: as Carl Sagan summarized it, "Extraordinary claims require extraordinary evidence."

Recommendations

Here are three experiments to illustrate when the different approaches to statistics are appropriate. In the first experiment, you are testing a plant extract on rabbits to see if it will lower their blood pressure. You already know that the plant extract is a diuretic (makes the rabbits pee more) and you already know that diuretics tend to lower blood pressure, so you think there's a good chance it will work. If it does work, you'll do more low-cost animal tests on it before you do expensive, potentially risky human trials. Your prior expectation is that the null hypothesis (that the plant extract has no effect) has a good chance of being false, and the cost of a false positive is fairly low. So you should do frequentist hypothesis testing, with a significance level of \(0.05\).

In the second experiment, you are going to put human volunteers with high blood pressure on a strict low-salt diet and see how much their blood pressure goes down. Everyone will be confined to a hospital for a month and fed either a normal diet, or the same foods with half as much salt. For this experiment, you wouldn't be very interested in the \(P\) value, as based on prior research in animals and humans, you are already quite certain that reducing salt intake will lower blood pressure; you're pretty sure that the null hypothesis that "Salt intake has no effect on blood pressure" is false. Instead, you are very interested to know how much the blood pressure goes down. Reducing salt intake in half is a big deal, and if it only reduces blood pressure by \(1mm\) Hg, the tiny gain in life expectancy wouldn't be worth a lifetime of bland food and obsessive label-reading. If it reduces blood pressure by \(20mm\) with a confidence interval of \(\pm 5mm\), it might be worth it. So you should estimate the effect size (the difference in blood pressure between the diets) and the confidence interval on the difference.

In the third experiment, you are going to put magnetic hats on guinea pigs and see if their blood pressure goes down (relative to guinea pigs wearing the kind of non-magnetic hats that guinea pigs usually wear). This is a really goofy experiment, and you know that it is very unlikely that the magnets will have any effect (it's not impossible—magnets affect the sense of direction of homing pigeons, and maybe guinea pigs have something similar in their brains and maybe it will somehow affect their blood pressure—it just seems really unlikely). You might analyze your results using Bayesian statistics, which will require specifying in numerical terms just how unlikely you think it is that the magnetic hats will work. Or you might use frequentist statistics, but require a \(P\) value much, much lower than \(0.05\) to convince yourself that the effect is real.

• Picture of giant concrete chicken from Sue and Tony's Photo Site.
• Picture of guinea pigs wearing hats from all over the internet; if you know the original photographer, please let me know.

Statistics Made Easy

Introduction to Hypothesis Testing

A statistical hypothesis is an assumption about a population parameter .

For example, we may assume that the mean height of a male in the U.S. is 70 inches.

The assumption about the height is the statistical hypothesis and the true mean height of a male in the U.S. is the population parameter .

A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.

The Two Types of Statistical Hypotheses

To test whether a statistical hypothesis about a population parameter is true, we obtain a random sample from the population and perform a hypothesis test on the sample data.

There are two types of statistical hypotheses:

The null hypothesis , denoted as H 0 , is the hypothesis that the sample data occurs purely from chance.

The alternative hypothesis , denoted as H 1 or H a , is the hypothesis that the sample data is influenced by some non-random cause.

Hypothesis Tests

A hypothesis test consists of five steps:

1. State the hypotheses. 

State the null and alternative hypotheses. These two hypotheses need to be mutually exclusive, so if one is true then the other must be false.

2. Determine a significance level to use for the hypothesis.

Decide on a significance level. Common choices are .01, .05, and .1. 

3. Find the test statistic.

Find the test statistic and the corresponding p-value. Often we are analyzing a population mean or proportion and the general formula to find the test statistic is: (sample statistic – population parameter) / (standard deviation of statistic)

4. Reject or fail to reject the null hypothesis.

Using the test statistic or the p-value, determine if you can reject or fail to reject the null hypothesis based on the significance level.

The p-value  tells us the strength of evidence in support of a null hypothesis. If the p-value is less than the significance level, we reject the null hypothesis.

5. Interpret the results. 

Interpret the results of the hypothesis test in the context of the question being asked. 

The Two Types of Decision Errors

There are two types of decision errors that one can make when doing a hypothesis test:

Type I error: You reject the null hypothesis when it is actually true. The probability of committing a Type I error is equal to the significance level, often called  alpha , and denoted as α.

Type II error: You fail to reject the null hypothesis when it is actually false. The probability of committing a Type II error is called the Power of the test or  Beta , denoted as β.

One-Tailed and Two-Tailed Tests

A statistical hypothesis can be one-tailed or two-tailed.

A one-tailed hypothesis involves making a “greater than” or “less than ” statement.

For example, suppose we assume the mean height of a male in the U.S. is greater than or equal to 70 inches. The null hypothesis would be H0: µ ≥ 70 inches and the alternative hypothesis would be Ha: µ < 70 inches.

A two-tailed hypothesis involves making an “equal to” or “not equal to” statement.

For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches. The null hypothesis would be H0: µ = 70 inches and the alternative hypothesis would be Ha: µ ≠ 70 inches.

Note: The “equal” sign is always included in the null hypothesis, whether it is =, ≥, or ≤.

Related:   What is a Directional Hypothesis?

Types of Hypothesis Tests

There are many different types of hypothesis tests you can perform depending on the type of data you’re working with and the goal of your analysis.

The following tutorials provide an explanation of the most common types of hypothesis tests:

Introduction to the One Sample t-test Introduction to the Two Sample t-test Introduction to the Paired Samples t-test Introduction to the One Proportion Z-Test Introduction to the Two Proportion Z-Test

Hey there. My name is Zach Bobbitt. I have a Master of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

• Number Theory
• Data Structures
• Cornerstones

Summary of the 3 Approaches to Hypothesis Testing

Steps to conduct a hypothesis test using $p$-values:.

Identify the null hypothesis and the alternative hypothesis (and decide which is the claim).

Ensure any necessary assumptions are met for the test to be conducted.

Find the test statistic.

Find the p-value associated with the test statistic as it relates to the alternative hypothesis.

Compare the p-value with the significance level, $\alpha$. If $p \lt \alpha$, conclude that the null hypothesis should be rejected based on what we saw. If not, conclude that we fail to reject the null hypothesis as a result of what we saw.

Make an inference.

Steps to Conduct a Hypothesis Test Using Critical Values:

Find the critical values associated with the significance level, $\alpha$, and the alternative hypothesis to establish the rejection region in the distribution.

If the test statistic falls in the rejection region, conclude that the null hypothesis should be rejected based on what we saw. If not, conclude that we fail to reject the null hypothesis as a result of what we saw.

Steps to Conduct a Hypothesis Test Using a Confidence Interval:

Construct a confidence interval with a confidence level of $(1-\alpha)$

If the hypothesized population parameter falls outside of the confidence interval, conclude that the null hypothesis should be rejected based on what we saw. If it falls within the confidence interval, conclude that we fail to reject the null hypothesis as a result of what we saw.

• > Machine Learning
• > Statistics

What is Hypothesis Testing? Types and Methods

• Soumyaa Rawat
• Jul 23, 2021

Hypothesis Testing  

Hypothesis testing is the act of testing a hypothesis or a supposition in relation to a statistical parameter. Analysts implement hypothesis testing in order to test if a hypothesis is plausible or not. 

In data science and statistics , hypothesis testing is an important step as it involves the verification of an assumption that could help develop a statistical parameter. For instance, a researcher establishes a hypothesis assuming that the average of all odd numbers is an even number. 

In order to find the plausibility of this hypothesis, the researcher will have to test the hypothesis using hypothesis testing methods. Unlike a hypothesis that is ‘supposed’ to stand true on the basis of little or no evidence, hypothesis testing is required to have plausible evidence in order to establish that a statistical hypothesis is true. 

Perhaps this is where statistics play an important role. A number of components are involved in this process. But before understanding the process involved in hypothesis testing in research methodology, we shall first understand the types of hypotheses that are involved in the process. Let us get started! 

Types of Hypotheses

In data sampling, different types of hypothesis are involved in finding whether the tested samples test positive for a hypothesis or not. In this segment, we shall discover the different types of hypotheses and understand the role they play in hypothesis testing.

Alternative Hypothesis

Alternative Hypothesis (H1) or the research hypothesis states that there is a relationship between two variables (where one variable affects the other). The alternative hypothesis is the main driving force for hypothesis testing. 

It implies that the two variables are related to each other and the relationship that exists between them is not due to chance or coincidence. 

When the process of hypothesis testing is carried out, the alternative hypothesis is the main subject of the testing process. The analyst intends to test the alternative hypothesis and verifies its plausibility.

Null Hypothesis

The Null Hypothesis (H0) aims to nullify the alternative hypothesis by implying that there exists no relation between two variables in statistics. It states that the effect of one variable on the other is solely due to chance and no empirical cause lies behind it. 

The null hypothesis is established alongside the alternative hypothesis and is recognized as important as the latter. In hypothesis testing, the null hypothesis has a major role to play as it influences the testing against the alternative hypothesis. 

(Must read: What is ANOVA test? )

Non-Directional Hypothesis

The Non-directional hypothesis states that the relation between two variables has no direction. 

Simply put, it asserts that there exists a relation between two variables, but does not recognize the direction of effect, whether variable A affects variable B or vice versa. 

Directional Hypothesis

The Directional hypothesis, on the other hand, asserts the direction of effect of the relationship that exists between two variables. 

Herein, the hypothesis clearly states that variable A affects variable B, or vice versa. 

Statistical Hypothesis

A statistical hypothesis is a hypothesis that can be verified to be plausible on the basis of statistics. 

By using data sampling and statistical knowledge, one can determine the plausibility of a statistical hypothesis and find out if it stands true or not. 

(Related blog: z-test vs t-test )

Performing Hypothesis Testing  

Now that we have understood the types of hypotheses and the role they play in hypothesis testing, let us now move on to understand the process in a better manner. 

In hypothesis testing, a researcher is first required to establish two hypotheses - alternative hypothesis and null hypothesis in order to begin with the procedure. 

To establish these two hypotheses, one is required to study data samples, find a plausible pattern among the samples, and pen down a statistical hypothesis that they wish to test. 

A random population of samples can be drawn, to begin with hypothesis testing. Among the two hypotheses, alternative and null, only one can be verified to be true. Perhaps the presence of both hypotheses is required to make the process successful. 

At the end of the hypothesis testing procedure, either of the hypotheses will be rejected and the other one will be supported. Even though one of the two hypotheses turns out to be true, no hypothesis can ever be verified 100%. 

(Read also: Types of data sampling techniques )

Therefore, a hypothesis can only be supported based on the statistical samples and verified data. Here is a step-by-step guide for hypothesis testing.

Establish the hypotheses

First things first, one is required to establish two hypotheses - alternative and null, that will set the foundation for hypothesis testing. 

These hypotheses initiate the testing process that involves the researcher working on data samples in order to either support the alternative hypothesis or the null hypothesis. 

Generate a testing plan

Once the hypotheses have been formulated, it is now time to generate a testing plan. A testing plan or an analysis plan involves the accumulation of data samples, determining which statistic is to be considered and laying out the sample size. 

All these factors are very important while one is working on hypothesis testing.

Analyze data samples

As soon as a testing plan is ready, it is time to move on to the analysis part. Analysis of data samples involves configuring statistical values of samples, drawing them together, and deriving a pattern out of these samples. 

While analyzing the data samples, a researcher needs to determine a set of things -

Significance Level - The level of significance in hypothesis testing indicates if a statistical result could have significance if the null hypothesis stands to be true.

Testing Method - The testing method involves a type of sampling-distribution and a test statistic that leads to hypothesis testing. There are a number of testing methods that can assist in the analysis of data samples. 

Test statistic - Test statistic is a numerical summary of a data set that can be used to perform hypothesis testing.

P-value - The P-value interpretation is the probability of finding a sample statistic to be as extreme as the test statistic, indicating the plausibility of the null hypothesis. 

Infer the results

The analysis of data samples leads to the inference of results that establishes whether the alternative hypothesis stands true or not. When the P-value is less than the significance level, the null hypothesis is rejected and the alternative hypothesis turns out to be plausible. 

Methods of Hypothesis Testing

As we have already looked into different aspects of hypothesis testing, we shall now look into the different methods of hypothesis testing. All in all, there are 2 most common types of hypothesis testing methods. They are as follows -

Frequentist Hypothesis Testing

The frequentist hypothesis or the traditional approach to hypothesis testing is a hypothesis testing method that aims on making assumptions by considering current data. 

The supposed truths and assumptions are based on the current data and a set of 2 hypotheses are formulated. A very popular subtype of the frequentist approach is the Null Hypothesis Significance Testing (NHST). 

The NHST approach (involving the null and alternative hypothesis) has been one of the most sought-after methods of hypothesis testing in the field of statistics ever since its inception in the mid-1950s. 

Bayesian Hypothesis Testing

A much unconventional and modern method of hypothesis testing, the Bayesian Hypothesis Testing claims to test a particular hypothesis in accordance with the past data samples, known as prior probability, and current data that lead to the plausibility of a hypothesis. 

The result obtained indicates the posterior probability of the hypothesis. In this method, the researcher relies on ‘prior probability and posterior probability’ to conduct hypothesis testing on hand. 

On the basis of this prior probability, the Bayesian approach tests a hypothesis to be true or false. The Bayes factor, a major component of this method, indicates the likelihood ratio among the null hypothesis and the alternative hypothesis. 

The Bayes factor is the indicator of the plausibility of either of the two hypotheses that are established for hypothesis testing.  

(Also read - Introduction to Bayesian Statistics ) 

To conclude, hypothesis testing, a way to verify the plausibility of a supposed assumption can be done through different methods - the Bayesian approach or the Frequentist approach. 

Although the Bayesian approach relies on the prior probability of data samples, the frequentist approach assumes without a probability. A number of elements involved in hypothesis testing are - significance level, p-level, test statistic, and method of hypothesis testing. 

(Also read: Introduction to probability distributions )

A significant way to determine whether a hypothesis stands true or not is to verify the data samples and identify the plausible hypothesis among the null hypothesis and alternative hypothesis. 

Share Blog :

Be a part of our Instagram community

Trending blogs

5 Factors Influencing Consumer Behavior

Elasticity of Demand and its Types

What is PESTLE Analysis? Everything you need to know about it

An Overview of Descriptive Analysis

What is Managerial Economics? Definition, Types, Nature, Principles, and Scope

5 Factors Affecting the Price Elasticity of Demand (PED)

6 Major Branches of Artificial Intelligence (AI)

Dijkstra’s Algorithm: The Shortest Path Algorithm

Scope of Managerial Economics

Different Types of Research Methods

Latest Comments

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings
• Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].

Hypothesis testing, p values, confidence intervals, and significance.

Jacob Shreffler ; Martin R. Huecker .

Affiliations

Last Update: March 13, 2023 .

• Definition/Introduction

Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting these findings, which may affect the adequate application of the data.

• Issues of Concern

Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. Therefore, an overview of these concepts is provided to allow medical professionals to use their expertise to determine if results are reported sufficiently and if the study outcomes are clinically appropriate to be applied in healthcare practice.

Hypothesis Testing

Investigators conducting studies need research questions and hypotheses to guide analyses. Starting with broad research questions (RQs), investigators then identify a gap in current clinical practice or research. Any research problem or statement is grounded in a better understanding of relationships between two or more variables. For this article, we will use the following research question example:

Research Question: Is Drug 23 an effective treatment for Disease A?

Research questions do not directly imply specific guesses or predictions; we must formulate research hypotheses. A hypothesis is a predetermined declaration regarding the research question in which the investigator(s) makes a precise, educated guess about a study outcome. This is sometimes called the alternative hypothesis and ultimately allows the researcher to take a stance based on experience or insight from medical literature. An example of a hypothesis is below.

Research Hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.

The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis.

Researchers should be aware of journal recommendations when considering how to report p values, and manuscripts should remain internally consistent.

Regarding p values, as the number of individuals enrolled in a study (the sample size) increases, the likelihood of finding a statistically significant effect increases. With very large sample sizes, the p-value can be very low significant differences in the reduction of symptoms for Disease A between Drug 23 and Drug 22. The null hypothesis is deemed true until a study presents significant data to support rejecting the null hypothesis. Based on the results, the investigators will either reject the null hypothesis (if they found significant differences or associations) or fail to reject the null hypothesis (they could not provide proof that there were significant differences or associations).

To test a hypothesis, researchers obtain data on a representative sample to determine whether to reject or fail to reject a null hypothesis. In most research studies, it is not feasible to obtain data for an entire population. Using a sampling procedure allows for statistical inference, though this involves a certain possibility of error. [1]  When determining whether to reject or fail to reject the null hypothesis, mistakes can be made: Type I and Type II errors. Though it is impossible to ensure that these errors have not occurred, researchers should limit the possibilities of these faults. [2]

Significance

Significance is a term to describe the substantive importance of medical research. Statistical significance is the likelihood of results due to chance. [3]  Healthcare providers should always delineate statistical significance from clinical significance, a common error when reviewing biomedical research. [4]  When conceptualizing findings reported as either significant or not significant, healthcare providers should not simply accept researchers' results or conclusions without considering the clinical significance. Healthcare professionals should consider the clinical importance of findings and understand both p values and confidence intervals so they do not have to rely on the researchers to determine the level of significance. [5]  One criterion often used to determine statistical significance is the utilization of p values.

P values are used in research to determine whether the sample estimate is significantly different from a hypothesized value. The p-value is the probability that the observed effect within the study would have occurred by chance if, in reality, there was no true effect. Conventionally, data yielding a p<0.05 or p<0.01 is considered statistically significant. While some have debated that the 0.05 level should be lowered, it is still universally practiced. [6]  Hypothesis testing allows us to determine the size of the effect.

An example of findings reported with p values are below:

Statement: Drug 23 reduced patients' symptoms compared to Drug 22. Patients who received Drug 23 (n=100) were 2.1 times less likely than patients who received Drug 22 (n = 100) to experience symptoms of Disease A, p<0.05.

Statement:Individuals who were prescribed Drug 23 experienced fewer symptoms (M = 1.3, SD = 0.7) compared to individuals who were prescribed Drug 22 (M = 5.3, SD = 1.9). This finding was statistically significant, p= 0.02.

For either statement, if the threshold had been set at 0.05, the null hypothesis (that there was no relationship) should be rejected, and we should conclude significant differences. Noticeably, as can be seen in the two statements above, some researchers will report findings with < or > and others will provide an exact p-value (0.000001) but never zero [6] . When examining research, readers should understand how p values are reported. The best practice is to report all p values for all variables within a study design, rather than only providing p values for variables with significant findings. [7]  The inclusion of all p values provides evidence for study validity and limits suspicion for selective reporting/data mining.  

While researchers have historically used p values, experts who find p values problematic encourage the use of confidence intervals. [8] . P-values alone do not allow us to understand the size or the extent of the differences or associations. [3]  In March 2016, the American Statistical Association (ASA) released a statement on p values, noting that scientific decision-making and conclusions should not be based on a fixed p-value threshold (e.g., 0.05). They recommend focusing on the significance of results in the context of study design, quality of measurements, and validity of data. Ultimately, the ASA statement noted that in isolation, a p-value does not provide strong evidence. [9]

When conceptualizing clinical work, healthcare professionals should consider p values with a concurrent appraisal study design validity. For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study [7] . The p-value debate has smoldered since the 1950s [10] , and replacement with confidence intervals has been suggested since the 1980s. [11]

Confidence Intervals

A confidence interval provides a range of values within given confidence (e.g., 95%), including the accurate value of the statistical constraint within a targeted population. [12]  Most research uses a 95% CI, but investigators can set any level (e.g., 90% CI, 99% CI). [13]  A CI provides a range with the lower bound and upper bound limits of a difference or association that would be plausible for a population. [14]  Therefore, a CI of 95% indicates that if a study were to be carried out 100 times, the range would contain the true value in 95, [15]  confidence intervals provide more evidence regarding the precision of an estimate compared to p-values. [6]

In consideration of the similar research example provided above, one could make the following statement with 95% CI:

Statement: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22; there was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

It is important to note that the width of the CI is affected by the standard error and the sample size; reducing a study sample number will result in less precision of the CI (increase the width). [14]  A larger width indicates a smaller sample size or a larger variability. [16]  A researcher would want to increase the precision of the CI. For example, a 95% CI of 1.43 – 1.47 is much more precise than the one provided in the example above. In research and clinical practice, CIs provide valuable information on whether the interval includes or excludes any clinically significant values. [14]

Null values are sometimes used for differences with CI (zero for differential comparisons and 1 for ratios). However, CIs provide more information than that. [15]  Consider this example: A hospital implements a new protocol that reduced wait time for patients in the emergency department by an average of 25 minutes (95% CI: -2.5 – 41 minutes). Because the range crosses zero, implementing this protocol in different populations could result in longer wait times; however, the range is much higher on the positive side. Thus, while the p-value used to detect statistical significance for this may result in "not significant" findings, individuals should examine this range, consider the study design, and weigh whether or not it is still worth piloting in their workplace.

Similarly to p-values, 95% CIs cannot control for researchers' errors (e.g., study bias or improper data analysis). [14]  In consideration of whether to report p-values or CIs, researchers should examine journal preferences. When in doubt, reporting both may be beneficial. [13]  An example is below:

Reporting both: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22, p = 0.009. There was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

• Clinical Significance

Recall that clinical significance and statistical significance are two different concepts. Healthcare providers should remember that a study with statistically significant differences and large sample size may be of no interest to clinicians, whereas a study with smaller sample size and statistically non-significant results could impact clinical practice. [14]  Additionally, as previously mentioned, a non-significant finding may reflect the study design itself rather than relationships between variables.

Healthcare providers using evidence-based medicine to inform practice should use clinical judgment to determine the practical importance of studies through careful evaluation of the design, sample size, power, likelihood of type I and type II errors, data analysis, and reporting of statistical findings (p values, 95% CI or both). [4]  Interestingly, some experts have called for "statistically significant" or "not significant" to be excluded from work as statistical significance never has and will never be equivalent to clinical significance. [17]

The decision on what is clinically significant can be challenging, depending on the providers' experience and especially the severity of the disease. Providers should use their knowledge and experiences to determine the meaningfulness of study results and make inferences based not only on significant or insignificant results by researchers but through their understanding of study limitations and practical implications.

• Nursing, Allied Health, and Interprofessional Team Interventions

All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts in this chapter. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care. 

• Review Questions
• Access free multiple choice questions on this topic.
• Comment on this article.

Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.

Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

• Cite this Page Shreffler J, Huecker MR. Hypothesis Testing, P Values, Confidence Intervals, and Significance. [Updated 2023 Mar 13]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

• Bulk download StatPearls data from FTP

Related information

• PMC PubMed Central citations
• PubMed Links to PubMed

Similar articles in PubMed

• The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). [PeerJ. 2021] The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). Messam LLM, Weng HY, Rosenberger NWY, Tan ZH, Payet SDM, Santbakshsing M. PeerJ. 2021; 9:e12453. Epub 2021 Nov 24.
• Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. [J Pharm Pract. 2010] Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. Ferrill MJ, Brown DA, Kyle JA. J Pharm Pract. 2010 Aug; 23(4):344-51. Epub 2010 Apr 13.
• Interpreting "statistical hypothesis testing" results in clinical research. [J Ayurveda Integr Med. 2012] Interpreting "statistical hypothesis testing" results in clinical research. Sarmukaddam SB. J Ayurveda Integr Med. 2012 Apr; 3(2):65-9.
• Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. [Dermatol Surg. 2005] Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. Alam M, Barzilai DA, Wrone DA. Dermatol Surg. 2005 Apr; 31(4):462-6.
• Review Is statistical significance testing useful in interpreting data? [Reprod Toxicol. 1993] Review Is statistical significance testing useful in interpreting data? Savitz DA. Reprod Toxicol. 1993; 7(2):95-100.

Recent Activity

• Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearl... Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 3: Hypothesis Testing

The previous two chapters introduced methods for organizing and summarizing sample data, and using sample statistics to estimate population parameters. This chapter introduces the next major topic of inferential statistics: hypothesis testing.

A hypothesis is a statement or claim about a property of a population.

The Fundamentals of Hypothesis Testing

When conducting scientific research, typically there is some known information, perhaps from some past work or from a long accepted idea. We want to test whether this claim is believable. This is the basic idea behind a hypothesis test:

• State what we think is true.
• Quantify how confident we are about our claim.
• Use sample statistics to make inferences about population parameters.

For example, past research tells us that the average life span for a hummingbird is about four years. You have been studying the hummingbirds in the southeastern United States and find a sample mean lifespan of 4.8 years. Should you reject the known or accepted information in favor of your results? How confident are you in your estimate? At what point would you say that there is enough evidence to reject the known information and support your alternative claim? How far from the known mean of four years can the sample mean be before we reject the idea that the average lifespan of a hummingbird is four years?

Hypothesis testing is a procedure, based on sample evidence and probability, used to test claims regarding a characteristic of a population.

A hypothesis is a claim or statement about a characteristic of a population of interest to us. A hypothesis test is a way for us to use our sample statistics to test a specific claim.

The population mean weight is known to be 157 lb. We want to test the claim that the mean weight has increased.

Two years ago, the proportion of infected plants was 37%. We believe that a treatment has helped, and we want to test the claim that there has been a reduction in the proportion of infected plants.

Components of a Formal Hypothesis Test

The null hypothesis is a statement about the value of a population parameter, such as the population mean (µ) or the population proportion ( p ). It contains the condition of equality and is denoted as H 0 (H-naught).

H 0 : µ = 157 or H 0 : p = 0.37

The alternative hypothesis is the claim to be tested, the opposite of the null hypothesis. It contains the value of the parameter that we consider plausible and is denoted as H 1 .

H 1 : µ > 157 or H 1 : p ≠ 0.37

The test statistic is a value computed from the sample data that is used in making a decision about the rejection of the null hypothesis. The test statistic converts the sample mean ( x̄ ) or sample proportion ( p̂ ) to a Z- or t-score under the assumption that the null hypothesis is true . It is used to decide whether the difference between the sample statistic and the hypothesized claim is significant.

The p-value is the area under the curve to the left or right of the test statistic. It is compared to the level of significance ( α ).

The critical value is the value that defines the rejection zone (the test statistic values that would lead to rejection of the null hypothesis). It is defined by the level of significance.

The level of significance ( α ) is the probability that the test statistic will fall into the critical region when the null hypothesis is true. This level is set by the researcher.

The conclusion is the final decision of the hypothesis test. The conclusion must always be clearly stated, communicating the decision based on the components of the test. It is important to realize that we never prove or accept the null hypothesis. We are merely saying that the sample evidence is not strong enough to warrant the rejection of the null hypothesis. The conclusion is made up of two parts:

1) Reject or fail to reject the null hypothesis, and 2) there is or is not enough evidence to support the alternative claim.

Option 1) Reject the null hypothesis (H 0 ). This means that you have enough statistical evidence to support the alternative claim (H 1 ).

Option 2) Fail to reject the null hypothesis (H 0 ). This means that you do NOT have enough evidence to support the alternative claim (H 1 ).

Another way to think about hypothesis testing is to compare it to the US justice system. A defendant is innocent until proven guilty (Null hypothesis—innocent). The prosecuting attorney tries to prove that the defendant is guilty (Alternative hypothesis—guilty). There are two possible conclusions that the jury can reach. First, the defendant is guilty (Reject the null hypothesis). Second, the defendant is not guilty (Fail to reject the null hypothesis). This is NOT the same thing as saying the defendant is innocent! In the first case, the prosecutor had enough evidence to reject the null hypothesis (innocent) and support the alternative claim (guilty). In the second case, the prosecutor did NOT have enough evidence to reject the null hypothesis (innocent) and support the alternative claim of guilty.

The Null and Alternative Hypotheses

There are three different pairs of null and alternative hypotheses:

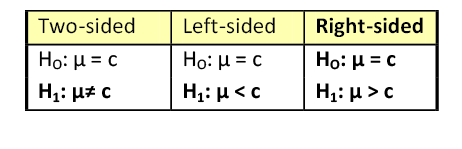
where c is some known value.

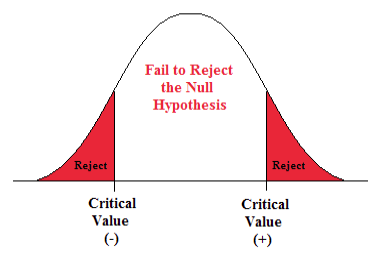
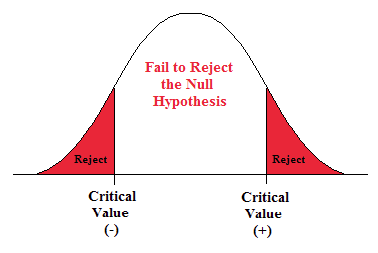
A Two-sided Test

This tests whether the population parameter is equal to, versus not equal to, some specific value.

H o : μ = 12 vs. H 1 : μ ≠ 12

The critical region is divided equally into the two tails and the critical values are ± values that define the rejection zones.

A forester studying diameter growth of red pine believes that the mean diameter growth will be different if a fertilization treatment is applied to the stand.

• H o : μ = 1.2 in./ year
• H 1 : μ ≠ 1.2 in./ year

This is a two-sided question, as the forester doesn’t state whether population mean diameter growth will increase or decrease.

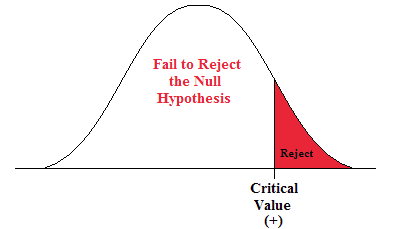
A Right-sided Test

This tests whether the population parameter is equal to, versus greater than, some specific value.

H o : μ = 12 vs. H 1 : μ > 12

The critical region is in the right tail and the critical value is a positive value that defines the rejection zone.

A biologist believes that there has been an increase in the mean number of lakes infected with milfoil, an invasive species, since the last study five years ago.

• H o : μ = 15 lakes
• H 1 : μ >15 lakes

This is a right-sided question, as the biologist believes that there has been an increase in population mean number of infected lakes.

A Left-sided Test

This tests whether the population parameter is equal to, versus less than, some specific value.

H o : μ = 12 vs. H 1 : μ < 12

The critical region is in the left tail and the critical value is a negative value that defines the rejection zone.

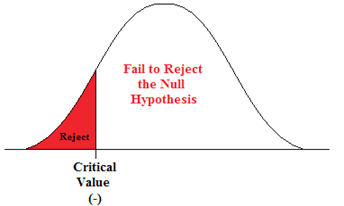
A scientist’s research indicates that there has been a change in the proportion of people who support certain environmental policies. He wants to test the claim that there has been a reduction in the proportion of people who support these policies.

• H o : p = 0.57
• H 1 : p < 0.57

This is a left-sided question, as the scientist believes that there has been a reduction in the true population proportion.

Statistically Significant

When the observed results (the sample statistics) are unlikely (a low probability) under the assumption that the null hypothesis is true, we say that the result is statistically significant, and we reject the null hypothesis. This result depends on the level of significance, the sample statistic, sample size, and whether it is a one- or two-sided alternative hypothesis.

Types of Errors

When testing, we arrive at a conclusion of rejecting the null hypothesis or failing to reject the null hypothesis. Such conclusions are sometimes correct and sometimes incorrect (even when we have followed all the correct procedures). We use incomplete sample data to reach a conclusion and there is always the possibility of reaching the wrong conclusion. There are four possible conclusions to reach from hypothesis testing. Of the four possible outcomes, two are correct and two are NOT correct.

A Type I error is when we reject the null hypothesis when it is true. The symbol α (alpha) is used to represent Type I errors. This is the same alpha we use as the level of significance. By setting alpha as low as reasonably possible, we try to control the Type I error through the level of significance.

A Type II error is when we fail to reject the null hypothesis when it is false. The symbol β (beta) is used to represent Type II errors.

In general, Type I errors are considered more serious. One step in the hypothesis test procedure involves selecting the significance level ( α ), which is the probability of rejecting the null hypothesis when it is correct. So the researcher can select the level of significance that minimizes Type I errors. However, there is a mathematical relationship between α, β , and n (sample size).

• As α increases, β decreases
• As α decreases, β increases
• As sample size increases (n), both α and β decrease

The natural inclination is to select the smallest possible value for α, thinking to minimize the possibility of causing a Type I error. Unfortunately, this forces an increase in Type II errors. By making the rejection zone too small, you may fail to reject the null hypothesis, when, in fact, it is false. Typically, we select the best sample size and level of significance, automatically setting β .

Power of the Test

A Type II error ( β ) is the probability of failing to reject a false null hypothesis. It follows that 1- β is the probability of rejecting a false null hypothesis. This probability is identified as the power of the test, and is often used to gauge the test’s effectiveness in recognizing that a null hypothesis is false.

The probability that at a fixed level α significance test will reject H 0 , when a particular alternative value of the parameter is true is called the power of the test.

Power is also directly linked to sample size. For example, suppose the null hypothesis is that the mean fish weight is 8.7 lb. Given sample data, a level of significance of 5%, and an alternative weight of 9.2 lb., we can compute the power of the test to reject μ = 8.7 lb. If we have a small sample size, the power will be low. However, increasing the sample size will increase the power of the test. Increasing the level of significance will also increase power. A 5% test of significance will have a greater chance of rejecting the null hypothesis than a 1% test because the strength of evidence required for the rejection is less. Decreasing the standard deviation has the same effect as increasing the sample size: there is more information about μ .

Hypothesis Test about the Population Mean ( μ ) when the Population Standard Deviation ( σ ) is Known

We are going to examine two equivalent ways to perform a hypothesis test: the classical approach and the p-value approach. The classical approach is based on standard deviations. This method compares the test statistic (Z-score) to a critical value (Z-score) from the standard normal table. If the test statistic falls in the rejection zone, you reject the null hypothesis. The p-value approach is based on area under the normal curve. This method compares the area associated with the test statistic to alpha ( α ), the level of significance (which is also area under the normal curve). If the p-value is less than alpha, you would reject the null hypothesis.

As a past student poetically said: If the p-value is a wee value, Reject Ho

Both methods must have:

• Data from a random sample.
• Verification of the assumption of normality.
• A null and alternative hypothesis.
• A criterion that determines if we reject or fail to reject the null hypothesis.
• A conclusion that answers the question.

There are four steps required for a hypothesis test:

• State the null and alternative hypotheses.
• State the level of significance and the critical value.
• Compute the test statistic.
• State a conclusion.

The Classical Method for Testing a Claim about the Population Mean ( μ ) when the Population Standard Deviation ( σ ) is Known

A forester studying diameter growth of red pine believes that the mean diameter growth will be different from the known mean growth of 1.35 inches/year if a fertilization treatment is applied to the stand. He conducts his experiment, collects data from a sample of 32 plots, and gets a sample mean diameter growth of 1.6 in./year. The population standard deviation for this stand is known to be 0.46 in./year. Does he have enough evidence to support his claim?

Step 1) State the null and alternative hypotheses.

• H o : μ = 1.35 in./year
• H 1 : μ ≠ 1.35 in./year

Step 2) State the level of significance and the critical value.

• We will choose a level of significance of 5% ( α = 0.05).
• For a two-sided question, we need a two-sided critical value – Z α /2 and + Z α /2 .
• The level of significance is divided by 2 (since we are only testing “not equal”). We must have two rejection zones that can deal with either a greater than or less than outcome (to the right (+) or to the left (-)).
• We need to find the Z-score associated with the area of 0.025. The red areas are equal to α /2 = 0.05/2 = 0.025 or 2.5% of the area under the normal curve.
• Go into the body of values and find the negative Z-score associated with the area 0.025.

• The negative critical value is -1.96. Since the curve is symmetric, we know that the positive critical value is 1.96.
• ±1.96 are the critical values. These values set up the rejection zone. If the test statistic falls within these red rejection zones, we reject the null hypothesis.

Step 3) Compute the test statistic.

• The test statistic is the number of standard deviations the sample mean is from the known mean. It is also a Z-score, just like the critical value.

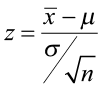
• For this problem, the test statistic is

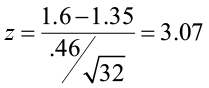
Step 4) State a conclusion.

• Compare the test statistic to the critical value. If the test statistic falls into the rejection zones, reject the null hypothesis. In other words, if the test statistic is greater than +1.96 or less than -1.96, reject the null hypothesis.

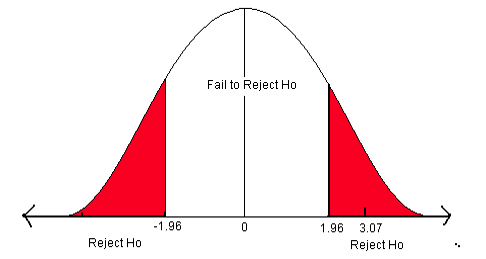
In this problem, the test statistic falls in the red rejection zone. The test statistic of 3.07 is greater than the critical value of 1.96.We will reject the null hypothesis. We have enough evidence to support the claim that the mean diameter growth is different from (not equal to) 1.35 in./year.

A researcher believes that there has been an increase in the average farm size in his state since the last study five years ago. The previous study reported a mean size of 450 acres with a population standard deviation ( σ ) of 167 acres. He samples 45 farms and gets a sample mean of 485.8 acres. Is there enough information to support his claim?

• H o : μ = 450 acres
• H 1 : μ >450 acres
• For a one-sided question, we need a one-sided positive critical value Z α .
• The level of significance is all in the right side (the rejection zone is just on the right side).
• We need to find the Z-score associated with the 5% area in the right tail.

• Go into the body of values in the standard normal table and find the Z-score that separates the lower 95% from the upper 5%.
• The critical value is 1.645. This value sets up the rejection zone.

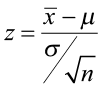
• Compare the test statistic to the critical value.

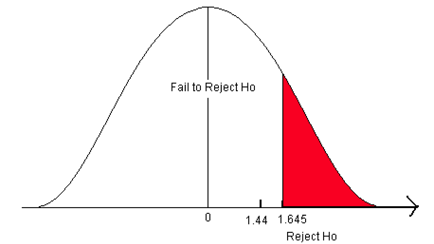
• The test statistic does not fall in the rejection zone. It is less than the critical value.

We fail to reject the null hypothesis. We do not have enough evidence to support the claim that the mean farm size has increased from 450 acres.

A researcher believes that there has been a reduction in the mean number of hours that college students spend preparing for final exams. A national study stated that students at a 4-year college spend an average of 23 hours preparing for 5 final exams each semester with a population standard deviation of 7.3 hours. The researcher sampled 227 students and found a sample mean study time of 19.6 hours. Does this indicate that the average study time for final exams has decreased? Use a 1% level of significance to test this claim.

• H o : μ = 23 hours
• H 1 : μ < 23 hours
• This is a left-sided test so alpha (0.01) is all in the left tail.

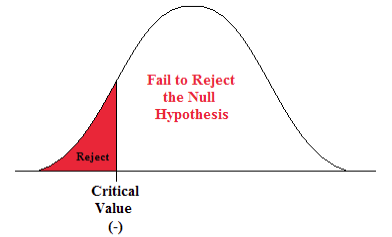
• Go into the body of values in the standard normal table and find the Z-score that defines the lower 1% of the area.
• The critical value is -2.33. This value sets up the rejection zone.

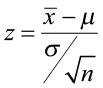
• The test statistic falls in the rejection zone. The test statistic of -7.02 is less than the critical value of -2.33.

We reject the null hypothesis. We have sufficient evidence to support the claim that the mean final exam study time has decreased below 23 hours.

Testing a Hypothesis using P-values

The p-value is the probability of observing our sample mean given that the null hypothesis is true. It is the area under the curve to the left or right of the test statistic. If the probability of observing such a sample mean is very small (less than the level of significance), we would reject the null hypothesis. Computations for the p-value depend on whether it is a one- or two-sided test.

Steps for a hypothesis test using p-values:

• State the level of significance.
• Compute the test statistic and find the area associated with it (this is the p-value).
• Compare the p-value to alpha ( α ) and state a conclusion.

Instead of comparing Z-score test statistic to Z-score critical value, as in the classical method, we compare area of the test statistic to area of the level of significance.

The Decision Rule: If the p-value is less than alpha, we reject the null hypothesis

Computing P-values

If it is a two-sided test (the alternative claim is ≠), the p-value is equal to two times the probability of the absolute value of the test statistic. If the test is a left-sided test (the alternative claim is “<”), then the p-value is equal to the area to the left of the test statistic. If the test is a right-sided test (the alternative claim is “>”), then the p-value is equal to the area to the right of the test statistic.

Let’s look at Example 6 again.

A forester studying diameter growth of red pine believes that the mean diameter growth will be different from the known mean growth of 1.35 in./year if a fertilization treatment is applied to the stand. He conducts his experiment, collects data from a sample of 32 plots, and gets a sample mean diameter growth of 1.6 in./year. The population standard deviation for this stand is known to be 0.46 in./year. Does he have enough evidence to support his claim?

Step 2) State the level of significance.

• For this problem, the test statistic is:

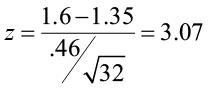
The p-value is two times the area of the absolute value of the test statistic (because the alternative claim is “not equal”).

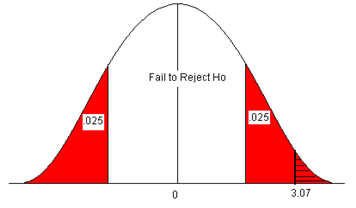
• Look up the area for the Z-score 3.07 in the standard normal table. The area (probability) is equal to 1 – 0.9989 = 0.0011.
• Multiply this by 2 to get the p-value = 2 * 0.0011 = 0.0022.

Step 4) Compare the p-value to alpha and state a conclusion.

• Use the Decision Rule (if the p-value is less than α , reject H 0 ).
• In this problem, the p-value (0.0022) is less than alpha (0.05).
• We reject the H 0 . We have enough evidence to support the claim that the mean diameter growth is different from 1.35 inches/year.

Let’s look at Example 7 again.

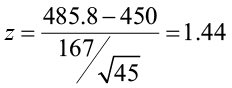
The p-value is the area to the right of the Z-score 1.44 (the hatched area).

• This is equal to 1 – 0.9251 = 0.0749.
• The p-value is 0.0749.

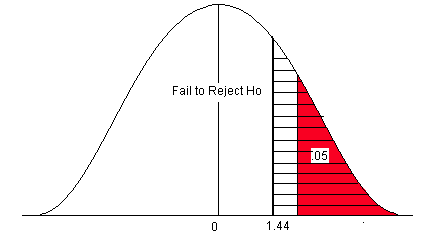
• Use the Decision Rule.
• In this problem, the p-value (0.0749) is greater than alpha (0.05), so we Fail to Reject the H 0 .
• The area of the test statistic is greater than the area of alpha ( α ).

We fail to reject the null hypothesis. We do not have enough evidence to support the claim that the mean farm size has increased.

Let’s look at Example 8 again.

• H 0 : μ = 23 hours

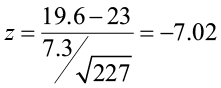
The p-value is the area to the left of the test statistic (the little black area to the left of -7.02). The Z-score of -7.02 is not on the standard normal table. The smallest probability on the table is 0.0002. We know that the area for the Z-score -7.02 is smaller than this area (probability). Therefore, the p-value is <0.0002.

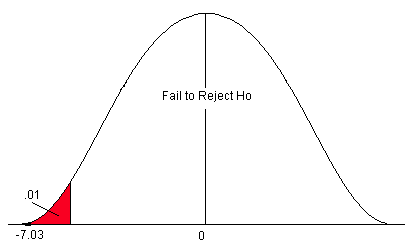
• In this problem, the p-value (p<0.0002) is less than alpha (0.01), so we Reject the H 0 .
• The area of the test statistic is much less than the area of alpha ( α ).

We reject the null hypothesis. We have enough evidence to support the claim that the mean final exam study time has decreased below 23 hours.

Both the classical method and p-value method for testing a hypothesis will arrive at the same conclusion. In the classical method, the critical Z-score is the number on the z-axis that defines the level of significance ( α ). The test statistic converts the sample mean to units of standard deviation (a Z-score). If the test statistic falls in the rejection zone defined by the critical value, we will reject the null hypothesis. In this approach, two Z-scores, which are numbers on the z-axis, are compared. In the p-value approach, the p-value is the area associated with the test statistic. In this method, we compare α (which is also area under the curve) to the p-value. If the p-value is less than α , we reject the null hypothesis. The p-value is the probability of observing such a sample mean when the null hypothesis is true. If the probability is too small (less than the level of significance), then we believe we have enough statistical evidence to reject the null hypothesis and support the alternative claim.

Software Solutions

(referring to Ex. 8)

One-Sample Z

Excel does not offer 1-sample hypothesis testing.

Hypothesis Test about the Population Mean ( μ ) when the Population Standard Deviation ( σ ) is Unknown

Frequently, the population standard deviation (σ) is not known. We can estimate the population standard deviation (σ) with the sample standard deviation (s). However, the test statistic will no longer follow the standard normal distribution. We must rely on the student’s t-distribution with n-1 degrees of freedom. Because we use the sample standard deviation (s), the test statistic will change from a Z-score to a t-score.

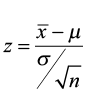
Steps for a hypothesis test are the same that we covered in Section 2.

Just as with the hypothesis test from the previous section, the data for this test must be from a random sample and requires either that the population from which the sample was drawn be normal or that the sample size is sufficiently large (n≥30). A t-test is robust, so small departures from normality will not adversely affect the results of the test. That being said, if the sample size is smaller than 30, it is always good to verify the assumption of normality through a normal probability plot.

We will still have the same three pairs of null and alternative hypotheses and we can still use either the classical approach or the p-value approach.

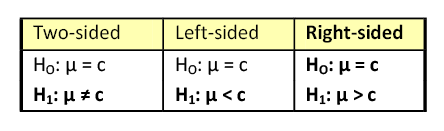
Selecting the correct critical value from the student’s t-distribution table depends on three factors: the type of test (one-sided or two-sided alternative hypothesis), the sample size, and the level of significance.

For a two-sided test (“not equal” alternative hypothesis), the critical value (t α /2 ), is determined by alpha ( α ), the level of significance, divided by two, to deal with the possibility that the result could be less than OR greater than the known value.

• If your level of significance was 0.05, you would use the 0.025 column to find the correct critical value (0.05/2 = 0.025).
• If your level of significance was 0.01, you would use the 0.005 column to find the correct critical value (0.01/2 = 0.005).

For a one-sided test (“a less than” or “greater than” alternative hypothesis), the critical value (t α ) , is determined by alpha ( α ), the level of significance, being all in the one side.

• If your level of significance was 0.05, you would use the 0.05 column to find the correct critical value for either a left or right-side question. If you are asking a “less than” (left-sided question, your critical value will be negative. If you are asking a “greater than” (right-sided question), your critical value will be positive.

Find the critical value you would use to test the claim that μ ≠ 112 with a sample size of 18 and a 5% level of significance.

In this case, the critical value (t α /2 ) would be 2.110. This is a two-sided question (≠) so you would divide alpha by 2 (0.05/2 = 0.025) and go down the 0.025 column to 17 degrees of freedom.

What would the critical value be if you wanted to test that μ < 112 for the same data?

In this case, the critical value would be 1.740. This is a one-sided question (<) so alpha would be divided by 1 (0.05/1 = 0.05). You would go down the 0.05 column with 17 degrees of freedom to get the correct critical value.

In 2005, the mean pH level of rain in a county in northern New York was 5.41. A biologist believes that the rain acidity has changed. He takes a random sample of 11 rain dates in 2010 and obtains the following data. Use a 1% level of significance to test his claim.

4.70, 5.63, 5.02, 5.78, 4.99, 5.91, 5.76, 5.54, 5.25, 5.18, 5.01

The sample size is small and we don’t know anything about the distribution of the population, so we examine a normal probability plot. The distribution looks normal so we will continue with our test.

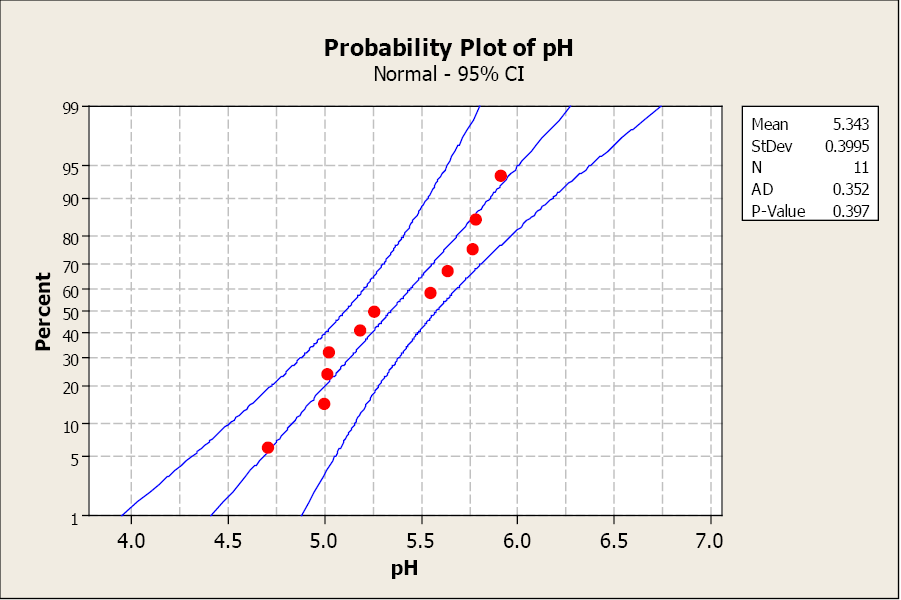
The sample mean is 5.343 with a sample standard deviation of 0.397.

• H o : μ = 5.41
• H 1 : μ ≠ 5.41
• This is a two-sided question so alpha is divided by two.

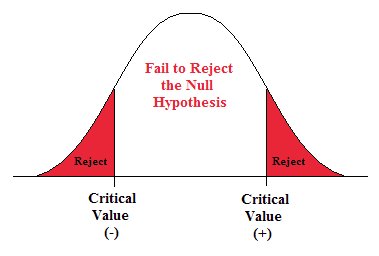
• t α /2 is found by going down the 0.005 column with 14 degrees of freedom.
• t α /2 = ±3.169.
• The test statistic is a t-score.

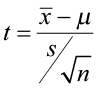
• The test statistic does not fall in the rejection zone.

We will fail to reject the null hypothesis. We do not have enough evidence to support the claim that the mean rain pH has changed.

A One-sided Test

Cadmium, a heavy metal, is toxic to animals. Mushrooms, however, are able to absorb and accumulate cadmium at high concentrations. The government has set safety limits for cadmium in dry vegetables at 0.5 ppm. Biologists believe that the mean level of cadmium in mushrooms growing near strip mines is greater than the recommended limit of 0.5 ppm, negatively impacting the animals that live in this ecosystem. A random sample of 51 mushrooms gave a sample mean of 0.59 ppm with a sample standard deviation of 0.29 ppm. Use a 5% level of significance to test the claim that the mean cadmium level is greater than the acceptable limit of 0.5 ppm.

The sample size is greater than 30 so we are assured of a normal distribution of the means.

• H o : μ = 0.5 ppm
• H 1 : μ > 0.5 ppm
• This is a right-sided question so alpha is all in the right tail.

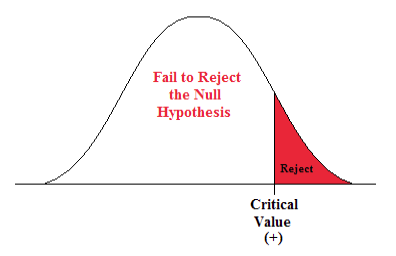
• t α is found by going down the 0.05 column with 50 degrees of freedom.
• t α = 1.676

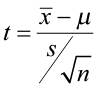
Step 4) State a Conclusion.

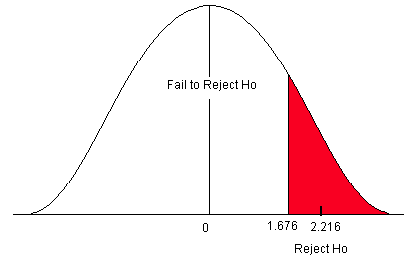
The test statistic falls in the rejection zone. We will reject the null hypothesis. We have enough evidence to support the claim that the mean cadmium level is greater than the acceptable safe limit.

BUT, what happens if the significance level changes to 1%?

The critical value is now found by going down the 0.01 column with 50 degrees of freedom. The critical value is 2.403. The test statistic is now LESS THAN the critical value. The test statistic does not fall in the rejection zone. The conclusion will change. We do NOT have enough evidence to support the claim that the mean cadmium level is greater than the acceptable safe limit of 0.5 ppm.

The level of significance is the probability that you, as the researcher, set to decide if there is enough statistical evidence to support the alternative claim. It should be set before the experiment begins.

P-value Approach

We can also use the p-value approach for a hypothesis test about the mean when the population standard deviation ( σ ) is unknown. However, when using a student’s t-table, we can only estimate the range of the p-value, not a specific value as when using the standard normal table. The student’s t-table has area (probability) across the top row in the table, with t-scores in the body of the table.

• To find the p-value (the area associated with the test statistic), you would go to the row with the number of degrees of freedom.
• Go across that row until you find the two values that your test statistic is between, then go up those columns to find the estimated range for the p-value.

Estimating P-value from a Student’s T-table

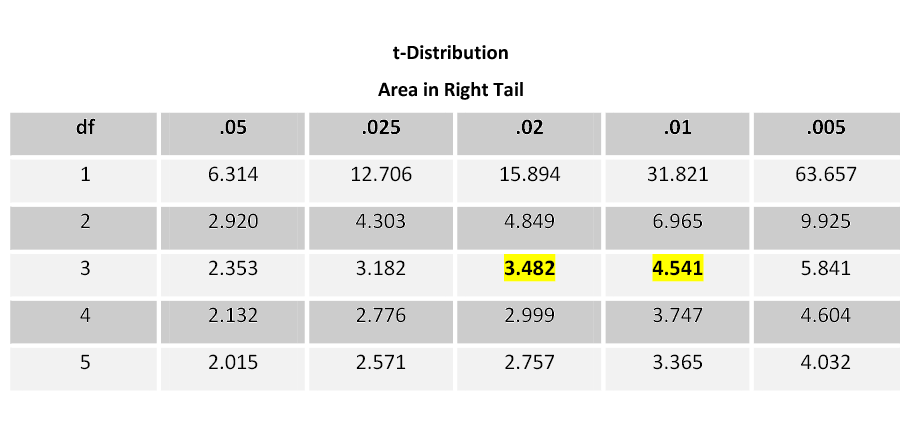
If your test statistic is 3.789 with 3 degrees of freedom, you would go across the 3 df row. The value 3.789 falls between the values 3.482 and 4.541 in that row. Therefore, the p-value is between 0.02 and 0.01. The p-value will be greater than 0.01 but less than 0.02 (0.01<p<0.02).

If your level of significance is 5%, you would reject the null hypothesis as the p-value (0.01-0.02) is less than alpha ( α ) of 0.05.

If your level of significance is 1%, you would fail to reject the null hypothesis as the p-value (0.01-0.02) is greater than alpha ( α ) of 0.01.

Software packages typically output p-values. It is easy to use the Decision Rule to answer your research question by the p-value method.

(referring to Ex. 12)

One-Sample T

Test of mu = 0.5 vs. > 0.5

Additional example: www.youtube.com/watch?v=WwdSjO4VUsg .

Hypothesis Test for a Population Proportion ( p )

Frequently, the parameter we are testing is the population proportion.

• We are studying the proportion of trees with cavities for wildlife habitat.
• We need to know if the proportion of people who support green building materials has changed.
• Has the proportion of wolves that died last year in Yellowstone increased from the year before?

Recall that the best point estimate of p , the population proportion, is given by

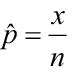
when np (1 – p )≥10. We can use both the classical approach and the p-value approach for testing.

The steps for a hypothesis test are the same that we covered in Section 2.

The test statistic follows the standard normal distribution. Notice that the standard error (the denominator) uses p instead of p̂ , which was used when constructing a confidence interval about the population proportion. In a hypothesis test, the null hypothesis is assumed to be true, so the known proportion is used.

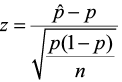
• The critical value comes from the standard normal table, just as in Section 2. We will still use the same three pairs of null and alternative hypotheses as we used in the previous sections, but the parameter is now p instead of μ :

• For a two-sided test, alpha will be divided by 2 giving a ± Z α /2 critical value.
• For a left-sided test, alpha will be all in the left tail giving a – Z α critical value.
• For a right-sided test, alpha will be all in the right tail giving a Z α critical value.

A botanist has produced a new variety of hybrid soy plant that is better able to withstand drought than other varieties. The botanist knows the seed germination for the parent plants is 75%, but does not know the seed germination for the new hybrid. He tests the claim that it is different from the parent plants. To test this claim, 450 seeds from the hybrid plant are tested and 321 have germinated. Use a 5% level of significance to test this claim that the germination rate is different from 75%.

• H o : p = 0.75
• H 1 : p ≠ 0.75

This is a two-sided question so alpha is divided by 2.

• Alpha is 0.05 so the critical values are ± Z α /2 = ± Z .025 .
• Look on the negative side of the standard normal table, in the body of values for 0.025.
• The critical values are ± 1.96.

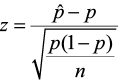
The test statistic does not fall in the rejection zone. We fail to reject the null hypothesis. We do not have enough evidence to support the claim that the germination rate of the hybrid plant is different from the parent plants.

Let’s answer this question using the p-value approach. Remember, for a two-sided alternative hypothesis (“not equal”), the p-value is two times the area of the test statistic. The test statistic is -1.81 and we want to find the area to the left of -1.81 from the standard normal table.

• On the negative page, find the Z-score -1.81. Find the area associated with this Z-score.
• The area = 0.0351.
• This is a two-sided test so multiply the area times 2 to get the p-value = 0.0351 x 2 = 0.0702.

Now compare the p-value to alpha. The Decision Rule states that if the p-value is less than alpha, reject the H 0 . In this case, the p-value (0.0702) is greater than alpha (0.05) so we will fail to reject H 0 . We do not have enough evidence to support the claim that the germination rate of the hybrid plant is different from the parent plants.

You are a biologist studying the wildlife habitat in the Monongahela National Forest. Cavities in older trees provide excellent habitat for a variety of birds and small mammals. A study five years ago stated that 32% of the trees in this forest had suitable cavities for this type of wildlife. You believe that the proportion of cavity trees has increased. You sample 196 trees and find that 79 trees have cavities. Does this evidence support your claim that there has been an increase in the proportion of cavity trees?

Use a 10% level of significance to test this claim.

• H o : p = 0.32
• H 1 : p > 0.32

This is a one-sided question so alpha is divided by 1.

• Alpha is 0.10 so the critical value is Z α = Z .10
• Look on the positive side of the standard normal table, in the body of values for 0.90.
• The critical value is 1.28.

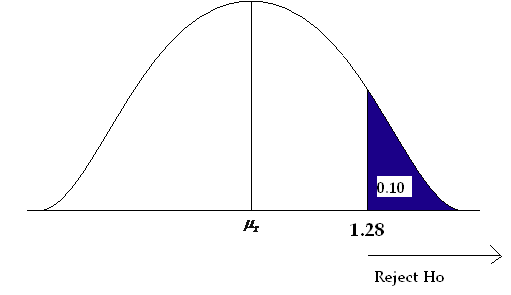
• The test statistic is the number of standard deviations the sample proportion is from the known proportion. It is also a Z-score, just like the critical value.

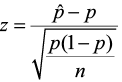
The test statistic is larger than the critical value (it falls in the rejection zone). We will reject the null hypothesis. We have enough evidence to support the claim that there has been an increase in the proportion of cavity trees.

Now use the p-value approach to answer the question. This is a right-sided question (“greater than”), so the p-value is equal to the area to the right of the test statistic. Go to the positive side of the standard normal table and find the area associated with the Z-score of 2.49. The area is 0.9936. Remember that this table is cumulative from the left. To find the area to the right of 2.49, we subtract from one.

p-value = (1 – 0.9936) = 0.0064

The p-value is less than the level of significance (0.10), so we reject the null hypothesis. We have enough evidence to support the claim that the proportion of cavity trees has increased.

(referring to Ex. 15)

Test and CI for One Proportion

Test of p = 0.32 vs. p > 0.32

Hypothesis Test about a Variance

When people think of statistical inference, they usually think of inferences involving population means or proportions. However, the particular population parameter needed to answer an experimenter’s practical questions varies from one situation to another, and sometimes a population’s variability is more important than its mean. Thus, product quality is often defined in terms of low variability.

Sample variance S 2 can be used for inferences concerning a population variance σ 2 . For a random sample of n measurements drawn from a normal population with mean μ and variance σ 2 , the value S 2 provides a point estimate for σ 2 . In addition, the quantity ( n – 1) S 2 / σ 2 follows a Chi-square ( χ 2 ) distribution, with df = n – 1.

The properties of Chi-square ( χ 2 ) distribution are:

• Unlike Z and t distributions, the values in a chi-square distribution are all positive.
• The chi-square distribution is asymmetric, unlike the Z and t distributions.
• There are many chi-square distributions. We obtain a particular one by specifying the degrees of freedom (df = n – 1) associated with the sample variances S 2 .

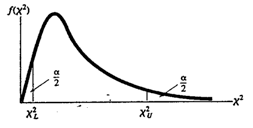
One-sample χ 2 test for testing the hypotheses:

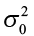
Alternative hypothesis:

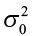
where the χ 2 critical value in the rejection region is based on degrees of freedom df = n – 1 and a specified significance level of α .

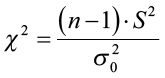
As with previous sections, if the test statistic falls in the rejection zone set by the critical value, you will reject the null hypothesis.

A forester wants to control a dense understory of striped maple that is interfering with desirable hardwood regeneration using a mist blower to apply an herbicide treatment. She wants to make sure that treatment has a consistent application rate, in other words, low variability not exceeding 0.25 gal./acre (0.06 gal. 2 ). She collects sample data (n = 11) on this type of mist blower and gets a sample variance of 0.064 gal. 2 Using a 5% level of significance, test the claim that the variance is significantly greater than 0.06 gal. 2

H 0 : σ 2 = 0.06

H 1 : σ 2 >0.06

The critical value is 18.307. Any test statistic greater than this value will cause you to reject the null hypothesis.

The test statistic is

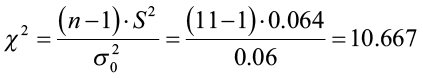
We fail to reject the null hypothesis. The forester does NOT have enough evidence to support the claim that the variance is greater than 0.06 gal. 2 You can also estimate the p-value using the same method as for the student t-table. Go across the row for degrees of freedom until you find the two values that your test statistic falls between. In this case going across the row 10, the two table values are 4.865 and 15.987. Now go up those two columns to the top row to estimate the p-value (0.1-0.9). The p-value is greater than 0.1 and less than 0.9. Both are greater than the level of significance (0.05) causing us to fail to reject the null hypothesis.

(referring to Ex. 16)

Test and CI for One Variance

The chi-square method is only for the normal distribution.

Excel does not offer 1-sample χ 2 testing.

Putting it all Together Using the Classical Method

To test a claim about μ when σ is known.

• Write the null and alternative hypotheses.
• State the level of significance and get the critical value from the standard normal table.

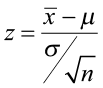
• Compare the test statistic to the critical value (Z-score) and write the conclusion.

To Test a Claim about μ When σ is Unknown

• State the level of significance and get the critical value from the student’s t-table with n-1 degrees of freedom.

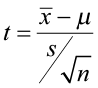
• Compare the test statistic to the critical value (t-score) and write the conclusion.

To Test a Claim about p

• State the level of significance and get the critical value from the standard normal distribution.

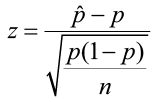
To Test a Claim about Variance

• State the level of significance and get the critical value from the chi-square table using n-1 degrees of freedom.

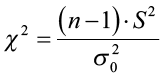
• Compare the test statistic to the critical value and write the conclusion.

Natural Resources Biometrics Copyright © 2014 by Diane Kiernan is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

• Machine Learning Tutorial
• Data Analysis Tutorial
• Python - Data visualization tutorial
• Machine Learning Projects
• Machine Learning Interview Questions
• Machine Learning Mathematics
• Deep Learning Tutorial
• Deep Learning Project
• Deep Learning Interview Questions
• Computer Vision Tutorial
• Computer Vision Projects
• NLP Project
• NLP Interview Questions
• Statistics with Python
• 100 Days of Machine Learning
• Data Analysis with Python

Introduction to Data Analysis

• What is Data Analysis?
• Data Analytics and its type
• How to Install Numpy on Windows?
• How to Install Pandas in Python?
• How to Install Matplotlib on python?
• How to Install Python Tensorflow in Windows?

Data Analysis Libraries

• Pandas Tutorial
• NumPy Tutorial - Python Library
• Data Analysis with SciPy
• Introduction to TensorFlow

Data Visulization Libraries

• Matplotlib Tutorial
• Python Seaborn Tutorial
• Plotly tutorial
• Introduction to Bokeh in Python

Exploratory Data Analysis (EDA)

• Univariate, Bivariate and Multivariate data and its analysis
• Measures of Central Tendency in Statistics
• Measures of spread - Range, Variance, and Standard Deviation
• Interquartile Range and Quartile Deviation using NumPy and SciPy
• Anova Formula
• Skewness of Statistical Data
• How to Calculate Skewness and Kurtosis in Python?
• Difference Between Skewness and Kurtosis
• Histogram | Meaning, Example, Types and Steps to Draw
• Interpretations of Histogram
• Quantile Quantile plots
• What is Univariate, Bivariate & Multivariate Analysis in Data Visualisation?
• Using pandas crosstab to create a bar plot
• Exploring Correlation in Python
• Mathematics | Covariance and Correlation
• Factor Analysis | Data Analysis
• Data Mining - Cluster Analysis
• MANOVA Test in R Programming
• Python - Central Limit Theorem
• Probability Distribution Function
• Probability Density Estimation & Maximum Likelihood Estimation
• Exponential Distribution in R Programming - dexp(), pexp(), qexp(), and rexp() Functions
• Mathematics | Probability Distributions Set 4 (Binomial Distribution)
• Poisson Distribution - Definition, Formula, Table and Examples
• P-Value: Comprehensive Guide to Understand, Apply, and Interpret
• Z-Score in Statistics
• How to Calculate Point Estimates in R?
• Confidence Interval
• Chi-square test in Machine Learning

Understanding Hypothesis Testing

Data preprocessing.

• ML | Data Preprocessing in Python
• ML | Overview of Data Cleaning
• ML | Handling Missing Values
• Detect and Remove the Outliers using Python

Data Transformation

• Data Normalization Machine Learning
• Sampling distribution Using Python

Time Series Data Analysis

• Data Mining - Time-Series, Symbolic and Biological Sequences Data
• Basic DateTime Operations in Python
• Time Series Analysis & Visualization in Python
• How to deal with missing values in a Timeseries in Python?
• How to calculate MOVING AVERAGE in a Pandas DataFrame?
• What is a trend in time series?
• How to Perform an Augmented Dickey-Fuller Test in R
• AutoCorrelation

Case Studies and Projects

• Top 8 Free Dataset Sources to Use for Data Science Projects
• Step by Step Predictive Analysis - Machine Learning
• 6 Tips for Creating Effective Data Visualizations

Hypothesis testing involves formulating assumptions about population parameters based on sample statistics and rigorously evaluating these assumptions against empirical evidence. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.

What is Hypothesis Testing?

Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. 

Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.

Defining Hypotheses

Key Terms of Hypothesis Testing

• P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
• Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
• Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
• Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.

Why do we use Hypothesis Testing?

Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing. 

One-Tailed and Two-Tailed Test

One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.

One-Tailed Test

There are two types of one-tailed test:

Two-Tailed Test

A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.

What are Type 1 and Type 2 errors in Hypothesis Testing?

In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.

How does Hypothesis Testing work?

Step 1: define null and alternative hypothesis.

We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.

Step 2 – Choose significance level

Step 3 – Collect and Analyze data.

Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.

Step 4-Calculate Test Statistic

The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.

There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.

• Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
• t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
• Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
• F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.

We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.

T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

Step 5 – Comparing Test Statistic:

In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.

Method A: Using Crtical values

Comparing the test statistic and tabulated critical value we have,

• If Test Statistic>Critical Value: Reject the null hypothesis.
• If Test Statistic≤Critical Value: Fail to reject the null hypothesis.

Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Method B: Using P-values

We can also come to an conclusion using the p-value,

Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Step 7- Interpret the Results

At last, we can conclude our experiment using method A or B.

Calculating test statistic

To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .

1. Z-statistics:

When population means and standard deviations are known.

• μ represents the population mean, 
• σ is the standard deviation
• and n is the size of the sample.

2. T-Statistics

T test is used when n<30,

t-statistic calculation is given by:

• t = t-score,
• x̄ = sample mean
• μ = population mean,
• s = standard deviation of the sample,
• n = sample size

3. Chi-Square Test

Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

• i,j are the rows and columns index respectively.

Real life Hypothesis Testing example

Let’s examine hypothesis testing using two real life situations,

Case A: D oes a New Drug Affect Blood Pressure?

Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.

• Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
• After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114

Step 1 : Define the Hypothesis

• Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
• Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.

Step 2: Define the Significance level

Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.

If the evidence suggests less than a 5% chance of observing the results due to random variation.

Step 3 : Compute the test statistic

Using paired T-test analyze the data to obtain a test statistic and a p-value.

The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.

t = m/(s/√n)

• m  = mean of the difference i.e X after, X before
• s  = standard deviation of the difference (d) i.e d i ​= X after, i ​− X before,
• n  = sample size,

then, m= -3.9, s= 1.8 and n= 10

we, calculate the , T-statistic = -9 based on the formula for paired t test

Step 4: Find the p-value

The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.

thus, p-value = 8.538051223166285e-06

Step 5: Result

• If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
• If the p-value is greater than 0.05, they fail to reject the null hypothesis.

Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

Python Implementation of Hypothesis Testing

Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.

Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.

We will implement our first real life problem via python,

In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05. 

• The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
• The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.

Case B : Cholesterol level in a population

Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.

Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.

Populations Mean = 200

Population Standard Deviation (σ): 5 mg/dL(given for this problem)

Step 1: Define the Hypothesis

• Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
• Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.

As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.

Step 4: Result

Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL

Limitations of Hypothesis Testing

• Although a useful technique, hypothesis testing does not offer a comprehensive grasp of the topic being studied. Without fully reflecting the intricacy or whole context of the phenomena, it concentrates on certain hypotheses and statistical significance.
• The accuracy of hypothesis testing results is contingent on the quality of available data and the appropriateness of statistical methods used. Inaccurate data or poorly formulated hypotheses can lead to incorrect conclusions.
• Relying solely on hypothesis testing may cause analysts to overlook significant patterns or relationships in the data that are not captured by the specific hypotheses being tested. This limitation underscores the importance of complimenting hypothesis testing with other analytical approaches.

Hypothesis testing stands as a cornerstone in statistical analysis, enabling data scientists to navigate uncertainties and draw credible inferences from sample data. By systematically defining null and alternative hypotheses, choosing significance levels, and leveraging statistical tests, researchers can assess the validity of their assumptions. The article also elucidates the critical distinction between Type I and Type II errors, providing a comprehensive understanding of the nuanced decision-making process inherent in hypothesis testing. The real-life example of testing a new drug’s effect on blood pressure using a paired T-test showcases the practical application of these principles, underscoring the importance of statistical rigor in data-driven decision-making.

Frequently Asked Questions (FAQs)

1. what are the 3 types of hypothesis test.

There are three types of hypothesis tests: right-tailed, left-tailed, and two-tailed. Right-tailed tests assess if a parameter is greater, left-tailed if lesser. Two-tailed tests check for non-directional differences, greater or lesser.

2.What are the 4 components of hypothesis testing?

Null Hypothesis ( ): No effect or difference exists. Alternative Hypothesis ( ): An effect or difference exists. Significance Level ( ): Risk of rejecting null hypothesis when it’s true (Type I error). Test Statistic: Numerical value representing observed evidence against null hypothesis.

3.What is hypothesis testing in ML?

Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.

4.What is the difference between Pytest and hypothesis in Python?

Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.

Please Login to comment...

Similar reads.

• data-science
• Data Science
• Machine Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Hypothesis Testing Approach (to Evaluation)

• Reference work entry
• Cite this reference work entry

• Shahal Rozenblatt 5  

288 Accesses

1 Altmetric

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

References and Readings

Goldberg, E. (2001). The executive brain: Frontal lobes and the civilized mind . New York: Oxford University Press.

Google Scholar  

Hale, J. B., & Fiorello, C. A. (2004). School neuropsychology: A practitioner’s handbook . New York: Guilford.

Lezak, M. D., Howieson, D. B., & Loring, D. W. (2004). Neuropsychological assessment , (4th ed.). New York: Oxford University Press.

Download references

Author information

Authors and affiliations.

Advanced Psychological Assessment, 50 Karl Avenue, Suite 104, 11787, P. C. Smithtown, NY, USA

Shahal Rozenblatt

You can also search for this author in PubMed   Google Scholar

Editor information

Editors and affiliations.

Physical Medicine and Rehabilitation, and Professor of Neurosurgery, and Psychiatry Virginia Commonwealth University – Medical Center Department of Physical Medicine and Rehabilitation, VCU, 980542, Richmond, Virginia, 23298-0542, USA

Jeffrey S. Kreutzer

Kessler Foundation Research Center, 1199 Pleasant Valley Way, West Orange, NJ, 07052, USA

John DeLuca

Professor of Physical Medicine and Rehabilitation, and Neurology and Neuroscience, University of Medicine and Dentistry of New Jersey – New Jersey Medical School, New Jersey, USA

Independent Practice, 564 M.O.B. East, 100 E. Lancaster Ave., Wynnewood, PA, 19096, USA

Bruce Caplan

Rights and permissions

Reprints and permissions

Copyright information

© 2011 Springer Science+Business Media, LLC

About this entry

Cite this entry.

Rozenblatt, S. (2011). Hypothesis Testing Approach (to Evaluation). In: Kreutzer, J.S., DeLuca, J., Caplan, B. (eds) Encyclopedia of Clinical Neuropsychology. Springer, New York, NY. https://doi.org/10.1007/978-0-387-79948-3_191

Download citation

DOI : https://doi.org/10.1007/978-0-387-79948-3_191

Publisher Name : Springer, New York, NY

Print ISBN : 978-0-387-79947-6

Online ISBN : 978-0-387-79948-3

eBook Packages : Behavioral Science

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3.1 hypothesis testing (critical value approach).

The critical value approach involves determining "likely" or "unlikely" by determining whether or not the observed test statistic is more extreme than would be expected if the null hypothesis were true. That is, it entails comparing the observed test statistic to some cutoff value, called the " critical value ." If the test statistic is more extreme than the critical value, then the null hypothesis is rejected in favor of the alternative hypothesis. If the test statistic is not as extreme as the critical value, then the null hypothesis is not rejected.

Specifically, the four steps involved in using the critical value approach to conducting any hypothesis test are:

• Specify the null and alternative hypotheses.
• Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic. To conduct the hypothesis test for the population mean μ , we use the t -statistic \(t^*=\frac{\bar{x}-\mu}{s/\sqrt{n}}\) which follows a t -distribution with n - 1 degrees of freedom.
• Determine the critical value by finding the value of the known distribution of the test statistic such that the probability of making a Type I error — which is denoted \(\alpha\) (greek letter "alpha") and is called the " significance level of the test " — is small (typically 0.01, 0.05, or 0.10).
• Compare the test statistic to the critical value. If the test statistic is more extreme in the direction of the alternative than the critical value, reject the null hypothesis in favor of the alternative hypothesis. If the test statistic is less extreme than the critical value, do not reject the null hypothesis.

Example S.3.1.1

Mean gpa section  .

In our example concerning the mean grade point average, suppose we take a random sample of n = 15 students majoring in mathematics. Since n = 15, our test statistic t * has n - 1 = 14 degrees of freedom. Also, suppose we set our significance level α at 0.05 so that we have only a 5% chance of making a Type I error.

Right-Tailed

The critical value for conducting the right-tailed test H 0 : μ = 3 versus H A : μ > 3 is the t -value, denoted t \(\alpha\) , n - 1 , such that the probability to the right of it is \(\alpha\). It can be shown using either statistical software or a t -table that the critical value t 0.05,14 is 1.7613. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ > 3 if the test statistic t * is greater than 1.7613. Visually, the rejection region is shaded red in the graph.

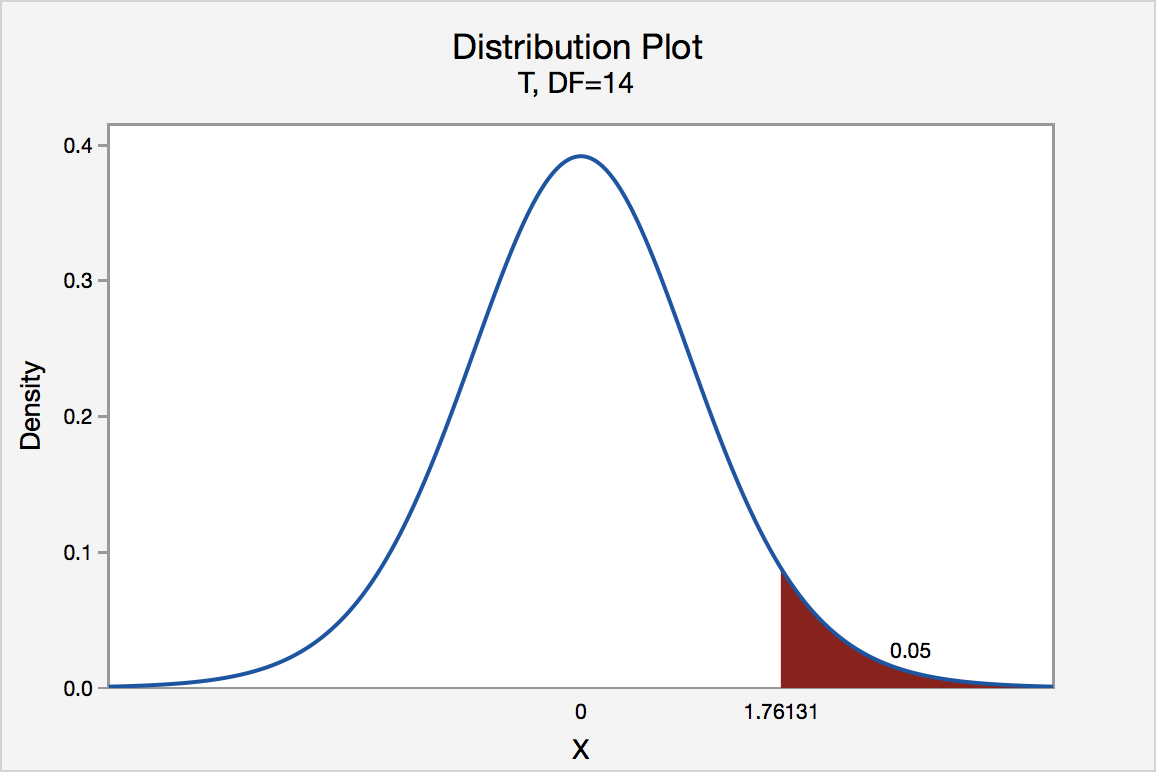
Left-Tailed

The critical value for conducting the left-tailed test H 0 : μ = 3 versus H A : μ < 3 is the t -value, denoted -t ( \(\alpha\) , n - 1) , such that the probability to the left of it is \(\alpha\). It can be shown using either statistical software or a t -table that the critical value -t 0.05,14 is -1.7613. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ < 3 if the test statistic t * is less than -1.7613. Visually, the rejection region is shaded red in the graph.

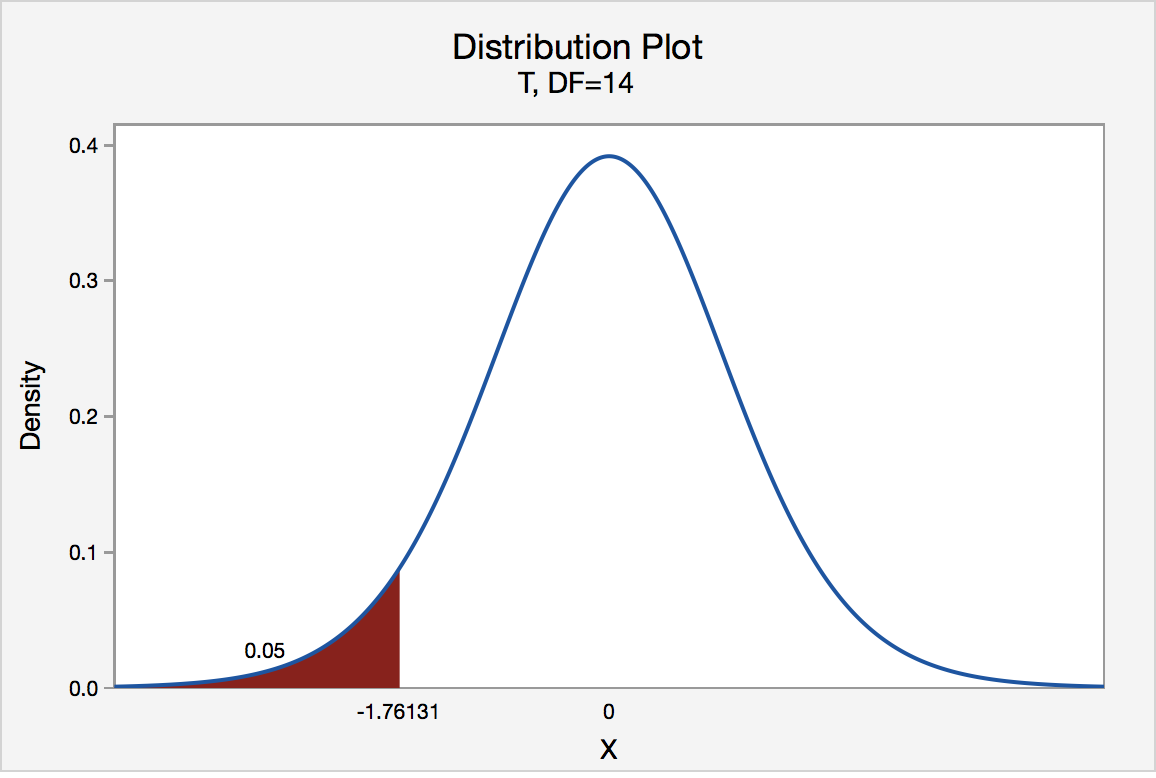
There are two critical values for the two-tailed test H 0 : μ = 3 versus H A : μ ≠ 3 — one for the left-tail denoted -t ( \(\alpha\) / 2, n - 1) and one for the right-tail denoted t ( \(\alpha\) / 2, n - 1) . The value - t ( \(\alpha\) /2, n - 1) is the t -value such that the probability to the left of it is \(\alpha\)/2, and the value t ( \(\alpha\) /2, n - 1) is the t -value such that the probability to the right of it is \(\alpha\)/2. It can be shown using either statistical software or a t -table that the critical value -t 0.025,14 is -2.1448 and the critical value t 0.025,14 is 2.1448. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ ≠ 3 if the test statistic t * is less than -2.1448 or greater than 2.1448. Visually, the rejection region is shaded red in the graph.

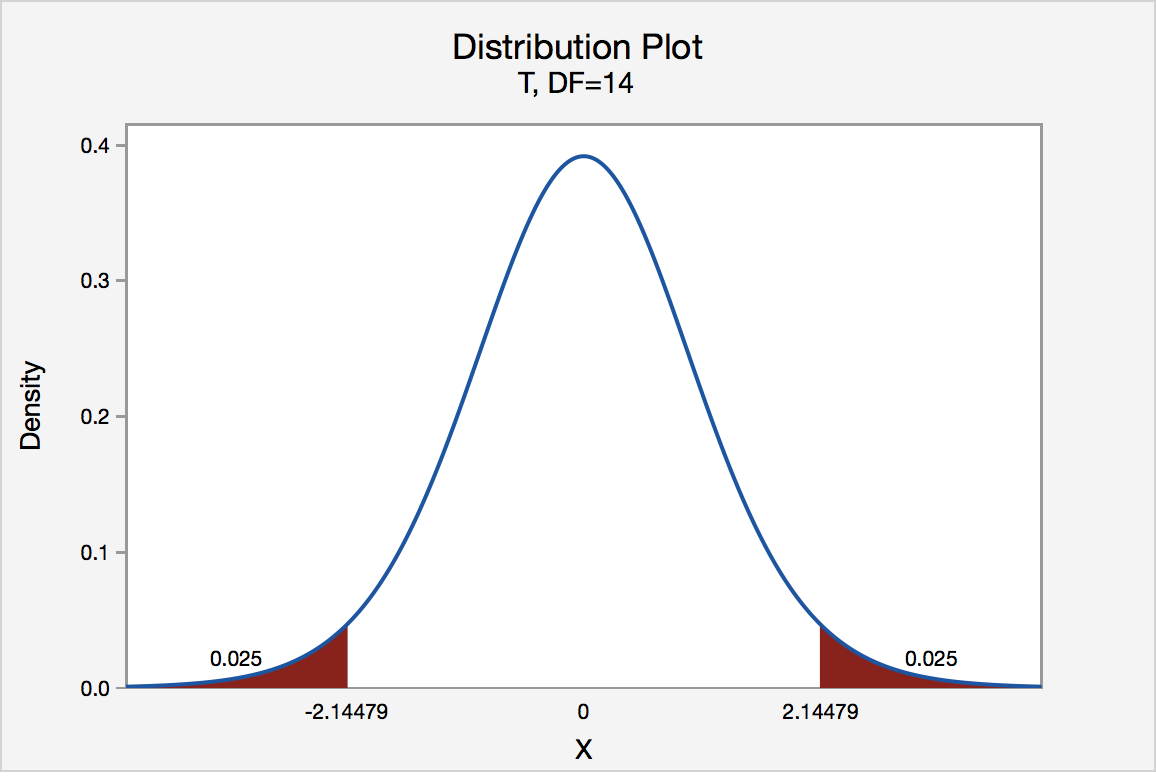
Click through the PLOS taxonomy to find articles in your field.

For more information about PLOS Subject Areas, click here .

Loading metrics

Open Access

Peer-reviewed

Research Article

User authentication system based on human exhaled breath physics

Roles Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing

Affiliation Department of Applied Mechanics and Biomedical Engineering, Indian Institute of Technology Madras, Chennai, Tamil Nadu, India

Roles Data curation, Formal analysis, Software, Visualization

Roles Conceptualization, Investigation, Methodology, Resources, Supervision, Writing – review & editing

* E-mail: [email protected]

Affiliation Department of Chemical Engineering, Indian Institute of Technology Madras, Chennai, Tamil Nadu, India

• Mukesh Karunanethy, 
• Rahul Tripathi, 
• Mahesh V. Panchagnula, 
• Raghunathan Rengaswamy

• Published: April 22, 2024
• https://doi.org/10.1371/journal.pone.0301971
• Reader Comments

This work, in a pioneering approach, attempts to build a biometric system that works purely based on the fluid mechanics governing exhaled breath. We test the hypothesis that the structure of turbulence in exhaled human breath can be exploited to build biometric algorithms. This work relies on the idea that the extrathoracic airway is unique for every individual, making the exhaled breath a biomarker. Methods including classical multi-dimensional hypothesis testing approach and machine learning models are employed in building user authentication algorithms, namely user confirmation and user identification. A user confirmation algorithm tries to verify whether a user is the person they claim to be. A user identification algorithm tries to identify a user’s identity with no prior information available. A dataset of exhaled breath time series samples from 94 human subjects was used to evaluate the performance of these algorithms. The user confirmation algorithms performed exceedingly well for the given dataset with over 97% true confirmation rate. The machine learning based algorithm achieved a good true confirmation rate, reiterating our understanding of why machine learning based algorithms typically outperform classical hypothesis test based algorithms. The user identification algorithm performs reasonably well with the provided dataset with over 50% of the users identified as being within two possible suspects. We show surprisingly unique turbulent signatures in the exhaled breath that have not been discovered before. In addition to discussions on a novel biometric system, we make arguments to utilise this idea as a tool to gain insights into the morphometric variation of extrathoracic airway across individuals. Such tools are expected to have future potential in the area of personalised medicines.

Citation: Karunanethy M, Tripathi R, Panchagnula MV, Rengaswamy R (2024) User authentication system based on human exhaled breath physics. PLoS ONE 19(4): e0301971. https://doi.org/10.1371/journal.pone.0301971

Editor: Sandip Varkey George, University of Aberdeen, UNITED KINGDOM

Received: September 14, 2023; Accepted: March 26, 2024; Published: April 22, 2024

Copyright: © 2024 Karunanethy et al. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Data Availability: All relevant data are available from the ‘Harvard Dataverse’ database (DOI: https://doi.org/10.7910/DVN/MKVJQT ).

Funding: The author(s) received no specific funding for this work.

Competing interests: The authors declare there is a patent application on the discussed technology filed at Indian Patent Office, under the title ‘Exhaled breath based user authentication and diagnosis’ (PATENT PENDING - 202241065024). This does not alter our adherence to PLoS ONE policies on sharing data and materials.

Introduction

Human exhaled breath is largely turbulent. During exhalation, air is forced out of the lung through trachea by the contracting diaphragm. To start with, the Reynolds number (a dimensionless quantity defined as the ratio of inertial to viscous forces within a fluid) associated with flow through trachea is sufficiently high, typically ranging from around 2300 for silent breathing to over 9000 for vigorous breathing indicating a highly turbulent flow [ 1 – 4 ]. In addition, as the air passes through the trachea, it interacts with the complex internal structures associated with the upper respiratory tract, leading to complexity in the flow [ 3 , 5 ]. The upper respiratory tract consists of the larynx, the pharynx, and the oral cavity. Owing to the complexity associated with the interaction between air that is already turbulent [ 3 , 4 ] with the upper respiratory tract, we hypothesize that the turbulent signatures in the exhaled air are unique and identifiable from person-to-person. A plausible way to test this hypothesis is to build a user authentication system that would answer the question of classifiability of a human subject purely based on the fluid dynamics of the exhaled breath, essentially serving the purpose of a biometric user authentication system. Such a system is a real-time system to verify a user’s identity using any measured feature pertaining to the user’s physiology or behaviour. Thus, authentication can be broadly seen as comprising two classes of methods: physiological biometrics (eg., fingerprints, iris scans, facial recognition, etc.) and behavioural biometrics (eg., gait analysis, voice ID, breathing gesture [ 6 ], etc.). There are two major modes of deployment of a user authentication/access system [ 7 ]: ( i ) user confirmation or verification , and ( ii ) user identification . In the confirmation mode, a user declares his or her identity, which is to be confirmed. In this case, the user’s biometric data is compared to a specific set of data of the same person obtained during an enrollment process. In the identification mode, a user does not disclose his or her identity. In that case, a user’s data is compared with all registered data in the database of bona fide users, and the user is identified. We will discuss algorithms for testing the two biometric modes in this manuscript and argue that exhaled breath contains sufficient information to implement both biometric modes.

Human exhaled breath has proven to be a non-invasive diagnostic tool for a spectrum of medical problems as well. [ 8 ] studied the diagnosis of malarial infection by analysing the breath composition, or “breathprint” which contains a series of volatile organic compounds (VOCs) produced by the P. falciparum -infected erythrocytes. They built a nearest mean binary classifier with leave-1-breath-sample-out cross-validation scheme to assign predictions. The European Respiratory Society (ERS) technical standard [ 9 ] reported that the fraction of nitric oxide in exhaled gas is a potential biomarker for lung diseases. [ 10 ] showed the potential of breath-based metabolomics (breathomics) in personalised medicine. Mass spectrometry is one of the main platforms used for data profiling in these techniques. In their study, [ 11 ] reported enhancements required in the analysis of single exhaled breath metabolomic data for the unique identification of patients with acute decompensated heart failure. [ 12 ] made attempts to develop a breath analyzer system to measure blood glucose levels and to classify diabetic/non-diabetic patients using a support vector machine (SVM) classifier based on acetone levels in breath measured using chemical sensors. [ 13 ] reviewed various breath sampling methods with a bibliometric study. [ 14 – 16 ] studied the potential advantages of breath tests as a non-invasive technique with potential biomarkers in disease diagnosis. The above efforts in the literature proving exhaled breath as a biomarker largely involve the analysis of its chemical composition by various techniques. In other words, these studies have shown that the compounds present in exhaled air produce a molecular signature. There exists no evidence in the literature of any attempt to develop an identifier purely based on the fluid dynamic aspects of the exhaled airflow.

Respiratory flow measurements are widely performed using spirometers and pneumotachographs. Inspirational flow patterns in humans were studied using measurements from a cycloergometer to theoretically estimate mechanical work during inhalation by [ 17 ]. [ 18 ] studied the human respiratory flow patterns using pneumotachographic flow measurements at the mouth. Hot wire anemometry (HWA) has been used by several researchers in the past for respiratory flow measurements. [ 19 ] demonstrated the application of HWA in respiratory flow measurements in small animals. [ 20 ] investigated the performance of a constant temperature hot wire anemometer (CT-HWA) system for respiratory gas flow rate measurements. The study demonstrated that a CT-HWA will meet the response requirements and be insensitive to changes in temperature and humidity that are frequently experienced in respiratory flows. In the research by [ 21 ] and later by [ 22 ], it was shown that CT-HWA can be used to measure fluid flow in the forced oscillations technique applied to the human respiratory system, as a substitute for the pneumotachograph. Other studies reporting the implementation of CT-HWA for measuring expiratory flow parameters are by [ 23 , 24 ]. [ 25 ] showed that CT-HWA can be used as a flow transducer for spirography. In conclusion, HWA is a robust tool for obtaining time-resolved turbulence signature measurements in flows. Most of the work in the literature has taken advantage of the HWA data for flow rate calculations, effectively using it only as an alternative for spirometry-based studies. We propose to use HWA measurements (the complete time series of instantaneous velocity data) of turbulence in human exhaled breath as input signals for the development of a biometric system.

Behavioural biometrics use a person’s gestures, such as gait patterns or breathing gestures. Recent work by [ 6 , 26 ] revealed the prospects of exploiting breathing acoustics for user authentication. They built a new behavioural biometric signature called BreathPrint based on audio features acquired from a microphone sensor in smartphones, wearables and other IoT devices. [ 6 ] deployed a conventional machine learning model based on the Gaussian mixture model (GMM), while [ 26 ] established the feasibility and performance evaluation of a Recurrent Neural Network (RNN)-based deep learning models. A novel WiFi-based breathing estimator UbiBreathe developed by [ 27 ] works as a respiratory monitoring system based on the received signal strength (RSS) data from a nearby WiFi-enabled device. A continuous user verification system was developed using this approach by [ 28 ] for round-the-clock user verification, built based on user-specific respiratory features derived based on waveform morphology analysis and fuzzy wavelet transformation. A deep learning-based scheme also detects the existence of spoofing attacks. [ 29 ] developed a speaker recognition system, BreathID based on breath biometrics. Breath during speech is considered trivial or a noise component. They showed that unique breath features can be formulated by a template matching technique for speaker recognition.

In summary, the use of HWA and, more broadly, breath turbulence measurements as a tool for biometric authentication has not been attempted in the literature. Conventional biometric systems such as voice, face, and fingerprint recognition have their own disadvantages. There is a need to develop more sophisticated biometric systems that could make use of internal physiological features of the human body. We attempt to build a novel user authentication system based on human exhaled breath, using the principles of multidimensional hypothesis testing and machine learning. This system is different from an acoustics-based biometric system, since it does not require vocal data from the human subject and is built solely on the fluid dynamic information contained in the exhaled breath.

The experimental dataset and methodology

A measurement-based study was employed to develop algorithms for biometric authentication. Measurements of the exhaled breath were made using a Dantec Dynamics ® 55P11 hot wire probe. It consists of a 5 μ m diameter, 1.25mm long platinum-coated tungsten wire, which acts as the sensor. A Dantec Dynamics MiniCTA ® 54T42 module housed the CT-HWA’s signal processing and output system. The hot wire probe was calibrated using a standard procedure of simultaneous measurement of the flow velocity and the anemometer voltage. The calibration was performed using a Dantec Dynamics StreamLine Pro ® automatic calibrator, between a velocity range of 0 − 5 m/s. Using this procedure, we were able to determine the calibration constants from an assumed velocity-voltage relation. This relation is a least-square polynomial fit of order-4 in the velocity-voltage space as shown in Fig 1 . In the current study, the raw voltage time series was itself used in all the analyses. This helps us avoid frequent re-calibration of the probe. The initial calibration was performed only to make sure that the voltage and velocity signals are monotonically positively correlated (as can be inferred from the least square fit from Fig 1 ).

• PPT PowerPoint slide
• PNG larger image
• TIFF original image

A fourth order least square fit of the experimental data (shown as maroon dotted line) becomes the calibration curve for the hot wire anemometer in use. The polynomial equation of the fourth order fit is shown inside the plot.

https://doi.org/10.1371/journal.pone.0301971.g001

Participants

94 participants were recruited to take part in this study, following the ethical approval from the Institutional Ethics Committee (IEC) of the Indian Institute of Technology Madras, Chennai, India (IITM—IEC Protocol No. IEC/2018–03/MP/01). The participants were students of the Indian Institute of Technology Madras. Their age ranged from 21 to 27 years. Data were collected only once (one set of 10 breath samples) per participant. Volunteers with epileptic disorder were excluded from participation. The experimental data collection was carried out between 8th and 17th January, 2019. All volunteers who participated in this study had given their written informed consent. The recorded time series data were analyzed anonymously.

Data collection and analysis

A schematic of the experimental setup is shown in Fig 2A . It consists of a mouthpiece assembled into an aluminium circular cross-section channel which housed the hot-wire probe aligned to its axis to measure the streamwise component of the turbulent exhaled flow velocity. The human subjects were allowed to exhale through their mouths into the experimental measurement setup. The nose was clipped during data recording to ensure that all the exhaled air passes through the oral cavity before entering the experimental setup. Each human subject was provided with a new disposable plastic mouth-piece to wrap their mouth around, through which the subjects exhaled. The obstruction of the tongue to the flow was avoided by placing the mouth-piece above the tongue. Data were obtained in each exhalation trial lasting about 1.5 seconds, with 10 trials recorded per subject. Each time series was recorded by sampling the voltage response at 10kHz. This effectively gives us 15000 data points in a time series, the relevance of which would be discussed in the following sections. The time series signal from a typical exhalation trial is shown in Fig 2B . In our study, we investigated the multifractal properties of the time series, since interestingly, human exhaled breath has been found to display multifractality, based on our analysis which is discussed in detail in Part 1 of S1 Text . This was performed using the well-known technique called multifractal detrended fluctuation analysis (MFDFA) developed by [ 30 ].

(A) Depiction of the experimental setup for data collection. It consists of a disposable mouth-piece, a mouth-piece mount housing a hot wire anemometer and a data acquisition system. (B) A typical human exhalation velocity signal measured using a standard hot wire anemometer. The time signals were sampled at 10kHz for 1.5 seconds.

https://doi.org/10.1371/journal.pone.0301971.g002

Given a set of time series signals from a library of users, our algorithm comprises of segmentation, normalization, feature extraction and subdivision of feature set into training and testing sets. The training dataset became part of the enrolled database, whereas the testing dataset was used for testing the performance of the authentication algorithms. The enrollment and algorithm testing depends on the type of algorithm being used. More details of user authentication systems are discussed in section titled User confirmation algorithms (page 8).

Time series segmentation, normalization and selection

Segmentation of time series is a standard practice in many data analysis techniques to obtain dividing points on a signal with or without stationarity. In machine learning problems with limited availability of time series samples, segmentation is of vital importance. By performing an efficient segmentation on the basis of certain statistical measures, we can obtain sufficient number of samples to train and test machine learning models. Fig 2B is a plot showing the instantaneous voltage response from the hot wire probe for 1.5 seconds. It was obtained by sampling at a frequency of 10kHz, giving us a sufficiently resolved long series to perform segmentation without losing any significant information on the flow physics.

MFDFA was performed on all normalised time series, and it revealed that not all spectra exhibit the expected shape. The general shape of a multifractal spectrum is convex or more precisely an inverted parabola, with the peak occurring at the central moment. This convex shape signifies the presence of multifractal scaling, indicating that different parts of the time series exhibit distinct scaling behaviors. Certain time segments were observed to result in a spectrum with folds or distortions. Fig 3 shows an example of such a distortion. The multifractal spectrum for a time signal and three randomly chosen segments X, Y and Z from the same time series are displayed. Fig 3A shows the entire time signal and the chosen segments. Out of the three segments, X and Z show a typical spectral shape, whereas segment Y consists of a fold towards the left hand side of the spectrum (see Fig 3B ).

The multifractal spectra corresponding to the entire time signal (maroon) and time segments X, Y and Z (black, bounded by gray band) in (A) are shown in (B). It is evident that few segments exhibit an inverted parabola shape and spectrum B has a distortion.

https://doi.org/10.1371/journal.pone.0301971.g003

There could be several reasons for the appearance of folds in the multifractal spectrum. ( i ) They could occur due to irregularities or data artifacts in the time series itself, such as noises, outliers, etc. which may arise due to inconsistent exhalation by the user during data acquisition. For example, during the period of 1.5 seconds, if the user exhales abruptly for the first 1 second of the trial, and then the breath velocity steadily decays for the remaining 0.5 seconds. The segment which falls between these two regions might contain irregularities within it. Such irregularities could introduce inconsistencies in the scaling behaviour. ( ii ) The spectrum may be affected by the non-stationarity of the time series, which is when the statistical properties change with time, such as due to change in breath velocity. ( iii ) Spectral folds might even arise due to the finite size of the time segment. Limited number of data points may not capture the scaling properties at different scales. Investigating the type of distortions or the reason behind this behaviour of the spectrum for certain time segments fell outside the scope of this work. Instead, we made use of this behaviour as an indicator to judge whether a segment is valid or not. All segments which showed non-convex singularity spectra were discarded in our analysis. Also, the segments which produce a spectral width less than 0.05 were rejected, since they exhibit a very low degree of multifractality. These two strategies effectively make MFDFA a tool for time series selection, for further feature extraction and analysis. Any time signal which contains significant number of segments with inconsistent scaling behaviour can be rejected using this tool during the data recording step itself. A numerical example discussing how a multifractal singularity spectrum can have non-convex shapes can be found in [ 31 ].

Feature extraction

Features were extracted from normalized time signals using various time series feature extraction techniques. Unlike other physiological biometric systems where image-based patterns or features are used as templates to match an individual’s identity, our input data is a time series from an individual, which requires feature extraction. Several features of the time series were studied in order to develop insights into the data. The multifractal spectral information was incorporated into our analysis by including them in the set of features. The fact that the time series contains information pertaining to the correlation structure becomes relevant to machine learning algorithms. In keeping with this principle, we extract a set of three important features from the spectrum: ( i ) β , the abscissa corresponding to the spectral maxima, ( ii ) ω , the width of the spectrum, and ( iii ) ϵ , the bias or asymmetry parameter of the spectrum. The parameters β , ω and ϵ are dimensionless. These features are visualised on the multifractal spectrum of an exhaled breath time signal in Fig 4 . It was also noted from our analysis that the spectra showed clear differences in their temporal structure; i.e., parameters such as β , ω and ϵ were different for different time signals. Several other multifractal spectral features have also been considered in the literature [ 31 – 33 ]. We chose these three features for simplicity and also they encompass the most important descriptions of a multifractal spectrum. Investigating how unique these features behave is of interest to this work.

Plot of the spectrum of singularities f ( α ) against the singularity strength α , computed for an exhalation time series segment. The parameters β , ω and ϵ are the features that characterize a multifractal spectrum.

https://doi.org/10.1371/journal.pone.0301971.g004

In addition to the use of MFDFA as a feature extraction algorithm, we also use an automated time series feature extraction algorithm named tsfresh (Time Series FeatuRe Extraction on the basis of Scalable Hypothesis tests) developed by [ 34 ]. The tool generates over 700 time series features using 63 different time series characterization methods. The following discussion pertains to the preparation of dataset for model building, training and testing of the algorithms. A consolidated pipeline of the algorithm towards model library building including time series normalization, and selection, followed by feature extraction and reduction, is shown in Fig 5 .

Flow chart showing the algorithm pipeline, including time series normalization, filtering, feature extraction, feature reduction, and data splitting into training and testing. The time signal shown here is one of the segments of the original time series. Note that the representation of blue bar for training dataset and green bar for testing dataset will be consistent in further discussions in this manuscript. The training data of all users were used for building n C 2 binary classifier models, which becomes the process known as enrollment .

https://doi.org/10.1371/journal.pone.0301971.g005

Features extracted by these algorithms from all available time series are concatenated and passed through a low-variance filter. This was done to remove those feature columns with a variance value below a given threshold, which in our case was 1%. The rationale behind applying this low variance filter was to eliminate features that exhibit very little variation across instances. Such low-variance features may not provide useful insights for classification tasks. Furthermore, highly correlated features were removed from the feature set. A correlation threshold of 80% was chosen for this purpose. Removing features by these techniques reduce the dimensionality, simplifies the model, and potentially improves model performance by focusing on more informative features. All features which were derived from the absolute values of the time series, such as maximum/minimum values, quantile information, etc., were disregarded. For example, inclusion of mean value of a signal will bias the algorithms and allow them to classify on the basis of the mean values itself, which was undesired. It was observed that different human subjects were able to exhale in different velocity bands depending on their lung capacity. The filtered feature matrix thus obtained is a stack of vectors from each time series sample available, and it consisted of approximately 450 time series features. This feature space is high dimensional and may contain redundant features that can be excluded. The reduced feature set will also reduce the computational complexity of the algorithms. We adopted a feature selection method using binary random forest classifiers. Binary classifiers were built on pairwise combinations of the users’ feature datasets. The importance of the features can be quantified for every random forest binary classifier by estimating how much the random forest’s performance would suffer if a given feature were to be eliminated. This impurity-based feature importance developed by [ 35 ] was used for picking the top features. The top 10 most prevalent features among users were chosen as the feature space after computing the top 10 features from each classifier. In the later sections of this manuscript, the methods used for model construction and the physical insights of these features will be described. The reduced feature matrix thus obtained contains features of all the users in the database. For each user, the dataset was split into training (60%) and test (40%) sets. It is important to note that this splitting was done after shuffling between groups of features corresponding to the 19 time blocks for each subject. We know that there were 190 time signals for each user in the database with each set of 19 signals coming from a single recorded time series (see subsection titled Time series segmentation, normalization and selection (page 5)). Shuffling without grouping would result in the same information being spread across the training and testing dataset, which was undesired. By doing this, we made sure that out of 10 exhaled breath samples, 6 became part of the training set and 4 became part of the test set. The training feature set was used to build the model library and the test feature set was used for user confirmation/identification tests.

Building of model library

This means that when a new user is added to the users’ database, n additional binary classifier models are to be built and stored in the model library. Expectedly, this follows a second-order power-law variation of the form y = ax m with the multiplication factor a ≈ 0.5 and exponent m ≈ 2.

User confirmation algorithms

Two different user confirmation algorithms were built using the extracted feature data. The first approach was based on statistical hypothesis testing, which involves the testing of a null hypothesis against an alternative hypothesis. The second approach was based on machine learning models. In case of a machine learning based algorithm development, the training data were used to build random forest binary classifier models, thereby creating a library of models. In the case of the hypothesis testing based algorithm, model building process is redundant, and the predictions are made based on the hypothesis test results between a user’s test data and available training data, making it an instance-based algorithm. These algorithms will be referred to as UCA.HT (User Confirmation Algorithm—Hypothesis Testing) and UCA.ML (User Confirmation Algorithm—Machine Learning) in later sections. The Hotelling’s T 2 test [ 40 ] was used in UCA.HT, which is a multidimensional version of the Student’s t -test.

Confirmation algorithm based on hypothesis testing

The use of hypothesis testing as an instance-based binary classifier has been attempted in the literature. [ 41 ] compared the machine learning approach and the statistical testing based on p − variations; and the idea of instance-based classification by hypothesis testing was investigated by [ 42 ]. [ 43 ] provided a detailed description on how binary decision problems can be formulated as hypothesis testing and/or binary classification. In a system based on hypothesis testing, the library comprises of the training datasets of all the users. Since we are building an algorithm which is intended to work alongside a machine learning algorithm, we formulate the hypothesis test based algorithm to work on binary pairs of users. To be more precise, the library will comprise of training datasets of pairs of users. It will be referred to as user-pair data in further discussions. Fig 6 shows a flow chart of the user confirmation algorithm which is based on hypothesis testing principles. The equality-of-means test was performed between a test data and each training data in pairs present in the library to infer whether the null hypothesis is to be rejected or not, as depicted in Fig 6 . Here, the null hypothesis states that the two samples come from the same distribution ( H 0 : μ a = μ b ), and the alternate hypothesis states that the samples come from different distributions ( H 1 : μ a ≠ μ b ). A detailed description on the test statistic and formulation of the Hotelling’s T 2 test can be found in the original work by [ 40 ].

A flow chart of the user confirmation algorithm based on hypothesis testing. The user confirmation block will be made use in the user identification algorithm later in this manuscript. An example of the hypothesis test against user-pair is illustrated inside the dotted box, directed from the user confirmation block by the red asterisk. Given a user i , the user confirmation block’s output was reposed to answer the question “Are you indeed User i ?” based on a threshold.

https://doi.org/10.1371/journal.pone.0301971.g006

When a test user, say ‘User i ’ was to provide the input, the pairwise Hotelling’s T 2 tests are performed between the test user’s data and the training data of n − 1 pairs of users which include ‘User i ’, where n is the number of users in the database. Let us look at one of those tests as shown inside dotted box in Fig 6 . By performing a hypothesis test against a user-pair, for example, (1, 2), we get a pair of p − values, ( p 1 , p 2 ). The tests were performed with a confidence level of 99.9%, and therefore a p − value of 0.001 or less was sufficient to reject the null hypothesis. At least one of the two p − values need to be above 0.001 for the algorithm to accept the null hypothesis. The predicted user is then the user corresponding to a higher p − value. If both p − values are either equal to or below 0.001, no predictions were made. After the test, the predictions made here are reposed as an answer to the question “Is it User i ? (Yes/No)”. The pipeline discussed so far becomes the ‘User Confirmation Block—HT’ for the hypothesis testing based algorithm. The output of this block is a scalar v which is equal to the count of model predictions which says ‘Yes’. Here, a threshold of 50% of the predictions was used for defining the minimum confidence of confirmation. This means that HT( i , i ) accepts the null hypothesis and HT( i , j ) ∀ j = 1, 2, … n and i ≠ j rejects the null hypothesis in at least 50% of the cases. Then, the User i is so confirmed. Here, HT( i , j ) stands for the hypothesis test between a User i and User j .

The equality-of-means test can actually be viewed from two perspectives: (a) Testing the distribution of test data against the distribution of n training data; (b) Testing the distribution of test data against the distribution of training data in pairs as discussed so far. The former strategy produces n test results and the algorithm would face one of three scenarios: ( i ) If only one test accepts the null hypothesis, the user identity is presumed to be of the user corresponding to that particular test; ( ii ) If more than one tests accept the null hypothesis, the user corresponding to the test which corresponds to highest p -value is presumed to be of the user identity (predicted user). In either case, if the predicted user matches with the test user, the user is confirmed, otherwise not; ( iii ) If all tests reject or no test rejects the null hypothesis, then the user is not confirmed. Although the former case (procedure (a)) is a computationally simpler formulation, the latter case (procedure (b)) becomes more relevant in our study since we are trying to build a multi-model approach for user identification. It was also noted that the latter approach gave better confirmation results (for UCA.HT) compared to the former approach.

Confirmation algorithm based on machine learning

Following the discussions from subsection titled Building of model library (page 8), generating n C 2 binary classifiers is necessary to handle the multiclass problem. The choice of a classifier depends on the specific characteristics of the dataset. A detailed discussion on the model-building procedure and the choice of a binary classifier can be found in Part 2 of S1 Text . Based on this analysis, we chose random forest as the appropriate binary classifier model for the model library. For the rest of this work, we will employ random forest as our machine learning algorithm and report results from this tool for both user confirmation and user identification.

Once the model building was complete and the entire library was stored, the test user data were given as input, say ‘User i ’. The algorithm selects those models from the library which were built using the same test user and makes predictions using each model as depicted in the flow chart in Fig 7 . The predictions made here are answers to the question “Is it User i ? (Yes/No)”. The pipeline discussed so far becomes the ‘User confirmation block—ML’. The output of this block is a scalar v which is equal to the count of model predictions which says ‘Yes’. Here, a threshold of (again) 50% of the predictions was used for defining the minimum confidence of confirmation. This means that if the algorithm confirms the user in more than half the classification trials, i.e., when v > ( n /2), the user is confirmed, else not.

A flow chart of the user confirmation algorithm based on machine learning. The user confirmation block will be made use in the user identification algorithm later in this manuscript. Given a user i , the user confirmation block’s output was reposed to answer the question “Are you indeed User i ?” based on a threshold.

https://doi.org/10.1371/journal.pone.0301971.g007

User identification algorithm

Given a test user j , the algorithm performs n confirmation trials. One confirmation trial is the equivalent to running the user confirmation block (either HT from Fig 6 or ML from Fig 7 ) for a trial user i . The identified user corresponds to the maximum prediction based on the n confirmation tests. Note that in the case where more than one confirmation trial results in the maximum prediction value, the algorithm does not identify a user.

https://doi.org/10.1371/journal.pone.0301971.g008

Results and discussions

User confirmation system.

Histograms of confidence of confirmation η i compared between (A) a machine learning based approach (random forest classifiers) and (B) a hypothesis testing based classification approach, for one trial of n confirmation tests. In the example shown here, the predictions from ML classifiers give a range of η i values distributed between ≈38% to 100%, whereas the predictions from HT based classifiers produce η i values only close to 0% and 100%.

https://doi.org/10.1371/journal.pone.0301971.g009

We shall now investigate why the machine learning based classification algorithm performs better in comparison with a hypothesis test based classification. In the case of hypothesis testing, we know that the rejection of null hypothesis is based on the confidence level chosen. The confidence level can be visualized as a demarcating hyper-surface between two n-dimensional normal distributions. For simplicity, let us have a look at the decision boundaries captured by the random forest classifier and the hypothesis test based classifier in a chosen two dimensional feature space. Fig 10 shows a visualisation in the ( β , ω ) plane for a randomly chosen user-pair. The blue and red markers are the training data points corresponding to two user classes, respectively. The class regions are computed using a structured synthetic dataset in the feature space.

Decision boundaries captured by (A) random forest classifier and (B) hypothesis testing based classifier for a randomly chosen user-pair. The scattered points are the training data points with red and blue labels denoting their true classes respectively. The line separating the two contour regions is the decision boundary. Accuracy of each model against the test data is displayed at the top right corner of their respective plots. The RF classifier captures a complex decision boundary compared to the HT based classifier.

https://doi.org/10.1371/journal.pone.0301971.g010

For the purpose of visualisation of a hypothesis test based classifier’s decision boundary, z − tests were performed in each dimension separately, for every data point from the synthetic dataset against one of the user’s training data. The tests were performed under the null hypothesis that the data point belongs to the distribution of the training data, under a confidence level of 99.9%. The overall null hypothesis is accepted only if the null hypothesis in both the dimensions are accepted. Comparing the decision boundaries captured by a hypothesis test based algorithm and a random forest model for the same pair of users, one can observe that the random forest model has the ability to capture a more complex decision boundary between two user classes. This lets the random forest classifier to achieve a test data accuracy of 90.9%, whereas the hypothesis testing based classifier achieves only 73.9%. Now that we have established that the machine learning based algorithm is better than the hypothesis test based algorithm for user confirmation, we will now investigate how these two algorithms perform for user identification in the following section.

User identification system

The identification algorithm discussed in Fig 8 shows that we obtain a vector V of favourable user predictions. Based on the values of vector V j with j = 1, 2, 3, … n , we can obtain the following outcomes:

• True positives ( t )—Number of users who were identified correctly.
• False positives ( f )—Number of users who were identified incorrectly.
• Not identified ( h )—Number of users who the algorithm was unable to identify.

We shall define the following performance metrics to evaluate the user identification algorithm:

The precision and accuracy values computed using Eqs 7 and 8 respectively, were 35±10.5% and 29±9.1% respectively, for the hypothesis test based algorithm. The results reported in this section are in the format ‘ μ p ±2 σ p ’ where μ p and σ p are mean and standard deviation of the performance metrics respectively. For the random forest based algorithm, we were able to observe precision and accuracy values of 26±7.2% and 22±6.4% respectively. These values were computed on the basis of the maximum votes received by a user among n confirmation trials, as described previously in Fig 8 . When we combine the results from both the algorithms using Eq 3 with w 1 = 0.3 and w 2 = 0.7, we get precision and accuracy values of 32±8.5% and 31±8.5% respectively. Note that the values reported here are also influenced by the threshold η t which in this case was set to 55%. The parameters w 1 , w 2 , and η t can be tweaked to make the algorithm behave on both extremes—( i ) to be very liberal (low precision, low accuracy); ( ii ) to be very conservative (high precision, low accuracy). Taking the example of a particular trial with n = 94, for a weights setting of w 1 = 0.3 and w 2 = 0.7, η t = 50% produces the outcomes ( t , f , h ) = (31, 58, 5), giving a precision of 34.8% and accuracy of 33.0%. For the same weights, η t = 96% produces the outcomes ( t , f , h ) = (18, 6, 70), giving a precision of 75.0% and accuracy of 19.1%. The former case allows for a lot of false positives by making judgements on most of the instances, whereas the latter case of the algorithm makes judgements stringently.

With the right set of hyperparameters ( w 1 , w 2 , … w r (in the general case from Eq 4 ) and η t ), a multi-modal approach is expected to improve the robustness of the overall algorithm. If one classifier produces incorrect predictions for certain trials, other classifiers in the ensemble can compensate for it and provide correct predictions. The contribution of each algorithm can be controlled by the weights. This robustness helps in improving the generalization of the ensemble model. The following discussion is based on results produced from this combined algorithm. We know that the highest voted user becomes the identified user from the algorithm. Based on the 66 shuffle trials, we have the following understanding of the user database. 21.3% to 42.6% of the users can be correctly identified by them being the highest voted users, 39.4% to 57.4% of the users can be correctly identified as at least the second highest voted users, and 50.0% to 66.0% of the users can be correctly identified as at least the third highest voted users. This is remarkable given that it is the first attempt in the literature to classify and uniquely identify individuals based solely on the fluid physics of the exhaled breath. We believe that this is conclusive evidence that the fluid dynamic structure of the exhaled breath contains uniquely identifiable information.

This algorithm holds tremendous potential for future use in the area of personalised medicine and also as a novel way to store biological data. This can be achieved by careful model selection and generalisation of classifier models. Advanced models such as deep neural networks can be made use to enhance the multi-model approach discussed in this manuscript.

Physical insights: Understanding the defining features

In order to make a physics-based argument for the uniqueness of human exhalation, it is important to investigate the physical significance of the most important features that result in robust classification. These would be the set of features or attributes which inherently differentiate the classes for a given training data. As we have seen, the importance of the features were quantified for every random forest binary classifier for choosing a reduced feature set in subsection titled Feature extraction (page 6). These features are to be investigated to understand their physical meaning in the context of the current problem in hand. A description of the most important classifying features (in the decreasing order of importance) are as follows.

• The singularity strength or Hölder exponent corresponding to the maximum ( β ) of the multifractal spectrum of the exhaled breath time series: This is a feature extracted using the MFDFA. β explains the long range correlation present in the time series. A low value indicates that the underlying process becomes correlated and loses fine structure, becoming more regular in appearance [ 30 ]. This, in our case, would relate to the organised motion of vortical structures in the turbulent exhaled air flow. For some subjects the vorticity pattern might be more irregular than the others, which could be attributed to the extrathoracic morphology.
• The sum over the absolute value of consecutive changes in the velocity time series: This feature represents the total magnitude of absolute differences between successive data points. In the context of our study, a higher value of this feature indicates a greater overall change in velocity between consecutive data points, i.e., the velocity changes rapidly and frequently. In contrast, a low value of this feature indicates that the velocity is smooth and consistent. It provides a quantitative measure of how much the velocity values fluctuate over successive time intervals, which in our case is 0.1 milliseconds. The detection of distinctive patterns in these fluctuations can provide insights into the presence of vortical structures in exhaled breath flow, contributing to the uniqueness of these patterns for individual subjects and enabling their classification by the algorithm.
• Third coefficient of the autoregressive AR ( r ) model with order parameter r = 10: The parameter r is the maximum lag of the autoregressive process. The AR model generally predicts future behavior based on past data. The importance of the third as well as fourth (point 8) coefficients show that there is some correlation between successive values in the time series for most of the users.
• The number of peaks in the time series with a support ( s ) of at least 1: A peak of support s is defined as a sub-sequence in the time series where a value occurs that is greater than its s neighbors to the left and to the right. When s is set to 1, this feature computes the number of peaks in the time series where a value is greater than its immediate neighbors. This feature can provide insights into the presence or intensity of localised fluctuations in the flow.
• The number of different Continuous Wavelet Transform (CWT) peaks present in the signal for smoothing width of 1: This feature was extracted from the time series by applying CWT using Ricker wavelet with width, w = 1. This method simultaneously evaluates the signal in the temporal and frequency domains. In the context of our study, the identified CWT peaks represent distinctive features in the breath signature. Physically, these peaks may correspond to specific events or patterns that are characterised by rapid changes in both time and frequency domains. For instance, a CWT peak could signify the presence of a sudden, localized change in the breath velocity with a particular frequency content. The number of distinct peaks across the considered width scales provides a quantitative measure of the breath signature’s complexity. It can be utilized to compare the signals based on their peak characteristics.
• The value of partial autocorrelation function at a lag of 3: The partial autocorrelation is a statistical measure that quantifies the linear relationship between a time series variable and its lagged values. In the context of our exhaled breath flow, the partial autocorrelation can provide insights into the temporal dependence and correlation structure of the breath velocity. This means that this feature can be useful in understanding the persistence or memory of the signal. It suggests that a strong linear relationship between the current flow state and its state 3 time steps ago have been important for the classification of human subjects. In our analysis, a ‘time step’ corresponds to the original sampling rate of 10kHz. Therefore, when we refer to a lag of 3 time steps, it signifies a duration of 0.3 milliseconds.
• Width of the multifractal spectrum ( ω ) of the exhaled breath time series: ω describes the richness of the multifractality present in the time series, i.e., wider the range of singularity strength, richer the structure of the signal. The spectral width can implicitly represent the intensity or the level of turbulence present in the flow of exhaled breath. Turbulence is characterized by fluctuations in velocity at different scales. A wider range of turbulence scales is reflected by a wider spectral width, indicating a more turbulent flow. This might be attributed to factors such as extrathoracic constriction, or increased turbulence due to specific breath patterns or breath dynamics.
• Fourth coefficient of the autoregressive AR ( r ) model with order parameter r = 10.
• The number of different continuous wavelet transform (CWT) peaks present in the signal for smoothing width of 5. This feature was extracted using the same technique as discussed in point 5, but with a width of w = 5. A larger smoothing width typically leads to a broader wavelet. A wider wavelet provides a smoother analysis that might emphasize broader features and lower-frequency components in the signal. Conversely, a smaller smoothing width of w = 1 (point 5) would result in a narrow wavelet, allowing for a more detailed examination of rapid changes in the signal (sensitive to high-frequency components).
• Kurtosis of the velocity time series calculated with the adjusted Fisher-Pearson standardized moment coefficient, g 2: We know that Kurtosis is a higher-order statistical attribute of velocity signals. The heaviness of the tails of the probability density functions of normalized time series could be distinct for each user. This feature will help us in assessing the degree of deviation from the Gaussian distribution and provides evidence of skewed behaviour of the time series.

Computational complexity of the algorithm

Run-time of an algorithm is an extremely important factor for a real-time biometric system. It was generally observed that the size of the input feature set affects the amount of computational resources required to run an algorithm. It was observed that the hypothesis test based algorithm performs predictions faster than the machine learning based algorithm which is because the former is an instance-based classifier. Since the user identification algorithm depends on the number of users and in turn the number of models in the model library, the identification time per user was expected to scale up with the size of the library. The identification time was observed to show a linear relationship with the size of the library (of the form y = ax , with slope a ≈ 1) as seen in the Fig 11 . The error bars show 95% confidence interval at every data point.

Plot showing the linear relation of user identification time with the growth of model library. This is applicable to the ML based algorithms which include building of binary classifier models (also known as enrollment in the context of biometrics). The error bars show 95% confidence interval at every data point.

https://doi.org/10.1371/journal.pone.0301971.g011

One of the advantages of building an algorithm which uses n C 2 binary classifiers instead of a single multi-class classifier is that it is massively parallelisable. As long as we have sufficient number of cores to run model loading and prediction, the parallelisation is possible. This significantly improves the computational time by several orders.

We have provided evidence for the feasibility of a novel biometric system that works based on the turbulence information present in human exhaled breath. The use of a hot-wire anemometer for data acquisition allowed us to build a compact working setup. The faster response time of a constant temperature hot wire anemometer and the real-time computation in combination will possibly make the setup implementable as a biometric authentication system. Since the input of the exhaled breath-based biometric system is correlated with the internal morphology of the human body, it is impossible for a hacker to spoof-authenticate a user. This is because it is difficult to reconstruct an original time series and subsequently the binary classifier models that consolidate all the relevant features (biometric traits) of the true user. Preliminary studies carried out and presented in this work based on time series data from 94 human subjects have shown promising results. We recommend the machine learning approach discussed in this work as a procedure to build a working user confirmation system, as it produces good accuracy in confirming users. It achieved a true confirmation rate of over 97%, which is because of the ability of random forest models to capture complex decision boundaries between the classes. Although the dataset performs really well for a user confirmation algorithm, the real test of a biometric system comes in for the user identification algorithm, where the test user’s identity is not revealed a priori. Building such an algorithm comes with more challenges and would require samples from a larger population to be evaluated. We recommend a multi-model approach for the user identification system, as discussed in this manuscript. The results from our study show that a user identification algorithm performs reasonably well with maximum precision and accuracy of ≈40% each for optimum parameter settings. 39.4% to 57.4% of the users were correctly identified as at least the second highest voted users.

Our study reveals the possibility that a system built solely on the basis of the fluid dynamics of human exhaled breath could be a potential tool to understand the person-to-person variation in turbulent signatures of exhaled breath. This uniqueness in observed signature could potentially be correlated to the morphometric variation present in the extrathoracic airway. To make comments on the intricate structures within the upper respiratory tract, we might need experimental proof on cadaver models, or simultaneous imaging of upper tract along with the HWA data. Such a study would give us insights on how the structures exhibit considerable morphological diversity among individuals. While our study does not involve direct experimentation with throat morphology, it prompts consideration of how these morphological variations could contribute to the surprisingly unique turbulent signatures found in exhaled breath. Further investigation would give us better understanding on the relationship between these morphological traits and the distinct fluid dynamic signatures. For example, it is possible that the turbulence information can be correlated to occlusion in the extrathoracic passage and its nature, which is a major source of deposition of aerosolised therapeutics. Such an understanding will help us delve deeper into the area of personalised medicines.

Supporting information

S1 text. supplementary materials for user authentication system based on human exhaled breath physics ..

The supporting information for this research article includes: Part 1: A statistical description which describes the Multifractal Detrended Fluctuation Analysis (MFDFA) of human exhaled breath velocity time series; Part 2: Model library building procedure and model selection for the machine learning based algorithm.

https://doi.org/10.1371/journal.pone.0301971.s001

S1 Checklist. Human participants research checklist.

https://doi.org/10.1371/journal.pone.0301971.s002

Acknowledgments

The authors acknowledge the HPCE, the Synchrony, and the SENAI of the Indian Institute of Technology Madras for providing the required high performance computing resources. The authors thank the NCCRD, IIT Madras, for providing the hot-wire anemometer setup and the calibration facility to carry out the experiments. The authors are also thankful to all the participants who volunteered to give their exhaled breath data for this study.

• View Article
• Google Scholar
• PubMed/NCBI
• 3. sen Wang C. Chapter 3 Airflow in the respiratory system. In: Inhaled Particles. vol. 5 of Interface Science and Technology. Elsevier; 2005. p. 31–54.
• 4. Finlay WH. The mechanics of inhaled pharmaceutical aerosols. San Diego, CA: Academic Press; 2001.
• 6. Chauhan J, Hu Y, Seneviratne S, Misra A, Seneviratne A, Lee Y. BreathPrint: Breathing Acoustics-Based User Authentication. In: Proceedings of the 15th Annual International Conference on Mobile Systems, Applications, and Services. MobiSys’17. New York, NY, USA: Association for Computing Machinery; 2017. p. 278–291.
• 7. Woodward JD, Webb KW, Newton EM, Bradley M, Rubenson D, Larson K, et al. In: A PRIMER ON BIOMETRIC TECHNOLOGY. 1st ed. RAND Corporation; 2001. p. 9–20.
• 12. Guo D, Zhang D, Li N, Zhang L, Yang J. Diabetes identification and classification by means of a breath analysis system. In: International conference on medical biometrics. Springer; 2010. p. 52–63.
• 21. Silva ISS, Freire RCS, Silva JF, Naviner JF, Sousa FR, Catunda SYC. Architectures of anemometers using the electric equivalence principle. In: IMTC/2002. Proceedings of the 19th IEEE Instrumentation and Measurement Technology Conference (IEEE Cat. No.00CH37276). vol. 1; 2002. p. 397–401 vol.1.
• 22. Araujo GA, Freire RC, Silva JF, Oliveira A, Jaguaribe E. Breathing flow measurement with constant temperature hot-wire anemometer for forced oscillations technique. In: Proceedings of the 21st IEEE Instrumentation and Measurement Technology Conference (IEEE Cat. No. 04CH37510). vol. 1. IEEE; 2004. p. 730–733.
• 23. Kandaswamy A, Kumar CS, Kiran TV. A virtual instrument for measurement of expiratory parameters. In: IMTC/2002. Proceedings of the 19th IEEE Instrumentation and Measurement Technology Conference (IEEE Cat. No.00CH37276). vol. 2; 2002. p. 1255–1258 vol.2.
• 27. Abdelnasser H, Harras KA, Youssef M. UbiBreathe: A ubiquitous non-invasive WiFi-based breathing estimator. In: Proceedings of the 16th ACM International Symposium on Mobile Ad Hoc Networking and Computing; 2015. p. 277–286.
• 28. Liu J, Chen Y, Dong Y, Wang Y, Zhao T, Yao YD. Continuous user verification via respiratory biometrics. In: IEEE INFOCOM 2020-IEEE Conference on Computer Communications. IEEE; 2020. p. 1–10.