law of sines assignment quizlet

The Law of Sines

The Law of Sines (or Sine Rule ) is very useful for solving triangles:

a sin A = b sin B = c sin C

It works for any triangle:

And it says that:

When we divide side a by the sine of angle A it is equal to side b divided by the sine of angle B , and also equal to side c divided by the sine of angle C

Well, let's do the calculations for a triangle I prepared earlier:

a sin A = 8 sin(62.2°) = 8 0.885... = 9.04...

b sin B = 5 sin(33.5°) = 5 0.552... = 9.06...

c sin C = 9 sin(84.3°) = 9 0.995... = 9.04...

The answers are almost the same! (They would be exactly the same if we used perfect accuracy).

So now you can see that:

Is This Magic?

Not really, look at this general triangle and imagine it is two right-angled triangles sharing the side h :

The sine of an angle is the opposite divided by the hypotenuse, so:

a sin(B) and b sin(A) both equal h , so we get:

a sin(B) = b sin(A)

Which can be rearranged to:

a sin A = b sin B

We can follow similar steps to include c/sin(C)

How Do We Use It?

Let us see an example:

Example: Calculate side "c"

Now we use our algebra skills to rearrange and solve:

Finding an Unknown Angle

In the previous example we found an unknown side ...

... but we can also use the Law of Sines to find an unknown angle .

In this case it is best to turn the fractions upside down ( sin A/a instead of a/sin A , etc):

sin A a = sin B b = sin C c

Example: Calculate angle B

Sometimes there are two answers .

There is one very tricky thing we have to look out for:

Two possible answers.

This only happens in the " Two Sides and an Angle not between " case, and even then not always, but we have to watch out for it.

Just think "could I swing that side the other way to also make a correct answer?"

Example: Calculate angle R

The first thing to notice is that this triangle has different labels: PQR instead of ABC. But that's OK. We just use P,Q and R instead of A, B and C in The Law of Sines.

But wait! There's another angle that also has a sine equal to 0.9215...

The calculator won't tell you this but sin(112.9°) is also equal to 0.9215...

So, how do we discover the value 112.9°?

Easy ... take 67.1° away from 180°, like this:

180° − 67.1° = 112.9°

So there are two possible answers for R: 67.1° and 112.9° :

Both are possible! Each one has the 39° angle, and sides of 41 and 28.

So, always check to see whether the alternative answer makes sense.

• ... sometimes it will (like above) and there are two solutions
• ... sometimes it won't (like below) and there is one solution

For example this triangle from before.

As you can see, we can try swinging the "5.5" line around, but no other solution makes sense.

So this has only one solution.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.2: The Law of Sines

• Last updated
• Save as PDF
• Page ID 113918

• Carl Stitz & Jeff Zeager
• Lakeland Community College & Lorain County Community College

Trigonometry literally means ‘measuring triangles’ and with Chapter 10 under our belts, we are more than prepared to do just that. The main goal of this section and the next is to develop theorems which allow us to ‘solve’ triangles – that is, find the length of each side of a triangle and the measure of each of its angles. In Sections 10.2 , 10.3 and 10.6 , we’ve had some experience solving right triangles. The following example reviews what we know.

Example 11.2.1

Given a right triangle with a hypotenuse of length 7 units and one leg of length 4 units, find the length of the remaining side and the measures of the remaining angles. Express the angles in decimal degrees, rounded to the nearest hundreth of a degree.

For definitiveness, we label the triangle below.

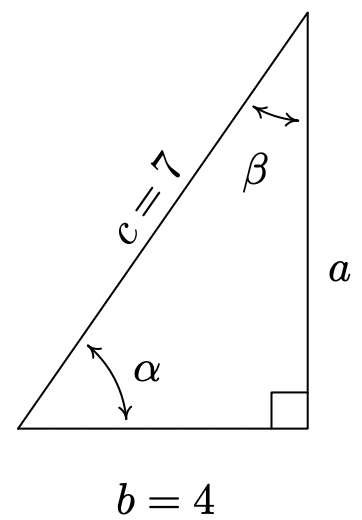
To find the length of the missing side \(a\), we use the Pythagorean Theorem to get \(a^{2}+4^{2}=7^{2}\) which then yields \(a=\sqrt{33}\) units. Now that all three sides of the triangle are known, there are several ways we can find \(\alpha\) using the inverse trigonometric functions. To decrease the chances of propagating error, however, we stick to using the data given to us in the problem. In this case, the lengths 4 and 7 were given, so we want to relate these to \(\alpha\). According to Theorem 10.4 , \(\cos (\alpha)=\frac{4}{7}\). Since \(\alpha\) is an acute angle, \(\alpha=\arccos \left(\frac{4}{7}\right)\) radians. Converting to degrees, we find \(\alpha \approx 55.15^{\circ}\). Now that we have the measure of angle \(\alpha\), we could find the measure of angle \(\beta\) using the fact that \(\alpha\) and \(\beta\) are complements so \(\alpha+\beta=90^{\circ}\). Once again, we opt to use the data given to us in the problem. According to Theorem 10.4 , we have that \(\sin (\beta)=\frac{4}{7}\) so \(\beta=\arcsin \left(\frac{4}{7}\right)\) radians and we have \(\beta \approx 34.85^{\circ}\).

A few remarks about Example 11.2.1 are in order. First, we adhere to the convention that a lower case Greek letter denotes an angle 1 and the corresponding lowercase English letter represents the side 2 opposite that angle. Thus, \(a\) is the side opposite \(\alpha, b\) is the side opposite \(\beta\) and \(c\) is the side opposite \(\gamma\). Taken together, the pairs \((\alpha, a)\), \((\beta, b)\) and \((\gamma, c)\) are called angle-side opposite pairs. Second, as mentioned earlier, we will strive to solve for quantities using the original data given in the problem whenever possible. While this is not always the easiest or fastest way to proceed, it minimizes the chances of propagated error. 3 Third, since many of the applications which require solving triangles ‘in the wild’ rely on degree measure, we shall adopt this convention for the time being. 4 The Pythagorean Theorem along with Theorems 10.4 and 10.10 allow us to easily handle any given right triangle problem, but what if the triangle isn’t a right triangle? In certain cases, we can use the Law of Sines to help.

Theorem 11.2. The Law of Sines

Given a triangle with angle-side opposite pairs \((\alpha, a)\), \((\beta, b)\) and \((\gamma, c)\), the following ratios hold

\(\frac{\sin (\alpha)}{a}=\frac{\sin (\beta)}{b}=\frac{\sin (\gamma)}{c}\)

or, equivalently,

\(\frac{a}{\sin (\alpha)}=\frac{b}{\sin (\beta)}=\frac{c}{\sin (\gamma)}\)

The proof of the Law of Sines can be broken into three cases. For our first case, consider the triangle \(\triangle A B C\) below, all of whose angles are acute, with angle-side opposite pairs \((\alpha, a)\), \((\beta, b)\) and \((\gamma, c)\). If we drop an altitude from vertex \(B\), we divide the triangle into two right triangles: \(\triangle A B Q\) and \(\triangle B C Q\). If we call the length of the altitude \(h\) (for height), we get from Theorem 10.4 that \(\sin (\alpha)=\frac{h}{c}\) and \(\sin (\gamma)=\frac{h}{a}\) so that \(h=c \sin (\alpha)=a \sin (\gamma)\). After some rearrangement of the last equation, we get \(\frac{\sin (\alpha)}{a}=\frac{\sin (\gamma)}{c}\). If we drop an altitude from vertex \(A\), we can proceed as above using the triangles \(\triangle A B Q\) and \(\triangle A C Q\) to get \(\frac{\sin (\beta)}{b}=\frac{\sin (\gamma)}{c}\), completing the proof for this case.

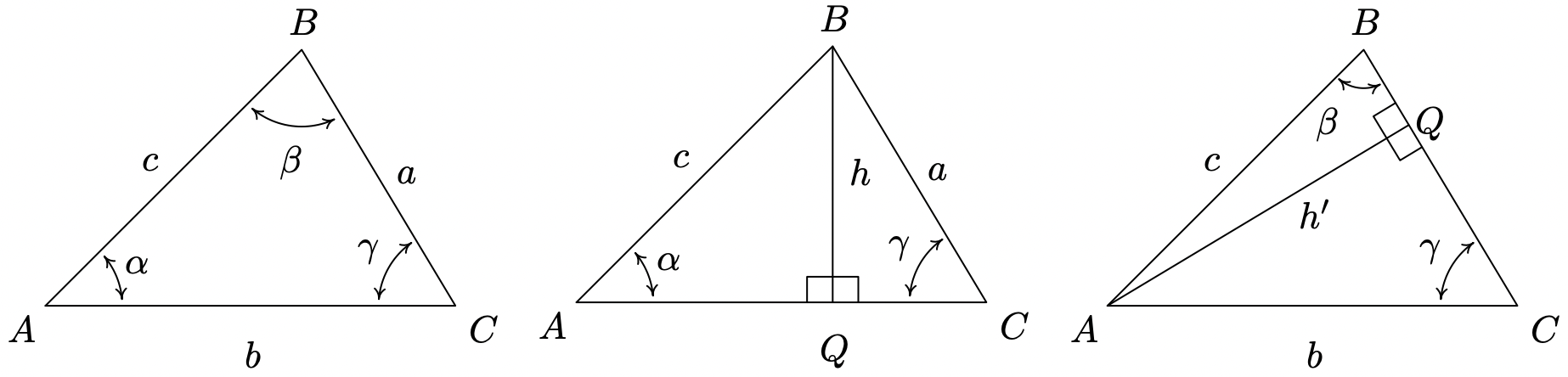
For our next case consider the triangle \(\triangle A B C\) below with obtuse angle \(\alpha\). Extending an altitude from vertex \(A\) gives two right triangles, as in the previous case: \(\triangle A B Q\) and \(\triangle A C Q\). Proceeding as before, we get \(h=b \sin (\gamma)\) and \(h=c \sin (\beta)\) so that \(\frac{\sin (\beta)}{b}=\frac{\sin (\gamma)}{c}\).

Dropping an altitude from vertex B also generates two right triangles, \(\triangle A B Q\) and \(\triangle B C Q\). We know that \(\sin \left(\alpha^{\prime}\right)=\frac{h^{\prime}}{c}\) so that \(h^{\prime}=c \sin \left(\alpha^{\prime}\right)\). Since \(\alpha^{\prime}=180^{\circ}-\alpha, \sin \left(\alpha^{\prime}\right)=\sin (\alpha)\), so in fact, we have \(h^{\prime}=c \sin (\alpha)\). Proceeding to \(\triangle B C Q\), we get \(\sin (\gamma)=\frac{h^{\prime}}{a} \text { so } h^{\prime}=a \sin (\gamma)\). Putting this together with the previous equation, we get \(\frac{\sin (\gamma)}{c}=\frac{\sin (\alpha)}{a}\), and we are finished with this case.

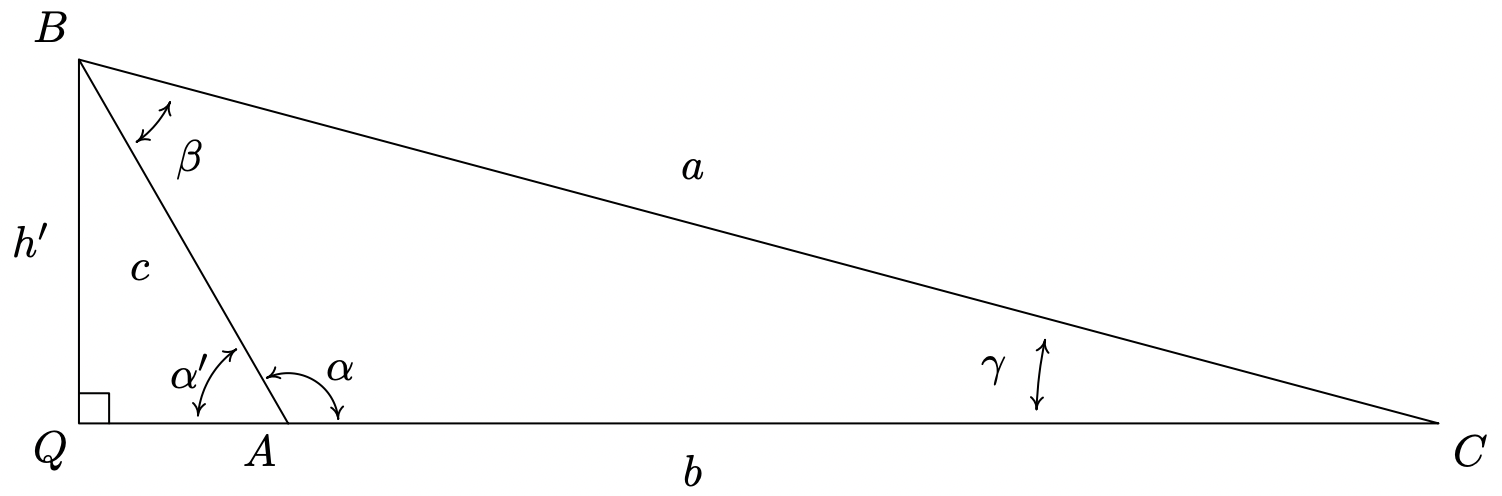
The remaining case is when \(\triangle A B C\) is a right triangle. In this case, the Law of Sines reduces to the formulas given in Theorem 10.4 and is left to the reader. In order to use the Law of Sines to solve a triangle, we need at least one angle-side opposite pair. The next example showcases some of the power, and the pitfalls, of the Law of Sines.

Example 11.2.2

Solve the following triangles. Give exact answers and decimal approximations (rounded to hundredths) and sketch the triangle.

• \(\alpha=120^{\circ}, a=7 \text { units, } \beta=45^{\circ}\)
• \(\alpha=85^{\circ}, \beta=30^{\circ}, c=5.25 \text { units }\)
• \(\alpha=30^{\circ}, a=1 \text { units, } c=4 \text { units }\)
• \(\alpha=30^{\circ}, a=2 \text { units, } c=4 \text { units }\)
• \(\alpha=30^{\circ}, a=3 \text { units, } c=4 \text { units }\)
• \(\alpha=30^{\circ}, a=4 \text { units, } c=4 \text { units }\)
• Knowing an angle-side opposite pair, namely \(\alpha\) and \(a\), we may proceed in using the Law of Sines. Since \(\beta=45^{\circ}\), we use \(\frac{b}{\sin \left(45^{\circ}\right)}=\frac{7}{\sin \left(120^{\circ}\right)}\) so \(b=\frac{7 \sin \left(45^{\circ}\right)}{\sin \left(120^{\circ}\right)}=\frac{7 \sqrt{6}}{3} \approx 5.72\) units. Now that we have two angle-side pairs, it is time to find the third. To find \(\gamma\), we use the fact that the sum of the measures of the angles in a triangle is \(180^{\circ}\). Hence, \(\gamma=180^{\circ}-120^{\circ}-45^{\circ}=15^{\circ}\). To find \(c\), we have no choice but to used the derived value \(\gamma=15^{\circ}\), yet we can minimize the propagation of error here by using the given angle-side opposite pair \((\alpha, a)\). The Law of Sines gives us \(\frac{c}{\sin \left(15^{\circ}\right)}=\frac{7}{\sin \left(120^{\circ}\right)}\) so that \(c=\frac{7 \sin \left(15^{\circ}\right)}{\sin \left(120^{\circ}\right)} \approx 2.09\) units. 5

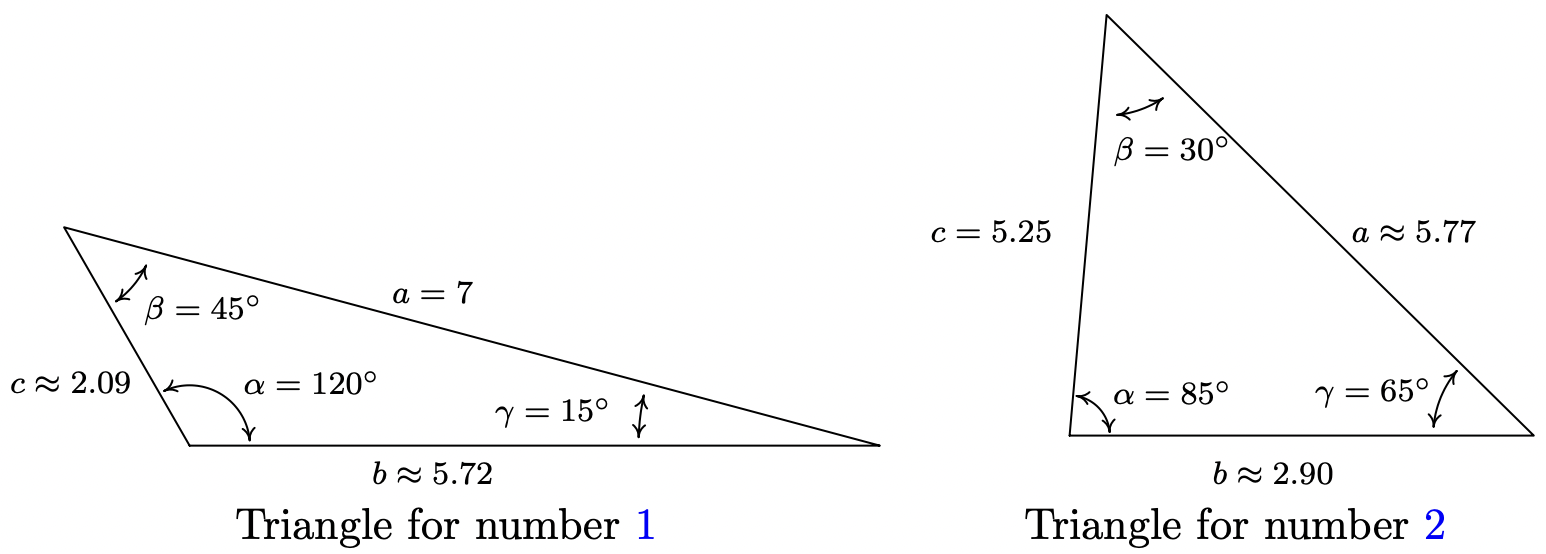
• Since we are given \((\alpha, a)\) and \(c\), we use the Law of Sines to find the measure of \(\gamma\). We start with \(\frac{\sin (\gamma)}{4}=\frac{\sin \left(30^{\circ}\right)}{1}\) and get \(\sin (\gamma)=4 \sin \left(30^{\circ}\right)=2\). Since the range of the sine function is [−1, 1], there is no real number with \(\sin (\gamma)=2\). Geometrically, we see that side \(a\) is just too short to make a triangle. The next three examples keep the same values for the measure of \(\alpha\) and the length of \(c\) while varying the length of \(a\). We will discuss this case in more detail after we see what happens in those examples.

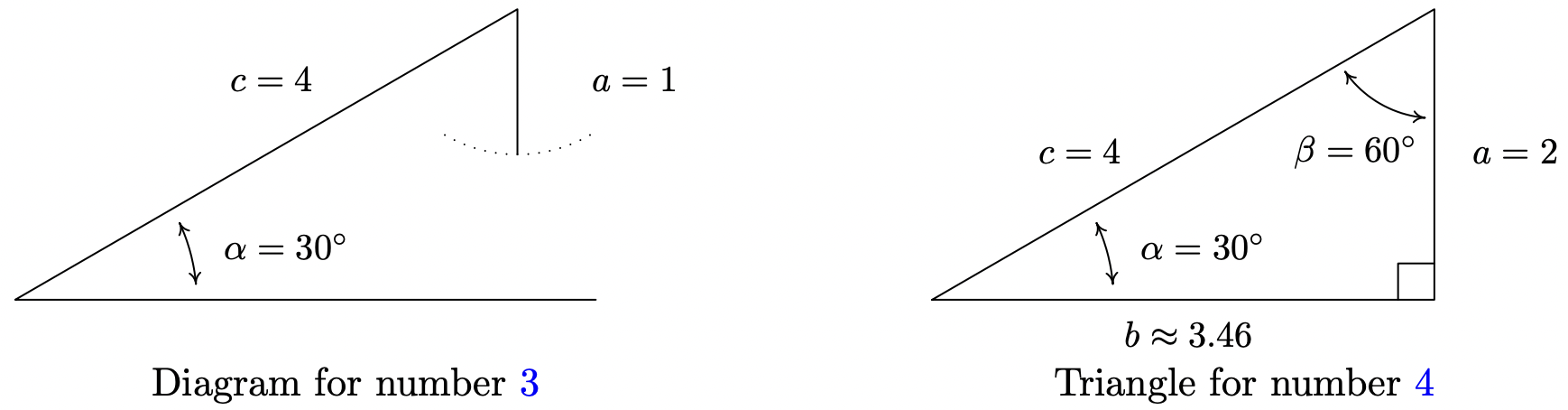
Some remarks about Example 11.2.2 are in order. We first note that if we are given the measures of two of the angles in a triangle, say \(\alpha\) and \(\beta\), the measure of the third angle \(\gamma\) uniquely determined using the equation \(\gamma=180^{\circ}-\alpha-\beta\). Knowing the measures of all three angles of a triangle completely determines its shape. If in addition we are given the length of one of the sides of the triangle, we can then use the Law of Sines to find the lengths of the remaining two sides to determine the size of the triangle. Such is the case in numbers 1 and 2 above. In number 1, the given side is adjacent to just one of the angles – this is called the ‘Angle-Angle-Side’ (AAS) case. 8 In number 2, the given side is adjacent to both angles which means we are in the so-called ‘Angle-Side-Angle’ (ASA) case. If, on the other hand, we are given the measure of just one of the angles in the triangle along with the length of two sides, only one of which is adjacent to the given angle, we are in the ‘Angle-Side-Side’ (ASS) case. 9 In number 3, the length of the one given side \(a\) was too short to even form a triangle; in number 4, the length of a was just long enough to form a right triangle; in 5, \(a\) was long enough, but not too long, so that two triangles were possible; and in number 6, side \(a\) was long enough to form a triangle but too long to swing back and form two. These four cases exemplify all of the possibilities in the Angle-Side-Side case which are summarized in the following theorem.

Theorem 11.3

Suppose \((\alpha, a)\) and \((\gamma, c)\) are intended to be angle-side pairs in a triangle where \(\alpha\), \(a\) and \(c\) are given. Let \(h=c \sin (\alpha)\).

• If \(a<h\), then no triangle exists which satisfies the given criteria.
• If \(a=h\), then \(\gamma=90^{\circ}\) so exactly one (right) triangle exists which satisfies the criteria.
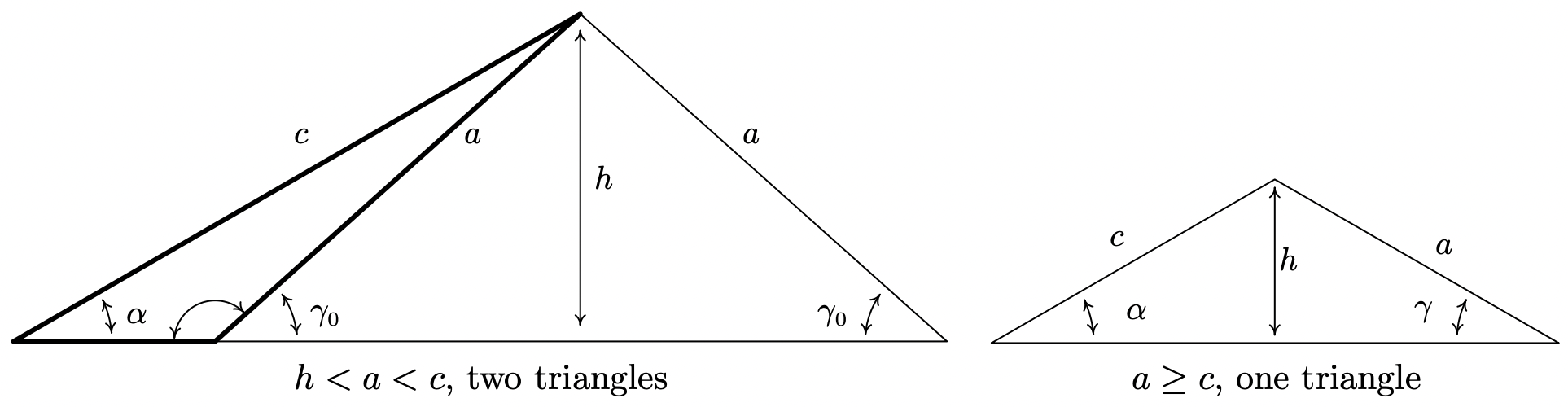
• If \(h<a<c\), then two distinct triangles exist which satisfy the given criteria.
• If \(a \geq c\), then \(\gamma\) is acute and exactly one triangle exists which satisfies the given criteria

Theorem 11.3 is proved on a case-by-case basis. If \(a<h\), then \(a<c \sin (\alpha)\). If a triangle were to exist, the Law of Sines would have \(\frac{\sin (\gamma)}{c}=\frac{\sin (\alpha)}{a}\) so that \(\sin (\gamma)=\frac{c \sin (\alpha)}{a}>\frac{a}{a}=1\), which is impossible. In the figure below, we see geometrically why this is the case.

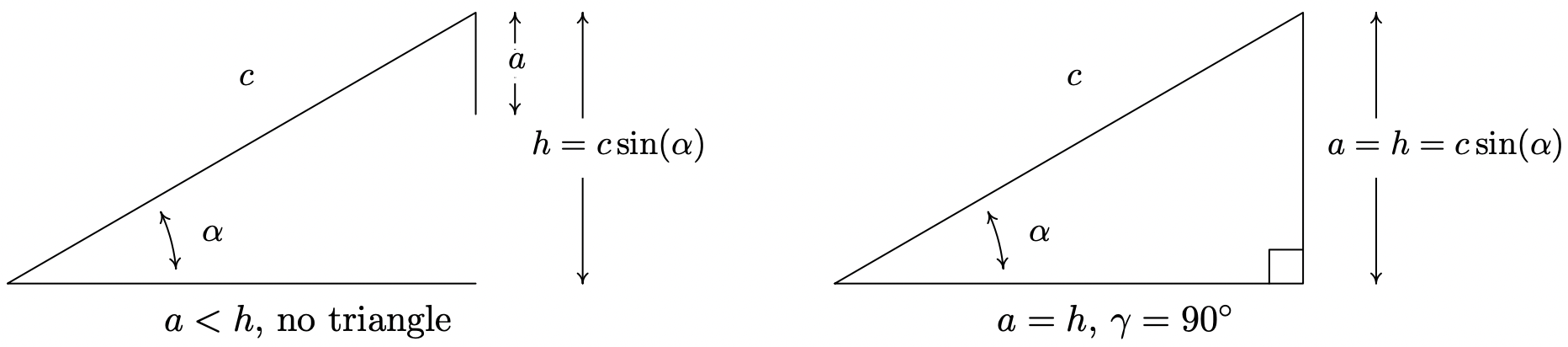
Simply put, if \(a<h\) the side \(a\) is too short to connect to form a triangle. This means if \(a \geq h\), we are always guaranteed to have at least one triangle, and the remaining parts of the theorem tell us what kind and how many triangles to expect in each case. If \(a = h\), then \(a=c \sin (\alpha)\) and the Law of Sines gives \(\frac{\sin (\alpha)}{a}=\frac{\sin (\gamma)}{c}\) so that \(\sin (\gamma)=\frac{c \sin (\alpha)}{a}=\frac{a}{a}=1\). Here, \(\gamma=90^{\circ}\) as required. Moving along, now suppose \(h<a<c\). As before, the Law of Sines 10 gives \(\sin (\gamma)=\frac{c \sin (\alpha)}{a}\). Since \(h<a\), \(c \sin (\alpha)<a\) or \(\frac{c \sin (\alpha)}{a}<1\) which means there are two solutions to \(\sin (\gamma)=\frac{c \sin (\alpha)}{a}\): an acute angle which we’ll call \(\gamma_{0}\), and its supplement, \(180^{\circ}-\gamma_{0}\). We need to argue that each of these angles ‘fit’ into a triangle with \(\alpha\). Since \((\alpha, a)\) and \(\left(\gamma_{0}, c\right)\) are angle-side opposite pairs, the assumption \(c>a\) a in this case gives us \(\gamma_{0}>\alpha\). Since \(\gamma_{0}\) is acute, we must have that \(\alpha\) is acute as well. This means one triangle can contain both \(\alpha\) and \(\gamma_{0}\), giving us one of the triangles promised in the theorem. If we manipulate the inequality \(\gamma_{0}>\alpha\) a bit, we have \(180^{\circ}-\gamma_{0}<180^{\circ}-\alpha\) which gives \(\left(180^{\circ}-\gamma_{0}\right)+\alpha<180^{\circ}\). This proves a triangle can contain both of the angles \(\alpha\) and \(\left(180^{\circ}-\gamma_{0}\right)\), giving us the second triangle predicted in the theorem. To prove the last case in the theorem, we assume \(a \geq c\). Then \(\alpha \geq \gamma\), which forces \(\gamma\) to be an acute angle. Hence, we get only one triangle in this case, completing the proof.

Example 11.2.3

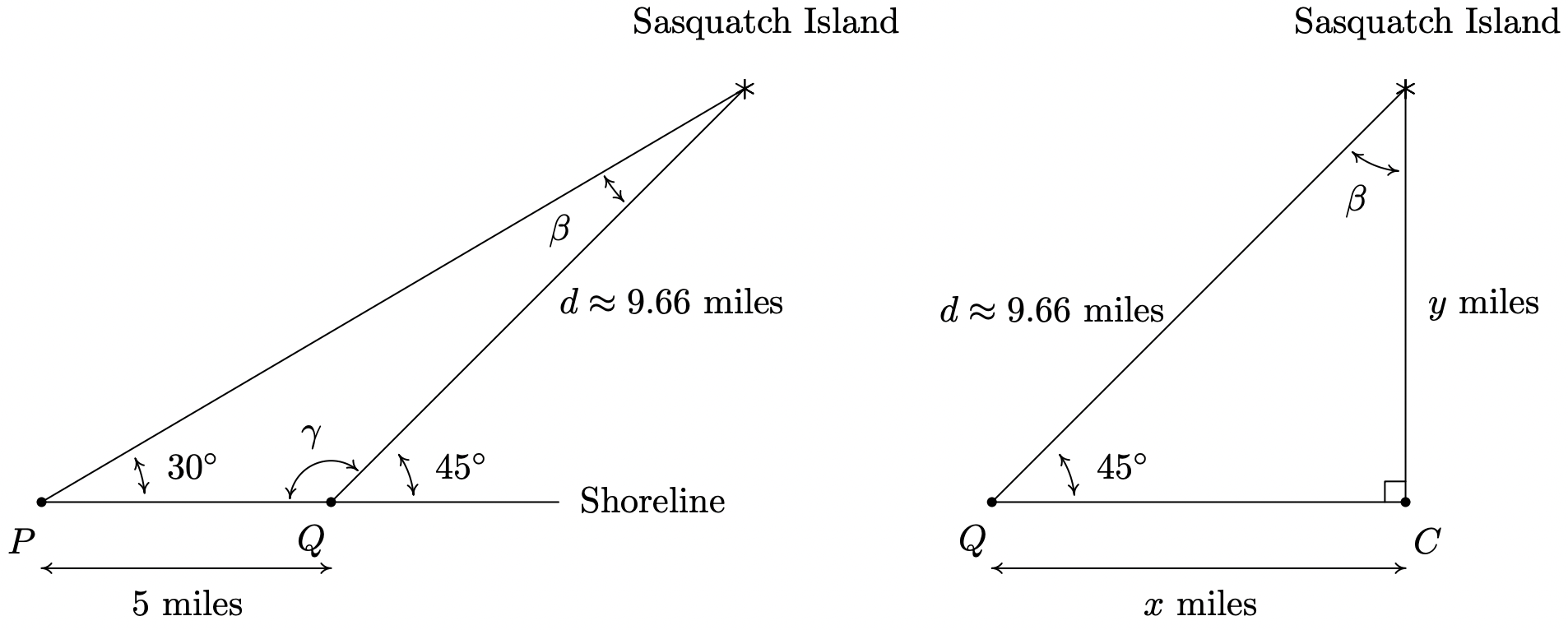
Sasquatch Island lies off the coast of Ippizuti Lake. Two sightings, taken 5 miles apart, are made to the island. The angle between the shore and the island at the first observation point is \(30^{\circ}\) and at the second point the angle is \(45^{\circ}\). Assuming a straight coastline, find the distance from the second observation point to the island. What point on the shore is closest to the island? How far is the island from this point?

We sketch the problem below with the first observation point labeled as \(P\) and the second as \(Q\). In order to use the Law of Sines to find the distance \(d\) from \(Q\) to the island, we first need to find the measure of \(\beta\) which is the angle opposite the side of length 5 miles. To that end, we note that the angles \(\gamma\) and \(45^{\circ}\) are supplemental, so that \(\gamma=180^{\circ}-45^{\circ}=135^{\circ}\). We can now find \(\beta=180^{\circ}-30^{\circ}-\gamma=180^{\circ}-30^{\circ}-135^{\circ}=15^{\circ}\). By the Law of Sines, we have \(\frac{d}{\sin \left(30^{\circ}\right)}=\frac{5}{\sin \left(15^{\circ}\right)}\) which gives \(d=\frac{5 \sin \left(30^{\circ}\right)}{\sin \left(15^{\circ}\right)} \approx 9.66\) miles. Next, to find the point on the coast closest to the island, which we’ve labeled as \(C\), we need to find the perpendicular distance from the island to the coast. 11

Let \(x\) denote the distance from the second observation point \(Q\) to the point \(C\) and let \(y\) denote the distance from \(C\) to the island. Using Theorem 10.4 , we get \(\sin \left(45^{\circ}\right)=\frac{y}{d}\). After some rearranging, we find \(y=d \sin \left(45^{\circ}\right) \approx 9.66\left(\frac{\sqrt{2}}{2}\right) \approx 6.83\) miles. Hence, the island is approximately 6.83 miles from the coast. To find the distance from \(Q\) to \(C\), we note that \(\beta=180^{\circ}-90^{\circ}-45^{\circ}=45^{\circ}\) so by symmetry, 12 we get \(x=y \approx 6.83\) miles. Hence, the point on the shore closest to the island is approximately 6.83 miles down the coast from the second observation point.

We close this section with a new formula to compute the area enclosed by a triangle. Its proof uses the same cases and diagrams as the proof of the Law of Sines and is left as an exercise.

Theorem 11.4

Suppose \((\alpha, a),(\beta, b) \text { and }(\gamma, c)\) are the angle-side opposite pairs of a triangle. Then the area \(A\) enclosed by the triangle is given by

\(A=\frac{1}{2} b c \sin (\alpha)=\frac{1}{2} a c \sin (\beta)=\frac{1}{2} a b \sin (\gamma)\)

Example 11.2.4

Find the area of the triangle in Example 11.2.2 number 1.

From our work in Example 11.2.2 number 1, we have all three angles and all three sides to work with. However, to minimize propagated error, we choose \(A=\frac{1}{2} a c \sin (\beta)\) from Theorem 11.4 because it uses the most pieces of given information. We are given \(a=7\) and \(\beta=45^{\circ}\), and we calculated \(c=\frac{7 \sin \left(15^{\circ}\right)}{\sin \left(120^{\circ}\right)}\). Using these values, we find \(A=\frac{1}{2}(7)\left(\frac{7 \sin \left(15^{\circ}\right)}{\sin \left(120^{\circ}\right)}\right) \sin \left(45^{\circ}\right)=\approx 5.18\) square units. The reader is encouraged to check this answer against the results obtained using the other formulas in Theorem 11.4 .

11.2.1 Exercises

In Exercises 1 - 20, solve for the remaining side(s) and angle(s) if possible. As in the text, \((\alpha, a)\), \((\beta, b)\) and \((\gamma, c)\) are angle-side opposite pairs.

• \(\alpha=13^{\circ}, \beta=17^{\circ}, a=5\)
• \(\alpha=73.2^{\circ}, \beta=54.1^{\circ}, a=117\)
• \(\alpha=95^{\circ}, \beta=85^{\circ}, a=33.33\)
• \(\alpha=95^{\circ}, \beta=62^{\circ}, a=33.33\)
• \(\alpha=117^{\circ}, a=35, b=42\)
• \(\alpha=117^{\circ}, a=45, b=42\)
• \(\alpha=68.7^{\circ}, a=88, b=92\)
• \(\alpha=42^{\circ}, a=17, b=23.5\)
• \(\alpha=68.7^{\circ}, a=70, b=90\)
• \(\alpha=30^{\circ}, a=7, b=14\)
• \(\alpha=42^{\circ}, a=39, b=23.5\)
• \(\gamma=53^{\circ}, \alpha=53^{\circ}, c=28.01\)
• \(\alpha=6^{\circ}, a=57, b=100\)
• \(\gamma=74.6^{\circ}, c=3, a=3.05\)
• \(\beta=102^{\circ}, b=16.75, c=13\)
• \(\beta=102^{\circ}, b=16.75, c=18\)
• \(\beta=102^{\circ}, \gamma=35^{\circ}, b=16.75\)
• \(\beta=29.13^{\circ}, \gamma=83.95^{\circ}, b=314.15\)
• \(\gamma=120^{\circ}, \beta=61^{\circ}, c=4\)
• \(\alpha=50^{\circ}, a=25, b=12.5\)
• Find the area of the triangles given in Exercises 1, 12 and 20 above.

(Another Classic Application: Grade of a Road) The grade of a road is much like the pitch of a roof (See Example 10.6.6 ) in that it expresses the ratio of rise/run. In the case of a road, this ratio is always positive because it is measured going uphill and it is usually given as a percentage. For example, a road which rises 7 feet for every 100 feet of (horizontal) forward progress is said to have a 7% grade. However, if we want to apply any Trigonometry to a story problem involving roads going uphill or downhill, we need to view the grade as an angle with respect to the horizontal. In Exercises 22 - 24, we first have you change road grades into angles and then use the Law of Sines in an application.

• Using a right triangle with a horizontal leg of length 100 and vertical leg with length 7, show that a \(7 \%\) grade means that the road (hypotenuse) makes about a \(4^{\circ}\) angle with the horizontal. (It will not be exactly \(4^{\circ}\), but it’s pretty close.)
• What grade is given by a \(9.65^{\circ}\) angle made by the road and the horizontal? 13
• Along a long, straight stretch of mountain road with a 7% grade, you see a tall tree standing perfectly plumb alongside the road. 14 From a point 500 feet downhill from the tree, the angle of inclination from the road to the top of the tree is \(6^{\circ}\). Use the Law of Sines to find the height of the tree. (Hint: First show that the tree makes a \(94^{\circ}\) angle with the road.)

(Another Classic Application: Bearings) In the next several exercises we introduce and work with the navigation tool known as bearings. Simply put, a bearing is the direction you are heading according to a compass. The classic nomenclature for bearings, however, is not given as an angle in standard position, so we must first understand the notation. A bearing is given as an acute angle of rotation (to the east or to the west) away from the north-south (up and down) line of a compass rose. For example, \(\mathrm{N} 40^{\circ} \mathrm{E}\) (read "\(40^{\circ}\) east of north”) is a bearing which is rotated clockwise \(40^{\circ}\) from due north. If we imagine standing at the origin in the Cartesian Plane, this bearing would have us heading into Quadrant I along the terminal side of \(\theta=50^{\circ}\). Similarly, \(\mathrm{S} 50^{\circ} \mathrm{W}\) would point into Quadrant III along the terminal side of \(\theta=220^{\circ}\) because we started out pointing due south (along \(\theta=270^{\circ}\)) and rotated clockwise \(50^{\circ}\) back to \(220^{\circ}\). Counter-clockwise rotations would be found in the bearings \(\mathrm{N} 60^{\circ} \mathrm{W}\) (which is on the terminal side of \(\theta=150^{\circ}\)) and \(\mathrm{S} 27^{\circ} \mathrm{E}\) (which lies along the terminal side of \(\theta=297^{\circ}\)). These four bearings are drawn in the plane below.

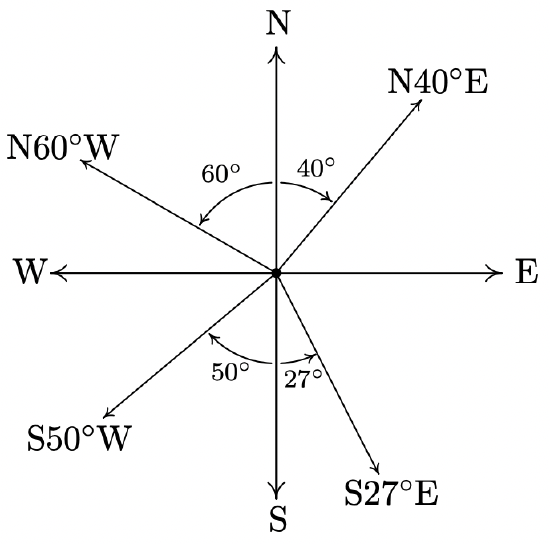
The cardinal directions north, south, east and west are usually not given as bearings in the fashion described above, but rather, one just refers to them as ‘due north’, ‘due south’, ‘due east’ and ‘due west’, respectively, and it is assumed that you know which quadrantal angle goes with each cardinal direction. (Hint: Look at the diagram above.)

• \(\mathrm{S} 83^{\circ} \mathrm{E}\)
• \(\mathrm{N} 5.5^{\circ} \mathrm{E}\)
• \(\mathrm{N} 31.25^{\circ} \mathrm{W}\)
• \(\mathrm{S}{72}^{\circ} 41^{\prime} 12^{\prime \prime} \mathrm{W}\) 15
• \(\mathrm{N} 45^{\circ} \mathrm{E}\)
• \(\mathrm{S}{45}{ }^{\circ} \mathrm{W}\)
• The Colonel spots a campfire at a of bearing \(\mathrm{N} 42^{\circ} \mathrm{E}\) from his current position. Sarge, who is positioned 3000 feet due east of the Colonel, reckons the bearing to the fire to be \(\mathrm{N} 20^{\circ} \mathrm{W}\) from his current position. Determine the distance from the campfire to each man, rounded to the nearest foot.
• A hiker starts walking due west from Sasquatch Point and gets to the Chupacabra Trailhead before she realizes that she hasn’t reset her pedometer. From the Chupacabra Trailhead she hikes for 5 miles along a bearing of \(\mathrm{N} 53^{\circ} \mathrm{W}\) which brings her to the Muffin Ridge Observatory. From there, she knows a bearing of \(\mathrm{S}6 5^{\circ} \mathrm{E}\) will take her straight back to Sasquatch Point. How far will she have to walk to get from the Muffin Ridge Observatory to Sasquach Point? What is the distance between Sasquatch Point and the Chupacabra Trailhead?
• The captain of the SS Bigfoot sees a signal flare at a bearing of \(\mathrm{N} 15^{\circ} \mathrm{E}\) from her current location. From his position, the captain of the HMS Sasquatch finds the signal flare to be at a bearing of \(\mathrm{N} 75^{\circ} \mathrm{W}\). If the SS Bigfoot is 5 miles from the HMS Sasquatch and the bearing from the SS Bigfoot to the HMS Sasquatch is \(\mathrm{N} 50^{\circ} \mathrm{E}\), find the distances from the flare to each vessel, rounded to the nearest tenth of a mile.
• Carl spies a potential Sasquatch nest at a bearing of \(\mathrm{N} 10^{\circ} \mathrm{E}\) and radios Jeff, who is at a bearing of \(\mathrm{N} 50^{\circ} \mathrm{E}\) from Carl’s position. From Jeff’s position, the nest is at a bearing of \(\mathrm{S} 70^{\circ} \mathrm{W}\). If Jeff and Carl are 500 feet apart, how far is Jeff from the Sasquatch nest? Round your answer to the nearest foot.
• A hiker determines the bearing to a lodge from her current position is \(\mathrm{S} 40^{\circ} \mathrm{W}\). She proceeds to hike 2 miles at a bearing of \(\mathrm{S} 20^{\circ} \mathrm{E}\) at which point she determines the bearing to the lodge is \(\mathrm{S}{75}{ }^{\circ} \mathrm{W}\). How far is she from the lodge at this point? Round your answer to the nearest hundredth of a mile.
• A watchtower spots a ship off shore at a bearing of \(\mathrm{N} 70^{\circ} \mathrm{E}\). A second tower, which is 50 miles from the first at a bearing of \(\mathrm{S} 80^{\circ} \mathrm{E}\) from the first tower, determines the bearing to the ship to be \(\mathrm{N} 25^{\circ} \mathrm{W}\). How far is the boat from the second tower? Round your answer to the nearest tenth of a mile.
• Skippy and Sally decide to hunt UFOs. One night, they position themselves 2 miles apart on an abandoned stretch of desert runway. An hour into their investigation, Skippy spies a UFO hovering over a spot on the runway directly between him and Sally. He records the angle of inclination from the ground to the craft to be \(75^{\circ}\) and radios Sally immediately to find the angle of inclination from her position to the craft is \(50^{\circ}\). How high off the ground is the UFO at this point? Round your answer to the nearest foot. (Recall: 1 mile is 5280 feet.)
• The angle of depression from an observer in an apartment complex to a gargoyle on the building next door is \(55^{\circ}\). From a point five stories below the original observer, the angle of inclination to the gargoyle is \(20^{\circ}\). Find the distance from each observer to the gargoyle and the distance from the gargoyle to the apartment complex. Round your answers to the nearest foot. (Use the rule of thumb that one story of a building is 9 feet.)
• Prove that the Law of Sines holds when \(\triangle A B C\) is a right triangle.
• Discuss with your classmates why knowing only the three angles of a triangle is not enough to determine any of the sides.
• Discuss with your classmates why the Law of Sines cannot be used to find the angles in the triangle when only the three sides are given. Also discuss what happens if only two sides and the angle between them are given. (Said another way, explain why the Law of Sines cannot be used in the SSS and SAS cases.)
• the information yields no triangle
• the information yields exactly one right triangle
• the information yields two distinct triangles
• the information yields exactly one obtuse triangle

Explain why you cannot choose \(a\) in such a way as to have \(\alpha=30^{\circ}, b=10\) and your choice of \(a\) yield only one triangle where that unique triangle has three acute angles.

• Use the cases and diagrams in the proof of the Law of Sines ( Theorem 11.2 ) to prove the area formulas given in Theorem 11.4 . Why do those formulas yield square units when four quantities are being multiplied together?

11.2.2 Answers

• \(\begin{array}{lll} \alpha=13^{\circ} & \beta=17^{\circ} & \gamma=150^{\circ} \\ a=5 & b \approx 6.50 & c \approx 11.11 \end{array}\)
• \(\begin{array}{lll} \alpha=73.2^{\circ} & \beta=54.1^{\circ} & \gamma=52.7^{\circ} \\ a=117 & b \approx 99.00 & c \approx 97.22 \end{array}\)
• Information does not produce a triangle
• \( \begin{array}{lll} \alpha=95^{\circ} & \beta=62^{\circ} & \gamma=23^{\circ} \\ a=33.33 & b \approx 29.54 & c \approx 13.07 \end{array}\)
• \(\begin{array}{lll} \alpha=117^{\circ} & \beta \approx 56.3^{\circ} & \gamma \approx 6.7^{\circ} \\ a=45 & b=42 & c \approx 5.89 \end{array}\)
• \(\begin{array}{lll} \alpha=68.7^{\circ} & \beta \approx 76.9^{\circ} & \gamma \approx 34.4^{\circ} \\ a=88 & b=92 & c \approx 53.36 \end{array}\)
• \(\begin{array}{lll} \alpha=42^{\circ} & \beta \approx 67.66^{\circ} & \gamma \approx 70.34^{\circ} \\ a=17 & b=23.5 & c \approx 23.93 \end{array}\)
• \(\begin{array}{lll} \alpha=30^{\circ} & \beta=90^{\circ} & \gamma=60^{\circ} \\ a=7 & b=14 & c=7 \sqrt{3} \end{array}\)
• \(\begin{array}{lll} \alpha=42^{\circ} & \beta \approx 23.78^{\circ} & \gamma \approx 114.22^{\circ} \\ a=39 & b=23.5 & c \approx 53.15 \end{array}\)
• \(\begin{array}{lll} \alpha=53^{\circ} & \beta=74^{\circ} & \gamma=53^{\circ} \\ a=28.01 & b \approx 33.71 & c=28.01 \end{array}\)
• \(\begin{array}{lll} \alpha=6^{\circ} & \beta \approx 169.43^{\circ} & \gamma \approx 4.57^{\circ} \\ a=57 & b=100 & c \approx 43.45 \end{array}\)
• \(\begin{array}{lll} \alpha \approx 78.59^{\circ} & \beta \approx 26.81^{\circ} & \gamma=74.6^{\circ} \\ a=3.05 & b \approx 1.40 & c=3 \end{array}\)
• \(\begin{array}{lll} \alpha \approx 28.61^{\circ} & \beta=102^{\circ} & \gamma \approx 49.39^{\circ} \\ a \approx 8.20 & b=16.75 & c=13 \end{array}\)
• \(\begin{array}{lll} \alpha=43^{\circ} & \beta=102^{\circ} & \gamma=35^{\circ} \\ a \approx 11.68 & b=16.75 & c \approx 9.82 \end{array}\)
• \(\begin{array}{lll} \alpha=66.92^{\circ} & \beta=29.13^{\circ} & \gamma=83.95^{\circ} \\ a \approx 593.69 & b=314.15 & c \approx 641.75 \end{array}\)
• \(\begin{array}{lll} \alpha=50^{\circ} & \beta \approx 22.52^{\circ} & \gamma \approx 107.48^{\circ} \\ a=25 & b=12.5 & c \approx 31.13 \end{array}\)

The area of the triangle from Exercise 12 is about 377.1 square units.

The area of the triangle from Exercise 20 is about 149 square units.

• \(\arctan \left(\frac{7}{100}\right) \approx 0.699 \text { radians }\), which is equivalent to \(\(4.004^{\circ}\)
• About 53 feet
• \(\theta=180^{\circ}\)
• \(\theta=353^{\circ}\)
• \(\theta=84.5^{\circ}\)
• \(\theta=270^{\circ}\)
• \(\theta=121.25^{\circ}\)
• \(\theta=197^{\circ} 18^{\prime} 48^{\prime \prime}\)
• \(\theta=45^{\circ}\)
• \(\theta=225^{\circ}\)

Sarge is about 2525 feet to the campfire.

The distance from Sasquatch Point to the Chupacabra Trailhead is about 2.46 miles.

The HMS Sasquatch is about 2.9 miles from the flare.

• Jeff is about 371 feet from the nest.
• She is about 3.02 miles from the lodge
• The boat is about 25.1 miles from the second tower.
• The UFO is hovering about 9539 feet above the ground.

The gargoyle is about 27 feet from the observer on the lower floor.

The gargoyle is about 25 feet from the other building.

1 as well as the measure of said angle

2 as well as the length of said side

3 Your Science teachers should thank us for this.

4 Don’t worry! Radians will be back before you know it!

5 The exact value of \(\sin \left(15^{\circ}\right)\) could be found using the difference identity for sine or a half-angle formula, but that becomes unnecessarily messy for the discussion at hand. Thus “exact” here means \(\frac{7 \sin \left(15^{\circ}\right)}{\sin \left(120^{\circ}\right)}\).

6 To find an exact expression for \(\beta\), we convert everything back to radians: \(\alpha=30^{\circ}=\frac{\pi}{6}\) radians, \(\gamma=\arcsin \left(\frac{2}{3}\right)\) radians and \(180^{\circ}=\pi\) radians. Hence, \(\beta=\pi-\frac{\pi}{6}-\arcsin \left(\frac{2}{3}\right)=\frac{5 \pi}{6}-\arcsin \left(\frac{2}{3}\right) \text { radians } \approx 108.19^{\circ}\).

7 An exact answer for \(\beta\) in this case is \(\beta=\arcsin \left(\frac{2}{3}\right)-\frac{\pi}{6} \text { radians } \approx 11.81^{\circ}\).

8 If this sounds familiar, it should. From high school Geometry, we know there are four congruence conditions for triangles: Angle-Angle-Side (AAS), Angle-Side-Angle (ASA), Side-Angle-Side (SAS) and Side-Side-Side (SSS). If we are given information about a triangle that meets one of these four criteria, then we are guaranteed that exactly one triangle exists which satisfies the given criteria.

9 In more reputable books, this is called the ‘Side-Side-Angle’ or SSA case.

10 Remember, we have already argued that a triangle exists in this case!

11 Do you see why \(C\) must lie to the right of \(Q\)?

12 Or by Theorem 10.4 again . . .

13 I have friends who live in Pacifica, CA and their road is actually this steep. It’s not a nice road to drive.

14 The word ‘plumb’ here means that the tree is perpendicular to the horizontal.

15 See Example 10.1.1 in Section 10.1 for a review of the DMS system.

Module 13: Non-Right Triangles

Introduction to law of sines, learning objectives.

By the end of this section, you will be able to:

• Use the Law of Sines to solve oblique triangles.
• Solve applied problems using the Law of Sines.

Suppose two radar stations located 20 miles apart each detect an aircraft between them. The angle of elevation measured by the first station is 35 degrees, whereas the angle of elevation measured by the second station is 15 degrees. How can we determine the altitude of the aircraft? We see in Figure 1 that the triangle formed by the aircraft and the two stations is not a right triangle, so we cannot use what we know about right triangles. In this section, we will find out how to solve problems involving non-right triangles .

• Precalculus. Authored by : OpenStax College. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:1/Preface . License : CC BY: Attribution

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 2: Trigonometric functions

About this unit.

Discover how to measure angles, distances, and heights using trigonometric ratios and the unit circle. Learn how to use sine, cosine, and tangent to solve real-world problems involving triangles and circular motion.

Unit circle introduction

• Unit circle (Opens a modal)
• The trig functions & right triangle trig ratios (Opens a modal)
• Trig unit circle review (Opens a modal)
• Trigonometric functions: FAQ (Opens a modal)
• Unit circle Get 3 of 4 questions to level up!
• Intro to radians (Opens a modal)
• Radians & degrees (Opens a modal)
• Degrees to radians (Opens a modal)
• Radians to degrees (Opens a modal)
• Radian angles & quadrants (Opens a modal)
• Radians & degrees Get 3 of 4 questions to level up!
• Unit circle (with radians) Get 3 of 4 questions to level up!

The Pythagorean identity

• Proof of the Pythagorean trig identity (Opens a modal)
• Using the Pythagorean trig identity (Opens a modal)
• Pythagorean identity review (Opens a modal)
• Use the Pythagorean identity Get 3 of 4 questions to level up!

Special trigonometric values in the first quadrant

• Cosine, sine and tangent of π/6 and π/3 (Opens a modal)
• Trig values of π/4 (Opens a modal)
• Trig values of π/6, π/4, and π/3 Get 3 of 4 questions to level up!

Trigonometric values on the unit circle

• Sine & cosine identities: symmetry (Opens a modal)
• Tangent identities: symmetry (Opens a modal)
• Sine & cosine identities: periodicity (Opens a modal)
• Tangent identities: periodicity (Opens a modal)
• Trig identities from reflections and rotations Get 3 of 4 questions to level up!
• Trig values of special angles Get 3 of 4 questions to level up!

Graphs of sin(x), cos(x), and tan(x)

• Graph of y=sin(x) (Opens a modal)
• Intersection points of y=sin(x) and y=cos(x) (Opens a modal)
• Graph of y=tan(x) (Opens a modal)

Amplitude, midline, and period

• Features of sinusoidal functions (Opens a modal)
• Midline, amplitude, and period review (Opens a modal)
• Midline of sinusoidal functions from graph Get 3 of 4 questions to level up!
• Amplitude of sinusoidal functions from graph Get 3 of 4 questions to level up!
• Period of sinusoidal functions from graph Get 3 of 4 questions to level up!

Transforming sinusoidal graphs

• Amplitude & period of sinusoidal functions from equation (Opens a modal)
• Transforming sinusoidal graphs: vertical stretch & horizontal reflection (Opens a modal)
• Transforming sinusoidal graphs: vertical & horizontal stretches (Opens a modal)
• Amplitude of sinusoidal functions from equation Get 3 of 4 questions to level up!
• Midline of sinusoidal functions from equation Get 3 of 4 questions to level up!
• Period of sinusoidal functions from equation Get 3 of 4 questions to level up!

Graphing sinusoidal functions

• Example: Graphing y=3⋅sin(½⋅x)-2 (Opens a modal)
• Example: Graphing y=-cos(π⋅x)+1.5 (Opens a modal)
• Sinusoidal function from graph (Opens a modal)
• Graph sinusoidal functions Get 3 of 4 questions to level up!
• Construct sinusoidal functions Get 3 of 4 questions to level up!
• Graph sinusoidal functions: phase shift Get 3 of 4 questions to level up!

Sinusoidal models

• Interpreting trigonometric graphs in context (Opens a modal)
• Trig word problem: modeling daily temperature (Opens a modal)
• Trig word problem: modeling annual temperature (Opens a modal)
• Trig word problem: length of day (phase shift) (Opens a modal)
• Interpreting trigonometric graphs in context Get 3 of 4 questions to level up!
• Modeling with sinusoidal functions Get 3 of 4 questions to level up!
• Modeling with sinusoidal functions: phase shift Get 3 of 4 questions to level up!

Long live Tau

• Tau versus pi (Opens a modal)
• Pi is (still) wrong (Opens a modal)

Have an account?

Laws of Sine and Cosine

9th - 12th grade, mathematics.

20 questions

Introducing new   Paper mode

No student devices needed.   Know more

• 1. Multiple Choice Edit 5 minutes 1 pt Given: B = 70°, a = 11, C = 40° Find: c 11 7.5 70 8
• 2. Multiple Choice Edit 5 minutes 1 pt A=122° c=22 a=31 find B 37 21 13.1 49
• 3. Multiple Choice Edit 5 minutes 1 pt Given: A = 45°, B = 65°, c = 25 Find: a 19 24.1 70 18.8
• 4. Multiple Choice Edit 5 minutes 1 pt Solve the Triangle B= 85°, C= 47°, and a=19 Find A, b, and c A= 48°, b=25.5, c= 17.8 A= 48°, b= 19.5, c= 23.4 A= 90°, b= 14, c= 23.6 A= 39°, b= 19, c= 19√2
• 5. Multiple Choice Edit 5 minutes 1 pt Solve the Triangle a=38, b= 31, c= 35 Find A, B and C A= 43°, B= 47°, C= 90° A= 70°, B= 50.1°, C= 59.9° A= 50.1°, B= 70°, C= 59.9° A= 60°, B= 70°, C= 50°
• 6. Multiple Choice Edit 5 minutes 1 pt A triangle has side lengths of 3, 8, and 9.  Find the angle measurement for the angle across from the side with length of 8. 19 o 80 o 61 o 53 o
• 7. Multiple Choice Edit 5 minutes 1 pt Angle C is 41 o , side AC is 13 and side CB is 29.  Find side AB. 18.5 32 30 21
• 19. Multiple Choice Edit 30 seconds 1 pt Will this make 1 triangle? 2 triangles? or no triangles? A= 37°, a=8, b=14 1 Trianlge 2 Triangles No Triangles
• 20. Multiple Choice Edit 30 seconds 1 pt Will this make 1 triangle? 2 Triangles? or No Triangles? B= 70°, b=85, c=88 1 Triangle 2 Triangles No Triangles

Explore all questions with a free account

Continue with email

Continue with phone

Law of Cosines Calculator

Table of contents

The law of cosines calculator can help you solve a vast number of triangular problems. You will learn what is the law of cosines (also known as the cosine rule), the law of cosines formula , and its applications. Scroll down to find out when and how to use the law of cosines, and check out the proofs of this law. Thanks to this triangle calculator, you will be able to find the properties of any arbitrary triangle quickly.

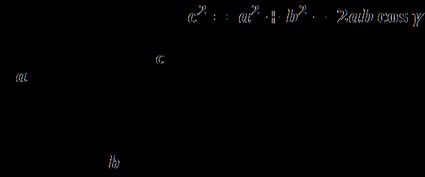
But if, somehow, you're wondering what the heck is cosine, better have a look at our cosine calculator .

Law of cosines formula

The law of cosines states that, for a triangle with sides and angles denoted with symbols as illustrated above,

a² = b² + c² - 2bc × cos(α)

b² = a² + c² - 2ac × cos(β)

c² = a² + b² - 2ab × cos(γ)

For a right triangle, the angle gamma, which is the angle between legs a and b , is equal to 90°. The cosine of 90° = 0, so in that special case, the law of cosines formula is reduced to the well-known equation of Pythagorean theorem :

a² = b² + c² - 2bc × cos(90°)

a² = b² + c²

What is the law of cosines?

The law of cosines (alternatively the cosine formula or cosine rule) describes the relationship between the lengths of a triangle's sides and the cosine of its angles. It can be applied to all triangles, not only the right triangles. This law generalizes the Pythagorean theorem, as it allows you to calculate the length of one of the sides, given you know the length of both the other sides and the angle between them.

The law appeared in Euclid's Element , a mathematical treatise containing definitions, postulates, and geometry theorems. Euclid didn't formulate it in the way we learn it today, as the concept of cosine had not been developed yet.

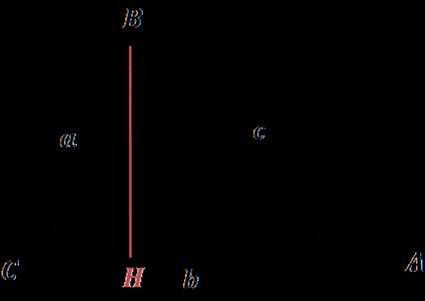
AB² = CA² + CB² - 2 × CA × CH (for acute angles, '+' for obtuse)

However, we may reformulate Euclid's theorem easily to the current cosine formula form:

CH = CB × cos(γ) , so AB² = CA² + CB² - 2 × CA × (CB × cos(γ))

Changing notation, we obtain the familiar expression:

The first explicit equation of the cosine rule was presented by Persian mathematician d'Al-Kashi in the 15th century. In the 16th century, the law was popularized by famous French mathematician Viète before it received its final shape in the 19th century.

Applications of the law of cosines

You can transform these law of cosines formulas to solve some problems of triangulation (solving a triangle). You can use them to find:

The third side of a triangle , knowing two sides and the angle between them (SAS):

a = √[b² + c² - 2bc × cos(α)]

b = √[a² + c² - 2ac × cos(β)]

c = √[a² + b² - 2ab × cos(γ)]

The angles of a triangle , knowing all three sides (SSS):

α = arccos [(b² + c² - a²)/(2bc)]

β = arccos [(a² + c² - b²)/(2ac)]

γ = arccos [(a² + b² - c²)/(2ab)]

The third side of a triangle , knowing two sides and an angle opposite to one of them (SSA):

a = b × cos(γ) ± √[c² - b² × sin²(γ)]

b = c × cos(α) ± √[a² - c² × sin²(α)]

c = a × cos(β) ± √[b² - a² × sin²(β)]

Just remember that knowing two sides and an adjacent angle can yield two distinct possible triangles (or one or zero positive solutions, depending on the given data). That's why we've decided to implement SAS and SSS in this tool, but not SSA.

The law of cosines is one of the basic laws, and it's widely used for many geometric problems. We also take advantage of that law in many Omnitools, to mention only a few:

• Triangle angle calculator
• Triangle area calculator
• Perimeter of a triangle calculator
• Triangular prism calculator

Also, you can combine the law of cosines calculator with the law of sines to solve other problems, for example, finding the side of the triangle, given two of the angles and one side (AAS and ASA).

Law of cosines proofs

There are many ways in which you can prove the law of cosines equation. You've already read about one of them – it comes directly from Euclid's formulation of the law and an application of the Pythagorean theorem. You can write the other proofs of the law of cosines using:

1. Trigonometry

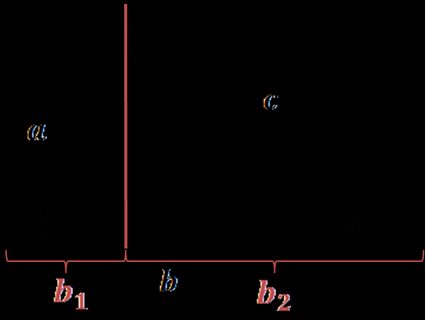
Draw a line for the height of the triangle and divide the side perpendicular to it into two parts:

b = b₁ + b₂

From sine and cosine definitions, b₁ might be expressed as a × cos(γ) and b₂ = c × cos(α) . Hence:

b = a × cos(γ) + c × cos(α) and by multiplying it by b , we get:

b² = ab × cos(γ) + bc × cos(α) (1)

Analogical equations may be derived for other two sides:

a² = ac × cos(β) + ab × cos(γ) (2)

c² = bc × cos(α) + ac × cos(β) (3)

To finish the law of cosines proof, you need to add the equation (1) and (2) and subtract (3):

a² + b² - c² = ac × cos(β) + ab × cos(γ) + bc × cos(α) + ab × cos(γ) - bc × cos(α) - ac × cos(β)

Reduction and simplification of the equation give one of the forms of the cosine rule:

a² + b² - c² = 2ab × cos(γ)

By changing the order in which they are added and subtracted, you can derive the other law of cosine formulas.

2. Distance formula

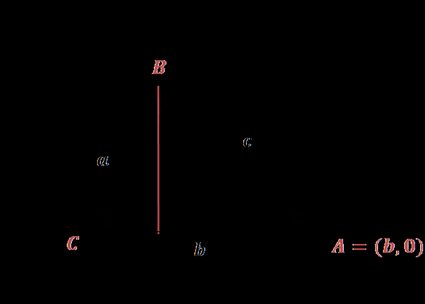
Let C = (0,0) , A = (b,0) , as in the image.

To find the coordinates of B, we can use the definition of sine and cosine:

B = (a × cos(γ), a × sin(γ))

From the distance formula , we can find that:

c = √[(x₂ - x₁)² + (y₂ - y₁)²] = √[(a × cos(γ) - b)² + (a × sin(γ) - 0)²]

c² = a² × cos(γ)² - 2ab × cos(γ) + b² + a² × sin(γ)²

c² = b² + a²(sin(γ)² + cos(γ)²) - 2ab × cos(γ)

As a sum of squares of sine and cosine is equal to 1, we obtain the final formula:

3. Ptolemy's theorem

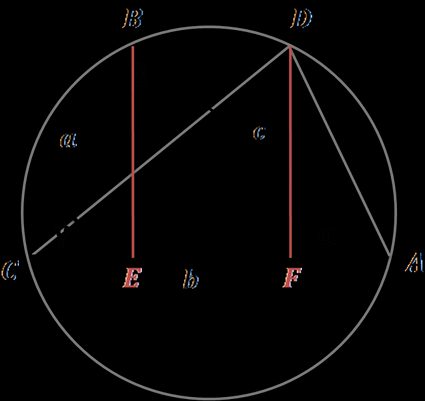
Another law of cosines proof that is relatively easy to understand uses Ptolemy's theorem:

Assume we have the triangle ABC drawn in its circumcircle, as in the picture.

Construct the congruent triangle ADC, where AD = BC and DC = BA

The heights from points B and D split the base AC by E and F, respectively. CE equals FA.

From the cosine definition, we can express CE as a × cos(γ) .

Thus, we can write that BD = EF = AC - 2 × CE = b - 2 × a × cos(γ) .

Then, for our quadrilateral ADBC, we can use Ptolemy's theorem , which explains the relation between the four sides and two diagonals. The theorem states that for cyclic quadrilaterals, the sum of products of opposite sides is equal to the product of the two diagonals:

BC × DA + CA × BD = AB × CD

so in our case:

a² + b × (b - 2 × a × cos(γ)) + a² = c²

After reduction, we get the final formula:

The great advantage of these three proofs is their universality – they work for acute, right, and obtuse triangles.

• Using the law of sines
• Using the definition of dot product
• Comparison of areas
• Geometry of the circle

The last two proofs require the distinction between different triangle cases. The one based on the definition of dot product is shown in another article, and the proof using the law of sines is quite complicated, so we have decided not to reproduce it here. If you're curious about these law of cosines proofs, check out the Wikipedia explanation.

How to use the law of cosines calculator

Start with formulating your problem. For example, you may know two sides of the triangle and the angle between them and are looking for the remaining side.

Input the known values into the appropriate boxes of this triangle calculator. Remember to double-check with the figure above whether you denoted the sides and angles with correct symbols.

Watch our law of cosines calculator perform all the calculations for you!

Law of cosines – SSS example

If your task is to find the angles of a triangle given all three sides, all you need to do is to use the transformed cosine rule formulas:

α = arccos [(b² + c² - a²)/(2bc)] β = arccos [(a² + c² - b²)/(2ac)] γ = arccos [(a² + b² - c²)/(2ab)]

Let's calculate one of the angles. Assume we have a = 4 in, b = 5 in and c = 6 in. We'll use the first equation to find α:

= arccos [(5² + 6² - 4²)/(2 × 5 × 6)]

= arccos [(25 + 36 - 16)/60]

= arccos [(45/60)] = arccos [0.75]

You may calculate the second angle from the second equation in an analogical way, and the third angle you can find by knowing that the sum of the angles in a triangle is equal to 180° (π).

If you want to save some time, type the side lengths into our law of cosines calculator - our tool is a safe bet! Just follow these simple steps:

Choose the option depending on given values . We need to pick the second option – SSS (3 sides) .

Enter the known values . Type the sides: a = 4 in, b = 5 in, and c = 6 in.

The calculator displays the result! In our case the angles are equal to α = 41.41°, β = 55.77° and γ = 82.82°.

After such an explanation, we're sure that you understand what the law of cosine is and when to use it. Give this tool a try, solve some exercises, and remember that practice makes permanent!

When should I use the law of cosines?

Use the law of cosines if you need to calculate:

• A side of a triangle given two other sides and the angle between them.
• The three angles of a triangle given its sides.
• A side of a triangle given two other sides and an angle opposite to one of these sides.

When should I use the law of cosines vs the Pythagorean theorem?

The law of cosines is a generalization of the Pythagorean theorem, so whenever the latter works, the former can be applied as well. Not the other way round, though!

Is the law of cosines valid only for right triangles?

No , the law of cosines is valid for all triangles. In fact, when you apply the law of cosines to a right triangle, you'll arrive at the good old Pythagorean theorem.

What is the third side of a triangle with sides 5 and 6?

Besides the two sides, you need to know one of the inner angles of the triangle. Let's say it's the angle γ = 30° between the sides 5 and 6 . Then:

• Recall the law of cosines formula c² = a² + b² - 2ab × cos(γ)
• Plug in the values a = 5 , b = 6 , γ = 30° .
• We obtain c² = 25 + 36 - 2 × 5 × 6 × cos(30) ≈ 9 .
• Therefore, c ≈ 3 . Remember to include the units if you were given any!

.css-slt4t3.css-slt4t3{color:#2B3148;background-color:transparent;font-family:"Roboto","Helvetica","Arial",sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-slt4t3.css-slt4t3:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-slt4t3 .js-external-link-button.link-like,.css-slt4t3 .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-slt4t3 .js-external-link-button.link-like:hover,.css-slt4t3 .js-external-link-anchor:hover,.css-slt4t3 .js-external-link-button.link-like:active,.css-slt4t3 .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-slt4t3 .js-external-link-button.link-like:focus-visible,.css-slt4t3 .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-slt4t3 p,.css-slt4t3 div{margin:0px;display:block;}.css-slt4t3 pre{margin:0px;display:block;}.css-slt4t3 pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-slt4t3 pre:not(:first-child){padding-top:8px;}.css-slt4t3 ul,.css-slt4t3 ol{display:block margin:0px;padding-left:20px;}.css-slt4t3 ul li,.css-slt4t3 ol li{padding-top:8px;}.css-slt4t3 ul ul,.css-slt4t3 ol ul,.css-slt4t3 ul ol,.css-slt4t3 ol ol{padding-top:0px;}.css-slt4t3 ul:not(:first-child),.css-slt4t3 ol:not(:first-child){padding-top:4px;} .css-4okk7a{margin:auto;background-color:white;overflow:auto;overflow-wrap:break-word;word-break:break-word;}.css-4okk7a code,.css-4okk7a kbd,.css-4okk7a pre,.css-4okk7a samp{font-family:monospace;}.css-4okk7a code{padding:2px 4px;color:#444;background:#ddd;border-radius:4px;}.css-4okk7a figcaption,.css-4okk7a caption{text-align:center;}.css-4okk7a figcaption{font-size:12px;font-style:italic;overflow:hidden;}.css-4okk7a h3{font-size:1.75rem;}.css-4okk7a h4{font-size:1.5rem;}.css-4okk7a .mathBlock{font-size:24px;-webkit-padding-start:4px;padding-inline-start:4px;}.css-4okk7a .mathBlock .katex{font-size:24px;text-align:left;}.css-4okk7a .math-inline{background-color:#f0f0f0;display:inline-block;font-size:inherit;padding:0 3px;}.css-4okk7a .videoBlock,.css-4okk7a .imageBlock{margin-bottom:16px;}.css-4okk7a .imageBlock__image-align--left,.css-4okk7a .videoBlock__video-align--left{float:left;}.css-4okk7a .imageBlock__image-align--right,.css-4okk7a .videoBlock__video-align--right{float:right;}.css-4okk7a .imageBlock__image-align--center,.css-4okk7a .videoBlock__video-align--center{display:block;margin-left:auto;margin-right:auto;clear:both;}.css-4okk7a .imageBlock__image-align--none,.css-4okk7a .videoBlock__video-align--none{clear:both;margin-left:0;margin-right:0;}.css-4okk7a .videoBlock__video--wrapper{position:relative;padding-bottom:56.25%;height:0;}.css-4okk7a .videoBlock__video--wrapper iframe{position:absolute;top:0;left:0;width:100%;height:100%;}.css-4okk7a .videoBlock__caption{text-align:left;}@font-face{font-family:'KaTeX_AMS';src:url(/katex-fonts/KaTeX_AMS-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_AMS-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_AMS-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Script';src:url(/katex-fonts/KaTeX_Script-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Script-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Script-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size1';src:url(/katex-fonts/KaTeX_Size1-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size1-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size1-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size2';src:url(/katex-fonts/KaTeX_Size2-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size2-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size2-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size3';src:url(/katex-fonts/KaTeX_Size3-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size3-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size3-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size4';src:url(/katex-fonts/KaTeX_Size4-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size4-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size4-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Typewriter';src:url(/katex-fonts/KaTeX_Typewriter-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Typewriter-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Typewriter-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}.css-4okk7a .katex{font:normal 1.21em KaTeX_Main,Times New Roman,serif;line-height:1.2;text-indent:0;text-rendering:auto;}.css-4okk7a .katex *{-ms-high-contrast-adjust:none!important;border-color:currentColor;}.css-4okk7a .katex .katex-version::after{content:'0.13.13';}.css-4okk7a .katex .katex-mathml{position:absolute;clip:rect(1px, 1px, 1px, 1px);padding:0;border:0;height:1px;width:1px;overflow:hidden;}.css-4okk7a .katex .katex-html>.newline{display:block;}.css-4okk7a .katex .base{position:relative;display:inline-block;white-space:nowrap;width:-webkit-min-content;width:-moz-min-content;width:-webkit-min-content;width:-moz-min-content;width:min-content;}.css-4okk7a .katex .strut{display:inline-block;}.css-4okk7a .katex .textbf{font-weight:bold;}.css-4okk7a .katex .textit{font-style:italic;}.css-4okk7a .katex .textrm{font-family:KaTeX_Main;}.css-4okk7a .katex .textsf{font-family:KaTeX_SansSerif;}.css-4okk7a .katex .texttt{font-family:KaTeX_Typewriter;}.css-4okk7a .katex .mathnormal{font-family:KaTeX_Math;font-style:italic;}.css-4okk7a .katex .mathit{font-family:KaTeX_Main;font-style:italic;}.css-4okk7a .katex .mathrm{font-style:normal;}.css-4okk7a .katex .mathbf{font-family:KaTeX_Main;font-weight:bold;}.css-4okk7a .katex .boldsymbol{font-family:KaTeX_Math;font-weight:bold;font-style:italic;}.css-4okk7a .katex .amsrm{font-family:KaTeX_AMS;}.css-4okk7a .katex .mathbb,.css-4okk7a .katex .textbb{font-family:KaTeX_AMS;}.css-4okk7a .katex .mathcal{font-family:KaTeX_Caligraphic;}.css-4okk7a .katex .mathfrak,.css-4okk7a .katex .textfrak{font-family:KaTeX_Fraktur;}.css-4okk7a .katex .mathtt{font-family:KaTeX_Typewriter;}.css-4okk7a .katex .mathscr,.css-4okk7a .katex .textscr{font-family:KaTeX_Script;}.css-4okk7a .katex .mathsf,.css-4okk7a .katex .textsf{font-family:KaTeX_SansSerif;}.css-4okk7a .katex .mathboldsf,.css-4okk7a .katex .textboldsf{font-family:KaTeX_SansSerif;font-weight:bold;}.css-4okk7a .katex .mathitsf,.css-4okk7a .katex .textitsf{font-family:KaTeX_SansSerif;font-style:italic;}.css-4okk7a .katex .mainrm{font-family:KaTeX_Main;font-style:normal;}.css-4okk7a .katex .vlist-t{display:inline-table;table-layout:fixed;border-collapse:collapse;}.css-4okk7a .katex .vlist-r{display:table-row;}.css-4okk7a .katex .vlist{display:table-cell;vertical-align:bottom;position:relative;}.css-4okk7a .katex .vlist>span{display:block;height:0;position:relative;}.css-4okk7a .katex .vlist>span>span{display:inline-block;}.css-4okk7a .katex .vlist>span>.pstrut{overflow:hidden;width:0;}.css-4okk7a .katex .vlist-t2{margin-right:-2px;}.css-4okk7a .katex .vlist-s{display:table-cell;vertical-align:bottom;font-size:1px;width:2px;min-width:2px;}.css-4okk7a .katex .vbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:column;-ms-flex-direction:column;flex-direction:column;-webkit-align-items:baseline;-webkit-box-align:baseline;-ms-flex-align:baseline;align-items:baseline;}.css-4okk7a .katex .hbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:100%;}.css-4okk7a .katex .thinbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:0;max-width:0;}.css-4okk7a .katex .msupsub{text-align:left;}.css-4okk7a .katex .mfrac>span>span{text-align:center;}.css-4okk7a .katex .mfrac .frac-line{display:inline-block;width:100%;border-bottom-style:solid;}.css-4okk7a .katex .mfrac .frac-line,.css-4okk7a .katex .overline .overline-line,.css-4okk7a .katex .underline .underline-line,.css-4okk7a .katex .hline,.css-4okk7a .katex .hdashline,.css-4okk7a .katex .rule{min-height:1px;}.css-4okk7a .katex .mspace{display:inline-block;}.css-4okk7a .katex .llap,.css-4okk7a .katex .rlap,.css-4okk7a .katex .clap{width:0;position:relative;}.css-4okk7a .katex .llap>.inner,.css-4okk7a .katex .rlap>.inner,.css-4okk7a .katex .clap>.inner{position:absolute;}.css-4okk7a .katex .llap>.fix,.css-4okk7a .katex .rlap>.fix,.css-4okk7a .katex .clap>.fix{display:inline-block;}.css-4okk7a .katex .llap>.inner{right:0;}.css-4okk7a .katex .rlap>.inner,.css-4okk7a .katex .clap>.inner{left:0;}.css-4okk7a .katex .clap>.inner>span{margin-left:-50%;margin-right:50%;}.css-4okk7a .katex .rule{display:inline-block;border:solid 0;position:relative;}.css-4okk7a .katex .overline .overline-line,.css-4okk7a .katex .underline .underline-line,.css-4okk7a .katex .hline{display:inline-block;width:100%;border-bottom-style:solid;}.css-4okk7a .katex .hdashline{display:inline-block;width:100%;border-bottom-style:dashed;}.css-4okk7a .katex .sqrt>.root{margin-left:0.27777778em;margin-right:-0.55555556em;}.css-4okk7a .katex .sizing.reset-size1.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size1{font-size:1em;}.css-4okk7a .katex .sizing.reset-size1.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size2{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size1.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size3{font-size:1.4em;}.css-4okk7a .katex .sizing.reset-size1.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size4{font-size:1.6em;}.css-4okk7a .katex .sizing.reset-size1.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size5{font-size:1.8em;}.css-4okk7a .katex .sizing.reset-size1.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size6{font-size:2em;}.css-4okk7a .katex .sizing.reset-size1.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size7{font-size:2.4em;}.css-4okk7a .katex .sizing.reset-size1.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size8{font-size:2.88em;}.css-4okk7a .katex .sizing.reset-size1.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size9{font-size:3.456em;}.css-4okk7a .katex .sizing.reset-size1.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size10{font-size:4.148em;}.css-4okk7a .katex .sizing.reset-size1.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size1.size11{font-size:4.976em;}.css-4okk7a .katex .sizing.reset-size2.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size1{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size2.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size2{font-size:1em;}.css-4okk7a .katex .sizing.reset-size2.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size3{font-size:1.16666667em;}.css-4okk7a .katex .sizing.reset-size2.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size4{font-size:1.33333333em;}.css-4okk7a .katex .sizing.reset-size2.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size5{font-size:1.5em;}.css-4okk7a .katex .sizing.reset-size2.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size6{font-size:1.66666667em;}.css-4okk7a .katex .sizing.reset-size2.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size7{font-size:2em;}.css-4okk7a .katex .sizing.reset-size2.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size8{font-size:2.4em;}.css-4okk7a .katex .sizing.reset-size2.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size9{font-size:2.88em;}.css-4okk7a .katex .sizing.reset-size2.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size10{font-size:3.45666667em;}.css-4okk7a .katex .sizing.reset-size2.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size2.size11{font-size:4.14666667em;}.css-4okk7a .katex .sizing.reset-size3.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size1{font-size:0.71428571em;}.css-4okk7a .katex .sizing.reset-size3.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size2{font-size:0.85714286em;}.css-4okk7a .katex .sizing.reset-size3.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size3{font-size:1em;}.css-4okk7a .katex .sizing.reset-size3.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size4{font-size:1.14285714em;}.css-4okk7a .katex .sizing.reset-size3.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size5{font-size:1.28571429em;}.css-4okk7a .katex .sizing.reset-size3.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size6{font-size:1.42857143em;}.css-4okk7a .katex .sizing.reset-size3.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size7{font-size:1.71428571em;}.css-4okk7a .katex .sizing.reset-size3.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size8{font-size:2.05714286em;}.css-4okk7a .katex .sizing.reset-size3.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size9{font-size:2.46857143em;}.css-4okk7a .katex .sizing.reset-size3.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size10{font-size:2.96285714em;}.css-4okk7a .katex .sizing.reset-size3.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size3.size11{font-size:3.55428571em;}.css-4okk7a .katex .sizing.reset-size4.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size1{font-size:0.625em;}.css-4okk7a .katex .sizing.reset-size4.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size2{font-size:0.75em;}.css-4okk7a .katex .sizing.reset-size4.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size3{font-size:0.875em;}.css-4okk7a .katex .sizing.reset-size4.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size4{font-size:1em;}.css-4okk7a .katex .sizing.reset-size4.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size5{font-size:1.125em;}.css-4okk7a .katex .sizing.reset-size4.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size6{font-size:1.25em;}.css-4okk7a .katex .sizing.reset-size4.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size7{font-size:1.5em;}.css-4okk7a .katex .sizing.reset-size4.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size8{font-size:1.8em;}.css-4okk7a .katex .sizing.reset-size4.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size9{font-size:2.16em;}.css-4okk7a .katex .sizing.reset-size4.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size10{font-size:2.5925em;}.css-4okk7a .katex .sizing.reset-size4.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size4.size11{font-size:3.11em;}.css-4okk7a .katex .sizing.reset-size5.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size1{font-size:0.55555556em;}.css-4okk7a .katex .sizing.reset-size5.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size2{font-size:0.66666667em;}.css-4okk7a .katex .sizing.reset-size5.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size3{font-size:0.77777778em;}.css-4okk7a .katex .sizing.reset-size5.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size4{font-size:0.88888889em;}.css-4okk7a .katex .sizing.reset-size5.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size5{font-size:1em;}.css-4okk7a .katex .sizing.reset-size5.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size6{font-size:1.11111111em;}.css-4okk7a .katex .sizing.reset-size5.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size7{font-size:1.33333333em;}.css-4okk7a .katex .sizing.reset-size5.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size8{font-size:1.6em;}.css-4okk7a .katex .sizing.reset-size5.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size9{font-size:1.92em;}.css-4okk7a .katex .sizing.reset-size5.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size10{font-size:2.30444444em;}.css-4okk7a .katex .sizing.reset-size5.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size5.size11{font-size:2.76444444em;}.css-4okk7a .katex .sizing.reset-size6.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size1{font-size:0.5em;}.css-4okk7a .katex .sizing.reset-size6.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size2{font-size:0.6em;}.css-4okk7a .katex .sizing.reset-size6.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size3{font-size:0.7em;}.css-4okk7a .katex .sizing.reset-size6.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size4{font-size:0.8em;}.css-4okk7a .katex .sizing.reset-size6.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size5{font-size:0.9em;}.css-4okk7a .katex .sizing.reset-size6.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size6{font-size:1em;}.css-4okk7a .katex .sizing.reset-size6.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size7{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size6.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size8{font-size:1.44em;}.css-4okk7a .katex .sizing.reset-size6.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size9{font-size:1.728em;}.css-4okk7a .katex .sizing.reset-size6.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size10{font-size:2.074em;}.css-4okk7a .katex .sizing.reset-size6.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size6.size11{font-size:2.488em;}.css-4okk7a .katex .sizing.reset-size7.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size1{font-size:0.41666667em;}.css-4okk7a .katex .sizing.reset-size7.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size2{font-size:0.5em;}.css-4okk7a .katex .sizing.reset-size7.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size3{font-size:0.58333333em;}.css-4okk7a .katex .sizing.reset-size7.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size4{font-size:0.66666667em;}.css-4okk7a .katex .sizing.reset-size7.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size5{font-size:0.75em;}.css-4okk7a .katex .sizing.reset-size7.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size6{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size7.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size7{font-size:1em;}.css-4okk7a .katex .sizing.reset-size7.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size8{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size7.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size9{font-size:1.44em;}.css-4okk7a .katex .sizing.reset-size7.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size10{font-size:1.72833333em;}.css-4okk7a .katex .sizing.reset-size7.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size7.size11{font-size:2.07333333em;}.css-4okk7a .katex .sizing.reset-size8.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size1{font-size:0.34722222em;}.css-4okk7a .katex .sizing.reset-size8.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size2{font-size:0.41666667em;}.css-4okk7a .katex .sizing.reset-size8.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size3{font-size:0.48611111em;}.css-4okk7a .katex .sizing.reset-size8.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size4{font-size:0.55555556em;}.css-4okk7a .katex .sizing.reset-size8.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size5{font-size:0.625em;}.css-4okk7a .katex .sizing.reset-size8.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size6{font-size:0.69444444em;}.css-4okk7a .katex .sizing.reset-size8.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size7{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size8.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size8{font-size:1em;}.css-4okk7a .katex .sizing.reset-size8.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size9{font-size:1.2em;}.css-4okk7a .katex .sizing.reset-size8.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size10{font-size:1.44027778em;}.css-4okk7a .katex .sizing.reset-size8.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size8.size11{font-size:1.72777778em;}.css-4okk7a .katex .sizing.reset-size9.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size1{font-size:0.28935185em;}.css-4okk7a .katex .sizing.reset-size9.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size2{font-size:0.34722222em;}.css-4okk7a .katex .sizing.reset-size9.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size3{font-size:0.40509259em;}.css-4okk7a .katex .sizing.reset-size9.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size4{font-size:0.46296296em;}.css-4okk7a .katex .sizing.reset-size9.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size5{font-size:0.52083333em;}.css-4okk7a .katex .sizing.reset-size9.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size6{font-size:0.5787037em;}.css-4okk7a .katex .sizing.reset-size9.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size7{font-size:0.69444444em;}.css-4okk7a .katex .sizing.reset-size9.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size8{font-size:0.83333333em;}.css-4okk7a .katex .sizing.reset-size9.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size9{font-size:1em;}.css-4okk7a .katex .sizing.reset-size9.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size10{font-size:1.20023148em;}.css-4okk7a .katex .sizing.reset-size9.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size9.size11{font-size:1.43981481em;}.css-4okk7a .katex .sizing.reset-size10.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size1{font-size:0.24108004em;}.css-4okk7a .katex .sizing.reset-size10.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size2{font-size:0.28929605em;}.css-4okk7a .katex .sizing.reset-size10.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size3{font-size:0.33751205em;}.css-4okk7a .katex .sizing.reset-size10.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size4{font-size:0.38572806em;}.css-4okk7a .katex .sizing.reset-size10.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size5{font-size:0.43394407em;}.css-4okk7a .katex .sizing.reset-size10.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size6{font-size:0.48216008em;}.css-4okk7a .katex .sizing.reset-size10.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size7{font-size:0.57859209em;}.css-4okk7a .katex .sizing.reset-size10.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size8{font-size:0.69431051em;}.css-4okk7a .katex .sizing.reset-size10.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size9{font-size:0.83317261em;}.css-4okk7a .katex .sizing.reset-size10.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size10{font-size:1em;}.css-4okk7a .katex .sizing.reset-size10.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size10.size11{font-size:1.19961427em;}.css-4okk7a .katex .sizing.reset-size11.size1,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size1{font-size:0.20096463em;}.css-4okk7a .katex .sizing.reset-size11.size2,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size2{font-size:0.24115756em;}.css-4okk7a .katex .sizing.reset-size11.size3,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size3{font-size:0.28135048em;}.css-4okk7a .katex .sizing.reset-size11.size4,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size4{font-size:0.32154341em;}.css-4okk7a .katex .sizing.reset-size11.size5,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size5{font-size:0.36173633em;}.css-4okk7a .katex .sizing.reset-size11.size6,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size6{font-size:0.40192926em;}.css-4okk7a .katex .sizing.reset-size11.size7,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size7{font-size:0.48231511em;}.css-4okk7a .katex .sizing.reset-size11.size8,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size8{font-size:0.57877814em;}.css-4okk7a .katex .sizing.reset-size11.size9,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size9{font-size:0.69453376em;}.css-4okk7a .katex .sizing.reset-size11.size10,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size10{font-size:0.83360129em;}.css-4okk7a .katex .sizing.reset-size11.size11,.css-4okk7a .katex .fontsize-ensurer.reset-size11.size11{font-size:1em;}.css-4okk7a .katex .delimsizing.size1{font-family:KaTeX_Size1;}.css-4okk7a .katex .delimsizing.size2{font-family:KaTeX_Size2;}.css-4okk7a .katex .delimsizing.size3{font-family:KaTeX_Size3;}.css-4okk7a .katex .delimsizing.size4{font-family:KaTeX_Size4;}.css-4okk7a .katex .delimsizing.mult .delim-size1>span{font-family:KaTeX_Size1;}.css-4okk7a .katex .delimsizing.mult .delim-size4>span{font-family:KaTeX_Size4;}.css-4okk7a .katex .nulldelimiter{display:inline-block;width:0.12em;}.css-4okk7a .katex .delimcenter{position:relative;}.css-4okk7a .katex .op-symbol{position:relative;}.css-4okk7a .katex .op-symbol.small-op{font-family:KaTeX_Size1;}.css-4okk7a .katex .op-symbol.large-op{font-family:KaTeX_Size2;}.css-4okk7a .katex .op-limits>.vlist-t{text-align:center;}.css-4okk7a .katex .accent>.vlist-t{text-align:center;}.css-4okk7a .katex .accent .accent-body{position:relative;}.css-4okk7a .katex .accent .accent-body:not(.accent-full){width:0;}.css-4okk7a .katex .overlay{display:block;}.css-4okk7a .katex .mtable .vertical-separator{display:inline-block;min-width:1px;}.css-4okk7a .katex .mtable .arraycolsep{display:inline-block;}.css-4okk7a .katex .mtable .col-align-c>.vlist-t{text-align:center;}.css-4okk7a .katex .mtable .col-align-l>.vlist-t{text-align:left;}.css-4okk7a .katex .mtable .col-align-r>.vlist-t{text-align:right;}.css-4okk7a .katex .svg-align{text-align:left;}.css-4okk7a .katex svg{display:block;position:absolute;width:100%;height:inherit;fill:currentColor;stroke:currentColor;fill-rule:nonzero;fill-opacity:1;stroke-width:1;stroke-linecap:butt;stroke-linejoin:miter;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1;}.css-4okk7a .katex svg path{stroke:none;}.css-4okk7a .katex img{border-style:none;min-width:0;min-height:0;max-width:none;max-height:none;}.css-4okk7a .katex .stretchy{width:100%;display:block;position:relative;overflow:hidden;}.css-4okk7a .katex .stretchy::before,.css-4okk7a .katex .stretchy::after{content:'';}.css-4okk7a .katex .hide-tail{width:100%;position:relative;overflow:hidden;}.css-4okk7a .katex .halfarrow-left{position:absolute;left:0;width:50.2%;overflow:hidden;}.css-4okk7a .katex .halfarrow-right{position:absolute;right:0;width:50.2%;overflow:hidden;}.css-4okk7a .katex .brace-left{position:absolute;left:0;width:25.1%;overflow:hidden;}.css-4okk7a .katex .brace-center{position:absolute;left:25%;width:50%;overflow:hidden;}.css-4okk7a .katex .brace-right{position:absolute;right:0;width:25.1%;overflow:hidden;}.css-4okk7a .katex .x-arrow-pad{padding:0 0.5em;}.css-4okk7a .katex .cd-arrow-pad{padding:0 0.55556em 0 0.27778em;}.css-4okk7a .katex .x-arrow,.css-4okk7a .katex .mover,.css-4okk7a .katex .munder{text-align:center;}.css-4okk7a .katex .boxpad{padding:0 0.3em 0 0.3em;}.css-4okk7a .katex .fbox,.css-4okk7a .katex .fcolorbox{box-sizing:border-box;border:0.04em solid;}.css-4okk7a .katex .cancel-pad{padding:0 0.2em 0 0.2em;}.css-4okk7a .katex .cancel-lap{margin-left:-0.2em;margin-right:-0.2em;}.css-4okk7a .katex .sout{border-bottom-style:solid;border-bottom-width:0.08em;}.css-4okk7a .katex .angl{box-sizing:border-box;border-top:0.049em solid;border-right:0.049em solid;margin-right:0.03889em;}.css-4okk7a .katex .anglpad{padding:0 0.03889em 0 0.03889em;}.css-4okk7a .katex .eqn-num::before{counter-increment:katexEqnNo;content:'(' counter(katexEqnNo) ')';}.css-4okk7a .katex .mml-eqn-num::before{counter-increment:mmlEqnNo;content:'(' counter(mmlEqnNo) ')';}.css-4okk7a .katex .mtr-glue{width:50%;}.css-4okk7a .katex .cd-vert-arrow{display:inline-block;position:relative;}.css-4okk7a .katex .cd-label-left{display:inline-block;position:absolute;right:calc(50% + 0.3em);text-align:left;}.css-4okk7a .katex .cd-label-right{display:inline-block;position:absolute;left:calc(50% + 0.3em);text-align:right;}.css-4okk7a .katex-display{display:block;margin:1em 0;text-align:center;}.css-4okk7a .katex-display>.katex{display:block;white-space:nowrap;}.css-4okk7a .katex-display>.katex>.katex-html{display:block;position:relative;}.css-4okk7a .katex-display>.katex>.katex-html>.tag{position:absolute;right:0;}.css-4okk7a .katex-display.leqno>.katex>.katex-html>.tag{left:0;right:auto;}.css-4okk7a .katex-display.fleqn>.katex{text-align:left;padding-left:2em;}.css-4okk7a body{counter-reset:katexEqnNo mmlEqnNo;}.css-4okk7a table{width:-webkit-max-content;width:-moz-max-content;width:max-content;}.css-4okk7a .tableBlock{max-width:100%;margin-bottom:1rem;overflow-y:scroll;}.css-4okk7a .tableBlock thead,.css-4okk7a .tableBlock thead th{border-bottom:1px solid #333!important;}.css-4okk7a .tableBlock th,.css-4okk7a .tableBlock td{padding:10px;text-align:left;}.css-4okk7a .tableBlock th{font-weight:bold!important;}.css-4okk7a .tableBlock caption{caption-side:bottom;color:#555;font-size:12px;font-style:italic;text-align:center;}.css-4okk7a .tableBlock caption>p{margin:0;}.css-4okk7a .tableBlock th>p,.css-4okk7a .tableBlock td>p{margin:0;}.css-4okk7a .tableBlock [data-background-color='aliceblue']{background-color:#f0f8ff;color:#000;}.css-4okk7a .tableBlock [data-background-color='black']{background-color:#000;color:#fff;}.css-4okk7a .tableBlock [data-background-color='chocolate']{background-color:#d2691e;color:#fff;}.css-4okk7a .tableBlock [data-background-color='cornflowerblue']{background-color:#6495ed;color:#fff;}.css-4okk7a .tableBlock [data-background-color='crimson']{background-color:#dc143c;color:#fff;}.css-4okk7a .tableBlock [data-background-color='darkblue']{background-color:#00008b;color:#fff;}.css-4okk7a .tableBlock [data-background-color='darkseagreen']{background-color:#8fbc8f;color:#000;}.css-4okk7a .tableBlock [data-background-color='deepskyblue']{background-color:#00bfff;color:#000;}.css-4okk7a .tableBlock [data-background-color='gainsboro']{background-color:#dcdcdc;color:#000;}.css-4okk7a .tableBlock [data-background-color='grey']{background-color:#808080;color:#fff;}.css-4okk7a .tableBlock [data-background-color='lemonchiffon']{background-color:#fffacd;color:#000;}.css-4okk7a .tableBlock [data-background-color='lightpink']{background-color:#ffb6c1;color:#000;}.css-4okk7a .tableBlock [data-background-color='lightsalmon']{background-color:#ffa07a;color:#000;}.css-4okk7a .tableBlock [data-background-color='lightskyblue']{background-color:#87cefa;color:#000;}.css-4okk7a .tableBlock [data-background-color='mediumblue']{background-color:#0000cd;color:#fff;}.css-4okk7a .tableBlock [data-background-color='omnigrey']{background-color:#f0f0f0;color:#000;}.css-4okk7a .tableBlock [data-background-color='white']{background-color:#fff;color:#000;}.css-4okk7a .tableBlock [data-text-align='center']{text-align:center;}.css-4okk7a .tableBlock [data-text-align='left']{text-align:left;}.css-4okk7a .tableBlock [data-text-align='right']{text-align:right;}.css-4okk7a .tableBlock [data-vertical-align='bottom']{vertical-align:bottom;}.css-4okk7a .tableBlock [data-vertical-align='middle']{vertical-align:middle;}.css-4okk7a .tableBlock [data-vertical-align='top']{vertical-align:top;}.css-4okk7a .tableBlock__font-size--xxsmall{font-size:10px;}.css-4okk7a .tableBlock__font-size--xsmall{font-size:12px;}.css-4okk7a .tableBlock__font-size--small{font-size:14px;}.css-4okk7a .tableBlock__font-size--large{font-size:18px;}.css-4okk7a .tableBlock__border--some tbody tr:not(:last-child){border-bottom:1px solid #e2e5e7;}.css-4okk7a .tableBlock__border--bordered td,.css-4okk7a .tableBlock__border--bordered th{border:1px solid #e2e5e7;}.css-4okk7a .tableBlock__border--borderless tbody+tbody,.css-4okk7a .tableBlock__border--borderless td,.css-4okk7a .tableBlock__border--borderless th,.css-4okk7a .tableBlock__border--borderless tr,.css-4okk7a .tableBlock__border--borderless thead,.css-4okk7a .tableBlock__border--borderless thead th{border:0!important;}.css-4okk7a .tableBlock:not(.tableBlock__table-striped) tbody tr{background-color:unset!important;}.css-4okk7a .tableBlock__table-striped tbody tr:nth-of-type(odd){background-color:#f9fafc!important;}.css-4okk7a .tableBlock__table-compactl th,.css-4okk7a .tableBlock__table-compact td{padding:3px!important;}.css-4okk7a .tableBlock__full-size{width:100%;}.css-4okk7a .textBlock{margin-bottom:16px;}.css-4okk7a .textBlock__text-formatting--finePrint{font-size:12px;}.css-4okk7a .textBlock__text-infoBox{padding:0.75rem 1.25rem;margin-bottom:1rem;border:1px solid transparent;border-radius:0.25rem;}.css-4okk7a .textBlock__text-infoBox p{margin:0;}.css-4okk7a .textBlock__text-infoBox--primary{background-color:#cce5ff;border-color:#b8daff;color:#004085;}.css-4okk7a .textBlock__text-infoBox--secondary{background-color:#e2e3e5;border-color:#d6d8db;color:#383d41;}.css-4okk7a .textBlock__text-infoBox--success{background-color:#d4edda;border-color:#c3e6cb;color:#155724;}.css-4okk7a .textBlock__text-infoBox--danger{background-color:#f8d7da;border-color:#f5c6cb;color:#721c24;}.css-4okk7a .textBlock__text-infoBox--warning{background-color:#fff3cd;border-color:#ffeeba;color:#856404;}.css-4okk7a .textBlock__text-infoBox--info{background-color:#d1ecf1;border-color:#bee5eb;color:#0c5460;}.css-4okk7a .textBlock__text-infoBox--dark{background-color:#d6d8d9;border-color:#c6c8ca;color:#1b1e21;}.css-4okk7a .text-overline{-webkit-text-decoration:overline;text-decoration:overline;}.css-4okk7a.css-4okk7a{color:#2B3148;background-color:transparent;font-family:"Roboto","Helvetica","Arial",sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-4okk7a.css-4okk7a:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-4okk7a .js-external-link-button.link-like,.css-4okk7a .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-4okk7a .js-external-link-button.link-like:hover,.css-4okk7a .js-external-link-anchor:hover,.css-4okk7a .js-external-link-button.link-like:active,.css-4okk7a .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-4okk7a .js-external-link-button.link-like:focus-visible,.css-4okk7a .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-4okk7a p,.css-4okk7a div{margin:0px;display:block;}.css-4okk7a pre{margin:0px;display:block;}.css-4okk7a pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-4okk7a pre:not(:first-child){padding-top:8px;}.css-4okk7a ul,.css-4okk7a ol{display:block margin:0px;padding-left:20px;}.css-4okk7a ul li,.css-4okk7a ol li{padding-top:8px;}.css-4okk7a ul ul,.css-4okk7a ol ul,.css-4okk7a ul ol,.css-4okk7a ol ol{padding-top:0px;}.css-4okk7a ul:not(:first-child),.css-4okk7a ol:not(:first-child){padding-top:4px;} Known values

Triangle solution.