homework 5 trigonometry finding sides and angles

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.2: Right Triangle Trigonometry

• Last updated
• Save as PDF
• Page ID 34917

Trigonometric Functions: Ratios of Sides of a Right Triangle

In this section we introduce right triangle trigonometry and explore right triangle applications of trigonometric functions. In later sections we will examine trigonometric functions as ratios of the sides of a triangle drawn inside a circle, and discuss the role of those functions in finding points on the circle. 

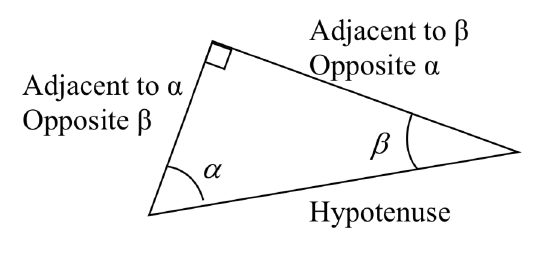
Trigonometric functions are ratios of two of the three sides of a right triangle. The longest side of the right triangle is the hypotenuse. The other two sides are defined in terms of their relationship to one of the acute angles in the right triangle -- the side opposite the chosen angle, and the side adjacent (next to) that angle. 

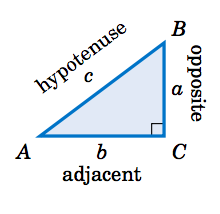
The triangle can be oriented any where in space, but when the triangle is placed in standard position with the chosen acute angle \( \theta\) at the origin, these sides can be expressed equivalently in terms of \(y\) for the opposite side, \(x\) for the adjacent side, and \(r\) for the hypotenuse. The point \( (x, y) \) is a point on the terminal side of the angle.

RIGHT TRIANGLE RELATIONSHIPS

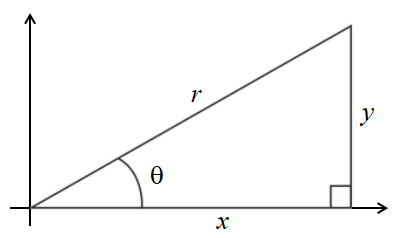
Given a right triangle with an angle of \(\theta\)

\( \begin{array}{rllrll}  \sin \theta &= \dfrac{\text{opposite}}{\text{hypotenuse}} &= \dfrac{y}{r}  \qquad &\csc \theta &= \dfrac{\text{hypotenuse}}{\text{opposite}} &= \dfrac{r}{y}  \\ \cos \theta &= \dfrac{\text{adjacent}}{\text{hypotenuse}} &= \dfrac{x}{r}  \qquad &\sec \theta &= \dfrac{\text{hypotenuse}}{\text{adjacent}} &= \dfrac{r}{x}  \\ \tan \theta &= \dfrac{\text{opposite}}{\text{adjacent}} &= \dfrac{y}{x}  \qquad &\cot \theta &= \dfrac{\text{adjacent}}{\text{opposite}}  &= \dfrac{x}{y} \\ \end{array}   \)

A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “ S ine is o pposite over h ypotenuse, C osine is a djacent over h ypotenuse, T angent is o pposite over a djacent.”

Example \(\PageIndex{1}\): Find trigonometric ratios given 3 sides of a right triangle

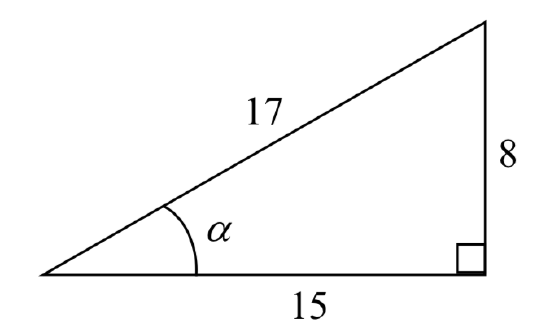
The side adjacent to the angle is 15, and the hypotenuse of the triangle is 17, so

\[\text{cos}(\alpha) = \dfrac{\text{adjacent}}{\text{hypotenuse}} = \dfrac{15}{17}\nonumber\]

Given Two Sides, Find the 3rd Side and All Trigonometric Ratios

It is not necessary that the lengths of all three sides of the right triangle be known initially. The Theorem of Pythagoras can be used to find the third side if we are given the lengths of only two sides of a right triangle.

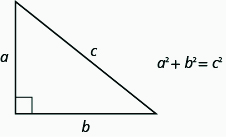
THE PYTHAGOREAN THEOREM

In any right triangle, where \(a\) and \(b\) are the lengths of the legs, and \(c\) is the length of the hypotenuse, the sum of the squares of the lengths of the two legs equals the square of the length of the hypotenuse.

We will use the Pythagorean Theorem in the next example.

Example \(\PageIndex{2}\): Find trigonometric ratios given 2 sides of a right triangle

Given a triangle with a hypotenuse of \(9\) and side opposite to angle \( \alpha\) of \(5\), find the sine, cosine and tangent for angle \( \alpha\).

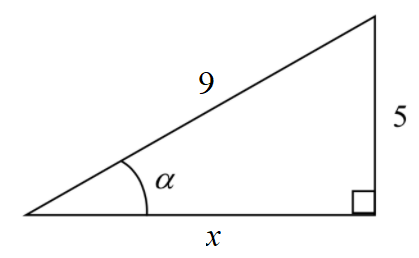
The triangle with the given information is illustrated on the right. The third side, which in this case is the "adjacent" side, can be found by using the Theorem of Pythagoras \( a^2 + b^2 = c^2\). Always remember that in the formula, \(c\) is the length of the hypotenuse. From \( x^2 + 5^2 = 9^2\) we obtain \(x^2 = 81-25 = 56\). So \(x = \sqrt{56} = 2\sqrt{14}\). 

Now that all three sides have been found, values for the trigonometric functions can be calculated. Always remember to rationalize denominators!

\( \sin \alpha = \dfrac{\text{opposite}}{\text{hypotenuse}} = \dfrac{5}{9} \) \( \qquad\)  \( \cos \alpha = \dfrac{\text{adjacent}}{\text{hypotenuse}} =\dfrac{2\sqrt{14}}{9}\) \( \qquad\)  \( \tan \alpha = \dfrac{\text{opposite}}{\text{adjacent}} = \dfrac{5}{2\sqrt{14}} =  \dfrac{5\sqrt{14}}{28} \)

Given a triangle with the side adjacent to angle \(\theta\) being \(x=2\) and the side opposite angle \(\theta\) being \(x=5\), find the secant, cosecant, and cotangent for angle \(\theta\).

From \(x^2 + y^2 = r^2\) we obtain \( r = \sqrt{x^2+y^2}\) and so \(r = \sqrt{29}\).

Therefore, \( \csc \theta = \dfrac{\sqrt{29}}{5} ,   \; \sec \theta = \dfrac{\sqrt{29}}{2},   \; \cot \theta = \dfrac{5}{2},  \)

Given One Trigonometric Ratio, find all others

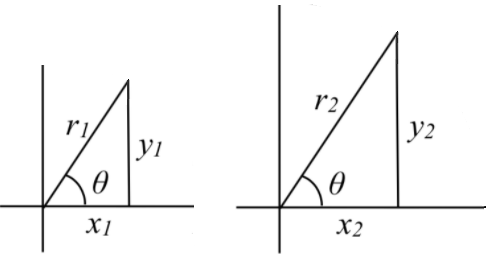
One important point to make here is that it is only the angle that determines the values of these trigonometric ratios, not the size of the triangle being used. This is because triangles constructed with the same angles but different length sides  are similar triangles, so their ratios will be the same.

Thus, \(  \dfrac{y_{1} }{r_{1} } =\dfrac{y_{2} }{r_{2} } \qquad \dfrac{x_{1} }{r_{1} } =\dfrac{x_{2} }{r_{2} }\)

A trigonometric ratio is the ratio of two sides of a right triangle. Since right triangles that are similar can be used to establish values for trigonometric functions,  the numerator of the trigonometric ratio can serve as the length of one of the sides; the denominator can serve as the length of another side. Whether these sides are the hypotenuse of the triangle or the side opposite or adjacent to the given angle depends on which trigonometric ratio is being used.

• Draw a right triangle with angle \(A\) and the two known sides labeled according to the diagram on the right. If the trigonometric ratio has no denominator, use \(1\) for the value of the denominator.
• Use the Pythagorean Theorem \( a^2 + b^2 = c^2 \) to find the value of the missing 3rd side of the right triangle.
• Use the definitions to find the values of the other trigonometric ratios.

Example \(\PageIndex{3}\): Find all trigonometric ratios given one ratio

Given \( \sec \theta = 4 \), find the other five trigonometric ratios for angle \( \theta \).

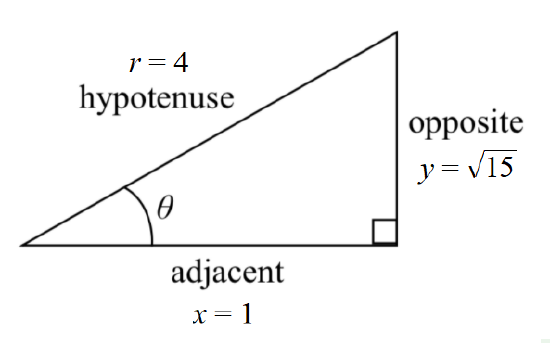
Draw a triangle to help visualize the relationships represented by this trigonometric ratio.

Using the Theorem of Pythagoras \( x^2 +y^2 = r^2\) and knowing \(r = 4\), \(x = 1\), we obtain \( 1^2 + y^2 = 4^2\).  Thus, \( y^2 = 16 - 1 = 15 \) and so \( y =  \sqrt{15} \).

Now that all three sides of the right triangle are known, the definitions can be used to find the other five trigonometric ratios.

\( \sin \theta = \dfrac{y}{r} = \dfrac{\sqrt{15}}{4} \)          \( \cos \theta = \dfrac{x}{r} = \dfrac{1}{4} \)          \( \tan \theta = \dfrac{y}{x} = \sqrt{15} \)

 \( \csc \theta = \dfrac{r}{y} = \dfrac{4}{\sqrt{15}} = \dfrac{4 \sqrt{15}}{15} \)                 \( \cot \theta = \dfrac{x}{y} = \dfrac{1}{\sqrt{15}} = \dfrac{\sqrt{15}}{15} \)

Given \( \tan \theta = \dfrac{\sqrt{3}}{2} \), find the other five trigonometric ratios for angle \( \theta \).

\( \sin \theta = \dfrac{\sqrt{21}}{7} ,  \; \cos \theta = \dfrac{2\sqrt{7}}{7},  \; \csc \theta = \dfrac{\sqrt{21}}{3},   \; \sec \theta = \dfrac{\sqrt{7}}{2},  \; \cot \theta = \dfrac{2\sqrt{3}}{3} \)

Given One Side and an Angle, Find all Other Sides and Angles

In previous examples, we evaluated the sine and cosine in triangles where we knew all three sides. But the real power of right-triangle trigonometry emerges when we look at triangles in which we know an angle but do not know all the sides.

• For each side, select the trigonometric function with the unknown side as either the numerator or the denominator and the known side as the corresponding denominator or the numerator.
• Write an equation setting the function value of the known angle equal to the ratio of the corresponding sides.
• Using the value of the trigonometric function and the known side length, solve for the missing side length.

Example \(\PageIndex{4}\): Finding Missing Side Lengths Using Trigonometric Ratios

Find the unknown sides of the triangle below.

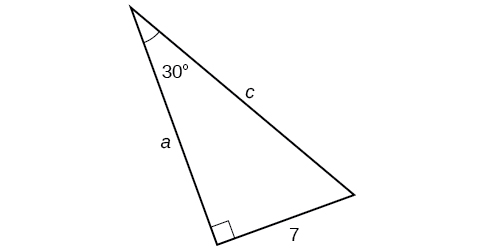
We are given the angle \(30^{\circ}\) and the opposite side (OPP).

To find the adjacent side (ADJ) choose the ratio that uses both OPP (given) and ADJ (unknown): \( \tan A = \frac{OPP}{ADJ}.\) 

Write the equation with the given and unknown values: \( \qquad \tan (30°)= \dfrac{7}{a} \)

Rearrange to solve for \(a\). \( \qquad a =\dfrac{7}{ \tan (30°)}  =12.1 \)

To find the hypotenuse (HYP), choose the ratio that uses both OPP (given) and HYP (unknown): \( \sin A = \frac{OPP}{HYP}.\)

Substitute: \( \qquad \sin (30°)= \dfrac{7}{c} \)

Rearrange to solve for \(c\). \( \qquad c = \dfrac{7}{\sin (30°)} =14 \)

Notice that if we know at least one of the non-right angles of a right triangle and one side, we can find the rest of the sides and angles.

A right triangle has one angle of \(\dfrac{\pi }{3}\) (radians) and a hypotenuse of 20. Find the unknown sides and angles of the triangle.

\[\text{cos} \left(\dfrac{\pi}{3} \right) = \dfrac{\text{adjacent}}{\text{hypoteuse}} = \dfrac{\text{Adj}}{20}  \quad \rightarrow \quad  \text{adjacent} = 20 \text{cos} \left(\dfrac{\pi}{3} \right) = 20 \left(\dfrac{1}{2} \right) = 10\nonumber\]

\[\text{sin} \left(\dfrac{\pi}{3} \right) = \dfrac{\text{Opposite}}{\text{hypotenuse}} = \dfrac{\text{Opp}}{20} \quad \rightarrow \quad  \text{opposite} = 20 \text{sin} \left(\dfrac{\pi}{3} \right) = 20 \left(\dfrac{\sqrt{3}}{2} \right) = 10\sqrt{3}\nonumber\]

Missing angle = \( \frac{\pi}{2} - \frac{\pi}{3} =  \frac{\pi}{6}\).

Right Triangle Trigonometry Used to Solve Applied Problems

Example \(\PageIndex{5}\)

To find the height of a tree, a person walks to a point 30 feet from the base of the tree, and measures the angle from the ground to the top of the tree to be 57 degrees. Find the height of the tree.

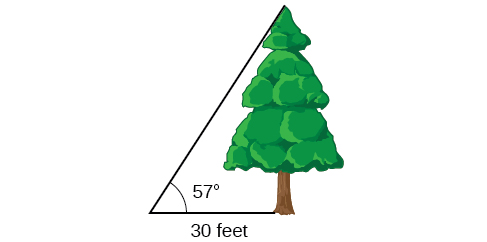
The trigonometric function which relates the side opposite of the angle and the side adjacent to the angle is the tangent.

\(\text{tan} (57^{\circ}) = \dfrac{\text{opposite}}{\text{adjacent}} = \dfrac{h}{30}\) 

Solving for \(h\), \(h=30\tan (57{}^\circ )\) 

Using a calculator, we can approximate a value for the height, \(h=30\tan (57{}^\circ )\approx 46.2\text{ feet}\)

The tree is approximately 46 feet tall.

Example \(\PageIndex{6}\)

A person standing on the roof of a 100 foot tall building is looking towards a skyscraper a few blocks away, wondering how tall it is. The angle of declination from the roof of the building to the base of the skyscraper is observed to be 20 degrees and the angle of inclination to the top of the skyscraper is 42 degrees.

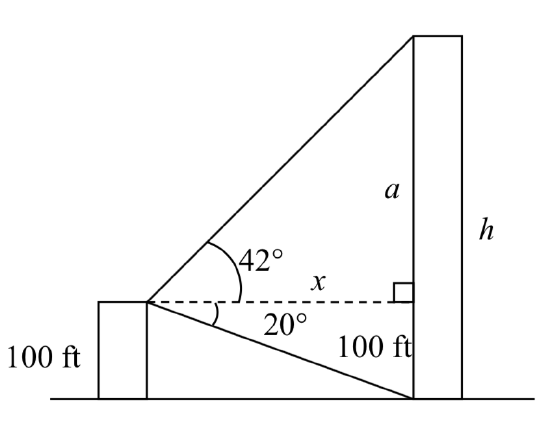
To start solving this problem, notice we have two right triangles. In the top triangle, we know one angle is 42 degrees, but we don’t know any of the sides of the triangle, so we don’t yet know enough to work with this triangle.

In the lower right triangle, we know one angle is 20 degrees, and we know the vertical height measurement of 100 ft. Since we know these two pieces of information, we can solve for the unknown distance \(x\).

\(\text{tan} (20^{\circ}) = \dfrac{\text{opposite}}{\text{adjacent}} = \dfrac{100}{x}\)

Solving for \(x\)

\(x \text{ tan} (20^{\circ}) = 100\) \(x = \dfrac{100}{\text{tan} (20^{\circ})}\)

Now that we have found the distance \(x\), we know enough information to solve the top right triangle.

\(\text{tan} (42^{\circ}) = \dfrac{\text{opposite}}{\text{adjacent}} = \dfrac{a}{x} = \dfrac{a}{100/\text{tan}(20^{\circ})}\) \(\text{tan} (42^{\circ}) = \dfrac{a\text{ tan} (20^{\circ})}{100} \quad \rightarrow \quad   100 \text{ tan} (42^{\circ}) = a\text{ tan} (20^{\circ}) \quad \rightarrow \quad  \dfrac{100 \text{ tan} (42^{\circ})}{\text{ tan} (20^{\circ})} = a\)

Approximating, \(a=\dfrac{100\tan (42{}^\circ )}{\tan (20{}^\circ )} \approx 247.4\text{ feet}\)

Adding the height of the first building, we determine that the skyscraper is about 347 feet tall.

Find an angle given two sides of a right triangle.

Sometimes an angle that has a particular trigonometric ratio is desired. In this situation we use the inverse trigonometric functions \( \sin^{-1},\) \( \cos^{-1},\) and  \( \tan^{-1}\) on a calculator to find an angle with a given trigonometric ratio.

Example \(\PageIndex{7}\)

Use a calculator to find the angle in degrees to the nearest tenth with the following trigonometric ratios.

a.    \( \sin A = .3877\)                    b.     \( \cos A = .6691\)             \( \tan A = 4.6543\)        

Use the inverse trigonometric function keys on a calculator. Be sure you are in degree mode in order to get an angle measurement in degrees!

a.    \( A =  \sin^{-1} (.3877) \approx 22.8^{\circ} \)                    b.     \( A =  \cos^{-1} (.6691) \approx 48.0^{\circ} \)                    c.    \( A =  \tan^{-1} (4.6543) \approx 77.9^{\circ} \) 

Example \(\PageIndex{8}\)

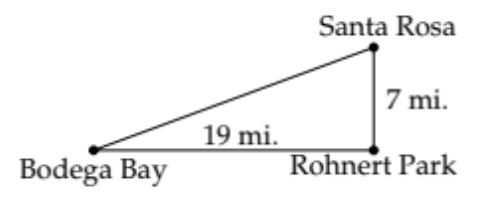
To answer the question we'll need another diagram:

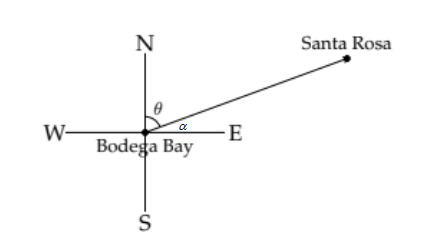
If we knew the angle \(\theta\), then we could conclude that the bearing of Santa Rosa from Bodega Bay is \(\theta\) degrees East of North. From the previous diagram we can see that we can't find \(\theta\) directly, but we can find \( \alpha,\) the complement of \(\theta\)

\( \tan \alpha=\frac{7}{19} \)     so       \(\alpha = \tan^{-1} \frac{7}{19} \approx 20.2^{\circ}\) \[ \text { Therefore, } \theta \approx 90^{\circ}-20.2^{\circ} \approx 69.8^{\circ} \nonumber \]

Thus the bearing of Santa Rosa from Bodega Bay is \(N 69.8^{\circ} E\), or \(69.8^{\circ}\) East of North.

Cofunction Identities

When working with general right triangles, the same rules apply regardless of the orientation of the triangle. In fact, we can evaluate the sine and cosine of either of the two acute angles in the triangle.

Example \(\PageIndex{9}\)

Using the triangle shown, evaluate \( \sin α, \cos α, \tan α, \sec α, \csc α,\) and \( \cot α\). Also evaluate  sin(\(\beta\)) and cos(\(\beta\)).

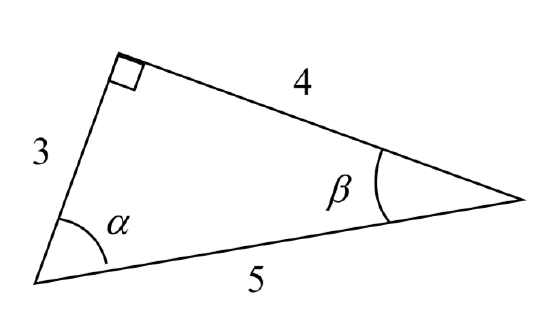
\( \sin α = \dfrac{\text{opposite } α}{\text{hypotenuse}} = \dfrac{4}{5} \; \qquad \cos α = \dfrac{\text{adjacent to }α}{\text{hypotenuse}}=\dfrac{3}{5} \; \qquad \tan α = \dfrac{\text{opposite }α}{\text{adjacent to }α}=\dfrac{4}{3} \) \( \csc α = \dfrac{\text{hypotenuse}}{\text{opposite }α}=\dfrac{5}{4} \qquad \sec α = \dfrac{\text{hypotenuse}}{\text{adjacent to }α}= \dfrac{5}{3} \qquad  \cot α = \dfrac{\text{adjacent to }α}{\text{opposite }α}=\dfrac{3}{4} \)

\(\text{sin}(\beta) = \dfrac{\text{opposite } \beta}{\text{hypotenuse}} = \dfrac{3}{5}\)   \(   \;\;  \text{cos}(\beta) = \dfrac{\text{adjacent to } \beta}{\text{hypotenuse}} = \dfrac{4}{5}   \)

A right triangle is drawn with angle \(\alpha\) opposite a side with length 33, angle \(\beta\) opposite a side with length 56, and hypotenuse 65. Evaluate \( \sin α, \cos α,\tan α, \sec α, \csc α,\) and \(\cot α\). Also, find the sine and cosine of \(\beta\)

\( \sin α = \frac{33}{65},  \; \cos α= \frac{56}{65},  \; \tan α= \frac{33}{56},   \; \sec α = \frac{65}{56},  \; \csc α= \frac{65}{33},  \; \cot α= \frac{56}{33} \) \( \qquad \) \(\text{sin} (\beta) = \frac{56}{65},  \; \text{cos} (\beta) = \frac{33}{65}\)

You may have noticed in the examples  above  that \(\cos (\alpha )=\sin (\beta )\) and \(\cos (\beta )=\sin (\alpha )\).

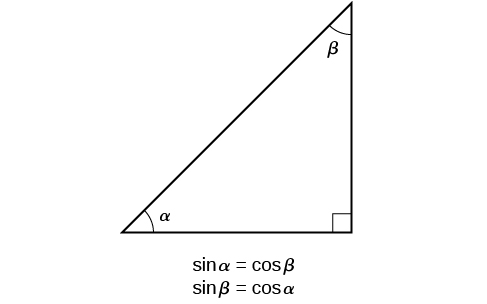
This makes sense since the side opposite \(\alpha\) is the same side that is adjacent to \(\beta\). Since the three angles in a right triangle need to add up to \(180^{\circ}\) (or \(\pi\) if angles are measured in radians), then the two acute angles in a right triangle must add to \(90^{\circ}\) (or \(\dfrac{\pi }{2}\) (radians). Therefore, \(\beta =90^{\circ} -\alpha\), and \(\alpha =90^{\circ} -\beta\). Since \(\cos (\alpha )=\sin (\beta )\), then \(\cos (\alpha )=\sin \left(90^{\circ} -\alpha \right)\).

So we may state a cofunction identity : If any two angles are complementary, the sine of one is the cosine of the other, and vice versa. This identity is illustrated in Figure \(\PageIndex{4}\).

Using this identity, we can state without calculating, for instance, that \(\sin (15^{\circ}) = \cos (90^{\circ}- 15^{\circ}) = \cos (75^{\circ}) \), and that \(\sin (75^{\circ}) = \cos (90^{\circ}- 75^{\circ}) =  \cos (15^{\circ}) \). 

In a similar manner it can be shown that \(\sec (\alpha )=\csc (\beta )\) and \(\sec (\beta )=\csc (\alpha )\). It can also be shown that \(\cot (\alpha )=\tan (\beta )\) and \(\cot (\beta )=\tan (\alpha )\). These relationships are summarized below.

COFUNCTION IDENTITIES

Cofunctions of complementary angles are equal.

The angles \(d^{\circ}\) and \((90 ^{\circ}-d^{\circ})\) are complementary angles .  Angles \(r\) and \(\left( \dfrac{π}{2} - r \right)\) are complementary angles .  Sine and co sine are cofunctions . Secant and co secant are cofunctions . Tangent and co tangent are cofunctions .

The cofunction identities  for an angle \(t\) in degrees are listed below. (If \(t\) is in radians, then use \( \dfrac{π}{2} \) in place of \(90^{\circ}).\)

• To find the sine of the complementary angle, find the cosine of the original angle.
• To find the cosine of the complementary angle, find the sine of the original angle.

Example \(\PageIndex{10}\): Using Cofunction Identities

If \( \sin t = \dfrac{5}{12},\) find \( \cos (90^{\circ}−t)\).

According to the cofunction identities for sine and cosine, \( \sin t= \cos (90^{\circ}−t). \) So \( \cos (90^{\circ}−t)= \dfrac{5}{12}. \)

If \(\csc (30^{\circ})=2,\) find \( \sec (60^{\circ}).\)

Key Concepts

• We can define trigonometric functions as ratios of the side lengths of a right triangle. 
• The same side lengths can be used to evaluate the trigonometric functions of either acute angle in a right triangle. 
• Any two complementary angles could be the two acute angles of a right triangle.
• If two angles are complementary, the cofunction identities state that the sine of one equals the cosine of the other and vice versa.
• We can use trigonometric functions of an angle to find unknown side lengths. Select the trigonometric function representing the ratio of the unknown side to the known side. 
• Right-triangle trigonometry permits the measurement of inaccessible heights and distances. The unknown height or distance can be found by creating a right triangle in which the unknown height or distance is one of the sides, and another side and angle are known. 

Snapsolve any problem by taking a picture. Try it in the Numerade app?

Finding a Side in a Right-Angled Triangle

Find a side when we know another side and angle.

We can find an unknown side in a right-angled triangle when we know:

• one length, and
• one angle (apart from the right angle).

Example: Depth to the Seabed

The ship is anchored on the seabed.

• the cable length (30 m), and
• the angle the cable makes with the seabed

So we should be able to find the depth!

The answer is to use Sine, Cosine or Tangent !

But Which One?

Which one of Sine, Cosine or Tangent to use?

To find out which, first we give names to the sides:

• Adjacent is adjacent (next to) to the angle,
• Opposite is opposite the angle,
• and the longest side is the Hypotenuse .

Now, for the side we already know and the side we are trying to find , we use the first letters of their names and the phrase "SOHCAHTOA" to decide which function:

Example: Depth to the Seabed (Continued)

Find the names of the two sides we are working on:

• the side we know is the Hypotenuse
• the side we want to find is Opposite the angle (check for yourself that "d" is opposite the angle 39°)

Now use the first letters of those two sides ( O pposite and H ypotenuse) and the phrase "SOHCAHTOA" which gives us " SOH cahtoa", which tells us we need to use Sine :

S ine: sin(θ) = O pposite / H ypotenuse

 Now put in the values we know:

sin(39°) = d / 30

And solve that equation!

But how do we calculate sin(39°) ... ?

sin(39°) = 0.6293...

 So now we have:

0.6293... = d / 30

 Now we rearrange it a little bit, and solve:

The depth the anchor ring lies beneath the hole is 18.88 m

Step By Step

These are the four steps to follow:

• Step 1 Find the names of the two sides we are using, one we are trying to find and one we already know, out of Opposite, Adjacent and Hypotenuse.
• Step 2 Use SOHCAHTOA to decide which one of Sine, Cosine or Tangent to use in this question.
• Step 3 For Sine write down Opposite/Hypotenuse, for Cosine write down Adjacent/Hypotenuse or for Tangent write down Opposite/Adjacent. One of the values is the unknown length.
• Step 4 Solve using your calculator and your skills with Algebra .

Let’s look at a few more examples:

Example: find the height of the plane.

We know the distance to the plane is 1000 And the angle is 60°

What is the plane's height?

Careful! The 60° angle is at the top, so the "h" side is Adjacent to the angle!

• Step 1 The two sides we are using are A djacent (h) and H ypotenuse (1000).
• Step 2 SOH CAH TOA tells us to use C osine.

cos 60° = Adjacent / Hypotenuse = h / 1000

• Step 4 Solve:

The height of the plane = 500 meters

Example: Find the length of the side y :

• Step 1 The two sides we are using are O pposite (y) and A djacent (7).
• Step 2 SOHCAH TOA tells us to use T angent.

tan 53° = Opposite/Adjacent  = y/7

Side y = 9.29

Example: Radio Mast

There is a mast that is 70 meters high.

A wire goes to the top of the mast at an angle of 68°.

How long is the wire?

• Step 1 The two sides we are using are O pposite (70) and H ypotenuse (w).
• Step 2 SOH CAHTOA tells us to use S ine.

sin 68° = 70/w

The unknown length is on the bottom (the denominator) of the fraction!

So we need to follow a slightly different approach when solving:

The length of the wire = 75.5 m

Chapter 1: Triangles and Circles

Exercises: 1.1 Triangles and Angles

Practice each skill in the Homework Problems listed.

• Sketch a triangle with given properties #1–6
• Find an unknown angle in a triangle #7–12, 17–20
• Find angles formed by parallel lines and a transversal #13–16, 35–44
• Find exterior angles of a triangle #21–24
• Find angles in isosceles, equilateral, and right triangles #25–34
• State reasons for conclusions #45–48

Suggested Problems

Exercises for 1.1 Triangles and Angles

Exercise group, 1. an isosceles triangle with a vertex angle [latex]306^{\circ}[/latex], 2. a scalene triangle with one obtuse angle ( scalene means three unequal sides.), 3. a right triangle with legs [latex]4[/latex] and [latex]7[/latex], 4. an isosceles right triangle, 5. an isosceles triangle with one obtuse angle, 6. a right triangle with one angle [latex]20°[/latex].

In parts (a) and (b), find the exterior angle [latex]\phi[/latex].

• Use your answer to part (c) to write a rule for finding an exterior angle of a triangle.

In Problems 25 and 26, the figures inscribed are regular polygons , which means that all their sides are the same length, and all the angles have the same measure. Find the angles [latex]\theta[/latex] and [latex]\phi[/latex].

In problems 27 and 28, triangle ABC is equilateral. Find the unknown angles.

a. [latex]2\theta + 2\phi =[/latex]

b. [latex]\theta + \phi =[/latex]

c. [latex]\triangle ABC[/latex] is

Find [latex]\alpha[/latex] and [latex]\beta[/latex]

• Explain why [latex]\angle OAB[/latex] and [latex]\angle ABO[/latex] are equal in measure.
• Explain why [latex]\angle OBC[/latex] and [latex]\angle BCO[/latex] are equal in measure.
• Explain why [latex]\angle ABC[/latex] is a right angle. (Hint: Use Problem 29.)
• Compare [latex]\theta[/latex] with [latex]\alpha + \beta[/latex] (Hint: What do you know about supplementary angles and the sum of angles in a triangle?)
• Compare [latex]\alpha[/latex] and [latex]\beta[/latex]
• Explain why the inscribed angle [latex]\angle BAO[/latex] is half the size of the central angle [latex]\angle BOD[/latex]

Find [latex]\alpha[/latex] and [latex]\beta[/latex]

• [latex]\angle 4 + \angle 2 + \angle 5 =[/latex]
• Use parts (a) and (b) to explain why the sum of the angles of a triangle is [latex]180^{\circ}[/latex]

ABCD is a rectangle. The diagonals of a rectangle bisect each other. In the figure,  [latex]\angle AQD = 130^{\circ}[/latex]. Find the angles labeled 1 through 5 in order, and give a reason for each answer.

A tangent meets the radius of a circle at a right angle. In the figure, [latex]\angle AOB = 140^{\circ}[/latex]. Find the angles labeled 1 through 5 in order, and give a reason for each answer.

Trigonometry Copyright © 2024 by Bimal Kunwor; Donna Densmore; Jared Eusea; and Yi Zhen. All Rights Reserved.

Share This Book

SOHCAHTOA Worksheet and Answer Key

Students will practice identifying adjacent, opposite sides (and hypotenuse) in right triangles and they will practice writing Sine Cosine Tangent (SOHCAHTOA) relationships. This sheet has model problems worked out, step by step -- as well as, 20 scaffolded questions that start out relatively easy and end with some real challenges.

Example Questions

Ii. identify sides opposite, adjacent to angles.

III. Use SOHCAHTOA

Visual Aids

Other Details

This is a 4 part worksheet:

• Part I Model Problems
• Part II Practice
• Part III Challenge Problems
• Part IV Answer Key
• Sine Cosine Calculator
• Arcsine Calculator

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.