assignment 1 real numbers

1.1 Real Numbers: Algebra Essentials

Learning objectives.

In this section, you will:

Classify a real number as a natural, whole, integer, rational, or irrational number.
Perform calculations using order of operations.
Use the following properties of real numbers: commutative, associative, distributive, inverse, and identity.
Evaluate algebraic expressions.
Simplify algebraic expressions.

It is often said that mathematics is the language of science. If this is true, then an essential part of the language of mathematics is numbers. The earliest use of numbers occurred 100 centuries ago in the Middle East to count, or enumerate items. Farmers, cattle herders, and traders used tokens, stones, or markers to signify a single quantity—a sheaf of grain, a head of livestock, or a fixed length of cloth, for example. Doing so made commerce possible, leading to improved communications and the spread of civilization.

Three to four thousand years ago, Egyptians introduced fractions. They first used them to show reciprocals. Later, they used them to represent the amount when a quantity was divided into equal parts.

But what if there were no cattle to trade or an entire crop of grain was lost in a flood? How could someone indicate the existence of nothing? From earliest times, people had thought of a “base state” while counting and used various symbols to represent this null condition. However, it was not until about the fifth century CE in India that zero was added to the number system and used as a numeral in calculations.

Clearly, there was also a need for numbers to represent loss or debt. In India, in the seventh century CE, negative numbers were used as solutions to mathematical equations and commercial debts. The opposites of the counting numbers expanded the number system even further.

Because of the evolution of the number system, we can now perform complex calculations using these and other categories of real numbers. In this section, we will explore sets of numbers, calculations with different kinds of numbers, and the use of numbers in expressions.

Classifying a Real Number

The numbers we use for counting, or enumerating items, are the natural numbers : 1, 2, 3, 4, 5, and so on. We describe them in set notation as { 1 , 2 , 3 , ... } { 1 , 2 , 3 , ... } where the ellipsis (…) indicates that the numbers continue to infinity. The natural numbers are, of course, also called the counting numbers . Any time we enumerate the members of a team, count the coins in a collection, or tally the trees in a grove, we are using the set of natural numbers. The set of whole numbers is the set of natural numbers plus zero: { 0 , 1 , 2 , 3 , ... } . { 0 , 1 , 2 , 3 , ... } .

The set of integers adds the opposites of the natural numbers to the set of whole numbers: { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } . { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } . It is useful to note that the set of integers is made up of three distinct subsets: negative integers, zero, and positive integers. In this sense, the positive integers are just the natural numbers. Another way to think about it is that the natural numbers are a subset of the integers.

The set of rational numbers is written as { m n | m and n are integers and n ≠ 0 } . { m n | m and n are integers and n ≠ 0 } . Notice from the definition that rational numbers are fractions (or quotients) containing integers in both the numerator and the denominator, and the denominator is never 0. We can also see that every natural number, whole number, and integer is a rational number with a denominator of 1.

Because they are fractions, any rational number can also be expressed as a terminating or repeating decimal. Any rational number can be represented as either:

ⓐ a terminating decimal: 15 8 = 1.875 , 15 8 = 1.875 , or
ⓑ a repeating decimal: 4 11 = 0.36363636 … = 0. 36 ¯ 4 11 = 0.36363636 … = 0. 36 ¯

We use a line drawn over the repeating block of numbers instead of writing the group multiple times.

Writing Integers as Rational Numbers

Write each of the following as a rational number.

Write a fraction with the integer in the numerator and 1 in the denominator.

ⓐ 7 = 7 1 7 = 7 1
ⓑ 0 = 0 1 0 = 0 1
ⓒ −8 = − 8 1 −8 = − 8 1

Identifying Rational Numbers

Write each of the following rational numbers as either a terminating or repeating decimal.

ⓐ − 5 7 − 5 7
ⓑ 15 5 15 5
ⓒ 13 25 13 25

Write each fraction as a decimal by dividing the numerator by the denominator.

ⓐ − 5 7 = −0. 714285 ——— , − 5 7 = −0. 714285 ——— , a repeating decimal
ⓑ 15 5 = 3 15 5 = 3 (or 3.0), a terminating decimal
ⓒ 13 25 = 0.52 , 13 25 = 0.52 , a terminating decimal
ⓐ 68 17 68 17
ⓑ 8 13 8 13
ⓒ − 17 20 − 17 20

Irrational Numbers

At some point in the ancient past, someone discovered that not all numbers are rational numbers. A builder, for instance, may have found that the diagonal of a square with unit sides was not 2 or even 3 2 , 3 2 , but was something else. Or a garment maker might have observed that the ratio of the circumference to the diameter of a roll of cloth was a little bit more than 3, but still not a rational number. Such numbers are said to be irrational because they cannot be written as fractions. These numbers make up the set of irrational numbers . Irrational numbers cannot be expressed as a fraction of two integers. It is impossible to describe this set of numbers by a single rule except to say that a number is irrational if it is not rational. So we write this as shown.

Differentiating Rational and Irrational Numbers

Determine whether each of the following numbers is rational or irrational. If it is rational, determine whether it is a terminating or repeating decimal.

ⓑ 33 9 33 9
ⓓ 17 34 17 34
ⓔ 0.3033033303333 … 0.3033033303333 …
ⓐ 25 : 25 : This can be simplified as 25 = 5. 25 = 5. Therefore, 25 25 is rational.

So, 33 9 33 9 is rational and a repeating decimal.

ⓒ 11 : 11 11 : 11 is irrational because 11 is not a perfect square and 11 11 cannot be expressed as a fraction.

So, 17 34 17 34 is rational and a terminating decimal.

ⓔ 0.3033033303333 … 0.3033033303333 … is not a terminating decimal. Also note that there is no repeating pattern because the group of 3s increases each time. Therefore it is neither a terminating nor a repeating decimal and, hence, not a rational number. It is an irrational number.
ⓐ 7 77 7 77
ⓒ 4.27027002700027 … 4.27027002700027 …
ⓓ 91 13 91 13

Real Numbers

Given any number n , we know that n is either rational or irrational. It cannot be both. The sets of rational and irrational numbers together make up the set of real numbers . As we saw with integers, the real numbers can be divided into three subsets: negative real numbers, zero, and positive real numbers. Each subset includes fractions, decimals, and irrational numbers according to their algebraic sign (+ or –). Zero is considered neither positive nor negative.

The real numbers can be visualized on a horizontal number line with an arbitrary point chosen as 0, with negative numbers to the left of 0 and positive numbers to the right of 0. A fixed unit distance is then used to mark off each integer (or other basic value) on either side of 0. Any real number corresponds to a unique position on the number line.The converse is also true: Each location on the number line corresponds to exactly one real number. This is known as a one-to-one correspondence. We refer to this as the real number line as shown in Figure 1 .

Classifying Real Numbers

Classify each number as either positive or negative and as either rational or irrational. Does the number lie to the left or the right of 0 on the number line?

ⓐ − 10 3 − 10 3
ⓒ − 289 − 289
ⓓ −6 π −6 π
ⓔ 0.615384615384 … 0.615384615384 …
ⓐ − 10 3 − 10 3 is negative and rational. It lies to the left of 0 on the number line.
ⓑ 5 5 is positive and irrational. It lies to the right of 0.
ⓒ − 289 = − 17 2 = −17 − 289 = − 17 2 = −17 is negative and rational. It lies to the left of 0.
ⓓ −6 π −6 π is negative and irrational. It lies to the left of 0.
ⓔ 0.615384615384 … 0.615384615384 … is a repeating decimal so it is rational and positive. It lies to the right of 0.
ⓑ −11.411411411 … −11.411411411 …
ⓒ 47 19 47 19
ⓓ − 5 2 − 5 2
ⓔ 6.210735 6.210735

Sets of Numbers as Subsets

Beginning with the natural numbers, we have expanded each set to form a larger set, meaning that there is a subset relationship between the sets of numbers we have encountered so far. These relationships become more obvious when seen as a diagram, such as Figure 2 .

Sets of Numbers

The set of natural numbers includes the numbers used for counting: { 1 , 2 , 3 , ... } . { 1 , 2 , 3 , ... } .

The set of whole numbers is the set of natural numbers plus zero: { 0 , 1 , 2 , 3 , ... } . { 0 , 1 , 2 , 3 , ... } .

The set of integers adds the negative natural numbers to the set of whole numbers: { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } . { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } .

The set of rational numbers includes fractions written as { m n | m and n are integers and n ≠ 0 } . { m n | m and n are integers and n ≠ 0 } .

The set of irrational numbers is the set of numbers that are not rational, are nonrepeating, and are nonterminating: { h | h is not a rational number } . { h | h is not a rational number } .

Differentiating the Sets of Numbers

Classify each number as being a natural number ( N ), whole number ( W ), integer ( I ), rational number ( Q ), and/or irrational number ( Q′ ).

ⓔ 3.2121121112 … 3.2121121112 …
ⓐ − 35 7 − 35 7
ⓔ 4.763763763 … 4.763763763 …

Performing Calculations Using the Order of Operations

When we multiply a number by itself, we square it or raise it to a power of 2. For example, 4 2 = 4 ⋅ 4 = 16. 4 2 = 4 ⋅ 4 = 16. We can raise any number to any power. In general, the exponential notation a n a n means that the number or variable a a is used as a factor n n times.

In this notation, a n a n is read as the n th power of a , a , or a a to the n n where a a is called the base and n n is called the exponent . A term in exponential notation may be part of a mathematical expression, which is a combination of numbers and operations. For example, 24 + 6 ⋅ 2 3 − 4 2 24 + 6 ⋅ 2 3 − 4 2 is a mathematical expression.

To evaluate a mathematical expression, we perform the various operations. However, we do not perform them in any random order. We use the order of operations . This is a sequence of rules for evaluating such expressions.

Recall that in mathematics we use parentheses ( ), brackets [ ], and braces { } to group numbers and expressions so that anything appearing within the symbols is treated as a unit. Additionally, fraction bars, radicals, and absolute value bars are treated as grouping symbols. When evaluating a mathematical expression, begin by simplifying expressions within grouping symbols.

The next step is to address any exponents or radicals. Afterward, perform multiplication and division from left to right and finally addition and subtraction from left to right.

Let’s take a look at the expression provided.

There are no grouping symbols, so we move on to exponents or radicals. The number 4 is raised to a power of 2, so simplify 4 2 4 2 as 16.

Next, perform multiplication or division, left to right.

Lastly, perform addition or subtraction, left to right.

Therefore, 24 + 6 ⋅ 2 3 − 4 2 = 12. 24 + 6 ⋅ 2 3 − 4 2 = 12.

For some complicated expressions, several passes through the order of operations will be needed. For instance, there may be a radical expression inside parentheses that must be simplified before the parentheses are evaluated. Following the order of operations ensures that anyone simplifying the same mathematical expression will get the same result.

Order of Operations

Operations in mathematical expressions must be evaluated in a systematic order, which can be simplified using the acronym PEMDAS :

P (arentheses) E (xponents) M (ultiplication) and D (ivision) A (ddition) and S (ubtraction)

Given a mathematical expression, simplify it using the order of operations.

Step 1. Simplify any expressions within grouping symbols.
Step 2. Simplify any expressions containing exponents or radicals.
Step 3. Perform any multiplication and division in order, from left to right.
Step 4. Perform any addition and subtraction in order, from left to right.

Using the Order of Operations

Use the order of operations to evaluate each of the following expressions.

ⓐ ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 ) ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 )
ⓑ 5 2 − 4 7 − 11 − 2 5 2 − 4 7 − 11 − 2
ⓒ 6 − | 5 − 8 | + 3 ( 4 − 1 ) 6 − | 5 − 8 | + 3 ( 4 − 1 )
ⓓ 14 − 3 ⋅ 2 2 ⋅ 5 − 3 2 14 − 3 ⋅ 2 2 ⋅ 5 − 3 2
ⓔ 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1
ⓐ ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 ) = ( 6 ) 2 − 4 ( 8 ) Simplify parentheses. = 36 − 4 ( 8 ) Simplify exponent. = 36 − 32 Simplify multiplication. = 4 Simplify subtraction. ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 ) = ( 6 ) 2 − 4 ( 8 ) Simplify parentheses. = 36 − 4 ( 8 ) Simplify exponent. = 36 − 32 Simplify multiplication. = 4 Simplify subtraction.

Note that in the first step, the radical is treated as a grouping symbol, like parentheses. Also, in the third step, the fraction bar is considered a grouping symbol so the numerator is considered to be grouped.

ⓒ 6 − | 5 − 8 | + 3 | 4 − 1 | = 6 − | −3 | + 3 ( 3 ) Simplify inside grouping symbols. = 6 - ( 3 ) + 3 ( 3 ) Simplify absolute value. = 6 - 3 + 9 Simplify multiplication. = 12 Simplify addition. 6 − | 5 − 8 | + 3 | 4 − 1 | = 6 − | −3 | + 3 ( 3 ) Simplify inside grouping symbols. = 6 - ( 3 ) + 3 ( 3 ) Simplify absolute value. = 6 - 3 + 9 Simplify multiplication. = 12 Simplify addition.

In this example, the fraction bar separates the numerator and denominator, which we simplify separately until the last step.

ⓔ 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1 = 7 ( 15 ) − 2 [ ( 3 ) − 4 2 ] + 1 Simplify inside parentheses. = 7 ( 15 ) − 2 ( 3 − 16 ) + 1 Simplify exponent. = 7 ( 15 ) − 2 ( −13 ) + 1 Subtract. = 105 + 26 + 1 Multiply. = 132 Add. 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1 = 7 ( 15 ) − 2 [ ( 3 ) − 4 2 ] + 1 Simplify inside parentheses. = 7 ( 15 ) − 2 ( 3 − 16 ) + 1 Simplify exponent. = 7 ( 15 ) − 2 ( −13 ) + 1 Subtract. = 105 + 26 + 1 Multiply. = 132 Add.
ⓐ 5 2 − 4 2 + 7 ( 5 − 4 ) 2 5 2 − 4 2 + 7 ( 5 − 4 ) 2
ⓑ 1 + 7 ⋅ 5 − 8 ⋅ 4 9 − 6 1 + 7 ⋅ 5 − 8 ⋅ 4 9 − 6
ⓒ | 1.8 − 4.3 | + 0.4 15 + 10 | 1.8 − 4.3 | + 0.4 15 + 10
ⓓ 1 2 [ 5 ⋅ 3 2 − 7 2 ] + 1 3 ⋅ 9 2 1 2 [ 5 ⋅ 3 2 − 7 2 ] + 1 3 ⋅ 9 2
ⓔ [ ( 3 − 8 ) 2 − 4 ] − ( 3 − 8 ) [ ( 3 − 8 ) 2 − 4 ] − ( 3 − 8 )

Using Properties of Real Numbers

For some activities we perform, the order of certain operations does not matter, but the order of other operations does. For example, it does not make a difference if we put on the right shoe before the left or vice-versa. However, it does matter whether we put on shoes or socks first. The same thing is true for operations in mathematics.

Commutative Properties

The commutative property of addition states that numbers may be added in any order without affecting the sum.

We can better see this relationship when using real numbers.

Similarly, the commutative property of multiplication states that numbers may be multiplied in any order without affecting the product.

Again, consider an example with real numbers.

It is important to note that neither subtraction nor division is commutative. For example, 17 − 5 17 − 5 is not the same as 5 − 17. 5 − 17. Similarly, 20 ÷ 5 ≠ 5 ÷ 20. 20 ÷ 5 ≠ 5 ÷ 20.

Associative Properties

The associative property of multiplication tells us that it does not matter how we group numbers when multiplying. We can move the grouping symbols to make the calculation easier, and the product remains the same.

Consider this example.

The associative property of addition tells us that numbers may be grouped differently without affecting the sum.

This property can be especially helpful when dealing with negative integers. Consider this example.

Are subtraction and division associative? Review these examples.

As we can see, neither subtraction nor division is associative.

Distributive Property

The distributive property states that the product of a factor times a sum is the sum of the factor times each term in the sum.

This property combines both addition and multiplication (and is the only property to do so). Let us consider an example.

Note that 4 is outside the grouping symbols, so we distribute the 4 by multiplying it by 12, multiplying it by –7, and adding the products.

To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.

A special case of the distributive property occurs when a sum of terms is subtracted.

For example, consider the difference 12 − ( 5 + 3 ) . 12 − ( 5 + 3 ) . We can rewrite the difference of the two terms 12 and ( 5 + 3 ) ( 5 + 3 ) by turning the subtraction expression into addition of the opposite. So instead of subtracting ( 5 + 3 ) , ( 5 + 3 ) , we add the opposite.

Now, distribute −1 −1 and simplify the result.

This seems like a lot of trouble for a simple sum, but it illustrates a powerful result that will be useful once we introduce algebraic terms. To subtract a sum of terms, change the sign of each term and add the results. With this in mind, we can rewrite the last example.

Identity Properties

The identity property of addition states that there is a unique number, called the additive identity (0) that, when added to a number, results in the original number.

The identity property of multiplication states that there is a unique number, called the multiplicative identity (1) that, when multiplied by a number, results in the original number.

For example, we have ( −6 ) + 0 = −6 ( −6 ) + 0 = −6 and 23 ⋅ 1 = 23. 23 ⋅ 1 = 23. There are no exceptions for these properties; they work for every real number, including 0 and 1.

Inverse Properties

The inverse property of addition states that, for every real number a , there is a unique number, called the additive inverse (or opposite), denoted by (− a ), that, when added to the original number, results in the additive identity, 0.

For example, if a = −8 , a = −8 , the additive inverse is 8, since ( −8 ) + 8 = 0. ( −8 ) + 8 = 0.

The inverse property of multiplication holds for all real numbers except 0 because the reciprocal of 0 is not defined. The property states that, for every real number a , there is a unique number, called the multiplicative inverse (or reciprocal), denoted 1 a , 1 a , that, when multiplied by the original number, results in the multiplicative identity, 1.

For example, if a = − 2 3 , a = − 2 3 , the reciprocal, denoted 1 a , 1 a , is − 3 2 − 3 2 because

Properties of Real Numbers

The following properties hold for real numbers a , b , and c .

Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.

ⓐ 3 ⋅ 6 + 3 ⋅ 4 3 ⋅ 6 + 3 ⋅ 4
ⓑ ( 5 + 8 ) + ( −8 ) ( 5 + 8 ) + ( −8 )
ⓒ 6 − ( 15 + 9 ) 6 − ( 15 + 9 )
ⓓ 4 7 ⋅ ( 2 3 ⋅ 7 4 ) 4 7 ⋅ ( 2 3 ⋅ 7 4 )
ⓔ 100 ⋅ [ 0.75 + ( −2.38 ) ] 100 ⋅ [ 0.75 + ( −2.38 ) ]
ⓐ 3 ⋅ 6 + 3 ⋅ 4 = 3 ⋅ ( 6 + 4 ) Distributive property. = 3 ⋅ 10 Simplify. = 30 Simplify. 3 ⋅ 6 + 3 ⋅ 4 = 3 ⋅ ( 6 + 4 ) Distributive property. = 3 ⋅ 10 Simplify. = 30 Simplify.
ⓑ ( 5 + 8 ) + ( −8 ) = 5 + [ 8 + ( −8 ) ] Associative property of addition. = 5 + 0 Inverse property of addition. = 5 Identity property of addition. ( 5 + 8 ) + ( −8 ) = 5 + [ 8 + ( −8 ) ] Associative property of addition. = 5 + 0 Inverse property of addition. = 5 Identity property of addition.
ⓒ 6 − ( 15 + 9 ) = 6 + [ ( −15 ) + ( −9 ) ] Distributive property. = 6 + ( −24 ) Simplify. = −18 Simplify. 6 − ( 15 + 9 ) = 6 + [ ( −15 ) + ( −9 ) ] Distributive property. = 6 + ( −24 ) Simplify. = −18 Simplify.
ⓓ 4 7 ⋅ ( 2 3 ⋅ 7 4 ) = 4 7 ⋅ ( 7 4 ⋅ 2 3 ) Commutative property of multiplication. = ( 4 7 ⋅ 7 4 ) ⋅ 2 3 Associative property of multiplication. = 1 ⋅ 2 3 Inverse property of multiplication. = 2 3 Identity property of multiplication. 4 7 ⋅ ( 2 3 ⋅ 7 4 ) = 4 7 ⋅ ( 7 4 ⋅ 2 3 ) Commutative property of multiplication. = ( 4 7 ⋅ 7 4 ) ⋅ 2 3 Associative property of multiplication. = 1 ⋅ 2 3 Inverse property of multiplication. = 2 3 Identity property of multiplication.
ⓔ 100 ⋅ [ 0.75 + ( − 2.38 ) ] = 100 ⋅ 0.75 + 100 ⋅ ( −2.38 ) Distributive property. = 75 + ( −238 ) Simplify. = −163 Simplify. 100 ⋅ [ 0.75 + ( − 2.38 ) ] = 100 ⋅ 0.75 + 100 ⋅ ( −2.38 ) Distributive property. = 75 + ( −238 ) Simplify. = −163 Simplify.
ⓐ ( − 23 5 ) ⋅ [ 11 ⋅ ( − 5 23 ) ] ( − 23 5 ) ⋅ [ 11 ⋅ ( − 5 23 ) ]
ⓑ 5 ⋅ ( 6.2 + 0.4 ) 5 ⋅ ( 6.2 + 0.4 )
ⓒ 18 − ( 7 −15 ) 18 − ( 7 −15 )
ⓓ 17 18 + [ 4 9 + ( − 17 18 ) ] 17 18 + [ 4 9 + ( − 17 18 ) ]
ⓔ 6 ⋅ ( −3 ) + 6 ⋅ 3 6 ⋅ ( −3 ) + 6 ⋅ 3

Evaluating Algebraic Expressions

So far, the mathematical expressions we have seen have involved real numbers only. In mathematics, we may see expressions such as x + 5 , 4 3 π r 3 , x + 5 , 4 3 π r 3 , or 2 m 3 n 2 . 2 m 3 n 2 . In the expression x + 5 , x + 5 , 5 is called a constant because it does not vary and x is called a variable because it does. (In naming the variable, ignore any exponents or radicals containing the variable.) An algebraic expression is a collection of constants and variables joined together by the algebraic operations of addition, subtraction, multiplication, and division.

We have already seen some real number examples of exponential notation, a shorthand method of writing products of the same factor. When variables are used, the constants and variables are treated the same way.

In each case, the exponent tells us how many factors of the base to use, whether the base consists of constants or variables.

Any variable in an algebraic expression may take on or be assigned different values. When that happens, the value of the algebraic expression changes. To evaluate an algebraic expression means to determine the value of the expression for a given value of each variable in the expression. Replace each variable in the expression with the given value, then simplify the resulting expression using the order of operations. If the algebraic expression contains more than one variable, replace each variable with its assigned value and simplify the expression as before.

Describing Algebraic Expressions

List the constants and variables for each algebraic expression.

ⓑ 4 3 π r 3 4 3 π r 3
ⓒ 2 m 3 n 2 2 m 3 n 2
ⓐ 2 π r ( r + h ) 2 π r ( r + h )
ⓑ 2( L + W )
ⓒ 4 y 3 + y 4 y 3 + y

Evaluating an Algebraic Expression at Different Values

Evaluate the expression 2 x − 7 2 x − 7 for each value for x.

ⓐ x = 0 x = 0
ⓑ x = 1 x = 1
ⓒ x = 1 2 x = 1 2
ⓓ x = −4 x = −4
ⓐ Substitute 0 for x . x . 2 x − 7 = 2 ( 0 ) − 7 = 0 − 7 = −7 2 x − 7 = 2 ( 0 ) − 7 = 0 − 7 = −7
ⓑ Substitute 1 for x . x . 2 x − 7 = 2 ( 1 ) − 7 = 2 − 7 = −5 2 x − 7 = 2 ( 1 ) − 7 = 2 − 7 = −5
ⓒ Substitute 1 2 1 2 for x . x . 2 x − 7 = 2 ( 1 2 ) − 7 = 1 − 7 = −6 2 x − 7 = 2 ( 1 2 ) − 7 = 1 − 7 = −6
ⓓ Substitute −4 −4 for x . x . 2 x − 7 = 2 ( − 4 ) − 7 = − 8 − 7 = −15 2 x − 7 = 2 ( − 4 ) − 7 = − 8 − 7 = −15

Evaluate the expression 11 − 3 y 11 − 3 y for each value for y.

ⓐ y = 2 y = 2
ⓑ y = 0 y = 0
ⓒ y = 2 3 y = 2 3
ⓓ y = −5 y = −5

Evaluate each expression for the given values.

ⓐ x + 5 x + 5 for x = −5 x = −5
ⓑ t 2 t −1 t 2 t −1 for t = 10 t = 10
ⓒ 4 3 π r 3 4 3 π r 3 for r = 5 r = 5
ⓓ a + a b + b a + a b + b for a = 11 , b = −8 a = 11 , b = −8
ⓔ 2 m 3 n 2 2 m 3 n 2 for m = 2 , n = 3 m = 2 , n = 3
ⓐ Substitute −5 −5 for x . x . x + 5 = ( −5 ) + 5 = 0 x + 5 = ( −5 ) + 5 = 0
ⓑ Substitute 10 for t . t . t 2 t − 1 = ( 10 ) 2 ( 10 ) − 1 = 10 20 − 1 = 10 19 t 2 t − 1 = ( 10 ) 2 ( 10 ) − 1 = 10 20 − 1 = 10 19
ⓒ Substitute 5 for r . r . 4 3 π r 3 = 4 3 π ( 5 ) 3 = 4 3 π ( 125 ) = 500 3 π 4 3 π r 3 = 4 3 π ( 5 ) 3 = 4 3 π ( 125 ) = 500 3 π
ⓓ Substitute 11 for a a and –8 for b . b . a + a b + b = ( 11 ) + ( 11 ) ( −8 ) + ( −8 ) = 11 − 88 − 8 = −85 a + a b + b = ( 11 ) + ( 11 ) ( −8 ) + ( −8 ) = 11 − 88 − 8 = −85
ⓔ Substitute 2 for m m and 3 for n . n . 2 m 3 n 2 = 2 ( 2 ) 3 ( 3 ) 2 = 2 ( 8 ) ( 9 ) = 144 = 12 2 m 3 n 2 = 2 ( 2 ) 3 ( 3 ) 2 = 2 ( 8 ) ( 9 ) = 144 = 12
ⓐ y + 3 y − 3 y + 3 y − 3 for y = 5 y = 5
ⓑ 7 − 2 t 7 − 2 t for t = −2 t = −2
ⓒ 1 3 π r 2 1 3 π r 2 for r = 11 r = 11
ⓓ ( p 2 q ) 3 ( p 2 q ) 3 for p = −2 , q = 3 p = −2 , q = 3
ⓔ 4 ( m − n ) − 5 ( n − m ) 4 ( m − n ) − 5 ( n − m ) for m = 2 3 , n = 1 3 m = 2 3 , n = 1 3

An equation is a mathematical statement indicating that two expressions are equal. The expressions can be numerical or algebraic. The equation is not inherently true or false, but only a proposition. The values that make the equation true, the solutions, are found using the properties of real numbers and other results. For example, the equation 2 x + 1 = 7 2 x + 1 = 7 has the solution of 3 because when we substitute 3 for x x in the equation, we obtain the true statement 2 ( 3 ) + 1 = 7. 2 ( 3 ) + 1 = 7.

A formula is an equation expressing a relationship between constant and variable quantities. Very often, the equation is a means of finding the value of one quantity (often a single variable) in terms of another or other quantities. One of the most common examples is the formula for finding the area A A of a circle in terms of the radius r r of the circle: A = π r 2 . A = π r 2 . For any value of r , r , the area A A can be found by evaluating the expression π r 2 . π r 2 .

Using a Formula

A right circular cylinder with radius r r and height h h has the surface area S S (in square units) given by the formula S = 2 π r ( r + h ) . S = 2 π r ( r + h ) . See Figure 3 . Find the surface area of a cylinder with radius 6 in. and height 9 in. Leave the answer in terms of π . π .

Evaluate the expression 2 π r ( r + h ) 2 π r ( r + h ) for r = 6 r = 6 and h = 9. h = 9.

The surface area is 180 π 180 π square inches.

A photograph with length L and width W is placed in a mat of width 8 centimeters (cm). The area of the mat (in square centimeters, or cm 2 ) is found to be A = ( L + 16 ) ( W + 16 ) − L ⋅ W . A = ( L + 16 ) ( W + 16 ) − L ⋅ W . See Figure 4 . Find the area of a mat for a photograph with length 32 cm and width 24 cm.

Simplifying Algebraic Expressions

Sometimes we can simplify an algebraic expression to make it easier to evaluate or to use in some other way. To do so, we use the properties of real numbers. We can use the same properties in formulas because they contain algebraic expressions.

Simplify each algebraic expression.

ⓐ 3 x − 2 y + x − 3 y − 7 3 x − 2 y + x − 3 y − 7
ⓑ 2 r − 5 ( 3 − r ) + 4 2 r − 5 ( 3 − r ) + 4
ⓒ ( 4 t − 5 4 s ) − ( 2 3 t + 2 s ) ( 4 t − 5 4 s ) − ( 2 3 t + 2 s )
ⓓ 2 m n − 5 m + 3 m n + n 2 m n − 5 m + 3 m n + n
ⓐ 3 x − 2 y + x − 3 y − 7 = 3 x + x − 2 y − 3 y − 7 Commutative property of addition. = 4 x − 5 y − 7 Simplify. 3 x − 2 y + x − 3 y − 7 = 3 x + x − 2 y − 3 y − 7 Commutative property of addition. = 4 x − 5 y − 7 Simplify.
ⓑ 2 r − 5 ( 3 − r ) + 4 = 2 r − 15 + 5 r + 4 Distributive property. = 2 r + 5 r − 15 + 4 Commutative property of addition. = 7 r − 11 Simplify. 2 r − 5 ( 3 − r ) + 4 = 2 r − 15 + 5 r + 4 Distributive property. = 2 r + 5 r − 15 + 4 Commutative property of addition. = 7 r − 11 Simplify.
ⓒ ( 4 t − 5 4 s ) − ( 2 3 t + 2 s ) = 4 t − 5 4 s − 2 3 t − 2 s Distributive property. = 4 t − 2 3 t − 5 4 s − 2 s Commutative property of addition. = 10 3 t − 13 4 s Simplify. ( 4 t − 5 4 s ) − ( 2 3 t + 2 s ) = 4 t − 5 4 s − 2 3 t − 2 s Distributive property. = 4 t − 2 3 t − 5 4 s − 2 s Commutative property of addition. = 10 3 t − 13 4 s Simplify.
ⓓ 2 m n − 5 m + 3 m n + n = 2 m n + 3 m n − 5 m + n Commutative property of addition. = 5 m n − 5 m + n Simplify. 2 m n − 5 m + 3 m n + n = 2 m n + 3 m n − 5 m + n Commutative property of addition. = 5 m n − 5 m + n Simplify.
ⓐ 2 3 y − 2 ( 4 3 y + z ) 2 3 y − 2 ( 4 3 y + z )
ⓑ 5 t − 2 − 3 t + 1 5 t − 2 − 3 t + 1
ⓒ 4 p ( q − 1 ) + q ( 1 − p ) 4 p ( q − 1 ) + q ( 1 − p )
ⓓ 9 r − ( s + 2 r ) + ( 6 − s ) 9 r − ( s + 2 r ) + ( 6 − s )

Simplifying a Formula

A rectangle with length L L and width W W has a perimeter P P given by P = L + W + L + W . P = L + W + L + W . Simplify this expression.

If the amount P P is deposited into an account paying simple interest r r for time t , t , the total value of the deposit A A is given by A = P + P r t . A = P + P r t . Simplify the expression. (This formula will be explored in more detail later in the course.)

Access these online resources for additional instruction and practice with real numbers.

Simplify an Expression.
Evaluate an Expression 1.
Evaluate an Expression 2.

1.1 Section Exercises

Is 2 2 an example of a rational terminating, rational repeating, or irrational number? Tell why it fits that category.

What is the order of operations? What acronym is used to describe the order of operations, and what does it stand for?

What do the Associative Properties allow us to do when following the order of operations? Explain your answer.

For the following exercises, simplify the given expression.

10 + 2 × ( 5 − 3 ) 10 + 2 × ( 5 − 3 )

6 ÷ 2 − ( 81 ÷ 3 2 ) 6 ÷ 2 − ( 81 ÷ 3 2 )

18 + ( 6 − 8 ) 3 18 + ( 6 − 8 ) 3

−2 × [ 16 ÷ ( 8 − 4 ) 2 ] 2 −2 × [ 16 ÷ ( 8 − 4 ) 2 ] 2

4 − 6 + 2 × 7 4 − 6 + 2 × 7

3 ( 5 − 8 ) 3 ( 5 − 8 )

4 + 6 − 10 ÷ 2 4 + 6 − 10 ÷ 2

12 ÷ ( 36 ÷ 9 ) + 6 12 ÷ ( 36 ÷ 9 ) + 6

( 4 + 5 ) 2 ÷ 3 ( 4 + 5 ) 2 ÷ 3

3 − 12 × 2 + 19 3 − 12 × 2 + 19

2 + 8 × 7 ÷ 4 2 + 8 × 7 ÷ 4

5 + ( 6 + 4 ) − 11 5 + ( 6 + 4 ) − 11

9 − 18 ÷ 3 2 9 − 18 ÷ 3 2

14 × 3 ÷ 7 − 6 14 × 3 ÷ 7 − 6

9 − ( 3 + 11 ) × 2 9 − ( 3 + 11 ) × 2

6 + 2 × 2 − 1 6 + 2 × 2 − 1

64 ÷ ( 8 + 4 × 2 ) 64 ÷ ( 8 + 4 × 2 )

9 + 4 ( 2 2 ) 9 + 4 ( 2 2 )

( 12 ÷ 3 × 3 ) 2 ( 12 ÷ 3 × 3 ) 2

25 ÷ 5 2 − 7 25 ÷ 5 2 − 7

( 15 − 7 ) × ( 3 − 7 ) ( 15 − 7 ) × ( 3 − 7 )

2 × 4 − 9 ( −1 ) 2 × 4 − 9 ( −1 )

4 2 − 25 × 1 5 4 2 − 25 × 1 5

12 ( 3 − 1 ) ÷ 6 12 ( 3 − 1 ) ÷ 6

For the following exercises, evaluate the expression using the given value of the variable.

8 ( x + 3 ) – 64 8 ( x + 3 ) – 64 for x = 2 x = 2

4 y + 8 – 2 y 4 y + 8 – 2 y for y = 3 y = 3

( 11 a + 3 ) − 18 a + 4 ( 11 a + 3 ) − 18 a + 4 for a = –2 a = –2

4 z − 2 z ( 1 + 4 ) – 36 4 z − 2 z ( 1 + 4 ) – 36 for z = 5 z = 5

4 y ( 7 − 2 ) 2 + 200 4 y ( 7 − 2 ) 2 + 200 for y = –2 y = –2

− ( 2 x ) 2 + 1 + 3 − ( 2 x ) 2 + 1 + 3 for x = 2 x = 2

For the 8 ( 2 + 4 ) − 15 b + b 8 ( 2 + 4 ) − 15 b + b for b = –3 b = –3

2 ( 11 c − 4 ) – 36 2 ( 11 c − 4 ) – 36 for c = 0 c = 0

4 ( 3 − 1 ) x – 4 4 ( 3 − 1 ) x – 4 for x = 10 x = 10

1 4 ( 8 w − 4 2 ) 1 4 ( 8 w − 4 2 ) for w = 1 w = 1

For the following exercises, simplify the expression.

4 x + x ( 13 − 7 ) 4 x + x ( 13 − 7 )

2 y − ( 4 ) 2 y − 11 2 y − ( 4 ) 2 y − 11

a 2 3 ( 64 ) − 12 a ÷ 6 a 2 3 ( 64 ) − 12 a ÷ 6

8 b − 4 b ( 3 ) + 1 8 b − 4 b ( 3 ) + 1

5 l ÷ 3 l × ( 9 − 6 ) 5 l ÷ 3 l × ( 9 − 6 )

7 z − 3 + z × 6 2 7 z − 3 + z × 6 2

4 × 3 + 18 x ÷ 9 − 12 4 × 3 + 18 x ÷ 9 − 12

9 ( y + 8 ) − 27 9 ( y + 8 ) − 27

( 9 6 t − 4 ) 2 ( 9 6 t − 4 ) 2

6 + 12 b − 3 × 6 b 6 + 12 b − 3 × 6 b

18 y − 2 ( 1 + 7 y ) 18 y − 2 ( 1 + 7 y )

( 4 9 ) 2 × 27 x ( 4 9 ) 2 × 27 x

8 ( 3 − m ) + 1 ( − 8 ) 8 ( 3 − m ) + 1 ( − 8 )

9 x + 4 x ( 2 + 3 ) − 4 ( 2 x + 3 x ) 9 x + 4 x ( 2 + 3 ) − 4 ( 2 x + 3 x )

5 2 − 4 ( 3 x ) 5 2 − 4 ( 3 x )

Real-World Applications

For the following exercises, consider this scenario: Fred earns $40 at the community garden. He spends $10 on a streaming subscription, puts half of what is left in a savings account, and gets another $5 for walking his neighbor’s dog.

Write the expression that represents the number of dollars Fred keeps (and does not put in his savings account). Remember the order of operations.

How much money does Fred keep?

For the following exercises, solve the given problem.

According to the U.S. Mint, the diameter of a quarter is 0.955 inches. The circumference of the quarter would be the diameter multiplied by π . π . Is the circumference of a quarter a whole number, a rational number, or an irrational number?

Jessica and her roommate, Adriana, have decided to share a change jar for joint expenses. Jessica put her loose change in the jar first, and then Adriana put her change in the jar. We know that it does not matter in which order the change was added to the jar. What property of addition describes this fact?

For the following exercises, consider this scenario: There is a mound of g g pounds of gravel in a quarry. Throughout the day, 400 pounds of gravel is added to the mound. Two orders of 600 pounds are sold and the gravel is removed from the mound. At the end of the day, the mound has 1,200 pounds of gravel.

Write the equation that describes the situation.

Solve for g .

For the following exercise, solve the given problem.

Ramon runs the marketing department at their company. Their department gets a budget every year, and every year, they must spend the entire budget without going over. If they spend less than the budget, then the department gets a smaller budget the following year. At the beginning of this year, Ramon got $2.5 million for the annual marketing budget. They must spend the budget such that 2,500,000 − x = 0. 2,500,000 − x = 0. What property of addition tells us what the value of x must be?

For the following exercises, use a graphing calculator to solve for x . Round the answers to the nearest hundredth.

0.5 ( 12.3 ) 2 − 48 x = 3 5 0.5 ( 12.3 ) 2 − 48 x = 3 5

( 0.25 − 0.75 ) 2 x − 7.2 = 9.9 ( 0.25 − 0.75 ) 2 x − 7.2 = 9.9

If a whole number is not a natural number, what must the number be?

Determine whether the statement is true or false: The multiplicative inverse of a rational number is also rational.

Determine whether the statement is true or false: The product of a rational and irrational number is always irrational.

Determine whether the simplified expression is rational or irrational: −18 − 4 ( 5 ) ( −1 ) . −18 − 4 ( 5 ) ( −1 ) .

Determine whether the simplified expression is rational or irrational: −16 + 4 ( 5 ) + 5 . −16 + 4 ( 5 ) + 5 .

The division of two natural numbers will always result in what type of number?

What property of real numbers would simplify the following expression: 4 + 7 ( x − 1 ) ? 4 + 7 ( x − 1 ) ?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites

Authors: Jay Abramson
Publisher/website: OpenStax
Book title: College Algebra 2e
Publication date: Dec 21, 2021
Location: Houston, Texas
Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
Section URL: https://openstax.org/books/college-algebra-2e/pages/1-1-real-numbers-algebra-essentials

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Module 1: Algebra Essentials

Real numbers, learning outcomes.

Classify a real number.
Perform calculations using order of operations.
Use the properties of real numbers.
Evaluate and simplify algebraic expressions.

Because of the evolution of the number system, we can now perform complex calculations using several categories of real numbers. In this section we will explore sets of numbers, perform calculations with different kinds of numbers, and begin to learn about the use of numbers in algebraic expressions.

Classify a Real Number

The numbers we use for counting, or enumerating items, are the natural numbers : 1, 2, 3, 4, 5, and so on. We describe them in set notation as {1, 2, 3, …} where the ellipsis (…) indicates that the numbers continue to infinity. The natural numbers are, of course, also called the counting numbers . Any time we enumerate the members of a team, count the coins in a collection, or tally the trees in a grove, we are using the set of natural numbers. The set of whole numbers is the set of natural numbers plus zero: {0, 1, 2, 3,…}.

The set of integers adds the opposites of the natural numbers to the set of whole numbers: {…,-3, -2, -1, 0, 1, 2, 3,…}. It is useful to note that the set of integers is made up of three distinct subsets: negative integers, zero, and positive integers. In this sense, the positive integers are just the natural numbers. Another way to think about it is that the natural numbers are a subset of the integers.

The set of rational numbers is written as [latex]\left\{\frac{m}{n}|m\text{ and }{n}\text{ are integers and }{n}\ne{ 0 }\right\}[/latex]. Notice from the definition that rational numbers are fractions (or quotients) containing integers in both the numerator and the denominator, and the denominator is never 0. We can also see that every natural number, whole number, and integer is a rational number with a denominator of 1.

Because they are fractions, any rational number can also be expressed in decimal form. Any rational number can be represented as either:

a terminating decimal: [latex]\frac{15}{8}=1.875[/latex], or
a repeating decimal: [latex]\frac{4}{11}=0.36363636\dots =0.\overline{36}[/latex]

We use a line drawn over the repeating block of numbers instead of writing the group multiple times.

Example: Writing Integers as Rational Numbers

Write each of the following as a rational number.

Write a fraction with the integer in the numerator and 1 in the denominator.

[latex]7=\dfrac{7}{1}[/latex]
[latex]0=\dfrac{0}{1}[/latex]
[latex]-8=-\dfrac{8}{1}[/latex]
[latex]\dfrac{11}{1}[/latex]
[latex]\dfrac{3}{1}[/latex]
[latex]-\dfrac{4}{1}[/latex]

Example: Identifying Rational Numbers

Write each of the following rational numbers as either a terminating or repeating decimal.

[latex]-\dfrac{5}{7}[/latex]
[latex]\dfrac{15}{5}[/latex]
[latex]\dfrac{13}{25}[/latex]

Write each fraction as a decimal by dividing the numerator by the denominator.

[latex]-\dfrac{5}{7}=-0.\overline{714285}[/latex], a repeating decimal
[latex]\dfrac{15}{5}=3[/latex] (or 3.0), a terminating decimal
[latex]\dfrac{13}{25}=0.52[/latex], a terminating decimal

Irrational Numbers

At some point in the ancient past, someone discovered that not all numbers are rational numbers. A builder, for instance, may have found that the diagonal of a square with unit sides was not 2 or even [latex]\frac{3}{2}[/latex], but was something else. Or a garment maker might have observed that the ratio of the circumference to the diameter of a roll of cloth was a little bit more than 3, but still not a rational number. Such numbers are said to be irrational because they cannot be written as fractions. These numbers make up the set of irrational numbers . Irrational numbers cannot be expressed as a fraction of two integers. It is impossible to describe this set of numbers by a single rule except to say that a number is irrational if it is not rational. So we write this as shown.

Example: Differentiating Rational and Irrational Numbers

Determine whether each of the following numbers is rational or irrational. If it is rational, determine whether it is a terminating or repeating decimal.

[latex]\sqrt{25}[/latex]
[latex]\dfrac{33}{9}[/latex]
[latex]\sqrt{11}[/latex]
[latex]\dfrac{17}{34}[/latex]
[latex]0.3033033303333\dots[/latex]
[latex]\sqrt{25}:[/latex] This can be simplified as [latex]\sqrt{25}=5[/latex]. Therefore, [latex]\sqrt{25}[/latex] is rational.
[latex]\sqrt{11}:[/latex] This cannot be simplified any further. Therefore, [latex]\sqrt{11}[/latex] is an irrational number.
0.3033033303333… is not a terminating decimal. Also note that there is no repeating pattern because the group of 3s increases each time. Therefore it is neither a terminating nor a repeating decimal and, hence, not a rational number. It is an irrational number.

The real numbers can be visualized on a horizontal number line with an arbitrary point chosen as 0, with negative numbers to the left of 0 and positive numbers to the right of 0. A fixed unit distance is then used to mark off each integer (or other basic value) on either side of 0. Any real number corresponds to a unique position on the number line. The converse is also true: each location on the number line corresponds to exactly one real number. This is known as a one-to-one correspondence. We refer to this as the real number line .

The real number line

Example: Classifying Real Numbers

Classify each number as either positive or negative and as either rational or irrational. Does the number lie to the left or the right of 0 on the number line?

[latex]-\dfrac{10}{3}[/latex]
[latex]\sqrt{5}[/latex]
[latex]-\sqrt{289}[/latex]
[latex]-6\pi[/latex]
[latex]0.616161\dots[/latex]
[latex] 0.13 [/latex]
[latex]-\dfrac{10}{3}[/latex] is negative and rational. It lies to the left of 0 on the number line.
[latex]\sqrt{5}[/latex] is positive and irrational. It lies to the right of 0.
[latex]-\sqrt{289}=-\sqrt{{17}^{2}}=-17[/latex] is negative and rational. It lies to the left of 0.
[latex]-6\pi [/latex] is negative and irrational. It lies to the left of 0.
[latex]0.616161\dots [/latex] is a repeating decimal so it is rational and positive. It lies to the right of 0.
[latex] 0.13 [/latex] is a finite decimal and may be written as 13/100. So it is rational and positive.
[latex]\sqrt{73}[/latex]
[latex]-11.411411411\dots [/latex]
[latex]\dfrac{47}{19}[/latex]
[latex]-\dfrac{\sqrt{5}}{2}[/latex]
[latex]6.210735[/latex]
positive, irrational; right
negative, rational; left
positive, rational; right
negative, irrational; left

Sets of Numbers as Subsets

A large box labeled: Real Numbers encloses five circles. Four of these circles enclose each other and the other is separate from the rest. The innermost circle contains: 1, 2, 3… N. The circle enclosing that circle contains: 0 W. The circle enclosing that circle contains: …, -3, -2, -1 I. The outermost circle contains: m/n, n not equal to zero Q. The separate circle contains: pi, square root of two, etc Q´.

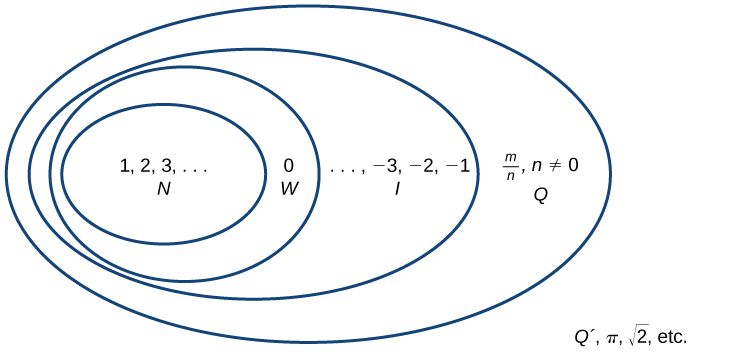
Sets of numbers. N : the set of natural numbers W : the set of whole numbers I : the set of integers Q : the set of rational numbers Q´ : the set of irrational numbers

A General Note: Sets of Numbers

The set of natural numbers includes the numbers used for counting: [latex]\{1,2,3,\dots\}[/latex].

The set of whole numbers is the set of natural numbers plus zero: [latex]\{0,1,2,3,\dots\}[/latex].

The set of integers adds the negative natural numbers to the set of whole numbers: [latex]\{\dots,-3,-2,-1,0,1,2,3,\dots\}[/latex].

The set of rational numbers includes fractions written as [latex]\{\frac{m}{n}|m\text{ and }n\text{ are integers and }n\ne 0\}[/latex].

The set of irrational numbers is the set of numbers that are not rational, are nonrepeating, and are nonterminating: [latex]\{h|h\text{ is not a rational number}\}[/latex].

Example: Differentiating the Sets of Numbers

Classify each number as being a natural number, whole number, integer, rational number, and/or irrational number.

[latex]\sqrt{36}[/latex]
[latex]\dfrac{8}{3}[/latex]
[latex]-6[/latex]
[latex]3.2121121112\dots [/latex]

Classify each number as being a natural number ( N ), whole number ( W ), integer ( I ), rational number ( Q ), and/or irrational number ( Q’ ).

[latex]-\dfrac{35}{7}[/latex]
[latex]0[/latex]
[latex]\sqrt{169}[/latex]
[latex]\sqrt{24}[/latex]
[latex]4.763763763\dots [/latex]

Properties of Real Numbers

When we multiply a number by itself, we square it or raise it to a power of 2. For example, [latex]{4}^{2}=4\cdot 4=16[/latex]. We can raise any number to any power. In general, the exponential notation [latex]{a}^{n}[/latex] means that the number or variable [latex]a[/latex] is used as a factor [latex]n[/latex] times.

In this notation, [latex]{a}^{n}[/latex] is read as the n th power of [latex]a[/latex], where [latex]a[/latex] is called the base and [latex]n[/latex] is called the exponent . A term in exponential notation may be part of a mathematical expression, which is a combination of numbers and operations. For example, [latex]24+6\cdot \frac{2}{3}-{4}^{2}[/latex] is a mathematical expression.

The next step is to address any exponents or radicals. Afterward, perform multiplication and division from left to right and finally addition and subtraction from left to right.

Let’s take a look at the expression provided.

There are no grouping symbols, so we move on to exponents or radicals. The number 4 is raised to a power of 2, so simplify [latex]{4}^{2}[/latex] as 16.

Next, perform multiplication or division, left to right.

Lastly, perform addition or subtraction, left to right.

Therefore, [latex]24+6\cdot \dfrac{2}{3}-{4}^{2}=12[/latex].

A General Note: Order of Operations

Operations in mathematical expressions must be evaluated in a systematic order, which can be simplified using the acronym PEMDAS :

P (arentheses)

E (xponents)

M (ultiplication) and D (ivision)

A (ddition) and S (ubtraction)

How To: Given a mathematical expression, simplify it using the order of operations.

Simplify any expressions within grouping symbols.
Simplify any expressions containing exponents or radicals.
Perform any multiplication and division in order, from left to right.
Perform any addition and subtraction in order, from left to right.

Example: Using the Order of Operations

Use the order of operations to evaluate each of the following expressions.

[latex]{\left(3\cdot 2\right)}^{2}-4\left(6+2\right)[/latex]
[latex]\dfrac{{5}^{2}-4}{7}-\sqrt{11 - 2}[/latex]
[latex]6-|5 - 8|+3\left(4 - 1\right)[/latex]
[latex]\dfrac{14 - 3\cdot 2}{2\cdot 5-{3}^{2}}[/latex]
[latex]7\left(5\cdot 3\right)-2\left[\left(6 - 3\right)-{4}^{2}\right]+1[/latex]

[latex]\begin{align}\left(3\cdot 2\right)^{2} & =\left(6\right)^{2}-4\left(8\right) && \text{Simplify parentheses} \\ & =36-4\left(8\right) && \text{Simplify exponent} \\ & =36-32 && \text{Simplify multiplication} \\ & =4 && \text{Simplify subtraction}\end{align}[/latex]

[latex]\begin{align}\frac{5^{2}-4}{7}-\sqrt{11-2} & =\frac{5^{2}-4}{7}-\sqrt{9} && \text{Simplify grouping systems (radical)} \\ & =\frac{5^{2}-4}{7}-3 && \text{Simplify radical} \\ & =\frac{25-4}{7}-3 && \text{Simplify exponent} \\ & =\frac{21}{7}-3 && \text{Simplify subtraction in numerator} \\ & =3-3 && \text{Simplify division} \\ & =0 && \text{Simplify subtraction}\end{align}[/latex]

[latex]\begin{align}6-|5-8|+3\left(4-1\right) & =6-|-3|+3\left(3\right) && \text{Simplify inside grouping system} \\ & =6-3+3\left(3\right) && \text{Simplify absolute value} \\ & =6-3+9 && \text{Simplify multiplication} \\ & =3+9 && \text{Simplify subtraction} \\ & =12 && \text{Simplify addition}\end{align}[/latex]

[latex]\begin{align}\frac{14-3\cdot2}{2\cdot5-3^{2}} & =\frac{14-3\cdot2}{2\cdot5-9} && \text{Simplify exponent} \\ & =\frac{14-6}{10-9} && \text{Simplify products} \\ & =\frac{8}{1} && \text{Simplify quotient} \\ & =8 && \text{Simplify quotient}\end{align}[/latex] In this example, the fraction bar separates the numerator and denominator, which we simplify separately until the last step.

[latex]\begin{align}7\left(5\cdot3\right)-2[\left(6-3\right)-4^{2}]+1 & =7\left(15\right)-2[\left(3\right)-4^{2}]+1 && \text{Simplify inside parentheses} \\ & 7\left(15\right)-2\left(3-16\right)+1 && \text{Simplify exponent} \\ & =7\left(15\right)-2\left(-13\right)+1 && \text{Subtract} \\ & =105+26+1 && \text{Multiply} \\ & =132 && \text{Add}\end{align}[/latex]

Watch the following video for more examples of using the order of operations to simplify an expression.

Using Properties of Real Numbers

Commutative Properties

The commutative property of addition states that numbers may be added in any order without affecting the sum.

We can better see this relationship when using real numbers.

Similarly, the commutative property of multiplication states that numbers may be multiplied in any order without affecting the product.

Again, consider an example with real numbers.

It is important to note that neither subtraction nor division is commutative. For example, [latex]17 - 5[/latex] is not the same as [latex]5 - 17[/latex]. Similarly, [latex]20\div 5\ne 5\div 20[/latex].

Associative Properties

Consider this example.

The associative property of addition tells us that numbers may be grouped differently without affecting the sum.

This property can be especially helpful when dealing with negative integers. Consider this example.

Are subtraction and division associative? Review these examples.

As we can see, neither subtraction nor division is associative.

Distributive Property

The distributive property states that the product of a factor times a sum is the sum of the factor times each term in the sum.

This property combines both addition and multiplication (and is the only property to do so). Let us consider an example.

The number four is separated by a multiplication symbol from a bracketed expression reading: twelve plus negative seven. Arrows extend from the four pointing to the twelve and negative seven separately. This expression equals four times twelve plus four times negative seven. Under this line the expression reads forty eight plus negative twenty eight. Under this line the expression reads twenty as the answer.

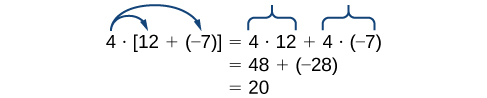
Note that 4 is outside the grouping symbols, so we distribute the 4 by multiplying it by 12, multiplying it by –7, and adding the products.

To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.

Multiplication does not distribute over subtraction, and division distributes over neither addition nor subtraction.

A special case of the distributive property occurs when a sum of terms is subtracted.

For example, consider the difference [latex]12-\left(5+3\right)[/latex]. We can rewrite the difference of the two terms 12 and [latex]\left(5+3\right)[/latex] by turning the subtraction expression into addition of the opposite. So instead of subtracting [latex]\left(5+3\right)[/latex], we add the opposite.

Now, distribute [latex]-1[/latex] and simplify the result.

Identity Properties

The identity property of addition states that there is a unique number, called the additive identity (0) that, when added to a number, results in the original number.

The identity property of multiplication states that there is a unique number, called the multiplicative identity (1) that, when multiplied by a number, results in the original number.

For example, we have [latex]\left(-6\right)+0=-6[/latex] and [latex]23\cdot 1=23[/latex]. There are no exceptions for these properties; they work for every real number, including 0 and 1.

Inverse Properties

The inverse property of addition states that, for every real number a , there is a unique number, called the additive inverse (or opposite), denoted− a , that, when added to the original number, results in the additive identity, 0.

For example, if [latex]a=-8[/latex], the additive inverse is 8, since [latex]\left(-8\right)+8=0[/latex].

The inverse property of multiplication holds for all real numbers except 0 because the reciprocal of 0 is not defined. The property states that, for every real number a , there is a unique number, called the multiplicative inverse (or reciprocal), denoted [latex]\frac{1}{a}[/latex], that, when multiplied by the original number, results in the multiplicative identity, 1.

For example, if [latex]a=-\frac{2}{3}[/latex], the reciprocal, denoted [latex]\frac{1}{a}[/latex], is [latex]-\frac{3}{2}[/latex] because

A General Note: Properties of Real Numbers

The following properties hold for real numbers a , b , and c .

Example: Using Properties of Real Numbers

Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.

[latex]3\cdot 6+3\cdot 4[/latex]
[latex]\left(5+8\right)+\left(-8\right)[/latex]
[latex]6-\left(15+9\right)[/latex]
[latex]\dfrac{4}{7}\cdot \left(\frac{2}{3}\cdot \dfrac{7}{4}\right)[/latex]
[latex]100\cdot \left[0.75+\left(-2.38\right)\right][/latex]

[latex]\begin{align}3\cdot6+3\cdot4 &=3\cdot\left(6+4\right) && \text{Distributive property} \\ &=3\cdot10 && \text{Simplify} \\ & =30 && \text{Simplify}\end{align}[/latex]

[latex]\begin{align}\left(5+8\right)+\left(-8\right) &=5+\left[8+\left(-8\right)\right] &&\text{Associative property of addition} \\ &=5+0 && \text{Inverse property of addition} \\ &=5 &&\text{Identity property of addition}\end{align}[/latex]

[latex]\begin{align}6-\left(15+9\right) & =6+(-15-9) && \text{Distributive property} \\ & =6+\left(-24\right) && \text{Simplify} \\ & =-18 && \text{Simplify}\end{align}[/latex]

[latex]\begin{align}\frac{4}{7}\cdot\left(\frac{2}{3}\cdot\frac{7}{4}\right) & =\frac{4}{7} \cdot\left(\frac{7}{4}\cdot\frac{2}{3}\right) && \text{Commutative property of multiplication} \\ & =\left(\frac{4}{7}\cdot\frac{7}{4}\right)\cdot\frac{2}{3} && \text{Associative property of multiplication} \\ & =1\cdot\frac{2}{3} && \text{Inverse property of multiplication} \\ & =\frac{2}{3} && \text{Identity property of multiplication}\end{align}[/latex]

[latex]\begin{align}100\cdot[0.75+\left(-2.38\right)] & =100\cdot0.75+100\cdot\left(-2.38\right) && \text{Distributive property} \\ & =75+\left(-238\right) && \text{Simplify} \\ & =-163 && \text{Simplify}\end{align}[/latex]

[latex]\left(-\dfrac{23}{5}\right)\cdot \left[11\cdot \left(-\dfrac{5}{23}\right)\right][/latex]
[latex]5\cdot \left(6.2+0.4\right)[/latex]
[latex]18-\left(7 - 15\right)[/latex]
[latex]\dfrac{17}{18}+\cdot \left[\dfrac{4}{9}+\left(-\dfrac{17}{18}\right)\right][/latex]
[latex]6\cdot \left(-3\right)+6\cdot 3[/latex]
11, commutative property of multiplication, associative property of multiplication, inverse property of multiplication, identity property of multiplication;
33, distributive property;
26, distributive property;
[latex]\dfrac{4}{9}[/latex], commutative property of addition, associative property of addition, inverse property of addition, identity property of addition;
0, distributive property, inverse property of addition, identity property of addition

Evaluate and Simplify Algebraic Expressions

So far, the mathematical expressions we have seen have involved real numbers only. In mathematics, we may see expressions such as [latex]x+5,\frac{4}{3}\pi {r}^{3}[/latex], or [latex]\sqrt{2{m}^{3}{n}^{2}}[/latex]. In the expression [latex]x+5, 5[/latex] is called a constant because it does not vary and x is called a variable because it does. (In naming the variable, ignore any exponents or radicals containing the variable.) An algebraic expression is a collection of constants and variables joined together by the algebraic operations of addition, subtraction, multiplication, and division.

In each case, the exponent tells us how many factors of the base to use, whether the base consists of constants or variables.

Example: Describing Algebraic Expressions

List the constants and variables for each algebraic expression.

[latex]\frac{4}{3}\pi {r}^{3}[/latex]
[latex]\sqrt{2{m}^{3}{n}^{2}}[/latex]

Example: Evaluating an Algebraic Expression at Different Values

Evaluate the expression [latex]2x - 7[/latex] for each value for x.

[latex]x=0[/latex]
[latex]x=1[/latex]
[latex]x=\dfrac{1}{2}[/latex]
[latex]x=-4[/latex]
Substitute 0 for [latex]x[/latex]. [latex]\begin{align}2x-7 & = 2\left(0\right)-7 \\ & =0-7 \\ & =-7\end{align}[/latex]
Substitute 1 for [latex]x[/latex]. [latex]\begin{align}2x-7 & = 2\left(1\right)-7 \\ & =2-7 \\ & =-5\end{align}[/latex]
Substitute [latex]\dfrac{1}{2}[/latex] for [latex]x[/latex]. [latex]\begin{align}2x-7 & = 2\left(\frac{1}{2}\right)-7 \\ & =1-7 \\ & =-6\end{align}[/latex]
Substitute [latex]-4[/latex] for [latex]x[/latex]. [latex]\begin{align}2x-7 & = 2\left(-4\right)-7 \\ & =-8-7 \\ & =-15\end{align}[/latex]

Example: Evaluating Algebraic Expressions

Evaluate each expression for the given values.

[latex]x+5[/latex] for [latex]x=-5[/latex]
[latex]\frac{t}{2t - 1}[/latex] for [latex]t=10[/latex]
[latex]\dfrac{4}{3}\pi {r}^{3}[/latex] for [latex]r=5[/latex]
[latex]a+ab+b[/latex] for [latex]a=11,b=-8[/latex]
[latex]\sqrt{2{m}^{3}{n}^{2}}[/latex] for [latex]m=2,n=3[/latex]
Substitute [latex]-5[/latex] for [latex]x[/latex]. [latex]\begin{align}x+5 &=\left(-5\right)+5 \\ &=0\end{align}[/latex]
Substitute 10 for [latex]t[/latex]. [latex]\begin{align}\frac{t}{2t-1} & =\frac{\left(10\right)}{2\left(10\right)-1} \\ & =\frac{10}{20-1} \\ & =\frac{10}{19}\end{align}[/latex]
Substitute 5 for [latex]r[/latex]. [latex]\begin{align}\frac{4}{3}\pi r^{3} & =\frac{4}{3}\pi\left(5\right)^{3} \\ & =\frac{4}{3}\pi\left(125\right) \\ & =\frac{500}{3}\pi\end{align}[/latex]
Substitute 11 for [latex]a[/latex] and –8 for [latex]b[/latex]. [latex]\begin{align}a+ab+b & =\left(11\right)+\left(11\right)\left(-8\right)+\left(-8\right) \\ & =11-8-8 \\ & =-85\end{align}[/latex]
Substitute 2 for [latex]m[/latex] and 3 for [latex]n[/latex]. [latex]\begin{align}\sqrt{2m^{3}n^{2}} & =\sqrt{2\left(2\right)^{3}\left(3\right)^{2}} \\ & =\sqrt{2\left(8\right)\left(9\right)} \\ & =\sqrt{144} \\ & =12\end{align}[/latex]

In the following video we present more examples of how to evaluate an expression for a given value.

An equation is a mathematical statement indicating that two expressions are equal. The expressions can be numerical or algebraic. The equation is not inherently true or false, but only a proposition. The values that make the equation true, the solutions, are found using the properties of real numbers and other results. For example, the equation [latex]2x+1=7[/latex] has the unique solution [latex]x=3[/latex] because when we substitute 3 for [latex]x[/latex] in the equation, we obtain the true statement [latex]2\left(3\right)+1=7[/latex].

A formula is an equation expressing a relationship between constant and variable quantities. Very often the equation is a means of finding the value of one quantity (often a single variable) in terms of another or other quantities. One of the most common examples is the formula for finding the area [latex]A[/latex] of a circle in terms of the radius [latex]r[/latex] of the circle: [latex]A=\pi {r}^{2}[/latex]. For any value of [latex]r[/latex], the area [latex]A[/latex] can be found by evaluating the expression [latex]\pi {r}^{2}[/latex].

Example: Using a Formula

A right circular cylinder with radius [latex]r[/latex] and height [latex]h[/latex] has the surface area [latex]S[/latex] (in square units) given by the formula [latex]S=2\pi r\left(r+h\right)[/latex]. Find the surface area of a cylinder with radius 6 in. and height 9 in. Leave the answer in terms of [latex]\pi[/latex].

Right circular cylinder

Evaluate the expression [latex]2\pi r\left(r+h\right)[/latex] for [latex]r=6[/latex] and [latex]h=9[/latex].

The surface area is [latex]180\pi [/latex] square inches.

/ An art frame with a piece of artwork in the center. The frame has a width of 8 centimeters. The artwork itself has a length of 32 centimeters and a width of 24 centimeters.

A photograph with length L and width W is placed in a mat of width 8 centimeters (cm). The area of the mat (in square centimeters, or cm 2 ) is found to be [latex]A=\left(L+16\right)\left(W+16\right)-L\cdot W[/latex]. Find the area of a mat for a photograph with length 32 cm and width 24 cm.

Simplify Algebraic Expressions

Example: Simplifying Algebraic Expressions

Simplify each algebraic expression.

[latex]3x - 2y+x - 3y - 7[/latex]
[latex]2r - 5\left(3-r\right)+4[/latex]
[latex]\left(4t-\dfrac{5}{4}s\right)-\left(\dfrac{2}{3}t+2s\right)[/latex]
[latex]2mn - 5m+3mn+n[/latex]
[latex]\begin{align}3x-2y+x-3y-7 & =3x+x-2y-3y-7 && \text{Commutative property of addition} \\ & =4x-5y-7 && \text{Simplify} \\ \text{ }\end{align}[/latex]
[latex]\begin{align}2r-5\left(3-r\right)+4 & =2r-15+5r+4 && \text{Distributive property}\\&=2r+5r-15+4 && \text{Commutative property of addition} \\ & =7r-11 && \text{Simplify} \\ \text{ }\end{align}[/latex]
[latex]\begin{align} 4t-\frac{5}{4}s -\left(\frac{2}{3}t+2s\right) &=4t-\frac{5}{4}s-\frac{2}{3}t-2s &&\text{Distributive property}\\&=4t-\frac{2}{3}t-\frac{5}{4}s-2s && \text{Commutative property of addition}\\&=\frac{12}{3}t-\frac{2}{3}t-\frac{5}{4}s-\frac{8}{4}s && \text{Common Denominators}\\ & =\frac{10}{3}t-\frac{13}{4}s && \text{Simplify} \\ \text{ }\end{align}[/latex]
[latex]\begin{align}mn-5m+3mn+n & =2mn+3mn-5m+n && \text{Commutative property of addition} \\ & =5mn-5m+n && \text{Simplify}\end{align}[/latex]

Example: Simplifying a Formula

A rectangle with length [latex]L[/latex] and width [latex]W[/latex] has a perimeter [latex]P[/latex] given by [latex]P=L+W+L+W[/latex]. Simplify this expression.

If the amount [latex]P[/latex] is deposited into an account paying simple interest [latex]r[/latex] for time [latex]t[/latex], the total value of the deposit [latex]A[/latex] is given by [latex]A=P+Prt[/latex]. Simplify the expression. (This formula will be explored in more detail later in the course.)

[latex]A=P\left(1+rt\right)[/latex]

Key Concepts

Rational numbers may be written as fractions or terminating or repeating decimals.
Determine whether a number is rational or irrational by writing it as a decimal.
The rational numbers and irrational numbers make up the set of real numbers. A number can be classified as natural, whole, integer, rational, or irrational.
The order of operations is used to evaluate expressions.
The real numbers under the operations of addition and multiplication obey basic rules, known as the properties of real numbers. These are the commutative properties, the associative properties, the distributive property, the identity properties, and the inverse properties.
Algebraic expressions are composed of constants and variables that are combined using addition, subtraction, multiplication, and division. They take on a numerical value when evaluated by replacing variables with constants.
Formulas are equations in which one quantity is represented in terms of other quantities. They may be simplified or evaluated as any mathematical expression.

algebraic expression constants and variables combined using addition, subtraction, multiplication, and division

associative property of addition the sum of three numbers may be grouped differently without affecting the result; in symbols, [latex]a+\left(b+c\right)=\left(a+b\right)+c[/latex]

associative property of multiplication the product of three numbers may be grouped differently without affecting the result; in symbols, [latex]a\cdot \left(b\cdot c\right)=\left(a\cdot b\right)\cdot c[/latex]

base in exponential notation, the expression that is being multiplied

commutative property of addition two numbers may be added in either order without affecting the result; in symbols, [latex]a+b=b+a[/latex]

commutative property of multiplication two numbers may be multiplied in any order without affecting the result; in symbols, [latex]a\cdot b=b\cdot a[/latex]

constant a quantity that does not change value

distributive property the product of a factor times a sum is the sum of the factor times each term in the sum; in symbols, [latex]a\cdot \left(b+c\right)=a\cdot b+a\cdot c[/latex]

equation a mathematical statement indicating that two expressions are equal

exponent in exponential notation, the raised number or variable that indicates how many times the base is being multiplied

exponential notation a shorthand method of writing products of the same factor

formula an equation expressing a relationship between constant and variable quantities

identity property of addition there is a unique number, called the additive identity, 0, which, when added to a number, results in the original number; in symbols, [latex]a+0=a[/latex]

identity property of multiplication there is a unique number, called the multiplicative identity, 1, which, when multiplied by a number, results in the original number; in symbols, [latex]a\cdot 1=a[/latex]

integers the set consisting of the natural numbers, their opposites, and 0: [latex]\{\dots ,-3,-2,-1,0,1,2,3,\dots \}[/latex]

inverse property of addition for every real number [latex]a[/latex], there is a unique number, called the additive inverse (or opposite), denoted [latex]-a[/latex], which, when added to the original number, results in the additive identity, 0; in symbols, [latex]a+\left(-a\right)=0[/latex]

inverse property of multiplication for every non-zero real number [latex]a[/latex], there is a unique number, called the multiplicative inverse (or reciprocal), denoted [latex]\dfrac{1}{a}[/latex], which, when multiplied by the original number, results in the multiplicative identity, 1; in symbols, [latex]a\cdot \dfrac{1}{a}=1[/latex]

irrational numbers the set of all numbers that are not rational; they cannot be written as either a terminating or repeating decimal; they cannot be expressed as a fraction of two integers

natural numbers the set of counting numbers: [latex]\{1,2,3,\dots \}[/latex]

order of operations a set of rules governing how mathematical expressions are to be evaluated, assigning priorities to operations

rational numbers the set of all numbers of the form [latex]\dfrac{m}{n}[/latex], where [latex]m[/latex] and [latex]n[/latex] are integers and [latex]n\ne 0[/latex]. Any rational number may be written as a fraction or a terminating or repeating decimal.

real number line a horizontal line used to represent the real numbers. An arbitrary fixed point is chosen to represent 0; positive numbers lie to the right of 0 and negative numbers to the left.

real numbers the sets of rational numbers and irrational numbers taken together

variable a quantity that may change value

whole numbers the set consisting of 0 plus the natural numbers: [latex]\{0,1,2,3,\dots \}[/latex]

Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
College Algebra. Authored by : Abramson, Jay et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
Question ID 92383, 109700, 110263, 109667. Authored by : Alyson Day. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
Question ID 13740. Authored by : David Lippman. License : CC BY: Attribution . License Terms : IMathAS Community License, CC-BY + GPL
Question ID 13741, 259. Authored by : James Sousa. License : CC BY: Attribution . License Terms : IMathAS Community License CC- BY + GPL
Identifying Sets of Real Numbers. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/htP2goe31MM . License : CC BY: Attribution
Simplifying Expressions With Square Roots. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/9suc63qB96o . License : CC BY: Attribution
Question ID 993379. Authored by : Desiree Davis. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
Question ID 92360, 92361, 92388. Authored by : Michael Jenck. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
Evaluating Algebraic Expressions. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/MkRdwV4n91g . License : CC BY: Attribution
Question ID 50617. Authored by : Brenda Gardner. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
Question ID 483. Authored by : Jeff Eldridge. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
Question ID 1976, 1980. Authored by : Lawrence Morales. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
Question ID 3616. Authored by : Shawn Triplett. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
College Algebra. Authored by : OpenStax College Algebra. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:1/Preface . License : CC BY: Attribution

1-1 Properties of Real Numbers

Here is your free content for this lesson!

Properties of Real Numbers - Word Docs & PowerPoints

1-1 Assignment - Properties of Real Numbers 1-1 Bellwork - Properties of real numbers 1-1 Exit Quiz - Properties of Real Numbers 1-1 Guided Notes SE - Properties of Real Numbers 1-1 Guided Notes TE - Properties of Real Numbers 1-1 Lesson Plan - Properties of Real Numbers 1-1 Online Activity - Properties of Real Numbers 1-1 Slide Show - Properties of Real Numbers

Properties of Real Numbers - PDFs

1-1 Assignment SE - Properties of Real Numbers 1-1 Assignment - Properties of Real Numbers 1-1 Bellwork SE - Properties of real numbers 1-1 Bellwork - Properties of real numbers 1-1 Exit Quiz SE - Properties of Real Numbers 1-1 Exit Quiz - Properties of Real Numbers 1-1 Guided Notes TE - Properties of Real Numbers 1-1 Guided Notes SE - Properties of Real Numbers 1-1 Lesson Plan - Properties of Real Numbers 1-1 Online Activity - Properties of Real Numbers 1-1 Slide Show - Properties of Real Numbers

Want access to everything? Simply click the image below to GET ALL OF OUR LESSONS!

Want more Great Algebra 2 Lessons? Check out our other posts…

Matrix multiplication, the properties of parabolas, organizing data into matrices, modeling data with quadratic functions, teaching linear equations, graphing systems of equations, teaching relations and functions, solving systems of linear inequalities, solving equations (algebra 2), simplifying algebraic expressions (algebra 2), angles and the unit circle – time to eat, properties of real numbers – the importance of differentiating directions in algebra, absolute value functions and graphs – real world applications, rational functions and their graphs – group activity, algebraic expressions worksheet and activity – mazing, holiday algebra 2 activities, how to make your math class paperless, i stopped letting my students use calculators in class, algebra 2 teacher hacks, conditional probability – call it in the air, area under a curve – is your umbrella big enough, properties of logarithms, adding and subtracting matrices – using rainbows, the nightmare of exploring conic sections, probability of multiple events – a coin and a card, roots and radical expressions – why so negative, solving systems of equations by substitution – sports and algebra 2, permutations and combinations using magic card tricks, angry birds parabola project, subscribe to blog via email.

Enter your email address to subscribe to this blog and receive notifications of new posts by email.

Join 2,704 other subscribers

Email Address

1.2: Order of Real Numbers

Last updated
Save as PDF
Page ID 1070

Order of Real Numbers

Suppose that you and three friends were playing a game where you each drew a number from a hat and the person with the highest number won. Let's say that you drew the number 32, while your friends drew the numbers 3–√, 1.7, and π3, respectively. Could you figure out who won the game?

Ordering Real Numbers

Classifying real numbers.

Let's use the chart to categorize the following numbers:

Zero is a whole number, an integer, a rational number , and a real number .

–1 is an integer, a rational number, and a real number.

π/3 is an irrational number and a real number.

√36/9

√36/9=6/9=2/3. This is a rational number and a real number.

Graphing and Ordering Real Numbers

Every real number can be positioned between two integers. Many times you will need to organize real numbers to determine the least value, greatest value, or both. This is usually done on a number line.

Let's plot the following rational numbers on a number line:

Now, let's compare π/15 and √3/√75:

First we simplify in order to better compare:

√3/√75=√3/(5√3)=1/5.

Now we rewrite π/15 to compare it to 1/5:

π/15=π/(3×5)=π/3×1/5.

Since π>3,

π/3>1

π/3×1/5>1/5.

Therefore, π/15>√3/√75.

Example 1 $\PageIndex{1}$

Earlier, you were asked to determine which number out of 3/2, √3, 1.7, and π/3 is the highest.

Notice that 3/2 = 1.5.

Also, since π≈3.14, π/3≈1.

Using a calculator, √3≈1.73.

Thus the order of the numbers is π/3 < 3/2 < 1.7 < √3 and √3 is the largest number.

Example 2 $\PageIndex{1}$

For the numbers: √12, (1.5)⋅(√3), 3/2, 2√5/√20, classify each number.

We need to simplify the numbers in order to classify them:

√12 = √((4x3)/2) = (2√3)/2 = √3. This is an irrational number. An irrational numbers is a type of real number.

(1.5)⋅(√3). This number cannot be simplified, but since it is a multiple of an irrational number, it is also irrational. In other words, we cannot get rid of the irrational part, and so we cannot write it as a rational number. It is also a real number.

3/2. Since this number is in the form of a proper fraction, it is also a rational number and real number.

(2√5)/√20 = (2√5)/(√4x5) = (2√5)/(2√5) = 1. This number can be simplified to an integer. All integers can be expressed as rational numbers and are a special kind of real number.

Example 3 $\PageIndex{1}$

For the numbers: √(12)/2, (1.5)⋅(√3), 3/2, (2√5)/√20, order the four numbers.

The four numbers are ordered as follows: 1<3/2<√3<(1.5)⋅√3.

1<3/2 since the numerator is larger then the denominator and 3/2=1.5.

3/2<√3 since we can see on our calculators that √3≈1.7

√3<(1.5)⋅√3 since multiplying by 1.5 makes any number larger.

Classify the following numbers. Include all the categories that apply to the number.

√0.25
√1.35
Place the following numbers in numerical order from lowest to highest. 6–√261501.5−−−√1613
Find the value of each marked point;

Mixed Review

Simplify (9/4)÷6.
The area of a triangle is given by the formula A=b(h)/2, where b= base of the triangle and h= height of the triangle. Determine the area of a triangle with base =3 feet and height =7 feet.
Reduce the fraction 144/6.
Construct a table for the following situation: Tracey jumps 60 times per minute. Let the minutes be {0,1,2,3,4,5,6}. What is the range of this function?

Review (Answers)

To see the Review answers, open this PDF file and look for section 2.13.

Additional Resources

PLIX: Play, Learn, Interact, eXplore: Number Lines: Freezing Cold Comparison

Real World Application: It's Elementary!

Practice: Order Real Numbers

Video: Graphing Real Numbers on a Number Line - Example 1

Class 10 Maths Chapter 1 Assignments

Class 10 Maths Chapter 1 Real Numbers Assignments and Worksheets with solutions and answers updated for academic session 2024-25. All the chapter is divided into 4 assignments taking easy, average, and difficult questions. These set of questions provide a complete revision for the preparation of CBSE and State board exams 2024-25.

CBSE NCERT Class 10 Maths Chapter 1 Real Numbers Assignments

Class 10 Maths Chapter 1 Real Numbers Assignments 1
Class 10 Maths Chapter 1 Real Numbers Assignments 1 Solutions
Class 10 Maths Chapter 1 Real Numbers Assignments 2
Class 10 Maths Chapter 1 Real Numbers Assignments 2 Solutions
Class 10 Maths Chapter 1 Real Numbers Assignments 3
Class 10 Maths Chapter 1 Real Numbers Assignments 3 Solutions
Class 10 Maths Chapter 1 Real Numbers Assignments 4
Class 10 Maths Chapter 1 Real Numbers Assignments 4 Solutions
Class 10 Maths Chapter 1 Real Numbers Solution Page

Download App for Class 10 all Subjects

There are 4 assignments and worksheets. Assignments contains MCQ, Fill in the Blanks, and True false questions. We have covered every topic in the chapter 1 of class 10 Maths. Answers and solutions of each assignment is also given free to use. Students can download these assignments and solve themselves. After solving they can check the answers given on website.

There are some easy questions based on understanding only. Some questions contains tricky methods and 17 percent questions are little bit difficult one. Students need to put effort to explore these questions. These assignments are guarantee to get good marks in exams. The questions based on Case Study will also be included in later chapters.

Download links are given for each assignments. Download and print it and solve it. Match the answers and solutions given on website to know the accuracy. Assignments are deign level wise, so do the first assignment first and the fourth assignment in the last.

Please suggest us, if any, about these assignments, so that we can improve the quality of the contents. We are preparing assignments for all the chapters. Gradually it will be uploaded before the final exams. Students are advised to solve these assignments to prepare the chapter and get confidence in topics.

Are assignments helpful in final exams?

Assignments are helpful in the revision of chapter as well as preparation for exams.

How many assignment should do to prepare the chapter?

At least 3 or 4 assignments which cover the entire chapter will be sufficient to know the chapter well.

How do solve the assignment?

Do yourself each assignment. If a part of assignment is not cleared or creating confusion, discuss with your classmate or teachers and solve it again.

Assignments for Class 10 Maths Chapter 1

Math Article
Real Numbers For Class 10

Real Numbers Class 10 Notes: Chapter 1

Cbse real numbers class 10 notes:- download pdf here, class 10 maths chapter 1 real number notes.

CBSE Class 10 Maths Chapter 1 Real Numbers Notes are provided here in detail. As we all know, any number, excluding complex numbers, is a real number. Positive and negative integers, irrational numbers, and fractions are all examples of real numbers. To put it another way, any number found in the real world is a real number. Numbers can be found all around us. Natural numbers are being used to count objects, integers are used to measure temperature, rational numbers are used to represent fractions, irrational numbers are used to calculate the square root of a number, etc. These various types of numbers form a collection of real numbers. Here, we are going to learn what a real number is, Euclid’s division algorithm, the fundamental theorem of arithmetic, methods of finding LCM and HCF and the complete explanation of rational and irrational numbers with examples.

Real Numbers

Positive integers, negative integers, irrational numbers, and fractions are all examples of real numbers. In other words, we can say that any number is a real number, except for complex numbers. Examples of real numbers include -1, ½, 1.75, √2, and so on. In general,

Real numbers constitute the union of all rational and irrational numbers.
Any real number can be plotted on the number line.

To know more about real numbers, visit here .

Students can refer to the short notes and MCQ questions along with a separate solution pdf of this chapter for quick revision from the links below.

Real Numbers Short Notes
Real Numbers MCQ Practice Questions
Real Numbers MCQ Practice Solutions

Euclid’s Division Lemma

Euclid’s Division Lemma states that given two integers a and b , there exists a unique pair of integers q and r such that a = b × q + r a n d 0 ≤ r < b .
This lemma is essentially equivalent to : dividend = divisor × quotient + remainder
In other words, for a given pair of dividend and divisor, the quotient and remainder obtained are going to be unique.

For more information on Euclid’s Division Lemma, watch the below video

To know more about Euclid’s Division Lemma, visit here .

Euclid’s Division Algorithm

Euclid’s Division Algorithm is a method used to find the H.C.F of two numbers, say a and b where a> b.
We apply Euclid’s Division Lemma to find two integers q and r such that a = b × q + r a n d 0 ≤ r < b .
If r = 0, the H.C.F is b; else, we apply Euclid’s division Lemma to b (the divisor) and r (the remainder) to get another pair of quotient and remainder.
The above method is repeated until a remainder of zero is obtained. The divisor in that step is the H.C.F. of the given set of numbers.

For more information on Euclid’s Division Algorithm, watch the below video

The Fundamental Theorem of Arithmetic

Prime Factorisation

Prime Factorisation is the method of expressing a natural number as a product of prime numbers.
Example: 36 = 2 × 2 × 3 × 3 is the prime factorisation of 36.

Fundamental Theorem of Arithmetic

The Fundamental Theorem of Arithmetic states that the prime factorisation for a given number is unique if the arrangement of the prime factors is ignored.
Example: 36 = 2 × 2 × 3 × 3 OR, 36 = 2 × 3 × 2 × 3
Therefore, 36 is represented as a product of prime factors (Two 2s and two 3s) ignoring the arrangement of the factors.

To know more about the Fundamental Theorem of Arithmetic, visit here .

Method of Finding LCM

As we know, the smallest of the common multiples of two or more numbers is called the lowest common multiple (LCM). Example: To find the Least Common Multiple ( L.C.M ) of 36 and 56,

36 = 2 × 2 × 3 × 3 56 = 2 × 2 × 2 × 7
The common prime factors are 2 × 2
The uncommon prime factors are 3 × 3 for 36 and 2 × 7 for 56.
LCM of 36 and 56 = 2 × 2 × 3 × 3 × 2 × 7 which is 504

To know more about LCM, visit here .

Method of Finding HCF

We know that the greatest number that divides each of the given numbers without leaving any remainder is the highest common factor (HCF) of two or more given numbers. H.C.F can be found using two methods – Prime factorisation and Euclid’s division algorithm.

Given two numbers, we express both of them as products of their respective prime factors. Then, we select the prime factors that are common to both the numbers
Example – To find the H.C.F of 20 and 24 20 = 2 × 2 × 5 and 24 = 2 × 2 × 2 × 3
The factor common to 20 and 24 is 2 × 2 , which is 4, which in turn is the H.C.F of 20 and 24.
It is the repeated use of Euclid’s division lemma to find the H.C.F of two numbers.

The required HCF is 6 .

To know more about HCF, visit here .

For more information on HCF and LCM, watch the below video

To know more about the Properties of HCF and LCM, visit here .

Product of Two Numbers = HCF X LCM of the Two Numbers

For any two positive integers a and b, a × b = H . C . F × L . C . M .
Example – For 36 and 56, the H.C.F is 4 and the L.C.M is 504 36 × 56 = 2016 4 × 504 = 2016 Thus, 36 × 56 = 4 × 504
Let us consider another example: For 5 and 6, the H.C.F is 1 and the L.C.M is 30 5 × 6 = 30 1 × 30 =30 Thus, 5 × 6 = 1 × 30
The above relationship, however, doesn’t hold true for 3 or more numbers

To know the Relationship between LCM and HCF, visit here .

Applications of HCF & LCM in Real-World Problems

L.C.M can be used to find the points of common occurrence. For example,ringing of bells that ring with different frequencies, the time at which two persons running at different speeds meet, and so on.

For more information on Applications Of LCM, watch the below video

Revisiting Irrational Numbers

Irrational numbers.

Any number that cannot be expressed in the form of p/q (where p and q are integers and q ≠ 0 .) is an irrational number. Examples √2 , π , e and so on.

To know more about Irrational Numbers, visit here .

Number theory: Interesting results

If a number p (a prime number) divides a 2 , then p divides a. Example: 3 divides 6 2 i.e 36, which implies that 3 divides 6.
The sum or difference of a rational and an irrational number is irrational
The product and quotient of a non-zero rational and irrational number are irrational.
√p is irrational when ‘p’ is a prime. For example, 7 is a prime number, and √7 is irrational. The above statement can be proved by the method of “Proof by contradiction”.

To know more about Number theory, visit here .

Proof by Contradiction

In the method of contradiction, to check whether a statement is TRUE (i) We assume that the given statement is TRUE. (ii) We arrive at some result which contradicts our assumption, thereby proving the contrary. Eg: Prove that √7 is irrational. Assumption: √7 is rational. Since it is rational √7 can be expressed as √7 = a/b , where a and b are co-prime Integers, b ≠ 0. On squaring, a 2 /b 2 = 7 ⇒ a 2 = 7 b 2 . Hence, 7 divides a. Then, there exists a number c such that a=7c. Then, a 2 = 49 c 2 . Hence, 7 b 2 = 49 c 2 or b 2 = 7 c 2 . Hence 7 divides b. Since 7 is a common factor for both a and b, it contradicts our assumption that a and b are coprime integers. Hence, our initial assumption that √7 is rational is wrong. Therefore, √7 is irrational.

Revisiting Rational Numbers and Their Decimal Expansions

Rational numbers.

Rational numbers are numbers that can be written in the form p/q, where p and q are integers and q ≠ 0 . Examples -1/2 , 4/5, 1 , 0 , − 3 and so on.

To know more about Rational Numbers, visit here .

Terminating and Non-Terminating Decimals

Terminating decimals are decimals that end at a certain point. Example: 0.2, 2.56 and so on. Non-terminating decimals are decimals where the digits after the decimal point don’t terminate. Example: 0.333333….., 0.13135235343… Non-terminating decimals can be : a) Recurring – a part of the decimal repeats indefinitely (0 . 142857 142857 …. ) b) Non-recurring – no part of the decimal repeats indefinitely. Example: π = 3.1415926535…

To know more about terminating and non-terminating decimals, click here .

Check if a given rational number is terminating or not

If a/b is a rational number, then its decimal expansion would terminate if both of the following conditions are satisfied : a) The H.C.F of a and b is 1. b) b can be expressed as a prime factorisation of 2 and 5 i.e b = 2 m × 5 n where either m or n, or both can = 0. If the prime factorisation of b contains any number other than 2 or 5, then the decimal expansion of that number will be recurring

1/40 = 0.025 is a terminating decimal, as the H.C.F of 1 and 40 is 1, and the denominator (40) can be expressed as 2 3 × 5 1 .

3/7 = 0.428571 is a recurring decimal as the H.C.F of 3 and 7 is 1 and the denominator (7) is equal to 7 1

Real Numbers for Class 10 Solved Examples

Find the largest number that divides 70 and 125 leaving the remainder 5 and 8 respectively.

First, subtract the remainder from the number.

(i.e) 70-5 = 65

125-8 = 117.

Thus, we need to find the largest number that divides 65 and 117 and leaves the remainder 0.

To find the largest number, take the HCF of 65 and 117.

Finding HCF of 65 and 117.

65 = 5×13

117 = 3×3×13.

Hence, HCF (65, 117) = 13.

Therefore, the largest number that divides 70 and 125 leaving the remainder 5 and 8 respectively is 13.

Find the LCM of 306 and 657, given that HCF (306, 657) = 9.

Given that, HCF (306, 657) = 9.

We know that HCF × LCM = Product of Numbers

Hence, 9×LCM = 306×657

9×LCM = 201042

LCM = 201042/9

LCM = 22338.

Therefore, LCM of 306 and 657 is 22338.

Prove that 1/√2 is an irrational number.

To prove 1/√2 is an irrational number.

Now, let us take the opposite assumption.

(i.e) Take 1/√2 is a rational number.

We know that rational numbers are the numbers that can be written in the form of p/q, where q is not equal to 0. (p and q are two co-prime numbers)

Hence, 1/√2 = p/q.

Now, simplify the above equation by multiplying √2 on both sides.

1 = (p√2)/q

q = p√2

Hence, we get q/p = √2.

Here, p and q are integers, and hence q/p is a rational number.

But, √2 is an irrational number.

Hence, our assumption is wrong.

Therefore, 1/√2 is an irrational number.

Hence, proved.

Frequently Asked Questions on Class 10 Real Numbers

What is euclid’s division algorithm, what does real numbers for class 10 explains, is 10i a real number, what does the fundamental theory of arithmetic explain.

Download BYJU’S – The Learning App and stay tuned with us to learn all Maths-related concepts easily by exploring more videos.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Register with BYJU'S & Download Free PDFs

Real Numbers

Real Numbers include all the rational and irrational numbers and can be positive, negative or zero. The Real Numbers had no name before Imaginary Numbers were thought of. They got called “Real” because they were not imaginary. The type of number we normally use, such as 1, 15.82, −0.1, 3/4, etc.

Positive or negative, large or small, whole numbers or decimal numbers are all Real Numbers. They are called “Real Numbers” because they are not Imaginary Numbers.

A real number is any element of the set R, which is the union of the set of rational numbers and the set of irrational numbers. In mathematical expressions, unknown or unspecified real numbers are usually represented by lowercase italic letters u through z. The set R gives rise to other sets such as the set of imaginary numbers and the set of complex numbers. The idea of a real number (and what makes it “real”) is primarily of interest to theoreticians.

A proper explanation of the real numbers nowadays is covered, if at all, in a course in “real analysis” in the junior or senior year of students who are majoring in mathematics. Surprisingly few students take such a course; perhaps that’s because it is too algebraic for the analysts’ taste and too analytic to please the algebraists.

Classification of Real Numbers

Natural Numbers– It includes all the counting numbers such as 1, 2, 3, 4,…
Whole Numbers– Numbers starting with zero are called whole numbers, like 0, 1, 2, 3, 4,…
Integers– Whole numbers and negative of all natural numbers are collectively known as integers, for example -3, -2, -1, 0, 1, 2,
Rational Numbers– All the numbers that can be written in the form of p/q, where q≠0 are known as Rational numbers.
Irrational Numbers– The numbers which cannot be written in the form of p/q (simple fraction) are known as irrational numbers. Irrational numbers are non-terminatin

Examples of Real Numbers

Natural numbers, whole numbers, integers, decimal numbers, rational numbers, and irrational numbers are the examples of real numbers.

Natural Numbers = {1, 2, 3,…}

Whole Numbers = {0, 1, 2, 3,…}

Integers Z = {…, -2, -1, 0, 1, 2,…}

Properties of Real Numbers

Real numbers can be ordered (this is not true, for instance, of imaginary numbers) They can be added, subtracted, multiplied and divided by nonzero numbers in an ordered way.

Commutative property- If we have real numbers m,n. The general form will be m + n = n + m for adaddition andmn = nm for multiplication
Associative property- If we have real numbers m,n,r. The general form will be m + (n + r) = (m + n) + r for addition(mn) r = m (nr) for multiplication
Distributive property- If we have real numbers m,n,r. The general form will be – m (n + r) = mn + mr and (m + n) r = mr + nr
Identity property- For addition: m + (- m) = 0

Define and Discuss on Central Limit Theorem

Inclination of a line, about deductive reasoning, relation between cartesian and polar co-ordinates, request letter to librarian to borrow books, arbitration process, lead-acid battery, venture debt, use of internet, light from space is brighter than expected, latest post, mid-ocean ridge (mor), harnessing hydrogen at the genesis of life, ngc 5728’s faint characteristics are exposed, astronomers discover the oldest black hole ever observed, atomic hydrogen welding, variable-frequency transformer (vft).

Watch CBS News

What customers should know about AT&T's massive data breach

By Khristopher J. Brooks

Edited By Anne Marie Lee

Updated on: April 11, 2024 / 3:23 PM EDT / CBS News

Millions of current and former AT&T customers learned over the weekend that hackers have likely stolen their personal information and are sharing it on the dark web .

AT&T on Saturday said it doesn't know if the massive data breach "originated from AT&T or one of its vendors," but that it has "launched a robust investigation" into what caused the incident. The data breach is the latest cyberattack AT&T has experienced since a leak in January of 2023 , that affected 9 million users. By contrast, Saturday's much larger breach impacts 73 million current and former AT&T account holders. AT&T has seen several data breaches over the years that range in size and impact.

The data breach prompted an Ohio man to file a class-action lawsuit against AT&T, accusing the telecommunications giant of negligence and breach of contract. Lawyers representing Alex Petroski of Summit County, Ohio, argued that the cyberattack could have been avoided and that AT&T's security failed to protect customer data.

Until more details of AT&T's investigation arise, here's what customers should know about the most recent data breach.

How many people were impacted by the AT&T data breach?

AT&T said the breach on Saturday affects about 7.6 million current and 65.4 million former AT&T customers.

What type of information was taken from AT&T?

AT&T said Saturday that a dataset found on the dark web contains information such as Social Security and passcodes. Unlike passwords, passcodes are numerical PINS that are typically four-digits long. Full names, email addresses, mailing addresses, phone numbers, dates of birth and AT&T account numbers may have also been compromised, the company said. The impacted data is from 2019 or earlier and does not appear to include financial information or call history, it added.

Was my information affected by the AT&T data breach?

Consumers impacted by this breach should be receiving an email or letter directly from AT&T about the incident. The email notices began going out on Saturday, an AT&T spokesperson confirmed .

What has AT&T done so far to help customers?

Beyond notifying customers, AT&T said that it had already reset the passcodes of current users. The company also said it would pay for credit-monitoring services where applicable.

What's the latest with AT&T's investigation into the breach?

AT&T hasn't disclosed details about its investigation into the data breach, but it is likely to be time-consuming and costly, according to Kevin Powers, the founding director of the Master of Science in Cybersecurity Policy and Governance Programs at Boston College.

The company will most likely bring in outside computer forensics specialists who will work with its on-site IT staff to determine exactly when and how the hackers got into the customer account information system, Powers said. But identifying the hackers' path of entry will be a big challenge for such a large company.

"You don't know where it came in from," Powers told CBS MoneyWatch, referring to the source of the breach. "It potentially could be from a customer or it could have been done from one of their outside contractors or someone else along their supply chain."

In addition, AT&T will have to scrub any malware out of the software that runs its customer account system, while also keeping the system running for customers who weren't impacted, he said. All these steps will have to be shared with lawyers, the outside consultants, and likely officials from the Federal Trade Commission.

What's the best way to protect my personal information?

Start by freezing your credit reports at all three major agencies — Equifax, Experience and TransUnion. Then sign up for 24-7 credit monitoring and enable two-factor authentication on your AT&T account, said WalletHub CEO Odysseas Papadimitriou, a former senior director at Capital One.

If you receive a notice about a breach, it's a good idea to change your password and monitor your account activity for any suspicious transactions. The Federal Trade Commission offers free credit freezes and fraud alerts that consumers can set up to help protect themselves from identity theft and other malicious activity.

—The Associated Press contributed to this report.

Khristopher J. Brooks is a reporter for CBS MoneyWatch. He previously worked as a reporter for the Omaha World-Herald, Newsday and the Florida Times-Union. His reporting primarily focuses on the U.S. housing market, the business of sports and bankruptcy.

More from CBS News

Costco now sells up to $200 million a month in gold and silver

Americans think they pay too much in taxes. Here's who pays the most.

Stamp prices poised to rise again, for the 2nd time this year

Delta is changing how it boards passengers starting May 1

Sports Betting
Sports Entertainment
New York Yankees
New York Mets
Transactions

Six real culprits for pitching-injury epidemic and pitch clock isn’t one of them

View Author Archive
Email the Author
Get author RSS feed

Contact The Author

Thanks for contacting us. We've received your submission.

MLB can look at the pitch clock as a possible factor as it continues to investigate the pitching-injury epidemic — and they’ve been investigating since October, with more than 100 interviewed so far — but here’s what folks around the game say are the real culprits.

1. Chasing velocity the wrong way (the rise of throwing academies that overemphasize velocity could be a culprit).

Yankees reliever Jonathan Loáisiga was one of the MLB pitchers to sustain an injury early into the 2024 season.

2. Violent, unhealthy deliveries.

3. Max-effort bullpens, even in spring (because data is being recorded).

4. High-pressure games starting at 10 years old.

Braves ace Spencer Strider sustained UCL damage in his throwing elbow.

5. Specializing in baseball only from an early age (few multisport athletes).

6. An emphasis on speed and strikeouts in deciding who to draft, who to sign and who to pay.

Share this article:

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

1.1: Sets of Real Numbers and the Cartesian Coordinate Plane

Last updated
Save as PDF
Page ID 80754

Carl Stitz & Jeff Zeager
Lakeland Community College & Lorain County Community College

Sets of Numbers

While the authors would like nothing more than to delve quickly and deeply into the sheer excitement that is Precalculus , experience 1 has taught us that a brief refresher on some basic notions is welcome, if not completely necessary, at this stage. To that end, we present a brief summary of ‘set theory’ and some of the associated vocabulary and notations we use in the text. Like all good Math books, we begin with a definition.

Definition 1.1

A set is a well-defined collection of objects which are called the ‘elements’ of the set. Here, ‘well-defined’ means that it is possible to determine if something belongs to the collection or not, without prejudice.

For example, the collection of letters that make up the word “smolko” is well-defined and is a set, but the collection of the worst math teachers in the world is not well-defined, and so is not a set. 2 In general, there are three ways to describe sets. They are

Ways to Describe Sets

The Verbal Method: Use a sentence to define a set.
The Roster Method: Begin with a left brace ‘$\{$’, list each element of the set only once and then end with a right brace ‘$\}$’.
The Set-Builder Method: A combination of the verbal and roster methods using a “dummy variable” such as $x$.

For example, let $S$ be the set described verbally as the set of letters that make up the word “smolko”. A roster description of $S$ would be $\left\{ s, m, o, l, k \right\}$. Note that we listed ‘o’ only once, even though it appears twice in “smolko.” Also, the order of the elements doesn’t matter, so $\left\{ k, l, m, o, s \right\}$ is also a roster description of $S$. A set-builder description of $S$ is: \[\{ x \, | \, \mbox{$x$ is a letter in the word ``smolko''.}\}\]

The way to read this is: ‘The set of elements $x$ $x$ is a letter in the word “smolko.”’ In each of the above cases, we may use the familiar equals sign ‘$=$’ and write $S = \left\{ s, m, o, l, k \right\}$ or $\ S=\{x \mid x \text { is a letter in the word "smolko". }\}$. Clearly $m$ is in $S$ and $q$ is not in $S$. We express these sentiments mathematically by writing $m \in S$ and $q \notin S$. Throughout your mathematical upbringing, you have encountered several famous sets of numbers. They are listed below.

The Empty Set : $\ \emptyset=\{\}=\{x \mid x \neq x\}$. This is the set with no elements. Like the number ‘$0$,’ it plays a vital role in mathematics. a
The Natural Numbers : $\mathbb N= \{ 1, 2, 3, \ldots\}$ The periods of ellipsis here indicate that the natural numbers contain $1$, $2$, $3$, ‘and so forth’.
The Whole Numbers : $\mathbb W = \{ 0, 1, 2, \ldots \}$
The Integers : $\mathbb Z=\{ \ldots, -3, -2, -1, 0, 1, 2, 3, \ldots \}$
The Rational Numbers : $\mathbb Q=\left\{\frac{a}{b} \, | \, a \in \mathbb Z \, \mbox{and} \, b \in \mathbb Z \right\}$. nal numbers are the s of integers (provided the denominator is not zero!) It turns out that another way to describe the rational numbers b is: \[\mathbb Q=\{x\,|\,\mbox{$x$ possesses a repeating or terminating decimal representation.}\}\]
The Real Numbers : $\ \mathbb{R}=\{x \mid x \text { possesses a decimal representation. }\}$
The Irrational Numbers : $\ \mathbb{P}=\{x \mid x \text { is a non-rational real number. }\}$ Said another way, an rational number is a decimal which neither repeats nor terminates. c
The Complex Numbers : $\ \mathbb{C}=\{a+b i \mid a, b \in \mathbb{R} \text { and } i=\sqrt{-1}\}$ Despite their importance, the complex numbers play only a minor role in the text. d

a . . . which, sadly, we will not explore in this text.

b See Section 9.2 .

c The classic example is the number $\ \pi$ (See Section 10.1 ), but numbers like $\ \sqrt{2}$ and 0.101001000100001 . . . are other fine representatives.

d They first appear in Section 3.4 and return in Section 11.7

It is important to note that every natural number is a whole number, which, in turn, is an integer. Each integer is a rational number (take $b =1$ in the above definition for $\mathbb Q$) and the rational numbers are all real numbers, since they possess decimal representations. 3 If we take $b=0$ in the above definition of $\mathbb C$, we see that every real number is a complex number. In this sense, the sets $\mathbb N$, $\mathbb W$, $\mathbb Z$, $\mathbb Q$, $\mathbb R$, and $\mathbb C$ are ‘nested’ like Matryoshka dolls .

For the most part, this textbook focuses on sets whose elements come from the real numbers $\mathbb R$. Recall that we may visualize $\mathbb R$ as a line. Segments of this line are called intervals of numbers. Below is a summary of the so-called interval notation associated with given sets of numbers. For intervals with finite endpoints, we list the left endpoint, then the right endpoint. We use square brackets, ‘$[$’ or ‘$]$’, if the endpoint is included in the interval and use a filled-in or ‘closed’ dot to indicate membership in the interval. Otherwise, we use parentheses, ‘$($’ or ‘$)$’ and an ‘open’ circle to indicate that the endpoint is not part of the set. If the interval does not have finite endpoints, we use the symbols $-\infty$ to indicate that the interval extends indefinitely to the left and $\infty$ to indicate that the interval extends indefinitely to the right. Since infinity is a concept, and not a number, we always use parentheses when using these symbols in interval notation, and use an appropriate arrow to indicate that the interval extends indefinitely in one (or both) directions.

Interval Notation

Let $a$ and $b$ be real numbers with $a<b$.

For an example, consider the sets of real numbers described below.

We will often have occasion to combine sets. There are two basic ways to combine sets: intersection and union . We define both of these concepts below.

Definition 1.2

Suppose $A$ and $B$ are two sets.

The intersection of $A$ and $B$: $A \cap B = \{ x \, | \, x \in A \, \text{and} \,\, x \in B \}$
The union of $A$ and $B$: $A \cup B = \{ x \, | \, x \in A \, \text{or} \,\, x \in B \, \, \text{(or both)} \}$

Said differently, the intersection of two sets is the overlap of the two sets – the elements which the sets have in common. The union of two sets consists of the totality of the elements in each of the sets, collected together. 4 For example, if $A = \{ 1,2,3 \}$ and $B = \{2,4,6 \}$, then $A \cap B = \{2\}$ and $A \cup B = \{1,2,3,4,6\}$. If $A = [-5,3)$ and $B = (1, \infty)$, then we can find $A \cap B$ and $A\cup B$ graphically. To find $A\cap B$, we shade the overlap of the two and obtain $A \cap B = (1,3)$. To find $A \cup B$, we shade each of $A$ and $B$ and describe the resulting shaded region to find $A \cup B = [-5,\infty)$.

$Screen Shot 2022-03-07 at 5.44.36 PM.png$

While both intersection and union are important, we have more occasion to use union in this text than intersection, simply because most of the sets of real numbers we will be working with are either intervals or are unions of intervals, as the following example illustrates.

Example 1.1.1

Express the following sets of numbers using interval notation.

$\ \{x \mid x \leq-2 \text { or } x \geq 2\}$
$\ \{x \mid x \neq 3\}$
$\ \{x \mid x \neq \pm 3\}$
$\ \{x \mid-1<x \leq 3 \text { or } x=5\}$

$Screen Shot 2022-03-07 at 5.52.21 PM.png$

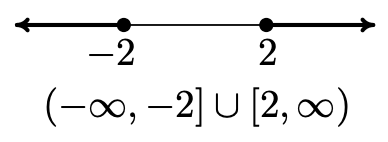
The Cartesian Coordinate Plane

In order to visualize the pure excitement that is Precalculus, we need to unite Algebra and Geometry. Simply put, we must find a way to draw algebraic things. Let’s start with possibly the greatest mathematical achievement of all time: the Cartesian Coordinate Plane . 5 Imagine two real number lines crossing at a right angle at $0$ as drawn below.

$Screen Shot 2022-03-07 at 6.24.19 PM.png$

The horizontal number line is usually called the $x$-axis while the vertical number line is usually called the $y$-axis . 6 As with the usual number line, we imagine these axes extending off indefinitely in both directions. 7 Having two number lines allows us to locate the positions of points off of the number lines as well as points on the lines themselves.

For example, consider the point $P$ on the next page. To use the numbers on the axes to label this point, we imagine dropping a vertical line from the $x$-axis to $P$ and extending a horizontal line from the $y$-axis to $P$. This process is sometimes called ‘projecting’ the point $P$ to the $x$- (respectively $y$-) axis. We then describe the point $P$ using the ordered pair $(2,-4)$. The first number in the ordered pair is called the abscissa or $x$-coordinate and the second is called the ordinate or $y$-coordinate . 8 Taken together, the ordered pair $(2,-4)$ comprise the Cartesian coordinates 9 of the point $P$. In practice, the distinction between a point and its coordinates is blurred; for example, we often speak of ‘the point $(2,-4)$.’ We can think of $(2,-4)$ as instructions on how to reach $P$ from the $(0, 0)$ by moving $2$ units to the right and $4$ units downwards. Notice that the order in the pair is important $-$ if we wish to plot the point $(-4,2)$, we would move to the left $4$ units from the origin and then move upwards $2$ units, as below on the right.

$Screen Shot 2022-03-07 at 6.29.23 PM.png$

When we speak of the Cartesian Coordinate Plane, we mean the set of all possible ordered pairs $(x,y)$ as $x$ and $y$ take values from the real numbers. Below is a summary of important facts about Cartesian coordinates.

Important Facts about the Cartesian Coordinate Plane

$(a,b)$ and $(c,d)$ represent the same point in the plane if and only if $a = c$ and $b = d$.
$(x,y)$ lies on the $x$-axis if and only if $y = 0$.
$(x,y)$ lies on the $y$-axis if and only if $x=0$.
The origin is the point $(0,0)$. It is the only point common to both axes.

Example 1.1.2

Plot the following points: $A(5,8)$, $B\left(-\frac{5}{2}, 3\right)$, $C(-5.8, -3)$, $D(4.5, -1)$, $E(5,0)$, $F(0,5)$, $G(-7,0)$, $H(0, -9)$, $O(0,0)$. 10

To plot these points, we start at the origin and move to the right if the $x$-coordinate is positive; to the left if it is negative. Next, we move up if the $y$-coordinate is positive or down if it is negative. If the $x$-coordinate is $0$, we start at the origin and move along the $y$-axis only. If the $y$-coordinate is $0$ we move along the $x$-axis only.

$Screen Shot 2022-03-07 at 7.54.43 PM.png$

The axes divide the plane into four regions called quadrants . They are labeled with Roman numerals and proceed counterclockwise around the plane

$Screen Shot 2022-03-07 at 7.56.14 PM.png$

For example, $(1,2)$ lies in Quadrant I, $(-1,2)$ in Quadrant II, $(-1,-2)$ in Quadrant III and $(1,-2)$ in Quadrant IV. If a point other than the origin happens to lie on the axes, we typically refer to that point as lying on the positive or negative $x$-axis (if $y = 0$) or on the positive or negative $y$-axis (if $x = 0$). For example, $(0,4)$ lies on the positive $y$-axis whereas $(-117,0)$ lies on the negative $x$-axis. Such points do not belong to any of the four quadrants.

One of the most important concepts in all of Mathematics is symmetry . 11 There are many types of symmetry in Mathematics, but three of them can be discussed easily using Cartesian Coordinates.

Definition 1.3

Two points $(a,b)$ and $(c,d)$ in the plane are said to be

symmetric about the $x$-axis if $a = c$ and $b = -d$
symmetric about the $y$-axis if $a = -c$ and $b = d$
symmetric about the origin if $a = -c$ and $b = -d$

Schematically,

$Screen Shot 2022-03-07 at 7.59.31 PM.png$

In the above figure, $P$ and $S$ are symmetric about the $x$-axis, as are $Q$ and $R$; $P$ and $Q$ are symmetric about the $y$-axis, as are $R$ and $S$; and $P$ and $R$ are symmetric about the origin, as are $Q$ and $S$.

Example 1.1.3

Let $P$ be the point $(-2,3)$. Find the points which are symmetric to $P$ about the:

Check your answer by plotting the points.

The figure after Definition 1.3 gives us a good way to think about finding symmetric points in terms of taking the opposites of the $x$- and/or $y$-coordinates of $P(-2,3)$.

To find the point symmetric about the $x$-axis, we replace the $y$-coordinate with its opposite to get $(-2,-3)$.
To find the point symmetric about the $y$-axis, we replace the $x$-coordinate with its opposite to get $(2,3)$.
To find the point symmetric about the origin, we replace the $x$- and $y$-coordinates with their opposites to get $(2,-3)$.

$Screen Shot 2022-03-07 at 8.06.12 PM.png$

One way to visualize the processes in the previous example is with the concept of a reflection . If we start with our point $(-2,3)$ and pretend that the $x$-axis is a mirror, then the reflection of $(-2,3)$ across the $x$-axis would lie at $(-2,-3)$. If we pretend that the $y$-axis is a mirror, the reflection of $(-2,3)$ across that axis would be $(2,3)$. If we reflect across the $x$-axis and then the $y$-axis, we would go from $(-2,3)$ to $(-2,-3)$ then to $(2,-3)$, and so we would end up at the point symmetric to $(-2,3)$ about the origin. We summarize and generalize this process below.

Reflections

To reflect a point $(x,y)$ about the:

$x$-axis, replace $y$ with $-y$.
$y$-axis, replace $x$ with $-x$.
origin, replace $x$ with $-x$ and $y$ with $-y$.

Distance in the Plane

Another important concept in Geometry is the notion of length. If we are going to unite Algebra and Geometry using the Cartesian Plane, then we need to develop an algebraic understanding of what distance in the plane means. Suppose we have two points, $P\left(x_0, y_0\right)$ and $Q\left(x_{1}, y_{1}\right),$ in the plane. By the distance $d$ between $P$ and $Q$, we mean the length of the line segment joining $P$ with $Q$. (Remember, given any two distinct points in the plane, there is a unique line containing both points.) Our goal now is to create an algebraic formula to compute the distance between these two points. Consider the generic situation below on the left.

$Screen Shot 2022-03-07 at 8.09.44 PM.png$

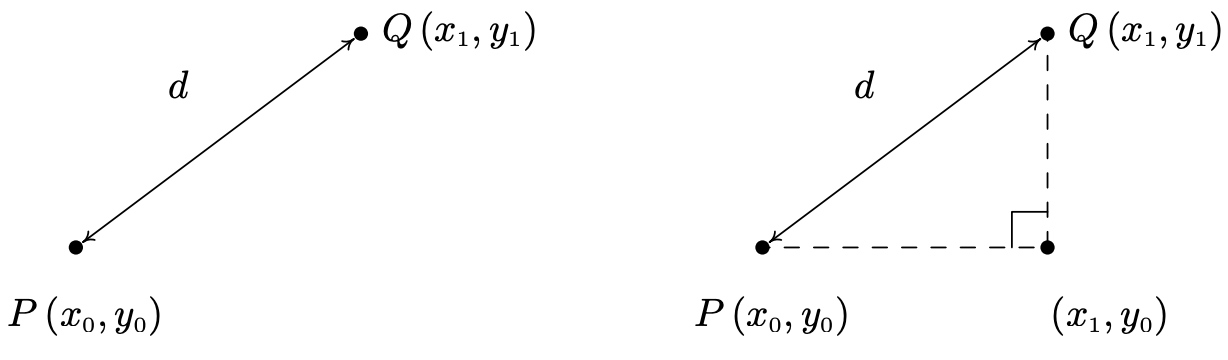
With a little more imagination, we can envision a right triangle whose hypotenuse has length $d$ as drawn above on the right. From the latter figure, we see that the lengths of the legs of the triangle are $\left|x_{1} - x_0\right|$ and $\left|y_{1} - y_0\right|$ so the Pythagorean Theorem gives us

\[\left|x_1 - x_0\right|^2 + \left|y_1 - y_0\right|^2 = d^2\] \[\left(x_1 - x_0\right)^2 + \left(y_1 - y_0\right)^2 = d^2\]

(Do you remember why we can replace the absolute value notation with parentheses?) By extracting the square root of both sides of the second equation and using the fact that distance is never negative, we get

Equation 1.1

The Distance Formula: The distance $d$ between the points $P\left(x_0, y_0\right)$ and $Q\left(x_{1}, y_{1}\right)$ is:

\[d = \sqrt{ \left(x_1 - x_0\right)^2 + \left(y_1 - y_0\right)^2}\]

It is not always the case that the points $P$ and $Q$ lend themselves to constructing such a triangle. If the points $P$ and $Q$ are arranged vertically or horizontally, or describe the exact same point, we cannot use the above geometric argument to derive the distance formula. It is left to the reader in Exercise 35 to verify Equation 1.1 for these cases.

Example 1.1.4

Find and simplify the distance between $P(-2,3)$ and $Q(1,-3)$.

\[\begin{array}{rcl} d & = & \sqrt{\left(x_1 - x_0 \right)^2 + \left(y_1 - y_0 \right)^2} \\ & = & \sqrt{ (1-(-2))^2 + (-3-3)^2} \\ & = & \sqrt{9 + 36} \\ & = & 3 \sqrt{5} \end{array}\]

So the distance is $3 \sqrt{5}$.

Example 1.1.5

Find all of the points with $x$-coordinate $1$ which are $4$ units from the point $(3,2)$.

We shall soon see that the points we wish to find are on the line $x=1$, but for now we’ll just view them as points of the form $(1,y)$. Visually,

$Screen Shot 2022-03-07 at 8.26.32 PM.png$

We require that the distance from $(3,2)$ to $(1,y)$ be $4$. The Distance Formula, Equation 1.1 , yields

\[\begin{array}{rclr} d & = & \sqrt{\left(x_1-x_0\right)^2+\left(y_1-y_0\right)^2} & \\ 4 & = & \sqrt{(1-3)^2+(y-2)^2} & \\ 4 & = & \sqrt{4+(y-2)^2} & \\ 4^2 & = & \left(\sqrt{4+(y-2)^2}\right)^2 & \mbox{squaring both sides} \\ 16 & = & 4+(y-2)^2 & \\ 12 & = & (y-2)^2 & \\ (y-2)^2 & = & 12 & \\ y - 2 & = & \pm \sqrt{12} & \mbox{extracting the square root} \\ y-2 & = & \pm 2 \sqrt{3} & \\ y & = & 2 \pm 2 \sqrt{3} & \end{array}\]

We obtain two answers: $(1, 2 + 2 \sqrt{3})$ and $(1, 2-2 \sqrt{3}).$ The reader is encouraged to think about why there are two answers.

Related to finding the distance between two points is the problem of finding the midpoint of the line segment connecting two points. Given two points, $P\left(x_0, y_0\right)$ and $Q\left(x_{1}, y_{1}\right)$, the midpoint $M$ of $P$ and $Q$ is defined to be the point on the line segment connecting $P$ and $Q$ whose distance from $P$ is equal to its distance from $Q$.

$Screen Shot 2022-03-07 at 8.29.27 PM.png$

If we think of reaching $M$ by going ‘halfway over’ and ‘halfway up’ we get the following formula.

Equation 1.2

The Midpoint Formula: The midpoint $M$ of the line segment connecting $P\left(x_0, y_0\right)$ and $Q\left(x_{1}, y_{1}\right)$ is:

\[M = \left( \dfrac{x_0 + x_1}{2} , \dfrac{y_0 + y_1}{2} \right)\]

If we let $d$ denote the distance between $P$ and $Q$, we leave it as Exercise 36 to show that the distance between $P$ and $M$ is $d/2$ which is the same as the distance between $M$ and $Q$. This suffices to show that Equation 1.2 gives the coordinates of the midpoint.

Example 1.1.6

Find the midpoint of the line segment connecting $P(-2,3)$ and $Q(1,-3)$.

\[\begin{array}{rcl} M & = & \left( \dfrac{x_0+x_1}{2}, \dfrac{y_0+y_1}{2} \right) \\ & = & \left( \dfrac{(-2)+1}{2}, \dfrac{3+(-3)}{2} \right) = \left(- \dfrac{1}{2}, \dfrac{0}{2} \right) \\ & = & \left(- \dfrac{1}{2}, 0 \right) \end{array}\]

The midpoint is $\left(- \frac{1}{2}, 0 \right)$.

We close with a more abstract application of the Midpoint Formula. We will revisit the following example in Exercise 72 in Section 2.1 .

Example 1.1.7

If $a \neq b$, prove that the line $y = x$ equally divides the line segment with endpoints $(a,b)$ and $(b,a)$.

Solution. To prove the claim, we use Equation 1.2 to find the midpoint

\[\begin{array}{rcl} M & = & \left( \dfrac{a+b}{2}, \dfrac{b+a}{2} \right) \\ & = & \left( \dfrac{a+b}{2}, \dfrac{a+b}{2} \right) \\ \end{array}\]

Since the $x$ and $y$ coordinates of this point are the same, we find that the midpoint lies on the line $y=x$, as required.

In Exercises 2 -7, find the indicated intersection or union and simplify if possible. Express your answers in interval notation.

$(-1,5] \cap [0,8)$ [findunionintfirst]
$(-1,1) \cup [0,6]$
$(-\infty,4]\cap (0,\infty)$
$(-\infty,0) \cap [1,5]$
$(-\infty, 0) \cup [1,5]$
$(-\infty, 5] \cap [5,8)$ [findunionintlast]

In Exercises 8 - 9, write the set using interval notation.

$\{x\,|\, x \neq 5 \}$ [writeintervalfirst]
$\{x\,|\, x \neq -1 \}$
$\{x\,|\, x \neq -3,\, 4 \}$
$\{x\,|\, x \neq 0, \, 2 \}$
$\{x\,|\, x \neq 2, \, -2 \}$
$\{x\,|\, x \neq 0,\, \pm 4 \}$
$\{x\,|\, x \leq -1 \, \text{or} \, x \geq 1 \}$
$\{x\,|\, x < 3 \, \text{or} \, x \geq 2 \}$
$\{x\,|\, x \leq -3 \, \text{or} \, x > 0 \}$
$\{x\,|\, x \leq 5 \, \text{or} \, x = 6 \}$
$\{x\,|\, x > 2 \, \text{or} \, x = \pm 1 \}$
$\{x\,|\, -3 < x < 3 \, \text{or} \, x = 4 \}$ [writeintervallast]
Plot and label the points $\;A(-3, -7)$, $\;B(1.3, -2)$, $\;C(\pi, \sqrt{10})$, $\;D(0, 8)$, $\;E(-5.5, 0)$, $\;F(-8, 4)$, $\;G(9.2, -7.8)$ and $H(7, 5)$ in the Cartesian Coordinate Plane given below.

$Screen Shot 2022-03-07 at 9.44.24 PM.png$

Identify the quadrant or axis in/on which the point lies.
Find the point symmetric to the given point about the $x$-axis.
Find the point symmetric to the given point about the $y$-axis.
Find the point symmetric to the given point about the origin.

In Exercises 22 - 29, find the distance $d$ between the points and the midpoint $M$ of the line segment which connects them.

$(1,2)$, $(-3,5)$ [distmidfirst]
$(3, -10)$, $(-1, 2)$
$\left( \dfrac{1}{2}, 4\right)$, $\left(\dfrac{3}{2}, -1\right)$
$\left(- \dfrac{2}{3}, \dfrac{3}{2} \right)$, $\left(\dfrac{7}{3}, 2\right)$
$\left( \dfrac{24}{5}, \dfrac{6}{5} \right)$, $\left( -\dfrac{11}{5}, -\dfrac{19}{5} \right)$.
$\left(\sqrt{2}, \sqrt{3}\right)$, $\left(-\sqrt{8}, -\sqrt{12}\right)$
$\left(2 \sqrt{45}, \sqrt{12} \right)$, $\left(\sqrt{20}, \sqrt{27} \right)$.
$(0, 0)$, $(x, y)$ [distmidlast]
Find all of the points of the form $(x, -1)$ which are $4$ units from the point $(3,2)$.
Find all of the points on the $y$-axis which are $5$ units from the point $(-5,3)$.
Find all of the points on the $x$-axis which are $2$ units from the point $(-1,1)$.
Find all of the points of the form $(x,-x)$ which are $1$ unit from the origin.
Let’s assume for a moment that we are standing at the origin and the positive $y$-axis points due North while the positive $x$-axis points due East. Our Sasquatch-o-meter tells us that Sasquatch is 3 miles West and 4 miles South of our current position. What are the coordinates of his position? How far away is he from us? If he runs 7 miles due East what would his new position be?
The points are arranged vertically. (Hint: Use $P(a, y_0)$ and $Q(a, y_{1})$.)
The points are arranged horizontally. (Hint: Use $P(x_0, b)$ and $Q(x_{1}, b)$.)
The points are actually the same point. (You shouldn’t need a hint for this one.)
Verify the Midpoint Formula by showing the distance between $P(x_{1}, y_{1})$ and $M$ and the distance between $M$ and $Q(x_{2}, y_{2})$ are both half of the distance between $P$ and $Q$.
$A(-3,2)$, $\;B(-6,4)$, and $C(1,8)$
$A(-3, 1)$, $\;B(4, 0)$ and $C(0, -3)$
Find a point $D(x, y)$ such that the points $A(-3, 1)$, $\;B(4, 0)$, $\;C(0, -3)$ and $D$ are the corners of a square. Justify your answer.
Discuss with your classmates how many numbers are in the interval $(0,1)$.
[orderedtripleexercise] The world is not flat. 12 Thus the Cartesian Plane cannot possibly be the end of the story. Discuss with your classmates how you would extend Cartesian Coordinates to represent the three dimensional world. What would the Distance and Midpoint formulas look like, assuming those concepts make sense at all?
$(-1,5] \cap [0,8) = [0,5]$
$(-1,1) \cup [0,6] = (-1,6]$
$(-\infty,4]\cap (0,\infty) = (0,4]$
$(-\infty,0) \cap [1,5] = \emptyset$
$(-\infty, 0) \cup [1,5] = (-\infty,0) \cup [1,5]$
$(-\infty, 5] \cap [5,8) = \left\{ 5\right\}$
$(-\infty, 5) \cup (5, \infty)$
$(-\infty, -1) \cup (-1, \infty)$
$(-\infty, -3) \cup (-3, 4)\cup (4, \infty)$
$(-\infty, 0) \cup (0, 2)\cup (2, \infty)$
$(-\infty, -2) \cup (-2, 2)\cup (2, \infty)$
$(-\infty, -4) \cup (-4, 0) \cup (0, 4) \cup (4, \infty)$
$(-\infty, -1] \cup [1, \infty)$
$(-\infty, \infty)$
$(-\infty, -3] \cup (0, \infty)$
$(-\infty, 5] \cup \{6\}$
$\{-1\} \cup \{1\} \cup (2, \infty)$
$(-3,3) \cup \{4\}$

$Screen Shot 2022-03-07 at 10.26.08 PM.png$

in Quadrant III
symmetric about $x$-axis with $(-3, 7)$
symmetric about $y$-axis with $(3, -7)$
symmetric about origin with $(3, 7)$
in Quadrant IV
symmetric about $x$-axis with $(1.3, 2)$
symmetric about $y$-axis with $(-1.3, -2)$
symmetric about origin with $(-1.3, 2)$
in Quadrant I
symmetric about $x$-axis with $(\pi, -\sqrt{10})$
symmetric about $y$-axis with $(-\pi, \sqrt{10})$
symmetric about origin with $(-\pi, -\sqrt{10})$
on the positive $y$-axis
symmetric about $x$-axis with $(0, -8)$
symmetric about $y$-axis with $(0, 8)$
symmetric about origin with $(0, -8)$
on the negative $x$-axis
symmetric about $x$-axis with $(-5.5, 0)$
symmetric about $y$-axis with $(5.5, 0)$
symmetric about origin with $(5.5, 0)$
in Quadrant II
symmetric about $x$-axis with $(-8, -4)$
symmetric about $y$-axis with $(8, 4)$
symmetric about origin with $(8, -4)$
symmetric about $x$-axis with $(9.2, 7.8)$
symmetric about $y$-axis with $(-9.2, -7.8)$
symmetric about origin with $(-9.2, 7.8)$
symmetric about $x$-axis with $(7, -5)$
symmetric about $y$-axis with $(-7, 5)$
symmetric about origin with $(-7, -5)$
$d = 5$, $M = \left(-1, \frac{7}{2} \right)$
$d = 4 \sqrt{10}$, $M = \left(1, -4 \right)$
$d = \sqrt{26}$, $M = \left(1, \frac{3}{2} \right)$
$d= \frac{\sqrt{37}}{2}$, $M = \left(\frac{5}{6}, \frac{7}{4} \right)$
$d = \sqrt{74}$, $M = \left(\frac{13}{10}, -\frac{13}{10} \right)$
$d= 3\sqrt{5}$, $M = \left(-\frac{\sqrt{2}}{2}, -\frac{\sqrt{3}}{2} \right)$
$d = \sqrt{83}$, $M = \left(4 \sqrt{5}, \frac{5 \sqrt{3}}{2} \right)$
$d = \sqrt{x^2 + y^2}$, $M = \left( \frac{x}{2}, \frac{y}{2}\right)$
$(3 + \sqrt{7}, -1)$, $(3-\sqrt{7}, -1)$
$(-1+\sqrt{3},0)$, $(-1-\sqrt{3},0)$
$\left(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2} \right)$, $\left(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)$
$(-3, -4)$, $5$ miles, $(4, -4)$
The distance from $A$ to $B$ is $|AB| = \sqrt{13}$, the distance from $A$ to $C$ is $|AC| = \sqrt{52}$, and the distance from $B$ to $C$ is $|BC| = \sqrt{65}$. Since $\left(\sqrt{13}\right)^2 + \left( \sqrt{52} \right)^2 = \left( \sqrt{65} \right)^2$, we are guaranteed by the that the triangle is a right triangle.
Show that $|AC|^{2} + |BC|^{2} = |AB|^{2}$

1 . . . to be read as ‘good, solid feedback from colleagues’ . . .

2 For a more thought-provoking example, consider the collection of all things that do not contain themselves - this leads to the famous Russell’s Paradox .

3 Long division, anyone?

4 The reader is encouraged to research Venn Diagrams for a nice geometric interpretation of these concepts.

5 So named in honor of René Descartes .

6 The labels can vary depending on the context of application.

7 Usually extending off towards infinity is indicated by arrows, but here, the arrows are used to indicate the direction of increasing values of $\ x$ and $\ y$.

8 Again, the names of the coordinates can vary depending on the context of the application. If, for example, the horizontal axis represented time we might choose to call it the t-axis. The first number in the ordered pair would then be the t-coordinate.

9 Also called the ‘rectangular coordinates’ of P – see Section 11.4 for more details.

10 The letter $\ O$ is almost always reserved for the origin.

11 According to Carl. Jeff thinks symmetry is overrated.

12 There are those who disagree with this statement. Look them up on the Internet some time when you’re bored.

We've detected unusual activity from your computer network

To continue, please click the box below to let us know you're not a robot.

Why did this happen?

Please make sure your browser supports JavaScript and cookies and that you are not blocking them from loading. For more information you can review our Terms of Service and Cookie Policy .

For inquiries related to this message please contact our support team and provide the reference ID below.

IMAGES

CBSE NCERT Class 10 Maths Chapter 1 Real Numbers Assignments Worksheet
NCERT Solutions for Class 10 Maths Chapter 1
a diagram on a piece of paper with markers and pencils sitting next to it
CBSE Class 10 Maths Chapter 1
CBSE NCERT Class 10 Maths Chapter 1 Real Numbers Assignments Worksheet
CBSE NCERT Class 10 Maths Chapter 1 Real Numbers Assignments Worksheet

VIDEO

Exercise 1.4 (Q-1) Real Number Class 10th(NCERT)
🔹️🔹️NCERT Solutions|Chapter 1 Real numbers|Exercise 1.1 Question-2|🔹️🔹️
Exercise
Chapter 1 Real Numbers Important 9 Questions || @gautammathsclasees1
Real Numbers
Real Numbers

COMMENTS

1.1 Real Numbers: Algebra Essentials
The property states that, for every real number a, there is a unique number, called the multiplicative inverse (or reciprocal), denoted 1 a, that, when multiplied by the original number, results in the multiplicative identity, 1. a ⋅ 1 a = 1. For example, if a = − 2 3, the reciprocal, denoted 1 a, is − 3 2 because.
1.1: Real Numbers
This page titled 1.1: Real Numbers - Algebra Essentials is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.
1.1E: Real Numbers
This page titled 1.1E: Real Numbers - Algebra Essentials (Exercises) is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.
PDF Name: Period: Date: Properties of Real Numbers Assignment
Find the additive inverse of each number. 1. 15 2. - 27 3. 7 9 4. 9 16 5. 0 1.-15 2. 27 3. - 4. 9 16 5. 0 Find the multiplicative inverse of each number. 1. 15 2. - 27 3. 7 9 4. 9 16 5. 1 1. 1 15 2. −1 27 3. 9 7 4. −16 9 5. 1
Real Numbers
We can also see that every natural number, whole number, and integer is a rational number with a denominator of 1. Because they are fractions, any rational number can also be expressed in decimal form. Any rational number can be represented as either: a terminating decimal: [latex]\frac {15} {8}=1.875 [/latex], or.
0.1: Review
To find the union of two intervals, use the portion of the number line representing the total collection of numbers in the two number line graphs. For example, Figure 0.1.3 Number Line Graph of x < 3 or x ≥ 6. Interval notation: ( − ∞, 3) ∪ [6, ∞) Set notation: {x | x < 3 or x ≥ 6}
Unit 1, Lesson 1: Real Numbers Flashcards
natural number. the set of all positive counting numbers starting with 1. irrational number. a number that cannot be written as a fraction, is a non-perfect square, is a non-terminating decimal, or is a non-repeating decimal. Study with Quizlet and memorize flashcards containing terms like real number, subset, rational number and more.
2.1 Real Numbers
A1.1.3 Explain the relationship between real numbers and the number line (including the density property) and compare and order real numbers with and without the number line; A1.1.6 Simplify numerical expressions, ... Corrective Assignment. 2.1_ca.pdf: File Size: 102 kb:
Properties of Real Numbers Worksheets ⋆ Algebra2Coach.com
Free Properties of Real Numbers Worksheets! Properties of Real Numbers Worksheet, Word Docs & PowerPoints. 1-1 Assignment. 1-1 Bell Work. 1-1 Exit Quiz. 1-1 Guided Notes SE. 1-1 Guided Notes TE. 1-1 Lesson Plan. 1-1 Online Activity. 1-1 Slide Show. Properties of Real Numbers - PDFs. 1-1 Assignment. 1-1 Assignment SE. 1-1 Bell Work. 1-1 Bell ...
PDF ASSIGNMENT 1
ASSIGNMENT 1 11 3. Section 1.3 - Properties of Real Numbers In the following exercises identify the property of real numbers illus-trated by the statement. 1.3.1: 18− 18 = 0 Additive Inverse Property 1.3.5: 13+12 = 12+13 Commutative Property of Addition 1.3.12: 1·9k = 9k Multiplicative Identity Property
1-1 Properties of Real Numbers
Here is your free content for this lesson! Properties of Real Numbers - Word Docs & PowerPoints. 1-1 Assignment - Properties of Real Numbers. 1-1 Bellwork - Properties of real numbers
Unit 1: Quiz 1
1/4c+5. Finding which number supports the idea that the rational numbers are dense in the real numbers? a terminating decimal between -3.14 and -3.15. Unit 1: Quiz 1 - Real Numbers. 4.5 (2 reviews) Which algebraic expression represents the phrase "six less than a number"? Click the card to flip 👆. x - 6.
1.2: Order of Real Numbers
It is also a real number. 3/2. Since this number is in the form of a proper fraction, it is also a rational number and real number. (2√5)/√20 = (2√5)/(√4x5) = (2√5)/(2√5) = 1. This number can be simplified to an integer. All integers can be expressed as rational numbers and are a special kind of real number.
1: Real Numbers and Their Operations
1.4: Fractions A fraction is a real number written as a quotient, or ratio, of two integers a and b , where b≠0 . 1.5: Review of Decimals and Percents In this section, we provide a brief review of the decimal system. A real number in decimal form, a decimal consists of a decimal point, digits (0 through 9) to the left of the decimal point ...
CBSE NCERT Class 10 Maths Chapter 1 Real Numbers Assignments Worksheet
Class 10 Maths Chapter 1 Real Numbers Assignments and Worksheets with solutions and answers updated for academic session 2024-25. All the chapter is divided into 4 assignments taking easy, average, and difficult questions. ... Assignments are deign level wise, so do the first assignment first and the fourth assignment in the last.
NCERT Solutions for Class 10 Maths Chapter 1- Real Numbers
There are four exercises in the NCERT Solutions for Class 10 Maths Real Numbers. These Solutions of NCERT Maths Class 10 Chapter 1 help the students in solving problems adroitly and efficiently. They also focus on cracking the Solutions of Maths in such a way that it is easy for the students to understand. Q3.
Properties of the Real Numbers Mathematics 800 Fundamentals
Unit 1. European Backgrounds, Assignment 10. The Dutch Claim New Land. 9 terms. QueenB218. Preview. History European backgrounds quiz 3. ... the number 1; when multiplied by any number, the value of the number does not change ... associative property. a property of the real numbers which states that how numbers are grouped in a sum or product ...
HW_ 1.3 The Real Numbers Assignment
= 7/4, and 16 = 16/1. Irrational numbers: 𝜋 𝜋 = 3.1415.. a nonterminating, nonrepeating decimal. Real numbers: 15 , 2 5, 0, −6, 1 3 4, 𝜋, 16 Every natural number, whole number, integer, rational number, and irrational number, is a real number. Self Check 1 Use the instructions for Example 1 with the following numbers. Natural numbers:
Real Numbers Class 10 Maths Chapter 1 Notes
Now, let us take the opposite assumption. (i.e) Take 1/√2 is a rational number. We know that rational numbers are the numbers that can be written in the form of p/q, where q is not equal to 0. (p and q are two co-prime numbers) Hence, 1/√2 = p/q. Now, simplify the above equation by multiplying √2 on both sides.
1.E: Review Exercises and Sample Exam
Exercise $\PageIndex{4}$ Real Numbers and the Number Line. Translate the following into a mathematical statement. Negative eight is less than or equal to zero. Seventy-eight is not equal to twelve. Negative nine is greater than negative ten. Zero is equal to zero. Answer. 1. $-8\leq 0$
Real Numbers
Article. Real Numbers include all the rational and irrational numbers and can be positive, negative or zero. The Real Numbers had no name before Imaginary Numbers were thought of. They got called "Real" because they were not imaginary. The type of number we normally use, such as 1, 15.82, −0.1, 3/4, etc. Positive or negative, large or ...
What customers should know about AT&T's massive data breach
AT&T said data found on the "dark web " contains information such as Social Security numbers and passcodes for roughly 73 million current and former customers. ... First published on April 1, 2024 ...
MLB pitch clock not one of real culprits for injury epidemic
1. Chasing velocity the wrong way (the rise of throwing academies that overemphasize velocity could be a culprit). Yankees reliever Jonathan Loáisiga was one of the MLB pitchers to sustain an ...
1.1: Sets of Real Numbers and the Cartesian Coordinate Plane
It is important to note that every natural number is a whole number, which, in turn, is an integer. Each integer is a rational number (take $b =1$ in the above definition for $\mathbb Q$) and the rational numbers are all real numbers, since they possess decimal representations. 3 If we take $b=0$ in the above definition of $\mathbb C$, we see that every real number is a complex number.
China Banks Say They Won't Blame Staff If Developer Loans Go Bad
A number of Chinese state banks are making their strongest effort yet to encourage credit officers to approve loans for developers, in a bid to heed the government's call to prop up the ...

1.1 Real Numbers: Algebra Essentials

Classifying a Real Number

Writing Integers as Rational Numbers

Identifying Rational Numbers

Irrational Numbers

Differentiating Rational and Irrational Numbers

Real Numbers

Classifying Real Numbers

Sets of Numbers as Subsets

Sets of Numbers

Differentiating the Sets of Numbers

Performing Calculations Using the Order of Operations

Order of Operations

Using the Order of Operations

Using Properties of Real Numbers

Commutative Properties

Associative Properties

Distributive Property

Identity Properties

Inverse Properties

Properties of Real Numbers

Evaluating Algebraic Expressions

Describing Algebraic Expressions

Evaluating an Algebraic Expression at Different Values

Using a Formula

Simplifying Algebraic Expressions

Simplifying a Formula

1.1 Section Exercises

Real-World Applications

Module 1: Algebra Essentials

Classify a Real Number

Example: Writing Integers as Rational Numbers

Example: Identifying Rational Numbers

Irrational Numbers

Example: Differentiating Rational and Irrational Numbers

Example: Classifying Real Numbers

Sets of Numbers as Subsets

A General Note: Sets of Numbers

Example: Differentiating the Sets of Numbers

Properties of Real Numbers

A General Note: Order of Operations

How To: Given a mathematical expression, simplify it using the order of operations.

Example: Using the Order of Operations

Using Properties of Real Numbers

Commutative Properties

Associative Properties

Distributive Property

Identity Properties

Inverse Properties

A General Note: Properties of Real Numbers

Example: Using Properties of Real Numbers

Evaluate and Simplify Algebraic Expressions

Example: Describing Algebraic Expressions

Example: Evaluating an Algebraic Expression at Different Values

Example: Evaluating Algebraic Expressions

Example: Using a Formula

Simplify Algebraic Expressions

Example: Simplifying Algebraic Expressions

Example: Simplifying a Formula

Key Concepts

1-1 Properties of Real Numbers

Properties of Real Numbers - Word Docs & PowerPoints

Properties of Real Numbers - PDFs

Want more Great Algebra 2 Lessons? Check out our other posts…

Share this:

1.2: Order of Real Numbers

Order of Real Numbers

Ordering Real Numbers

Let's use the chart to categorize the following numbers:

Graphing and Ordering Real Numbers

Let's plot the following rational numbers on a number line:

Now, let's compare π/15 and √3/√75:

Review (Answers)

Additional Resources

Class 10 Maths Chapter 1 Assignments

CBSE NCERT Class 10 Maths Chapter 1 Real Numbers Assignments

Are assignments helpful in final exams?

How many assignment should do to prepare the chapter?

How do solve the assignment?

Real Numbers Class 10 Notes: Chapter 1