problem solving lesson 1.12

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.12: Chapter 1 Review Exercises

• Last updated
• Save as PDF
• Page ID 49861

Chapter Review Exercises

Introduction to whole numbers.

Use Place Value with Whole Number

In the following exercises find the place value of each digit.

Exercise \(\PageIndex{1}\)

• ten thousands

Exercise \(\PageIndex{2}\)

Exercise \(\pageindex{3}\).

• ten millions
• hundred thousands

Exercise \(\PageIndex{4}\)

9,430,286,157

In the following exercises, name each number.

Exercise \(\PageIndex{5}\)

six thousand, one hundred four

Exercise \(\PageIndex{6}\)

Exercise \(\pageindex{7}\).

three million, nine hundred seventy-five thousand, two hundred eighty-four

Exercise \(\PageIndex{8}\)

In the following exercises, write each number as a whole number using digits.

Exercise \(\PageIndex{9}\)

three hundred fifteen

Exercise \(\PageIndex{10}\)

sixty-five thousand, nine hundred twelve

Exercise \(\PageIndex{11}\)

ninety million, four hundred twenty-five thousand, sixteen

Exercise \(\PageIndex{12}\)

one billion, forty-three million, nine hundred twenty-two thousand, three hundred eleven

In the following exercises, round to the indicated place value.

Exercise \(\PageIndex{13}\)

Round to the nearest ten.

Exercise \(\PageIndex{14}\)

Round to the nearest hundred.

In the following exercises, round each number to the nearest 1. hundred 2. thousand 3. ten thousand.

Exercise \(\PageIndex{15}\)

• 865,000865,000

Exercise \(\PageIndex{16}\)

Identify Multiples and Factors

In the following exercises, use the divisibility tests to determine whether each number is divisible by 2, by 3, by 5, by 6, and by 10.

Exercise \(\PageIndex{17}\)

Exercise \(\pageindex{18}\), exercise \(\pageindex{19}\), exercise \(\pageindex{20}\), exercise \(\pageindex{21}\), exercise \(\pageindex{22}\).

Find Prime Factorizations and Least Common Multiples

In the following exercises, find the prime factorization.

Exercise \(\PageIndex{23}\)

2\(\cdot 2 \cdot 3 \cdot 5 \cdot 7\)

Exercise \(\PageIndex{24}\)

Exercise \(\pageindex{25}\).

3\(\cdot 3 \cdot 5 \cdot 5\)

Exercise \(\PageIndex{26}\)

Exercise \(\pageindex{27}\).

\(2 \cdot 2 \cdot 2 \cdot 3 \cdot 5 \cdot 13\)

Exercise \(\PageIndex{28}\)

Exercise \(\pageindex{29}\).

\(2 \cdot 2 \cdot 2 \cdot 3 \cdot 3\)

Exercise \(\PageIndex{30}\)

Exercise \(\pageindex{31}\).

\(2 \cdot 2 \cdot 3 \cdot 3 \cdot 7\)

Exercise \(\PageIndex{32}\)

In the following exercises, find the least common multiple of the following numbers using the multiples method.

Exercise \(\PageIndex{33}\)

Exercise \(\pageindex{34}\).

In the following exercises, find the least common multiple of the following numbers using the prime factors method.

Exercise \(\PageIndex{35}\)

Exercise \(\pageindex{36}\), use the language of algebra.

Use Variables and Algebraic Symbols

In the following exercises, translate the following from algebra to English.

Exercise \(\PageIndex{37}\)

25 minus 7, the difference of twenty-five and seven

Exercise \(\PageIndex{38}\)

5\(\cdot 6\)

Exercise \(\PageIndex{39}\)

\(45 \div 5\)

45 divided by 5, the quotient of forty-five and five

Exercise \(\PageIndex{40}\)

Exercise \(\pageindex{41}\).

\(42 \geq 27\)

forty-two is greater than or equal to twenty-seven

Exercise \(\PageIndex{42}\)

Exercise \(\pageindex{43}\).

\(3 \leq 20 \div 4\)

3 is less than or equal to 20 divided by 4, three is less than or equal to the quotient of twenty and four

Exercise \(\PageIndex{44}\)

\(a \neq 7 \cdot 4\)

In the following exercises, determine if each is an expression or an equation.

Exercise \(\PageIndex{45}\)

\(6 \cdot 3+5\)

Exercise \(\PageIndex{46}\)

y−8=32

Simplify Expressions Using the Order of Operations

In the following exercises, simplify each expression.

Exercise \(\PageIndex{47}\)

Exercise \(\pageindex{48}\).

In the following exercises, simplify

Exercise \(\PageIndex{49}\)

Exercise \(\pageindex{50}\), exercise \(\pageindex{51}\).

\(20 \div(4+6) \cdot 5\)

Exercise \(\PageIndex{52}\)

\(33 \div(3+8) \cdot 2\)

Exercise \(\PageIndex{53}\)

\(4^{2}+5^{2}\)

Exercise \(\PageIndex{54}\)

\((4+5)^{2}\)

Evaluate an Expression

In the following exercises, evaluate the following expressions.

Exercise \(\PageIndex{55}\)

9x+7 when x=3

Exercise \(\PageIndex{56}\)

5x−4 when x=6

Exercise \(\PageIndex{57}\)

\(x^{4}\) when \(x=3\)

Exercise \(\PageIndex{58}\)

\(3^{x}\) when \(x=3\)

Exercise \(\PageIndex{59}\)

\(x^{2}+5 x-8\) when \(x=6\)

Exercise \(\PageIndex{60}\)

\(2 x+4 y-5\) when \(x=7, y=8\)

Simplify Expressions by Combining Like Terms

In the following exercises, identify the coefficient of each term.

Exercise \(\PageIndex{61}\)

Exercise \(\pageindex{62}\).

In the following exercises, identify the like terms.

Exercise \(\PageIndex{63}\)

\(3 n, n^{2}, 12,12 p^{2}, 3,3 n^{2}\)

12 and \(3, n^{2}\) and 3\(n^{2}\)

Exercise \(\PageIndex{64}\)

\(5,18 r^{2}, 9 s, 9 r, 5 r^{2}, 5 s\)

In the following exercises, identify the terms in each expression.

Exercise \(\PageIndex{65}\)

\(11 x^{2}+3 x+6\)

\(11 x^{2}, 3 x, 6\)

Exercise \(\PageIndex{66}\)

\(22 y^{3}+y+15\)

In the following exercises, simplify the following expressions by combining like terms.

Exercise \(\PageIndex{67}\)

Exercise \(\pageindex{68}\), exercise \(\pageindex{69}\), exercise \(\pageindex{70}\), exercise \(\pageindex{71}\).

7p+6+5p−4

Exercise \(\PageIndex{72}\)

8x+7+4x−5

Translate an English Phrase to an Algebraic Expression

In the following exercises, translate the following phrases into algebraic expressions.

Exercise \(\PageIndex{73}\)

the sum of 8 and 12

Exercise \(\PageIndex{74}\)

the sum of 9 and 1

Exercise \(\PageIndex{75}\)

the difference of x and 4

Exercise \(\PageIndex{76}\)

the difference of x and 3

Exercise \(\PageIndex{77}\)

the product of 6 and y

Exercise \(\PageIndex{78}\)

the product of 9 and y

Exercise \(\PageIndex{79}\)

Adele bought a skirt and a blouse. The skirt cost $15 more than the blouse. Let bb represent the cost of the blouse. Write an expression for the cost of the skirt.

Exercise \(\PageIndex{80}\)

Marcella has 6 fewer boy cousins than girl cousins. Let g represent the number of girl cousins. Write an expression for the number of boy cousins.

Add and Subtract Integers

Use Negatives and Opposites of Integers

In the following exercises, order each of the following pairs of numbers, using < or >.

Exercise \(\PageIndex{81}\)

• −7___4
• −9___−1
• 9___−3

Exercise \(\PageIndex{82}\)

• −5___1
• −4___−9
• 3___−8

In the following exercises,, find the opposite of each number.

Exercise \(\PageIndex{83}\)

Exercise \(\pageindex{84}\).

In the following exercises, simplify.

Exercise \(\PageIndex{85}\)

−(−19)

Exercise \(\PageIndex{86}\)

−(−53)

Exercise \(\PageIndex{87}\)

−m when

Exercise \(\PageIndex{88}\)

−p when

Simplify Expressions with Absolute Value

In the following exercises,, simplify.

Exercise \(\PageIndex{89}\)

• |−25|

Exercise \(\PageIndex{90}\)

• |−19|

In the following exercises, fill in <, >, or = for each of the following pairs of numbers.

Exercise \(\PageIndex{91}\)

• −8___|−8|
• −|−2|___−2

Exercise \(\PageIndex{92}\)

• |−3|___−|−3|
• 4___−|−4|

Exercise \(\PageIndex{93}\)

|8−4|

Exercise \(\PageIndex{94}\)

|9−6|

Exercise \(\PageIndex{95}\)

8(14−2|−2|)

Exercise \(\PageIndex{96}\)

6(13−4|−2|)

In the following exercises, evaluate.

Exercise \(\PageIndex{97}\)

1. |x| when x=−28

Exercise \(\PageIndex{98}\)

• ∣y∣ when y=−37
• |−z| when z=−24

Add Integers

Exercise \(\PageIndex{99}\)

−200+65

Exercise \(\PageIndex{100}\)

−150+45

Exercise \(\PageIndex{101}\)

2+(−8)+6

Exercise \(\PageIndex{102}\)

4+(−9)+7

Exercise \(\PageIndex{103}\)

140+(−75)+67

Exercise \(\PageIndex{104}\)

−32+24+(−6)+10

Subtract Integers

Exercise \(\PageIndex{105}\)

Exercise \(\pageindex{106}\).

−5−(−1)

Exercise \(\PageIndex{107}\)

• 15+(−6)

Exercise \(\PageIndex{108}\)

• 12+(−9)

Exercise \(\PageIndex{109}\)

• 8−(−9)

Exercise \(\PageIndex{110}\)

• 4−(−4)

Exercise \(\PageIndex{111}\)

10−(−19)

Exercise \(\PageIndex{112}\)

11−(−18)

Exercise \(\PageIndex{113}\)

31−79

Exercise \(\PageIndex{114}\)

39−81

Exercise \(\PageIndex{115}\)

−31−11

Exercise \(\PageIndex{116}\)

−32−18

Exercise \(\PageIndex{117}\)

−15−(−28)+5

Exercise \(\PageIndex{118}\)

71+(−10)−8

Exercise \(\PageIndex{119}\)

−16−(−4+1)−7

Exercise \(\PageIndex{120}\)

−15−(−6+4)−3

Multiply Integers

In the following exercises, multiply.

Exercise \(\PageIndex{121}\)

−5(7)

Exercise \(\PageIndex{122}\)

−8(6)

Exercise \(\PageIndex{123}\)

−18(−2)

Exercise \(\PageIndex{124}\)

−10(−6)

Divide Integers

In the following exercises, divide.

Exercise \(\PageIndex{125}\)

\(-28 \div 7\)

Exercise \(\PageIndex{126}\)

\(56 \div(-7)\)

Exercise \(\PageIndex{127}\)

\(-120 \div(-20)\)

Exercise \(\PageIndex{128}\)

\(-200 \div 25\)

Simplify Expressions with Integers

Exercise \(\PageIndex{129}\)

−8(−2)−3(−9)

Exercise \(\PageIndex{130}\)

−7(−4)−5(−3)

Exercise \(\PageIndex{131}\)

\((-5)^{3}\)

Exercise \(\PageIndex{132}\)

\((-4)^{3}\)

Exercise \(\PageIndex{133}\)

\(-4 \cdot 2 \cdot 11\)

Exercise \(\PageIndex{134}\)

\(-5 \cdot 3 \cdot 10\)

Exercise \(\PageIndex{135}\)

\(-10(-4) \div(-8)\)

Exercise \(\PageIndex{136}\)

\(-8(-6) \div(-4)\)

Exercise \(\PageIndex{137}\)

31−4(3−9)

Exercise \(\PageIndex{138}\)

24−3(2−10)

Evaluate Variable Expressions with Integers

In the following exercises, evaluate each expression.

Exercise \(\PageIndex{139}\)

• x=−26
• x=−95

Exercise \(\PageIndex{140}\)

• y=−29
• y=−84

Exercise \(\PageIndex{141}\)

When b=−11, evaluate:

Exercise \(\PageIndex{142}\)

When c=−9, evaluate:

• c+(−4)c+(−4)
• −c+(−4)

Exercise \(\PageIndex{143}\)

\(p^{2}-5 p+2\) when \(p=-1\)

Exercise \(\PageIndex{144}\)

\(q^{2}-2 q+9\) when \(q=-2\)

Exercise \(\PageIndex{145}\)

\(6 x-5 y+15\) when \(x=3\) and \(y=-1\)

Exercise \(\PageIndex{146}\)

\(3 p-2 q+9\) when \(p=8\) and \(q=-2\)

Translate English Phrases to Algebraic Expressions

In the following exercises, translate to an algebraic expression and simplify if possible.

Exercise \(\PageIndex{147}\)

the sum of −4 and −17, increased by 32

(−4+(−17))+32;11

Exercise \(\PageIndex{148}\)

• the difference of 15 and −7
• subtract 15 from −7

Exercise \(\PageIndex{149}\)

the quotient of −45 and −9

\(\frac{-45}{-9} ; 5\)

Exercise \(\PageIndex{150}\)

the product of −12 and the difference of c and d

Use Integers in Applications

In the following exercises, solve.

Exercise \(\PageIndex{151}\)

Temperature The high temperature one day in Miami Beach, Florida, was 76°. That same day, the high temperature in Buffalo, New York was −8°. What was the difference between the temperature in Miami Beach and the temperature in Buffalo?

Exercise \(\PageIndex{152}\)

Checking Account Adrianne has a balance of −$22 in her checking account. She deposits $301 to the account. What is the new balance?

Visualize Fractions

Find Equivalent Fractions

In the following exercises, find three fractions equivalent to the given fraction. Show your work, using figures or algebra.

Exercise \(\PageIndex{153}\)

\(\frac{1}{4}\)

\(\frac{2}{8}, \frac{3}{12}, \frac{4}{16}\) answers may vary

Exercise \(\PageIndex{154}\)

• \(\frac{1}{3}\)

Exercise \(\PageIndex{155}\)

\(\frac{5}{6}\)

\(\frac{10}{12}, \frac{15}{18}, \frac{20}{24}\) answers may vary

Exercise \(\PageIndex{156}\)

\(\frac{2}{7}\)

Simplify Fractions

Exercise \(\PageIndex{157}\)

\(\frac{7}{21}\)

Exercise \(\PageIndex{158}\)

\(\frac{8}{24}\)

Exercise \(\PageIndex{159}\)

\(\frac{15}{20}\)

\(\frac{3}{4}\)

Exercise \(\PageIndex{160}\)

\(\frac{12}{18}\)

Exercise \(\PageIndex{161}\)

\(-\frac{168}{192}\)

• \(-\frac{7}{8}\)

Exercise \(\PageIndex{162}\)

\(-\frac{140}{224}\)

Exercise \(\PageIndex{163}\)

\(\frac{11 x}{11 y}\)

\(\frac{x}{y}\)

Exercise \(\PageIndex{164}\)

\(\frac{15 a}{15 b}\)

Multiply Fractions

Exercise \(\PageIndex{165}\)

\(\frac{2}{5} \cdot \frac{1}{3}\)

\(\frac{2}{15}\)

Exercise \(\PageIndex{166}\)

\(\frac{1}{2} \cdot \frac{3}{8}\)

Exercise \(\PageIndex{167}\)

\(\frac{7}{12}\left(-\frac{8}{21}\right)\)

\(-\frac{2}{9}\)

Exercise \(\PageIndex{168}\)

\(\frac{5}{12}\left(-\frac{8}{15}\right)\)

Exercise \(\PageIndex{169}\)

\(-28 p\left(-\frac{1}{4}\right)\)

Exercise \(\PageIndex{170}\)

\(-51 q\left(-\frac{1}{3}\right)\)

Exercise \(\PageIndex{172}\)

\(\frac{14}{5}(-15)\)

Exercise \(\PageIndex{173}\)

\(-1\left(-\frac{3}{8}\right)\)

Divide Fractions

In the following exercises, divide

Exercise \(\PageIndex{174}\)

\(\frac{1}{2} \div \frac{1}{4}\)

Exercise \(\PageIndex{175}\)

\(\frac{1}{2} \div \frac{1}{8}\)

Exercise \(\PageIndex{176}\)

\(-\frac{4}{5} \div \frac{4}{7}\)

\(-\frac{7}{5}\)

Exercise \(\PageIndex{177}\)

\(-\frac{3}{4} \div \frac{3}{5}\)

Exercise \(\PageIndex{178}\)

\(\frac{5}{8} \div \frac{a}{10}\)

\(\frac{25}{4 a}\)

Exercise \(\PageIndex{179}\)

\(\frac{5}{6} \div \frac{c}{15}\)

Exercise \(\PageIndex{180}\)

\(\frac{7 p}{12} \div \frac{21 p}{8}\)

\(\frac{2}{9}\)

Exercise \(\PageIndex{181}\)

\(\frac{5 q}{12} \div \frac{15 q}{8}\)

Exercise \(\PageIndex{182}\)

\(\frac{2}{5} \div(-10)\)

\(-\frac{1}{25}\)

Exercise \(\PageIndex{183}\)

\(-18 \div-\left(\frac{9}{2}\right)\)

Exercise \(\PageIndex{184}\)

\(\frac{\frac{2}{3}}{\frac{8}{9}}\)

Exercise \(\PageIndex{185}\)

\(\frac{\frac{4}{5}}{\frac{8}{15}}\)

Exercise \(\PageIndex{186}\)

\(\frac{-\frac{9}{10}}{3}\)

\(-\frac{3}{10}\)

Exercise \(\PageIndex{187}\)

\(\frac{2}{\frac{5}{8}}\)

Exercise \(\PageIndex{188}\)

\(\frac{\frac{r}{5}}{\frac{s}{3}}\)

\(\frac{3 r}{5 s}\)

Exercise \(\PageIndex{189}\)

\(\frac{-\frac{x}{6}}{-\frac{8}{9}}\)

Simplify Expressions Written with a Fraction Bar

Exercise \(\PageIndex{190}\)

\(\frac{4+11}{8}\)

\(\frac{15}{8}\)

Exercise \(\PageIndex{191}\)

\(\frac{9+3}{7}\)

Exercise \(\PageIndex{192}\)

\(\frac{30}{7-12}\)

Exercise \(\PageIndex{193}\)

\(\frac{15}{4-9}\)

Exercise \(\PageIndex{194}\)

\(\frac{22-14}{19-13}\)

\(\frac{4}{3}\)

Exercise \(\PageIndex{195}\)

\(\frac{15+9}{18+12}\)

Exercise \(\PageIndex{196}\)

\(\frac{5 \cdot 8}{-10}\)

Exercise \(\PageIndex{197}\)

\(\frac{3 \cdot 4}{-24}\)

Exercise \(\PageIndex{198}\)

\(\frac{15 \cdot 5-5^{2}}{2 \cdot 10}\)

\(\frac{5}{2}\)

Exercise \(\PageIndex{199}\)

\(\frac{12 \cdot 9-3^{2}}{3 \cdot 18}\)

Exercise \(\PageIndex{200}\)

\(\frac{2+4(3)}{-3-2^{2}}\)

Exercise \(\PageIndex{201}\)

\(\frac{7+3(5)}{-2-3^{2}}\)

Translate Phrases to Expressions with Fractions

In the following exercises, translate each English phrase into an algebraic expression.

Exercise \(\PageIndex{202}\)

the quotient of c and the sum of d and 9.

\(\frac{c}{d+9}\)

Exercise \(\PageIndex{203}\)

the quotient of the difference of h and k , and −5.

Add and Subtract Fractions

Add and Subtract Fractions with a Common Denominator

In the following exercises, add.

Exercise \(\PageIndex{204}\)

\(\frac{4}{9}+\frac{1}{9}\)

\(\frac{5}{9}\)

Exercise \(\PageIndex{205}\)

\(\frac{2}{9}+\frac{5}{9}\)

Exercise \(\PageIndex{206}\)

\(\frac{y}{3}+\frac{2}{3}\)

\(\frac{y+2}{3}\)

Exercise \(\PageIndex{207}\)

\(\frac{7}{p}+\frac{9}{p}\)

Exercise \(\PageIndex{208}\)

\(-\frac{1}{8}+\left(-\frac{3}{8}\right)\)

\(-\frac{1}{2}\)

Exercise \(\PageIndex{209}\)

\(-\frac{1}{8}+\left(-\frac{5}{8}\right)\)

In the following exercises, subtract.

Exercise \(\PageIndex{210}\)

\(\frac{4}{5}-\frac{1}{5}\)

\(\frac{3}{5}\)

Exercise \(\PageIndex{211}\)

\(\frac{4}{5}-\frac{3}{5}\)

Exercise \(\PageIndex{212}\)

\(\frac{y}{17}-\frac{9}{17}\)

\(\frac{y-9}{17}\)

Exercise \(\PageIndex{213}\)

\(\frac{x}{19}-\frac{8}{19}\)

Exercise \(\PageIndex{214}\)

\(-\frac{8}{d}-\frac{3}{d}\)

\(-\frac{11}{d}\)

Exercise \(\PageIndex{215}\)

\(-\frac{7}{c}-\frac{7}{c}\)

Add or Subtract Fractions with Different Denominators

In the following exercises, add or subtract.

Exercise \(\PageIndex{216}\)

\(\frac{1}{3}+\frac{1}{5}\)

\(\frac{8}{15}\)

Exercise \(\PageIndex{217}\)

\(\frac{1}{4}+\frac{1}{5}\)

Exercise \(\PageIndex{218}\)

\(\frac{1}{5}-\left(-\frac{1}{10}\right)\)

\(\frac{3}{10}\)

Exercise \(\PageIndex{219}\)

\(\frac{1}{2}-\left(-\frac{1}{6}\right)\)

Exercise \(\PageIndex{220}\)

\(\frac{2}{3}+\frac{3}{4}\)

\(\frac{17}{12}\)

Exercise \(\PageIndex{221}\)

\(\frac{3}{4}+\frac{2}{5}\)

Exercise \(\PageIndex{222}\)

\(\frac{11}{12}-\frac{3}{8}\)

\(\frac{13}{24}\)

Exercise \(\PageIndex{223}\)

\(\frac{5}{8}-\frac{7}{12}\)

Exercise \(\PageIndex{224}\)

\(-\frac{9}{16}-\left(-\frac{4}{5}\right)\)

\(\frac{19}{80}\)

Exercise \(\PageIndex{225}\)

\(-\frac{7}{20}-\left(-\frac{5}{8}\right)\)

Exercise \(\PageIndex{226}\)

\(1+\frac{5}{6}\)

\(\frac{11}{6}\)

Exercise \(\PageIndex{227}\)

\(1-\frac{5}{9}\)

Use the Order of Operations to Simplify Complex Fractions

Exercise \(\PageIndex{228}\)

\(\frac{\left(\frac{1}{5}\right)^{2}}{2+3^{2}}\)

\(\frac{1}{275}\)

Exercise \(\PageIndex{229}\)

\(\frac{\left(\frac{1}{3}\right)^{2}}{5+2^{2}}\)

Exercise \(\PageIndex{230}\)

\(\frac{\frac{2}{3}+\frac{1}{2}}{\frac{3}{4}-\frac{2}{3}}\)

Exercise \(\PageIndex{231}\)

\(\frac{\frac{3}{4}+\frac{1}{2}}{\frac{5}{6}-\frac{2}{3}}\)

Evaluate Variable Expressions with Fractions

Exercise \(\PageIndex{232}\)

\(x+\frac{1}{2}\) when

• \(x=-\frac{1}{8}\)
• \(x=-\frac{1}{2}\)
• \(\frac{3}{8}\)

Exercise \(\PageIndex{233}\)

\(x+\frac{2}{3}\) when

• \(x=-\frac{1}{6}\)
• \(x=-\frac{5}{3}\)

Exercise \(\PageIndex{234}\)

4\(p^{2} q\) when \(p=-\frac{1}{2}\) and \(q=\frac{5}{9}\)

Exercise \(\PageIndex{235}\)

5\(m^{2} n\) when \(m=-\frac{2}{5}\) and \(n=\frac{1}{3}\)

Exercise \(\PageIndex{236}\)

\(\frac{u+v}{w}\) when \(u=-4, v=-8, w=2\)

Exercise \(\PageIndex{237}\)

\(\frac{m+n}{p}\) when \(m=-6, n=-2, p=4\)

Name and Write Decimals

In the following exercises, write as a decimal.

Exercise \(\PageIndex{238}\)

Eight and three hundredths

Exercise \(\PageIndex{239}\)

Nine and seven hundredths

Exercise \(\PageIndex{240}\)

One thousandth

Exercise \(\PageIndex{241}\)

Nine thousandths

In the following exercises, name each decimal.

Exercise \(\PageIndex{242}\)

seven and eight tenths

Exercise \(\PageIndex{243}\)

Exercise \(\pageindex{244}\).

five thousandths

Exercise \(\PageIndex{245}\)

Round Decimals

In the following exercises, round each number to the nearest

• whole number.

Exercise \(\PageIndex{246}\)

Exercise \(\pageindex{247}\), exercise \(\pageindex{248}\), exercise \(\pageindex{249}\).

Add and Subtract Decimals

Exercise \(\PageIndex{250}\)

Exercise \(\pageindex{251}\).

256.37−85.49

Exercise \(\PageIndex{252}\)

15.35−20.88

−5.53

Exercise \(\PageIndex{253}\)

Exercise \(\pageindex{254}\).

−4.2+(−9.3)

−13.5

Exercise \(\PageIndex{255}\)

−8.6+(−8.6)

Exercise \(\PageIndex{256}\)

100−64.2

Exercise \(\PageIndex{257}\)

100−65.83

Exercise \(\PageIndex{258}\)

Exercise \(\pageindex{259}\).

Multiply and Divide Decimals

Exercise \(\PageIndex{260}\)

Exercise \(\pageindex{261}\), exercise \(\pageindex{262}\).

(8.52)(3.14)

Exercise \(\PageIndex{263}\)

(5.32)(4.86)

Exercise \(\PageIndex{264}\)

(0.09)(24.78)

Exercise \(\PageIndex{265}\)

(0.04)(36.89)

Exercise \(\PageIndex{266}\)

\(0.15 \div 5\)

Exercise \(\PageIndex{267}\)

\(0.27 \div 3\)

Exercise \(\PageIndex{268}\)

\(\$ 8.49 \div 12\)

Exercise \(\PageIndex{269}\)

\(\$ 16.99 \div 9\)

Exercise \(\PageIndex{270}\)

\(12 \div 0.08\)

Exercise \(\PageIndex{271}\)

\(5 \div 0.04\)

Convert Decimals, Fractions, and Percents

In the following exercises, write each decimal as a fraction.

Exercise \(\PageIndex{272}\)

\(\frac{2}{25}\)

Exercise \(\PageIndex{273}\)

Exercise \(\pageindex{274}\).

\(\frac{17}{40}\)

Exercise \(\PageIndex{275}\)

Exercise \(\pageindex{276}\).

\(\frac{7}{4}\)

Exercise \(\PageIndex{277}\)

In the following exercises, convert each fraction to a decimal.

Exercise \(\PageIndex{278}\)

\(\frac{2}{5}\)

Exercise \(\PageIndex{279}\)

\(\frac{4}{5}\)

Exercise \(\PageIndex{280}\)

\(-\frac{3}{8}\)

−0.375

Exercise \(\PageIndex{281}\)

\(-\frac{5}{8}\)

Exercise \(\PageIndex{282}\)

\(0 . \overline{5}\)

Exercise \(\PageIndex{283}\)

Exercise \(\pageindex{284}\).

\(\frac{1}{2}+6.5\)

Exercise \(\PageIndex{285}\)

\(\frac{1}{4}+10.75\)

In the following exercises, convert each percent to a decimal.

Exercise \(\PageIndex{286}\)

Exercise \(\pageindex{287}\), exercise \(\pageindex{288}\), exercise \(\pageindex{289}\), exercise \(\pageindex{290}\), exercise \(\pageindex{291}\).

In the following exercises, convert each decimal to a percent.

Exercise \(\PageIndex{292}\)

Exercise \(\pageindex{293}\), exercise \(\pageindex{294}\), exercise \(\pageindex{295}\), exercise \(\pageindex{296}\), exercise \(\pageindex{297}\), the real numbers.

Simplify Expressions with Square Roots

Exercise \(\PageIndex{298}\)

\(\sqrt{64}\)

Exercise \(\PageIndex{299}\)

\(\sqrt{144}\)

Exercise \(\PageIndex{300}\)

\(-\sqrt{25}\)

Exercise \(\PageIndex{301}\)

• \(-\sqrt{81}\)

Identify Integers, Rational Numbers, Irrational Numbers, and Real Numbers

In the following exercises, write as the ratio of two integers.

Exercise \(\PageIndex{302}\)

• \(\frac{9}{1}\)
• \(\frac{847}{100}\)

Exercise \(\PageIndex{303}\)

In the following exercises, list the

• rational numbers,
• irrational numbers.

Exercise \(\PageIndex{304}\)

\(0.84,0.79132 \ldots, 1 . \overline{3}\)

• \(0.84,1.3\)
• \(0.79132 \ldots\)

Exercise \(\PageIndex{305}\)

\(2.3 \overline{8}, 0.572,4.93814 \ldots\)

In the following exercises, identify whether each number is rational or irrational.

Exercise \(\PageIndex{306}\)

• \(\sqrt{121}\)
• \(\sqrt{48}\)

Exercise \(\PageIndex{307}\)

• \(\sqrt{56}\)
• \(\sqrt{16}\)

In the following exercises, identify whether each number is a real number or not a real number.

Exercise \(\PageIndex{308}\)

• \(\sqrt{-9}\)
• \(-\sqrt{169}\)
• not a real number
• real number

Exercise \(\PageIndex{309}\)

• \(\sqrt{-64}\)
• whole numbers,
• irrational numbers,
• real numbers for each set of numbers.

Exercise \(\PageIndex{310}\)

• \(-4,0, \frac{5}{6}, \sqrt{16}, \sqrt{18}, 5.2537 \ldots\)
• \(0, \sqrt{16}\)
• \(-4,0, \sqrt{16}\)
• \(-4,0, \frac{5}{6}, \sqrt{16}\)
• \(\sqrt{18}, 5.2537 \ldots\)

Exercise \(\PageIndex{311}\)

\(-\sqrt{4}, 0 . \overline{36}, \frac{13}{3}, 6.9152 \ldots, \sqrt{48}, 10 \frac{1}{2}\)

Locate Fractions on the Number Line

In the following exercises, locate the numbers on a number line.

Exercise \(\PageIndex{312}\)

\(\frac{2}{3}, \frac{5}{4}, \frac{12}{5}\)

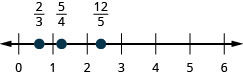
Exercise \(\PageIndex{313}\)

\(\frac{1}{3}, \frac{7}{4}, \frac{13}{5}\)

Exercise \(\PageIndex{314}\)

\(2 \frac{1}{3},-2 \frac{1}{3}\)

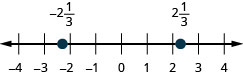
Exercise \(\PageIndex{315}\)

\(1 \frac{3}{5},-1 \frac{3}{5}\)

Exercise \(\PageIndex{316}\)

−1___\(-\frac{1}{8}\)

Exercise \(\PageIndex{317}\)

\(-3 \frac{1}{4}\)___−4

Exercise \(\PageIndex{318}\)

\(-\frac{7}{9}\) ___ \(\frac{4}{9}\)

Exercise \(\PageIndex{319}\)

\(-2\) ___ \(\frac{19}{8}\)

Locate Decimals on the Number Line

In the following exercises, locate on the number line.

Exercise \(\PageIndex{320}\)

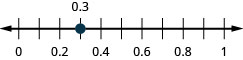
Exercise \(\PageIndex{321}\)

Exercise \(\pageindex{322}\).

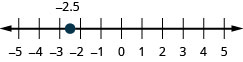
Exercise \(\PageIndex{323}\)

Exercise \(\pageindex{324}\), exercise \(\pageindex{325}\), exercise \(\pageindex{326}\).

−0.6___−0.59

Exercise \(\PageIndex{327}\)

−0.27___−0.3

Properties of Real Numbers

Use the Commutative and Associative Properties

In the following exercises, use the Associative Property to simplify.

Exercise \(\PageIndex{328}\)

−12(4m)

Exercise \(\PageIndex{329}\)

30\(\left(\frac{5}{6} q\right)\)

Exercise \(\PageIndex{330}\)

Exercise \(\pageindex{331}\).

(c+0.2)+0.7

Exercise \(\PageIndex{332}\)

6y+37+(−6y)

Exercise \(\PageIndex{333}\)

\(\frac{1}{4}+\frac{11}{15}+\left(-\frac{1}{4}\right)\)

Exercise \(\PageIndex{334}\)

\(\frac{14}{11} \cdot \frac{35}{9} \cdot \frac{14}{11}\)

\(\frac{35}{9}\)

Exercise \(\PageIndex{335}\)

\(-18 \cdot 15 \cdot \frac{2}{9}\)

Exercise \(\PageIndex{336}\)

\(\left(\frac{7}{12}+\frac{4}{5}\right)+\frac{1}{5}\)

1\(\frac{7}{12}\)

Exercise \(\PageIndex{337}\)

(3.98d+0.75d)+1.25d

Exercise \(\PageIndex{338}\)

11x+8y+16x+15y

Exercise \(\PageIndex{339}\)

52m+(−20n)+(−18m)+(−5n)

Use the Identity and Inverse Properties of Addition and Multiplication

In the following exercises, find the additive inverse of each number.

Exercise \(\PageIndex{340}\)

• \(-\frac{8}{5}\)
• \(-\frac{1}{3}\)

Exercise \(\PageIndex{341}\)

• \(\frac{12}{5}\)

In the following exercises, find the multiplicative inverse of each number.

Exercise \(\PageIndex{342}\)

• \(-\frac{4}{9}\)
• \(\frac{1}{10}\)
• \(-\frac{9}{4}\)
• \(\frac{5}{3}\)

Exercise \(\PageIndex{343}\)

• \(-\frac{9}{2}\)

Use the Properties of Zero

Exercise \(\PageIndex{344}\)

83\(\cdot 0\)

Exercise \(\PageIndex{345}\)

\(\frac{0}{9}\)

Exercise \(\PageIndex{346}\)

\(\frac{5}{0}\)

Exercise \(\PageIndex{347}\)

\(0 \div \frac{2}{3}\)

Exercise \(\PageIndex{348}\)

43+39+(−43)

Exercise \(\PageIndex{349}\)

(n+6.75)+0.25

Exercise \(\PageIndex{350}\)

\(\frac{5}{13} \cdot 57 \cdot \frac{13}{5}\)

Exercise \(\PageIndex{351}\)

\(\frac{1}{6} \cdot 17 \cdot 12\)

Exercise \(\PageIndex{352}\)

\(\frac{2}{3} \cdot 28 \cdot \frac{3}{7}\)

Exercise \(\PageIndex{353}\)

\(9(6 x-11)+15\)

Simplify Expressions Using the Distributive Property

In the following exercises, simplify using the Distributive Property.

Exercise \(\PageIndex{354}\)

Exercise \(\pageindex{355}\).

9(u−4)

Exercise \(\PageIndex{356}\)

−3(6m−1)

−18m+3

Exercise \(\PageIndex{357}\)

−8(−7a−12)

Exercise \(\PageIndex{358}\)

\(\frac{1}{3}(15 n-6)\)

Exercise \(\PageIndex{359}\)

\((y+10) \cdot p\)

Exercise \(\PageIndex{360}\)

(a−4)−(6a+9)

−5a−13

Exercise \(\PageIndex{361}\)

4(x+3)−8(x−7)

Systems of Measurement

1.1 Define U.S. Units of Measurement and Convert from One Unit to Another

In the following exercises, convert the units. Round to the nearest tenth.

Exercise \(\PageIndex{362}\)

A floral arbor is 7 feet tall. Convert the height to inches.

Exercise \(\PageIndex{363}\)

A picture frame is 42 inches wide. Convert the width to feet.

Exercise \(\PageIndex{364}\)

Kelly is 5 feet 4 inches tall. Convert her height to inches.

Exercise \(\PageIndex{365}\)

A playground is 45 feet wide. Convert the width to yards.

Exercise \(\PageIndex{366}\)

The height of Mount Shasta is 14,179 feet. Convert the height to miles.

Exercise \(\PageIndex{367}\)

Shamu weights 4.5 tons. Convert the weight to pounds.

Exercise \(\PageIndex{368}\)

The play lasted \(1\frac{3}{4}\) hours. Convert the time to minutes.

105 minutes

Exercise \(\PageIndex{369}\)

How many tablespoons are in a quart?

Exercise \(\PageIndex{370}\)

Naomi’s baby weighed 5 pounds 14 ounces at birth. Convert the weight to ounces.

Exercise \(\PageIndex{371}\)

Trinh needs 30 cups of paint for her class art project. Convert the volume to gallons.

Use Mixed Units of Measurement in the U.S. System.

Exercise \(\PageIndex{372}\)

John caught 4 lobsters. The weights of the lobsters were 1 pound 9 ounces, 1 pound 12 ounces, 4 pounds 2 ounces, and 2 pounds 15 ounces. What was the total weight of the lobsters?

10 lbs. 6 oz.

Exercise \(\PageIndex{373}\)

Every day last week Pedro recorded the number of minutes he spent reading. The number of minutes were 50, 25, 83, 45, 32, 60, 135. How many hours did Pedro spend reading?

Exercise \(\PageIndex{374}\)

Fouad is 6 feet 2 inches tall. If he stands on a rung of a ladder 8 feet 10 inches high, how high off the ground is the top of Fouad’s head?

Exercise \(\PageIndex{375}\)

Dalila wants to make throw pillow covers. Each cover takes 30 inches of fabric. How many yards of fabric does she need for 4 covers?

Make Unit Conversions in the Metric System

In the following exercises, convert the units.

Exercise \(\PageIndex{376}\)

Donna is 1.7 meters tall. Convert her height to centimeters.

170 centimeters

Exercise \(\PageIndex{377}\)

Mount Everest is 8,850 meters tall. Convert the height to kilometers.

Exercise \(\PageIndex{378}\)

One cup of yogurt contains 488 milligrams of calcium. Convert this to grams.

0.488 grams

Exercise \(\PageIndex{379}\)

One cup of yogurt contains 13 grams of protein. Convert this to milligrams.

Exercise \(\PageIndex{380}\)

Sergio weighed 2.9 kilograms at birth. Convert this to grams.

2,900 grams

Exercise \(\PageIndex{381}\)

A bottle of water contained 650 milliliters. Convert this to liters.

Use Mixed Units of Measurement in the Metric System

In the following exerices, solve.

Exercise \(\PageIndex{382}\)

Minh is 2 meters tall. His daughter is 88 centimeters tall. How much taller is Minh than his daughter?

Exercise \(\PageIndex{383}\)

Selma had a 1 liter bottle of water. If she drank 145 milliliters, how much water was left in the bottle?

Exercise \(\PageIndex{384}\)

One serving of cranberry juice contains 30 grams of sugar. How many kilograms of sugar are in 30 servings of cranberry juice?

0.9 kilograms

Exercise \(\PageIndex{385}\)

One ounce of tofu provided 2 grams of protein. How many milligrams of protein are provided by 5 ounces of tofu?

Convert between the U.S. and the Metric Systems of Measurement

In the following exercises, make the unit conversions. Round to the nearest tenth.

Exercise \(\PageIndex{386}\)

Majid is 69 inches tall. Convert his height to centimeters.

175.3 centimeters

Exercise \(\PageIndex{387}\)

A college basketball court is 84 feet long. Convert this length to meters.

Exercise \(\PageIndex{388}\)

Caroline walked 2.5 kilometers. Convert this length to miles.

Exercise \(\PageIndex{389}\)

Lucas weighs 78 kilograms. Convert his weight to pounds.

Exercise \(\PageIndex{390}\)

Steve’s car holds 55 liters of gas. Convert this to gallons.

14.6 gallons

Exercise \(\PageIndex{391}\)

A box of books weighs 25 pounds. Convert the weight to kilograms.

Convert between Fahrenheit and Celsius Temperatures

In the following exercises, convert the Fahrenheit temperatures to degrees Celsius. Round to the nearest tenth.

Exercise \(\PageIndex{392}\)

95° Fahrenheit

Exercise \(\PageIndex{393}\)

23° Fahrenheit

Exercise \(\PageIndex{394}\)

20° Fahrenheit

–6.7° C

Exercise \(\PageIndex{395}\)

64° Fahrenheit

In the following exercises, convert the Celsius temperatures to degrees Fahrenheit. Round to the nearest tenth.

Exercise \(\PageIndex{396}\)

30° Celsius

Exercise \(\PageIndex{397}\)

–5° Celsius

Exercise \(\PageIndex{398}\)

–12° Celsius

10.4° F

Exercise \(\PageIndex{399}\)

24° Celsius

Chapter Practice Test

Write as a whole number using digits: two hundred five thousand, six hundred seventeen.

Find the prime factorization of 504.

Find the Least Common Multiple of 18 and 24.

Combine like terms: 5n+8+2n−1.

\(-|x|\) when \(x=-2\)

11−a when a=−3

Translate to an algebraic expression and simplify: twenty less than negative 7.

−7−20;−27

Monique has a balance of −$18 in her checking account. She deposits $152 to the account. What is the new balance?

Round 677.1348 to the nearest hundredth.

Convert \(\frac{4}{5}\) to a decimal.

Convert 1.85 to a percent.

Locate \(\frac{2}{3},-1.5,\) and \(\frac{9}{4}\) on a number line.

\(4+10(3+9)-5^{2}\)

−85+42

−19−25

\((-2)^{4}\)

\(-5(-9) \div 15\)

\(\frac{3}{8} \cdot \frac{11}{12}\)

\(\frac{4}{5} \div \frac{9}{20}\)

\(\frac{16}{9}\)

\(\frac{12+3 \cdot 5}{15-6}\)

\(\frac{m}{7}+\frac{10}{7}\)

\(\frac{m+10}{7}\)

\(\frac{7}{12}-\frac{3}{8}\)

\(-5.8+(-4.7)\)

−10.5

100−64.25

(0.07)(31.95)

\(9 \div 0.05\)

\(-14\left(\frac{5}{7} p\right)\)

(u+8)−9

6x+(−4y)+9x+8y

\(\frac{0}{23}\)

\(\frac{75}{0}\)

−2(13q−5)

A movie lasted 1\(\frac{2}{3}\) hours. How many minutes did it last? ( 1 hour \(=60\) minutes)

100 minutes

Mike’s SUV is 5 feet 11 inches tall. He wants to put a rooftop cargo bag on the the SUV. The cargo bag is 1 foot 6 inches tall. What will the total height be of the SUV with the cargo bag on the roof? (1 foot = 12 inches)

Jennifer ran 2.8 miles. Convert this length to kilometers. (1 mile = 1.61 kilometers)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.12: Scientific Problem Solving

• Last updated
• Save as PDF
• Page ID 52325

How can we use problem solving in our everyday routines?

One day you wake up and realize your clock radio did not turn on to get you out of bed. You are puzzled, so you decide to find out what happened. You list three possible explanations:

• There was a power failure and your radio cannot turn on.
• Your little sister turned it off as a joke.
• You did not set the alarm last night.

Upon investigation, you find that the clock is on, so there is no power failure. Your little sister was spending the night with a friend and could not have turned the alarm off. You notice that the alarm is not set—your forgetfulness made you late. You have used the scientific method to answer a question.

Scientific Problem Solving

Humans have always wondered about the world around them. One of the questions of interest was (and still is): what is this world made of? Chemistry has been defined in various ways as the study of matter. What matter consists of has been a source of debate over the centuries. One of the key areas for this debate in the Western world was Greek philosophy.

The basic approach of the Greek philosophers was to discuss and debate the questions they had about the world. There was no gathering of information to speak of, just talking. As a result, several ideas about matter were put forth, but never resolved. The first philosopher to carry out the gathering of data was Aristotle (384-322 B.C.). He recorded many observations on the weather, on plant and animal life and behavior, on physical motions, and a number of other topics. Aristotle could probably be considered the first "real" scientist, because he made systematic observations of nature and tried to understand what he was seeing.

Inductive and Deductive Reasoning

Two approaches to logical thinking developed over the centuries. These two methods are inductive reasoning and deductive reasoning . Inductive reasoning involves getting a collection of specific examples and drawing a general conclusion from them. Deductive reasoning takes a general principle and then draws a specific conclusion from the general concept. Both are used in the development of scientific ideas.

Inductive reasoning first involves the collection of data: "If I add sodium metal to water, I observe a very violent reaction. Every time I repeat the process, I see the same thing happen." A general conclusion is drawn from these observations: the addition of sodium to water results in a violent reaction.

In deductive reasoning, a specific prediction is made based on a general principle. One general principle is that acids turn blue litmus paper red. Using the deductive reasoning process, one might predict: "If I have a bottle of liquid labeled 'acid', I expect the litmus paper to turn red when I immerse it in the liquid."

The Idea of the Experiment

Inductive reasoning is at the heart of what is now called the " scientific method ." In European culture, this approach was developed mainly by Francis Bacon (1561-1626), a British scholar. He advocated the use of inductive reasoning in every area of life, not just science. The scientific method, as developed by Bacon and others, involves several steps:

• Ask a question - identify the problem to be considered.
• Make observations - gather data that pertains to the question.
• Propose an explanation (a hypothesis) for the observations.
• Make new observations to test the hypothesis further.

Note that this should not be considered a "cookbook" for scientific research. Scientists do not sit down with their daily "to do" list and write down these steps. The steps may not necessarily be followed in order. But this does provide a general idea of how scientific research is usually done.

When a hypothesis is confirmed repeatedly, it eventually becomes a theory—a general principle that is offered to explain natural phenomena. Note a key word— explain , or  explanation . A theory offers a description of why something happens. A law, on the other hand, is a statement that is always true, but offers no explanation as to why. The law of gravity says a rock will fall when dropped, but does not explain why (gravitational theory is very complex and incomplete at present). The kinetic molecular theory of gases, on the other hand, states what happens when a gas is heated in a closed container (the pressure increases), but also explains why (the motions of the gas molecules are increased due to the change in temperature). Theories do not get "promoted" to laws, because laws do not answer the "why" question.

• The early Greek philosophers spent their time talking about nature, but did little or no actual exploration or investigation.
• Inductive reasoning - to develop a general conclusion from a collection of observations.
• Deductive reasoning - to make a specific statement based on a general principle.
• Scientific method - a process of observation, developing a hypothesis, and testing that hypothesis.
• What was the basic shortcoming of the Greek philosophers approach to studying the material world?
• How did Aristotle improve the approach?
• Define “inductive reasoning” and give an example.
• Define “deductive reasoning” and give an example.
• What is the difference between a hypothesis and a theory?
• What is the difference between a theory and a law?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.12: Solving Problems in Physics

• Last updated
• Save as PDF
• Page ID 18100

Learning Objectives

• Describe the process for developing a problem-solving strategy.
• Explain how to find the numerical solution to a problem.
• Summarize the process for assessing the significance of the numerical solution to a problem.

Problem-solving skills are clearly essential to success in a quantitative course in physics. More important, the ability to apply broad physical principles—usually represented by equations—to specific situations is a very powerful form of knowledge. It is much more powerful than memorizing a list of facts. Analytical skills and problem-solving abilities can be applied to new situations whereas a list of facts cannot be made long enough to contain every possible circumstance. Such analytical skills are useful both for solving problems in this text and for applying physics in everyday life.

As you are probably well aware, a certain amount of creativity and insight is required to solve problems. No rigid procedure works every time. Creativity and insight grow with experience. With practice, the basics of problem solving become almost automatic. One way to get practice is to work out the text’s examples for yourself as you read. Another is to work as many end-of-section problems as possible, starting with the easiest to build confidence and then progressing to the more difficult. After you become involved in physics, you will see it all around you, and you can begin to apply it to situations you encounter outside the classroom, just as is done in many of the applications in this text.

Although there is no simple step-by-step method that works for every problem, the following three-stage process facilitates problem solving and makes it more meaningful. The three stages are strategy, solution, and significance. This process is used in examples throughout the book. Here, we look at each stage of the process in turn.

Strategy is the beginning stage of solving a problem. The idea is to figure out exactly what the problem is and then develop a strategy for solving it. Some general advice for this stage is as follows:

• Examine the situation to determine which physical principles are involved . It often helps to draw a simple sketch at the outset. You often need to decide which direction is positive and note that on your sketch. When you have identified the physical principles, it is much easier to find and apply the equations representing those principles. Although finding the correct equation is essential, keep in mind that equations represent physical principles, laws of nature, and relationships among physical quantities. Without a conceptual understanding of a problem, a numerical solution is meaningless.
• Make a list of what is given or can be inferred from the problem as stated (identify the “knowns”) . Many problems are stated very succinctly and require some inspection to determine what is known. Drawing a sketch be very useful at this point as well. Formally identifying the knowns is of particular importance in applying physics to real-world situations. For example, the word stopped means the velocity is zero at that instant. Also, we can often take initial time and position as zero by the appropriate choice of coordinate system.
• Identify exactly what needs to be determined in the problem (identify the unknowns). In complex problems, especially, it is not always obvious what needs to be found or in what sequence. Making a list can help identify the unknowns.
• Determine which physical principles can help you solve the problem . Since physical principles tend to be expressed in the form of mathematical equations, a list of knowns and unknowns can help here. It is easiest if you can find equations that contain only one unknown—that is, all the other variables are known—so you can solve for the unknown easily. If the equation contains more than one unknown, then additional equations are needed to solve the problem. In some problems, several unknowns must be determined to get at the one needed most. In such problems it is especially important to keep physical principles in mind to avoid going astray in a sea of equations. You may have to use two (or more) different equations to get the final answer.

The solution stage is when you do the math. Substitute the knowns (along with their units) into the appropriate equation and obtain numerical solutions complete with units . That is, do the algebra, calculus, geometry, or arithmetic necessary to find the unknown from the knowns, being sure to carry the units through the calculations. This step is clearly important because it produces the numerical answer, along with its units. Notice, however, that this stage is only one-third of the overall problem-solving process.

Significance

After having done the math in the solution stage of problem solving, it is tempting to think you are done. But, always remember that physics is not math. Rather, in doing physics, we use mathematics as a tool to help us understand nature. So, after you obtain a numerical answer, you should always assess its significance:

• Check your units . If the units of the answer are incorrect, then an error has been made and you should go back over your previous steps to find it. One way to find the mistake is to check all the equations you derived for dimensional consistency. However, be warned that correct units do not guarantee the numerical part of the answer is also correct.
• Check the answer to see whether it is reasonable. Does it make sense? This step is extremely important: –the goal of physics is to describe nature accurately. To determine whether the answer is reasonable, check both its magnitude and its sign, in addition to its units. The magnitude should be consistent with a rough estimate of what it should be. It should also compare reasonably with magnitudes of other quantities of the same type. The sign usually tells you about direction and should be consistent with your prior expectations. Your judgment will improve as you solve more physics problems, and it will become possible for you to make finer judgments regarding whether nature is described adequately by the answer to a problem. This step brings the problem back to its conceptual meaning. If you can judge whether the answer is reasonable, you have a deeper understanding of physics than just being able to solve a problem mechanically.
• Check to see whether the answer tells you something interesting. What does it mean? This is the flip side of the question: Does it make sense? Ultimately, physics is about understanding nature, and we solve physics problems to learn a little something about how nature operates. Therefore, assuming the answer does make sense, you should always take a moment to see if it tells you something about the world that you find interesting. Even if the answer to this particular problem is not very interesting to you, what about the method you used to solve it? Could the method be adapted to answer a question that you do find interesting? In many ways, it is in answering questions such as these science that progresses.

Standard Deviation

Lesson Narrative

The mathematical purpose of this lesson is to introduce standard deviation and understand that it is a measure of variability. Previously, students understood the meaning of MAD and IQR; standard deviation fits into their understanding as another measure of variability. Future lessons build on this lesson when students interpret standard deviation in context. Standard deviation is a measure of variability calculated by:

• Finding the square of the distance from the mean to each value.
• Then finding the sum of these square distances and dividing by n (the number of values in the data set).
• Finally, finding the square root of this sum.

When students manipulate data to achieve various specified measures of center or variability they are engaging in MP2 because they have to make use of the structure underlying standard deviation as a measure of variability.

Note that in this unit, all standard deviations refer to the population standard deviation ( \(\sigma\) ) calculation rather than the sample standard deviation ( \(s\) ).

Learning Goals

Teacher Facing

• Comprehend (in spoken and written language) standard deviation as a measure of variability.
• Use technology to compute standard deviation.

Student Facing

• Let’s learn about standard deviation, another measure of variability.

Required Materials

• Statistical technology

Required Preparation

Acquire devices that can run GeoGebra (recommended) or other spreadsheet technology. It is ideal if each student has their own device. (A GeoGebra Spreadsheet is available under Math Tools.)

Students should have access to technology for calculating standard deviation and mean. Optional activities require technology for creating dot plots and calculating standard deviation, mean, and IQR.

Learning Targets

• I can describe standard deviation as a measure of variability.
• I can use technology to compute standard deviation.

CCSS Standards

Building On

Glossary Entries

A measure of the variability, or spread, of a distribution, calculated by a method similar to the method for calculating the MAD (mean absolute deviation). The exact method is studied in more advanced courses.

Print Formatted Materials

Teachers with a valid work email address can  click here to register or sign in for free access to Cool Down, Teacher Guide, and PowerPoint materials.

Additional Resources

• 888-309-8227
• 732-384-0146

New User Registration

Forgot Password

Go Math! 5 Common Core, Grade: 5 Publisher: Houghton Mifflin Harcourt

Go math 5 common core, title : go math 5 common core, publisher : houghton mifflin harcourt, isbn : 547587813, isbn-13 : 9780547587813, use the table below to find videos, mobile apps, worksheets and lessons that supplement go math 5 common core., textbook resources.

• Call us toll-free
• FAQs – Frequently Asked Questions
• Contact Lumos Learning – Proven Study Programs by Expert Teachers

Follow us: Lumos Learning -->

• 2024 © Lumos Learning
• Privacy Policy - Terms of Service - Disclaimers

PARCC® is a registered trademark of PARCC, Inc. Lumos Learning, is not owned by or affiliated in any fashion with PARCC, Inc... Read More

PARCC® is a registered trademark of PARCC, Inc. Lumos Learning, is not owned by or affiliated in any fashion with PARCC, Inc., the Partnership for the Assessment of Readiness for College and Careers, nor any state of the Union. Neither PARCC, Inc., nor The Partnership for the Assessment of Readiness for College and Careers, nor any member state has endorsed this product. No portion of any fees or charges paid for any products or services Lumos Learning offers will be paid or inure to the benefit of PARCC, Inc., or any state of the Union

SBAC is a copyright of The Regents of the University of California – Smarter Balanced Assessment Consortium, which is not aff... Read More

SBAC is a copyright of The Regents of the University of California – Smarter Balanced Assessment Consortium, which is not affiliated to Lumos Learning. The Regents of the University of California – Smarter Balanced Assessment Consortium, was not involved in the production of, and does not endorse these products or this site.

ACT® Aspire™ is a registered trademark of ACT Aspire LLC., which is not affiliated to Lumos Learning. ACT Aspire LLC, was not... Read More

ACT® Aspire™ is a registered trademark of ACT Aspire LLC., which is not affiliated to Lumos Learning. ACT Aspire LLC,was not involved in the production of, and does not endorse these products or this site.

Florida Department of Education is not affiliated to Lumos Learning. Florida department of education, was not involved in the... Read More

Florida Department of Education is not affiliated to Lumos Learning. Florida department of education, was not involved in the production of, and does not endorse these products or this site.

Indiana Department of Education is not affiliated to Lumos Learning. Indiana department of education, was not involved in the... Read More

Indiana Department of Education is not affiliated to Lumos Learning. Indiana department of education, was not involved in the production of, and does not endorse these products or this site.

Mississippi Department of Education is not affiliated to Lumos Learning. Mississippi department of education, was not involved... Read More

Mississippi Department of Education is not affiliated to Lumos Learning. Mississippi department of education, was not involved in the production of, and does not endorse these products or this site.

Ohio Department of Education is not affiliated to Lumos Learning. Ohio department of education, was not involved in the prod... Read More

Ohio Department of Education is not affiliated to Lumos Learning. Ohio department of education, was not involved in the production of, and does not endorse these products or this site.

Tennessee Department of Education is not affiliated to Lumos Learning. Tennessee department of education, was not involved... Read More

Tennessee Department of Education is not affiliated to Lumos Learning. Tennessee department of education, was not involved in the production of, and does not endorse these products or this site.

Georgia Department of Education is not affiliated to Lumos Learning. Georgia department of education, was not involved... Read More

Georgia Department of Education is not affiliated to Lumos Learning. Georgia department of education, was not involved in the production of, and does not endorse these products or this site.

Missouri Department of Education is not affiliated to Lumos Learning. Missouri department of education, was not involved... Read More

Missouri Department of Education is not affiliated to Lumos Learning. Missouri department of education, was not involved in the production of, and does not endorse these products or this site.

Louisiana Department of Education is not affiliated to Lumos Learning. Louisiana department of education, was not involved... Read More

Louisiana Department of Education is not affiliated to Lumos Learning. Louisiana department of education, was not involved in the production of, and does not endorse these products or this site.

Be Prepared

180 , 096 180 , 096

1 , 024 1 , 024

x − 8 x − 8

4 4 and 215 215

2 , 3 , 5 , 6 , 10 2 , 3 , 5 , 6 , 10

• ⓐ 18 plus 11; the sum of eighteen and eleven
• ⓑ 27 times 9; the product of twenty-seven and nine
• ⓒ 84 divided by 7; the quotient of eighty-four and seven
• ⓓ p minus q ; the difference of p and q
• ⓐ 47 minus 19; the difference of forty-seven and nineteen
• ⓑ 72 divided by 9; the quotient of seventy-two and nine
• ⓒ m plus n ; the sum of m and n
• ⓓ 13 times 7; the product of thirteen and seven
• ⓐ fourteen is less than or equal to twenty-seven
• ⓑ nineteen minus two is not equal to eight
• ⓒ twelve is greater than four divided by two
• ⓓ x minus seven is less than one
• ⓐ nineteen is greater than or equal to fifteen
• ⓑ seven is equal to twelve minus five
• ⓒ fifteen divided by three is less than eight
• ⓓ y minus three is greater than six
• ⓑ expression
• ⓐ expression
• ⓐ 4 · 4 · 4 · 4 · 4 · 4 · 4 · 4
• ⓑ a · a · a · a · a · a · a
• ⓐ 8 · 8 · 8 · 8 · 8 · 8 · 8 · 8
• ⓑ b · b · b · b · b · b

The terms are 4 x , 3 b , and 2. The coefficients are 4, 3, and 2.

The terms are 9 a , 13 a 2 , and a 3 , The coefficients are 9, 13, and 1.

9 and 15; 2 x 3 and 8 x 3 ; y 2 and 11 y 2

4 x 3 and 6 x 3 ; 8 x 2 and 3 x 2 ; 19 and 24

4 x 2 + 14 x

12 y 2 + 15 y

• ⓑ 11 a − 14
• ⓐ 4( p + q )
• ⓑ 2( x − 8)

x + 1 = 7; x = 6

x + 3 = 4; x = 1

21 ⋅ 3 = 63

2( x − 5) = 30

2( y − 4) = 16

x + 7 = 37; x = 30

y + 11 = 28; y = 17

z − 17 = 37; z = 54

x − 19 = 45; x = 64

Divisible by 2, 3, 5, and 10

Divisible by 2 and 3, not 5 or 10.

Divisible by 2, 3, not 5 or 10.

Divisible by 3 and 5.

1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96

1, 2, 4, 5, 8, 10, 16, 20, 40, 80

2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5, or 2 4 ⋅ 5

2 ⋅ 2 ⋅ 3 ⋅ 5, or 2 2 ⋅ 3 ⋅ 5

2 ⋅ 3 ⋅ 3 ⋅ 7, or 2 ⋅ 3 2 ⋅ 7

2 ⋅ 3 ⋅ 7 ⋅ 7, or 2 ⋅ 3 ⋅ 7 2

Section 2.1 Exercises

16 minus 9, the difference of sixteen and nine

5 times 6, the product of five and six

28 divided by 4, the quotient of twenty-eight and four

x plus 8, the sum of x and eight

2 times 7, the product of two and seven

fourteen is less than twenty-one

thirty-six is greater than or equal to nineteen

3 times n equals 24, the product of three and n equals twenty-four

y minus 1 is greater than 6, the difference of y and one is greater than six

2 is less than or equal to 18 divided by 6; 2 is less than or equal to the quotient of eighteen and six

a is not equal to 7 times 4, a is not equal to the product of seven and four

5 · 5 · 5 5 · 5 · 5

2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2

Section 2.2 Exercises

15 x 2 , 6 x , 2

10 y 3 , y , 2

x 3 and 8 x 3 ; 14 and 5

16 ab and 4 ab ; 16 b 2 and 9 b 2

17 x 2 + 20 x + 16

5 ( x + y )

He will pay $750. His insurance company will pay $1350.

Section 2.3 Exercises

x + 2 = 5; x = 3

x + 3 = 6; x = 3

23 − 19 = 4

2( n − 10) = 52

3 y + 10 = 100

p + 5 = 21; p = 16

r + 18 = 73; r = 55

d − 30 = 52; d = 82

u − 12 = 89; u = 101

c − 325 = 799; c = 1124

Section 2.4 Exercises

2, 4, 6, 8, 10 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48

4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48

6, 12, 18, 24, 30, 36, 42, 48

8, 16, 24, 32, 40, 48

10, 20, 30, 40

Divisible by 2, 3, 4, 6

Divisible by 3, 5

Divisible by 2, 3, 4, 5, 6, 10

Divisible by 2, 4

Divisible by 2, 5, 10

1, 2, 3, 4, 6, 9, 12, 18, 36

1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72,144

1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 49, 84, 98, 147, 196, 294, 588

Section 2.5 Exercises

2 ⋅ 2 ⋅ 3 ⋅ 11

3 ⋅ 3 ⋅ 7 ⋅ 11

3 ⋅ 3 ⋅ 5 ⋅ 5 ⋅ 11

2 ⋅ 2 ⋅ 2 ⋅ 7

2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 7

2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3

2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 5

2 ⋅ 3 ⋅ 5 ⋅ 5

3 ⋅ 5 ⋅ 5 ⋅ 7

2 ⋅ 2 ⋅ 3 ⋅ 3

2 ⋅ 5 ⋅ 5 ⋅ 7

Review Exercises

3 times 8, the product of three and eight.

24 divided by 6, the quotient of twenty-four and six.

50 is greater than or equal to 47

The sum of n and 4 is equal to 13

8 ⋅ 8 ⋅ 8 ⋅ 8

y ⋅ y ⋅ y ⋅ y ⋅ y

12 n 2 ,3 n , 1

3 and 4; 3 x and x

10 y 2 + 2 y + 3

x + 3 = 5; x = 2

7 + 33 = 40

2( n − 3) = 76

x + 8 = 35; x = 27

q − 18 = 57; q = 75

3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48

2, 3, 5, 6, 10

1, 2, 3, 5, 6, 10, 15, 30

1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180

2 ⋅ 2 ⋅ 3 ⋅ 7

Answers will vary

Practice Test

15 minus x , the difference of fifteen and x .

• ⓑ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 243

y − 15 = 32; y = 47

2 3 ⋅ 3 3 ⋅ 5

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction

• Authors: Lynn Marecek, MaryAnne Anthony-Smith, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Prealgebra 2e
• Publication date: Mar 11, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/prealgebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/prealgebra-2e/pages/chapter-2

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.