hypothesis testing normal distribution p value

P-Value And Statistical Significance: What It Is & Why It Matters

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

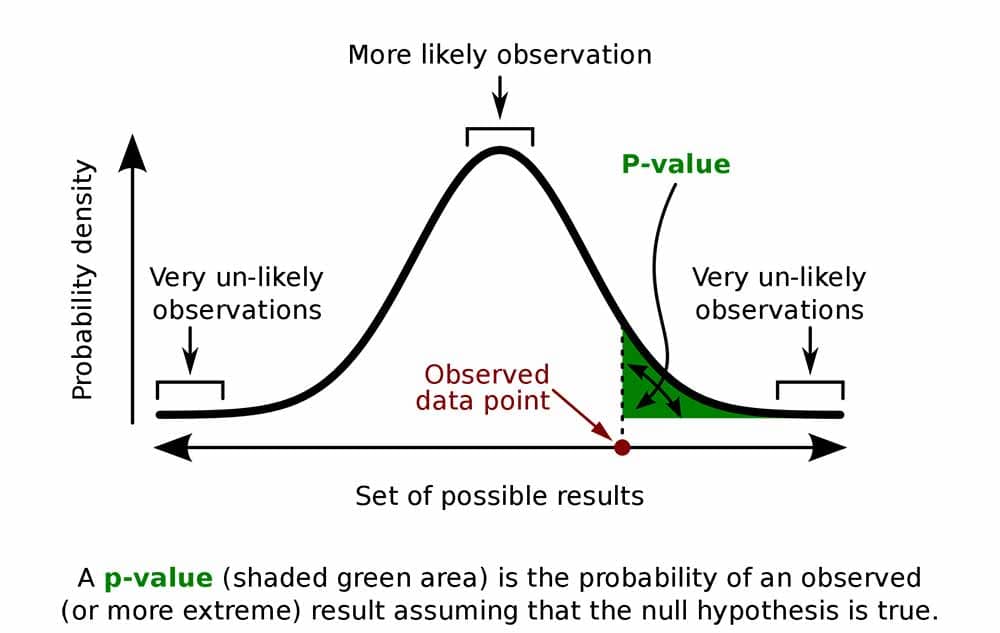
The p-value in statistics quantifies the evidence against a null hypothesis. A low p-value suggests data is inconsistent with the null, potentially favoring an alternative hypothesis. Common significance thresholds are 0.05 or 0.01.

Hypothesis testing

When you perform a statistical test, a p-value helps you determine the significance of your results in relation to the null hypothesis.

The null hypothesis (H0) states no relationship exists between the two variables being studied (one variable does not affect the other). It states the results are due to chance and are not significant in supporting the idea being investigated. Thus, the null hypothesis assumes that whatever you try to prove did not happen.

The alternative hypothesis (Ha or H1) is the one you would believe if the null hypothesis is concluded to be untrue.

The alternative hypothesis states that the independent variable affected the dependent variable, and the results are significant in supporting the theory being investigated (i.e., the results are not due to random chance).

What a p-value tells you

A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true).

The level of statistical significance is often expressed as a p-value between 0 and 1.

The smaller the p -value, the less likely the results occurred by random chance, and the stronger the evidence that you should reject the null hypothesis.

Remember, a p-value doesn’t tell you if the null hypothesis is true or false. It just tells you how likely you’d see the data you observed (or more extreme data) if the null hypothesis was true. It’s a piece of evidence, not a definitive proof.

Example: Test Statistic and p-Value

Suppose you’re conducting a study to determine whether a new drug has an effect on pain relief compared to a placebo. If the new drug has no impact, your test statistic will be close to the one predicted by the null hypothesis (no difference between the drug and placebo groups), and the resulting p-value will be close to 1. It may not be precisely 1 because real-world variations may exist. Conversely, if the new drug indeed reduces pain significantly, your test statistic will diverge further from what’s expected under the null hypothesis, and the p-value will decrease. The p-value will never reach zero because there’s always a slim possibility, though highly improbable, that the observed results occurred by random chance.

P-value interpretation

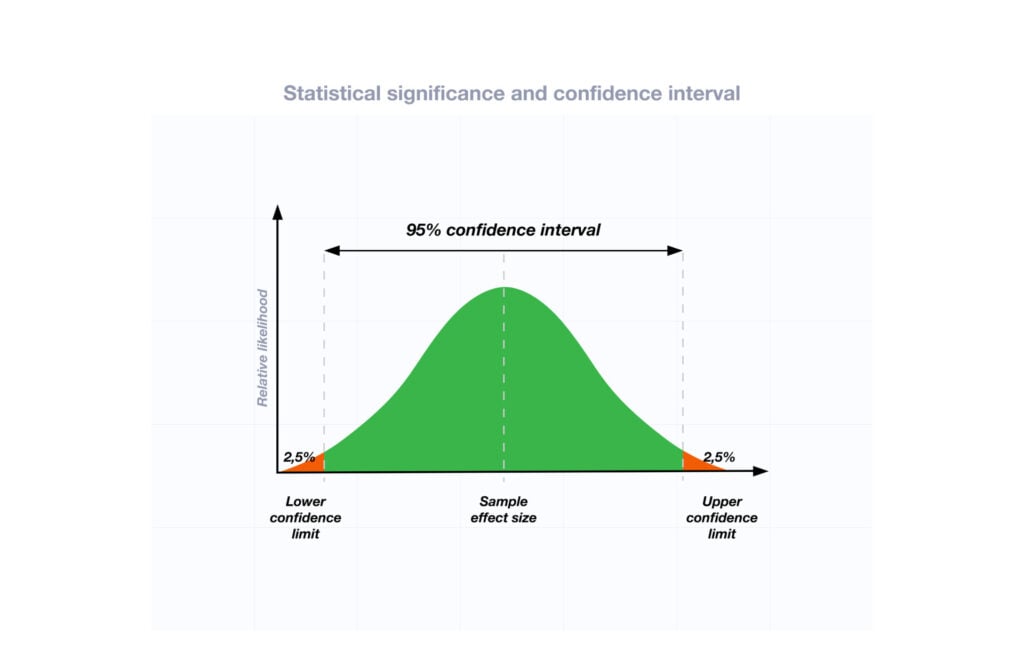
The significance level (alpha) is a set probability threshold (often 0.05), while the p-value is the probability you calculate based on your study or analysis.

A p-value less than or equal to your significance level (typically ≤ 0.05) is statistically significant.

A p-value less than or equal to a predetermined significance level (often 0.05 or 0.01) indicates a statistically significant result, meaning the observed data provide strong evidence against the null hypothesis.

This suggests the effect under study likely represents a real relationship rather than just random chance.

For instance, if you set α = 0.05, you would reject the null hypothesis if your p -value ≤ 0.05. 

It indicates strong evidence against the null hypothesis, as there is less than a 5% probability the null is correct (and the results are random).

Therefore, we reject the null hypothesis and accept the alternative hypothesis.

Example: Statistical Significance

Upon analyzing the pain relief effects of the new drug compared to the placebo, the computed p-value is less than 0.01, which falls well below the predetermined alpha value of 0.05. Consequently, you conclude that there is a statistically significant difference in pain relief between the new drug and the placebo.

What does a p-value of 0.001 mean?

A p-value of 0.001 is highly statistically significant beyond the commonly used 0.05 threshold. It indicates strong evidence of a real effect or difference, rather than just random variation.

Specifically, a p-value of 0.001 means there is only a 0.1% chance of obtaining a result at least as extreme as the one observed, assuming the null hypothesis is correct.

Such a small p-value provides strong evidence against the null hypothesis, leading to rejecting the null in favor of the alternative hypothesis.

A p-value more than the significance level (typically p > 0.05) is not statistically significant and indicates strong evidence for the null hypothesis.

This means we retain the null hypothesis and reject the alternative hypothesis. You should note that you cannot accept the null hypothesis; we can only reject it or fail to reject it.

Note : when the p-value is above your threshold of significance,  it does not mean that there is a 95% probability that the alternative hypothesis is true.

One-Tailed Test

Two-Tailed Test

How do you calculate the p-value ?

Most statistical software packages like R, SPSS, and others automatically calculate your p-value. This is the easiest and most common way.

Online resources and tables are available to estimate the p-value based on your test statistic and degrees of freedom.

These tables help you understand how often you would expect to see your test statistic under the null hypothesis.

Understanding the Statistical Test:

Different statistical tests are designed to answer specific research questions or hypotheses. Each test has its own underlying assumptions and characteristics.

For example, you might use a t-test to compare means, a chi-squared test for categorical data, or a correlation test to measure the strength of a relationship between variables.

Be aware that the number of independent variables you include in your analysis can influence the magnitude of the test statistic needed to produce the same p-value.

This factor is particularly important to consider when comparing results across different analyses.

Example: Choosing a Statistical Test

If you’re comparing the effectiveness of just two different drugs in pain relief, a two-sample t-test is a suitable choice for comparing these two groups. However, when you’re examining the impact of three or more drugs, it’s more appropriate to employ an Analysis of Variance ( ANOVA) . Utilizing multiple pairwise comparisons in such cases can lead to artificially low p-values and an overestimation of the significance of differences between the drug groups.

How to report

A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty).

Instead, we may state our results “provide support for” or “give evidence for” our research hypothesis (as there is still a slight probability that the results occurred by chance and the null hypothesis was correct – e.g., less than 5%).

Example: Reporting the results

In our comparison of the pain relief effects of the new drug and the placebo, we observed that participants in the drug group experienced a significant reduction in pain ( M = 3.5; SD = 0.8) compared to those in the placebo group ( M = 5.2; SD  = 0.7), resulting in an average difference of 1.7 points on the pain scale (t(98) = -9.36; p < 0.001).

The 6th edition of the APA style manual (American Psychological Association, 2010) states the following on the topic of reporting p-values:

“When reporting p values, report exact p values (e.g., p = .031) to two or three decimal places. However, report p values less than .001 as p < .001.

The tradition of reporting p values in the form p < .10, p < .05, p < .01, and so forth, was appropriate in a time when only limited tables of critical values were available.” (p. 114)

• Do not use 0 before the decimal point for the statistical value p as it cannot equal 1. In other words, write p = .001 instead of p = 0.001.
• Please pay attention to issues of italics ( p is always italicized) and spacing (either side of the = sign).
• p = .000 (as outputted by some statistical packages such as SPSS) is impossible and should be written as p < .001.
• The opposite of significant is “nonsignificant,” not “insignificant.”

Why is the p -value not enough?

A lower p-value  is sometimes interpreted as meaning there is a stronger relationship between two variables.

However, statistical significance means that it is unlikely that the null hypothesis is true (less than 5%).

To understand the strength of the difference between the two groups (control vs. experimental) a researcher needs to calculate the effect size .

When do you reject the null hypothesis?

In statistical hypothesis testing, you reject the null hypothesis when the p-value is less than or equal to the significance level (α) you set before conducting your test. The significance level is the probability of rejecting the null hypothesis when it is true. Commonly used significance levels are 0.01, 0.05, and 0.10.

Remember, rejecting the null hypothesis doesn’t prove the alternative hypothesis; it just suggests that the alternative hypothesis may be plausible given the observed data.

The p -value is conditional upon the null hypothesis being true but is unrelated to the truth or falsity of the alternative hypothesis.

What does p-value of 0.05 mean?

If your p-value is less than or equal to 0.05 (the significance level), you would conclude that your result is statistically significant. This means the evidence is strong enough to reject the null hypothesis in favor of the alternative hypothesis.

Are all p-values below 0.05 considered statistically significant?

No, not all p-values below 0.05 are considered statistically significant. The threshold of 0.05 is commonly used, but it’s just a convention. Statistical significance depends on factors like the study design, sample size, and the magnitude of the observed effect.

A p-value below 0.05 means there is evidence against the null hypothesis, suggesting a real effect. However, it’s essential to consider the context and other factors when interpreting results.

Researchers also look at effect size and confidence intervals to determine the practical significance and reliability of findings.

How does sample size affect the interpretation of p-values?

Sample size can impact the interpretation of p-values. A larger sample size provides more reliable and precise estimates of the population, leading to narrower confidence intervals.

With a larger sample, even small differences between groups or effects can become statistically significant, yielding lower p-values. In contrast, smaller sample sizes may not have enough statistical power to detect smaller effects, resulting in higher p-values.

Therefore, a larger sample size increases the chances of finding statistically significant results when there is a genuine effect, making the findings more trustworthy and robust.

Can a non-significant p-value indicate that there is no effect or difference in the data?

No, a non-significant p-value does not necessarily indicate that there is no effect or difference in the data. It means that the observed data do not provide strong enough evidence to reject the null hypothesis.

There could still be a real effect or difference, but it might be smaller or more variable than the study was able to detect.

Other factors like sample size, study design, and measurement precision can influence the p-value. It’s important to consider the entire body of evidence and not rely solely on p-values when interpreting research findings.

Can P values be exactly zero?

While a p-value can be extremely small, it cannot technically be absolute zero. When a p-value is reported as p = 0.000, the actual p-value is too small for the software to display. This is often interpreted as strong evidence against the null hypothesis. For p values less than 0.001, report as p < .001

Further Information

• P-values and significance tests (Kahn Academy)
• Hypothesis testing and p-values (Kahn Academy)
• Wasserstein, R. L., Schirm, A. L., & Lazar, N. A. (2019). Moving to a world beyond “ p “< 0.05”.
• Criticism of using the “ p “< 0.05”.
• Publication manual of the American Psychological Association
• Statistics for Psychology Book Download

Bland, J. M., & Altman, D. G. (1994). One and two sided tests of significance: Authors’ reply.  BMJ: British Medical Journal ,  309 (6958), 874.

Goodman, S. N., & Royall, R. (1988). Evidence and scientific research.  American Journal of Public Health ,  78 (12), 1568-1574.

Goodman, S. (2008, July). A dirty dozen: twelve p-value misconceptions . In  Seminars in hematology  (Vol. 45, No. 3, pp. 135-140). WB Saunders.

Lang, J. M., Rothman, K. J., & Cann, C. I. (1998). That confounded P-value.  Epidemiology (Cambridge, Mass.) ,  9 (1), 7-8.

p-value Calculator

What is p-value, how do i calculate p-value from test statistic, how to interpret p-value, how to use the p-value calculator to find p-value from test statistic, how do i find p-value from z-score, how do i find p-value from t, p-value from chi-square score (χ² score), p-value from f-score.

Welcome to our p-value calculator! You will never again have to wonder how to find the p-value, as here you can determine the one-sided and two-sided p-values from test statistics, following all the most popular distributions: normal, t-Student, chi-squared, and Snedecor's F.

P-values appear all over science, yet many people find the concept a bit intimidating. Don't worry – in this article, we will explain not only what the p-value is but also how to interpret p-values correctly . Have you ever been curious about how to calculate the p-value by hand? We provide you with all the necessary formulae as well!

🙋 If you want to revise some basics from statistics, our normal distribution calculator is an excellent place to start.

Formally, the p-value is the probability that the test statistic will produce values at least as extreme as the value it produced for your sample . It is crucial to remember that this probability is calculated under the assumption that the null hypothesis H 0 is true !

More intuitively, p-value answers the question:

Assuming that I live in a world where the null hypothesis holds, how probable is it that, for another sample, the test I'm performing will generate a value at least as extreme as the one I observed for the sample I already have?

It is the alternative hypothesis that determines what "extreme" actually means , so the p-value depends on the alternative hypothesis that you state: left-tailed, right-tailed, or two-tailed. In the formulas below, S stands for a test statistic, x for the value it produced for a given sample, and Pr(event | H 0 ) is the probability of an event, calculated under the assumption that H 0 is true:

Left-tailed test: p-value = Pr(S ≤ x | H 0 )

Right-tailed test: p-value = Pr(S ≥ x | H 0 )

Two-tailed test:

p-value = 2 × min{Pr(S ≤ x | H 0 ), Pr(S ≥ x | H 0 )}

(By min{a,b} , we denote the smaller number out of a and b .)

If the distribution of the test statistic under H 0 is symmetric about 0 , then: p-value = 2 × Pr(S ≥ |x| | H 0 )

or, equivalently: p-value = 2 × Pr(S ≤ -|x| | H 0 )

As a picture is worth a thousand words, let us illustrate these definitions. Here, we use the fact that the probability can be neatly depicted as the area under the density curve for a given distribution. We give two sets of pictures: one for a symmetric distribution and the other for a skewed (non-symmetric) distribution.

• Symmetric case: normal distribution:

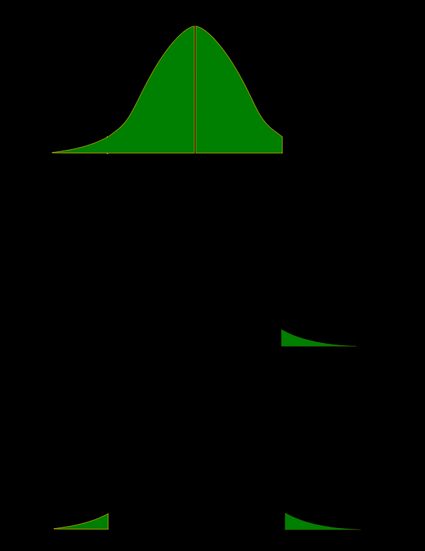
• Non-symmetric case: chi-squared distribution:

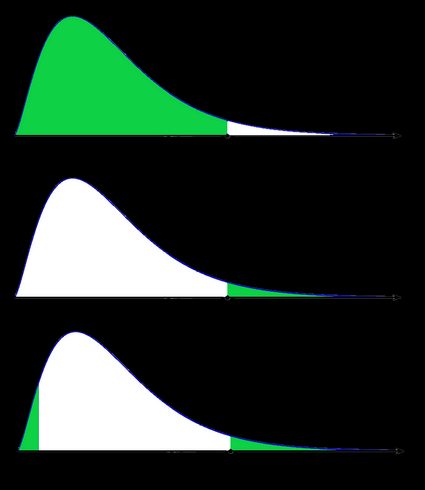
In the last picture (two-tailed p-value for skewed distribution), the area of the left-hand side is equal to the area of the right-hand side.

To determine the p-value, you need to know the distribution of your test statistic under the assumption that the null hypothesis is true . Then, with the help of the cumulative distribution function ( cdf ) of this distribution, we can express the probability of the test statistics being at least as extreme as its value x for the sample:

Left-tailed test:

p-value = cdf(x) .

Right-tailed test:

p-value = 1 - cdf(x) .

p-value = 2 × min{cdf(x) , 1 - cdf(x)} .

If the distribution of the test statistic under H 0 is symmetric about 0 , then a two-sided p-value can be simplified to p-value = 2 × cdf(-|x|) , or, equivalently, as p-value = 2 - 2 × cdf(|x|) .

The probability distributions that are most widespread in hypothesis testing tend to have complicated cdf formulae, and finding the p-value by hand may not be possible. You'll likely need to resort to a computer or to a statistical table, where people have gathered approximate cdf values.

Well, you now know how to calculate the p-value, but… why do you need to calculate this number in the first place? In hypothesis testing, the p-value approach is an alternative to the critical value approach . Recall that the latter requires researchers to pre-set the significance level, α, which is the probability of rejecting the null hypothesis when it is true (so of type I error ). Once you have your p-value, you just need to compare it with any given α to quickly decide whether or not to reject the null hypothesis at that significance level, α. For details, check the next section, where we explain how to interpret p-values.

As we have mentioned above, the p-value is the answer to the following question:

What does that mean for you? Well, you've got two options:

• A high p-value means that your data is highly compatible with the null hypothesis; and
• A small p-value provides evidence against the null hypothesis , as it means that your result would be very improbable if the null hypothesis were true.

However, it may happen that the null hypothesis is true, but your sample is highly unusual! For example, imagine we studied the effect of a new drug and got a p-value of 0.03 . This means that in 3% of similar studies, random chance alone would still be able to produce the value of the test statistic that we obtained, or a value even more extreme, even if the drug had no effect at all!

The question "what is p-value" can also be answered as follows: p-value is the smallest level of significance at which the null hypothesis would be rejected. So, if you now want to make a decision on the null hypothesis at some significance level α , just compare your p-value with α :

• If p-value ≤ α , then you reject the null hypothesis and accept the alternative hypothesis; and
• If p-value ≥ α , then you don't have enough evidence to reject the null hypothesis.

Obviously, the fate of the null hypothesis depends on α . For instance, if the p-value was 0.03 , we would reject the null hypothesis at a significance level of 0.05 , but not at a level of 0.01 . That's why the significance level should be stated in advance and not adapted conveniently after the p-value has been established! A significance level of 0.05 is the most common value, but there's nothing magical about it. Here, you can see what too strong a faith in the 0.05 threshold can lead to. It's always best to report the p-value, and allow the reader to make their own conclusions.

Also, bear in mind that subject area expertise (and common reason) is crucial. Otherwise, mindlessly applying statistical principles, you can easily arrive at statistically significant, despite the conclusion being 100% untrue.

As our p-value calculator is here at your service, you no longer need to wonder how to find p-value from all those complicated test statistics! Here are the steps you need to follow:

Pick the alternative hypothesis : two-tailed, right-tailed, or left-tailed.

Tell us the distribution of your test statistic under the null hypothesis: is it N(0,1), t-Student, chi-squared, or Snedecor's F? If you are unsure, check the sections below, as they are devoted to these distributions.

If needed, specify the degrees of freedom of the test statistic's distribution.

Enter the value of test statistic computed for your data sample.

Our calculator determines the p-value from the test statistic and provides the decision to be made about the null hypothesis. The standard significance level is 0.05 by default.

Go to the advanced mode if you need to increase the precision with which the calculations are performed or change the significance level .

In terms of the cumulative distribution function (cdf) of the standard normal distribution, which is traditionally denoted by Φ , the p-value is given by the following formulae:

Left-tailed z-test:

p-value = Φ(Z score )

Right-tailed z-test:

p-value = 1 - Φ(Z score )

Two-tailed z-test:

p-value = 2 × Φ(−|Z score |)

p-value = 2 - 2 × Φ(|Z score |)

🙋 To learn more about Z-tests, head to Omni's Z-test calculator .

We use the Z-score if the test statistic approximately follows the standard normal distribution N(0,1) . Thanks to the central limit theorem, you can count on the approximation if you have a large sample (say at least 50 data points) and treat your distribution as normal.

A Z-test most often refers to testing the population mean , or the difference between two population means, in particular between two proportions. You can also find Z-tests in maximum likelihood estimations.

The p-value from the t-score is given by the following formulae, in which cdf t,d stands for the cumulative distribution function of the t-Student distribution with d degrees of freedom:

Left-tailed t-test:

p-value = cdf t,d (t score )

Right-tailed t-test:

p-value = 1 - cdf t,d (t score )

Two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

p-value = 2 - 2 × cdf t,d (|t score |)

Use the t-score option if your test statistic follows the t-Student distribution . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails – the exact shape depends on the parameter called the degrees of freedom . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from the normal distribution N(0,1).

The most common t-tests are those for population means with an unknown population standard deviation, or for the difference between means of two populations , with either equal or unequal yet unknown population standard deviations. There's also a t-test for paired (dependent) samples .

🙋 To get more insights into t-statistics, we recommend using our t-test calculator .

Use the χ²-score option when performing a test in which the test statistic follows the χ²-distribution .

This distribution arises if, for example, you take the sum of squared variables, each following the normal distribution N(0,1). Remember to check the number of degrees of freedom of the χ²-distribution of your test statistic!

How to find the p-value from chi-square-score ? You can do it with the help of the following formulae, in which cdf χ²,d denotes the cumulative distribution function of the χ²-distribution with d degrees of freedom:

Left-tailed χ²-test:

p-value = cdf χ²,d (χ² score )

Right-tailed χ²-test:

p-value = 1 - cdf χ²,d (χ² score )

Remember that χ²-tests for goodness-of-fit and independence are right-tailed tests! (see below)

Two-tailed χ²-test:

p-value = 2 × min{cdf χ²,d (χ² score ), 1 - cdf χ²,d (χ² score )}

(By min{a,b} , we denote the smaller of the numbers a and b .)

The most popular tests which lead to a χ²-score are the following:

Testing whether the variance of normally distributed data has some pre-determined value. In this case, the test statistic has the χ²-distribution with n - 1 degrees of freedom, where n is the sample size. This can be a one-tailed or two-tailed test .

Goodness-of-fit test checks whether the empirical (sample) distribution agrees with some expected probability distribution. In this case, the test statistic follows the χ²-distribution with k - 1 degrees of freedom, where k is the number of classes into which the sample is divided. This is a right-tailed test .

Independence test is used to determine if there is a statistically significant relationship between two variables. In this case, its test statistic is based on the contingency table and follows the χ²-distribution with (r - 1)(c - 1) degrees of freedom, where r is the number of rows, and c is the number of columns in this contingency table. This also is a right-tailed test .

Finally, the F-score option should be used when you perform a test in which the test statistic follows the F-distribution , also known as the Fisher–Snedecor distribution. The exact shape of an F-distribution depends on two degrees of freedom .

To see where those degrees of freedom come from, consider the independent random variables X and Y , which both follow the χ²-distributions with d 1 and d 2 degrees of freedom, respectively. In that case, the ratio (X/d 1 )/(Y/d 2 ) follows the F-distribution, with (d 1 , d 2 ) -degrees of freedom. For this reason, the two parameters d 1 and d 2 are also called the numerator and denominator degrees of freedom .

The p-value from F-score is given by the following formulae, where we let cdf F,d1,d2 denote the cumulative distribution function of the F-distribution, with (d 1 , d 2 ) -degrees of freedom:

Left-tailed F-test:

p-value = cdf F,d1,d2 (F score )

Right-tailed F-test:

p-value = 1 - cdf F,d1,d2 (F score )

Two-tailed F-test:

p-value = 2 × min{cdf F,d1,d2 (F score ), 1 - cdf F,d1,d2 (F score )}

Below we list the most important tests that produce F-scores. All of them are right-tailed tests .

A test for the equality of variances in two normally distributed populations . Its test statistic follows the F-distribution with (n - 1, m - 1) -degrees of freedom, where n and m are the respective sample sizes.

ANOVA is used to test the equality of means in three or more groups that come from normally distributed populations with equal variances. We arrive at the F-distribution with (k - 1, n - k) -degrees of freedom, where k is the number of groups, and n is the total sample size (in all groups together).

A test for overall significance of regression analysis . The test statistic has an F-distribution with (k - 1, n - k) -degrees of freedom, where n is the sample size, and k is the number of variables (including the intercept).

With the presence of the linear relationship having been established in your data sample with the above test, you can calculate the coefficient of determination, R 2 , which indicates the strength of this relationship . You can do it by hand or use our coefficient of determination calculator .

A test to compare two nested regression models . The test statistic follows the F-distribution with (k 2 - k 1 , n - k 2 ) -degrees of freedom, where k 1 and k 2 are the numbers of variables in the smaller and bigger models, respectively, and n is the sample size.

You may notice that the F-test of an overall significance is a particular form of the F-test for comparing two nested models: it tests whether our model does significantly better than the model with no predictors (i.e., the intercept-only model).

Can p-value be negative?

No, the p-value cannot be negative. This is because probabilities cannot be negative, and the p-value is the probability of the test statistic satisfying certain conditions.

What does a high p-value mean?

A high p-value means that under the null hypothesis, there's a high probability that for another sample, the test statistic will generate a value at least as extreme as the one observed in the sample you already have. A high p-value doesn't allow you to reject the null hypothesis.

What does a low p-value mean?

A low p-value means that under the null hypothesis, there's little probability that for another sample, the test statistic will generate a value at least as extreme as the one observed for the sample you already have. A low p-value is evidence in favor of the alternative hypothesis – it allows you to reject the null hypothesis.

Pearson correlation

Specificity.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (570)
• Health (440)
• Physics (510)
• Sports (105)
• Statistics (182)
• Other (182)
• Discover Omni (40)

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Statistics and probability

Course: statistics and probability   >   unit 12, hypothesis testing and p-values.

• One-tailed and two-tailed tests
• Z-statistics vs. T-statistics
• Small sample hypothesis test
• Large sample proportion hypothesis testing

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.3: A Single Population Mean using the Normal Distribution

• Last updated
• Save as PDF
• Page ID 20074

All hypotheses tests have the same basic steps:

• The alternative hypothesis, \(H_{a}\), never has a symbol that contains an equal sign.
• The alternative hypothesis, \(H_{a}\), tells you if the test is left, right, or two-tailed. It is the key to conducting the appropriate test.
• In a hypothesis test problem, you may see words such as "the level of significance is 1%." The "1%" is the preconceived or preset \(\alpha\). The statistician setting up the hypothesis test selects the value of α to use before collecting the sample data. If no level of significance is given, a common standard to use is \(\alpha = 0.05\).
• When you calculate the \(p\)-value and draw the picture, the \(p\)-value is the area in the left tail, the right tail, or split evenly between the two tails. For this reason, we call the hypothesis test left, right, or two tailed.
• Never, ever, Accept the Null Hypothesis.
• Thinking about the meaning of the \(p\)-value: A data analyst (and anyone else) should have more confidence that he made the correct decision to reject the null hypothesis with a smaller \(p\)-value (for example, 0.001 as opposed to 0.04) even if using the 0.05 level for alpha. Similarly, for a large p -value such as 0.4, as opposed to a \(p\)-value of 0.056 (\(\alpha = 0.05\) is less than either number), a data analyst should have more confidence that she made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.
• Determine the conclusion : What does the decision mean in terms of the problem given?

Direction of Tail

Example \(\pageindex{1}\).

\(H_{0}: \mu \geq 5, H_{a}: \mu < 5\)

Test of a single population mean. \(H_{a}\) tells you the test is left-tailed. The picture of the \(p\)-value is as follows:

Exercise \(\PageIndex{1}\)

\(H_{0}: \mu \geq 10, H_{a}: \mu < 10\)

Assume the \(p\)-value is 0.0935. What type of test is this? Draw the picture of the \(p\)-value.

left-tailed test

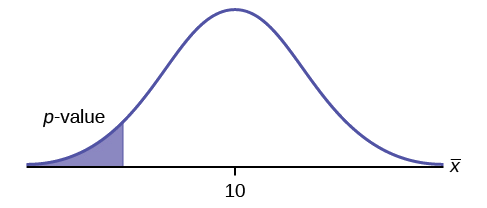
Example \(\PageIndex{2}\)

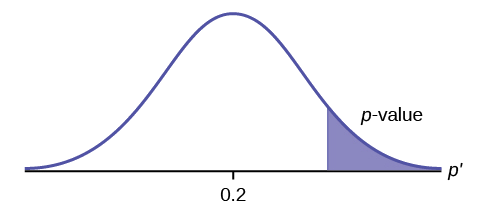
\(H_{0}: \mu \leq 0.2, H_{a}: \mu > 0.2\)

This is a test of a single population proportion. \(H_{a}\) tells you the test is right-tailed . The picture of the p -value is as follows:

Exercise \(\PageIndex{2}\)

\(H_{0}: \mu \leq 1, H_{a}: \mu > 1\)

Assume the \(p\)-value is 0.1243. What type of test is this? Draw the picture of the \(p\)-value.

right-tailed test

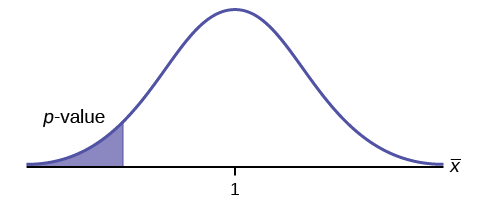
Example \(\PageIndex{3}\)

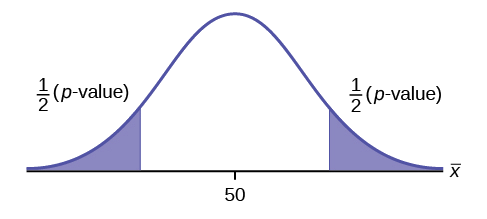
\(H_{0}: \mu = 50, H_{a}: \mu \neq 50\)

This is a test of a single population mean. \(H_{a}\) tells you the test is two-tailed . The picture of the \(p\)-value is as follows.

Exercise \(\PageIndex{3}\)

\(H_{0}: \mu = 0.5, H_{a}: \mu \neq 0.5\)

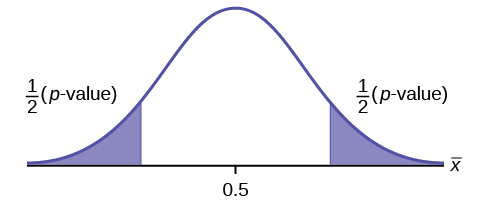
Assume the p -value is 0.2564. What type of test is this? Draw the picture of the \(p\)-value.

two-tailed test

Full Hypothesis Test Examples

Example \(\pageindex{4}\).

Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle, with a standard deviation of 0.8 seconds. His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles. Frank bought Jeffrey a new pair of expensive goggles and timed Jeffrey for 15 25-yard freestyle swims. For the 15 swims, Jeffrey's mean time was 16 seconds. Frank thought that the goggles helped Jeffrey to swim faster than the 16.43 seconds. Conduct a hypothesis test using a preset α = 0.05. Assume that the swim times for the 25-yard freestyle are normal.

\(P\)-value Solution

Determine the hypothesis :

Since the problem is about a mean, this is a test of a single population mean.

For Jeffrey to swim faster, his time will be less than 16.43 seconds. So the claim will be that he can swim it in less time than 16.43 seconds.

\(H_{0}: \mu \geq 16.43\)

\(H_{a}: \mu < 16.43\) (claim)

The "\(<\)" in the alternative hypothesis tells you this is left-tailed.

Calculate the evidence :

Use the Standard Normal Distribution since the population standard deviation is given.

Calculate the test statistic using the same formula as a \(z\)-score using the Central Limit Theorem.

\[z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\nonumber\]

\(\mu = 16.43\) comes from \(H_{0}\) and not the data. \(\sigma = 0.8\) and \(n = 15\). Which gives

\[z=\frac{16-16.43}{\frac{0.8}{\sqrt{15}}}=\frac{-0.43}{\frac{0.8}{3.87298}}=\frac{-0.43}{0.20656}=-2.0817\nonumber\]

Now calculate the p-value based on the test statistic found.

This is a left-tailed test, so use the Excel formula \(=\text{NORM.S.DIST}(z,\text{true})\).

In this case, we found \(z\), which is the test statistic, to be \(z=-2.0817\).

Use the Excel formula \(=\text{NORM.S.DIST}(-2.0817,\text{true})=0.0187\).

So the \(p\text{-value} = 0.0187\). This is the area to the left of the sample mean, which is given as 16.

Make a decision:

Interpretation of the \(p-\text{value}\): If \(H_{0}\) is true, there is a 0.0187 probability (1.87%) that Jeffrey's mean time to swim the 25-yard freestyle is 16 seconds or less. Because a 1.87% chance is small, the mean time of 16 seconds or less is unlikely to have happened randomly. It is a rare event.

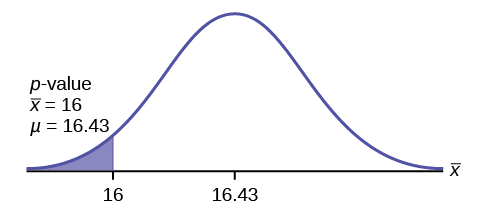
\(\mu = 16.43\) comes from \(H_{0}\). Our assumption gives \(\mu = 16.43\).

\(\alpha\) is the minimum area that could be considered to make our result significant.

Compare \(\alpha\) and the \(p\text{-value}\)

• If \(p\text{-value}\) is less than the \(\alpha\) then we will Reject \(H_0\).
• If \(\alpha\) is less than the \(p\text{-value}\) then we will Fail to Reject \(H_0\).

\(\alpha = 0.05\) and \(p\text{-value} = 0.0187\), so \(p\text{-value}<\alpha\)

Since \(p\text{-value}<\alpha\), reject \(H_{0}\).

Conclusion:

This means that you reject \(\mu \geq 16.43\).

There is sufficient evidence to support the claim that Jeffrey's mean swim time for the 25-yard freestyle is less than 16.43 seconds.

Critical Value Solution

Determine the hypothesis (Same as the \(P\)-value solution) :

Calculate the critical value. Use the Standard Normal Distribution, Critical Value, Right-tail Excel formula: \(=\text{NORM.S.INV}(\alpha)\).

In this problem, the \(\alpha=0.05\), so use \(=\text{NORM.S.INV}(0.05)=-1.64485\)

Graph the critical value and the test statistic along the number line of the Standard Normal Distribution graph.

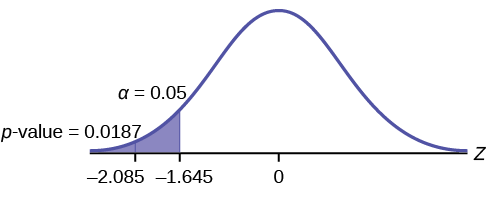
Since this is left-tailed, everything less than the critical value, \(\text{CV}=-1.64485\) will be the rejection region.

Since the test statistic, \(z=-2.0817\) is less than the critical value, \(\text{CV}=-1.64485, the decision will be to Reject the Null Hypothesis.

Conclusion (Same as the \(P\)-value solution):

The Type I and Type II errors for this problem are as follows :

The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on average, in 16.43 seconds. (Reject the null hypothesis when the null hypothesis is true.)

The Type II error is that there is not evidence to conclude that Jeffrey swims the 25-yard free-style, on average, in less than 16.43 seconds when, in fact, he actually does swim the 25-yard free-style, on average, in less than 16.43 seconds. (Do not reject the null hypothesis when the null hypothesis is false.)

Exercise \(\PageIndex{4}\)

The mean throwing distance of a football for a Marco, a high school freshman quarterback, is 40 yards, with a standard deviation of two yards. The team coach tells Marco to adjust his grip to get more distance. The coach records the distances for 20 throws. For the 20 throws, Marco’s mean distance was 45 yards. The coach thought the different grip helped Marco throw farther than 40 yards. Conduct a hypothesis test using a preset \(\alpha = 0.01\). Assume the throw distances for footballs are normal. Use the critical value method.

For Marco to throw farther, his distance will be greater than 40 yards. So the claim will be that he can throw farther than 40 yards.

\(H_{0}: \mu \leq 40\)

\(H_{a}: \mu > 40\) (claim)

The "\(>\)" in the alternative hypothesis tells you this is right-tailed.

Calculate the critical value. Use the Standard Normal Distribution, Critical Value, Right-tail Excel formula: \(=\text{NORM.S.INV}(1-\alpha)\).

In this problem, the \(\alpha=0.01\), so use \(=\text{NORM.S.INV}(1-0.01)=2.3263\)

\(\mu = 40\) comes from \(H_{0}\) and not the data. \(\sigma = 2\) and \(n = 20\). Which gives

\[z=\frac{45-40}{\frac{2}{\sqrt{20}}}=\frac{5}{\frac{2}{4.4721}}=\frac{5}{0.4472}=11.1803\nonumber\]

Since this is right-tailed, everything greater than the critical value, \(\text{CV}=2.3263\) will be the rejection region.

Since the test statistic, \(z=11.1803\) is greater than the critical value, \(\text{CV}=2.3263\), the decision will be to Reject the Null Hypothesis.

This means that you reject \(\mu \leq 40\).

There is sufficient evidence to support the claim that the change in Marco's grip improved his throwing distance to give a mean throw distance is greater than 40 yards.

Example \(\PageIndex{5}\)

A college football coach thought that his players could bench press a mean weight of 275 pounds. It is known that the standard deviation is 55 pounds. Three of his players thought that the mean weight was great than that amount. They asked 30 of their teammates for their estimated maximum lift on the bench press exercise. The data ranged from 205 pounds to 385 pounds. The actual different weights are given below

Conduct a \(p\)-value hypothesis test using a 2.5% level of significance to determine if the bench press mean is more than 275 pounds.

Since the problem is about a mean weight, this is a test of a single population mean.

\(H_{0}: \mu \leq 275\)

\(H_{a}: \mu > 275\) (claim)

The "\(>\)" in the alternative hypothesis tells you this is a right-tailed test.

Calculate the test statistic using the same formula as the \(z\)-score using the Central Limit Theorem.

\(\mu = 275\) comes from \(H_{0}\) and not the data. \(\sigma=55\) and \(n=30\). The problem does not give the sample mean, so that will need to be calculated using the data.

Enter the data into Excel, and use the Excel formula \(=\text{AVERAGE}()\) to find \(\bar{x}=286.2\).

\[z=\frac{286.2-275}{\frac{55}{\sqrt{30}}}=\frac{11.2}{\frac{2}{5.4772}}=\frac{11.2}{10.04}=1.11536\nonumber\]

Now calculate the \(p\)-value based on the test statistic found.

This is a right-tailed test, so use the Excel formula \(=1-\text{NORM.S.DIST}(z,\text{true})\).

In this case, we found \(z\), which is the test statistic, to be \(z=1.11536\).

Use the Excel formula \(=1-\text{NORM.S.DIST}(1.11536,\text{true})=0.132348\).

So the \(p\text{-value} = 0.132348\).

Interpretation of the p -value: If \(H_{0}\) is true, then there is a 0.1331 probability (13.23%) that the football players can lift a mean weight of 286.2 pounds or more. Because a 13.23% chance is large enough, a mean weight lift of 286.2 pounds or more is not a rare event.

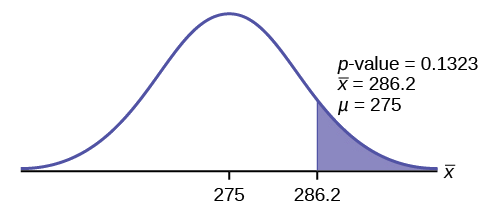
Make a decision :

\(\alpha = 0.025\) and \(p\)-value \(= 0.1323\)

Since \(\alpha < p\text{-value}\), do not reject \(H_{0}\).

Conclusion: At the 2.5% level of significance, from the sample data, there is not sufficient evidence to conclude that the true mean weight lifted is more than 275 pounds.

The hypothesis test itself has an established process. This can be summarized as follows:

• Determine \(H_{0}\) and \(H_{a}\). Remember, they are contradictory.
• Find the evidence: Draw a graph, calculate the test statistic, and use the test statistic to calculate the \(p\text{-value}\). (A z -score and a t -score are examples of test statistics.)
• Compare the preconceived α with the p -value, make a decision (reject or do not reject H 0 ).
• Write a clear conclusion using English sentences.

Notice that in performing the hypothesis test, you use \(\alpha\) and not \(\beta\). \(\beta\) is needed to help determine the sample size of the data that is used in calculating the \(p\text{-value}\). Remember that the quantity \(1 – \beta\) is called the Power of the Test . A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.

Exercise \(\PageIndex{5}\)

Assume \(H_{0}: \mu = 9\) and \(H_{a}: \mu < 9\). Is this a left-tailed, right-tailed, or two-tailed test?

This is a left-tailed test.

Exercise \(\PageIndex{6}\)

Assume \(H_{0}: \mu \leq 6\) and \(H_{a}: \mu > 6\). Is this a left-tailed, right-tailed, or two-tailed test?

Exercise \(\PageIndex{7}\)

Assume \(H_{0}: p = 0.25\) and \(H_{a}: p \neq 0.25\). Is this a left-tailed, right-tailed, or two-tailed test?

This is a two-tailed test.

Exercise \(\PageIndex{8}\)

Draw the general graph of a left-tailed test.

Exercise \(\PageIndex{9}\)

Draw the graph of a two-tailed test.

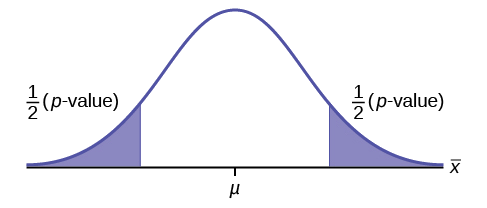
Exercise \(\PageIndex{10}\)

A bottle of water is labeled as containing 16 fluid ounces of water. You believe it is less than that. What type of test would you use?

Exercise \(\PageIndex{11}\)

Your friend claims that his mean golf score is 63. You want to show that it is higher than that. What type of test would you use?

a right-tailed test

Exercise \(\PageIndex{12}\)

A bathroom scale claims to be able to identify correctly any weight within a pound. You think that it cannot be that accurate. What type of test would you use?

Exercise \(\PageIndex{13}\)

You flip a coin and record whether it shows heads or tails. You know the probability of getting heads is 50%, but you think it is less for this particular coin. What type of test would you use?

a left-tailed test

Exercise \(\PageIndex{14}\)

If the alternative hypothesis has a not equals ( \(\neq\) ) symbol, you know to use which type of test?

Exercise \(\PageIndex{15}\)

Assume the null hypothesis states that the mean is at least 18. Is this a left-tailed, right-tailed, or two-tailed test?

Exercise \(\PageIndex{16}\)

Assume the null hypothesis states that the mean is at most 12. Is this a left-tailed, right-tailed, or two-tailed test?

Exercise \(\PageIndex{17}\)

Assume the null hypothesis states that the mean is equal to 88. The alternative hypothesis states that the mean is not equal to 88. Is this a left-tailed, right-tailed, or two-tailed test?

• Data from Amit Schitai. Director of Instructional Technology and Distance Learning. LBCC.
• Data from Bloomberg Businessweek . Available online at www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
• Data from energy.gov. Available online at http://energy.gov (accessed June 27. 2013).
• Data from Gallup®. Available online at www.gallup.com (accessed June 27, 2013).
• Data from Growing by Degrees by Allen and Seaman.
• Data from La Leche League International. Available online at www.lalecheleague.org/Law/BAFeb01.html.
• Data from the American Automobile Association. Available online at www.aaa.com (accessed June 27, 2013).
• Data from the American Library Association. Available online at www.ala.org (accessed June 27, 2013).
• Data from the Bureau of Labor Statistics. Available online at http://www.bls.gov/oes/current/oes291111.htm .
• Data from the Centers for Disease Control and Prevention. Available online at www.cdc.gov (accessed June 27, 2013)
• Data from the U.S. Census Bureau, available online at quickfacts.census.gov/qfd/states/00000.html (accessed June 27, 2013).
• Data from the United States Census Bureau. Available online at www.census.gov/hhes/socdemo/language/.
• Data from Toastmasters International. Available online at http://toastmasters.org/artisan/deta...eID=429&Page=1 .
• Data from Weather Underground. Available online at www.wunderground.com (accessed June 27, 2013).
• Federal Bureau of Investigations. “Uniform Crime Reports and Index of Crime in Daviess in the State of Kentucky enforced by Daviess County from 1985 to 2005.” Available online at http://www.disastercenter.com/kentucky/crime/3868.htm (accessed June 27, 2013).
• “Foothill-De Anza Community College District.” De Anza College, Winter 2006. Available online at research.fhda.edu/factbook/DA...t_da_2006w.pdf.
• Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Cellular Telephones and Cancer—a Nationwide Cohort Study in Denmark.” Institute of Cancer Epidemiology and the Danish Cancer Society, 93(3):203-7. Available online at http://www.ncbi.nlm.nih.gov/pubmed/11158188 (accessed June 27, 2013).
• Rape, Abuse & Incest National Network. “How often does sexual assault occur?” RAINN, 2009. Available online at www.rainn.org/get-information...sexual-assault (accessed June 27, 2013).

Contributors and Attributions

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] .

8.1.2 - Hypothesis Testing

A hypothesis test for a proportion is used when you are comparing one group to a known or hypothesized population proportion value. In other words, you have one sample with one categorical variable. The hypothesized value of the population proportion is symbolized by \(p_0\) because this is the value in the null hypothesis (\(H_0\)).

If \(np_0 \ge 10\) and \(n(1-p_0) \ge 10\) then the distribution of sample proportions is approximately normal and can be estimated using the normal distribution. That sampling distribution will have a mean of \(p_0\) and a standard deviation (i.e., standard error) of \(\sqrt{\frac{p_0 (1-p_0)}{n}}\)

Recall that the standard normal distribution is also known as the z distribution. Thus, this is known as a "single sample proportion z test" or "one sample proportion z test." 

If \(np_0 < 10\) or \(n(1-p_0) < 10\) then the distribution of sample proportions follows a binomial distribution. We will not be conducting this test by hand in this course, however you will learn how this can be conducted using Minitab using the exact method.

8.1.2.1 - Normal Approximation Method Formulas

Here we will be using the five step hypothesis testing procedure to compare the proportion in one random sample to a specified population proportion using the normal approximation method.

In order to use the normal approximation method, the assumption is that both \(n p_0 \geq 10\) and \(n (1-p_0) \geq 10\). Recall that \(p_0\) is the population proportion in the null hypothesis.

Where \(p_0\) is the hypothesized population proportion that you are comparing your sample to.

When using the normal approximation method we will be using a z test statistic. The z test statistic tells us how far our sample proportion is from the hypothesized population proportion in standard error units. Note that this formula follows the basic structure of a test statistic that you learned in the last lesson:

\(test\;statistic=\dfrac{sample\;statistic-null\;parameter}{standard\;error}\)

\(\widehat{p}\) = sample proportion \(p_{0}\) = hypothesize population proportion \(n\) = sample size

Given that the null hypothesis is true, the p value is the probability that a randomly selected sample of n would have a sample proportion as different, or more different, than the one in our sample, in the direction of the alternative hypothesis. We can find the p value by mapping the test statistic from step 2 onto the z distribution. 

Note that p-values are also symbolized by \(p\). Do not confuse this with the population proportion which shares the same symbol.

We can look up the \(p\)-value using Minitab by constructing the sampling distribution.  Because we are using the normal approximation here, we have a \(z\) test statistic that we can map onto the \(z\) distribution. Recall, the z distribution is a normal distribution with a mean of 0 and standard deviation of 1. If we are conducting a one-tailed (i.e., right- or left-tailed) test, we look up the area of the sampling distribution that is beyond our test statistic. If we are conducting a two-tailed (i.e., non-directional) test there is one additional step: we need to multiple the area by two to take into account the possibility of being in the right or left tail. 

We can decide between the null and alternative hypotheses by examining our p-value. If \(p \leq \alpha\) reject the null hypothesis. If \(p>\alpha\) fail to reject the null hypothesis. Unless stated otherwise, assume that \(\alpha=.05\).

When we reject the null hypothesis our results are said to be statistically significant.

Based on our decision in step 4, we will write a sentence or two concerning our decision in relation to the original research question.

8.1.2.1.1 - Video Example: Male Babies

8.1.2.1.2 - Example: Handedness

Research Question : Are more than 80% of American's right handed?

In a sample of 100 Americans, 87 were right handed.

\(np_0 = 100(0.80)=80\)

\(n(1-p_0) = 100 (1-0.80) = 20\)

Both \(np_0\) and \(n(1-p_0)\) are at least 10 so we can use the normal approximation method. 

This is a right-tailed test because we want to know if the proportion is greater than 0.80.

\(H_{0}\colon p=0.80\) \(H_{a}\colon p>0.80\)

\(z=\dfrac{\widehat{p}- p_0 }{\sqrt{\frac{p_0 (1- p_0)}{n}}}\)

\(\widehat{p}=\dfrac{87}{100}=0.87\), \(p_{0}=0.80\), \(n=100\)

\(z= \dfrac{\widehat{p}- p_0 }{\sqrt{\frac{p_0 (1- p_0)}{n}}}= \dfrac{0.87-0.80}{\sqrt{\frac{0.80 (1-0.80)}{100}}}=1.75\)

Our \(z\) test statistic is 1.75.

This is a right-tailed test so we need to find the area to the right of the test statistic, \(z=1.75\), on the z distribution.

Using Minitab , we find the probability \(P(z\geq1.75)=0.0400592\) which may be rounded to \(p\; value=0.0401\).

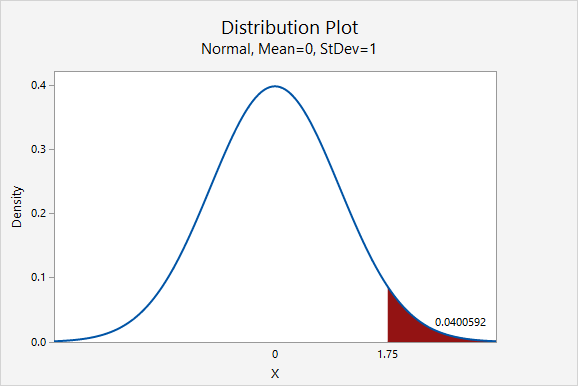
\(p\leq .05\), therefore our decision is to reject the null hypothesis

Yes, there is statistical evidence to state that more than 80% of all Americans are right handed.

8.1.2.1.3 - Example: Ice Cream

Research Question : Is the percentage of Creamery customers who prefer chocolate ice cream over vanilla less than 80%?

In a sample of 50 customers 60% preferred chocolate over vanilla.

\(np_0 = 50(0.80) = 40\)

\(n(1-p_0)=50(1-0.80) = 10\)

Both \(np_0\) and \(n(1-p_0)\) are at least 10. We can use the normal approximation method.

This is a left-tailed test because we want to know if the proportion is less than 0.80.

\(H_{0}\colon p=0.80\) \(H_{a}\colon p<0.80\)

\(\widehat{p}=0.60\), \(p_{0}=0.80\), \(n=50\)

\(z= \dfrac{\widehat{p}- p_0 }{\sqrt{\frac{p_0 (1- p_0)}{n}}}= \dfrac{0.60-0.80}{\sqrt{\frac{0.80 (1-0.80)}{50}}}=-3.536\)

Our \(z\) test statistic is -3.536.

This is a left-tailed test so we need to find the area to the right of our test statistic, \(z=-3.536\).

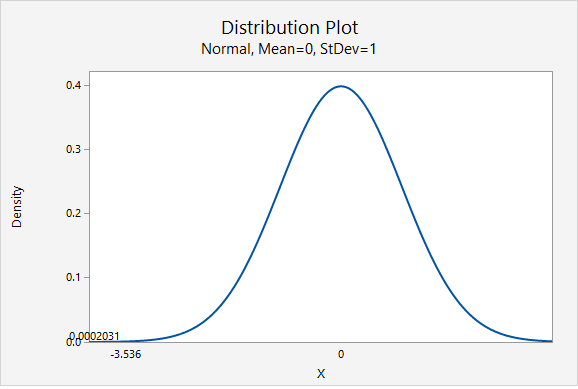
From the Minitab output above, the p-value is 0.0002031

\(p \leq.05\), therefore our decision is to reject the null hypothesis.

Yes, there is evidence that the percentage of all Creamery customers who prefer chocolate ice cream over vanilla is less than 80%.

8.1.2.1.4 - Example: Overweight Citizens

According to the Center for Disease Control (CDC), the percent of adults 20 years of age and over in the United States who are overweight is 69.0% (see  http://www.cdc.gov/nchs/fastats/obesity-overweight.htm ). One city’s council wants to know if the proportion of overweight citizens in their city is different from this known national proportion. They take a random sample of 150 adults 20 years of age or older in their city and find that 98 are classified as overweight. Let’s use the five step hypothesis testing procedure to determine if there is evidence that the proportion in this city is different from the known national proportion.

\(np_0 =150 (0.690)=103.5 \)

\(n (1-p_0) =150 (1-0.690)=46.5\)

Both \(n p_0\) and \(n (1-p_0)\) are at least 10, this assumption has been met.

Research question: Is this city’s proportion of overweight individuals different from 0.690?

This is a non-directional test because our question states that we are looking for a differences as opposed to a specific direction. This will be a two-tailed test.

\(H_{0}\colon p=0.690\) \(H_{a}\colon p\neq 0.690\)

\(\widehat{p}=\dfrac{98}{150}=.653\)

\( z =\dfrac{0.653- 0.690 }{\sqrt{\frac{0.690 (1- 0.690)}{150}}} = -0.980 \)

Our test statistic is \(z=-0.980\)

This is a non-directional (i.e., two-tailed) test, so we need to find the area under the z distribution that is more extreme than \(z=-0.980\).

In Minitab, we find the proportion of a normal curve beyond \(\pm0.980\):

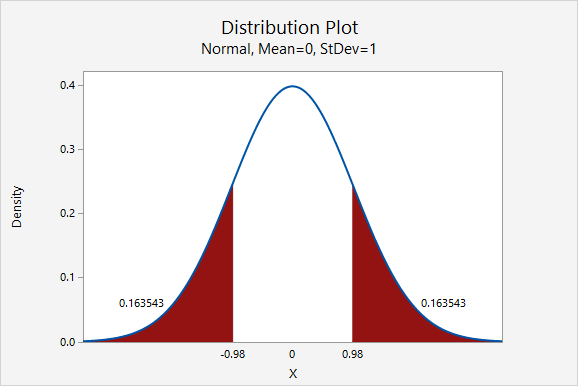
\(p-value=0.163543+0.163543=0.327086\)

\(p>\alpha\), therefore we fail to reject the null hypothesis

There is not sufficient evidence to state that the proportion of citizens of this city who are overweight is different from the national proportion of 0.690.

8.1.2.2 - Minitab: Hypothesis Tests for One Proportion

A hypothesis test for one proportion can be conducted in Minitab. This can be done using raw data or summarized data.

• If you have a data file with every individual's observation, then you have  raw data .
• If you do not have each individual observation, but rather have the sample size and number of successes in the sample, then you have summarized data.

The next two pages will show you how to use Minitab to conduct this analysis using either raw data or summarized data .

Note that the default method for constructing the sampling distribution in Minitab is to use the exact method.  If \(np_0 \geq 10\) and \(n(1-p_0) \geq 10\) then you will need to change this to the normal approximation method.  This must be done manually.  Minitab will use the method that you select, it will not check assumptions for you!

8.1.2.2.1 - Minitab: 1 Proportion z Test, Raw Data

If you have data in a Minitab worksheet, then you have what we call "raw data."  This is in contrast to "summarized data" which you'll see on the next page.

In order to use the normal approximation method both \(np_0 \geq 10\) and \(n(1-p_0) \geq 10\). Before we can conduct our hypothesis test we must check this assumption to determine if the normal approximation method or exact method should be used. This must be checked manually.  Minitab will not check assumptions for you.

In the example below, we want to know if there is evidence that the proportion of students who are male is different from 0.50.

\(n=226\) and \(p_0=0.50\)

\(np_0 = 226(0.50)=113\) and \(n(1-p_0) = 226(1-0.50)=113\)

Both \(np_0 \geq 10\) and \(n(1-p_0) \geq 10\) so we can use the normal approximation method. 

Minitab ®  – Conducting a One Sample Proportion z Test: Raw Data

Research question:  Is the proportion of students who are male different from 0.50?

• class_survey.mpx
• In Minitab, select Stat > Basic Statistics > 1 Proportion
• Select One or more samples, each in a column from the dropdown
• Double-click the variable  Biological Sex  to insert it into the box
• Check the box next to  Perform hypothesis test and enter  0.50  in the  Hypothesized proportion  box
• Select Options
• Use the default  Alternative hypothesis  setting of  Proportion ≠ hypothesized proportion value 
• Use the default  Confidence level  of 95
• Select  Normal approximation method
• Click OK and OK

The result should be the following output:

Event: Biological Sex = Male p: proportion where Biological Sex = Male Normal approximation is used for this analysis.

Summary of Results

We could summarize these results using the five-step hypothesis testing procedure:

\(np_0 = 226(0.50)=113\) and \(n(1-p_0) = 226(1-0.50)=113\) therefore the normal approximation method will be used.

 \(H_0\colon p = 0.50\)

 \(H_a\colon p \ne 0.50\)

From the Minitab output, \(z\) = -1.86

From the Minitab output, \(p\) = 0.0625

\(p > \alpha\), fail to reject the null hypothesis

There is NOT enough evidence that the proportion of all students in the population who are male is different from 0.50.

8.1.2.2.2 - Minitab: 1 Sample Proportion z test, Summary Data

Example: overweight.

The following example uses a scenario in which we want to know if the proportion of college women who think they are overweight is less than 40%. We collect data from a random sample of 129 college women and 37 said that they think they are overweight.

First, we should check assumptions to determine if the normal approximation method or exact method should be used:

\(np_0=129(0.40)=51.6\) and \(n(1-p_0)=129(1-0.40)=77.4\) both values are at least 10 so we can use the normal approximation method.

Minitab ®  – Performing a One Proportion z Test with Summarized Data

To perform a one sample proportion  z  test with summarized data in Minitab:

• Select Summarized data from the dropdown
• For number of events, add 37 and for number of trials add 129.
• Check the box next to  Perform hypothesis test and enter  0.40  in the  Hypothesized proportion  box
• Use the default  Alternative hypothesis  setting of  Proportion < hypothesized proportion value 

Event: Event proportion Normal approximation is used for this analysis.

\(H_0\colon p = 0.40\)

\(H_a\colon p < 0.40\)

From output, \(z\) = -2.62

From output, \(p\) = 0.004

\(p \leq \alpha\), reject the null hypothesis

There is evidence that the proportion of women in the population who think they are overweight is less than 40%.

8.1.2.2.2.1 - Minitab Example: Normal Approx. Method

Example: gym membership.

Research question:  Are less than 50% of all individuals with a membership at one gym female?

A simple random sample of 60 individuals with a membership at one gym was collected. Each individual's biological sex was recorded. There were 24 females. 

First we have to check the assumptions:

  np = 60 (0.50) = 30

  n(1-p) = 60(1-0.50) = 30

The assumptions are met to use the normal approximation method.

• For number of events, add 24 and for number of trials add 60.

\(np_0=60(0.50)=30\) and \(n(1-p_0)=60(1-0.50)=30\) both values are at least 10 so we can use the normal approximation method.

\(H_0\colon p = 0.50\)

\(H_a\colon p < 0.50\)

From output, \(z\) = -1.55

From output, \(p\) = 0.061

\(p \geq \alpha\), fail to reject the null hypothesis

There is not enough evidence to support the alternative that the proportion of women memberships at this gym is less than 50%.