hypothesis test meaning in psychology

All Subjects

Intro to Psychology

Study guides for every class, that actually explain what's on your next test, hypothesis testing, from class:.

Hypothesis testing is a statistical method used to determine whether a particular claim or hypothesis about a population parameter is likely to be true or false. It involves using sample data to evaluate the plausibility of a hypothesis and make inferences about the population.

congrats on reading the definition of Hypothesis Testing . now let's actually learn it.

5 Must Know Facts For Your Next Test

• Hypothesis testing is a fundamental component of the scientific method, allowing researchers to draw conclusions about population parameters based on sample data.
• The process of hypothesis testing involves formulating a null hypothesis, collecting sample data, calculating a test statistic, and determining the probability of obtaining the observed results under the null hypothesis.
• Researchers use hypothesis testing to assess the strength of evidence against the null hypothesis, and to make decisions about whether to reject or fail to reject the null hypothesis.
• The level of statistical significance, often represented by the p-value, determines the likelihood that the observed results would occur by chance if the null hypothesis is true.
• Hypothesis testing is crucial in psychological research, as it allows researchers to evaluate the effectiveness of interventions, the relationships between variables, and the validity of theoretical models.

Review Questions

• Hypothesis testing is a central component of the scientific method in psychology. It allows researchers to systematically evaluate the plausibility of a proposed claim or hypothesis about a population parameter, using sample data to draw conclusions. By formulating a null hypothesis and an alternative hypothesis, researchers can design studies to collect empirical evidence that supports or contradicts the initial hypothesis. This process of hypothesis testing is fundamental to the scientific approach, as it enables researchers to make informed decisions about the validity of their theories and the generalizability of their findings.
• Statistical significance is a key concept in hypothesis testing, as it quantifies the likelihood that the observed results in a study are due to chance, rather than a true effect or relationship in the population. The p-value, which represents the probability of obtaining the observed results if the null hypothesis is true, is used to determine the statistical significance of the findings. A low p-value (typically less than 0.05) indicates that the observed results are unlikely to have occurred by chance, and researchers can then reject the null hypothesis in favor of the alternative hypothesis. The level of statistical significance guides the interpretation of research findings, helping researchers draw conclusions about the strength of the evidence and the potential real-world implications of their study.
• Hypothesis testing is a powerful tool for evaluating the effectiveness of psychological interventions and the relationships between variables. By formulating a null hypothesis that states there is no significant difference or relationship, and an alternative hypothesis that proposes a specific effect or relationship, researchers can design studies to collect data and statistically test these hypotheses. For example, in evaluating the effectiveness of a new therapy for depression, the null hypothesis might be that the therapy has no effect on symptoms, while the alternative hypothesis would be that the therapy significantly reduces depressive symptoms. Through the process of hypothesis testing, researchers can determine the probability of obtaining the observed results if the null hypothesis is true, and make informed decisions about whether to reject or fail to reject the null hypothesis. This, in turn, allows them to draw conclusions about the effectiveness of the intervention and the potential real-world implications for clinical practice.

Related terms

Null Hypothesis : The null hypothesis represents the claim or statement that is being tested, typically stating that there is no significant difference or relationship between the variables being studied.

Alternative Hypothesis : The alternative hypothesis is the statement that contradicts the null hypothesis, representing the claim that the researcher believes to be true or wants to demonstrate.

Statistical significance refers to the probability that the observed results in a study are due to chance, and not due to a true effect or relationship in the population.

" Hypothesis Testing " also found in:

Subjects ( 122 ).

• AP Psychology
• AP Statistics
• Advanced Communication Research Methods
• Advanced Design Strategy and Software
• Advanced Signal Processing
• Advanced quantitative methods
• Advertising Strategy & Consumer Insights
• Bayesian Statistics
• Big Data Analytics and Visualization
• Bioengineering Signals and Systems
• Biostatistics
• Brand Experience Marketing
• Business Analytics
• Business Decision Making
• Business Incubation and Acceleration
• Business Process Optimization
• Business of Healthcare
• Causal Inference
• Cognitive Computing in Business
• College Introductory Statistics
• Combinatorics
• Communication Research Methods
• Computational Chemistry
• Computational Geometry
• Computational Neuroscience
• Contemporary Mathematics for Non-Math Majors
• Covering Politics
• Criminology
• Customer Insights
• Data Journalism
• Data, Inference, and Decisions
• Digital Transformation Strategies
• E-commerce Strategies
• Economic Geography
• Engineering Applications of Statistics
• Engineering Probability
• Environmental Chemistry I
• Epidemiology
• Exoplanetary Science
• Experimental Design
• Financial Mathematics
• Forecasting
• Foundations of Data Science
• Fundamentals of Marketing
• Healthcare Quality and Outcomes
• History of Mathematics
• Honors Algebra II
• Honors Statistics
• Human-Computer Interaction
• Information Theory
• Intro to Anthropology
• Intro to Astronomy
• Intro to Business Statistics
• Intro to Political Science
• Intro to Python Programming
• Introduction to Advanced Programming in R
• Introduction to Archaeology
• Introduction to Biostatistics
• Introduction to Business Analytics
• Introduction to Econometrics
• Introduction to Engineering
• Introduction to Epidemiology
• Introduction to Industrial Engineering
• Introduction to Journalism
• Introduction to Plato
• Introduction to Political Research
• Introduction to Probabilistic Methods in Mathematics and the Sciences
• Introduction to Probability
• Introduction to Programming in R
• Introduction to Public Health
• Introduction to Scientific Computing
• Introductory Probability and Statistics for Business
• Investigative Reporting
• Journalism Research
• Leading Nonprofit and Social Enterprises
• Linear Modeling: Theory and Applications
• Logic and Formal Reasoning
• Market Research: Tools and Techniques for Data Collection and Analysis
• Marketing Research
• Marketing Strategy
• Mathematical Modeling
• Mathematical Probability Theory
• Mathematical and Computational Methods in Molecular Biology
• Mechatronic Systems Integration
• Media Expression and Communication
• Methods of Mathematics: Calculus, Statistics, and Combinatorics
• Model-Based Systems Engineering
• Modern Statistical Prediction and Machine Learning
• Numerical Analysis for Data Science and Statistics
• Numerical Solution of Differential Equations
• Organization Design
• Particle Physics
• Philosophy of Science
• Physical Science
• Planetary Science
• Predictive Analytics in Business
• Principles & Techniques of Data Science
• Principles of Finance
• Principles of Marketing
• Probabilistic & Statistical Decision-Making for Management
• Probability and Mathematical Statistics in Data Science
• Probability and Statistics
• Production and Operations Management
• Public Health Policy and Administration
• Public Policy Analysis
• Reproducible and Collaborative Statistical Data Science
• Risk Management and Insurance
• Sampling Surveys
• Science Education
• Smart Grid Optimization
• Statistical Inference
• Statistical Methods for Data Science
• Stochastic Processes
• Strategic Improvisation in Business
• Structural Health Monitoring
• Supply Chain Management
• Theoretical Statistics
• Thinking Like a Mathematician
• Vibrations of Mechanical Systems
• World Geography

© 2024 Fiveable Inc. All rights reserved.

Ap® and sat® are trademarks registered by the college board, which is not affiliated with, and does not endorse this website..

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

How to Write a Great Hypothesis

Hypothesis Definition, Format, Examples, and Tips

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Amy Morin, LCSW, is a psychotherapist and international bestselling author. Her books, including "13 Things Mentally Strong People Don't Do," have been translated into more than 40 languages. Her TEDx talk,  "The Secret of Becoming Mentally Strong," is one of the most viewed talks of all time.

Verywell / Alex Dos Diaz

• The Scientific Method

Hypothesis Format

Falsifiability of a hypothesis.

• Operationalization

Hypothesis Types

Hypotheses examples.

• Collecting Data

A hypothesis is a tentative statement about the relationship between two or more variables. It is a specific, testable prediction about what you expect to happen in a study. It is a preliminary answer to your question that helps guide the research process.

Consider a study designed to examine the relationship between sleep deprivation and test performance. The hypothesis might be: "This study is designed to assess the hypothesis that sleep-deprived people will perform worse on a test than individuals who are not sleep-deprived."

At a Glance

A hypothesis is crucial to scientific research because it offers a clear direction for what the researchers are looking to find. This allows them to design experiments to test their predictions and add to our scientific knowledge about the world. This article explores how a hypothesis is used in psychology research, how to write a good hypothesis, and the different types of hypotheses you might use.

The Hypothesis in the Scientific Method

In the scientific method , whether it involves research in psychology, biology, or some other area, a hypothesis represents what the researchers think will happen in an experiment. The scientific method involves the following steps:

• Forming a question
• Performing background research
• Creating a hypothesis
• Designing an experiment
• Collecting data
• Analyzing the results
• Drawing conclusions
• Communicating the results

The hypothesis is a prediction, but it involves more than a guess. Most of the time, the hypothesis begins with a question which is then explored through background research. At this point, researchers then begin to develop a testable hypothesis.

Unless you are creating an exploratory study, your hypothesis should always explain what you  expect  to happen.

In a study exploring the effects of a particular drug, the hypothesis might be that researchers expect the drug to have some type of effect on the symptoms of a specific illness. In psychology, the hypothesis might focus on how a certain aspect of the environment might influence a particular behavior.

Remember, a hypothesis does not have to be correct. While the hypothesis predicts what the researchers expect to see, the goal of the research is to determine whether this guess is right or wrong. When conducting an experiment, researchers might explore numerous factors to determine which ones might contribute to the ultimate outcome.

In many cases, researchers may find that the results of an experiment  do not  support the original hypothesis. When writing up these results, the researchers might suggest other options that should be explored in future studies.

In many cases, researchers might draw a hypothesis from a specific theory or build on previous research. For example, prior research has shown that stress can impact the immune system. So a researcher might hypothesize: "People with high-stress levels will be more likely to contract a common cold after being exposed to the virus than people who have low-stress levels."

In other instances, researchers might look at commonly held beliefs or folk wisdom. "Birds of a feather flock together" is one example of folk adage that a psychologist might try to investigate. The researcher might pose a specific hypothesis that "People tend to select romantic partners who are similar to them in interests and educational level."

Elements of a Good Hypothesis

So how do you write a good hypothesis? When trying to come up with a hypothesis for your research or experiments, ask yourself the following questions:

• Is your hypothesis based on your research on a topic?
• Can your hypothesis be tested?
• Does your hypothesis include independent and dependent variables?

Before you come up with a specific hypothesis, spend some time doing background research. Once you have completed a literature review, start thinking about potential questions you still have. Pay attention to the discussion section in the  journal articles you read . Many authors will suggest questions that still need to be explored.

How to Formulate a Good Hypothesis

To form a hypothesis, you should take these steps:

• Collect as many observations about a topic or problem as you can.
• Evaluate these observations and look for possible causes of the problem.
• Create a list of possible explanations that you might want to explore.
• After you have developed some possible hypotheses, think of ways that you could confirm or disprove each hypothesis through experimentation. This is known as falsifiability.

In the scientific method ,  falsifiability is an important part of any valid hypothesis. In order to test a claim scientifically, it must be possible that the claim could be proven false.

Students sometimes confuse the idea of falsifiability with the idea that it means that something is false, which is not the case. What falsifiability means is that  if  something was false, then it is possible to demonstrate that it is false.

One of the hallmarks of pseudoscience is that it makes claims that cannot be refuted or proven false.

The Importance of Operational Definitions

A variable is a factor or element that can be changed and manipulated in ways that are observable and measurable. However, the researcher must also define how the variable will be manipulated and measured in the study.

Operational definitions are specific definitions for all relevant factors in a study. This process helps make vague or ambiguous concepts detailed and measurable.

For example, a researcher might operationally define the variable " test anxiety " as the results of a self-report measure of anxiety experienced during an exam. A "study habits" variable might be defined by the amount of studying that actually occurs as measured by time.

These precise descriptions are important because many things can be measured in various ways. Clearly defining these variables and how they are measured helps ensure that other researchers can replicate your results.

Replicability

One of the basic principles of any type of scientific research is that the results must be replicable.

Replication means repeating an experiment in the same way to produce the same results. By clearly detailing the specifics of how the variables were measured and manipulated, other researchers can better understand the results and repeat the study if needed.

Some variables are more difficult than others to define. For example, how would you operationally define a variable such as aggression ? For obvious ethical reasons, researchers cannot create a situation in which a person behaves aggressively toward others.

To measure this variable, the researcher must devise a measurement that assesses aggressive behavior without harming others. The researcher might utilize a simulated task to measure aggressiveness in this situation.

Hypothesis Checklist

• Does your hypothesis focus on something that you can actually test?
• Does your hypothesis include both an independent and dependent variable?
• Can you manipulate the variables?
• Can your hypothesis be tested without violating ethical standards?

The hypothesis you use will depend on what you are investigating and hoping to find. Some of the main types of hypotheses that you might use include:

• Simple hypothesis : This type of hypothesis suggests there is a relationship between one independent variable and one dependent variable.
• Complex hypothesis : This type suggests a relationship between three or more variables, such as two independent and dependent variables.
• Null hypothesis : This hypothesis suggests no relationship exists between two or more variables.
• Alternative hypothesis : This hypothesis states the opposite of the null hypothesis.
• Statistical hypothesis : This hypothesis uses statistical analysis to evaluate a representative population sample and then generalizes the findings to the larger group.
• Logical hypothesis : This hypothesis assumes a relationship between variables without collecting data or evidence.

A hypothesis often follows a basic format of "If {this happens} then {this will happen}." One way to structure your hypothesis is to describe what will happen to the  dependent variable  if you change the  independent variable .

The basic format might be: "If {these changes are made to a certain independent variable}, then we will observe {a change in a specific dependent variable}."

A few examples of simple hypotheses:

• "Students who eat breakfast will perform better on a math exam than students who do not eat breakfast."
• "Students who experience test anxiety before an English exam will get lower scores than students who do not experience test anxiety."​
• "Motorists who talk on the phone while driving will be more likely to make errors on a driving course than those who do not talk on the phone."
• "Children who receive a new reading intervention will have higher reading scores than students who do not receive the intervention."

Examples of a complex hypothesis include:

• "People with high-sugar diets and sedentary activity levels are more likely to develop depression."
• "Younger people who are regularly exposed to green, outdoor areas have better subjective well-being than older adults who have limited exposure to green spaces."

Examples of a null hypothesis include:

• "There is no difference in anxiety levels between people who take St. John's wort supplements and those who do not."
• "There is no difference in scores on a memory recall task between children and adults."
• "There is no difference in aggression levels between children who play first-person shooter games and those who do not."

Examples of an alternative hypothesis:

• "People who take St. John's wort supplements will have less anxiety than those who do not."
• "Adults will perform better on a memory task than children."
• "Children who play first-person shooter games will show higher levels of aggression than children who do not." 

Collecting Data on Your Hypothesis

Once a researcher has formed a testable hypothesis, the next step is to select a research design and start collecting data. The research method depends largely on exactly what they are studying. There are two basic types of research methods: descriptive research and experimental research.

Descriptive Research Methods

Descriptive research such as  case studies ,  naturalistic observations , and surveys are often used when  conducting an experiment is difficult or impossible. These methods are best used to describe different aspects of a behavior or psychological phenomenon.

Once a researcher has collected data using descriptive methods, a  correlational study  can examine how the variables are related. This research method might be used to investigate a hypothesis that is difficult to test experimentally.

Experimental Research Methods

Experimental methods  are used to demonstrate causal relationships between variables. In an experiment, the researcher systematically manipulates a variable of interest (known as the independent variable) and measures the effect on another variable (known as the dependent variable).

Unlike correlational studies, which can only be used to determine if there is a relationship between two variables, experimental methods can be used to determine the actual nature of the relationship—whether changes in one variable actually  cause  another to change.

The hypothesis is a critical part of any scientific exploration. It represents what researchers expect to find in a study or experiment. In situations where the hypothesis is unsupported by the research, the research still has value. Such research helps us better understand how different aspects of the natural world relate to one another. It also helps us develop new hypotheses that can then be tested in the future.

Thompson WH, Skau S. On the scope of scientific hypotheses .  R Soc Open Sci . 2023;10(8):230607. doi:10.1098/rsos.230607

Taran S, Adhikari NKJ, Fan E. Falsifiability in medicine: what clinicians can learn from Karl Popper [published correction appears in Intensive Care Med. 2021 Jun 17;:].  Intensive Care Med . 2021;47(9):1054-1056. doi:10.1007/s00134-021-06432-z

Eyler AA. Research Methods for Public Health . 1st ed. Springer Publishing Company; 2020. doi:10.1891/9780826182067.0004

Nosek BA, Errington TM. What is replication ?  PLoS Biol . 2020;18(3):e3000691. doi:10.1371/journal.pbio.3000691

Aggarwal R, Ranganathan P. Study designs: Part 2 - Descriptive studies .  Perspect Clin Res . 2019;10(1):34-36. doi:10.4103/picr.PICR_154_18

Nevid J. Psychology: Concepts and Applications. Wadworth, 2013.

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Introduction to Hypothesis Testing (Psychology)

Contents Toggle Main Menu 1 What is a Hypothesis test? 2 The Null and Alternative Hypotheses 3 The Structure of a Hypothesis Test 3.1 Summary of Steps for a Hypothesis Test 4 P -Values 5 Parametric and Non-Parametric Hypothesis Tests 6 One and two tailed tests 7 Type I and Type II Errors 8 See Also 9 Worksheets

What is a Hypothesis test?

A statistical hypothesis is an unproven statement which can be tested. A hypothesis test is used to test whether this statement is true.

The Null and Alternative Hypotheses

• The null hypothesis $H_0$, is where you assume that the observations are statistically independent i.e. no difference in the populations you are testing. If the null hypothesis is true, it suggests that any changes witnessed in an experiment are because of random chance and not because of changes made to variables in the experiment. For example, serotonin levels have no effect on ability to cope with stress. See also Null and alternative hypotheses .
• The alternative hypothesis $H_1$, is a theory that the observations are related (not independent) in some way. We only adopt the alternative hypothesis if we have rejected the null hypothesis. For example, serotonin levels affect a person's ability to cope with stress. You do not necessarily have to specify in what way they are related but can do (see one and two tailed tests for more information).

The Structure of a Hypothesis Test

• The first step of a hypothesis test is to state the null hypothesis $H_0$ and the alternative hypothesis $H_1$ . The null hypothesis is the statement or claim being made (which we are trying to disprove) and the alternative hypothesis is the hypothesis that we are trying to prove and which is accepted if we have sufficient evidence to reject the null hypothesis.

For example, consider a person in court who is charged with murder. The jury needs to decide whether the person in innocent (the null hypothesis) or guilty (the alternative hypothesis). As usual, we assume the person is innocent unless the jury can provide sufficient evidence that the person is guilty. Similarly, we assume that $H_0$ is true unless we can provide sufficient evidence that it is false and that $H_1$ is true, in which case we reject $H_0$ and accept $H_1$.

To decide if we have sufficient evidence against the null hypothesis to reject it (in favour of the alternative hypothesis), we must first decide upon a significance level . The significance level is the probability of rejecting the null hypothesis when it the null hypothesis is true and is denoted by $\alpha$. The $5\%$ significance level is a common choice for statistical test.

The next step is to collect data and calculate the test statistic and associated $p$-value using the data. Assuming that the null hypothesis is true, the $p$-value is the probability of obtaining a sample statistic equal to or more extreme than the observed test statistic.

Next we must compare the $p$-value with the chosen significance level. If $p \lt \alpha$ then we reject $H_0$ and accept $H_1$. The lower $p$, the more evidence we have against $H_0$ and so the more confidence we can have that $H_0$ is false. If $p \geq \alpha$ then we do not have sufficient evidence to reject the $H_0$ and so must accept it.

Alternatively, we can compare our test statistic with the appropriate critical value for the chosen significance level. We can look up critical values in distribution tables (see worked examples below). If our test statistic is:

• positive and greater than the critical value, then we have sufficient evidence to reject the null hypothesis and accept the alternative hypothesis.
• positive and lower than or equal to the critical value, we must accept the null hypothesis.
• negative and lower than the critical value, then we have sufficient evidence to reject the null hypothesis and accept the alternative hypothesis.
• negative and greater than or equal to the critical value, we must accept the null hypothesis.

For either method:

Significant difference found: Reject the null hypothesis No significant difference found: Accept the null hypothesis

Finally, we must interpret our results and come to a conclusion. Returning to the example of the person in court, if the result of our hypothesis test indicated that we should accept $H_1$ and reject $H_0$, our conclusion would be that the jury should declare the person guilty of murder.

Summary of Steps for a Hypothesis Test

• Specify the null and the alternative hypothesis
• Decide upon the significance level.
• Comparing the $p$-value to the significance level $\alpha$, or
• Comparing the test statistic to the critical value.
• Interpret your results and draw a conclusion

P -Values"> P -Values

The $p$ -value is the probability of the test statistic (e.g. t -value or Chi-Square value) occurring given the null hypothesis is true. Since it is a probability, the $p$-value is a number between $0$ and $1$.

• Typically $p \leq 0.05$ shows that there is strong evidence for $H_1$ so we can accept it and reject $H_0$. Any $p$-value less than $0.05$ is significant and $p$-values less than $0.01$ are very significant .
• Typically $ p > 0.05$ shows that there is poor evidence for $H_1$ so we reject it and accept $H_0$.
• The smaller the $p$-value the more evidence there is supporting the hypothesis.
• The rule for accepting and rejecting the hypothesis is:

\begin{align} \text {Significant difference found} &= \textbf{Reject}\text{ the null hypothesis}\\ \text {No Significant difference found} &= \textbf{Accept}\text{ the null hypothesis}\\ \end{align}

• Note : The significance level is not always $0.05$. It can differ depending on the application and is often subjective (different people will have different opinions on what values are appropriate). For example, if lives are at stake then the $p$-value must be very small for safety reasons.
• See $P$-values for further detail on this topic.

Parametric and Non-Parametric Hypothesis Tests

There are parametric and non-parametric hypothesis tests.

• A parametric hypothesis assumes that the data follows a Normal probability distribution (with equal variances if we are working with more than one set of data) . A parametric hypothesis test is a statement about the parameters of this distribution (typically the mean). This can be seen in more detail in the Parametric Hypotheses Tests section .
• A non-parametric test assumes that the data does not follow any distribution and usually bases its calculations on the median . Note that although we assume the data does not follow a particular distribution it may do anyway. This can be seen in more detail in the Non-Parametric Hypotheses Tests section .

One and two tailed tests

Whether a test is One-tailed or Two-tailed is appropriate depends upon the alternative hypothesis $H_1$.

• One-tailed tests are used when the alternative hypothesis states that the parameter of interest is either bigger or smaller than the value stated in the null hypothesis. For example, the null hypothesis might state that the average weight of chocolate bars produced by a chocolate factory in Slough is 35g (as is printed on the wrapper), while the alternative hypothesis might state that the average weight of the chocolate bars is in fact lower than 35g.
• Two-tailed tests are used when the hypothesis states that the parameter of interest differs from the null hypothesis but does not specify in which direction. In the above example, a Two-tailed alternative hypothesis would be that the average weight of the chocolate bars is not equal to 35g.

Type I and Type II Errors

• A Type I error is made if we reject the null hypothesis when it is true (so should have been accepted). Returning to the example of the person in court, a Type I error would be made if the jury declared the person guilty when they are in fact innocent. The probability of making a Type I error is equal to the significance level $\alpha$.
• A Type II error is made if we accept the null hypothesis when it is false i.e. we should have rejected the null hypothesis and accepted the alternative hypothesis. This would occur if the jury declared the person innocent when they are in fact guilty.

For more information about the topics covered here see hypothesis testing .

• Introduction to hypothesis testing
• Binomial tests

P-Value And Statistical Significance: What It Is & Why It Matters

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

The p-value in statistics quantifies the evidence against a null hypothesis. A low p-value suggests data is inconsistent with the null, potentially favoring an alternative hypothesis. Common significance thresholds are 0.05 or 0.01.

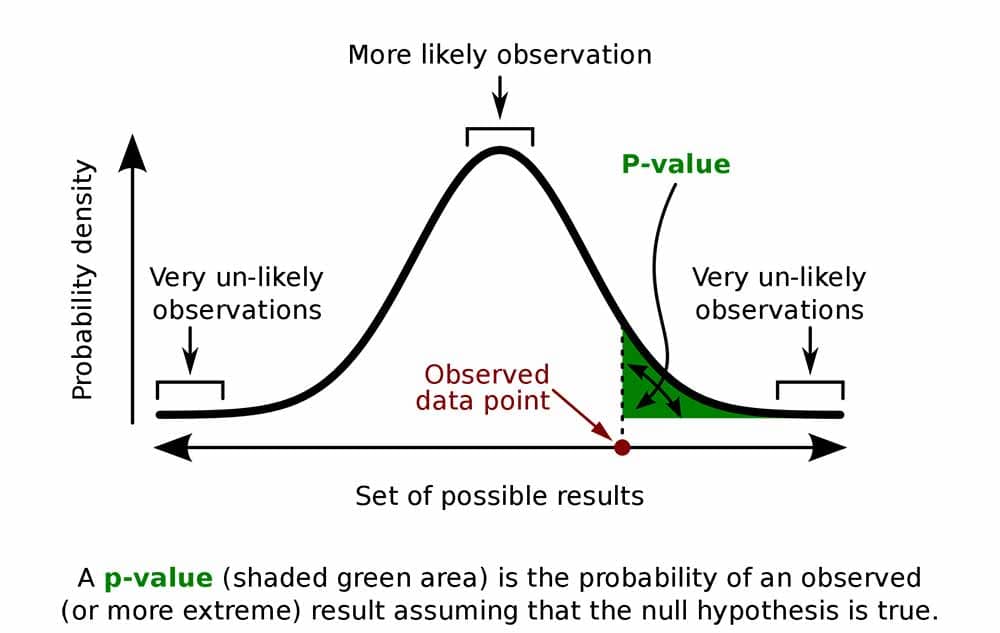
Hypothesis testing

When you perform a statistical test, a p-value helps you determine the significance of your results in relation to the null hypothesis.

The null hypothesis (H0) states no relationship exists between the two variables being studied (one variable does not affect the other). It states the results are due to chance and are not significant in supporting the idea being investigated. Thus, the null hypothesis assumes that whatever you try to prove did not happen.

The alternative hypothesis (Ha or H1) is the one you would believe if the null hypothesis is concluded to be untrue.

The alternative hypothesis states that the independent variable affected the dependent variable, and the results are significant in supporting the theory being investigated (i.e., the results are not due to random chance).

What a p-value tells you

A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true).

The level of statistical significance is often expressed as a p-value between 0 and 1.

The smaller the p -value, the less likely the results occurred by random chance, and the stronger the evidence that you should reject the null hypothesis.

Remember, a p-value doesn’t tell you if the null hypothesis is true or false. It just tells you how likely you’d see the data you observed (or more extreme data) if the null hypothesis was true. It’s a piece of evidence, not a definitive proof.

Example: Test Statistic and p-Value

Suppose you’re conducting a study to determine whether a new drug has an effect on pain relief compared to a placebo. If the new drug has no impact, your test statistic will be close to the one predicted by the null hypothesis (no difference between the drug and placebo groups), and the resulting p-value will be close to 1. It may not be precisely 1 because real-world variations may exist. Conversely, if the new drug indeed reduces pain significantly, your test statistic will diverge further from what’s expected under the null hypothesis, and the p-value will decrease. The p-value will never reach zero because there’s always a slim possibility, though highly improbable, that the observed results occurred by random chance.

P-value interpretation

The significance level (alpha) is a set probability threshold (often 0.05), while the p-value is the probability you calculate based on your study or analysis.

A p-value less than or equal to your significance level (typically ≤ 0.05) is statistically significant.

A p-value less than or equal to a predetermined significance level (often 0.05 or 0.01) indicates a statistically significant result, meaning the observed data provide strong evidence against the null hypothesis.

This suggests the effect under study likely represents a real relationship rather than just random chance.

For instance, if you set α = 0.05, you would reject the null hypothesis if your p -value ≤ 0.05. 

It indicates strong evidence against the null hypothesis, as there is less than a 5% probability the null is correct (and the results are random).

Therefore, we reject the null hypothesis and accept the alternative hypothesis.

Example: Statistical Significance

Upon analyzing the pain relief effects of the new drug compared to the placebo, the computed p-value is less than 0.01, which falls well below the predetermined alpha value of 0.05. Consequently, you conclude that there is a statistically significant difference in pain relief between the new drug and the placebo.

What does a p-value of 0.001 mean?

A p-value of 0.001 is highly statistically significant beyond the commonly used 0.05 threshold. It indicates strong evidence of a real effect or difference, rather than just random variation.

Specifically, a p-value of 0.001 means there is only a 0.1% chance of obtaining a result at least as extreme as the one observed, assuming the null hypothesis is correct.

Such a small p-value provides strong evidence against the null hypothesis, leading to rejecting the null in favor of the alternative hypothesis.

A p-value more than the significance level (typically p > 0.05) is not statistically significant and indicates strong evidence for the null hypothesis.

This means we retain the null hypothesis and reject the alternative hypothesis. You should note that you cannot accept the null hypothesis; we can only reject it or fail to reject it.

Note : when the p-value is above your threshold of significance,  it does not mean that there is a 95% probability that the alternative hypothesis is true.

One-Tailed Test

Two-Tailed Test

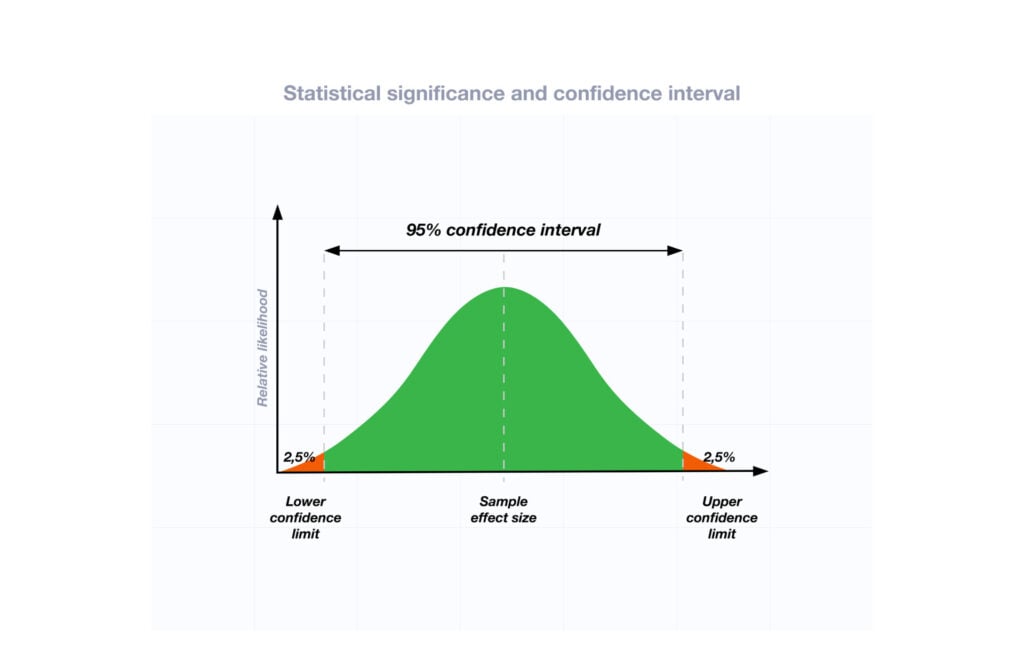
How do you calculate the p-value ?

Most statistical software packages like R, SPSS, and others automatically calculate your p-value. This is the easiest and most common way.

Online resources and tables are available to estimate the p-value based on your test statistic and degrees of freedom.

These tables help you understand how often you would expect to see your test statistic under the null hypothesis.

Understanding the Statistical Test:

Different statistical tests are designed to answer specific research questions or hypotheses. Each test has its own underlying assumptions and characteristics.

For example, you might use a t-test to compare means, a chi-squared test for categorical data, or a correlation test to measure the strength of a relationship between variables.

Be aware that the number of independent variables you include in your analysis can influence the magnitude of the test statistic needed to produce the same p-value.

This factor is particularly important to consider when comparing results across different analyses.

Example: Choosing a Statistical Test

If you’re comparing the effectiveness of just two different drugs in pain relief, a two-sample t-test is a suitable choice for comparing these two groups. However, when you’re examining the impact of three or more drugs, it’s more appropriate to employ an Analysis of Variance ( ANOVA) . Utilizing multiple pairwise comparisons in such cases can lead to artificially low p-values and an overestimation of the significance of differences between the drug groups.

How to report

A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty).

Instead, we may state our results “provide support for” or “give evidence for” our research hypothesis (as there is still a slight probability that the results occurred by chance and the null hypothesis was correct – e.g., less than 5%).

Example: Reporting the results

In our comparison of the pain relief effects of the new drug and the placebo, we observed that participants in the drug group experienced a significant reduction in pain ( M = 3.5; SD = 0.8) compared to those in the placebo group ( M = 5.2; SD  = 0.7), resulting in an average difference of 1.7 points on the pain scale (t(98) = -9.36; p < 0.001).

The 6th edition of the APA style manual (American Psychological Association, 2010) states the following on the topic of reporting p-values:

“When reporting p values, report exact p values (e.g., p = .031) to two or three decimal places. However, report p values less than .001 as p < .001.

The tradition of reporting p values in the form p < .10, p < .05, p < .01, and so forth, was appropriate in a time when only limited tables of critical values were available.” (p. 114)

• Do not use 0 before the decimal point for the statistical value p as it cannot equal 1. In other words, write p = .001 instead of p = 0.001.
• Please pay attention to issues of italics ( p is always italicized) and spacing (either side of the = sign).
• p = .000 (as outputted by some statistical packages such as SPSS) is impossible and should be written as p < .001.
• The opposite of significant is “nonsignificant,” not “insignificant.”

Why is the p -value not enough?

A lower p-value  is sometimes interpreted as meaning there is a stronger relationship between two variables.

However, statistical significance means that it is unlikely that the null hypothesis is true (less than 5%).

To understand the strength of the difference between the two groups (control vs. experimental) a researcher needs to calculate the effect size .

When do you reject the null hypothesis?

In statistical hypothesis testing, you reject the null hypothesis when the p-value is less than or equal to the significance level (α) you set before conducting your test. The significance level is the probability of rejecting the null hypothesis when it is true. Commonly used significance levels are 0.01, 0.05, and 0.10.

Remember, rejecting the null hypothesis doesn’t prove the alternative hypothesis; it just suggests that the alternative hypothesis may be plausible given the observed data.

The p -value is conditional upon the null hypothesis being true but is unrelated to the truth or falsity of the alternative hypothesis.

What does p-value of 0.05 mean?

If your p-value is less than or equal to 0.05 (the significance level), you would conclude that your result is statistically significant. This means the evidence is strong enough to reject the null hypothesis in favor of the alternative hypothesis.

Are all p-values below 0.05 considered statistically significant?

No, not all p-values below 0.05 are considered statistically significant. The threshold of 0.05 is commonly used, but it’s just a convention. Statistical significance depends on factors like the study design, sample size, and the magnitude of the observed effect.

A p-value below 0.05 means there is evidence against the null hypothesis, suggesting a real effect. However, it’s essential to consider the context and other factors when interpreting results.

Researchers also look at effect size and confidence intervals to determine the practical significance and reliability of findings.

How does sample size affect the interpretation of p-values?

Sample size can impact the interpretation of p-values. A larger sample size provides more reliable and precise estimates of the population, leading to narrower confidence intervals.

With a larger sample, even small differences between groups or effects can become statistically significant, yielding lower p-values. In contrast, smaller sample sizes may not have enough statistical power to detect smaller effects, resulting in higher p-values.

Therefore, a larger sample size increases the chances of finding statistically significant results when there is a genuine effect, making the findings more trustworthy and robust.

Can a non-significant p-value indicate that there is no effect or difference in the data?

No, a non-significant p-value does not necessarily indicate that there is no effect or difference in the data. It means that the observed data do not provide strong enough evidence to reject the null hypothesis.

There could still be a real effect or difference, but it might be smaller or more variable than the study was able to detect.

Other factors like sample size, study design, and measurement precision can influence the p-value. It’s important to consider the entire body of evidence and not rely solely on p-values when interpreting research findings.

Can P values be exactly zero?

While a p-value can be extremely small, it cannot technically be absolute zero. When a p-value is reported as p = 0.000, the actual p-value is too small for the software to display. This is often interpreted as strong evidence against the null hypothesis. For p values less than 0.001, report as p < .001

Further Information

• P Value Calculator From T Score
• P-Value Calculator For Chi-Square
• P-values and significance tests (Kahn Academy)
• Hypothesis testing and p-values (Kahn Academy)
• Wasserstein, R. L., Schirm, A. L., & Lazar, N. A. (2019). Moving to a world beyond “ p “< 0.05”.
• Criticism of using the “ p “< 0.05”.
• Publication manual of the American Psychological Association
• Statistics for Psychology Book Download

Bland, J. M., & Altman, D. G. (1994). One and two sided tests of significance: Authors’ reply.  BMJ: British Medical Journal ,  309 (6958), 874.

Goodman, S. N., & Royall, R. (1988). Evidence and scientific research.  American Journal of Public Health ,  78 (12), 1568-1574.

Goodman, S. (2008, July). A dirty dozen: twelve p-value misconceptions . In  Seminars in hematology  (Vol. 45, No. 3, pp. 135-140). WB Saunders.

Lang, J. M., Rothman, K. J., & Cann, C. I. (1998). That confounded P-value.  Epidemiology (Cambridge, Mass.) ,  9 (1), 7-8.