minimization in assignment problem

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures

Hungarian Algorithm for Assignment Problem | Set 1 (Introduction)

• Hungarian Algorithm for Assignment Problem | Set 2 (Implementation)
• Job Assignment Problem using Branch And Bound
• Channel Assignment Problem
• OLA Interview Experience | Set 11 ( For Internship)
• Minimizing Total Manhattan Distances for Driver-Package Allocation
• Quadratic Assignment Problem (QAP)
• Find minimum time to finish all jobs with given constraints
• Minimum Number of Platforms Required for a Railway/Bus Station | Set 2 (Set based approach)
• Assign N tasks to N persons to minimize total time
• Maximum points collected by two persons allowed to meet once
• Find the Platform at which the given Train arrives
• Data Structures and Algorithms | Set 21
• Algorithms | Dynamic Programming | Question 7
• Sprinklr Interview Experience | (On Campus for Internship)
• OYO Rooms Interview Experience | Set 7
• Amazon Internship Interview Experience | On-Campus 2021
• Zoho Interview Experience | Set 9 (On-Campus)
• Zoho Interview | Set 5 (On-Campus Drive)
• Gameskraft Technologies Interview Experience
• Merge Sort - Data Structure and Algorithms Tutorials
• Must Do Coding Questions for Companies like Amazon, Microsoft, Adobe, ...
• QuickSort - Data Structure and Algorithm Tutorials
• Bubble Sort - Data Structure and Algorithm Tutorials
• Tree Traversal Techniques - Data Structure and Algorithm Tutorials
• Binary Search - Data Structure and Algorithm Tutorials
• Insertion Sort - Data Structure and Algorithm Tutorials
• Selection Sort – Data Structure and Algorithm Tutorials
• Understanding the basics of Linked List
• Breadth First Search or BFS for a Graph

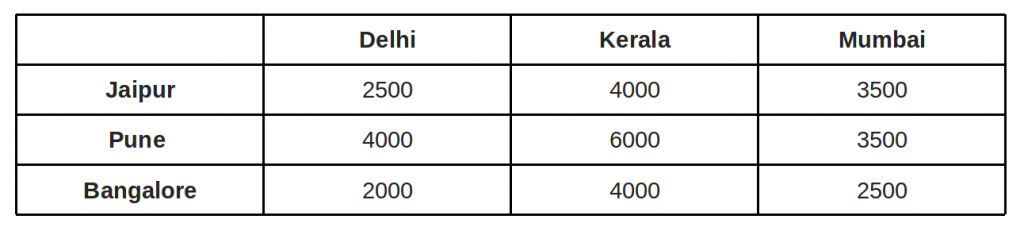
• For each row of the matrix, find the smallest element and subtract it from every element in its row.
• Do the same (as step 1) for all columns.
• Cover all zeros in the matrix using minimum number of horizontal and vertical lines.
• Test for Optimality: If the minimum number of covering lines is n, an optimal assignment is possible and we are finished. Else if lines are lesser than n, we haven’t found the optimal assignment, and must proceed to step 5.
• Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.

Try it before moving to see the solution

Explanation for above simple example:

  An example that doesn’t lead to optimal value in first attempt: In the above example, the first check for optimality did give us solution. What if we the number covering lines is less than n.

Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3).

Space complexity :   O(n^2), where n is the number of workers and jobs. This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional arrays of size n to store the labels, matches, and auxiliary information needed for the algorithm.

In the next post, we will be discussing implementation of the above algorithm. The implementation requires more steps as we need to find minimum number of lines to cover all 0’s using a program. References: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY

Please Login to comment...

Similar reads.

• Mathematical

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Hungarian Method Examples

Now we will examine a few highly simplified illustrations of Hungarian Method for solving an assignment problem .

Later in the chapter, you will find more practical versions of assignment models like Crew assignment problem , Travelling salesman problem , etc.

Example-1, Example-2

Example 1: Hungarian Method

The Funny Toys Company has four men available for work on four separate jobs. Only one man can work on any one job. The cost of assigning each man to each job is given in the following table. The objective is to assign men to jobs in such a way that the total cost of assignment is minimum.

This is a minimization example of assignment problem . We will use the Hungarian Algorithm to solve this problem.

Identify the minimum element in each row and subtract it from every element of that row. The result is shown in the following table.

"A man has one hundred dollars and you leave him with two dollars, that's subtraction." -Mae West

On small screens, scroll horizontally to view full calculation

Identify the minimum element in each column and subtract it from every element of that column.

Make the assignments for the reduced matrix obtained from steps 1 and 2 in the following way:

• For every zero that becomes assigned, cross out (X) all other zeros in the same row and the same column.
• If for a row and a column, there are two or more zeros and one cannot be chosen by inspection, choose the cell arbitrarily for assignment.

An optimal assignment is found, if the number of assigned cells equals the number of rows (and columns). In case you have chosen a zero cell arbitrarily, there may be alternate optimal solutions. If no optimal solution is found, go to step 5.

Use Horizontal Scrollbar to View Full Table Calculation

Draw the minimum number of vertical and horizontal lines necessary to cover all the zeros in the reduced matrix obtained from step 3 by adopting the following procedure:

• Mark all the rows that do not have assignments.
• Mark all the columns (not already marked) which have zeros in the marked rows.
• Mark all the rows (not already marked) that have assignments in marked columns.
• Repeat steps 5 (ii) and (iii) until no more rows or columns can be marked.
• Draw straight lines through all unmarked rows and marked columns.

You can also draw the minimum number of lines by inspection.

Select the smallest element (i.e., 1) from all the uncovered elements. Subtract this smallest element from all the uncovered elements and add it to the elements, which lie at the intersection of two lines. Thus, we obtain another reduced matrix for fresh assignment.

Now again make the assignments for the reduced matrix.

Final Table: Hungarian Method

Since the number of assignments is equal to the number of rows (& columns), this is the optimal solution.

The total cost of assignment = A1 + B4 + C2 + D3

Substituting values from original table: 20 + 17 + 17 + 24 = Rs. 78.

Share This Article

Operations Research Simplified Back Next

Goal programming Linear programming Simplex Method Transportation Problem

The assignment problem revisited

• Original Paper
• Published: 16 August 2021
• Volume 16 , pages 1531–1548, ( 2022 )

Cite this article

• Carlos A. Alfaro   ORCID: orcid.org/0000-0001-9783-8587 1 ,
• Sergio L. Perez 2 ,
• Carlos E. Valencia 3 &
• Marcos C. Vargas 1  

970 Accesses

4 Citations

4 Altmetric

Explore all metrics

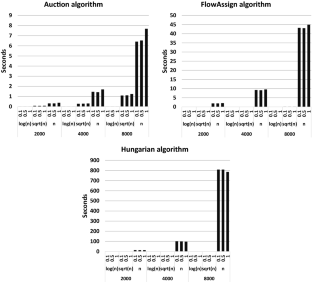
First, we give a detailed review of two algorithms that solve the minimization case of the assignment problem, the Bertsekas auction algorithm and the Goldberg & Kennedy algorithm. It was previously alluded that both algorithms are equivalent. We give a detailed proof that these algorithms are equivalent. Also, we perform experimental results comparing the performance of three algorithms for the assignment problem: the \(\epsilon \) - scaling auction algorithm , the Hungarian algorithm and the FlowAssign algorithm . The experiment shows that the auction algorithm still performs and scales better in practice than the other algorithms which are harder to implement and have better theoretical time complexity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Some results on an assignment problem variant

Integer Programming

A Full Description of Polytopes Related to the Index of the Lowest Nonzero Row of an Assignment Matrix

Bertsekas, D.P.: The auction algorithm: a distributed relaxation method for the assignment problem. Annal Op. Res. 14 , 105–123 (1988)

Article   MathSciNet   Google Scholar  

Bertsekas, D.P., Castañon, D.A.: Parallel synchronous and asynchronous implementations of the auction algorithm. Parallel Comput. 17 , 707–732 (1991)

Article   Google Scholar  

Bertsekas, D.P.: Linear network optimization: algorithms and codes. MIT Press, Cambridge, MA (1991)

MATH   Google Scholar  

Bertsekas, D.P.: The auction algorithm for shortest paths. SIAM J. Optim. 1 , 425–477 (1991)

Bertsekas, D.P.: Auction algorithms for network flow problems: a tutorial introduction. Comput. Optim. Appl. 1 , 7–66 (1992)

Bertsekas, D.P., Castañon, D.A., Tsaknakis, H.: Reverse auction and the solution of inequality constrained assignment problems. SIAM J. Optim. 3 , 268–299 (1993)

Bertsekas, D.P., Eckstein, J.: Dual coordinate step methods for linear network flow problems. Math. Progr., Ser. B 42 , 203–243 (1988)

Bertsimas, D., Tsitsiklis, J.N.: Introduction to linear optimization. Athena Scientific, Belmont, MA (1997)

Google Scholar  

Burkard, R., Dell’Amico, M., Martello, S.: Assignment Problems. Revised reprint. SIAM, Philadelphia, PA (2011)

Gabow, H.N., Tarjan, R.E.: Faster scaling algorithms for network problems. SIAM J. Comput. 18 (5), 1013–1036 (1989)

Goldberg, A.V., Tarjan, R.E.: A new approach to the maximum flow problem. J. Assoc. Comput. Mach. 35 , 921–940 (1988)

Goldberg, A.V., Tarjan, R.E.: Finding minimum-cost circulations by successive approximation. Math. Op. Res. 15 , 430–466 (1990)

Goldberg, A.V., Kennedy, R.: An efficient cost scaling algorithm for the assignment problem. Math. Programm. 71 , 153–177 (1995)

MathSciNet   MATH   Google Scholar  

Goldberg, A.V., Kennedy, R.: Global price updates help. SIAM J. Discr. Math. 10 (4), 551–572 (1997)

Kuhn, H.W.: The Hungarian method for the assignment problem. Naval Res. Logist. Quart. 2 , 83–97 (1955)

Kuhn, H.W.: Variants of the Hungarian method for the assignment problem. Naval Res. Logist. Quart. 2 , 253–258 (1956)

Lawler, E.L.: Combinatorial optimization: networks and matroids, Holt. Rinehart & Winston, New York (1976)

Orlin, J.B., Ahuja, R.K.: New scaling algorithms for the assignment ad minimum mean cycle problems. Math. Programm. 54 , 41–56 (1992)

Ramshaw, L., Tarjan, R.E., Weight-Scaling Algorithm, A., for Min-Cost Imperfect Matchings in Bipartite Graphs, : IEEE 53rd Annual Symposium on Foundations of Computer Science. New Brunswick, NJ 2012 , 581–590 (2012)

Zaki, H.: A comparison of two algorithms for the assignment problem. Comput. Optim. Appl. 4 , 23–45 (1995)

Download references

Acknowledgements

This research was partially supported by SNI and CONACyT.

Author information

Authors and affiliations.

Banco de México, Mexico City, Mexico

Carlos A. Alfaro & Marcos C. Vargas

Mountain View, CA, 94043, USA

Sergio L. Perez

Departamento de Matemáticas, CINVESTAV del IPN, Apartado postal 14-740, 07000, Mexico City, Mexico

Carlos E. Valencia

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Carlos A. Alfaro .

Ethics declarations

Conflict of interest.

There is no conflict of interest.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The authors were partially supported by SNI and CONACyT.

Rights and permissions

Reprints and permissions

About this article

Alfaro, C.A., Perez, S.L., Valencia, C.E. et al. The assignment problem revisited. Optim Lett 16 , 1531–1548 (2022). https://doi.org/10.1007/s11590-021-01791-4

Download citation

Received : 26 March 2020

Accepted : 03 August 2021

Published : 16 August 2021

Issue Date : June 2022

DOI : https://doi.org/10.1007/s11590-021-01791-4

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Assignment problem
• Bertsekas auction algorithm
• Combinatorial optimization and matching
• Find a journal
• Publish with us
• Track your research

Assignment problem: Hungarian method 3

Assignment problem: Hungarian Method Nui Ruppert (Mtk_Nr.: 373224) David Lenh (Mtk_Nr.: 368343) Amir Farshchi Tabrizi (Mtk-Nr.: 372894)

In this OR-Wiki entry we're going to explain the Hungarian method with 3 examples. In the first example you'll find the optimal solution after a few steps with the help of the reduced matrix. The second example illustrates a complex case where you need to proceed all the steps of the algorithm to get to an optimal solution. Finally in the third example we will show how to solve a maximization problem with the Hungarian method.

Inhaltsverzeichnis

• 1 Introduction
• 2 Example 1 – Minimization problem
• 3 Example 2 – Minimazation problem
• 4 Example 3 – Maximization problem
• 6 References

Introduction

The Hungarian method is a combinatorial optimization algorithm which was developed and published by Harold Kuhn in 1955. This method was originally invented for the best assignment of a set of persons to a set of jobs. It is a special case of the transportation problem. The algorithm finds an optimal assignment for a given “n x n” cost matrix. “Assignment problems deal with the question how to assign n items (e.g. jobs) to n machines (or workers) in the best possible way. […] Mathematically an assignment is nothing else than a bijective mapping of a finite set into itself […]” [1]

The assignment constraints are mathematically defined as:

To make clear how to solve an assignment problem with the Hungarian algorithm we will show you the different cases with several examples which can occur .

Example 1 – Minimization problem

In this example we have to assign 4 workers to 4 machines. Each worker causes different costs for the machines. Your goal is to minimize the total cost to the condition that each machine goes to exactly 1 person and each person works at exactly 1 machine. For comprehension: Worker 1 causes a cost of 6 for machine 1 and so on …

To solve the problem we have to perform the following steps:

Step 1 – Subtract the row minimum from each row.

Step 2 – Subtract the column minimum from each column from the reduced matrix.

The idea behind these 2 steps is to simplify the matrix since the solution of the reduced matrix will be exactly the same as of the original matrix.

Step 3 – Assign one “0” to each row & column.

Now that we have simplified the matrix we can assign each worker with the minimal cost to each machine which is represented by a “0”.

- In the first row we have one assignable “0” therefore we assign it to worker 3 .

- In the second row we also only have one assignable “0” therefore we assign it to worker 4 .

- In the third row we have two assignable “0”. We leave it as it is for now.

- In the fourth row we have one assignable “0” therefore we assign it. Consider that we can only assign each worker to each machine hence we can’t allocate any other “0” in the first column.

- Now we go back to the third row which now only has one assignable “0” for worker 2 .

As soon as we can assign each worker to one machine, we have the optimal solution . In this case there is no need to proceed any further steps. Remember also, if we decide on an arbitrary order in which we start allocating the “0”s then we may get into a situation where we have 3 assignments as against the possible 4. If we assign a “0” in the third row to worker 1 we wouldn’t be able to allocate any “0”s in column one and row two.

The rule to assign the “0”:

- If there is an assignable “0”, only 1 assignable “0” in any row or any column, assign it.

- If there are more than 1, leave it and proceed.

This rule would try to give us as many assignments as possible.

Now there are also cases where you won’t get an optimal solution for a reduced matrix after one iteration. The following example will explain it.

Example 2 – Minimazation problem

In this example we have the fastest taxi company that has to assign each taxi to each passenger as fast as possible. The numbers in the matrix represent the time to reach the passenger.

We proceed as in the first example.

Iteration 1:

Now we have to assign the “0”s for every row respectively to the rule that we described earlier in example 1.

- In the first row we have one assignable “0” therefore we assign it and no other allocation in column 2 is possible.

- In the second row we have one assignable “0” therefore we assign it.

- In the third row we have several assignable “0”s. We leave it as it is for now and proceed.

- In the fourth and fifth row we have no assignable “0”s.

Now we proceed with the allocations of the “0”s for each column .

- In the first column we have one assignable “0” therefore we assign it. No other “0”s in row 3 are assignable anymore.

Now we are unable to proceed because all the “0”s either been assigned or crossed. The crosses indicate that they are not fit for assignments because assignments are already made.

We realize that we have 3 assignments for this 5x5 matrix. In the earlier example we were able to get 4 assignments for a 4x4 matrix. Now we have to follow another procedure to get the remaining 2 assignments (“0”).

Step 4 – Tick all unassigned rows.

Step 5 – If a row is ticked and has a “0”, then tick the corresponding column (if the column is not yet ticked).

Step 6 – If a column is ticked and has an assignment, then tick the corresponding row (if the row is not yet ticked).

Step 7 - Repeat step 5 and 6 till no more ticking is possible.

In this case there is no more ticking possible and we proceed with the next step.

Step 8 – Draw lines through unticked rows and ticked columns. The number of lines represents the maximum number of assignments possible.

Step 9 – Find out the smallest number which does not have any line passing through it. We call it Theta. Subtract theta from all the numbers that do not have any lines passing through them and add theta to all those numbers that have two lines passing through them. Keep the rest of them the same.

(With this step we create a new “0”)

With the new assignment matrix we start to assign the “0”s after the explained rules. Nevertheless we have 4 assignments against the required 5 for an optimal solution. Therefore we have to repeat step 4 – 9.

Iteration 2:

Step 4 – Tick all unassigned row.

Note: The indices of the ticks show you the order we added them.

Iteration 3:

Iteration 4:

After the fourth iteration we assign the “0”s again and now we have an optimal solution with 5 assignments.

The solution:

- Taxi1 => Passenger1 - duration 12

- Taxi2 => Passenger4 - duration 11

- Taxi3 => Passenger2 - duration 8

- Taxi4 => Passenger3 - duration 14

- Taxi5 => Passenger5 - duration 11

If we define the needed duration as costs, the minimal cost for this problem is 56.

Example 3 – Maximization problem

Furthermore the Hungarian algorithm can also be used for a maximization problem in which case we first have to transform the matrix. For example a company wants to assign different workers to different machines. Each worker is more or less efficient with each machine. The efficiency can be defined as profit. The higher the number, the higher the profit.

As you can see, the maximal profit of the matrix is 13. The simple twist that we do is rather than try to maximize the profit, we’re going to try to minimize the profit that you don’t get. If every value is taken away from 13, then we can minimize the amount of profit lost. We receive the following matrix:

From now on we proceed as usual with the steps to get to an optimal solution.

With the determined optimal solution we can compute the maximal profit:

- Worker1 => Machine2 - 9

- Worker2 => Machine4 - 11

- Worker3 => Machine3 - 13

- Worker4 => Machine1 - 7

Maximal profit is 40.

The optimal solution is found if there is one assigned “0” for each row and each column.

[1] Linear Assignment Problems and Extensions, Rainer E. Burkard, Eranda Cela

[2] Operations Research Skript TU Kaiserslautern, Prof. Dr. Oliver Wendt

[3] The Hungarian method for the assignment problem, H. W. Kuhn, Bryn Mawr College

Fundamental of Operations Research, Lec. 16, Prof. G. Srinivasan

Navigationsmenü

• Quelltext anzeigen
• Versionsgeschichte

Meine Werkzeuge

• Gemeinschaftsportal
• Operations Research
• Studentenbeiträge zum Thema Operations Research
• Wirtschaftsinformatik
• Aktuelle Ereignisse
• Letzte Änderungen
• Zufällige Seite
• Links auf diese Seite
• Änderungen an verlinkten Seiten
• Spezialseiten
• Druckversion
• Permanenter Link
• Seiten­informationen

• Diese Seite wurde zuletzt am 1. Juli 2013 um 11:03 Uhr geändert.
• Datenschutz
• Über Operations-Research-Wiki

• MapReduce Algorithm
• Linear Programming using Pyomo
• Networking and Professional Development for Machine Learning Careers in the USA
• Predicting Employee Churn in Python
• Airflow Operators

Solving Assignment Problem using Linear Programming in Python

Learn how to use Python PuLP to solve Assignment problems using Linear Programming.

In earlier articles, we have seen various applications of Linear programming such as transportation, transshipment problem, Cargo Loading problem, and shift-scheduling problem. Now In this tutorial, we will focus on another model that comes under the class of linear programming model known as the Assignment problem. Its objective function is similar to transportation problems. Here we minimize the objective function time or cost of manufacturing the products by allocating one job to one machine.

If we want to solve the maximization problem assignment problem then we subtract all the elements of the matrix from the highest element in the matrix or multiply the entire matrix by –1 and continue with the procedure. For solving the assignment problem, we use the Assignment technique or Hungarian method, or Flood’s technique.

The transportation problem is a special case of the linear programming model and the assignment problem is a special case of transportation problem, therefore it is also a special case of the linear programming problem.

In this tutorial, we are going to cover the following topics:

Assignment Problem

A problem that requires pairing two sets of items given a set of paired costs or profit in such a way that the total cost of the pairings is minimized or maximized. The assignment problem is a special case of linear programming.

For example, an operation manager needs to assign four jobs to four machines. The project manager needs to assign four projects to four staff members. Similarly, the marketing manager needs to assign the 4 salespersons to 4 territories. The manager’s goal is to minimize the total time or cost.

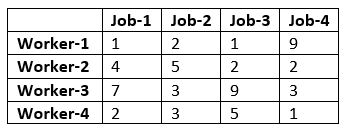
Problem Formulation

A manager has prepared a table that shows the cost of performing each of four jobs by each of four employees. The manager has stated his goal is to develop a set of job assignments that will minimize the total cost of getting all 4 jobs.  

Initialize LP Model

In this step, we will import all the classes and functions of pulp module and create a Minimization LP problem using LpProblem class.

Define Decision Variable

In this step, we will define the decision variables. In our problem, we have two variable lists: workers and jobs. Let’s create them using  LpVariable.dicts()  class.  LpVariable.dicts()  used with Python’s list comprehension.  LpVariable.dicts()  will take the following four values:

• First, prefix name of what this variable represents.
• Second is the list of all the variables.
• Third is the lower bound on this variable.
• Fourth variable is the upper bound.
• Fourth is essentially the type of data (discrete or continuous). The options for the fourth parameter are  LpContinuous  or  LpInteger .

Let’s first create a list route for the route between warehouse and project site and create the decision variables using LpVariable.dicts() the method.

Define Objective Function

In this step, we will define the minimum objective function by adding it to the LpProblem  object. lpSum(vector)is used here to define multiple linear expressions. It also used list comprehension to add multiple variables.

Define the Constraints

Here, we are adding two types of constraints: Each job can be assigned to only one employee constraint and Each employee can be assigned to only one job. We have added the 2 constraints defined in the problem by adding them to the LpProblem  object.

Solve Model

In this step, we will solve the LP problem by calling solve() method. We can print the final value by using the following for loop.

From the above results, we can infer that Worker-1 will be assigned to Job-1, Worker-2 will be assigned to job-3, Worker-3 will be assigned to Job-2, and Worker-4 will assign with job-4.

In this article, we have learned about Assignment problems, Problem Formulation, and implementation using the python PuLp library. We have solved the Assignment problem using a Linear programming problem in Python. Of course, this is just a simple case study, we can add more constraints to it and make it more complicated. You can also run other case studies on Cargo Loading problems , Staff scheduling problems . In upcoming articles, we will write more on different optimization problems such as transshipment problem, balanced diet problem. You can revise the basics of mathematical concepts in  this article  and learn about Linear Programming  in this article .

• Solving Blending Problem in Python using Gurobi
• Transshipment Problem in Python Using PuLP

You May Also Like

apply() in Pandas

Understanding Random Forest Classification and Building a Model in Python

Text Analytics for Beginner using Python TextBlob

• Google OR-Tools
• Español – América Latina
• Português – Brasil
• Tiếng Việt

Solving an Assignment Problem

This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver.

In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview .

The costs of assigning workers to tasks are shown in the following table.

The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost. Since there are more workers than tasks, one worker will not be assigned a task.

MIP solution

The following sections describe how to solve the problem using the MPSolver wrapper .

Import the libraries

The following code imports the required libraries.

Create the data

The following code creates the data for the problem.

The costs array corresponds to the table of costs for assigning workers to tasks, shown above.

Declare the MIP solver

The following code declares the MIP solver.

Create the variables

The following code creates binary integer variables for the problem.

Create the constraints

Create the objective function.

The following code creates the objective function for the problem.

The value of the objective function is the total cost over all variables that are assigned the value 1 by the solver.

Invoke the solver

The following code invokes the solver.

Print the solution

The following code prints the solution to the problem.

Here is the output of the program.

Complete programs

Here are the complete programs for the MIP solution.

CP SAT solution

The following sections describe how to solve the problem using the CP-SAT solver.

Declare the model

The following code declares the CP-SAT model.

The following code sets up the data for the problem.

The following code creates the constraints for the problem.

Here are the complete programs for the CP-SAT solution.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-02 UTC.

How to Solve the Assignment Problem: A Complete Guide

Table of Contents

Assignment problem is a special type of linear programming problem that deals with assigning a number of resources to an equal number of tasks in the most efficient way. The goal is to minimize the total cost of assignments while ensuring that each task is assigned to only one resource and each resource is assigned to only one task. In this blog, we will discuss the solution of the assignment problem using the Hungarian method, which is a popular algorithm for solving the problem.

Understanding the Assignment Problem

Before we dive into the solution, it is important to understand the problem itself. In the assignment problem, we have a matrix of costs, where each row represents a resource and each column represents a task. The objective is to assign each resource to a task in such a way that the total cost of assignments is minimized. However, there are certain constraints that need to be satisfied – each resource can be assigned to only one task and each task can be assigned to only one resource.

Solving the Assignment Problem

There are various methods for solving the assignment problem, including the Hungarian method, the brute force method, and the auction algorithm. Here, we will focus on the steps involved in solving the assignment problem using the Hungarian method, which is the most commonly used and efficient method.

Step 1: Set up the cost matrix

The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.

Step 2: Subtract the smallest element from each row and column

To simplify the calculations, we need to reduce the size of the cost matrix by subtracting the smallest element from each row and column. This step is called matrix reduction.

Step 3: Cover all zeros with the minimum number of lines

The next step is to cover all zeros in the matrix with the minimum number of horizontal and vertical lines. This step is called matrix covering.

Step 4: Test for optimality and adjust the matrix

To test for optimality, we need to calculate the minimum number of lines required to cover all zeros in the matrix. If the number of lines equals the number of rows or columns, the solution is optimal. If not, we need to adjust the matrix and repeat steps 3 and 4 until we get an optimal solution.

Step 5: Assign the tasks to the agents

The final step is to assign the tasks to the agents based on the optimal solution obtained in step 4. This will give us the most cost-effective or profit-maximizing assignment.

Solution of the Assignment Problem using the Hungarian Method

The Hungarian method is an algorithm that uses a step-by-step approach to find the optimal assignment. The algorithm consists of the following steps:

• Subtract the smallest entry in each row from all the entries of the row.
• Subtract the smallest entry in each column from all the entries of the column.
• Draw the minimum number of lines to cover all zeros in the matrix. If the number of lines drawn is equal to the number of rows, we have an optimal solution. If not, go to step 4.
• Determine the smallest entry not covered by any line. Subtract it from all uncovered entries and add it to all entries covered by two lines. Go to step 3.

The above steps are repeated until an optimal solution is obtained. The optimal solution will have all zeros covered by the minimum number of lines. The assignments can be made by selecting the rows and columns with a single zero in the final matrix.

Applications of the Assignment Problem

The assignment problem has various applications in different fields, including computer science, economics, logistics, and management. In this section, we will provide some examples of how the assignment problem is used in real-life situations.

Applications in Computer Science

The assignment problem can be used in computer science to allocate resources to different tasks, such as allocating memory to processes or assigning threads to processors.

Applications in Economics

The assignment problem can be used in economics to allocate resources to different agents, such as allocating workers to jobs or assigning projects to contractors.

Applications in Logistics

The assignment problem can be used in logistics to allocate resources to different activities, such as allocating vehicles to routes or assigning warehouses to customers.

Applications in Management

The assignment problem can be used in management to allocate resources to different projects, such as allocating employees to tasks or assigning budgets to departments.

Let’s consider the following scenario: a manager needs to assign three employees to three different tasks. Each employee has different skills, and each task requires specific skills. The manager wants to minimize the total time it takes to complete all the tasks. The skills and the time required for each task are given in the table below:

The assignment problem is to determine which employee should be assigned to which task to minimize the total time required. To solve this problem, we can use the Hungarian method, which we discussed in the previous blog.

Using the Hungarian method, we first subtract the smallest entry in each row from all the entries of the row:

Next, we subtract the smallest entry in each column from all the entries of the column:

We draw the minimum number of lines to cover all the zeros in the matrix, which in this case is three:

Since the number of lines is equal to the number of rows, we have an optimal solution. The assignments can be made by selecting the rows and columns with a single zero in the final matrix. In this case, the optimal assignments are:

• Emp 1 to Task 3
• Emp 2 to Task 2
• Emp 3 to Task 1

This assignment results in a total time of 9 units.

I hope this example helps you better understand the assignment problem and how to solve it using the Hungarian method.

Solving the assignment problem may seem daunting, but with the right approach, it can be a straightforward process. By following the steps outlined in this guide, you can confidently tackle any assignment problem that comes your way.

How useful was this post?

Click on a star to rate it!

Average rating 0 / 5. Vote count: 0

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you! 😔

Let us improve this post!

Tell us how we can improve this post?

Operations Research

1 Operations Research-An Overview

• History of O.R.
• Approach, Techniques and Tools
• Phases and Processes of O.R. Study
• Typical Applications of O.R
• Limitations of Operations Research
• Models in Operations Research
• O.R. in real world

2 Linear Programming: Formulation and Graphical Method

• General formulation of Linear Programming Problem
• Optimisation Models
• Basics of Graphic Method
• Important steps to draw graph
• Multiple, Unbounded Solution and Infeasible Problems
• Solving Linear Programming Graphically Using Computer
• Application of Linear Programming in Business and Industry

3 Linear Programming-Simplex Method

• Principle of Simplex Method
• Computational aspect of Simplex Method
• Simplex Method with several Decision Variables
• Two Phase and M-method
• Multiple Solution, Unbounded Solution and Infeasible Problem
• Sensitivity Analysis
• Dual Linear Programming Problem

4 Transportation Problem

• Basic Feasible Solution of a Transportation Problem
• Modified Distribution Method
• Stepping Stone Method
• Unbalanced Transportation Problem
• Degenerate Transportation Problem
• Transhipment Problem
• Maximisation in a Transportation Problem

5 Assignment Problem

• Solution of the Assignment Problem
• Unbalanced Assignment Problem
• Problem with some Infeasible Assignments
• Maximisation in an Assignment Problem
• Crew Assignment Problem

6 Application of Excel Solver to Solve LPP

• Building Excel model for solving LP: An Illustrative Example

7 Goal Programming

• Concepts of goal programming
• Goal programming model formulation
• Graphical method of goal programming
• The simplex method of goal programming
• Using Excel Solver to Solve Goal Programming Models
• Application areas of goal programming

8 Integer Programming

• Some Integer Programming Formulation Techniques
• Binary Representation of General Integer Variables
• Unimodularity
• Cutting Plane Method
• Branch and Bound Method
• Solver Solution

9 Dynamic Programming

• Dynamic Programming Methodology: An Example
• Definitions and Notations
• Dynamic Programming Applications

10 Non-Linear Programming

• Solution of a Non-linear Programming Problem
• Convex and Concave Functions
• Kuhn-Tucker Conditions for Constrained Optimisation
• Quadratic Programming
• Separable Programming
• NLP Models with Solver

11 Introduction to game theory and its Applications

• Important terms in Game Theory
• Saddle points
• Mixed strategies: Games without saddle points
• 2 x n games
• Exploiting an opponent’s mistakes

12 Monte Carlo Simulation

• Reasons for using simulation
• Monte Carlo simulation
• Limitations of simulation
• Steps in the simulation process
• Some practical applications of simulation
• Two typical examples of hand-computed simulation
• Computer simulation

13 Queueing Models

• Characteristics of a queueing model
• Notations and Symbols
• Statistical methods in queueing
• The M/M/I System
• The M/M/C System
• The M/Ek/I System
• Decision problems in queueing

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.3: Minimization By The Simplex Method

• Last updated
• Save as PDF
• Page ID 38581

• Rupinder Sekhon and Roberta Bloom
• De Anza College

Learning Objectives

In this section, you will learn to solve linear programming minimization problems using the simplex method.

• Identify and set up a linear program in standard minimization form
• Formulate a dual problem in standard maximization form
• Use the simplex method to solve the dual maximization problem
• Identify the optimal solution to the original minimization problem from the optimal simplex tableau.

In this section, we will solve the standard linear programming minimization problems using the simplex method. Once again, we remind the reader that in the standard minimization problems all constraints are of the form \(ax + by ≥ c\).

The procedure to solve these problems was developed by Dr. John Von Neuman. It involves solving an associated problem called the dual problem . To every minimization problem there corresponds a dual problem. The solution of the dual problem is used to find the solution of the original problem. The dual problem is a maximization problem, which we learned to solve in the last section. We first solve the dual problem by the simplex method.

From the final simplex tableau, we then extract the solution to the original minimization problem.

Before we go any further, however, we first learn to convert a minimization problem into its corresponding maximization problem called its dual .

Example \(\PageIndex{1}\)

Convert the following minimization problem into its dual.

\[\begin{array}{ll} \textbf { Minimize } & \mathrm{Z}=12 \mathrm{x}_{1}+16 \mathrm{x}_{2} \\ \textbf { Subject to: } & \mathrm{x}_{1}+2 \mathrm{x}_{2} \geq 40 \\ & \mathrm{x}_{1}+\mathrm{x}_2 \geq 30 \\ & \mathrm{x}_{1} \geq 0 ; \mathrm{x}_{2} \geq 0 \end{array} \nonumber \]

To achieve our goal, we first express our problem as the following matrix.

\[\begin{array}{cc|c} 1 & 2 & 40 \\ 1 & 1 & 30 \\ \hline 12 & 16 & 0 \end{array} \nonumber \]

Observe that this table looks like an initial simplex tableau without the slack variables. Next, we write a matrix whose columns are the rows of this matrix, and the rows are the columns. Such a matrix is called a transpose of the original matrix. We get:

\[\begin{array}{cc|c} 1 & 1 & 12 \\ 2 & 1 & 16 \\ \hline 40 & 30 & 0 \end{array} \nonumber \]

The following maximization problem associated with the above matrix is called its dual.

\[\begin{array}{ll} \textbf { Maximize } & \mathrm{Z}=40 \mathrm{y}_{1}+30 \mathrm{y}_{2} \\ \textbf { Subject to: } & \mathrm{y}_{1}+\mathrm{y}_{2} \leq 12 \\ & 2 \mathrm{y}_1+\mathrm{y}_2 \leq 16 \\ & \mathrm{y}_{1} \geq 0 ; \mathrm{y}_{2} \geq 0 \end{array} \nonumber \]

Note that we have chosen the variables as y's, instead of x's, to distinguish the two problems.

Example \(\PageIndex{2}\)

Solve graphically both the minimization problem and its dual maximization problem.

Our minimization problem is as follows.

\[\begin{array}{ll} \textbf { Minimize } & \mathrm{Z}=12 \mathrm{x}_1+16 \mathrm{x}_2 \\ \textbf { Subject to: } & \mathrm{x}_{1}+2 \mathrm{x}_{2} \geq 40 \\ & \mathrm{x}_{1}+\mathrm{x}_{2} \geq 30 \\ & \mathrm{x}_{1} \geq 0 ; \mathrm{x}_{2} \geq 0 \end{array} \nonumber \]

We now graph the inequalities:

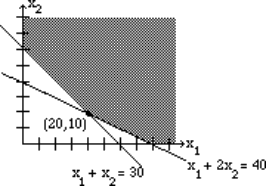
We have plotted the graph, shaded the feasibility region, and labeled the corner points. The corner point (20, 10) gives the lowest value for the objective function and that value is 400.

Now its dual is:

\[\begin{array}{ll} \textbf { Maximize } & \mathrm{Z}=40 \mathrm{y}_1+30 \mathrm{y}_{2} \\ \textbf { Subject to: } & \mathrm{y}_{1}+\mathrm{y}_{2} \leq 12 \\ & 2 \mathrm{y}_1+\mathrm{y} 2 \leq 16 \\ & \mathrm{y}_{1} \geq 0 ; \mathrm{y}_{2} \geq 0 \end{array}\nonumber \]

We graph the inequalities:

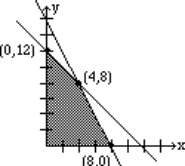
Again, we have plotted the graph, shaded the feasibility region, and labeled the corner points. The corner point (4, 8) gives the highest value for the objective function, with a value of 400.

The reader may recognize that Example \(\PageIndex{2}\) above is the same as Example 3.1.1, in section 3.1. It is also the same problem as Example 4.1.1 in section 4.1, where we solved it by the simplex method.

We observe that the minimum value of the minimization problem is the same as the maximum value of the maximization problem; in Example \(\PageIndex{2}\) the minimum and maximum are both 400. This is not a coincident. We state the duality principle.

The Duality Principle

The objective function of the minimization problem reaches its minimum if and only if the objective function of its dual reaches its maximum. And when they do, they are equal.

Our next goal is to extract the solution for our minimization problem from the corresponding dual. To do this, we solve the dual by the simplex method.

Example \(\PageIndex{3}\)

Find the solution to the minimization problem in Example \(\PageIndex{1}\) by solving its dual using the simplex method. We rewrite our problem.

\[\begin{array}{ll} \textbf { Minimize } & \mathrm{Z}=12 \mathrm{x}_{1}+16 \mathrm{x}_{2} \\ \textbf { Subject to: } & \mathrm{x}_{1}+2 \mathrm{x}_{2} \geq 40 \\ & \mathrm{x}_{1}+\mathrm{x}_{2} \geq 30 \\ & \mathrm{x}_{1} \geq 0 ; \mathrm{x}_{2} \geq 0 \end{array} \nonumber \]

\[\begin{array}{ll} \textbf { Maximize } & \mathrm{Z}=40 \mathrm{y}_{1}+30 \mathrm{y}_{2} \\ \textbf { Subject to: } & \mathrm{y}_{1}+\mathrm{y}_{2} \leq 12 \\ & 2 \mathrm{y}_{1}+\mathrm{y}_{2} \leq 16 \\ & \mathrm{y}_{1} \geq 0 ; \mathrm{y}_{2} \geq 0 \end{array} \nonumber \]

Recall that we solved the above problem by the simplex method in Example 4.1.1, section 4.1. Therefore, we only show the initial and final simplex tableau.

The initial simplex tableau is

\[\begin{array}{ccccc|c} \mathrm{y}_1 & \mathrm{y}_2 & \mathrm{x}_{1} & \mathrm{x}_{2} & \mathrm{Z} & \mathrm{C} \\ 1 & 1 & 1 & 0 & 0 & 12 \\ 2 & 1 & 0 & 1 & 0 & 16 \\ \hline-40 & -30 & 0 & 0 & 1 & 0 \end{array}\nonumber \]

Observe an important change. Here our main variables are \(\mathrm{y}_1\) and \(\mathrm{y}_2\) and the slack variables are \(\mathrm{x}_1 and \mathrm{x}_2\).

The final simplex tableau reads as follows:

\[\begin{array}{ccccc|c} \mathrm{y}_1 & \mathrm{y}_2 & \mathrm{x}_{1} & \mathrm{x}_{2} & \mathrm{Z} & \\ 0 & 1 & 2 & -1 & 0 & 8 \\ 1 & 0 & -1 & 1 & 0 & 4 \\ \hline 0 & 0 & 20 & 10 & 1 & 400 \end{array} \nonumber \]

A closer look at this table reveals that the \(\mathrm{x}_1\) and \(\mathrm{x}_2\) values along with the minimum value for the minimization problem can be obtained from the last row of the final tableau. We have highlighted these values by the arrows.

\[\begin{array}{ccccc|c} \mathrm{y}_1 & \mathrm{y}_2 & \mathrm{x}_{1} & \mathrm{x}_{2} & \mathrm{Z} & \\ 0 & 1 & 2 & -1 & 0 & 8 \\ 1 & 0 & -1 & 1 & 0 & 4 \\ \hline 0 & 0 & 20 & 10 & 1 & 400 \\ & & \uparrow & \uparrow & & \uparrow \end{array} \nonumber \]

We restate the solution as follows:

The minimization problem has a minimum value of 400 at the corner point (20, 10)

We now summarize our discussion.

Minimization by the Simplex Method

• Set up the problem.
• Write a matrix whose rows represent each constraint with the objective function as its bottom row.
• Write the transpose of this matrix by interchanging the rows and columns.
• Now write the dual problem associated with the transpose.
• Solve the dual problem by the simplex method learned in section 4.1.
• The optimal solution is found in the bottom row of the final matrix in the columns corresponding to the slack variables, and the minimum value of the objective function is the same as the maximum value of the dual.

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

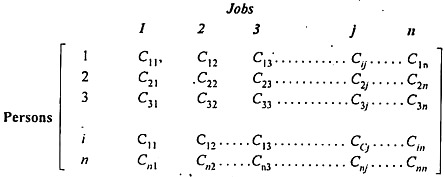
5. Maximization case in Assignment Problem

Secret Service removes agent from Kamala Harris' detail after 'distressing' behavior

WASHINGTON — A Secret Service special agent was removed from Vice President Kamala Harris' detail after having exhibited "distressing" behavior this week, a spokesperson confirmed Thursday.

The agent, whose identity has not been disclosed, had been involved with the Harris' departure from Joint Base Andrews, Maryland, on Monday morning, when Harris was headed to Wisconsin.

The agent "began displaying behavior their colleagues found distressing," Anthony Guglielmi, chief of communications for the Secret Service, said in a statement Thursday. "The agent was removed from their assignment while medical personnel were summoned."

Harris was not present when the incident took place. She was at the Naval Observatory, the vice president's residence, and Guglielmi said her departure was not affected.

“The U.S. Secret Service takes the safety and health of our employees very seriously,” Guglielmi said. “As this was a medical matter, we will not disclose any further details.”

Additional information about the incident, which was first reported by the Washington Examiner , was not released. The vice president's office did not comment Thursday.

Megan Lebowitz is a politics reporter for NBC News.

Help | Advanced Search

Quantum Physics

Title: optimization of quantum systems emulation via a variant of the bandwidth minimization problem.

Abstract: This paper introduces weighted-BMP, a variant of the Bandwidth Minimization Problem (BMP), with a significant application in optimizing quantum emulation. Weighted-BMP optimizes particles ordering to reduce the emulation costs, by designing a particle interaction matrix where strong interactions are placed as close as possible to the diagonal. We formulate the problem using a Mixed Integer Linear Program (MILP) and solve it to optimality with a state of the art solver. To strengthen our MILP model, we introduce symmetry-breaking inequalities and establish a lower bound. Through extensive numerical analysis, we examine the impacts of these enhancements on the solver's performance. The introduced reinforcements result in an average CPU time reduction of 25.61 percent. Additionally, we conduct quantum emulations of realistic instances. Our numerical tests show that the weighted-BMP approach outperforms the Reverse Cuthill-McKee (RCM) algorithm, an efficient heuristic used for site ordering tasks in quantum emulation, achieving an average memory storage reduction of 24.48 percent. From an application standpoint, this study is the first to apply an exact optimization method, weighted-BMP, that considers interactions for site ordering in quantum emulation pre-processing, and shows its crucial role in cost reduction. From an algorithmic perspective, it contributes by introducing important reinforcements and lays the groundwork for future research on further enhancements, particularly on strengthening the weak linear relaxation of the MILP.

Submission history

Access paper:.

• Other Formats

References & Citations

• INSPIRE HEP
• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .