critical region for the hypothesis test

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.4: Hypothesis Tests about μ- Critical Region Approach

• Last updated
• Save as PDF
• Page ID 26095

Establishing the type of distribution, sample size, and known or unknown standard deviation can help you figure out how to go about a hypothesis test. However, there are several other factors you should consider when working out a hypothesis test.

Rare Events

Suppose you make an assumption about a property of the population (this assumption is the null hypothesis). Then you gather sample data randomly. If the sample has properties that would be very unlikely to occur if the assumption is true, then you would conclude that your assumption about the population is probably incorrect. (Remember that your assumption is just an assumption—it is not a fact and it may or may not be true. But your sample data are real and the data are showing you a fact that seems to contradict your assumption.)

For example, Didi and Ali are at a birthday party of a very wealthy friend. They hurry to be first in line to grab a prize from a tall basket that they cannot see inside because they will be blindfolded. There are 200 plastic bubbles in the basket and Didi and Ali have been told that there is only one with a $100 bill. Didi is the first person to reach into the basket and pull out a bubble. Her bubble contains a $100 bill. The probability of this happening is \(\frac{1}{200} = 0.005\). Because this is so unlikely, Ali is hoping that what the two of them were told is wrong and there are more $100 bills in the basket. A "rare event" has occurred (Didi getting the $100 bill) so Ali doubts the assumption about only one $100 bill being in the basket.

Using the Sample to Test the Null Hypothesis

Use the sample data to calculate the actual probability of getting the test result, called the \(p\)-value. The \(p\)-value is the probability that, if the null hypothesis is true, the results from another randomly selected sample will be as extreme or more extreme as the results obtained from the given sample.

A large \(p\)-value calculated from the data indicates that we should not reject the null hypothesis. The smaller the \(p\)-value, the more unlikely the outcome, and the stronger the evidence is against the null hypothesis. We would reject the null hypothesis if the evidence is strongly against it.

Draw a graph that shows the \(p\)-value. The hypothesis test is easier to perform if you use a graph because you see the problem more clearly.

Example \(\PageIndex{1}\)

Suppose a baker claims that his bread height is more than 15 cm, on average. Several of his customers do not believe him. To persuade his customers that he is right, the baker decides to do a hypothesis test. He bakes 10 loaves of bread. The mean height of the sample loaves is 17 cm. The baker knows from baking hundreds of loaves of bread that the standard deviation for the height is 0.5 cm. and the distribution of heights is normal.

• The null hypothesis could be \(H_{0}: \mu \leq 15\)
• The alternate hypothesis is \(H_{a}: \mu > 15\)

The words "is more than" translates as a "\(>\)" so "\(\mu > 15\)" goes into the alternate hypothesis. The null hypothesis must contradict the alternate hypothesis.

Since \(\sigma\) is known (\(\sigma = 0.5 cm.\)), the distribution for the population is known to be normal with mean \(μ = 15\) and standard deviation

\[\dfrac{\sigma}{\sqrt{n}} = \frac{0.5}{\sqrt{10}} = 0.16. \nonumber\]

Suppose the null hypothesis is true (the mean height of the loaves is no more than 15 cm). Then is the mean height (17 cm) calculated from the sample unexpectedly large? The hypothesis test works by asking the question how unlikely the sample mean would be if the null hypothesis were true. The graph shows how far out the sample mean is on the normal curve. The p -value is the probability that, if we were to take other samples, any other sample mean would fall at least as far out as 17 cm.

The \(p\) -value, then, is the probability that a sample mean is the same or greater than 17 cm. when the population mean is, in fact, 15 cm. We can calculate this probability using the normal distribution for means.

\(p\text{-value} = P(\bar{x} > 17)\) which is approximately zero.

A \(p\)-value of approximately zero tells us that it is highly unlikely that a loaf of bread rises no more than 15 cm, on average. That is, almost 0% of all loaves of bread would be at least as high as 17 cm. purely by CHANCE had the population mean height really been 15 cm. Because the outcome of 17 cm. is so unlikely (meaning it is happening NOT by chance alone) , we conclude that the evidence is strongly against the null hypothesis (the mean height is at most 15 cm.). There is sufficient evidence that the true mean height for the population of the baker's loaves of bread is greater than 15 cm.

Exercise \(\PageIndex{1}\)

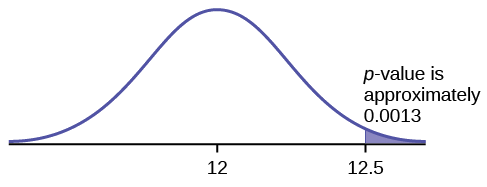
A normal distribution has a standard deviation of 1. We want to verify a claim that the mean is greater than 12. A sample of 36 is taken with a sample mean of 12.5.

• \(H_{0}: \mu leq 12\)
• \(H_{a}: \mu > 12\)

The \(p\)-value is 0.0013

Draw a graph that shows the \(p\)-value.

\(p\text{-value} = 0.0013\)

Decision and Conclusion

A systematic way to make a decision of whether to reject or not reject the null hypothesis is to compare the \(p\)-value and a preset or preconceived \(\alpha\) (also called a " significance level "). A preset \(\alpha\) is the probability of a Type I error (rejecting the null hypothesis when the null hypothesis is true). It may or may not be given to you at the beginning of the problem.

When you make a decision to reject or not reject \(H_{0}\), do as follows:

• If \(\alpha > p\text{-value}\), reject \(H_{0}\). The results of the sample data are significant. There is sufficient evidence to conclude that \(H_{0}\) is an incorrect belief and that the alternative hypothesis, \(H_{a}\), may be correct.
• If \(\alpha \leq p\text{-value}\), do not reject \(H_{0}\). The results of the sample data are not significant.There is not sufficient evidence to conclude that the alternative hypothesis,\(H_{a}\), may be correct.

When you "do not reject \(H_{0}\)", it does not mean that you should believe that H 0 is true. It simply means that the sample data have failed to provide sufficient evidence to cast serious doubt about the truthfulness of \(H_{0}\).

Conclusion: After you make your decision, write a thoughtful conclusion about the hypotheses in terms of the given problem.

Example \(\PageIndex{2}\)

When using the \(p\)-value to evaluate a hypothesis test, it is sometimes useful to use the following memory device

• If the \(p\)-value is low, the null must go.
• If the \(p\)-value is high, the null must fly.

This memory aid relates a \(p\)-value less than the established alpha (the \(p\) is low) as rejecting the null hypothesis and, likewise, relates a \(p\)-value higher than the established alpha (the \(p\) is high) as not rejecting the null hypothesis.

Fill in the blanks.

Reject the null hypothesis when ______________________________________.

The results of the sample data _____________________________________.

Do not reject the null when hypothesis when __________________________________________.

The results of the sample data ____________________________________________.

Reject the null hypothesis when the \(p\) -value is less than the established alpha value . The results of the sample data support the alternative hypothesis .

Do not reject the null hypothesis when the \(p\) -value is greater than the established alpha value . The results of the sample data do not support the alternative hypothesis .

When the probability of an event occurring is low, and it happens, it is called a rare event. Rare events are important to consider in hypothesis testing because they can inform your willingness not to reject or to reject a null hypothesis. To test a null hypothesis, find the p -value for the sample data and graph the results. When deciding whether or not to reject the null the hypothesis, keep these two parameters in mind:

• \(\alpha > p-value\), reject the null hypothesis
• \(\alpha \leq p-value\), do not reject the null hypothesis

WeBWorK Problems

Query \(\PageIndex{1}\)

Query \(\PageIndex{2}\)

Query \(\PageIndex{3}\)

Contributors and Attributions

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] .

Chapter 2: Summarizing and Visualizing Data

Chapter 3: measure of central tendency, chapter 4: measures of variation, chapter 5: measures of relative standing, chapter 6: probability distributions, chapter 7: estimates, chapter 8: distributions, chapter 9: hypothesis testing, chapter 10: analysis of variance, chapter 11: correlation and regression, chapter 12: statistics in practice.

The JoVE video player is compatible with HTML5 and Adobe Flash. Older browsers that do not support HTML5 and the H.264 video codec will still use a Flash-based video player. We recommend downloading the newest version of Flash here, but we support all versions 10 and above.

Hypothesis testing requires the sample statistics—such as proportion, mean, or standard deviation—to be converted into a value or score known as the test statistics.

Assuming that the null hypothesis is true, the test statistic for each sample statistic is calculated using the following equations.

As samples assume a particular distribution, a given test statistic value would fall into a specific area under the curve with some probability.

Such an area, which includes all the values of a test statistic that indicates that the null hypothesis must be rejected, is termed the rejection region or critical region.

The value that separates a critical region from the rest is termed the critical value. The critical values are the  z, t,  or chi-square values calculated at the desired confidence level.

The probability that the test statistic will fall in the critical region when the null hypothesis is actually true is called the significance level.

In the example of testing the proportion of healthy and scabbed apples, if the sample proportion is 0.9, the hypothesis can be tested as follows.

9.3: Critical Region, Critical Values and Significance Level

The critical region, critical value, and significance level are interdependent concepts crucial in hypothesis testing.

In hypothesis testing, a sample statistic is converted to a test statistic using z , t , or chi-square distribution. A critical region is an area under the curve in  probability distributions demarcated by the critical value. When the test statistic falls in this region, it suggests that the null hypothesis must be rejected. As this region contains all those values of the test statistic (calculated using the sample data) that suggest rejecting the null hypothesis, it is also known as the rejection region or region of rejection. The critical region may fall at the right, left, or both tails of the distribution based on the direction indicated in the alternative hypothesis and the calculated critical value.

A critical value is calculated using the z , t, or chi-square distribution table at a specific significance level. It is a fixed value for the given sample size and the significance level. The critical value creates a demarcation between all those values that suggest rejection of the null hypothesis and all those other values that indicate the opposite. A critical value is  based on a pre-decided significance level.

A significance level or level of significance or statistical significance is defined as the probability that the calculated test statistic will fall in the critical region. In other words, it is a statistical measure that indicates that the evidence for rejecting a true null hypothesis is strong enough. The significance level is indicated by α, and it is commonly 0.05 or 0.01.

Get cutting-edge science videos from J o VE sent straight to your inbox every month.

mktb-description

We use cookies to enhance your experience on our website.

By continuing to use our website or clicking “Continue”, you are agreeing to accept our cookies.

Critical Value Approach in Hypothesis Testing

by Nathan Sebhastian

Posted on Jun 05, 2023

Reading time: 5 minutes

The critical value is the cut-off point to determine whether to accept or reject the null hypothesis for your sample distribution.

The critical value approach provides a standardized method for hypothesis testing, enabling you to make informed decisions based on the evidence obtained from sample data.

After calculating the test statistic using the sample data, you compare it to the critical value(s) corresponding to the chosen significance level ( α ).

The critical value(s) represent the boundary beyond which you reject the null hypothesis. You will have rejection regions and non-rejection region as follows:

Two-sided test

A two-sided hypothesis test has 2 rejection regions, so you need 2 critical values on each side. Because there are 2 rejection regions, you must split the significance level in half.

Each rejection region has a probability of α / 2 , making the total likelihood for both areas equal the significance level.

In this test, the null hypothesis H0 gets rejected when the test statistic is too small or too large.

Left-tailed test

The left-tailed test has 1 rejection region, and the null hypothesis only gets rejected when the test statistic is too small.

Right-tailed test

The right-tailed test is similar to the left-tailed test, only the null hypothesis gets rejected when the test statistic is too large.

Now that you understand the definition of critical values, let’s look at how to use critical values to construct a confidence interval.

Using Critical Values to Construct Confidence Intervals

Confidence Intervals use the same Critical values as the test you’re running.

If you’re running a z-test with a 95% confidence interval, then:

• For a two-sided test, The CVs are -1.96 and 1.96
• For a one-tailed test, the critical value is -1.65 (left) or 1.65 (right)

To calculate the upper and lower bounds of the confidence interval, you need to calculate the sample mean and then add or subtract the margin of error from it.

To get the Margin of Error, multiply the critical value by the standard error:

Let’s see an example. Suppose you are estimating the population mean with a 95% confidence level.

You have a sample mean of 50, a sample size of 100, and a standard deviation of 10. Using a z-table, the critical value for a 95% confidence level is approximately 1.96.

Calculate the standard error:

Determine the margin of error:

Compute the lower bound and upper bound:

The 95% confidence interval is (48.04, 51.96). This means that we are 95% confident that the true population mean falls within this interval.

Finding the Critical Value

The formula to find critical values depends on the specific distribution associated with the hypothesis test or confidence interval you’re using.

Here are the formulas for some commonly used distributions.

Standard Normal Distribution (Z-distribution):

The critical value for a given significance level ( α ) in the standard normal distribution is found using the cumulative distribution function (CDF) or a standard normal table.

z(α) represents the z-score corresponding to the desired significance level α .

Student’s t-Distribution (t-distribution):

The critical value for a given significance level (α) and degrees of freedom (df) in the t-distribution is found using the inverse cumulative distribution function (CDF) or a t-distribution table.

t(α, df) represents the t-score corresponding to the desired significance level α and degrees of freedom df .

Chi-Square Distribution (χ²-distribution):

The critical value for a given significance level (α) and degrees of freedom (df) in the chi-square distribution is found using the inverse cumulative distribution function (CDF) or a chi-square distribution table.

where χ²(α, df) represents the chi-square value corresponding to the desired significance level α and degrees of freedom df .

F-Distribution:

The critical value for a given significance level (α), degrees of freedom for the numerator (df₁), and degrees of freedom for the denominator (df₂) in the F-distribution is found using the inverse cumulative distribution function (CDF) or an F-distribution table.

F(α, df₁, df₂) represents the F-value corresponding to the desired significance level α , df₁ , and df₂ .

As you can see, the specific formula to find critical values depends on the distribution and the parameters associated with the problem at hand.

Usually, you don’t calculate the critical values manually as you can use statistical tables or statistical software to determine the critical values.

I will update this tutorial with statistical tables that you can use later.

The critical value is as a threshold where you make a decision based on the observed test statistic and its relation to the significance level.

It provides a predetermined point of reference to objectively evaluate the strength of the evidence against the null hypothesis and guide the acceptance or rejection of the hypothesis.

If the test statistic falls in the critical region (beyond the critical value), it means the observed data provide strong evidence against the null hypothesis.

In this case, you reject the null hypothesis in favor of the alternative hypothesis, indicating that there is sufficient evidence to support the claim or relationship stated in the alternative hypothesis.

On the other hand, if the test statistic falls in the non-critical region (within the critical value), it means the observed data do not provide enough evidence to reject the null hypothesis.

In this case, you fail to reject the null hypothesis, indicating that there is insufficient evidence to support the alternative hypothesis.

Take your skills to the next level ⚡️

I'm sending out an occasional email with the latest tutorials on programming, web development, and statistics. Drop your email in the box below and I'll send new stuff straight into your inbox!

Hello! This website is dedicated to help you learn tech and data science skills with its step-by-step, beginner-friendly tutorials. Learn statistics, JavaScript and other programming languages using clear examples written for people.

Learn more about this website

Connect with me on Twitter

Or LinkedIn

Type the keyword below and hit enter

Click to see all tutorials tagged with:

Critical Region and Confidence Interval

Contents Toggle Main Menu 1 Confidence Interval 2 Significance Levels 3 Critical Region 4 Critical Values 5 Constructing a Confidence Interval 5.1 Binomial Distribution 5.2 Normal Distribution 5.3 Student $t$-distribution 6 Video Examples

Confidence Interval

A confidence interval , also known as the acceptance region, is a set of values for the test statistic for which the null hypothesis is accepted. i.e. if the observed test statistic is in the confidence interval then we accept the null hypothesis and reject the alternative hypothesis .

Significance Levels

Confidence intervals can be calculated at different significance levels . We use $\alpha$ to denote the level of significance and perform a hypothesis test with a $100(1- \alpha)$% confidence interval.

Confidence intervals are usually calculated at $5$% or $1$% significance levels, for which $\alpha = 0.05$ and $\alpha = 0.01$ respectively. Note that a $95$% confidence interval does not mean there is a $95$% chance that the true value being estimated is in the calculated interval. Rather, given a population, there is a $95$% chance that choosing a random sample from this population results in a confidence interval which contains the true value being estimated.

Critical Region

A critical region , also known as the rejection region, is a set of values for the test statistic for which the null hypothesis is rejected. i.e. if the observed test statistic is in the critical region then we reject the null hypothesis and accept the alternative hypothesis.

Critical Values

The critical value at a certain significance level can be thought of as a cut-off point. If a test statistic on one side of the critical value results in accepting the null hypothesis, a test statistic on the other side will result in rejecting the null hypothesis.

Constructing a Confidence Interval

Binomial distribution.

Usually, the easiest way to perform a hypothesis test with the binomial distribution is to use the $p$-value and see whether it is larger or smaller than $\alpha$, the significance level used.

Sometimes, if we have observed a large number of Bernoulli Trials, we can use the observed probability of success $\hat{p}$, based entirely on the data obtained, to approximate the distribution of error using the normal distribution. We do this using the formula \[\hat{p} \pm z_{1-\frac{\alpha}{2} } \sqrt{ \frac{1}{n} \hat{p} (1-\hat {p})}\] where $\hat{p}$ is the estimated probability of success, $z_{1- \frac{\alpha}{2} }$ is obtained from the normal distribution tables , $\alpha$ is the significance level and $n$ is the sample size.

Worked Example

A coin is tossed $1050$ times and lands on heads $500$ times. Construct a $90$% confidence interval for the probability $p$ of getting a head.

Here the observed probability of success $\hat{p} = \dfrac{500}{1050}$, $n=1050$ and $\alpha = 0.1$ so $z_{1-\frac{\alpha}{2} } = z_{0.95} = 1.645$. This is because $\Phi^{-1} (0.95) = 1.645$ .

So the confidence interval will be between $\hat{p} + z_{1-\frac{\alpha}{2} } \sqrt{ \frac{1}{n} \hat{p} (1-\hat {p})} \text{ and } \hat{p} - z_{1-\frac{\alpha}{2} } \sqrt{ \frac{1}{n} \hat{p} (1-\hat {p})} . $ By substituting into these expressions, we find that the confidence interval is between \begin{align} &\dfrac{500}{1050} + 1.645 \sqrt{ \frac{1}{1050} \times \dfrac{500}{1050} \times \left(1- \dfrac{500}{1050}\right) }\\ \text{ and } &\dfrac{500}{1050} - 1.645 \sqrt{ \frac{1}{1050} \times \dfrac{500}{1050} \times \left(1- \dfrac{500}{1050}\right) }\\\\ &=0.47619 + (1.645 \times \sqrt{0.00024} ) \text{ and } 0.47619 - (1.645 \times \sqrt{0.00024} ) \\ &=0.50155 \text{ and } 0.45084 . \end{align} So the confidence interval is $(0.45084, 0.50155)$.

Normal Distribution

We can use either the $z$-score or the sample mean $\bar{x}$ as the test statistic. If the $z$-score is used then reading straight from the tables gives the critical values.

For example, the critical values for a $5$% significance test are:

To obtain a confidence interval for the mean, use the following procedure:

For a two-tailed test with a $5$% significance level we need to consider \begin{align} 0.95 &= \mathrm{P}[-k< Z < k] \\ &= \mathrm{P}\left[-k<\dfrac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n} } } \mu+1.96\frac{\sigma}{\sqrt{n} }. \]

Student $t$-distribution

Given the number of degrees of freedom $v$ and the significance level $\alpha$, the critical values can be obtained from the tables. Critical regions can then be computed from these.

If we are performing a hypothesis test at a $1$% significance level with $15$ degrees of freedom using the Student $t$-distribution then there are three cases, depending on the alternative hypothesis.

If we are performing a two-tailed test, the critical values are $\pm2.9467$ so the confidence interval is $-2.9467 \leq t \leq 2.9467$ where $t$ is the test statistic. The critical regions will be $t< -2.9467$ and $t>2.9467$.

If we are performing a one-tailed test, the critical value is $2.6025$:

Video Examples

In this video, Daniel Organisciak calculates a one-tailed confidence interval for the normal distribution.

In this video Daniel Organisciak calculates a two-tailed confidence interval for the normal distribution.

Critical Value Calculator

How to use critical value calculator, what is a critical value, critical value definition, how to calculate critical values, z critical values, t critical values, chi-square critical values (χ²), f critical values, behind the scenes of the critical value calculator.

Welcome to the critical value calculator! Here you can quickly determine the critical value(s) for two-tailed tests, as well as for one-tailed tests. It works for most common distributions in statistical testing: the standard normal distribution N(0,1) (that is when you have a Z-score), t-Student, chi-square, and F-distribution .

What is a critical value? And what is the critical value formula? Scroll down – we provide you with the critical value definition and explain how to calculate critical values in order to use them to construct rejection regions (also known as critical regions).

The critical value calculator is your go-to tool for swiftly determining critical values in statistical tests, be it one-tailed or two-tailed. To effectively use the calculator, follow these steps:

In the first field, input the distribution of your test statistic under the null hypothesis: is it a standard normal N (0,1), t-Student, chi-squared, or Snedecor's F? If you are not sure, check the sections below devoted to those distributions, and try to localize the test you need to perform.

In the field What type of test? choose the alternative hypothesis : two-tailed, right-tailed, or left-tailed.

If needed, specify the degrees of freedom of the test statistic's distribution. If you need more clarification, check the description of the test you are performing. You can learn more about the meaning of this quantity in statistics from the degrees of freedom calculator .

Set the significance level, α \alpha α . By default, we pre-set it to the most common value, 0.05, but you can adjust it to your needs.

The critical value calculator will display your critical value(s) and the rejection region(s).

Click the advanced mode if you need to increase the precision with which the critical values are computed.

For example, let's envision a scenario where you are conducting a one-tailed hypothesis test using a t-Student distribution with 15 degrees of freedom. You have opted for a right-tailed test and set a significance level (α) of 0.05. The results indicate that the critical value is 1.7531, and the critical region is (1.7531, ∞). This implies that if your test statistic exceeds 1.7531, you will reject the null hypothesis at the 0.05 significance level.

👩‍🏫 Want to learn more about critical values? Keep reading!

In hypothesis testing, critical values are one of the two approaches which allow you to decide whether to retain or reject the null hypothesis. The other approach is to calculate the p-value (for example, using the p-value calculator ).

The critical value approach consists of checking if the value of the test statistic generated by your sample belongs to the so-called rejection region , or critical region , which is the region where the test statistic is highly improbable to lie . A critical value is a cut-off value (or two cut-off values in the case of a two-tailed test) that constitutes the boundary of the rejection region(s). In other words, critical values divide the scale of your test statistic into the rejection region and the non-rejection region.

Once you have found the rejection region, check if the value of the test statistic generated by your sample belongs to it :

• If so, it means that you can reject the null hypothesis and accept the alternative hypothesis; and
• If not, then there is not enough evidence to reject H 0 .

But how to calculate critical values? First of all, you need to set a significance level , α \alpha α , which quantifies the probability of rejecting the null hypothesis when it is actually correct. The choice of α is arbitrary; in practice, we most often use a value of 0.05 or 0.01. Critical values also depend on the alternative hypothesis you choose for your test , elucidated in the next section .

To determine critical values, you need to know the distribution of your test statistic under the assumption that the null hypothesis holds. Critical values are then points with the property that the probability of your test statistic assuming values at least as extreme at those critical values is equal to the significance level α . Wow, quite a definition, isn't it? Don't worry, we'll explain what it all means.

First, let us point out it is the alternative hypothesis that determines what "extreme" means. In particular, if the test is one-sided, then there will be just one critical value; if it is two-sided, then there will be two of them: one to the left and the other to the right of the median value of the distribution.

Critical values can be conveniently depicted as the points with the property that the area under the density curve of the test statistic from those points to the tails is equal to α \alpha α :

Left-tailed test: the area under the density curve from the critical value to the left is equal to α \alpha α ;

Right-tailed test: the area under the density curve from the critical value to the right is equal to α \alpha α ; and

Two-tailed test: the area under the density curve from the left critical value to the left is equal to α / 2 \alpha/2 α /2 , and the area under the curve from the right critical value to the right is equal to α / 2 \alpha/2 α /2 as well; thus, total area equals α \alpha α .

As you can see, finding the critical values for a two-tailed test with significance α \alpha α boils down to finding both one-tailed critical values with a significance level of α / 2 \alpha/2 α /2 .

The formulae for the critical values involve the quantile function , Q Q Q , which is the inverse of the cumulative distribution function ( c d f \mathrm{cdf} cdf ) for the test statistic distribution (calculated under the assumption that H 0 holds!): Q = c d f − 1 Q = \mathrm{cdf}^{-1} Q = cdf − 1 .

Once we have agreed upon the value of α \alpha α , the critical value formulae are the following:

• Left-tailed test :
• Right-tailed test :
• Two-tailed test :

In the case of a distribution symmetric about 0 , the critical values for the two-tailed test are symmetric as well:

Unfortunately, the probability distributions that are the most widespread in hypothesis testing have somewhat complicated c d f \mathrm{cdf} cdf formulae. To find critical values by hand, you would need to use specialized software or statistical tables. In these cases, the best option is, of course, our critical value calculator! 😁

Use the Z (standard normal) option if your test statistic follows (at least approximately) the standard normal distribution N(0,1) .

In the formulae below, u u u denotes the quantile function of the standard normal distribution N(0,1):

Left-tailed Z critical value: u ( α ) u(\alpha) u ( α )

Right-tailed Z critical value: u ( 1 − α ) u(1-\alpha) u ( 1 − α )

Two-tailed Z critical value: ± u ( 1 − α / 2 ) \pm u(1- \alpha/2) ± u ( 1 − α /2 )

Check out Z-test calculator to learn more about the most common Z-test used on the population mean. There are also Z-tests for the difference between two population means, in particular, one between two proportions.

Use the t-Student option if your test statistic follows the t-Student distribution . This distribution is similar to N(0,1) , but its tails are fatter – the exact shape depends on the number of degrees of freedom . If this number is large (>30), which generically happens for large samples, then the t-Student distribution is practically indistinguishable from N(0,1). Check our t-statistic calculator to compute the related test statistic.

In the formulae below, Q t , d Q_{\text{t}, d} Q t , d ​ is the quantile function of the t-Student distribution with d d d degrees of freedom:

Left-tailed t critical value: Q t , d ( α ) Q_{\text{t}, d}(\alpha) Q t , d ​ ( α )

Right-tailed t critical value: Q t , d ( 1 − α ) Q_{\text{t}, d}(1 - \alpha) Q t , d ​ ( 1 − α )

Two-tailed t critical values: ± Q t , d ( 1 − α / 2 ) \pm Q_{\text{t}, d}(1 - \alpha/2) ± Q t , d ​ ( 1 − α /2 )

Visit the t-test calculator to learn more about various t-tests: the one for a population mean with an unknown population standard deviation , those for the difference between the means of two populations (with either equal or unequal population standard deviations), as well as about the t-test for paired samples .

Use the χ² (chi-square) option when performing a test in which the test statistic follows the χ²-distribution .

You need to determine the number of degrees of freedom of the χ²-distribution of your test statistic – below, we list them for the most commonly used χ²-tests.

Here we give the formulae for chi square critical values; Q χ 2 , d Q_{\chi^2, d} Q χ 2 , d ​ is the quantile function of the χ²-distribution with d d d degrees of freedom:

Left-tailed χ² critical value: Q χ 2 , d ( α ) Q_{\chi^2, d}(\alpha) Q χ 2 , d ​ ( α )

Right-tailed χ² critical value: Q χ 2 , d ( 1 − α ) Q_{\chi^2, d}(1 - \alpha) Q χ 2 , d ​ ( 1 − α )

Two-tailed χ² critical values: Q χ 2 , d ( α / 2 ) Q_{\chi^2, d}(\alpha/2) Q χ 2 , d ​ ( α /2 ) and Q χ 2 , d ( 1 − α / 2 ) Q_{\chi^2, d}(1 - \alpha/2) Q χ 2 , d ​ ( 1 − α /2 )

Several different tests lead to a χ²-score:

Goodness-of-fit test : does the empirical distribution agree with the expected distribution?

This test is right-tailed . Its test statistic follows the χ²-distribution with k − 1 k - 1 k − 1 degrees of freedom, where k k k is the number of classes into which the sample is divided.

Independence test : is there a statistically significant relationship between two variables?

This test is also right-tailed , and its test statistic is computed from the contingency table. There are ( r − 1 ) ( c − 1 ) (r - 1)(c - 1) ( r − 1 ) ( c − 1 ) degrees of freedom, where r r r is the number of rows, and c c c is the number of columns in the contingency table.

Test for the variance of normally distributed data : does this variance have some pre-determined value?

This test can be one- or two-tailed! Its test statistic has the χ²-distribution with n − 1 n - 1 n − 1 degrees of freedom, where n n n is the sample size.

Finally, choose F (Fisher-Snedecor) if your test statistic follows the F-distribution . This distribution has a pair of degrees of freedom .

Let us see how those degrees of freedom arise. Assume that you have two independent random variables, X X X and Y Y Y , that follow χ²-distributions with d 1 d_1 d 1 ​ and d 2 d_2 d 2 ​ degrees of freedom, respectively. If you now consider the ratio ( X d 1 ) : ( Y d 2 ) (\frac{X}{d_1}):(\frac{Y}{d_2}) ( d 1 ​ X ​ ) : ( d 2 ​ Y ​ ) , it turns out it follows the F-distribution with ( d 1 , d 2 ) (d_1, d_2) ( d 1 ​ , d 2 ​ ) degrees of freedom. That's the reason why we call d 1 d_1 d 1 ​ and d 2 d_2 d 2 ​ the numerator and denominator degrees of freedom , respectively.

In the formulae below, Q F , d 1 , d 2 Q_{\text{F}, d_1, d_2} Q F , d 1 ​ , d 2 ​ ​ stands for the quantile function of the F-distribution with ( d 1 , d 2 ) (d_1, d_2) ( d 1 ​ , d 2 ​ ) degrees of freedom:

Left-tailed F critical value: Q F , d 1 , d 2 ( α ) Q_{\text{F}, d_1, d_2}(\alpha) Q F , d 1 ​ , d 2 ​ ​ ( α )

Right-tailed F critical value: Q F , d 1 , d 2 ( 1 − α ) Q_{\text{F}, d_1, d_2}(1 - \alpha) Q F , d 1 ​ , d 2 ​ ​ ( 1 − α )

Two-tailed F critical values: Q F , d 1 , d 2 ( α / 2 ) Q_{\text{F}, d_1, d_2}(\alpha/2) Q F , d 1 ​ , d 2 ​ ​ ( α /2 ) and Q F , d 1 , d 2 ( 1 − α / 2 ) Q_{\text{F}, d_1, d_2}(1 -\alpha/2) Q F , d 1 ​ , d 2 ​ ​ ( 1 − α /2 )

Here we list the most important tests that produce F-scores: each of them is right-tailed .

ANOVA : tests the equality of means in three or more groups that come from normally distributed populations with equal variances. There are ( k − 1 , n − k ) (k - 1, n - k) ( k − 1 , n − k ) degrees of freedom, where k k k is the number of groups, and n n n is the total sample size (across every group).

Overall significance in regression analysis . The test statistic has ( k − 1 , n − k ) (k - 1, n - k) ( k − 1 , n − k ) degrees of freedom, where n n n is the sample size, and k k k is the number of variables (including the intercept).

Compare two nested regression models . The test statistic follows the F-distribution with ( k 2 − k 1 , n − k 2 ) (k_2 - k_1, n - k_2) ( k 2 ​ − k 1 ​ , n − k 2 ​ ) degrees of freedom, where k 1 k_1 k 1 ​ and k 2 k_2 k 2 ​ are the number of variables in the smaller and bigger models, respectively, and n n n is the sample size.

The equality of variances in two normally distributed populations . There are ( n − 1 , m − 1 ) (n - 1, m - 1) ( n − 1 , m − 1 ) degrees of freedom, where n n n and m m m are the respective sample sizes.

I'm Anna, the mastermind behind the critical value calculator and a PhD in mathematics from Jagiellonian University .

The idea for creating the tool originated from my experiences in teaching and research. Recognizing the need for a tool that simplifies the critical value determination process across various statistical distributions, I built a user-friendly calculator accessible to both students and professionals. After publishing the tool, I soon found myself using the calculator in my research and as a teaching aid.

Trust in this calculator is paramount to me. Each tool undergoes a rigorous review process , with peer-reviewed insights from experts and meticulous proofreading by native speakers. This commitment to accuracy and reliability ensures that users can be confident in the content. Please check the Editorial Policies page for more details on our standards.

What is a Z critical value?

A Z critical value is the value that defines the critical region in hypothesis testing when the test statistic follows the standard normal distribution . If the value of the test statistic falls into the critical region, you should reject the null hypothesis and accept the alternative hypothesis.

How do I calculate Z critical value?

To find a Z critical value for a given confidence level α :

Check if you perform a one- or two-tailed test .

For a one-tailed test:

Left -tailed: critical value is the α -th quantile of the standard normal distribution N(0,1).

Right -tailed: critical value is the (1-α) -th quantile.

Two-tailed test: critical value equals ±(1-α/2) -th quantile of N(0,1).

No quantile tables ? Use CDF tables! (The quantile function is the inverse of the CDF.)

Verify your answer with an online critical value calculator.

Is a t critical value the same as Z critical value?

In theory, no . In practice, very often, yes . The t-Student distribution is similar to the standard normal distribution, but it is not the same . However, if the number of degrees of freedom (which is, roughly speaking, the size of your sample) is large enough (>30), then the two distributions are practically indistinguishable , and so the t critical value has practically the same value as the Z critical value.

What is the Z critical value for 95% confidence?

The Z critical value for a 95% confidence interval is:

• 1.96 for a two-tailed test;
• 1.64 for a right-tailed test; and
• -1.64 for a left-tailed test.

Black hole collision

Order from least to greatest, social media time alternatives.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (292)
• Ecology (30)
• Everyday life (261)
• Finance (569)
• Health (440)
• Physics (509)
• Sports (104)
• Statistics (182)
• Other (181)
• Discover Omni (40)

Teach yourself statistics

Region of Acceptance

For a hypothesis test , a researcher collects sample data. From the sample data, the researcher computes a test statistic . If the statistic falls within a specified range of values, the researcher cannot reject the null hypothesis. That range of values is called the region of acceptance.

In this lesson, we describe how to find the region of acceptance for a hypothesis test.

One-Tailed and Two-Tailed Hypothesis Tests

The steps taken to define the region of acceptance will vary, depending on whether the null hypothesis calls for a one- or a two-tailed hypothesis test.

The table below shows three sets of hypotheses. Each makes a statement about how the population mean μ is related to a specified value M . (In the table, the symbol ≠ means " not equal to ".)

The first set of hypotheses (Set 1) is an example of a two-tailed test , since an extreme value on either side of the sampling distribution would cause a researcher to reject the null hypothesis. That is, if the sample mean were much bigger or much smaller than M, we would reject the null hypothesis.

The other two sets of hypotheses (Sets 2 and 3) are one-tailed tests , since an extreme value on only one side of the sampling distribution would cause a researcher to reject the null hypothesis. For example, for Set 2, we would reject the null hypothesis only if the sample mean were much smaller than M. And for Set 2, we would reject the null hypothesis only if the sample mean were much bigger than M.

How to Find the Region of Acceptance

We define the region of acceptance in such a way that the chance of making a Type I error is equal to the significance level . Here is how that is done.

s 2 = P * (1 - P)

where s 2 is an estimate of population variance, and P is the value of the proportion in the null hypothesis.

s 2 = Σ ( x i - x ) 2 / ( n - 1 )

where s 2 is a sample estimate of population variance, x is the sample mean, x i is the i th element from the sample, and n is the number of elements in the sample.

s 2 h = Σ ( x i h - x h ) 2 / ( n h - 1 )

where s 2 h is a sample estimate of population variance in stratum h , x i h is the value of the i th element from stratum h, x h is the sample mean from stratum h , and n h is the number of sample observations from stratum h .

s 2 h = Σ ( x i h - x h ) 2 / ( m h - 1 )

where s 2 h is a sample estimate of population variance in cluster h , x i h is the value of the i th element from cluster h, x h is the sample mean from cluster h , and m h is the number of observations sampled from cluster h .

s 2 b = Σ ( t h - t/N ) 2 / ( n - 1 )

where s 2 b is a sample estimate of the variance between sampled clusters, t h is the total from cluster h, t is the sample estimate of the population total, N is the number of clusters in the population, and n is the number of clusters in the sample.

You can estimate the population total (t) from the following formula:

Population total = t = N/n * ΣM h * x h

where M h is the number of observations in the population from cluster h , and x h is the sample mean from cluster h .

SE = sqrt [ (1 - n/N) * s 2 / n ]

where n is the sample size, N is the population size, and s is a sample estimate of the population standard deviation.

SE = sqrt [ N 2 * (1 - n/N) * s 2 / n ]

where N is the population size, n is the sample size, and s 2 is a sample estimate of the population variance.

SE = (1 / N) * sqrt { Σ [ N 2 h * ( 1 - n h /N h ) * s 2 h / n h ] }

where n h is the number of sample observations from stratum h, N h is the number of elements from stratum h in the population, N is the number of elements in the population, and s 2 h is a sample estimate of the population variance in stratum h.

SE = sqrt { Σ [ N 2 h * ( 1 - n h /N h ) * s 2 h / n h ] }

where N h is the number of elements from stratum h in the population, n h is the number of sample observations from stratum h, and s 2 h is a sample estimate of the population variance in stratum h.

where M is the number of observations in the population, N is the number of clusters in the population, n is the number of clusters in the sample, M h is the number of elements from cluster h in the population, m h is the number of elements from cluster h in the sample, x h is the sample mean from cluster h, s 2 h is a sample estimate of the population variance in stratum h, and t is a sample estimate of the population total. For the equation above, use the following formula to estimate the population total.

t = N/n * Σ M h x h

With one-stage cluster sampling, the formula for the standard error reduces to:

where M is the number of observations in the population, N is the number of clusters in the population, n is the number of clusters in the sample, M h is the number of elements from cluster h in the population, m h is the number of elements from cluster h in the sample, p h is the value of the proportion from cluster h, and t is a sample estimate of the population total. For the equation above, use the following formula to estimate the population total.

t = N/n * Σ M h p h

where N is the number of clusters in the population, n is the number of clusters in the sample, s 2 b is a sample estimate of the variance between clusters, m h is the number of elements from cluster h in the sample, M h is the number of elements from cluster h in the population, and s 2 h is a sample estimate of the population variance in cluster h.

SE = N * sqrt { [ ( 1 - n/N ) / n ] * s 2 b /n }

• Choose a significance level. The significance level (denoted by α) is the probability of committing a Type I error . Researchers often set the significance level equal to 0.05 or 0.01.

When the null hypothesis is one-tailed, the critical value is the z-score or t-score that has a cumulative probability equal to 1 - α/2. When the null hypothesis is one-tailed, the critical value has a cumulative probability equal to 1 - α.

Researchers use a t-score when sample size is small; a z-score when it is large (at least 30). You can use the Normal Distribution Calculator to find the critical z-score, and the t Distribution Calculator to find the critical t-score.

If you use a t-score, you will have to find the degrees of freedom (df). With simple random samples, df is often equal to the sample size minus one.

Note: The critical value for a one-tailed hypothesis does not equal the critical value for a two-tailed hypothesis. The critical value for a one-tailed hypothesis is smaller.

UL = M + SE * CV

• If the null hypothesis is μ > M: The theoretical upper limit of the region of acceptance is plus infinity, unless the parameter in the null hypothesis is a proportion or a percentage. The upper limit is 1 for a proportion, and 100 for a percentage.

LL = M - SE * CV

• If the null hypothesis is μ < M: The theoretical lower limit of the region of acceptance is minus infinity, unless the test statistic is a proportion or a percentage. The lower limit for a proportion or a percentage is zero.

The region of acceptance is defined by the range between LL and UL.

Test Your Understanding

In this section, three sample problems illustrate step-by-step how to define the region of acceptance. The first problem shows how to find the standard error; the second problem, how to find the critical value; and the third problem, how to find upper and lower limits for the region of acceptance.

Sample Size Calculator

As you probably noticed, defining the region of acceptance can be complex and time-consuming. Stat Trek's Sample Size Calculator can do the same job quickly, easily, and error-free.The calculator is easy to use, and it is free. You can find the Sample Size Calculator in Stat Trek's main menu under the Stat Tools tab. Or you can tap the button below.

An inventor has developed a new, energy-efficient lawn mower engine. Suppose a simple random sample of 50 engines is tested. The engines run for an average of 295 minutes, with a standard deviation of 20 minutes.

What is the standard error of the estimate?

Solution: The right formula to compute standard error will vary, depending on the sampling method and the parameter under study. Here, we are using simple random sampling to estimate a mean score; so the right formula for the standard error (SE) is:

For this problem, we know that the sample size is 50, and the standard deviation is 20. The population size is not stated explicitly; but, in theory, the manufacturer could produce an infinite number of motors. Therefore, the population size is a very large number. For the purpose of the analysis, we'll assume that the population size is 100,000. Plugging those values into the formula, we find that the standard error is:

SE = sqrt [ (1 - 50/100,000) * 20 2 / 50 ]

SE = sqrt(0.9995 * 8) = 2.828

An inventor has developed a new, energy-efficient lawn mower engine. He hypothesizes that the engine will run continuously for at least 300 minutes on a single ounce of regular gasoline.

What are the null and alternative hypotheses for this test? Given these hypotheses, find the critical value. Assume the significance level (α) is 0.05.

Solution: In this problem, the inventor states that his engine will run at least 300 minutes. That is the null hypothesis. The alternative hypothesis is that the engine will run less than 300 minutes. These hypotheses can be expressed as:

Notice that this is a one-tailed test, since an extreme value on only one side of the sampling distribution would cause the inventor to reject the null hypothesis. That is, he would reject the null hypothesis only if the mean running time were much less than 300 minutes.

When the sample size is large (at least 30), researchers can express the critical value as a t-score or as a z-score. Here, the sample size is much larger than 30 (n=50), so we will express the critical value as a z-score.

Since the null hypothesis is one-tailed, the critical value is the z-score that has a cumulative probability equal to 1 - α. For this problem, the significance level (α) is 0.05, so the critical value will be the z-score that has a cumulative probability equal to 0.95.

We use the Normal Distribution Calculator to find that the z-score with a cumulative probability of 0.95 is 1.645. Thus, the critical value is 1.645.

Use the findings from Problems 1 and 2 to define the region of acceptance for the hypothesis test described in Problem 2. In the tests, the engines run for an average of 295 minutes. Based on these findings and your analysis of the region of acceptance, should the inventor reject his hypothesis that the engine will run continuously for 300 minutes on a single ounce of gasoline?

Solution: From the previous problems, we know three important facts:

• The null hypothesis is: μ > 300.
• The standard error is 2.828.
• The critical value is 1.645.

For this type of one-tailed hypothesis, the theoretical upper limit of the region of acceptance is plus infinity; since any run time greater than 300 is consistent with the null hypothesis. The lower limit (LL) of the region of acceptance will be:

where M is the parameter value in the null hypothesis, SE is the standard error, and CV is the critical value. So, for this problem, we compute the lower limit of the region of acceptance as:

LL = 300 - 2.828 * 1.645

LL = 300 - 4.652

LL = 295.35

Therefore, the region of acceptance for this hypothesis test is 295.35 to plus infinity. Any run time within that range is consistent with the null hypothesis. In the tests, the engines ran for an average of 295 minutes. That value is outside the region of acceptance, so the inventor should reject the null hypothesis that the engines run for at least 300 minutes.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

26.2 - uniformly most powerful tests.

The Neyman Pearson Lemma is all well and good for deriving the best hypothesis tests for testing a simple null hypothesis against a simple alternative hypothesis, but the reality is that we typically are interested in testing a simple null hypothesis, such as \(H_0 \colon \mu = 10\) against a composite alternative hypothesis, such as \(H_A \colon \mu > 10\). The good news is that we can extend the Neyman Pearson Lemma to account for composite alternative hypotheses, providing we take into account each simple alternative specified in H_A. Doing so creates what is called a uniformly most powerful (or UMP ) test .

A test defined by a critical region C of size \(\alpha\) is a uniformly most powerful (UMP) test if it is a most powerful test against each simple alternative in the alternative hypothesis \(H_A\). The critical region C is called a uniformly most powerful critical region of size \(\alpha\) .

Let's demonstrate by returning to the normal example from the previous page, but this time specifying a composite alternative hypothesis.

Example 26-6 Section  

Suppose \(X_1, X_2, \colon, X_n\) is a random sample from a normal population with mean \(\mu\) and variance 16. Find the test with the best critical region, that is, find the uniformly most powerful test, with a sample size of \(n = 16\) and a significance level \(\alpha\) = 0.05 to test the simple null hypothesis \(H_0: \mu = 10\) against the composite alternative hypothesis \(H_A: \mu > 10\).

For each simple alternative in \(H_A , \mu = \mu_a\), say, the ratio of the likelihood functions is:

\( \dfrac{L(10)}{L(\mu_\alpha)}= \dfrac{(32\pi)^{-16/2} exp \left[ -(1/32)\sum_{i=1}^{16}(x_i -10)^2 \right]}{(32\pi)^{-16/2} exp \left[ -(1/32)\sum_{i=1}^{16}(x_i -\mu_\alpha)^2 \right]} \le k \)

Simplifying, we get:

\(exp \left[ - \left(\dfrac{1}{32} \right) \left(\sum_{i=1}^{16}(x_i -10)^2 - \sum_{i=1}^{16}(x_i -\mu_\alpha)^2 \right) \right] \le k \)

And, simplifying yet more, we get:

Taking the natural logarithm of both sides of the inequality, collecting like terms, and multiplying through by 32, we get:

\( -2(\mu_\alpha - 10) \sum x_i +16 (\mu_{\alpha}^{2} - 10^2) \le 32 ln(k) \)

Moving the constant term on the left-side of the inequality to the right-side, and dividing through by \(-16(2(\mu_\alpha - 10)) \), we get:

\( \dfrac{1}{16} \sum x_i \ge - \dfrac{1}{16(2(\mu_\alpha - 10))}(32 ln(k) - 16(\mu_{\alpha}^{2} - 10^2)) = k^* \)

In summary, we have shown that the ratio of the likelihoods is small, that is:

\(\dfrac{L(10)}{L(\mu_\alpha)} \le k \)

if and only if:

\( \bar{x} \ge k^*\)

Therefore, the best critical region of size \(\alpha\) for testing \(H_0: \mu = 10\) against each simple alternative \(H_A \colon \mu = \mu_a\), where \(\mu_a > 10\), is given by:

\( C= \left\{ (x_1, x_1, ... , x_n): \bar{x} \ge k^* \right\} \)

where \(k^*\) is selected such that the probability of committing a Type I error is \(\alpha\), that is:

\( \alpha = P(\bar{X} \ge k^*) \text{ when } \mu = 10 \)

Because the critical region C defines a test that is most powerful against each simple alternative \(\mu_a > 10\), this is a uniformly most powerful test, and C is a uniformly most powerful critical region of size \(\alpha\).

One and Two Tailed Tests

Suppose we have a null hypothesis H 0 and an alternative hypothesis H 1 . We consider the distribution given by the null hypothesis and perform a test to determine whether or not the null hypothesis should be rejected in favour of the alternative hypothesis.

There are two different types of tests that can be performed. A one-tailed test looks for an increase or decrease in the parameter whereas a two-tailed test looks for any change in the parameter (which can be any change- increase or decrease).

We can perform the test at any level (usually 1%, 5% or 10%). For example, performing the test at a 5% level means that there is a 5% chance of wrongly rejecting H 0 .

If we perform the test at the 5% level and decide to reject the null hypothesis, we say "there is significant evidence at the 5% level to suggest the hypothesis is false".

One-Tailed Test

We choose a critical region. In a one-tailed test, the critical region will have just one part (the red area below). If our sample value lies in this region, we reject the null hypothesis in favour of the alternative.

Suppose we are looking for a definite decrease. Then the critical region will be to the left. Note, however, that in the one-tailed test the value of the parameter can be as high as you like.

Suppose we are given that X has a Poisson distribution and we want to carry out a hypothesis test on the mean, l, based upon a sample observation of 3.

Suppose the hypotheses are: H 0 : l = 9 H 1 : l < 9

We want to test if it is "reasonable" for the observed value of 3 to have come from a Poisson distribution with parameter 9. So what is the probability that a value as low as 3 has come from a Po(9)?

P(X < 3) = 0.0212 (this has come from a Poisson table)

The probability is less than 0.05, so there is less than a 5% chance that the value has come from a Poisson(3) distribution. We therefore reject the null hypothesis in favour of the alternative at the 5% level.

However, the probability is greater than 0.01, so we would not reject the null hypothesis in favour of the alternative at the 1% level.

Two-Tailed Test

In a two-tailed test, we are looking for either an increase or a decrease. So, for example, H 0 might be that the mean is equal to 9 (as before). This time, however, H 1 would be that the mean is not equal to 9. In this case, therefore, the critical region has two parts:

Lets test the parameter p of a Binomial distribution at the 10% level.

Suppose a coin is tossed 10 times and we get 7 heads. We want to test whether or not the coin is fair. If the coin is fair, p = 0.5 . Put this as the null hypothesis:

H 0 : p = 0.5 H 1 : p =(doesn' equal) 0.5

Now, because the test is 2-tailed, the critical region has two parts. Half of the critical region is to the right and half is to the left. So the critical region contains both the top 5% of the distribution and the bottom 5% of the distribution (since we are testing at the 10% level).

If H 0 is true, X ~ Bin(10, 0.5).

If the null hypothesis is true, what is the probability that X is 7 or above? P(X > 7) = 1 - P(X < 7) = 1 - P(X < 6) = 1 - 0.8281 = 0.1719

Is this in the critical region? No- because the probability that X is at least 7 is not less than 0.05 (5%), which is what we need it to be.

So there is not significant evidence at the 10% level to reject the null hypothesis.