literature review particle swarm optimization

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 10 April 2024

A hybrid particle swarm optimization algorithm for solving engineering problem

• Jinwei Qiao 1 , 2 ,
• Guangyuan Wang 1 , 2 ,
• Zhi Yang 1 , 2 ,
• Xiaochuan Luo 3 ,
• Jun Chen 1 , 2 ,
• Kan Li 4 &
• Pengbo Liu 1 , 2  

Scientific Reports volume  14 , Article number:  8357 ( 2024 ) Cite this article

94 Accesses

Metrics details

• Computational science
• Mechanical engineering

To overcome the disadvantages of premature convergence and easy trapping into local optimum solutions, this paper proposes an improved particle swarm optimization algorithm (named NDWPSO algorithm) based on multiple hybrid strategies. Firstly, the elite opposition-based learning method is utilized to initialize the particle position matrix. Secondly, the dynamic inertial weight parameters are given to improve the global search speed in the early iterative phase. Thirdly, a new local optimal jump-out strategy is proposed to overcome the "premature" problem. Finally, the algorithm applies the spiral shrinkage search strategy from the whale optimization algorithm (WOA) and the Differential Evolution (DE) mutation strategy in the later iteration to accelerate the convergence speed. The NDWPSO is further compared with other 8 well-known nature-inspired algorithms (3 PSO variants and 5 other intelligent algorithms) on 23 benchmark test functions and three practical engineering problems. Simulation results prove that the NDWPSO algorithm obtains better results for all 49 sets of data than the other 3 PSO variants. Compared with 5 other intelligent algorithms, the NDWPSO obtains 69.2%, 84.6%, and 84.6% of the best results for the benchmark function ( \({f}_{1}-{f}_{13}\) ) with 3 kinds of dimensional spaces (Dim = 30,50,100) and 80% of the best optimal solutions for 10 fixed-multimodal benchmark functions. Also, the best design solutions are obtained by NDWPSO for all 3 classical practical engineering problems.

Similar content being viewed by others

A clustering-based competitive particle swarm optimization with grid ranking for multi-objective optimization problems

Qianlin Ye, Zheng Wang, … Mengjiao Yu

A modified shuffled frog leaping algorithm with inertia weight

Zhuanzhe Zhao, Mengxian Wang, … Zhibo Liu

Appropriate noise addition to metaheuristic algorithms can enhance their performance

Kwok Pui Choi, Enzio Hai Hong Kam, … Weng Kee Wong

Introduction

In the ever-changing society, new optimization problems arise every moment, and they are distributed in various fields, such as automation control 1 , statistical physics 2 , security prevention and temperature prediction 3 , artificial intelligence 4 , and telecommunication technology 5 . Faced with a constant stream of practical engineering optimization problems, traditional solution methods gradually lose their efficiency and convenience, making it more and more expensive to solve the problems. Therefore, researchers have developed many metaheuristic algorithms and successfully applied them to the solution of optimization problems. Among them, Particle swarm optimization (PSO) algorithm 6 is one of the most widely used swarm intelligence algorithms.

However, the basic PSO has a simple operating principle and solves problems with high efficiency and good computational performance, but it suffers from the disadvantages of easily trapping in local optima and premature convergence. To improve the overall performance of the particle swarm algorithm, an improved particle swarm optimization algorithm is proposed by the multiple hybrid strategy in this paper. The improved PSO incorporates the search ideas of other intelligent algorithms (DE, WOA), so the improved algorithm proposed in this paper is named NDWPSO. The main improvement schemes are divided into the following 4 points: Firstly, a strategy of elite opposition-based learning is introduced into the particle population position initialization. A high-quality initialization matrix of population position can improve the convergence speed of the algorithm. Secondly, a dynamic weight methodology is adopted for the acceleration coefficients by combining the iterative map and linearly transformed method. This method utilizes the chaotic nature of the mapping function, the fast convergence capability of the dynamic weighting scheme, and the time-varying property of the acceleration coefficients. Thus, the global search and local search of the algorithm are balanced and the global search speed of the population is improved. Thirdly, a determination mechanism is set up to detect whether the algorithm falls into a local optimum. When the algorithm is “premature”, the population resets 40% of the position information to overcome the local optimum. Finally, the spiral shrinking mechanism combined with the DE/best/2 position mutation is used in the later iteration, which further improves the solution accuracy.

The structure of the paper is given as follows: Sect. “ Particle swarm optimization (PSO) ” describes the principle of the particle swarm algorithm. Section “ Improved particle swarm optimization algorithm ” shows the detailed improvement strategy and a comparison experiment of inertia weight is set up for the proposed NDWPSO. Section “ Experiment and discussion ” includes the experimental and result discussion sections on the performance of the improved algorithm. Section “ Conclusions and future works ” summarizes the main findings of this study.

Literature review

This section reviews some metaheuristic algorithms and other improved PSO algorithms. A simple discussion about recently proposed research studies is given.

Metaheuristic algorithms

A series of metaheuristic algorithms have been proposed in recent years by using various innovative approaches. For instance, Lin et al. 7 proposed a novel artificial bee colony algorithm (ABCLGII) in 2018 and compared ABCLGII with other outstanding ABC variants on 52 frequently used test functions. Abed-alguni et al. 8 proposed an exploratory cuckoo search (ECS) algorithm in 2021 and carried out several experiments to investigate the performance of ECS by 14 benchmark functions. Brajević 9 presented a novel shuffle-based artificial bee colony (SB-ABC) algorithm for solving integer programming and minimax problems in 2021. The experiments are tested on 7 integer programming problems and 10 minimax problems. In 2022, Khan et al. 10 proposed a non-deterministic meta-heuristic algorithm called Non-linear Activated Beetle Antennae Search (NABAS) for a non-convex tax-aware portfolio selection problem. Brajević et al. 11 proposed a hybridization of the sine cosine algorithm (HSCA) in 2022 to solve 15 complex structural and mechanical engineering design optimization problems. Abed-Alguni et al. 12 proposed an improved Salp Swarm Algorithm (ISSA) in 2022 for single-objective continuous optimization problems. A set of 14 standard benchmark functions was used to evaluate the performance of ISSA. In 2023, Nadimi et al. 13 proposed a binary starling murmuration optimization (BSMO) to select the effective features from different important diseases. In the same year, Nadimi et al. 14 systematically reviewed the last 5 years' developments of WOA and made a critical analysis of those WOA variants. In 2024, Fatahi et al. 15 proposed an Improved Binary Quantum-based Avian Navigation Optimizer Algorithm (IBQANA) for the Feature Subset Selection problem in the medical area. Experimental evaluation on 12 medical datasets demonstrates that IBQANA outperforms 7 established algorithms. Abed-alguni et al. 16 proposed an Improved Binary DJaya Algorithm (IBJA) to solve the Feature Selection problem in 2024. The IBJA’s performance was compared against 4 ML classifiers and 10 efficient optimization algorithms.

Improved PSO algorithms

Many researchers have constantly proposed some improved PSO algorithms to solve engineering problems in different fields. For instance, Yeh 17 proposed an improved particle swarm algorithm, which combines a new self-boundary search and a bivariate update mechanism, to solve the reliability redundancy allocation problem (RRAP) problem. Solomon et al. 18 designed a collaborative multi-group particle swarm algorithm with high parallelism that was used to test the adaptability of Graphics Processing Units (GPUs) in distributed computing environments. Mukhopadhyay and Banerjee 19 proposed a chaotic multi-group particle swarm optimization (CMS-PSO) to estimate the unknown parameters of an autonomous chaotic laser system. Duan et al. 20 designed an improved particle swarm algorithm with nonlinear adjustment of inertia weights to improve the coupling accuracy between laser diodes and single-mode fibers. Sun et al. 21 proposed a particle swarm optimization algorithm combined with non-Gaussian stochastic distribution for the optimal design of wind turbine blades. Based on a multiple swarm scheme, Liu et al. 22 proposed an improved particle swarm optimization algorithm to predict the temperatures of steel billets for the reheating furnace. In 2022, Gad 23 analyzed the existing 2140 papers on Swarm Intelligence between 2017 and 2019 and pointed out that the PSO algorithm still needs further research. In general, the improved methods can be classified into four categories:

Adjusting the distribution of algorithm parameters. Feng et al. 24 used a nonlinear adaptive method on inertia weights to balance local and global search and introduced asynchronously varying acceleration coefficients.

Changing the updating formula of the particle swarm position. Both papers 25 and 26 used chaotic mapping functions to update the inertia weight parameters and combined them with a dynamic weighting strategy to update the particle swarm positions. This improved approach enables the particle swarm algorithm to be equipped with fast convergence of performance.

The initialization of the swarm. Alsaidy and Abbood proposed 27 a hybrid task scheduling algorithm that replaced the random initialization of the meta-heuristic algorithm with the heuristic algorithms MCT-PSO and LJFP-PSO.

Combining with other intelligent algorithms: Liu et al. 28 introduced the differential evolution (DE) algorithm into PSO to increase the particle swarm as diversity and reduce the probability of the population falling into local optimum.

Particle swarm optimization (PSO)

The particle swarm optimization algorithm is a population intelligence algorithm for solving continuous and discrete optimization problems. It originated from the social behavior of individuals in bird and fish flocks 6 . The core of the PSO algorithm is that an individual particle identifies potential solutions by flight in a defined constraint space adjusts its exploration direction to approach the global optimal solution based on the shared information among the group, and finally solves the optimization problem. Each particle \(i\) includes two attributes: velocity vector \({V}_{i}=\left[{v}_{i1},{v}_{i2},{v}_{i3},{...,v}_{ij},{...,v}_{iD},\right]\) and position vector \({X}_{i}=[{x}_{i1},{x}_{i2},{x}_{i3},...,{x}_{ij},...,{x}_{iD}]\) . The velocity vector is used to modify the motion path of the swarm; the position vector represents a potential solution for the optimization problem. Here, \(j=\mathrm{1,2},\dots ,D\) , \(D\) represents the dimension of the constraint space. The equations for updating the velocity and position of the particle swarm are shown in Eqs. ( 1 ) and ( 2 ).

Here \({Pbest}_{i}^{k}\) represents the previous optimal position of the particle \(i\) , and \({Gbest}\) is the optimal position discovered by the whole population. \(i=\mathrm{1,2},\dots ,n\) , \(n\) denotes the size of the particle swarm. \({c}_{1}\) and \({c}_{2}\) are the acceleration constants, which are used to adjust the search step of the particle 29 . \({r}_{1}\) and \({r}_{2}\) are two random uniform values distributed in the range \([\mathrm{0,1}]\) , which are used to improve the randomness of the particle search. \(\omega\) inertia weight parameter, which is used to adjust the scale of the search range of the particle swarm 30 . The basic PSO sets the inertia weight parameter as a time-varying parameter to balance global exploration and local seeking. The updated equation of the inertia weight parameter is given as follows:

where \({\omega }_{max}\) and \({\omega }_{min}\) represent the upper and lower limits of the range of inertia weight parameter. \(k\) and \(Mk\) are the current iteration and maximum iteration.

Improved particle swarm optimization algorithm

According to the no free lunch theory 31 , it is known that no algorithm can solve every practical problem with high quality and efficiency for increasingly complex and diverse optimization problems. In this section, several improvement strategies are proposed to improve the search efficiency and overcome this shortcoming of the basic PSO algorithm.

Improvement strategies

The optimization strategies of the improved PSO algorithm are shown as follows:

The inertia weight parameter is updated by an improved chaotic variables method instead of a linear decreasing strategy. Chaotic mapping performs the whole search at a higher speed and is more resistant to falling into local optimal than the probability-dependent random search 32 . However, the population may result in that particles can easily fly out of the global optimum boundary. To ensure that the population can converge to the global optimum, an improved Iterative mapping is adopted and shown as follows:

Here \({\omega }_{k}\) is the inertia weight parameter in the iteration \(k\) , \(b\) is the control parameter in the range \([\mathrm{0,1}]\) .

The acceleration coefficients are updated by the linear transformation. \({c}_{1}\) and \({c}_{2}\) represent the influential coefficients of the particles by their own and population information, respectively. To improve the search performance of the population, \({c}_{1}\) and \({c}_{2}\) are changed from fixed values to time-varying parameter parameters, that are updated by linear transformation with the number of iterations:

where \({c}_{max}\) and \({c}_{min}\) are the maximum and minimum values of acceleration coefficients, respectively.

The initialization scheme is determined by elite opposition-based learning . The high-quality initial population will accelerate the solution speed of the algorithm and improve the accuracy of the optimal solution. Thus, the elite backward learning strategy 33 is introduced to generate the position matrix of the initial population. Suppose the elite individual of the population is \({X}=[{x}_{1},{x}_{2},{x}_{3},...,{x}_{j},...,{x}_{D}]\) , and the elite opposition-based solution of \(X\) is \({X}_{o}=[{x}_{{\text{o}}1},{x}_{{\text{o}}2},{x}_{{\text{o}}3},...,{x}_{oj},...,{x}_{oD}]\) . The formula for the elite opposition-based solution is as follows:

where \({k}_{r}\) is the random value in the range \((\mathrm{0,1})\) . \({ux}_{oij}\) and \({lx}_{oij}\) are dynamic boundaries of the elite opposition-based solution in \(j\) dimensional variables. The advantage of dynamic boundary is to reduce the exploration space of particles, which is beneficial to the convergence of the algorithm. When the elite opposition-based solution is out of bounds, the out-of-bounds processing is performed. The equation is given as follows:

After calculating the fitness function values of the elite solution and the elite opposition-based solution, respectively, \(n\) high quality solutions were selected to form a new initial population position matrix.

The position updating Eq. ( 2 ) is modified based on the strategy of dynamic weight. To improve the speed of the global search of the population, the strategy of dynamic weight from the artificial bee colony algorithm 34 is introduced to enhance the computational performance. The new position updating equation is shown as follows:

Here \(\rho\) is the random value in the range \((\mathrm{0,1})\) . \(\psi\) represents the acceleration coefficient and \({\omega }{\prime}\) is the dynamic weight coefficient. The updated equations of the above parameters are as follows:

where \(f(i)\) denotes the fitness function value of individual particle \(i\) and u is the average of the population fitness function values in the current iteration. The Eqs. ( 11 , 12 ) are introduced into the position updating equation. And they can attract the particle towards positions of the best-so-far solution in the search space.

New local optimal jump-out strategy is added for escaping from the local optimal. When the value of the fitness function for the population optimal particles does not change in M iterations, the algorithm determines that the population falls into a local optimal. The scheme in which the population jumps out of the local optimum is to reset the position information of the 40% of individuals within the population, in other words, to randomly generate the position vector in the search space. M is set to 5% of the maximum number of iterations.

New spiral update search strategy is added after the local optimal jump-out strategy. Since the whale optimization algorithm (WOA) was good at exploring the local search space 35 , the spiral update search strategy in the WOA 36 is introduced to update the position of the particles after the swarm jumps out of local optimal. The equation for the spiral update is as follows:

Here \(D=\left|{x}_{i}\left(k\right)-Gbest\right|\) denotes the distance between the particle itself and the global optimal solution so far. \(B\) is the constant that defines the shape of the logarithmic spiral. \(l\) is the random value in \([-\mathrm{1,1}]\) . \(l\) represents the distance between the newly generated particle and the global optimal position, \(l=-1\) means the closest distance, while \(l=1\) means the farthest distance, and the meaning of this parameter can be directly observed by Fig.  1 .

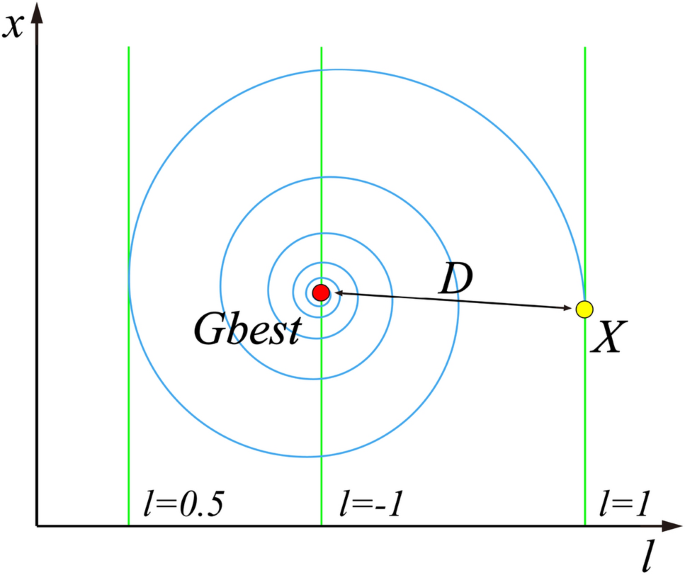
Spiral updating position.

The DE/best/2 mutation strategy is introduced to form the mutant particle. 4 individuals in the population are randomly selected that differ from the current particle, then the vector difference between them is rescaled, and the difference vector is combined with the global optimal position to form the mutant particle. The equation for mutation of particle position is shown as follows:

where \({x}^{*}\) is the mutated particle, \(F\) is the scale factor of mutation, \({r}_{1}\) , \({r}_{2}\) , \({r}_{3}\) , \({r}_{4}\) are random integer values in \((0,n]\) and not equal to \(i\) , respectively. Specific particles are selected for mutation with the screening conditions as follows:

where \(Cr\) represents the probability of mutation, \(rand\left(\mathrm{0,1}\right)\) is a random number in \(\left(\mathrm{0,1}\right)\) , and \({i}_{rand}\) is a random integer value in \((0,n]\) .

The improved PSO incorporates the search ideas of other intelligent algorithms (DE, WOA), so the improved algorithm proposed in this paper is named NDWPSO. The pseudo-code for the NDWPSO algorithm is given as follows:

The main procedure of NDWPSO.

Comparing the distribution of inertia weight parameters

There are several improved PSO algorithms (such as CDWPSO 25 , and SDWPSO 26 ) that adopt the dynamic weighted particle position update strategy as their improvement strategy. The updated equations of the CDWPSO and the SDWPSO algorithm for the inertia weight parameters are given as follows:

where \({\text{A}}\) is a value in \((\mathrm{0,1}]\) . \({r}_{max}\) and \({r}_{min}\) are the upper and lower limits of the fluctuation range of the inertia weight parameters, \(k\) is the current number of algorithm iterations, and \(Mk\) denotes the maximum number of iterations.

Considering that the update method of inertia weight parameters by our proposed NDWPSO is comparable to the CDWPSO, and SDWPSO, a comparison experiment for the distribution of inertia weight parameters is set up in this section. The maximum number of iterations in the experiment is \(Mk=500\) . The distributions of CDWPSO, SDWPSO, and NDWPSO inertia weights are shown sequentially in Fig.  2 .

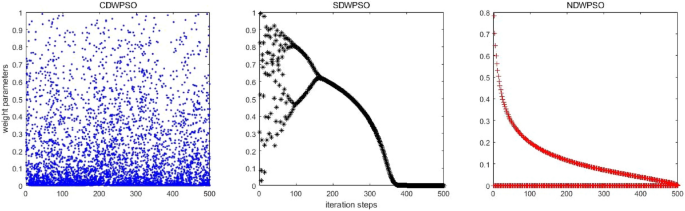
The inertial weight distribution of CDWPSO, SDWPSO, and NDWPSO.

In Fig.  2 , the inertia weight value of CDWPSO is a random value in (0,1]. It may make individual particles fly out of the range in the late iteration of the algorithm. Similarly, the inertia weight value of SDWPSO is a value that tends to zero infinitely, so that the swarm no longer can fly in the search space, making the algorithm extremely easy to fall into the local optimal value. On the other hand, the distribution of the inertia weights of the NDWPSO forms a gentle slope by two curves. Thus, the swarm can faster lock the global optimum range in the early iterations and locate the global optimal more precisely in the late iterations. The reason is that the inertia weight values between two adjacent iterations are inversely proportional to each other. Besides, the time-varying part of the inertial weight within NDWPSO is designed to reduce the chaos characteristic of the parameters. The inertia weight value of NDWPSO avoids the disadvantages of the above two schemes, so its design is more reasonable.

Experiment and discussion

In this section, three experiments are set up to evaluate the performance of NDWPSO: (1) the experiment of 23 classical functions 37 between NDWPSO and three particle swarm algorithms (PSO 6 , CDWPSO 25 , SDWPSO 26 ); (2) the experiment of benchmark test functions between NDWPSO and other intelligent algorithms (Whale Optimization Algorithm (WOA) 36 , Harris Hawk Algorithm (HHO) 38 , Gray Wolf Optimization Algorithm (GWO) 39 , Archimedes Algorithm (AOA) 40 , Equilibrium Optimizer (EO) 41 and Differential Evolution (DE) 42 ); (3) the experiment for solving three real engineering problems (welded beam design 43 , pressure vessel design 44 , and three-bar truss design 38 ). All experiments are run on a computer with Intel i5-11400F GPU, 2.60 GHz, 16 GB RAM, and the code is written with MATLAB R2017b.

The benchmark test functions are 23 classical functions, which consist of indefinite unimodal (F1–F7), indefinite dimensional multimodal functions (F8–F13), and fixed-dimensional multimodal functions (F14–F23). The unimodal benchmark function is used to evaluate the global search performance of different algorithms, while the multimodal benchmark function reflects the ability of the algorithm to escape from the local optimal. The mathematical equations of the benchmark functions are shown and found as Supplementary Tables S1 – S3 online.

Experiments on benchmark functions between NDWPSO, and other PSO variants

The purpose of the experiment is to show the performance advantages of the NDWPSO algorithm. Here, the dimensions and corresponding population sizes of 13 benchmark functions (7 unimodal and 6 multimodal) are set to (30, 40), (50, 70), and (100, 130). The population size of 10 fixed multimodal functions is set to 40. Each algorithm is repeated 30 times independently, and the maximum number of iterations is 200. The performance of the algorithm is measured by the mean and the standard deviation (SD) of the results for different benchmark functions. The parameters of the NDWPSO are set as: \({[{\omega }_{min},\omega }_{max}]=[\mathrm{0.4,0.9}]\) , \(\left[{c}_{max},{c}_{min}\right]=\left[\mathrm{2.5,1.5}\right],{V}_{max}=0.1,b={e}^{-50}, M=0.05\times Mk, B=1,F=0.7, Cr=0.9.\) And, \(A={\omega }_{max}\) for CDWPSO; \({[r}_{max},{r}_{min}]=[\mathrm{4,0}]\) for SDWPSO.

Besides, the experimental data are retained to two decimal places, but some experimental data will increase the number of retained data to pursue more accuracy in comparison. The best results in each group of experiments will be displayed in bold font. The experimental data is set to 0 if the value is below 10 –323 . The experimental parameter settings in this paper are different from the references (PSO 6 , CDWPSO 25 , SDWPSO 26 , so the final experimental data differ from the ones within the reference.

As shown in Tables 1 and 2 , the NDWPSO algorithm obtains better results for all 49 sets of data than other PSO variants, which include not only 13 indefinite-dimensional benchmark functions and 10 fixed-multimodal benchmark functions. Remarkably, the SDWPSO algorithm obtains the same accuracy of calculation as NDWPSO for both unimodal functions f 1 –f 4 and multimodal functions f 9 –f 11 . The solution accuracy of NDWPSO is higher than that of other PSO variants for fixed-multimodal benchmark functions f 14 -f 23 . The conclusion can be drawn that the NDWPSO has excellent global search capability, local search capability, and the capability for escaping the local optimal.

In addition, the convergence curves of the 23 benchmark functions are shown in Figs. 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 and 19 . The NDWPSO algorithm has a faster convergence speed in the early stage of the search for processing functions f1-f6, f8-f14, f16, f17, and finds the global optimal solution with a smaller number of iterations. In the remaining benchmark function experiments, the NDWPSO algorithm shows no outstanding performance for convergence speed in the early iterations. There are two reasons of no outstanding performance in the early iterations. On one hand, the fixed-multimodal benchmark function has many disturbances and local optimal solutions in the whole search space. on the other hand, the initialization scheme based on elite opposition-based learning is still stochastic, which leads to the initial position far from the global optimal solution. The inertia weight based on chaotic mapping and the strategy of spiral updating can significantly improve the convergence speed and computational accuracy of the algorithm in the late search stage. Finally, the NDWPSO algorithm can find better solutions than other algorithms in the middle and late stages of the search.

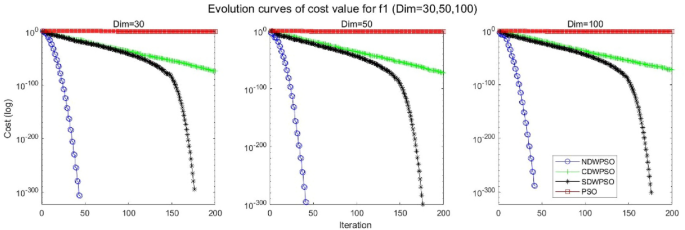
Evolution curve of NDWPSO and other PSO algorithms for f1 (Dim = 30,50,100).

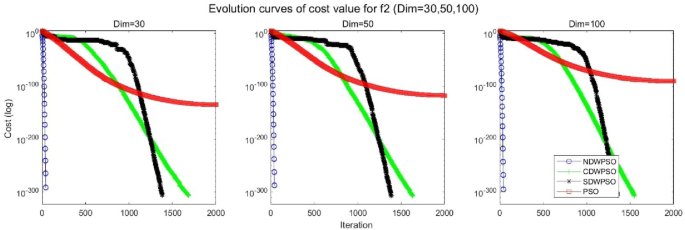
Evolution curve of NDWPSO and other PSO algorithms for f2 (Dim = 30,50,100).

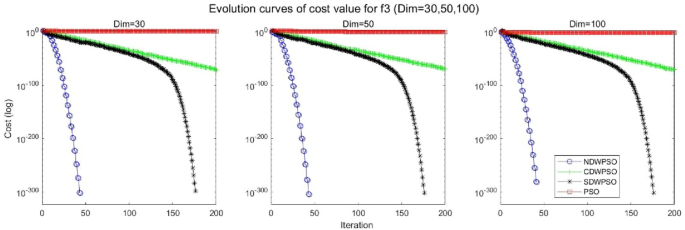
Evolution curve of NDWPSO and other PSO algorithms for f3 (Dim = 30,50,100).

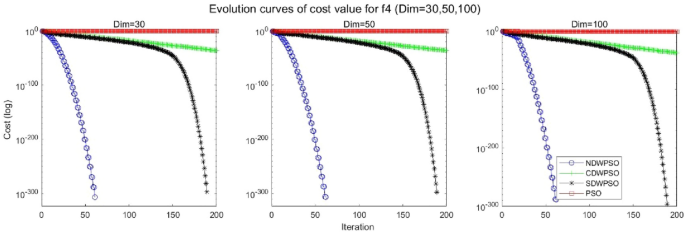
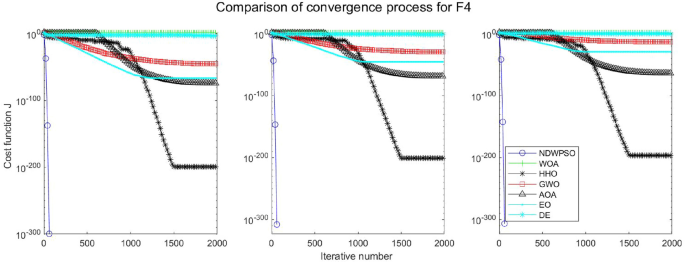
Evolution curve of NDWPSO and other PSO algorithms for f4 (Dim = 30,50,100).

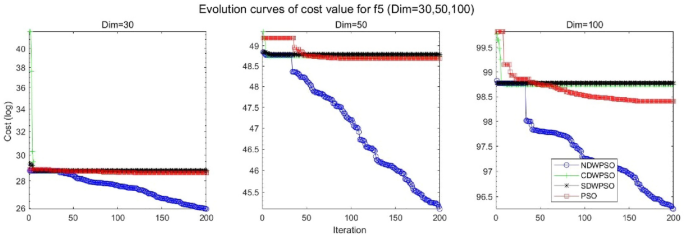
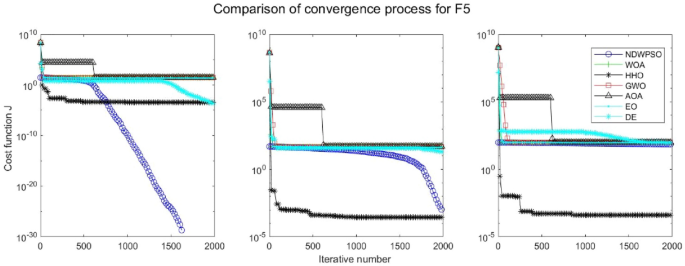
Evolution curve of NDWPSO and other PSO algorithms for f5 (Dim = 30,50,100).

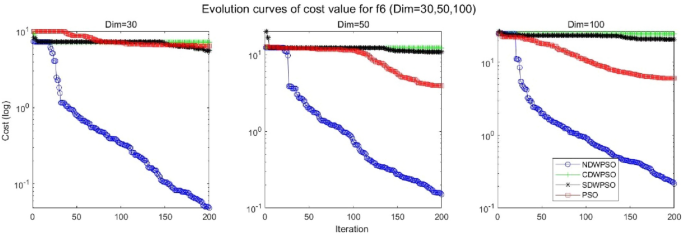
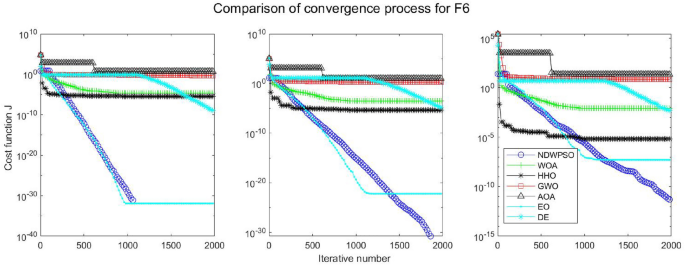
Evolution curve of NDWPSO and other PSO algorithms for f6 (Dim = 30,50,100).

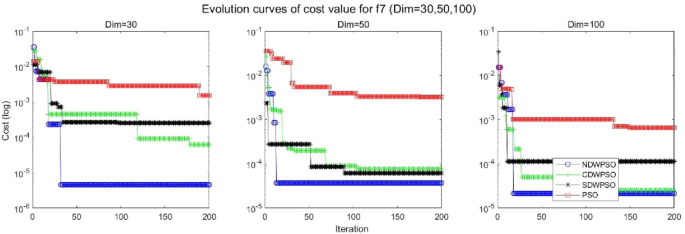
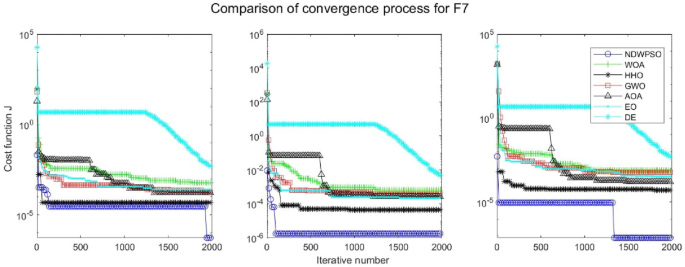
Evolution curve of NDWPSO and other PSO algorithms for f7 (Dim = 30,50,100).

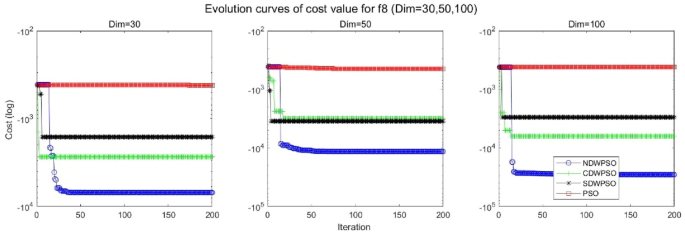
Evolution curve of NDWPSO and other PSO algorithms for f8 (Dim = 30,50,100).

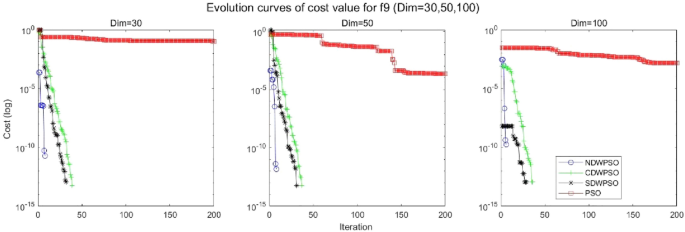
Evolution curve of NDWPSO and other PSO algorithms for f9 (Dim = 30,50,100).

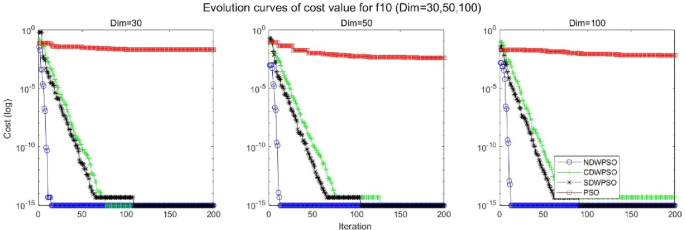
Evolution curve of NDWPSO and other PSO algorithms for f10 (Dim = 30,50,100).

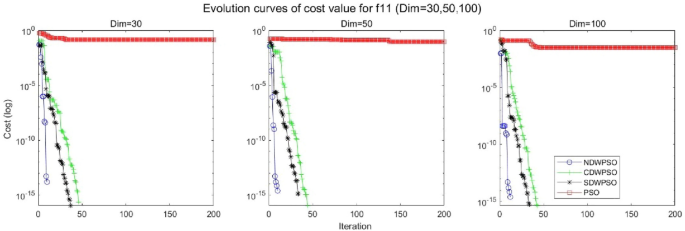
Evolution curve of NDWPSO and other PSO algorithms for f11(Dim = 30,50,100).

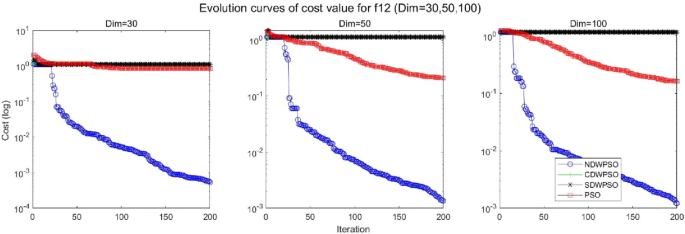
Evolution curve of NDWPSO and other PSO algorithms for f12 (Dim = 30,50,100).

Evolution curve of NDWPSO and other PSO algorithms for f13 (Dim = 30,50,100).

Evolution curve of NDWPSO and other PSO algorithms for f14, f15, f16.

Evolution curve of NDWPSO and other PSO algorithms for f17, f18, f19.

Evolution curve of NDWPSO and other PSO algorithms for f20, f21, f22.

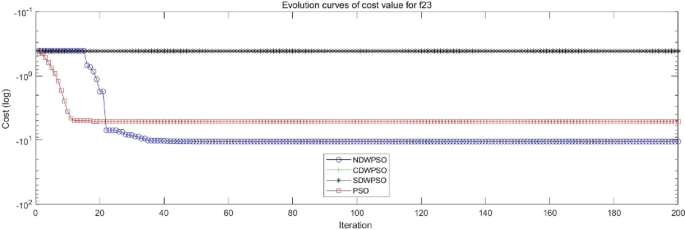
Evolution curve of NDWPSO and other PSO algorithms for f23.

To evaluate the performance of different PSO algorithms, a statistical test is conducted. Due to the stochastic nature of the meta-heuristics, it is not enough to compare algorithms based on only the mean and standard deviation values. The optimization results cannot be assumed to obey the normal distribution; thus, it is necessary to judge whether the results of the algorithms differ from each other in a statistically significant way. Here, the Wilcoxon non-parametric statistical test 45 is used to obtain a parameter called p -value to verify whether two sets of solutions are different to a statistically significant extent or not. Generally, it is considered that p  ≤ 0.5 can be considered as a statistically significant superiority of the results. The p -values calculated in Wilcoxon’s rank-sum test comparing NDWPSO and other PSO algorithms are listed in Table  3 for all benchmark functions. The p -values in Table  3 additionally present the superiority of the NDWPSO because all of the p -values are much smaller than 0.5.

In general, the NDWPSO has the fastest convergence rate when finding the global optimum from Figs. 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 and 19 , and thus we can conclude that the NDWPSO is superior to the other PSO variants during the process of optimization.

Comparison experiments between NDWPSO and other intelligent algorithms

Experiments are conducted to compare NDWPSO with several other intelligent algorithms (WOA, HHO, GWO, AOA, EO and DE). The experimental object is 23 benchmark functions, and the experimental parameters of the NDWPSO algorithm are set the same as in Experiment 4.1. The maximum number of iterations of the experiment is increased to 2000 to fully demonstrate the performance of each algorithm. Each algorithm is repeated 30 times individually. The parameters of the relevant intelligent algorithms in the experiments are set as shown in Table 4 . To ensure the fairness of the algorithm comparison, all parameters are concerning the original parameters in the relevant algorithm literature. The experimental results are shown in Tables 5 , 6 , 7 and 8 and Figs. 20 , 21 , 22 , 23 , 24 , 25 , 26 , 27 , 28 , 29 , 30 , 31 , 32 , 33 , 34 , 35 and 36 .

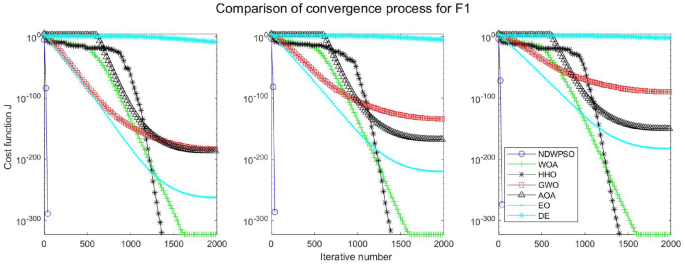
Evolution curve of NDWPSO and other algorithms for f1 (Dim = 30,50,100).

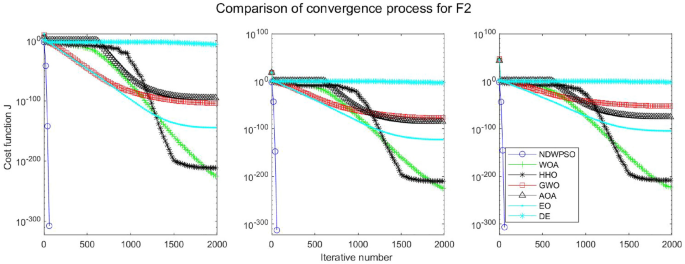
Evolution curve of NDWPSO and other algorithms for f2 (Dim = 30,50,100).

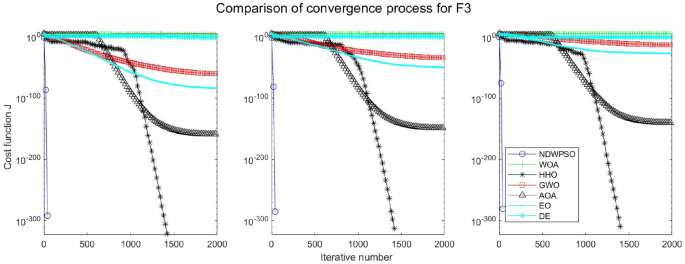
Evolution curve of NDWPSO and other algorithms for f3(Dim = 30,50,100).

Evolution curve of NDWPSO and other algorithms for f4 (Dim = 30,50,100).

Evolution curve of NDWPSO and other algorithms for f5 (Dim = 30,50,100).

Evolution curve of NDWPSO and other algorithms for f6 (Dim = 30,50,100).

Evolution curve of NDWPSO and other algorithms for f7 (Dim = 30,50,100).

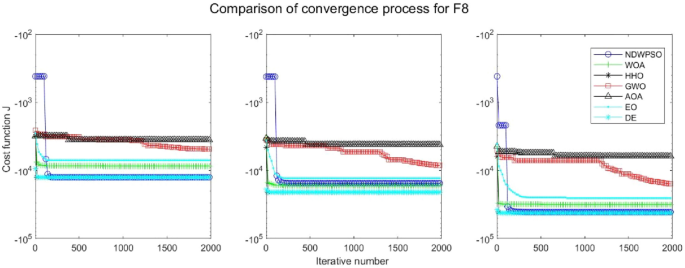
Evolution curve of NDWPSO and other algorithms for f8 (Dim = 30,50,100).

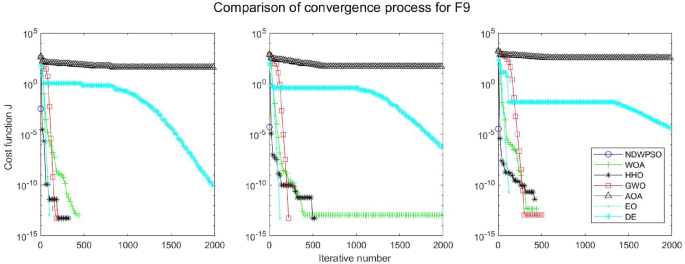
Evolution curve of NDWPSO and other algorithms for f9(Dim = 30,50,100).

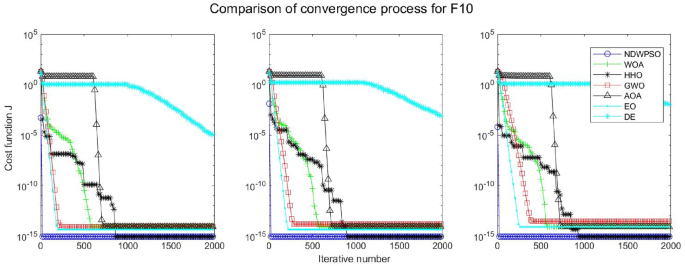
Evolution curve of NDWPSO and other algorithms for f10 (Dim = 30,50,100).

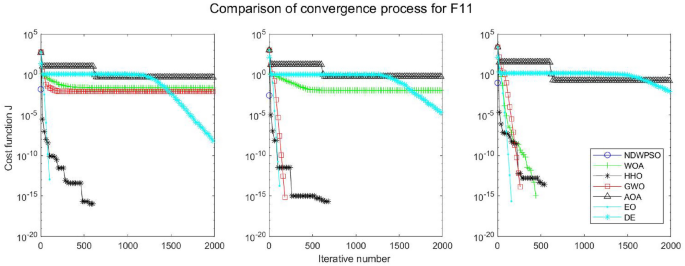
Evolution curve of NDWPSO and other algorithms for f11 (Dim = 30,50,100).

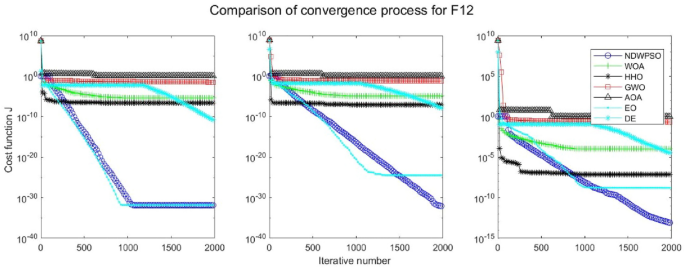
Evolution curve of NDWPSO and other algorithms for f12 (Dim = 30,50,100).

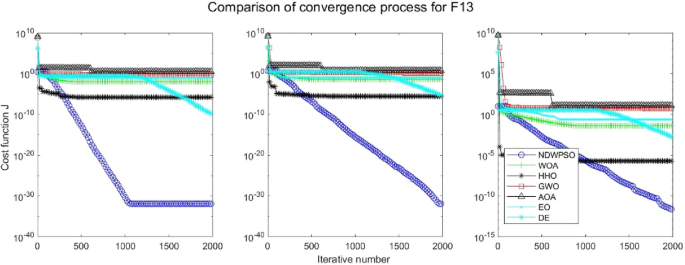
Evolution curve of NDWPSO and other algorithms for f13 (Dim = 30,50,100).

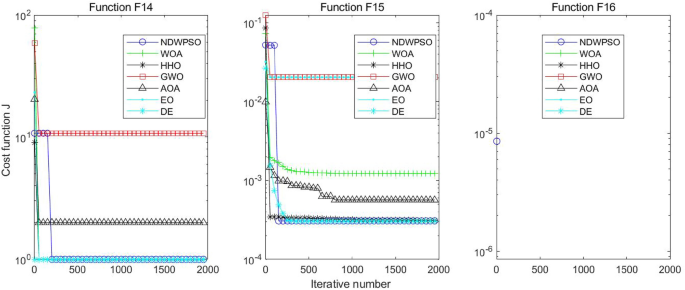
Evolution curve of NDWPSO and other algorithms for f14, f15, f16.

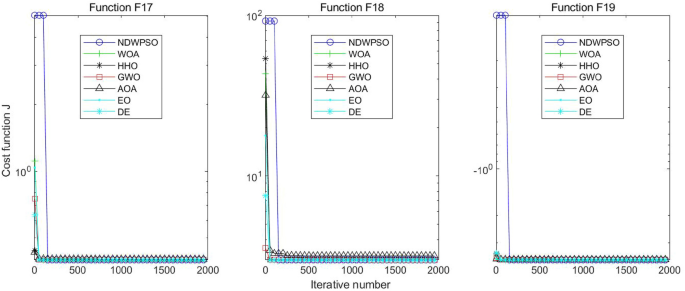
Evolution curve of NDWPSO and other algorithms for f17, f18, f19.

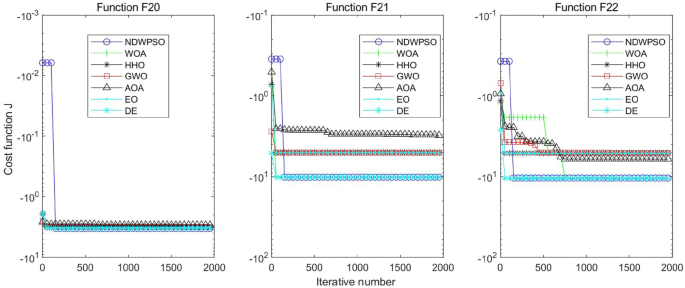
Evolution curve of NDWPSO and other algorithms for f20, f21, f22.

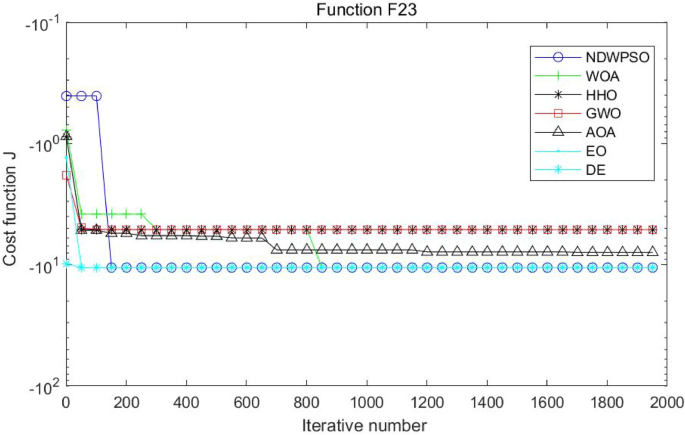
Evolution curve of NDWPSO and other algorithms for f23.

The experimental data of NDWPSO and other intelligent algorithms for handling 30, 50, and 100-dimensional benchmark functions ( \({f}_{1}-{f}_{13}\) ) are recorded in Tables 8 , 9 and 10 , respectively. The comparison data of fixed-multimodal benchmark tests ( \({f}_{14}-{f}_{23}\) ) are recorded in Table 11 . According to the data in Tables 5 , 6 and 7 , the NDWPSO algorithm obtains 69.2%, 84.6%, and 84.6% of the best results for the benchmark function ( \({f}_{1}-{f}_{13}\) ) in the search space of three dimensions (Dim = 30, 50, 100), respectively. In Table 8 , the NDWPSO algorithm obtains 80% of the optimal solutions in 10 fixed-multimodal benchmark functions.

The convergence curves of each algorithm are shown in Figs. 20 , 21 , 22 , 23 , 24 , 25 , 26 , 27 , 28 , 29 , 30 , 31 , 32 , 33 , 34 , 35 and 36 . The NDWPSO algorithm demonstrates two convergence behaviors when calculating the benchmark functions in 30, 50, and 100-dimensional search spaces. The first behavior is the fast convergence of NDWPSO with a small number of iterations at the beginning of the search. The reason is that the Iterative-mapping strategy and the position update scheme of dynamic weighting are used in the NDWPSO algorithm. This scheme can quickly target the region in the search space where the global optimum is located, and then precisely lock the optimal solution. When NDWPSO processes the functions \({f}_{1}-{f}_{4}\) , and \({f}_{9}-{f}_{11}\) , the behavior can be reflected in the convergence trend of their corresponding curves. The second behavior is that NDWPSO gradually improves the convergence accuracy and rapidly approaches the global optimal in the middle and late stages of the iteration. The NDWPSO algorithm fails to converge quickly in the early iterations, which is possible to prevent the swarm from falling into a local optimal. The behavior can be demonstrated by the convergence trend of the curves when NDWPSO handles the functions \({f}_{6}\) , \({f}_{12}\) , and \({f}_{13}\) , and it also shows that the NDWPSO algorithm has an excellent ability of local search.

Combining the experimental data with the convergence curves, it is concluded that the NDWPSO algorithm has a faster convergence speed, so the effectiveness and global convergence of the NDWPSO algorithm are more outstanding than other intelligent algorithms.

Experiments on classical engineering problems

Three constrained classical engineering design problems (welded beam design, pressure vessel design 43 , and three-bar truss design 38 ) are used to evaluate the NDWPSO algorithm. The experiments are the NDWPSO algorithm and 5 other intelligent algorithms (WOA 36 , HHO, GWO, AOA, EO 41 ). Each algorithm is provided with the maximum number of iterations and population size ( \({\text{Mk}}=500,\mathrm{ n}=40\) ), and then repeats 30 times, independently. The parameters of the algorithms are set the same as in Table 4 . The experimental results of three engineering design problems are recorded in Tables 9 , 10 and 11 in turn. The result data is the average value of the solved data.

Welded beam design

The target of the welded beam design problem is to find the optimal manufacturing cost for the welded beam with the constraints, as shown in Fig.  37 . The constraints are the thickness of the weld seam ( \({\text{h}}\) ), the length of the clamped bar ( \({\text{l}}\) ), the height of the bar ( \({\text{t}}\) ) and the thickness of the bar ( \({\text{b}}\) ). The mathematical formulation of the optimization problem is given as follows:

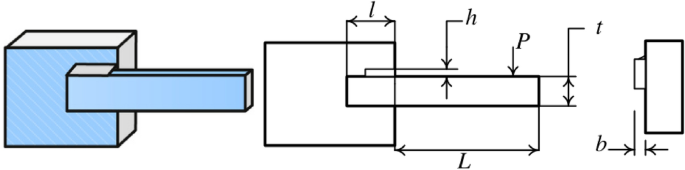
Welded beam design.

In Table 9 , the NDWPSO, GWO, and EO algorithms obtain the best optimal cost. Besides, the standard deviation (SD) of t NDWPSO is the lowest, which means it has very good results in solving the welded beam design problem.

Pressure vessel design

Kannan and Kramer 43 proposed the pressure vessel design problem as shown in Fig.  38 to minimize the total cost, including the cost of material, forming, and welding. There are four design optimized objects: the thickness of the shell \({T}_{s}\) ; the thickness of the head \({T}_{h}\) ; the inner radius \({\text{R}}\) ; the length of the cylindrical section without considering the head \({\text{L}}\) . The problem includes the objective function and constraints as follows:

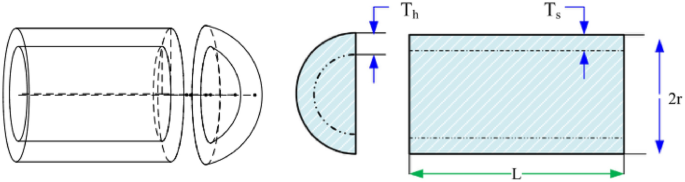
Pressure vessel design.

The results in Table 10 show that the NDWPSO algorithm obtains the lowest optimal cost with the same constraints and has the lowest standard deviation compared with other algorithms, which again proves the good performance of NDWPSO in terms of solution accuracy.

Three-bar truss design

This structural design problem 44 is one of the most widely-used case studies as shown in Fig.  39 . There are two main design parameters: the area of the bar1 and 3 ( \({A}_{1}={A}_{3}\) ) and area of bar 2 ( \({A}_{2}\) ). The objective is to minimize the weight of the truss. This problem is subject to several constraints as well: stress, deflection, and buckling constraints. The problem is formulated as follows:

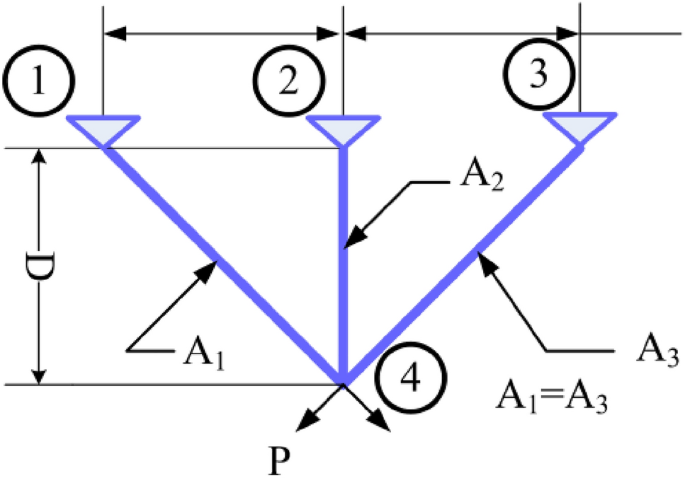
Three-bar truss design.

From Table 11 , NDWPSO obtains the best design solution in this engineering problem and has the smallest standard deviation of the result data. In summary, the NDWPSO can reveal very competitive results compared to other intelligent algorithms.

Conclusions and future works

An improved algorithm named NDWPSO is proposed to enhance the solving speed and improve the computational accuracy at the same time. The improved NDWPSO algorithm incorporates the search ideas of other intelligent algorithms (DE, WOA). Besides, we also proposed some new hybrid strategies to adjust the distribution of algorithm parameters (such as the inertia weight parameter, the acceleration coefficients, the initialization scheme, the position updating equation, and so on).

23 classical benchmark functions: indefinite unimodal (f1-f7), indefinite multimodal (f8-f13), and fixed-dimensional multimodal(f14-f23) are applied to evaluate the effective line and feasibility of the NDWPSO algorithm. Firstly, NDWPSO is compared with PSO, CDWPSO, and SDWPSO. The simulation results can prove the exploitative, exploratory, and local optima avoidance of NDWPSO. Secondly, the NDWPSO algorithm is compared with 5 other intelligent algorithms (WOA, HHO, GWO, AOA, EO). The NDWPSO algorithm also has better performance than other intelligent algorithms. Finally, 3 classical engineering problems are applied to prove that the NDWPSO algorithm shows superior results compared to other algorithms for the constrained engineering optimization problems.

Although the proposed NDWPSO is superior in many computation aspects, there are still some limitations and further improvements are needed. The NDWPSO performs a limit initialize on each particle by the strategy of “elite opposition-based learning”, it takes more computation time before speed update. Besides, the” local optimal jump-out” strategy also brings some random process. How to reduce the random process and how to improve the limit initialize efficiency are the issues that need to be further discussed. In addition, in future work, researchers will try to apply the NDWPSO algorithm to wider fields to solve more complex and diverse optimization problems.

Data availability

The datasets used and/or analyzed during the current study available from the corresponding author on reasonable request.

Sami, F. Optimize electric automation control using artificial intelligence (AI). Optik 271 , 170085 (2022).

Article   ADS   Google Scholar  

Li, X. et al. Prediction of electricity consumption during epidemic period based on improved particle swarm optimization algorithm. Energy Rep. 8 , 437–446 (2022).

Article   Google Scholar  

Sun, B. Adaptive modified ant colony optimization algorithm for global temperature perception of the underground tunnel fire. Case Stud. Therm. Eng. 40 , 102500 (2022).

Bartsch, G. et al. Use of artificial intelligence and machine learning algorithms with gene expression profiling to predict recurrent nonmuscle invasive urothelial carcinoma of the bladder. J. Urol. 195 (2), 493–498 (2016).

Article   PubMed   Google Scholar  

Bao, Z. Secure clustering strategy based on improved particle swarm optimization algorithm in internet of things. Comput. Intell. Neurosci. 2022 , 1–9 (2022).

Google Scholar  

Kennedy, J. & Eberhart, R. Particle swarm optimization. In: Proceedings of ICNN'95-International Conference on Neural Networks . IEEE, 1942–1948 (1995).

Lin, Q. et al. A novel artificial bee colony algorithm with local and global information interaction. Appl. Soft Comput. 62 , 702–735 (2018).

Abed-alguni, B. H. et al. Exploratory cuckoo search for solving single-objective optimization problems. Soft Comput. 25 (15), 10167–10180 (2021).

Brajević, I. A shuffle-based artificial bee colony algorithm for solving integer programming and minimax problems. Mathematics 9 (11), 1211 (2021).

Khan, A. T. et al. Non-linear activated beetle antennae search: A novel technique for non-convex tax-aware portfolio optimization problem. Expert Syst. Appl. 197 , 116631 (2022).

Brajević, I. et al. Hybrid sine cosine algorithm for solving engineering optimization problems. Mathematics 10 (23), 4555 (2022).

Abed-Alguni, B. H., Paul, D. & Hammad, R. Improved Salp swarm algorithm for solving single-objective continuous optimization problems. Appl. Intell. 52 (15), 17217–17236 (2022).

Nadimi-Shahraki, M. H. et al. Binary starling murmuration optimizer algorithm to select effective features from medical data. Appl. Sci. 13 (1), 564 (2022).

Nadimi-Shahraki, M. H. et al. A systematic review of the whale optimization algorithm: Theoretical foundation, improvements, and hybridizations. Archiv. Comput. Methods Eng. 30 (7), 4113–4159 (2023).

Fatahi, A., Nadimi-Shahraki, M. H. & Zamani, H. An improved binary quantum-based avian navigation optimizer algorithm to select effective feature subset from medical data: A COVID-19 case study. J. Bionic Eng. 21 (1), 426–446 (2024).

Abed-alguni, B. H. & AL-Jarah, S. H. IBJA: An improved binary DJaya algorithm for feature selection. J. Comput. Sci. 75 , 102201 (2024).

Yeh, W.-C. A novel boundary swarm optimization method for reliability redundancy allocation problems. Reliab. Eng. Syst. Saf. 192 , 106060 (2019).

Solomon, S., Thulasiraman, P. & Thulasiram, R. Collaborative multi-swarm PSO for task matching using graphics processing units. In: Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation 1563–1570 (2011).

Mukhopadhyay, S. & Banerjee, S. Global optimization of an optical chaotic system by chaotic multi swarm particle swarm optimization. Expert Syst. Appl. 39 (1), 917–924 (2012).

Duan, L. et al. Improved particle swarm optimization algorithm for enhanced coupling of coaxial optical communication laser. Opt. Fiber Technol. 64 , 102559 (2021).

Sun, F., Xu, Z. & Zhang, D. Optimization design of wind turbine blade based on an improved particle swarm optimization algorithm combined with non-gaussian distribution. Adv. Civ. Eng. 2021 , 1–9 (2021).

Liu, M. et al. An improved particle-swarm-optimization algorithm for a prediction model of steel slab temperature. Appl. Sci. 12 (22), 11550 (2022).

Article   MathSciNet   CAS   Google Scholar  

Gad, A. G. Particle swarm optimization algorithm and its applications: A systematic review. Archiv. Comput. Methods Eng. 29 (5), 2531–2561 (2022).

Article   MathSciNet   Google Scholar  

Feng, H. et al. Trajectory control of electro-hydraulic position servo system using improved PSO-PID controller. Autom. Constr. 127 , 103722 (2021).

Chen, Ke., Zhou, F. & Liu, A. Chaotic dynamic weight particle swarm optimization for numerical function optimization. Knowl. Based Syst. 139 , 23–40 (2018).

Bai, B. et al. Reliability prediction-based improved dynamic weight particle swarm optimization and back propagation neural network in engineering systems. Expert Syst. Appl. 177 , 114952 (2021).

Alsaidy, S. A., Abbood, A. D. & Sahib, M. A. Heuristic initialization of PSO task scheduling algorithm in cloud computing. J. King Saud Univ. –Comput. Inf. Sci. 34 (6), 2370–2382 (2022).

Liu, H., Cai, Z. & Wang, Y. Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization. Appl. Soft Comput. 10 (2), 629–640 (2010).

Deng, W. et al. A novel intelligent diagnosis method using optimal LS-SVM with improved PSO algorithm. Soft Comput. 23 , 2445–2462 (2019).

Huang, M. & Zhen, L. Research on mechanical fault prediction method based on multifeature fusion of vibration sensing data. Sensors 20 (1), 6 (2019).

Article   ADS   PubMed   PubMed Central   Google Scholar  

Wolpert, D. H. & Macready, W. G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1 (1), 67–82 (1997).

Gandomi, A. H. et al. Firefly algorithm with chaos. Commun. Nonlinear Sci. Numer. Simul. 18 (1), 89–98 (2013).

Article   ADS   MathSciNet   Google Scholar  

Zhou, Y., Wang, R. & Luo, Q. Elite opposition-based flower pollination algorithm. Neurocomputing 188 , 294–310 (2016).

Li, G., Niu, P. & Xiao, X. Development and investigation of efficient artificial bee colony algorithm for numerical function optimization. Appl. Soft Comput. 12 (1), 320–332 (2012).

Xiong, G. et al. Parameter extraction of solar photovoltaic models by means of a hybrid differential evolution with whale optimization algorithm. Solar Energy 176 , 742–761 (2018).

Mirjalili, S. & Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 95 , 51–67 (2016).

Yao, X., Liu, Y. & Lin, G. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 3 (2), 82–102 (1999).

Heidari, A. A. et al. Harris hawks optimization: Algorithm and applications. Fut. Gener. Comput. Syst. 97 , 849–872 (2019).

Mirjalili, S., Mirjalili, S. M. & Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 69 , 46–61 (2014).

Hashim, F. A. et al. Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Appl. Intell. 51 , 1531–1551 (2021).

Faramarzi, A. et al. Equilibrium optimizer: A novel optimization algorithm. Knowl. -Based Syst. 191 , 105190 (2020).

Pant, M. et al. Differential evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 90 , 103479 (2020).

Coello, C. A. C. Use of a self-adaptive penalty approach for engineering optimization problems. Comput. Ind. 41 (2), 113–127 (2000).

Kannan, B. K. & Kramer, S. N. An augmented lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design. J. Mech. Des. 116 , 405–411 (1994).

Derrac, J. et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 1 (1), 3–18 (2011).

Download references

Acknowledgements

This work was supported by Key R&D plan of Shandong Province, China (2021CXGC010207, 2023CXGC01020); First batch of talent research projects of Qilu University of Technology in 2023 (2023RCKY116); Introduction of urgently needed talent projects in Key Supported Regions of Shandong Province; Key Projects of Natural Science Foundation of Shandong Province (ZR2020ME116); the Innovation Ability Improvement Project for Technology-based Small- and Medium-sized Enterprises of Shandong Province (2022TSGC2051, 2023TSGC0024, 2023TSGC0931); National Key R&D Program of China (2019YFB1705002), LiaoNing Revitalization Talents Program (XLYC2002041) and Young Innovative Talents Introduction & Cultivation Program for Colleges and Universities of Shandong Province (Granted by Department of Education of Shandong Province, Sub-Title: Innovative Research Team of High Performance Integrated Device).

Author information

Authors and affiliations.

School of Mechanical and Automotive Engineering, Qilu University of Technology (Shandong Academy of Sciences), Jinan, 250353, China

Jinwei Qiao, Guangyuan Wang, Zhi Yang, Jun Chen & Pengbo Liu

Shandong Institute of Mechanical Design and Research, Jinan, 250353, China

School of Information Science and Engineering, Northeastern University, Shenyang, 110819, China

Xiaochuan Luo

Fushun Supervision Inspection Institute for Special Equipment, Fushun, 113000, China

You can also search for this author in PubMed   Google Scholar

Contributions

Z.Y., J.Q., and G.W. wrote the main manuscript text and prepared all figures and tables. J.C., P.L., K.L., and X.L. were responsible for the data curation and software. All authors reviewed the manuscript.

Corresponding author

Correspondence to Zhi Yang .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Supplementary information., rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Qiao, J., Wang, G., Yang, Z. et al. A hybrid particle swarm optimization algorithm for solving engineering problem. Sci Rep 14 , 8357 (2024). https://doi.org/10.1038/s41598-024-59034-2

Download citation

Received : 11 January 2024

Accepted : 05 April 2024

Published : 10 April 2024

DOI : https://doi.org/10.1038/s41598-024-59034-2

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Particle swarm optimization
• Elite opposition-based learning
• Iterative mapping
• Convergence analysis

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

A comparative review of current optimization algorithms for maximizing overcurrent relay selectivity and speed

Ieee account.

• Change Username/Password
• Update Address

Purchase Details

• Payment Options
• Order History
• View Purchased Documents

Profile Information

• Communications Preferences
• Profession and Education
• Technical Interests
• US & Canada: +1 800 678 4333
• Worldwide: +1 732 981 0060
• Contact & Support
• About IEEE Xplore
• Accessibility
• Terms of Use
• Nondiscrimination Policy
• Privacy & Opting Out of Cookies

A not-for-profit organization, IEEE is the world's largest technical professional organization dedicated to advancing technology for the benefit of humanity. © Copyright 2024 IEEE - All rights reserved. Use of this web site signifies your agreement to the terms and conditions.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Comput Intell Neurosci
• v.2022; 2022

An Improved Particle Swarm Optimization Algorithm and Its Application to the Extreme Value Optimization Problem of Multivariable Function

School of Mathematical and Statistics, Xuzhou University of Technology, Xuzhou 221008, China

Associated Data

The datasets generated and/or analyzed in the current study are available from the corresponding author upon reasonable request.

It is proposed to improve the study of particle optimization and its application in order to solve the problem of inefficiency and lack of local optimization skills in the use of particle herd optimization. Firstly, the basic principle, mathematical description, algorithm parameters, and flow of the original (Particle Swarm Optimization, PSO) algorithm are introduced, and then the standard PSO algorithm is introduced; thirdly, over the last 10 years, four types of improvements have been proposed through the study of improved particle algorithms. The improved algorithm is applied to the extreme value optimization problem of multivariable function. The simulation results show that the basic (Cloud Particle Swarm Optimization, CPSO) algorithm within 500 generations has not reached convergence for 8 times, 6 times, 4 times, and 5 times, respectively. In the case of convergence, the average number of steps is much higher than ICPSO, and the improved algorithm converges completely. In terms of time performance, the convergence time of ICPSO is much better than that of CPSO algorithm. Therefore, the improved particle optimization algorithm ensures the effectiveness of the improvement measures, such as small optimization algebra, fast merging speed, high efficiency, and good population diversity.

1. Introduction

An optimization problem involves finding a set of parameter values under certain constraints so that some measure of optimization is met, even if some performance indexes of the system reach the minimum or maximum. It is an ancient subject based on mathematics. It widely exists in agriculture, chemical industry, national defense, finance, transportation, electric power, communication, and many other fields [ 1 ]. The application of optimization technology in the above fields has brought great economic and social benefits. Long-term practice shows that under the same conditions, the treatment of optimization technology has significant effects on the reduction of system energy consumption, the improvement of efficiency, and the rational utilization of resources, and this advantage is more obvious with the increase of the scale of treatment objects. The emergence of bionic algorithm provides a powerful tool for a large number of problems that cannot be well optimized by traditional optimization algorithms. Bionic algorithm is an algorithm model based on human and biological behavior or material movement form [ 2 ]. Since this kind of algorithm was put forward, because of its universality in solving the optimization problem, it does not need some information of the objective function or even the explicit expression of the optimized object. It only needs to know the input and output of the optimized problem so as to avoid the computational complexity and difficult operability of the algorithm based on the properties of the optimized function. Currently, bionic algorithms include genetic algorithms, artificial immunity algorithms, ant colony optimization algorithms, particle herd optimization algorithms, community location algorithms, and more [ 3 , 4 ].

Particle swarm optimization (PSO) is a new type of bionic optimization algorithm that is similar to the genetic algorithm and is a repetitive optimization algorithm (see Figure 1 ). It initiates a set of random solutions and repeatedly searches for the optimal solution. However, this is different from the evolutionary idea in the genetic algorithm that “the best survives, the best survives.” Compared to other bionic algorithms, such as genetic algorithms, particle herd algorithms are simpler to understand, have fewer parameters that can be adjusted, and are easier to implement. Convergence analysis of particle herd optimization algorithms is the basis of PSO algorithms. Currently, most improved particle herd optimization algorithms lack convergence models and convergence analysis. Second, the particle optimization algorithm is easy to get into the local optimization problem; that is, there is a problem of incomplete integration [ 5 ]. Particle optimization when solving the problem of optimizing high-dimensional or ultra-high-dimensional complex functions, particle swarm optimization often has the problem of premature convergence; that is, limited by the particle update mechanism, the particles have gathered to a point and stagnated when the population has not found the optimal solution. Therefore, it is urgent to find an effective mechanism to make the algorithm escape from local minima and overcome the problem of premature convergence. Third, it is necessary to expand the theory of discrete particle optimization and its application, as the results of discrete particle optimization studies lag far behind continuous particle optimization. Fourth, the expansion of research on the application of particle herd algorithms, how to use particle herd algorithms, and the integration of other algorithms to solve practical problems are the research topics of domestic and foreign scientists [ 6 ].

An improved particle swarm optimization algorithm.

2. Literature Review

Numerous scientists are devoted to the study of optimization problems, and as a result, optimization theories and algorithms are developing rapidly. Currently, traditional optimization methods include Newton's method, simplex method, and conjugate gradient method, trust region method, pattern search method, Rosenbrock method, and Powell method. When facing some large-scale problems, these methods need to traverse the whole search space and produce a combination explosion of search, which makes them “helpless” in the face of these problems; that is, the calculation speed, convergence, and initial sensitivity are far from meeting the requirements. Therefore, efficient optimization algorithm has become one of the research objectives of scientists [ 7 ]. Sun et al.'s model has been proposed to convert uncertainty between the definition of qualitative knowledge, the concept of quality, and its numerical representation, and it has been used in many fields, such as intelligent management and fuzzy evaluation. Because the cloud model has the characteristics of uncertainty, uncertainty, stability, and change in the expression of knowledge, it reflects the basic principles of species evolution in nature. Therefore, the field of evolutionary computing has also begun to focus on cloud design [ 8 ]. Song's algorithm for high-dimensional functions and nonlinear distribution particle optimization has been proposed to overcome the poor performance of particle optimization. The algorithm performs scattering operations on particles in a nonlinear increment so that a large number of unnecessary scattering operations can be avoided at the beginning of the algorithm iteration, and the probability of scattering operations at the end is high iteration, thus ensuring the efficiency of the algorithm's operation. This can effectively improve the algorithm's global search capability [ 9 ]. Zeng et al. proposed a cloud genetic algorithm by using cloud generator to replace the traditional crossover and mutation operators in genetic algorithm, which has achieved good results in function optimization [ 10 ]. Kumari et al. combining genetic algorithms with cloud models offers a cloud-based evolutionary algorithm that effectively solves the problem of genetic algorithms and easily facilitates local optimization and early convergence [ 11 ]. Omidinasab and Goodarzimehr proposed an adaptive cloud particle swarm optimization algorithm using particle fitness and different inertia weight evolution strategies, which effectively solved the problems of local optimization and too fast convergence speed of the algorithm [ 12 ]. Zhu et al. suggest that the current condition and space of a particle in an entire population should be explored, evaluated by the fitness value of the particle, and its speed adjusted by the fitness value so that the particle itself can be active locally and globally search [ 13 ].

Based on this study, this paper proposes to improve the study of particle herd algorithms and their applications. By means of solution space transformation, the local optimization and global optimization are combined, a simple cloud operator is used to study the evolution of particles and to perform mutations to accelerate the integration speed of the algorithm. From the simulation results, it can be seen that the improvement measures improve the accuracy of the population diversity, search capabilities, and algorithm integrity.

3. Research Methods

3.1. particle herd algorithm.

Particle herd optimization (PSO) is a new type of bionic optimization algorithm based on modeling the behavior of birds of prey according to certain assumptions. The discovery of the algorithm is based on the modeling of simplified social models. It originated from complex adaptive system. CAS particle swarm optimization algorithm is developed based on the following four characteristics of CAS: firstly, the subject is active and active. Secondly, the subject interacts with the environment and other subjects, which is the main driving force for the development and change of the system. Moreover, the influence of environment is macro, the influence between subjects is micro, and macro and micro should be organically combined. Finally, the whole system may also be affected by some random factors [ 14 ].

3.1.1. Standard Particle Swarm Optimization Algorithm

In order to better explore the solution space, Shi introduced the concept of inertia weight based on the original particle herd algorithm and gradually developed the standard particle herd algorithm currently in use. The speed-position update mode is as follows:

The standard particle herd algorithm described in this section is a linearly tuned particle herd algorithm. Its formula is

where ω max indicates the value of the maximum mass of inertia, ω min indicates the minimum value of the mass of inertia, Gen represents the maximum number of iterations, and iter represents the current number of iterations. A particle herd algorithm involves inertial motion of a particle along its own velocity and thinking about the behavior of the particle itself. At the same time, it also participates in group information sharing and mutual cooperation so as to find the best position in the particle swarm. The interaction and restriction of these three parts determine the optimization performance of the algorithm [ 15 , 16 ]. For its movement process, see Figure 2 .

The schematic diagram of the update process.

3.1.2. Discrete Particle Swarm Optimization

To solve the problem of optimizing a separate combinator with a PSO algorithm, two completely different technical routes were developed: one based on the classical continuous particle herd algorithm, and for a specific problem, a discrete policy space for continuous particle motion, space, and appropriate adjustments is made. The PSO algorithm to be solved still retains the speed-position update algorithm of the classical particle herd algorithm in the calculation. His representative, Eberhart, proposed a discrete binary version of the PSO based on the first particle herd algorithm. The model they proposed is to limit the historical and global optimization of each dimension of the particle and the particle itself to 1 or 0, but the speed is not limited. When updating the position with speed, set an off value. When the speed is higher than the off value, the position of particles is taken as 1; otherwise, it is taken as 0. The speed and position update equations are expressed as follows:

Consider S v i d = 1 1 + exp − v i d , (7) where

S ( v id ) is the sigmoid function and r  and () is the random number between [0, 1]. The velocity component v id determines the probability that the position component x id takes 1 or 0. The greater the v id , the greater the probability that x id takes 1.

Another approach is to solve the discrete optimization problem based on the basic information update mechanism of the PSO algorithm, as well as to redefine the basic idea of the classical particle optimization algorithm, the unique representation of the particle herd, and the operation algorithm within the algorithm, for example, the discrete binary PSO algorithm proposed by Farzane in Clerc's Traveler Trading Policy (TSP) and the 0–1 planning policy. The difference between the two methods lies in the following: the former maps the actual discrete problem to the particle continuous motion space and then calculates and solves it in the continuous space. The latter is to map PSO algorithm to discrete space and calculate and solve it in discrete space [ 17 , 18 ].

3.2. Improved Particle Swarm Optimization (ICPSO)

3.2.1. cloud design.

The cloud model is a mathematical model that transforms deterministic knowledge into qualitative and quantitative forms and mainly reflects the ambiguity and randomness of knowledge about things and people in the objective world and provides a combination of qualitative and quantitative processing of things.

Definition 1 . —

(clouds and cloud drops). Let U be a numerical world represented by numerical values, and C be a qualitative concept over U . If the numerical value of x  ∈  U is a random embodiment of the concept of quality C , then C µ ( x ) ∈ [0, 1] of the degree of certainty is a random number that tends to be constant: μ : ∪⟶[0,1],   x ∈ ∪, x ⟶ μ ( x ). The distribution of x in the U universe is then called a cloud, which is denoted by a C ( X ) cloud, and each x is called a cloud drop. The cloud model and its numerical properties are shown in Figure 3 , and Ex  = 20, En  = 3, He  = 0.1.

Cloud model and its digital features.

Definition 2 . —

One-dimensional simple cloud operator ArForward ( C ( Ex , En , He )) is a mapping of π that converts the general properties of quality concepts into digital representations. C ⟶Π. The following conditions are met:

In, Norm( μ , δ ) is a normal random variable with expected value µ and variance δ , and N is the number of cloud droplets. Using a simple cloud operator, it is possible to convert a concept into a set of cloud droplets numerically represented by C ( Ex , En , He ) realizing the transformation from conceptual space to numerical space. The one-dimensional simple cloud operator can be extended to the n -dimensional simple cloud operator.

3.2.2. Basic Particle Swarm Optimization (CPSO)

Let the size of the particle swarm be N , the fitness value of the particle X i in the t th iteration is f i , and the average fitness value of the particle is equations ( 8 )∼( 10 ):

Equations ( 9 ) and ( 10 ) are speed update formula and position update formula, respectively. The fitness value better than f avg is averaged to get f avg ′, the fitness value less than f avg is averaged to get f avg ″ , and the fitness value of the optimal particle is f min . If f i is better than f avg ′, the fitness value of particles is small and close to the optimal solution. Small inertia weight is adopted, and the evolution strategy adopts “social model” to speed up the speed of global convergence. If f i is inferior to f avg ″ , the fitness value of particles is large and far from the optimal solution. Large inertia weight is adopted, and the evolution strategy adopts “cognitive model” so that these particles with poor performance can accelerate the convergence speed. If f i is better than f avg ″ and inferior to f avg ′, the fitness value of particles is moderate, the inertia weight adopts cloud adaptive inertia weight, and the evolution strategy adopts “complete model” [ 19 ].

Definition 3 . —

(evolutionary model). The process that each particle generates a new generation of particles through the normal cloud generator according to its individual extreme value is called evolutionary model.

Definition 4 . —

(mutation). Given the thresholds N and K in advance, when the global extreme value has not evolved for N consecutive generations or the amplitude of the evolution process is less than k , it is considered that the particles fall into the local optimum, and all particles are mutated through the normal cloud generator according to the global extreme value.

3.2.3. ICPSO Algorithm

Aiming at the problems of the above basic CPSO, this paper puts forward the following two improvement methods.

• (1) With the help of group substitution and spatial transformation, the global search and local search are combined.
• Most of the running time of the basic CPSO algorithm is consumed in the updating of the population. In addition, the limitation of slow evolution often appears in the later stage of evolution. For this, group substitution and space transformation are introduced. The particle swarm optimization algorithm of group substitution mainly searches the solution space through several particle swarm optimization using different search methods. One particle swarm is the main search group and the other is the auxiliary search group. Under some conditions in the search process, some auxiliary search group particles and main search group particles are replaced to maintain the diversity of main search group particles so that the main search group can avoid stagnation or premature due to lack of diversity so as to ensure that the main search group can search the global optimal value point. In order to calculate the advantages and disadvantages of the current position of cloud particles, it is necessary to transform the solution space and map the two positions occupied by each particle from the unit space I =[−1,1] n to the solution space of the optimization problem. Note that the i th cloud operator on particle P j is [ α i j β i j ] T ; then, the corresponding solution space variables are as follows: X k j = 1 2 b i 1 + α i j + a i 1 − α i j , (12) X i δ j = 1 2 b i 1 + β i j + a i 1 − β i j . (13)
• Then, if the optimal value obtained is greater than the modern optimal solution, the spatial transformation of the solution is optimized. After each iteration, the improved algorithm performs local search near the contemporary optimal solution and improves the ability to search algorithms, and the basic CPSO algorithm improves errors that do not change over several generations [ 20 ].
• (2) According to a simple cloud operator, particle mutations are used to improve the algorithmic search method. Nonmodern optimal solutions focus on phenomena that are common in the evolutionary process of the CPSO basic algorithm, and the greater the evolution, the greater the deviation from the optimal solution, and the following improvement measures are taken: calculate the initial value of the current position and velocity of each particle, and then calculate whether the fitness of each particle has reached the mutation threshold N , and if so, perform a mutation operation on each particle according to Definition 4 ; otherwise, the particle renewal is performed according to equations ( 9 ) and ( 10 ).

3.2.4. Algorithm Flow of ICPSO

The ICPSO algorithm flow using the above two improvement measures is as follows:

• Initialize the population. That is, initialize the position of each particle, individual extreme value PBEST, local extreme value GBEST, and so on.
• Calculate the fitness value for each particle and update Pbest and Gbest.
• Judge whether the mutation threshold n is reached. If it is reached, the mutation operation is carried out according to Definition 4 . Let the local best (minimum) of all particles be Gbest and make ex  = Gbest, en  = 2gbest, h e = en/10 in normal cloud computing a ( C ( ex , en , he )). According to Definition 2 , the normal cloud generator completes the mutation operation of all particles and fails to reach the mutation threshold (4).
• Evolve each particle. Let the individual minimum of particle I be Pbest, let ex  = Pbest, en  = 2pbest, he  = en/10 in normal cloud computing a ( C ( ex , en , he )), generate a new particle J according to the normal cloud generator in Definition 2 , and let I  =  J to complete the evolution operation.
• If the iteration limit is reached, the Gbest output will end; otherwise, go to (2).

3.3. Analysis of Influence of Parameter Selection on Algorithm Performance

In the mutation operation, select the global extreme value Gbest as ex . Because at this time, the algorithm may have fallen into local optimization, and according to the sociological principle, there are often better individuals around the current excellent individuals, so there is more chance to find the optimal solution around them. en represents the horizontal width of the cloud. The larger the en , the larger the horizontal width and the larger the particle search range. The scope of the search should be expanded in the first stage of evolution, the search accuracy should be improved in the next stage of evolution, and en should be reduced dynamically. The global extreme (small) value Gbest of particle evolution gradually approaches the actual extreme value from large to small. In this paper, en  = 2gbest is taken to realize the dynamic mediation of en to a certain extent [ 21 ].

It is proportional to the degree of distribution of the cloud droplets. The larger it is, the greater the degree of distribution, and the more the cloud droplets spread. If it is too large, the algorithm loses its stability, and if it is too large, the algorithm loses its stability. The smallness and randomness will be lost to a certain extent. he  =  en /10 is taken to mediate the stability of the algorithm.

If the parameter K is too large, the mutation will be too high, which will affect the efficiency of the algorithm, and if it is too low, reduce the accuracy of the solution. Also, because the particle herd algorithm has a rapid fusion rate in the first stage of evolution, the fusion rate in the next stage is gradually slowed down, it is difficult to set a completely reasonable fixed value for parameter k . In this paper, let k  = Gbest/2 so that the value of K decreases dynamically with the global optimal value Gbest so as to realize adaptive adjustment. To select the change threshold N , consider the SpHere function as an example to test the effect of different N values on the resolution accuracy of the ICPSO algorithm. The experimental parameters were set as follows: the population size was 100, the initial value range was [−5, 5], the maximum iterative algebra was 1000, and the SpHere function was 5, 10, 30, 50, 100. Take 2 for N , respectively. Run 5, 10, and 20 50 times to get the mean, and the quantity is K  = Gbest/2. For the test results, see Table 1 .

Solutions of sphere function under different N values.

As can be seen from Table 1 , the smaller the threshold n of low-dimensional function with dimension less than 10, the higher the accuracy of the solution, but the more time-consuming. The smaller the threshold n of 10∼100-dimensional function, the more time-consuming, but the accuracy of the solution is not necessarily high. There is an inflection point in the solution accuracy at 5 out of n . It can be seen that the selection of n value has a certain correlation with the dimension of the function [ 22 ].

4. Result Discussion

Check the effectiveness of the improvement measures, the following typical function extreme value optimization problem is introduced.

• (1) RA-Rastrigin function is shown in formula ( 13 ): f 1 x , y = x 2 + y 2 − cos    18    x − cos    18    y , (14)

Variation of Rastrigin function optimization results with dimension.

• (2) The generalized raster function is shown in equation ( 14 ): f 2 x = ∑ i = 1 30 x i 2 − 10    cos 2 π x i + 10 . (15)
• Here, x i ∈ [−5.12, 5.12], the optimization objective is to find the minimum of the function, the global minimum of f 2 is 0, and there are about 45 local minimum points in the feasible region.
• (3) Br-Branin function is shown in equation ( 15 ): f 3 x , y = x − 5.1 4 π 2 y 2 + 5 π y − 6 2 + 10 1 − 1 8 π cos    y + 10 , (16)
• where X ∈ [0,15]; y ∈[−5,10].The optimization objective is to find the minimum of the function, the global minimum of F3 is 0.3979, and the three global minimum points are (−3.031, 1.164), (3.031, 1.164), and (9.3425, 2.425).
• (4) The six-hump camel-back function is as follows ( 16 ): f 4 x , y = 4 x 2 − 2.1 x 4 + 1 3 x 6 + x y − 4 y 2 + 4 y 4 . (17)

Here, x , y ∈ [−5,5], the optimization objective is to find the minimum of the function, the global minimum of F4 is −1.0205, and the two global minimum points are (0.0884, −0.7014) and (−0.0884, 0.7014). The above functions are optimized 50 times with basic CPSO and ICPSO, respectively. For comparison, the initial values of the two algorithms are the same. Then, count the maximum/minimum steps, convergence times, and average steps of each algorithm. The simulation results are shown in Figure 5  ∼  Figure 8 and Table 2 .

RA-Rastrigin function optimization curve.

Optimization curve of six-hump camel-back function.

Performance comparison between PSO and ICPSO algorithms.

Figures ​ Figures5 5 ​ 5 ​ – 8 show the comparison curve of CPSO and ICPSO optimization. From the figures, it can be seen that the calculation accuracy of ICPSO is significantly improved and the iteration algebra is reduced. In Figure 5 , CPSO does not converge, which verifies the problem of poor optimization ability. After step 10 of ICPSO, it begins to converge stably and gradually approaches the global optimal value −2. In Figures ​ Figures6 6 and ​ and7, 7 , the curve after CPSO optimization drops relatively slowly, and the speed gradually approaches 0 due to the algorithm itself, and the speed update correspondingly becomes slower and slower. At this time, the particles will gather at several points and cannot conduct larger-scale local search, making the optimization trapped in local convergence. As can be seen from Figure 8 , the optimization goal was achieved in step 46, and ICPSO reduced the number of particle iterations and improved the optimization accuracy by transforming the solution space and mutating the normal cloud operator and achieves the optimization goal in step 10 and step 7, respectively. In Figure 8 , it can be seen from the optimization curves of CPSO and ICPSO that although the curve change is not very obvious, it is obvious from the number of optimization steps that ICPSO reaches the optimization goal in step 9 and CPSO reaches the optimization goal in step 23. Table 2 shows the performance simulation results of ICPSO combined with two improvement measures and basic CPSO, in which the average number of steps is the average value under convergence. It can be seen from Table 2 that the basic CPSO algorithm within 500 generations has not reached convergence for 8 times, 6 times, 4 times, and 5 times, respectively. In the case of convergence, the average number of steps is much higher than ICPSO, and all the improved algorithms converge. In terms of time performance, the convergence time of ICPSO is much better than that of CPSO algorithm. Comparing the simulation results, the ICPSO algorithm is better than the CPSO algorithm, indicating that the improved method is effective.

Optimization curve of generalized Rastrigin function.

BR-Branin function optimization curve.

5. Conclusion

Particle herd optimization is a global research hotspot. Its research includes the analysis of algorithm mechanism, the improvement of algorithm performance and the expansion of algorithm application. CPSO algorithm is based on cloud digital feature coding to better describe the dynamic behavior of cloud particles. Focusing on key CPSO current issues, this paper proposes two improvement measures to improve algorithm search capabilities, population diversity, and algorithm integration speed and accuracy. Experiments have shown that the improved method is effective. The successful combination of cloud model, cloud particle swarm optimization, and mutation idea makes a new exploration and attempt for the research of solving the optimal value. Although some of these issues have been addressed in this paper and some step-by-step results have been achieved, there is still a need for further discussion and in-depth research on some of the issues encountered during the study: Create as many types of problems as possible, or develop algorithms that are more appropriate to the specific situation? There is currently no unified design standard. In this regard, it is necessary to develop a flexible algorithm that can use the properties of the particle herd optimization algorithm for different problems and combine it with the specifics of the problem, and it needs to be adapted.

Acknowledgments

This study was supported by Jiangsu Natural Science Foundation (BK20170248).

Data Availability

Conflicts of interest.

The author declares that there are no conflicts of interest regarding the publication of this paper.

I. INTRODUCTION

Ii. propaedeutics, iii. fractional order model of hev, iv. model analysis, a. positivity and boundedness, b. stability, v. fractional optimal control problem, a. optimization method, vi. numerical simulation and results, a. the fractional adams–bashforth–moulton prediction correction algorithm, b. strategy and results, vii. conclusions, acknowledgments, author declarations, conflict of interest, author contributions, data availability, a caputo fractional derivative dynamic model of hepatitis e with optimal control based on particle swarm optimization.

Email: [email protected]

Email: [email protected]

Email: [email protected]

• Split-Screen
• Article contents
• Figures & tables
• Supplementary Data
• Peer Review
• Open the PDF for in another window
• Reprints and Permissions
• Cite Icon Cite
• Search Site

Jia Li , Xuewen Tan , Wanqin Wu , Xiufen Zou; A Caputo fractional derivative dynamic model of hepatitis E with optimal control based on particle swarm optimization. AIP Advances 1 April 2024; 14 (4): 045125. https://doi.org/10.1063/5.0193463

Download citation file:

• Ris (Zotero)
• Reference Manager

Hepatitis E, as a zoonotic disease, has been a great challenge to global public health. Therefore, it has important research value and practical significance for the transmission and control of hepatitis E virus (HEV). In the exploration of infectious disease transmission dynamics and optimal control, mathematical models are often applied. Among them, the fractional differential model has become an important and practical tool because of its good memory and genetic characteristics. In this paper, an HEV propagation dynamic model is constructed by the Caputo fractional derivative. First, the properties of the model are analyzed, including the existence, non-negativity, boundedness, and stability of the equilibrium points. Then, from the perspective of fractional optimal control (FOC), control measures were proposed, including improving the awareness and prevention of hepatitis E among susceptible people, strengthening the treatment of infected people, and improving environmental hygiene. Then, an FOC model of HEV was constructed. After analyzing the necessary conditions for optimality, the particle swarm optimization is introduced to optimize the control function. In addition, four control strategies are applied. Finally, the numerical simulation is completed by the fractional Adams–Bashforth–Moulton prediction correction algorithm. The four strategies and no control were compared and analyzed. The numerical simulation results of different fractional orders are also compared and analyzed. The results illustrate that the optimal strategy, compared with no control, reduces the HEV control time by nearly 60 days. Therefore, this method would contribute to the study of HEV transmission dynamics and control mechanisms, thus contributing to the development of global public health.

Viral infectious diseases have always been a great challenge to global public health security and are one of the serious problems facing mankind. 1 Viral hepatitis is one of the most prevalent and harmful viral infectious diseases in the world, and hepatitis E virus (HEV) is the main pathogen causing acute viral hepatitis worldwide. 2 According to the World Health Organization (WHO), ∼20 × 10 6 HEV infections occur worldwide every year, of which about 3.3 × 10 6 people develop symptoms of hepatitis E. In a study on hepatitis E, according to the World Trade Organization (WTO) Regional Office for South-East Asia, 6.5 × 10 6 people are infected with symptomatic HEV in Asia alone and 160 000 people die each year, including 2700 deaths due to HEV infection during pregnancy. 3 In a separate study, about one in eight people worldwide, equivalent to about 939 × 10 6 people, were infected with hepatitis E and between 15 × 10 6 and 110 × 10 6 people are currently or recently infected with hepatitis E. 4 Therefore, it has important research value and practical significance for the transmission and control of HEV.

To understand the transmission route and mechanism of HEV, researchers have done a lot of detailed research and found that HEV is an icosahedral symmetric spherical non-enveloped virus. The virus particles are about 32–34 nm in diameter and have a 7.2 kb single-stranded RNA genome with a polyadenylate 3′ end. 5,6 Smith and colleagues proposed a new classification of HEV, which was later adopted by the International Committee on Taxonomy of Viruses (ICTV) in 2015. 7 The major type A orthohepatitis viruses have eight identified genotypes, detailed in Table I . Among them, the main hosts of HEV1 and HEV2 are humans. These genotypes are mainly transmitted by water sources, especially in areas with poor water supply and sanitation. 8 A water source contaminated by HEV excreted in the feces of a clinically or subclinically infected person can be a route of transmission of the virus. 9 The main reservoirs of HEV3 and HEV4 include humans, pigs, and some other animals, which are considered zoonotic viruses. 10 These genotypes are mainly transmitted through food, especially infected meat that has not been fully cooked. 11 In the study of HEV thermal stability, it was found that heating food at 71 °C for 20 min completely inactivated HEV. 12 HEV5 and HEV6 are two novel genotypes identified in Japanese wild boars. 13 HEV7 and HEV8 are two novel genotypes identified in camels. 14 The main hosts of these genotypes are wild boars, camels, and other wild animals. Their risk of transmission to humans is relatively low, but one human infection with HEV7 was reported in 2016 after consuming camel food, so more research is needed to understand the potential threat. 15 Although HEV has not been globally prevalent and only large-scale epidemics have occurred in regions, it is a particular pathogen affecting humans and animals and has become an increasingly serious global public health problem. Therefore, it is very critical to study the transmission dynamics and control mechanisms.

Main distribution, host, and transmission route of HEV genotypes.

At present, the application of various mathematical models in the dynamic model of infectious diseases has provided great help in explaining the transmission mechanism and developing control strategies. Among them, fractional order models are more suitable for analyzing the dynamics of real-world problems than integer order models because of their good properties, such as memory and genetic characteristics. 16 Therefore, the fractional model has a wide application prospect in the dynamics of hepatitis E transmission. It can help researchers better understand the mechanisms of HEV transmission from person to person, human to animal, and animal to animal and develop effective and low-cost control strategies, so as to promote the development of global public health security. Alzahrani and Khan first explored the dynamic model of hepatitis E and carried out the analysis of optimal control and then introduced the fractional Atangana–Baleanu (AB) derivative to discuss the dynamical properties of the model. 17 Prakasha et al. developed a fractional model of HEV with the fractional AB derivatives and studied the dynamic properties of the model, which showed that fractional calculus was effective. 18 Khan et al. discussed the hepatitis B virus (HBV) epidemic model in the AB fractional derivative, analyzed the stability and important parameters, and verified the feasibility of the fractional model. 19 Fu et al. introduced the Caputo fractional derivative into an infectious disease model on a complex network, studied the model dynamics and parameter effects, and analyzed the optimal control problem. 20 Sümeyra established a new epidemic model by using the fractional dimension operator. In the process of analyzing the basic reproductive number (BRN), he studied and obtained the threshold of the parameter and found that the numerical arrangement was an effective method when facing the problem of predicting and investigating complex phenomena. 21 Zhang et al. proposed an optimal control model for hepatitis B with the Caputo operator. The study of the model provides a strong theoretical basis for revealing the importance of long-term memory effects in disease treatment. 22 Sadki et al. introduced the Caputo fractional derivative (CFD) to study the dynamics of HCV, investigated the global stability of the steady states, and verified the theory with numerical simulations. 23  

Based on the above studies, we proposed a HEV transmission dynamics model based on the CFD and added control functions for optimal control. The introduction of the CFD would result in a mismatch of the order of the times on either side of the model equation. We introduce fractional parameters to solve this problem. First, we analyze the existence, non-negativity, and boundedness of the equilibrium points (EPs) and prove their stability. Then, we introduce the control function according to the actual situation and formulate four strategies. Finally, the optimal control function is obtained by particle swarm optimization (PSO). The following major contributions are addressed: (1) To better fit the realistic situation of hepatitis E transmission, Caputo fractional calculus with temporal memory was used to construct a transmission model of hepatitis E. (2) To ensure the practical significance of the model, the existence, boundedness, non-negativity, and stability of the model EPs were analyzed. (3) To better control the transmission of hepatitis E, we developed four different control strategies and optimized the control function using PSO. (4) To better explain the biological significance of our model, we used the fractional Adams–Bashforth–Moulton (ABM) prediction correction algorithm for numerical simulations and compared the influence of different fractional order and control effects of different strategies.

The remaining sections are as follows: Sec.  II gives the relevant preparatory knowledge of fractional calculus. Section  III describes the process of establishing the HEV fractional propagation dynamics model. Section  IV proves some properties of this model. Section  V introduces the fractional optimal control (FOC) problem and presents the optimization algorithm. Numerical simulation and results are presented in Sec.  VI , and conclusion is made in Sec.  VII .

Here, some definitions and properties of fractional calculus related to this article are mainly introduced. 24  

Definition II.1. The left Riemann–Liouville fractional integral (order α > 0 ) is D t − α t 0 f ( t ) = 1 Γ ( α ) ∫ t 0 t ( t − s ) α − 1 f ( s ) d s or I t α t 0 f ( t ) = 1 Γ ( α ) ∫ t 0 t ( t − s ) α − 1 f ( s ) d s ,

where Γ(⋅) denotes the gamma function. The left Caputo fractional integral definition is the same as Definition II.1, and their difference is mainly in fractional derivative.

where n is a positive integer.

Definition II.3. Let F ( s ) be the Laplace transform of f ( t ) , then the Laplace transform of the left CFD of order α ∈ ( n − 1, n ] ( where n is a positive integer ) is L D α C f ( t ) , s = s α F ( s ) − ∑ i = 0 n − 1 s α − i − 1 f ( i ) ( 0 ) .

Definition II.4. The two-parameter Mittag-Leffler function is E l , m ( z ) = ∑ n = 0 ∞ z n Γ ( ln + m ) , l > 0 , m > 0 .

Definition II.5. The Laplace transform of the function t m −1 E l , m (± λt l ) is defined as follows: L t m − 1 E l , m ( ± λ t l ) = s l − m s l ∓ λ . (2)

Here, the total population N ( t ) consists of four compartments: susceptible, exposed, infected, and recovered, namely N ( t ) = S ( t ) + E ( t ) + I ( t ) + R ( t ). An additional compartment represents the density P ( t ) of HEV in the environment. The susceptible individual is recruited by b . The contact rate between the susceptible and infected individuals is β . Susceptible individuals acquire HEV from the environment through γ . The parameters ρ and υ denote the transmission rate of the exposed and the recovery rate of the infected, respectively. The parameter ω represents the rate at which an infected population releases the virus into the environment, and the parameter η represents the rate of virus decay in the environment. The mortality rate is denoted through θ .

Here, the existence, non-negativity, and boundedness of the EPs are proved, and the stability of the disease-free equilibrium point (DFEP) and the endemic equilibrium point (EEP) is analyzed.

Before the proof, the generalized mean value theorem is introduced. 28  

Lemma IV.1 (Generalized mean value theorem). Let f ( t ) ∈ C [ a , b ] and D a α f ( t ) ∈ C [ a , b ] , for 0 < α ≤ 1 , then we have f ( t ) = f ( a ) + 1 Γ ( α ) D a α f ( ξ ) ( t − a ) α with a ≤ ξ ≤ t and ∀t ∈ ( a , b ].

Let f ( t ) ∈ C [ a , b ] , D a α f ( t ) ∈ C [ a , b ] , and α ∈ (0, 1] . It is obvious from Lemma IV.1 that ∀t ∈ ( a , b ] if D a α f ( t ) ≥ 0 ⁠ , then f ( t ) is non-decreasing, and if D a α f ( t ) ≤ 0 , then f ( t ) is non-increasing.

With the above-mentioned lemma, we are ready to prove the non-negativity of the EPs.

Theorem IV.1. The region Ω + = S ̄ , E ̄ , I ̄ , P ̄ ; S ̄ ≥ 0 , E ̄ ≥ 0 , I ̄ ≥ 0 , P ̄ ≥ 0 is a positivity invariant set for model (8) .

According to Remark IV.1, the region Ω + for this model is a positive invariant set.□

Next, we show that the EPs are boundedness.

Theorem IV.2. The region Ω = S ̄ , E ̄ , I ̄ , P ̄ ; 0 ≤ S ̄ + E ̄ + I ̄ ≤ 1 , 0 ≤ P ̄ ≤ ω α η α + b α − θ α is a positivity invariant set for model (8) .

Similar to the proof above, we can get the boundedness of P ̄ ( t ) as 0 ≤ P ̄ ≤ ω α η α + b α − θ α ⁠ . This shows that the solution is bounded.□

Here, κ 1 = b α + ρ α , κ 2 = b α + υ α , κ 3 = η α + b α − θ α .

The meaning of the BRN R 0 is that if R 0 < 1 ⁠ , the disease will disappear. Meanwhile, if R 0 > 1 ⁠ , there will always be disease. The values of R 0 at the DFEP and EEP are R 0 | X 0 = ρ α β α κ 3 + γ α ω α κ 1 κ 2 κ 3 and R 0 | X * = b α ρ α S ̄ * β α κ 3 + γ α ω α κ 1 κ 2 κ 3 b α + β I ̄ * + γ P ̄ * ⁠ , respectively.

Now, we illustrate the stability of the DFEP X 0 = (1, 0, 0, 0) and the EEP X * = ( S ̄ * , E ̄ * , I ̄ * , P ̄ * ) and have the following conclusions:

Model (8) is locally asymptotically stable at the DFEP if R 0 < 1 ⁠ .

In addition, ρ 1 ρ 2 ≥ ρ 3 , so the condition of Routh–Hurwitz is satisfied. Therefore, if R 0 ≤ 1 ⁠ , it is locally asymptotically stable for the DFEP.□

Next, we study the stability of the EEP X *.

Model (8) EEP X * is locally asymptotically stable if R 0 ≥ 1 ⁠ .

It is possible to verify the eigenequations τ i > 0( i = 1, 2, 3, 4), τ 1 τ 2 > τ 3 , and τ 1 τ 2 τ 3 > τ 3 2 + τ 4 τ 1 2 if R 0 > 1 ⁠ . Thus, due to the Routh–Hurwitz stability condition, the EEP is locally asymptotically stable if R 0 > 1 ⁠ .□

The global stability of the EPs is discussed below. Before the proof, we introduce a lemma, which is convenient for us to construct the Lyapunov function. 33,34

Lemma IV.2. Let Φ ( t ) ∈ R + be a continuously differentiable function. Then, for t ≥ 0 , 1 2 D t α 0 C Φ 2 ( t ) ≤ Φ ( t ) D t α 0 C Φ ( t ) (10) and D t α 0 C Φ ( t ) − Φ * − Φ * ⁡ ln Φ ( t ) Φ * ≤ 1 − Φ * Φ ( t ) D t α 0 C Φ ( t ) , (11) where α ∈ (0, 1).

Note that the above inequality is equal when α = 1. For the stability of the DFEP X 0 , the following conclusion follows:

Model (8) at the DFEP X 0 is globally asymptotically stable, if R 0 < 1 ⁠ .

So, if R 0 < 1 ⁠ , then D t α 0 C V 1 ( t ) ≤ 0 ⁠ . In addition, D t α 0 C V 1 ( t ) = 0 if and only if S ̄ ( t ) = S ̄ 0 = 1 and I ̄ ( t ) = I ̄ 0 = 0 ⁠ . In addition, if I ̄ ( t ) = 0 ⁠ , then E ̄ ( t ) = 0 and P ̄ ( t ) = 0 ⁠ . Therefore, the maximum invariant set for ( S ̄ , E ̄ , I ̄ , R ̄ ) : 0 C D t α V 1 ( t ) = 0 is the singleton set { X 0 }. Therefore, according to LaSalle’s invariance principle, 35,36 in the domain of definition, all the solutions converge to X 0 . Therefore, the DFEP is globally asymptotically stable when R 0 < 1 ⁠ .□

Model (8) at the EEP X * = ( S ̄ * , E ̄ * , I ̄ * , P ̄ * ) is globally asymptotically stable, if R 0 > 1 ⁠ .

So, if R 0 > 1 ⁠ , then D t α 0 C V 1 ( t ) ≤ 0 ⁠ . In addition, D t α 0 C V 1 ( t ) = 0 if and only if S ̄ ( t ) = S ̄ * , E ̄ ( t ) = E ̄ * , I ̄ ( t ) = I ̄ * and P ̄ ( t ) = P ̄ * ⁠ . Therefore, the maximum invariant set for ( S ̄ , E ̄ , I ̄ , R ̄ ) : 0 C D t α V 1 ( t ) = 0 is the singleton set { X *}. So, according to LaSalle’s invariance principle, all the solutions of this model converge to X * in the domain of definition. Therefore, the EEP is globally asymptotically stable when R 0 > 1 ⁠ .□

In summary, model (8) is both mathematically and epidemiologically appropriate.

The control effects of u 1 , u 2 , and u 3 were reflected in model (12) as follows: u 1 would reduce the probability that the susceptible population are exposed to HEV and the influence of environmental virus on susceptible population, reducing the contact rate by u 1 factors; u 2 would increase the treatment rate of HEV, and the recovery rate would increase by u 2 factors; and u 3 would reduce HEV load in the environment, reducing the release rate by u 3 factors, where the control set is defined as U = ( u 1 , u 2 , u 3 ) | u i i s L e b e s g u e m e a s u r a b l e o n [ 0 , 1 ] , i = 1 , 2 , 3 ⁠ .

Theorem V.1. Let the optimal control variables of the problem be u 1 * , u 2 * , and u 3 * . Then, the optimal control variable can be obtained from u 1 * = max 0 , min 1 , ν 1 − ν 2 β α I ̄ ( t ) + γ α P ̄ ( t ) S ̄ ( t ) n 1 , u 2 * = max 0 , min 1 , ν 3 − ν 4 I ̄ ( t ) n 2 , u 3 * = max 0 , min 1 , ν 5 ω α I ̄ ( t ) n 3 , (15) where the adjoint variables ν 1 , ν 2 , ν 3 , ν 4 , and ν 5 satisfy ν 1 ′ = ν 1 − ν 2 1 − u 1 β α I ̄ ( t ) + γ α P ̄ ( t ) + ν 1 b α , ν 2 ′ = − m 1 + ν 1 − ν 2 ρ α + ν 2 b α , ν 3 ′ = − m 2 + ν 1 − ν 2 1 − u 1 β α S ̄ ( t ) + ν 3 − ν 4 υ α + u 2 + ν 5 1 − u 3 ω α + ν 3 b α , ν 4 ′ = ν 4 b α , ν 5 ′ = − m 3 + ν 1 − ν 2 1 − u 1 γ α S ̄ ( t ) , (16) with transversality conditions or boundary conditions, ν 1 ( t f ) = 0 , ν 2 ( t f ) = 0 , ν 3 ( t f ) = 0 , ν 4 ( t f ) = 0 , a n d ν 5 ( t f ) = 0 .

Thus, the theorem is proved.□

The above-mentioned theorem states the NCO of the model FOC problem. However, one approach to computing the optimal control variables is to consider Eq.  (15) as iterative formulas. 39 Although this treatment has some feasibility, the expressions in Eq.  (15) are not strictly iterative formulas. Therefore, for this problem, we use the PSO to optimize the control variables.

Optimal control algorithm for the fractional HEV model.

Here, four control strategies are developed for the HEV transmission model and the numerical simulation results and comparative analysis are presented. The fractional ABM prediction correction algorithm is used for numerical calculation. 42 At the same time, the results of fractional models with different orders are compared, as well as the differences between different strategies. All numerical simulations of the HEV fractional dynamics model were implemented by MATLAB (R2017a) on a laptop with Intel Core i5.

For the fractional ABM prediction correction algorithm, we first consider the general form of the nonlinear CFD equation. 25  

Definition VI.1. The general mathematical form of the monomial nonlinear CFD equation is D t α 0 C y ( t ) = f t , y ( t ) , (19) with initial conditions y ( i ) ( 0 ) = y i , i = 1 , 2 , 3 , … , [ α ] − 1 . (20)

Step 1: The number of subintervals N and the step size h are determined to obtain node t n = nh ;

Step 2: Loop through each n , and the estimated coefficient b i , n +1 is obtained from Eq.  (25) ;

Step 3: The correction coefficient a i , n +1 is obtained from Eq.  (23) , and then, the estimated solution y p ( t n +1 ) is calculated from Eq.  (24) ;

Step 4: The solution y ( t n +1 ) of the equation is calculated from Eq.  (22) ;

Step 5: Output y ( t n +1 ) when y ( t n + 1 ) − y p ( t n + 1 ) is less than a certain precision, otherwise set y p ( t n +1 ) = y ( t n +1 ), and return to step 4.

Strategy A : Combining individual prevention, patient treatment, and environmental control ( i . e ., u 1 , u 2 , u 3 ≠ 0).

Strategy B : Combining patient treatment and environmental control ( i . e ., u 2 , u 3 ≠ 0 and  u 1 = 0).

Strategy C : Combining individual prevention and environmental control ( i . e ., u 1 , u 3 ≠ 0 and  u 2 = 0).

Strategy D : Combining individual prevention and patient treatment ( i . e ., u 1 , u 2 ≠ 0 and  u 3 = 0).

The parameter values in the numerical simulation are given in Table II . The weight constants in the minimization objective functional J ( u ) are set to m 1 = 80 ⁠ , m 2 = 60 ⁠ , m 3 = 500 ⁠ , n 1 = 20 ⁠ , n 2 = 30 ⁠ , and n 3 = 50 ⁠ . For the PSO, the population size is 50 and the number of iterations is 100. The other hyperparameters are set to the inertia weight ω = 1, and both the individual learning factor c 1 and the group learning factor c 2 are 1.5.

Interpretation and values of the parameters. 17,43

Figure 1 presents the changes in the five variables S , E , I , R , and P over time for HEV fractional models with different orders α without control. In this case, the hepatitis E susceptible population was well controlled ( S ̄ ≥ 0.99 ) after 166 days, the infected people gradually cleared ( I ̄ ≤ 0.001 ) after 131 days, the number of recovery reached a peak after 26 days, and the environmental viral load gradually disappeared ( P ̄ ≤ 0.0005 ) after 101 days. In addition, by comparing different orders α , it is obtained that the application of CFD in the HEV propagation dynamics model makes the model change more stable due to its time memory.

Numerical simulation results of different fractional orders α for the uncontrolled state. (a) Changes in the susceptible population S ̄ ( t ) ⁠ . (b) Changes in the exposed population E ̄ ( t ) ⁠ . (c) Changes in the infected population I ̄ ( t ) ⁠ . (d) Changes in the recovered population R ̄ ( t ) ⁠ . (e) Changes in the environmental viral load P ̄ ( t ) ⁠ .

Figure 2 shows the changes in the five variables S , E , I , R , and P over time for the HEV fractional model with different orders under strategy A. Figure 3 illustrates the change in the five variables S , E , I , R , and P of the HEV fractional model over time when different strategies are used for control. Among them, the adoption of strategy A can make the susceptible population of hepatitis E better controlled after 105 days, the number of infected and recovered patients can reach a good situation within 10 days, and the environmental viral load gradually disappears after 59 days. It can be seen that strategy A, which is implemented with all three control measures, has good control of the hepatitis E infectious disease. If strategy B was adopted, the susceptible population of hepatitis E could be well controlled after 144 days, the number of infected and recovered people could reach a better situation within 10 days, and the environmental viral load could gradually disappear after 73 days. It can be seen that strategy B implementing patient treatment and environmental control has almost the same results as strategy A in controlling the number of infected and recovered hepatitis E infections. However, because individual prevention was not implemented, the improvement in the susceptible persons, exposed persons, and environmental viral load was delayed for some time. If strategy C was adopted, the susceptible population of hepatitis E could be well controlled after 128 days, the infection would gradually clear to zero after 74 days, the number of recovered people would reach a peak at 25 days, and the environmental viral load would gradually disappear after 75 days. Therefore, strategy C implementing individual prevention and environmental control has a good effect on the control of hepatitis E transmission, but the effect on the control of hepatitis E infection and recovery is not ideal. If strategy D was adopted, the susceptible population of hepatitis E could be well controlled after 128 days, the number of infected and recovered patients could reach a good situation within 10 days, and the environmental viral load could gradually disappear after 73 days. It can be seen that strategy D, which implemented patient treatment and environmental control, had almost the same effect as strategy A in controlling hepatitis E infection and the number of people recovered. In summary, strategy A had the best effect on hepatitis E infection control.

Numerical simulation results of different fractional orders α for strategy A . (a) Changes in the susceptible population S ̄ ( t ) ⁠ . (b) Changes in the exposed population E ̄ ( t ) ⁠ . (c) Changes in the infected population I ̄ ( t ) ⁠ . (d) Changes in the recovered population R ̄ ( t ) ⁠ . (e) Changes in the environmental viral load P ̄ ( t ) ⁠ .

Comparison of numerical simulation results of different strategies. [(a) Changes in the susceptible population S ̄ ( t ) ⁠ . (b) Changes in the exposed population E ̄ ( t ) ⁠ . (c) Changes in the infected population I ̄ ( t ) ⁠ . (d) Changes in the recovered population R ̄ ( t ) ⁠ . (e) Changes in the environmental viral load P ̄ ( t ) ⁠ . α = 0.95.

Figure 4 illustrates the change in the control function over time for the four strategies when PSO is used to optimize the control function. In addition, from Fig. 4(a) , it can be seen that for strategy A, the control measure u 1 (individual prevention) is required to maintain the maximum control intensity until 50 days, after which it begins to decline, and the control measure u 1 can be stopped after 145 days. Control measures u 2 (patient treatment) should be maintained at maximum control for about 10 days, after which control measures can be reduced as appropriate, but control measures u 2 should be maintained for more than 200 days. For control measure u 3 (environmental control), large-scale control should be carried out for the first few days, and then, appropriate local control can be carried out according to the location of the infected person. Figure 4(b) shows that compared with strategy A, the maximum control strength of the control measure u 2 of strategy B was maintained for about 20 days, after which the control strength also increased. The control time and intensity of the control measure u 3 were also increased accordingly. From Fig. 4(c) , it can be concluded that the control measures u 1 and u 3 of strategy C have a large improvement in control time and intensity compared with strategy A. Figure 4(d) shows that compared with strategy A, the control measures u 1 and u 2 of strategy D have an increase in control time and intensity, but the increase is not as large as that of strategy C. Therefore, it can be obtained that the control effect of control measure u 2 is better than that of control measure u 3 .

Numerical results of the optimal control functions u 1 , u 2 , u 3 for different strategies. (a) Changes in the control functions u 1 , u 2 , u 3 of strategy A . (b) Changes in the control functions u 2 , u 3 of strategy B . (c) Changes in the control functions u 1 , u 3 of strategy C . (d) Changes in the control functions u 1 , u 2 of Strategy D . α = 0.95.

Figure 5 also shows the change in the objective functional J ( u ) value when the four strategies use PSO to optimize the control function ( u 1 , u 2 , u 3 ). It can be seen that the convergence speed of PSO is faster. It can also be concluded that strategy A has the best control effect. The effects of control measures u 1 and u 2 on the objective functional J ( u ) value are close and better than those of control measure u 3 .

Optimal individual fitness of different strategies ( α = 0.95).

Table III shows the values of objective functional J ( u ) for different fractional orders α under no control and implementation of the four strategies. It can be concluded that J ( u ) is smaller in all strategies than without control. Moreover, J ( u ) in strategy A is smaller than that in other strategies under different fractional orders α . In addition, in the four strategies, J ( u ) decreases as the fractional order α becomes smaller, which is an effect of the fractional order.

Results of the objective functional values of different strategies and different fractional orders α .

In this paper, we study the HEV propagation dynamics model based on the CFD. First, to ensure the practical significance of this study, we analyze the dynamic properties in the fractional sense, including the existence, non-negativity, boundedness, and stability of the EPs. Then, from the perspective of FOC, we select appropriate control measures according to the actual situation of HEV transmission to construct an FOC model. The control measures include promoting awareness and prevention of hepatitis E among susceptible people (such as not eating raw food and paying attention to hygiene), strengthening the treatment of infected people (such as drug treatment and physical isolation), and improving environmental sanitation (such as purifying sewage resources and managing human and animal waste). In addition, we use the PMP to analyze the NCO. Then, we illustrate the shortcomings of treating the NCO as iterative formulas and introduce PSO to optimize the control function. To control the transmission of HEV, we develop four control strategies according to the actual situation and make a comparative analysis of them. The numerical simulation results using the ABM predictive correction method show that strategy A is the best strategy to control HEV transmission, and it shorelines the HEV control time by nearly 60 days compared with the absence of control. In addition, the numerical simulation results also show the effect of fractional derivatives on the model. These results indicated that the CFD could be well applied to the study of HEV transmission mechanism and explain the complex transmission dynamics in reality. At the same time, it also shows that the PSO can optimize the control function of the fractional optimal control problem, which can play a certain role in the development of HEV control strategy. Therefore, we hope that this work would be helpful to the study of HEV transmission dynamics and control mechanisms, thereby promoting the development of global public health.

Our research can be improved in the following aspects in the future. First of all, there are not enough realistic data in this paper, so we can collect more realistic data to verify and improve our method in the next step. In addition, when solving the problem of order mismatch on both ends of the equation due to the introduction of CFD, we adopt the introduction of fractional parameters to solve the problem. However, this method can only reduce the impact of the problem, not eliminate the error. So, the next step can be to study more accurately or even eliminate this error method.

We would like to thank the editor and the anonymous referees for their valuable comments and suggestions that greatly improved the presentation of this work. This work was supported by the National Natural Science Foundation of China (Grant No. 12361104), the Youth Talent Program of Xingdian Talent Support Plan (Grant No. XDYC-QNRC-2022-0514), the Yunnan Provincial Basic Research Program Project (Grant No. 202301AT070016), and the Science Research Fund of Education Department of Yunnan Province (Grant No. 2024Y468).

The authors have no conflicts to disclose.

Jia Li : Formal analysis (equal); Methodology (equal); Software (equal); Writing – original draft (equal). Xuewen Tan : Conceptualization (equal); Visualization (equal); Writing – review & editing (equal). Wanqin Wu : Project administration (equal); Validation (equal). Xiufen Zou : Supervision (equal); Writing – review & editing (equal).

Data sharing is not applicable to this article as no new data were created or analyzed in this study.

Citing articles via

Submit your article.

Sign up for alerts

• Online ISSN 2158-3226
• For Researchers
• For Librarians
• For Advertisers
• Our Publishing Partners  
• Physics Today
• Conference Proceedings
• Special Topics

pubs.aip.org

• Privacy Policy
• Terms of Use

Connect with AIP Publishing

This feature is available to subscribers only.

Sign In or Create an Account

Multi-objective Particle Swarm Optimization: Theory, Literature Review, and Application in Feature Selection for Medical Diagnosis

• First Online: 12 November 2019

Cite this chapter

• Maria Habib 7 ,
• Ibrahim Aljarah 7 ,
• Hossam Faris 7 &
• Seyedali Mirjalili 8 , 9  

Part of the book series: Algorithms for Intelligent Systems ((AIS))

2805 Accesses

15 Citations

Disease prediction has a vital role in health informatics. The early detection of diseases assists in taking preventive steps and more functional treatment. Incorporating intelligent classification models and data analysis methods has intrinsic impact on converting such trivial, row data into worthy useful knowledge. Due to the explosion in computational and medical technologies, we observe an explosion in the volume of health- and medical-related data. Medical datasets are high-dimensional datasets, which make the process of building a classification model that searches for optimal set of features a hard, yet more challenging task. Hence, this chapter introduces a fundamental class of optimization known as the multi-objective evolutionary algorithms (MOEA) for optimization, which handles the feature selection for classification in medical applications. The chapter presents an introduction to multi-objective optimization and their related mathematical models. Furthermore, this chapter investigates the utilization of a well-regarded multi-objective particle swarm optimization (MOPSO) as wrapper-based feature selection method, in order to detect the presence or absence of different types of diseases. Therefore, the performance of MOPSO and its behavior are examined by comparing it with other well-regarded MOEAs on several medical datasets. The experimental results on most of the medical datasets show that the MOPSO algorithm outperforms other algorithms such as non-dominated sorting genetic algorithm (NSGA-II) and multi-objective evolutionary algorithm based on decomposition (MOEA/D) in terms of classification accuracy and minimum number of features.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Abbass HA (2002) An evolutionary artificial neural networks approach for breast cancer diagnosis. Artif Intell Med 25(3):265–281

Article   Google Scholar  

Ahmed S, Mafarja M, Faris H, Aljarah I (2018) Feature selection using salp swarm algorithm with chaos. In: Proceedings of the 2nd international conference on intelligent systems, metaheuristics & swarm intelligence. ACM, pp 65–69

Google Scholar  

Aljarah I, Al-Zoubi AM, Faris H, Hassonah MA, Mirjalili S, Saadeh H (2018) Simultaneous feature selection and support vector machine optimization using the grasshopper optimization algorithm. Cogn Comput 1–18

Aljarah I, Faris H, Mirjalili S, Al-Madi N, Sheta A, Mafarja M (2019) Evolving neural networks using bird swarm algorithm for data classification and regression applications. Clust Comput 1–29

Aljarah I, Ludwig SA (2013) Towards a scalable intrusion detection system based on parallel pso clustering using mapreduce. In: Proceedings of the 15th annual conference companion on Genetic and evolutionary computation. ACM, pp 169–170

Aljarah I, Mafarja M, Heidari AA, Faris H, Zhang Y, Mirjalili S (2018) Asynchronous accelerating multi-leader salp chains for feature selection. Appl Soft Comput 71:964–979

Alnemer LM, Rajab L, Aljarah I (2016) Conformal prediction technique to predict breast cancer survivability. Int J Adv Sci Technol 96:1–10

Alon U, Barkai N, Notterman DA, Gish K, Ybarra S, Mack D, Levine AJ (1999) Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc Natl Acad Sci 96(12):6745–6750

Berner ES (2007) Clinical decision support systems, vol 233. Springer

Blum AL, Langley P (1997) Selection of relevant features and examples in machine learning. Artif Intell 97(1–2):245–271

Article   MathSciNet   Google Scholar  

Bramer M (2007) Principles of data mining, vol 180. Springer

Coello CAC, Lechuga MS (2002) Mopso: a proposal for multiple objective particle swarm optimization. In: Proceedings of the 2002 congress on evolutionary computation. CEC’02 (Cat. No. 02TH8600), vol 2. pp 1051–1056, IEEE

Coello CA, Lamont GB, Van Veldhuizen DA et al (2007) Evolutionary algorithms for solving multi-objective problems, vol 5. Springer

Corne DW, Knowles JD, Oates MJ (2000) The pareto envelope-based selection algorithm for multiobjective optimization. In: International conference on parallel problem solving from nature. Springer, pp 839–848

Deb K, Agrawal S, Pratap A, Meyarivan T (2000) A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: Nsga-ii. In: International conference on parallel problem solving from nature. Springer, pp 849–858

Deb K, Kalyanmoy D (2001) Multi-objective optimization using evolutionary algorithms. Wiley, New York, NY, USA

MATH   Google Scholar  

Dua D, Efi KT (2017) UCI machine learning repository

Dioşan L, Andreica A (2015) Multi-objective breast cancer classification by using multi-expression programming. Appl Intell 43(3):499–511

Dos Santos BC, Nobre CN, Zárate LE (2018) Multi-objective genetic algorithm for feature selection in a protein function prediction context. In: 2018 IEEE congress on evolutionary computation (CEC). IEEE, pp 1–6

Dubey AK, Gupta U, Jain S (2016) Analysis of k-means clustering approach on the breast cancer wisconsin dataset. Int J Comput Assist Radiol Surg 11(11):2033–2047

Dudoit S, Fridlyand J, Speed TP (2002) Comparison of discrimination methods for the classification of tumors using gene expression data. J Am Stat Assoc 97(457):77–87

Dussaut JS, Vidal PJ, Ponzoni I, Olivera AC (2018) Comparing multiobjective evolutionary algorithms for cancer data microarray feature selection. In: 2018 IEEE congress on evolutionary computation (CEC). IEEE, pp 1–8

Eberhart R, Kennedy J (1995) A new optimizer using particle swarm theory. In: Micro machine and human science, 1995. MHS’95. Proceedings of the Sixth International Symposium on. IEEE, pp 39–43

Faris H, Aljarah I, Al-Betar MA, Mirjalili S (2018) Grey wolf optimizer: a review of recent variants and applications. Neural Comput Appl, pp 1–23

Faris H, Aljarah I, Al-Shboul B (2016) A hybrid approach based on particle swarm optimization and random forests for e-mail spam filtering. In: International Conference on Computational Collective Intelligence. Springer, pp 498–508

Faris H, Hassonah MA, Al-Zoubi AM, Mirjalili S, Aljarah I (2018) A multi-verse optimizer approach for feature selection and optimizing svm parameters based on a robust system architecture. Neural Comput Appl 30(8):2355–2369

Faris H, Mafarja MM, Heidari AA, Aljarah I, Al-Zoubi AM, Mirjalili S, Fujita H (2018) An efficient binary salp swarm algorithm with crossover scheme for feature selection problems. Knowl-Based Syst 154:43–67

Faris H, Mirjalili S, Aljarah I (2019) Automatic selection of hidden neurons and weights in neural networks using grey wolf optimizer based on a hybrid encoding scheme. Int J Mach Learn Cybern 1–20

Friedman N, Linial M, Nachman I, Pe’Er D (2000) Using bayesian networks to analyze expression data. J Comput Biol 7(3–4):601–620

Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA et al (1999) Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 286(5439):531–537

Han J, Pei J, Kamber M (2011) Data mining: concepts and techniques. Elsevier

Haque MR, Islam MM, Iqbal H, Reza MS, Hasan MK (2018) Performance evaluation of random forests and artificial neural networks for the classification of liver disorder. In: 2018 international conference on computer, communication, chemical, material and electronic engineering (IC4ME2). IEEE pp 1–5

Holland JH et al (1992) Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence. MIT press

Ibrahim AO, Shamsuddin SM, Saleh AY, Abdelmaboud A, Ali A (2015) Intelligent multi-objective classifier for breast cancer diagnosis based on multilayer perceptron neural network and differential evolution. In: 2015 international conference on computing, control, networking, electronics and embedded systems engineering (ICCNEEE). IEEE pp 422–427

Kennedy J, Eberhart RC (1997) A discrete binary version of the particle swarm algorithm. In: 1997 IEEE international conference on systems, man, and cybernetics. Computational cybernetics and simulation, vol 5. IEEE pp 4104–4108

Knowles J, Corne D (1999) The pareto archived evolution strategy: a new baseline algorithm for pareto multiobjective optimisation. In: Congress on Evolutionary Computation (CEC99), vol 1, pp 98–105

Kong Q, Wang D, Wang Y, Jin Y, Jiang B (2018) Multi-objective neural network-based diagnostic model of prostatic cancer. Xitong Gongcheng Lilun Yu Shijian/Syst Eng Theory Pract 38(2):532–544. cited By 0

Kuhn M, Johnson K (2013) Applied predictive modeling, vol 26. Springer

Kumar S, Katyal S (2018) Effective analysis and diagnosis of liver disorder by data mining. In: 2018 international conference on inventive research in computing applications (ICIRCA). IEEE pp 1047–1051

Kurgan LA, Cios KJ, Tadeusiewicz R, Ogiela M, Goodenday LS (2001) Knowledge discovery approach to automated cardiac spect diagnosis. Artif Intell Med 23(2):149–169

Kursawe F (1990) A variant of evolution strategies for vector optimization. In: International conference on parallel problem solving from nature. Springer, pp 193–197

Li X, Yin M (2013) Multiobjective binary biogeography based optimization for feature selection using gene expression data. IEEE Trans NanoBioscience 12(4):343–353

Little MA, McSharry PE, Hunter EJ, Spielman J, Ramig LO (2009) Suitability of dysphonia measurements for telemonitoring of parkinson’s disease. IEEE Trans Bio-Med Eng 56(4):1015

Mafarja M, Aljarah I, Faris H, Hammouri AI, Al-Zoubi AM, Mirjalili S (2019) Binary grasshopper optimisation algorithm approaches for feature selection problems. Expert Syst Appl 117:267–286

Mafarja M, Aljarah I, Heidari AA, Faris H, Fournier-Viger P, Li X, Mirjalili S (2018) Binary dragonfly optimization for feature selection using time-varying transfer functions. Knowl-Based Syst 161:185–204

Mafarja M, Aljarah I, Heidari AA, Hammouri AI, Faris H, A-Zoubi AM, Mirjalili S (2018) Evolutionary population dynamics and grasshopper optimization approaches for feature selection problems. Knowl-Based Syst 145:25–45

Mafarja M, Heidari AA, Faris H, Mirjalili S, Aljarah I (2020) Dragonfly algorithm: theory, literature review, and application in feature selection. In: Nature-inspired optimizers. Springer, pp 47–67

Mafarja MM, Mirjalili S (2018) Hybrid binary ant lion optimizer with rough set and approximate entropy reducts for feature selection. Soft Comput 1–17

Mirjalili S, Jangir P, Saremi S (2017) Multi-objective ant lion optimizer: a multi-objective optimization algorithm for solving engineering problems. Appl Intell 46(1):79–95

Mirjalili S, Lewis A (2013) S-shaped versus v-shaped transfer functions for binary particle swarm optimization. Swarm Evol Comput 9:1–14

Mirjalili S, Saremi S, Mirjalili SM, Coelho LDS (2016) Multi-objective grey wolf optimizer: a novel algorithm for multi-criterion optimization. Expert Syst Appl 47:106–119

Mirjalili SZ, Mirjalili S, Saremi S, Faris H, Aljarah I (2018) Grasshopper optimization algorithm for multi-objective optimization problems. Appl Intell 48(4):805–820

Mitra S, Banka H (2006) Multi-objective evolutionary biclustering of gene expression data. Pattern Recognit 39(12):2464–2477

Mohemmed AW, Zhang M (2008) Evaluation of particle swarm optimization based centroid classifier with different distance metrics. In: 2008 IEEE congress on evolutionary computation (IEEE world congress on computational intelligence). IEEE, pp 2929–2932

Mugambi EM, Hunter A (2003) Multi-objective genetic programming optimization of decision trees for classifying medical data. In: International conference on knowledge-based and intelligent information and engineering systems. Springer, pp 293–299

Murata T, Ishibuchi H (1995) Moga: multi-objective genetic algorithms. IEEE Int Conf Evol Comput 1:289–294

rey Horn J, Nafpliotis N, Goldberg DE (1994) A niched pareto genetic algorithm for multiobjective optimization. In: Proceedings of the first IEEE conference on evolutionary computation, IEEE world congress on computational intelligence, vol 1. Citeseer, pp 82–87

Sahoo A, Chandra S (2017) Multi-objective grey wolf optimizer for improved cervix lesion classification. Appl Soft Comput 52:64–80

Santhosh J, Bhatia M, Sahu S, Anand S (2004) Quantitative eeg analysis for assessment to plana task in amyotrophic lateral sclerosis patients: a study of executive functions (planning) in als patients. Cogn Brain Res 22(1):59–66

Schaffer JD (1985) Multiple objective optimization with vector evaluated genetic algorithms. In: Proceedings of the first international conference on genetic algorithms and their applications (1985) Lawrence Erlbaum Associates. Publishers, Inc., p 1985

Shahbeig S, Rahideh A, Helfroush MS, Kazemi K (2018) Gene selection from large-scale gene expression data based on fuzzy interactive multi-objective binary optimization for medical diagnosis. Biocybern Biomed Eng 38(2):313–328

Sarah S, Hossam F, Ibrahim A, Seyedali M, Ajith A (2018) Evolutionary static and dynamic clustering algorithms based on multi-verse optimizer. Eng Appl Artif Intell 72:54–66

Sohrabi MK, Tajik A (2017) Multi-objective feature selection for warfarin dose prediction. Comput Biol Chem 69:126–133

Srinivas N, Deb K (1994) Muiltiobjective optimization using nondominated sorting in genetic algorithms. Evol Comput 2(3):221–248

Turing AM, Lerner A, (1987) Aaai 1991 spring symposium series reports. 12(4): Winter 1991, 31–37 aaai 1993 fall symposium reports. 15(1): Spring, (1994) 14–17 aaai 1994 spring symposium series. Intelligence 1(49):8

Yang X-S (2010) Nature-inspired metaheuristic algorithms. Luniver press

Zhang Q, Li H (2007) Moea/d: a multiobjective evolutionary algorithm based on decomposition. IEEE Trans Evol Comput 11(6):712–731

Download references

Author information

Authors and affiliations.

King Abdullah II School for Information Technology, The University of Jordan, Amman, Jordan

Maria Habib, Ibrahim Aljarah & Hossam Faris

Torrens University Australia, Brisbane, QLD, 4006, Australia

Seyedali Mirjalili

Griffith University, Brisbane, QLD, 4111, Australia

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Seyedali Mirjalili .

Editor information

Editors and affiliations.

Torrens University Australia, Brisbane, QLD, Australia

Hossam Faris

Ibrahim Aljarah

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Singapore Pte Ltd.

About this chapter

Habib, M., Aljarah, I., Faris, H., Mirjalili, S. (2020). Multi-objective Particle Swarm Optimization: Theory, Literature Review, and Application in Feature Selection for Medical Diagnosis. In: Mirjalili, S., Faris, H., Aljarah, I. (eds) Evolutionary Machine Learning Techniques. Algorithms for Intelligent Systems. Springer, Singapore. https://doi.org/10.1007/978-981-32-9990-0_9

Download citation

DOI : https://doi.org/10.1007/978-981-32-9990-0_9

Published : 12 November 2019

Publisher Name : Springer, Singapore

Print ISBN : 978-981-32-9989-4

Online ISBN : 978-981-32-9990-0

eBook Packages : Intelligent Technologies and Robotics Intelligent Technologies and Robotics (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research