research paper with null and alternative hypothesis

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base
• Null and Alternative Hypotheses | Definitions & Examples

Null and Alternative Hypotheses | Definitions & Examples

Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

• Null hypothesis (H 0 ): There’s no effect in the population .
• Alternative hypothesis (H A ): There’s an effect in the population.

The effect is usually the effect of the independent variable on the dependent variable .

Table of contents

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.

Null and alternative hypotheses are similar in some ways:

• They’re both answers to the research question
• They both make claims about the population
• They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

• Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
• Alternative hypothesis (H A ): Independent variable affects dependent variable .

Test-specific

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 14 May 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/

Is this article helpful?

Shaun Turney

Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.

Statistics Resources

• Excel - Tutorials
• Basic Probability Rules
• Single Event Probability
• Complement Rule
• Intersections & Unions
• Compound Events
• Levels of Measurement
• Independent and Dependent Variables
• Entering Data
• Central Tendency
• Data and Tests
• Displaying Data
• Discussing Statistics In-text
• SEM and Confidence Intervals
• Two-Way Frequency Tables
• Empirical Rule
• Finding Probability
• Accessing SPSS
• Chart and Graphs
• Frequency Table and Distribution
• Descriptive Statistics
• Converting Raw Scores to Z-Scores
• Converting Z-scores to t-scores
• Split File/Split Output
• Partial Eta Squared
• Downloading and Installing G*Power: Windows/PC
• Correlation
• Testing Parametric Assumptions
• One-Way ANOVA
• Two-Way ANOVA
• Repeated Measures ANOVA
• Goodness-of-Fit
• Test of Association
• Pearson's r
• Point Biserial
• Mediation and Moderation
• Simple Linear Regression
• Multiple Linear Regression
• Binomial Logistic Regression
• Multinomial Logistic Regression
• Independent Samples T-test
• Dependent Samples T-test
• Testing Assumptions
• T-tests using SPSS
• T-Test Practice
• Predictive Analytics This link opens in a new window
• Quantitative Research Questions
• Null & Alternative Hypotheses
• One-Tail vs. Two-Tail
• Alpha & Beta
• Associated Probability
• Decision Rule
• Statement of Conclusion
• Statistics Group Sessions

ASC Chat Hours

ASC Chat is usually available at the following times ( Pacific Time):

If there is not a coach on duty, submit your question via one of the below methods:

  928-440-1325

  Ask a Coach

  [email protected]

Search our FAQs on the Academic Success Center's  Ask a Coach   page.

Once you have developed a clear and focused research question or set of research questions, you’ll be ready to conduct further research, a literature review, on the topic to help you make an educated guess about the answer to your question(s). This educated guess is called a hypothesis.

In research, there are two types of hypotheses: null and alternative. They work as a complementary pair, each stating that the other is wrong.

• Null Hypothesis (H 0 ) – This can be thought of as the implied hypothesis. “Null” meaning “nothing.”  This hypothesis states that there is no difference between groups or no relationship between variables. The null hypothesis is a presumption of status quo or no change.
• Alternative Hypothesis (H a ) – This is also known as the claim. This hypothesis should state what you expect the data to show, based on your research on the topic. This is your answer to your research question.

Null Hypothesis:   H 0 : There is no difference in the salary of factory workers based on gender. Alternative Hypothesis :  H a : Male factory workers have a higher salary than female factory workers.

Null Hypothesis :  H 0 : There is no relationship between height and shoe size. Alternative Hypothesis :  H a : There is a positive relationship between height and shoe size.

Null Hypothesis :  H 0 : Experience on the job has no impact on the quality of a brick mason’s work. Alternative Hypothesis :  H a : The quality of a brick mason’s work is influenced by on-the-job experience.

Was this resource helpful?

• << Previous: Hypothesis Testing
• Next: One-Tail vs. Two-Tail >>
• Last Updated: Apr 19, 2024 3:09 PM
• URL: https://resources.nu.edu/statsresources

Our websites may use cookies to personalize and enhance your experience. By continuing without changing your cookie settings, you agree to this collection. For more information, please see our University Websites Privacy Notice .

Neag School of Education

Educational Research Basics by Del Siegle

Null and alternative hypotheses.

Converting research questions to hypothesis is a simple task. Take the questions and make it a positive statement that says a relationship exists (correlation studies) or a difference exists between the groups (experiment study) and you have the alternative hypothesis. Write the statement such that a relationship does not exist or a difference does not exist and you have the null hypothesis. You can reverse the process if you have a hypothesis and wish to write a research question.

When you are comparing two groups, the groups are the independent variable. When you are testing whether something affects something else, the cause is the independent variable. The independent variable is the one you manipulate.

Teachers given higher pay will have more positive attitudes toward children than teachers given lower pay. The first step is to ask yourself “Are there two or more groups being compared?” The answer is “Yes.” What are the groups? Teachers who are given higher pay and teachers who are given lower pay. The independent variable is teacher pay. The dependent variable (the outcome) is attitude towards school.

You could also approach is another way. “Is something causing something else?” The answer is “Yes.”  What is causing what? Teacher pay is causing attitude towards school. Therefore, teacher pay is the independent variable (cause) and attitude towards school is the dependent variable (outcome).

By tradition, we try to disprove (reject) the null hypothesis. We can never prove a null hypothesis, because it is impossible to prove something does not exist. We can disprove something does not exist by finding an example of it. Therefore, in research we try to disprove the null hypothesis. When we do find that a relationship (or difference) exists then we reject the null and accept the alternative. If we do not find that a relationship (or difference) exists, we fail to reject the null hypothesis (and go with it). We never say we accept the null hypothesis because it is never possible to prove something does not exist. That is why we say that we failed to reject the null hypothesis, rather than we accepted it.

Del Siegle, Ph.D. Neag School of Education – University of Connecticut [email protected] www.delsiegle.com

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

10.1 - setting the hypotheses: examples.

A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or differences between means or proportions or correlations or odds ratios or any other numerical summary of the population. The alternative hypothesis is typically the research hypothesis of interest. Here are some examples.

Example 10.2: Hypotheses with One Sample of One Categorical Variable Section  

About 10% of the human population is left-handed. Suppose a researcher at Penn State speculates that students in the College of Arts and Architecture are more likely to be left-handed than people found in the general population. We only have one sample since we will be comparing a population proportion based on a sample value to a known population value.

• Research Question : Are artists more likely to be left-handed than people found in the general population?
• Response Variable : Classification of the student as either right-handed or left-handed

State Null and Alternative Hypotheses

• Null Hypothesis : Students in the College of Arts and Architecture are no more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Art and Architecture = 10% or p = .10).
• Alternative Hypothesis : Students in the College of Arts and Architecture are more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Arts and Architecture > 10% or p > .10). This is a one-sided alternative hypothesis.

Example 10.3: Hypotheses with One Sample of One Measurement Variable Section  

A generic brand of the anti-histamine Diphenhydramine markets a capsule with a 50 milligram dose. The manufacturer is worried that the machine that fills the capsules has come out of calibration and is no longer creating capsules with the appropriate dosage.

• Research Question : Does the data suggest that the population mean dosage of this brand is different than 50 mg?
• Response Variable : dosage of the active ingredient found by a chemical assay.
• Null Hypothesis : On the average, the dosage sold under this brand is 50 mg (population mean dosage = 50 mg).
• Alternative Hypothesis : On the average, the dosage sold under this brand is not 50 mg (population mean dosage ≠ 50 mg). This is a two-sided alternative hypothesis.

Example 10.4: Hypotheses with Two Samples of One Categorical Variable Section  

Many people are starting to prefer vegetarian meals on a regular basis. Specifically, a researcher believes that females are more likely than males to eat vegetarian meals on a regular basis.

• Research Question : Does the data suggest that females are more likely than males to eat vegetarian meals on a regular basis?
• Response Variable : Classification of whether or not a person eats vegetarian meals on a regular basis
• Explanatory (Grouping) Variable: Sex
• Null Hypothesis : There is no sex effect regarding those who eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis = population percent of males who eat vegetarian meals on a regular basis or p females = p males ).
• Alternative Hypothesis : Females are more likely than males to eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis > population percent of males who eat vegetarian meals on a regular basis or p females > p males ). This is a one-sided alternative hypothesis.

Example 10.5: Hypotheses with Two Samples of One Measurement Variable Section  

Obesity is a major health problem today. Research is starting to show that people may be able to lose more weight on a low carbohydrate diet than on a low fat diet.

• Research Question : Does the data suggest that, on the average, people are able to lose more weight on a low carbohydrate diet than on a low fat diet?
• Response Variable : Weight loss (pounds)
• Explanatory (Grouping) Variable : Type of diet
• Null Hypothesis : There is no difference in the mean amount of weight loss when comparing a low carbohydrate diet with a low fat diet (population mean weight loss on a low carbohydrate diet = population mean weight loss on a low fat diet).
• Alternative Hypothesis : The mean weight loss should be greater for those on a low carbohydrate diet when compared with those on a low fat diet (population mean weight loss on a low carbohydrate diet > population mean weight loss on a low fat diet). This is a one-sided alternative hypothesis.

Example 10.6: Hypotheses about the relationship between Two Categorical Variables Section  

• Research Question : Do the odds of having a stroke increase if you inhale second hand smoke ? A case-control study of non-smoking stroke patients and controls of the same age and occupation are asked if someone in their household smokes.
• Variables : There are two different categorical variables (Stroke patient vs control and whether the subject lives in the same household as a smoker). Living with a smoker (or not) is the natural explanatory variable and having a stroke (or not) is the natural response variable in this situation.
• Null Hypothesis : There is no relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is = 1).
• Alternative Hypothesis : There is a relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is > 1). This is a one-tailed alternative.

This research question might also be addressed like example 11.4 by making the hypotheses about comparing the proportion of stroke patients that live with smokers to the proportion of controls that live with smokers.

Example 10.7: Hypotheses about the relationship between Two Measurement Variables Section  

• Research Question : A financial analyst believes there might be a positive association between the change in a stock's price and the amount of the stock purchased by non-management employees the previous day (stock trading by management being under "insider-trading" regulatory restrictions).
• Variables : Daily price change information (the response variable) and previous day stock purchases by non-management employees (explanatory variable). These are two different measurement variables.
• Null Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) = 0.
• Alternative Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) > 0. This is a one-sided alternative hypothesis.

Example 10.8: Hypotheses about comparing the relationship between Two Measurement Variables in Two Samples Section  

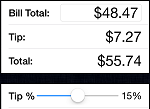
• Research Question : Is there a linear relationship between the amount of the bill (\$) at a restaurant and the tip (\$) that was left. Is the strength of this association different for family restaurants than for fine dining restaurants?
• Variables : There are two different measurement variables. The size of the tip would depend on the size of the bill so the amount of the bill would be the explanatory variable and the size of the tip would be the response variable.
• Null Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the same at family restaurants as it is at fine dining restaurants.
• Alternative Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the difference at family restaurants then it is at fine dining restaurants. This is a two-sided alternative hypothesis.

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• College University and Postgraduate
• Academic Writing

Writing Null Hypotheses in Research and Statistics

Last Updated: January 17, 2024 Fact Checked

This article was co-authored by Joseph Quinones and by wikiHow staff writer, Jennifer Mueller, JD . Joseph Quinones is a High School Physics Teacher working at South Bronx Community Charter High School. Joseph specializes in astronomy and astrophysics and is interested in science education and science outreach, currently practicing ways to make physics accessible to more students with the goal of bringing more students of color into the STEM fields. He has experience working on Astrophysics research projects at the Museum of Natural History (AMNH). Joseph recieved his Bachelor's degree in Physics from Lehman College and his Masters in Physics Education from City College of New York (CCNY). He is also a member of a network called New York City Men Teach. There are 7 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 25,573 times.

Are you working on a research project and struggling with how to write a null hypothesis? Well, you've come to the right place! Start by recognizing that the basic definition of "null" is "none" or "zero"—that's your biggest clue as to what a null hypothesis should say. Keep reading to learn everything you need to know about the null hypothesis, including how it relates to your research question and your alternative hypothesis as well as how to use it in different types of studies.

Things You Should Know

• Write a research null hypothesis as a statement that the studied variables have no relationship to each other, or that there's no difference between 2 groups.

• Adjust the format of your null hypothesis to match the statistical method you used to test it, such as using "mean" if you're comparing the mean between 2 groups.

What is a null hypothesis?

• Research hypothesis: States in plain language that there's no relationship between the 2 variables or there's no difference between the 2 groups being studied.
• Statistical hypothesis: States the predicted outcome of statistical analysis through a mathematical equation related to the statistical method you're using.

Examples of Null Hypotheses

Null Hypothesis vs. Alternative Hypothesis

• For example, your alternative hypothesis could state a positive correlation between 2 variables while your null hypothesis states there's no relationship. If there's a negative correlation, then both hypotheses are false.

• You need additional data or evidence to show that your alternative hypothesis is correct—proving the null hypothesis false is just the first step.
• In smaller studies, sometimes it's enough to show that there's some relationship and your hypothesis could be correct—you can leave the additional proof as an open question for other researchers to tackle.

How do I test a null hypothesis?

• Group means: Compare the mean of the variable in your sample with the mean of the variable in the general population. [6] X Research source
• Group proportions: Compare the proportion of the variable in your sample with the proportion of the variable in the general population. [7] X Research source
• Correlation: Correlation analysis looks at the relationship between 2 variables—specifically, whether they tend to happen together. [8] X Research source
• Regression: Regression analysis reveals the correlation between 2 variables while also controlling for the effect of other, interrelated variables. [9] X Research source

Templates for Null Hypotheses

• Research null hypothesis: There is no difference in the mean [dependent variable] between [group 1] and [group 2].

• Research null hypothesis: The proportion of [dependent variable] in [group 1] and [group 2] is the same.

• Research null hypothesis: There is no correlation between [independent variable] and [dependent variable] in the population.

• Research null hypothesis: There is no relationship between [independent variable] and [dependent variable] in the population.

Expert Q&A

You Might Also Like

Expert Interview

Thanks for reading our article! If you’d like to learn more about physics, check out our in-depth interview with Joseph Quinones .

• ↑ https://online.stat.psu.edu/stat100/lesson/10/10.1
• ↑ https://online.stat.psu.edu/stat501/lesson/2/2.12
• ↑ https://support.minitab.com/en-us/minitab/21/help-and-how-to/statistics/basic-statistics/supporting-topics/basics/null-and-alternative-hypotheses/
• ↑ https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5635437/
• ↑ https://online.stat.psu.edu/statprogram/reviews/statistical-concepts/hypothesis-testing
• ↑ https://education.arcus.chop.edu/null-hypothesis-testing/
• ↑ https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_hypothesistest-means-proportions/bs704_hypothesistest-means-proportions_print.html

About This Article

• Send fan mail to authors

Reader Success Stories

Dec 3, 2022

Did this article help you?

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Develop the tech skills you need for work and life

Statistics Made Easy

How to Write a Null Hypothesis (5 Examples)

A hypothesis test uses sample data to determine whether or not some claim about a population parameter is true.

Whenever we perform a hypothesis test, we always write a null hypothesis and an alternative hypothesis, which take the following forms:

H 0 (Null Hypothesis): Population parameter =,  ≤, ≥ some value

H A  (Alternative Hypothesis): Population parameter <, >, ≠ some value

Note that the null hypothesis always contains the equal sign .

We interpret the hypotheses as follows:

Null hypothesis: The sample data provides no evidence to support some claim being made by an individual.

Alternative hypothesis: The sample data  does provide sufficient evidence to support the claim being made by an individual.

For example, suppose it’s assumed that the average height of a certain species of plant is 20 inches tall. However, one botanist claims the true average height is greater than 20 inches.

To test this claim, she may go out and collect a random sample of plants. She can then use this sample data to perform a hypothesis test using the following two hypotheses:

H 0 : μ ≤ 20 (the true mean height of plants is equal to or even less than 20 inches)

H A : μ > 20 (the true mean height of plants is greater than 20 inches)

If the sample data gathered by the botanist shows that the mean height of this species of plants is significantly greater than 20 inches, she can reject the null hypothesis and conclude that the mean height is greater than 20 inches.

Read through the following examples to gain a better understanding of how to write a null hypothesis in different situations.

Example 1: Weight of Turtles

A biologist wants to test whether or not the true mean weight of a certain species of turtles is 300 pounds. To test this, he goes out and measures the weight of a random sample of 40 turtles.

Here is how to write the null and alternative hypotheses for this scenario:

H 0 : μ = 300 (the true mean weight is equal to 300 pounds)

H A : μ ≠ 300 (the true mean weight is not equal to 300 pounds)

Example 2: Height of Males

It’s assumed that the mean height of males in a certain city is 68 inches. However, an independent researcher believes the true mean height is greater than 68 inches. To test this, he goes out and collects the height of 50 males in the city.

H 0 : μ ≤ 68 (the true mean height is equal to or even less than 68 inches)

H A : μ > 68 (the true mean height is greater than 68 inches)

Example 3: Graduation Rates

A university states that 80% of all students graduate on time. However, an independent researcher believes that less than 80% of all students graduate on time. To test this, she collects data on the proportion of students who graduated on time last year at the university.

H 0 : p ≥ 0.80 (the true proportion of students who graduate on time is 80% or higher)

H A : μ < 0.80 (the true proportion of students who graduate on time is less than 80%)

Example 4: Burger Weights

A food researcher wants to test whether or not the true mean weight of a burger at a certain restaurant is 7 ounces. To test this, he goes out and measures the weight of a random sample of 20 burgers from this restaurant.

H 0 : μ = 7 (the true mean weight is equal to 7 ounces)

H A : μ ≠ 7 (the true mean weight is not equal to 7 ounces)

Example 5: Citizen Support

A politician claims that less than 30% of citizens in a certain town support a certain law. To test this, he goes out and surveys 200 citizens on whether or not they support the law.

H 0 : p ≥ .30 (the true proportion of citizens who support the law is greater than or equal to 30%)

H A : μ < 0.30 (the true proportion of citizens who support the law is less than 30%)

Additional Resources

Introduction to Hypothesis Testing Introduction to Confidence Intervals An Explanation of P-Values and Statistical Significance

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

2 Replies to “How to Write a Null Hypothesis (5 Examples)”

you are amazing, thank you so much

Say I am a botanist hypothesizing the average height of daisies is 20 inches, or not? Does T = (ave – 20 inches) / √ variance / (80 / 4)? … This assumes 40 real measures + 40 fake = 80 n, but that seems questionable. Please advise.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

How to Write a Null and Alternative Hypothesis: A Guide With Examples

• Icon Calendar 18 May 2024
• Icon Page 1229 words
• Icon Clock 6 min read

When undertaking a qualitative or quantitative research project, researchers must first formulate a research question, from which they develop a hypothesis. By definition, a hypothesis is a prediction that a researcher makes about the research question and can either be affirmative or negative. In this case, a research question has three main components: variables (independent and dependent), a population sample, and the relation between the variables. When the prediction contradicts the research question, it is referred to as a null hypothesis. In short, a null hypothesis is a statement that implies there is no relationship between independent and dependent variables. Hence, researchers need to learn how to write a good null and alternative hypothesis to present quality studies.

General Aspect of Writing a Null and Alternative Hypothesis

Students with qualitative or quantitative research assignments must learn how to formulate and write a good research question and hypothesis. By definition, a hypothesis is an assumption or prediction that a researcher makes before undertaking an experimental investigation. Basically, academic standards require such a prediction to be a precise and testable statement, meaning that researchers must prove or disapprove of it in the course of the assignment. In this case, the main components of a hypothesis are variables (independent and dependent), a population sample, and the relation between the variables. Therefore, a research hypothesis is a prediction that researchers write about the relationship between two or more variables. In turn, the research inquiry is the process that seeks to answer the research question and, in the process, test the hypothesis by confirming or disapproving it.

Types of Hypotheses

There are several types of hypotheses, including an alternative hypothesis, a null hypothesis, a directional hypothesis, and a non-directional hypothesis. Basically, the directional hypothesis is a prediction of how the independent variable affects the dependent variable. In contrast, the non-directional hypothesis predicts that the independent variable influences the dependent variable, but does not specify how. Regardless of the type, all hypotheses are about predicting the relationship between the independent and dependent variables.

What Is a Null and Alternative Hypothesis

A null hypothesis, usually symbolized as “H0,” is a statement that contradicts the research hypothesis. In other words, it is a negative statement, indicating that there is no relationship between the independent and dependent variables. By testing the null hypothesis, a researcher can determine whether the inquiry results are due to the chance or the effect of manipulating the dependent variable. In most instances, a null hypothesis corresponds with an alternative hypothesis, a positive statement that covers a relationship that exists between the independent and dependent variables. Also, it is highly recommended that a researcher should write the alternative hypothesis first before the null hypothesis.

10 Examples of Research Questions Цith H0 and H1 Hypotheses

Before developing a hypothesis, a researcher must formulate the research question. Then, the next step is to transform the question into a negative statement that claims the lack of a relationship between the independent and dependent variables. Alternatively, researchers can change the question into a positive statement that includes a relationship that exists between the variables. In turn, this latter statement becomes the alternative hypothesis and is symbolized as H1. Hence, some of the examples of research questions and hull and alternative hypotheses are as follows:

1. Do physical exercises help individuals to age gracefully?

A Null Hypothesis (H0): Physical exercises are not a guarantee for graceful old age.

An Alternative Hypothesis (H1): Engaging in physical exercises enables individuals to remain healthy and active into old age.

2. What are the implications of therapeutic interventions in the fight against substance abuse?

H0: Therapeutic interventions are of no help in the fight against substance abuse.

H1: Exposing individuals with substance abuse disorders to therapeutic interventions helps to control and even stop their addictions.

3. How do sexual orientation and gender identity affect the experiences of late adolescents in foster care?

H0: Sexual orientation and gender identity have no effects on the experiences of late adolescents in foster care.

H1: The reality of stereotypes in society makes sexual orientation and gender identity factors complicate the experiences of late adolescents in foster care.

4. Does income inequality contribute to crime in high-density urban areas?

H0: There is no correlation between income inequality and incidences of crime in high-density urban areas.

H1: The high crime rates in high-density urban areas are due to the incidence of income inequality in those areas.

5. Does placement in foster care impact individuals’ mental health?

H0: There is no correlation between being in foster care and having mental health problems.

H1: Individuals placed in foster care experience anxiety and depression at one point in their life.

6. Do assistive devices and technologies lessen the mobility challenges of older adults with a stroke?

H0: Assistive devices and technologies do not provide any assistance to the mobility of older adults diagnosed with a stroke.

H1: Assistive devices and technologies enhance the mobility of older adults diagnosed with a stroke.

7. Does race identity undermine classroom participation?

H0: There is no correlation between racial identity and the ability to participate in classroom learning.

H1: Students from racial minorities are not as active as white students in classroom participation.

8. Do high school grades determine future success?

H0: There is no correlation between how one performs in high school and their success level in life.

H1: Attaining high grades in high school positions one for greater success in the future personal and professional lives.

9. Does critical thinking predict academic achievement?

H0: There is no correlation between critical thinking and academic achievement.

H1: Being a critical thinker is a pathway to academic success.

10. What benefits does group therapy provide to victims of domestic violence?

H0: Group therapy does not help victims of domestic violence because individuals prefer to hide rather than expose their shame.

H1: Group therapy provides domestic violence victims with a platform to share their hurt and connect with others with similar experiences.

Summing Up on How to Write a Null and Alternative Hypothesis

The formulation of research questions in qualitative and quantitative assignments helps students develop a hypothesis for their experiment. In this case, learning how to write a good hypothesis helps students and researchers to make their research relevant. Basically, the difference between a null and alternative hypothesis is that the former contradicts the research question, while the latter affirms it. In short, a null hypothesis is a negative statement relative to the research question, and an alternative hypothesis is a positive statement. Moreover, it is important to note that developing the null hypothesis at the beginning of the assignment is for prediction purposes. As such, the research work answers the research question and confirms or disapproves of the hypothesis. Hence, some of the tips that students and researchers need to know when developing a null hypothesis include:

• Formulate a research question that specifies the relationship between an independent variable and a dependent variable.
• Develop an alternative hypothesis that says a relationship that exists between the variables.
• Develop a null hypothesis that says a relationship that does not exist between the variables.
• Conduct the research to answer the research question, which allows the confirmation of a disapproval of a null hypothesis.

To Learn More, Read Relevant Articles

SAT Essay Examples With Explanations and Recommendations

• 29 July 2020

How to Cite Lecture Notes in APA: Basic Guidelines

• 27 July 2020

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Research Hypothesis In Psychology: Types, & Examples

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A research hypothesis, in its plural form “hypotheses,” is a specific, testable prediction about the anticipated results of a study, established at its outset. It is a key component of the scientific method .

Hypotheses connect theory to data and guide the research process towards expanding scientific understanding

Some key points about hypotheses:

• A hypothesis expresses an expected pattern or relationship. It connects the variables under investigation.
• It is stated in clear, precise terms before any data collection or analysis occurs. This makes the hypothesis testable.
• A hypothesis must be falsifiable. It should be possible, even if unlikely in practice, to collect data that disconfirms rather than supports the hypothesis.
• Hypotheses guide research. Scientists design studies to explicitly evaluate hypotheses about how nature works.
• For a hypothesis to be valid, it must be testable against empirical evidence. The evidence can then confirm or disprove the testable predictions.
• Hypotheses are informed by background knowledge and observation, but go beyond what is already known to propose an explanation of how or why something occurs.

Predictions typically arise from a thorough knowledge of the research literature, curiosity about real-world problems or implications, and integrating this to advance theory. They build on existing literature while providing new insight.

Types of Research Hypotheses

Alternative hypothesis.

The research hypothesis is often called the alternative or experimental hypothesis in experimental research.

It typically suggests a potential relationship between two key variables: the independent variable, which the researcher manipulates, and the dependent variable, which is measured based on those changes.

The alternative hypothesis states a relationship exists between the two variables being studied (one variable affects the other).

A hypothesis is a testable statement or prediction about the relationship between two or more variables. It is a key component of the scientific method. Some key points about hypotheses:

• Important hypotheses lead to predictions that can be tested empirically. The evidence can then confirm or disprove the testable predictions.

In summary, a hypothesis is a precise, testable statement of what researchers expect to happen in a study and why. Hypotheses connect theory to data and guide the research process towards expanding scientific understanding.

An experimental hypothesis predicts what change(s) will occur in the dependent variable when the independent variable is manipulated.

It states that the results are not due to chance and are significant in supporting the theory being investigated.

The alternative hypothesis can be directional, indicating a specific direction of the effect, or non-directional, suggesting a difference without specifying its nature. It’s what researchers aim to support or demonstrate through their study.

Null Hypothesis

The null hypothesis states no relationship exists between the two variables being studied (one variable does not affect the other). There will be no changes in the dependent variable due to manipulating the independent variable.

It states results are due to chance and are not significant in supporting the idea being investigated.

The null hypothesis, positing no effect or relationship, is a foundational contrast to the research hypothesis in scientific inquiry. It establishes a baseline for statistical testing, promoting objectivity by initiating research from a neutral stance.

Many statistical methods are tailored to test the null hypothesis, determining the likelihood of observed results if no true effect exists.

This dual-hypothesis approach provides clarity, ensuring that research intentions are explicit, and fosters consistency across scientific studies, enhancing the standardization and interpretability of research outcomes.

Nondirectional Hypothesis

A non-directional hypothesis, also known as a two-tailed hypothesis, predicts that there is a difference or relationship between two variables but does not specify the direction of this relationship.

It merely indicates that a change or effect will occur without predicting which group will have higher or lower values.

For example, “There is a difference in performance between Group A and Group B” is a non-directional hypothesis.

Directional Hypothesis

A directional (one-tailed) hypothesis predicts the nature of the effect of the independent variable on the dependent variable. It predicts in which direction the change will take place. (i.e., greater, smaller, less, more)

It specifies whether one variable is greater, lesser, or different from another, rather than just indicating that there’s a difference without specifying its nature.

For example, “Exercise increases weight loss” is a directional hypothesis.

Falsifiability

The Falsification Principle, proposed by Karl Popper , is a way of demarcating science from non-science. It suggests that for a theory or hypothesis to be considered scientific, it must be testable and irrefutable.

Falsifiability emphasizes that scientific claims shouldn’t just be confirmable but should also have the potential to be proven wrong.

It means that there should exist some potential evidence or experiment that could prove the proposition false.

However many confirming instances exist for a theory, it only takes one counter observation to falsify it. For example, the hypothesis that “all swans are white,” can be falsified by observing a black swan.

For Popper, science should attempt to disprove a theory rather than attempt to continually provide evidence to support a research hypothesis.

Can a Hypothesis be Proven?

Hypotheses make probabilistic predictions. They state the expected outcome if a particular relationship exists. However, a study result supporting a hypothesis does not definitively prove it is true.

All studies have limitations. There may be unknown confounding factors or issues that limit the certainty of conclusions. Additional studies may yield different results.

In science, hypotheses can realistically only be supported with some degree of confidence, not proven. The process of science is to incrementally accumulate evidence for and against hypothesized relationships in an ongoing pursuit of better models and explanations that best fit the empirical data. But hypotheses remain open to revision and rejection if that is where the evidence leads.

• Disproving a hypothesis is definitive. Solid disconfirmatory evidence will falsify a hypothesis and require altering or discarding it based on the evidence.
• However, confirming evidence is always open to revision. Other explanations may account for the same results, and additional or contradictory evidence may emerge over time.

We can never 100% prove the alternative hypothesis. Instead, we see if we can disprove, or reject the null hypothesis.

If we reject the null hypothesis, this doesn’t mean that our alternative hypothesis is correct but does support the alternative/experimental hypothesis.

Upon analysis of the results, an alternative hypothesis can be rejected or supported, but it can never be proven to be correct. We must avoid any reference to results proving a theory as this implies 100% certainty, and there is always a chance that evidence may exist which could refute a theory.

How to Write a Hypothesis

• Identify variables . The researcher manipulates the independent variable and the dependent variable is the measured outcome.
• Operationalized the variables being investigated . Operationalization of a hypothesis refers to the process of making the variables physically measurable or testable, e.g. if you are about to study aggression, you might count the number of punches given by participants.
• Decide on a direction for your prediction . If there is evidence in the literature to support a specific effect of the independent variable on the dependent variable, write a directional (one-tailed) hypothesis. If there are limited or ambiguous findings in the literature regarding the effect of the independent variable on the dependent variable, write a non-directional (two-tailed) hypothesis.
• Make it Testable : Ensure your hypothesis can be tested through experimentation or observation. It should be possible to prove it false (principle of falsifiability).
• Clear & concise language . A strong hypothesis is concise (typically one to two sentences long), and formulated using clear and straightforward language, ensuring it’s easily understood and testable.

Consider a hypothesis many teachers might subscribe to: students work better on Monday morning than on Friday afternoon (IV=Day, DV= Standard of work).

Now, if we decide to study this by giving the same group of students a lesson on a Monday morning and a Friday afternoon and then measuring their immediate recall of the material covered in each session, we would end up with the following:

• The alternative hypothesis states that students will recall significantly more information on a Monday morning than on a Friday afternoon.
• The null hypothesis states that there will be no significant difference in the amount recalled on a Monday morning compared to a Friday afternoon. Any difference will be due to chance or confounding factors.

More Examples

• Memory : Participants exposed to classical music during study sessions will recall more items from a list than those who studied in silence.
• Social Psychology : Individuals who frequently engage in social media use will report higher levels of perceived social isolation compared to those who use it infrequently.
• Developmental Psychology : Children who engage in regular imaginative play have better problem-solving skills than those who don’t.
• Clinical Psychology : Cognitive-behavioral therapy will be more effective in reducing symptoms of anxiety over a 6-month period compared to traditional talk therapy.
• Cognitive Psychology : Individuals who multitask between various electronic devices will have shorter attention spans on focused tasks than those who single-task.
• Health Psychology : Patients who practice mindfulness meditation will experience lower levels of chronic pain compared to those who don’t meditate.
• Organizational Psychology : Employees in open-plan offices will report higher levels of stress than those in private offices.
• Behavioral Psychology : Rats rewarded with food after pressing a lever will press it more frequently than rats who receive no reward.

Related Articles

Research Methodology

Qualitative Data Coding

What Is a Focus Group?

Cross-Cultural Research Methodology In Psychology

What Is Internal Validity In Research?

Research Methodology , Statistics

What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples

• Research article
• Open access
• Published: 19 May 2010

The null hypothesis significance test in health sciences research (1995-2006): statistical analysis and interpretation

• Luis Carlos Silva-Ayçaguer 1 ,
• Patricio Suárez-Gil 2 &
• Ana Fernández-Somoano 3  

BMC Medical Research Methodology volume  10 , Article number:  44 ( 2010 ) Cite this article

38k Accesses

23 Citations

18 Altmetric

Metrics details

The null hypothesis significance test (NHST) is the most frequently used statistical method, although its inferential validity has been widely criticized since its introduction. In 1988, the International Committee of Medical Journal Editors (ICMJE) warned against sole reliance on NHST to substantiate study conclusions and suggested supplementary use of confidence intervals (CI). Our objective was to evaluate the extent and quality in the use of NHST and CI, both in English and Spanish language biomedical publications between 1995 and 2006, taking into account the International Committee of Medical Journal Editors recommendations, with particular focus on the accuracy of the interpretation of statistical significance and the validity of conclusions.

Original articles published in three English and three Spanish biomedical journals in three fields (General Medicine, Clinical Specialties and Epidemiology - Public Health) were considered for this study. Papers published in 1995-1996, 2000-2001, and 2005-2006 were selected through a systematic sampling method. After excluding the purely descriptive and theoretical articles, analytic studies were evaluated for their use of NHST with P-values and/or CI for interpretation of statistical "significance" and "relevance" in study conclusions.

Among 1,043 original papers, 874 were selected for detailed review. The exclusive use of P-values was less frequent in English language publications as well as in Public Health journals; overall such use decreased from 41% in 1995-1996 to 21% in 2005-2006. While the use of CI increased over time, the "significance fallacy" (to equate statistical and substantive significance) appeared very often, mainly in journals devoted to clinical specialties (81%). In papers originally written in English and Spanish, 15% and 10%, respectively, mentioned statistical significance in their conclusions.

Conclusions

Overall, results of our review show some improvements in statistical management of statistical results, but further efforts by scholars and journal editors are clearly required to move the communication toward ICMJE advices, especially in the clinical setting, which seems to be imperative among publications in Spanish.

Peer Review reports

The null hypothesis statistical testing (NHST) has been the most widely used statistical approach in health research over the past 80 years. Its origins dates back to 1279 [ 1 ] although it was in the second decade of the twentieth century when the statistician Ronald Fisher formally introduced the concept of "null hypothesis" H 0 - which, generally speaking, establishes that certain parameters do not differ from each other. He was the inventor of the "P-value" through which it could be assessed [ 2 ]. Fisher's P-value is defined as a conditional probability calculated using the results of a study. Specifically, the P-value is the probability of obtaining a result at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. The Fisherian significance testing theory considered the p-value as an index to measure the strength of evidence against the null hypothesis in a single experiment. The father of NHST never endorsed, however, the inflexible application of the ultimately subjective threshold levels almost universally adopted later on (although the introduction of the 0.05 has his paternity also).

A few years later, Jerzy Neyman and Egon Pearson considered the Fisherian approach inefficient, and in 1928 they published an article [ 3 ] that would provide the theoretical basis of what they called hypothesis statistical testing . The Neyman-Pearson approach is based on the notion that one out of two choices has to be taken: accept the null hypothesis taking the information as a reference based on the information provided, or reject it in favor of an alternative one. Thus, one can incur one of two types of errors: a Type I error, if the null hypothesis is rejected when it is actually true, and a Type II error, if the null hypothesis is accepted when it is actually false. They established a rule to optimize the decision process, using the p-value introduced by Fisher, by setting the maximum frequency of errors that would be admissible.

The null hypothesis statistical testing, as applied today, is a hybrid coming from the amalgamation of the two methods [ 4 ]. As a matter of fact, some 15 years later, both procedures were combined to give rise to the nowadays widespread use of an inferential tool that would satisfy none of the statisticians involved in the original controversy. The present method essentially goes as follows: given a null hypothesis, an estimate of the parameter (or parameters) is obtained and used to create statistics whose distribution, under H 0 , is known. With these data the P-value is computed. Finally, the null hypothesis is rejected when the obtained P-value is smaller than a certain comparative threshold (usually 0.05) and it is not rejected if P is larger than the threshold.

The first reservations about the validity of the method began to appear around 1940, when some statisticians censured the logical roots and practical convenience of Fisher's P-value [ 5 ]. Significance tests and P-values have repeatedly drawn the attention and criticism of many authors over the past 70 years, who have kept questioning its epistemological legitimacy as well as its practical value. What remains in spite of these criticisms is the lasting legacy of researchers' unwillingness to eradicate or reform these methods.

Although there are very comprehensive works on the topic [ 6 ], we list below some of the criticisms most universally accepted by specialists.

The P-values are used as a tool to make decisions in favor of or against a hypothesis. What really may be relevant, however, is to get an effect size estimate (often the difference between two values) rather than rendering dichotomous true/false verdicts [ 7 – 11 ].

The P-value is a conditional probability of the data, provided that some assumptions are met, but what really interests the investigator is the inverse probability: what degree of validity can be attributed to each of several competing hypotheses, once that certain data have been observed [ 12 ].

The two elements that affect the results, namely the sample size and the magnitude of the effect, are inextricably linked in the value of p and we can always get a lower P-value by increasing the sample size. Thus, the conclusions depend on a factor completely unrelated to the reality studied (i.e. the available resources, which in turn determine the sample size) [ 13 , 14 ].

Those who defend the NHST often assert the objective nature of that test, but the process is actually far from being so. NHST does not ensure objectivity. This is reflected in the fact that we generally operate with thresholds that are ultimately no more than conventions, such as 0.01 or 0.05. What is more, for many years their use has unequivocally demonstrated the inherent subjectivity that goes with the concept of P, regardless of how it will be used later [ 15 – 17 ].

In practice, the NHST is limited to a binary response sorting hypotheses into "true" and "false" or declaring "rejection" or "no rejection", without demanding a reasonable interpretation of the results, as has been noted time and again for decades. This binary orthodoxy validates categorical thinking, which results in a very simplistic view of scientific activity that induces researchers not to test theories about the magnitude of effect sizes [ 18 – 20 ].

Despite the weakness and shortcomings of the NHST, they are frequently taught as if they were the key inferential statistical method or the most appropriate, or even the sole unquestioned one. The statistical textbooks, with only some exceptions, do not even mention the NHST controversy. Instead, the myth is spread that NHST is the "natural" final action of scientific inference and the only procedure for testing hypotheses. However, relevant specialists and important regulators of the scientific world advocate avoiding them.

Taking especially into account that NHST does not offer the most important information (i.e. the magnitude of an effect of interest, and the precision of the estimate of the magnitude of that effect), many experts recommend the reporting of point estimates of effect sizes with confidence intervals as the appropriate representation of the inherent uncertainty linked to empirical studies [ 21 – 25 ]. Since 1988, the International Committee of Medical Journal Editors (ICMJE, known as the Vancouver Group ) incorporates the following recommendation to authors of manuscripts submitted to medical journals: "When possible, quantify findings and present them with appropriate indicators of measurement error or uncertainty (such as confidence intervals). Avoid relying solely on statistical hypothesis testing, such as P-values, which fail to convey important information about effect size" [ 26 ].

As will be shown, the use of confidence intervals (CI), occasionally accompanied by P-values, is recommended as a more appropriate method for reporting results. Some authors have noted several shortcomings of CI long ago [ 27 ]. In spite of the fact that calculating CI could be complicated indeed, and that their interpretation is far from simple [ 28 , 29 ], authors are urged to use them because they provide much more information than the NHST and do not merit most of its criticisms of NHST [ 30 ]. While some have proposed different options (for instance, likelihood-based information theoretic methods [ 31 ], and the Bayesian inferential paradigm [ 32 ]), confidence interval estimation of effect sizes is clearly the most widespread alternative approach.

Although twenty years have passed since the ICMJE began to disseminate such recommendations, systematically ignored by the vast majority of textbooks and hardly incorporated in medical publications [ 33 ], it is interesting to examine the extent to which the NHST is used in articles published in medical journals during recent years, in order to identify what is still lacking in the process of eradicating the widespread ceremonial use that is made of statistics in health research [ 34 ]. Furthermore, it is enlightening in this context to examine whether these patterns differ between English- and Spanish-speaking worlds and, if so, to see if the changes in paradigms are occurring more slowly in Spanish-language publications. In such a case we would offer various suggestions.

In addition to assessing the adherence to the above cited statistical recommendation proposed by ICMJE relative to the use of P-values, we consider it of particular interest to estimate the extent to which the significance fallacy is present, an inertial deficiency that consists of attributing -- explicitly or not -- qualitative importance or practical relevance to the found differences simply because statistical significance was obtained.

Many authors produce misleading statements such as "a significant effect was (or was not) found" when it should be said that "a statistically significant difference was (or was not) found". A detrimental consequence of this equivalence is that some authors believe that finding out whether there is "statistical significance" or not is the aim, so that this term is then mentioned in the conclusions [ 35 ]. This means virtually nothing, except that it indicates that the author is letting a computer do the thinking. Since the real research questions are never statistical ones, the answers cannot be statistical either. Accordingly, the conversion of the dichotomous outcome produced by a NHST into a conclusion is another manifestation of the mentioned fallacy.

The general objective of the present study is to evaluate the extent and quality of use of NHST and CI, both in English- and in Spanish-language biomedical publications, between 1995 and 2006 taking into account the International Committee of Medical Journal Editors recommendations, with particular focus on accuracy regarding interpretation of statistical significance and the validity of conclusions.

We reviewed the original articles from six journals, three in English and three in Spanish, over three disjoint periods sufficiently separated from each other (1995-1996, 2000-2001, 2005-2006) as to properly describe the evolution in prevalence of the target features along the selected periods.

The selection of journals was intended to get representation for each of the following three thematic areas: clinical specialties ( Obstetrics & Gynecology and Revista Española de Cardiología) ; Public Health and Epidemiology ( International Journal of Epidemiology and Atención Primaria) and the area of general and internal medicine ( British Medical Journal and Medicina Clínica ). Five of the selected journals formally endorsed ICMJE guidelines; the remaining one ( Revista Española de Cardiología ) suggests observing ICMJE demands in relation with specific issues. We attempted to capture journal diversity in the sample by selecting general and specialty journals with different degrees of influence, resulting from their impact factors in 2007, which oscillated between 1.337 (MC) and 9.723 (BMJ). No special reasons guided us to choose these specific journals, but we opted for journals with rather large paid circulations. For instance, the Spanish Cardiology Journal is the one with the largest impact factor among the fourteen Spanish Journals devoted to clinical specialties that have impact factor and Obstetrics & Gynecology has an outstanding impact factor among the huge number of journals available for selection.

It was decided to take around 60 papers for each biennium and journal, which means a total of around 1,000 papers. As recently suggested [ 36 , 37 ], this number was not established using a conventional method, but by means of a purposive and pragmatic approach in choosing the maximum sample size that was feasible.

Systematic sampling in phases [ 38 ] was used in applying a sampling fraction equal to 60/N, where N is the number of articles, in each of the 18 subgroups defined by crossing the six journals and the three time periods. Table 1 lists the population size and the sample size for each subgroup. While the sample within each subgroup was selected with equal probability, estimates based on other subsets of articles (defined across time periods, areas, or languages) are based on samples with various selection probabilities. Proper weights were used to take into account the stratified nature of the sampling in these cases.

Forty-nine of the 1,092 selected papers were eliminated because, although the section of the article in which they were assigned could suggest they were originals, detailed scrutiny revealed that in some cases they were not. The sample, therefore, consisted of 1,043 papers. Each of them was classified into one of three categories: (1) purely descriptive papers, those designed to review or characterize the state of affairs as it exists at present, (2) analytical papers, or (3) articles that address theoretical, methodological or conceptual issues. An article was regarded as analytical if it seeks to explain the reasons behind a particular occurrence by discovering causal relationships or, even if self-classified as descriptive, it was carried out to assess cause-effect associations among variables. We classify as theoretical or methodological those articles that do not handle empirical data as such, and focus instead on proposing or assessing research methods. We identified 169 papers as purely descriptive or theoretical, which were therefore excluded from the sample. Figure 1 presents a flow chart showing the process for determining eligibility for inclusion in the sample.

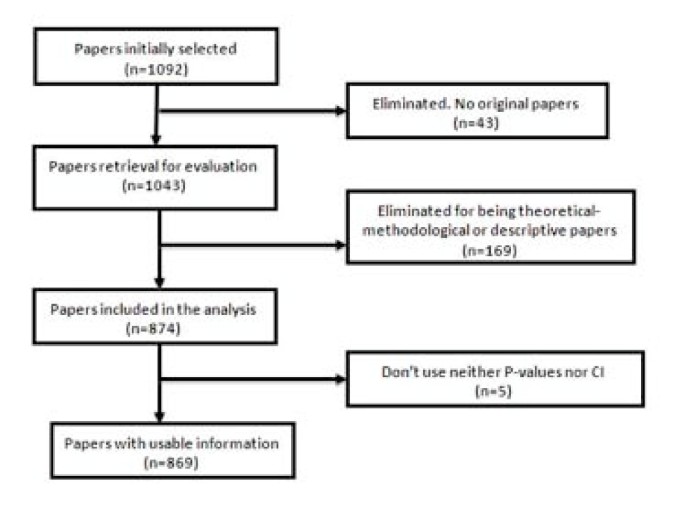
Flow chart of the selection process for eligible papers .

To estimate the adherence to ICMJE recommendations, we considered whether the papers used P-values, confidence intervals, and both simultaneously. By "the use of P-values" we mean that the article contains at least one P-value, explicitly mentioned in the text or at the bottom of a table, or that it reports that an effect was considered as statistically significant . It was deemed that an article uses CI if it explicitly contained at least one confidence interval, but not when it only provides information that could allow its computation (usually by presenting both the estimate and the standard error). Probability intervals provided in Bayesian analysis were classified as confidence intervals (although conceptually they are not the same) since what is really of interest here is whether or not the authors quantify the findings and present them with appropriate indicators of the margin of error or uncertainty.

In addition we determined whether the "Results" section of each article attributed the status of "significant" to an effect on the sole basis of the outcome of a NHST (i.e., without clarifying that it is strictly statistical significance). Similarly, we examined whether the term "significant" (applied to a test) was mistakenly used as synonymous with substantive , relevant or important . The use of the term "significant effect" when it is only appropriate as a reference to a "statistically significant difference," can be considered a direct expression of the significance fallacy [ 39 ] and, as such, constitutes one way to detect the problem in a specific paper.

We also assessed whether the "Conclusions," which sometimes appear as a separate section in the paper or otherwise in the last paragraphs of the "Discussion" section mentioned statistical significance and, if so, whether any of such mentions were no more than an allusion to results.

To perform these analyses we considered both the abstract and the body of the article. To assess the handling of the significance issue, however, only the body of the manuscript was taken into account.

The information was collected by four trained observers. Every paper was assigned to two reviewers. Disagreements were discussed and, if no agreement was reached, a third reviewer was consulted to break the tie and so moderate the effect of subjectivity in the assessment.

In order to assess the reliability of the criteria used for the evaluation of articles and to effect a convergence of criteria among the reviewers, a pilot study of 20 papers from each of three journals ( Clinical Medicine , Primary Care , and International Journal of Epidemiology) was performed. The results of this pilot study were satisfactory. Our results are reported using percentages together with their corresponding confidence intervals. For sampling errors estimations, used to obtain confidence intervals, we weighted the data using the inverse of the probability of selection of each paper, and we took into account the complex nature of the sample design. These analyses were carried out with EPIDAT [ 40 ], a specialized computer program that is readily available.

A total of 1,043 articles were reviewed, of which 874 (84%) were found to be analytic, while the remainders were purely descriptive or of a theoretical and methodological nature. Five of them did not employ either P-values or CI. Consequently, the analysis was made using the remaining 869 articles.

Use of NHST and confidence intervals

The percentage of articles that use only P-values, without even mentioning confidence intervals, to report their results has declined steadily throughout the period analyzed (Table 2 ). The percentage decreased from approximately 41% in 1995-1996 to 21% in 2005-2006. However, it does not differ notably among journals of different languages, as shown by the estimates and confidence intervals of the respective percentages. Concerning thematic areas, it is highly surprising that most of the clinical articles ignore the recommendations of ICMJE, while for general and internal medicine papers such a problem is only present in one in five papers, and in the area of Public Health and Epidemiology it occurs only in one out of six. The use of CI alone (without P-values) has increased slightly across the studied periods (from 9% to 13%), but it is five times more prevalent in Public Health and Epidemiology journals than in Clinical ones, where it reached a scanty 3%.

Ambivalent handling of the significance

While the percentage of articles referring implicitly or explicitly to significance in an ambiguous or incorrect way - that is, incurring the significance fallacy -- seems to decline steadily, the prevalence of this problem exceeds 69%, even in the most recent period. This percentage was almost the same for articles written in Spanish and in English, but it was notably higher in the Clinical journals (81%) compared to the other journals, where the problem occurs in approximately 7 out of 10 papers (Table 3 ). The kappa coefficient for measuring agreement between observers concerning the presence of the "significance fallacy" was 0.78 (CI95%: 0.62 to 0.93), which is considered acceptable in the scale of Landis and Koch [ 41 ].

Reference to numerical results or statistical significance in Conclusions

The percentage of papers mentioning a numerical finding as a conclusion is similar in the three periods analyzed (Table 4 ). Concerning languages, this percentage is nearly twice as large for Spanish journals as for those published in English (approximately 21% versus 12%). And, again, the highest percentage (16%) corresponded to clinical journals.

A similar pattern is observed, although with less pronounced differences, in references to the outcome of the NHST (significant or not) in the conclusions (Table 5 ). The percentage of articles that introduce the term in the "Conclusions" does not appreciably differ between articles written in Spanish and in English. Again, the area where this insufficiency is more often present (more than 15% of articles) is the Clinical area.

There are some previous studies addressing the degree to which researchers have moved beyond the ritualistic use of NHST to assess their hypotheses. This has been examined for areas such as biology [ 42 ], organizational research [ 43 ], or psychology [ 44 – 47 ]. However, to our knowledge, no recent research has explored the pattern of use P-values and CI in medical literature and, in any case, no efforts have been made to study this problem in a way that takes into account different languages and specialties.

At first glance it is puzzling that, after decades of questioning and technical warnings, and after twenty years since the inception of ICMJE recommendation to avoid NHST, they continue being applied ritualistically and mindlessly as the dominant doctrine. Not long ago, when researchers did not observe statistically significant effects, they were unlikely to write them up and to report "negative" findings, since they knew there was a high probability that the paper would be rejected. This has changed a bit: editors are more prone to judge all findings as potentially eloquent. This is probably the frequent denunciations of the tendency for those papers presenting a significant positive result to receive more favorable publication decisions than equally well-conducted ones that report a negative or null result, the so-called publication bias [ 48 – 50 ]. This new openness is consistent with the fact that if the substantive question addressed is really relevant, the answer (whether positive or negative) will also be relevant.

Consequently, even though it was not an aim of our study, we found many examples in which statistical significance was not obtained. However, many of those negative results were reported with a comment of this type: " The results did not show a significant difference between groups; however, with a larger sample size, this difference would have probably proved to be significant ". The problem with this statement is that it is true; more specifically, it will always be true and it is, therefore, sterile. It is not fortuitous that one never encounters the opposite, and equally tautological, statement: " A significant difference between groups has been detected; however, perhaps with a smaller sample size, this difference would have proved to be not significant" . Such a double standard is itself an unequivocal sign of the ritual application of NHST.

Although the declining rates of NHST usage show that, gradually, ICMJE and similar recommendations are having a positive impact, most of the articles in the clinical setting still considered NHST as the final arbiter of the research process. Moreover, it appears that the improvement in the situation is mostly formal, and the percentage of articles that fall into the significance fallacy is huge.

The contradiction between what has been conceptually recommended and the common practice is sensibly less acute in the area of Epidemiology and Public Health, but the same pattern was evident everywhere in the mechanical way of applying significance tests. Nevertheless, the clinical journals remain the most unmoved by the recommendations.

The ICMJE recommendations are not cosmetic statements but substantial ones, and the vigorous exhortations made by outstanding authorities [ 51 ] are not mere intellectual exercises due to ingenious and inopportune methodologists, but rather they are very serious epistemological warnings.

In some cases, the role of CI is not as clearly suitable (e.g. when estimating multiple regression coefficients or because effect sizes are not available for some research designs [ 43 , 52 ]), but when it comes to estimating, for example, an odds ratio or a rates difference, the advantage of using CI instead of P values is very clear, since in such cases it is obvious that the goal is to assess what has been called the "effect size."

The inherent resistance to change old paradigms and practices that have been entrenched for decades is always high. Old habits die hard. The estimates and trends outlined are entirely consistent with Alvan Feinstein's warning 25 years ago: "Because the history of medical research also shows a long tradition of maintaining loyalty to established doctrines long after the doctrines had been discredited, or shown to be valueless, we cannot expect a sudden change in this medical policy merely because it has been denounced by leading connoisseurs of statistics [ 53 ]".

It is possible, however, that the nature of the problem has an external explanation: it is likely that some editors prefer to "avoid troubles" with the authors and vice versa, thus resorting to the most conventional procedures. Many junior researchers believe that it is wise to avoid long back-and-forth discussions with reviewers and editors. In general, researchers who want to appear in print and survive in a publish-or-perish environment are motivated by force, fear, and expedience in their use of NHST [ 54 ]. Furthermore, it is relatively natural that simple researchers use NHST when they take into account that some theoretical objectors have used this statistical analysis in empirical studies, published after the appearance of their own critiques [ 55 ].

For example, Journal of the American Medical Association published a bibliometric study [ 56 ] discussing the impact of statisticians' co-authorship of medical papers on publication decisions by two major high-impact journals: British Medical Journal and Annals of Internal Medicine . The data analysis is characterized by methodological orthodoxy. The authors just use chi-square tests without any reference to CI, although the NHST had been repeatedly criticized over the years by two of the authors:

Douglas Altman, an early promoter of confidence intervals as an alternative [ 57 ], and Steve Goodman, a critic of NHST from a Bayesian perspective [ 58 ]. Individual authors, however, cannot be blamed for broader institutional problems and systemic forces opposed to change.

The present effort is certainly partial in at least two ways: it is limited to only six specific journals and to three biennia. It would be therefore highly desirable to improve it by studying the problem in a more detailed way (especially by reviewing more journals with different profiles), and continuing the review of prevailing patterns and trends.

Curran-Everett D: Explorations in statistics: hypothesis tests and P values. Adv Physiol Educ. 2009, 33: 81-86. 10.1152/advan.90218.2008.

Article   PubMed   Google Scholar  

Fisher RA: Statistical Methods for Research Workers. 1925, Edinburgh: Oliver & Boyd

Google Scholar  

Neyman J, Pearson E: On the use and interpretation of certain test criteria for purposes of statistical inference. Biometrika. 1928, 20: 175-240.

Silva LC: Los laberintos de la investigación biomédica. En defensa de la racionalidad para la ciencia del siglo XXI. 2009, Madrid: Díaz de Santos

Berkson J: Test of significance considered as evidence. J Am Stat Assoc. 1942, 37: 325-335. 10.2307/2279000.

Article   Google Scholar  

Nickerson RS: Null hypothesis significance testing: A review of an old and continuing controversy. Psychol Methods. 2000, 5: 241-301. 10.1037/1082-989X.5.2.241.

Article   CAS   PubMed   Google Scholar  

Rozeboom WW: The fallacy of the null hypothesissignificance test. Psychol Bull. 1960, 57: 418-428. 10.1037/h0042040.

Callahan JL, Reio TG: Making subjective judgments in quantitative studies: The importance of using effect sizes and confidenceintervals. HRD Quarterly. 2006, 17: 159-173.

Nakagawa S, Cuthill IC: Effect size, confidence interval and statistical significance: a practical guide for biologists. Biol Rev. 2007, 82: 591-605. 10.1111/j.1469-185X.2007.00027.x.

Breaugh JA: Effect size estimation: factors to consider and mistakes to avoid. J Manage. 2003, 29: 79-97. 10.1177/014920630302900106.

Thompson B: What future quantitative social science research could look like: confidence intervals for effect sizes. Educ Res. 2002, 31: 25-32.

Matthews RA: Significance levels for the assessment of anomalous phenomena. Journal of Scientific Exploration. 1999, 13: 1-7.

Savage IR: Nonparametric statistics. J Am Stat Assoc. 1957, 52: 332-333.

Silva LC, Benavides A, Almenara J: El péndulo bayesiano: Crónica de una polémica estadística. Llull. 2002, 25: 109-128.

Goodman SN, Royall R: Evidence and scientific research. Am J Public Health. 1988, 78: 1568-1574. 10.2105/AJPH.78.12.1568.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Berger JO, Berry DA: Statistical analysis and the illusion of objectivity. Am Sci. 1988, 76: 159-165.

Hurlbert SH, Lombardi CM: Final collapse of the Neyman-Pearson decision theoretic framework and rise of the neoFisherian. Ann Zool Fenn. 2009, 46: 311-349.

Fidler F, Thomason N, Cumming G, Finch S, Leeman J: Editors can lead researchers to confidence intervals but they can't make them think: Statistical reform lessons from Medicine. Psychol Sci. 2004, 15: 119-126. 10.1111/j.0963-7214.2004.01502008.x.

Balluerka N, Vergara AI, Arnau J: Calculating the main alternatives to null-hypothesis-significance testing in between-subject experimental designs. Psicothema. 2009, 21: 141-151.

Cumming G, Fidler F: Confidence intervals: Better answers to better questions. J Psychol. 2009, 217: 15-26.

Jones LV, Tukey JW: A sensible formulation of the significance test. Psychol Methods. 2000, 5: 411-414. 10.1037/1082-989X.5.4.411.

Dixon P: The p-value fallacy and how to avoid it. Can J Exp Psychol. 2003, 57: 189-202.

Nakagawa S, Cuthill IC: Effect size, confidence interval and statistical significance: a practical guide for biologists. Biol Rev Camb Philos Soc. 2007, 82: 591-605. 10.1111/j.1469-185X.2007.00027.x.

Brandstaetter E: Confidence intervals as an alternative to significance testing. MPR-Online. 2001, 4: 33-46.

Masson ME, Loftus GR: Using confidence intervals for graphically based data interpretation. Can J Exp Psychol. 2003, 57: 203-220.

International Committee of Medical Journal Editors: Uniform requirements for manuscripts submitted to biomedical journals. Update October 2008. Accessed July 11, 2009, [ http://www.icmje.org ]

Feinstein AR: P-Values and Confidence Intervals: two sides of the same unsatisfactory coin. J Clin Epidemiol. 1998, 51: 355-360. 10.1016/S0895-4356(97)00295-3.

Haller H, Kraus S: Misinterpretations of significance: A problem students share with their teachers?. MRP-Online. 2002, 7: 1-20.

Gigerenzer G, Krauss S, Vitouch O: The null ritual: What you always wanted to know about significance testing but were afraid to ask. The Handbook of Methodology for the Social Sciences. Edited by: Kaplan D. 2004, Thousand Oaks, CA: Sage Publications, Chapter 21: 391-408.

Curran-Everett D, Taylor S, Kafadar K: Fundamental concepts in statistics: elucidation and illustration. J Appl Physiol. 1998, 85: 775-786.

CAS   PubMed   Google Scholar  

Royall RM: Statistical evidence: a likelihood paradigm. 1997, Boca Raton: Chapman & Hall/CRC

Goodman SN: Of P values and Bayes: A modest proposal. Epidemiology. 2001, 12: 295-297. 10.1097/00001648-200105000-00006.

Sarria M, Silva LC: Tests of statistical significance in three biomedical journals: a critical review. Rev Panam Salud Publica. 2004, 15: 300-306.

Silva LC: Una ceremonia estadística para identificar factores de riesgo. Salud Colectiva. 2005, 1: 322-329.

Goodman SN: Toward Evidence-Based Medical Statistics 1: The p Value Fallacy. Ann Intern Med. 1999, 130: 995-1004.

Schulz KF, Grimes DA: Sample size calculations in randomised clinical trials: mandatory and mystical. Lancet. 2005, 365: 1348-1353. 10.1016/S0140-6736(05)61034-3.

Bacchetti P: Current sample size conventions: Flaws, harms, and alternatives. BMC Med. 2010, 8: 17-10.1186/1741-7015-8-17.

Article   PubMed   PubMed Central   Google Scholar  

Silva LC: Diseño razonado de muestras para la investigación sanitaria. 2000, Madrid: Díaz de Santos

Barnett ML, Mathisen A: Tyranny of the p-value: The conflict between statistical significance and common sense. J Dent Res. 1997, 76: 534-536. 10.1177/00220345970760010201.

Santiago MI, Hervada X, Naveira G, Silva LC, Fariñas H, Vázquez E, Bacallao J, Mújica OJ: [The Epidat program: uses and perspectives] [letter]. Pan Am J Public Health. 2010, 27: 80-82. Spanish.

Landis JR, Koch GG: The measurement of observer agreement for categorical data. Biometrics. 1977, 33: 159-74. 10.2307/2529310.

Fidler F, Burgman MA, Cumming G, Buttrose R, Thomason N: Impact of criticism of null-hypothesis significance testing on statistical reporting practices in conservation biology. Conserv Biol. 2005, 20: 1539-1544. 10.1111/j.1523-1739.2006.00525.x.

Kline RB: Beyond significance testing: Reforming data analysis methods in behavioral research. 2004, Washington, DC: American Psychological Association

Book   Google Scholar  

Curran-Everett D, Benos DJ: Guidelines for reporting statistics in journals published by the American Physiological Society: the sequel. Adv Physiol Educ. 2007, 31: 295-298. 10.1152/advan.00022.2007.

Hubbard R, Parsa AR, Luthy MR: The spread of statistical significance testing: The case of the Journal of Applied Psychology. Theor Psychol. 1997, 7: 545-554. 10.1177/0959354397074006.

Vacha-Haase T, Nilsson JE, Reetz DR, Lance TS, Thompson B: Reporting practices and APA editorial policies regarding statistical significance and effect size. Theor Psychol. 2000, 10: 413-425. 10.1177/0959354300103006.

Krueger J: Null hypothesis significance testing: On the survival of a flawed method. Am Psychol. 2001, 56: 16-26. 10.1037/0003-066X.56.1.16.

Rising K, Bacchetti P, Bero L: Reporting Bias in Drug Trials Submitted to the Food and Drug Administration: Review of Publication and Presentation. PLoS Med. 2008, 5: e217-10.1371/journal.pmed.0050217. doi:10.1371/journal.pmed.0050217

Sridharan L, Greenland L: Editorial policies and publication bias the importance of negative studies. Arch Intern Med. 2009, 169: 1022-1023. 10.1001/archinternmed.2009.100.

Falagas ME, Alexiou VG: The top-ten in journal impact factor manipulation. Arch Immunol Ther Exp (Warsz). 2008, 56: 223-226. 10.1007/s00005-008-0024-5.

Rothman K: Writing for Epidemiology. Epidemiology. 1998, 9: 98-104. 10.1097/00001648-199805000-00019.

Fidler F: The fifth edition of the APA publication manual: Why its statistics recommendations are so controversial. Educ Psychol Meas. 2002, 62: 749-770. 10.1177/001316402236876.

Feinstein AR: Clinical epidemiology: The architecture of clinical research. 1985, Philadelphia: W.B. Saunders Company

Orlitzky M: Institutionalized dualism: statistical significance testing as myth and ceremony. Accessed Feb 8, 2010, [ http://ssrn.com/abstract=1415926 ]

Greenwald AG, González R, Harris RJ, Guthrie D: Effect sizes and p-value. What should be reported and what should be replicated?. Psychophysiology. 1996, 33: 175-183. 10.1111/j.1469-8986.1996.tb02121.x.

Altman DG, Goodman SN, Schroter S: How statistical expertise is used in medical research. J Am Med Assoc. 2002, 287: 2817-2820. 10.1001/jama.287.21.2817.

Gardner MJ, Altman DJ: Statistics with confidence. Confidence intervals and statistical guidelines. 1992, London: BMJ

Goodman SN: P Values, Hypothesis Tests and Likelihood: implications for epidemiology of a neglected historical debate. Am J Epidemiol. 1993, 137: 485-496.

Pre-publication history

The pre-publication history for this paper can be accessed here: http://www.biomedcentral.com/1471-2288/10/44/prepub

Download references

Acknowledgements

The authors would like to thank Tania Iglesias-Cabo and Vanesa Alvarez-González for their help with the collection of empirical data and their participation in an earlier version of the paper. The manuscript has benefited greatly from thoughtful, constructive feedback by Carlos Campillo-Artero, Tom Piazza and Ann Séror.

Author information

Authors and affiliations.

Centro Nacional de Investigación de Ciencias Médicas, La Habana, Cuba

Luis Carlos Silva-Ayçaguer

Unidad de Investigación. Hospital de Cabueñes, Servicio de Salud del Principado de Asturias (SESPA), Gijón, Spain

Patricio Suárez-Gil

CIBER Epidemiología y Salud Pública (CIBERESP), Spain and Departamento de Medicina, Unidad de Epidemiología Molecular del Instituto Universitario de Oncología, Universidad de Oviedo, Spain

Ana Fernández-Somoano

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Patricio Suárez-Gil .

Additional information

Competing interests.

The authors declare that they have no competing interests.

Authors' contributions

LCSA designed the study, wrote the paper and supervised the whole process; PSG coordinated the data extraction and carried out statistical analysis, as well as participated in the editing process; AFS extracted the data and participated in the first stage of statistical analysis; all authors contributed to and revised the final manuscript.

Authors’ original submitted files for images

Below are the links to the authors’ original submitted files for images.

Authors’ original file for figure 1

Rights and permissions.

Open Access This article is published under license to BioMed Central Ltd. This is an Open Access article is distributed under the terms of the Creative Commons Attribution License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and permissions

About this article

Cite this article.

Silva-Ayçaguer, L.C., Suárez-Gil, P. & Fernández-Somoano, A. The null hypothesis significance test in health sciences research (1995-2006): statistical analysis and interpretation. BMC Med Res Methodol 10 , 44 (2010). https://doi.org/10.1186/1471-2288-10-44

Download citation

Received : 29 December 2009

Accepted : 19 May 2010

Published : 19 May 2010

DOI : https://doi.org/10.1186/1471-2288-10-44

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Clinical Specialty
• Significance Fallacy
• Null Hypothesis Statistical Testing
• Medical Journal Editor
• Clinical Journal

BMC Medical Research Methodology

ISSN: 1471-2288

• General enquiries: [email protected]

Module 9: Hypothesis Testing With One Sample

Null and alternative hypotheses, learning outcomes.

• Describe hypothesis testing in general and in practice

The actual test begins by considering two  hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make adecision. There are two options for a  decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in  H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

H a : p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40

• H 0 : p = 0.40
• H a : p > 0.40

Concept Review

In a  hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

H 0 and H a are contradictory.

• OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License

What Is A Research (Scientific) Hypothesis? A plain-language explainer + examples

By:  Derek Jansen (MBA)  | Reviewed By: Dr Eunice Rautenbach | June 2020

If you’re new to the world of research, or it’s your first time writing a dissertation or thesis, you’re probably noticing that the words “research hypothesis” and “scientific hypothesis” are used quite a bit, and you’re wondering what they mean in a research context .

“Hypothesis” is one of those words that people use loosely, thinking they understand what it means. However, it has a very specific meaning within academic research. So, it’s important to understand the exact meaning before you start hypothesizing. 

Research Hypothesis 101

• What is a hypothesis ?
• What is a research hypothesis (scientific hypothesis)?
• Requirements for a research hypothesis
• Definition of a research hypothesis
• The null hypothesis

What is a hypothesis?

Let’s start with the general definition of a hypothesis (not a research hypothesis or scientific hypothesis), according to the Cambridge Dictionary:

Hypothesis: an idea or explanation for something that is based on known facts but has not yet been proved.

In other words, it’s a statement that provides an explanation for why or how something works, based on facts (or some reasonable assumptions), but that has not yet been specifically tested . For example, a hypothesis might look something like this:

Hypothesis: sleep impacts academic performance.

This statement predicts that academic performance will be influenced by the amount and/or quality of sleep a student engages in – sounds reasonable, right? It’s based on reasonable assumptions , underpinned by what we currently know about sleep and health (from the existing literature). So, loosely speaking, we could call it a hypothesis, at least by the dictionary definition.

But that’s not good enough…

Unfortunately, that’s not quite sophisticated enough to describe a research hypothesis (also sometimes called a scientific hypothesis), and it wouldn’t be acceptable in a dissertation, thesis or research paper . In the world of academic research, a statement needs a few more criteria to constitute a true research hypothesis .

What is a research hypothesis?

A research hypothesis (also called a scientific hypothesis) is a statement about the expected outcome of a study (for example, a dissertation or thesis). To constitute a quality hypothesis, the statement needs to have three attributes – specificity , clarity and testability .

Let’s take a look at these more closely.

Need a helping hand?

Hypothesis Essential #1: Specificity & Clarity

A good research hypothesis needs to be extremely clear and articulate about both what’ s being assessed (who or what variables are involved ) and the expected outcome (for example, a difference between groups, a relationship between variables, etc.).

Let’s stick with our sleepy students example and look at how this statement could be more specific and clear.

Hypothesis: Students who sleep at least 8 hours per night will, on average, achieve higher grades in standardised tests than students who sleep less than 8 hours a night.

As you can see, the statement is very specific as it identifies the variables involved (sleep hours and test grades), the parties involved (two groups of students), as well as the predicted relationship type (a positive relationship). There’s no ambiguity or uncertainty about who or what is involved in the statement, and the expected outcome is clear.

Contrast that to the original hypothesis we looked at – “Sleep impacts academic performance” – and you can see the difference. “Sleep” and “academic performance” are both comparatively vague , and there’s no indication of what the expected relationship direction is (more sleep or less sleep). As you can see, specificity and clarity are key.

Hypothesis Essential #2: Testability (Provability)

A statement must be testable to qualify as a research hypothesis. In other words, there needs to be a way to prove (or disprove) the statement. If it’s not testable, it’s not a hypothesis – simple as that.

For example, consider the hypothesis we mentioned earlier:

Hypothesis: Students who sleep at least 8 hours per night will, on average, achieve higher grades in standardised tests than students who sleep less than 8 hours a night.  

We could test this statement by undertaking a quantitative study involving two groups of students, one that gets 8 or more hours of sleep per night for a fixed period, and one that gets less. We could then compare the standardised test results for both groups to see if there’s a statistically significant difference. 

Again, if you compare this to the original hypothesis we looked at – “Sleep impacts academic performance” – you can see that it would be quite difficult to test that statement, primarily because it isn’t specific enough. How much sleep? By who? What type of academic performance?

So, remember the mantra – if you can’t test it, it’s not a hypothesis 🙂

Defining A Research Hypothesis

You’re still with us? Great! Let’s recap and pin down a clear definition of a hypothesis.

A research hypothesis (or scientific hypothesis) is a statement about an expected relationship between variables, or explanation of an occurrence, that is clear, specific and testable.

So, when you write up hypotheses for your dissertation or thesis, make sure that they meet all these criteria. If you do, you’ll not only have rock-solid hypotheses but you’ll also ensure a clear focus for your entire research project.

What about the null hypothesis?

You may have also heard the terms null hypothesis , alternative hypothesis, or H-zero thrown around. At a simple level, the null hypothesis is the counter-proposal to the original hypothesis.

For example, if the hypothesis predicts that there is a relationship between two variables (for example, sleep and academic performance), the null hypothesis would predict that there is no relationship between those variables.

At a more technical level, the null hypothesis proposes that no statistical significance exists in a set of given observations and that any differences are due to chance alone.

And there you have it – hypotheses in a nutshell. 

If you have any questions, be sure to leave a comment below and we’ll do our best to help you. If you need hands-on help developing and testing your hypotheses, consider our private coaching service , where we hold your hand through the research journey.

Psst... there’s more!

This post was based on one of our popular Research Bootcamps . If you're working on a research project, you'll definitely want to check this out ...

You Might Also Like:

16 Comments

Very useful information. I benefit more from getting more information in this regard.

Very great insight,educative and informative. Please give meet deep critics on many research data of public international Law like human rights, environment, natural resources, law of the sea etc

In a book I read a distinction is made between null, research, and alternative hypothesis. As far as I understand, alternative and research hypotheses are the same. Can you please elaborate? Best Afshin

This is a self explanatory, easy going site. I will recommend this to my friends and colleagues.

Very good definition. How can I cite your definition in my thesis? Thank you. Is nul hypothesis compulsory in a research?

It’s a counter-proposal to be proven as a rejection

Please what is the difference between alternate hypothesis and research hypothesis?

It is a very good explanation. However, it limits hypotheses to statistically tasteable ideas. What about for qualitative researches or other researches that involve quantitative data that don’t need statistical tests?

In qualitative research, one typically uses propositions, not hypotheses.

could you please elaborate it more

I’ve benefited greatly from these notes, thank you.

This is very helpful

well articulated ideas are presented here, thank you for being reliable sources of information

Excellent. Thanks for being clear and sound about the research methodology and hypothesis (quantitative research)

I have only a simple question regarding the null hypothesis. – Is the null hypothesis (Ho) known as the reversible hypothesis of the alternative hypothesis (H1? – How to test it in academic research?

this is very important note help me much more

Trackbacks/Pingbacks

• What Is Research Methodology? Simple Definition (With Examples) - Grad Coach - […] Contrasted to this, a quantitative methodology is typically used when the research aims and objectives are confirmatory in nature. For example,…

Submit a Comment Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

• Print Friendly

• Open access
• Published: 13 May 2024

SCIPAC: quantitative estimation of cell-phenotype associations

• Dailin Gan 1 ,
• Yini Zhu 2 ,
• Xin Lu 2 , 3 &
• Jun Li   ORCID: orcid.org/0000-0003-4353-5761 1  

Genome Biology volume  25 , Article number:  119 ( 2024 ) Cite this article

175 Accesses

2 Altmetric

Metrics details

Numerous algorithms have been proposed to identify cell types in single-cell RNA sequencing data, yet a fundamental problem remains: determining associations between cells and phenotypes such as cancer. We develop SCIPAC, the first algorithm that quantitatively estimates the association between each cell in single-cell data and a phenotype. SCIPAC also provides a p -value for each association and applies to data with virtually any type of phenotype. We demonstrate SCIPAC’s accuracy in simulated data. On four real cancerous or noncancerous datasets, insights from SCIPAC help interpret the data and generate new hypotheses. SCIPAC requires minimum tuning and is computationally very fast.

Single-cell RNA sequencing (scRNA-seq) technologies are revolutionizing biomedical research by providing comprehensive characterizations of diverse cell populations in heterogeneous tissues [ 1 , 2 ]. Unlike bulk RNA sequencing (RNA-seq), which measures the average expression profile of the whole tissue, scRNA-seq gives the expression profiles of thousands of individual cells in the tissue [ 3 , 4 , 5 , 6 , 7 ]. Based on this rich data, cell types may be discovered/determined in an unsupervised (e.g., [ 8 , 9 ]), semi-supervised (e.g., [ 10 , 11 , 12 , 13 ]), or supervised manner (e.g., [ 14 , 15 , 16 ]). Despite the fast development, there are still limitations with scRNA-seq technologies. Notably, the cost for each scRNA-seq experiment is still high; as a result, most scRNA-seq data are from a single or a few biological samples/tissues. Very few datasets consist of large numbers of samples with different phenotypes, e.g., cancer vs. normal. This places great difficulties in determining how a cell type contributes to a phenotype based on single-cell studies (especially if the cell type is discovered in a completely unsupervised manner or if people have limited knowledge of this cell type). For example, without having single-cell data from multiple cancer patients and multiple normal controls, it could be hard to computationally infer whether a cell type may promote or inhibit cancer development. However, such association can be critical for cancer research [ 17 ], disease diagnosis [ 18 ], cell-type targeted therapy development [ 19 ], etc.

Fortunately, this difficulty may be overcome by borrowing information from bulk RNA-seq data. Over the past decade, a considerable amount of bulk RNA-seq data from a large number of samples with different phenotypes have been accumulated and made available through databases like The Cancer Genome Atlas (TCGA) [ 20 ] and cBioPortal [ 21 , 22 ]. Data in these databases often contain comprehensive patient phenotype information, such as cancer status, cancer stages, survival status and time, and tumor metastasis. Combining single-cell data from a single or a few individuals and bulk data from a relatively large number of individuals regarding a particular phenotype can be a cost-effective way to determine how a cell type contributes to the phenotype. A recent method Scissor [ 23 ] took an essential step in this direction. It uses single-cell and bulk RNA-seq data with phenotype information to classify the cells into three discrete categories: Scissor+, Scissor−, and null cells, corresponding to cells that are positively associated, negatively associated, and not associated with the phenotype.

Here, we present a method that takes another big step in this direction, which is called Single-Cell and bulk data-based Identifier for Phenotype Associated Cells or SCIPAC for short. SCIPAC enables quantitative estimation of the strength of association between each cell in a scRNA-seq data and a phenotype, with the help of bulk RNA-seq data with phenotype information. Moreover, SCIPAC also enables the estimation of the statistical significance of the association. That is, it gives a p -value for the association between each cell and the phenotype. Furthermore, SCIPAC enables the estimation of association between cells and an ordinal phenotype (e.g., different stages of cancer), which could be informative as people may not only be interested in the emergence/existence of cancer (cancer vs. healthy, a binary problem) but also in the progression of cancer (different stages of cancer, an ordinal problem).

To study the performance of SCIPAC, we first apply SCIPAC to simulated data under three schemes. SCIPAC shows high accuracy with low false positive rates. We further show the broad applicability of SCIPAC on real datasets across various diseases, including prostate cancer, breast cancer, lung cancer, and muscular dystrophy. The association inferred by SCIPAC is highly informative. In real datasets, some cell types have definite and well-studied functions, while others are less well-understood: their functions may be disease-dependent or tissue-dependent, and they may contain different sub-types with distinct functions. In the former case, SCIPAC’s results agree with current biological knowledge. In the latter case, SCIPAC’s discoveries inspire the generation of new hypotheses regarding the roles and functions of cells under different conditions.

An overview of the SCIPAC algorithm

SCIPAC is a computational method that identifies cells in single-cell data that are associated with a given phenotype. This phenotype can be binary (e.g., cancer vs. normal), ordinal (e.g., cancer stage), continuous (e.g., quantitative traits), or survival (i.e., survival time and status). SCIPAC uses input data consisting of three parts: single-cell RNA-seq data that measures the expression of p genes in m cells, bulk RNA-seq data that measures the expression of the same set of p genes in n samples/tissues, and the statuses/values of the phenotype of the n bulk samples/tissues. The output of SCIPAC is the strength and the p -value of the association between each cell and the phenotype.

SCIPAC proposes the following definition of “association” between a cell and a phenotype: A group of cells that are likely to play a similar role in the phenotype (such as cells of a specific cell type or sub-type, cells in a particular state, cells in a cluster, cells with similar expression profiles, or cells with similar functions) is considered to be positively/negatively associated with a phenotype if an increase in their proportion within the tissue likely indicates an increased/decreased probability of the phenotype’s presence. SCIPAC assigns the same association to all cells within such a group. Taking cancer as the phenotype as an example, if increasing the proportion of a cell type indicates a higher chance of having cancer (binary), having a higher cancer stage (ordinal), or a higher hazard rate (survival), all cells in this cell type is positively associated with cancer.

The algorithm of SCIPAC follows the following four steps. First, the cells in the single-cell data are grouped into clusters according to their expression profiles. The Louvain algorithm from the Seurat package [ 24 , 25 ] is used as the default clustering algorithm, but the user may choose any clustering algorithm they prefer. Or if information of the cell types or other groupings of cells is available a priori, it may be supplied to SCIPAC as the cell clusters, and this clustering step can be skipped. In the second step, a regression model is learned from bulk gene expression data with the phenotype. Depending on the type of the phenotype, this model can be logistic regression, ordinary linear regression, proportional odds model, or Cox proportional hazards model. To achieve a higher prediction power with less variance, by default, the elastic net (a blender of Lasso and ridge regression [ 26 ]) is used to fit the model. In the third step, SCIPAC computes the association strength \(\Lambda\) between each cell cluster and the phenotype based on a mathematical formula that we derive. Finally, the p -values are computed. The association strength and its p -value between a cell cluster and the phenotype are given to all cells in the cluster.

SCIPAC requires minimum tuning. When the cell-type information is given in step 1, SCIPAC does not have any (hyper)parameter. Otherwise, the Louvain algorithm used in step 1 has a “resolution” parameter that controls the number of cell clusters: a larger resolution results in more clusters. SCIPAC inherits this parameter as its only parameter. Since SCIPAC gives the same association strength and p -value to cells from the same cluster, this parameter also determines the resolution of results provided by SCIPAC. Thus, we still call it “resolution” in SCIPAC. Because of its meaning, we recommend setting it so that the number of cell clusters given by the clustering algorithm is comparable to, or reasonably larger than, the number of cell types (or sub-types) in the data. We will see that the performance of SCIPAC is insensitive to this resolution parameter, and the default value 2.0 typically works well.

The details of the SCIPAC algorithm are given in the “ Methods ” section.

Performance in simulated data

We assess the performance of SCIPAC in simulated data under three different schemes. The first scheme is simple and consists of only three cell types. The second scheme is more complicated and consists of seven cell types, which better imitates actual scRNA-seq data. In the third scheme, we simulate cells under different cell development stages to test the performance of SCIPAC under an ordinal phenotype. Details of the simulation are given in Additional file 1.

Simulation scheme I

Under this scheme, the single-cell data consists of three cell types: one is positively associated with the phenotype, one is negatively associated, and the third is not associated (we call it “null”). Figure 1 a gives the UMAP [ 27 ] plot of the three cell types, and Fig. 1 b gives the true associations of these three cell types with the phenotype, with red, blue, and light gray denoting positive, negative, and null associations.

UMAP visualization and numeric measures of the simulated data under scheme I. All the plots in a–e  are scatterplots of the two dimensional single-cell data given by UMAP. The x and y axes represent the two dimensions, and their scales are not shown as their specific values are not directly relevant. Points in the plots represents single cells, and they are colored differently in each subplot to reflect different information/results. a  Cell types. b  True associations. The association between cell types 1, 2, and 3 and the phenotype are positive, negative, and null, respectively. c  Association strengths \(\Lambda\) given by SCIPAC under different resolutions. Red/blue represents the sign of \(\Lambda\) , and the shade gives the absolute value of \(\Lambda\) . Every cell is colored red or blue since no \(\Lambda\) is exactly zero. Below each subplot, Res stands for resolution, and K stands for the number of cell clusters given by this resolution. d   p -values given by SCIPAC. Only cells with p -value \(< 0.05\) are colored red (positive association) or blue (negative association); others are colored white. e  Results given by Scissor under different \(\alpha\) values. Red, blue, and light gray stands for Scissor+, Scissor−, and background (i.e., null) cells. f  F1 scores and g  FSC for SCIPAC and Scissor under different parameter values. For SCIPAC, each bar is the value under a resolution/number of clusters. For Scissor, each bar is the value under an \(\alpha\)

We apply SCIPAC to the simulated data. For the resolution parameter (see the “ Methods ” section), values 0.5, 1.0, and 1.5 give 3, 4, and 4 clusters, respectively, close to the actual number of cell types. They are good choices based on the guidance for choosing this parameter. To show how SCIPAC behaves under parameter misspecification, we also set the resolution up to 4.0, which gives a whopping 61 clusters. Figure 1 c and d give the association strengths \(\Lambda\) and the p -values given by four different resolutions (results under other resolutions are provided in Additional file 1: Fig. S1 and S2). In Fig. 1 c, red and blue denote positive and negative associations, respectively, and the shade of the color represents the strength of the association, i.e., the absolute value of \(\Lambda\) . Every cell is colored blue or red, as none of \(\Lambda\) is exactly zero. In Fig. 1 d, red and blue denote positive and negative associations that are statistically significant ( p -value \(< 0.05\) ). Cells whose associations are not statistically significant ( p -value \(\ge 0.05\) ) are shown in white. To avoid confusion, it is worth repeating that cells that are colored in red/blue in Fig. 1 c are shown in red/blue in Fig. 1 d only if they are statistically significant; otherwise, they are colored white in Fig. 1 d.

From Fig. 1 c, d (as well as Additional file 1: Fig. S1 and S2), it is clear that the results of SCIPAC are highly consistent under different resolution values, including both the estimated association strengths and the p -values. It is also clear that SCIPAC is highly accurate: most truly associated cells are identified as significant, and most, if not all, truly null cells are identified as null.

As the first algorithm that quantitatively estimates the association strength and the first algorithm that gives the p -value of the association, SCIPAC does not have a real competitor. A previous algorithm, Scissor, is able to classify cells into three discrete categories according to their associations with the phenotype. So, we compare SCIPAC with Scissor in respect of the ability to differentiate positively associated, negatively associated, and null cells.

Running Scissor requires tuning a parameter called \(\alpha\) , which is a number between 0 and 1 that balances the amount of regularization for the smoothness and for the sparsity of the associations. The Scissor R package does not provide a default value for this \(\alpha\) or a function to help select this value. The Scissor paper suggests the following criterion: “the number of Scissor-selected cells should not exceed a certain percentage of total cells (default 20%) in the single-cell data. In each experiment, a search on the above searching list is performed from the smallest to the largest until a value of \(\alpha\) meets the above criteria.” In practice, we have found that this criterion does not often work properly, as the truly associated cells may not compose 20% of all cells in actual data. Therefore, instead of setting \(\alpha\) to any particular value, we set \(\alpha\) values that span the whole range of \(\alpha\) to see the best possible performance of Scissor.

The performance of Scissor in our simulation data under four different \(\alpha\) values are shown in Fig. 1 e, and results under more \(\alpha\) values are shown in Additional file 1: Fig. S3. In the figures, red, blue, and light gray denote Scissor+, Scissor−, and null (called “background” in Scissor) cells, respectively. The results of Scissor have several characteristics different from SCIPAC. First, Scissor does not give the strength or statistical significance of the association, and thus the colors of the cells in the figures do not have different shades. Second, different \(\alpha\) values give very different results. Greater \(\alpha\) values generally give fewer Scissor+ and Scissor− cells, but there are additional complexities. One complexity is that the Scissor+ (or Scissor−) cells under a greater \(\alpha\) value are not a strict subset of Scissor+ (or Scissor−) cells under a smaller \(\alpha\) value. For example, the number of truly negatively associated cells detected as Scissor− increases when \(\alpha\) increases from 0.01 to 0.30. Another complexity is that the direction of the association may flip as \(\alpha\) increases. For example, most cells of cell type 2 are identified as Scissor+ under \(\alpha =0.01\) , but many of them are identified as Scissor− under larger \(\alpha\) values. Third, Scissor does not achieve high power and low false-positive rate at the same time under any \(\alpha\) . No matter what the \(\alpha\) value is, there is only a small proportion of cells from cell type 2 that are correctly identified as negatively associated, and there is always a non-negligible proportion of null cells (i.e., cells from cell type 3) that are incorrectly identified as positively or negatively associated. Fourth, Scissor+ and Scissor− cells can be close to each other in the figure, even under a large \(\alpha\) value. This means that cells with nearly identical expression profiles are detected to be associated with the phenotype in opposite directions, which can place difficulties in interpreting the results.

SCIPAC overcomes the difficulties of Scissor and gives results that are more informative (quantitative strengths with p -values), more accurate (both high power and low false-positive rate), less sensitive to the tuning parameter, and easier to interpret (cells with similar expression typically have similar associations to the phenotype).

SCIPAC’s higher accuracy in differentiating positively associated, negatively associated, and null cells than Scissors can also be measured numerically using the F1 score and the fraction of sign correctness (FSC). F1, which is the harmonic mean of precision and recall, is a commonly used measure of calling accuracy. Note that precision and recall are only defined for two-class problems, which try to classify desired signals/discoveries (so-called “positives”) against noises/trivial results (so-called “negatives”). Our case, on the other hand, is a three-class problem: positive association, negative association, and null. To compute F1, we combine the positive and negative associations and treat them as “positives,” and treat null as “negatives.” This F1 score ignores the direction of the association; thus, it alone is not enough to describe the performance of an association-detection algorithm. For example, an algorithm may have a perfect F1 score even if it incorrectly calls all negative associations positive. To measure an algorithm’s ability to determine the direction of the association, we propose a statistic called FSC, defined as the fraction of true discoveries that also have the correct direction of the association. The F1 score and FSC are numbers between 0 and 1, and higher values are preferred. A mathematical definition of these two measures is given in Additional file 1.

Figure 1 f, g show the F1 score and FSC of SCIPAC and Scissor under different values of tuning parameters. The F1 score of Scissor is between 0.2 and 0.7 under different \(\alpha\) ’s. The FSC of Scissor increases from around 0.5 to nearly 1 as \(\alpha\) increases, but Scissor does not achieve high F1 and FSC scores at the same time under any \(\alpha\) . On the other hand, the F1 score of SCIPAC is close to perfection when the resolution parameter is properly set, and it is still above 0.90 even if the resolution parameter is set too large. The FSC of SCIPAC is always above 0.96 under different resolutions. That is, SCIPAC achieves high F1 and FSC scores simultaneously under a wide range of resolutions, representing a much higher accuracy than Scissor.

Simulation scheme II

This more complicated simulation scheme has seven cell types, which are shown in Fig. 2 a. As shown in Fig. 2 b, cell types 1 and 3 are negatively associated (colored blue), 2 and 4 are positively associated (colored red), and 5, 6, and 7 are not associated (colored light gray).

UMAP visualization of the simulated data under a–g  scheme II and h–k  scheme III. a  Cell types. b  True associations. c , d  Association strengths \(\Lambda\) and p -values given by SCIPAC under the default resolution. e  Results given by Scissor under different \(\alpha\) values. f  F1 scores and g  FSC for SCIPAC and Scissor under different parameter values. h  Cell differentiation paths. The four paths have the same starting location, which is in the center, but different ending locations. This can be considered as a progenitor cell type differentiating into four specialized cell types. i  Cell differentiation steps. These steps are used to create four stages, each containing 500 steps. Thus, this plot of differentiation steps can also be viewed as the plot of true association strengths. j , k  Association strengths \(\Lambda\) and p -values given by SCIPAC under the default resolution

The association strengths and p -values given by SCIPAC under the default resolution are illustrated in Fig. 2 c, d, respectively. Results under several other resolutions are given in Additional file 1: Fig. S4 and S5. Again, we find that SCIPAC gives highly consistent results under different resolutions. SCIPAC successfully identifies three out of the four truly associated cell types. For the other truly associated cell type, cell type 1, SCIPAC correctly recognizes its association with the phenotype as negative, although the p -values are not significant enough. The F1 score is 0.85, and the FSC is greater than 0.99, as shown in Fig. 2 f, g.

The results of Scissor under four different \(\alpha\) values are given in Fig. 2 e. (More shown in Additional file 1: Fig. S6.) Under this highly challenging simulation scheme, Scissor can only identify one out of four truly associated cell types. Its F1 score is below 0.4.

Simulation scheme III

This simulation scheme is to assess the performance of SCIPAC for ordinal phenotypes. We simulate cells along four cell-differentiation paths with the same starting location but different ending locations, as shown in Fig. 2 h. These cells can be considered as a progenitor cell population differentiating into four specialized cell types. In Fig. 2 i, the “step” reflects their position in the differentiation path, with step 0 meaning the start and step 2000 meaning the end of the differentiation. Then, the “stage” is generated according to the step: cells in steps 0 \(\sim\) 500, 501 \(\sim\) 1000, 1001 \(\sim\) 1500, and 1501 \(\sim\) 2000 are assigned to stages I, II, III, and IV, respectively. This stage is treated as the ordinal phenotype. Under this simulation scheme, Fig. 2 i also gives the actual associations, and all cells are associated with the phenotype.

The results of SCIPAC under the default resolution are shown in Fig. 2 j, k. Clearly, the associations SCIPAC identifies are highly consistent with the truth. Particularly, it successfully identifies the cells in the center as early-stage cells and most cells at the end of branches as last-stage cells. The results of SCIPAC under other resolutions are given in Additional file 1: Fig. S7 and S8, which are highly consistent. Scissor does not work with ordinal phenotypes; thus, no results are reported here.

Performance in real data

We consider four real datasets: a prostate cancer dataset, a breast cancer dataset, a lung cancer dataset, and a muscular dystrophy dataset. The bulk RNA-seq data of the three cancer datasets are obtained from the TCGA database, and that of the muscular dystrophy dataset is obtained from a published paper [ 28 ]. A detailed description of these datasets is given in Additional file 1. We will use these datasets to assess the performance of SCIPAC on different types of phenotypes. The cell type information (i.e., which cell belongs to which cell type) is available for the first three datasets, but we ignore this information so that we can make a fair comparison with Scissor, which cannot utilize this information.

Prostate cancer data with a binary phenotype

We use the single-cell expression of 8,700 cells from prostate-cancer tumors sequenced by [ 29 ]. The cell types of these cells are known and given in Fig. 3 a. The bulk data comprises 550 TCGA-PRAD (prostate adenocarcinoma) samples with phenotype (cancer vs. normal) information. Here the phenotype is cancer, and it is binary: present or absent.

UMAP visualization of the prostate cancer data, with a zoom-in view for the red-circled region (cell type MNP). a  True cell types. BE, HE, and CE stand for basal, hillock, club epithelial cells, LE-KLK3 and LE-KLK4 stand for luminal epithelial cells with high levels of kallikrein related peptidase 3 and 4, and MNP stands for mononuclear phagocytes. In the zoom-in view, the sub-types of MNP cells are given. b  Association strengths \(\Lambda\) given by SCIPAC under the default resolution. The cyan-circled cells are B cells, which are estimated by SCIPAC as negatively associated with cancer but estimated by Scissor as Scissor+ or null. c   p -values given by SCIPAC. The MNP cell type, which is red-circled in the plot, is estimated by SCIPAC to be strongly negatively associated with cancer but estimated by Scissor to be positively associated with cancer. d  Results given by Scissor under different \(\alpha\) values

Results from SCIPAC with the default resolution are shown in Fig. 3 b, c (results with other resolutions, given in Additional file 1: Fig. S9 and S10, are highly consistent with results here.) Compared with results from Scissor, shown in Fig. 3 d, results from SCIPAC again show three advantages. First, results from SCIPAC are richer and more comprehensive. SCIPAC gives estimated associations and the corresponding p -values, and the estimated associations are quantitative (shown in Fig. 3 b as different shades to the red or blue color) instead of discrete (shown in Fig. 3 d as a uniform shade to the red, blue, or light gray color). Second, SCIPAC’s results can be easier to interpret as the red and blue colors are more block-wise instead of scattered. Third, unlike Scissor, which produces multiple sets of results varying based on the parameter \(\alpha\) —a parameter without a default value or tuning guidance—typically, a single set of results from SCIPAC under its default settings suffices.

Comparing the results from our SCIPAC method with those from Scissor is non-trivial, as the latter’s outcomes are scattered and include multiple sets. We propose the following solutions to summarize the inferred association of a known cell type with the phenotype using a specific method (Scissor under a specific \(\alpha\) value, or SCIPAC with the default setting). We first calculate the proportion of cells in this cell type identified as Scissor+ (by Scissor at a specific \(\alpha\) value) or as significantly positively associated (by SCIPAC), denoted by \(p_{+}\) . We also calculate the proportion of all cells, encompassing any cell type, which are identified as Scissor+ or significantly positively associated, serving as the average background strength, denoted by \(p_{a}\) . Then, we compute the log odds ratio for this cell type to be positively associated with the phenotype compared to the background, represented as:

Similarly, the log odds ratio for the cell type to be negatively associated with the phenotype, \(\rho _-\) , is computed in a parallel manner.

For SCIPAC, a cell type is summarized as positively associated with the phenotype if \(\rho _+ \ge 1\) and \(\rho _- < 1\)  and negatively associated if \(\rho _- \ge 1\) and \(\rho _+ < 1\) . If neither condition is met, the association is inconclusive. For Scissor, we apply it under six different \(\alpha\) values: 0.01, 0.05, 0.10, 0.15, 0.20, and 0.25. A cell type is summarized as positively associated with the phenotype if \(\rho _+ \ge 1\) and \(\rho _- < 1\) in at least four of these \(\alpha\) values and negatively associated if \(\rho _- \ge 1\) and \(\rho _+ < 1\) in at least four \(\alpha\) values. If these criteria are not met, the association is deemed inconclusive. The above computation of log odds ratios and the determination of associations are performed only on cell types that each compose at least 1% of the cell population, to ensure adequate power.

For the prostate cancer data, the log odds ratios for each cell type using each method are presented in Tables S1 and S2. The final associations determined for each cell type are summarized in Table S3. In the last column of this table, we also indicate whether the conclusions drawn from SCIPAC and Scissor are consistent or not.

We find that SCIPAC’s results agree with Scissor on most cell types. However, there are three exceptions: mononuclear phagocytes (MNPs), B cells, and LE-KLK4.

MNPs are red-circled and zoomed in in each sub-figure of Fig. 3 . Most cells in this cell type are colored red in Fig. 3 d but colored dark blue in Fig. 3 b. In other words, while Scissor determines that this cell type is Scissor+, SCIPAC makes the opposite inference. Moreover, SCIPAC is confident about its judgment by giving small p -values, as shown in Fig. 3 c. To see which inference is closer to the biological fact is not easy, as biologically MNPs contain a number of sub-types that each have different functions [ 30 , 31 ]. Fortunately, this cell population has been studied in detail in the original paper that generated this dataset [ 29 ], and the sub-type information of each cell is provided there: this MNP population contains six sub-types, which are dendritic cells (DC), M1 macrophages (Mac1), metallothionein-expressing macrophages (Mac-MT), M2 macrophages (Mac2), proliferating macrophages (Mac-cycling), and monocytes (Mono), as shown in the zoom-in view of Fig. 3 a. Among these six sub-types, DC, Mac1, and Mac-MT are believed to inhibit cancer development and can serve as targets in cancer immunotherapy [ 29 ]; they compose more than 60% of all MNP cells in this dataset. SCIPAC makes the correct inference on this majority of MNP cells. Another cell type, Mac2, is reported to promote tumor development [ 32 ], but it only composes less than \(15\%\) of the MNPs. How the other two cell types, Mac-cycling and Mono, are associated with cancer is less studied. Overall, the results given by SCIPAC are more consistent with the current biological knowledge.

B cells are cyan-circled in Fig. 3 b. B cells are generally believed to have anti-tumor activity by producing tumor-reactive antibodies and forming tertiary lymphoid structures [ 29 , 33 ]. This means that B cells are likely to be negatively associated with cancer. SCIPAC successfully identifies this negative association, while Scissor fails.

LE-KLK4, a subtype of cancer cells, is thought to be positively associated with the tumor phenotype [ 29 ]. SCIPAC successfully identified this positive association, in contrast to Scissor, which failed to do so (in the figure, a proportion of LE-KLK4 cells are identified as Scissor+, especially under the smallest \(\alpha\) value; however, this proportion is not significantly higher than the background Scissor+ level under the majority of \(\alpha\) values).

In summary, across all three cell types, the results from SCIPAC appear to be more consistent with current biological knowledge. For more discussions regarding this dataset, refer to Additional file 1.

Breast cancer data with an ordinal phenotype

The scRNA-seq data for breast cancer are from [ 34 ], and we use the 19,311 cells from the five HER2+ tumor tissues. The true cell types are shown in Fig. 4 a. The bulk data include 1215 TCGA-BRCA samples with information on the cancer stage (I, II, III, or IV), which is treated as an ordinal phenotype.

UMAP visualization of the breast cancer data. a  True cell types. CAFs stand for cancer-associated fibroblasts, PB stands for plasmablasts and PVL stands for perivascular-like cells. b , c  Association strengths \(\Lambda\) and p -values given by SCIPAC under the default resolution. Cyan-circled are a group of T cells that are estimated by SCIPAC to be most significantly associated with the cancer stage in the negative direction, and orange-circled are a group of T cells that are estimated by SCIPAC to be significantly positively associated with the cancer stage. d  DE analysis of the cyan-circled T cells vs. all the other T cells. e  DE analysis of the cyan-circled T cells vs. all the other cells. f  Expression of CD8+ T cell marker genes in the cyan-circled cells and all the other cells. g  DE analysis of the orange-circled T cells vs. all the other cells. h  Expression of regulatory T cell marker genes in the orange-circled cells and all the other cells

Association strengths and p -values given by SCIPAC under the default resolution are shown in Fig. 4 b, c. Results under other resolutions are given in Additional file 1: Fig. S11 and S12, and again they are highly consistent with results under the default resolution. We do not present the results from Scissor, as Scissor does not take ordinal phenotypes.

In the SCIPAC results, cells that are most strongly and statistically significantly associated with the phenotype in the positive direction are the cancer-associated fibroblasts (CAFs). This finding agrees with the literature: CAFs contribute to therapy resistance and metastasis of cancer cells via the production of secreted factors and direct interaction with cancer cells [ 35 ], and they are also active players in breast cancer initiation and progression [ 36 , 37 , 38 , 39 ]. Another large group of cells identified as positively associated with the phenotype is the cancer epithelial cells. They are malignant cells in breast cancer tissues and are thus expected to be associated with severe cancer stages.

Of the cells identified as negatively associated with severe cancer stages, a large portion of T cells is the most noticeable. Biologically, T cells contain many sub-types, including CD4+, CD8+, regulatory T cells, and more, and their functions are diverse in the tumor microenvironment [ 40 ]. To explore SCIPAC’s discoveries, we compare T cells that are identified as most statistically significant, with p -values \(< 10^{-6}\) and circled in Fig. 4 d, with the other T cells. Differential expression (DE) analysis (details about DE analysis and other analyses are given in Additional file 1) identifies seven genes upregulated in these most significant T cells. Of these seven genes, at least five are supported by the literature: CCL4, XCL1, IFNG, and GZMB are associated with CD8+ T cell infiltration; they have been shown to have anti-tumor functions and are involved in cancer immunotherapy [ 41 , 42 , 43 ]. Also, IL2 has been shown to serve an important role in combination therapies for autoimmunity and cancer [ 44 ]. We also perform an enrichment analysis [ 45 ], in which a pathway called Myc stands out with a \(\textit{p}\text{-value}<10^{-7}\) , much smaller than all other pathways. Myc is downregulated in the T cells that are identified as most negatively associated with cancer stage progress. This agrees with current biological knowledge about this pathway: Myc is known to contribute to malignant cell transformation and tumor metastasis [ 46 , 47 , 48 ].

On the above, we have compared T cells that are most significantly associated with cancer stages in the negative direction with the other T cells using DE and pathway analysis, and the results could suggest that these cells are tumor-infiltrated CD8+ T cells with tumor-inhibition functions. To check this hypothesis, we perform DE analysis of these cells against all other cells (i.e., the other T cells and all the other cell types). The DE genes are shown in Fig. 4 e. It can be noted that CD8+ T cell marker genes such as CD8A, CD8B, and GZMK are upregulated. We further obtain CD8+ T cell marker genes from CellMarker [ 49 ] and check their expression, as illustrated in Fig. 4 f. Marker genes CD8A, CD8B, CD3D, GZMK, and CD7 show significantly higher expression in these T cells. This again supports our hypothesis that these cells are tumor-infiltrated CD8+ T cells that have anti-tumor functions.

Interestingly, not all T cells are identified as negatively associated with severe cancer stages; a group of T cells is identified as positively associated, as circled in Fig. 4 c. To explore the function of this group of T cells, we perform DE analysis of these T cells against the other T cells. The DE genes are shown in Fig. 4 g. Based on the literature, six out of eight over-expressed genes are associated with cancer development. The high expression of NUSAP1 gene is associated with poor patient overall survival, and this gene also serves as a prognostic factor in breast cancer [ 50 , 51 , 52 ]. Gene MKI67 has been treated as a candidate prognostic prediction for cancer proliferation [ 53 , 54 ]. The over-expression of RRM2 has been linked to higher proliferation and invasiveness of malignant cells [ 55 , 56 ], and the upregulation of RRM2 in breast cancer suggests it to be a possible prognostic indicator [ 57 , 58 , 59 , 60 , 61 , 62 ]. The high expression of UBE2C gene always occurs in cancers with a high degree of malignancy, low differentiation, and high metastatic tendency [ 63 ]. For gene TOP2A, it has been proposed that the HER2 amplification in HER2 breast cancers may be a direct result of the frequent co-amplification of TOP2A [ 64 , 65 , 66 ], and there is a high correlation between the high expressions of TOP2A and the oncogene HER2 [ 67 , 68 ]. Gene CENPF is a cell cycle-associated gene, and it has been identified as a marker of cell proliferation in breast cancers [ 69 ]. The over-expression of these genes strongly supports the correctness of the association identified by SCIPAC. To further validate this positive association, we perform DE analysis of these cells against all the other cells. We find that the top marker genes obtained from CellMarker [ 49 ] for the regulatory T cells, which are known to be immunosuppressive and promote cancer progression [ 70 ], are over-expressed with statistical significance, as shown in Fig. 4 h. This finding again provides strong evidence that the positive association identified by SCIPAC for this group of T cells is correct.

Lung cancer data with survival information

The scRNA-seq data for lung cancer are from [ 71 ], and we use two lung adenocarcinoma (LUAD) patients’ data with 29,888 cells. The true cell types are shown in Fig. 5 a. The bulk data consist of 576 TCGA-LUAD samples with survival status and time.

UMAP visualization of a–d  the lung cancer data and e–g  the muscular dystrophy data. a  True cell types. b , c  Association strengths \(\Lambda\) and p -values given by SCIPAC under the default resolution. d  Results given by Scissor under different \(\alpha\) values. e , f  Association strengths \(\Lambda\) and p -values given by SCIPAC under the default resolution. Circled are a group of cells that are identified by SCIPAC as significantly positively associated with the disease but identified by Scissor as null. g  Results given by Scissor under different \(\alpha\) values

Association strengths and p -values given by SCIPAC are given in Fig. 5 b, c (results under other resolutions are given in Additional file 1: Fig. S13 and S14). In Fig. 5 c, most cells with statistically significant associations are CD4+ T cells or B cells. These associations are negative, meaning that the abundance of these cells is associated with a reduced death rate, i.e., longer survival time. This agrees with the literature: CD4+ T cells primarily mediate anti-tumor immunity and are associated with favorable prognosis in lung cancer patients [ 72 , 73 , 74 ]; B cells also show anti-tumor functions in all stages of human lung cancer development and play an essential role in anti-tumor responses [ 75 , 76 ].

The results by Scissor under different \(\alpha\) values are shown in Fig. 5 d. The highly scattered Scissor+ and Scissor− cells make identifying and interpreting meaningful phenotype-associated cell groups difficult.

Muscular dystrophy data with a binary phenotype

This dataset contains cells from four facioscapulohumeral muscular dystrophy (FSHD) samples and two control samples [ 77 ]. We pool all the 7047 cells from these six samples together. The true cell types of these cells are unknown. The bulk data consists of 27 FSHD patients and eight controls from [ 28 ]. Here the phenotype is FSHD, and it is binary: present or absent.

The results of SCIPAC with the default resolution are given in Fig. 5 e, f. Results under other resolutions are highly similar (shown in Additional file 1: Fig. S15 and S16). For comparison, results given by Scissor under different \(\alpha\) values are presented in Fig. 5 g. The agreements between the results of SCIPAC and Scissor are clear. For example, both methods identify cells located at the top and lower left part of UMAP plots to be negatively associated with FSHD, and cells located at the center and right parts of UMAP plots to be positively associated. However, the discrepancies in their results are also evident. The most pronounced one is a large group of cells (circled in Fig. 5 f) that are identified by SCIPAC as significantly positively associated but are completely ignored by Scissor. Checking into this group of cells, we find that over 90% (424 out of 469) come from the FSHD patients, and less than 10% come from the control samples. However, cells from FSHD patients only compose 73% (5133) of all the 7047 cells. This statistically significant ( p -value \(<10^{-15}\) , Fisher’s exact test) over-representation (odds ratio = 3.51) suggests that the positive association identified SCIPAC is likely to be correct.

SCIPAC is computationally highly efficient. On an 8-core machine with 2.50 GHz CPU and 16 GB RAM, SCIPAC takes 7, 24, and 2 s to finish all the computation and give the estimated association strengths and p -values on the prostate cancer, lung cancer, and muscular dystrophy datasets, respectively. As a reference, Scissor takes 314, 539, and 171 seconds, respectively.

SCIPAC works with various phenotype types, including binary, continuous, survival, and ordinal. It can easily accommodate other types by using a proper regression model with a systematic component in the form of Eq. 3 (see the “ Methods ” section). For example, a Poisson or negative binomial log-linear model can be used if the phenotype is a count (i.e., non-negative integer).

In SCIPAC’s definition of association, a cell type is associated with the phenotype if increasing the proportion of this cell type leads to a change of probability of the phenotype occurring. The strength of association represents the extent of the increase or decrease in this probability. In the case of binary-response, this change is measured by the log odds ratio. For example, if the association strength of cell type A is twice that of cell type B, increasing cell type A by a certain proportion leads to twice the amount of change in the log odds ratio of having the phenotype compared to increasing cell type B by the same proportion. The association strength under other types of phenotypes can be interpreted similarly, with the major difference lying in the measure of change in probability. For quantitative, ordinal, and survival outcomes, the difference in the quantitative outcome, log odds ratio of the right-tail probability, and log hazard ratio respectively are used. Despite the differences in the exact form of the association strength under different types of phenotypes, the underlying concept remains the same: a larger (absolute value of) association strength indicates that the same increase/decrease in a cell type leads to a larger change in the occurrence of the phenotype.

As SCIPAC utilizes both bulk RNA-seq data with phenotype and single-cell RNA-seq data, the estimated associations for the cells are influenced by the choice of the bulk data. Although different bulk data can yield varying estimations of the association for the same single cells, the estimated associations appear to be reasonably robust even when minor changes are made to the bulk data. See Additional file 1 for further discussions.

When using the Louvain algorithm in the Seurat package to cluster cells, SCIPAC’s default resolution is 2.0, larger than the default setting of Seurat. This allows for the identification of potential subtypes within the major cell type and enables the estimation of individual association strengths. Consequently, a more detailed and comprehensive description of the association between single cells and the phenotype can be obtained by SCIPAC.

When applying SCIPAC to real datasets, we made a deliberate choice to disregard the cell annotation provided by the original publications and instead relied on the inferred cell clusters produced by the Louvain algorithm. We made this decision for several reasons. Firstly, we aimed to ensure a fair comparison with Scissor, as it does not utilize cell-type annotations. Secondly, the original annotation might not be sufficiently comprehensive or detailed. Presumed cell types could potentially encompass multiple subtypes, each of which may exhibit distinct associations with the phenotype under investigation. In such cases, employing the Louvain algorithm with a relatively high resolution, which is the default setting in SCIPAC, enables us to differentiate between these subtypes and allows SCIPAC to assign varying association strengths to each subtype.

SCIPAC fits the regression model using the elastic net, a machine-learning algorithm that maximizes a penalized version of the likelihood. The elastic net can be replaced by other penalized estimates of regression models, such as SCAD [ 78 ], without altering the rest of the SCIPAC algorithm. The combination of a regression model and a penalized estimation algorithm such as the elastic net has shown comparable or higher prediction power than other sophisticated methods such as random forests, boosting, or neural networks in numerous applications, especially for gene expression data [ 79 ]. However, there can still be datasets where other models have higher prediction power. It will be future work to incorporate these models into SCIPAC.

The use of metacells is becoming an efficient way to handle large single-cell datasets [ 80 , 81 , 82 , 83 ]. Conceptually, SCIPAC can incorporate metacells and their representatives as an alternative to its default setting of using cell clusters/types and their centroids. We have explored this aspect using metacells provided by SEACells [ 81 ]. Details are given in Additional file 1. Our comparative analysis reveals that combining SCIPAC with SEACells results in significantly reduced performance compared to using SCIPAC directly on original single-cell data. The primary reason for this appears to be the subpar performance of SEACells in cell grouping, especially when contrasted with the Louvain algorithm. Given these findings, we do not suggest using metacells provided by SEACells for SCIPAC applications in the current stage.

Conclusions

SCIPAC is a novel algorithm for studying the associations between cells and phenotypes. Compared to the previous algorithm, SCIPAC gives a much more detailed and comprehensive description of the associations by enabling a quantitative estimation of the association strength and by providing a quality control—the p -value. Underlying SCIPAC are a general statistical model that accommodates virtually all types of phenotypes, including ordinal (and potentially count) phenotypes that have never been considered before, and a concise and closed-form mathematical formula that quantifies the association, which minimizes the computational load. The mathematical conciseness also largely frees SCIPAC from parameter tuning. The only parameter (i.e., the resolution) barely changes the results given by SCIPAC. Overall, compared with its predecessor, SCIPAC represents a substantially more capable software by being much more informative, versatile, robust, and user-friendly.

The improvement in accuracy is also remarkable. In simulated data, SCIPAC achieves high power and low false positives, which is evident from the UMAP plot, F1 score, and FSC score. In real data, SCIPAC gives results that are consistent with current biological knowledge for cell types whose functions are well understood. For cell types whose functions are less studied or more multifaceted, SCIPAC gives support to certain biological hypotheses or helps identify/discover cell sub-types.

SCIPAC’s identification of cell-phenotype associations closely follows its definition of association: when increasing the fraction of a cell type increases (or decreases) the probability for a phenotype to be present, this cell type is positively (or negatively) associated with the phenotype.

The increase of the fraction of a cell type

For a bulk sample, let vector \(\varvec{G} \in \mathbb {R}^p\) be its expression profile, that is, its expression on the p genes. Suppose there are K cell types in the tissue, and let \(\varvec{g}_{k}\) be the representative expression of the k ’th cell type. Usually, people assume that \(\varvec{G}\) can be decomposed by

where \(\gamma _{k}\) is the proportion of cell type k in the bulk tissue, with \(\sum _{k = 1}^{K}\gamma _{k} = 1\) . This equation links the bulk and single-cell expression data.

Now consider increasing cells from cell type k by \(\Delta \gamma\) proportion of the original number of cells. Then, the new proportion of cell type k becomes \(\frac{\gamma _{k} + \Delta \gamma }{1 + \Delta \gamma }\) , and the new proportion of cell type \(j \ne k\) becomes \(\frac{\gamma _{j}}{1 + \Delta \gamma }\)  (note that the new proportions of all cell types should still add up to 1). Thus, the bulk expression profile with the increase of cell type k becomes

Plugging Eq. 1 , we get

Interestingly, this expression of \(\varvec{G}^*\) does not include \(\gamma _{1}, \ldots , \gamma _{K}\) . This means that there is no need actually to compute \(\gamma _{1}, \ldots , \gamma _{K}\) in Eq. 1 , which could otherwise be done using a cell-type-decomposition software, but an accurate and robust decomposition is non-trivial [ 84 , 85 , 86 ]. See Additional file 1 for a more in-depth discussion on the connections of SCIPAC with decomposition/deconvolution.

The change in chance of a phenotype

In this section, we consider how the increase in the fraction of a cell type will change the chance for a binary phenotype such as cancer to occur. Other types of phenotypes will be considered in the next section.

Let \(\pi (\varvec{G})\) be the chance of an individual with gene expression profile \(\varvec{G}\) for this phenotype to occur. We assume a logistic regression model to describe the relationship between \(\pi (\varvec{G})\) and \(\varvec{G}\) :

here the left-hand side is the log odds of \(\pi (\varvec{G})\) , \(\beta _{0}\) is the intercept, and \(\varvec{\beta }\) is a length- p vector of coefficients. In the section after the next, we will describe how we obtain \(\beta _{0}\) and \(\varvec{\beta }\) from the data.

When increasing cells from cell type k by \(\Delta \gamma\) , \(\varvec{G}\) becomes \(\varvec{G}^*\) in Eq. 3 . Plugging Eq. 2 , we get

We further take the difference between Eqs. 4 and 3 and get

The left-hand side of this equation is the log odds ratio (i.e., the change of log odds). On the right-hand side, \(\frac{\Delta \gamma }{1 + \Delta \gamma }\) is an increasing function with respect to \(\Delta \gamma\) , and \(\varvec{\beta }^T(\varvec{g}_{k} - \varvec{G})\) is independent of \(\Delta \gamma\) . This indicates that given any specific \(\Delta \gamma\) , the log odds ratio under over-representation of cell type k is proportional to

\(\lambda _k\) describes the strength of the effect of increasing cell type k to a bulk sample with expression profile \(\varvec{G}\) . Given the presence of numerous bulk samples, employing multiple \(\lambda _k\) ’s could be cumbersome and obscure the overall effect of a particular cell type. To concisely summarize the association of cell type k , we propose averaging their effects. The average effect on all bulk samples can be obtained by

where \(\bar{\varvec{G}}\) is the average expression profile of all bulk samples.

\(\Lambda _k\) gives an overall impression of how strong the effect is when cell type k over-represents to the probability for the phenotype to be present. Its sign represents the direction of the change: a positive value means an increase in probability, and a negative value means a decrease in probability. Its absolute value represents the strength of the effect. In SCIPAC, we call \(\Lambda _k\) the association strength of cell type k and the phenotype.

Note that this derivation does not involve likelihood, although the computation of \(\varvec{\beta }\) does. Here, it serves more as a definitional approach.

Definition of the association strength for other types of phenotype

Our definition of \(\Lambda _k\) relies on vector \(\varvec{\beta }\) . In the case of a binary phenotype, \(\varvec{\beta }\) are the coefficients of a logistic regression that describes a linear relationship between the expression profile and the log odds of having the phenotype, as shown in Eq. 3 . For other types of phenotype, \(\varvec{\beta }\) can be defined/computed similarly.

For a quantitative (i.e., continuous) phenotype, an ordinary linear regression can be used, and the left-hand side of Eq. 3 is changed to the quantitative value of the phenotype.

For a survival phenotype, a Cox proportional hazards model can be used, and the left-hand side of Eq. 3 is changed to the log hazard ratio.

For an ordinal phenotype, we use a proportional odds model

where \(j \in \{1, 2, ..., (J - 1)\}\) and J is the number of ordinal levels. It should be noted that here we use the right-tail probability \(\Pr (Y_{i} \ge j + 1 | X)\) instead of the commonly used cumulative probability (left-tail probability) \(\Pr (Y_{i} \le j | X)\) . Such a change makes the interpretation consistent with other types of phenotypes: in our model, a larger value on the right-hand side indicates a larger chance for \(Y_{i}\) to have a higher level, which in turn guarantees that the sign of the association strength defined according to this \(\varvec{\beta }\) has the usual meaning: a positive \(\Lambda _k\) value means a positive association with the phenotype-using the cancer stage as an example. A positive \(\Lambda _k\) means the over-representation of cell type k increases the chance of a higher cancer stage. In contrast, using the commonly used cumulative probability leads to a counter-intuitive, reversed interpretation.

Computation of the association strength in practice

In practice, \(\varvec{\beta }\) in Eq. 3 needs to be learned from the bulk data. By default, SCIPAC uses the elastic net, a popular and powerful penalized regression method:

In this model, \(l(\beta _{0}, \varvec{\beta })\) is a log-likelihood of the linear model (i.e., logistic regression for a binary phenotype, ordinary linear regression for a quantitative phenotype, Cox proportional odds model for a survival phenotype, and proportional odds model for an ordinal phenotype). \(\alpha\) is a number between 0 and 1, denoting a combination of \(\ell _1\) and \(\ell _2\) penalties, and \(\lambda\) is the penalty strength. SCIPAC fixes \(\alpha\) to be 0.4 (see Additional file 1 for discussions on this choice) and uses 10-fold cross-validation to decide \(\lambda\) automatically. This way, they do not become hyperparameters.

In SCIPAC, the fitting and cross-validation of the elastic net are done by calling the ordinalNet [ 87 ] R package for the ordinal phenotype and by calling the glmnet R package [ 88 , 89 , 90 , 91 ] for other types of phenotypes.

The computation of the association strength, as defined by Eq. 7 , does not only require \(\varvec{\beta }\) , but also \(\varvec{g}_k\) and \(\bar{\varvec{G}}\) . \(\bar{\varvec{G}}\) is simply the average expression profile of all bulk samples. On the other hand, \(\varvec{g}_k\) requires knowing the cell type of each cell. By default, SCIPAC does not assume this information to be given, and it uses the Louvain clustering implemented in the Seurat [ 24 , 25 ] R package to infer it. This clustering algorithm has one tuning parameter called “resolution.” SCIPAC sets its default value as 2.0, and the user can use other values. With the inferred or given cell types, \(\varvec{g}_k\) is computed as the centroid (i.e., the mean expression profile) of cells in cluster k .

Given \(\varvec{\beta }\) , \(\bar{\varvec{G}}\) , and \(\varvec{g}_k\) , the association strength can be computed using Eq. 7 . Knowing the association strength for each cell type and the cell-type label for each cell, we also know the association strength for every single cell. In practice, we standardize the association strengths for all cells. That is, we compute the mean and standard deviation of the association strengths of all cells and use them to centralize and scale the association strength, respectively. We have found such standardization makes SCIPAC more robust to the possible unbalance in sample size of bulk data in different phenotype groups.

Computation of the p -value

SCIPAC uses non-parametric bootstrap [ 92 ] to compute the standard deviation and hence the p -value of the association. Fifty bootstrap samples, which are believed to be enough to compute the standard error of most statistics [ 93 ], are generated for the bulk expression data, and each is used to compute (standardized) \(\Lambda\) values for all the cells. For cell i , let its original \(\Lambda\) values be \(\Lambda _i\) , and the bootstrapped values be \(\Lambda _i^{(1)}, \ldots , \Lambda _i^{(50)}\) . A z -score is then computed using

and then the p -value is computed according to the cumulative distribution function of the standard Gaussian distribution. See Additional file 1 for more discussions on the calculation of p -value.

Availability of data and materials

The simulated datasets [ 94 ] under three schemes are available at Zenodo with DOI 10.5281/zenodo.11013320 [ 95 ]. The SCIPAC package is available at GitHub website https://github.com/RavenGan/SCIPAC under the MIT license [ 96 ]. The source code of SCIPAC is also deposited at Zenodo with DOI 10.5281/zenodo.11013696 [ 97 ]. A vignette of the R package is available on the GitHub page and in the Additional file 2. The prostate cancer scRNA-seq data is obtained from the Prostate Cell Atlas https://www.prostatecellatlas.org [ 29 ]; the scRNA-seq data for the breast cancer are from the Gene Expression Omnibus (GEO) under accession number GSE176078 [ 34 , 98 ]; the scRNA-seq data for the lung cancer are from E-MTAB-6149 [ 99 ] and E-MTAB-6653 [ 71 , 100 ]; the scRNA-seq data for facioscapulohumeral muscular dystrophy data are from the GEO under accession number GSE122873 [ 101 ]. The bulk RNA-seq data are obtained from the TCGA database via TCGAbiolinks (ver. 2.25.2) R package [ 102 ]. More details about the simulated and real scRNA-seq and bulk RNA-seq data can be found in the Additional file 1.

Yofe I, Dahan R, Amit I. Single-cell genomic approaches for developing the next generation of immunotherapies. Nat Med. 2020;26(2):171–7.

Article   CAS   PubMed   Google Scholar  

Zhang Q, He Y, Luo N, Patel SJ, Han Y, Gao R, et al. Landscape and dynamics of single immune cells in hepatocellular carcinoma. Cell. 2019;179(4):829–45.

Fan J, Slowikowski K, Zhang F. Single-cell transcriptomics in cancer: computational challenges and opportunities. Exp Mol Med. 2020;52(9):1452–65.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Klein AM, Mazutis L, Akartuna I, Tallapragada N, Veres A, Li V, et al. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell. 2015;161(5):1187–201.

Macosko EZ, Basu A, Satija R, Nemesh J, Shekhar K, Goldman M, et al. Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets. Cell. 2015;161(5):1202–14.

Rosenberg AB, Roco CM, Muscat RA, Kuchina A, Sample P, Yao Z, et al. Single-cell profiling of the developing mouse brain and spinal cord with split-pool barcoding. Science. 2018;360(6385):176–82.

Zheng GX, Terry JM, Belgrader P, Ryvkin P, Bent ZW, Wilson R, et al. Massively parallel digital transcriptional profiling of single cells. Nat Commun. 2017;8(1):1–12.

Article   Google Scholar  

Abdelaal T, Michielsen L, Cats D, Hoogduin D, Mei H, Reinders MJ, et al. A comparison of automatic cell identification methods for single-cell RNA sequencing data. Genome Biol. 2019;20(1):1–19.

Article   CAS   Google Scholar  

Luecken MD, Theis FJ. Current best practices in single-cell RNA-seq analysis: a tutorial. Mol Syst Biol. 2019;15(6):e8746.

Article   PubMed   PubMed Central   Google Scholar  

Guo H, Li J. scSorter: assigning cells to known cell types according to marker genes. Genome Biol. 2021;22(1):1–18.

Pliner HA, Shendure J, Trapnell C. Supervised classification enables rapid annotation of cell atlases. Nat Methods. 2019;16(10):983–6.

Zhang AW, O’Flanagan C, Chavez EA, Lim JL, Ceglia N, McPherson A, et al. Probabilistic cell-type assignment of single-cell RNA-seq for tumor microenvironment profiling. Nat Methods. 2019;16(10):1007–15.

Zhang Z, Luo D, Zhong X, Choi JH, Ma Y, Wang S, et al. SCINA: a semi-supervised subtyping algorithm of single cells and bulk samples. Genes. 2019;10(7):531.

Johnson TS, Wang T, Huang Z, Yu CY, Wu Y, Han Y, et al. LAmbDA: label ambiguous domain adaptation dataset integration reduces batch effects and improves subtype detection. Bioinformatics. 2019;35(22):4696–706.

Ma F, Pellegrini M. ACTINN: automated identification of cell types in single cell RNA sequencing. Bioinformatics. 2020;36(2):533–8.

Tan Y, Cahan P. SingleCellNet: a computational tool to classify single cell RNA-Seq data across platforms and across species. Cell Syst. 2019;9(2):207–13.

Salcher S, Sturm G, Horvath L, Untergasser G, Kuempers C, Fotakis G, et al. High-resolution single-cell atlas reveals diversity and plasticity of tissue-resident neutrophils in non-small cell lung cancer. Cancer Cell. 2022;40(12):1503–20.

Good Z, Sarno J, Jager A, Samusik N, Aghaeepour N, Simonds EF, et al. Single-cell developmental classification of B cell precursor acute lymphoblastic leukemia at diagnosis reveals predictors of relapse. Nat Med. 2018;24(4):474–83.

Wagner J, Rapsomaniki MA, Chevrier S, Anzeneder T, Langwieder C, Dykgers A, et al. A single-cell atlas of the tumor and immune ecosystem of human breast cancer. Cell. 2019;177(5):1330–45.

Weinstein JN, Collisson EA, Mills GB, Shaw KR, Ozenberger BA, Ellrott K, et al. The cancer genome atlas pan-cancer analysis project. Nat Genet. 2013;45(10):1113–20.

Cerami E, Gao J, Dogrusoz U, Gross BE, Sumer SO, Aksoy BA, et al. The cBio cancer genomics portal: an open platform for exploring multidimensional cancer genomics data. Cancer Disc. 2012;2(5):401–4.

Gao J, Aksoy BA, Dogrusoz U, Dresdner G, Gross B, Sumer SO, et al. Integrative analysis of complex cancer genomics and clinical profiles using the cBioPortal. Sci Signal. 2013;6(269):1.

Sun D, Guan X, Moran AE, Wu LY, Qian DZ, Schedin P, et al. Identifying phenotype-associated subpopulations by integrating bulk and single-cell sequencing data. Nat Biotechnol. 2022;40(4):527–38.

Blondel VD, Guillaume JL, Lambiotte R, Lefebvre E. Fast unfolding of communities in large networks. J Stat Mech Theory Exp. 2008;2008(10):P10008.

Stuart T, Butler A, Hoffman P, Hafemeister C, Papalexi E, Mauck WM III, et al. Comprehensive integration of single-cell data. Cell. 2019;177(7):1888–902.

Zou H, Hastie T. Regularization and variable selection via the elastic net. J R Stat Soc Ser B Stat Methodol. 2005;67(2):301–20.

McInnes L, Healy J, Melville J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. 2018. arXiv preprint arXiv:1802.03426 .

Wong CJ, Wang LH, Friedman SD, Shaw D, Campbell AE, Budech CB, et al. Longitudinal measures of RNA expression and disease activity in FSHD muscle biopsies. Hum Mol Genet. 2020;29(6):1030–43.

Tuong ZK, Loudon KW, Berry B, Richoz N, Jones J, Tan X, et al. Resolving the immune landscape of human prostate at a single-cell level in health and cancer. Cell Rep. 2021;37(12):110132.

Hume DA. The mononuclear phagocyte system. Curr Opin Immunol. 2006;18(1):49–53.

Hume DA, Ross IL, Himes SR, Sasmono RT, Wells CA, Ravasi T. The mononuclear phagocyte system revisited. J Leukoc Biol. 2002;72(4):621–7.

Raggi F, Bosco MC. Targeting mononuclear phagocyte receptors in cancer immunotherapy: new perspectives of the triggering receptor expressed on myeloid cells (TREM-1). Cancers. 2020;12(5):1337.

Largeot A, Pagano G, Gonder S, Moussay E, Paggetti J. The B-side of cancer immunity: the underrated tune. Cells. 2019;8(5):449.

Wu SZ, Al-Eryani G, Roden DL, Junankar S, Harvey K, Andersson A, et al. A single-cell and spatially resolved atlas of human breast cancers. Nat Genet. 2021;53(9):1334–47.

Fernández-Nogueira P, Fuster G, Gutierrez-Uzquiza Á, Gascón P, Carbó N, Bragado P. Cancer-associated fibroblasts in breast cancer treatment response and metastasis. Cancers. 2021;13(13):3146.

Ao Z, Shah SH, Machlin LM, Parajuli R, Miller PC, Rawal S, et al. Identification of cancer-associated fibroblasts in circulating blood from patients with metastatic breast cancer. Identification of cCAFs from metastatic cancer patients. Cancer Res. 2015;75(22):4681–7.

Arcucci A, Ruocco MR, Granato G, Sacco AM, Montagnani S. Cancer: an oxidative crosstalk between solid tumor cells and cancer associated fibroblasts. BioMed Res Int. 2016;2016.  https://pubmed.ncbi.nlm.nih.gov/27595103/ .

Buchsbaum RJ, Oh SY. Breast cancer-associated fibroblasts: where we are and where we need to go. Cancers. 2016;8(2):19.

Ruocco MR, Avagliano A, Granato G, Imparato V, Masone S, Masullo M, et al. Involvement of breast cancer-associated fibroblasts in tumor development, therapy resistance and evaluation of potential therapeutic strategies. Curr Med Chem. 2018;25(29):3414–34.

Savas P, Virassamy B, Ye C, Salim A, Mintoff CP, Caramia F, et al. Single-cell profiling of breast cancer T cells reveals a tissue-resident memory subset associated with improved prognosis. Nat Med. 2018;24(7):986–93.

Bassez A, Vos H, Van Dyck L, Floris G, Arijs I, Desmedt C, et al. A single-cell map of intratumoral changes during anti-PD1 treatment of patients with breast cancer. Nat Med. 2021;27(5):820–32.

Romero JM, Grünwald B, Jang GH, Bavi PP, Jhaveri A, Masoomian M, et al. A four-chemokine signature is associated with a T-cell-inflamed phenotype in primary and metastatic pancreatic cancer. Chemokines in Pancreatic Cancer. Clin Cancer Res. 2020;26(8):1997–2010.

Tamura R, Yoshihara K, Nakaoka H, Yachida N, Yamaguchi M, Suda K, et al. XCL1 expression correlates with CD8-positive T cells infiltration and PD-L1 expression in squamous cell carcinoma arising from mature cystic teratoma of the ovary. Oncogene. 2020;39(17):3541–54.

Hernandez R, Põder J, LaPorte KM, Malek TR. Engineering IL-2 for immunotherapy of autoimmunity and cancer. Nat Rev Immunol. 2022:22:1–15.  https://pubmed.ncbi.nlm.nih.gov/35217787/ .

Korotkevich G, Sukhov V, Budin N, Shpak B, Artyomov MN, Sergushichev A. Fast gene set enrichment analysis. BioRxiv. 2016:060012.  https://www.biorxiv.org/content/10.1101/060012v3.abstract .

Dang CV. MYC on the path to cancer. Cell. 2012;149(1):22–35.

Gnanaprakasam JR, Wang R. MYC in regulating immunity: metabolism and beyond. Genes. 2017;8(3):88.

Oshi M, Takahashi H, Tokumaru Y, Yan L, Rashid OM, Matsuyama R, et al. G2M cell cycle pathway score as a prognostic biomarker of metastasis in estrogen receptor (ER)-positive breast cancer. Int J Mol Sci. 2020;21(8):2921.

Zhang X, Lan Y, Xu J, Quan F, Zhao E, Deng C, et al. Cell Marker: a manually curated resource of cell markers in human and mouse. Nucleic Acids Res. 2019;47(D1):D721–8.

Chen L, Yang L, Qiao F, Hu X, Li S, Yao L, et al. High levels of nucleolar spindle-associated protein and reduced levels of BRCA1 expression predict poor prognosis in triple-negative breast cancer. PLoS ONE. 2015;10(10):e0140572.

Li M, Yang B. Prognostic value of NUSAP1 and its correlation with immune infiltrates in human breast cancer. Crit Rev TM Eukaryot Gene Expr. 2022;32(3).  https://pubmed.ncbi.nlm.nih.gov/35695609/ .

Zhang X, Pan Y, Fu H, Zhang J. Nucleolar and spindle associated protein 1 (NUSAP1) inhibits cell proliferation and enhances susceptibility to epirubicin in invasive breast cancer cells by regulating cyclin D kinase (CDK1) and DLGAP5 expression. Med Sci Monit: Int Med J Exp Clin Res. 2018;24:8553.

Geyer FC, Rodrigues DN, Weigelt B, Reis-Filho JS. Molecular classification of estrogen receptor-positive/luminal breast cancers. Adv Anat Pathol. 2012;19(1):39–53.

Karamitopoulou E, Perentes E, Tolnay M, Probst A. Prognostic significance of MIB-1, p53, and bcl-2 immunoreactivity in meningiomas. Hum Pathol. 1998;29(2):140–5.

Duxbury MS, Whang EE. RRM2 induces NF- \(\kappa\) B-dependent MMP-9 activation and enhances cellular invasiveness. Biochem Biophys Res Commun. 2007;354(1):190–6.

Zhou BS, Tsai P, Ker R, Tsai J, Ho R, Yu J, et al. Overexpression of transfected human ribonucleotide reductase M2 subunit in human cancer cells enhances their invasive potential. Clin Exp Metastasis. 1998;16(1):43–9.

Zhang H, Liu X, Warden CD, Huang Y, Loera S, Xue L, et al. Prognostic and therapeutic significance of ribonucleotide reductase small subunit M2 in estrogen-negative breast cancers. BMC Cancer. 2014;14(1):1–16.

Putluri N, Maity S, Kommagani R, Creighton CJ, Putluri V, Chen F, et al. Pathway-centric integrative analysis identifies RRM2 as a prognostic marker in breast cancer associated with poor survival and tamoxifen resistance. Neoplasia. 2014;16(5):390–402.

Koleck TA, Conley YP. Identification and prioritization of candidate genes for symptom variability in breast cancer survivors based on disease characteristics at the cellular level. Breast Cancer Targets Ther. 2016;8:29.

Li Jp, Zhang Xm, Zhang Z, Zheng Lh, Jindal S, Liu Yj. Association of p53 expression with poor prognosis in patients with triple-negative breast invasive ductal carcinoma. Medicine. 2019;98(18).  https://pubmed.ncbi.nlm.nih.gov/31045815/ .

Gong MT, Ye SD, Lv WW, He K, Li WX. Comprehensive integrated analysis of gene expression datasets identifies key anti-cancer targets in different stages of breast cancer. Exp Ther Med. 2018;16(2):802–10.

PubMed   PubMed Central   Google Scholar  

Chen Wx, Yang Lg, Xu Ly, Cheng L, Qian Q, Sun L, et al. Bioinformatics analysis revealing prognostic significance of RRM2 gene in breast cancer. Biosci Rep. 2019;39(4).  https://pubmed.ncbi.nlm.nih.gov/30898978/ .

Hao Z, Zhang H, Cowell J. Ubiquitin-conjugating enzyme UBE2C: molecular biology, role in tumorigenesis, and potential as a biomarker. Tumor Biol. 2012;33(3):723–30.

Arriola E, Rodriguez-Pinilla SM, Lambros MB, Jones RL, James M, Savage K, et al. Topoisomerase II alpha amplification may predict benefit from adjuvant anthracyclines in HER2 positive early breast cancer. Breast Cancer Res Treat. 2007;106(2):181–9.

Knoop AS, Knudsen H, Balslev E, Rasmussen BB, Overgaard J, Nielsen KV, et al. Retrospective analysis of topoisomerase IIa amplifications and deletions as predictive markers in primary breast cancer patients randomly assigned to cyclophosphamide, methotrexate, and fluorouracil or cyclophosphamide, epirubicin, and fluorouracil: Danish Breast Cancer Cooperative Group. J Clin Oncol. 2005;23(30):7483–90.

Tanner M, Isola J, Wiklund T, Erikstein B, Kellokumpu-Lehtinen P, Malmstrom P, et al. Topoisomerase II \(\alpha\) gene amplification predicts favorable treatment response to tailored and dose-escalated anthracycline-based adjuvant chemotherapy in HER-2/neu-amplified breast cancer: Scandinavian Breast Group Trial 9401. J Clin Oncol. 2006;24(16):2428–36.

Arriola E, Moreno A, Varela M, Serra JM, Falo C, Benito E, et al. Predictive value of HER-2 and topoisomerase II \(\alpha\) in response to primary doxorubicin in breast cancer. Eur J Cancer. 2006;42(17):2954–60.

Järvinen TA, Tanner M, Bärlund M, Borg Å, Isola J. Characterization of topoisomerase II \(\alpha\) gene amplification and deletion in breast cancer. Gene Chromosome Cancer. 1999;26(2):142–50.

Landberg G, Erlanson M, Roos G, Tan EM, Casiano CA. Nuclear autoantigen p330d/CENP-F: a marker for cell proliferation in human malignancies. Cytom J Int Soc Anal Cytol. 1996;25(1):90–8.

CAS   Google Scholar  

Bettelli E, Carrier Y, Gao W, Korn T, Strom TB, Oukka M, et al. Reciprocal developmental pathways for the generation of pathogenic effector TH17 and regulatory T cells. Nature. 2006;441(7090):235–8.

Lambrechts D, Wauters E, Boeckx B, Aibar S, Nittner D, Burton O, et al. Phenotype molding of stromal cells in the lung tumor microenvironment. Nat Med. 2018;24(8):1277–89.

Bremnes RM, Busund LT, Kilvær TL, Andersen S, Richardsen E, Paulsen EE, et al. The role of tumor-infiltrating lymphocytes in development, progression, and prognosis of non-small cell lung cancer. J Thorac Oncol. 2016;11(6):789–800.

Article   PubMed   Google Scholar  

Schalper KA, Brown J, Carvajal-Hausdorf D, McLaughlin J, Velcheti V, Syrigos KN, et al. Objective measurement and clinical significance of TILs in non–small cell lung cancer. J Natl Cancer Inst. 2015;107(3):dju435.

Tay RE, Richardson EK, Toh HC. Revisiting the role of CD4+ T cells in cancer immunotherapy—new insights into old paradigms. Cancer Gene Ther. 2021;28(1):5–17.

Dieu-Nosjean MC, Goc J, Giraldo NA, Sautès-Fridman C, Fridman WH. Tertiary lymphoid structures in cancer and beyond. Trends Immunol. 2014;35(11):571–80.

Wang Ss, Liu W, Ly D, Xu H, Qu L, Zhang L. Tumor-infiltrating B cells: their role and application in anti-tumor immunity in lung cancer. Cell Mol Immunol. 2019;16(1):6–18.

van den Heuvel A, Mahfouz A, Kloet SL, Balog J, van Engelen BG, Tawil R, et al. Single-cell RNA sequencing in facioscapulohumeral muscular dystrophy disease etiology and development. Hum Mol Genet. 2019;28(7):1064–75.

Fan J, Li R. Variable selection via nonconcave penalized likelihood and its oracle properties. J Am Stat Assoc. 2001;96(456):1348–60.

Hastie T, Tibshirani R, Friedman JH, Friedman JH. The elements of statistical learning: data mining, inference, and prediction, vol. 2. New York: Springer; 2009.

Book   Google Scholar  

Baran Y, Bercovich A, Sebe-Pedros A, Lubling Y, Giladi A, Chomsky E, et al. MetaCell: analysis of single-cell RNA-seq data using K-nn graph partitions. Genome Biol. 2019;20(1):1–19.

Persad S, Choo ZN, Dien C, Sohail N, Masilionis I, Chaligné R, et al. SEACells infers transcriptional and epigenomic cellular states from single-cell genomics data. Nat Biotechnol. 2023;41:1–12.  https://pubmed.ncbi.nlm.nih.gov/36973557/ .

Ben-Kiki O, Bercovich A, Lifshitz A, Tanay A. Metacell-2: a divide-and-conquer metacell algorithm for scalable scRNA-seq analysis. Genome Biol. 2022;23(1):100.

Bilous M, Tran L, Cianciaruso C, Gabriel A, Michel H, Carmona SJ, et al. Metacells untangle large and complex single-cell transcriptome networks. BMC Bioinformatics. 2022;23(1):336.

Avila Cobos F, Alquicira-Hernandez J, Powell JE, Mestdagh P, De Preter K. Benchmarking of cell type deconvolution pipelines for transcriptomics data. Nat Commun. 2020;11(1):1–14.

Jin H, Liu Z. A benchmark for RNA-seq deconvolution analysis under dynamic testing environments. Genome Biol. 2021;22(1):1–23.

Wang X, Park J, Susztak K, Zhang NR, Li M. Bulk tissue cell type deconvolution with multi-subject single-cell expression reference. Nat Commun. 2019;10(1):380.

Wurm MJ, Rathouz PJ, Hanlon BM. Regularized ordinal regression and the ordinalNet R package. 2017. arXiv preprint arXiv:1706.05003 .

Friedman J, Hastie T, Tibshirani R. Regularization paths for generalized linear models via coordinate descent. J Stat Softw. 2010;33(1):1.

Simon N, Friedman J, Hastie T. A blockwise descent algorithm for group-penalized multiresponse and multinomial regression. 2013. arXiv preprint arXiv:1311.6529 .

Simon N, Friedman J, Hastie T, Tibshirani R. Regularization paths for Cox’s proportional hazards model via coordinate descent. J Stat Softw. 2011;39(5):1.

Tibshirani R, Bien J, Friedman J, Hastie T, Simon N, Taylor J, et al. Strong rules for discarding predictors in lasso-type problems. J R Stat Soc Ser B Stat Methodol. 2012;74(2):245–66.

Efron B. Bootstrap methods: another look at the jackknife. In: Breakthroughs in statistics. New York: Springer; 1992. pp. 569–593.

Efron B, Tibshirani RJ. An introduction to the bootstrap. London: CRC Press; 1994.

Zappia L, Phipson B, Oshlack A. Splatter: simulation of single-cell RNA sequencing data. Genome Biol. 2017;18(1):174.

Gan D, Zhu Y, Lu X, Li J. Simulated datasets used in SCIPAC analysis. Zenodo. 2024. https://doi.org/10.5281/zenodo.11013320 .

Gan D, Zhu Y, Lu X, Li J. SCIPAC R package. GitHub. 2024. https://github.com/RavenGan/SCIPAC . Accessed 24 Apr 2024.

Gan D, Zhu Y, Lu X, Li J. SCIPAC source code. Zenodo. 2024. https://doi.org/10.5281/zenodo.11013696 .

Wu SZ, Al-Eryani G, Roden DL, Junankar S, Harvey K, Andersson A, et al. A single-cell and spatially resolved atlas of human breast cancers. Datasets. 2021. https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE176078 . Gene Expression Omnibus. Accessed 1 Oct 2022.

Lambrechts D, Wauters E, Boeckx B, Aibar S, Nittner D, Burton O, et al. Phenotype molding of stromal cells in the lung tumor microenvironment. Datasets. 2018. https://www.ebi.ac.uk/biostudies/arrayexpress/studies/E-MTAB-6149 . ArrayExpress. Accessed 24 July 2022.

Lambrechts D, Wauters E, Boeckx B, Aibar S, Nittner D, Burton O, et al. Phenotype molding of stromal cells in the lung tumor microenvironment. Datasets. 2018. https://www.ebi.ac.uk/biostudies/arrayexpress/studies/E-MTAB-6653 . ArrayExpress. Accessed 24 July 2022.

van den Heuvel A, Mahfouz A, Kloet SL, Balog J, van Engelen BG, Tawil R, et al. Single-cell RNA sequencing in facioscapulohumeral muscular dystrophy disease etiology and development. Datasets. 2019. https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE122873 . Gene Expression Omnibus. Accessed 13 Aug 2022.

Colaprico A, Silva TC, Olsen C, Garofano L, Cava C, Garolini D, et al. TCGAbiolinks: an R/Bioconductor package for integrative analysis of TCGA data. Nucleic Acids Res. 2016;44(8):e71.

Download references

Review history

The review history is available as Additional file 3.

Peer review information

Veronique van den Berghe was the primary editor of this article and managed its editorial process and peer review in collaboration with the rest of the editorial team.

This work is supported by the National Institutes of Health (R01CA280097 to X.L. and J.L, R01CA252878 to J.L.) and the DOD BCRP Breakthrough Award, Level 2 (W81XWH2110432 to J.L.).

Author information

Authors and affiliations.

Department of Applied and Computational Mathematics and Statistics, University of Notre Dame, Notre Dame, 46556, IN, USA

Dailin Gan & Jun Li

Department of Biological Sciences, Boler-Parseghian Center for Rare and Neglected Diseases, Harper Cancer Research Institute, Integrated Biomedical Sciences Graduate Program, University of Notre Dame, Notre Dame, 46556, IN, USA

Yini Zhu & Xin Lu

Tumor Microenvironment and Metastasis Program, Indiana University Melvin and Bren Simon Comprehensive Cancer Center, Indianapolis, 46202, IN, USA

You can also search for this author in PubMed   Google Scholar

Contributions

J.L. conceived and supervised the study. J.L. and D.G. proposed the methods. D.G. implemented the methods and analyzed the data. D.G. and J.L. drafted the paper. D.G., Y.Z., X.L., and J.L. interpreted the results and revised the paper.

Corresponding author

Correspondence to Jun Li .

Ethics declarations

Ethics approval and consent to participate.

Not applicable.

Consent for publication

Competing interests.

The authors declare that they have no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Additional file 1. supplementary materials that include additional results and plots., additional file 2. a vignette of the scipac package., additional file 3. review history., rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Gan, D., Zhu, Y., Lu, X. et al. SCIPAC: quantitative estimation of cell-phenotype associations. Genome Biol 25 , 119 (2024). https://doi.org/10.1186/s13059-024-03263-1

Download citation

Received : 30 January 2023

Accepted : 30 April 2024

Published : 13 May 2024

DOI : https://doi.org/10.1186/s13059-024-03263-1

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Phenotype association
• Single cell
• RNA sequencing
• Cancer research

Genome Biology

ISSN: 1474-760X

• Submission enquiries: [email protected]
• General enquiries: [email protected]

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Food Sci Biotechnol
• v.32(11); 2023 Oct
• PMC10227784

Problems and alternatives of testing significance using null hypothesis and P -value in food research

Won-seok choi.

Department of Food Science and Technology, Korea National University of Transportation, Jeungpyeong-gun, 27909 Chungbuk Republic of Korea

A testing method to identify statistically significant differences by comparing the significance level and the probability value based on the Null Hypothesis Significance Test (NHST) has been used in food research. However, problems with this testing method have been discussed. Several alternatives to the NHST and the P -value test methods have been proposed including lowering the P -value threshold and using confidence interval (CI), effect size, and Bayesian statistics. The CI estimates the extent of the effect or difference and determines the presence or absence of statistical significance. The effect size index determines the degree of effect difference and allows for the comparison of various statistical results. Bayesian statistics enable predictions to be made even when only a small amount of data is available. In conclusion, CI, effect size, and Bayesian statistics can complement or replace traditional statistical tests in food research by replacing the use of NHST and P -value.

Introduction

In food of animal or plant resources research, quantitative methods such as experimental research are mainly used. After food research became a separate field of applied science, the use of statistical methods that use the null hypothesis and the P -value increased. This was due in part to Fisher, a pioneer in the field of statistics, who mentioned these methods in a tea- tasting sensory test (Fisher, 1935 , 1936 ). In food research, statistical significance at a P -value of 0.05 (5%) first appeared in the early 1940s (Eheart and Sholes, 1945 ; Griswold and Wharton, 1941 ). Only in the early 1970s, the statistical test procedure was described in the materials and methods of papers (Bouton et al., 1975 ; Froning et al., 1971 ; Reddy et al., 1970 ). In Korea, it was not until the 1990s that statistical tests began to be used in food research papers using animal or plant materials on a variety of topics beyond just sensory tests (Chung et al., 1991 ; Kim and Lee, 1998 ; Shin et al., 1991 ).

The expression “showed a significant difference (at a significance level of 0.05 (5%))” was used to determine whether difference between the control and the experimental groups was statistically significant by comparing the significance level (α) and probability ( P ) based on the Null Hypothesis Significance Test (NHST) (Goodman, 1999 ; Wasserstein et al., 2019 ). As previously mentioned, this statistical verification method was started in the early 20th century by Fisher (Bandit and Boen, 1972 ).

In food research, the significance of the differences is determined using the P -value based on the NHST theory when comparing the experimental group of a new method or material to the control group. This statistical reasoning method is a common practice in food research, especially in Korean food research. However, the problems with NHST were actually raised 50 years ago in 1972 (Edwards, 1972 ). While there has been more recent attention drawn to these problems. In 1988, the International Medical Journal Editors' Committee recognized the problem of using NHST and P -value and requested that statistics be reported using confidence interval (CI) instead (Bailar and Mosteller, 1988 ). Some social science journals even banned using the NHST method in 2015 (Trafimow and Marks, 2015 ). In addition, the American Statistical Association (ASA) has published a statement on statistical significance and P- value, arguing that passing a certain threshold (significance level) the P -value should not be the basis for making scientific conclusions, business, or policy decisions (Ronald and Nicole, 2016 ).

Although there are many reasons for the continued use of NHST and P -values in food research despite these controversies, one of the key reasons is that using NHST and P -value in statistical testing has become universal and commonplace as a mathematical formula for the solution. In addition, it may be because of the denying the results of numerous published papers or acknowledging that there may be errors by judging whether there is a difference from the control group only with the P -value based on the NHST theory. The author is no exception to this conventional behavior and burden. Nevertheless, it is clear that there is a problem in blindly using NHST and P values, and there is a need for gradual improvement.

Several methods have been proposed as alternatives to using NHST and P -value. However, the most prominent ones include lowering the P -value threshold and using confidence interval (CI), effect size, and Bayesian statistics (Benjamin et al., 2018 ; Joo et al., 1994 ; Lee, 2013 , 2016 ; Sullivan and Feinn, 2012 ; Yeo, 2021 ).

In this paper, I will discuss the problems of using NHST and P -value. I will also provide an introduction to basic knowledge and related details on complementary or alternative methods for food researchers who may not have a strong background in statistics. These methods include lowering the P -value threshold, and using CI, effect size, and Bayesian statistics. I will argue that using dichotomous statistical tests based solely on NHST and P -value should be avoided in food research, and that researchers should gradually incorporate supplementary or alternative statistical testing methods such as CI, effect size, and Bayesian statistics, which can provide more diverse information from the same data.

Meaning of NHST and P -value

The NHST used in statistics is a part of the verification method for inferring the characteristics of the entire population. NHST is used to estimate the characteristics of the population from samples collected from the entire population when it is not possible to obtain information (data) from the entire population, and testing is conducted based on hypotheses such as “no difference” or “no effect” (null hypothesis). The null hypothesis is generally the opposite of the hypothesis the researcher intends to infer (alternative hypothesis), which the researcher wants to reject (Joo et al., 1994 ; Verdam et al., 2014 ; Yeo, 2021 ).

In general, rejection of the null hypothesis in NHST is determined by comparing the significance level and the P value. Here, the P value refers to the probability value at which the data value of the sample can be obtained under the condition that the null hypothesis is true (Cohen, 2011 ; Goodman, 1999 ; Trafimow and Rice, 2009 ). That is, a P value of 0.01 means that the probability of obtaining a sample data value (with a difference or effect greater than or equal to the usual level) from the population for which the null hypothesis is true is a very rare (based on significance level of 0.05) with a probability of 1% (0.01), and a P -value of 0.10 is interpreted as the probability of obtaining a sample statistic (sample data value) from the population for which the null hypothesis is true is a relatively high probability (based on significance level of 0.05) with a probability of 10% (0.1). Very high or very rare is a relative concept that requires a criterion and the criterion is called the significance level (generally 0.05 (5%)). If the P -value is smaller than the significance level, it is considered that an unlikely event has occurred. As a result, the null hypothesis is rejected and deemed to have statistical significance.

In fact, NHST is a test method that combines Fisher's significance test and Neyman and Pearson's hypothesis test (Lee, 2013 ). These masters of statistics belonged to different schools, and Fisher, the founder of the concept of the null hypothesis, used the P -value only to reject the null hypothesis, and set the rejection criterion (significance level) at a “convenient and flexible” value of 0.05. On the other hand, Neyman and Pearson supplemented Fisher’s theory and formulated the concept of alternative hypotheses in order to draw mathematical and scientific conclusions, providing a “fixed” criterion for the selection (adoption of the null hypothesis) and rejection (adoption of the alternative hypothesis) of the hypothesis with the use of Type I error (false rejection) probability as α. In other words, if Fisher’s test recommended flexible conclusions, Neyman and Pearson insisted on making strict conclusions. The problem arose when a new theory emerged amid the confrontation and debate between the two schools of thought. Fisher’s P value began to be used with Neyman and Pearson's α, which corresponded to Fisher’s significance level to draw a mathematically rigorous conclusion (Perezgonzalez, 2015 ). Many current problems are the result of blindly using this testing method, which is a simple blend of different schools of thought in an attempt to unify theories.

Problems with using NHST and P -values

As mentioned in the introduction, the problems of making statistical inference using NHST and P -value are as follows (Lee, 2013 ; Sullivan and Feinn, 2012 ; Yeo, 2021 ).

First of all, the most problematic of misunderstandings about the P -value is that it misinterprets “the probability of observing the data value of the sample under the condition that the null hypothesis is correct (true)” as “the probability of the null hypothesis being true based on the observed sample statistic” (Carver, 1978 ; Nickerson, 2000 ). Since the value of P is calculated on the premise that the null hypothesis is true, it cannot be a value of the probability that the null hypothesis is true. A P -value of 0.01 means that the probability of obtaining a sample data value is 1% (0.01) from the population for which the null hypothesis is true, which is a very rare (based on significance level of 0.05) probability and does not mean that there is only a 1% chance that the null hypothesis is true. In other words, when the null hypothesis is rejected, the interpretation that the probability of this being an error is 1% (a very rare probability based on the significance level of 0.05) is an incorrect interpretation. In general, it is wrong to think of the P -value as the probability of making an error, i.e., the error rate, and Sellke et al. ( 2001 ) reported that for a P value of 0.05, the error rate is estimated as “at least 29% (typically around 50%).”

Second, the NHST lacks an explanation of the results, and may sometimes provide no meaning at all. When establishing a null hypothesis such as “there is no (performance) effect of the program” or “there is no difference between the two groups” in a study, the researcher might be interested in the extent of the effect, i.e., effect size along with the presence or absence of an effect, if indeed there was one. When the null hypothesis is rejected, the effect is “statistically” significant, but it is not known whether this effect is “actually” meaningful or meaningless. The same is true for the analysis of differences between the two groups. In the natural sciences, especially in physics, theoretically, the effect can have a value of 0 (zero), but in reality, the case where the effect of a program is 0 is extremely rare; particularly, in the field of social science, it is almost impossible for an effect to have a value of zero. Between the two groups, it is highly probable that there will be a difference of 0 or more mostly due to the surrounding conditions other than the essence, such as the difference in the test method and the number of samples in the groups (McShane and Gal, 2017 ; Yeo, 2021 ).

Third, the P -value is inevitably affected by the number of samples (cases). The larger the number of samples, the smaller the P -value, and conversely, the smaller the number of samples, the higher the P -value. Therefore, if the researcher intends to show a significant effect or difference by lowering the P -value, the researcher has a higher probability of probabilistic success if the number of samples is increased, which leads to the misunderstanding that the smaller the P -value, the greater the effect. That is, the usefulness of the P -value decreases as the number of samples increases (Sullivan and Feinn, 2012 ).

Fourth, papers that performed statistical inference using NHST and P -value have no choice but to interpret the results dichotomously. Determining significance by the size of the P -value at a specific statistical significance level (generally 0.05) has the advantage of being simple and clear to judge the result, but can it be said that the effect is 0 or there is no difference if the P -value is 0.051 at the significance level of 0.05? In other words, can we say that the 0.002 difference between the P -values 0.051 and 0.049 is the absolute difference that will decide the fate? Also, the significance level of 0.05 was an arbitrary and reference only value suggested by Fisher, but now many researchers regard it as an almost absolute reference point (McShane and Gal, 2017 ).

Fifth, it leads to publication bias. Publication bias refers to the selection and publication of only papers with favorable results by an academic organization (Gerber and Malhotra, 2008 ). The use of NHST and P -value is likely to categorize various studies dichotomously into successful and failed studies, leading to the publication of only the studies with so-called statistical significance showing a P -value that is lower than the significance level (Bruns and Ioannidis, 2016 ; Fanelli, 2012 ). This could further lead to side effects such as over-interpretation of study results or preventing various results from being published (Simonsohn et al., 2014 ).

Sixth, NHST and P -value are not correlated with the reproducibility of results, which refers to the ability to obtain the same or similar results when published studies are repeatedly performed in the same way (Plucker and Makel, 2021 ). The majority of readers believe that papers that use NHST and P -value to publish statistically significant results have reproducibility. However, unfortunately, according to the study by Ioannidis (Ioannidis, 2005 ), although there are differences between studies, a significant number of papers published in the medical field did not reproduce the statistical significance. This paper is currently cited more than 7000 times (PLOS MEDICINE, 2023 ). Even when the P value of the research results is 0.001, the reproducibility of the research results cannot be guaranteed (Yeo, 2021 ).

Meanwhile, the American Statistical Association (ASA) mentioned the following principles regarding P -values (Ronald and Nicole, 2016 ).

• The P -value indicates how much the data is inconsistent with a specific statistical model (hypothesis) rather than interpreting it as a probability that a given hypothesis is true based on the sample dataset. In other words, if the basic assumption used to calculate the P -value is maintained, the smaller the P -value, the greater the statistical discrepancy between the null hypothesis and the data;
• The P -value does not measure the probability that the research hypothesis is true or the probability that the data were created by chance;
• One should not make any scientific conclusion, business or policy decisions based only on the passing of a specific threshold (significance level) of the P -value;
• For proper inference, it is necessary to report all statistics transparently and completely in addition to the P -value;
• The P -value or statistical significance does not measure the size of the effect or the importance of the outcome;
• The P -value by itself is not a good evidence for a statistical model or hypothesis (e.g., whether the null hypothesis is true or false).

As an alternative to the problem of using NHST and P -value, several researchers have proposed lowering the P -value threshold, and using CIs, effect sizes, and Bayesian statistics (Benjamin et al., 2018 ; Joo et al., 1994 ; Lee, 2013 , 2016 ; Lin et al., 2013 ).

Lowering the P -value threshold

Benjamin et al. ( 2018 ) numerically analyzed the problems that occur when using a P -value of 0.05. As a result, when the two-sided P -value is 0.05, the minimum probability that the alternative (research) hypothesis is true is 75%, which means that the maximum probability that the null hypothesis is also true is also 25%. In order to solve this problem, they argued that the significance level should be lowered and the P -value should be 0.005. According to the simulation results of these researchers, when the P -value is 0.005, the probability that the alternative (research) hypothesis is true increased about 6.8 times compared to when the P -value was 0.05, and the percentage of false positives decreased by about 6.6 times (33% → 5%). In addition, it was argued that the study results with a P -value of 0.05 to 0.005 are suggestive results, which are inadequate and should be treated as a study that requires further research. Opposition to this argument has also been published. Ioannidis ( 2018 ) argued that lowering the threshold of P -value to 0.005 is a temporary measure, a lower threshold may be preferred, and the magnitude of the effect may be more exaggerated than in the previous case. The power (1-β) corresponding to a P -value of 0.0001 was reported to be about 0.85 (sample size 100) (Norman, 2019 ).

Confidence interval

When estimating population parameters from study data (sample), the best estimate is a single value, which is called point estimation. This is one of the infinitely possible numbers, and the probability of being able to estimate the single value is very low. Therefore, it is more preferable to present the estimate as a value of a range (interval), and when the expected values of an unknown parameter, consistent with the observed data (within a limited range), are expressed as a series of ranges, it is called a CI and this estimation is called interval estimation (Langman, 1986 ). The range of the CI is affected by the number of variables and the confidence level, which is an arbitrary number (Lee, 2016 ; So, 2016 ). Confidence level of 95% is mainly used, and it is directly related to the significance level, so it corresponds to a value of (1–significance level) × 100. That is, the 95% CI corresponds to a significance level of 0.05. In interpreting this, if the 95% confidence level interval for the population mean difference or population ratio between the two groups does not include the null value (0 or 1, respectively) of the parameter and is included in the 99% CI, the P -value of this parameter can be said to be greater than 0.01 and less than 0.05. That is, it is not statistically significant at the significance level of 0.01, but is at the significance level of 0.05. However, the interpretation of this requires attention as in the interpretation of the P value. In calculating the 95% CI of the mean value from the sample, it should be interpreted as meaning that the population mean value is included in 95 CI s (that is, 95% CI) among the CIs calculated from 100 samples obtained by the same method from the same population; it would be erroneous to interpret this as a 95% probability (or the population mean is included with 95% probability) that the 95% CI of the mean value calculated from a “single sample” contains the population mean value.

If two groups with a small sample size satisfy the assumption of normal distribution and equal variance, the CI for the difference in mean values between the two groups can be obtained from the following equation using t-statistics (Lee, 2016 ).

( s pooled , n i ; pooled sample variance at equal variance assumption, sample size of group i)

Confidence interval;

( Xi ¯ , n i , t α df ; mean of group i, sample size of group i, critical value of the t-distribution for the probability α and degrees of freedom)

I would like to explain the difference between using NHST and P -value and using CIs. When comparing the effects of the existing treatment A and the new treatment B, if the NHST-based P value is 0.06, it is generally concluded that “there is no significant difference between the two treatments”. In this case, when the P -value is expressed as P  = 0.06 rather than P  > 0.05, a more diverse meaning can be provided. Nevertheless, the P -value only judges the significance of the difference in the treatment effect between the two treatments, but does not explain the extent of the difference in the treatment effect (Joo et al., 1994 ).

In Fig.  1 . the individual 95% CIs for the study results of A and B and the 95% CI for the difference between the population means of the two studies was shown (Choi and Han, 2017 ). It can be thought that there is no significant difference between A and B at the 0.05 (5%) significance level because the individual CIs of A and B partially overlap, but this would be an incorrect interpretation; given the 95% CI (far right, B-A) for the population mean value difference between A and B, the correct interpretation would be that there is a statistically significant difference at the significance level of 0.05 because 0 (null value for the mean value difference) is not included. Also, since each CI represents the expected size of the effect, which means that it can have an effect within the range, it can be estimated that B is more effective than A (Choi and Han, 2017 ; Joo et al., 1994 ; Lee, 2016 ). In other words, the CI provides information on the extent (size) as well as the statistical significance of the effect or difference. It is possible to compare more than 3 groups by this method.

95% confidence intervals.

Adapted from Choi and Han ( 2017 )

Usually, the distribution of numerical values in the CI is not uniformly distributed but roughly follows a normal distribution, so it can be estimated that the data are mainly located in the center rather than at the boundary, which is both ends of the CI. That is, the boundary values of the CI mean that the frequency of the data is small and does not significantly affect the interpretation. Different interpretations may occur depending on the location of the boundary value, but this is not a big problem because such cases are rare. That is, comparing the P value with the significance level (e.g., 0.05) is equivalent to focusing all on the boundary value of the CI while ignoring information on the extent (size) of the effect or difference (Joo et al., 1994 ).

As a result of using CIs to re-interpret 71 clinical trial papers published with the conclusion that there was no effect based on the NHST and P value, Freiman et al. ( 1978 ) reported that the results of many studies were misinterpreted and that there were actually effects.

Effect size

CIs provide some information about the magnitude of effects that NHST and P value do not, but they only provide a range of possibilities.

Effect size refers to the difference in standardized scores between groups, i.e., the size of the difference when testing for differences between groups. For example, if the test scores in each subject increased by an average of 30 points (based on 100 points) through a series of programs, the absolute effect size would be 30 points or 30%. Absolute effect sizes are useful when variables are numerical values that have intrinsic meaning (such as sleep time) while the calculated effect size, such as Cohen's d, is used for numerical values that have no intrinsic meaning, such as the Likert scale (Sullivan and Feinn, 2012 ). The calculated effect size is commonly used in meta-analysis as it enables the comparison of statistical results by solving the difficulty of comparison due to inconsistency in measurement units or using other measurement methods (Kim, 2011 ; Lee, 2016 ).

The process of obtaining the effect size index calculated to confirm the difference in the effect between two independent groups (control group and experimental group, etc.) is simple and has the advantage of leading to a more direct interpretation of results. Several types of effect size indices exist, and are mentioned in Table ​ Table1 1 (Lee, 2016 ; Sullivan and Feinn, 2012 ).

Effect size indices

Adapted from Sullivan and Feinn ( 2012 )

The formula for calculating the d value, which is a representative effect size index, is as follows.

( X i ¯ , s pooled ; mean of group I, pooled sample variance at equal variance assumption)

According to the criteria proposed by Cohen ( 1988 ), a d value of 0.2 is considered a small effect size, a value of 0.5 is considered a medium effect size, and a value of 0.8 is considered a large effect size; however, just as significance level criterion P value of 0.05 is a value proposed by Fisher for reference, this value should not be interpreted as an absolute value. Cohen's d = 0.5 means that the mean score of the experimental group is 0.5 SD (standard deviation) higher than the mean score of the control group, which means that about 69% of the control group (standard normal cumulative distribution function value 0.5) is lower than the mean score of the experimental group (Kim, 2015 ).

A typical example of using an effect size is the following. When aspirin was administered to prevent myocardial infarction to 22,000 subjects for 5 years, a statistically significant result of P  < 0.00001 was found. Based on this, aspirin was recommended for the prevention of myocardial infarction. However, the effect size of this study was very small, and further studies showed much smaller effects, so the recommendation for aspirin use was revised (Bartolucci et al., 2011 ). In addition, using the effect size can save us from the dichotomous conclusion resulting from the use of NHST and P value; it is also independent of the sample size (Sullivan and Feinn, 2012 ).

In the paper titled Concept and application of effect size, Kim ( 2011 ) asserted that attention should be paid not only to statistical significance but also to practical effect (usefulness), as the calculated effect size, Cohen’s d, ranged between 0.40 and 0.72 for the studies that did not have statistically significant results because the P value slightly deviated from 0.05 (0.055 to 0.066).

Despite these various advantages, there are criticisms that another effect not related to the effect size can be ignored by oversimplifying the interpretation of Cohen's d. For example, if there is a drug that is inexpensive and safe, although the effect size is small for curing the patient's disease, the effect size for the patient may be small in the medical aspect, but the effect in terms of economic and social aspect is not so small (McGough and Faraone, 2009 ).

Bayesian statistics

Whereas the aforementioned frequentist statistics of Fisher and Neyman–Pearson are a method of estimating fixed-value parameters based on the statistical distribution of a repeated sample, Bayesian statistics is a method of estimating parameters based on the posterior probability that combines the priori probability of parameters with new data (sample) after assuming that the parameter has a probability distribution (prior probability). Therefore, sequential inference is possible, and it is similar to the human thought-judgment process. In other words, the strength of Bayesian statistics is that the previous research data (prior probability) and new research data are placed on a continuous flow line without distinction, therefore are updated (posterior probability) in response to new data in real time; as the data accumulates, the estimation becomes more accurate. In addition, Bayesian statistics have the advantage of being able to make estimates in various environments as there is no null or alternative hypotheses; they provide reliable results even when the sample size is small, do not require a significance level, and do not depend on the limits of assumption of multivariate normality and assumption of equal variance. On the other hand, since prior probabilities are used, the subjectivity of the researcher may be involved and there is the disadvantage of using very complex mathematics; however, these shortcomings can be overcome by using uninformative prior probability or by the development of computer calculation functions (Kim et al., 2016 ; Lee, 2013 ; Noh et al., 2014 ).

By overcoming these limitations, Bayesian statistics are being used in various fields such as IT business for estimating the behavior or search form of Internet consumers, imaging for noise removal, diagnosis through prediction in the medical field, analysis and prediction of surveys and agricultural production, and climate factor analysis. In addition, as the basic study of deep learning model, it is gaining popularity (Kim et al., 2016 ; Nurminen and Mutanen, 1987 ; Wang and Campbell, 2013 ).

Nevertheless, Bayesian statistics is a completely different concept from the existing frequentist statistics, and it is not easy to understand and utilize it for researchers in the food field who do not have a deep academic depth in the statistics.

A typical example of using Bayesian statistics is a case related to COVID-19. It involves calculating the probability of a person who tested positive on a diagnostic kit actually being infected with the disease. The core of the kit is sensitivity and specificity, where sensitivity is “the probability that the diagnostic kit will determine that an infected person has the infection (positive)”, and specificity is “the probability that a person who is not infected will be determined as not infected (negative)”.

Assuming a prevalence rate of (the number of patients with a specific disease/total population) 50% for COVID-19, and sensitivity of 99% and specificity of 90% for the test kit, the probability of actually having the disease when the test result is positive is calculated as follows (Lee, 2013 ).

Here, P(disease│positive) is the probability of having the disease, given a positive test, (corresponds to the “posterior probability” of the disease), P(positive│disease) is sensitivity (“referred to as likelihood”), P(disease) is the probability of having the disease (corresponds to the “prior probability” of the disease, referred to as prevalence), P(positive) is the probability of testing positive, (“marginal probability”). This expression is Bayes’ theorem in Bayesian statistics.

P(positive) can be expressed as the sum of P(positive│D) × P(D), i.e., the probability of true positive and P(positive│not D) × P(not D), i.e., the probability of false positive.

Here, P(positive│not D) is the probability that a healthy person may test positive, referred to as false positive, and is calculated as ‘1- specificity’; P(not D) is the probability of being healthy and is calculated as ‘1-prevalence’.

If the test result came out to be positive using this formula, P(D│positive) = 0.99 × 0.5/((0.99 × 0.5) + (0.1 × 0.5)) = 0.908, i.e., 90.8% is the probability of actually having COVID-19.

Unlike the calculated value of 90.8%, many may think that the probability of actually having the disease to be 99%, but this is the result of confusing the sensitivity of the kit (P(positive│D)) with the probability of actually having the disease (P(D│positive)) when test result is positive. The posterior probability, P(D│positive) is directly and decisively influenced by the prior probability, P(D), so if it is assumed that the prevalence is low (P(disease) = 10%), the probability of actually having the disease may drop significantly (52.4%) even when the positive result is obtained using the diagnostic kit having the same sensitivity (99%) and specificity (90%).

In Bayesian statistics, various statistical analysis programs such as SPSS and JAMOVI can still be used to perform common statistical analyses like correlation, regression, and ANOVA.

Bayesian statistics can express both subjective concepts, such as “approximately,” and objective concepts, such as “numerical values,” which can be advantageous for statistical estimation in fields related to food, such as sensory science, that encompass many social scientific aspects.

In recent years, food research has increasingly utilized large datasets. Bayesian statistics, as a fusion of artificial intelligence and statistics, is one of the techniques that can solve the problem of time-consuming and difficult to manage classical (frequentist) statistical analysis. Due to its advantages, Bayesian statistics is widely used in a variety of fields. However, it has only recently made its presence felt in the food industry (Van Boekel, 2004 ).

Initially, modeling with Bayesian statistics was primarily focused on microbial risk assessment in food production, using structured and simple models that added new information in an organized manner (Barker et al., 2002 ). Bayesian statistics is also used in kinetics to understand food reactions and influence product and process design. Bayesian statistics has the benefit of being easy to interpret and can be applied to a wide variety of complex models with varying degrees of complexity (Van Boekel, 2020 ).

Bayesian statistics can be applied in various ways to the food industry. It can estimate the shelf life of food products by analyzing data on degradation and considering factors such as temperature, humidity, and pH (Calle et al., 2006 ; Luong et al., 2022 ). In sensory analysis, Bayesian statistics can evaluate food samples and estimate the distribution of sensory attributes in the population, helping food companies make informed decisions about product development (Calle et al., 2006 ). Bayesian statistics is also useful for assessing the risk of foodborne illness from microbial contamination (Oishi et al., 2021 ). By incorporating uncertainty, Bayesian statistics can provide more accurate estimates and predictions in all these applications. Overall, Bayesian statistics is a powerful tool for food scientists to draw more reliable conclusions and make more accurate predictions in their studies.

To summarize, the contents are as follows. Although the statistical testing method of determining statistically significant differences by comparing significance level (α) and probability (P) based on the NHST has been commonly used in food research, problems with this testing method have been identified, and some social science journals even banned the use of the NHST method in 2015. Given the limitations of NHST and P -value, several alternative methods have been proposed, including lowering the P -value threshold and utilizing measures such as CI, effect size, and Bayesian statistics. Lowering the threshold for P -value to 0.005, increases the probability that the alternative hypothesis is true by about 6.8 times compared to when the P -value is 0.05, while reducing the ratio of false positives by approximately 6.6 times (33% → 5%). The CI is another alternative, that provides information about the extent of effect or difference and the presence or absence of statistical significance unlike the P -value, which only determines the statistical significance of an effect or difference. The third alternative is the use of effect size. Using an effect size index such as Cohen's d can distinguish the extent of effect difference and enables the comparison of various statistical results by solving the difficulty in comparison due to the inconsistency of measurement units and the use of different measurement methods. Lastly, Bayesian statistics can be used. Bayesian statistics can express the subjective concept of “approximately” as an objective concept of “numerical value”, which can be useful for statistical estimation in the food field, such as sensory science, which involves many social scientific aspects. Additionally, Bayesian statistics can be updated in real time by incorporating new data into the previous research data (prior probability), resulting in increasingly accurate as more data is accumulated.

In conclusion, dichotomous statistical analysis using NHST and P -values in food research is problematic. As a complement or alternative, it is worth considering a gradual transition to using relatively simple statistical concepts such as CI and effect size, which can provide more information about your results compared to dichotomous statistical analysis using NHST and P -values. Additionally, although Bayesian statistics are more complex, it can also be a valuable alternative to consider.

This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (Grant Number NRF-2018R1D1A1B07048619).

Declarations

The author declare no conflict of interest.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

• Bailar JC, Mosteller F. Guideline for statistical reporting in articles for medical journals. Annals of Internal Medicine. 1988; 108 :266–273. doi: 10.7326/0003-4819-108-2-266. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Bandit CL, Boen JR. A prevalent misconception about sample size, statistical significance and clinical importance. Journal of Periodontology. 1972; 43 :181–183. doi: 10.1902/jop.1972.43.3.181. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Barker GC, Talbot NLC, Peck MW. Risk assessment for Clostridium botulinum : A network approach. International Biodeterioration and Biodegradation. 2002; 50 :167–175. doi: 10.1016/S0964-8305(02)00083-5. [ CrossRef ] [ Google Scholar ]
• Bartolucci AA, Tendera M, Howard G. Meta-analysis of multiple primary prevention trials of cardiovascular events using aspirin. American Journal of Cardiology. 2011; 107 :1796–1801. doi: 10.1016/j.amjcard.2011.02.325. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Benjamin DJ, Berger JO, Johannesson M, Nosek BA, Wagenmakers EJ, Berk R, Bollen KA, Brembs B, Brown L, Camerer C, Cesarini D, et al. Redefine statistical significance. Nature Human Behaviour. 2018; 2 :6–10. doi: 10.1038/s41562-017-0189-z. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Bouton PE, Harris PV, Shorthose WR. Changes in shear parameters of meat associated with structural changes produced by aging, cooking and myofibrillar contraction. Journal of Food Science. 1975; 40 :1122–1126. doi: 10.1111/j.1365-2621.1975.tb01032.x. [ CrossRef ] [ Google Scholar ]
• Bruns SB, Ioannidis JPA. P-curve and p-hacking in observational research. PLoS ONE. 2016; 11 :1–13. doi: 10.1371/journal.pone.0149144. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Calle ML, Hough G, Curia A, Gomez G. Bayesian survival analysis modeling applied to sensory shelf life of foods. Food Quality and Preference. 2006; 17 :307–312. doi: 10.1016/j.foodqual.2005.03.012. [ CrossRef ] [ Google Scholar ]
• Carver R. The case against statistical significance testing. Harvard Educational Review. 1978; 48 :378–399. doi: 10.17763/haer.48.3.t490261645281841. [ CrossRef ] [ Google Scholar ]
• Choi SH, Han KS. Visual inspection of overlapping confidence intervals for comparison of normal population means. The Korean Journal of Applied Statistics. 2017; 30 :691–699. doi: 10.5351/KJAS.2017.30.5.691. [ CrossRef ] [ Google Scholar ]
• Chung SY, Kim SH, Kim HS, Cheong HS, Kim HJ, Kang JS. Effects of water soluble extract of Ganoderma lucidum , kale juice and sodium dextrothyroxine on hormone and lipid. Journal of Korean Society of Food and Nutrition. 1991; 20 :59–64. [ Google Scholar ]
• Cohen J. Statistical power analysis for the behavioral sciences. 2. Mahwah : Lawrence Erlbaum Associates Publishers; 1988. pp. 19–27. [ Google Scholar ]
• Cohen HW. P values: Use and misuse in medical literature. American Journal of Hypertension. 2011; 24 :18–23. doi: 10.1038/ajh.2010.205. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Edwards AWF. Likelihood: An account of the statistical concept of likelihood and its application to scientific inference. Cambridge: Cambridge University Press; 1972. pp. 8–23. [ Google Scholar ]
• Eheart MS, Sholes ML. Effects of methods of blanching, storage, and cooking on calcium, phosphorus, and ascorbic acid contents of dehydrated green beans. Journal of Food Science. 1945; 10 :342–350. doi: 10.1111/j.1365-2621.1945.tb16177.x. [ CrossRef ] [ Google Scholar ]
• Fanelli D. Negative results are disappearing from most disciplines and countries. Scientometrics. 2012; 90 :891–904. doi: 10.1007/s11192-011-0494-7. [ CrossRef ] [ Google Scholar ]
• Fisher RA. The design of experiments. 1. Edinburgh.: Oliver and Boyd; 1935. p. 252. [ Google Scholar ]
• Fisher RA. Statistical methods for research worker. 6. Edinburgh: Oliver and Boyd; 1936. pp. 125–128. [ Google Scholar ]
• Freiman JA, Chalmers TC, Smith HA, Kuebler RR. The importance of beta, the type II error and sample size in the design and interpretation of the randomized controlled trial: Survey of 71 “negative” trials. New England Journal of Medicine. 1978; 299 :690–694. doi: 10.1056/NEJM197809282991304. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Froning GW, Arnold RG, Mandigo RW, Neth CE, Hartung TE. Quality and storage stability of frankfurters containing 15% mechanically deboned turkey meat. Journal of Food Science. 1971; 36 :974–978. doi: 10.1111/j.1365-2621.1971.tb03324.x. [ CrossRef ] [ Google Scholar ]
• Gerber AS, Malhotra N. Publication bias in empirical sociological research: Do arbitrary significance levels distort published results? Sociological Methods & Research. 2008; 37 :3–30. doi: 10.1177/0049124108318973. [ CrossRef ] [ Google Scholar ]
• Goodman SN. Toward evidence-based medical statistics. 1: The p value fallacy. Annals of Internal Medicine. 1999; 130 :995–1004. doi: 10.7326/0003-4819-130-12-199906150-00008. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Griswold RM, Wharton MA. Effect of storage conditions on palatability of beef. Journal of Food Science. 1941; 6 :517–528. doi: 10.1111/j.1365-2621.1941.tb16310.x. [ CrossRef ] [ Google Scholar ]
• Ioannidis JPA. Why most published research findings are false. PLoS Medicine. 2005; 2 :696–701. doi: 10.1371/journal.pmed.0020124. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Ioannidis JPA. The proposal to lower p value thresholds to 0.005. Journal of the American Medical Association. 2018; 319 :1429–1430. doi: 10.1001/jama.2018.1536. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Joo JS, Kim DH, Yoo KY. How should we present the result of statistical analysis? The meaning of p value. Annals of Surgical Treatment and Research. 1994; 46 :155–162. [ Google Scholar ]
• Kim MS. Quantitative methods in geography education research: Concept and application of effect size. The Journal of the Korean Association of Geographic and Environmental Education. 2011; 19 :205–220. doi: 10.17279/jkagee.2011.19.2.205. [ CrossRef ] [ Google Scholar ]
• Kim TK. T-test as a parametric statistic. Korean Journal of Anesthesiology. 2015; 68 :540–546. doi: 10.4097/kjae.2015.68.6.540. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Kim MJ, Lee CH. The effects of extracts from mugwort on the blood ethanol concentration and liver function. Korean Journal for Food Science Animal Resources. 1998; 18 :348–357. [ Google Scholar ]
• Kim MJ, Jeon MH, Sung KI, Kim YJ. Bayesian structural equation modeling for analysis of climate effect on whole crop barley yield. The Korean Journal of Applied Statistics. 2016; 29 :331–344. doi: 10.5351/KJAS.2016.29.2.331. [ CrossRef ] [ Google Scholar ]
• Langman MJ. Toward estimation and confidence intervals. British Medical Journal. 1986; 292 :716. doi: 10.1136/bmj.292.6522.716. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lee KH. Review on problems with null hypothesis significance testing in dental research and its alternatives. Journal of Korean Academy of Pediatric Dentistry. 2013; 40 :223–232. doi: 10.5933/JKAPD.2013.40.3.223. [ CrossRef ] [ Google Scholar ]
• Lee DK. Alternatives to a p value: Confidence interval and effect size. Korean Journal of Anesthesiology. 2016; 69 :555–562. doi: 10.4097/kjae.2016.69.6.555. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lin M, Lucas HC, Shmueli G. Too big to fail: Large samples and the p value problem. Information Systems Research. 2013; 24 :906–917. doi: 10.1287/isre.2013.0480. [ CrossRef ] [ Google Scholar ]
• Luong N-DM, Coroller L, Zagorec M, Moriceau N, Anthoine V, Guillou S, Membre J-M. A Bayesian approach to describe and simulate the pH evolution of fresh meat products depending on the preservation conditions. Foods. 2022; 11 :1114. doi: 10.3390/foods11081114. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• McGough JJ, Faraone SV. Estimating the size of treatment effects: Moving beyond p values. Psychiatry (Edgmont). 2009; 6 :21–29. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• McShane BB, Gal D. Statistical significance and the dichotomization of evidence. Journal of American Statistical Association. 2017; 112 :885–895. doi: 10.1080/01621459.2017.1289846. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Nickerson RS. Null hypothesis statistical testing: A review of an old and continuing controversy. Psychological Methods. 2000; 5 :241–331. doi: 10.1037/1082-989X.5.2.241. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Noh HS, Park JS, Sim GS, Yu JE, Chung YS. Nonparametric Bayesian statistical model in biomedical research. The Korean Journal of Applied Statistics. 2014; 27 :867–889. doi: 10.5351/KJAS.2014.27.6.867. [ CrossRef ] [ Google Scholar ]
• Norman G. Statistics 101. Advances in Health Sciences Education. 2019; 24 :637–642. doi: 10.1007/s10459-019-09915-3. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Nurminen M, Mutanen P. Exact Bayesian analysis of two proportions. Scandinavian Journal Statistics, Theory and Applications. 1987; 14 :67–77. [ Google Scholar ]
• Oishi W, Kadoya S-S, Nishimura O, Rose JB, Sano D. Hierarchical Bayesian modeling for predictive environmental microbiology toward a safe use of human excreta. Journal of Environmental Management. 2021; 284 :112088. doi: 10.1016/j.jenvman.2021.112088. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Perezgonzalez JD. Fisher, Neyman–Pearson or NHST? A tutorial for teaching data testing. Frontiers Psychology. 2015; 6 :1–11. doi: 10.3389/fpsyg.2015.00223. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• PLOS MEDICINE. Why most published research findings are false. https://journals.plos.org/plosmedicine/article?id=https://doi.org/10.1371/journal.pmed.0020124 Accessed 09 Mar 2023
• Plucker JA, Makel MC. Replication is important for educational psychology: Recent developments and key issues. Journal of Educational Psychology. 2021; 56 :90–100. doi: 10.1080/00461520.2021.1895796. [ CrossRef ] [ Google Scholar ]
• Reddy SG, Henrickson RL, Olson HC. The influence of lactic cultures on ground beef quality. Journal of Food Science. 1970; 35 :787–791. doi: 10.1111/j.1365-2621.1970.tb01995.x. [ CrossRef ] [ Google Scholar ]
• Ronald LW, Nicole AL. The ASA statement on p-values: context, process, and purpose. The American Statistician. 2016; 70 :129–133. doi: 10.1080/00031305.2016.1154108. [ CrossRef ] [ Google Scholar ]
• Sellke T, Bayarri MJ, Berger JO. Calibration of p values for testing precise null hypotheses. The American Statistician. 2001; 55 :62–71. doi: 10.1198/000313001300339950. [ CrossRef ] [ Google Scholar ]
• Shin DH, Choi U, Lee HY. Yukwa quality on mixing of non-waxy rice to waxy rice. Korean Journal of Food Science and Technology. 1991; 23 :619–621. [ Google Scholar ]
• Simonsohn U, Nelson LD, Simmons JP. P-curve: A key to the file-draw. Journal of Experimental Psychology. 2014; 143 :534–547. doi: 10.1037/a0033242. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• So YS. Selection and interpretation of standard deviation, standard error and confidence interval in the data analysis of crop breeding research. Korean Journal of Breeding Science. 2016; 48 :102–110. doi: 10.9787/KJBS.2016.48.2.102. [ CrossRef ] [ Google Scholar ]
• Sullivan GM, Feinn R. Using effect size or why the p value is not enough. Journal of Graduate Medical Education. 2012; 4 :279–282. doi: 10.4300/JGME-D-12-00156.1. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Trafimow D, Marks M. Editorial in basic and applied social psychology. Basic and Applied Social Psychology. 2015; 37 :1–2. doi: 10.1080/01973533.2015.1012991. [ CrossRef ] [ Google Scholar ]
• Trafimow D, Rice S. A test of the null hypothesis significance testing procedure correlation argument. Journal of General Psychology. 2009; 136 :261–270. doi: 10.3200/GENP.136.3.261-270. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Van Boekel MAJS. Bayesian solutions for food-science problems?: Bayesian statistics and quality modelling in the agro-food production chain. Dordrecht: Kluwer Academic Publishers; 2004. pp. 17–27. [ Google Scholar ]
• Van Boekel MAJS. On the pros and cons of Bayesian kinetic modeling in food science. Trends in Food Science & Technology. 2020; 99 :181–193. doi: 10.1016/j.tifs.2020.02.027. [ CrossRef ] [ Google Scholar ]
• Verdam MG, Oort FJ, Sparangers MA. Significance, truth and proof of p value: Reminders about common misconceptions regarding null hypothesis significance testing. Quality of Life Research. 2014; 23 :5–7. doi: 10.1007/s11136-013-0437-2. [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wang S, Campbell B. Mr. Bayes Goes to Washington. Science. 2013; 339 :758–759. doi: 10.1126/science.1232290. [ CrossRef ] [ Google Scholar ]
• Wasserstein RL, Schirm AL, Lazar NA. Moving to a world beyond “p<0.05” The American Statistician. 2019; 73 :1–19. doi: 10.1080/00031305.2019.1583913. [ CrossRef ] [ Google Scholar ]
• Yeo SS. Innovation on quantitative research in education: Beyond “null hypothesis” and “p value” Education Review. 2021; 48 :270–296. [ Google Scholar ]