- Texas Go Math
- Big Ideas Math
- Engageny Math
- McGraw Hill My Math
- enVision Math
- 180 Days of Math
- Math in Focus Answer Key
- Math Expressions Answer Key
- Privacy Policy

McGraw Hill My Math Grade 5 Chapter 1 Lesson 9 Answer Key Problem-Solving Investigation: Use the Four-Step Plan
All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 1 Lesson 9 Problem-Solving Investigation: Use the Four-Step Plan will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 1 Lesson 9 Problem-Solving Investigation: Use the Four-Step Plan
1. Understand
What facts do you know?

2. Plan To solve this problem, I can work backwards.
3. Solve The smallest size is ___ centimeter. Victor spent 2 × ___ or ____. Subtract to find the remaining amount spent: $61 – ___ = ____ The largest size is 0.011 centimeter. Each package costs $7. Victor bought $21 ÷ $7, or ___ packages of the largest grain sandpaper.
4. Check Does your answer make sense? Explain.
What facts do you know? ________________ ________________
What do you need to find? ________________
2. Plan ________________ ________________
4. Check Is your answer reasonable ? Explain. ________________
Apply the Strategy
Solve each problem using the four-step plan.
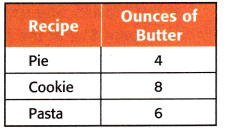
Question 3. Mathematical PRACTICE Keep Trying You divide a number by 3, add 6, and then subtract 7. The result ¡s 4. What is the number? Answer: Let the number be ‘n’ Now divide the number(n) by 3. n/3 + 6 – 7 = 4 Now solve the equation. n/3 – 1 = 4 n – 3/3 = 4 n – 3 = 12 n = 12 + 3 n = 15 Now substitute n value in the equation. 15 – 3 = 12 12 = 12 LHS = RHS
Question 4. Mr Toshio lent out 11 rulers at the beginning of class, collected 4 rulers in the middle of class, and gave out 7 at the end of class. He had 18 at the end of the day. How many rulers did he start with? Answer: The number of rulers Mr Toshio lent out at the beginning of the class is 11 The number of rulers Mr Toshio collected in the middle of class = 4 The number of rulers he gave out at the end of the class = 7 The number of rulers he had at the end of the day was 18 The number of rulers he had at the beginning = X X = (11 – 4) + 18 + 7 X = 7 + 18 + 7 X = 32 Therefore, he started with 32 rulers.

Review the Strategies
Use any strategy to solve each problem.
- Use the four-step plan.
- Make a table.
- Act it out.
Question 6. Mathematical PRACTICE Make a Plan Ming-Li spent $15 at the movies. She then earned $30 babysitting. She spent $12 at the bookstore. She now has $18 left. How much money did Ming-Li have to begin with? Answer: The amount she spent on movies = $15 The amount she earned on babysitting = $30 The amount she spent at the bookstore = $12 The amount she has left = $18 The amount she has to begin with = X X – 15 + 30 – 12 = 18 X – 15 + 18 = 18 After solving the equation, we get 18 gets cancelled. X – 15 = 0 X = 15 Therefore, the money she begin with $15.
Question 7. Mr. Jenkins bought payers for some landscaping projects. He used 120 for a small patio, 86 for the border of a flower bed, and 70 for a wall. He has 24 payers left. How many payers did Mr. Jenkins buy? Answer: The number of payers he used for the small patio = 120 The number of payers he used for the flower bed = 86 The number of payers he used for the wall = 70 The number of payers left = 24 The number of payers he buys = X X = 120 + 86 + 70 + 24 X = 300 Therefore, he bought 300 payers.
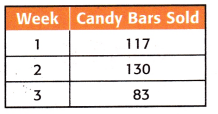
Question 9. You multiply a number by 3, subtract 6 and then add 2. The result is 20. What is the number? Answer: Let the number be n 3n – 6 + 2 = 20 Solve the equation. 3n – 4 = 20 3n = 20 + 4 3n = 24 n = 24/3 n = 8

McGraw Hill My Math Grade 5 Chapter 1 Lesson 9 My Homework Answer Key
Problem Solving
Question 2. The volleyball team sold 16 items on the first day of a bake sale, 28 items on the second day, and 12 items on the last day. There were 4 items left that had not been purchased. How many total items were for sale at the bake sale? Answer: The number of items sold by the Volleyball team on the first day = 16 The number of items sold by the Volleyball team on the second day = 28 The number of items sold by the Volleyball team on the third day = 12 The number of items left that are not purchased = 4 The number of total items = x x = add all the items to get the total x = 16 + 28 + 12 + 4 x = 60 Therefore, the total items are 60.

Question 4. The distance between Cincinnati, Ohio, and Charlotte, North Carolina, is about 336 miles. The distance between Cincinnati and Chicago, Illinois, is about 247 miles. If Perry drove from Charlotte to Chicago by way of Cincinnati, find the distance he drove. Answer: Cincinnati, Ohio, and Charlotte, North Carolina all are considered as x1 Cincinnati and Chicago, Illinois are considered as x2 The distance between the cities(x1) = 336 The distance between the cities(x2) = 247 The distance we need to find out for Charlotte to Chicago by way of Cincinnati = D D = 336 – 247 D = 89 Therefore, the distance he dove is 89 miles.
Question 5. Mathematical PRACTICE Plan Your Solution Adison earned $25 mowing her neighbor’s lawn. Then she loaned her friend $18, and got $50 from her grandmother for her birthday. She now has $86. How much money did Adison have to begin with? Answer: Let x be the beginning amount of money The amount earned by Addison by mowing her neighbour’s lawn = $25 The amount she loaned from her friend = $18 The amount she got a birthday gift from her grandmother = $50 the amount she has present = $86 the expression to solve this question is x + 25 – 18 + 50 = 86 x + 75 – 18 = 86 x + 57 = 86 x = 86 – 57 x = 29 Therefore, the beginning amount of money is $29
Leave a Comment Cancel Reply
You must be logged in to post a comment.

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

2.3.1: George Polya's Four Step Problem Solving Process
- Last updated
- Save as PDF
- Page ID 90483
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Step 1: Understand the Problem
- Do you understand all the words?
- Can you restate the problem in your own words?
- Do you know what is given?
- Do you know what the goal is?
- Is there enough information?
- Is there extraneous information?
- Is this problem similar to another problem you have solved?
Step 2: Devise a Plan: Below are some strategies one might use to solve a problem. Can one (or more) of the following strategies be used? (A strategy is defined as an artful means to an end.)
- A. Robison Elementary
- Adam Elementary School
- Andre' Elementary School
- Anthony Middle School
- Aragon Middle School
- Arnold Middle School
- Ault Elementary School
- Bane Elementary School
- Bang Elementary School
- Birkes Elementary School
- Black Elementary School
- Bleyl Middle School
- Byrd Elementary
- Brautigam Center
- Bridgeland High School
- Brosnahan Elementary School
- Campbell Middle School
- Carlton Center
- Carpenter Center
- Cook Middle School
- Copeland Elementary
- Cy-Fair High School
- Cypress Creek High School
- Cypress Falls High School
- Cypress Lakes High School
- Cypress Park High School
- Cypress Ranch High School
- Cypress Ridge High School
- Cypress Springs High School
- Cypress Woods High School
- Danish Elementary School
- Dean Middle School
- Duryea Elementary School
- Emery Elementary School
- Emmott Elementary School
- Farney Elementary School
- Fiest Elementary School
- Francone Elementary School
- Frazier Elementary School
- Gleason Elementary School
- Goodson Middle School
- Hairgrove Elementary School
- Hamilton Elementary School
- Hamilton Middle School
- Hancock Elementary School
- Hemmenway Elementary School
- Holbrook Elementary School
- Holmsley Elementary School
- Hoover Elementary (PK-2) School
- Hopper Middle School
- Horne Elementary School
- Jersey Village High School
- Jowell Elementary (3-5) School
- Kahla Middle School
- Keith Elementary School
- Kirk Elementary School
- Labay Middle School
- Lamkin Elementary School
- Langham Creek High School
- Lee Elementary School
- Lieder Elementary School
- Lowery Elementary School
- M. Robinson Elementary School
- Matzke Elementary School
- McFee Elementary
- McGown Elementary School
- Metcalf Elementary School
- Millsap Elementary School
- Moore Elementary School
- Owens Elementary School
- Pope Elementary School
- Post Elementary School
- Postma Elementary School
- Reed Elementary School
- Rennell Elementary School
- Rowe Middle School
- Salyards Middle School
- Sampson Elementary School
- Sheridan Elementary School
- Smith Middle School
- Spillane Middle School
- Sprague Middle School
- Swenke Elementary School
- Thornton Middle School
- Tipps Elementary School
- Truitt Middle School
- Walker Elementary School
- Warner Elementary School
- Watkins Middle School
- Wells Elementary School
- Willbern Elementary School
- Wilson Elementary School
- Woodard Elementary School
- Yeager Elementary School

THE FOUR-STEP PROBLEM SOLVING PLAN
Overview of “Four-Step Problem Solving”
The “Four-Step Problem Solving” plan helps elementary math students to employ sound reasoning and to develop mathematical language while they complete a four-step problem-solving process. This problem-solving plan consists of four steps: details, main idea, strategy, and how. As students work through each step, they may use “graphic representations” to organize their ideas, to provide evidence of their mathematical thinking, and to show their strategy for arriving at a solution.
In this step, the student is a reader, a thinker, and an analyzer. First, the student reads over the problem and finds any proper nouns (capitalized words). If unusual names of people or places cause confusion, the student may substitute a familiar name and see if the question now makes sense. It may help the student to re-read the problem, summarize the problem, or visualize what is happening. When the student identifies the main idea, he or she should write it down, using words or phrases; that is, complete sentences are unnecessary. Students need to ask themselves questions such as the ones shown below.
- “What is the main idea in the question of this problem?”
- “What are we looking for?”
- “What do we want to find out?”
The student reads the problem again, sentence by sentence, slowly and carefully. The student identifies and records any details, using numbers, words, and phrases. The student looks for extra information—that is, facts in the reading that do not figure into the answer. In this step, the student should also look for hidden numbers, which may be indicated but not clearly expressed. (Example: The problem may refer to “Frank and his three friends.” In solving the problem, the student needs to understand that there are actually four people, even though “four” or “4” is not mentioned in the reading.) Students ask themselves the following kinds of questions.
- “What are the details needed to answer the question?”
- “What are the important details?”
- “What is going on that can help me answer the question?”
- “What details do I need?”
The student chooses a math strategy (or strategies) to find a solution to the problem and uses that strategy to find the answer/solve the problem. Possible strategies, as outlined in the Texas Essential Knowledge and Skills (TEKS) curriculum, include the following.
- use or draw a picture
- look for a pattern
- write a number sentence
- use actions (operations) such as add, subtract, multiply, divide
- make or use a table
- make or use a list
- work a simpler problem
- work backwards to solve a problem
- act out the situation
The preceding list is just a sampling of the strategies used in elementary mathematics. There are many strategies that students can employ related to questions such as the following.
- “What am I going to do to solve this problem?”
- “What is my strategy?”
- “What can I do with the details to get the answer?”
To make sure that their answer is reasonable and that they understand the process clearly, students use words or phrases to describe how they solved the problem. Students may ask themselves questions such as the following.
- “How did I solve the problem?”
- “What strategy did I use?”
- “What were my steps?”
In this step, students must explain the solution strategy they have selected. They must provide reasons for and offer proof of the soundness of their strategy. This step gives students the opportunity to communicate their understanding of math concepts and math vocabulary represented in the problem they solved and to justify their thinking.
Responses on these four parts need not be lengthy—a list of words and numbers might be used for the details, and phrases might be used for the “Main Idea” and “How.”
Benefits of Using “Four-Step Problem Solving Plan”
One of the method's major benefits to students is that it forces them to operate at high levels of thinking. Teachers, using the tried-and-true Bloom’s Taxonomy to describe levels of thinking, want to take students beyond the lower levels and help them reach the upper levels of thinking. Doing the multiple step method requires students to record their thinking about three steps in the process, in addition to actually "working the problem."
A second benefit of extending the process from three steps to four is that having students think at these levels will deepen their understanding of mathematics and improve their fluency in using math language. In the short term, students' performance on assessments will improve, and confidence in their mathematical ability will grow. In the long term, this rigor in elementary school mathematics will prepare students for increased rigor in secondary mathematics, beginning particularly in grade 7.
Another benefit of using “Four-Step Problem Solving” is that it will increase teachers’ ability to identify specific problems students are having and provide them with information to give specific corrective feedback to students.
Extracting and writing the main idea and details and then showing the strategies to solve problems should also help students establish good test-taking habits for online testing.
Educational Research Supporting “Four-Step Problem Solving”
Although scholarly articles do not mention “Four-Step Problem Solving” by name, most educational experts do advocate the use of multi-step problem-solving methods that foster students’ performing at complex levels of thinking. The number of steps often ranges from four to eight.
Conclusions drawn from studying the work of meta-researcher Dr. Robert Marzano published in the book Classroom Instruction That Works (Marzano, Pickering, Pollock) as well as numerous other research studies, indicate that significant improvement in student achievement occurs when teachers use these strategies.
The National Council of Teachers of Mathematics endorses the use of such strategies as those appearing in “Four-Step Problem Solving”—particularly the step requiring students to explain their answers—as effective for producing students’ math competency, as described in NCTM publications such as Principles and Standards for School Mathematics. Excerpts from NCTM documents validate the district's problem-solving strategy. Some of the key ideas and teaching standards identified include the following.
- Teachers need to investigate how their students arrive at answers. Correct answers don't necessarily equate to correct thinking.
- Students need to explore various ways to think about math problems and their solutions.
- Students need to learn to analyze and solve problems on their own.
- Students' discourse in a mathematics classroom should focus on their thinking process as they solved a problem.
Relationship of “Four-Step Problem Solving” and the TEKS
Although the TEKS for elementary math do not mention a graphic organizer for problem-solving, they do require that students in grades 1-5 learn and do the following things in the area of “Underlying Processes and Mathematical Tools.”
- The student applies mathematics to solve problems connected to everyday experiences and activities in and outside of school.
- Identify the mathematics in everyday situations.
- Solve problems that incorporate understanding the problem, making a plan, carrying out the plan, and evaluating the solution for reasonableness.
- Select or develop an appropriate problem-solving plan or strategy, including drawing a picture, looking for a pattern, systematic guessing and checking, acting it out, making a table, working a simpler problem, or working backwards to solve a problem.
- Use tools such as real objects, manipulatives, and technology to solve problems.
- The student communicates about mathematics using informal language.
- Explain and record observations using objects, words, pictures, numbers, and technology.
- Relate informal language to mathematical language and symbols.
- The student uses logical reasoning to make sense of his or her world.
- Make generalizations from patterns or sets of examples and nonexamples.
- Justify why an answer is reasonable and explain the solution process.
Instructional Methods Behind “Four-Step Problem Solving”
Teachers will use a variety of techniques as they instruct students regarding “Four-Step Problem Solving.” They will
- model use of the “Four-Step Problem Solving Plan” with graphic representations as they guide students through the four-step problem-solving process;
- use a think-aloud method to share their reasoning with students;
- employ questioning strategies that provoke students to higher levels of thinking; and
- foster rich dialogue, both in whole-class discussions and for partner/table activities.
For success with “Four-Step Problem Solving,” talking must occur prior to writing. Students will be shown how to bridge the span between math and language to express their reasoning in a way that uses logical sequences and proper math vocabulary terms. Once students have mastered the ability to communicate out loud with the teacher and with peers, they can transition to developing the skill of conducting an “internal dialogue” for solving problems independently.
Students Using “Four-Step Problem Solving”
Use of a common graphic organizer at all schools would greatly benefit our ever-shifting population of students—not only those whose families move often, but also those affected by boundary changes we continue to experience as we grow. District-wide staff development has focused on acquainting all elementary math teaching staff with “Four-Step Problem Solving,” and outlining expectations for students’ problem-solving knowledge and skills outlined in the TEKS at each grade-level.
Because it is the steps in the problem that are important, not the graphic representation itself, vertical math teams on each campus, working with the building principal, have the option of selecting or designing a graphic organizer, as long as it fulfills the four-step approach. Alternatives to “The Q” include a four-pane “window pane” or a simple list of the four steps. Another scheme adopted by some schools is being called SQ-RQ-CQ-HQ, which uses the old three steps plus a new fourth step—the “HQ” is the "how" step. Schools using SQ-RQ-CQ-HQ should consider how the advent of online testing will impact its use.
Putting “The Four-Step Problem Solving Plan” into Action
In class, students will use “Four-Step Problem Solving” in a variety of circumstances.
- Students will participate in whole-class discussion and completion of “Four-Step Problem Solving” pages as the teacher explains math problems to the group. To guide students through the steps, teachers may place a “Four-Step Problem Solving Organizer” transparency on the overhead, affix a “Four-Step Problem Solving Organizer” visual aid to the white board, use a “Four-Step Problem Solving Organizer” poster, or simply draw a “Four-Step Problem Solving Organizer” on the board to fill in the areas of the graphic organizer so that students observe how to solve the problems.
- Students will work in pairs to complete daily work with a partner using four-step problem solving. Having a partner allows the students to discuss aspects of the problem-solving process, a grouping arrangement which helps them develop the language skills needed for completing the steps of the problem-solving process.
- Students will complete assignments on their own using the four steps, allowing teachers to gauge their ability to master the steps needed to complete the problem-solving process.
Students can expect to see “Four-Step Problem Solving” used in all phases of math instruction, including assessments. Students will be given problems and asked to identify the main idea, details, and process used, as well as solve for a calculation.
The district’s expectation is that students will ultimately use “Four-Step Problem Solving” for all story problems, unless directed otherwise. When students clearly understand the process and concepts they are studying, teachers may choose to limit the writing of the “how.” Improved student achievement comes in classrooms that routinely and consistently use all four steps of the process.
Using this approach should reduce the number of problems students are assigned. Completing the “Four-Step Problem Solving” should take only a few minutes. As students become familiar with the graphic organizer, they will be able to increase the pace of their work. Students can save time by writing only the main idea (instead of copying the entire question) and by using words or phrases in describing the “how” (instead of complete sentences).
For years, researchers of results on the National Assessment of Educational Progress ( NAEP ) and the Trends in International Mathematics and Science Study ( TIMSS ) have cited curricular and instructional differences between U.S. schools and schools in countries that outperform us in mathematics. For example, Japanese students study fewer concepts and work fewer problems than American students do. In Japan , students spend their time in exploring multiple approaches to solving a problem, thereby deepening their understanding of mathematics. Depth of understanding is our goal for students, too, and we believe that the four-step problem-solving plan will help us achieve this goal.
The ultimate goal is that students learn to do the four steps without the use of a pre-printed form. This ability becomes necessary on assessments such as TAKS, since security rules prohibit the teacher from distributing any materials. In 2007, when students may first be expected to take TAKS online, students will need a plan for problem-solving on blank paper to ensure that they don’t just, randomly select an answer—they can’t underline and circle on the computer monitor’s glass.
Assessment and Grading with “The Four-Step Problem Solving Plan”
Assignments using “The Four-Step Problem Solving Plan” may include daily work, homework, quizzes, and tests (including district-developed benchmarks). CFISD’s grade-averaging software includes options for all these categories. As with other assignments, grades may be taken for individuals or for partners/groups. Experienced teachers are already familiar with all these grading scenarios.
Teachers may use a rubric for evaluating student work. The rubric describes expectations for students’ responses and guides teachers in giving feedback. Rubrics may be used in many subjects in school, especially for reviewing students’ written compositions in language arts.
A range of “partial credit” options is possible, depending on the teacher’s judgment regarding the student’s reasoning and thoroughness. Students may be asked to redo incomplete portions to earn back points. Each campus makes a decision about whether the process will be included in one grade or if process will be a separate grade.
Knowledge of students’ thinking will help the teacher to provide the feedback and/or the re-teaching that will get a struggling student back on track, or it will allow the teacher to identify students who have advanced understanding in mathematics so that their curriculum can be adjusted. Looking at students' work and giving feedback may require additional time because the teacher is examining each student's thought processes, not just checking for a correct numeric answer.
Because students’ success in communicating their understanding of a math concept does not require that they use formal language mechanics (complete sentences, perfect spelling, etc.) when completing “The Four-Step Problem Solving Plan,” the rubric does not address these skills, leading math teachers to focus and assign grades that represent the students’ mastery of math concepts.
- Questions or Feedback? |
- Web Community Manager Privacy Policy (Updated) |

- Share on Facebook
- Tweet This Resource
- Pin This Resource

Using a Four-Step Plan to Solve Problems
This using a four-step plan to solve problems lesson plan also includes:.
- Join to access all included materials
Students examine the four-step plan. For this current events lesson, students solve problems using the four-step plan of exploring, planning, solving, and examining.
Start Your Free Trial
Save time and discover engaging curriculum for your classroom. Reviewed and rated by trusted, credentialed teachers.
- Collection Types
- Activities & Projects
- Assessments
- Graphics & Images
- Handouts & References
- Interactives
- Lab Resources
- Learning Games
- Lesson Plans
- Presentations
- Primary Sources
- Printables & Templates
- Professional Documents
- Study Guides
- Instructional Videos
- Performance Tasks
- Graphic Organizers
- Writing Prompts
- Constructed Response Items
- AP Test Preps
- Lesson Planet Articles
- Online Courses
- Interactive Whiteboards
- Home Letters
- Unknown Types
- Stock Footages
- All Resource Types
See similar resources:
The notorious four-color problem, the four-color problem: concept and solution, exploring borderlands, the marshall plan: the vision of a family of nations, indigenous peoples’ day lesson plan, early history and exploration unit, loc: teaching with primary sources: hispanic exploration in america [pdf], island rotation: lesson plan 3, exploring "my market", lesson plan: montgomery bus boycott.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

79 Problem-Based Lesson Plan Template
Problem-based lesson plan template.
For additional information on Problem-based instruction, please visit our Teaching Strategies page of the MNSU Instructional Design Services . In order to implement a problem-based instruction lesson in your classroom, there are a few planning steps to consider. Fill in the blanks with your lesson-specific information in order to plan your problem-based lesson.
1. Develop clear and measurable learning objectives (including cognitive and behavioral objectives) – based on Bloom’s Taxonomy
- Students will be able to {verb} {noun}.
Ex: Students will demonstrate the methods of organismal biologists, including observation, phylogenetics, experimentation, and form/function studies.
2. Identify the learning resources students will need to access at home before coming to class. These resources are generally what you would normally do in a traditional lecture format class (lecture, videos, etc)
- Reading materials
- Watch instructional video xxx (name of the video) for xx minutes http://www …
- Exercise on worksheets, if any
- Suggest other learning resources
Ex: Before class on Thursday, please watch instructional video #1.
Learning Resources my lesson will include:
- __________________________________
Technology Resources I will need to create the pre-class learning resources:
3. Prepare the real-world, contextual problem that students will use to explore the content. You can either create a problem or select one from an existing problem bank. Follow the guidelines below for both selecting and creating a problem.
Garner’s (2010) suggested PBL problem elements:
- The topic of concern captures the attention and interest of participating students.
- Students are required to make judgments and decisions by analyzing a variety of options in choosing their best course of action.
- The proposed problem has a level of complexity that involves all team members in the data gathering and decision-making phases.
- Questions are open-ended and invite group members to participate.
- There is a direct connection between the PBL scenario and course learning outcomes.
Students should be able to answer the following four questions when working towards a problem solution:
- What do I know (about the problem or issue)
- What do I need to know to solve it?
- How do I get that information?
- How do I apply that information to determine a solution?
You can also use created problems from resources like the University of Delaware’s PBL Clearninghouse
My problem:
Ex: (From A Principles of Organismal Biology course)
200,000 people applied to be a part of the Mars colonization project. The 40 candidates that were selected have asked you, a biologist, to describe for them what plant or animal life might exist on Mars or what life might exist on Mars eventually through colonization, adaptation, and mutation. Based on your knowledge of Earth biology, what might a Mars plant or animal look like? How could you prepare the colonist for creatures or life they might encounter?
4. Define the procedures for in-Class problem analysis that your students will be completing. Let students know if they need to bring or prepare anything before class. The idea is to create an active learning environment where students interact with the content and the instructor acts as a guide. Activities should scaffold the students into the problem solution.
- Establish ground rules for participation
- Assign discussion groups or roles in the problem-solving process
- Students define facts and significant information surrounding the problem
- Pose challenging questions to further discussion
- Students define objectives and possible solutions
Activities students will complete analyzing the problem:
Technology Resources my students will need to complete the analysis:
Ex: Create a graphic organizer of your choice (graphic, infographic, flyer, blog, etc) that illustrates the lineages of life. Categorize them by one of the following: their biodiversity, anatomy, physiology, development, behavior, biogeography, fossil record, or ecology. Then hypothesize how the lineage might be extended to include extraterrestrial life and add those branches to your organizer.
5. Identify any post-analysis activities that your students will be completing.
- Shift context – students see problem or solution from another point of view
- Follow up discussion
- Shift time frame – “what’s next?”, “How could this situation be different?”
Activities students will complete post-analysis:
Technology Resources my students will need to complete the post-analysis activities:
Ex: Write a counterargument to your problem solution. Take the side of those who might not agree with your conclusions. What alternatives or arguments against your theories exist?
- Create the assessments that you will use for determining students’ mastery of the learning objectives.
- Formative/Summative
- Challenging questions
- Interactive quizzes
- Problem solution presentations
Ex: Using what you have learned in this class, present and describe a lifeform colonist might encounter in the Martian environment. Visuals, such as a drawing, would be useful to help the colonists identify possible lifeforms. Use the scientific method to present your lifeform hypothesis.
Assessment(s) I will use in my problem-based lesson:
Technology Resources my students will need to complete the assessment(s):
7. Verify that your assessments and activities align to the learning objectives. Do they allow your students to demonstrate that they have achieved the learning objectives?
Maverick Learning and Educational Applied Research Nexus Copyright © 2021 by Minnesota State University, Mankato is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License , except where otherwise noted.
Share This Book
4th Grade Resources - Use the four operations with whole numbers to solve problems.
Interpret a multiplication equation as a comparison, e.g., interpret 35 = 5 x 7 as a statement that 35 is 5 times as many as 7 and 7 times as many as 5. Represent verbal statements of multiplicative comparisons as multiplication equations.
Multiply or divide to solve word problems involving multiplicative comparison, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem, distinguishing multiplicative comparison from additive comparison.
Solve multistep word problems posed with whole numbers and having whole-number answers using the four operations, including problems in which remainders must be interpreted. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding.
Newest 4th Grade Resources - Use the four operations with whole numbers to solve problems.
(Click on a resource to see our full catalog)
Operator Arithmetic
Use the four operators to solve multi-step equations
Mixed matching
Match pairs of equivalent equations to score points

Balloon Pop Mixed Operators
Pop ballons with mixed operators from smallest to largest
Calculator Chaos
Use knowledge of operations to solve several math problems using a single set of numbers.

Rate and keep track of your favorite activities! Sign Up to Rate Activities!
Create an Account!
Please pick a grade, elementary school math games, middle school math games, elementary school videos, middle school videos, elementary school worksheets, middle school worksheets, elementary school activities, middle school activities.

Engage your students with effective distance learning resources. ACCESS RESOURCES>>
Solve two-step word problems using the four operations. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding. This standard is limited to problems posed with whole numbers and having whole-number answers; students should know how to perform operations in the conventional order when there are no parentheses to specify a particular order (Order of Operations).

IMAGES
VIDEO
COMMENTS
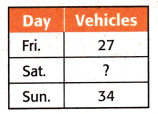
McGraw Hill My Math Grade 5 Chapter 1 Lesson 9 My Homework Answer Key. Problem Solving. Solve each problem using the four-step plan. Question 1. The table shows the number of vehicles washed at a car wash fundraiser over the weekend. If there were a total of 94 vehicles, how many were washed on Saturday? Answer: The above-given information:
Problem Solving Solve each problem using the four-step plan. 1. The table shows the number of vehicles washed at a car wash fundraiser over the weekend. If there were a total of 94 vehicles, how many were washed on Saturday? 2. The volleyball team sold 16 items on the first day of a bake sale, 28 items the second day, and 12 items the last day.
Lesson 9: Problem Solving Investigation: Use the Four Step Plan 1. Add and subtract whole numbers: word problems 2 Chapter 2. Multiply Whole Numbers ... Lesson 4: Problem Solving Investigation: Guess, Check, and Revise 1. Guess-and-check problems
Step 1: Understanding the problem. We are given in the problem that there are 25 chickens and cows. All together there are 76 feet. Chickens have 2 feet and cows have 4 feet. We are trying to determine how many cows and how many chickens Mr. Jones has on his farm. Step 2: Devise a plan.
Consider the problem-solving steps applied in the following example. I know that I want to say "I don't eat eggs" to my Mexican waiter. That's the problem. I don't know how to say that, but last night I told my date "No bebo alcohol" ("I don't drink alcohol"). I also know the infinitive for "eat" in Spanish (comer).
Step 2: Devise a Plan: Below are some strategies one might use to solve a problem. Can one (or more) of the following strategies be used? (A strategy is defined as an artful means to an end.) 1. Guess and test. 11. Solve an equivalent problem. 2. Use a variable.
This problem-solving plan consists of four steps: details, main idea, strategy, and how. As students work through each step, they may use "graphic representations" to organize their ideas, to provide evidence of their mathematical thinking, and to show their strategy for arriving at a solution. Main Idea. In this step, the student is a ...
Lesson 9: Problem Solving Investigation: Use the Four Step Plan 1.Add and subtract whole numbers: word problems JYY My Math - 5th grade ... Lesson 2: Estimate Sums and Differences 1.Estimate sums and differences of decimals using rounding YGG Lesson 3: Problem Solving Investigation: Estimate or Exact Answer 1.Compare, order, and round decimals ...
If not, solve the problem another way. FOUR-STEP PLAN FOR PROBLEM SOLVING The table shows the average number of meals and snacks children prepare for themselves each week. How many times per month does the average 11-year-old ... For use with Lesson 9 3-1 0 4 ones tenths 0 77 ones tenths hundredths
qacblogs.org
After discussing the four-step plan and completing an example as a class, Behavioral Verb SW solve word problems Criteria Using the four-step plan. 10. Criteria for student achievement of objective: Students use the four-step plan to solve word problems, and must successfully complete at least three problems during this lesson. 11.
The 4-Step Problem-Solving Process. This document is the third in a series intended to help school and district leaders maximize the effectiveness and fluidity of their multi-tiered system of supports (MTSS) across different learning environments. Specifically, the document is designed to support the use of problem solving to improve outcomes ...
Word Problem Practice A Plan for Problem Solving Use the four-step plan to solve each problem. SKATEBOARDING For Exercises 1 and 2, use the table at the right. It shows the results of a recent survey in which teenagers were asked who the best professional skateboarder is. Skater Votes Bob Burnquist 18 Danny Way 15 Bam Margera 11 Arto Saari 9 1.
Polya's four step method for problem solving is. 1) Understand the Problem-Make sure you understand what the question is asking and what information will be used to solve the problem. 2) Devise a ...
Lesson 6 Problem Solving: Use the Four-Step Plan Homework Helper A six-digit number has a 2 in the thousands place, a 5 in the tens place, a 3 in the hundred thousands place, and zeros in each of the remaining places. What is the number? Use the four-step plan to solve this problem. Understand I know that there is a number with six digits.
Solve problems involving the four operations, and identify and explain patterns in arithmetic. 3.OA.D.8. Fully covered. Solve two-step word problems using the four operations. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation ...
Lesson Plans the four steps of problem solving subject teacher grade mat150 kendal tucker 00 date overview students are to solve word problems using the four. ... LESSON I will explain what the four steps in the problem-solving process are and the reason why each step is important. I will use the dry erase board to discuss and brainstorm with ...
This Using a Four-Step Plan to Solve Problems Lesson Plan is suitable for 9th - 10th Grade. Students examine the four-step plan. In this current events instructional activity, students solve problems using the four-step plan of exploring, planning, solving, and examining.
Introduction. (10 minutes) Bring students together in a circle, either seated or standing. Bring blocks with you to the circle. Show the student the blocks and ask them to watch you build a tall castle. After you build it, bring out two figurines that you would like to play with in the castle. Say out loud, "Hmm....there seems to be a problem.
In order to implement a problem-based instruction lesson in your classroom, there are a few planning steps to consider. Fill in the blanks with your lesson-specific information in order to plan your problem-based lesson. 1. Develop clear and measurable learning objectives (including cognitive and behavioral objectives) - based on Bloom's ...
4th Grade Resources - Use the four operations with whole numbers to solve problems. Interpret a multiplication equation as a comparison, e.g., interpret 35 = 5 x 7 as a statement that 35 is 5 times as many as 7 and 7 times as many as 5. Represent verbal statements of multiplicative comparisons as multiplication equations. Multiply or divide to ...
3.OA.D.8. Solve two-step word problems using the four operations. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding. View all 3.OA.D.8 Tasks Download all tasks for this grade.
Key learning points. In this lesson, we will solve a multi-step problem using all four operations; addition, subtraction, multiplication and division. Licence. This content is made available by Oak National Academy Limited and its partners and licensed under Oak's terms & conditions (Collection 1), except where otherwise stated.