hypothesis testing d

• Comprehensive Learning Paths
• 150+ Hours of Videos
• Complete Access to Jupyter notebooks, Datasets, References.

Hypothesis Testing – A Deep Dive into Hypothesis Testing, The Backbone of Statistical Inference

• September 21, 2023

Explore the intricacies of hypothesis testing, a cornerstone of statistical analysis. Dive into methods, interpretations, and applications for making data-driven decisions.

In this Blog post we will learn:

• What is Hypothesis Testing?
• Steps in Hypothesis Testing 2.1. Set up Hypotheses: Null and Alternative 2.2. Choose a Significance Level (α) 2.3. Calculate a test statistic and P-Value 2.4. Make a Decision
• Example : Testing a new drug.
• Example in python

1. What is Hypothesis Testing?

In simple terms, hypothesis testing is a method used to make decisions or inferences about population parameters based on sample data. Imagine being handed a dice and asked if it’s biased. By rolling it a few times and analyzing the outcomes, you’d be engaging in the essence of hypothesis testing.

Think of hypothesis testing as the scientific method of the statistics world. Suppose you hear claims like “This new drug works wonders!” or “Our new website design boosts sales.” How do you know if these statements hold water? Enter hypothesis testing.

2. Steps in Hypothesis Testing

• Set up Hypotheses : Begin with a null hypothesis (H0) and an alternative hypothesis (Ha).
• Choose a Significance Level (α) : Typically 0.05, this is the probability of rejecting the null hypothesis when it’s actually true. Think of it as the chance of accusing an innocent person.
• Calculate Test statistic and P-Value : Gather evidence (data) and calculate a test statistic.
• p-value : This is the probability of observing the data, given that the null hypothesis is true. A small p-value (typically ≤ 0.05) suggests the data is inconsistent with the null hypothesis.
• Decision Rule : If the p-value is less than or equal to α, you reject the null hypothesis in favor of the alternative.

2.1. Set up Hypotheses: Null and Alternative

Before diving into testing, we must formulate hypotheses. The null hypothesis (H0) represents the default assumption, while the alternative hypothesis (H1) challenges it.

For instance, in drug testing, H0 : “The new drug is no better than the existing one,” H1 : “The new drug is superior .”

2.2. Choose a Significance Level (α)

When You collect and analyze data to test H0 and H1 hypotheses. Based on your analysis, you decide whether to reject the null hypothesis in favor of the alternative, or fail to reject / Accept the null hypothesis.

The significance level, often denoted by $α$, represents the probability of rejecting the null hypothesis when it is actually true.

In other words, it’s the risk you’re willing to take of making a Type I error (false positive).

Type I Error (False Positive) :

• Symbolized by the Greek letter alpha (α).
• Occurs when you incorrectly reject a true null hypothesis . In other words, you conclude that there is an effect or difference when, in reality, there isn’t.
• The probability of making a Type I error is denoted by the significance level of a test. Commonly, tests are conducted at the 0.05 significance level , which means there’s a 5% chance of making a Type I error .
• Commonly used significance levels are 0.01, 0.05, and 0.10, but the choice depends on the context of the study and the level of risk one is willing to accept.

Example : If a drug is not effective (truth), but a clinical trial incorrectly concludes that it is effective (based on the sample data), then a Type I error has occurred.

Type II Error (False Negative) :

• Symbolized by the Greek letter beta (β).
• Occurs when you accept a false null hypothesis . This means you conclude there is no effect or difference when, in reality, there is.
• The probability of making a Type II error is denoted by β. The power of a test (1 – β) represents the probability of correctly rejecting a false null hypothesis.

Example : If a drug is effective (truth), but a clinical trial incorrectly concludes that it is not effective (based on the sample data), then a Type II error has occurred.

Balancing the Errors :

In practice, there’s a trade-off between Type I and Type II errors. Reducing the risk of one typically increases the risk of the other. For example, if you want to decrease the probability of a Type I error (by setting a lower significance level), you might increase the probability of a Type II error unless you compensate by collecting more data or making other adjustments.

It’s essential to understand the consequences of both types of errors in any given context. In some situations, a Type I error might be more severe, while in others, a Type II error might be of greater concern. This understanding guides researchers in designing their experiments and choosing appropriate significance levels.

2.3. Calculate a test statistic and P-Value

Test statistic : A test statistic is a single number that helps us understand how far our sample data is from what we’d expect under a null hypothesis (a basic assumption we’re trying to test against). Generally, the larger the test statistic, the more evidence we have against our null hypothesis. It helps us decide whether the differences we observe in our data are due to random chance or if there’s an actual effect.

P-value : The P-value tells us how likely we would get our observed results (or something more extreme) if the null hypothesis were true. It’s a value between 0 and 1. – A smaller P-value (typically below 0.05) means that the observation is rare under the null hypothesis, so we might reject the null hypothesis. – A larger P-value suggests that what we observed could easily happen by random chance, so we might not reject the null hypothesis.

2.4. Make a Decision

Relationship between $α$ and P-Value

When conducting a hypothesis test:

We then calculate the p-value from our sample data and the test statistic.

Finally, we compare the p-value to our chosen $α$:

• If $p−value≤α$: We reject the null hypothesis in favor of the alternative hypothesis. The result is said to be statistically significant.
• If $p−value>α$: We fail to reject the null hypothesis. There isn’t enough statistical evidence to support the alternative hypothesis.

3. Example : Testing a new drug.

Imagine we are investigating whether a new drug is effective at treating headaches faster than drug B.

Setting Up the Experiment : You gather 100 people who suffer from headaches. Half of them (50 people) are given the new drug (let’s call this the ‘Drug Group’), and the other half are given a sugar pill, which doesn’t contain any medication.

• Set up Hypotheses : Before starting, you make a prediction:
• Null Hypothesis (H0): The new drug has no effect. Any difference in healing time between the two groups is just due to random chance.
• Alternative Hypothesis (H1): The new drug does have an effect. The difference in healing time between the two groups is significant and not just by chance.

Calculate Test statistic and P-Value : After the experiment, you analyze the data. The “test statistic” is a number that helps you understand the difference between the two groups in terms of standard units.

For instance, let’s say:

• The average healing time in the Drug Group is 2 hours.
• The average healing time in the Placebo Group is 3 hours.

The test statistic helps you understand how significant this 1-hour difference is. If the groups are large and the spread of healing times in each group is small, then this difference might be significant. But if there’s a huge variation in healing times, the 1-hour difference might not be so special.

Imagine the P-value as answering this question: “If the new drug had NO real effect, what’s the probability that I’d see a difference as extreme (or more extreme) as the one I found, just by random chance?”

For instance:

• P-value of 0.01 means there’s a 1% chance that the observed difference (or a more extreme difference) would occur if the drug had no effect. That’s pretty rare, so we might consider the drug effective.
• P-value of 0.5 means there’s a 50% chance you’d see this difference just by chance. That’s pretty high, so we might not be convinced the drug is doing much.
• If the P-value is less than ($α$) 0.05: the results are “statistically significant,” and they might reject the null hypothesis , believing the new drug has an effect.
• If the P-value is greater than ($α$) 0.05: the results are not statistically significant, and they don’t reject the null hypothesis , remaining unsure if the drug has a genuine effect.

4. Example in python

For simplicity, let’s say we’re using a t-test (common for comparing means). Let’s dive into Python:

Making a Decision : “The results are statistically significant! p-value < 0.05 , The drug seems to have an effect!” If not, we’d say, “Looks like the drug isn’t as miraculous as we thought.”

5. Conclusion

Hypothesis testing is an indispensable tool in data science, allowing us to make data-driven decisions with confidence. By understanding its principles, conducting tests properly, and considering real-world applications, you can harness the power of hypothesis testing to unlock valuable insights from your data.

More Articles

Correlation – connecting the dots, the role of correlation in data analysis, sampling and sampling distributions – a comprehensive guide on sampling and sampling distributions, law of large numbers – a deep dive into the world of statistics, central limit theorem – a deep dive into central limit theorem and its significance in statistics, skewness and kurtosis – peaks and tails, understanding data through skewness and kurtosis”, similar articles, complete introduction to linear regression in r, how to implement common statistical significance tests and find the p value, logistic regression – a complete tutorial with examples in r.

Subscribe to Machine Learning Plus for high value data science content

© Machinelearningplus. All rights reserved.

Machine Learning A-Z™: Hands-On Python & R In Data Science

Free sample videos:.

Hypothesis Testing

When you conduct a piece of quantitative research, you are inevitably attempting to answer a research question or hypothesis that you have set. One method of evaluating this research question is via a process called hypothesis testing , which is sometimes also referred to as significance testing . Since there are many facets to hypothesis testing, we start with the example we refer to throughout this guide.

An example of a lecturer's dilemma

Two statistics lecturers, Sarah and Mike, think that they use the best method to teach their students. Each lecturer has 50 statistics students who are studying a graduate degree in management. In Sarah's class, students have to attend one lecture and one seminar class every week, whilst in Mike's class students only have to attend one lecture. Sarah thinks that seminars, in addition to lectures, are an important teaching method in statistics, whilst Mike believes that lectures are sufficient by themselves and thinks that students are better off solving problems by themselves in their own time. This is the first year that Sarah has given seminars, but since they take up a lot of her time, she wants to make sure that she is not wasting her time and that seminars improve her students' performance.

The research hypothesis

The first step in hypothesis testing is to set a research hypothesis. In Sarah and Mike's study, the aim is to examine the effect that two different teaching methods – providing both lectures and seminar classes (Sarah), and providing lectures by themselves (Mike) – had on the performance of Sarah's 50 students and Mike's 50 students. More specifically, they want to determine whether performance is different between the two different teaching methods. Whilst Mike is skeptical about the effectiveness of seminars, Sarah clearly believes that giving seminars in addition to lectures helps her students do better than those in Mike's class. This leads to the following research hypothesis:

Before moving onto the second step of the hypothesis testing process, we need to take you on a brief detour to explain why you need to run hypothesis testing at all. This is explained next.

Sample to population

If you have measured individuals (or any other type of "object") in a study and want to understand differences (or any other type of effect), you can simply summarize the data you have collected. For example, if Sarah and Mike wanted to know which teaching method was the best, they could simply compare the performance achieved by the two groups of students – the group of students that took lectures and seminar classes, and the group of students that took lectures by themselves – and conclude that the best method was the teaching method which resulted in the highest performance. However, this is generally of only limited appeal because the conclusions could only apply to students in this study. However, if those students were representative of all statistics students on a graduate management degree, the study would have wider appeal.

In statistics terminology, the students in the study are the sample and the larger group they represent (i.e., all statistics students on a graduate management degree) is called the population . Given that the sample of statistics students in the study are representative of a larger population of statistics students, you can use hypothesis testing to understand whether any differences or effects discovered in the study exist in the population. In layman's terms, hypothesis testing is used to establish whether a research hypothesis extends beyond those individuals examined in a single study.

Another example could be taking a sample of 200 breast cancer sufferers in order to test a new drug that is designed to eradicate this type of cancer. As much as you are interested in helping these specific 200 cancer sufferers, your real goal is to establish that the drug works in the population (i.e., all breast cancer sufferers).

As such, by taking a hypothesis testing approach, Sarah and Mike want to generalize their results to a population rather than just the students in their sample. However, in order to use hypothesis testing, you need to re-state your research hypothesis as a null and alternative hypothesis. Before you can do this, it is best to consider the process/structure involved in hypothesis testing and what you are measuring. This structure is presented on the next page .

Statistics Made Easy

Introduction to Hypothesis Testing

A statistical hypothesis is an assumption about a population parameter .

For example, we may assume that the mean height of a male in the U.S. is 70 inches.

The assumption about the height is the statistical hypothesis and the true mean height of a male in the U.S. is the population parameter .

A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.

The Two Types of Statistical Hypotheses

To test whether a statistical hypothesis about a population parameter is true, we obtain a random sample from the population and perform a hypothesis test on the sample data.

There are two types of statistical hypotheses:

The null hypothesis , denoted as H 0 , is the hypothesis that the sample data occurs purely from chance.

The alternative hypothesis , denoted as H 1 or H a , is the hypothesis that the sample data is influenced by some non-random cause.

Hypothesis Tests

A hypothesis test consists of five steps:

1. State the hypotheses. 

State the null and alternative hypotheses. These two hypotheses need to be mutually exclusive, so if one is true then the other must be false.

2. Determine a significance level to use for the hypothesis.

Decide on a significance level. Common choices are .01, .05, and .1. 

3. Find the test statistic.

Find the test statistic and the corresponding p-value. Often we are analyzing a population mean or proportion and the general formula to find the test statistic is: (sample statistic – population parameter) / (standard deviation of statistic)

4. Reject or fail to reject the null hypothesis.

Using the test statistic or the p-value, determine if you can reject or fail to reject the null hypothesis based on the significance level.

The p-value  tells us the strength of evidence in support of a null hypothesis. If the p-value is less than the significance level, we reject the null hypothesis.

5. Interpret the results. 

Interpret the results of the hypothesis test in the context of the question being asked. 

The Two Types of Decision Errors

There are two types of decision errors that one can make when doing a hypothesis test:

Type I error: You reject the null hypothesis when it is actually true. The probability of committing a Type I error is equal to the significance level, often called  alpha , and denoted as α.

Type II error: You fail to reject the null hypothesis when it is actually false. The probability of committing a Type II error is called the Power of the test or  Beta , denoted as β.

One-Tailed and Two-Tailed Tests

A statistical hypothesis can be one-tailed or two-tailed.

A one-tailed hypothesis involves making a “greater than” or “less than ” statement.

For example, suppose we assume the mean height of a male in the U.S. is greater than or equal to 70 inches. The null hypothesis would be H0: µ ≥ 70 inches and the alternative hypothesis would be Ha: µ < 70 inches.

A two-tailed hypothesis involves making an “equal to” or “not equal to” statement.

For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches. The null hypothesis would be H0: µ = 70 inches and the alternative hypothesis would be Ha: µ ≠ 70 inches.

Note: The “equal” sign is always included in the null hypothesis, whether it is =, ≥, or ≤.

Related:   What is a Directional Hypothesis?

Types of Hypothesis Tests

There are many different types of hypothesis tests you can perform depending on the type of data you’re working with and the goal of your analysis.

The following tutorials provide an explanation of the most common types of hypothesis tests:

Introduction to the One Sample t-test Introduction to the Two Sample t-test Introduction to the Paired Samples t-test Introduction to the One Proportion Z-Test Introduction to the Two Proportion Z-Test

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Statistics and probability

Course: statistics and probability   >   unit 12, hypothesis testing and p-values.

• One-tailed and two-tailed tests
• Z-statistics vs. T-statistics
• Small sample hypothesis test
• Large sample proportion hypothesis testing

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• Search Search Please fill out this field.

What Is Hypothesis Testing?

• How It Works

4 Step Process

The bottom line.

• Fundamental Analysis

Hypothesis Testing: 4 Steps and Example

Hypothesis testing, sometimes called significance testing, is an act in statistics whereby an analyst tests an assumption regarding a population parameter. The methodology employed by the analyst depends on the nature of the data used and the reason for the analysis.

Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data. Such data may come from a larger population or a data-generating process. The word "population" will be used for both of these cases in the following descriptions.

Key Takeaways

• Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data.
• The test provides evidence concerning the plausibility of the hypothesis, given the data.
• Statistical analysts test a hypothesis by measuring and examining a random sample of the population being analyzed.
• The four steps of hypothesis testing include stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.

How Hypothesis Testing Works

In hypothesis testing, an  analyst  tests a statistical sample, intending to provide evidence on the plausibility of the null hypothesis. Statistical analysts measure and examine a random sample of the population being analyzed. All analysts use a random population sample to test two different hypotheses: the null hypothesis and the alternative hypothesis.

The null hypothesis is usually a hypothesis of equality between population parameters; e.g., a null hypothesis may state that the population mean return is equal to zero. The alternative hypothesis is effectively the opposite of a null hypothesis. Thus, they are mutually exclusive , and only one can be true. However, one of the two hypotheses will always be true.

The null hypothesis is a statement about a population parameter, such as the population mean, that is assumed to be true.

• State the hypotheses.
• Formulate an analysis plan, which outlines how the data will be evaluated.
• Carry out the plan and analyze the sample data.
• Analyze the results and either reject the null hypothesis, or state that the null hypothesis is plausible, given the data.

Example of Hypothesis Testing

If an individual wants to test that a penny has exactly a 50% chance of landing on heads, the null hypothesis would be that 50% is correct, and the alternative hypothesis would be that 50% is not correct. Mathematically, the null hypothesis is represented as Ho: P = 0.5. The alternative hypothesis is shown as "Ha" and is identical to the null hypothesis, except with the equal sign struck-through, meaning that it does not equal 50%.

A random sample of 100 coin flips is taken, and the null hypothesis is tested. If it is found that the 100 coin flips were distributed as 40 heads and 60 tails, the analyst would assume that a penny does not have a 50% chance of landing on heads and would reject the null hypothesis and accept the alternative hypothesis.

If there were 48 heads and 52 tails, then it is plausible that the coin could be fair and still produce such a result. In cases such as this where the null hypothesis is "accepted," the analyst states that the difference between the expected results (50 heads and 50 tails) and the observed results (48 heads and 52 tails) is "explainable by chance alone."

When Did Hypothesis Testing Begin?

Some statisticians attribute the first hypothesis tests to satirical writer John Arbuthnot in 1710, who studied male and female births in England after observing that in nearly every year, male births exceeded female births by a slight proportion. Arbuthnot calculated that the probability of this happening by chance was small, and therefore it was due to “divine providence.”

What are the Benefits of Hypothesis Testing?

Hypothesis testing helps assess the accuracy of new ideas or theories by testing them against data. This allows researchers to determine whether the evidence supports their hypothesis, helping to avoid false claims and conclusions. Hypothesis testing also provides a framework for decision-making based on data rather than personal opinions or biases. By relying on statistical analysis, hypothesis testing helps to reduce the effects of chance and confounding variables, providing a robust framework for making informed conclusions.

What are the Limitations of Hypothesis Testing?

Hypothesis testing relies exclusively on data and doesn’t provide a comprehensive understanding of the subject being studied. Additionally, the accuracy of the results depends on the quality of the available data and the statistical methods used. Inaccurate data or inappropriate hypothesis formulation may lead to incorrect conclusions or failed tests. Hypothesis testing can also lead to errors, such as analysts either accepting or rejecting a null hypothesis when they shouldn’t have. These errors may result in false conclusions or missed opportunities to identify significant patterns or relationships in the data.

Hypothesis testing refers to a statistical process that helps researchers determine the reliability of a study. By using a well-formulated hypothesis and set of statistical tests, individuals or businesses can make inferences about the population that they are studying and draw conclusions based on the data presented. All hypothesis testing methods have the same four-step process, which includes stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.

Sage. " Introduction to Hypothesis Testing ," Page 4.

Elder Research. " Who Invented the Null Hypothesis? "

Formplus. " Hypothesis Testing: Definition, Uses, Limitations and Examples ."

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

• z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
• t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
• \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

• One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
• Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

• One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
• Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

\(H_{0}\): The population parameter is ≤ some value

\(H_{1}\): The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

Left Tailed Hypothesis Testing

The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

\(H_{0}\): The population parameter is ≥ some value

\(H_{1}\): The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

Two Tailed Hypothesis Testing

In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

\(H_{0}\): the population parameter = some value

\(H_{1}\): the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

• Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
• Step 2: Set up the alternative hypothesis.
• Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
• Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
• Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.

Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.

Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.

1 - \(\alpha\) = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).

\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15

z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Related Articles:

• Probability and Statistics
• Data Handling

Important Notes on Hypothesis Testing

• Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
• It involves the setting up of a null hypothesis and an alternate hypothesis.
• There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
• Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

• Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
• Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
• Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes
• Data Analysis with Python

Introduction to Data Analysis

• What is Data Analysis?
• Data Analytics and its type
• How to Install Numpy on Windows?
• How to Install Pandas in Python?
• How to Install Matplotlib on python?
• How to Install Python Tensorflow in Windows?

Data Analysis Libraries

• Pandas Tutorial
• NumPy Tutorial - Python Library
• Data Analysis with SciPy
• Introduction to TensorFlow

Data Visulization Libraries

• Matplotlib Tutorial
• Python Seaborn Tutorial
• Plotly tutorial
• Introduction to Bokeh in Python

Exploratory Data Analysis (EDA)

• Univariate, Bivariate and Multivariate data and its analysis
• Measures of Central Tendency in Statistics
• Measures of spread - Range, Variance, and Standard Deviation
• Interquartile Range and Quartile Deviation using NumPy and SciPy
• Anova Formula
• Skewness of Statistical Data
• How to Calculate Skewness and Kurtosis in Python?
• Difference Between Skewness and Kurtosis
• Histogram | Meaning, Example, Types and Steps to Draw
• Interpretations of Histogram
• Quantile Quantile plots
• What is Univariate, Bivariate & Multivariate Analysis in Data Visualisation?
• Using pandas crosstab to create a bar plot
• Exploring Correlation in Python
• Mathematics | Covariance and Correlation
• Factor Analysis | Data Analysis
• Data Mining - Cluster Analysis
• MANOVA Test in R Programming
• Python - Central Limit Theorem
• Probability Distribution Function
• Probability Density Estimation & Maximum Likelihood Estimation
• Exponential Distribution in R Programming - dexp(), pexp(), qexp(), and rexp() Functions
• Mathematics | Probability Distributions Set 4 (Binomial Distribution)
• Poisson Distribution - Definition, Formula, Table and Examples
• P-Value: Comprehensive Guide to Understand, Apply, and Interpret
• Z-Score in Statistics
• How to Calculate Point Estimates in R?
• Confidence Interval
• Chi-square test in Machine Learning

Understanding Hypothesis Testing

Data preprocessing.

• ML | Data Preprocessing in Python
• ML | Overview of Data Cleaning
• ML | Handling Missing Values
• Detect and Remove the Outliers using Python

Data Transformation

• Data Normalization Machine Learning
• Sampling distribution Using Python

Time Series Data Analysis

• Data Mining - Time-Series, Symbolic and Biological Sequences Data
• Basic DateTime Operations in Python
• Time Series Analysis & Visualization in Python
• How to deal with missing values in a Timeseries in Python?
• How to calculate MOVING AVERAGE in a Pandas DataFrame?
• What is a trend in time series?
• How to Perform an Augmented Dickey-Fuller Test in R
• AutoCorrelation

Case Studies and Projects

• Top 8 Free Dataset Sources to Use for Data Science Projects
• Step by Step Predictive Analysis - Machine Learning
• 6 Tips for Creating Effective Data Visualizations

Hypothesis testing involves formulating assumptions about population parameters based on sample statistics and rigorously evaluating these assumptions against empirical evidence. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.

What is Hypothesis Testing?

Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. 

Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.

Defining Hypotheses

Key Terms of Hypothesis Testing

• P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
• Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
• Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
• Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.

Why do we use Hypothesis Testing?

Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing. 

One-Tailed and Two-Tailed Test

One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.

One-Tailed Test

There are two types of one-tailed test:

Two-Tailed Test

A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.

What are Type 1 and Type 2 errors in Hypothesis Testing?

In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.

How does Hypothesis Testing work?

Step 1: define null and alternative hypothesis.

We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.

Step 2 – Choose significance level

Step 3 – Collect and Analyze data.

Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.

Step 4-Calculate Test Statistic

The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.

There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.

• Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
• t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
• Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
• F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.

We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.

T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

Step 5 – Comparing Test Statistic:

In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.

Method A: Using Crtical values

Comparing the test statistic and tabulated critical value we have,

• If Test Statistic>Critical Value: Reject the null hypothesis.
• If Test Statistic≤Critical Value: Fail to reject the null hypothesis.

Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Method B: Using P-values

We can also come to an conclusion using the p-value,

Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Step 7- Interpret the Results

At last, we can conclude our experiment using method A or B.

Calculating test statistic

To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .

1. Z-statistics:

When population means and standard deviations are known.

• μ represents the population mean, 
• σ is the standard deviation
• and n is the size of the sample.

2. T-Statistics

T test is used when n<30,

t-statistic calculation is given by:

• t = t-score,
• x̄ = sample mean
• μ = population mean,
• s = standard deviation of the sample,
• n = sample size

3. Chi-Square Test

Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

• i,j are the rows and columns index respectively.

Real life Hypothesis Testing example

Let’s examine hypothesis testing using two real life situations,

Case A: D oes a New Drug Affect Blood Pressure?

Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.

• Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
• After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114

Step 1 : Define the Hypothesis

• Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
• Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.

Step 2: Define the Significance level

Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.

If the evidence suggests less than a 5% chance of observing the results due to random variation.

Step 3 : Compute the test statistic

Using paired T-test analyze the data to obtain a test statistic and a p-value.

The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.

t = m/(s/√n)

• m  = mean of the difference i.e X after, X before
• s  = standard deviation of the difference (d) i.e d i ​= X after, i ​− X before,
• n  = sample size,

then, m= -3.9, s= 1.8 and n= 10

we, calculate the , T-statistic = -9 based on the formula for paired t test

Step 4: Find the p-value

The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.

thus, p-value = 8.538051223166285e-06

Step 5: Result

• If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
• If the p-value is greater than 0.05, they fail to reject the null hypothesis.

Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

Python Implementation of Hypothesis Testing

Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.

Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.

We will implement our first real life problem via python,

In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05. 

• The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
• The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.

Case B : Cholesterol level in a population

Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.

Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.

Populations Mean = 200

Population Standard Deviation (σ): 5 mg/dL(given for this problem)

Step 1: Define the Hypothesis

• Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
• Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.

As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.

Step 4: Result

Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL

Limitations of Hypothesis Testing

• Although a useful technique, hypothesis testing does not offer a comprehensive grasp of the topic being studied. Without fully reflecting the intricacy or whole context of the phenomena, it concentrates on certain hypotheses and statistical significance.
• The accuracy of hypothesis testing results is contingent on the quality of available data and the appropriateness of statistical methods used. Inaccurate data or poorly formulated hypotheses can lead to incorrect conclusions.
• Relying solely on hypothesis testing may cause analysts to overlook significant patterns or relationships in the data that are not captured by the specific hypotheses being tested. This limitation underscores the importance of complimenting hypothesis testing with other analytical approaches.

Hypothesis testing stands as a cornerstone in statistical analysis, enabling data scientists to navigate uncertainties and draw credible inferences from sample data. By systematically defining null and alternative hypotheses, choosing significance levels, and leveraging statistical tests, researchers can assess the validity of their assumptions. The article also elucidates the critical distinction between Type I and Type II errors, providing a comprehensive understanding of the nuanced decision-making process inherent in hypothesis testing. The real-life example of testing a new drug’s effect on blood pressure using a paired T-test showcases the practical application of these principles, underscoring the importance of statistical rigor in data-driven decision-making.

Frequently Asked Questions (FAQs)

1. what are the 3 types of hypothesis test.

There are three types of hypothesis tests: right-tailed, left-tailed, and two-tailed. Right-tailed tests assess if a parameter is greater, left-tailed if lesser. Two-tailed tests check for non-directional differences, greater or lesser.

2.What are the 4 components of hypothesis testing?

Null Hypothesis ( ): No effect or difference exists. Alternative Hypothesis ( ): An effect or difference exists. Significance Level ( ): Risk of rejecting null hypothesis when it’s true (Type I error). Test Statistic: Numerical value representing observed evidence against null hypothesis.

3.What is hypothesis testing in ML?

Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.

4.What is the difference between Pytest and hypothesis in Python?

Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.

Please Login to comment...

Similar reads.

• data-science
• Data Science
• Machine Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

RSC Advances

Testing the hypothesis that solvent exchange limits the rates of calcite growth and dissolution †.

* Corresponding authors

a Chemical Sciences Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA E-mail: [email protected] , [email protected] , [email protected]

b Department of Chemical Engineering, Columbia University, New York, NY 10027, USA

c Computer Science and Mathematics Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA

d Central European Institute of Technology, Masaryk University, Kamenice 5, 625 00 Brno, Czech Republic

e Neutron Sciences Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA

It is established that the rates of solvent exchange at interfaces correlate with the rates of a number of mineral reactions, including growth, dissolution and ion sorption. To test if solvent exchange is limiting these rates, quasi-elastic neutron scattering (QENS) is used here to benchmark classical molecular dynamics (CMD) simulations of water bound to nanoparticulate calcite. Four distributions of solvent exchanges are found with residence times of 8.9 ps for water bound to calcium sites, 14 ps for that bound to carbonate sites and 16.7 and 85.1 ps for two bound waters in a shared calcium-carbonate conformation. By comparing rates and activation energies, it is found that solvent exchange limits reaction rates neither for growth nor dissolution, likely due to the necessity to form intermediate states during ion sorption. However, solvent exchange forms the ceiling for reaction rates and yields insight into more complex reaction pathways.

Supplementary files

• Supplementary information PDF (4102K)

Article information

Download Citation

Permissions.

Testing the hypothesis that solvent exchange limits the rates of calcite growth and dissolution

N. Rampal, H. Wang, A. B. Brady, J. M. Borreguero, D. Biriukov, E. Mamontov and A. G. Stack, RSC Adv. , 2024,  14 , 15743 DOI: 10.1039/D4RA00565A

This article is licensed under a Creative Commons Attribution 3.0 Unported Licence . You can use material from this article in other publications without requesting further permissions from the RSC, provided that the correct acknowledgement is given.

Read more about how to correctly acknowledge RSC content .

Social activity

Search articles by author, advertisements.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3.2 hypothesis testing (p-value approach).

The P -value approach involves determining "likely" or "unlikely" by determining the probability — assuming the null hypothesis was true — of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed. If the P -value is small, say less than (or equal to) \(\alpha\), then it is "unlikely." And, if the P -value is large, say more than \(\alpha\), then it is "likely."

If the P -value is less than (or equal to) \(\alpha\), then the null hypothesis is rejected in favor of the alternative hypothesis. And, if the P -value is greater than \(\alpha\), then the null hypothesis is not rejected.

Specifically, the four steps involved in using the P -value approach to conducting any hypothesis test are:

• Specify the null and alternative hypotheses.
• Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic. Again, to conduct the hypothesis test for the population mean μ , we use the t -statistic \(t^*=\frac{\bar{x}-\mu}{s/\sqrt{n}}\) which follows a t -distribution with n - 1 degrees of freedom.
• Using the known distribution of the test statistic, calculate the P -value : "If the null hypothesis is true, what is the probability that we'd observe a more extreme test statistic in the direction of the alternative hypothesis than we did?" (Note how this question is equivalent to the question answered in criminal trials: "If the defendant is innocent, what is the chance that we'd observe such extreme criminal evidence?")
• Set the significance level, \(\alpha\), the probability of making a Type I error to be small — 0.01, 0.05, or 0.10. Compare the P -value to \(\alpha\). If the P -value is less than (or equal to) \(\alpha\), reject the null hypothesis in favor of the alternative hypothesis. If the P -value is greater than \(\alpha\), do not reject the null hypothesis.

Example S.3.2.1

Mean gpa section  .

In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t * equaling 2.5. Since n = 15, our test statistic t * has n - 1 = 14 degrees of freedom. Also, suppose we set our significance level α at 0.05 so that we have only a 5% chance of making a Type I error.

Right Tailed

The P -value for conducting the right-tailed test H 0 : μ = 3 versus H A : μ > 3 is the probability that we would observe a test statistic greater than t * = 2.5 if the population mean \(\mu\) really were 3. Recall that probability equals the area under the probability curve. The P -value is therefore the area under a t n - 1 = t 14 curve and to the right of the test statistic t * = 2.5. It can be shown using statistical software that the P -value is 0.0127. The graph depicts this visually.

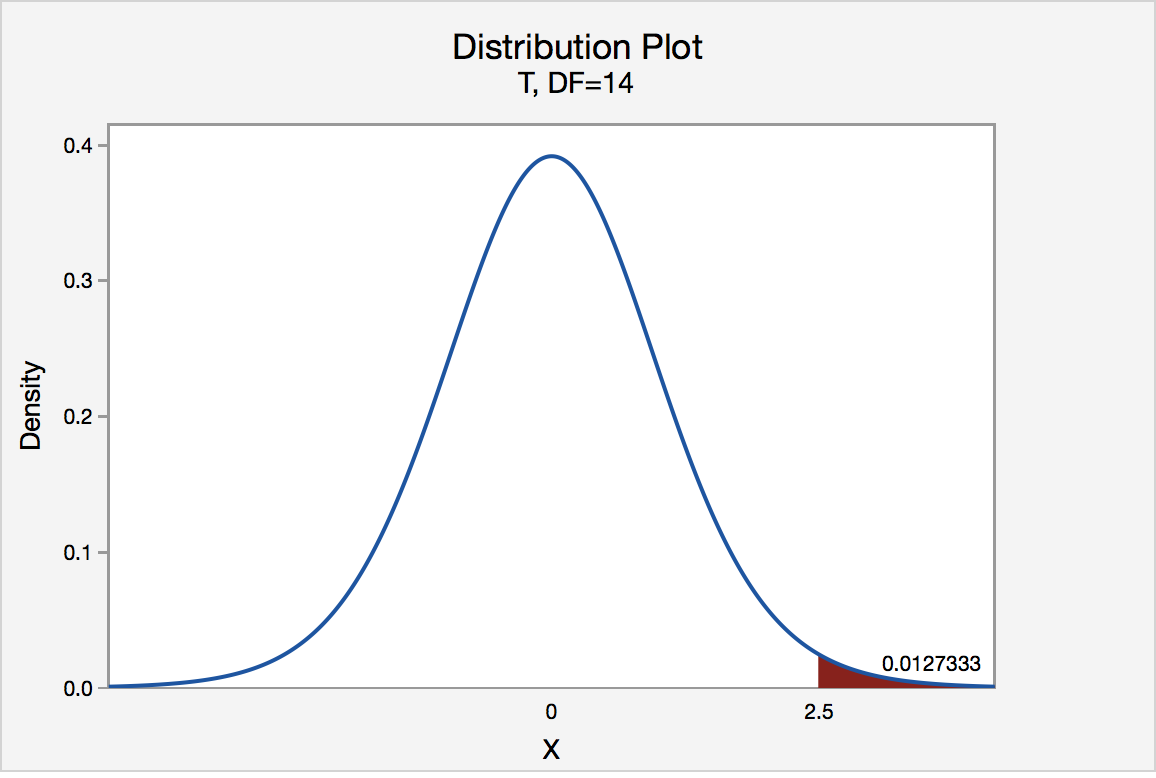
The P -value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0127, is less than \(\alpha\) = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ > 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ > 3 if we lowered our willingness to make a Type I error to \(\alpha\) = 0.01 instead, as the P -value, 0.0127, is then greater than \(\alpha\) = 0.01.

Left Tailed

In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t * instead of equaling -2.5. The P -value for conducting the left-tailed test H 0 : μ = 3 versus H A : μ < 3 is the probability that we would observe a test statistic less than t * = -2.5 if the population mean μ really were 3. The P -value is therefore the area under a t n - 1 = t 14 curve and to the left of the test statistic t* = -2.5. It can be shown using statistical software that the P -value is 0.0127. The graph depicts this visually.

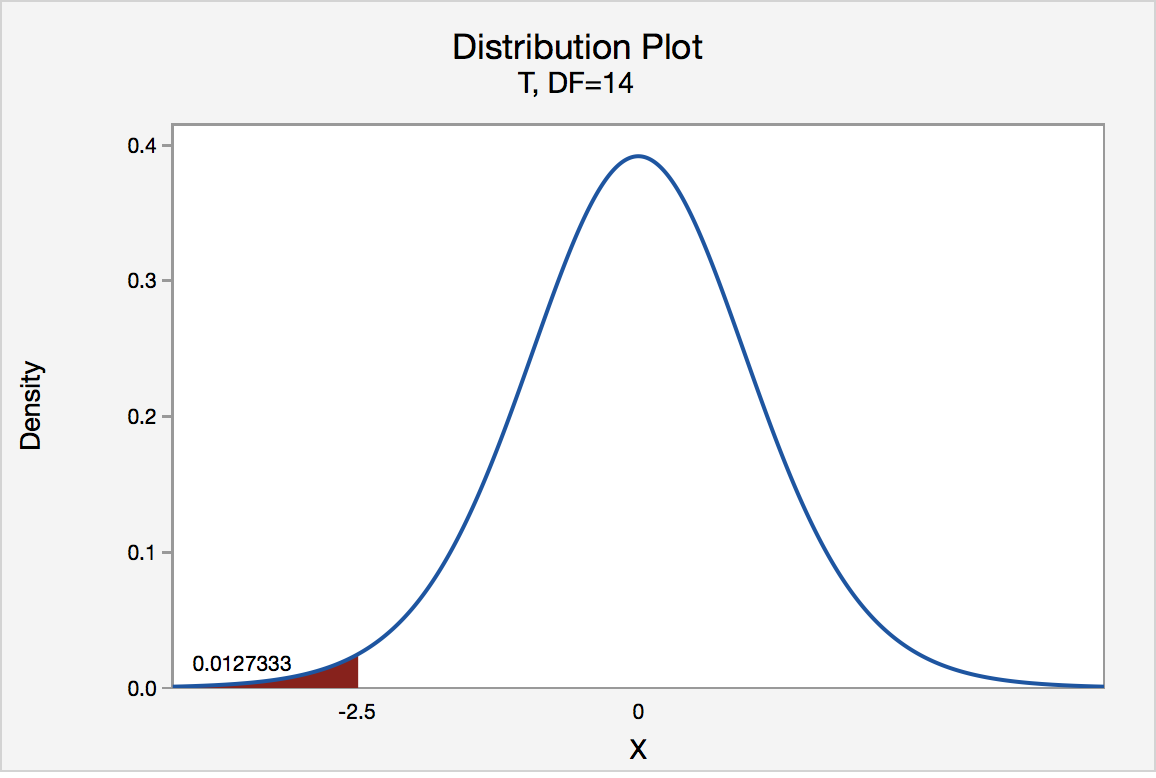
The P -value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0127, is less than α = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ < 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ < 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P -value, 0.0127, is then greater than \(\alpha\) = 0.01.

In our example concerning the mean grade point average, suppose again that our random sample of n = 15 students majoring in mathematics yields a test statistic t * instead of equaling -2.5. The P -value for conducting the two-tailed test H 0 : μ = 3 versus H A : μ ≠ 3 is the probability that we would observe a test statistic less than -2.5 or greater than 2.5 if the population mean μ really was 3. That is, the two-tailed test requires taking into account the possibility that the test statistic could fall into either tail (hence the name "two-tailed" test). The P -value is, therefore, the area under a t n - 1 = t 14 curve to the left of -2.5 and to the right of 2.5. It can be shown using statistical software that the P -value is 0.0127 + 0.0127, or 0.0254. The graph depicts this visually.

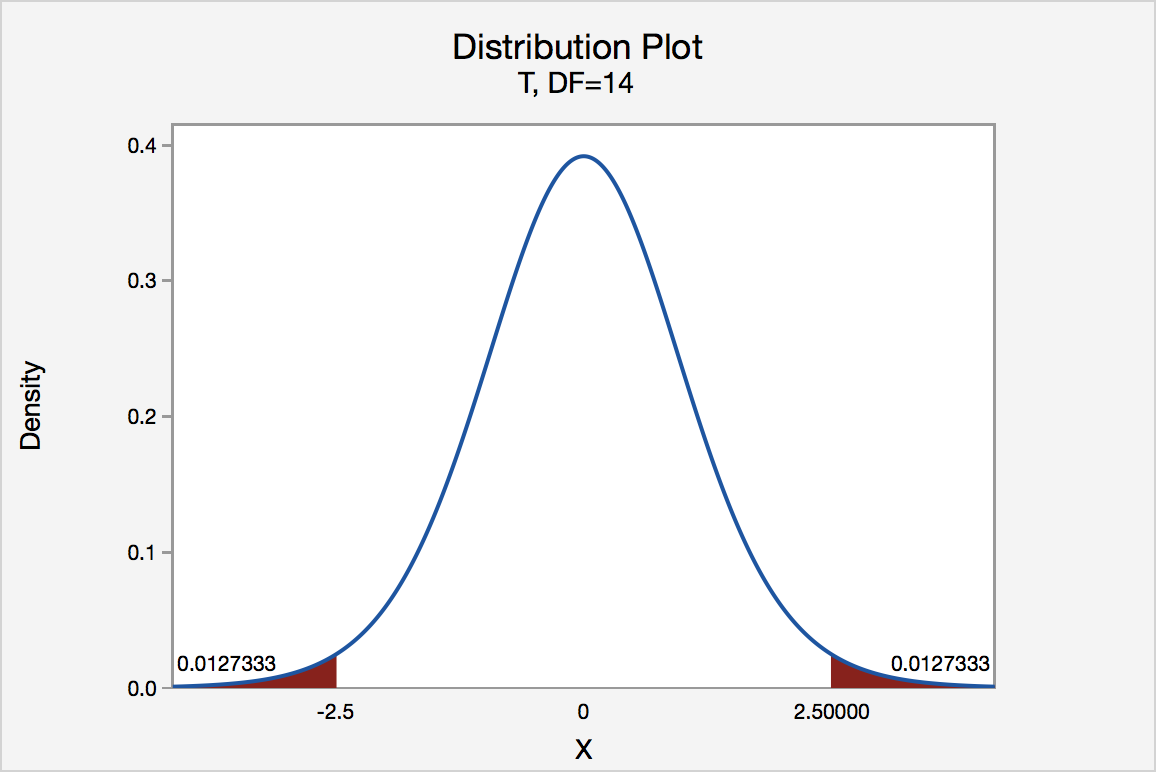
Note that the P -value for a two-tailed test is always two times the P -value for either of the one-tailed tests. The P -value, 0.0254, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0254, is less than α = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ ≠ 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ ≠ 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P -value, 0.0254, is then greater than \(\alpha\) = 0.01.

Now that we have reviewed the critical value and P -value approach procedures for each of the three possible hypotheses, let's look at three new examples — one of a right-tailed test, one of a left-tailed test, and one of a two-tailed test.

The good news is that, whenever possible, we will take advantage of the test statistics and P -values reported in statistical software, such as Minitab, to conduct our hypothesis tests in this course.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.E: Hypothesis Testing with One Sample (Exercises)

• Last updated
• Save as PDF
• Page ID 1146

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

These are homework exercises to accompany the Textmap created for "Introductory Statistics" by OpenStax.

9.1: Introduction

9.2: null and alternative hypotheses.

Some of the following statements refer to the null hypothesis, some to the alternate hypothesis.

State the null hypothesis, \(H_{0}\), and the alternative hypothesis. \(H_{a}\), in terms of the appropriate parameter \((\mu \text{or} p)\).

• The mean number of years Americans work before retiring is 34.
• At most 60% of Americans vote in presidential elections.
• The mean starting salary for San Jose State University graduates is at least $100,000 per year.
• Twenty-nine percent of high school seniors get drunk each month.
• Fewer than 5% of adults ride the bus to work in Los Angeles.
• The mean number of cars a person owns in her lifetime is not more than ten.
• About half of Americans prefer to live away from cities, given the choice.
• Europeans have a mean paid vacation each year of six weeks.
• The chance of developing breast cancer is under 11% for women.
• Private universities' mean tuition cost is more than $20,000 per year.
• \(H_{0}: \mu = 34; H_{a}: \mu \neq 34\)
• \(H_{0}: p \leq 0.60; H_{a}: p > 0.60\)
• \(H_{0}: \mu \geq 100,000; H_{a}: \mu < 100,000\)
• \(H_{0}: p = 0.29; H_{a}: p \neq 0.29\)
• \(H_{0}: p = 0.05; H_{a}: p < 0.05\)
• \(H_{0}: \mu \leq 10; H_{a}: \mu > 10\)
• \(H_{0}: p = 0.50; H_{a}: p \neq 0.50\)
• \(H_{0}: \mu = 6; H_{a}: \mu \neq 6\)
• \(H_{0}: p ≥ 0.11; H_{a}: p < 0.11\)
• \(H_{0}: \mu \leq 20,000; H_{a}: \mu > 20,000\)

Over the past few decades, public health officials have examined the link between weight concerns and teen girls' smoking. Researchers surveyed a group of 273 randomly selected teen girls living in Massachusetts (between 12 and 15 years old). After four years the girls were surveyed again. Sixty-three said they smoked to stay thin. Is there good evidence that more than thirty percent of the teen girls smoke to stay thin? The alternative hypothesis is:

• \(p < 0.30\)
• \(p \leq 0.30\)
• \(p \geq 0.30\)
• \(p > 0.30\)

A statistics instructor believes that fewer than 20% of Evergreen Valley College (EVC) students attended the opening night midnight showing of the latest Harry Potter movie. She surveys 84 of her students and finds that 11 attended the midnight showing. An appropriate alternative hypothesis is:

• \(p = 0.20\)
• \(p > 0.20\)
• \(p < 0.20\)
• \(p \leq 0.20\)

Previously, an organization reported that teenagers spent 4.5 hours per week, on average, on the phone. The organization thinks that, currently, the mean is higher. Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test. The null and alternative hypotheses are:

• \(H_{0}: \bar{x} = 4.5, H_{a}: \bar{x} > 4.5\)
• \(H_{0}: \mu \geq 4.5, H_{a}: \mu < 4.5\)
• \(H_{0}: \mu = 4.75, H_{a}: \mu > 4.75\)
• \(H_{0}: \mu = 4.5, H_{a}: \mu > 4.5\)

9.3: Outcomes and the Type I and Type II Errors

State the Type I and Type II errors in complete sentences given the following statements.

• The mean number of cars a person owns in his or her lifetime is not more than ten.
• Private universities mean tuition cost is more than $20,000 per year.
• Type I error: We conclude that the mean is not 34 years, when it really is 34 years. Type II error: We conclude that the mean is 34 years, when in fact it really is not 34 years.
• Type I error: We conclude that more than 60% of Americans vote in presidential elections, when the actual percentage is at most 60%.Type II error: We conclude that at most 60% of Americans vote in presidential elections when, in fact, more than 60% do.
• Type I error: We conclude that the mean starting salary is less than $100,000, when it really is at least $100,000. Type II error: We conclude that the mean starting salary is at least $100,000 when, in fact, it is less than $100,000.
• Type I error: We conclude that the proportion of high school seniors who get drunk each month is not 29%, when it really is 29%. Type II error: We conclude that the proportion of high school seniors who get drunk each month is 29% when, in fact, it is not 29%.
• Type I error: We conclude that fewer than 5% of adults ride the bus to work in Los Angeles, when the percentage that do is really 5% or more. Type II error: We conclude that 5% or more adults ride the bus to work in Los Angeles when, in fact, fewer that 5% do.
• Type I error: We conclude that the mean number of cars a person owns in his or her lifetime is more than 10, when in reality it is not more than 10. Type II error: We conclude that the mean number of cars a person owns in his or her lifetime is not more than 10 when, in fact, it is more than 10.
• Type I error: We conclude that the proportion of Americans who prefer to live away from cities is not about half, though the actual proportion is about half. Type II error: We conclude that the proportion of Americans who prefer to live away from cities is half when, in fact, it is not half.
• Type I error: We conclude that the duration of paid vacations each year for Europeans is not six weeks, when in fact it is six weeks. Type II error: We conclude that the duration of paid vacations each year for Europeans is six weeks when, in fact, it is not.
• Type I error: We conclude that the proportion is less than 11%, when it is really at least 11%. Type II error: We conclude that the proportion of women who develop breast cancer is at least 11%, when in fact it is less than 11%.
• Type I error: We conclude that the average tuition cost at private universities is more than $20,000, though in reality it is at most $20,000. Type II error: We conclude that the average tuition cost at private universities is at most $20,000 when, in fact, it is more than $20,000.

For statements a-j in Exercise 9.109 , answer the following in complete sentences.

• State a consequence of committing a Type I error.
• State a consequence of committing a Type II error.

When a new drug is created, the pharmaceutical company must subject it to testing before receiving the necessary permission from the Food and Drug Administration (FDA) to market the drug. Suppose the null hypothesis is “the drug is unsafe.” What is the Type II Error?

• To conclude the drug is safe when in, fact, it is unsafe.
• Not to conclude the drug is safe when, in fact, it is safe.
• To conclude the drug is safe when, in fact, it is safe.
• Not to conclude the drug is unsafe when, in fact, it is unsafe.

A statistics instructor believes that fewer than 20% of Evergreen Valley College (EVC) students attended the opening midnight showing of the latest Harry Potter movie. She surveys 84 of her students and finds that 11 of them attended the midnight showing. The Type I error is to conclude that the percent of EVC students who attended is ________.

• at least 20%, when in fact, it is less than 20%.
• 20%, when in fact, it is 20%.
• less than 20%, when in fact, it is at least 20%.
• less than 20%, when in fact, it is less than 20%.

It is believed that Lake Tahoe Community College (LTCC) Intermediate Algebra students get less than seven hours of sleep per night, on average. A survey of 22 LTCC Intermediate Algebra students generated a mean of 7.24 hours with a standard deviation of 1.93 hours. At a level of significance of 5%, do LTCC Intermediate Algebra students get less than seven hours of sleep per night, on average?

The Type II error is not to reject that the mean number of hours of sleep LTCC students get per night is at least seven when, in fact, the mean number of hours

• is more than seven hours.
• is at most seven hours.
• is at least seven hours.
• is less than seven hours.

Previously, an organization reported that teenagers spent 4.5 hours per week, on average, on the phone. The organization thinks that, currently, the mean is higher. Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test, the Type I error is:

• to conclude that the current mean hours per week is higher than 4.5, when in fact, it is higher
• to conclude that the current mean hours per week is higher than 4.5, when in fact, it is the same
• to conclude that the mean hours per week currently is 4.5, when in fact, it is higher
• to conclude that the mean hours per week currently is no higher than 4.5, when in fact, it is not higher

9.4: Distribution Needed for Hypothesis Testing

It is believed that Lake Tahoe Community College (LTCC) Intermediate Algebra students get less than seven hours of sleep per night, on average. A survey of 22 LTCC Intermediate Algebra students generated a mean of 7.24 hours with a standard deviation of 1.93 hours. At a level of significance of 5%, do LTCC Intermediate Algebra students get less than seven hours of sleep per night, on average? The distribution to be used for this test is \(\bar{X} \sim\) ________________

• \(N\left(7.24, \frac{1.93}{\sqrt{22}}\right)\)
• \(N\left(7.24, 1.93\right)\)

9.5: Rare Events, the Sample, Decision and Conclusion

The National Institute of Mental Health published an article stating that in any one-year period, approximately 9.5 percent of American adults suffer from depression or a depressive illness. Suppose that in a survey of 100 people in a certain town, seven of them suffered from depression or a depressive illness. Conduct a hypothesis test to determine if the true proportion of people in that town suffering from depression or a depressive illness is lower than the percent in the general adult American population.

• Is this a test of one mean or proportion?
• State the null and alternative hypotheses. \(H_{0}\) : ____________________ \(H_{a}\) : ____________________
• Is this a right-tailed, left-tailed, or two-tailed test?
• What symbol represents the random variable for this test?
• In words, define the random variable for this test.
• \(x =\) ________________
• \(n =\) ________________
• \(p′ =\) _____________
• Calculate \(\sigma_{x} =\) __________. Show the formula set-up.
• State the distribution to use for the hypothesis test.
• Find the \(p\text{-value}\).
• Reason for the decision:
• Conclusion (write out in a complete sentence):

9.6: Additional Information and Full Hypothesis Test Examples

For each of the word problems, use a solution sheet to do the hypothesis test. The solution sheet is found in [link] . Please feel free to make copies of the solution sheets. For the online version of the book, it is suggested that you copy the .doc or the .pdf files.

If you are using a Student's \(t\) - distribution for one of the following homework problems, you may assume that the underlying population is normally distributed. (In general, you must first prove that assumption, however.)

A particular brand of tires claims that its deluxe tire averages at least 50,000 miles before it needs to be replaced. From past studies of this tire, the standard deviation is known to be 8,000. A survey of owners of that tire design is conducted. From the 28 tires surveyed, the mean lifespan was 46,500 miles with a standard deviation of 9,800 miles. Using \(\alpha = 0.05\), is the data highly inconsistent with the claim?

• \(H_{0}: \mu \geq 50,000\)
• \(H_{a}: \mu < 50,000\)
• Let \(\bar{X} =\) the average lifespan of a brand of tires.
• normal distribution
• \(z = -2.315\)
• \(p\text{-value} = 0.0103\)
• Check student’s solution.
• alpha: 0.05
• Decision: Reject the null hypothesis.
• Reason for decision: The \(p\text{-value}\) is less than 0.05.
• Conclusion: There is sufficient evidence to conclude that the mean lifespan of the tires is less than 50,000 miles.
• \((43,537, 49,463)\)

From generation to generation, the mean age when smokers first start to smoke varies. However, the standard deviation of that age remains constant of around 2.1 years. A survey of 40 smokers of this generation was done to see if the mean starting age is at least 19. The sample mean was 18.1 with a sample standard deviation of 1.3. Do the data support the claim at the 5% level?

The cost of a daily newspaper varies from city to city. However, the variation among prices remains steady with a standard deviation of 20¢. A study was done to test the claim that the mean cost of a daily newspaper is $1.00. Twelve costs yield a mean cost of 95¢ with a standard deviation of 18¢. Do the data support the claim at the 1% level?

• \(H_{0}: \mu = $1.00\)
• \(H_{a}: \mu \neq $1.00\)
• Let \(\bar{X} =\) the average cost of a daily newspaper.
• \(z = –0.866\)
• \(p\text{-value} = 0.3865\)
• \(\alpha: 0.01\)
• Decision: Do not reject the null hypothesis.
• Reason for decision: The \(p\text{-value}\) is greater than 0.01.
• Conclusion: There is sufficient evidence to support the claim that the mean cost of daily papers is $1. The mean cost could be $1.
• \(($0.84, $1.06)\)

An article in the San Jose Mercury News stated that students in the California state university system take 4.5 years, on average, to finish their undergraduate degrees. Suppose you believe that the mean time is longer. You conduct a survey of 49 students and obtain a sample mean of 5.1 with a sample standard deviation of 1.2. Do the data support your claim at the 1% level?

The mean number of sick days an employee takes per year is believed to be about ten. Members of a personnel department do not believe this figure. They randomly survey eight employees. The number of sick days they took for the past year are as follows: 12; 4; 15; 3; 11; 8; 6; 8. Let \(x =\) the number of sick days they took for the past year. Should the personnel team believe that the mean number is ten?

• \(H_{0}: \mu = 10\)
• \(H_{a}: \mu \neq 10\)
• Let \(\bar{X}\) the mean number of sick days an employee takes per year.
• Student’s t -distribution
• \(t = –1.12\)
• \(p\text{-value} = 0.300\)
• \(\alpha: 0.05\)
• Reason for decision: The \(p\text{-value}\) is greater than 0.05.
• Conclusion: At the 5% significance level, there is insufficient evidence to conclude that the mean number of sick days is not ten.
• \((4.9443, 11.806)\)

In 1955, Life Magazine reported that the 25 year-old mother of three worked, on average, an 80 hour week. Recently, many groups have been studying whether or not the women's movement has, in fact, resulted in an increase in the average work week for women (combining employment and at-home work). Suppose a study was done to determine if the mean work week has increased. 81 women were surveyed with the following results. The sample mean was 83; the sample standard deviation was ten. Does it appear that the mean work week has increased for women at the 5% level?

Your statistics instructor claims that 60 percent of the students who take her Elementary Statistics class go through life feeling more enriched. For some reason that she can't quite figure out, most people don't believe her. You decide to check this out on your own. You randomly survey 64 of her past Elementary Statistics students and find that 34 feel more enriched as a result of her class. Now, what do you think?

• \(H_{0}: p \geq 0.6\)
• \(H_{a}: p < 0.6\)
• Let \(P′ =\) the proportion of students who feel more enriched as a result of taking Elementary Statistics.
• normal for a single proportion
• \(p\text{-value} = 0.1308\)
• Conclusion: There is insufficient evidence to conclude that less than 60 percent of her students feel more enriched.

The “plus-4s” confidence interval is \((0.411, 0.648)\)

A Nissan Motor Corporation advertisement read, “The average man’s I.Q. is 107. The average brown trout’s I.Q. is 4. So why can’t man catch brown trout?” Suppose you believe that the brown trout’s mean I.Q. is greater than four. You catch 12 brown trout. A fish psychologist determines the I.Q.s as follows: 5; 4; 7; 3; 6; 4; 5; 3; 6; 3; 8; 5. Conduct a hypothesis test of your belief.

Refer to Exercise 9.119 . Conduct a hypothesis test to see if your decision and conclusion would change if your belief were that the brown trout’s mean I.Q. is not four.

• \(H_{0}: \mu = 4\)
• \(H_{a}: \mu \neq 4\)
• Let \(\bar{X}\) the average I.Q. of a set of brown trout.
• two-tailed Student's t-test
• \(t = 1.95\)
• \(p\text{-value} = 0.076\)
• Reason for decision: The \(p\text{-value}\) is greater than 0.05
• Conclusion: There is insufficient evidence to conclude that the average IQ of brown trout is not four.
• \((3.8865,5.9468)\)

According to an article in Newsweek , the natural ratio of girls to boys is 100:105. In China, the birth ratio is 100: 114 (46.7% girls). Suppose you don’t believe the reported figures of the percent of girls born in China. You conduct a study. In this study, you count the number of girls and boys born in 150 randomly chosen recent births. There are 60 girls and 90 boys born of the 150. Based on your study, do you believe that the percent of girls born in China is 46.7?

A poll done for Newsweek found that 13% of Americans have seen or sensed the presence of an angel. A contingent doubts that the percent is really that high. It conducts its own survey. Out of 76 Americans surveyed, only two had seen or sensed the presence of an angel. As a result of the contingent’s survey, would you agree with the Newsweek poll? In complete sentences, also give three reasons why the two polls might give different results.

• \(H_{a}: p < 0.13\)
• Let \(P′ =\) the proportion of Americans who have seen or sensed angels
• –2.688
• \(p\text{-value} = 0.0036\)
• Reason for decision: The \(p\text{-value}\)e is less than 0.05.
• Conclusion: There is sufficient evidence to conclude that the percentage of Americans who have seen or sensed an angel is less than 13%.

The“plus-4s” confidence interval is (0.0022, 0.0978)

The mean work week for engineers in a start-up company is believed to be about 60 hours. A newly hired engineer hopes that it’s shorter. She asks ten engineering friends in start-ups for the lengths of their mean work weeks. Based on the results that follow, should she count on the mean work week to be shorter than 60 hours?

Data (length of mean work week): 70; 45; 55; 60; 65; 55; 55; 60; 50; 55.

Use the “Lap time” data for Lap 4 (see [link] ) to test the claim that Terri finishes Lap 4, on average, in less than 129 seconds. Use all twenty races given.

• \(H_{0}: \mu \geq 129\)
• \(H_{a}: \mu < 129\)
• Let \(\bar{X} =\) the average time in seconds that Terri finishes Lap 4.
• Student's t -distribution
• \(t = 1.209\)
• Conclusion: There is insufficient evidence to conclude that Terri’s mean lap time is less than 129 seconds.
• \((128.63, 130.37)\)

Use the “Initial Public Offering” data (see [link] ) to test the claim that the mean offer price was $18 per share. Do not use all the data. Use your random number generator to randomly survey 15 prices.

The following questions were written by past students. They are excellent problems!

"Asian Family Reunion," by Chau Nguyen

Every two years it comes around.

We all get together from different towns.

In my honest opinion,

It's not a typical family reunion.

Not forty, or fifty, or sixty,

But how about seventy companions!

The kids would play, scream, and shout

One minute they're happy, another they'll pout.

The teenagers would look, stare, and compare

From how they look to what they wear.

The men would chat about their business

That they make more, but never less.

Money is always their subject

And there's always talk of more new projects.

The women get tired from all of the chats

They head to the kitchen to set out the mats.

Some would sit and some would stand

Eating and talking with plates in their hands.

Then come the games and the songs

And suddenly, everyone gets along!

With all that laughter, it's sad to say

That it always ends in the same old way.

They hug and kiss and say "good-bye"

And then they all begin to cry!

I say that 60 percent shed their tears

But my mom counted 35 people this year.

She said that boys and men will always have their pride,

So we won't ever see them cry.

I myself don't think she's correct,

So could you please try this problem to see if you object?

• \(H_{0}: p = 0.60\)
• \(H_{a}: p < 0.60\)
• Let \(P′ =\) the proportion of family members who shed tears at a reunion.
• –1.71
• Reason for decision: \(p\text{-value} < \alpha\)
• Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the proportion of family members who shed tears at a reunion is less than 0.60. However, the test is weak because the \(p\text{-value}\) and alpha are quite close, so other tests should be done.
• We are 95% confident that between 38.29% and 61.71% of family members will shed tears at a family reunion. \((0.3829, 0.6171)\). The“plus-4s” confidence interval (see chapter 8) is \((0.3861, 0.6139)\)

Note that here the “large-sample” \(1 - \text{PropZTest}\) provides the approximate \(p\text{-value}\) of 0.0438. Whenever a \(p\text{-value}\) based on a normal approximation is close to the level of significance, the exact \(p\text{-value}\) based on binomial probabilities should be calculated whenever possible. This is beyond the scope of this course.

"The Problem with Angels," by Cyndy Dowling

Although this problem is wholly mine,

The catalyst came from the magazine, Time.

On the magazine cover I did find

The realm of angels tickling my mind.

Inside, 69% I found to be

In angels, Americans do believe.

Then, it was time to rise to the task,

Ninety-five high school and college students I did ask.

Viewing all as one group,

Random sampling to get the scoop.

So, I asked each to be true,

"Do you believe in angels?" Tell me, do!

Hypothesizing at the start,

Totally believing in my heart

That the proportion who said yes

Would be equal on this test.

Lo and behold, seventy-three did arrive,

Out of the sample of ninety-five.

Now your job has just begun,

Solve this problem and have some fun.

"Blowing Bubbles," by Sondra Prull

Studying stats just made me tense,

I had to find some sane defense.

Some light and lifting simple play

To float my math anxiety away.

Blowing bubbles lifts me high

Takes my troubles to the sky.

POIK! They're gone, with all my stress

Bubble therapy is the best.

The label said each time I blew

The average number of bubbles would be at least 22.

I blew and blew and this I found

From 64 blows, they all are round!

But the number of bubbles in 64 blows

Varied widely, this I know.

20 per blow became the mean

They deviated by 6, and not 16.

From counting bubbles, I sure did relax

But now I give to you your task.

Was 22 a reasonable guess?

Find the answer and pass this test!

• \(H_{0}: \mu \geq 22\)
• \(H_{a}: \mu < 22\)
• Let \(\bar{X} =\) the mean number of bubbles per blow.
• –2.667
• \(p\text{-value} = 0.00486\)
• Conclusion: There is sufficient evidence to conclude that the mean number of bubbles per blow is less than 22.
• \((18.501, 21.499)\)

"Dalmatian Darnation," by Kathy Sparling

A greedy dog breeder named Spreckles

Bred puppies with numerous freckles

The Dalmatians he sought

Possessed spot upon spot

The more spots, he thought, the more shekels.

His competitors did not agree

That freckles would increase the fee.

They said, “Spots are quite nice

But they don't affect price;

One should breed for improved pedigree.”

The breeders decided to prove

This strategy was a wrong move.

Breeding only for spots

Would wreak havoc, they thought.

His theory they want to disprove.

They proposed a contest to Spreckles

Comparing dog prices to freckles.

In records they looked up

One hundred one pups:

Dalmatians that fetched the most shekels.

They asked Mr. Spreckles to name

An average spot count he'd claim

To bring in big bucks.

Said Spreckles, “Well, shucks,

It's for one hundred one that I aim.”

Said an amateur statistician

Who wanted to help with this mission.

“Twenty-one for the sample

Standard deviation's ample:

They examined one hundred and one

Dalmatians that fetched a good sum.

They counted each spot,

Mark, freckle and dot

And tallied up every one.

Instead of one hundred one spots

They averaged ninety six dots

Can they muzzle Spreckles’

Obsession with freckles

Based on all the dog data they've got?

"Macaroni and Cheese, please!!" by Nedda Misherghi and Rachelle Hall

As a poor starving student I don't have much money to spend for even the bare necessities. So my favorite and main staple food is macaroni and cheese. It's high in taste and low in cost and nutritional value.

One day, as I sat down to determine the meaning of life, I got a serious craving for this, oh, so important, food of my life. So I went down the street to Greatway to get a box of macaroni and cheese, but it was SO expensive! $2.02 !!! Can you believe it? It made me stop and think. The world is changing fast. I had thought that the mean cost of a box (the normal size, not some super-gigantic-family-value-pack) was at most $1, but now I wasn't so sure. However, I was determined to find out. I went to 53 of the closest grocery stores and surveyed the prices of macaroni and cheese. Here are the data I wrote in my notebook:

Price per box of Mac and Cheese:

• 5 stores @ $2.02
• 15 stores @ $0.25
• 3 stores @ $1.29
• 6 stores @ $0.35
• 4 stores @ $2.27
• 7 stores @ $1.50
• 5 stores @ $1.89
• 8 stores @ 0.75.

I could see that the cost varied but I had to sit down to figure out whether or not I was right. If it does turn out that this mouth-watering dish is at most $1, then I'll throw a big cheesy party in our next statistics lab, with enough macaroni and cheese for just me. (After all, as a poor starving student I can't be expected to feed our class of animals!)

• \(H_{0}: \mu \leq 1\)
• \(H_{a}: \mu > 1\)
• Let \(\bar{X} =\) the mean cost in dollars of macaroni and cheese in a certain town.
• Student's \(t\)-distribution
• \(t = 0.340\)
• \(p\text{-value} = 0.36756\)
• Conclusion: The mean cost could be $1, or less. At the 5% significance level, there is insufficient evidence to conclude that the mean price of a box of macaroni and cheese is more than $1.
• \((0.8291, 1.241)\)

"William Shakespeare: The Tragedy of Hamlet, Prince of Denmark," by Jacqueline Ghodsi

THE CHARACTERS (in order of appearance):

• HAMLET, Prince of Denmark and student of Statistics
• POLONIUS, Hamlet’s tutor
• HOROTIO, friend to Hamlet and fellow student

Scene: The great library of the castle, in which Hamlet does his lessons

(The day is fair, but the face of Hamlet is clouded. He paces the large room. His tutor, Polonius, is reprimanding Hamlet regarding the latter’s recent experience. Horatio is seated at the large table at right stage.)

POLONIUS: My Lord, how cans’t thou admit that thou hast seen a ghost! It is but a figment of your imagination!

HAMLET: I beg to differ; I know of a certainty that five-and-seventy in one hundred of us, condemned to the whips and scorns of time as we are, have gazed upon a spirit of health, or goblin damn’d, be their intents wicked or charitable.

POLONIUS If thou doest insist upon thy wretched vision then let me invest your time; be true to thy work and speak to me through the reason of the null and alternate hypotheses. (He turns to Horatio.) Did not Hamlet himself say, “What piece of work is man, how noble in reason, how infinite in faculties? Then let not this foolishness persist. Go, Horatio, make a survey of three-and-sixty and discover what the true proportion be. For my part, I will never succumb to this fantasy, but deem man to be devoid of all reason should thy proposal of at least five-and-seventy in one hundred hold true.

HORATIO (to Hamlet): What should we do, my Lord?

HAMLET: Go to thy purpose, Horatio.

HORATIO: To what end, my Lord?

HAMLET: That you must teach me. But let me conjure you by the rights of our fellowship, by the consonance of our youth, but the obligation of our ever-preserved love, be even and direct with me, whether I am right or no.

(Horatio exits, followed by Polonius, leaving Hamlet to ponder alone.)

(The next day, Hamlet awaits anxiously the presence of his friend, Horatio. Polonius enters and places some books upon the table just a moment before Horatio enters.)

POLONIUS: So, Horatio, what is it thou didst reveal through thy deliberations?

HORATIO: In a random survey, for which purpose thou thyself sent me forth, I did discover that one-and-forty believe fervently that the spirits of the dead walk with us. Before my God, I might not this believe, without the sensible and true avouch of mine own eyes.

POLONIUS: Give thine own thoughts no tongue, Horatio. (Polonius turns to Hamlet.) But look to’t I charge you, my Lord. Come Horatio, let us go together, for this is not our test. (Horatio and Polonius leave together.)

HAMLET: To reject, or not reject, that is the question: whether ‘tis nobler in the mind to suffer the slings and arrows of outrageous statistics, or to take arms against a sea of data, and, by opposing, end them. (Hamlet resignedly attends to his task.)

(Curtain falls)

"Untitled," by Stephen Chen

I've often wondered how software is released and sold to the public. Ironically, I work for a company that sells products with known problems. Unfortunately, most of the problems are difficult to create, which makes them difficult to fix. I usually use the test program X, which tests the product, to try to create a specific problem. When the test program is run to make an error occur, the likelihood of generating an error is 1%.

So, armed with this knowledge, I wrote a new test program Y that will generate the same error that test program X creates, but more often. To find out if my test program is better than the original, so that I can convince the management that I'm right, I ran my test program to find out how often I can generate the same error. When I ran my test program 50 times, I generated the error twice. While this may not seem much better, I think that I can convince the management to use my test program instead of the original test program. Am I right?

• \(H_{0}: p = 0.01\)
• \(H_{a}: p > 0.01\)
• Let \(P′ =\) the proportion of errors generated
• Normal for a single proportion
• Decision: Reject the null hypothesis
• Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the proportion of errors generated is more than 0.01.

The“plus-4s” confidence interval is \((0.004, 0.144)\).

"Japanese Girls’ Names"

by Kumi Furuichi

It used to be very typical for Japanese girls’ names to end with “ko.” (The trend might have started around my grandmothers’ generation and its peak might have been around my mother’s generation.) “Ko” means “child” in Chinese characters. Parents would name their daughters with “ko” attaching to other Chinese characters which have meanings that they want their daughters to become, such as Sachiko—happy child, Yoshiko—a good child, Yasuko—a healthy child, and so on.

However, I noticed recently that only two out of nine of my Japanese girlfriends at this school have names which end with “ko.” More and more, parents seem to have become creative, modernized, and, sometimes, westernized in naming their children.

I have a feeling that, while 70 percent or more of my mother’s generation would have names with “ko” at the end, the proportion has dropped among my peers. I wrote down all my Japanese friends’, ex-classmates’, co-workers, and acquaintances’ names that I could remember. Following are the names. (Some are repeats.) Test to see if the proportion has dropped for this generation.

Ai, Akemi, Akiko, Ayumi, Chiaki, Chie, Eiko, Eri, Eriko, Fumiko, Harumi, Hitomi, Hiroko, Hiroko, Hidemi, Hisako, Hinako, Izumi, Izumi, Junko, Junko, Kana, Kanako, Kanayo, Kayo, Kayoko, Kazumi, Keiko, Keiko, Kei, Kumi, Kumiko, Kyoko, Kyoko, Madoka, Maho, Mai, Maiko, Maki, Miki, Miki, Mikiko, Mina, Minako, Miyako, Momoko, Nana, Naoko, Naoko, Naoko, Noriko, Rieko, Rika, Rika, Rumiko, Rei, Reiko, Reiko, Sachiko, Sachiko, Sachiyo, Saki, Sayaka, Sayoko, Sayuri, Seiko, Shiho, Shizuka, Sumiko, Takako, Takako, Tomoe, Tomoe, Tomoko, Touko, Yasuko, Yasuko, Yasuyo, Yoko, Yoko, Yoko, Yoshiko, Yoshiko, Yoshiko, Yuka, Yuki, Yuki, Yukiko, Yuko, Yuko.

"Phillip’s Wish," by Suzanne Osorio

My nephew likes to play

Chasing the girls makes his day.

He asked his mother

If it is okay

To get his ear pierced.

She said, “No way!”

To poke a hole through your ear,

Is not what I want for you, dear.

He argued his point quite well,

Says even my macho pal, Mel,

Has gotten this done.

It’s all just for fun.

C’mon please, mom, please, what the hell.

Again Phillip complained to his mother,

Saying half his friends (including their brothers)

Are piercing their ears

And they have no fears

He wants to be like the others.

She said, “I think it’s much less.

We must do a hypothesis test.

And if you are right,

I won’t put up a fight.

But, if not, then my case will rest.”

We proceeded to call fifty guys

To see whose prediction would fly.

Nineteen of the fifty

Said piercing was nifty

And earrings they’d occasionally buy.

Then there’s the other thirty-one,

Who said they’d never have this done.

So now this poem’s finished.

Will his hopes be diminished,

Or will my nephew have his fun?

• \(H_{0}: p = 0.50\)
• \(H_{a}: p < 0.50\)
• Let \(P′ =\) the proportion of friends that has a pierced ear.
• –1.70
• \(p\text{-value} = 0.0448\)
• Reason for decision: The \(p\text{-value}\) is less than 0.05. (However, they are very close.)
• Conclusion: There is sufficient evidence to support the claim that less than 50% of his friends have pierced ears.
• Confidence Interval: \((0.245, 0.515)\): The “plus-4s” confidence interval is \((0.259, 0.519)\).

"The Craven," by Mark Salangsang

Once upon a morning dreary

In stats class I was weak and weary.

Pondering over last night’s homework

Whose answers were now on the board

This I did and nothing more.

While I nodded nearly napping

Suddenly, there came a tapping.

As someone gently rapping,

Rapping my head as I snore.

Quoth the teacher, “Sleep no more.”

“In every class you fall asleep,”

The teacher said, his voice was deep.

“So a tally I’ve begun to keep

Of every class you nap and snore.

The percentage being forty-four.”

“My dear teacher I must confess,

While sleeping is what I do best.

The percentage, I think, must be less,

A percentage less than forty-four.”

This I said and nothing more.

“We’ll see,” he said and walked away,

And fifty classes from that day

He counted till the month of May

The classes in which I napped and snored.

The number he found was twenty-four.

At a significance level of 0.05,

Please tell me am I still alive?

Or did my grade just take a dive

Plunging down beneath the floor?

Upon thee I hereby implore.

Toastmasters International cites a report by Gallop Poll that 40% of Americans fear public speaking. A student believes that less than 40% of students at her school fear public speaking. She randomly surveys 361 schoolmates and finds that 135 report they fear public speaking. Conduct a hypothesis test to determine if the percent at her school is less than 40%.

• \(H_{0}: p = 0.40\)
• \(H_{a}: p < 0.40\)
• Let \(P′ =\) the proportion of schoolmates who fear public speaking.
• –1.01
• \(p\text{-value} = 0.1563\)
• Conclusion: There is insufficient evidence to support the claim that less than 40% of students at the school fear public speaking.
• Confidence Interval: \((0.3241, 0.4240)\): The “plus-4s” confidence interval is \((0.3257, 0.4250)\).

Sixty-eight percent of online courses taught at community colleges nationwide were taught by full-time faculty. To test if 68% also represents California’s percent for full-time faculty teaching the online classes, Long Beach City College (LBCC) in California, was randomly selected for comparison. In the same year, 34 of the 44 online courses LBCC offered were taught by full-time faculty. Conduct a hypothesis test to determine if 68% represents California. NOTE: For more accurate results, use more California community colleges and this past year's data.

According to an article in Bloomberg Businessweek , New York City's most recent adult smoking rate is 14%. Suppose that a survey is conducted to determine this year’s rate. Nine out of 70 randomly chosen N.Y. City residents reply that they smoke. Conduct a hypothesis test to determine if the rate is still 14% or if it has decreased.

• \(H_{0}: p = 0.14\)
• \(H_{a}: p < 0.14\)
• Let \(P′ =\) the proportion of NYC residents that smoke.
• –0.2756
• \(p\text{-value} = 0.3914\)
• At the 5% significance level, there is insufficient evidence to conclude that the proportion of NYC residents who smoke is less than 0.14.
• Confidence Interval: \((0.0502, 0.2070)\): The “plus-4s” confidence interval (see chapter 8) is \((0.0676, 0.2297)\).

The mean age of De Anza College students in a previous term was 26.6 years old. An instructor thinks the mean age for online students is older than 26.6. She randomly surveys 56 online students and finds that the sample mean is 29.4 with a standard deviation of 2.1. Conduct a hypothesis test.

Registered nurses earned an average annual salary of $69,110. For that same year, a survey was conducted of 41 California registered nurses to determine if the annual salary is higher than $69,110 for California nurses. The sample average was $71,121 with a sample standard deviation of $7,489. Conduct a hypothesis test.

• \(H_{0}: \mu = 69,110\)
• \(H_{0}: \mu > 69,110\)
• Let \(\bar{X} =\) the mean salary in dollars for California registered nurses.
• \(t = 1.719\)
• \(p\text{-value}: 0.0466\)
• Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the mean salary of California registered nurses exceeds $69,110.
• \(($68,757, $73,485)\)

La Leche League International reports that the mean age of weaning a child from breastfeeding is age four to five worldwide. In America, most nursing mothers wean their children much earlier. Suppose a random survey is conducted of 21 U.S. mothers who recently weaned their children. The mean weaning age was nine months (3/4 year) with a standard deviation of 4 months. Conduct a hypothesis test to determine if the mean weaning age in the U.S. is less than four years old.

Over the past few decades, public health officials have examined the link between weight concerns and teen girls' smoking. Researchers surveyed a group of 273 randomly selected teen girls living in Massachusetts (between 12 and 15 years old). After four years the girls were surveyed again. Sixty-three said they smoked to stay thin. Is there good evidence that more than thirty percent of the teen girls smoke to stay thin?

After conducting the test, your decision and conclusion are

• Reject \(H_{0}\): There is sufficient evidence to conclude that more than 30% of teen girls smoke to stay thin.
• Do not reject \(H_{0}\): There is not sufficient evidence to conclude that less than 30% of teen girls smoke to stay thin.
• Do not reject \(H_{0}\): There is not sufficient evidence to conclude that more than 30% of teen girls smoke to stay thin.
• Reject \(H_{0}\): There is sufficient evidence to conclude that less than 30% of teen girls smoke to stay thin.

A statistics instructor believes that fewer than 20% of Evergreen Valley College (EVC) students attended the opening night midnight showing of the latest Harry Potter movie. She surveys 84 of her students and finds that 11 of them attended the midnight showing.

At a 1% level of significance, an appropriate conclusion is:

• There is insufficient evidence to conclude that the percent of EVC students who attended the midnight showing of Harry Potter is less than 20%.
• There is sufficient evidence to conclude that the percent of EVC students who attended the midnight showing of Harry Potter is more than 20%.
• There is sufficient evidence to conclude that the percent of EVC students who attended the midnight showing of Harry Potter is less than 20%.
• There is insufficient evidence to conclude that the percent of EVC students who attended the midnight showing of Harry Potter is at least 20%.

Previously, an organization reported that teenagers spent 4.5 hours per week, on average, on the phone. The organization thinks that, currently, the mean is higher. Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test.

At a significance level of \(a = 0.05\), what is the correct conclusion?

• There is enough evidence to conclude that the mean number of hours is more than 4.75
• There is enough evidence to conclude that the mean number of hours is more than 4.5
• There is not enough evidence to conclude that the mean number of hours is more than 4.5
• There is not enough evidence to conclude that the mean number of hours is more than 4.75

Instructions: For the following ten exercises,

Hypothesis testing: For the following ten exercises, answer each question.

State the null and alternate hypothesis.

State the \(p\text{-value}\).

State \(\alpha\).

What is your decision?

Write a conclusion.

Answer any other questions asked in the problem.

According to the Center for Disease Control website, in 2011 at least 18% of high school students have smoked a cigarette. An Introduction to Statistics class in Davies County, KY conducted a hypothesis test at the local high school (a medium sized–approximately 1,200 students–small city demographic) to determine if the local high school’s percentage was lower. One hundred fifty students were chosen at random and surveyed. Of the 150 students surveyed, 82 have smoked. Use a significance level of 0.05 and using appropriate statistical evidence, conduct a hypothesis test and state the conclusions.

A recent survey in the N.Y. Times Almanac indicated that 48.8% of families own stock. A broker wanted to determine if this survey could be valid. He surveyed a random sample of 250 families and found that 142 owned some type of stock. At the 0.05 significance level, can the survey be considered to be accurate?

• \(H_{0}: p = 0.488\) \(H_{a}: p \neq 0.488\)
• \(p\text{-value} = 0.0114\)
• \(\alpha = 0.05\)
• Reject the null hypothesis.
• At the 5% level of significance, there is enough evidence to conclude that 48.8% of families own stocks.
• The survey does not appear to be accurate.

Driver error can be listed as the cause of approximately 54% of all fatal auto accidents, according to the American Automobile Association. Thirty randomly selected fatal accidents are examined, and it is determined that 14 were caused by driver error. Using \(\alpha = 0.05\), is the AAA proportion accurate?

The US Department of Energy reported that 51.7% of homes were heated by natural gas. A random sample of 221 homes in Kentucky found that 115 were heated by natural gas. Does the evidence support the claim for Kentucky at the \(\alpha = 0.05\) level in Kentucky? Are the results applicable across the country? Why?

• \(H_{0}: p = 0.517\) \(H_{0}: p \neq 0.517\)
• \(p\text{-value} = 0.9203\).
• \(\alpha = 0.05\).
• Do not reject the null hypothesis.
• At the 5% significance level, there is not enough evidence to conclude that the proportion of homes in Kentucky that are heated by natural gas is 0.517.
• However, we cannot generalize this result to the entire nation. First, the sample’s population is only the state of Kentucky. Second, it is reasonable to assume that homes in the extreme north and south will have extreme high usage and low usage, respectively. We would need to expand our sample base to include these possibilities if we wanted to generalize this claim to the entire nation.

For Americans using library services, the American Library Association claims that at most 67% of patrons borrow books. The library director in Owensboro, Kentucky feels this is not true, so she asked a local college statistic class to conduct a survey. The class randomly selected 100 patrons and found that 82 borrowed books. Did the class demonstrate that the percentage was higher in Owensboro, KY? Use \(\alpha = 0.01\) level of significance. What is the possible proportion of patrons that do borrow books from the Owensboro Library?

The Weather Underground reported that the mean amount of summer rainfall for the northeastern US is at least 11.52 inches. Ten cities in the northeast are randomly selected and the mean rainfall amount is calculated to be 7.42 inches with a standard deviation of 1.3 inches. At the \(\alpha = 0.05 level\), can it be concluded that the mean rainfall was below the reported average? What if \(\alpha = 0.01\)? Assume the amount of summer rainfall follows a normal distribution.

• \(H_{0}: \mu \geq 11.52\) \(H_{a}: \mu < 11.52\)
• \(p\text{-value} = 0.000002\) which is almost 0.
• At the 5% significance level, there is enough evidence to conclude that the mean amount of summer rain in the northeaster US is less than 11.52 inches, on average.
• We would make the same conclusion if alpha was 1% because the \(p\text{-value}\) is almost 0.

A survey in the N.Y. Times Almanac finds the mean commute time (one way) is 25.4 minutes for the 15 largest US cities. The Austin, TX chamber of commerce feels that Austin’s commute time is less and wants to publicize this fact. The mean for 25 randomly selected commuters is 22.1 minutes with a standard deviation of 5.3 minutes. At the \(\alpha = 0.10\) level, is the Austin, TX commute significantly less than the mean commute time for the 15 largest US cities?

A report by the Gallup Poll found that a woman visits her doctor, on average, at most 5.8 times each year. A random sample of 20 women results in these yearly visit totals

3; 2; 1; 3; 7; 2; 9; 4; 6; 6; 8; 0; 5; 6; 4; 2; 1; 3; 4; 1

At the \(\alpha = 0.05\) level can it be concluded that the sample mean is higher than 5.8 visits per year?

• \(H_{0}: \mu \leq 5.8\) \(H_{a}: \mu > 5.8\)
• \(p\text{-value} = 0.9987\)
• At the 5% level of significance, there is not enough evidence to conclude that a woman visits her doctor, on average, more than 5.8 times a year.

According to the N.Y. Times Almanac the mean family size in the U.S. is 3.18. A sample of a college math class resulted in the following family sizes:

5; 4; 5; 4; 4; 3; 6; 4; 3; 3; 5; 5; 6; 3; 3; 2; 7; 4; 5; 2; 2; 2; 3; 2

At \(\alpha = 0.05\) level, is the class’ mean family size greater than the national average? Does the Almanac result remain valid? Why?

The student academic group on a college campus claims that freshman students study at least 2.5 hours per day, on average. One Introduction to Statistics class was skeptical. The class took a random sample of 30 freshman students and found a mean study time of 137 minutes with a standard deviation of 45 minutes. At α = 0.01 level, is the student academic group’s claim correct?

• \(H_{0}: \mu \geq 150\) \(H_{0}: \mu < 150\)
• \(p\text{-value} = 0.0622\)
• \(\alpha = 0.01\)
• At the 1% significance level, there is not enough evidence to conclude that freshmen students study less than 2.5 hours per day, on average.
• The student academic group’s claim appears to be correct.

9.7: Hypothesis Testing of a Single Mean and Single Proportion

• Open access
• Published: 07 May 2024

Effects of improved amino acid balance diet on lysine mammary utilization, whole body protein turnover and muscle protein breakdown on lactating sows

• Sai Zhang 1 , 2 ,
• Juan C. Marini 3 ,
• Vengai Mavangira 4 ,
• Andrew Claude 4 ,
• Julie Moore 1 ,
• Mahmoud A. Mohammad 3 &
• Nathalie L. Trottier 1 , 5  

Journal of Animal Science and Biotechnology volume  15 , Article number:  65 ( 2024 ) Cite this article

256 Accesses

Metrics details

The study objective was to test the hypothesis that low crude protein (CP) diet with crystalline amino acids (CAA) supplementation improves Lys utilization efficiency for milk production and reduces protein turnover and muscle protein breakdown. Eighteen lactating multiparous Yorkshire sows were allotted to 1 of 2 isocaloric diets (10.80 MJ/kg net energy): control (CON; 19.24% CP) and reduced CP with “optimal” AA profile (OPT; 14.00% CP). Sow body weight and backfat were recorded on d 1 and 21 of lactation and piglets were weighed on d 1, 14, 18, and 21 of lactation. Between d 14 and 18, a subset of 9 sows (CON = 4, OPT = 5) was infused with a mixed solution of 3-[methyl- 2 H 3 ]histidine (bolus injection) and [ 13 C]bicarbonate (priming dose) first, then a constant 2-h [ 13 C]bicarbonate infusion followed by a 6-h primed constant [1- 13 C]lysine infusion. Serial blood and milk sampling were performed to determine plasma and milk Lys enrichment, Lys oxidation rate, whole body protein turnover, and muscle protein breakdown.

Over the 21-d lactation period, compared to CON, sows fed OPT had greater litter growth rate ( P < 0.05). Compared to CON, sows fed OPT had greater efficiency of Lys ( P < 0.05), Lys mammary flux ( P < 0.01) and whole-body protein turnover efficiency ( P < 0.05). Compared to CON, sows fed OPT tended to have lower whole body protein breakdown rate ( P = 0.069). Muscle protein breakdown rate did not differ between OPT and CON ( P = 0.197).

Feeding an improved AA balance diet increased efficiency of Lys and reduced whole-body protein turnover and protein breakdown. These results imply that the lower maternal N retention observed in lactating sows fed improved AA balance diets in previous studies may be a result of greater partitioning of AA towards milk rather than greater body protein breakdown.

The increasing availability of crystalline amino acid (CAA) at competitive costs relative to protein ingredients allows for reduction of excessive dietary nitrogen (N) and improving AA balance [ 1 ]. Several studies have shown that improving dietary AA balance in lactating sows leads to greater milk casein yield [ 2 , 3 ] and utilization efficiency of N and essential amino acid (EAA) [ 4 , 5 ] while dramatically mitigating N losses and ammonia emissions to the environment [ 2 ]. Lysine efficiency values previously reported [ 4 , 5 , 6 ] were estimated based on lean mass change during lactation. This approach yielded similar efficiency estimates for Val based on isotopic method [ 7 ]. Lysine utilization efficiency values in lactation using an isotopic approach have not been reported.

The increased apparent AA efficiency may be at the expense of sow body weight (BW) loss and reduced maternal N retention whereby partitioning of dietary AA and energy towards the mammary glands appears to be favoured [ 3 , 5 , 8 ]. Preserving maternal N pool during the lactation period is important since maternal body protein and lipid loss can affect subsequent production performance. Loss in performances may include delayed estrus [ 9 ], reduction of piglet birth weight and litter uniformity [ 10 , 11 ], and prolonged interval from weaning to successful pregnancy [ 12 ], thus compromising the overall life span production efficiency. It is unknown whether the reduced maternal N retention previously reported [ 3 , 5 ] in sows fed an improved AA balance diet was a result of greater maternal body protein breakdown. In addition, whole body and muscle protein breakdown rates in lactating sows are unknown and such values are critical to assess at a mechanistic level the impact of improved dietary AA balance on body protein dynamic. Isotope technique allows for better mechanistic understanding of protein dynamics, including protein turnover rate, AA flux and muscle protein breakdown in humans [ 13 ] and animals [ 14 ].

We hypothesized that low CP diet with improved AA balance would increase milk yield through improving efficiency of Lys for milk and increasing maternal body and muscle protein breakdown. The objectives were to (1) measure whole body protein dynamics and (2) estimate Lys utilization efficiency for milk synthesis.

Materials and methods

Dietary treatments.

The NRC model [ 6 ] was used to estimate requirements for AA, net energy (NE), calcium (Ca) and phosphorus (P). The requirements were predicted based on the following parameters: sow BW of 210 kg after parturition, parity number of 2 and above, average daily intake of 6 kg/d, litter size of 10, piglet average daily gain (ADG) of 280 g/d over a 21-d lactation period, and an ambient temperature of 20 °C. The model predicted a minimum sow BW loss of 7.5 kg and the protein to lipid ratio in the model was adjusted to the minimum allowable value of near zero. The model predicted SID Lys requirement of 0.90% and NE requirement of 2,580 kcal/kg.

A control diet (CON) was formulated using corn and soybean meal as the only sources of Lys to meet the SID Lys requirement (0.90%) and consequently contained 19.24% CP and a SID Val concentration 0.77% which was near the NRC (2012) requirement of 0.79%. All other EAA SID contents were in excess relative to NRC (2012). The SID AA values of feed ingredients were referred to NRC (2012). A second diet was formulated to improve AA balance [ 5 ], and referred to as optimal diet (OPT) throughout the manuscript. Fermentable fiber was high in CON due to high content of soybean meal with 24.88% fermentable fiber [ 6 ]. Thus, the same fiber source (soy hulls) was supplemented in OPT, and levels of fermentable fiber were consistent between CON and OPT. Ingredients and calculated nutrient composition of CON and OPT diets are presented in Table 1 . Analyzed total (hydrolysate) and free AA concentrations are presented in Table 2 , in order to verify the precision of diet formulation. The analyzed N concentration corresponded to a CP% of 18.44 compared to a calculated value of 19.24% CP. Therefore, the analyzed CP concentration value is used in the heading for the remainder of tables.

Animals and feeding

The study was conducted at the Michigan State University Swine Teaching and Research Center. A total of 18 purebred multiparous (parity 2+) Yorkshire sows were moved to conventional farrowing crates between d 105 and 107 of gestation, grouped by parity, and randomly assigned to 1 of 2 dietary treatments within parity groups (CON, n = 9; OPT, n = 9). The study was conducted over 3 blocks of time, with 6, 6, and 5 sows in each block, respectively. One sow in CON from block 3 was removed due to poor feed intake that was deemed unrelated to the dietary treatments. Sows were adapted to the experimental diets (2.2 kg/d) 4 to 6 d before the expected farrowing date. Following farrowing, sows feed allowance progressively increased from 1.88 kg/d on d 1 to 7.44 kg/d at d 21, according to the NRC model [ 6 ], with a targeted ADFI of 6.0 kg/d over the 21-d lactation period. Feed was provided daily in 3 equal meals (0700, 1300, and 1900) with feed intake and refusal recorded daily before the morning meal. On infusion days (between d 14 and 18), the 0700 and 1300 meals were divided into 6 aliquots fed every 2 h from 0700 to 1700. Water was freely accessible to sows and piglets. Litters were aimed to be standardized to 11 piglets within the first 24 h after farrowing with the objective of weaning 10 piglets per sow. Injection of iron and surgical castration of male were conducted on d 1 and 7, respectively, according to the institutional research farm protocol. No creep feed was supplied to the piglets. Body weight and backfat thickness [ 5 ] of sows were recorded on d 1 and 21, and litter weights were recorded on d 1, 14, 18 and 21. Milk yield was estimated for peak lactation (between d 14 and 18) [ 5 ]. Prediction equation for milk yield during peak lactation is as follows [ 15 ]: \(\mathrm{Daily}\;\mathrm{milk}\;\mathrm{yield}\;(\text{g}/\text{d})=\mathrm{littersize}\times(582+1.168\times\text{ADG}+0.00425\times\text{ADG}^2)\)

Bilateral ear vein catheterization

A subset of 10 sows (5 sows per treatment) was used for the catheterization and infusion protocol. An ear vein catheter was placed in each ear, with one ear serving as the infusion line and the other as the sampling line. For the length of the catheterization procedure, piglets were removed and transferred to an empty adjacent stall with a heat lamp. The sows were restrained with a rope snare and remained in their farrowing stall where sedation was induced. For sedation, Telazol was reconstituted with 2.5 mL of 100 mg/mL ketamine and 2.5 mL of 100 mg/mL xylazine to a volume of 5 mL. This sedative mixture was administered i.m. in the brachiocephalicus muscle approximately 6 cm caudal to the ear, at a dosage of 0.1 mL/4.537 kg body weight. Sows were carefully assisted to facilitate laying in ventral recumbence. Sedation lasted for 45 to 60 min. The depth of anesthesia was monitored by the degree of muscle relaxation and respiration rate (i.e., 10 to 25 breaths/min).

The entire dorsal surface of both ears was prepared for aseptic placement of the ear vein catheters. The skin was scrubbed gently with 10% betadine solution followed with 70% isopropyl alcohol. The hair covering the skin area caudal to the ear and dorsal to the neck was clipped using a professional clipper to ensure a good adhesion of veterinary adhesive tape to the skin (described below).

A pre-cut 61-cm, round tip, medical grade microbore intravascular tubing (1.65 mm o.d., 1.02 mm i.d.) with hydromer coating (Access Technology Corp., Skokie, IL, USA) was prefilled at the time of catheterization with heparinized saline (30 IU/mL) before insertion. A hand tourniquet was applied at the base of the ear to distend the medial and lateral branches of the auricular vein. Either vein was used for catheterization. A short-term stylet catheter (14G, 5.08 cm, Safety IV catheter; B. Braun Melsungen AG, Germany) was inserted into the vein with the needle bevel facing up. Upon appearance of blood, the vein was gently occluded, and the needle rotated 180° to angle the bevel facing down. While holding the needle in place, the stylet catheter was gently pushed into the vein through the needle. Once the stylet was in place, the needle was removed, and the intravascular tubing was inserted through the stylet and pushed for approximately 30 cm caudally to reach the external jugular vein, and the catheter verified for patency at this point. Small sections of tape (5.1 cm wide, ZONAS® porous tape, Johnson & Johnson Consumer Companies, Inc., Skillman, NJ, USA) were affixed to the remaining section of intravascular tubing and sutured to the skin to secure the tubing in place. The stylet catheter was also sutured (Monocryl, CP-1, 36 mm, 1/2c; Ethicon Inc., USA) to the skin at the point of entry. Gauze was placed over each sutured sites and held in position by wrapping the ear with elastic adhesive tape. A connector was used to join the intravascular tubing to a long tubing extension (approximately 120 cm). A blunt-end needle adapter with an adaptor injection cap and a male luer lock was placed onto the distal end of the tubing extension. The same vein catheterization procedure was done on the other ear. A final layer of elastic adhesive tape (7.5 cm wide, 3M veterinary adhesive tape) was used to wrap each ear into a gently folded cone shape and to affix extension tubing directly onto the clipped skin surface. The extension tubing ran from the ears to the dorsal region of the neck, caudally to the ears and cranial to the shoulders and the free end (approximately 100 cm) rolled up and placed in a handmade denim protective pouch mounted on 4.0-cm thick foam material. The pouch was kept in place by gluing the foam directly onto the skin with Livestock ID Tag Cement (W.J. Ruscoe Company, Akron, OH, USA). Catheters were verified for patency once more and the lines were filled with sterile saline, coiled, and placed in the pouch until used for infusion and blood sampling. The entire procedure was done following sterile techniques and lasted 45 to 90 min per sow. As soon as sows were able to stand, 15-cm wide elastic bandage (Novation ® , Hartmann USA, Inc., Rock Hill, SC, USA) was wrapped over the pouch and around the neck and thorax in at least 3 layers in the shape of a life vest (crisscross) to protect the pouch. Thereafter, the catheters were verified for patency and flushed with sterilized heparinized saline (30 IU/mL) twice per day.

Catheters were removed after all infusions and blood sampling were completed (blood sampling lasted for 3 d for 3MH; Fig. 1 ). The elastic bandaging was removed, and the elastic adhesive tape was carefully pulled to expose the sutures. The sutures were cut with small surgical scissors, the catheters were gently pulled out of the ear veins, and pressure was applied over the insertion sites to accelerate coagulation. The remaining adhesive tape was then carefully removed, and the pouch was freed from the foam which remained on the sow. Rectal temperature was recorded from the day of catheterization and for 3 d following removal of catheters.

Plasma isotopic enrichment of 3-[methyl- 2 H 3 ]histidine following 3-[methyl- 2 H 3 ]histidine bolus infusion during peak lactation (between d 14 and 18) for sows fed control (CON; 18.4% CP; n = 4) and optimal (OPT; 14.0% CP; n = 4) diets. Plasma isotopic enrichment of 3-[methyl- 2 H 3 ]histidine differed between diets ( P < 0.001) and time points ( P < 0.001), with no interaction between diet and time ( P = 0.894). Standard error of the mean (SEM) = 0.214

Preparation of isotope solutions

Tracers were weighed, dissolved in saline and the solution sterilized by filtration through Millipore Steriflip filters (0.22 μm). For each sow, the following stock solutions were prepared: 3-[methyl- 2 H 3 ]histidine (183 μmol in 20 mL saline for bolus injection), [ 13 C]bicarbonate (368 μmol in 20 mL saline for prime and 736 μmol in 30 mL saline for 2-h infusion), and [1- 13 C]lysine (1.28 mmol in 30 mL saline for prime and 9.00 mmol in 60 mL saline for 6-h infusion). The bolus dose of 3-[methyl- 2 H 3 ]histidine (3MH) was calculated based on 20% pool size of 3MH in sows [ 16 , 17 ]. The infusion rate of [1- 13 C]lysine was calculated based on average flux of lysine (25 mmol/h) in lactating sows [ 7 ] with the aim of 2% enrichment. The priming dose of [1- 13 C]lysine was aiming for 1.5 mmol (1 h of infusion), and 1.28 mmol was the actual amount according to weight balance.

The solution of [ 13 C]bicarbonate was freshly prepared to minimize loss of 13 CO 2 . Specifically, [ 13 C]bicarbonate was weighed and dissolved in 20-mL 3-[methyl- 2 H 3 ]histidine solution in the morning of infusion day (Fig. 2 ). The 3-[methyl- 2 H 3 ]histidine (3MH) was used to estimate muscle protein breakdown, and the [ 13 C]bicarbonate was used to prime the CO 2 pool to accelerate the estimation of lysine oxidation rate. The primed-constant infusion of [1- 13 C]lysine was used to estimate lysine utilization by the mammary gland and the lysine flux in the whole body.

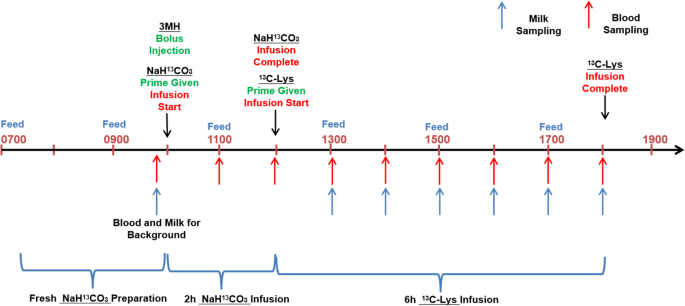
Timeline of isotope infusion and sampling (infusion day was within d 18–21)

Infusion protocol

The timeline for infusion is presented in Fig. 2 . Actual infusion day varied between d 14 and 18 due to real time patency of catheter. For lysine balance (Table 3 ) and body protein kinetics (Table 6 ), the actual infusion days were 17.0 ± 1.0 for CON and 17.0 ± 1.4 for OPT. For 3MH kinetics, the actual infusion days were 17.3 ± 1.0 for CON and 16.8 ± 1.5 for OPT. Pumps (Genie Touch TM , Kent Scientific Corp, Torrington, CT, USA) and syringes were placed on a large and stable plastic board laid above the farrowing stall. Following the priming dose, the infusion line was immediately attached to the syringe mounted to the pump to begin the constant infusion. The sampling line was coiled and stored in the pouch until used for blood sampling.

The mixed 20 mL saline solution containing 3-[methyl- 2 H 3 ]histidine (183 μmol) and [ 13 C]bicarbonate (368 μmol) was given through the infusion line as a bolus injection. The [ 13 C]bicarbonate in this infusate was used as a priming dose. After bolus injection, a constant 2-h infusion of [ 13 C]bicarbonate (368 μmol/h) began. The 2-h [ 13 C]bicarbonate infusion was followed by a 6-h primed constant [1- 13 C]lysine infusion (1.50 mmol/h) (Fig. 2 ).

Blood sampling

The timeline for blood sampling is presented in Fig. 2 . For analysis of plasma 3-[methyl- 2 H 3 ]histidine concentrations and estimation of muscle protein breakdown rate, blood samples were collected through the sampling line at 0 (immediately after termination of the bolus infusion), 5, 10, 15, 30 and 45 min and 1, 2, 3, 4, 5, 6, 7, 8, 24, 34, 48, 58 and 72 h post bolus infusion. Blood samples (0.5 mL) were transferred into 500-μL BD microtainer tubes (K 2 EDTA) and centrifuged (1,500 × g at 4 °C for 5 min). The plasma was extracted and stored in 1.5-mL microcentrifuge tubes at −20 °C until analysis.

For analysis of plasma [1- 13 C]lysine concentrations and estimation of whole-body Lys flux, blood samples (0.5 mL) were collected prior to infusion for background enrichment and at 1, 2, 3, 4, 5 and 6 h from the start of [1- 13 C]lysine infusion (Fig. 2 ).

For analysis of blood CO 2 concentrations, blood samples (2 mL) were collected prior to [ 13 C]bicarbonate-prime infusion for background, and at 1, 2, 3, 4, 5, 6, 7 and 8 h following the prime infusion. Blood samples were injected into evacuated vacutainer tubes (Becton Dickinson, Plymouth, UK) previously prepared with 2 mL of phosphoric acid, immediately mixed, and cooled to room temperature. The CO 2 was then transferred from evacuated vacutainers to Exetainer tubes (Labco Breath Tube, UK) by using pure nitrogen gas as medium until analysis.

Milk sampling protocol

The timeline for milk sampling is presented in Fig. 2 . Milk samples were taken between d 14 and 18 during the infusion protocol. Milk was sampled before infusion for background enrichment, and at 1, 2, 3, 4, 5 and 6 h of primed constant infusion of Lys.

For each milk sampling period, piglets were separated from the sows for 1 h in an empty adjacent farrowing crate with no access to water, and sows were administered 1 mL of oxytocin (20 IU/mL oxytocin, sodium chloride 0.9% w/v, and chlorobutanol 0.5% w/v, VetTek, Blue Springs, MO, USA) through the sampling catheter immediately after blood sampling. The catheter was rinsed with 2 mL of saline solution to ensure oxytocin reached the blood circulation. A total of 30-mL milk was manually collected across all glands and stored in 2 separate 15-mL tubes (polypropylene centrifuge tubes with screw cap, Denville Scientific, Swedesboro, NJ, USA). Piglets were immediately returned to sows to complete nursing and empty the mammary glands. Piglets were removed after nursing and kept separate from the sow until the next milk sampling time, 1 h later.

Isotope analysis

Plasma and milk [1- 13 C]lysine and 3-[methyl- 2 H 3 ]histidine (after acid hydrolysis) were determined as their dansyl derivatives by HESI LC-MS as previously described [ 18 ]. The following m/z transitions were monitored: 613→379 and 614→380 for [1- 13 C]lysine and 403→124 and 406→127 for 3-[methyl- 2 H 3 ]histidine. Determination of blood 13 CO 2 enrichment was performed by IRMS (Delta+XL IRMS coupled with GasBench-II peripheral device, Thermo-Quest Finnigan, Bremen, Germany) as previously described [ 19 ].

Nutrient analysis

Feed samples were analyzed for gross energy (GE) by bomb calorimetry (Parr Instrument Inc., Moline, IL, USA). Dry matter and N in feed samples were analyzed as previously described [ 5 ]. Dietary AA analysis [AOAC Official Method 982.30 E (a,b,c), 45.3.05, 2006] was performed by the Agricultural Experiment Station Chemical Laboratories (University of Missouri-Columbia, Columbia, MO, USA) as outlined in previous reports [ 5 ].

Calculations

The following assumptions were made during calculation:

Priming dose of isotope was assumed to mix with pool instantly.

The appearance of unlabeled bicarbonate was constant during the time of primed-constant infusion of bicarbonate (2 h) and that of [1- 13 C]lysine (6 h).

[1- 13 C]lysine cannot be synthesized once 1-carbon was lost to CO 2 , thus rate of lysine decarboxylation represented rate of lysine breakdown.

Kinetics of plasma lysine was an indicator of kinetics of whole body protein.

The indicator AA (lysine) was assumed to be oxidised for maintenance or incorporated into milk protein without other metabolic pathway.

Lysine oxidation

The enrichment of CO 2 during the period of primed-constant infusion of [ 13 C]bicarbonate was calculated as follows (Eq. 1 ):

Where “infusion \({\text{rate}}_{\text{H}{}^{13}\text{CO}_3^-}\) ” represents the infusion rate (368 μmol/h) of [ 13 C]bicarbonate, and “ \(\text{Ra}_{\text{HCO}_{3}^-}\) ” represents the rate of appearance of unlabeled bicarbonate (baseline) in the body.

The enrichment of CO 2 during the period of primed-constant infusion of [1- 13 C]lysine was calculated as follows (Eq. 2 ):

Where “ \({\text{Ra}}_{\text{H}{}^{13}\text{CO}_3^-}\) ” represents the rate of appearance of labeled bicarbonate from [1- 13 C]lysine oxidation, and “ \(\text{Ra}_{\text{HCO}_{3}^-}\) ” represents the rate of appearance of unlabeled bicarbonate (baseline) in the body as in Eq. 1 .

The enrichment of lysine during the period of primed-constant infusion of [1- 13 C]lysine was calculated as follows (Eq. 3 ):

Where Ra Lys represents the rate of appearance of unlabeled lysine in the body.

Lysine oxidation was estimated as follows (Eq. 4 ):

Whole body protein breakdown and synthesis

Whole body protein breakdown (PB) and synthesis (PS) were mirrored by Lys dynamics (Table 3 and Fig. 3 ).

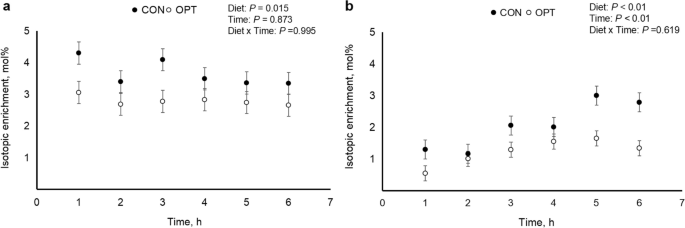
Isotopic enrichment of [1- 13 C]lysine in plasma (panel a ) and milk (panel b ) over 6 h during peak lactation (d 14 to 18) for sows fed control (CON; 18.4% CP; n = 3) and optimal (OPT; 14.0% CP; n = 5) diets

The PB and PS were calculated as follows (Eqs. 5 and 6 ):

Where 146.19 g/mol is the molar weight of isotopic Lys, 6.74% is the average weight percentage of Lys in the sow’s body protein [ 6 ].

The average milk protein concentration of 5.16% was used [ 6 ]. Milk yield was estimated according to Theil et al. [ 15 ].

Muscle protein breakdown

Data was expressed as tracer to tracee ratio (TTR). Multiexponential models were fitted to the data (Eq. 10 and Fig. 1 ). Residual inspection and pseudo-R 2 were used to determine the most parsimonious model that best fitted the data from each individual sow. Area under the curve (AUC; TTR•h) was calculated using the parameters from the multiexponential equation (Eq. 11 and Table 4 ) and 3MH rate of appearance (Ra; μmol/kg/h) was calculated by dividing the dose administered (μmol/kg) by AUC (Eq. 12 and Table 4 ). Half-life (h) was determined using the rate constant corresponding to the tail of the curve (Eq. 13 , Table 4 , and Fig. 1 ).

Muscle protein breakdown rate (%/d) was calculated as follows (Eq. 14 ):

Where total protein bound 3MH pool = muscle protein mass (g) × 3.8742 μmol 3MH/g protein and muscle protein mass = 8.21% × sow BW (kg) [ 20 ].

Muscle protein breakdown (g/d), was calculated as follows (Eq. 15 ):

Efficiency of lysine for lactation

Lysine utilization efficiency for lactation was calculated as follows (Eq. 16 ):

Statistical analysis

Data were confirmed for homogeneity of residual variance and normality of residuals by Mixed Procedures and Univariate Procedures of SAS 9.4 (SAS Inst. Inc., Cary, NC, USA) before ANOVA analysis (Mixed model procedures).

For the lysine balance and protein kinetic estimation, two sows from CON were removed from the data set. In one case, both ear vein catheters lost patency at the time of infusion, and in the other case, one of the 2 ear vein catheters lost patency. The latter sow, however, was used for the estimation of muscle protein breakdown, which only required one catheter. Therefore, the number of sows for the lysine balance data and protein kinetic estimation were 5 and 3 for OPT and CON, respectively.

For the analysis of lysine enrichment in plasma and milk, the following model was used:

The Enrichment of lysine depended on the fixed effects of diet ( OPT vs. CON ) , and sampling hour, with hour included as repeated measurement. The random effects included block and individual sow . The interactive effect of diet × hour was also included .

For the analysis of lysine balance, body protein breakdown and synthesis, and muscle protein breakdown rate, identified as “Response”, the following model was used:

The Response depended on the fixed effects of diet ( OPT vs. CON ) . The random effects included block and individual sow .

Differences between treatments were declared at P < 0.05 and tendencies at P ≤ 0.1.

Lactation performance

Lactation performance during the 21-d period and milk yield and nutrient concentrations between d 14 and 18 are presented in Table 5 . Sow initial BW and ADFI did not differ between OPT and CON diets. Litter growth rate of sows fed OPT diet was greater than those fed CON diet ( P < 0.05).

Lysine balance and efficiency of utilization

Lysine balance values are presented in Table 3 . The SID Lys intake, Lys oxidation, flux and Lys associated with protein synthesis did not differ between OPT and CON diets (Table 3 ). Compared to sows fed CON, those fed OPT had greater efficiency of Lys (0.62 vs. 0.50; P < 0.05) and tended to have a lower ( P = 0.069) released Lys associated with protein breakdown.

Whole body protein synthesis, whole body protein breakdown and fractional muscle protein breakdown

Whole body protein breakdown rate and synthesis rate tended to be lower ( P = 0.069 and P = 0.109, respectively) and protein turnover efficiency (synthesis: breakdown) tended to be greater ( P = 0.060) in sows fed OPT compared to those fed CON (Table 6 ). Whole body protein net synthesis (i.e., whole body protein synthesis − whole body protein breakdown) did not differ between OPT and CON diets.

For estimation of muscle protein breakdown rate, an additional sow in OPT treatment lost patency of both catheters, therefore the number of sows was 4 in each of the treatment. A 3-exponential model best fitted the 3MH decaying curve (Fig. 1 ) and pseudo- R 2 were > 0.995. Muscle protein breakdown rate and fractional muscle protein breakdown rate (%) did not differ ( P = 0.197) between sows fed OPT and CON diets (4.84% and 5.59%, respectively) (Table 6 ).

Enrichment of lysine

Lysine enrichment in plasma (panel a) and milk (panel b) is presented in Fig. 3 . The lysine enrichment in plasma did not differ between diets and time. Lysine enrichment in milk was lower ( P < 0.01) in sows fed OPT compared to sows fed CON diets and differed over time ( P < 0.01). There was no interaction between diets and time.

fDynamics of 3-[methyl- 2 H 3 ]histidine

Plasma isotopic enrichment of 3-MH following 3-MH bolus infusion is presented in Fig. 1 , and relevant dynamic parameters are presented in Table 4 . Plasma isotopic enrichment of 3-MH of sows fed CON was lower ( P < 0.001) than that for OPT diet. Time effects of 3-MH were significant ( P < 0.001) in both treatments of CON and OPT, and no interaction effect between diet and time ( P = 0.894) was detected.

Previous studies showed that lactating sows fed low CP diets with CAA supplementation had greater milk casein yield [ 2 , 3 ], and utilization efficiency of N and EAA [ 4 , 5 ]. The improvement of milk yield however was at the expense of sow BW and maternal N retention [ 3 , 5 ]. Zhang et al. [ 8 ] suggested that feeding diets with improved AA balance triggered nutrient repartitioning to milk at the expense of maternal adipose tissue rather than protein tissue. Maternal body fat loss affects subsequent reproductive performance and compromises the overall production efficiency during the sow’s life span [ 21 ]. Therefore, commercial implementation of diets with aggressing reduction in CP with CAA supplementation to achieve improved AA balance will not only depend on their impact on lactation performance and production efficiency but also on ensuring that long-term maternal body protein and lipid reserves are not compromised.

The mechanisms behind the reduced maternal N retention in sows fed improved AA balance diets reported in earlier studies [ 4 , 5 ] are unclear. Reduced maternal body protein synthesis, greater body protein breakdown, or a combination of thereof can dictate maternal N balance during lactation. In this study however, BW and backfat change during lactation did not differ between OPT and CON sows. Of note, sows fed OPT had no change in BW with a small loss in backfat while sows fed CON gained 5.5 kg with no change in backfat. Body protein kinetics in this study (Table 6 ) dictated that whole body protein net synthesis (whole body protein synthesis − whole body protein breakdown) of sows fed CON and OPT were close (1,041.72 vs. 1,022.90 g/d), but note that whole body protein net synthesis of lactating sows included milk protein yield and maternal protein deposition. Milk protein yield was greater in OPT than CON as mirrored by litter growth rate (Table 5 ). Consequently, maternal protein deposition was greater in CON than OPT which aligns with the observation that body weight increased in sows fed CON while there was no change of body weight in sows fed OPT (Table 5 ). In addition, increased milk production in sows fed OPT suggest that OPT diet led sows to partition more dietary nutrient towards milk than maternal reserves, in other words, sows fed OPT were more motivated to produce milk even at the expense of maternal deposition.

This study used Lys as representative AA of body protein to analyze whole body protein turnover. In essence, Lys flux in the blood was contributed by dietary Lys intake and Lys released by body protein breakdown, and free Lys in the blood could be directed to either Lys oxidation or Lys incorporation into body protein (Fig. 4 ). Thus, body protein breakdown and synthesis could be estimated by measuring Lys flux in blood and Lys oxidation. The carbon dioxide released by Lys oxidation remains in the blood bicarbonate pool and mixed with carbon dioxide from other substrate oxidation (Fig. 5 ). By priming the bicarbonate pool, the baseline production rate of carbon dioxide can be estimated based on bicarbonate enrichment and constant infusion rate of labeled bicarbonate during prime-constant infusion of bicarbonate (Eq. 1 ). The release of labeled carbon dioxide due to labeled Lys oxidation was proportional to the baseline production rate of carbon dioxide according to enrichment of bicarbonate during prime-constant infusion of Lys (Eqs. 2 and  3 ).

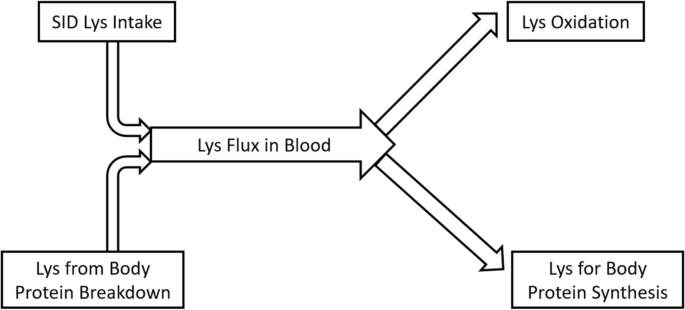
Diagram of lysine balance in lactating sows at fed state

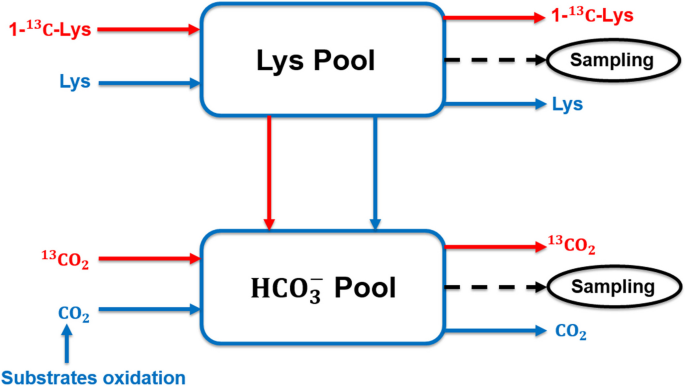
Representation of a two-pool model to estimate lysine oxidation

Milk protein synthesis represents the difference between whole body protein synthesis and breakdown, assuming that maternal protein retention is close to zero, since maternal tissue mobilization is majorly comprised of body fat rather than body protein [ 5 , 8 ]. According to this assumption, milk protein output rate measured by isotopic technique (Eq. 8 ) was 1,023 to 1,042 g/d, which aligns well with a previous study where 957 g/d milk protein synthesis was reported using a N balance approach [ 5 ]. When compared to traditional method where milk protein synthesis is the product of milk yield and milk protein concentration (645 to 675 g/d; Eq. 9 ), the isotopic-predicted milk protein synthesis (1,023 to 1,042 g/d) appears overestimated. Guan et al. [ 7 ] reported milk protein synthesis of 575 g/d as the net balance between sow whole mammary protein synthesis (975 g/d) and breakdown rate (400 g/d), corroborating the values reported here (645–675 g/d) using the traditional method. Nitrogen balance techniques tend to overestimate actual nitrogen retention [ 22 , 23 ], as observed herein with the isotope technique (Eq. 8 ). Note that the estimated muscle protein breakdown rate according to 3MH method in this study was 960 to 1,261 g/d (Eq. 15 ), which was greater than the protein breakdown rate (650 to 1,051 g/d; Eq. 8 ) based on the Lys flux. On the other hand, milk protein synthesis rate per metabolic BW (BW 0.75 ) were 10.25 and 9.85 g/d/kg 0.75 for OPT and CON, respectively in this study, supporting a previously reported value of 11.57 g/d/kg 0.75 (using Val as representative AA) [ 24 ]. Thus, overestimation of milk protein synthesis (Eq. 8 ) was majorly attributed to an underestimation of protein breakdown rather than overestimation of protein synthesis. The underestimation of body protein breakdown according to Lys flux (Eq. 5 ) may be partially due to the tendency to overestimate feed intake [ 23 ], although feed waste was minimized in this study. Nevertheless, it is also important to note that estimated muscle protein breakdown (15.4 to 17.8 μmol/kg/d; Eq. 15 ; Table 6 ) and fractional breakdown (4.84–5.59%/d; Eq. 14 ; Table 6 ) in this study was greater than those reported for lactating gilt (3.4%/d, 12.0 μmol/kg/d) using the same 3MH method [ 17 ]. It is speculated that the multiparous lactating sow may mobilize body protein more readily compared to the lactating gilt.

In this study, milk protein yield of lactating sows fed OPT diet did not differ from those fed control diet neither when an isotopic method nor the traditional method were used. Although there was no difference between whole body protein synthesis and breakdown, the absolute values of protein synthesis and breakdown were both lower in sows fed OPT diet compared to CON diet, suggesting less whole-body protein turnover in sows fed the OPT diet. In support of this view, previous studies also showed a decreased protein breakdown rate reflected by lower urea nitrogen output when sows were fed reduced protein diets [ 3 , 5 ]. The biological process of protein turnover is energetically costly [ 1 , 25 ]. Zhang et al. [ 5 ] reported feeding sows with an improved AA balance diet was associated with higher energy efficiency, lending support to the current observation.

The Lys efficiency for sows fed different levels of dietary protein based on the NRC [ 6 ] approach was previously determined [ 4 , 5 ], with greater efficiency values (0.68 and 0.66, respectively) found during peak lactation (d 14–18) in sows fed low CP diets balanced with CAA. Herein, greater Lys utilization efficiency values, determined using a different approach, were also found in sows fed OPT (0.62) compared to CON (0.50). The estimation of Lys utilization efficiency was based on Lys balance parameters, i.e., Lys flux in blood, SID Lys intake and Lys oxidation (Fig. 4 ), and the assumption that net protein synthesis (protein synthesis − protein breakdown) represents milk protein synthesis, with negligible maternal body retention. The true Lys utilization efficiency is the ratio between “Lys in milk” and “Lys for milk”, thus Lys utilized for maintenance should be excluded in the denominator [ 6 ] as follows:

In this study, the whole-body Lys flux was corrected by excluding Lys oxidation (Eq. 16 ), which corresponds to the Lys requirement for maintenance. Guan et al. [ 7 ] reported that Lys flux partitioned to the mammary glands as percentage of whole-body Lys flux was 56% in sows fed a conventional diet, which is comparable to the Lys efficiency values of 50% to 62% observed in this study.

Feeding lactation sows with an improved AA balance diet did not affect milk protein yield and reduced whole-body protein turnover. The reduced whole-body protein turnover resulted from a decrease in both whole-body protein synthesis and breakdown rate, with a tendency for greater protein synthesis to protein breakdown ratio (2.65 vs. 2.02).

Efficiency of Lys was also greater during peak lactation, together suggesting higher efficiency of energy use. These results imply that the lower maternal N retention observed in lactating sows fed improved AA balance diets in previous studies may be a result of greater partitioning of AA towards milk rather than greater body protein breakdown.

Availability of data and materials

All data generated or analyzed during this study are available from the corresponding author on request.

Abbreviations

Average daily gain

Area under the curve

Body weight

Crystalline amino acid

Crude protein

Essential amino acid

Standard error of the mean

Standardized ileal digestibility

3-[methyl- 2 H 3 ]histidine

Zhang S, Trottier NL. Dietary protein reduction improves the energetic and amino acid efficiency in lactating sows. Anim Prod Sci. 2019;59:1980–90.

Article   CAS   Google Scholar  

Chamberlin DP. Impacts of reducing dietary crude protein with crystalline amino acid supplementation on lactating sow performance, nitrogen utilization and heat production. East Lansing: MS Thesis, Michigan State University; 2017.

Google Scholar  

Huber L, de Lange CFM, Krogh U, Chamberlin D, Trottier NL. Impact of feeding reduced crude protein diets to lactating sows on nitrogen utilization. J Anim Sci. 2015;93:5254–64.

Article   CAS   PubMed   Google Scholar  

Huber L, de Lange CFM, Ernst CW, Krogh U, Trottier NL. Impact of improving dietary amino acid balance for lactating sows on efficiency of dietary amino acid utilization and transcript abundance of genes encoding lysine transporters in mammary tissue. J Anim Sci. 2016;94:4654–65.

Zhang S, Qiao M, Trottier NL. Feeding a reduced protein diet with a near ideal amino acid profile improves amino acid efficiency and nitrogen utilization for milk production in sows. J Anim Sci. 2019;97:3882–97.

Article   PubMed   PubMed Central   Google Scholar  

NRC. Nutrient requirements of swine. 11th ed. Washington, DC: National Academy Press; 2012.

Guan X, Bequette BJ, Calder G, Ku PK, Ames KN, Trottier NL. Amino acid availability affects amino acid flux and protein metabolism in the porcine mammary gland. J Nutr. 2002;132:1224–34.

Zhang S, Johnson JS, Qiao M, Trottier NL. Reduced protein diet with near ideal amino acid profile improves energy efficiency and mitigate heat production associated with lactation in sows. J Anim Sci Biotechno. 2020;11:4.

Article   Google Scholar  

Quesnel H. Nutritional and lactational effects on follicular development in the pig. In: Rodriguez Martinez H, Vallet JL, Ziecik AJ, editors. Control of pig reproduction VIII. Nottingham: Notthingham University Press; 2009. p. 121–34.

Wientjes JGM, Soede NM, van den Brand H, Kemp B. Nutritionally induced relationships between insulin levels during the weaning-to-ovulation interval and reproductive characteristics in multiparous sows: I. Luteinizing hormone, follicle development, oestrus and ovulation. Reprod Domest Anim. 2012;47:53–61.

Wientjes JGM, Soede NM, van den Brand H, Kemp B. Nutritionally induced relationships between insulin levels during the weaning-to-ovulation interval and reproductive characteristics in multiparous sows: II. Luteal development, progesterone and conceptus development and uniformity. Reprod Domest Anim. 2012;47:62–8.

Wientjes JGM, Soede NM, Knol EF, van den Brand H, Kemp B. Piglet birth weight and litter uniformity: effects of weaning-to-pregnancy interval and body condition changes in sows of different parities and crossbred lines. J Anim Sci. 2013;91(5):2099–107.

Kim IY, Schutzler S, Schrader A, Spencer H, Kortebein P, Deutz NEP, et al. Quantity of dietary protein intake, but not pattern of intake, affects net protein balance primarily through differences in protein synthesis in older adults. Am J Physiol-Endoc M. 2015;308(1):E21.

CAS   Google Scholar  

Claydon AJ, Thom MD, Hurst JL, Beynon RJ. Protein turnover: measurement of proteome dynamics by whole animal metabolic labelling with stable isotope labelled amino acids. Proteomics. 2012;12(8):1194–206.

Theil PK, Nielsen TT, Kristensen NB, Labouriau R, Danielsen V, Lauridsen C, et al. Estimation of milk production in lactating sows by determination of deuterated water turnover in three piglets per litter. Acta Agric Scand. 2002;52:221–32.

Rathmacher JA, Link GA, Nissen SL. Measuring of 3-methylhistidine production in lambs by using compartmental-kinetic analysis. Br J Nutr. 1993;69:1.

Trottier NL. Protein metabolism in the lactating sow. Urbana-Champaign: PhD Dissertation, University of Illinois; 1995.

Marini JC. Quantitative analysis of 15 N-labeled positional isomers of glutamine and citrulline via electrospray ionization tandem mass spectrometry of their dansyl derivatives. Rapid Commun Mass Spectrom. 2011;25(9):1291–6.

Verbruggen S, Sy J, Gordon WE, Hsu J, Wu M, Chacko S, et al. Ontogeny of methionine utilization and splanchnic uptake in critically ill children. Am J Physiol Endocrinol Metab. 2009;297(5):E1046–55.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Rathmacher JA, Nissen SL, Paxton RE, Anderson DB. Estimation of 3-methylhistidine production in pigs by compartmental analysis. J Anim Sci. 1996;74(1):46–56.

De Rensis F, Gherpelli M, Superchi P, Kirkwood RN. Relationships between backfat depth and plasma leptin during lactation and sow reproductive performance after weaning. Anim Reprod Sci. 2005;90(1–2):95–100.

Article   PubMed   Google Scholar  

Kopple JD. Uses and limitations of the balance technique. JPEN J Parenter Enteral Nutr. 1987;11(5 Suppl):79S–85S.

CAS   PubMed   Google Scholar  

Spanghero M, Kowalski ZM. Updating analysis of nitrogen balance experiments in dairy cows. J Dairy Sci. 2021;104(7):7725–37.

Hanigan MD, France J, Mabjeesh SJ, McNabb WC, Bequette BJ. High rates of mammary tissue protein turnover in lactating goats are energetically costly. J Nutr. 2009;139(6):1118–27.

Wolfe RR. Radioactive and stable isotope tracers in biomedicine: principles and practice of kinetic analysis. Somerset, NJ: John Wiley & Sons Inc; 1992.

Download references

This work was financially supported by funds from the USDA-NIFA (award number 2014-67015-21832).

Author information

Authors and affiliations.

Department of Animal Science, Michigan State University, East Lansing, 48824, USA

Sai Zhang, Julie Moore & Nathalie L. Trottier

State Key Laboratory of Swine and Poultry Breeding Industry, Key Laboratory of Animal Nutrition and Feed Science in South China, Ministry of Agriculture and Rural Affairs, Guangdong Provincial Key Laboratory of Animal Breeding and Nutrition, Institute of Animal Science, Guangdong Academy of Agricultural Sciences, Guangzhou, 510640, PR China

USDA/ARS Children’s Nutrition Research Center and Pediatric Critical Care Medicine, Department of Pediatrics, Baylor College of Medicine, Houston, TX, 77030, USA

Juan C. Marini & Mahmoud A. Mohammad

Department of Large Animal Clinical Sciences, Michigan State University, East Lansing, MI, 48824, USA

Vengai Mavangira & Andrew Claude

Present address: Department of Animal Science, Cornell University, Frank Morrison Hall, 507 Tower Road, Ithaca, NY, 14853-4801, USA

Nathalie L. Trottier

You can also search for this author in PubMed   Google Scholar

Contributions

Conceptualization, NLT and SZ; Methodology, NLT, SZ, JCM, VM, AC, JM, and MAM; Formal analysis, SZ and JCM; Writing, SZ and NLT; Supervision, NLT; Funding acquisition, NLT.

Corresponding author

Correspondence to Nathalie L. Trottier .

Ethics declarations

Ethics approval and consent to participate.

All procedures were approved by the Michigan State University Institutional Animal Care and Use Committee (AUF # 05/16-091-00) and followed the American Association for Laboratory Animal Science guidelines.

Consent for publication

Not applicable.

Competing interests

The authors declare that they have no competing interests.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Zhang, S., Marini, J.C., Mavangira, V. et al. Effects of improved amino acid balance diet on lysine mammary utilization, whole body protein turnover and muscle protein breakdown on lactating sows. J Animal Sci Biotechnol 15 , 65 (2024). https://doi.org/10.1186/s40104-024-01020-9

Download citation

Received : 07 December 2023

Accepted : 05 March 2024

Published : 07 May 2024

DOI : https://doi.org/10.1186/s40104-024-01020-9

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Lactating sows
• Protein breakdown
• Protein turnover
• Reduced protein diet

Journal of Animal Science and Biotechnology

ISSN: 2049-1891

• Submission enquiries: Access here and click Contact Us
• General enquiries: [email protected]