Difference between Random Selection and Random Assignment
Random selection and random assignment are commonly confused or used interchangeably, though the terms refer to entirely different processes. Random selection refers to how sample members (study participants) are selected from the population for inclusion in the study. Random assignment is an aspect of experimental design in which study participants are assigned to the treatment or control group using a random procedure.
Random selection requires the use of some form of random sampling (such as stratified random sampling , in which the population is sorted into groups from which sample members are chosen randomly). Random sampling is a probability sampling method, meaning that it relies on the laws of probability to select a sample that can be used to make inference to the population; this is the basis of statistical tests of significance .


Discover How We Assist to Edit Your Dissertation Chapters
Aligning theoretical framework, gathering articles, synthesizing gaps, articulating a clear methodology and data plan, and writing about the theoretical and practical implications of your research are part of our comprehensive dissertation editing services.
- Bring dissertation editing expertise to chapters 1-5 in timely manner.
- Track all changes, then work with you to bring about scholarly writing.
- Ongoing support to address committee feedback, reducing revisions.
Random assignment takes place following the selection of participants for the study. In a true experiment, all study participants are randomly assigned either to receive the treatment (also known as the stimulus or intervention) or to act as a control in the study (meaning they do not receive the treatment). Although random assignment is a simple procedure (it can be accomplished by the flip of a coin), it can be challenging to implement outside of controlled laboratory conditions.
A study can use both, only one, or neither. Here are some examples to illustrate each situation:
A researcher gets a list of all students enrolled at a particular school (the population). Using a random number generator, the researcher selects 100 students from the school to participate in the study (the random sample). All students’ names are placed in a hat and 50 are chosen to receive the intervention (the treatment group), while the remaining 50 students serve as the control group. This design uses both random selection and random assignment.
A study using only random assignment could ask the principle of the school to select the students she believes are most likely to enjoy participating in the study, and the researcher could then randomly assign this sample of students to the treatment and control groups. In such a design the researcher could draw conclusions about the effect of the intervention but couldn’t make any inference about whether the effect would likely to be found in the population.
A study using only random selection could randomly select students from the overall population of the school, but then assign students in one grade to the intervention and students in another grade to the control group. While any data collected from this sample could be used to make inference to the population of the school, the lack of random assignment to be in the treatment or control group would make it impossible to conclude whether the intervention had any effect.
Random selection is thus essential to external validity, or the extent to which the researcher can use the results of the study to generalize to the larger population. Random assignment is central to internal validity, which allows the researcher to make causal claims about the effect of the treatment. Nonrandom assignment often leads to non-equivalent groups, meaning that any effect of the treatment might be a result of the groups being different at the outset rather than different at the end as a result of the treatment. The consequences of random selection and random assignment are clearly very different, and a strong research design will employ both whenever possible to ensure both internal and external validity .
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Statistics and probability
Course: statistics and probability > unit 6.
- Introduction to experiment design
- Matched pairs experiment design
- The language of experiments
- Principles of experiment design
- Experiment designs
Random sampling vs. random assignment (scope of inference)
- (Choice A) Just the residents involved in Hilary's study. A Just the residents involved in Hilary's study.
- (Choice B) All residents in Hilary's town. B All residents in Hilary's town.
- (Choice C) All residents in Hilary's country. C All residents in Hilary's country.
- (Choice A) Yes A Yes
- (Choice B) No B No
- (Choice A) Just the residents in Hilary's study. A Just the residents in Hilary's study.
| Random sampling | Not random sampling | |
|---|---|---|
| Can determine causal relationship in population. | Can determine causal relationship in that sample only. | |
| Can detect relationships in population, but cannot determine causality. | Can detect relationships in that sample only, but cannot determine causality. |
Want to join the conversation?
Random Allocation & Random Selection | Definition & Examples
Jennifer Roling is a seasoned educator with nearly 30 years of teaching and curriculum development experience. She earned her undergraduate degree in childhood development from Truman State University and followed that up with a MA in Language Education from Indiana University. She has designed dozens of courses for students of all ages.
Chelsea has a bachelor's degree in biology and works in online content writing.
Are random selection and random allocation the same thing?
No. Random selection, also called random sampling, is the process of choosing all the participants in a study. After the participants are chosen, random allocation, also called random assignment, can be used to choose which participants will be in the control group and which participants will receive the experimental treatment.
What is an example of random selection?
A high school wants to interview students about their experience with online bullying. The principal pulls 20 names out of a hat that was filled with the names of all the students in the school and interviews those students.
Table of Contents
What is random selection, random allocation, random allocation vs random selection, lesson summary.
Because it is impossible for researchers to conduct a study on every single person in the world, they use smaller selections of people to predict the results for everyone. The entire group of people that the researcher is trying to describe is called the population. This may be all humans, but it may also be a subset of people such as all post-menopausal women or all college students or even Mr. Garrett's fourth-grade class.
Once the population has been defined, the researchers must figure out how they will choose who will participate in the study. This is where random selection comes in. Random selection , also called random sampling , is a way of choosing who participates in a study in which each member of the population has an equal chance of being selected. There are several types of random selection.
- Simple Random Sampling - This is the easiest method of random selection. Subjects are randomly chosen either manually or by a computer. For example, all members are written on pieces of paper and put in a hat. The researcher pulls out names to select the participants. Computer programs are able to do the same thing.
- Stratified Random Sampling - In this method, the population is first divided into subgroups before the names are drawn from the hats. For example, a given population may have an equal number of men and women. If researchers want to be sure that the final sample has an equal number of male and female participants, they will first put the male participants' names in one hat and the female participants' names in another hat. Then they will pick half their sample from the female hat and half from the female hat.
- Cluster Random Sampling - This method is similar to stratified in that the population is first divided into subgroups then the sample is randomly chosen from the subgroups. Often these clusters are naturally occurring. For example, the school board may choose to use homerooms as clusters for a questionnaire. The name of each homeroom will be put into a hat and the required number of clusters will be randomly drawn. Then the questionnaire will be administered to the students in the selected homerooms.
- Systematic Random Sampling- If researchers have a list of names, they may select participants by simply choosing them based on their position in the list. For example, they might decide every third name will be a participant.
To unlock this lesson you must be a Study.com Member. Create your account

An error occurred trying to load this video.
Try refreshing the page, or contact customer support.
You must c C reate an account to continue watching
Register to view this lesson.
As a member, you'll also get unlimited access to over 88,000 lessons in math, English, science, history, and more. Plus, get practice tests, quizzes, and personalized coaching to help you succeed.
Get unlimited access to over 88,000 lessons.
Already registered? Log in here for access
Resources created by teachers for teachers.
I would definitely recommend Study.com to my colleagues. It’s like a teacher waved a magic wand and did the work for me. I feel like it’s a lifeline.
You're on a roll. Keep up the good work!
Just checking in. are you still watching.
- 0:05 Random Selection
- 1:53 Random Allocation
- 3:27 Differences and Uses
- 5:00 Lesson Summary
In an experiment, there will be another step after the sample has been determined. Experimental design always requires at least two separate groups: The control group that receives no treatment, and the experimental, or treatment, group that receives the treatment. In a well-designed experiment, the researcher will want to randomly decide who gets the treatment and who does not. This helps prevent systemic differences in the groups and improves the validity of the study. This is random allocation , or random assignment , and all the methods used for random selection can be used for random allocation.
For example, a pharmacy company may choose every other name on its sample list to choose who gets the new medication and who gets the placebo (systematic). If the company is interested in tracking gender differences in the new drug, it may choose to first separate the list into male and female groups before randomly selecting the control and experimental subjects (stratified).
Although there are similarities between random selection and random allocation, they are used to accomplish different goals and the terms should not be used interchangeably. Random selection is used to choose all the participants in a study; random allocation, on the other hand, is used to decide who will receive treatment in an experiment. It is important to note that observational or correlational studies do not issue any treatment so random allocation is never used in them, although random selection can be used. Additionally, individual studies may utilize both random selection and random allocation, just one of them, or neither. The example below illustrates this.
Research Example
A company that makes dietary supplements wants to see the effects of using its new product on blood sugar. Here are some potential ways the participants could be selected:
- 100 names are chosen at random from the company's client list. From those 100 names, 50 are randomly chosen to test the new supplement and the other 50 receive a placebo, and all 100 subjects have their blood sugar levels tested multiple times throughout the study. RANDOM SELECTION and RANDOM ALLOCATION
- 100 names are chosen at random from the company's client list. The company allows the first 50 clients that respond to get the new supplement for free. The remaining 50 receive a placebo, and all 100 subjects have their blood sugar levels tested multiple times throughout the study. RANDOM SELECTION ONLY
- The company sends out an email asking for volunteers to try a new product. They accept the first 100 as participants, then randomly pick 50 to get the new supplement and 50 to get the placebo, all 100 subjects have their blood sugar levels tested multiple times throughout the study. RANDOM ALLOCATION ONLY
- The company sends out an email asking for volunteers to try a new product. The company allows the first 50 clients that respond to get the new supplement for free. The next 50 receive a placebo, and all 100 subjects have their blood sugar levels tested multiple times throughout the study. NEITHER
Random selection and random allocation are sometimes confused by people who do not understand them. Although similar methods of randomization can be used in both situations, they are not the same thing. Random selection , or random sampling, is a method used to choose a sample from a larger population. For example, when senators want to know how their constituents feel about an issue, they may call randomly selected phone numbers from their state to get a general idea of what people think.
Random allocation , or random assignment, is useful in experimental situations in which different people will be administered different treatments or conditions. By using randomization to choose which participants will receive which conditions, researchers are able to minimize any differences between the groups. In any research situation, researchers will have to decide whether using random selection and/or using random allocation are practical. Since randomization increases the validity of an experiment, researchers should strive to use it as often as possible.
Video Transcript
Random selection.
Aubree is conducting an experiment. She wants to find out if oranges consumed on a regular basis will help improve the chances of someone staying healthy during the winter months. Aubree will have to design a research experiment to find the answer to this question. As she is designing her research, she will need to understand random selection and random allocation .
In this lesson, you will learn about random selection and random allocation, how to use them and the differences between the two. First, let's discuss random selection.
Random selection is the method of choosing a sample of members from the population to participate in a study. Basically, random selection is the way Aubree will choose who will be a part of her study. Most studies use some sort of random sampling to select participants. There are different ways you can select participants for a study.
First, Aubree will need to decide on her population. A population is all members of a specified group. For example, let's say that Aubree wants to study the effects of oranges on college students. This means that her population will be all college students in the world. Of course, it's hard to conduct a study of this size. We can solve this problem using random selection. Aubree can get a sample of her population by selecting students at a local college for her study.
A sample is a part of a population used to describe the whole group. For example, Aubree can conduct her study with a random selection of students in certain classes at the college, or she can select every other student that is willing to be a part of the study.
There are many different ways you can get a sample from your population. These include random sampling, simple random sampling, cluster sampling, stratified sampling, and systematic sampling. Now that we have covered random selection, let's move on to random allocation.
Remember, Aubree is studying the effects of orange consumption on college students. She wants to know if consuming oranges on a regular basis will help improve the chances of someone staying healthy during the winter months.
As such, Aubree has to compare two groups of students: those that consume oranges on a regular basis and those that consume oranges on an irregular basis or not at all. Aubree will have to use a control group and a treatment group because she wants to see the effects of orange consumption and will need to compare two groups.
The control group is the group that remains untreated throughout the duration of an experiment. For example, in Aubree's experiment the students that do not consume oranges on a regular basis would be the control group.
The treatment is the variable in an experiment that is used on an experimental group. For example, the oranges in Aubree's experiment would be the treatment, and the experimental group would be whomever is selected to receive the treatment. This is where random allocation comes in.
Random allocation is the method used to select members of a sample to receive the treatment in an experiment. Random allocation is the way Aubree will select her experimental group, or the group that will consume oranges in the experiment. She can select this group using similar methods that she used with random sampling. For example, she can write all of the participants' names on a piece of paper and randomly select half of the names from a hat. The names selected would be the experimental group. Now let's discuss the differences and uses of random selection and random allocation.
Differences and Uses
You can use random allocation, random selection, both, or neither in a study. Aubree's experiment used both methods. There are a few things to keep in mind with this. Random allocation is only used for experimental studies with a control and a treatment. If you only use this method, then you did not randomly select the sample of your study. For example, let's say that out of convenience, Aubree asks people that do not eat oranges to participate in her study. This would not be random selection because she isn't selecting members randomly out of her population, but she could still use random allocation to find the experimental and control groups.
If Aubree did not want to find the cause and effect of orange consumption but simply wanted to see if there is a correlation between people that consume oranges, those that don't consume oranges, and the person's overall health, then she could use random selection for her participants. This would be an observational study because she would only be collecting data from the participant's natural eating patterns, not experimenting with the effects of orange consumption. Observational studies only use random selection; they do not use random allocation.
Aubree could also potentially use neither random selection nor random allocation in her study. For example, she could ask a few of her college friends to participate in the study. Then, she could have the participants that like eating oranges be part of the experimental group and the participants that do not like eating oranges be part of the control group. This study uses neither random selection nor random allocation.
Both random selection and random allocation are important parts of research and collecting data. Random selection is the method of selecting a sample from the population to participate in a study. Basically, random selection is the way a researcher chooses the participants in a study. This requires the researcher to identify the population and the sample. A population is all members of a specified group. Once you know the population, you can use random selection to determine the sample. A sample is a part of a population used to describe the whole group.
Random allocation is the method used to select members of a sample to receive the treatment in an experiment. This is how a researcher will determine the control and the experimental group. The control group is the group that remains untreated throughout the duration of an experiment, and the treatment is the variable in an experiment that is used on an experimental group.
A study can have any combination of random allocation and random selection or have neither. Remember, random allocation is only used for experimental studies with a control and a treatment, and observational studies only use random selection.
Unlock Your Education
See for yourself why 30 million people use study.com, become a study.com member and start learning now..
Already a member? Log In
Recommended Lessons and Courses for You
Related lessons, related courses, recommended lessons for you.

Random Allocation & Random Selection | Definition & Examples Related Study Materials
- Related Topics
Browse by Courses
- High School Algebra II: Homeschool Curriculum
- College Mathematics Remediation
- High School Geometry: Homeschool Curriculum
- Geometry: Credit Recovery
- High School Geometry Textbook
- Algebra I: Credit Recovery
- Remedial Algebra I
- High School Precalculus: Homeschool Curriculum
- Calculus: Homework Help Resource
- Study.com SAT Math Test Section: Review & Practice
- Holt McDougal Larson Geometry: Online Textbook Help
- College Algebra Textbook
- College Preparatory Mathematics: Help and Review
- Calculus: Tutoring Solution
- Precalculus: High School
Browse by Lessons
- Random Sampling in Psychology | Definition, Purpose & Benefits
- Random Assignment in Psychology | Definition, Purpose & Examples
- Random Assignment in Research: Definition and Importance
- Operations with Fractions | Steps & Examples
- Solving Polynomial Equations in the Complex Field
- How to Model & Solve Problems Using Nonlinear Functions
- Linear Programming Definition, Model & Examples
- Interpreting Computer Solutions of Linear Programming Models
- The Role of Probability Distributions, Random Numbers & the Computer in Simulations
- Monte Carlo Simulation | Overview, Analysis & Examples
- Applications of Integer Linear Programming: Fixed Charge, Capital Budgeting & Distribution System Design Problems
- Using Linear Programming to Solve Problems
- The Importance of Extreme Points in Problem Solving
- Graphical Sensitivity Analysis for Variable Linear Programming Problems
- Handling Transportation Problems & Special Cases
Create an account to start this course today Used by over 30 million students worldwide Create an account
Explore our library of over 88,000 lessons
- Foreign Language
- Social Science
- See All College Courses
- Common Core
- High School
- See All High School Courses
- College & Career Guidance Courses
- College Placement Exams
- Entrance Exams
- General Test Prep
- K-8 Courses
- Skills Courses
- Teacher Certification Exams
- See All Other Courses
- Create a Goal
- Create custom courses
- Get your questions answered
Random Assignment in Psychology: Definition & Examples
Julia Simkus
Editor at Simply Psychology
BA (Hons) Psychology, Princeton University
Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.
Learn about our Editorial Process
Saul Mcleod, PhD
Editor-in-Chief for Simply Psychology
BSc (Hons) Psychology, MRes, PhD, University of Manchester
Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.
Olivia Guy-Evans, MSc
Associate Editor for Simply Psychology
BSc (Hons) Psychology, MSc Psychology of Education
Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.
In psychology, random assignment refers to the practice of allocating participants to different experimental groups in a study in a completely unbiased way, ensuring each participant has an equal chance of being assigned to any group.
In experimental research, random assignment, or random placement, organizes participants from your sample into different groups using randomization.
Random assignment uses chance procedures to ensure that each participant has an equal opportunity of being assigned to either a control or experimental group.
The control group does not receive the treatment in question, whereas the experimental group does receive the treatment.
When using random assignment, neither the researcher nor the participant can choose the group to which the participant is assigned. This ensures that any differences between and within the groups are not systematic at the onset of the study.
In a study to test the success of a weight-loss program, investigators randomly assigned a pool of participants to one of two groups.
Group A participants participated in the weight-loss program for 10 weeks and took a class where they learned about the benefits of healthy eating and exercise.
Group B participants read a 200-page book that explains the benefits of weight loss. The investigator randomly assigned participants to one of the two groups.
The researchers found that those who participated in the program and took the class were more likely to lose weight than those in the other group that received only the book.
Importance
Random assignment ensures that each group in the experiment is identical before applying the independent variable.
In experiments , researchers will manipulate an independent variable to assess its effect on a dependent variable, while controlling for other variables. Random assignment increases the likelihood that the treatment groups are the same at the onset of a study.
Thus, any changes that result from the independent variable can be assumed to be a result of the treatment of interest. This is particularly important for eliminating sources of bias and strengthening the internal validity of an experiment.
Random assignment is the best method for inferring a causal relationship between a treatment and an outcome.
Random Selection vs. Random Assignment
Random selection (also called probability sampling or random sampling) is a way of randomly selecting members of a population to be included in your study.
On the other hand, random assignment is a way of sorting the sample participants into control and treatment groups.
Random selection ensures that everyone in the population has an equal chance of being selected for the study. Once the pool of participants has been chosen, experimenters use random assignment to assign participants into groups.
Random assignment is only used in between-subjects experimental designs, while random selection can be used in a variety of study designs.
Random Assignment vs Random Sampling
Random sampling refers to selecting participants from a population so that each individual has an equal chance of being chosen. This method enhances the representativeness of the sample.
Random assignment, on the other hand, is used in experimental designs once participants are selected. It involves allocating these participants to different experimental groups or conditions randomly.
This helps ensure that any differences in results across groups are due to manipulating the independent variable, not preexisting differences among participants.
When to Use Random Assignment
Random assignment is used in experiments with a between-groups or independent measures design.
In these research designs, researchers will manipulate an independent variable to assess its effect on a dependent variable, while controlling for other variables.
There is usually a control group and one or more experimental groups. Random assignment helps ensure that the groups are comparable at the onset of the study.
How to Use Random Assignment
There are a variety of ways to assign participants into study groups randomly. Here are a handful of popular methods:
- Random Number Generator : Give each member of the sample a unique number; use a computer program to randomly generate a number from the list for each group.
- Lottery : Give each member of the sample a unique number. Place all numbers in a hat or bucket and draw numbers at random for each group.
- Flipping a Coin : Flip a coin for each participant to decide if they will be in the control group or experimental group (this method can only be used when you have just two groups)
- Roll a Die : For each number on the list, roll a dice to decide which of the groups they will be in. For example, assume that rolling 1, 2, or 3 places them in a control group and rolling 3, 4, 5 lands them in an experimental group.
When is Random Assignment not used?
- When it is not ethically permissible: Randomization is only ethical if the researcher has no evidence that one treatment is superior to the other or that one treatment might have harmful side effects.
- When answering non-causal questions : If the researcher is just interested in predicting the probability of an event, the causal relationship between the variables is not important and observational designs would be more suitable than random assignment.
- When studying the effect of variables that cannot be manipulated: Some risk factors cannot be manipulated and so it would not make any sense to study them in a randomized trial. For example, we cannot randomly assign participants into categories based on age, gender, or genetic factors.
Drawbacks of Random Assignment
While randomization assures an unbiased assignment of participants to groups, it does not guarantee the equality of these groups. There could still be extraneous variables that differ between groups or group differences that arise from chance. Additionally, there is still an element of luck with random assignments.
Thus, researchers can not produce perfectly equal groups for each specific study. Differences between the treatment group and control group might still exist, and the results of a randomized trial may sometimes be wrong, but this is absolutely okay.
Scientific evidence is a long and continuous process, and the groups will tend to be equal in the long run when data is aggregated in a meta-analysis.
Additionally, external validity (i.e., the extent to which the researcher can use the results of the study to generalize to the larger population) is compromised with random assignment.
Random assignment is challenging to implement outside of controlled laboratory conditions and might not represent what would happen in the real world at the population level.
Random assignment can also be more costly than simple observational studies, where an investigator is just observing events without intervening with the population.
Randomization also can be time-consuming and challenging, especially when participants refuse to receive the assigned treatment or do not adhere to recommendations.
What is the difference between random sampling and random assignment?
Random sampling refers to randomly selecting a sample of participants from a population. Random assignment refers to randomly assigning participants to treatment groups from the selected sample.
Does random assignment increase internal validity?
Yes, random assignment ensures that there are no systematic differences between the participants in each group, enhancing the study’s internal validity .
Does random assignment reduce sampling error?
Yes, with random assignment, participants have an equal chance of being assigned to either a control group or an experimental group, resulting in a sample that is, in theory, representative of the population.
Random assignment does not completely eliminate sampling error because a sample only approximates the population from which it is drawn. However, random sampling is a way to minimize sampling errors.
When is random assignment not possible?
Random assignment is not possible when the experimenters cannot control the treatment or independent variable.
For example, if you want to compare how men and women perform on a test, you cannot randomly assign subjects to these groups.
Participants are not randomly assigned to different groups in this study, but instead assigned based on their characteristics.
Does random assignment eliminate confounding variables?
Yes, random assignment eliminates the influence of any confounding variables on the treatment because it distributes them at random among the study groups. Randomization invalidates any relationship between a confounding variable and the treatment.
Why is random assignment of participants to treatment conditions in an experiment used?
Random assignment is used to ensure that all groups are comparable at the start of a study. This allows researchers to conclude that the outcomes of the study can be attributed to the intervention at hand and to rule out alternative explanations for study results.
Further Reading
- Bogomolnaia, A., & Moulin, H. (2001). A new solution to the random assignment problem . Journal of Economic theory , 100 (2), 295-328.
- Krause, M. S., & Howard, K. I. (2003). What random assignment does and does not do . Journal of Clinical Psychology , 59 (7), 751-766.
Related Articles
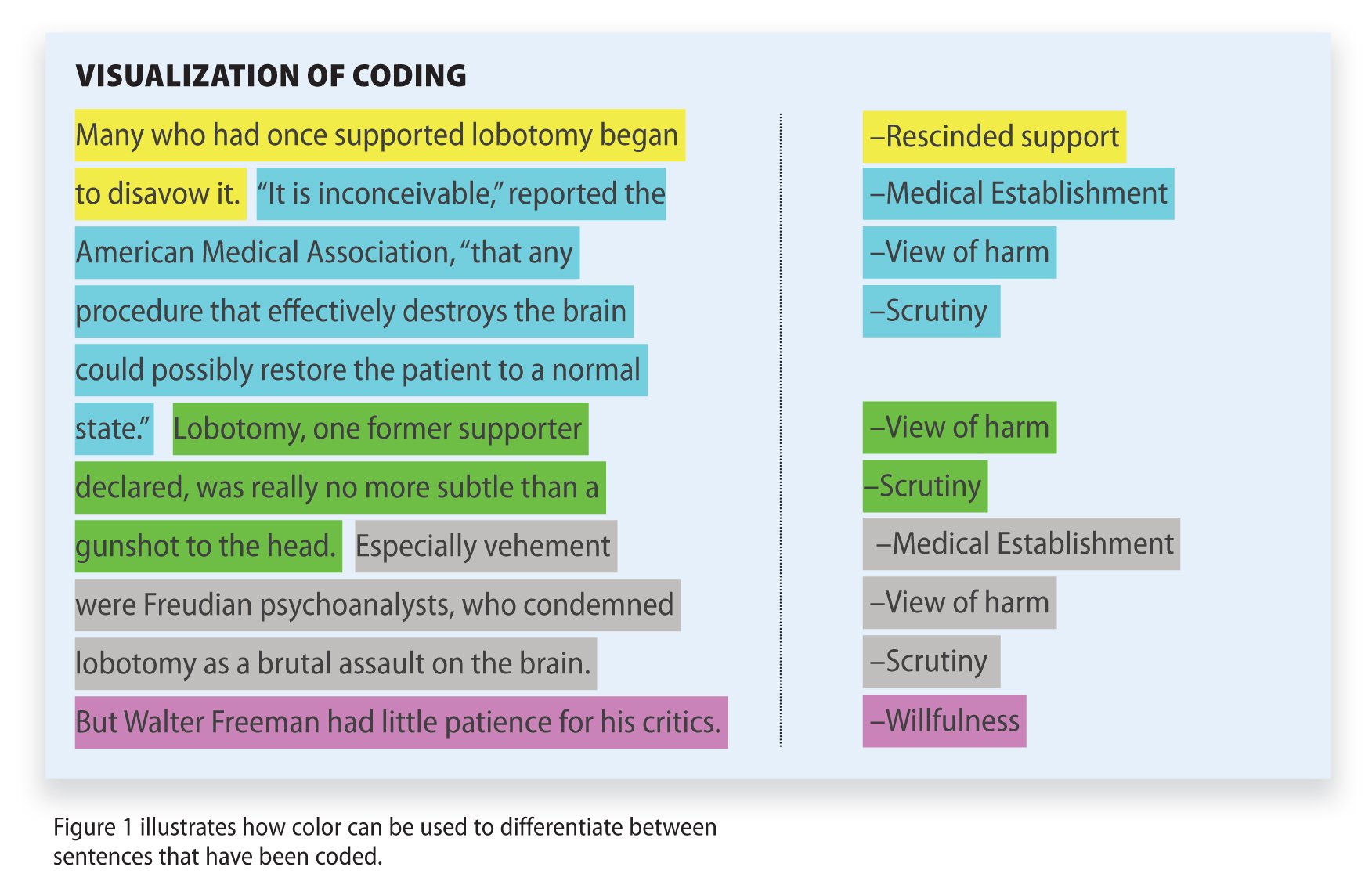
Research Methodology
Qualitative Data Coding

What Is a Focus Group?

Cross-Cultural Research Methodology In Psychology

What Is Internal Validity In Research?

Research Methodology , Statistics
What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples
Random Assignment
- Reference work entry
- First Online: 01 January 2020
- pp 4260–4262
- Cite this reference work entry

- Sven Hilbert 3 , 4 , 5
105 Accesses
Random assignment defines the assignment of participants of a study to their respective group strictly by chance.
Introduction
Statistical inference is based on the theory of probability, and effects investigated in psychological studies are defined by measures that are treated as random variables. The inference about the probability of a given result with regard to an assumed population and the popular term “significance” are only meaningful and without bias if the measure of interest is really a random variable. To achieve the creation of a random variable in form of a measure derived from a sample of participants, these participants have to be randomly drawn. In an experimental study involving different groups of participants, these participants have to additionally be randomly assigned to one of the groups.
Why Is Random Assignment Crucial for Statistical Inference?
Many psychological investigations, such as clinical treatment studies or neuropsychological training...
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Available as EPUB and PDF
- Durable hardcover edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Gigerenzer, G., Swijtink, Z., Porter, T., Daston, L., Beatty, J., & Kruger, L. (1989). The empire of chance: How probability changed science and everyday-life . Cambridge: New York.
Book Google Scholar
Download references
Author information
Authors and affiliations.
Department of Psychology, Psychological Methods and Assessment, Münich, Germany
Sven Hilbert
Faculty of Psychology, Educational Science, and Sport Science, University of Regensburg, Regensburg, Germany
Psychological Methods and Assessment, LMU Munich, Munich, Germany
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Sven Hilbert .
Editor information
Editors and affiliations.
Oakland University, Rochester, MI, USA
Virgil Zeigler-Hill
Todd K. Shackelford
Section Editor information
Humboldt University, Germany, Berlin, Germany
Matthias Ziegler
Rights and permissions
Reprints and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this entry
Cite this entry.
Hilbert, S. (2020). Random Assignment. In: Zeigler-Hill, V., Shackelford, T.K. (eds) Encyclopedia of Personality and Individual Differences. Springer, Cham. https://doi.org/10.1007/978-3-319-24612-3_1343
Download citation
DOI : https://doi.org/10.1007/978-3-319-24612-3_1343
Published : 22 April 2020
Publisher Name : Springer, Cham
Print ISBN : 978-3-319-24610-9
Online ISBN : 978-3-319-24612-3
eBook Packages : Behavioral Science and Psychology Reference Module Humanities and Social Sciences Reference Module Business, Economics and Social Sciences

Share this entry
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research

Statistics Made Easy
Randomization in Statistics: Definition & Example
In the field of statistics, randomization refers to the act of randomly assigning subjects in a study to different treatment groups.
For example, suppose researchers recruit 100 subjects to participate in a study in which they hope to understand whether or not two different pills have different effects on blood pressure.
They may decide to use a random number generator to randomly assign each subject to use either pill #1 or pill #2.

Benefits of Randomization
The point of randomization is to control for lurking variables – variables that are not directly included in an analysis, yet impact the analysis in some way.
For example, if researchers are studying the effects of two different pills on blood pressure then the following lurking variables could affect the analysis:
- Smoking habits
By randomly assigning subjects to treatment groups, we maximize the chances that the lurking variables will affect both treatment groups equally.
This means any differences in blood pressure can be attributed to the type of pill, rather than the effect of a lurking variable.
Block Randomization
An extension of randomization is known as block randomization . This is the process of first separating subjects into blocks, then using randomization to assign subjects within blocks to different treatments.
For example, if researchers want to know whether or not two different pills affect blood pressure differently then they may first separate all subjects into one of two blocks based on gender: Male or Female.
Then, within each block they can use randomization to randomly assign subjects to use either Pill #1 or Pill #2.

The benefit of this approach is that researchers can directly control for any effect that gender may have on blood pressure since we know that males and females are likely to respond to each pill differently.
By using gender as a block, we’re able to eliminate this variable as a potential source of variation. If there are differences in blood pressure between the two pills then we can know that gender is not the underlying cause of these differences.
Additional Resources
Blocking in Statistics: Definition & Example Permuted Block Randomization: Definition & Example Lurking Variables: Definition & Examples
Featured Posts
Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Join the Statology Community
Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!
By subscribing you accept Statology's Privacy Policy.
MA121: Introduction to Statistics
Descriptive and Inferential Statistics
Read these sections and complete the questions at the end of each section. Here, we introduce descriptive statistics using examples and discuss the difference between descriptive and inferential statistics. We also talk about samples and populations, explain how you can identify biased samples, and define differential statistics.
Inferential Statistics
Random assignment.
In experimental research, populations are often hypothetical. For example, in an experiment comparing the effectiveness of a new anti-depressant drug with a placebo, there is no actual population of individuals taking the drug. In this case, a specified population of people with some degree of depression is defined and a random sample is taken from this population. The sample is then randomly divided into two groups; one group is assigned to the treatment condition (drug) and the other group is assigned to the control condition (placebo). This random division of the sample into two groups is called random assignment . Random assignment is critical for the validity of an experiment. For example, consider the bias that could be introduced if the first 20 subjects to show up at the experiment were assigned to the experimental group and the second 20 subjects were assigned to the control group. It is possible that subjects who show up late tend to be more depressed than those who show up early, thus making the experimental group less depressed than the control group even before the treatment was administered.
In experimental research of this kind, failure to assign subjects randomly to groups is generally more serious than having a non-random sample. Failure to randomize (the former error) invalidates the experimental findings. A non-random sample (the latter error) simply restricts the generalizability of the results.
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Simple Random Sampling: Definition & Examples
By Jim Frost Leave a Comment
What is Simple Random Sampling?
Simple random sampling (SRS) is a probability sampling method where researchers randomly choose participants from a population . All population members have an equal probability of being selected. This method tends to produce representative, unbiased samples.
For example, if you randomly select 1000 people from a town with a population of 100,000 residents, each person has a 1000/100000 = 0.01 probability. That’s a simple calculation requiring no additional knowledge about the population’s composition. Hence, simple random sampling.
Simple random sampling is a probability sampling method that helps ensure the sample mirrors the population. The process proportionately samples from larger subpopulations more frequently than smaller subpopulations.
Suppose the town contains subpopulation A with 40,000 people and subpopulation B with 10,000. Using SRS with a probability of 0.01, the process will tend to enlist 400 from subpopulation A and 100 from B. Hence, the process tends to produce a proportionate representation in the sample that reflects the entire population. You don’t need to know the details about the subpopulations for this process to work!
Learn more about Types of Sampling Methods in Research .
How to Use Simple Random Sampling
Performing simple random sampling requires that you have a sampling frame that contains a complete list of all population members and the ability to contact and involve them in your study. Learn more about Sampling Frames: Definition, Examples & Uses .

- Define the population.
- Create a list of all population members.
- Assign random numbers to each member.
- Use a random number generator to select participants until you reach your target sample size.
Alternatively, if the population is not too large, you can use a lottery system for drawing the sample. Place all the names in a hat and randomly draw your sample. For large populations, researchers typically use computers to select participants randomly from a database.
Example of Simple Random Sampling
Imagine we are studying the town with 100,000 residents. We want to perform simple random sampling to obtain a sample size of 1000. We first need to define the population. We’ll define it as residents of the town who pay township taxes and are at least 18 years old.
Next, we need to create a complete list of residents who meet those criteria. Perhaps we’ll work with the township tax office to make the list. We’ll add all eligible residents to our list.
Finally, we need to select participants randomly from the list. We can use a computer program to do that. Alternatively, we can print out names on slips of paper and draw them from a basket. We keep drawing from the list until we have 1000 names.
Benefits of Simple Random Sampling
Many statisticians consider simple random sampling to be the gold standard for producing representative samples. Because it is entirely random, it minimizes the potential for researchers biasing the results, even if unintentionally. As you’ll read, there are alternative sampling methods that provide concessions to real-world sampling difficulties. Unfortunately, the alternatives can unwittingly produce a biased sample. Learn more about representative samples .
Procedurally, SRS is the simplest method for obtaining an unbiased sample. While the researchers need a list of the entire population, they don’t need other information about that population, its subpopulations, and its features.
Conversely, other more complex forms of sampling require researchers to understand the population’s characteristics. Then, using that knowledge and a lot of preplanning, they divide the population into strata or clusters and perform other procedures before sampling. With SRS, you just randomly draw from the list until you have enough subjects.
Because simple random sampling tends to produce unbiased samples that mirror the population, it’s excellent for analysts who need to use a sample to infer the properties of a population (i.e., inferential statistics ). In a study, having a representative sample improves both its internal and external validity . After simple random sampling, you can use statistical hypothesis tests to use the sample to draw conclusions about the population.
For more information about inferential statistics, read my articles about Populations, Parameters, and Samples in Inferential Statistics and Descriptive versus Inferential Statistics .
Drawbacks of Simple Random Sampling
Even though there are great benefits to using this method, simple random sampling has some significant drawbacks.
Population List
First and foremost, this method can be quite cumbersome and require ample resources for large populations. You’ll need a list of all population members, which can be a tremendous hurdle by itself. If that list doesn’t exist, you might need to expend considerable resources to create it. An incomplete list can bias your results. Only a complete list allows the researchers to have an equal probability of selecting all population members.
Attempting to perform SRS with an incomplete population list causes undercoverage bias and a nonrepresentative sample.
Learn more about Undercoverage Bias: Definition & Examples .
Then you’ll need to contact and interact with everyone you randomly select. Depending on the nature of your study, that process can be pretty expensive and time-consuming if your participants span a wide geographic range, particularly when you need a large sample size.
Insufficient Representation of Subpopulations
Despite being entirely random, simple random sampling can miss important subpopulations and features in the population. For example, in our town with 100,000 residents, imagine that we’re particularly interested in surveying those who are at least 90 years old. You plan to obtain a sample size of 1000, which is 1 out of 100 residents. However, there are only 50 people in town who are older than 90. Your sample might not include anyone in this vital group! If it does, it’ll be a tiny number that doesn’t provide a clear picture of this subgroup.
Simple random sampling can fail to provide precise data about particular subgroups and differences between subgroups. Other sampling methods can ensure sufficient numbers from small subgroups that produce a clear picture and increase the ability to compare subgroups.
Simple Random Sampling vs. Other Methods
Because you need a list of the entire population, simple random sampling is most feasible when working with a relatively small population that is already defined. For example, if you’re surveying a company and can easily obtain a list of employees from Human Resources, SRS isn’t too difficult. Large populations can require extensive amounts of time and resources just to create the complete list. Simple random sampling is a great option when you don’t know much about your population other than its membership.
However, other sampling methods can be more efficient when creating the population list is difficult, your population is large and dispersed, or you need to guarantee sufficient data for specific subpopulations. Alternative methods can reduce the need for a complete list and reduce the logistical headaches of a geographically extensive study.
For example, a national opinion poll company might consider an alternative method to assess differences between subpopulations, such as gender, race, and age.
These other methods frequently require you to have a greater understanding of your population than SRS requires. Consider the following alternatives to simple random sampling that can also obtain representative samples:
- Systematic sampling : Uses a random starting point but then samples at a fixed interval. Does not require a complete population list.
- Stratified sampling: Divides the population into dissimilar strata. Ensures that the sample includes specific subpopulations and facilitates comparisons between them.
- Cluster sampling : Divides the population into clusters that mirror the entire population. Then you randomly select from a subset of clusters. Reduces the need for a complete list of the population and eases logistics issues.
For a contrast to representative sampling methods, learn about convenience sampling , which tends to produce biased samples.
Learn about the specialized random sampling process that Political Polls use, allowing a relatively small sample to predict an election.
Sampling in Developmental Science: Situations, Shortcomings, Solutions, and Standards (nih.gov)
Share this:

Reader Interactions
Comments and questions cancel reply.
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Methodology
- Simple Random Sampling | Definition, Steps & Examples
Simple Random Sampling | Definition, Steps & Examples
Published on August 28, 2020 by Lauren Thomas . Revised on December 18, 2023.
A simple random sample is a randomly selected subset of a population. In this sampling method, each member of the population has an exactly equal chance of being selected.
This method is the most straightforward of all the probability sampling methods , since it only involves a single random selection and requires little advance knowledge about the population. Because it uses randomization, any research performed on this sample should have high internal and external validity, and be at a lower risk for research biases like sampling bias and selection bias .
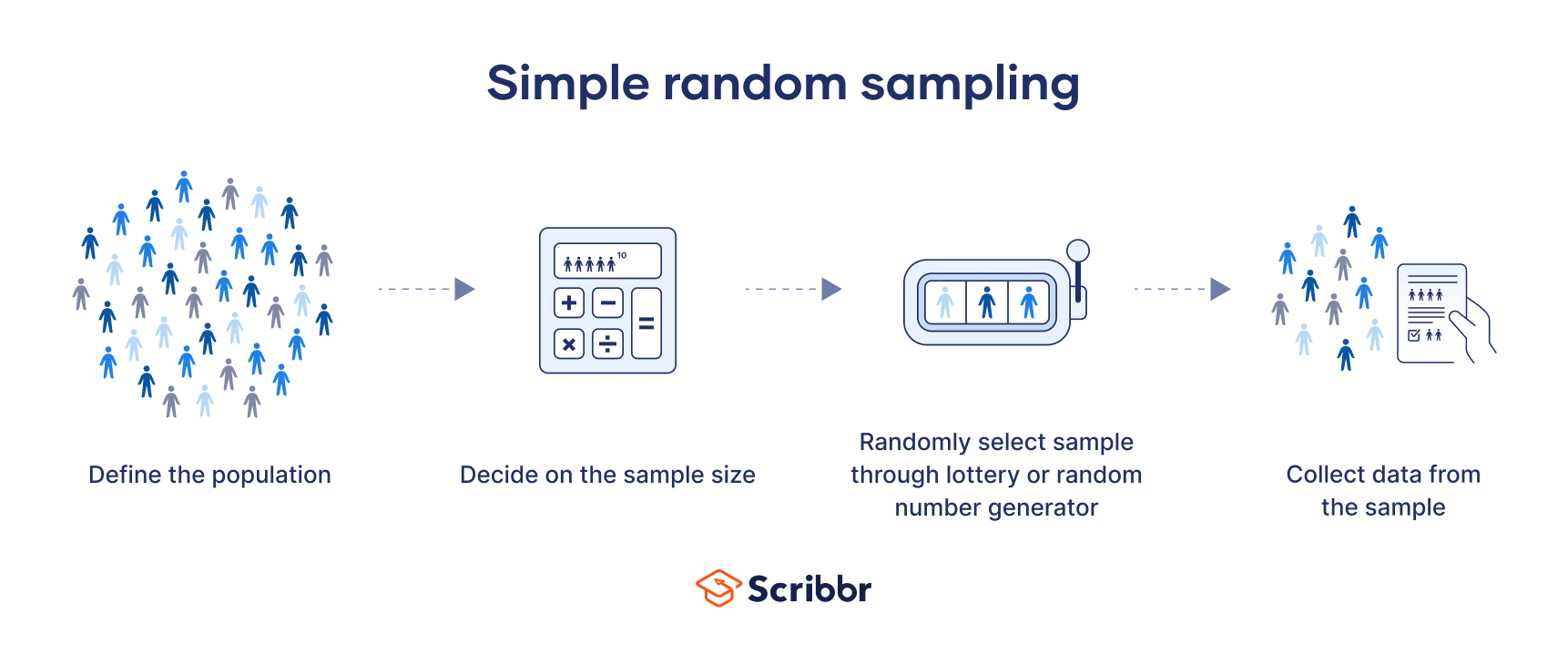
Table of contents
When to use simple random sampling, how to perform simple random sampling, other interesting articles, frequently asked questions about simple random sampling.
Simple random sampling is used to make statistical inferences about a population. It helps ensure high internal validity : randomization is the best method to reduce the impact of potential confounding variables .
In addition, with a large enough sample size, a simple random sample has high external validity : it represents the characteristics of the larger population.
However, simple random sampling can be challenging to implement in practice. To use this method, there are some prerequisites:
- You have a complete list of every member of the population .
- You can contact or access each member of the population if they are selected.
- You have the time and resources to collect data from the necessary sample size.
Simple random sampling works best if you have a lot of time and resources to conduct your study, or if you are studying a limited population that can easily be sampled.
In some cases, it might be more appropriate to use a different type of probability sampling:
- Systematic sampling involves choosing your sample based on a regular interval, rather than a fully random selection. It can also be used when you don’t have a complete list of the population.
- Stratified sampling is appropriate when you want to ensure that specific characteristics are proportionally represented in the sample. You split your population into strata (for example, divided by gender or race), and then randomly select from each of these subgroups.
- Cluster sampling is appropriate when you are unable to sample from the entire population. You divide the sample into clusters that approximately reflect the whole population, and then choose your sample from a random selection of these clusters.
Prevent plagiarism. Run a free check.
There are 4 key steps to select a simple random sample.
Step 1: Define the population
Start by deciding on the population that you want to study.
It’s important to ensure that you have access to every individual member of the population, so that you can collect data from all those who are selected for the sample.
Step 2: Decide on the sample size
Next, you need to decide how large your sample size will be. Although larger samples provide more statistical certainty, they also cost more and require far more work.
There are several potential ways to decide upon the size of your sample, but one of the simplest involves using a formula with your desired confidence interval and confidence level , estimated size of the population you are working with, and the standard deviation of whatever you want to measure in your population.
The most common confidence interval and levels used are 0.05 and 0.95, respectively. Since you may not know the standard deviation of the population you are studying, you should choose a number high enough to account for a variety of possibilities (such as 0.5).
You can then use a sample size calculator to estimate the necessary sample size.
Step 3: Randomly select your sample
This can be done in one of two ways: the lottery or random number method.
In the lottery method , you choose the sample at random by “drawing from a hat” or by using a computer program that will simulate the same action.
In the random number method , you assign every individual a number. By using a random number generator or random number tables, you then randomly pick a subset of the population. You can also use the random number function (RAND) in Microsoft Excel to generate random numbers.
Step 4: Collect data from your sample
Finally, you should collect data from your sample.
To ensure the validity of your findings, you need to make sure every individual selected actually participates in your study. If some drop out or do not participate for reasons associated with the question that you’re studying, this could bias your findings.
For example, if young participants are systematically less likely to participate in your study, your findings might not be valid due to the underrepresentation of this group.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Student’s t -distribution
- Normal distribution
- Null and Alternative Hypotheses
- Chi square tests
- Confidence interval
- Quartiles & Quantiles
- Cluster sampling
- Stratified sampling
- Data cleansing
- Reproducibility vs Replicability
- Peer review
- Prospective cohort study
Research bias
- Implicit bias
- Cognitive bias
- Placebo effect
- Hawthorne effect
- Hindsight bias
- Affect heuristic
- Social desirability bias
Probability sampling means that every member of the target population has a known chance of being included in the sample.
Probability sampling methods include simple random sampling , systematic sampling , stratified sampling , and cluster sampling .
Simple random sampling is a type of probability sampling in which the researcher randomly selects a subset of participants from a population . Each member of the population has an equal chance of being selected. Data is then collected from as large a percentage as possible of this random subset.
The American Community Survey is an example of simple random sampling . In order to collect detailed data on the population of the US, the Census Bureau officials randomly select 3.5 million households per year and use a variety of methods to convince them to fill out the survey.
If properly implemented, simple random sampling is usually the best sampling method for ensuring both internal and external validity . However, it can sometimes be impractical and expensive to implement, depending on the size of the population to be studied,
If you have a list of every member of the population and the ability to reach whichever members are selected, you can use simple random sampling.
Samples are used to make inferences about populations . Samples are easier to collect data from because they are practical, cost-effective, convenient, and manageable.
Sampling bias occurs when some members of a population are systematically more likely to be selected in a sample than others.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Thomas, L. (2023, December 18). Simple Random Sampling | Definition, Steps & Examples. Scribbr. Retrieved June 7, 2024, from https://www.scribbr.com/methodology/simple-random-sampling/
Is this article helpful?

Lauren Thomas
Other students also liked, sampling methods | types, techniques & examples, stratified sampling | definition, guide & examples, sampling bias and how to avoid it | types & examples, get unlimited documents corrected.
✔ Free APA citation check included ✔ Unlimited document corrections ✔ Specialized in correcting academic texts

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

15.1: Random Selection
- Last updated
- Save as PDF
- Page ID 10844

- Paul Pfeiffer
- Rice University
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Introduction
The usual treatments deal with a single random variable or a fixed, finite number of random variables, considered jointly. However, there are many common applications in which we select at random a member of a class of random variables and observe its value, or select a random number of random variables and obtain some function of those selected. This is formulated with the aid of a counting or selecting random variable \(N\), which is nonegative, integer valued. It may be independent of the class selected, or may be related in some sequential way to members of the class. We consider only the independent case. Many important problems require optional random variables, sometimes called Markov times . These involve more theory than we develop in this treatment.
Some common examples:
Total demand of \(N\) customers— \(N\) independent of the individual demands. Total service time for \(N\) units— \(N\) independent of the individual service times. Net gain in \(N\) plays of a game— \(N\) independent of the individual gains. Extreme values of \(N\) random variables— \(N\) independent of the individual values. Random sample of size \(N\)— \(N\) is usually determined by propereties of the sample observed. Decide when to play on the basis of past results— \(N\) dependent on past
A useful model—random sums
As a basic model, we consider the sum of a random number of members of an iid class. In order to have a concrete interpretation to help visualize the formal patterns, we think of the demand of a random number of customers. We suppose the number of customers N is independent of the individual demands. We formulate a model to be used for a variety of applications.
A basic sequence \(\{X_n: 0 \le n\}\) [Demand of \(n\) customers] An incremental sequence \(\{Y_n:0 \le n\}\) [Individual demands] These are related as follows:
\(X_n = \sum_{k = 0}^{n} Y_k\) for \(n \ge 0\) and \(X_n = 0\) for \(n < 0\) \(Y_n = X_n - X_{n - 1}\) for all \(n\)
A counting random variable \(N\). If \(N = n\) then \(n\) of the \(Y_k\) are added to give the compound demand \(D\) (the random sum)
\(D = \sum_{k = 0}^{N} Y_k = \sum_{k = 0}^{\infty} I_{[N = k]} X_k = \sum_{k = 0}^{\infty} I_{\{k\}} (N) X_k\)
Note . In some applications the counting random variable may take on the idealized value \(\infty\). For example, in a game that is played until some specified result occurs, this may never happen, so that no finite value can be assigned to \(N\). In such a case, it is necessary to decide what value \(X_{\infty}\) is to be assigned. For \(N\) independent of the \(Y_n\) (hence of the \(X_n\)), we rarely need to consider this possibility.
Independent selection from an iid incremental sequence
We assume throughout , unless specifically stated otherwise, that: \(X_0 = Y_0 = 0\) \(\{Y_k: 1 \le k\}\) is iid \(\{N, Y_k: 0 \le k\}\) is an independent class
We utilize repeatedly two important propositions: \(E[h(D)|N = n] = E[h(X_n)]\), \(n \ge 0\) \(M_D (s) = g_N [M_Y (s)]\). If the \(Y_n\) are nonnegative integer valued, then so is \(D\) and \(g_D (s) = g_N[g_Y (s)]\)
We utilize properties of generating functions, moment generating functions, and conditional expectation. \(E[I_{\{n\}} (N) h(D)] = E[h(D)|N = n] P(N = n)\) by definition of conditional expectation, given an event, Now, \(I_{\{n\}} (N) h(D) = I_{\{n\}} (N) h(X_n)\) and \(E[I_{\{n\}} (N) h(X_n)] = P(N = n) E[h(X_n)]\). Hence \(E[h(D) |N = n] P(N = n) = P(N = n) E[h(X_n)]\). Division by \(P(N = n)\) gives the desired result. By the law of total probability (CE1b), \(M_D(s)= E[e^{sD}] = E\{E[e^{sD} |N]\}\). By proposition 1 and the product rule for moment generating functions,
\(E[e^{sD}|N = n] = E[e^{sX_n}] = \prod_{k = 1}^{n} E[e^{sY_k}] = M_Y^n (s)\)
\(M_D(s) = \sum_{n = 0}^{\infty} M_Y^n (s) P(N = n) = g_N[M_Y (s)]\)
A parallel argument holds for \(g_D\)
— □
Remark . The result on \(M_D\) and \(g_D\) may be developed without use of conditional expectation.
in the integer-valued case.
\(M_D(s) = E[e^{sD}] = \sum_{k = 0}^{\infty} E[I_{\{N = n\}} e^{sX_n}] = \sum_{k = 0}^{\infty} P(N = n) E[e^{sX_n}]\)
\(= \sum_{k = 0}^{\infty} P(N = n) M_Y^n (s) = g_N [M_Y (s)]\)
Example \(\PageIndex{1}\) A service shop
Suppose the number \(N\) of jobs brought to a service shop in a day is Poisson (8). One fourth of these are items under warranty for which no charge is made. Others fall in one of two categories. One half of the arriving jobs are charged for one hour of shop time; the remaining one fourth are charged for two hours of shop time. Thus, the individual shop hour charges \(Y_k\) have the common distribution
\(Y =\) [0 1 2] with probabilities \(PY =\) [1/4 1/2 1/4]
Make the basic assumptions of our model. Determine \(P(D \le 4)\).
\(g_N(s) = e^{8(s - 1)} g_Y (s) = \dfrac{1}{4} (1 + 2s + s^2)\)
According to the formula developed above,
\(g_D (s) = g_N [g_Y (s)] = \text{exp} ((8/4) (1 + 2s + s^2) - 8) = e^{4s} e^{2s^2} e^{-6}\)
Expand the exponentials in power series about the origin, multiply out to get enough terms. The result of straightforward but somewhat tedious calculations is
\(g_D (s) = e^{-6} ( 1 + 4s + 10s^2 + \dfrac{56}{3} s^3 + \dfrac{86}{3} s^4 + \cdot\cdot\cdot)\)
Taking the coefficients of the generating function, we get
\(P(D \le 4) \approx e^{-6} (1 + 4 + 10 + \dfrac{56}{3} + \dfrac{86}{3}) = e^{-6} \dfrac{187}{3} \approx 0.1545\)
Example \(\PageIndex{2}\) A result on Bernoulli trials
Suppose the counting random variable \(N\) ~ binomial \((n, p)\) and \(Y_i = I_{E_i}\), with \(P(E_i) = p_0\). Then
\(g_N = (q + ps)^n\) and \(g_Y (s) = q_0 + p_0 s\)
By the basic result on random selection, we have
\(g_D (s) = g_N [g_Y(s)] = [q + p(q_0 + p_0 s)]^n = [(1 - pp_0) + pp_0 s]^n\)
so that \(D\) ~ binomial \((n, pp_0)\).
In the next section we establish useful m-procedures for determining the generating function g D and the moment generating function \(M_D\) for the compound demand for simple random variables, hence for determining the complete distribution. Obviously, these will not work for all problems. It may helpful, if not entirely sufficient, in such cases to be able to determine the mean value \(E[D]\) and variance \(\text{Var} [D]\). To this end, we establish the following expressions for the mean and variance.
Example \(\PageIndex{3}\) Mean and variance of the compound demand
\(E[D] = E[N]E[Y]\) and \(\text{Var} [D] = E[N] \text{Var} [Y] + \text{Var} [N] E^2 [Y]\)
\(E[D] = E[\sum_{n = 0}^{\infty} I_{\{N = n\}} X_n] = \sum_{n = 0}^{\infty} P(N = n) E[X_n]\)
\(= E[Y] \sum_{n = 0}^{\infty} n P(N = n) = E[Y] E[N]\)
\(E[D^2] = \sum_{n = 0}^{\infty} P(N = n) E[X_n^2] = \sum_{n = 0}^{\infty} P(N = n) \{\text{Var} [X_n] + E^2 [X_n]\}\)
\(= \sum_{n = 0}^{\infty} P(N = n) \{n \text{Var} [Y] = n^2 E^2 [Y]\} = E[N] \text{Var} [Y] + E[N^2] E^2[Y]\)
\(\text{Var} [D] = E[N] \text{Var} [Y] + E[N^2] E^2 [Y] - E[N]^2 E^2[Y] = E[N] \text{Var} [Y] + \text{Var} [N] E^2[Y]\)
Example \(\PageIndex{4}\) Mean and variance for Example 15.1.1
\(E[N] = \text{Var} [N] = 9\). By symmetry \(E[Y] = 1\). \(\text{Var} [Y] = 0.25(0 + 2 + 4) - 1 = 0.5\). Hence,
\(E[D] = 8 \cdot 1 = 8\), \(\text{Var} [D] = 8 \cdot 0.5 + 8 \cdot 1 = 12\)
Calculations for the compound demand
We have m-procedures for performing the calculations necessary to determine the distribution for a composite demand \(D\) when the counting random variable \(N\) and the individual demands \(Y_k\) are simple random variables with not too many values. In some cases, such as for a Poisson counting random variable, we are able to approximate by a simple random variable.
The procedure gend
If the \(Y_i\) are nonnegative, integer valued, then so is \(D\), and there is a generating function. We examine a strategy for computation which is implemented in the m-procedure gend . Suppose
\(g_N (s) = p_0 + p_1 s + p_2 s^2 + \cdot\cdot\cdot p_n s^n\)
\(g_Y (s) = \pi_0 + \pi_1 s + \pi_2 s^2 + \cdot\cdot\cdot \pi_m s^m\)
The coefficients of \(g_N\) and \(g_Y\) are the probabilities of the values of \(N\) and \(Y\), respectively. We enter these and calculate the coefficients for powers of \(g_Y\):
\(\begin{array} {lcr} {gN = [p_0\ p_1\ \cdot\cdot\cdot\ p_n]} & {1 \times (n + 1)} & {\text{Coefficients of } g_N} \\ {y = [\pi_0\ \pi_1\ \cdot\cdot\cdot\ \pi_n]} & {1 \times (m + 1)} & {\text{Coefficients of } g_Y} \\ {\ \ \ \ \ \cdot\cdot\cdot} & { } & { } \\ {y2 = \text{conv}(y,y)} & {1 \times (2m + 1)} & {\text{Coefficients of } g_Y^2} \\ {y3 = \text{conv}(y,y2)} & {1 \times (3m + 1)} & {\text{Coefficients of } g_Y^3} \\ {\ \ \ \ \ \cdot\cdot\cdot} & { } & { } \\ {yn = \text{conv}(y,y(n - 1))} & {1 \times (nm + 1)} & {\text{Coefficients of } g_Y^n}\end{array}\)
We wish to generate a matrix \(P\) whose rows contain the joint probabilities. The probabilities in the \(i\)th row consist of the coefficients for the appropriate power of \(g_Y\) multiplied by the probability \(N\) has that value. To achieve this, we need a matrix, each of whose \(n + 1\) rows has \(nm + 1\) elements, the length of \(yn\). We begin by “preallocating” zeros to the rows. That is, we set \(P = \text{zeros}(n + 1, n\ ^*\ m + 1)\). We then replace the appropriate elements of the successive rows. The replacement probabilities for the \(i\)th row are obtained by the convolution of \(g_Y\) and the power of \(g_Y\) for the previous row. When the matrix \(P\) is completed, we remove zero rows and columns, corresponding to missing values of \(N\) and \(D\) (i.e., values with zero probability). To orient the joint probabilities as on the plane, we rotate \(P\) ninety degrees counterclockwise. With the joint distribution, we may then calculate any desired quantities.
Example \(\PageIndex{5}\) A compound demand
The number of customers in a major appliance store is equally likely to be 1, 2, or 3. Each customer buys 0, 1, or 2 items with respective probabilities 0.5, 0.4, 0.1. Customers buy independently, regardless of the number of customers. First we determine the matrices representing \(g_N\) and \(g_Y\). The coefficients are the probabilities that each integer value is observed. Note that the zero coefficients for any missing powers must be included.
Example \(\PageIndex{6}\) A numerical example
\(g_N (s) = \dfrac{1}{5} (1 + s + s^2 + s^3 + s^4)\) \(g_Y (s) = 0.1 (5s + 3s^2 + 2s^3\)
Note that the zero power is missing from \(gY\). corresponding to the fact that \(P(Y = 0) = 0\).
Example \(\PageIndex{7}\) Number of successes for random number \(N\) of trials.
We are interested in the number of successes in \(N\) trials for a general counting random variable. This is a generalization of the Bernoulli case in Example 15.1.2 . Suppose, as in Example 15.1.2 , the number of customers in a major appliance store is equally likely to be 1, 2, or 3, and each buys at least one item with probability \(p = 0.6\). Determine the distribution for the number \(D\) of buying customers.
We use \(gN\), \(gY\), and gend.
The procedure gend is limited to simple \(N\) and \(Y_k\), with nonnegative integer values. Sometimes, a random variable with unbounded range may be approximated by a simple random variable. The solution in the following example utilizes such an approximation procedure for the counting random variable \(N\).
Example \(\PageIndex{8}\) Solution of the shop time Example 15.1.1
The number \(N\) of jobs brought to a service shop in a day is Poisson (8). The individual shop hour charges \(Y_k\) have the common distribution \(Y =\) [0 1 2] with probabilities \(PY =\) [1/4 1/2 1/4].
Under the basic assumptions of our model, determine \(P(D \le 4)\).
Since Poisson \(N\) is unbounded, we need to check for a sufficient number of terms in a simple approximation. Then we proceed as in the simple case.
The m-procedures mgd and jmgd
The next example shows a fundamental limitation of the gend procedure. The values for the individual demands are not limited to integers, and there are considerable gaps between the values. In this case, we need to implement the moment generating function \(M_D\) rather than the generating function \(g_D\).
In the generating function case, it is as easy to develop the joint distribution for \(\{N, D\}\) as to develop the marginal distribution for \(D\). For the moment generating function, the joint distribution requires considerably more computation. As a consequence, we find it convenient to have two m-procedures: mgd for the marginal distribution and jmgd for the joint distribution.
Instead of the convolution procedure used in gend to determine the distribution for the sums of the individual demands, the m-procedure mgd utilizes the m-function mgsum to obtain these distributions. The distributions for the various sums are concatenated into two row vectors, to which csort is applied to obtain the distribution for the compound demand. The procedure requires as input the generating function for \(N\) and the actual distribution, \(Y\) and \(PY\), for the individual demands. For \(gN\), it is necessary to treat the coefficients as in gend. However, the actual values and probabilities in the distribution for Y are put into a pair of row matrices. If \(Y\) is integer valued, there are no zeros in the probability matrix for missing values.
Example \(\PageIndex{9}\) Noninteger values
A service shop has three standard charges for a certain class of warranty services it performs: $10, $12.50, and $15. The number of jobs received in a normal work day can be considered a random variable \(N\) which takes on values 0, 1, 2, 3, 4 with equal probabilities 0.2. The job types for arrivals may be represented by an iid class \(\{Y_i: 1 \le i \le 4\}\), independent of the arrival process. The \(Y_i\) take on values 10, 12.5, 15 with respective probabilities 0.5, 0.3, 0.2. Let \(C\) be the total amount of services rendered in a day. Determine the distribution for \(C\).
We next recalculate Example 15.1.6 , above, using mgd rather than gend.
Example \(\PageIndex{10}\) Recalculation of Example 15.1.6
In Example 15.1.6, we have
\(g_N (s) = \dfrac{1}{5} (1 + s + s^2 + s^3 + s^4)\) \(g_Y (s) = 0.1 (5s + 3s^2 + 2s^3)\)
The means that the distribution for \(Y\) is \(Y =\) [1 2 3] and \(PY =\) 0.1 * [5 3 2].
We use the same expression for \(gN\) as in Example 15.1.6.
As expected, the results are the same as those obtained with gend.
If it is desired to obtain the joint distribution for \(\{N, D\}\), we use a modification of mgd called jmgd . The complications come in placing the probabilities in the \(P\) matrix in the desired positions. This requires some calculations to determine the appropriate size of the matrices used as well as a procedure to put each probability in the position corresponding to its \(D\) value. Actual operation is quite similar to the operation of mgd, and requires the same data format.
A principle use of the joint distribution is to demonstrate features of the model, such as \(E[D|N = n] = nE[Y]\), etc. This, of course, is utilized in obtaining the expressions for \(M_D (s)\) in terms of \(g_N (s)\) and \(M_Y (s)\). This result guides the development of the computational procedures, but these do not depend upon this result. However, it is usually helpful to demonstrate the validity of the assumptions in typical examples.
Remark . In general, if the use of gend is appropriate, it is faster and more efficient than mgd (or jmgd). And it will handle somewhat larger problems. But both m-procedures work quite well for problems of moderate size, and are convenient tools for solving various “compound demand” type problems.
- Bipolar Disorder
- Therapy Center
- When To See a Therapist
- Types of Therapy
- Best Online Therapy
- Best Couples Therapy
- Best Family Therapy
- Managing Stress
- Sleep and Dreaming
- Understanding Emotions
- Self-Improvement
- Healthy Relationships
- Student Resources
- Personality Types
- Guided Meditations
- Verywell Mind Insights
- 2024 Verywell Mind 25
- Mental Health in the Classroom
- Editorial Process
- Meet Our Review Board
- Crisis Support
The Definition of Random Assignment According to Psychology
Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."
:max_bytes(150000):strip_icc():format(webp)/IMG_9791-89504ab694d54b66bbd72cb84ffb860e.jpg)
Emily is a board-certified science editor who has worked with top digital publishing brands like Voices for Biodiversity, Study.com, GoodTherapy, Vox, and Verywell.
:max_bytes(150000):strip_icc():format(webp)/Emily-Swaim-1000-0f3197de18f74329aeffb690a177160c.jpg)
Materio / Getty Images
Random assignment refers to the use of chance procedures in psychology experiments to ensure that each participant has the same opportunity to be assigned to any given group in a study to eliminate any potential bias in the experiment at the outset. Participants are randomly assigned to different groups, such as the treatment group versus the control group. In clinical research, randomized clinical trials are known as the gold standard for meaningful results.
Simple random assignment techniques might involve tactics such as flipping a coin, drawing names out of a hat, rolling dice, or assigning random numbers to a list of participants. It is important to note that random assignment differs from random selection .
While random selection refers to how participants are randomly chosen from a target population as representatives of that population, random assignment refers to how those chosen participants are then assigned to experimental groups.
Random Assignment In Research
To determine if changes in one variable will cause changes in another variable, psychologists must perform an experiment. Random assignment is a critical part of the experimental design that helps ensure the reliability of the study outcomes.
Researchers often begin by forming a testable hypothesis predicting that one variable of interest will have some predictable impact on another variable.
The variable that the experimenters will manipulate in the experiment is known as the independent variable , while the variable that they will then measure for different outcomes is known as the dependent variable. While there are different ways to look at relationships between variables, an experiment is the best way to get a clear idea if there is a cause-and-effect relationship between two or more variables.
Once researchers have formulated a hypothesis, conducted background research, and chosen an experimental design, it is time to find participants for their experiment. How exactly do researchers decide who will be part of an experiment? As mentioned previously, this is often accomplished through something known as random selection.
Random Selection
In order to generalize the results of an experiment to a larger group, it is important to choose a sample that is representative of the qualities found in that population. For example, if the total population is 60% female and 40% male, then the sample should reflect those same percentages.
Choosing a representative sample is often accomplished by randomly picking people from the population to be participants in a study. Random selection means that everyone in the group stands an equal chance of being chosen to minimize any bias. Once a pool of participants has been selected, it is time to assign them to groups.
By randomly assigning the participants into groups, the experimenters can be fairly sure that each group will have the same characteristics before the independent variable is applied.
Participants might be randomly assigned to the control group , which does not receive the treatment in question. The control group may receive a placebo or receive the standard treatment. Participants may also be randomly assigned to the experimental group , which receives the treatment of interest. In larger studies, there can be multiple treatment groups for comparison.
There are simple methods of random assignment, like rolling the die. However, there are more complex techniques that involve random number generators to remove any human error.
There can also be random assignment to groups with pre-established rules or parameters. For example, if you want to have an equal number of men and women in each of your study groups, you might separate your sample into two groups (by sex) before randomly assigning each of those groups into the treatment group and control group.
Random assignment is essential because it increases the likelihood that the groups are the same at the outset. With all characteristics being equal between groups, other than the application of the independent variable, any differences found between group outcomes can be more confidently attributed to the effect of the intervention.
Example of Random Assignment
Imagine that a researcher is interested in learning whether or not drinking caffeinated beverages prior to an exam will improve test performance. After randomly selecting a pool of participants, each person is randomly assigned to either the control group or the experimental group.
The participants in the control group consume a placebo drink prior to the exam that does not contain any caffeine. Those in the experimental group, on the other hand, consume a caffeinated beverage before taking the test.
Participants in both groups then take the test, and the researcher compares the results to determine if the caffeinated beverage had any impact on test performance.
A Word From Verywell
Random assignment plays an important role in the psychology research process. Not only does this process help eliminate possible sources of bias, but it also makes it easier to generalize the results of a tested sample of participants to a larger population.
Random assignment helps ensure that members of each group in the experiment are the same, which means that the groups are also likely more representative of what is present in the larger population of interest. Through the use of this technique, psychology researchers are able to study complex phenomena and contribute to our understanding of the human mind and behavior.
Lin Y, Zhu M, Su Z. The pursuit of balance: An overview of covariate-adaptive randomization techniques in clinical trials . Contemp Clin Trials. 2015;45(Pt A):21-25. doi:10.1016/j.cct.2015.07.011
Sullivan L. Random assignment versus random selection . In: The SAGE Glossary of the Social and Behavioral Sciences. SAGE Publications, Inc.; 2009. doi:10.4135/9781412972024.n2108
Alferes VR. Methods of Randomization in Experimental Design . SAGE Publications, Inc.; 2012. doi:10.4135/9781452270012
Nestor PG, Schutt RK. Research Methods in Psychology: Investigating Human Behavior. (2nd Ed.). SAGE Publications, Inc.; 2015.
By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Statistics and probability
Course: statistics and probability > unit 9, random variables.
- Discrete and continuous random variables
- Constructing a probability distribution for random variable
- Constructing probability distributions
- Probability models example: frozen yogurt
- Probability models
- Valid discrete probability distribution examples
- Probability with discrete random variable example
- Probability with discrete random variables
- Mean (expected value) of a discrete random variable
- Expected value
- Expected value (basic)
- Variance and standard deviation of a discrete random variable
- Standard deviation of a discrete random variable
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page

Video transcript
Applied Causal Analysis (with R)
4.23 independence assumption & random assignment.
- = a statistical solution (Holland 1986 , 948f)
- Units randomly assigned to treatment/control have identical distributions of covariates/potential outcomes in both groups ( (infinite) long run! ) 25
- Random assignment induces independence between treatment status and potential outcomes
- Contrast a randomized experiment here in the class (e.g., N = 4) with a bigger sample (e.g., N = 1000).
- Compare average outcome among treatment units with average outcome among control units
Holland, Paul W. 1986. “Statistics and Causal Inference.” J. Am. Stat. Assoc. 81 (396): 945–60.
“When units are assigned at random either to cause t or to cause c, certain physical randomization processes are carried out so that the determination of which cause (t or c) u is exposed to is regarded as statistically independent of all other variables, including Y t and Y c . This means that if the physical randomization is carried out correctly, then it is plausible that S [= treatment D] is independent of Y, and Y, and all other variables over U. This is the independence assumption” (Holland 1986 , 948) . ↩

IMAGES
VIDEO
COMMENTS
Random sampling (also called probability sampling or random selection) is a way of selecting members of a population to be included in your study. In contrast, random assignment is a way of sorting the sample participants into control and experimental groups. While random sampling is used in many types of studies, random assignment is only used ...
Random selection and random assignment are two techniques in statistics that are commonly used, but are commonly confused.. Random selection refers to the process of randomly selecting individuals from a population to be involved in a study.. Random assignment refers to the process of randomly assigning the individuals in a study to either a treatment group or a control group.
Random sampling Not random sampling; Random assignment: Can determine causal relationship in population. This design is relatively rare in the real world. Can determine causal relationship in that sample only. This design is where most experiments would fit. No random assignment: Can detect relationships in population, but cannot determine ...
Random assignment is a fundamental part of a "true" experiment because it helps ensure that any differences found between the groups are attributable to the treatment, rather than a confounding variable. So, to summarize, random sampling refers to how you select individuals from the population to participate in your study.
Correlation, Causation, and Confounding Variables. Random assignment helps you separate causation from correlation and rule out confounding variables. As a critical component of the scientific method, experiments typically set up contrasts between a control group and one or more treatment groups. The idea is to determine whether the effect, which is the difference between a treatment group and ...
Random selection is thus essential to external validity, or the extent to which the researcher can use the results of the study to generalize to the larger population. Random assignment is central to internal validity, which allows the researcher to make causal claims about the effect of the treatment. Nonrandom assignment often leads to non ...
Random assignment or random placement is an experimental technique for assigning human participants or animal subjects to different groups in an experiment (e.g., a treatment group versus a control group) using randomization, such as by a chance procedure (e.g., flipping a coin) or a random number generator. This ensures that each participant or subject has an equal chance of being placed in ...
Random sampling Not random sampling; Random assignment: Can determine causal relationship in population. This design is relatively rare in the real world. Can determine causal relationship in that sample only. This design is where most experiments would fit. No random assignment: Can detect relationships in population, but cannot determine ...
Random allocation, or random assignment, is useful in experimental situations in which different people will be administered different treatments or conditions. By using randomization to choose ...
Random sampling allows us to obtain a sample representative of the population. Therefore, results of the study can be generalized to the population. Random assignment allows us to make sure that the only difference between the various treatment groups is what we are studying. For example, in the serif/sans serif example, random assignment helps ...
Random selection (also called probability sampling or random sampling) is a way of randomly selecting members of a population to be included in your study. On the other hand, random assignment is a way of sorting the sample participants into control and treatment groups. Random selection ensures that everyone in the population has an equal ...
Definition. Random assignment defines the assignment of participants of a study to their respective group strictly by chance. Introduction. Statistical inference is based on the theory of probability, and effects investigated in psychological studies are defined by measures that are treated as random variables. The inference about the ...
by Zach Bobbitt February 9, 2021. In the field of statistics, randomization refers to the act of randomly assigning subjects in a study to different treatment groups. For example, suppose researchers recruit 100 subjects to participate in a study in which they hope to understand whether or not two different pills have different effects on blood ...
Random assignment is critical for the validity of an experiment. For example, consider the bias that could be introduced if the first 20 subjects to show up at the experiment were assigned to the experimental group and the second 20 subjects were assigned to the control group. It is possible that subjects who show up late tend to be more ...
Simple random sampling (SRS) is a probability sampling method where researchers randomly choose participants from a population. All population members have an equal probability of being selected. This method tends to produce representative, unbiased samples. For example, if you randomly select 1000 people from a town with a population of ...
Revised on December 18, 2023. A simple random sample is a randomly selected subset of a population. In this sampling method, each member of the population has an exactly equal chance of being selected. This method is the most straightforward of all the probability sampling methods, since it only involves a single random selection and requires ...
Unit 8: Random variables and probability distributions. A random variable is some outcome from a chance process, like how many heads will occur in a series of 20 flips, or how many seconds it took someone to read this sentence. Calculate probabilities and expected value of random variables, and look at ways to ransform and combine random variables.
Cluster sampling- she puts 50 into random groups of 5 so we get 10 groups then randomly selects 5 of them and interviews everyone in those groups --> 25 people are asked. 2. Stratified sampling- she puts 50 into categories: high achieving smart kids, decently achieving kids, mediumly achieving kids, lower poorer achieving kids and clueless ...
A useful model—random sums. As a basic model, we consider the sum of a random number of members of an iid class. In order to have a concrete interpretation to help visualize the formal patterns, we think of the demand of a random number of customers. We suppose the number of customers Nis independent of the individual demands. We formulate a ...
Randomization is a statistical process in which a random mechanism is employed to select a sample from a population or assign subjects to different groups. The process is crucial in ensuring the random allocation of experimental units or treatment protocols, thereby minimizing selection bias and enhancing the statistical validity. It facilitates the objective comparison of treatment effects in ...
Random assignment refers to the use of chance procedures in psychology experiments to ensure that each participant has the same opportunity to be assigned to any given group in a study to eliminate any potential bias in the experiment at the outset. Participants are randomly assigned to different groups, such as the treatment group versus the ...
Random (Statistics): Governed by or involving equal chances for each of the actual or hypothetical members of a population; (also) produced or obtained by a such a process, and therefore unpredictable in detail. Arbitrary: Derived from mere opinion or preference; not based on the nature of things; hence, capricious, uncertain, varying.
"Statistics and Causal Inference." J. Am. Stat. Assoc. 81 (396): 945-60. "When units are assigned at random either to cause t or to cause c, certain physical randomization processes are carried out so that the determination of which cause (t or c) u is exposed to is regarded as statistically independent of all other variables, including ...