case study questions in integers

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 7 Maths Chapter 1 Integers

Last modified on: 8 months ago
Reading Time: 7 Minutes

Here in this article, we are providing case study questions for Class 7 Maths Chapter 1 Integers.

Maths Class 7 Chapter List

Latest chapter list (2023-24).

There is total 13 chapters.

Chapter 1 Integers Case Study Questions Chapter 2 Fractions and Decimals Case Study Questions Chapter 3 Data Handling Case Study Questions Chapter 4 Simple Equations Case Study Questions Chapter 5 Lines and Angles Case Study Questions Chapter 6 The Triangles and its Properties Case Study Questions Chapter 7 Comparing Quantities Case Study Questions Chapter 8 Rational Numbers Case Study Questions Chapter 9 Perimeter and Area Case Study Questions Chapter 10 Algebraic Expressions Case Study Questions Chapter 11 Exponents and Powers Case Study Questions Chapter 12 Symmetry Case Study Questions Chapter 13 Visualising Solid Shapes Case Study Questions

Old Chapter List

Chapter 1 Integers Chapter 2 Fractions and Decimals Chapter 3 Data Handling Chapter 4 Simple Equations Chapter 5 Lines and Angles Chapter 6 The Triangles and its Properties Chapter 7 Congruence of Triangles Chapter 8 Comparing Quantities Chapter 9 Rational Numbers Chapter 10 Practical Geometry Chapter 11 Perimeter and Area Chapter 12 Algebraic Expressions Chapter 13 Exponents and Powers Chapter 14 Symmetry Chapter 15 Visualising Solid Shapes

Deleted Chapter:

Chapter 7 Congruence of Triangles
Chapter 10 Practical Geometry

Tips for Answering Case Study Questions for Class 7 Maths in Exam

1. Comprehensive Reading for Context: Prioritize a thorough understanding of the provided case study. Absorb the contextual details and data meticulously to establish a strong foundation for your solution.

2. Relevance Identification: Pinpoint pertinent mathematical concepts applicable to the case study. By doing so, you can streamline your thinking process and apply appropriate methods with precision.

3. Deconstruction of the Problem: Break down the complex problem into manageable components or steps. This approach enhances clarity and facilitates organized problem-solving.

4. Highlighting Key Data: Emphasize critical information and data supplied within the case study. This practice aids quick referencing during the problem-solving process.

5. Application of Formulas: Leverage pertinent mathematical formulas, theorems, and principles to solve the case study. Accuracy in formula selection and unit usage is paramount.

6. Transparent Workflow Display: Document your solution with transparency, showcasing intermediate calculations and steps taken. This not only helps track progress but also offers insight into your analytical process.

7. Variable Labeling and Definition: For introduced variables or unknowns, offer clear labels and definitions. This eliminates ambiguity and reinforces a structured solution approach.

8. Step Explanation: Accompany each step with an explanatory note. This reinforces your grasp of concepts and demonstrates effective application.

9. Realistic Application: When the case study pertains to real-world scenarios, infuse practical reasoning and logic into your solution. This ensures alignment with real-life implications.

10. Thorough Answer Review: Post-solving, meticulously review your answer for accuracy and coherence. Assess its compatibility with the case study’s context.

11. Solution Recap: Before submission, revisit your solution to guarantee comprehensive coverage of the problem and a well-organized response.

12. Previous Case Study Practice: Boost your confidence by practicing with past case study questions from exams or textbooks. This familiarity enhances your readiness for the question format.

13. Efficient Time Management: Strategically allocate time for each case study question based on its complexity and the overall exam duration.

14. Maintain Composure and Confidence: Approach questions with poise and self-assurance. Your preparation equips you to conquer the challenges presented.

Download CBSE Books

Exam Special Series:

Sample Question Paper for CBSE Class 10 Science (for 2024)
Sample Question Paper for CBSE Class 10 Maths (for 2024)
CBSE Most Repeated Questions for Class 10 Science Board Exams
CBSE Important Diagram Based Questions Class 10 Physics Board Exams
CBSE Important Numericals Class 10 Physics Board Exams
CBSE Practical Based Questions for Class 10 Science Board Exams
CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
Sample Question Papers for CBSE Class 12 Physics (for 2024)
Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
Sample Question Papers for CBSE Class 12 Maths (for 2024)
Sample Question Papers for CBSE Class 12 Biology (for 2024)
CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
Master Organic Conversions CBSE Class 12 Chemistry Board Exams
CBSE Important Numericals Class 12 Physics Board Exams
CBSE Important Definitions Class 12 Physics Board Exams
CBSE Important Laws & Principles Class 12 Physics Board Exams
10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
ICSE Important Functions and Locations Based Questions Class 10 Biology
ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

New QB365-SLMS
NEET Materials
JEE Materials
Banking first yr Materials
TNPSC Materials
DIPLOMA COURSE Materials
5th Standard Materials
12th Standard Materials
11th Standard Materials
10th Standard Materials
9th Standard Materials
8th Standard Materials
7th Standard Materials
6th Standard Materials
12th Standard CBSE Materials
11th Standard CBSE Materials
10th Standard CBSE Materials
9th Standard CBSE Materials
8th Standard CBSE Materials
7th Standard CBSE Materials
6th Standard CBSE Materials
Tamilnadu Stateboard
Scholarship Exams
Scholarships

CBSE 7th Standard CBSE Mathematics question papers, important notes , study materials , Previuous Year questions, Syllabus and exam patterns. Free 7th Standard CBSE Mathematics books and syllabus online. Practice Online test for free in QB365 Study Material. Important keywords, Case Study Questions and Solutions. Updates about latest education news and Scholorships in one place.

7th Standard CBSE Subjects

7th standard cbse study materials.

Class VI to XII

Tn state board / cbse, 3000+ q&a's per subject, score high marks.

Latest CBSE 7th Standard CBSE Study Material Updates

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Here you will learn about integers, including how to identify integers, integers on a horizontal number line, and integers on a vertical number line.

Students will first learn about integers as part of the number system in 6th grade.

What are integers?

Integers are a set of numbers that include all whole numbers (zero and positive numbers) as well as negative numbers. Integers do not include fractions or decimals.

For example, here are some integers on a horizontal number line

All whole numbers are integers, but not all integers are whole numbers since integers also include negative numbers. Both whole numbers and integers are rational numbers and real numbers.

Natural numbers (also known as counting numbers) are a subset of integers.

For example,

Common Core State Standards

How does this relate to 6th grade math?

Grade 6 – The Number System (6.NS.6c) Find and position integers and other rational numbers on a horizontal or vertical number line diagram; find and position pairs of integers and other rational numbers on a coordinate plane.

How to identify integers

In order to identify integers:

Recall the definition of the type of number needed.

Show whether the number fits or does not fit the definition.

[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)

Use this quiz to check your grade 6 students’ understanding of types of numbers. 10+ questions with answers covering a range of 2nd, 4th and 6th grade types of numbers topics to identify areas of strength and support!

Integers examples

Example 1: identifying integers.

Which of the following are integers?

Integers include all whole numbers (positive numbers and zero) and their corresponding negative numbers. You can eliminate the following numbers based on this definition:

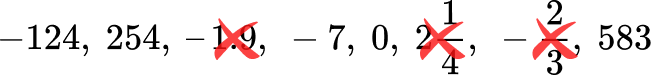
2 Show whether the number fits or does not fit the definition.

The remaining numbers are –124, 254, –7, 0, and 583, all of which are integers.

Example 2: identifying integers

Grace says –21 is not an integer, but it is a whole number. Her friend Isaiah says –21 is not a whole number but an integer. Who is correct?

Integers include all whole numbers (positive numbers and zero) and their corresponding negative numbers. Integers do not include fractions or decimals.

Isaiah is correct because –21 is a negative number; it does not include a decimal or a fractional part.

Whole numbers only include zero and positive numbers. Therefore, it is an integer.

Example 3: integers on a number line

Find the missing integer on the number line.

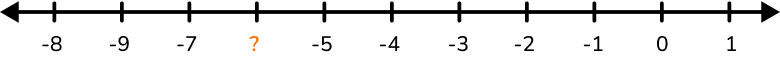
This means the missing number will not be a fraction or decimal and will be a negative number.

The missing number is –6.

If you continue counting on the number line, the number in between –7 and –5 would be –6.

Example 4: integers on a number line

There are two integers missing from the number line. Which missing integer is a positive integer?

In this case, you are looking for a non-negative integer or positive integer only.

The missing integers are –15 and 20.

The missing positive integer is 20.

Example 5: integers on a vertical number line

The vertical number line is missing two integers; one positive integer and one negative integer. What are they?

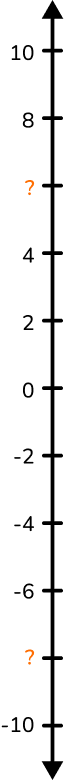
There is one negative number and one positive number missing from the vertical number line.

The negative numbers are on the bottom half (counting downwards from zero by 2 ) and the positive numbers are on the top half (counting upwards from zero by 2 ).

Therefore, the missing integers are –8 and 6.

Example 6: integers on a vertical number line

Look at the set of integers on the vertical number line. Fill in the boxes to complete the set.

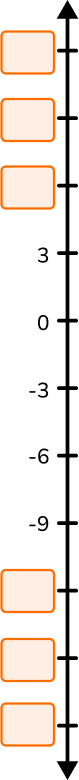
The set of integers included on the number line is, in numeric order, –9, –6, –3, 0, 3.

This means you are counting by 3.

So the missing positive numbers are 6, 9, and 12.

The missing negative numbers are –12, –15, and –18.

Teaching tips for integers

Using a horizontal or vertical number line will help students build their foundation of understanding integers, especially negative numbers. It will also help them understand that negative numbers are the additive inverses of positive numbers.
Students should master identifying and understanding integers on a number line before moving on to performing arithmetic operations with negative numbers and including negative numbers in algebraic equations.

Easy mistakes to make

Thinking that integers and whole numbers are the same Integers and whole numbers are similar, but they are not the same. Whole numbers are a subset of integers. While whole numbers and integers include zero and positive numbers and do not include fractions or decimals, integers also include negative numbers.
Thinking that zero is not an integer Zero, while not negative or positive, is an integer as well as a whole number.

Related types of numbers lessons

Types of numbers
Irrational numbers
Absolute value
Even numbers
Odd numbers
Number sets
Prime and composite numbers
Prime numbers
Natural numbers
Rational numbers
Whole numbers

Practice integers questions

1. Which of the following is a non-negative integer?

Integers include all whole numbers (positive numbers and zero) and all negative numbers.

Integers do not include fractions or decimals.

2. Which set of numbers are all integers?

The last set of numbers is the only set that does not contain any fractions or decimals and is therefore, a set of integers.

3. Amir’s teacher asked him to plot all of the integers from –4 to 6 on a number line. Which number line is correct?

Integers include all negative numbers, positive numbers, and zero.

On a horizontal number line, the negative numbers are shown to the left of zero while the positive numbers are shown to the right.

Since negative numbers are the additive inverse of positive numbers, the negative and positive numbers should mirror each other on opposite sides of the zero.

4. Fill in the missing integers to complete the number line.

On the horizontal number line, negative numbers count left from zero while positive numbers count right from zero.

The scale, or amount between each number, should be the same.

On this number line, you are counting by 10.

So the missing integers in numeric order are –70, –60, –40, 0, and 20.

5. Plot the numbers –8 to 2 on a vertical number line.

On the vertical number line, negative numbers count down from zero, while positive numbers count up from zero.

On this number line, you are counting by 1.

So in numeric order starting at the top of the number line, the integers should be 2, 1, 0, –1, –2, –3, –4, –5, –6, –7, –8.

6. Fill in the missing integers to complete the vertical number line.

On this number line, you are counting by 5.

So in numeric order starting at the top of the number line, the missing integers should be 15, 5, –5, 20 .

Integers FAQs

An integer is a positive number, a negative number, or the number zero. An integer does not contain decimal digits or fractional parts.

Negative numbers are the additive inverses of the corresponding positive numbers. For example, the additive inverse of –3 is 3, the additive inverse of –12 is 12, etc.

All four basic arithmetic operations – addition, subtraction, multiplication, and division – can be performed on integers. However, mathematicians performing these arithmetic operations on negative numbers may follow different rules than performing them on whole numbers.

The next lessons are

Rounding numbers
Factors and multiples
Adding and subtracting integers
Multiplying and dividing integers

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

$One on one math tuition$

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

Class 10 Maths Case Study Questions of Chapter 1 Real Numbers

Post author: studyrate
Post published:
Post category: class 10th
Post comments: 0 Comments

Case study Questions in the Class 10 Mathematics Chapter 1 are very important to solve for your exam. Class 10 Maths Chapter 1 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving Class 10 Maths Case Study Questions Chapter 1 Real Numbers

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

In CBSE Class 10 Maths Paper, Students will have to answer some questions based on Assertion and Reason . There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

Real Numbers Case Study Questions With Answers

Here, we have provided case-based/passage-based questions for Class 10 Maths Chapter 1 Real Numbers

Case Study/Passage-Based Questions

Case Study 1: Srikanth has made a project on real numbers, where he finely explained the applicability of exponential laws and divisibility conditions on real numbers. He also included some assessment questions at the end of his project as listed below. (i) For what value of n, 4 n ends in 0?

Answer: (d) no value of n

(ii) If a is a positive rational number and n is a positive integer greater than 1, then for what value of n, a n is a rational number?

Answer: (c) for all n > 1

(iii) If x and yare two odd positive integers, then which of the following is true?

Answer: (d) both (a) and (b)

(iv) The statement ‘One of every three consecutive positive integers is divisible by 3’ is

Answer: (a) always true

(v) If n is any odd integer, then n2 – 1 is divisible by

Answer: (d) 8

Case Study 2: HCF and LCM are widely used in number system especially in real numbers in finding relationship between different numbers and their general forms. Also, product of two positive integers is equal to the product of their HCF and LCM Based on the above information answer the following questions.

(i) If two positive integers x and y are expressible in terms of primes as x =p 2 q 3 and y=p 3 q, then which of the following is true? (a) HCF = pq 2 x LCM (b) LCM = pq 2 x HCF (c) LCM = p 2 q x HCF (d) HCF = p 2 q x LCM

Answer: (b) LCM = pq2 x HCF

ii) A boy with collection of marbles realizes that if he makes a group of 5 or 6 marbles, there are always two marbles left, then which of the following is correct if the number of marbles is p? (a) p is odd (b) p is even (c) p is not prime (d) both (b) and (c)

Answer: (d) both (b) and (c)

(iii) Find the largest possible positive integer that will divide 398, 436 and 542 leaving remainder 7, 11, 15 respectively. (a) 3 (b) 1 (c) 34 (d) 17

Answer: (d) 17

(iv) Find the least positive integer that on adding 1 is exactly divisible by 126 and 600. (a) 12600 (b) 12599 (C) 12601 (d) 12500

Answer: (b) 12599

(v) If A, B and C are three rational numbers such that 85C – 340A = 109, 425A + 85B = 146, then the sum of A, B and C is divisible by (a) 3 (b) 6 (c) 7 (d) 9

Answer: (a) 3

Case Study 3: Real numbers are an essential concept in mathematics that encompasses both rational and irrational numbers. Rational numbers are those that can be expressed as fractions, where the numerator and denominator are integers and the denominator is not zero. Examples of rational numbers include integers, decimals, and fractions. On the other hand, irrational numbers are those that cannot be expressed as fractions and have non-terminating and non-repeating decimal expansions. Examples of irrational numbers include √2, π (pi), and e. Real numbers are represented on the number line, which extends infinitely in both positive and negative directions. The set of real numbers is closed under addition, subtraction, multiplication, and division, making it a fundamental number system used in various mathematical operations and calculations.

Which numbers can be classified as rational numbers? a) Fractions b) Integers c) Decimals d) All of the above Answer: d) All of the above

What are rational numbers? a) Numbers that can be expressed as fractions b) Numbers that have non-terminating decimal expansions c) Numbers that extend infinitely in both positive and negative directions d) Numbers that cannot be expressed as fractions Answer: a) Numbers that can be expressed as fractions

What are examples of irrational numbers? a) √2, π (pi), e b) Integers, decimals, fractions c) Numbers with terminating decimal expansions d) Numbers that can be expressed as fractions Answer: a) √2, π (pi), e

How are real numbers represented? a) On the number line b) In complex mathematical formulas c) In algebraic equations d) In geometric figures Answer: a) On the number line

What operations are closed under the set of real numbers? a) Addition, subtraction, multiplication b) Subtraction, multiplication, division c) Addition, multiplication, division d) Addition, subtraction, multiplication, division Answer: d) Addition, subtraction, multiplication, division

Hope the information shed above regarding Case Study and Passage Based Questions for Class 10 Maths Chapter 1 Real Numbers with Answers Pdf free download has been useful to an extent. If you have any other queries about CBSE Class 10 Maths Real Numbers Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible By Team Study Rate

Extra questions of class 10 science chapter 12 electricity pdf download, mcq class 10 english from the diary of anne frank questions with answers english chapter 4, case study questions class 10 science chapter 5 periodic classification of elements, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

NCERT Exemplar
NCERT Exemplar Class 7
Class 7 Maths
Class 7 Maths Chapter 1

NCERT Exemplar Solutions for Class 7 Maths Chapter 1 Integers

NCERT Exemplar Solutions for Class 7 Maths Chapter 1 Integers are the best study materials for students who find difficulties in solving problems. These solutions can help students clear doubts quickly and help in understanding topics effectively. Our subject experts formulate these exercises to assist you with your exam preparation to attain good marks in the subject. Students can score good marks in Maths by practising NCERT Exemplar Solutions for Class 7 Maths.

Chapter 1 – Integers solutions are available for download in PDF format, which provides answers to all questions in the NCERT Exemplar Class 7 Maths textbook. An integer is a whole number that can be positive, negative or zero. Positive integers are used in many ways in our daily lives. One such instance is highway numbers, along with roadway speed limits. Negative integers are used in thermometer readings, keeping scores in some games, etc. Now, let us have a look at some of the concepts discussed in this chapter.

Representation of integers on the number line and their addition and subtraction.
Properties of addition and subtraction of integers
Multiplication of integers
Multiplication of a positive and negative integer
Division of a positive and negative integer

Download the PDF of NCERT Exemplar Solutions for Class 7 Maths Chapter 1 Integers

ncert exemplar nov2020 class 7 maths solutions chapter 1 01

Access Answers to Maths NCERT Exemplar Solutions for Class 7 Chapter 1 Integers

Exercise Page No: 8

In the Questions 1 to 25, there are four options, out of which only one is correct. Write the correct one.

1. When the integers 10, 0, 5, – 5, – 7 are arranged in descending or ascending order, then find out which of the following integers always remains in the middle of the arrangement.

(a) 0 (b) 5 (c) – 7 (d) – 5

When the given integers are arranged in descending order we have: 10, 5, 0, -5, -7

When the given integers are arranged in an ascending order we have: -7, -5, 0, 5, 10

It’s seen that in both the orders 0 always remains in the middle of the arrangement.

2. By observing the number line (Fig. 1.2), state which of the following statements is not true.

NCERT Exemplars Class 7 Maths Solutions Chapter 1 Image 1

(a) B is greater than –10 (b) A is greater than 0

Since, B lies to the left of zero and A lies to the right of zero on the number line clearly, A has to be greater than B.

3. By observing the above number line (Fig. 1.2), state which of the following statements is true.

(a) B is 2 (b) A is – 4 (c) B is –13 (d) B is – 4

(d) B is -4

Each division on the number line is 1 unit apart. Then, B is 4 units from the left of zero.

4. Next three consecutive numbers in the pattern 11, 8, 5, 2, –, –, — are

(a) 0, – 3, – 6 (b) – 1, – 5, – 8 (c) – 2, – 5, – 8 (d) – 1, – 4, – 7

(d) -1, -4, -7

In the given sequence of numbers, each number differs by 3 from the previous number.

5. The next number in the pattern – 62, – 37, – 12 _________ is

(a) 25 (b) 13 (c) 0 (d) –13

It’s found that the pattern is -62 + 25 = -37, -37 + 25 = -12

So, similarly -12 + 25 = 13

6. Which of the following statements is not true?

(a) When two positive integers are added, we always get a positive integer.

(b) When two negative integers are added we always get a negative integer.

(d) Additive inverse of an integer 2 is (– 2) and additive inverse of (– 2) is 2.

The above statement is false as when a positive and a negative integer is added we may get a positive number or even zero.

7. On the following number line value ‘Zero’ is shown by the point

NCERT Exemplars Class 7 Maths Solutions Chapter 1 Image 2

(a) X (b) Y (c) Z (d) W

It’s observed that each division on the number line is 5 units. So, from 10 taking two division to its left we get zero.

8. If ⊗, O, and • represent some integers on number line, then descending order of these numbers is

NCERT Exemplars Class 7 Maths Solutions Chapter 1 Image 3

The descending order of these numbers is as in option (c).

9. On the number line, the value of (–3) × 3 lies on right hand side of

(a) – 10 (b) – 4 (c) 0 (d) 9

As (-3) x 3 = -9

So, -9 lies to the right to -10.

10. The value of 5 ÷ (–1) does not lie between

(a) 0 and – 10 (b) 0 and 10 (c) – 4 and – 15 (d) – 6 and 6

(b) 0 and 10

The value of 5 ÷ (–1) = -5

As it is a negative number it doesn’t lie between 0 and 10.

11. Water level in a well was 20m below ground level. During rainy season, rain water collected in different water tanks was drained into the well and the water level rises 5 m above the previous level. The wall of the well is 1m 20 cm high and a pulley is fixed at a height of 80 cm. Raghu wants to draw water from the well. The minimum length of the rope that he can use is

NCERT Exemplars Class 7 Maths Solutions Chapter 1 Image 4

(a) 17 m (b) 18 m (c) 96 m (d) 97 m

Height of the wall of the well = 1m 20 cm = 1.2 m

Height of the fixed pulley = 80 cm = 0.8 m

Initially water was available at a depth of 20 m below ground level.

Later, due to rain the water level was raised by 5 m.

Hence, the new depth at which water is available = 20 – 5 = 15 m

The minimum length of the rope required to draw water from the well will be

(1.2 + 0.8 + 15) m = 17 m

12. (– 11) × 7 is not equal to

(a) 11 × (– 7) (b) – (11 × 7) (c) (– 11) × (– 7) (d) 7 × (– 11)

11 x (-7) = -77

– (11 x 7) = -77 and

7 x (-11) = -77

But, (-11) x (-7) = 77

13. (– 10) × (– 5) + (– 7) is equal to

(a) – 57 (b) 57 (c) – 43 (d) 43

Using BODMAS rule,

(-10) x (-5) + (-7) = 50 – 7 = 43

14. Which of the following is not the additive inverse of a?

(a) – (– a) (b) a × (– 1) (c) – a (d) a ÷ (–1)

The additive inverse of a is – a

But, – (-a) = a

15. Which of the following is the multiplicative identity for an integer a?

(a) a (b) 1 (c) 0 (d) – 1

16. [(– 8) × (– 3)] × (– 4) is not equal to

(a) (– 8) × [(– 3) × (– 4)] (b) [(– 8) × (– 4)] × (– 3)

(d) (– 8) × (– 3) – (– 8) × (– 4)

= [(– 8) × (– 4)] × (– 3)

= [(– 3) × (– 8)] × (– 4)

But, [(– 8) × (– 3)] × (– 4) ≠ (– 8) × (– 3) – (-8) × (– 4)

17. (– 25) × [6 + 4] is not same as

(a) (– 25) × 10 (b) (– 25) × 6 + (– 25) × 4 (c) (– 25) × 6 × 4 (d) – 250

= (– 25) × 10

= (– 25) × 6 + (– 25) × 4

But, (– 25) × [6 + 4] ≠ (– 25) × 6 × 4

18. – 35 × 107 is not same as

(a) – 35 × (100 + 7) (b) (– 35) × 7 + ( – 35) × 100

– 35 × 107 = (– 30 – 5) × 107 = – 35 × (100 + 7) = (– 35) × 7 + ( – 35) × 100

But, – 35 × 107 ≠ – 35 × 7 + 100

19. (– 43) × (– 99) + 43 is equal to

(a) 4300 (b) – 4300 (c) 4257 (d) – 4214

By BODMAS rule,

(– 43) × (– 99) + 43 = [(– 43) × (– 99)] + 43 = 4257 + 43 = 4300

20. (– 16) ÷ 4 is not same as

(a) ( – 4) ÷ 16 (b) – ( 16 ÷ 4) (c) 16 ÷ (– 4) (d) – 4

(a) ( – 4) ÷ 16

(– 16) ÷ 4 = -4

But, ( – 4) ÷ 16 = -1/4

21. Which of the following does not represent an integer?

(a) 0 ÷ (– 7) (b) 20 ÷ (– 4) (c) (– 9) ÷ 3 (d) (– 12) ÷ 5

(d) (– 12) ÷ 5

0 ÷ (– 7) = 0, an integer

20 ÷ (– 4) = -5, an integer

(– 9) ÷ 3 = -3, an integer

But, (– 12) ÷ 5 = -2.4, which is a decimal and not an integer

22. Which of the following is different from the others?

(a) 20 + (–25) (b) (– 37) – (– 32) (c) (– 5) × (–1) (d) ( 45 ) ÷ (– 9)

As all the remaining options give a value of -5

20 + (–25) = (– 37) – (– 32) = ( 45 ) ÷ (– 9) = -5

But, (– 5) × (–1) = 5

23. Which of the following shows the maximum rise in temperature?

(a) 23° to 32° (b) – 10° to + 1° (c) – 18° to – 11° (d) – 5° to 5°

(b) – 10° to + 1°

As the difference in the temperature = 1° – (10°) = 11° (maximum)

23° to 32° = 32° – 23° = 9°

– 18° to – 11° = -11° – (-18)° = 7°

– 5° to 5° = 5° – (-5)° = 10°

24. If a and b are two integers, then which of the following may not be an integer?

(a) a + b (b) a – b (c) a × b (d) a ÷ b

If a and b are two integers, then

a + b will always be an integer

a – b will always be an integer

a × b will always be an integer

25. For a non-zero integer a, which of the following is not defined?

(a) a ÷ 0 (b) 0 ÷ a (c) a ÷ 1 (d) 1 ÷ a

a ÷ 0 = a/0 is undefined

Encircle the odd one of the following (Questions 26 to 30).

26. (a) (–3, 3) (b) (–5, 5) (c) (–6, 1) (d) (–8, 8)

–6 + 1 = -5

Hence, (–6, 1) is the odd one.

27. (a) (–1, –2) (b) (–5, +2) (c) (–4, +1) (d) (–9, +7)

(d) (–9, +7)

–1 + (–2) = -3

–5 + 2 = -3

–4 + 1 = -3

–9 + 7 = -2

Hence, (–9, +7) is the odd one.

28. (a) (–9) × 5 × 6 × (–3) (b) 9 × (–5) × 6 × (–3)

(–9) × 5 × 6 × (–3) = 810

9 × (–5) × 6 × (–3) = 810

(–9) × (–5) × (–6) × 3 = -810

9 × (–5) × (–6) × 3 = 810

Hence, (–9) × (–5) × (–6) × 3 is the odd one.

29. (a) (–100) ÷ 5 (b) (–81) ÷ 9 (c) (–75) ÷ 5 (d) (–32) ÷ 9

(d) (–32) ÷ 9

Since, only (–32) ÷ 9 doesn’t give an integer i.e. -32/9 = -3.5555555556

Hence, (–32) ÷ 9 is the odd one.

30. (a) (–1) × (–1) (b) (–1) × (–1) × (–1)

(b) (–1) × (–1) × (–1)

(–1) × (–1) = 1

(–1) × (–1) × (–1) × (–1) = 1

(–1) × (–1) × (–1) × (–1) × (–1) × (–1) = 1

But, (–1) × (–1) × (–1) = -1

Hence, (–1) × (–1) × (–1) is the odd one.

In Questions 31 to 71, fill in the blanks to make the statements true.

31. (–a) + b = b + Additive inverse of __________.

(–a) + b = b + (-a)

(–a) + b = b + Additive inverse of (a)

32. ________ ÷ (–10) = 0

0 ÷ (–10) = 0/(-10) = 0

33. (–157) × (–19) + 157 = ___________

(–157) × (–19) + 157 = (2983) + 157 = 3140

34. [(–8) + ______ ] + ________ = ________ + [(–3) + ________ ] = –3

-3, 8, -8, 8:

35. On the following number line, (–4) × 3 is represented by the point _________.

NCERT Exemplars Class 7 Maths Solutions Chapter 1 Imag 5

(-4) x 3 = -12

Each division on the number line is 2 units. So, D represent -12

36. If x, y and z are integers then (x +___ ) + z = _____ + (y + _____ )

By associative property of integers, we have

(x + y) + z = x + (y + z)

37. (– 43) + _____ = – 43

(– 43) + 0 = – 43

38. (– 8) + (– 8) + (– 8) = _____ × (– 8)

(– 8) + (– 8) + (– 8) = -24 = 3 × (– 8)

39. 11 × (– 5) = – ( _____ × _____ ) = _____

11, 5, -55:

11 × (– 5) = – (11 × 5 ) = -55

40. (– 9) × 20 = _____

(– 9) × 20 = -180

41. (– 23) × (42) = (– 42) × _____

(– 23) × (42) = (– 42) × 23 = 966

42. While multiplying a positive integer and a negative integer, we multiply them as ________ numbers and put a ________ sign before the product.

whole, negative

43. If we multiply ________ number of negative integers, then the resulting integer is positive.

44. If we multiply six negative integers and six positive integers, then the resulting integer is _______

positive integer

When even number of negative integers are multiplied the resulting integer is positive and when six positive integers are multiplied the resulting integer is also a positive.

45. If we multiply five positive integers and one negative integer, then the resulting integer is _______.

When odd number of negative integers are multiplied the resulting integer is negative. Also, when a negative and positive integer are multiplied the resulting integer is negative.

46. _______ is the multiplicative identity for integers.

1 is the multiplicative identity for integers.

i.e. 1 x a = a

47. We get additive inverse of an integer a when we multiply it by _________.

a x (-1) = -a = additive inverse of (a)

48. ( – 25) × ( – 2) =

( – 25) × ( – 2) = 25 x 2 = 50

49. (– 5) × ( – 6) × ( – 7) =

(– 5) × ( – 6) × ( – 7) = – (5 × 6 × 7) = -210

50. 3 × ( – 1) × ( – 15) =

3 × ( – 1 ) × ( – 15) = (-3) x (-15) = 45

51. [12 × ( – 7)] × 5 = ___ × [(– 7) × ___ ]

52. 23 × ( – 99) = ___ × ( – 100 + ___ ) = 23 × ___ + 23 × ___

23, 1, -100, 1:

23 × ( – 99) = 23 × ( – 100 + 1 ) = 23 × (-100) + 23 × 1 (Distributive property of integers)

53. ___ × ( – 1) = – 35

35 × ( – 1) = – 35

54. ____ × ( – 1) = 47

-47 × ( – 1) = 47 (product of even number of negative integers is a positive integer)

55. 88 × ___ = – 88

88 × -1 = – 88

56. ___ × (–93) = 93

-1 × (–93) = 93

57. ( – 40) × __ = 80

( – 40) × (-2) = 80

58. ___ × (–23) = – 920

40 × (–23) = – 920

59. When we divide a negative integer by a positive integer, we divide them as whole numbers and put a ______ sign before quotient.

60. When –16 is divided by _________ the quotient is 4.

Let -16 be divided by x and the quotient is 4

So, -16/x = 4

61. Division is the inverse operation of ____________

Multiplication

62. 65 ÷ ( – 13) =

65 ÷ (– 13) = 65/ (-13) = -5

63. ( – 100) ÷ ( – 10) =

( – 100) ÷ ( – 10) = ( – 100)/ ( – 10) = 10

64. ( – 225) ÷ 5 =

( – 225) ÷ 5 = -45

65. _____÷ ( – 1 ) = – 83

83 ÷ ( – 1 ) = – 83

66. _____ ÷ ( – 1) = 75

(-75) ÷ ( – 1) = 75

67. 51 ÷ _____ = – 51

51 ÷ (-1) = – 51

68. 113 ÷ _____ = – 1

113 ÷ (-113) = – 1

69. (– 95) ÷ _____ = 95

(– 95) ÷ (-1) = 95

70. ( – 69) ÷ ( 69) = _____

( – 69) ÷ ( 69) = (-69)/ 69 = -1

71. ( – 28) ÷ ( – 28) = _____

( – 28) ÷ ( – 28) = (-28)/ (-28) = 1

In Questions 72 to 83, state whether the statements are True or False.

72. 5 – ( – 8) is same as 5 + 8.

5 – ( – 8) = 5 + 8

73. (– 9) + (– 11) is greater than (– 9) – ( – 11).

(– 9) + (– 11) = – 19

But, (– 9) – ( – 11) = – 9 + 11 = 2

So, -19 < 2

Hence, (– 9) + (– 11) < (– 9) – ( – 11)

74. Sum of two negative integers always gives a number smaller than both the integers.

-4 + (-5) = -9

-4 > -9 and -5 > -9

75. Difference of two negative integers cannot be a positive integer.

E.g.: -2 – (-5) = -2 + 5 = 3 (positive integer)

76. We can write a pair of integers whose sum is not an integer.

Sum of two integers is always an integer.

77. Integers are closed under subtraction.

The difference of two integers is always an integer.

78. (– 23) + 47 is same as 47 + (– 23).

In case of addition even if the orders of integers are changed, as the values are equal both are equal.

(– 23) + 47 = 24 and 47 + (– 23) = 24

79. When we change the order of integers, their sum remains the same.

80. When we change the order of integers their difference remains the same.

E.g., 4 – 5 – 8 = -9

But, 5 – 4 – 8 = -7

81. Going 500 m towards east first and then 200 m back is same as going 200 m towards west first and then going 500 m back.

Considering the originating point to the zero of a number line

In the first scenario: 500 – 200 = 300 m to the right from the starting point (0)

In the second scenario: -200 + 500 = 300 m to the right from the starting point (0)

82. (– 5) × (33) = 5 × (– 33)

(– 5) × (33) = -165 and 5 × (– 33) = -165

83. (– 19) × (– 11) = 19 × 11

As the product of numbers with same signs are equal to the absolute value

(– 19) × (– 11) = 19 × 11 = 209

Register with BYJU'S & Download Free PDFs

Bihar Board

RBSE Result 2024

Srm university.

Goa Board Result 2024
Maharashtra HSC Result
Maharashtra SSC Result
RBSE 10th Result 2024
RBSE 12th Result 2024
CBSE Board Result 2024
Shiv Khera Special
Education News
Web Stories
Current Affairs
नए भारत का नया उत्तर प्रदेश
School & Boards
College Admission
Govt Jobs Alert & Prep
GK & Aptitude
CBSE Class 10 Study Material

CBSE Class 10 Maths Case Study Questions for Chapter 2 - Polynomials (Published by CBSE)

Check the case study questions published by cbse for class 10 maths chapter 2 - polynomials. these questions are important for the preparation of cbse class 10 maths exam 2021-22..

CBSE Class 10 Maths paper in Board Exam 2022 will have some questions based on the case study. These questions are entirely new for the class 10 students. Therefore, the board has released a question bank to help the students get familiarised with the case study questions. We have provided here the case study questions for CBSE Class 10 Maths Chapter 2 - Polynomials. All the questions have sub-questions of MCQ type. You can find the answer (correct option) written against each question. Practice all the case study based questions right after you finish with the chapter - Polynomials. This will help you prepare for your Maths exam easily and effectively.

Case Study Questions for Class 10 Maths Chapter 2 - Polynomials

CASE STUDY 1:

The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.

1. In the standard form of quadratic polynomial, ax 2 + bx + c, a, b and c are

a) All are Polynomials.

b) All are rational numbers.

c) ‘a’ is a non zero real number and b and c are any Polynomials.

d) All are integers.

Answers: c) ‘a’ is a non zero real number and b and c are any Polynomials.

2. If the roots of the quadratic polynomial are equal, where the discriminant D = b 2 – 4ac, then

a) D > 0

b) D < 0

c) D ≥ 0

Answers: d) D = 0

3. If α and 1/α are the zeroes of the quadratic polynomial 2x2 – x + 8k, then k is

c) –1/4

Answers: b) 1/4

4. The graph of x 2 +1 = 0

a) Intersects x‐axis at two distinct points.

b)Touches x‐axis at a point.

c) Neither touches nor intersects x‐axis.

d)Either touches or intersects x‐ axis.

Answers: c) Neither touches nor intersects x‐axis.

5. If the sum of the roots is –p and product of the roots is –1/p, then the quadratic polynomial is

a) k(–px 2 + x/p + 1)

b) k(px 2 – x/p – 1)

c) k(x 2 + px – 1/p)

d) k(x 2 – px + 1/p)

Answers: c) k(x 2 + px – 1/p)

CASE STUDY 2:

An asana is a body posture, originally and still a general term for a sitting meditation pose, and later extended in hatha yoga and modern yoga as exercise, to any type of pose or position, adding reclining, standing, inverted, twisting, and balancing poses. In the figure, one can observe that poses can be related to representation of quadratic polynomial.

1. The shape of the poses shown is

d) Parabola

Answer: d) Parabola

2. The graph of parabola opens downwards, if _______

a) a ≥ 0

c) a < 0

d) a > 0

Answer: c) a < 0

3. In the graph, how many zeroes are there for the polynomial?

Answer: c) 2

4. The two zeroes in the above shown graph are

Answer: b) -2, 4

CASE STUDY 3:

Basketball and soccer are played with a spherical ball. Even though an athlete dribbles the ball in both sports, a basketball player uses his hands and a soccer player uses his feet. Usually, soccer is played outdoors on a large field and basketball is played indoor on a court made out of wood. The projectile (path traced) of soccer ball and basketball are in the form of parabola representing quadratic polynomial.

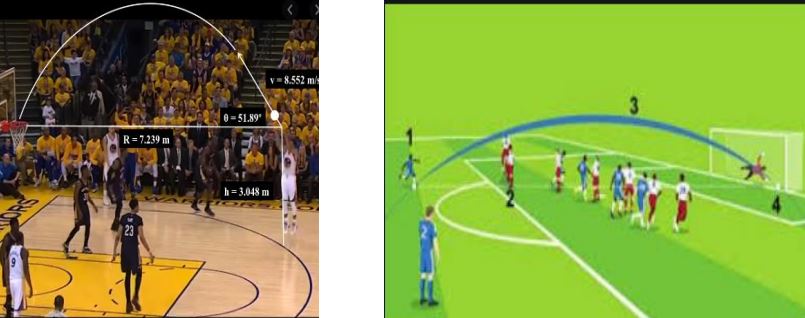
1. The shape of the path traced shown is

2. The graph of parabola opens upwards, if _______

b) a < 0

c) a > 0

d) a ≥ 0

Answer: c) a > 0

3. Observe the following graph and answer

In the above graph, how many zeroes are there for the polynomial?

Answer: d) 3

4. The three zeroes in the above shown graph are

b) -2, 3, 1

c) -3, -1, 2

d) -2, -3, -1

Answer: c) -3, -1, 2

5. What will be the expression of the polynomial?

a) x 3 + 2x 2 – 5x – 6

b) x 3 + 2x 2 – 5x + 6

c) x 3 + 2x 2 + 5x – 6

d) x 3 + 2x 2 + 5x + 6

Answer: a) x 3 + 2x 2 – 5x – 6

Also Check:

CBSE Case Study Questions for Class 10 Maths - All Chapters

Tips to Solve Case Study Based Questions Accurately

Get here latest School , CBSE and Govt Jobs notification in English and Hindi for Sarkari Naukari and Sarkari Result . Download the Jagran Josh Sarkari Naukri App . Check Board Result 2024 for Class 10 and Class 12 like CBSE Board Result , UP Board Result , Bihar Board Result , MP Board Result , Rajasthan Board Result and Other States Boards.

JAC 9th, 11th रिजल्ट 2024
JAC 9th रिजल्ट 2024
JAC Result 2024
jac.jharkhand.gov.in 11th Result 2024
JAC 11वीं रिजल्ट 2024 रोल नंबर
GBSHSE SSC Result 2024
SSC Result 2024 Goa
CDS 2 Notification 2024
results.gbshsegoa.net Result 2024
CBSE 10th Result 2024
CBSE Study Material
CBSE Class 10

Latest Education News

Who Won Yesterday IPL Match: LSG vs MI, Match 67, Check All Details and Latest Points Table

IPL 2024 CSK Players: चेन्नई सुपर किंग्स के खिलाड़ियों की पूरी लिस्ट यहां देखें

IPL 2024 Qualifier, Eliminator: कब, कहां और किसके बीच होगा क्वालीफायर और एलिमिनेटर, Tickets और Live Streaming कैसे देखें

IPL 2024 Playoffs Teams: इन 4 टीमों का प्लेऑफ टिकट कन्फर्म! KKR, SRH और RR के बाद किसका नंबर

Pakistan T20 World Cup Squad 2024: पाक की विश्व कप टीम में किसे मिला मौका कौन हुआ बाहर देखें यहां

ICC T20 World Cup 2024: T20 वर्ल्ड कप का शेड्यूल जारी, कब और किससे है India का Match देखें यहां

RBSE Result 2024 Kab Aayega: आज आ सकता है राजस्थान बोर्ड 10वीं के परिणाम का नोटिफिकेशन, rajresults.nic.in पर मिलेगा Result Link

[रिजल्ट लिंक] JAC 9th Result 2024 OUT: कोडरमा जिला रहा अव्वल, jac.jharkhand.gov.in पर Result Link से तुरंत डाउनलोड करें Marksheet

CUET UG Exam Analysis 2024, May 17: Check Detailed Paper Review, Difficulty Level, and Good Attempts

CUET UG Answer Key May 17, 2024: Download Set Wise Answer Sheet PDF

BTEUP Result 2024 OUT on bteup.ac.in; Direct Link to Download Odd Semester Revaluation Marksheet PDF

TSPSC Group 4 Certificate Update 2024: Check Details Here

CUET UG Question Paper 2024, May 17: Download Question Paper PDF (SET A, B, C, D)

BTEUP Result 2024 OUT on bteup.ac.in: Download Odd Semester Revaluation Result

PSEB Class 11 Computer Science Syllabus 2024-2025: Download in PDF

PSEB 12th Economics Syllabus 2025: Download Punjab Board Class 12 Economics Syllabus 2024-2025 PDF Here

CBSE Class 12 2024 Marks Verification Application Begins, Check Important Dates And Fees Here

South Africa T20 World Cup Squad 2024: Complete List of Team Players and Name

Afghanistan T20 World Cup Squad 2024: Complete List of Team Players and Name

Bangladesh T20 World Cup Squad 2024: Complete List of Team Players and Name

School Solutions
Star Program
NCERT Solutions Class 12 Maths
NCERT Solutions Class 12 Physics
NCERT Solutions Class 12 Chemistry
NCERT Solutions Class 12 Biology
NCERT Solutions Class 12 Commerce
NCERT Solutions Class 12 Economics
NCERT Solutions Class 12 Accountancy
NCERT Solutions Class 12 English
NCERT Solutions Class 12 Hindi
NCERT Solutions Class 11 Maths
NCERT Solutions Class 11 Physics
NCERT Solutions Class 11 Chemistry
NCERT Solutions Class 11 Biology
NCERT Solutions Class 11 Commerce
NCERT Solutions Class 11 Accountancy
NCERT Solutions Class 11 English
NCERT Solutions Class 11 Hindi
NCERT Solutions Class 11 Statistics
NCERT Solutions Class 10 Maths
NCERT Solutions Class 10 Science
NCERT Solutions Class 10 English
NCERT Solutions Class 10 Hindi
NCERT Solutions Class 10 Social Science
NCERT Solutions Class 9 Maths
NCERT Solutions Class 9 Science
NCERT Solutions Class 9 English
NCERT Solutions Class 9 Hindi
NCERT Solutions Class 9 Social Science
NCERT Solutions Class 8 Maths
NCERT Solutions Class 8 Science
NCERT Solutions Class 8 English
NCERT Solutions Class 8 Hindi
NCERT Solutions Class 8 Social Science
NCERT Solutions Class 7 Maths
NCERT Solutions Class 7 Science
NCERT Solutions Class 7 English
NCERT Solutions Class 7 Hindi
NCERT Solutions Class 7 Social Science
NCERT Solutions Class 6 Maths
NCERT Solutions Class 6 Science
NCERT Solutions Class 6 English
NCERT Solutions Class 6 Hindi
NCERT Solutions Class 6 Social Science
NCERT Solutions Class 5 Maths
NCERT Solutions Class 5 English
NCERT Solutions Class 5 EVS
NCERT Solutions Class 4 Maths
NCERT Solutions Class 4 English
NCERT Solutions Class 4 EVS
NCERT Solutions Class 4 Hindi
NCERT Solutions Class 3 Maths
NCERT Solutions Class 3 English
NCERT Solutions Class 3 EVS
NCERT Solutions Class 3 Hindi
NCERT Solutions Class 2 Maths
NCERT Solutions Class 2 English
NCERT Solutions Class 2 Hindi
NCERT Solutions Class 1 Maths
NCERT Solutions Class 1 English
NCERT Solutions Class 1 Hindi
NCERT Books Class 12
NCERT Books Class 11
NCERT Books Class 10
NCERT Books Class 9
NCERT Books Class 8
NCERT Books Class 7
NCERT Books Class 6
NCERT Books Class 5
NCERT Books Class 4
NCERT Books Class 3
NCERT Books Class 2
NCERT Books Class 1
Important Questions Class 12
Important Questions Class 11
Important Questions Class 10
Important Questions Class 9
Important Questions Class 8
Important Questions Class 7
important questions class 6
CBSE Class 12 Revision Notes
CBSE Class 11 Revision Notes
CBSE Class 10 Revision Notes
CBSE Class 9 Revision Notes
CBSE Class 8 Revision Notes
CBSE Class 7 Revision Notes
CBSE Class 6 Revision Notes
CBSE Class 12 Syllabus
CBSE Class 11 Syllabus
CBSE Class 10 Syllabus
CBSE Class 9 Syllabus
CBSE Class 8 Syllabus
CBSE Class 7 Syllabus
CBSE Class 6 Syllabus
CBSE Class 5 Syllabus
CBSE Class 4 Syllabus
CBSE Class 3 Syllabus
CBSE Class 2 Syllabus
CBSE Class 1 Syllabus
CBSE Sample Question Papers For Class 12
CBSE Sample Question Papers For Class 11
CBSE Sample Question Papers For Class 10
CBSE Sample Question Papers For Class 9
CBSE Sample Question Papers For Class 8
CBSE Sample Question Papers For Class 7
CBSE Sample Question Papers For Class 6
CBSE Sample Question Papers For Class 5
CBSE Sample Question Papers For Class 4
CBSE Sample Question Papers For Class 3
CBSE Sample Question Papers For Class 2
CBSE Sample Question Papers For Class 1
CBSE Previous Year Question Papers Class 12
CBSE Previous Year Question Papers Class 10
Extra Questions For Class 8 Maths
Extra Questions For Class 8 Science
Extra Questions For Class 9 Maths
Extra Questions For Class 9 Science
Extra Questions For Class 10 Maths
Extra Questions For Class 10 Science
NEET 2021 Question Paper
NEET 2020 Question Paper
NEET 2019 Question Paper
NEET 2018 Question Paper
NEET 2017 Question Paper
NEET 2016 Question Paper
NEET 2015 Question Paper
NEET Physics Questions
NEET Chemistry Questions
NEET Biology Questions
NEET Sample Papers
NEET Physics Syllabus
NEET Chemistry Syllabus
NEET Biology Syllabus
NEET Mock Test
NEET Eligibility Criteria
JEE Main 2021 Question Paper
JEE Main 2020 Question Paper
JEE Main 2019 Question Paper
JEE Main 2018 Question Paper
JEE Main 2017 Question Paper
JEE Main 2016 Question Paper
JEE Main 2015 Question Paper
JEE Main Sample Papers
JEE Main Physics Syllabus
JEE Main Chemistry Syllabus
JEE Main Maths Syllabus
JEE Main Physics Questions
JEE Main Chemistry Questions
JEE Main Maths Questions
JEE main revision notes
JEE Main Mock Test
JEE Advanced Physics Questions
JEE Advanced Chemistry Questions
JEE Advanced Maths Questions
JEE Advanced 2021 Question Paper
JEE Advanced 2020 Question Paper
JEE Advanced 2019 Question Paper
JEE Advanced 2018 Question Paper
JEE Advanced 2017 Question Paper
JEE Advanced 2016 Question Paper
JEE Advanced 2015 Question Paper
JEE Advanced Physics Syllabus
JEE Advanced Chemistry Syllabus
JEE Advanced Maths Syllabus
JEE Advanced Mock Test
ISC Class 12 Syllabus
ISC Class 11 Syllabus
ICSE Class 10 Syllabus
ICSE Class 9 Syllabus
ICSE Class 8 Syllabus
ICSE Class 7 Syllabus
ICSE Class 6 Syllabus
ISC Sample Question Papers for Class 12
ISC Sample Question Papers for Class 11
ICSE Sample Question Papers for Class 10
ICSE Sample Question Papers for Class 9
ICSE Sample Question Papers for Class 8
ICSE Sample Question Papers for Class 7
ICSE Sample Question Papers for Class 6
ICSE Class 10 Revision Notes
ICSE Class 9 Revision Notes
ISC Important Questions for Class 12
ISC Important Questions for Class 11
ICSE Important Questions for Class 10
ICSE Important Questions for Class 9
ICSE Important Questions for Class 8
ICSE Important Questions for Class 7
ICSE Important Questions for Class 6
ISC Class 12 Question Paper
ICSE Class 10 Question Paper
Maharashtra Board Syllabus
Maharashtra Board Sample Question Paper
Maharashtra Board Previous Year Question Paper
AP Board Syllabus
AP Board Sample Question Paper
AP Board Previous Year Question Paper
Tamilnadu Board Syllabus
Tamilnadu Board Sample Question Paper
Tamilnadu Board Previous Year Question Paper
Telangana Board Syllabus
Telangana Board Sample Question Paper
Telangana Board Previous Year Question Paper
Karnataka Board Syllabus
Karnataka Board Sample Question Paper
Karnataka Board Previous Year Question Paper
Examination Full Forms
Physics Full Forms
Chemistry Full Forms
Biology Full Forms
Educational Full Form
CUET Eligibility Criteria
CUET Exam Pattern
CUET Cutoff
CUET Syllabus
CUET Admit Card
CUET Counselling
CUET Previous Year Question Papers
CUET Application Form
CUET Sample Papers
CUET Exam Centers
CUET Exam Dates
CUET Results
Physics Formulas
Chemistry Formulas
Math Formulas
Algebra Formulas
Geometry Formulas
Trigonometry Formulas
Subscription

CBSE Important Questions Class 7 Maths Chapter 1

Home » CBSE » CBSE Important Questions Class 7 Maths Chapter 1

CBSE Important Questions
Important Questions Class 6
CBSE Previous Year Question Papers
CBSE Revision Notes
CBSE Syllabus
CBSE Extra Questions
CBSE Sample Papers
ISC & ICSE Syllabus
ICSE Syllabus Class 9
ICSE Syllabus Class 8
ICSE Syllabus Class 7
ICSE Syllabus Class 6
ICSE Syllabus Class 10
ICSE Question Paper
ICSE Sample Question Papers
ISC Sample Question Papers For Class 12
ISC Sample Question Papers For Class 11
ICSE Sample Question Papers For Class 10
ICSE Sample Question Papers For Class 9
ICSE Sample Question Papers For Class 8
ICSE Sample Question Papers For Class 7
ICSE Sample Question Papers For Class 6
ICSE Revision Notes
ICSE Important Questions
ISC Important Questions For Class 12
ISC Important Questions For Class 11
ICSE Important Questions For Class 10
ICSE Important Questions For Class 9
ICSE Important Questions For Class 8
ICSE Important Questions For Class 7
ICSE Important Questions For Class 6
Maharashtra board
Rajasthan-Board
Andhrapradesh Board
AP Board syllabus
Telangana Board
Tamilnadu Board
Tamilnadu Sample Question Paper
Tamilnadu Syllabus
Tamilnadu Previous Year Question Paper
NCERT Solutions Class 12
NCERT Solutions Class 10
NCERT Solutions Class 11
NCERT Solutions Class 9
NCERT Solutions Class 8
NCERT Solutions Class 7
NCERT Solutions Class 6
NCERT Solutions Class 5
NCERT Solutions Class 4
NCERT Solutions Class 3
NCERT Solutions Class 2
NCERT Solutions Class 1
JEE Main Question Papers
JEE Main Syllabus
JEE Main Questions
JEE Main Revision Notes
JEE Advanced Question Papers
JEE Advanced Syllabus
JEE Advanced Questions
JEE Advanced Sample Papers
NEET Question Papers
Neet 2021 Question Paper
Neet 2020 Question Paper
Neet 2019 Question Paper
Neet 2018 Question Paper
Neet 2017 Question Paper
Neet 2016 Question Paper
Neet 2015 Question Paper
NEET Syllabus

Important Questions Class 7 Mathematics Chapter 1 – Integers

Mathematics is an important subject that we need in our daily life too. Students must solve questions to clear their concepts and boost their confidence. The first chapter of Class 7 Mathematics under CBSE curriculum is integers.

Quick Links

Students have learned integers in their previous class. In this chapter, they will learn how to put the integers on the number line, their properties, and the addition and multiplication of integers. It is a very important chapter. Students must practice the textbook exercise and questions from other sources to build their concepts.

Extramarks is a leading company that provides a wide range of study materials related to CBSE and NCERT. Our experts have made the Important Questions Class 7 Mathematics Chapter 1 to help students in regular practice. They collected the questions from different sources such as the textbook exercises, CBSE sample papers, CBSE past years’ question papers and important reference books. They have solved the questions too. Hence, the question series will help students increase their exam marks.

Extramarks is a leading company that helps students by providing all the important study materials related to CBSE and NCERT. You may register on our official website and download these study materials. You will find the CBSE syllabus, NCERT textbooks, CBSE past years’ question papers, CBSE sample papers, CBSE revision notes, CBSE extra questions, NCERT solutions, NCERT important questions, vital formulas and many more.

Important Questions Class 7 Mathematics Chapter 1 – With Solutions

The experts of Extramarks have made this question series so that students can solve the questions daily. They collected the questions from the textbook exercises, CBSE sample papers and important reference books. They have included a few questions from the past years’ question papers so that students may have an idea regarding questions in exams. Experienced professionals have further checked the answers to ensure the best quality of the content. Thus, the Important Questions Class 7 Mathematics Chapter 1 will help students to score better in exams. The questions are-

Question 1. Following number line given below shows the temperature present in degree celsius at different places on a particular day.

Image Source: Internet / NCERT Textbook

(i) Observe the number line and write down the temperature of the places marked on it.

By observing the above number line, we can find out the temperature of the cities as follows,

The temperature in the city of Lahulspiti is -8°C.

The temperature in the city of Srinagar is -2°C

The temperature in the city of Shimla is 5°C.

The temperature in the city of Ooty is 14°C.

The temperature in the city of Bengaluru is 22°C.

(ii) What is the temperature difference between the hottest and the coldest places among the cities stated above?

From the above number line, we can observe that,

The temperature at the given hottest place, that is, Bengaluru, is 22°C.

The temperature at the given coldest place, that is, Lahulspiti, is -8°C

The temperature difference between the hottest and the coldest place is given as = 22°C – (-8°C)

= 22°C + 8°C

= 30° Celsius

Hence, the total temperature difference between the hottest and the coldest place is 30oC.

(iii) What is the temperature difference between the cities of Lahulspiti and Srinagar?

From the above-given number line,

∴The temperature difference between the cities Lahulspiti and Srinagar is = -2oC – (8oC)

= – 2°C + 8°C

(iv) Can we say that the temperature of Srinagar and Shimla taken together is less than the temperature present at Shimla? Is it also less than the temperature present at Srinagar?

The temperature in the city of Srinagar =-2°C

The temperature in the city of Shimla = 5°C

The temperature of the cities Srinagar and Shimla taken together becomes = – 2°C + 5°C

= 3° degree C

5°C > 3°C

Hence, the temperature of the cities Srinagar and Shimla taken together is indeed less than the temperature present at Shimla.

3° > -2°

And No, the temperature of the cities Srinagar and Shimla taken together is not less than the temperature of the city Srinagar.

Question 2. Mohan deposits ₹ 2,000 in his bank account and then withdraws ₹ 1,642 from it the following day. Now, if the withdrawal of the amount from the account is represented by a negative integer, then how will you represent the total amount deposited? Also, Find the balance in Mohan’s account after the withdrawal.

Withdrawal of these amounts from the account is represented by a negative integer.

Then, the deposit of the amount to the account is represented by a positive integer.

From the above question,

The total amount that is deposited in the bank account by the Mohan = ₹ 2000

The total amount that is withdrawn from the bank account by the Mohan is = – ₹ 1642

Final Balance in Mohan’s account after the withdrawal = amount deposited + amount is withdrawn

= ₹ 2000 + (-₹ 1642)

= ₹ 2000 – ₹ 1642

Hence, the total balance in Mohan’s account after the withdrawal is ₹ 358

Question 3. In the following quiz, positive marks are given for every correct answer and negative marks are given for each incorrect answer. If Jack’s scores in the quiz for five successive rounds were 25, – 5, – 10, 10, and 15 so, what was his total at the end?

Jack’s scores in the five successive rounds are 25, -5, -10, 15 and 10

Hence, Their total score of Jack at the end will be = 25 + (-5) + (-10) + 15 + 10

= 25 – 5 – 10 + 15 + 10

∴ Now, Jack’s total score at the end is 35.

Question 4. In the city of Srinagar, temperature was – 5°C on Monday, and then it dropped by two °C on Tuesday. What was the temperature of the city of Srinagar on Tuesday? On Wednesday, the temperature rose by 4°C. What was the temperature on this day?

The temperature on Monday at Srinagar is = -5C

The temperature on Tuesday at the city of Srinagar is dropped by 2C = Temperature on Monday – 2C

= -7 celsius

The temperature on Wednesday at the city Srinagar rose by 4C = Temperature on Tuesday + 4C.

= -3 celsius

Thus, the temperature on days Tuesday and Wednesday was found to be -7C and -3C, respectively.

Question 5. In a magic square, every row, column and diagonal has the same sum. Check which of these following is a magic square.

Firstly we consider the square (i)

Now By adding these numbers in each of the rows, we get,

= 5 + (- 1) + (- 4) equals to 5 – 1 – 4 = 5 – 5 = 0

= -5 + (-2) + 7 equals to – 5 – 2 + 7 = -7 + 7 = 0

= 0 + 3 + (-3) = 3 – 3 = 0

By adding these numbers in every column we receive,

= 5 + (- 5) + 0 is equal to 5 – 5 = 0

= (-1) + (-2) + 3 equals to -1 – 2 + 3 = -3 + 3 = 0

= -4 + 7 + (-3) equals to -4 + 7 – 3 = -7 + 7 = 0

By adding these numbers in diagonals, we receive,

= 5 + (-2) + (-3) is equal to 5 – 2 – 3 = 5 – 5 = 0

= -4 + (-2) + 0 is equal to – 4 – 2 = -6

Because the sum of one diagonal is not always equal to zero,

Hence, (i) is not a magic square.

Now, we should consider the square (ii)

By adding these numbers to each rows we receive,

= 1 + (-10) + 0 is equal to 1 – 10 + 0 = -9

= (-4) + (-3) + (-2) equal to -4 – 3 – 2 = -9

= (-6) + 4 + (-7) becomes equal to -6 + 4 – 7 = -13 + 4 = -9

By adding these numbers in each column we receive,

= 1 + (-4) + (-6) equals to 1 – 4 – 6 = 1 – 10 = -9

= (-10) + (-3) + 4 equals to -10 – 3 + 4 = -13 + 4

= 0 + (-2) + (-7) equals to 0 – 2 – 7 = -9

= 1 + (-3) + (-7) equals to 1 – 3 – 7 = 1 – 10 = -9

= 0 + (-3) + (-6) equal to 0 – 3 – 6 = -9

Hence This (ii) square is a magic square because the sum of each row, each column and the diagonal becomes equal to -9 (negative).

Question 6. Verify a – (– b) is equal to a + b for the following values of alphabets a and b.

(i) a = 21, b = 18

a = 21 and b = 18

So To verify a – (- b) is equal to a + b

Let us take the Left Hand Side (LHS) = a – (- b)

= 21 – (- 18)

Now, lets take Right Hand Side (RHS) = a + b

By comparing both the LHS and the RHS.

Hence, the value of a and b are verified.

(ii) a = 118, b = 125

a = 118 and b = 125

To verify this a – (- b) = a + b

= 118 – (- 125)

= 118 + 125

Now, take the Right Hand Side (RHS) = a + b

By comparing both the LHS and the RHS

Hence, the values of a and b are verified.

(iii) a = 75, b = 84

a = 75 and b = 84

To verify that the a – (- b) = a + b

= 75 – (- 84)

Now, the Right Hand Side (RHS) = a + b

By comparing both LHS and RHS, we find that,

Hence, the value of a and b is verified as.

(iv) a = 28, b = 11

a = 28 and b = 11

To verify that a – (- b) = a + b

Let us now take Left Hand Side (LHS) = a – (- b)

= 28 – (- 11)

Now, Right Hand Side (RHS) = a + b

Question 7 . A water tank has stepped inside it. A monkey is sitting on the utter topmost step (which is the first step). The water level is present at the ninth step.

(i) He jumps three steps down the stairs and then successively jumps back two steps upwards. In how many jumps will the Monkey reach the following water level?

Let us consider the steps moved down are represented by a positive integer, and then the steps moved up are represented by a negative integer.

Initially, the Monkey is sitting on the topmost step, which is the first step.

In the 1st jump monkey will be at the step = 1 + 3 = 4 steps

In the 2nd jump monkey will be at the step = 4 + (-2) = 4 – 2 = 2 steps

In the 3rd jump monkey will be at the step = 2 + 3 = 5 steps

In the 4th jump monkey will be at the step = 5 + (-2) = 5 – 2 = 3 steps

In the 5th jump monkey will be at the step = 3 + 3 = 6 steps

In the 6th jump monkey will be at the step = 6 + (-2) = 6 – 2 = 4 steps

In the 7th jump monkey will be at the step = 4 + 3 = 7 steps

In the 8th jump monkey will be at the step = 7 + (-2) = 7 – 2 = 5 steps

In the 9th jump monkey will be at the step = 5 + 3 = 8 steps

In the 10th jump monkey will be at the step = 8 + (-2) = 8 – 2 = 6 steps

In the 11th jump monkey will be at the step = 6 + 3 = 9 steps

∴Monkey took a total of 11 jumps (i.e., 9th step) to reach the water level.

(ii) After drinking water, the Monkey wants to go back. For this, the Monkey jumps four steps up and then successively jumps back two steps down in his every move. In how many total jumps will he reach back to the top step?

Let us consider the steps moved down are represented by the positive integers, and then the steps moved up are represented by the negative integers.

Initially, the Monkey is sitting on the ninth step, i.e., at the water level.

In the 1st jump monkey will be at the step = 9 + (-4) = 9 – 4 = 5 steps

In the 2nd jump monkey will be at the step = 5 + 2 = 7 steps

In the 3rd jump monkey will be at the step = 7 + (-4) = 7 – 4 = 3 steps

In the 4th jump monkey will be at the step = 3 + 2 = 5 steps

In the 5th jump monkey will be at the step = 5 + (-4) = 5 – 4 = 1 step

∴ Hence the Monkey took five jumps to reach back to the top step, i.e., the first step.

Question 8. Fill in the blanks to make the following statements true:

(i) (–5) + (– 8) = (– 8) + (…………)

Let us assume that the missing integer is x,

= (–5) + (– 8) which equals to (– 8) + (x)

= – 5 – 8 = – 8 + x

= – 13 = – 8 + x

By sending – 8 from the RHS to the LHS, it becomes 8,

= – 13 + 8 = x

Now substitute the x value in the place of the blank place present,

(–5) + (– 8) = (– 8) + (- 5) … [This following equation is present in the form of the Commutative law of Addition]

(ii) –53 + ………… = –53

= –53 + x = –53

By sending – 53 from the LHS to the RHS, it becomes 53,

= x = -53 + 53

Now substitute the following x value in the blank place,

= –53 + 0 = –53 … [This equation is present in the form of Closure property of Addition]

(iii) 17 + ………… = 0

= 17 + x = 0

By sending 17 from the LHS to the RHS, it becomes -17,

= x = 0 – 17

Now substitute this x value in the blank place,

= 17 + (-17) = 0 … [This equation is present in the form of Closure property of Addition]

= 17 – 17 = 0

(iv) [13 + (– 12)] + (…………) = 13 + [(–12) + (–7)]

= [13 + (– 12)] + (x) = 13 + [(–12) + (–7)]

= [13 – 12] + (x) = 13 + [–12 –7]

= [1] + (x) = 13 + [-19]

= 1 + (x) = 13 – 19

= 1 + (x) = -6

By sending one from the LHS to the RHS, it becomes -1,

= x = -6 – 1

Now substitute the following x value in the blank place value,

= [13 + (– 12)] + (-7) equals to 13 + [(–12) + (–7)] … [This equation is present in the form of the Associative Property of Addition]

(v) (– 4) + [15 + (–3)] equals to [– 4 + 15] +…………

= (– 4) + [15 + (–3)] is equal to [– 4 + 15] + x

= (– 4) + [15 – 3)] equals to [– 4 + 15] + x

= (-4) + [12] = [11] + x

= 8 = 11 + x

Now, By sending 11 from the RHS to the LHS, it becomes -11,

= 8 – 11 = x

Now substitute the x value in the place of the blank place,

= (– 4) + [15 + (–3)] equals to [– 4 + 15] + -3 … [The following equation is in the form of the Associative property of the Addition]

Question 9. Find the product using the suitable properties:

(i) 26 × (– 48) + (– 48) × (–36)

This given equation is in the form of the Distributive law of the Multiplication property over Addition.

= a × (b + c) becomes equal to (a × b) + (a × c)

Let, a = -48, b = 26, c = -36

= 26 × (– 48) + (– 48) × (–36)

= -48 × (26 + (-36)

= -48 × (26 – 36)

= -48 × (-10)

= 480 … [∵ (- × – = +)

(ii) 8 × 53 × (–125)

The given equation is present in the form of the Commutative law of Multiplication.

= a × b = b × a

= 8 × [53 × (-125)]

= 8 × [(-125) × 53]

= [8 × (-125)] × 53

= [-1000] × 53

(iii) 15 × (–25) × (– 4) × (–10)

This given equation is in the form of the Commutative law of the Multiplication property.

= 15 × [(–25) × (– 4)] × (–10)

= 15 × [100] × (–10)

= 15 × [-1000]

(iv) (– 41) × 102

This given equation is in the form of a Distributive law of the Multiplication property over Addition.

= a × (b + c) = (a × b) + (a × c)

= (-41) × (100 + 2)

= (-41) × 100 + (-41) × 2

= – 4100 – 82

(v) 625 × (–35) + (– 625) × 65

This given equation is in the form of the Distributive law of Multiplication over Addition.

= 625 × [(-35) + (-65)]

= 625 × [-100]

Question 10. A certain freezing process requires that the room temperature be lowered from 40°C at the rate of 5°C every hour. What will be the final room temperature 10 hours after the actual process begins?

Answer 10:-

From the above question, it is given that

Let us take the lowered temperature as a negative integer,

Initial temperature will be= 40oC

Change in temperature per hour is = -5oC

Change in temperature after 10 hours will be = (-5) × 10 = -50oC

∴The final room temperature after the 10 hours of freezing process = 40oC + (-50oC)

Question 11. In a class test containing about ten questions, five marks are awarded for each correct answer and (–2) marks are awarded for every incorrect answer and 0 for questions which are not attempted.

(i) Mohan gets four correct answers and six incorrect answers on his test. What is his total score?

Marks awarded for one correct answer is = 5

The total marks awarded for his four correct answers are = four × 5 = 20 marks.

Marks awarded for 1 wrong answer = -2 (negative)

Total marks awarded for 6 wrong answers is = 6 × -2 = -12

∴Total score obtained by Mohan = 20 + (-12)

(ii) Reshma gets five correct answers and similarly five incorrect answers; what is her total score?

Total marks awarded for 5 correct answer becomes = 5 × 5 = 25

Marks awarded for one wrong answer is = -2

Total marks awarded for 5 wrong answer becomes = 5 × -2 = -10

∴Total score obtained by Reshma is = 25 + (-10)

(iii) Heena gets two correct answers and five incorrect answers out of the seven questions she attempts. What is her final score?

Total marks awarded for 2 correct answer is = 2 × 5 = 10

Marks awarded for the questions which are not attempted is = 0

∴Total score obtained by Heena is = 10 + (-10)

Question 12. A cement company earns a profit of around ₹ 8 per bag of white cement that is sold and simultaneously a loss of ₹ 5 per bag of grey cement that is sold.

(i) The company sells 3,000 bags of white cement and 5,000 bags of grey cement in a month. What is its profit or loss?

We denote profit by a positive integer and loss by a negative integer,

So From the above question,

The Cement company earns a profit on selling one bag of white cement = ₹ 8 per bag.

The cement company earns a total profit on selling 3000 bags of white cement = 3000 × ₹ 8

And also the,

Loss on selling one bag of grey cement is = – ₹ 5 per bag.

Loss on selling the 5000 bags of the grey cement = 5000 × – ₹ 5

= – ₹ 25000

Total loss or profit earned by these cement companies is = profit + loss.

= 24000 + (-25000)

Hence, a loss of ₹ 1000 will be incurred by the company.

(ii) What is the number of white cement bags that must sell to have neither a profit nor loss if the total number of grey bags sold is 6,400 bags?

We denote the profit as a positive integer and the loss as a negative integer,

The cement company earns the profit on selling one bag of white cement as = ₹ 8 per bag.

Now Let the number of white cement bags present be x.

The cement company earns a profit on selling these x bags of white cement as = (x) × ₹ 8

Loss on selling one bag of grey cement becomes = – ₹ 5 per bag.

Loss on selling 6400 bags of grey cement becomes = 6400 × – ₹ 5

= – ₹ 32000

According to the above question,

Company to have neither profit nor loss, must sell,

= Profit + loss = 0

= 8x + (-32000) =0

By sending -32000 from the LHS to the RHS, it becomes 32000

= 8x = 32000

= x = 32000/8

Hence, the 4000 bags of white cement should sell to have neither profit nor loss.

Question 13. Evaluate each of the following:

(i) (–30) ÷ 10

= (–30) ÷ 10

When we divide the negative integer by a positive integer, we first divide them as whole numbers and then put the minus sign (-) before the quotient.

(ii) 50 ÷ (–5)

= (50) ÷ (-5)

When we divide the positive integer by a negative integer, we first divide them as whole numbers and then apply the minus sign (-) before the quotient.

(iii) (–36) ÷ (–9)

= (-36) ÷ (-9)

When we divide the negative integer by a similar negative integer, we first divide these as whole numbers and then put the positive sign (+) before the quotient.

(iv) (– 49) ÷ (49)

= (–49) ÷ 49

When we divide the negative integer by a positive integer, we first divide these as whole numbers and then put the minus sign (-) before the quotient.

(e) 13 ÷ [(–2) + 1]

= 13 ÷ [(–2) + 1]

= 13 ÷ (-1)

When we divide the positive integer by a negative integer, we first divide these as whole numbers and then put the minus sign (-) before the quotient.

(f) 0 ÷ (–12)

= 0 ÷ (-12)

When we divide zero by a negative integer, it gives zero.

(g) (–31) ÷ [(–30) + (–1)]

= (–31) ÷ [(–30) + (–1)]

= (-31) ÷ [-30 – 1]

= (-31) ÷ (-31)

When we divide the negative integer by a negative integer, we first divide these as whole numbers and then put the positive sign (+) before the quotient.

(h) [(–36) ÷ 12] ÷ 3

First, we have to solve these integers within the bracket,

= [(–36) ÷ 12]

= (–36) ÷ 12

When we divide a negative integer by a positive integer, we first divide them as whole numbers and then put the minus sign (-) before the quotient.

(i) [(– 6) + 5)] ÷ [(–2) + 1]

The given question can be written as,

= [-1] ÷ [-1]

Question 14. Verify that a ÷ (b + c) is not equal to (a ÷ b) + (a ÷ c) for each of the following symbols of a, b and c.

(i) a = 12, b = – 4, c = 2

From the above question, a ÷ (b + c) ≠ (a ÷ b) + (a ÷ c)

Given, a = 12, b = – 4 (negative), c = 2

Now, consider that the LHS = a ÷ (b + c)

= 12 ÷ (-4 + 2)

= 12 ÷ (-2)

When we divide a following positive integer by any of the negative integers, we first divide them as a whole number and then put the minus sign (-) before their quotient.

Then, consider that the RHS is equal to = (a ÷ b) + (a ÷ c)

= (12 ÷ (-4)) + (12 ÷ 2)

= (-3) + (6)

By comparing the LHS and RHS, we get,

= LHS ≠ RHS

Hence, the given values have been verified.

(ii) a = (–10), b = 1, c = 1

Given, a = (-10), b = 1, c = 1

= (-10) ÷ (1 + 1)

= (-10) ÷ (2)

When we divide a negative integer by any other positive integer, we first divide them as a whole number and then put the minus sign (-) before the quotient.

Then, consider RHS = (a ÷ b) + (a ÷ c)

= ((-10) ÷ (1)) + ((-10) ÷ 1)

= (-10) + (-10)

By comparing LHS and RHS

Hence, the given values are verified.

Question. Fill in the following blanks:

(a) 369 ÷ _____ = 369

= 369 ÷ x = 369

= x = (369/369)

Hence, put the valve of x in the blank place.

= 369 ÷ 1 = 369

(b) (–75) ÷ _____ = –1

= (-75) ÷ x = -1

= x = (-75/-1)

Now, put the above valve of x in the blank place.

= (-75) ÷ 75 = -1

= (-206) ÷ x = 1

= x = (-206/1)

= (-206) ÷ (-206) = 1

(d) – 87 ÷ _____ = 87

= (-87) ÷ x = 87

= x = (-87)/87

= (-87) ÷ (-1) = 87

(e) _____ ÷ 1 = – 87

= (x) ÷ 1 = -87

= x = (-87) × 1

So, put the valve of x in the blank.

= (-87) ÷ 1 = -87

(f) _____ ÷ 48 = –1

= (x) ÷ 48 = -1

= x = (-1) × 48

Now, put the above valve of x in the following blank.

= (-48) ÷ 48 = -1

Question 15. The temperature at 12 noon was 10 degrees C above zero. If it decreases at the rate of 2C per hour until midnight, at what time would the temperature be eight °C below zero? Also, What would be the temperature at midnight?

From the above question, it is given that,

The temperature at the beginning, which is, at 12 noon, is = 10C

The rate of change of temperature becomes = – 2C per hour.

Temperature present at 1 PM = 10 + (-2) = 10 – 2 = 8° C

Temperature present at 2 PM = 8 + (-2) = 8 – 2 = 6° C

Temperature present at 3 PM = 6 + (-2) = 6 – 2 = 4°C

Temperature present at 4 PM = 4 + (-2) = 4 – 2 = 2°C

Temperature present at 5 PM = 2 + (-2) = 2 – 2 = 0°C

Temperature present at 6 PM = 0 + (-2) = 0 – 2 = -2°C

Temperature present at 7 PM = -2 + (-2) = -2 -2 = -4°C

Temperature present at 8 PM = -4 + (-2) = -4 – 2 = -6°C

Temperature present at 9 PM = -6 + (-2) = -6 – 2 = -8°C

∴At 9 PM, the temperature will be 8° C below zero.

The temperature at mid-night which is at 12 AM

Change in the temperature in every 12 hours = -2°C × 12 = – 24°C

So, at midnight the temperature will be = 10 + (-24)

At midnight the temperature will be 14°C below 0.

Question 16. In the following class test, (+ 3) marks are given for every correct answer, (–2) marks are given for every the incorrect answer and no marks are given for not attempting any question.

(i) Radhika scored 20 marks. If she has got around 12 correct answers, then how many questions has she attempted that are incorrect?

(ii) Mohini scores –5 (negative) marks on this test, and though she has got seven correct answers. How many questions has she attempted incorrectly?

Marks awarded for 1 correct answer is = + 3

(i) Radhika, in the test, scored 20 marks

Total marks awarded for every 12 correct answers is = 12 × 3 = 36

Marks awarded for every incorrect answer = Total score – Total marks awarded for 12 correct questions.

So, the number of incorrect answers done by Radhika = (-16) ÷ (-2)

(ii) Mohini scored a total of -5 marks

Total marks awarded for her 7 correct answers is = 7 × 3 = 21

Marks awarded for her incorrect answers = Total score – Total marks awarded for the 12 correct answers.

Hence, the number of incorrect answers made by Mohini = (-26) ÷ (-2)

Question 17. An elevator descends down into a mine shaft at the rate of 6 m per min. If the descent starts from 10 meters above the ground level, how much time will it take to reach – 350 m?

The initial height of the elevator becomes = 10 m

Final depth of elevator is = – 350 m … [the distance descended is denoted by a negative integer]

The total distance to descend by the elevator becomes = (-350) – (10)

Time taken by the elevator to descend (negative) -6 m is = 1 min

So, the total time taken by the elevator to descend – 360 m becomes = (-360) ÷ (-60)

= 60 minutes

= 1 hour Benefits of Solving Important Questions Class 7 Mathematics Chapter 1

Practice is the key to success. The practice habit is very important for students because it will help them in many ways. It will help them to score better in exams. Apart from this, practice will clear doubts, generate interest in the subject matter, and strengthen the concepts. Thus, students must practice sums regularly to improve their exam preparation. The Important Questions Class 7 Mathematics Chapter 1 will help students in many ways. These are-

The experts have collated the questions from various sources. They have accumulated the questions from the textbook exercises, CBSE sample papers, CBSE past years’ question papers and important reference books. Thus, students will find all the vital questions In this article, and they can solve the questions regularly. Thus, students don’t have to search for questions in different books, but they will find them here. Thus, Chapter 1, Class 7 Mathematics Important Questions includes all the important concepts.
The experts have not only collated the questions but also provided the solutions. They have given a step-by-step solution for each chapter to help students. Experienced professionals have further checked the answers. Thus, we have ensured the best quality of content for the students. They can follow the solutions and check their answers with the experts’ answers. So, the Mathematics Class 7 Chapter 1 Important Questions will help students to clarify their doubts, boost their confidence and build their concepts.
The subject matter experts of Extramarks understand the student’s needs. They have built the question series to help students with their exam preparation. They have collected all the vital questions so students can find them in a single article. Sometimes, students need more than the textbook. Hence, they can follow the Class 7 Mathematics Chapter 1 Important Questions because they will find chapter-wise questions for each subject. Regular practice will strengthen their ideas, and they can solve any question that comes in exams. Thus, the question series will help them to score better in exams.

Extramarks is a leading company that provides all the important study materials related to CBSE and NCERT. You can download these after registering on our official website. We provide CBSE syllabus, CBSE past years, question papers, CBSE sample papers, NCERT books, NCERT exemplar, NCERT solutions, important questions, CBSE revision notes, CBSE extra questions, vital formulas and many more. Like the Important Questions Class 7 Mathematics Chapter 1, you will also find important questions for other chapters. The links to study materials are given below-

NCERT books
Important questions
CBSE syllabus
CBSE sample papers
CBSE past years’ question papers
Important formulas
CBSE extra questions
Click to share on Facebook (Opens in new window)
Click to share on Twitter (Opens in new window)
Click to share on LinkedIn (Opens in new window)
Click to share on WhatsApp (Opens in new window)

Q.1 Which one of the following statements is false?

1. For any two positive integers a and b, a ÷ (–b) = – a ÷ b, where b ≠ 0.

2. The commutativity, associativity and distributivity of integers help to make calculations simpler.

3. The product of three integers does not depend upon the grouping of integers.

4. Division is closed for integers.

Option 4. Explanation

Division is not closed for integers. For example: 2 ÷ 6 =

is not an integer.

Q.2 Which one of the following is false?

Marks: 1 1. Sum of integers a and b is an integer.

2. a + b = b + a, for all integers a and b

3. a – b = b – a, for all integers a and b

4. a + (b + c) = (a + b) + c, for all integers a, b and c

Ans Option3 Explanation

a – b = b – a, for all integers a and b is false. For example, 2 – 4 = – 2 and 4 – 2 = 2 Thus, 2 – 4 ≠ 4 – 2

Q.3 What is the difference between a temperature of 7º C above zero and a temperature of 3º C below zero?

Ans Option 1. Explanation

Difference between a temperature of 7º C above zero and a temperature of 3º C below zero = 7º C – (– 3º C) = 7º C + 3º C = 10º C

Q.4 A plane is flying at the height of 8750 m above sea level. At a particular point, it is exactly above a submarine floating 1340 m below sea level. What is the vertical distance between them?

Marks: 2 Ans

Height of the plane above sea level = 8750 m Distance of submarine below sea level = – 1340 m Vertical distance = 8750 m – (– 1340 m) = 8750 m + 1340 m = 10,090 m

Q.5 A man walks 22 m towards east and then 17 m towards west. The position of the man with respect to his starting point is ______________.

1.5 m towards west

2.5 m towards east

3.39 m towards east

4.39 m towards west

Ans Option 2. Explanation

Let 22 m towards east be represented by +22, then –17 m represents 17 m towards west. On adding, +22 – 17 = +5 (positive) The position of the man with respect to his starting point = 5 m towards east

Please register to view this section

Faqs (frequently asked questions), 1. is class 7 mathematics chapter 1 easy.

Class 7 Mathematics Chapter 1 under CBSE curriculum is about integers. Students will study the properties of integers, how to add and multiply integers and how to put them on the number line. The concepts may be new to them, but they have studied integers in Class 6. They can easily understand the concepts if they follow the textbook seriously. The chapter is relatively easy. Students can take help from the Important Questions Class 7 Mathematics Chapter 1 to solve questions from the chapter.

2. How can the Important Questions Class 7 Mathematics Chapter 1 help students?

The experts of Extramarks have made the question series after taking help from several sources. They have collated the questions from the textbook exercise, CBSE sample papers, important reference books and NCERT exemplar. They have included questions from CBSE past years’ question papers too. Apart from this, they have solved the questions for students, and experienced professionals have further checked the answers. Thus, the Important Questions Class 7 Mathematics Chapter 1 will help the students to practice the sums regularly. It will boost their confidence and increase their marks in exams.

CBSE Related Links

Fill this form to view question paper

Otp verification.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 4: Integers

Integers on the number line.

Intro to negative numbers (Opens a modal)
Number opposites (Opens a modal)
Negative symbol as opposite (Opens a modal)
Number opposites Get 5 of 7 questions to level up!
Negative numbers on the number line Get 5 of 7 questions to level up!

Ordering of integers

Ordering negative numbers (Opens a modal)
Negative numbers, variables, number line (Opens a modal)
Ordering small negative numbers Get 5 of 7 questions to level up!
Ordering rational numbers Get 3 of 4 questions to level up!
Compare rational numbers using a number line Get 3 of 4 questions to level up!

Adding and subtracting integers

Adding & subtracting negative numbers (Opens a modal)
Subtracting a negative = adding a positive (Opens a modal)
Adding numbers with different signs (Opens a modal)
Adding negative numbers Get 5 of 7 questions to level up!
Subtracting negative numbers Get 5 of 7 questions to level up!
Adding & subtracting negative numbers Get 5 of 7 questions to level up!

Talk to our experts

1800-120-456-456

Important Questions for CBSE Class 6 Maths Chapter 6 - Integers

CBSE Class 6 Maths Important Questions Chapter 6 - Integers - Free PDF Download

Important Questions for Class 6 Chapter 6 - Integers deals with the basic concepts of Integers and the questions given in the segment created by Vedantu will help students prepare for final exams. Students can practice these questions to score good marks. Chapter 6 of Class 6 Maths deals with the number system. Children will also learn addition, subtraction, multiplication and division of positive and negative integers. Students can refer to CBSE Solutions Important Questions for Class 6 Maths to get a hold of important questions that they can expect in exams. You can download the PDF version of important questions for Class 6 Maths Chapter 6 from Vedantu’s website anytime on any device and refer to them at your pace. You can also reach out to the teachers on the panel by enrolling with us. You can also register Online for NCERT Class 6 Science tuition on Vedantu.com to score more marks in CBSE board examination .

Download CBSE Class 6 Maths Important Questions 2024-25 PDF

Also, check CBSE Class 6 Maths Important Questions for other chapters:

Study Important Questions for Class 6 Maths Chapter 6 Integers

1 Mark Questions

1. Integers are denoted using the alphabet ___?

Ans: Integers are denoted using the alphabet Z.

2. $-9$__$5$. Fill in the blanks.

Ans: $-9<5$

3. Compare \[-\mathbf{815}\] and \[-\mathbf{814}\].

Ans: $-815<-814$

4. Say true or false. The absolute value of an integer is always greater than the integer.

Ans: True

5. The predecessor of\[~\mathbf{219}\] is \[\mathbf{218}\]. Say true or false.

Ans: Predecessor of a number is the one that comes before the number.

\[\begin{align} & \text{Predecessor of a number} \\ & =\text{Number}1 \\ & =\left( -219 \right)1 \\ & =220. \\ \end{align}\]

Hence the statement is false.

6. ___ is called the Additive identity.

Ans: 0 is called the additive identity. This is because addition of zero to any number bears the same number.

7. \[-\mathbf{3}\] is the ___ of \[\mathbf{3}\].

Ans: $-3$ is the additive inverse of $3$. This is because on adding the numbers, we get zero, i.e., $\left( -3 \right)+3=0$.

8. \[\_\_\_\div \mathbf{483}=\mathbf{0}\]

9. \[-\mathbf{843}\div \_\_\_=\mathbf{1}\]

2 Marks Questions

1. Write opposite of each of the following:

(a) A decrease of 9

(b) Spending Rs.500

Ans: (a) An increase of $9$.

(b) Saving Rs.$500$.

2. Indicate using ‘$+$‘ or ‘$-$‘ sign

(a) 10km before sea level

(b) loss of Rs.900

Ans: (a) $-10$km

(b)$-$Rs.$900$

3. Write in ascending order: \[\mathbf{365}\], \[\mathbf{515}\], \[\mathbf{102}\], \[\mathbf{413}\], \[\mathbf{7}\].

Ans: $-515$, $-365$, $7$, $102$, $413$.

4. Write in descending order: \[\mathbf{21}\], \[\mathbf{501}\], \[\mathbf{2}\], \[\mathbf{16}\], \[\mathbf{81}\], \[\mathbf{363}\].

Ans: $21$, $-2$, $-16$, $-81$, $-363$, $-501$.

5. Find the value of the following:

(a)$-\left| -4 \right|$

(b)$\left| 7-4 \right|$

(c)$8-\left| 7 \right|$

Ans: (a)$-\left| -4 \right|=-4$

(b)$\left| 7-4 \right|=\left| 3 \right|=3$

(c)$8-\left| 7 \right|=8-7=1$

6. Add \[-\mathbf{82}\] and \[+\mathbf{45}\].

Ans: Adding $-82$ and $45$,

$\begin{align} & -82 \\ & +\underline{45} \\ & -37 \\ \end{align}$

Hence, the answer is $-37$.

7. Add \[-\mathbf{9568}\] and \[-\mathbf{695}\].

Ans: Adding $-9568$ and $-695$,

\[\begin{align} & -\text{ }9568 \\ & -\underline{\text{ }695} \\ & -10263 \\ \end{align}\]

Hence, the answer is $-10,263$.

8. Add

(a) \[-\mathbf{19}+\mathbf{36}\]

(b) \[-\mathbf{49}+\mathbf{27}\]

Ans: (a) Adding $-19$ and $36$,

$\begin{align} & -19 \\ & +\underline{36} \\ & \text{ 17} \\ \end{align}$

Hence, the answer is $17$.

(b) Adding $-49$ and $27$,

$\begin{align} & -49 \\ & +\underline{27} \\ & -22 \\ \end{align}$

Hence, the answer is $-22$.

9. \[\left( -14+6 \right)\] ___$\left( -38-\left( -9 \right) \right)$ . Use >, <, =

Ans: Solving both sides, we get

$\left( -14+6 \right)$__$\left( -38-\left( -9 \right) \right)$

$-8>-29$

3 Marks Questions

1. Mark the following on the number line:

(a) \[\mathbf{4}\]

(b) \[\mathbf{0}\]

(d) \[\mathbf{6}\]

Numbers marked on the Number line are -10,-4, 0 and +6

2. Write all integers between

(a) \[\mathbf{4}\] and \[\mathbf{4}\]

(b) \[\mathbf{8}\] and \[\mathbf{3}\]

Ans: (a) $-3$,$-2$, $-1$, $0$, $1$, $2$. $3$

(b) $-7$, $-6$, $-5$, $-4$

3. Subtract the following:

(a) \[-\mathbf{842}\] from \[\mathbf{0}\]

(b) \[-\mathbf{2959}\] from \[\mathbf{8158}\]

Ans: (a) Subtracting $-842$ from $0$,

$\begin{align} & 0-\left( -842 \right) \\ & =0+842 \\ & =842 \\ \end{align}$

Hence, the answer is $842$.

(b) Subtracting $-2959$ from $8158$,

$\begin{align} & 8158-\left( -2959 \right) \\ & =8158+2959 \\ & =11117 \\ \end{align}$

Hence, the answer is $11,117$.

4. The sum of two integers is – 38. If one of them is 240. Find the other.

Ans: We know that, $\text{addend+addend=sum}$

From given,

$\begin{align} & 240+X=-38 \\ & X=-38-240 \\ & X=-278 \\ \end{align}$

Hence, the other number is $-278$.

5. Find the product of \[\left( -27 \right)\times 18\times 30\].

Ans: The product of \[\left( -27 \right)\times 18\times 30\] is

\[\begin{align} & \left( -27 \right)\times 30\times 18 \\ & =-810\times 18 \\ & =-14580 \\ \end{align}\]

Hence, the answer is \[-14,580\].

6. Simplify: $\left( -37 \right)\times \left( -16 \right)+\left( -37 \right)\times \left( -14 \right)$.

Ans: $\left( -37 \right)\times \left( -16 \right)+\left( -37 \right)\times \left( -14 \right)$…(1)

We know that by distributive property,

$a\times b+a\times c=a\times \left( b+c \right)$

Hence, by (1),

$a=-37$, $b=-16$, $c=-14$

$\begin{align} & \left( -37 \right)\left[ \left( -16 \right)+\left( -14 \right) \right] \\ & =\left( -37 \right)\left[ -30 \right] \\ & =-1110 \\ \end{align}$

The answer after simplification is $-1110$.

7. Divide \[\left( +\mathbf{3251} \right)\] by \[\left( -\mathbf{27} \right)\].

Ans: We know that,

$\frac{\left( +3251 \right)}{\left( -27 \right)}=-\left( \frac{3251}{27} \right)$

By long division, we get,

Hence, we get,

$\begin{align} & \text{Quotient=-120} \\ & \text{Remainder=11} \\ \end{align}$

4 Marks Questions

1. Using number line, write the following

(a) \[\mathbf{4}\] more than \[\mathbf{6}\]

(b) \[\mathbf{5}\] more than \[\mathbf{2}\]

(d) \[\mathbf{3}\] less than \[\mathbf{2}\]

Ans: (a) $4\text{ more than 6}=6+4=10$

Number line showing the operation “4 more than 6”

(b) \[\text{5 more than -2}=5+\left( -2 \right)=5-2=3\]

Number line showing the operation “5 more than -2”

Number line showing the operation “6 less than 4”

(d)$3\text{ less than }-2=\left( -2 \right)-3=-2-3=-5$

Number line showing the operation “3 less than -2”

2. A bus travelled 30km to south, then 40km to north and from 30km to west. How for did the bus travel?

Illustration of the distance of a bus traveled 30km to south, then 40km to north and from 30km to west

Distance travelled south = \[-30\]km

Distance travelled North = \[40\]km

Distance travelled West = $-30$km

Hence, Total distance travelled

\[\begin{array}{*{35}{l}} =\left( -30 \right)+40+\left( 30 \right) \\ \begin{align} & =60+40 \\ & =-20 \\ \end{align} \\ \end{array}\]

Thus, the total distance travelled is $20$km towards the south.

5 Marks Questions

1. In a class test containing \[\mathbf{25}\] questions, \[\mathbf{4}\] marks are given for every correct answer and \[\left( \mathbf{2} \right)\] marks are given for every wrong answer. A student attempts all questions and \[\mathbf{20}\] of his answers are correct. What is the total score of a student?

Ans: Total questions in test \[=25\]

Marks are given for 1 correct answer \[=4\]

Marks are given for 1 incorrect answer \[=2\]

Marks given for 20 correct answers \[=20\times 4=80\]

Total incorrect answers \[=\left( 2520 \right)=5\]

Marks given for incorrect answers \[=5\times \left( 2 \right)=10\]

Total score in test

\[\begin{align} & =80+\left( 10 \right) \\ & =70 \\ \end{align}\]

Hence, the total score in the test is $70$ marks.

CBSE Class 6 Maths Important Questions Chapter 6 - Free PDF Download

Let’s Revise

Integers is a set of all natural numbers, 0 and negatives of natural numbers are called integers, i.e., we can represent the integers on the number line.

Integers range from { ………, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, …….. }

The absolute value of an integer is the numerical value of the integer in any case regardless of its sign.

Successors and predecessor of an integer: Let abe an integer, then:

(a + 1) is called the successor of a.

(a - 1) is called the predecessor of a.

Properties of addition of integers:

(i) Closure property of addition: The total of two integers is always an integer.

(ii) Commutative law of addition: a + b = b + a

(iii) Associative law of addition: the sum remains the same even if the grouping of addends change.

Properties of subtraction of integers:

(i) If two integers a and b are given then (a - b) is also an integer.

(ii) If a is considered an integer, then a - 0 = a.

(iii) if a, b, c are integers and a＞b, then (a - c)＞(b - c)

Properties of multiplication of integers:

(i) Closure property: The result of two integers is always an integer after multiplication.

(ii) Commutative law: a x b = b x a.

(iii) Associative law: a x (b x c) = (a x b) x c.

(iv) Distributive law: a x (b + c) = a x b + a x c.

Properties of division of integers:

(i) If two integers are a and b, then a ÷ b is not necessarily an integer.

(ii) If a ≠ 0, then a ÷ a = 1

(iii) a ÷ 1 = a.

(iv) If a is a non-zero integer, then 0 ÷ a = 0, but a ÷ 0 is not meaningful.

(v) (a ÷ b) ÷ c ≠ a ÷ (b ÷ c) unless c = 1.

Representation of Integers on Number line: To represent integers on a number line, draw a line and mark some points at equal distances on it. Mark a point as 0 on it. Points to the right of 0 are positive integers and are marked as +1, +2, +3, etc. or simply 1, 2, 3, etc. Points to the left of are negative integers and are marked as -1, -2, -3, etc.

Ordering of Integers: On the number line, integers are grouped in such a way that when we move to the right the numbers increase and when we move to the left, the numbers decrease.

We add the corresponding positive integers and retain the negative sign with the sum when adding two negative integers, Ex: Find the sum of -3 and -3.

-3 + (-3) = - (3+ 3) = -6.

To add a positive integer and a negative integer, we ignore the signs and subtract integers with smaller numerical value from the integer with a larger numerical value and take the sign of the larger one.

Ex: (a) Consider -6 and + 4

As 6 -4 = 2, therefore -6 + (+4) = -2

(b) Consider + 5 and -2

5 + (-2) = 5 - 2 = 3

Two integers whose sum is 0 are called additive inverse of each other.

In order to subtract an integer from a given integer, we add an additive opposite of the integer to the given integer.

Ex: (a) Subtract 3 from -4

The additive inverse of 3 is -3

So, -4, -3 = -4 + (-3) = (4 + 3) = -7

(b) -2 from -4

The additive inverse of -3 is 3

So, -4 - (-2) = -4 + 2 = -2

Addition/ Subtraction of Integers on Number line: Firstly draw the number line and represent the first number on it. Then to add/ subtract the second number in first, we move left/ right to the first number according to the second integer (either -ve or +ve)

Chapter 6 Integers for Class 6 teaches the concepts of Integers that you have learnt the basics of in your previous grade. The chapter Integers is the foundation of mathematics. Revising the chapter of Integers along with important questions will help you with other topics in mathematics. The important questions are prepared based on the topics that are discussed in this chapter. The reference notes for the chapter given above will benefit you in solving the Important Questions Of Chapter 6 of Maths for Class 6 Integers . The important questions of the chapter and the reference notes related to the chapter provided by Vedantu will not only help you to understand the concept better but also solve the questions successfully. If you still have any doubts then you can get answers to all your queries by reaching out to our experienced teachers. You can register on www.vedantu.com and master the topic.

Why Should You Opt for Vedantu?

Vedantu is one of the foremost eLearning education forums of the country, where our team has worked very hard to create an awesome technology platform that enables learning in a very interactive and engaging manner. It is an online tutoring platform that connects teachers and students. Vedantu focuses on the quality of teachers because we believe a teacher can shape up the overall personality of a child. So our main priority is having good, qualified and experienced teachers on board. With the help of new technology, Vedantu has brought a revolution in all the traditional methods of teachings. Our experienced teachers have designed the courses with the latest technology called WAVE in which the teachers can teach while writing on the whiteboard. This will give a feeling of offline classes to the students.

Students can avail abundant solutions and study materials affiliated to all the Boards of the country. These solutions for each subject, notes and study materials not only give you enough practice for the exams but also magnify your confidence and strengthen your conceptual understanding of the subject. You can also learn the shortcuts and tricks to solve the difficult questions from our master teachers. Our subject matter experts have done extensive research and have developed the NCERT Solution for all subjects.

The solutions to the exercises in the course books are 100% verified and developed as per the latest edition CBSE textbooks. The online sessions are designed with in-class quizzes which enables master teachers to get real-time feedback on students' understanding. To prepare for advanced exams like IIT-JEE , KVPY and NEET examinations , you can count on Vedantu’s experienced teachers who are from some reputed institutions of the country. The USP of Vedantu is the live interactive sessions and innumerable students have been benefited from the courses that Vedantu provides. Take the right decision today to register with Vedantu and shape your career through us.

Important Related Links for CBSE Class 6 Maths

Vedantu's provision of important questions for CBSE Class 6 Maths Chapter 6 - "Integers" is a crucial aid for young learners. These questions are thoughtfully designed to help students navigate the world of integers with ease. They encourage critical thinking, problem-solving skills, and a deeper understanding of numerical concepts. Vedantu's commitment to quality education is evident, as these important questions empower students to excel in their mathematics studies. By practising these questions, students can build a robust foundation in integer mathematics, fostering confidence and competence in mathematical reasoning. These questions are a valuable resource for both exam preparation and lifelong mathematical learning.

FAQs on Important Questions for CBSE Class 6 Maths Chapter 6 - Integers

1. What is integer in maths for class 6?

Integers, which do not include decimal or fractional numbers, are a collection of whole numbers and their negatives. Positive and negative integers are the two different sorts of integers. Positive integers are all positive values, whereas negative integers are all negative numbers. In short, any number—aside from decimal or fractional numbers—can be referred to as an integer.

2. How can I prepare Chapter 6 integers for my exam?

You should practice as many questions as possible. You can seek help in your doubts online from Vedantu.com . You should solve as many questions as you can. Moreover, you can find many questions for practice on Vedantu. Vedantu provides you many Important questions for CBSE to boost your exam preparations as well.

3. Can I download important questions for CBSE board of Chapter 6 Integers for class 6?

Yes, definitely you can download the important questions for CBSE class 6 and not only questions but all the necessary notes and study material needed for the preparation of your chapter from Vedantu.com which is one of the finest and student friendly

4. What is the role of zero?

In mathematics, zero serves two very different purposes. It extends the theory of numbers from the natural numbers to integers and acts as a placeholder for writing numbers. It has a "1," the first counting symbol, as well as a "0," thus indicating that the number is ten times larger than a plain "1."

5. Which is the best platform to study the Integers chapter for class 6 for CBSE board?

The best platform to study about Integers would be Vedantu where you can have access across the best lectures on whatever topic you need to study. You will be provided with worksheets, notes, Important questions that are going to help you strengthen your concepts and will make you secure good marks.

6. Do these questions come with answers and explanations?

Depending on the source, these questions may or may not come with answers and explanations. It's essential to attempt the questions first and then refer to your textbook or teacher for explanations if needed.

7. Can I find these questions in a downloadable format?

Yes, many educational websites offer downloadable PDFs of important questions for various subjects and chapters. You may check Vedantu or other educational platforms for downloadable versions.

8. How can I best utilise these important questions for exam preparation?

Use these questions as part of your study plan. Attempt them regularly, time yourself, and simulate exam conditions to build confidence and improve your performance in the actual exams.

Chapter wise Important Questions for CBSE Class 6 Maths

Cbse study materials.

The Site is down as we are performing important server maintenance, during which time the server will be unavailable for approximately 24 hours. Please hold off on any critical actions until we are finished. As always your feedback is appreciated.

Study Packages
NCERT Solutions
Sample Papers
Online Test

Questions Bank
Mathematics
Test Series
Ncert Solutions
Solved Papers
Current Affairs
JEE Main & Advanced
Pre-Primary
MP State Exams
UP State Exams
Rajasthan State Exams
Jharkhand State Exams
Chhattisgarh State Exams
Bihar State Exams
Haryana State Exams
Gujarat State Exams
MH State Exams
Himachal State Exams
Delhi State Exams
Uttarakhand State Exams
Punjab State Exams
J&K State Exams

7th Class Mathematics Integers Question Bank

Done integers total questions - 41.

question_answer 1) What do we call the set of negative numbers and whole numbers?

A) Natural numbers done clear

B) Integers done clear

C) Positive numbers done clear

D) The set of whole numbers. done clear

question_answer 2) Which of the following is the smallest positive integer?

A) 0 done clear

B) 100 done clear

C) 1 done clear

D) 9 done clear

question_answer 3) Where are the negative numbers located on a horizontal number line?

A) On the right of 0 done clear

B) On the left of 0 done clear

C) Above 0 done clear

D) Below 0 done clear

question_answer 4) What is the opposite of earning Rs. 100?

A) \[+\] Rs. 100 done clear

B) Profit of Rs. 100 done clear

C) Gain of Rs. 100 done clear

D) Spending Rs. 100 done clear

question_answer 5) How is the withdrawal of RS. 200 represented?

A) Depositing Rs. 200 done clear

B) \[-\]Rs. 200 done clear

C) Rs. 200 done clear

D) \[-200\] done clear

question_answer 6) Which of the following is true with respect to \[-28\] and \[-32\]?

A) \[-28<-32\] done clear

B) \[~-28=-32\] done clear

C) \[-32>-28\] done clear

D) \[-28>-32\] done clear

question_answer 7) Where do we place the positive numbers on a vertical number line with respect to O?

A) Above done clear

B) On its left side done clear

C) On its right side done clear

D) Below done clear

question_answer 8) What is the representation of 30 km towards the west?

A) 30 km east done clear

B) \[-30\] km done clear

C) 30 km done clear

D) 30 done clear

question_answer 9) What is the nature of the product of a negative integer by itself, odd number of times?

A) Positive done clear

B) Negative done clear

C) Non negative done clear

D) Cannot be determined done clear

question_answer 10) What is the nature of the product of a negative number by itself even number of times?

A) Negative done clear

B) 0 done clear

C) Positive done clear

D) Non-negative done clear

question_answer 11) A Calculate \[(-32)\times (-4)\times (-3)\times 0\times (-6)\]

A) 27648 done clear

B) 276480 done clear

C) 0 done clear

D) \[-27648\] done clear

question_answer 12) If the dividend and the divisor have like signs, what is the sign of the quotient?

A) Positive done clear

B) Negative done clear

C) Zero done clear

D) Indeterminate done clear

question_answer 13) If the dividend and divisor have unlike signs, what is the sign of the quotient?

A) Positive done clear

A) \[\left( i \right)-\left( b \right),\left( ii \right)-\left( a \right),\left( iii \right)-\left( c \right),\left( iv \right)-\left( d \right)\] done clear

B) \[\left( i \right)-\left( a \right),\left( ii \right)-\left( b \right),\left( iii \right)-\left( d \right),\left( iv \right)-\left( c \right)\] done clear

C) \[\left( i \right)-\left( d \right),\left( ii \right)-\left( c \right),\left( iii \right)-\left( b \right),\left( iv \right)-\left( a \right)\] done clear

D) \[\left( i \right)-\left( c \right),\left( ii \right)-\left( d \right),\left( iii \right)-\left( a \right),\left( iv \right)-\left( b \right)\] done clear

question_answer 15) With respect to which of the following operations is closure property satisfied by the set of integers?

A) \[+,\times \] done clear

B) \[+,\div ,\times \] done clear

C) \[+,\times ,-\] done clear

D) \[+,-,\div \] done clear

question_answer 16) What is the additive identity for the set of integers?

A) \[0\] done clear

B) \[(-1)\] done clear

C) \[1\] done clear

D) \[+10\] done clear

question_answer 17) Which of the following is the multiplicative identity in the set of integers?

A) \[1\] done clear

C) \[0\] done clear

D) \[(-10)\] done clear

question_answer 18) What is the value of\[124\times 4-3+118\div 2\]?

A) \[552\] done clear

B) \[496\] done clear

C) \[553\] done clear

D) \[-553\] done clear

question_answer 19) Which of the following orders is used while evaluating an expression?

A) \[[\,],\,\,(\,),\,\,\{\,\}\] done clear

B) \[\{\,\},\,\,(\,),\,\,[\,]\] done clear

C) \[(\,),\,\,\{\,\},\,\,[\,]\] done clear

D) \[(\,),\,\,[\,],\,\,\{\,\}\] done clear

question_answer 20) If a negative sign precedes a bracket, what happens to the terms inside it?

A) Their signs are changed. done clear

B) The terms are reciprocated. done clear

C) The signs remain the same. done clear

D) The terms are doubled. done clear

question_answer 21) If a positive sign precedes a bracket, what happens to the terms inside it?

A) Signs of the terms will be changed. done clear

B) Every term is reciprocated. done clear

C) Every term will become zero. done clear

D) No change occurs in any of the terms. done clear

question_answer 22) What is the value of the expression \[7-[13-\{-2-6(6\,\,of\,\,-5)\}]\]?

A) \[-172\] done clear

B) \[180\] done clear

C) \[172\] done clear

D) \[0\] done clear

question_answer 23) What is the sign of the product of two integers with like signs?

A) Negative done clear

B) Positive done clear

C) 0 done clear

D) Cannot be determined done clear

question_answer 24) What is the sign of the product of two integers with unlike signs?

A) Negative done clear

C) Positive done clear

question_answer 25) Which of the following operations on integers satisfy the commutative property?

A) \[-,\,\div \] done clear

B) \[-,\,\times \] done clear

C) \[+,\,-\] done clear

D) \[+,\,\times \] done clear

question_answer 26) Over which of the following operations is multiplication distributed in the set of integers?

C) \[+,\,-\] done clear

D) \[\times ,\,\div \] done clear

question_answer 27) What is the sign of the product obtained when a positive integer is multiplied by \[-1\]?

A) Positive done clear

C) 0 done clear

D) Non negative done clear

question_answer 28) The sum of two integers is 62. If one o1 the integers is \[-48\] what is the other?

A) \[14\] done clear

B) \[-14\] done clear

C) \[-110\] done clear

D) \[110\] done clear

question_answer 29) The product of two integers is \[-48\]. If one of the integers is \[-6,\]what is the value of the other?

A) \[1\] done clear

B) \[288\] done clear

D) \[8\] done clear

question_answer 30) A man walked 3 km towards North then 8 km towards South. What is his final position with respect to his initial position?

A) 5 km towards East done clear

B) 3 km towards South done clear

C) 8 km towards North done clear

D) 5 km towards South done clear

question_answer 31) What is the smallest negative integer?

A) \[-1\] done clear

B) \[-10\] done clear

C) \[0\] done clear

D) Does not exist done clear

question_answer 32) In a quiz, positive marks were given for correct answers and negative marks for incorrect answers. If Guru's scores in five successive rounds were \[35,-10,-15,\text{ }20\]and 5, what is his total score at the end?

A) \[25\] done clear

B) \[35\] done clear

C) \[45\] done clear

D) \[55\] done clear

question_answer 33) A deep well has steps inside it. A monkey is sitting on the topmost step (i.e., the first step). The water level is at the ninth step. If the monkey jumps 3 steps down and then jumps back 2 steps up, how many jumps does it have to make to reach the water level?

A) \[11\] done clear

B) \[9\] done clear

C) \[7\] done clear

D) \[5\] done clear

question_answer 34) A certain freezing process requires that room temperature be lowered from \[{{4}^{o}}C\]at the rate of \[{{5}^{o}}C\] every hour. What is the room temperature after 10 hours?

A) \[{{0}^{o}}C\] done clear

B) \[-{{5}^{o}}C\] done clear

C) \[-{{10}^{o}}C\] done clear

D) \[-{{15}^{o}}C\] done clear

question_answer 35) In a class test containing 10 questions, 3 marks are awarded for every correct answer and \[(-1)\] mark is awarded for every incorrect answer and 0 for the questions not attempted. Srinu gets two correct and six incorrect answers out of eight questions he attempts. What is his total score?

A) \[0\] done clear

B) \[2\] done clear

C) \[-2\] done clear

D) \[6\] done clear

question_answer 36) What should be multiplied by \[(-12)\] in order to get 180?

A) \[15\] done clear

B) \[-15\] done clear

C) \[16\] done clear

D) \[-16\] done clear

question_answer 37) A lift descends into an underground floor at the rate of 6 metres per minute. If the descent starts from 10 metres above the ground level, how much time will it take to descend 350 metres?

A) 30 minutes done clear

B) 50 minutes done clear

C) 1 hour done clear

D) 1 hour 30 minutes done clear

question_answer 38) The temperature at 12 noon was \[{{10}^{o}}C\] above zero. If it decreases at the rate of \[{{2}^{o}}C\] per hour until midnight, what would be the temperature at 9 p.m.?

A) \[-{{8}^{o}}C\] done clear

B) \[-{{6}^{o}}C\] done clear

C) \[{{8}^{o}}C\] done clear

D) \[{{6}^{o}}C\] done clear

question_answer 39) What is the identity element with respect to subtraction in integers?

A) \[0\] done clear

B) \[1\] done clear

C) \[-1\] done clear

D) Does not exist done clear

question_answer 40) Which of the following statements holds correct?

A) \[N\subset W\subset Z\] done clear

B) \[Z\subset N\subset W\] done clear

C) \[W\subset N\subset Z\] done clear

D) \[Z\subset W\subset N\] done clear

question_answer 41) The quotient of two numbers is \[(-17)\]. If one of the numbers is \[(-340),\]what is the other number?

A) \[20\] done clear

B) \[17\] done clear

C) \[(-20)\] done clear

D) \[(-30)\] done clear

Study Package

Question - Integers

Reset Password.

OTP has been sent to your mobile number and is valid for one hour

Mobile Number Verified

Your mobile number is verified.

School Guide
Mathematics
Number System and Arithmetic
Trigonometry
Probability
Mensuration
Maths Formulas
Class 8 Maths Notes
Class 9 Maths Notes
Class 10 Maths Notes
Class 11 Maths Notes
Class 12 Maths Notes
Real Life Applications of Functions
Real Life Applications of Area
Real-Life Applications of Euclidean Geometry
Real-life Applications of Numbers
Real Life Applications of Number Lines
Real Life Application of Maths in Engineering
Applications of Prime Numbers in Real Life
Real-life Applications of Negative Numbers
Real-Life Applications of Real Numbers
Real-Life Applications of Irrational Numbers
Real Life Applications of Volume
Real-life Applications of Algebraic Geometry
Real Life Application of Simple Equations
Real-Life Applications of Whole Numbers
Real-Life Applications of Discrete Mathematics
Real Life Applications of Arithmetic Operations
Real-Life Applications of Number Theory
Real-life Applications of Arithmetic Progression
Real Life Application of Maths in Computer Science

Applications of Integers in Real Life

Integers, a fundamental concept of mathematics representing whole numbers and their opposite versions with negative signs, have a variety of real-world benefits even beyond their usage in schools. Number theory helps design various useful solutions for solving practical issues as well as effective process optimization.

This article explores, applications of integers in various fields, highlighting their importance in shaping our daily lives and advancing technology.

Table of Content

What are Integers?

Applications of integers, real-life applications of integers, financial transactions, temperature readings, inventory control, engineering calculations, sports scores and rankings, transportation and distance measurement.

Integers are a fundamental concept of mathematics representing whole numbers and their opposite versions with negative signs. In other terms, integers are numbers that cannot have a decimal component or fractional part. The set of integers is a collection of positive whole numbers (1, 2, 3, …) and their opposite partners (-1, -2, -3, …) and zero.

They are used in various mathematical operations, for example, addition, subtraction, multiplication and division, which are used to represent discrete quantities or values numbers that are counted in whole numbers. They serve as operational math tools in the process of solving equations, representing directions or positions, and analyzing data in many real-life applications.

Various applications of Integers includes:

Finance and Accounting: In finance, we use the integers to designate money values, profits, and losses and analyze deals. Integers may either have the positive meaning of credits or deposits or the negative meaning of debts and withdrawals.
Temperature and Weather Forecasting: The integers are used to signify the temperature through the Celsius or Fahrenheit units. Positive numbers are associated with temperatures above zero degrees Celsius, while negative integers show temperatures below zero.
Sports and Games: The scoring and ranking system makes use of integers in sports and games. Points, scores, rankings, and player statistics are often represented using integers.
Inventory Management: Integral functions are involved in inventory management systems as they help trace stock levels, monitor product amounts and make order processing possible.
Engineering and Construction: Every instance of an integer is critical in measuring, dimensioning and calculations in engineering and construction work. Here they are utilized to designate the amount to be expended by weight and height of the hard goods.

Integers as used in real life scenarios are:

In Banking and accounting, integers serve as utilities in banking transactions, budgeting and accounting practices. Credits (depicting deposits or increases) are represented by positive integers whereas negative integers indicate debits (withdrawals or decreases). Take for instance a situation where you have a bank account with a balance of +$500; you deposited the money. On the other hand, in case the balance is -$200; you withdrew the money.

Example: In case with personal finance, a budgeting app can utilize a measure of income, spending, and fund, which will have an impact on the ability of an individual to manage his/her finances and achieve financial goals.

Integers are applied for representing temperature readings in weather forecasts and climate monitoring. The positive integers shows temperatures above zero degrees Celsius or Fahrenheit, while the negative integers correspond to the temperatures which are lower than zero in the Celsius or Fahrenheit. For instance, + 25 degrees would be warm; – 5 degree Celsius would mean freezing.

Example: Meteorologists use integer-based data to analyze temperature trends used in the analysis and predictions about the weather, and the advisories issued for different types of climate change are all based on integer data.

Integers belong among the list of essential in this system that is used to track the amount of stock available and to always have a product availability. Positive numbers show that the stocks are available while negative numbers indicate that there is a product shortage or a backorder. Retailers relying on integer-valued algorithms enhance stock rotation and avoid disappointing customers and prevent overstocking or understocking.

Example: E-commerce platforms utilize integers for purposes such as product catalog management, stock level monitoring in warehouses, and finalization of order shipment, that ensures orders are delivered on time.

In general, integers play a decisive role in the arithmetic computations concerning the measure of the quantity, dimensions, and structures. They are used to show the distances, weights and the amount of materials in any kind of projects and production process. Integer-based algorithms sell resource allocation and draw a line between overconsumption and sustainability in engineering services.

Example: Integral numbers are the unit that civil engineers use in designing bridges, buildings, and projects of infrastructure. The safety standards and structural integrity of each project are achieved on the basis of this required precision.

Integers are often used in sports and games to express scores, points, rankings, and player statistics. Positive integers represent the points gained by teams or players, which can be diminished by negative integers, that represent penalties. Through application oriented statistics in Sports analysis, Integer based data regarding performance metrics is used for forecasting of game projections.

Example: In basketball when we show the result of the winning team it could be +90 points and the one which lost the game can have a result of -70 points whose discrepancy is owing to the integer-based scoring system.

Integers are the important part of the transport and distance measurement where natural numbers are used to depict distance, motion, speed and the quantities related to travelling. Integer-based mathematics is used to perform route planning, fuel consumption, scheduling, and logistics controls while operating transport systems.

Example: Road traffic application involves integer to represent the distance between two cities or landmarks. There may be a number of cities showing on the map not that far away from each other like 150 miles which would be easy to spot and plan your route using the map and the number would be easier from a driver’s point of view.

Real-life Applications of Numbers Real-Life Applications of Real Numbers Real-Life Applications of Whole Numbers

FAQs on Applications of Integers

How are integers used in financial accounting.

Integer is used in financial accounting for budgeting, and accounting which are based on the area of monetary values. Positive integers shows deposits and credits whereas negative integers indicate withdrawal and debit. So it helps to trace and organize the account.

What is the significance of integers in temperature readings?

Positive integers indicate temperatures more than zero degree Celsius (or Fahrenheit), while negative integers represent temperatures less than zero; such representation is very helpful in predicting weather variations and climate patterns.

How do integers contribute to inventory management?

Integers play the decisive role in inventory monitoring by providing stock levels and product availability. Positive integers means there is enough stock to service the retailer, on the contrary negative integers mean a short supply or back order.

How are integers used in engineering calculations?

We use integers in engineering for calculations such as length, width, speed, and structure formulas. They aid in planning and engineering of industrial and manufacturing process by representing distances, weights, and quantities of materials in construction projects.

What role do integers play in sports scoring and rankings?

Integers forms the basis in sports by representing results such as points, ranks, and player statistics in sports and games. Positive integers express the achievements of teams as well as athletes, while negative integers can stand for penalties or deductions and thus enable the evaluation of performance and outcome parameters in competitive sports.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Share full article

Supported by

When Is the Best Time to Work Out?

It’s an age-old question. But a few recent studies have brought us closer to an answer.

A silhouetted woman running along a body of water with the sun glistening behind her.

By Alexander Nazaryan

What is the best time of day to exercise?

It’s a straightforward question with a frustrating number of answers, based on research results that can be downright contradictory.

The latest piece of evidence came last month from a group of Australian researchers, who argued that evening was the healthiest time to break a sweat, at least for those who are overweight. Their study looked at 30,000 middle-aged people with obesity and found that evening exercisers were 28 percent less likely to die of any cause than those who worked out in the morning or afternoon.

“We were surprised by the gap,” said Angelo Sabag, an exercise physiologist at the University of Sydney who led the study. The team expected to see a benefit from evening workouts, but “we didn’t think the risk reduction would be as pronounced as it was.”

So does that mean that evening swimmers and night runners had the right idea all along?

“It’s not settled,” said Juleen Zierath, a physiologist at the Karolinska Institute in Sweden. “It’s an emerging area of research. We haven’t done all the experiments. We’re learning a lot every month.”

No single study can dictate when you should exercise. For many people, the choice comes down to fitness goals, work schedules and plain old preferences. That said, certain times of day may offer slight advantages, depending on what you hope to achieve.

The case for morning exercise

According to a 2022 study , morning exercise may be especially beneficial for heart health. It may also lead to better sleep .

And when it comes to weight loss, there have been good arguments made for morning workouts. Last year, a study published in the journal Obesity found that people who exercised between the hours of 7 a.m. and 9 a.m. had a lower body mass index than counterparts who exercised in the afternoon or at night, though it did not track them over time, unlike the Australian study, which followed participants for an average of eight years.

Of course, the biggest argument for morning exercise may be purely practical. “For a lot of people, the morning is more convenient,” said Shawn Youngstedt, an exercise science professor at Arizona State University. Even if rising early to work out can be challenging at first , morning exercise won’t get in the way of Zoom meetings, play dates or your latest Netflix binge.

The case for afternoon exercise

A few small studies suggest that the best workout time, at least for elite athletes, might be the least convenient for many of us.

Body temperature, which is lower in the morning but peaks in late afternoon, plays a role in athletic performance. Several recent small studies with competitive athletes suggest that lower body temperature reduces performance (though warm-ups exercises help counter that) and afternoon workouts help them play better and sleep longer .

If you have the luxury of ample time, one small New Zealand study found that it can help to nap first. As far as the rest of us are concerned, a Chinese study of 92,000 people found that the best time to exercise for your heart was between 11 a.m. and 5 p.m.

“The main difference is our population,” Dr. Sabag said. While his study was restricted to obese people, the Chinese study was not. “Individuals with obesity may be more sensitive to the time-of-day effects of exercise,” he said.

The case for evening exercise

This latest study may not settle the debate, but it certainly suggests that those struggling with obesity might benefit from a later workout.

Exercise makes insulin more effective at lowering blood sugar levels, which in turn fends off weight gain and Type 2 diabetes, a common and devastating consequence of obesity.

“In the evening, you are most insulin resistant,” Dr. Sabag said. “So if you can compensate for that natural change in insulin sensitivity by doing exercise,” he explained, you can lower your blood glucose levels, and thus help keep diabetes and cardiovascular disease at bay.

One persistent concern about evening exercise is that vigorous activity can disturb sleep. However, some experts have argued that these concerns have been overstated.

The case that it may not matter

While many of these studies are fascinating, none of them is definitive. For one thing, most are simply showing a correlation between exercise times and health benefits, not identifying them as the cause.

“The definitive study would be to actually randomize people to different times,” Dr. Youngstedt said, which would be phenomenally expensive and difficult for academics.

One thing public health experts do agree on is that most Americans are far too sedentary. And that any movement is good movement.

“Whenever you can exercise,” Dr. Sabag urged. “That is the answer.”

In a recent edition of his newsletter that discussed the Australian study, Arnold Schwarzenegger — bodybuilder, actor, former governor — seemed to agree. He cited a 2023 study suggesting that there really isn’t any difference in outcomes based on which time of day you exercise. In which case, it’s all about what works best for you.

“I will continue to train in the morning,” the former Mr. Universe wrote. “It’s automatic for me.”

Alexander Nazaryan is a science and culture writer who prefers to run in the early evening.

Let Us Help You Pick Your Next Workout

Looking for a new way to get moving we have plenty of options..

To get the most out of your strength training, you need to let go of routine and try progressive overload .

What is the best time of day to exercise? A few recent studies have brought us closer to an answer .

Sprinting, at least for short distances, can be a great way to level up your workout routine .

Cycling isn’t just fun. It can also deliver big fitness gains with the right gear and strategy .

Is your workout really working for you? Take our quiz to find out .

Pick the Right Equipment With Wirecutter’s Recommendations

Want to build a home gym? These five things can help you transform your space into a fitness center.

Transform your upper-body workouts with a simple pull-up bar and an adjustable dumbbell set .

Choosing the best running shoes and running gear can be tricky. These tips make the process easier.

A comfortable sports bra can improve your overall workout experience. These are the best on the market .

Few things are more annoying than ill-fitting, hard-to-use headphones. Here are the best ones for the gym and for runners .

COMMENTS

Case Study Questions for Class 7 Maths Chapter 1 Integers
There is total 13 chapters. Chapter 1 Integers Case Study Questions. Chapter 2 Fractions and Decimals Case Study Questions. Chapter 3 Data Handling Case Study Questions. Chapter 4 Simple Equations Case Study Questions. Chapter 5 Lines and Angles Case Study Questions. Chapter 6 The Triangles and its Properties Case Study Questions.
CBSE 7th Standard CBSE Mathematics Case study Questions
CBSE 7th Standard CBSE Mathematics English medium question papers, important notes , study materials , Previuous Year questions, Syllabus and exam patterns. Free 7th Standard CBSE Mathematics books and syllabus online. Practice Online test for free in QB365 Study Material. Important keywords, Case Study Questions and Solutions. Updates about latest education news and Scholorships in one place
PDF Real Numbers- Case Study Case Study 1
REAL NUMBERS- CASE STUDY CASE STUDY 1. To enhance the reading skills of grade X students, the school nominates you and ... If the product of two positive integers is equal to the product of their HCF and LCM is true then, the HCF (32 , 36) is a) 2 b) 4 ... A test consists of 'True' or 'False' questions. One mark is awarded for every correct
Integers
Amir's teacher asked him to plot all of the integers from -4 -4 to 6 6 on a number line. Which number line is correct? 4. Fill in the missing integers to complete the number line. 5. Plot the numbers -8 -8 to 2 2 on a vertical number line. 6. Fill in the missing integers to complete the vertical number line.
Integers Questions
Properties of Integers. Closure Property: For any a and b integers, a * b is also an integer, where * represents arithmetic operations ( +, -, × ) For example: -2 + 3 = 1 is an integer - 34 - 4 = - 38 is an integer - 6 × 2 = - 12 is an integer ; 3 ÷ 2 = 1.5 is not an integer ; Hence, integers are not closed with respect to ...
Integers
Learn how to use integers to represent positive and negative numbers, and how to perform operations with them. This unit covers the concepts of addition, subtraction, multiplication, and division of integers, as well as the properties of these operations. You will also practice solving word problems involving integers and applying them to real-world situations.
CBSE Class 10 Maths Case Study Questions for Class 10 Maths Chapter 1
4. 7 × 11 × 13 × 15 + 15 is a. a) Prime number. b) Composite number. c) Neither prime nor composite. d) None of the above. Answer: b) Composite number. 5. If p and q are positive integers such ...
Class 10 Maths Case Study Questions of Chapter 1 Real Numbers
Case Study 2: HCF and LCM are widely used in number system especially in real numbers in finding relationship between different numbers and their general forms. Also, product of two positive integers is equal to the product of their HCF and LCM Based on the above information answer the following questions.
Integers
Integers: Unit test; Adding and subtracting integers. Learn. Intro to negative numbers (Opens a modal) Adding & subtracting negative numbers (Opens a modal) ... Multiplying & dividing negative numbers word problems Get 3 of 4 questions to level up! Up next for you: Unit test. Level up on all the skills in this unit and collect up to 700 Mastery ...
CBSE Class 7 Maths Important Questions Chapter 1
There are four exercises in Chapter 1 "Integers" of Class 7 Maths. These four exercises contain a total of 30 questions. For more practice of Chapter 1 of Class 7 Maths, students can refer to the Important Questions of Chapter 1 of Class 7 Maths, prepared by experts at Vedantu for the benefit of the students. 7.
Classroom Case Studies, 3-5
Classroom Case Studies, 3-5. Watch this program in the 10th session for grade 3-5 teachers. Explore how the concepts developed in this course can be applied through case studies of grade 3-5 teachers (former course participants) who have adapted their new knowledge to their classrooms. 0 seconds of 26 minutes, 35 secondsVolume 90%. 00:00. 26:35.
Integers
Integers: Unit test; Addition and subtraction of integers (Recap) Learn. Adding numbers with different signs (Opens a modal) Commutative law of addition ... Multiplying & dividing negative numbers word problems Get 3 of 4 questions to level up! Up next for you: Unit test. Level up on all the skills in this unit and collect up to 1,000 Mastery ...
NCERT Exemplar Solutions for Class 7 Maths Chapter 1 Integers
Chapter 1 - Integers solutions are available for download in PDF format, which provides answers to all questions in the NCERT Exemplar Class 7 Maths textbook. An integer is a whole number that can be positive, negative or zero. Positive integers are used in many ways in our daily lives. One such instance is highway numbers, along with roadway ...
RD Sharma (2016) Solutions for Class 7 Math Chapter 1
math. Integers. RD Sharma (2016) Solutions for Class 7 Math Chapter 1 Integers are provided here with simple step-by-step explanations. These solutions for Integers are extremely popular among class 7 students for Math Integers Solutions come handy for quickly completing your homework and preparing for exams. All questions and answers from the ...
Integers Class 7 Extra Questions Maths Chapter 1
Integers Class 7 Extra Questions Very Short Answer Type. Question 1. Fill in the blanks using < or >. Question 2. Question 3. Question 4. Question 5. Write five pair of integers (m, n ) such that m ÷ n = -3. One of such pair is (-6, 2).
6th Class Mathematics Integers Question Bank
View Solution play_arrow. question_answer 57) Direction: David and Dravid started from a place denoted by 0, in opposite directions. After Dravid walked for 8 m, he met Sajid. After 7 m from the starting point David met Sahid. Dravid went back 2 m to buy a book. David went ahead 3 m to the library.
CBSE Class 10 Maths Case Study Questions for Chapter 2
1. In the standard form of quadratic polynomial, ax2 + bx + c, a, b and c are. a) All are Polynomials. b) All are rational numbers. c) 'a' is a non zero real number and b and c are any ...
Integers Questions for Class 7 Maths CBSE
1. For any two positive integers a and b, a ÷ (-b) = - a ÷ b, where b ≠ 0. 2. The commutativity, associativity and distributivity of integers help to make calculations simpler. 3. The product of three integers does not depend upon the grouping of integers. 4. Division is closed for integers. Marks: 1. Ans. Option 4. Explanation
Integers
Integers: Unit test; Integers on the number line. Learn. Intro to negative numbers (Opens a modal) Number opposites (Opens a modal) Negative symbol as opposite (Opens a modal) ... Compare rational numbers using a number line Get 3 of 4 questions to level up! Quiz 1. Level up on the above skills and collect up to 400 Mastery points Start quiz ...
Important Questions for CBSE Class 6 Maths Chapter 6
Important Questions for Class 6 Chapter 6 - Integers deals with the basic concepts of Integers and the questions given in the segment created by Vedantu will help students prepare for final exams. Students can practice these questions to score good marks. Chapter 6 of Class 6 Maths deals with the number system. Children will also learn addition, subtraction, multiplication and division of ...
7th Class Mathematics Integers Question Bank
View Solution play_arrow. question_answer 32) In a quiz, positive marks were given for correct answers and negative marks for incorrect answers. If Guru's scores in five successive rounds were. 35, −10, −15, 20. and 5, what is his total score at the end? A) 25.
Applications of Integers in Real Life
What are Integers? Integers are a fundamental concept of mathematics representing whole numbers and their opposite versions with negative signs. In other terms, integers are numbers that cannot have a decimal component or fractional part. The set of integers is a collection of positive whole numbers (1, 2, 3, …) and their opposite partners (-1, -2, -3, …) and zero.
PDF THE LARGE INTEGER CASE STUDY
Large Integer Case Study in C++ for AP Computer Science Introduction This document describes the process of producing a solution to a programming problem. It is intended to provide an opportunity for "apprenticeship learning." The narrative is written as instruction from an expert to an apprentice, and study questions represent places where the
Should You Exercise in the Morning or the Evening ...
The case for morning exercise. According to a 2022 study, morning exercise may be especially beneficial for heart health.It may also lead to better sleep.. And when it comes to weight loss, there ...

Case Study Questions for Class 7 Maths Chapter 1 Integers

Maths Class 7 Chapter List

Old Chapter List

Tips for Answering Case Study Questions for Class 7 Maths in Exam

Download CBSE Books

Leave a Reply Cancel reply

Discover more from Gurukul of Excellence

7th Standard CBSE Subjects

Class VI to XII

Latest CBSE 7th Standard CBSE Study Material Updates

What are integers?

Common Core State Standards

How to identify integers

[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)

Integers examples

Example 2: identifying integers

Example 3: integers on a number line

Example 4: integers on a number line

Example 5: integers on a vertical number line

Example 6: integers on a vertical number line

Teaching tips for integers

Easy mistakes to make

Related types of numbers lessons

Practice integers questions

Integers FAQs

The next lessons are

Still stuck?

[FREE] Common Core Practice Tests (Grades 3 to 6)

Privacy Overview

Class 10 Maths Case Study Questions of Chapter 1 Real Numbers

Real Numbers Case Study Questions With Answers

You Might Also Like

NCERT Exemplar Solutions for Class 7 Maths Chapter 1 Integers

Download the PDF of NCERT Exemplar Solutions for Class 7 Maths Chapter 1 Integers

Access Answers to Maths NCERT Exemplar Solutions for Class 7 Chapter 1 Integers

Leave a Comment Cancel reply

Register with BYJU'S & Download Free PDFs

RBSE Result 2024

CBSE Class 10 Maths Case Study Questions for Chapter 2 - Polynomials (Published by CBSE)

Latest Education News

CBSE Important Questions Class 7 Maths Chapter 1

Important Questions Class 7 Mathematics Chapter 1 – Integers

Important Questions Class 7 Mathematics Chapter 1 – With Solutions

= 1 hour Benefits of Solving Important Questions Class 7 Mathematics Chapter 1

Please register to view this section

2. How can the Important Questions Class 7 Mathematics Chapter 1 help students?

CBSE Related Links

Fill this form to view question paper

Unit 4: Integers

Ordering of integers

Adding and subtracting integers

CBSE Class 6 Maths Important Questions Chapter 6 - Integers - Free PDF Download

Download CBSE Class 6 Maths Important Questions 2024-25 PDF

Study Important Questions for Class 6 Maths Chapter 6 Integers

CBSE Class 6 Maths Important Questions Chapter 6 - Free PDF Download

Why Should You Opt for Vedantu?

Important Related Links for CBSE Class 6 Maths

FAQs on Important Questions for CBSE Class 6 Maths Chapter 6 - Integers

Chapter wise Important Questions for CBSE Class 6 Maths

The Site is down as we are performing important server maintenance, during which time the server will be unavailable for approximately 24 hours. Please hold off on any critical actions until we are finished. As always your feedback is appreciated.

7th Class Mathematics Integers Question Bank

Study Package

Question - Integers

Reset Password.

Mobile Number Verified

Applications of Integers in Real Life

What are Integers?

FAQs on Applications of Integers

What is the significance of integers in temperature readings?

How do integers contribute to inventory management?

How are integers used in engineering calculations?

What role do integers play in sports scoring and rankings?

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

When Is the Best Time to Work Out?

The case for morning exercise

The case for afternoon exercise

The case for evening exercise

The case that it may not matter