applied math research

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals

Applied mathematics articles from across Nature Portfolio

Applied mathematics is the application of mathematical techniques to describe real-world systems and solve technologically relevant problems. This can include the mechanics of a moving body, the statistics governing the atoms in a gas or developing more efficient algorithms for computational analysis. These ideas are closely linked with those of theoretical physics.

Latest Research and Reviews

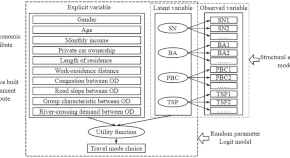
A study on commuters’ public transportation mode choice behavior in river valley-type cities considering terrain spatial perception: evidence from Lanzhou, China

• Mengxing Fan

A multivariate process quality correlation diagnosis method based on grouping technique

• Shujie Cheng

Scalable design of orthogonal DNA barcode libraries

Seqwalk is a scalable method for designing orthogonal DNA barcode libraries, producing one million barcodes in 20 s on a standard laptop.

• Gokul Gowri
• Kuanwei Sheng

The role of promiscuous molecular recognition in the evolution of RNase-based self-incompatibility in plants

Self-incompatibility evolved to avoid self-fertilization among hermaphroditic plants, yet it remains murky how this compatibility recognition evolved. This study constructs a theoretical framework incorporating promiscuous molecular recognition into the evolutionary model of incompatibility.

• Amit Jangid
• Tamar Friedlander

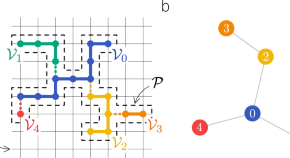
Physical networks as network-of-networks

In analysis of physically embedded complex networks, their nodes are usually considered as localized spheres connected by links, neglecting possible differences of nodes spatial shapes. The authors develop a representation of physical networks that captures arbitrary node shapes to characterize structural and dynamical network properties.

• Márton Pósfai

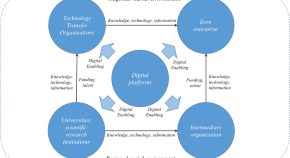
Dynamic analysis and optimal control of knowledge diffusion model in regional innovation ecosystem under digitalization

• Haijun Wang
• Huiyan Zhao

News and Comment

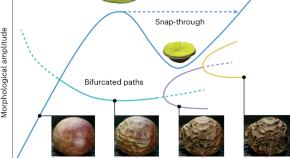
Computational morphology and morphogenesis for empowering soft-matter engineering

Morphing soft matter, which is capable of changing its shape and function in response to stimuli, has wide-ranging applications in robotics, medicine and biology. Recently, computational models have accelerated its development. Here, we highlight advances and challenges in developing computational techniques, and explore the potential applications enabled by such models.

Long ties across networks accelerate the spread of social contagions

Long ties that bridge socially separate regions of networks are critical for the spread of contagions, such as innovations or adoptions of new norms. Contrary to previous thinking, long ties have now been found to accelerate social contagions, even for behaviours that involve the social reinforcement of adoption by network neighbours.

The curious case of the test set AUROC

The area under the receiver operating characteristic curve (AUROC) of the test set is used throughout machine learning (ML) for assessing a model’s performance. However, when concordance is not the only ambition, this gives only a partial insight into performance, masking distribution shifts of model outputs and model instability.

• Michael Roberts
• Carola-Bibiane Schönlieb

The role of computational science in digital twins

Digital twins hold immense promise in accelerating scientific discovery, but the publicity currently outweighs the evidence base of success. We summarize key research opportunities in the computational sciences to enable digital twin technologies, as identified by a recent National Academies of Sciences, Engineering, and Medicine consensus study report.

• Karen Willcox
• Brittany Segundo

Distilling data into code

One of the greatest limitations of deep neural networks is the difficulty of interpreting what they learn from the data. Deep distilling addresses this problem by extracting human-comprehensible and executable code from observations.

• Joseph Bakarji

Why even specialists struggle with black hole proofs

Mathematical proofs of black hole physics are becoming too complex even for specialists.

• Alejandro Penuela Diaz

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Quick links

• Directories

Recent Research

•   LinkedIn
•   Mailing List
•   YouTube
•   News Feed

Research areas

Research in Applied Mathematics has changed dramatically over the past 30 years, with revolutionary developments in traditional areas, together with the emergence of exciting new areas. These changes have been triggered by the development of more powerful computers allowing researchers to address previously intractable problems, and developments in other fields which have led to new mathematical problems.

The department has strong research programs in:   

• Control and Dynamical Systems  (including differential equations)
• Fluid Mechanics
• Mathematical Medicine and Biology
• Mathematical Physics
• Mathematics of Data Science and Machine Learning
• Scientific Computing

Researchers in our department are at the forefront of a number of exciting research areas. Here are some examples:

• Math and Water
• Carbon Nanotubes
• Mathematics and medicine are powerful partners
• Saving the whales with mathematics
• Quantum sounds could reveal the shape of the universe

Using social media to help prevent the spread of disease

The following links give further examples of research conducted in the department:

• Recent PhD Theses in the Applied Mathematics Department
• Recent Master's Theses in the Applied Mathematics Department
• Conference Posters on Research Conducted in the Applied Mathematics Department

• Ph.D. Program
• Minor in Applied Math
• Postdoc Program

Research Areas

• Graduate Field Faculty
• Postdocs and Visitors
• Graduate Students
• Previous Special Talks and Events
• Related Colloquia/Lecture Series
• Alumni Directory
• Alumni Spotlights
• Giving Opportunities
• Get Involved

CAM students draw on resources from a variety of disciplines and departments in developing their particular programs of study. The links on this page provide an introduction to the most common research areas, examples of a couple specific research projects, and a brief guide to the computational resources available to CAM students.

• Applied Mathematics

The students and faculty of the Department of Applied Mathematics are active in five research areas of modern applied mathematics: applied analysis, computational mathematics, discrete mathematics, stochastics (including financial mathematics), and statistics. As part of developing new collaborations, research groups meet in seminars   and reading groups to explore mathematics, where student participation is always welcome.

Undergraduate and graduate students are actively involved in faculty research projects. Graduate students regularly publish papers, present their projects at the department’s research seminars, and attend and present research at regional and international conferences. Undergraduate students have the opportunity to conduct research through course projects as well as independent research, which may take place during the summer. Summer research can be funded by department and College of Computing stipend awards or faculty research grants. Several courses in the department offer independent or group research opportunities.

Elevate Experience

Illinois Tech’s Elevate initiative is a one-of-a-kind program that combines a world-class education with guaranteed experiences and a customized plan that set you on the pathway to an amazing career. By taking part in guaranteed hands-on experiences like research projects, internships, study away, competitions, and short courses, you’ll gain the twenty-first century skills essential for professional success.

Learn more about Elevate and how your team of career, academic, and alumni advisers can help you create your personalized Elevate Your Future plan for academic and career success.

Questions about summer research opportunities?  Email  [email protected] du  or call 312.567.3849.

Summer Undergraduate Research Experience (SURE)

Spend the summer with a computer science or applied mathematics research team in a College of Computing Summer Undergraduate Research Experience (SURE) program. SURE offers insight and learning in some of the hottest topics including big data, machine learning in financial markets, cybersecurity, data analytics, and more.

Research Possibilities with a Math Degree

Mathematics is at the heart of analyzing data in the sciences, tech, finance and banking, and even government. Victoria Beloit (AMAT/STATS/M.S. CDSOR '22) used her mathematics skills during internships in credit modeling and climatology.

Chance Encounter Leads Applied to Award-Winning Research Collaboration

Min-Jhe Lu (Ph.D. AMAT 3rd Year) was presenting his research on solid tumor carcinomas at a poster session when the student presenting next him, Yifan Wang from the University of California, Berkeley, commented on Lu’s work and asked if he would be interested in collaborating with him.

Learn more...

Applied Math

Applied mathematics at the Stanford Department of Mathematics focuses, very broadly, on the areas of scientific computing, stochastic modeling, and applied analysis. 

Some of the more specific areas of interest are, again broadly, signal processing, compressed sensing, imaging, fast numerical algorithms, and mathematical analysis of the physical phenomena in random media. Much of the applied mathematics at Stanford happens outside of the Mathematics Department, at places such as the Statistics Department, the Institute for Computational Mathematics and Engineering, the Center for Turbulence Research, and various other science and engineering departments. The connection between “theoretical applied mathematics” and “engineering applied mathematics” is what keeps the life of the applied mathematics group vibrant.

Emmanuel Candès

Alice Cortinovis

Donald Knuth

George Papanicolaou

Lenya Ryzhik

Tadashi Tokieda

Lexing Ying

• Research & Faculty
• Offices & Services
• Information for:
• Faculty & Staff
• News & Events
• Contact & Visit
• Open Positions
• Message from the Chair
• What is Applied Mathematics?
• Quick Facts
• Undergraduate Study
• Bachelor of Science Degree
• Curriculum & Requirements
• Dual Degrees
• Combined BS/MS Program
• Special Programs
• Student Organizations
• Graduate Study
• Master's Degree
• Typical PhD Sequence
• Information Events
• First-Year Graduate Workshop
• All Department Courses
• Affiliated Centers & Institutes
• Research Areas
• Asymptotic Analysis
• Biological Systems
• Complex Systems
• Diffusive Processes
• Earth Sciences
• Fluid Dynamics
• Materials Science
• Mathematical Biology
• Scientific Computing
• Social Systems
• Wave Propagation
• Stellar Astrophysics
• Core Faculty
• Affiliated Faculty
• Emeritus Faculty
• Advisory Board
• Graduate Students
• Visiting Faculty & Postdocs
• Undergraduate Alumni
• News Archive
• Department & Student Events
• Colloquia & Seminars
• Past Colloquia
• Recorded Talks
• Edward L. Reiss Memorial Lectures
• The Stephen H. Davis Symposium
• Current Students
• Career Resources
• Forms & Documents
• Student Handbooks
• Computing Resources
• Working Offline
• Working Remotely
• Travel and Purchase Reimbursements
• Student Groups
• Northwestern Engineering

The applied mathematics faculty is involved in research that utilizes and invents a variety of mathematical methods associated with asymptotic analysis, bifurcation theory, graph theory, numerical analysis, optimal control, ordinary and partial differential equations, probability and statistics, singular perturbations, stability theory, and stochastic processess.

These methods are employed in the investigation of problems arising in biomechanics, fluid mechanics, geophysics, interfacial phenomena, molecular biology, neuroscience, solid mechanics, statistical mechanics, transport theory, and wave phenomena, to name a few.

Collaboration

Strong interdisciplinary research is a hallmark of the Department of Engineering Sciences and Applied Mathematics at Northwestern.

The educational component of research is held in high regard, with considerable emphasis placed on the mentoring relationship between faculty members , undergraduates , and graduate students .

Browse our areas of research

Learn about our affiliated centers and institutes

Meet our award-winning faculty

More in this section

• Engineering Home
• ESAM Department

Related Links

• Research at McCormick
• Meet our Faculty
• Northwestern Research Overview

Contact Info

Department of Engineering Sciences and Applied Mathematics McCormick School of Engineering and Applied Science 2145 Sheridan Road, Room M426 Evanston, IL 60208 Phone: 847-491-3345 Fax: 847-491-2178 Email Department Department Linkedin

Department of Mathematics

College of science, main navigation.

The Mathematics Department has world class researchers in a broad spectrum of pure and applied mathematics. Faculty research and research groups provide faculty, graduate and undergraduate students with excellent opportunities for collaboration. Each week seminars, colloquia and other events contribute to the research environment. Research Training Grants (RTG) fund programs, projects and activities for undergraduates, graduate students and postdoctoral scholars.

FACULTY/UNDERGRADUATE RESEARCH

• Faculty Research Specialties
• Faculty Distinctions
• Undergraduate Research

RESEARCH AND RESOURCES

• Algebra Geometry/Topology RTG
• Applied Math RTG
• Research Groups
• Research Resources

News & Highlights

Friday  

Summer 2024 First Half Last Day to Reverse CR/NC Option

Tuesday 10am - 4pm

Summer Mathematics Program for High School Students begins

Wednesday  

Holiday: Juneteenth

Thursday  

Summer 2024 First Half Classes End

Summer 2024 full-term last day to withdraw from classes, university of utah stem safety day.

Alumni House - Eccles (ALUMNI)

View All Events

Applied Mathematics

Academic & research opportunities.

• Undergraduate Program

Academic & Research Opportunities

Academic opportunities in apma.

• Senior Seminars - The Division usually offers at least two senior seminars with varying topics each year (193X and 194X series, such as APMA 1941D). Please check Courses@Brown for current information on the senior seminars being offered.
• Independent Study  - Independent studies (APMA 1970) offer the opportunity to study specific topics or areas that are not represented in our course offerings. These are scheduled with individual sponsoring faculty members, who develop a syllabus and forms of assessment with the student and advise them over the course of the semester. Your concentration advisor can help with identifying potential faculty sponsors if you need help or advice.
• Honors - Each of the APMA-related concentrations allow exceptional students to pursue honors. Honors requirements and guidelines can be found on the Honors page.
• Directed Reading Program - The Directed Reading Program (DRP) is a one-on-one mathematics mentoring program that allows undergraduates to work on semester-long independent reading projects under the guidance of graduate students. The first DRP was founded by two graduate students at the University of Chicago in 2003 and has now spread to over a dozen institutions across the United States. Visit the Directed Reading Program page for more information.

Research Opportunities at Brown and Beyond

• Research with APMA Faculty - Many of our faculty are interested in working with undergraduates during the summer. If you would like to participate in these opportunities, please contact individual faculty (ideally in late fall) to inquire about who would be interested in working with you on a research project. Your concentration advisor can help with identifying potential faculty sponsors.
• Research with non-APMA Faculty - You may also search for opportunities outside of applied math, including biostatistics, computer science, economics, engineering, CLPS, neuroscience, CCMB, biology, etc. There are a lot of labs outside of applied math that could really use people with good math/computing skills. In fact, there tends to be a lot more opportunities for undergrad math/computer research outside of applied math than inside of it. The College's page on Undergraduate Research and Teaching Awards (UTRAs) contains a list of faculty-offered opportunities for the upcoming summer.
• Summer@ICERM - the Summer@ICERM program is an eight-week residential program designed for a select group of 18-22 undergraduate scholars. Every year, faculty organizers develop a variety of topical research projects that are interdisciplinary in nature. They begin the program with brief introductory talks about each project. Throughout the eight-week program, students work on their assigned projects in groups of two-to-four, mentored by faculty advisors and teaching assistants. Students meet daily, give regular talks about their findings, attend mini-courses and guest talks, and participate in professional development seminars. Visit the Summer@ICERM page for more details on upcoming programming.
• REUs - Many universities across the US offer REUs (Research Experiences for Undergraduates) during the summer. The National Science Foundation  and the  American Mathematical Society  maintain lists of REUs that are updated regularly.

Brown provides support for summer research through SPRINT awards .

Internships

Many companies and national labs offer internship opportunities for undergraduate students: please visit SIAM's list of internship and job opportunities .

Brown also runs the Summer Research Early Identification Program (SR-EIP), which finds internships for rising sophomores, juniors, and seniors who plan to pursue a Ph.D. in the biomedical and physical sciences, engineering, social sciences, or humanities. Sponsored by the Leadership Alliance, a consortium of 31 institutions of higher education, SR-EIP allows students to work for eight to ten weeks under the guidance of a faculty or research mentor at a participating Alliance institution.

Applied Mathematics

Faculty and students interested in the applications of mathematics are an integral part of the department of mathematics; there is no formal separation between pure and applied mathematics, and the department takes pride in the many ways in which they enrich each other. we also benefit tremendously from close collaborations with faculty and students in other departments at uc berkeley as well as scientists at  lawrence berkeley national laboratory  and visitors to the  mathematical sciences research institute.

The Department regularly offers courses in ordinary and partial differential equations and their numerical solution, discrete applied mathematics, the methods of mathematical physics, mathematical biology, the mathematical aspects of fluid and solid mechanics, approximation theory, scientific computing, numerical linear algebra, and mathematical aspects of computer science. Courses in probability theory, stochastic processes, data analysis and bioinformatics are offered by the Department of Statistics, while courses in combinatorial and convex optimization are offered by the Department of Industrial Engineering and Operations Research. Our students are encouraged to take courses of mathematical interest in these and many other departments. Topics explored intensively by our faculty and students in recent years include scientific computation and the mathematical aspects of quantum theory, computational genomics, image processing and medical imaging, inverse problems, combinatorial optimization, control, robotics, shape optimization, turbulence, hurricanes, microchip failure, MEMS, biodemography, population genetics, phylogenetics, and computational approaches to historical linguistics. Within the department we also have a  Laboratory for Mathematical and Computational Biology .

Chair:   Per-Olof Persson

Applied Mathematics Faculty, Courses, Dissertations

Senate faculty, graduate students, visiting faculty, meet our faculty, mina aganagic, david aldous, robert m. anderson, sunčica čanić, jennifer chayes, alexandre j. chorin, paul concus, james w. demmel, l. craig evans, steven n. evans, f. alberto grünbaum, venkatesan guruswami, ole h. hald, william m. kahan, richard karp, michael j. klass, hendrik w. lenstra, jr., lin lin (林霖), michael j. lindsey, c. keith miller, john c. neu, beresford n. parlett.

• 1 of 2 Grid: People (Current page)
• 2 of 2 Grid: People
• next › Grid: People
• last » Grid: People

Emory College of Arts and Sciences Department of Mathematics

Research areas, algebra and number theory, analysis & differential geometry, computational and data enabled science, discrete mathematics & theoretical computer science, imaging informatics.

• Mission Statement
• All Faculty
• Tenured and Tenure Track Faculty
• Courtesy Appointments
• Instructional Faculty
• Postdoctoral Researchers
• Emeritus Faculty
• Graduate Students
• In Memoriam
• Undergraduate
• Textbook Listing
• Student Organizations
• Actuarial Studies
• Research Interests

Research Groups

• Research Training Groups
• UT Portugal CoLab
• Online Videos
• Administration
• Business Forms
• Computer Facilities
• Quick Links
• Recent Ph. D. Alumni with Placement
• Ph. D. Alumni 1883 to Present
• Search Alumni Database
• Support UT Math

The department has internationally recognized research groups in a number of overlapping areas.

Click on the topics below to see a list of our senior faculty with research interests in that area.

• Applied Math
• Dynamical Systems
• Groups and Dynamics
• Mathematical Physics
• Number Theory
• Numerical Analysis
• Partial Differential Equations

Department of Mathematics The University of Texas at Austin 2515 Speedway, PMA 8.100 Austin, TX 78712

Quick Links for UT Math

• Employment Opportunities
• Graduate Students
• Undergraduate Program FAQ’s
• Why Major in Mathematics, Applied Mathematics and Statistics
• Bachelor and Minor Requirements
• Transfer Credit Policy
• Tutoring Schedule
• Mathematics (MATH) Courses
• Statistics (STAT) Courses
• Math Tutoring Center
• Math Proficiency Exams
• Frequently Asked Questions
• Financial Aid
• Masters and PhD Requirements
• Integrated Graduate Studies Program
• Graduate Courses
• Mathematics Graduate Student Association
• News and Events
• Department of MAMS Newsletter
• Upcoming Colloquia
• Past Colloquia
• Upcoming Seminars
• Past Seminars
• DataFest 2024
• DataFest 2023
• DataFest 2020
• DataFest 2019
• DataFest 2018
• DataFest 2017
• DataFest FAQ
• DataFest Testimonials
• Past Sponsors
• The annual Elizabeth S. Meckes Memorial Lecture
• Past Student Presentations
• Research Areas
• Publications
• Presentations
• Undergraduate Student Resources
• Graduate Student Resources
• Faculty Resources

Shopping cart

College of Arts and Sciences

Department of mathematics, applied mathematics, and statistics, the department of mathematics, applied mathematics, and statistics conduct research in the following areas:.

Algebra is the mathematics of operations like addition and    multiplication of numbers, or composition and convolution of functions. Traditional objects of study in algebra include groups,  rings, fields, and vector spaces, but any well-defined system of operations and equations can be subjected to algebraic manipulations  and arguments. For example, one can study logic (via the  connectives  “ and,” “or,” “implies,” and negation “not”) or differential equations  (by algebraically defining a derivative and asking it to satisfy  product and chain rules) in a purely algebraic fashion. Of  particular  interest  in the department is category theory, in which the rules for  composition of functions (the existence of identities and  associativity) are abstracted to give a flexible system for studying  problems in many areas of mathematics including traditional algebra, algebraic topology, or algebraic geometry.  

Nick Gurski

Eva Belmont

Analysis and Applied Analysis

Julia Dobsrosotskaya

Mary Ann Horn

Mark Meckes

Stanislaw Szarek

Elisabeth Werner

Anuj Abhishek

Bayesian Statistics

Bayesian statistics is a field of statistics which relies on the Bayesian interpretation of probability where probability expresses a degree of belief in an unknown quantity. The degree of belief is often based on prior knowledge, such as the result of previous experiments or personal belief, and can be updated after observing new data. The updated belief is mathematically expressed through the posterior distribution and Bayesian inferences are typically based on this. While the elegance of the Bayesian paradigm is undeniable, it has been regarded as a minor area in statistics until the late 20th century, mainly due to the difficulty of the posterior computation. With the development of high computational technology, however, it became one of the most rapidly growing fields in modern statistics.  

Jenny Brynjarsdottir

Anirban Mondal

Patricia Williamson

Continuum and Fluid Mechanics

Continuum mechanics describe how a composite material or structure, rather than discrete particles, responds to applied forces. Mathematical models formulated using continuum mechanics are typically applied to systems with length scales ranging from a micron (cellular structures) to large (e.g. geophysical, planetary) scales. The equations of continuum mechanics involve conservation laws (of mass, energy, momentum et al) and maps from  undeformed  to deformed configurations. Continuum mechanics can be used to describe the deformation of elastic bodies, fluid motion, and more complex systems with micro-structure as well as fluid-structure interaction problems. Faculty interests include continuum modeling applied to physical, chemical, biological systems and numerical methods for simulating geophysical turbulence, transport and chemistry, cellular motility, and fluid-structure interaction models.  

David Gurarie

Wanda Strychalski

Longhua Zhao

Convex and Differential Geometry

Joel Langer

David Singer

Dynamical Systems

Dynamical system theory is the study of processes that evolve over time. This evolution can be deterministic or stochastic discrete or continuous. Deterministic evolution means that all future states of the process are uniquely determined by its current state, stochastic evolution allows random transitions among system’s states. This concept encompasses a broad range of systems, models and applications in physics, chemistry, biology, engineering, life and social Sciences, and more.  

In general, a dynamical system involves a state space and a rule, the generator of the system, that expresses how a choice of a current state determines its future states, system’s trajectory or  called orbit Typical questions deal with structure and patterns of solutions,  They include, sensitivity to initial state and/or other inputs (model parameters, external/driving sources et al); local and global dynamic patterns; parameter space analysis and qualitative  changes that go under the name “bifurcation theory” , problems of control and optimization (can a dynamical system be brought to a desired state by external driving, what are efficient or optimal ways to accomplish it).  Different concepts, methods and tools are employed in the study of dynamical systems from foundational mathematical tool, to numeric simulations, experiment, data analysis.  

The faculty’s research interests cover a wide range of topics, including dynamical systems based modeling of biological systems ranging from networks of nerve cells to schooling fish, infectious diseases (individual and community level), chemistry and physiology .  

Michael Hurley

Peter Thomas

Imaging and Inverse Problems

In inverse problems, the goal is to estimate unknown parameters from noisy observations of quantities that a related to the unknowns through a mathematical model. A characteristic feature of the inverse problems is their ill- posedness :  the problem may have no solution, the solution may not be unique, and small errors in the data may propagate to huge errors in the estimated quantity. Inverse problems research addresses these problems in a systematic manner, either by appropriate regularization of the problem, or by using statistical methods recasting the problem as a question of inference. Inverse problems arise often in imaging or in context where the unknown of interest can be represent as an image, and many techniques developed for imaging science are closely related to those in inverse problems. However, the challenges in imaging problems have their specific nature, making imaging science an active research area of its own.   

F rom pictures taken by smart phones to x-rays  doctors  use for diagnosis, images become an important part of our life. Imaging science addresses various problems related to images:  image formation, image processing,  image  analysis. Image formation focuses on obtaining high quality images from indirect information such as hardware measurements. It is usually solved from an inverse problem perspective. Image processing refers to removing flaws such as blur, noise,  scratch  from images for better visualization or analysis. Automatic extraction of features of interest from images is one example of   image  analysis.  Imaging research uses tools from a variety of mathematical and statistical  subdisciplines  such as  variational  analysis,   partial  differential equations, optimization,  Bayesian statistics and more.  

Daniela Calvetti

Julia Dobrosotskaya

Weihong Guo

Steven Izen

Erkki Somersalo

Life Sciences and Biomedical Research

Modeling and understanding living systems in quantitative terms is the new frontier in applied mathematics, characterized by the extreme complexity of the object of interest. In life sciences the analytic approach of dividing a system into well-understood simple units is often only a first step, as life itself is an emergent phenomenon based on a complex interplay of different simultaneous and interacting processes. For this reason, mathematical research in life sciences requires new ideas, and meaningful research is often the fruit of clos e collaboration with experts in  biology  and  medical sciences.  

The faculty’s research interests cover a wide range of topics, including complex adaptive biological systems, perinatal development of respiratory rhythms, signal transduction pathways (for gradient sensing chemotaxis and pattern formation), the development of the nervous system: modeling cellular level metabolism; connection of metabolic processes with medical imaging; infectious disease modeling (immunology, ecology of transmission, disease control,  ployparasitism , drug resistance and genotyping techniques for monitoring drug-resistant mutants).  

Methodologically, the mathematical research in biosciences is very wide, requiring skills from various areas such as differential equations, probability and statistics, dynamical systems and scientific computing.  

Mathematical Physics

Numerical analysis and scientific computing.

Numerical analysis is the study of the properties of algorithms for the computational solution of mathematical problems, including convergence rates and numerical stability when implemented in finite precision arithmetic. Scientific computing is concerned with the details of efficient and stable implementation of numerical schemes. Numerical analysis and scientific computing are very important in the design and implementation of algorithms for the simulation physical systems, in particular when analytic solutions are not available.   

Probability and Stochastic Processes

Spatial statistics.

Spatial Statistics is a branch of Statistics where the spatial location of the phenomena under study is of intrinsic interest or where spatial location is an integral part of a statistical model for the phenomena. Spatial data can be geo-statistical, aerial, or point patterns. Geo-statistical data arise when observations are made at fixed or pre-determined locations, and location coordinates are recorded as well as the phenomena of interest. For data where observations that are close tend to be more alike than  observations that are further away, it is often useful to model dependence between observations as a function of the distance between them. Areal data arise when data are available on an aggregated level (sometimes for privacy reasons), such as zip-code of county level data. For such data it is often reasonable to assume that neighboring areas are more alike than areas that do not share a boundary.  Point pattern data arise when the observed locations of a phenomenon is of main interest.  

Uncertainty Quantification

Uncertainty quantification (UQ) aims at providing systematic methods to characterize and quantify the uncertainties   arising  when using complex models to analyze data. Uncertainties may arise from noise in the data, unknown or uncertain parameters, incompleteness of the model, discrepancies between the model and the reality, or from the turbulent or chaotic behavior of the system. Since UQ relies on analytic methods, probability theory, statistics, and numerical analysis, it bridges a wide range of different fields of statistics, mathematics and its applications. The UQ expertise in the department comprises Bayesian statistics, probability, chaotic and turbulent systems, and numerical analysis.   

Sakshi Arya

Abdul-Nasah Soale

View Publications

• Student intranet /
• Staff intranet

Department of Mathematics

Research projects

Find a postgraduate research project in your area of interest by exploring the research projects we offer in the Department of Mathematics.

Programme directors

If you are not sure which supervisors are the best match for your interests, contact the postgraduate programme directors:

• Sean Holman  (applied mathematics and numerical analysis)
• Olatunji Johnson (probability, statistics and financial mathematics)
• Marcus Tressl  (pure mathematics)

You can also get in touch with the postgraduate research leads through our  research themes  page.

Opportunities within the department are advertised by supervisors as either:

• Specific, well-defined individual projects : which you can apply for directly after contacting the named supervisor
• Research fields with suggestions for possible projects : where you can discuss a range of potential projects available in a specific area with the supervisor.

Choosing the right PhD project depends on matching your interests to those of your supervisor.

Our  research themes  page gives an overview of the research taking place in the Department and contacts for each area. Potential supervisors can also be contacted directly through the academic staff list . They will be able to tell you more about the type of projects they offer and/or you can suggest a research project yourself.

Please note that all PhD projects are eligible for funding via a variety of scholarships from the Department, the Faculty of Science and Engineering and/or the University; see our  funding page  for further details. All scholarships are awarded competitively by the relevant postgraduate funding committees.

Academics regularly apply for research grants and may therefore be able to offer funding for specific projects without requiring approval from these committees. Some specific funded projects are listed below, but many of our students instead arrive at a project through discussion with potential supervisors.

Specific, individual projects

Browse all of our specific, individual projects listed on FindAPhD:

Research field projects

In addition to individual projects listed on FindAPhD, we are also looking for postgraduate researchers for potential projects within a number of other research fields.

Browse these fields below and get in contact with the named supervisor to find out more.

Applied Mathematics and Numerical Analysis

Adaptive finite element approximation strategies.

Theme: Numerical analytics and scientific computing | Supervisor: David Silvester

I would be happy to supervise projects in the general area of efficient solution of elliptic and parabolic partial differential equations using finite elements. PhD projects would involve a mix of theoretical analysis and the development of proof-of-concept software written in MATLAB or Python. The design of robust and efficient error estimators is an open problem in computational fluid dynamics. Recent papers on this topic include Alex Bespalov, Leonardo Rocchi and David Silvester, T--IFISS: a toolbox for adaptive FEM computation, Computers and Mathematics with Applications, 81: 373--390, 2021. https://doi.org/10.1016/j.camwa.2020.03.005 Arbaz Khan, Catherine Powell and David Silvester, Robust a posteriori error estimators for mixed approximation of nearly incompressible elasticity, International Journal for Numerical Methods in Engineering, 119: 1--20, 2019. https://doi.org/10.1002/nme.6040 John Pearson, Jen Pestana and David Silvester, Refined saddle-point preconditioners for discretized Stokes problems, Numerische Mathematik, 138: 331--363, 2018. https://doi.org/10.1007/s00211-017-0908-4

Bayesian and machine learning methods for statistical inverse problems

Theme: Statistics, inverse problems, uncertainty quantification and data science | Supervisor: Simon Cotter

A range of projects are available on the topic of statistical inverse problems, in particular with application to problems in applied mathematics. Our aim is to construct new methods for the solution of statistical inverse problems, and to apply them to real problems from science, biology, engineering, etc. These may be more traditional Markov chain Monte Carlo (MCMC) methods, Piecewise-deterministic Markov processes (PDMPs), gradient flows (e.g. Stein gradient descent), or entirely new families of methods. Where possible the methods will be flexible and widely applicable, which will enable us to also apply them to real problems and datasets. Some recent applications involve cell matching in biology, and characterisation of physical properties of materials, for example the thermal properties of a manmade material, or the Young's modulus of a tendon or artery. The project will require the candidate to be proficient in a modern programming language (e.g. Python).

Complex deformations of biological soft tissues

Theme: Continuum mechanics | Supervisor: Tom Shearer , Andrew Hazel

The answers to many open questions in medicine depend on understanding the mechanical behaviour of biological soft tissues. For example, which tendon is most appropriate to replace the anterior cruciate ligament in reconstruction surgery? what causes the onset of aneurysms in the aorta? and how does the mechanics of the bladder wall affect afferent nerve firing? Current work at The University of Manchester seeks to understand how the microstructure of a biological soft tissue affects its macroscale mechanical properties. We have previously focused on developing non-linear elastic models of tendons and are now seeking to incorporate more complex physics such as viscoelasticity, and to consider other biological soft tissues, using our “in house” finite element software oomph-lib. The work will require development and implementation of novel constitutive equations as well as formulation of non-standard problems in solid mechanics. The project is likely to appeal to students with an interest in continuum mechanics, computational mathematics and interdisciplinary science.

Efficient solution for PDEs with random data

I would be happy to supervise projects in the general area of efficient solution of elliptic and parabolic partial differential equations with random data. PhD projects would involve a mix of theoretical analysis and the development of proof-of-concept software written in MATLAB or Python. The design of robust and efficient error estimators for stochastic collocation approximation methods is an active area of research within the uncertainty quantification community. Recent papers on this topic include Alex Bespalov, David Silvester and Feng Xu. Error estimation and adaptivity for stochastic collocation finite elements Part I: single-level approximation, SIAM J. Scientific Computing, 44: A3393--A3412, 2022. {\tt https://doi.org/10.1137/21M1446745} Arbaz Khan, Alex Bespalov, Catherine Powell and David Silvester, Robust a posteriori error estimators for stochastic Galerkin formulations of parameter-dependent linear elasticity equations, Mathematics of Computation, 90: 613--636, 2021. https://doi.org/10.1090/mcom/3572 Jens Lang, Rob Scheichl and David Silvester, A fully adaptive multilevel collocation strategy for solving elliptic PDEs with random data, J. Computational Physics, 419, 109692, 2020. https://doi.org/10.1016/j.jcp.2020.109692

Fluid flow, interfaces, bifurcations, continuation and control

Theme: Continuum mechanics | Supervisor: Alice Thompson

My research interests are in fluid dynamical systems with deformable interfaces, for example bubbles in very viscous fluid, or inkjet printed droplets. The deformability of the interface can lead to complex nonlinear behaviour, and often occurs in configurations where full numerical simulation of the three-dimensional system is computationally impossible. This computational difficulty leaves an important role for mathematical modelling, in using asymptotic or physical arguments to devise simpler models which can help us understand underlying physical mechanisms, make testable predictions, and to directly access control problems for active (feedback) or passive control mechanisms. Most recently I am interested in how different modelling methodologies affect whether models are robust in the forward or control problems. I am also interested in how control-based continuation methods can be used in continuum mechanics to directly observe unstable dynamical behaviour in experiments, even without access to a physical model. This research combines fluid dynamics, mathematical modelling, computational methods (e.g. with the finite-element library oomph-lib), experiments conducted in the Manchester Centre for Nonlinear Dynamics, control theory and nonlinear dynamics. I would not expect any student to have experience in all these areas and there is scope to shape any project to your interests.

Granular materials in industry and nature

Theme: Continuum mechanics | Supervisor: Chris Johnson

The field of granular materials encompasses a vast range of materials and processes, from the formation of sand dunes on a beach and snow avalanches in the mountains, to the roasting of coffee beans and the manufacture of pharmaceutical tablets. The science of granular materials is still in its relative infancy, and many aspects of flowing grains cannot yet be predicted with a continuum rheology. Insights into granular material behaviour come from a range of methods, and my research therefore combines mathematical modelling, computation, and laboratory experiments, undertaken at the Manchester Centre for Nonlinear Dynamics laboratories. Some example areas of work suitable for a PhD project include: - Debris flows and their deposits Debris flows are rapid avalanches of rock and water, which are triggered on mountainsides when erodible sediment is destabilised by heavy rainfall or snowmelt. These flows cause loss of life and infrastructure across the world, but many of the physical mechanisms underlying their motion remain poorly understood. Because it is difficult to predict where and when a debris flow will occur, scientific observations are rarely made on an active flow. More often, all we have to work from is the deposit left behind, and some detective work is required to infer properties of the flow (such as its speed and composition) from this deposit. This project focuses on developing theoretical models for debris flows that predict both a debris flow and its deposit -- in particular the way in which grains of different sizes are distributed throughout the deposit. The aim is then to invert such models, allowing observations of a deposit, when combined with model simulations, to constrain what must have happened during the flow. - Modelling polydispersity Much of the current theory of granular materials has been formulated with the assumption of a single type of grain. When grains vary in size, shape or density, it opens up the possibility that such grains with different properties separate from one another, a process called segregation. A fundamental question in this area is predicting the rate of segregation from a description of a granular material, such as the distribution of particle sizes. Thanks to some recent developments, we are approaching a point where this can be done for very simple granular materials (in particular those containing only two, similar, sizes sizes of grain), but many practical granular materials are much more complex. For example, it is common for mixtures of grains used in industry to vary in diameter by a factor of more than 100, and the complex segregation that can occur in these mixtures is poorly understood. This project will make measurements of the segregation behaviour of such mixtures and use these to put together a theoretical framework for describing segregation in complex granular materials.

Machine learning with partial differential equations

Theme: Statistics, inverse problems, uncertainty quantification and data science | Supervisor: Jonas Latz

Machine learning and artificial intelligence play a major part in our everyday life. Self-driving cars, automatic diagnoses from medical images, face recognition, or fraud detection, all profit especially from the universal applicability of deep neural networks. Their use in safety critical applications, however, is problematic: no interpretability, missing mathematical guarantees for network or learning process, and no quantification of the uncertainties in the neural network output. Recently, models that are based on partial differential equations (PDEs) have gained popularity in machine learning. In a classification problem, for instance, a PDE is constructed whose solution correctly classifies the training data and gives a suitable model to classify unlabelled feature vectors. In practice, feature vectors tend to be high dimensional and the natural space on which they live tends to have a complicated geometry. Therefore, partial differential equations on graphs are particularly suitable and popular. The resulting models are interpretable, mathematically well-understood, and uncertainty quantification is possible. In addition, they can be employed in a semi-supervised fashion, making them highly applicable in small data settings. I am interested in various mathematical, statistical, and computational aspects of PDE-based machine learning. Many of those aspects translate easily into PhD projects; examples are - Efficient algorithms for p-Laplacian-based regression and clustering - Bayesian identification of graphs from flow data - PDEs on random graphs - Deeply learned PDEs in data science Depending on the project, applicants should be familiar with at least one of: (a) numerical analysis and numerical linear algebra; (b) probability theory and statistics; (c) machine learning and deep learning.

Mathematical modelling of nano-reinforced foams

Theme: Maths: Continuum mechanics | Supervisor: William Parnell

Complex materials are important in almost every aspect of our lives, whether that is using a cell phone, insulating a house, ensuring that transport is environmentally friendly or that packaging is sustainable. An important facet of this is to ensure that materials are optimal in some sense. This could be an optimal stiffness for a given weight or an optimal conductivity for a given stiffness. Foams are an important class of material that are lightweight but also have the potential for unprecedented mechanical properties by adding nano-reinforcements (graphene flakes or carbon nanotubes) into the background or matrix material from which the foam is fabricated. When coupled with experimentation such as imaging and mechanical testing, mathematical models allow us to understand how to improve the design and properties of such foams. A number of projects are available in this broad area and interested parties can discuss these by making contact with the supervisor.

Multiscale modelling of structure-function relationships in biological tissues

Theme: Maths: Mathematics in the life sciences | Supervisor: Oliver Jensen

Biological tissues have an intrinsically multiscale structure. They contain components that range in size from individual molecules to the scale of whole organs. The organisation of individual components of a tissue, which often has a stochastic component, is intimately connected to biological function. Examples include exchange organs such as the lung and placenta, and developing multicellular tissues where mechanical forces play an crucial role in growth. To describe such materials mathematically, new multiscale approaches are needed that retain essential elements of tissue organisation at small scales, while providing tractable descriptions of function at larger scales. Projects are available in these areas that offer opportunities to collaborate with life scientists while developing original mathematical models relating tissue structure to its biological function.

Pure Mathematics and Logic

Algebraic differential equations and model theory.

Theme: Algebra, logic and number theory | Supervisor: Omar Leon sanchez

Differential rings and algebraic differential equations have been a crucial source of examples for model theory (more specifically, geometric stability theory), and have had numerous application in number theory, algebraic geometry, and combinatorics (to name a few). In this project we propose to establish and analyse deep structural results on the model theory of (partial) differential fields. In particular, in the setup of differentially large fields. There are interesting questions around inverse problems in differential Galois theory that can be address as part of this project. On the other hand, there are (still open) questions related to the different notions of rank in differentially closed fields; for instance: are there infinite dimensional types that are also strongly minimal? This is somewhat related to the understanding of regular types, which interestingly are quite far from being fully classified. A weak version of Zilber's dichotomy have been established for such types, but is the full dichotomy true?

Algebraic invariants of abelian varieties

Theme: Algebra, logic and number theory | Supervisor: Martin Orr

Project: Algebraic invariants of abelian varieties Abelian varieties are higher-dimensional generalisations of elliptic curves, objects of algebraic geometry which are of great interest to number theorists. There are various open questions about how properties of abelian varieties vary across a families of abelian varieties. The aim of this project is to study the variation of algebraic objects attached to abelian varieties, such as endomorphism algebras, Mumford-Tate groups or isogenies. These algebraic objects control much of the behaviour of the abelian variety. We aim to bound their complexity in terms of the equations defining the abelian variety. Potential specific projects include: (1) Constructing "relations between periods" from the Mumford-Tate group. This involves concrete calculations of polynomials, similar in style to classical invariant theory of reductive groups. (2) Understanding the interactions between isogenies and polarisations of abelian varieties. This involves calculations with fundamental sets for arithmetic group actions, generalising reduction theory for quadratic forms. A key tool is the theory of reductive groups and their finite-dimensional representations (roots and weights).

Algebraic Model Theory of Fields with Operators

Model theory is a branch of Mathematical Logic that has had several remarkable applications with other areas of mathematics, such as Combinatorics, Algebraic Geometry, Number Theory, Arithmetic Geometry, Complex and Real Analysis, Functional Analysis, and Algebra (to name a few). Some of these applications have come from the study of model-theoretic properties of fields equipped with a family of operators. For instance, this includes differential/difference fields. In this project, we look at the model theory of fields equipped with general classes of operators and also within certain natural classes of arithmetic fields (such as large fields). Several foundational questions remain open around what is called "model-companion", "elimination of imaginaries", and the "trichotomy", this is a small sample of the problems that can be tackled.

Homeomorphism groups from a geometric viewpoint

Theme: Algebra, logic and number theory | Supervisor: Richard Webb

A powerful technique for studying groups is to use their actions by isometries on metric spaces. Properties of the action can be translated into algebraic properties of the group, and vice versa. This is called geometric group theory, and has played a key role in different fields of mathematics e.g. random groups, mapping class groups of surfaces, fundamental groups of 3-manifolds, the Cremona group. In this project we will study the homeomorphisms of a surface by using geometric group theoretic techniques recently introduced by Bowden, Hensel, and myself. This is a new research initiative at the frontier between dynamics, topology, and geometric group theory, and there are many questions waiting to be explored using these tools. These range from new questions on the relationship between the topology/dynamics of homeomorphisms and their action on metric spaces, to older questions regarding the algebraic structure of the homeomorphism group.

The Existential Closedness problem for exponential and automorphic functions

Theme: Maths: Algebra, logic and number theory | Supervisor: Vahagn Aslanyan

The Existential Closedness problem asks when systems of equations involving field operations and certain classical functions of a complex variable, such as exponential and modular functions, have solutions in the complex numbers. There are conjectures predicting when such systems should have solutions. The general philosophy is that when a system is not "overdetermined" (e.g. more equations than variables) then it should have a solution. The notion of an overdetermined system of equations is related to Schanuel's conjecture and its analogues and is captured by some purely algebraic conditions. The aim of this project is to make progress towards the Existential Closedness conjectures (EC for short) for exponential and automorphic functions (and the derivatives of automorphic functions). These include the usual complex exponential function, as well as the exponential functions of semi-abelian varieties, and modular functions such as the j-invariant. Significant progress has been made towards EC in recent years, but the full conjectures are open. There are many special cases which are within reach and could be tackled as part of a PhD project. Methods used to approach EC come from complex analysis and geometry, differential algebra, model theory (including o-minimality), tropical geometry. Potential specific projects are: (1) proving EC in low dimensions (e.g. for 2 or 3 variables), (2) proving EC for certain relations defined in terms of the function under consideration, e.g. establishing new EC results for "blurred" exponential and/or modular functions, (3) proving EC under additional geometric assumptions on the system of equations, (4) using EC to study the model-theoretic properties of exponential and automorphic functions.

Statistics and Probability

Distributional approximation by stein's method theme.

Theme: Probability, financial mathematics and actuarial science | Supervisor: Robert Gaunt

Stein's method is a powerful (and elegant) technique for deriving bounds on the distance between two probability distributions with respect to a probability metric. Such bounds are of interest, for example, in statistical inference when samples sizes are small; indeed, obtaining bounds on the rate of convergence of the central limit theorem was one of the most important problems in probability theory in the first half of the 20th century. The method is based on differential or difference equations that in a sense characterise the limit distribution and coupling techniques that allow one to derive approximations whilst retaining the probabilistic intuition. There is an active area of research concerning the development of Stein's method as a probabilistic tool and its application in areas as diverse as random graph theory, statistical mechanics and queuing theory. There is an excellent survey of Stein's method (see below) and, given a strong background in probability, the basic method can be learnt quite quickly, so it would be possible for the interested student to make progress on new problems relatively shortly into their PhD. Possible directions for research (although not limited) include: extend Stein's method to new limit distributions; generalisations of the central limit theorem; investigate `faster than would be expected' convergence rates and establish necessary and sufficient conditions under which they occur; applications of Stein's method to problems from, for example, statistical inference. Literature: Ross, N. Fundamentals of Stein's method. Probability Surveys 8 (2011), pp. 210-293.

Long-term behaviour of Markov Chains

Theme: Probability, financial mathematics and actuarial science | Supervisor: Malwina Luczak

Several projects are available, studying idealised Markovian models of epidemic, population and network processes. The emphasis will mostly be on theoretical aspects of the models, involving advanced probability theory. For instance, there are a number of stochastic models of epidemics where the course of the epidemic is known to follow the solution of a differential equation over short time intervals, but where little or nothing has been proved about the long-term behaviour of the stochastic process. Techniques have been developed for studying such problems, and a project might involve adapting these methods to new settings. Depending on the preference of the candidate, a project might involve a substantial computational component, gaining insights into the behaviour of a model, via simulations, ahead of proving rigorous theoretical results.

Mathematical Epidemiology

Theme: Mathematics in the life sciences | Supervisor: Thomas House

Understanding patterns of disease at the population level - Epidemiology - is inherently a quantitative problem, and increasingly involves sophisticated research-level mathematics and statistics in both infectious and chronic diseases. The details of which diseases and mathematics offer the best PhD directions are likely to vary over time, but this broad area is available for PhD research.

Spatial and temporal modelling for crime

Theme: Maths: Statistics, inverse problems, uncertainty quantification and data science | Supervisor: Ines Henriques-Cadby , Olatunji Johnson

A range of projects are available on the topic of statistical spatial and temporal modelling for crime. These projects will focus on developing novel methods for modelling crime related events in space and time, and applying these to real world datasets, mostly within the UK, but with the possibility to use international datasets. Some examples of recent applications include spatio-temporal modelling of drug overdoses and related crime. These projects will aim to use statistical spatio-temporalpoint processes methods, Bayesian methods, and machine learning methods. The project will require the candidate to be proficient in a modern programming language (e.g., R or Python). Applicants should have achieved a first-class degree in Statistics or Mathematics, with a significant component of Statistics, and be proficient in a statistical programming language (e.g., R, Python, Stata, S). We strongly recommend that you contact the supervisor(s) for this project before you apply. Please send your CV and a brief cover letter to [email protected] before you apply. At Manchester we offer a range of scholarships, studentships and awards at university, faculty and department level, to support both UK and overseas postgraduate researchers. For more information, visit our funding page or search our funding database for specific scholarships, studentships and awards you may be eligible for.

Applied Mathematics

Applied Mathematics at Harvard School of Engineering is an interdisciplinary field that focuses on the creation and imaginative use of mathematical concepts to pose and solve problems over the entire gamut of the physical and biomedical sciences and engineering, and increasingly, the social sciences and humanities.

Working individually and as part of teams collaborating across the University and beyond, faculty and students in Applied Mathematics seek to quantitatively describe, predict, design and control phenomena in a range of fields. This involves the study of relations between models and observations, while examining the mathematical foundations and limitations of these models and techniques.

Research and educational activities have particularly close links to Harvard's efforts in  Mathematics ,  Economics ,  Computer Science , and  Statistics . 

Applied Math Programs

Undergraduate

Bachelor of Arts (AB)

Bachelor of Arts (AB) / Master of Science (SM)

• Secondary Field

Applied Mathematics Leadership

In applied mathematics.

• First-Year Exploration
• Areas of Application
• AM & Economics
• How to Declare
• Who are my Advisors?
• Senior Thesis
• Research for Course Credit (AM 91R & AM 99R)
• AB/SM Information
• Peer Concentration Advisors (PCA) Program
• Student Organizations
• How to Apply
• PhD Timeline
• PhD Model Program (Course Guidelines)
• Oral Qualifying Examination
• Committee Meetings
• Committee on Higher Degrees
• Research Interest Comparison
• Collaborations
• Cross-Harvard Engagement
• Clubs & Organizations
• Centers & Initiatives
• Alumni Stories

Research Areas

• Active Matter
• Applied Algebra and Geometry
• Computational Neuroscience
• Computational Science and Engineering
• Control Theory and Stochastic Systems
• Data Science
• Economics and Computation
• Fluid Mechanics
• Machine Learning
• Modeling Physical/Biological Phenomena and Systems
• Numerical Analysis
• Science and Engineering for ClimateTech
• Theory of Computation

Featured Stories

2024 Commencement photos

Images from the 373rd Harvard Commencement on Thursday, May 23

Academics , Applied Computation , Applied Mathematics , Applied Physics , Bioengineering , Computer Science , Environmental Science & Engineering , Events , Materials Science & Mechanical Engineering , Robotics

Ph.D. student Monteiro Paes named Apple Scholar in AI/ML

Monteiro Paes studies fairness and arbitrariness in machine learning models

AI / Machine Learning , Applied Mathematics , Awards , Graduate Student Profile

Rhodes Scholars want to improve life around the world

SEAS students Morales, Chang ready for Oxford

Academics , Applied Mathematics , Awards , Computer Science

Unfortunately we don't fully support your browser. If you have the option to, please upgrade to a newer version or use Mozilla Firefox , Microsoft Edge , Google Chrome , or Safari 14 or newer. If you are unable to, and need support, please send us your feedback .

We'd appreciate your feedback. Tell us what you think! opens in new tab/window

CRediT author statement

CRediT (Contributor Roles Taxonomy) was introduced with the intention of recognizing individual author contributions, reducing authorship disputes and facilitating collaboration. The idea came about following a 2012 collaborative workshop led by Harvard University and the Wellcome Trust, with input from researchers, the International Committee of Medical Journal Editors (ICMJE) and publishers, including Elsevier, represented by Cell Press.

CRediT offers authors the opportunity to share an accurate and detailed description of their diverse contributions to the published work.

The corresponding author is responsible for ensuring that the descriptions are accurate and agreed by all authors

The role(s) of all authors should be listed, using the relevant above categories

Authors may have contributed in multiple roles

CRediT in no way changes the journal’s criteria to qualify for authorship

CRediT statements should be provided during the submission process and will appear above the acknowledgment section of the published paper as shown further below.

*Reproduced from Brand et al. (2015), Learned Publishing 28(2), with permission of the authors.

Sample CRediT author statement

Zhang San:  Conceptualization, Methodology, Software  Priya Singh. : Data curation, Writing- Original draft preparation.  Wang Wu : Visualization, Investigation.  Jan Jansen :  Supervision. : Ajay Kumar : Software, Validation.:  Sun Qi:  Writing- Reviewing and Editing,

Read more about CRediT  here opens in new tab/window  or check out this  article from  Authors' Updat e:  CRediT where credit's due .

• Browse All Articles
• Newsletter Sign-Up

Marketing →

• 07 May 2024
• Cold Call Podcast

Lessons in Business Innovation from Legendary Restaurant elBulli

Ferran Adrià, chef at legendary Barcelona-based restaurant elBulli, was facing two related decisions. First, he and his team must continue to develop new and different dishes for elBulli to guarantee a continuous stream of innovation, the cornerstone of the restaurant's success. But they also need to focus on growing the restaurant’s business. Can the team balance both objectives? Professor Michael I. Norton discusses the connections between creativity, emotions, rituals, and innovation – and how they can be applied to other domains – in the case, “elBulli: The Taste of Innovation,” and his new book, The Ritual Effect.

• 29 Feb 2024

Beyond Goals: David Beckham's Playbook for Mobilizing Star Talent

Reach soccer's pinnacle. Become a global brand. Buy a team. Sign Lionel Messi. David Beckham makes success look as easy as his epic free kicks. But leveraging world-class talent takes discipline and deft decision-making, as case studies by Anita Elberse reveal. What could other businesses learn from his ascent?

• 17 Jan 2024

Psychological Pricing Tactics to Fight the Inflation Blues

Inflation has slowed from the epic rates of 2021 and 2022, but many consumers still feel pinched. What will it take to encourage them to spend? Thoughtful pricing strategies that empower customers as they make purchasing decisions, says research by Elie Ofek.

• 05 Dec 2023

What Founders Get Wrong about Sales and Marketing

Which sales candidate is a startup’s ideal first hire? What marketing channels are best to invest in? How aggressively should an executive team align sales with customer success? Senior Lecturer Mark Roberge discusses how early-stage founders, sales leaders, and marketing executives can address these challenges as they grow their ventures in the case, “Entrepreneurial Sales and Marketing Vignettes.”

Tommy Hilfiger’s Adaptive Clothing Line: Making Fashion Inclusive

In 2017, Tommy Hilfiger launched its adaptive fashion line to provide fashion apparel that aims to make dressing easier. By 2020, it was still a relatively unknown line in the U.S. and the Tommy Hilfiger team was continuing to learn more about how to serve these new customers. Should the team make adaptive clothing available beyond the U.S., or is a global expansion premature? Assistant Professor Elizabeth Keenan discusses the opportunities and challenges that accompanied the introduction of a new product line that effectively serves an entirely new customer while simultaneously starting a movement to provide fashion for all in the case, “Tommy Hilfiger Adaptive: Fashion for All.”

• Research & Ideas

Are Virtual Tours Still Worth It in Real Estate? Evidence from 75,000 Home Sales

Many real estate listings still feature videos and interactive tools that simulate the experience of walking through properties. But do they help homes sell faster? Research by Isamar Troncoso probes the post-pandemic value of virtual home tours.

• 17 Oct 2023

With Subscription Fatigue Setting In, Companies Need to Think Hard About Fees

Subscriptions are available for everything from dental floss to dog toys, but are consumers tiring of monthly fees? Elie Ofek says that subscription revenue can provide stability, but companies need to tread carefully or risk alienating customers.

• 29 Aug 2023

As Social Networks Get More Competitive, Which Ones Will Survive?

In early 2023, TikTok reached close to 1 billion users globally, placing it fourth behind the leading social networks: Facebook, YouTube, and Instagram. Meanwhile, competition in the market for videos had intensified. Can all four networks continue to attract audiences and creators? Felix Oberholzer-Gee discusses competition and imitation among social networks in his case “Hey, Insta & YouTube, Are You Watching TikTok?”

• 26 Jun 2023

Want to Leave a Lasting Impression on Customers? Don't Forget the (Proverbial) Fireworks

Some of the most successful customer experiences end with a bang. Julian De Freitas provides three tips to help businesses invest in the kind of memorable moments that will keep customers coming back.

• 31 May 2023

With Predictive Analytics, Companies Can Tap the Ultimate Opportunity: Customers’ Routines

Armed with more data than ever, many companies know what key customers need. But how many know exactly when they need it? An analysis of 2,000 ridesharing commuters by Eva Ascarza and colleagues shows what's possible for companies that can anticipate a customer's routine.

• 30 May 2023

Can AI Predict Whether Shoppers Would Pick Crest Over Colgate?

Is it the end of customer surveys? Definitely not, but research by Ayelet Israeli sheds light on the potential for generative AI to improve market research. But first, businesses will need to learn to harness the technology.

• 24 Apr 2023

What Does It Take to Build as Much Buzz as Booze? Inside the Epic Challenge of Cannabis-Infused Drinks

The market for cannabis products has exploded as more states legalize marijuana. But the path to success is rife with complexity as a case study about the beverage company Cann by Ayelet Israeli illustrates.

• 07 Apr 2023

When Celebrity ‘Crypto-Influencers’ Rake in Cash, Investors Lose Big

Kim Kardashian, Lindsay Lohan, and other entertainers have been accused of promoting crypto products on social media without disclosing conflicts. Research by Joseph Pacelli shows what can happen to eager investors who follow them.

• 10 Feb 2023

COVID-19 Lessons: Social Media Can Nudge More People to Get Vaccinated

Social networks have been criticized for spreading COVID-19 misinformation, but the platforms have also helped public health agencies spread the word on vaccines, says research by Michael Luca and colleagues. What does this mean for the next pandemic?

• 02 Feb 2023

Why We Still Need Twitter: How Social Media Holds Companies Accountable

Remember the viral video of the United passenger being removed from a plane? An analysis of Twitter activity and corporate misconduct by Jonas Heese and Joseph Pacelli reveals the power of social media to uncover questionable situations at companies.

• 06 Dec 2022

Latest Isn’t Always Greatest: Why Product Updates Capture Consumers

Consumers can't pass up a product update—even if there's no improvement. Research by Leslie John, Michael Norton, and Ximena Garcia-Rada illustrates the powerful allure of change. Are we really that naïve?

• 29 Nov 2022

How Much More Would Holiday Shoppers Pay to Wear Something Rare?

Economic worries will make pricing strategy even more critical this holiday season. Research by Chiara Farronato reveals the value that hip consumers see in hard-to-find products. Are companies simply making too many goods?

• 26 Oct 2022

How Paid Promos Take the Shine Off YouTube Stars (and Tips for Better Influencer Marketing)

Influencers aspire to turn "likes" into dollars through brand sponsorships, but these deals can erode their reputations, says research by Shunyuan Zhang. Marketers should seek out authentic voices on YouTube, not necessarily those with the most followers.

• 25 Oct 2022

Is Baseball Ready to Compete for the Next Generation of Fans?

With its slower pace and limited on-field action, major league baseball trails football in the US, basketball, and European soccer in revenue and popularity. Stephen Greyser discusses the state of "America's pastime."

• 18 Oct 2022

When Bias Creeps into AI, Managers Can Stop It by Asking the Right Questions

Even when companies actively try to prevent it, bias can sway algorithms and skew decision-making. Ayelet Israeli and Eva Ascarza offer a new approach to make artificial intelligence more accurate.