null hypothesis and alternative hypothesis ppt

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Module 9: Hypothesis Testing With One Sample

Null and alternative hypotheses, learning outcomes.

• Describe hypothesis testing in general and in practice

The actual test begins by considering two  hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make adecision. There are two options for a  decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in  H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

H a : p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40

• H 0 : p = 0.40
• H a : p > 0.40

Concept Review

In a  hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

H 0 and H a are contradictory.

• OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License

Privacy Policy

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base
• Null and Alternative Hypotheses | Definitions & Examples

Null and Alternative Hypotheses | Definitions & Examples

Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

• Null hypothesis (H 0 ): There’s no effect in the population .
• Alternative hypothesis (H A ): There’s an effect in the population.

The effect is usually the effect of the independent variable on the dependent variable .

Table of contents

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.

Null and alternative hypotheses are similar in some ways:

• They’re both answers to the research question
• They both make claims about the population
• They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

• Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
• Alternative hypothesis (H A ): Independent variable affects dependent variable .

Test-specific

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 6 May 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/

Is this article helpful?

Shaun Turney

Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.

Hypothesis Testing: Null Hypothesis and Alternative Hypothesis

Join over 2 million students who advanced their careers with 365 Data Science. Learn from instructors who have worked at Meta, Spotify, Google, IKEA, Netflix, and Coca-Cola and master Python, SQL, Excel, machine learning, data analysis, AI fundamentals, and more.

Figuring out exactly what the null hypothesis and the alternative hypotheses are is not a walk in the park. Hypothesis testing is based on the knowledge that you can acquire by going over what we have previously covered about statistics in our blog.

So, if you don’t want to have a hard time keeping up, make sure you have read all the tutorials about confidence intervals , distributions , z-tables and t-tables .

We've also made a video on null hypothesis vs alternative hypothesis - you can watch it below or just scroll down if you prefer reading.

Confidence intervals provide us with an estimation of where the parameters are located. You can obtain them with our confidence interval calculator and learn more about them in the related article.

However, when we are making a decision, we need a yes or no answer. The correct approach, in this case, is to use a test .

Here we will start learning about one of the fundamental tasks in statistics - hypothesis testing !

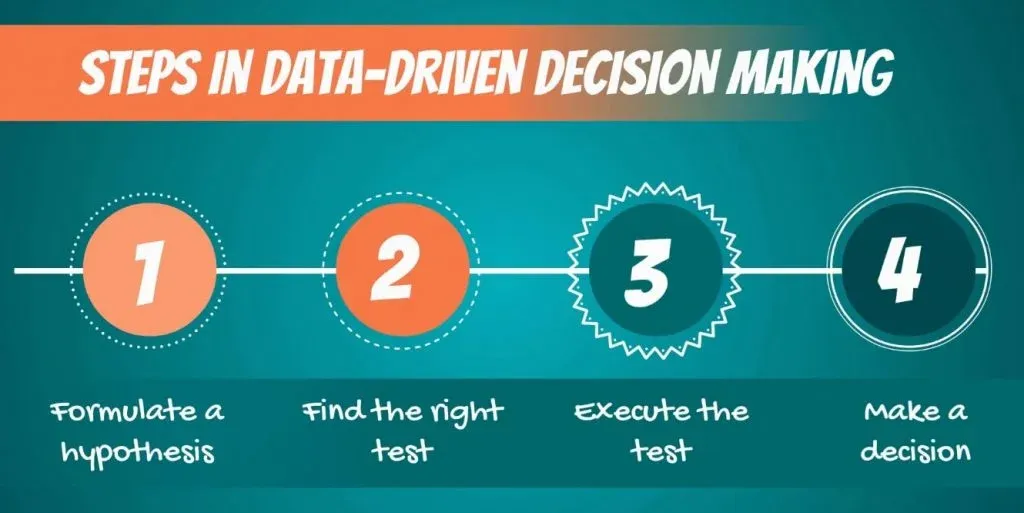
The Hypothesis Testing Process

  First off, let’s talk about data-driven decision-making. It consists of the following steps:

• First, we must formulate a hypothesis .
• After doing that, we have to find the right test for our hypothesis .
• Then, we execute the test.
• Finally, we make a decision based on the result.

Let’s start from the beginning.

What is a Hypothesis?

Though there are many ways to define it, the most intuitive must be:

“A hypothesis is an idea that can be tested.”

This is not the formal definition, but it explains the point very well.

So, if we say that apples in New York are expensive, this is an idea or a statement. However, it is not testable, until we have something to compare it with.

For instance, if we define expensive as: any price higher than $1.75 dollars per pound, then it immediately becomes a hypothesis .

What Cannot Be a Hypothesis?

An example may be: would the USA do better or worse under a Clinton administration, compared to a Trump administration? Statistically speaking, this is an idea , but there is no data to test it. Therefore, it cannot be a hypothesis of a statistical test.

Actually, it is more likely to be a topic of another discipline.

Conversely, in statistics, we may compare different US presidencies that have already been completed. For example, the Obama administration and the Bush administration, as we have data on both.

A Two-Sided Test

Alright, let’s get out of politics and get into hypotheses . Here’s a simple topic that CAN be tested.

According to Glassdoor (the popular salary information website), the mean data scientist salary in the US is 113,000 dollars.

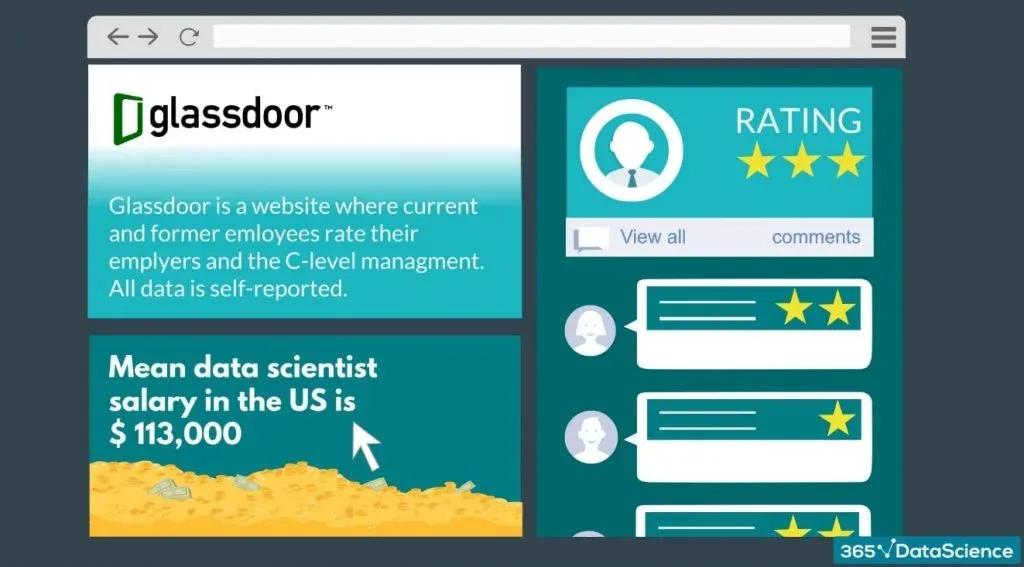
So, we want to test if their estimate is correct.

The Null and Alternative Hypotheses

There are two hypotheses that are made: the null hypothesis , denoted H 0 , and the alternative hypothesis , denoted H 1 or H A .

The null hypothesis is the one to be tested and the alternative is everything else. In our example:

The null hypothesis would be: The mean data scientist salary is 113,000 dollars.

While the alternative : The mean data scientist salary is not 113,000 dollars.

Author's note: If you're interested in a data scientist career, check out our articles Data Scientist Career Path , 5 Business Basics for Data Scientists , Data Science Interview Questions , and 15 Data Science Consulting Companies Hiring Now .

An Example of a One-Sided Test

You can also form one-sided or one-tailed tests.

Say your friend, Paul, told you that he thinks data scientists earn more than 125,000 dollars per year. You doubt him, so you design a test to see who’s right.

The null hypothesis of this test would be: The mean data scientist salary is more than 125,000 dollars.

The alternative will cover everything else, thus: The mean data scientist salary is less than or equal to 125,000 dollars.

Important: The outcomes of tests refer to the population parameter rather than the sample statistic! So, the result that we get is for the population.

Important: Another crucial consideration is that, generally, the researcher is trying to reject the null hypothesis . Think about the null hypothesis as the status quo and the alternative as the change or innovation that challenges that status quo. In our example, Paul was representing the status quo, which we were challenging.

Let’s go over it once more. In statistics, the null hypothesis is the statement we are trying to reject. Therefore, the null hypothesis is the present state of affairs, while the alternative is our personal opinion.

Why Hypothesis Testing Works

Right now, you may be feeling a little puzzled. This is normal because this whole concept is counter-intuitive at the beginning. However, there is an extremely easy way to continue your journey of exploring it. By diving into the linked tutorial, you will find out why hypothesis testing actually works.

Interested in learning more? You can take your skills from good to great with our statistics course!

Try statistics course for free

Next Tutorial:  Hypothesis Testing: Significance Level and Rejection Region

World-Class

Data Science

Learn with instructors from:

Iliya Valchanov

Co-founder of 365 Data Science

Iliya is a finance graduate with a strong quantitative background who chose the exciting path of a startup entrepreneur. He demonstrated a formidable affinity for numbers during his childhood, winning more than 90 national and international awards and competitions through the years. Iliya started teaching at university, helping other students learn statistics and econometrics. Inspired by his first happy students, he co-founded 365 Data Science to continue spreading knowledge. He authored several of the program’s online courses in mathematics, statistics, machine learning, and deep learning.

We Think you'll also like

Statistics Tutorials

False Positive vs. False Negative: Type I and Type II Errors in Statistical Hypothesis Testing

Hypothesis Testing with Z-Test: Significance Level and Rejection Region

Calculating and Using Covariance and Linear Correlation Coefficient

Examples of Numerical and Categorical Variables

Chapter 9 Hypothesis Tests

Mar 16, 2019

580 likes | 989 Views

Chapter 9 Hypothesis Tests. Developing Null and Alternative Hypotheses. Type I and Type II Errors. Population Mean: σ Known. Population Mean: σ Unknown. Population Proportion. 9.1 Developing Null and Alternative Hypotheses. Hypothesis testing can be used to determine whether

Share Presentation

• tailed test
• hypothesis testing
• tailed hypothesis testing
• chapter 9 hypothesis tests

Presentation Transcript

Chapter 9 Hypothesis Tests • Developing Null and Alternative Hypotheses • Type I and Type II Errors • Population Mean: σ Known • Population Mean: σ Unknown • Population Proportion

9.1 Developing Null and Alternative Hypotheses • Hypothesis testing can be used to determine whether • a statement about the value of a population parameter • should or should not be rejected. • The null hypothesis, denoted by H0 , is a tentative • assumption about a population parameter. • The alternative hypothesis, denoted by Ha, is the • opposite of what is stated in the null hypothesis. • The alternative hypothesis is what the test is attempting to establish.

Developing Null and Alternative Hypotheses • Testing Research Hypotheses • The research hypothesis should be expressed as • the alternative hypothesis. • The conclusion that the research hypothesis is true • comes from sample data that contradict the null • hypothesis.

Developing Null and Alternative Hypotheses • Testing the Validity of a Claim • Manufacturers’ claims are usually given the benefit • of the doubt and stated as the null hypothesis. • The conclusion that the claim is false comes from • sample data that contradict the null hypothesis.

Developing Null and Alternative Hypotheses • Testing in Decision-Making Situations • A decision maker might have to choose between • two courses of action, one associated with the null • hypothesis and another associated with the • alternative hypothesis. • Example: Accepting a shipment of goods from a • supplier or returning the shipment of goods to the • supplier

Summary of Forms for Null and Alternative Hypotheses about a Population Mean • The equality part of the hypotheses always appears in the null hypothesis. • In general, a hypothesis test about the value of a • population mean must take one of the following • three forms (where0is the hypothesized value of • the population mean). One-tailed (upper-tail) Two-tailed One-tailed (lower-tail)

Null and Alternative Hypotheses • Example: Metro EMS A major west coast city provides one of the most comprehensive emergency medical services in the world. Operating in a multiple hospital system with approximately 20 mobile medical units, the service goal is to respond to medical emergencies with a mean time of 12 minutes or less.

Null and Alternative Hypotheses • Example: Metro EMS The director of medical services wants to formulate a hypothesis test that could use a sample of emergency response times to determine whether or not the service goal of 12 minutes or less is being achieved.

Null and Alternative Hypotheses The emergency service is meeting the response goal; no follow-up action is necessary. H0: The emergency service is not meeting the response goal; appropriate follow-up action is necessary. Ha: where:= mean response time for the population of medical emergency requests

9.2 Type I Error • Because hypothesis tests are based on sample data, • we must allow for the possibility of errors. • A Type I error is rejecting H0 when it is true. • The probability of making a Type I error when the null hypothesis is true as an equality is called the level of significance. • Applications of hypothesis testing that only control the Type I error are often called significance tests.

Type II Error • A Type II error is accepting H0 when it is false. • It is difficult to control for the probability of making a Type II error. • Statisticians avoid the risk of making a Type II error by using “do not reject H0” and not “accept H0”.

Type I and Type II Errors Population Condition H0 True (m< 12) H0 False (m> 12) Conclusion AcceptH0 (Concludem< 12) Correct Decision Type II Error Type I Error Correct Decision RejectH0 (Concludem> 12)

9.3 p-Value Approach to One-Tailed Hypothesis Testing • The p-value is the probability, computed using the test statistic, that measures the support (or lack of support) provided by the sample for the null hypothesis. • If the p-value is less than or equal to the level of significance, the value of the test statistic is in the rejection region. • Reject H0 if the p-value <.

Lower-Tailed Test About a Population Mean: s Known p-Value <a, so reject H0. • p-Value Approach a= .10 Sampling distribution of p-value 72 z z = -1.46 -za = -1.28 0

Sampling distribution of Upper-Tailed Test About a Population Mean: σKnown p-Value <a, so reject H0. • p-Value Approach a= .04 p-Value 11 z za = 1.75 z = 2.29 0

Critical Value Approach to One-Tailed Hypothesis Testing • The test statistic z has a standard normal probability • distribution. • We can use the standard normal probability • distribution table to find the z-value with an area • of a in the lower (or upper) tail of the distribution. • The value of the test statistic that established the • boundary of the rejection region is called the • critical value for the test. • The rejection rule is: • Lower tail: Reject H0 if z< -z • Upper tail: Reject H0 if z>z

Sampling distribution of Lower-Tailed Test About a Population Mean: σKnown • Critical Value Approach Reject H0 a 1 Do Not Reject H0 z -za = -1.28 0

Sampling distribution of Upper-Tailed Test About a Population Mean: σ Known • Critical Value Approach Reject H0  Do Not Reject H0 z za = 1.645 0

Steps of Hypothesis Testing Step 1. Develop the null and alternative hypotheses. Step 2. Specify the level of significance α. Step 3. Collect the sample data and compute the test statistic. p-Value Approach Step 4. Use the value of the test statistic to compute the p-value. Step 5. Reject H0 if p-value <a.

Steps of Hypothesis Testing Critical Value Approach Step 4. Use the level of significance to determine the critical value and the rejection rule. Step 5. Use the value of the test statistic and the rejection rule to determine whether to reject H0.

One-Tailed Tests About a Population Mean: σKnown • Example: Metro EMS The response times for a random sample of 40 medical emergencies were tabulated. The sample mean is 13.25 minutes. The population standard deviation is believed to be 3.2 minutes. The EMS director wants to perform a hypothesis test, with a .05 level of significance, to determine whether the service goal of 12 minutes or less is being achieved.

One-Tailed Tests About a Population Mean: σ Known • p -Value and Critical Value Approaches 1. Develop the hypotheses. H0: Ha: a = .05 2. Specify the level of significance. 3. Compute the value of the test statistic.

One-Tailed Tests About a Population Mean: σ Known • p –Value Approach 4. Compute the p –value. For z = 2.47, cumulative probability = .9932. p–value = 1 - .9932 = .0068 5. Determine whether to reject H0. Because p–value = .0068<a= .05, we reject H0. We are at least 95% confident that Metro EMS is not meeting the response goal of 12 minutes.

Sampling distribution of One-Tailed Tests About a Population Mean: σ Known • p –Value Approach a = .05 p-value  z za = 1.645 z = 2.47 0

One-Tailed Tests About a Population Mean: σKnown • Critical Value Approach 4. Determine the critical value and rejection rule. For a= .05, z.05 = 1.645 Reject H0 if z> 1.645 5. Determine whether to reject H0. Because 2.47 > 1.645, we reject H0. We are at least 95% confident that Metro EMS is not meeting the response goal of 12 minutes.

p-Value Approach to Two-Tailed Hypothesis Testing • Compute the p-value using the following three steps: 1. Compute the value of the test statistic z. 2. If z is in the upper tail (z > 0), find the area under the standard normal curve to the right of z. If z is in the lower tail (z < 0), find the area under the standard normal curve to the left of z. 3. Double the tail area obtained in step 2 to obtain the p –value. • The rejection rule: Reject H0 if the p-value <.

Critical Value Approach to Two-Tailed Hypothesis Testing • The critical values will occur in both the lower and upper tails of the standard normal curve. • Use the standard normal probability distribution table to find z/2 (the z-value with an area of a/2 in the upper tail of the distribution). • The rejection rule is: • Reject H0 if z< -z/2or z>z/2.

oz. Glow Example: Glow Toothpaste • Two-Tailed Test About a Population Mean: s Known The production line for Glow toothpaste is designed to fill tubes with a mean weight of 6 oz. Periodically, a sample of 30 tubes will be selected in order to check the filling process. Quality assurance procedures call for the continuation of the filling process if the sample results are consistent with the assumption that the mean filling weight for the population of toothpaste tubes is 6 oz.; otherwise the process will be adjusted.

oz. Glow Example: Glow Toothpaste • Two-Tailed Test About a Population Mean: σ Known Assume that a sample of 30 toothpaste tubes provides a sample mean of 6.1 oz. The population standard deviation is believed to be 0.2 oz. Perform a hypothesis test, at the .03 level of significance, to help determine whether the filling process should continue operating or be stopped and corrected.

Glow H0:= 6 Ha: Two-Tailed Tests About a Population Mean: σ Known • p –Value and Critical Value Approaches 1. Determine the hypotheses. a = .03 2. Specify the level of significance. 3. Compute the value of the test statistic.

Glow Two-Tailed Tests About a Population Mean: σ Known • p –Value Approach 4. Compute the p –value. For z = 2.74, cumulative probability = .9969 p–value = 2(1 - .9969) = .0062 5. Determine whether to reject H0. Because p–value = .0062 <a = .03, we reject H0. We are at least 97% confident that the mean filling weight of the toothpaste tubes is not 6 oz.

Glow Two-Tailed Tests About a Population Mean: σ Known • p-Value Approach 1/2 p -value = .0031 1/2 p -value = .0031 a/2 = .015 a/2 = .015 z z = -2.74 0 z = 2.74 -za/2 = -2.17 za/2 = 2.17

Glow Two-Tailed Tests About a Population Mean: σ Known • Critical Value Approach 4. Determine the critical value and rejection rule. For a/2 = .03/2 = .015, z.015 = 2.17 Reject H0 if z< -2.17 or z> 2.17 5. Determine whether to reject H0. Because 2.47 > 2.17, we reject H0. We are at least 97% confident that the mean filling weight of the toothpaste tubes is not 6 oz.

Glow Sampling distribution of Two-Tailed Tests About a Population Mean: σ Known • Critical Value Approach Reject H0 Reject H0 Do Not Reject H0 a/2 = .015 a/2 = .015 z 0 2.17 -2.17

Confidence Interval Approach toTwo-Tailed Tests About a Population Mean • Select a simple random sample from the population and use the value of the sample mean to develop the confidence interval for the population mean μ. (Confidence intervals are covered in Chapter 8.) • If the confidence interval contains the hypothesized • value0, do not reject H0. Otherwise, reject H0.

Glow Confidence Interval Approach toTwo-Tailed Tests About a Population Mean The 97% confidence interval for μis or 6.02076 to 6.17924 Because the hypothesized value for the population mean,0= 6, is not in this interval, the hypothesis-testing conclusion is that the null hypothesis, H0:= 6, can be rejected.

9.4 Tests About a Population Mean:s Unknown • Test Statistic This test statistic has a t distribution with n - 1 degrees of freedom.

Tests About a Population Mean:s Unknown • Rejection Rule: p -Value Approach Reject H0 if p –value<a • Rejection Rule: Critical Value Approach H0: Reject H0 if t< -t H0: Reject H0 if t>t H0: Reject H0 if t< - tor t>t

p -Values and the t Distribution • The format of the t distribution table provided in most • statistics textbooks does not have sufficient detail • to determine the exact p-value for a hypothesis test. • However, we can still use the t distribution table to identify a range for the p-value. • An advantage of computer software packages is that the computer output will provide the p-value for the t distribution.

Example: Highway Patrol • One-Tailed Test About a Population Mean: s Unknown A State Highway Patrol periodically samples vehicle speeds at various locations on a particular roadway. The sample of vehicle speeds is used to test the hypothesis H0:m< 65 The locations where H0 is rejected are deemed the best locations for radar traps.

Example: Highway Patrol • One-Tailed Test About a Population Mean: σ Unknown At Location F, a sample of 64 vehicles shows a mean speed of 66.2 mph with a standard deviation of 4.2 mph. Use α = .05 to test the hypothesis.

One-Tailed Test About a Population Mean:σ Unknown • p –Value and Critical Value Approaches 1. Determine the hypotheses. H0:< 65 Ha:m > 65 a = .05 2. Specify the level of significance. 3. Compute the value of the test statistic.

One-Tailed Test About a Population Mean:σ Unknown • p –Value Approach 4. Compute the p –value. For t = 2.286, the p–value must be less than .025 (for t = 1.998) and greater than .01 (for t = 2.387). .01 < p–value < .025 5. Determine whether to reject H0. Because p–value<a= .05, we reject H0. We are at least 95% confident that the mean speed of vehicles at Location F is greater than 65 mph.

One-Tailed Test About a Population Mean:σ Unknown • Critical Value Approach 4. Determine the critical value and rejection rule. For a = .05 and d.f. = 64 – 1 = 63, t.05 = 1.669 Reject H0 if t> 1.669 5. Determine whether to reject H0. Because 2.286 > 1.669, we reject H0. We are at least 95% confident that the mean speed of vehicles at Location F is greater than 65 mph. Location F is a good candidate for a radar trap.

One-Tailed Test About a Population Mean:σUnknown Reject H0 Do Not Reject H0  t ta = 1.669 0

9.5 A Summary of Forms for Null and Alternative Hypotheses About a Population Proportion • The equality part of the hypotheses always appears in the null hypothesis. • In general, a hypothesis test about the value of a population proportion pmust take one of the following three forms (where p0 is the hypothesized value of the population proportion). One-tailed (lower tail) One-tailed (upper tail) Two-tailed

Tests About a Population Proportion • Test Statistic where: assuming np> 5 and n(1 – p) > 5

Tests About a Population Proportion • Rejection Rule: p –Value Approach Reject H0 if p –value <a • Rejection Rule: Critical Value Approach H0: pp Reject H0 if z>zα H0: pp Reject H0 if z< -z H0: pp Reject H0 if z< -zor z>z

Two-Tailed Test About a Population Proportion • Example: National Safety Council For a Christmas and New Year’s week, the National Safety Council estimated that 500 people would be killed and 25,000 injured on the nation’s roads. The NSC claimed that 50% of the accidents would be caused by drunk driving.

Two-Tailed Test About a Population Proportion • Example: National Safety Council A sample of 120 accidents showed that 67 were caused by drunk driving. Use these data to test the NSC’s claim with a = .05.

• More by User

Chapter 9 Hypothesis Testing

Chapter 9 Hypothesis Testing. 9.1 The Language of Hypothesis Testing. Example: Illustrating Hypothesis Testing.

934 views • 32 slides

Chapter 9 Hypothesis Testing. 9.1 The Language of Hypothesis Testing. Steps in Hypothesis Testing 1. A claim is made. Steps in Hypothesis Testing 1. A claim is made. 2. Evidence (sample data) is collected in order to test the claim. Steps in Hypothesis Testing 1. A claim is made.

674 views • 30 slides

Chapter 9 Hypothesis Testing. Developing Null and Alternative Hypotheses Type I and Type II Errors One-Tailed Tests About a Population Mean: Large-Sample Case Two-Tailed Tests About a Population Mean: Large-Sample Case Tests About a Population Mean: Small-Sample Case

658 views • 43 slides

Chapter 9 Hypothesis Testing. Testing Hypothesis about µ, when the s.t of population is known. THREE WAYS TO STRUCTURE THE HYPOTHESIS TEST:.

526 views • 36 slides

Chapter 9 - Hypothesis Tests

Chapter 9 - Hypothesis Tests. Hypothesis and Test Procedures A statistical test of hypothesis consist of : 1. The Null hypothesis, 2. The Alternative hypothesis, 3. The test statistic and its p -value 4. The rejection region 5. The conclusion. Definition 9.1:

779 views • 38 slides

Hypothesis Tests

Hypothesis Tests. Structure of hypothesis tests 1. choose the appropriate test based on: data characteristics, study objectives parametric or nonparametric two-sided, one-sided t-test, rank-sum test, others… 2. establish the null and alternate hypothesis

369 views • 15 slides

Chapter 9 – Hypothesis Tests concerning One Population Mean

Chapter 9 – Hypothesis Tests concerning One Population Mean. Two different conclusions based on different values. Who picks ? What is ?. The value of is picked by the researcher. Recall: Step 2 : Decide upon a level of significance for the test

304 views • 18 slides

Hypothesis Tests. BUAD820 Chapters 9. Problem #1: Quality improvement and salad dressings.

180 views • 6 slides

Chapter 9 Hypothesis Testing. Developing Null and Alternative Hypotheses. Type I and Type II Errors. Population Mean: s Known. Population Mean: s Unknown. Developing Null and Alternative Hypotheses. Hypothesis testing can be used to determine whether

486 views • 21 slides

Hypothesis Tests. In statistics a hypothesis is a statement that something is true. Selecting the population parameter being tested (mean, proportion, variance, ect.) Using p-values for hypothesis tests Using Critical Regions for hypothesis tests One tailed vs. two tailed tests.

366 views • 16 slides

Hypothesis Tests. In statistics a hypothesis is a statement that something is true. Hypothesis Tests. In statistics a hypothesis is a statement that something is true. For example:

342 views • 18 slides

Hypothesis tests Hypothesis

Hypothesis tests Hypothesis. H 0 : Null-hypothesis is an conjecture which we assume is true until we have too much evidence against it. H 1 : The alternative hypothesis covers the alternative to H 0

543 views • 15 slides

Hypothesis Tests. IEF 217a: Lecture 2.b Fall 2002. Hypothesis Testing. Correct models? Data similar? Use one series to predict another Has something changed in the data? Quality control, portfolio strategies. Outline. Introduction (Basketball) Proportion changes (Political polls)

414 views • 33 slides

Chapter 9 Hypothesis Testing. Introduction to Statistical Tests Testing the Mean µ Testing a Proportion p Tests Involving Paired Differences Testing µ1-µ2 and p1-p2. 9.1 Introduction to Statistical Tests. We can draw inference on a population parameter in two ways: Estimation (Chapter 8)

984 views • 78 slides

Chapter 9 -Hypothesis Testing

Chapter 9 -Hypothesis Testing. Hypothesis testing can be used to determine whether a statement about the value of a population parameter should or should not be rejected. The null hypothesis , denoted by H 0 , is a tentative assumption about a population parameter.

556 views • 40 slides

Hypothesis Tests. 2014/3/3. Purpose of hypothesis test. Hypothesis test is used to determine whether a statement about the value of of a population parameter should or should not be rejected. Ex. P.340 soft drink. Process of hypothesis test.

259 views • 13 slides

Chapter 8 Hypothesis Tests

Chapter 8 Hypothesis Tests. What are Hypothesis Tests ? A set of methods and procedure to s tudy the reliability of claim s about population parameter s. Examples of Hypotheses :. The mean monthly cell phone bill of this city is $42.

458 views • 18 slides

Chapter 9 – Hypothesis Tests concerning One Population Mean. Hypothesis testing is basic to the scientific method and statistical theory gives us a way of conducting tests of scientific hypotheses.

767 views • 67 slides

Hypothesis tests

Hypothesis tests. Hypothesis tests.

334 views • 32 slides

Chapter 9 Hypothesis Testing. Chapter Outline. Developing Null and Alternative Hypothesis Type I and Type II Errors Population Mean: Known Population Mean: Unknown Population Proportion. Hypothesis Testing.

638 views • 46 slides

Chapter 8 Hypothesis Tests. What are Hypothesis Tests ? A set of methods and procedure to s tudy the reliability of claim s about population parameter s. Examples of Hypotheses :. The air quality of San Diego meets federal standards.

213 views • 20 slides

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 10.

• Idea behind hypothesis testing

Examples of null and alternative hypotheses

• Writing null and alternative hypotheses
• P-values and significance tests
• Comparing P-values to different significance levels
• Estimating a P-value from a simulation
• Estimating P-values from simulations
• Using P-values to make conclusions

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Null Hypothesis and Alternative Hypothesis

• Inferential Statistics
• Statistics Tutorials
• Probability & Games
• Descriptive Statistics
• Applications Of Statistics
• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade
• Ph.D., Mathematics, Purdue University
• M.S., Mathematics, Purdue University
• B.A., Mathematics, Physics, and Chemistry, Anderson University

Hypothesis testing involves the careful construction of two statements: the null hypothesis and the alternative hypothesis. These hypotheses can look very similar but are actually different.

How do we know which hypothesis is the null and which one is the alternative? We will see that there are a few ways to tell the difference.

The Null Hypothesis

The null hypothesis reflects that there will be no observed effect in our experiment. In a mathematical formulation of the null hypothesis, there will typically be an equal sign. This hypothesis is denoted by H 0 .

The null hypothesis is what we attempt to find evidence against in our hypothesis test. We hope to obtain a small enough p-value that it is lower than our level of significance alpha and we are justified in rejecting the null hypothesis. If our p-value is greater than alpha, then we fail to reject the null hypothesis.

If the null hypothesis is not rejected, then we must be careful to say what this means. The thinking on this is similar to a legal verdict. Just because a person has been declared "not guilty", it does not mean that he is innocent. In the same way, just because we failed to reject a null hypothesis it does not mean that the statement is true.

For example, we may want to investigate the claim that despite what convention has told us, the mean adult body temperature is not the accepted value of 98.6 degrees Fahrenheit . The null hypothesis for an experiment to investigate this is “The mean adult body temperature for healthy individuals is 98.6 degrees Fahrenheit.” If we fail to reject the null hypothesis, then our working hypothesis remains that the average adult who is healthy has a temperature of 98.6 degrees. We do not prove that this is true.

If we are studying a new treatment, the null hypothesis is that our treatment will not change our subjects in any meaningful way. In other words, the treatment will not produce any effect in our subjects.

The Alternative Hypothesis

The alternative or experimental hypothesis reflects that there will be an observed effect for our experiment. In a mathematical formulation of the alternative hypothesis, there will typically be an inequality, or not equal to symbol. This hypothesis is denoted by either H a or by H 1 .

The alternative hypothesis is what we are attempting to demonstrate in an indirect way by the use of our hypothesis test. If the null hypothesis is rejected, then we accept the alternative hypothesis. If the null hypothesis is not rejected, then we do not accept the alternative hypothesis. Going back to the above example of mean human body temperature, the alternative hypothesis is “The average adult human body temperature is not 98.6 degrees Fahrenheit.”

If we are studying a new treatment, then the alternative hypothesis is that our treatment does, in fact, change our subjects in a meaningful and measurable way.

The following set of negations may help when you are forming your null and alternative hypotheses. Most technical papers rely on just the first formulation, even though you may see some of the others in a statistics textbook.

• Null hypothesis: “ x is equal to y .” Alternative hypothesis “ x is not equal to y .”
• Null hypothesis: “ x is at least y .” Alternative hypothesis “ x is less than y .”
• Null hypothesis: “ x is at most y .” Alternative hypothesis “ x is greater than y .”
• An Example of a Hypothesis Test
• Hypothesis Test for the Difference of Two Population Proportions
• What Is a P-Value?
• How to Conduct a Hypothesis Test
• Hypothesis Test Example
• Chi-Square Goodness of Fit Test
• What Level of Alpha Determines Statistical Significance?
• How to Do Hypothesis Tests With the Z.TEST Function in Excel
• The Difference Between Type I and Type II Errors in Hypothesis Testing
• Type I and Type II Errors in Statistics
• The Runs Test for Random Sequences
• What 'Fail to Reject' Means in a Hypothesis Test
• What Is the Difference Between Alpha and P-Values?
• An Example of Chi-Square Test for a Multinomial Experiment
• Example of a Chi-Square Goodness of Fit Test
• Null Hypothesis Definition and Examples

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.1: Null and Alternative Hypotheses

• Last updated
• Save as PDF
• Page ID 36712

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

\(H_0\): The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.

\(H_a\): The alternative hypothesis: It is a claim about the population that is contradictory to \(H_0\) and what we conclude when we reject \(H_0\). This is usually what the researcher is trying to prove.

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject \(H_0\)" if the sample information favors the alternative hypothesis or "do not reject \(H_0\)" or "decline to reject \(H_0\)" if the sample information is insufficient to reject the null hypothesis.

\(H_{0}\) always has a symbol with an equal in it. \(H_{a}\) never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example \(\PageIndex{1}\)

• \(H_{0}\): No more than 30% of the registered voters in Santa Clara County voted in the primary election. \(p \leq 30\)
• \(H_{a}\): More than 30% of the registered voters in Santa Clara County voted in the primary election. \(p > 30\)

Exercise \(\PageIndex{1}\)

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

• \(H_{0}\): The drug reduces cholesterol by 25%. \(p = 0.25\)
• \(H_{a}\): The drug does not reduce cholesterol by 25%. \(p \neq 0.25\)

Example \(\PageIndex{2}\)

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

• \(H_{0}: \mu = 2.0\)
• \(H_{a}: \mu \neq 2.0\)

Exercise \(\PageIndex{2}\)

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol \((=, \neq, \geq, <, \leq, >)\) for the null and alternative hypotheses.

• \(H_{0}: \mu \_ 66\)
• \(H_{a}: \mu \_ 66\)
• \(H_{0}: \mu = 66\)
• \(H_{a}: \mu \neq 66\)

Example \(\PageIndex{3}\)

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

• \(H_{0}: \mu \geq 5\)
• \(H_{a}: \mu < 5\)

Exercise \(\PageIndex{3}\)

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• \(H_{0}: \mu \_ 45\)
• \(H_{a}: \mu \_ 45\)
• \(H_{0}: \mu \geq 45\)
• \(H_{a}: \mu < 45\)

Example \(\PageIndex{4}\)

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

• \(H_{0}: p \leq 0.066\)
• \(H_{a}: p > 0.066\)

Exercise \(\PageIndex{4}\)

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (\(=, \neq, \geq, <, \leq, >\)) for the null and alternative hypotheses.

• \(H_{0}: p \_ 0.40\)
• \(H_{a}: p \_ 0.40\)
• \(H_{0}: p = 0.40\)
• \(H_{a}: p > 0.40\)

COLLABORATIVE EXERCISE

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:

• Evaluate the null hypothesis , typically denoted with \(H_{0}\). The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality \((=, \leq \text{or} \geq)\)
• Always write the alternative hypothesis , typically denoted with \(H_{a}\) or \(H_{1}\), using less than, greater than, or not equals symbols, i.e., \((\neq, >, \text{or} <)\).
• If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis.
• Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

\(H_{0}\) and \(H_{a}\) are contradictory.

• If \(\alpha \leq p\)-value, then do not reject \(H_{0}\).
• If\(\alpha > p\)-value, then reject \(H_{0}\).

\(\alpha\) is preconceived. Its value is set before the hypothesis test starts. The \(p\)-value is calculated from the data.References

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm .

• Preferences

Null and alternative hypotheses - PowerPoint PPT Presentation

• Null and alternative hypotheses

... test of hypothesis is a procedure, based on data, for deciding between two ... Type I: process on target, but we say it is out of control. ... – PowerPoint PPT presentation

• Errors in decision making
• Strategy for statistical hypothesis testing
• Many decision problems involve making a choice between two possibilities
• Process is in control or not in control
• Defendant is guilty or not guilty
• Drug is effective or not effective
• Food product is safe for consumption or not safe
• 2. Statistical Hypotheses
• A statistical hypothesis is a conjecture about the state of nature of something we are studying.
• A statistical test of hypothesis is a procedure, based on data, for deciding between two statistical hypotheses called the null hypothesis (denoted H0) and the alternative hypothesis (denoted Ha).
• 3. Illustrations
• Suppose a target value for the amount of liquid in a bottle of soft drink is 20 oz. In running a control chart for the mean, we decide between
• H0 the process mean is 20 oz. (on target)
• Ha the process mean is not 20 oz. (off target)
• In a jury trial we decide between
• H0 the defendant is not guilty
• Ha the defendant is guilty
• 4. Two Types of Errors in Hypothesis Testing
• Type I The null hypothesis is true but we say the alternative is true.
• Type II The alternative hypothesis is true but we say the null hypothesis is true.
• H0 process on target, Ha process out of control
• Type I process on target, but we say it is out of control.
• Type II process out of control, but we say it is on target.
• 5. Representation of Errors
• We say this
• H0 is true Ha is true
• H0 is true o.k. Type I
• Ha is true Type II o.k.
• 6. Consequences of Making Errors
• Consequences of making a Type I error are not the same as those of making a Type II error.
• H0 defendant not guilty, Ha defendant guilty
• Jury convicts an innocent person (Type I error).
• Jury frees a guilty person (Type II error).
• Ideally we would like both errors to have a small chance of occurring. If that is not possible we have to decide which error is most important to protect against.
• 7. Strategy in Statistical Hypothesis Testing
• Define the null hypothesis and use the decision procedure so that the chance of a Type I error small, typically 5.
• For instance, in a jury trial we do not want to convict an innocent person, so we require guilt beyond a reasonable doubt.
• In statistical terms we let not guilty be the null hypothesis, and require a small chance of a Type I error.
• A regulatory agency in charge of drug safety would not want an unsafe drug to enter the marketplace even if it meant some safe drug is rejected (error on the side of caution).
• From a statistical point of view, the agency would set the null hypothesis as drug is not safe, and require a small chance of a Type I error. This has the practical effect of requiring strong evidence that the drug is safe before it is approved for use.

PowerShow.com is a leading presentation sharing website. It has millions of presentations already uploaded and available with 1,000s more being uploaded by its users every day. Whatever your area of interest, here you’ll be able to find and view presentations you’ll love and possibly download. And, best of all, it is completely free and easy to use.

You might even have a presentation you’d like to share with others. If so, just upload it to PowerShow.com. We’ll convert it to an HTML5 slideshow that includes all the media types you’ve already added: audio, video, music, pictures, animations and transition effects. Then you can share it with your target audience as well as PowerShow.com’s millions of monthly visitors. And, again, it’s all free.

About the Developers

PowerShow.com is brought to you by  CrystalGraphics , the award-winning developer and market-leading publisher of rich-media enhancement products for presentations. Our product offerings include millions of PowerPoint templates, diagrams, animated 3D characters and more.

• My presentations

Auth with social network:

Download presentation

We think you have liked this presentation. If you wish to download it, please recommend it to your friends in any social system. Share buttons are a little bit lower. Thank you!

Presentation is loading. Please wait.

HYPOTHESES Null hypothesis (H1) Alternative hypothesis (H0)

Published by Noel George Modified over 6 years ago

Similar presentations

Presentation on theme: "HYPOTHESES Null hypothesis (H1) Alternative hypothesis (H0)"— Presentation transcript:

Differentiating between directional and non-directional hypotheses.

Mr. Mason’s Cruel Experiment (or Mason’s version of the scientific method…)

Hypothesis testing Week 10 Lecture 2.

Chapter 9 Hypothesis Testing 9.4 Testing a Hypothesis about a Population Proportion.

A hypothesis is a statement of expected relationship between two or more variables. - Theoretical and empirical justifications. - Testable. - Brief wording.

C82MCP Diploma Statistics School of Psychology University of Nottingham 1 Overview of Lecture Independent and Dependent Variables Between and Within Designs.

Inferences about two proportions Assumptions 1.We have proportions from two simple random samples that are independent (not paired) 2.For both samples,

T-Tests Lecture: Nov. 6, 2002.

© LOUIS COHEN, LAWRENCE MANION & KEITH MORRISON

PLANNING AND DESIGNING A RESEARCH STUDY

Pearson Correlation Example A researcher wants to determine if there is a relationship between the annual number of lost workdays for each plant and the.

Point Biserial Correlation Example

Overview of Statistical Hypothesis Testing: The z-Test

Causal Hypotheses. l Statement of relationship between an independent and dependent variable l Describes a cause and effect l Usually stated in two forms.

User Study Evaluation Human-Computer Interaction.

What we have learnt Independent Variable dependent Variable Extraneous Variables Laboratory Experiments Natural Experiment (Field)

Jeopardy Hypothesis Testing t-test Basics t for Indep. Samples Related Samples t— Didn’t cover— Skip for now Ancient History $100 $200$200 $300 $500 $400.

Hypotheses and operationalisation By Mr Daniel Hansson.

Research Methods. What is Involved in Research? Research Why was it done? What was the research question? How did the psychologist carry out the research?

Hypotheses. What is a hypothesis? A precise and testable statement A prediction about what the outcome of an experiment will be Usually derived from a.

About project

© 2024 SlidePlayer.com Inc. All rights reserved.