completion of assignment dga

Bradley DeRuiter

The ultimate guide to dga theatrical rates.

When your feature or short film production hires crew from the Directors Guild of America, you know your cast and crew are getting top notch expertise. With that level of excellence.comes a lot of terms like, completion of assignment pay, wrap allowance production fees, and other daunting details. So it is not just about the DGA rates alone. Whether you are shooting a feature film or a short film, this article will help guide you through, the information you need to know, when working with the DGA.

If you want to ensure your production goes fast and smooth, use Topsheet , our automated app will ensure all those daunting details are covered. Sign Up Today!

Here is a layout of what you will find in the order of appearance:

DGA Basic Agreement Theatrical Rates Table Directors
DGA Theatrical Director Fringe Rates
DGA Basic Agreement Theatrical Rates Table UPM, AD’s
DGA Basic Agreement Completion of Assignment UPM, AD’s
DGA Basic Agreement UPM, AD’s Fringe Rates
DGA Low Budget Agreement Director Rates Table
DGA Low Budget Agreement Levels 1-3 UPM, AD’s Rates Table
DGA Low Budget Agreement Levels 1-3 UPM, AD’s Other Terms
DGA Low Budget Agreement Level 4 UPM, AD’s Rates Table
DGA Low Budget Agreement Level 4 UPM, AD’s Other Terms
DGA Low Budget Agreement Extended Workdays

Important DGA rates and dates

Latest DGA rates effective July 1st, 2019 and remain in effect until June 30th, 2020. When the subsequent season DGA rates come in we will update our blog.

DGA Basic Agreement Director Rate Table

Basic Agreement is for films with budgets $11 million and over.

Shooting a feature film, Documentary or Short Film? You can always find the latest union rates on our website with our easy Union Rates Search tool .

DGA Rate Card for Film Directors Theatrical Basic Agreement Directors

6th and 7th Days Worked; Holidays Worked

The workweek for Studio locations is 5 days, with the 6th and 7th days off. The workweek for Distant locations is 6 days, with the 7th day off.

Film directors will be paid 1/5 of their weekly salary plus $3,609 for work on a 7th day in a workweek or on New Year’s Day, Presidents’ Day, Good Friday, Memorial Day, Independence Day, Labor Day, Thanksgiving Day, the day after Thanksgiving or Christmas Day. If compensation is less than $3,609 per day, then they are paid 200% of scale.

If required to work a 6th day studio, Directors will be paid 150% of actual pro rata daily salary or an additional 200% of scale, whichever is lower.

Director Fringe Rates for Basic and Low Budget

Pension & Health Employer Contributions:

Pension Plan 7%, Health Plan 10.5%

Pension & Health Ceilings:

Theatrical: Pension ceiling = $200,000; Health ceiling = $400,000

Unit Production Managers & Assistant Directors Minimum Rates

DGA Rate Card for Theatrical Basic Agreement UPM and AD's

Topsheet helps feature films, commercials, and (soon) television so you can submit payroll like never before. Our flat fee is 2% of the gross payroll. Let us help smooth out your production affairs. Talk to us today to set up your project automations

Extended Workday

Rest periods.

The rest period is 9 hours, if the rest period is invaded the employee receives ¼ days pay for every hour invaded.

UPM & AD’S Completion Of Assignment Pay

UPMs, 1st ADs, Key 2nd ADs and 2nd 2nd ADs are entitled to an additional week’s salary upon completion of assignment if employed two or more consecutive weeks or 2 1/2 days salary if employed at least five consecutive days but less than two consecutive weeks. COA pay shall be based on actual (including overscale) salary paid, excluding production fee, extended day, and rest period invasion payments, and shall be computed by totaling all compensation earned (including upgrade salaries) and dividing the total thereof by the number of weeks worked.

No COA is paid for a hiatus of at least one week over Christmas/New Years so long as (1) the Employee receives unworked holiday pay for Christmas Day and New Years Day; (2) the hiatus is a maximum of two consecutive weeks; and (3) if on location, the Employer will provide travel to/from location or will provide per diem and housing if the Employer agrees that Employee remains on location.

UPM and AD’s Employer Contributions Fring Rates

Pension & Health Contributions

Pension Plan 7%, Health Plan 10.5%, Vacation 4%, Holiday Accrual 3.719%

Pension & Health Ceilings

Theatrical: Pension ceiling = $200,000, UPM Health ceiling = $350,000, AD’s Health ceiling = $250,000

Topsheet is serving the entertainment industry from Los Angeles, CA. Our company is born in technology and catered towards entertainment payroll. Our mobile app helps you run and wrap your sets up to 25X faster than traditional payroll processing.

Low Budget Agreement Director Rates Table

DGA Rate Card Theatrical Low Budget Directors

*For Second Unit Directors

Low Budget UPM & AD's Minimum Rates

DGA Rate Card Low Budget Theatrical UPM’s and AD’s

Low Budget Agreement Levels 1 - 3

Low budget levels 1-3 upm, ad’s other terms.

**COA is Completion of Assignment

At Topsheet, we are passionate about serving the entertainment industry. Topsheet provides payroll processing for features, commercials, music, and television. We know you don’t want to spend endless hours on administrative payroll tasks. That is why we developed our innovative and automated app, so you can spend time telling stories while we take care of all the payroll compliance .

Low Budget Agreement Level 4 UPM, AD’s Rate Table

Low budget level 4a $3.75m-5.5m, low budget level 4b $5.5m-8.5m, low budget level 4c $8.5m-11m, low budget agreement level 4 upm, ad’s other terms, all level 4: 6th and 7th days worked; holidays worked.

Workweeks for all Low Budget levels for Directors, UPM’s, AD’s are the same as the Basic Agreement, Studio locations 5 day workweek, Distant locations 6 day workweek.

For studio locations, 5 day workweek, employees working on the 6th day get 150% of their daily salary including any production fee. Daily salary for weekly employees is ⅕ their weekly salary. Employees who work on the 7th day get 200% of their daily salary and production fee, if any.

For distant locations employees working on the 7th get an addition ⅕ of their studio salary and an addition ⅙ of their production fee. Distant weekly salaries equal 7/5 of the studio salary.

For Holidays worked employees get 200% of their daily pay, for holidays not worked employees get paid their daily pay.

Low Budget Agreement Extended Workdays

Employer fringe contributions.

Same as Basic Agreement:

DGA Basic Agreement Theatrical Director’s Fringe Rates

Commercial rate information will be coming soon in a future blog. Topsheet is here to handle all the details of working with a union like the DGA. Whether you are doing a feature film, documentary, short film, commercial or industrial video, we got you covered. We are also here so that you can run your payroll up to 25X faster, eliminating hundreds of hours of grunt work on your weekly payroll, giving you more time to do your thing. So get started now!

Topsheet is an entertainment tech company specializing in production payroll. We service clients from commercials for Fortune 500 to feature films. We are born in technology, built with filmmakers in mind.

Do you need production payroll ?

Hi. We are Topsheet. We are determined to revolutionize production payroll. Our only question is, will it be your production?

Don't foget to share this post

Assignments: why you need to serve a notice of assignment

It's the day of completion; security is taken, assignments are completed and funds move. Everyone breathes a sigh of relief. At this point, no-one wants to create unnecessary paperwork - not even the lawyers! Notices of assignment are, in some circumstances, optional. However, in other transactions they could be crucial to a lender's enforcement strategy. In the article below, we have given you the facts you need to consider when deciding whether or not you need to serve notice of assignment.

What issues are there with serving notice of assignment?

Assignments are useful tools for adding flexibility to banking transactions. They enable the transfer of one party's rights under a contract to a new party (for example, the right to receive an income stream or a debt) and allow security to be taken over intangible assets which might be unsuitable targets for a fixed charge. A lender's security net will often include assignments over contracts (such as insurance or material contracts), intellectual property rights, investments or receivables.

An assignment can be a legal assignment or an equitable assignment. If a legal assignment is required, the assignment must comply with a set of formalities set out in s136 of the Law of Property Act 1925, which include the requirement to give notice to the contract counterparty.

The main difference between legal and equitable assignments (other than the formalities required to create them) is that with a legal assignment, the assignee can usually bring an action against the contract counterparty in its own name following assignment. However, with an equitable assignment, the assignee will usually be required to join in proceedings with the assignor (unless the assignee has been granted specific powers to circumvent that). That may be problematic if the assignor is no longer available or interested in participating.

Why should we serve a notice of assignment?

The legal status of the assignment may affect the credit scoring that can be given to a particular class of assets. It may also affect a lender's ability to effect part of its exit strategy if that strategy requires the lender to be able to deal directly with the contract counterparty.

The case of General Nutrition Investment Company (GNIC) v Holland and Barrett International Ltd and another (H&B) provides an example of an equitable assignee being unable to deal directly with a contract counterparty as a result of a failure to provide a notice of assignment.

The case concerned the assignment of a trade mark licence to GNIC . The other party to the licence agreement was H&B. H&B had not received notice of the assignment. GNIC tried to terminate the licence agreement for breach by serving a notice of termination. H&B disputed the termination. By this point in time the original licensor had been dissolved and so was unable to assist.

At a hearing of preliminary issues, the High Court held that the notices of termination served by GNIC , as an equitable assignee, were invalid, because no notice of the assignment had been given to the licensee. Although only a High Court decision, this follows a Court of Appeal decision in the Warner Bros Records Inc v Rollgreen Ltd case, which was decided in the context of the attempt to exercise an option.

In both cases, an equitable assignee attempted to exercise a contractual right that would change the contractual relationship between the parties (i.e. by terminating the contractual relationship or exercising an option to extend the term of a licence). The judge in GNIC felt that "in each case, the counterparty (the recipient of the relevant notice) is entitled to see that the potential change in his contractual position is brought about by a person who is entitled, and whom he can see to be entitled, to bring about that change".

In a security context, this could hamper the ability of a lender to maximise the value of the secured assets but yet is a constraint that, in most transactions, could be easily avoided.

Why not serve notice?

Sometimes it's just not necessary or desirable. For example:

If security is being taken over a large number of low value receivables or contracts, the time and cost involved in giving notice may be disproportionate to the additional value gained by obtaining a legal rather than an equitable assignment.
If enforcement action were required, the equitable assignee typically has the option to join in the assignor to any proceedings (if it could not be waived by the court) and provision could be made in the assignment deed for the assignor to assist in such situations. Powers of attorney are also typically granted so that a lender can bring an action in the assignor's name.
Enforcement is often not considered to be a significant issue given that the vast majority of assignees will never need to bring claims against the contract counterparty.

Care should however, be taken in all circumstances where the underlying contract contains a ban on assignment, as the contract counterparty would not have to recognise an assignment that is made in contravention of that ban. Furthermore, that contravention in itself may trigger termination and/or other rights in the assigned contract, that could affect the value of any underlying security.

What about acknowledgements of notices?

A simple acknowledgement of service of notice is simply evidence of the notice having been received. However, these documents often contain commitments or assurances by the contract counterparty which increase their value to the assignee.

Best practice for serving notice of assignment

Each transaction is different and the weighting given to each element of the security package will depend upon the nature of the debt and the borrower's business. The service of a notice of assignment may be a necessity or an optional extra. In each case, the question of whether to serve notice is best considered with your advisers at the start of a transaction to allow time for the lender's priorities to be highlighted to the borrowers and captured within the documents.

For further advice on serving notice of assignment please contact Kirsty Barnes or Catherine Phillips from our Banking & Finance team.

[email protected]
T: +44 (0)370 733 0605
Download vCard for Catherine Phillips

Related Insights & Resources

The Space: Leadership and law - episode five - with Navin Prabhakar, partner

Gowling WLG updates

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Publications
Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

Advanced Search
Journal List
Health Inf Sci Syst
v.11(1); 2023 Dec
PMC10307766

Patient assignment optimization in cloud healthcare systems: a distributed genetic algorithm

1 Guangdong Technion Israel Institute of Technology, Shantou, China

Yong-Feng Ge

2 Institute for Sustainable Industries and Liveable Cities, Victoria University, Melbourne, Australia

3 School of Health and Biomedical Sciences, RMIT University, Melbourne, Australia

Agma J. M. Traina

4 Institute of Mathematics and Computer Sciences, University of São Paulo, São Paulo, Brazil

Integrating Internet technologies with traditional healthcare systems has enabled the emergence of cloud healthcare systems. These systems aim to optimize the balance between online diagnosis and offline treatment to effectively reduce patients’ waiting times and improve the utilization of idle medical resources. In this paper, a distributed genetic algorithm (DGA) is proposed as a means to optimize the balance of patient assignment (PA) in cloud healthcare systems. The proposed DGA utilizes individuals as solutions for the PA optimization problem and generates better solutions through the execution of crossover, mutation, and selection operators. Besides, the distributed framework in the DGA is proposed to improve its population diversity and scalability. Experimental results demonstrate the effectiveness of the proposed DGA in optimizing the PA problem within the cloud healthcare systems.

Introduction

The rapid advancement of Internet and information technologies [ 1 – 7 ] has led to a growing demand for cloud healthcare systems [ 8 – 13 ] that can effectively provide all medical services [ 14 – 16 ]. These systems are based on integrating online diagnosis [ 17 – 21 ] and offline treatment to reduce patients’ waiting time and improve the utilization of idle medical resources. However, the development of such systems [ 22 – 25 ] is contingent upon the successful resolution of the patient assignment (PA) problem. The PA problem is a crucial aspect of cloud healthcare systems, as it directly impacts the efficiency and effectiveness of the system. Therefore, it is paramount that the PA problem is carefully considered and appropriately addressed in the design and implementation of cloud healthcare systems.

The PA problem in cloud healthcare systems has been the subject of ongoing research, with various strategies proposed to address it. One such approach is the use of discrete event simulation to develop a queuing model [ 26 ]. This strategy aims to reduce patient waiting time and increase the system’s overall throughput. Another approach uses Petri nets to describe the relationship between medical processes and resources [ 9 ]. A hybrid ant agent algorithm has also been proposed [ 27 ], which aims to identify the optimal path for patients, thus reducing both waiting and cycle time. Previous studies have emphasized the importance of reducing patients’ waiting time. However, it should be noted that a continuous influx of patients characterizes cloud healthcare systems. The balance of assignments among doctors is also crucial in improving the system’s efficiency. Therefore, in this paper, we optimize the balance of assignments among doctors in the cloud healthcare systems.

The optimization of the PA problem can be achieved through the utilization of genetic algorithms (GAs) [ 28 , 29 ]. GAs are a type of evolutionary algorithm (EA) [ 30 – 33 ] that have been widely used in the field of computational mathematics to solve optimization problems. Evolutionary biology concepts such as heredity, mutation, natural selection, and hybridization are used to construct EAs [ 34 – 36 ]. GAs are beneficial for finding reasonable solutions quickly, even in complex spatial solutions, by using parallel studies, selection operations, alteration operations, and mutation functions [ 37 – 39 ]. Previous studies have demonstrated the advantages of using EAs, including GAs, in various scenarios, such as reliability and performance. They have been applied to various fields such as computer science, engineering, and operations research and have consistently shown to be effective in solving optimization problems [ 40 – 42 ]. Previously, GA has been utilized in the optimization of the PA problem [ 43 ] and its advantages in terms of convergence speed and scalability have been verified.

This paper proposes a distributed genetic algorithm (DGA) to optimize the PA problem. Over the previous approaches for the PA problem, DGA shows its advantages of global optimization performance and diversity maintenance (not easily trapped by local optima), robustness and scalability (the capability of handling complex and noisy problem spaces), flexibility (easily fits different problem formulation), and increased parallelism (enables faster convergence and reduces running time). Each individual in the proposed DGA represents a solution to the PA optimization problem. Several individuals in the proposed DGA form multiple sub-populations. During the evolution of each sub-population, information included in all the individuals is exchanged by the crossover operator. Individuals are randomly adjusted in the mutation operator. After that, the selection operator evaluates the competitiveness of different solutions. The more competitive solutions are kept in the population, and the less competitive individuals are gradually eliminated. Then, with a predefined interval, the elite individuals of all the sub-populations are exchanged to accelerate the convergence. Finally, the optimal solution to the PA problem is outputted.

More specifically, the contributions of this paper are listed as follows.

We propose the DGA to optimize the PA balance in cloud healthcare systems.
We propose a distributed framework in the DGA to improve population diversity and scalability.
We utilize the operators in DGA to improve the competitiveness of the solutions to the PA problem.

The organization of this paper is as follows. In Sect. 2, a formal problem formulation of the PA problem is illustrated. Then, we review the related work of the PA problem and the application of GA. In Sect. 4, we introduce the DGA. Afterward, the proposed DGA is introduced in detail. In Sects. 6 and 7, the experimental study is executed, and the experimental results are analyzed. Finally, we conclude this paper.

Problem formulation

In Fig. 1 , an example of patient assessment and assignment modules is given. In the given example, the condition of four patients is assessed at the beginning. Accordingly, the estimated diagnosis time and available doctor lists are produced. Our optimization objective in the patient assignment module is to minimize the diagnosis time difference among different doctors. Finally, the patients are assigned to the corresponding doctors for further diagnosis.

An external file that holds a picture, illustration, etc.
Object name is 13755_2023_230_Fig1_HTML.jpg

Illustration of the patient assignment in the cloud healthcare systems

Specifically, in PA, the i -th patient is represented by P i ; D j represents the j -th doctor. The estimated diagnosis time of i -th patient is indicated by T i ~ .

The total diagnosis time of j -th doctor (represented by T j ) is calculated as follows:

where nP is the number of patients; S indicates a status matrix. S i j equals to one when the i -th patient is allocated to the j -th doctor; S i j equals to zero when the i -th patient is not allocated to the j -th doctor.

Thus, the mean value of diagnosis time is calculated as:

where nD is the number of doctors.

The time factor (TF) is then obtained by calculating the standard deviation of diagnosis time of all the doctors. Formally,

As mentioned above, the optimization objective is to balance the doctors’ diagnosis time. Therefore, the optimization objective is to minimize the value of TF.

Related work

In [ 44 ], a positive model of the public hospital waiting lists was established. According to the studies, doctors did not necessarily treat the mildest cases on the waiting list to have the shortest overall hospital stay. In [ 45 ], Takakuwa and Wijewickrama created a discrete-time simulation model and integrated the simulation model into the optimization algorithm to reduce patient waiting and physician idle time without adding any additional resources. In [ 46 ], the dynamic patient scheduling with different priorities in a public healthcare setting was tackled. The proposed method dynamically assigns available capacity to incoming demand to achieve cost-effective wait-time targets. This study collected real-time data from Nagoya University Hospital’s outpatient clinic to create a simulation. In [ 47 ], the Lean Six Sigma (LSS) method was used to solve the problem of the long waiting time of patients. The entire procedure was covered, from patient registration to prescription distribution. A causal map was created for patients with longer waiting times, and data collected during the process were used to verify the reasons. In [ 26 ], a queuing model was developed using discrete event simulation, which could reduce the patient waiting time and improve the system’s overall throughput. To resolve ambiguities in the present system, required data was collected, and alternative scenarios were generated and examined. Furthermore, the best solution concerning patient satisfaction was proposed. In [ 48 ], a system was designed to reduce the doctors’ idle time instead of the patients’ waiting time. It provides an alternative perspective on this problem. This study aimed to improve resource efficiency and modify how doctors schedule visits. The results showed that patients’ waiting time might be lowered without affecting doctors’ work efficiency. In [ 9 ], a Petri net was presented to describe the relationship between the medical process and resources in this integrated healthcare system. A PA scheduling problem was investigated and studied to allocate this system’s bottleneck medical resource efficiently. A mathematical model was established, and a greedy-based heuristic algorithm was designed. In [ 49 ], Chawasemerwa et al. developed a constraint satisfaction and penalty minimization scheduling model that satisfied “hard constraints” and minimized the cost of “soft constraints” violations. Furthermore, since multiple schedules may be obtained using the same parameters defined by users, an optimization protocol can be added to the system to reduce the search space and obtain the optimal schedule while satisfying the constraints. In [ 27 ], the real-time walk-in patient scheduling optimization problem was addressed. An overall patient scheduling model was integrated. The status and information of all outpatient departments were combined. The hybrid and agent algorithm was developed to identify the best path for the patient while also lowering cycle time (from registration to exit). In [ 50 ], similar issues have been further refined. Conforti et al. defined that the scheduling objective of radiotherapy patients in the oncology department was to ensure the best treatment in the shortest possible time. As a result, the waiting time should be minimized, and device utilization should be maximized. Various criteria were added to the optimization model.

The limitations of previous PA approaches are manifold. Firstly, previous PA approaches emphasized the importance of reducing patients’ waiting time, ignoring the balance of assignments among doctors, which is crucial for cloud healthcare systems’ efficiency and scalability. Secondly, previous optimization approaches did not provide sufficient global optimization performance, easily trapped by the local optima. Thirdly, no distributed computation framework was proposed. Therefore, the convergence speed is limited and the running time cannot be reduced.

The application of GAs also has remarkable achievements in the medical and healthcare fields. Yadav et al. [ 51 ] focused on optimizing blood bank inventory control, a healthcare system, on enhancing its determinism. The problems of inbound and outbound logistics and inventory inflation were solved by a multi-objective GA and reliability application using minimum cost optimization of other parameters. Ahmed et al. [ 52 ] improved the modeling of building degradation to alleviate budgetary constraints on the maintenance of medical resources and to reduce the incidence of accidents. Developing a fuzzy Markov model based on a hybrid GA with a nonhomogeneous transition probability matrix based on fuzzy membership functions representing the hospital system’s condition, age, and relative deterioration rate is utilized to address the inherited uncertainties. Mutingi and Mbohwa [ 53 ] tackled the home healthcare worker scheduling problem. Considering the accelerating demand for home care requires careful task allocation and scheduling of limited healthcare resources, Mutingi and Mbohwa proposed a group GA for scheduling the dispatch of healthcare while considering the minimum economic cost of time.

Genetic algorithm

GAs are potent meta-heuristics that improve and refine Darwin’s theory of natural evolution. Based on initialization methods, GAs usually start by constructing initial populations in a randomized and uniform manner. Each population is evaluated for its fit to the target problem using a fitness function. New populations are formed through a series of processes, such as crossover and mutation, and new individuals replace the original ones to form a new population. The great advantage of GAs is that they can process problems of different dimensions in parallel, considering several factors and characteristics simultaneously. It is possible to optimize the computational speed by managing the task allocation between off-the-shelf. In terms of application areas and problem areas, we focus on the typical characteristics of applications and the classification of GAs, respectively, and optimize solutions from different dimensions through examples. The overall procedure of GA is given as follows.

First, the program creates a set number of individuals representing the solutions to the optimized problem at random. When the operator interferes with this randomly produced process to increase the quality of the first population, the quality of the initial population improves. After that, each generation’s individuals are given a value, and the fitness value is calculated using the fitness function. Dominant populations obtain a higher degree of adaptation compared to disadvantaged populations.

The next step is to generate the next generation of individuals to form the population. This process is done by selection and replication, which involves crossover and mutation in algorithmic studies. Selecting the winners from the population and eliminating the inferior ones is called selection. The goal of selection is to pass on their directly optimized genes to the next generation or generate new individuals through crossover pairing and generation, which are then passed on to the next generation. Selectivity is based on assessing the individual’s physical condition in the population. Selection is based on the fitness of new individuals. However, it does not mean at the same time that it is entirely oriented toward fitness because simply selecting individuals with high fitness will lead to a rapid local conversion of the algorithm to the optimal solution rather than to the optimal global solution, which we call the initial stage. As a compromise, GAs follow the principle that the higher the fitness, the higher the chance of being selected, and the lower the fitness, the lower the chance of being selected. The initial data can be selected to form a relatively optimal group.

After that, the selected individuals enter the mating process. The core of biological evolution in nature is the recombination of biogenetics (coupled with mutation). After this series of processes (selection, crossover, mutation), a new generation of individuals differs from the first generation. Each generation moves toward improved overall fitness Because individuals with greater adaptability are more likely to survive and produce the next generation. Conversely, poorly adapted individuals are gradually eliminated.

Distributed genetic algorithm for patient assignment

This section illustrates the proposed DGA for optimizing the PA problem. Firstly, we introduce the representation manner and initialization strategy of DGA. Secondly, the distributed framework of DGA is illustrated in detail. Afterward, the crossover and mutation operators of DGA are described. Finally, the entire procedure of DGA is described.

Representation and initialization

In GA, each individual represents a solution for PA. In each individual, each gene indicates the assignment of each patient. An example of this representation manner is given in Fig. 2 . In this example, three doctors allocated to for each patient (represented by A, B,..., F). Different digits with different colors represent different doctors. In total, six doctors are included in this example. Therefore, one doctor is chosen from the candidature lists for each patient. In this example, two individuals are given (represented by I 1 and I 2 ). For the first patient (patient A), doctor 1 is allocated to in individual I 1 , while doctor 2 is allocated to individual I 2 . For each complete individual, it can be directly evaluated according to the definition of the PA problem.

An external file that holds a picture, illustration, etc.
Object name is 13755_2023_230_Fig2_HTML.jpg

Illustration of the representation manner in DGA

In the initial population of the proposed DGA, all the individuals are generated randomly according to the above manner. More specifically, the doctor is randomly chosen from the corresponding candidature list for each patient listed in each individual.

Distributed framework

As we introduced, GA with the distributed framework has shown its advantages in terms of population diversity, convergence speed, and optimization speed. The initial population is divided into several sub-populations in the distributed framework, each completing the evolutionary process independently. Based on the predefined topology, sub-populations share their elite individuals (e.g., the best individuals) with the predefined migration interval ( MI ). Once one sub-population receives the elite individual from the neighbors in the topology, the current sub-population will randomly select an existing individual (not the best one) to replace.

The proposed DGA uses a distributed framework with a ring communication topology. An example of the distributed framework is given in Fig. 3 . As shown in this figure, each big hexagon represents a sub-population. The small triangle and five hexagons represent the best individual and the other five individuals in each big hexagon. During the migration operator, the best individuals in sub-populations are sent to the corresponding neighbor sub-populations according to the ring topology with the predefined migration topology. Afterward, one hexagon in the sub-population is replaced by the triangle, representing one random individual replaced by the best individual.

An external file that holds a picture, illustration, etc.
Object name is 13755_2023_230_Fig3_HTML.jpg

Illustration of distributed framework in DGA

In DGA, the distributed framework is effective in maintaining population diversity. Thus, the exploration search ability of DGA is guaranteed. Besides, by migrating elite individuals among the sub-populations, the population quality of each sub-population is improved, which helps improve the exploitation search ability of DGA. With the help of the distributed framework and migration operator, DGA is likely to achieve the trade-off between exploration and exploitation during the evolution. Furthermore, the distributed framework helps improve the execution speed of DGA.

Crossover operator

In genetics, the crossover operator is an algorithmic procedure that encapsulates the phenomena of chromosomal crossover exchange and biological hybridization. For example, the act of recombining and assigning genes on the chromosomes of two parents to form the next generation of humans may combine the dominant genomes of the two parents to produce new individuals more adaptable and closer to the ideal solution via crossing over.

Similarly, the core of GAs is the internal operation of genetic manipulation. By crossover, we mean the function of replacement and recombination of parts of the structure of biparental individuals, resulting in new individuals. The searchability of GAs is greatly improved by crossover. First, general GAs have a mating probability (crossover probability). This mating probability reflects the probability of two selected individuals mating. Each pair of parent individuals produces one or multiple new individuals as the offspring, while the unmated individuals remain unchanged. In the produced child individual, part of the information comes from the father individual, while the left comes from the mother individual.

An example of the crossover operator in GA is given in Fig. 4 . In the example, two individuals (represented by I 1 and I 2 ). The information included these two individuals is then exchanged. In this example, each individual includes six genes representing six patients. The values on six genes indicate the assignment of these six patients. For each gene, with the same possibility, one value is randomly chosen from two individuals during the crossover operator. For instance, on the first gene (gene A), the value in individual I 1 is chosen. Thus, in the child individual (represented by C), the value on the first bit is 1. Similarly, on the second gene (gene B), the value in C comes from individual I 2 .

An external file that holds a picture, illustration, etc.
Object name is 13755_2023_230_Fig4_HTML.jpg

Illustration of crossover operator in DGA

Mutation operator

There are always individual differences between the parents and offspring of an organism, i.e., differences in the genetic material of different individuals in the same gene pool are called mutations.

The mutation operator’s primary goal is to change the gene values at a specific location in individual strings in the population. The probability of the mutation operator is represented by a constant in the general GA for fixed mutations (the probability of mutation). Based on this probability, a random mutation on the chromosome of a new individual is usually a change of one byte of the chromosome. There are two reasons for introducing mutations into GAs: First, give the GA a local random search function. The variation operator’s local random search capability can speed up the convergence in the optimal solution when the GA approximates the optimal solution neighborhood by the crossover operator. In this case, the variance probability should take a small value. Otherwise, the variation will destroy the building blocks close to the optimal solution. The second is to enable the GA to maintain population diversity and prevent premature convergence. In this case, the convergence probability should take a more meaningful value.

In Fig. 5 , an example of the mutation operator is given. With the mutation rate MR , each gene of the child individual (represented by C) is randomly adjusted. The third gene (gene C) is chosen randomly in this example. Therefore, its value is randomly adjusted, and its value is changed from 5 to 4.

An external file that holds a picture, illustration, etc.
Object name is 13755_2023_230_Figa_HTML.jpg

Illustration of mutation operator in DGA

Overall procedure

The pseudo-code of DGA is given in Algorithm 1. As shown in the pseudo-code, a master–slave model is utilized to implement the DGA algorithm. At the master node, the generation index g is set as zero. Then the entire population is divided into NSP sub-populations and sent to the corresponding NSP slave nodes. With the predefined migration interval MI , the master node receives the elite individuals from all the slave nodes. Then it sends these elite individuals to the corresponding slave nodes according to the ring topology. The migration process is executed until the terminal condition is satisfied. Finally, the best solution to the PA problem is outputted.

At the slave node, each sub-population evolves independently. During the evolution, in each generation, for each pair of parent individuals, the crossover operator is executed to exchange the allocation information in parent individuals and generate the child individual. Afterward, the mutation operator is carried out on the child individual to improve the population diversity. After the mutation operator, the mutant child individual is evaluated and compared with the parent individuals by the selection operator. If the mutant child individual is better than any parent individual, one of the parent individuals will be replaced. Otherwise, the mutant child individual will not be kept in the population. Then, the migration operator is carried out with the predefined mutation interval MI . Each slave node sends the best individual to the master node and receives one elite individual from the master node. Afterward, one randomly chosen individual in the sub-population that is not the best individual will be replaced by the received migrated individual. Finally, the best individual is returned to the master node.

Experimental setup

This section illustrates the test instances, parameter settings, and algorithm implementation in the following experiments.

In the subsequent experimental studies, 16 test instances are utilized to investigate the performance of the proposed DGA. Table Table1 1 outlines the properties of these test instances, including the number of patients nP , the number of doctors nD , and the range of estimated diagnosis time T .

Properties of 16 test instances

In the proposed DGA, the sub-population size SPS is set as 20; the number of sub-population NSP is set as 4; the mutation rate MR is set as 0.1; the migration interval MI is set as 5. For all the algorithms, the maximum fitness evaluation number is set as n P × n D .

The distributed framework of DGA is implemented by the Message Passing Interface (MPI). Each sub-population is assigned to an independent computation core in the CPU. The communication between sub-populations is implemented by the message passing between CPU cores. DGA and all the compared algorithms in this paper are implemented in C++.

Experimental result

Comparison with existing approaches.

To verify the performance of the proposed DGA, it is compared with three existing algorithms, i.e., Random, Greedy, differential evolution (DE) [ 54 ], and GA [ 43 ]. These algorithms are described as follows:

Random: This algorithm uses a random manner to solve the PA problem. Random solutions are continuously generated and compared with the best solution. The best solution is replaced once a more competitive solution is generated.
Greedy: This algorithm uses a greedy manner to solve the PA problem. Each patient is greedily allocated to a doctor.
DE [ 54 ]: This DE algorithm utilizes the “DE/best/1” mutation schema to generate the mutant individuals, which can help accelerate the exploitation search ability during the optimization of the PA problem.
GA [ 43 ]: In this algorithm, a GA is specifically designed for the PA problem, including the representation manner, crossover operator, and mutation operator.

Table Table2 2 lists the mean (Avg) and standard deviation (Std) of TF values (defined in Sect. 2 ) over 25 independent runs. Therefore, a lower TF value indicates that the corresponding algorithm can provide better optimization performance with regard to the balance of doctors’ diagnosis time. The best results (i.e., the lowest Avg values) in Table Table2 2 are highlighted in boldface. The Greedy approach only lists its results since it can generate deterministic results. The proposed DGA can achieve significant advantages on all 16 test instances. The benefits of DGA in heuristic strategies are confirmed compared to Random. With the help of the crossover and mutation operators, information allocation among different individuals is effectively exchanged, and more competitive individuals are generated and inserted into the population. Compared with Greedy, the stronger feasibility of DGA in population diversity is verified. The greedy technique is more likely to get trapped by the local optima during the PA problem optimization. Unlike the Greedy approach, the population diversity of DGA can effectively guarantee the exploration search ability of DGA. The benefit of DGA in discrete-domain optimization is demonstrated when compared to DE. The mutation strategy of DE, such as “DE/best/1”, is efficient in the continuous-domain calculation. For this discrete PA problem, its mutation strategies are challenging to transfer information among individuals. Compared with GA, the advantage of the distributed framework in DGA is verified. Moreover, with the architecture of the distribution framework, the population diversity in DGA is maintained. Furthermore, the migration of elite individuals among sub-populations accelerates the optimization process. As a result, the advantage of convergence speed is based on the ring topology.

TF values of DGA and compared algorithms on all text instances

† indicates that the difference among the compared results is significant based on the Wilcoxon rank-sum test with a 5% level

Besides, the Wilcoxon rank-sum test with a 0.05 level is utilized to investigate the performance of these algorithms in a statistical sense. In Table Table2, 2 , the symbol † shows that the corresponding result is significantly better than the other compared results. The advantage of DGA obtained in all the test instances is significant.

According to the problem formulation in Sect. 2 , the time complexity of calculating a given solution to the PA problem is O ( n P ) . Therefore, the time complexity of the proposed DGA is O ( n P 2 × n D ) . Similarly, the time complexity of Random, DE, and GA is O ( n P 2 × n D ) , the same as DGA. Different from these algorithms, the time complexity of the Greedy method is O ( n P × n D ) . Although the Greedy method is of lower time complexity, due to the limitation of search diversity, its optimization performance is significantly worse than the proposed DGA. Regarding the space complexity, the space complexity of Random and Greedy is O ( n P × n D ) , while the space complexity of DE, GA, and the proposed DGA is O ( n P × ( n D + S P S ) ) .

In Fig. 6 , the convergence curves of Random, DE, GA, and DGA on six typical test instances are plotted. A line with unique color indicates each approach. The number of fitness evaluations is indicated on the horizontal axis, and the value of TF is represented on the vertical axis for each point on the line. The Greedy approach is not given in the figure since no eligible solution is generated during the greedy construction. Compared with the Random approach, the advantage of DGA in search efficiency is verified. Furthermore, with the help of the population crossover and mutation operators, DGA is more likely to achieve the trade-off between exploration and exploitation. Compared with DE, the advantage of DGA in discrete-domain optimization is verified. In addition, compared with GA, the advantage of DGA in information exchange efficiency and population diversity is shown. In summary, DGA achieves the best convergence performance in all six test instances.

An external file that holds a picture, illustration, etc.
Object name is 13755_2023_230_Fig6_HTML.jpg

Convergence curves of DGA and compared algorithms on six typical test instances

Impact of proposed components

In this section, we will experiment to verify the impact of the proposed components in the DGA. Besides the proposed DGA, we have implemented three variants.

DGA-no-crossover: This variant is implemented by removing the crossover operator from DGA.
DGA-no-mutation: In this variant, the mutation operator is removed. Accordingly, the crossover operator and distributed framework are kept.
DGA-no-distributed: In this variant, the proposed distributed framework is proposed. Therefore, this variant is implemented serially.

Table Table3 3 lists the average (Avg) and standard deviation (Std) values of TF (defined in Sect. 2 ) obtained by three variants and DGA. The best results (i.e., the lowest Avg values) in all the test instances are labeled in boldface. Overall, the complete-version DGA can outperform the compared variants on all 16 test instances. Compared with DGA-no-crossover, DGA shows its advantage in terms of the crossover operator, effectively exchanging allocation between parent individuals. Compared with DGA-no-mutation, DGA shows its advantage in terms of the mutation operator, which can effectively improve population diversity. Finally, compared with the variant DGA-no-distributed, DGA shows the advantage of the distributed framework, which can effectively balance the exploration and exploitation searching abilities.

TF values of DGA and three variants on all text instances

Besides, the Wilcoxon rank-sum (significance level 0.05) is employed to verify DGA’s advantage in a statistical sense. As shown in the table, the symbol † shows that the labeled results are significantly better than the compared results. In all 16 test instances, the advantages of the complete DGA are significant.

In this paper, a DGA has been proposed to optimize the balance of PA schedules. Each individual in the proposed DGA represents a solution for the PA optimization problem. Furthermore, three operators in the proposed DGA, i.e., crossover, mutation, and selection, have been utilized to improve the competitiveness of these solutions. The distributed framework in the proposed DGA helps improve population diversity and scalability. Through the analysis of the experimental results, we have verified that the proposed DGA effectively optimizes the PA problem. In addition, we have verified the effectiveness of all the proposed components.

In the future, it would be crucial to include more objectives in the PA problem. Thus, some practical multi-objective optimization algorithms should be designed accordingly.

Open Access funding enabled and organized by CAUL and its Member Institutions.

Declarations

The authors have no competing interests to declare that are relevant to the content of this article.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Patient assignment optimization in cloud healthcare systems: a distributed genetic algorithm

Open access
Published: 29 June 2023
Volume 11 , article number 30 , ( 2023 )

Cite this article

You have full access to this open access article

Xinyu Pang 1 ,
Yong-Feng Ge ORCID: orcid.org/0000-0002-5955-6295 2 ,
Kate Wang 3 ,
Agma J. M. Traina 4 &
Hua Wang 2

1914 Accesses

7 Citations

Explore all metrics

A review on genetic algorithm: past, present, and future

Genetic algorithms: theory, genetic operators, solutions, and applications

Evolutionary algorithms and their applications to engineering problems

Avoid common mistakes on your manuscript.

Introduction

The rapid advancement of Internet and information technologies [ 1 , 2 , 3 , 4 , 5 , 6 , 7 ] has led to a growing demand for cloud healthcare systems [ 8 , 9 , 10 , 11 , 12 , 13 ] that can effectively provide all medical services [ 14 , 15 , 16 ]. These systems are based on integrating online diagnosis [ 17 , 18 , 19 , 20 , 21 ] and offline treatment to reduce patients’ waiting time and improve the utilization of idle medical resources. However, the development of such systems [ 22 , 23 , 24 , 25 ] is contingent upon the successful resolution of the patient assignment (PA) problem. The PA problem is a crucial aspect of cloud healthcare systems, as it directly impacts the efficiency and effectiveness of the system. Therefore, it is paramount that the PA problem is carefully considered and appropriately addressed in the design and implementation of cloud healthcare systems.

The optimization of the PA problem can be achieved through the utilization of genetic algorithms (GAs) [ 28 , 29 ]. GAs are a type of evolutionary algorithm (EA) [ 30 , 31 , 32 , 33 ] that have been widely used in the field of computational mathematics to solve optimization problems. Evolutionary biology concepts such as heredity, mutation, natural selection, and hybridization are used to construct EAs [ 34 , 35 , 36 ]. GAs are beneficial for finding reasonable solutions quickly, even in complex spatial solutions, by using parallel studies, selection operations, alteration operations, and mutation functions [ 37 , 38 , 39 ]. Previous studies have demonstrated the advantages of using EAs, including GAs, in various scenarios, such as reliability and performance. They have been applied to various fields such as computer science, engineering, and operations research and have consistently shown to be effective in solving optimization problems [ 40 , 41 , 42 ]. Previously, GA has been utilized in the optimization of the PA problem [ 43 ] and its advantages in terms of convergence speed and scalability have been verified.

More specifically, the contributions of this paper are listed as follows.

We propose the DGA to optimize the PA balance in cloud healthcare systems.

We propose a distributed framework in the DGA to improve population diversity and scalability.

We utilize the operators in DGA to improve the competitiveness of the solutions to the PA problem.

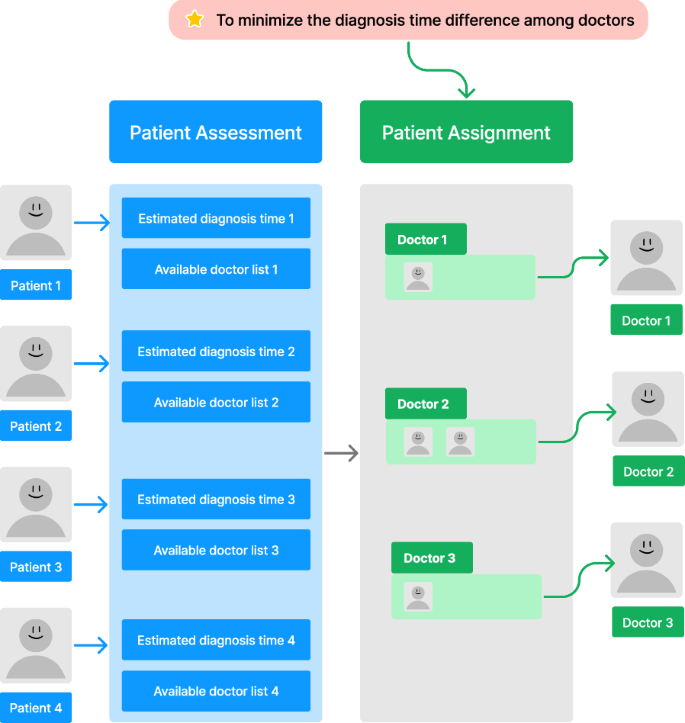
Illustration of the patient assignment in the cloud healthcare systems

Problem formulation

Specifically, in PA, the i -th patient is represented by $P_i$ ; $D_j$ represents the j -th doctor. The estimated diagnosis time of i -th patient is indicated by $\widetilde{T_i}$ .

The total diagnosis time of j -th doctor (represented by $T_j$ ) is calculated as follows:

where nP is the number of patients; S indicates a status matrix. $S_i^j$ equals to one when the i -th patient is allocated to the j -th doctor; $S_i^j$ equals to zero when the i -th patient is not allocated to the j -th doctor.

Thus, the mean value of diagnosis time is calculated as:

where nD is the number of doctors.

The time factor (TF) is then obtained by calculating the standard deviation of diagnosis time of all the doctors. Formally,

As mentioned above, the optimization objective is to balance the doctors’ diagnosis time. Therefore, the optimization objective is to minimize the value of TF.

Related work

Genetic algorithm

Distributed genetic algorithm for patient assignment

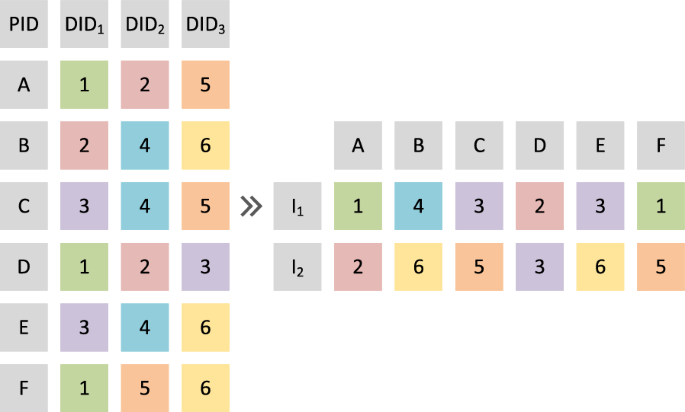
Illustration of the representation manner in DGA

Representation and initialization

In GA, each individual represents a solution for PA. In each individual, each gene indicates the assignment of each patient. An example of this representation manner is given in Fig. 2 . In this example, three doctors allocated to for each patient (represented by A, B,..., F). Different digits with different colors represent different doctors. In total, six doctors are included in this example. Therefore, one doctor is chosen from the candidature lists for each patient. In this example, two individuals are given (represented by $\mathrm {I_1}$ and $\mathrm {I_2}$ ). For the first patient (patient A), doctor 1 is allocated to in individual $\mathrm {I_1}$ , while doctor 2 is allocated to individual $\mathrm {I_2}$ . For each complete individual, it can be directly evaluated according to the definition of the PA problem.

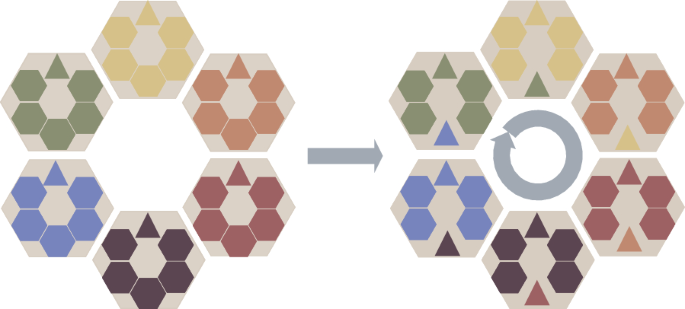
Illustration of distributed framework in DGA

Distributed framework

Crossover operator

An example of the crossover operator in GA is given in Fig. 4 . In the example, two individuals (represented by $\mathrm {I_1}$ and $\mathrm {I_2}$ ). The information included these two individuals is then exchanged. In this example, each individual includes six genes representing six patients. The values on six genes indicate the assignment of these six patients. For each gene, with the same possibility, one value is randomly chosen from two individuals during the crossover operator. For instance, on the first gene (gene A), the value in individual $\mathrm {I_1}$ is chosen. Thus, in the child individual (represented by C), the value on the first bit is 1. Similarly, on the second gene (gene B), the value in C comes from individual $\mathrm {I_2}$ .

Illustration of crossover operator in DGA

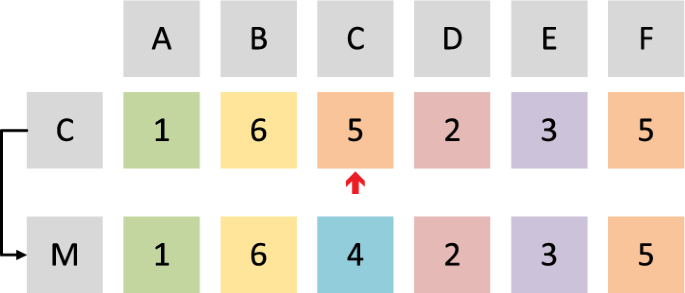
Illustration of mutation operator in DGA

Mutation operator

Overall procedure

Experimental setup

This section illustrates the test instances, parameter settings, and algorithm implementation in the following experiments.

In the subsequent experimental studies, 16 test instances are utilized to investigate the performance of the proposed DGA. Table 1 outlines the properties of these test instances, including the number of patients nP , the number of doctors nD , and the range of estimated diagnosis time T .

Experimental result

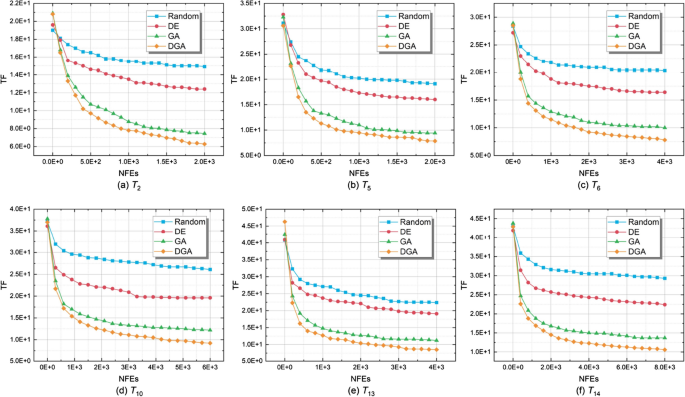
Convergence curves of DGA and compared algorithms on six typical test instances

Comparison with existing approaches

Random: This algorithm uses a random manner to solve the PA problem. Random solutions are continuously generated and compared with the best solution. The best solution is replaced once a more competitive solution is generated.

Greedy: This algorithm uses a greedy manner to solve the PA problem. Each patient is greedily allocated to a doctor.

DE [ 54 ]: This DE algorithm utilizes the “DE/best/1” mutation schema to generate the mutant individuals, which can help accelerate the exploitation search ability during the optimization of the PA problem.

GA [ 43 ]: In this algorithm, a GA is specifically designed for the PA problem, including the representation manner, crossover operator, and mutation operator.

Table 2 lists the mean (Avg) and standard deviation (Std) of TF values (defined in Sect. 2 ) over 25 independent runs. Therefore, a lower TF value indicates that the corresponding algorithm can provide better optimization performance with regard to the balance of doctors’ diagnosis time. The best results (i.e., the lowest Avg values) in Table 2 are highlighted in boldface. The Greedy approach only lists its results since it can generate deterministic results. The proposed DGA can achieve significant advantages on all 16 test instances. The benefits of DGA in heuristic strategies are confirmed compared to Random. With the help of the crossover and mutation operators, information allocation among different individuals is effectively exchanged, and more competitive individuals are generated and inserted into the population. Compared with Greedy, the stronger feasibility of DGA in population diversity is verified. The greedy technique is more likely to get trapped by the local optima during the PA problem optimization. Unlike the Greedy approach, the population diversity of DGA can effectively guarantee the exploration search ability of DGA. The benefit of DGA in discrete-domain optimization is demonstrated when compared to DE. The mutation strategy of DE, such as “DE/best/1”, is efficient in the continuous-domain calculation. For this discrete PA problem, its mutation strategies are challenging to transfer information among individuals. Compared with GA, the advantage of the distributed framework in DGA is verified. Moreover, with the architecture of the distribution framework, the population diversity in DGA is maintained. Furthermore, the migration of elite individuals among sub-populations accelerates the optimization process. As a result, the advantage of convergence speed is based on the ring topology.

Besides, the Wilcoxon rank-sum test with a 0.05 level is utilized to investigate the performance of these algorithms in a statistical sense. In Table 2 , the symbol $^\dagger$ shows that the corresponding result is significantly better than the other compared results. The advantage of DGA obtained in all the test instances is significant.

According to the problem formulation in Sect. 2 , the time complexity of calculating a given solution to the PA problem is $\mathcal {O}(nP)$ . Therefore, the time complexity of the proposed DGA is $\mathcal {O}(nP^2\times nD)$ . Similarly, the time complexity of Random, DE, and GA is $\mathcal {O}(nP^2\times nD)$ , the same as DGA. Different from these algorithms, the time complexity of the Greedy method is $\mathcal {O}(nP\times nD)$ . Although the Greedy method is of lower time complexity, due to the limitation of search diversity, its optimization performance is significantly worse than the proposed DGA. Regarding the space complexity, the space complexity of Random and Greedy is $\mathcal {O}(nP\times nD)$ , while the space complexity of DE, GA, and the proposed DGA is $\mathcal {O}(nP\times (nD+SPS))$ .

Impact of proposed components

In this section, we will experiment to verify the impact of the proposed components in the DGA. Besides the proposed DGA, we have implemented three variants.

DGA-no-crossover: This variant is implemented by removing the crossover operator from DGA.

DGA-no-mutation: In this variant, the mutation operator is removed. Accordingly, the crossover operator and distributed framework are kept.

DGA-no-distributed: In this variant, the proposed distributed framework is proposed. Therefore, this variant is implemented serially.

Table 3 lists the average (Avg) and standard deviation (Std) values of TF (defined in Sect. 2 ) obtained by three variants and DGA. The best results (i.e., the lowest Avg values) in all the test instances are labeled in boldface. Overall, the complete-version DGA can outperform the compared variants on all 16 test instances. Compared with DGA-no-crossover, DGA shows its advantage in terms of the crossover operator, effectively exchanging allocation between parent individuals. Compared with DGA-no-mutation, DGA shows its advantage in terms of the mutation operator, which can effectively improve population diversity. Finally, compared with the variant DGA-no-distributed, DGA shows the advantage of the distributed framework, which can effectively balance the exploration and exploitation searching abilities.

Besides, the Wilcoxon rank-sum (significance level 0.05) is employed to verify DGA’s advantage in a statistical sense. As shown in the table, the symbol $^\dagger$ shows that the labeled results are significantly better than the compared results. In all 16 test instances, the advantages of the complete DGA are significant.

In the future, it would be crucial to include more objectives in the PA problem. Thus, some practical multi-objective optimization algorithms should be designed accordingly.

Du J, Michalska S, Subramani S, et al. Neural attention with character embeddings for hay fever detection from twitter. Health Inf Sci Syst. 2019;7(1):1–7. https://doi.org/10.1007/s13755-019-0084-2 .

Article Google Scholar

He J, Rong J, Sun L, et al. A framework for cardiac arrhythmia detection from IoT-based ECGs. World Wide Web. 2020;23(5):2835–50. https://doi.org/10.1007/s11280-019-00776-9 .

Hong W, Yin J, You M, et al. Graph intelligence enhanced bi-channel insider threat detection. In: Network and System Security. Springer Nature Switzerland; 2022. pp. 86–102. https://doi.org/10.1007/978-3-031-23020-2_5 .

Jiang H, Zhou R, Zhang L, et al. Sentence level topic models for associated topics extraction. World Wide Web. 2018;22(6):2545–60. https://doi.org/10.1007/s11280-018-0639-1 .

Siuly S, Alcin OF, Kabir E, et al. A new framework for automatic detection of patients with mild cognitive impairment using resting-state EEG signals. IEEE Trans Neural Syst Rehabil Eng. 2020;28(9):1966–76. https://doi.org/10.1109/tnsre.2020.3013429 .

Vimalachandran P, Liu H, Lin Y, et al. Improving accessibility of the Australian my health records while preserving privacy and security of the system. Health Inf Sci Syst. 2020;8(1):1–9. https://doi.org/10.1007/s13755-020-00126-4 .

Yin J, Tang M, Cao J, et al. Knowledge-driven cybersecurity intelligence: software vulnerability coexploitation behavior discovery. IEEE Trans Ind Inf. 2023;19(4):5593–601. https://doi.org/10.1109/tii.2022.3192027 .

Lee J, Park J, Wang K, et al. The use of telehealth during the coronavirus (COVID-19) pandemic in oral and maxillofacial surgery: a qualitative analysis. In: ICST Transactions on Scalable Information Systems; 2021. p. 172361. https://doi.org/10.4108/eai.2-12-2021.172361 .

Wang H, Li Y, Li Y, et al. Patient assignment scheduling in a cloud healthcare system based on petri net and greedy-based heuristic. Enterp Inf Syst. 2018;13(4):515–33. https://doi.org/10.1080/17517575.2018.1526323 .

Sarki R, Ahmed K, Wang H, et al. Convolutional neural network for multi-class classification of diabetic eye disease. In: ICST Transactions on Scalable Information Systems; 2021. p. 172436. https://doi.org/10.4108/eai.16-12-2021.172436 .

Singh R, Zhang Y, Wang H, et al. Investigation of social behaviour patterns using location-based data: a melbourne case study. In: ICST Transactions on Scalable Information Systems; 2020. p. 166767. https://doi.org/10.4108/eai.26-10-2020.166767 .

Yin J, Tang M, Cao J, et al. Apply transfer learning to cybersecurity: predicting exploitability of vulnerabilities by description. Knowl-Based Syst. 2020;210(106):529. https://doi.org/10.1016/j.knosys.2020.106529 .

You M, Yin J, Wang H, et al. A knowledge graph empowered online learning framework for access control decision-making. World Wide Web. 2022;26(2):827–48. https://doi.org/10.1007/s11280-022-01076-5 .

Pandey D, Wang H, Yin X, et al. Automatic breast lesion segmentation in phase preserved DCE-MRIs. Health Inf Sci Syst. 2022;10(1):9. https://doi.org/10.1007/s13755-022-00176-w .

Sarki R, Ahmed K, Wang H, et al. Automated detection of mild and multi-class diabetic eye diseases using deep learning. Health Inf Sci Syst. 2020;8(1):32. https://doi.org/10.1007/s13755-020-00125-5 .

Supriya S, Siuly S, Wang H, et al. Automated epilepsy detection techniques from electroencephalogram signals: a review study. Health Inf Sci Syst. 2020;8(1):1–15. https://doi.org/10.1007/s13755-020-00129-1 .

Chenthara S, Ahmed K, Wang H, et al. Healthchain: a novel framework on privacy preservation of electronic health records using blockchain technology. PLoS ONE. 2020;15(12):e0243043. https://doi.org/10.1371/journal.pone.0243043 .

Hu H, Li J, Wang H, et al. Combined gene selection methods for microarray data analysis. In: Lecture Notes in Computer Science. Springer Berlin Heidelberg; 2006. pp. 976–83. https://doi.org/10.1007/11892960_117 .

Malhotra V, Sandhu M. Improved ECG based stress prediction using optimization and machine learning techniques. In: ICST Transactions on Scalable Information Systems; 2018. p. 169175. https://doi.org/10.4108/eai.6-4-2021.169175 .

Nigam K, Godani K, Sharma D, et al. An improved approach for stress detection using physiological signals. ICST Trans Scalable Inf Syst. 2021;8(33):169,919. https://doi.org/10.4108/eai.14-5-2021.169919 .

Sarki R, Ahmed K, Wang H, et al. Automatic detection of diabetic eye disease through deep learning using fundus images: a survey. IEEE Access. 2020;8:151133–49. https://doi.org/10.1109/access.2020.3015258 .

Hu H, Li J, Wang H, et al. A maximally diversified multiple decision tree algorithm for microarray data classification. In: Proceedings of the 2006 Workshop on Intelligent Systems for Bioinformatics. Australian Computer Society; 2006. pp. 35–38.

Khalil F, Li J, Wang H. An integrated model for next page access prediction. Int J Knowl Web Intell. 2009;1(1/2):48. https://doi.org/10.1504/ijkwi.2009.027925 .

Peng M, Zhu J, Wang H, et al. Mining event-oriented topics in microblog stream with unsupervised multi-view hierarchical embedding. ACM Trans Knowl Discov Data. 2018;12(3):1–26. https://doi.org/10.1145/3173044 .

Subramani S, Wang H, Vu HQ, et al. Domestic violence crisis identification from facebook posts based on deep learning. IEEE Access. 2018;6:54075–85. https://doi.org/10.1109/access.2018.2871446 .

Hossain NUI, Debusk H, Hasan MM. Reducing patient waiting time in an outpatient clinic: a discrete event simulation (des) based approach. In: Proceedings of the IIE Annual Conference. Institute of Industrial and Systems Engineers (IISE); 2017. pp. 241–46.

Munavalli JR, Rao SV, Srinivasan A, et al. Integral patient scheduling in outpatient clinics under demand uncertainty to minimize patient waiting times. Health Inf J. 2019;26(1):435–48. https://doi.org/10.1177/1460458219832044 .

Ge YF, Cao J, Wang H, et al. A benefit-driven genetic algorithm for balancing privacy and utility in database fragmentation. In: Proceedings of the Genetic and Evolutionary Computation Conference. ACM; 2019. pp 771–76. https://doi.org/10.1145/3321707.3321778 .

Srinivas M, Patnaik L. Genetic algorithms: a survey. Computer. 1994;27(6):17–26. https://doi.org/10.1109/2.294849 .

Chen ZG, Zhan ZH, Wang H, et al. Distributed individuals for multiple peaks: a novel differential evolution for multimodal optimization problems. IEEE Trans Evol Comput. 2020;24(4):708–19. https://doi.org/10.1109/tevc.2019.2944180 .

Ge YF, Yu WJ, Zhang J. Diversity-based multi-population differential evolution for large-scale optimization. In: Proceedings of the 2016 on Genetic and Evolutionary Computation Conference Companion. ACM; 2016. https://doi.org/10.1145/2908961.2908995 .

Ge YF, Orlowska M, Cao J, et al. MDDE: multitasking distributed differential evolution for privacy-preserving database fragmentation. VLDB J. 2022. https://doi.org/10.1007/s00778-021-00718-w .

Wang ZJ, Zhan ZH, Lin Y, et al. Automatic niching differential evolution with contour prediction approach for multimodal optimization problems. IEEE Trans Evol Comput. 2020;24(1):114–28. https://doi.org/10.1109/tevc.2019.2910721 .

Ge YF, Yu WJ, Zhan ZH, (2018) Competition-based distributed differential evolution. In: IEEE Congress on Evolutionary Computation (CEC). IEEE; 2018. https://doi.org/10.1109/cec.2018.8477758 .

Ge YF, Yu WJ, Cao J, et al. Distributed memetic algorithm for outsourced database fragmentation. IEEE Trans Cybern. 2021;51(10):4808–21. https://doi.org/10.1109/tcyb.2020.3027962 .

Mirjalili S. Evolutionary algorithms and neural networks. New York: Springer; 2018.

Google Scholar

Ge YF, Wang H, Cao J, et al. An information-driven genetic algorithm for privacy-preserving data publishing. In: Web Information Systems Engineering—WISE 2022. Springer International Publishing; 2022. pp. 340–354. https://doi.org/10.1007/978-3-031-20891-1_24 .

Ge YF, Zhan ZH, Cao J, et al. DSGA: a distributed segment-based genetic algorithm for multi-objective outsourced database partitioning. Inf Sci. 2022;612:864–86. https://doi.org/10.1016/j.ins.2022.09.003 .

Huang T, Gong YJ, Kwong S, et al. A niching memetic algorithm for multi-solution traveling salesman problem. In: IEEE Transactions on Evolutionary Computation; 2019. pp. 1–1. https://doi.org/10.1109/tevc.2019.2936440 .

Ge YF, Cao J, Wang H, et al. Distributed differential evolution for anonymity-driven vertical fragmentation in outsourced data storage. In: Web Information Systems Engineering—WISE 2020. Springer International Publishing; 2020. pp. 213–26. https://doi.org/10.1007/978-3-030-62008-0_15 .

Ge YF, Orlowska M, Cao J, et al. Knowledge transfer-based distributed differential evolution for dynamic database fragmentation. Knowl-Based Syst. 2021;229(107):325. https://doi.org/10.1016/j.knosys.2021.107325 .

Li JY, Du KJ, Zhan ZH, et al. Distributed differential evolution with adaptive resource allocation. IEEE Trans Cybern 2022. https://doi.org/10.1109/tcyb.2022.3153964 .

Pang X, Ge YF, Wang K. Genetic algorithm for patient assignment optimization in cloud healthcare system. In: Health Information Science. Springer Nature Switzerland; 2022, pp. 197–208. https://doi.org/10.1007/978-3-031-20627-6_19 .

Barros PP, Olivella P. Waiting lists and patient selection. J Econ Manag Strategy. 2005;14(3):623–46. https://doi.org/10.1111/j.1530-9134.2005.00076.x .

Takakuwa S, Wijewickrama A. Optimizing staffing schedule in light of patient satisfaction for the whole outpatient hospital ward. In: Winter Simulation Conference. IEEE; 2008. https://doi.org/10.1109/wsc.2008.4736230 .

Patrick J, Puterman ML, Queyranne M. Dynamic multipriority patient scheduling for a diagnostic resource. Oper Res. 2008;56(6):1507–25. https://doi.org/10.1287/opre.1080.0590 .

Article MathSciNet Google Scholar

Gijo EV, Antony J. Reducing patient waiting time in outpatient department using lean six sigma methodology. Qual Reliab Eng Int. 2013;30(8):1481–91. https://doi.org/10.1002/qre.1552 .

Mardiah FP, Basri MH. The analysis of appointment system to reduce outpatient waiting time at Indonesia’s public hospital. Hum Resour Manag Res. 2013;3(1):27–33.

Chawasemerwa T, Taifa I, Hartmann D. Development of a doctor scheduling system: a constraint satisfaction and penalty minimisation scheduling model. Int J Res Ind Eng 2018;7(4):396–422. https://doi.org/10.22105/riej.2018.160257.1068

Conforti D, Guerriero F, Guido R. Optimization models for radiotherapy patient scheduling. 4OR. 2007;6(3):263–78. https://doi.org/10.1007/s10288-007-0050-8 .

Yadav AS, Ahlawat N, Sharma N, et al. Healthcare system of inventory control for blood bank storage with reliability applications using genetic algorithm. Adv Math. 2020;9(7):5133–42. https://doi.org/10.37418/amsj.9.7.80 .

Ahmed R, Zayed T, Nasiri F. A hybrid genetic algorithm-based fuzzy Markovian model for the deterioration modeling of healthcare facilities. Algorithms. 2020;13(9):210. https://doi.org/10.3390/a13090210 .

Mutingi M, Mbohwa C. Home healthcare worker scheduling: a group genetic algorithm approach. In: Proceedings of the World Congress on Engineering 2013; 2013.

Price KV. Differential evolution. In: Zelinka I, Snasael V, Abraham A, editors. Handbook of optimization. Berlin Heidelberg: Springer; 2013. p. 187–214.

Chapter Google Scholar

Download references

Open Access funding enabled and organized by CAUL and its Member Institutions.

Author information

Authors and affiliations.

Guangdong Technion Israel Institute of Technology, Shantou, China

Institute for Sustainable Industries and Liveable Cities, Victoria University, Melbourne, Australia

Yong-Feng Ge & Hua Wang

School of Health and Biomedical Sciences, RMIT University, Melbourne, Australia

Institute of Mathematics and Computer Sciences, University of São Paulo, São Paulo, Brazil

Agma J. M. Traina

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yong-Feng Ge .

Ethics declarations

Conflict of interest.

The authors have no competing interests to declare that are relevant to the content of this article.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Pang, X., Ge, YF., Wang, K. et al. Patient assignment optimization in cloud healthcare systems: a distributed genetic algorithm. Health Inf Sci Syst 11 , 30 (2023). https://doi.org/10.1007/s13755-023-00230-1

Download citation

Received : 15 February 2023

Accepted : 21 June 2023

Published : 29 June 2023

DOI : https://doi.org/10.1007/s13755-023-00230-1

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Patient assignment
Distributed genetic algorithm
Cloud healthcare system
Evolutionary algorithm
Find a journal
Publish with us
Track your research

6 ways to use Microsoft Copilot for end-of-school-year tasks

May 14, 2024.

By Microsoft Education Team

Share this article

The end of the school year is a hectic time for educators everywhere. Between reviewing content, completing assessments, and maintaining classroom management, it’s easy to feel the pressure of too many responsibilities and not enough time to accomplish everything.

Whether closing out the academic year in the northern hemisphere or preparing for the next one in the southern hemisphere, Microsoft Copilot offers innovative and efficient ways to complete many of the tasks that occupy these transitional times of year. From drafting student feedback to composing newsletters and offering planning suggestions for events, Copilot adapts to whatever task it’s asked. To get started, all you need is a basic understanding of how to access and use Copilot.

Start using Copilot for your end-of-school-year tasks

You can learn how to use Copilot by visiting Meet your AI assistant for education: Microsoft Copilot .

When you’re ready to get started, go to copilot.microsoft.com or download the iOS or Android mobile app.

Writing prompts for the end of the school year

Prompting Copilot to generate content requires practice. Including specific information in your prompt helps produce more relevant responses.

An effective Copilot prompt:

Asks the tool to take on a role called a persona .
Provides an objective that tells the tool what to do or produce.
Defines the audience who will be using whatever Copilot generates.
Includes context that gives the tool background information.
Sets boundaries that limit or constrain responses.

Elements of a Good Prompt infographic which includes tips for writing prompts that produce more relevant responses.

Throughout this post, you’ll find sample prompts that include these components. We recommend borrowing inspiration from them and adjusting to make them fit your own classroom, or you can copy and paste the examples without modifications if you are just beginning.

Now let’s learn how Copilot can help you complete six common end-of-school-year tasks.

1. Craft student feedback at the end of the school year

Copilot can help you write end-of-school-year feedback in a style and tone that all students can understand. Simply craft a prompt that includes the subject area and details about the feedback you want to provide, and Copilot can draft a constructive, supportive statement written specifically for students. For example:

You are a fourth-grade teacher who is writing feedback on a student’s current reading skills. The student uses details to explain what text means but is unable to draw inferences in fiction. The student can identify in-text examples that illustrate a given theme but is unable to independently produce a theme without guidance. Write a short statement that explains this feedback to a student. Include a description about why using details is important and 1-2 ways to develop this skill. The paragraph should be written with plain text so that a fourth-grade student will understand.

You can always refine your prompt if the response is not what you expected. Simply include something like, “Re-write this feedback in Spanish” without selecting New topic , and Copilot will continue where you left off. Give it a try.

2. Write end-of-school-year reflections

Educators often write end-of-school-year newsletters for families, update class blogs with a final post, and draft reflections on school year goals. Copilot can assist with all these tasks and can help you create personalized, engaging visuals for your content. For example, you can use the following prompt to produce a summer newsletter for families.

You are the science department leader for a middle school in New York City. Draft a summer newsletter for families that includes an introduction that talks about the past year and 5 sections: Science Books for Young Adults, Science at Home, Science Summer Camps, Science Events in NYC, and NY Science Museums. Only include information that can be linked to a website to learn more. The newsletter should be written in plain text using an informal tone.

You can also share your experiences, memorable moments, and insights from the school year and Copilot will help you find creative ways to share this information with colleagues, families, and students.

3. Organize classroom materials at the end of the school year

The last few weeks of a school year includes packing up classrooms for the summer, collecting books and devices, and organizing materials for the next year. Copilot can create checklists or reminders for end-of-school-year tasks like these and offer suggestions that you might not even consider. For example:

You are a high school media specialist who checks out technology to administrators and educators. Write a checklist of the 3 most important things to do before returning each of the following devices: document camera, tablet, digital projector, games, and wires. Make each device a section heading and use bulleted lists for the content. Write the checklists so that the content is easily understood by people with varying levels of technological expertise.

Another way to use Copilot when you are organizing classroom materials is to ask for suggestions for efficient ways to declutter and prepare your classroom for the next school year.

4. Plan an end-of-school-year celebration

Many schools celebrate major milestones like the start of summer or moving from lower grades to higher grades with a party or ceremony. Copilot can be your personal planner and assist with brainstorming ideas for end-of-school-year events, awards ceremonies, or virtual gatherings. It can even suggest ways to be more inclusive in areas you might not have considered, like food options in the prompt below.

You are a guidance counselor in charge of helping rising eighth-grade students transition from middle school to high school. Draft a letter to middle school teachers that shares the biggest differences between middle school and high school. Include paragraphs on class schedules, touring the high school, meeting educators, extracurricular activities, and summer reading books. The letter should be written in a formal, conversational tone.

Whether you are creating invitations, planning activities, or drafting speeches, Copilot can be your creative collaborator.

5. Develop transition materials at the end of the school year

When students enter elementary school or move to middle or high school, everyone involved in the transition needs to know how to prepare for this change. Students need to know what to expect, families need to know how to support their children, and current educators need to provide relevant information. Copilot can help create transition materials so that everyone stays informed using a prompt like this example:

You can also use Copilot to write welcome letters, tips for success, or information about what to expect in the upcoming year.

6. Streamline parent communication at the end of the school year

Copilot can help you create templates for parent-teacher conferences at the end of the school year, as well as student progress updates, and letters to families. For example, you can ask Copilot to create a message to families about signing up for conferences with the following prompt.

You are a high school math teacher who teaches introductory algebra. Write a letter to families about parent-teacher conferences. Include an introductory paragraph that thanks families for their ongoing support and paragraphs about what will happen during the conferences, why conferences are important, who should attend, and how to prepare for the meeting. Conclude the letter with a paragraph about how to sign up for a conference slot. Write the letter using an approachable, informal tone.

Microsoft Copilot is a versatile AI tool for educators that adapts to your specific needs. To learn more about Microsoft’s AI solutions and resources, check out Smart learning: AI resources every educator should know and the AI for educators learning path on Microsoft Learn. Most importantly, enjoy the end of the school year with your students and the time you saved by using Copilot.

Explore insights from the AI in Education Report

The swift rise of generative AI is reshaping how schools approach creation, problem-solving, learning, and communication. Your schools are in a pivotal moment when critical thinking and metacognitive skills are more important than ever as new technology develops

How to celebrate Earth Day 2024 with your students

Spark your students' curiosity with Earth Day activities and more from Microsoft. From video games to projects, try these fun Earth Day activities for your class.

Kickstart your school’s AI journey with the Microsoft Education AI Toolkit

AI is igniting enthusiasm in classrooms, department meetings, board rooms, and administrative offices across the country. For many, generative AI is changing what it means to create, solve problems, communicate, and even learn. It’s not just teachers and students embracing this new technology; education leaders are also turning to AI to improve operational processes and provide equitable access to resources among other opportunities.

SCHOOL STORIES
MICROSOFT EDUCATOR CENTER
CONTACT SALES

IMAGES

Dga completion of assignment pay by donuijwn
Ntr 320 practice
Assignment Completion Sheet by Indiana Teacher's Hub
Что такое Dynamic Group Assignment (DGA) на DIGI
Fillable Online Completion of Assignment Form
Assignment 5 operations

VIDEO

Fuse box location and diagrams: Hyundai Matrix (2002-2008)
CSC TEC Exam कैसे पास करें । CSC TEC Certificate Exam Kaise Pass Kare । Exam Questions and Answers
Mere Sai
Hogwarts Legacy
mmpo 008 solved assignment 2023 in english / mmpo 8 solved assignment 2022-23 / ignou mba 2022-23
Nostalgia Digimon Card Battle (ps1) 100% Completion : Igloo City Battle Arena Whamon #part168

COMMENTS

PDF Article 10. Basic Minimum Compensation and Conditions for Associate
1. Completion of Assignment Pay (a) All freelance Associate Directors and Stage Managers, upon completion of an assignment, shall receive Completion of Assignment Pay as follows: (i) Those employed for at least four (4) days per week shall receive one (1) week's pay if employed for two (2) or more consecutive weeks or two and one-half (2½) days
The Ultimate Guide to DGA Theatrical Rates 2020
UPM & AD'S Completion Of Assignment Pay UPMs, 1st ADs, Key 2nd ADs and 2nd 2nd ADs are entitled to an additional week's salary upon completion of assignment if employed two or more consecutive weeks or 2 1/2 days salary if employed at least five consecutive days but less than two consecutive weeks.
PDF ARTICLE 13 Minimum Salary Schedules and Working Conditions of UPMs
upon completion of an assignment, shall receive Completion of Assignment Pay of one (1) week's pay at their respective salary if employed two (2) or more consecutive weeks, and of two (2) and one-half days' pay if employed under two (2) weeks, except in the case of those employed on a daily basis for less than five (5) days.
Essential Guide to the DGA Rate Card 2024
When it comes to DGA commercials, the DGA Rate Card is simple and easy to understand. Regardless of the commercial's scale, the DGA commercial rates for directors must be at least $1,620 for the day or $6,480 for a 5-day week. As with all DGA rates, you should expect to pay an additional 19.4% into the DGA health and pension plan.
Employers / Deal Memos & Reports Compliance Forms
Completion of Assignment ; ... Pursuant to Article 15 of the DGA Basic Agreement and Article 19 of the DGA Freelance Live & Tape Television Agreement, Employers must submit an Employment Data Report identifying the gender and ethnicity of persons employed in DGA-covered categories. The report must also identify Directors employed on prime time ...
Directors Guild of America
The Directors Guild of America (DGA) ... Gross income includes but is not limited to base salary, overtime, residuals, deferments, percentage compensation, completion of assignment, vacation and holiday pay, profit participation and fees of all kinds in any Guild category. DGA members must report all gross earnings from Guild-covered employment ...
What the New DGA Contracts Mean For You
For complete information, review the new contract directly or reach out directly to the Directors Guild of America. With that in mind, let's start with a change that could affect your bottom line. General wages increase. The new DGA contracts effectively update the DGA rate card. It guarantees a series of annual increases to minimum salaries ...
PDF 1) . 3) A d s. dsben p n. tk 6) (L for d. Basic Agreement/Freelance
DGA -Producer Pension ... Please indicate ^ V_ for Vacation Pay or ^ C_ for Completion of Assignment Pay in the V or C column. 5) Refer to Article 12 of the Basic Agreement or Articles 11 and 12 of the Freelance Live & Tape Television Agreement for definition of salary and contribution ceilings.
PDF 2024 JEFFORDS RULES
DGA. Daily or weekly with appropriate completion of assignment pay and guaranteed prep. Basic cable dramatic program: Season 1 - 85% of BA rates, Season 2 & 3 90% of BA rates, for budgets on 1/2 hour between $550,000 & $937,660; 1 hour between $1,200,000 & $1,493,500; 2 hour between $2,750,000 & $4,635,000. All Season 4 - 100%.
Dga
The Directors Guild has established a Producer Training Plan for training a sufficient number of qualified Assistant Directors and UPMs to meet the needs of the industry. ... Completion of Assignment Pay Completion of Assignment Pay is based on actual salary paid and will be computed by totaling all compensation earned and dividing the total by ...
PDF DirectorsGuild of America -Producer Pension and Health Plans
(do not use for Vacation Pay or Completion of Assignment Pay) For projects produced on or after July 1, 2013 under the Basic Agreement/Freelance Live & Tape Television Agreement (do not use for commercials or projects produced under other agreements ... DGA-ProducerPension and Health Plans 5055 Wilshire Boulevard, 6th Floor Los Angeles, CA ...
PDF 75 DGA Policy Guidance-1
The current norm, per the Guidelines, states between three and five selectees each year. With that in mind, the goal of the 1975 DGA Committee is to put forth those most deserving and whose package is both compelling and competitive for that selection cycle. All members of the 1975 DGA Committee will be selected by the Class President.
Assignments: why you need to serve a notice of assignment
It's the day of completion; security is taken, assignments are completed and funds move. Everyone breathes a sigh of relief. At this point, no-one wants to create unnecessary paperwork - not even the lawyers! Notices of assignment are, in some circumstances, optional. ... An assignment can be a legal assignment or an equitable assignment. If a ...
PDF DGA Plans Signatory Guide
5055 Wilshire Blvd, Suite 600 Los Angeles, CA 90036 (323) 866-2200 (877) 866-2200 www.dgaplans.org. Updated February 2024. The Directors Guild of America-Producer Pension and Health Plans (Plans) are Employee benefit plans created by tax exempt trusts established through collective bargaining between the Directors Guild of America (DGA) and ...
PDF Research: The Assignment Completion Strategy
assignment completion per week. During the instructional and maintenance conditions, they earned an average of 28% and 60% of the points, respectively. With regard to actual assignment completion, students turned in an average of 54% of their assignments during baseline and an average of 58% of their assignments during instruction in the strategy.
PDF ADDITIONAL INFORMATION FOR ADs and UPMs
There is no cap on the number of Completion of Assignment events. Except as defined below, UPMs, 1st ADs, Key 2nd ADs, 2nd 2ADs, and Associate Directors employed on a "tape style" show (where there is a line cut) are entitled to 50% of Completion of Assignment pay for all hiatus periods or periods of layoffs. The final Completion of Assignment
PDF Effects of Instruction in an Assignment Completion Strategy on the
Teacher Ratings. At the beginning of the study, the mean teacher ratings (on a six-point scale) for all the students were 3.3 for organization, 3.7 for turning assignments in on time, 3.8 for quality of work, and 3.9 for accuracy. At the end of the study, the mean ratings were 4.7, 5.0, 4.8, and 5.2, respectively.
Dga completion of assignment pay by donuijwn
Read Dga completion of assignment pay by donuijwn on Issuu and browse thousands of other publications on our platform. Start here!
Patient assignment optimization in cloud healthcare systems: a
These systems aim to optimize the balance between online diagnosis and offline treatment to effectively reduce patients' waiting times and improve the utilization of idle medical resources. In this paper, a distributed genetic algorithm (DGA) is proposed as a means to optimize the balance of patient assignment (PA) in cloud healthcare systems.
Patient assignment optimization in cloud healthcare systems ...
The best results (i.e., the lowest Avg values) in all the test instances are labeled in boldface. Overall, the complete-version DGA can outperform the compared variants on all 16 test instances. Compared with DGA-no-crossover, DGA shows its advantage in terms of the crossover operator, effectively exchanging allocation between parent individuals.
6 ways to use Microsoft Copilot for end-of-school-year tasks
Give it a try. 2. Write end-of-school-year reflections. Educators often write end-of-school-year newsletters for families, update class blogs with a final post, and draft reflections on school year goals. Copilot can assist with all these tasks and can help you create personalized, engaging visuals for your content.

Bradley DeRuiter

Here is a layout of what you will find in the order of appearance:

Important DGA rates and dates

DGA Basic Agreement Director Rate Table

6th and 7th Days Worked; Holidays Worked

Director Fringe Rates for Basic and Low Budget

Unit Production Managers & Assistant Directors Minimum Rates

Extended Workday

UPM & AD’S Completion Of Assignment Pay

UPM and AD’s Employer Contributions Fring Rates

Low Budget Agreement Director Rates Table

Low Budget UPM & AD's Minimum Rates

Low Budget Agreement Levels 1 - 3

Low Budget Agreement Level 4 UPM, AD’s Rate Table

Low Budget Agreement Extended Workdays

Do you need production payroll ?

Don't foget to share this post

Assignments: why you need to serve a notice of assignment

What issues are there with serving notice of assignment?

Why should we serve a notice of assignment?

Why not serve notice?

What about acknowledgements of notices?

Best practice for serving notice of assignment

Related Insights & Resources

Patient assignment optimization in cloud healthcare systems: a distributed genetic algorithm

Yong-Feng Ge

Agma J. M. Traina

Introduction

Problem formulation

Related work

Genetic algorithm

Distributed genetic algorithm for patient assignment

Representation and initialization

Distributed framework

Crossover operator

Mutation operator

Overall procedure

Experimental setup

Experimental result

Impact of proposed components

Declarations

Patient assignment optimization in cloud healthcare systems: a distributed genetic algorithm

Cite this article

Similar content being viewed by others

A review on genetic algorithm: past, present, and future

Genetic algorithms: theory, genetic operators, solutions, and applications

Evolutionary algorithms and their applications to engineering problems

Introduction

Problem formulation

Related work

Genetic algorithm

Distributed genetic algorithm for patient assignment

Representation and initialization

Distributed framework

Crossover operator

Mutation operator

Overall procedure

Experimental setup

Experimental result

Comparison with existing approaches

Impact of proposed components

Author information

Corresponding author

Ethics declarations

Additional information

Rights and permissions

About this article

Share this article

6 ways to use Microsoft Copilot for end-of-school-year tasks

Share this article

Start using Copilot for your end-of-school-year tasks

Writing prompts for the end of the school year

1. Craft student feedback at the end of the school year

2. Write end-of-school-year reflections

3. Organize classroom materials at the end of the school year

4. Plan an end-of-school-year celebration

5. Develop transition materials at the end of the school year

6. Streamline parent communication at the end of the school year

Related stories

Explore insights from the AI in Education Report