cubic equations problem solving

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Solving Cubic Equations – Methods & Examples

Solving Cubic Equations – Methods & Examples

This article will discuss how to solve the cubic equations using different methods such as the division method, Factor Theorem, and factoring by grouping.

But before getting into this topic, let’s discuss what a polynomial and cubic equation is.

A polynomial is an algebraic expression with one or more terms in which an addition or a subtraction sign separates a constant and a variable.

How to Solve Cubic Equations?

The traditional way of solving a cubic equation is to reduce it to a quadratic equation and then solve it either by factoring or quadratic formula.

Like a quadratic equation has two real roots , a cubic equation may have possibly three real roots. But unlike a quadratic equation, which may have no real solution, a cubic equation has at least one real root.

The other two roots might be real or imaginary.

Whenever you are given a cubic equation or any equation, you always have to arrange it in a standard form first.

For example, if you are given something like this, 3x 2 + x – 3 = 2/x, you will re-arrange into the standard form and write it like, 3x 3 + x 2 – 3x – 2 = 0. Then you can solve this by any suitable method.

Let’s see a few examples below for better understanding:

Determine the roots of the cubic equation 2x 3  + 3x 2  – 11x – 6 = 0

Since d = 6, then the possible factors are 1, 2, 3 and 6.

Now apply the Factor Theorem to check the possible values by trial and error.

f (1) = 2 + 3 – 11 – 6 ≠ 0 f (–1) = –2 + 3 + 11 – 6 ≠ 0 f (2) = 16 + 12 – 22 – 6 = 0

Hence, x = 2 is the first root.

We can get the other roots of the equation using synthetic division method. = (x – 2) (ax 2  + bx + c) = (x – 2) (2x 2  + bx + 3) = (x – 2) (2x 2  + 7x + 3) = (x – 2) (2x + 1) (x +3)

Therefore, the solutions are x = 2, x = -1/2 and x = -3.

Find the roots of the cubic equation x 3 − 6x 2 + 11x – 6 = 0

x 3 − 6x 2 + 11x – 6

(x – 1) is one of the factors.

By dividing x 3 − 6x 2 + 11x – 6 by (x – 1),

⟹ (x – 1) (x 2 – 5x + 6) = 0

⟹ (x – 1) (x – 2) (x – 3) = 0

This of the cubic equation solutions are x = 1, x = 2 and x = 3.

Solve x 3  – 2x 2  – x + 2

Factorize the equation.

x 3  – 2x 2  – x + 2 = x 2 (x – 2) – (x – 2)

= (x 2  – 1) (x – 2)

= (x + 1) (x – 1) (x – 2)

x = 1, -1 and 2.

Solve the cubic equation x 3  – 23x 2  + 142x – 120

First factorize the polynomial.

x 3  – 23x 2  + 142x – 120 = (x – 1) (x 2  – 22x + 120)

But x 2  – 22x + 120 = x 2  – 12x – 10x + 120

= x (x – 12) – 10(x – 12) = (x – 12) (x – 10)

Therefore, x 3  – 23x 2  + 142x – 120 = (x – 1) (x – 10) (x – 12)

Equate each factor to zero.

x – 10 = 10

The roots of the equation are x = 1, 10 and 12.

Solve the cubic equation x 3  – 6 x 2  + 11x – 6 = 0.

To solve this problem using division method, take any factor of the constant 6;

Divide the polynomial by x-2 to

(x 2  – 4x + 3) = 0.

Now solve the quadratic equation (x 2  – 4x + 3) = 0 to get x= 1 or x = 3

Therefore, the solutions are x = 2, x= 1 and x =3.

Solve the cubic equation x 3  – 7x 2  + 4x + 12 = 0

Let f(x) = x 3  – 7x 2  + 4x + 12

Since d = 12, the possible values are 1, 2, 3, 4, 6 and 12.

By trial and error, we find that f (–1) = –1 – 7 – 4 + 12 = 0

So, (x + 1) is a factor of the function.

x 3  – 7x 2  + 4x + 12 = (x + 1) (x 2  – 8x + 12) = (x + 1) (x – 2) (x – 6)

Therefore x = –1, 2, 6

Solve the following cubic equation:

x 3  + 3x 2  + x + 3 = 0.

x 3  + 3x 2  + x + 3 = (x 3  + 3x 2 ) + (x + 3) = x 2 (x + 3) + 1(x + 3) = (x + 3) (x 2  + 1)

Therefore, x = -1 ,1 -3.

Solve x 3 − 6x 2 + 11x − 6 = 0

x 3 − 6x 2 + 11x − 6 = 0 ⟹ (x − 1) (x − 2) (x − 3) = 0

Equating each factor to zero gives;

x = 1, x = 2 and x = 3

Solve x 3 − 4x 2 − 9x + 36 = 0

Factorize each set of two terms.

x 2 (x − 4) − 9(x − 4) = 0

Extract the common factor (x − 4) to give

(x 2 − 9) (x − 4) = 0

Now factorize the difference of two squares

(x + 3) (x − 3) (x − 4) = 0

By equating each factor to zero, we get;

x = −3, 3 or 4

Solve the equation 3x 3  −16x 2  + 23x − 6 = 0

Divide 3x 3  −16x 2  + 23x – 6 by x -2 to get 3x 2  – 1x – 9x + 3

= x (3x – 1) – 3(3x – 1)

= (x – 3) (3x – 1)

Therefore, 3x 3  −16x 2  + 23x − 6 = (x- 2) (x – 3) (3x – 1)

Equate each factor to zero to get,

x = 2, 3 and 1/3

Find the roots of 3x 3  – 3x 2  – 90x=0

factor it out 3x

3x 3  – 3x 2  – 90x ⟹3x (x 2  – x – 30)

Find a pair of factors whose product is −30 and sum is −1.

⟹- 6 * 5 =-30

⟹ −6 + 5 = -1

Rewrite the equation by replacing the term “bx” with the chosen factors.

⟹ 3x [(x 2  – 6x) + (5x – 30)]

Factor the equation;

⟹ 3x [(x (x – 6) + 5(x – 6)]

= 3x (x – 6) (x + 5)

x = 0, 6, -5

Solving cubic equations using graphical method

If you cannot solve the cubic equation by any of the above methods, you can solve it graphically. For that, you need to have an accurate sketch of the given cubic equation.

The point(s) where its graph crosses the x-axis, is a solution of the equation. The number of real solutions of the cubic equations is same as the number of times its graph crosses the x-axis.

Find the roots of x 3  + 5x 2  + 2x – 8 = 0 graphically.

Simply draw the graph of the following function by substituting random values of x:

f (x) = x 3  + 5x 2  + 2x – 8

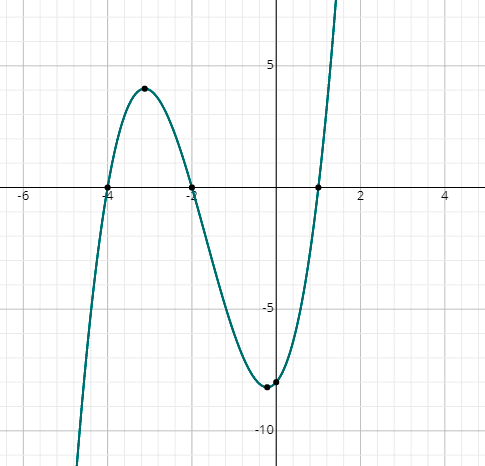
You can see the graph cuts the x-axis at 3 points, therefore, there are 3 real solutions.

From the graph, the solutions are:

x = 1, x = -2 & x = -4.

Practice Questions

Previous Lesson  |  Main Page | Next Lesson

Solving Cubic Equations

In these lessons, we will learn how to solve cubic equations using the Remainder Theorem and the Factor Theorem.

Related Pages Cubic Functions Factor Theorem Remainder Theorem More Algebra Lessons More Algebra Worksheets More Algebra Games

What is the Remainder Theorem?

If a polynomial, f(x), is divided by x - k, the remainder is equal to f(k).

What is the Factor Theorem?

x - k is a factor of the polynomial f(x) if and only if f(k) = 0

How to solve cubic equations using the Factor Theorem?

In these lessons, we will consider how to solve cubic equations of the form px 3 + qx 2 + rx + s = 0 where p, q, r and s are constants by using the Factor Theorem and Synthetic Division.

The following diagram shows an example of solving cubic equations. Scroll down the page for more examples and solutions on how to solve cubic equations.

Example: Find the roots of f(x) = 2x 3 + 3x 2 – 11x – 6 = 0, given that it has at least one integer root.

Step 1: Use the factor theorem to test the possible values by trial and error.

f(1) = 2 + 3 – 11 – 6 ≠ 0 f(–1) = –2 + 3 + 11 – 6 ≠ 0 f(2) = 16 + 12 – 22 – 6 = 0 We find that the integer root is 2.

Step 2: Find the other roots either by inspection or by synthetic division .

2x 3 + 3x 2 – 11x – 6 = (x – 2)(ax 2 + bx + c) = (x – 2)(2x 2 + bx + 3) = (x – 2)(2x 2 + 7x + 3) = (x – 2)(2x + 1)(x +3)

Example: Solve the cubic equation x 3 – 7x 2 + 4x + 12 = 0

Solution: Let f(x) = x 3 – 7x 2 + 4x + 12

We find that f(–1) = –1 – 7 – 4 + 12 = 0

So, (x + 1) is a factor of f(x)

x 3 – 7x 2 + 4x + 12 = (x + 1)(x 2 – 8x + 12) = (x + 1)(x – 2)(x – 6) So, the roots are –1, 2, 6

What are The Remainder Theorem and the Factor Theorem? How to use the Theorems to find the linear factorization of a polynomial? Example: Factor F(x) = 2x 3 − 3x 2 − 5x + 6

How to use the Factor Theorem to factor polynomials? Examples:

• Factor P(x) = 3x 3 − x 2 − 10x + 8
• Factor P(x) = 2x 3 − 9x 2 + x + 12

How to use the Factor Theorem to solve a cubic equation? If f(x) is a polynomial and f(p) = 0 then x - p is a factor of f(x) Example: Solve the equation 2x 3 −5x 2 − 10 = 23x

How to solve Cubic Equations using the Factor theorem and Long Division? Example: Find the roots of the cubic equation 2x 3 − 6x 2 + 7x − 1 = 0

How to solve Cubic Equations using the Factor theorem and Synthetic Division? Example: Show that x + 3 is a factor of x 3 − 19x − 30 = 0. Then find the remaining factors of f(x)

How to solve cubic equation problems? Example: 3x 3 −4x 2 − 17x = x 3 + 3x 2 − 10 Step 1: Set one side of equation equal to 0. Step 2: Collect like terms. Step 3: Factorize using the Factor Theorem and Long Division

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve a Cubic Equation

Last Updated: August 15, 2023 Fact Checked

This article was co-authored by David Jia and by wikiHow staff writer, Christopher M. Osborne, PhD . David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math. There are 10 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 1,127,294 times.

Solving Cubic Equations without a Constant

• You can also factor it by grouping .

Finding Integer Solutions with Factor Lists

• Synthetic division is a complex topic that’s beyond the scope of describing fully here. However, here's a sample of how to find one of the solutions to your cubic equation with synthetic division: -1 | 2 9 13 6 __| -2-7-6 __| 2 7 6 0

Using a Discriminant Approach

• A cubic equation always has at least one real solution, because the graph will always cross the x-axis at least once.

• You can solve the example by checking the answer when n is equal to 1 , 2 , and 3 . The answers you get from these tests are the possible answers to the cubic equation — any that give an answer of 0 when plugged into the equation are correct.

Practice Problems and Answers

Expert Q&A

You Might Also Like

• ↑ https://brilliant.org/wiki/cubic-equations/
• ↑ https://www.mathcentre.ac.uk/resources/uploaded/mc-ty-cubicequations-2009-1.pdf
• ↑ https://sciencing.com/solve-cubic-equations-8136094.html
• ↑ https://www.purplemath.com/modules/quadform.htm
• ↑ https://math.vanderbilt.edu/schectex/courses/cubic/
• ↑ https://www.geeksforgeeks.org/solving-cubic-equations/
• ↑ https://mathworld.wolfram.com/CubicFormula.html
• ↑ https://courses.cs.washington.edu/courses/cse590b/13au/lecture_notes/cubic.pdf

About This Article

To solve a cubic equation, start by determining if your equation has a constant. If it doesn't, factor an x out and use the quadratic formula to solve the remaining quadratic equation. If it does have a constant, you won't be able to use the quadratic formula. Instead, find all of the factors of a and d in the equation and then divide the factors of a by the factors of d. Then, plug each answer into the equation to see which one equals 0. Whichever integer equals 0 is your answer. Read on to learn how to solve a cubic equation using a discriminant approach! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Sep 14, 2017

Did this article help you?

Feb 5, 2017

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Get all the best how-tos!

Sign up for wikiHow's weekly email newsletter

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.5: Cubic equations

• Last updated
• Save as PDF
• Page ID 23468

• Alexandre Borovik & Tony Gardiner
• University of Manchester & University of Birmingham via Open Book Publishers

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

The first recorded procedure for finding the positive roots of any given quadratic equation dates from around 1700 BC (ancient Babylonian). A corresponding procedure for cubic equations had to wait until the early sixteenth century AD. The story is a slightly complicated one - involving public contests, betrayal, and much else besides.

In Section 4.4 we saw that the cubic equation x 3 = 1 has three solutions - two of which are complex numbers. But in the sixteenth century, even negative numbers were viewed with suspicion, and complex numbers were still unknown. Moreover, symbolical algebra had not yet been invented, so everything was carried out in words: constants were “numbers”; a given multiple of the unknown was referred to as so many “things”; a given multiple of the square of the unknown was simply referred to as “squares”; and so on.

In short, we know that an improved method for sometimes finding a (positive) unknown which satisfied a cubic equation was devised by Scipione del Ferro (1465–1526) around 1515. He kept his method secret until just before his death, when he told his student Antonio del Fiore (1506-??). Niccolo Tartaglia (1499–1557) then made some independent progress in solving cubic equations. At some stage (around 1535) Fiore challenged Tartaglia to a public “cubic solving contest”. In preparing for this event, Tartaglia managed to improve on his method, and he seems to have triumphed in the contest. Tartaglia naturally hesitated to divulge his method in order to preserve his superiority, but was later persuaded to communicate what he knew to Girolamo Cardano (1501–1576) after Cardano promised not to publish it (either never, or not before Tartaglia himself had done so). Cardano improved the method, and his student Ferrari (1522–1565) extended the idea to give a method for solving quartic equations - all of which Cardano then published, contrary to his promise, but with full attribution to the rightful discoverers, in his groundbreaking book Ars Magna (1545 -just two years after Copernicus (1473–1543) published his De revolutionibus ...). Problem 134 illustrates the necessary first move in solving any cubic equation. Problem 135 then illustrates the general method in a relatively simple case.

Problem 134

(a) Given the equation x 3 + 3 x 2 − 4 = 0, choose a constant a, and then change variable by substituting y = x + a to produce an equation of the form y 3 + ky = constant.

(b) In general, given any cubic equation ax 3 + bx 2 + c x + d = 0 with a ≠ 0 , show how to change variable so as to reduce this to a cubic equation with no quadratic term.

Problem 135 The equation x 3 + 3 x 2 − 4 = 0 clearly has “ x = 1” as a positive solution. (The other two solutions are x = −2, and x = −2 - a repeated root; however negatives were viewed with suspicion in the sixteenth century, so this root might well have been ignored.) Try to understand how the following sequence of moves “finds the root x = 1”:

(i) substitute y = x + 1 to get a cubic equation in y with no term in y 2 ;

(ii) imagine y = u + v and interpret the identity for

( u + v ) 3 = u 3 + 3 u v ( u + v ) + v 3

as your cubic equation in y ;

(iii) solve the simultaneous equations “3 uv = 3”, “ u 3 + v 3 = 2” (not by guessing, but by substituting v = 1 u from the first equation into the second to get a quadratic equation in “ u 3 ”, which you can then solve for u 3 before taking cube roots);

(iv) then find the corresponding value of v , hence the value of y = u + v , and hence the value of x .

The simple method underlying Problem 135 is in fact completely general. Given any cubic equation

a x 3 + b x 2 + c x + d = 0   ( with   a ≠ 0 )

we can divide through by a to reduce this to

x 3 + p x 2 + q x + r = 0

with leading coefficient = 1. Then we can substitute y = x + p 3 and reduce this to a cubic equation in y

y 3 − 3 ( p 3 ) 2 y + q y + [ r + 2 ( p 3 ) 3 − q ( p 3 ) ] = 0

which we can treat as having the form

y 3 − m y − n = 0.

So we can set y = u + v (for some unknown u and v yet to be chosen), and treat the last equation as an instance of the identity

( u + v ) 3 − 3 u v ( u + v ) − ( u 3 + v 3 ) = 0

which it will become if we simply choose u and v to solve the simultaneous equations

3 u v = m ,   u 3 + v 3 = n .

We can then solve these equations to find u , then v - and hence find y = u + v and x = y − p 3 .

• Number Theory
• Data Structures
• Cornerstones

Solving The General Cubic Equation

The tschirnhause-vieta approach.

Having now covered the basics of trigonometry, let's see how we can put this together with the depressed terms method of solving quadratic equations to solve cubic equations whose roots are all real. As a concrete example, let us consider the following cubic equation: $$x^3 - 2x^2 - 5x + 6 = 0$$ Note that we have $3$ occurences of $x$ in the above. We hope to eliminate $2$ of them, so that we can apply the socks and shoes principle.

Francois Viete (whom we've discussed before) and German mathematician Ehrenfried Walther von Tschirnhaus realized that the method of depressed terms provides the opportunity to eliminate $1$ of these fairly easily.

Suppose that the function $f(x)$ outputs the value of the left side of our equation. Then consider the function $g(x) = f(x+h)$, whose graph is some shift of the graph of $y=f(x)$. As when we applied this method to solving quadratics, note that the graph of $y=g(x)$ is simply a horizontal shift of the graph of $y=f(x)$.

While the sign of $h$ determines whether this shift is to the left or right, should we find any roots to $g(x) = 0$ we can deduce corresponding roots to $f(x)=0$ by simply adding $h$ to each of the found roots to $g(x) = 0$.

Plugging in $(x+h)$ as input to $f$ and expanding the result as quadratic in $x$, we find $$\begin{array}{rcl} g(x) &=& f(x+h)\\ &=& (x+h)^3 - 2(x+h)^2 - 5(x+h) + 6\\ &=& x^3 + 3x^2 h + 3xh^2 + h^3 -2x^2 - 4xh - 2h^2 - 5x - 5h + 6\\ &=& x^3 + (3h-2)x^2 + (3h^2 - 4h - 5)x + (h^3 - 2h^2 - 5h + 6)\\ \end{array}$$ As before, we may find it useful to note that the constant term of $g(x)$ must always be $f(h)$, given the way it was defined.

Note the coefficient on the quadratic term, however. Just as we can depress the linear term in a quadratic to find its solutions, let us here depress the quadratic term for the resulting cubic to solve this problem. That is to say, let us find $h$ so that $(3h-2) = 0$, so that $g(x)$ has no quadratic term.

This of course is almost immediate, as $3h-2 = 0$ implies $h=\frac{2}{3}$

Now, finding the rest of $g(x)$ for this special $h$ value, we have $$\begin{array}{rcl} g(x) &=& x^3 + \left(3 (\frac{2}{3})^2 - 4 (\frac{2}{3}) - 5\right) x + \left((\frac{2}{3})^3 - 2(\frac{2}{3})^2 - 5(\frac{2}{3}) + 6\right)\\ &=& x^3 + \left(\frac{4}{3} - \frac{8}{3} - \frac{15}{3}\right) x + \left( \frac{8}{27} - \frac{24}{27} - \frac{90}{27} + \frac{162}{27}\right)\\ &=& x^3 - \frac{19}{3} x + \frac{56}{27}\\ \end{array}$$ As such, the roots of $f(x) = 0$ can be found by adding $h=\frac{2}{3}$ to each root of $x^3 - \frac{19}{3} x + \frac{56}{27} = 0$. The problem, however, is that this last equation still has more than one occurrence of $x$. This is where trigonometry can help!

Notice that if we solve for the constant in this equation, we get $$-\frac{56}{27} = x^3 - \frac{19}{3}x$$ Now recall the triple-angle formula for the cosine: $$\cos 3\theta = 4\cos^3 \theta - 3\cos \theta$$ Notice the similarities between the two. On their right sides, we have in both situations a cubic and a linear term -- in terms of $x$ for the first, and in terms of $\cos \theta$ for the second.

Our aim is to make these two look even closer in form, and then assume some nice relationship exists between them (i.e., one where we can solve for either in terms of the other), allowing us to make a clever substitution (more on that in a minute).

With this in mind, and noting that there is a coefficient on the $\cos^3 \theta$ term but not on the $x^3$ term, -- let's divide the equation in $\theta$ by $4$ to get $$\frac{\cos 3\theta}{4} = \cos^3 \theta - \frac{3}{4} \cos \theta$$ Now for the clever substitution! Suppose we choose $\theta$ and some real value $a$ so that $x = a\cos \theta$. There are lots of $(a,\theta)$ pairs possible here. To see this, note that when $0 \lt \theta \lt \frac{\pi}{2}$, increasing $\theta$ by a "smidge" will require decreasing $a$ by some amount to keep their product equal to $x$. Similar things happen when $\theta$ is in other ranges.

The many options we have for the particular pair of $\theta$ and $a$ values we will use gives us some flexibility to make some desired thing happen -- just as there were many $h$ we could have used to define $g(x)$, so we picked the one that would make the quadratic term disappear.

Let's consider what happens if $x = a\cos \theta$ and we use this to rewrite our equation currently in terms of $x$ to be in terms of $\cos \theta$: $$-\frac{56}{27} = (a \cos \theta)^3 - \frac{19}{3}(a \cos \theta)$$ Dividing both sides by $a^3$ (to return the coefficient on $\cos^3 \theta$ to $1$, we have $$-\frac{56}{27a^3} = \cos^3 \theta - \frac{19}{3a^2} \cos \theta$$ Recall again the earlier relationship stemming from the triple-angle formula: $$\frac{\cos 3\theta}{4} = \cos^3 \theta - \frac{3}{4} \cos \theta$$ If we can make the right side of our equation look exactly like the right side of the equation immediately above, then we could replace it with $\frac{1}{4} \cos 3\theta$. This would reduce the number of occurrences of our variable down to a single occurrence -- allowing us to solve the rest with the socks and shoes principle. Given this, let us choose the value $a$ to be the one that will make the coefficient on $\cos \theta$ equal to $\frac{3}{4}$.

We should pause for a moment here and consider what could have happened just now had we attacked a slightly different cubic equation. Suppose the $19$ above had been negative. This could easily happen! (Can you make a cubic where it does?) In such a case, the two values associated with the variable $a$ will then be complex. As will be seen in the paragraphs coming, such a situation would require we consider when the cosine of an angle is complex! Certainly this never happens when the input to the cosine is real -- but what if the cosine function (and others) could accept complex-valued inputs? Lest we get ahead of ourselves, let us leave those exciting possibilities linger for now. But don't worry, we'll pick them up again soon!

With two options for $a$ that both accomplish what we seek to do, let us pick the positive one. With $a = \frac{2}{3}\sqrt{19}$, we then have $$ \frac{-56}{27 ( \frac{2}{3} \sqrt{19} )^3} = \cos^3 \theta - \frac{3}{4} \cos \theta $$ Simplifying the left side and then swapping sides (just to make it look prettier), we have $$\cos^3 \theta - \frac{3}{4} \cos \theta = -\frac{7}{19^{3/2}}$$ Finally, we have thus set ourselves up to replace the two occurrences of $\theta$ with a single one -- using the relationship resulting from the triple-angle formula for cosine: $$\frac{\cos 3\theta}{4} = -\frac{7}{19^{3/2}}$$ From here, we use socks and shoes. Of course, we must be careful when navigating the one "wrinkle" that the cosine function is technically not invertible. That said, we know how to find (using the arccosine function, $\cos^{-1}$) all angles for which their cosine equals some given value. $$\begin{array}{rcl} \displaystyle{\frac{\cos 3\theta}{4}} &=& -\displaystyle{\frac{7}{19^{3/2}}}\\\\ \cos 3\theta &=& \displaystyle{-\frac{28}{19^{3/2}}}\\\\ 3\theta &=& \pm \displaystyle{\cos^{-1} \left(\frac{-28}{19^{3/2}}\right)+2\pi n \quad \textrm{where $n$ is an integer}}\\\\ \theta &=& \pm \displaystyle{\frac{1}{3} \cos^{-1} \left(\frac{-28}{19^{3/2}}\right)+\frac{2\pi n}{3} \quad \textrm{where $n$ is an integer}}\\\\ \end{array}$$ Our last steps are to work backwards from this solution for $\theta$, first to a solution $x$ to $g(x)=0$, and then to a solution $x$ to $f(x)=0$.

Recall that we let $x = a \cos \theta$, except now we know the value of $a$ we wanted -- namely, $a = \frac{2}{3}\sqrt{19}$. As such, the following $x$ solves $g(x)=0$: $$x = \frac{2}{3}\sqrt{19} \cos \left(\pm \frac{1}{3} \cos^{-1} \left(\frac{-28}{19^{3/2}}\right)+\frac{2\pi n}{3}\right) \quad \textrm{where $n$ is an integer}$$ All that remains is to add $h=\frac{2}{3}$ to these solutions to find the $x$ values that solve $f(x)=0$ $$x = \frac{2}{3}\sqrt{19} \cos \left(\pm \frac{1}{3} \cos^{-1} \left(\frac{-28}{19^{3/2}}\right)+\frac{2\pi n}{3}\right) + \frac{2}{3}\quad \textrm{where $n$ is an integer}$$ Of course, we probably want to simplify these if we can! Evaluating the above with a calculator for $n=0$, $n=1$, and $n=2$ and the "$+$" option (things start to repeat after that), we shockingly get the below as our solution! $$x = 1, x = -2, \textrm{ or } x = 3$$ Note we can easily verify this, as if true our original polynomial should factor into: $$x^2 - 2x^2 - 5x + 6 = (x-1)(x+2)(x-3)$$ Expanding the right side, we see that this is true. Wow! 😀

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}
• Is there a step by step calculator for math?
• Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. It shows you the solution, graph, detailed steps and explanations for each problem.
• Is there a step by step calculator for physics?
• Symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and magnetism, and thermodynamics. It shows you the steps and explanations for each problem, so you can learn as you go.
• How to solve math problems step-by-step?
• To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem.

cubic-equation-calculator

• Practice Makes Perfect Learning math takes practice, lots of practice. Just like running, it takes practice and dedication. If you want...

Please add a message.

Message received. Thanks for the feedback.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 2   >   Unit 10

Solving cube-root equations, want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Reset password New user? Sign up

Existing user? Log in

Solving Cubic Equations - Lagrange's Resolvent

Already have an account? Log in here.

We all can solve quadratic equations of the form \(ax^2 + bx + c = 0\) where \(a \neq 0\). Simple, isn't it. Even, we have also devised formulaes like:

\[x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]

for that general quadratic. Has anyone wondered about solving higher degree equations? Cubics (of degree 3), quartics (of degree 4), quintics (of degree 5), sextics (of degree 6), etc.? Probably. We might have heard about Cardano's formula in cubics and Ferrari's solution in quartics. Even, we might know about the Tschirnhausen transformation and all to obtain depressed equations to solve the original. Hey wait, we also have a solution for cubics using trigonometry.

We'll discuss here a way to solve cubics. One is the Traditional Cardano's Solution as we all know. Let's explore the rest.

• Lagrange's Resolvents ( A Brief Idea ) :

Guys, do you know about the Abel-Ruffini Theorem ? Maybe. Forget that. I'm presenting you a statement, and if you don't know it, just accept it for the present moment.

Galois theory has established that formulas using a finite number of arithmetic operations and root extractions are impossible for general equations of degree greater than four.

What? Really? So, can't we generalize formulas for degree 5+ equations?

Joseph-Louis Lagrange (1736-1813) had something in store. What Lagrange realized was that to solve equations of prime degree \(n\) with rational coefficients, one has to solve a resolvent equation of degree \(n-1\) also with rational coefficients, which are now called Lagrange resolvents. Please remember that he is talking about prime degrees, like cubics, quintics, heptics, degrees - 11, 13, and so on.

Now here comes our Mathematics!

Using Lagrange's resolvents, to solve the cubic, one has to first solve a quadratic.

Given the general cubic, \(x^3 + ax^2 + bx + c = 0\)

it's resolvent equation is given by

\[z^2 + (2a^3 - 9ab + 27c)z + (a^2-3b)^3 = 0\]

such that the solution to the cubic is \[x= \dfrac{-a + z_1^{1/3} + z_2^{1/3}}{3}\] where \(z_1, z_2\) are roots of the resolvent.

One can note two things. First, the solution is analogous to the quadratic formula. And while Galois theory has established that formulas using a finite number of arithmetic operations and root extractions are impossible for general equations of degree greater than four, there are particular equations solvable as such. So the solution to the solvable quintic should be similar in form, namely,

\[x = \dfrac{-a + z_1^{1/5} + z_2^{1/5} + z_3^{1/5} + z_4^{1/5} }{5}\]

where \(z_i\) are the roots of the Lagrange's quartic resolvent.

We can obtain similar solutions for solvable degrees - 7, 11, 13, 17, ..

Let's take an example:

Let the cubic be \(x^3 - 5x^2 + x - 7 = 0\)

Resolvent is \(z^2 -394z + 22^3 = 0\)

with roots \(z_i = 197 \pm \sqrt{3129}\)

Thus \(x = \large{\boxed{ \dfrac{5 + \left(197 + \sqrt{3129} \right)^{1/3} + \left(197 - \sqrt{3129} \right)^{1/3}}{3} }} \approx 5.07475\)

And we know how to obtain the rest two roots of a cubic if we are presented with one of the roots.

The important issue here is to find the Lagrange's Resolvents for other higher degrees. Can you think of some?

In the subsequent issues, I'll be posting various other ways to solve a cubic like - Cardano's solution, Translation, Linear Fractional Transformations.

Problem Loading...

Note Loading...

Set Loading...

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes
• Algebra in Math: Definition, Branches, Basics and Examples

Basics of Algebra

• What is a variable in algebra?
• Algebraic Expressions in Math: Definition, Example and Equation
• Like and Unlike Algebraic Terms: Definition and Examples
• Mathematical Operations on Algebraic Expressions - Algebraic Expressions and Identities | Class 8 Maths

Algebraic Expression

• Algebra | Set -1
• Algebraic Identities
• Factorization of Polynomial
• Division of Algebraic Expressions

Polynomials

• Polynomials - Definition, Standard Form, Types, Identities, Zeroes
• Types of Polynomials
• Zeros of Polynomial
• Geometrical meaning of the Zeroes of a Polynomial
• Multiplying Polynomials
• Dividing Polynomials - Long Division Algorithm
• Division Algorithm for Polynomials
• Division Algorithm Problems and Solutions
• Remainder Theorem
• Factor Theorem
• Algebraic Identities of Polynomials
• Factoring Polynomials
• Relationship between Zeroes and Coefficients of a Polynomial

Linear Equations

• Linear Equations in One Variable
• Solve Linear Equations with Variable on both Sides
• Graphical Methods of Solving Pair of Linear Equations in Two Variables
• Reducing Equations to Simpler Form | Class 8 Maths
• Linear Equation in Two Variables
• Graph of Linear Equations in Two Variables
• Equations of Lines Parallel to the x-axis and y-axis
• Pair of Linear Equations in Two Variables
• Number of Solutions to a System of Equations Algebraically
• Solve the Linear Equation using Substitution Method
• Cross Multiplication Method
• Equations Reducible to Linear Form

Quadratic Equations

• Quadratic Equations - Roots, Solution, Formula and Examples
• Solving Quadratic Equations
• Roots of Quadratic Equation

Cubic Equations

• Cubic Equation Formula

Solving Cubic Equations

Sequence and series.

• Arithmetic Progression
• Arithmetic Series
• Arithmetic Sequence
• Geometric Progression
• Geometric Series
• Representation of a Set
• Types Of Sets
• Universal Sets
• Venn Diagram
• Operations on Sets
• Union of Sets
• Cartesian Product of Sets

Relations and Functions

• Relation and Function
• What is a Function?
• Types of Functions
• Composite functions - Relations and functions
• Invertible Functions
• Composition of Functions
• Inverse Functions
• Verifying Inverse Functions by Composition
• Domain and Range of a Function
• Piecewise Function
• Linear Function
• Exponential Functions | Definition, Formula, Examples
• Six Trigonometric Functions
• Inverse Trigonometric Functions
• Increasing and Decreasing Functions

Matrices and Determinants

• Types of Matrices
• Matrix Operations
• Matrix Addition
• Matrix Multiplication: How to Multiply Matrices, Methods, Examples
• Transpose of a Matrix
• Symmetric and Skew Symmetric Matrices
• Elementary Operations on Matrices
• Inverse of a Matrix
• Invertible Matrix
• Determinant of a Matrix
• Properties of Determinants
• Area of a Triangle using Determinants
• Minors and Cofactors
• Adjoint of a Matrix
• Applications of Matrices and Determinants
• Vector Algebra
• Vector Addition
• Vector Operations
• Scalar Product of Vectors
• Dot and Cross Products on Vectors
• How to Find the Angle Between Two Vectors?
• Magnitude of a Vector
• Direction Cosines and Direction Ratios
• Resultant Vector Formula
• Vector Projection - Formula, Derivation & Examples
• Orthogonal and Orthonormal Vectors in Linear Algebra
• Distance Formula in Coordinate Geometry
• Direction of a Vector Formula
• Section Formula - Vector Algebra
• Angle between Two Vectors Formula
• Program to find equation of a plane passing through 3 points
• Cartesian Plane
• What is a plane in geometry?
• Boolean Algebra
• Properties of Boolean Algebra
• Boolean Algebraic Theorems

Cubic Equation is a mathematical equation in which a polynomial of degree 3 is equated to a constant or another polynomial of maximum degree 2. The standard representation of the cubic equation is ax 3 +bx 2 +cx+d = 0 where a, b, c, and d are real numbers. Some examples of cubic equation are x 3 – 4x 2 + 15x – 9 = 0, 2x 3 – 4x 2 = 0 etc.

Table of Content

Polynomial Definition

Degree of equation, cubic equation definition, how to solve cubic equations, solving cubic equation using factors, solving cubic equation using graphical method, problems based on solving cubic equations, practice problems on solving cubic equations.

For learning How to Solve Cubic Equations we must first learn about polynomials, the degree of the polynomial, and others. In this article, we will learn about, Polynomials, Polynomial Equations, Solving Cubic Equations Or how to solve cubic equations, and others in detail.

Polynomial is defined as follows,

A polynomial is an algebraic expression in which the power of a variable is a non-negative integer. The general form of a polynomial is a 0 x n + a 1 x n-1 + a 2 x n-2 +… + a n . Depending upon the maximum power of the variable, a polynomial can be classified as a monomial, binomial, trinomial, and so on.

What is an Equation?

An Equation is defined as follows,

An equation is a polynomial that is equated to a numerical value or any other polynomial. For Example, x + 2 is a polynomial but x + 2 = 5 is an equation. Similarly, 2x + 3 = x + 1 is also an equation whereas, 2x + 3 and x + 1 are polynomials individually.

The definition of the Degree of Equation is stated below:

Degree of a Equation is defined as the maximum power possessed by the variable in an Equation.

Based on the degree of the Equation, an Equation can be classified as follows:

Linear Equation

• Quadratic Equation

Cubic Equation

• Biquadratic Equation

The Equation in which the maximum power of the variable is 1 is called a Linear Equation.

• For example 3x +1 = 0

Quadratic Polynomial

The Equation in which the maximum power of the variable is 2 is a Quadratic Equation.

• For example 3x 2 +x+1 = 0

The Equation in which the maximum power of the variable is 3 is called a Cubic Equation.

• For example 5x 3 +3x 2 +x+1 = 0

Biquadratic Polynomial

The Equation in which the maximum power of the variable is 4 is called a Biquadratic Polynomial or Quartic Polynomial.

• For example 5x 4 +4x 3 +3x 2 +2x+1 = 0

Cubic Equation is an algebraic equation where the highest degree of the polynomial is 3. Some examples of cubic equations are 5x 3 +3x 2 +x+1 = 0, 2x 3 +8 = x ⇒ 2x 3 -x+8 = 0, etc.

 The general form of a cubic equation is,

ax 3 + bx 2 + cx + d = 0, a ≠ 0 Where, a, b, and c are the coefficients of variable and their exponenats and d is the constant, and a, b, c and d are real numbers.

A cubic equation is a equation with degree three. It has three solution and it can be solved easily by following the steps added below,

Step 1: Find one solution to the cubic equation by hit and try method. Suppose we have a cubic equation P(x) then find for any x = a, P(a) = 0 by taking, x = 0, ±1, ±2, ±3, … and so. Step 2: When we get, P(a) = 0, find the factor (x – a) of P(x) Step 3: Divide P(x) by (x – a) to get a quadratic equation say Q(x) using polynomial division. Step 4: Factarize the quadratic equation Q(x) to get the factors as (x – b), and (x – c). Step 5: (x – a), (x – b), and (x – c) are the factors of P(x) and solving each factors we gets the roots of equation as, a, b, and c.

Learn more about, Dividing Polynomial

A Cubic Equation can be solved by two methods

By reducing it into a quadratic equation and then solving it either by factoring or the quadratic formula  By Graphical Method

A Cubic Equation has three roots. These roots may be real or imaginary. Also, there can be there distinct roots or two same and one different root and all three same roots.

Point to be noted that for any equation, including Cubic Equations , the equation must always be arranged in its standard form first before solving the equation. 

For instance, if the given equation is 2x 2 -5 = x + 4/x, then we have to re-arrange this into its standard form, i.e., 2x 3 -x 2 -5x-4 = 0. Now, we can solve the equation using any appropriate method.

The solution of cubic equation using factor theorem is explained using the example added below,

Example:  Find the roots of equation f(x) = 3x 3 −16x 2 + 23x − 6 = 0.

Given expression: f(x) = 3x 3 −16x 2 + 23x − 6 = 0 First, factorize the polynomial to get roots Since the constant is -6 the possible factors are 1, 2, 3, 6 f(1) = 3 – 16 + 23 – 6 ≠ 0 f(2) = 24 – 64 + 46 – 6 = 0 f(3) = 81 – 144 + 69 – 6 = 0 f(6) = 648 – 576 + 138 – 6 ≠ 0 We know that, iaccording to Factor Theorem if f(a) = 0, then (x-a) is a factor of f(x) So, (x – 2) and (x – 3) are factors of f(x). Therefore, the product of (x – 2) and (x – 3) will also be factor of f(x). Now to find the remaining factors use the long division method and divide f(x) by product of (x – 2) and (x – 3) Hence, Divisor = (x – 2)(x – 3) = (x 2 – 5x + 6) and Dividend = 3x 3 −16x 2 + 23x − 6. Now divide as shown below, After division we obtain (3x- 1) as quotient and remainder is 0. Now as per Division Algorithm we know that Dividend = Divisor×Quotient+Remainder. ⇒ f(x) = (3x 3 −16x 2 + 23x − 6) =  (x 2 – 5x + 6)(3x-1) Since f(x) = 0 ⇒ (x 2 – 5x + 6)(3x-1) = 0 ⇒ x 2 – 5x + 6 = 0 or 3x-1 = 0 Now we will take 3x-1 = 0 ⇒ x = 1/3 as we already know two roots from x 2 – 5x + 6 which are 2 and 3 So, Roots of the given Cubic Equation are 1/3, 2, and 3.

A cubic equation is solved graphically when you cannot solve the given equation using other techniques. So, we need an accurate drawing of the given cubic equation. The equation’s roots are the point(s) at which the graph crosses the X-axis if the equation is in the terms of x and if the equation is in the terms of y then the roots of the equation are the points at which the graph cuts the Y-axis.

The number of real solutions to the cubic equation is equal to the number of times the graph of the cubic equation crosses the X-axis. 

Example: Find the roots of equation f(x) = x 3 − 4x 2 − 9x + 36 = 0, using the graphical method.

Given expression: f(x) = x 3 − 4x 2 − 9x + 36 = 0. Now, simply substitute random values for x in the graph for the given function: x -4 -3 -2 -1 0 1 2 3 4 5 f(x) -56‬ 0 19‬ 40 36 24‬ 10‬ 0 0 16 We can see that the graph has cut the X-axis at 3 points, therefore, there are 3 real solutions. From the graph, the solutions are: x = -3, x = 3, and x = 4. Hence, the roots of the given equation are -3, 3, and 4.

Linear Equation Solving Quadratic Equation Factoring Polynomials

Problem 1: Find the roots of f(x) = x 3 – 4x 2 -3x + 6 = 0.

Given expression:  f(x) = x 3 – 4x 2 -3x + 6 = 0. First, factorize the polynomial to get roots. Since the constant is +6 the possible factors are 1, 2, 3, 6. f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0 f(2) = 8 – 16 – 6 + 6 ≠ 0 f(3) = 27 – 36 – 9 + 6 ≠ 0 f(6) = 216 – 144 -18 + 6 = -48 ≠ 0 So,  according to Factor Theorem (x – 1) is a factor of the given equation. Now to find the remaining factors use the long division method. According to Division Algorithm we can write, So, f(x) = x 3 – 4x 2 -3x + 6 = (x – 1) (x 2 – 3x – 6) = 0 ⇒ (x – 1) = 0 or (x 2 – 3x – 6) = 0 We know that the roots of a quadratic equation ax 2 + bx + c = 0 are, x = [-b ± √(b 2 -4ac)]/2a Hence, for (x 2 – 3x – 6) = 0 x = [3 ± √(3 2 – 4(1)(-6)]/2(1) x = (3 ± √33)/2 Hence, the roots of the given cubic equation are 1, (3+√33)/2, and (3–√33)/2.

Problem 2: Find the roots of equation f(x) = 4x 3 – 10x 2 + 4x = 0.

Given expression:  f(x) = 4x 3 – 10x 2 + 4x = 0 ⇒ x (4x 2 – 10x + 4) = 0 ⇒ x (4x 2 – 8x – 2x + 4) = 0 ⇒ x(4x(x – 2) – 2(x – 2)) = 0 ⇒ x (4x – 2) (x – 2) = 0 ⇒ x = 0 or 4x – 2 = 0, x – 2 = 0 ⇒ x = 0 or x = 1/2 or x = 2 Hence, the roots of the given equation are 0, 1/2 and 2.

Problem 3: Find the roots of equation f(x) = x 3 + 3x 2 + x + 3 = 0.

Given expression:  f(x) = x 3 + 3x 2 + x + 3 = 0. ⇒ x 2 (x + 3) + 1(x + 3) = 0 ⇒ (x + 3) (x 2 + 1) = 0 ⇒ x + 3 = 0 or x 2 + 1 = 0 ⇒ x = -3, ±i So, the given equation has a real root, i.e., -3, and two imaginary roots, i.e., ±i.

Problem 4: Find the roots of equation f(x) = x 3 – 7x 2 – x + 7 = 0.

Given expressions, f(x) = x 3 – 3x 2 – 5x + 7 = 0 First, factorize the equation, f(x): x 3 – 3x 2 – 5x + 7= 0 It can be factored into (x-7)(x+1)(x-1) = 0 After factoring the polynomial, we can find the roots by equating each factor to zero. For example: x – 7 = 0, so x = 7 x + 1 = 0, so x = -1 x – 1 = 0, so x = 1 So the roots of the equation f(x): x 3 – 3x 2 – 5x + 7 = 0 are x = 7 x = -1 x = 1

Problem 5: Find the roots of equation f(x) = x 3 − 6x 2 + 11x − 6 = 0, using the graphical method.

Given expression: f(x) = x 3 − 6x 2 + 11x − 6 = 0. Now, simply substitute random values for x in the graph for the given function: x 1 2 3 4 5 f(x) 0 0 0 6 24 We can see that the graph has cut the X-axis at 3 points, therefore, there are 3 real solutions. From the graph, the solutions are: x = 1, x = 2, and x = 3. Hence, the roots of the given equation are 1, 2, and 3.

Various practise problems related to cubic equations are added below. Solve these problems to fully grasp the concept of How to Solve Cubic Equation?

P1. Solve the cubic equation, 3x 3 + 2x 2 – 11x + 7 = 0.

P2. Find the roots of cubic equation, 4x 3 – 12x 2 + 17 = 0.

P3. Solve the cubic equation, x 3 + 4x 2 – x + 3 = 0 using graphical method.

P4. Find the number which satisfy, -9x 3 + 11x 2 – 8x + 2 = 0.

FAQs on Solving Cubic Equations

1. what are cubic equations.

Cubic Equations are the algebraic equations in which the maximum power of a variable is 3

2. How do you Factor a Cubic Equation?

We can factor a cubic equation in two ways. First by taking a linear expression common from the given cubic equation, then we will have a linear and a quadratic expression as a product. This quadratic equation can be further factorized to get all the factors. The second method is to find a zero of the given cubic equation by putting random values. The value for which we get the value of the equation to be zero will be one of the zeros of the given cubic equation. Now using the factor theorem form a linear expression let’s say x-a and divide the given cubic equation by this expression which will give a quadratic equation as quotient. This obtained quadratic equation can be further factorized to get all the factors.

3. How do you Solve a Cubic Equation Graphically?

To solve a cubic equation graphically put random values for x in the given cubic equation and solve, you will get the values of y. Plot these obtained values on the graph. Find the coordinates at which the graph is intersecting the x-axis. These coordinates are the solution of the cubic equation.

4. Can all Cubic Equations be Solved Exactly?

Any equation that has odd power must have one real root. Hence, a cubic equation must have at least one real root, unlike a quadratic equation where both roots can be imaginary when the discriminant is less than zero.

5. Can a Cubic Equation have Multiple Solutions?

Yes, cubic equations can have multiple solutions as a cubic equation can have up to three distinct real roots.

6. What do you mean by the Degree of an Equation?

The maximum power possessed by the variable in an equation is called the degree of a polynomial.

7. What is the Difference between a Polynomial and an Equation?

Polynomial is simply an algebraic equation in which the power of the variable is non-negative integer. This polynomial when equated (=) with a numerical value or another polynomial then it is called an Equation.

8. What is the Factor Theorem for cubic equations?

Factor Theorem states that if r is a root (solution) of the cubic equation ax 3 + bx 2 + cx + d = 0, then x – r is a factor of the equation.

9. What if I can’t find exact solutions using formulas?

If finding exact solutions seems impossible, we can use the numerical methods like iterative methods (e.g., Newton’s method) to approximate the roots of the equation. Learn more about Newton Raphson’s Method .

Please Login to comment...

Similar reads.

• Maths-Class-12
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• Math Formulas

Cubic Equation Formula

The cubic equation formula expresses the cubic equation in Mathematics. An equation with degree three is called a cubic equation. The nature of roots of all cubic equations is either one real root and two imaginary roots or three real roots. If the polynomials have degree three, they are known as cubic polynomials. 

What is Cubic Equation Formula?

To plot the curve of a cubic equation, we need cubic equation formula. This formula helps to find the roots of a cubic equation. If the degree of the polynomial is n, then there will be n number of roots. The roots of cubic equation are also called zeros.

The  cubic  equation formula is given by:

Depressing the Cubic Equation

Substitute  \(\begin{array}{l}\large x= y-\frac{b}{3a}\end{array} \) in the above cubic equation, then we get,

Simplifying further, we obtain the following depressed cubic equation –

It must have the term in x 3   or it would not be cubic ( and so a≠0 ), but any or all of b, c and d  can be zero. For instance:

The examples of cubic equations are:

• x 3  – 6x 2  + 11x – 6 = 0
• 4x 3  + 57 = 0
• x 3  + 9x = 0

Solved Examples on Cubic Equation Formula

(x-1)(x-2)(x-3)=0

This equation has three real roots, all different – the solutions are x = 1, x = 2 and x = 3.

Question 2: Solve the cubic equation x 3 – 23x 2 + 142x – 120.

Solution:  First factorize the polynomial to get;

x 3 – 23x 2 + 142x – 120 = (x – 1) (x 2 – 22x + 120)

But x 2 – 22x + 120 = x 2 – 12x – 10x + 120

= x (x – 12) – 10(x – 12)

= (x – 12) (x – 10)

Therefore, x3 – 23×2 + 142x – 120 = (x – 1) (x – 10) (x – 12)

Equate each factor to zero to get;

The roots of the equation are x = 1, 10 and 12.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

PROBLEMS BASED ON CUBIC EQUATIONS

(1)  If the sides of a cubic box are increased by 1, 2, 3 units respectively to form a cuboid, then the volume is increased by 52 cubic units. Find the volume of the cuboid.              Solution

(2)  Construct a cubic equation with roots

(i) 1, 2 and 3      (ii) 1,1, and −2         (iii) 2, 1/2 and 1.

(3)  If α , β and γ are the roots of the cubic equation x 3  + 2x 2  + 3x + 4 = 0 , form a cubic equation whose roots are

(i) 2α , 2β , 2γ

(ii)  1/α, 1/β, 1/γ

(iii) −α, -β, -γ          Solution

(4)   Solve the equation 3x 3  −16x 2  + 23x − 6 = 0 if the product of two roots is 1.          Solution

(5)   Find the sum of squares of roots of the equation 2x 4  −8x 3  + 6x 2  − 3 = 0.          Solution

(6)   Solve the equation x 3  − 9x 2  + 14x + 24 = 0 if it is given that two of its roots are in the ratio 3: 2.    Solution

(7)   If α, β  and γ are the roots of the polynomial equation ax 3  + bx 2  + cx + d = 0 , find the Value of  ∑  α/βγ in terms of the coefficients          Solution

(8)   If  α, β, γ  and δ are the roots of the polynomial equation 2x 4 + 5x 3  − 7x 2  + 8 = 0 , find a quadratic equation with integer coefficients whose roots are  α + β + γ +  δ and  αβγ δ.       Solution

(9)   If p and q are the roots of the equation lx 2  + nx + n = 0, show that  √(p/q) +  √(q/p) +  √(n/l)  =  0       Solution

(10)   If the equations x 2  + px + q = 0 and x 2  + p'x + q' = 0 have a common root, show that it must be equal to (pq'-p'q)/q q' or (q - q') / (p' - p)       Solution

(11)  Formalate into a mathematical problem to find a number such that when its cube root is added to it, the result is 6.       Solution

(12)  A 12 metre tall tree was broken into two parts. It was found that the height of the part which was left standing was the cube root of the length of the part that was cut away. Formulate this into a mathematical problem to find the height of the part which was cut away       Solution

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

Simplifying Algebraic Expressions with Fractional Coefficients

May 17, 24 08:12 AM

The Mean Value Theorem Worksheet

May 14, 24 08:53 AM

Mean Value Theorem

May 14, 24 02:48 AM