case study questions for class 11 maths chapter 3

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 11 Maths Chapter 3 Trigonometric Functions

• Last modified on: 9 months ago
• Reading Time: 8 Minutes

Table of Contents

[PDF] Download Case Study Questions for Class 11 Maths Chapter 3 Trigonometric Functions

Here we are providing case study questions for class 11 maths. In this article, we are sharing Class 11 Maths Chapter 3 Trigonometric Functions. All case study questions of class 11 maths are solved so that students can check their solutions after attempting questions.

What is meant by Case Study Question?

In the context of CBSE (Central Board of Secondary Education), a case study question is a type of question that requires students to analyze a given scenario or situation and apply their knowledge and skills to solve a problem or answer a question related to the case study.

Case study questions typically involve a real-world situation that requires students to identify the problem or issue, analyze the relevant information, and apply their understanding of the relevant concepts to propose a solution or answer a question. These questions may involve multiple steps and require students to think critically, apply their problem-solving skills, and communicate their reasoning effectively.

Importance of Solving Case Study Questions for Class 11 Maths

Case study questions are an important aspect of mathematics education at the Class 11 level. These questions require students to apply their knowledge and skills to real-world scenarios, helping them develop critical thinking, problem-solving, and analytical skills. Here are some reasons why case study questions are important in Class 11 maths education:

• Real-world application: Case study questions allow students to see how the concepts they are learning in mathematics can be applied in real-life situations. This helps students understand the relevance and importance of mathematics in their daily lives.
• Higher-order thinking: Case study questions require students to think critically, analyze data, and make connections between different concepts. This helps develop higher-order thinking skills, which are essential for success in both academics and real-life situations.
• Collaborative learning: Case study questions often require students to work in groups, which promotes collaborative learning and helps students develop communication and teamwork skills.
• Problem-solving skills: Case study questions require students to apply their knowledge and skills to solve complex problems. This helps develop problem-solving skills, which are essential in many careers and in everyday life.
• Exam preparation: Case study questions are included in exams and tests, so practicing them can help students prepare for these assessments.

Overall, case study questions are an important component of Class 11 mathematics education, as they help students develop critical thinking, problem-solving, and analytical skills, which are essential for success in both academics and real-life situations.

Feature of Case Study Questions on This Website

Here are some features of a Class 11 Maths Case Study Questions Booklet:

Many Case Study Questions: This website contains many case study questions, each with a unique scenario and problem statement.

Different types of problems: The booklet includes different types of problems, such as optimization problems, application problems, and interpretation problems, to test students’ understanding of various mathematical concepts and their ability to apply them to real-world situations.

Multiple-choice questions: Questions contains multiple-choice questions to assess students’ knowledge, understanding, and critical thinking skills.

Focus on problem-solving skills: The questions are designed to test students’ problem-solving skills, requiring them to identify the problem, select appropriate mathematical tools, and analyze and interpret the results.

Emphasis on practical applications: The case studies in the booklet focus on practical applications of mathematical concepts, allowing students to develop an understanding of how mathematics is used in real-life situations.

Comprehensive answer key: The booklet includes a comprehensive answer key that provides detailed explanations and step-by-step solutions for all the questions, helping students to understand the concepts and methods used to solve each problem.

Download CBSE Books

Exam Special Series:

• Sample Question Paper for CBSE Class 10 Science (for 2024)
• Sample Question Paper for CBSE Class 10 Maths (for 2024)
• CBSE Most Repeated Questions for Class 10 Science Board Exams
• CBSE Important Diagram Based Questions Class 10 Physics Board Exams
• CBSE Important Numericals Class 10 Physics Board Exams
• CBSE Practical Based Questions for Class 10 Science Board Exams
• CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
• Sample Question Papers for CBSE Class 12 Physics (for 2024)
• Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
• Sample Question Papers for CBSE Class 12 Maths (for 2024)
• Sample Question Papers for CBSE Class 12 Biology (for 2024)
• CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
• Master Organic Conversions CBSE Class 12 Chemistry Board Exams
• CBSE Important Numericals Class 12 Physics Board Exams
• CBSE Important Definitions Class 12 Physics Board Exams
• CBSE Important Laws & Principles Class 12 Physics Board Exams
• 10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
• ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
• ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
• ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
• ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
• ICSE Important Functions and Locations Based Questions Class 10 Biology
• ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Leave a Reply Cancel reply

Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

myCBSEguide

• Mathematics
• Class 11 Mathematics Case...

Class 11 Mathematics Case Study Questions

Table of Contents

myCBSEguide App

Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.

If you’re seeking a comprehensive and dependable study resource with Class 11 mathematics case study questions for CBSE, myCBSEguide is the place to be. It has a wide range of study notes, case study questions, previous year question papers, and practice questions to help you ace your examinations. Furthermore, it is routinely updated to bring you up to speed with the newest CBSE syllabus. So, why delay? Begin your path to success with myCBSEguide now!

The rationale behind teaching Mathematics

The general rationale to teach Mathematics at the senior secondary level is to assist students:

• In knowledge acquisition and cognitive understanding of basic ideas, words, principles, symbols, and mastery of underlying processes and abilities, notably through motivation and visualization.
• To experience the flow of arguments while demonstrating a point or addressing an issue.
• To use the information and skills gained to address issues using several methods wherever possible.
• To cultivate a good mentality in order to think, evaluate, and explain coherently.
• To spark interest in the subject by taking part in relevant tournaments.
• To familiarise pupils with many areas of mathematics utilized in daily life.
• To pique students’ interest in studying mathematics as a discipline.

Case studies in Class 11 Mathematics

A case study in mathematics is a comprehensive examination of a specific mathematical topic or scenario. Case studies are frequently used to investigate the link between theory and practise, as well as the connections between different fields of mathematics. A case study will frequently focus on a specific topic or circumstance and will investigate it using a range of methodologies. These approaches may incorporate algebraic, geometric, and/or statistical analysis.

Sample Class 11 Mathematics case study questions

When it comes to preparing for Class 11 Mathematics, one of the best things Class 11 Mathematics students can do is to look at some Class 11 Mathematics sample case study questions. Class 11 Mathematics sample case study questions will give you a good idea of the types of Class 11 Mathematics sample case study questions that will be asked in the exam and help you to prepare more effectively.

Looking at sample questions is also a good way to identify any areas of weakness in your knowledge. If you find that you struggle with a particular topic, you can then focus your revision on that area.

myCBSEguide offers ample Class 11 Mathematics case study questions, so there is no excuse. With a little bit of preparation, Class 11 Mathematics students can boost their chances of getting the grade they deserve.

Some samples of Class 11 Mathematics case study questions are as follows:

Class 11 Mathematics case study question 1

• 9 km and 13 km
• 9.8 km and 13.8 km
• 9.5 km and 13.5 km
• 10 km and 14 km
• x  ≤   −1913
• x <  −1613
• −1613  < x <  −1913
• There are no solution.
• y  ≤   12 x+2
• y >  12 x+2
• y  ≥   12 x+2
• y <  12 x+2

Answer Key:

• (b) 9.8 km and 13.8 km
• (a) −1913   ≤  x 
• (b)  y >  12 x+2
• (d) (-5, 5)

Class 11 Mathematics case study question 2

• 2 C 1 × 13 C 10
• 2 C 1 × 10 C 13
• 1 C 2 × 13 C 10
• 2 C 10 × 13 C 10
• 6 C 2​ × 3 C 4   × 11 C 5 ​
• 6 C 2​ × 3 C 4   × 11 C 5
• 6 C 2​ × 3 C 5 × 11 C 4 ​
• 6 C 2 ​  ×   3 C 1 ​  × 11 C 5 ​
• (b) (13) 4  ways
• (c) 2860 ways.

Class 11 Mathematics case study question 3

Read the Case study given below and attempt any 4 sub parts: Father of Ashok is a builder, He planned a 12 story building in Gurgaon sector 5. For this, he bought a plot of 500 square yards at the rate of Rs 1000 /yard². The builder planned ground floor of 5 m height, first floor of 4.75 m and so on each floor is 0.25 m less than its previous floor.

Class 11 Mathematics case study question 4

Read the Case study given below and attempt any 4 sub parts: villages of Shanu and Arun’s are 50km apart and are situated on Delhi Agra highway as shown in the following picture. Another highway YY’ crosses Agra Delhi highway at O(0,0). A small local road PQ crosses both the highways at pints A and B such that OA=10 km and OB =12 km. Also, the villages of Barun and Jeetu are on the smaller high way YY’. Barun’s village B is 12km from O and that of Jeetu is 15 km from O.

Now answer the following questions:

• 5x + 6y = 60
• 6x + 5y = 60
• (a) (10, 0)
• (b) 6x + 5y = 60
• (b) 60/√ 61 km
• (d) 2√61 km

A peek at the Class 11 Mathematics curriculum

The Mathematics Syllabus has evolved over time in response to the subject’s expansion and developing societal requirements. The Senior Secondary stage serves as a springboard for students to pursue higher academic education in Mathematics or professional subjects such as Engineering, Physical and Biological Science, Commerce, or Computer Applications. The current updated curriculum has been prepared in compliance with the National Curriculum Framework 2005 and the instructions provided by the Focus Group on Teaching Mathematics 2005 in order to satisfy the rising demands of all student groups. Greater focus has been placed on the application of various principles by motivating the themes from real-life events and other subject areas.

Class 11 Mathematics (Code No. 041)

Design of Class 11 Mathematics exam paper

CBSE Class 11 mathematics question paper is designed to assess students’ understanding of the subject’s essential concepts. Class 11 mathematics question paper will assess their problem-solving and analytical abilities. Before beginning their test preparations, students in Class 11 maths should properly review the question paper format. This will assist Class 11 mathematics students in better understanding the paper and achieving optimum scores. Refer to the Class 11 Mathematics question paper design provided.

 Class 11 Mathematics Question Paper Design

• No chapter-wise weightage. Care to be taken to cover all the chapters.
• Suitable internal variations may be made for generating various templates keeping the overall weightage to different forms of questions and typology of questions the same.  

Choice(s): There will be no overall choice in the question paper. However, 33% of internal choices will be given in all the sections.

  Prescribed Books:

• Mathematics Textbook for Class XI, NCERT Publications
• Mathematics Exemplar Problem for Class XI, Published by NCERT
• Mathematics Lab Manual class XI, published by NCERT

myCBSEguide guarantees LHS=RHS

With myCBSEguide it will always be LHS=RHS, Hence Proved!

myCBSEguide is a prominent streaming resource for students studying for CBSE examinations. The site offers extensive study material, practice papers, case study questions, online examinations, and other resources at the push of a click. myCBSEguide also has a mobile app for learning on the move. There’s no excuse not to try myCBSEguide with so much convenience and simplicity of access! Hence Proved!

Test Generator

Create question paper PDF and online tests with your own name & logo in minutes.

Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes

Related Posts

• Competency Based Learning in CBSE Schools
• Class 11 Physical Education Case Study Questions
• Class 11 Sociology Case Study Questions
• Class 12 Applied Mathematics Case Study Questions
• Class 11 Applied Mathematics Case Study Questions
• Class 11 Biology Case Study Questions
• Class 12 Physical Education Case Study Questions
• Class 12 Computer Science Case Study Questions

1 thought on “Class 11 Mathematics Case Study Questions”

teri meri meri teri prem kahani hai muskil dolabjo main sayana hop jaye ek ladka aur ek ladki ki prem kahani hai muskil

Leave a Comment

Save my name, email, and website in this browser for the next time I comment.

• Class 6 Maths
• Class 6 Science
• Class 6 Social Science
• Class 6 English
• Class 7 Maths
• Class 7 Science
• Class 7 Social Science
• Class 7 English
• Class 8 Maths
• Class 8 Science
• Class 8 Social Science
• Class 8 English
• Class 9 Maths
• Class 9 Science
• Class 9 Social Science
• Class 9 English
• Class 10 Maths
• Class 10 Science
• Class 10 Social Science
• Class 10 English
• Class 11 Maths
• Class 11 Computer Science (Python)
• Class 11 English
• Class 12 Maths
• Class 12 English
• Class 12 Economics
• Class 12 Accountancy
• Class 12 Physics
• Class 12 Chemistry
• Class 12 Biology
• Class 12 Computer Science (Python)
• Class 12 Physical Education
• GST and Accounting Course
• Excel Course
• Tally Course
• Finance and CMA Data Course
• Payroll Course

Interesting

• Learn English
• Learn Excel
• Learn Tally
• Learn GST (Goods and Services Tax)
• Learn Accounting and Finance
• GST Tax Invoice Format
• Accounts Tax Practical
• Tally Ledger List
• GSTR 2A - JSON to Excel

Are you in school ? Do you love Teachoo?

We would love to talk to you! Please fill this form so that we can contact you

You are learning...

Chapter 3 Class 11 Trigonometric Functions

Click on any of the links below to start learning from Teachoo ...

NCERT Solutions of Chapter 3 Class 11 Trigonometry is available free at teachoo. You can check the detailed explanation of all questions of exercises, examples and miscellaneous by clicking on the Exercise link below.

We had learned Basics of Trigonometry in Class 10. In this chapter, we will learn

• What is a positive or a negative angle
• Measuring angles in Degree , Minutes and Seconds
• Radian measure of an angle
• Converting Degree to Radians , and vice-versa
• Sign of sin, cos, tan in all 4 quadrants
• Finding values of trigonometric functions when one value is given (Example: Finding value of sin, cot, cosec, tan, sec, when cos x = -3/5 is given)
• Finding Value of trigonometric functions, given angle
• Solving questions by formula like  (x + y) formula, 2x 3x formula, Cos x + cos y formula , 2 sin x sin y formula 
• Finding principal and general solutions of a trigonometric equation
• Sin and Cosine Formula with supplementary Questions

Important questions are marked, and Formula sheet is also provided. Click on an exercise or topic to begin.

Serial order wise

Concept wise.

What's in it?

Hi, it looks like you're using AdBlock :(

Please login to view more pages. it's free :), solve all your doubts with teachoo black.

CBSE Class 11 Maths – Chapter 3 Trigonometric Functions- Study Materials

NCERT Solutions Class 11 All Subjects Sample Papers Past Years Papers

Sets : Notes and Study Materials -pdf

• Concepts of  Trigonometric Functions
• Trigonometric Functions Master File
• Trigonometric Functions Revision Notes
• R D Sharma Solution of Trigonometric Functions
• NCERT Solution  Trigonometric Functions
• NCERT  Exemplar Solution Trigonometric Functions
• Trigonometric Functions : Solved Example 1

CBSE Class 11 Maths Notes Chapter 3 Trigonometric Functions

Angle Angle is a measure of rotation of a given ray about its initial point. The original ray is called the initial side and the final position of ray after rotation is called terminal side of the angle. The point of rotation is called vertex. If the direction of rotation is anti-clockwise, the angle is said to be positive and if the direction of rotation is clockwise, then the angle is negative.

Measuring Angles There are two systems of measuring angles Sexagesimal system (degree measure): If a rotation from the initial side to terminal side is  ( 1 360 ) t h  of a revolution, the angle is said to have a measure of one degree, written as 1°. One sixtieth of a degree is called a minute, written as 1′ and one-sixtieth of a minute is called a second, written as 1″ Thus, 1° = 60′ and 1′ = 60″

Circular system (radian measure):  A radian is an angle subtended at the centre of a circle by an arc, whose length is equal to the radius of the circle. We denote 1 radian by 1°.

Relation Between Radian and Degree We know that a complete circle subtends at its centre an angle whose measure is 2π radians as well as 360°. 2π radian = 360°. Hence, π radian = 180° or 1 radian = 57° 16′ 21″ (approx) 1 degree = 0.01746 radian

Six Fundamental Trigonometric Identities

• sinx =  1 c o s e c x
• cos x =  1 s e c x
• tan x =  1 c o t x
• sin 2  x + cos 2  x = 1
• 1 + tan 2 x = sec 2  x
• 1 + cot 2  x = cosec 2  x

Trigonometric Functions – Class 11 Maths Notes

Trigonometric ratios are defined for acute angles as the ratio of the sides of a right angled triangle. The extension of trigonometric ratios to any angle in terms of radian measure (real number) are called trigonometric function. The signs of trigonometric function in different quadrants have been given in following table.

Domain and Range of Trigonometric Functions

Sine, Cosine, and Tangent of Some Angles Less Than 90°

Allied or Related Angles The angles  n π 2 ± θ  are called allied or related angle and θ ± n × (2π) are called coterminal angles. For general reduction, we have following rules, the value of trigonometric function for ( n π 2 ± θ ) is numerically equal to

• the value of the same function, if n is an even integer with the algebraic sign of the function as per the quadrant in which angle lies.
• the corresponding co-function of θ, if n is an odd integer with the algebraic sign of the function for the quadrant in which it lies, here sine and cosine, tan and cot, sec and cosec are cofunctions of each other.

Functions of Negative Angles

For any acute angle of θ. We have,

• sin(-θ) = – sinθ
• cos (-θ) = cosθ
• tan (-θ) = – tanθ
• cot (-θ) = – cotθ
• sec (-θ) = secθ
• cosec (-θ) = – cosecθ

Some Formulae Regarding Compound Angles

An angle made up of the sum or difference of two or more angles is called compound angles. The basic results in direction are called trigonometric identities as given below: (i) sin (x + y) = sin x cos y + cos x sin y (ii) sin (x – y) = sin x cos y – cos x sin y (iii) cos (x + y) = cos x cos y – sin x sin y (iv) cos (x – y) = cos x cos y + sin x sin y

(ix) sin(x + y) sin (x – y) = sin 2  x – sin 2  y = cos 2  y – cos 2  x (x) cos (x + y) cos (x – y) = cos 2  x – sin 2  y = cos 2  y – sin 2  x

Transformation Formulae

• 2 sin x cos y = sin (x + y) + sin (x – y)
• 2 cos x sin y = sin (x + y) – sin (x – y)
• 2 cos x cos y = cos (x + y) + cos (x – y)
• 2 sin x sin y = cos (x – y) – cos (x + y)
• sin x + sin y = 2 sin( x + y 2 ) cos( x − y 2 )
• sin x – sin y = 2 cos( x + y 2 ) sin( x − y 2 )
• cos x + cos y = 2 cos( x + y 2 ) cos( x − y 2 )
• cos x – cos y = -2 sin( x + y 2 ) sin( x − y 2 )

Trigonometric Ratios of Multiple Angles

Product of Trigonometric Ratios

• sin x sin (60° – x) sin (60° + x) =  1 4  sin 3x
• cos x cos (60° – x) cos (60° + x) =  1 4  cos 3x
• tan x tan (60° – x) tan (60° + x) = tan 3x
• cos 36° cos 72° =  1 4
• cos x . cos 2x . cos 2 2 x . cos 2 3 x … cos 2 n-1  =  s i n 2 n x 2 n s i n x

Sum of Trigonometric Ratio, if Angles are in A.P.

Trigonometric Equations Equation which involves trigonometric functions of unknown angles is known as the trigonometric equation.

Solution of a Trigonometric Equation A solution of a trigonometric equation is the value of the unknown angle that satisfies the equation. A trigonometric equation may have an infinite number of solutions.

Principal Solution The solutions of a trigonometric equation for which 0 ≤ x ≤ 2π are called principal solutions.

General Solutions A solution of a trigonometric equation, involving ‘n’ which gives all solution of a trigonometric equation is called the general solutions.

General Solutions of Trigonometric Equation

• sin x = 0 ⇔ x = nπ, n ∈ Z
• cos x = 0 ⇔ x = (2n + 1)  π 2  , n ∈ Z
• tan x = 0 ⇔ x = nπ, n ∈ Z
• sin x = sin y ⇔ x = nπ + (-1) n  y, n ∈ Z
• cos x = cos y ⇔ x = 2nπ ± y, n ∈ Z
• tan x = tan y ⇔ x = nπ ± y, n ∈ Z
• sin 2  x = sin 2  y ⇔ x = nπ ± y, n ∈ Z
• cos 2  x = cos 2  y ⇔ x = nπ ± y, n ∈ Z
• tan 2  x = tan 2  y ⇔ x = nπ ± y, n ∈ Z

Basic Rules of Triangle

In a triangle ABC, the angles are denoted by capital letters A, B and C and the lengths of sides of opposite to these angles are denoted by small letters a, b and c, respectively. Sine Rule s i n A a = s i n B b = s i n C c

Cosine Rule a 2  = b 2  + c 2  – 2bc cos A b 2  = c 2  + a 2  – 2ac cos B c 2  = a 2  + b 2  – 2ab cos C

Projection Rule a = b cos C + c cos B b = c cos A + a cos C c = a cos B + b cos A

Trigonometric Functions Class 11 MCQs Questions with Answers

Question 1. The value of cos² x + cos² y – 2cos x × cos y × cos (x + y) is (a) sin (x + y) (b) sin² (x + y) (c) sin³ (x + y) (d) sin 4 (x + y)

Answer: (b) sin² (x + y) Hint: cos² x + cos² y – 2cos x × cos y × cos(x + y) {since cos(x + y) = cos x × cos y – sin x × sin y } = cos² x + cos² y – 2cos x × cos y × (cos x × cos y – sin x × sin y) = cos² x + cos² y – 2cos² x × cos² y + 2cos x × cos y × sin x × sin y = cos² x + cos² y – cos² x × cos² y – cos² x × cos² y + 2cos x × cos y × sin x × sin y = (cos² x – cos² x × cos² y) + (cos² y – cos² x × cos² y) + 2cos x × cos y × sin x × sin y = cos² x(1- cos² y) + cos² y(1 – cos² x) + 2cos x × cos y × sin x × sin y = sin² y × cos² x + sin² x × cos² y + 2cos x × cos y × sin x × sin y (since sin² x + cos² x = 1 ) = sin² x × cos² y + sin² y × cos² x + 2cos x × cos y × sin x × sin y = (sin x × cos y)² + (sin y × cos x)² + 2cos x × cos y × sin x × sin y = (sin x × cos y + sin y × cos x)² = {sin (x + y)}² = sin² (x + y)

Question 2. If a×cos x + b × cos x = c, then the value of (a × sin x – b²cos x)² is (a) a² + b² + c² (b) a² – b² – c² (c) a² – b² + c² (d) a² + b² – c²

Answer: (d) a² + b² – c² Hint: We have (a×cos x + b × sin x)² + (a × sin x – b × cos x)² = a² + b² ⇒ c² + (a × sin x – b × cos x)² = a² + b² ⇒ (a × sin x – b × cos x)² = a² + b² – c²

Question 3. If cos a + 2cos b + cos c = 2 then a, b, c are in (a) 2b = a + c (b) b² = a × c (c) a = b = c (d) None of these

Answer: (a) 2b = a + c Hint: Given, cos A + 2 cos B + cos C = 2 ⇒ cos A + cos C = 2(1 – cos B) ⇒ 2 cos((A + C)/2) × cos((A-C)/2 = 4 sin²(B/2) ⇒ 2 sin(B/2)cos((A-C)/2) = 4sin² (B/2) ⇒ cos((A-C)/2) = 2sin (B/2) ⇒ cos((A-C)/2) = 2cos((A+C)/2) ⇒ cos((A-C)/2) – cos((A+C)/2) = cos((A+C)/2) ⇒ 2sin(A/2)sin(C/2) = sin(B/2) ⇒ 2{√(s-b)(s-c)√bc} × {√(s-a)(s-b)√ab} = √(s-a)(s-c)√ac ⇒ 2(s – b) = b ⇒ a + b + c – 2b = b ⇒ a + c – b = b ⇒ a + c = 2b

Question 4. The value of cos 5π is (a) 0 (b) 1 (c) -1 (d) None of these

Answer: (c) -1 Hint: Given, cos 5π = cos (π + 4π) = cos π = -1

Question 5. In a triangle ABC, cosec A (sin B cos C + cos B sin C) equals (a) none of these (b) c/a (c) 1 (d) a/c

Answer: (c) 1 Hint: Given cosec A (sin B cos C + cos B sin C) = cosec A × sin(B+C) = cosec A × sin(180 – A) = cosec A × sin A = cosec A × 1/cosec A = 1

Question 6. If the angles of a triangle be in the ratio 1 : 4 : 5, then the ratio of the greatest side to the smallest side is (a) 4 : (√5 – 1) (b) 5 : 4 (c) (√5 – 1) : 4 (d) none of these

Answer: (a) 4 : (√5 – 1) Hint: Given, the angles of a triangle be in the ratio 1 : 4 : 5 ⇒ x + 4x + 5x = 180 ⇒ 10x = 180 ⇒ x = 180/10 ⇒ x = 18 So, the angle are: 18, 72, 90 Since a : b : c = sin A : sin B : sin C ⇒ a : b : c = sin 18 : sin 72 : sin 90 ⇒ a : b : c = (√5 – 1)/4 : {√(10 + 2√5)}/4 : 1 ⇒ a : b : c = (√5 – 1) : {√(10 + 2√5)} : 4 Now, c /a = 4/(√5 – 1) ⇒ c : a = 4 : (√5 – 1)

Question 7. The value of cos 180° is (a) 0 (b) 1 (c) -1 (d) infinite

Answer: (c) -1 Hint: 180 is a standard degree generally we all know their values but if we want to go theoretically then cos(90 + x) = – sin(x) So, cos 180 = cos(90 + 90) = -sin 90 = -1 {sin 90 = 1} So, cos 180 = -1

Question 8. The perimeter of a triangle ABC is 6 times the arithmetic mean of the sines of its angles. If the side b is 2, then the angle B is (a) 30° (b) 90° (c) 60° (d) 120°

Answer: (b) 90° Hint: Let the lengths of the sides if ∆ABC be a, b and c Perimeter of the triangle = 2s = a + b + c = 6(sinA + sinB + sinC)/3 ⇒ (sinA + sinB + sinC) = ( a + b + c)/2 ⇒ (sinA + sinB + sinC)/( a + b + c) = 1/2 From sin formula,Using sinA/a = sinB/b = sinC/c = (sinA + sinB + sinC)/(a + b + c) = 1/2 Now, sinB/b = 1/2 Given b = 2 So, sinB/2 = 1/2 ⇒ sinB = 1 ⇒ B = π/2

Question 9: If 3 × tan(x – 15) = tan(x + 15), then the value of x is (a) 30 (b) 45 (c) 60 (d) 90

Answer: (b) 45 Hint: Given, 3×tan(x – 15) = tan(x + 15) ⇒ tan(x + 15)/tan(x – 15) = 3/1 ⇒ {tan(x + 15) + tan(x – 15)}/{tan(x + 15) – tan(x – 15)} = (3 + 1)/(3 – 1) ⇒ {tan(x + 15) + tan(x – 15)}/{tan(x + 15) – tan(x – 15)} = 4/2 ⇒ {tan(x + 15) + tan(x – 15)}/{tan(x + 15) – tan(x – 15)} = 2 ⇒ sin(x + 15 + x – 15)/sin(x + 15 – x + 15) = 2 ⇒ sin 2x/sin 30 = 2 ⇒ sin 2x/(1/2) = 2 ⇒ 2 × sin 2x = 2 ⇒ sin 2x = 1 ⇒ sin 2x = sin 90 ⇒ 2x = 90 ⇒ x = 45

Question 10. If the sides of a triangle are 13, 7, 8 the greatest angle of the triangle is (a) π/3 (b) π/2 (c) 2π/3 (d) 3π/2

Answer: (c) 2π/3 Hint: Given, the sides of a triangle are 13, 7, 8 Since greatest side has greatest angle, Now Cos A = (b² + c² – a²)/2bc ⇒ Cos A = (7² + 8² – 13²)/(2×7×8) ⇒ Cos A = (49 + 64 – 169)/(2×7×8) ⇒ Cos A = (113 – 169)/(2×7×8) ⇒ Cos A = -56/(2×56) ⇒ Cos A = -1/2 ⇒ Cos A = Cos 2π/3 ⇒ A = 2π/3 So, the greatest angle is = 2π/3

Question 11. The value of tan 20 × tan 40 × tan 80 is (a) tan 30 (b) tan 60 (c) 2 tan 30 (d) 2 tan 60

Answer: (b) tan 60 Hint: Given, tan 20 × tan 40 × tan 80 = tan 40 × tan 80 × tan 20 = [{sin 40 × sin 80}/{cos 40 × cos 80}] × (sin 20/cos 20) = [{2 * sin 40 × sin 80}/{2 × cos 40 × cos 80}] × (sin 20/cos 20) = [{cos 40 – cos 120}/{cos 120 + cos 40}] × (sin 20/cos 20) = [{cos 40 – cos (90 + 30)}/{cos (90 + 30) + cos 40}] × (sin 20/cos 20) = [{cos 40 + sin30}/{-sin30 + cos 40}] × (sin 20/cos 20) = [{(2 × cos 40 + 1)/2}/{(-1 + cos 40)/2}] × (sin 20/cos 20) = [{2 × cos 40 + 1}/{-1 + cos 40}] × (sin 20/cos 20) = [{2 × cos 40 × sin 20 + sin 20}/{-cos 20 + cos 40 × cos 20}] = (sin 60 – sin 20 + sin 20)/(-cos 20 + cos 60 + cos 20) = sin 60/cos 60 = tan 60 So, tan 20 × tan 40 × tan 80 = tan 60

Question 12. If the angles of a triangle be in the ratio 1 : 4 : 5, then the ratio of the greatest side to the smallest side is (a) 4 : (√5 – 1) (b) 5 : 4 (c) (√5 – 1) : 4 (d) none of these

Question 13. The general solution of √3 cos x – sin x = 1 is (a) x = n × π + (-1)n × (π/6) (b) x = π/3 – n × π + (-1)n × (π/6) (c) x = π/3 + n × π + (-1)n × (π/6) (d) x = π/3 – n × π + (π/6)

Answer: (c) x = π/3 + n × π + (-1)n × (π/6) Hint: √3 cos x-sin x=1 ⇒ (√3/2)cos x – (1/2)sin x = 1/2 ⇒ sin 60 × cos x – cos 60 × sin x = 1/2 ⇒ sin (x – 60) = 1/2 ⇒ sin (x – π/3) = sin 30 ⇒ sin (x – π/3) = sinπ/6 ⇒ x – π/3 = n × π + (-1)n × (π/6) {where n ∈ Z} ⇒ x = π/3 + n × π + (-1)n × (π/6)

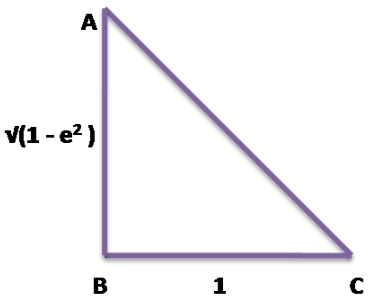
Question 14. If tan² θ = 1 – e², then the value of sec θ + tan³ θ × cosec θ is (a) 2 – e² (b) (2 – e²) 1/2 (c) (2 – e²)² (d) (2 – e²) 3/2

Question 15. The value of cos 20 + 2sin² 55 – √2 sin65 is (a) 0 (b) 1 (c) -1 (d) None of these

Answer: (b) 1 Hint: Given, cos 20 + 2sin² 55 – √2 sin65 = cos 20 + 1 – cos 110 – √2 sin65 {since cos 2x = 1 – 2sin² x} = 1 + cos 20 – cos 110 – √2 sin65 = 1 – 2 × sin {(20 + 110)/2 × sin{(20 – 110)/2} – √2 sin65 {Apply cos C – cos D formula} = 1 – 2 × sin 65 × sin (-45) – √2 sin65 = 1 + 2 × sin 65 × sin 45 – √2 sin65 = 1 + (2 × sin 65)/√2 – √2 sin65 = 1 + √2 ( sin 65 – √2 sin 65 = 1 So, cos 20 + 2sin² 55 – √2 sin65 = 1

Question 16. If the radius of the circumcircle of an isosceles triangle PQR is equal to PQ ( = PR), then the angle P is (a) 2π/3 (b) π/3 (c) π/2 (d) π/6

Answer: (a) 2π/3 Hint: Let S be the center of the circumcircle of triangle PQR. So, SP = SQ = SR = PQ = PR, where SP, SQ & SR are radii. Thus SPQ & SPR are equilateral triangles. ⇒ ∠QSP = 60°; Similarly ∠RQP = 60° ⇒ Angle at the center QSP = 120° So, SRPQ is a rhombus, since all the four sides are equal. Hence, its opposite angles are equal; so ∠P = ∠QSP = 120°

Question 17. If cos a + 2cos b + cos c = 2 then a, b, c are in (a) 2b = a + c (b) b² = a × c (c) a = b = c (d) None of these

Answer: (a) 2b = a + c Hint: Given, cos A + 2 cos B + cos C = 2 ⇒ cos A + cos C = 2(1 – cos B) ⇒ 2 cos((A + C)/2) × cos((A-C)/2 = 4 sin² (B/2) ⇒ 2 sin(B/2)cos((A-C)/2) = 4sin² (B/2) ⇒ cos((A-C)/2) = 2sin (B/2) ⇒ cos((A-C)/2) = 2cos((A+C)/2) ⇒ cos((A-C)/2) – cos((A+C)/2) = cos((A+C)/2) ⇒ 2sin(A/2)sin(C/2) = sin(B/2) ⇒ 2{√(s-b)(s-c)√bc} × {√(s-a)(s-b)√ab} = √(s-a)(s-c)√ac ⇒ 2(s – b) = b ⇒ a + b + c – 2b = b ⇒ a + c – b = b ⇒ a + c = 2b

Question 18. The value of 4 × sin x × sin(x + π/3) × sin(x + 2π/3) is (a) sin x (b) sin 2x (c) sin 3x (d) sin 4x

Answer: (c) sin 3x Hint: Given, 4 × sin x × sin(x + π/3) × sin(x + 2π/3) = 4 × sin x × {sin x × cos π/3 + cos x × sin π/3} × {sin x × cos 2π/3 + cos x × sin 2π/3} = 4 × sin x × {(sin x)/2 + (√3 × cos x)/2} × {-(sin x)/2 + (√3 × cos x)/2} = 4 × sin x × {-(sin 2x)/4 + (3 × cos 2x)/4} = sin x × {-sin 2x + 3 × cos 2x} = sin x × {-sin 2x + 3 × (1 – sin 2x)} = sin x × {-sin 2x + 3 – 3 × sin 2x} = sin x × {3 – 4 × sin 2x} = 3 × sin x – 4 sin 3x = sin 3x So, 4 × sin x × sin(x + π/3) × sin(x + 2π/3) = sin 3x

Question 19. If tan A – tan B = x and cot B – cot A = y, then the value of cot (A – B) is (a) x + y (b) 1/x + y (c) x + 1/y (d) 1/x + 1/y

Answer: (d) 1/x + 1/y Hint: Given, tan A – tan B = x ……………. 1 and cot B – cot A = y ……………. 2 From equation, 1/cot A – 1/cot B = x ⇒ (cot B – cot A)/(cot A × cot B) = x ⇒ y/(cot A × cot B) = x {from equation 2} ⇒ y = x × (cot A × cot B) ⇒ cot A × cot B = y/x Now, cot (A – B) = (cot A × cot B + 1)/(cot B – cot A) ⇒ cot (A – B) = (y/x + 1)/y ⇒ cot (A – B) = (y/x) × (1/y) + 1/y ⇒ cot (A – B) = 1/x + 1/y

Question 20. The value of (sin 7x + sin 5x) /(cos 7x + cos 5x) + (sin 9x + sin 3x) / (cos 9x + cos 3x) is (a) tan 6x (b) 2 tan 6x (c) 3 tan 6x (d) 4 tan 6x

Answer: (b) 2 tan 6x Hint: Given, (sin 7x + sin 5x) /(cos 7x + cos 5x) + (sin 9x + sin 3x) / (cos 9x + cos 3x) ⇒ [{2 × sin(7x+5x)/2 × cos(7x-5x)/2}/{2 × cos(7x+5x)/2 × cos(7x-5x)/2}] + [{2 × sin(9x+3x)/2 × cos(9x-3x)/2}/{2 × cos(9x+3x)/2 × cos(9x-3x)/2}] ⇒ [{2 × sin 6x × cosx}/{2 × cos 6x × cosx}] + [{2 × sin 6x × cosx}/{2 × cos 6x × cosx}] ⇒ (sin 6x/cos 6x) + (sin 6x/cos 6x) ⇒ tan 6x + tan 6x ⇒ 2 tan 6x

Important Questions for Class 11 Maths Chapter 3 Trigonometric Functions - PDF Download

CBSE class 11 maths chapter 3 Trigonometric Functions important questions are prepared for the students who are preparing for class 11 maths exams. Trigonometric functions class 11th maths important questions have been developed by subject experts of eSaral for enhancing the problem-solving ability to score good marks in exams. You can go through the trigonometry questions for class 11 which are based on the updated syllabus of CBSE. These important questions are solved in a step by step method which helps you to understand the concepts easily.

Class 11 maths chapter 3 Trigonometric Functions is one of the easiest chapters which includes questions based on different formulas. To solve trigonometric questions for class 11, you have to learn and remember all the essential formulas of trigonometric functions. Each and every concept of trigonometric functions has been covered in important questions of class 11 mathematics chapter 3 curated by eSaral that will help you to achieve great marks in final exams. 

Students can refer to trigonometry questions with answers pdf provided by experts of mathematics. In class 11th trigonometry important questions, all the concepts are explained in precise language. This will give you a quick understanding of all the concepts and formulas while solving these important questions. Our expert teachers of mathematics at eSaral have also provided important questions of trigonometry class 11 in free PDF format which you can download from the official website of eSaral and practice these questions even before the main exam.  

Important Topics & Sub-topics of Trigonometric Functions Class 11 Maths

Chapter 3 Trigonometric Functions deals with the relation between angles and sides of triangles. This chapter is essential and a scoring one for the students of class 11. Thus, it is vital for students to have a thorough understanding of all the significant topics and sub-topics of trigonometric functions. In class 11 maths chapter 3, you will delve into the difficulties of trigonometric functions and concepts based on them. Our subject experts of eSaral have combined all the topics and sub-topics of trigonometric functions in the tabulated structure mentioned below.

Class 11 Maths Chapter 3 Trigonometric Functions Weightage

CBSE class 11 maths chapter 3 Trigonometric Functions forms solid foundations for advance level concepts of mathematical studies. In chapter 3, understanding the weightage of significant topics helps you to prioritize your preparations in an effective way. This chapter carries the highest marks in unit one. Thus, students should be thorough with the concepts of trigonometric functions chapter 3 class 11 maths to score desired marks in examination.

The weightage and marks distribution can vary from one education board to another one so students are advised to check the official website of CBSE to get the correct information regarding weightage of chapter 3. Chapter 3 Trigonometric Functions has topics angles, domain and range of trigonometric functions, and trigonometric functions of sum and difference of two angles which you must be well-versed to solve questions effectively and easily in exam. In order to score full marks in trigonometric functions, practice important questions of trigonometry class 11 maths provided on eSaral. You can also solve examples and questions mentioned in exercises of chapter 3 to grasp the knowledge of essential topics of trigonometric functions. 

Tips to Solve Class 11 Maths Chapter 3 Trigonometric Functions

Class 11 maths chapter 3 Trigonometric Functions is an easy chapter where you can score full marks by deeply analyzing and comprehending the main concepts of trigonometry. By solving 11th class trigonometry important questions, you will get to know some tips and tricks that help you to solve the questions quickly. Check out some useful tips provided below by eSaral’s subject experts of mathematics.

Firstly, Students should never miss the formulas of trigonometric functions as these formulas are crucial to solve the questions correctly.  

To understand the concepts of trigonometry deeply, you should use the resources like trigonometry important questions for class 11 available on eSaral.  

Trigonometric formulas are an essential part of chapter 3. Thus, forming a formula chart can be a helpful tool for students whenever they need to practice trigonometry based questions. 

There are some significant topics such as domain and range of trigonometric functions, relation between degree and radian, degree measure of angles etc. which students need to understand to solve questions without any error.

Benefits of Solving Class 11 Maths Chapter 3 Important Questions with Answers

Downloading and practicing important questions class 11 maths chapter 3 will give you an in-depth understanding of trigonometric functions. Students must solve trigonometry problems for class 11 by eSaral for better preparation of exams. Here, our subject experts of mathematics have provided numerous benefits of solving class 11 maths chapter 3 important questions which can be checked below.

Conceptual Understanding - By practicing class 11 maths important questions solidify the fundamental concepts of trigonometric functions. All the important questions of trigonometric functions class 11th have deeply included each question which describes the core principles of trigonometry. This process helps you to revise the concepts which you have studied in theoretical knowledge acquired in the classroom. 

Preparing for Examination - Class 11 maths chapter 3 important questions not only help you to reinforce the theoretical knowledge of trigonometric functions but also familiarize you with question format and type of questions asked in board exams. 

Boost Confidence - Solving class 11 maths chapter 3 important questions help students to recall all the vital concepts of trigonometry. You also get to learn the easy methods of solving trigonometric functions that boost your self-confidence.

Improve Time Management - By frequently practicing important questions of trigonometry class 11 maths chapter 3, You will be able to solve questions within the time allotted for question paper in the main exam. This will help you to improve your time management skills. 

Frequently Asked Questions

Answer 1. To solve trigonometry based questions, students must memorize all the formulas of trigonometric functions which help you to solve any question asked in examinations related to trigonometric functions. You should also practice questions of exercises mentioned in chapter 3. This provides deep comprehension of concepts of trigonometric functions.

Answer 2. There are a total of 3 exercises as well as one miscellaneous exercise which must be solved to score good marks in the final exam.

Click here to get exam-ready with eSaral

For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.

Download Now

eSaral Gurukul

• JEE Coaching in Kota
• NEET Coaching in Kota
• NEET 2024 Exam Date
• JEE Main Question Paper
• JEE Main 2024 Question Paper
• JEE Main 2023 Question Paper
• JEE Main 2022 Question Paper
• JEE Main 2021 Question Paper

JEE Advanced

• JEE Advanced Question Paper
• JEE Advanced 2023 Question Paper

Our Telegram Channel

• eSaral Class 9-10

All Study Material

NCERT Solutions for Class 11 Maths Chapter 3 Free PDF Download

Ncert solutions for class 11 maths chapter 3 – trigonometric functions.

NCERT Solutions for Class 11 Maths Chapter 3 help you to solve the unsolved problems of the NCERT maths book prescribed by the CBSE. It breaks down into detailed steps and explains the answer, which helps you to understand the pattern of questioning. NCERT Solutions also contain questions, answers, images, explanations of questions given in the books.

NCERT Solutions for Class 11 Maths Chapter 3 are formed by our team of highly experienced and qualified faculties. Our NCERT Solutions will give you a complete grasp over the subject and shall help you in scoring higher marks. However, in case of doubts, we have a team of teachers who are ready to solve your doubts any time and are just a click away.

Toppr provides free study materials, the last 10 years of question papers, 1000+ hours of video lectures. Download Toppr app for  Android ,  iOS  or  signup  for free.

Download NCERT Solutions for Class 11 Maths.

Download NCERT Solutions for Class 11 here.

Download NCERT Solutions for all subjects here.

CBSE Class 11 Maths Chapter 3 Trigonometric Functions NCERT Solutions

In NCERT Solutions for Class 11 Maths Chapter 3, you will learn about trigonometric functions and their representations, empty set, finite and infinite trigonometric functions, equal trigonometric functions. Sub trigonometric functions, union, and the intersection of trigonometric functions, the difference of trigonometric functions, the complement of a set, properties of complement trigonometric functions.

Sub topics covered under NCERT Solutions for Class 11 Maths Chapter 3

3.1 – Introduction

3.2 – Angles

3.2.1- Degree measure

3.2.2 – Radian measure

3.2.3 – Relation between radian and real numbers

3.2.4 – Relation between degree and radian

3.3 – Trigonometric Functions

3.3.1- Sign of trigonometric functions

3.3.2 – Domain and range of trigonometric functions

3.4 – Trigonometric Functions of Sum and Difference of Two Angles

3.5 – Trigonometric Equations

NCERT Solutions for Class 11 Maths Chapter 3

In NCERT Solutions for Class 11 Maths Chapter 3 you will learn about radian measure – conversion, arc length,  finding the value of trigonometric functions, given other functions, finding the value of trigonometric functions, given angle, (x + y) formula, finding principal solutions, general solutions, sine, and cosine formula. Let us now discuss the subtopics included in Chapter 3.

3.1 – Introduction

In this, you will study about trigonometric function.

3.2 – Angles

In this, you will study the angles formed.

In this, you will study the measure of the degree of angle.

In this, you will study the measure of the degree of angle by radian.

In this, you will study the relation between radian and real number.

In this, you will study the relationship between degree and radian

In this, you will study about trigonometric functions such as sin, cos, tan, cosec, sec, cot, the relation between them.

In this, you will study the sign of trigonometric functions in all four quadrants i.e. in the first quadrant all functions are positive, in II quadrant only sin and cosec are positive, in III quadrant only tan and cot are positive, in IV quadrant only cos and sec are positive.

In this, you will study about domain and range of trigonometric functions i.e. tan x increases from 0 to infinity, sin increases from 0 to 1 and increases from –1 to 0, cos increases from –1 to 0 increases from 0 to 1.

In this, you will derive expressions for trigonometric functions of the sum and difference of two numbers (angles) and related expressions, trigonometric identities.

In this, you will study about trigonometric equations are equations involving trigonometric functions of a variable, principal solution of a trigonometric equation is a solution for which 0≤x<2π, the expression involving integer ‘n’ that gives all solutions of a trigonometric equation is called the general solution.

You can download NCERT Solutions for Class 11 Maths Chapter 3 PDF by clicking on the button below.

Download Toppr – Best Learning App for Class 5 to 12

With Toppr App, you get free pdf downloads, free videos and free doubt solving sessions by our highly qualifies faculties. With Toppr app you also get free online classes and mock tests which help you to perform well in your exams. So Download the Toppr App now or visit Toppr website.

Customize your course in 30 seconds

Which class are you in.

NCERT Solutions for Class 11

• NCERT Solutions for Class 11 Chemistry Chapter 7 Free PDF Download
• NCERT Solutions for Class 11 Physics Chapter 6
• NCERT Solutions for Class 11 Biology Chapter 6 Free PDF Download
• NCERT Solutions for Class 11 Biology Chapter 2 Free PDF Download
• NCERT Solutions for Class 11 Biology Chapter 18 Free PDF Download
• NCERT Solutions for Class 11 Biology Chapter 10 Free PDF Download
• NCERT Solutions for Class 11 Biology Chapter 22 Free PDF Download
• NCERT Solutions for Class 11 Biology Chapter 16 Free PDF Download
• NCERT Solutions for Class 11 Biology Chapter 20 Free PDF Download
• NCERT Solutions for Class 11 Biology Chapter 19 Free PDF Download

One response to “NCERT Solutions for Class 11 Biology Chapter 19 Free PDF Download”

Iam student pls help me

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Download the App

Talk to our experts

1800-120-456-456

NCERT Solutions for Class 11 Maths Chapter 3: Trigonometric Functions - Exercise 3.3

• NCERT Solutions
• Chapter 3 Trigonometric Functions Exercise 3.3

CBSE NCERT Solutions Class 11 Maths Chapter 3 Exercise 3.3 - Trignometry

Chapter 3 of Maths explains the concept of trigonometric ratios to trigonometric functions. The students will study the properties of trigonometric functions like sin theta, cos theta, tan theta, and more in a comprehensive way. In class 11 maths chapter 3 exercise 3.3, students have to solve problems on radian measure, arc length, conversion, finding the values of trigonometric functions, and more. Additionally, students will learn general solutions like sine and cosine, their identity, and another formula in ex 3.3 class 11 maths NCERT. 

Access NCERT solutions for Class 11 Maths Chapter 3 - Trigonometric Functions

Exercise 3.3

1. Prove that $\text{si}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{+co}{{\text{s}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\text{-ta}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{=-}\dfrac{\text{1}}{\text{2}}$

Ans: Substituting the values of  $\text{sin}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{,cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{,tan}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}$ on left hand side,

$\text{si}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{+co}{{\text{s}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\text{-ta}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{=}{{\left( \dfrac{\text{1}}{\text{2}} \right)}^{\text{2}}}\text{+}{{\left( \dfrac{\text{1}}{\text{2}} \right)}^{\text{2}}}\text{-}{{\left( \text{1} \right)}^{\text{2}}}$

$\text{=}\dfrac{\text{1}}{\text{4}}\text{+}\dfrac{\text{1}}{\text{4}}\text{-1}$

$=-\dfrac{1}{2}$

Hence proved.

2. Prove that $\text{2si}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{+cose}{{\text{c}}^{\text{2}}}\dfrac{\text{7 }\!\!\pi\!\!\text{ }}{\text{6}}\text{co}{{\text{s}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\text{=}\dfrac{\text{3}}{\text{2}}$

Substituting the values of  $\text{sin}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{,cosec}\dfrac{\text{7 }\!\!\pi\!\!\text{ }}{\text{6}}\text{,cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}$ on left hand side,

L.H.S.$\text{=2si}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{+cose}{{\text{c}}^{\text{2}}}\dfrac{\text{7 }\!\!\pi\!\!\text{ }}{\text{6}}\text{co}{{\text{s}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}$

$\text{=2}{{\left( \dfrac{\text{1}}{\text{2}} \right)}^{\text{2}}}\text{+cose}{{\text{c}}^{\text{2}}}\left( \text{ }\!\!\pi\!\!\text{ +}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}} \right){{\left( \dfrac{\text{1}}{\text{2}} \right)}^{\text{2}}}$

$\text{=2 }\!\!\times\!\!\text{ }\dfrac{\text{1}}{\text{4}}\text{+}{{\left( \text{-cosec}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}} \right)}^{\text{2}}}\left( \dfrac{\text{1}}{\text{4}} \right)$

$\text{=}\dfrac{\text{1}}{\text{2}}\text{+}{{\left( \text{-2} \right)}^{\text{2}}}\left( \dfrac{\text{1}}{\text{4}} \right)$

Since $\text{cosec x}$ repeat its value after an interval of $\text{2 }\!\!\pi\!\!\text{ }$ , 

we have, $\text{cosec}\dfrac{\text{7 }\!\!\pi\!\!\text{ }}{\text{6}}\text{=-cosec}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}$  

L.H.S  $=\dfrac{1}{2}+\dfrac{4}{4}$

$=\dfrac{3}{2}$ 

3. Prove that $\text{co}{{\text{t}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{+cosec}\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{6}}\text{+3ta}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{=6}$

Substituting the values of  $\text{cot}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{,cosec}\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{6}}\text{,tan}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}$ on left hand side,

L.H.S.$\text{=co}{{\text{t}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{+cosec}\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{6}}\text{+3ta}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}$

$\text{=}{{\left( \sqrt{\text{3}} \right)}^{\text{2}}}\text{+cosec}\left( \text{ }\!\!\pi\!\!\text{ -}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}} \right)\text{+3}{{\left( \dfrac{\text{1}}{\sqrt{\text{3}}} \right)}^{\text{2}}}$

$\text{=3+cosec}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{+3 }\!\!\times\!\!\text{ }\dfrac{\text{1}}{\text{3}}$

we have, $\text{cosec}\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{6}}\text{=cosec}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}$  

L.H.S $=3+2+1$ 

4. Prove that $\text{2si}{{\text{n}}^{\text{2}}}\dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{+2co}{{\text{s}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{+2se}{{\text{c}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\text{=10}$

Substituting the values of  $\text{sin}\dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{,cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{,sec}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}$ on left hand side,

L.H.S.$\text{=2si}{{\text{n}}^{\text{2}}}\dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{+2co}{{\text{s}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{+2se}{{\text{c}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}$

$\text{=2}{{\left\{ \text{sin}\left( \text{ }\!\!\pi\!\!\text{ -}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}} \right) \right\}}^{\text{2}}}\text{+2}{{\left( \dfrac{\text{1}}{\sqrt{\text{2}}} \right)}^{\text{2}}}\text{+2}{{\left( \text{2} \right)}^{\text{2}}}$

$\text{=2}{{\left\{ \text{sin}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}} \right\}}^{\text{2}}}\text{+2 }\!\!\times\!\!\text{ }\dfrac{\text{1}}{\text{2}}\text{+8}$

Since $\text{sin x}$ repeats its value after an interval of $\text{2 }\!\!\pi\!\!\text{ }$ , 

we have, $\text{sin}\dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{=sin}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}$  

 L.H.S  $=1+1+8$ 

5. Find the value of :

(i) Sin 75°

Ans: We have,

Sin 75°= Sin ( 45°+ 30° )

Sin 75°= Sin 45° Cos 30° + Cos 45° Sin 30° 

Since we know that, $\text{sin}\left( \text{x+y} \right)\text{=sin x cos y+cos x sin y}$ 

Therefore we have,

$Sin 75^o = \dfrac{1}{\sqrt 2}\times \dfrac{\sqrt 3}{2}\times+ \dfrac{1}{\sqrt 2}\times\dfrac{1}{2}$

$Sin 75^o = \dfrac{{\sqrt 3}+1}{2\sqrt 2}$

(ii) tan 15°

tan 15°= tan ( 45°- 30° )

= $\dfrac{( tan 45°- tan 30° )}{1+( tan 45° tan 30° )}$

Since we know, $\text{tan}\left( \text{x-y} \right)\text{=}\dfrac{\text{tan x-tan y}}{\text{1+tan x tan y}}$

$tan 15°=\dfrac{\text{1-}\dfrac{\text{1}}{\sqrt{\text{3}}}}{\text{1+1}\left( \dfrac{\text{1}}{\sqrt{\text{3}}} \right)}$

$\text{=}\dfrac{\dfrac{\sqrt{\text{3}}\text{-1}}{\sqrt{\text{3}}}}{\dfrac{\sqrt{\text{3}}\text{+1}}{\sqrt{\text{3}}}}$

$\text{=}\dfrac{\sqrt{\text{3}}\text{-1}}{\sqrt{\text{3}}\text{+1}}$

$\text{=}\dfrac{{{\left( \sqrt{\text{3}}\text{-1} \right)}^{\text{2}}}}{\left( \sqrt{\text{3}}\text{+1} \right)\left( \sqrt{\text{3}}\text{-1} \right)}$ 

Further computing we have,

$\text{tan1}{{\text{5}}^{\text{o}}}\text{=}\dfrac{\text{3+1-2}\sqrt{\text{3}}}{{{\left( \sqrt{\text{3}} \right)}^{\text{2}}}\text{-}{{\left( \text{1} \right)}^{\text{2}}}}$ 

$\text{=}\dfrac{\text{4-2}\sqrt{\text{3}}}{\text{3-1}}$

$\text{=2-}\sqrt{\text{3}}$

6. Prove that $\text{cos}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)\text{cos}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-y} \right)\text{-sin}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)\text{sin}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-y} \right)\text{=sin}\left( \text{x+y} \right)$

Ans: We know that, $\text{cos}\left( \text{x+y} \right)\text{=cos xcos y-sin xsin y}$ 

$\text{cos}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)\text{cos}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-y} \right)\text{-sin}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)\text{sin}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-y} \right)\text{=cos}\left[ \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x+}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-y} \right]$

$\text{=cos}\left[ \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}\text{-}\left( \text{x+y} \right) \right]$

$\text{=sin}\left( \text{x+y} \right)$ 

L.H.S  $=$ R.H.S.

Hence  proved.

7. Prove that $\dfrac{\text{tan}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{+x} \right)}{\text{tan}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)}\text{=}{{\left( \dfrac{\text{1+tanx}}{\text{1-tanx}} \right)}^{\text{2}}}$

We  know that ,$\text{tan}\left( \text{A+B} \right)\text{=}\dfrac{\text{tan A+tan B}}{\text{1-tan Atan B}}$

and $\text{tan}\left( \text{A-B} \right)\text{=}\dfrac{\text{tan A-tan B}}{\text{1+tan Atan B}}$

L.H.S.$\text{=}\dfrac{\text{tan}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{+x} \right)}{\text{tan}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)}$

Using the above formula,

$\text{L}\text{.H}\text{.S=}\dfrac{\left( \dfrac{\text{tan}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{+tanx}}{\text{1-tan}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{tanx}} \right)}{\dfrac{\text{tan}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-tanx}}{\text{1+tan}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{tanx}}}$

$\text{=}\dfrac{\left( \dfrac{\text{1+tan x}}{\text{1-tan x}} \right)}{\left( \dfrac{\text{1-tan x}}{\text{1+tan x}} \right)}$      

Substituting $\text{tan}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{=1}$

$\text{=}{{\left( \dfrac{\text{1+tan x}}{\text{1-tan x}} \right)}^{\text{2}}}$

8.  Prove that  $\dfrac{\text{cos}\left( \text{ }\!\!\pi\!\!\text{ +x} \right)\text{cos}\left( \text{-x} \right)}{\text{sin}\left( \text{ }\!\!\pi\!\!\text{ -x} \right)\text{cos}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}\text{+x} \right)}\text{=co}{{\text{t}}^{\text{2}}}\text{x}$

Ans: Observe that $\text{cos x}$ repeats the same value after an interval $\text{2 }\!\!\pi\!\!\text{ }$ and $\text{sin x}$ repeat the same value after an interval  $\text{2 }\!\!\pi\!\!\text{ }$.

L.H.S. $\text{=}\dfrac{\text{cos}\left( \text{ }\!\!\pi\!\!\text{ +x} \right)\text{cos}\left( \text{-x} \right)}{\text{sin}\left( \text{ }\!\!\pi\!\!\text{ -x} \right)\text{cos}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}\text{+x} \right)}$

$\text{=}\dfrac{\left[ \text{-cos x} \right]\left[ \text{cos x} \right]}{\left( \text{sin x} \right)\left( \text{-sin x} \right)}$

$\text{=}\dfrac{\text{-co}{{\text{s}}^{\text{2}}}\text{x}}{\text{-si}{{\text{n}}^{\text{2}}}\text{x}}$

$\text{=co}{{\text{t}}^{\text{2}}}\text{x}$

9. Prove that,

$\text{Cos}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{2}}\text{+x} \right)\text{Cos}\left( \text{2 }\!\!\pi\!\!\text{ +x} \right)\left[ \text{cot}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{2}}\text{-x} \right)\text{+cot}\left( \text{2 }\!\!\pi\!\!\text{ +x} \right) \right]\text{=1}$

We know that $\text{cot x}$  repeats the same value after an interval $2\pi $ .

L.H.S $=Cos\left( \dfrac{3\pi }{2}+x \right)Cos\left( 2\pi +x \right)\left[ cot\left( \dfrac{3\pi }{2}-x \right)+cot\left( 2\pi +x \right) \right]$

$\text{=sin x cos x}\left[ \text{tan x+cot x} \right]$

Substituting $\text{tan x=}\dfrac{\text{sin x}}{\text{cos x}}$ and

$\text{cot x=}\dfrac{\text{cos x}}{\text{sin x}}$ ,

$\text{L}\text{.H}\text{.S=sin xcos x}\left( \dfrac{\text{sin x}}{\text{cos x}}\text{+}\dfrac{\text{cos x}}{\text{sin x}} \right)$

$\text{=}\left( \text{sin x cos x} \right)\left[ \dfrac{\text{si}{{\text{n}}^{\text{2}}}\text{x+co}{{\text{s}}^{\text{2}}}\text{x}}{\text{sin x cos x}} \right]$

$\text{=1}$ 

$\text{=}$ R.H.S.

10. Prove that $\text{sin}\left( \text{n+1} \right)\text{xsin}\left( \text{n+2} \right)\text{x+cos (n+1)x cos (n+2)x=cos x}$

We know that , $\text{cos}\left( \text{x-y} \right)\text{=cosxcosy+sinxsiny}$ 

L.H.S.$\text{=sin}\left( \text{n+1} \right)\text{xsin}\left( \text{n+2} \right)\text{x+cos (n+1)x cos (n+2)x}$

$\text{=cos}\left[ \left( \text{n+1} \right)\text{x-}\left( \text{n+2} \right)\text{x} \right]$ 

$\text{=cos}\left( \text{-x} \right)$ 

$\text{=cosx}$ 

=  R.H.S

11. Prove that $\text{cos}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{+x} \right)\text{-cos}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)\text{=-}\sqrt{\text{2}}\text{sinx}$

Ans: We  know that , $\text{cos A-cos B=-2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{.sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)$

$\therefore $ L.H.S.$\text{=cos}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{+x} \right)\text{-cos}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)$

$\text{=-2sin}\left\{ \dfrac{\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{+x} \right)\text{+}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)}{\text{2}} \right\}\text{.sin}\left\{ \dfrac{\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{+x} \right)\text{-}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)}{\text{2}} \right\}$

$\text{=-2sin}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}} \right)\text{sin x}$ 

Since $\text{sin x}$ repeats the same value after an interval $\text{2 }\!\!\pi\!\!\text{ }$ , 

we have, $\text{sin}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}} \right)\text{=sin}\left( \text{ }\!\!\pi\!\!\text{ -}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}} \right)$ 

Therefore, $\text{L}\text{.H}\text{.S=-2sin}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{sin x}$ 

$\text{=-2 }\!\!\times\!\!\text{ }\dfrac{\text{1}}{\sqrt{\text{2}}}\text{ }\!\!\times\!\!\text{ sinx}$

$\text{=-}\sqrt{\text{2}}\text{sin x}$

12. Prove that $\text{si}{{\text{n}}^{\text{2}}}\text{6x-si}{{\text{n}}^{\text{2}}}\text{4x=sin 2x sin 10x}$

Ans: We know that,$\text{sinA+sinB=2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)$

And $\text{sin A-sin B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)$

$\therefore$ L.H.S $\text{=si}{{\text{n}}^{\text{2}}}\text{6x-si}{{\text{n}}^{\text{2}}}\text{4xa}$

$\text{=}\left( \text{sin 6x+sin 4x} \right)\left( \text{sin 6x-sin 4x} \right)$

$\text{=}\left[ \text{2sin}\left( \dfrac{\text{6x+4x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{6x-4x}}{\text{2}} \right) \right]\left[ \text{2cos}\left( \dfrac{\text{6x+4x}}{\text{2}} \right)\text{.sin}\left( \dfrac{\text{6x-4x}}{\text{2}} \right) \right]$

$\text{=}\left( \text{2sin 5x cos x} \right)\left( \text{2cos 5x sin x} \right)$

Now we know that, $\text{sin 2x=2sin x cos x}$ ,

$\text{L}\text{.H}\text{.S=}\left( \text{2sin 5x cos 5x} \right)\left( \text{2sin x cos x} \right)$ 

$\text{=sin 10x sin 2x}$

13. Prove that $\text{co}{{\text{s}}^{\text{2}}}\text{2x-co}{{\text{s}}^{\text{2}}}\text{6x=sin 4x sin 8x}$

Ans: We  know that,

$\text{cos A+cos B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)$

And $\text{cos A-cos B=-2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)$

 L.H.S.$\text{=co}{{\text{s}}^{\text{2}}}\text{2x-co}{{\text{s}}^{\text{2}}}\text{6x}$

$\text{=}\left( \text{cos 2x+cos 6x} \right)\left( \text{cos 2x-6x} \right)$

$\text{=}\left[ \text{2cos}\left( \dfrac{\text{2x+6x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{2x-6x}}{\text{2}} \right) \right]\left[ \text{-2sin}\left( \dfrac{\text{2x+6x}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{2x-6x}}{\text{2}} \right) \right]$

Further computing, we have,

$\text{L}\text{.H}\text{.S=}\left[ \text{2cos 4x cos}\left( \text{-2x} \right) \right]\left[ \text{-2sin 4xsin}\left( \text{-2x} \right) \right]$

$\text{=}\left[ \text{2cos  4x cos 2x} \right]\left[ \text{-2sin 4x}\left( \text{-sin 2x} \right) \right]$

$\text{=}\left( \text{2sin 4x cos 4x} \right)\left( \text{2sin 2xcos 2x} \right)$

Now we know that, $\text{sin 2x=2sin x cos x}$ 

Therefore we have,                

$\text{L}\text{.H}\text{.S=sin 8x sin 4x}$

14. Prove that $\text{sin 2x+2sin 4x+sin6=4co}{{\text{s}}^{\text{2}}}\text{xsin 4x}$

Ans: We know that, $\text{sin A+sin B=2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)$

L.H.S $\text{=sin 2x+2sin 4x+sin 6x}$

$\text{=}\left[ \text{sin 2x+sin 6x} \right]\text{+2sin 4x}$

$\text{=}\left[ \text{2sin}\left( \dfrac{\text{2x+6x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{2x-6x}}{\text{2}} \right) \right]\text{+2sin4x}$

$\text{=2sin 4xcos}\left( \text{-2x} \right)\text{+2sin 4x}$

Further computing,

We have, $\text{L}\text{.H}\text{.S=2sin 4x cos 2x+2sin 4x}$ 

$\text{=2sin 4x}\left( \text{cos 2x+1} \right)$ 

Now we know that, $\text{cos 2x+1=2co}{{\text{s}}^{\text{2}}}\text{x}$ 

$\text{L}\text{.H}\text{.S=2sin 4x}\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x} \right)$ 

$\text{=4co}{{\text{s}}^{\text{2}}}\text{xsin 4x}$

15. Prove that $\text{cot 4x}\left( \text{sin 5x+sin 3x} \right)\text{=cot x}\left( \text{sin 5x-sin 3x} \right)$

L.H.S.$\text{=cot 4x}\left( \text{sin 5x+sin 3x} \right)$

$\text{=}\dfrac{\text{cot 4x}}{\text{sin 4x}}\left[ \text{2sin}\left( \dfrac{\text{5x+3x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{5x+3x}}{\text{2}} \right) \right]$

$\text{=}\left( \dfrac{\text{cos 4x}}{\text{sin 4x}} \right)\left[ \text{2sin 4x cos x} \right]$

$\text{=2cos 4x cos x}$

Now also ,we know that, $\text{sin A-sin B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)$

 R.H.S $\text{=cot x}\left( \text{sin 5x-sin 3x} \right)$

$\text{=}\dfrac{\text{cos x}}{\text{sin x}}\left[ \text{2cos}\left( \dfrac{\text{5x+3x}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{5x-3x}}{\text{2}} \right) \right]$

$\text{=}\dfrac{\text{cos x}}{\text{sin x}}\left[ \text{2cos 4x sin x} \right]$

Therefore , we can conclude that,

L.H.S = R.H.S

16. Prove that $\dfrac{\text{cos 9x-cos 5x}}{\text{sin 17x-sin 3x}}\text{=-}\dfrac{\text{sin 2x}}{\text{cos 10x}}$

Ans: We know that,

$\text{cos A-cos B=-2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)$

And  $\text{sin A-sin B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)$

 L.H.S $\text{=}\dfrac{\text{cos 9x-cos 5x}}{\text{sin 17x-sin 3x}}$

$\text{=}\dfrac{\text{-2sin}\left( \dfrac{\text{9x+5x}}{\text{2}} \right)\text{.sin}\left( \dfrac{\text{9x-5x}}{\text{2}} \right)}{\text{2cos}\left( \dfrac{\text{17x+3x}}{\text{2}} \right)\text{.sin}\left( \dfrac{\text{17x-3x}}{\text{2}} \right)}$                    

(Following the formula)

$\text{=}\dfrac{\text{-2sin 7x}\text{.sin 2x}}{\text{2cos 10x}\text{.sin 7x}}$

$\text{=-}\dfrac{\text{sin 2x}}{\text{cos 10x}}$ 

17. Prove that:$\dfrac{\text{sin 5x+sin 3x}}{\text{cos 5x+cos 3x}}\text{=tan 4x}$

Ans: We know that

$\text{sin A+sin B=2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)\text{,}$

Now , L.H.S.$\text{=}\dfrac{\text{sin 5x+sin 3x}}{\text{cos 5x+cos 3x}}$

$\text{=}\dfrac{\text{2sin}\left( \dfrac{\text{5x+3x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{5x-3x}}{\text{2}} \right)}{\text{2cos}\left( \dfrac{\text{5x+3x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{5x-3x}}{\text{2}} \right)}$                  

(Using the formula)

$\text{=}\dfrac{\text{2sin}\left( \dfrac{\text{5x+3x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{5x-3x}}{\text{2}} \right)}{\text{2cos}\left( \dfrac{\text{5x+3x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{5x-3x}}{\text{2}} \right)}$

$\text{=}\dfrac{\text{2sin 4x cos x}}{\text{2cos 4x cos x}}$

$\text{L}\text{.H}\text{.S=tan 4x}$ 

18. Prove that $\dfrac{\text{sin x-sin y}}{\text{cos x+cos y}}\text{=tan}\dfrac{\text{x-y}}{\text{2}}$

$\text{sin A-sin B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)\text{,}$

L.H.S.$\text{=}\dfrac{\text{sin x-sin y}}{\text{cosx+cosy}}$

$\text{=}\dfrac{\text{2cos}\left( \dfrac{\text{x+y}}{\text{2}} \right)\text{.sin}\left( \dfrac{\text{x-y}}{\text{2}} \right)}{\text{2cos}\left( \dfrac{\text{x+y}}{\text{2}} \right)\text{.cos}\left( \dfrac{\text{x-y}}{\text{2}} \right)}$

$\text{=}\dfrac{\text{sin}\left( \dfrac{\text{x-y}}{\text{2}} \right)}{\text{cos}\left( \dfrac{\text{x-y}}{\text{2}} \right)}$

$\text{=tan}\left( \dfrac{\text{x-y}}{\text{2}} \right)$

Therefore $\text{L}\text{.H}\text{.S=R}\text{.H}\text{.S}$ 

19. Prove that $\dfrac{\text{sin x+sin 3x}}{\text{cos x+cos 3x}}\text{=tan 2x}$

Ans: We  know that

$\text{sin A+sin B=2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{,}$

Now , L.H.S $\text{=}\dfrac{\text{sinx+sin3x}}{\text{cos x+cos 3x}}$

$\text{=}\dfrac{\text{2sin}\left( \dfrac{\text{x+3x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{x-3x}}{\text{2}} \right)}{\text{2cos}\left( \dfrac{\text{x+3x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{x-3x}}{\text{2}} \right)}$                   

( Using the formula )

$\text{=}\dfrac{\text{sin 2x}}{\text{cos 2x}}$

$\text{=tan 2x}$

Therefore,  L.H.S = R.H.S.

20. Prove that $\dfrac{\text{sin x-sin 3x}}{\text{si}{{\text{n}}^{\text{2}}}\text{x-co}{{\text{s}}^{\text{2}}}\text{x}}\text{=2sin x}$

$\text{sin A-sin B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)$

And $\text{co}{{\text{s}}^{\text{2}}}\text{A-si}{{\text{n}}^{\text{2}}}\text{A=cos 2A}$

 L.H.S $\text{=}\dfrac{\text{sin x-sin 3x}}{\text{si}{{\text{n}}^{\text{2}}}\text{x-co}{{\text{s}}^{\text{2}}}\text{x}}$

$\text{=}\dfrac{\text{2cos}\left( \dfrac{\text{x+3x}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{x-3x}}{\text{2}} \right)}{\text{-cos2x}}$

$\text{=}\dfrac{\text{2cos2xsin}\left( \text{-x} \right)}{\text{-cos 2x}}$

$\text{=-2 }\!\!\times\!\!\text{ }\left( \text{-sinx} \right)$

Therefore , we have,

$\text{L}\text{.H}\text{.S=2sin x}$

21. Prove that $\dfrac{\text{cos 4x+cos 3x+cos 2x}}{\text{sin 4x+sin 3x+sin 2x}}\text{=cot 3x}$

And, $\text{sin A+sin B=2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)$

Now, L.H.S.$\text{=}\dfrac{\text{cos 4x+cos 3x+cos 2x}}{\text{sin 4x+sin 3x+sin 2x}}$

$\text{=}\dfrac{\left( \text{cos 4x+cos 2x} \right)\text{+cos 3x}}{\left( \text{sin4x+sin2x} \right)\text{+sin 3x}}$

$\text{=}\dfrac{\text{2cos}\left( \dfrac{\text{4x+2x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{4x-2x}}{\text{2}} \right)\text{+cos3x}}{\text{2sin}\left( \dfrac{\text{4x+2x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{4x-2x}}{\text{2}} \right)\text{+sin 3x}}$   

(Using the Formulas)

$\text{=}\dfrac{\text{2cos 3x cos x+cos 3x}}{\text{2sin 3x cos x+sin 3x}}$

Further computing, we obtain,

L.H.S $\text{=}\dfrac{\text{cos 3x}\left( \text{2cos x+1} \right)}{\text{sin 3x}\left( \text{2cos x+1} \right)}$ 

$\text{=cot 3x}$ 

22. Prove that $\text{cot x cot 2x-cot 2x cot 3x-cot 3x cot x=1}$

We know that, $\text{cot}\left( \text{A+B} \right)\text{=}\dfrac{\text{cotAcotB-1}}{\text{cot A+cot B}}$

Now , L.H.S.$\text{=cot xcot 2x-cot 2x cot 3x-cot 3x cot x}$

$\text{=cot x cot 2x-cot 3x}\left( \text{cot 2x+cot x} \right)$

$\text{=cot x cot 2x-cot}\left( \text{2x+x} \right)\left( \text{cot 2x+cot x} \right)$

$\text{=cot x cot 2x-}\left[ \dfrac{\text{cot 2x cot x-1}}{\text{cot x+cot 2x}} \right]\left( \text{cot 2x+cot x} \right)$

Further computing we obtain,

$\text{L}\text{.H}\text{.S=cot x cot 2x-}\left( \text{cot 2x cot x-1} \right)$ 

$\text{=1}$

23. Prove that $\text{tan 4x=}\dfrac{\text{4tan x}\left( \text{1-ta}{{\text{n}}^{\text{2}}}\text{x} \right)}{\text{1-6ta}{{\text{n}}^{\text{2}}}\text{x+ta}{{\text{n}}^{\text{4}}}\text{x}}$

We  know that $\text{tan 2A=}\dfrac{\text{2tan A}}{\text{1-ta}{{\text{n}}^{\text{2}}}\text{A}}$

L.H.S.$\text{=tan 4x}$

$\text{=tan2}\left( \text{2x} \right)$

$\text{=}\dfrac{\text{2tan 2x}}{\text{1-ta}{{\text{n}}^{\text{2}}}\left( \text{2x} \right)}$

$\text{=}\dfrac{\left( \dfrac{\text{4tan x}}{\text{1-ta}{{\text{n}}^{\text{2}}}\text{x}} \right)}{\left[ \text{1-}\dfrac{\text{4ta}{{\text{n}}^{\text{2}}}\text{x}}{{{\left( \text{1-ta}{{\text{n}}^{\text{2}}}\text{x} \right)}^{\text{2}}}} \right]}$

Further  computing, we obtain,

L.H.S $\text{=}\dfrac{\left( \dfrac{\text{4tan x}}{\text{1-ta}{{\text{n}}^{\text{2}}}\text{x}} \right)}{\left[ \dfrac{{{\left( \text{1-ta}{{\text{n}}^{\text{2}}}\text{x} \right)}^{\text{2}}}\text{4ta}{{\text{n}}^{\text{2}}}\text{x}}{{{\left( \text{1-ta}{{\text{n}}^{\text{2}}}\text{x} \right)}^{\text{2}}}} \right]}$$$$$

$\text{=}\dfrac{\text{4tan x}\left( \text{1-ta}{{\text{n}}^{\text{2}}}\text{x} \right)}{\text{1+ta}{{\text{n}}^{\text{4}}}\text{x-2ta}{{\text{n}}^{\text{2}}}\text{x-4ta}{{\text{n}}^{\text{2}}}\text{x}}$

$\text{=}\dfrac{\text{4tan x}\left( \text{1-ta}{{\text{n}}^{\text{2}}}\text{x} \right)}{\text{1-6ta}{{\text{n}}^{\text{2}}}\text{x+ta}{{\text{n}}^{\text{4}}}\text{x}}$ 

24. Prove that $\text{cos 4x=1-8si}{{\text{n}}^{\text{2}}}\text{xco}{{\text{s}}^{\text{2}}}\text{x}$

We know that, $\text{cos 2x=1-2si}{{\text{n}}^{\text{2}}}\text{x}$ 

And $\text{sin 2x=2sin x cos x}$ 

L.H.S.$\text{=cos 4x}$

$\text{=cos 2}\left( \text{2x} \right)$

$\text{=1-2si}{{\text{n}}^{\text{2}}}\text{2x}$

$\text{=1-2}{{\left( \text{2sin x cos x} \right)}^{\text{2}}}$

Further computing we get,

L.H.S $\text{=1-8si}{{\text{n}}^{\text{2}}}\text{xco}{{\text{s}}^{\text{2}}}\text{x}$ 

25. Prove that $\text{cos 6x=32xco}{{\text{s}}^{\text{6}}}\text{x-48co}{{\text{s}}^{\text{4}}}\text{x+18co}{{\text{s}}^{\text{2}}}\text{x-1}$

We know that, $\text{cos 3A=4co}{{\text{s}}^{\text{3}}}\text{A-3cosA}$

and  $\text{cos 2x=1-2si}{{\text{n}}^{\text{2}}}\text{x}$

L.H.S $\text{=cos 6x}$

$\text{=cos 3}\left( \text{2x} \right)$

$\text{=4co}{{\text{s}}^{\text{3}}}\text{2x-3cos 2x}$

$\text{=4}\left[ {{\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x-1} \right)}^{\text{3}}}\text{-3}\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x-1} \right) \right]$

L.H.S $\text{=4}\left[ {{\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x} \right)}^{\text{3}}}\text{-}{{\left( \text{1} \right)}^{\text{3}}}\text{-3}\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x} \right) \right]\text{-6co}{{\text{s}}^{\text{2}}}\text{x+3}$

$\text{=4}\left[ {{\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x} \right)}^{\text{3}}}\text{-}{{\left( \text{1} \right)}^{\text{3}}}\text{-3}{{\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x} \right)}^{\text{2}}}\text{+3}\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x} \right) \right]\text{-6co}{{\text{s}}^{\text{2}}}\text{x+3}$

$\text{=4}\left[ \text{8co}{{\text{s}}^{\text{6}}}\text{x-1-12co}{{\text{s}}^{\text{4}}}\text{x+6co}{{\text{s}}^{\text{2}}}\text{x} \right]\text{-6co}{{\text{s}}^{\text{2}}}\text{x+3}$    $\text{=32co}{{\text{s}}^{\text{6}}}\text{x-48co}{{\text{s}}^{\text{4}}}\text{x+18co}{{\text{s}}^{\text{2}}}\text{x-1}$

NCERT Solutions For Class 11 Maths Chapter 3 Exercise 3.3 Trigonometry-

Ncert solutions for class 11 maths chapter 3 trigonometric functions exercise 3.3 have been provided here for students to prepare well for their academic and competitive examinations. the steps given in the examples have been followed while providing the ncert solutions for class 11 exercise 3.3. for all the questions present in this exercise. these solutions have been prepared by the subject experts at vedantu and are in accordance with the latest syllabus issued by the cbse board., topic covered in class 11 maths chapter 3 exercise 3.3, class 11 maths chapter 3 exercise 3.3. is based on the topic of the trigonometry function of  sum and difference of two angles., free pdf download.

The experts offer these solutions after a detailed analysis of the marking pattern plus the model answer sheet issued by CBSE. It is recommendable for class 11 students to go through with these solutions and enhance their speed for attempting Trigonometry questions. Class 11 Maths exercise 3.3 solutions can help students throughout the journey of their board and competitive exams.  

NCERT Solutions Class 11 Maths Chapter 3 Exercise 3.3 - Trigonometry

In class 11 Trigonometry exercise 3.3, students will learn about the representation and properties of trigonometric functions. Students will get to know about the empty set, equal trigonometric functions, finite and infinite trigonometric functions, and more. The chapter educates students about principal solutions, general solutions, (x + y) formula, sine and cosine formula, and more. In chapter 3 exercise 3.3 Trigonometric Functions, students will acknowledge the concepts like a sign of trigonometric functions, domain and range of trigonometric functions, sum and difference of two angles formed by trigonometric functions, and more. There are four quadrants; all trigonometric functions are positive in the first quadrant. In the second quadrant, sine and cosec functions are positive. In the third, tan and cot functions are positive, and in the last quadrant, cos and sec functions are positive. 

The chapter introduces students to sub trigonometric functions, intersection, and union of trigonometric functions, the complement of a set, and more. In the section domain and range of trigonometric functions, students will study about domain and range of functions ranging from 0 to 1. The sine function increases from -1 to 0 and from 0 to 1. The cosine function increases from 0 to 1 and -1 to 0. The tan function ranges from 0 to infinity. Students should practice maths class 11 chapter 3 exercise 3.3 questions based on the concepts like trigonometric functions, properties of complement trigonometric functions, and more. 

By using the identity and properties of trigonometric functions, students will study how to derive expressions for the sum and difference of two numbers. Apart from it, students will come across problems based on trigonometric identities, basic applications, related expressions, and more. With the help of class 11 maths NCERT solutions chapter 3 exercise 3.3, students can practice a greater number of questions.

NCERT Solutions for Class 11 Maths Chapters

Chapter 1 - Sets

Chapter 2 - Relations and Functions

Chapter 3 - Trigonometric Functions

Chapter 4 - Principle of Mathematical Induction

Chapter 5 - Complex Numbers and Quadratic Equations

Chapter 6 - Linear Inequalities

Chapter 7 - Permutations and Combinations

Chapter 8 - Binomial Theorem

Chapter 9 - Sequences and Series

Chapter 10 - Straight Lines

Chapter 11 - Conic Sections

Chapter 12 - Introduction to Three Dimensional Geometry

Chapter 13 - Limits and Derivatives

Chapter 14 - Mathematical Reasoning

Chapter 15 - Statistics

Chapter 16 - Probability

Along with this, students can also download additional study materials provided by Vedantu, for Chapter 3 of CBSE Class 11 Maths Solutions –

Chapter 3: Important Questions

Chapter 3: Important Formulas

Chapter 3: Revision Notes

Chapter 3: NCERT Exemplar Solutions  

Chapter 3: RD Sharma Solutions

Class 11 Maths Chapter 3 Exercise 3.3- Weightage Marks

Out of 80 marks, the Sets and Functions chapter hold a weight of 23 marks. Trigonometric Function is a part of this unit. 

Benefits of Maths Chapter 3 Class 11 NCERT Solutions

Class 11th leads to several career-making decisions as students have to go through some crucial competitive exams to get the desired college. Class 11 Maths NCERT solutions chapter 3 exercise 3.3 offers a better knowledge of the chapter that will help students to study deeper into basics. These solutions can be of great value for those trying to outshine in their regular school examinations. Some of the benefits of referring class 11 maths exercise 3.3 solutions include:

The students can gain the confidence to attempt an advanced level of questions asked from the exercise 3.3 maths class 11. 

Maths Class 11 NCERT solutions are a one-stop destination for all the possible questions with proved answers that will help students to secure a high percentage. 

The students can understand the properties of Trigonometry in a better way by going through these solutions. They get all the crucial contents required in one place. 

Exercise 3.3 class 11 maths solutions offered by Vedantu are in a well-organized format. It helps students to analyze the paper attempting method for Trigonometry questions asked in the exam.

The use of user-friendly language makes it trouble-free for students to study the problems based on Trigonometry. 

FAQs on NCERT Solutions for Class 11 Maths Chapter 3: Trigonometric Functions - Exercise 3.3

1. How to prove 2(𝜋/6) + (7𝜋 6)(𝜋/3)  =3/2?

Let us first solve the Left-hand side of the problem mentioned. 

Given equation at the left-hand side is 2(π/6) +(7π b)(π/3).

Using the properties of trigonometric functions: 

sin sin (𝜋/6) = ½ 𝜋/3 = ½ and = (π+ 𝜋/6) 

Hence, (𝜋/6) = (½) 2 =¼ (𝜋/3)  = (½) 2 = ¼ 

The given equation becomes 2(¼) + (π+ π/6)(¼) 

Hence, the equation becomes 2(¼) + (-π/6)(¼)

L.H.S. becomes 1/2 + (-2) 2 (1/4)

Here, 1/2 + 4/4 = 1/2 + 1= 3/2 = R.H.S.

Hence proved L.H.S = R.H.S

2. How to find the value of tan 15 o ?

tan 15 o can be written as tan (45 o – 30 o )

By using the Trigonometry formula for tan (x – y):

tan (x – y) = (tan x – tan y)/ (1 + tan x tan y)

tan (45 o – 30 o ) = (tan 45 o – tan 30 o )/ (1 + tan 45 o tan 30 o )

Now, tan 45 o = 1 and tan 30 o = 1/√3; we get:

tan (45 o – 30 o ) = (1 - 1/√3) / (1 + 1/√3)

tan 15 o = ((√3 – 1)/√3)/ ((√3 + 1)/√3)

tan 15 o = (√3 – 1)/ (√3 + 1) = (√3– 1)/ (√3 + 1) (√3 – 1)

By further calculations:

tan 15 o = 4 - 2√3/ 3 – 1 = 2 - √3

3. How do I solve Class 11 Maths Chapter 3 Exercise 3.3?

Ans: You can refer to the NCERT Solutions Class 11 Maths Chapter 3 Exercise 3.3 available on Vedantu to solve the sums. This NCERT Solutions to Trigonometric Functions is available for downloading as well so now, you can solve this exercise even without the internet! Hurry up and download the NCERT Solutions from the page NCERT Solutions for Class 11 Maths Chapter 3 Exercise 3.3 on the Vedantu website at free of cost. You can also download these solutions from the Vedantu app for free.

4. What is a radian measure?

A radian measure, in simple words, is the angle in a circle. For example, in a circle of one unit radius, the angle made at the centre by a one-unit arc will be equal to one radian. A radian measure is used to express the measure of an angle in a circle. For more clarity on the topic, you can consider using the NCERT Solutions for Class 11 Maths Chapter 3 Exercise 3.3. 

5. Where can I get the full solutions to Class 11 Maths Chapter 3 Exercise 3.3?

Vedantu is the best place for you. Here you can get the full solutions to Class 11 Maths Chapter Exercise 3.3. You can check out the NCERT Solutions for complete step by step answers to all the questions present in the exercise. Practice the complete solution to get full marks on your test. Since they are explained in simple language and in detail, the students will be able to grasp them easily. 

6. Is Class 11 Maths Chapter 3 very difficult?

No, Class 11 Maths Chapter 3 “Trigonometric Functions” is not at all difficult. Success can be easily achieved from practice. The best guide for practice is Vedantu’s NCERT Solutions Class 11 Maths Chapter 3. You will get a complete solution to all the questions from all the different exercises that are there in the chapter. These answers are precise and step by step so you will learn a lot while practising. 

7. How to complete the Class 11 Maths 3.3 Exercise?

You can successfully complete Class 11 Maths Chapter 3 Exercise 3.3. By referring to Vedantu’s NCERT Solutions. This solution is the best that you will get as it has all questions solved by experts, who have provided step by step precise answers. Moreover, all the important questions from the miscellaneous exercise have also been explained in detail. So, download the notes today and practise well.

Syllabus for the Session 2023-24

CBSE Syllabus

Case Study Questions

Case Study on Sets      CS-2   CS-3   CS-4   CS-5

Case Study on Relations & Functions   CS-2   CS-3

Case Study on Trigonometric Functions

Case Study on Complex Numbers

Case Study on Linear Inequalities

Case Study on Permutations and Combinations

Case Study on Sequences & Series

Case Study on Straight Lines

Case Study on Conic Sections

Case Study on Statistics

Case Study on Probability

Pdf of  Case Studies

MCQs for Practice

Chapter 1 - Sets     

Chapter 2 - Relations & Functions

Chapter 3 - Trigonometric Functions

Chapter 4 - Complex Numbers & Quadratic Equations

Chapter 5 - Linear Inequalities

Chapter 6 - Permutations & Combinations

Chapter 7 - Binomial Theorem

Chapter 8 - Sequences & Series

Chapter 9 - Straight Line

Chapter 1 0 - Conic Sections

Chapter 1 1 - Introduction to Three-dimensional Geometry

Chapter 12 - Limits & D erivatives

Chapter 13 - Statistics

Chapter 14 - Probability

Answers of MCQs

Assertion & Reasoning Questions

Relations & Functions

Trigonometric Functions

Complex Numbers

Linear Inequalities

Permutations & Combinations

Binomial Theorem

Sequences & Series

Straight Lines

Conic Sections

Introduction to Three-Dimensional Geometry

Limits & derivatives

Probability

Topic Wise Assignments of Previous Year Questions

Relations and Functions

Straight Line

Limits & Derivatives

Question Papers - DoE, Delhi

Session 2015-2016

            SA2(QP)         SA2(MS)         COMP(QP)         COMP(MS)

Session 201 6 -20 17

            SA1(QP)      SA2(QP)         SA2(MS)         COMP(QP)        COMP(MS)

Session 201 7 -201 8

            SA2(QP)          SA2(MS)         COMP(QP)         COMP(MS)

Session 201 8 -201 9

            SA2(QP)          SA2(MS)         COMP(QP)         COMP(MS)

Session 201 9 -20 20

            SA2(QP)          SA2(MS)        

Session 2020-21

    Video Explanation:  Part A     Part B Section III     Part B Section IV   Part B Section V

Session 2021-22

Question Paper 

Video Explanation:  Section A     Section B     Section C

Session 2022-23

  Sample Question Paper for Mid-Term Exam

Video Explanation: Section A     Section B    Section C     Section D     Section E

Mid-Term Exam:  Question Paper

Video Explanation: Section A     Section B     Section C     Section D    Section E

Practice Paper for Final Exam

Video Explanation: Section A     Section B     Section C     Section D     Section E

Final Exam:  Question Paper     Marking Scheme

Video Explanation: Section A     Section B     Section C     Section D     Section E

Support Material Issued by DoE, Delhi

Session 202 3 -24

 Mid-Term Exam:  Question Paper

Video Explanation:   Section A    Section B     Section C     Section D     Section E

Practice Paper 1 for Final Exam: Question Paper

Practice Paper 2 for Final Exam: Question Paper

Short Capsules (Notes to Revise Concepts)

Chapter 1 - Sets

Chapter 4 - Mathematical Induction

Chapter 5 - Complex Numbers & Quadratic Equations

Chapter 6 - Linear Inequalities

Chapter 7 - Permutations & Combinations

Chapter 8 - Binomial Theorem

Chapter 9 - Sequences & Series

Chapter 10 - Straight Line

Chapter 11 - Conic Sections

Chapter 12 - Introduction to Three-dimensional Geometry

Chapter 13 - Limits & derivatives

Chapter 14 - Mathematical Reasoning

Chapter 15 - Statistics

Chapter 16 - Probability

Some Basic Concepts to Revise:

Number System

Mensuration Results

Quadratic Equations

Solution of Polynomial Inequality - Wavy Curve Method

Probability__Revision of the Topics studied in Earlier Classes  

Result Sheets

Trigonometric Identities

CBSE Case Study Questions for Class 11 Maths Complex Numbers Free PDF

Mere Bacchon, you must practice the CBSE Case Study Questions Class 11 Maths Complex Numbers  in order to fully complete your preparation . They are very very important from exam point of view. These tricky Case Study Based Questions can act as a villain in your heroic exams!

I have made sure the questions (along with the solutions) prepare you fully for the upcoming exams. To download the latest CBSE Case Study Questions , just click ‘ Download PDF ’.

CBSE Case Study Questions for Class 11 Maths Complex Numbers PDF

Checkout our case study questions for other chapters.

• Chapter 3 Trigonometric Functions Case Study Questions
• Chapter 4 Principle of Mathematical Induction Case Study Questions
• Chapter 6 Linear Inequalities Case Study Questions
• Chapter 7 Permutations and Combinations Case Study Questions

How should I study for my upcoming exams?

First, learn to sit for at least 2 hours at a stretch

Solve every question of NCERT by hand, without looking at the solution.

Solve NCERT Exemplar (if available)

Sit through chapter wise FULLY INVIGILATED TESTS

Practice MCQ Questions (Very Important)

Practice Assertion Reason & Case Study Based Questions

Sit through FULLY INVIGILATED TESTS involving MCQs. Assertion reason & Case Study Based Questions

After Completing everything mentioned above, Sit for atleast 6 full syllabus TESTS.

Comments are closed.

Contact Form

Privacy Policy

• Privacy Policy
• Terms and Conditions

• Web Stories

Friday, December 17, 2021

Class 11 maths case study based questions chapter 1 sets term 1 with answer key.

Hello students, Welcome to Maths Easy Institute.  

0 comments:

Post a comment.

Please do not enter any spam link in the comment box.

Warning: Do Not Copy!

• Blog Archives

• Best Books for IIT JEE
• Best Colleges Of India
• class 10 Case Study Based questions
• Class 10 Maths MCQ
• Class 11 Maths Case Study Questions
• Class 11 Maths MCQ
• Class 12 Math Case Study questions
• Class 12 Maths MCQ
• JEE MAIN MCQ
• Maths Strategy JEE
• News for Students

Blog Archive

• ►  April (3)
• ►  March (2)
• ►  February (1)
• ►  January (5)
• JEE MAIN Maths MCQ Chapter Application Of Derivati...
• JEE MAIN Maths MCQ Chapter Relations and Functions...
• JEE MAIN Maths MCQ Chapter SETS with Answers
• Class 11 Maths MCQ Chapter 11 Conic Section CBSE B...
• Class 11 Maths Case Study Based Questions Chapter ...
• Class 11 Maths MCQ Chapter 7 Permutation and Combi...
• Class 12 Maths MCQ Chapter 7 Integration with Answ...
• Class 10 Maths MCQ chapter 7 Coordinate Geometry C...
• Class 10 Maths MCQ chapter 5 Arithmetic Progressio...
• ►  November (5)
• ►  October (6)
• ►  September (5)
• ►  April (4)
• ►  March (3)
• ►  October (2)
• ►  September (7)
• ►  August (2)
• ►  July (4)

NCERT Solutions for Class 11 Maths Chapter 3 Exercise 3.3

Ncert solutions for class 11 maths chapter 3 trigonometric functions ex 3.3.

Free PDF of NCERT Solutions for Class 11 Maths Chapter 3 Exercise 3.3 prepared by expert Mathematics teacher at Mathongo.com as per CBSE (NCERT) books guidelines. Download our Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.3 Questions with Solutions to help you to revise complete Syllabus and Score More marks in your exams.

Share with friends:

• CBSE Maths Important Questions
• Class 11 Maths

CBSE Important Questions for Class 11 Maths

CBSE Important Questions for Class 11 Maths is crucial for the students as there is sudden progress in the level of challenge in the subject. This article will help you get an idea of the different types of questions that can be framed in the examination. Students will find chapter-wise sets of CBSE Important Questions in our question bank that will enhance their level of understanding of the subject. Also, some of these questions are expected to be asked in the exam. So, practise daily to excel in the examination.

CBSE Class 11 Maths Important Questions

There are a total of 16 chapters in the Class 11 Maths textbook. Students can get the Maths chapter-wise CBSE Important Questions of Class 11 by clicking on the links below.

Solving these questions will boost the student’s exam preparation. They will feel more confident while writing the Maths CBSE Class 11 exam. So, students must keep practising and continue with their studies.

For more study material and the latest updates on CBSE/ICSE/State Board/Competitive exams, keep visiting BYJU’S. Also, download the BYJU’S App, to watch interactive study videos.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.