simple equations case study questions class 7

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 7 Maths Chapter 4 Simple Equations

Last modified on: 8 months ago
Reading Time: 7 Minutes

Case Study Questions for Class 7 Maths Chapter 1 Integers

Here in this article, we are providing case study questions for Class 7 Maths Chapter 4 Simple Equations.

Maths Class 7 Chapter List

Latest chapter list (2023-24).

There is total 13 chapters.

Chapter 1 Integers Case Study Questions Chapter 2 Fractions and Decimals Case Study Questions Chapter 3 Data Handling Case Study Questions Chapter 4 Simple Equations Case Study Questions Chapter 5 Lines and Angles Case Study Questions Chapter 6 The Triangles and its Properties Case Study Questions Chapter 7 Comparing Quantities Case Study Questions Chapter 8 Rational Numbers Case Study Questions Chapter 9 Perimeter and Area Case Study Questions Chapter 10 Algebraic Expressions Case Study Questions Chapter 11 Exponents and Powers Case Study Questions Chapter 12 Symmetry Case Study Questions Chapter 13 Visualising Solid Shapes Case Study Questions

Old Chapter List

Chapter 1 Integers Chapter 2 Fractions and Decimals Chapter 3 Data Handling Chapter 4 Simple Equations Chapter 5 Lines and Angles Chapter 6 The Triangles and its Properties Chapter 7 Congruence of Triangles Chapter 8 Comparing Quantities Chapter 9 Rational Numbers Chapter 10 Practical Geometry Chapter 11 Perimeter and Area Chapter 12 Algebraic Expressions Chapter 13 Exponents and Powers Chapter 14 Symmetry Chapter 15 Visualising Solid Shapes

Deleted Chapter:

Chapter 7 Congruence of Triangles
Chapter 10 Practical Geometry

Tips for Answering Case Study Questions for Class 7 Maths in Exam

1. Comprehensive Reading for Context: Prioritize a thorough understanding of the provided case study. Absorb the contextual details and data meticulously to establish a strong foundation for your solution.

2. Relevance Identification: Pinpoint pertinent mathematical concepts applicable to the case study. By doing so, you can streamline your thinking process and apply appropriate methods with precision.

3. Deconstruction of the Problem: Break down the complex problem into manageable components or steps. This approach enhances clarity and facilitates organized problem-solving.

4. Highlighting Key Data: Emphasize critical information and data supplied within the case study. This practice aids quick referencing during the problem-solving process.

5. Application of Formulas: Leverage pertinent mathematical formulas, theorems, and principles to solve the case study. Accuracy in formula selection and unit usage is paramount.

6. Transparent Workflow Display: Document your solution with transparency, showcasing intermediate calculations and steps taken. This not only helps track progress but also offers insight into your analytical process.

7. Variable Labeling and Definition: For introduced variables or unknowns, offer clear labels and definitions. This eliminates ambiguity and reinforces a structured solution approach.

8. Step Explanation: Accompany each step with an explanatory note. This reinforces your grasp of concepts and demonstrates effective application.

9. Realistic Application: When the case study pertains to real-world scenarios, infuse practical reasoning and logic into your solution. This ensures alignment with real-life implications.

10. Thorough Answer Review: Post-solving, meticulously review your answer for accuracy and coherence. Assess its compatibility with the case study’s context.

11. Solution Recap: Before submission, revisit your solution to guarantee comprehensive coverage of the problem and a well-organized response.

12. Previous Case Study Practice: Boost your confidence by practicing with past case study questions from exams or textbooks. This familiarity enhances your readiness for the question format.

13. Efficient Time Management: Strategically allocate time for each case study question based on its complexity and the overall exam duration.

14. Maintain Composure and Confidence: Approach questions with poise and self-assurance. Your preparation equips you to conquer the challenges presented.

Download CBSE Books

Exam Special Series:

Sample Question Paper for CBSE Class 10 Science (for 2024)
Sample Question Paper for CBSE Class 10 Maths (for 2024)
CBSE Most Repeated Questions for Class 10 Science Board Exams
CBSE Important Diagram Based Questions Class 10 Physics Board Exams
CBSE Important Numericals Class 10 Physics Board Exams
CBSE Practical Based Questions for Class 10 Science Board Exams
CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
Sample Question Papers for CBSE Class 12 Physics (for 2024)
Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
Sample Question Papers for CBSE Class 12 Maths (for 2024)
Sample Question Papers for CBSE Class 12 Biology (for 2024)
CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
Master Organic Conversions CBSE Class 12 Chemistry Board Exams
CBSE Important Numericals Class 12 Physics Board Exams
CBSE Important Definitions Class 12 Physics Board Exams
CBSE Important Laws & Principles Class 12 Physics Board Exams
10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
ICSE Important Functions and Locations Based Questions Class 10 Biology
ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations and Class 7 Maths Chapter 4 Try These Solutions in Hindi and English Medium updated for session 2024-25. Class 7 Maths Chapter 4, which deals with simple equations, is a fundamental topic that has real-life applications and serves as a foundation for more complex algebraic concepts. According to new syllabus and revised books for 2024-25, the class 7th mathematics chapter 4 simple equations has only three exercises in course.

7th Maths Chapter 4 Solutions in English Medium

Class 7 Maths Chapter 4 Try These
Class 7 Maths Exercise 4.1 in English
Class 7 Maths Exercise 4.2 in English
Class 7 Maths Exercise 4.3 in English

7th Maths Chapter 4 Solutions in Hindi Medium

Class 7 Maths Exercise 4.1 in Hindi
Class 7 Maths Exercise 4.2 in Hindi
Class 7 Maths Exercise 4.3 in Hindi
Class 7 Maths Chapter 4 NCERT Book
Class 7 Maths Solutions Page
Class 7 all Subjects Solutions

Simple equations are used to solve a wide range of everyday problems. Whether it’s calculating expenses, determining quantities, or finding missing values, equations help you solve various real-life situations. Working with equations develops your mathematical thinking and problem-solving skills. Class 7 Maths chapter 4 teaches students how to translate word problems into mathematical expressions and equations.

Class 7 Maths Chapter 4 Simple Equations

7th Maths Exercise 4.1, Exercise 4.2 and Exercise 4.3 in English Medium updated for new academic session based on new NCERT Books. Download Solutions of Prashnavali 4.1, Prashnavali 4.2 and Prashnavali 4.3 in Hindi Medium free to use in PDF format. Class 7 Maths NCERT (https://ncert.nic.in/) Solutions are updated according to NCERT Books 2024-25. View these solutions in Video Format to study online or in PDF file format for offline use. Simple equations lay the groundwork for more advanced algebraic concepts you’ll encounter in higher grades. They provide a bridge between arithmetic and algebra, helping you transition to more abstract mathematical thinking. Download NCERT Solutions Offline Apps for class 7 all subjects in Hindi and English Medium.

Free App for Class 7 all Subjects

As students work with equations, they will start recognizing patterns and relationships between different variables. This skill is valuable not only in math but also in other subjects and analytical tasks. Equations are used to manage budgets, calculate expenses, and plan savings. They help learners make informed financial decisions by understanding how different variables affect your finances.

Important Questions on Class 7 Maths Chapter 4

Check whether the value given in the brackets is a solution to the given equation or not: n + 5 = 19 [ n = 1]..

n + 5 = 19 Putting n = 1 in L.H.S., 1 + 5 = 6 L.H.S. R.H.S., n = 1 is not the solution of given equation.

Write equations for the following statement: The sum of numbers x and 4 is 9.

Write the following equations in statement form: 4 p – 2 = 18..

If you take away 2 from 4 times p you get 18.

Class 7 Maths all three exercises of Chapter 4 Simple Equations solutions with step by step complete explanation are given below. Equations are used extensively in science and engineering fields to model and analyze various phenomena. From physics to chemistry to engineering, equations play a crucial role in understanding the natural world. No login or password is required to access these solutions for the session 2024-25. Class 7 Maths chapter 4 Simple Equations are used to analyze and interpret data. They help in making predictions, drawing conclusions, and understanding trends in various data sets.

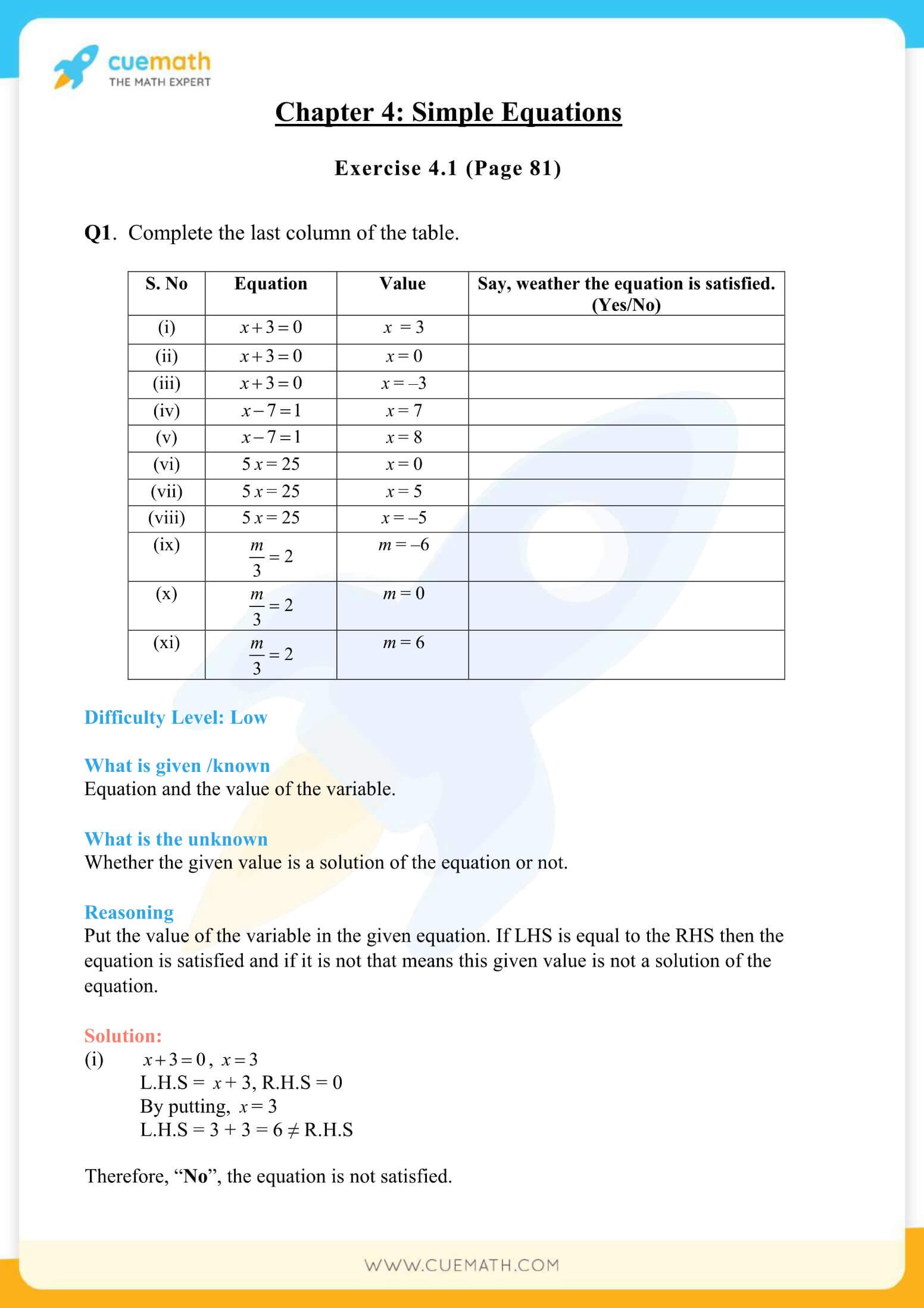
In 7 Maths Chapter 4 Simple Equations, we will study about the formation of linear equations in one variable (A variable takes on different numerical values; its value is not fixed. Variables are denoted usually by letters of the alphabets, such as x, y, z, l, m, n, p, etc.). In an equation there is always an equality sign. In computer programming, equations are used to write algorithms, create simulations, and solve computational problems. The equality sign shows that the value of expression to the left hand side or LHS is equal to the value of the expression to the right hand side or RHS. Remember the following things for an equation: 1. If we subtract the same number from both sides of an equality, it still holds. 2. If we multiply or divide both sides of the equality by the same non-zero number, it still holds. 3. Transposing a number (changing the side of the number) is the same as adding or subtracting the number from both sides. Note: If we fail to do the same mathematical operation on both sides of an equality, the equality does not hold. Learning to solve equations involves abstracting real-life situations into mathematical symbols and relationships, which is a valuable cognitive skill. To solve the practical problems based on equations, first convert the situation into equation and then apply the mathematical operation on it.

Solving equations involves trial and error, deduction, and careful analysis of the problem. This cultivates your critical thinking skills. Hindi Medium NCERT Solutions 2024-25 are now prepared for the new session 2024-25 and available for all the users. The skills and concepts you learn in this chapter set the stage for more advanced algebraic topics you’ll encounter in higher grades. Hindi & English Medium solutions are in Online as well as offline mode. Working with equations enhances your logical thinking by requiring you to follow a step-by-step process to arrive at a solution. These all are as per students suggestions. Download Class 7 Offline App for offline use. In essence, understanding simple equations is about developing problem-solving skills, logical reasoning, and an appreciation for how math is applied in various contexts. While the chapter might deal with “simple” equations, the skills you acquire here are foundational and will continue to be relevant as you progress in your mathematical journey.

Class 7 Maths Chapter 4 Try These Solutions

« Chapter 3: Data Handling

Chapter 5: lines and angles ».

NCERT Solutions
NCERT Class 7
NCERT 7 Maths
Chapter 4: Simple Equations

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations are provided to aid the students while preparing for their exams as well as assignments. For students who feel stressed about solving the most comprehensive and detailed NCERT Solutions for Class 7 Maths, we at BYJU’S, have prepared step-by-step solutions with detailed descriptions. We suggest students who aspire to score good marks in Maths go through these solutions and increase their knowledge.

Download Exclusively Curated Chapter Notes for Class 7 Maths Chapter – 4 Simple Equations

Download most important questions for class 7 maths chapter – 4 simple equations.

Chapter 4 – Simple Equations of NCERT Solutions for Class 7 Maths contains 4 exercises. Let’s now look at the important topics covered in this chapter mentioned below.

What Is Equation
Solving an Equation
More Equations
From Solution to Equation
Applications of Simple Equations to Practical Situations

carouselExampleControls111

ncert solutions for class 7 maths 5may chapter 4 simple equations 01

Previous Next

Access other exercises of NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations

Exercise 4.1 Solutions

Exercise 4.2 Solutions

Exercise 4.3 Solutions

Exercise 4.4 Solutions

Access answers to Maths NCERT Solutions for Class 7 Chapter 4 – Simple Equations

Exercise 4.1 Page: 81

1. Complete the last column of the table.

(i) x + 3 = 0

LHS = x + 3

By substituting the value of x = 3

LHS = 3 + 3 = 6

By comparing LHS and RHS,

∴ No, the equation is not satisfied.

(ii) x + 3 = 0

By substituting the value of x = 0,

LHS = 0 + 3 = 3

(iii) x + 3 = 0

By substituting the value of x = – 3,

LHS = – 3 + 3 = 0

∴ Yes, the equation is satisfied.

(iv) x – 7 = 1

LHS = x – 7

By substituting the value of x = 7,

LHS = 7 – 7 = 0

simple equations case study questions class 7

(v) x – 7 = 1

By substituting the value of x = 8,

LHS = 8 – 7 = 1

(vi) 5x = 25

LHS = 5 × 0 = 0

(vii) 5x = 25

By substituting the value of x = 5,

LHS = 5 × 5 = 25

(viii) 5x = 25

By substituting the value of x = -5,

LHS = 5 × (-5) = – 25

(ix) m/3 = 2

By substituting the value of m = – 6,

LHS = -6/3 = – 2

(x) m/3 = 2

By substituting the value of m = 0,

LHS = 0/3 = 0

(xi) m/3 = 2

By substituting the value of m = 6,

LHS = 6/3 = 2

2. Check whether the value given in the brackets is a solution to the given equation or not.

(a) n + 5 = 19 (n = 1)

LHS = n + 5

By substituting the value of n = 1,

Hence, the value of n = 1 is not a solution to the given equation n + 5 = 19.

(b) 7n + 5 = 19 (n = – 2)

LHS = 7n + 5

By substituting the value of n = -2,

= (7 × (-2)) + 5

Hence, the value of n = -2 is not a solution to the given equation 7n + 5 = 19.

By substituting the value of n = 2,

= (7 × (2)) + 5

Hence, the value of n = 2 is a solution to the given equation 7n + 5 = 19.

(d) 4p – 3 = 13 (p = 1)

LHS = 4p – 3

By substituting the value of p = 1,

= (4 × 1) – 3

Hence, the value of p = 1 is not a solution to the given equation 4p – 3 = 13.

(e) 4p – 3 = 13 (p = – 4)

By substituting the value of p = – 4,

= (4 × (-4)) – 3

Hence, the value of p = -4 is not a solution to the given equation 4p – 3 = 13.

(f) 4p – 3 = 13 (p = 0)

By substituting the value of p = 0,

= (4 × 0) – 3

Hence, the value of p = 0 is not a solution to the given equation 4p – 3 = 13.

3. Solve the following equations by trial and error method.

(i) 5p + 2 = 17

LHS = 5p + 2

= (5 × 0) + 2

Hence, the value of p = 0 is not a solution to the given equation.

= (5 × 1) + 2

Hence, the value of p = 1 is not a solution to the given equation.

= (5 × 2) + 2

Hence, the value of p = 2 is not a solution to the given equation.

= (5 × 3) + 2

Hence, the value of p = 3 is a solution to the given equation.

(ii) 3m – 14 = 4

LHS = 3m – 14

By substituting the value of m = 3,

= (3 × 3) – 14

Hence, the value of m = 3 is not a solution to the given equation.

= (3 × 4) – 14

Hence, the value of m = 4 is not a solution to the given equation.

= (3 × 5) – 14

Hence, the value of m = 5 is not a solution to the given equation.

= (3 × 6) – 14

Hence, the value of m = 6 is a solution to the given equation.

4. Write equations for the following statements.

(i) The sum of numbers x and 4 is 9.

The above statement can be written in the equation form as,

= x + 4 = 9

(ii) 2 subtracted from y is 8.

= y – 2 = 8

(iii) Ten times a is 70.

(iv) The number b divided by 5 gives 6.

= (b/5) = 6

(v) Three-fourths of t is 15.

(vi) Seven times m plus 7 gets you 77.

Seven times m is 7m.

= 7m + 7 = 77

(vii) One-fourth of a number x minus 4 gives 4.

One-fourth of a number x is x/4.

= x/4 – 4 = 4

(viii) If you take away 6 from 6 times y, you get 60.

6 times y is 6y.

= 6y – 6 = 60

(ix) If you add 3 to one-third of z, you get 30.

One-third of z is z/3.

= 3 + z/3 = 30

5. Write the following equations in statement forms.

(i) p + 4 = 15

The sum of numbers p and 4 is 15.

(ii) m – 7 = 3

7 subtracted from m is 3.

(iii) 2m = 7

Twice of number m is 7.

(iv) m/5 = 3

The number m divided by 5 gives 3.

(v) (3m)/5 = 6

Three-fifth of m is 6.

(vi) 3p + 4 = 25

Three times p plus 4 gives you 25.

(vii) 4p – 2 = 18

Four times p minus 2 gives you 18.

(viii) p/2 + 2 = 8

If you add half of a number p to 2, you get 8.

6. Set up an equation in the following cases.

(i) Irfan says that he has 7 marbles, more than five times the marbles Parmit has. Irfan has 37 marbles (Take m to be the number of Parmit’s marbles).

From the question, it is given that

Number of Parmit’s marbles = m

Irfan has 7 marbles, more than five times the marbles Parmit has.

= 5 × Number of Parmit’s marbles + 7 = Total number of marbles Irfan having

= (5 × m) + 7 = 37

= 5m + 7 = 37

(ii) Laxmi’s father is 49 years old. He is 4 years older than three times Laxmi’s age (Take Laxmi’s age to be y years).

Let Laxmi’s age be = y years old

Lakshmi’s father is 4 years older than three times her age.

= 3 × Laxmi’s age + 4 = Age of Lakshmi’s father

= (3 × y) + 4 = 49

= 3y + 4 = 49

(iii) The teacher tells the class that the highest marks obtained by a student in her class are twice the lowest marks plus 7. The highest score is 87 (Take the lowest score to be l).

Highest score in the class = 87

Let the lowest score be l.

= 2 × Lowest score + 7 = Highest score in the class

= (2 × l) + 7 = 87

= 2l + 7 = 87

(iv) In an isosceles triangle, the vertex angle is twice either base angle (Let the base angle be b in degrees. Remember that the sum of angles of a triangle is 180 degrees).

We know that the sum of angles of a triangle is 180 o

Let the base angle be b.

Vertex angle = 2 × base angle = 2b

= b + b + 2b = 180 o

= 4b = 180 o

Exercise 4.2 Page: 86

1. Give first the step you will use to separate the variable and then solve the equation.

(a) x – 1 = 0

We have to add 1 to both sides of the given equation.

Then, we get

= x – 1 + 1 = 0 + 1

(b) x + 1 = 0

We have to subtract 1 from both sides of the given equation.

= x + 1 – 1 = 0 – 1

= x – 1 + 1 = 5 + 1

(d) x + 6 = 2

We have to subtract 6 from both sides of the given equation.

= x + 6 – 6 = 2 – 6

(e) y – 4 = – 7

We have to add 4 to both sides of the given equation.

= y – 4 + 4 = – 7 + 4

(f) y – 4 = 4

= y – 4 + 4 = 4 + 4

(g) y + 4 = 4

We have to subtract 4 from both sides of the given equation.

= y + 4 – 4 = 4 – 4

(h) y + 4 = – 4

= y + 4 – 4 = – 4 – 4

2. Give first the step you will use to separate the variable and then solve the equation.

(a) 3l = 42

Now, we have to divide both sides of the equation by 3.

= 3l/3 = 42/3

(b) b/2 = 6

Now, we have to multiply both sides of the equation by 2.

= b/2 × 2= 6 × 2

Now, we have to multiply both sides of the equation by 7.

= p/7 × 7= 4 × 7

(d) 4x = 25

Now, we have to divide both sides of the equation by 4

= 4x/4 = 25/4

(e) 8y = 36

Now, we have to divide both sides of the equation by 8.

= 8y/8 = 36/8

(f) (z/3) = (5/4)

Now, we have to multiply both sides of the equation by 3.

= (z/3) × 3 = (5/4) × 3

(g) (a/5) = (7/15)

Now, we have to multiply both sides of the equation by 5.

= (a/5) × 5 = (7/15) × 5

(h) 20t = – 10

Now, we have to divide both sides of the equation by 20.

= 20t/20 = -10/20

3. Give the steps you will use to separate the variable and then solve the equation.

(a) 3n – 2 = 46

First, we have to add 2 to both sides of the equation.

= 3n – 2 + 2 = 46 + 2

We have to divide both sides of the equation by 3.

= 3n/3 = 48/3

(b) 5m + 7 = 17

First, we have to subtract 7 from both sides of the equation.

= 5m + 7 – 7 = 17 – 7

We have to divide both sides of the equation by 5.

= 5m/5 = 10/5

First, we have to multiply both sides of the equation by 3.

= (20p/3) × 3 = 40 × 3

= 20p = 120

We have to divide both sides of the equation by 20.

= 20p/20 = 120/20

(d) 3p/10 = 6

First, we have to multiply both sides of the equation by 10.

= (3p/10) × 10 = 6 × 10

= 3p/3 = 60/3

4. Solve the following equations.

(a) 10p = 100

We have to divide both sides of the equation by 10.

= 10p/10 = 100/10

(b) 10p + 10 = 100

First, we have to subtract 10 from both sides of the equation.

= 10p + 10 – 10 = 100 – 10

= 10p/10 = 90/10

We have to multiply both sides of the equation by 4.

= p/4 × 4 = 5 × 4

(d) – p/3 = 5

We have to multiply both sides of the equation by – 3.

= – p/3 × (- 3) = 5 × (- 3)

(e) 3p/4 = 6

First, we have to multiply both sides of the equation by 4.

= (3p/4) × (4) = 6 × 4

= 3p/3 = 24/3

(f) 3s = – 9

= 3s/3 = -9/3

(g) 3s + 12 = 0

First, we have to subtract 12 from both sides of the equation.

= 3s + 12 – 12 = 0 – 12

= 3s/3 = -12/3

= 3s/3 = 0/3

We have to divide both sides of the equation by 2.

= 2q/2 = 6/2

(j) 2q – 6 = 0

First, we have to add 6 to both sides of the equation.

= 2q – 6 + 6 = 0 + 6

(k) 2q + 6 = 0

First, we have to subtract 6 from both sides of the equation.

= 2q + 6 – 6 = 0 – 6

= 2q/2 = – 6/2

(l) 2q + 6 = 12

= 2q + 6 – 6 = 12 – 6

Exercise 4.3 Page: 89

1. Solve the following equations.

(a) 2y + (5/2) = (37/2)

By transposing (5/2) from LHS to RHS, it becomes -5/2

= 2y = (37/2) – (5/2)

= 2y = (37-5)/2

= 2y = 32/2

Divide both sides by 2.

= 2y/2 = (32/2)/2

= y = (32/2) × (1/2)

(b) 5t + 28 = 10

By transposing 28 from LHS to RHS, it becomes -28

= 5t = 10 – 28

= 5t = – 18

Divide both sides by 5.

= 5t/5= -18/5

= t = -18/5

By transposing 3 from LHS to RHS, it becomes -3

= a/5 = 2 – 3

= a/5 = – 1

Multiply both sides by 5.

= (a/5) × 5= -1 × 5

(d) (q/4) + 7 = 5

By transposing 7 from LHS to RHS, it becomes -7

= q/4 = 5 – 7

= q/4 = – 2

Multiply both sides by 4.

= (q/4) × 4= -2 × 4

(e) (5/2) x = -5

First, we have to multiply both sides by 2.

= (5x/2) × 2 = – 5 × 2

= 5x = – 10

We have to divide both sides by 5.

= 5x/5 = -10/5

(f) (5/2) x = 25/4

= (5x/2) × 2 = (25/4) × 2

= 5x = (25/2)

= 5x/5 = (25/2)/5

= x = (25/2) × (1/5)

= x = (5/2)

(g) 7m + (19/2) = 13

By transposing (19/2) from LHS to RHS, it becomes -19/2

= 7m = 13 – (19/2)

= 7m = (26 – 19)/2

Divide both sides by 7.

= 7m/7 = (7/2)/7

= m = (7/2) × (1/7)

(h) 6z + 10 = – 2

By transposing 10 from LHS to RHS, it becomes – 10

= 6z = -2 – 10

= 6z = – 12

Divide both sides by 6.

= 6z/6 = -12/6

(i) (3/2) l = 2/3

= (3l/2) × 2 = (2/3) × 2

= 3l = (4/3)

We have to divide both sides by 3.

= 3l/3 = (4/3)/3

= l = (4/3) × (1/3)

= x = (4/9)

(j) (2b/3) – 5 = 3

By transposing -5 from LHS to RHS, it becomes 5

= 2b/3 = 3 + 5

Multiply both sides by 3.

= (2b/3) × 3= 8 × 3

= 2b/2 = 24/2

2. Solve the following equations.

(a) 2(x + 4) = 12

Let us divide both sides by 2.

= (2(x + 4))/2 = 12/2

= x + 4 = 6

By transposing 4 from LHS to RHS, it becomes -4

= x = 6 – 4

(b) 3(n – 5) = 21

Let us divide both sides by 3.

= (3(n – 5))/3 = 21/3

= n – 5 = 7

= n = 7 + 5

= (3(n – 5))/3 = – 21/3

= n – 5 = -7

= n = – 7 + 5

(d) – 4(2 + x) = 8

Let us divide both sides by -4.

= (-4(2 + x))/ (-4) = 8/ (-4)

= 2 + x = -2

By transposing 2 from LHS to RHS, it becomes – 2

= x = -2 – 2

(e) 4(2 – x) = 8

Let us divide both sides by 4.

= (4(2 – x))/ 4 = 8/ 4

= 2 – x = 2

= – x = 2 – 2

3. Solve the following equations.

(a) 4 = 5(p – 2)

Let us divide both sides by 5.

= 4/5 = (5(p – 2))/5

= 4/5 = p -2

By transposing – 2 from RHS to LHS, it becomes 2

= (4/5) + 2 = p

= (4 + 10)/ 5 = p

(b) – 4 = 5(p – 2)

= – 4/5 = (5(p – 2))/5

= – 4/5 = p -2

= – (4/5) + 2 = p

= (- 4 + 10)/ 5 = p

By transposing 4 from RHS to LHS, it becomes – 4

= 16 – 4 = 3(t + 2)

= 12 = 3(t + 2)

= 12/3 = (3(t + 2))/ 3

= 4 = t + 2

By transposing 2 from RHS to LHS, it becomes – 2

= 4 – 2 = t

(d) 4 + 5(p – 1) =34

By transposing 4 from LHS to RHS, it becomes – 4

= 5(p – 1) = 34 – 4

= 5(p – 1) = 30

= (5(p – 1))/ 5 = 30/5

= p – 1 = 6

By transposing – 1 from RHS to LHS, it becomes 1

= p = 6 + 1

(e) 0 = 16 + 4(m – 6)

By transposing 16 from RHS to LHS, it becomes – 16

= 0 – 16 = 4(m – 6)

= – 16 = 4(m – 6)

= – 16/4 = (4(m – 6))/ 4

= – 4 = m – 6

By transposing – 6 from RHS to LHS, it becomes 6

= – 4 + 6 = m

4. (a) Construct 3 equations starting with x = 2

The first equation is,

Multiply both sides by 6.

= 6x = 12 … [equation 1]

The second equation is,

Subtracting 4 from both sides,

= 6x – 4 = 12 -4

= 6x – 4 = 8 … [equation 2]

The third equation is,

= (6x/6) – (4/6) = (8/6)

= x – (4/6) = (8/6) … [equation 3]

(b) Construct 3 equations starting with x = – 2

= 5x = -10 … [equation 1]

Subtracting 3 from both sides,

= 5x – 3 = – 10 – 3

= 5x – 3 = – 13 … [equation 2]

Dividing both sides by 2.

= (5x/2) – (3/2) = (-13/2) … [equation 3]

Exercise 4.4 Page: 91

1. Set up equations and solve them to find the unknown numbers in the following cases.

(a) Add 4 to eight times a number; you get 60.

Let us assume the required number is x.

Eight times a number = 8x

The given above statement can be written in the equation form as,

= 8x + 4 = 60

= 8x = 60 – 4

Divide both sides by 8.

= (8x/8) = 56/8

(b) One-fifth of a number minus 4 gives 3.

One-fifth of a number = (1/5) x = x/5

= (x/5) – 4 = 3

By transposing – 4 from LHS to RHS, it becomes 4

= x/5 = 3 + 4

Then. we get

= (x/5) × 5 = 7 × 5

Three-fourths of a number = (3/4) x

= (3/4) x + 3 = 21

By transposing 3 from LHS to RHS, it becomes – 3

= (3/4) x = 21 – 3

= (3/4) x = 18

= (3x/4) × 4 = 18 × 4

Divide both sides by 3.

= (3x/3) = 72/3

(d) When I subtracted 11 from twice a number, the result was 15.

Twice a number = 2x

= 2x –11 = 15

By transposing -11 from LHS to RHS, it becomes 11

= 2x = 15 + 11

= (2x/2) = 26/2

(e) Munna subtracts thrice the number of notebooks he has from 50, and he finds the result to be 8.

Thrice the number = 3x

= 50 – 3x = 8

By transposing 50 from LHS to RHS, it becomes – 50

= – 3x = 8 – 50

= -3x = – 42

Divide both sides by -3.

= (-3x/-3) = – 42/-3

(f) Ibenhal thinks of a number. If she adds 19 to it and divides the sum by 5, she will get 8.

= (x + 19)/5 = 8

= ((x + 19)/5) × 5 = 8 × 5

= x + 19 = 40

By transposing 19 from LHS to RHS, it becomes – 19

= x = 40 – 19

(g) Anwar thinks of a number. If he takes away 7 from 5/2 of the number, the result is 23.

Let us assume the required number is x

5/2 of the number = (5/2) x

= (5/2) x – 7 = 23

By transposing -7 from LHS to RHS, it becomes 7

= (5/2) x = 23 + 7

= (5/2) x = 30

Multiply both sides by 2,

= ((5/2) x) × 2 = 30 × 2

= 5x/5 = 60/5

2. Solve the following.

(a) The teacher tells the class that the highest marks obtained by a student in her class are twice the lowest marks plus 7. The highest score is 87. What is the lowest score?

Let us assume the lowest score is x.

The highest score is = 87

The highest marks obtained by a student in her class are twice the lowest marks plus 7= 2x + 7

= 2x + 7 = Highest score

= 2x + 7 = 87

= 2x = 87 – 7

= 2x/2 = 80/2

Hence, the lowest score is 40.

(b) In an isosceles triangle, the base angles are equal. The vertex angle is 40°.

What are the base angles of the triangle? (Remember, the sum of three angles of a triangle is 180°.)

= b + b + 40 o = 180 o

= 2b + 40 = 180 o

By transposing 40 from LHS to RHS, it becomes -40

= 2b = 180 – 40

= 2b/2 = 140/2

Hence, 70 o is the base angle of an isosceles triangle.

(c) Sachin scored twice as many runs as Rahul. Together, their runs fell two short of a double century. How many runs did each one score?

Let us assume Rahul’s score is x.

Sachin scored twice as many runs as Rahul is 2x.

Together, their runs fell two short of a double century.

= Rahul’s score + Sachin’s score = 200 – 2

= x + 2x = 198

= 3x/3 = 198/3

So, Rahul’s score is 66.

And Sachin’s score is 2x = 2 × 66 = 132

3. Solve the following:

(i) Irfan says that he has 7 marbles, more than five times the marbles Parmit has.

Irfan has 37 marbles. How many marbles does Parmit have?

Let us assume the number of Parmit’s marbles = m

= 5m = 37 – 7

= 5m/5 = 30/5

So, Permit has 6 marbles.

(ii) Laxmi’s father is 49 years old. He is 4 years older than three times Laxmi’s age.

What is Laxmi’s age?

= 3y = 49 – 4

= 3y/3 = 45/3

So, Lakshmi’s age is 15 years.

(iii) People of Sundargram planted trees in the village garden. Some of the trees were fruit trees. The number of non-fruit trees was two more than three times the number of fruit trees. What was the number of fruit trees planted if the number of non-fruit trees planted was 77?

Let the number of fruit trees be f.

3 × number of fruit trees + 2 = number of non-fruit trees

= 3f + 2 = 77

By transposing 2 from LHS to RHS, it becomes -2

=3f = 77 – 2

= 3f/3 = 75/3

So, the number of fruit trees was 25.

4. Solve the following riddle.

I am a number,

Tell my identity!

Take me seven times over

And add a fifty!

To reach a triple century

You still need forty!

Let us assume the number is x.

Take me seven times over and add a fifty = 7x + 50

To reach a triple century you still need forty = (7x + 50) + 40 = 300

= 7x + 50 + 40 = 300

= 7x + 90 = 300

By transposing 90 from LHS to RHS, it becomes -90

= 7x = 300 – 90

= 7x/7 = 210/7

Hence, the number is 30.

Disclaimer:

Dropped Topics – 4.6 From solution to equation

Frequently Asked Questions on NCERT Solutions for Class 7 Maths Chapter 4

List out the frequently asked topics of chapter 4 of ncert solutions in the exam of class 7 maths., why should we download ncert solutions for class 7 maths chapter 4 from byju’s, are ncert solutions for class 7 maths chapter 4 from an exam point of view, leave a comment cancel reply.

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Share Share

Register with BYJU'S & Download Free PDFs

Counselling

NCERT Solutions Class 7 Maths Chapter 4 Simple Equations

Algebra is all about the study of the unknown, and the fact that any condition on this unknown variable is called an equation has been covered in NCERT solutions for class 7 maths chapter 4 simple equations. When there are certain conditions on a variable, and the two expressions are supposed to be equal or have the same values, then that is defined as an equation. And once the value of the variable has been found out, which holds for the equation, that value is its solution. The NCERT solutions class 7 maths chapter 4 simple equations start from the basics of defining a variable to how an algebraic expression can be built around it and solved.

The students will come across the concepts like for any given conditions when equations are framed the right-hand side expression and the left-hand expression if interchanged, the equation will remain the same. The class 7 maths NCERT solutions chapter 4 simple equations can be accessed through the link below and also find some of these in the exercises given below.

NCERT Solutions Class 7 Maths Chapter 4 Ex 4.1
NCERT Solutions Class 7 Maths Chapter 4 Ex 4.2
NCERT Solutions Class 7 Maths Chapter 4 Ex 4.3
NCERT Solutions Class 7 Maths Chapter 4 Ex 4.4

NCERT Solutions for Class 7 Maths Chapter 4 PDF

The NCERT solutions for class 7 maths chapter 4 has exercises about the balancing of equations, performing arithmetic operations on them, and also about how transposing is done in an equation. The exercise links are given below and are available for free download in the form of pdf files:

☛ Download Class 7 Maths NCERT Solutions Chapter 4 Simple Equations

NCERT Class 7 Maths Chapter 4 Download PDF

$NCERT Solutions Class 7 Math Chapter 4 Simple Equations 1$

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations

The basics of algebra , if learned well, are helpful in real-life situations and also in learning higher mathematics too; hence, students should make use of this resource of exercises. The count of exercise questions under each chapter in NCERT Solutions Class 7 Maths Chapter 4 Simple Equations are as seen below:

Class 7 Maths Chapter 4 Ex 4.1 - 6 Questions
Class 7 Maths Chapter 4 Ex 4.2 - 4 Questions
Class 7 Maths Chapter 4 Ex 4.3 - 4 Questions
Class 7 Maths Chapter 4 Ex 4.4 - 4 Questions

☛ Download Class 7 Maths Chapter 4 NCERT Book

Topics Covered: The chapter starts from the basics of what is variable, and how to frame algebraic expressions around it, the definition of the equation. The topics in class 7 maths NCERT solutions chapter 4 further expand into how to solve the equation, carrying out arithmetic operations in an equation, the transposing concept, and how to build up simple algebraic expressions from practical, real-world scenarios.

Total Questions: Class 7 maths chapter 4 has in total 18 questions, of which 12 are easy, 4 are moderately challenging, while 2 would require some conceptual thinking from the students' side.

List of Formulas in NCERT Solutions Class 7 Maths Chapter 4

NCERT solutions class 7 maths chapter 4 has lots of simple yet basic concepts regarding solving equations. The students need to understand how to balance out an equation, and an equation remains unchanged when the left-hand side and right-hand side of the equation are interchanged. Below are some of the important pointers covered in the NCERT solutions class 7 maths chapter 4 :

In case the right-hand side of the equation is changed to the left-hand side and vice versa, the equation remains unchanged. So, x + 5 = y + 2 is the same as y + 2 = x + 5.
Transposing refers to moving on to the other side. The transposing of a number leads to the change of sign when the number is brought to the other side.

Like, in following equation if 5 is transposed:

y + 5 = 6 ; then y = 6 -5 ; it leads to y = 1

Important Questions for Class 7 Maths NCERT Solutions Chapter 4

Ncert solutions for class 7 maths video chapter 4, faqs on ncert solutions class 7 maths chapter 4, why is ncert solutions class 7 maths chapter 4 important.

NCERT Class 7 maths chapter 4 simple equations hold an important place in the math curriculum as they are prepared by experts. The content put up by them is well researched. Also, the explanations are in an easy language that can be understood by everyone. The CBSE board recommends studying the NCERT solutions, making them important again.

What are the Important Formulas in class 7 maths NCERT Solutions chapter 4?

The NCERT Solutions class 7 maths chapter 4 elaborately covers the simple equations, wherein the important concepts like the left-hand side and right-hand side of the equation, if interchanged, the equation remains unchanged. Also, the concept of transposing, which makes equation solving easier. The concept of transposing involves the shift of numbers to the other side of the equation with a change of sign.

What are the Important Topics Covered in NCERT Solutions class 7 maths chapter 4?

The topics covered in the NCERT Solutions class 7 maths chapter 4 range from the very basics of what is variable, framing of algebraic expressions, equations, how to solve the equation, how to deal with arithmetic operations in an equation, the transposing technique, and constructing simple algebraic expressions from practical situations.

How Many Questions are there in NCERT Solutions class 7 maths chapter 4 simple equations?

Class 7 maths chapter 4 features simple equations and all their relevant concepts. The exercise has a total of 18 problems, 12 of which are straightforward, 4 of which are fairly difficult, and 2 of which will take some conceptual thinking on the part of the students.

How the CBSE students can utilize NCERT Solutions class 7 maths chapter 4 effectively?

The CBSE board recommends the NCERT solutions class 7 maths; hence the probability of the occurrence of the questions in the chapter becomes higher. To effectively utilize this resource, the students must go through the chapters in detail and practice the solved examples on their own. This will help them memorize the basic concepts. Also, students can refer to the highlights presented in the chapter for their quick revision.

Do I Need to Practice all Questions Provided in NCERT Solutions Class 7 Maths simple equations?

The students should go through all the questions which are presented in the NCERT Solutions Class 7 Maths as they cover all the aspects of simple equations. The students should make use of this wonderful resource which is in the form of solved examples and exercises to explore the fundamentals of algebra.

Talk to our experts

1800-120-456-456

Simple Equations Class 7 Notes CBSE Maths Chapter 4 (Free PDF Download)
Revision Notes

Revision Notes for CBSE Class 7 Maths Chapter 4 - Free PDF Download

CBSE Class 7 Maths Revision Notes are prepared by an expert team at Vedantu. These solutions will help students to address their doubts in a better way, and they can understand the concept in an easy way. Students can go through these CBSE Class 7 Simple Equation Revision Notes to secure good scores in their board examination. The subject experts at Vedantu have prepared these revision notes on Class 7 Maths Chapter 4 as per the latest CBSE syllabus and following the Board’s guidelines. In order to have a thorough understanding of the chapter, download Simple Equation Class 7 Revision Notes Maths which is available in PDF format.

Vedantu is a platform that provides free CBSE Solutions (NCERT) and other study materials for students. You can also register Online for NCERT Solutions Class 7 Science tuition on Ved antu.com to score more marks in CBSE board examination.

Download CBSE Class 7 Maths Revision Notes 2024-25 PDF

Also, check CBSE Class 7 Maths revision notes for All chapters:

Access Class VII Mathematics Chapter 4 - Simple Equations Notes in 30 Minutes

The value of a variable can take on a variety of numerical values whose value is not fixed.

Vari ables can be represented as alphabetical letters such as $\text{a, b, c, x, y, z}$ etc.

Expressions are made up of variables.

The expressions are created by performing operations on the variables such as addition, subtraction, multiplication, and division .

An equation is a condition on a variable that demands that two expressions in the variable have the same value.

The solution of the equation is the value of the variable for which the equation is satisfied.

If the $\text{LHS}$ and $\text{RHS}$ are swapped or interchanged, the equation remains the same.

In the case of the balanced equation, if we

Add the same number to both the sides, or

Subtract the same number from both sides, or

Multiply both sides by the same number, or

Divide both sides by the same number, the balance remains undisturbed, i.e., the value of the $\text{LHS}$ remains equal to the value of the $\text{RHS}$ .

Consider an equality $\text{16 - 5 = 8 + 3}$ .

The above equality holds, since both its sides are equal (each is equal to $\text{11}$).

1. Let us now add $3$ to both sides; as a result

$\text{LHS = 16 - 5 + 3}$

$\text{LHS = 11 + 3}$

$\text{LHS = 14}$

$\text{RHS = 8 + 3 + 3}$

$\text{RHS = 11 + 3}$

$\text{RHS = 14}$

That is

$\text{LHS = RHS}$ , Here equality holds.

2. Let us now subtract $3$ to both sides; as a result

$\text{LHS = 16 - 5 - 3}$

$\text{LHS = 11 - 3}$

$\text{LHS = 8}$

$\text{RHS = 8 + 3 - 3}$

$\text{RHS = 8}$

$\text{LHS = RHS}$

Here equality holds.

3. Let us now multiply by $5$ to both sides; we get

$\text{LHS = }\left( \text{16 - 5} \right)\times 5$

$\text{LHS = 11}\times 5$

$\text{LHS = 55}$

$\text{RHS = }\left( \text{8 + 3} \right)\times \text{5}$

$\text{RHS = 11}\times \text{5}$

$\text{RHS = }55$

4. Let us now divide by $5$ to both sides; we get

$\text{LHS = }\left( \text{16 - 5} \right)\div 5$

$\text{LHS = 11}\div 5$

$\text{LHS = }\dfrac{11}{5}$

$\text{RHS = }\left( \text{8 + 3} \right)\div \text{5}$

$\text{RHS = 11}\div \text{5}$

$\text{RHS = }\dfrac{11}{5}$

The equality may not hold if we do not do the same mathematical operation with the same integer on both sides of an equivalence.

The above property provides a method for solving an equation in a systematic manner.

On both sides of the equation, we perform a series of identical mathematical operations in such a way that one side yields only the variable.

The equation's solution is the final step.

Changing the side of a number (that is transposing it) is the same as adding or subtracting the number from both sides.

Moving to the opposite side is referred to as transposing.

The effect of transposing a number is the same as adding (or removing) the same number to both sides of the equation.

You can change the sign of a number when you move it from one side of an equation to the other.

In the equation $\text{y - 7 = 15}$, transposing $\text{- 7}$ from the $\text{LHS}$ to the $\text{RHS}$ which gives,

$\text{y = 15 + 7}$

$\text{y = 22}$

The transposition of an expression can be done in the same way that the transposition of a number can be done.

We learned how to write simple algebraic expressions that correspond to real-life situations.

We also learned how to build an equation from its solution by employing the concept of doing the same mathematical operation (for example, adding the same integer) on both sides.

We also learned that we might apply a given equation to a specific practical scenario and use the equation to create a practical word problem or puzzle.

1. Nita’s father’s age is $10$ years more than twice times Nita’s age. Find Nita’s age, if her father is $\text{54}$ years old.

Consider Nita’s age will be $\text{x}$

We know that, Nita’s father’s age is $10$ years more than twice times Nita’s age and now he is $\text{54}$ years old.

Therefore, we can express as;

$\text{2x + 10 = 54}$

By transposing $\text{+ 10}$ from $\text{LHS}$ to $\text{RHS}$ , we get

$\text{2x = 54 - 10}$

$\text{2x = 44}$

$\text{ x = }\dfrac{44}{2}$

$\text{ x = 22}$

Therefore, Nita’s age is $\text{22}$ years.

Simple Equations Class 7 Notes Maths Chapter 4- PDF Download

Let’s revise the concepts in the chapter briefly:

Simple Equations

A simple equation is the set of variables, constants, and mathematical operations like addition, subtraction, multiplication, or division which are balanced by an equal sign. The left side of the equation is called the left-hand side (LHS) and the right side of the equation is called the right-hand side (RHS).

Consider an example x + 3 = 8. So, this letter x which is unknown is said to be a variable. A variable can be represented by any letter from a to z. We can write a general equation in one variable x in the form of ax+b=c

Here the Variable ‘a’ Represents the Coefficient of x, and the Variables b and c Represents the Constant Term

Variables: The letters used to express the unknown values are known as variables.

Constants: Constants are the values that remain constant throughout the solution. In other words, it is a symbol that has any fixed numeric value.

Equal to Sign: An equal to sign represents the balanced status between the left-hand-side(LHS) and the right-hand-side(RHS) of the equation.

Solving Simple Equations

In many cases solving simple equations requires rearrangement. This means that we need to move all the terms or numbers to one side of the equality symbol (such as =, >, or <) and x on the other side of the equality symbol. We can also refer to this process as isolating x.

We Can Always Rearrange the Equations for Solving Simple Equations Using a Set of Extremely Simple Rules:

Whatever we do to one side of the equation, we must do the same to the other. That way you preserve the relationship between them. It doesn’t matter what you do, whether it’s take away 2, add 57, multiply by 150, or divide by x.

As long as we do operations on both sides, the equation remains correct. It can help to think of your equation as a set of scales or a see-saw, which must always balance.

Solving simple equations is also done according to the BODMAS rule. So always remember to do the calculation in the right order.

Make equations as simple as possible: multiply the brackets, divide, cancel out the fractions, and add or subtract all the like terms.

Importances of Solving Simple Equations of Class 7 Notes CBSE Maths Chapter 4 (Free PDF Download)

The "Simple Equations Class 7 Notes CBSE Maths Chapter 4 (Free PDF Download)" are of paramount importance in a student's mathematical journey. This chapter introduces fundamental concepts of algebraic equations, laying a strong foundation for more advanced mathematical topics in the future. These notes provide a structured and clear explanation of how to formulate and solve simple equations, a skill essential for solving a wide range of real-world problems.

Moreover, understanding equations is not just about mathematics; it promotes critical thinking and problem-solving skills. It encourages students to translate practical scenarios into mathematical expressions, fostering logical reasoning and analytical abilities. The free PDF download of these notes makes quality education accessible to all, transcending geographical and economic barriers. In essence, these notes empower students with a versatile mathematical toolset that not only aids in academic success but also in making informed decisions in various aspects of life, making them well-rounded and equipped individuals.

Advantages of Revision Notes of CBSE Class 7 Chapter 4

Following are the advantages of referring to the Revision Notes by Vedantu:

Students will be able to revise the important concepts and formulas.

Students can have a quick revision of all the topics of this chapter which are important from an exam point of view.

The revision notes are very essential for last-minute examination preparation.

Studying from revision notes will minimise chances of making simple, but conspicuous mistakes

These revision notes are highly beneficial as all the important topics of CBSE Class 7 Maths Notes of Simple Equations are covered systematically in this PDF.

"Simple Equations Class 7 Notes CBSE Maths Chapter 4 [Free PDF Download]" plays a pivotal role in shaping students' mathematical acumen. This chapter serves as a crucial stepping stone in the realm of algebra, introducing students to the essential concept of solving equations. These free PDF notes provide a comprehensive and accessible resource, making quality education available to a wider audience. Beyond academic excellence, the significance of these notes lies in their ability to nurture critical thinking, problem-solving skills, and logical reasoning. They empower students to approach real-world challenges with mathematical precision, equipping them with lifelong skills that extend far beyond the classroom.

FAQs on Simple Equations Class 7 Notes CBSE Maths Chapter 4 (Free PDF Download)

1. How Vedantu has helped CBSE Class 7 students to make their revision easy?

While preparing for examinations it is very important to have good study material for revision. To make your preparation ace up, we at Vedantu offer you the most refined and effective CBSE revision notes. Revision Notes Class 7 Maths Chapter 4 will provide you a summary of all the important and relevant topics as well as highlight the significant references from chapter 4 Simple Equations.

2. Is there any order to consider while adding or subtracting numbers?

No. Addition demonstrates that it doesn’t matter what order we do the addition, the answer will still be the same. This means that we can always rearrange the expression to put together the like terms and therefore make it easier to add up. The same applies to Subtraction too, as long as we remember that subtracting is the same as adding a negative number. So, for example, 10 − 3 = 10 + (-3).

3. How are CBSE Class 7 Maths Revision Notes prepared?

Class 7 Maths Chapter 4 Revision Notes provided by Vedantu help students revise each and every important concepts related to simple equations in detail. The Vedantu revision notes for class 7 are prepared by collecting extracts from NCERT books as well as some standard books strictly based on the CBSE pattern.

4. Can I download the PDF of Notes for Chapter 4 of Class 7 “Simple Equations”?

The Revision Notes for Chapter 4 “Simple Equations” of Maths of Class 7 are available on the internet as well as in the solution books such as an NCERT exemplar, exam idea, and U-like. You can find a digital copy of Revision Notes to download from the official site of Vedantu. Vedantu is a highly recommended and trusted site for study material by students and teachers. Vedantu provides Revision Notes in a PDF format that is accessible to students without costing them any money.

5. Is Chapter 4 of Class 7 Mathematics difficult to understand?

Chapter 4 “Simple Equations” is a very important chapter for higher standards. The difficulty of the chapter is a subjective concept but since it is a new concept, some students may find the chapter hard to understand. Revision Notes help you understand these complex and new concepts. Revision Notes provide you with formulas and methods to solve simple equations effectively. These notes also provide you with extra practice which opens up your mind to new questions related to simple equations.

6. Are Chapter 4 of Class 7 Revision Notes of Maths good for study purposes?

NCERT Revision Notes are highly factual and knowledgeable to strengthen your basics in Mathematics. Chapter 4 talks about simple equations which are one of the most important base chapters for algebra-based chapters in the future. Revision notes provide all the formulas, methods, and theorems in one place which saves students’ time and energy. Revision notes also provide you with chapter summaries which is a great way to revise a chapter quickly the night before the exam. These notes are also available on Vedantu Mobile app.

7. Are NCERT examples of Chapter 4 of Maths of Class 7 students important to practice?

The NCERT examples are very necessary for the preparation of the exam. The concept of simple equations is relatively new for the students of Class 7. Before diving into the exercises of the chapter, it is always better to practice the examples and how the method has been followed. Examples of NCERT are a nice warm-up, before trying your hand on NCERT exercises. NCERT examples are also important for the preparation of examinations as many times examples are asked with a change in digits here and there.

8. How many questions are there for Chapter 4 of Maths of Class 7?

There are a total of four exercises and combined questions of all the four exercises sum up to a total of 18 questions.

Exercise 4.1 - six questions with further subdivisions in each question

Exercise 4.2 - four questions with subdivisions in each question

Exercise 4.3 - four questions

Exercise 4.4 consists of four questions as well with a further division in subdivisions.

Revision Notes provide you with all the concepts on which these 18 questions are based, in a PDF format.

NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations are provided below. Our solutions covered each questions of the chapter and explains every concept with a clarified explanation. It helps the students to understand slowly and to get practice well to become perfect and again a good score in their examination. Below we have listed NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Exercise 4.1, Ex 4.2, Ex 4.3 and Ex 4.4.

These materials are prepared based on Class 7 NCERT syllabus, taking the types of questions asked in the NCERT textbook into consideration. Further, all the CBSE Class 7 Solutions Maths Chapter 4 Simple Equations are in accordance with the latest CBSE guidelines and marking schemes

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.1

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Exercise 4.1 00001

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.2

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Exercise 4.2 001

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.3

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Exercise 4.3 00001

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.4

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Exercise 4.4 00001

Class 7 Maths Chapter 4 Simple Equations Textbook Solutions

Chapter 4 – Simple Equations of NCERT Solutions for Class 7 Maths contains 4 exercises. Let’s now look at the important topics covered in this chapter are mentioned below.

What is Equation
Solving an Equation
More Equations
From Solution to Equation
Applications of Simple Equations To Practical Situations

NCERT Solutions Class 7 Maths Chapter 4

Home » NCERT Solutions » NCERT Solutions Class 7 Maths Chapter 4

CBSE Important Questions
Important Questions Class 6
CBSE Previous Year Question Papers
CBSE Revision Notes
CBSE Syllabus
CBSE Extra Questions
CBSE Sample Papers
ISC & ICSE Syllabus
ICSE Syllabus Class 9
ICSE Syllabus Class 8
ICSE Syllabus Class 7
ICSE Syllabus Class 6
ICSE Syllabus Class 10
ICSE Question Paper
ICSE Sample Question Papers
ISC Sample Question Papers For Class 12
ISC Sample Question Papers For Class 11
ICSE Sample Question Papers For Class 10
ICSE Sample Question Papers For Class 9
ICSE Sample Question Papers For Class 8
ICSE Sample Question Papers For Class 7
ICSE Sample Question Papers For Class 6
ICSE Revision Notes
ICSE Important Questions
ISC Important Questions For Class 12
ISC Important Questions For Class 11
ICSE Important Questions For Class 10
ICSE Important Questions For Class 9
ICSE Important Questions For Class 8
ICSE Important Questions For Class 7
ICSE Important Questions For Class 6
Maharashtra board
Rajasthan-Board
Andhrapradesh Board
AP Board syllabus
Telangana Board
Tamilnadu Board
Tamilnadu Sample Question Paper
Tamilnadu Syllabus
Tamilnadu Previous Year Question Paper
NCERT Solutions Class 12
NCERT Solutions Class 10
NCERT Solutions Class 11
NCERT Solutions Class 9
NCERT Solutions Class 8
NCERT Solutions Class 7
NCERT Solutions Class 6
NCERT Solutions Class 5
NCERT Solutions Class 4
NCERT Solutions Class 3
NCERT Solutions Class 2
NCERT Solutions Class 1
JEE Main Question Papers
JEE Main Syllabus
JEE Main Questions
JEE Main Revision Notes
JEE Advanced Question Papers
JEE Advanced Syllabus
JEE Advanced Questions
JEE Advanced Sample Papers
NEET Question Papers
Neet 2021 Question Paper
Neet 2020 Question Paper
Neet 2019 Question Paper
Neet 2018 Question Paper
Neet 2017 Question Paper
Neet 2016 Question Paper
Neet 2015 Question Paper
NEET Syllabus

NCERT Solutions for Class 7 Mathematics Chapter 4

Ncert solutions for class 7 mathematics chapter 4 simple equations .

The NCERT Solutions for Class 7 Mathematics Chapter 4 by Extramarks is a compilation of detailed step-by-step solutions to all exercises included in this chapter.

Quick Links

Students should practise all the exercise questions to get in-depth knowledge about the topics. The solutions are crafted by the subject matter experts, who have framed solutions in a systematic and organised manner which is easy to understand. Students who refer to these materials will be able to prepare confidently for their exams and achieve desired results.

NCERT Solutions for Class 7 Mathematics Chapter 4 Simple equations

Access ncert solutions for class 7 mathematics chapter 4 – simple equations .

Chapter 4 of Class 7 Mathematics is on simple equations divided into five major sections. It is one of the most important chapters in Class 7 Mathematics, as it brushes-up basic concepts of algebraic equations.

Students are advised to go through the chapter to get a clear understanding of the concepts in simple equations. The solutions to the questions in this chapter provided by Extramarks will help students to clarify the concepts and they will be able to solve any questions in the term tests and exams confidently.

Following are the important topics covered under NCERT Class 7 Mathematics Chapter 4.

Stepping up of an equation
Review of what we know
What Equation is?
Solving an equation
More Equations
From Solution to Equation
Application of Simple Equations to practical situations

NCERT Solutions for Class 7 Mathematics Chapter 4 Exercises

The total number of questions in each of the chapter’s exercises are given in the table below.

A variable takes on different numerical values whereas a constant has a fixed value.
An equation is a statement of a variable in which two expressions of the variable should have equal value.
An equation remains unchanged if its LHS and RHS are interchanged.
Transposing a number means moving it to the other side.
The equations remain unchanged when we:
Add the same number to both sides.
Subtract the same number from both sides.
Multiply and divide both sides by the same number.
When we transpose a number from one side of the equation to the other its sign changes

A variable does not have a fixed value. The numerical value of the variable changes. These variables are denoted by letters of the alphabet such as l, m, n, p, q, r, s, t, u, v, w, x, y, z, etc. Expressions are formed when we perform operations such as addition, subtraction, multiplication, and division on variables.

The value of an expression depends upon the chosen value of the variable. If there is only one term in an expression then it is called a monomial expression.
If there are two terms in an expression then it is called a binomial expression.
If there are three terms in an expression then it is called a trinomial expression.
A polynomial expression is an expression that has four terms.

Note : A polynomial expression can have many terms but none of the terms can have a negative exponent for any variable.

An Equation

An equation is a mathematical statement on a variable where two expressions on either side of the equal sign should have equal value. At least one of the expressions must contain the variable.

Note : An equation does not change when the expression on the left-hand side or the right-hand side is interchanged.

In an equation, there is always an equality sign between two expressions.

Example : Write the following statements in the form of equations.

The difference of five times x and 11 is 28.
One-fourth of a number minus 8 is 18.
We have five times x that is 5x

The difference of 5x-11 is 5x-11

Thus, the required equation is 5x-11=28

Let the number be x

One-fourth of x is ¼(x)

Now, one-fourth of x minus 8 is 1/4(x) – 8

Thus, the required equation is ¼(x) – 8=18

Let us see one more example which will help you with Exercise 4.1 of NCERT solutions chapter 4

Example : Write a statement for the equation 2x-5=15

Solution : 2x-5=15

Taking away 5 from twice a number is 15

Solving an Equation

We use this principle when we solve an equation. The equality sign between the LHS and RHS corresponds to the horizontal beam of the balance.

An equation remains undisturbed or unchanged:

If LHS and RHS are interchanged.
To both the sides, if the same number is added
From both sides if the same number is subtracted.
When both LHS and RHS are multiplied by the same number
When both LHS and RHS are divided by the same number

To understand the concept better, let us try to solve an example. This will help you with exercise 4.2 of NCERT Solutions Chapter 4.

Example : Solve 5x-3=12

Adding 3 to both sides, we get

5x-3+3=12+3

Dividing both sides by 5, we get 5x/5=15/5

x=3, which is the required solution.

Note : For checking the answer, we substitute the value of the variable in the given equation

i.e., L.H.S = (5*3)-3= 15-3= 12= R.H.S

or L.H.S = R.H.S

Example : ½(x) + 5= 65

Subtracting 5 from both sides we have,

½(x) +5-5 = 65-5

Multiplying 2 on both sides, we have

½(x) *2 = 60*2

x = 120, is the required solution.

Forming an Equation

We have learned how to solve an equation. Now we shall form or construct the equation when the solution(root) is given. Let us know the following successive steps:

Start with x = 9
Multiply both sides by 3
Subtract 2 from both sides

3x – 2 = 27-2

3x – 2 = 25, which is an equation.

Note : For a given equation, you get one solution; but for a given solution, one can make many equations.

Let us understand this with more examples so that you can solve exercise 4.3 of NCERT Solutions Chapter 4.

Example: Solve 5(x-3) = 25

(Or) x-3 = 25/5 (Dividing both sides by 5)

(Or) x – 3 = 5

(or) x = 5+3 (Transposing -3 to R.H.S)

x = 8, which is the required solution.

Example: Solve 3(x+1)/2 = 18

Solution : 3(x+1)/2 = 18

(or) (x+1)/2 = 18/2 (Dividing both sides by 2)

(or) (x+1)/2 = 6

(or) x/2 = (6-1)/2 (Transposing 1 to R.H.S)

(or) x = (12-1)/2 = 11/2, which is the required solution.

Application of Simple Equations to Practical Situations

Let us understand this with more examples so that you can solve exercise 4.4 of NCERT Solutions Chapter 4.

Example : The sum of five times a number and 18 is 63. Find the number

Let the required number be x

5 times the number is 5x

According to the condition, we have

5x + 18 = 63

5x = 63 – 18 (Transposing 18 form L.H.S to R.H.S)

(or) dividing both sides by 5, we have

5x/5 = 45/5

Thus, the required number is = 9

Related Questions

Question: If 2x-3 = 5, then

Solution: x = 4

Question: If both sides of the equation are divided by the same (non–zero) quantity, the equality –

Does not change
May or may not change
None of these

Solutions: Does not change

NCERT Solutions Class 7 Maths Chapter-wise List

Click to share on Facebook (Opens in new window)
Click to share on Twitter (Opens in new window)
Click to share on LinkedIn (Opens in new window)
Click to share on WhatsApp (Opens in new window)

Q.1 Complete the last column of the table .

Q.2 Check whether the value given in the brackets is a solution to the given equation or not : ( a ) n + 5 = 19 ( n = 1 ) ( b ) 7 n + 5 = 19 ( n = – 2 ) ( c ) 7 n + 5 = 19 ( n = 2 ) ( d ) 4 p – 3 = 13 ( p = 1 ) ( e ) 4 p – 3 = 13 ( p = – 4 ) ( f ) 4 p – 3 = 13 ( p = 0 )

( a ) n + 5 = 19 ( n = 1 ) Put n = 1 in L .H .S to get n+5 = 1 + 5 = 6 ≠ R .H .S So, the given value in the bracket is not a solution to the given equation . ( b ) 7n + 5 = 19 ( n = − 2 ) Put n = − 2 in L .H .S to get 7n+5 = 7 ( − 2 ) + 5 = − 14 + 5 = − 9 ≠ R .H .S So, the given value in the bracket is not a solution to the given equation . ( c ) 7n + 5 = 19 ( n = 2 ) Put n = 2 in L .H .S to get 7n+5 = 7 ( 2 ) + 5 = 14 + 5 = 19 = R .H .S So, the given value in the bracket is a solution to the given equation . ( d ) 4p − 3 = 13 ( p = 1 ) Put p = 1 in L .H .S to get 4p − 3 = 4 ( 1 ) − 3 = 4 − 3 = 1 ≠ R .H .S So, the given value in the bracket is not a solution to the given equation . ( e ) 4p − 3 = 13 ( p = − 4 ) Put p = − 4 in L .H .S to get 4p − 3 = 4 ( − 4 ) − 3 = − 16 − 3 = − 19 ≠ R .H .S So, the given value in the bracket is not a solution to the given equation . ( f ) 4p − 3 = 13 ( p = 0 ) Put p = 0 in L .H .S to get 4p − 3 = 4 ( 0 ) − 3 = 0 − 3 = − 3 ≠ R .H .S So, the given value in the bracket is not a solution to the given equation . MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqeduuDJXwAKbYu51MyVXgaruWqVvNCPvMCG4uz3bqefqvATv2C G4uz3bIuV1wyUbqeeuuDJXwAKbsr4rNCHbGeaGqiVz0xg9vqqrpepC 0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yq aqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabe qaamaaeaqbaaGceaqabeaadaqadaqaaiaabggaaiaawIcacaGLPaaa caqGUbGaey4kaSIaaeynaiabg2da9iaabgdacaqG5aGaaeiiaiaacI cacaqGUbGaeyypa0JaaeymaiaacMcaaeaacaqGqbGaaeyDaiaabsha caqGGaGaaeOBaiabg2da9iaabgdacaqGGaGaaeyAaiaab6gacaqGGa Gaaeitaiaab6cacaqGibGaaeOlaiaabofacaqGGaGaaeiDaiaab+ga caqGGaGaae4zaiaabwgacaqG0baabaGaaeOBaiaabUcacaqG1aGaey ypa0JaaGymaiabgUcaRiaaiwdacqGH9aqpcaaI2aGaeyiyIKRaaeOu aiaab6cacaqGibGaaeOlaiaabofaaeaacaqGtbGaae4BaiaabYcaca qGGaGaaeiDaiaabIgacaqGLbGaaeiiaiaabEgacaqGPbGaaeODaiaa bwgacaqGUbGaaeiiaiaabAhacaqGHbGaaeiBaiaabwhacaqGLbGaae iiaiaabMgacaqGUbGaaeiiaiaabshacaqGObGaaeyzaiaabccacaqG IbGaaeOCaiaabggacaqGJbGaae4AaiaabwgacaqG0bGaaeiiaiaabM gacaqGZbGaaeiiaiaab6gacaqGVbGaaeiDaiaabccacaqGHbGaaeii aiaabohacaqGVbGaaeiBaiaabwhacaqG0bGaaeyAaiaab+gacaqGUb GaaeiiaiaabshacaqGVbGaaeiiaiaabshacaqGObGaaeyzaaqaaiaa bEgacaqGPbGaaeODaiaabwgacaqGUbGaaeiiaiaabwgacaqGXbGaae yDaiaabggacaqG0bGaaeyAaiaab+gacaqGUbGaaeOlaaqaamaabmaa baGaaeOyaaGaayjkaiaawMcaaiaabccacaqG3aGaaeOBaiabgUcaRi aabwdacqGH9aqpcaqGXaGaaeyoaiaabccacaGGOaGaaeOBaiabg2da 9iabgkHiTiaabccacaqGYaGaaiykaaqaaiaabcfacaqG1bGaaeiDai aabccacaqGUbGaeyypa0JaeyOeI0IaaeOmaiaabccacaqGPbGaaeOB aiaabccacaqGmbGaaeOlaiaabIeacaqGUaGaae4uaiaabccacaqG0b Gaae4BaiaabccacaqGNbGaaeyzaiaabshaaeaacaqG3aGaaeOBaiaa bUcacaqG1aGaeyypa0JaaG4namaabmaabaGaeyOeI0IaaGOmaaGaay jkaiaawMcaaiabgUcaRiaaiwdacqGH9aqpcqGHsislcaaIXaGaaGin aiabgUcaRiaaiwdacqGH9aqpcqGHsislcaaI5aGaeyiyIKRaaeOuai aab6cacaqGibGaaeOlaiaabofaaeaacaqGtbGaae4BaiaabYcacaqG GaGaaeiDaiaabIgacaqGLbGaaeiiaiaabEgacaqGPbGaaeODaiaabw gacaqGUbGaaeiiaiaabAhacaqGHbGaaeiBaiaabwhacaqGLbGaaeii aiaabMgacaqGUbGaaeiiaiaabshacaqGObGaaeyzaiaabccacaqGIb GaaeOCaiaabggacaqGJbGaae4AaiaabwgacaqG0bGaaeiiaiaabMga caqGZbGaaeiiaiaab6gacaqGVbGaaeiDaiaabccacaqGHbGaaeiiai aabohacaqGVbGaaeiBaiaabwhacaqG0bGaaeyAaiaab+gacaqGUbGa aeiiaiaabshacaqGVbGaaeiiaiaabshacaqGObGaaeyzaaqaaiaabE gacaqGPbGaaeODaiaabwgacaqGUbGaaeiiaiaabwgacaqGXbGaaeyD aiaabggacaqG0bGaaeyAaiaab+gacaqGUbGaaeOlaaqaamaabmaaba Gaae4yaaGaayjkaiaawMcaaiaabccacaqG3aGaaeOBaiabgUcaRiaa bwdacaqGGaGaeyypa0JaaeymaiaabMdacaqGGaGaaiikaiaab6gacq GH9aqpcaqGYaGaaiykaaqaaiaabcfacaqG1bGaaeiDaiaabccacaqG UbGaeyypa0JaaeOmaiaabccacaqGPbGaaeOBaiaabccacaqGmbGaae OlaiaabIeacaqGUaGaae4uaiaabccacaqG0bGaae4BaiaabccacaqG NbGaaeyzaiaabshaaeaacaqG3aGaaeOBaiaabUcacaqG1aGaeyypa0 JaaG4namaabmaabaGaaGOmaaGaayjkaiaawMcaaiabgUcaRiaaiwda cqGH9aqpcaaIXaGaaGinaiabgUcaRiaaiwdacqGH9aqpcaaIXaGaaG yoaiabg2da9iaabkfacaqGUaGaaeisaiaab6cacaqGtbaabaGaae4u aiaab+gacaqGSaGaaeiiaiaabshacaqGObGaaeyzaiaabccacaqGNb GaaeyAaiaabAhacaqGLbGaaeOBaiaabccacaqG2bGaaeyyaiaabYga caqG1bGaaeyzaiaabccacaqGPbGaaeOBaiaabccacaqG0bGaaeiAai aabwgacaqGGaGaaeOyaiaabkhacaqGHbGaae4yaiaabUgacaqGLbGa aeiDaiaabccacaqGPbGaae4CaiaabccacaqGHbGaaeiiaiaabohaca qGVbGaaeiBaiaabwhacaqG0bGaaeyAaiaab+gacaqGUbGaaeiiaiaa bshacaqGVbGaaeiiaiaabshacaqGObGaaeyzaaqaaiaabEgacaqGPb GaaeODaiaabwgacaqGUbGaaeiiaiaabwgacaqGXbGaaeyDaiaabgga caqG0bGaaeyAaiaab+gacaqGUbGaaeOlaaqaamaabmaabaGaaeizaa GaayjkaiaawMcaaiaabccacaqG0aGaaeiCaiabgkHiTiaabodacqGH 9aqpcaqGXaGaae4maiaabccacaGGOaGaaeiCaiabg2da9iaabgdaca GGPaaabaGaaeiuaiaabwhacaqG0bGaaeiiaiaabchacqGH9aqpcaaI XaGaaeiiaiaabMgacaqGUbGaaeiiaiaabYeacaqGUaGaaeisaiaab6 cacaqGtbGaaeiiaiaabshacaqGVbGaaeiiaiaabEgacaqGLbGaaeiD aaqaaiaabsdacaqGWbGaeyOeI0IaaG4maiabg2da9iaaisdadaqada qaaiaaigdaaiaawIcacaGLPaaacqGHsislcaaIZaGaeyypa0JaaGin aiabgkHiTiaaiodacqGH9aqpcaaIXaGaeyiyIKRaaeOuaiaab6caca qGibGaaeOlaiaabofaaeaacaqGtbGaae4BaiaabYcacaqGGaGaaeiD aiaabIgacaqGLbGaaeiiaiaabEgacaqGPbGaaeODaiaabwgacaqGUb GaaeiiaiaabAhacaqGHbGaaeiBaiaabwhacaqGLbGaaeiiaiaabMga caqGUbGaaeiiaiaabshacaqGObGaaeyzaiaabccacaqGIbGaaeOCai aabggacaqGJbGaae4AaiaabwgacaqG0bGaaeiiaiaabMgacaqGZbGa aeiiaiaab6gacaqGVbGaaeiDaiaabccacaqGHbGaaeiiaiaabohaca qGVbGaaeiBaiaabwhacaqG0bGaaeyAaiaab+gacaqGUbGaaeiiaiaa bshacaqGVbGaaeiiaiaabshacaqGObGaaeyzaaqaaiaabEgacaqGPb GaaeODaiaabwgacaqGUbGaaeiiaiaabwgacaqGXbGaaeyDaiaabgga caqG0bGaaeyAaiaab+gacaqGUbGaaeOlaaqaamaabmaabaGaaeyzaa GaayjkaiaawMcaaiaabccacaqG0aGaaeiCaiabgkHiTiaabodacqGH 9aqpcaqGXaGaae4maiaabccacaGGOaGaaeiCaiabg2da9iabgkHiTi aabccacaqG0aGaaiykaaqaaiaabcfacaqG1bGaaeiDaiaabccacaqG WbGaeyypa0JaeyOeI0IaaeinaiaabccacaqGPbGaaeOBaiaabccaca qGmbGaaeOlaiaabIeacaqGUaGaae4uaiaabccacaqG0bGaae4Baiaa bccacaqGNbGaaeyzaiaabshaaeaacaqG0aGaaeiCaiabgkHiTiaaio dacqGH9aqpcaaI0aWaaeWaaeaacqGHsislcaaI0aaacaGLOaGaayzk aaGaeyOeI0IaaG4maiabg2da9iabgkHiTiaaigdacaaI2aGaeyOeI0 IaaG4maiabg2da9iabgkHiTiaaigdacaaI5aGaeyiyIKRaaeOuaiaa b6cacaqGibGaaeOlaiaabofaaeaacaqGtbGaae4BaiaabYcacaqGGa GaaeiDaiaabIgacaqGLbGaaeiiaiaabEgacaqGPbGaaeODaiaabwga caqGUbGaaeiiaiaabAhacaqGHbGaaeiBaiaabwhacaqGLbGaaeiiai aabMgacaqGUbGaaeiiaiaabshacaqGObGaaeyzaiaabccacaqGIbGa aeOCaiaabggacaqGJbGaae4AaiaabwgacaqG0bGaaeiiaiaabMgaca qGZbGaaeiiaiaab6gacaqGVbGaaeiDaiaabccacaqGHbGaaeiiaiaa bohacaqGVbGaaeiBaiaabwhacaqG0bGaaeyAaiaab+gacaqGUbGaae iiaiaabshacaqGVbGaaeiiaiaabshacaqGObGaaeyzaaqaaiaabEga caqGPbGaaeODaiaabwgacaqGUbGaaeiiaiaabwgacaqGXbGaaeyDai aabggacaqG0bGaaeyAaiaab+gacaqGUbGaaeOlaaqaamaabmaabaGa aeOzaaGaayjkaiaawMcaaiaabccacaqG0aGaaeiCaiabgkHiTiaabo dacqGH9aqpcaqGXaGaae4maiaabccacaGGOaGaaeiCaiabg2da9iaa icdacaGGPaaabaGaaeiuaiaabwhacaqG0bGaaeiiaiaabchacqGH9a qpcaqGWaGaaeiiaiaabMgacaqGUbGaaeiiaiaabYeacaqGUaGaaeis aiaab6cacaqGtbGaaeiiaiaabshacaqGVbGaaeiiaiaabEgacaqGLb GaaeiDaaqaaiaabsdacaqGWbGaeyOeI0IaaG4maiabg2da9iaaisda daqadaqaaiaaicdaaiaawIcacaGLPaaacqGHsislcaaIZaGaeyypa0 JaaGimaiabgkHiTiaaiodacqGH9aqpcqGHsislcaaIZaGaeyiyIKRa aeOuaiaab6cacaqGibGaaeOlaiaabofaaeaacaqGtbGaae4BaiaabY cacaqGGaGaaeiDaiaabIgacaqGLbGaaeiiaiaabEgacaqGPbGaaeOD aiaabwgacaqGUbGaaeiiaiaabAhacaqGHbGaaeiBaiaabwhacaqGLb GaaeiiaiaabMgacaqGUbGaaeiiaiaabshacaqGObGaaeyzaiaabcca caqGIbGaaeOCaiaabggacaqGJbGaae4AaiaabwgacaqG0bGaaeiiai aabMgacaqGZbGaaeiiaiaab6gacaqGVbGaaeiDaiaabccacaqGHbGa aeiiaiaabohacaqGVbGaaeiBaiaabwhacaqG0bGaaeyAaiaab+gaca qGUbGaaeiiaiaabshacaqGVbGaaeiiaiaabshacaqGObGaaeyzaaqa aiaabEgacaqGPbGaaeODaiaabwgacaqGUbGaaeiiaiaabwgacaqGXb GaaeyDaiaabggacaqG0bGaaeyAaiaab+gacaqGUbGaaeOlaaaaaa@FE43@

Q.3 Solve the following equations by trial and error method : ( i ) 5 p + 2 = 17 ( ii ) 3 m – 14 = 4

( i ) 5p + 2 = 17 Put p = 1 to L .H .S to get 5 ( 1 ) +2 = 5+2 = 7 ≠ R .H .S Put p = 2 to L .H .S to get 5 ( 2 ) +2 = 10+2 = 12 ≠ R .H .S Put p = 3 to L .H .S to get 5 ( 3 ) +2 = 15+2 = 17 = R .H .S Thus, p = 3 is a solution to the given equation ( ii ) 3m − 14 = 4 Put m = 4 in L .H .S to get 3 ( 4 ) − 14 = 12 − 14 = − 2 ≠ R .H .S Put m = 5 in L .H .S to get 3 ( 5 ) − 14 = 15 − 14 = − 1 ≠ R .H .S Put m = 6 in L .H .S to get 3 ( 4 ) − 14 = 18 − 14 = 4 = R .H .S Thus, m = 6 is a solution to the given equation MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqeduuDJXwAKbYu51MyVXgaruWqVvNCPvMCG4uz3bqefqvATv2C G4uz3bIuV1wyUbqeeuuDJXwAKbsr4rNCHbGeaGqiVz0xg9vqqrpepC 0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yq aqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabe qaamaaeaqbaaGceaqabeaadaqadaqaaiaabMgaaiaawIcacaGLPaaa caqGGaGaaeynaiaabchacqGHRaWkcaqGGaGaaeOmaiabg2da9iaabg dacaqG3aaabaGaaeiuaiaabwhacaqG0bGaaeiiaiaabchacqGH9aqp caqGXaGaaeiiaiaabshacaqGVbGaaeiiaiaabYeacaqGUaGaaeisai aab6cacaqGtbGaaeiiaiaabshacaqGVbGaaeiiaiaabEgacaqGLbGa aeiDaaqaaiaabwdadaqadaqaaiaaigdaaiaawIcacaGLPaaacaqGRa GaaeOmaiabg2da9iaabwdacaqGRaGaaeOmaiabg2da9iaabEdacqGH GjsUcaqGsbGaaeOlaiaabIeacaqGUaGaae4uaaqaaiaabcfacaqG1b GaaeiDaiaabccacaqGWbGaeyypa0JaaeOmaiaabccacaqG0bGaae4B aiaabccacaqGmbGaaeOlaiaabIeacaqGUaGaae4uaiaabccacaqG0b Gaae4BaiaabccacaqGNbGaaeyzaiaabshaaeaacaqG1aWaaeWaaeaa caaIYaaacaGLOaGaayzkaaGaae4kaiaabkdacqGH9aqpcaqGXaGaae imaiaabUcacaqGYaGaeyypa0JaaeymaiaabkdacqGHGjsUcaqGsbGa aeOlaiaabIeacaqGUaGaae4uaaqaaiaabcfacaqG1bGaaeiDaiaabc cacaqGWbGaeyypa0Jaae4maiaabccacaqG0bGaae4BaiaabccacaqG mbGaaeOlaiaabIeacaqGUaGaae4uaiaabccacaqG0bGaae4Baiaabc cacaqGNbGaaeyzaiaabshaaeaacaqG1aWaaeWaaeaacaaIZaaacaGL OaGaayzkaaGaae4kaiaabkdacqGH9aqpcaqGXaGaaeynaiaabUcaca qGYaGaeyypa0JaaeymaiaabEdacqGH9aqpcaqGsbGaaeOlaiaabIea caqGUaGaae4uaaqaaiaabsfacaqGObGaaeyDaiaabohacaqGSaGaae iiaiaabchacqGH9aqpcaqGZaGaaeiiaiaabMgacaqGZbGaaeiiaiaa bggacaqGGaGaae4Caiaab+gacaqGSbGaaeyDaiaabshacaqGPbGaae 4Baiaab6gacaqGGaGaaeiDaiaab+gacaqGGaGaaeiDaiaabIgacaqG LbGaaeiiaiaabEgacaqGPbGaaeODaiaabwgacaqGUbGaaeiiaiaabw gacaqGXbGaaeyDaiaabggacaqG0bGaaeyAaiaab+gacaqGUbGaaeii aaqaamaabmaabaGaaeyAaiaabMgaaiaawIcacaGLPaaacaqGGaGaae 4maiaab2gacqGHsislcaqGXaGaaeinaiabg2da9iaabsdaaeaacaqG qbGaaeyDaiaabshacaqGGaGaaeyBaiabg2da9iaabsdacaqGGaGaae yAaiaab6gacaqGGaGaaeitaiaab6cacaqGibGaaeOlaiaabofacaqG GaGaaeiDaiaab+gacaqGGaGaae4zaiaabwgacaqG0baabaGaae4mam aabmaabaGaaGinaaGaayjkaiaawMcaaiabgkHiTiaaigdacaaI0aGa eyypa0JaaGymaiaaikdacqGHsislcaaIXaGaaGinaiabg2da9iabgk HiTiaaikdacqGHGjsUcaqGsbGaaeOlaiaabIeacaqGUaGaae4uaaqa aiaabcfacaqG1bGaaeiDaiaabccacaqGTbGaeyypa0Jaaeynaiaabc cacaqGPbGaaeOBaiaabccacaqGmbGaaeOlaiaabIeacaqGUaGaae4u aiaabccacaqG0bGaae4BaiaabccacaqGNbGaaeyzaiaabshaaeaaca qGZaWaaeWaaeaacaaI1aaacaGLOaGaayzkaaGaeyOeI0IaaGymaiaa isdacqGH9aqpcaaIXaGaaGynaiabgkHiTiaaigdacaaI0aGaeyypa0 JaeyOeI0IaaGymaiabgcMi5kaabkfacaqGUaGaaeisaiaab6cacaqG tbaabaGaaeiuaiaabwhacaqG0bGaaeiiaiaab2gacqGH9aqpcaqG2a GaaeiiaiaabMgacaqGUbGaaeiiaiaabYeacaqGUaGaaeisaiaab6ca caqGtbGaaeiiaiaabshacaqGVbGaaeiiaiaabEgacaqGLbGaaeiDaa qaaiaabodadaqadaqaaiaaisdaaiaawIcacaGLPaaacqGHsislcaaI XaGaaGinaiabg2da9iaaigdacaaI4aGaeyOeI0IaaGymaiaaisdacq GH9aqpcaaI0aGaeyypa0JaaeOuaiaab6cacaqGibGaaeOlaiaabofa aeaacaqGubGaaeiAaiaabwhacaqGZbGaaeilaiaabccacaqGTbGaey ypa0JaaeOnaiaabccacaqGPbGaae4CaiaabccacaqGHbGaaeiiaiaa bohacaqGVbGaaeiBaiaabwhacaqG0bGaaeyAaiaab+gacaqGUbGaae iiaiaabshacaqGVbGaaeiiaiaabshacaqGObGaaeyzaiaabccacaqG NbGaaeyAaiaabAhacaqGLbGaaeOBaiaabccacaqGLbGaaeyCaiaabw hacaqGHbGaaeiDaiaabMgacaqGVbGaaeOBaaaaaa@76BD@

Q.4 Write equations for the following statements : ( i ) The sum of numbers x and 4 is 9 . ( ii ) The difference between y and 2 is 8 . ( iii ) Ten times a is 70 . ( iv ) The number b divided by 5 gives 6 . ( v ) Three fourth of t is 15 . ( vi ) Seven times m plus 7 gets you 77 . ( vii ) One fourth of a number minus 4 gives 4 . ( viii ) If you take away 6 from 6 times y , you get 60 . ( ix ) If you add 3 toone third of z , you get 30 .

( i ) x + 4 = 9 ( ii) y − 2 = 8 (iii) 10 a = 70 (iv) b 5 = 6 (v) 3 4 t = 15 ( vi ) 7 m + 7 = 77 ( vii ) x 4 − 4 = 4 ( viii ) 6 y − 6 = 60 ( ix ) z 3 + 3 = 30 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqeduuDJXwAKbYu51MyVXgaruWqVvNCPvMCG4uz3bqefqvATv2C G4uz3bIuV1wyUbqeeuuDJXwAKbsr4rNCHbGeaGqiVz0xg9vqqrpepC 0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yq aqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabe qaamaaeaqbaaGceaqabeaadaqadaqaaiaabMgaaiaawIcacaGLPaaa caaMe8UaamiEaiabgUcaRiaaisdacqGH9aqpcaaI5aaabaGaaiikai aabMgacaqGPbGaaeykaiaaysW7caWG5bGaeyOeI0IaaGOmaiabg2da 9iaaiIdaaeaacaqGOaGaaeyAaiaabMgacaqGPbGaaeykaiaaysW7ca aIXaGaaGimaiaadggacqGH9aqpcaaI3aGaaGimaaqaaiaabIcacaqG PbGaaeODaiaabMcacaaMe8+aaSaaaeaacaWGIbaabaGaaGynaaaacq GH9aqpcaaI2aaabaGaaeikaiaabAhacaqGPaGaaGjbVpaalaaabaGa aG4maaqaaiaaisdaaaGaamiDaiabg2da9iaaigdacaaI1aaabaWaae WaaeaacaqG2bGaaeyAaaGaayjkaiaawMcaaiaaysW7caaI3aGaamyB aiabgUcaRiaaiEdacqGH9aqpcaaI3aGaaG4naaqaamaabmaabaGaae ODaiaabMgacaqGPbaacaGLOaGaayzkaaGaaGjbVpaalaaabaGaamiE aaqaaiaaisdaaaGaeyOeI0IaaGinaiabg2da9iaaisdaaeaadaqada qaaiaabAhacaqGPbGaaeyAaiaabMgaaiaawIcacaGLPaaacaaMe8Ua aGOnaiaadMhacqGHsislcaaI2aGaeyypa0JaaGOnaiaaicdaaeaada qadaqaaiaabMgacaqG4baacaGLOaGaayzkaaGaaGjbVpaalaaabaGa amOEaaqaaiaaiodaaaGaey4kaSIaaG4maiabg2da9iaaiodacaaIWa aaaaa@9828@

Write the following equations in statement forms : ( i ) p + 4 = 15 ( ii ) m – 7 = 3 ( iii ) 2 m = 7 ( iv ) m 5 = 3 ( v ) 3 5 m = 6 ( vi ) 3 p + 4 = 25 ( vii ) 4 p – 2 = 18 ( viii ) p 2 + 2 = 8

( i ) The sum of p and 4 is 15 . (ii) 7 subtracted from m is 3 . (iii) Twice of a number m is 7 . (iv) One-fifth of m is 3 . (v) Three-fifth of m is 6 . (vi) Three times of a number p, when add to 4 gives 25 . (vii) When 2 is subtracted from four times of a number p, it gives 18 . (viii) When 2 is added to half of a number p, it gives 8 . MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqeduuDJXwAKbYu51MyVXgaruWqVvNCPvMCG4uz3bqefqvATv2C G4uz3bIuV1wyUbqeeuuDJXwAKbsr4rNCHbGeaGqiVz0xg9vqqrpepC 0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yq aqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabe qaamaaeaqbaaGceaqabeaacaGGOaGaamyAaiaacMcacaqGGaGaaeiv aiaabIgacaqGLbGaaeiiaiaabohacaqG1bGaaeyBaiaabccacaqGVb GaaeOzaiaabccacaqGWbGaaeiiaiaabggacaqGUbGaaeizaiaabcca caqG0aGaaeiiaiaabMgacaqGZbGaaeiiaiaabgdacaqG1aGaaeOlaa qaaiaabIcacaqGPbGaaeyAaiaabMcacaqGGaGaae4naiaabccacaqG ZbGaaeyDaiaabkgacaqG0bGaaeOCaiaabggacaqGJbGaaeiDaiaabw gacaqGKbGaaeiiaiaabAgacaqGYbGaae4Baiaab2gacaqGGaGaaeyB aiaabccacaqGPbGaae4CaiaabccacaqGZaGaaeOlaaqaaiaabIcaca qGPbGaaeyAaiaabMgacaqGPaGaaeiiaiaabsfacaqG3bGaaeyAaiaa bogacaqGLbGaaeiiaiaab+gacaqGMbGaaeiiaiaabggacaqGGaGaae OBaiaabwhacaqGTbGaaeOyaiaabwgacaqGYbGaaeiiaiaab2gacaqG GaGaaeyAaiaabohacaqGGaGaae4naiaab6caaeaacaqGOaGaaeyAai aabAhacaqGPaGaaeiiaiaab+eacaqGUbGaaeyzaiaab2cacaqGMbGa aeyAaiaabAgacaqG0bGaaeiAaiaabccacaqGVbGaaeOzaiaabccaca qGTbGaaeiiaiaabMgacaqGZbGaaeiiaiaabodacaqGUaaabaGaaeik aiaabAhacaqGPaGaaeiiaiaabsfacaqGObGaaeOCaiaabwgacaqGLb GaaeylaiaabAgacaqGPbGaaeOzaiaabshacaqGObGaaeiiaiaab+ga caqGMbGaaeiiaiaab2gacaqGGaGaaeyAaiaabohacaqGGaGaaeOnai aab6caaeaacaqGOaGaaeODaiaabMgacaqGPaGaaeiiaiaabsfacaqG ObGaaeOCaiaabwgacaqGLbGaaeiiaiaabshacaqGPbGaaeyBaiaabw gacaqGZbGaaeiiaiaab+gacaqGMbGaaeiiaiaabggacaqGGaGaaeOB aiaabwhacaqGTbGaaeOyaiaabwgacaqGYbGaaeiiaiaabchacaqGSa GaaeiiaiaabEhacaqGObGaaeyzaiaab6gacaqGGaGaaeyyaiaabsga caqGKbGaaeiiaiaabshacaqGVbGaaeiiaiaabsdacaqGGaGaae4zai aabMgacaqG2bGaaeyzaiaabohacaqGGaGaaeOmaiaabwdacaqGUaaa baGaaeikaiaabAhacaqGPbGaaeyAaiaabMcacaqGGaGaae4vaiaabI gacaqGLbGaaeOBaiaabccacaqGYaGaaeiiaiaabMgacaqGZbGaaeii aiaabohacaqG1bGaaeOyaiaabshacaqGYbGaaeyyaiaabogacaqG0b GaaeyzaiaabsgacaqGGaGaaeOzaiaabkhacaqGVbGaaeyBaiaabcca caqGMbGaae4BaiaabwhacaqGYbGaaeiiaiaabshacaqGPbGaaeyBai aabwgacaqGZbGaaeiiaiaab+gacaqGMbGaaeiiaiaabggacaqGGaGa aeOBaiaabwhacaqGTbGaaeOyaiaabwgacaqGYbGaaeiiaiaabchaca qGSaaabaGaaGjbVlaaysW7caaMe8UaaGjbVlaaysW7caaMe8UaaeyA aiaabshacaqGGaGaae4zaiaabMgacaqG2bGaaeyzaiaabohacaqGGa GaaeymaiaabIdacaqGUaaabaGaaeikaiaabAhacaqGPbGaaeyAaiaa bMgacaqGPaGaaeiiaiaabEfacaqGObGaaeyzaiaab6gacaqGGaGaae OmaiaabccacaqGPbGaae4CaiaabccacaqGHbGaaeizaiaabsgacaqG LbGaaeizaiaabccacaqG0bGaae4BaiaabccacaqGObGaaeyyaiaabY gacaqGMbGaaeiiaiaab+gacaqGMbGaaeiiaiaabggacaqGGaGaaeOB aiaabwhacaqGTbGaaeOyaiaabwgacaqGYbGaaeiiaiaabchacaqGSa GaaeiiaiaabMgacaqG0bGaaeiiaiaabEgacaqGPbGaaeODaiaabwga caqGZbGaaeiiaiaabIdacaqGUaaaaaa@52BE@

Q.6 Set up an equation in the following cases : i Irfan says that he has 7 marbles more than five times the marbles Parmit has . Irfan has 37 marbles . ( Take m to be the number of Parmit ’ s marbles . ( ii ) Laxmi ’ s father is 49 years old . He is 4 years older than three times Laxmi ’ s age .( Take Laxmi ’ s age to be y years .) iii The teacher tells the class that the highest marks obtained by a student in her class is twice the lowest marks plus 7. The highest score is 87. ( Take the lowest score to be l ). iv In an isosceles triangle , the vertex angle is twice either base angle .( Let the base angle be b in degrees . Remember that the sum of angles of a triangle is 180 degrees ).

(i) Let Parmit has m marbles . Then, according to the question, we have 5 × Number of marbles Parmit has +7 = Number of marbles Irfan has 5 × m + 7 = 37 So, we get 5 m + 7 = 37 (ii) Let Laxmi be y years old Then, according to the question, we have 3 × Laxmi’s age + 4 = Laxmi’s father age 3 × y +4 = 49 3 y + 4 = 49 (iii) Let the lowest marks be l . Then, according to the question, we have 2 × lowest marks + 7 = Highest marks 2 × l + 7 = 87 2 l + 7 = 87 (iv) An isoceles triangle has two angles equal . Let the base angle be b . Then, according to the question, we have b + b + 2 b = 180 ° 4 b = 180 ° MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqeduuDJXwAKbYu51MyVXgaruWqVvNCPvMCG4uz3bqefqvATv2C G4uz3bIuV1wyUbqeeuuDJXwAKbsr4rNCHbGeaGqiVz0xg9vqqrpepC 0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yq aqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabe qaamaaeaqbaaGceaqabeaacaqGOaGaaeyAaiaabMcacaqGGaGaaeit aiaabwgacaqG0bGaaeiiaiaabcfacaqGHbGaaeOCaiaab2gacaqGPb GaaeiDaiaabccacaqGObGaaeyyaiaabohacaqGGaGaamyBaiaabcca caqGTbGaaeyyaiaabkhacaqGIbGaaeiBaiaabwgacaqGZbGaaeOlaa qaaiaabsfacaqGObGaaeyzaiaab6gacaqGSaGaaeiiaiaabggacaqG JbGaae4yaiaab+gacaqGYbGaaeizaiaabMgacaqGUbGaae4zaiaabc cacaqG0bGaae4BaiaabccacaqG0bGaaeiAaiaabwgacaqGGaGaaeyC aiaabwhacaqGLbGaae4CaiaabshacaqGPbGaae4Baiaab6gacaqGSa GaaeiiaiaabEhacaqGLbGaaeiiaiaabIgacaqGHbGaaeODaiaabwga aeaacaqG1aGaey41aqRaaeOtaiaabwhacaqGTbGaaeOyaiaabwgaca qGYbGaaeiiaiaab+gacaqGMbGaaeiiaiaab2gacaqGHbGaaeOCaiaa bkgacaqGSbGaaeyzaiaabohacaqGGaGaaeiuaiaabggacaqGYbGaae yBaiaabMgacaqG0bGaaeiiaiaabIgacaqGHbGaae4CaiaabccacaqG RaGaae4naiabg2da9iaab6eacaqG1bGaaeyBaiaabkgacaqGLbGaae OCaiaabccacaqGVbGaaeOzaiaabccacaqGTbGaaeyyaiaabkhacaqG IbGaaeiBaiaabwgacaqGZbaabaGaaCzcaiaaxMaacaWLjaGaaCzcai aaxMaacaWLjaGaaCzcaiaaxMaacaWLjaGaaeysaiaabkhacaqGMbGa aeyyaiaab6gacaqGGaGaaeiAaiaabggacaqGZbaabaGaaCzcaiaaxM aacaWLjaGaaCzcaiaaxMaacaWLjaGaaGjbVlaaysW7caqG1aGaey41 aqRaamyBaiabgUcaRiaabEdacqGH9aqpcaqGZaGaae4naaqaaiaabo facaqGVbGaaeilaiaabccacaqG3bGaaeyzaiaabccacaqGNbGaaeyz aiaabshaaeaacaWLjaGaaCzcaiaaxMaacaWLjaGaaCzcaiaaxMaaca aMe8UaaGjbVlaaysW7daqjEaqaaiaabwdacaWGTbGaey4kaSIaae4n aiabg2da9iaabodacaqG3aaaaaqaaiaabIcacaqGPbGaaeyAaiaabM cacaqGGaGaaeitaiaabwgacaqG0bGaaeiiaiaabYeacaqGHbGaaeiE aiaab2gacaqGPbGaaeiiaiaabkgacaqGLbGaaeiiaiaadMhacaqGGa GaaeyEaiaabwgacaqGHbGaaeOCaiaabohacaqGGaGaae4BaiaabYga caqGKbaabaGaaeivaiaabIgacaqGLbGaaeOBaiaabYcacaqGGaGaae yyaiaabogacaqGJbGaae4BaiaabkhacaqGKbGaaeyAaiaab6gacaqG NbGaaeiiaiaabshacaqGVbGaaeiiaiaabshacaqGObGaaeyzaiaabc cacaqGXbGaaeyDaiaabwgacaqGZbGaaeiDaiaabMgacaqGVbGaaeOB aiaabYcacaqGGaGaae4DaiaabwgacaqGGaGaaeiAaiaabggacaqG2b GaaeyzaaqaaiaabodacqGHxdaTcaqGmbGaaeyyaiaabIhacaqGTbGa aeyAaiaabEcacaqGZbGaaeiiaiaabggacaqGNbGaaeyzaiabgUcaRi aabsdacqGH9aqpcaqGmbGaaeyyaiaabIhacaqGTbGaaeyAaiaabEca caqGZbGaaeiiaiaabAgacaqGHbGaaeiDaiaabIgacaqGLbGaaeOCai aabccacaqGHbGaae4zaiaabwgaaeaacaqGZaGaey41aqRaamyEaiaa bUcacaqG0aGaeyypa0JaaeinaiaabMdaaeaadaqjEaqaaiaabodaca WG5bGaey4kaSIaaeinaiabg2da9iaabsdacaqG5aaaaaqaaiaabIca caqGPbGaaeyAaiaabMgacaqGPaGaaeiiaiaabYeacaqGLbGaaeiDai aabccacaqG0bGaaeiAaiaabwgacaqGGaGaaeiBaiaab+gacaqG3bGa aeyzaiaabohacaqG0bGaaeiiaiaab2gacaqGHbGaaeOCaiaabUgaca qGZbGaaeiiaiaabkgacaqGLbGaaeiiaiaadYgacaqGUaaabaGaaeiv aiaabIgacaqGLbGaaeOBaiaabYcacaqGGaGaaeyyaiaabogacaqGJb Gaae4BaiaabkhacaqGKbGaaeyAaiaab6gacaqGNbGaaeiiaiaabsha caqGVbGaaeiiaiaabshacaqGObGaaeyzaiaabccacaqGXbGaaeyDai aabwgacaqGZbGaaeiDaiaabMgacaqGVbGaaeOBaiaabYcacaqGGaGa ae4DaiaabwgacaqGGaGaaeiAaiaabggacaqG2bGaaeyzaaqaaiaaik dacqGHxdaTcaqGSbGaae4BaiaabEhacaqGLbGaae4CaiaabshacaqG GaGaaeyBaiaabggacaqGYbGaae4AaiaabohacaqGGaGaey4kaSIaae 4naiabg2da9iaabIeacaqGPbGaae4zaiaabIgacaqGLbGaae4Caiaa bshacaqGGaGaaeyBaiaabggacaqGYbGaae4AaiaabohaaeaacaqGYa Gaey41aqRaamiBaiabgUcaRiaabEdacqGH9aqpcaqG4aGaae4naaqa amaaL4babaGaaGOmaiaadYgacqGHRaWkcaaI3aGaeyypa0JaaGioai aaiEdaaaaabaGaaeikaiaabMgacaqG2bGaaeykaiaabccacaqGbbGa aeOBaiaabccacaqGPbGaae4Caiaab+gacaqGJbGaaeyzaiaabYgaca qGLbGaae4CaiaabccacaqG0bGaaeOCaiaabMgacaqGHbGaaeOBaiaa bEgacaqGSbGaaeyzaiaabccacaqGObGaaeyyaiaabohacaqGGaGaae iDaiaabEhacaqGVbGaaeiiaiaabggacaqGUbGaae4zaiaabYgacaqG LbGaae4CaiaabccacaqGLbGaaeyCaiaabwhacaqGHbGaaeiBaiaab6 caaeaacaqGmbGaaeyzaiaabshacaqGGaGaaeiDaiaabIgacaqGLbGa aeiiaiaabkgacaqGHbGaae4CaiaabwgacaqGGaGaaeyyaiaab6gaca qGNbGaaeiBaiaabwgacaqGGaGaaeOyaiaabwgacaqGGaGaamOyaiaa b6caaeaacaqGubGaaeiAaiaabwgacaqGUbGaaeilaiaabccacaqGHb Gaae4yaiaabogacaqGVbGaaeOCaiaabsgacaqGPbGaaeOBaiaabEga caqGGaGaaeiDaiaab+gacaqGGaGaaeiDaiaabIgacaqGLbGaaeiiai aabghacaqG1bGaaeyzaiaabohacaqG0bGaaeyAaiaab+gacaqGUbGa aeilaiaabccacaqG3bGaaeyzaiaabccacaqGObGaaeyyaiaabAhaca qGLbaabaGaamOyaiabgUcaRiaadkgacqGHRaWkcaWGYaGaamOyaiab g2da9iaabgdacaqG4aGaaeimaiabgclaWcqaamaaL4babaGaaGinai aadkgacqGH9aqpcaaIXaGaaGioaiaaicdacqGHWcaSaaaaaaa@1B6D@

Q.7 Give first the step you will use to separate the variable and then solve the equation : ( a ) x – 1 = 0 ( b ) x + 1 = 0 ( c ) x – 1 = 5 ( d ) x + 6 = 2 ( e ) y – 4 = – 7 ( f ) y – 4 = 4 ( g ) y + 4 = 4 ( h ) y + 4 = – 4

( a ) x − 1 = 0 Add 1 to both sides to get x = 1 ( b ) x + 1 = 0 Subtract 1 from both sides to get x = − 1 ( c ) x − 1 = 5 Add 1 to both sides to get x = 6 ( d ) x + 6 = 2 Subtract 6 from both sides to get x = − 4 ( e ) y − 4 = − 7 Add 4 to both sides to get y = − 3 ( f ) y − 4 = 4 Add 4 to both sides to get y = 0 ( g ) y + 4 = 4 Subtract 4 from both sides to get y = 0 ( h ) y + 4 = − 4 Subtract 4 from both sides to get y = − 8 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqeduuDJXwAKbYu51MyVXgaruWqVvNCPvMCG4uz3bqefqvATv2C G4uz3bIuV1wyUbqeeuuDJXwAKbsr4rNCHbGeaGqiVz0xg9vqqrpepC 0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yq aqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabe qaamaaeaqbaaGceaqabeaadaqadaqaaiaabggaaiaawIcacaGLPaaa caWG4bGaeyOeI0Iaaeymaiabg2da9iaaicdaaeaacaqGbbGaaeizai aabsgacaqGGaGaaeymaiaabccacaqG0bGaae4BaiaabccacaqGIbGa ae4BaiaabshacaqGObGaaeiiaiaabohacaqGPbGaaeizaiaabwgaca qGZbGaaeiiaiaabshacaqGVbGaaeiiaiaabEgacaqGLbGaaeiDaaqa amaaL4babaGaamiEaiabg2da9iaaigdaaaaabaWaaeWaaeaacaqGIb aacaGLOaGaayzkaaGaaeiEaiabgUcaRiaabgdacqGH9aqpcaaIWaaa baGaae4uaiaabwhacaqGIbGaaeiDaiaabkhacaqGHbGaae4yaiaabs hacaqGGaGaaeymaiaabccacaqGMbGaaeOCaiaab+gacaqGTbGaaeii aiaabkgacaqGVbGaaeiDaiaabIgacaqGGaGaae4CaiaabMgacaqGKb GaaeyzaiaabohacaqGGaGaaeiDaiaab+gacaqGGaGaae4zaiaabwga caqG0baabaWaauIhaeaacaqG4bGaeyypa0JaeyOeI0Iaaeymaaaaae aadaqadaqaaiaabogaaiaawIcacaGLPaaacaqG4bGaeyOeI0Iaaeym aiabg2da9iaabwdaaeaacaqGbbGaaeizaiaabsgacaqGGaGaaeymai aabccacaqG0bGaae4BaiaabccacaqGIbGaae4BaiaabshacaqGObGa aeiiaiaabohacaqGPbGaaeizaiaabwgacaqGZbGaaeiiaiaabshaca qGVbGaaeiiaiaabEgacaqGLbGaaeiDaaqaamaaL4babaGaamiEaiab g2da9iaaiAdaaaaabaWaaeWaaeaacaqGKbaacaGLOaGaayzkaaGaae iEaiabgUcaRiaabccacaqG2aGaaeiiaiabg2da9iaabccacaqGYaaa baGaae4uaiaabwhacaqGIbGaaeiDaiaabkhacaqGHbGaae4yaiaabs hacaqGGaGaaeOnaiaabccacaqGMbGaaeOCaiaab+gacaqGTbGaaeii aiaabkgacaqGVbGaaeiDaiaabIgacaqGGaGaae4CaiaabMgacaqGKb GaaeyzaiaabohacaqGGaGaaeiDaiaab+gacaqGGaGaae4zaiaabwga caqG0baabaWaauIhaeaacaqG4bGaeyypa0JaeyOeI0Iaaeinaaaaae aadaqadaqaaiaabwgaaiaawIcacaGLPaaacaqG5bGaeyOeI0Iaaeii aiaabsdacqGH9aqpcqGHsislcaqGGaGaae4naaqaaiaabgeacaqGKb GaaeizaiaabccacaqG0aGaaeiiaiaabshacaqGVbGaaeiiaiaabkga caqGVbGaaeiDaiaabIgacaqGGaGaae4CaiaabMgacaqGKbGaaeyzai aabohacaqGGaGaaeiDaiaab+gacaqGGaGaae4zaiaabwgacaqG0baa baWaauIhaeaacaqG5bGaeyypa0JaeyOeI0IaaG4maaaaaeaadaqada qaaiaabAgaaiaawIcacaGLPaaacaqG5bGaeyOeI0Iaaeinaiabg2da 9iaabsdaaeaacaqGbbGaaeizaiaabsgacaqGGaGaaeinaiaabccaca qG0bGaae4BaiaabccacaqGIbGaae4BaiaabshacaqGObGaaeiiaiaa bohacaqGPbGaaeizaiaabwgacaqGZbGaaeiiaiaabshacaqGVbGaae iiaiaabEgacaqGLbGaaeiDaaqaamaaL4babaGaamyEaiabg2da9iaa icdaaaaabaWaaeWaaeaacaqGNbaacaGLOaGaayzkaaGaaeyEaiabgU caRiaabsdacqGH9aqpcaqG0aaabaGaae4uaiaabwhacaqGIbGaaeiD aiaabkhacaqGHbGaae4yaiaabshacaqGGaGaaeinaiaabccacaqGMb GaaeOCaiaab+gacaqGTbGaaeiiaiaabkgacaqGVbGaaeiDaiaabIga caqGGaGaae4CaiaabMgacaqGKbGaaeyzaiaabohacaqGGaGaaeiDai aab+gacaqGGaGaae4zaiaabwgacaqG0baabaWaauIhaeaacaWG5bGa eyypa0JaaGimaaaaaeaadaqadaqaaiaabIgaaiaawIcacaGLPaaaca qG5bGaey4kaSIaaeinaiabg2da9iabgkHiTiaabccacaqG0aaabaGa ae4uaiaabwhacaqGIbGaaeiDaiaabkhacaqGHbGaae4yaiaabshaca qGGaGaaeinaiaabccacaqGMbGaaeOCaiaab+gacaqGTbGaaeiiaiaa bkgacaqGVbGaaeiDaiaabIgacaqGGaGaae4CaiaabMgacaqGKbGaae yzaiaabohacaqGGaGaaeiDaiaab+gacaqGGaGaae4zaiaabwgacaqG 0baabaWaauIhaeaacaWG5bGaeyypa0JaeyOeI0IaaGioaaaaaaaa@605F@

Q.8 Give first the step you will use to separate the variable and then solve the equation : ( a ) 3 l = 42 ( b ) b 2 = 6 ( c ) p 7 = 4 ( d ) 4 x = 25 ( e ) 8 y = 36 ( f ) z 3 = 5 4 ( g ) a 5 = 7 15 ( h ) 2 t = – 10

( a ) 3 l = 42 Divide both sides by 3 to get l = 42 3 = 14 ( b ) b 2 = 6 Multiply both sides by 3 to get b = 12 ( c ) p 7 = 4 Multiply both sides by 7 to get p = 28 ( d ) 4x = 25 Divide both sides by 4 to get x = 25 4 ( e ) 8y = 36 Divide both sides by 8 to get y = 36 8 = 9 2 ( f ) z 3 = 5 4 Multiply both sides by 3 to get z = 15 4 ( g ) a 5 = 7 15 Multiply both sides by 5 to get a= 7 × 5 15 = 7 × 5 3 × 5 = 7 3 ( h ) 2 t = − 10 Divide both sides by 2 to get t= − 10 2 = − 5 × 2 2 = − 5

Q.9 Give the steps you will use to separate the variable and then solve the equation : ( a ) 3 n -2 = 46 ( b ) 5 m +7 = 17 ( c ) 20 p 3 = 40 ( d ) 3 p 10 = 6

(a) 3 n − 2 = 46 Add 2 to both sides to get 3 n = 48 Now, divide both sides by 3 to get n = 16 (b) 5 m + 7 = 17 Subtract 7 from both sides to get 5 m = 10 Now, divide both sides by 5 to get m = 2 (c) 20 p 3 = 40 Multiply both sides by 3 to get 20 p = 120 Now divide both sides by 20, to get p = 120 20 = 20 × 3 20 Thus , p = 3 (d) 3 p 10 = 6 Multiply both sides by 10 to get 3 p = 60 Now divide both sides by 3, to get p = 60 3 = 20 × 3 3 Thus , p = 20 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqeduuDJXwAKbYu51MyVXgaruWqVvNCPvMCG4uz3bqefqvATv2C G4uz3bIuV1wyUbqeeuuDJXwAKbsr4rNCHbGeaGqiVz0xg9vqqrpepC 0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yq aqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabe qaamaaeaqbaaGceaqabeaacaqGOaGaaeyyaiaabMcacaqGGaGaaG4m aiaad6gacqGHsislcaaIYaGaeyypa0JaaGinaiaaiAdaaeaacaqGbb GaaeizaiaabsgacaqGGaGaaeOmaiaabccacaqG0bGaae4Baiaabcca caqGIbGaae4BaiaabshacaqGObGaaeiiaiaabohacaqGPbGaaeizai aabwgacaqGZbGaaeiiaiaabshacaqGVbGaaeiiaiaabEgacaqGLbGa aeiDaaqaaiaaiodacaWGUbGaeyypa0JaaGinaiaaiIdaaeaacaqGob Gaae4BaiaabEhacaqGSaGaaeiiaiaabsgacaqGPbGaaeODaiaabMga caqGKbGaaeyzaiaabccacaqGIbGaae4BaiaabshacaqGObGaaeiiai aabohacaqGPbGaaeizaiaabwgacaqGZbGaaeiiaiaabkgacaqG5bGa aeiiaiaabodacaqGGaGaaeiDaiaab+gacaqGGaGaae4zaiaabwgaca qG0baabaWaauIhaeaacaWGUbGaeyypa0JaaGymaiaaiAdaaaaabaGa aeikaiaabkgacaqGPaGaaeiiaiaaiwdacaWGTbGaey4kaSIaaG4nai abg2da9iaaigdacaaI3aaabaGaae4uaiaabwhacaqGIbGaaeiDaiaa bkhacaqGHbGaae4yaiaabshacaqGGaGaae4naiaabccacaqGMbGaae OCaiaab+gacaqGTbGaaeiiaiaabkgacaqGVbGaaeiDaiaabIgacaqG GaGaae4CaiaabMgacaqGKbGaaeyzaiaabohacaqGGaGaaeiDaiaab+ gacaqGGaGaae4zaiaabwgacaqG0baabaGaaGynaiaad2gacqGH9aqp caaIXaGaaGimaaqaaiaab6eacaqGVbGaae4DaiaabYcacaqGGaGaae izaiaabMgacaqG2bGaaeyAaiaabsgacaqGLbGaaeiiaiaabkgacaqG VbGaaeiDaiaabIgacaqGGaGaae4CaiaabMgacaqGKbGaaeyzaiaabo hacaqGGaGaaeOyaiaabMhacaqGGaGaaeynaiaabccacaqG0bGaae4B aiaabccacaqGNbGaaeyzaiaabshaaeaadaqjEaqaaiaad2gacqGH9a qpcaaIYaaaaaqaaiaabIcacaqGJbGaaeykaiaabccadaWcaaqaaiaa ikdacaaIWaGaamiCaaqaaiaaiodaaaGaeyypa0JaaGinaiaaicdaae aacaqGnbGaaeyDaiaabYgacaqG0bGaaeyAaiaabchacaqGSbGaaeyE aiaabccacaqGIbGaae4BaiaabshacaqGObGaaeiiaiaabohacaqGPb GaaeizaiaabwgacaqGZbGaaeiiaiaabkgacaqG5bGaaeiiaiaaboda caqGGaGaaeiDaiaab+gacaqGGaGaae4zaiaabwgacaqG0baabaGaaG OmaiaaicdacaWGWbGaeyypa0JaaGymaiaaikdacaaIWaaabaGaaeOt aiaab+gacaqG3bGaaeiiaiaabsgacaqGPbGaaeODaiaabMgacaqGKb GaaeyzaiaabccacaqGIbGaae4BaiaabshacaqGObGaaeiiaiaaboha caqGPbGaaeizaiaabwgacaqGZbGaaeiiaiaabkgacaqG5bGaaeiiai aabkdacaqGWaGaaeilaiaabccacaqG0bGaae4BaiaabccacaqGNbGa aeyzaiaabshaaeaacaWGWbGaeyypa0ZaaSaaaeaacaaIXaGaaGOmai aaicdaaeaacaaIYaGaaGimaaaacqGH9aqpdaWcaaqaamaaKiaabaGa aGOmaiaaicdaaaGaey41aqRaaG4maaqaamaaKiaabaGaaGOmaiaaic daaaaaaaqaaiaabsfacaqGObGaaeyDaiaabohacaGGSaGaaGjbVpaa L4babaGaamiCaiabg2da9iaaiodaaaaabaGaaeikaiaabsgacaqGPa GaaGjbVpaalaaabaGaaG4maiaadchaaeaacaaIXaGaaGimaaaacqGH 9aqpcaaI2aaabaGaaeytaiaabwhacaqGSbGaaeiDaiaabMgacaqGWb GaaeiBaiaabMhacaqGGaGaaeOyaiaab+gacaqG0bGaaeiAaiaabcca caqGZbGaaeyAaiaabsgacaqGLbGaae4CaiaabccacaqGIbGaaeyEai aabccacaqGXaGaaeimaiaabccacaqG0bGaae4BaiaabccacaqGNbGa aeyzaiaabshaaeaacaaIZaGaamiCaiabg2da9iaaiAdacaaIWaaaba GaaeOtaiaab+gacaqG3bGaaeiiaiaabsgacaqGPbGaaeODaiaabMga caqGKbGaaeyzaiaabccacaqGIbGaae4BaiaabshacaqGObGaaeiiai aabohacaqGPbGaaeizaiaabwgacaqGZbGaaeiiaiaabkgacaqG5bGa aeiiaiaabodacaqGSaGaaeiiaiaabshacaqGVbGaaeiiaiaabEgaca qGLbGaaeiDaaqaaiaadchacqGH9aqpdaWcaaqaaiaaiAdacaaIWaaa baGaaG4maaaacqGH9aqpdaWcaaqaaiaaikdacaaIWaGaey41aqRabG 4mayaawaaabaGabG4mayaawaaaaaqaaiaabsfacaqGObGaaeyDaiaa bohacaGGSaGaaGjbVpaaL4babaGaamiCaiabg2da9iaaikdacaaIWa aaaaaaaa@817B@

Q.10 Solve the following equations : ( a ) 10 p = 100 ( b ) 10 p + 10 = 100 ( c ) p 4 = 5 ( d ) p 3 = 5 ( e ) 3 p 4 = 6 ( f ) 3 s = – 9 ( g ) 3 s + 12 = 0 ( h ) 3 s = 0 ( i ) 2 q = 6 ( j ) 2 q – 6 = 0 ( k ) 2 q + 6 = 0 ( l ) 2 q + 6 = 12

( a ) 10 p = 100 p = 100 10 = 10 (b) 10 p + 10 = 100 10 p = 90 p = 90 10 = 9 (c) p 4 = 5 p = 5 × 4 = 20 (d) p 3 = 5 p = 5 × 3 = 15 ( e ) 3 p 4 = 6 3 p = 6 × 4 = 24 p = 24 3 = 8 ( f ) 3 s = − 9 s = − 9 3 = − 3 ( g ) 3 s + 12 = 0 3 s = − 12 s = − 12 3 = − 4 ( h ) 3 s = 0 s = 0 3 = 0 ( i ) 2 q = 6 q = 6 2 = 3 ( j ) 2 q − 6 = 0 2 q = 6 q = 6 2 = 3 ( k ) 2 q + 6 = 0 2 q = − 6 q = − 6 2 = − 3 ( l ) 2 q + 6 = 12 2 q = 12 − 6 2 q = 6 q = 6 3 = 2 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqeduuDJXwAKbYu51MyVXgaruWqVvNCPvMCG4uz3bqefqvATv2C G4uz3bIuV1wyUbqeeuuDJXwAKbsr4rNCHbGeaGqiVz0xg9vqqrpepC 0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yq aqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabe qaamaaeaqbaaGceaqabeaacaGGOaGaamyyaiaacMcacaqGGaGaaGym aiaaicdacaWGWbGaeyypa0JaaGymaiaaicdacaaIWaaabaGaamiCai abg2da9maalaaabaGaaGymaiaaicdacaaIWaaabaGaaGymaiaaicda aaGaeyypa0ZaauIhaeaacaaIXaGaaGimaaaaaeaacaqGOaGaaeOyai aabMcacaqGGaGaaGymaiaaicdacaWGWbGaey4kaSIaaGymaiaaicda cqGH9aqpcaaIXaGaaGimaiaaicdaaeaacaaIXaGaaGimaiaadchacq GH9aqpcaaI5aGaaGimaaqaaiaadchacqGH9aqpdaWcaaqaaiaaiMda caaIWaaabaGaaGymaiaaicdaaaGaeyypa0ZaauIhaeaacaaI5aaaaa qaaiaabIcacaqGJbGaaeykaiaabccadaWcaaqaaiaadchaaeaacaaI 0aaaaiabg2da9iaaiwdaaeaacaWGWbGaeyypa0JaaGynaiabgEna0k aaisdacqGH9aqpdaqjEaqaaiaaikdacaaIWaaaaaqaaiaabIcacaqG KbGaaeykaiaabccadaWcaaqaaiaadchaaeaacaaIZaaaaiabg2da9i aaiwdaaeaacaWGWbGaeyypa0JaaGynaiabgEna0kaaiodacqGH9aqp daqjEaqaaiaaigdacaaI1aaaaaqaaiaacIcacaWGLbGaaiykaiaabc cadaWcaaqaaiaaiodacaWGWbaabaGaaGinaaaacqGH9aqpcaaI2aaa baGaaG4maiaadchacqGH9aqpcaaI2aGaey41aqRaaGinaiabg2da9i aaikdacaaI0aaabaGaamiCaiabg2da9maalaaabaGaaGOmaiaaisda aeaacaaIZaaaaiabg2da9maaL4babaGaaGioaaaaaeaacaGGOaGaam OzaiaacMcacaaMe8UaaG4maiaadohacqGH9aqpcqGHsislcaaI5aaa baGaam4Caiabg2da9maalaaabaGaeyOeI0IaaGyoaaqaaiaaiodaaa Gaeyypa0ZaauIhaeaacqGHsislcaaIZaaaaaqaaiaacIcacaWGNbGa aiykaiaaysW7caaIZaGaam4CaiabgUcaRiaaigdacaaIYaGaeyypa0 JaaGimaaqaaiaaiodacaWGZbGaeyypa0JaeyOeI0IaaGymaiaaikda aeaacaWGZbGaeyypa0ZaaSaaaeaacqGHsislcaaIXaGaaGOmaaqaai aaiodaaaGaeyypa0ZaauIhaeaacqGHsislcaaI0aaaaaqaaiaacIca caWGObGaaiykaiaaysW7caaIZaGaam4Caiabg2da9iaaicdaaeaaca WGZbGaeyypa0ZaaSaaaeaacaaIWaaabaGaaG4maaaacqGH9aqpdaqj EaqaaiaaicdaaaaabaGaaiikaiaadMgacaGGPaGaaGjbVlaaikdaca WGXbGaeyypa0JaaGOnaaqaaiaadghacqGH9aqpdaWcaaqaaiaaiAda aeaacaaIYaaaaiabg2da9maaL4babaGaaG4maaaaaeaacaGGOaGaam OAaiaacMcacaaMe8UaaGOmaiaadghacqGHsislcaaI2aGaeyypa0Ja aGimaaqaaiaaikdacaWGXbGaeyypa0JaaGOnaaqaaiaadghacqGH9a qpdaWcaaqaaiaaiAdaaeaacaaIYaaaaiabg2da9maaL4babaGaaG4m aaaaaeaacaGGOaGaam4AaiaacMcacaaMe8UaaGOmaiaadghacqGHRa WkcaaI2aGaeyypa0JaaGimaaqaaiaaikdacaWGXbGaeyypa0JaeyOe I0IaaGOnaaqaaiaadghacqGH9aqpdaWcaaqaaiabgkHiTiaaiAdaae aacaaIYaaaaiabg2da9maaL4babaGaeyOeI0IaaG4maaaaaeaacaGG OaGaamiBaiaacMcacaaMe8UaaGOmaiaadghacqGHRaWkcaaI2aGaey ypa0JaaGymaiaaikdaaeaacaaIYaGaamyCaiabg2da9iaaigdacaaI YaGaeyOeI0IaaGOnaaqaaiaaikdacaWGXbGaeyypa0JaaGOnaaqaai aadghacqGH9aqpdaWcaaqaaiaaiAdaaeaacaaIZaaaaiabg2da9maa L4babaGaaGOmaaaaaaaa@1872@

Q.11 Solve the following equations : ( a ) 2 y + 5 2 = 37 2 ( b ) 5 t + 28 = 10 ( c ) a 5 + 3 = 2 ( d ) q 4 + 7 = 5 ( e ) 5 2 x = 10 ( f ) 5 2 x = 25 4 ( g ) 7 m + 19 2 = 13 ( h ) 6 z + 10 = − 2 ( i ) 3 l 2 = 2 3 ( j ) 2 b 3 − 5 = 3

( a ) 2 y + 5 2 = 37 2 2 y = 37 2 − 5 2 = 37 − 5 2 = 32 2 = 16 2 y = 16 y = 16 2 = 8 T h u s , y = 8 ( b ) 5t + 28 = 1 0 5 t = 10 − 28 5 t = − 18 t = − 18 5 ( c ) a 5 + 3 = 2 a 5 = 2 − 3 a 5 = − 1 a = − 5 ( d ) q 4 + 7 = 5 q 4 = 5 − 7 q 4 = − 2 q = − 8 ( e ) 5 2 x = − 10 5 x = − 10 × 2 x = − 10 × 2 5 = − 5 × 2 × 2 5 = − 4 T h u s , x = − 4 ( f ) 5 2 x = 25 4 5 x = 25 × 2 4 x = 5 × 5 × 2 2 × 2 × 5 T h u s , x = 5 2 ( g ) 7 m + 19 2 = 13 7 m = 13 − 19 2 = 26 − 19 2 = 7 2 7 m = 7 2 m = 7 2 × 7 T h u s , m = 1 2 ( h ) 6z + 1 0 = − 2 6 z = − 2 − 10 6 z = − 12 z = − 12 6 = − 2 × 6 6 0 T h u s , z = − 2 ( i ) 3 l 2 = 2 3 3 l = 4 3 l = 4 9 ( j ) 2 b 3 − 5 = 3 2 b 3 = 8 2 b = 24 b = 24 2 = 2 × 12 2 T h u s , b = 12 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqeduuDJXwAKbYu51MyVXgaruWqVvNCPvMCG4uz3bqefqvATv2C G4uz3bIuV1wyUbqeeuuDJXwAKbsr4rNCHbGeaGqiVz0xg9vqqrpepC 0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yq aqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabe qaamaaeaqbaaGceaqabeaadaqadaqaaiaabggaaiaawIcacaGLPaaa caqGYaGaamyEaiabgUcaRmaalaaabaGaaGynaaqaaiaaikdaaaGaey ypa0ZaaSaaaeaacaaIZaGaaG4naaqaaiaaikdaaaaabaGaaGOmaiaa dMhacqGH9aqpdaWcaaqaaiaaiodacaaI3aaabaGaaGOmaaaacqGHsi sldaWcaaqaaiaaiwdaaeaacaaIYaaaaiabg2da9maalaaabaGaaG4m aiaaiEdacqGHsislcaaI1aaabaGaaGOmaaaacqGH9aqpdaWcaaqaai aaiodacaaIYaaabaGaaGOmaaaacqGH9aqpcaaIXaGaaGOnaaqaaiaa ikdacaWG5bGaeyypa0JaaGymaiaaiAdaaeaacaWG5bGaeyypa0ZaaS aaaeaacaaIXaGaaGOnaaqaaiaaikdaaaGaeyypa0JaaGioaaqaaiaa dsfacaWGObGaamyDaiaadohacaGGSaGaaGjbVpaaL4babaGaamyEai abg2da9iaaiIdaaaaabaWaaeWaaeaacaqGIbaacaGLOaGaayzkaaGa aeiiaiaabwdacaqG0bGaey4kaSIaaeOmaiaabIdacqGH9aqpcaqGXa GaaGimaaqaaiaaiwdacaWG0bGaeyypa0JaaGymaiaaicdacqGHsisl caaIYaGaaGioaaqaaiaaiwdacaWG0bGaeyypa0JaeyOeI0IaaGymai aaiIdaaeaadaqjEaqaaiaadshacqGH9aqpdaWcaaqaaiabgkHiTiaa igdacaaI4aaabaGaaGynaaaaaaaabaWaaeWaaeaacaqGJbaacaGLOa GaayzkaaWaaSaaaeaacaqGHbaabaGaaGynaaaacqGHRaWkcaaIZaGa eyypa0JaaGOmaaqaamaalaaabaGaamyyaaqaaiaaiwdaaaGaeyypa0 JaaGOmaiabgkHiTiaaiodaaeaadaWcaaqaaiaadggaaeaacaaI1aaa aiabg2da9iabgkHiTiaaigdaaeaadaqjEaqaaiaadggacqGH9aqpcq GHsislcaaI1aaaaaqaamaabmaabaGaaeizaaGaayjkaiaawMcaamaa laaabaGaamyCaaqaaiaaisdaaaGaey4kaSIaaG4naiabg2da9iaaiw daaeaadaWcaaqaaiaadghaaeaacaaI0aaaaiabg2da9iaaiwdacqGH sislcaaI3aaabaWaaSaaaeaacaWGXbaabaGaaGinaaaacqGH9aqpcq GHsislcaaIYaaabaWaauIhaeaacaWGXbGaeyypa0JaeyOeI0IaaGio aaaaaeaadaqadaqaaiaabwgaaiaawIcacaGLPaaadaWcaaqaaiaaiw daaeaacaaIYaaaaiaadIhacqGH9aqpcqGHsislcaaIXaGaaGimaaqa aiaaiwdacaWG4bGaeyypa0JaeyOeI0IaaGymaiaaicdacqGHxdaTca aIYaaabaGaamiEaiabg2da9maalaaabaGaeyOeI0IaaGymaiaaicda cqGHxdaTcaaIYaaabaGaaGynaaaacqGH9aqpdaWcaaqaaiabgkHiTi qaiwdagaGfaiabgEna0kaaikdacqGHxdaTcaaIYaaabaGabGynayaa waaaaiabg2da9iabgkHiTiaaisdaaeaacaWGubGaamiAaiaadwhaca WGZbGaaiilaiaaysW7daqjEaqaaiaadIhacqGH9aqpcqGHsislcaaI 0aaaaaqaamaabmaabaGaaeOzaaGaayjkaiaawMcaamaalaaabaGaaG ynaaqaaiaaikdaaaGaamiEaiabg2da9maalaaabaGaaGOmaiaaiwda aeaacaaI0aaaaaqaaiaaiwdacaWG4bGaeyypa0ZaaSaaaeaacaaIYa GaaGynaiabgEna0kaaikdaaeaacaaI0aaaaaqaaiaadIhacqGH9aqp daWcaaqaaiqaiwdagaGfaiabgEna0kaaiwdacqGHxdaTceaIYaGbay baaeaaceaIYaGbaybacqGHxdaTcaaIYaGaey41aqRabGynayaawaaa aaqaaiaadsfacaWGObGaamyDaiaadohacaGGSaGaaGjbVpaaL4baba GaamiEaiabg2da9maalaaabaGaaGynaaqaaiaaikdaaaaaaaqaamaa bmaabaGaae4zaaGaayjkaiaawMcaaiaaiEdacaWGTbGaey4kaSYaaS aaaeaacaaIXaGaaGyoaaqaaiaaikdaaaGaeyypa0JaaGymaiaaioda aeaacaaI3aGaamyBaiabg2da9iaaigdacaaIZaGaeyOeI0YaaSaaae aacaaIXaGaaGyoaaqaaiaaikdaaaGaeyypa0ZaaSaaaeaacaaIYaGa aGOnaiabgkHiTiaaigdacaaI5aaabaGaaGOmaaaacqGH9aqpdaWcaa qaaiaaiEdaaeaacaaIYaaaaaqaaiaaiEdacaWGTbGaeyypa0ZaaSaa aeaacaaI3aaabaGaaGOmaaaaaeaacaWGTbGaeyypa0ZaaSaaaeaace aI3aGbaybaaeaacaaIYaGaey41aqRabG4nayaawaaaaaqaaiaadsfa caWGObGaamyDaiaadohacaGGSaGaaGjbVpaaL4babaGaamyBaiabg2 da9maalaaabaGaaGymaaqaaiaaikdaaaaaaaqaamaabmaabaGaaeiA aaGaayjkaiaawMcaaiaabccacaqG2aGaaeOEaiabgUcaRiaabgdaca aIWaGaeyypa0JaeyOeI0IaaeOmaaqaaiaaiAdacaWG6bGaeyypa0Ja eyOeI0IaaGOmaiabgkHiTiaaigdacaaIWaaabaGaaGOnaiaadQhacq GH9aqpcqGHsislcaaIXaGaaGOmaaqaaiaadQhacqGH9aqpdaWcaaqa aiabgkHiTiaaigdacaaIYaaabaGaaGOnaaaacqGH9aqpdaWcaaqaai abgkHiTiaaikdacqGHxdaTceaI2aGbaybaaeaaceaI2aGbaybaaaGa aGimaaqaaiaadsfacaWGObGaamyDaiaadohacaGGSaGaaGjbVpaaL4 babaGaamOEaiabg2da9iabgkHiTiaaikdaaaaabaWaaeWaaeaacaqG PbaacaGLOaGaayzkaaWaaSaaaeaacaaIZaGaamiBaaqaaiaaikdaaa Gaeyypa0ZaaSaaaeaacaaIYaaabaGaaG4maaaaaeaacaaIZaGaamiB aiabg2da9maalaaabaGaaGinaaqaaiaaiodaaaaabaWaauIhaeaaca WGSbGaeyypa0ZaaSaaaeaacaaI0aaabaGaaGyoaaaaaaaabaWaaeWa aeaacaqGQbaacaGLOaGaayzkaaWaaSaaaeaacaaIYaGaamOyaaqaai aaiodaaaGaeyOeI0IaaGynaiabg2da9iaaiodaaeaadaWcaaqaaiaa ikdacaWGIbaabaGaaG4maaaacqGH9aqpcaaI4aaabaGaaGOmaiaadk gacqGH9aqpcaaIYaGaaGinaaqaaiaadkgacqGH9aqpdaWcaaqaaiaa ikdacaaI0aaabaGaaGOmaaaacqGH9aqpdaWcaaqaaiqaikdagaGfai abgEna0kaaigdacaaIYaaabaGabGOmayaawaaaaaqaaiaadsfacaWG ObGaamyDaiaadohacaGGSaGaaGjbVpaaL4babaGaamOyaiabg2da9i aaigdacaaIYaaaaaaaaa@981B@

Q.12 Solve the following equations : ( a ) 2 ( x + 4 ) = 12 ( b ) 3 ( n − 5 ) = 21 ( c ) 3 ( n − 5 ) = 21 ( d ) 3 − 2 ( 2 − y ) = 7 ( e ) − 4 ( 2 − x ) = 9 ( f ) 4 ( 2 − x ) = 9 ( g ) 4 + 5 ( p − 1 ) = 34 ( h ) 34 − 5 ( p − 1 ) = 4

(a ) 2 ( x + 4 ) = 12 Divide both sides by 2 to get x + 4 = 6 Thus, x = 2 ( b ) 3 ( n − 5 ) = − 21 Divide both sides by 3 to get n − 5 = − 7 Thus, n = − 2 ( c ) 3 ( n − 5 ) = − 21 Divide both sides by 2 to get n − 5 = − 7 T h u s , n = − 12 ( d ) 3 − 2 ( 2 − y ) = 7 − 2 ( 2 − y ) = 4 Divide both sides by − 2 to get 2 − y = − 2 Multiply both sides by − 1 to get y − 2 = 2 Thus, y = 4 ( e ) − 4 ( 2 − x ) = 9 Divide both sides by − 4 to get 2 − x = − 9 4 Multiply both sides by − 1 to get x − 2 = 9 4 x = 9 4 + 2 = 9 + 8 4 T h u s , x = 17 4 ( f ) 4 ( 2 − x ) = 9 Divide both sides by 4 to get 2 − x = 9 4 Multiply both sides by -1 to get x − 2 = − 9 4 x = − 9 4 + 2 = − 9 + 8 4 Thus , x = − 1 4 ( g ) 4 + 5 ( p − 1 ) = 34 5 ( p − 1 ) = 30 Divide both sides by 5 to get p − 1 = 6 p = 6 + 1 = 7 Thus , p = 7 ( h ) 34 − 5 ( p − 1 ) = 4 − 5 ( p − 1 ) = − 30 Divide both sides by − 5 to get p − 1 = 6 p = 6 + 1 = 7 Thus, p = 7 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqeduuDJXwAKbYu51MyVXgaruWqVvNCPvMCG4uz3bqefqvATv2C G4uz3bIuV1wyUbqeeuuDJXwAKbsr4rNCHbGeaGqiVz0xg9vqqrpepC 0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yq aqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabe qaamaaeaqbaaGceaqabeaacaqGOaGaaeyyaiaacMcacaqGGaGaaGOm aiaacIcacaWG4bGaey4kaSIaaeiiaiaaisdacaGGPaGaeyypa0JaaG ymaiaaikdaaeaacaqGebGaaeyAaiaabAhacaqGPbGaaeizaiaabwga caqGGaGaaeOyaiaab+gacaqG0bGaaeiAaiaabccacaqGZbGaaeyAai aabsgacaqGLbGaae4CaiaabccacaqGIbGaaeyEaiaabccacaqGYaGa aeiiaiaabshacaqGVbGaaeiiaiaabEgacaqGLbGaaeiDaaqaaiaadI hacqGHRaWkcaaI0aGaeyypa0JaaGOnaaqaaiaabsfacaqGObGaaeyD aiaabohacaqGSaGaaGjbVpaaL4babaGaamiEaiabg2da9iaaikdaaa aabaWaaeWaaeaacaqGIbaacaGLOaGaayzkaaGaaeiiaiaaiodacaGG OaGaamOBaiabgkHiTiaaiwdacaGGPaGaeyypa0JaeyOeI0IaaGOmai aaigdaaeaacaqGebGaaeyAaiaabAhacaqGPbGaaeizaiaabwgacaqG GaGaaeOyaiaab+gacaqG0bGaaeiAaiaabccacaqGZbGaaeyAaiaabs gacaqGLbGaae4CaiaabccacaqGIbGaaeyEaiaabccacaqGZaGaaeii aiaabshacaqGVbGaaeiiaiaabEgacaqGLbGaaeiDaaqaaiaad6gacq GHsislcaaI1aGaeyypa0JaeyOeI0Iaae4naaqaaiaabsfacaqGObGa aeyDaiaabohacaqGSaWaauIhaeaacaqGGaGaamOBaiabg2da9iabgk HiTiaaikdaaaaabaWaaeWaaeaacaqGJbaacaGLOaGaayzkaaGaaeii aiaaiodacaGGOaGaamOBaiabgkHiTiaaiwdacaGGPaGaeyypa0Jaey OeI0IaaeOmaiaabgdaaeaacaqGebGaaeyAaiaabAhacaqGPbGaaeiz aiaabwgacaqGGaGaaeOyaiaab+gacaqG0bGaaeiAaiaabccacaqGZb GaaeyAaiaabsgacaqGLbGaae4CaiaabccacaqGIbGaaeyEaiaabcca caqGYaGaaeiiaiaabshacaqGVbGaaeiiaiaabEgacaqGLbGaaeiDaa qaaiaad6gacqGHsislcaaI1aGaeyypa0JaeyOeI0IaaG4naaqaaiaa dsfacaWGObGaamyDaiaadohacaGGSaGaaGjbVpaaL4babaGaamOBai abg2da9iabgkHiTiaaigdacaaIYaaaaaqaamaabmaabaGaaeizaaGa ayjkaiaawMcaaiaabccacaqGZaGaeyOeI0IaaeOmaiaacIcacaqGYa GaeyOeI0IaamyEaiaacMcacqGH9aqpcaqG3aaabaGaeyOeI0IaaGOm amaabmaabaGaaGOmaiabgkHiTiaadMhaaiaawIcacaGLPaaacqGH9a qpcaaI0aaabaGaaeiraiaabMgacaqG2bGaaeyAaiaabsgacaqGLbGa aeiiaiaabkgacaqGVbGaaeiDaiaabIgacaqGGaGaae4CaiaabMgaca qGKbGaaeyzaiaabohacaqGGaGaaeOyaiaabMhacqGHsislcaqGYaGa aeiiaiaabshacaqGVbGaaeiiaiaabEgacaqGLbGaaeiDaaqaaiaaik dacqGHsislcaWG5bGaeyypa0JaeyOeI0IaaGOmaaqaaiaab2eacaqG 1bGaaeiBaiaabshacaqGPbGaaeiCaiaabYgacaqG5bGaaeiiaiaabk gacaqGVbGaaeiDaiaabIgacaqGGaGaae4CaiaabMgacaqGKbGaaeyz aiaabohacaqGGaGaaeOyaiaabMhacqGHsislcaqGXaGaaeiiaiaabs hacaqGVbGaaeiiaiaabEgacaqGLbGaaeiDaaqaaiaadMhacqGHsisl caaIYaGaeyypa0JaaGOmaaqaaiaabsfacaqGObGaaeyDaiaabohaca qGSaGaaeiiamaaL4babaGaamyEaiabg2da9iaaisdaaaaabaWaaeWa aeaacaqGLbaacaGLOaGaayzkaaGaaeiiaiabgkHiTiaaisdacaGGOa GaaGOmaiabgkHiTiaadIhacaGGPaGaeyypa0Jaaeyoaaqaaiaabsea caqGPbGaaeODaiaabMgacaqGKbGaaeyzaiaabccacaqGIbGaae4Bai aabshacaqGObGaaeiiaiaabohacaqGPbGaaeizaiaabwgacaqGZbGa aeiiaiaabkgacaqG5bGaeyOeI0IaaeinaiaabccacaqG0bGaae4Bai aabccacaqGNbGaaeyzaiaabshaaeaacaqGYaGaeyOeI0IaamiEaiab g2da9maalaaabaGaeyOeI0IaaGyoaaqaaiaaisdaaaaabaGaaeytai aabwhacaqGSbGaaeiDaiaabMgacaqGWbGaaeiBaiaabMhacaqGGaGa aeOyaiaab+gacaqG0bGaaeiAaiaabccacaqGZbGaaeyAaiaabsgaca qGLbGaae4CaiaabccacaqGIbGaaeyEaiabgkHiTiaabgdacaqGGaGa aeiDaiaab+gacaqGGaGaae4zaiaabwgacaqG0baabaGaamiEaiabgk HiTiaaikdacqGH9aqpdaWcaaqaaiaaiMdaaeaacaaI0aaaaaqaaiaa dIhacqGH9aqpdaWcaaqaaiaaiMdaaeaacaaI0aaaaiabgUcaRiaaik dacqGH9aqpdaWcaaqaaiaaiMdacqGHRaWkcaaI4aaabaGaaGinaaaa aeaacaWGubGaamiAaiaadwhacaWGZbGaaiilaiaaysW7daqjEaqaai aadIhacqGH9aqpdaWcaaqaaiaaigdacaaI3aaabaGaaGinaaaaaaaa baWaaeWaaeaacaqGMbaacaGLOaGaayzkaaGaaeiiaiaaisdacaGGOa GaaGOmaiabgkHiTiaadIhacaGGPaGaeyypa0Jaaeyoaaqaaiaabsea caqGPbGaaeODaiaabMgacaqGKbGaaeyzaiaabccacaqGIbGaae4Bai aabshacaqGObGaaeiiaiaabohacaqGPbGaaeizaiaabwgacaqGZbGa aeiiaiaabkgacaqG5bGaaeiiaiaabsdacaqGGaGaaeiDaiaab+gaca qGGaGaae4zaiaabwgacaqG0baabaGaaeOmaiabgkHiTiaadIhacqGH 9aqpdaWcaaqaaiaaiMdaaeaacaaI0aaaaaqaaiaab2eacaqG1bGaae iBaiaabshacaqGPbGaaeiCaiaabYgacaqG5bGaaeiiaiaabkgacaqG VbGaaeiDaiaabIgacaqGGaGaae4CaiaabMgacaqGKbGaaeyzaiaabo hacaqGGaGaaeOyaiaabMhacaqGGaGaaeylaiaabgdacaqGGaGaaeiD aiaab+gacaqGGaGaae4zaiaabwgacaqG0baabaGaaeiEaiabgkHiTi aaikdacqGH9aqpdaWcaaqaaiabgkHiTiaaiMdaaeaacaaI0aaaaaqa aiaadIhacqGH9aqpdaWcaaqaaiabgkHiTiaaiMdaaeaacaaI0aaaai abgUcaRiaaikdacqGH9aqpdaWcaaqaaiabgkHiTiaaiMdacqGHRaWk caaI4aaabaGaaGinaaaaaeaacaqGubGaaeiAaiaabwhacaqGZbGaai ilaiaaysW7daqjEaqaaiaadIhacqGH9aqpdaWcaaqaaiabgkHiTiaa igdaaeaacaaI0aaaaaaaaeaadaqadaqaaiaabEgaaiaawIcacaGLPa aacaqGGaGaaGinaiabgUcaRiaaiwdacaqGGaGaaiikaiaadchacqGH sislcaaIXaGaaiykaiabg2da9iaaiodacaaI0aaabaGaaGynamaabm aabaGaamiCaiabgkHiTiaaigdaaiaawIcacaGLPaaacqGH9aqpcaaI ZaGaaGimaaqaaiaabseacaqGPbGaaeODaiaabMgacaqGKbGaaeyzai aabccacaqGIbGaae4BaiaabshacaqGObGaaeiiaiaabohacaqGPbGa aeizaiaabwgacaqGZbGaaeiiaiaabkgacaqG5bGaaeiiaiaabwdaca qGGaGaaeiDaiaab+gacaqGGaGaae4zaiaabwgacaqG0baabaGaaeiC aiabgkHiTiaaigdacqGH9aqpcaaI2aaabaGaamiCaiabg2da9iaaiA dacqGHRaWkcaaIXaGaeyypa0JaaG4naaqaaiaabsfacaqGObGaaeyD aiaabohacaGGSaGaaGjbVpaaL4babaGaamiCaiabg2da9iaaiEdaaa aabaWaaeWaaeaacaqGObaacaGLOaGaayzkaaGaaeiiaiaaiodacaaI 0aGaeyOeI0IaaGynaiaacIcacaWGWbGaeyOeI0IaaGymaiaacMcacq GH9aqpcaaI0aaabaGaeyOeI0IaaGynamaabmaabaGaamiCaiabgkHi TiaaigdaaiaawIcacaGLPaaacqGH9aqpcqGHsislcaaIZaGaaGimaa qaaiaabseacaqGPbGaaeODaiaabMgacaqGKbGaaeyzaiaabccacaqG IbGaae4BaiaabshacaqGObGaaeiiaiaabohacaqGPbGaaeizaiaabw gacaqGZbGaaeiiaiaabkgacaqG5bGaeyOeI0IaaeynaiaabccacaqG 0bGaae4BaiaabccacaqGNbGaaeyzaiaabshaaeaacaWGWbGaeyOeI0 IaaGymaiabg2da9iaaiAdaaeaacaWGWbGaeyypa0JaaGOnaiabgUca RiaaigdacqGH9aqpcaaI3aaabaGaaeivaiaabIgacaqG1bGaae4Cai aabYcacaaMe8+aauIhaeaacaWGWbGaeyypa0JaaG4naaaaaaaa@6D42@

Q.13 Solve the following equations . ( a ) 4 = 5 ( p − 2 ) ( b ) − 4 = 5 ( p − 2 ) ( c ) − 16 = − 5 ( 2 − p ) ( d ) 10 = 4 + 3 ( t + 2 ) ( e ) 28 = 4 + 3 ( t + 5 ) ( f ) 0 = 16 + 4 ( m − 6 )

( a ) 4 = 5 ( p − 2 ) Divide both sides by 5 to get 4 5 = p − 2 p = 4 5 + 2 = 4 + 10 5 Thus , p = 14 5 ( b ) − 4 = 5 ( p − 2 ) Divide both sides by 5 to get − 4 5 = p − 2 p = − 4 5 + 2 = − 4 + 10 5 Thus , p = 6 5 ( c ) − 16 = − 5 ( 2 − p ) Divide both sides by − 5 to get 16 5 = 2 − p Multiply both sides by − 1 to get − 16 5 = p − 2 p = − 16 5 + 2 = − 16 + 10 5 Thus , p = − 6 5 ( d ) 1 0 = 4 + 3 ( t + 2 ) 6 = 3 ( t + 2 ) Divide both sides by 3 to get 2 = t + 2 Thus, t = 0 ( e ) 28 = 4 + 3 ( t + 5 ) 24 = 3 ( t + 5 ) Divide both sides by 3 to get 8 = t + 5 Thus, t = 3 ( f ) 0 = 16 + 4 ( m − 6 ) − 16 = 4 ( m − 6 ) Divide both sides by 4 to get − 4 = m − 6 Thus, m = 2 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqeduuDJXwAKbYu51MyVXgaruWqVvNCPvMCG4uz3bqefqvATv2C G4uz3bIuV1wyUbqeeuuDJXwAKbsr4rNCHbGeaGqiVz0xg9vqqrpepC 0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yq aqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabe qaamaaeaqbaaGceaqabeaadaqadaqaaiaabggaaiaawIcacaGLPaaa caqGGaGaaeinaiabg2da9iaabwdacaGGOaGaamiCaiabgkHiTiaabk dacaGGPaaabaGaaeiraiaabMgacaqG2bGaaeyAaiaabsgacaqGLbGa aeiiaiaabkgacaqGVbGaaeiDaiaabIgacaqGGaGaae4CaiaabMgaca qGKbGaaeyzaiaabohacaqGGaGaaeOyaiaabMhacaqGGaGaaeynaiaa bccacaqG0bGaae4BaiaabccacaqGNbGaaeyzaiaabshaaeaadaWcaa qaaiaaisdaaeaacaaI1aaaaiabg2da9iaadchacqGHsislcaaIYaaa baGaamiCaiabg2da9maalaaabaGaaGinaaqaaiaaiwdaaaGaey4kaS IaaGOmaiabg2da9maalaaabaGaaGinaiabgUcaRiaaigdacaaIWaaa baGaaGynaaaaaeaacaqGubGaaeiAaiaabwhacaqGZbGaaiilaiaays W7daqjEaqaaiaadchacqGH9aqpdaWcaaqaaiaaigdacaaI0aaabaGa aGynaaaaaaaabaWaaeWaaeaacaqGIbaacaGLOaGaayzkaaGaeyOeI0 Iaaeinaiabg2da9iaabwdacaGGOaGaamiCaiabgkHiTiaaikdacaGG PaaabaGaaeiraiaabMgacaqG2bGaaeyAaiaabsgacaqGLbGaaeiiai aabkgacaqGVbGaaeiDaiaabIgacaqGGaGaae4CaiaabMgacaqGKbGa aeyzaiaabohacaqGGaGaaeOyaiaabMhacaqGGaGaaeynaiaabccaca qG0bGaae4BaiaabccacaqGNbGaaeyzaiaabshaaeaadaWcaaqaaiab gkHiTiaaisdaaeaacaaI1aaaaiabg2da9iaadchacqGHsislcaaIYa aabaGaamiCaiabg2da9maalaaabaGaeyOeI0IaaGinaaqaaiaaiwda aaGaey4kaSIaaGOmaiabg2da9maalaaabaGaeyOeI0IaaGinaiabgU caRiaaigdacaaIWaaabaGaaGynaaaaaeaacaqGubGaaeiAaiaabwha caqGZbGaaiilaiaaysW7daqjEaqaaiaadchacqGH9aqpdaWcaaqaai aaiAdaaeaacaaI1aaaaaaaaeaadaqadaqaaiaabogaaiaawIcacaGL PaaacqGHsislcaaIXaGaaGOnaiabg2da9iabgkHiTiaaiwdacaqGGa GaaiikaiaaikdacqGHsislcaWGWbGaaiykaaqaaiaabseacaqGPbGa aeODaiaabMgacaqGKbGaaeyzaiaabccacaqGIbGaae4Baiaabshaca qGObGaaeiiaiaabohacaqGPbGaaeizaiaabwgacaqGZbGaaeiiaiaa bkgacaqG5bGaaeiiaiabgkHiTiaabwdacaqGGaGaaeiDaiaab+gaca qGGaGaae4zaiaabwgacaqG0baabaWaaSaaaeaacaaIXaGaaGOnaaqa aiaaiwdaaaGaeyypa0JaaGOmaiabgkHiTiaadchaaeaacaqGnbGaae yDaiaabYgacaqG0bGaaeyAaiaabchacaqGSbGaaeyEaiaabccacaqG IbGaae4BaiaabshacaqGObGaaeiiaiaabohacaqGPbGaaeizaiaabw gacaqGZbGaaeiiaiaabkgacaqG5bGaaeiiaiabgkHiTiaabgdacaqG GaGaaeiDaiaab+gacaqGGaGaae4zaiaabwgacaqG0baabaWaaSaaae aacqGHsislcaqGXaGaaeOnaaqaaiaaiwdaaaGaeyypa0JaamiCaiab gkHiTiaaikdaaeaacaWGWbGaeyypa0ZaaSaaaeaacqGHsislcaaIXa GaaGOnaaqaaiaaiwdaaaGaey4kaSIaaGOmaiabg2da9maalaaabaGa eyOeI0IaaGymaiaaiAdacqGHRaWkcaaIXaGaaGimaaqaaiaaiwdaaa aabaGaaeivaiaabIgacaqG1bGaae4CaiaacYcacaaMe8+aauIhaeaa caWGWbGaeyypa0ZaaSaaaeaacqGHsislcaaI2aaabaGaaGynaaaaaa aabaWaaeWaaeaacaqGKbaacaGLOaGaayzkaaGaaeiiaiaabgdacaaI WaGaeyypa0JaaeinaiabgUcaRiaabodacaGGOaGaamiDaiabgUcaRi aaikdacaGGPaaabaGaaGOnaiabg2da9iaaiodadaqadaqaaiaadsha cqGHRaWkcaaIYaaacaGLOaGaayzkaaaabaGaaeiraiaabMgacaqG2b GaaeyAaiaabsgacaqGLbGaaeiiaiaabkgacaqGVbGaaeiDaiaabIga caqGGaGaae4CaiaabMgacaqGKbGaaeyzaiaabohacaqGGaGaaeOyai aabMhacaqGGaGaae4maiaabccacaqG0bGaae4BaiaabccacaqGNbGa aeyzaiaabshaaeaacaaIYaGaeyypa0JaamiDaiabgUcaRiaaikdaae aacaqGubGaaeiAaiaabwhacaqGZbGaaeilaiaabccadaqjEaqaaiaa dshacqGH9aqpcaaIWaaaaaqaamaabmaabaGaaeyzaaGaayjkaiaawM caaiaabccacaqGYaGaaeioaiabg2da9iaabsdacqGHRaWkcaqGZaGa aiikaiaadshacqGHRaWkcaqG1aGaaiykaaqaaiaaikdacaaI0aGaey ypa0JaaG4mamaabmaabaGaamiDaiabgUcaRiaaiwdaaiaawIcacaGL PaaaaeaacaqGebGaaeyAaiaabAhacaqGPbGaaeizaiaabwgacaqGGa GaaeOyaiaab+gacaqG0bGaaeiAaiaabccacaqGZbGaaeyAaiaabsga caqGLbGaae4CaiaabccacaqGIbGaaeyEaiaabccacaqGZaGaaeiiai aabshacaqGVbGaaeiiaiaabEgacaqGLbGaaeiDaaqaaiaaiIdacqGH 9aqpcaWG0bGaey4kaSIaaGynaaqaaiaabsfacaqGObGaaeyDaiaabo hacaqGSaGaaeiiamaaL4babaGaamiDaiabg2da9iaaiodaaaaabaWa aeWaaeaacaqGMbaacaGLOaGaayzkaaGaaGimaiabg2da9iaabgdaca qG2aGaey4kaSIaaeinaiaacIcacaWGTbGaeyOeI0IaaeOnaiaacMca aeaacqGHsislcaaIXaGaaGOnaiabg2da9iaaisdadaqadaqaaiaad2 gacqGHsislcaaI2aaacaGLOaGaayzkaaaabaGaaeiraiaabMgacaqG 2bGaaeyAaiaabsgacaqGLbGaaeiiaiaabkgacaqGVbGaaeiDaiaabI gacaqGGaGaae4CaiaabMgacaqGKbGaaeyzaiaabohacaqGGaGaaeOy aiaabMhacaqGGaGaaeinaiaabccacaqG0bGaae4BaiaabccacaqGNb GaaeyzaiaabshaaeaacqGHsislcaaI0aGaeyypa0JaamyBaiabgkHi TiaaiAdaaeaacaqGubGaaeiAaiaabwhacaqGZbGaaeilaiaabccada qjEaqaaiaad2gacqGH9aqpcaaIYaaaaaaaaa@C843@

Q.14 ( a ) Construct 3 equations starting with x = 2 ( b ) Construct 3 equations starting with x = − 2

( a ) Construct 3 equations starting with x = 2 ( b ) Construct 3 equations starting with x = − 2

Q.15 Set up equations and solve them to find the unknown numbers in the following case : a Add 4 to eight times a number ; you get 60. b One fifth of a number minus 4 gives 3. c If I take three fourths of a number and count up 3 more , I get 21. ( d ) When I subtracted 11 from twice a number , the result was 15. ( e ) Munna subtracts thrice the number of notebooks he has from 50, he finds the result to be 8. f Ibenhal thinks of a number . If she adds 19 to it and divides the sum by 5, she will get 8. g Anwar thinks of a number . If he takes away 7 from 52 of the number , the result is 11 2 .

(a) Let the number be x . 8 times of this number = 8x So, we get 8 x + 4 = 6 0 8 x = 56 x= 56 8 T h u s , x = 7 (b) Let the number be x . One-fifth of this number= x 5 So, we get x 5 − 4 = 3 x 5 = 7 x = 35 (c) Let the number be x . Three-fourth of this number = 3 x 4 So, we get 3 x 4 + 3 = 21 3 x 4 = 18 3 x = 72 x = 72 3 T h u s , x = 24 ( d ) Let the number be x . So, we have 2x-11=15 2x=26 x= 26 13 = 13 T h u s , x = 13 ( e ) Let the number be x Thrice the number of books = 3 x So, we get 50 − 3 x = 8 − 3 x = 8 − 50 = − 42 Divide both sides by -3 to get x= − 42 − 3 = 14 T h u s , x = 14 ( f ) Let the number be x . We, have x + 19 5 = 8 x + 19 = 8 × 5 = 40 x = 40 − 19 = 21 Thus, x = 21 ( g ) Let the number be x . S o , w e h a v e 5 x 2 − 7 = 23 5 x 2 = 23 + 7 = 30 5 x = 30 × 2 = 60 x = 60 5 = 12 Thus , x = 12 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqeduuDJXwAKbYu51MyVXgaruWqVvNCPvMCG4uz3bqefqvATv2C G4uz3bIuV1wyUbqeeuuDJXwAKbsr4rNCHbGeaGqiVz0xg9vqqrpepC 0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yq aqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabe qaamaaeaqbaaGceaqabeaacaqGOaGaaeyyaiaabMcacaqGGaGaaeit aiaabwgacaqG0bGaaeiiaiaabshacaqGObGaaeyzaiaabccacaqGUb GaaeyDaiaab2gacaqGIbGaaeyzaiaabkhacaqGGaGaaeOyaiaabwga caqGGaGaaeiEaiaab6caaeaacaqG4aGaaeiiaiaabshacaqGPbGaae yBaiaabwgacaqGZbGaaeiiaiaab+gacaqGMbGaaeiiaiaabshacaqG ObGaaeyAaiaabohacaqGGaGaaeOBaiaabwhacaqGTbGaaeOyaiaabw gacaqGYbGaaeiiaiaab2dacaqGGaGaaeioaiaabIhaaeaacaqGtbGa ae4BaiaabYcacaqGGaGaae4DaiaabwgacaqGGaGaae4zaiaabwgaca qG0baabaGaaGioaiaadIhacqGHRaWkcaaI0aGaeyypa0JaaGOnaiaa bcdaaeaacaaI4aGaamiEaiabg2da9iaabwdacaqG2aaabaGaaeiEai aab2dadaWcaaqaaiaaiwdacaaI2aaabaGaaGioaaaaaeaacaWGubGa amiAaiaadwhacaWGZbGaaiilamaaL4babaGaamiEaiabg2da9iaaiE daaaaabaGaaeikaiaabkgacaqGPaGaaeiiaiaabYeacaqGLbGaaeiD aiaabccacaqG0bGaaeiAaiaabwgacaqGGaGaaeOBaiaabwhacaqGTb GaaeOyaiaabwgacaqGYbGaaeiiaiaabkgacaqGLbGaaeiiaiaadIha caGGUaaabaGaae4taiaab6gacaqGLbGaaeylaiaabAgacaqGPbGaae OzaiaabshacaqGObGaaeiiaiaab+gacaqGMbGaaeiiaiaabshacaqG ObGaaeyAaiaabohacaqGGaGaaeOBaiaabwhacaqGTbGaaeOyaiaabw gacaqGYbGaaeypamaalaaabaGaamiEaaqaaiaaiwdaaaaabaGaae4u aiaab+gacaqGSaGaaeiiaiaabEhacaqGLbGaaeiiaiaabEgacaqGLb GaaeiDaaqaamaalaaabaGaamiEaaqaaiaaiwdaaaGaeyOeI0IaaGin aiabg2da9iaaiodaaeaadaWcaaqaaiaadIhaaeaacaaI1aaaaiabg2 da9iaaiEdaaeaadaqjEaqaaiaadIhacqGH9aqpcaaIZaGaaGynaaaa aeaacaqGOaGaae4yaiaabMcacaqGGaGaaeitaiaabwgacaqG0bGaae iiaiaabshacaqGObGaaeyzaiaabccacaqGUbGaaeyDaiaab2gacaqG IbGaaeyzaiaabkhacaqGGaGaaeOyaiaabwgacaqGGaGaamiEaiaac6 caaeaacaqGubGaaeiAaiaabkhacaqGLbGaaeyzaiaab2cacaqGMbGa ae4BaiaabwhacaqGYbGaaeiDaiaabIgacaqGGaGaae4BaiaabAgaca qGGaGaaeiDaiaabIgacaqGPbGaae4CaiaabccacaqGUbGaaeyDaiaa b2gacaqGIbGaaeyzaiaabkhacqGH9aqpdaWcaaqaaiaaiodacaWG4b aabaGaaGinaaaaaeaacaqGtbGaae4BaiaabYcacaaMe8Uaae4Daiaa bwgacaaMe8Uaae4zaiaabwgacaqG0baabaWaaSaaaeaacaaIZaGaam iEaaqaaiaaisdaaaGaey4kaSIaaG4maiabg2da9iaaikdacaaIXaaa baWaaSaaaeaacaaIZaGaamiEaaqaaiaaisdaaaGaeyypa0JaaGymai aaiIdaaeaacaaIZaGaamiEaiabg2da9iaaiEdacaaIYaaabaGaamiE aiabg2da9maalaaabaGaaG4naiaaikdaaeaacaaIZaaaaaqaaiaads facaWGObGaamyDaiaadohacaGGSaGaaGjbVpaaL4babaGaamiEaiab g2da9iaaikdacaaI0aaaaaqaaiaacIcacaWGKbGaaiykaiaaysW7ca qGmbGaaeyzaiaabshacaqGGaGaaeiDaiaabIgacaqGLbGaaeiiaiaa b6gacaqG1bGaaeyBaiaabkgacaqGLbGaaeOCaiaabccacaqGIbGaae yzaiaabccacaWG4bGaaiOlaaqaaiaabofacaqGVbGaaeilaiaabcca caqG3bGaaeyzaiaabccacaqGObGaaeyyaiaabAhacaqGLbaabaGaae OmaiaabIhacaqGTaGaaeymaiaabgdacaqG9aGaaeymaiaabwdaaeaa caqGYaGaaeiEaiaab2dacaqGYaGaaeOnaaqaaiaabIhacaqG9aWaaS aaaeaacaaIYaGaaGOnaaqaaiaaigdacaaIZaaaaiabg2da9iaaigda caaIZaaabaGaamivaiaadIgacaWG1bGaam4CaiaacYcadaqjEaqaai aadIhacqGH9aqpcaaIXaGaaG4maaaaaeaacaGGOaGaamyzaiaacMca caaMe8UaaeitaiaabwgacaqG0bGaaeiiaiaabshacaqGObGaaeyzai aabccacaqGUbGaaeyDaiaab2gacaqGIbGaaeyzaiaabkhacaqGGaGa aeOyaiaabwgacaqGGaGaamiEaaqaaiaabsfacaqGObGaaeOCaiaabM gacaqGJbGaaeyzaiaabccacaqG0bGaaeiAaiaabwgacaqGGaGaaeOB aiaabwhacaqGTbGaaeOyaiaabwgacaqGYbGaaeiiaiaab+gacaqGMb GaaeiiaiaabkgacaqGVbGaae4BaiaabUgacaqGZbGaaeiiaiabg2da 9iaabodacaWG4baabaGaae4uaiaab+gacaqGSaGaaeiiaiaabEhaca qGLbGaaeiiaiaabEgacaqGLbGaaeiDaaqaaiaabwdacaqGWaGaeyOe I0IaaG4maiaadIhacqGH9aqpcaqG4aaabaGaeyOeI0IaaG4maiaadI hacqGH9aqpcaaI4aGaeyOeI0IaaGynaiaaicdacqGH9aqpcqGHsisl caaI0aGaaGOmaaqaaiaabseacaqGPbGaaeODaiaabMgacaqGKbGaae yzaiaabccacaqGIbGaae4BaiaabshacaqGObGaaeiiaiaabohacaqG PbGaaeizaiaabwgacaqGZbGaaeiiaiaabkgacaqG5bGaaeiiaiaab2 cacaqGZaGaaeiiaiaabshacaqGVbGaaeiiaiaabEgacaqGLbGaaeiD aaqaaiaabIhacaqG9aWaaSaaaeaacqGHsislcaaI0aGaaGOmaaqaai abgkHiTiaaiodaaaGaeyypa0JaaGymaiaaisdaaeaacaWGubGaamiA aiaadwhacaWGZbGaaiilamaaL4babaGaamiEaiabg2da9iaaigdaca aI0aaaaaqaaiaacIcacaWGMbGaaiykaiaaysW7caqGmbGaaeyzaiaa bshacaqGGaGaaeiDaiaabIgacaqGLbGaaeiiaiaab6gacaqG1bGaae yBaiaabkgacaqGLbGaaeOCaiaabccacaqGIbGaaeyzaiaabccacaWG 4bGaaiOlaaqaaiaabEfacaqGLbGaaeilaiaabccacaqGObGaaeyyai aabAhacaqGLbaabaWaaSaaaeaacaWG4bGaey4kaSIaaGymaiaaiMda aeaacaaI1aaaaiabg2da9iaaiIdaaeaacaWG4bGaey4kaSIaaGymai aaiMdacqGH9aqpcaaI4aGaey41aqRaaGynaiabg2da9iaaisdacaaI WaaabaGaamiEaiabg2da9iaaisdacaaIWaGaeyOeI0IaaGymaiaaiM dacqGH9aqpcaaIYaGaaGymaaqaaiaabsfacaqGObGaaeyDaiaaboha caqGSaGaaGjbVpaaL4babaGaamiEaiabg2da9iaaikdacaaIXaaaaa qaaiaacIcacaWGNbGaaiykaiaaysW7caqGmbGaaeyzaiaabshacaqG GaGaaeiDaiaabIgacaqGLbGaaeiiaiaab6gacaqG1bGaaeyBaiaabk gacaqGLbGaaeOCaiaabccacaqGIbGaaeyzaiaabccacaWG4bGaaiOl aaqaamaaL4babaGaam4uaiaad+gacaGGSaGaaGjbVlaadEhacaWGLb GaaGjbVlaadIgacaWGHbGaamODaiaadwgaaaaabaWaaSaaaeaacaaI 1aGaamiEaaqaaiaaikdaaaGaeyOeI0IaaG4naiabg2da9iaaikdaca aIZaaabaWaaSaaaeaacaaI1aGaamiEaaqaaiaaikdaaaGaeyypa0Ja aGOmaiaaiodacqGHRaWkcaaI3aGaeyypa0JaaG4maiaaicdaaeaaca aI1aGaamiEaiabg2da9iaaiodacaaIWaGaey41aqRaaGOmaiabg2da 9iaaiAdacaaIWaaabaGaamiEaiabg2da9maalaaabaGaaGOnaiaaic daaeaacaaI1aaaaiabg2da9iaaigdacaaIYaaabaGaaeivaiaabIga caqG1bGaae4CaiaacYcacaaMe8+aauIhaeaacaWG4bGaeyypa0JaaG ymaiaaikdaaaaaaaa@4FA1@

Q.16 Solve the following : a The teacher tells the class that the highest marks obtained by a student in her class is twice the lowest marks plus 7. The highest score is 87. What is the lowest score ? b In an isosceles triangle , the base angles are equal . The vertex angle is 40°. What are the base angles of the triangle ? ( Remember , the sum of three angles of a triangle is 180°)

Solve the following : a The teacher tells the class that the highest marks obtained by a student in her class is twice the lowest marks plus 7. The highest score is 87. What is the lowest score ? b In an isosceles triangle , the base angles are equal . The vertex angle is 40°. What are the base angles of the triangle ? ( Remember , the sum of three angles of a triangle is 180°)

Q.17 Solve the following : ( i ) Irfan says that he has 7 marbles more than five times the marbles Parmithas . Irfan has 37 marbles . How many marbles does Parmit have ? ( ii ) Laxmi ‘ s father is 49 year sold . He is 4 years older than three times Laxmi ‘ s age . What is Laxmi ‘ sage ? ( iii ) Maya , Madhura and Mohsina are friends studying in the same class . In a class testin geography , Maya got 16 out of 25 . Madhura got 20 . Their average score was 19 . How much did Mohsina score ?

( iv ) People of Sundargram planted a total of 102 trees in the village garden . Some of the trees were fruit trees . The number of non − fruit trees were two more than three times the number of fruit trees . What was the number of fruit trees planted ?

(i) Let Parmit has m marbles . Then, according to the question, we have 5 × Number of marbles Parmit has +7 = Number of marbles Irfan has 5 × m + 7 = 37 So, we get 5 m + 7 = 37 5 m = 37 − 7 = 30 5 m = 30 m = 30 5 = 6 Therefore, Parmit has 6 marbles . (ii) Let Laxmi be y years old Then, according to the question, we have 3 × Laxmi’s age + 4 = Laxmi’s father age 3 × y + 4 = 49 3 y + 4 = 49 3 y = 49 − 4 = 45 3 y = 45 y = 45 3 = 15 Therefore, laxmi’s age is 15 years . (iii) Let the number of fruit trees be x . So, we have 3 × Number of fruit trees + 2 = Number of non-fruit trees 3 x + 2 = 77 3 x = 77 – 2 = 75 3 x = 75 x = 75 3 = 25 Therefore, the number of fruit trees was 25 . MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqeduuDJXwAKbYu51MyVXgaruWqVvNCPvMCG4uz3bqefqvATv2C G4uz3bIuV1wyUbqeeuuDJXwAKbsr4rNCHbGeaGqiVz0xg9vqqrpepC 0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yq aqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabe qaamaaeaqbaaGceaqabeaacaqGOaGaaeyAaiaabMcacaqGGaGaaeit aiaabwgacaqG0bGaaeiiaiaabcfacaqGHbGaaeOCaiaab2gacaqGPb GaaeiDaiaabccacaqGObGaaeyyaiaabohacaqGGaGaamyBaiaabcca caqGTbGaaeyyaiaabkhacaqGIbGaaeiBaiaabwgacaqGZbGaaeOlaa qaaiaabsfacaqGObGaaeyzaiaab6gacaqGSaGaaeiiaiaabggacaqG JbGaae4yaiaab+gacaqGYbGaaeizaiaabMgacaqGUbGaae4zaiaabc cacaqG0bGaae4BaiaabccacaqG0bGaaeiAaiaabwgacaqGGaGaaeyC aiaabwhacaqGLbGaae4CaiaabshacaqGPbGaae4Baiaab6gacaqGSa GaaeiiaiaabEhacaqGLbGaaeiiaiaabIgacaqGHbGaaeODaiaabwga aeaacaqG1aGaey41aqRaaeOtaiaabwhacaqGTbGaaeOyaiaabwgaca qGYbGaaeiiaiaab+gacaqGMbGaaeiiaiaab2gacaqGHbGaaeOCaiaa bkgacaqGSbGaaeyzaiaabohacaqGGaGaaeiuaiaabggacaqGYbGaae yBaiaabMgacaqG0bGaaeiiaiaabIgacaqGHbGaae4CaiaabccacaqG RaGaae4naiabg2da9iaab6eacaqG1bGaaeyBaiaabkgacaqGLbGaae OCaiaabccacaqGVbGaaeOzaiaabccacaqGTbGaaeyyaiaabkhacaqG IbGaaeiBaiaabwgacaqGZbaabaGaaCzcaiaaxMaacaWLjaGaaCzcai aaxMaacaWLjaGaaCzcaiaaxMaacaWLjaGaaeysaiaabkhacaqGMbGa aeyyaiaab6gacaqGGaGaaeiAaiaabggacaqGZbaabaGaaCzcaiaaxM aacaWLjaGaaCzcaiaaxMaacaWLjaGaaGjbVlaaysW7caqG1aGaey41 aqRaamyBaiabgUcaRiaabEdacqGH9aqpcaqGZaGaae4naaqaaiaabo facaqGVbGaaeilaiaabccacaqG3bGaaeyzaiaabccacaqGNbGaaeyz aiaabshaaeaacaWLjaGaaCzcaiaaxMaacaWLjaGaaCzcaiaaxMaaca aMe8UaaGjbVlaaysW7caqG1aGaamyBaiabgUcaRiaabEdacqGH9aqp caqGZaGaae4naaqaaiaaiwdacaWGTbGaeyypa0JaaG4maiaaiEdacq GHsislcaaI3aGaeyypa0JaaG4maiaaicdaaeaacaaI1aGaamyBaiab g2da9iaaiodacaaIWaaabaGaamyBaiabg2da9maalaaabaGaaG4mai aaicdaaeaacaaI1aaaaiabg2da9iaaiAdaaeaacaqGubGaaeiAaiaa bwgacaqGYbGaaeyzaiaabAgacaqGVbGaaeOCaiaabwgacaqGSaGaaG zaVlaabcfacaqGHbGaaeOCaiaab2gacaqGPbGaaeiDaiaaysW7caqG ObGaaeyyaiaabohacaaMe8+aauIhaeaacaqG2aGaaGjbVlaab2gaca qGHbGaaeOCaiaabkgacaqGSbGaaeyzaiaabohaaaGaaeOlaaqaaiaa bIcacaqGPbGaaeyAaiaabMcacaqGGaGaaeitaiaabwgacaqG0bGaae iiaiaabYeacaqGHbGaaeiEaiaab2gacaqGPbGaaeiiaiaabkgacaqG LbGaaeiiaiaadMhacaqGGaGaaeyEaiaabwgacaqGHbGaaeOCaiaabo hacaqGGaGaae4BaiaabYgacaqGKbaabaGaaeivaiaabIgacaqGLbGa aeOBaiaabYcacaqGGaGaaeyyaiaabogacaqGJbGaae4Baiaabkhaca qGKbGaaeyAaiaab6gacaqGNbGaaeiiaiaabshacaqGVbGaaeiiaiaa bshacaqGObGaaeyzaiaabccacaqGXbGaaeyDaiaabwgacaqGZbGaae iDaiaabMgacaqGVbGaaeOBaiaabYcacaqGGaGaae4DaiaabwgacaqG GaGaaeiAaiaabggacaqG2bGaaeyzaaqaaiaabodacqGHxdaTcaqGmb GaaeyyaiaabIhacaqGTbGaaeyAaiaabEcacaqGZbGaaeiiaiaabgga caqGNbGaaeyzaiabgUcaRiaabsdacqGH9aqpcaqGmbGaaeyyaiaabI hacaqGTbGaaeyAaiaabEcacaqGZbGaaeiiaiaabAgacaqGHbGaaeiD aiaabIgacaqGLbGaaeOCaiaabccacaqGHbGaae4zaiaabwgaaeaaca qGZaGaey41aqRaamyEaiabgUcaRiaaisdacqGH9aqpcaqG0aGaaeyo aaqaaiaabodacaWG5bGaey4kaSIaaeinaiabg2da9iaabsdacaqG5a aabaGaaG4maiaadMhacqGH9aqpcaaI0aGaaGyoaiabgkHiTiaaisda cqGH9aqpcaaI0aGaaGynaaqaaiaaiodacaWG5bGaeyypa0JaaGinai aaiwdaaeaacaWG5bGaeyypa0ZaaSaaaeaacaaI0aGaaGynaaqaaiaa iodaaaGaeyypa0JaaGymaiaaiwdaaeaacaqGubGaaeiAaiaabwgaca qGYbGaaeyzaiaabAgacaqGVbGaaeOCaiaabwgacaqGSaGaaGjbVlaa bYgacaqGHbGaaeiEaiaab2gacaqGPbGaae4jaiaabohacaaMe8Uaae yyaiaabEgacaqGLbGaaGjbVlaabMgacaqGZbGaaGjbVpaaL4babaGa aeymaiaabwdacaaMe8UaaeyEaiaabwgacaqGHbGaaeOCaiaabohaaa GaaeOlaaqaaiaabIcacaqGPbGaaeyAaiaabMgacaqGPaGaaeiiaiaa bYeacaqGLbGaaeiDaiaabccacaqG0bGaaeiAaiaabwgacaqGGaGaae OBaiaabwhacaqGTbGaaeOyaiaabwgacaqGYbGaaeiiaiaab+gacaqG MbGaaeiiaiaabAgacaqGYbGaaeyDaiaabMgacaqG0bGaaeiiaiaabs hacaqGYbGaaeyzaiaabwgacaqGZbGaaeiiaiaabkgacaqGLbGaaeii aiaadIhacaGGUaaabaGaae4uaiaab+gacaqGSaGaaeiiaiaabEhaca qGLbGaaeiiaiaabIgacaqGHbGaaeODaiaabwgaaeaacaqGZaGaey41 aqRaaeiiaiaab6eacaqG1bGaaeyBaiaabkgacaqGLbGaaeOCaiaabc cacaqGVbGaaeOzaiaabccacaqGMbGaaeOCaiaabwhacaqGPbGaaeiD aiaabccacaqG0bGaaeOCaiaabwgacaqGLbGaae4CaiabgUcaRiaaik dacqGH9aqpcaqGobGaaeyDaiaab2gacaqGIbGaaeyzaiaabkhacaqG GaGaae4BaiaabAgacaqGGaGaaeOBaiaab+gacaqGUbGaaeylaiaabA gacaqGYbGaaeyDaiaabMgacaqG0bGaaeiiaiaabshacaqGYbGaaeyz aiaabwgacaqGZbaabaGaaG4maiaadIhacqGHRaWkcaaIYaGaeyypa0 JaaG4naiaaiEdaaeaacaaIZaGaamiEaiabg2da9iaaiEdacaaI3aGa aiylaiaaikdacqGH9aqpcaaI3aGaaGynaaqaaiaaiodacaWG4bGaey ypa0JaaG4naiaaiwdaaeaacaWG4bGaeyypa0ZaaSaaaeaacaaI3aGa aGynaaqaaiaaiodaaaGaeyypa0JaaGOmaiaaiwdaaeaacaqGubGaae iAaiaabwgacaqGYbGaaeyzaiaabAgacaqGVbGaaeOCaiaabwgacaqG SaGaaGjbVlaabshacaqGObGaaeyzaiaaysW7caqGUbGaaeyDaiaab2 gacaqGIbGaaeyzaiaabkhacaaMe8Uaae4BaiaabAgacaaMe8UaaeOz aiaabkhacaqG1bGaaeyAaiaabshacaaMe8UaaeiDaiaabkhacaqGLb GaaeyzaiaabohacaaMe8Uaae4DaiaabggacaqGZbGaaGjbVpaaL4ba baGaaGOmaiaaiwdaaaGaaiOlaaaaaa@4A61@

Q.18 Solve the following riddle . I am a number , Tell my identity ! Take me seven times over And add a fifty ! To reach a triple century You still need forty

Let the number be x . Then we have ( 7 x + 50 ) + 40 = 300 7 x + 50 + 40 = 300 7 x + 90 + 300 7 x = 300 − 90 7 x = 210 x = 210 7 = 30 . Therefore , the number is 30 .

Please register to view this section

Faqs (frequently asked questions), 1. what are the important topics covered in ncert solutions class 7 mathematics chapter 4.

A few of the important topics covered under Chapter 7 are given below:

Constants and variables
L.H.S and R.H.S

2. How do you avail the study materials for NCERT Solutions for Class 7 Mathematics?

NCERT Solutions for Class 7 Mathematics are available on Extramarks. Subject matter experts have crafted the solutions in a step-by-step method that is easy to understand. Students can revise and solve the questions to master this chapter.

3. Are there any theoretical questions in chapter Simple Equations of Class 7 Mathematics?

There aren’t any theoretical questions in this chapter. The questions in this chapter are mostly practical. Even if a theoretical question is asked, the response will be one line or one word long. As a result, your primary focus should be on problem solving rather than learning theory.

4. How many questions are there in NCERT Solutions for class 11 chapter 4?

There are a variety of questions found in NCERT solutions for Class 11 Chapter 4. The chapter is divided into four exercises. Exercise 4.1 has a total of 6 questions, exercise 4.2 has 4 questions, exercise 4.3 has four questions and exercise 4.4 has four questions.

NCERT Solutions Related Links

Fill this form to view question paper

Otp verification.

Join NOW to get access to exclusive study material for best results

CBSE Class 7 Textbook Solutions
Ncert Solutions
Chapter 4 Simple Equations

Please Login or Sign up to continue!

Class 7 NCERT Solutions Maths Chapter 4 - Simple Equations

Simple equations exercise ex. 4.1.

Simple Equations Exercise Ex. 4.3

CBSE Class 10 Maths MIQs, Subjective Questions & More

Once you complete your vast syllabus, you can continue to revise the concepts learned in your class. Once you complete your vast syllabus, you can continue to revise the concepts learned in your class. Once you complete your vast syllabus, you can continue to revise the concepts learned in your class. Once you complete your vast syllabus, you can continue to revise the concepts learned in your class.

Once you complete your vast syllabus, you can continue to revise the concepts learned in your class.

Frequently Asked Questions

Get in Touch

Call / Whats App

- Class 11 Science
- Class 11 Commerce
- Class 12 Science
- Class 12 Commerce

Register here

In case you want to be notified about school in your locality then please register here.

Are you a Parent or Student?
Are you a Teacher?
Are you a School Supplier?

Our other Domains Olympiad Preparation Math Square Science Square English Square Cyber Square School Square Scholar Square Global Olympiads NCERT Solutions CBSE Sample Papers
Join WhatsApp Channel
Apply for CREST Olympiads

Simple Equations

An equation which has only one variable is called Linear Equation

Maths class 8 Linear equations and variables

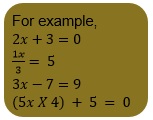
Solving equations which have linear equations on one side and numbers on the other side

EXAMPLE 1: Solve 3x + 15 = 1

We need to keep the variable on the left side and numerical terms on the right side. Because of this, we have to transport 15 to the right side by changing its sign i.e., -15. => 3x + 15 = 1 => 3x = 1-15

We need to keep the variable on the left side and numerical terms on the right side. Because of this, we have to transport -12 to the other side by changing its sign i.e., +12.

Solving equations having variables having the variable on both sides

EXAMPLE 1: Solve .

Simplify the given equation. => =>
Bring the variable terms on the left side of the equation and the other numerical terms on the right side of the equation. => =>
Now, to find the value of ‘x’ we need to divide both sides of the equation by 6 to maintain equality.

Application of Linear Equations

Linear equations are used to find the value of an unknown quantity. Have a look at the following examples:

EXAMPLE 1: The sum of the digits of a 2 digit number 13. The numbers obtained by interchanging the digits is 14 more than the given number. Find the number.

SOLUTION: Let the digit at units place be x and the number at tens place be y.

=> y + x = 13 [sum is 13 given] => y = 13 – x [Transposing x to the other side by changing its sign] Thus, the formed number is= [Since x is at ones place and y=13-x is at tens place] After interchanging the digits, the number is= [Now x is at tens place & y=13-x is at one's place] The interchanged number is greater than the original number by 14. [Given]

New number Old number Difference

Simplify => => => =>
Transpose the variable term ‘x’ on the left side of the equation and other numerical terms on the right side of the equation by changing their sign. => 18x – 117 = 14 => 18x = 131

EXAMPLE 2: The distance between town A and town B is 123 km. Two buses begin their journey from these towns and move directly toward each other. From town A, the bus is moving at a speed of 45 km per hour and from town B, the bus is moving at 67 km per hour. Assuming the buses start at the same time, find how far is their meeting point from town A. SOLUTION: Let the buses meet after t hours.

We know that distance= speed X time Distance covered by bus 1 = 45 X t Distance covered by bus 2 = 67 X t Therefore, 45t + 67t = 123

The distance travelled by bus 1 from city A to the meeting point= speed of bus 1 X time taken by it to reach the meeting point. =45 X 1.098= 49.41 km Thus, the distance of reaching point from town A is 49.41km. [ANS]

Reducing Equation to Simpler Form

Equations reducible to linear form

Now, simplify => 6x + 12 + 12x + 15 = 14x + 16 => 18x + 27 = 14x +16
Transpose the variable term ‘x’ to the left side and the numerical terms on the right side of the equation by changing their sign. => 18x – 14x = 16 – 27 => 4x = 11

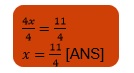
Practice these questions

Q3) Three numbers are in the ratio 1:2:3. If the sum of the largest and the smallest equals the second and 45. Find the numbers.

Q4) Find the number whose 1/6 th part decreased 7 equals its 8/9 th part diminished by 1.

Q5) The difference between two numbers is 23. And the quotient obtained by dividing the larger number by the smaller one is 4. Find the numbers.

Q6) A man cycles to the office from his house at a speed of 5km per hour and reaches 6 minutes late. If he cycles at a speed of 7km/hr, he reaches 8 minutes early. What is the distance between the office and his house? Q7) Suraj is now half as old as his father. 20 years ago, Suraj’s father was six times Suraj’s age. What are their ages now? Q8) The perimeter of an isosceles triangle is 91cm. If the length of each equal side is 2cm more than the length of its base. Find the lengths of the sides of the triangle. Q9) The age of a boy in months is equal to the age of his grandfather in years. If the difference between their ages is 66 years, find their ages.

The basic principle used in solving any linear equation is that any operation performed on one side of the equation must also be performed on the other side of the equation.
Any term in an equation can be transposed from one side to other side by changing its sign.
In cross multiplication, we multiply the numerator of LHS by the denominator of RHS and the denominator of LHS by the numerator of RHS and the resultant expression are equal to each other.
Practical problems are based on the relations between some known and unknown quantities. We convert such problems into equations and then solve them.

Quiz for Simple Equations

Your Score: 0 /10

Other Chapters of Class 7

Number System Integers and Rational Numbers image

Quick Links

SchoolPlus Program

Yearlong program for Olympiads preparation & to build necessary skills for future.

Olympiad Exam Dates

Time to mark your calendar with the upcoming Olympiads exam schedule.

LIVE Classes for Olympiads

Take your Olympiad preparation to next-level by taking LIVE Classes.

Olympiad Test Series

Assess your performance by taking topic-wise and full length mock tests.

India’s First Summer Olympiads

Know your true potential by participating in Unicus Olympiads for classes 1-11.

Asia’s Biggest Winter Olympiads

Give wings to your innovation by appearing in CREST Olympiads for Prep/KG to classes 1-10.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Class 7 > Unit 4

Unit test Simple Equations

The Site is down as we are performing important server maintenance, during which time the server will be unavailable for approximately 24 hours. Please hold off on any critical actions until we are finished. As always your feedback is appreciated.

Study Packages
NCERT Solutions
Sample Papers
Online Test

Questions Bank
Mathematics
Simple Equations
Test Series
Ncert Solutions
Solved Papers
Current Affairs
JEE Main & Advanced
Pre-Primary
MP State Exams
UP State Exams
Rajasthan State Exams
Jharkhand State Exams
Chhattisgarh State Exams
Bihar State Exams
Haryana State Exams
Gujarat State Exams
MH State Exams
Himachal State Exams
Delhi State Exams
Uttarakhand State Exams
Punjab State Exams
J&K State Exams

7th Class Mathematics Simple Equations Question Bank

Done simple equations total questions - 45.

question_answer 1) What is the value of 'x' in \[\frac{3x-1}{5}-\frac{1+x}{2}=3-\frac{x-1}{2}\]?

A) \[5\] done clear

B) \[-7\] done clear

C) \[7\] done clear

D) \[-5\] done clear

question_answer 2) If \[0.2(2x-1)-0.5(3x-1)=0.4,\] what is the value of x'?

A) \[\frac{1}{11}\] done clear

B) \[-\frac{1}{11}\] done clear

C) \[\frac{3}{11}\] done clear

D) \[-\frac{3}{11}\] done clear

question_answer 3) In each of these figures the solution of an equation is given in brackets. Which of them is correct?

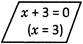
question_answer 4) Sunil wrote an equation as \[\frac{m}{5}=4\]. Ravi wrote a statement for Sunil's equation. Which of these is the statement of Ravi if he has written correctly?

A) One-fifth of m' is 4. done clear

B) One-fifth of a number is 5. done clear

C) One-fourth of 'm' is 4. done clear

D) One-fourth of a number is 4. done clear

question_answer 5) In which of the following cases does an equality NOT hold?

A) Adding the same number on both the sides. done clear

B) Not performing the same operation on both the sides. done clear

C) Subtracting the same number from both the sides. done clear

D) Multiplying both the sides by the same non-zero number. done clear

question_answer 6) What are the two steps involved in solving the equation\[15x+4=26\]?

A) Subtracting 4 from both the sides and then dividing both sides by 15. done clear

B) Adding 4 on both sides & then multiplying both sides by 15. done clear

C) Subtracting 4 on the L.H.S. and multiplying by 15 on the R.H.S. done clear

D) Adding 4 on the L.H.S. and dividing by 15 on the R.H.S. done clear

question_answer 7) Which of the following equations can be constructed with \[x=2\]?

A) \[3x+4=8\] done clear

B) \[3x-4=2\] done clear

C) \[3x+4=2\] done clear

D) \[3x-4=8\] done clear

question_answer 8) 7 subtracted from \[\frac{5}{2}\]of a number results in 23. What is the number?

A) \[-10\] done clear

B) \[10\] done clear

C) \[12\] done clear

D) \[-12\] done clear

question_answer 9) In a coconut grove, \[(x+2)\] trees yield 60 coconuts per year, x trees yield 120 coconuts per year and \[(x-2)\] trees yield 180 coconuts per year. If the average yield per year per tree is 100, find x.

A) \[4\] done clear

B) \[3\] done clear

C) \[2\] done clear

D) \[1\] done clear

question_answer 10) 4 is added to a number and the sum is multiplied by 5. If 20 is subtracted from the product and the difference is divided by 8, the result is equal to 10. Find the number.

A) \[16\] done clear

B) \[12\] done clear

C) \[8\] done clear

D) \[20\] done clear

question_answer 11) A number is 3 less than two times the other. If their sum is increased by 7, the result is 37. Find the numbers.

A) \[9,\,\,11\] done clear

B) \[11,\,\,13\] done clear

C) \[11,\,\,19\] done clear

D) \[9,\,\,13\] done clear

question_answer 12) \[\frac{1}{2}\] is subtracted from a number and the difference is multiplied by 4. If 25 is added to the product and the sum is divided by 3, the result is equal to 10. Find the number.

A) \[\frac{3}{5}\] done clear

B) \[\frac{7}{4}\] done clear

C) \[\frac{6}{7}\] done clear

D) \[\frac{2}{3}\] done clear

question_answer 13) The present age of A is twice that of B. 30 years from now, age of A will be \[1{}^{1}/{}_{2}\]times that of B. Find the present ages (in years) of A and B respectively.

A) \[60,\,\,30\] done clear

B) \[30,\,\,60\] done clear

C) \[40,\,\,50\] done clear

D) \[50,\,\,40\] done clear

question_answer 14) A person travelled \[{{\frac{5}{8}}^{th}}\] of the distance by train, \[{{\frac{1}{4}}^{th}}\] by bus and the remaining 15 km by boat. Find the total distance travelled by him.

A) \[90\,\,km\] done clear

B) \[120\,\,km\] done clear

C) \[150\,\,km\] done clear

D) \[180\,\,km\] done clear

question_answer 15) The total cost of three prizes is Rs.2550. If the value of second prize is \[{{\frac{3}{4}}^{th}}\]of the first and the value of 3rd prize is \[\frac{1}{2}\]of the second prize, find the value of first prize.

A) \[Rs.\,900\] done clear

B) \[Rs.\,1500\] done clear

C) \[Rs.\,1200\] done clear

D) \[Rs.\,450\] done clear

question_answer 16) Which of the following is an equation?

A) \[4x+5=65\] done clear

B) \[4x+5<65\] done clear

C) \[4x+5>65\] done clear

D) \[4x+5\ne 65\] done clear

question_answer 17) Which of the following is an algebraic expression for the statement "The sum of \[3x\] and 11 is 32."?

A) \[11x+3=32\] done clear

B) \[3x+11=32\] done clear

C) \[3x+32=11\] done clear

D) \[11x+32=11\] done clear

question_answer 18) Choose the statement that best describes the equation \[\frac{1}{4}m=10\].

A) One - fourth of 10 is m. done clear

B) One - fourth of m is 3 more than 3. done clear

C) One - fourth of m is 10. done clear

D) Four times m is 10. done clear

question_answer 19) Vinay's father is 44 years old. If he is 5 years older than thrice Vinay's age, which of these equations gives, the age of Vinay's father?

A) \[3x+5=44\] done clear

B) \[44+5x=3x\] done clear

C) \[44-3y=5+3y\] done clear

D) \[3x-5=44\] done clear

question_answer 20) Which of the following statements is false?

A) The solution of \[4x=60\] is 12. done clear

B) \[y=7\] satisfies the equation \[y+0=7\]. done clear

C) \[p=\frac{5}{2}\] is the solution of \[12p-5=25\]. done clear

D) \[m=\frac{3}{2}\] is the solution of \[4(m+3)=18\]. done clear

question_answer 21) Which of the following does not affect the given equation?

A) Adding 0 on the L.H.S. and 1 on the R. H. S. done clear

B) Adding 1 on the L.H.S. and \[(-1)\] on the R.H.S. done clear

C) Adding the same number on both sides of the equation. done clear

D) Adding 0 on the R.H.S. and 1 on the L.H.S. done clear

question_answer 22) P is a linear equation. How many solutions does P have?

A) 1 done clear

B) 0 done clear

C) 3 done clear

D) Infinitely many done clear

question_answer 23) Ramesh got 5 marks more than Sonu in a test. If the total marks secured by them is 15, how many marks did Ramesh get?

A) \[25\] done clear

B) \[5\] done clear

C) \[15\] done clear

D) \[10\] done clear

question_answer 24) In a test match, Sach in scored twice as many runs as Sehwag. Together, their runs fell two short of a double century. How many runs did Sachin score?

A) \[66\] done clear

B) \[132\] done clear

C) \[198\] done clear

D) \[200\] done clear

question_answer 25) In a math test, the highest marks obtained by a student in the class is twice the lowest marks plus 7. If the highest score is 87, what is the lowest score?

A) \[42\] done clear

B) \[39\] done clear

C) \[40\] done clear

D) \[44\] done clear

A) (i) only done clear

B) (ii) only done clear

C) (iii) only done clear

D) Both [b] and [c]. done clear

question_answer 27) On transposing terms from one side of the equation to the other, which of these changes takes place?

A) Addition becomes subtraction. done clear

B) Multiplication becomes addition. done clear

C) Addition becomes multiplication. done clear

D) Multiplication becomes subtraction. done clear

question_answer 28) \[M=\frac{2x+5}{7}\]and \[N=\frac{3x-2}{4}\]. What value of x makes\[M=N\]?

A) \[\frac{-17}{3}\] done clear

B) \[\frac{-34}{13}\] done clear

C) \[\frac{34}{13}\] done clear

D) \[\frac{17}{3}\] done clear

question_answer 29) Given \[A=P(1+rt),\] what is the value of 'r' when \[A=27,\text{ }P=18\]and \[t=5\]?

A) \[\frac{1}{2}\] done clear

B) \[\frac{1}{5}\] done clear

C) \[\frac{27}{5}\] done clear

D) \[\frac{1}{10}\] done clear

question_answer 30) Given \[\frac{1}{u}+\frac{1}{v}=\frac{1}{f},\] find the value of 'v' when \[f=20\] and \[u=30\].

A) \[-20\] done clear

B) \[-60\] done clear

C) \[60\] done clear

D) \[-30\] done clear

question_answer 31) The sum of three consecutive integers is 75. Which is the largest among them?

A) 26 done clear

B) 25 done clear

C) 24 done clear

D) 23 done clear

question_answer 32) The lengths of the sides of a triangle are \[(2a+1)\,\,cm,\,\,(3a+2)\,\,cm\] and \[(4a-1)\,\,cm\]. For what value of 'a' is the perimeter of the triangle \[92\,cm\]?

A) \[5\] done clear

B) \[9\] done clear

C) \[8\] done clear

D) \[10\] done clear

question_answer 33) A father is 26 years older than his son. In 3 years' time, the son's age will be one-third his father's age. What is the present age of the son?

A) 10 years done clear

B) 13 years done clear

C) 39 years done clear

D) 29 years done clear

question_answer 34) Pankaj has 96 marbles and Arun has 63 marbles. How many marbles should run give Pankaj so that Pankaj will have twice as many marbles as Arun?

A) \[9\] done clear

C) \[7\] done clear

question_answer 35) If \[\frac{3p+2}{5}-\frac{4p-3}{7}+\frac{p-1}{35}=4,\] find the value of p.

A) \[65\] done clear

B) \[63\] done clear

C) \[36\] done clear

D) \[56\] done clear

question_answer 36) The sum of five times a number and 13 is 48. What is the number?

A) \[3\] done clear

B) \[5\] done clear

C) \[7\] done clear

D) \[9\] done clear

question_answer 37) Guru is 20 years older than his son. If the sum of their ages is 50 years, how old is his son?

A) 5 years done clear

B) 10 years done clear

C) 15 years done clear

D) 20 years done clear

question_answer 38) If one-fourth of a number decreased by 12 is 30, what is the number?

A) \[168\] done clear

B) \[186\] done clear

C) \[148\] done clear

D) \[184\] done clear

question_answer 39) lf \[C=\frac{5}{9}(F-32),\] what is the value F?

A) \[\frac{5C}{9}-32\] done clear

B) \[\frac{9C}{5}-32\] done clear

C) \[\frac{9C}{5}+32\] done clear

D) \[\frac{5C}{9}+32\] done clear

A) 1 gram done clear

B) 4 grams done clear

C) 5 grams done clear

D) 20 grams done clear

A) \[26\] done clear

B) \[22\] done clear

C) \[19\] done clear

D) \[16\] done clear

question_answer 42) The sum of two-thirds of a number and one-fifth of the same number is 13. Find the number.

A) \[15\] done clear

C) \[13\] done clear

D) \[5\] done clear

question_answer 43) Evaluate \[\frac{x-4}{3}-\frac{2x+1}{6}=\frac{5x+1}{2}\]

A) \[\frac{3}{5}\] done clear

B) \[\frac{4}{5}\] done clear

C) \[\frac{5}{6}\] done clear

D) \[\frac{-4}{5}\] done clear

question_answer 44) The denominator of a fraction is 3 more than its numerator. If 2 is added to both the numerator and the denominator, the new fraction is equivalent to \[\frac{2}{3}\] What is the original fraction?

A) \[\frac{3}{7}\] done clear

B) \[\frac{4}{7}\] done clear

C) \[\frac{2}{3}\] done clear

D) \[\frac{3}{5}\] done clear

question_answer 45) 144 beads were shared equally among some children. If there were 3 children fewer, each child would have 16 beads each. How many children were there?

A) \[8\] done clear

B) \[9\] done clear

C) \[12\] done clear

D) \[11\] done clear

Study Package

Question - Simple Equations

Reset Password.

OTP has been sent to your mobile number and is valid for one hour

Mobile Number Verified

Your mobile number is verified.

Andhra Pradesh
Chhattisgarh
West Bengal
Madhya Pradesh
Maharashtra
Jammu & Kashmir
NCERT Books 2022-23
NCERT Solutions
NCERT Notes
NCERT Exemplar Books
NCERT Exemplar Solution
States UT Book
School Kits & Lab Manual
NCERT Books 2021-22
NCERT Books 2020-21
NCERT Book 2019-2020
NCERT Book 2015-2016
RD Sharma Solution
TS Grewal Solution
TR Jain Solution
Selina Solution
Frank Solution
ML Aggarwal Solution
Lakhmir Singh and Manjit Kaur Solution
I.E.Irodov solutions
ICSE - Goyal Brothers Park
ICSE - Dorothy M. Noronhe
Sandeep Garg Textbook Solution
Micheal Vaz Solution
S.S. Krotov Solution
Evergreen Science
KC Sinha Solution
ICSE - ISC Jayanti Sengupta, Oxford
ICSE Focus on History
ICSE GeoGraphy Voyage
ICSE Hindi Solution
ICSE Treasure Trove Solution
Thomas & Finney Solution
SL Loney Solution
SB Mathur Solution
P Bahadur Solution
Narendra Awasthi Solution
MS Chauhan Solution
LA Sena Solution
Integral Calculus Amit Agarwal Solution
IA Maron Solution
Hall & Knight Solution
Errorless Solution
Pradeep's KL Gogia Solution
OP Tandon Solutions
Sample Papers
Previous Year Question Paper
Value Based Questions
CBSE Syllabus
CBSE MCQs PDF
Assertion & Reason
New Revision Notes
Revision Notes
HOTS Question
Marks Wise Question
Toppers Answer Sheets
Exam Paper Aalysis
Concept Map
CBSE Text Book
Additional Practice Questions
Vocational Book
CBSE - Concept
KVS NCERT CBSE Worksheets
Formula Class Wise
Formula Chapter Wise
JEE Crash Course
JEE Previous Year Paper
Important Info
JEE Mock Test
JEE Sample Papers
SRM-JEEE Mock Test
VITEEE Mock Test
BITSAT Mock Test
Manipal Engineering Mock Test
AP EAMCET Previous Year Paper
COMEDK Previous Year Paper
GUJCET Previous Year Paper
KCET Previous Year Paper
KEAM Previous Year Paper
Manipal Previous Year Paper
MHT CET Previous Year Paper
WBJEE Previous Year Paper
AMU Previous Year Paper
TS EAMCET Previous Year Paper
SRM-JEEE Previous Year Paper
VITEEE Previous Year Paper
BITSAT Previous Year Paper
UPSEE Previous Year Paper
CGPET Previous Year Paper
CUSAT Previous Year Paper
AEEE Previous Year Paper
Crash Course
Previous Year Paper
NCERT Based Short Notes
NCERT Based Tests
NEET Sample Paper
Previous Year Papers
Quantitative Aptitude
Numerical Aptitude Data Interpretation
General Knowledge
Mathematics
Agriculture
Accountancy
Business Studies
Political science
Enviromental Studies
Mass Media Communication
Teaching Aptitude
NAVODAYA VIDYALAYA
SAINIK SCHOOL (AISSEE)
Mechanical Engineering
Electrical Engineering
Electronics & Communication Engineering
Civil Engineering
Computer Science Engineering
CBSE Board News
Scholarship Olympiad
School Admissions
Entrance Exams
All Board Updates
Miscellaneous
State Wise Books
Engineering Exam

Simple Equations Class 7 MCQ Test (Online Available)

Free mcq test, table of content, simple equations test - 20.

Duration: 10 Mins

Maximum Marks: 10

Read the following instructions carefully.

1. The test contains 10 total questions.

2. Each question has 4 options out of which only one is correct .

3. You have to finish the test in 10 minutes.

4. You will be awarded 1 mark for each correct answer.

5. You can view your Score & Rank after submitting the test.

6. Check detailed Solution with explanation after submitting the test.

7. Rank is calculated on the basis of Marks Scored & Time

Simple Equations Test - 19

Simple equations test - 18, simple equations test - 17, simple equations test - 16, simple equations test - 15, simple equations test - 14, simple equations test - 13, simple equations test - 12, simple equations test - 11, simple equations test - 10, simple equations test - 9, simple equations test - 8, simple equations test - 7, simple equations test - 6, simple equations test - 5, simple equations test - 4, simple equations test - 3, simple equations test - 2, simple equations test - 1.

Objective questions have become the norm now, those students who are studying in class 7 must be well versed with all kinds of MCQ Questions; therefore, the link to access Simple Equations MCQ Class 7 is mentioned here on this page.

Simple Equations Class 7 MCQ questions are curated by subject experts referring to the prescribed NCERT Class 7 Maths Book. Those students who have studied the lesson Simple Equations must practise the CBSE Class 7 MCQ Questions as it helps in deepening the understanding of the topics.

Class 7 Simple Equations MCQ with Answers Online

For the ease of students, the subject experts have simplified the practice process of the class 7 Simple Equations MCQ as they have solved each and every question given. The answers are detailed and easy to grasp. Students who want to practise the questions of Class 7 Simple Equations MCQ with Answers online can use the Selfstudys website.

The MCQ Questions of Simple Equations with answers are also given so that students can understand the methods of solving the concepts based questions. As well as, the solutions are helpful to understand where the students are making mistakes and need to improve.

How to Practise MCQ from NCERT Chapter Simple Equations?

There are several ways to practise the MCQ from NCERT Chapter Simple Equations; one is by solving questions from the chapter’s end and another is by using online medium. In this section, we have mentioned the steps to Practise MCQ from NCERT Chapter Simple Equations online.

First of all open Selfstudys.com on your Smartphone, PC/Laptop

Simple Equations Class 7 MCQ, Simple Equations Class 7 MCQ Test, MCQ on Simple Equations Class 7, Simple Equations Class 7 Online MCQ Test, Simple Equations Online MCQ Test, Class 7 Simple Equations MCQ with Answers, Delhi Sultans MCQ Class 7

Navigate to the CBSE by Tapping/clicking on the navigation bar or button
It will open a new lists where you can find MCQ Test - Click on that

Then, a new page will load containing the lists of classes; just Tap or click on Class 7. *In Smartphone, you may require to scroll the given classes name towards left.

Now, after selecting the Class 7, the same page will reload, make sure you select the Maths to access the MCQ Questions of Class 7 Simple Equations.

Note: The online MCQ Questions of Simple Equations can’t be downloaded, those who want to access the PDF of Simple Equations MCQ can refer to the CBSE Class 7 MCQ PDF section within the CBSE menu.

What is Simple Equations MCQ and How to Use it?

Since class 7 students are in their early stage of academics they may have questions regarding What is Simple Equations MCQ and How to Use it. So, the answer is MCQ Questions are objective questions which contain questions followed by 4 options where only one is considered the correct answer and remaining as a distraction. Why is it so, because MCQ questions are ideal to assess a student’s conceptual knowledge.

Those who want to use the Simple Equations MCQ can use this website to access the online MCQ questions to practise.

Top 5 Benefits of Simple Equations MCQ Class 7

Simple Equations MCQ Class 7 questions benefit students in several ways; however, here we have mentioned a total of 5 benefits that a student will get if they are using the MCQ from NCERT Chapter Simple Equations.

Helps in Practising Questions: Sometimes, it's hard to get the questions to practise; therefore, the Selfstudys team has curated various sets of MCQ Questions of Class 7 Simple Equations. Having access to the objective questions of Class 7 Simple Equations helps students practising various questions for free of cost.
Boosts the Critical Thinking Capability: The MCQs or objective questions must be answered in lesser time; therefore, those who will regularly solve Simple Equations MCQ Class 7 will benefit by having a great boost in the critical thinking capability as the questions are in the objective format which can be answered if one has a good command over the concepts of Simple Equations.
Assists in Covering the Class 7 Maths Syllabus: Simple Equations is a chapter of Class 7 Maths and those who are going to solve the MCQs of Class 7 Simple Equations will be able to practise all the questions as per their Maths Syllabus.
Helps in Exam Preparation: If a student solves the objective questions from class 7 Simple Equations, they will be able to be prepared for the annual examination too. It is because the questions that are asked in the online MCQ of Simple Equations are asked in the final exam question papers too.
A Deeper Understanding of Simple Equations: All the important points that are discussed in Simple Equations must be memorised by students as it helps in deepening the understanding of the Delhi Sultans. One of the great benefits of solving Simple Equations MCQ Class 7 is that one can be thorough with the topics and can develop a deeper understanding of Simple Equations chapter of class 7.

Apply These Techniques To Better Answer the MCQ Questions of Simple Equations

Although, there is no wrong or right method to answer the MCQ Questions, those who are interested in knowing the techniques to better answer the MCQ Questions of Simple Equations can follow the below given methods.

Read the Question Carefully: Questions in Simple Equations MCQ Class 7 can be asked from tricky to hard to understand. In this case, you must read the questions of Simple Equations MCQ carefully. By paying attention to the questions, it will help you connect the dots and assist you recall the studied concepts to answer the MCQs easily.

Eliminate Obviously Wrong Answers: Many questions of Simple Equations MCQ Class 7 will be so familiar that you can be certain for the wrong answer but uncertain for the right answer, in that situation obviously eliminate wrong answers first. By eliminating irrelevant or incorrect answers, it will help you find the one correct answer from all the given four options.

Look for Clues in the Question: As we have discussed the first technique is to read the questions carefully, it is vital for looking for the clues in the questions of Simple Equations MCQ Class 7. Every single question contains some kind of clues that help you answer them easily, but due to running out of time many don’t pay attention to it. In order to solve Simple Equations MCQ Class 7 by using this technique you may have to do a thorough practice of Class 7 MCQ Questions.

Use the Process of Elimination: There is not much difference in the elimination method and eliminating the wrong answer (discussed in point number 2) first, but one difference that makes the elimination process different is you can eliminate the right or wrong answer first.

This means that when you are confused between two options, you can separate them and then you try to focus on only those 2 options to find out the correct answer of Simple Equations MCQ Class 7. This elimination process works best in most of the scenarios.

Don't Spend too Much Time on One Question: It is never a good idea to be rigid on one question and spend most of your time answering them. When you are practising Simple Equations MCQ Class 7 questions, you have limited time and you have to make sure that you use your time smartly to attempt all the questions as asked in the Simple Equations Class 7 MCQ.

Double-check your Answer: Before submitting the Online test of Class 7 Simple Equations MCQ, you should double check your answer if the test time hasn't completed. When you do a double check of your answers, you may find some silly mistakes that you have made due to which you could have lost some marks. Therefore, be conscious and double check your answers before submitting Simple Equations MCQ Class 7.

*As per the Selfstudys Online MCQ Test instructions the time plays a crucial role in calculating your test rank so, be conscious when you use any single minute during your test.

Manage your Time: Having great time management skills doesn’t only help you quickly answer the questions, but gives you the ability to save time to review the questions or in doing a last minute cross-checking. Thus, when you start solving Simple Equations MCQ Class 7 questions, try to manage time and some of your test time to review the answers you have ticked throughout the test.

Apart from this, time management skills give you peace of mind and keep you calm.

Stay Calm to Recall Previously Studied Topics: When you struggle to come up with the correct answer of Simple Equations MCQ Class 7 Questions try to stay calm as it will help you recall previously studied topics. Research says, being calm and relaxed helps in saving energy. Thus, staying calm while solving the MCQ from NCERT Chapter Simple Equations helps you be more focused and answer the questions efficiently. The saved energy can be channelized to increase the focus and concentration to better recall the topics and subtopics of Simple Equations.

There is a high possibility of having more techniques of Simple Equations MCQ Class 7 as mentioned, but these given methods work well in most of the cases.

Manipal MET 2024 Application (Released) (All Pages)

NCERT Solutions for Class 12 Maths
NCERT Solutions for Class 10 Maths
CBSE Syllabus 2023-24
Social Media Channels
Login Customize Your Notification Preferences

Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

Question and Answer forum for K12 Students

MCQ Questions for Class 7 Maths Chapter 4 Simple Equations with Answers

We have compiled the NCERT MCQ Questions for Class 7 Maths Chapter 4 Simple Equations with Answers Pdf free download covering the entire syllabus. Practice MCQ Questions for Class 7 Maths with Answers on a daily basis and score well in exams. Refer to the Simple Equations Class 7 MCQs Questions with Answers here along with a detailed explanation.

Simple Equations Class 7 MCQs Questions with Answers

Choose the correct option.

Question 1. Write the following statement in the form of an equation. “The sum of three times x and 10 is 23. (a) 3x – 10 = 23 (b) 3x + 23 = 10 (c) 3x + 10 = 23 (d) 3x – 23 = 10

Answer: (c) 3x + 10 = 23

Question 2. Write the following statement in the form of an equation “The number b divided by 6 gives 5”. (a) b – 5 = 6 (b) 5b = 6 (c) b + 5 = 6 (d) $\frac {b}{6}$ = 5

Answer: (d) $\frac {b}{6}$ = 5

Question 3. The solution of the equation 4p – 3 = 13 is ………. (a) 1 (b) 2 (c) 3 (d) 4

Answer: (d) 4

Question 4. In an isosceles triangle, the base angles are equal to 50°. The vertex angle is (a) 45° (b) 80° (c) 75° (d) 85°

Answer: (b) 80°

Question 5. What value of p makes the given equation true. $\frac {p}{5}$ + 19 = 20 (a) 5 (b) 10 (c) 15 (d) 20

Answer: (a) 5

Question 6. Which of the following is the value of x such that 5x – 12 = -2? (a) 2 (b) -2 (c) $\frac {2}{3}$ (d) 10

Answer: (a) 2

Question 7. The solution of the equation 12p – 11 = 13 is (a) 1 (b) 2 (c) 3 (d) 4

Answer: (b) 2

Question 8. The solution of the equation -2(x + 3) = 4 is (a) -2 (b) -3 (c) -4 (d) -5

Answer: (d) -5

Question 9. The solution of the equation 0 = 4 + 4 (m + 1) is (a) 1 (b) -1 (c) 2 (d) -2

Answer: (d) -2

Question 10. The solution of the equation 4(2 – x) = 4 is (a) 1 (b) 2 (c) 3 (d) 4

Question 11. The value of the variable that we get on solving an equation is: (a) degree of the equation (b) root of the equation (c) co-efficient of the variable (d) none of these

Answer: (b) root of the equation

Question 12. If the LHS and RHS of an equation are interchanged, then (a) The equation remains the same. (b) The value of the variable becomes half. (c) The value of the variable becomes double. (d) The value of the variable becomes zero.

Answer: (a) The equation remains the same.

Fill in the blanks

Question 1. 9 + 3x –$\frac {4}{3}$ = $\frac {11}{3}$ then x = ……………..

Answer: $\frac {4}{3}$

Question 2. x + $\frac {3}{4}$ = $\frac {5}{4}$ then x = ……………..

Answer: $\frac {1}{2}$

Question 3. 9 + 2x + $\frac {3}{4}$ = $\frac {5}{4}$ then x = ……………..

Answer: –$\frac {17}{4}$

Question 4. $\frac {x}{2}$ + $\frac {3}{4}$ =$\frac {5}{4}$ then x = …………….

Question 5. $\frac {x}{4}$ + 1 = 2 then x = ………………..

Question 6. When 2x + 3 = 5, then x = ………………….

Question 7. When $\frac {2x}{3}$ = 4, then x = ………………….

Question 8. If 9x = 27, then x = ………………….

Question 9. If 4x + 1 = 17, then x = ………………….

Question 10. If 5x – $\frac {3}{4}$ = 2x, then x = ………………..

Answer: $\frac {1}{4}$

Question 11. If $\frac {4x}{5}$ – $\frac {1}{4}$ = $\frac {3x}{5}$, then x = …………………..

Answer: $\frac {5}{4}$

Question 12. If 3x – $\frac {4}{3}$ = $\frac {11}{3}$, then x = …………………

Answer: $\frac {5}{3}$

Question 13. If X + $\frac {3}{4}$ = $\frac {5}{4}$, then x = ……………….

Question 14. If $\frac {x}{4}$ – 3 = 1 then x = …………………..

Question 15. If $\frac {x}{4}$ + 4 = 3, then x = ……………………

Question 16. If 2x – 4 = 5 – x, then x = ………………..

Question 17. If 2x + 4 = 5 – x, then x = ……………………

Question 18. If 4($\frac {1}{4}$x + $\frac {1}{4}$) = 2, then x = ……………….

Question 19. If 4($\frac {1}{4}$x) + $\frac {1}{4}$ = 2, then x = ……………….

Answer: $\frac {7}{4}$

Question 20. If $\frac {1}{x}$ + 1 = 2, then x = …………………..

Question 21. If $\frac {2}{x}$ + 1 = 2, then x = …………………

Answer: $\frac {1}{3}$

Question 22. If 1 – $\frac {1}{x}$ = 4, then x = ………………….

Answer: –$\frac {1}{3}$

Question 23. If 2 – $\frac {2}{x}$ = 4, then x = …………………

Answer: –$\frac {1}{2}$

Question 24. If 3x – $\frac {1}{3}$ = $\frac {2}{3}$, then x = ………………….

Question 25. If 5x – $\frac {4}{5}$ = $\frac {1}{5}$, then x = ……………………

Answer: $\frac {1}{5}$

Match the following

Hope the information shed above regarding NCERT MCQ Questions for Class 7 Maths Chapter 4 Simple Equations with Answers Pdf free download has been useful to an extent. If you have any other queries of CBSE Class 7 Maths Simple Equations MCQs Multiple Choice Questions with Answers, feel free to reach us so that we can revert back to us at the earliest possible.

IMAGES

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations
CBSE Class 7 Maths Simple Equations Worksheets
NCERT Exemplar Solutions for Class 7 Maths Chapter 4 Simple Equations
NCERT Solutions for Class 7 Maths Ch 4 Simple Equations Exercise 4.4
class 7 maths case based study questions
Chapter 4 Simple Equations

VIDEO

Simple Equations
Simple Equations
Simple Equations
Simple Equations Ex-4.4 Chapter -4 || Class 7th Maths
Simple Equations in 1 Shot
Simple Equations

COMMENTS

Case Study Questions for Class 7 Maths Chapter 4 Simple Equations
There is total 13 chapters. Chapter 1 Integers Case Study Questions. Chapter 2 Fractions and Decimals Case Study Questions. Chapter 3 Data Handling Case Study Questions. Chapter 4 Simple Equations Case Study Questions. Chapter 5 Lines and Angles Case Study Questions. Chapter 6 The Triangles and its Properties Case Study Questions.
PDF CLASS 7 MATHS SIMPLE EQUATION HOTS
CASE STUDY 1. Two persons start moving from two points A and B in opposite directions toward each other . One person starts moving from A at the speed of 4km/h and meets the other person coming from B after 6 hours. If the distance between A and B is 42km, find the speed of other person. 2. There are some benches in a classroom.
Important Questions for CBSE Class 7 Maths Chapter 4
5. The Equation Having 5 as a Solution is: (a) 4x + 1 = 2 (b) 3 - x = 8 (c) x - 5 = 3 (d) 3 + x = 8. The 4th chapter of the class 7 maths textbook is all about simple equations. This is a chapter that can be considered as really important since it helps the students in gaining some important information about equations and much more. By ...
Simple Equations Class 7 Maths Notes
Methods of Solving an Equation. Method 1: performing the same operations on the expressions on either side of the "=" sign so that the value of the variable is found without disturbing the balance. Opertions involve Adding, subtracting, multipling or dividing on both sides. Example: x+2=6. Subtract 2 from LHS and RHS. ⇒ LHS: x+2−2=x ...
Simple Equations
Class 7. 11 units · 47 skills. Unit 1. Integers. Unit 2. Fractions and Decimals. Unit 3. Data Handling. Unit 4. Simple Equations. Unit 5. Lines and Angles. ... Simple Equations 4.3 Get 9 of 12 questions to level up! Up next for you: Unit test. Level up on all the skills in this unit and collect up to 300 Mastery points!
NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations
About NCERT Solutions for Class 7 Maths Chapter 4. In 7 Maths Chapter 4 Simple Equations, we will study about the formation of linear equations in one variable (A variable takes on different numerical values; its value is not fixed. Variables are denoted usually by letters of the alphabets, such as x, y, z, l, m, n, p, etc.).
NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations
The highest score is = 87. The highest marks obtained by a student in her class are twice the lowest marks plus 7= 2x + 7. 5/2 of the number = (5/2) x. The given above statement can be written in the equation form as, Then, = 2x + 7 = Highest score. = 2x + 7 = 87. By transposing 7 from LHS to RHS, it becomes -7.
NCERT Solutions Class 7 Maths Chapter 4 Simple Equations
Below are some of the important pointers covered in the NCERT solutions class 7 maths chapter 4 : In case the right-hand side of the equation is changed to the left-hand side and vice versa, the equation remains unchanged. So, x + 5 = y + 2 is the same as y + 2 = x + 5. Transposing refers to moving on to the other side.
NCERT Solutions for Class 7 Maths Chapter 4
There are a variety of questions found in the NCERT Solutions for Class 7 Maths, Chapter 4, Simple Equations. This chapter consists of four exercises. In Exercise 4.1, there are a total of six questions, Exercise 4.2 has four questions, Exercise 4.3 has four questions and lastly Exercise 4.4 has four questions.
Simple Equations Class 7 Extra Questions Maths Chapter 4
Question 1. Write the following statements in the form of equations. (a) The sum of four times a number and 5 gives a number five times of it. (b) One-fourth of a number is 2 more than 5. (a) Let the number be x. The sum is 5x. The equation is 4x + 5 = 5x as required. (b) Let the number be x. ⇒ \frac { 1 } { 4 } x = 7 as required.
Simple Equations Class 7 Notes CBSE Maths Chapter 4 [PDF]
Importances of Solving Simple Equations of Class 7 Notes CBSE Maths Chapter 4 (Free PDF Download) The "Simple Equations Class 7 Notes CBSE Maths Chapter 4 (Free PDF Download)" are of paramount importance in a student's mathematical journey. This chapter introduces fundamental concepts of algebraic equations, laying a strong foundation for more advanced mathematical topics in the future.
Simple equations
Class 7 (Old) 12 units · 100 skills. Unit 1. Integers. Unit 2. Fractions and decimals. Unit 3. Data handling. ... Simple equations: Unit test; Setting up an equation (Recap) Learn. Writing expressions with variables ... Two-step equations Get 5 of 7 questions to level up! Two-step equations with decimals and fractions Get 5 of 7 questions to ...
NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations
It helps the students to understand slowly and to get practice well to become perfect and again a good score in their examination. Below we have listed NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Exercise 4.1, Ex 4.2, Ex 4.3 and Ex 4.4. These materials are prepared based on Class 7 NCERT syllabus, taking the types of questions ...
NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations
This will help you with exercise 4.2 of NCERT Solutions Chapter 4. Example: Solve 5x-3=12. Adding 3 to both sides, we get. 5x-3+3=12+3. 5x=15. Dividing both sides by 5, we get 5x/5=15/5. x=3, which is the required solution. Note: For checking the answer, we substitute the value of the variable in the given equation.
NCERT Solutions for Class 7 Math Chapter 4
Question 4: Write equations for the following statements: (i) The sum of numbers x and 4 is 9. (ii) 2 subtracted from y is 8. (iii) Ten times a is 70. (iv) The number b divided by 5 gives 6. (v) Three-fourth of t is 15. (vi) Seven times m plus 7 gets you 77. (vii) One-fourth of a number x minus 4 gives 4.
Question Bank for 7th Class Mathematics Simple Equations
Free Question Bank for 7th Class Mathematics Simple Equations. Customer Care : 6267349244. ... Question Bank for 7th Class Mathematics Simple Equations Linear Equation in one Variable Practice Now. Simple Equation ... Study Packages Question Bank Online Test Rajasthan State Exams ; Videos Sample Papers
Class 7 NCERT Solutions Maths Chapter 4
NCERT Solutions for Class 7 Maths CBSE Chapter 4: Get free access to Simple Equations Class 7 Solutions which includes all the exercises with solved solutions. Visit TopperLearning now!
Class 7 Simple Equations
Have a look at the following examples: EXAMPLE 1: The sum of the digits of a 2 digit number 13. The numbers obtained by interchanging the digits is 14 more than the given number. Find the number. SOLUTION: Let the digit at units place be x and the number at tens place be y. => y + x = 13 [sum is 13 given]
Simple Equations: Unit test
Please help keep Khan Academy free, for anyone, anywhere forever. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
7th Class Mathematics Simple Equations Question Bank
question_answer 15) The total cost of three prizes is Rs.2550. If the value of second prize is. 3 4th. of the first and the value of 3rd prize is. 1 2. of the second prize, find the value of first prize. A) Rs. 900.
Simple Equations Class 7 MCQ Test (Online Available)
Helps in Practising Questions: Sometimes, it's hard to get the questions to practise; therefore, the Selfstudys team has curated various sets of MCQ Questions of Class 7 Simple Equations. Having access to the objective questions of Class 7 Simple Equations helps students practising various questions for free of cost.
MCQ Questions for Class 7 Maths Chapter 4 Simple Equations with Answers
Simple Equations Class 7 MCQs Questions with Answers. Choose the correct option. Question 1. Write the following statement in the form of an equation. "The sum of three times x and 10 is 23. Question 2. Write the following statement in the form of an equation "The number b divided by 6 gives 5". Question 3.

Case Study Questions for Class 7 Maths Chapter 4 Simple Equations

Maths Class 7 Chapter List

Old Chapter List

Tips for Answering Case Study Questions for Class 7 Maths in Exam

Download CBSE Books

Leave a Reply Cancel reply

Discover more from Gurukul of Excellence

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations

7th Maths Chapter 4 Solutions in English Medium

7th Maths Chapter 4 Solutions in Hindi Medium

Important Questions on Class 7 Maths Chapter 4

Write equations for the following statement: The sum of numbers x and 4 is 9.

« Chapter 3: Data Handling

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations

Download Exclusively Curated Chapter Notes for Class 7 Maths Chapter – 4 Simple Equations

Access other exercises of NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations

Access answers to Maths NCERT Solutions for Class 7 Chapter 4 – Simple Equations

Frequently Asked Questions on NCERT Solutions for Class 7 Maths Chapter 4

Register with BYJU'S & Download Free PDFs

NCERT Solutions Class 7 Maths Chapter 4 Simple Equations

NCERT Solutions for Class 7 Maths Chapter 4 PDF

☛ Download Class 7 Maths NCERT Solutions Chapter 4 Simple Equations

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations

List of Formulas in NCERT Solutions Class 7 Maths Chapter 4

Important Questions for Class 7 Maths NCERT Solutions Chapter 4

What are the Important Formulas in class 7 maths NCERT Solutions chapter 4?

What are the Important Topics Covered in NCERT Solutions class 7 maths chapter 4?

How Many Questions are there in NCERT Solutions class 7 maths chapter 4 simple equations?

How the CBSE students can utilize NCERT Solutions class 7 maths chapter 4 effectively?

Do I Need to Practice all Questions Provided in NCERT Solutions Class 7 Maths simple equations?

Revision Notes for CBSE Class 7 Maths Chapter 4 - Free PDF Download

Download CBSE Class 7 Maths Revision Notes 2024-25 PDF

Access Class VII Mathematics Chapter 4 - Simple Equations Notes in 30 Minutes

Simple Equations Class 7 Notes Maths Chapter 4- PDF Download

Simple Equations

Solving Simple Equations

Importances of Solving Simple Equations of Class 7 Notes CBSE Maths Chapter 4 (Free PDF Download)

Advantages of Revision Notes of CBSE Class 7 Chapter 4

FAQs on Simple Equations Class 7 Notes CBSE Maths Chapter 4 (Free PDF Download)

NCERT Solutions

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.1

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.2

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.3

NCERT Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.4

Class 7 Maths Chapter 4 Simple Equations Textbook Solutions

Leave a Reply Cancel reply

NCERT Solutions Class 7 Maths Chapter 4

NCERT Solutions for Class 7 Mathematics Chapter 4

NCERT Solutions for Class 7 Mathematics Chapter 4 Simple equations

NCERT Solutions for Class 7 Mathematics Chapter 4 Exercises

An Equation

Please register to view this section

2. How do you avail the study materials for NCERT Solutions for Class 7 Mathematics?

3. Are there any theoretical questions in chapter Simple Equations of Class 7 Mathematics?

4. How many questions are there in NCERT Solutions for class 11 chapter 4?

NCERT Solutions Related Links

Fill this form to view question paper

Class 7 NCERT Solutions Maths Chapter 4 - Simple Equations

Simple Equations Exercise Ex. 4.3

CBSE Class 10 Maths MIQs, Subjective Questions & More

Frequently Asked Questions

Get in Touch

Call / Whats App

Register here

Simple Equations

Solving equations which have linear equations on one side and numbers on the other side

Solving equations having variables having the variable on both sides

Application of Linear Equations

Reducing Equation to Simpler Form

Equations reducible to linear form

Practice these questions

Quiz for Simple Equations

Other Chapters of Class 7

Quick Links

SchoolPlus Program

Olympiad Exam Dates

LIVE Classes for Olympiads

Olympiad Test Series

India’s First Summer Olympiads