scientific method observation hypothesis

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Mechanics (Essentials) - Class 11th

Course: mechanics (essentials) - class 11th   >   unit 2.

• Introduction to physics
• What is physics?

The scientific method

• Models and Approximations in Physics

Introduction

• Make an observation.
• Ask a question.
• Form a hypothesis , or testable explanation.
• Make a prediction based on the hypothesis.
• Test the prediction.
• Iterate: use the results to make new hypotheses or predictions.

Scientific method example: Failure to toast

1. make an observation..

• Observation: the toaster won't toast.

2. Ask a question.

• Question: Why won't my toaster toast?

3. Propose a hypothesis.

• Hypothesis: Maybe the outlet is broken.

4. Make predictions.

• Prediction: If I plug the toaster into a different outlet, then it will toast the bread.

5. Test the predictions.

• Test of prediction: Plug the toaster into a different outlet and try again.
• If the toaster does toast, then the hypothesis is supported—likely correct.
• If the toaster doesn't toast, then the hypothesis is not supported—likely wrong.

Logical possibility

Practical possibility, building a body of evidence, 6. iterate..

• Iteration time!
• If the hypothesis was supported, we might do additional tests to confirm it, or revise it to be more specific. For instance, we might investigate why the outlet is broken.
• If the hypothesis was not supported, we would come up with a new hypothesis. For instance, the next hypothesis might be that there's a broken wire in the toaster.

Want to join the conversation?

• Table of Contents
• Random Entry
• Chronological
• Editorial Information
• About the SEP
• Editorial Board
• How to Cite the SEP
• Special Characters
• Advanced Tools
• Support the SEP
• PDFs for SEP Friends
• Make a Donation
• SEPIA for Libraries
• Entry Contents

Bibliography

Academic tools.

• Friends PDF Preview
• Author and Citation Info
• Back to Top

Scientific Method

Science is an enormously successful human enterprise. The study of scientific method is the attempt to discern the activities by which that success is achieved. Among the activities often identified as characteristic of science are systematic observation and experimentation, inductive and deductive reasoning, and the formation and testing of hypotheses and theories. How these are carried out in detail can vary greatly, but characteristics like these have been looked to as a way of demarcating scientific activity from non-science, where only enterprises which employ some canonical form of scientific method or methods should be considered science (see also the entry on science and pseudo-science ). Others have questioned whether there is anything like a fixed toolkit of methods which is common across science and only science. Some reject privileging one view of method as part of rejecting broader views about the nature of science, such as naturalism (Dupré 2004); some reject any restriction in principle (pluralism).

Scientific method should be distinguished from the aims and products of science, such as knowledge, predictions, or control. Methods are the means by which those goals are achieved. Scientific method should also be distinguished from meta-methodology, which includes the values and justifications behind a particular characterization of scientific method (i.e., a methodology) — values such as objectivity, reproducibility, simplicity, or past successes. Methodological rules are proposed to govern method and it is a meta-methodological question whether methods obeying those rules satisfy given values. Finally, method is distinct, to some degree, from the detailed and contextual practices through which methods are implemented. The latter might range over: specific laboratory techniques; mathematical formalisms or other specialized languages used in descriptions and reasoning; technological or other material means; ways of communicating and sharing results, whether with other scientists or with the public at large; or the conventions, habits, enforced customs, and institutional controls over how and what science is carried out.

While it is important to recognize these distinctions, their boundaries are fuzzy. Hence, accounts of method cannot be entirely divorced from their methodological and meta-methodological motivations or justifications, Moreover, each aspect plays a crucial role in identifying methods. Disputes about method have therefore played out at the detail, rule, and meta-rule levels. Changes in beliefs about the certainty or fallibility of scientific knowledge, for instance (which is a meta-methodological consideration of what we can hope for methods to deliver), have meant different emphases on deductive and inductive reasoning, or on the relative importance attached to reasoning over observation (i.e., differences over particular methods.) Beliefs about the role of science in society will affect the place one gives to values in scientific method.

The issue which has shaped debates over scientific method the most in the last half century is the question of how pluralist do we need to be about method? Unificationists continue to hold out for one method essential to science; nihilism is a form of radical pluralism, which considers the effectiveness of any methodological prescription to be so context sensitive as to render it not explanatory on its own. Some middle degree of pluralism regarding the methods embodied in scientific practice seems appropriate. But the details of scientific practice vary with time and place, from institution to institution, across scientists and their subjects of investigation. How significant are the variations for understanding science and its success? How much can method be abstracted from practice? This entry describes some of the attempts to characterize scientific method or methods, as well as arguments for a more context-sensitive approach to methods embedded in actual scientific practices.

1. Overview and organizing themes

2. historical review: aristotle to mill, 3.1 logical constructionism and operationalism, 3.2. h-d as a logic of confirmation, 3.3. popper and falsificationism, 3.4 meta-methodology and the end of method, 4. statistical methods for hypothesis testing, 5.1 creative and exploratory practices.

• 5.2 Computer methods and the ‘new ways’ of doing science

6.1 “The scientific method” in science education and as seen by scientists

6.2 privileged methods and ‘gold standards’, 6.3 scientific method in the court room, 6.4 deviating practices, 7. conclusion, other internet resources, related entries.

This entry could have been given the title Scientific Methods and gone on to fill volumes, or it could have been extremely short, consisting of a brief summary rejection of the idea that there is any such thing as a unique Scientific Method at all. Both unhappy prospects are due to the fact that scientific activity varies so much across disciplines, times, places, and scientists that any account which manages to unify it all will either consist of overwhelming descriptive detail, or trivial generalizations.

The choice of scope for the present entry is more optimistic, taking a cue from the recent movement in philosophy of science toward a greater attention to practice: to what scientists actually do. This “turn to practice” can be seen as the latest form of studies of methods in science, insofar as it represents an attempt at understanding scientific activity, but through accounts that are neither meant to be universal and unified, nor singular and narrowly descriptive. To some extent, different scientists at different times and places can be said to be using the same method even though, in practice, the details are different.

Whether the context in which methods are carried out is relevant, or to what extent, will depend largely on what one takes the aims of science to be and what one’s own aims are. For most of the history of scientific methodology the assumption has been that the most important output of science is knowledge and so the aim of methodology should be to discover those methods by which scientific knowledge is generated.

Science was seen to embody the most successful form of reasoning (but which form?) to the most certain knowledge claims (but how certain?) on the basis of systematically collected evidence (but what counts as evidence, and should the evidence of the senses take precedence, or rational insight?) Section 2 surveys some of the history, pointing to two major themes. One theme is seeking the right balance between observation and reasoning (and the attendant forms of reasoning which employ them); the other is how certain scientific knowledge is or can be.

Section 3 turns to 20 th century debates on scientific method. In the second half of the 20 th century the epistemic privilege of science faced several challenges and many philosophers of science abandoned the reconstruction of the logic of scientific method. Views changed significantly regarding which functions of science ought to be captured and why. For some, the success of science was better identified with social or cultural features. Historical and sociological turns in the philosophy of science were made, with a demand that greater attention be paid to the non-epistemic aspects of science, such as sociological, institutional, material, and political factors. Even outside of those movements there was an increased specialization in the philosophy of science, with more and more focus on specific fields within science. The combined upshot was very few philosophers arguing any longer for a grand unified methodology of science. Sections 3 and 4 surveys the main positions on scientific method in 20 th century philosophy of science, focusing on where they differ in their preference for confirmation or falsification or for waiving the idea of a special scientific method altogether.

In recent decades, attention has primarily been paid to scientific activities traditionally falling under the rubric of method, such as experimental design and general laboratory practice, the use of statistics, the construction and use of models and diagrams, interdisciplinary collaboration, and science communication. Sections 4–6 attempt to construct a map of the current domains of the study of methods in science.

As these sections illustrate, the question of method is still central to the discourse about science. Scientific method remains a topic for education, for science policy, and for scientists. It arises in the public domain where the demarcation or status of science is at issue. Some philosophers have recently returned, therefore, to the question of what it is that makes science a unique cultural product. This entry will close with some of these recent attempts at discerning and encapsulating the activities by which scientific knowledge is achieved.

Attempting a history of scientific method compounds the vast scope of the topic. This section briefly surveys the background to modern methodological debates. What can be called the classical view goes back to antiquity, and represents a point of departure for later divergences. [ 1 ]

We begin with a point made by Laudan (1968) in his historical survey of scientific method:

Perhaps the most serious inhibition to the emergence of the history of theories of scientific method as a respectable area of study has been the tendency to conflate it with the general history of epistemology, thereby assuming that the narrative categories and classificatory pigeon-holes applied to the latter are also basic to the former. (1968: 5)

To see knowledge about the natural world as falling under knowledge more generally is an understandable conflation. Histories of theories of method would naturally employ the same narrative categories and classificatory pigeon holes. An important theme of the history of epistemology, for example, is the unification of knowledge, a theme reflected in the question of the unification of method in science. Those who have identified differences in kinds of knowledge have often likewise identified different methods for achieving that kind of knowledge (see the entry on the unity of science ).

Different views on what is known, how it is known, and what can be known are connected. Plato distinguished the realms of things into the visible and the intelligible ( The Republic , 510a, in Cooper 1997). Only the latter, the Forms, could be objects of knowledge. The intelligible truths could be known with the certainty of geometry and deductive reasoning. What could be observed of the material world, however, was by definition imperfect and deceptive, not ideal. The Platonic way of knowledge therefore emphasized reasoning as a method, downplaying the importance of observation. Aristotle disagreed, locating the Forms in the natural world as the fundamental principles to be discovered through the inquiry into nature ( Metaphysics Z , in Barnes 1984).

Aristotle is recognized as giving the earliest systematic treatise on the nature of scientific inquiry in the western tradition, one which embraced observation and reasoning about the natural world. In the Prior and Posterior Analytics , Aristotle reflects first on the aims and then the methods of inquiry into nature. A number of features can be found which are still considered by most to be essential to science. For Aristotle, empiricism, careful observation (but passive observation, not controlled experiment), is the starting point. The aim is not merely recording of facts, though. For Aristotle, science ( epistêmê ) is a body of properly arranged knowledge or learning—the empirical facts, but also their ordering and display are of crucial importance. The aims of discovery, ordering, and display of facts partly determine the methods required of successful scientific inquiry. Also determinant is the nature of the knowledge being sought, and the explanatory causes proper to that kind of knowledge (see the discussion of the four causes in the entry on Aristotle on causality ).

In addition to careful observation, then, scientific method requires a logic as a system of reasoning for properly arranging, but also inferring beyond, what is known by observation. Methods of reasoning may include induction, prediction, or analogy, among others. Aristotle’s system (along with his catalogue of fallacious reasoning) was collected under the title the Organon . This title would be echoed in later works on scientific reasoning, such as Novum Organon by Francis Bacon, and Novum Organon Restorum by William Whewell (see below). In Aristotle’s Organon reasoning is divided primarily into two forms, a rough division which persists into modern times. The division, known most commonly today as deductive versus inductive method, appears in other eras and methodologies as analysis/​synthesis, non-ampliative/​ampliative, or even confirmation/​verification. The basic idea is there are two “directions” to proceed in our methods of inquiry: one away from what is observed, to the more fundamental, general, and encompassing principles; the other, from the fundamental and general to instances or implications of principles.

The basic aim and method of inquiry identified here can be seen as a theme running throughout the next two millennia of reflection on the correct way to seek after knowledge: carefully observe nature and then seek rules or principles which explain or predict its operation. The Aristotelian corpus provided the framework for a commentary tradition on scientific method independent of science itself (cosmos versus physics.) During the medieval period, figures such as Albertus Magnus (1206–1280), Thomas Aquinas (1225–1274), Robert Grosseteste (1175–1253), Roger Bacon (1214/1220–1292), William of Ockham (1287–1347), Andreas Vesalius (1514–1546), Giacomo Zabarella (1533–1589) all worked to clarify the kind of knowledge obtainable by observation and induction, the source of justification of induction, and best rules for its application. [ 2 ] Many of their contributions we now think of as essential to science (see also Laudan 1968). As Aristotle and Plato had employed a framework of reasoning either “to the forms” or “away from the forms”, medieval thinkers employed directions away from the phenomena or back to the phenomena. In analysis, a phenomena was examined to discover its basic explanatory principles; in synthesis, explanations of a phenomena were constructed from first principles.

During the Scientific Revolution these various strands of argument, experiment, and reason were forged into a dominant epistemic authority. The 16 th –18 th centuries were a period of not only dramatic advance in knowledge about the operation of the natural world—advances in mechanical, medical, biological, political, economic explanations—but also of self-awareness of the revolutionary changes taking place, and intense reflection on the source and legitimation of the method by which the advances were made. The struggle to establish the new authority included methodological moves. The Book of Nature, according to the metaphor of Galileo Galilei (1564–1642) or Francis Bacon (1561–1626), was written in the language of mathematics, of geometry and number. This motivated an emphasis on mathematical description and mechanical explanation as important aspects of scientific method. Through figures such as Henry More and Ralph Cudworth, a neo-Platonic emphasis on the importance of metaphysical reflection on nature behind appearances, particularly regarding the spiritual as a complement to the purely mechanical, remained an important methodological thread of the Scientific Revolution (see the entries on Cambridge platonists ; Boyle ; Henry More ; Galileo ).

In Novum Organum (1620), Bacon was critical of the Aristotelian method for leaping from particulars to universals too quickly. The syllogistic form of reasoning readily mixed those two types of propositions. Bacon aimed at the invention of new arts, principles, and directions. His method would be grounded in methodical collection of observations, coupled with correction of our senses (and particularly, directions for the avoidance of the Idols, as he called them, kinds of systematic errors to which naïve observers are prone.) The community of scientists could then climb, by a careful, gradual and unbroken ascent, to reliable general claims.

Bacon’s method has been criticized as impractical and too inflexible for the practicing scientist. Whewell would later criticize Bacon in his System of Logic for paying too little attention to the practices of scientists. It is hard to find convincing examples of Bacon’s method being put in to practice in the history of science, but there are a few who have been held up as real examples of 16 th century scientific, inductive method, even if not in the rigid Baconian mold: figures such as Robert Boyle (1627–1691) and William Harvey (1578–1657) (see the entry on Bacon ).

It is to Isaac Newton (1642–1727), however, that historians of science and methodologists have paid greatest attention. Given the enormous success of his Principia Mathematica and Opticks , this is understandable. The study of Newton’s method has had two main thrusts: the implicit method of the experiments and reasoning presented in the Opticks, and the explicit methodological rules given as the Rules for Philosophising (the Regulae) in Book III of the Principia . [ 3 ] Newton’s law of gravitation, the linchpin of his new cosmology, broke with explanatory conventions of natural philosophy, first for apparently proposing action at a distance, but more generally for not providing “true”, physical causes. The argument for his System of the World ( Principia , Book III) was based on phenomena, not reasoned first principles. This was viewed (mainly on the continent) as insufficient for proper natural philosophy. The Regulae counter this objection, re-defining the aims of natural philosophy by re-defining the method natural philosophers should follow. (See the entry on Newton’s philosophy .)

To his list of methodological prescriptions should be added Newton’s famous phrase “ hypotheses non fingo ” (commonly translated as “I frame no hypotheses”.) The scientist was not to invent systems but infer explanations from observations, as Bacon had advocated. This would come to be known as inductivism. In the century after Newton, significant clarifications of the Newtonian method were made. Colin Maclaurin (1698–1746), for instance, reconstructed the essential structure of the method as having complementary analysis and synthesis phases, one proceeding away from the phenomena in generalization, the other from the general propositions to derive explanations of new phenomena. Denis Diderot (1713–1784) and editors of the Encyclopédie did much to consolidate and popularize Newtonianism, as did Francesco Algarotti (1721–1764). The emphasis was often the same, as much on the character of the scientist as on their process, a character which is still commonly assumed. The scientist is humble in the face of nature, not beholden to dogma, obeys only his eyes, and follows the truth wherever it leads. It was certainly Voltaire (1694–1778) and du Chatelet (1706–1749) who were most influential in propagating the latter vision of the scientist and their craft, with Newton as hero. Scientific method became a revolutionary force of the Enlightenment. (See also the entries on Newton , Leibniz , Descartes , Boyle , Hume , enlightenment , as well as Shank 2008 for a historical overview.)

Not all 18 th century reflections on scientific method were so celebratory. Famous also are George Berkeley’s (1685–1753) attack on the mathematics of the new science, as well as the over-emphasis of Newtonians on observation; and David Hume’s (1711–1776) undermining of the warrant offered for scientific claims by inductive justification (see the entries on: George Berkeley ; David Hume ; Hume’s Newtonianism and Anti-Newtonianism ). Hume’s problem of induction motivated Immanuel Kant (1724–1804) to seek new foundations for empirical method, though as an epistemic reconstruction, not as any set of practical guidelines for scientists. Both Hume and Kant influenced the methodological reflections of the next century, such as the debate between Mill and Whewell over the certainty of inductive inferences in science.

The debate between John Stuart Mill (1806–1873) and William Whewell (1794–1866) has become the canonical methodological debate of the 19 th century. Although often characterized as a debate between inductivism and hypothetico-deductivism, the role of the two methods on each side is actually more complex. On the hypothetico-deductive account, scientists work to come up with hypotheses from which true observational consequences can be deduced—hence, hypothetico-deductive. Because Whewell emphasizes both hypotheses and deduction in his account of method, he can be seen as a convenient foil to the inductivism of Mill. However, equally if not more important to Whewell’s portrayal of scientific method is what he calls the “fundamental antithesis”. Knowledge is a product of the objective (what we see in the world around us) and subjective (the contributions of our mind to how we perceive and understand what we experience, which he called the Fundamental Ideas). Both elements are essential according to Whewell, and he was therefore critical of Kant for too much focus on the subjective, and John Locke (1632–1704) and Mill for too much focus on the senses. Whewell’s fundamental ideas can be discipline relative. An idea can be fundamental even if it is necessary for knowledge only within a given scientific discipline (e.g., chemical affinity for chemistry). This distinguishes fundamental ideas from the forms and categories of intuition of Kant. (See the entry on Whewell .)

Clarifying fundamental ideas would therefore be an essential part of scientific method and scientific progress. Whewell called this process “Discoverer’s Induction”. It was induction, following Bacon or Newton, but Whewell sought to revive Bacon’s account by emphasising the role of ideas in the clear and careful formulation of inductive hypotheses. Whewell’s induction is not merely the collecting of objective facts. The subjective plays a role through what Whewell calls the Colligation of Facts, a creative act of the scientist, the invention of a theory. A theory is then confirmed by testing, where more facts are brought under the theory, called the Consilience of Inductions. Whewell felt that this was the method by which the true laws of nature could be discovered: clarification of fundamental concepts, clever invention of explanations, and careful testing. Mill, in his critique of Whewell, and others who have cast Whewell as a fore-runner of the hypothetico-deductivist view, seem to have under-estimated the importance of this discovery phase in Whewell’s understanding of method (Snyder 1997a,b, 1999). Down-playing the discovery phase would come to characterize methodology of the early 20 th century (see section 3 ).

Mill, in his System of Logic , put forward a narrower view of induction as the essence of scientific method. For Mill, induction is the search first for regularities among events. Among those regularities, some will continue to hold for further observations, eventually gaining the status of laws. One can also look for regularities among the laws discovered in a domain, i.e., for a law of laws. Which “law law” will hold is time and discipline dependent and open to revision. One example is the Law of Universal Causation, and Mill put forward specific methods for identifying causes—now commonly known as Mill’s methods. These five methods look for circumstances which are common among the phenomena of interest, those which are absent when the phenomena are, or those for which both vary together. Mill’s methods are still seen as capturing basic intuitions about experimental methods for finding the relevant explanatory factors ( System of Logic (1843), see Mill entry). The methods advocated by Whewell and Mill, in the end, look similar. Both involve inductive generalization to covering laws. They differ dramatically, however, with respect to the necessity of the knowledge arrived at; that is, at the meta-methodological level (see the entries on Whewell and Mill entries).

3. Logic of method and critical responses

The quantum and relativistic revolutions in physics in the early 20 th century had a profound effect on methodology. Conceptual foundations of both theories were taken to show the defeasibility of even the most seemingly secure intuitions about space, time and bodies. Certainty of knowledge about the natural world was therefore recognized as unattainable. Instead a renewed empiricism was sought which rendered science fallible but still rationally justifiable.

Analyses of the reasoning of scientists emerged, according to which the aspects of scientific method which were of primary importance were the means of testing and confirming of theories. A distinction in methodology was made between the contexts of discovery and justification. The distinction could be used as a wedge between the particularities of where and how theories or hypotheses are arrived at, on the one hand, and the underlying reasoning scientists use (whether or not they are aware of it) when assessing theories and judging their adequacy on the basis of the available evidence. By and large, for most of the 20 th century, philosophy of science focused on the second context, although philosophers differed on whether to focus on confirmation or refutation as well as on the many details of how confirmation or refutation could or could not be brought about. By the mid-20 th century these attempts at defining the method of justification and the context distinction itself came under pressure. During the same period, philosophy of science developed rapidly, and from section 4 this entry will therefore shift from a primarily historical treatment of the scientific method towards a primarily thematic one.

Advances in logic and probability held out promise of the possibility of elaborate reconstructions of scientific theories and empirical method, the best example being Rudolf Carnap’s The Logical Structure of the World (1928). Carnap attempted to show that a scientific theory could be reconstructed as a formal axiomatic system—that is, a logic. That system could refer to the world because some of its basic sentences could be interpreted as observations or operations which one could perform to test them. The rest of the theoretical system, including sentences using theoretical or unobservable terms (like electron or force) would then either be meaningful because they could be reduced to observations, or they had purely logical meanings (called analytic, like mathematical identities). This has been referred to as the verifiability criterion of meaning. According to the criterion, any statement not either analytic or verifiable was strictly meaningless. Although the view was endorsed by Carnap in 1928, he would later come to see it as too restrictive (Carnap 1956). Another familiar version of this idea is operationalism of Percy William Bridgman. In The Logic of Modern Physics (1927) Bridgman asserted that every physical concept could be defined in terms of the operations one would perform to verify the application of that concept. Making good on the operationalisation of a concept even as simple as length, however, can easily become enormously complex (for measuring very small lengths, for instance) or impractical (measuring large distances like light years.)

Carl Hempel’s (1950, 1951) criticisms of the verifiability criterion of meaning had enormous influence. He pointed out that universal generalizations, such as most scientific laws, were not strictly meaningful on the criterion. Verifiability and operationalism both seemed too restrictive to capture standard scientific aims and practice. The tenuous connection between these reconstructions and actual scientific practice was criticized in another way. In both approaches, scientific methods are instead recast in methodological roles. Measurements, for example, were looked to as ways of giving meanings to terms. The aim of the philosopher of science was not to understand the methods per se , but to use them to reconstruct theories, their meanings, and their relation to the world. When scientists perform these operations, however, they will not report that they are doing them to give meaning to terms in a formal axiomatic system. This disconnect between methodology and the details of actual scientific practice would seem to violate the empiricism the Logical Positivists and Bridgman were committed to. The view that methodology should correspond to practice (to some extent) has been called historicism, or intuitionism. We turn to these criticisms and responses in section 3.4 . [ 4 ]

Positivism also had to contend with the recognition that a purely inductivist approach, along the lines of Bacon-Newton-Mill, was untenable. There was no pure observation, for starters. All observation was theory laden. Theory is required to make any observation, therefore not all theory can be derived from observation alone. (See the entry on theory and observation in science .) Even granting an observational basis, Hume had already pointed out that one could not deductively justify inductive conclusions without begging the question by presuming the success of the inductive method. Likewise, positivist attempts at analyzing how a generalization can be confirmed by observations of its instances were subject to a number of criticisms. Goodman (1965) and Hempel (1965) both point to paradoxes inherent in standard accounts of confirmation. Recent attempts at explaining how observations can serve to confirm a scientific theory are discussed in section 4 below.

The standard starting point for a non-inductive analysis of the logic of confirmation is known as the Hypothetico-Deductive (H-D) method. In its simplest form, a sentence of a theory which expresses some hypothesis is confirmed by its true consequences. As noted in section 2 , this method had been advanced by Whewell in the 19 th century, as well as Nicod (1924) and others in the 20 th century. Often, Hempel’s (1966) description of the H-D method, illustrated by the case of Semmelweiss’ inferential procedures in establishing the cause of childbed fever, has been presented as a key account of H-D as well as a foil for criticism of the H-D account of confirmation (see, for example, Lipton’s (2004) discussion of inference to the best explanation; also the entry on confirmation ). Hempel described Semmelsweiss’ procedure as examining various hypotheses explaining the cause of childbed fever. Some hypotheses conflicted with observable facts and could be rejected as false immediately. Others needed to be tested experimentally by deducing which observable events should follow if the hypothesis were true (what Hempel called the test implications of the hypothesis), then conducting an experiment and observing whether or not the test implications occurred. If the experiment showed the test implication to be false, the hypothesis could be rejected. If the experiment showed the test implications to be true, however, this did not prove the hypothesis true. The confirmation of a test implication does not verify a hypothesis, though Hempel did allow that “it provides at least some support, some corroboration or confirmation for it” (Hempel 1966: 8). The degree of this support then depends on the quantity, variety and precision of the supporting evidence.

Another approach that took off from the difficulties with inductive inference was Karl Popper’s critical rationalism or falsificationism (Popper 1959, 1963). Falsification is deductive and similar to H-D in that it involves scientists deducing observational consequences from the hypothesis under test. For Popper, however, the important point was not the degree of confirmation that successful prediction offered to a hypothesis. The crucial thing was the logical asymmetry between confirmation, based on inductive inference, and falsification, which can be based on a deductive inference. (This simple opposition was later questioned, by Lakatos, among others. See the entry on historicist theories of scientific rationality. )

Popper stressed that, regardless of the amount of confirming evidence, we can never be certain that a hypothesis is true without committing the fallacy of affirming the consequent. Instead, Popper introduced the notion of corroboration as a measure for how well a theory or hypothesis has survived previous testing—but without implying that this is also a measure for the probability that it is true.

Popper was also motivated by his doubts about the scientific status of theories like the Marxist theory of history or psycho-analysis, and so wanted to demarcate between science and pseudo-science. Popper saw this as an importantly different distinction than demarcating science from metaphysics. The latter demarcation was the primary concern of many logical empiricists. Popper used the idea of falsification to draw a line instead between pseudo and proper science. Science was science because its method involved subjecting theories to rigorous tests which offered a high probability of failing and thus refuting the theory.

A commitment to the risk of failure was important. Avoiding falsification could be done all too easily. If a consequence of a theory is inconsistent with observations, an exception can be added by introducing auxiliary hypotheses designed explicitly to save the theory, so-called ad hoc modifications. This Popper saw done in pseudo-science where ad hoc theories appeared capable of explaining anything in their field of application. In contrast, science is risky. If observations showed the predictions from a theory to be wrong, the theory would be refuted. Hence, scientific hypotheses must be falsifiable. Not only must there exist some possible observation statement which could falsify the hypothesis or theory, were it observed, (Popper called these the hypothesis’ potential falsifiers) it is crucial to the Popperian scientific method that such falsifications be sincerely attempted on a regular basis.

The more potential falsifiers of a hypothesis, the more falsifiable it would be, and the more the hypothesis claimed. Conversely, hypotheses without falsifiers claimed very little or nothing at all. Originally, Popper thought that this meant the introduction of ad hoc hypotheses only to save a theory should not be countenanced as good scientific method. These would undermine the falsifiabililty of a theory. However, Popper later came to recognize that the introduction of modifications (immunizations, he called them) was often an important part of scientific development. Responding to surprising or apparently falsifying observations often generated important new scientific insights. Popper’s own example was the observed motion of Uranus which originally did not agree with Newtonian predictions. The ad hoc hypothesis of an outer planet explained the disagreement and led to further falsifiable predictions. Popper sought to reconcile the view by blurring the distinction between falsifiable and not falsifiable, and speaking instead of degrees of testability (Popper 1985: 41f.).

From the 1960s on, sustained meta-methodological criticism emerged that drove philosophical focus away from scientific method. A brief look at those criticisms follows, with recommendations for further reading at the end of the entry.

Thomas Kuhn’s The Structure of Scientific Revolutions (1962) begins with a well-known shot across the bow for philosophers of science:

History, if viewed as a repository for more than anecdote or chronology, could produce a decisive transformation in the image of science by which we are now possessed. (1962: 1)

The image Kuhn thought needed transforming was the a-historical, rational reconstruction sought by many of the Logical Positivists, though Carnap and other positivists were actually quite sympathetic to Kuhn’s views. (See the entry on the Vienna Circle .) Kuhn shares with other of his contemporaries, such as Feyerabend and Lakatos, a commitment to a more empirical approach to philosophy of science. Namely, the history of science provides important data, and necessary checks, for philosophy of science, including any theory of scientific method.

The history of science reveals, according to Kuhn, that scientific development occurs in alternating phases. During normal science, the members of the scientific community adhere to the paradigm in place. Their commitment to the paradigm means a commitment to the puzzles to be solved and the acceptable ways of solving them. Confidence in the paradigm remains so long as steady progress is made in solving the shared puzzles. Method in this normal phase operates within a disciplinary matrix (Kuhn’s later concept of a paradigm) which includes standards for problem solving, and defines the range of problems to which the method should be applied. An important part of a disciplinary matrix is the set of values which provide the norms and aims for scientific method. The main values that Kuhn identifies are prediction, problem solving, simplicity, consistency, and plausibility.

An important by-product of normal science is the accumulation of puzzles which cannot be solved with resources of the current paradigm. Once accumulation of these anomalies has reached some critical mass, it can trigger a communal shift to a new paradigm and a new phase of normal science. Importantly, the values that provide the norms and aims for scientific method may have transformed in the meantime. Method may therefore be relative to discipline, time or place

Feyerabend also identified the aims of science as progress, but argued that any methodological prescription would only stifle that progress (Feyerabend 1988). His arguments are grounded in re-examining accepted “myths” about the history of science. Heroes of science, like Galileo, are shown to be just as reliant on rhetoric and persuasion as they are on reason and demonstration. Others, like Aristotle, are shown to be far more reasonable and far-reaching in their outlooks then they are given credit for. As a consequence, the only rule that could provide what he took to be sufficient freedom was the vacuous “anything goes”. More generally, even the methodological restriction that science is the best way to pursue knowledge, and to increase knowledge, is too restrictive. Feyerabend suggested instead that science might, in fact, be a threat to a free society, because it and its myth had become so dominant (Feyerabend 1978).

An even more fundamental kind of criticism was offered by several sociologists of science from the 1970s onwards who rejected the methodology of providing philosophical accounts for the rational development of science and sociological accounts of the irrational mistakes. Instead, they adhered to a symmetry thesis on which any causal explanation of how scientific knowledge is established needs to be symmetrical in explaining truth and falsity, rationality and irrationality, success and mistakes, by the same causal factors (see, e.g., Barnes and Bloor 1982, Bloor 1991). Movements in the Sociology of Science, like the Strong Programme, or in the social dimensions and causes of knowledge more generally led to extended and close examination of detailed case studies in contemporary science and its history. (See the entries on the social dimensions of scientific knowledge and social epistemology .) Well-known examinations by Latour and Woolgar (1979/1986), Knorr-Cetina (1981), Pickering (1984), Shapin and Schaffer (1985) seem to bear out that it was social ideologies (on a macro-scale) or individual interactions and circumstances (on a micro-scale) which were the primary causal factors in determining which beliefs gained the status of scientific knowledge. As they saw it therefore, explanatory appeals to scientific method were not empirically grounded.

A late, and largely unexpected, criticism of scientific method came from within science itself. Beginning in the early 2000s, a number of scientists attempting to replicate the results of published experiments could not do so. There may be close conceptual connection between reproducibility and method. For example, if reproducibility means that the same scientific methods ought to produce the same result, and all scientific results ought to be reproducible, then whatever it takes to reproduce a scientific result ought to be called scientific method. Space limits us to the observation that, insofar as reproducibility is a desired outcome of proper scientific method, it is not strictly a part of scientific method. (See the entry on reproducibility of scientific results .)

By the close of the 20 th century the search for the scientific method was flagging. Nola and Sankey (2000b) could introduce their volume on method by remarking that “For some, the whole idea of a theory of scientific method is yester-year’s debate …”.

Despite the many difficulties that philosophers encountered in trying to providing a clear methodology of conformation (or refutation), still important progress has been made on understanding how observation can provide evidence for a given theory. Work in statistics has been crucial for understanding how theories can be tested empirically, and in recent decades a huge literature has developed that attempts to recast confirmation in Bayesian terms. Here these developments can be covered only briefly, and we refer to the entry on confirmation for further details and references.

Statistics has come to play an increasingly important role in the methodology of the experimental sciences from the 19 th century onwards. At that time, statistics and probability theory took on a methodological role as an analysis of inductive inference, and attempts to ground the rationality of induction in the axioms of probability theory have continued throughout the 20 th century and in to the present. Developments in the theory of statistics itself, meanwhile, have had a direct and immense influence on the experimental method, including methods for measuring the uncertainty of observations such as the Method of Least Squares developed by Legendre and Gauss in the early 19 th century, criteria for the rejection of outliers proposed by Peirce by the mid-19 th century, and the significance tests developed by Gosset (a.k.a. “Student”), Fisher, Neyman & Pearson and others in the 1920s and 1930s (see, e.g., Swijtink 1987 for a brief historical overview; and also the entry on C.S. Peirce ).

These developments within statistics then in turn led to a reflective discussion among both statisticians and philosophers of science on how to perceive the process of hypothesis testing: whether it was a rigorous statistical inference that could provide a numerical expression of the degree of confidence in the tested hypothesis, or if it should be seen as a decision between different courses of actions that also involved a value component. This led to a major controversy among Fisher on the one side and Neyman and Pearson on the other (see especially Fisher 1955, Neyman 1956 and Pearson 1955, and for analyses of the controversy, e.g., Howie 2002, Marks 2000, Lenhard 2006). On Fisher’s view, hypothesis testing was a methodology for when to accept or reject a statistical hypothesis, namely that a hypothesis should be rejected by evidence if this evidence would be unlikely relative to other possible outcomes, given the hypothesis were true. In contrast, on Neyman and Pearson’s view, the consequence of error also had to play a role when deciding between hypotheses. Introducing the distinction between the error of rejecting a true hypothesis (type I error) and accepting a false hypothesis (type II error), they argued that it depends on the consequences of the error to decide whether it is more important to avoid rejecting a true hypothesis or accepting a false one. Hence, Fisher aimed for a theory of inductive inference that enabled a numerical expression of confidence in a hypothesis. To him, the important point was the search for truth, not utility. In contrast, the Neyman-Pearson approach provided a strategy of inductive behaviour for deciding between different courses of action. Here, the important point was not whether a hypothesis was true, but whether one should act as if it was.

Similar discussions are found in the philosophical literature. On the one side, Churchman (1948) and Rudner (1953) argued that because scientific hypotheses can never be completely verified, a complete analysis of the methods of scientific inference includes ethical judgments in which the scientists must decide whether the evidence is sufficiently strong or that the probability is sufficiently high to warrant the acceptance of the hypothesis, which again will depend on the importance of making a mistake in accepting or rejecting the hypothesis. Others, such as Jeffrey (1956) and Levi (1960) disagreed and instead defended a value-neutral view of science on which scientists should bracket their attitudes, preferences, temperament, and values when assessing the correctness of their inferences. For more details on this value-free ideal in the philosophy of science and its historical development, see Douglas (2009) and Howard (2003). For a broad set of case studies examining the role of values in science, see e.g. Elliott & Richards 2017.

In recent decades, philosophical discussions of the evaluation of probabilistic hypotheses by statistical inference have largely focused on Bayesianism that understands probability as a measure of a person’s degree of belief in an event, given the available information, and frequentism that instead understands probability as a long-run frequency of a repeatable event. Hence, for Bayesians probabilities refer to a state of knowledge, whereas for frequentists probabilities refer to frequencies of events (see, e.g., Sober 2008, chapter 1 for a detailed introduction to Bayesianism and frequentism as well as to likelihoodism). Bayesianism aims at providing a quantifiable, algorithmic representation of belief revision, where belief revision is a function of prior beliefs (i.e., background knowledge) and incoming evidence. Bayesianism employs a rule based on Bayes’ theorem, a theorem of the probability calculus which relates conditional probabilities. The probability that a particular hypothesis is true is interpreted as a degree of belief, or credence, of the scientist. There will also be a probability and a degree of belief that a hypothesis will be true conditional on a piece of evidence (an observation, say) being true. Bayesianism proscribes that it is rational for the scientist to update their belief in the hypothesis to that conditional probability should it turn out that the evidence is, in fact, observed (see, e.g., Sprenger & Hartmann 2019 for a comprehensive treatment of Bayesian philosophy of science). Originating in the work of Neyman and Person, frequentism aims at providing the tools for reducing long-run error rates, such as the error-statistical approach developed by Mayo (1996) that focuses on how experimenters can avoid both type I and type II errors by building up a repertoire of procedures that detect errors if and only if they are present. Both Bayesianism and frequentism have developed over time, they are interpreted in different ways by its various proponents, and their relations to previous criticism to attempts at defining scientific method are seen differently by proponents and critics. The literature, surveys, reviews and criticism in this area are vast and the reader is referred to the entries on Bayesian epistemology and confirmation .

5. Method in Practice

Attention to scientific practice, as we have seen, is not itself new. However, the turn to practice in the philosophy of science of late can be seen as a correction to the pessimism with respect to method in philosophy of science in later parts of the 20 th century, and as an attempted reconciliation between sociological and rationalist explanations of scientific knowledge. Much of this work sees method as detailed and context specific problem-solving procedures, and methodological analyses to be at the same time descriptive, critical and advisory (see Nickles 1987 for an exposition of this view). The following section contains a survey of some of the practice focuses. In this section we turn fully to topics rather than chronology.

A problem with the distinction between the contexts of discovery and justification that figured so prominently in philosophy of science in the first half of the 20 th century (see section 2 ) is that no such distinction can be clearly seen in scientific activity (see Arabatzis 2006). Thus, in recent decades, it has been recognized that study of conceptual innovation and change should not be confined to psychology and sociology of science, but are also important aspects of scientific practice which philosophy of science should address (see also the entry on scientific discovery ). Looking for the practices that drive conceptual innovation has led philosophers to examine both the reasoning practices of scientists and the wide realm of experimental practices that are not directed narrowly at testing hypotheses, that is, exploratory experimentation.

Examining the reasoning practices of historical and contemporary scientists, Nersessian (2008) has argued that new scientific concepts are constructed as solutions to specific problems by systematic reasoning, and that of analogy, visual representation and thought-experimentation are among the important reasoning practices employed. These ubiquitous forms of reasoning are reliable—but also fallible—methods of conceptual development and change. On her account, model-based reasoning consists of cycles of construction, simulation, evaluation and adaption of models that serve as interim interpretations of the target problem to be solved. Often, this process will lead to modifications or extensions, and a new cycle of simulation and evaluation. However, Nersessian also emphasizes that

creative model-based reasoning cannot be applied as a simple recipe, is not always productive of solutions, and even its most exemplary usages can lead to incorrect solutions. (Nersessian 2008: 11)

Thus, while on the one hand she agrees with many previous philosophers that there is no logic of discovery, discoveries can derive from reasoned processes, such that a large and integral part of scientific practice is

the creation of concepts through which to comprehend, structure, and communicate about physical phenomena …. (Nersessian 1987: 11)

Similarly, work on heuristics for discovery and theory construction by scholars such as Darden (1991) and Bechtel & Richardson (1993) present science as problem solving and investigate scientific problem solving as a special case of problem-solving in general. Drawing largely on cases from the biological sciences, much of their focus has been on reasoning strategies for the generation, evaluation, and revision of mechanistic explanations of complex systems.

Addressing another aspect of the context distinction, namely the traditional view that the primary role of experiments is to test theoretical hypotheses according to the H-D model, other philosophers of science have argued for additional roles that experiments can play. The notion of exploratory experimentation was introduced to describe experiments driven by the desire to obtain empirical regularities and to develop concepts and classifications in which these regularities can be described (Steinle 1997, 2002; Burian 1997; Waters 2007)). However the difference between theory driven experimentation and exploratory experimentation should not be seen as a sharp distinction. Theory driven experiments are not always directed at testing hypothesis, but may also be directed at various kinds of fact-gathering, such as determining numerical parameters. Vice versa , exploratory experiments are usually informed by theory in various ways and are therefore not theory-free. Instead, in exploratory experiments phenomena are investigated without first limiting the possible outcomes of the experiment on the basis of extant theory about the phenomena.

The development of high throughput instrumentation in molecular biology and neighbouring fields has given rise to a special type of exploratory experimentation that collects and analyses very large amounts of data, and these new ‘omics’ disciplines are often said to represent a break with the ideal of hypothesis-driven science (Burian 2007; Elliott 2007; Waters 2007; O’Malley 2007) and instead described as data-driven research (Leonelli 2012; Strasser 2012) or as a special kind of “convenience experimentation” in which many experiments are done simply because they are extraordinarily convenient to perform (Krohs 2012).

5.2 Computer methods and ‘new ways’ of doing science

The field of omics just described is possible because of the ability of computers to process, in a reasonable amount of time, the huge quantities of data required. Computers allow for more elaborate experimentation (higher speed, better filtering, more variables, sophisticated coordination and control), but also, through modelling and simulations, might constitute a form of experimentation themselves. Here, too, we can pose a version of the general question of method versus practice: does the practice of using computers fundamentally change scientific method, or merely provide a more efficient means of implementing standard methods?

Because computers can be used to automate measurements, quantifications, calculations, and statistical analyses where, for practical reasons, these operations cannot be otherwise carried out, many of the steps involved in reaching a conclusion on the basis of an experiment are now made inside a “black box”, without the direct involvement or awareness of a human. This has epistemological implications, regarding what we can know, and how we can know it. To have confidence in the results, computer methods are therefore subjected to tests of verification and validation.

The distinction between verification and validation is easiest to characterize in the case of computer simulations. In a typical computer simulation scenario computers are used to numerically integrate differential equations for which no analytic solution is available. The equations are part of the model the scientist uses to represent a phenomenon or system under investigation. Verifying a computer simulation means checking that the equations of the model are being correctly approximated. Validating a simulation means checking that the equations of the model are adequate for the inferences one wants to make on the basis of that model.

A number of issues related to computer simulations have been raised. The identification of validity and verification as the testing methods has been criticized. Oreskes et al. (1994) raise concerns that “validiation”, because it suggests deductive inference, might lead to over-confidence in the results of simulations. The distinction itself is probably too clean, since actual practice in the testing of simulations mixes and moves back and forth between the two (Weissart 1997; Parker 2008a; Winsberg 2010). Computer simulations do seem to have a non-inductive character, given that the principles by which they operate are built in by the programmers, and any results of the simulation follow from those in-built principles in such a way that those results could, in principle, be deduced from the program code and its inputs. The status of simulations as experiments has therefore been examined (Kaufmann and Smarr 1993; Humphreys 1995; Hughes 1999; Norton and Suppe 2001). This literature considers the epistemology of these experiments: what we can learn by simulation, and also the kinds of justifications which can be given in applying that knowledge to the “real” world. (Mayo 1996; Parker 2008b). As pointed out, part of the advantage of computer simulation derives from the fact that huge numbers of calculations can be carried out without requiring direct observation by the experimenter/​simulator. At the same time, many of these calculations are approximations to the calculations which would be performed first-hand in an ideal situation. Both factors introduce uncertainties into the inferences drawn from what is observed in the simulation.

For many of the reasons described above, computer simulations do not seem to belong clearly to either the experimental or theoretical domain. Rather, they seem to crucially involve aspects of both. This has led some authors, such as Fox Keller (2003: 200) to argue that we ought to consider computer simulation a “qualitatively different way of doing science”. The literature in general tends to follow Kaufmann and Smarr (1993) in referring to computer simulation as a “third way” for scientific methodology (theoretical reasoning and experimental practice are the first two ways.). It should also be noted that the debates around these issues have tended to focus on the form of computer simulation typical in the physical sciences, where models are based on dynamical equations. Other forms of simulation might not have the same problems, or have problems of their own (see the entry on computer simulations in science ).

In recent years, the rapid development of machine learning techniques has prompted some scholars to suggest that the scientific method has become “obsolete” (Anderson 2008, Carrol and Goodstein 2009). This has resulted in an intense debate on the relative merit of data-driven and hypothesis-driven research (for samples, see e.g. Mazzocchi 2015 or Succi and Coveney 2018). For a detailed treatment of this topic, we refer to the entry scientific research and big data .

6. Discourse on scientific method

Despite philosophical disagreements, the idea of the scientific method still figures prominently in contemporary discourse on many different topics, both within science and in society at large. Often, reference to scientific method is used in ways that convey either the legend of a single, universal method characteristic of all science, or grants to a particular method or set of methods privilege as a special ‘gold standard’, often with reference to particular philosophers to vindicate the claims. Discourse on scientific method also typically arises when there is a need to distinguish between science and other activities, or for justifying the special status conveyed to science. In these areas, the philosophical attempts at identifying a set of methods characteristic for scientific endeavors are closely related to the philosophy of science’s classical problem of demarcation (see the entry on science and pseudo-science ) and to the philosophical analysis of the social dimension of scientific knowledge and the role of science in democratic society.

One of the settings in which the legend of a single, universal scientific method has been particularly strong is science education (see, e.g., Bauer 1992; McComas 1996; Wivagg & Allchin 2002). [ 5 ] Often, ‘the scientific method’ is presented in textbooks and educational web pages as a fixed four or five step procedure starting from observations and description of a phenomenon and progressing over formulation of a hypothesis which explains the phenomenon, designing and conducting experiments to test the hypothesis, analyzing the results, and ending with drawing a conclusion. Such references to a universal scientific method can be found in educational material at all levels of science education (Blachowicz 2009), and numerous studies have shown that the idea of a general and universal scientific method often form part of both students’ and teachers’ conception of science (see, e.g., Aikenhead 1987; Osborne et al. 2003). In response, it has been argued that science education need to focus more on teaching about the nature of science, although views have differed on whether this is best done through student-led investigations, contemporary cases, or historical cases (Allchin, Andersen & Nielsen 2014)

Although occasionally phrased with reference to the H-D method, important historical roots of the legend in science education of a single, universal scientific method are the American philosopher and psychologist Dewey’s account of inquiry in How We Think (1910) and the British mathematician Karl Pearson’s account of science in Grammar of Science (1892). On Dewey’s account, inquiry is divided into the five steps of

(i) a felt difficulty, (ii) its location and definition, (iii) suggestion of a possible solution, (iv) development by reasoning of the bearing of the suggestions, (v) further observation and experiment leading to its acceptance or rejection. (Dewey 1910: 72)

Similarly, on Pearson’s account, scientific investigations start with measurement of data and observation of their correction and sequence from which scientific laws can be discovered with the aid of creative imagination. These laws have to be subject to criticism, and their final acceptance will have equal validity for “all normally constituted minds”. Both Dewey’s and Pearson’s accounts should be seen as generalized abstractions of inquiry and not restricted to the realm of science—although both Dewey and Pearson referred to their respective accounts as ‘the scientific method’.

Occasionally, scientists make sweeping statements about a simple and distinct scientific method, as exemplified by Feynman’s simplified version of a conjectures and refutations method presented, for example, in the last of his 1964 Cornell Messenger lectures. [ 6 ] However, just as often scientists have come to the same conclusion as recent philosophy of science that there is not any unique, easily described scientific method. For example, the physicist and Nobel Laureate Weinberg described in the paper “The Methods of Science … And Those By Which We Live” (1995) how

The fact that the standards of scientific success shift with time does not only make the philosophy of science difficult; it also raises problems for the public understanding of science. We do not have a fixed scientific method to rally around and defend. (1995: 8)

Interview studies with scientists on their conception of method shows that scientists often find it hard to figure out whether available evidence confirms their hypothesis, and that there are no direct translations between general ideas about method and specific strategies to guide how research is conducted (Schickore & Hangel 2019, Hangel & Schickore 2017)

Reference to the scientific method has also often been used to argue for the scientific nature or special status of a particular activity. Philosophical positions that argue for a simple and unique scientific method as a criterion of demarcation, such as Popperian falsification, have often attracted practitioners who felt that they had a need to defend their domain of practice. For example, references to conjectures and refutation as the scientific method are abundant in much of the literature on complementary and alternative medicine (CAM)—alongside the competing position that CAM, as an alternative to conventional biomedicine, needs to develop its own methodology different from that of science.

Also within mainstream science, reference to the scientific method is used in arguments regarding the internal hierarchy of disciplines and domains. A frequently seen argument is that research based on the H-D method is superior to research based on induction from observations because in deductive inferences the conclusion follows necessarily from the premises. (See, e.g., Parascandola 1998 for an analysis of how this argument has been made to downgrade epidemiology compared to the laboratory sciences.) Similarly, based on an examination of the practices of major funding institutions such as the National Institutes of Health (NIH), the National Science Foundation (NSF) and the Biomedical Sciences Research Practices (BBSRC) in the UK, O’Malley et al. (2009) have argued that funding agencies seem to have a tendency to adhere to the view that the primary activity of science is to test hypotheses, while descriptive and exploratory research is seen as merely preparatory activities that are valuable only insofar as they fuel hypothesis-driven research.

In some areas of science, scholarly publications are structured in a way that may convey the impression of a neat and linear process of inquiry from stating a question, devising the methods by which to answer it, collecting the data, to drawing a conclusion from the analysis of data. For example, the codified format of publications in most biomedical journals known as the IMRAD format (Introduction, Method, Results, Analysis, Discussion) is explicitly described by the journal editors as “not an arbitrary publication format but rather a direct reflection of the process of scientific discovery” (see the so-called “Vancouver Recommendations”, ICMJE 2013: 11). However, scientific publications do not in general reflect the process by which the reported scientific results were produced. For example, under the provocative title “Is the scientific paper a fraud?”, Medawar argued that scientific papers generally misrepresent how the results have been produced (Medawar 1963/1996). Similar views have been advanced by philosophers, historians and sociologists of science (Gilbert 1976; Holmes 1987; Knorr-Cetina 1981; Schickore 2008; Suppe 1998) who have argued that scientists’ experimental practices are messy and often do not follow any recognizable pattern. Publications of research results, they argue, are retrospective reconstructions of these activities that often do not preserve the temporal order or the logic of these activities, but are instead often constructed in order to screen off potential criticism (see Schickore 2008 for a review of this work).

Philosophical positions on the scientific method have also made it into the court room, especially in the US where judges have drawn on philosophy of science in deciding when to confer special status to scientific expert testimony. A key case is Daubert vs Merrell Dow Pharmaceuticals (92–102, 509 U.S. 579, 1993). In this case, the Supreme Court argued in its 1993 ruling that trial judges must ensure that expert testimony is reliable, and that in doing this the court must look at the expert’s methodology to determine whether the proffered evidence is actually scientific knowledge. Further, referring to works of Popper and Hempel the court stated that

ordinarily, a key question to be answered in determining whether a theory or technique is scientific knowledge … is whether it can be (and has been) tested. (Justice Blackmun, Daubert v. Merrell Dow Pharmaceuticals; see Other Internet Resources for a link to the opinion)

But as argued by Haack (2005a,b, 2010) and by Foster & Hubner (1999), by equating the question of whether a piece of testimony is reliable with the question whether it is scientific as indicated by a special methodology, the court was producing an inconsistent mixture of Popper’s and Hempel’s philosophies, and this has later led to considerable confusion in subsequent case rulings that drew on the Daubert case (see Haack 2010 for a detailed exposition).

The difficulties around identifying the methods of science are also reflected in the difficulties of identifying scientific misconduct in the form of improper application of the method or methods of science. One of the first and most influential attempts at defining misconduct in science was the US definition from 1989 that defined misconduct as

fabrication, falsification, plagiarism, or other practices that seriously deviate from those that are commonly accepted within the scientific community . (Code of Federal Regulations, part 50, subpart A., August 8, 1989, italics added)

However, the “other practices that seriously deviate” clause was heavily criticized because it could be used to suppress creative or novel science. For example, the National Academy of Science stated in their report Responsible Science (1992) that it

wishes to discourage the possibility that a misconduct complaint could be lodged against scientists based solely on their use of novel or unorthodox research methods. (NAS: 27)

This clause was therefore later removed from the definition. For an entry into the key philosophical literature on conduct in science, see Shamoo & Resnick (2009).

The question of the source of the success of science has been at the core of philosophy since the beginning of modern science. If viewed as a matter of epistemology more generally, scientific method is a part of the entire history of philosophy. Over that time, science and whatever methods its practitioners may employ have changed dramatically. Today, many philosophers have taken up the banners of pluralism or of practice to focus on what are, in effect, fine-grained and contextually limited examinations of scientific method. Others hope to shift perspectives in order to provide a renewed general account of what characterizes the activity we call science.

One such perspective has been offered recently by Hoyningen-Huene (2008, 2013), who argues from the history of philosophy of science that after three lengthy phases of characterizing science by its method, we are now in a phase where the belief in the existence of a positive scientific method has eroded and what has been left to characterize science is only its fallibility. First was a phase from Plato and Aristotle up until the 17 th century where the specificity of scientific knowledge was seen in its absolute certainty established by proof from evident axioms; next was a phase up to the mid-19 th century in which the means to establish the certainty of scientific knowledge had been generalized to include inductive procedures as well. In the third phase, which lasted until the last decades of the 20 th century, it was recognized that empirical knowledge was fallible, but it was still granted a special status due to its distinctive mode of production. But now in the fourth phase, according to Hoyningen-Huene, historical and philosophical studies have shown how “scientific methods with the characteristics as posited in the second and third phase do not exist” (2008: 168) and there is no longer any consensus among philosophers and historians of science about the nature of science. For Hoyningen-Huene, this is too negative a stance, and he therefore urges the question about the nature of science anew. His own answer to this question is that “scientific knowledge differs from other kinds of knowledge, especially everyday knowledge, primarily by being more systematic” (Hoyningen-Huene 2013: 14). Systematicity can have several different dimensions: among them are more systematic descriptions, explanations, predictions, defense of knowledge claims, epistemic connectedness, ideal of completeness, knowledge generation, representation of knowledge and critical discourse. Hence, what characterizes science is the greater care in excluding possible alternative explanations, the more detailed elaboration with respect to data on which predictions are based, the greater care in detecting and eliminating sources of error, the more articulate connections to other pieces of knowledge, etc. On this position, what characterizes science is not that the methods employed are unique to science, but that the methods are more carefully employed.

Another, similar approach has been offered by Haack (2003). She sets off, similar to Hoyningen-Huene, from a dissatisfaction with the recent clash between what she calls Old Deferentialism and New Cynicism. The Old Deferentialist position is that science progressed inductively by accumulating true theories confirmed by empirical evidence or deductively by testing conjectures against basic statements; while the New Cynics position is that science has no epistemic authority and no uniquely rational method and is merely just politics. Haack insists that contrary to the views of the New Cynics, there are objective epistemic standards, and there is something epistemologically special about science, even though the Old Deferentialists pictured this in a wrong way. Instead, she offers a new Critical Commonsensist account on which standards of good, strong, supportive evidence and well-conducted, honest, thorough and imaginative inquiry are not exclusive to the sciences, but the standards by which we judge all inquirers. In this sense, science does not differ in kind from other kinds of inquiry, but it may differ in the degree to which it requires broad and detailed background knowledge and a familiarity with a technical vocabulary that only specialists may possess.

• Aikenhead, G.S., 1987, “High-school graduates’ beliefs about science-technology-society. III. Characteristics and limitations of scientific knowledge”, Science Education , 71(4): 459–487.
• Allchin, D., H.M. Andersen and K. Nielsen, 2014, “Complementary Approaches to Teaching Nature of Science: Integrating Student Inquiry, Historical Cases, and Contemporary Cases in Classroom Practice”, Science Education , 98: 461–486.
• Anderson, C., 2008, “The end of theory: The data deluge makes the scientific method obsolete”, Wired magazine , 16(7): 16–07
• Arabatzis, T., 2006, “On the inextricability of the context of discovery and the context of justification”, in Revisiting Discovery and Justification , J. Schickore and F. Steinle (eds.), Dordrecht: Springer, pp. 215–230.
• Barnes, J. (ed.), 1984, The Complete Works of Aristotle, Vols I and II , Princeton: Princeton University Press.
• Barnes, B. and D. Bloor, 1982, “Relativism, Rationalism, and the Sociology of Knowledge”, in Rationality and Relativism , M. Hollis and S. Lukes (eds.), Cambridge: MIT Press, pp. 1–20.
• Bauer, H.H., 1992, Scientific Literacy and the Myth of the Scientific Method , Urbana: University of Illinois Press.
• Bechtel, W. and R.C. Richardson, 1993, Discovering complexity , Princeton, NJ: Princeton University Press.
• Berkeley, G., 1734, The Analyst in De Motu and The Analyst: A Modern Edition with Introductions and Commentary , D. Jesseph (trans. and ed.), Dordrecht: Kluwer Academic Publishers, 1992.
• Blachowicz, J., 2009, “How science textbooks treat scientific method: A philosopher’s perspective”, The British Journal for the Philosophy of Science , 60(2): 303–344.
• Bloor, D., 1991, Knowledge and Social Imagery , Chicago: University of Chicago Press, 2 nd edition.
• Boyle, R., 1682, New experiments physico-mechanical, touching the air , Printed by Miles Flesher for Richard Davis, bookseller in Oxford.
• Bridgman, P.W., 1927, The Logic of Modern Physics , New York: Macmillan.
• –––, 1956, “The Methodological Character of Theoretical Concepts”, in The Foundations of Science and the Concepts of Science and Psychology , Herbert Feigl and Michael Scriven (eds.), Minnesota: University of Minneapolis Press, pp. 38–76.
• Burian, R., 1997, “Exploratory Experimentation and the Role of Histochemical Techniques in the Work of Jean Brachet, 1938–1952”, History and Philosophy of the Life Sciences , 19(1): 27–45.
• –––, 2007, “On microRNA and the need for exploratory experimentation in post-genomic molecular biology”, History and Philosophy of the Life Sciences , 29(3): 285–311.
• Carnap, R., 1928, Der logische Aufbau der Welt , Berlin: Bernary, transl. by R.A. George, The Logical Structure of the World , Berkeley: University of California Press, 1967.
• –––, 1956, “The methodological character of theoretical concepts”, Minnesota studies in the philosophy of science , 1: 38–76.
• Carrol, S., and D. Goodstein, 2009, “Defining the scientific method”, Nature Methods , 6: 237.
• Churchman, C.W., 1948, “Science, Pragmatics, Induction”, Philosophy of Science , 15(3): 249–268.
• Cooper, J. (ed.), 1997, Plato: Complete Works , Indianapolis: Hackett.
• Darden, L., 1991, Theory Change in Science: Strategies from Mendelian Genetics , Oxford: Oxford University Press
• Dewey, J., 1910, How we think , New York: Dover Publications (reprinted 1997).
• Douglas, H., 2009, Science, Policy, and the Value-Free Ideal , Pittsburgh: University of Pittsburgh Press.
• Dupré, J., 2004, “Miracle of Monism ”, in Naturalism in Question , Mario De Caro and David Macarthur (eds.), Cambridge, MA: Harvard University Press, pp. 36–58.
• Elliott, K.C., 2007, “Varieties of exploratory experimentation in nanotoxicology”, History and Philosophy of the Life Sciences , 29(3): 311–334.
• Elliott, K. C., and T. Richards (eds.), 2017, Exploring inductive risk: Case studies of values in science , Oxford: Oxford University Press.
• Falcon, Andrea, 2005, Aristotle and the science of nature: Unity without uniformity , Cambridge: Cambridge University Press.
• Feyerabend, P., 1978, Science in a Free Society , London: New Left Books
• –––, 1988, Against Method , London: Verso, 2 nd edition.
• Fisher, R.A., 1955, “Statistical Methods and Scientific Induction”, Journal of The Royal Statistical Society. Series B (Methodological) , 17(1): 69–78.
• Foster, K. and P.W. Huber, 1999, Judging Science. Scientific Knowledge and the Federal Courts , Cambridge: MIT Press.
• Fox Keller, E., 2003, “Models, Simulation, and ‘computer experiments’”, in The Philosophy of Scientific Experimentation , H. Radder (ed.), Pittsburgh: Pittsburgh University Press, 198–215.
• Gilbert, G., 1976, “The transformation of research findings into scientific knowledge”, Social Studies of Science , 6: 281–306.
• Gimbel, S., 2011, Exploring the Scientific Method , Chicago: University of Chicago Press.
• Goodman, N., 1965, Fact , Fiction, and Forecast , Indianapolis: Bobbs-Merrill.
• Haack, S., 1995, “Science is neither sacred nor a confidence trick”, Foundations of Science , 1(3): 323–335.
• –––, 2003, Defending science—within reason , Amherst: Prometheus.
• –––, 2005a, “Disentangling Daubert: an epistemological study in theory and practice”, Journal of Philosophy, Science and Law , 5, Haack 2005a available online . doi:10.5840/jpsl2005513
• –––, 2005b, “Trial and error: The Supreme Court’s philosophy of science”, American Journal of Public Health , 95: S66-S73.
• –––, 2010, “Federal Philosophy of Science: A Deconstruction-and a Reconstruction”, NYUJL & Liberty , 5: 394.
• Hangel, N. and J. Schickore, 2017, “Scientists’ conceptions of good research practice”, Perspectives on Science , 25(6): 766–791
• Harper, W.L., 2011, Isaac Newton’s Scientific Method: Turning Data into Evidence about Gravity and Cosmology , Oxford: Oxford University Press.
• Hempel, C., 1950, “Problems and Changes in the Empiricist Criterion of Meaning”, Revue Internationale de Philosophie , 41(11): 41–63.
• –––, 1951, “The Concept of Cognitive Significance: A Reconsideration”, Proceedings of the American Academy of Arts and Sciences , 80(1): 61–77.
• –––, 1965, Aspects of scientific explanation and other essays in the philosophy of science , New York–London: Free Press.
• –––, 1966, Philosophy of Natural Science , Englewood Cliffs: Prentice-Hall.
• Holmes, F.L., 1987, “Scientific writing and scientific discovery”, Isis , 78(2): 220–235.
• Howard, D., 2003, “Two left turns make a right: On the curious political career of North American philosophy of science at midcentury”, in Logical Empiricism in North America , G.L. Hardcastle & A.W. Richardson (eds.), Minneapolis: University of Minnesota Press, pp. 25–93.
• Hoyningen-Huene, P., 2008, “Systematicity: The nature of science”, Philosophia , 36(2): 167–180.
• –––, 2013, Systematicity. The Nature of Science , Oxford: Oxford University Press.
• Howie, D., 2002, Interpreting probability: Controversies and developments in the early twentieth century , Cambridge: Cambridge University Press.
• Hughes, R., 1999, “The Ising Model, Computer Simulation, and Universal Physics”, in Models as Mediators , M. Morgan and M. Morrison (eds.), Cambridge: Cambridge University Press, pp. 97–145
• Hume, D., 1739, A Treatise of Human Nature , D. Fate Norton and M.J. Norton (eds.), Oxford: Oxford University Press, 2000.
• Humphreys, P., 1995, “Computational science and scientific method”, Minds and Machines , 5(1): 499–512.
• ICMJE, 2013, “Recommendations for the Conduct, Reporting, Editing, and Publication of Scholarly Work in Medical Journals”, International Committee of Medical Journal Editors, available online , accessed August 13 2014
• Jeffrey, R.C., 1956, “Valuation and Acceptance of Scientific Hypotheses”, Philosophy of Science , 23(3): 237–246.
• Kaufmann, W.J., and L.L. Smarr, 1993, Supercomputing and the Transformation of Science , New York: Scientific American Library.
• Knorr-Cetina, K., 1981, The Manufacture of Knowledge , Oxford: Pergamon Press.
• Krohs, U., 2012, “Convenience experimentation”, Studies in History and Philosophy of Biological and BiomedicalSciences , 43: 52–57.
• Kuhn, T.S., 1962, The Structure of Scientific Revolutions , Chicago: University of Chicago Press
• Latour, B. and S. Woolgar, 1986, Laboratory Life: The Construction of Scientific Facts , Princeton: Princeton University Press, 2 nd edition.
• Laudan, L., 1968, “Theories of scientific method from Plato to Mach”, History of Science , 7(1): 1–63.
• Lenhard, J., 2006, “Models and statistical inference: The controversy between Fisher and Neyman-Pearson”, The British Journal for the Philosophy of Science , 57(1): 69–91.
• Leonelli, S., 2012, “Making Sense of Data-Driven Research in the Biological and the Biomedical Sciences”, Studies in the History and Philosophy of the Biological and Biomedical Sciences , 43(1): 1–3.
• Levi, I., 1960, “Must the scientist make value judgments?”, Philosophy of Science , 57(11): 345–357
• Lindley, D., 1991, Theory Change in Science: Strategies from Mendelian Genetics , Oxford: Oxford University Press.
• Lipton, P., 2004, Inference to the Best Explanation , London: Routledge, 2 nd edition.
• Marks, H.M., 2000, The progress of experiment: science and therapeutic reform in the United States, 1900–1990 , Cambridge: Cambridge University Press.
• Mazzochi, F., 2015, “Could Big Data be the end of theory in science?”, EMBO reports , 16: 1250–1255.
• Mayo, D.G., 1996, Error and the Growth of Experimental Knowledge , Chicago: University of Chicago Press.
• McComas, W.F., 1996, “Ten myths of science: Reexamining what we think we know about the nature of science”, School Science and Mathematics , 96(1): 10–16.
• Medawar, P.B., 1963/1996, “Is the scientific paper a fraud”, in The Strange Case of the Spotted Mouse and Other Classic Essays on Science , Oxford: Oxford University Press, 33–39.
• Mill, J.S., 1963, Collected Works of John Stuart Mill , J. M. Robson (ed.), Toronto: University of Toronto Press
• NAS, 1992, Responsible Science: Ensuring the integrity of the research process , Washington DC: National Academy Press.
• Nersessian, N.J., 1987, “A cognitive-historical approach to meaning in scientific theories”, in The process of science , N. Nersessian (ed.), Berlin: Springer, pp. 161–177.
• –––, 2008, Creating Scientific Concepts , Cambridge: MIT Press.
• Newton, I., 1726, Philosophiae naturalis Principia Mathematica (3 rd edition), in The Principia: Mathematical Principles of Natural Philosophy: A New Translation , I.B. Cohen and A. Whitman (trans.), Berkeley: University of California Press, 1999.
• –––, 1704, Opticks or A Treatise of the Reflections, Refractions, Inflections & Colors of Light , New York: Dover Publications, 1952.
• Neyman, J., 1956, “Note on an Article by Sir Ronald Fisher”, Journal of the Royal Statistical Society. Series B (Methodological) , 18: 288–294.
• Nickles, T., 1987, “Methodology, heuristics, and rationality”, in Rational changes in science: Essays on Scientific Reasoning , J.C. Pitt (ed.), Berlin: Springer, pp. 103–132.
• Nicod, J., 1924, Le problème logique de l’induction , Paris: Alcan. (Engl. transl. “The Logical Problem of Induction”, in Foundations of Geometry and Induction , London: Routledge, 2000.)
• Nola, R. and H. Sankey, 2000a, “A selective survey of theories of scientific method”, in Nola and Sankey 2000b: 1–65.
• –––, 2000b, After Popper, Kuhn and Feyerabend. Recent Issues in Theories of Scientific Method , London: Springer.
• –––, 2007, Theories of Scientific Method , Stocksfield: Acumen.
• Norton, S., and F. Suppe, 2001, “Why atmospheric modeling is good science”, in Changing the Atmosphere: Expert Knowledge and Environmental Governance , C. Miller and P. Edwards (eds.), Cambridge, MA: MIT Press, 88–133.
• O’Malley, M., 2007, “Exploratory experimentation and scientific practice: Metagenomics and the proteorhodopsin case”, History and Philosophy of the Life Sciences , 29(3): 337–360.
• O’Malley, M., C. Haufe, K. Elliot, and R. Burian, 2009, “Philosophies of Funding”, Cell , 138: 611–615.
• Oreskes, N., K. Shrader-Frechette, and K. Belitz, 1994, “Verification, Validation and Confirmation of Numerical Models in the Earth Sciences”, Science , 263(5147): 641–646.
• Osborne, J., S. Simon, and S. Collins, 2003, “Attitudes towards science: a review of the literature and its implications”, International Journal of Science Education , 25(9): 1049–1079.
• Parascandola, M., 1998, “Epidemiology—2 nd -Rate Science”, Public Health Reports , 113(4): 312–320.
• Parker, W., 2008a, “Franklin, Holmes and the Epistemology of Computer Simulation”, International Studies in the Philosophy of Science , 22(2): 165–83.
• –––, 2008b, “Computer Simulation through an Error-Statistical Lens”, Synthese , 163(3): 371–84.
• Pearson, K. 1892, The Grammar of Science , London: J.M. Dents and Sons, 1951
• Pearson, E.S., 1955, “Statistical Concepts in Their Relation to Reality”, Journal of the Royal Statistical Society , B, 17: 204–207.
• Pickering, A., 1984, Constructing Quarks: A Sociological History of Particle Physics , Edinburgh: Edinburgh University Press.
• Popper, K.R., 1959, The Logic of Scientific Discovery , London: Routledge, 2002
• –––, 1963, Conjectures and Refutations , London: Routledge, 2002.
• –––, 1985, Unended Quest: An Intellectual Autobiography , La Salle: Open Court Publishing Co..
• Rudner, R., 1953, “The Scientist Qua Scientist Making Value Judgments”, Philosophy of Science , 20(1): 1–6.
• Rudolph, J.L., 2005, “Epistemology for the masses: The origin of ‘The Scientific Method’ in American Schools”, History of Education Quarterly , 45(3): 341–376
• Schickore, J., 2008, “Doing science, writing science”, Philosophy of Science , 75: 323–343.
• Schickore, J. and N. Hangel, 2019, “‘It might be this, it should be that…’ uncertainty and doubt in day-to-day science practice”, European Journal for Philosophy of Science , 9(2): 31. doi:10.1007/s13194-019-0253-9
• Shamoo, A.E. and D.B. Resnik, 2009, Responsible Conduct of Research , Oxford: Oxford University Press.
• Shank, J.B., 2008, The Newton Wars and the Beginning of the French Enlightenment , Chicago: The University of Chicago Press.
• Shapin, S. and S. Schaffer, 1985, Leviathan and the air-pump , Princeton: Princeton University Press.
• Smith, G.E., 2002, “The Methodology of the Principia”, in The Cambridge Companion to Newton , I.B. Cohen and G.E. Smith (eds.), Cambridge: Cambridge University Press, 138–173.
• Snyder, L.J., 1997a, “Discoverers’ Induction”, Philosophy of Science , 64: 580–604.
• –––, 1997b, “The Mill-Whewell Debate: Much Ado About Induction”, Perspectives on Science , 5: 159–198.
• –––, 1999, “Renovating the Novum Organum: Bacon, Whewell and Induction”, Studies in History and Philosophy of Science , 30: 531–557.
• Sober, E., 2008, Evidence and Evolution. The logic behind the science , Cambridge: Cambridge University Press
• Sprenger, J. and S. Hartmann, 2019, Bayesian philosophy of science , Oxford: Oxford University Press.
• Steinle, F., 1997, “Entering New Fields: Exploratory Uses of Experimentation”, Philosophy of Science (Proceedings), 64: S65–S74.
• –––, 2002, “Experiments in History and Philosophy of Science”, Perspectives on Science , 10(4): 408–432.
• Strasser, B.J., 2012, “Data-driven sciences: From wonder cabinets to electronic databases”, Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences , 43(1): 85–87.
• Succi, S. and P.V. Coveney, 2018, “Big data: the end of the scientific method?”, Philosophical Transactions of the Royal Society A , 377: 20180145. doi:10.1098/rsta.2018.0145
• Suppe, F., 1998, “The Structure of a Scientific Paper”, Philosophy of Science , 65(3): 381–405.
• Swijtink, Z.G., 1987, “The objectification of observation: Measurement and statistical methods in the nineteenth century”, in The probabilistic revolution. Ideas in History, Vol. 1 , L. Kruger (ed.), Cambridge MA: MIT Press, pp. 261–285.
• Waters, C.K., 2007, “The nature and context of exploratory experimentation: An introduction to three case studies of exploratory research”, History and Philosophy of the Life Sciences , 29(3): 275–284.
• Weinberg, S., 1995, “The methods of science… and those by which we live”, Academic Questions , 8(2): 7–13.
• Weissert, T., 1997, The Genesis of Simulation in Dynamics: Pursuing the Fermi-Pasta-Ulam Problem , New York: Springer Verlag.
• William H., 1628, Exercitatio Anatomica de Motu Cordis et Sanguinis in Animalibus , in On the Motion of the Heart and Blood in Animals , R. Willis (trans.), Buffalo: Prometheus Books, 1993.
• Winsberg, E., 2010, Science in the Age of Computer Simulation , Chicago: University of Chicago Press.
• Wivagg, D. & D. Allchin, 2002, “The Dogma of the Scientific Method”, The American Biology Teacher , 64(9): 645–646

How to cite this entry . Preview the PDF version of this entry at the Friends of the SEP Society . Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers , with links to its database.

• Blackmun opinion , in Daubert v. Merrell Dow Pharmaceuticals (92–102), 509 U.S. 579 (1993).
• Scientific Method at philpapers. Darrell Rowbottom (ed.).
• Recent Articles | Scientific Method | The Scientist Magazine

al-Kindi | Albert the Great [= Albertus magnus] | Aquinas, Thomas | Arabic and Islamic Philosophy, disciplines in: natural philosophy and natural science | Arabic and Islamic Philosophy, historical and methodological topics in: Greek sources | Arabic and Islamic Philosophy, historical and methodological topics in: influence of Arabic and Islamic Philosophy on the Latin West | Aristotle | Bacon, Francis | Bacon, Roger | Berkeley, George | biology: experiment in | Boyle, Robert | Cambridge Platonists | confirmation | Descartes, René | Enlightenment | epistemology | epistemology: Bayesian | epistemology: social | Feyerabend, Paul | Galileo Galilei | Grosseteste, Robert | Hempel, Carl | Hume, David | Hume, David: Newtonianism and Anti-Newtonianism | induction: problem of | Kant, Immanuel | Kuhn, Thomas | Leibniz, Gottfried Wilhelm | Locke, John | Mill, John Stuart | More, Henry | Neurath, Otto | Newton, Isaac | Newton, Isaac: philosophy | Ockham [Occam], William | operationalism | Peirce, Charles Sanders | Plato | Popper, Karl | rationality: historicist theories of | Reichenbach, Hans | reproducibility, scientific | Schlick, Moritz | science: and pseudo-science | science: theory and observation in | science: unity of | scientific discovery | scientific knowledge: social dimensions of | simulations in science | skepticism: medieval | space and time: absolute and relational space and motion, post-Newtonian theories | Vienna Circle | Whewell, William | Zabarella, Giacomo

Copyright © 2021 by Brian Hepburn < brian . hepburn @ wichita . edu > Hanne Andersen < hanne . andersen @ ind . ku . dk >

• Accessibility

Support SEP

Mirror sites.

View this site from another server:

• Info about mirror sites

The Stanford Encyclopedia of Philosophy is copyright © 2023 by The Metaphysics Research Lab , Department of Philosophy, Stanford University

Library of Congress Catalog Data: ISSN 1095-5054

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.4: The Scientific Method- How Chemists Think

• Last updated
• Save as PDF
• Page ID 97965

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Identify the components of the scientific method.

Scientists search for answers to questions and solutions to problems by using a procedure called the scientific method. This procedure consists of making observations, formulating hypotheses, and designing experiments; which leads to additional observations, hypotheses, and experiments in repeated cycles (Figure \(\PageIndex{1}\)).

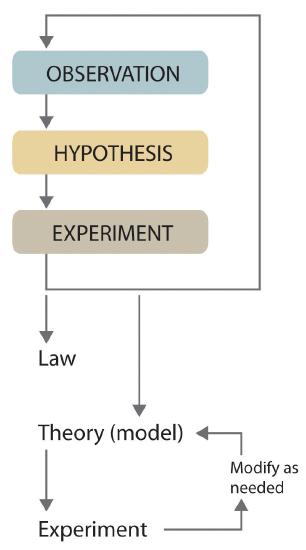
Step 1: Make observations

Observations can be qualitative or quantitative. Qualitative observations describe properties or occurrences in ways that do not rely on numbers. Examples of qualitative observations include the following: "the outside air temperature is cooler during the winter season," "table salt is a crystalline solid," "sulfur crystals are yellow," and "dissolving a penny in dilute nitric acid forms a blue solution and a brown gas." Quantitative observations are measurements, which by definition consist of both a number and a unit. Examples of quantitative observations include the following: "the melting point of crystalline sulfur is 115.21° Celsius," and "35.9 grams of table salt—the chemical name of which is sodium chloride—dissolve in 100 grams of water at 20° Celsius." For the question of the dinosaurs’ extinction, the initial observation was quantitative: iridium concentrations in sediments dating to 66 million years ago were 20–160 times higher than normal.

Step 2: Formulate a hypothesis

After deciding to learn more about an observation or a set of observations, scientists generally begin an investigation by forming a hypothesis, a tentative explanation for the observation(s). The hypothesis may not be correct, but it puts the scientist’s understanding of the system being studied into a form that can be tested. For example, the observation that we experience alternating periods of light and darkness corresponding to observed movements of the sun, moon, clouds, and shadows is consistent with either one of two hypotheses:

• Earth rotates on its axis every 24 hours, alternately exposing one side to the sun.
• The sun revolves around Earth every 24 hours.

Suitable experiments can be designed to choose between these two alternatives. For the disappearance of the dinosaurs, the hypothesis was that the impact of a large extraterrestrial object caused their extinction. Unfortunately (or perhaps fortunately), this hypothesis does not lend itself to direct testing by any obvious experiment, but scientists can collect additional data that either support or refute it.

Step 3: Design and perform experiments

After a hypothesis has been formed, scientists conduct experiments to test its validity. Experiments are systematic observations or measurements, preferably made under controlled conditions—that is—under conditions in which a single variable changes.

Step 4: Accept or modify the hypothesis

A properly designed and executed experiment enables a scientist to determine whether or not the original hypothesis is valid. If the hypothesis is valid, the scientist can proceed to step 5. In other cases, experiments often demonstrate that the hypothesis is incorrect or that it must be modified and requires further experimentation.

Step 5: Development into a law and/or theory

More experimental data are then collected and analyzed, at which point a scientist may begin to think that the results are sufficiently reproducible (i.e., dependable) to merit being summarized in a law, a verbal or mathematical description of a phenomenon that allows for general predictions. A law simply states what happens; it does not address the question of why.

One example of a law, the law of definite proportions , which was discovered by the French scientist Joseph Proust (1754–1826), states that a chemical substance always contains the same proportions of elements by mass. Thus, sodium chloride (table salt) always contains the same proportion by mass of sodium to chlorine, in this case 39.34% sodium and 60.66% chlorine by mass, and sucrose (table sugar) is always 42.11% carbon, 6.48% hydrogen, and 51.41% oxygen by mass.

Whereas a law states only what happens, a theory attempts to explain why nature behaves as it does. Laws are unlikely to change greatly over time unless a major experimental error is discovered. In contrast, a theory, by definition, is incomplete and imperfect, evolving with time to explain new facts as they are discovered.

Because scientists can enter the cycle shown in Figure \(\PageIndex{1}\) at any point, the actual application of the scientific method to different topics can take many different forms. For example, a scientist may start with a hypothesis formed by reading about work done by others in the field, rather than by making direct observations.

Example \(\PageIndex{1}\)

Classify each statement as a law, a theory, an experiment, a hypothesis, an observation.

• Ice always floats on liquid water.
• Birds evolved from dinosaurs.
• Hot air is less dense than cold air, probably because the components of hot air are moving more rapidly.
• When 10 g of ice were added to 100 mL of water at 25°C, the temperature of the water decreased to 15.5°C after the ice melted.
• The ingredients of Ivory soap were analyzed to see whether it really is 99.44% pure, as advertised.
• This is a general statement of a relationship between the properties of liquid and solid water, so it is a law.
• This is a possible explanation for the origin of birds, so it is a hypothesis.
• This is a statement that tries to explain the relationship between the temperature and the density of air based on fundamental principles, so it is a theory.
• The temperature is measured before and after a change is made in a system, so these are observations.
• This is an analysis designed to test a hypothesis (in this case, the manufacturer’s claim of purity), so it is an experiment.

Exercise \(\PageIndex{1}\) 

Classify each statement as a law, a theory, an experiment, a hypothesis, a qualitative observation, or a quantitative observation.

• Measured amounts of acid were added to a Rolaids tablet to see whether it really “consumes 47 times its weight in excess stomach acid.”
• Heat always flows from hot objects to cooler ones, not in the opposite direction.
• The universe was formed by a massive explosion that propelled matter into a vacuum.
• Michael Jordan is the greatest pure shooter to ever play professional basketball.
• Limestone is relatively insoluble in water, but dissolves readily in dilute acid with the evolution of a gas.

The scientific method is a method of investigation involving experimentation and observation to acquire new knowledge, solve problems, and answer questions. The key steps in the scientific method include the following:

• Step 1: Make observations.
• Step 2: Formulate a hypothesis.
• Step 3: Test the hypothesis through experimentation.
• Step 4: Accept or modify the hypothesis.
• Step 5: Develop into a law and/or a theory.

Contributions & Attributions

What Are The Steps Of The Scientific Method?

Julia Simkus

Editor at Simply Psychology

BA (Hons) Psychology, Princeton University

Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.

Learn about our Editorial Process

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

Science is not just knowledge. It is also a method for obtaining knowledge. Scientific understanding is organized into theories.

The scientific method is a step-by-step process used by researchers and scientists to determine if there is a relationship between two or more variables. Psychologists use this method to conduct psychological research, gather data, process information, and describe behaviors.

It involves careful observation, asking questions, formulating hypotheses, experimental testing, and refining hypotheses based on experimental findings.

How it is Used

The scientific method can be applied broadly in science across many different fields, such as chemistry, physics, geology, and psychology. In a typical application of this process, a researcher will develop a hypothesis, test this hypothesis, and then modify the hypothesis based on the outcomes of the experiment.

The process is then repeated with the modified hypothesis until the results align with the observed phenomena. Detailed steps of the scientific method are described below.

Keep in mind that the scientific method does not have to follow this fixed sequence of steps; rather, these steps represent a set of general principles or guidelines.

7 Steps of the Scientific Method

Psychology uses an empirical approach.

Empiricism (founded by John Locke) states that the only source of knowledge comes through our senses – e.g., sight, hearing, touch, etc.

Empirical evidence does not rely on argument or belief. Thus, empiricism is the view that all knowledge is based on or may come from direct observation and experience.

The empiricist approach of gaining knowledge through experience quickly became the scientific approach and greatly influenced the development of physics and chemistry in the 17th and 18th centuries.

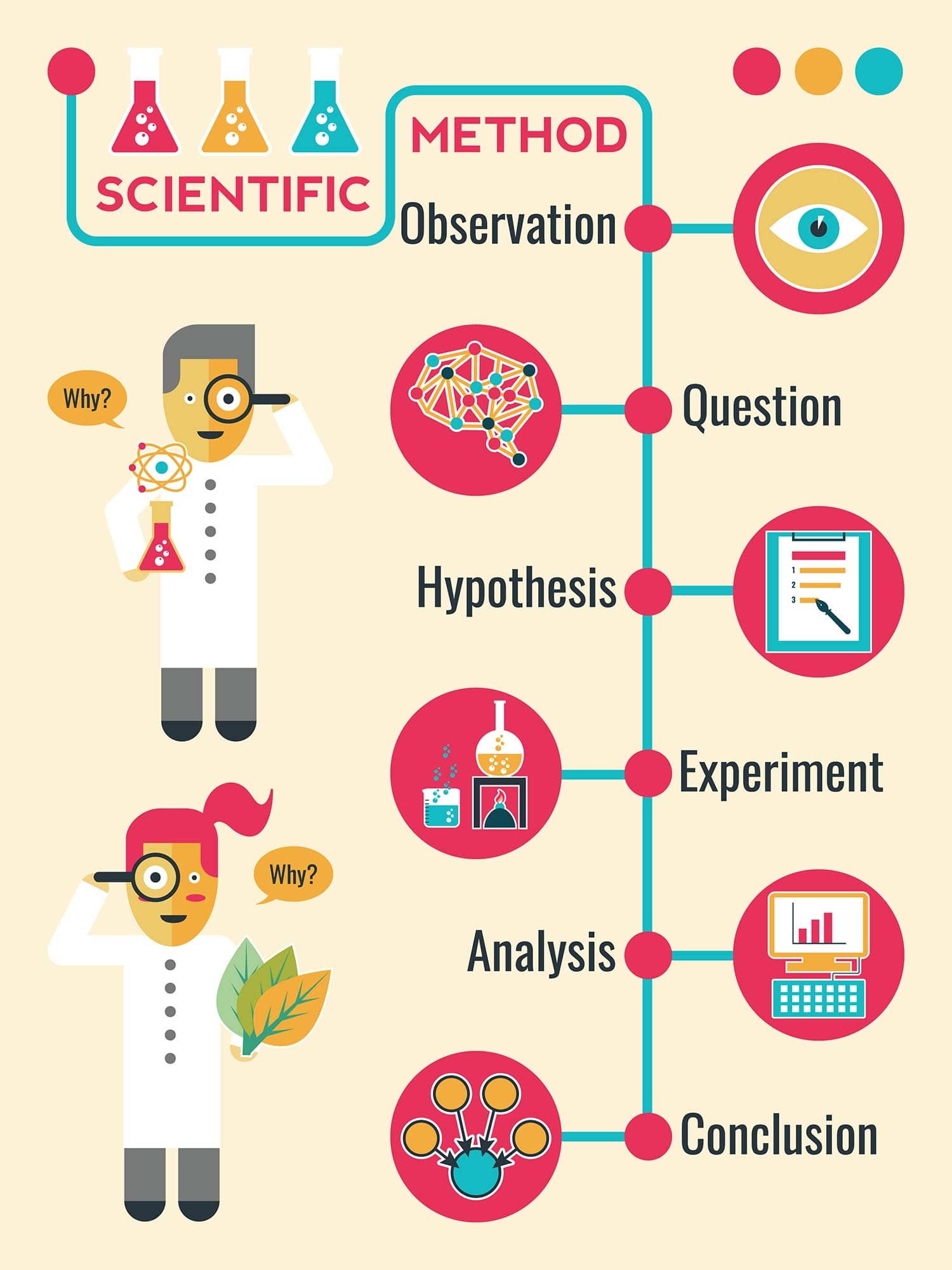
Step 1: Make an Observation (Theory Construction)

Every researcher starts at the very beginning. Before diving in and exploring something, one must first determine what they will study – it seems simple enough!

By making observations, researchers can establish an area of interest. Once this topic of study has been chosen, a researcher should review existing literature to gain insight into what has already been tested and determine what questions remain unanswered.

This assessment will provide helpful information about what has already been comprehended about the specific topic and what questions remain, and if one can go and answer them.

Specifically, a literature review might implicate examining a substantial amount of documented material from academic journals to books dating back decades. The most appropriate information gathered by the researcher will be shown in the introduction section or abstract of the published study results.

The background material and knowledge will help the researcher with the first significant step in conducting a psychology study, which is formulating a research question.

This is the inductive phase of the scientific process. Observations yield information that is used to formulate theories as explanations. A theory is a well-developed set of ideas that propose an explanation for observed phenomena.

Inductive reasoning moves from specific premises to a general conclusion. It starts with observations of phenomena in the natural world and derives a general law.

Step 2: Ask a Question

Once a researcher has made observations and conducted background research, the next step is to ask a scientific question. A scientific question must be defined, testable, and measurable.

A useful approach to develop a scientific question is: “What is the effect of…?” or “How does X affect Y?”

To answer an experimental question, a researcher must identify two variables: the independent and dependent variables.

The independent variable is the variable manipulated (the cause), and the dependent variable is the variable being measured (the effect).

An example of a research question could be, “Is handwriting or typing more effective for retaining information?” Answering the research question and proposing a relationship between the two variables is discussed in the next step.

Step 3: Form a Hypothesis (Make Predictions)

A hypothesis is an educated guess about the relationship between two or more variables. A hypothesis is an attempt to answer your research question based on prior observation and background research. Theories tend to be too complex to be tested all at once; instead, researchers create hypotheses to test specific aspects of a theory.

For example, a researcher might ask about the connection between sleep and educational performance. Do students who get less sleep perform worse on tests at school?

It is crucial to think about different questions one might have about a particular topic to formulate a reasonable hypothesis. It would help if one also considered how one could investigate the causalities.

It is important that the hypothesis is both testable against reality and falsifiable. This means that it can be tested through an experiment and can be proven wrong.

The falsification principle, proposed by Karl Popper , is a way of demarcating science from non-science. It suggests that for a theory to be considered scientific, it must be able to be tested and conceivably proven false.

To test a hypothesis, we first assume that there is no difference between the populations from which the samples were taken. This is known as the null hypothesis and predicts that the independent variable will not influence the dependent variable.

Examples of “if…then…” Hypotheses:

• If one gets less than 6 hours of sleep, then one will do worse on tests than if one obtains more rest.
• If one drinks lots of water before going to bed, one will have to use the bathroom often at night.
• If one practices exercising and lighting weights, then one’s body will begin to build muscle.

The research hypothesis is often called the alternative hypothesis and predicts what change(s) will occur in the dependent variable when the independent variable is manipulated.

It states that the results are not due to chance and that they are significant in terms of supporting the theory being investigated.

Although one could state and write a scientific hypothesis in many ways, hypotheses are usually built like “if…then…” statements.

Step 4: Run an Experiment (Gather Data)

The next step in the scientific method is to test your hypothesis and collect data. A researcher will design an experiment to test the hypothesis and gather data that will either support or refute the hypothesis.

The exact research methods used to examine a hypothesis depend on what is being studied. A psychologist might utilize two primary forms of research, experimental research, and descriptive research.

The scientific method is objective in that researchers do not let preconceived ideas or biases influence the collection of data and is systematic in that experiments are conducted in a logical way.

Experimental Research

Experimental research is used to investigate cause-and-effect associations between two or more variables. This type of research systematically controls an independent variable and measures its effect on a specified dependent variable.

Experimental research involves manipulating an independent variable and measuring the effect(s) on the dependent variable. Repeating the experiment multiple times is important to confirm that your results are accurate and consistent.

One of the significant advantages of this method is that it permits researchers to determine if changes in one variable cause shifts in each other.

While experiments in psychology typically have many moving parts (and can be relatively complex), an easy investigation is rather fundamental. Still, it does allow researchers to specify cause-and-effect associations between variables.

Most simple experiments use a control group, which involves those who do not receive the treatment, and an experimental group, which involves those who do receive the treatment.

An example of experimental research would be when a pharmaceutical company wants to test a new drug. They give one group a placebo (control group) and the other the actual pill (experimental group).

Descriptive Research

Descriptive research is generally used when it is challenging or even impossible to control the variables in question. Examples of descriptive analysis include naturalistic observation, case studies , and correlation studies .

One example of descriptive research includes phone surveys that marketers often use. While they typically do not allow researchers to identify cause and effect, correlational studies are quite common in psychology research. They make it possible to spot associations between distinct variables and measure the solidity of those relationships.

Step 5: Analyze the Data and Draw Conclusions

Once a researcher has designed and done the investigation and collected sufficient data, it is time to inspect this gathered information and judge what has been found. Researchers can summarize the data, interpret the results, and draw conclusions based on this evidence using analyses and statistics.

Upon completion of the experiment, you can collect your measurements and analyze the data using statistics. Based on the outcomes, you will either reject or confirm your hypothesis.

Analyze the Data

So, how does a researcher determine what the results of their study mean? Statistical analysis can either support or refute a researcher’s hypothesis and can also be used to determine if the conclusions are statistically significant.

When outcomes are said to be “statistically significant,” it is improbable that these results are due to luck or chance. Based on these observations, investigators must then determine what the results mean.

An experiment will support a hypothesis in some circumstances, but sometimes it fails to be truthful in other cases.

What occurs if the developments of a psychology investigation do not endorse the researcher’s hypothesis? It does mean that the study was worthless. Simply because the findings fail to defend the researcher’s hypothesis does not mean that the examination is not helpful or instructive.

This kind of research plays a vital role in supporting scientists in developing unexplored questions and hypotheses to investigate in the future. After decisions have been made, the next step is to communicate the results with the rest of the scientific community.

This is an integral part of the process because it contributes to the general knowledge base and can assist other scientists in finding new research routes to explore.

If the hypothesis is not supported, a researcher should acknowledge the experiment’s results, formulate a new hypothesis, and develop a new experiment.

We must avoid any reference to results proving a theory as this implies 100% certainty, and there is always a chance that evidence may exist that could refute a theory.

Draw Conclusions and Interpret the Data

When the empirical observations disagree with the hypothesis, a number of possibilities must be considered. It might be that the theory is incorrect, in which case it needs altering, so it fully explains the data.

Alternatively, it might be that the hypothesis was poorly derived from the original theory, in which case the scientists were expecting the wrong thing to happen.

It might also be that the research was poorly conducted, or used an inappropriate method, or there were factors in play that the researchers did not consider. This will begin the process of the scientific method again.

If the hypothesis is supported, the researcher can find more evidence to support their hypothesis or look for counter-evidence to strengthen their hypothesis further.

In either scenario, the researcher should share their results with the greater scientific community.

Step 6: Share Your Results

One of the final stages of the research cycle involves the publication of the research. Once the report is written, the researcher(s) may submit the work for publication in an appropriate journal.

Usually, this is done by writing up a study description and publishing the article in a professional or academic journal. The studies and conclusions of psychological work can be seen in peer-reviewed journals such as  Developmental Psychology , Psychological Bulletin, the  Journal of Social Psychology, and numerous others.

Scientists should report their findings by writing up a description of their study and any subsequent findings. This enables other researchers to build upon the present research or replicate the results.

As outlined by the American Psychological Association (APA), there is a typical structure of a journal article that follows a specified format. In these articles, researchers:

• Supply a brief narrative and background on previous research
• Give their hypothesis
• Specify who participated in the study and how they were chosen
• Provide operational definitions for each variable
• Explain the measures and methods used to collect data
• Describe how the data collected was interpreted
• Discuss what the outcomes mean

A detailed record of psychological studies and all scientific studies is vital to clearly explain the steps and procedures used throughout the study. So that other researchers can try this experiment too and replicate the results.

The editorial process utilized by academic and professional journals guarantees that each submitted article undergoes a thorough peer review to help assure that the study is scientifically sound. Once published, the investigation becomes another piece of the current puzzle of our knowledge “base” on that subject.

This last step is important because all results, whether they supported or did not support the hypothesis, can contribute to the scientific community. Publication of empirical observations leads to more ideas that are tested against the real world, and so on. In this sense, the scientific process is circular.

The editorial process utilized by academic and professional journals guarantees that each submitted article undergoes a thorough peer review to help assure that the study is scientifically sound.

Once published, the investigation becomes another piece of the current puzzle of our knowledge “base” on that subject.

By replicating studies, psychologists can reduce errors, validate theories, and gain a stronger understanding of a particular topic.

Step 7: Repeat the Scientific Method (Iteration)

Now, if one’s hypothesis turns out to be accurate, find more evidence or find counter-evidence. If one’s hypothesis is false, create a new hypothesis or try again.

One may wish to revise their first hypothesis to make a more niche experiment to design or a different specific question to test.

The amazingness of the scientific method is that it is a comprehensive and straightforward process that scientists, and everyone, can utilize over and over again.

So, draw conclusions and repeat because the scientific method is never-ending, and no result is ever considered perfect.

The scientific method is a process of:

• Making an observation.
• Forming a hypothesis.
• Making a prediction.
• Experimenting to test the hypothesis.

The procedure of repeating the scientific method is crucial to science and all fields of human knowledge.

Further Information

• Karl Popper – Falsification
• Thomas – Kuhn Paradigm Shift
• Positivism in Sociology: Definition, Theory & Examples
• Is Psychology a Science?
• Psychology as a Science (PDF)

List the 6 steps of the scientific methods in order

• Make an observation (theory construction)
• Ask a question. A scientific question must be defined, testable, and measurable.
• Form a hypothesis (make predictions)
• Run an experiment to test the hypothesis (gather data)
• Analyze the data and draw conclusions
• Share your results so that other researchers can make new hypotheses

What is the first step of the scientific method?

The first step of the scientific method is making an observation. This involves noticing and describing a phenomenon or group of phenomena that one finds interesting and wishes to explain.

Observations can occur in a natural setting or within the confines of a laboratory. The key point is that the observation provides the initial question or problem that the rest of the scientific method seeks to answer or solve.

What is the scientific method?

The scientific method is a step-by-step process that investigators can follow to determine if there is a causal connection between two or more variables.

Psychologists and other scientists regularly suggest motivations for human behavior. On a more casual level, people judge other people’s intentions, incentives, and actions daily.

While our standard assessments of human behavior are subjective and anecdotal, researchers use the scientific method to study psychology objectively and systematically.

All utilize a scientific method to study distinct aspects of people’s thinking and behavior. This process allows scientists to analyze and understand various psychological phenomena, but it also provides investigators and others a way to disseminate and debate the results of their studies.

The outcomes of these studies are often noted in popular media, which leads numerous to think about how or why researchers came to the findings they did.

Why Use the Six Steps of the Scientific Method

The goal of scientists is to understand better the world that surrounds us. Scientific research is the most critical tool for navigating and learning about our complex world.

Without it, we would be compelled to rely solely on intuition, other people’s power, and luck. We can eliminate our preconceived concepts and superstitions through methodical scientific research and gain an objective sense of ourselves and our world.

All psychological studies aim to explain, predict, and even control or impact mental behaviors or processes. So, psychologists use and repeat the scientific method (and its six steps) to perform and record essential psychological research.

So, psychologists focus on understanding behavior and the cognitive (mental) and physiological (body) processes underlying behavior.

In the real world, people use to understand the behavior of others, such as intuition and personal experience. The hallmark of scientific research is evidence to support a claim.

Scientific knowledge is empirical, meaning it is grounded in objective, tangible evidence that can be observed repeatedly, regardless of who is watching.

The scientific method is crucial because it minimizes the impact of bias or prejudice on the experimenter. Regardless of how hard one tries, even the best-intentioned scientists can’t escape discrimination. can’t

It stems from personal opinions and cultural beliefs, meaning any mortal filters data based on one’s experience. Sadly, this “filtering” process can cause a scientist to favor one outcome over another.

For an everyday person trying to solve a minor issue at home or work, succumbing to these biases is not such a big deal; in fact, most times, it is important.

But in the scientific community, where results must be inspected and reproduced, bias or discrimination must be avoided.

When to Use the Six Steps of the Scientific Method ?

One can use the scientific method anytime, anywhere! From the smallest conundrum to solving global problems, it is a process that can be applied to any science and any investigation.

Even if you are not considered a “scientist,” you will be surprised to know that people of all disciplines use it for all kinds of dilemmas.

Try to catch yourself next time you come by a question and see how you subconsciously or consciously use the scientific method.

Related Articles

Research Methodology

Qualitative Data Coding

What Is a Focus Group?

Cross-Cultural Research Methodology In Psychology

What Is Internal Validity In Research?

Research Methodology , Statistics

What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples

1.2 The Scientific Methods

Section learning objectives.

By the end of this section, you will be able to do the following:

• Explain how the methods of science are used to make scientific discoveries
• Define a scientific model and describe examples of physical and mathematical models used in physics
• Compare and contrast hypothesis, theory, and law

Teacher Support

The learning objectives in this section will help your students master the following standards:

• (A) know the definition of science and understand that it has limitations, as specified in subsection (b)(2) of this section;
• (B) know that scientific hypotheses are tentative and testable statements that must be capable of being supported or not supported by observational evidence. Hypotheses of durable explanatory power which have been tested over a wide variety of conditions are incorporated into theories;
• (C) know that scientific theories are based on natural and physical phenomena and are capable of being tested by multiple independent researchers. Unlike hypotheses, scientific theories are well-established and highly-reliable explanations, but may be subject to change as new areas of science and new technologies are developed;
• (D) distinguish between scientific hypotheses and scientific theories.

Section Key Terms

[OL] Pre-assessment for this section could involve students sharing or writing down an anecdote about when they used the methods of science. Then, students could label their thought processes in their anecdote with the appropriate scientific methods. The class could also discuss their definitions of theory and law, both outside and within the context of science.

[OL] It should be noted and possibly mentioned that a scientist , as mentioned in this section, does not necessarily mean a trained scientist. It could be anyone using methods of science.

Scientific Methods

Scientists often plan and carry out investigations to answer questions about the universe around us. These investigations may lead to natural laws. Such laws are intrinsic to the universe, meaning that humans did not create them and cannot change them. We can only discover and understand them. Their discovery is a very human endeavor, with all the elements of mystery, imagination, struggle, triumph, and disappointment inherent in any creative effort. The cornerstone of discovering natural laws is observation. Science must describe the universe as it is, not as we imagine or wish it to be.

We all are curious to some extent. We look around, make generalizations, and try to understand what we see. For example, we look up and wonder whether one type of cloud signals an oncoming storm. As we become serious about exploring nature, we become more organized and formal in collecting and analyzing data. We attempt greater precision, perform controlled experiments (if we can), and write down ideas about how data may be organized. We then formulate models, theories, and laws based on the data we have collected, and communicate those results with others. This, in a nutshell, describes the scientific method that scientists employ to decide scientific issues on the basis of evidence from observation and experiment.

An investigation often begins with a scientist making an observation . The scientist observes a pattern or trend within the natural world. Observation may generate questions that the scientist wishes to answer. Next, the scientist may perform some research about the topic and devise a hypothesis . A hypothesis is a testable statement that describes how something in the natural world works. In essence, a hypothesis is an educated guess that explains something about an observation.

[OL] An educated guess is used throughout this section in describing a hypothesis to combat the tendency to think of a theory as an educated guess.

Scientists may test the hypothesis by performing an experiment . During an experiment, the scientist collects data that will help them learn about the phenomenon they are studying. Then the scientists analyze the results of the experiment (that is, the data), often using statistical, mathematical, and/or graphical methods. From the data analysis, they draw conclusions. They may conclude that their experiment either supports or rejects their hypothesis. If the hypothesis is supported, the scientist usually goes on to test another hypothesis related to the first. If their hypothesis is rejected, they will often then test a new and different hypothesis in their effort to learn more about whatever they are studying.

Scientific processes can be applied to many situations. Let’s say that you try to turn on your car, but it will not start. You have just made an observation! You ask yourself, "Why won’t my car start?" You can now use scientific processes to answer this question. First, you generate a hypothesis such as, "The car won’t start because it has no gasoline in the gas tank." To test this hypothesis, you put gasoline in the car and try to start it again. If the car starts, then your hypothesis is supported by the experiment. If the car does not start, then your hypothesis is rejected. You will then need to think up a new hypothesis to test such as, "My car won’t start because the fuel pump is broken." Hopefully, your investigations lead you to discover why the car won’t start and enable you to fix it.

A model is a representation of something that is often too difficult (or impossible) to study directly. Models can take the form of physical models, equations, computer programs, or simulations—computer graphics/animations. Models are tools that are especially useful in modern physics because they let us visualize phenomena that we normally cannot observe with our senses, such as very small objects or objects that move at high speeds. For example, we can understand the structure of an atom using models, without seeing an atom with our own eyes. Although images of single atoms are now possible, these images are extremely difficult to achieve and are only possible due to the success of our models. The existence of these images is a consequence rather than a source of our understanding of atoms. Models are always approximate, so they are simpler to consider than the real situation; the more complete a model is, the more complicated it must be. Models put the intangible or the extremely complex into human terms that we can visualize, discuss, and hypothesize about.

Scientific models are constructed based on the results of previous experiments. Even still, models often only describe a phenomenon partially or in a few limited situations. Some phenomena are so complex that they may be impossible to model them in their entirety, even using computers. An example is the electron cloud model of the atom in which electrons are moving around the atom’s center in distinct clouds ( Figure 1.12 ), that represent the likelihood of finding an electron in different places. This model helps us to visualize the structure of an atom. However, it does not show us exactly where an electron will be within its cloud at any one particular time.

As mentioned previously, physicists use a variety of models including equations, physical models, computer simulations, etc. For example, three-dimensional models are often commonly used in chemistry and physics to model molecules. Properties other than appearance or location are usually modelled using mathematics, where functions are used to show how these properties relate to one another. Processes such as the formation of a star or the planets, can also be modelled using computer simulations. Once a simulation is correctly programmed based on actual experimental data, the simulation can allow us to view processes that happened in the past or happen too quickly or slowly for us to observe directly. In addition, scientists can also run virtual experiments using computer-based models. In a model of planet formation, for example, the scientist could alter the amount or type of rocks present in space and see how it affects planet formation.

Scientists use models and experimental results to construct explanations of observations or design solutions to problems. For example, one way to make a car more fuel efficient is to reduce the friction or drag caused by air flowing around the moving car. This can be done by designing the body shape of the car to be more aerodynamic, such as by using rounded corners instead of sharp ones. Engineers can then construct physical models of the car body, place them in a wind tunnel, and examine the flow of air around the model. This can also be done mathematically in a computer simulation. The air flow pattern can be analyzed for regions smooth air flow and for eddies that indicate drag. The model of the car body may have to be altered slightly to produce the smoothest pattern of air flow (i.e., the least drag). The pattern with the least drag may be the solution to increasing fuel efficiency of the car. This solution might then be incorporated into the car design.

Using Models and the Scientific Processes

Be sure to secure loose items before opening the window or door.

In this activity, you will learn about scientific models by making a model of how air flows through your classroom or a room in your house.

• One room with at least one window or door that can be opened
• Work with a group of four, as directed by your teacher. Close all of the windows and doors in the room you are working in. Your teacher may assign you a specific window or door to study.
• Before opening any windows or doors, draw a to-scale diagram of your room. First, measure the length and width of your room using the tape measure. Then, transform the measurement using a scale that could fit on your paper, such as 5 centimeters = 1 meter.
• Your teacher will assign you a specific window or door to study air flow. On your diagram, add arrows showing your hypothesis (before opening any windows or doors) of how air will flow through the room when your assigned window or door is opened. Use pencil so that you can easily make changes to your diagram.
• On your diagram, mark four locations where you would like to test air flow in your room. To test for airflow, hold a strip of single ply tissue paper between the thumb and index finger. Note the direction that the paper moves when exposed to the airflow. Then, for each location, predict which way the paper will move if your air flow diagram is correct.
• Now, each member of your group will stand in one of the four selected areas. Each member will test the airflow Agree upon an approximate height at which everyone will hold their papers.
• When you teacher tells you to, open your assigned window and/or door. Each person should note the direction that their paper points immediately after the window or door was opened. Record your results on your diagram.
• Did the airflow test data support or refute the hypothetical model of air flow shown in your diagram? Why or why not? Correct your model based on your experimental evidence.
• With your group, discuss how accurate your model is. What limitations did it have? Write down the limitations that your group agreed upon.
• Yes, you could use your model to predict air flow through a new window. The earlier experiment of air flow would help you model the system more accurately.
• Yes, you could use your model to predict air flow through a new window. The earlier experiment of air flow is not useful for modeling the new system.
• No, you cannot model a system to predict the air flow through a new window. The earlier experiment of air flow would help you model the system more accurately.
• No, you cannot model a system to predict the air flow through a new window. The earlier experiment of air flow is not useful for modeling the new system.

This Snap Lab! has students construct a model of how air flows in their classroom. Each group of four students will create a model of air flow in their classroom using a scale drawing of the room. Then, the groups will test the validity of their model by placing weathervanes that they have constructed around the room and opening a window or door. By observing the weather vanes, students will see how air actually flows through the room from a specific window or door. Students will then correct their model based on their experimental evidence. The following material list is given per group:

• One room with at least one window or door that can be opened (An optimal configuration would be one window or door per group.)
• Several pieces of construction paper (at least four per group)
• Strips of single ply tissue paper
• One tape measure (long enough to measure the dimensions of the room)
• Group size can vary depending on the number of windows/doors available and the number of students in the class.
• The room dimensions could be provided by the teacher. Also, students may need a brief introduction in how to make a drawing to scale.
• This is another opportunity to discuss controlled experiments in terms of why the students should hold the strips of tissue paper at the same height and in the same way. One student could also serve as a control and stand far away from the window/door or in another area that will not receive air flow from the window/door.
• You will probably need to coordinate this when multiple windows or doors are used. Only one window or door should be opened at a time for best results. Between openings, allow a short period (5 minutes) when all windows and doors are closed, if possible.

Answers to the Grasp Check will vary, but the air flow in the new window or door should be based on what the students observed in their experiment.

Scientific Laws and Theories

A scientific law is a description of a pattern in nature that is true in all circumstances that have been studied. That is, physical laws are meant to be universal , meaning that they apply throughout the known universe. Laws are often also concise, whereas theories are more complicated. A law can be expressed in the form of a single sentence or mathematical equation. For example, Newton’s second law of motion , which relates the motion of an object to the force applied ( F ), the mass of the object ( m ), and the object’s acceleration ( a ), is simply stated using the equation

Scientific ideas and explanations that are true in many, but not all situations in the universe are usually called principles . An example is Pascal’s principle , which explains properties of liquids, but not solids or gases. However, the distinction between laws and principles is sometimes not carefully made in science.

A theory is an explanation for patterns in nature that is supported by much scientific evidence and verified multiple times by multiple researchers. While many people confuse theories with educated guesses or hypotheses, theories have withstood more rigorous testing and verification than hypotheses.

[OL] Explain to students that in informal, everyday English the word theory can be used to describe an idea that is possibly true but that has not been proven to be true. This use of the word theory often leads people to think that scientific theories are nothing more than educated guesses. This is not just a misconception among students, but among the general public as well.

As a closing idea about scientific processes, we want to point out that scientific laws and theories, even those that have been supported by experiments for centuries, can still be changed by new discoveries. This is especially true when new technologies emerge that allow us to observe things that were formerly unobservable. Imagine how viewing previously invisible objects with a microscope or viewing Earth for the first time from space may have instantly changed our scientific theories and laws! What discoveries still await us in the future? The constant retesting and perfecting of our scientific laws and theories allows our knowledge of nature to progress. For this reason, many scientists are reluctant to say that their studies prove anything. By saying support instead of prove , it keeps the door open for future discoveries, even if they won’t occur for centuries or even millennia.

[OL] With regard to scientists avoiding using the word prove , the general public knows that science has proven certain things such as that the heart pumps blood and the Earth is round. However, scientists should shy away from using prove because it is impossible to test every single instance and every set of conditions in a system to absolutely prove anything. Using support or similar terminology leaves the door open for further discovery.

Check Your Understanding

• Models are simpler to analyze.
• Models give more accurate results.
• Models provide more reliable predictions.
• Models do not require any computer calculations.
• They are the same.
• A hypothesis has been thoroughly tested and found to be true.
• A hypothesis is a tentative assumption based on what is already known.
• A hypothesis is a broad explanation firmly supported by evidence.
• A scientific model is a representation of something that can be easily studied directly. It is useful for studying things that can be easily analyzed by humans.
• A scientific model is a representation of something that is often too difficult to study directly. It is useful for studying a complex system or systems that humans cannot observe directly.
• A scientific model is a representation of scientific equipment. It is useful for studying working principles of scientific equipment.
• A scientific model is a representation of a laboratory where experiments are performed. It is useful for studying requirements needed inside the laboratory.
• The hypothesis must be validated by scientific experiments.
• The hypothesis must not include any physical quantity.
• The hypothesis must be a short and concise statement.
• The hypothesis must apply to all the situations in the universe.
• A scientific theory is an explanation of natural phenomena that is supported by evidence.
• A scientific theory is an explanation of natural phenomena without the support of evidence.
• A scientific theory is an educated guess about the natural phenomena occurring in nature.
• A scientific theory is an uneducated guess about natural phenomena occurring in nature.
• A hypothesis is an explanation of the natural world with experimental support, while a scientific theory is an educated guess about a natural phenomenon.
• A hypothesis is an educated guess about natural phenomenon, while a scientific theory is an explanation of natural world with experimental support.
• A hypothesis is experimental evidence of a natural phenomenon, while a scientific theory is an explanation of the natural world with experimental support.
• A hypothesis is an explanation of the natural world with experimental support, while a scientific theory is experimental evidence of a natural phenomenon.

Use the Check Your Understanding questions to assess students’ achievement of the section’s learning objectives. If students are struggling with a specific objective, the Check Your Understanding will help identify which objective and direct students to the relevant content.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-physics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/physics/pages/1-introduction

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: Physics
• Publication date: Mar 26, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/physics/pages/1-introduction
• Section URL: https://openstax.org/books/physics/pages/1-2-the-scientific-methods

© Jan 19, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

The Scientific Method by Science Made Simple

Understanding and using the scientific method.

The Scientific Method is a process used to design and perform experiments. It's important to minimize experimental errors and bias, and increase confidence in the accuracy of your results.

In the previous sections, we talked about how to pick a good topic and specific question to investigate. Now we will discuss how to carry out your investigation.

Steps of the Scientific Method

• Observation/Research
• Experimentation

Now that you have settled on the question you want to ask, it's time to use the Scientific Method to design an experiment to answer that question.

If your experiment isn't designed well, you may not get the correct answer. You may not even get any definitive answer at all!

The Scientific Method is a logical and rational order of steps by which scientists come to conclusions about the world around them. The Scientific Method helps to organize thoughts and procedures so that scientists can be confident in the answers they find.

OBSERVATION is first step, so that you know how you want to go about your research.

HYPOTHESIS is the answer you think you'll find.

PREDICTION is your specific belief about the scientific idea: If my hypothesis is true, then I predict we will discover this.

EXPERIMENT is the tool that you invent to answer the question, and

CONCLUSION is the answer that the experiment gives.

Don't worry, it isn't that complicated. Let's take a closer look at each one of these steps. Then you can understand the tools scientists use for their science experiments, and use them for your own.

OBSERVATION

This step could also be called "research." It is the first stage in understanding the problem.

After you decide on topic, and narrow it down to a specific question, you will need to research everything that you can find about it. You can collect information from your own experiences, books, the internet, or even smaller "unofficial" experiments.

Let's continue the example of a science fair idea about tomatoes in the garden. You like to garden, and notice that some tomatoes are bigger than others and wonder why.

Because of this personal experience and an interest in the problem, you decide to learn more about what makes plants grow.

For this stage of the Scientific Method, it's important to use as many sources as you can find. The more information you have on your science fair topic, the better the design of your experiment is going to be, and the better your science fair project is going to be overall.

Also try to get information from your teachers or librarians, or professionals who know something about your science fair project. They can help to guide you to a solid experimental setup.

The next stage of the Scientific Method is known as the "hypothesis." This word basically means "a possible solution to a problem, based on knowledge and research."

The hypothesis is a simple statement that defines what you think the outcome of your experiment will be.

All of the first stage of the Scientific Method -- the observation, or research stage -- is designed to help you express a problem in a single question ("Does the amount of sunlight in a garden affect tomato size?") and propose an answer to the question based on what you know. The experiment that you will design is done to test the hypothesis.

Using the example of the tomato experiment, here is an example of a hypothesis:

TOPIC: "Does the amount of sunlight a tomato plant receives affect the size of the tomatoes?"

HYPOTHESIS: "I believe that the more sunlight a tomato plant receives, the larger the tomatoes will grow.

This hypothesis is based on:

(1) Tomato plants need sunshine to make food through photosynthesis, and logically, more sun means more food, and;

(2) Through informal, exploratory observations of plants in a garden, those with more sunlight appear to grow bigger.

The hypothesis is your general statement of how you think the scientific phenomenon in question works.

Your prediction lets you get specific -- how will you demonstrate that your hypothesis is true? The experiment that you will design is done to test the prediction.

An important thing to remember during this stage of the scientific method is that once you develop a hypothesis and a prediction, you shouldn't change it, even if the results of your experiment show that you were wrong.

An incorrect prediction does NOT mean that you "failed." It just means that the experiment brought some new facts to light that maybe you hadn't thought about before.

Continuing our tomato plant example, a good prediction would be: Increasing the amount of sunlight tomato plants in my experiment receive will cause an increase in their size compared to identical plants that received the same care but less light.

This is the part of the scientific method that tests your hypothesis. An experiment is a tool that you design to find out if your ideas about your topic are right or wrong.

It is absolutely necessary to design a science fair experiment that will accurately test your hypothesis. The experiment is the most important part of the scientific method. It's the logical process that lets scientists learn about the world.

On the next page, we'll discuss the ways that you can go about designing a science fair experiment idea.

The final step in the scientific method is the conclusion. This is a summary of the experiment's results, and how those results match up to your hypothesis.

You have two options for your conclusions: based on your results, either:

(1) YOU CAN REJECT the hypothesis, or

(2) YOU CAN NOT REJECT the hypothesis.

This is an important point!

You can not PROVE the hypothesis with a single experiment, because there is a chance that you made an error somewhere along the way.

What you can say is that your results SUPPORT the original hypothesis.

If your original hypothesis didn't match up with the final results of your experiment, don't change the hypothesis.

Instead, try to explain what might have been wrong with your original hypothesis. What information were you missing when you made your prediction? What are the possible reasons the hypothesis and experimental results didn't match up?

Remember, a science fair experiment isn't a failure simply because does not agree with your hypothesis. No one will take points off if your prediction wasn't accurate. Many important scientific discoveries were made as a result of experiments gone wrong!

A science fair experiment is only a failure if its design is flawed. A flawed experiment is one that (1) doesn't keep its variables under control, and (2) doesn't sufficiently answer the question that you asked of it.

Search This Site:

Science Fairs

• Introduction
• Project Ideas
• Types of Projects
• Pick a Topic
• Scientific Method
• Design Your Experiment
• Present Your Project
• What Judges Want
• Parent Info

Recommended *

• Sample Science Projects - botany, ecology, microbiology, nutrition

* This site contains affiliate links to carefully chosen, high quality products. We may receive a commission for purchases made through these links.

• Terms of Service

Copyright © 2006 - 2023, Science Made Simple, Inc. All Rights Reserved.

The science fair projects & ideas, science articles and all other material on this website are covered by copyright laws and may not be reproduced without permission.

The Scientific Method Tutorial

The scientific method, steps in the scientific method.

There is a great deal of variation in the specific techniques scientists use explore the natural world. However, the following steps characterize the majority of scientific investigations:

Step 1: Make observations Step 2: Propose a hypothesis to explain observations Step 3: Test the hypothesis with further observations or experiments Step 4: Analyze data Step 5: State conclusions about hypothesis based on data analysis

Each of these steps is explained briefly below, and in more detail later in this section.

Step 1: Make observations

A scientific inquiry typically starts with observations. Often, simple observations will trigger a question in the researcher's mind.

Example: A biologist frequently sees monarch caterpillars feeding on milkweed plants, but rarely sees them feeding on other types of plants. She wonders if it is because the caterpillars prefer milkweed over other food choices.

Step 2: Propose a hypothesis

The researcher develops a hypothesis (singular) or hypotheses (plural) to explain these observations. A hypothesis is a tentative explanation of a phenomenon or observation(s) that can be supported or falsified by further observations or experimentation.

Example: The researcher hypothesizes that monarch caterpillars prefer to feed on milkweed compared to other common plants. (Notice how the hypothesis is a statement, not a question as in step 1.)

Step 3: Test the hypothesis

The researcher makes further observations and/or may design an experiment to test the hypothesis. An experiment is a controlled situation created by a researcher to test the validity of a hypothesis. Whether further observations or an experiment is used to test the hypothesis will depend on the nature of the question and the practicality of manipulating the factors involved.

Example: The researcher sets up an experiment in the lab in which a number of monarch caterpillars are given a choice between milkweed and a number of other common plants to feed on.

Step 4: Analyze data

The researcher summarizes and analyzes the information, or data, generated by these further observations or experiments.

Example: In her experiment, milkweed was chosen by caterpillars 9 times out of 10 over all other plant selections.

Step 5: State conclusions

The researcher interprets the results of experiments or observations and forms conclusions about the meaning of these results. These conclusions are generally expressed as probability statements about their hypothesis.

Example: She concludes that when given a choice, 90 percent of monarch caterpillars prefer to feed on milkweed over other common plants.

Often, the results of one scientific study will raise questions that may be addressed in subsequent research. For example, the above study might lead the researcher to wonder why monarchs seem to prefer to feed on milkweed, and she may plan additional experiments to explore this question. For example, perhaps the milkweed has higher nutritional value than other available plants.

Return to top of page

The Scientific Method Flowchart

The steps in the scientific method are presented visually in the following flow chart. The question raised or the results obtained at each step directly determine how the next step will proceed. Following the flow of the arrows, pass the cursor over each blue box. An explanation and example of each step will appear. As you read the example given at each step, see if you can predict what the next step will be.

Activity: Apply the Scientific Method to Everyday Life Use the steps of the scientific method described above to solve a problem in real life. Suppose you come home one evening and flick the light switch only to find that the light doesn’t turn on. What is your hypothesis? How will you test that hypothesis? Based on the result of this test, what are your conclusions? Follow your instructor's directions for submitting your response.

The above flowchart illustrates the logical sequence of conclusions and decisions in a typical scientific study. There are some important points to note about this process:

1. The steps are clearly linked.

The steps in this process are clearly linked. The hypothesis, formed as a potential explanation for the initial observations, becomes the focus of the study. The hypothesis will determine what further observations are needed or what type of experiment should be done to test its validity. The conclusions of the experiment or further observations will either be in agreement with or will contradict the hypothesis. If the results are in agreement with the hypothesis, this does not prove that the hypothesis is true! In scientific terms, it "lends support" to the hypothesis, which will be tested again and again under a variety of circumstances before researchers accept it as a fairly reliable description of reality.

2. The same steps are not followed in all types of research.

The steps described above present a generalized method followed in a many scientific investigations. These steps are not carved in stone. The question the researcher wishes to answer will influence the steps in the method and how they will be carried out. For example, astronomers do not perform many experiments as defined here. They tend to rely on observations to test theories. Biologists and chemists have the ability to change conditions in a test tube and then observe whether the outcome supports or invalidates their starting hypothesis, while astronomers are not able to change the path of Jupiter around the Sun and observe the outcome!

3. Collected observations may lead to the development of theories.

When a large number of observations and/or experimental results have been compiled, and all are consistent with a generalized description of how some element of nature operates, this description is called a theory. Theories are much broader than hypotheses and are supported by a wide range of evidence. Theories are important scientific tools. They provide a context for interpretation of new observations and also suggest experiments to test their own validity. Theories are discussed in more detail in another section.

The Scientific Method in Detail

In the sections that follow, each step in the scientific method is described in more detail.

Step 1: Observations

Observations in science.

An observation is some thing, event, or phenomenon that is noticed or observed. Observations are listed as the first step in the scientific method because they often provide a starting point, a source of questions a researcher may ask. For example, the observation that leaves change color in the fall may lead a researcher to ask why this is so, and to propose a hypothesis to explain this phenomena. In fact, observations also will provide the key to answering the research question.

In science, observations form the foundation of all hypotheses, experiments, and theories. In an experiment, the researcher carefully plans what observations will be made and how they will be recorded. To be accepted, scientific conclusions and theories must be supported by all available observations. If new observations are made which seem to contradict an established theory, that theory will be re-examined and may be revised to explain the new facts. Observations are the nuts and bolts of science that researchers use to piece together a better understanding of nature.

Observations in science are made in a way that can be precisely communicated to (and verified by) other researchers. In many types of studies (especially in chemistry, physics, and biology), quantitative observations are used. A quantitative observation is one that is expressed and recorded as a quantity, using some standard system of measurement. Quantities such as size, volume, weight, time, distance, or a host of others may be measured in scientific studies.

Some observations that researchers need to make may be difficult or impossible to quantify. Take the example of color. Not all individuals perceive color in exactly the same way. Even apart from limiting conditions such as colorblindness, the way two people see and describe the color of a particular flower, for example, will not be the same. Color, as perceived by the human eye, is an example of a qualitative observation.

Qualitative observations note qualities associated with subjects or samples that are not readily measured. Other examples of qualitative observations might be descriptions of mating behaviors, human facial expressions, or "yes/no" type of data, where some factor is present or absent. Though the qualities of an object may be more difficult to describe or measure than any quantities associated with it, every attempt is made to minimize the effects of the subjective perceptions of the researcher in the process. Some types of studies, such as those in the social and behavioral sciences (which deal with highly variable human subjects), may rely heavily on qualitative observations.

Question: Why are observations important to science?

Limits of Observations

Because all observations rely to some degree on the senses (eyes, ears, or steady hand) of the researcher, complete objectivity is impossible. Our human perceptions are limited by the physical abilities of our sense organs and are interpreted according to our understanding of how the world works, which can be influenced by culture, experience, or education. According to science education specialist, George F. Kneller, "Surprising as it may seem, there is no fact that is not colored by our preconceptions" ("A Method of Enquiry," from Science and Its Ways of Knowing [Upper Saddle River: Prentice-Hall Inc., 1997], 15).

Observations made by a scientist are also limited by the sensitivity of whatever equipment he is using. Research findings will be limited at times by the available technology. For example, Italian physicist and philosopher Galileo Galilei (1564–1642) was reportedly the first person to observe the heavens with a telescope. Imagine how it must have felt to him to see the heavens through this amazing new instrument! It opened a window to the stars and planets and allowed new observations undreamed of before.

In the centuries since Galileo, increasingly more powerful telescopes have been devised that dwarf the power of that first device. In the past decade, we have marveled at images from deep space , courtesy of the Hubble Space Telescope, a large telescope that orbits Earth. Because of its view from outside the distorting effects of the atmosphere, the Hubble can look 50 times farther into space than the best earth-bound telescopes, and resolve details a tenth of the size (Seeds, Michael A., Horizons: Exploring the Universe , 5 th ed. [Belmont: Wadsworth Publishing Company, 1998], 86-87).

Construction is underway on a new radio telescope that scientists say will be able to detect electromagnetic waves from the very edges of the universe! This joint U.S.-Mexican project may allow us to ask questions about the origins of the universe and the beginnings of time that we could never have hoped to answer before. Completion of the new telescope is expected by the end of 2001.

Although the amount of detail observed by Galileo and today's astronomers is vastly different, the stars and their relationships have not changed very much. Yet with each technological advance, the level of detail of observation has been increased, and with it, the power to answer more and more challenging questions with greater precision.

Question: What are some of the differences between a casual observation and a 'scientific observation'?

Step 2: The Hypothesis

A hypothesis is a statement created by the researcher as a potential explanation for an observation or phenomena. The hypothesis converts the researcher's original question into a statement that can be used to make predictions about what should be observed if the hypothesis is true. For example, given the hypothesis, "exposure to ultraviolet (UV) radiation increases the risk of skin cancer," one would predict higher rates of skin cancer among people with greater UV exposure. These predictions could be tested by comparing skin cancer rates among individuals with varying amounts of UV exposure. Note how the hypothesis itself determines what experiments or further observations should be made to test its validity. Results of tests are then compared to predictions from the hypothesis, and conclusions are stated in terms of whether or not the data supports the hypothesis. So the hypothesis serves a guide to the full process of scientific inquiry.

The Qualities of a Good Hypothesis

• A hypothesis must be testable or provide predictions that are testable. It can potentially be shown to be false by further observations or experimentation.
• A hypothesis should be specific. If it is too general it cannot be tested, or tests will have so many variables that the results will be complicated and difficult to interpret. A well-written hypothesis is so specific it actually determines how the experiment should be set up.
• A hypothesis should not include any untested assumptions if they can be avoided. The hypothesis itself may be an assumption that is being tested, but it should be phrased in a way that does not include assumptions that are not tested in the experiment.
• It is okay (and sometimes a good idea) to develop more than one hypothesis to explain a set of observations. Competing hypotheses can often be tested side-by-side in the same experiment.

Question: Why is the hypothesis important to the scientific method?

Step 3: Testing the Hypothesis

A hypothesis may be tested in one of two ways: by making additional observations of a natural situation, or by setting up an experiment. In either case, the hypothesis is used to make predictions, and the observations or experimental data collected are examined to determine if they are consistent or inconsistent with those predictions. Hypothesis testing, especially through experimentation, is at the core of the scientific process. It is how scientists gain a better understanding of how things work.

Testing a Hypothesis by Observation

Some hypotheses may be tested through simple observation. For example, a researcher may formulate the hypothesis that the sun always rises in the east. What might an alternative hypothesis be? If his hypothesis is correct, he would predict that the sun will rise in the east tomorrow. He can easily test such a prediction by rising before dawn and going out to observe the sunrise. If the sun rises in the west, he will have disproved the hypothesis. He will have shown that it does not hold true in every situation. However, if he observes on that morning that the sun does in fact rise in the east, he has not proven the hypothesis. He has made a single observation that is consistent with, or supports, the hypothesis. As a scientist, to confidently state that the sun will always rise in the east, he will want to make many observations, under a variety of circumstances. Note that in this instance no manipulation of circumstance is required to test the hypothesis (i.e., you aren't altering the sun in any way).

Testing a Hypothesis by Experimentation

An experiment is a controlled series of observations designed to test a specific hypothesis. In an experiment, the researcher manipulates factors related to the hypothesis in such a way that the effect of these factors on the observations (data) can be readily measured and compared. Most experiments are an attempt to define a cause-and-effect relationship between two factors or events—to explain why something happens. For example, with the hypothesis "roses planted in sunny areas bloom earlier than those grown in shady areas," the experiment would be testing a cause-and-effect relationship between sunlight and time of blooming.

A major advantage of setting up an experiment versus making observations of what is already available is that it allows the researcher to control all the factors or events related to the hypothesis, so that the true cause of an event can be more easily isolated. In all cases, the hypothesis itself will determine the way the experiment will be set up. For example, suppose my hypothesis is "the weight of an object is proportional to the amount of time it takes to fall a certain distance." How would you test this hypothesis?

The Qualities of a Good Experiment

• The experiment must be conducted on a group of subjects that are narrowly defined and have certain aspects in common. This is the group to which any conclusions must later be confined. (Examples of possible subjects: female cancer patients over age 40, E. coli bacteria, red giant stars, the nicotine molecule and its derivatives.)
• All subjects of the experiment should be (ideally) completely alike in all ways except for the factor or factors that are being tested. Factors that are compared in scientific experiments are called variables. A variable is some aspect of a subject or event that may differ over time or from one group of subjects to another. For example, if a biologist wanted to test the effect of nitrogen on grass growth, he would apply different amounts of nitrogen fertilizer to several plots of grass. The grass in each of the plots should be as alike as possible so that any difference in growth could be attributed to the effect of the nitrogen. For example, all the grass should be of the same species, planted at the same time and at the same density, receive the same amount of water and sunlight, and so on. The variable in this case would be the amount of nitrogen applied to the plants. The researcher would not compare differing amounts of nitrogen across different grass species to determine the effect of nitrogen on grass growth. What is the problem with using different species of plants to compare the effect of nitrogen on plant growth? There are different kinds of variables in an experiment. A factor that the experimenter controls, and changes intentionally to determine if it has an effect, is called an independent variable . A factor that is recorded as data in the experiment, and which is compared across different groups of subjects, is called a dependent variable . In many cases, the value of the dependent variable will be influenced by the value of an independent variable. The goal of the experiment is to determine a cause-and-effect relationship between independent and dependent variables—in this case, an effect of nitrogen on plant growth. In the nitrogen/grass experiment, (1) which factor was the independent variable? (2) Which factor was the dependent variable?
• Nearly all types of experiments require a control group and an experimental group. The control group generally is not changed in any way, but remains in a "natural state," while the experimental group is modified in some way to examine the effect of the variable which of interest to the researcher. The control group provides a standard of comparison for the experimental groups. For example, in new drug trials, some patients are given a placebo while others are given doses of the drug being tested. The placebo serves as a control by showing the effect of no drug treatment on the patients. In research terminology, the experimental groups are often referred to as treatments , since each group is treated differently. In the experimental test of the effect of nitrogen on grass growth, what is the control group? In the example of the nitrogen experiment, what is the purpose of a control group?
• In research studies a great deal of emphasis is placed on repetition. It is essential that an experiment or study include enough subjects or enough observations for the researcher to make valid conclusions. The two main reasons why repetition is important in scientific studies are (1) variation among subjects or samples and (2) measurement error.

Variation among Subjects

There is a great deal of variation in nature. In a group of experimental subjects, much of this variation may have little to do with the variables being studied, but could still affect the outcome of the experiment in unpredicted ways. For example, in an experiment designed to test the effects of alcohol dose levels on reflex time in 18- to 22-year-old males, there would be significant variation among individual responses to various doses of alcohol. Some of this variation might be due to differences in genetic make-up, to varying levels of previous alcohol use, or any number of factors unknown to the researcher.

Because what the researcher wants to discover is average dose level effects for this group, he must run the test on a number of different subjects. Suppose he performed the test on only 10 individuals. Do you think the average response calculated would be the same as the average response of all 18- to 22-year-old males? What if he tests 100 individuals, or 1,000? Do you think the average he comes up with would be the same in each case? Chances are it would not be. So which average would you predict would be most representative of all 18- to 22-year-old males?

A basic rule of statistics is, the more observations you make, the closer the average of those observations will be to the average for the whole population you are interested in. This is because factors that vary among a population tend to occur most commonly in the middle range, and least commonly at the two extremes. Take human height for example. Although you may find a man who is 7 feet tall, or one who is 4 feet tall, most men will fall somewhere between 5 and 6 feet in height. The more men we measure to determine average male height, the less effect those uncommon extreme (tall or short) individuals will tend to impact the average. Thus, one reason why repetition is so important in experiments is that it helps to assure that the conclusions made will be valid not only for the individuals tested, but also for the greater population those individuals represent.

"The use of a sample (or subset) of a population, an event, or some other aspect of nature for an experimental group that is not large enough to be representative of the whole" is called sampling error (Starr, Cecie, Biology: Concepts and Applications , 4 th ed. [Pacific Cove: Brooks/Cole, 2000], glossary). If too few samples or subjects are used in an experiment, the researcher may draw incorrect conclusions about the population those samples or subjects represent.

Use the jellybean activity below to see a simple demonstration of samping error.

Directions: There are 400 jellybeans in the jar. If you could not see the jar and you initially chose 1 green jellybean from the jar, you might assume the jar only contains green jelly beans. The jar actually contains both green and black jellybeans. Use the "pick 1, 5, or 10" buttons to create your samples. For example, use the "pick" buttons now to create samples of 2, 13, and 27 jellybeans. After you take each sample, try to predict the ratio of green to black jellybeans in the jar. How does your prediction of the ratio of green to black jellybeans change as your sample changes?

Measurement Error

The second reason why repetition is necessary in research studies has to do with measurement error. Measurement error may be the fault of the researcher, a slight difference in measuring techniques among one or more technicians, or the result of limitations or glitches in measuring equipment. Even the most careful researcher or the best state-of-the-art equipment will make some mistakes in measuring or recording data. Another way of looking at this is to say that, in any study, some measurements will be more accurate than others will. If the researcher is conscientious and the equipment is good, the majority of measurements will be highly accurate, some will be somewhat inaccurate, and a few may be considerably inaccurate. In this case, the same reasoning used above also applies here: the more measurements taken, the less effect a few inaccurate measurements will have on the overall average.

Step 4: Data Analysis

In any experiment, observations are made, and often, measurements are taken. Measurements and observations recorded in an experiment are referred to as data . The data collected must relate to the hypothesis being tested. Any differences between experimental and control groups must be expressed in some way (often quantitatively) so that the groups may be compared. Graphs and charts are often used to visualize the data and to identify patterns and relationships among the variables.

Statistics is the branch of mathematics that deals with interpretation of data. Data analysis refers to statistical methods of determining whether any differences between the control group and experimental groups are too great to be attributed to chance alone. Although a discussion of statistical methods is beyond the scope of this tutorial, the data analysis step is crucial because it provides a somewhat standardized means for interpreting data. The statistical methods of data analysis used, and the results of those analyses, are always included in the publication of scientific research. This convention limits the subjective aspects of data interpretation and allows scientists to scrutinize the working methods of their peers.

Why is data analysis an important step in the scientific method?

Step 5: Stating Conclusions

The conclusions made in a scientific experiment are particularly important. Often, the conclusion is the only part of a study that gets communicated to the general public. As such, it must be a statement of reality, based upon the results of the experiment. To assure that this is the case, the conclusions made in an experiment must (1) relate back to the hypothesis being tested, (2) be limited to the population under study, and (3) be stated as probabilities.

The hypothesis that is being tested will be compared to the data collected in the experiment. If the experimental results contradict the hypothesis, it is rejected and further testing of that hypothesis under those conditions is not necessary. However, if the hypothesis is not shown to be wrong, that does not conclusively prove that it is right! In scientific terms, the hypothesis is said to be "supported by the data." Further testing will be done to see if the hypothesis is supported under a number of trials and under different conditions.

If the hypothesis holds up to extensive testing then the temptation is to claim that it is correct. However, keep in mind that the number of experiments and observations made will only represent a subset of all the situations in which the hypothesis may potentially be tested. In other words, experimental data will only show part of the picture. There is always the possibility that a further experiment may show the hypothesis to be wrong in some situations. Also, note that the limits of current knowledge and available technologies may prevent a researcher from devising an experiment that would disprove a particular hypothesis.

The researcher must be sure to limit his or her conclusions to apply only to the subjects tested in the study. If a particular species of fish is shown to consume their young 90 percent of the time when raised in captivity, that doesn't necessarily mean that all fish will do so, or that this fish's behavior would be the same in its native habitat.

Finally, the conclusions of the experiment are generally stated as probabilities. A careful scientist would never say, "drug x kills cancer cells;" she would more likely say, "drug x was shown to destroy 85 percent of cancerous skin cells in rats in lab trials." Notice how very different these two statements are. There is a tendency in the media and in the general public to gravitate toward the first statement. This makes a terrific headline and is also easy to interpret; it is absolute. Remember though, in science conclusions must be confined to the population under study; broad generalizations should be avoided. The second statement is sound science. There is data to back it up. Later studies may reveal a more universal effect of the drug on cancerous cells, or they may not. Most researchers would be unwilling to stake their reputations on the first statement.

As a student, you should read and interpret popular press articles about research studies very carefully. From the text, can you determine how the experiment was set up and what variables were measured? Are the observations and data collected appropriate to the hypothesis being tested? Are the conclusions supported by the data? Are the conclusions worded in a scientific context (as probability statements) or are they generalized for dramatic effect? In any researched-based assignment, it is a good idea to refer to the original publication of a study (usually found in professional journals) and to interpret the facts for yourself.

Qualities of a Good Experiment

• narrowly defined subjects
• all subjects treated alike except for the factor or variable being studied
• a control group is used for comparison
• measurements related to the factors being studied are carefully recorded
• enough samples or subjects are used so that conclusions are valid for the population of interest
• conclusions made relate back to the hypothesis, are limited to the population being studied, and are stated in terms of probabilities

1.3: The Scientific Method

Chapter 1: scientific inquiry, chapter 2: chemistry of life, chapter 3: macromolecules, chapter 4: cell structure and function, chapter 5: membranes and cellular transport, chapter 6: cell signaling, chapter 7: metabolism, chapter 8: cellular respiration, chapter 9: photosynthesis, chapter 10: cell cycle and division, chapter 11: meiosis, chapter 12: classical and modern genetics, chapter 13: dna structure and function, chapter 14: gene expression, chapter 15: biotechnology, chapter 16: viruses, chapter 17: nutrition and digestion, chapter 18: nervous system, chapter 19: sensory systems, chapter 20: musculoskeletal system, chapter 21: endocrine system, chapter 22: circulatory and pulmonary systems, chapter 23: osmoregulation and excretion, chapter 24: immune system, chapter 25: reproduction and development, chapter 26: behavior, chapter 27: ecosystems, chapter 28: population and community ecology, chapter 29: biodiversity and conservation, chapter 30: speciation and diversity, chapter 31: natural selection, chapter 32: population genetics, chapter 33: evolutionary history, chapter 34: plant structure, growth, and nutrition, chapter 35: plant reproduction, chapter 36: plant responses to the environment.

The JoVE video player is compatible with HTML5 and Adobe Flash. Older browsers that do not support HTML5 and the H.264 video codec will still use a Flash-based video player. We recommend downloading the newest version of Flash here, but we support all versions 10 and above.

The scientific method is a detailed, stepwise process for answering questions. For example, a scientist makes an observation that the slugs destroy some cabbages but not those near garlic.

Such observations lead to asking questions, "Could garlic be used to deter slugs from ruining a cabbage patch?" After formulating questions, the scientist can then develop hypotheses —potential explanations for the observations that lead to specific, testable predictions.

In this case, a hypothesis could be that garlic repels slugs, which predicts that cabbages surrounded by garlic powder will suffer less damage than the ones without it. 

The hypothesis is then tested through a series of experiments designed to eliminate hypotheses.

The experimental setup involves defining variables. An independent variable is an item that is being tested, in this case, garlic addition. The dependent variable describes the measurement used to determine the outcome, such as the number of slugs on the cabbages.

In addition, the slugs must be divided into groups, experimental and control. These groups are identical, except that the experimental group is exposed to garlic powder.

After data are collected and analyzed, conclusions are made, and results are communicated to other scientists.

The scientific method is a detailed, empirical problem-solving process used by biologists and other scientists. This iterative approach involves formulating a question based on observation, developing a testable potential explanation for the observation (called a hypothesis), making and testing predictions based on the hypothesis, and using the findings to create new hypotheses and predictions.

Generally, predictions are tested using carefully-designed experiments. Based on the outcome of these experiments, the original hypothesis may need to be refined, and new hypotheses and questions can be generated. Importantly, this illustrates that the scientific method is not a stepwise recipe. Instead, it is a continuous refinement and testing of ideas based on new observations, which is the crux of scientific inquiry.

Science is mutable and continuously changes as scientists learn more about the world, physical phenomena and how organisms interact with their environment. For this reason, scientists avoid claiming to ‘prove' a specific idea. Instead, they gather evidence that either supports or refutes a given hypothesis.

Making Observations and Formulating Hypotheses

A hypothesis is preceded by an initial observation, during which information is gathered by the senses (e.g., vision, hearing) or using scientific tools and instruments. This observation leads to a question that prompts the formation of an initial hypothesis, a (testable) possible answer to the question. For example, the observation that slugs eat some cabbage plants but not cabbage plants located near garlic may prompt the question: why do slugs selectively not eat cabbage plants near garlic? One possible hypothesis, or answer to this question, is that slugs have an aversion to garlic. Based on this hypothesis, one might predict that slugs will not eat cabbage plants surrounded by a ring of garlic powder.

A hypothesis should be falsifiable, meaning that there are ways to disprove it if it is untrue. In other words, a hypothesis should be testable. Scientists often articulate and explicitly test for the opposite of the hypothesis, which is called the null hypothesis. In this case, the null hypothesis is that slugs do not have an aversion to garlic. The null hypothesis would be supported if, contrary to the prediction, slugs eat cabbage plants that are surrounded by garlic powder.

Testing a Hypothesis

When possible, scientists test hypotheses using controlled experiments that include independent and dependent variables, as well as control and experimental groups.

An independent variable is an item expected to have an effect (e.g., the garlic powder used in the slug and cabbage experiment or treatment given in a clinical trial). Dependent variables are the measurements used to determine the outcome of an experiment. In the experiment with slugs, cabbages, and garlic, the number of slugs eating cabbages is the dependent variable. This number is expected to depend on the presence or absence of garlic powder rings around the cabbage plants.

Experiments require experimental and control groups. An experimental group is treated with or exposed to the independent variable (i.e., the manipulation or treatment). For example, in the garlic aversion experiment with slugs, the experimental group is a group of cabbage plants surrounded by a garlic powder ring. A control group is subject to the same conditions as the experimental group, with the exception of the independent variable. Control groups in this experiment might include a group of cabbage plants in the same area that is surrounded by a non-garlic powder ring (to control for powder aversion) and a group that is not surrounded by any particular substance (to control for cabbage aversion). It is essential to include a control group because, without one, it is unclear whether the outcome is the result of the treatment or manipulation.

Refining a Hypothesis

If the results of an experiment support the hypothesis, further experiments may be designed and carried out to provide support for the hypothesis. The hypothesis may also be refined and made more specific. For example, additional experiments could determine whether slugs also have an aversion to other plants of the Allium genus, like onions.

If the results do not support the hypothesis, then the original hypothesis may be modified based on the new observations. It is important to rule out potential problems with the experimental design before modifying the hypothesis. For example, if slugs demonstrate an aversion to both garlic and non-garlic powder, the experiment can be carried out again using fresh garlic instead of powdered garlic. If the slugs still exhibit no aversion to garlic, then the original hypothesis can be modified.

Communication

The results of the experiments should be communicated to other scientists and the public, regardless of whether the data support the original hypothesis. This information can guide the development of new hypotheses and experimental questions.

Get cutting-edge science videos from J o VE sent straight to your inbox every month.

mktb-description

We use cookies to enhance your experience on our website.

By continuing to use our website or clicking “Continue”, you are agreeing to accept our cookies.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.2: Part One- The Scientific Method

• Last updated
• Save as PDF
• Page ID 134868

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

All rigorous scientific inquiry follows the scientific method. Understanding this process is essential when devising and carrying out your own experiments and critically analyzing the results of other experiments. T here are two types of scientific inquiry: discovery-based and hypothesis-based. Discovery-based science is often exploratory or descriptive, whereas hypothesis-based inquiry is used to answer ‘how’ and ‘why’ questions. Hypothesis-based science follows the steps scientific method. 

The scientific method is a systematic process that scientists use to gather information and test their ideas about the world. It typically involves the following steps: 

• Observing and asking questions: Scientists observe the natural world and ask questions about what they observe with their senses. Both types of scientific inquiry use this. 
• Forming a hypothesis: A hypothesis is a testable explanation for the observations, it is NOT an educated guess. Scientists form a hypothesis based on their observations and background knowledge. 
• Designing an experiment: Scientists design an experiment to test their hypothesis. They must control all other variables so that they can isolate the effects of the variable they are studying. 
• Collecting data: Scientists collect data by performing their experiments. They measure and record the results. Being able to measure something is a key component of science. Scientists have invented and developed many tools to aid in making measurements with a high degree of accuracy and measuring things that are impossible to measure with just human senses. 
• Analyzing data: Scientists analyze their data to see if it supports or disproves their hypothesis. They look for patterns and relationships in their data.
• Drawing conclusions: Based on the data, scientists draw conclusions about the validity of their hypothesis. If the data support the hypothesis, scientists must form a new hypothesis and start the process over again. 
• Communicating results: Scientists communicate their results to others through publications, conferences, and other means. Other scientists can then attempt to replicate the results to verify their validity. 

To write a good hypothesis , first answer your question: is it ‘yes’, or ‘no’? Then, explain why you think this is the answer. Then write this into a clear statement. For example, you may suspect that the abundance of birds is related to the number of trees. You think this is because more trees = more food and nesting sites: 

‘Bird abundance increases with the number of trees in a habitat because more trees increase the amount of food and nesting sites.’ 

You must explain HOW bird abundance varies with tree density. A mediocre hypothesis would be ‘bird density changes with tree density’ because it doesn’t address how it may happen and doesn’t account for increases or decreases. Another example that could use improvement might be: ‘the number of leaves in a forest positively correlates to bird abundance’ because it doesn’t try to explain why that happens not to mention that it would be extremely difficult to make an experiment to test this. 

Test your understanding: hypothesis  

You notice that your dog prefers chicken to vegetables. Research tells you that dogs were selectively bred from wolves: efficient predators with a meat-based diet. 

Write a hypothesis for this observation: 

Make a prediction . There are many ways to test your hypothesis. You could count the number of birds you see in an hour; you could count the number of nests or feathers you find; put out bird feeders and count how much food is eaten per bird visit… likewise, there are many ways of counting the number of trees.

Your prediction is what you think you will see in the ACTUAL RESULT(S) that you will collect in YOUR experiment if your hypothesis is not proven wrong . It also helps to restate the hypothesis in your prediction: 

Example predictions:  

If your methods were to walk in a forest and observe the number of birds seen in a day and then count all of the trees, your prediction would be: ‘if bird density increases with tree density then more birds will be counted in one day in habitats with more trees compared to habitats with fewer trees.’ 

If instead you put out bird feeders and used the amount of food eaten to indicate how many birds there are, your prediction would be: ‘if bird density increases with tree density then more food will be eaten from bird feeders in habitats with more trees compared to habitats with fewer trees.’ 

Test your understanding: Prediction  

You test whether dogs prefer chicken to vegetables by giving dogs two bowls of food: one with 200g of chicken, the other with 200g of boiled vegetables. After 1 minute you record how much food is left in each bowl. 

Write a prediction for this experiment based on the hypothesis you wrote earlier: 

Carry out an experiment . Use accurate and precise methods that enable you to collect unbiased, accurate data and test your hypothesis. A variable is anything that can be measured or controlled in an experiment. An independent variable is a variable that you will manipulate. The dependent variable is the variable being tested and that often ‘depends’ i.e. responds to the independent variable. In our example, we think that the number of birds depends on the number of trees. The independent variable is the number of trees and the dependent variable is the number of birds . 

A control variable is something that is kept constant, such as temperature, or the type of binoculars you use to observe birds. A control group is a group in which you will compare your experimental group with. For example, if you wanted to test the impact of eating sugar on tooth decay, your control group will be the group not given extra sugar, whereas the experimental group is given extra sugar. 

Only test one variable at a time! Otherwise, you will not be able to see what is impacting your dependent variable. If we tested both tree density and insect abundance at the same time, we would not know which one was affecting bird density.

Test your understanding: variables  

Identify the independent and dependent variables for your experiment testing food preferences in dogs: 

Independent: 

Dependent: 

7. Form a conclusion . What did you find? What does your data show? What is the answer to your question? Your conclusion is always based on your results and analyses and states whether your hypothesis and predictions were supported. Remember: it is ok to not support your hypothesis or to not reach a concrete conclusion! This is all part of the scientific process. If your hypothesis is disproven, go back and formulate and test a new one! This is often the time when you would write your entire experiment into a lab report. 

6. Analyze your data. You now need to examine and analyze your findings to find out what they mean. This could be as simple as plotting a graph of your results or calculating means and ranges. The method you chose should reveal the answer to your question. For our example, we could plot a graph of the number of trees vs. the number of birds in an area. 

Science and the scientific method: Definitions and examples

Here's a look at the foundation of doing science — the scientific method.

The scientific method

Hypothesis, theory and law, a brief history of science, additional resources, bibliography.

Science is a systematic and logical approach to discovering how things in the universe work. It is also the body of knowledge accumulated through the discoveries about all the things in the universe. 

The word "science" is derived from the Latin word "scientia," which means knowledge based on demonstrable and reproducible data, according to the Merriam-Webster dictionary . True to this definition, science aims for measurable results through testing and analysis, a process known as the scientific method. Science is based on fact, not opinion or preferences. The process of science is designed to challenge ideas through research. One important aspect of the scientific process is that it focuses only on the natural world, according to the University of California, Berkeley . Anything that is considered supernatural, or beyond physical reality, does not fit into the definition of science.

When conducting research, scientists use the scientific method to collect measurable, empirical evidence in an experiment related to a hypothesis (often in the form of an if/then statement) that is designed to support or contradict a scientific theory .

"As a field biologist, my favorite part of the scientific method is being in the field collecting the data," Jaime Tanner, a professor of biology at Marlboro College, told Live Science. "But what really makes that fun is knowing that you are trying to answer an interesting question. So the first step in identifying questions and generating possible answers (hypotheses) is also very important and is a creative process. Then once you collect the data you analyze it to see if your hypothesis is supported or not."

The steps of the scientific method go something like this, according to Highline College :

• Make an observation or observations.
• Form a hypothesis — a tentative description of what's been observed, and make predictions based on that hypothesis.
• Test the hypothesis and predictions in an experiment that can be reproduced.
• Analyze the data and draw conclusions; accept or reject the hypothesis or modify the hypothesis if necessary.
• Reproduce the experiment until there are no discrepancies between observations and theory. "Replication of methods and results is my favorite step in the scientific method," Moshe Pritsker, a former post-doctoral researcher at Harvard Medical School and CEO of JoVE, told Live Science. "The reproducibility of published experiments is the foundation of science. No reproducibility — no science."

Some key underpinnings to the scientific method:

• The hypothesis must be testable and falsifiable, according to North Carolina State University . Falsifiable means that there must be a possible negative answer to the hypothesis.
• Research must involve deductive reasoning and inductive reasoning . Deductive reasoning is the process of using true premises to reach a logical true conclusion while inductive reasoning uses observations to infer an explanation for those observations.
• An experiment should include a dependent variable (which does not change) and an independent variable (which does change), according to the University of California, Santa Barbara .
• An experiment should include an experimental group and a control group. The control group is what the experimental group is compared against, according to Britannica .

The process of generating and testing a hypothesis forms the backbone of the scientific method. When an idea has been confirmed over many experiments, it can be called a scientific theory. While a theory provides an explanation for a phenomenon, a scientific law provides a description of a phenomenon, according to The University of Waikato . One example would be the law of conservation of energy, which is the first law of thermodynamics that says that energy can neither be created nor destroyed. 

A law describes an observed phenomenon, but it doesn't explain why the phenomenon exists or what causes it. "In science, laws are a starting place," said Peter Coppinger, an associate professor of biology and biomedical engineering at the Rose-Hulman Institute of Technology. "From there, scientists can then ask the questions, 'Why and how?'"

Laws are generally considered to be without exception, though some laws have been modified over time after further testing found discrepancies. For instance, Newton's laws of motion describe everything we've observed in the macroscopic world, but they break down at the subatomic level.

This does not mean theories are not meaningful. For a hypothesis to become a theory, scientists must conduct rigorous testing, typically across multiple disciplines by separate groups of scientists. Saying something is "just a theory" confuses the scientific definition of "theory" with the layperson's definition. To most people a theory is a hunch. In science, a theory is the framework for observations and facts, Tanner told Live Science.

The earliest evidence of science can be found as far back as records exist. Early tablets contain numerals and information about the solar system , which were derived by using careful observation, prediction and testing of those predictions. Science became decidedly more "scientific" over time, however.

1200s: Robert Grosseteste developed the framework for the proper methods of modern scientific experimentation, according to the Stanford Encyclopedia of Philosophy. His works included the principle that an inquiry must be based on measurable evidence that is confirmed through testing.

1400s: Leonardo da Vinci began his notebooks in pursuit of evidence that the human body is microcosmic. The artist, scientist and mathematician also gathered information about optics and hydrodynamics.

1500s: Nicolaus Copernicus advanced the understanding of the solar system with his discovery of heliocentrism. This is a model in which Earth and the other planets revolve around the sun, which is the center of the solar system.

1600s: Johannes Kepler built upon those observations with his laws of planetary motion. Galileo Galilei improved on a new invention, the telescope, and used it to study the sun and planets. The 1600s also saw advancements in the study of physics as Isaac Newton developed his laws of motion.

1700s: Benjamin Franklin discovered that lightning is electrical. He also contributed to the study of oceanography and meteorology. The understanding of chemistry also evolved during this century as Antoine Lavoisier, dubbed the father of modern chemistry , developed the law of conservation of mass.

1800s: Milestones included Alessandro Volta's discoveries regarding electrochemical series, which led to the invention of the battery. John Dalton also introduced atomic theory, which stated that all matter is composed of atoms that combine to form molecules. The basis of modern study of genetics advanced as Gregor Mendel unveiled his laws of inheritance. Later in the century, Wilhelm Conrad Röntgen discovered X-rays , while George Ohm's law provided the basis for understanding how to harness electrical charges.

1900s: The discoveries of Albert Einstein , who is best known for his theory of relativity, dominated the beginning of the 20th century. Einstein's theory of relativity is actually two separate theories. His special theory of relativity, which he outlined in a 1905 paper, " The Electrodynamics of Moving Bodies ," concluded that time must change according to the speed of a moving object relative to the frame of reference of an observer. His second theory of general relativity, which he published as " The Foundation of the General Theory of Relativity ," advanced the idea that matter causes space to curve.

In 1952, Jonas Salk developed the polio vaccine , which reduced the incidence of polio in the United States by nearly 90%, according to Britannica . The following year, James D. Watson and Francis Crick discovered the structure of DNA , which is a double helix formed by base pairs attached to a sugar-phosphate backbone, according to the National Human Genome Research Institute .

2000s: The 21st century saw the first draft of the human genome completed, leading to a greater understanding of DNA. This advanced the study of genetics, its role in human biology and its use as a predictor of diseases and other disorders, according to the National Human Genome Research Institute .

• This video from City University of New York delves into the basics of what defines science.
• Learn about what makes science science in this book excerpt from Washington State University .
• This resource from the University of Michigan — Flint explains how to design your own scientific study.

Merriam-Webster Dictionary, Scientia. 2022. https://www.merriam-webster.com/dictionary/scientia

University of California, Berkeley, "Understanding Science: An Overview." 2022. ​​ https://undsci.berkeley.edu/article/0_0_0/intro_01  

Highline College, "Scientific method." July 12, 2015. https://people.highline.edu/iglozman/classes/astronotes/scimeth.htm  

North Carolina State University, "Science Scripts." https://projects.ncsu.edu/project/bio183de/Black/science/science_scripts.html  

University of California, Santa Barbara. "What is an Independent variable?" October 31,2017. http://scienceline.ucsb.edu/getkey.php?key=6045  

Encyclopedia Britannica, "Control group." May 14, 2020. https://www.britannica.com/science/control-group  

The University of Waikato, "Scientific Hypothesis, Theories and Laws." https://sci.waikato.ac.nz/evolution/Theories.shtml  

Stanford Encyclopedia of Philosophy, Robert Grosseteste. May 3, 2019. https://plato.stanford.edu/entries/grosseteste/  

Encyclopedia Britannica, "Jonas Salk." October 21, 2021. https://www.britannica.com/ biography /Jonas-Salk

National Human Genome Research Institute, "​Phosphate Backbone." https://www.genome.gov/genetics-glossary/Phosphate-Backbone  

National Human Genome Research Institute, "What is the Human Genome Project?" https://www.genome.gov/human-genome-project/What  

‌ Live Science contributor Ashley Hamer updated this article on Jan. 16, 2022.

Sign up for the Live Science daily newsletter now

Get the world’s most fascinating discoveries delivered straight to your inbox.

Warm ocean water is rushing beneath Antarctica's 'Doomsday Glacier,' making its collapse more likely

Earth from space: Rare phenomenon transforms African thunderstorm into giant ethereal 'jellyfish'

Scientists grow diamonds from scratch in 15 minutes thanks to groundbreaking new process

Most Popular

• 2 James Webb telescope confirms there is something seriously wrong with our understanding of the universe
• 3 Earth from space: Rare phenomenon transforms African thunderstorm into giant ethereal 'jellyfish'
• 4 Some of the oldest stars in the universe found hiding near the Milky Way's edge — and they may not be alone
• 5 See May's full 'Flower Moon' rise this week close to a red supergiant star
• 2 Creepy Deep-Sea Anglerfish Captured in Rare Video
• 3 Can a commercial airplane do a barrel roll?
• 4 Mysterious L-shaped structure found near Egyptian pyramids of Giza baffles scientists
• 5 In a 1st, HIV vaccine triggers rare and elusive antibodies in human patients

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• PLoS Comput Biol
• v.15(9); 2019 Sep

Perspective: Dimensions of the scientific method

Eberhard o. voit.

Department of Biomedical Engineering, Georgia Institute of Technology and Emory University, Atlanta, Georgia, United States of America

The scientific method has been guiding biological research for a long time. It not only prescribes the order and types of activities that give a scientific study validity and a stamp of approval but also has substantially shaped how we collectively think about the endeavor of investigating nature. The advent of high-throughput data generation, data mining, and advanced computational modeling has thrown the formerly undisputed, monolithic status of the scientific method into turmoil. On the one hand, the new approaches are clearly successful and expect the same acceptance as the traditional methods, but on the other hand, they replace much of the hypothesis-driven reasoning with inductive argumentation, which philosophers of science consider problematic. Intrigued by the enormous wealth of data and the power of machine learning, some scientists have even argued that significant correlations within datasets could make the entire quest for causation obsolete. Many of these issues have been passionately debated during the past two decades, often with scant agreement. It is proffered here that hypothesis-driven, data-mining–inspired, and “allochthonous” knowledge acquisition, based on mathematical and computational models, are vectors spanning a 3D space of an expanded scientific method. The combination of methods within this space will most certainly shape our thinking about nature, with implications for experimental design, peer review and funding, sharing of result, education, medical diagnostics, and even questions of litigation.

The traditional scientific method: Hypothesis-driven deduction

Research is the undisputed core activity defining science. Without research, the advancement of scientific knowledge would come to a screeching halt. While it is evident that researchers look for new information or insights, the term “research” is somewhat puzzling. Never mind the prefix “re,” which simply means “coming back and doing it again and again,” the word “search” seems to suggest that the research process is somewhat haphazard, that not much of a strategy is involved in the process. One might argue that research a few hundred years ago had the character of hoping for enough luck to find something new. The alchemists come to mind in their quest to turn mercury or lead into gold, or to discover an elixir for eternal youth, through methods we nowadays consider laughable.

Today’s sciences, in stark contrast, are clearly different. Yes, we still try to find something new—and may need a good dose of luck—but the process is anything but unstructured. In fact, it is prescribed in such rigor that it has been given the widely known moniker “scientific method.” This scientific method has deep roots going back to Aristotle and Herophilus (approximately 300 BC), Avicenna and Alhazen (approximately 1,000 AD), Grosseteste and Robert Bacon (approximately 1,250 AD), and many others, but solidified and crystallized into the gold standard of quality research during the 17th and 18th centuries [ 1 – 7 ]. In particular, Sir Francis Bacon (1561–1626) and René Descartes (1596–1650) are often considered the founders of the scientific method, because they insisted on careful, systematic observations of high quality, rather than metaphysical speculations that were en vogue among the scholars of the time [ 1 , 8 ]. In contrast to their peers, they strove for objectivity and insisted that observations, rather than an investigator’s preconceived ideas or superstitions, should be the basis for formulating a research idea [ 7 , 9 ].

Bacon and his 19th century follower John Stuart Mill explicitly proposed gaining knowledge through inductive reasoning: Based on carefully recorded observations, or from data obtained in a well-planned experiment, generalized assertions were to be made about similar yet (so far) unobserved phenomena [ 7 ]. Expressed differently, inductive reasoning attempts to derive general principles or laws directly from empirical evidence [ 10 ]. An example is the 19th century epigram of the physician Rudolf Virchow, Omnis cellula e cellula . There is no proof that indeed “every cell derives from a cell,” but like Virchow, we have made the observation time and again and never encountered anything suggesting otherwise.

In contrast to induction, the widely accepted, traditional scientific method is based on formulating and testing hypotheses. From the results of these tests, a deduction is made whether the hypothesis is presumably true or false. This type of hypotheticodeductive reasoning goes back to William Whewell, William Stanley Jevons, and Charles Peirce in the 19th century [ 1 ]. By the 20th century, the deductive, hypothesis-based scientific method had become deeply ingrained in the scientific psyche, and it is now taught as early as middle school in order to teach students valid means of discovery [ 8 , 11 , 12 ]. The scientific method has not only guided most research studies but also fundamentally influenced how we think about the process of scientific discovery.

Alas, because biology has almost no general laws, deduction in the strictest sense is difficult. It may therefore be preferable to use the term abduction, which refers to the logical inference toward the most plausible explanation, given a set of observations, although this explanation cannot be proven and is not necessarily true.

Over the decades, the hypothesis-based scientific method did experience variations here and there, but its conceptual scaffold remained essentially unchanged ( Fig 1 ). Its key is a process that begins with the formulation of a hypothesis that is to be rigorously tested, either in the wet lab or computationally; nonadherence to this principle is seen as lacking rigor and can lead to irreproducible results [ 1 , 13 – 15 ].

The central concept of the traditional scientific method is a falsifiable hypothesis regarding some phenomenon of interest. This hypothesis is to be tested experimentally or computationally. The test results support or refute the hypothesis, triggering a new round of hypothesis formulation and testing.

Going further, the prominent philosopher of science Sir Karl Popper argued that a scientific hypothesis can never be verified but that it can be disproved by a single counterexample. He therefore demanded that scientific hypotheses had to be falsifiable, because otherwise, testing would be moot [ 16 , 17 ] (see also [ 18 ]). As Gillies put it, “successful theories are those that survive elimination through falsification” [ 19 ]. Kelley and Scott agreed to some degree but warned that complete insistence on falsifiability is too restrictive as it would mark many computational techniques, statistical hypothesis testing, and even Darwin’s theory of evolution as nonscientific [ 20 ].

While the hypothesis-based scientific method has been very successful, its exclusive reliance on deductive reasoning is dangerous because according to the so-called Duhem–Quine thesis, hypothesis testing always involves an unknown number of explicit or implicit assumptions, some of which may steer the researcher away from hypotheses that seem implausible, although they are, in fact, true [ 21 ]. According to Kuhn, this bias can obstruct the recognition of paradigm shifts [ 22 ], which require the rethinking of previously accepted “truths” and the development of radically new ideas [ 23 , 24 ]. The testing of simultaneous alternative hypotheses [ 25 – 27 ] ameliorates this problem to some degree but not entirely.

The traditional scientific method is often presented in discrete steps, but it should really be seen as a form of critical thinking, subject to review and independent validation [ 8 ]. It has proven very influential, not only by prescribing valid experimentation, but also for affecting the way we attempt to understand nature [ 18 ], for teaching [ 8 , 12 ], reporting, publishing, and otherwise sharing information [ 28 ], for peer review and the awarding of funds by research-supporting agencies [ 29 , 30 ], for medical diagnostics [ 7 ], and even in litigation [ 31 ].

A second dimension of the scientific method: Data-mining–inspired induction

A major shift in biological experimentation occurred with the–omics revolution of the early 21st century. All of a sudden, it became feasible to perform high-throughput experiments that generated thousands of measurements, typically characterizing the expression or abundances of very many—if not all—genes, proteins, metabolites, or other biological quantities in a sample.

The strategy of measuring large numbers of items in a nontargeted fashion is fundamentally different from the traditional scientific method and constitutes a new, second dimension of the scientific method. Instead of hypothesizing and testing whether gene X is up-regulated under some altered condition, the leading question becomes which of the thousands of genes in a sample are up- or down-regulated. This shift in focus elevates the data to the supreme role of revealing novel insights by themselves ( Fig 2 ). As an important, generic advantage over the traditional strategy, this second dimension is free of a researcher’s preconceived notions regarding the molecular mechanisms governing the phenomenon of interest, which are otherwise the key to formulating a hypothesis. The prominent biologists Patrick Brown and David Botstein commented that “the patterns of expression will often suffice to begin de novo discovery of potential gene functions” [ 32 ].

Data-driven research begins with an untargeted exploration, in which the data speak for themselves. Machine learning extracts patterns from the data, which suggest hypotheses that are to be tested in the lab or computationally.

This data-driven, discovery-generating approach is at once appealing and challenging. On the one hand, very many data are explored simultaneously and essentially without bias. On the other hand, the large datasets supporting this approach create a genuine challenge to understanding and interpreting the experimental results because the thousands of data points, often superimposed with a fair amount of noise, make it difficult to detect meaningful differences between sample and control. This situation can only be addressed with computational methods that first “clean” the data, for instance, through the statistically valid removal of outliers, and then use machine learning to identify statistically significant, distinguishing molecular profiles or signatures. In favorable cases, such signatures point to specific biological pathways, whereas other signatures defy direct explanation but may become the launch pad for follow-up investigations [ 33 ].

Today’s scientists are very familiar with this discovery-driven exploration of “what’s out there” and might consider it a quaint quirk of history that this strategy was at first widely chastised and ridiculed as a “fishing expedition” [ 30 , 34 ]. Strict traditionalists were outraged that rigor was leaving science with the new approach and that sufficient guidelines were unavailable to assure the validity and reproducibility of results [ 10 , 35 , 36 ].

From the view point of philosophy of science, this second dimension of the scientific method uses inductive reasoning and reflects Bacon’s idea that observations can and should dictate the research question to be investigated [ 1 , 7 ]. Allen [ 36 ] forcefully rejected this type of reasoning, stating “the thinking goes, we can now expect computer programs to derive significance, relevance and meaning from chunks of information, be they nucleotide sequences or gene expression profiles… In contrast with this view, many are convinced that no purely logical process can turn observation into understanding.” His conviction goes back to the 18th century philosopher David Hume and again to Popper, who identified as the overriding problem with inductive reasoning that it can never truly reveal causality, even if a phenomenon is observed time and again [ 16 , 17 , 37 , 38 ]. No number of observations, even if they always have the same result, can guard against an exception that would violate the generality of a law inferred from these observations [ 1 , 35 ]. Worse, Popper argued, through inference by induction, we cannot even know the probability of something being true [ 10 , 17 , 36 ].

Others argued that data-driven and hypothesis-driven research actually do not differ all that much in principle, as long as there is cycling between developing new ideas and testing them with care [ 27 ]. In fact, Kell and Oliver [ 34 ] maintained that the exclusive acceptance of hypothesis-driven programs misrepresents the complexities of biological knowledge generation. Similarly refuting the prominent rule of deduction, Platt [ 26 ] and Beard and Kushmerick [ 27 ] argued that repeated inductive reasoning, called strong inference, corresponds to a logically sound decision tree of disproving or refining hypotheses that can rapidly yield firm conclusions; nonetheless, Platt had to admit that inductive inference is not as certain as deduction, because it projects into the unknown. Lander compared the task of obtaining causality by induction to the problem of inferring the design of a microprocessor from input-output readings, which in a strict sense is impossible, because the microprocessor could be arbitrarily complicated; even so, inference often leads to novel insights and therefore is valuable [ 39 ].

An interesting special case of almost pure inductive reasoning is epidemiology, where hypothesis-driven reasoning is rare and instead, the fundamental question is whether data-based evidence is sufficient to associate health risks with specific causes [ 31 , 34 ].

Recent advances in machine learning and “big-data” mining have driven the use of inductive reasoning to unprecedented heights. As an example, machine learning can greatly assist in the discovery of patterns, for instance, in biological sequences [ 40 ]. Going a step further, a pithy article by Andersen [ 41 ] proffered that we may not need to look for causality or mechanistic explanations anymore if we just have enough correlation: “With enough data, the numbers speak for themselves, correlation replaces causation, and science can advance even without coherent models or unified theories.”

Of course, the proposal to abandon the quest for causality caused pushback on philosophical as well as mathematical grounds. Allen [ 10 , 35 ] considered the idea “absurd” that data analysis could enhance understanding in the absence of a hypothesis. He felt confident “that even the formidable combination of computing power with ease of access to data cannot produce a qualitative shift in the way that we do science: the making of hypotheses remains an indispensable component in the growth of knowledge” [ 36 ]. Succi and Coveney [ 42 ] refuted the “most extravagant claims” of big-data proponents very differently, namely by analyzing the theories on which machine learning is founded. They contrasted the assumptions underlying these theories, such as the law of large numbers, with the mathematical reality of complex biological systems. Specifically, they carefully identified genuine features of these systems, such as nonlinearities, nonlocality of effects, fractal aspects, and high dimensionality, and argued that they fundamentally violate some of the statistical assumptions implicitly underlying big-data analysis, like independence of events. They concluded that these discrepancies “may lead to false expectations and, at their nadir, even to dangerous social, economical and political manipulation.” To ameliorate the situation, the field of big-data analysis would need new strong theorems characterizing the validity of its methods and the numbers of data required for obtaining reliable insights. Succi and Coveney go as far as stating that too many data are just as bad as insufficient data [ 42 ].

While philosophical doubts regarding inductive methods will always persist, one cannot deny that -omics-based, high-throughput studies, combined with machine learning and big-data analysis, have been very successful [ 43 ]. Yes, induction cannot truly reveal general laws, no matter how large the datasets, but they do provide insights that are very different from what science had offered before and may at least suggest novel patterns, trends, or principles. As a case in point, if many transcriptomic studies indicate that a particular gene set is involved in certain classes of phenomena, there is probably some truth to the observation, even though it is not mathematically provable. Kepler’s laws of astronomy were arguably derived solely from inductive reasoning [ 34 ].

Notwithstanding the opposing views on inductive methods, successful strategies shape how we think about science. Thus, to take advantage of all experimental options while ensuring quality of research, we must not allow that “anything goes” but instead identify and characterize standard operating procedures and controls that render this emerging scientific method valid and reproducible. A laudable step in this direction was the wide acceptance of “minimum information about a microarray experiment” (MIAME) standards for microarray experiments [ 44 ].

A third dimension of the scientific method: Allochthonous reasoning

Parallel to the blossoming of molecular biology and the rapid rise in the power and availability of computing in the late 20th century, the use of mathematical and computational models became increasingly recognized as relevant and beneficial for understanding biological phenomena. Indeed, mathematical models eventually achieved cornerstone status in the new field of computational systems biology.

Mathematical modeling has been used as a tool of biological analysis for a long time [ 27 , 45 – 48 ]. Interesting for the discussion here is that the use of mathematical and computational modeling in biology follows a scientific approach that is distinctly different from the traditional and the data-driven methods, because it is distributed over two entirely separate domains of knowledge. One consists of the biological reality of DNA, elephants, and roses, whereas the other is the world of mathematics, which is governed by numbers, symbols, theorems, and abstract work protocols. Because the ways of thinking—and even the languages—are different in these two realms, I suggest calling this type of knowledge acquisition “allochthonous” (literally Greek: in or from a “piece of land different from where one is at home”; one could perhaps translate it into modern lingo as “outside one’s comfort zone”). De facto, most allochthonous reasoning in biology presently refers to mathematics and computing, but one might also consider, for instance, the application of methods from linguistics in the analysis of DNA sequences or proteins [ 49 ].

One could argue that biologists have employed “models” for a long time, for instance, in the form of “model organisms,” cell lines, or in vitro experiments, which more or less faithfully reflect features of the organisms of true interest but are easier to manipulate. However, this type of biological model use is rather different from allochthonous reasoning, as it does not leave the realm of biology and uses the same language and often similar methodologies.

A brief discussion of three experiences from our lab may illustrate the benefits of allochthonous reasoning. (1) In a case study of renal cell carcinoma, a dynamic model was able to explain an observed yet nonintuitive metabolic profile in terms of the enzymatic reaction steps that had been altered during the disease [ 50 ]. (2) A transcriptome analysis had identified several genes as displaying significantly different expression patterns during malaria infection in comparison to the state of health. Considered by themselves and focusing solely on genes coding for specific enzymes of purine metabolism, the findings showed patterns that did not make sense. However, integrating the changes in a dynamic model revealed that purine metabolism globally shifted, in response to malaria, from guanine compounds to adenine, inosine, and hypoxanthine [ 51 ]. (3) Data capturing the dynamics of malaria parasites suggested growth rates that were biologically impossible. Speculation regarding possible explanations led to the hypothesis that many parasite-harboring red blood cells might “hide” from circulation and therewith from detection in the blood stream. While experimental testing of the feasibility of the hypothesis would have been expensive, a dynamic model confirmed that such a concealment mechanism could indeed quantitatively explain the apparently very high growth rates [ 52 ]. In all three cases, the insights gained inductively from computational modeling would have been difficult to obtain purely with experimental laboratory methods. Purely deductive allochthonous reasoning is the ultimate goal of the search for design and operating principles [ 53 – 55 ], which strives to explain why certain structures or functions are employed by nature time and again. An example is a linear metabolic pathway, in which feedback inhibition is essentially always exerted on the first step [ 56 , 57 ]. This generality allows the deduction that a so far unstudied linear pathway is most likely (or even certain to be) inhibited at the first step. Not strictly deductive—but rather abductive—was a study in our lab in which we analyzed time series data with a mathematical model that allowed us to infer the most likely regulatory structure of a metabolic pathway [ 58 , 59 ].

A typical allochthonous investigation begins in the realm of biology with the formulation of a hypothesis ( Fig 3 ). Instead of testing this hypothesis with laboratory experiments, the system encompassing the hypothesis is moved into the realm of mathematics. This move requires two sets of ingredients. One set consists of the simplification and abstraction of the biological system: Any distracting details that seem unrelated to the hypothesis and its context are omitted or represented collectively with other details. This simplification step carries the greatest risk of the entire modeling approach, as omission of seemingly negligible but, in truth, important details can easily lead to wrong results. The second set of ingredients consists of correspondence rules that translate every biological component or process into the language of mathematics [ 60 , 61 ].

This mathematical and computational approach is distributed over two realms, which are connected by correspondence rules.

Once the system is translated, it has become an entirely mathematical construct that can be analyzed purely with mathematical and computational means. The results of this analysis are also strictly mathematical. They typically consist of values of variables, magnitudes of processes, sensitivity patterns, signs of eigenvalues, or qualitative features like the onset of oscillations or the potential for limit cycles. Correspondence rules are used again to move these results back into the realm of biology. As an example, the mathematical result that “two eigenvalues have positive real parts” does not make much sense to many biologists, whereas the interpretation that “the system is not stable at the steady state in question” is readily explained. New biological insights may lead to new hypotheses, which are tested either by experiments or by returning once more to the realm of mathematics. The model design, diagnosis, refinements, and validation consist of several phases, which have been discussed widely in the biomathematical literature. Importantly, each iteration of a typical modeling analysis consists of a move from the biological to the mathematical realm and back.

The reasoning within the realm of mathematics is often deductive, in the form of an Aristotelian syllogism, such as the well-known “All men are mortal; Socrates is a man; therefore, Socrates is mortal.” However, the reasoning may also be inductive, as it is the case with large-scale Monte-Carlo simulations that generate arbitrarily many “observations,” although they cannot reveal universal principles or theorems. An example is a simulation randomly drawing numbers in an attempt to show that every real number has an inverse. The simulation will always attest to this hypothesis but fail to discover the truth because it will never randomly draw 0. Generically, computational models may be considered sets of hypotheses, formulated as equations or as algorithms that reflect our perception of a complex system [ 27 ].

Impact of the multidimensional scientific method on learning

Almost all we know in biology has come from observation, experimentation, and interpretation. The traditional scientific method not only offered clear guidance for this knowledge gathering, but it also fundamentally shaped the way we think about the exploration of nature. When presented with a new research question, scientists were trained to think immediately in terms of hypotheses and alternatives, pondering the best feasible ways of testing them, and designing in their minds strong controls that would limit the effects of known or unknown confounders. Shaped by the rigidity of this ever-repeating process, our thinking became trained to move forward one well-planned step at a time. This modus operandi was rigid and exact. It also minimized the erroneous pursuit of long speculative lines of thought, because every step required testing before a new hypothesis was formed. While effective, the process was also very slow and driven by ingenuity—as well as bias—on the scientist’s part. This bias was sometimes a hindrance to necessary paradigm shifts [ 22 ].

High-throughput data generation, big-data analysis, and mathematical-computational modeling changed all that within a few decades. In particular, the acceptance of inductive principles and of the allochthonous use of nonbiological strategies to answer biological questions created an unprecedented mix of successes and chaos. To the horror of traditionalists, the importance of hypotheses became minimized, and the suggestion spread that the data would speak for themselves [ 36 ]. Importantly, within this fog of “anything goes,” the fundamental question arose how to determine whether an experiment was valid.

Because agreed-upon operating procedures affect research progress and interpretation, thinking, teaching, and sharing of results, this question requires a deconvolution of scientific strategies. Here I proffer that the single scientific method of the past should be expanded toward a vector space of scientific methods, with spanning vectors that correspond to different dimensions of the scientific method ( Fig 4 ).

The traditional hypothesis-based deductive scientific method is expanded into a 3D space that allows for synergistic blends of methods that include data-mining–inspired, inductive knowledge acquisition, and mathematical model-based, allochthonous reasoning.

Obviously, all three dimensions have their advantages and drawbacks. The traditional, hypothesis-driven deductive method is philosophically “clean,” except that it is confounded by preconceptions and assumptions. The data-mining–inspired inductive method cannot offer universal truths but helps us explore very large spaces of factors that contribute to a phenomenon. Allochthonous, model-based reasoning can be performed mentally, with paper and pencil, through rigorous analysis, or with a host of computational methods that are precise and disprovable [ 27 ]. At the same time, they are incomparable faster, cheaper, and much more comprehensive than experiments in molecular biology. This reduction in cost and time, and the increase in coverage, may eventually have far-reaching consequences, as we can already fathom from much of modern physics.

Due to its long history, the traditional dimension of the scientific method is supported by clear and very strong standard operating procedures. Similarly, strong procedures need to be developed for the other two dimensions. The MIAME rules for microarray analysis provide an excellent example [ 44 ]. On the mathematical modeling front, no such rules are generally accepted yet, but trends toward them seem to emerge at the horizon. For instance, it seems to be becoming common practice to include sensitivity analyses in typical modeling studies and to assess the identifiability or sloppiness of ensembles of parameter combinations that fit a given dataset well [ 62 , 63 ].

From a philosophical point of view, it seems unlikely that objections against inductive reasoning will disappear. However, instead of pitting hypothesis-based deductive reasoning against inductivism, it seems more beneficial to determine how the different methods can be synergistically blended ( cf . [ 18 , 27 , 34 , 42 ]) as linear combinations of the three vectors of knowledge acquisition ( Fig 4 ). It is at this point unclear to what degree the identified three dimensions are truly independent of each other, whether additional dimensions should be added [ 24 ], or whether the different versions could be amalgamated into a single scientific method [ 18 ], especially if it is loosely defined as a form of critical thinking [ 8 ]. Nobel Laureate Percy Bridgman even concluded that “science is what scientists do, and there are as many scientific methods as there are individual scientists” [ 8 , 64 ].

Combinations of the three spanning vectors of the scientific method have been emerging for some time. Many biologists already use inductive high-throughput methods to develop specific hypotheses that are subsequently tested with deductive or further inductive methods [ 34 , 65 ]. In terms of including mathematical modeling, physics and geology have been leading the way for a long time, often by beginning an investigation in theory, before any actual experiment is performed. It will benefit biology to look into this strategy and to develop best practices of allochthonous reasoning.

The blending of methods may take quite different shapes. Early on, Ideker and colleagues [ 65 ] proposed an integrated experimental approach for pathway analysis that offered a glimpse of new experimental strategies within the space of scientific methods. In a similar vein, Covert and colleagues [ 66 ] included computational methods into such an integrated approach. Additional examples of blended analyses in systems biology can be seen in other works, such as [ 43 , 67 – 73 ]. Generically, it is often beneficial to start with big data, determine patterns in associations and correlations, then switch to the mathematical realm in order to filter out spurious correlations in a high-throughput fashion. If this procedure is executed in an iterative manner, the “surviving” associations have an increased level of confidence and are good candidates for further experimental or computational testing (personal communication from S. Chandrasekaran).

If each component of a blended scientific method follows strict, commonly agreed guidelines, “linear combinations” within the 3D space can also be checked objectively, per deconvolution. In addition, guidelines for synergistic blends of component procedures should be developed. If we carefully monitor such blends, time will presumably indicate which method is best for which task and how the different approaches optimally inform each other. For instance, it will be interesting to study whether there is an optimal sequence of experiments along the three axes for a particular class of tasks. Big-data analysis together with inductive reasoning might be optimal for creating initial hypotheses and possibly refuting wrong speculations (“we had thought this gene would be involved, but apparently it isn’t”). If the logic of an emerging hypotheses can be tested with mathematical and computational tools, it will almost certainly be faster and cheaper than an immediate launch into wet-lab experimentation. It is also likely that mathematical reasoning will be able to refute some apparently feasible hypothesis and suggest amendments. Ultimately, the “surviving” hypotheses must still be tested for validity through conventional experiments. Deconvolving current practices and optimizing the combination of methods within the 3D or higher-dimensional space of scientific methods will likely result in better planning of experiments and in synergistic blends of approaches that have the potential capacity of addressing some of the grand challenges in biology.

Acknowledgments

The author is very grateful to Dr. Sriram Chandrasekaran and Ms. Carla Kumbale for superb suggestions and invaluable feedback.

Funding Statement

This work was supported in part by grants from the National Science Foundation ( https://www.nsf.gov/div/index.jsp?div=MCB ) grant NSF-MCB-1517588 (PI: EOV), NSF-MCB-1615373 (PI: Diana Downs) and the National Institute of Environmental Health Sciences ( https://www.niehs.nih.gov/ ) grant NIH-2P30ES019776-05 (PI: Carmen Marsit). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Six Steps of the Scientific Method

Learn What Makes Each Stage Important

ThoughtCo. / Hugo Lin 

• Scientific Method
• Chemical Laws
• Periodic Table
• Projects & Experiments
• Biochemistry
• Physical Chemistry
• Medical Chemistry
• Chemistry In Everyday Life
• Famous Chemists
• Activities for Kids
• Abbreviations & Acronyms
• Weather & Climate
• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

The scientific method is a systematic way of learning about the world around us and answering questions. The key difference between the scientific method and other ways of acquiring knowledge are forming a hypothesis and then testing it with an experiment.

The Six Steps

The number of steps can vary from one description to another (which mainly happens when data and analysis are separated into separate steps), however, this is a fairly standard list of the six scientific method steps that you are expected to know for any science class:

• Purpose/Question Ask a question.
• Research Conduct background research. Write down your sources so you can cite your references. In the modern era, a lot of your research may be conducted online. Scroll to the bottom of articles to check the references. Even if you can't access the full text of a published article, you can usually view the abstract to see the summary of other experiments. Interview experts on a topic. The more you know about a subject, the easier it will be to conduct your investigation.
• Hypothesis Propose a hypothesis . This is a sort of educated guess about what you expect. It is a statement used to predict the outcome of an experiment. Usually, a hypothesis is written in terms of cause and effect. Alternatively, it may describe the relationship between two phenomena. One type of hypothesis is the null hypothesis or the no-difference hypothesis. This is an easy type of hypothesis to test because it assumes changing a variable will have no effect on the outcome. In reality, you probably expect a change but rejecting a hypothesis may be more useful than accepting one.
• Experiment Design and perform an experiment to test your hypothesis. An experiment has an independent and dependent variable. You change or control the independent variable and record the effect it has on the dependent variable . It's important to change only one variable for an experiment rather than try to combine the effects of variables in an experiment. For example, if you want to test the effects of light intensity and fertilizer concentration on the growth rate of a plant, you're really looking at two separate experiments.
• Data/Analysis Record observations and analyze the meaning of the data. Often, you'll prepare a table or graph of the data. Don't throw out data points you think are bad or that don't support your predictions. Some of the most incredible discoveries in science were made because the data looked wrong! Once you have the data, you may need to perform a mathematical analysis to support or refute your hypothesis.
• Conclusion Conclude whether to accept or reject your hypothesis. There is no right or wrong outcome to an experiment, so either result is fine. Accepting a hypothesis does not necessarily mean it's correct! Sometimes repeating an experiment may give a different result. In other cases, a hypothesis may predict an outcome, yet you might draw an incorrect conclusion. Communicate your results. The results may be compiled into a lab report or formally submitted as a paper. Whether you accept or reject the hypothesis, you likely learned something about the subject and may wish to revise the original hypothesis or form a new one for a future experiment.

When Are There Seven Steps?

Sometimes the scientific method is taught with seven steps instead of six. In this model, the first step of the scientific method is to make observations. Really, even if you don't make observations formally, you think about prior experiences with a subject in order to ask a question or solve a problem.

Formal observations are a type of brainstorming that can help you find an idea and form a hypothesis. Observe your subject and record everything about it. Include colors, timing, sounds, temperatures, changes, behavior, and anything that strikes you as interesting or significant.

When you design an experiment, you are controlling and measuring variables. There are three types of variables:

• Controlled Variables:  You can have as many  controlled variables  as you like. These are parts of the experiment that you try to keep constant throughout an experiment so that they won't interfere with your test. Writing down controlled variables is a good idea because it helps make your experiment  reproducible , which is important in science! If you have trouble duplicating results from one experiment to another, there may be a controlled variable that you missed.
• Independent Variable:  This is the variable you control.
• Dependent Variable:  This is the variable you measure. It is called the dependent variable because it  depends  on the independent variable.
• Examples of Independent and Dependent Variables
• Null Hypothesis Examples
• Difference Between Independent and Dependent Variables
• Scientific Method Flow Chart
• What Is an Experiment? Definition and Design
• How To Design a Science Fair Experiment
• What Is a Hypothesis? (Science)
• Scientific Variable
• What Are the Elements of a Good Hypothesis?
• Scientific Method Vocabulary Terms
• Understanding Simple vs Controlled Experiments
• What Is a Variable in Science?
• Null Hypothesis Definition and Examples
• Independent Variable Definition and Examples
• Scientific Method Lesson Plan