assignment problem with dummy column

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

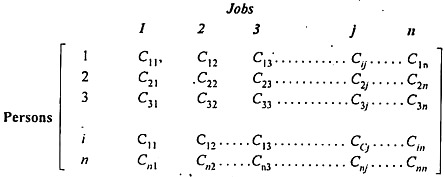
Step :4 If each row and each column contains exactly one assignment, then the solution is optimal.

Example 10.7

Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV.

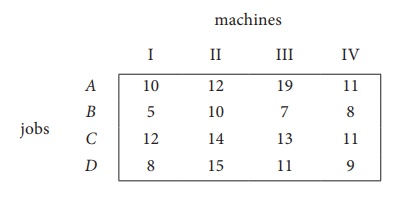
Here the number of rows and columns are equal.

∴ The given assignment problem is balanced. Now let us find the solution.

Step 1: Select a smallest element in each row and subtract this from all the elements in its row.

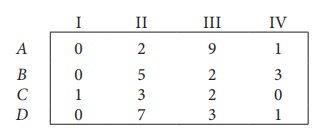
Look for atleast one zero in each row and each column.Otherwise go to step 2.

Step 2: Select the smallest element in each column and subtract this from all the elements in its column.

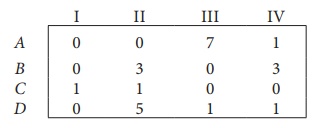
Since each row and column contains atleast one zero, assignments can be made.

Step 3 (Assignment):

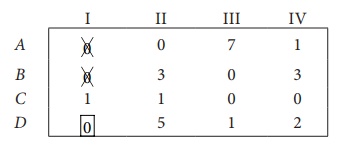
Thus all the four assignments have been made. The optimal assignment schedule and total cost is

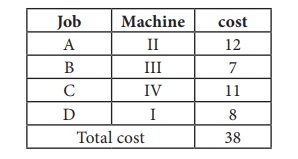
The optimal assignment (minimum) cost

Example 10.8

Consider the problem of assigning five jobs to five persons. The assignment costs are given as follows. Determine the optimum assignment schedule.

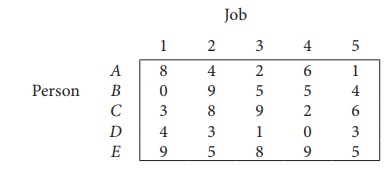
∴ The given assignment problem is balanced.

Now let us find the solution.

The cost matrix of the given assignment problem is

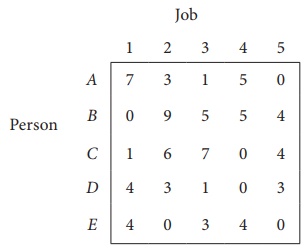
Column 3 contains no zero. Go to Step 2.

Thus all the five assignments have been made. The Optimal assignment schedule and total cost is

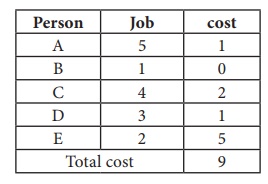
The optimal assignment (minimum) cost = ` 9

Example 10.9

Solve the following assignment problem.

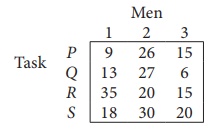
Since the number of columns is less than the number of rows, given assignment problem is unbalanced one. To balance it , introduce a dummy column with all the entries zero. The revised assignment problem is

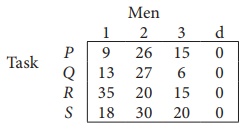
Here only 3 tasks can be assigned to 3 men.

Step 1: is not necessary, since each row contains zero entry. Go to Step 2.

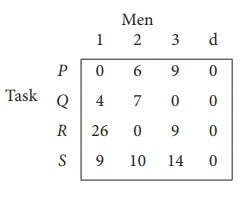
Step 3 (Assignment) :

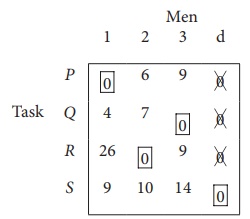
Since each row and each columncontains exactly one assignment,all the three men have been assigned a task. But task S is not assigned to any Man. The optimal assignment schedule and total cost is

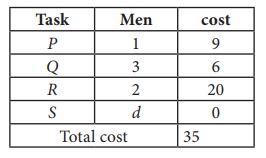
The optimal assignment (minimum) cost = ₹ 35

Related Topics

Privacy Policy , Terms and Conditions , DMCA Policy and Compliant

Copyright © 2018-2024 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures

Hungarian Algorithm for Assignment Problem | Set 1 (Introduction)

• Hungarian Algorithm for Assignment Problem | Set 2 (Implementation)
• Introduction to Exact Cover Problem and Algorithm X
• Greedy Approximate Algorithm for Set Cover Problem
• Job Assignment Problem using Branch And Bound
• Implementation of Exhaustive Search Algorithm for Set Packing
• Channel Assignment Problem
• Chocolate Distribution Problem | Set 2
• Transportation Problem | Set 1 (Introduction)
• OLA Interview Experience | Set 11 ( For Internship)
• Top 20 Greedy Algorithms Interview Questions
• Job Sequencing Problem - Loss Minimization
• Prim's Algorithm (Simple Implementation for Adjacency Matrix Representation)
• Data Structures and Algorithms | Set 21
• Adobe Interview Experience | Set 55 (On-Campus Full Time for MTS profile)
• Amazon Interview Experience | Set 211 (On-Campus for Internship)
• OYO Rooms Interview Experience | Set 3 (For SDE-II, Gurgaon)
• C# Program for Dijkstra's shortest path algorithm | Greedy Algo-7
• Algorithms | Dynamic Programming | Question 7
• Amazon Interview | Set 46 (On-campus for Internship)

• For each row of the matrix, find the smallest element and subtract it from every element in its row.
• Do the same (as step 1) for all columns.
• Cover all zeros in the matrix using minimum number of horizontal and vertical lines.
• Test for Optimality: If the minimum number of covering lines is n, an optimal assignment is possible and we are finished. Else if lines are lesser than n, we haven’t found the optimal assignment, and must proceed to step 5.
• Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.

Try it before moving to see the solution

Explanation for above simple example:

  An example that doesn’t lead to optimal value in first attempt: In the above example, the first check for optimality did give us solution. What if we the number covering lines is less than n.

Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3).

Space complexity :   O(n^2), where n is the number of workers and jobs. This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional arrays of size n to store the labels, matches, and auxiliary information needed for the algorithm.

In the next post, we will be discussing implementation of the above algorithm. The implementation requires more steps as we need to find minimum number of lines to cover all 0’s using a program. References: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY

Please Login to comment...

Similar reads.

• Mathematical

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Assignment Problem

• Feb 20, 2024

The assignment problem is a special case of transportation problem.

Suppose there are $n$ jobs to be performed and $n$ persons are available for these jobs. Assume that each person can do each job at a time, though with varying degree of efficiency.

Let $c_{ij}$ be the cost if the $i^{th}$ person is assigned the $j^{th}$ job. Then the problem is to find an assignment so that the total cost of performing all jobs is minimum. (i.e., which job should be assigned to which person with minimum cost). Such problem is called an Assignment Problem (AP).

The tabular form of the assignment problem is as follows

The above table is called the $n\times n$ cost-matrix, where $c_{ij}$ are real numbers.

Thus the objective in the Assignment Problem is to assign a number of jobs to the equal number of persons at a minimum cost or maximum profit. e.g. assigning men to offices, classes to rooms, drivers to trucks, problems to research teams etc.

Mathematical Formulation of AP

Mathematically, the AP can be stated as $$ \begin{equation}\label{eq2.4} \min z = \sum_{i=1}^n\sum_{j=1}^n x_{ij} c_{ij}. \end{equation} $$ subject to $$ \begin{equation}\label{eq2.5} \sum_{j=1}^n x_{ij} =1,; \text{ for } i=1,2,\ldots, n \end{equation} $$

$$ \begin{equation}\label{eq2.6} \sum_{i=1}^n x_{ij} =1,; \text{ for } j=1,2,\ldots,n \end{equation} $$ where $$ \begin{equation*} x_{ij}=\left{ \begin{array}{ll} 1, & \hbox{if $i^{th}$ person is assigned $j^{th}$ job;} \ 0, & \hbox{otherwise.} \end{array} \right. \end{equation*} $$ Constraint \eqref{eq2.5} indicate that one job is done by $i^{th}$ person $i=1,2,\ldots, n$ and constraint \eqref{eq2.6} indicate that one person should be assigned $j^{th}$ job $j=1,2,\ldots, n$.

It may be observed from the above formulation that AP is a special type of Linear programming problem.

Unbalanced Assignment Problem

If the cost matrix of an assignment problem is not a square matrix, the assignment problem is called an Unbalanced Assignment Problem . In such a case, add dummy row or dummy column with zero cost in the cost matrix so as to form a square matrix. Then apply the usual assignment method to find the optimal solution.

Maximal Assignment Problem

Sometimes, the assignment problem deals with the maximization of an objective function instead of minimization.. For example, it may be required to assign persons to jobs in such a way that the expected profit is maximum. In such a case, first convert the problem of maximization to minimization and apply the usual procedure of assignment.

The assignment problem of maximization type can be converted to minimization type by subtracting all the elements of the given profit matrix from the largest element.

Restrictions on Assignment

Sometimes due to technical or other difficulties do not permit the assignment of a particular facility to a particular job. In such a situation, the difficulty can be overcome by assigning a very high cost (say, infinity i.e. $\infty$) to the corresponding cell.

Because of assigning an infinite penalty to such a cell the activity will be automatically excluded from the optimal solution. Then apply the usual procedure to find the optimal assignment.

Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.

Hungarian Method to Solve Assignment Problems

The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.

What is an Assignment Problem?

A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.

Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.

Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.

Hungarian Method Steps

Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.

Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.

Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.

Step 3 – Assign zeros

• Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
• Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.

Step 4 – Perform the Optimal Test

• The present assignment is optimal if each row and column has exactly one encircled zero.
• The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.

Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:

(a) Highlight the rows that aren’t assigned.

(b) Label the columns with zeros in marked rows (if they haven’t already been marked).

(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).

(d) Continue with (b) and (c) until no further marking is needed.

(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.

Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.

Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.

Hungarian Method Example

Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.

\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)

With 5 jobs and 5 men, the stated problem is balanced.

\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)

Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.

\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)

Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.

\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)

When the zeros are assigned, we get the following:

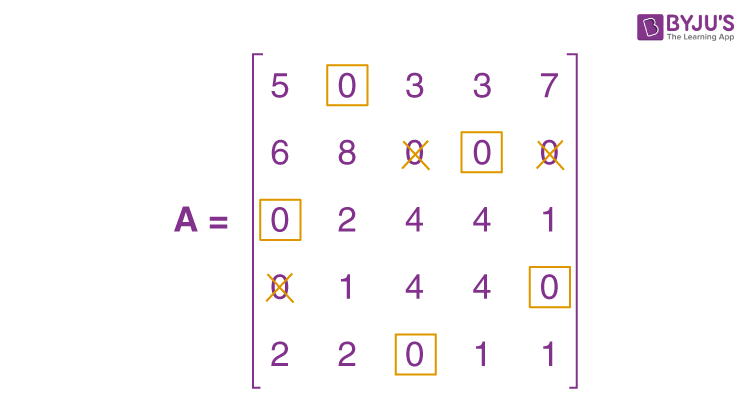
The present assignment is optimal because each row and column contain precisely one encircled zero.

Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.

Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.

Practice Question on Hungarian Method

Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.

\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)

Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.

Frequently Asked Questions on Hungarian Method

What is hungarian method.

The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.

What are the steps involved in Hungarian method?

The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.

What is the purpose of the Hungarian method?

When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

A-level Mathematics/Edexcel/Decision 2/Assignment Problems

Assignment Problems (AP) (also known as Allocation Problems, although they will be known as the former throughout this article) are a common form of problem. A distinguishing feature of AP is that one agent is assigned to one and only one task. Examples in real-life situations could be:

• Assigning contracts
• Assigning tasks to machinery
• Assigning agents to tasks
• Assigning Sales Personnel to Territories

An example of such a problem would be three lorries, A, B and C, and three loads that need to be transported, 1, 2 and 3. An example arrangement would be A → 1, B → 2 and C → 3. This means that Lorry A transports Load 1, Lorry B transports Load 2 and Lorry C transports Load 3.

• 1.1 Formulation as a Linear Programming Problem
• 2.1.1 Finding the Opportunity Cost Matrix
• 2.1.2 Interpreting The Opportunity Cost Matrix
• 2.2.1 Revision of the Opportunity Cost Matrix
• 3 Solutions of Unbalanced Assignment Problems
• 4 Maximisation Problems

Balanced Problems [ edit | edit source ]

A balanced AP is one in which:

(number of agents) = (number of tasks)

Consider again our lorry and load example. In this example, the number of agents (lorries) was 3 and the number of tasks (loads to be transported) is also equal to 3. Thus, it is a balanced problem . Initially, one will consider only balanced problems and how they are to be solved.

Upon expansion of the earlier problem, it was revealed that the cost for each lorry to transport each load is different. These are represented in Table 1.

The manager of the fleet of lorries wishes to minimise to total cost to complete all three jobs. How would one allocate the lorries to the loads? The table of numbers given is called the cost matrix of the problem.

Formulation as a Linear Programming Problem [ edit | edit source ]

Thus, one can obtain the contraints for the Linear Programming Problem by considering each agent/task in turn:

As each agent is assigned to exactly one job, we can deduce:

Similarly, since each job is assigned to exactly one agent, one can deduce:

The obtain the objective function for this example, we must consider the total costs.

The means, therefore, that the objection function, Z , for this example is to minimise Z where:

Finally, this means that one can conclude the LPP to be:

Minimise Z, where Z = 15 x {\displaystyle x} A1 + {\displaystyle +} 10 x {\displaystyle x} A2 + {\displaystyle +} 12 x {\displaystyle x} A3 + {\displaystyle +} 10 x {\displaystyle x} B1 + {\displaystyle +} 7 x {\displaystyle x} B2 + {\displaystyle +} 11 x {\displaystyle x} B3 + {\displaystyle +} 15 x {\displaystyle x} C1 + {\displaystyle +} 6 x {\displaystyle x} C2 + {\displaystyle +} 9 x {\displaystyle x} C3 , subject to: x {\displaystyle x} A1 + x {\displaystyle x} A2 + x {\displaystyle x} A3 = 1 x {\displaystyle x} B1 + x {\displaystyle x} B2 + x {\displaystyle x} B3 = 1 x {\displaystyle x} C1 + x {\displaystyle x} C2 + x {\displaystyle x} C3 = 1 x {\displaystyle x} A1 + x {\displaystyle x} B1 + x {\displaystyle x} C1 = 1 x {\displaystyle x} A2 + x {\displaystyle x} B2 + x {\displaystyle x} C2 = 1 x {\displaystyle x} A3 + x {\displaystyle x} B3 + x {\displaystyle x} C3 = 1

Solution of the Balanced Assignment Problem [ edit | edit source ]

An algorithm was developed by Harold Kuhn in the 1950s, and was named the Hungarian Algorithm. Its name is a reference to Dénes Kőnig and Jenő Egerváry, a pair of prominent Hungarian Mathematicians whose techniques are applied in this algorithm.

The Hungarian Algorithm [ edit | edit source ]

For the Hungarian Algorithm to work, the assignment problem must meet the following criteria:

• Each worker must be assigned, as we previously saw, to exactly one job.
• Each job must be assigned to exactly one worker.
• In the cost matrix, a constant can be added or subtracted from all cost values in any row or column without having any effect on the optimal assignments.

There are three stages in the implementation of the Hungarian Algorithm:

• Find the opportunity cost matrix
• Test for an optimal assignment. If one can be made, use it and stop.
• If an optimal assignment cannot be made, revise the opportunity cost matrix and return to the previous step.

To demonstrate these three steps, let us consider again the lorry example:

Finding the Opportunity Cost Matrix [ edit | edit source ]

The Opportunity Cost Matrix (OCM) is essentially a modified version of our initial Cost Matrix. In order to change the Cost Matrix into the OCM, one must carry out two stages.

• Carry out row reduction
• Carry out column reduction

Row reduction is the operation in which the smallest number in each row is subtracted from every number in that row. With our earlier example:

Next, one completes the column reduction. This is the same as row reduction, only with the smallest number in each column being subtracted from each value within that column. Thus:

Thus, the completed Opportunity Cost Matrix is:

Interpreting The Opportunity Cost Matrix [ edit | edit source ]

Since the aim of an assignment problem is to assign exactly one agent to exactly one task, one must match each agent up to the task which best minimises overall cost. After completing the row reduction and column reduction, it is logical to assume that the values that remain in the table are the minimum possible. Similarly, since the values in the table are the cost-values, the lowest values in the table are, surely, those of lowest cost. In order to find a solution, one must select one zero from each row and one zero from each column. However, one cannot select more than one value from any row or column, as it will result in one agent/task being assigned twice, which cannot occur in an Assignment Problem.

Again, let's consider the earlier example. If we were to select one zero from each column/row without any doubles occurring, the only possible solution is (with selected costs marked by asterices):

If we then assign this solution to our original cost matrix, one can see the following:

Thus, the final assignment is:

It is interesting to see that, despite this being the cheapest solution, it doesn't actually utilise all of the lowest values within the table.

Optimality of a Solution [ edit | edit source ]

An important issue with AP is the optimality of solution - when one obtains a solution, how can one be sure it truly is the best solution available? With the Hungarian algorithm, there is a fairly straightforward test for optimality that concerns drawing lines through the zeros in the Opportunity Cost Matrix. If the number of lines (horizontal and vertical only) is equal to the number of rows/columns, the solution obtained is optimal. If, however, the number of lines needed does not equal the number of rows/columns, the solution is not optimal, and can be improved. This is a somewhat perplexing technique, but one that is straightforward to implement and clear to interpret.

Consider the following OCM:

It is fairly easy to see that it would require only two lines to draw through all of the zeros - one could use a horizontal line through row B, and a vertical line through column 2, for instance. 2≠3 (the number of rows/columns), thus an optimal solution cannot be made.

Consider, on the other hand, our lorry example. Is the solution that we obtained optimal?

One can see that, in order to strike through each zero, one would need three lines (for instance, one through column 2, one through row B and one through row A). 3 = 3, thus we have an optimal solution that cannot be improved upon.

Revision of the Opportunity Cost Matrix [ edit | edit source ]

In the event of achieving a non-optimal assignment, one must revise the OCM. There are several steps in this process:

• Check the costs uncovered by the drawn lines
• Identify the smallest uncovered value
• Subtract this value from all of the uncovered costs
• Add this value to any costs that are at the intersection of any two drawn lines

Take our non-optimal solution from earlier. The smallest uncovered value was one. Subtracting one from each uncovered value gives:

Adding one to the point of intersection of the two lines (in this example, one could have drawn them through row B and column 2, therefore the point of intersection is cell B2) gives:

Again, only two lines (this time, they must be through row A and column 3) are needed. They intersect at cell A3. The smallest uncovered value is, again, 1. So, subtracting one from each uncovered cell and adding one to cell A3 gives:

Finally, the minimum number of lines needed to draw through all of the zeros is 3, which is the number of rows/columns. This means any assignment made will be optimal.

Solutions of Unbalanced Assignment Problems [ edit | edit source ]

The definition of a balanced AP was one in which the number of agents was the same as the number of tasks. In reality, this is unlikely to be the case - that is, it is unlikely that one would have the same number of taxi drivers to the number of customers, for example. In the event of an unbalanced problem, one must add a dummy , which is a blank/empty row, added to the Cost Matrix, in order to 'balance' the rows, for the sake of the algorithm. If one had, for instance, three agents and four tasks, one would add a dummy row . On the other hand, if one had four agents and three tasks, one would add a dummy task . This helps as it means that one agent or task will be left without a 'real' assignment, as using them would increase the total cost of the assignment.

Consider the following example:

A taxi company has four drivers (A, B, C, D), each currently at different locations. Three customers (1, 2, 3) have called the taxi company and need to be driven to their destinations. The total distance that would be travelled, by the driver, is represented in the cost matrix below:

The Taxi Company wishes to minimise the total distance travelled by its drivers. Find an optimal solution to this Assignment Problem.

Solution: Initially, one must add a dummy column, in order to make this a 'balanced' problem. Let this column be called "Row 4". Since there isn't actually a fourth customer, all of the costs in this matrix will be zero. This will mean that the otherwise most expensive taxi in the matrix will result in being assigned the dummy - in other words, it won't be used in the problem. First, let's carry out row and column reduction: Cost Matrix with Row Minima 1 2 3 4 Row Minimum A 11 19 17 0 0 C 15 18 21 0 0 D 18 15 17 0 0 ... with Column Minima 1 2 3 4 A 11 19 17 0 B 21 15 13 0 C 15 18 21 0 D 18 15 17 0 Column Minimum 11 15 13 0 Opportunity Cost Matrix 1 2 3 4 A 0 4 4 0 B 10 0 0 0 C 4 3 8 0 D 7 4 0 0 As one can see, all of the zeros in the Opportunity Cost Matrix can only be struck through using 4 lines (for instance, 1 line vertically through Column 4, 3 lines horizontally through Rows A, B & D). Thus, we've already arrived at the optimal solution because 4 lines can be used to mark through the entire matrix. The only possible solution is: A → 1 B → 3 C → 2 D → 4* Z = 11 + 13 + 18 = 42

• Of course, customer 4 is in fact a 'dummy' - i.e., D doesn't actually transport any customer. Thus, the only three drivers needed are drivers A, B and C. Driver A will transport Passenger 1, Driver B will transport Passenger 3 and Driver C will transport Passenger 2.

Maximisation Problems [ edit | edit source ]

All of the examples that have been considered so far have been Minimisation problems - in other words, they've been ones in which the aim of the problem was to minimise a cost. Assignment problems can, however, be used for the opposite reason - to maximise a gain or a profit. Consider the example of ice-cream seller. They know that, in certain towns, they will sell more icecream than others. The day, too, changes how much ice-cream s/he sells - they only drive the van on Monday, Wednesday and Saturday (M, W and S respectively). Taking into account that the ice-cream van can only visit one town at a time, which town should the ice-cream van visit on which day, in order to maximise his/her profit.

The following cost-matrix represents the earnings (in £100s) for each town (A, B, C) on each day (M, W, S):

After completing this process for the whole matrix, we achieve the following:

We can now carry out row and column reduction, as we usually would. This, eventually, results in the following Opportunity Cost Matrix:

Since the smallest number of lines that can be used to strike-through each of the zeros in this matrix is 3 (which is equal to the number of rows/columns), an optimal assignment can be made. The only possible assignment is:

On the cost matrix, this gives us:

This means that:

The total profit gives:

Thus the maximum total profit of the ice-cream van is £3500.

• Book:A-level Mathematics

Navigation menu

the intact one

Read MBA, BBA, B.COM Notes

Unbalanced Assignment Problems

Whenever the cost matrix of an assignment problem is not a square matrix, that is, whenever the number of sources is not equal to the number of destinations, the assignment problem is called an unbalanced assignment problem. In such problems, dummy rows (or columns) are added in the matrix so as to complete it to form a square matrix. The dummy rows or columns will contain all costs elements as zeroes. The Hungarian method may be used to solve the problem.

Example :  A company has five machines that are used for four jobs. Each job can be assigned to one and only one machine. The cost of each job on each machine is given in the following Table.

Unbalanced Maximization Assignment problem example

Assignment Problem

Solution:  Convert the 4 × 5 matrix into a square matrix by adding a dummy row D5.

Dummy Row D5 Added

Row-wise Reduction of the Matrix

Column-wise reduction is not necessary since all columns contain a single zero. Now, draw minimum number of lines to cover all the zeros, as shown in Table.

All Zeros in the Matrix Covered

Number of lines drawn ≠ Order of matrix. Hence not optimal.

Select the least uncovered element, i.e., 1, subtract it from other uncovered elements, add to the elements at intersection of lines and leave the elements that are covered with single line unchanged as shown in Table.

Subtracted or Added to Elements

Again Added or Subtracted 1 from Elements

Number of lines drawn = Order of matrix. Hence optimality is reached. Now assign the jobs to machines, as shown in Table.

Assigning Jobs to Machines

Example :  In a plant layout, four different machines M1, M2, M3 and M4 are to be erected in a machine shop. There are five vacant areas A, B, C, D and E. Because of limited space, Machine M2 cannot be erected at area C and Machine M4 cannot be erected at area A. The cost of erection of machines is given in the Table.

Find the optimal assignment plan.

Solution:  As the given matrix is not balanced, add a dummy row D5 with zero cost values. Assign a high cost H for (M2, C) and (M4, A). While selecting the lowest cost element neglect the high cost assigned H, as shown in Table below.

– Row-wise reduction of the matrix is shown in Table.

Matrix Reduced Row-wise

Note:  Column-wise reduction is not necessary, as each column has at least one single zero. Now, draw minimum number of lines to cover all the zeros, see Table.

Lines Drawn to Cover all Zeros

Number of lines drawn ≠ Order of matrix. Hence not Optimal. Select the smallest uncovered element, in this case 1. Subtract 1 from all other uncovered element and add 1 with the elements at the intersection. The element covered by single line remains unchanged. These changes are shown in Table. Now try to draw minimum number of lines to cover all the zeros.

Added or Subtracted 1 from Elements

Now number of lines drawn = Order of matrix, hence optimality is reached. Optimal assignment of machines to areas are shown in Table.

Optimal Assignment

Hence, the optimal solution is:

Share this:

You might also like, building information’s systems: systems analysis and design, principal methodology, trade dealings and retail promotions, definition: income, 2 thoughts on “ unbalanced assignment problems ”.

• Pingback: GGSIPU(NEW DELHI) QUANTITATIVE TECHNIQUE – 2ND SEMESTER – STUDY MBA & BBA NOTES
• Pingback: CCSU(BBA) 406 Operation Research – Home | Management

Leave a Reply Cancel reply

2. Algorithm & Example-1