what is hypothesis testing in quality

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings
• Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].

Hypothesis testing, p values, confidence intervals, and significance.

Jacob Shreffler ; Martin R. Huecker .

Affiliations

Last Update: March 13, 2023 .

• Definition/Introduction

Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting these findings, which may affect the adequate application of the data.

• Issues of Concern

Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. Therefore, an overview of these concepts is provided to allow medical professionals to use their expertise to determine if results are reported sufficiently and if the study outcomes are clinically appropriate to be applied in healthcare practice.

Hypothesis Testing

Investigators conducting studies need research questions and hypotheses to guide analyses. Starting with broad research questions (RQs), investigators then identify a gap in current clinical practice or research. Any research problem or statement is grounded in a better understanding of relationships between two or more variables. For this article, we will use the following research question example:

Research Question: Is Drug 23 an effective treatment for Disease A?

Research questions do not directly imply specific guesses or predictions; we must formulate research hypotheses. A hypothesis is a predetermined declaration regarding the research question in which the investigator(s) makes a precise, educated guess about a study outcome. This is sometimes called the alternative hypothesis and ultimately allows the researcher to take a stance based on experience or insight from medical literature. An example of a hypothesis is below.

Research Hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.

The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis.

Researchers should be aware of journal recommendations when considering how to report p values, and manuscripts should remain internally consistent.

Regarding p values, as the number of individuals enrolled in a study (the sample size) increases, the likelihood of finding a statistically significant effect increases. With very large sample sizes, the p-value can be very low significant differences in the reduction of symptoms for Disease A between Drug 23 and Drug 22. The null hypothesis is deemed true until a study presents significant data to support rejecting the null hypothesis. Based on the results, the investigators will either reject the null hypothesis (if they found significant differences or associations) or fail to reject the null hypothesis (they could not provide proof that there were significant differences or associations).

To test a hypothesis, researchers obtain data on a representative sample to determine whether to reject or fail to reject a null hypothesis. In most research studies, it is not feasible to obtain data for an entire population. Using a sampling procedure allows for statistical inference, though this involves a certain possibility of error. [1]  When determining whether to reject or fail to reject the null hypothesis, mistakes can be made: Type I and Type II errors. Though it is impossible to ensure that these errors have not occurred, researchers should limit the possibilities of these faults. [2]

Significance

Significance is a term to describe the substantive importance of medical research. Statistical significance is the likelihood of results due to chance. [3]  Healthcare providers should always delineate statistical significance from clinical significance, a common error when reviewing biomedical research. [4]  When conceptualizing findings reported as either significant or not significant, healthcare providers should not simply accept researchers' results or conclusions without considering the clinical significance. Healthcare professionals should consider the clinical importance of findings and understand both p values and confidence intervals so they do not have to rely on the researchers to determine the level of significance. [5]  One criterion often used to determine statistical significance is the utilization of p values.

P values are used in research to determine whether the sample estimate is significantly different from a hypothesized value. The p-value is the probability that the observed effect within the study would have occurred by chance if, in reality, there was no true effect. Conventionally, data yielding a p<0.05 or p<0.01 is considered statistically significant. While some have debated that the 0.05 level should be lowered, it is still universally practiced. [6]  Hypothesis testing allows us to determine the size of the effect.

An example of findings reported with p values are below:

Statement: Drug 23 reduced patients' symptoms compared to Drug 22. Patients who received Drug 23 (n=100) were 2.1 times less likely than patients who received Drug 22 (n = 100) to experience symptoms of Disease A, p<0.05.

Statement:Individuals who were prescribed Drug 23 experienced fewer symptoms (M = 1.3, SD = 0.7) compared to individuals who were prescribed Drug 22 (M = 5.3, SD = 1.9). This finding was statistically significant, p= 0.02.

For either statement, if the threshold had been set at 0.05, the null hypothesis (that there was no relationship) should be rejected, and we should conclude significant differences. Noticeably, as can be seen in the two statements above, some researchers will report findings with < or > and others will provide an exact p-value (0.000001) but never zero [6] . When examining research, readers should understand how p values are reported. The best practice is to report all p values for all variables within a study design, rather than only providing p values for variables with significant findings. [7]  The inclusion of all p values provides evidence for study validity and limits suspicion for selective reporting/data mining.  

While researchers have historically used p values, experts who find p values problematic encourage the use of confidence intervals. [8] . P-values alone do not allow us to understand the size or the extent of the differences or associations. [3]  In March 2016, the American Statistical Association (ASA) released a statement on p values, noting that scientific decision-making and conclusions should not be based on a fixed p-value threshold (e.g., 0.05). They recommend focusing on the significance of results in the context of study design, quality of measurements, and validity of data. Ultimately, the ASA statement noted that in isolation, a p-value does not provide strong evidence. [9]

When conceptualizing clinical work, healthcare professionals should consider p values with a concurrent appraisal study design validity. For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study [7] . The p-value debate has smoldered since the 1950s [10] , and replacement with confidence intervals has been suggested since the 1980s. [11]

Confidence Intervals

A confidence interval provides a range of values within given confidence (e.g., 95%), including the accurate value of the statistical constraint within a targeted population. [12]  Most research uses a 95% CI, but investigators can set any level (e.g., 90% CI, 99% CI). [13]  A CI provides a range with the lower bound and upper bound limits of a difference or association that would be plausible for a population. [14]  Therefore, a CI of 95% indicates that if a study were to be carried out 100 times, the range would contain the true value in 95, [15]  confidence intervals provide more evidence regarding the precision of an estimate compared to p-values. [6]

In consideration of the similar research example provided above, one could make the following statement with 95% CI:

Statement: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22; there was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

It is important to note that the width of the CI is affected by the standard error and the sample size; reducing a study sample number will result in less precision of the CI (increase the width). [14]  A larger width indicates a smaller sample size or a larger variability. [16]  A researcher would want to increase the precision of the CI. For example, a 95% CI of 1.43 – 1.47 is much more precise than the one provided in the example above. In research and clinical practice, CIs provide valuable information on whether the interval includes or excludes any clinically significant values. [14]

Null values are sometimes used for differences with CI (zero for differential comparisons and 1 for ratios). However, CIs provide more information than that. [15]  Consider this example: A hospital implements a new protocol that reduced wait time for patients in the emergency department by an average of 25 minutes (95% CI: -2.5 – 41 minutes). Because the range crosses zero, implementing this protocol in different populations could result in longer wait times; however, the range is much higher on the positive side. Thus, while the p-value used to detect statistical significance for this may result in "not significant" findings, individuals should examine this range, consider the study design, and weigh whether or not it is still worth piloting in their workplace.

Similarly to p-values, 95% CIs cannot control for researchers' errors (e.g., study bias or improper data analysis). [14]  In consideration of whether to report p-values or CIs, researchers should examine journal preferences. When in doubt, reporting both may be beneficial. [13]  An example is below:

Reporting both: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22, p = 0.009. There was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

• Clinical Significance

Recall that clinical significance and statistical significance are two different concepts. Healthcare providers should remember that a study with statistically significant differences and large sample size may be of no interest to clinicians, whereas a study with smaller sample size and statistically non-significant results could impact clinical practice. [14]  Additionally, as previously mentioned, a non-significant finding may reflect the study design itself rather than relationships between variables.

Healthcare providers using evidence-based medicine to inform practice should use clinical judgment to determine the practical importance of studies through careful evaluation of the design, sample size, power, likelihood of type I and type II errors, data analysis, and reporting of statistical findings (p values, 95% CI or both). [4]  Interestingly, some experts have called for "statistically significant" or "not significant" to be excluded from work as statistical significance never has and will never be equivalent to clinical significance. [17]

The decision on what is clinically significant can be challenging, depending on the providers' experience and especially the severity of the disease. Providers should use their knowledge and experiences to determine the meaningfulness of study results and make inferences based not only on significant or insignificant results by researchers but through their understanding of study limitations and practical implications.

• Nursing, Allied Health, and Interprofessional Team Interventions

All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts in this chapter. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care. 

• Review Questions
• Access free multiple choice questions on this topic.
• Comment on this article.

Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.

Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

• Cite this Page Shreffler J, Huecker MR. Hypothesis Testing, P Values, Confidence Intervals, and Significance. [Updated 2023 Mar 13]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

• Bulk download StatPearls data from FTP

Related information

• PMC PubMed Central citations
• PubMed Links to PubMed

Similar articles in PubMed

• The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). [PeerJ. 2021] The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). Messam LLM, Weng HY, Rosenberger NWY, Tan ZH, Payet SDM, Santbakshsing M. PeerJ. 2021; 9:e12453. Epub 2021 Nov 24.
• Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. [J Pharm Pract. 2010] Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. Ferrill MJ, Brown DA, Kyle JA. J Pharm Pract. 2010 Aug; 23(4):344-51. Epub 2010 Apr 13.
• Interpreting "statistical hypothesis testing" results in clinical research. [J Ayurveda Integr Med. 2012] Interpreting "statistical hypothesis testing" results in clinical research. Sarmukaddam SB. J Ayurveda Integr Med. 2012 Apr; 3(2):65-9.
• Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. [Dermatol Surg. 2005] Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. Alam M, Barzilai DA, Wrone DA. Dermatol Surg. 2005 Apr; 31(4):462-6.
• Review Is statistical significance testing useful in interpreting data? [Reprod Toxicol. 1993] Review Is statistical significance testing useful in interpreting data? Savitz DA. Reprod Toxicol. 1993; 7(2):95-100.

Recent Activity

• Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearl... Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

• Hypothesis Testing: Definition, Uses, Limitations + Examples

Hypothesis testing is as old as the scientific method and is at the heart of the research process. 

Research exists to validate or disprove assumptions about various phenomena. The process of validation involves testing and it is in this context that we will explore hypothesis testing. 

What is a Hypothesis? 

A hypothesis is a calculated prediction or assumption about a population parameter based on limited evidence. The whole idea behind hypothesis formulation is testing—this means the researcher subjects his or her calculated assumption to a series of evaluations to know whether they are true or false. 

Typically, every research starts with a hypothesis—the investigator makes a claim and experiments to prove that this claim is true or false . For instance, if you predict that students who drink milk before class perform better than those who don’t, then this becomes a hypothesis that can be confirmed or refuted using an experiment.  

Read: What is Empirical Research Study? [Examples & Method]

What are the Types of Hypotheses? 

1. simple hypothesis.

Also known as a basic hypothesis, a simple hypothesis suggests that an independent variable is responsible for a corresponding dependent variable. In other words, an occurrence of the independent variable inevitably leads to an occurrence of the dependent variable. 

Typically, simple hypotheses are considered as generally true, and they establish a causal relationship between two variables. 

Examples of Simple Hypothesis  

• Drinking soda and other sugary drinks can cause obesity. 
• Smoking cigarettes daily leads to lung cancer.

2. Complex Hypothesis

A complex hypothesis is also known as a modal. It accounts for the causal relationship between two independent variables and the resulting dependent variables. This means that the combination of the independent variables leads to the occurrence of the dependent variables . 

Examples of Complex Hypotheses  

• Adults who do not smoke and drink are less likely to develop liver-related conditions.
• Global warming causes icebergs to melt which in turn causes major changes in weather patterns.

3. Null Hypothesis

As the name suggests, a null hypothesis is formed when a researcher suspects that there’s no relationship between the variables in an observation. In this case, the purpose of the research is to approve or disapprove this assumption. 

Examples of Null Hypothesis

• This is no significant change in a student’s performance if they drink coffee or tea before classes. 
• There’s no significant change in the growth of a plant if one uses distilled water only or vitamin-rich water. 

Read: Research Report: Definition, Types + [Writing Guide]

4. Alternative Hypothesis 

To disapprove a null hypothesis, the researcher has to come up with an opposite assumption—this assumption is known as the alternative hypothesis. This means if the null hypothesis says that A is false, the alternative hypothesis assumes that A is true. 

An alternative hypothesis can be directional or non-directional depending on the direction of the difference. A directional alternative hypothesis specifies the direction of the tested relationship, stating that one variable is predicted to be larger or smaller than the null value while a non-directional hypothesis only validates the existence of a difference without stating its direction. 

Examples of Alternative Hypotheses  

• Starting your day with a cup of tea instead of a cup of coffee can make you more alert in the morning. 
• The growth of a plant improves significantly when it receives distilled water instead of vitamin-rich water. 

5. Logical Hypothesis

Logical hypotheses are some of the most common types of calculated assumptions in systematic investigations. It is an attempt to use your reasoning to connect different pieces in research and build a theory using little evidence. In this case, the researcher uses any data available to him, to form a plausible assumption that can be tested. 

Examples of Logical Hypothesis

• Waking up early helps you to have a more productive day. 
• Beings from Mars would not be able to breathe the air in the atmosphere of the Earth. 

6. Empirical Hypothesis  

After forming a logical hypothesis, the next step is to create an empirical or working hypothesis. At this stage, your logical hypothesis undergoes systematic testing to prove or disprove the assumption. An empirical hypothesis is subject to several variables that can trigger changes and lead to specific outcomes. 

Examples of Empirical Testing 

• People who eat more fish run faster than people who eat meat.
• Women taking vitamin E grow hair faster than those taking vitamin K.

7. Statistical Hypothesis

When forming a statistical hypothesis, the researcher examines the portion of a population of interest and makes a calculated assumption based on the data from this sample. A statistical hypothesis is most common with systematic investigations involving a large target audience. Here, it’s impossible to collect responses from every member of the population so you have to depend on data from your sample and extrapolate the results to the wider population. 

Examples of Statistical Hypothesis  

• 45% of students in Louisiana have middle-income parents. 
• 80% of the UK’s population gets a divorce because of irreconcilable differences.

What is Hypothesis Testing? 

Hypothesis testing is an assessment method that allows researchers to determine the plausibility of a hypothesis. It involves testing an assumption about a specific population parameter to know whether it’s true or false. These population parameters include variance, standard deviation, and median. 

Typically, hypothesis testing starts with developing a null hypothesis and then performing several tests that support or reject the null hypothesis. The researcher uses test statistics to compare the association or relationship between two or more variables. 

Explore: Research Bias: Definition, Types + Examples

Researchers also use hypothesis testing to calculate the coefficient of variation and determine if the regression relationship and the correlation coefficient are statistically significant.

How Hypothesis Testing Works

The basis of hypothesis testing is to examine and analyze the null hypothesis and alternative hypothesis to know which one is the most plausible assumption. Since both assumptions are mutually exclusive, only one can be true. In other words, the occurrence of a null hypothesis destroys the chances of the alternative coming to life, and vice-versa. 

Interesting: 21 Chrome Extensions for Academic Researchers in 2021

What Are The Stages of Hypothesis Testing?  

To successfully confirm or refute an assumption, the researcher goes through five (5) stages of hypothesis testing; 

• Determine the null hypothesis
• Specify the alternative hypothesis
• Set the significance level
• Calculate the test statistics and corresponding P-value
• Draw your conclusion
• Determine the Null Hypothesis

Like we mentioned earlier, hypothesis testing starts with creating a null hypothesis which stands as an assumption that a certain statement is false or implausible. For example, the null hypothesis (H0) could suggest that different subgroups in the research population react to a variable in the same way. 

• Specify the Alternative Hypothesis

Once you know the variables for the null hypothesis, the next step is to determine the alternative hypothesis. The alternative hypothesis counters the null assumption by suggesting the statement or assertion is true. Depending on the purpose of your research, the alternative hypothesis can be one-sided or two-sided. 

Using the example we established earlier, the alternative hypothesis may argue that the different sub-groups react differently to the same variable based on several internal and external factors. 

• Set the Significance Level

Many researchers create a 5% allowance for accepting the value of an alternative hypothesis, even if the value is untrue. This means that there is a 0.05 chance that one would go with the value of the alternative hypothesis, despite the truth of the null hypothesis. 

Something to note here is that the smaller the significance level, the greater the burden of proof needed to reject the null hypothesis and support the alternative hypothesis.

Explore: What is Data Interpretation? + [Types, Method & Tools]

• Calculate the Test Statistics and Corresponding P-Value 

Test statistics in hypothesis testing allow you to compare different groups between variables while the p-value accounts for the probability of obtaining sample statistics if your null hypothesis is true. In this case, your test statistics can be the mean, median and similar parameters. 

If your p-value is 0.65, for example, then it means that the variable in your hypothesis will happen 65 in100 times by pure chance. Use this formula to determine the p-value for your data: 

• Draw Your Conclusions

After conducting a series of tests, you should be able to agree or refute the hypothesis based on feedback and insights from your sample data.  

Applications of Hypothesis Testing in Research

Hypothesis testing isn’t only confined to numbers and calculations; it also has several real-life applications in business, manufacturing, advertising, and medicine. 

In a factory or other manufacturing plants, hypothesis testing is an important part of quality and production control before the final products are approved and sent out to the consumer. 

During ideation and strategy development, C-level executives use hypothesis testing to evaluate their theories and assumptions before any form of implementation. For example, they could leverage hypothesis testing to determine whether or not some new advertising campaign, marketing technique, etc. causes increased sales. 

In addition, hypothesis testing is used during clinical trials to prove the efficacy of a drug or new medical method before its approval for widespread human usage. 

What is an Example of Hypothesis Testing?

An employer claims that her workers are of above-average intelligence. She takes a random sample of 20 of them and gets the following results: 

Mean IQ Scores: 110

Standard Deviation: 15 

Mean Population IQ: 100

Step 1: Using the value of the mean population IQ, we establish the null hypothesis as 100.

Step 2: State that the alternative hypothesis is greater than 100.

Step 3: State the alpha level as 0.05 or 5% 

Step 4: Find the rejection region area (given by your alpha level above) from the z-table. An area of .05 is equal to a z-score of 1.645.

Step 5: Calculate the test statistics using this formula

Z = (110–100) ÷ (15÷√20) 

10 ÷ 3.35 = 2.99 

If the value of the test statistics is higher than the value of the rejection region, then you should reject the null hypothesis. If it is less, then you cannot reject the null. 

In this case, 2.99 > 1.645 so we reject the null. 

Importance/Benefits of Hypothesis Testing 

The most significant benefit of hypothesis testing is it allows you to evaluate the strength of your claim or assumption before implementing it in your data set. Also, hypothesis testing is the only valid method to prove that something “is or is not”. Other benefits include: 

• Hypothesis testing provides a reliable framework for making any data decisions for your population of interest. 
• It helps the researcher to successfully extrapolate data from the sample to the larger population. 
• Hypothesis testing allows the researcher to determine whether the data from the sample is statistically significant. 
• Hypothesis testing is one of the most important processes for measuring the validity and reliability of outcomes in any systematic investigation. 
• It helps to provide links to the underlying theory and specific research questions.

Criticism and Limitations of Hypothesis Testing

Several limitations of hypothesis testing can affect the quality of data you get from this process. Some of these limitations include: 

• The interpretation of a p-value for observation depends on the stopping rule and definition of multiple comparisons. This makes it difficult to calculate since the stopping rule is subject to numerous interpretations, plus “multiple comparisons” are unavoidably ambiguous. 
• Conceptual issues often arise in hypothesis testing, especially if the researcher merges Fisher and Neyman-Pearson’s methods which are conceptually distinct. 
• In an attempt to focus on the statistical significance of the data, the researcher might ignore the estimation and confirmation by repeated experiments.
• Hypothesis testing can trigger publication bias, especially when it requires statistical significance as a criterion for publication.
• When used to detect whether a difference exists between groups, hypothesis testing can trigger absurd assumptions that affect the reliability of your observation.

Connect to Formplus, Get Started Now - It's Free!

• alternative hypothesis
• alternative vs null hypothesis
• complex hypothesis
• empirical hypothesis
• hypothesis testing
• logical hypothesis
• simple hypothesis
• statistical hypothesis
• busayo.longe

You may also like:

Internal Validity in Research: Definition, Threats, Examples

In this article, we will discuss the concept of internal validity, some clear examples, its importance, and how to test it.

What is Pure or Basic Research? + [Examples & Method]

Simple guide on pure or basic research, its methods, characteristics, advantages, and examples in science, medicine, education and psychology

Type I vs Type II Errors: Causes, Examples & Prevention

This article will discuss the two different types of errors in hypothesis testing and how you can prevent them from occurring in your research

Alternative vs Null Hypothesis: Pros, Cons, Uses & Examples

We are going to discuss alternative hypotheses and null hypotheses in this post and how they work in research.

Formplus - For Seamless Data Collection

Collect data the right way with a versatile data collection tool. try formplus and transform your work productivity today..

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3 hypothesis testing.

In reviewing hypothesis tests, we start first with the general idea. Then, we keep returning to the basic procedures of hypothesis testing, each time adding a little more detail.

The general idea of hypothesis testing involves:

• Making an initial assumption.
• Collecting evidence (data).
• Based on the available evidence (data), deciding whether to reject or not reject the initial assumption.

Every hypothesis test — regardless of the population parameter involved — requires the above three steps.

Example S.3.1

Is normal body temperature really 98.6 degrees f section  .

Consider the population of many, many adults. A researcher hypothesized that the average adult body temperature is lower than the often-advertised 98.6 degrees F. That is, the researcher wants an answer to the question: "Is the average adult body temperature 98.6 degrees? Or is it lower?" To answer his research question, the researcher starts by assuming that the average adult body temperature was 98.6 degrees F.

Then, the researcher went out and tried to find evidence that refutes his initial assumption. In doing so, he selects a random sample of 130 adults. The average body temperature of the 130 sampled adults is 98.25 degrees.

Then, the researcher uses the data he collected to make a decision about his initial assumption. It is either likely or unlikely that the researcher would collect the evidence he did given his initial assumption that the average adult body temperature is 98.6 degrees:

• If it is likely , then the researcher does not reject his initial assumption that the average adult body temperature is 98.6 degrees. There is not enough evidence to do otherwise.
• either the researcher's initial assumption is correct and he experienced a very unusual event;
• or the researcher's initial assumption is incorrect.

In statistics, we generally don't make claims that require us to believe that a very unusual event happened. That is, in the practice of statistics, if the evidence (data) we collected is unlikely in light of the initial assumption, then we reject our initial assumption.

Example S.3.2

Criminal trial analogy section  .

One place where you can consistently see the general idea of hypothesis testing in action is in criminal trials held in the United States. Our criminal justice system assumes "the defendant is innocent until proven guilty." That is, our initial assumption is that the defendant is innocent.

In the practice of statistics, we make our initial assumption when we state our two competing hypotheses -- the null hypothesis ( H 0 ) and the alternative hypothesis ( H A ). Here, our hypotheses are:

• H 0 : Defendant is not guilty (innocent)
• H A : Defendant is guilty

In statistics, we always assume the null hypothesis is true . That is, the null hypothesis is always our initial assumption.

The prosecution team then collects evidence — such as finger prints, blood spots, hair samples, carpet fibers, shoe prints, ransom notes, and handwriting samples — with the hopes of finding "sufficient evidence" to make the assumption of innocence refutable.

In statistics, the data are the evidence.

The jury then makes a decision based on the available evidence:

• If the jury finds sufficient evidence — beyond a reasonable doubt — to make the assumption of innocence refutable, the jury rejects the null hypothesis and deems the defendant guilty. We behave as if the defendant is guilty.
• If there is insufficient evidence, then the jury does not reject the null hypothesis . We behave as if the defendant is innocent.

In statistics, we always make one of two decisions. We either "reject the null hypothesis" or we "fail to reject the null hypothesis."

Errors in Hypothesis Testing Section  

Did you notice the use of the phrase "behave as if" in the previous discussion? We "behave as if" the defendant is guilty; we do not "prove" that the defendant is guilty. And, we "behave as if" the defendant is innocent; we do not "prove" that the defendant is innocent.

This is a very important distinction! We make our decision based on evidence not on 100% guaranteed proof. Again:

• If we reject the null hypothesis, we do not prove that the alternative hypothesis is true.
• If we do not reject the null hypothesis, we do not prove that the null hypothesis is true.

We merely state that there is enough evidence to behave one way or the other. This is always true in statistics! Because of this, whatever the decision, there is always a chance that we made an error .

Let's review the two types of errors that can be made in criminal trials:

Table S.3.2 shows how this corresponds to the two types of errors in hypothesis testing.

Note that, in statistics, we call the two types of errors by two different  names -- one is called a "Type I error," and the other is called  a "Type II error." Here are the formal definitions of the two types of errors:

There is always a chance of making one of these errors. But, a good scientific study will minimize the chance of doing so!

Making the Decision Section  

Recall that it is either likely or unlikely that we would observe the evidence we did given our initial assumption. If it is likely , we do not reject the null hypothesis. If it is unlikely , then we reject the null hypothesis in favor of the alternative hypothesis. Effectively, then, making the decision reduces to determining "likely" or "unlikely."

In statistics, there are two ways to determine whether the evidence is likely or unlikely given the initial assumption:

• We could take the " critical value approach " (favored in many of the older textbooks).
• Or, we could take the " P -value approach " (what is used most often in research, journal articles, and statistical software).

In the next two sections, we review the procedures behind each of these two approaches. To make our review concrete, let's imagine that μ is the average grade point average of all American students who major in mathematics. We first review the critical value approach for conducting each of the following three hypothesis tests about the population mean $\mu$:

In Practice

• We would want to conduct the first hypothesis test if we were interested in concluding that the average grade point average of the group is more than 3.
• We would want to conduct the second hypothesis test if we were interested in concluding that the average grade point average of the group is less than 3.
• And, we would want to conduct the third hypothesis test if we were only interested in concluding that the average grade point average of the group differs from 3 (without caring whether it is more or less than 3).

Upon completing the review of the critical value approach, we review the P -value approach for conducting each of the above three hypothesis tests about the population mean \(\mu\). The procedures that we review here for both approaches easily extend to hypothesis tests about any other population parameter.

• Guide: Hypothesis Testing

Daniel Croft

Daniel Croft is an experienced continuous improvement manager with a Lean Six Sigma Black Belt and a Bachelor's degree in Business Management. With more than ten years of experience applying his skills across various industries, Daniel specializes in optimizing processes and improving efficiency. His approach combines practical experience with a deep understanding of business fundamentals to drive meaningful change.

• Last Updated: September 8, 2023
• Learn Lean Sigma

In the world of data-driven decision-making, Hypothesis Testing stands as a cornerstone methodology. It serves as the statistical backbone for a multitude of sectors, from manufacturing and logistics to healthcare and finance. But what exactly is Hypothesis Testing, and why is it so indispensable? Simply put, it’s a technique that allows you to validate or invalidate claims about a population based on sample data. Whether you’re looking to streamline a manufacturing process, optimize logistics, or improve customer satisfaction, Hypothesis Testing offers a structured approach to reach conclusive, data-supported decisions.

The graphical example above provides a simplified snapshot of a hypothesis test. The bell curve represents a normal distribution, the green area is where you’d accept the null hypothesis ( H 0​), and the red area is the “rejection zone,” where you’d favor the alternative hypothesis ( Ha ​). The vertical blue line represents the threshold value or “critical value,” beyond which you’d reject H 0​.

Here’s a graphical example of a hypothesis test, which you can include in the introduction section of your guide. In this graph:

• The curve represents a standard normal distribution, often encountered in hypothesis tests.
• The green-shaded area signifies the “Acceptance Region,” where you would fail to reject the null hypothesis ( H 0​).
• The red-shaded areas are the “Rejection Regions,” where you would reject H 0​ in favor of the alternative hypothesis ( Ha ​).
• The blue dashed lines indicate the “Critical Values” (±1.96), which are the thresholds for rejecting H 0​.

This graphical representation serves as a conceptual foundation for understanding the mechanics of hypothesis testing. It visually illustrates what it means to accept or reject a hypothesis based on a predefined level of significance.

Table of Contents

What is hypothesis testing.

Hypothesis testing is a structured procedure in statistics used for drawing conclusions about a larger population based on a subset of that population, known as a sample. The method is widely used across different industries and sectors for a variety of purposes. Below, we’ll dissect the key components of hypothesis testing to provide a more in-depth understanding.

The Hypotheses: H 0 and Ha

In every hypothesis test, there are two competing statements:

• Null Hypothesis ( H 0) : This is the “status quo” hypothesis that you are trying to test against. It is a statement that asserts that there is no effect or difference. For example, in a manufacturing setting, the null hypothesis might state that a new production process does not improve the average output quality.
• Alternative Hypothesis ( Ha or H 1) : This is what you aim to prove by conducting the hypothesis test. It is the statement that there is an effect or difference. Using the same manufacturing example, the alternative hypothesis might state that the new process does improve the average output quality.

Significance Level ( α )

Before conducting the test, you decide on a “Significance Level” ( α ), typically set at 0.05 or 5%. This level represents the probability of rejecting the null hypothesis when it is actually true. Lower α values make the test more stringent, reducing the chances of a ‘false positive’.

Data Collection

You then proceed to gather data, which is usually a sample from a larger population. The quality of your test heavily relies on how well this sample represents the population. The data can be collected through various means such as surveys, observations, or experiments.

Statistical Test

Depending on the nature of the data and what you’re trying to prove, different statistical tests can be applied (e.g., t-test, chi-square test , ANOVA , etc.). These tests will compute a test statistic (e.g., t , 2 χ 2, F , etc.) based on your sample data.

Here are graphical examples of the distributions commonly used in three different types of statistical tests: t-test, Chi-square test, and ANOVA (Analysis of Variance), displayed side by side for comparison.

• Graph 1 (Leftmost): This graph represents a t-distribution, often used in t-tests. The t-distribution is similar to the normal distribution but tends to have heavier tails. It is commonly used when the sample size is small or the population variance is unknown.

Chi-square Test

• Graph 2 (Middle): The Chi-square distribution is used in Chi-square tests, often for testing independence or goodness-of-fit. Unlike the t-distribution, the Chi-square distribution is not symmetrical and only takes on positive values.

ANOVA (F-distribution)

• Graph 3 (Rightmost): The F-distribution is used in Analysis of Variance (ANOVA), a statistical test used to analyze the differences between group means. Like the Chi-square distribution, the F-distribution is also not symmetrical and takes only positive values.

These visual representations provide an intuitive understanding of the different statistical tests and their underlying distributions. Knowing which test to use and when is crucial for conducting accurate and meaningful hypothesis tests.

Decision Making

The test statistic is then compared to a critical value determined by the significance level ( α ) and the sample size. This comparison will give you a p-value. If the p-value is less than α , you reject the null hypothesis in favor of the alternative hypothesis. Otherwise, you fail to reject the null hypothesis.

Interpretation

Finally, you interpret the results in the context of what you were investigating. Rejecting the null hypothesis might mean implementing a new process or strategy, while failing to reject it might lead to a continuation of current practices.

To sum it up, hypothesis testing is not just a set of formulas but a methodical approach to problem-solving and decision-making based on data. It’s a crucial tool for anyone interested in deriving meaningful insights from data to make informed decisions.

Why is Hypothesis Testing Important?

Hypothesis testing is a cornerstone of statistical and empirical research, serving multiple functions in various fields. Let’s delve into each of the key areas where hypothesis testing holds significant importance:

Data-Driven Decisions

In today’s complex business environment, making decisions based on gut feeling or intuition is not enough; you need data to back up your choices. Hypothesis testing serves as a rigorous methodology for making decisions based on data. By setting up a null hypothesis and an alternative hypothesis, you can use statistical methods to determine which is more likely to be true given a data sample. This structured approach eliminates guesswork and adds empirical weight to your decisions, thereby increasing their credibility and effectiveness.

Risk Management

Hypothesis testing allows you to assign a ‘p-value’ to your findings, which is essentially the probability of observing the given sample data if the null hypothesis is true. This p-value can be directly used to quantify risk. For instance, a p-value of 0.05 implies there’s a 5% risk of rejecting the null hypothesis when it’s actually true. This is invaluable in scenarios like product launches or changes in operational processes, where understanding the risk involved can be as crucial as the decision itself.

Here’s an example to help you understand the concept better.

The graph above serves as a graphical representation to help explain the concept of a ‘p-value’ and its role in quantifying risk in hypothesis testing. Here’s how to interpret the graph:

Elements of the Graph

• The curve represents a Standard Normal Distribution , which is often used to represent z-scores in hypothesis testing.
• The red-shaded area on the right represents the Rejection Region . It corresponds to a 5% risk ( α =0.05) of rejecting the null hypothesis when it is actually true. This is the area where, if your test statistic falls, you would reject the null hypothesis.
• The green-shaded area represents the Acceptance Region , with a 95% level of confidence. If your test statistic falls in this region, you would fail to reject the null hypothesis.
• The blue dashed line is the Critical Value (approximately 1.645 in this example). If your standardized test statistic (z-value) exceeds this point, you enter the rejection region, and your p-value becomes less than 0.05, leading you to reject the null hypothesis.

Relating to Risk Management

The p-value can be directly related to risk management. For example, if you’re considering implementing a new manufacturing process, the p-value quantifies the risk of that decision. A low p-value (less than α ) would mean that the risk of rejecting the null hypothesis (i.e., going ahead with the new process) when it’s actually true is low, thus indicating a lower risk in implementing the change.

Quality Control

In sectors like manufacturing, automotive, and logistics, maintaining a high level of quality is not just an option but a necessity. Hypothesis testing is often employed in quality assurance and control processes to test whether a certain process or product conforms to standards. For example, if a car manufacturing line claims its error rate is below 5%, hypothesis testing can confirm or disprove this claim based on a sample of products. This ensures that quality is not compromised and that stakeholders can trust the end product.

Resource Optimization

Resource allocation is a significant challenge for any organization. Hypothesis testing can be a valuable tool in determining where resources will be most effectively utilized. For instance, in a manufacturing setting, you might want to test whether a new piece of machinery significantly increases production speed. A hypothesis test could provide the statistical evidence needed to decide whether investing in more of such machinery would be a wise use of resources.

In the realm of research and development, hypothesis testing can be a game-changer. When developing a new product or process, you’ll likely have various theories or hypotheses. Hypothesis testing allows you to systematically test these, filtering out the less likely options and focusing on the most promising ones. This not only speeds up the innovation process but also makes it more cost-effective by reducing the likelihood of investing in ideas that are statistically unlikely to be successful.

In summary, hypothesis testing is a versatile tool that adds rigor, reduces risk, and enhances the decision-making and innovation processes across various sectors and functions.

This graphical representation makes it easier to grasp how the p-value is used to quantify the risk involved in making a decision based on a hypothesis test.

Step-by-Step Guide to Hypothesis Testing

To make this guide practical and helpful if you are new learning about the concept we will explain each step of the process and follow it up with an example of the method being applied to a manufacturing line, and you want to test if a new process reduces the average time it takes to assemble a product.

Step 1: State the Hypotheses

The first and foremost step in hypothesis testing is to clearly define your hypotheses. This sets the stage for your entire test and guides the subsequent steps, from data collection to decision-making. At this stage, you formulate two competing hypotheses:

Null Hypothesis ( H 0)

The null hypothesis is a statement that there is no effect or no difference, and it serves as the hypothesis that you are trying to test against. It’s the default assumption that any kind of effect or difference you suspect is not real, and is due to chance. Formulating a clear null hypothesis is crucial, as your statistical tests will be aimed at challenging this hypothesis.

In a manufacturing context, if you’re testing whether a new assembly line process has reduced the time it takes to produce an item, your null hypothesis ( H 0) could be:

H 0:”The new process does not reduce the average assembly time.”

Alternative Hypothesis ( Ha or H 1)

The alternative hypothesis is what you want to prove. It is a statement that there is an effect or difference. This hypothesis is considered only after you find enough evidence against the null hypothesis.

Continuing with the manufacturing example, the alternative hypothesis ( Ha ) could be:

Ha :”The new process reduces the average assembly time.”

Types of Alternative Hypothesis

Depending on what exactly you are trying to prove, the alternative hypothesis can be:

• Two-Sided : You’re interested in deviations in either direction (greater or smaller).
• One-Sided : You’re interested in deviations only in one direction (either greater or smaller).

Scenario: Reducing Assembly Time in a Car Manufacturing Plant

You are a continuous improvement manager at a car manufacturing plant. One of the assembly lines has been struggling with longer assembly times, affecting the overall production schedule. A new assembly process has been proposed, promising to reduce the assembly time per car. Before rolling it out on the entire line, you decide to conduct a hypothesis test to see if the new process actually makes a difference. Null Hypothesis ( H 0​) In this context, the null hypothesis would be the status quo, asserting that the new assembly process doesn’t reduce the assembly time per car. Mathematically, you could state it as: H 0:The average assembly time per car with the new process ≥ The average assembly time per car with the old process. Or simply: H 0​:”The new process does not reduce the average assembly time per car.” Alternative Hypothesis ( Ha ​ or H 1​) The alternative hypothesis is what you aim to prove — that the new process is more efficient. Mathematically, it could be stated as: Ha :The average assembly time per car with the new process < The average assembly time per car with the old process Or simply: Ha ​:”The new process reduces the average assembly time per car.” Types of Alternative Hypothesis In this example, you’re only interested in knowing if the new process reduces the time, making it a One-Sided Alternative Hypothesis .

Step 2: Determine the Significance Level ( α )

Once you’ve clearly stated your null and alternative hypotheses, the next step is to decide on the significance level, often denoted by α . The significance level is a threshold below which the null hypothesis will be rejected. It quantifies the level of risk you’re willing to accept when making a decision based on the hypothesis test.

What is a Significance Level?

The significance level, usually expressed as a percentage, represents the probability of rejecting the null hypothesis when it is actually true. Common choices for α are 0.05, 0.01, and 0.10, representing 5%, 1%, and 10% levels of significance, respectively.

• 5% Significance Level ( α =0.05) : This is the most commonly used level and implies that you are willing to accept a 5% chance of rejecting the null hypothesis when it is true.
• 1% Significance Level ( α =0.01) : This is a more stringent level, used when you want to be more sure of your decision. The risk of falsely rejecting the null hypothesis is reduced to 1%.
• 10% Significance Level ( α =0.10) : This is a more lenient level, used when you are willing to take a higher risk. Here, the chance of falsely rejecting the null hypothesis is 10%.

Continuing with the manufacturing example, let’s say you decide to set α =0.05, meaning you’re willing to take a 5% risk of concluding that the new process is effective when it might not be.

How to Choose the Right Significance Level?

Choosing the right significance level depends on the context and the consequences of making a wrong decision. Here are some factors to consider:

• Criticality of Decision : For highly critical decisions with severe consequences if wrong, a lower α like 0.01 may be appropriate.
• Resource Constraints : If the cost of collecting more data is high, you may choose a higher α to make a decision based on a smaller sample size.
• Industry Standards : Sometimes, the choice of α may be dictated by industry norms or regulatory guidelines.

By the end of Step 2, you should have a well-defined significance level that will guide the rest of your hypothesis testing process. This level serves as the cut-off for determining whether the observed effect or difference in your sample is statistically significant or not.

Continuing the Scenario: Reducing Assembly Time in a Car Manufacturing Plant

After formulating the hypotheses, the next step is to set the significance level ( α ) that will be used to interpret the results of the hypothesis test. This is a critical decision as it quantifies the level of risk you’re willing to accept when making a conclusion based on the test. Setting the Significance Level Given that assembly time is a critical factor affecting the production schedule, and ultimately, the company’s bottom line, you decide to be fairly stringent in your test. You opt for a commonly used significance level: α = 0.05 This means you are willing to accept a 5% chance of rejecting the null hypothesis when it is actually true. In practical terms, if you find that the p-value of the test is less than 0.05, you will conclude that the new process significantly reduces assembly time and consider implementing it across the entire line. Why α = 0.05 ? Industry Standard : A 5% significance level is widely accepted in many industries, including manufacturing, for hypothesis testing. Risk Management : By setting  α = 0.05 , you’re limiting the risk of concluding that the new process is effective when it may not be to just 5%. Balanced Approach : This level offers a balance between being too lenient (e.g., α=0.10) and too stringent (e.g., α=0.01), making it a reasonable choice for this scenario.

Step 3: Collect and Prepare the Data

After stating your hypotheses and setting the significance level, the next vital step is data collection. The data you collect serves as the basis for your hypothesis test, so it’s essential to gather accurate and relevant data.

Types of Data

Depending on your hypothesis, you’ll need to collect either:

• Quantitative Data : Numerical data that can be measured. Examples include height, weight, and temperature.
• Qualitative Data : Categorical data that represent characteristics. Examples include colors, gender, and material types.

Data Collection Methods

Various methods can be used to collect data, such as:

• Surveys and Questionnaires : Useful for collecting qualitative data and opinions.
• Observation : Collecting data through direct or participant observation.
• Experiments : Especially useful in scientific research where control over variables is possible.
• Existing Data : Utilizing databases, records, or any other data previously collected.

Sample Size

The sample size ( n ) is another crucial factor. A larger sample size generally gives more accurate results, but it’s often constrained by resources like time and money. The choice of sample size might also depend on the statistical test you plan to use.

Continuing with the manufacturing example, suppose you decide to collect data on the assembly time of 30 randomly chosen products, 15 made using the old process and 15 made using the new process. Here, your sample size n =30.

Data Preparation

Once data is collected, it often needs to be cleaned and prepared for analysis. This could involve:

• Removing Outliers : Outliers can skew the results and provide an inaccurate picture.
• Data Transformation : Converting data into a format suitable for statistical analysis.
• Data Coding : Categorizing or labeling data, necessary for qualitative data.

By the end of Step 3, you should have a dataset that is ready for statistical analysis. This dataset should be representative of the population you’re interested in and prepared in a way that makes it suitable for hypothesis testing.

With the hypotheses stated and the significance level set, you’re now ready to collect the data that will serve as the foundation for your hypothesis test. Given that you’re testing a change in a manufacturing process, the data will most likely be quantitative, representing the assembly time of cars produced on the line. Data Collection Plan You decide to use a Random Sampling Method for your data collection. For two weeks, assembly times for randomly selected cars will be recorded: one week using the old process and another week using the new process. Your aim is to collect data for 40 cars from each process, giving you a sample size ( n ) of 80 cars in total. Types of Data Quantitative Data : In this case, you’re collecting numerical data representing the assembly time in minutes for each car. Data Preparation Data Cleaning : Once the data is collected, you’ll need to inspect it for any anomalies or outliers that could skew your results. For example, if a significant machine breakdown happened during one of the weeks, you may need to adjust your data or collect more. Data Transformation : Given that you’re dealing with time, you may not need to transform your data, but it’s something to consider, depending on the statistical test you plan to use. Data Coding : Since you’re dealing with quantitative data in this scenario, coding is likely unnecessary unless you’re planning to categorize assembly times into bins (e.g., ‘fast’, ‘medium’, ‘slow’) for some reason. Example Data Points: Car_ID Process_Type Assembly_Time_Minutes 1 Old 38.53 2 Old 35.80 3 Old 36.96 4 Old 39.48 5 Old 38.74 6 Old 33.05 7 Old 36.90 8 Old 34.70 9 Old 34.79 … … … The complete dataset would contain 80 rows: 40 for the old process and 40 for the new process.

Step 4: Conduct the Statistical Test

After you have your hypotheses, significance level, and collected data, the next step is to actually perform the statistical test. This step involves calculations that will lead to a test statistic, which you’ll then use to make your decision regarding the null hypothesis.

Choose the Right Test

The first task is to decide which statistical test to use. The choice depends on several factors:

• Type of Data : Quantitative or Qualitative
• Sample Size : Large or Small
• Number of Groups or Categories : One-sample, Two-sample, or Multiple groups

For instance, you might choose a t-test for comparing means of two groups when you have a small sample size. Chi-square tests are often used for categorical data, and ANOVA is used for comparing means across more than two groups.

Calculation of Test Statistic

Once you’ve chosen the appropriate statistical test, the next step is to calculate the test statistic. This involves using the sample data in a specific formula for the chosen test.

Obtain the p-value

After calculating the test statistic, the next step is to find the p-value associated with it. The p-value represents the probability of observing the given test statistic if the null hypothesis is true.

• A small p-value (< α ) indicates strong evidence against the null hypothesis, so you reject the null hypothesis.
• A large p-value (> α ) indicates weak evidence against the null hypothesis, so you fail to reject the null hypothesis.

Make the Decision

You now compare the p-value to the predetermined significance level ( α ):

• If p < α , you reject the null hypothesis in favor of the alternative hypothesis.
• If p > α , you fail to reject the null hypothesis.

In the manufacturing case, if your calculated p-value is 0.03 and your α is 0.05, you would reject the null hypothesis, concluding that the new process effectively reduces the average assembly time.

By the end of Step 4, you will have either rejected or failed to reject the null hypothesis, providing a statistical basis for your decision-making process.

Now that you have collected and prepared your data, the next step is to conduct the actual statistical test to evaluate the null and alternative hypotheses. In this case, you’ll be comparing the mean assembly times between cars produced using the old and new processes to determine if the new process is statistically significantly faster. Choosing the Right Test Given that you have two sets of independent samples (old process and new process), a Two-sample t-test for Equality of Means seems appropriate for comparing the average assembly times. Preparing Data for Minitab Firstly, you would prepare your data in an Excel sheet or CSV file with one column for the assembly times using the old process and another column for the assembly times using the new process. Import this file into Minitab. Steps to Perform the Two-sample t-test in Minitab Open Minitab : Launch the Minitab software on your computer. Import Data : Navigate to File > Open and import your data file. Navigate to the t-test Menu : Go to Stat > Basic Statistics > 2-Sample t... . Select Columns : In the dialog box, specify the columns corresponding to the old and new process assembly times under “Sample 1” and “Sample 2.” Options : Click on Options and make sure that you set the confidence level to 95% (which corresponds to α = 0.05 ). Run the Test : Click OK to run the test. In this example output, the p-value is 0.0012, which is less than the significance level α = 0.05 . Hence, you would reject the null hypothesis. The t-statistic is -3.45, indicating that the mean of the new process is statistically significantly less than the mean of the old process, which aligns with your alternative hypothesis. Showing the data displayed as a Box plot in the below graphic it is easy to see the new process is statistically significantly better.

Why do a Hypothesis test?

You might ask, after all this why do a hypothesis test and not just look at the averages, which is a good question. While looking at average times might give you a general idea of which process is faster, hypothesis testing provides several advantages that a simple comparison of averages doesn’t offer:

Statistical Significance

Account for Random Variability : Hypothesis testing considers not just the averages, but also the variability within each group. This allows you to make more robust conclusions that account for random chance.

Quantify the Evidence : With hypothesis testing, you obtain a p-value that quantifies the strength of the evidence against the null hypothesis. A simple comparison of averages doesn’t provide this level of detail.

Control Type I Error : Hypothesis testing allows you to control the probability of making a Type I error (i.e., rejecting a true null hypothesis). This is particularly useful in settings where the consequences of such an error could be costly or risky.

Quantify Risk : Hypothesis testing provides a structured way to make decisions based on a predefined level of risk (the significance level, α ).

Decision-making Confidence

Objective Decision Making : The formal structure of hypothesis testing provides an objective framework for decision-making. This is especially useful in a business setting where decisions often have to be justified to stakeholders.

Replicability : The statistical rigor ensures that the results are replicable. Another team could perform the same test and expect to get similar results, which is not necessarily the case when comparing only averages.

Additional Insights

Understanding of Variability : Hypothesis testing often involves looking at measures of spread and distribution, not just the mean. This can offer additional insights into the processes you’re comparing.

Basis for Further Analysis : Once you’ve performed a hypothesis test, you can often follow it up with other analyses (like confidence intervals for the difference in means, or effect size calculations) that offer more detailed information.

In summary, while comparing averages is quicker and simpler, hypothesis testing provides a more reliable, nuanced, and objective basis for making data-driven decisions.

Step 5: Interpret the Results and Make Conclusions

Having conducted the statistical test and obtained the p-value, you’re now at a stage where you can interpret these results in the context of the problem you’re investigating. This step is crucial for transforming the statistical findings into actionable insights.

Interpret the p-value

The p-value you obtained tells you the significance of your results:

• Low p-value ( p < α ) : Indicates that the results are statistically significant, and it’s unlikely that the observed effects are due to random chance. In this case, you generally reject the null hypothesis.
• High p-value ( p > α ) : Indicates that the results are not statistically significant, and the observed effects could well be due to random chance. Here, you generally fail to reject the null hypothesis.

Relate to Real-world Context

You should then relate these statistical conclusions to the real-world context of your problem. This is where your expertise in your specific field comes into play.

In our manufacturing example, if you’ve found a statistically significant reduction in assembly time with a p-value of 0.03 (which is less than the α level of 0.05), you can confidently conclude that the new manufacturing process is more efficient. You might then consider implementing this new process across the entire assembly line.

Make Recommendations

Based on your conclusions, you can make recommendations for action or further study. For example:

• Implement Changes : If the test results are significant, consider making the changes on a larger scale.
• Further Research : If the test results are not clear or not significant, you may recommend further studies or data collection.
• Review Methodology : If you find that the results are not as expected, it might be useful to review the methodology and see if the test was conducted under the right conditions and with the right test parameters.

Document the Findings

Lastly, it’s essential to document all the steps taken, the methodology used, the data collected, and the conclusions drawn. This documentation is not only useful for any further studies but also for auditing purposes or for stakeholders who may need to understand the process and the findings.

By the end of Step 5, you’ll have turned the raw statistical findings into meaningful conclusions and actionable insights. This is the final step in the hypothesis testing process, making it a complete, robust method for informed decision-making.

You’ve successfully conducted the hypothesis test and found strong evidence to reject the null hypothesis in favor of the alternative: The new assembly process is statistically significantly faster than the old one. It’s now time to interpret these results in the context of your business operations and make actionable recommendations. Interpretation of Results Statistical Significance : The p-value of 0.0012 is well below the significance level of = 0.05   α = 0.05 , indicating that the results are statistically significant. Practical Significance : The boxplot and t-statistic (-3.45) suggest not just statistical, but also practical significance. The new process appears to be both consistently and substantially faster. Risk Assessment : The low p-value allows you to reject the null hypothesis with a high degree of confidence, meaning the risk of making a Type I error is minimal. Business Implications Increased Productivity : Implementing the new process could lead to an increase in the number of cars produced, thereby enhancing productivity. Cost Savings : Faster assembly time likely translates to lower labor costs. Quality Control : Consider monitoring the quality of cars produced under the new process closely to ensure that the speedier assembly does not compromise quality. Recommendations Implement New Process : Given the statistical and practical significance of the findings, recommend implementing the new process across the entire assembly line. Monitor and Adjust : Implement a control phase where the new process is monitored for both speed and quality. This could involve additional hypothesis tests or control charts. Communicate Findings : Share the results and recommendations with stakeholders through a formal presentation or report, emphasizing both the statistical rigor and the potential business benefits. Review Resource Allocation : Given the likely increase in productivity, assess if resources like labor and parts need to be reallocated to optimize the workflow further.

By following this step-by-step guide, you’ve journeyed through the rigorous yet enlightening process of hypothesis testing. From stating clear hypotheses to interpreting the results, each step has paved the way for making informed, data-driven decisions that can significantly impact your projects, business, or research.

Hypothesis testing is more than just a set of formulas or calculations; it’s a holistic approach to problem-solving that incorporates context, statistics, and strategic decision-making. While the process may seem daunting at first, each step serves a crucial role in ensuring that your conclusions are both statistically sound and practically relevant.

• McKenzie, C.R., 2004. Hypothesis testing and evaluation .  Blackwell handbook of judgment and decision making , pp.200-219.
• Park, H.M., 2015. Hypothesis testing and statistical power of a test.
• Eberhardt, L.L., 2003. What should we do about hypothesis testing? .  The Journal of wildlife management , pp.241-247.

Q: What is hypothesis testing in the context of Lean Six Sigma?

A: Hypothesis testing is a statistical method used in Lean Six Sigma to determine whether there is enough evidence in a sample of data to infer that a certain condition holds true for the entire population. In the Lean Six Sigma process, it’s commonly used to validate the effectiveness of process improvements by comparing performance metrics before and after changes are implemented. A null hypothesis ( H 0 ​ ) usually represents no change or effect, while the alternative hypothesis ( H 1 ​ ) indicates a significant change or effect.

Q: How do I determine which statistical test to use for my hypothesis?

A: The choice of statistical test for hypothesis testing depends on several factors, including the type of data (nominal, ordinal, interval, or ratio), the sample size, the number of samples (one sample, two samples, paired), and whether the data distribution is normal. For example, a t-test is used for comparing the means of two groups when the data is normally distributed, while a Chi-square test is suitable for categorical data to test the relationship between two variables. It’s important to choose the right test to ensure the validity of your hypothesis testing results.

Q: What is a p-value, and how does it relate to hypothesis testing?

A: A p-value is a probability value that helps you determine the significance of your results in hypothesis testing. It represents the likelihood of obtaining a result at least as extreme as the one observed during the test, assuming that the null hypothesis is true. In hypothesis testing, if the p-value is lower than the predetermined significance level (commonly α = 0.05 ), you reject the null hypothesis, suggesting that the observed effect is statistically significant. If the p-value is higher, you fail to reject the null hypothesis, indicating that there is not enough evidence to support the alternative hypothesis.

Q: Can you explain Type I and Type II errors in hypothesis testing?

A: Type I and Type II errors are potential errors that can occur in hypothesis testing. A Type I error, also known as a “false positive,” occurs when the null hypothesis is true, but it is incorrectly rejected. It is equivalent to a false alarm. On the other hand, a Type II error, or a “false negative,” happens when the null hypothesis is false, but it is erroneously failed to be rejected. This means a real effect or difference was missed. The risk of a Type I error is represented by the significance level ( α ), while the risk of a Type II error is denoted by β . Minimizing these errors is crucial for the reliability of hypothesis tests in continuous improvement projects.

Daniel Croft is a seasoned continuous improvement manager with a Black Belt in Lean Six Sigma. With over 10 years of real-world application experience across diverse sectors, Daniel has a passion for optimizing processes and fostering a culture of efficiency. He's not just a practitioner but also an avid learner, constantly seeking to expand his knowledge. Outside of his professional life, Daniel has a keen Investing, statistics and knowledge-sharing, which led him to create the website learnleansigma.com, a platform dedicated to Lean Six Sigma and process improvement insights.

Free Lean Six Sigma Templates

Improve your Lean Six Sigma projects with our free templates. They're designed to make implementation and management easier, helping you achieve better results.

Other Guides

• Business Essentials
• Leadership & Management
• Credential of Leadership, Impact, and Management in Business (CLIMB)
• Entrepreneurship & Innovation
• Digital Transformation
• Finance & Accounting
• Business in Society
• For Organizations
• Support Portal
• Media Coverage
• Founding Donors
• Leadership Team

• Harvard Business School →
• HBS Online →
• Business Insights →

Business Insights

Harvard Business School Online's Business Insights Blog provides the career insights you need to achieve your goals and gain confidence in your business skills.

• Career Development
• Communication
• Decision-Making
• Earning Your MBA
• Negotiation
• News & Events
• Productivity
• Staff Spotlight
• Student Profiles
• Work-Life Balance
• AI Essentials for Business
• Alternative Investments
• Business Analytics
• Business Strategy
• Business and Climate Change
• Design Thinking and Innovation
• Digital Marketing Strategy
• Disruptive Strategy
• Economics for Managers
• Entrepreneurship Essentials
• Financial Accounting
• Global Business
• Launching Tech Ventures
• Leadership Principles
• Leadership, Ethics, and Corporate Accountability
• Leading with Finance
• Management Essentials
• Negotiation Mastery
• Organizational Leadership
• Power and Influence for Positive Impact
• Strategy Execution
• Sustainable Business Strategy
• Sustainable Investing
• Winning with Digital Platforms

A Beginner’s Guide to Hypothesis Testing in Business

• 30 Mar 2021

Becoming a more data-driven decision-maker can bring several benefits to your organization, enabling you to identify new opportunities to pursue and threats to abate. Rather than allowing subjective thinking to guide your business strategy, backing your decisions with data can empower your company to become more innovative and, ultimately, profitable.

If you’re new to data-driven decision-making, you might be wondering how data translates into business strategy. The answer lies in generating a hypothesis and verifying or rejecting it based on what various forms of data tell you.

Below is a look at hypothesis testing and the role it plays in helping businesses become more data-driven.

Access your free e-book today.

What Is Hypothesis Testing?

To understand what hypothesis testing is, it’s important first to understand what a hypothesis is.

A hypothesis or hypothesis statement seeks to explain why something has happened, or what might happen, under certain conditions. It can also be used to understand how different variables relate to each other. Hypotheses are often written as if-then statements; for example, “If this happens, then this will happen.”

Hypothesis testing , then, is a statistical means of testing an assumption stated in a hypothesis. While the specific methodology leveraged depends on the nature of the hypothesis and data available, hypothesis testing typically uses sample data to extrapolate insights about a larger population.

Hypothesis Testing in Business

When it comes to data-driven decision-making, there’s a certain amount of risk that can mislead a professional. This could be due to flawed thinking or observations, incomplete or inaccurate data , or the presence of unknown variables. The danger in this is that, if major strategic decisions are made based on flawed insights, it can lead to wasted resources, missed opportunities, and catastrophic outcomes.

The real value of hypothesis testing in business is that it allows professionals to test their theories and assumptions before putting them into action. This essentially allows an organization to verify its analysis is correct before committing resources to implement a broader strategy.

As one example, consider a company that wishes to launch a new marketing campaign to revitalize sales during a slow period. Doing so could be an incredibly expensive endeavor, depending on the campaign’s size and complexity. The company, therefore, may wish to test the campaign on a smaller scale to understand how it will perform.

In this example, the hypothesis that’s being tested would fall along the lines of: “If the company launches a new marketing campaign, then it will translate into an increase in sales.” It may even be possible to quantify how much of a lift in sales the company expects to see from the effort. Pending the results of the pilot campaign, the business would then know whether it makes sense to roll it out more broadly.

Related: 9 Fundamental Data Science Skills for Business Professionals

Key Considerations for Hypothesis Testing

1. alternative hypothesis and null hypothesis.

In hypothesis testing, the hypothesis that’s being tested is known as the alternative hypothesis . Often, it’s expressed as a correlation or statistical relationship between variables. The null hypothesis , on the other hand, is a statement that’s meant to show there’s no statistical relationship between the variables being tested. It’s typically the exact opposite of whatever is stated in the alternative hypothesis.

For example, consider a company’s leadership team that historically and reliably sees $12 million in monthly revenue. They want to understand if reducing the price of their services will attract more customers and, in turn, increase revenue.

In this case, the alternative hypothesis may take the form of a statement such as: “If we reduce the price of our flagship service by five percent, then we’ll see an increase in sales and realize revenues greater than $12 million in the next month.”

The null hypothesis, on the other hand, would indicate that revenues wouldn’t increase from the base of $12 million, or might even decrease.

Check out the video below about the difference between an alternative and a null hypothesis, and subscribe to our YouTube channel for more explainer content.

2. Significance Level and P-Value

Statistically speaking, if you were to run the same scenario 100 times, you’d likely receive somewhat different results each time. If you were to plot these results in a distribution plot, you’d see the most likely outcome is at the tallest point in the graph, with less likely outcomes falling to the right and left of that point.

With this in mind, imagine you’ve completed your hypothesis test and have your results, which indicate there may be a correlation between the variables you were testing. To understand your results' significance, you’ll need to identify a p-value for the test, which helps note how confident you are in the test results.

In statistics, the p-value depicts the probability that, assuming the null hypothesis is correct, you might still observe results that are at least as extreme as the results of your hypothesis test. The smaller the p-value, the more likely the alternative hypothesis is correct, and the greater the significance of your results.

3. One-Sided vs. Two-Sided Testing

When it’s time to test your hypothesis, it’s important to leverage the correct testing method. The two most common hypothesis testing methods are one-sided and two-sided tests , or one-tailed and two-tailed tests, respectively.

Typically, you’d leverage a one-sided test when you have a strong conviction about the direction of change you expect to see due to your hypothesis test. You’d leverage a two-sided test when you’re less confident in the direction of change.

4. Sampling

To perform hypothesis testing in the first place, you need to collect a sample of data to be analyzed. Depending on the question you’re seeking to answer or investigate, you might collect samples through surveys, observational studies, or experiments.

A survey involves asking a series of questions to a random population sample and recording self-reported responses.

Observational studies involve a researcher observing a sample population and collecting data as it occurs naturally, without intervention.

Finally, an experiment involves dividing a sample into multiple groups, one of which acts as the control group. For each non-control group, the variable being studied is manipulated to determine how the data collected differs from that of the control group.

Learn How to Perform Hypothesis Testing

Hypothesis testing is a complex process involving different moving pieces that can allow an organization to effectively leverage its data and inform strategic decisions.

If you’re interested in better understanding hypothesis testing and the role it can play within your organization, one option is to complete a course that focuses on the process. Doing so can lay the statistical and analytical foundation you need to succeed.

Do you want to learn more about hypothesis testing? Explore Business Analytics —one of our online business essentials courses —and download our Beginner’s Guide to Data & Analytics .

About the Author

Statistics Made Easy

Introduction to Hypothesis Testing

A statistical hypothesis is an assumption about a population parameter .

For example, we may assume that the mean height of a male in the U.S. is 70 inches.

The assumption about the height is the statistical hypothesis and the true mean height of a male in the U.S. is the population parameter .

A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.

The Two Types of Statistical Hypotheses

To test whether a statistical hypothesis about a population parameter is true, we obtain a random sample from the population and perform a hypothesis test on the sample data.

There are two types of statistical hypotheses:

The null hypothesis , denoted as H 0 , is the hypothesis that the sample data occurs purely from chance.

The alternative hypothesis , denoted as H 1 or H a , is the hypothesis that the sample data is influenced by some non-random cause.

Hypothesis Tests

A hypothesis test consists of five steps:

1. State the hypotheses. 

State the null and alternative hypotheses. These two hypotheses need to be mutually exclusive, so if one is true then the other must be false.

2. Determine a significance level to use for the hypothesis.

Decide on a significance level. Common choices are .01, .05, and .1. 

3. Find the test statistic.

Find the test statistic and the corresponding p-value. Often we are analyzing a population mean or proportion and the general formula to find the test statistic is: (sample statistic – population parameter) / (standard deviation of statistic)

4. Reject or fail to reject the null hypothesis.

Using the test statistic or the p-value, determine if you can reject or fail to reject the null hypothesis based on the significance level.

The p-value  tells us the strength of evidence in support of a null hypothesis. If the p-value is less than the significance level, we reject the null hypothesis.

5. Interpret the results. 

Interpret the results of the hypothesis test in the context of the question being asked. 

The Two Types of Decision Errors

There are two types of decision errors that one can make when doing a hypothesis test:

Type I error: You reject the null hypothesis when it is actually true. The probability of committing a Type I error is equal to the significance level, often called  alpha , and denoted as α.

Type II error: You fail to reject the null hypothesis when it is actually false. The probability of committing a Type II error is called the Power of the test or  Beta , denoted as β.

One-Tailed and Two-Tailed Tests

A statistical hypothesis can be one-tailed or two-tailed.

A one-tailed hypothesis involves making a “greater than” or “less than ” statement.

For example, suppose we assume the mean height of a male in the U.S. is greater than or equal to 70 inches. The null hypothesis would be H0: µ ≥ 70 inches and the alternative hypothesis would be Ha: µ < 70 inches.

A two-tailed hypothesis involves making an “equal to” or “not equal to” statement.

For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches. The null hypothesis would be H0: µ = 70 inches and the alternative hypothesis would be Ha: µ ≠ 70 inches.

Note: The “equal” sign is always included in the null hypothesis, whether it is =, ≥, or ≤.

Related:   What is a Directional Hypothesis?

Types of Hypothesis Tests

There are many different types of hypothesis tests you can perform depending on the type of data you’re working with and the goal of your analysis.

The following tutorials provide an explanation of the most common types of hypothesis tests:

Introduction to the One Sample t-test Introduction to the Two Sample t-test Introduction to the Paired Samples t-test Introduction to the One Proportion Z-Test Introduction to the Two Proportion Z-Test

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Tutorial Playlist

Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability.

A Comprehensive Look at Percentile in Statistics

The Best Guide to Understand Bayes Theorem

Everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, a complete guide to chi-square test, a complete guide on hypothesis testing in statistics, understanding the fundamentals of arithmetic and geometric progression, the definitive guide to understand spearman’s rank correlation, a comprehensive guide to understand mean squared error, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution.

All You Need to Know About Bias in Statistics

A Complete Guide to Get a Grasp of Time Series Analysis

The Key Differences Between Z-Test Vs. T-Test

The Complete Guide to Understand Pearson's Correlation

A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, what is hypothesis testing in statistics types and examples.

Lesson 10 of 24 By Avijeet Biswal

Table of Contents

In today’s data-driven world , decisions are based on data all the time. Hypothesis plays a crucial role in that process, whether it may be making business decisions, in the health sector, academia, or in quality improvement. Without hypothesis & hypothesis tests, you risk drawing the wrong conclusions and making bad decisions. In this tutorial, you will look at Hypothesis Testing in Statistics.

What Is Hypothesis Testing in Statistics?

Hypothesis Testing is a type of statistical analysis in which you put your assumptions about a population parameter to the test. It is used to estimate the relationship between 2 statistical variables.

Let's discuss few examples of statistical hypothesis from real-life - 

• A teacher assumes that 60% of his college's students come from lower-middle-class families.
• A doctor believes that 3D (Diet, Dose, and Discipline) is 90% effective for diabetic patients.

Now that you know about hypothesis testing, look at the two types of hypothesis testing in statistics.

Hypothesis Testing Formula

Z = ( x̅ – μ0 ) / (σ /√n)

• Here, x̅ is the sample mean,
• μ0 is the population mean,
• σ is the standard deviation,
• n is the sample size.

How Hypothesis Testing Works?

An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis. Measurements and analyses are conducted on a random sample of the population to test a theory. Analysts use a random population sample to test two hypotheses: the null and alternative hypotheses.

The null hypothesis is typically an equality hypothesis between population parameters; for example, a null hypothesis may claim that the population means return equals zero. The alternate hypothesis is essentially the inverse of the null hypothesis (e.g., the population means the return is not equal to zero). As a result, they are mutually exclusive, and only one can be correct. One of the two possibilities, however, will always be correct.

Your Dream Career is Just Around The Corner!

Null Hypothesis and Alternate Hypothesis

The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.

H0 is the symbol for it, and it is pronounced H-naught.

The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.

Let's understand this with an example.

A sanitizer manufacturer claims that its product kills 95 percent of germs on average. 

To put this company's claim to the test, create a null and alternate hypothesis.

H0 (Null Hypothesis): Average = 95%.

Alternative Hypothesis (H1): The average is less than 95%.

Another straightforward example to understand this concept is determining whether or not a coin is fair and balanced. The null hypothesis states that the probability of a show of heads is equal to the likelihood of a show of tails. In contrast, the alternate theory states that the probability of a show of heads and tails would be very different.

Become a Data Scientist with Hands-on Training!

Hypothesis Testing Calculation With Examples

Let's consider a hypothesis test for the average height of women in the United States. Suppose our null hypothesis is that the average height is 5'4". We gather a sample of 100 women and determine that their average height is 5'5". The standard deviation of population is 2.

To calculate the z-score, we would use the following formula:

z = ( x̅ – μ0 ) / (σ /√n)

z = (5'5" - 5'4") / (2" / √100)

z = 0.5 / (0.045)

 We will reject the null hypothesis as the z-score of 11.11 is very large and conclude that there is evidence to suggest that the average height of women in the US is greater than 5'4".

Steps of Hypothesis Testing

Step 1: specify your null and alternate hypotheses.

It is critical to rephrase your original research hypothesis (the prediction that you wish to study) as a null (Ho) and alternative (Ha) hypothesis so that you can test it quantitatively. Your first hypothesis, which predicts a link between variables, is generally your alternate hypothesis. The null hypothesis predicts no link between the variables of interest.

Step 2: Gather Data

For a statistical test to be legitimate, sampling and data collection must be done in a way that is meant to test your hypothesis. You cannot draw statistical conclusions about the population you are interested in if your data is not representative.

Step 3: Conduct a Statistical Test

Other statistical tests are available, but they all compare within-group variance (how to spread out the data inside a category) against between-group variance (how different the categories are from one another). If the between-group variation is big enough that there is little or no overlap between groups, your statistical test will display a low p-value to represent this. This suggests that the disparities between these groups are unlikely to have occurred by accident. Alternatively, if there is a large within-group variance and a low between-group variance, your statistical test will show a high p-value. Any difference you find across groups is most likely attributable to chance. The variety of variables and the level of measurement of your obtained data will influence your statistical test selection.

Step 4: Determine Rejection Of Your Null Hypothesis

Your statistical test results must determine whether your null hypothesis should be rejected or not. In most circumstances, you will base your judgment on the p-value provided by the statistical test. In most circumstances, your preset level of significance for rejecting the null hypothesis will be 0.05 - that is, when there is less than a 5% likelihood that these data would be seen if the null hypothesis were true. In other circumstances, researchers use a lower level of significance, such as 0.01 (1%). This reduces the possibility of wrongly rejecting the null hypothesis.

Step 5: Present Your Results 

The findings of hypothesis testing will be discussed in the results and discussion portions of your research paper, dissertation, or thesis. You should include a concise overview of the data and a summary of the findings of your statistical test in the results section. You can talk about whether your results confirmed your initial hypothesis or not in the conversation. Rejecting or failing to reject the null hypothesis is a formal term used in hypothesis testing. This is likely a must for your statistics assignments.

Types of Hypothesis Testing

To determine whether a discovery or relationship is statistically significant, hypothesis testing uses a z-test. It usually checks to see if two means are the same (the null hypothesis). Only when the population standard deviation is known and the sample size is 30 data points or more, can a z-test be applied.

A statistical test called a t-test is employed to compare the means of two groups. To determine whether two groups differ or if a procedure or treatment affects the population of interest, it is frequently used in hypothesis testing.

Chi-Square 

You utilize a Chi-square test for hypothesis testing concerning whether your data is as predicted. To determine if the expected and observed results are well-fitted, the Chi-square test analyzes the differences between categorical variables from a random sample. The test's fundamental premise is that the observed values in your data should be compared to the predicted values that would be present if the null hypothesis were true.

Hypothesis Testing and Confidence Intervals

Both confidence intervals and hypothesis tests are inferential techniques that depend on approximating the sample distribution. Data from a sample is used to estimate a population parameter using confidence intervals. Data from a sample is used in hypothesis testing to examine a given hypothesis. We must have a postulated parameter to conduct hypothesis testing.

Bootstrap distributions and randomization distributions are created using comparable simulation techniques. The observed sample statistic is the focal point of a bootstrap distribution, whereas the null hypothesis value is the focal point of a randomization distribution.

A variety of feasible population parameter estimates are included in confidence ranges. In this lesson, we created just two-tailed confidence intervals. There is a direct connection between these two-tail confidence intervals and these two-tail hypothesis tests. The results of a two-tailed hypothesis test and two-tailed confidence intervals typically provide the same results. In other words, a hypothesis test at the 0.05 level will virtually always fail to reject the null hypothesis if the 95% confidence interval contains the predicted value. A hypothesis test at the 0.05 level will nearly certainly reject the null hypothesis if the 95% confidence interval does not include the hypothesized parameter.

Simple and Composite Hypothesis Testing

Depending on the population distribution, you can classify the statistical hypothesis into two types.

Simple Hypothesis: A simple hypothesis specifies an exact value for the parameter.

Composite Hypothesis: A composite hypothesis specifies a range of values.

A company is claiming that their average sales for this quarter are 1000 units. This is an example of a simple hypothesis.

Suppose the company claims that the sales are in the range of 900 to 1000 units. Then this is a case of a composite hypothesis.

One-Tailed and Two-Tailed Hypothesis Testing

The One-Tailed test, also called a directional test, considers a critical region of data that would result in the null hypothesis being rejected if the test sample falls into it, inevitably meaning the acceptance of the alternate hypothesis.

In a one-tailed test, the critical distribution area is one-sided, meaning the test sample is either greater or lesser than a specific value.

In two tails, the test sample is checked to be greater or less than a range of values in a Two-Tailed test, implying that the critical distribution area is two-sided.

If the sample falls within this range, the alternate hypothesis will be accepted, and the null hypothesis will be rejected.

Become a Data Scientist With Real-World Experience

Right Tailed Hypothesis Testing

If the larger than (>) sign appears in your hypothesis statement, you are using a right-tailed test, also known as an upper test. Or, to put it another way, the disparity is to the right. For instance, you can contrast the battery life before and after a change in production. Your hypothesis statements can be the following if you want to know if the battery life is longer than the original (let's say 90 hours):

• The null hypothesis is (H0 <= 90) or less change.
• A possibility is that battery life has risen (H1) > 90.

The crucial point in this situation is that the alternate hypothesis (H1), not the null hypothesis, decides whether you get a right-tailed test.

Left Tailed Hypothesis Testing

Alternative hypotheses that assert the true value of a parameter is lower than the null hypothesis are tested with a left-tailed test; they are indicated by the asterisk "<".

Suppose H0: mean = 50 and H1: mean not equal to 50

According to the H1, the mean can be greater than or less than 50. This is an example of a Two-tailed test.

In a similar manner, if H0: mean >=50, then H1: mean <50

Here the mean is less than 50. It is called a One-tailed test.

Type 1 and Type 2 Error

A hypothesis test can result in two types of errors.

Type 1 Error: A Type-I error occurs when sample results reject the null hypothesis despite being true.

Type 2 Error: A Type-II error occurs when the null hypothesis is not rejected when it is false, unlike a Type-I error.

Suppose a teacher evaluates the examination paper to decide whether a student passes or fails.

H0: Student has passed

H1: Student has failed

Type I error will be the teacher failing the student [rejects H0] although the student scored the passing marks [H0 was true]. 

Type II error will be the case where the teacher passes the student [do not reject H0] although the student did not score the passing marks [H1 is true].

Level of Significance

The alpha value is a criterion for determining whether a test statistic is statistically significant. In a statistical test, Alpha represents an acceptable probability of a Type I error. Because alpha is a probability, it can be anywhere between 0 and 1. In practice, the most commonly used alpha values are 0.01, 0.05, and 0.1, which represent a 1%, 5%, and 10% chance of a Type I error, respectively (i.e. rejecting the null hypothesis when it is in fact correct).

Future-Proof Your AI/ML Career: Top Dos and Don'ts

A p-value is a metric that expresses the likelihood that an observed difference could have occurred by chance. As the p-value decreases the statistical significance of the observed difference increases. If the p-value is too low, you reject the null hypothesis.

Here you have taken an example in which you are trying to test whether the new advertising campaign has increased the product's sales. The p-value is the likelihood that the null hypothesis, which states that there is no change in the sales due to the new advertising campaign, is true. If the p-value is .30, then there is a 30% chance that there is no increase or decrease in the product's sales.  If the p-value is 0.03, then there is a 3% probability that there is no increase or decrease in the sales value due to the new advertising campaign. As you can see, the lower the p-value, the chances of the alternate hypothesis being true increases, which means that the new advertising campaign causes an increase or decrease in sales.

Why is Hypothesis Testing Important in Research Methodology?

Hypothesis testing is crucial in research methodology for several reasons:

• Provides evidence-based conclusions: It allows researchers to make objective conclusions based on empirical data, providing evidence to support or refute their research hypotheses.
• Supports decision-making: It helps make informed decisions, such as accepting or rejecting a new treatment, implementing policy changes, or adopting new practices.
• Adds rigor and validity: It adds scientific rigor to research using statistical methods to analyze data, ensuring that conclusions are based on sound statistical evidence.
• Contributes to the advancement of knowledge: By testing hypotheses, researchers contribute to the growth of knowledge in their respective fields by confirming existing theories or discovering new patterns and relationships.

Limitations of Hypothesis Testing

Hypothesis testing has some limitations that researchers should be aware of:

• It cannot prove or establish the truth: Hypothesis testing provides evidence to support or reject a hypothesis, but it cannot confirm the absolute truth of the research question.
• Results are sample-specific: Hypothesis testing is based on analyzing a sample from a population, and the conclusions drawn are specific to that particular sample.
• Possible errors: During hypothesis testing, there is a chance of committing type I error (rejecting a true null hypothesis) or type II error (failing to reject a false null hypothesis).
• Assumptions and requirements: Different tests have specific assumptions and requirements that must be met to accurately interpret results.

After reading this tutorial, you would have a much better understanding of hypothesis testing, one of the most important concepts in the field of Data Science . The majority of hypotheses are based on speculation about observed behavior, natural phenomena, or established theories.

If you are interested in statistics of data science and skills needed for such a career, you ought to explore Simplilearn’s Post Graduate Program in Data Science.

If you have any questions regarding this ‘Hypothesis Testing In Statistics’ tutorial, do share them in the comment section. Our subject matter expert will respond to your queries. Happy learning!

1. What is hypothesis testing in statistics with example?

Hypothesis testing is a statistical method used to determine if there is enough evidence in a sample data to draw conclusions about a population. It involves formulating two competing hypotheses, the null hypothesis (H0) and the alternative hypothesis (Ha), and then collecting data to assess the evidence. An example: testing if a new drug improves patient recovery (Ha) compared to the standard treatment (H0) based on collected patient data.

2. What is hypothesis testing and its types?

Hypothesis testing is a statistical method used to make inferences about a population based on sample data. It involves formulating two hypotheses: the null hypothesis (H0), which represents the default assumption, and the alternative hypothesis (Ha), which contradicts H0. The goal is to assess the evidence and determine whether there is enough statistical significance to reject the null hypothesis in favor of the alternative hypothesis.

Types of hypothesis testing:

• One-sample test: Used to compare a sample to a known value or a hypothesized value.
• Two-sample test: Compares two independent samples to assess if there is a significant difference between their means or distributions.
• Paired-sample test: Compares two related samples, such as pre-test and post-test data, to evaluate changes within the same subjects over time or under different conditions.
• Chi-square test: Used to analyze categorical data and determine if there is a significant association between variables.
• ANOVA (Analysis of Variance): Compares means across multiple groups to check if there is a significant difference between them.

3. What are the steps of hypothesis testing?

The steps of hypothesis testing are as follows:

• Formulate the hypotheses: State the null hypothesis (H0) and the alternative hypothesis (Ha) based on the research question.
• Set the significance level: Determine the acceptable level of error (alpha) for making a decision.
• Collect and analyze data: Gather and process the sample data.
• Compute test statistic: Calculate the appropriate statistical test to assess the evidence.
• Make a decision: Compare the test statistic with critical values or p-values and determine whether to reject H0 in favor of Ha or not.
• Draw conclusions: Interpret the results and communicate the findings in the context of the research question.

4. What are the 2 types of hypothesis testing?

• One-tailed (or one-sided) test: Tests for the significance of an effect in only one direction, either positive or negative.
• Two-tailed (or two-sided) test: Tests for the significance of an effect in both directions, allowing for the possibility of a positive or negative effect.

The choice between one-tailed and two-tailed tests depends on the specific research question and the directionality of the expected effect.

5. What are the 3 major types of hypothesis?

The three major types of hypotheses are:

• Null Hypothesis (H0): Represents the default assumption, stating that there is no significant effect or relationship in the data.
• Alternative Hypothesis (Ha): Contradicts the null hypothesis and proposes a specific effect or relationship that researchers want to investigate.
• Nondirectional Hypothesis: An alternative hypothesis that doesn't specify the direction of the effect, leaving it open for both positive and negative possibilities.

Find our Data Analyst Online Bootcamp in top cities:

About the author.

Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.

Recommended Resources

Free eBook: Top Programming Languages For A Data Scientist

Normality Test in Minitab: Minitab with Statistics

Machine Learning Career Guide: A Playbook to Becoming a Machine Learning Engineer

• PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.

• Automation-Analytics-AI
• [email protected]
• +91 80 40109783

Hypothesis Testing

Introduction.

In any process scenarios – either manufacturing or service, we collect sample from a large set of data (population) for analysis and draw inferences. To determine whether the results are statistically significant or not – “We use Hypothesis Testing”. In simpler words, the process of drawing inferences (making decisions) about the sample with regards to population as a whole.

For example, manufacturer wants to check the product’s quality meets the pre-specified criteria. Here, it is not possible to check the whole population to make a decision. We collect a sample data from the population. Based on the sample data, we need to make an inference for a population – This process is called as “Hypothesis Testing”. It is basically an assumption that we make about the population parameter.

Basic Terminology

• Sampling – It is a procedure of selecting a sample from a large set of data (Population). For e.g. a manufacturer industry wants to check the quality of a product. It is not possible to check on each and every item it manufactured. So we will take some part of it for inspecting the quality.
• Null Hypothesis (H0) – It is a type of hypothesis which is presumed to be true i.e. no statistical significance exists in a set of given observations. In simpler words, everything is okay and the process is fine. For e.g. quality inspector is sure that product is good and has no defects.
• Alternative Hypothesis (H1) – It is alternative or contradictory to null hypothesis. There is a significant difference in a process. In simpler words, everything is not okay and the process is bad. For e.g. product is bad and has defects.
• Level of significance (α) – It represents the probability of making wrong decision when the null hypothesis is true. The common alpha values are 1% (0.01), 5% (0.05) and 10% (0.1). An alpha value of 0.05 indicates that we are willing to accept a 5% chance that we are wrong when we reject the null hypothesis. To lower this risk, we must use a lower value for α.
• p value – It is a probability value and is calculated using the test statistic. It is used in hypothesis testing for making decision whether to accept or reject the null hypothesis. In simpler words, to determine the significance of a results and is compared to the level of significance. It lies between 0 and 1.

Procedure for Hypothesis Testing

• Null hypothesis (H0) – The products are good and has no defects.
• Alternative hypothesis (H1) – The products are bad and has defects.
• Set the criteria for decision – To set the criteria for decision, we set a level of significance (α). It represents the probability of making wrong decision when the null hypothesis is true. The common alpha values are 1% (0.01), 5% (0.05) and 10% (0.1).
• Compute the test statistic – A test statistic is a random variable that is calculated from sample data and used in a hypothesis test. We compute test statistic based on hypothesis tests we perform. It can be z test, t test, F test, Chi-square and so on. For these tests, test statistic are called as Z statistic (or Z score), t statistic (t Score), F statistic and chi square statistic. We use test statistic to determine whether to accept or reject the null hypothesis. The test statistic compares data with what is expected under the null hypothesis.
• Calculate p value – It is a probability value and is calculated using the test statistic. It is used in hypothesis testing for making decision whether to accept or reject the null hypothesis. In simpler words, to determine the significance of a results and is compared to the level of significance. It lies between 0 and 1.
• p value < α -> Reject null hypothesis
• p value > α -> Accept null hypothesis

For e.g. when the p value is less than 0.05 (alpha value), we reject the null hypothesis and accept the alternative hypothesis. When the p value is greater than 0.05, we accept the null hypothesis and reject the alternative hypothesis.

Before doing an analysis of data, we often have questions like – “How much data is needed and how reliable our collected data is?” To understand this concept, Check our blogs

• “Is your Sample Size enough for doing the Analysis?”
• “Is your Data Reliable enough to do the Analysis?”

What are the types of error in Hypothesis testing?

While making conclusion in a hypothesis testing, there is always a possibility to occur errors – known as type I and type II errors. Since the test is based on probabilities, there is always a chance of making an incorrect conclusion. 

• Type I error – We reject the null hypothesis when it is true. Then we commit a type I error. The probability of making the wrong decision when the null hypothesis is true is known as α (level of significance).
• Type II error – We accept the null hypothesis when it is false. Then we commit a type II error. The probability of accepting the null hypothesis when it is false is known as β.

Suppose in a cosmetic manufacturing industry, when the UV level of sun screen is at the appropriate level – they reject the lot (Type I error). And when the UV level of sun screen is not at the appropriate level – they accept the lot (Type II error).

What are types of Hypothesis testing (Based on sample)?

Let us have a brief overview; in real life manufacturing or service processes, we first do sampling (to collect samples) because it is not always possible to do analysis on whole data (population). Suppose in a beverage manufacturing industry, they produce lakhs of bottle cans – it is time consuming to measure the quality dimensions of whole outputs and in such cases we apply sampling to collect samples. Here, we do not know the population standard deviation and hence we have to use t test.

The commonly used sample test methods are

• One sample t test – We use one sample t test when we have one sample group. By doing so, we would be able to find whether the mean is significantly different or not with regards to our target specification.

For e.g. in a pharmaceutical company, QA officer collects a samples of 10 tablets to measure the dissolution rate of a drug. Here, we can find whether the mean of a dissolution rate is significant to our target dissolution rate or not.

• Two sample t test – We use two sample t test when we have two independent sample groups. By doing so, we would be able to find whether the means are significantly different or not with regards to our target specification. And we would be able to compare which one is good.

For e.g. in a pharmaceutical company, QA officer collects a two sample groups (A and B) each of 10 tablets to measure the dissolution rate of a drug. We can compare which of these types have a better dissolution rate and hence we able to choose the best one.

By now we know the basic concepts of sample tests, when we have one sample we use one sample t – test and when we have two samples we use two sample t – test. In many scenarios, we will have more than two sample groups say three or four sample groups then “What can we do?” We can go for ANOVA test. Here, we can use more than two sample groups for analysis.

To discover the importance of t-tests and ANOVA, check our blogs 

• “What role do t-tests play in Pharmaceutical Processes? When can we apply it?”
• “What are the applications of ANOVA in the field of Healthcare and Pharmaceutical Industry?”

Understanding Hypothesis Testing – based on example

Suppose in a beverage manufacturing company, a quality inspector wants to know whether the bottle caps diameters are equal to 3 cm or not. If the bottle caps diameters are not equal to 3 cm then it won’t fit during the filling process.

(One sample t-test)

• The first step is to do sampling . We collected a sample of 50 bottles (n=50) and measured the diameters of all the bottles.
• Based on the measurement, we got mean (ȳ)=3.3 and standard deviation (s)=1.3
• Null hypothesis (H0) = the bottle diameter is equal to 3 cm.
• Alternative hypothesis (H1) = the bottle diameter is not equal to 3 cm.
• We set the level of significance (α) as 0.05 (5%).

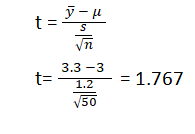
• Now say p value = 0.023 (based on test statistic)
• Making conclusion –

Since we know,

• p value < α, Reject Null Hypothesis
• p value > α, Accept Null Hypothesis

Here, p value < alpha value (i.e. 0.023 < 0.05) and hence we reject the null hypothesis. Therefore the bottle diameter is not equal to 3 cm.

Attend our Training Program, to know more about Statistics and Statistical Software. We conduct various training programs – Statistical Training and Minitab Software Training. Some of the Statistical training certified courses are Predictive Analytics Masterclass,   Essential Statistics For Business Analytics,   SPC Masterclass, DOE Masterclass, etc. (Basic to Advanced Level). Some of the Minitab software training certified courses are Minitab Essentials, Statistical Tools for Pharmaceuticals, Statistical Quality Analysis & Factorial Designs, etc. (Basic to Advanced Level).

We also provide a wide range of Business Analytics Solutions and Business Consulting Services for Organisations to make data-driven decisions and thus enhance their decision support systems.

Perform Hypothesis Testing at Ease in Minitab

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.2: The 7-Step Process of Statistical Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 33320

• Penn State's Department of Statistics
• The Pennsylvania State University

We will cover the seven steps one by one.

Step 1: State the Null Hypothesis

The null hypothesis can be thought of as the opposite of the "guess" the researchers made: in this example, the biologist thinks the plant height will be different for the fertilizers. So the null would be that there will be no difference among the groups of plants. Specifically, in more statistical language the null for an ANOVA is that the means are the same. We state the null hypothesis as: \[H_{0}: \ \mu_{1} = \mu_{2} = \ldots = \mu_{T}\] for \(T\) levels of an experimental treatment.

Why do we do this? Why not simply test the working hypothesis directly? The answer lies in the Popperian Principle of Falsification. Karl Popper (a philosopher) discovered that we can't conclusively confirm a hypothesis, but we can conclusively negate one. So we set up a null hypothesis which is effectively the opposite of the working hypothesis. The hope is that based on the strength of the data, we will be able to negate or reject the null hypothesis and accept an alternative hypothesis. In other words, we usually see the working hypothesis in \(H_{A}\).

Step 2: State the Alternative Hypothesis

\[H_{A}: \ \text{treatment level means not all equal}\]

The reason we state the alternative hypothesis this way is that if the null is rejected, there are many possibilities.

For example, \(\mu_{1} \neq \mu_{2} = \ldots = \mu_{T}\) is one possibility, as is \(\mu_{1} = \mu_{2} \neq \mu_{3} = \ldots = \mu_{T}\). Many people make the mistake of stating the alternative hypothesis as \(mu_{1} \neq mu_{2} \neq \ldots \neq \mu_{T}\), which says that every mean differs from every other mean. This is a possibility, but only one of many possibilities. To cover all alternative outcomes, we resort to a verbal statement of "not all equal" and then follow up with mean comparisons to find out where differences among means exist. In our example, this means that fertilizer 1 may result in plants that are really tall, but fertilizers 2, 3, and the plants with no fertilizers don't differ from one another. A simpler way of thinking about this is that at least one mean is different from all others.

Step 3: Set \(\alpha\)

If we look at what can happen in a hypothesis test, we can construct the following contingency table:

You should be familiar with type I and type II errors from your introductory course. It is important to note that we want to set \(\alpha\) before the experiment ( a priori ) because the Type I error is the more grievous error to make. The typical value of \(\alpha\) is 0.05, establishing a 95% confidence level. For this course, we will assume \(\alpha\) =0.05, unless stated otherwise.

Step 4: Collect Data

Remember the importance of recognizing whether data is collected through an experimental design or observational study.

Step 5: Calculate a test statistic

For categorical treatment level means, we use an \(F\) statistic, named after R.A. Fisher. We will explore the mechanics of computing the \(F\) statistic beginning in Chapter 2. The \(F\) value we get from the data is labeled \(F_{\text{calculated}}\).

Step 6: Construct Acceptance / Rejection regions

As with all other test statistics, a threshold (critical) value of \(F\) is established. This \(F\) value can be obtained from statistical tables or software and is referred to as \(F_{\text{critical}}\) or \(F_{\alpha}\). As a reminder, this critical value is the minimum value for the test statistic (in this case the F test) for us to be able to reject the null.

The \(F\) distribution, \(F_{\alpha}\), and the location of acceptance and rejection regions are shown in the graph below:

Step 7: Based on steps 5 and 6, draw a conclusion about H0

If the \(F_{\text{\calculated}}\) from the data is larger than the \(F_{\alpha}\), then you are in the rejection region and you can reject the null hypothesis with \((1 - \alpha)\) level of confidence.

Note that modern statistical software condenses steps 6 and 7 by providing a \(p\)-value. The \(p\)-value here is the probability of getting an \(F_{\text{calculated}}\) even greater than what you observe assuming the null hypothesis is true. If by chance, the \(F_{\text{calculated}} = F_{\alpha}\), then the \(p\)-value would exactly equal \(\alpha\). With larger \(F_{\text{calculated}}\) values, we move further into the rejection region and the \(p\) - value becomes less than \(\alpha\). So the decision rule is as follows:

If the \(p\) - value obtained from the ANOVA is less than \(\alpha\), then reject \(H_{0}\) and accept \(H_{A}\).

If you are not familiar with this material, we suggest that you review course materials from your basic statistics course.

• Search Search Please fill out this field.

What Is Hypothesis Testing?

• How It Works

4 Step Process

The bottom line.

• Fundamental Analysis

Hypothesis Testing: 4 Steps and Example

Hypothesis testing, sometimes called significance testing, is an act in statistics whereby an analyst tests an assumption regarding a population parameter. The methodology employed by the analyst depends on the nature of the data used and the reason for the analysis.

Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data. Such data may come from a larger population or a data-generating process. The word "population" will be used for both of these cases in the following descriptions.

Key Takeaways

• Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data.
• The test provides evidence concerning the plausibility of the hypothesis, given the data.
• Statistical analysts test a hypothesis by measuring and examining a random sample of the population being analyzed.
• The four steps of hypothesis testing include stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.

How Hypothesis Testing Works

In hypothesis testing, an  analyst  tests a statistical sample, intending to provide evidence on the plausibility of the null hypothesis. Statistical analysts measure and examine a random sample of the population being analyzed. All analysts use a random population sample to test two different hypotheses: the null hypothesis and the alternative hypothesis.

The null hypothesis is usually a hypothesis of equality between population parameters; e.g., a null hypothesis may state that the population mean return is equal to zero. The alternative hypothesis is effectively the opposite of a null hypothesis. Thus, they are mutually exclusive , and only one can be true. However, one of the two hypotheses will always be true.

The null hypothesis is a statement about a population parameter, such as the population mean, that is assumed to be true.

• State the hypotheses.
• Formulate an analysis plan, which outlines how the data will be evaluated.
• Carry out the plan and analyze the sample data.
• Analyze the results and either reject the null hypothesis, or state that the null hypothesis is plausible, given the data.

Example of Hypothesis Testing

If an individual wants to test that a penny has exactly a 50% chance of landing on heads, the null hypothesis would be that 50% is correct, and the alternative hypothesis would be that 50% is not correct. Mathematically, the null hypothesis is represented as Ho: P = 0.5. The alternative hypothesis is shown as "Ha" and is identical to the null hypothesis, except with the equal sign struck-through, meaning that it does not equal 50%.

A random sample of 100 coin flips is taken, and the null hypothesis is tested. If it is found that the 100 coin flips were distributed as 40 heads and 60 tails, the analyst would assume that a penny does not have a 50% chance of landing on heads and would reject the null hypothesis and accept the alternative hypothesis.

If there were 48 heads and 52 tails, then it is plausible that the coin could be fair and still produce such a result. In cases such as this where the null hypothesis is "accepted," the analyst states that the difference between the expected results (50 heads and 50 tails) and the observed results (48 heads and 52 tails) is "explainable by chance alone."

When Did Hypothesis Testing Begin?

Some statisticians attribute the first hypothesis tests to satirical writer John Arbuthnot in 1710, who studied male and female births in England after observing that in nearly every year, male births exceeded female births by a slight proportion. Arbuthnot calculated that the probability of this happening by chance was small, and therefore it was due to “divine providence.”

What are the Benefits of Hypothesis Testing?

Hypothesis testing helps assess the accuracy of new ideas or theories by testing them against data. This allows researchers to determine whether the evidence supports their hypothesis, helping to avoid false claims and conclusions. Hypothesis testing also provides a framework for decision-making based on data rather than personal opinions or biases. By relying on statistical analysis, hypothesis testing helps to reduce the effects of chance and confounding variables, providing a robust framework for making informed conclusions.

What are the Limitations of Hypothesis Testing?

Hypothesis testing relies exclusively on data and doesn’t provide a comprehensive understanding of the subject being studied. Additionally, the accuracy of the results depends on the quality of the available data and the statistical methods used. Inaccurate data or inappropriate hypothesis formulation may lead to incorrect conclusions or failed tests. Hypothesis testing can also lead to errors, such as analysts either accepting or rejecting a null hypothesis when they shouldn’t have. These errors may result in false conclusions or missed opportunities to identify significant patterns or relationships in the data.

Hypothesis testing refers to a statistical process that helps researchers determine the reliability of a study. By using a well-formulated hypothesis and set of statistical tests, individuals or businesses can make inferences about the population that they are studying and draw conclusions based on the data presented. All hypothesis testing methods have the same four-step process, which includes stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.

Sage. " Introduction to Hypothesis Testing ," Page 4.

Elder Research. " Who Invented the Null Hypothesis? "

Formplus. " Hypothesis Testing: Definition, Uses, Limitations and Examples ."

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

Data Science Central

• Author Portal
• 3D Printing
• AI Data Stores
• AI Hardware
• AI Linguistics
• AI User Interfaces and Experience
• AI Visualization
• Cloud and Edge
• Cognitive Computing
• Containers and Virtualization
• Data Science
• Data Security
• Digital Factoring
• Drones and Robot AI
• Internet of Things
• Knowledge Engineering
• Machine Learning
• Quantum Computing
• Robotic Process Automation
• The Mathematics of AI
• Tools and Techniques
• Virtual Reality and Gaming
• Blockchain & Identity
• Business Agility
• Business Analytics
• Data Lifecycle Management
• Data Privacy
• Data Strategist
• Data Trends
• Digital Communications
• Digital Disruption
• Digital Professional
• Digital Twins
• Digital Workplace
• Marketing Tech
• Sustainability
• Agriculture and Food AI
• AI and Science
• AI in Government
• Autonomous Vehicles
• Education AI
• Energy Tech
• Financial Services AI
• Healthcare AI
• Logistics and Supply Chain AI
• Manufacturing AI
• Mobile and Telecom AI
• News and Entertainment AI
• Smart Cities
• Social Media and AI
• Functional Languages
• Other Languages
• Query Languages
• Web Languages
• Education Spotlight
• Newsletters
• O’Reilly Media

Importance of Hypothesis Testing in Quality Management

• January 27, 2017 at 1:00 pm

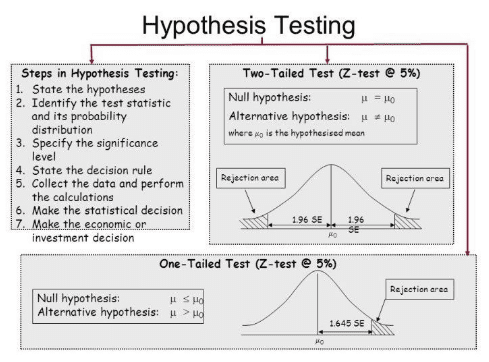
Essentially good hypotheses lead decision-makers like you to new and better ways to achieve your business goals. When you need to make decisions such as how much you should spend on advertising or what effect a price increase will have your customer base, it’s easy to make wild assumptions or get lost in analysis paralysis. A business hypothesis solves this problem, because, at the start, it’s based on some foundational information. In all of science, hypotheses are grounded in theory. Theory tells you what you can generally expect from a certain line of inquiry. A hypothesis based on years of business research in a particular area, then, helps you focus, define and appropriately direct your research. You won’t go on a wild goose chase to prove or disprove it. A hypothesis predicts the relationship between two variables. If you want to study pricing and customer loyalty, you won’t waste your time and resources studying tangential areas.

Data collection establishes the foundation for appraising quality of a product or service. But without correct data processing, it becomes challenging to make an objective conclusion. Sometimes, the observation is wrongly interpreted

Hypothesis testing is the process of using statistics to determine the probability that a specific hypothesis is true. it’s is an essential procedure in statistics. A hypothesis test evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data.

Hypothesis testing is categorized as parametric test and nonparametric test. The parametric test includes z-test, t-test, f-test. The nonparametric test includes sign test, Wilcoxon Rank-sum test, Kruskal-Wallis test and permutation test.

Application of Parametric Test:

This test is used for testing the population mean when the population standard deviation is known and the population under study is normal or non-normal for the large sample. But when the sample size is small, we apply the Z-test only when the population under study is normal. However if sample size is less than 30 then use t-test for testing the population mean when the population standard deviation (σ) is unknown and the population under study is normal

We first formulate the null hypothesis (H0) and alternative hypothesis (H1) and then calculate the value of the test statistics using the below formula:

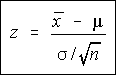
We obtain the critical(cut-off or tabulated) value(s) of the test statistics Z corresponding to the given level of significance(α)

Now take a decision about the null hypothesis as follows:

• Using the Critical region Approach — In this approach, compare the calculated value of the test statistics(z) with the critical value(s) obtained above
• Using p-value approach — Compare the calculated p-value with the given level of significance. if p-value is less than or equal to α, we reject the null hypothesis and if it is greater than α, we do not reject the null hypothesis.

So finally if null hypothesis is rejected, we conclude that the sample provides us sufficient evidence against the null hypothesis at α% level of significance.

Related Content

We are in the process of writing and adding new material (compact eBooks) exclusively available to our members, and written in simple English, by world leading experts in AI, data science, and machine learning.

Welcome to the newly launched Education Spotlight page! View Listings

• Data Science
• Data Analysis
• Data Visualization
• Machine Learning
• Deep Learning
• Computer Vision
• Artificial Intelligence
• AI ML DS Interview Series
• AI ML DS Projects series
• Data Engineering
• Web Scrapping
• Data Analysis with Python

Introduction to Data Analysis

• What is Data Analysis?
• Data Analytics and its type
• How to Install Numpy on Windows?
• How to Install Pandas in Python?
• How to Install Matplotlib on python?
• How to Install Python Tensorflow in Windows?

Data Analysis Libraries

• Pandas Tutorial
• NumPy Tutorial - Python Library
• Data Analysis with SciPy
• Introduction to TensorFlow

Data Visulization Libraries

• Matplotlib Tutorial
• Python Seaborn Tutorial
• Plotly tutorial
• Introduction to Bokeh in Python

Exploratory Data Analysis (EDA)

• Univariate, Bivariate and Multivariate data and its analysis
• Measures of Central Tendency in Statistics
• Measures of spread - Range, Variance, and Standard Deviation
• Interquartile Range and Quartile Deviation using NumPy and SciPy
• Anova Formula
• Skewness of Statistical Data
• How to Calculate Skewness and Kurtosis in Python?
• Difference Between Skewness and Kurtosis
• Histogram | Meaning, Example, Types and Steps to Draw
• Interpretations of Histogram
• Quantile Quantile plots
• What is Univariate, Bivariate & Multivariate Analysis in Data Visualisation?
• Using pandas crosstab to create a bar plot
• Exploring Correlation in Python
• Mathematics | Covariance and Correlation
• Factor Analysis | Data Analysis
• Data Mining - Cluster Analysis
• MANOVA Test in R Programming
• Python - Central Limit Theorem
• Probability Distribution Function
• Probability Density Estimation & Maximum Likelihood Estimation
• Exponential Distribution in R Programming - dexp(), pexp(), qexp(), and rexp() Functions
• Mathematics | Probability Distributions Set 4 (Binomial Distribution)
• Poisson Distribution - Definition, Formula, Table and Examples
• P-Value: Comprehensive Guide to Understand, Apply, and Interpret
• Z-Score in Statistics
• How to Calculate Point Estimates in R?
• Confidence Interval
• Chi-square test in Machine Learning

Understanding Hypothesis Testing

Data preprocessing.

• ML | Data Preprocessing in Python
• ML | Overview of Data Cleaning
• ML | Handling Missing Values
• Detect and Remove the Outliers using Python

Data Transformation

• Data Normalization Machine Learning
• Sampling distribution Using Python

Time Series Data Analysis

• Data Mining - Time-Series, Symbolic and Biological Sequences Data
• Basic DateTime Operations in Python
• Time Series Analysis & Visualization in Python
• How to deal with missing values in a Timeseries in Python?
• How to calculate MOVING AVERAGE in a Pandas DataFrame?
• What is a trend in time series?
• How to Perform an Augmented Dickey-Fuller Test in R
• AutoCorrelation

Case Studies and Projects

• Top 8 Free Dataset Sources to Use for Data Science Projects
• Step by Step Predictive Analysis - Machine Learning
• 6 Tips for Creating Effective Data Visualizations

Hypothesis testing involves formulating assumptions about population parameters based on sample statistics and rigorously evaluating these assumptions against empirical evidence. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.

What is Hypothesis Testing?

Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. 

Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.

Defining Hypotheses

Key Terms of Hypothesis Testing

• P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
• Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
• Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
• Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.

Why do we use Hypothesis Testing?

Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing. 

One-Tailed and Two-Tailed Test

One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.

One-Tailed Test

There are two types of one-tailed test:

Two-Tailed Test

A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.

What are Type 1 and Type 2 errors in Hypothesis Testing?

In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.

How does Hypothesis Testing work?

Step 1: define null and alternative hypothesis.

We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.

Step 2 – Choose significance level

Step 3 – Collect and Analyze data.

Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.

Step 4-Calculate Test Statistic

The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.

There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.

• Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
• t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
• Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
• F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.

We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.

T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

Step 5 – Comparing Test Statistic:

In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.

Method A: Using Crtical values

Comparing the test statistic and tabulated critical value we have,

• If Test Statistic>Critical Value: Reject the null hypothesis.
• If Test Statistic≤Critical Value: Fail to reject the null hypothesis.

Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Method B: Using P-values

We can also come to an conclusion using the p-value,

Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Step 7- Interpret the Results

At last, we can conclude our experiment using method A or B.

Calculating test statistic

To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .

1. Z-statistics:

When population means and standard deviations are known.

• μ represents the population mean, 
• σ is the standard deviation
• and n is the size of the sample.

2. T-Statistics

T test is used when n<30,

t-statistic calculation is given by:

• t = t-score,
• x̄ = sample mean
• μ = population mean,
• s = standard deviation of the sample,
• n = sample size

3. Chi-Square Test

Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

• i,j are the rows and columns index respectively.

Real life Hypothesis Testing example

Let’s examine hypothesis testing using two real life situations,

Case A: D oes a New Drug Affect Blood Pressure?

Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.

• Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
• After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114

Step 1 : Define the Hypothesis

• Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
• Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.

Step 2: Define the Significance level

Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.

If the evidence suggests less than a 5% chance of observing the results due to random variation.

Step 3 : Compute the test statistic

Using paired T-test analyze the data to obtain a test statistic and a p-value.

The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.

t = m/(s/√n)

• m  = mean of the difference i.e X after, X before
• s  = standard deviation of the difference (d) i.e d i ​= X after, i ​− X before,
• n  = sample size,

then, m= -3.9, s= 1.8 and n= 10

we, calculate the , T-statistic = -9 based on the formula for paired t test

Step 4: Find the p-value

The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.

thus, p-value = 8.538051223166285e-06

Step 5: Result

• If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
• If the p-value is greater than 0.05, they fail to reject the null hypothesis.

Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

Python Implementation of Hypothesis Testing

Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.

Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.

We will implement our first real life problem via python,

In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05. 

• The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
• The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.

Case B : Cholesterol level in a population

Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.

Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.

Populations Mean = 200

Population Standard Deviation (σ): 5 mg/dL(given for this problem)

Step 1: Define the Hypothesis

• Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
• Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.

As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.

Step 4: Result

Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL

Limitations of Hypothesis Testing

• Although a useful technique, hypothesis testing does not offer a comprehensive grasp of the topic being studied. Without fully reflecting the intricacy or whole context of the phenomena, it concentrates on certain hypotheses and statistical significance.
• The accuracy of hypothesis testing results is contingent on the quality of available data and the appropriateness of statistical methods used. Inaccurate data or poorly formulated hypotheses can lead to incorrect conclusions.
• Relying solely on hypothesis testing may cause analysts to overlook significant patterns or relationships in the data that are not captured by the specific hypotheses being tested. This limitation underscores the importance of complimenting hypothesis testing with other analytical approaches.

Hypothesis testing stands as a cornerstone in statistical analysis, enabling data scientists to navigate uncertainties and draw credible inferences from sample data. By systematically defining null and alternative hypotheses, choosing significance levels, and leveraging statistical tests, researchers can assess the validity of their assumptions. The article also elucidates the critical distinction between Type I and Type II errors, providing a comprehensive understanding of the nuanced decision-making process inherent in hypothesis testing. The real-life example of testing a new drug’s effect on blood pressure using a paired T-test showcases the practical application of these principles, underscoring the importance of statistical rigor in data-driven decision-making.

Frequently Asked Questions (FAQs)

1. what are the 3 types of hypothesis test.

There are three types of hypothesis tests: right-tailed, left-tailed, and two-tailed. Right-tailed tests assess if a parameter is greater, left-tailed if lesser. Two-tailed tests check for non-directional differences, greater or lesser.

2.What are the 4 components of hypothesis testing?

Null Hypothesis ( ): No effect or difference exists. Alternative Hypothesis ( ): An effect or difference exists. Significance Level ( ): Risk of rejecting null hypothesis when it’s true (Type I error). Test Statistic: Numerical value representing observed evidence against null hypothesis.

3.What is hypothesis testing in ML?

Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.

4.What is the difference between Pytest and hypothesis in Python?

Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.

Please Login to comment...

Similar reads.

• data-science

Improve your Coding Skills with Practice

What kind of Experience do you want to share?