name five strategies for problem solving in math and science

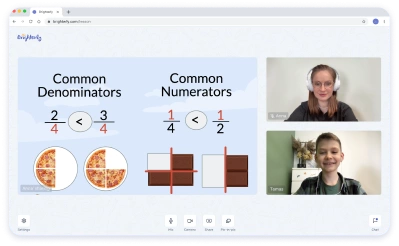
High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving 

Katie Keeton

Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.  

Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.

This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations. 

What are problem-solving strategies?

Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies: 

• Draw a model
• Use different approaches
• Check the inverse to make sure the answer is correct

Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better. 

Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques

Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.

20 Math Strategies For Problem-Solving

Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem. 

Here are 20 strategies to help students develop their problem-solving skills. 

Strategies to understand the problem

Strategies that help students understand the problem before solving it helps ensure they understand: 

• The context
• What the key information is
• How to form a plan to solve it

Following these steps leads students to the correct solution and makes the math word problem easier .

Here are five strategies to help students understand the content of the problem and identify key information. 

1. Read the problem aloud

Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.

2. Highlight keywords 

When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed.  For example, if the word problem asks how many are left, the problem likely requires subtraction.  Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.

3. Summarize the information

Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary.  Summaries should include only the important information and be in simple terms that help contextualize the problem.

4. Determine the unknown

A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer.  Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.

5. Make a plan

Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it.  The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer.  Encourage students to make a list of each step they need to take to solve the problem before getting started.

Strategies for solving the problem 

1. draw a model or diagram.

Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process.  It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out

This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives .  When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts.  The examples below show how 1st-grade students could “act out” an addition and subtraction problem:

3. Work backwards

Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution.  This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.

For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71.  Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.

4. Write a number sentence

When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved.  It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.

5. Use a formula

Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve.   Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.

Strategies for checking the solution 

Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense. 

There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.

Here are five strategies to help students check their solutions. 

1. Use the Inverse Operation

For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work. 

2. Estimate to check for reasonableness

Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable.  Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten.  For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10.  When the estimate is clear the two numbers are close. This means your answer is reasonable. 

3. Plug-In Method

This method is particularly useful for algebraic equations. Specifically when working with variables.  To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓

4. Peer Review

Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly.   Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills.  If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.

5. Use a Calculator

A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.  

Step-by-step problem-solving processes for your classroom

In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems. 

Polya’s 4 steps include:

• Understand the problem
• Devise a plan
• Carry out the plan

Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall. 

Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom. 

Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving 

Resources .

Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking. 

Explore the range of problem solving resources for 2nd to 8th grade students. 

One-on-one tutoring 

Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards. 

Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice. 

Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving

Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra. 

Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.

READ MORE : 8 Common Core math examples

There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model  • act it out  • work backwards  • write a number sentence • use a formula

Here are 10 strategies of problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model  • Act it out  • Work backwards  • Write a number sentence • Use a formula

1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back

Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.

Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers 

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• Knowledge Base
• Math for kids

10 Strategies for Problem Solving in Math

Created on May 19, 2022

Updated on January 6, 2024

When faced with problem-solving, children often get stuck. Word puzzles and math questions with an unknown variable, like x, usually confuse them. Therefore, this article discusses math strategies and how your students may use them since instructors often have to lead students through this problem-solving maze.

What Are Problem Solving Strategies in Math?

If you want to fix a problem, you need a solid plan. Math strategies for problem solving are ways of tackling math in a way that guarantees better outcomes. These strategies simplify math for kids so that less time is spent figuring out the problem. Both those new to mathematics and those more knowledgeable about the subject may benefit from these methods.

There are several methods to apply problem-solving procedures in math, and each strategy is different. While none of these methods failsafe, they may help your student become a better problem solver, particularly when paired with practice and examples. The more math problems kids tackle, the more math problem solving skills they acquire, and practice is the key.

Strategies for Problem-solving in Math

Even if a student is not a math wiz, a suitable solution to mathematical problems in math may help them discover answers. There is no one best method for helping students solve arithmetic problems, but the following ten approaches have shown to be very effective.

Understand the Problem

Understanding the nature of math problems is a prerequisite to solving them. They need to specify what kind of issue it is ( fraction problem , word problem, quadratic equation, etc.). Searching for keywords in the math problem, revisiting similar questions, or consulting the internet are all great ways to strengthen their grasp of the material. This step keeps the pupil on track.

1:1 Math Lessons

Want to raise a genius? Start learning Math with Brighterly

Guess and check.

One of the time-intensive strategies for resolving mathematical problems is the guess and check method. In this approach, students keep guessing until they get the answer right.

After assuming how to solve a math issue, students should reintroduce that assumption to check for correctness. While the approach may appear cumbersome, it is typically successful in revealing patterns in a child’s thought process.

Work It Out

Encourage pupils to record their thinking process as they go through a math problem. Since this technique requires an initial comprehension of the topic, it serves as a self-monitoring method for mathematics students. If they immediately start solving the problem, they risk making mistakes.

Students may keep track of their ideas and fix their math problems as they go along using this method. A youngster may still need you to explain their methods of solving the arithmetic questions on the extra page. This confirmation stage etches the steps they took to solve the problem in their minds.

Work Backwards

In mathematics, a fresh perspective is sometimes the key to a successful solution. Young people need to know that the ability to recreate math problems is valuable in many professional fields, including project management and engineering.

Students may better prepare for difficulties in real-world circumstances by using the “Work Backwards” technique. The end product may be used as a start-off point to identify the underlying issue.

In most cases, a visual representation of a math problem may help youngsters understand it better. Some of the most helpful math tactics for kids include having them play out the issue and picture how to solve it.

One way to visualize a workout is to use a blank piece of paper to draw a picture or make tally marks. Students might also use a marker and a whiteboard to draw as they demonstrate the technique before writing it down.

Find a Pattern

Kids who use pattern recognition techniques can better grasp math concepts and retain formulae. The most remarkable technique for problem solving in mathematics is to help students see patterns in math problems by instructing them how to extract and list relevant details. This method may be used by students when learning shapes and other topics that need repetition.

Students may use this strategy to spot patterns and fill in the blanks. Over time, this strategy will help kids answer math problems quickly.

When faced with a math word problem, it might be helpful to ask, “What are some possible solutions to this issue?” It encourages you to give the problem more thought, develop creative solutions, and prevent you from being stuck in a rut. So, tell the pupils to think about the math problems and not just go with the first solution that comes to mind.

Draw a Picture or Diagram

Drawing a picture of a math problem can help kids understand how to solve it, just like picturing it can help them see it. Shapes or numbers could be used to show the forms to keep things easy. Kids might learn how to use dots or letters to show the parts of a pattern or graph if you teach them.

Charts and graphs can be useful even when math isn’t involved. Kids can draw pictures of the ideas they read about to help them remember them after they’ve learned them. The plan for how to solve the mathematical problem will help kids understand what the problem is and how to solve it.

Trial and Error Method

The trial and error method may be one of the most common problem solving strategies for kids to figure out how to solve problems. But how well this strategy is used will determine how well it works. Students have a hard time figuring out math questions if they don’t have clear formulas or instructions.

They have a better chance of getting the correct answer, though, if they first make a list of possible answers based on rules they already know and then try each one. Don’t be too quick to tell kids they shouldn’t learn by making mistakes.

Review Answers with Peers

It’s fun to work on your math skills with friends by reviewing the answers to math questions together. If different students have different ideas about how to solve the same problem, get them to share their thoughts with the class.

During class time, kids’ ways of working might be compared. Then, students can make their points stronger by fixing these problems.

Check out the Printable Math Worksheets for Your Kids!

There are different ways to solve problems that can affect how fast and well students do on math tests. That’s why they need to learn the best ways to do things. If students follow the steps in this piece, they will have better experiences with solving math questions.

Jessica is a a seasoned math tutor with over a decade of experience in the field. With a BSc and Master’s degree in Mathematics, she enjoys nurturing math geniuses, regardless of their age, grade, and skills. Apart from tutoring, Jessica blogs at Brighterly. She also has experience in child psychology, homeschooling and curriculum consultation for schools and EdTech websites.

As adults, we take numbers for granted, but preschoolers and kindergartners have no idea what these symbols mean. Yet, we often demand instant understanding and flawless performance when we start teaching numbers to our children. If you don’t have a clue about how to teach numbers for kids, browse no more. You will get four […]

May 19, 2022

Teaching children is a complex process because they require more attention than an adult person. You may need to employ different teaching strategies when teaching kids. But what are teaching strategies? Teaching strategies are the methods to ensure your kids or students learn efficiently. But not all strategies yield similarly, and if the one you […]

Book 1 to 1 Math Lesson

Kid’s grade

Summer Math Program Boost Your Child's Math Abilities! Ideal for 1st-12th Graders, Perfectly Synced with School Curriculum!

Online Summer Math Camp

Related posts.

16 Math Magic Tricks for Kids to Calculate Numbers in a Split Second

Over 50% of Americans have math anxiety that often originates from insufficient school practice and a lack of math understanding. In fact, math is much simpler than you think. What if we say that you can add, subtract, multiply, and divide any number by solving simple 5 + 5 or 7 + 2? Check 16 […]

Feb 22, 2022

How to Manage Test Anxiety and Perform Better?

When students have an actual test to write, most of them are a bit nervous, but others develop an intense fear known as test anxiety. This fear could impact anyone even if a student is prepared well. Test anxiety affects performance due to the pressure it creates and one’s wish to perform better. The stress […]

Jun 10, 2022

Safe Learning Environment

The learning environment of students has an immense impact on their learning ability. Whether young or old, you will be affected by how they think if these learners are not in security because psychological influence is there. The following article entails strategies on how to create a safe environment for students in the classroom. What […]

Jun 03, 2022

We use cookies to help give you the best service possible. If you continue to use the website we will understand that you consent to the Terms and Conditions. These cookies are safe and secure. We will not share your history logs with third parties. Learn More

You are using an outdated browser. Please upgrade your browser to improve your experience.

Math Problem Solving Strategies That Make Students Say “I Get It!”

Even students who are quick with math facts can get stuck when it comes to problem solving.

As soon as a concept is translated to a word problem, or a simple mathematical sentence contains an unknown, they’re stumped.

That’s because problem solving requires us to  consciously choose the strategies most appropriate for the problem   at hand . And not all students have this metacognitive ability.

But you can teach these strategies for problem solving.  You just need to know what they are.

We’ve compiled them here divided into four categories:

Strategies for understanding a problem

Strategies for solving the problem, strategies for working out, strategies for checking the solution.

Get to know these strategies and then model them explicitly to your students. Next time they dive into a rich problem, they’ll be filling up their working out paper faster than ever!

Before students can solve a problem, they need to know what it’s asking them. This is often the first hurdle with word problems that don’t specify a particular mathematical operation.

Encourage your students to:

Read and reread the question

They say they’ve read it, but have they  really ? Sometimes students will skip ahead as soon as they’ve noticed one familiar piece of information or give up trying to understand it if the problem doesn’t make sense at first glance.

Teach students to interpret a question by using self-monitoring strategies such as:

• Rereading a question more slowly if it doesn’t make sense the first time
• Asking for help
• Highlighting or underlining important pieces of information.

Identify important and extraneous information

John is collecting money for his friend Ari’s birthday. He starts with $5 of his own, then Marcus gives him another $5. How much does he have now?

As adults looking at the above problem, we can instantly look past the names and the birthday scenario to see a simple addition problem. Students, however, can struggle to determine what’s relevant in the information that’s been given to them.

Teach students to sort and sift the information in a problem to find what’s relevant. A good way to do this is to have them swap out pieces of information to see if the solution changes. If changing names, items or scenarios has no impact on the end result, they’ll realize that it doesn’t need to be a point of focus while solving the problem.

Schema approach

This is a math intervention strategy that can make problem solving easier for all students, regardless of ability.

Compare different word problems of the same type and construct a formula, or mathematical sentence stem, that applies to them all. For example, a simple subtraction problems could be expressed as:

[Number/Quantity A] with [Number/Quantity B] removed becomes [end result].

This is the underlying procedure or  schema  students are being asked to use. Once they have a list of schema for different mathematical operations (addition, multiplication and so on), they can take turns to apply them to an unfamiliar word problem and see which one fits.

Struggling students often believe math is something you either do automatically or don’t do at all. But that’s not true. Help your students understand that they have a choice of problem-solving strategies to use, and if one doesn’t work, they can try another.

Here are four common strategies students can use for problem solving.

Visualizing

Visualizing an abstract problem often makes it easier to solve. Students could draw a picture or simply draw tally marks on a piece of working out paper.

Encourage visualization by modeling it on the whiteboard and providing graphic organizers that have space for students to draw before they write down the final number.

Guess and check

Show students how to make an educated guess and then plug this answer back into the original problem. If it doesn’t work, they can adjust their initial guess higher or lower accordingly.

Find a pattern

To find patterns, show students how to extract and list all the relevant facts in a problem so they can be easily compared. If they find a pattern, they’ll be able to locate the missing piece of information.

Work backward

Working backward is useful if students are tasked with finding an unknown number in a problem or mathematical sentence. For example, if the problem is 8 + x = 12, students can find x by:

• Starting with 12
• Taking the 8 from the 12
• Being left with 4
• Checking that 4 works when used instead of x

Now students have understood the problem and formulated a strategy, it’s time to put it into practice. But if they just launch in and do it, they might make it harder for themselves. Show them how to work through a problem effectively by:

Documenting working out

Model the process of writing down every step you take to complete a math problem and provide working out paper when students are solving a problem. This will allow students to keep track of their thoughts and pick up errors before they reach a final solution.

Check along the way

Checking work as you go is another crucial self-monitoring strategy for math learners. Model it to them with think aloud questions such as:

• Does that last step look right?
• Does this follow on from the step I took before?
• Have I done any ‘smaller’ sums within the bigger problem that need checking?

Students often make the mistake of thinking that speed is everything in math — so they’ll rush to get an answer down and move on without checking.

But checking is important too. It allows them to pinpoint areas of difficulty as they come up, and it enables them to tackle more complex problems that require multiple checks  before  arriving at a final answer.

Here are some checking strategies you can promote:

Check with a partner

Comparing answers with a peer leads is a more reflective process than just receiving a tick from the teacher. If students have two different answers, encourage them to talk about how they arrived at them and compare working out methods. They’ll figure out exactly where they went wrong, and what they got right.

Reread the problem with your solution

Most of the time, students will be able to tell whether or not their answer is correct by putting it back into the initial problem. If it doesn’t work or it just ‘looks wrong’, it’s time to go back and fix it up.

Fixing mistakes

Show students how to backtrack through their working out to find the exact point where they made a mistake. Emphasize that they can’t do this if they haven’t written down everything in the first place — so a single answer with no working out isn’t as impressive as they might think!

Need more help developing problem solving skills?

Read up on  how to set a problem solving and reasoning activity  or explore Mathseeds and Mathletics, our award winning online math programs. They’ve got over 900 teacher tested problem solving activities between them!

Get access to 900+ unique problem solving activities

You might like....

• Skip to main content
• Skip to primary sidebar
• Skip to footer

Additional menu

Khan Academy Blog

Unlocking the Power of Math Learning: Strategies and Tools for Success

posted on September 20, 2023

Mathematics, the foundation of all sciences and technology, plays a fundamental role in our everyday lives. Yet many students find the subject challenging, causing them to shy away from it altogether. This reluctance is often due to a lack of confidence, a misunderstanding of unclear concepts, a move ahead to more advanced skills before they are ready, and ineffective learning methods. However, with the right approach, math learning can be both rewarding and empowering. This post will explore different approaches to learning math, strategies for success, and cutting-edge tools to help you achieve your goals.

Math Learning

Math learning can take many forms, including traditional classroom instruction, online courses, and self-directed learning. A multifaceted approach to math learning can improve understanding, engage students, and promote subject mastery. A 2014 study by the National Council of Teachers of Mathematics found that the use of multiple representations, such as visual aids, graphs, and real-world examples, supports the development of mathematical connections, reasoning, and problem-solving skills.

Moreover, the importance of math learning goes beyond solving equations and formulas. Advanced math skills are essential for success in many fields, including science, engineering, finance, health care, and technology. In fact, a report by Burning Glass Technologies found that 71% of high-salary, entry-level positions require advanced math skills.

Benefits of Math Learning

In today’s 21st-century world, having a broad knowledge base and strong reading and math skills is essential. Mathematical literacy plays a crucial role in this success. It empowers individuals to comprehend the world around them and make well-informed decisions based on data-driven understanding. More than just earning good grades in math, mathematical literacy is a vital life skill that can open doors to economic opportunities, improve financial management, and foster critical thinking. We’re not the only ones who say so:

• Math learning enhances problem-solving skills, critical thinking, and logical reasoning abilities. (Source: National Council of Teachers of Mathematics )
• It improves analytical skills that can be applied in various real-life situations, such as budgeting or analyzing data. (Source: Southern New Hampshire University )
• Math learning promotes creativity and innovation by fostering a deep understanding of patterns and relationships. (Source: Purdue University )
• It provides a strong foundation for careers in fields such as engineering, finance, computer science, and more. These careers generally correlate to high wages. (Source: U.S. Bureau of Labor Statistics )
• Math skills are transferable and can be applied across different academic disciplines. (Source: Sydney School of Education and Social Work )

How to Know What Math You Need to Learn

Often students will find gaps in their math knowledge; this can occur at any age or skill level. As math learning is generally iterative, a solid foundation and understanding of the math skills that preceded current learning are key to success. The solution to these gaps is called mastery learning, the philosophy that underpins Khan Academy’s approach to education .

Mastery learning is an educational philosophy that emphasizes the importance of a student fully understanding a concept before moving on to the next one. Rather than rushing students through a curriculum, mastery learning asks educators to ensure that learners have “mastered” a topic or skill, showing a high level of proficiency and understanding, before progressing. This approach is rooted in the belief that all students can learn given the appropriate learning conditions and enough time, making it a markedly student-centered method. It promotes thoroughness over speed and encourages individualized learning paths, thus catering to the unique learning needs of each student.

Students will encounter mastery learning passively as they go through Khan Academy coursework, as our platform identifies gaps and systematically adjusts to support student learning outcomes. More details can be found in our Educators Hub . 

Try Our Free Confidence Boosters

How to learn math.

Learning at School

One of the most common methods of math instruction is classroom learning. In-class instruction provides students with real-time feedback, practical application, and a peer-learning environment. Teachers can personalize instruction by assessing students’ strengths and weaknesses, providing remediation when necessary, and offering advanced instruction to students who need it.

Learning at Home

Supplemental learning at home can complement traditional classroom instruction. For example, using online resources that provide additional practice opportunities, interactive games, and demonstrations, can help students consolidate learning outside of class. E-learning has become increasingly popular, with a wealth of online resources available to learners of all ages. The benefits of online learning include flexibility, customization, and the ability to work at one’s own pace. One excellent online learning platform is Khan Academy, which offers free video tutorials, interactive practice exercises, and a wealth of resources across a range of mathematical topics.

Moreover, parents can encourage and monitor progress, answer questions, and demonstrate practical applications of math in everyday life. For example, when at the grocery store, parents can ask their children to help calculate the price per ounce of two items to discover which one is the better deal. Cooking and baking with your children also provides a lot of opportunities to use math skills, like dividing a recipe in half or doubling the ingredients. 

Learning Math with the Help of Artificial Intelligence (AI) 

AI-powered tools are changing the way students learn math. Personalized feedback and adaptive practice help target individual needs. Virtual tutors offer real-time help with math concepts while AI algorithms identify areas for improvement. Custom math problems provide tailored practice, and natural language processing allows for instant question-and-answer sessions. 

Using Khan Academy’s AI Tutor, Khanmigo

Transform your child’s grasp of mathematics with Khanmigo , the 24/7 AI-powered tutor that specializes in tailored, one-on-one math instruction. Available at any time, Khanmigo provides personalized support that goes beyond mere answers to nurture genuine mathematical understanding and critical thinking. Khanmigo can track progress, identify strengths and weaknesses, and offer real-time feedback to help students stay on the right track. Within a secure and ethical AI framework, your child can tackle everything from basic arithmetic to complex calculus, all while you maintain oversight using robust parental controls.

Get Math Help with Khanmigo Right Now

You can learn anything .

Math learning is essential for success in the modern world, and with the right approach, it can also be enjoyable and rewarding. Learning math requires curiosity, diligence, and the ability to connect abstract concepts with real-world applications. Strategies for effective math learning include a multifaceted approach, including classroom instruction, online courses, homework, tutoring, and personalized AI support. 

So, don’t let math anxiety hold you back; take advantage of available resources and technology to enhance your knowledge base and enjoy the benefits of math learning.

National Council of Teachers of Mathematics, “Principles to Actions: Ensuring Mathematical Success for All” , April 2014

Project Lead The Way Research Report, “The Power of Transportable Skills: Assessing the Demand and Value of the Skills of the Future” , 2020

Page. M, “Why Develop Quantitative and Qualitative Data Analysis Skills?” , 2016

Mann. EL, Creativity: The Essence of Mathematics, Journal for the Education of the Gifted. Vol. 30, No. 2, 2006, pp. 236–260, http://www.prufrock.com ’

Nakakoji Y, Wilson R.” Interdisciplinary Learning in Mathematics and Science: Transfer of Learning for 21st Century Problem Solving at University ”. J Intell. 2020 Sep 1;8(3):32. doi: 10.3390/jintelligence8030032. PMID: 32882908; PMCID: PMC7555771.

Get Khanmigo

The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo. 

For learners     For teachers     For parents

Think back to the first problem in this chapter, the ABC Problem . What did you do to solve it? Even if you did not figure it out completely by yourself, you probably worked towards a solution and figured out some things that did not work.

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.

Pólya’s How to Solve It

George Pólya was a great champion in the field of teaching effective problem solving skills.  He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities).  He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985. [1]

 In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

• Understand the problem.
• Devise a plan.
• Carry out the plan.
• Looking back.

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

We have already seen one problem solving strategy, which we call “Wishful Thinking.” Do not be afraid to change the problem! Ask yourself “what if” questions:

• What if the picture was different?
• What if the numbers were simpler?
• What if I just made up some numbers?

You need to be sure to go back to the original problem at the end, but wishful thinking can be a powerful strategy for getting started.

This brings us to the most important problem solving strategy of all:

Problem Solving Strategy 2 (Try Something!). If you are really trying to solve a problem, the whole point is that you do not know what to do right out of the starting gate. You need to just try something! Put pencil to paper (or stylus to screen or chalk to board or whatever!) and try something. This is often an important step in understanding the problem; just mess around with it a bit to understand the situation and figure out what is going on.

And equally important: If what you tried first does not work, try something else! Play around with the problem until you have a feel for what is going on.

Problem 2 (Payback)

Last week, Alex borrowed money from several of his friends. He finally got paid at work, so he brought cash to school to pay back his debts. First he saw Brianna, and he gave her 1/4 of the money he had brought to school. Then Alex saw Chris and gave him 1/3 of what he had left after paying Brianna. Finally, Alex saw David and gave him 1/2 of what he had remaining. Who got the most money from Alex?

Think/Pair/Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What did you figure out about the problem?

This problem lends itself to two particular strategies. Did you try either of these as you worked on the problem? If not, read about the strategy and then try it out before watching the solution.

Problem Solving Strategy 3 (Draw a Picture). Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric, like this one, thinking visually can help! Can you represent something in the situation by a picture?

Draw a square to represent all of Alex’s money. Then shade 1/4 of the square — that’s what he gave away to Brianna. How can the picture help you finish the problem?

After you have worked on the problem yourself using this strategy (or if you are completely stuck), you can watch someone else’s solution.

Problem Solving Strategy 4 (Make Up Numbers). Part of what makes this problem difficult is that it is about money, but there are no numbers given. That means the numbers must not be important. So just make them up!

You can work forwards: Assume Alex had some specific amount of money when he showed up at school, say $100. Then figure out how much he gives to each person. Or you can work backwards: suppose he has some specific amount left at the end, like $10. Since he gave Chris half of what he had left, that means he had $20 before running into Chris. Now, work backwards and figure out how much each person got.

Watch the solution only after you tried this strategy for yourself.

If you use the “Make Up Numbers” strategy, it is really important to remember what the original problem was asking! You do not want to answer something like “Everyone got $10.” That is not true in the original problem; that is an artifact of the numbers you made up. So after you work everything out, be sure to re-read the problem and answer what was asked!

Problem 3 (Squares on a Chess Board)

How many squares, of any possible size, are on a 8 × 8 chess board? (The answer is not 64… It’s a lot bigger!)

Remember Pólya’s first step is to understand the problem. If you are not sure what is being asked, or why the answer is not just 64, be sure to ask someone!

Think / Pair / Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What did you figure out about the problem, even if you have not solved it completely?

It is clear that you want to draw a picture for this problem, but even with the picture it can be hard to know if you have found the correct answer. The numbers get big, and it can be hard to keep track of your work. Your goal at the end is to be absolutely positive that you found the right answer. You should never ask the teacher, “Is this right?” Instead, you should declare, “Here’s my answer, and here is why I know it is correct!”

Problem Solving Strategy 5 (Try a Simpler Problem). Pólya suggested this strategy: “If you can’t solve a problem, then there is an easier problem you can solve: find it.” He also said: “If you cannot solve the proposed problem, try to solve first some related problem. Could you imagine a more accessible related problem?” In this case, an 8 × 8 chess board is pretty big. Can you solve the problem for smaller boards? Like 1 × 1? 2 × 2? 3 × 3?

Of course the ultimate goal is to solve the original problem. But working with smaller boards might give you some insight and help you devise your plan (that is Pólya’s step (2)).

Problem Solving Strategy 6 (Work Systematically). If you are working on simpler problems, it is useful to keep track of what you have figured out and what changes as the problem gets more complicated.

For example, in this problem you might keep track of how many 1 × 1 squares are on each board, how many 2 × 2 squares on are each board, how many 3 × 3 squares are on each board, and so on. You could keep track of the information in a table:

Problem Solving Strategy 7 (Use Manipulatives to Help You Investigate). Sometimes even drawing a picture may not be enough to help you investigate a problem. Having actual materials that you move around can sometimes help a lot!

For example, in this problem it can be difficult to keep track of which squares you have already counted. You might want to cut out 1 × 1 squares, 2 × 2 squares, 3 × 3 squares, and so on. You can actually move the smaller squares across the chess board in a systematic way, making sure that you count everything once and do not count anything twice.

Problem Solving Strategy 8 (Look for and Explain Patterns). Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand! It would be much more appealing to find a pattern in the smaller boards and then extend that pattern to solve the problem for a 100 × 100 chess board just with a calculation.

If you have not done so already, extend the table above all the way to an 8 × 8 chess board, filling in all the rows and columns. Use your table to find the total number of squares in an 8 × 8 chess board. Then:

• Describe all of the patterns you see in the table.
• Can you explain and justify any of the patterns you see? How can you be sure they will continue?
• What calculation would you do to find the total number of squares on a 100 × 100 chess board?

(We will come back to this question soon. So if you are not sure right now how to explain and justify the patterns you found, that is OK.)

Problem 4 (Broken Clock)

This clock has been broken into three pieces. If you add the numbers in each piece, the sums are consecutive numbers. ( Consecutive numbers are whole numbers that appear one after the other, such as 1, 2, 3, 4 or 13, 14, 15.)

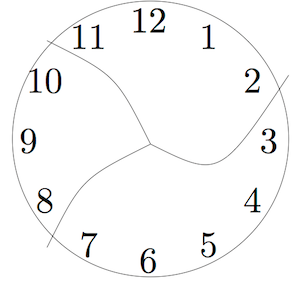
Can you break another clock into a different number of pieces so that the sums are consecutive numbers? Assume that each piece has at least two numbers and that no number is damaged (e.g. 12 isn’t split into two digits 1 and 2.)

Remember that your first step is to understand the problem. Work out what is going on here. What are the sums of the numbers on each piece? Are they consecutive?

After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What progress have you made?

Problem Solving Strategy 9 (Find the Math, Remove the Context). Sometimes the problem has a lot of details in it that are unimportant, or at least unimportant for getting started. The goal is to find the underlying math problem, then come back to the original question and see if you can solve it using the math.

In this case, worrying about the clock and exactly how the pieces break is less important than worrying about finding consecutive numbers that sum to the correct total. Ask yourself:

• What is the sum of all the numbers on the clock’s face?
• Can I find two consecutive numbers that give the correct sum? Or four consecutive numbers? Or some other amount?
• How do I know when I am done? When should I stop looking?

Of course, solving the question about consecutive numbers is not the same as solving the original problem. You have to go back and see if the clock can actually break apart so that each piece gives you one of those consecutive numbers. Maybe you can solve the math problem, but it does not translate into solving the clock problem.

Problem Solving Strategy 10 (Check Your Assumptions). When solving problems, it is easy to limit your thinking by adding extra assumptions that are not in the problem. Be sure you ask yourself: Am I constraining my thinking too much?

In the clock problem, because the first solution has the clock broken radially (all three pieces meet at the center, so it looks like slicing a pie), many people assume that is how the clock must break. But the problem does not require the clock to break radially. It might break into pieces like this:

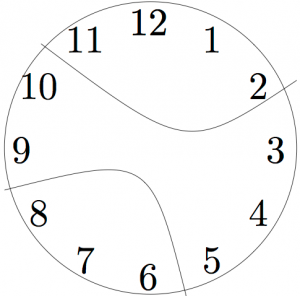
Were you assuming the clock would break in a specific way? Try to solve the problem now, if you have not already.

• Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY 2.0 (http://creativecommons.org/licenses/by/2.0)], via Wikimedia Commons ↵

Mathematics for Elementary Teachers Copyright © 2018 by Michelle Manes is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

5 Essential Problem Solving Techniques

• Critical Thinking

In the first post in this series, I talked about the difference between solving problems and problem solving. This week, I will continue my series on problem solving and share five essential problem solving techniques for your problem solving routines.

A strong problem-solving routine is essential for helping students develop their problem-solving strategy toolboxes. Over the years, I have used a variety of routines that have helped my students develop problem-solving strategies and critical thinking skills. (Read more about my favorite routine here !) Through a lot of trial and error, I found several routines that worked well for my students. (I will share more about them next week!) Today, I want to share some trade secrets with you to help you get the most from your problem-solving routines with five essential problem-solving techniques.

Five Essential Problem Solving Techniques

1. share student thinking and strategies..

This is essential! I can’t tell you how many times I have seen teachers give a great problem solving or critical thinking task and then never allow students to share their responses. Sometimes, our students are the best teachers and they can get a message across when we struggle to do so. Also, providing an opportunity for students to talk to other students about their thinking increases math vocabulary and builds communication skills.

After students have had an opportunity to share their thinking with a group member or partner, I encourage you to discuss the task as a class. This gives the teacher an opportunity to reiterate correct thinking, modify incorrect thinking, ask questions, build math vocabulary, and increase students’ communication skills.

Read more about getting started with math talk in the classroom here .

2. Solve non-routine problems.

In an earlier blog post, I emphasized the importance of using non-routine problems with students. Not only are students typically more engaged, but students have the opportunity to use strategies beyond writing an equation/number sentence or drawing a picture. If you’re interested in some fun, non-routine tasks, please check out my Solve It! Friday page.

One of the things many people say they love about math is the fact that there is a right and wrong answer. While there certainly are wrong answers, sometimes, there can be more than one right answer. These types of tasks really stretch some kids’ thinking. They also provide a natural venue for discussion. Students can debate the answers only to discover that more than one works!

3. Discuss efficiency.

During problem-solving experiences, students will often use beautiful and complicated solution strategies to solve problems. While we want to encourage outside-of-the-box thinking, we also want students to attend to efficiency. One way to do this is to have several students share their solutions. They can then discuss what strategies are best for specific types of problems. When discussing difficulty becomes a regular part of your routine, students will begin to utilize their problem-solving strategies in a way that not only gets them to the correct answer but also using an efficient method.

4. Make connections.

Recently, I wrote about making connections as part of my Summer PD series. Read it here ! When students make connects, it deepens their understanding of other content and skills. One way to do this is to connect the problem-solving task to grade-level content and skills. Another way is to have students represent problems in a variety of ways, i.e. pictures, numbers, words, or equations. Each representation is crafted in a specific way, so being able to translate words into an equation or numbers into a picture is a big skill that has many benefits.

5. Use “high ceiling, low floor tasks.”

The term “high ceiling, low floor” refers to a task having multiple entry points to allow all students a way to access the task; however, it also includes ways to extend the tasks for those students who are ready for more of a challenge. These types of tasks increase participation because students can participate at a level that is comfortable for them. Students are also able to showcase what they can do instead of what they are unable to do. Even better, these tasks provide instant opportunities for differentiation because all students can participate in a way that allows them to be most successful.

Using a regular problem-solving routine can help students develop the tools necessary to be powerful thinkers of mathematics; however, in order to get the most from the routines, certain problem-solving techniques must be included. While you may not want to add all of the above techniques to your routine, I encourage you to commit to adding one or two of them this year. I highly recommended starting with “sharing student thinking and strategies.” It’s probably the most important technique of all of the problem-solving routines. It will get you the most bang for your buck!

Sound Off! How do get the most from your problem-solving routine? Which problem-solving techniques do you think are most important?

Shametria Routt Banks

• Assessment Tools
• Content and Standards
• Differentiation
• Math & Literature
• Math & Technology
• Math Routines
• Math Stations
• Virtual Learning
• Writing in Math

You may also like...

3 Responses

Hi, can you provide an example of a high ceiling, low floor task? Thank you!

Hi Jen! Great question! The high ceiling, low floor tasks give all students a chance to engage in the task but have places to go to extend the learning for students. One problem that comes to mind is a task where students are asked to find combinations of numbers to achieve a goal, like the following problem: Farmer Brown’s niece Angie is in charge of her uncle’s farm while he is on vacation. He gave her strict instructions to make sure none of the animals ran away. When Angie counted the pigs and chickens, she counted 32 legs. How many pigs and chickens did she count? All students should be able to determine a combination of pigs and chickens; however, what if I added a new condition to say: Angie counted a total of 12 animals. This changes the level of rigor because students are now looking for a specific combination. Some students will struggle with this but others may be ready to tackle it; so, using tasks that have a high-ceiling allow for this flexibility. Check out more high ceiling, low floor tasks here: https://www.youcubed.org/task-grades/low-floor-high-ceiling/ .

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed .

©2024 The Routty Math Teacher.   All Rights Reserved.  Designed by Ashley Hughes.

Privacy overview.

How to Improve Problem-Solving Skills: Mathematics and Critical Thinking

In today’s rapidly changing world, problem-solving has become a quintessential skill. When we discuss the topic, it’s natural to ask, “What is problem-solving?” and “How can we enhance this skill, particularly in children?” The discipline of mathematics offers a rich platform to explore these questions. Through math, not only do we delve into numbers and equations, but we also explore how to improve problem-solving skills and how to develop critical thinking skills in math. Let’s embark on this enlightening journey together.

What is Problem-Solving?

At its core, problem-solving involves identifying a challenge and finding a solution. But it’s not always as straightforward as it sounds. So, what is problem-solving? True problem-solving requires a combination of creative thinking and logical reasoning. Mathematics, in many ways, embodies this blend. When a student approaches a math problem, they must discern the issue at hand, consider various methods to tackle it, and then systematically execute their chosen strategy.

But what is problem-solving in a broader context? It’s a life skill. Whether we’re deciding the best route to a destination, determining how to save for a big purchase, or even figuring out how to fix a broken appliance, we’re using problem-solving.

How to Develop Critical Thinking Skills in Math

Critical thinking goes hand in hand with problem-solving. But exactly how to develop critical thinking skills in math might not be immediately obvious. Here are a few strategies:

• Contextual Learning: Teaching math within a story or real-life scenario makes it relevant. When students see math as a tool to navigate the world around them, they naturally begin to think critically about solutions.
• Open-ended Questions: Instead of merely seeking the “right” answer, encourage students to explain their thought processes. This nudges them to think deeply about their approach.
• Group Discussions: Collaborative learning can foster different perspectives, prompting students to consider multiple ways to solve a problem.
• Challenging Problems: Occasionally introducing problems that are a bit beyond a student’s current skill level can stimulate critical thinking. They will have to stretch their understanding and think outside the box.

What are the Six Basic Steps of the Problem-Solving Process?

Understanding how to improve problem-solving skills often comes down to familiarizing oneself with the systematic approach to challenges. So, what are the six basic steps of the problem-solving process?

• Identification: Recognize and define the problem.
• Analysis: Understand the problem’s intricacies and nuances.
• Generation of Alternatives: Think of different ways to approach the challenge.
• Decision Making: Choose the most suitable method to address the problem.
• Implementation: Put the chosen solution into action.
• Evaluation: Reflect on the solution’s effectiveness and learn from the outcome.

By embedding these steps into mathematical education, we provide students with a structured framework. When they wonder about how to improve problem-solving skills or how to develop critical thinking skills in math, they can revert to this process, refining their approach with each new challenge.

Making Math Fun and Relevant

At Wonder Math, we believe that the key to developing robust problem-solving skills lies in making math enjoyable and pertinent. When students see math not just as numbers on a page but as a captivating story or a real-world problem to be solved, their engagement skyrockets. And with heightened engagement comes enhanced understanding.

As educators and parents, it’s crucial to continuously ask ourselves: how can we demonstrate to our children what problem-solving is? How can we best teach them how to develop critical thinking skills in math? And how can we instill in them an understanding of the six basic steps of the problem-solving process?

The answer, we believe, lies in active learning, contextual teaching, and a genuine passion for the beauty of mathematics.

The Underlying Beauty of Mathematics

Often, people perceive mathematics as a rigid discipline confined to numbers and formulas. However, this is a limited view. Math, in essence, is a language that describes patterns, relationships, and structures. It’s a medium through which we can communicate complex ideas, describe our universe, and solve intricate problems. Understanding this deeper beauty of math can further emphasize how to develop critical thinking skills in math.

Why Mathematics is the Ideal Playground for Problem-Solving

Math provides endless opportunities for problem-solving. From basic arithmetic puzzles to advanced calculus challenges, every math problem offers a chance to hone our problem-solving skills. But why is mathematics so effective in this regard?

• Structured Challenges: Mathematics presents problems in a structured manner, allowing learners to systematically break them down. This format mimics real-world scenarios where understanding the structure of a challenge can be half the battle.
• Multiple Approaches: Most math problems can be approached in various ways . This teaches learners flexibility in thinking and the ability to view a single issue from multiple angles.
• Immediate Feedback: Unlike many real-world problems where solutions might take time to show results, in math, students often get immediate feedback. They can quickly gauge if their approach works or if they need to rethink their strategy.

Enhancing the Learning Environment

To genuinely harness the power of mathematics in developing problem-solving skills, the learning environment plays a crucial role. A student who is afraid of making mistakes will hesitate to try out different approaches, stunting their critical thinking growth.

However, in a nurturing, supportive environment where mistakes are seen as learning opportunities, students thrive. They become more willing to take risks, try unconventional solutions, and learn from missteps. This mindset, where failure is not feared but embraced as a part of the learning journey, is pivotal for developing robust problem-solving skills.

Incorporating Technology

In our digital age, technology offers innovative ways to explore math. Interactive apps and online platforms can provide dynamic problem-solving scenarios, making the process even more engaging. These tools can simulate real-world challenges, allowing students to apply their math skills in diverse contexts, further answering the question of how to improve problem-solving skills.

More than Numbers 

In summary, mathematics is more than just numbers and formulas—it’s a world filled with challenges, patterns, and beauty. By understanding its depth and leveraging its structured nature, we can provide learners with the perfect platform to develop critical thinking and problem-solving skills. The key lies in blending traditional techniques with modern tools, creating a holistic learning environment that fosters growth, curiosity, and a lifelong love for learning.

Join us on this transformative journey at Wonder Math. Let’s make math an adventure, teaching our children not just numbers and equations, but also how to improve problem-solving skills and navigate the world with confidence. Enroll your child today and witness the magic of mathematics unfold before your eyes!

FAQ: Mathematics and Critical Thinking

1. what is problem-solving in the context of mathematics.

Problem-solving in mathematics refers to the process of identifying a mathematical challenge and systematically working through methods and strategies to find a solution.

2. Why is math considered a good avenue for developing problem-solving skills?

Mathematics provides structured challenges and allows for multiple approaches to find solutions. This promotes flexibility in thinking and encourages learners to view problems from various angles.

3. How does contextual learning enhance problem-solving abilities?

By teaching math within a story or real-life scenario, it becomes more relevant for the learner. This helps them see math as a tool to navigate real-world challenges , thereby promoting critical thinking.

4. What are the six basic steps of the problem-solving process in math?

The six steps are: Identification, Analysis, Generation of Alternatives, Decision Making, Implementation, and Evaluation.

5. How can parents support their children in developing mathematical problem-solving skills?

Parents can provide real-life contexts for math problems , encourage open discussions about different methods, and ensure a supportive environment where mistakes are seen as learning opportunities.

6. Are there any tools or apps that can help in enhancing problem-solving skills in math?

Yes, there are various interactive apps and online platforms designed specifically for math learning. These tools provide dynamic problem-solving scenarios and simulate real-world challenges, making the learning process engaging.

7. How does group discussion foster critical thinking in math?

Group discussions allow students to hear different perspectives and approaches to a problem. This can challenge their own understanding and push them to think about alternative methods.

8. Is it necessary to always follow the six steps of the problem-solving process sequentially?

While the six steps provide a structured approach, real-life problem-solving can sometimes be more fluid. It’s beneficial to know the steps, but adaptability and responsiveness to the situation are also crucial.

9. How does Wonder Math incorporate active learning in teaching mathematics?

Wonder Math integrates mathematics within engaging stories and real-world scenarios, making it fun and relevant. This active learning approach ensures that students are not just passive recipients but active participants in the learning process.

10. What if my child finds a math problem too challenging and becomes demotivated?

It’s essential to create a supportive environment where challenges are seen as growth opportunities. Remind them that every problem is a chance to learn, and it’s okay to seek help or approach it differently.

Related posts

Summer Math Programs: How They Can Prevent Learning Loss in Young Students

As summer approaches, parents and educators alike turn their attention to how they can support young learners during the break. Summer is a time for relaxation, fun, and travel, yet it’s also a critical period when learning loss can occur. This phenomenon, often referred to as the “summer slide,” impacts students’ progress, especially in foundational subjects like mathematics. It’s reported…

Math Programs 101: What Every Parent Should Know When Looking For A Math Program

  As a parent, you know that a solid foundation in mathematics is crucial for your child’s success, both in school and in life. But with so many math programs and math help services out there, how do you choose the right one? Whether you’re considering Outschool classes, searching for “math tutoring near me,” or exploring tutoring services online, understanding…

• Our Mission

6 Tips for Teaching Math Problem-Solving Skills

Solving word problems is tougher than computing with numbers, but elementary teachers can guide students to do the deep thinking involved.

A growing concern with students is the ability to problem-solve, especially with complex, multistep problems. Data shows that students struggle more when solving word problems than they do with computation , and so problem-solving should be considered separately from computation. Why?

Consider this. When we’re on the way to a new destination and we plug in our location to a map on our phone, it tells us what lane to be in and takes us around any detours or collisions, sometimes even buzzing our watch to remind us to turn. When I experience this as a driver, I don’t have to do the thinking. I can think about what I’m going to cook for dinner, not paying much attention to my surroundings other than to follow those directions. If I were to be asked to go there again, I wouldn’t be able to remember, and I would again seek help.

If we can switch to giving students strategies that require them to think instead of giving them too much support throughout the journey to the answer, we may be able to give them the ability to learn the skills to read a map and have several ways to get there.

Here are six ways we can start letting students do this thinking so that they can go through rigorous problem-solving again and again, paving their own way to the solution. 

1. Link problem-solving to reading

When we can remind students that they already have many comprehension skills and strategies they can easily use in math problem-solving, it can ease the anxiety surrounding the math problem. For example, providing them with strategies to practice, such as visualizing, acting out the problem with math tools like counters or base 10 blocks, drawing a quick sketch of the problem, retelling the story in their own words, etc., can really help them to utilize the skills they already have to make the task less daunting.

We can break these skills into specific short lessons so students have a bank of strategies to try on their own. Here's an example of an anchor chart that they can use for visualizing . Breaking up comprehension into specific skills can increase student independence and help teachers to be much more targeted in their problem-solving instruction. This allows students to build confidence and break down the barriers between reading and math to see they already have so many strengths that are transferable to all problems.

2. Avoid boxing students into choosing a specific operation

It can be so tempting to tell students to look for certain words that might mean a certain operation. This might even be thoroughly successful in kindergarten and first grade, but just like when our map tells us where to go, that limits students from becoming deep thinkers. It also expires once they get into the upper grades, where those words could be in a problem multiple times, creating more confusion when students are trying to follow a rule that may not exist in every problem.

We can encourage a variety of ways to solve problems instead of choosing the operation first. In first grade, a problem might say, “Joceline has 13 stuffed animals and Jordan has 17. How many more does Jordan have?” Some students might choose to subtract, but a lot of students might just count to find the amount in between. If we tell them that “how many more” means to subtract, we’re taking the thinking out of the problem altogether, allowing them to go on autopilot without truly solving the problem or using their comprehension skills to visualize it. 

3. Revisit ‘representation’

The word “representation” can be misleading. It seems like something to do after the process of solving. When students think they have to go straight to solving, they may not realize that they need a step in between to be able to support their understanding of what’s actually happening in the problem first.

Using an anchor chart like one of these ( lower grade , upper grade ) can help students to choose a representation that most closely matches what they’re visualizing in their mind. Once they sketch it out, it can give them a clearer picture of different ways they could solve the problem.

Think about this problem: “Varush went on a trip with his family to his grandmother’s house. It was 710 miles away. On the way there, three people took turns driving. His mom drove 214 miles. His dad drove 358 miles. His older sister drove the rest. How many miles did his sister drive?”

If we were to show this student the anchor chart, they would probably choose a number line or a strip diagram to help them understand what’s happening.

If we tell students they must always draw base 10 blocks in a place value chart, that doesn’t necessarily match the concept of this problem. When we ask students to match our way of thinking, we rob them of critical thinking practice and sometimes confuse them in the process. 

4. Give time to process

Sometimes as educators, we can feel rushed to get to everyone and everything that’s required. When solving a complex problem, students need time to just sit with a problem and wrestle with it, maybe even leaving it and coming back to it after a period of time.

This might mean we need to give them fewer problems but go deeper with those problems we give them. We can also speed up processing time when we allow for collaboration and talk time with peers on problem-solving tasks. 

5. Ask questions that let Students do the thinking

Questions or prompts during problem-solving should be very open-ended to promote thinking. Telling a student to reread the problem or to think about what tools or resources would help them solve it is a way to get them to try something new but not take over their thinking.

These skills are also transferable across content, and students will be reminded, “Good readers and mathematicians reread.” 

6. Spiral concepts so students frequently use problem-solving skills

When students don’t have to switch gears in between concepts, they’re not truly using deep problem-solving skills. They already kind of know what operation it might be or that it’s something they have at the forefront of their mind from recent learning. Being intentional within their learning stations and assessments about having a variety of rigorous problem-solving skills will refine their critical thinking abilities while building more and more resilience throughout the school year as they retain content learning in the process. 

Problem-solving skills are so abstract, and it can be tough to pinpoint exactly what students need. Sometimes we have to go slow to go fast. Slowing down and helping students have tools when they get stuck and enabling them to be critical thinkers will prepare them for life and allow them multiple ways to get to their own destination.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

CHAPTER 5 Solving First Degree Equations in One Variable

5.7 Use a Problem-Solving Strategy

Learning Objectives

By the end of this section, you will be able to:

• Approach word problems with a positive attitude
• Use a problem-solving strategy for word problems
• Solve number problems

Approach Word Problems with a Positive Attitude

“If you think you can… or think you can’t… you’re right.”—Henry Ford

The world is full of word problems! Will my income qualify me to rent that apartment? How much punch do I need to make for the party? What size diamond can I afford to buy my girlfriend? Should I fly or drive to my family reunion?

How much money do I need to fill the car with gas? How much tip should I leave at a restaurant? How many socks should I pack for vacation? What size turkey do I need to buy for Thanksgiving dinner, and then what time do I need to put it in the oven? If my sister and I buy our mother a present, how much does each of us pay?

Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student below?

When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.

Start with a fresh slate and begin to think positive thoughts. If we take control and believe we can be successful, we will be able to master word problems! Read the positive thoughts in (Figure 2) and say them out loud.

Think of something, outside of school, that you can do now but couldn’t do 3 years ago. Is it driving a car? Snowboarding? Cooking a gourmet meal? Speaking a new language? Your past experiences with word problems happened when you were younger—now you’re older and ready to succeed!

Use a Problem-Solving Strategy for Word Problems

We have reviewed translating English phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. We have also translated English sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. We restated the situation in one sentence, assigned a variable, and then wrote an equation to solve the problem. This method works as long as the situation is familiar and the math is not too complicated.

Now, we’ll expand our strategy so we can use it to successfully solve any word problem. We’ll list the strategy here, and then we’ll use it to solve some problems. We summarize below an effective strategy for problem solving.

Use a Problem-Solving Strategy to Solve Word Problems.

• Read the problem. Make sure all the words and ideas are understood.
• Identify what we are looking for.
• Name what we are looking for. Choose a variable to represent that quantity.
• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
• Solve the equation using good algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

Pilar bought a purse on sale for $18, which is one-half of the original price. What was the original price of the purse?

Step 1. Read the problem. Read the problem two or more times if necessary. Look up any unfamiliar words in a dictionary or on the internet.

• In this problem, is it clear what is being discussed? Is every word familiar?

Step 2. Identify what you are looking for. Did you ever go into your bedroom to get something and then forget what you were looking for? It’s hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!

• In this problem, the words “what was the original price of the purse” tell us what we need to find.

Step 3. Name what we are looking for. Choose a variable to represent that quantity. We can use any letter for the variable, but choose one that makes it easy to remember what it represents.

Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Translate the English sentence into an algebraic equation.

Reread the problem carefully to see how the given information is related. Often, there is one sentence that gives this information, or it may help to write one sentence with all the important information. Look for clue words to help translate the sentence into algebra. Translate the sentence into an equation.

Step 5. Solve the equation using good algebraic techniques. Even if you know the solution right away, using good algebraic techniques here will better prepare you to solve problems that do not have obvious answers.

• Does $36 make sense in the problem? Yes, because 18 is one-half of 36, and the purse was on sale at half the original price.

Step 7. Answer the question with a complete sentence. The problem asked “What was the original price of the purse?”

• The answer to the question is: “The original price of the purse was $36.”

If this were a homework exercise, our work might look like this:

Pilar bought a purse on sale for $18, which is one-half the original price. What was the original price of the purse?

Joaquin bought a bookcase on sale for $120, which was two-thirds of the original price. What was the original price of the bookcase?

Two-fifths of the songs in Mariel’s playlist are country. If there are 16 country songs, what is the total number of songs in the playlist?

Let’s try this approach with another example.

Ginny and her classmates formed a study group. The number of girls in the study group was three more than twice the number of boys. There were 11 girls in the study group. How many boys were in the study group?

Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was 3 more than twice the number of notebooks. He bought 7 textbooks. How many notebooks did he buy?

Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is eight more than twice the number of crossword puzzles. He completed 22 Sudoku puzzles. How many crossword puzzles did he do?

Solve Number Problems

Now that we have a problem solving strategy, we will use it on several different types of word problems. The first type we will work on is “number problems.” Number problems give some clues about one or more numbers. We use these clues to write an equation. Number problems don’t usually arise on an everyday basis, but they provide a good introduction to practicing the problem solving strategy outlined above.

The difference of a number and six is 13. Find the number.

The difference of a number and eight is 17. Find the number.

The sum of twice a number and seven is 15. Find the number.

Did you notice that we left out some of the steps as we solved this equation? If you’re not yet ready to leave out these steps, write down as many as you need.

The sum of four times a number and two is 14. Find the number.

The sum of three times a number and seven is 25. Find the number.

Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.

One number is five more than another. The sum of the numbers is 21. Find the numbers.

One number is six more than another. The sum of the numbers is twenty-four. Find the numbers.

The sum of two numbers is fifty-eight. One number is four more than the other. Find the numbers.

The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.

The sum of two numbers is negative twenty-three. One number is seven less than the other. Find the numbers.

One number is ten more than twice another. Their sum is one. Find the numbers.

One number is eight more than twice another. Their sum is negative four. Find the numbers.

Some number problems involve consecutive integers. Consecutive integers are integers that immediately follow each other.

 Examples of consecutive integers are:

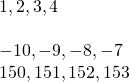
The sum of two consecutive integers is 47. Find the numbers.

Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers. Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:

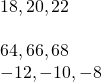
Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers 77, 79, and 81

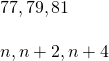
Does it seem strange to add 2 (an even number) to get from one odd integer to the next? Do you get an odd number or an even number when we add 2 to 3? to 11? to 47?

Whether the problem asks for consecutive even numbers or odd numbers, you don’t have to do anything different. The pattern is still the same—to get from one odd or one even integer to the next, add 2

Find three consecutive even integers whose sum is 84

TRY IT 10.1

Find three consecutive even integers whose sum is 102

TRY IT 10.2

A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?

TRY IT 11.1

According to the National Automobile Dealers Association, the average cost of a car in 2014 was 28,500. This was 1,500 less than 6 times the cost in 1975. What was the average cost of a car in 1975?

TRY IT 11.2

The Canadian Real Estate Association (CREA) data shows that the median price of new home in the Canada in December 2018 was $470,000. This was $14,000 more than 19 times the price in December 1967. What was the median price of a new home in December 1967?

$24,000

Key Concepts

• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.

Consecutive even integers are even integers that immediately follow one another.

Consecutive odd integers are odd integers that immediately follow one another.

Practice Makes Perfect

Use the approach word problems with a positive attitude.

In the following exercises, prepare the lists described.

In the following exercises, solve using the problem solving strategy for word problems. Remember to write a complete sentence to answer each question.

In the following exercises, solve each number word problem.

Everyday Math

Writing exercises, attributions.

This chapter has been adapted from “Use a Problem-Solving Strategy” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence . Adapted by Izabela Mazur. See the Copyright page for more information.

Introductory Algebra Copyright © 2021 by Izabela Mazur is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Problem-Solving Strategies

There are many different ways to solve a math problem, and equipping students with problem-solving strategies is just as important as teaching computation and algorithms. Problem-solving strategies help students visualize the problem or present the given information in a way that can lead them to the solution. Solving word problems using strategies works great as a number talks activity and helps to revise many skills.

Problem-solving strategies

1. create a diagram/picture, 2. guess and check., 3. make a table or a list., 4. logical reasoning., 5. find a pattern, 6. work backward, 1. create a diagram/draw a picture.

Creating a diagram helps students visualize the problem and reach the solution. A diagram can be a picture with labels, or a representation of the problem with objects that can be manipulated. Role-playing and acting out the problem like a story can help get to the solution.

Alice spent 3/4 of her babysitting money on comic books. She is left with $6. How much money did she make from babysitting?

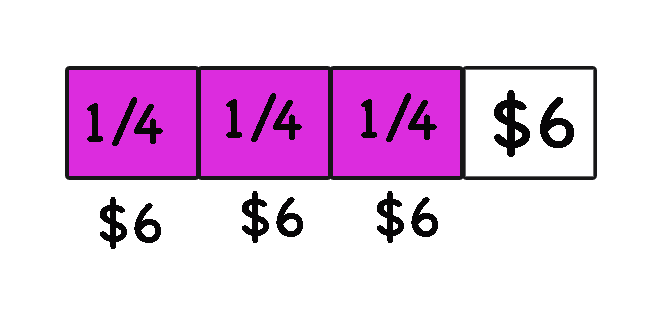
2. Guess and check

Teach students the same strategy research mathematicians use.

With this strategy, students solve problems by making a reasonable guess depending on the information given. Then they check to see if the answer is correct and they improve it accordingly.  By repeating this process, a student can arrive at a correct answer that has been checked. It is recommended that the students keep a record of their guesses by making a chart, a table or a list. This is a flexible strategy that works for many types of problems. When students are stuck, guessing and checking helps them start and explore the problem. However, there is a trap. Exactly because it is such a simple strategy to use, some students find it difficult to consider other strategies. As problems get more complicated, other strategies become more important and more effective.

Find two numbers that have sum 11 and product 24.

Try/guess  5 and 6  the product is 30 too high

  adjust  to 4 and 7 with product 28 still high

  adjust  again 3 and 8 product 24

3. Make a table or a list

Carefully organize the information on a table or list according to the problem information. It might be a table of numbers, a table with ticks and crosses to solve a logic problem or a list of possible answers. Seeing the given information sorted out on a table or a list will help find patterns and lead to the correct solution.

To make sure you are listing all the information correctly read the problem carefully.

Find the common factors of 24, 30 and 18

Logical reasoning is the process of using logical, systemic steps to arrive at a conclusion based on given facts and mathematic principles. Read and understand the problem. Then find the information that helps you start solving the problem. Continue with each piece of information and write possible answers.

Thomas, Helen, Bill, and Mary have cats that are black, brown, white, or gray. The cats’ names are Buddy, Lucky, Fifi, and Moo. Buddy is brown. Thoma’s cat, Lucky, is not gray. Helen’s cat is white but is not named Moo. The gray cat belongs to Bill. Which cat belongs to each student, and what is its color?

A table or list is useful in solving logic problems.

Since Lucky is not gray it can be black or brown. However, Buddy is brown so Lucky has to be black.

Buddy is brown so it cannot be Helen’s cat. Helen’s cat cannot be Moo, Buddy or Lucky, so it is Fifi.

Therefore, Moo is Bill’s cat and Buddy is Mary’s cat.

5. Find a pattern.

Finding a pattern is a strategy in which students look for patterns in the given information in order to solve the problem. When the problem consists of data like numbers or events that are repeated then it can be solved using the “find a pattern” problem-solving strategy. Data can be organized in a table or a list to reveal the pattern and help discover the “rule” of the pattern.

 The “rule” can then be used to find the answer to the question and complete the table/list.

Shannon’s Pizzeria made 5 pizzas on Sunday, 10 pizzas on Monday, 20 pizzas on Tuesday, and 40 pizzas on Wednesday. If this pattern continues, how many pizzas will the pizzeria make on Saturday?

6. Working backward

Problems that can be solved with this strategy are the ones that  list a series of events or a sequence of steps .

In this strategy, the students must start with the solution and work back to the beginning. Each operation must be reversed to get back to the beginning. So if working forwards requires addition, when students work backward they will need to subtract. And if they multiply working forwards, they must divide when working backward.

Mom bought a box of candy. Mary took 5 of them, Nick took 4 of them and 31 were given out on Halloween night. The next morning they found 8 pieces of candy in the box. How many candy pieces were in the box when mom bought it.

For this problem, we know that the final number of candy was 8, so if we work backward to “put back” the candy that was taken from the box we can reach the number of candy pieces that were in the box, to begin with.

The candy was taken away so we will normally subtract them. However, to get back to the original number of candy we need to work backward and do the opposite, which is to add them.

8 candy pieces were left + the 31 given out + plus the ones Mary took + the ones Nick took

8+31+5+4= 48   Answer: The box came with 48 pieces of candy.

Selecting the best strategy for a problem comes with practice and often problems will require the use of more than one strategies.

Print and digital activities

I have created a collection of print and digital activity cards and worksheets with word problems (print and google slides) to solve using the strategies above. The collection includes 70 problems (5 challenge ones) and their solution s and explanations.

sample below

How to use the activity cards

Allow the students to use manipulatives to solve the problems. (counters, shapes, lego blocks, Cuisenaire blocks, base 10 blocks, clocks) They can use manipulatives to create a picture and visualize the problem. They can use counters for the guess and check strategy. Discuss which strategy/strategies are better for solving each problem. Discuss the different ways. Use the activities as warm-ups, number talks, initiate discussions, group work, challenge, escape rooms, and more.

Ask your students to write their own problems using the problems in this resource, and more, as examples. Start with a simple type. Students learn a lot when trying to compose a problem. They can share the problem with their partner or the whole class. Make a collection of problems to share with another class.

For the google slides the students can use text boxes to explain their thinking with words, add shapes and lines to create diagrams, and add (insert) tables and diagrams.

Many of the problems can be solved faster by using algebraic expressions. However, since I created this resource for grades 4 and up I chose to show simple conceptual ways of solving the problems using the strategies above. You can suggest different ways of solving the problems based on the grade level.

Find the free and premium versions of the resource below. The premium version includes 70 problems (challenge problems included) and their solutions

There are 2 versions of the resource

70 google slides with explanations + 70 printable task cards

70 google slides with explanations + 11 worksheets

5 Tips for Maths Problem Solving

Mathematics is one subject that you cannot avoid. Some love it and some loathe it. The truth is, the importance of mathematics cannot be any greater in this tech-savvy world we live in. Mathematics forms the basis of future technological advancement. 

The problem that many students have is that they do not know how to approach maths problem solving to get good results. No matter how much time you spend studying for your math paper, if you cannot solve the problem on the day of the test, you are lost. Thankfully, five math problem-solving techniques can make your work way easier.

Image 1;  https://unsplash.com/photos/aG-pvyMsbis  

1. Create time and a peaceful environment to study

Maths is a complex subject that requires your utmost concentration. Avoid the temptation to multi-task or studying in a distracting environment. 

Some common distractions may include housework, assignments, television, food, your phone, etc. Where you have lots of assignments such as essay writing right before a math test, you can  hire personal statement writer . The expert writers have great skills and they help you to prepare your essays as you set time apart to study for your maths test. 

You can also create a peaceful ambiance for studying by finding a quiet space to study or applying other techniques that resonate with you. Some studies show that listening to slow and soothing music while studying can improve your concentration. Try adding such music to your playlist and find a distraction-free space to study.

2. Practice, practice and more practice!

There are many ways to learn maths skills. You can learn math problem-solving skills in school, with the help of a tutor or use apps to improve maths skills. However, without practice, it is impossible to learn how to tackle a maths problem. 

Practice makes perfect and helps you to do maths tasks accurately. Use your spare time to practice simple math problems and exercises. Your maths problem-solving skills will develop in time.

The more you practice answering maths problems, the more confidence you build. Most students cannot do maths accurately because of a lack of confidence.

3. Review your work and identify errors

If you get a wrong answer while practicing, do not give up. Review your workings and identify where you've made errors. Understanding where you went wrong will help you sharpen your skills and avoid similar mistakes. Apply different solutions until you find the right answer. 

Where further clarification is needed, don't be shy to consult with your peers and teachers. Consulting opens up opportunities for learning new concepts and ideas to approach a similar problem. You will get to explore many techniques for solving the maths problem until you arrive at the right one. 

4. Understand the logic behind key concepts

Learning maths skills is a sequential process. Learn one basic concept then move to a more complex concept with time. If you understand how a formula came about, you will be in a better position to apply it while solving maths problems.

It is futile to memorize the processes and formulae. It is better to understand the logic behind the process. This will help you understand how to approach similar problems.

Image 2:  https://unsplash.com/photos/05A-kdOH6Hw  

5. Apportion adequate time for each problem

One of the most common complaints from students when sitting for an exam is that they ran out of time. Math is a complex subject with complicated problems that require understanding before a solution could be reached. It is up to the student to figure out techniques to solve the problems more quickly. 

When sitting for your math test, the first step is reading the math problem carefully from the beginning to the end. Underline the important numbers and facts as you read. As you are reading, your brain is taking in all the facts and developing the blueprint of the solution. 

Your subconscious will help in processing prior knowledge and choosing those formulae and processes that are more applicable to the problem at hand. You will recall similar techniques and theorems that could help you solve the problem.

After this process, you should be able to translate all the data into equations. Think of any formula or procedure that could help shorten the solution. Make sure that the formula or procedure applies to the problem at hand. Put down all your workings in a simplified and logical format.

The last step is to go through your work and confirm if your answer fits. Do not declare that you are done simply because you got an answer. Only submit the paper if you understand the answer you got.

Once you get good at it, you will not have to think about the above steps when solving math problems. The steps will come naturally to you. Try as much as possible to apply mathematical techniques in solving real-world problems. Looking for practical ideas can help you disassociate math with complexity and make it a more fun concept to you. 

Applying maths to real-world problems will also increase your interest and understanding. Parents should also help in fostering positive attitudes about maths to students as much as possible. They can find mentors for their kids where they cannot answer questions.

Author Bio:

Connie Elser is a competitive exam tutor who specializes in maths, reasoning and English. Her teaching methodology and innovative approach to tackle entrance exams has helped numerous students make it to a university of their choice. In her free time, she works on her education blog, writes poems, and goes to the gym.

Most Popular

What Dissolves Ear Wax Fast?

Different Feline? New Type of Cat Results From Genetic Mutation, Study Reveals

Murdered by UFOs? Expert Explains Bizarre Fatality Cases Linked to These Unidentified Flying Objects

Major Solar Storm Headed for Earth This Week; Powerful Eruption Could Cause 60% Chance of Radio Blackouts and Northern Light Displays

Ozempic's Semaglutide Shows Promise in Reducing Kidney Disease Risk for Type 2 Diabetes Patients

Latest stories.

Cloacibacterium in Action: Tiny Organism Shows Potential in Fighting Climate Change by Reducing Nitrous Oxide in Farm Field

7 More Rogue Planets Discovered by Euclid Space Telescope; Could They Be the Key in the Search for Extraterrestrial Life?

World’s First Wooden Satellite Built by Japanese Researchers To Fight Space Pollution; How Does LignoSat Probe Differ From Other Spacecraft?

Tauonium: The Hunt for a New Atom in Quantum Physics

China’s BYD Releases New Hybrid Cars With Lowest Fuel Consumption, Longest Range

Subscribe to the science times.

Sign up for our free newsletter for the Latest coverage!

Recommended Stories

Moon in Broad Daylight: Here's Why We Can Sometimes See Earth's Natural Satellite in the Daytime Sky

Sandblasting by Lunar Dust Poses Serious Risk to Cargo and Crew on the Moon [Studies]

High-Speed UFO Spotted in NYC During Blue Angels Demonstration, Sighting Only Lasted a Nanosecond [Report]

• Research Article

7 Strategies to Solve the Biggest Math Challenges

Teaching Strategies

National Assessment of Educational Progress ( NAEP ) long-term trend assessment data from the 2022-23 school year revealed the average 13-year-old’s math scores dropped by 9 points, significantly lower than in 2020, with a 14-point drop compared to a decade ago. Declines were even greater for lower-performing students. To ensure academic recovery for all students, this math challenge needs a solution.

What will it take to solve learning loss caused by the pandemic?

Today, scores show just 36% of 4th graders are proficient in math. And in districts experiencing deep poverty, such as Detroit, this number falls to just 4% . While some students may know simple arithmetic facts, fewer can take on more complex math, like adding fractions. Research shows that foundational math, like fraction knowledge and math fact fluency skills , predicts math success in high school, as well as on standardized tests. So what does this mean?

Students who can’t move past these math basics will face long-term struggles, including negative impacts to their academic success and career paths. They may struggle to graduate high school or attend college. Besides these challenges, basic math skills are just as important as literacy for navigating our everyday lives.

Help your students overcome the mathematics struggle and achieve math success with our strategies.

• Extend The School Day. NAEP results show how much school closures during the pandemic hurt students. Get your students excited about learning outside of school and extend the school day. Use engaging digital solutions that satisfy kids’ love of technology, and allow students to continue working on key skills at home. The best solutions allow students to work independently without support from staff. And of course, it should be fun.
• Support SEL in Your Class. Skills that are important in math class, like problem-solving and decision-making, are also crucial social-emotional learning skills. Help your students tackle math and real-world problems with our math class SEL guide .
• Choose Evidence-Based Solutions. Considering adding digital solutions to your classroom? Make sure they can produce real outcomes. Programs should be based on research with measurable outcomes and quantifiable data, like all ExploreLearning products . Learn how to gamify learning in your classroom and how to choose evidence-based edtech for real results.
• Invest in Classroom Reporting. Without a reporting strategy, it’s much more difficult to identify and address gaps in student knowledge. But reporting should go beyond student worksheets or quizzes. With ExploreLearning Reflex ’s intuitive reporting features , you can easily track your entire class’ math fact fluency without assigning one test. Each Reflex session is carefully monitored, adapted to students’ levels, and produces measurable results. Now that’s powerful!
• Individualize Student’s Learning. Not all students learn at the same pace. Make sure students are engaged and challenged at the right level with adaptive and individualized instruction. Reflex and Frax include personalized instruction to help students overcome the biggest math challenges at their own pace.
• Nurture Growth Mindsets. Math skills aren’t fixed skills, but many students believe they are. Mindset can make a huge difference in how students approach math, giving them the confidence to tackle obstacles. Use growth mindset strategies to encourage students to stop the negative self-talk and think positively about their math abilities.
• Close the Achievement Gap with Math Fact Fluency. Math fact fluency is the foundation for future math success. And the achievement gap existed before the pandemic, with students requiring math intervention. Our studies show that Reflex engages students at every level and gives them the skills needed to get back on the fast track to math achievement.

To see what happens when the students at Title I schools use Reflex for 60 days, watch this video .

In this graph, we compare average fluency in Reflex (the y-axis) to the percentage of students on free or reduced lunch (the x-axis) over the school year. Each dot represents a Title I eligible school with at least 100 students with recommended Reflex usage. The size represents the number of kids at the school who used Reflex. Read the full article .

Explore our math solutions free for 30 days when you sign up for a trial.

You might also like these stories...

Sign up to get the latest updates from ExploreLearning via occasional email.

Top 10 Challenges to Teaching Math and Science Using Real Problems

• Share article

Nine in ten educators believe that using a problem-solving approach to teaching math and science can be motivating for students, according to an EdWeek Research Center survey.

But that doesn’t mean it’s easy.

Teachers perceive lack of time as a big hurdle. In fact, a third of educators—35 percent—worry that teaching math or science through real-world problems—rather than focusing on procedures—eats up too many precious instructional minutes.

Other challenges: About another third of educators said they weren’t given sufficient professional development in how to teach using a real-world problem-solving approach. Nearly a third say reading and writing take priority over STEM, leaving little bandwidth for this kind of instruction. About a quarter say that it’s tough to find instructional materials that embrace a problem-solving perspective.

Nearly one in five cited teachers’ lack of confidence in their own problem solving, the belief that this approach isn’t compatible with standardized tests, low parent support, and the belief that student behavior is so poor that this approach would not be feasible.

The nationally representative survey included 1,183 district leaders, school leaders, and teachers, and was conducted from March 27 to April 14. (Note: The chart below lists 11 challenges because the last two on the list—dealing with teacher preparation and student behavior—received the exact percentage of responses.)

Trying to incorporate a problem-solving approach to tackling math can require rethinking long-held beliefs about how students learn, said Elham Kazemi, a professor in the teacher education program at the University of Washington.

Most teachers were taught math using a procedural perspective when they were in school. While Kazemi believes that approach has merit, she advocates for exposing students to both types of instruction.

Many educators have “grown up around a particular model of thinking of teaching and learning as the teacher in the front of the room, imparting knowledge, showing kids how to do things,” Kazemi said.

To be sure, some teachers have figured out how to incorporate some real-world problem solving alongside more traditional methods. But it can be tough for their colleagues to learn from them because “teachers don’t have a lot of time to collaborate with one another and see each other teach,” Kazemi said.

What’s more, there are limited instructional materials emphasizing problem solving, Kazemi said.

Though that’s changing, many of the resources available have “reinforced the idea that the teacher demonstrates solutions for kids,” Kazemi said.

Molly Daley, a regional math coordinator for Education Service District 112, which serves about 30 districts near Vancouver, Wash., has heard teachers raise concerns that teaching math from a problem-solving perspective takes too long—particularly given the pressure to get through all the material students will need to perform well on state tests.

Daley believes, however, that being taught to think about math in a deeper way will help students tackle math questions on state assessments that may look different from what they’ve seen before.

“It’s myth that it’s possible to cover everything that will be on the test,” as it will appear, she said. “There’s actually no way to make sure that kids have seen every single possible thing the way it will show up. That’s kind of a losing proposition.”

But rushing through the material in a purely procedural way may actually be counterproductive, she said.

Teachers don’t want kids to “sit down at the test and say, ‘I haven’t seen this and therefore I can’t do it,’” Daley said. “I think a lot of times teachers can unintentionally foster that because they’re so urgently trying to cover everything. That’s where the kind of mindless [teaching] approaches come in.”

Teachers may think to themselves: “’OK, I’m gonna make this as simple as possible, make sure everyone knows how to follow the steps and then when they see it, they can follow it,” Daley said.

But that strategy might “take away their students’ confidence that they can figure out what to do when they don’t know what to do, which is really what you want them to be thinking when they go to approach a test,” Daley said.

Sign Up for EdWeek Update

Edweek top school jobs.

Sign Up & Sign In

• Share full article

Advertisement

Supported by

The Algebra Problem: How Middle School Math Became a National Flashpoint

Top students can benefit greatly by being offered the subject early. But many districts offer few Black and Latino eighth graders a chance to study it.

By Troy Closson

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system. Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly four in five poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class. San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’s administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12 percent of Black and Latino eighth graders do, compared with roughly 24 percent of white pupils, a federal report found .

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research . A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Mass., the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside of school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, Mr. de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80 percent from 60 percent. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s current schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won both support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Mr. Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Mr. Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100 percent, yes,” he added. “That was not something that I could live with.”

Troy Closson reports on K-12 schools in New York City for The Times. More about Troy Closson

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.9: Strategies for Solving Applications and Equations

• Last updated
• Save as PDF
• Page ID 113697

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Use a problem solving strategy for word problems
• Solve number word problems
• Solve percent applications
• Solve simple interest applications

Before you get started, take this readiness quiz.

• Translate “six less than twice x ” into an algebraic expression. If you missed this problem, review [link] .
• Convert 4.5% to a decimal. If you missed this problem, review [link] .
• Convert 0.6 to a percent. If you missed this problem, review [link] .

Have you ever had any negative experiences in the past with word problems? When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. Realize that your negative experiences with word problems are in your past. To move forward you need to calm your fears and change your negative feelings.

Start with a fresh slate and begin to think positive thoughts. Repeating some of the following statements may be helpful to turn your thoughts positive. Thinking positive thoughts is a first step towards success.

• I think I can! I think I can!
• While word problems were hard in the past, I think I can try them now.
• I am better prepared now—I think I will begin to understand word problems.
• I am able to solve equations because I practiced many problems and I got help when I needed it—I can try that with word problems.
• It may take time, but I can begin to solve word problems.
• You are now well prepared and you are ready to succeed. If you take control and believe you can be successful, you will be able to master word problems.

Use a Problem Solving Strategy for Word Problems

Now that we can solve equations, we are ready to apply our new skills to word problems. We will develop a strategy we can use to solve any word problem successfully.

EXAMPLE \(\PageIndex{1}\)

Normal yearly snowfall at the local ski resort is 12 inches more than twice the amount it received last season. The normal yearly snowfall is 62 inches. What was the snowfall last season at the ski resort?

EXAMPLE \(\PageIndex{2}\)

Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was three more than twice the number of notebooks. He bought seven textbooks. How many notebooks did he buy?

He bought two notebooks

EXAMPLE \(\PageIndex{3}\)

Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is eight more than twice the number of crossword puzzles. He completed 22 Sudoku puzzles. How many crossword puzzles did he do?

He did seven crosswords puzzles

We summarize an effective strategy for problem solving.

PROBLEM SOLVING STRATEGY FOR WORD PROBLEMS

• Read the problem. Make sure all the words and ideas are understood.
• Identify what you are looking for.
• Name what you are looking for. Choose a variable to represent that quantity.
• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
• Solve the equation using proper algebra techniques.
• Check the answer in the problem to make sure it makes sense.
• Answer the question with a complete sentence.

Solve Number Word Problems

We will now apply the problem solving strategy to “number word problems.” Number word problems give some clues about one or more numbers and we use these clues to write an equation. Number word problems provide good practice for using the Problem Solving Strategy.

EXAMPLE \(\PageIndex{4}\)

The sum of seven times a number and eight is thirty-six. Find the number.

Did you notice that we left out some of the steps as we solved this equation? If you’re not yet ready to leave out these steps, write down as many as you need.

EXAMPLE \(\PageIndex{5}\)

The sum of four times a number and two is fourteen. Find the number.

EXAMPLE \(\PageIndex{6}\)

The sum of three times a number and seven is twenty-five. Find the number.

Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far, we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.

EXAMPLE \(\PageIndex{7}\)

The sum of two numbers is negative fifteen. One number is nine less than the other. Find the numbers.

EXAMPLE \(\PageIndex{8}\)

The sum of two numbers is negative twenty-three. One number is seven less than the other. Find the numbers.

\(−15,−8\)

EXAMPLE \(\PageIndex{9}\)

The sum of two numbers is negative eighteen. One number is forty more than the other. Find the numbers.

\(−29,11\)

Consecutive Integers (optional)

Some number problems involve consecutive integers . Consecutive integers are integers that immediately follow each other. Examples of consecutive integers are:

\[\begin{array}{rrrr} 1, & 2, & 3, & 4 \\ −10, & −9, & −8, & −7\\ 150, & 151, & 152, & 153 \end{array}\]

Notice that each number is one more than the number preceding it. Therefore, if we define the first integer as n , the next consecutive integer is \(n+1\). The one after that is one more than \(n+1\), so it is \(n+1+1\), which is \(n+2\).

\[\begin{array}{ll} n & 1^{\text{st}} \text{integer} \\ n+1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; & 2^{\text{nd}}\text{consecutive integer} \\ n+2 & 3^{\text{rd}}\text{consecutive integer} \;\;\;\;\;\;\;\; \text{etc.} \end{array}\]

We will use this notation to represent consecutive integers in the next example.

EXAMPLE \(\PageIndex{10}\)

Find three consecutive integers whose sum is \(−54\).

EXAMPLE \(\PageIndex{11}\)

Find three consecutive integers whose sum is \(−96\).

\(−33,−32,−31\)

EXAMPLE \(\PageIndex{12}\)

Find three consecutive integers whose sum is \(−36\).

\(−13,−12,−11\)

Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers . Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:

\[24, 26, 28\]

\[−12,−10,−8\]

Notice each integer is two more than the number preceding it. If we call the first one n , then the next one is \(n+2\). The one after that would be \(n+2+2\) or \(n+4\).

Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers 63, 65, and 67.

\[63, 65, 67\]

\[n,n+2,n+4\]

Does it seem strange to have to add two (an even number) to get the next odd number? Do we get an odd number or an even number when we add 2 to 3? to 11? to 47?

Whether the problem asks for consecutive even numbers or odd numbers, you do not have to do anything different. The pattern is still the same—to get to the next odd or the next even integer, add two.

EXAMPLE \(\PageIndex{13}\)

Find three consecutive even integers whose sum is \(120\).

EXAMPLE \(\PageIndex{14}\)

Find three consecutive even integers whose sum is 102.

\(32, 34, 36\)

EXAMPLE \(\PageIndex{15}\)

Find three consecutive even integers whose sum is \(−24\).

\(−10,−8,−6\)

When a number problem is in a real life context, we still use the same strategies that we used for the previous examples.

EXAMPLE \(\PageIndex{16}\)

A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?

According to the National Automobile Dealers Association, the average cost of a car in 2014 was $28,400. This was $1,600 less than six times the cost in 1975. What was the average cost of a car in 1975?

The average cost was $5,000.

EXAMPLE \(\PageIndex{18}\)

US Census data shows that the median price of new home in the U.S. in November 2014 was $280,900. This was $10,700 more than 14 times the price in November 1964. What was the median price of a new home in November 1964?

The median price was $19,300.

Solve Percent Applications

There are several methods to solve percent equations. In algebra, it is easiest if we just translate English sentences into algebraic equations and then solve the equations. Be sure to change the given percent to a decimal before you use it in the equation.

EXAMPLE \(\PageIndex{19}\)

Translate and solve:

• What number is 45% of 84?
• 8.5% of what amount is $4.76?
• 168 is what percent of 112?
• What number is 45% of 80?
• 7.5% of what amount is $1.95?
• 110 is what percent of 88?

ⓐ 36 ⓑ $26 ⓒ \(125 \% \)

EXAMPLE \(\PageIndex{21}\)

• What number is 55% of 60?
• 8.5% of what amount is $3.06?
• 126 is what percent of 72?

ⓐ 33 ⓑ $36 ⓐ \(175 \% \)

Now that we have a problem solving strategy to refer to, and have practiced solving basic percent equations, we are ready to solve percent applications. Be sure to ask yourself if your final answer makes sense—since many of the applications we will solve involve everyday situations, you can rely on your own experience.

EXAMPLE \(\PageIndex{22}\)

The label on Audrey’s yogurt said that one serving provided 12 grams of protein, which is 24% of the recommended daily amount. What is the total recommended daily amount of protein?

EXAMPLE \(\PageIndex{23}\)

One serving of wheat square cereal has 7 grams of fiber, which is 28% of the recommended daily amount. What is the total recommended daily amount of fiber?

EXAMPLE \(\PageIndex{24}\)

One serving of rice cereal has 190 mg of sodium, which is 8% of the recommended daily amount. What is the total recommended daily amount of sodium?

Remember to put the answer in the form requested. In the next example we are looking for the percent.

EXAMPLE \(\PageIndex{25}\)

Veronica is planning to make muffins from a mix. The package says each muffin will be 240 calories and 60 calories will be from fat. What percent of the total calories is from fat?

EXAMPLE \(\PageIndex{26}\)

Mitzi received some gourmet brownies as a gift. The wrapper said each 28% brownie was 480 calories, and had 240 calories of fat. What percent of the total calories in each brownie comes from fat? Round the answer to the nearest whole percent.

EXAMPLE \(\PageIndex{27}\)

The mix Ricardo plans to use to make brownies says that each brownie will be 190 calories, and 76 calories are from fat. What percent of the total calories are from fat? Round the answer to the nearest whole percent.

It is often important in many fields—business, sciences, pop culture—to talk about how much an amount has increased or decreased over a certain period of time. This increase or decrease is generally expressed as a percent and called the percent change .

To find the percent change, first we find the amount of change, by finding the difference of the new amount and the original amount. Then we find what percent the amount of change is of the original amount.

FIND PERCENT CHANGE

\[\text{change}= \text{new amount}−\text{original amount}\]

change is what percent of the original amount?

EXAMPLE \(\PageIndex{28}\)

Recently, the California governor proposed raising community college fees from $36 a unit to $46 a unit. Find the percent change. (Round to the nearest tenth of a percent.)

EXAMPLE \(\PageIndex{29}\)

Find the percent change. (Round to the nearest tenth of a percent.) In 2011, the IRS increased the deductible mileage cost to 55.5 cents from 51 cents.

\(8.8 \% \)

EXAMPLE \(\PageIndex{30}\)

Find the percent change. (Round to the nearest tenth of a percent.) In 1995, the standard bus fare in Chicago was $1.50. In 2008, the standard bus fare was 2.25.

Applications of discount and mark-up are very common in retail settings.

When you buy an item on sale, the original price has been discounted by some dollar amount. The discount rate , usually given as a percent, is used to determine the amount of the discount . To determine the amount of discount, we multiply the discount rate by the original price.

The price a retailer pays for an item is called the original cost . The retailer then adds a mark-up to the original cost to get the list price , the price he sells the item for. The mark-up is usually calculated as a percent of the original cost. To determine the amount of mark-up, multiply the mark-up rate by the original cost.

\[ \begin{align} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align}\]

The sale price should always be less than the original price.

\[\begin{align} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align}\]

The list price should always be more than the original cost.

EXAMPLE \(\PageIndex{31}\)

Liam’s art gallery bought a painting at an original cost of $750. Liam marked the price up 40%. Find

• the amount of mark-up and
• the list price of the painting.

EXAMPLE \(\PageIndex{32}\)

Find ⓐ the amount of mark-up and ⓑ the list price: Jim’s music store bought a guitar at original cost $1,200. Jim marked the price up 50%.

ⓐ $600 ⓑ $1,800

EXAMPLE \(\PageIndex{33}\)

Find ⓐ the amount of mark-up and ⓑ the list price: The Auto Resale Store bought Pablo’s Toyota for $8,500. They marked the price up 35%.

ⓐ $2,975 ⓑ $11,475

Solve Simple Interest Applications

Interest is a part of our daily lives. From the interest earned on our savings to the interest we pay on a car loan or credit card debt, we all have some experience with interest in our lives.

The amount of money you initially deposit into a bank is called the principal , P , and the bank pays you interest, I. When you take out a loan, you pay interest on the amount you borrow, also called the principal.

In either case, the interest is computed as a certain percent of the principal, called the rate of interest , r . The rate of interest is usually expressed as a percent per year, and is calculated by using the decimal equivalent of the percent. The variable t , (for time) represents the number of years the money is saved or borrowed.

Interest is calculated as simple interest or compound interest. Here we will use simple interest.

SIMPLE INTEREST

If an amount of money, P , called the principal, is invested or borrowed for a period of t years at an annual interest rate r , the amount of interest, I , earned or paid is

\[ \begin{array}{ll} I=Prt \; \; \; \; \; \; \; \; \; \; \; \; \text{where} & { \begin{align} I &= \text{interest} \\ P &= \text{principal} \\ r &= \text{rate} \\ t &= \text{time} \end{align}} \end{array}\]

Interest earned or paid according to this formula is called simple interest .

The formula we use to calculate interest is \(I=Prt\). To use the formula we substitute in the values for variables that are given, and then solve for the unknown variable. It may be helpful to organize the information in a chart.

EXAMPLE \(\PageIndex{34}\)

Areli invested a principal of $950 in her bank account that earned simple interest at an interest rate of 3%. How much interest did she earn in five years?

\( \begin{aligned} I & = \; ? \\ P & = \; \$ 950 \\ r & = \; 3 \% \\ t & = \; 5 \text{ years} \end{aligned}\)

\(\begin{array}{ll} \text{Identify what you are asked to find, and choose a} & \text{What is the simple interest?} \\ \text{variable to represent it.} & \text{Let } I= \text{interest.} \\ \text{Write the formula.} & I=Prt \\ \text{Substitute in the given information.} & I=(950)(0.03)(5) \\ \text{Simplify.} & I=142.5 \\ \text{Check.} \\ \text{Is } \$142.50 \text{ a reasonable amount of interest on } \$ \text{ 950?} \; \;\;\;\;\; \;\;\;\;\;\; \\ \text{Yes.} \\ \text{Write a complete sentence.} & \text{The interest is } \$ \text{142.50.} \end{array}\)

EXAMPLE \(\PageIndex{35}\)

Nathaly deposited $12,500 in her bank account where it will earn 4% simple interest. How much interest will Nathaly earn in five years?

He will earn $2,500.

EXAMPLE \(\PageIndex{36}\)

Susana invested a principal of $36,000 in her bank account that earned simple interest at an interest rate of 6.5%.6.5%. How much interest did she earn in three years?

She earned $7,020.

There may be times when we know the amount of interest earned on a given principal over a certain length of time, but we do not know the rate.

EXAMPLE \(\PageIndex{37}\)

Hang borrowed $7,500 from her parents to pay her tuition. In five years, she paid them $1,500 interest in addition to the $7,500 she borrowed. What was the rate of simple interest?

\( \begin{aligned} I & = \; \$ 1500 \\ P & = \; \$ 7500 \\ r & = \; ? \\ t & = \; 5 \text{ years} \end{aligned}\)

Identify what you are asked to find, and choose What is the rate of simple interest? a variable to represent it. Write the formula. Substitute in the given information. Multiply. Divide. Change to percent form. Let r = rate of interest. I = P r t 1,500 = ( 7,500 ) r ( 5 ) 1,500 = 37,500 r 0.04 = r 4 % = r Check. I = P r t 1,500 = ? ( 7,500 ) ( 0.04 ) ( 5 ) 1,500 = 1,500 ✓ Write a complete sentence. The rate of interest was 4%. Identify what you are asked to find, and choose What is the rate of simple interest? a variable to represent it. Write the formula. Substitute in the given information. Multiply. Divide. Change to percent form. Let r = rate of interest. I = P r t 1 ,500 = ( 7,500 ) r ( 5 ) 1,500 = 37,500 r 0.04 = r 4 % = r Check. I = P r t 1 ,500 = ? ( 7,500 ) ( 0.04 ) ( 5 ) 1,500 = 1, 500 ✓ Write a complete sentence. The rate of interest was 4%.

EXAMPLE \(\PageIndex{38}\)

Jim lent his sister $5,000 to help her buy a house. In three years, she paid him the $5,000, plus $900 interest. What was the rate of simple interest?

The rate of simple interest was 6%.

EXAMPLE \(\PageIndex{39}\)

Loren lent his brother $3,000 to help him buy a car. In four years, his brother paid him back the $3,000 plus $660 in interest. What was the rate of simple interest?

The rate of simple interest was 5.5%.

In the next example, we are asked to find the principal—the amount borrowed.

EXAMPLE \(\PageIndex{40}\)

Sean’s new car loan statement said he would pay $4,866,25 in interest from a simple interest rate of 8.5% over five years. How much did he borrow to buy his new car?

\( \begin{aligned} I & = \; 4,866.25 \\ P & = \; ? \\ r & = \; 8.5 \% \\ t & = \; 5 \text{ years} \end{aligned}\)

Identify what you are asked to find, What is the amount borrowed (the principal)? and choose a variable to represent it. Write the formula. Substitute in the given information. Multiply. Divide. Let P = principal borrowed. I = P r t 4,866.25 = P ( 0.085 ) ( 5 ) 4,866.25 = 0.425 P 11,450 = P Check. I = P r t 4,866.25 = ? ( 11,450 ) ( 0.085 ) ( 5 ) 4,866.25 = 4,866.25 ✓ Write a complete sentence. The principal was $11,450. Identify what you are asked to find, What is the amount borrowed (the principal)? and choose a variable to represent it. Write the formula. Substitute in the given information. Multiply. Divide. Let P = principal borrowed. I = P r t 4 ,866.25 = P ( 0.085 ) ( 5 ) 4,866.25 = 0.425 P 11,450 = P Check. I = P r t 4 ,866.25 = ? ( 11,450 ) ( 0.085 ) ( 5 ) 4,866.25 = 4,866.25 ✓ Write a complete sentence. The principal was $11,450.

EXAMPLE \(\PageIndex{41}\)

Eduardo noticed that his new car loan papers stated that with a 7.5% simple interest rate, he would pay $6,596.25 in interest over five years. How much did he borrow to pay for his car?

He paid $17,590.

EXAMPLE \(\PageIndex{42}\)

In five years, Gloria’s bank account earned $2,400 interest at 5% simple interest. How much had she deposited in the account?

She deposited $9,600.

Access this online resource for additional instruction and practice with using a problem solving strategy.

• Begining Arithmetic Problems

Key Concepts

\(\text{change}=\text{new amount}−\text{original amount}\)

\(\text{change is what percent of the original amount?}\)

• \( \begin{align} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align}\)
• \(\begin{align} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align}\)
• If an amount of money, P , called the principal, is invested or borrowed for a period of t years at an annual interest rate r , the amount of interest, I , earned or paid is: \[\begin{aligned} &{} &{} &{I=interest} \nonumber\\ &{I=Prt} &{\text{where} \space} &{P=principal} \nonumber\\ &{} &{\space} &{r=rate} \nonumber\\ &{} &{\space} &{t=time} \nonumber \end{aligned}\]

Practice Makes Perfect

1. List five positive thoughts you can say to yourself that will help you approach word problems with a positive attitude. You may want to copy them on a sheet of paper and put it in the front of your notebook, where you can read them often.

Answers will vary.

2. List five negative thoughts that you have said to yourself in the past that will hinder your progress on word problems. You may want to write each one on a small piece of paper and rip it up to symbolically destroy the negative thoughts.

In the following exercises, solve using the problem solving strategy for word problems. Remember to write a complete sentence to answer each question.

3. There are \(16\) girls in a school club. The number of girls is four more than twice the number of boys. Find the number of boys.

4. There are \(18\) Cub Scouts in Troop 645. The number of scouts is three more than five times the number of adult leaders. Find the number of adult leaders.

5. Huong is organizing paperback and hardback books for her club’s used book sale. The number of paperbacks is \(12\) less than three times the number of hardbacks. Huong had \(162\) paperbacks. How many hardback books were there?

58 hardback books

6. Jeff is lining up children’s and adult bicycles at the bike shop where he works. The number of children’s bicycles is nine less than three times the number of adult bicycles. There are \(42\) adult bicycles. How many children’s bicycles are there?

In the following exercises, solve each number word problem.

7. The difference of a number and \(12\) is three. Find the number.

8. The difference of a number and eight is four. Find the number.

9. The sum of three times a number and eight is \(23\). Find the number.

10. The sum of twice a number and six is \(14\). Find the number.

11 . The difference of twice a number and seven is \(17\). Find the number.

12. The difference of four times a number and seven is \(21\). Find the number.

13. Three times the sum of a number and nine is \(12\). Find the number.

14. Six times the sum of a number and eight is \(30\). Find the number.

15. One number is six more than the other. Their sum is \(42\). Find the numbers.

\(18, \;24\)

16. One number is five more than the other. Their sum is \(33\). Find the numbers.

17. The sum of two numbers is \(20\). One number is four less than the other. Find the numbers.

\(8, \;12\)

18 . The sum of two numbers is \(27\). One number is seven less than the other. Find the numbers.

19. One number is \(14\) less than another. If their sum is increased by seven, the result is \(85\). Find the numbers.

\(32,\; 46\)

20 . One number is \(11\) less than another. If their sum is increased by eight, the result is \(71\). Find the numbers.

21. The sum of two numbers is \(14\). One number is two less than three times the other. Find the numbers.

\(4,\; 10\)

22. The sum of two numbers is zero. One number is nine less than twice the other. Find the numbers.

23. The sum of two consecutive integers is \(77\). Find the integers.

\(38,\; 39\)

24. The sum of two consecutive integers is \(89\). Find the integers.

25. The sum of three consecutive integers is \(78\). Find the integers.

\(25,\; 26,\; 27\)

26. The sum of three consecutive integers is \(60\). Find the integers.

27. Find three consecutive integers whose sum is \(−36\).

\(−11,\;−12,\;−13\)

28. Find three consecutive integers whose sum is \(−3\).

29. Find three consecutive even integers whose sum is \(258\).

\(84,\; 86,\; 88\)

30. Find three consecutive even integers whose sum is \(222\).

31. Find three consecutive odd integers whose sum is \(−213\).

\(−69,\;−71,\;−73\)

32. Find three consecutive odd integers whose sum is \(−267\).

33. Philip pays \($1,620\) in rent every month. This amount is \($120\) more than twice what his brother Paul pays for rent. How much does Paul pay for rent?

34. Marc just bought an SUV for \($54,000\). This is \($7,400\) less than twice what his wife paid for her car last year. How much did his wife pay for her car?

35. Laurie has \($46,000\) invested in stocks and bonds. The amount invested in stocks is \($8,000\) less than three times the amount invested in bonds. How much does Laurie have invested in bonds?

\($13,500\)

36. Erica earned a total of \($50,450\) last year from her two jobs. The amount she earned from her job at the store was \($1,250\) more than three times the amount she earned from her job at the college. How much did she earn from her job at the college?

In the following exercises, translate and solve.

37. a. What number is 45% of 120? b. 81 is 75% of what number? c. What percent of 260 is 78?

a. 54 b. 108 c. 30%

38. a. What number is 65% of 100? b. 93 is 75% of what number? c. What percent of 215 is 86?

39. a. 250% of 65 is what number? b. 8.2% of what amount is $2.87? c. 30 is what percent of 20?

a. 162.5 b. $35 c. 150%

40. a. 150% of 90 is what number? b. 6.4% of what amount is $2.88? c. 50 is what percent of 40?

In the following exercises, solve.

41. Geneva treated her parents to dinner at their favorite restaurant. The bill was $74.25. Geneva wants to leave 16% of the total bill as a tip. How much should the tip be?

42. When Hiro and his co-workers had lunch at a restaurant near their work, the bill was $90.50. They want to leave 18% of the total bill as a tip. How much should the tip be?

43. One serving of oatmeal has 8 grams of fiber, which is 33% of the recommended daily amount. What is the total recommended daily amount of fiber?

44. One serving of trail mix has 67 grams of carbohydrates, which is 22% of the recommended daily amount. What is the total recommended daily amount of carbohydrates?

45. A bacon cheeseburger at a popular fast food restaurant contains 2070 milligrams (mg) of sodium, which is 86% of the recommended daily amount. What is the total recommended daily amount of sodium?

46. A grilled chicken salad at a popular fast food restaurant contains 650 milligrams (mg) of sodium, which is 27% of the recommended daily amount. What is the total recommended daily amount of sodium?

47. The nutrition fact sheet at a fast food restaurant says the fish sandwich has 380 calories, and 171 calories are from fat. What percent of the total calories is from fat?

48. The nutrition fact sheet at a fast food restaurant says a small portion of chicken nuggets has 190 calories, and 114 calories are from fat. What percent of the total calories is from fat?

49. Emma gets paid $3,000 per month. She pays $750 a month for rent. What percent of her monthly pay goes to rent?

50. Dimple gets paid $3,200 per month. She pays $960 a month for rent. What percent of her monthly pay goes to rent?

51. Tamanika received a raise in her hourly pay, from $15.50 to $17.36. Find the percent change.

52. Ayodele received a raise in her hourly pay, from $24.50 to $25.48. Find the percent change.

53. Annual student fees at the University of California rose from about $4,000 in 2000 to about $12,000 in 2010. Find the percent change.

54. The price of a share of one stock rose from $12.50 to $50. Find the percent change.

55. A grocery store reduced the price of a loaf of bread from $2.80 to $2.73. Find the percent change.

−2.5%

56. The price of a share of one stock fell from $8.75 to $8.54. Find the percent change.

57. Hernando’s salary was $49,500 last year. This year his salary was cut to $44,055. Find the percent change.

58. In ten years, the population of Detroit fell from 950,000 to about 712,500. Find the percent change.

In the following exercises, find a. the amount of discount and b. the sale price.

59. Janelle bought a beach chair on sale at 60% off. The original price was $44.95.

a. $26.97 b. $17.98

60. Errol bought a skateboard helmet on sale at 40% off. The original price was $49.95.

In the following exercises, find a. the amount of discount and b. the discount rate (Round to the nearest tenth of a percent if needed.)

61. Larry and Donna bought a sofa at the sale price of $1,344. The original price of the sofa was $1,920.

a. $576 b. 30%

62. Hiroshi bought a lawnmower at the sale price of $240. The original price of the lawnmower is $300.

In the following exercises, find a. the amount of the mark-up and b. the list price.

63. Daria bought a bracelet at original cost $16 to sell in her handicraft store. She marked the price up 45%. What was the list price of the bracelet?

a. $7.20 b. $23.20

64. Regina bought a handmade quilt at original cost $120 to sell in her quilt store. She marked the price up 55%. What was the list price of the quilt?

65. Tom paid $0.60 a pound for tomatoes to sell at his produce store. He added a 33% mark-up. What price did he charge his customers for the tomatoes?

a. $0.20 b. $0.80

66. Flora paid her supplier $0.74 a stem for roses to sell at her flower shop. She added an 85% mark-up. What price did she charge her customers for the roses?

67. Casey deposited $1,450 in a bank account that earned simple interest at an interest rate of 4%. How much interest was earned in two years?

68 . Terrence deposited $5,720 in a bank account that earned simple interest at an interest rate of 6%. How much interest was earned in four years?

69. Robin deposited $31,000 in a bank account that earned simple interest at an interest rate of 5.2%. How much interest was earned in three years?

70. Carleen deposited $16,400 in a bank account that earned simple interest at an interest rate of 3.9% How much interest was earned in eight years?

71. Hilaria borrowed $8,000 from her grandfather to pay for college. Five years later, she paid him back the $8,000, plus $1,200 interest. What was the rate of simple interest?

72. Kenneth lent his niece $1,200 to buy a computer. Two years later, she paid him back the $1,200, plus $96 interest. What was the rate of simple interest?

73. Lebron lent his daughter $20,000 to help her buy a condominium. When she sold the condominium four years later, she paid him the $20,000, plus $3,000 interest. What was the rate of simple interest?

74. Pablo borrowed $50,000 to start a business. Three years later, he repaid the $50,000, plus $9,375 interest. What was the rate of simple interest?

75. In 10 years, a bank account that paid 5.25% simple interest earned $18,375 interest. What was the principal of the account?

76. In 25 years, a bond that paid 4.75% simple interest earned $2,375 interest. What was the principal of the bond?

77. Joshua’s computer loan statement said he would pay $1,244.34 in simple interest for a three-year loan at 12.4%. How much did Joshua borrow to buy the computer?

78. Margaret’s car loan statement said she would pay $7,683.20 in simple interest for a five-year loan at 9.8%. How much did Margaret borrow to buy the car?

Everyday Math

79 . Tipping At the campus coffee cart, a medium coffee costs $1.65. MaryAnne brings $2.00 with her when she buys a cup of coffee and leaves the change as a tip. What percent tip does she leave?

80 . Tipping Four friends went out to lunch and the bill came to $53.75 They decided to add enough tip to make a total of $64, so that they could easily split the bill evenly among themselves. What percent tip did they leave?

Writing Exercises

81. What has been your past experience solving word problems? Where do you see yourself moving forward?

82. Without solving the problem “44 is 80% of what number” think about what the solution might be. Should it be a number that is greater than 44 or less than 44? Explain your reasoning.

83. After returning from vacation, Alex said he should have packed 50% fewer shorts and 200% more shirts. Explain what Alex meant.

84. Because of road construction in one city, commuters were advised to plan that their Monday morning commute would take 150% of their usual commuting time. Explain what this means.

a. After completing the exercises, use this checklist to evaluate your mastery of the objective of this section.

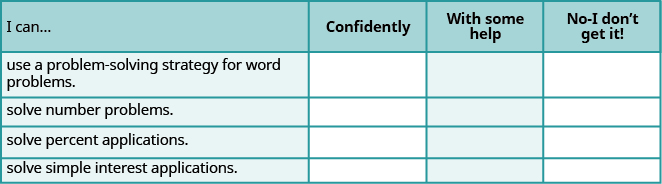
b. After reviewing this checklist, what will you do to become confident for all objectives?

• SUGGESTED TOPICS
• The Magazine
• Newsletters
• Managing Yourself
• Managing Teams
• Work-life Balance
• The Big Idea
• Data & Visuals
• Reading Lists
• Case Selections
• HBR Learning
• Topic Feeds
• Account Settings
• Email Preferences

Share Podcast

A Better Framework for Solving Tough Problems

Start with trust and end with speed.

• Apple Podcasts

When it comes to solving complicated problems, the default for many organizational leaders is to take their time to work through the issues at hand. Unfortunately, that often leads to patchwork solutions or problems not truly getting resolved.

But Anne Morriss offers a different framework. In this episode, she outlines a five-step process for solving any problem and explains why starting with trust and ending with speed is so important for effective change leadership. As she says, “Let’s get into dialogue with the people who are also impacted by the problem before we start running down the path of solving it.”

Morriss is an entrepreneur and leadership coach. She’s also the coauthor of the book, Move Fast and Fix Things: The Trusted Leader’s Guide to Solving Hard Problems .

Key episode topics include: strategy, decision making and problem solving, strategy execution, managing people, collaboration and teams, trustworthiness, organizational culture, change leadership, problem solving, leadership.

HBR On Strategy curates the best case studies and conversations with the world’s top business and management experts, to help you unlock new ways of doing business. New episodes every week.

• Listen to the full HBR IdeaCast episode: How to Solve Tough Problems Better and Faster (2023)
• Find more episodes of HBR IdeaCast
• Discover 100 years of Harvard Business Review articles, case studies, podcasts, and more at HBR.org .

HANNAH BATES: Welcome to HBR On Strategy , case studies and conversations with the world’s top business and management experts, hand-selected to help you unlock new ways of doing business.

When it comes to solving complicated problems, many leaders only focus on the most apparent issues. Unfortunately that often leads to patchwork or partial solutions. But Anne Morriss offers a different framework that aims to truly tackle big problems by first leaning into trust and then focusing on speed.

Morriss is an entrepreneur and leadership coach. She’s also the co-author of the book, Move Fast and Fix Things: The Trusted Leader’s Guide to Solving Hard Problems . In this episode, she outlines a five-step process for solving any problem. Some, she says, can be solved in a week, while others take much longer. She also explains why starting with trust and ending with speed is so important for effective change leadership.

This episode originally aired on HBR IdeaCast in October 2023. Here it is.

CURT NICKISCH: Welcome to the HBR IdeaCast from Harvard Business Review. I’m Curt Nickisch.

Problems can be intimidating. Sure, some problems are fun to dig into. You roll up your sleeves, you just take care of them; but others, well, they’re complicated. Sometimes it’s hard to wrap your brain around a problem, much less fix it.

And that’s especially true for leaders in organizations where problems are often layered and complex. They sometimes demand technical, financial, or interpersonal knowledge to fix. And whether it’s avoidance on the leaders’ part or just the perception that a problem is systemic or even intractable, problems find a way to endure, to keep going, to keep being a problem that everyone tries to work around or just puts up with.

But today’s guest says that just compounds it and makes the problem harder to fix. Instead, she says, speed and momentum are key to overcoming a problem.

Anne Morriss is an entrepreneur, leadership coach and founder of the Leadership Consortium and with Harvard Business School Professor Francis Frei, she wrote the new book, Move Fast and Fix Things: The Trusted Leaders Guide to Solving Hard Problems . Anne, welcome back to the show.

ANNE MORRISS: Curt, thank you so much for having me.

CURT NICKISCH: So, to generate momentum at an organization, you say that you really need speed and trust. We’ll get into those essential ingredients some more, but why are those two essential?

ANNE MORRISS: Yeah. Well, the essential pattern that we observed was that the most effective change leaders out there were building trust and speed, and it didn’t seem to be a well-known observation. We all know the phrase, “Move fast and break things,” but the people who were really getting it right were moving fast and fixing things, and that was really our jumping off point. So when we dug into the pattern, what we observed was they were building trust first and then speed. This foundation of trust was what allowed them to fix more things and break fewer.

CURT NICKISCH: Trust sounds like a slow thing, right? If you talk about building trust, that is something that takes interactions, it takes communication, it takes experiences. Does that run counter to the speed idea?

ANNE MORRISS: Yeah. Well, this issue of trust is something we’ve been looking at for over a decade. One of the headlines in our research is it’s actually something we’re building and rebuilding and breaking all the time. And so instead of being this precious, almost farbege egg, it’s this thing that is constantly in motion and this thing that we can really impact when we’re deliberate about our choices and have some self-awareness around where it’s breaking down and how it’s breaking down.

CURT NICKISCH: You said break trust in there, which is intriguing, right? That you may have to break trust to build trust. Can you explain that a little?

ANNE MORRISS:  Yeah, well, I’ll clarify. It’s not that you have to break it in order to build it. It’s just that we all do it some of the time. Most of us are trusted most of the time. Most of your listeners I imagine are trusted most of the time, but all of us have a pattern where we break trust or where we don’t build as much as could be possible.

CURT NICKISCH: I want to talk about speed, this other essential ingredient that’s so intriguing, right? Because you think about solving hard problems as something that just takes a lot of time and thinking and coordination and planning and designing. Explain what you mean by it? And also, just  how we maybe approach problems wrong by taking them on too slowly?

ANNE MORRISS: Well, Curt, no one has ever said to us, “I wish I had taken longer and done less.” We hear the opposite all the time, by the way. So what we really set out to do was to create a playbook that anyone can use to take less time to do more of the things that are going to make your teams and organizations stronger.

And the way we set up the book is okay, it’s really a five step process. Speed is the last step. It’s the payoff for the hard work you’re going to do to figure out your problem, build or rebuild trust, expand the team in thoughtful and strategic ways, and then tell a real and compelling story about the change you’re leading.

Only then do you get to go fast, but that’s an essential part of the process, and we find that either people under emphasize it or speed has gotten a bad name in this world of moving fast and breaking things. And part of our mission for sure was to rehabilitate speed’s reputation because it is an essential part of the change leader’s equation. It can be the difference between good intentions and getting anything done at all.

CURT NICKISCH: You know, the fact that nobody ever tells you, “I wish we had done less and taken more time.” I think we all feel that, right? Sometimes we do something and then realize, “Oh, that wasn’t that hard and why did it take me so long to do it? And I wish I’d done this a long time ago.” Is it ever possible to solve a problem too quickly?

ANNE MORRISS: Absolutely. And we see that all the time too. What we push people to do in those scenarios is really take a look at the underlying issue because in most cases, the solution is not to take your foot off the accelerator per se and slow down. The solution is to get into the underlying problem. So if it’s burnout or a strategic disconnect between what you’re building and the marketplace you’re serving, what we find is the anxiety that people attach to speed or the frustration people attach to speed is often misplaced.

CURT NICKISCH: What is a good timeline to think about solving a problem then? Because if we by default take too long or else jump ahead and we don’t fix it right, what’s a good target time to have in your mind for how long solving a problem should take?

ANNE MORRISS: Yeah. Well, we’re playful in the book and talking about the idea that many problems can be solved in a week. We set the book up five chapters. They’re titled Monday, Tuesday, Wednesday, Thursday, Friday, and we’re definitely having fun with that. And yet, if you count the hours in a week, there are a lot of them. Many of our problems, if you were to spend a focused 40 hours of effort on a problem, you’re going to get pretty far.

But our main message is, listen, of course it’s going to depend on the nature of the problem, and you’re going to take weeks and maybe even some cases months to get to the other side. What we don’t want you to do is take years, which tends to be our default timeline for solving hard problems.

CURT NICKISCH: So you say to start with identifying the problem that’s holding you back, seems kind of obvious. But where do companies go right and wrong with this first step of just identifying the problem that’s holding you back?

ANNE MORRISS: And our goal is that all of these are going to feel obvious in retrospect. The problem is we skip over a lot of these steps and this is why we wanted to underline them. So this one is really rooted in our observation and I think the pattern of our species that we tend to be overconfident in the quality of our thoughts, particularly when it comes to diagnosing problems.

And so we want to invite you to start in a very humble and curious place, which tends not to be our default mode when we’re showing up for work. We convince ourselves that we’re being paid for our judgment. That’s exactly what gets reinforced everywhere. And so we tend to counterintuitively, given what we just talked about, we tend to move too quickly through the diagnostic phase.

CURT NICKISCH: “I know what to do, that’s why you hired me.”

ANNE MORRISS: Exactly. “I know what to do. That’s why you hired me. I’ve seen this before. I have a plan. Follow me.” We get rewarded for the expression of confidence and clarity. And so what we’re inviting people to do here is actually pause and really lean into what are the root causes of the problem you’re seeing? What are some alternative explanations? Let’s get into dialogue with the people who are also impacted by the problem before we start running down the path of solving it.

CURT NICKISCH: So what do you recommend for this step, for getting to the root of the problem? What are questions you should ask? What’s the right thought process? What do you do on Monday of the week?

ANNE MORRISS: In our experience of doing this work, people tend to undervalue the power of conversation, particularly with other people in the organization. So we will often advocate putting together a team of problem solvers, make it a temporary team, really pull in people who have a particular perspective on the problem and create the space, make it as psychologically safe as you can for people to really, as Chris Argyris so beautifully articulated, discuss the undiscussable.

And so the conditions for that are going to look different in every organization depending on the problem, but if you can get a space where smart people who have direct experience of a problem are in a room and talking honestly with each other, you can make an extraordinary amount of progress, certainly in a day.

CURT NICKISCH: Yeah, that gets back to the trust piece.

ANNE MORRISS: Definitely.

CURT NICKISCH: How do you like to start that meeting, or how do you like to talk about it? I’m just curious what somebody on that team might hear in that meeting, just to get the sense that it’s psychologically safe, you can discuss the undiscussable and you’re also focusing on the identification part. What’s key to communicate there?

ANNE MORRISS: Yeah. Well, we sometimes encourage people to do a little bit of data gathering before those conversations. So the power of a quick anonymous survey around whatever problem you’re solving, but also be really thoughtful about the questions you’re going to ask in the moment. So a little bit of preparation can go a long way and a little bit of thoughtfulness about the power dynamic. So who’s going to walk in there with license to speak and who’s going to hold back? So being thoughtful about the agenda, about the questions you’re asking about the room, about the facilitation, and then courage is a very infectious emotion.

So if you can early on create the conditions for people to show up bravely in that conversation, then the chance that you’re going to get good information and that you’re going to walk out of that room with new insight in the problem that you didn’t have when you walked in is extraordinarily high.

CURT NICKISCH: Now, in those discussions, you may have people who have different perspectives on what the problem really is. They also bear different costs of addressing the problem or solving it. You talked about the power dynamic, but there’s also an unfairness dynamic of who’s going to actually have to do the work to take care of it, and I wonder how you create a culture in that meeting where it’s the most productive?

ANNE MORRISS: For sure, the burden of work is not going to be equitably distributed around the room. But I would say, Curt, the dynamic that we see most often is that people are deeply relieved that hard problems are being addressed. So it really can create, and more often than not in our experience, it does create this beautiful flywheel of action, creativity, optimism. Often when problems haven’t been addressed, there is a fair amount of anxiety in the organization, frustration, stagnation. And so credible movement towards action and progress is often the best antidote. So even if the plan isn’t super clear yet, if it’s credible, given who’s in the room and their decision rights and mandate, if there’s real momentum coming out of that to make progress, then that tends to be deeply energizing to people.

CURT NICKISCH: I wonder if there’s an organization that you’ve worked with that you could talk about how this rolled out and how this took shape?

ANNE MORRISS: When we started working with Uber, that was wrestling with some very public issues of culture and trust with a range of stakeholders internally, the organization, also external, that work really started with a campaign of listening and really trying to understand where trust was breaking down from the perspective of these stakeholders?

So whether it was female employees or regulators or riders who had safety concerns getting into the car with a stranger. This work, it starts with an honest internal dialogue, but often the problem has threads that go external. And so bringing that same commitment to curiosity and humility and dialogue to anyone who’s impacted by the problem is the fastest way to surface what’s really going on.

CURT NICKISCH: There’s a step in this process that you lay out and that’s communicating powerfully as a leader. So we’ve heard about listening and trust building, but now you’re talking about powerful communication. How do you do this and why is it maybe this step in the process rather than the first thing you do or the last thing you do?

ANNE MORRISS: So in our process, again, it’s the days of the week. On Monday you figured out the problem. Tuesday you really got into the sandbox in figuring out what a good enough plan is for building trust. Wednesday, step three, you made it better. You created an even better plan, bringing in new perspectives. Thursday, this fourth step is the day we’re saying you got to go get buy-in. You got to bring other people along. And again, this is a step where we see people often underinvest in the power and payoff of really executing it well.

CURT NICKISCH: How does that go wrong?

ANNE MORRISS: Yeah, people don’t know the why. Human behavior and the change in human behavior really depends on a strong why. It’s not just a selfish, “What’s in it for me?” Although that’s helpful, but where are we going? I may be invested in a status quo and I need to understand, okay, if you’re going to ask me to change, if you’re going to invite me into this uncomfortable place of doing things differently, why am I here? Help me understand it and articulate the way forward and language that not only I can understand, but also that’s going to be motivating to me.

CURT NICKISCH: And who on my team was part of this process and all that kind of stuff?

ANNE MORRISS: Oh, yeah. I may have some really important questions that may be in the way of my buy-in and commitment to this plan. So certainly creating a space where those questions can be addressed is essential. But what we found is that there is an architecture of a great change story, and it starts with honoring the past, honoring the starting place. Sometimes we’re so excited about the change and animated about the change that what has happened before or what is even happening in the present tense is low on our list of priorities.

Or we want to label it bad, because that’s the way we’ve thought about the change, but really pausing and honoring what came before you and all the reasonable decisions that led up to it, I think can be really helpful to getting people emotionally where you want them to be willing to be guided by you. Going back to Uber, when Dara Khosrowshahi came in.

CURT NICKISCH: This is the new CEO.

ANNE MORRISS: The new CEO.

CURT NICKISCH: Replaced Travis Kalanick, the founder and first CEO, yeah.

ANNE MORRISS: Yeah, and had his first all-hands meeting. One of his key messages, and this is a quote, was that he was going to retain the edge that had made Uber, “A force of nature.” And in that meeting, the crowd went wild because this is also a company that had been beaten up publicly for months and months and months, and it was a really powerful choice. And his predecessor, Travis was in the room, and he also honored Travis’ incredible work and investment in bringing the company to the place where it was.

And I would use words like grace to also describe those choices, but there’s also an incredible strategic value to naming the starting place for everybody in the room because in most cases, most people in that room played a role in getting to that starting place, and you’re acknowledging that.

CURT NICKISCH: You can call it grace. Somebody else might call it diplomatic or strategic. But yeah, I guess like it or not, it’s helpful to call out and honor the complexity of the way things have been done and also the change that’s happening.

ANNE MORRISS: Yeah, and the value. Sometimes honoring the past is also owning what didn’t work or what wasn’t working for stakeholders or segments of the employee team, and we see that around culture change. Sometimes you’ve got to acknowledge that it was not an equitable environment, but whatever the worker, everyone in that room is bringing that pass with them. So again, making it discussable and using it as the jumping off place is where we advise people to start.

Then you’ve earned the right to talk about the change mandate, which we suggest using clear and compelling language about the why. “This is what happened, this is where we are, this is the good and the bad of it, and here’s the case for change.”

And then the last part, which is to describe a rigorous and optimistic way forward. It’s a simple past, present, future arc, which will be familiar to human beings. We love stories as human beings. It’s among the most powerful currency we have to make sense of the world.

CURT NICKISCH: Yeah. Chronological is a pretty powerful order.

ANNE MORRISS: Right. But again, the change leaders we see really get it right, are investing an incredible amount of time into the storytelling part of their job. Ursula Burns, the Head of Xerox is famous for the months and years she spent on the road just telling the story of Xerox’s change, its pivot into services to everyone who would listen, and that was a huge part of her success.

CURT NICKISCH: So Friday or your fifth step, you end with empowering teams and removing roadblocks. That seems obvious, but it’s critical. Can you dig into that a little bit?

ANNE MORRISS: Yeah. Friday is the fun day. Friday’s the release of energy into the system. Again, you’ve now earned the right to go fast. You have a plan, you’re pretty confident it’s going to work. You’ve told the story of change the organization, and now you get to sprint. So this is about really executing with urgency, and it’s about a lot of the tactics of speed is where we focus in the book. So the tactics of empowerment, making tough strategic trade-offs so that your priorities are clear and clearly communicated, creating mechanisms to fast-track progress. At Etsy, CEO Josh Silverman, he labeled these projects ambulances. It’s an unfortunate metaphor, but it’s super memorable. These are the products that get to speed out in front of the other ones because the stakes are high and the clock is sticking.

CURT NICKISCH: You pull over and let it go by.

ANNE MORRISS: Yeah, exactly. And so we have to agree as an organization on how to do something like that. And so we see lots of great examples both in young organizations and big complex biotech companies with lots of regulatory guardrails have still found ways to do this gracefully.

And I think we end with this idea of conflict debt, which is a term we really love. Leanne Davey, who’s a team scholar and researcher, and anyone in a tech company will recognize the idea of tech debt, which is this weight the organization drags around until they resolve it. Conflict debt is a beautiful metaphor because it is this weight that we drag around and slows us down until we decide to clean it up and fix it. The organizations that are really getting speed right have figured out either formally or informally, how to create an environment where conflict and disagreements can be gracefully resolved.

CURT NICKISCH: Well, let’s talk about this speed more, right? Because I think this is one of those places that maybe people go wrong or take too long, and then you lose the awareness of the problem, you lose that urgency. And then that also just makes it less effective, right? It’s not just about getting the problem solved as quickly as possible. It’s also just speed in some ways helps solve the problem.

ANNE MORRISS: Oh, yeah. It really is the difference between imagining the change you want to lead and really being able to bring it to life. Speed is the thing that unlocks your ability to lead change. It needs a foundation, and that’s what Monday through Thursday is all about, steps one through four, but the finish line is executing with urgency, and it’s that urgency that releases the system’s energy, that communicates your priorities, that creates the conditions for your team to make progress.

CURT NICKISCH: Moving fast is something that entrepreneurs and tech companies certainly understand, but there’s also this awareness that with big companies, the bigger the organization, the harder it is to turn the aircraft carrier around, right? Is speed relative when you get at those levels, or do you think this is something that any company should be able to apply equally?

ANNE MORRISS: We think this applies to any company. The culture really lives at the level of team. So we believe you can make a tremendous amount of progress even within your circle of control as a team leader. I want to bring some humility to this and careful of words like universal, but we do think there’s some universal truths here around the value of speed, and then some of the byproducts like keeping fantastic people. Your best people want to solve problems, they want to execute, they want to make progress and speed, and the ability to do that is going to be a variable in their own equation of whether they stay or they go somewhere else where they can have an impact.

CURT NICKISCH: Right. They want to accomplish something before they go or before they retire or finish something out. And if you’re able to just bring more things on the horizon and have it not feel like it’s going to be another two years to do something meaningful.

ANNE MORRISS: People – I mean, they want to make stuff happen and they want to be around the energy and the vitality of making things happen, which again, is also a super infectious phenomenon. One of the most important jobs of a leader, we believe, is to set the metabolic pace of their teams and organizations. And so what we really dig into on Friday is, well, what does that look like to speed something up? What are the tactics of that?

CURT NICKISCH: I wonder if that universal truth, that a body in motion stays in motion applies to organizations, right? If an organization in motion stays in motion, there is something to that.

ANNE MORRISS: Absolutely.

CURT NICKISCH: Do you have a favorite client story to share, just where you saw speed just become a bit of a flywheel or just a positive reinforcement loop for more positive change at the organization?

ANNE MORRISS: Yeah. We work with a fair number of organizations that are on fire. We do a fair amount of firefighting, but we also less dramatically do a lot of fire prevention. So we’re brought into organizations that are working well and want to get better, looking out on the horizon. That work is super gratifying, and there is always a component of, well, how do we speed this up?

What I love about that work is there’s often already a high foundation of trust, and so it’s, well, how do we maintain that foundation but move this flywheel, as you said, even faster? And it’s really energizing because often there’s a lot of pent-up energy that… There’s a lot of loyalty to the organization, but often it’s also frustration and pent-up energy. And so when that gets released, when good people get the opportunity to sprint for the first time in a little while, it’s incredibly energizing, not just for us, but for the whole organization.

CURT NICKISCH: Anne, this is great. I think finding a way to solve problems better but also faster is going to be really helpful. So thanks for coming on the show to talk about it.

ANNE MORRISS:  Oh, Curt, it was such a pleasure. This is my favorite conversation. I’m delighted to have it anytime.

HANNAH BATES: That was entrepreneur, leadership coach, and author Anne Morriss – in conversation with Curt Nickisch on HBR IdeaCast.

We’ll be back next Wednesday with another hand-picked conversation about business strategy from Harvard Business Review. If you found this episode helpful, share it with your friends and colleagues, and follow our show on Apple Podcasts, Spotify, or wherever you get your podcasts. While you’re there, be sure to leave us a review.

When you’re ready for more podcasts, articles, case studies, books, and videos with the world’s top business and management experts, you’ll find it all at HBR.org.

This episode was produced by Mary Dooe, Anne Saini, and me, Hannah Bates. Ian Fox is our editor. Special thanks to Rob Eckhardt, Maureen Hoch, Erica Truxler, Ramsey Khabbaz, Nicole Smith, Anne Bartholomew, and you – our listener. See you next week.

• Subscribe On:

Latest in this series

This article is about strategy.

• Decision making and problem solving
• Strategy execution
• Leadership and managing people
• Collaboration and teams
• Trustworthiness
• Organizational culture

Partner Center