problem solving with mean median mode and range

How to Find Mean, Mean, Mode and Range: Your Complete Guide

August 25, 2021 by Anthony Persico

Central Tendency: Mean, Median, Mode, and Range

Welcome to this complete step-by-step guide to central tendency and how to find the mean, median, and mode of a data set.

This post will share key information, formulas, and vocabulary so that you can use math to determine the mean, median, mode, and range of any data set and understand what these values represent.

After working through two examples, you will also have access to a free mean, median, and mode pdf practice worksheet that includes an answer key.

Key Questions

Now let’s go ahead and begin this lesson by raising two key questions:

For a given set of data…

What does the mean, median, mode, and range represent?

How can you find the mean, median, mode, and range of a data set?

What is Central Tendency?

Mean, median, and mode are measures of central tendency and are three different ways of expressing averages of a set of data.

The key term here is average . In math, central tendency is a number or value that can be used to describe a central position, or average value, within a data set.

Furthermore, the range of a set of data is the difference between the highest and lowest values.

With this key math vocabulary in mind, let’s take a look at two examples

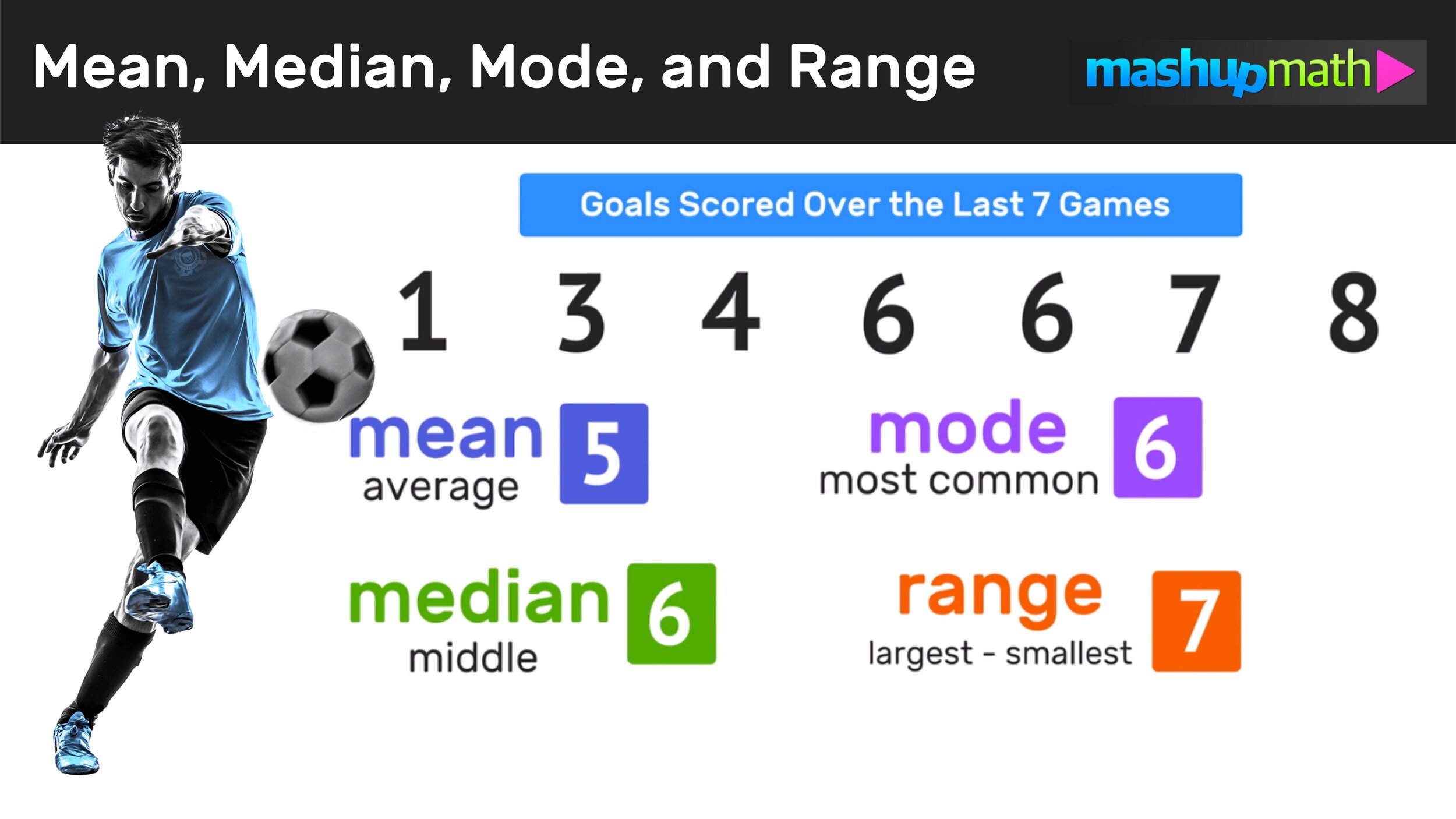
Example 01: Find the Mean, Median Mode, and Range

Find the mean, median, mode and range of the data set: 1, 6, 7, 4, 6, 8, 3

*Before you find the mean, median, mode, and range of a data set, be sure to rewrite the list of values in either ascending (least to greatest) or descending (greatest to least) form.

For today’s examples, we will be rearranging the original data set into ascending form where the values are placed in order from least to greatest as follows:

Now that we have rearranged the values of the data set in ascending order, we are ready to find values of central tendency.

Step 01: Find the Mean

how to find the mean of a data set.

The mean is the numerical average of a data set.

To determine the mean of the data set, divide the total sum by the total amount of numbers.

In this example, to find the total sum, add all seven values in the data set together as follows:

1 + 3 + 4 + 6 + 6 + 7 + 8 = 35

The total sum is 35.

Next, divide the total sum by the total amount of numbers in the data set (which, in this example is 7).

35/7 =5 >>> The mean is 5 goals per game.

Mean Formula

For future reference, here is a handy formula that you can always use to find the mean of a data set. To determine the mean, simply divide the total sum of all of the values in the data set by the total number of values as follows:

Step 02: Find the Median

The median is the middle number or value of a data set.

To determine the median of numbers in the data set, simply find the middle value.

In this example, notice that there is an odd number of values in the data set (7 total). To find the median of numbers, start crossing the “bookend values” on each side of the data set as you make your way towards the middle until only one value remains as follows…

Clearly, the middle value is 6, so you can conclude that the median of the data set is equal to 6.

*Note that when there is an even number of values in the data set, using this strategy to find the median will require one extra step (we will go more in depth in example 2).

Median Calculator

Looking for a quick way to central tendency values? This median calculator (which is really a mean, median, mode calculator from Calculator Soup ) is an excellent tool for quickly finding these values. However, this website should only be used a tool for checking your work and not a substitute for understanding how to actually find the mean, median, mode, and range of a data set.

Step 03: Find the Mode

The mode of a data set is the most common number. It is possible to have more than one mode, or no mode at all.

If you’re looking for a simple answer to how to find the mode of a data set, then you’re in the right place. To find the mode, simply look for the value that occurs the most often (i.e. the value that repeats more than any other value).

In this example, notice that the only value that repeats is 6…

Therefore, you can conclude that the mode for this data set is 6 .

How to find the mode of a data set…

Just like in example 01, you can find the mode of a data set by determining which value is the most common. You can find this value by looking for numbers that repeat.

And remember that it is possible to have more than one mode or no mode at all!

Step 04: Find the Range

The range is the difference between the highest and lowest values in the data set (the largest number minus the smallest number).

To calculate range math, simply determine the largest and smallest values and then find the difference by subtracting (rearranging the numbers in ascending order at the very start of this example males calculating the range very easy).

In this example, the largest number in the data set is 8 and the smallest number in the data set is 1.

To find the range, simply perform 8 – 1 = 7

Therefore, the range is 7 goals.

Quick Summary:

And now we have found all values of central tendency for this example. Here is a quick summary of what you just did!

Keep in mind that the process for determining mean, median, mode, and range of any data set is pretty much always the same. So, now let’s try a second example that involves a larger data set!

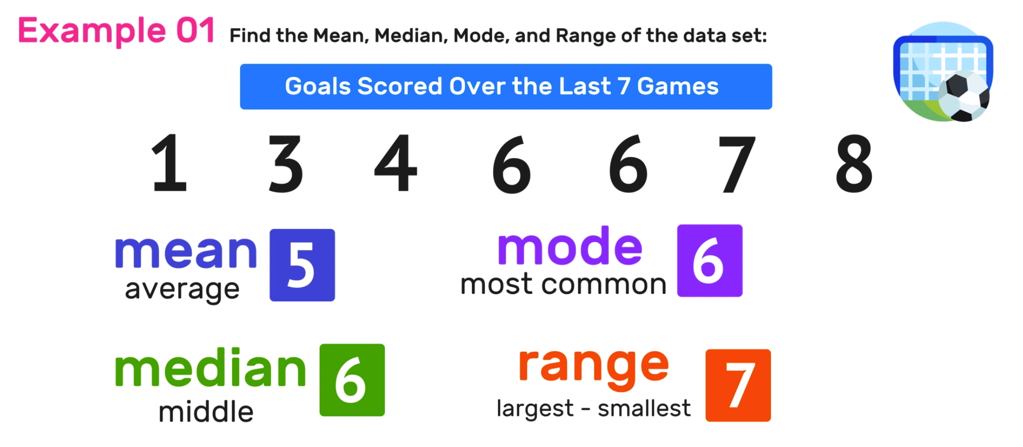
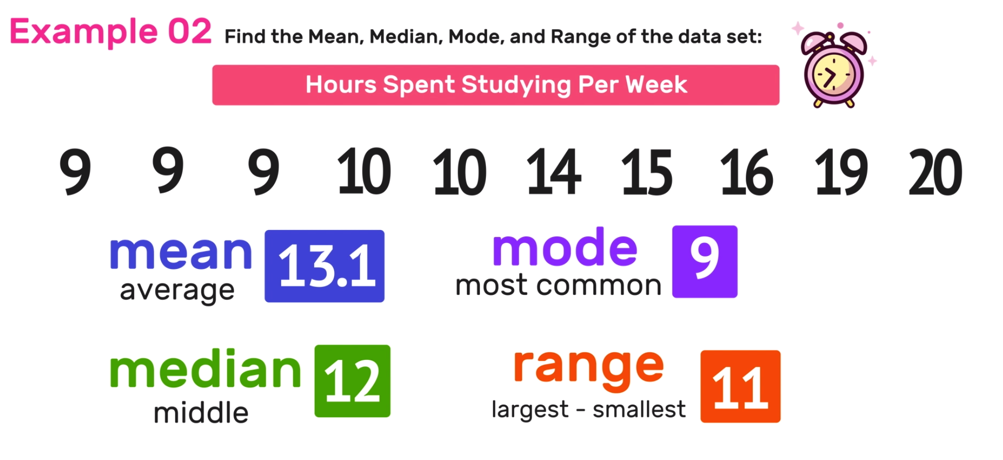
Example 02: Find the Mean, Median Mode, and Range

Find the mean, median, mode and range of the data set: 15, 9, 16, 9, 20, 14, 10, 9, 10, 9

Again, just like in Example 01, start by rearranging the numbers in the data set so that they are in ascending order from left to right…

*Note that the values in the data set have not changed. All that you did was rewrite them in order from least to greatest, which will make finding the mean, median, mode, and range much easier for you (with or without a calculator).

Now you are ready to find the mean, median, mode, and range of this data set.

Step 01: Determine the Mean

To find the mean of the data set, remember to apply the mean formula, where you find the total sum of all of the numbers and divide it by the total number of values in the data set.

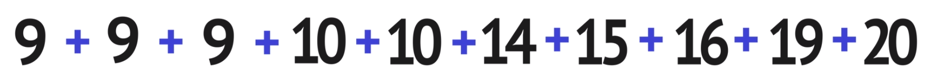
In this case…

9 + 9 + 9 + 10 + 10 + 14 +15 + 16 + 19 + 20 = 131 (the total sum)

and there are 10 total numbers.

131/10 =13.1 >>> The mean is 13.1 hours studying

*Note that it will often be the case that the mean value is decimal.

Remember that the median represents the middle value of a data set.

To determine the median of numbers in the data set, you perform the same process of crossing out the “bookend values” on the left and right of the data set until you reach the middle. Unlike the last example where the data set had an odd number of values, this data set has an even number of values (ten in total), which means that there will one be extra step involved to find the median.

After crossing out the outside values and working your way to the middle, you will notice that, because the data set has an even number of values, there are two values in the middle (in this case, 10 and 14).

So, which value is the median?

In cases like this, the median is the average of the two values . To find the average, simply add the two values together and divide the sum by two as follows:

10+ 14 = 24 >>> 24/2 =12

The median of the data set is 12 hours.

Remember that the mode of any data set is the most common number and that the key to finding the mode is to look for repeat values.

Notice that this data set has two values that occur more than once: 9 and 10. In this case, 9 shows up three times and 10 shows up twice. Since 9 shows up more often than 10, you can conclude that 9 is the most common number in the data set and that the mode is 9.

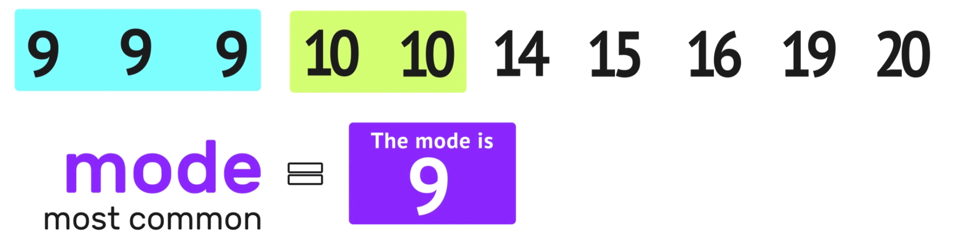
Step 04: Find the Range Math

The last remaining measure of central tendency that you must find is the range, which is the difference between the largest number and the smallest number.

To calculate range for this example, look at the data set and identify the largest value (20) and the smallest value (9) and then find the difference as follows

20 -9 = 11 >>> The range of the data set is 11.

Example 02 Conclusion

You can click the link below to watch the animated video that accompanies this lesson.

Have thoughts? Share your thoughts in the comments section below!

(Never miss a Mashup Math blog--click here to get our weekly newsletter!)

Mean Median Mode Range Worksheets and Help

Welcome to the Math Salamanders Mean Median Mode Range Worksheets. Here you will find a wide range of free printable Worksheets, which will help your child learn how to find the mean, median, mode and range of a set of data points.

These worksheets are aimed at students in 5th and 6th grade.

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

Mean Median Mode Range Quicklinks

Quicklinks to ...

Median Help

Mean Median Mode Range Worksheets

Mean Median Mode Range Online Quiz
More related Math resources

What is the Mean?

The mean is the average of a set of numbers.

It is found by adding up the set of numbers and then dividing the total by the number of data points in the set.

How to find the mean

Step 1) Add up all the numbers in the set.

Step 2) Divide the total by the total number of data points in the set.

Example 1) Find the mean of 5, 7, 8 and 4

Step 1) Add up the numbers to give a total of 5+7+8+4=24

Step 2) Divide the total by the number of data points. 24 ÷ 4 = 6

Answer: the mean is 6.

Example 2) Find the mean of 8, 2, 5, 7 and 13

Step 1) Add up the numbers to give a total of 8+2+5+7+13=35

Step 2) Divide by the number of data points. 35 ÷ 5 = 7

Answer: the mean is 7.

What is the Median?

The median is the midpoint (or middle value) of a set of numbers.

It is found by ordering the set of numbers and then finding the middle value in the set.

How to find the median

Step 1) Order the numbers in the set from smallest to largest.

Step 2) Find the middle number.

- If there is an odd number of values in the set, then the median is the middle value.

- If there is an even number of values in the set, then the median is the average of the two middle values.

Example 1) Find the median of 5, 7, 8, 2 and 4

Step 1) Put the numbers in order: 2, 4, 5, 7, 8

Step 2) There is an odd number of values in the set so the median is the middle value which is 5.

Answer: the median is 5.

Example 2) Find the median of 23, 27, 16, 31

Step 1) Put the numbers in order: 16, 23, 27, 31

Step 2) There is an even number of values in the set, so the median is the average of the middle two values.

(23+27) ÷ 2 = 25

Answer: the mean is 25

Example 3) Find the median of 7, -4, 9, -7, -2, 5

Step 1) Order the numbers: -7, -4, -2, 5, 7, 9

To get the average, simply add the two values together and divide by 2:

(-2 + 5) ÷ 2 = 1.5

Answer: the mean is 1.5

What is the Mode?

The mode is the most common (or the data point that appears most often) in a set of data.

It can be found by putting the data into an ordered list and seeing which data point occurs most often.

How to find the mode

Step 1) Put the data into an ordered list.

Step 2) Check that you have got the same number of data points.

Step 3) The mode is the data point which is the most common.

Finding the Mode Examples

Example 1) Find the mode of 3, 6, 4, 3, 2, 4, 7, 8, 6, 3, 9

This gives us: 2, 3, 3, 3, 4, 4, 6, 6, 7, 8, 9

Step 2) Check the number of data points in both lists is the same.

Both lists have 11 data points.

Step 3) The mode is the number which occurs most often.

Answer: the mode is 3.

Example 2) Find the mode of 0.6, 0.3, 0.4, 0.2, 0.4, 0.7, 0.6, 0.1, 0.4, 0.9

This gives us: 0.1, 0.2, 0.3, 0.4, 0.4, 0.4, 0.6, 0.6, 0.7, 0.9

Both lists have 10 data points.

Answer: the mode is 0.4.

What is the Range?

The range is the gap between the smallest and largest data point.

It is found by putting the data into an ordered list and find the difference between the largest and smallest amount.

How to find the range

Step 3) The range is the difference between the largest and smallest data point.

To find the range simply subtract the smallest number from the largest number.

Finding the Range Examples

Example 1) Find the range of 14, 21, 9, 32, 27, 15, 12, 30

This gives us: 9, 12, 14, 15, 21, 27, 30, 32

Both lists have 8 data points.

Step 3) The range is the difference or gap between the largest and smallest numbers.

Answer: the range is 32-9=23.

Example 2) Find the range of 6, 2, -7, 2, -5, 11, 3, -4, 0, 9

This gives us: -7, -5, -4, 0, 2, 2, 3, 6, 9, 11

Answer: the range is 11-(-7)=18.

These printable mean median mode range worksheets have been carefully graded to ensure a progression in the level of difficulty.

Sheets 1, 2 and 3 are designed for 5th graders involve ordering and calculating using positive integers and decimals.

Sheets 4, 5 and 6 are designed for 6th graders and involve ordering and calculating with positive and negative numbers and decimals.

The first sheet involve finding the mean, median, mode and range of some positive whole numbers.

The 2nd sheet involves the use of decimals to 1dp.

The 3rd sheet is similar to the 2nd sheet but has many more data points.

The 4th sheet involves decimals and negative numbers.

The 5th and 6th sheets are similar to the 4th sheets but with increased number of data points.

Mean Median Mode and Range Sheet 1
PDF version
Median Mean Mode and Range Sheet 2
Median Mean Mode and Range Sheet 3
Median Mean Mode and Range Sheet 4
Median Mean Mode and Range Sheet 5
Median Mean Mode and Range Sheet 6

Mean Median Mode Range Problems

These printable mean median mode range problem sheets will help your child to use and apply their skills to solve problems.

The first problem sheet is more suitable for 5th grade and the second sheet is aimed at 6th graders.

Median Mean Mode and Range Problems 1
Median Mean Mode and Range Problems 2

Mean Median Mode Range Walkthrough Video

This short video walkthrough shows the problems from our Median Mean Mode and Range Problems Sheet 2 being solved and has been produced by the West Explains Best math channel.

If you would like some support in solving the problems on these sheets, check out the video!

More Recommended Math Worksheets

Take a look at some more of our worksheets similar to these.

Mean Worksheets

The sheets in this section will help you to find the mean of a range of numbers, including negative numbers and decimals.

There are a range of sheets involving finding the mean, and also finding a missing data point when the mean is given.

Median Worksheets

The sheets in this section will help you to find the median of a range of numbers, including negative numbers and decimals.

On some of the easier sheets, only odd numbers of data points have been used.

On the harder sheets, both odd and even numbers of data points have been included.

Mode and Range Worksheets

The sheets in this section will help you to find the mode and range of a set of numbers, including negative numbers and decimals.

There are easier sheets involving fewer data points, and harder ones with more data points.

The sheets in this section will help you to solve problems involving bar graphs and picture graphs.

There are a range of sheet involving reading and interpreting graphs as well as drawing your own graphs.

Box Plot Worksheets

Here are our selection of box plot worksheets to help you practice creating and interpreting box plots.

Mean, Median, Mode and Range Online Quiz

Our quizzes have been created using Google Forms.

At the end of the quiz, you will get the chance to see your results by clicking 'See Score'.

This will take you to a new webpage where your results will be shown. You can print a copy of your results from this page, either as a pdf or as a paper copy.

For incorrect responses, we have added some helpful learning points to explain which answer was correct and why.

We do not collect any personal data from our quizzes, except in the 'First Name' and 'Group/Class' fields which are both optional and only used for teachers to identify students within their educational setting.

We also collect the results from the quizzes which we use to help us to develop our resources and give us insight into future resources to create.

For more information on the information we collect, please take a look at our Privacy Policy

We would be grateful for any feedback on our quizzes, please let us know using our Contact Us link, or use the Facebook Comments form at the bottom of the page.

This quick quiz tests your knowledge and skill at finding and using the mean, median, mode and range of a set of data.

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

$math salamanders news image$

Newsletter Signup

Return to 6th Grade Math Worksheets

Return to Statistics Hub page

Return from Mean Median Mode Range to Math Salamanders Homepage

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Negative numbers

Averages & range

Mean median mode

Mean, Median, Mode

Here you will learn about the measures of central tendency, which is the mean, median and mode of data sets, including what they are and how to find them.

Students first learn about measures of central tendency in the 6 th grade and expand this knowledge as they move through middle school and high school statistics.

What is mean median mode?

The mean, median and mode are different measures of center of a numerical data set. They are a way of summarizing a data set with a single number.

The mean is the average of a numerical data set.

To calculate the mean, find the total of the values and divide the total by the number of values .

The “number of values” is sometimes referred to as the “number of numbers”.

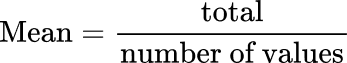
Let’s find the mean of this data set.

The mean is 4.57 (rounded to 2 decimal places)

The median is the middle number of a numerical data set.

To find the median, we need to arrange the values in numerical order, from the smallest value to the highest value, and find the middle value .

The middle value is the median value.

Let’s find the median of the same data set.

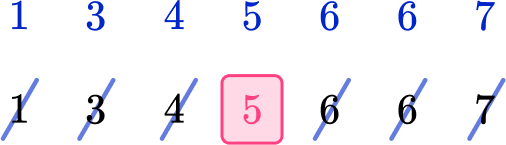
The median is 5 because it is the middle number of data points.

The mode is the most common number. To find the mode, we need to find the value in the data set that occurs the most number of times.

Let’s find the mode of the data set.

The number that occurs the most or is most frequent is 6.

The mode is 6.

[FREE] Mean, Median, and Mode Worksheet (Grade 6)

Use this quiz to check your 6th grade students’ understanding of mean, median, and mode. 10+ questions with answers covering a range of 6th grade topics on mean, median, and mode to identify areas of strength and support!

The range is the difference between the greatest value and the least value of a data set. It is a measure of variability not a measure of center.

Let’s find the range of the data set.

The range is 6.

Common Core State Standards

How does this apply to 6 th grade math?

Grade 6 – Statistics and Probability 6.SP.A.3 Recognize that a measure of center for a numerical data set summarizes all of its values with a single number, while a measure of variation describes how its values vary with a single number.
Grade 6 – Statistics and Probability 6.SP.A2 Understand that a set of data collected to answer a statistical question has a distribution which can be described by its center, spread, and overall shape.
Grade 6 – Statistics and Probability 6.SP.B.5c Giving quantitative measures of center (median and/or mean) and variability (interquartile range and/or mean absolute deviation), as well as describing any overall pattern and any striking deviations from the overall pattern with reference to the context in which the data were gathered.

How to find the mean median mode

In order to find the mean, median or mode:

List the numbers in order from least to greatest.

To find the mean, find the total of the numbers in the data set and divide by the number of values in the data set.

To find the median, find value(s) in the middle of the data set.

To find the mode, look for the value(s) that occur the most; there may be more than one mode.

To find the range, find the difference between the largest value and the smallest value.

Mean median mode examples

Example 1: finding the mode.

Find the mode for the given data set.

List the numbers in order from least to greatest.

4 To find the mode, look for the value(s) that occur the most; there may be more than one mode.

7 occurs the most, so the mode is 7.

Example 2: finding the median

Find the median for the given data set.

List the numbers in order from least to greatest

To find the median, find values in the middle of the data set.

The value in the middle is 9. The median is 9.

Example 3: finding the median

Find the median of the given data set.

Find the middle of the data set. There is an even number of values, so we have a middle pair. To find the median, find the average of the two middle numbers or the midpoint of 4 and 6.

The average of 4 and 6 or the midpoint between 4 and 6 is 5. So, the median is 5.

Example 4: finding the mean

Find the mean of the given data set.

Although not necessary, it can be helpful to put the values in order.

To find mean, find the total of the numbers in the data set and divide by the number of values in the data set.

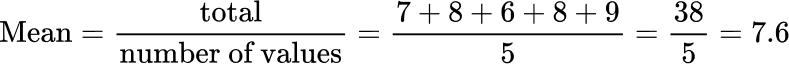
The mean is 7.6.

Example 5: finding the mean, median, and mode

Find the mean, median, and mode of the data set.

The mean is 13.

There are an even number of data points in the data set, so there are two values in the middle, 12 and 13. To find the median, find the average of the two numbers of the midpoint.

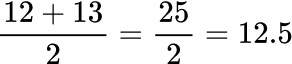
The median is 12.5.

12 is the value that occurs the most which means it is the mode.

Example 6: finding the mean, median, mode, and range

The mean is 4.875.

There are an even amount of values in the data set, 4 and 6 are in the middle. To find the median find the average of 4 and 6 or find the midpoint of 4 and 6.

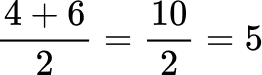
The median is 5.

3 and 6 both occur twice, so there are two modes, 3 and 6. Since there are two modes, the data is bimodal.

The modes are 3 and 6.

Teaching tips for mean, median, mode

Incorporate project based data science learning activities where students have opportunity to collect their own data, as well as do data analysis/statistical analysis on the collected data.
Although worksheets and paper-based quizzes have their place, consider alternate forms of formative assessments that engage students to gain a global perspective by having them summarize data in real time with real world data points.

Easy mistakes to make

Mixing up the measures of center For example, if a student is asked to find the median and they find the mean.
Listing the numbers in descending order instead of ascending order When summarizing data, the best way to list the data is in ascending order (from least to greatest) not descending order (greatest to least).

10, \, 8, \, 5, \, 5, \, 6, \, 7, \, 5, \, 11, \, 4, \, 9, \, 3

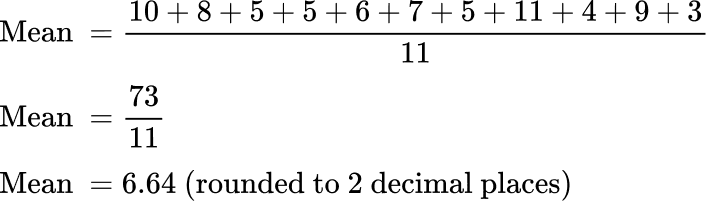
Related averages and range lessons

Averages and range
Range in math
Mean in math
Mode in math

Practice mean median mode questions

1. Find the mode of the given data set.

The value that occurs the most in the data set is 18. The other numbers only occur once.

2. Find the mode of the given data set.

The most common values are 19 and 23. These two values occur twice within the data set. The other values only occur once.

3. Find the median of the given data set.

Put the numbers in order from the smallest number to largest number. Then find the middle value.

The middle value is 17, so this is the median.

4. Find the median of the given data set.

Put the numbers in order from the smallest to largest. Then find the middle value.

The middle pairs of values are 35 and 37. The average of these is 36. The median is 36.

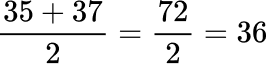
5. Find the mean of the given data set.

To find the mean, add up all the values in the data set and divide by the number of values in the data set.

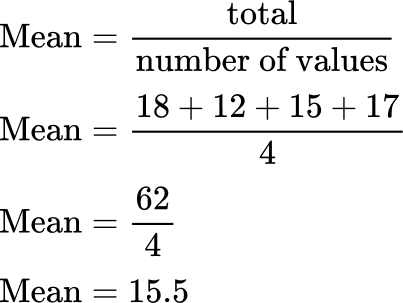
6. Find the mean, median, mode, and range for the given data set (round to two decimal places when necessary).

Mean = 6.23, Median = 7.2, Mode = 7.2, Range = 7.9

Mean = 6, Median = 6.2, Mode = 7.2, Range = 8

Mean = 7, Median = 7.2, Mode = 7.2, Range = 7

Mean = 6.2, Median = 7, Mode = 7, Range = 7.2

The value in the middle is 7.2.

The median is 7.2.

The value that occurs the most is 7.2. The mode is 7.2.

Range = 9.1-1.2 = 7.9

Range = 7.9

Mean, median, mode FAQs

Yes, data sets can be made up of whole numbers (odd numbers and even numbers), integers, decimals, and fractions.

The arithmetic mean is the mean (average value) where you add all the values and divide by the number of values in the set of data.

An outlier is an extremely high or low data point in relation to the rest of the set of numbers in the data set.

The geometric mean is the square root of a product of two numbers.

The standard deviation is a statistical measure that measures the dispersion of data points relative to the mean.

Descriptive statistics is a method of summarizing data. Measures of central tendency are descriptive statistics.

The next lessons are

Frequency table
Representing data
Frequency graph
Cumulative frequency

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

$One on one math tuition$

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

8.3 Mean, Median and Mode

Learning objectives.

After completing this section, you should be able to:

Calculate the mode of a dataset.
Calculate the median of a dataset.
Calculate the mean of a dataset.
Contrast measures of central tendency to identify the most representative average.
Solve application problems involving mean, median, and mode.

What exactly do we mean when we describe something as "average"? Is the height of an average person the height that more people share than any other? What if we line up every person in the world, in order from shortest to tallest, and find the person right in the middle: Is that person’s height the average? Or maybe it’s something more complicated.

Imagine a game where you and a friend are trying to guess the typical person’s height. Once the guesses are made, you bring in every person and measure their height. You and your friend figure out how far off each of your guesses were from the actual value, then square that number. The result is the number of points you earn for that person. After we check every height and award points accordingly, the person with the lower score wins (because a lower score means that person’s guess was, overall, closer to the actual values). Could we define the average height to be the number that you should guess to give you the smallest possible score?

Each of these three methods of determining the “average” is commonly used. They are all methods of measuring centrality (or central tendency ). Centrality is just a word that describes the middle of a set of data. All give potentially different results, and all are useful for different reasons. In this section, we’ll explore each of these methods of finding the “average.”

In our discussion of average heights, the first possible definition we offered was the height that more people share than any other. This is the mode , or the value that appears most often. If there are two modes, the data are bimodal .

Let’s look at some examples.

Example 8.15

Finding the mode using a stem-and-leaf plot.

In Example 8.9 , we looked at a stem-and-leaf plot of the sale prices (in dollars) of a particular collectible trading card:

What is the mode price?

The mode is the price that appears most often. Both 15 and 20 appear 4 times, more than any other values. So, they are the modes (and we can conclude that this set of data is bimodal).

Your Turn 8.15

When we have a complete list of the data or a stem-and-leaf plot, it’s pretty straightforward to find the mode; we just need to find the number that appears most often. If we’re given a frequency distribution instead, the technique is different (but just as straightforward): we’re looking for the number with the highest frequency.

Example 8.16

Finding the mode using a frequency distribution.

In Example 8.3 , we created a frequency distribution of the number of siblings of conflict resolution class attendees.

What is the mode of the number of siblings?

The mode is the value that appears the most often, which means it has the greatest frequency. Thirteen of the respondents have one sibling, more than any other number. So, the mode is 1.

Your Turn 8.16

What happens if there is no number in the data that appears more than once? In that case, by our definition, every data value is a mode. But according to some other definitions, the data would have no mode. In practice, though, it doesn’t really matter; if no data value appears more than once, then the mode is not helpful at all as a measure of centrality.

Let's revisit our example of trying to identify the height of the “average” person. If we lined everyone up in order by height and found the person right in the middle, that person’s height is called the median , or the value that is greater than no more than half and less than no more than half of the values.

Let’s look at a really simple example. Consider the following list of numbers: 11, 12, 13, 13, 14. Is the first number on the list, 11, the median? There are no values less than 11 (that’s 0%), and there are four values greater than 11 (that’s 80%). Since more than 50% of the data are greater than 11, the definition is violated; it’s not the median. Here’s a chart with the rest of the data, with red shading to show where the definition is violated:

Only 13 has no violations, so it’s the median according to the definition. In practice, we find the median just like we described in the average height example: by lining up all the data values in order from smallest to largest and picking the value in the middle. For our easy example (with data values 11, 12, 13, 13, 14), that first 13 is right in the middle; there are two values to the left and two values to the right. If there’s not one value right in the middle, we pick the two closest, then choose the number exactly between them. For example, let’s say we have the data 41, 44, 46, 53. Since there are an even number of data values in our list, we can’t pick the one right in the middle. The two closest to the middle are 44 and 46, so we’ll choose the number halfway between those to be the median: 45. As this example shows, the median (unlike the mode) doesn’t have to be a number in our original set of data.

In the examples we’ve looked at so far, it’s been pretty easy to identify which number is right in the middle. If we had a very large dataset, though, it might be harder. Fortunately, we have some formulas to help us with that.

Suppose we have a set of data with n n values, ordered from smallest to largest. If n n is odd, then the median is the data value at position n + 1 2 n + 1 2 . If n n is even, then we find the values at positions n 2 n 2 and n 2 + 1 n 2 + 1 . If those values are named a a and b b , then the median is defined to be a + b 2 a + b 2 .

Let’s put those formulas to work in an example.

Example 8.17

Finding the median using a stem-and-leaf plot.

In Example 8.9 , we looked at a stem-and-leaf plot that contained 33 sale prices (in dollars) of a particular collectible trading card:

What is the median price?

Step 1: Since 33 is odd, the median is the data value at position n + 1 2 n + 1 2 , where n n is the number of values in the dataset. There are 33 total values, so our formula becomes 33 + 1 2 = 17 33 + 1 2 = 17 . That means we want to look for the 17th number in the dataset.

Step 2: We'll want to count from the lowest value to the 17th number. We can use our stem and leaf plot to do this.

The seventeenth number is 20, so the median is 20.

Your Turn 8.17

Now, let’s tackle an example with an even number of values.

Example 8.18

Finding the median.

In Example 8.10 , we looked at the number of times different crickets (of differing species, genders, etc.) chirped in a one-minute span. That data is again provided below:

Find the median.

Step 1 : In order to find the median, we first need to sort the data so that they’re in order, smallest to largest:

Step 2 : Next, we figure out how many data values we have. Counting them up, we see there are 30, which is even.

Step 3 : Since we have an even number of data values, we need to find the values in positions 30 2 = 15 30 2 = 15 and 30 2 + 1 = 16 30 2 + 1 = 16 . These are 101 and 102.

Step 4 : We use the formula to compute the median: 101 + 102 2 = 101.5 101 + 102 2 = 101.5 .

Your Turn 8.18

Example 8.19, finding the median using a frequency distribution.

In Example 8.3 , we created a frequency distribution of the number of siblings of the people who attended a conflict resolution class. Let's review that data again:

What is the median of the number of siblings?

There are 30 data values total, so the median is between the 15th and 16th values in the ordered list. There are five 0s and thirteen 1s according to the frequency distribution, so items one through five are all 0s and items six through eighteen are all 1s. Since both items fifteen and sixteen are 1s, the median is 1.

Your Turn 8.19

Recall our example of ways we could identify the “average” height of an individual. The last method we discussed was also the most complicated. It involved a game where the player guesses a height, then figures out how far off that guess is from every single person’s height. Those differences get squared and added together to get a score. Our next measure of centrality gives the lowest possible score: No other guess would beat it in the game. Given a dataset containing n total values, the mean of the dataset is the sum of all the data values, divided by n .

This is a computation you have likely done before. In many places, including spreadsheet programs like Microsoft Excel and Google Sheets, this number is called the average . For statisticians, though, the word average has too many possible meanings, so they prefer the one we’ll use: mean.

Example 8.20

Finding the mean.

Compute the mean of the numbers 12, 15, 17, 18, 18, and 19.

The mean is the sum of the values, divided by the number of values on the list. So, we get:

Your Turn 8.20

Example 8.21, finding the mean using a frequency distribution.

Refer again to the frequency distribution of the number of siblings people who attended a conflict resolution class reported:

What is the mean of the number of siblings?

Step 1: We compute the mean by adding up all the data values and then dividing by the number of data values on the list.

Step 2: Adding up the frequencies, we get 5 + 13 + 6 + 3 + 2 + 1 = 30 5 + 13 + 6 + 3 + 2 + 1 = 30 data values in our list.

Step 3: Now, to find the sum of all the data values, we could simply reconstruct the raw data and add up all the numbers there. But, there’s an easier way: Remember that repeatedly adding a number to itself is the definition of multiplication. So, for example, since there are six 2s in our data, the sum of all those 2s must be 6 × 2 = 12 6 × 2 = 12 .

Step 4: Let’s add a column to our distribution for these products:

Step 5: So, the sum of all our data values is 0 + 13 + 12 + 9 + 8 + 5 = 47 0 + 13 + 12 + 9 + 8 + 5 = 47 . The mean is 47 30 ≈ 1.567 47 30 ≈ 1.567 .

Your Turn 8.21

As the number of data values we are considering grows, the computation for the mean gets more and more complicated. That’s why people generally trust technology to perform that computation.

Compute Measures of Centrality Using Google Sheets

Note that a recent update to Google Sheets introduced a new function called “MODE.MULT,” which will find every mode (not just the first one on the list).

Example 8.22

Using google sheets to compute measures of centrality.

The dataset "InState" contains the in-state tuitions of every college and university in the country that reported that data to the Department of Education. Find the mode, median, and mean of those in-state tuition values.

Step 1: To find the mode, we select an empty cell type “=MODE(”, click on the header of the column to insert a reference to the column into our formula, and then close the parentheses. When we hit the enter key, our formula is replaced with the mode: $13,380.

Step 2: We can find the median and mean using the same process, except using the functions “MEDIAN” and “AVERAGE” in place of “MODE”. We find that the median is $11,207 and the mean is $15,476.79.

Your Turn 8.22

Which is better: mode, median, or mean.

If the mode, median, and mean all purport to measure the same thing (centrality), why do we need all three? The answer is complicated, as each measure has its own strengths and weaknesses. The mode is simple to compute, but there may be more than one. Further, if no data value appears more than once, the mode is entirely unhelpful. As for the mean and median, the main difference between these two measures is how each is affected by extreme values.

Consider this example: the mean and median of 1, 2, 3, 4, 5 are both 3. But what if the dataset is instead 1, 2, 3, 4, 10? The median is still 3, but the mean is now 4. What this example shows is that the mean is sensitive to extreme values, while the median isn’t. This knowledge can help us decide which of the two is more relevant for a given dataset. If it is important that the really high or really low values are reflected in the measure of centrality, then the mean is the better option. If very high or low values are not important, however, then we should stick with the median.

The decision between mean and median only really matters if the data are skewed. If the data are symmetric, then the mean and median are going to be approximately equal, and the distinction between them is irrelevant. If the data are skewed, the mean gets pulled in the direction of the skew (i.e., if the data are right-skewed, then the mean will be bigger than the median; if the data are left-skewed, the opposite relation is true).

Example 8.23

Choosing which measure of centrality to use.

For the following situations, decide which measure(s) of centrality would be best:

You found a used car that you like, and you want to know if the price is too high or too low. You find a list of sale prices for that make and model, and you see that the distribution of those prices is skewed to the right. Some of the prices at the high end are close to the original sale price of the car, so you guess that those cars might have really low mileage, or have other enhancements added on that increased the value (but which don’t apply to the car you found).
You are asked to analyze the responses to a survey. One of the questions asked, “How strongly do you agree with the statement, ‘I believe my elected representatives have my best interests in mind when they vote’?” Responses are a number between 1 and 5, with 1 representing “strongly disagree” and 5 representing “strongly agree.”
You are asked to find the “average” household income for a zip code. Those values are skewed right.
Thinking back to the situation at the beginning of this section: you want to find “average” height. The data you’ve collected seem to be distributed symmetrically.
In this situation, the high values are not comparable to the value of the car you found and we don’t want them to affect the results. Also, we’re unlikely to find many repeated values, so the mode is probably not useful. Median is best.
Here, we want to know what a typical result is. The mean doesn’t really make sense; it involves adding the numbers together, so it would treat two “strongly disagree” and two “strongly agree” responses (those add to 1 + 1 + 5 + 5 = 12 1 + 1 + 5 + 5 = 12 ) as exactly the same as four “neutral” responses ( 3 + 3 + 3 + 3 = 12 3 + 3 + 3 + 3 = 12 ). But those are really different situations; the first shows a strong polarization in the responses, while the second represents strong indifference. The mode is probably the best choice (because the data are actually categorical), but the median would be good too.
The mode isn’t going to be useful in this situation because it’s unlikely you will find many households that have exactly the same income. The mean and median will be different because of the skew, so the choice comes down to the extreme values. Remember that the data are skewed right, so high values are prevalent. Because these high values are important for our analysis, we want them to be reflected in the results. Thus, the mean is best. That being said, the median is also useful; it allows us to say something like “50% of the households surveyed make more than” the median.
Because we aren’t likely to find many people with exactly the same height, the mode won’t be useful. Since the data are symmetric, the mean and the median will be about the same. So, it doesn’t really matter which of those two we choose.

Your Turn 8.23

Check your understanding.

A survey of college students asked how many courses those students were currently taking. The results are summarized in this frequency distribution:

Section 8.3 Exercises

The dataset “AvgSAT” gives the average SAT score for incoming students (the use of “average” here stands in for “mean” to avoid confusion in the following problems) for every institution in the United States that reported the data (from data.ed.gov). Use that dataset to answer the following questions.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction

Authors: Donna Kirk
Publisher/website: OpenStax
Book title: Contemporary Mathematics
Publication date: Mar 22, 2023
Location: Houston, Texas
Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
Section URL: https://openstax.org/books/contemporary-mathematics/pages/8-3-mean-median-and-mode

© Dec 21, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Topic Specification

Mean, Median, Mode and Range Revision

Try it yourself.

Example Questions
Worksheets 2

Supercharge your learning

Filter by Level

Filter by exam board, mean, median, mode and range, mean, median, mode, and range.

The mean , median , and mode are different types of average and the range tells us how spread out our data is.

To find the mean we must add up all the numbers we’re finding the average of, and then divide by how many numbers there are in that list:

\text{Mean} = \dfrac{\text{Sum of items}}{\text{Total number of items}}

Advantages and Disadvantages

Advantage – every bit of data is used in calculating the mean , so it represents all the data.
Disadvantage – it is highly affected by outliers. An outlier is a piece of data that doesn’t quite fit with the rest of them.

Note: A better way to calculate the mean is to remove outliers before calculating it. The question will specifically tell you to do this if it is required.

The median is often referred to as “the middle”, which is precisely what it is.

There are two common ways of finding the middle value(s):

Method 1: Put the numbers in order from smallest to largest and find the middle value/middle two values. Cross out the smallest number and the largest number, then cross out the next smallest and largest, keeping going crossing out pairs of number like this until you have one or two left. If there is one left, then that is the median ; if there are two values, left then the median is the halfway point between the two.

Method 2: If n is the number of values in the list, then work out the value of \frac{n+1}{2} . The median is that number of values along in the list.

Advantage – it is not affected by outliers.
Disadvantage – it does not consider all the data.

Your 2024 Revision Partner

The mode is the most common value. To find it, look for which value appears most often . There might be two values which are tied for the most appearances, in which case we say the data is bimodal , or alternatively there might be no repeats at all, in which case there is simply no mode .

Disadvantage(s) – Firstly, there may not actually be a mode. Secondly, it does not consider all of the data. Consider the values 32, 35, 35, 128, 201, 176, 295 – what is the mode? Does it represent the “average” of the data?

The range is not another average – it is a measure of spread. This means the range is a way of telling us how spread out the data is.

To calculate it, we subtract the smallest value from the biggest value.

\text{Range} = \text{Biggest value} - \text{Smallest Value}

Note: The range is highly affected by outliers. So a better way to calculate the range is to remove outliers before calculating it. The question will specifically tell you if this is required.

Comparing Two Data Sets

You may need to use what you have learnt about averages to compare two given sets of data.

The things to look out for when comparing data are:

Averages ( mean , median , mode ) – which set of data has the higher or lower averages.
Spread (interquartile range , quartiles, range , minimum/maximum values) – which set of data is more varied , or less consistent .

Example 1: Finding the Mean, Median and Mode

9 people take a test. Their scores out of 100 are:

56, 79, 77, 48, 90, 68, 79, 92, 71

Work out the mean , median , and mode of their scores.

Mean: There are 9 data points. First add the numbers together and then divide the result by 9 .

56 + 79 + 77 + 48 + 90 + 68 + 79 + 92 + 71 = 660

\text{Mean} = \dfrac{660}{9}=73.3 ( 1 dp)

Median: Firstly, put the numbers in ascending order.

48, 56, 68, 71, 77, 79, 79, 90, 92

There are 9 numbers, and \frac{9+1}{2}=5 , so the median must be the 5 th term along.

\xcancel{48}, \xcancel{56}, \xcancel{68}, \xcancel{71}, 77, 79, 79, 90, 92

Counting along the list, we get that the median is 77 .

Mode: We can see very clearly from the ordered list that there is only one repeat, 79 , so the mode is 79 .

Example 2: Calculating the Range

Find the range of 12, 8, 4, 16, 15, 15, 5, 15, 10, 8

A good way to make sure you haven’t missed any numbers in determining the biggest and smallest value is to order them. Doing this, we get

4, 5, 8, 8, 10, 12, 15, 15, 15, 16

Largest - Smallest = 16-4=12 , so the range is 12

Example 3: Finding the Mean – Applied Questions

There were 5 members of a basketball team who had a mean points score of 12 points each per game.

One of the team members left, causing the mean point score to reduce to 10 points each per game.

What was the mean score of the player that left?

Step 1: Find the total for the original number of players: 5\times12=60

Step 2: Find the total after once the mean has changed, so 4\times10=40

Step 3: Calculate the difference between these two totals as that difference has been caused by the person who left: 60-40=20

Therefore the mean score of the person who left was 20 points per game. The same method applies if a new person/amount is added, you find the old and new totals and the difference is always due to the thing which caused the change.

Example 4: Comparing Two Data Sets

Two Maths teachers are comparing how their Year 9 classes performed in the end of year exams.

Their results are as follows:

Class A: 76, 35, 47, 64, 95, 66, 89, 36, 84

Class B: 51, 56, 84, 60, 59, 70, 63, 66, 50

Give 3 comparisons between the results of these 2 maths classes

Let’s firstly think about averages. We can start with the mean,

Mean of Class A: \dfrac{76+35+47+64+95+66+89+36+84}{9}=65.\dot{7}

Mean of Class B: \dfrac{51+56+84+60+59+70+63+66+50}{9}=62.\dot{1}

So, Class A has a higher mean.

As neither of the classes have any repeated scores, we can’t use the mode. Therefore, let’s look at median,

Order Class A: 35, 36, 47, 64, 66, 76, 84, 89, 95

Middle score: 66

Order Class B: 50, 51, 56, 59, 60, 63, 66, 70, 84

Middle score: 60

So, Class A has a higher median.

Now, let’s look at range to consider the spread of data:

Class A range: 95-35=60

Class B range: 84-50=34

Class A has a bigger range.

In conclusion, Class A generally has higher scores, with both the mean and median being higher than class B. Class B’s scores are more concentrated and less spread out than Class A.

Mean, Median, Mode and Range Example Questions

Question 1: Find the mode and range of the list of numbers below:

\begin{aligned}&280, 350, 320, 400, 350,\\&490, 590, 470, 280, 410, 350\end{aligned}

It is not necessary to order the numbers, but it may help, especially in working out the range. In ascending order, these values are:

280, 280, 320, 350, 350, 350, 400, 410, 470, 490, 590

Since the number 350 occurs 3 times, it is the most common value, so:

\text{mode} = 350

The range is the difference between the lowest and the highest value. The lowest value is 280 and the highest is 590 , so:

\text{range} = 590-280=310 .

Save your answers with

Gold Standard Education

Question 2: Dani recorded the heights of members of her extended family, to the nearest cm. Find the median of their heights (listed below):

163, 185, 164, 170, 188, 154, 168, 179

First of all, since we have been asked to work out the median, we need to order the set of values:

154, 163, 164, 168, 170, 179, 185, 188

There are 8 values in total, so we need to know which value, or values, we need in order to find the median.

Since there is an even number of values, there is not one single middle value, so you will need to find the two middle values. To find the median value, we can use the following formula:

\dfrac{n + 1}{2} where n represents the total number of values.

In this question, we have 8 values, so:

\frac{8 + 1}{2}=4.5

The answer 4.5 tells us that the median is half-way between the 4 th value and the 5 th value. The 4 th value is 168 and the 5 th value is 170 , so the median is 169 .

NOTE: if you struggle to work out the half-way value, add up the two numbers and divide by 2 (in other words, work out the mean of these two values).

Question 3: Below is a list of recorded reaction times in seconds.

\begin{aligned}&0.25, 0.34, 0.39, 0.38, 0.39,\\&1.67, 0.28, 0.30, 0.42, 0.46\end{aligned}

a) Calculate the mean of these values.

b) Identify any outliers and explain how the value of the mean would change if any outliers were to be removed from the calculation of the mean.

a) In order to calculate the mean, we need to add up all the values and divide by 10 (since there are 10 values in total). The sum of the reaction times is

0.25+0.34+0.39+0.38+0.39 +\, 1.67+0.28+0.3+0.42+0.46 = 4.88

\text{Mean}=\dfrac{4.88}{10}=0.488

b) 1.67 is the outlier as it is vastly higher than all the other values.

If this outlier were removed, then the mean would be lower.

Question 4: The mean length of 7 planks of wood is 1.35 m. When an extra plank of wood is added, the mean length of a plank of wood increased to 1.4 m.

What is the length of the extra plank of wood that was added?

In most questions involving the mean, we are given the total and need to work out the mean from the total. In this question, we have been given the mean, so we are going to have to calculate the total from the mean.

If the mean length of 7 planks of wood is 1.35 m, then the total length of all these planks of wood combined can be calculated as follows:

7 \times 1.35 m = 9.45 m

When the extra plank of wood is added, the mean length of a plank of wood increases to 1.4 m. This means there are now 8 planks of wood, with a combined length of:

8 \times 1.40 m = 11.2 m

Therefore, by adding this additional plank of wood, the combined length has increased from 9.45 m to 11.2 m, so the length of this extra plank of wood is therefore:

11.2 m - \, 9.45 m = 1.75 m

Question 5: In a rowing team, the weight of 8 women, in kilograms, is:

63, \, 60, \, 57, \, 66, \, 62, \, 65, \, 69, \, 58

In order to be a more competitive team, the coach has said that each team member should try to increase their overall muscle mass which will result in a 2\% gain in overall body weight.

What will be the mean weight of the team if all 8 are successful in precisely meeting this 2\% weight gain?

In this question, we do not need to work out a 2\% increase in weight for each individual team member (it would not be wrong to do so, just unnecessarily time-consuming).

The combined weight of all 8 members is:

63 + 60+57+66+62+65+69+58 = 500 kg

If each team member increases their weight by 2\% , then this is the same as the team increasing their combined weight by 2\% . Therefore, if the team is successful in achieving this 2\% weight gain, then the combined weight of the team can be calculated as follows:

1.02\times500 = 510 kg

Since there are 8 team members in total, then mean weight following this weight gain is:

510 kg \div \, 8 =63.75 kg

Question 6 : A farmer is growing potatoes. He grows some in a greenhouse and some outside and wants to compare which environment produces bigger potatoes. Here are the results of measuring his potatoes, in \text{cm} :

Outside potatoes: 9, 8, 11, 14, 16, 13, 12

Greenhouse potatoes: 5, 6, 17, 16, 14, 4, 8

The farmer looks at the data and says “the greenhouse has the largest potato so this must be the best growing conditions”.

Decide whether you agree with the farmer, giving 2 reasons. Describe how his experiment could be improved.

As the farmer wants to know the best conditions, it’s better to look at averages rather than range.

We cannot use mode as there are no repeated values.

Let’s use mean first,

Outside potatoes: \dfrac{9+8+11+14+16+13+12}{7}=11.8...

Greenhouse potatoes: \dfrac{5+6+17+16+14+4+8}{7}=10

Therefore, the outside potatoes had a higher mean size.

Now, let’s look at median:

Outside potatoes ordered: 8, 9, 11, 12, 13, 14, 16

Greenhouse potatoes ordered: 4, 5, 6, 8, 14, 16, 17

Therefore, the farmer is wrong as both the mean and median are higher for the potatoes outside so it is likely this is the best growing environment. However, to be more sure on his conclusion, it would be helpful to use more potatoes to get a more accurate average.

Mean, Median, Mode and Range Worksheet and Example Questions

(NEW) Mean, Median, Mode and Range 1 Exam Style Questions - MME

(new) mean, median, mode and range 2 exam style questions - mme, mean, median, mode and range drill questions, mean median mode range - drill questions, mean median mode range and iqr - drill questions, estimate of mean - drill questions, averages from frequency tables - drill questions.

MME Premium Membership

Learn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.

Where next?

Previous gcse maths topic, types of data, gcse maths revision home, go back to the main gcse maths topic list, next gcse maths topic, data sampling and questionnaires.

By clicking continue and using our website you are consenting to our use of cookies in accordance with our Cookie Policy

Report a Question

You must be logged in to vote for this question..

Your personal data will be used to support your experience throughout this website, to manage access to your account, and for other purposes described in our privacy policy .

Child Login

Kindergarten
Number charts
Skip Counting
Place Value
Number Lines
Subtraction
Multiplication
Word Problems
Comparing Numbers
Ordering Numbers
Odd and Even
Prime and Composite
Roman Numerals
Ordinal Numbers
In and Out Boxes
Number System Conversions
More Number Sense Worksheets
Size Comparison
Measuring Length
Metric Unit Conversion
Customary Unit Conversion
Temperature
More Measurement Worksheets
Writing Checks
Profit and Loss
Simple Interest
Compound Interest
Tally Marks
Mean, Median, Mode, Range
Mean Absolute Deviation
Stem-and-leaf Plot
Box-and-whisker Plot
Permutation and Combination
Probability
Venn Diagram
More Statistics Worksheets
Shapes - 2D
Shapes - 3D
Lines, Rays and Line Segments
Points, Lines and Planes
Transformation
Quadrilateral
Ordered Pairs
Midpoint Formula
Distance Formula
Parallel, Perpendicular and Intersecting Lines
Scale Factor
Surface Area
Pythagorean Theorem
More Geometry Worksheets
Converting between Fractions and Decimals
Significant Figures
Convert between Fractions, Decimals, and Percents
Proportions
Direct and Inverse Variation
Order of Operations
Squaring Numbers
Square Roots
Scientific Notations
Speed, Distance, and Time
Absolute Value
More Pre-Algebra Worksheets
Translating Algebraic Phrases
Evaluating Algebraic Expressions
Simplifying Algebraic Expressions
Algebraic Identities
Quadratic Equations
Systems of Equations
Polynomials
Inequalities
Sequence and Series
Complex Numbers
More Algebra Worksheets
Trigonometry
Math Workbooks
English Language Arts
Summer Review Packets
Social Studies
Holidays and Events
Worksheets >
Statistics >
Mean, Median, Mode and Range

Central Tendency Worksheets: Mean, Median, Mode and Range

Mean, median, mode and range worksheets contain printable practice pages to determine the mean, median, mode, range, lower quartile and upper quartile for the given set of data. The pdf exercises are curated for students of grade 3 through grade 8. Interesting word problems are included in each section. Sample some of these worksheets for free!

Finding Average

Average or mean worksheets have plentiful exercises to find the average of numbers, numbers with practical units and decimals.

(49 Worksheets)

Finding Range

Identify the maximum and minimum values to find the range of the given data. Word problems are included for practice.

Download the set

Finding Median

In these worksheets, 3rd grade and 4th grade children identify the median (middle value) of the represented data. Two word problems included.

Finding Quartiles

Determine the first (lower) quartile, second (median) quartile and the third (upper) quartile of the given data. One word problem included in each pdf worksheet for 5th grade and 6th grade students.

Mean, Median, Mode and Range: Level 1

These printable central tendency worksheets contain a mixed review of mean, median, mode and range concepts. Around 8 data are used in level 1.

Mean, Median, Mode and Range: Level 2

Find the mean, median, mode and range of each set of data. Each sheet has six problems with around 15 data.

Word Problems: Level 1

This exclusive section has five word problems to find the mean, median, mode and range of the given data.

Word Problems: Level 2

A variety of informative data are included as word problems in these central tendency worksheet pdfs requires 7th grade and 8th grade students to determine the values of mean, median, mode and range.

Related Worksheets

» Line Plot

» Mean Absolute Deviation

» Stem and Leaf Plot

» Box and Whisker Plot

Become a Member

Membership Information

What's New?

Printing Help

Testimonial

This is a members-only feature!

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 6th grade > Unit 11

Statistics intro: Mean, median, & mode

Mean, median, & mode example

Calculating the mean
Calculating the median
Calculating the mean: data displays
Calculating the median: data displays

Want to join the conversation?

Upvote Button navigates to signup page
Downvote Button navigates to signup page
Flag Button navigates to signup page

Video transcript

Mean, Median, Mode and Range

These lessons help GMAT students review mean, median, mode and range.

Related Pages Mean Median Mode Central Tendency More Statistics Lessons

The following diagrams show how to find the mean, median, mode and range. Scroll down the page for examples and solutions.

Statistics: The Average

Introduction to descriptive statistics and central tendency. Ways to measure the average of a set: median, mean, mode

Mean, Median, and Mode

Learn about Mean, Median, and Mode Mean, median and mode are measures of central tendency. Mean: add together and divide by how many there are. Median: the middle number when the data is listed in order from smallest to largest. If there are 2 middle number, add them and divide by 2. Mode: the most frequent number.

Example: Find the mean, median and mode of this set of data. 35,8,12,50,55,22,34,22,34

Mean, Median and Mode

This lesson shows how to calculate Mean, Median and Mode and some tricks to help you remember the differences of these methods of finding the Center.

The mean is the average. To calculate the mean, you add add the values and divide by the number of values.

If you had 20 pencils in one box and 30 pencils in a second box, what is the average number of pencils in your boxes?
Your grades out of 20 are all listed below. What is your average grade out of 20? 15, 16, 20, 12, 18, 20, 17

The median is the center. List the numbers in order and pick the center one. If there are an even number of numbers find the mean of the two middle numbers.

The mode is the number that shows up the most. There can be more than one mode. If the values all appear the same number of times, there is no mode.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Or search by topic

Number and algebra

The Number System and Place Value
Calculations and Numerical Methods
Fractions, Decimals, Percentages, Ratio and Proportion
Properties of Numbers
Patterns, Sequences and Structure
Algebraic expressions, equations and formulae
Coordinates, Functions and Graphs

Geometry and measure

Angles, Polygons, and Geometrical Proof
3D Geometry, Shape and Space
Measuring and calculating with units
Transformations and constructions
Pythagoras and Trigonometry
Vectors and Matrices

Probability and statistics

Handling, Processing and Representing Data
Probability

Working mathematically

Thinking mathematically
Mathematical mindsets
Cross-curricular contexts
Physical and digital manipulatives

For younger learners

Early Years Foundation Stage

Advanced mathematics

Decision Mathematics and Combinatorics
Advanced Probability and Statistics

All about Averages

problem solving with mean median mode and range

About Average Age 11 to 14 Challenge Level

Unequal Averages Age 11 to 14 Challenge Level

Wipeout Age 11 to 16 Challenge Level

The Lives of Presidents Age 11 to 16 Challenge Level

Statistics - Stage 3
Statistics - Stage 4

Math Article

Mean Median Mode Questions

Mean, Median and Mode are three measures of central tendency, and these are the important topics in statistics. In this article, you will get mean, median, and mode questions and answers, along with some practice questions. These questions and answers will help you to practise for the board exams. Also, these questions cover various types of problems asked on mean, median and mode for Classes 9 and 10.

What is the mean formula?

As we know, the mean is the average of the given data set. This can be calculated using the formula given below.

Mean for ungrouped data = Sum of observations/Number of observations

Click here to get more information about mean .

What is the formula for the median?

The median is the middlemost data value of an ordered data set. This can be estimated using the formulas given below.

When n is odd:

Median = (n + 1)/2th observation

When n is even:

Median = [(n/2)th observation + {(n/2)+1}th observation]/2

Learn more about median here.

What is the mode?

Mode is the most frequently occurring value in the data set.

Get more information about mode here.

Mean Median Mode Questions and Answers

1. Find the mean of the first 10 odd integers.

First 10 odd integers: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19

Mean = Sum of the first 10 odd integers/Number of such integers

= (1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19)/10

Therefore, the mean of the first 10 odd integers is 10.

2. What is the median of the following data set?

32, 6, 21, 10, 8, 11, 12, 36, 17, 16, 15, 18, 40, 24, 21, 23, 24, 24, 29, 16, 32, 31, 10, 30, 35, 32, 18, 39, 12, 20

The ascending order of the given data set is:

6, 8, 10, 10, 11, 12, 12, 15, 16, 16, 17, 18, 18, 20, 21, 21, 23, 24, 24, 24, 29, 30, 31, 32, 32, 32, 35, 36, 39, 40

Number of values in the data set = n = 30

n/2 = 30/2 = 15

15th data value = 21

(n/2) +1 = 16

16th data value = 21

= (15th data value + 16th data value)/2

= (21 + 21)/2

3. Identify the mode for the following data set:

21, 19, 62, 21, 66, 28, 66, 48, 79, 59, 28, 62, 63, 63, 48, 66, 59, 66, 94, 79, 19 94

Let us write the given data set in ascending order as follows:

19, 19, 21, 21, 28, 28, 48, 48, 59, 59, 62, 62, 63, 63, 66, 66, 66, 66, 79, 79, 94, 94

Here, we can observe that the number 66 occurred the maximum number of times.

Thus, the mode of the given data set is 66.

4. Consider the following frequency distribution. Calculate the mean weight of students.

The given distribution has discontinuous class intervals, so we need to make them continuous.

Here, ∑f i = 40 and ∑f i d i = 35

By Assumed mean method,

Mean = a + (∑f i d i /∑f i )

= 43 + (35/40)

= 43 + 0.875

Therefore, the mean weight of the students is 43.875 kg.

5. Find the mean for the following distribution.

Mean = ∑f i x i /∑f i

6. Calculate the median marks of students from the following distribution.

N/2 = 90/2 = 45

Cumulative frequency greater and nearer to 45 is 47, which lies in the interval 40 – 50

Median class is 40 – 50.

Lower limit of the median class = l = 40

Class size = h = 10

Frequency of the median class = f = 20

Cumulative frequency of the class preceding the median class = cf = 27

As we know,

Median = 40 + [(45 – 27)/20] × 10

= 40 + (18/2)

Hence, the median marks of the students = 49.

7. The given distribution shows the number of runs scored by some top batsmen of the world in one-day international cricket matches.

Find the mode of the above distribution.

From the given,

Modal class = 4000 – 5000

Lower limit of the modal class = l = 4000

Class width (h) = 1000

Frequency of the modal class = f 1 = 18,

Frequency of the class preceding the modal class = f 0 = 4

Frequency of the class succeeding the modal class = f 2 = 9

Mode = l + [(f 1 – f 0 )/ (2f 1 – f 0 – f 2 )] × h

Mode = 4000 + [(18 – 4)/(36 – 4 – 9)] × 1000

= 4000 + (14000/23)

= 4000 + 608.695

= 4608.7 (approximately)

Thus, the mode of the given data is 4608.7 runs

8. If the median of a distribution given below is 28.5, then find the value of x and y.

N/2 = 60/2 = 30

Median of the given data = 28.5

Median class is 20 – 30 with a cumulative frequency = 25 + x.

Lower limit of median class = l = 20

Cumulative frequency of the class preceding the median class = cf = 5 + x

28.5 = 20 + [(30 − 5 − x)/ 20] × 10

28.5 – 20 = (25 – x)/2

8.5 × 2 = 25 – x

17 = 25 – x

x = 25 – 17

Therefore, x = 8

60 = 5 + 20 + 15 + 5 + x + y

60 = 5 + 20 + 15 + 5 + 8 + y

y = 60 – 53

Therefore, the value of x = 8 and y = 7.

9. For a moderately skewed distribution, the mean and median are respectively 26.8 and 27.9. What is the mode of the distribution?

Mean = 26.8

Median = 27.9

Using the relationship between mean, median and mode,

Mode = 3 Median – 2 Mean

= 3 × 27.9 – 2 × 26.8

= 83.7 – 53.6

Therefore, the mode of the distribution is 30.1.

10. If the mean of the given frequency distribution is 35, then find the missing frequency y. Also, calculate the median and mode for the distribution.

Given that the mean of the distribution is 35.

So, (430 + 45y)/(14 + y) = 35

430 + 45y = (14 + y)35

430 + 45y = 490 + 35y

45y – 35y = 490 – 430

Thus, the missing frequency is 6.

Now, we can calculate the mode as follows:

Mode = 30 + [(7 – 4)/(14 – 4 – 6)] × 10

= 30 + (30/4)

Now, using the formula Mode = 3Median – 2 Mean, we can get the value of median.

37.5 = 3 Median – 2 (35)

3 Median = 37.5 + 70

Median = 107.7/3

Practice Questions on Mean Median Mode

1. Find the mean, median and mode of the following data:

23, 18, 24, 23, 31, 37, 28, 30, 25, 40, 35, 35, 27, 25

2. The mileage (km per litre) of 50 cars of the same model was tested by a manufacturer, and details are tabulated as given below:

Find the mean mileage.

The manufacturer claimed that the mileage of the model was 16 km/litre. Do you agree with this claim?

3. Find the median of the following frequency distribution.

4. Calculate the mode for the following distribution.

5. Suppose the mean and median of distribution are 10.14 and 8, respectively. Find the mode of the distribution using the empirical relationship between mean, median and mode.

Keep visiting byjus.com to get solved questions on various Maths topics. Also, download BYJU’S – The Learning App today!

Register with BYJU'S & Download Free PDFs

HW Guidelines
Study Skills Quiz
Find Local Tutors
Demo MathHelp.com
Join MathHelp.com

Select a Course Below

ACCUPLACER Math
Math Placement Test
PRAXIS Math
+ more tests
5th Grade Math
6th Grade Math
Pre-Algebra
College Pre-Algebra
Introductory Algebra
Intermediate Algebra
College Algebra

Mean, Median, Mode, and Range

Mean, median, and mode are three kinds of "averages". There are many "averages" in statistics, but these are, I think, the three most common, and are certainly the three you are most likely to encounter in your pre-statistics courses, if the topic comes up at all.

Why do we need different kinds of averages?

The average that we're used to is found by adding all the values in a data set, and then dividing the sum by the number of values in that data set; but this average might be misleading.

Content Continues Below

MathHelp.com

Median, Mode, and Range

A typical example would be the case where nearly every person in a given population lives on about two dollars a day, but there is a small elite with incomes in the millions. The numerical average can mislead by suggesting that the average (in this case, we mean "typical") person earns a few tens of thousands per year.

But this does not accurately reflect what we mean when we're trying to discuss the "average" income. This is why the average income is almost always expressed by a different sort of average.

What are the three averages?

The three averages are:

The "mean" is the "average" you're used to, where you add up all the numbers and then divide by the number of numbers.
The "median" is the "middle" value in the list of numbers. To find the median, your numbers have to be listed in numerical order from smallest to largest, so you may have to rewrite your list before you can find the median.
The "mode" is the value that occurs most often. If no number in the list is repeated, then there is no mode for the list.

The "range" of a list a numbers is just the difference between the largest and smallest values. It expresses "spread", being how far the values are distributed (or how concentrated they are).

Find the mean, median, mode, and range for the following list of values:

13, 18, 13, 14, 13, 16, 14, 21, 13

The mean is the usual average, so I'll add and then divide:

(13 + 18 + 13 + 14 + 13 + 16 + 14 + 21 + 13) ÷ 9 = 15

Note that the mean, in this case, isn't a value from the original list. This is a common result. You should not assume that your mean will be one of your original numbers; you should not be surprised when it isn't.

The median is the middle value, so first I'll have to rewrite the list in numerical order:

13, 13, 13, 13, 14, 14, 16, 18, 21

There are nine numbers in the list, so the middle one will be the (9 + 1) ÷ 2 = 10 ÷ 2 = 5 th number:

So the median is 14 .

The mode is the number that is repeated more often than any other, so 13 , I see from my listing above, is the mode.

The largest value in the list is 21 , and the smallest is 13 , so the range is 21 − 13 = 8 .

mean: 15 median: 14 mode: 13 range: 8

Note: The formula for the place to find the median is " ( [the number of data points] + 1) ÷ 2 ", but you don't have to use this formula. You can just count in from both ends of the list until you meet in the middle, if you prefer, especially if your list is short. Either way will work.

The mean is the usual average:

(1 + 2 + 4 + 7) ÷ 4 = 14 ÷ 4 = 3.5

The median is the middle number. In this example, the numbers are already listed in numerical order, so I don't have to rewrite the list. But there is no "middle" number, because there are an even number of numbers.

Because of this, the median of the list will be the mean (that is, the usual average) of the middle two values within the list. The middle two numbers are 2 and 4 , so:

(2 + 4) ÷ 2 = 6 ÷ 2 = 3

So the median of this list is 3 , a value that isn't in the list at all.

The mode is the number that is repeated most often, but all the numbers in this list appear only once, so there is no mode.

The largest value in the list is 7 , the smallest is 1 , and their difference is 6 , so the range is 6 .

mean: 3.5 median: 3 mode: none range: 6

The values in the list above were all whole numbers, but the mean of the list was a decimal value. Getting a decimal value for the mean (or for the median, if you have an even number of data points) is perfectly okay; don't round your answers to try to match the format of the other numbers.

8, 9, 10, 10, 10, 11, 11, 11, 12, 13

The mean is the usual average, so I'll add up and then divide:

(8 + 9 + 10 + 10 + 10 + 11 + 11 + 11 + 12 + 13) ÷ 10 = 105 ÷ 10 = 10.5

The median is the middle value. In a list of ten values, that will be the (10 + 1) ÷ 2 = 5.5 -th value; the formula is reminding me, with that "point-five", that I'll need to average the fifth and sixth numbers to find the median. The fifth and sixth numbers are the last 10 and the first 11 , so:

(10 + 11) ÷ 2 = 21 ÷ 2 = 10.5

The mode is the number repeated most often. This list has two values that are repeated three times; namely, 10 and 11 , each repeated three times.

The largest value is 13 and the smallest is 8 , so the range is 13 − 8 = 5 .

mean: 10.5 median: 10.5 modes: 10 and 11 range: 5

As you can see, it is possible for two of the averages (the mean and the median, in this case) to have the same value. But this is not usual, and you should not expect it.

Note: Depending on your text or your instructor, the above data set may be viewed as having no mode rather than having two modes, because no single solitary number was repeated more often than any other. I've seen books that go either way on this; there doesn't seem to be a consensus on the "right" definition of "mode" in the above case. So if you're not certain how you should answer the "mode" part of the above example, ask your instructor before the next test.

How can I keep straight which average is which?

About the only hard part of finding the mean, median, and mode is keeping straight which "average" is which. Use this list:

mean: regular meaning of "average"
median: middle value
mode: most often

(In the above, I've used the term "average" rather casually. The technical definition of what we commonly refer to as the "average" is technically called "the arithmetic mean": adding up the values and then dividing by the number of values. Since you're probably more familiar with the concept of "average" than with "measure of central tendency", I used the more comfortable term.)

A student has gotten the following grades on his tests: 87, 95, 76, and 88 . He wants an 85 or better overall for the course. Assuming all tests are evenly weighted, what is the minimum grade he must get on the last test in order to achieve that overall average?

The minimum grade for the last test is what I need to find. To find the average of all his grades (the known ones, plus the unknown one), I have to add up all the grades, and then divide by the number of grades. Since I don't have a score for the last test yet, I'll use a variable to stand for this unknown value: " x ". Then, setting the expression for the average equal to the desired average, the computation is:

(87 + 95 + 76 + 88 + x ) ÷ 5 = 85

Multiplying through by 5 and simplifying, I get:

87 + 95 + 76 + 88 + x = 425

346 + x = 425

This is the score that he needs on the last test in order to get the overall grade that he is wanting. (If I doubt myself, I can always plug this value into the formula for the average, and confirm that I get 85 as the result.)

He needs to get at least a 79 on the last test.

You can use the Mathway widget below to practice finding the median. Try the entered exercise, or type in your own exercise. Or try entering any list of numbers, and then selecting the option — mean, median, mode, etc — from what the widget offers you. Then click the button to compare your answer to Mathway's.

Please accept "preferences" cookies in order to enable this widget.

(Click here to be taken directly to the Mathway site, if you'd like to check out their software or get further info.)

URL: https://www.purplemath.com/modules/meanmode.htm

Standardized Test Prep

College math, homeschool math, share this page.

Terms of Use
About Purplemath
About the Author
Tutoring from PM
Advertising
Linking to PM
Site licencing

Visit Our Profiles

Mean, Median, Mode, Range Calculator

Please provide numbers separated by comma to calculate.

Related Statistics Calculator | Standard Deviation Calculator | Sample Size Calculator

The word mean, which is a homonym for multiple other words in the English language, is similarly ambiguous even in the area of mathematics. Depending on the context, whether mathematical or statistical, what is meant by the "mean" changes. In its simplest mathematical definition regarding data sets, the mean used is the arithmetic mean, also referred to as mathematical expectation, or average. In this form, the mean refers to an intermediate value between a discrete set of numbers, namely, the sum of all values in the data set, divided by the total number of values. The equation for calculating the arithmetic mean is virtually identical to that for calculating the statistical concepts of population and sample mean, with slight variations in the variables used:

The mean is often denoted as x̄ , pronounced "x bar," and even in other uses when the variable is not x , the bar notation is a common indicator of some form of the mean. In the specific case of the population mean, rather than using the variable x̄ , the Greek symbol mu, or μ , is used. Similarly, or rather confusingly, the sample mean in statistics is often indicated with a capital X̄ . Given the data set 10, 2, 38, 23, 38, 23, 21, applying the summation above yields:

As previously mentioned, this is one of the simplest definitions of the mean, and some others include the weighted arithmetic mean (which only differs in that certain values in the data set contribute more value than others), and geometric mean . Proper understanding of given situations and contexts can often provide a person with the tools necessary to determine what statistically relevant method to use. In general, mean, median, mode and range should ideally all be computed and analyzed for a given sample or data set since they elucidate different aspects of the given data, and if considered alone, can lead to misrepresentations of the data, as will be demonstrated in the following sections.

The statistical concept of the median is a value that divides a data sample, population, or probability distribution into two halves. Finding the median essentially involves finding the value in a data sample that has a physical location between the rest of the numbers. Note that when calculating the median of a finite list of numbers, the order of the data samples is important. Conventionally, the values are listed in ascending order, but there is no real reason that listing the values in descending order would provide different results. In the case where the total number of values in a data sample is odd, the median is simply the number in the middle of the list of all values. When the data sample contains an even number of values, the median is the mean of the two middle values. While this can be confusing, simply remember that even though the median sometimes involves the computation of a mean, when this case arises, it will involve only the two middle values, while a mean involves all the values in the data sample. In the odd cases where there are only two data samples or there is an even number of samples where all the values are the same, the mean and median will be the same. Given the same data set as before, the median would be acquired in the following manner:

2,10,21, 23 ,23,38,38

After listing the data in ascending order, and determining that there are an odd number of values, it is clear that 23 is the median given this case. If there were another value added to the data set:

2,10,21, 23 , 23 ,38,38,1027892

Since there are an even number of values, the median will be the average of the two middle numbers, in this case, 23 and 23, the mean of which is 23. Note that in this particular data set, the addition of an outlier (a value well outside the expected range of values), the value 1,027,892, has no real effect on the data set. If, however, the mean is computed for this data set, the result is 128,505.875. This value is clearly not a good representation of the seven other values in the data set that are far smaller and closer in value than the average and the outlier. This is the main advantage of using the median in describing statistical data when compared to the mean. While both, as well as other statistical values, should be calculated when describing data, if only one can be used, the median can provide a better estimate of a typical value in a given data set when there are extremely large variations between values.

In statistics, the mode is the value in a data set that has the highest number of recurrences. It is possible for a data set to be multimodal, meaning that it has more than one mode. For example:

2,10,21,23,23,38,38

Both 23 and 38 appear twice each, making them both a mode for the data set above.

Similar to mean and median, the mode is used as a way to express information about random variables and populations. Unlike mean and median, however, the mode is a concept that can be applied to non-numerical values such as the brand of tortilla chips most commonly purchased from a grocery store. For example, when comparing the brands Tostitos, Mission, and XOCHiTL, if it is found that in the sale of tortilla chips, XOCHiTL is the mode and sells in a 3:2:1 ratio compared to Tostitos and Mission brand tortilla chips respectively, the ratio could be used to determine how many bags of each brand to stock. In the case where 24 bags of tortilla chips sell during a given period, the store would stock 12 bags of XOCHiTL chips, 8 of Tostitos, and 4 of Mission if using the mode. If, however, the store simply used an average and sold 8 bags of each, it could potentially lose 4 sales if a customer desired only XOCHiTL chips and not any other brand. As is evident from this example, it is important to take all manners of statistical values into account when attempting to draw conclusions about any data sample.

The range of a data set in statistics is the difference between the largest and the smallest values. While range does have different meanings within different areas of statistics and mathematics, this is its most basic definition, and is what is used by the provided calculator. Using the same example:

2,10,21,23,23,38,38 38 - 2 = 36

The range in this example is 36. Similar to the mean, range can be significantly affected by extremely large or small values. Using the same example as previously:

The range, in this case, would be 1,027,890 compared to 36 in the previous case. As such, it is important to extensively analyze data sets to ensure that outliers are accounted for.

Averages and Range Textbook Exercise

Click here for questions.

means, modes, medians, mean, mode, median

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Terms and Conditions

IMAGES

MEAN, MEDIAN, MODE, & RANGE Word Problems with Graphic Organizer
Mean Median Mode Range Worksheets
Mean Median Mode Range Worksheets
$problem solving with mean median mode and range$
Get your students successfully understanding and solving MEAN, MEDIAN
Mean Median Mode Range Worksheets
Statistics: Mode (solutions, examples, videos)

VIDEO

Measures of center MODE AND MIDRANGE
Mean, Median, Mode, Range -3
How to Find Mean, Median, Mode, and Range
Problem Solving Mean Median Mode
Data handling
Mean Median Mode || Statistics || Part 1 || RR BANKING ADDA

COMMENTS

Mean Median Mode and Range
To find the range: Range is equal to maximum value minus minimum value which gives us: 12 − 2 = 10. Example 3:Find the mean, median, mode and range for the following list of values. To determine the value of the mean, obtain the total of all the numbers and then divide by the number of numbers in the list.
How to Find Mean, Mean, Mode and Range: Your Complete Guide
This post will share key information, formulas, and vocabulary so that you can use math to determine the mean, median, mode, and range of any data set and understand what these values represent. After working through two examples, you will also have access to a free mean, median, and mode pdf practice worksheet that includes an answer key.
Mean, Mode, Median, Range Practice Questions
averages, average, means, modes, medians, ranges. Practice Questions. Previous: Area of a Triangle Practice Questions
Mean Median Mode Range Worksheets
Step 1) Put the data into an ordered list. This gives us: 9, 12, 14, 15, 21, 27, 30, 32. Step 2) Check the number of data points in both lists is the same. Both lists have 8 data points. Step 3) The range is the difference or gap between the largest and smallest numbers. Answer: the range is 32-9=23.
Mean, median, and mode (practice)
Mean, median, and mode. What is the mode of the following numbers? Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
Mean, median, and mode review (article)
Mean: The "average" number; found by adding all data points and dividing by the number of data points. Example: The mean of 4 , 1 , and 7 is ( 4 + 1 + 7) / 3 = 12 / 3 = 4 . Median: The middle number; found by ordering all data points and picking out the one in the middle (or if there are two middle numbers, taking the mean of those two numbers).
Mean Median Mode
To find the median find the average of 4 4 and 6 6 or find the midpoint of 4 4 and 6. 6. The median is 5. 5. To find the mode, look for the value (s) that occur the most; there may be more than one mode. Show step. 3 3 and 6 6 both occur twice, so there are two modes, 3 3 and 6. 6.
8.3 Mean, Median and Mode
Suppose we have a set of data with n n values, ordered from smallest to largest. If n n is odd, then the median is the data value at position n+1 2 n + 1 2. If n n is even, then we find the values at positions n 2 n 2 and n 2 + 1 n 2 + 1. If those values are named a a and b b, then the median is defined to be a+b 2 a + b 2.
Mean Median Mode and Range Questions and Revision
Median. The median is often referred to as "the middle", which is precisely what it is.. There are two common ways of finding the middle value(s): Method 1: Put the numbers in order from smallest to largest and find the middle value/middle two values. Cross out the smallest number and the largest number, then cross out the next smallest and largest, keeping going crossing out pairs of ...
Mean, Median, Mode, and Range
This central tendency statistics math video tutorial explains how to calculate the mean, median, mode, and range given a data set of odd numbers and even num...
IXL
Follow us. Learn how to find the mean, median, mode, and range of a data set in this free, interactive math lesson. Practice, get feedback, and have fun learning!
Mean, Median, Mode and Range Worksheets
These printable central tendency worksheets contain a mixed review of mean, median, mode and range concepts. Around 8 data are used in level 1. Download the set. Mean, Median, Mode and Range: Level 2. Find the mean, median, mode and range of each set of data. Each sheet has six problems with around 15 data. Download the set.
Mean, median, & mode example (video)
Find the mean, median, and mode of the following sets of numbers. And they give us the numbers right over here. So if someone just says the mean, they're really referring to what we typically, in everyday language, call the average. Sometimes it's called the arithmetic mean because you'll learn that there's other ways of actually calculating a ...
Mean, Median, Mode and Range
Mean: add together and divide by how many there are. Median: the middle number when the data is listed in order from smallest to largest. If there are 2 middle number, add them and divide by 2. Mode: the most frequent number. Example: Find the mean, median and mode of this set of data. 35,8,12,50,55,22,34,22,34. Show Video Lesson.
All about Averages
All about Averages. How well do you really understand mean, median and mode? In these puzzling problems we invite you to be playful with numbers and discover how averages change when data sets are tweaked. About Average. Age 11 to 14. Challenge Level. Can you find sets of numbers which satisfy each of our mean, median, mode and range conditions?
Mean, Median, and Mode: Measures of Central Tendency
The mean is the arithmetic average, and it is probably the measure of central tendency that you are most familiar. Calculating the mean is very simple. You just add up all of the values and divide by the number of observations in your dataset. The calculation of the mean incorporates all values in the data.
Mean, Median, Mode, and Range
Welcome to Mean, Median, Mode, and Range with Mr. J! Need help with mean, median, mode, and range? You're in the right place!Whether you're just starting out...
Mean Mode Median and Range Worksheets
These Mean Mode Median and Range Worksheets are great for practicing how to compute mean, mode, median, and range for data sets of numbers. These Mean Mode Median and Range Worksheets will generate 10 Mean Mode Median and Range problems per worksheet. These Mean Mode Median and Range Worksheets are perfect for mastering the math topic of means ...
Mean Median Mode Questions with Solutions
Mean = 26.8. Median = 27.9. Using the relationship between mean, median and mode, Mode = 3 Median - 2 Mean = 3 × 27.9 - 2 × 26.8 = 83.7 - 53.6 = 30.1. Therefore, the mode of the distribution is 30.1. 10. If the mean of the given frequency distribution is 35, then find the missing frequency y. Also, calculate the median and mode for the ...
Mean, median, and mode: they're ALL averages...?
Because of this, the median of the list will be the mean (that is, the usual average) of the middle two values within the list. The middle two numbers are 2 and 4, so: (2 + 4) ÷ 2 = 6 ÷ 2 = 3. So the median of this list is 3, a value that isn't in the list at all. The mode is the number that is repeated most often, but all the numbers in this ...
Calculating the Mean, Median, Mode & Range: Practice Problems
The mean of a data set tells us on average how much gas cost in the year 2000. We can find the mean by adding all of the numbers up and dividing by 12, which is the number of months in the year ...
Mean, Median, Mode, Range Calculator
Using the same example as previously: 2,10,21, 23, 23 ,38,38,1027892. The range, in this case, would be 1,027,890 compared to 36 in the previous case. As such, it is important to extensively analyze data sets to ensure that outliers are accounted for. This calculator determines the mean, median, mode, and range of a given data set.
Averages and Range Textbook Exercise
The Corbettmaths Textbook Exercise on the Mean, Median, Mode and Range. Welcome; Videos and Worksheets; Primary; 5-a-day. 5-a-day GCSE 9-1; 5-a-day Primary; 5-a-day Further Maths ... Click here for Questions . means, modes, medians, mean, mode, median. Textbook Exercise. Previous: Median from a Frequency Table Textbook Exercise. Next: Area of a ...