hypothesis testing without statistics

Statistics Resources

• Excel - Tutorials
• Basic Probability Rules
• Single Event Probability
• Complement Rule
• Intersections & Unions
• Compound Events
• Levels of Measurement
• Independent and Dependent Variables
• Entering Data
• Central Tendency
• Data and Tests
• Displaying Data
• Discussing Statistics In-text
• SEM and Confidence Intervals
• Two-Way Frequency Tables
• Empirical Rule
• Finding Probability
• Accessing SPSS
• Chart and Graphs
• Frequency Table and Distribution
• Descriptive Statistics
• Converting Raw Scores to Z-Scores
• Converting Z-scores to t-scores
• Split File/Split Output
• Partial Eta Squared
• Downloading and Installing G*Power: Windows/PC
• Correlation
• Testing Parametric Assumptions
• One-Way ANOVA
• Two-Way ANOVA
• Repeated Measures ANOVA
• Goodness-of-Fit
• Test of Association
• Pearson's r
• Point Biserial
• Mediation and Moderation
• Simple Linear Regression
• Multiple Linear Regression
• Binomial Logistic Regression
• Multinomial Logistic Regression
• Independent Samples T-test
• Dependent Samples T-test
• Testing Assumptions
• T-tests using SPSS
• T-Test Practice
• Predictive Analytics This link opens in a new window
• Quantitative Research Questions
• Null & Alternative Hypotheses
• One-Tail vs. Two-Tail
• Alpha & Beta
• Associated Probability
• Decision Rule
• Statement of Conclusion
• Statistics Group Sessions

ASC Chat Hours

ASC Chat is usually available at the following times ( Pacific Time):

If there is not a coach on duty, submit your question via one of the below methods:

  928-440-1325

  Ask a Coach

  [email protected]

Search our FAQs on the Academic Success Center's  Ask a Coach   page.

Reading List

In quantitative research, we can’t make claims without having some statistics to support it. In other words, it can’t be determined if the null or the alternative hypothesis is supported until the hypothesis has been explored, using the data that was collected.

There are numerous tests that can be used to test a hypothesis. Which test you use will depend on a number of factors. The purpose of this section is to discuss the basics of hypothesis testing.

Steps of Hypothesis Testing:

• State the Null & Alternative Hypotheses. These should reflect the hypothesis test that you anticipate conducting. For example, an alternative hypothesis for an ANOVA will state that there are significant differences between one or more means.
• Determine α. This refers to the amount of Type I error you are willing to make or the chance of determining that the null hypothesis is false when it is in fact true.
• State the decision rule. The decision rule states the circumstances under which the null hypothesis will be rejected. For a research paper, this will be comparing the obtained p-value (level of significance) of the test statistic to the alpha set for the hypothesis. For example, “If p < .05, the null hypothesis will be rejected.”
• Calculate the test statistic. In other words, conduct your hypothesis test with the appropriate statistical analysis. In most cases, this will be done using a statistical analysis tool, like SPSS.
• Reject the null hypothesis – In this case, the p-value for the test statistic is less than alpha. There is evidence to suggest the alternative is true.
• Fail to reject the null hypothesis – The p-value from the hypothesis test was greater than alpha. There is not sufficient evidence to suggest the null is not true.
• State the conclusion of the test in layman’s terms. This is where you connect the statistics back to the specific hypothesis being tested. For example, “The results of the hypothesis test indicate that the salary of factory workers varies based on gender.”

Was this resource helpful?

• << Previous: Quantitative Research Questions
• Next: Null & Alternative Hypotheses >>
• Last Updated: Apr 19, 2024 3:09 PM
• URL: https://resources.nu.edu/statsresources

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Statistics and probability

Course: statistics and probability   >   unit 12, hypothesis testing and p-values.

• One-tailed and two-tailed tests
• Z-statistics vs. T-statistics
• Small sample hypothesis test
• Large sample proportion hypothesis testing

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• Comprehensive Learning Paths
• 150+ Hours of Videos
• Complete Access to Jupyter notebooks, Datasets, References.

Hypothesis Testing – A Deep Dive into Hypothesis Testing, The Backbone of Statistical Inference

• September 21, 2023

Explore the intricacies of hypothesis testing, a cornerstone of statistical analysis. Dive into methods, interpretations, and applications for making data-driven decisions.

In this Blog post we will learn:

• What is Hypothesis Testing?
• Steps in Hypothesis Testing 2.1. Set up Hypotheses: Null and Alternative 2.2. Choose a Significance Level (α) 2.3. Calculate a test statistic and P-Value 2.4. Make a Decision
• Example : Testing a new drug.
• Example in python

1. What is Hypothesis Testing?

In simple terms, hypothesis testing is a method used to make decisions or inferences about population parameters based on sample data. Imagine being handed a dice and asked if it’s biased. By rolling it a few times and analyzing the outcomes, you’d be engaging in the essence of hypothesis testing.

Think of hypothesis testing as the scientific method of the statistics world. Suppose you hear claims like “This new drug works wonders!” or “Our new website design boosts sales.” How do you know if these statements hold water? Enter hypothesis testing.

2. Steps in Hypothesis Testing

• Set up Hypotheses : Begin with a null hypothesis (H0) and an alternative hypothesis (Ha).
• Choose a Significance Level (α) : Typically 0.05, this is the probability of rejecting the null hypothesis when it’s actually true. Think of it as the chance of accusing an innocent person.
• Calculate Test statistic and P-Value : Gather evidence (data) and calculate a test statistic.
• p-value : This is the probability of observing the data, given that the null hypothesis is true. A small p-value (typically ≤ 0.05) suggests the data is inconsistent with the null hypothesis.
• Decision Rule : If the p-value is less than or equal to α, you reject the null hypothesis in favor of the alternative.

2.1. Set up Hypotheses: Null and Alternative

Before diving into testing, we must formulate hypotheses. The null hypothesis (H0) represents the default assumption, while the alternative hypothesis (H1) challenges it.

For instance, in drug testing, H0 : “The new drug is no better than the existing one,” H1 : “The new drug is superior .”

2.2. Choose a Significance Level (α)

When You collect and analyze data to test H0 and H1 hypotheses. Based on your analysis, you decide whether to reject the null hypothesis in favor of the alternative, or fail to reject / Accept the null hypothesis.

The significance level, often denoted by $α$, represents the probability of rejecting the null hypothesis when it is actually true.

In other words, it’s the risk you’re willing to take of making a Type I error (false positive).

Type I Error (False Positive) :

• Symbolized by the Greek letter alpha (α).
• Occurs when you incorrectly reject a true null hypothesis . In other words, you conclude that there is an effect or difference when, in reality, there isn’t.
• The probability of making a Type I error is denoted by the significance level of a test. Commonly, tests are conducted at the 0.05 significance level , which means there’s a 5% chance of making a Type I error .
• Commonly used significance levels are 0.01, 0.05, and 0.10, but the choice depends on the context of the study and the level of risk one is willing to accept.

Example : If a drug is not effective (truth), but a clinical trial incorrectly concludes that it is effective (based on the sample data), then a Type I error has occurred.

Type II Error (False Negative) :

• Symbolized by the Greek letter beta (β).
• Occurs when you accept a false null hypothesis . This means you conclude there is no effect or difference when, in reality, there is.
• The probability of making a Type II error is denoted by β. The power of a test (1 – β) represents the probability of correctly rejecting a false null hypothesis.

Example : If a drug is effective (truth), but a clinical trial incorrectly concludes that it is not effective (based on the sample data), then a Type II error has occurred.

Balancing the Errors :

In practice, there’s a trade-off between Type I and Type II errors. Reducing the risk of one typically increases the risk of the other. For example, if you want to decrease the probability of a Type I error (by setting a lower significance level), you might increase the probability of a Type II error unless you compensate by collecting more data or making other adjustments.

It’s essential to understand the consequences of both types of errors in any given context. In some situations, a Type I error might be more severe, while in others, a Type II error might be of greater concern. This understanding guides researchers in designing their experiments and choosing appropriate significance levels.

2.3. Calculate a test statistic and P-Value

Test statistic : A test statistic is a single number that helps us understand how far our sample data is from what we’d expect under a null hypothesis (a basic assumption we’re trying to test against). Generally, the larger the test statistic, the more evidence we have against our null hypothesis. It helps us decide whether the differences we observe in our data are due to random chance or if there’s an actual effect.

P-value : The P-value tells us how likely we would get our observed results (or something more extreme) if the null hypothesis were true. It’s a value between 0 and 1. – A smaller P-value (typically below 0.05) means that the observation is rare under the null hypothesis, so we might reject the null hypothesis. – A larger P-value suggests that what we observed could easily happen by random chance, so we might not reject the null hypothesis.

2.4. Make a Decision

Relationship between $α$ and P-Value

When conducting a hypothesis test:

We then calculate the p-value from our sample data and the test statistic.

Finally, we compare the p-value to our chosen $α$:

• If $p−value≤α$: We reject the null hypothesis in favor of the alternative hypothesis. The result is said to be statistically significant.
• If $p−value>α$: We fail to reject the null hypothesis. There isn’t enough statistical evidence to support the alternative hypothesis.

3. Example : Testing a new drug.

Imagine we are investigating whether a new drug is effective at treating headaches faster than drug B.

Setting Up the Experiment : You gather 100 people who suffer from headaches. Half of them (50 people) are given the new drug (let’s call this the ‘Drug Group’), and the other half are given a sugar pill, which doesn’t contain any medication.

• Set up Hypotheses : Before starting, you make a prediction:
• Null Hypothesis (H0): The new drug has no effect. Any difference in healing time between the two groups is just due to random chance.
• Alternative Hypothesis (H1): The new drug does have an effect. The difference in healing time between the two groups is significant and not just by chance.

Calculate Test statistic and P-Value : After the experiment, you analyze the data. The “test statistic” is a number that helps you understand the difference between the two groups in terms of standard units.

For instance, let’s say:

• The average healing time in the Drug Group is 2 hours.
• The average healing time in the Placebo Group is 3 hours.

The test statistic helps you understand how significant this 1-hour difference is. If the groups are large and the spread of healing times in each group is small, then this difference might be significant. But if there’s a huge variation in healing times, the 1-hour difference might not be so special.

Imagine the P-value as answering this question: “If the new drug had NO real effect, what’s the probability that I’d see a difference as extreme (or more extreme) as the one I found, just by random chance?”

For instance:

• P-value of 0.01 means there’s a 1% chance that the observed difference (or a more extreme difference) would occur if the drug had no effect. That’s pretty rare, so we might consider the drug effective.
• P-value of 0.5 means there’s a 50% chance you’d see this difference just by chance. That’s pretty high, so we might not be convinced the drug is doing much.
• If the P-value is less than ($α$) 0.05: the results are “statistically significant,” and they might reject the null hypothesis , believing the new drug has an effect.
• If the P-value is greater than ($α$) 0.05: the results are not statistically significant, and they don’t reject the null hypothesis , remaining unsure if the drug has a genuine effect.

4. Example in python

For simplicity, let’s say we’re using a t-test (common for comparing means). Let’s dive into Python:

Making a Decision : “The results are statistically significant! p-value < 0.05 , The drug seems to have an effect!” If not, we’d say, “Looks like the drug isn’t as miraculous as we thought.”

5. Conclusion

Hypothesis testing is an indispensable tool in data science, allowing us to make data-driven decisions with confidence. By understanding its principles, conducting tests properly, and considering real-world applications, you can harness the power of hypothesis testing to unlock valuable insights from your data.

More Articles

Correlation – connecting the dots, the role of correlation in data analysis, sampling and sampling distributions – a comprehensive guide on sampling and sampling distributions, law of large numbers – a deep dive into the world of statistics, central limit theorem – a deep dive into central limit theorem and its significance in statistics, skewness and kurtosis – peaks and tails, understanding data through skewness and kurtosis”, similar articles, complete introduction to linear regression in r, how to implement common statistical significance tests and find the p value, logistic regression – a complete tutorial with examples in r.

Subscribe to Machine Learning Plus for high value data science content

© Machinelearningplus. All rights reserved.

Machine Learning A-Z™: Hands-On Python & R In Data Science

Free sample videos:.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.4: Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 283

• David Diez, Christopher Barr, & Mine Çetinkaya-Rundel
• OpenIntro Statistics

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Is the typical US runner getting faster or slower over time? We consider this question in the context of the Cherry Blossom Run, comparing runners in 2006 and 2012. Technological advances in shoes, training, and diet might suggest runners would be faster in 2012. An opposing viewpoint might say that with the average body mass index on the rise, people tend to run slower. In fact, all of these components might be influencing run time.

In addition to considering run times in this section, we consider a topic near and dear to most students: sleep. A recent study found that college students average about 7 hours of sleep per night.15 However, researchers at a rural college are interested in showing that their students sleep longer than seven hours on average. We investigate this topic in Section 4.3.4.

Hypothesis Testing Framework

The average time for all runners who finished the Cherry Blossom Run in 2006 was 93.29 minutes (93 minutes and about 17 seconds). We want to determine if the run10Samp data set provides strong evidence that the participants in 2012 were faster or slower than those runners in 2006, versus the other possibility that there has been no change. 16 We simplify these three options into two competing hypotheses :

• H 0 : The average 10 mile run time was the same for 2006 and 2012.
• H A : The average 10 mile run time for 2012 was different than that of 2006.

We call H 0 the null hypothesis and H A the alternative hypothesis.

Null and alternative hypotheses

• The null hypothesis (H 0 ) often represents either a skeptical perspective or a claim to be tested.
• The alternative hypothesis (H A ) represents an alternative claim under consideration and is often represented by a range of possible parameter values.

15 theloquitur.com/?p=1161

16 While we could answer this question by examining the entire population data (run10), we only consider the sample data (run10Samp), which is more realistic since we rarely have access to population data.

The null hypothesis often represents a skeptical position or a perspective of no difference. The alternative hypothesis often represents a new perspective, such as the possibility that there has been a change.

Hypothesis testing framework

The skeptic will not reject the null hypothesis (H 0 ), unless the evidence in favor of the alternative hypothesis (H A ) is so strong that she rejects H 0 in favor of H A .

The hypothesis testing framework is a very general tool, and we often use it without a second thought. If a person makes a somewhat unbelievable claim, we are initially skeptical. However, if there is sufficient evidence that supports the claim, we set aside our skepticism and reject the null hypothesis in favor of the alternative. The hallmarks of hypothesis testing are also found in the US court system.

Exercise \(\PageIndex{1}\)

A US court considers two possible claims about a defendant: she is either innocent or guilty. If we set these claims up in a hypothesis framework, which would be the null hypothesis and which the alternative? 17

Jurors examine the evidence to see whether it convincingly shows a defendant is guilty. Even if the jurors leave unconvinced of guilt beyond a reasonable doubt, this does not mean they believe the defendant is innocent. This is also the case with hypothesis testing: even if we fail to reject the null hypothesis, we typically do not accept the null hypothesis as true. Failing to find strong evidence for the alternative hypothesis is not equivalent to accepting the null hypothesis.

17 H 0 : The average cost is $650 per month, \(\mu\) = $650.

In the example with the Cherry Blossom Run, the null hypothesis represents no difference in the average time from 2006 to 2012. The alternative hypothesis represents something new or more interesting: there was a difference, either an increase or a decrease. These hypotheses can be described in mathematical notation using \(\mu_{12}\) as the average run time for 2012:

• H 0 : \(\mu_{12} = 93.29\)
• H A : \(\mu_{12} \ne 93.29\)

where 93.29 minutes (93 minutes and about 17 seconds) is the average 10 mile time for all runners in the 2006 Cherry Blossom Run. Using this mathematical notation, the hypotheses can now be evaluated using statistical tools. We call 93.29 the null value since it represents the value of the parameter if the null hypothesis is true. We will use the run10Samp data set to evaluate the hypothesis test.

Testing Hypotheses using Confidence Intervals

We can start the evaluation of the hypothesis setup by comparing 2006 and 2012 run times using a point estimate from the 2012 sample: \(\bar {x}_{12} = 95.61\) minutes. This estimate suggests the average time is actually longer than the 2006 time, 93.29 minutes. However, to evaluate whether this provides strong evidence that there has been a change, we must consider the uncertainty associated with \(\bar {x}_{12}\).

1 6 The jury considers whether the evidence is so convincing (strong) that there is no reasonable doubt regarding the person's guilt; in such a case, the jury rejects innocence (the null hypothesis) and concludes the defendant is guilty (alternative hypothesis).

We learned in Section 4.1 that there is fluctuation from one sample to another, and it is very unlikely that the sample mean will be exactly equal to our parameter; we should not expect \(\bar {x}_{12}\) to exactly equal \(\mu_{12}\). Given that \(\bar {x}_{12} = 95.61\), it might still be possible that the population average in 2012 has remained unchanged from 2006. The difference between \(\bar {x}_{12}\) and 93.29 could be due to sampling variation, i.e. the variability associated with the point estimate when we take a random sample.

In Section 4.2, confidence intervals were introduced as a way to find a range of plausible values for the population mean. Based on run10Samp, a 95% confidence interval for the 2012 population mean, \(\mu_{12}\), was calculated as

\[(92.45, 98.77)\]

Because the 2006 mean, 93.29, falls in the range of plausible values, we cannot say the null hypothesis is implausible. That is, we failed to reject the null hypothesis, H 0 .

Double negatives can sometimes be used in statistics

In many statistical explanations, we use double negatives. For instance, we might say that the null hypothesis is not implausible or we failed to reject the null hypothesis. Double negatives are used to communicate that while we are not rejecting a position, we are also not saying it is correct.

Example \(\PageIndex{1}\)

Next consider whether there is strong evidence that the average age of runners has changed from 2006 to 2012 in the Cherry Blossom Run. In 2006, the average age was 36.13 years, and in the 2012 run10Samp data set, the average was 35.05 years with a standard deviation of 8.97 years for 100 runners.

First, set up the hypotheses:

• H 0 : The average age of runners has not changed from 2006 to 2012, \(\mu_{age} = 36.13.\)
• H A : The average age of runners has changed from 2006 to 2012, \(\mu _{age} 6 \ne 36.13.\)

We have previously veri ed conditions for this data set. The normal model may be applied to \(\bar {y}\) and the estimate of SE should be very accurate. Using the sample mean and standard error, we can construct a 95% con dence interval for \(\mu _{age}\) to determine if there is sufficient evidence to reject H 0 :

\[\bar{y} \pm 1.96 \times \dfrac {s}{\sqrt {100}} \rightarrow 35.05 \pm 1.96 \times 0.90 \rightarrow (33.29, 36.81)\]

This confidence interval contains the null value, 36.13. Because 36.13 is not implausible, we cannot reject the null hypothesis. We have not found strong evidence that the average age is different than 36.13 years.

Exercise \(\PageIndex{2}\)

Colleges frequently provide estimates of student expenses such as housing. A consultant hired by a community college claimed that the average student housing expense was $650 per month. What are the null and alternative hypotheses to test whether this claim is accurate? 18

H A : The average cost is different than $650 per month, \(\mu \ne\) $650.

18 Applying the normal model requires that certain conditions are met. Because the data are a simple random sample and the sample (presumably) represents no more than 10% of all students at the college, the observations are independent. The sample size is also sufficiently large (n = 75) and the data exhibit only moderate skew. Thus, the normal model may be applied to the sample mean.

Exercise \(\PageIndex{3}\)

The community college decides to collect data to evaluate the $650 per month claim. They take a random sample of 75 students at their school and obtain the data represented in Figure 4.11. Can we apply the normal model to the sample mean?

If the court makes a Type 1 Error, this means the defendant is innocent (H 0 true) but wrongly convicted. A Type 2 Error means the court failed to reject H 0 (i.e. failed to convict the person) when she was in fact guilty (H A true).

Example \(\PageIndex{2}\)

The sample mean for student housing is $611.63 and the sample standard deviation is $132.85. Construct a 95% confidence interval for the population mean and evaluate the hypotheses of Exercise 4.22.

The standard error associated with the mean may be estimated using the sample standard deviation divided by the square root of the sample size. Recall that n = 75 students were sampled.

\[ SE = \dfrac {s}{\sqrt {n}} = \dfrac {132.85}{\sqrt {75}} = 15.34\]

You showed in Exercise 4.23 that the normal model may be applied to the sample mean. This ensures a 95% confidence interval may be accurately constructed:

\[\bar {x} \pm z*SE \rightarrow 611.63 \pm 1.96 \times 15.34 \times (581.56, 641.70)\]

Because the null value $650 is not in the confidence interval, a true mean of $650 is implausible and we reject the null hypothesis. The data provide statistically significant evidence that the actual average housing expense is less than $650 per month.

Decision Errors

Hypothesis tests are not flawless. Just think of the court system: innocent people are sometimes wrongly convicted and the guilty sometimes walk free. Similarly, we can make a wrong decision in statistical hypothesis tests. However, the difference is that we have the tools necessary to quantify how often we make such errors.

There are two competing hypotheses: the null and the alternative. In a hypothesis test, we make a statement about which one might be true, but we might choose incorrectly. There are four possible scenarios in a hypothesis test, which are summarized in Table 4.12.

A Type 1 Error is rejecting the null hypothesis when H0 is actually true. A Type 2 Error is failing to reject the null hypothesis when the alternative is actually true.

Exercise 4.25

In a US court, the defendant is either innocent (H 0 ) or guilty (H A ). What does a Type 1 Error represent in this context? What does a Type 2 Error represent? Table 4.12 may be useful.

To lower the Type 1 Error rate, we might raise our standard for conviction from "beyond a reasonable doubt" to "beyond a conceivable doubt" so fewer people would be wrongly convicted. However, this would also make it more difficult to convict the people who are actually guilty, so we would make more Type 2 Errors.

Exercise 4.26

How could we reduce the Type 1 Error rate in US courts? What influence would this have on the Type 2 Error rate?

To lower the Type 2 Error rate, we want to convict more guilty people. We could lower the standards for conviction from "beyond a reasonable doubt" to "beyond a little doubt". Lowering the bar for guilt will also result in more wrongful convictions, raising the Type 1 Error rate.

Exercise 4.27

How could we reduce the Type 2 Error rate in US courts? What influence would this have on the Type 1 Error rate?

A skeptic would have no reason to believe that sleep patterns at this school are different than the sleep patterns at another school.

Exercises 4.25-4.27 provide an important lesson:

If we reduce how often we make one type of error, we generally make more of the other type.

Hypothesis testing is built around rejecting or failing to reject the null hypothesis. That is, we do not reject H 0 unless we have strong evidence. But what precisely does strong evidence mean? As a general rule of thumb, for those cases where the null hypothesis is actually true, we do not want to incorrectly reject H 0 more than 5% of the time. This corresponds to a significance level of 0.05. We often write the significance level using \(\alpha\) (the Greek letter alpha): \(\alpha = 0.05.\) We discuss the appropriateness of different significance levels in Section 4.3.6.

If we use a 95% confidence interval to test a hypothesis where the null hypothesis is true, we will make an error whenever the point estimate is at least 1.96 standard errors away from the population parameter. This happens about 5% of the time (2.5% in each tail). Similarly, using a 99% con dence interval to evaluate a hypothesis is equivalent to a significance level of \(\alpha = 0.01\).

A confidence interval is, in one sense, simplistic in the world of hypothesis tests. Consider the following two scenarios:

• The null value (the parameter value under the null hypothesis) is in the 95% confidence interval but just barely, so we would not reject H 0 . However, we might like to somehow say, quantitatively, that it was a close decision.
• The null value is very far outside of the interval, so we reject H 0 . However, we want to communicate that, not only did we reject the null hypothesis, but it wasn't even close. Such a case is depicted in Figure 4.13.

In Section 4.3.4, we introduce a tool called the p-value that will be helpful in these cases. The p-value method also extends to hypothesis tests where con dence intervals cannot be easily constructed or applied.

Formal Testing using p-Values

The p-value is a way of quantifying the strength of the evidence against the null hypothesis and in favor of the alternative. Formally the p-value is a conditional probability.

definition: p-value

The p-value is the probability of observing data at least as favorable to the alternative hypothesis as our current data set, if the null hypothesis is true. We typically use a summary statistic of the data, in this chapter the sample mean, to help compute the p-value and evaluate the hypotheses.

A poll by the National Sleep Foundation found that college students average about 7 hours of sleep per night. Researchers at a rural school are interested in showing that students at their school sleep longer than seven hours on average, and they would like to demonstrate this using a sample of students. What would be an appropriate skeptical position for this research?

This is entirely based on the interests of the researchers. Had they been only interested in the opposite case - showing that their students were actually averaging fewer than seven hours of sleep but not interested in showing more than 7 hours - then our setup would have set the alternative as \(\mu < 7\).

We can set up the null hypothesis for this test as a skeptical perspective: the students at this school average 7 hours of sleep per night. The alternative hypothesis takes a new form reflecting the interests of the research: the students average more than 7 hours of sleep. We can write these hypotheses as

• H 0 : \(\mu\) = 7.
• H A : \(\mu\) > 7.

Using \(\mu\) > 7 as the alternative is an example of a one-sided hypothesis test. In this investigation, there is no apparent interest in learning whether the mean is less than 7 hours. (The standard error can be estimated from the sample standard deviation and the sample size: \(SE_{\bar {x}} = \dfrac {s_x}{\sqrt {n}} = \dfrac {1.75}{\sqrt {110}} = 0.17\)). Earlier we encountered a two-sided hypothesis where we looked for any clear difference, greater than or less than the null value.

Always use a two-sided test unless it was made clear prior to data collection that the test should be one-sided. Switching a two-sided test to a one-sided test after observing the data is dangerous because it can inflate the Type 1 Error rate.

TIP: One-sided and two-sided tests

If the researchers are only interested in showing an increase or a decrease, but not both, use a one-sided test. If the researchers would be interested in any difference from the null value - an increase or decrease - then the test should be two-sided.

TIP: Always write the null hypothesis as an equality

We will find it most useful if we always list the null hypothesis as an equality (e.g. \(\mu\) = 7) while the alternative always uses an inequality (e.g. \(\mu \ne 7, \mu > 7, or \mu < 7)\).

The researchers at the rural school conducted a simple random sample of n = 110 students on campus. They found that these students averaged 7.42 hours of sleep and the standard deviation of the amount of sleep for the students was 1.75 hours. A histogram of the sample is shown in Figure 4.14.

Before we can use a normal model for the sample mean or compute the standard error of the sample mean, we must verify conditions. (1) Because this is a simple random sample from less than 10% of the student body, the observations are independent. (2) The sample size in the sleep study is sufficiently large since it is greater than 30. (3) The data show moderate skew in Figure 4.14 and the presence of a couple of outliers. This skew and the outliers (which are not too extreme) are acceptable for a sample size of n = 110. With these conditions veri ed, the normal model can be safely applied to \(\bar {x}\) and the estimated standard error will be very accurate.

What is the standard deviation associated with \(\bar {x}\)? That is, estimate the standard error of \(\bar {x}\). 25

The hypothesis test will be evaluated using a significance level of \(\alpha = 0.05\). We want to consider the data under the scenario that the null hypothesis is true. In this case, the sample mean is from a distribution that is nearly normal and has mean 7 and standard deviation of about 0.17. Such a distribution is shown in Figure 4.15.

The shaded tail in Figure 4.15 represents the chance of observing such a large mean, conditional on the null hypothesis being true. That is, the shaded tail represents the p-value. We shade all means larger than our sample mean, \(\bar {x} = 7.42\), because they are more favorable to the alternative hypothesis than the observed mean.

We compute the p-value by finding the tail area of this normal distribution, which we learned to do in Section 3.1. First compute the Z score of the sample mean, \(\bar {x} = 7.42\):

\[Z = \dfrac {\bar {x} - \text {null value}}{SE_{\bar {x}}} = \dfrac {7.42 - 7}{0.17} = 2.47\]

Using the normal probability table, the lower unshaded area is found to be 0.993. Thus the shaded area is 1 - 0.993 = 0.007. If the null hypothesis is true, the probability of observing such a large sample mean for a sample of 110 students is only 0.007. That is, if the null hypothesis is true, we would not often see such a large mean.

We evaluate the hypotheses by comparing the p-value to the significance level. Because the p-value is less than the significance level \((p-value = 0.007 < 0.05 = \alpha)\), we reject the null hypothesis. What we observed is so unusual with respect to the null hypothesis that it casts serious doubt on H 0 and provides strong evidence favoring H A .

p-value as a tool in hypothesis testing

The p-value quantifies how strongly the data favor H A over H 0 . A small p-value (usually < 0.05) corresponds to sufficient evidence to reject H 0 in favor of H A .

TIP: It is useful to First draw a picture to find the p-value

It is useful to draw a picture of the distribution of \(\bar {x}\) as though H 0 was true (i.e. \(\mu\) equals the null value), and shade the region (or regions) of sample means that are at least as favorable to the alternative hypothesis. These shaded regions represent the p-value.

The ideas below review the process of evaluating hypothesis tests with p-values:

• The null hypothesis represents a skeptic's position or a position of no difference. We reject this position only if the evidence strongly favors H A .
• A small p-value means that if the null hypothesis is true, there is a low probability of seeing a point estimate at least as extreme as the one we saw. We interpret this as strong evidence in favor of the alternative.
• We reject the null hypothesis if the p-value is smaller than the significance level, \(\alpha\), which is usually 0.05. Otherwise, we fail to reject H 0 .
• We should always state the conclusion of the hypothesis test in plain language so non-statisticians can also understand the results.

The p-value is constructed in such a way that we can directly compare it to the significance level ( \(\alpha\)) to determine whether or not to reject H 0 . This method ensures that the Type 1 Error rate does not exceed the significance level standard.

If the null hypothesis is true, how often should the p-value be less than 0.05?

About 5% of the time. If the null hypothesis is true, then the data only has a 5% chance of being in the 5% of data most favorable to H A .

Exercise 4.31

Suppose we had used a significance level of 0.01 in the sleep study. Would the evidence have been strong enough to reject the null hypothesis? (The p-value was 0.007.) What if the significance level was \(\alpha = 0.001\)? 27

27 We reject the null hypothesis whenever p-value < \(\alpha\). Thus, we would still reject the null hypothesis if \(\alpha = 0.01\) but not if the significance level had been \(\alpha = 0.001\).

Exercise 4.32

Ebay might be interested in showing that buyers on its site tend to pay less than they would for the corresponding new item on Amazon. We'll research this topic for one particular product: a video game called Mario Kart for the Nintendo Wii. During early October 2009, Amazon sold this game for $46.99. Set up an appropriate (one-sided!) hypothesis test to check the claim that Ebay buyers pay less during auctions at this same time. 28

28 The skeptic would say the average is the same on Ebay, and we are interested in showing the average price is lower.

Exercise 4.33

During early October, 2009, 52 Ebay auctions were recorded for Mario Kart.29 The total prices for the auctions are presented using a histogram in Figure 4.17, and we may like to apply the normal model to the sample mean. Check the three conditions required for applying the normal model: (1) independence, (2) at least 30 observations, and (3) the data are not strongly skewed. 30

30 (1) The independence condition is unclear. We will make the assumption that the observations are independent, which we should report with any nal results. (2) The sample size is sufficiently large: \(n = 52 \ge 30\). (3) The data distribution is not strongly skewed; it is approximately symmetric.

H 0 : The average auction price on Ebay is equal to (or more than) the price on Amazon. We write only the equality in the statistical notation: \(\mu_{ebay} = 46.99\).

H A : The average price on Ebay is less than the price on Amazon, \(\mu _{ebay} < 46.99\).

29 These data were collected by OpenIntro staff.

Example 4.34

The average sale price of the 52 Ebay auctions for Wii Mario Kart was $44.17 with a standard deviation of $4.15. Does this provide sufficient evidence to reject the null hypothesis in Exercise 4.32? Use a significance level of \(\alpha = 0.01\).

The hypotheses were set up and the conditions were checked in Exercises 4.32 and 4.33. The next step is to find the standard error of the sample mean and produce a sketch to help find the p-value.

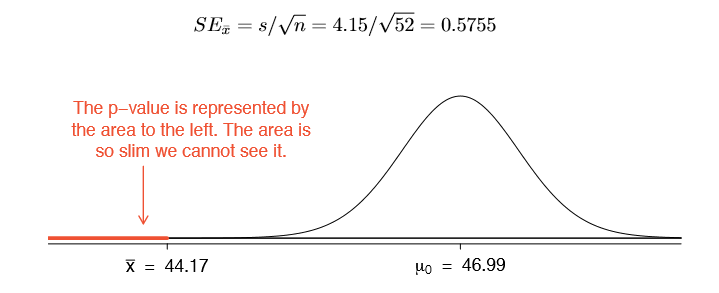
Because the alternative hypothesis says we are looking for a smaller mean, we shade the lower tail. We find this shaded area by using the Z score and normal probability table: \(Z = \dfrac {44.17 \times 46.99}{0.5755} = -4.90\), which has area less than 0.0002. The area is so small we cannot really see it on the picture. This lower tail area corresponds to the p-value.

Because the p-value is so small - specifically, smaller than = 0.01 - this provides sufficiently strong evidence to reject the null hypothesis in favor of the alternative. The data provide statistically signi cant evidence that the average price on Ebay is lower than Amazon's asking price.

Two-sided hypothesis testing with p-values

We now consider how to compute a p-value for a two-sided test. In one-sided tests, we shade the single tail in the direction of the alternative hypothesis. For example, when the alternative had the form \(\mu\) > 7, then the p-value was represented by the upper tail (Figure 4.16). When the alternative was \(\mu\) < 46.99, the p-value was the lower tail (Exercise 4.32). In a two-sided test, we shade two tails since evidence in either direction is favorable to H A .

Exercise 4.35 Earlier we talked about a research group investigating whether the students at their school slept longer than 7 hours each night. Let's consider a second group of researchers who want to evaluate whether the students at their college differ from the norm of 7 hours. Write the null and alternative hypotheses for this investigation. 31

Example 4.36 The second college randomly samples 72 students and nds a mean of \(\bar {x} = 6.83\) hours and a standard deviation of s = 1.8 hours. Does this provide strong evidence against H 0 in Exercise 4.35? Use a significance level of \(\alpha = 0.05\).

First, we must verify assumptions. (1) A simple random sample of less than 10% of the student body means the observations are independent. (2) The sample size is 72, which is greater than 30. (3) Based on the earlier distribution and what we already know about college student sleep habits, the distribution is probably not strongly skewed.

Next we can compute the standard error \((SE_{\bar {x}} = \dfrac {s}{\sqrt {n}} = 0.21)\) of the estimate and create a picture to represent the p-value, shown in Figure 4.18. Both tails are shaded.

31 Because the researchers are interested in any difference, they should use a two-sided setup: H 0 : \(\mu\) = 7, H A : \(\mu \ne 7.\)

An estimate of 7.17 or more provides at least as strong of evidence against the null hypothesis and in favor of the alternative as the observed estimate, \(\bar {x} = 6.83\).

We can calculate the tail areas by rst nding the lower tail corresponding to \(\bar {x}\):

\[Z = \dfrac {6.83 - 7.00}{0.21} = -0.81 \xrightarrow {table} \text {left tail} = 0.2090\]

Because the normal model is symmetric, the right tail will have the same area as the left tail. The p-value is found as the sum of the two shaded tails:

\[ \text {p-value} = \text {left tail} + \text {right tail} = 2 \times \text {(left tail)} = 0.4180\]

This p-value is relatively large (larger than \(\mu\)= 0.05), so we should not reject H 0 . That is, if H 0 is true, it would not be very unusual to see a sample mean this far from 7 hours simply due to sampling variation. Thus, we do not have sufficient evidence to conclude that the mean is different than 7 hours.

Example 4.37 It is never okay to change two-sided tests to one-sided tests after observing the data. In this example we explore the consequences of ignoring this advice. Using \(\alpha = 0.05\), we show that freely switching from two-sided tests to onesided tests will cause us to make twice as many Type 1 Errors as intended.

Suppose the sample mean was larger than the null value, \(\mu_0\) (e.g. \(\mu_0\) would represent 7 if H 0 : \(\mu\) = 7). Then if we can ip to a one-sided test, we would use H A : \(\mu > \mu_0\). Now if we obtain any observation with a Z score greater than 1.65, we would reject H 0 . If the null hypothesis is true, we incorrectly reject the null hypothesis about 5% of the time when the sample mean is above the null value, as shown in Figure 4.19.

Suppose the sample mean was smaller than the null value. Then if we change to a one-sided test, we would use H A : \(\mu < \mu_0\). If \(\bar {x}\) had a Z score smaller than -1.65, we would reject H 0 . If the null hypothesis is true, then we would observe such a case about 5% of the time.

By examining these two scenarios, we can determine that we will make a Type 1 Error 5% + 5% = 10% of the time if we are allowed to swap to the "best" one-sided test for the data. This is twice the error rate we prescribed with our significance level: \(\alpha = 0.05\) (!).

Caution: One-sided hypotheses are allowed only before seeing data

After observing data, it is tempting to turn a two-sided test into a one-sided test. Avoid this temptation. Hypotheses must be set up before observing the data. If they are not, the test must be two-sided.

Choosing a Significance Level

Choosing a significance level for a test is important in many contexts, and the traditional level is 0.05. However, it is often helpful to adjust the significance level based on the application. We may select a level that is smaller or larger than 0.05 depending on the consequences of any conclusions reached from the test.

• If making a Type 1 Error is dangerous or especially costly, we should choose a small significance level (e.g. 0.01). Under this scenario we want to be very cautious about rejecting the null hypothesis, so we demand very strong evidence favoring H A before we would reject H 0 .
• If a Type 2 Error is relatively more dangerous or much more costly than a Type 1 Error, then we should choose a higher significance level (e.g. 0.10). Here we want to be cautious about failing to reject H 0 when the null is actually false. We will discuss this particular case in greater detail in Section 4.6.

Significance levels should reflect consequences of errors

The significance level selected for a test should reflect the consequences associated with Type 1 and Type 2 Errors.

Example 4.38

A car manufacturer is considering a higher quality but more expensive supplier for window parts in its vehicles. They sample a number of parts from their current supplier and also parts from the new supplier. They decide that if the high quality parts will last more than 12% longer, it makes nancial sense to switch to this more expensive supplier. Is there good reason to modify the significance level in such a hypothesis test?

The null hypothesis is that the more expensive parts last no more than 12% longer while the alternative is that they do last more than 12% longer. This decision is just one of the many regular factors that have a marginal impact on the car and company. A significancelevel of 0.05 seems reasonable since neither a Type 1 or Type 2 error should be dangerous or (relatively) much more expensive.

Example 4.39

The same car manufacturer is considering a slightly more expensive supplier for parts related to safety, not windows. If the durability of these safety components is shown to be better than the current supplier, they will switch manufacturers. Is there good reason to modify the significance level in such an evaluation?

The null hypothesis would be that the suppliers' parts are equally reliable. Because safety is involved, the car company should be eager to switch to the slightly more expensive manufacturer (reject H 0 ) even if the evidence of increased safety is only moderately strong. A slightly larger significance level, such as \(\mu = 0.10\), might be appropriate.

Exercise 4.40

A part inside of a machine is very expensive to replace. However, the machine usually functions properly even if this part is broken, so the part is replaced only if we are extremely certain it is broken based on a series of measurements. Identify appropriate hypotheses for this test (in plain language) and suggest an appropriate significance level. 32

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Statistics Made Easy

How to Write Hypothesis Test Conclusions (With Examples)

A   hypothesis test is used to test whether or not some hypothesis about a population parameter is true.

To perform a hypothesis test in the real world, researchers obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:

• Null Hypothesis (H 0 ): The sample data occurs purely from chance.
• Alternative Hypothesis (H A ): The sample data is influenced by some non-random cause.

If the p-value of the hypothesis test is less than some significance level (e.g. α = .05), then we reject the null hypothesis .

Otherwise, if the p-value is not less than some significance level then we fail to reject the null hypothesis .

When writing the conclusion of a hypothesis test, we typically include:

• Whether we reject or fail to reject the null hypothesis.
• The significance level.
• A short explanation in the context of the hypothesis test.

For example, we would write:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that…

Or, we would write:

We fail to reject the null hypothesis at the 5% significance level.   There is not sufficient evidence to support the claim that…

The following examples show how to write a hypothesis test conclusion in both scenarios.

Example 1: Reject the Null Hypothesis Conclusion

Suppose a biologist believes that a certain fertilizer will cause plants to grow more during a one-month period than they normally do, which is currently 20 inches. To test this, she applies the fertilizer to each of the plants in her laboratory for one month.

She then performs a hypothesis test at a 5% significance level using the following hypotheses:

• H 0 : μ = 20 inches (the fertilizer will have no effect on the mean plant growth)
• H A : μ > 20 inches (the fertilizer will cause mean plant growth to increase)

Suppose the p-value of the test turns out to be 0.002.

Here is how she would report the results of the hypothesis test:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that this particular fertilizer causes plants to grow more during a one-month period than they normally do.

Example 2: Fail to Reject the Null Hypothesis Conclusion

Suppose the manager of a manufacturing plant wants to test whether or not some new method changes the number of defective widgets produced per month, which is currently 250. To test this, he measures the mean number of defective widgets produced before and after using the new method for one month.

He performs a hypothesis test at a 10% significance level using the following hypotheses:

• H 0 : μ after = μ before (the mean number of defective widgets is the same before and after using the new method)
• H A : μ after ≠ μ before (the mean number of defective widgets produced is different before and after using the new method)

Suppose the p-value of the test turns out to be 0.27.

Here is how he would report the results of the hypothesis test:

We fail to reject the null hypothesis at the 10% significance level.   There is not sufficient evidence to support the claim that the new method leads to a change in the number of defective widgets produced per month.

Additional Resources

The following tutorials provide additional information about hypothesis testing:

Introduction to Hypothesis Testing 4 Examples of Hypothesis Testing in Real Life How to Write a Null Hypothesis

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

6a.2 - steps for hypothesis tests, the logic of hypothesis testing section  .

A hypothesis, in statistics, is a statement about a population parameter, where this statement typically is represented by some specific numerical value. In testing a hypothesis, we use a method where we gather data in an effort to gather evidence about the hypothesis.

How do we decide whether to reject the null hypothesis?

• If the sample data are consistent with the null hypothesis, then we do not reject it.
• If the sample data are inconsistent with the null hypothesis, but consistent with the alternative, then we reject the null hypothesis and conclude that the alternative hypothesis is true.

Six Steps for Hypothesis Tests Section  

In hypothesis testing, there are certain steps one must follow. Below these are summarized into six such steps to conducting a test of a hypothesis.

• Set up the hypotheses and check conditions : Each hypothesis test includes two hypotheses about the population. One is the null hypothesis, notated as \(H_0 \), which is a statement of a particular parameter value. This hypothesis is assumed to be true until there is evidence to suggest otherwise. The second hypothesis is called the alternative, or research hypothesis, notated as \(H_a \). The alternative hypothesis is a statement of a range of alternative values in which the parameter may fall. One must also check that any conditions (assumptions) needed to run the test have been satisfied e.g. normality of data, independence, and number of success and failure outcomes.
• Decide on the significance level, \(\alpha \): This value is used as a probability cutoff for making decisions about the null hypothesis. This alpha value represents the probability we are willing to place on our test for making an incorrect decision in regards to rejecting the null hypothesis. The most common \(\alpha \) value is 0.05 or 5%. Other popular choices are 0.01 (1%) and 0.1 (10%).
• Calculate the test statistic: Gather sample data and calculate a test statistic where the sample statistic is compared to the parameter value. The test statistic is calculated under the assumption the null hypothesis is true and incorporates a measure of standard error and assumptions (conditions) related to the sampling distribution.
• Calculate probability value (p-value), or find the rejection region: A p-value is found by using the test statistic to calculate the probability of the sample data producing such a test statistic or one more extreme. The rejection region is found by using alpha to find a critical value; the rejection region is the area that is more extreme than the critical value. We discuss the p-value and rejection region in more detail in the next section.
• Make a decision about the null hypothesis: In this step, we decide to either reject the null hypothesis or decide to fail to reject the null hypothesis. Notice we do not make a decision where we will accept the null hypothesis.
• State an overall conclusion : Once we have found the p-value or rejection region, and made a statistical decision about the null hypothesis (i.e. we will reject the null or fail to reject the null), we then want to summarize our results into an overall conclusion for our test.

We will follow these six steps for the remainder of this Lesson. In the future Lessons, the steps will be followed but may not be explained explicitly.

Step 1 is a very important step to set up correctly. If your hypotheses are incorrect, your conclusion will be incorrect. In this next section, we practice with Step 1 for the one sample situations.

Tutorial Playlist

Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability.

A Comprehensive Look at Percentile in Statistics

The Best Guide to Understand Bayes Theorem

Everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, a complete guide to chi-square test, a complete guide on hypothesis testing in statistics, understanding the fundamentals of arithmetic and geometric progression, the definitive guide to understand spearman’s rank correlation, a comprehensive guide to understand mean squared error, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution.

All You Need to Know About Bias in Statistics

A Complete Guide to Get a Grasp of Time Series Analysis

The Key Differences Between Z-Test Vs. T-Test

The Complete Guide to Understand Pearson's Correlation

A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, what is hypothesis testing in statistics types and examples.

Lesson 10 of 24 By Avijeet Biswal

Table of Contents

In today’s data-driven world , decisions are based on data all the time. Hypothesis plays a crucial role in that process, whether it may be making business decisions, in the health sector, academia, or in quality improvement. Without hypothesis & hypothesis tests, you risk drawing the wrong conclusions and making bad decisions. In this tutorial, you will look at Hypothesis Testing in Statistics.

What Is Hypothesis Testing in Statistics?

Hypothesis Testing is a type of statistical analysis in which you put your assumptions about a population parameter to the test. It is used to estimate the relationship between 2 statistical variables.

Let's discuss few examples of statistical hypothesis from real-life - 

• A teacher assumes that 60% of his college's students come from lower-middle-class families.
• A doctor believes that 3D (Diet, Dose, and Discipline) is 90% effective for diabetic patients.

Now that you know about hypothesis testing, look at the two types of hypothesis testing in statistics.

Hypothesis Testing Formula

Z = ( x̅ – μ0 ) / (σ /√n)

• Here, x̅ is the sample mean,
• μ0 is the population mean,
• σ is the standard deviation,
• n is the sample size.

How Hypothesis Testing Works?

An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis. Measurements and analyses are conducted on a random sample of the population to test a theory. Analysts use a random population sample to test two hypotheses: the null and alternative hypotheses.

The null hypothesis is typically an equality hypothesis between population parameters; for example, a null hypothesis may claim that the population means return equals zero. The alternate hypothesis is essentially the inverse of the null hypothesis (e.g., the population means the return is not equal to zero). As a result, they are mutually exclusive, and only one can be correct. One of the two possibilities, however, will always be correct.

Your Dream Career is Just Around The Corner!

Null Hypothesis and Alternate Hypothesis

The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.

H0 is the symbol for it, and it is pronounced H-naught.

The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.

Let's understand this with an example.

A sanitizer manufacturer claims that its product kills 95 percent of germs on average. 

To put this company's claim to the test, create a null and alternate hypothesis.

H0 (Null Hypothesis): Average = 95%.

Alternative Hypothesis (H1): The average is less than 95%.

Another straightforward example to understand this concept is determining whether or not a coin is fair and balanced. The null hypothesis states that the probability of a show of heads is equal to the likelihood of a show of tails. In contrast, the alternate theory states that the probability of a show of heads and tails would be very different.

Become a Data Scientist with Hands-on Training!

Hypothesis Testing Calculation With Examples

Let's consider a hypothesis test for the average height of women in the United States. Suppose our null hypothesis is that the average height is 5'4". We gather a sample of 100 women and determine that their average height is 5'5". The standard deviation of population is 2.

To calculate the z-score, we would use the following formula:

z = ( x̅ – μ0 ) / (σ /√n)

z = (5'5" - 5'4") / (2" / √100)

z = 0.5 / (0.045)

 We will reject the null hypothesis as the z-score of 11.11 is very large and conclude that there is evidence to suggest that the average height of women in the US is greater than 5'4".

Steps of Hypothesis Testing

Step 1: specify your null and alternate hypotheses.

It is critical to rephrase your original research hypothesis (the prediction that you wish to study) as a null (Ho) and alternative (Ha) hypothesis so that you can test it quantitatively. Your first hypothesis, which predicts a link between variables, is generally your alternate hypothesis. The null hypothesis predicts no link between the variables of interest.

Step 2: Gather Data

For a statistical test to be legitimate, sampling and data collection must be done in a way that is meant to test your hypothesis. You cannot draw statistical conclusions about the population you are interested in if your data is not representative.

Step 3: Conduct a Statistical Test

Other statistical tests are available, but they all compare within-group variance (how to spread out the data inside a category) against between-group variance (how different the categories are from one another). If the between-group variation is big enough that there is little or no overlap between groups, your statistical test will display a low p-value to represent this. This suggests that the disparities between these groups are unlikely to have occurred by accident. Alternatively, if there is a large within-group variance and a low between-group variance, your statistical test will show a high p-value. Any difference you find across groups is most likely attributable to chance. The variety of variables and the level of measurement of your obtained data will influence your statistical test selection.

Step 4: Determine Rejection Of Your Null Hypothesis

Your statistical test results must determine whether your null hypothesis should be rejected or not. In most circumstances, you will base your judgment on the p-value provided by the statistical test. In most circumstances, your preset level of significance for rejecting the null hypothesis will be 0.05 - that is, when there is less than a 5% likelihood that these data would be seen if the null hypothesis were true. In other circumstances, researchers use a lower level of significance, such as 0.01 (1%). This reduces the possibility of wrongly rejecting the null hypothesis.

Step 5: Present Your Results 

The findings of hypothesis testing will be discussed in the results and discussion portions of your research paper, dissertation, or thesis. You should include a concise overview of the data and a summary of the findings of your statistical test in the results section. You can talk about whether your results confirmed your initial hypothesis or not in the conversation. Rejecting or failing to reject the null hypothesis is a formal term used in hypothesis testing. This is likely a must for your statistics assignments.

Types of Hypothesis Testing

To determine whether a discovery or relationship is statistically significant, hypothesis testing uses a z-test. It usually checks to see if two means are the same (the null hypothesis). Only when the population standard deviation is known and the sample size is 30 data points or more, can a z-test be applied.

A statistical test called a t-test is employed to compare the means of two groups. To determine whether two groups differ or if a procedure or treatment affects the population of interest, it is frequently used in hypothesis testing.

Chi-Square 

You utilize a Chi-square test for hypothesis testing concerning whether your data is as predicted. To determine if the expected and observed results are well-fitted, the Chi-square test analyzes the differences between categorical variables from a random sample. The test's fundamental premise is that the observed values in your data should be compared to the predicted values that would be present if the null hypothesis were true.

Hypothesis Testing and Confidence Intervals

Both confidence intervals and hypothesis tests are inferential techniques that depend on approximating the sample distribution. Data from a sample is used to estimate a population parameter using confidence intervals. Data from a sample is used in hypothesis testing to examine a given hypothesis. We must have a postulated parameter to conduct hypothesis testing.

Bootstrap distributions and randomization distributions are created using comparable simulation techniques. The observed sample statistic is the focal point of a bootstrap distribution, whereas the null hypothesis value is the focal point of a randomization distribution.

A variety of feasible population parameter estimates are included in confidence ranges. In this lesson, we created just two-tailed confidence intervals. There is a direct connection between these two-tail confidence intervals and these two-tail hypothesis tests. The results of a two-tailed hypothesis test and two-tailed confidence intervals typically provide the same results. In other words, a hypothesis test at the 0.05 level will virtually always fail to reject the null hypothesis if the 95% confidence interval contains the predicted value. A hypothesis test at the 0.05 level will nearly certainly reject the null hypothesis if the 95% confidence interval does not include the hypothesized parameter.

Simple and Composite Hypothesis Testing

Depending on the population distribution, you can classify the statistical hypothesis into two types.

Simple Hypothesis: A simple hypothesis specifies an exact value for the parameter.

Composite Hypothesis: A composite hypothesis specifies a range of values.

A company is claiming that their average sales for this quarter are 1000 units. This is an example of a simple hypothesis.

Suppose the company claims that the sales are in the range of 900 to 1000 units. Then this is a case of a composite hypothesis.

One-Tailed and Two-Tailed Hypothesis Testing

The One-Tailed test, also called a directional test, considers a critical region of data that would result in the null hypothesis being rejected if the test sample falls into it, inevitably meaning the acceptance of the alternate hypothesis.

In a one-tailed test, the critical distribution area is one-sided, meaning the test sample is either greater or lesser than a specific value.

In two tails, the test sample is checked to be greater or less than a range of values in a Two-Tailed test, implying that the critical distribution area is two-sided.

If the sample falls within this range, the alternate hypothesis will be accepted, and the null hypothesis will be rejected.

Become a Data Scientist With Real-World Experience

Right Tailed Hypothesis Testing

If the larger than (>) sign appears in your hypothesis statement, you are using a right-tailed test, also known as an upper test. Or, to put it another way, the disparity is to the right. For instance, you can contrast the battery life before and after a change in production. Your hypothesis statements can be the following if you want to know if the battery life is longer than the original (let's say 90 hours):

• The null hypothesis is (H0 <= 90) or less change.
• A possibility is that battery life has risen (H1) > 90.

The crucial point in this situation is that the alternate hypothesis (H1), not the null hypothesis, decides whether you get a right-tailed test.

Left Tailed Hypothesis Testing

Alternative hypotheses that assert the true value of a parameter is lower than the null hypothesis are tested with a left-tailed test; they are indicated by the asterisk "<".

Suppose H0: mean = 50 and H1: mean not equal to 50

According to the H1, the mean can be greater than or less than 50. This is an example of a Two-tailed test.

In a similar manner, if H0: mean >=50, then H1: mean <50

Here the mean is less than 50. It is called a One-tailed test.

Type 1 and Type 2 Error

A hypothesis test can result in two types of errors.

Type 1 Error: A Type-I error occurs when sample results reject the null hypothesis despite being true.

Type 2 Error: A Type-II error occurs when the null hypothesis is not rejected when it is false, unlike a Type-I error.

Suppose a teacher evaluates the examination paper to decide whether a student passes or fails.

H0: Student has passed

H1: Student has failed

Type I error will be the teacher failing the student [rejects H0] although the student scored the passing marks [H0 was true]. 

Type II error will be the case where the teacher passes the student [do not reject H0] although the student did not score the passing marks [H1 is true].

Level of Significance

The alpha value is a criterion for determining whether a test statistic is statistically significant. In a statistical test, Alpha represents an acceptable probability of a Type I error. Because alpha is a probability, it can be anywhere between 0 and 1. In practice, the most commonly used alpha values are 0.01, 0.05, and 0.1, which represent a 1%, 5%, and 10% chance of a Type I error, respectively (i.e. rejecting the null hypothesis when it is in fact correct).

Future-Proof Your AI/ML Career: Top Dos and Don'ts

A p-value is a metric that expresses the likelihood that an observed difference could have occurred by chance. As the p-value decreases the statistical significance of the observed difference increases. If the p-value is too low, you reject the null hypothesis.

Here you have taken an example in which you are trying to test whether the new advertising campaign has increased the product's sales. The p-value is the likelihood that the null hypothesis, which states that there is no change in the sales due to the new advertising campaign, is true. If the p-value is .30, then there is a 30% chance that there is no increase or decrease in the product's sales.  If the p-value is 0.03, then there is a 3% probability that there is no increase or decrease in the sales value due to the new advertising campaign. As you can see, the lower the p-value, the chances of the alternate hypothesis being true increases, which means that the new advertising campaign causes an increase or decrease in sales.

Why is Hypothesis Testing Important in Research Methodology?

Hypothesis testing is crucial in research methodology for several reasons:

• Provides evidence-based conclusions: It allows researchers to make objective conclusions based on empirical data, providing evidence to support or refute their research hypotheses.
• Supports decision-making: It helps make informed decisions, such as accepting or rejecting a new treatment, implementing policy changes, or adopting new practices.
• Adds rigor and validity: It adds scientific rigor to research using statistical methods to analyze data, ensuring that conclusions are based on sound statistical evidence.
• Contributes to the advancement of knowledge: By testing hypotheses, researchers contribute to the growth of knowledge in their respective fields by confirming existing theories or discovering new patterns and relationships.

Limitations of Hypothesis Testing

Hypothesis testing has some limitations that researchers should be aware of:

• It cannot prove or establish the truth: Hypothesis testing provides evidence to support or reject a hypothesis, but it cannot confirm the absolute truth of the research question.
• Results are sample-specific: Hypothesis testing is based on analyzing a sample from a population, and the conclusions drawn are specific to that particular sample.
• Possible errors: During hypothesis testing, there is a chance of committing type I error (rejecting a true null hypothesis) or type II error (failing to reject a false null hypothesis).
• Assumptions and requirements: Different tests have specific assumptions and requirements that must be met to accurately interpret results.

After reading this tutorial, you would have a much better understanding of hypothesis testing, one of the most important concepts in the field of Data Science . The majority of hypotheses are based on speculation about observed behavior, natural phenomena, or established theories.

If you are interested in statistics of data science and skills needed for such a career, you ought to explore Simplilearn’s Post Graduate Program in Data Science.

If you have any questions regarding this ‘Hypothesis Testing In Statistics’ tutorial, do share them in the comment section. Our subject matter expert will respond to your queries. Happy learning!

1. What is hypothesis testing in statistics with example?

Hypothesis testing is a statistical method used to determine if there is enough evidence in a sample data to draw conclusions about a population. It involves formulating two competing hypotheses, the null hypothesis (H0) and the alternative hypothesis (Ha), and then collecting data to assess the evidence. An example: testing if a new drug improves patient recovery (Ha) compared to the standard treatment (H0) based on collected patient data.

2. What is hypothesis testing and its types?

Hypothesis testing is a statistical method used to make inferences about a population based on sample data. It involves formulating two hypotheses: the null hypothesis (H0), which represents the default assumption, and the alternative hypothesis (Ha), which contradicts H0. The goal is to assess the evidence and determine whether there is enough statistical significance to reject the null hypothesis in favor of the alternative hypothesis.

Types of hypothesis testing:

• One-sample test: Used to compare a sample to a known value or a hypothesized value.
• Two-sample test: Compares two independent samples to assess if there is a significant difference between their means or distributions.
• Paired-sample test: Compares two related samples, such as pre-test and post-test data, to evaluate changes within the same subjects over time or under different conditions.
• Chi-square test: Used to analyze categorical data and determine if there is a significant association between variables.
• ANOVA (Analysis of Variance): Compares means across multiple groups to check if there is a significant difference between them.

3. What are the steps of hypothesis testing?

The steps of hypothesis testing are as follows:

• Formulate the hypotheses: State the null hypothesis (H0) and the alternative hypothesis (Ha) based on the research question.
• Set the significance level: Determine the acceptable level of error (alpha) for making a decision.
• Collect and analyze data: Gather and process the sample data.
• Compute test statistic: Calculate the appropriate statistical test to assess the evidence.
• Make a decision: Compare the test statistic with critical values or p-values and determine whether to reject H0 in favor of Ha or not.
• Draw conclusions: Interpret the results and communicate the findings in the context of the research question.

4. What are the 2 types of hypothesis testing?

• One-tailed (or one-sided) test: Tests for the significance of an effect in only one direction, either positive or negative.
• Two-tailed (or two-sided) test: Tests for the significance of an effect in both directions, allowing for the possibility of a positive or negative effect.

The choice between one-tailed and two-tailed tests depends on the specific research question and the directionality of the expected effect.

5. What are the 3 major types of hypothesis?

The three major types of hypotheses are:

• Null Hypothesis (H0): Represents the default assumption, stating that there is no significant effect or relationship in the data.
• Alternative Hypothesis (Ha): Contradicts the null hypothesis and proposes a specific effect or relationship that researchers want to investigate.
• Nondirectional Hypothesis: An alternative hypothesis that doesn't specify the direction of the effect, leaving it open for both positive and negative possibilities.

Find our Data Analyst Online Bootcamp in top cities:

About the author.

Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.

Recommended Resources

Free eBook: Top Programming Languages For A Data Scientist

Normality Test in Minitab: Minitab with Statistics

Machine Learning Career Guide: A Playbook to Becoming a Machine Learning Engineer

• PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.