hypothesis for water quality testing

Montana Science Partnership

• How to Navigate MSP Modules
• What Are Maps?
• How Are Maps Used in Science?
• Schoolyard Mapping Activity
• Mapping With Google Earth
• Extension Activities
• Mapping Glossary
• Sample Field Map Sketches
• Mapping Resources
• The Shape of Landscapes
• Tectonic Extension
• Transcurrent Tectonics
• Compressional Tectonics
• Weathering & Erosion
• Tectonics, Weathering & Erosion
• Time & Landscape
• Landform Examples
• Landscape Glossary
• Landscape Resources
• What Is Living in the Soil?
• Soil Profiles
• Understanding Soils
• The Tree of Life: Part 2
• The Tree of Life: Part 3
• Microbes & Biofilms
• Colonizing & Culturing Microbes
• Isolating a Colony from a Soil Sample
• Wrapping Petri Dishes in Parafilm
• Soil Glossary
• Soil Resources
• An Introduction to Water
• Polar Molecules
• Polarity of Water
• Conductivity: Pure Water + NaCl
• Conductivity: Pure Water + CaCO3
• Conductivity: Pure Water + Acetic Acid
• Conductivity: Pure Water + Sulfuric Acid
• An Introduction to Water Quality
• The Water Cycle
• Water Quality Parameters: pH
• Water Quality Parameters: Turbidity
• Water Quality Parameters: Temperature
• Water Quality Parameters: Dissolved Oxygen
• Water Quality Parameters: Conductivity & Hardness
• Water Quality Impacts: Point Source
• Water Quality Impacts: Nonpoint Source
• Step 1: Observation & Research
• Step 2: Formulate a Hypothesis & Make Predictions
• Step 3: Observe, Collect Data & Evaluate Results
• Step 4: Analyze & Communicate Your Data
• Water Glossary
• Water Resources
• Snowflake Shapes
• Snowflakes: Symmetry
• Water Phase Change
• Earth’s Energy Budget
• Absorption & Reflection of Energy
• Snow as an Insulator: Snow Density
• Heat Flow in Water
• Heat Flux Through the Snow Cover
• Calculating Heat Flux
• Calculating Data with Excel
• The Impact of Global Climate Change on Snow & Ice
• The Science of Ice Freeze-up & Break-up
• Snow Glossary
• Snow Resources
• What Is a Bird?
• Bird Classification
• From the Outside In
• Bird Legs & Feet
• Bird Locomotion
• How Do Birds Fly?
• Heart Rate & Breathing
• Diet & Beak Shape
• Bird Vocalizations
• Nests & Eggs
• Parental Care
• Orientation & Navigation
• The Evolution of Birds
• Creating Good Backyard Bird Habitat
• Bird Legends & Indigenous People
• Birds & Climate Change
• Bird Extremes
• Birds Glossary
• Birds Resources
• Life History
• Photosynthesis
• Respiration
• Stems & Vascular Tissue
• Flower Parts
• Flower Types
• Fruit Types
• Types of Plants
• Plant Diseases & Pests
• Community Assembly
• Unique Adaptations of Plants
• Parts of a Flower
• General Pollination Syndromes
• Specialized Pollination Syndromes
• Mutualisms & Cheaters
• Pollination Constancy Exercise
• Vegetation Assessment Activity
• Plants & Pollen Glossary
• Plants & Pollen Resources
• What is an Insect?
• Body Segment: The Head
• Body Segment: The Thorax
• Body Segment: The Abdomen
• Courtship & Mating
• Larva ID Tips: Dragonflies & Damselflies
• Larva ID Tips: Mayflies
• Larva ID Tips: Stoneflies
• Larva ID Tips: Caddisflies
• Larva ID Tips: Beetles
• Larva ID Tips: Flies
• Larva ID Tips: Moths
• Food Webs & Trophic Levels
• Functional Feeding Groups: Shredders
• Functional Feeding Groups: Collectors
• Functional Feeding Groups: Scrapers
• Functional Feeding Groups: Piercers
• Functional Feeding Groups: Predators
• Primary Defenses: Reducing Encounters with Predators
• Insect Vision: The Compound Eye
• Insects Glossary
• Insects Resources
• Impacts on Landscape
• Impacts on Soils
• Impacts on Bacteria
• Impacts on Water Quality
• Impacts on Insects
• Impacts on Snow
• Impacts on Birds
• Impacts on Plants & Pollen
• Mapping Human Impacts
• The Process of Science
• Human Impacts Resources

What do you want to find out about your study site’s water quality, how will I measure it and what are your predictions?

Check Your Thinking: Scenario: There is an abandoned mine dump within 5 meters of your study site stream. How might contaminants in the mine waste be impacting your stream? When would be the best time of year/day to collect water monitoring data that could help answer this question? What tests should you conduct?

Using your recorded observations and information compiled in the first step, the next step is to come up with a testable question. You can use the previously mentioned question (Based on what I know about the pH, DO, temperature and turbidity of my site, is the water of a good enough quality to support aquatic life?) as it relates to the limitations of the World Water Monitoring Day kit, or come up with one of your own.

What results do you predict? For example, your hypothesis may be “I believe the pH, DO, temperature and turbidity of the water at my study site are of good enough quality to support aquatic life because there are no visible impacts to water quality upstream or on the site.” Once you’ve formulated your question, begin planning the experiment or, in this case, the water monitoring you will conduct .

Leave A Comment

Name (required)

Mail (will not be published) (required)

XHTML: You can use these tags: <a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <s> <strike> <strong>

The MSP project is funded by an ESEA, Title II Part B Mathematics and Science Partnership Grant through the Montana Office of Public Instruction. MSP was developed by the Clark Fork Watershed Education Program and faculty from Montana Tech of The University of Montana and Montana State University , with support from other Montana University System Faculty.

• Entries RSS
• Comments RSS

Recent Comments

• jt beatty on Wrapping Petri Dishes in Parafilm
• admin on What Are Maps?
• A Teacher on What Are Maps?
• A Teacher on What is the Montana Science Partnership?

Explore MSP

Copyright © 2024 · All Rights Reserved · Montana Science Partnership

Design by Red Mountain Communications · RSS Feed · Log in

4. Test Hypotheses Using Epidemiologic and Environmental Investigation

Once a hypothesis is generated, it should be tested to determine if the source has been correctly identified. Investigators use several methods to test their hypotheses.

Epidemiologic Investigation

Case-control studies and cohort studies are the most common type of analytic studies conducted to assist investigators in determining statistical association of exposures to ill persons. These types of studies compare information collected from ill persons with comparable well persons.

Cohort studies use well-defined groups and compare the risk of developing of illness among people who were exposed to a source with the risk of developing illness among the unexposed. In a cohort study, you are determining the risk of developing illness among the exposed.

Case-control studies compare the exposures between ill persons with exposures among well persons (called controls). Controls for a case-control study should have the same risk of exposure as the cases. In a case-control study, the comparison is the odds of illness among those exposed with those not exposed.

Using statistical tests, the investigators can determine the strength of the association to the implicated water source instead of how likely it is to have occurred by chance alone. Investigators look at many factors when interpreting results from these studies:

• Frequencies of exposure
• Strength of the statistical association
• Dose-response relationships
• Biologic /toxicological plausibility

For more information and examples on designing and conducting analytic studies in the field, please see The CDC Field Epidemiology Manual .

Information on the clinical course of illness and results of clinical laboratory testing are very important for outbreak investigations. Evaluating symptoms and sequelae across patients can guide formulation of a clinical diagnosis. Results of advance molecular diagnostics can be evaluated to compare isolates from patient and the outbreak sources (e.g., water).

Environmental Investigation

Investigating an implicated water source with an onsite environmental investigation is often important for determining the outbreak’s cause and for pinpointing which factors at the water source were responsible. This requires understanding the implicated water system, potential contamination sources, the environmental controls in effect (e.g., water disinfection), and the ways that people interact with the water source. The factors considered in this investigation will differ depending on the type of implicated water source (e.g., drinking water system, swimming pool). Environmental investigation tools for different settings and venues are available.

The investigation might include collecting water samples. Sampling strategy should include the goal of water testing and what information will be gained by evaluating water quality parameters including measurement of disinfection residuals, and/or possible detection of particular contaminants. The epidemiology of each situation will typically inform the sampling effort.

• Drinking Water
• Healthy Swimming
• Water, Sanitation, and Environmentally-related Hygiene
• Harmful Algal Blooms
• Global WASH
• WASH Surveillance
• WASH-related Emergencies and Outbreaks
• Other Uses of Water

To receive updates highlighting our recent work to prevent infectious disease, enter your email address:

Exit Notification / Disclaimer Policy

• The Centers for Disease Control and Prevention (CDC) cannot attest to the accuracy of a non-federal website.
• Linking to a non-federal website does not constitute an endorsement by CDC or any of its employees of the sponsors or the information and products presented on the website.
• You will be subject to the destination website's privacy policy when you follow the link.
• CDC is not responsible for Section 508 compliance (accessibility) on other federal or private website.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 30 March 2020

Novel methods for global water safety monitoring: comparative analysis of low-cost, field-ready E. coli assays

• Joe Brown   ORCID: orcid.org/0000-0002-5200-4148 1 ,
• Arjun Bir 1 &
• Robert E. S. Bain   ORCID: orcid.org/0000-0001-6577-2923 2  

npj Clean Water volume  3 , Article number:  9 ( 2020 ) Cite this article

4077 Accesses

11 Citations

8 Altmetric

Metrics details

• Environmental chemistry
• Environmental sciences

Current microbiological water safety testing methods are not feasible in many settings because of laboratory, cost, and other constraints, particularly in low-income countries where water quality monitoring is most needed to protect public health. We evaluated two promising E. coli methods that may have potential in at-scale global water quality monitoring: a modified membrane filtration test followed by incubation on pre-prepared plates with dehydrated culture medium (CompactDry TM ), and 10 and 100 ml presence–absence tests using the open-source Aquatest medium (AT). We compared results to membrane filtration followed by incubation on MI agar as the standard test. We tested 315 samples in triplicate of drinking water in Bangalore, India, where E. coli counts by the standard method ranged from non-detect in 100 ml samples to TNTC (>200). Results suggest high sensitivity and specificity for E. coli detection of candidate tests compared with the standard method: sensitivity and specificity of the 100 ml AT test was 97% and 96% when incubated for 24 h at standard temperature and 97% and 97% when incubated 48 h at ambient temperatures (mean: 27 °C). Sensitivity and specificity of the CompactDry TM test was >99 and 97% when incubated for 24 h at standard temperature and >99 and 97% when incubated 48 h at ambient temperatures. Good agreement between these candidate tests compared with the reference method suggests they are suitable for E. coli monitoring to indicate water safety.

Similar content being viewed by others

Molecular testing devices for on-site detection of E. coli in water samples

Bluephage, a method for efficient detection of somatic coliphages in one hundred milliliter water samples

Rapid, sensitive, and low-cost detection of Escherichia coli bacteria in contaminated water samples using a phage-based assay

Introduction.

Water quality monitoring has the potential to serve as a critical feedback mechanism to support the development and operation of safe water supplies that promote public health 1 . In many settings, particularly in low- and middle-income countries (LMICs), water quality testing may be limited because the available methods for microbiological testing require dedicated hygienic laboratory space, specialized and expensive equipment, consumables that may be difficult or costly to source locally, and trained personnel. The resource constraints that limit laboratory testing are, in many cases, co-located with resource constraints that limit water safety. There is a pressing need for simple, scalable microbiological water safety tests that can be used in even the most basic settings by non-experts 2 , 3 , 4 , 5 .

Simpler, potentially low-cost alternatives to standard membrane filtration assays are now available for detection of Escherichia coli and other faecal indicator bacteria (FIB). Some are supported by systematic comparative testing 6 , 7 , 8 , 9 . Based on criteria of total cost per test of ≤US$2 per sample and a lower limit of detection of 1 colony-forming unit (cfu) E. coli in 100 ml of drinking-water by culture, we selected two novel assays for evaluation as microbial water safety tests in comparison with EPA Method 1604 (membrane filtration followed by incubation on MI agar) 10 . Our hypothesis was that candidate low-cost assays could yield E. coli detection data with high (≥90%) specificity and sensitivity compared with the reference test, both under standard and ambient incubation conditions. Such tests may hold promise for global water quality monitoring such as that required in documenting progress toward Sustainable Development Goal (SDG) 6, to “ensure availability and sustainable management of water and sanitation for all” 11 .

Systematic comparison across methods

For systematic comparison testing between methods, we collected 315 bulk tap water samples, each assayed in triplicate by all methods ( n  = 945). According to the reference method, the arithmetic mean total coliform count was 70 cfu 100 ml −1 (standard deviation: 82 cfu 100 ml −1 ) and the arithmetic mean E. coli count was 57 cfu 100 ml −1 (standard deviation 75 cfu 100 ml −1 ). The range of recorded values was <1 cfu 100 ml −1 to 200 cfu 100 ml −1 as an upper limit of quantification; therefore, computed means using this upper limit are underestimates of the true mean. Approximately 35% of samples met criteria for “safe” (<1 cfu E. coli 100 ml −1 ) and 26% of samples for “high risk” (101+ cfu E. coli 100 ml −1 ), according to mean counts from MF-MI.

The proportion of samples positive for both CompactDry TM and the AT 100 ml test are shown in Fig. 1 , stratified by log 10 E. coli counts in the MF-MI reference assay. We plotted receiver-operator characteristic (ROC) curves comparing these two tests to samples taken at the same time and of the same water and assayed by membrane filtration (MF-MI), to provide a measure of replicability of the standard measure of E. coli in water (Fig. 2 ). The ROC curves show the diagnostic performance of the CompactDry and AT tests compared to the MF-MI reference method as the detection limit is varied from ≥1 per 100 mL to the upper limit of detection. We then calculated the Area Under the Curve (AUC), a measure of diagnostic performance based on the ROC curves. For both standard and ambient temperature incubation conditions, the AUC estimates for AT exceed 0.97 and 0.99 for CompactDry TM , indicating near-ideal performance compared with the reference method of MF-MI. Tables 1 and 2 provide an overview of test performance characteristics for CompactDry TM and AT assays, respectively. A comparison of results (of individual assays and means of assay replicates) with triplicate means of the reference test is provided in Supplementary Tables 1 and 2 .

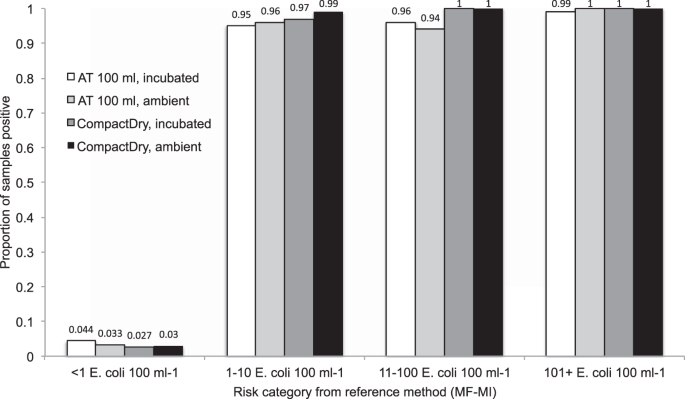
Proportion of samples positive with AT and CompactDry candidate test, incubated at 37 °C for 24 h or ambient temperature for 48 h, stratified by risk category of the reference test (MF-MI).

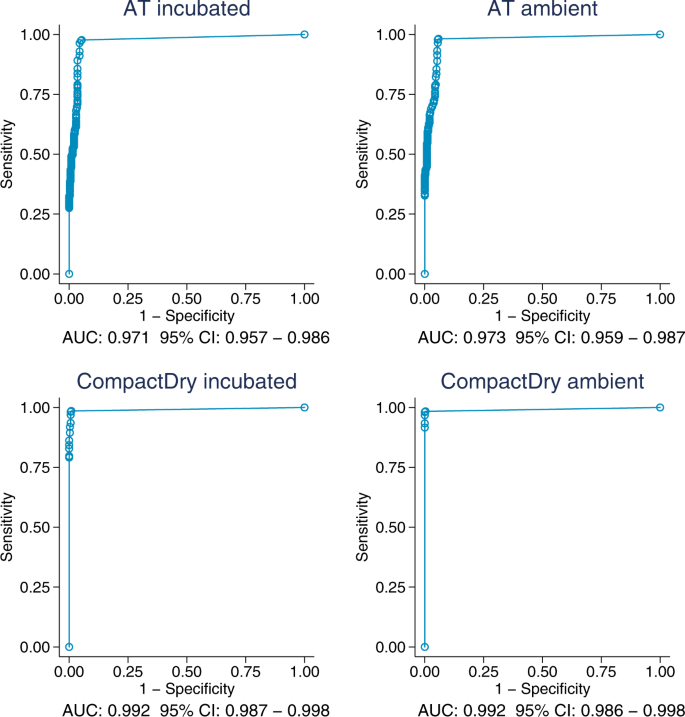
E. coli ROC curves for candidate tests versus the reference test (MF-MI).

In quantitative estimation, E. coli count estimates from the CompactDry TM method showed good agreement with the reference method across a wide range of values, as seen in raw count data plots (Fig. 3 ), log 10 transformed count data (Fig. 4 ), and in Bland-Altman plots (Fig. 5 ). Spearman’s correlation coefficients and Bland-Altman 95% limits of agreement demonstrate that both the ambient temperature and standard incubation conditions yielded consistent agreement between CompactDry TM and MF-MI.

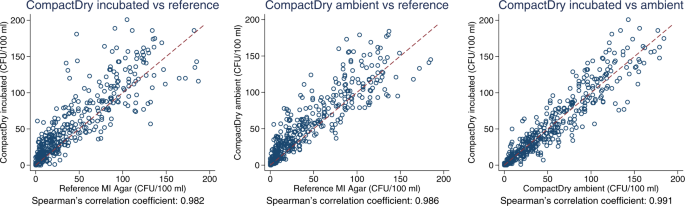
Scatter plot of E. coli count data from a CompactDry TM versus the reference test, incubated; b CompactDry TM versus the reference test, ambient; and c CompactDry TM incubated versus ambient.

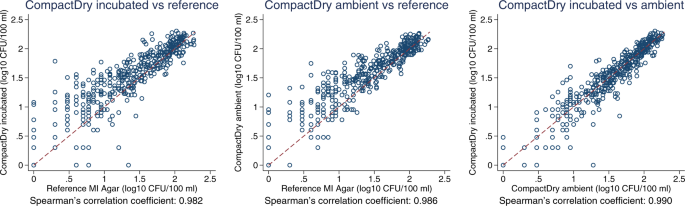
Scatter plot of log 10 transformed E. coli count data from a CompactDry TM versus the reference test, incubated; b CompactDry TM versus the reference test, ambient; and c CompactDry TM incubated versus ambient.

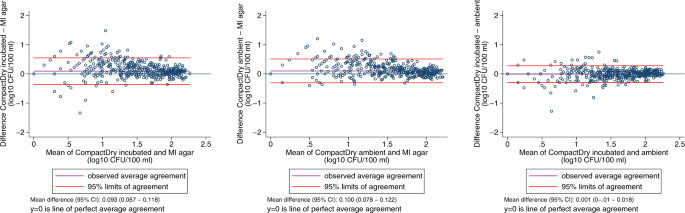
Bland-Altman plots showing log10-transformed microbial count data for a CompactDryTM versus the reference test, incubated; b CompactDry TM versus the reference test, ambient; and ( c ) CompactDry TM incubated versus ambient.

For both novel methods, we noted comparable sensitivity and specificity for sample duplicates incubated at ambient temperature in the testing space, generally (Tables 1 and 2 ), suggesting these ambient temperature conditions would yield equivalent results to standard incubation for these methods.

For 10 ml AT tests, poor sensitivity at both standard and ambient incubation temperatures (51.4 and 51.6%, respectively) suggests that 10 ml tests are not likely to be reliable for detection of E. coli counts at ≥11 cfu 100 ml −1 (the theoretical detection limit for a 10 ml test) when compared to a reference method using 100 ml samples. Among AT 10 ml tests, almost half (49%) of samples were negative when the reference method yielded counts of ≥11 cfu 100 ml −1 (Table 2 ).

The SDGs aim to track global progress in drinking-water safety. SDG global targets include measurement of E. coli in drinking-water sources, a reasonably reliable and widely used indicator of microbiological water safety 12 , 13 , 14 . Current methods for measuring microbial water safety at scale are not feasible, given the specialized training, resources, and facilities required for E. coli assays used in water safety monitoring and regulation in economically rich countries 2 . New, globally scalable approaches are needed that can provide equivalent water safety information at lower cost where these resources are lacking.

Based on criteria of cost, specificity of culturable E. coli as a target, and ease of use, we identified two novel water quality tests that represent potential for scale in international monitoring programs. These two tests join a suite of available methods that may be suitable to measure progress toward SDG 6.1, which calls for “universal and equitable access to safe and affordable drinking water for all” by 2030. We hypothesized that these methods could yield sensitive and specific estimates of E. coli in drinking water samples compared with an internationally accepted standard method for E. coli enumeration. Overall, our results from the ROC analysis on 945 data points from drinking water sources in Bangalore, India, suggest that both candidate tests, at ambient temperature and standard-temperature incubation, yield comparable estimates for E. coli presence in 100 ml samples. The CompactDry TM method shows good quantitative agreement with MF-MI across risk categories, and both methods provide highly sensitive and specific information on the presence or absence of E. coli in 100 ml sample volumes. Because CompactDry TM requires the use of sterile membrane filtration or another concentration step for any assay volume greater than 1 ml, this method will probably find greatest use in applications where quantitative E. coli counts are the desired endpoint. A presence-absence 100 ml AT assay is likely to be the most efficient and field-ready 15 option when quantal (presence-absence) data will suffice.

Our results also demonstrate the importance of using an appropriate volume for adequate sensitivity in quantal tests, as 10 ml was not sufficient for many of the samples tested in this study to yield information consistent with the reference method. Even though a 10 ml test should have a lower limit of detection of 10 cfu 100 ml −1 , the performance of 10 ml quantal AT tests was poor in reliably detecting ≥11 cfu 100 ml −1 E. coli (medium or high risk) in drinking water samples. This finding has potential implications for other methods that have been proposed for use in field surveillance, including a similar novel 10 ml E. coli method 16 and a 30 ml H 2 S test 17 proposed as lower-cost alternatives to more standard methods. Though these methods may be important tools for rapid surveys and to identify high-risk sources, any test using less than 100 ml assay volume will not be able to yield reliable estimates of drinking water safety at scale where the normative goal remains absence of culturable E. coli in 100 ml samples.

Our results are consistent with and complementary to one recent study comparing the use of AT for E. coli monitoring in environmental waters in Switzerland and Uganda 18 . This study compared quantitative results from AT with other, more standard tests: IDEXX Colilert-18®, m-TEC, and m-ColiBlue24®. In the previous study, AT showed high sensitivity (≥97%) for E. coli detection compared with reference methods, with an estimated 6% of AT samples being false positives. In our study, sensitivity of 100 ml AT tests was 97.1% among samples at standard incubation temperature and 96.7% under ambient incubation conditions, with 14 (4.2%) and 11 (3.3%) false positives, respectively. A finding that is potentially divergent between the studies, however, relates to performance at ambient temperatures. In Bangalore, where the range of ambient incubation temperatures was 25–30 °C (mean: 27 °C), we observed good agreement between test results at the two temperatures with ambient-temperature plates read at 48 h, concluding that ambient temperature incubation consistent with these conditions would yield comparable E. coli count data. Genter et al. 18 reported reduced performance at lower than standard incubation temperatures, though the condition tested was 24 °C with plates counted at 42 h post-inoculation. A comparison of results between these studies suggests that 25 °C may be a minimum recommended threshold for ambient temperature incubation using AT media. If possible, incubation at 37 °C for 24 h is likely to yield optimal results.

Sample collection and processing

We collected drinking water samples from 14 locations in Peenya, approximately 11 km from the city centre of Bangalore, India. Peenya has a resident population of ~800,000 people and a population density of ~1300 people per square km. We collected water samples from taps at businesses and public taps across an area of 15 km 2 ; all sources were from the mains water supply serving residential, commercial, and industrial areas. We collected samples across 37 non-consecutive sampling days in 2017–2018, typically visiting 10 or fewer tap sources per day. At each sample point, we collected three samples of water totalling ~2000 ml from the tap into sterile Whirl-Pak bags containing sodium thiosulfate. Following collection, samples were placed on ice until microbiological testing by all methods within 5 h of collection. Each sample was tested in triplicate by (1) the standard reference method (MF-MI), (2) the AT presence-absence test (100 and 10 ml volumes), (3) and a modified CompactDry TM test. On each sample day, we ran negative controls of each method using sterile dilution water.

As a standard method and basis for comparison, we measured E. coli in samples by filtering undiluted and diluted samples through 47-mm diameter, 0.45 µm pore size cellulose ester filters in sterile magnetic membrane filter funnels; membranes were incubated on MI agar for 24 h at 35 °C (this method is abbreviated throughout as “MF-MI”). MI agar detects E. coli by cleavage of a chromogenic β-galactoside substrate to detect total coliforms (TC) and a fluorogenic β–glucuronide substrate to detect E. coli , producing distinctive color TC colonies and blue fluorescing E. coli colonies under long-wave UV light at 366 nm 19 , 20 , 21 . Our methods conform to EPA Method 1604 10 , widely used globally as a standard method for detection of E. coli in water. E. coli and TC count data were reported as colony forming units (cfu) per unit volume of water. As the sources tested were drinking water sources, we assayed only 100 ml volumes, assigning an upper limit of quantification of 200 cfu per plate, deeming colonies “too numerous to count” beyond this number (TNTC).

The AT presence-absence E. coli test was developed and piloted as part of a behavior-change randomized controlled trial (RCT) in rural India 1 . The semi-quantitative test uses the open-source Aquatest (AT) broth medium 22 with a resorufin methyl ester chromogen 23 (Biosynth AG, Switzerland) and subsequent incubation. Briefly, water samples are measured to 10 and 100 ml volumes using single-use volumetric cylinders containing pre-measured AT medium. Following incubation for 24 h at 37 °C or 48 hat ambient temperature (mean: 27 °C, range 25–30 °C), a color change from yellow-beige to pink-red indicates the presence of E. coli , and the combination of the two containers is used to determine the test result. Results can be interpreted as <1 E. coli per 100 ml (both containers negative, “safe”); 1–10 E. coli per 100 ml (large container positive, small container negative, “unsafe–low to medium risk”); or ≥10 E. coli per 100 ml (small container positive, “unsafe–medium to high risk”).

The CompactDry™ E. coli test (Nissui Pharmaceutical, Japan) used membrane filtration as in Method 1604 10 , except 99 ml of sample water was filtered through the filter and this was placed on a pre-sterilized, single-use plate with dehydrated culture medium. The method allows for straightforward identification of E. coli and total coliforms (TC) via chromogenic media 24 , 25 , 26 . Plates were rehydrated with 1 ml of sample water (for 100 ml sample volume), allowing for computation of cfu per 100 ml. When testing 10 ml samples, 9 ml of sample was filtered and the filter placed on the plate rehydrated with 1 ml of sample water. As in the reference method, the use of a filtration column is necessary, requiring the use of a suction pump, sidearm flask or manifold, and sterile filtration column for each sample. By using inexpensive, single-use, pre-sterilized plates, however, the method does not require the preparation and sterilization of microbiological media or the re-sterilization of plates. Results were recorded after 24 h incubation at 35+/−2 °C and after 48 h at ambient temperature (mean: 27 °C, range 25–30 °C). As for MF-MI, E. coli and TC count data were reported as colony forming units (cfu) per 100 ml sample. Values above 200 cfu were recorded as TNTC and assigned a figure of 200 cfu when used in computing means.

Statistical analysis

We performed each method in triplicate in each bulk tap water sample. Our primary analysis assesses comparability of the methods across all individual replicates in parallel. We also compared data from each candidate test with the arithmetic means of three replicates of the reference test as a “true” value for that sample. We calculated sensitivity, specificity, and positive predictive values for detection of E. coli (≥1 E. coli per 100 ml) in both candidate tests and for both temperatures compared with the reference method.

After entering all data in Excel, we used Stata 16 (StataCorp, College Station, TX, USA) for primary data analysis, with further visualization and calculations in R. Descriptive statistics were used to characterize the water quality testing results from standard-temperature‐ and ambient-temperature-incubated samples using both continuous and categorical data, in unmodified and log 10 form. Of particular interest were the correlations between estimates within a priori risk strata for E. coli : <1 cfu 100 ml −1 (very low risk), 1–10 cfu 100 ml −1 (low risk), 11–100 cfu 100 ml −1 (moderate risk), 101+ cfu 100 ml −1 (high risk). These categories are commonly used to indicate levels of waterborne disease risk; existing evidence suggests an association between E. coli counts and diarrheal disease though the correlation may be non-monotonic, weak, and not necessarily always present 12 , 13 , 14 , 27 .

We used Bland-Altman and scatter plots to visualize results across tests. In data analysis of log 10 -transformed counts, we replaced non-detects with an integer value of “1” as the lower detection limit in assays. In Bland-Altman plots, we used linear regression to calculate mean differences accounting for replicate samples. To further compare results of candidate tests with the reference method, we used receiver operating characteristic (ROC) curves 28 . The ROC curves describe how the sensitivity and specificity of CompactDry and AT tests vary as the threshold used to define a positive reference test result increases from ≥1 per 100 ml to the upper limit of detection. Accuracy of a novel assay compared with the standard is measured by the area under the ROC curve (AUC), combining both sensitivity and specificity to evaluate the overall performance of the candidate tests compared with the reference method. We calculated confidence intervals for AUC estimates accounting for clustering of replicates for each water sample 29 .

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary .

Data availability

All data generated during this study are available at Open Science Framework: https://osf.io/k637w/

Trent, M. et al. AccEss To Household Water Quality Information Leads To Safer Water: a cluster randomized controlled trial in india. Environ. Sci. Technol. 52 , 5319–5329 (2018).

Article   CAS   Google Scholar  

Bain, R. et al. A summary catalogue of microbial drinking water tests for low and medium resource settings. Int. J. Environ. Res. Public Health 9 , 1609–1625 (2012).

Article   Google Scholar  

Delaire, C. et al. How much will it cost to monitor microbial drinking water quality in sub-Saharan Africa? Environ. Sci. Technol. 51 , 5869–5878 (2017).

Khan, S. M. et al. Optimizing household survey methods to monitor the Sustainable Development Goals targets 6.1 and 6.2 on drinking water, sanitation and hygiene: a mixed-methods field-test in Belize. PloS ONE 12 , e0189089 (2017).

Wright, J. et al. Water quality laboratories in Colombia: a GIS-based study of urban and rural accessibility. Sci. Total Environ. 485–486 , 643–652 (2014).

Wang, A. et al. Household microbial water quality testing in a Peruvian demographic and health survey: evaluation of the compartment bag test for Escherichia coli. Am. J. Tropical Med. Hyg. 96 , 970–975 (2017).

Baum, R., Kayser, G., Stauber, C. & Sobsey, M. Assessing the microbial quality of improved drinking water sources: results from the Dominican Republic. Am. J. Tropical Med. Hyg. 90 , 121–123 (2014).

Stauber, C., Miller, C., Cantrell, B. & Kroell, K. Evaluation of the compartment bag test for the detection of Escherichia coli in water. J. Microbiol. Methods 99 , 66–70 (2014).

Brown, J. et al. Ambient-temperature incubation for the field detection of Escherichia coli in drinking water. J. Appl. Microbiol. 110 , 915–923 (2011).

Agency, U. S. E. P. Vol. Publication EPA-821-R-02-024 (USEPA Office of Water (4303T), Washington, D.C., 2002).

WHO/UNICEF. Progress on drinking water, sanitation and hygiene: 2017 update and SDG baselines. doi:Licence: CC BY-NC-SA 3.0 IGO (2017).

Gruber, J. S., Ercumen, A. & Colford, J. M. Jr Coliform bacteria as indicators of diarrheal risk in household drinking water: systematic review and meta-analysis. PLoS ONE 9 , e107429 (2014).

Moe, C. L., Sobsey, M. D., Samsa, G. P. & Mesolo, V. Bacterial indicators of risk of diarrhoeal disease from drinking-water in the Philippines. Bull. World Health Organ. 69 , 305–317 (1991).

CAS   Google Scholar  

Brown, J. M., Proum, S. & Sobsey, M. D. Escherichia coli in household drinking water and diarrheal disease risk: evidence from Cambodia. Water Sci. Technol. 58 , 757–763 (2008).

Rocha-Melogno, L. et al. Rapid drinking water safety estimation in cities: piloting a globally scalable method in Cochabamba, Bolivia. Sci. Total Environ. 654 , 1132–1145 (2018).

Loo, A. et al. Development and field testing of low-cost, quantal microbial assays with volunteer reporting as scalable means of drinking water safety estimation. J. Appl. Microbiol. 126 , 1944–1954 (2019).

Khush, R. S. et al. H2S as an indicator of water supply vulnerability and health risk in low-resource settings: a prospective cohort study. Am. J. Tropical Med. Hyg. 89 , 251–259 (2013).

Franziska Genter, S. J. M., Clair-Caliot, G., Mugume, D. S., Johnston, R. B., Bain, R. E. S. & Timothy, R. J. Evaluation of the novel substrate RUGTM for the detection of Escherichia coli in water from temperate (Zurich, Switzerland) and tropical (Bushenyi, Uganda) field sites. Environ. Sci.: Water Res. Technol. 5 , 1082–1091 (2019).

Google Scholar  

Geissler, K., Manafi, M., Amoros, I. & Alonso, J. L. Quantitative determination of total coliforms and Escherichia coli in marine waters with chromogenic and fluorogenic media. J. Appl. Microbiol. 88 , 280–285 (2000).

Manafi, M. & Kneifel, W. [A combined chromogenic-fluorogenic medium for the simultaneous detection of coliform groups and E. coli in water]. Zentralblatt fur Hyg. und Umweltmed. 189 , 225–234 (1989).

Manafi, M., Kneifel, W. & Bascomb, S. Fluorogenic and chromogenic substrates used in bacterial diagnostics. Microbiological Rev. 55 , 335–348 (1991).

Bain, R. E. et al. Evaluation of an inexpensive growth medium for direct detection of Escherichia coli in temperate and sub-tropical waters. PloS ONE 10 , e0140997 (2015).

Magro, G. et al. Synthesis and application of resorufin beta-D-glucuronide, a low-cost chromogenic substrate for detecting Escherichia coli in drinking water. Environ. Sci. Technol. 48 , 9624–9631 (2014).

Mizuochi, S. et al. Matrix extension study: validation of the compact dry EC method for enumeration of Escherichia coli and non-E. coli coliform bacteria in selected foods. J. AOAC Int. 99 , 451–460 (2016).

Mizuochi, S. et al. Matrix extension study: validation of the compact Dry CF method for enumeration of total coliform bacteria in selected foods. J. AOAC Int. 99 , 444–450 (2016).

Mizuochi, S. et al. Matrix extension study: validation of the compact dry TC method for enumeration of total aerobic bacteria in selected foods. J. AOAC Int. 99 , 461–468 (2016).

Ercumen, A. et al. Potential sources of bias in the use of Escherichia coli to measure waterborne diarrhoea risk in low-income settings. Tropical Med. Int. Health. 22 , 2–11 (2017).

Lasko, T. A., Bhagwat, J. G., Zou, K. H. & Ohno-Machado, L. The use of receiver operating characteristic curves in biomedical informatics. J. Biomed. Inform. 38 , 404–415 (2005).

Newson, R. Parameters behind “Nonparametric” Statistics: Kendall’s tau, Somers’ D and Median Differences. Stata J. 2 , 45–64 (2002).

Clopper, C. J. & Pearson, E. S. The use of confidence or fiducial limits illustrated in the case of the binomial. Biometrika 26 , 404–413 (1934).

Mercaldo, N. D., Lau, K. F. & Zhou, X. H. Confidence intervals for predictive values with an emphasis to case-control studies. Stat. Med. 26 , 2170–2183 (2007).

Download references

Acknowledgements

Thermo Fisher Scientific (Waltham, MA, USA) provided AT medium for this study. We gratefully acknowledge assistance from Punith Kakaraddi for assistance in field sampling and laboratory analysis.

Author information

Authors and affiliations.

School of Civil and Environmental Engineering, Georgia Institute of Technology, 311 Ferst Drive, Atlanta, GA, 30332, USA

Joe Brown & Arjun Bir

Division of Data, Analysis, Planning and Monitoring, UNICEF, New York, NY, USA

Robert E. S. Bain

You can also search for this author in PubMed   Google Scholar

Contributions

JB and RB conceived and designed the study. AB processed all water samples. JB and RB analyzed the data and JB, AB, and RB wrote the manuscript.

Corresponding author

Correspondence to Joe Brown .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Npj reporting summary document, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Brown, J., Bir, A. & Bain, R.E.S. Novel methods for global water safety monitoring: comparative analysis of low-cost, field-ready E. coli assays. npj Clean Water 3 , 9 (2020). https://doi.org/10.1038/s41545-020-0056-8

Download citation

Received : 18 November 2019

Accepted : 20 February 2020

Published : 30 March 2020

DOI : https://doi.org/10.1038/s41545-020-0056-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Multi-model exploration of groundwater quality and potential health risk assessment in jajpur district, eastern india.

• Sushree Sabinaya
• Biswanath Mahanty
• Naresh Kumar Sahoo

Environmental Geochemistry and Health (2024)

Drinking water quality and the SDGs

• Robert Bain
• Rick Johnston
• Tom Slaymaker

npj Clean Water (2020)

Microbial Indicators of Fecal Pollution: Recent Progress and Challenges in Assessing Water Quality

• David A. Holcomb
• Jill R. Stewart

Current Environmental Health Reports (2020)

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

8   Hypothesis Testing

This section introduces some statistical approaches commonly used in out projects. For an in depth discussion and examples of statistical approaches commonly employed across surface water quality studies, the reader is highly encouraged to review Helsel et al. ( 2020 ) .

8.1 Hypothesis Tests

Hypothesis tests are an approach for testing for differences between groups of data. Typically, we are interested in differences in the mean, geometric mean, or median of two or more different groups of data. It is useful to become familiar with several terms prior to conducting a hypothesis test:

Null hypothesis : or \(H_0\) is what is assumed true about a system prior to testing and collecting data. It usually states there is no difference between groups or no relationship between variables. Differences or correlations in groups should be unlikely unless presented with evidence to reject the null.

Alternative hypothesis : or \(H_1\) is assumed true if the data show strong evidence to reject the null. \(H_1\) is stated as a negation of \(H_0\) .

\(\alpha\) -value : or significance level, is the probability of incorrectly rejecting the null hypothesis. While this is traditionally set at 0.05 (5%) or 0.01 (1%), other values can be chosen based on the acceptable risk of rejecting the null hypothesis when in fact the null is true (also called a Type I error ).

\(\beta\) -value : the probability of failing to reject the null hypothesis when is is in fact false (also called a Type II error ).

Power : Is the probability of rejecting the null when is is in fact false. This is equivalent to \(1-\beta\) .

The first step for an analysis is to establish the acceptable \(\alpha\) value. Next, we want to minimize the possibility of a Type II error or \(\beta\) by (1) choosing the test with the greatest power for the type of data being analyzed; and/or, (2) increasing the sample size.

With an infinite sample size we can detect nearly any difference or correlation in two groups of data. The increase in sample size comes at a financial and human resource cost. So it is important to identify what magnitude difference needs to be detected for relevance to the system being detected 1 . After establishing \(H_0\) , \(H_1\) , and the acceptable \(\alpha\) -value, choose the test and sample size needed to reach the desired power.

1  See Helsel et al. ( 2020 ) (Chapter 13) and Schramm ( 2021 ) for more about power calculations.

The probability of obtaining the calculated test statistic when the null is true the p -value. The smaller the p -value the less likely the test statistic value would be obtained if the null hypothesis were true. We reject the null hypothesis when the p -value is less than or equal to our predetermined \(\alpha\) -value. When the p -value is greater than the \(\alpha\) -value, we do no reject the null (we also do no accept the null).

8.2 Choice of test

Maximize statistical power by choosing the hypothesis test appropriate for the characteristics of the data you are analyzing. Table  8.1 provides an overview of potential tests covered in Helsel et al. ( 2020 ) . There are many more tests and methods available than are covered here, but these cover the most likely scenarios.

Comparison types:

Two independent groups: Testing for differences between two different datasets. For example, water quality at two different sites or water quality at one site before and after treatment.

Matched pairs: Testing differences in matched pairs of data. For example, water quality between watersheds or sites when the data are collected on the same days, or comparing before and after measurements of many sites.

Three of more groups: Testing differences in data collected at three or more groups. For example, comparing runoff at 3 treatment plots and one control plot.

Two-factor group comparison: Testing for difference in observations between groups when more than one factor might influence results. For example, testing for difference in water quality at an upstream and downstream site and before and after an intervention.

Correlation: Looking for linear or monotonic correlations between two independent and continuous variables. For example, testing the relationship between two simulatanesouly measured water quality parameters.

We also select test by the characteristics of the data. Non-skewed and normally distributed data can be assessed using parametric tests. Data following other distributions or that are skewed can be assessed with non-parametric tests. Often, we transform skewed data and apply parametric tests. This is appropriate but the test no longer tell us if there are differences in means, instead it tells us if there is a difference in geometric means. Similarly, nonparametric test tell us if there is shift in the distribution of the data, not if there is a difference in the means. Finally, we can utilize permutation tests to apply parametric test procedures to skewed datasets without loss of statistical power.

8.2.1 Plot your data

Data should, at minimum, be plotted using histograms and probability (Q-Q) plots to assess distributions and characteristics. If your data includes treatment blocks or levels, the data should be subset to explore each block and the overall distribution. The information from these plots will assist in chosing the correct type of tests described above.

8.3 Two independent groups

This set of tests compares two independent groups of samples. The data should be formatted as either two vectors of numeric data of any length, or as one vector of numeric data and a second vector of the same length indicating which group each data observation is in (also called long or tidy format). The example below shows random data drawn from the normal distribution using the rnorm() function. The first sample was drawn from a normal distribution with mean ( \(\mu\) )=0.5 and standard deviation ( \(\sigma\) )= 0.25. The second sample is drawn from a normal distribution with \(\mu\) =1.0 and \(\sigma\) = 0.5.

In the example above sample_1 and sample_2 are numeric vectors with the observations of interest. These can be stored in long or tidy format. The advantage to storing in long format, is that plotting and data exploration is much easier:

8.3.1 Two sample t-test

A test for the difference in the means is conducted using the t.test() function:

For the t -test, the null hypothesis ( \(H_0\) ) is that the difference in means is equal to zero, the alternative hypothesis ( \(H_1\) ) is that the difference in means is not equal to zero. By default t.test() prints some information about your test results, including the t-statistic, degrees of freedom for the t-statistic calculation, p-value, and confidence intervals 2 .

2  By assigning the output of t.test() to the results object it is easier to obtain or store the values printed in the console. For example, results$p.value returns the \(p\) -value. This is useful for for plotting or exporting results to other files. See the output of str(results) for a list of values.

The example above uses “formula” notation. In formula notation, y ~ x , the left hand side of ~ represents the response variable or column and the right hand side represents the grouping variable. The same thing can be achieved with:

In this example, we do not have the evidence to reject \(H_0\) at an \(\alpha\) = 0.05 (t-stat = -0.887, \(p\) = 0.387).

Since this example uses randomly drawn data, we can examine what happens when sample size is increased to \(n\) = 100:

Now we have evidence to reject \(H_0\) due to the larger sample size which increased the statistical power for detecting a smaller effect size at a cost of increasing the risk of detecting an effect that is not actually there or is not environmentally relevant and of course increased monitoring costs if this were an actual water quality monitoring project.

The t -test assumes underlying data is normally distributed. However, hydrology and water quality data is often skewed and log-normally distributed. While, a simple log-transformation in the data can correct this, it is suggested to use a non-parametric or permutation test instead.

8.3.2 Rank-Sum test

The Wilcoxon Rank Sum (also called Mann-Whitney) tests can be considered a non-parametric versions of the two-sample t -test. This example uses the bacteria data first shown in Chapter 6 . The heavily skewed data observed in fecal indicator bacteria are well suited for non-parametric statistical analysis. The Wilcoxon test is conducted using the wilcox.test() function.

8.3.3 Two-sample permutation test

Chapter 5.2 in Helsel et al. ( 2020 ) provide an excellent explanation of permutation tests. The permutation test works by resampling the data for all (or thousands of) possible permutations. Assuming the null hypothesis is true, we can draw a population distribution of the null statistic all the resampled combinations. The proportion of permutation results that equal or exceed the difference calculated in the original data is the permutation p -value.

The coin package provides functions for using the permutation test approach with different statistical tests.

We get roughly similar results with the permutation test and the Wilcoxon. However, the Wilcoxon tells us about the medians, while the permutation test tells us about the means.

8.4 Matched pairs

Matched pairs test evalute the differences in matched pairs of data. Typically, this might include watersheds in which you measured water quality before and after an intervention or event; paired upstream and downstream data; or looking at pre- and post-evaluation scores at an extension event. Since data has to be matched, the data format is typically two vectors with observed numeric data. The examples below use mean annual streamflow measurements from 2021 and 2022 at a random subset of stream gages in Travis County obtained from the dataRetrieval package.

8.4.1 Paired t -test

The paired t-test assumes a normal distribution, so the observations are log transformed in this example. The resulting difference are differences in log-means.

8.4.2 Signed rank test

Instead of the t-test, the sign rank test is more appropriate for skewed datasets. Keep in mind this does not report a difference in means because it is a test on the ranked values.

8.4.3 Paired permutation test

The permutation test is appropriate for skewed datasets where there is not a desire to transform data. The function below evaluates the mean difference in the paired data, then randomly reshuffles observations between 2021 and 2022 to create a distribution of mean differences under null conditions. The observed mean and the null distribution are compared to derive a \(p\) -value or the probability of obtaining the observed value if the null were true.

8.5 Three of more independent groups

8.5.1 anova, 8.5.2 kruskal-walis, 8.5.3 one-way permutation, 8.6 two-factor group comparisons, 8.6.1 two-factor anova.

When you have two-(non-nested)factors that may simultaneously influence observations, the factorial ANOVA and non-parametric alternatives can be used.

In 2011, an artificial wetland was completed to treat wastewater effluent discharged between stations 13079 (upstream side) and 13074 (downstream side). The first factor is station location, either upstream or downstream of the effluent discharge. We expect the upstream station to have “better” water quality than the downstream station. The second factor is before and after the wetland was completed. We expect the downstream station to have better water quality after the wetland than before, but no impact on the upstream water quality.

The aov() function fits the ANOVA model using the formula notation. The formula notation is of form response ~ factor where factor is a series of factors specified in the model. The specification factor1 + factor2 indicates all the factors are taken together, while factor1:factor2 indicates the interactions. The notation factor1*factor2 is equivalent to factor1 + factor2 + factor1:factor2 .

Here we fit the ANOVA to log-transformed ammonia values. The results indicate a difference in geometric means (because we used the log values in the ANOVA) between upstream and downstream location and a difference in the interaction terms.

We follow up the ANOVA with a multiple comparisons test (Tukey’s Honest Significant Difference, or Tukey’s HSD) on the factor(s) of interest.

The TukeyHSD() function takes the output from aov() and optionally the factor you are interested in evaluating the difference in means. The output provide the estimate difference in means between each level of the factor, the 95% confidence interval and the multiple comparisons adjusted p-value. Figure  8.3 is an example of how the data can be plotted for easier interpretation.

8.6.2 Two-factor Brunner-Dette-Munk

The non-parametric version of the ANOVA model is the two-factor Brunner-Dette-Munk (BDM) test. The BDM test is implemented in the asbio package using the BDM.2way() function:

The BMD output indicates there is evidence to reject the null hypothesis (no difference in concentration) for each factor and the interaction. We can conduct a multiple comparisons test following the BDM test using the Wilcoxon rank-sum test on all possible pairs and use the Benjamini and Hochberg correction to account for multiple comparisons.

Since we are interested in the impact of the wetland specifically, group the data by location (upstream, downstream) and subtract the median of each group from the observed values. Subtraction of the median values defined by the location factor adjusts for difference attributed to location. The pairwise.wilcox.test() function provides the pairwise compairson with corrections for multiple comparisons:

8.6.3 Two-factor permutation test

In Section 8.6.1 we identified a significant differencs in ammonia geometric means for each factor and interaction. If the interest is to identify difference in means, a permutation test can be used. The perm.fact.test() function from the asbio package can be used:

8.7 Correlation between two independent variables

8.7.1 pearson’s r.

Using the estuary water quality example data from #sec-plotclean we will explore correlations between two independent variables:

Pearson’s r is the linear correlation coefficient that measures the linear association between two variables. Values of r range from -1 to 1 (indicate perfectly positive or negative linear relationships). Use the cor.test() function to return Pearson’s r and associated p-value:

The results indicate we have strong evidence to reject the null hypothesis of no correlation between Temperature and dissolved oxygen (Pearson’s r = -0.83, p < 0.001).

8.7.2 Spearman’s p

Spearman’s p is a non-parametric correlation test using the ranked values. The following example looks at the correlation between TSS and TN concentrations.

The cor.test() function is also used to calculate Spearman’s p , but the method argument must be specified:

Using Spearman’s p there isn’t evidence to reject the null hypothesis at \(\alpha = 0.05\) .

8.7.3 Permutation test for Pearson’s r

If you want to use a permutation approach for Pearson’s r we need to write a function to calculate r for the observed data, then calculate r for the permutation resamples. The following function does that and provides the outputs along with the permutation results so we can plot them:

Now, use the function permutate_cor() to conduct Pearson’s r on the observed data and resamples:

Using the permutation approach, we don’t have evidence to reject the null hypothesis at \(\alpha = 0.05\) .

The following code produces a plot of the mull distribution of test statistic values and the test statistic value for the observed data:

JavaScript seems to be disabled in your browser. For the best experience on our site, be sure to turn on Javascript in your browser.

How to Interpret a Water Analysis Report

Whether your water causes illness, stains on plumbing, scaly deposits, or a bad taste, a water analysis identifies the problem and enables you to make knowledgeable decisions about water treatment.

Features of a Sample Report

Once the lab has completed testing your water, you will receive a report that looks similar to Figure 1. It will contain a list of contaminants tested, the concentrations, and, in some cases, highlight any problem contaminants. An important feature of the report is the units used to measure the contaminant level in your water. Milligrams per liter (mg/l) of water are used for substances like metals and nitrates. A milligram per liter is also equal to one part per million (ppm)--that is one part contaminant to one million parts water. About 0.03 of a teaspoon of sugar dissolved in a bathtub of water is an approximation of one ppm. For extremely toxic substances like pesticides, the units used are even smaller. In these cases, parts per billion (ppb) are used. Another unit found on some test reports is that used to measure radon--picocuries per liter. Some values like pH, hardness, conductance, and turbidity are reported in units specific to the test.

In addition to the test results, a lab may make notes on any contaminants that exceeded the PA DEP drinking water standards. For example, in Figure 1 the lab noted that total coliform bacteria and iron both exceeded the standards.

Retain your copy of the report in a safe place as a record of the quality of your water supply. If polluting activities such as mining occur in your area, you may need a record of past water quality to prove that your supply has been damaged.

Water test parameters

The following tables provide a general guideline to common water quality parameters that may appear on your water analysis report. The parameters are divided into three categories: health risk parameters, general indicators, and nuisance parameters. These guidelines are by no means exhaustive. However, they will provide you with acceptable limits and some information about symptoms, sources of the problem and effects.

Health Risk Parameters

The parameters in Table 1 are some commons ones that have known health effects. The table lists acceptable limits, potential health effects, and possible uses and sources of the contaminant.

General Water Quality Indicators

General Water Quality Indicators are parameters used to indicate the presence of harmful contaminants. Testing for indicators can eliminate costly tests for specific contaminants. Generally, if the indicator is present, the supply may contain the contaminant as well. For example, turbidity or the lack of clarity in a water sample usually indicates that bacteria may be present. The pH value is also considered a general water quality indicator. High or low pHs can indicate how corrosive water is. Corrosive water may further indicate that metals like lead or copper are being dissolved in the water as it passes through distribution pipes. Table 2 shows some of the common general indicators.

Nuisance contaminants are a third category of contaminants. While these have no adverse health effects, they may make water unpallatable or reduce the effectiveness of soaps and detergents. Some nuisance contaminants also cause staining. Nuisance contaminants may include iron bacteria, hydrogen sulfide, and hardness . Table 3 shows some typical nuisance contaminants you may see on your water analysis report.

Hardness is one contaminant you will also commonly see on the report. Hard water is a purely aesthetic problem that causes soap and scaly deposits in plumbing and decreased cleaning action of soaps and detergents. Hard water can also cause scale buildup in hot water heaters and reduce their effective lifetime. Table 4 will help you interpret the hardness parameters cited on your analysis. Note that the units used in this table differ from those indicated in Figure 1. Hardness can be expressed by either mg/l or a grains per gallon (gpg). A gpg is used exclusively as a hardness unit and equals approximately 17 mg/l or ppm. Most people object to water falling in the "hard" or "very hard" categories in Table 4. However, as with all water treatment, you should carefully consider the advantages and disadvantages to softening before making a purchasing a water softener.

Additional Resources

For more detailed information about water testing ask for publication Water Tests: What Do the Numbers Mean? at your local extension office or from this website.

Prepared by Paul D. Robillard, Assistant Professor of Agricultural Engineering, William E. Sharpe, Professor of Forest Hydrology and Bryan R. Swistock, Senior Extension Associate, Department of Ecosystem Science and Management

You may also be interested in ...

Private Water Supply Education and Water Testing

Water Tests: What Do the Numbers Mean?

Private Wells and Water Systems Management

Solving Bacteria Problems in Wells and Springs

Testing Your Drinking Water

Plomo en el Agua Potable

Interpreting Irrigation Water Tests

Roadside Dumps and Water Quality

Spring Development and Protection

Resources for Water Well, Spring, and Cistern Owners

Personalize your experience with penn state extension and stay informed of the latest in agriculture..

Open Access is an initiative that aims to make scientific research freely available to all. To date our community has made over 100 million downloads. It’s based on principles of collaboration, unobstructed discovery, and, most importantly, scientific progression. As PhD students, we found it difficult to access the research we needed, so we decided to create a new Open Access publisher that levels the playing field for scientists across the world. How? By making research easy to access, and puts the academic needs of the researchers before the business interests of publishers.

We are a community of more than 103,000 authors and editors from 3,291 institutions spanning 160 countries, including Nobel Prize winners and some of the world’s most-cited researchers. Publishing on IntechOpen allows authors to earn citations and find new collaborators, meaning more people see your work not only from your own field of study, but from other related fields too.

Brief introduction to this section that descibes Open Access especially from an IntechOpen perspective

Want to get in touch? Contact our London head office or media team here

Our team is growing all the time, so we’re always on the lookout for smart people who want to help us reshape the world of scientific publishing.

Home > Books > Research and Practices in Water Quality

Validity and Errors in Water Quality Data — A Review

Submitted: 13 May 2014 Published: 09 September 2015

DOI: 10.5772/59059

Cite this chapter

There are two ways to cite this chapter:

From the Edited Volume

Research and Practices in Water Quality

Edited by Teang Shui Lee

To purchase hard copies of this book, please contact the representative in India: CBS Publishers & Distributors Pvt. Ltd. www.cbspd.com | [email protected]

Chapter metrics overview

2,728 Chapter Downloads

Impact of this chapter

Total Chapter Downloads on intechopen.com

Total Chapter Views on intechopen.com

Author Information

Innocent rangeti.

• Department of Environmental Health, Durban University of Technology, Durban, South Africa

Bloodless Dzwairo

• Institute for Water and Wastewater Technology, Durban University of Technology, Durban, South Africa

Graham J. Barratt

Fredrick a.o. otieno.

• DVC: Technology, Innovation and Partnerships, Durban University of Technology, Durban, South Africa

*Address all correspondence to: [email protected]

1. Introduction

While it is essential for every researcher to obtain data that is highly accurate, complete, representative and comparable, it is known that missing values, outliers and censored values are common characteristics of a water quality data-set. Random and systematic errors at various stages of a monitoring program tend to produce erroneous values, which complicates statistical analysis. For example, the central tendency statistics, particularly the mean and standard deviation, are distorted by a single grossly inaccurate data point. An error, which is initially identified and is later incorporated into a decision making tool, like a water quality index (WQI) or a model, could subsequently lead to costly consequences to humans and the environment.

Checking for erroneous and anomalous data points should be routine, and an initial stage of any data analysis study. However, distinguishing between a data-point and an error requires experience. For example, outliers may actually be results which might require statistical attention before a decision can be made to either discard or retain them. Human judgement, based on knowledge, experience and intuition thus continue to be important in assessing the integrity and validity of a given data-set. It is therefore essential for water resources practitioners to be knowledgeable regarding the identification and treatment of errors and anomalies in water quality data before undertaking an in-depth analysis.

On the other hand, although the advent of computers and various software have made it easy to analyse large amounts of data, lack of basic statistical knowledge could result in the application of an inappropriate technique. This could ultimately lead to wrong conclusions that are costly to humans and the environment [ 1 ]. Such necessitate the need for some basic understanding of data characteristics and statistics methods that are commonly applied in the water quality sector. This chapter, discusses common anomalies and errors in water quality data-sets, methods of their identification and treatment. Knowledge reviewed could assist with building appropriate and validated data-sets which might suit the statistical method under consideration for data analysis and/or modelling.

2. Data errors and anomalies

Referring to water quality studies, an error can be defined as a value that does not represent the true concentration of a variable such as turbidity. These may arise from both human and technical error during sample collection, preparation, analysis and recording of results [ 2 ]. Erroneous values can be recorded even where an organisation has a clearly defined monitoring protocol. If invalid values are subsequently combined with valid data, the integrity of the latter is also impaired [ 1 ]. Incorporating erroneous values into a management tool like a WQI or model, could result in wrong conclusions that might be costly to the environment or humans.

Data validation is a rigorous process of reviewing the quality of data. It assists in determining errors and anomalies that might need attention during analysis. Validation is crucial especially where a study depends on secondary data as it increases confidence in the integrity of the obtained data. Without such confidence, further data manipulation is fruitless [ 3 ]. Though data validation is usually performed by a quality control personnel in most organisations, it is important for any water resource practitioner to understand the common characteristics that may affect in-depth analysis of a water quality data-sets.

3. Visual scan

Among the common methods of assessing the integrity of a data-set is visual scan. This approach assists to identify values that are distinct and, which might require attention during statistical analysis and model building. The ability to visually assess the integrity of data depends on both the monitoring objectives and experience [ 4 ]. Transcription errors, erroneous values (e.g. a pH value of greater than 14, or a negative reading) and inaccurate sample information (e.g. units of mg/L for specific conductivity data) are common errors that can be easily noted by a visual scan. A major source of transcription errors is during data entry or when converting data from one format to another [ 5 , 6 ]. This is common when data is transferred from a manually recorded spreadsheet to a computer oriented format. The incorrect positioning of a decimal point during data entry is also a common transcription error [ 7 , 8 ].

A report by [ 7 ] suggested that transcription errors can be reduced by minimising the number of times that data is copied before a final report is compiled. [ 9 ] recommended the read-aloud technique as an effective way of reducing transcription errors. Data is printed and read-aloud by one individual, while the second individual simultaneously compares the spoken values with the ones on the original sheet. Even though the double data-entry method has been described as an effective method of reducing transcription errors, its main limitation is of being laborious [ 9 - 11 ]. [ 12 ], however, recommended slow and careful entry of results as an effective approach of reducing transcription errors.

While it might be easy to detect some of the erroneous values by a general visual scan, more subtle errors, for example outliers, may only be ascertained by statistical methods [ 13 ]. Censored values, missing values, seasonality, serial correlation and outliers are common characteristics in data-sets that need identification and treatment [ 14 ]. The following sections review the common characteristics in water quality data namely; outliers, missing values and censored values. Methods of their identification and treatment are discussed.

3.1. Outliers (extreme values)

The presence of values that are far smaller or larger than the usual results is a common feature of water quality data. An outlier is defined as a value that has a low probability of originating from the same statistical distribution as the rest of observations in a data-set [ 15 ]. Outlying values should be examined to ascertain if they are possibly erroneous. If erroneous, the value can be discarded or corrected, where possible. Extreme values may arise from an imprecise measurement tool, sample contamination, incorrect laboratory analysis technique, mistakes made during data transfer, incorrect statistical distribution assumption or a novel phenomenon, [ 15 , 16 ]. Since many ecological phenomena (e.g., floods, storms) are known to produce extreme values, their removal assumes that the phenomenon did not occur when actually it did. A decision must thus be made as to whether an outlying datum is an occasional value and an appropriate member of the data-set or whether it should be amended, or excluded from subsequent statistical analyses as it might introduce bias [ 1 ].

An outlying value should only be objectively rejected as erroneous after a statistical test indicates that it is not real or when it is desired to make the statistical testing more sensitive [ 17 ]. In figure 1 , for example, simple inspection might mean that the two spikes are erroneous, but in-depth analysis might correlate the spikes to very poor water quality for those two days, which would make the two observations valid. The model, however, does not pick the extreme values, which negatively affects the R 2 value, and ultimately the accuracy and usefulness of the model in predicting polymer dosage.

Data inspection during validation and treatment

Both observational (graphical) and statistical techniques have been applied to identify outliers. Among the common observational methods are the box-plots, time series, histogram, ranked data plots and normal probability plots [ 18 , 19 ]. These methods basically detect an outlier value by quantifying how far it lies from the other values. This could be the difference between the outlier and the mean of all points, between the outlier and the next closest value or between the outlier and the mean of the remaining values [ 20 ].

3.2. Box-plot

The box-plot, a graphical representation of data dispersion, is considered to be a simple observation method for screening outliers. It has been recommended as a primary exploratory tool of identifying outlying values in large data-sets (15). Since the technique basically uses the median value and not the mean, it poses a greater advantage by allowing data analysis disregarding its distribution. [ 21 ] and [ 22 ] categorised potential outliers using the box-plot as:

data points between 1.5 and 3 times the Inter Quantile Range (IQR) above the 75 th percentile or between 1.5 and 3 times the IQR below the 25 th percentile, and

data points that exceed 3 times the IQR above the 75 th percentile or exceed 3 times the IQR below the 25 th percentile.

The limitation of a box plot is that it is basically a descriptive method that does not allow for hypothesis testing, and thus cannot determine the significance of a potential outlier [ 15 ].

3.3. Normal probability plot

The probability plot method identifies outliers as values that do not closely fit a normal distribution curve. The points located along the probability plot line represent ‘normal’,observation, while those at the upper or lower extreme of the line, indicates the suspected outliers as depicted in Figure 2 .

Normal probability plot showing outliers

The approach assumes that if an extreme value is removed, the resulting population becomes normally distributed [ 21 ]. If, however, the data still does not appear normally distributed after the removal of outlying values, a researcher might have to consider normalising it by transformation techniques, such as using logarithms [ 21 , 23 ]. However, it should be highlighted that data transformation tends to shrink large values (see the two extreme values in Figure 1 , before transformation), thus suppressing their effect which might be of interest for further analysis [ 23 , 24 ]. Data should thus not be simply transformed for the sole purpose of eliminating or reducing the impact of outliers. Furthermore, since some data transformation techniques require non-negative values only (e.g. square root function) and a value greater than zero (e.g. logarithm function), transformation should not be considered as an automatic way of reducing the effect of outliers [ 23 ].

Since observational methods might fail to identify some of the subtle outliers, statistical tests may be performed to identify a data point as an outlier. However a decision still has to be made on whether to exclude or retain an outlying data point. The section below describes the common statistical test for identifying outliers.

3.4. Grubbs test

The Grubb’s test, also known as the Studentised Deviate test, compares outlying data points with the average and standard deviation of a data-set [ 25 - 27 ]. Before applying the Grubbs test, one should firstly verify that the data can be reasonably approximated by a normal distribution. The test detects and removes one outlier at a time until all are removed. The test is two sided as shown in the two equations below.

To test whether the maximum value is an outlier, the test:

To test whether the minimum value is an outlier, the test is:

Where X 1 or X n =the suspected single outlier (max or min)

s=standard deviation of the whole data set

The main limitation of Grubbs test is of being invalid when data assumes non-normal distribution [ 28 ]. Multiple iterations of data also tends to change the probabilities of detection. Grubbs test is only recommended for sample sizes of not more than six, since it frequently tags most of the points as outliers. It suffers from masking, which is failure to identify more than one outlier in a data-set [ 28 , 29 ]. For instance, for a data-set consisting of the following points; 3, 5, 7, 13, 15, 150, 153, the identification of 153 (maximum value) as an outlier might fail because it is not extreme with respect to the next highest value (150). However, it is clear that both values (150 and 153) are much higher than the rest of the data-set and could jointly be considered as outliers.

3.5. Dixon test

Dixon’s test is considered an effective technique of identifying an outlier in a data-set containing not more than 25 values [ 21 , 30 ]. It is based on the ratio of the ranges of a potential outlier to the range of the whole data set as shown in equation 1 [ 31 ]. The observations are arranged in ascending order and if the distance between the potential outlier to its nearest value (Q gap ) is large enough, relative to the range of all values (Q range ), the value is considered an outlier.

The calculated Q exp value is then compared to a critical Q-value (Qcrit) found in tables. If Q exp is greater than the suspect value, the suspected value can be characterised as an outlier. Since the Dixon test is based on ordered statistics, it tends to counter-act the normality assumption [ 15 ]. The test assumes that if the suspected outlier is removed, the data becomes normally distributed. However, Dixon’s test also suffers the masking effect when the population contains more than one outlier.

[ 32 ] recommended the use of multivariate techniques like Jackknife distance and Mahalanobis distance [ 33 , 34 ]. The strength of multivariate methods is on their ability to incorporation of the correlation or covariance between variables thus making them more correct as compared to univariate methods. [ 34 ] introduced the chi-square plot, which draws the empirical distribution function of the robust Mahalanobis distances against the chi-square distribution. A value that is out of distribution tail indicates that it is an outlier [ 33 ].

For an on-going study, an outlier can be ascertained by re-analysis of the sample, if still available and valid. [ 28 ] and [ 2 ] advised the practise of triplicate sampling as an effective method of verifying the unexpected results. When conducting a long-term study, researchers might consider re-sampling when almost similar conditions prevail again. Nevertheless, this option might not be feasible when carrying out a retrospective study since it generally depend on secondary data from past events.

For data intended for trend analysis, studies have recommended the application of nonparametric techniques such as the Seasonal Kendal test where transformation techniques do not yield symmetric data [ 19 ]. Should a parametric test be preferred on a data-set that includes outliers, practitioners may evaluate the influence of outliers by performing the test twice, once using the full data-set (including the outliers) and again on the reduced data-set (excluding the outliers). If the conclusions are essentially the same, then the suspect datum may be retained, failing which a nonparametric test is recommended.

4. Missing values

While most statistical methods presumes a complete data-set for analysis, missing values are frequently encountered problems in water quality studies [ 35 , 36 ]. Handling missing values can be a challenge as it requires a careful examination of the data to identify the type and pattern of missingness, and also have a clear understanding of the most appropriate imputation method. Gaps in water quality data-sets may arise due to several reasons, among which are imperfect data entry, equipment error, loss of sample before analysis and incorrect measurements [ 37 ]. Missing values complicate data analysis, cause loss of statistical efficiency and reduces statistical estimation power [ 37 - 39 ]. For data intended for time-series analysis and model building, gaps become a significant obstacle since both generally require continuous data [ 40 , 41 ]. Any estimation of missing values should be done in a manner that minimise the introduction of more bias in order to preserve the structure of original data-set [ 41 , 42 ].

The best way to estimate missing values is to repeat the experiment and produce a complete data-set. This option is however, not feasible when conducting a retrospective study since it depend on historical data. Where it is not possible to re-sample, a model or non-model techniques may be applied to estimate missing values [ 43 ].

If the proportion of missing values is relatively small, listwise deletion has been recommended. This approach, which is considered the easiest and simplest, discards the entire case where any of the variables are missing. Its major advantage is that it produce a complete data-set, which in turn allows for the use of standard analysis techniques [ 44 ]. The method also does not require special computational techniques. However, as the proportion of missing data increases, deletion tends to introduce biasness and inaccuracies in subsequent analyses. This tends to reduce the power of significance test and is more pronounced particularly if the pattern of missing data is not completely random. Furthermore, listwise deletion also decreases the sample size which tends to reduce the ability to detect a true association. For example, suppose a data-set with 1,000 samples and 20 variables and each of the variables has missing data for 5% of the cases, then, one could expect to have complete data for only about 360 individuals, thus discarding the other 640.

On the other hand, pairwise deletion removes incomplete cases on an analysis-by-analysis basis, such that any given case may contribute to some analyses but not to others [ 44 ]. This approach is considered an improvement over listwise deletion because it minimises the number of cases discarded in any given analysis. However, it also tend to produce bias if the data is not completely random.

Several studies have applied imputation techniques to estimate missing values. A common assumption with these methods is that data should be missing randomly [ 45 ]. The most common and easiest imputation technique is replacing the missing values with an arithmetic mean for the rest of the data [ 35 , 41 ]. This is recommended where the frequency distribution of a variable is reasonably symmetric, or has been made so by data transformation methods. The advantage of arithmetic mean imputation is generation of unbiased estimates if the data is completely random because the mean lands on the regression line. Even though the insertion of mean value does not add information, it tends to improve subsequent analysis. However, while simple to execute, this method does not take into consideration the subjects patterns of scores across all the other variables. It changes the distribution of the original data by narrowing the variance [ 46 ]. If the data assumes an asymmetric distribution, the median has been recommended as a more representative estimate of the central tendency and should be used instead of the mean.

[ 47 ], recommended model-based substitution techniques as more flexible and less ad hoc approach of estimating missing values as compared to non-model methods. A simple modelling technique is to regress the previous observations into an equation which estimates missing values [ 35 , 48 ]. The time-series auto-regressive model has been described as an improvement and more accurate method of estimating missing values [ 25 ]. Unlike the arithmetic mean and median replacement methods, regression imputation techniques estimates missing values of a given variable using data of other parameters. This tends to reduce the variance problem, which is common with the arithmetic mean imputation and median replacement methods [ 41 , 49 ].

On the other hand, the maximum likelihood technique uses all the available complete and incomplete data to identify the parameter values that have the highest probability of producing the sample data [ 44 ]. It runs a series of data iterations by replacing different values for the unknown parameters and converges to a single set of parameters with the highest probability of matching the observed data [ 41 ]. The method has been recommended as it tends to give efficient estimates with correct standard errors. However, just like other imputation methods, the maximum likelihood estimates can be heavily biased if the sample size is small. In addition, the technique requires a specialised software which may be expensive, challenging to use and time consuming.

Some studies have considered the relationship between parameters as an effective approach of estimating missing values [ 50 ]. For instance, missing conductivity values can be calculated from the total dissolved solids value (TDS) by a simple linear regression where p-value and r-value are known to exist and the missing value lies between the two variables. Equation 2 , where a is in the range 1.2-1.8, has been described as an equally important estimator of missing conductivity values [ 1 , 51 ].

The constant, a , is high in water of high chloride and low sulphate [ 51 ]. [ 52 ] estimated missing potassium values by using a linear relationship between potassium and sodium. The relationship gave a high correlation coefficient of 0.904 (p<0.001).

As of late, research has explored the application of artificial intelligence (AI) techniques to handle missing values in the water quality sector. Among the major AI techniques that have been applied is the Artificial Neural Networks (ANN) and Hybrid Evolutionary Algorithms (HEA) (48, 53, 54). Nevertheless, it should also be highlighted that all techniques for estimating missing values invariably affect the results. This is more pronounced when missing values characterise a significant proportion of the data being analysed. A research should thus consider the sample size when choosing the most appropriate imputation method.

5. Scientific facts

The integrity of water quality data can also be assessed by checking whether the results are inline with known scientific facts. To ascertain that, a researcher must have some scientific knowledge regarding the characteristics of water quality variables. Below are some scientific facts that can be used to assess data integrity [ 1 ].

Presence of nitrate in the absence of dissolved oxygen may indicate an error since nitrate is rapidly reduced in the absence of oxygen. The dissolved oxygen meter might have malfunctioned or oxygen might have escaped from the sample before analysis.

Component parts of a water-quality variable must not be greater than the total variable. For example:

Total phosphorus ≥Total dissolved phosphorus>Ortho-phosphate.

Total Kjeldahl nitrogen ≥Total dissolved Kjeldahl nitrogen>ammonia.

Total organic carbon ≥Dissolved organic carbon.

Species in a water body should be described correctly with regards to original pH of the water sample. For example, carbonate species will normally exist as HCO 3 - while CO 3 2- cannot co-exist with H 2 CO 3.

6. Censored data

A common problem faced by researchers analysing environmental data is the presence of observations reported to have non-detectable levels of a contaminant. Data which are either less than the lower detection limit, or greater than the upper detection limit of the analytical method applied are normally artificially curtailed at the end of a distribution, and are termed “censored values” [ 14 ]. Multiple censored results may be recorded when the laboratory has changed levels of detection, possibly as a result of an instrument having gained more accuracy, or the laboratory protocol having established new limits. If the values are below the detection limit, they are abbreviated as BDL, and when above the limit, as ADL [ 55 , 56 ].

Various methods of treating censored values have been developed to reduce the complication generally brought about by censored values [ 57 ]. The application of an incorrect method may introduce bias especially when estimating the mean and variance of data distribution [ 58 ]. This may consequently distort the regression coefficients and their standard errors, and further reduce the hypothesis testing power. A researcher must thus decide on the most appropriate method to analyse censored values. One might reason that since these values are extra ordinarly small, they are not important and discard them while some might be tempted to remove them inorder to ease statistical analysis. Deletion has however been described as the worst practise as it tends to introduce a strong upward bias of the central tendency which lead to inaccurate interpretation of data [ 19 , 59 - 62 ].

The relatively easiest and most common method of handling censored values is to replace them with a real number value so that they conform to the rest of data. The United State Environmental Agency suggested substitution if censored data is less than 15% of the total data-set (63, 64). [ 8 ], BDL, for example x < 1.1, were multiplied by the factor 0.75 to give 0.825. ADL values, for example 500 < x, were recorded as one magnitude higher than the limit values to give 501. [ 65 ] recommended substituting with 1   2 DL or 1 2 DL if the sample size is less than 20 and contains less than 45% of its data as censored values. [ 66 ] suggested substitution by 1 √ 2 D L if the data are not highly skewed and substitution by 1 2 DL otherwise. [ 67 ], however, criticised the substitution approach and illustrated how the practice could produces poor estimates of correlation coefficients and regression slopes. [ 68 ] further explained that substitution is not suitable if the data has multiple detection limits [ 68 , 69 ].

A second approach for handling censored values is the maximum likelihood estimation (MLE). It is recommended for a large data-set which assumes normality and contains censored results [ 38 , 65 , 70 , 71 ]. This approach basically uses the statistical properties of non-censored portion of the data-set, and an iterative process to determine the means and variance. The MLE technique generates an equation that calculates mean and standard deviation from values assumed to represent both the detects and non-detect results [ 69 ]. The equation can be used to estimate values that can replace censored values. However, the technique is reportedly ineffective for a small data-set that has fewer than 50 BDLs [ 69 ].

When data assumes an independent distribution and contain censored values, non-parametric methods like the Kaplan-Meir method, can be considered for analysis [ 59 ]. The Kaplan-Meir method creates an estimate of the population mean and standard deviation, which is adjusted for data censoring, based on the fitted distribution model. Just like any non-parametric techniques for analysing censored data, the Kaplan-Meier is only applicable to right-censored results (i.e. greater than) [ 72 ]. To use Kaplan-Meier on left-censored values, the censored values must be converted to right-censored by flipping them over to the largest observed value [ 65 , 71 , 72 ]. To ease the process, [ 73 ] have developed a computer program that does the conversion. [ 71 ], however, found the Kaplan-Meier method to be effective when summarising a data-set containing up to 70% of censored results.

In between the parametric and non-parametric methods is a robust technique called Regression on Order Statistics (ROS) [ 38 ]. It treats BDLs based on the probability plot of detects. The technique is applicable where the response variable (concentration) is a linear function of the explanatory variable (the normal quartiles) and if the error variance of the model is constant. It also assumes that all censoring thresholds are left-censored and is effective for a data-set which contains up to 80% censored values [ 59 ]. The ROS technique uses data plots on a modelling distribution to predict censored values. [ 59 ] and [ 68 ] evaluated ROS as a reliable method for summarising multiply censored data. Helsel and Cohn (38) also described ROS as a better estimator of the mean and standard deviation as compared to MLE, when the sample size is less than 50 and contains censored values.

7. Statistical methods

The success of an analysis of water quality data primarily depends on the selection of the right statistical method which considers common data characteristics such as normality, seasonality, outliers, missing values, censoring, etc., [ 74 ]. If the data assumes an understandable and describable distribution, parametric methods can be used [ 14 ]. However, non-parametric techniques are slowly replacing parametric techniques mainly because the latter are sensitive to common water characteristics like outliers, missing values and censored value [ 75 ].

7.1. Computer application in data treatment

The increase in various computer programs has made it easy to detect and treat erroneous data. Computers now provide flexibility and speedy methods of data analysis, tabulation, graph preparation or running models, among others. Various software such as Microsoft Excel, Minitab, Stata and MATLAB have become indispensable tools for analysing environmental data. These software perform various computations associated with checking assumptions about statistical distributions, error detection and their treatment. However, the major problem encountered by researchers, is lack of guidance regarding selection of the most appropriate software. Computer-aided statistical analysis should be undertaken with some understanding of the techniques being used. For example, some statistical software packages might replace missing values with the means of the variable, or prompt the user for case-wise deletion of analytical data, both of which might be considered undesirable [ 52 ].

Lately, machine learning algorithms like the artificial neural networks (ANNs) [ 67 , 76 - 78 ], and genetic algorithms (GA) [ 76 , 79 ] have gained momentum in water quality monitoring studies. [ 41 ] pointed out that these technique generally yields the best parameter estimates in the data set with the least amount of missing data. Nevertheless, as the percentage of missing data increases, the performance of ANN which is generally measured by the errors in the parameter estimates, decreases and may reach performance levels similar to those obtained by the general substitution methods. However, in all cases the effectiveness of these methods lies on the user’s ability to manipulate and display data correctly.

8. Conclusion

This chapter discussed the common data characteristics which tend to affect statistical analysis. It is recommended that practitioners should explore for outliers, missing values and censored values in a data-set before undertaking in-depth analysis. Although an analyst might not be able to establish the causal of such characteristic, eliminate or overcome some of the errors, having knowledge of their existence assists in establishing some level of confidence in drawing meaningful conclusions. It is recommended that water quality monitoring programs should strive to collect data of high quality. Common methods of ascertaining data quality are practising duplicate samples, using blanks or reference samples, and running performance audits. If a researcher is not sure of how to treat a characteristic of interest, a non-parametric method like Seasonal Kendal test could provide a better alternative since it is insensitive to common water quality data characteristics like outliers.

• 1. Steel A, Clarke M, Whitfield P. Use and Reporting of Monitoring Data. In: Bartram J, Ballance R, editors. Water Quality Monitoring-A Practical Guide to the Design and Implementation of Freshwater Quality Studies and Monitoring Programmes: United Nations Environment Programme and the World Health Organization; 1996.
• 2. Mitchell P. Guidelines for Quality Assurance and Quality Control in Surface Water Quality Programs in Alberta. Alberta Environment, 2006.
• 3. Tasić S, Feruh MB. Errors and Issues in Secondary Data used in marketing research. The Scientific Journal for Theory and Practice of Socioeconomic Development. 2012;1(2).
• 4. Doong DJ, Chen SH, Kao CC, Lee BC, Yeh SP. Data quality check procedures of an operational coastal ocean monitoring network. Ocean Engineering. 2007;34(2):234-46.
• 5. Taylor S, Bogdan R. Introduction to research methods: New York: Wiley; 1984.
• 6. Wahi MM, Parks DV, Skeate RC, Goldin SB. Reducing errors from the electronic transcription of data collected on paper forms: a research data case study. Journal of the American Medical Informatics Association. 2008;15(3):386-9.
• 7. UNEP-WHO. Use and Reporting of monitoring data. In: Bartram J, Ballace R, editors. Water Quality Monitoring A practical Guide to the Design and Implementation of Freshwater Quality Studies and Monitoring Programmes. London: United Nations Environmental program, World Health Organisation; 1996.
• 8. Dzwairo B. Modelling raw water quality variability in order to predict cost of water treatment. Pretoria: Tshwane University of Technology; 2011.
• 9. Kawado M, Hinotsu S, Matsuyama Y, Yamaguchi T, Hashimoto S, Ohashi Y. A comparison of error detection rates between the reading aloud method and the double data entry method. Controlled Clinical Trials. 24. 2003:560–9.
• 10. Cummings J, Masten J. Customized dual data entry for computerized analysis. Quality Assurance: Good Practice, Regulation, and Law. 1994;3:300-3.
• 11. Brown ML, Austen DJ. Data management and statistical techniques. Murphy BR, Willis DW, editors. Bethesda, Maryland: America Fisheries Society; 1996.
• 12. Rajaraman V. Self study guide to Analysis and Design of Information Systems. New Delhi: Asoke K. Ghosh; 2006.
• 13. Data Analysis and Interpretation. Rhe Monitoring Guideline. Austria2000.
• 14. Helsel DR, Hirsch RM. Statistical Methods in Water Resources. Amsterdam, Netherlands: Elsevier Science Publisher B.V; 1992.
• 15. Köster D, Hutchinson N. Review of Long-Term Water Quality Data for the Lake System Health Program. Ontario: 2008 Contract No.: GLL 80398.
• 16. Iglewicz B, Hoaglin DC. How to Detect and Handle Outliers1993.
• 17. Zar JH. Biostatistical Analysis. Upper Saddle River, NJ.: Prentice-Hall Inc; 1996.
• 18. Silva-Ramírez E-L, Pino-Mejías R, López-Coello M, Cubiles-de-la-Vega M-D. Missing value imputation on missing completely at random data using multilayer perceptrons. Neural Networks. 2011;24(1):121-9.
• 19. USEPA., Ecology. Do. Technical Guidance for Exploring TMDL Effectiveness Monitoring Data. 2011.
• 20. Stoimenova E, Mateev P, Dobreva M. Outlier detection as a method for knowledge extraction from digital resources. Review of the National Center for Digitization. 2006;9:1-11.
• 21. US-EPA. Statistical Analysis of Groundwater Monitoring Data at RCRA Facilities, Unified Guidance (Unified Guidance). US-Environmetal Protection Agency, 2009.
• 22. US-EPA. Data Quality Assessment: Statistical Methods for Practitioners. In: Agency USEP, editor: United States Environmental Protection Agency; 2006.
• 23. Osoborne JW. Improving your data transformations: Applying the Box-Cox transformation. Practical Assessment, Research and Evaluation. 2010;15(12).
• 24. High R. Dealing with 'Outlier': How to Maintain your data's integrity.
• 25. Chi Fung DS. Methods for the Estimation of Missing Values in Time Series. Western Australia: Edith Cowan University; 2006.
• 26. US-EPA. Statistical Training Course for Ground-Water Monitoring Data Analysis.. Washington D.C.: Environmental Protection Agency, 1992.
• 27. Grubbs FE, Beck G. Extension of sample sizes and percentage points for significance tests of outlying observations. Technometric. 1972;14:847-54.
• 28. Tiwari RC, Dienes TP. The Kalman filter model and Bayesian outlier detection for time series analysis of BOD data. Ecological Modelling 1994;73:159-65.
• 29. De Muth JE. Basic statistics and pharmaceutical statistical applications: CRC Press; 2014.
• 30. Gibbons RD. Statistical Methods for Groundwater Monitoring. New York: John Wiley & Sons; 1994.
• 31. Walfish S. A Review of Statistical Outlier Methods. Pharmaceutical Technology. 2006.
• 32. Robinson RB, Cox CD, Odom K. Identifying Outliers in Correlated Water Quality Data. Journal of Environmental Engineering. 2005;131(4):651-7.
• 33. Filzmoser P, editor A multivariate outlier detection method. Proceedings of the seventh international conference on computer data analysis and modeling; 2004: Minsk: Belarusian State University.
• 34. Garret D. The Chi-square plot: A tool for multivariate recognition. Journal of Geochemical Exploration. 1989;32:319-41.
• 35. Ssali G, Marwala T. Estimation of Missing Data Using Computational Intelligence and Decision Trees. n.d.
• 36. Noor NM, Zainudin ML. A Review: Missing Values in Environmental Data Sets. International Conference on Environment 2008 (ICENV 2008); Pulau Pinang2008.
• 37. Calcagno G, Staiano A, Fortunato G, Brescia-Morra V, Salvatore E, Liguori R, et al. A multilayer perceptron neural network-based approach for the identification of responsiveness to interferon therapy in multiple sclerosis patients. Information Sciences. 2010;180(21):4153-63.
• 38. Helsel DR, Cohn T. Estimation of description statistics for multiply censored water quality data. Water Resource Research. 1988; 24:1997-2004.
• 39. Little RJ, Rubin DB. Statistical analysis with missing data. New York: John Wiley and Sons; 1987.
• 40. Junninen H, Niska H, Tuppurainen K, Ruuskanen J, Kolehmainen M. Methods for imputation of missing values in air quality data sets. Atmospheric Environment. 2004; 38:2895–907.
• 41. Nieh C. Using Mass Balance, Factor Analysis, and Multiple Imputation to Assess Health Effects of Water Quality. Chicago, Illinois: University of Illinois 2011.
• 42. Luengo J, Garcia S, Herrera F. A study on the use of imputation methods for experimentation with Radial Basis Function Network classifiers handling missing attribute values: The good synergy between RBFNs and EventCovering methodI. Neural Networks. 2010; 23:406-18.
• 43. Lakshminarayan K, Harp S, Samad T. Imputation of missing data in industrial databases. Applied Intelligence. 1999;11(3):259-75.
• 44. Baraldi AN, Enders CK. An introduction to modern missing data analyses. Journal of School Psychology. 2010;48(1):5-37.
• 45. Rubin DB. Inference and missing data. Biometrika. 1976;63(3):581-92.
• 46. Enders CK. A primer on the use of modern missing-data methods in psychosomatic medicine research. PsychosomaticMedicine. 2006;68:427–36.
• 47. Fogarty DJ. Multiple imputation as a missing data approach to reject inference on consumer credit scoring. Intersat. 2006.
• 48. Smits A, Baggelaar PK. Estimating missing values in time series. Netherlands: Association of River Waterworks – RIWA; 2010.
• 49. Sartori N, Salvan A, Thomaseth K. Multiple imputation of missing values in a cancer mortality analysis with estimated exposure dose. ComputationalStatistics and DataAnalysis. 2005;49(3):937–53.
• 50. Güler C, Thyne GD, McCray JE, Turner AK. Evaluation of graphical and multivariate statistical methods for classification of water chemistry data. Hydrogeology 2002;10:455–74.
• 51. Dzwairo B, Otieno FAO, Ochieng' GM. Incorporating surface raw water quality into the cost chain for water services: Vaal catchment, South Africa. Research Journal of Chemistry and Environment. 2010;14(1):29-35.
• 52. Guler C, Thyne GD, McCray JE, Turner AK. Evaluation of graphical and multivariate statistical methods for classification of water chemistry data. Hydrogeology. 2002;10:455-74.
• 53. Starret KS, Starret KS, Heier T, Su Y, Tuan D, Bandurraga M. Filling in Missing Peakflow data using Artificial Neural Networks. Journal of Engineering and Applied Science. 2010;5(1).
• 54. Aitkenhead MJ, Coull MC. An application based on neural networks for replacing missing data in large datasets n.d.
• 55. Lin P-E, Niu X-F. Comparison of Statistical Methods In Handling Minimum Detection Limits. Department of Statistics,, Florida State University, 1998.
• 56. Darken PF. Testing for changes in trend in water quality data. Blacksburg, Virginia: Virginia Polytechnic Institute and State University; 1999.
• 57. Farnham IM, Stetzenbach KJ, Singh AS, Johannesson KH. Treatment of nondetects in multivariate analysis of groundwatervgeochemistry data. Chemometrics Intelligent Lab Sys. 2002;60(265-281).
• 58. Lyles RH, Fan D, Chuachoowong R. Correlation coefficient estimation involving a left censored laboratory assay variable. Statist Med. 2001;20:2921-33.
• 59. Lopaka L, Helsel D. Statistical analysis of water-quality data containing multiple detection limits: S-language software for regression on order statistics. Computers & Geosciences. 2005;31:1241-8.
• 60. Gheyas IA, Smith LS. A neural network-based framework for the reconstruction of incomplete data sets. Neurocomputing. 2010;73(16–18):3039-65.
• 61. Nishanth KJ, Ravi V, Ankaiah N, Bose I. Soft computing based imputation and hybrid data and text mining: The case of predicting the severity of phishing alerts. Expert Systems with Applications. 2012;39(12):10583-9.
• 62. Helsel D. Fabricating data: How substituting values for nondetects can ruin results, and what can be done about it. Chemosphere. 2006;65:2434-9.
• 63. Kalderstam J, Edén P, Bendahl P-O, Strand C, Fernö M, Ohlsson M. Training artificial neural networks directly on the concordance index for censored data using genetic algorithms. Artificial Intelligence in Medicine. 2013;58(2):125-32.
• 64. Environmental Protection Agency. Data Quality Assessment: Statistical Methods for Practitioners. Agency USEP, editor. Washington: United States Environmental Protection Agency, Office of Environmental Information, 2006; 2006 14 June 2013. 198 p.
• 65. Hewett P, Ganser GH. A Comparison of Several Methods for Analyzing Censored Data. British Occupational Hygiene. 2007;57(7):611-32.
• 66. Hornung RW, Reed LD. Estimation of Average Concentration in the Presence of Nondetectable Values. Applied Occupational and Environmental Hygiene. 1990;5(1):46-51.
• 67. Kang P. Locally linear reconstruction based missing value imputation for supervised learning. Neurocomputing. 2013(0).
• 68. Shumway RH, Azari RS, Kayhanian M. Statistical approaches to estimating mean water quality concentrations with detection limits. Environmental Science and Technology. 2002;36:3345-53.
• 69. Helsel D. Less than obvious-statistical treatment data below the detection limit. Environmental Science and Technology. 1990;24(12):1766-44.
• 70. Sanford RF, Pierson CT, Crovelli RA. An objective replacement method for censored geochemical data. Math Geol. 1993;25:59-80.
• 71. Antweiler RC, Taylor HE. Evaluation of Statistical Treatments of Left-Censored Environmental Data using Coincident Uncensored Data Sets. Environmental Science and Technology. 2008;42(10):3732-8.
• 72. Fu L, Wang Y-G. Statistical tools for analysing water quality data2012.
• 73. Silva JdA, Hruschka ER. An experimental study on the use of nearest neighbor-based imputation algorithms for classification tasks. Data & Knowledge Engineering. 2013;84(0):47-58.
• 74. Visser A, Dubus I, Broers HP, Brouyere S, Korcz M, Orban P, et al. Comparison of methods for the detection and extrapolation of trends in groundwater quality. Journal of Environmental Monitoring. 2009;11(11):2030-43.
• 75. Schertzer TL, Alexander RB, Ohe DJ. The Computer Program Estimate Trend (ESTREND), a system for the detection of trends in water-quality data Water Resources investigation report. 1991;91-4040:56-7.
• 76. Recknagel F, Bobbin J, Whigham P, Wilson H. Comparative application of artificial neural networks and genetic algorithms for multivariate time-series modelling of algal blooms in freshwater lakes. Journal of Hydroinformatics. 2002;4(2):125-34.
• 77. Lee JHW, Huang Y, Dickman M, Jayawardena AW. Neural network modelling of coastal algal blooms.Ecological Modelling. 2003;159(179-201).
• 78. Singh KP, Basant A, Malik A, Jain G. Artificial neural network modeling of the river water quality—a case study. Ecological Modelling. 2009;220(6):888-95.
• 79. Muttil N, Lee JHW. Genetic programming for analysis and real-time prediction of coastal algal blooms. Ecological Modelling. 2005;189:363-76.

© 2015 The Author(s). Licensee IntechOpen. This chapter is distributed under the terms of the Creative Commons Attribution 3.0 License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Continue reading from the same book

Published: 09 September 2015

By Nataša Gros

1747 downloads

By Marco André da Silva Costa and Magda Sofia Valério...

2147 downloads

By A.M. Taiwo, A.T. Towolawi, A.A. Olanigan, O.O. Olu...

2920 downloads

Advertisement

Testing a Dynamic Complex Hypothesis in the Analysis of Land Use Impact on Lake Water Quality

• Published: 18 August 2009
• Volume 24 , pages 1313–1332, ( 2010 )

Cite this article

• QingHai Guo 1 ,
• KeMing Ma 1 ,
• Liu Yang 2 &
• Kate He 3  

477 Accesses

38 Citations

Explore all metrics

In this study, we proposed a dynamic complex hypothesis that the impact of land use on water quality could vary along the expansion of the buffer size, and there should be an effective buffer zone where the strongest linkage occurs between land use and water quality. The hypothesis was tested and supported by a case study carried out in four watersheds in Hanyang District, China. More specific, buffer analysis and regression model were applied for studying the impacts of land use type, area proportion of land use type, and spatial pattern of land use on water quality. We conclude that not only the proportion of land use but also the spatial pattern moderates the impact of land use on water quality. Our study indicates that the identification of the effective buffer zones can provide new information and ideas for planning and management. Moreover, this study could also partially help to explain the conflicting results on the impact of land use on water quality in buffer versus in catchments in the literatures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

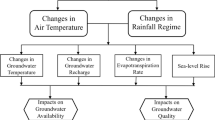
Impact of climate change on groundwater hydrology: a comprehensive review and current status of the Indian hydrogeology

Local determinants influencing stream water quality

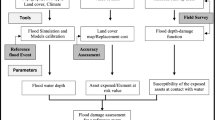
Analysis of flood damage and influencing factors in urban catchments: case studies in Manila, Philippines, and Jakarta, Indonesia

Alberti M, Booth D, Hill K, Coburn B, Avolio C, Coe S, Spirandelli D (2007) The impact of urban patterns on aquatic ecosystems: an empirical analysis in Puget lowland sub-basins. Landscape Urban Plan 80(4):345–361

Article   Google Scholar  

Amiri BJ, Nakane K (2009) Modeling the linkage between river water quality and landscape metrics in the Chugoku District of Japan. Water Resour Manag 23(5):931–956

Bannerman RT, Owens DW, Dodds RB, Hornewer NJ (1993) Sources of pollutants in Wisconsin stormwater. Water Sci Technol 28(3–5):241–259

Google Scholar  

Basnyat P, Teeter LD, Lockaby BG (1999) Relationships between landscape characteristics and nonpoint source pollution inputs to coastal estuaries. Environ Manage 23(4):539–549

Basnyat P, Teeter LD, Lockaby BG, Flynn KM (2000) The use of remote sensing and GIS in watershed level analyses of non-point source pollution problems. Forest Ecol Manag 128:65–73

Brezonik PL, Stadelmann TH (2002) Analysis and predictive models of stormwater runoff volumes, loads, and pollutant concentrations from watersheds in the Twin Cities metropolitan area, Minnesota, USA. Water Res 36(7):1743–1757

Cao WZ, Bowden WB, Davie T, Fenemor A (2009) Modelling impacts of land cover change on critical water resources in the Motueka river catchment, New Zealand. Water Resour Manag 23(1):137–151

Chang HJ (2008) Spatial analysis of water quality trends in the Han River basin, South Korea. Water Res 42:3285–3304

Changnon SA, Demissie M (1996) Detection of changes in streamflow and floods resulting from climate fluctuations and land-use drainage changes. Climatic Change 32:411–421

Conway TM, Lathrop RG (2005) Alternative land-use regulations and environmental impacts: assessing future land-use in an urbanizing watershed. Landscape Urban Plan 71:1–15

Donohue I, McGarrigle ML, Mills P (2006) Linking catchment characteristics and water chemistry with the ecological status of Irish rivers. Water Res 40(1):91–98

EPA China (2002) GB3838-2002. Available on: http://www.sepa.gov.cn/image20010518/3391.pdf (in Chinese, accessed 15 Aug 2008)

ESRI (2001) ArcGIS 8.1. Environmental Systems Research Institute Inc., Redlands, California

Fang JY, Rao S, Zhao SQ (2005) Human-induced long-term changes in the lakes of the Jianghan Plain, Central Yangtze. Front Ecol Environ 3(4):186–192

Foley JA, Ruth D, Asner GP et al (2005) Global consequences of land use. Science 309:570–574

Gburek WJ, Folmar GJ (1999) Flow and chemical contributions to streamflow in an upland watershed: a baseflow survey. J Hydrol 217:1–18

Gillies RR, Box JB, Symanzik J, Rodemaker EJ (2003) Effects of urbanization on the aquatic fauna of the Line Creek watershed, Atlanta—a satellite perspective. Remote Sens Environ 86:411–422

Grassland, Soil & Water Research Laboratory (2001). Soil & Water Assessment Tool. Available on: http://www.brc.tamus.edu/swat/soft_model_2000soft.html (accessed 20 May 2009)

Grimm NB, Faeth SH, Golubiewski NE, Redman CL, Wu JG, Bai XM, Briggs JM (2008) Global change and the ecology of cities. Science 319:756–760

Gustafson EJ (1998) Quantifying landscape spatial pattern: what is the state of the art? Ecosystems 1:143–156

Ha HJ, Stenstrom MK (2003) Identification of land use with water quality data in stormwater using a neural network. Water Res 37(17):4222–4230

Hanratty MP, Stefan HG (1998) Simulating climate change effects in a Minnesota agricultural watershed. J Environ Qual 27:1524–1532

Hunsaker CT, Levine DA (1995) Hierarchical approaches to the study of water quality in rivers. BioScience 45:193–202

Johnson LB, Richards C, Host GE, Arthur JW (1997) Landscape influences on water chemistry in Midwestern stream ecosystems. Freshwater Biol 37:193–208

Kim G, Choi E, Lee D (2005) Diffuse and point pollution impacts on the pathogen indicator organism level in the Geum River, Korea. Sci Total Environ 350:94–105

Leitch C, Harbor J (1999) Impacts of land-use change on freshwater runoff into the near-coastal zone, Holetown Catchments, Barbados: comparisons of long-term to single-storm effects. J Soil Water Conserv 3:584–592

Liu Y, Yu YJ, Guo HC, Yang PJ (2009) Optimal land-use management for surface source water protection under uncertainty: a case study of Songhuaba Watershed (Southwestern China). Water Resour Manag 23(10):2069–2083

Mander U, Kull A, Tamm V, Kuusemets V, Karjus R (1998) Impact of climatic fluctuations and land use change on runoff and nutrient losses in rural landscape. Landscape Urban Plan 41:229–238

Mattikalli NM, Richards KS (1996) Estimation of surface water quality changes in response to land-use change: application of the export coefficient model using remote sensing and geographical information system. J Environ Manage 48:263–282

McGarigal K, Marks BJ (1995) FRAGSTATS: spatial pattern analysis program for quantifying landscape structure. Forest Science Department, Oregon State University, Corvallis

Mehaffey MH, Nash MS, Wade TG et al (2005) Linking land cover and water quality in New York City’s water supply watersheds. Environ Monit Assess 107:29–44

Moreno JL, Navarro C, De Las Heras J (2006) Abiotic ecotypes in south-central Spanish rivers: reference conditions and pollution. Environ Pollut 143:388–396

O’Neill RV, Hunsaker CT, Jones KB, Riitters KH, Wickham JD, Schwartz PM, Goodman IA, Jackson BL, Baillargeon WS (1997) Monitoring environmental quality at the landscape scale. BioScience 47(8):513–519

Palmer M, Bernhardt E, Chornesky E et al (2004) Ecology for a crowded planet. Science 304:1251–1252

Phillips JD (1989) Evaluation of North Carolina’s estuarine shoreline area of environmental concern from a water quality perspective. Coastal Manage 17:103–117

Rai SE, Sharma E (1998) Comparative assessment of runoff characteristics under different land-use patterns within a Himalayan watershed. Hydrol Process 12:2235–2248

Ren WW, Zhong Y, Meligrana J, Anderson B, Watt WE, Chen JK, Leung HL (2003) Urbanization, land use, and water quality in Shanghai 1947–1996. Environ Int 29(5):649–659

Sawyer JA, Stewart PM, Mullen MM, Simon TP, Bennett HH (2004) Influence of habitat, water quality, and land use on macro-invertebrate and fish assemblages of a southeastern coastal plain watershed, USA. Aquat Ecosyst Health 7(1):85–99

Sieker H, Klein M (1998) Best management practices for stormwater runoff with alternative methods in a large urban catchment in Berlin, Germany. Water Sci Technol 38(10):91–97

Shao M, Tang XY, Zhang YH, Li WJ (2006) City clusters in China: air and surface water pollution. Front Ecol Environ 4(7):353–361

Sliva L, Williams DD (2001) Buffer zone versus whole catchment approaches to studying land-use impact on river water quality. Water Res 35(14):3462–3472

Sonzogni WC (1980) Pollution from land runoff. Environ Sci Technol 14(2):148–153

Tang Z, Engel BA, Pijanowski BC, Lim KJ (2005) Forecasting land use change and its environmental impact at a watershed scale. J Environ Manage 76(1):35–45

Tomer MD, as Principal Investigator (2002) Optimizing the placement of practices that improve water quality within a watershed. Research Project 01-024—Final Report. USDA/ARS–National Soil Tilth Laboratory

Tong STY, Chen WL (2002) Modeling the relationship between land-use and surface water quality. J Environ Manage 66:377–393

Tsihrintzis VA, Hamid R (1998) Runoff quality prediction from small urban catchments using SWMM. Hydrol Process 12:311–329

Van Dessel W, Van Rompaey A, Poelmans L, Szilassi P (2008) Predicting land cover changes and their impact on the sediment influx in the Lake Balaton catchment. Landscape Ecol 23(6):645–656

Wang X (2001) Integrating water-quality management and land-use planning in a watershed context. J Environ Manage 61:25–36

Wiens JA (2002) Riverine landscapes: taking landscape ecology into the water. Freshwater Biol 47(4):501–515

Download references

Author information

Authors and affiliations.

State Key Laboratory of Urban and Regional Ecology, Research Center for Eco-Environmental Sciences, Chinese Academy of Sciences, Beijing, 100085, China

QingHai Guo & KeMing Ma

School of Resource and Safety Engineering, China University of Mining and Technology (Beijing), Beijing, 100083, China

Department of Biological Sciences, Murray State University, Murray, KY, 42071, USA

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to KeMing Ma .

Rights and permissions

Reprints and permissions

About this article

Guo, Q., Ma, K., Yang, L. et al. Testing a Dynamic Complex Hypothesis in the Analysis of Land Use Impact on Lake Water Quality. Water Resour Manage 24 , 1313–1332 (2010). https://doi.org/10.1007/s11269-009-9498-y

Download citation

Received : 10 November 2008

Accepted : 07 August 2009

Published : 18 August 2009

Issue Date : May 2010

DOI : https://doi.org/10.1007/s11269-009-9498-y

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Spatial pattern
• Effective buffer
• Water quality
• Hanyang District
• Find a journal
• Publish with us
• Track your research

Sciencing_Icons_Science SCIENCE

Sciencing_icons_biology biology, sciencing_icons_cells cells, sciencing_icons_molecular molecular, sciencing_icons_microorganisms microorganisms, sciencing_icons_genetics genetics, sciencing_icons_human body human body, sciencing_icons_ecology ecology, sciencing_icons_chemistry chemistry, sciencing_icons_atomic &amp; molecular structure atomic & molecular structure, sciencing_icons_bonds bonds, sciencing_icons_reactions reactions, sciencing_icons_stoichiometry stoichiometry, sciencing_icons_solutions solutions, sciencing_icons_acids &amp; bases acids & bases, sciencing_icons_thermodynamics thermodynamics, sciencing_icons_organic chemistry organic chemistry, sciencing_icons_physics physics, sciencing_icons_fundamentals-physics fundamentals, sciencing_icons_electronics electronics, sciencing_icons_waves waves, sciencing_icons_energy energy, sciencing_icons_fluid fluid, sciencing_icons_astronomy astronomy, sciencing_icons_geology geology, sciencing_icons_fundamentals-geology fundamentals, sciencing_icons_minerals &amp; rocks minerals & rocks, sciencing_icons_earth scructure earth structure, sciencing_icons_fossils fossils, sciencing_icons_natural disasters natural disasters, sciencing_icons_nature nature, sciencing_icons_ecosystems ecosystems, sciencing_icons_environment environment, sciencing_icons_insects insects, sciencing_icons_plants &amp; mushrooms plants & mushrooms, sciencing_icons_animals animals, sciencing_icons_math math, sciencing_icons_arithmetic arithmetic, sciencing_icons_addition &amp; subtraction addition & subtraction, sciencing_icons_multiplication &amp; division multiplication & division, sciencing_icons_decimals decimals, sciencing_icons_fractions fractions, sciencing_icons_conversions conversions, sciencing_icons_algebra algebra, sciencing_icons_working with units working with units, sciencing_icons_equations &amp; expressions equations & expressions, sciencing_icons_ratios &amp; proportions ratios & proportions, sciencing_icons_inequalities inequalities, sciencing_icons_exponents &amp; logarithms exponents & logarithms, sciencing_icons_factorization factorization, sciencing_icons_functions functions, sciencing_icons_linear equations linear equations, sciencing_icons_graphs graphs, sciencing_icons_quadratics quadratics, sciencing_icons_polynomials polynomials, sciencing_icons_geometry geometry, sciencing_icons_fundamentals-geometry fundamentals, sciencing_icons_cartesian cartesian, sciencing_icons_circles circles, sciencing_icons_solids solids, sciencing_icons_trigonometry trigonometry, sciencing_icons_probability-statistics probability & statistics, sciencing_icons_mean-median-mode mean/median/mode, sciencing_icons_independent-dependent variables independent/dependent variables, sciencing_icons_deviation deviation, sciencing_icons_correlation correlation, sciencing_icons_sampling sampling, sciencing_icons_distributions distributions, sciencing_icons_probability probability, sciencing_icons_calculus calculus, sciencing_icons_differentiation-integration differentiation/integration, sciencing_icons_application application, sciencing_icons_projects projects, sciencing_icons_news news.

• Share Tweet Email Print
• Home ⋅
• Science Fair Project Ideas for Kids, Middle & High School Students ⋅

How to Test Water Quality for a Science Project

Science Projects on Bottled Water Vs. Tap Water

The United States Geological Survey defines water quality as "the chemical, physical and biological characteristics of water." Quality determines the best uses for water. Students who are interested in the environment benefit from experimenting with water from a variety of sources. Water quality experiments are informative, but not too difficult. They're easy to set up at a science fair. Whether you're testing water quality for its pH balance, chlorine or nitrate levels, or hardness, create a science fair experiment using one or all of these tests.

Chlorine and Nitrate Tests, pH Balance

Put 40 mL of tap water from the sink into a 50 mL beaker. This water will be used in all four tests.

Lower the 4.5 to 7.0 pH paper into the water. Pull it right back out and hold it next to the color-coded charts for pH papers. If the colors don't appear on the chart, use the 6.5 to 10 pH paper. Repeat the experiment and check the chart. Write your water's pH balance on the paper.

Swirl the chlorine strip in the tap water three or four times and remove it. Wait for 10 seconds and hold the paper next to the color chart section for chlorine. You'll find that most city water contains a certain level of chlorine. Record your results on the paper.

Stick the nitrate strip into the water for two seconds and remove it. Wait one minute and check the test strip against the colors on the chart for nitrates. Nitrates are found in the soil--too much nitrate in the drinking water can cause health issues. Write your results on the paper.

Hardness Test

Dip a water hardness strip into the tap water. Wait 15 seconds and hold it next to the chart to check for the hardness level. The chart only goes up to 180 parts per million (ppm). If your results appear to be 180 ppm, continue on to Step 2. If it's less than 180 ppm, record your answer. The water's hardness indicates its levels of calcium carbonate and magnesium.

Squeeze a plastic pipette into the 50 ml of tap water and withdraw 2 mL of water. Place the water into the 10 mL graduated cylinder.

Add 4 mL of distilled water to the 10 mL cylinder. You should have a total of 6 mL of water in the cylinder. Empty and dry the 50 mL beaker and pour the 6 mL of diluted water into the beaker.

Place another water hardness strip into the water. Wait for 15 seconds and hold it next to the chart. Check for your results and multiply the answer by three because the tap water has been diluted to one-third of the original water's contents. Now you have a more accurate result for your water. Record your score.

Things You'll Need

• Test strip kits are available online. Some strips are available through pool companies or home and garden supply stores.

Save your test strips to use on your display board during the science fair. Research your findings so you can explain your results.

Related Articles

How to measure the salinity of sea water, how to standardize a ph meter, how to measure iron in water, how to convert water hardness in mg/l to gpg, how to use beet juice to make a ph scale, what do the colors indicate on a ph test strip paper, how to convert tds to conductivity, different ways to raise the ph of drinking water, what are the uses of a level titration, how to measure ph levels, methods on how to determine ph in ph paper, how to convert ppm to grains in water hardness, electricity conductor science projects, what is ph of sodium carbonate in water, how to tell if a sample of water is pure or mixed, how to raise the alkalinity in a freshwater aquarium, how to make bromine water in the chemistry lab, how to measure the conductivity of water with a multimeter.

• USGS: Water Quality for Schools
• Washington University in Saint Louis: Water Hardness
• Save your test strips to use on your display board during the science fair.
• Research your findings so you can explain your results.

About the Author

Joan Collins began writing in 2008. Specializing in health, marriage, crafts and money, her articles appear on eHow. Collins earned a Bachelor of Arts in education from the University of Northern Colorado and a Master of Arts in instructional technology from American InterContinental University.

Photo Credits

glass image by Mikhail Olykainen from Fotolia.com

Find Your Next Great Science Fair Project! GO