problem solving examples factoring

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Here you will learn strategies for factoring algebraic expressions, including quadratics and polynomials. Factoring is a vital tool when simplifying expressions and solving quadratic equations.

Students first learn how to factor in the 6 th grade with their work in expressions and equations and expand that knowledge as they progress through algebra and beyond.

What is factoring?

Factoring is writing the algebraic expression as a product of its factors. It is the inverse process of multiplying algebraic expressions using the distributive property.

There are several strategies to factor algebraic expressions.

Step-by-step guide : Factoring out the GCF

Step-by-step guide : How to factor quadratic equations

Step-by-step guide : Factoring the difference of two squares

Step-by-step guide : Factor by grouping

Common Core State Standards

How does this relate to 6 th grade math – high school math?

• Grade 6: Expressions and Equations (6.EE.A.3) Apply the properties of operations to generate equivalent expressions. For example, apply the distributive property to the expression 3(2+x) to produce the equivalent expression 6+3x; apply the distributive property to the expression 24x+18y to produce the equivalent expression 6(4x+3y) .
• Grade 7: Expressions and Equations (7.EE.A.1)   Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients.
• High School Algebra: Seeing Structure in Equations (HSA-SSE.B.3a) Factor a quadratic expression to reveal the zeros of the function it defines.

[FREE] Algebra Worksheet (Grade 6 to 8)

Use this quiz to check your grade 6 – grade 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th to 8th grade algebra topics to identify areas of strength and support!

How to factor algebraic expressions using the GCF

In order to factor out the GCF from algebraic expressions:

Find the \textbf{GCF} of all terms in the expression and place it in front of parentheses.

Divide each term in the expression by the \textbf{GCF}.

Put the divided terms in the parentheses.

Express the \textbf{GCF} and the other factors as a product.

Factoring GCF examples

Example 1: factor the algebraic expression.

The greatest common factor in the expression is 4.

2 Divide each term in the expression by the \textbf{GCF}.

Since 4 is the GCF,

3 Put the divided terms in the parentheses.

4 Express the \textbf{GCF} and the other factors as a product.

Example 2: factor the algebraic expression

The GCF is 2x.

2x(\ \ \ \ \ \ \ \ \ \ )

Since 2x is the GCF,

2x^{2} \div {2x}=x

-4x \div {2x}=-2

How to factor algebraic expressions with a equal to 1

In order to factor an algebraic expression in the form x^2+bx+c\text{:}

Find two factors of the constant, \textbf{c} term, that sum to equal the coefficient of the \textbf{b} term.

Write the quadratic in factored form with two sets of parentheses.

Check your work and write the quadratic equation in factored form.

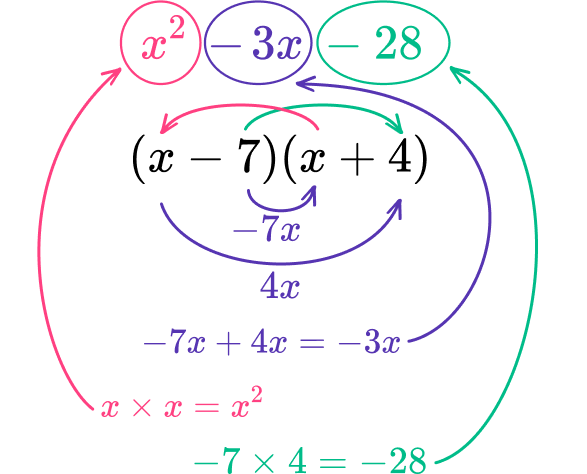
Example 3: factor the expression

The constant, c term, is -28 so one factor must be negative. The factors of -28 are:

\begin{array}{rl}1,&-28 \\\\ -1,&28 \\\\ 2,&-14 \\\\ -2,&14 \\\\ 4,&-7 \\\\ -4,&7 \end{array}

The coefficient of the b term is -3.

The two factors that multiply to -28 and add to -3 are -7 and 4.

\begin{aligned}-7\cdot4&=-28 \\\\ -7+4&=-3 \end{aligned}

The a term breaks up to be x\cdot{x} because x\cdot{x}=x^{2}

x^{2}-3x-28=(x-7)(x+4)

You can check your work through distributive property.

Example 4: factor the expression

The constant, c term, is + \; 12. As the b term is also positive, both factors are positive. The factors of 12 are:

\begin{array}{rl}1,&12 \\\\ 2,&6 \\\\ 3,&4 \end{array}

The coefficient of the b term is + \; 7.

The two factors that multiply to + \; 12 and add to 7 are 3 and 4.

\begin{aligned} 3\cdot4&=12 \\\\ 3+4&=7 \end{aligned}

x^{2}+7x+12=(x+3)(x+4)

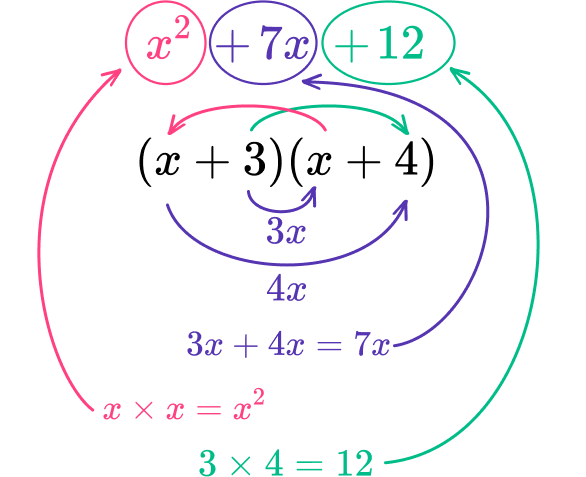
How to factor algebraic expressions with a not equal to 1

In order to factor an algebraic expression in the form ax^{2}+bx+c\text{:}

Find the factors of \textbf{ac} that sum to equal the coefficient of the \textbf{b} term.

Place the factors in the parentheses and check to make sure the product of the inside terms and outside terms sum to the \textbf{b} term.

Write the quadratic equation in factored form.

Example 5: factor the expression

The value of ac is 2 \times 5=10. As the b term is negative and the c term is positive, both factors must be negative.

The factors of 10 are:

\begin{array}{cc}-1,&-10 \\\\ -2,&-5 \end{array}

The coefficient of the b term is -11. The factors of 10 that sum to -11 are -1 and -10.

The a term is 2x^{2} which you can factor into 2x and x.

So far, the factored quadratic looks like: (2x\ \ \ \ \ )(x\ \ \ \ \ \ )

As one of the parentheses contains 2x, the factor in the other bracket is multiplied by 2, therefore you must divide the factor by 2 in the other bracket.

As -10 is a negative multiple of 2, you can easily divide this by 2 to get -5 so you need to place the factor of -1 in the first pair of parentheses and -5 into the second pair of parentheses to get (2x-1)(x-5).

Now check the expansion.

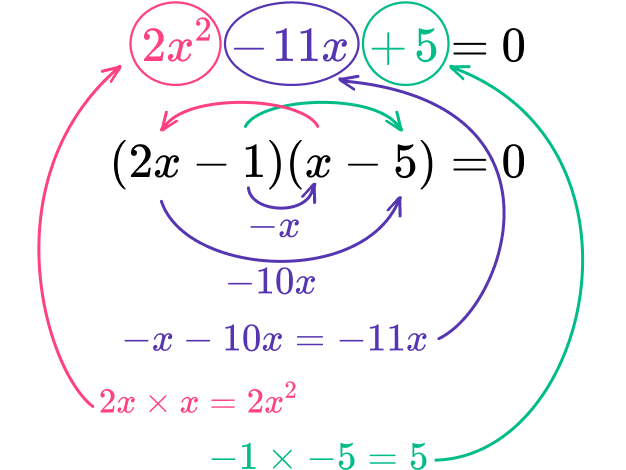
Each term is correct.

Example 6: factor the expression

The value of ac is 2 \times 3=6. As the b term is positive and the c term is positive, both factors must be positive.

The factors of 6 are:

\begin{array}{cc}1,&6 \\\\ 2,&3 \end{array}

The coefficient of the b term is + \; 5. The factors of 6 that sum to 5 are 2 and 3.

As 2 is a multiple of 2, you can easily divide this by 2 to get 1 so you need to place the factor of 3 in the first pair of parentheses and 1 into the second pair of parentheses to get (2x+3)(x+1).

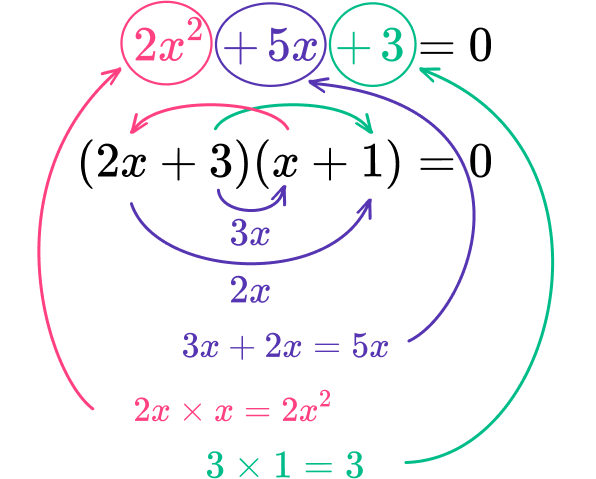
How to factor algebraic expressions (difference of two squares)

In order to factor the difference of two squares.

Write two sets of parentheses.

• Square root the first term and write it on the left hand side of both brackets
• Square root the last term and write it on the right hand side of both brackets.

Example 7: factor the expression

Square root the first term and write it on the left hand side of both brackets.

The first term is 4x^{2}. Square root this to get

\sqrt{4x^{2}}=2x

(2x\ \ \ \ \ \ )(2x\ \ \ \ \ \ )

Square root the last term and write the two values on the right hand side of each bracket.

The last term is 25. Square root this to get

\sqrt{25}=\pm5

(2x+5)(2x-5)

How to factor algebraic expressions by grouping

In order to factor by grouping:

Group the first two terms together and the last two terms together.

Factor out the \textbf{GCF} from each binomial.

Factor out the common binomial.

Example 8: factor the expression

Teaching tips for factoring.

• Use visual tools such as algebra tiles or digital algebra tiles so students can connect the area model with arrays to factoring.
• Although worksheets have their place, having students work in collaborative groups to problem solve is essential to the math classroom.

Easy mistakes to make

• Using the wrong factors For example, factoring x^{2}+5x+6, by using the incorrect factors of 6. \; (x+1)(x+6) ≠ {x^{2}}+5x+6 as 1+6=7, not 5. Here, the correct factored form is (x+2)(x+3).
• Not factoring out the greatest common factor For example, factoring 4x^{2}-16x to be 2(2x^{2}-8x). \; 2 is not the GCF of the expression, 4x is the GCF. So, the correct factored expression is 4x(x-4).
• Not finding the square root when factoring the difference of squares For example, factoring 16x^{2}-4 to be (8x-2)(8x+2). The correct factored expression should be (4x-2)(4x+2) as \sqrt{16x^{2}}=4x.

Practice factoring questions

1. Factor the expression.

The greatest common factor of 10 and 5 is 5. Divide both terms by 5 to get 10-5y=5(2-y).

2. Factor the expression.

The greatest common factor of 20x^{2} and 8x is 4x. Divide both terms by 4x to get 20x^{2}-8x=4x(5x-2).

3. Factor the expression.

The factors of -6 that sum to -1 are -3 and 2.

4. Factor the expression.

For the quadratic, 3x^{2}-2x-5, the value of ac is 3\times{-5}=-15. The factors of -15 that have a sum of -2 are -5 and 3. The a term can be factored into 3x and x so the factored form is currently (3x\ \ \ \ \ )(x\ \ \ \ \ \ ).

As one of the parentheses contains 3x, the factor in the other bracket is multiplied by 3, therefore divide the factor by 3 in the other bracket.

As 3 is a multiple of 3, you can easily divide this by 3 to get 1 so -5 is in the first pair of parentheses and 1 is in the second pair to get (3x-5)(x+1).

5. Factor the expression.

The expression is the difference of two perfect squares. To factor this expression, take the square root of the first term and place it in the first position of each parenthesis.

Take the square root of the second term and place the values in the second position of each parenthesis.

6. Fully factor the expression,

Group the first two terms and second two terms together.

The GCF of the first set is x^{2} and the GCF of the second set is positive 4.

Factoring FAQs

Yes, you can factor polynomial expressions with more than one variable. For example, xy-3y, factors to be y(x-3).

Yes, sometimes when factoring expressions completely, you might have to apply more than one strategy. For example, when factoring 3x^{2}-27, you first factor out the GCF. 3(x^{2}-9). Then you factor the parenthesis by using the strategy of the difference of two perfect squares. \sqrt{x^{2}}=x and \sqrt{9}=\pm3. So, the expression completely factored is 3(x-3)(x+3).

Yes, there are strategies you will learn to factor the difference of cubes and the sum of cubes in Algebra 2.

No, the sum of two squares is considered to be prime which means it cannot be factored. Quadratic polynomials can be prime meaning the only factors it has is itself and 1, like prime numbers.

Applying strategies of factoring helps to make solving equations easier. It can also help when finding the x -intercepts of polynomial functions.

The leading coefficient of algebraic expressions can be fractions and they can be factored. For example, \cfrac{1}{2}x-\cfrac{3}{4} factors to be \cfrac{1}{2}\left(x-\cfrac{3}{2}\right).

The next lessons are

• Radical functions

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

Calcworkshop

Factoring Fundamentals Tutorials & Examples

Boost your math confidence—Master factoring techniques—Solve complex problems with ease

Integer Factorization

1 hr 5 min 21 Examples

• Introduction to Video: Prime Factorization
• What is Prime Factorization and GCF for Integers?
• Examples #1-6: Give the prime Factorization of each number
• Examples #7-12: List all the pairs of integral factors
• Examples #13-21: Find the GCF for two numbers

Greatest Common Factor

1 hr 25 min 26 Examples

• Introduction to Video: Greatest Common Factor
• Overview of Factoring Out the GCF and Reducing Fractions with Examples #1-2
• Examples #3-8: Divide by the common factor
• Examples #9-14: Find the GCF of each monomial
• Examples #15-20: Factor the polynomial by pulling out the GCF
• Examples #21-26: Factor by pulling out the GCF

Difference of Squares

1 hr 28 min 31 Examples

• Introduction to Video: Difference of Two Squares
• Steps for Factoring the Difference of Squares
• Examples #1-6: Square each monomial
• Examples #7-12: Express as a product of squares
• Examples #13-31: Factor the binomial, if possible

Trinomial Coefficient One

1 hr 15 min 17 Examples

• Introduction to Video: Factoring Trinomials
• Steps for Factoring Trinomials with Leading Coefficient of 1
• Examples #1-8: Factor the trinomial
• Examples #9-17: Factor the trinomial completely

Trinomial Coefficient Not One

1 hr 33 min 12 Examples

• Introduction to Video: Factoring Trinomials with leading coefficient greater than 1
• Steps for Factoring Trinomials with leading coefficient greater than 1
• Examples #1-4: Factor the trinomial
• Examples #5-8: Factor the trinomial completely, if possible
• Examples #9-13: Factor the trinomial completely

Factor by Grouping

1 hr 30 min 16 Examples

• Introduction to Video: Factoring by Grouping
• How to factor a trinomial using grouping method? Examples #1-2
• Factoring by Grouping Steps with Example #3
• Examples #4-7: Factor each polynomial by grouping
• Example #8: Factor the polynomial by grouping
• Examples #9-12: Factor by Grouping and Difference of Squares
• Examples #13-16: Factor completely, using more than one factoring method

Factoring Cubes

1 hr 2 min 11 Examples

• Introduction to Video: Factoring Cubes
• Factoring Sum/Difference of Cubes Formulas with Example #1
• Examples #2-7: Factor using the sum or difference of cubes
• Examples #8-11: Factor completely

Solve By Factoring

1 hr 57 min 18 Examples

• Introduction to Video: Solve by Factoring
• Steps for Solving a Polynomial Equation by Factoring
• Examples #1-17: Solve by Factoring
• Example #18: Solve by Factoring using two different factoring techniques

Factoring Word Problems

1 hr 22 min 9 Examples

• Introduction to Video: Factoring Word Problems
• Steps for Solving Factoring Word Problems with Example #1
• Examples #2-3: Finding two numbers that satisfy the given conditions
• Examples #4-5: Find the area
• Example #6: Find the dimension of a picture given area of border
• Example #7: Find the width of the picture frame
• Example #8: Find the side of a box given the surface area
• Example #9: Find time when the ball will reach a specific height

Chapter Test

1 hr 30 min 31 Examples

• Examples #1-3: Give the prime factorization
• Examples #4-5: List the pairs of integral factors
• Examples #6-21: Factor completely, if possible
• Examples #22-24: Factor completely
• Examples #25-28: Solve the polynomial equation by factoring
• Example #29: Solve the polynomial equation
• Examples #30-31: Solve the word problem by factoring

Factoring Methods

In this mini-lesson, we will explore the world of factoring methods in math. You will get to learn about the way to factorize an expression, solving quadratic equations by factoring and other interesting facts around the topic. You can try your hand at solving a few interesting practice questions at the end of the page.

Now, look at the picture given below.

Hey! Don't start thinking which one out of these is your favorite flavor.

Think about the ingredients which are combined together to make such yummy ice-creams.

Similarly, in algebra, we mix a few expressions together to form a new expression.

You can't take out each ingredient from these ice-creams but you can factor all the terms out from the expression.

In this lesson, we will learn various factoring methods and the way to factor quadratic equations.

Lesson Plan

What is factoring.

The process of finding the factors is called factoring.

All numbers have factors.

For example, 7 and 3 are the factors of 21 .

Algebraic expressions also have factors.

For example, \(x\) and \(x-2\) are the factors of \(x^2-2x\)

Here, \(x\times 2x\) is the factored form of \(x^2-2x\).

So, factors can be numbers, algebraic expressions , or algebraic variables .

Experiment with the following simulation to see the factors of a few expressions.

Methods of Factoring

We will discuss some systematic methods of factoring algebraic expressions.

Method of Common Factors

Consider a simple example: \(3x+9\)

By factorizing each term we get, \((3\times x)+(3 \times 3)\)

By distributive law, \(3x+9=(3\times x)+(3 \times 3)=3(x+3)\).

Method of Regrouping

Regrouping allows us to rearrange the terms of the expression that leads to factorization. 

Consider an expression: \(2ab+2b+7a+7\)

Notice that there is no single factor common to all the terms.

Let us write \(2ab+2b\) and \(7a+7\) in the factor form separately.

\[\begin{align}2ab+2b&=2b(a+1)\\7a+7&=7(a+1)\end{align}\]

So, \(2ab+2b+7a+7=2b(a+1)+7(a+1)\).

Now, we have a common factor \((a+1)\) on the right-hand side.

The given expression is factorized as \(2ab+2b+7a+7=2b(a+1)+7(a+1)=(2b+7)(a+1)\).

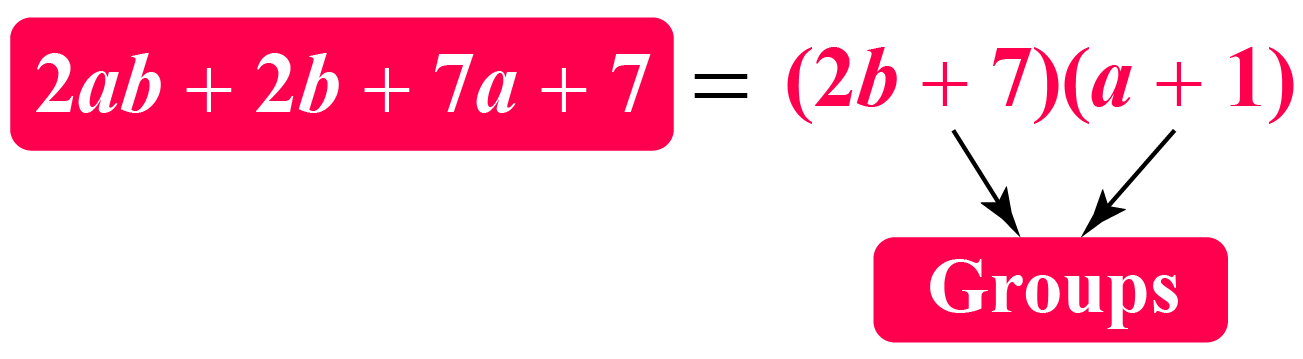
Method Using Algebraic Identities

Remember a few identities that are used for factorization.

Let's factorize \(4z^{2}-12z+9\)

Observe that \(4z^{2}=(2z)^{2}\), \(12z=2\times 3\times 2z\), and \(9=3^{2}\)

So, we can write \(4z^{2}-12z+9=(2z)^{2}-2\times 2z\times 3+3^{2}=(2z-3)^2\)

How to Factor Trinomials?

Solving Quadratic Equations By Factoring

We’ll do a few examples on solving quadratic equations by factorization.

Example 1:  \[4x-12x^2=0\]

Given any quadratic equation, first check for the common factors.

In this example, check for the common factors among \(4x\) and \(12x^2\)

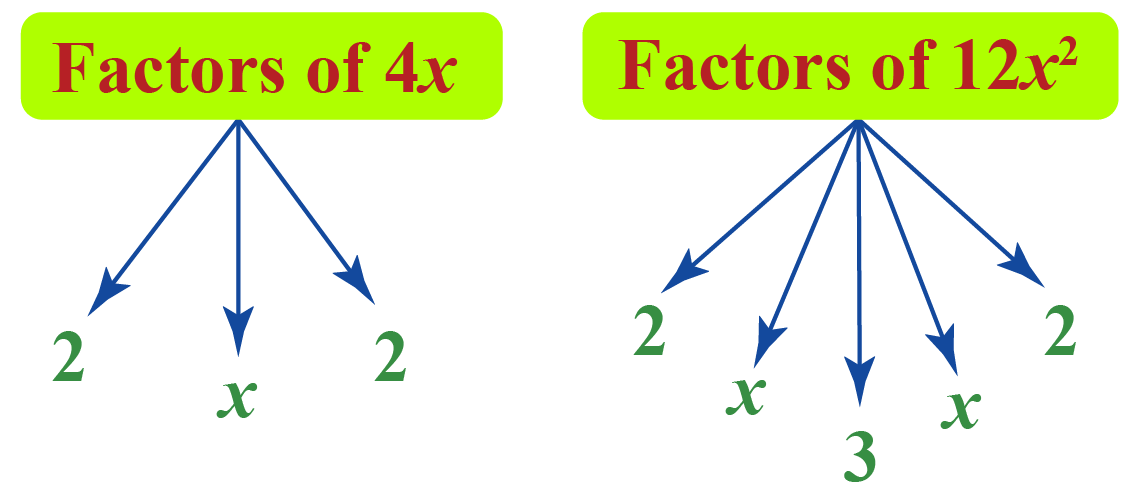
We can observe that \(4x\) is a common factor. Let’s take that common factor from the quadratic equation.

\[\begin{align}4x-12x^2&=0\\4x(1-3x)&=0\end{align}\]

Thus, by factoring the quadratic equation, we get \(4x(1-3x)=0\).

In other words, the quadratic equation can be factored as \((4x)(1-3x)=0\).

Example 2:  \[x^2+5x+6=0\]

We’ll factor this in two binomials, namely \((x+a)\) and \((x+b)\).

Expand \((x+a)(x+b)=0\).

\[\begin{align}(x+a)(x+b)&=0\\x(x+b)+a(x+b)&=0\\x^2+bx+ax+ab&=0\\x^2+(a+b)x+ab&=0\end{align}\]    

Let’s try to find \(a\) and \(b\) such that \((a+b)\) is mapped to 5 and \(ab\) is mapped to 6. 

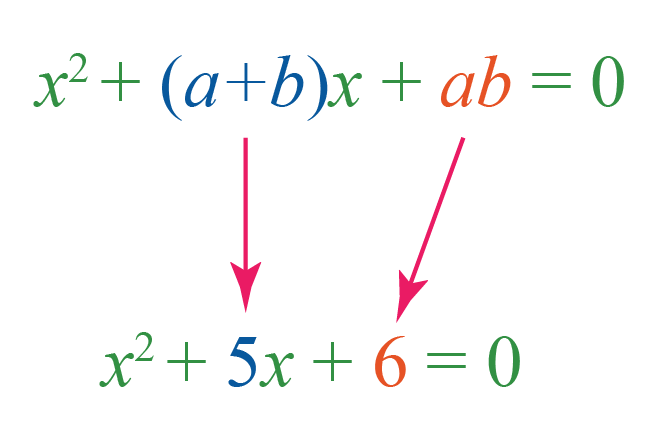
The factors of \(6\) are \(1\), \(2\), \(3\) and \(6\). Find the pairs \(a\) and \(b\) from \(1\), \(2\), \(3\) and \(6\) such that \(a+b=5\) and \(ab=6\)

This is the right pair: \(2\) and \(3\), because, \(2+3 = 5\) and \(2 \times 3=6\)

Thus, the quadratic equation can be factored as \((x+2)(x+3)=0\).

Calculator For Factoring

Here is a calculator for factoring different expressions.

Factoring helps us to find the solution of any algebraic expression.

Factoring allows us to express an expression in a simpler form.

Solved Examples

George has a huge rectangular farm.

He knows that the area of the farm is \(528\;\text{ft}^{2}\)

He says "The length of the farm is one more than twice its breadth."

Can you use this information to write the factored form of 528?

Let the breadth of the farm be \(x\) feet.

So, the length of the farm would be \(2x+1\) feet.

The area of a rectangle is the product of its length and breadth.

According to the question,

\[\begin{align}\text{Area of Farm}&=\text{Breadth} \times \text{Length}\\528&=x\times (2x+1)\end{align}\]

Jenny asked Jolly to factorize \(6xy-4y+6-9x\)

Jolly wants to factorize it using the method of regrouping.

Can you help them?

We observe that we have no common factor among all the terms in the expression \(6xy-4y+6-9x\)

Let's deal with \(6xy-4y\) and \(6-9x\) separately.

\[\begin{align}6xy-4y&=2y(3x-2)\\6-9x&=-3(3x-2)\end{align}\]

So, the given expression can be written as 

\[\begin{align}6xy-4y+6-9x&=2y(3x-2)-3(3x-2)\\&=(2y-3)(3x-2)\end{align}\]

Mia is a fitness enthusiast who runs every morning.

The park where she jogs is rectangular in shape and measures 12 feet by 8 feet.

An environmentalist group plans to revamp the park and decides to build a pathway surrounding the park.

This would increase the total area to 140 sq. ft.

What will be the width of the pathway?

Let’s denote the width of the pathway as \(x\).

Then, the length and breadth of the outer rectangle is \((12+2x)\;\text{ft.}\) and \((8+2x)\;\text{ft.}\)

According to the question, \[\begin{align}(12+2x)(8+2x)&=140\\2(6+x)\cdot 2(4+x)&=140\\(x+6)(x+4)&=35\\x^2+10x-11&=0\end{align}\]

So, we have to find the solution of the quadratic equation \(x^2+10x-11=0\)

\[\begin{align}x^2+11x-x-11&=0\\x(x+11)-(x+11)&=0\\(x+11)(x-1)&=0\\x&=1,-11\end{align}\]

Since the length can’t be negative, we take \(x=1\)

Sometimes working with a hard expression is difficult. But don’t worry! 

Here are a few tips and tricks for you to follow while factoring.

• Check out for any common terms in an expression and take the greatest common factor .
• Check if any algebraic identities are applicable in the expression.
• Keep factoring the expression until you reach the simplest form, that is, the form that is not further divisible.

Interactive Questions

Here are a few activities for you to practice.

Select/type your answer and click the "Check Answer" button to see the result.

Let's Summarize

The mini-lesson targeted the fascinating concept of factoring methods. The math journey around factoring methods starts with what a student already knows, and goes on to creatively crafting a fresh concept in the young minds. Done in a way that not only it is relatable and easy to grasp, but also will stay with them forever. Here lies the magic with Cuemath.

About Cuemath

At  Cuemath , our team of math experts is dedicated to making learning fun for our favorite readers, the students!

Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.

Be it worksheets, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we, at Cuemath, believe in.

Frequently Asked Questions (FAQs)

1. how to factor trinomials with a leading coefficient.

The following steps show how to factor trinomials with a leading coefficient.

• Write the trinomial in the standard form.
• Take the greatest common factor out if it exists.
• Find the product of the leading coefficient and the constant term.
• Determine the factors of the product found in step 3 and check which factor pair will result in the coefficient of \(x\).
• After choosing the appropriate factor pair, keep the sign in each number such that while operating them we get the result as the coefficient of \(x\) and on finding their product the number is equal to the number found in step 3.
• Now, you have 4 terms in the expression and so we use the method of regrouping to factorize.

2. How to factor perfect square trinomials?

Use the algebraic identities mentioned below to factor perfect square trinomials.

• \((a+b)^2=a^2+b^2+2ab\)
• \((a-b)^2=a^2+b^2-2ab\)

Factoring in Algebra

Numbers have factors :

And expressions (like x 2 +4x+3 ) also have factors:

Factoring (called " Factorising " in the UK) is the process of finding the factors :

Factoring: Finding what to multiply together to get an expression.

It is like "splitting" an expression into a multiplication of simpler expressions.

Example: factor 2y+6

Both 2y and 6 have a common factor of 2:

So we can factor the whole expression into:

2y+6 = 2(y+3)

So 2y+6 has been "factored into" 2 and y+3

Factoring is also the opposite of Expanding :

Common Factor

In the previous example we saw that 2y and 6 had a common factor of 2

But to do the job properly we need the highest common factor , including any variables

Example: factor 3y 2 +12y

Firstly, 3 and 12 have a common factor of 3 .

So we could have:

3y 2 +12y = 3(y 2 +4y)

But we can do better!

3y 2 and 12y also share the variable y .

Together that makes 3y :

• 3y 2 is 3y × y
• 12y is 3y × 4

3y 2 +12y = 3y(y+4)

Check: 3y(y+4) = 3y × y + 3y × 4 = 3y 2 +12y

More Complicated Factoring

Factoring can be hard .

The examples have been simple so far, but factoring can be very tricky.

Because we have to figure what got multiplied to produce the expression we are given!

Experience Helps

With more experience factoring becomes easier.

Example: Factor 4x 2 − 9

Hmmm... there don't seem to be any common factors.

But knowing the Special Binomial Products gives us a clue called the "difference of squares" :

Because 4x 2 is (2x) 2 , and 9 is (3) 2 ,

So we have:

4x 2 − 9 = (2x) 2 − (3) 2

And that can be produced by the difference of squares formula:

(a+b)(a−b) = a 2 − b 2

Where a is 2x, and b is 3.

So let us try doing that:

(2x+3)(2x−3) = (2x) 2 − (3) 2 = 4x 2 − 9

So the factors of 4x 2 − 9 are (2x+3) and (2x−3) :

Answer: 4x 2 − 9 = (2x+3)(2x−3)

How can you learn to do that? By getting lots of practice, and knowing "Identities"!

Remember these Identities

Here is a list of common "Identities" (including the "difference of squares" used above).

It is worth remembering these, as they can make factoring easier.

There are many more like those, but those are the most useful ones.

The factored form is usually best.

When trying to factor, follow these steps:

• "Factor out" any common terms
• See if it fits any of the identities, plus any more you may know
• Keep going till you can't factor any more

There are also Computer Algebra Systems (called "CAS") such as Axiom, Derive, Macsyma, Maple, Mathematica, MuPAD, Reduce and others that can do factoring.

More Examples

Experience does help, so here are more examples to help you on the way:

Example: w 4 − 16

An exponent of 4? Maybe we could try an exponent of 2:

w 4 − 16 = (w 2 ) 2 − 4 2

Yes, it is the difference of squares

w 4 − 16 = (w 2 + 4)(w 2 − 4)

And "(w 2 − 4)" is another difference of squares

w 4 − 16 = (w 2 + 4)(w+ 2)(w− 2)

That is as far as I can go (unless I use imaginary numbers)

Example: 3u 4 − 24uv 3

Remove common factor "3u":

3u 4 − 24uv 3 = 3u(u 3 − 8v 3 )

Then a difference of cubes:

3u 4 − 24uv 3 = 3u(u 3 − (2v) 3 )

= 3u(u−2v)(u 2 +2uv+4v 2 )

That is as far as I can go.

Example: z 3 − z 2 − 9z + 9

Try factoring the first two and second two separately:

z 2 (z−1) − 9(z−1)

Wow, (z-1) is on both, so let us use that:

(z 2 −9)(z−1)

And z 2 −9 is a difference of squares

(z−3)(z+3)(z−1)

Now get some more experience:

Factoring by Common Factors & by Grouping

In these lessons, we will look at factoring by common factors and factoring of polynomials by grouping.

Related Pages More Factoring and Algebra Lessons Algebra Worksheets Algebra Games

The following diagram shows the steps to factor a polynomial with four terms using grouping. Scroll down the page for examples and solutions.

The following diagram shows the steps to factor a trinomial using grouping. Scroll down the page for examples and solutions.

Factoring By Common Factors

The first step in factorizing is to find and extract the GCF of all the terms.

Example: Factorize the following algebraic expressions: a) xyz – x 2 z b) 6a 2 b + 4bc

Solution: a) xyz – x 2 z = xz(y – x) b) 6a 2 b + 4bc = 2b(3a 2 + 2c)

Factoring Out The Greatest Common Factor Factoring is a technique that is useful when trying to solve polynomial equations algebraically. We begin by looking for the Greatest Common Factor (GCF) of a polynomial expression. The GCF is the largest monomial that divides (is a factor of) each term of of the polynomial. The following video shows an example of simple factoring or factoring by common factors. To find the GCF of a Polynomial

• Write each term in prime factored form
• Identify the factors common in all terms
• Factor out the GCF

Examples: Factor out the GCF

• 2x 4 - 16x 3
• 4x 2 y 3 + 20xy 2 + 12xy
• -2x 3 + 8x 2 - 4x
• -y 3 - 2y 2 + y - 7

Factoring Using the Great Common Factor, GCF - Example 1 Two examples of factoring out the greatest common factor to rewrite a polynomial expression.

Example: Factor out the GCF: a) 2x 3 y 8 + 6x 4 y 2 + 10x 5 y 10 b) 6a 10 b 8 + 3a 7 b 4 - 24a 5 b 6

Factoring Using the Great Common Factor, GCF - Example 2

Example: Factor out binomial expressions. a) 3x 2 (2x + 5y) + 7y 2 (2x + 5y) b) 5x 2 (x + 3y) - 15x 3 (x + 3y)

Factoring Polynomials with Common Factors This video provides examples of how to factor polynomials that require factoring out the GCF as the first step. Then other methods are used to completely factor the polynomial.

Example: Factor 4x 2 - 64 3x 2 + 3x - 36 2x 2 - 28x + 98

Factoring By Grouping

When an expression has an even number of terms and there are no common factors for all the terms, we may group the terms into pairs and find the common factor for each pair:

Example: Factorize the following expressions:

a) ax + ay + bx + by b) 2x + 8y – 3px –12py c) 3x – 3y + 4ay – 4ax

Solution: a) ax + ay + bx + by = a(x + y) + b(x + y) = (a + b)(x + y)

b) 2x + 8y – 3px –12py = 2(x + 4y) –3p(x + 4y) = (2 – 3p)(x + 4y)

c) 3x – 3y + 4ay – 4ax = 3(x – y) + 4a(y – x) = 3(x – y) – 4a(x – y) = (3 – 4a)( x – y)

How to Factor by Grouping? 3 complete examples of solving quadratic equations using factoring by grouping are shown.

• Factor x(x + 1) - 5(x + 1)
• Solve 2x 2 + 5x + 2 = 0
• Solve 7x 2 + 16x + 4 = 0
• Solve 6x 2 - 17x + 12 = 0

Factoring by Grouping - Ex 1

Example: Factor: a) 2x 2 + 7x 2 + 2x + 7 b) 10x 2 + 2xy + 15xy + 3y 2

Factoring By Grouping - Ex 2

Example: Factor: 12u 2 + 15uv + 24uv 2 + 30v 3

Factoring Trinomials: Factor by Grouping - ex 1

Example: Factor 12x 2 + 34x + 10

Factoring Trinomials: Factor by Grouping - ex 2

Example: Factor 6x 2 + 15x - 21

Factoring by grouping - Prime Factorization

Example: 12a 3 - 9a 2 b - 8ab 2 + 6b 3

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.1: Quadratic Equations and Solving by Factoring

• Last updated
• Save as PDF
• Page ID 142781

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Solve quadratic equations by using the Zero Product Property
• Solve quadratic equations factoring
• Solve applications modeled by quadratic equations

Before you get started, take this readiness quiz.

• Solve: \(5y−3=0\). If you missed this problem, review Example 2.3.1 .
• Solve: \(10a=0\). If you missed this problem, review Example 2.2.1 .
• Combine like terms: \(12 x^{2}-6 x+4 x\). If you missed this problem, review Example 1.3.37 .
• Factor \(n^{3}-9 n^{2}-22 n\) completely. If you missed this problem, review Example 7.3.10 .

We have already solved linear equations, equations of the form \(a x+b y=c\). In linear equations, the variables have no exponents. Quadratic equations are equations in which the variable is squared. Listed below are some examples of quadratic equations:

\[x^{2}+5 x+6=0 \quad 3 y^{2}+4 y=10 \quad 64 u^{2}-81=0 \quad n(n+1)=42\]

The last equation doesn’t appear to have the variable squared, but when we simplify the expression on the left we will get \(n^{2}+n\).

The general form of a quadratic equation is \(a x^{2}+b x+c=0\),with \(a \neq 0\).

QUADRATIC EQUATION

An equation of the form \(a x^{2}+b x+c=0\) is called a quadratic equation.

\[a, b, \text { and } c \text { are real numbers and } a \neq 0\]

To solve quadratic equations we need methods different than the ones we used in solving linear equations. We will look at one method here and then several others in a later chapter.

Solve Quadratic Equations Using the Zero Product Property

We will first solve some quadratic equations by using the Zero Product Property. The Zero Product Property says that if the product of two quantities is zero, it must be that at least one of the quantities is zero. The only way to get a product equal to zero is to multiply by zero itself.

ZERO PRODUCT PROPERTY

\(\text { If } a \cdot b=0, \text { then either } a=0 \text { or } b=0 \text { or both. }\)

We will now use the Zero Product Property , to solve a quadratic equation.

Example \(\PageIndex{1}\): How to Use the Zero Product Property to Solve a Quadratic Equation

Solve: \((x+1)(x-4)=0\)

Try It \(\PageIndex{2}\)

Solve: \((x-3)(x+5)=0\)

\(x=3, x=-5\)

Try It \(\PageIndex{3}\)

Solve: \((y-6)(y+9)=0\)

\(y=6, y=-9\)

We usually will do a little more work than we did in this last example to solve the linear equations that result from using the Zero Product Property.

Example \(\PageIndex{4}\)

Solve: \((5 n-2)(6 n-1)=0\)

Try It \(\PageIndex{5}\)

Solve: \((3 m-2)(2 m+1)=0\)

\(m=\frac{2}{3}, m=-\frac{1}{2}\)

Try It \(\PageIndex{6}\)

Solve: \((4 p+3)(4 p-3)=0\)

\(p=-\frac{3}{4}, p=\frac{3}{4}\)

Notice when we checked the solutions that each of them made just one factor equal to zero. But the product was zero for both solutions.

Example \(\PageIndex{7}\)

Solve: \(3 p(10 p+7)=0\)

Try It \(\PageIndex{8}\)

Solve: \(2 u(5 u-1)=0\)

\(u=0, u=\frac{1}{5}\)

Try It \(\PageIndex{9}\)

Solve: \(w(2 w+3)=0\)

\(w=0, w=-\frac{3}{2}\)

It may appear that there is only one factor in the next example. Remember, however, that \((y-8)^{2}\) means \((y-8)(y-8)\).

Example \(\PageIndex{10}\)

Solve: \((y-8)^{2}=0\)

Try It \(\PageIndex{11}\)

Solve: \((x+1)^{2}=0\)

Try It \(\PageIndex{12}\)

Solve: \((v-2)^{2}=0\)

Solve Quadratic Equations by Factoring

Each of the equations we have solved in this section so far had one side in factored form. In order to use the Zero Product Property, the quadratic equation must be factored, with zero on one side. So we be sure to start with the quadratic equation in standard form, \(a x^{2}+b x+c=0\). Then we factor the expression on the left.

Example \(\PageIndex{13}\)

Solve: \(x^{2}+2 x-8=0\)

Try It \(\PageIndex{14}\)

Solve: \(x^{2}-x-12=0\)

\(x=4, x=-3\)

Try It \(\PageIndex{15}\)

Solve: \(b^{2}+9 b+14=0\)

\(b=-2, b=-7\)

SOLVE A QUADRATIC EQUATION BY FACTORING.

• Write the quadratic equation in standard form, \(a x^{2}+b x+c=0\).
• Factor the quadratic expression.
• Use the Zero Product Property.
• Solve the linear equations.

Before we factor, we must make sure the quadratic equation is in standard form.

Example \(\PageIndex{16}\)

Solve: \(2 y^{2}=13 y+45\)

Try It \(\PageIndex{17}\)

Solve: \(3 c^{2}=10 c-8\)

\(c=0, c=\frac{4}{3}\)

Try It \(\PageIndex{18}\)

Solve: \(2 d^{2}-5 d=3\)

\(d=3, d=-\frac{1}{2}\)

Example \(\PageIndex{19}\)

Solve: \(5 x^{2}-13 x=7 x\)

Try It \(\PageIndex{20}\)

Solve: \(6 a^{2}+9 a=3 a\)

\(a=0, a=-1\)

Try It \(\PageIndex{21}\)

Solve: \(45 b^{2}-2 b=-17 b\)

\(b=0, b=-\frac{1}{3}\)

Solving quadratic equations by factoring will make use of all the factoring techniques you have learned in this chapter! Do you recognize the special product pattern in the next example?

Example \(\PageIndex{22}\)

Solve: \(144 q^{2}=25\)

\(\begin{array}{lrllrl} & 144 q^{2}&=&25 \\ \text { Write the quadratic equation in standard form. }& 144 q^{2}-25&=& 0 \\ \text { Factor. It is a difference of squares. } & (12 q-5)(12 q+5) & = & 0 \\ \text { Use the Zero Product Property to set each factor to } 0 . & 12 q-5&=&0 & 12 q+5&=&0 \\\text { Solve each equation. } & 12 q & = & 5 & 12 q&=&-5 \\ & q&=&\frac{5}{12} & q & =&-\frac{5}{12} \\ \text { Check your answers. }\end{array}\)

Try It \(\PageIndex{23}\)

Solve: \(25 p^{2}=49\)

\(p=\frac{7}{5}, p=-\frac{7}{5}\)

Try It \(\PageIndex{24}\)

Solve: \(36 x^{2}=121\)

\(x=\frac{11}{6}, x=-\frac{11}{6}\)

The left side in the next example is factored, but the right side is not zero. In order to use the Zero Product Property, one side of the equation must be zero. We’ll multiply the factors and then write the equation in standard form.

Example \(\PageIndex{25}\)

Solve: \((3 x-8)(x-1)=3 x\)

\(\begin{array}{ll} & (3 x-8)(x-1)=3 x \\ \text { Multiply the binomials. }& 3 x^{2}-11 x+8=3 x \\ \text { Write the quadratic equation in standard form. }& 3 x^{2}-14 x+8=0\\ \text { Factor the trinomial. }& (3 x-2)(x-4)=0\\\text { Use the Zero Product Property to set each factor to } 0 . & 3 x-2=0 \quad x-4=0 \\ \text { Solve each equation. } & 3 x=2 \quad x=4 \\ & x=\frac{2}{3} \\ \text { Check your answers. } & \text {The check is left to you! } \end{array}\)

Try It \(\PageIndex{26}\)

Solve: \((2 m+1)(m+3)=12 m\)

\(m=1, m=\frac{3}{2}\)

Try It \(\PageIndex{27}\)

Solve: \((k+1)(k-1)=8\)

\(k=3, k=-3\)

The Zero Product Property also applies to the product of three or more factors. If the product is zero, at least one of the factors must be zero. We can solve some equations of degree more than two by using the Zero Product Property, just like we solved quadratic equations.

Example \(\PageIndex{28}\)

Solve: \(9 m^{3}+100 m=60 m^{2}\)

\(\begin{array}{lrllrl} & 9 m^{3}+100 m&=&60 m^{2}\\ \text { Bring all the terms to one side so that the other side is zero. } & 9 m^{3}-60 m^{2}+100 m&=&0 \\ \text { Factor the greatest common factor first. } & m\left(9 m^{2}-60 m+100\right)&=&0 \\ \text { Factor the trinomial. } & m(3 m-10)(3 m-10)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & m&=&0 & 3 m-10&=&0 & 3 m-10&=&0 \\ \text { Solve each equation. } & m&=&0 & m&=&\frac{10}{3}& m&=&\frac{10}{3} \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)

Try It \(\PageIndex{29}\)

Solve: \(8 x^{3}=24 x^{2}-18 x\)

\(x=0, x=\frac{3}{2}\)

Try It \(\PageIndex{30}\)

Solve: \(16 y^{2}=32 y^{3}+2 y\)

\(y=0, y=\frac{1}{4}\)

When we factor the quadratic equation in the next example we will get three factors. However the first factor is a constant. We know that factor cannot equal 0.

Example \(\PageIndex{31}\)

Solve: \(4 x^{2}=16 x+84\)

\(\begin{array}{lrllrl} & 4 x^{2}&=&16 x+84\\ \text { Write the quadratic equation in standard form. }& 4 x^{2}-16 x-84&=&0 \\ \text { Factor the greatest common factor first. }& 4\left(x^{2}-4 x-21\right)&=&0 \\ \text { Factor the trinomial. } & 4(x-7)(x+3)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & 4&\neq&0 & x-7&=&0 & x +3&=&0 \\ \text { Solve each equation. } & 4&\neq&0 & x&=&7& x&=&-3 \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)

Try It \(\PageIndex{32}\)

Solve: \(18 a^{2}-30=-33 a\)

\(a=-\frac{5}{2}, a=\frac{2}{3}\)

Try It \(\PageIndex{33}\)

Solve: \(123 b=-6-60 b^{2}\)

\(b=2, b=\frac{1}{20}\)

Solve Applications Modeled by Quadratic Equations

The problem solving strategy we used earlier for applications that translate to linear equations will work just as well for applications that translate to quadratic equations. We will copy the problem solving strategy here so we can use it for reference.

USE A PROBLEM-SOLVING STRATEGY TO SOLVE WORD PROBLEMS

• Read the problem. Make sure all the words and ideas are understood.
• Identify what we are looking for.
• Name what we are looking for. Choose a variable to represent that quantity.
• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
• Solve the equation using good algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

We will start with a number problem to get practice translating words into a quadratic equation.

Example \(\PageIndex{34}\)

The product of two consecutive integers is \(132 .\) Find the integers.

\(\begin{array}{ll} \textbf { Step 1. Read} \text { the problem. } \\ \textbf { Step 2. Identify} \text { what we are looking for. } & \text { We are looking for two consecutive integers. } \\ \textbf { Step 3. Name} \text{ what we are looking for. } & \begin{array}{l}{\text { Let } n=\text { the first integer }} \\ {\space n+1=\text { the next consecutive integer }}\end{array} \\\textbf { Step 4. Translate} \text { into an equation. Restate the } & \text { The product of the two consecutive integers is } 132 . \\ \text { problem in a sentence. } \\ \text { Translate to an equation. } & \begin{array}{c}{\text { The first integer times the next integer is } 132 .} \\ {n(n+1)=132}\end{array} \\ \textbf { Step 5. Solve}\text { the equation. } & n^{2}+n=132 \\ \text { Bring all the terms to one side. } & n^{2}+n-132=0 \\ \text { Factor the trinomial. } & (n-11)(n+12)=0 \\ \text { Use the zero product property. } & n-11=0 \quad n+12=0 \\ \text { Solve the equations. } & n=11 \quad n=-12 \end{array}\)

Try It \(\PageIndex{35}\)

The product of two consecutive integers is \(240 .\) Find the integers.

\(-15,-16\) and \(15,16\)

Try It \(\PageIndex{36}\)

The product of two consecutive integers is \(420 .\) Find the integers.

\(-21,-20\) and \(20,21\)

Were you surprised by the pair of negative integers that is one of the solutions to the previous example? The product of the two positive integers and the product of the two negative integers both give 132.

In some applications, negative solutions will result from the algebra, but will not be realistic for the situation.

Example \(\PageIndex{37}\)

A rectangular garden has an area of 15 square feet. The length of the garden is two feet more than the width. Find the length and width of the garden.

Try It \(\PageIndex{38}\)

A rectangular sign has an area of 30 square feet. The length of the sign is one foot more than the width. Find the length and width of the sign.

55 feet and 66 feet

Try It \(\PageIndex{39}\)

A rectangular patio has an area of 180 square feet. The width of the patio is three feet less than the length. Find the length and width of the patio.

12 feet and 15 feet

In an earlier chapter, we used the Pythagorean Theorem \(\left(a^{2}+b^{2}=c^{2}\right)\). It gave the relation between the legs and the hypotenuse of a right triangle.

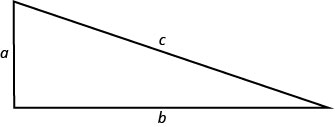
We will use this formula to in the next example.

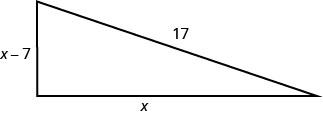
Example \(\PageIndex{40}\)

Justine wants to put a deck in the corner of her backyard in the shape of a right triangle, as shown below. The hypotenuse will be 17 feet long. The length of one side will be 7 feet less than the length of the other side. Find the lengths of the sides of the deck.

Try It \(\PageIndex{41}\)

A boat’s sail is a right triangle. The length of one side of the sail is 7 feet more than the other side. The hypotenuse is 13. Find the lengths of the two sides of the sail.

5 feet and 12 feet

Try It \(\PageIndex{42}\)

A meditation garden is in the shape of a right triangle, with one leg 7 feet. The length of the hypotenuse is one more than the length of one of the other legs. Find the lengths of the hypotenuse and the other leg.

24 feet and 25 feet

Key Concepts

• Zero Product Property If \(a \cdot b=0\), then either a=0 or b=0 or both. See Example .

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Solving & Factoring Polynomials: Examples

Solving Factoring Examples

These exercises can be very long, so I've only shown three examples so far. Here are a few more, for practice:

Find the real-number solutions to x 6 + 9 x 5 + 11 x 4 − 22 x 3 − 9 x 2 − 11 x + 21 = 0 .

They've given me an equation, and have asked for the solutions to that equation. So I'll be finding x -values, rather than factors.

First, I'll try the trick with 1 and −1 . Trying x  = 1 , I get:

1 + 9 + 11 − 22 − 9 − 11 + 21 = 0

Content Continues Below

MathHelp.com

Excellent! So x  = 1 is one of the zeroes. Trying x  = −1 , I get:

1 − 9 + 11 + 22 − 9 + 11 + 21 = 48

Okay; so that one isn't a zero. But, to reduce my polynomial by the one factor corresponding to this zero, I'll do my first synthetic division:

So my reduced polynomial is equation is:

x 5 + 10 x 4 + 21 x 3 − x 2 − 10 x − 21 = 0

This is so nasty... I'm gonna try the trick with x  = 1 again, just in case it's a root twice:

1 + 10 + 21 − 1 − 10 − 21 = 0

Nice! Okay; here's my second synthetic division:

Alright. My new polynomial equation now is:

x 4 + 11 x 3 + 32 x 2 + 31 x + 21 = 0

All the coefficients are positive, so +1 cannot be a zero again. Now it's time for the Rational Roots Test:

x = ±1, 3, 7, 21

Hm... I've already scratched off ±1 directly. Because all the coefficients are positive, then I know that +3, +7, and +21 are out, too. I'd rather stay small, if I can, so I'll try −3 next:

So now my polynonial equation is:

x 3 + 8 x 2 + 8 x + 7 = 0

From this reduced polynomial, I can see that I can cross −21 and −3 off the list of possible roots; they clearly won't work in this reduced polynomial. So I guess I'm left with −7 :

And now I'm down to a quadratic, which I can easily solve:

x 2 + x + 1 = 0

x = (−1 ± sqrt[−3])/2

Because there's a minus inside the radical, I know that the solutions of this quadratic are complex numbers; it has no real zeroes. Since they asked for just the real-valued roots of the original polynomial, then I can ignore these last two zeroes. Then my answer is:

x = 1, −3, −7

I didn't check the graph when I did the above, but it does confirm my answer:

The intercepts at x  = −7 and at x  = −3 are clear. The intercept at x  = 1 is clearly repeated, because of how the curve bounces off the x -axis at this point, and goes back the way it came.

Note: This polynomial's graph is so steep in places that it sometimes disappeared in my graphing software. I had to fiddle with the axis values and window size to get the whole curve to show up. When using your calculator, don't stick only with the default screen for graphs; play with the axis values until you get a picture that's useful.

Factor completely: 2 x 5 − 3 x 4 − 9 x 3 + 3 x 2 − 11 x + 6

They've given me an expression rather than an equation, and have told me to factor. So I'll be finding factors rather than x -values, and I'll need to keep track of everything I pull out, from beginning to end.

There is no factor common to all terms, so there is nothing to pull out yet. I'll check for zeroes of the associated polynomial equation (setting the original expression equal to zero), and see what I can find. Then I'll convert the zeroes to factors, and pull them out.

First, I'll try the usual shortcut with ±1 ; the positive first:

2 − 3 − 9 + 3 − 11 + 6 = −12

No joy. I'll try the negative now:

−2 − 3 + 9 + 3 + 11 + 6 = 90

That's even worse. Okay, now I'll use the Rational Roots Test to create a list of maybe-solution values:

±(1, 2, 3, 6)/(1, 2)

= ±1/2, 1, 3/2, 2, 3, 6

I already know that I can ignore ±1 . Descartes' Rule of Signs tells me that there will be four, two, or zero positive roots; and one (definite) negative root. So I'll start with the negative integers:

Okay; I've found that x  = −2 is a root, which means that x  + 2 is a factor. Also, I've reduced the expression still needing to be factored to:

2 x 4 − 7 x 3 + 5 x 2 − 7 x + 3

The constant term is 3 , so I know that ±2 cannot be a solution to what's left, nor can ±6 . Also, I've already found the one negative zero. So this leaves me with:

1/2, 3/2, 3

I'm trying to avoid fractions, so I'll try the last integer possibility:

The last row above is a four-term polynomial that looks like it can be factored in pairs:

(2 x 3 − x 2 ) + (2 x − 1)

x 2 (2 x − 1) + 1(2 x − 1)

(2 x − 1)( x 2 + 1)

The quadratic factor is the sum of squares, so it isn't factorable. This means I'm done, and my complete factorization is:

( x  + 2)​( x  − 3)​(2 x  − 1)​( x 2  + 1)

The method for answering the two exercises above is the method that I learned, back in the olden times when dinosaurs ruled the world and calculators were made with bear skins and stone knives. It's probably at least similar to the method that you've seen in your book, and your instructor likely expects you do show work along the lines of what I did above.

However, if you have a graphing calculator (and nearly everybody does, nowadays), you can avoid wasting quite so much time on maybe-solution values that turn out not to work.

Find all zeroes of y = 8 x 5 − 58 x 4 + 137 x 3 − 118 x 2 + 33 x + 18

Before doing anything else, I'll do a quick graph:

Looking at the graph, I know to check x  = 3 twice:

The original polynomial was degree-five. I've found one zero of multiplicity two, which leaves at most three more zeroes. Looking at the polynomial represented by the last row above, the Rational Roots Test says that any remaining "nice" zeroes will be among these:

±(1, 2)/(1, 2, 4, 8)

= ±1/8, 1/4, 1/2, 1, 2

Now I can see that there's a common factor of four that can be divided out and discarded, leaving me with:

2 x 2 − 3 x + 2 = 0

x = (−(−3) ± sqrt[(−3) 2 − 4(2)(2)])/(2(2))

= (3 ± sqrt[9 − 16])/4

= (3 ± sqrt[−7])/4

They asked me for all of the zeroes, not just all of the real-valued ones, so I have to include these two roots that don't show up on the graph. However, by checking the graph first, I was able to save a lot of time in arriving at my answer:

x = −(1/4), 3, (3 ± sqrt[−7])/4

Advertisement

There is a variant of these exercises, where they provide one or more factors (of an expression) or zeroes (of an equation or function), and they want you to find the rest of them. I've got examples of how this works in the last page of the lesson on synthetic division. Varient exercises are often a bit messier and, to answer them, you're expected to have a deeper understanding of how the Quadratic Formula generates solutions in pairs, because of the " ± ". Otherwise, they work in pretty much the same way.

URL: https://www.purplemath.com/modules/solvpoly3.htm

Page 1 Page 2 Page 3

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

Factoring to Solve Problems

Let's get started.

TEKS Standards and Student Expectations

A(10)  Number and algebraic methods. The student applies the mathematical process standards and algebraic methods to rewrite in equivalent forms and perform operations on polynomial expressions. The student is expected to:

A(10)(E) factor, if possible, trinomials with real factors in the form a x 2 + b x + c including perfect square trinomials of degree two

A(10)(F)  decide if a binomial can be written as the difference of two squares and if possible, use the structure of a difference of two squares to rewrite the binomial

A(10)(D) rewrite polynomial expressions of degree one and degree two in equivalent forms using the distributive property

A(8)  Quadratic functions and equations. The student applies the mathematical process standards to solve, with and without technology, quadratic equations and evaluate the reasonableness of their solutions. The student formulates statistical relationships and evaluates their reasonableness based on real-world data. The student is expected to:

A(8)(A) solve quadratic equations having real solutions by factoring, taking square roots, completing the square, and applying the quadratic formula

Resource Objective(s)

The student will use a variety of methods to solve problems by factoring, including models, guess and check, grouping, and special cases.

Essential Questions

What is the process for factoring a trinomial with a leading coefficient of 1?

What is the process for factoring a trinomial when the leading coefficient is not 1?

How can you determine if the rules for difference of two squares, difference of two cubes, or perfect squares  can be used to factor?

When does the grouping method for factoring apply?

• GCF (Greatest Common Factor)
• Leading Coefficient
• Quadratic Equation

Introduction: Factoring by Modeling

One way to find the factors of a value is to use models to create a rectangle. The length and width represent the factors.

Example 1 : Factors of 12 can be shown three different ways. 

12 has a total of 6 different factors: 1, 2, 3, 4, 6, and 12.

Example 2:  Algebraic expressions can also be factored using algebra tiles to create rectangles. In the example below, 2 x + 4 is used to create a rectangle. 

As you can see, the length and width of the rectangle represent the factors of 2 x + 4. The length is ( x + 2) and the width is 2. 

The factors of 2 x + 4 are 2 and ( x + 2).

Example 3:  Trinomials can also be factored using algebra tiles. The trinomial x 2 + x - 6 can be modeled by the following rectangle.

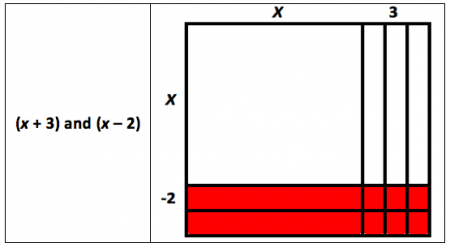
The side lengths of the rectangle show the factors of x 2  + x - 6  are ( x + 3) and ( x - 2) .

When you are ready, complete the two practice examples below to check your understanding.

Factoring Rule 1: Greatest Common Factor (GCF)

Always check to see if you can factor something out!

The first rule to factoring is to find the greatest common factor (GCF) of each term in the polynomial .

• If there is any factor in common in the polynomial, divide each term by that factor.
• Then, rewrite the polynomial using the distributive property with the common factor on the outside of the parenthesis.

2 x 3 -   2 x 2 - 12 x

All terms in the example have a coefficient that is divisible by 2. Each term also has an x . Therefore, the GCF is 2 x .

When 2 x  is factored out and the distributive property is applied the result is 

2 x ( x 2 -   x   -   6 ) .

Check your understanding with the two practice examples  below.

Factoring Rule 2: Special Products

If you are given a binomial to factor, the first special product to check for is the difference of two squares.

Difference of Two Squares:

  a 2 - b 2 =   ( a   -   b ) ( a   +   b ) .

If both terms are separated by a subtraction symbol and they are both perfect squares, the square roots can be used to write the factors.

Example 1: Factor  4 x 2 - 9 y 2 :

• The terms are separated by a subtraction symbol.
• Both terms are perfect squares.

    ( 2 x ) 2   a n d   ( 3 y ) 2

According to the rule for the difference of two squares, the factors will be  ( 2 x - 3 y ) ( 2 x + 3 y ) .

If you are given a trinomial to factor, the first special product to check for is a perfect square trinomial.

Perfect Square Trinomials:

a 2 + 2 a b + b 2   =   ( a + b ) 2   o r   a 2 - 2 a b + b 2   =   ( a - b ) 2

If the first term is a square, the last term is a square, and the middle term is two times the square root of the first and the last term, then it is a perfect square. There are two forms: one with a positive middle term and one with a negative middle term.

Example 2: Factor  x 2 + 6 x + 9

Notice the first and last terms are both perfect squares. When you multiply the square roots of x  and 3 times 2, you get 6 x   which is the middle term. According to the rule, t he factors are 

( x + 3 ) ( x + 3 )   o r   ( x + 3 ) 2

Example 3: Factor  4 x 2 - 20 x + 25

Notice the first and last terms are both perfect squares. When you multiply the square roots of 2 x and 5 times -2, you get -20 x which is the middle term. According to the rule, the factors are 

( 2 x - 5 ) ( 2 x - 5 )   o r   ( 2 x - 5 ) 2

Check your understanding by completing the practice example below. Determine which polynomials can be factored with a special product rule. Match each polynomial with the type of special product (first blank) and its factors (second blank).

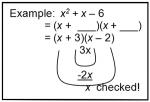
Factoring Rule 3: Trinomials with a Leading Coefficient of 1

After checking for a GCF and Special Products, look for polynomials with three terms that have a leading coefficient of 1. If the leading coefficient is 1, put x 's as the first term in each set of parentheses. Then you factor the last term and find the two factors that add or subtract to make the middle term.

Use the practice example to complete the activity below.

Factoring Rule 4: Other Trinomials

If the leading coefficient is not 1, you factor both the first and last terms and find the two products that add or subtract to make the middle term. Check your answer by using the smiley face check.

Factoring Rule 5: Four or More Terms

If there are four or more terms, you need to group them together, and then factor each part.

You can do this two ways—either by using the box method or parentheses.

Box Method: 

• Put all four terms in a two by two box.
• Look for the GCF in each column and row.
• Include signs for each of the factors.
• The result will be two factors: one on the length and the other on the width.

Parentheses Method: 

• Put parentheses around the first two terms and another set around the last two terms.
• Find the GCF of each set of parentheses. 
• Once the GCF is factored out, the terms inside each set of parentheses should match. 
• The factors will be the terms inside the parentheses (from step 3) and the GCF outside each set of parentheses (in step 2). 

Check your understanding by factoring the following polynomial (using either method) and answer the questions below. 

Solving Problems by Factoring

Some problems may ask for the solution of a quadratic equation . To solve these problems, set the factors equal to 0 and solve for x . 

     2 x 3   -    2 x 2   - 12 x   =   2 x   ( x 2   -    x   -    6 )   =   2 x   ( x   -    3 ) ( x   +   2 )

To solve this problem, you would need to set all factors to 0 and solve for x . There will be three solutions.

Fill in the blanks below to find the three solutions to the polynomial. 

Check polynomials in your graphing calculator:

Your solutions will be the x -intercepts on the graph.

• Input your equation using the equation editor [ Y  =] key on the graphing calculator.
• Press [GRAPH].
• Press [2nd] [TRACE] to access the CALC menu.
• Press [2] to select the zero command.
• Use the arrow keys to select a left bound and a right bound.

Vocabulary Activity

Journal activity.

Copy and paste the link code above.

Related Items

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 3: Polynomial factorization

About this unit.

Let's get equipped with a variety of key strategies for breaking down higher degree polynomials. From taking out common factors to using special products, we'll build a strong foundation to help us investigate polynomial functions and prove identities.

Factoring monomials

• Introduction to factoring higher degree polynomials (Opens a modal)
• Introduction to factoring higher degree monomials (Opens a modal)
• Which monomial factorization is correct? (Opens a modal)
• Worked example: finding the missing monomial factor (Opens a modal)
• Worked example: finding missing monomial side in area model (Opens a modal)
• Factoring monomials (Opens a modal)
• Factor monomials Get 3 of 4 questions to level up!

Greatest common factor

• Greatest common factor of monomials (Opens a modal)
• Greatest common factor of monomials Get 3 of 4 questions to level up!

Taking common factors

• Taking common factor from binomial (Opens a modal)
• Taking common factor from trinomial (Opens a modal)
• Taking common factor: area model (Opens a modal)
• Factoring polynomials by taking a common factor (Opens a modal)
• Factor polynomials: common factor Get 3 of 4 questions to level up!

Factoring higher degree polynomials

• Factoring higher degree polynomials (Opens a modal)
• Factoring higher-degree polynomials: Common factor (Opens a modal)
• Factor higher degree polynomials Get 3 of 4 questions to level up!

Factoring using structure

• Identifying quadratic patterns (Opens a modal)
• Factorization with substitution (Opens a modal)
• Factoring using the perfect square pattern (Opens a modal)
• Factoring using the difference of squares pattern (Opens a modal)
• Identify quadratic patterns Get 3 of 4 questions to level up!
• Factorization with substitution Get 3 of 4 questions to level up!
• Factor polynomials using structure Get 3 of 4 questions to level up!

Polynomial identities

• Polynomial identities introduction (Opens a modal)
• Analyzing polynomial identities (Opens a modal)
• Describing numerical relationships with polynomial identities (Opens a modal)
• Polynomial identities Get 3 of 4 questions to level up!

Geometric series

• Geometric series introduction (Opens a modal)
• Finite geometric series formula (Opens a modal)
• Worked examples: finite geometric series (Opens a modal)
• Geometric series word problems: swing (Opens a modal)
• Geometric series word problems: hike (Opens a modal)
• Polynomial factorization: FAQ (Opens a modal)
• Geometric series formula Get 3 of 4 questions to level up!
• Finite geometric series word problems Get 3 of 4 questions to level up!

Into all problem-solving, a little dissent must fall

Events of the past several years have reiterated for executives the importance of collaboration and of welcoming diverse perspectives when trying to solve complicated workplace problems. Companies weren’t fully prepared for the onset of a global pandemic, for instance, and all that it engendered—including supply chain snarls and the resulting Great Attrition  and shift to remote (and now hybrid) work, which required employers to fundamentally rethink their talent strategies . But in most cases leaders have been able to collaborate their way through the uncertainty, engage in rigorous debate and analyses about the best steps to take, and work with employees, suppliers, partners, and other critical stakeholders to react and, ultimately, recover.

And It’s not just COVID-19: many organisations have had to rethink their business strategies and practices in the wake of environmental concerns, the war in Ukraine, and social movements sparked by racial injustice, sexual misconduct, and widespread economic inequity . Ours are fast-moving, complex times, rich not just in worrisome challenges but also in exciting potential—organisations that enable innovation will find ample opportunities to thrive. So now more than ever, decision makers can’t act alone; they must bring diverse perspectives to the table and ensure that those voices are fully heard . 1 Sundiatu Dixon-Fyle, Kevin Dolan, Vivian Hunt, and Sara Prince, “ Diversity wins: How inclusion matters ,” McKinsey, May 19, 2020.

But while many leaders say they welcome dissent, their reactions often change when they actually get some. They may feel defensive. They may question their own judgment. They may resent having to take time to revisit the decision-making process. These are natural responses, of course; employees’ loyalty and affirmation are more reassuring to leaders than robust challenges from the group. There is discomfort, too, for potential dissenters; it is much safer to keep your thoughts to yourself and conform  than to risk expulsion from the group. 2 Derived from this work on the evolutionary origins of social and political behavior: Christopher Boehm, Hierarchy in the Forest: The Evolution of Egalitarian Behavior , Cambridge, Massachusetts: Harvard University Press, 2001.

What’s missing in many companies, in our experience, is the use of “contributory dissent” or the capabilities required to engage in healthy if divergent discussions about critical business problems. Contributory dissent allows individuals and groups to air their differences in a way that moves the discussion toward a positive outcome and doesn’t undermine leadership or group cohesion . 3 McKinsey itself has established obligation to dissent as one of its core values alongside those focused on client service and talent development. For more, see Bill Taylor, “True leaders believe dissent is an obligation,” Harvard Business Review , January 12, 2017.

McKinsey’s research and experience in the field point to several steps leaders can take to engage in healthy dissent and build a culture where constructive feedback is expected and where communication is forthright. These include modeling “open” behaviors, embedding psychological safety  and robust debate into decision-making processes, and equipping employees with the communication skills that will allow them to contribute dissenting opinions effectively.

In this article we outline the steps leaders can take to encourage healthy dissent, and the actions teams and individuals can take to share their voices and perspectives most effectively. It takes both sides, after all, to engage in robust debate, find the right solutions, and enable lasting, positive change.

How leaders can encourage contributory dissent

Senior leaders in an organisation play a central role in ensuring that individuals and teams see contributory dissent as a normal part of any discussion. They can signal the importance of dissent by taking a series of steps to institutionalise the practice within an organisation and empower employees to share their ideas freely and productively. Specifically, senior leaders should strive to inspire rather than direct employees to collaborate, explicitly demand dissent and, taking that one step further, actively engage with naysayers (see sidebar “How to encourage healthy dissent”). 4 Leaders can also draw on McKinsey’s “influence model” for changing mindsets and behaviors: role modeling, fostering understanding and conviction, reinforcing with formal mechanisms, and developing talent and skills. For more, see Tessa Basford and Bill Schaninger, “ The four building blocks of change ,” McKinsey Quarterly , April 11, 2016.

Inspire, don’t direct

How to encourage healthy dissent.

To encourage dissent through personal leadership:

Lead to inspire, not to direct:

• Empower the group to come up with ideas: “None of us knows the answer yet, but we can work it out together if we harness the best of everyone’s thinking.”

Foster dissent by actively seeking it:

• Explicitly seek dissent; give people permission and encouragement.
• Consider including dissent as a stated organisational value.
• Make provision for open discussion in the buildup to decisions.

Welcome open discussion when it comes:

• Listen to dissenters and naysayers, and thank them for their insights.
• Recognise this as a usefully unfiltered channel for understanding the organisation’s perceptions on issues.
• Seek to bring dissenters along the decision journey, so they become positive influencers later during implementation.
• Employ deliberate techniques such as red teaming and pre-mortems to widen the debate and mitigate groupthink.

As the inspirational speaker Simon Sinek put it, “The role of a leader is not to come up with all the great ideas. The role of a leader is to create an environment in which great ideas can happen.” 5 Simon Sinek, Start with Why: How Great Leaders Inspire Everyone to Take Action , New York, NY: Portfolio, 2009. That is especially important for fostering an atmosphere of collaboration and contributory dissent. Rather than immediately jump into a discussion about solutions, one senior leader in an international organisation addressed his team’s anxiety in the wake of a crisis. “Let me guess,” he said, “you’re all feeling confused and uncertain about the way ahead. Terrific. I’m so glad we are of one mind and that we all understand our situation correctly! I’m sure that we can work it out together, but it’s going to require the best of everyone’s thinking. Let’s get started.” His authenticity and understated humor allowed him to connect with the group and inspired them to keep calm, carry on, and generate solutions that the leader alone couldn’t have come up with. Harvard professor Ron Heifetz describes this as creating a holding environment, a key element of adaptive leadership. 6 Ronald A. Heifetz and Mary Linksy, Leadership on the Line: Staying Alive through the Dangers of Leading , Boston, MA: Harvard Business School Press, 2002; Ronald Heifetz, Alexander Grashow, and Marty Linksy, The Practice of Adaptive Leadership: Tools and Tactics for Changing Your Organization and the World , Boston, MA: Harvard Business Press, 2009.

Explicitly demand dissent

It’s not enough for leaders to give people permission to dissent; they must demand it of people. In many companies, individuals and teams may (understandably) default to collegiality, not realizing that there are ways to challenge ideas while still respecting colleagues’ roles and intellect. It’s on senior leaders, then, to help employees understand where the boundaries are. In World War 1, Australia’s General Sir John Monash was determined to develop better tactics to overcome the catastrophic impasse of trench warfare. He knew there were answers to be found from the experience of soldiers in the trenches, but he needed to loosen the military discipline of blind obedience: “I don’t care a damn for your loyal service when you think I am right; when I really want it most is when you think I am wrong.” Monash scheduled open battle planning sessions and pulled in advice from whoever offered it. In doing so, he built ownership of and confidence in his plans among all ranks. The resulting orchestration of tanks, artillery, aircraft, and troops led to rapid advances along the Somme Valley, and Monash garnered respect and appreciation from his troops, whose chances of survival and ultimate victory had increased markedly.

Actively engage with naysayers

Taking the demand imperative one step further, it’s beneficial for leaders to actively seek out the views of vocal naysayers , who can turn into influential champions just by being part of the conversation. They can immediately improve the nature of business debate and may boost the quality of the final decision, although engaging with naysayers can be tough. Some dissenting opinions can be ill-informed or uncomfortable to hear. The objective for senior leaders, then, is to put their discomfort aside and listen for signs of cognitive dissonance within an organisation. As an example, front-line employees may say things like “We’re not considered strategic thinkers,” or “The company doesn’t put people first,” while senior management may actually feel as though they have made strides in both of those areas. Still, leaders need to absorb such comments, treat them as useful data points, assess their validity, and engage in what may be a challenging discussion. They may want to use red teams  and premortems , in which teams at the outset anticipate all the ways a project could fail, to frame up dissenting opinions, mitigate groupthink, and find a positive resolution. These behaviours also serve to enhance organizational agility and resilience .

How leaders can establish psychological safety

Senior leaders need to establish a work environment in which it is safe to offer dissenting views. The McKinsey Health Institute’s work on employee well-being points to a strong correlation between leadership behaviors, collaborative culture, and resistance to mental health problems and burnout : only 15 percent of employees in environments with low inclusivity and low support for personal growth are highly engaged, compared with 38 percent in high-scoring environments. 7 “ Addressing employee burnout: Are you solving the right problem? ,” McKinsey, May 27, 2022. Leaders can build psychological safety (where team members feel they can take interpersonal risks and remain respected and accepted) and set the conditions for contributory dissent by rethinking how they engage in debate—both the dynamics and the choreography of it.

The dynamics of debate

The poet and playwright Oscar Wilde described a healthy debating culture as one in which people are “playing gracefully with ideas”— listening to, and even nourishing, opposing points of view in a measured and respectful way. 8 The Complete Works of Oscar Wilde, Volume 2: De Profundis, “Epistola: In Carcere et Vinculis,” Oxford, United Kingdom: Clarendon Press, 2005. Indeed, the best ideas can emerge at the intersection of cultures and opinions. In 15th century Florence, for instance, the Medici family attracted and funded creators from across the arts and sciences to establish an epicenter of innovative thinking that sparked the Renaissance. 9 Frans Johansson, The Medici Effect: Breakthrough Insights at the Intersection of Ideas, Concepts, and Culture , Boston, MA: Harvard Business School Press, 2004. Closer to this century, we have seen cross-discipline innovations like the application of biologists’ research on ant colonies to solve problems in telecommunications routing. And in the business world, extraordinary innovations have been achieved by open-minded leaders bringing together smart people and creating the conditions for playful exploration.

To achieve a state of “graceful play,” senior leaders must carefully manage group dynamics during debates. Rather than lead with their own opinions, for instance, which might immediately carry outsize weight in the group and stifle discussion, senior leaders can hold back and let others lead the discussion . They can lean in to show genuine curiosity or to explicitly recognise when a dissenting view has changed their thinking. But by letting other, more junior voices carry the agenda and work through ideas, however imperfect, senior leaders can establish a climate of psychological safety—and garner more respect from colleagues long term. 10 Amy C. Edmondson, The Fearless Organization: Creating Psychological Safety in the Workplace for Learning, Innovation, and Growth , Hoboken, NJ: John Wiley & Sons, 2019.

Leaders will also need to be aware of cultural differences that may crop up during debates. For example, many Australians speak candidly and are happy to address issues squarely. By contrast, the concept of “face” is so important in many Asian cultures that a more circumspect approach is taken. And the Pacific and Maori cultures emphasize displays of both strength and respect. 11 Erin Meyer, The Culture Map: Breaking through the Invisible Boundaries of Global Business , Philadelphia, PA: PublicAffairs, 2014. These differences in debate dynamics really matter. They can be a great source of hybrid vigour, 12 “Heterosis, also called hybrid vigour: the increase in such characteristics as size, growth rate, fertility, and yield of a hybrid organism over those of its parents. The first-generation offspring generally show, in greater measure, the desired characteristics of both parents.” Encyclopedia Britannica , accessed September 19, 2022. if sensitively managed, or a source of conflict and disenfranchisement if not. To approach these differences in a positive way, senior leaders could undertake a mapping exercise that identifies the different styles of the cultures present, thereby providing validation and enabling pragmatic measures to integrate them.

Choreographing debate

Beyond just managing debate dynamics, business leaders must take a hand in choreographing the debate and, specifically, in helping to design collective-thinking processes  so people know how best to play their part. Business leaders may adopt a structured approach  to brainstorming, for instance, or plan strategic off-site schedules that combine deliberate thinking with “distracted” thinking—taking time to engage in a social activity, for instance—to take advantage of employees’ deep-thinking processes.

How deliberate choices by the leader can optimise a decision-making process

A leader must consciously assess each new situation and design the collective-thinking process accordingly, then articulate this so that people know how best to play their part.

In doing so, the leader should consider an array of questions, the answers to which will determine the context, for example:

• What does success look like?
• Will the organisation underwrite initial failures in the interests of agility and innovation?
• How broad and freethinking an analysis is required?
• What are the explicit expectations for contributory dissent?
• Are any topics and behaviours out of bounds?
• Who will lead the discussion, and how will comments be captured?
• Does urgency mean that it’s better to be directive?
• Who will be consulted?
• Which decisions can be delegated, and to whom?
• Whose support needs to be built?
• What parameters and boundaries exist?
• Are there interim decisions and communications required?
• What form should the deliverable outcomes take?
• When are the deliverables required?
• Direction setting on these parameters by the leader focuses the team, while also creating space for creativity and iterative learning.

To create a sustainable structure for debate, business leaders will need to consider questions relating to team structure and rules of engagement: What does success look like when it comes to contributory dissent? What topics and behaviors are out of bounds? Who will lead the discussion, and how will comments be captured? Who has the final say on decisions, or which decisions can be delegated, and to whom? (For a more comprehensive explanation, see sidebar “How deliberate choices by the leader can optimise a decision-making process.”)

Having these parameters in place can free up the team to think more creatively about the issue at hand. Establishing such protocols can also make it easier to raise dissenting opinions. At one company, people are asked to call out their underlying values or potential biases when expressing a dissenting view. During meetings of the promotion committee, for instance, a statement like “I think we are making the wrong decision” would be rephrased as “I am someone who values experience over collaboration, and this decision would risk losing too much institutional knowledge.”

How individuals and teams can engage and dissent

As we’ve shared, senior leaders can take steps to set conditions for robust discussion and problem-solving, but individuals and teams themselves must also have the right mindsets and skills for contributory dissent to work well (see sidebar “How teams and individuals can dissent effectively”). In particular, they must embrace the obligation to dissent, actively make space to analyse ideas that are different from their own, and then find ways to either iterate on others’ ideas or respectfully agree to disagree.

Embrace the obligation to dissent

How teams and individuals can dissent effectively.

For dissent to be effective, its delivery requires courage and tactical skills underpinned by sincere respect and grace. Speaking up with respect is the right thing to do, and the responsibility to do so exists, even if there is uncertainty. The following guidelines are useful in enabling effective dissent:

Prepare a welcome for dissenting views:

• Understand the context and motivations of others, appreciate their views, and syndicate your own.
• Stop and strategise before wading into the conversations, establish a solid platform for agreement, and explicitly seek permission to dissent.

Play the long game:

• Be open minded and iterative. Don’t expect to succeed on the first try.
• Listen to others for what their views might add rather than to defend your own.

Withhold assent if you need to, but do it carefully:

• Withholding assent is a legitimate option if done judiciously.
• Minimise offense to and loss of face for the decision maker.
• If principles or legality is at stake, document your dissent.

Individuals and teams need to exhibit a certain amount of humility and confidence in order to speak truth to power with respect; they must be sure for themselves that doing so is the right thing to do. To build this confidence, individuals and teams should remember that the very act of dissent can be valuable, even if the contribution itself isn’t 100 percent baked. Others can react or build on the dissenting view—which, in itself, can be a satisfying process for a dissenter. If the ultimate decision isn’t what they proposed, they still helped shape it by offering and testing a worthy possibility.

Make space to analyse different views

Individuals and teams may need time to determine their positions on an issue. During this period, it’s important to be (and seen to be) open-minded and respectful of others’ views. That means asking lots of questions, gathering information, assessing others’ motivations, and acknowledging their views before syndicating alternatives of your own. Much of this fact gathering can be done one-on-one, in a nonconfrontational way, in offline conversations rather than in a tension-filled meeting room. In these conversations, individuals could start by reaffirming a shared commitment to finding a solution to the issue at hand, their respect for the decision-making process and the group, and areas of broad agreement. They could also signal their possible intention to dissent and seek permission to do so rather than confronting people head-on. People will find it harder to refuse that permission, and will be less likely to get defensive, when approached with statements like “This is a great discussion, and I love the vision of where we are headed, but would it be OK for us to explore some alternatives for how to get there?”

Agree to iterate …

Individuals and teams that decide to offer dissenting views should agree to iterate on other solutions, rather than digging in. Their dissenting opinions should be cogent, persuasive, and open-minded—but dissenters shouldn’t expect to change hearts and minds on the first try. They should plant seeds gently and bide their time; they might even see their idea come back as someone else’s. The critical skill required here is active, open listening: dissenters should listen carefully for others’ additive insights and find ways to build on them. In their contributory dissent, individuals and teams can take a moment to summarize what others have said and then use statements like “Can I offer another take?” and then allow the momentum of the conversation to take over.

… or agree to disagree

But what happens if, after all the considered and tactful input, the dissenter still believes a decision is heading in the wrong direction? In our experience, withholding assent then becomes a legitimate option: people shouldn’t agree if they don’t agree. This is where all the careful, respectful groundwork the dissenter has done can pay dividends. In fact, a dissenting view gains even more power when an individual can say something like, “I still believe in my alternate solution, but I’m grateful for the opportunity to contribute to this process, and I respect that you have the final say.” In this case, the dissenter is supporting the leader while flagging that the open debate hasn’t convinced them to change their initial view.

Of course, withholding assent should be a relatively rare action, taken only after an individual or team has shown that they can accommodate other views and have aligned with the consensus when they believe it’s right to do so. Think of US Supreme Court associate justice Ruth Bader Ginsburg, who joined the consensus view on many decisions but who is especially celebrated for the positive changes that arose from her highly influential dissenting opinions on issues such as gender equity, human rights, and religious freedom.

Contributory dissent can help strengthen employee engagement, unlock hidden insights, and help organisations solve tough challenges. But putting it into practice takes courage and humility, and it won’t just happen by accident. Leaders need to be intentional about welcoming challenges to their plans and opinions, even when it’s uncomfortable to do so. They need to establish cultures and structures where respectful debate can occur and where individuals and teams feel free to bring innovative—and often better—alternative solutions to the table.

Ben Fletcher is a senior partner in McKinsey’s Sydney office, Chris Hartley is a partner in the Melbourne office, Rupe Hoskin is a senior expert in the Canberra office, and Dana Maor is a senior partner in the Tel Aviv office.

The authors wish to thank Jacqueline Brassey, Nikki Dines, Richard Fitzgerald, Sam Hemphill, Ayush Jain, Jemma King, and Martin Nimmo for their contributions to this article.

Explore a career with us

Related articles.

Psychological safety and the critical role of leadership development

How to demonstrate calm and optimism in a crisis

The four building blocks of change