what is maximization assignment problem

Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.

Hungarian Method to Solve Assignment Problems

The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.

What is an Assignment Problem?

A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.

Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.

Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.

Hungarian Method Steps

Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.

Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.

Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.

Step 3 – Assign zeros

• Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
• Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.

Step 4 – Perform the Optimal Test

• The present assignment is optimal if each row and column has exactly one encircled zero.
• The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.

Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:

(a) Highlight the rows that aren’t assigned.

(b) Label the columns with zeros in marked rows (if they haven’t already been marked).

(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).

(d) Continue with (b) and (c) until no further marking is needed.

(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.

Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.

Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.

Hungarian Method Example

Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.

\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)

With 5 jobs and 5 men, the stated problem is balanced.

\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)

Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.

\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)

Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.

\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)

When the zeros are assigned, we get the following:

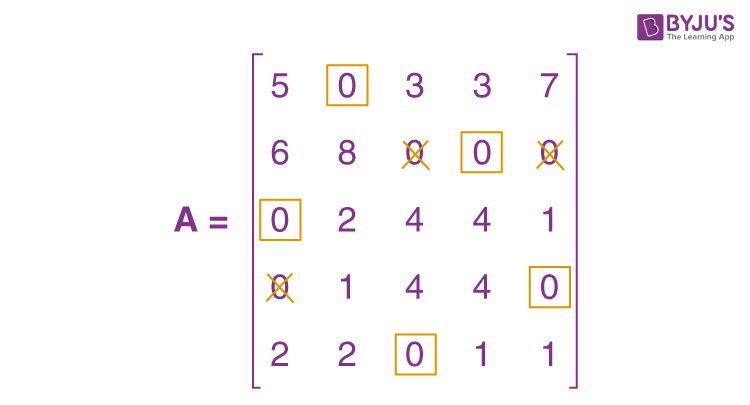
The present assignment is optimal because each row and column contain precisely one encircled zero.

Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.

Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.

Practice Question on Hungarian Method

Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.

\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)

Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.

Frequently Asked Questions on Hungarian Method

What is hungarian method.

The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.

What are the steps involved in Hungarian method?

The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.

What is the purpose of the Hungarian method?

When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

4.7 Applied Optimization Problems

Learning objectives.

• 4.7.1 Set up and solve optimization problems in several applied fields.

One common application of calculus is calculating the minimum or maximum value of a function. For example, companies often want to minimize production costs or maximize revenue. In manufacturing, it is often desirable to minimize the amount of material used to package a product with a certain volume. In this section, we show how to set up these types of minimization and maximization problems and solve them by using the tools developed in this chapter.

Solving Optimization Problems over a Closed, Bounded Interval

The basic idea of the optimization problems that follow is the same. We have a particular quantity that we are interested in maximizing or minimizing. However, we also have some auxiliary condition that needs to be satisfied. For example, in Example 4.32 , we are interested in maximizing the area of a rectangular garden. Certainly, if we keep making the side lengths of the garden larger, the area will continue to become larger. However, what if we have some restriction on how much fencing we can use for the perimeter? In this case, we cannot make the garden as large as we like. Let’s look at how we can maximize the area of a rectangle subject to some constraint on the perimeter.

Example 4.32

Maximizing the area of a garden.

A rectangular garden is to be constructed using a rock wall as one side of the garden and wire fencing for the other three sides ( Figure 4.62 ). Given 100 100 ft of wire fencing, determine the dimensions that would create a garden of maximum area. What is the maximum area?

Let x x denote the length of the side of the garden perpendicular to the rock wall and y y denote the length of the side parallel to the rock wall. Then the area of the garden is

We want to find the maximum possible area subject to the constraint that the total fencing is 100 ft . 100 ft . From Figure 4.62 , the total amount of fencing used will be 2 x + y . 2 x + y . Therefore, the constraint equation is

Solving this equation for y , y , we have y = 100 − 2 x . y = 100 − 2 x . Thus, we can write the area as

Before trying to maximize the area function A ( x ) = 100 x − 2 x 2 , A ( x ) = 100 x − 2 x 2 , we need to determine the domain under consideration. To construct a rectangular garden, we certainly need the lengths of both sides to be positive. Therefore, we need x > 0 x > 0 and y > 0 . y > 0 . Since y = 100 − 2 x , y = 100 − 2 x , if y > 0 , y > 0 , then x < 50 . x < 50 . Therefore, we are trying to determine the maximum value of A ( x ) A ( x ) for x x over the open interval ( 0 , 50 ) . ( 0 , 50 ) . We do not know that a function necessarily has a maximum value over an open interval. However, we do know that a continuous function has an absolute maximum (and absolute minimum) over a closed interval. Therefore, let’s consider the function A ( x ) = 100 x − 2 x 2 A ( x ) = 100 x − 2 x 2 over the closed interval [ 0 , 50 ] . [ 0 , 50 ] . If the maximum value occurs at an interior point, then we have found the value x x in the open interval ( 0 , 50 ) ( 0 , 50 ) that maximizes the area of the garden. Therefore, we consider the following problem:

Maximize A ( x ) = 100 x − 2 x 2 A ( x ) = 100 x − 2 x 2 over the interval [ 0 , 50 ] . [ 0 , 50 ] .

As mentioned earlier, since A A is a continuous function on a closed, bounded interval, by the extreme value theorem, it has a maximum and a minimum. These extreme values occur either at endpoints or critical points. At the endpoints, A ( x ) = 0 . A ( x ) = 0 . Since the area is positive for all x x in the open interval ( 0 , 50 ) , ( 0 , 50 ) , the maximum must occur at a critical point. Differentiating the function A ( x ) , A ( x ) , we obtain

Therefore, the only critical point is x = 25 x = 25 ( Figure 4.63 ). We conclude that the maximum area must occur when x = 25 . x = 25 . Then we have y = 100 − 2 x = 100 − 2 ( 25 ) = 50 . y = 100 − 2 x = 100 − 2 ( 25 ) = 50 . To maximize the area of the garden, let x = 25 x = 25 ft and y = 50 ft . y = 50 ft . The area of this garden is 1250 ft 2 . 1250 ft 2 .

Checkpoint 4.31

Determine the maximum area if we want to make the same rectangular garden as in Figure 4.63 , but we have 200 200 ft of fencing.

Now let’s look at a general strategy for solving optimization problems similar to Example 4.32 .

Problem-Solving Strategy

Problem-solving strategy: solving optimization problems.

• Introduce all variables. If applicable, draw a figure and label all variables.
• Determine which quantity is to be maximized or minimized, and for what range of values of the other variables (if this can be determined at this time).
• Write a formula for the quantity to be maximized or minimized in terms of the variables. This formula may involve more than one variable.
• Write any equations relating the independent variables in the formula from step 3 . 3 . Use these equations to write the quantity to be maximized or minimized as a function of one variable.
• Identify the domain of consideration for the function in step 4 4 based on the physical problem to be solved.
• Locate the maximum or minimum value of the function from step 4 . 4 . This step typically involves looking for critical points and evaluating a function at endpoints.

Now let’s apply this strategy to maximize the volume of an open-top box given a constraint on the amount of material to be used.

Example 4.33

Maximizing the volume of a box.

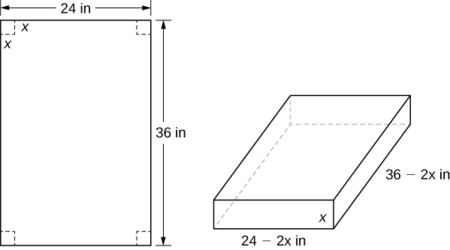
An open-top box is to be made from a 24 24 in. by 36 36 in. piece of cardboard by removing a square from each corner of the box and folding up the flaps on each side. What size square should be cut out of each corner to get a box with the maximum volume?

Step 1: Let x x be the side length of the square to be removed from each corner ( Figure 4.64 ). Then, the remaining four flaps can be folded up to form an open-top box. Let V V be the volume of the resulting box.

Step 2: We are trying to maximize the volume of a box. Therefore, the problem is to maximize V . V .

Step 3: As mentioned in step 2 , 2 , we are trying to maximize the volume of a box. The volume of a box is V = L · W · H , V = L · W · H , where L , W , and H L , W , and H are the length, width, and height, respectively.

Step 4: From Figure 4.64 , we see that the height of the box is x x inches, the length is 36 − 2 x 36 − 2 x inches, and the width is 24 − 2 x 24 − 2 x inches. Therefore, the volume of the box is

Step 5: To determine the domain of consideration, let’s examine Figure 4.64 . Certainly, we need x > 0 . x > 0 . Furthermore, the side length of the square cannot be greater than or equal to half the length of the shorter side, 24 24 in.; otherwise, one of the flaps would be completely cut off. Therefore, we are trying to determine whether there is a maximum volume of the box for x x over the open interval ( 0 , 12 ) . ( 0 , 12 ) . Since V V is a continuous function over the closed interval [ 0 , 12 ] , [ 0 , 12 ] , we know V V will have an absolute maximum over the closed interval. Therefore, we consider V V over the closed interval [ 0 , 12 ] [ 0 , 12 ] and check whether the absolute maximum occurs at an interior point.

Step 6: Since V ( x ) V ( x ) is a continuous function over the closed, bounded interval [ 0 , 12 ] , [ 0 , 12 ] , V V must have an absolute maximum (and an absolute minimum). Since V ( x ) = 0 V ( x ) = 0 at the endpoints and V ( x ) > 0 V ( x ) > 0 for 0 < x < 12 , 0 < x < 12 , the maximum must occur at a critical point. The derivative is

To find the critical points, we need to solve the equation

Dividing both sides of this equation by 12 , 12 , the problem simplifies to solving the equation

Using the quadratic formula, we find that the critical points are

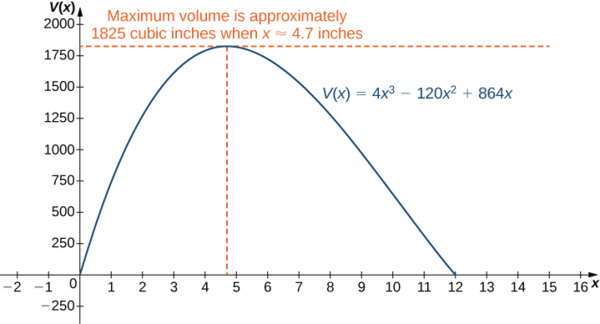
Since 10 + 2 7 10 + 2 7 is not in the domain of consideration, the only critical point we need to consider is 10 − 2 7 . 10 − 2 7 . Therefore, the volume is maximized if we let x = 10 − 2 7 in . x = 10 − 2 7 in . The maximum volume is V ( 10 − 2 7 ) = 640 + 448 7 ≈ 1825 in . 3 V ( 10 − 2 7 ) = 640 + 448 7 ≈ 1825 in . 3 as shown in the following graph.

Watch a video about optimizing the volume of a box.

Checkpoint 4.32

Suppose the dimensions of the cardboard in Example 4.33 are 20 in. by 30 in. Let x x be the side length of each square and write the volume of the open-top box as a function of x . x . Determine the domain of consideration for x . x .

Example 4.34

Minimizing travel time.

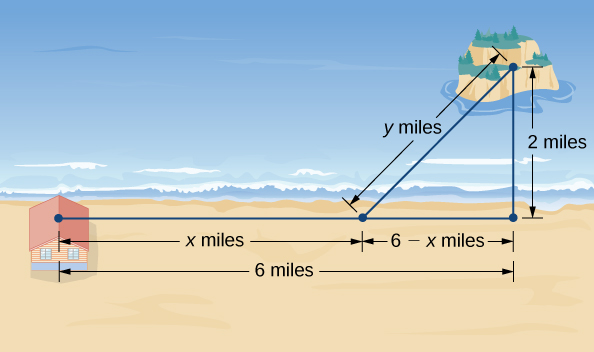
An island is 2 mi 2 mi due north of its closest point along a straight shoreline. A visitor is staying at a cabin on the shore that is 6 mi 6 mi west of that point. The visitor is planning to go from the cabin to the island. Suppose the visitor runs at a rate of 8 mph 8 mph and swims at a rate of 3 mph . 3 mph . How far should the visitor run before swimming to minimize the time it takes to reach the island?

Step 1: Let x x be the distance running and let y y be the distance swimming ( Figure 4.66 ). Let T T be the time it takes to get from the cabin to the island.

Step 2: The problem is to minimize T . T .

Step 3: To find the time spent traveling from the cabin to the island, add the time spent running and the time spent swimming. Since Distance = = Rate × × Time ( D = R × T ) , ( D = R × T ) , the time spent running is

and the time spent swimming is

Therefore, the total time spent traveling is

Step 4: From Figure 4.66 , the line segment of y y miles forms the hypotenuse of a right triangle with legs of length 2 mi 2 mi and 6 − x mi . 6 − x mi . Therefore, by the Pythagorean theorem, 2 2 + ( 6 − x ) 2 = y 2 , 2 2 + ( 6 − x ) 2 = y 2 , and we obtain y = ( 6 − x ) 2 + 4 . y = ( 6 − x ) 2 + 4 . Thus, the total time spent traveling is given by the function

Step 5: From Figure 4.66 , we see that 0 ≤ x ≤ 6 . 0 ≤ x ≤ 6 . Therefore, [ 0 , 6 ] [ 0 , 6 ] is the domain of consideration.

Step 6: Since T ( x ) T ( x ) is a continuous function over a closed, bounded interval, it has a maximum and a minimum. Let’s begin by looking for any critical points of T T over the interval [ 0 , 6 ] . [ 0 , 6 ] . The derivative is

If T ′ ( x ) = 0 , T ′ ( x ) = 0 , then

Squaring both sides of this equation, we see that if x x satisfies this equation, then x x must satisfy

which implies

We conclude that if x x is a critical point, then x x satisfies

Therefore, the possibilities for critical points are

Since x = 6 + 6 / 55 x = 6 + 6 / 55 is not in the domain, it is not a possibility for a critical point. On the other hand, x = 6 − 6 / 55 x = 6 − 6 / 55 is in the domain. Since we squared both sides of Equation 4.6 to arrive at the possible critical points, it remains to verify that x = 6 − 6 / 55 x = 6 − 6 / 55 satisfies Equation 4.6 . Since x = 6 − 6 / 55 x = 6 − 6 / 55 does satisfy that equation, we conclude that x = 6 − 6 / 55 x = 6 − 6 / 55 is a critical point, and it is the only one. To justify that the time is minimized for this value of x , x , we just need to check the values of T ( x ) T ( x ) at the endpoints x = 0 x = 0 and x = 6 , x = 6 , and compare them with the value of T ( x ) T ( x ) at the critical point x = 6 − 6 / 55 . x = 6 − 6 / 55 . We find that T ( 0 ) ≈ 2.108 h T ( 0 ) ≈ 2.108 h and T ( 6 ) ≈ 1.417 h, T ( 6 ) ≈ 1.417 h, whereas T ( 6 − 6 / 55 ) ≈ 1.368 h . T ( 6 − 6 / 55 ) ≈ 1.368 h . Therefore, we conclude that T T has a local minimum at x ≈ 5.19 x ≈ 5.19 mi.

Checkpoint 4.33

Suppose the island is 1 1 mi from shore, and the distance from the cabin to the point on the shore closest to the island is 15 mi . 15 mi . Suppose a visitor swims at the rate of 2.5 mph 2.5 mph and runs at a rate of 6 mph . 6 mph . Let x x denote the distance the visitor will run before swimming, and find a function for the time it takes the visitor to get from the cabin to the island.

In business, companies are interested in maximizing revenue . In the following example, we consider a scenario in which a company has collected data on how many cars it is able to lease, depending on the price it charges its customers to rent a car. Let’s use these data to determine the price the company should charge to maximize the amount of money it brings in.

Example 4.35

Maximizing revenue.

Owners of a car rental company have determined that if they charge customers p p dollars per day to rent a car, where 50 ≤ p ≤ 200 , 50 ≤ p ≤ 200 , the number of cars n n they rent per day can be modeled by the linear function n ( p ) = 1000 − 5 p . n ( p ) = 1000 − 5 p . If they charge $ 50 $ 50 per day or less, they will rent all their cars. If they charge $ 200 $ 200 per day or more, they will not rent any cars. Assuming the owners plan to charge customers between $50 per day and $ 200 $ 200 per day to rent a car, how much should they charge to maximize their revenue?

Step 1: Let p p be the price charged per car per day and let n n be the number of cars rented per day. Let R R be the revenue per day.

Step 2: The problem is to maximize R . R .

Step 3: The revenue (per day) is equal to the number of cars rented per day times the price charged per car per day—that is, R = n × p . R = n × p .

Step 4: Since the number of cars rented per day is modeled by the linear function n ( p ) = 1000 − 5 p , n ( p ) = 1000 − 5 p , the revenue R R can be represented by the function

Step 5: Since the owners plan to charge between $ 50 $ 50 per car per day and $ 200 $ 200 per car per day, the problem is to find the maximum revenue R ( p ) R ( p ) for p p in the closed interval [ 50 , 200 ] . [ 50 , 200 ] .

Step 6: Since R R is a continuous function over the closed, bounded interval [ 50 , 200 ] , [ 50 , 200 ] , it has an absolute maximum (and an absolute minimum) in that interval. To find the maximum value, look for critical points. The derivative is R ′ ( p ) = −10 p + 1000 . R ′ ( p ) = −10 p + 1000 . Therefore, the critical point is p = 100 p = 100 When p = 100 , p = 100 , R ( 100 ) = $ 50,000 . R ( 100 ) = $ 50,000 . When p = 50 , p = 50 , R ( p ) = $ 37,500 . R ( p ) = $ 37,500 . When p = 200 , p = 200 , R ( p ) = $ 0 . R ( p ) = $ 0 . Therefore, the absolute maximum occurs at p = $ 100 . p = $ 100 . The car rental company should charge $ 100 $ 100 per day per car to maximize revenue as shown in the following figure.

Checkpoint 4.34

A car rental company charges its customers p p dollars per day, where 60 ≤ p ≤ 150 . 60 ≤ p ≤ 150 . It has found that the number of cars rented per day can be modeled by the linear function n ( p ) = 750 − 5 p . n ( p ) = 750 − 5 p . How much should the company charge each customer to maximize revenue?

Example 4.36

Maximizing the area of an inscribed rectangle.

A rectangle is to be inscribed in the ellipse

What should the dimensions of the rectangle be to maximize its area? What is the maximum area?

Step 1: For a rectangle to be inscribed in the ellipse, the sides of the rectangle must be parallel to the axes. Let L L be the length of the rectangle and W W be its width. Let A A be the area of the rectangle.

Step 2: The problem is to maximize A . A .

Step 3: The area of the rectangle is A = L W . A = L W .

Step 4: Let ( x , y ) ( x , y ) be the corner of the rectangle that lies in the first quadrant, as shown in Figure 4.68 . We can write length L = 2 x L = 2 x and width W = 2 y . W = 2 y . Since x 2 4 + y 2 = 1 x 2 4 + y 2 = 1 and y > 0 , y > 0 , we have y = 1 − x 2 4 . y = 1 − x 2 4 . Therefore, the area is

Step 5: From Figure 4.68 , we see that to inscribe a rectangle in the ellipse, the x x -coordinate of the corner in the first quadrant must satisfy 0 < x < 2 . 0 < x < 2 . Therefore, the problem reduces to looking for the maximum value of A ( x ) A ( x ) over the open interval ( 0 , 2 ) . ( 0 , 2 ) . Since A ( x ) A ( x ) will have an absolute maximum (and absolute minimum) over the closed interval [ 0 , 2 ] , [ 0 , 2 ] , we consider A ( x ) = 2 x 4 − x 2 A ( x ) = 2 x 4 − x 2 over the interval [ 0 , 2 ] . [ 0 , 2 ] . If the absolute maximum occurs at an interior point, then we have found an absolute maximum in the open interval.

Step 6: As mentioned earlier, A ( x ) A ( x ) is a continuous function over the closed, bounded interval [ 0 , 2 ] . [ 0 , 2 ] . Therefore, it has an absolute maximum (and absolute minimum). At the endpoints x = 0 x = 0 and x = 2 , x = 2 , A ( x ) = 0 . A ( x ) = 0 . For 0 < x < 2 , 0 < x < 2 , A ( x ) > 0 . A ( x ) > 0 . Therefore, the maximum must occur at a critical point. Taking the derivative of A ( x ) , A ( x ) , we obtain

To find critical points, we need to find where A ′ ( x ) = 0 . A ′ ( x ) = 0 . We can see that if x x is a solution of

then x x must satisfy

Therefore, x 2 = 2 . x 2 = 2 . Thus, x = ± 2 x = ± 2 are the possible solutions of Equation 4.7 . Since we are considering x x over the interval [ 0 , 2 ] , [ 0 , 2 ] , x = 2 x = 2 is a possibility for a critical point, but x = − 2 x = − 2 is not. Therefore, we check whether 2 2 is a solution of Equation 4.7 . Since x = 2 x = 2 is a solution of Equation 4.7 , we conclude that 2 2 is the only critical point of A ( x ) A ( x ) in the interval [ 0 , 2 ] . [ 0 , 2 ] . Therefore, A ( x ) A ( x ) must have an absolute maximum at the critical point x = 2 . x = 2 . To determine the dimensions of the rectangle, we need to find the length L L and the width W . W . If x = 2 x = 2 then

Therefore, the dimensions of the rectangle are L = 2 x = 2 2 L = 2 x = 2 2 and W = 2 y = 2 2 = 2 . W = 2 y = 2 2 = 2 . The area of this rectangle is A = L W = ( 2 2 ) ( 2 ) = 4 . A = L W = ( 2 2 ) ( 2 ) = 4 .

Checkpoint 4.35

Modify the area function A A if the rectangle is to be inscribed in the unit circle x 2 + y 2 = 1 . x 2 + y 2 = 1 . What is the domain of consideration?

Solving Optimization Problems when the Interval Is Not Closed or Is Unbounded

In the previous examples, we considered functions on closed, bounded domains. Consequently, by the extreme value theorem, we were guaranteed that the functions had absolute extrema. Let’s now consider functions for which the domain is neither closed nor bounded.

Many functions still have at least one absolute extrema, even if the domain is not closed or the domain is unbounded. For example, the function f ( x ) = x 2 + 4 f ( x ) = x 2 + 4 over ( − ∞ , ∞ ) ( − ∞ , ∞ ) has an absolute minimum of 4 4 at x = 0 . x = 0 . Therefore, we can still consider functions over unbounded domains or open intervals and determine whether they have any absolute extrema. In the next example, we try to minimize a function over an unbounded domain. We will see that, although the domain of consideration is ( 0 , ∞ ) , ( 0 , ∞ ) , the function has an absolute minimum.

In the following example, we look at constructing a box of least surface area with a prescribed volume. It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the smallest surface area. Consequently, we consider the modified problem of determining which open-topped box with a specified volume has the smallest surface area.

Example 4.37

Minimizing surface area.

A rectangular box with a square base, an open top, and a volume of 216 216 in. 3 is to be constructed. What should the dimensions of the box be to minimize the surface area of the box? What is the minimum surface area?

Step 1: Draw a rectangular box and introduce the variable x x to represent the length of each side of the square base; let y y represent the height of the box. Let S S denote the surface area of the open-top box.

Step 2: We need to minimize the surface area. Therefore, we need to minimize S . S .

Step 3: Since the box has an open top, we need only determine the area of the four vertical sides and the base. The area of each of the four vertical sides is x · y . x · y . The area of the base is x 2 . x 2 . Therefore, the surface area of the box is

Step 4: Since the volume of this box is x 2 y x 2 y and the volume is given as 216 in . 3 , 216 in . 3 , the constraint equation is

Solving the constraint equation for y , y , we have y = 216 x 2 . y = 216 x 2 . Therefore, we can write the surface area as a function of x x only:

Therefore, S ( x ) = 864 x + x 2 . S ( x ) = 864 x + x 2 .

Step 5: Since we are requiring that x 2 y = 216 , x 2 y = 216 , we cannot have x = 0 . x = 0 . Therefore, we need x > 0 . x > 0 . On the other hand, x x is allowed to have any positive value. Note that as x x becomes large, the height of the box y y becomes correspondingly small so that x 2 y = 216 . x 2 y = 216 . Similarly, as x x becomes small, the height of the box becomes correspondingly large. We conclude that the domain is the open, unbounded interval ( 0 , ∞ ) . ( 0 , ∞ ) . Note that, unlike the previous examples, we cannot reduce our problem to looking for an absolute maximum or absolute minimum over a closed, bounded interval. However, in the next step, we discover why this function must have an absolute minimum over the interval ( 0 , ∞ ) . ( 0 , ∞ ) .

Step 6: Note that as x → 0 + , x → 0 + , S ( x ) → ∞ . S ( x ) → ∞ . Also, as x → ∞ , x → ∞ , S ( x ) → ∞ . S ( x ) → ∞ . Since S S is a continuous function that approaches infinity at the ends, it must have an absolute minimum at some x ∈ ( 0 , ∞ ) . x ∈ ( 0 , ∞ ) . This minimum must occur at a critical point of S . S . The derivative is

Therefore, S ′ ( x ) = 0 S ′ ( x ) = 0 when 2 x = 864 x 2 . 2 x = 864 x 2 . Solving this equation for x , x , we obtain x 3 = 432 , x 3 = 432 , so x = 432 3 = 6 2 3 . x = 432 3 = 6 2 3 . Since this is the only critical point of S , S , the absolute minimum must occur at x = 6 2 3 x = 6 2 3 (see Figure 4.70 ). When x = 6 2 3 , x = 6 2 3 , y = 216 ( 6 2 3 ) 2 = 3 2 3 in . y = 216 ( 6 2 3 ) 2 = 3 2 3 in . Therefore, the dimensions of the box should be x = 6 2 3 in . x = 6 2 3 in . and y = 3 2 3 in . y = 3 2 3 in . With these dimensions, the surface area is

Checkpoint 4.36

Consider the same open-top box, which is to have volume 216 in . 3 . 216 in . 3 . Suppose the cost of the material for the base is 20 ¢ / in . 2 20 ¢ / in . 2 and the cost of the material for the sides is 30 ¢ / in . 2 30 ¢ / in . 2 and we are trying to minimize the cost of this box. Write the cost as a function of the side lengths of the base. (Let x x be the side length of the base and y y be the height of the box.)

Section 4.7 Exercises

For the following exercises, answer by proof, counterexample, or explanation.

When you find the maximum for an optimization problem, why do you need to check the sign of the derivative around the critical points?

Why do you need to check the endpoints for optimization problems?

True or False . For every continuous nonlinear function, you can find the value x x that maximizes the function.

True or False . For every continuous nonconstant function on a closed, finite domain, there exists at least one x x that minimizes or maximizes the function.

For the following exercises, set up and evaluate each optimization problem.

To carry a suitcase on an airplane, the length + width + + width + height of the box must be less than or equal to 62 in . 62 in . Assuming the base of the suitcase is square, show that the volume is V = h ( 31 − ( 1 2 ) h ) 2 . V = h ( 31 − ( 1 2 ) h ) 2 . What height allows you to have the largest volume?

You are constructing a cardboard box with the dimensions 2 m by 4 m . 2 m by 4 m . You then cut equal-size squares from each corner so you may fold the edges. What are the dimensions of the box with the largest volume?

Find the positive integer that minimizes the sum of the number and its reciprocal.

Find two positive integers such that their sum is 10 , 10 , and minimize and maximize the sum of their squares.

For the following exercises, consider the construction of a pen to enclose an area.

You have 400 ft 400 ft of fencing to construct a rectangular pen for cattle. What are the dimensions of the pen that maximize the area?

You have 800 ft 800 ft of fencing to make a pen for hogs. If you have a river on one side of your property, what is the dimension of the rectangular pen that maximizes the area?

You need to construct a fence around an area of 1600 ft 2 . 1600 ft 2 . What are the dimensions of the rectangular pen to minimize the amount of material needed?

Two poles are connected by a wire that is also connected to the ground. The first pole is 20 ft 20 ft tall and the second pole is 10 ft 10 ft tall. There is a distance of 30 ft 30 ft between the two poles. Where should the wire be anchored to the ground to minimize the amount of wire needed?

[T] You are moving into a new apartment and notice there is a corner where the hallway narrows from 8 ft to 6 ft . 8 ft to 6 ft . What is the length of the longest item that can be carried horizontally around the corner?

A patient’s pulse measures 70 bpm, 80 bpm, then 120 bpm . 70 bpm, 80 bpm, then 120 bpm . To determine an accurate measurement of pulse, the doctor wants to know what value minimizes the expression ( x − 70 ) 2 + ( x − 80 ) 2 + ( x − 120 ) 2 ? ( x − 70 ) 2 + ( x − 80 ) 2 + ( x − 120 ) 2 ? What value minimizes it?

In the previous problem, assume the patient was nervous during the third measurement, so we only weight that value half as much as the others. What is the value that minimizes ( x − 70 ) 2 + ( x − 80 ) 2 + 1 2 ( x − 120 ) 2 ? ( x − 70 ) 2 + ( x − 80 ) 2 + 1 2 ( x − 120 ) 2 ?

You can run at a speed of 6 6 mph and swim at a speed of 3 3 mph and are located on the shore, 4 4 miles east of an island that is 1 1 mile north of the shoreline. How far should you run west to minimize the time needed to reach the island?

For the following problems, consider a lifeguard at a circular pool with diameter 40 m . 40 m . He must reach someone who is drowning on the exact opposite side of the pool, at position C . C . The lifeguard swims with a speed v v and runs around the pool at speed w = 3 v . w = 3 v .

Find a function that measures the total amount of time it takes to reach the drowning person as a function of the swim angle, θ . θ .

Find at what angle θ θ the lifeguard should swim to reach the drowning person in the least amount of time.

A truck uses gas as g ( v ) = a v + b v , g ( v ) = a v + b v , where v v represents the speed of the truck and g g represents the gallons of fuel per mile. Assuming a a and b b are positive, at what speed is fuel consumption minimized?

For the following exercises, consider a limousine that gets m ( v ) = ( 120 − 2 v ) 5 mi/gal m ( v ) = ( 120 − 2 v ) 5 mi/gal at speed v , v , the chauffeur costs $15/h , $15/h , and gas is $ 3.5 / gal . $ 3.5 / gal .

Find the cost per mile at speed v . v .

Find the cheapest driving speed.

For the following exercises, consider a pizzeria that sell pizzas for a revenue of R ( x ) = a x R ( x ) = a x and costs C ( x ) = b + c x + d x 2 , C ( x ) = b + c x + d x 2 , where x x represents the number of pizzas ;   a   >   c ;   a   >   c .

Find the profit function for the number of pizzas. How many pizzas gives the largest profit per pizza?

Assume that R ( x ) = 10 x R ( x ) = 10 x and C ( x ) = 2 x + x 2 . C ( x ) = 2 x + x 2 . How many pizzas sold maximizes the profit?

Assume that R ( x ) = 15 x , R ( x ) = 15 x , and C ( x ) = 60 + 3 x + 1 2 x 2 . C ( x ) = 60 + 3 x + 1 2 x 2 . How many pizzas sold maximizes the profit?

For the following exercises, consider a wire 4 ft 4 ft long cut into two pieces. One piece forms a circle with radius r r and the other forms a square of side x . x .

Choose x x to maximize the sum of their areas.

Choose x x to minimize the sum of their areas.

For the following exercises, consider two nonnegative numbers x x and y y such that x + y = 10 . x + y = 10 . Maximize and minimize the quantities.

x 2 y 2 x 2 y 2

y − 1 x y − 1 x

x 2 − y x 2 − y

For the following exercises, draw the given optimization problem and solve.

Find the volume of the largest right circular cylinder that fits in a sphere of radius 1 . 1 .

Find the volume of the largest right cone that fits in a sphere of radius 1 . 1 .

Find the area of the largest rectangle that fits into the triangle with sides x = 0 , y = 0 x = 0 , y = 0 and x 4 + y 6 = 1 . x 4 + y 6 = 1 .

Find the largest volume of a cylinder that fits into a cone that has base radius R R and height h . h .

Find the dimensions of the closed cylinder volume V = 16 π V = 16 π that has the least amount of surface area.

Find the dimensions of a right cone with surface area S = 4 π S = 4 π that has the largest volume.

For the following exercises, consider the points on the given graphs. Use a calculator to graph the functions.

[T] Where is the line y = 5 − 2 x y = 5 − 2 x closest to the origin?

[T] Where is the line y = 5 − 2 x y = 5 − 2 x closest to point ( 1 , 1 ) ? ( 1 , 1 ) ?

[T] Where is the parabola y = x 2 y = x 2 closest to point ( 2 , 0 ) ? ( 2 , 0 ) ?

[T] Where is the parabola y = x 2 y = x 2 closest to point ( 0 , 3 ) ? ( 0 , 3 ) ?

For the following exercises, set up, but do not evaluate, each optimization problem.

A window is composed of a semicircle placed on top of a rectangle. If you have 20 ft 20 ft of window-framing materials for the outer frame, what is the maximum size of the window you can create? Use r r to represent the radius of the semicircle.

You have a garden row of 20 20 watermelon plants that produce an average of 30 30 watermelons apiece. For any additional watermelon plants planted, the output per watermelon plant drops by one watermelon. How many extra watermelon plants should you plant?

You are constructing a box for your cat to sleep in. The plush material for the square bottom of the box costs $ 5 / ft 2 $ 5 / ft 2 and the material for the sides costs $ 2 / ft 2 . $ 2 / ft 2 . You need a box with volume 4 ft 3 . 4 ft 3 . Find the dimensions of the box that minimize cost. Use x x to represent the length of the side of the box.

You are building five identical pens adjacent to each other with a total area of 1000 m 2 , 1000 m 2 , as shown in the following figure. What dimensions should you use to minimize the amount of fencing?

You are the manager of an apartment complex with 50 50 units. When you set rent at $ 800 / month, $ 800 / month, all apartments are rented. As you increase rent by $ 25 / month, $ 25 / month, one fewer apartment is rented. Maintenance costs run $ 50 / month $ 50 / month for each occupied unit. What is the rent that maximizes the total amount of profit?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution-NonCommercial-ShareAlike License and you must attribute OpenStax.

Access for free at https://openstax.org/books/calculus-volume-1/pages/1-introduction

• Authors: Gilbert Strang, Edwin “Jed” Herman
• Publisher/website: OpenStax
• Book title: Calculus Volume 1
• Publication date: Mar 30, 2016
• Location: Houston, Texas
• Book URL: https://openstax.org/books/calculus-volume-1/pages/1-introduction
• Section URL: https://openstax.org/books/calculus-volume-1/pages/4-7-applied-optimization-problems

© Feb 5, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures

Hungarian Algorithm for Assignment Problem | Set 1 (Introduction)

• Hungarian Algorithm for Assignment Problem | Set 2 (Implementation)
• Job Assignment Problem using Branch And Bound
• Channel Assignment Problem
• OLA Interview Experience | Set 11 ( For Internship)
• Minimizing Total Manhattan Distances for Driver-Package Allocation
• Quadratic Assignment Problem (QAP)
• Find minimum time to finish all jobs with given constraints
• Minimum Number of Platforms Required for a Railway/Bus Station | Set 2 (Set based approach)
• Assign N tasks to N persons to minimize total time
• Maximum points collected by two persons allowed to meet once
• Find the Platform at which the given Train arrives
• Data Structures and Algorithms | Set 21
• Algorithms | Dynamic Programming | Question 7
• Sprinklr Interview Experience | (On Campus for Internship)
• OYO Rooms Interview Experience | Set 7
• Amazon Internship Interview Experience | On-Campus 2021
• Zoho Interview Experience | Set 9 (On-Campus)
• Zoho Interview | Set 5 (On-Campus Drive)
• Gameskraft Technologies Interview Experience
• Merge Sort - Data Structure and Algorithms Tutorials
• Must Do Coding Questions for Companies like Amazon, Microsoft, Adobe, ...
• QuickSort - Data Structure and Algorithm Tutorials
• Bubble Sort - Data Structure and Algorithm Tutorials
• Tree Traversal Techniques - Data Structure and Algorithm Tutorials
• Binary Search - Data Structure and Algorithm Tutorials
• Insertion Sort - Data Structure and Algorithm Tutorials
• Selection Sort – Data Structure and Algorithm Tutorials
• Understanding the basics of Linked List
• Breadth First Search or BFS for a Graph

• For each row of the matrix, find the smallest element and subtract it from every element in its row.
• Do the same (as step 1) for all columns.
• Cover all zeros in the matrix using minimum number of horizontal and vertical lines.
• Test for Optimality: If the minimum number of covering lines is n, an optimal assignment is possible and we are finished. Else if lines are lesser than n, we haven’t found the optimal assignment, and must proceed to step 5.
• Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.

Try it before moving to see the solution

Explanation for above simple example:

  An example that doesn’t lead to optimal value in first attempt: In the above example, the first check for optimality did give us solution. What if we the number covering lines is less than n.

Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3).

Space complexity :   O(n^2), where n is the number of workers and jobs. This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional arrays of size n to store the labels, matches, and auxiliary information needed for the algorithm.

In the next post, we will be discussing implementation of the above algorithm. The implementation requires more steps as we need to find minimum number of lines to cover all 0’s using a program. References: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY

Please Login to comment...

Similar reads.

• Mathematical

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

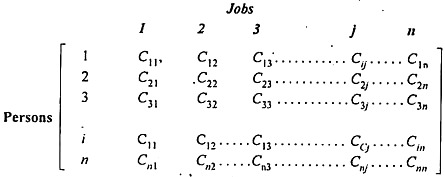
5. Maximization case in Assignment Problem

Quadratic assignment problem

Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)

• 1 Introduction
• 2.1 Koopmans-Beckman Mathematical Formulation
• 2.2.1 Parameters
• 2.3.1 Optimization Problem
• 2.4 Computational Complexity
• 2.5 Algorithmic Discussions
• 2.6 Branch and Bound Procedures
• 2.7 Linearizations
• 3.1 QAP with 3 Facilities
• 4.1 Inter-plant Transportation Problem
• 4.2 The Backboard Wiring Problem
• 4.3 Hospital Layout
• 4.4 Exam Scheduling System
• 5 Conclusion
• 6 References

Introduction

The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 [1] , is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, inter-plant transportation, hospital transportation, exam scheduling, along with many other applications not described within this page.

Theory, Methodology, and/or Algorithmic Discussions

Koopmans-beckman mathematical formulation.

Economists Koopmans and Beckman began their investigation of the QAP to ascertain the optimal method of locating important economic resources in a given area. The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org.

Quadratic Assignment Problem Formulation

Inner Product

Note: The true objective cost function only requires summing entries above the diagonal in the matrix comprised of elements

Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.

Optimization Problem

With all of this information, the QAP can be summarized as:

Computational Complexity

QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who states that of all combinatorial optimization problems, QAP is the “hardest of the hard”. [2]

Algorithmic Discussions

While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:

• Dynamic Program
• Cutting Plane

Branch and Bound Procedures

The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.

The Branch and Bound method was first proposed by Ailsa Land and Alison Doig in 1960 and is the most commonly used tool for solving NP-hard optimization problems.

A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before one lists all of the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and the branch is eliminated if it cannot produce a better solution than the best one found so far by the algorithm.

Linearizations

The first attempts to solve the QAP eliminated the quadratic term in the objective function of

in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be applied. The very large number of new variables and constraints, however, usually poses an obstacle for efficiently solving the resulting linear integer programs. MILP formulations provide LP relaxations of the problem which can be used to compute lower bounds.

Numerical Example

Qap with 3 facilities.

Applications

Inter-plant transportation problem.

The QAP was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations. [1] Factoring in the location of each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.

The Backboard Wiring Problem

As the QAP is focused on minimizing the cost of traveling from one location to another, it is an ideal approach to determining the placement of components in many modern electronics. Leon Steinberg proposed a QAP solution to optimize the layout of elements on a blackboard by minimizing the total amount of wiring required. [4]

When defining the problem Steinberg states that we have a set of n elements

as well as a set of r points

In his paper he derives the below formula:

In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation, he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.

The initial placement of components is shown below:

After the initial placement of elements, it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.

Hospital Layout

Building new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem". [5] With the high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create an optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Outpatient ward was acting as a bottleneck in the hospital and focused his efforts on optimizing the 17 departments there.

Elshafei identified the following QAP to determine where clinics should be placed:

For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 based on the original hospital layout.

Exam Scheduling System

The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross-program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.” [6]

• ↑ 1.0 1.1 1.2 Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
• ↑ 2.0 2.1 Quadratic Assignment Problem. (2020). Retrieved December 14, 2020, from https://neos-guide.org/content/quadratic-assignment-problem
• ↑ 3.0 3.1 3.2 Burkard, R. E., Çela, E., Pardalos, P. M., & Pitsoulis, L. S. (2013). The Quadratic Assignment Problem. https://www.opt.math.tugraz.at/~cela/papers/qap_bericht.pdf .
• ↑ 4.0 4.1 Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review . 1961;3(1):37.
• ↑ 5.0 5.1 Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977) . 1977;28(1):167. doi:10.2307/300878
• ↑ 6.0 6.1 Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.

Navigation menu

Maximization Transportation Problem

There are certain types of transportation problems where the objective function is to be maximized instead of being minimized.

These problems can be solved by converting the maximization problem into a minimization problem.

"Profit maximization is the single universal objective for most commercial organizations." -Vinay Chhabra & Manish Dewan

Example: Maximization Problem in Transportation

Surya Roshni Ltd. has three factories - X, Y, and Z. It supplies goods to four dealers spread all over the country. The production capacities of these factories are 200, 500 and 300 per month respectively.

Determine a suitable allocation to maximize the total net return.

Maximization transportation problem can be converted into minimization transportation problem by subtracting each transportation cost from maximum transportation cost.

Here, the maximum transportation cost is 25. So subtract each value from 25. The revised transportation problem is shown below.

An initial basic feasible solution is obtained by matrix minimum method and is shown in the final table.

Final table

Use Horizontal Scrollbar to View Full Table Calculation.

The maximum net return is

25 X 200 + 8 X 80 + 7 X 320 + 10 X 100 + 14 X 100 + 20 X 200 = 14280.

Share this article with your friends

Operations Research Simplified Back Next

Goal programming Linear programming Simplex Method Assignment Problem

Secret Service removes agent from Kamala Harris' detail after 'distressing' behavior

WASHINGTON — A Secret Service special agent was removed from Vice President Kamala Harris' detail after having exhibited "distressing" behavior this week, a spokesperson confirmed Thursday.

The agent, whose identity has not been disclosed, had been involved with the Harris' departure from Joint Base Andrews, Maryland, on Monday morning, when Harris was headed to Wisconsin.

The agent "began displaying behavior their colleagues found distressing," Anthony Guglielmi, chief of communications for the Secret Service, said in a statement Thursday. "The agent was removed from their assignment while medical personnel were summoned."

Harris was not present when the incident took place. She was at the Naval Observatory, the vice president's residence, and Guglielmi said her departure was not affected.

“The U.S. Secret Service takes the safety and health of our employees very seriously,” Guglielmi said. “As this was a medical matter, we will not disclose any further details.”

Additional information about the incident, which was first reported by the Washington Examiner , was not released. The vice president's office did not comment Thursday.

Megan Lebowitz is a politics reporter for NBC News.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.6: Applied Optimization Problems

• Last updated
• Save as PDF
• Page ID 43652

Learning Objectives

• Set up and solve optimization problems in several applied fields.

One common application of calculus is calculating the minimum or maximum value of a function. For example, companies often want to minimize production costs or maximize revenue. In manufacturing, it is often desirable to minimize the amount of material used to package a product with a certain volume. In this section, we show how to set up these types of minimization and maximization problems and solve them by using the tools developed in this chapter.

Solving Optimization Problems over a Closed, Bounded Interval

The basic idea of the optimization problems that follow is the same. We have a particular quantity that we are interested in maximizing or minimizing. However, we also have some auxiliary condition that needs to be satisfied. For example, in Example \(\PageIndex{1}\), we are interested in maximizing the area of a rectangular garden. Certainly, if we keep making the side lengths of the garden larger, the area will continue to become larger. However, what if we have some restriction on how much fencing we can use for the perimeter? In this case, we cannot make the garden as large as we like. Let’s look at how we can maximize the area of a rectangle subject to some constraint on the perimeter.

Example \(\PageIndex{1}\): Maximizing the Area of a Garden

A rectangular garden is to be constructed using a rock wall as one side of the garden and wire fencing for the other three sides (Figure \(\PageIndex{1}\)). Given \(100\,\text{ft}\) of wire fencing, determine the dimensions that would create a garden of maximum area. What is the maximum area?

Let \(x\) denote the length of the side of the garden perpendicular to the rock wall and \(y\) denote the length of the side parallel to the rock wall. Then the area of the garden is

\(A=x⋅y.\)

We want to find the maximum possible area subject to the constraint that the total fencing is \(100\,\text{ft}\). From Figure \(\PageIndex{1}\), the total amount of fencing used will be \(2x+y.\) Therefore, the constraint equation is

\(2x+y=100.\)

Solving this equation for \(y\), we have \(y=100−2x.\) Thus, we can write the area as

\(A(x)=x⋅(100−2x)=100x−2x^2.\)

Before trying to maximize the area function \(A(x)=100x−2x^2,\) we need to determine the domain under consideration. To construct a rectangular garden, we certainly need the lengths of both sides to be positive. Therefore, we need \(x>0\) and \(y>0\). Since \(y=100−2x\), if \(y>0\), then \(x<50\). Therefore, we are trying to determine the maximum value of \(A(x)\) for \(x\) over the open interval \((0,50)\). We do not know that a function necessarily has a maximum value over an open interval. However, we do know that a continuous function has an absolute maximum (and absolute minimum) over a closed interval. Therefore, let’s consider the function \(A(x)=100x−2x^2\) over the closed interval \([0,50]\). If the maximum value occurs at an interior point, then we have found the value \(x\) in the open interval \((0,50)\) that maximizes the area of the garden.

Therefore, we consider the following problem:

Maximize \(A(x)=100x−2x^2\) over the interval \([0,50].\)

As mentioned earlier, since \(A\) is a continuous function on a closed, bounded interval, by the extreme value theorem, it has a maximum and a minimum. These extreme values occur either at endpoints or critical points. At the endpoints, \(A(x)=0\). Since the area is positive for all \(x\) in the open interval \((0,50)\), the maximum must occur at a critical point. Differentiating the function \(A(x)\), we obtain

\(A′(x)=100−4x.\)

Therefore, the only critical point is \(x=25\) (Figure \(\PageIndex{2}\)). We conclude that the maximum area must occur when \(x=25\).

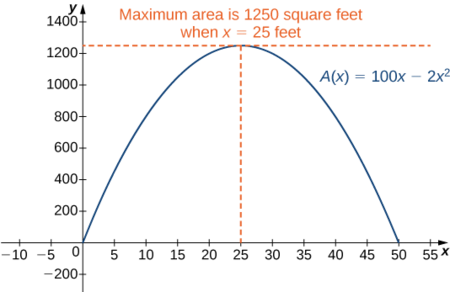
Then we have \(y=100−2x=100−2(25)=50.\) To maximize the area of the garden, let \(x=25\,\text{ft}\) and \(y=50\,\text{ft}\). The area of this garden is \(1250\, \text{ft}^2\).

Exercise \(\PageIndex{1}\)

Determine the maximum area if we want to make the same rectangular garden as in Figure \(\PageIndex{2}\), but we have \(200\,\text{ft}\) of fencing.

We need to maximize the function \(A(x)=200x−2x^2\) over the interval \([0,100].\)

The maximum area is \(5000\, \text{ft}^2\).

Now let’s look at a general strategy for solving optimization problems similar to Example \(\PageIndex{1}\).

Problem-Solving Strategy: Solving Optimization Problems

• Introduce all variables. If applicable, draw a figure and label all variables.
• Determine which quantity is to be maximized or minimized, and for what range of values of the other variables (if this can be determined at this time).
• Write a formula for the quantity to be maximized or minimized in terms of the variables. This formula may involve more than one variable.
• Write any equations relating the independent variables in the formula from step \(3\). Use these equations to write the quantity to be maximized or minimized as a function of one variable.
• Identify the domain of consideration for the function in step \(4\) based on the physical problem to be solved.
• Locate the maximum or minimum value of the function from step \(4.\) This step typically involves looking for critical points and evaluating a function at endpoints.

Now let’s apply this strategy to maximize the volume of an open-top box given a constraint on the amount of material to be used.

Example \(\PageIndex{2}\): Maximizing the Volume of a Box

An open-top box is to be made from a \(24\,\text{in.}\) by \(36\,\text{in.}\) piece of cardboard by removing a square from each corner of the box and folding up the flaps on each side. What size square should be cut out of each corner to get a box with the maximum volume?

Step 1: Let \(x\) be the side length of the square to be removed from each corner (Figure \(\PageIndex{3}\)). Then, the remaining four flaps can be folded up to form an open-top box. Let \(V\) be the volume of the resulting box.

Step 2: We are trying to maximize the volume of a box. Therefore, the problem is to maximize \(V\).

Step 3: As mentioned in step 2, are trying to maximize the volume of a box. The volume of a box is

\[V=L⋅W⋅H \nonumber, \nonumber \]

where \(L,\,W,\)and \(H\) are the length, width, and height, respectively.

Step 4: From Figure \(\PageIndex{3}\), we see that the height of the box is \(x\) inches, the length is \(36−2x\) inches, and the width is \(24−2x\) inches. Therefore, the volume of the box is

\[ \begin{align*} V(x) &=(36−2x)(24−2x)x \\[4pt] &=4x^3−120x^2+864x \end{align*}. \nonumber \]

Step 5: To determine the domain of consideration, let’s examine Figure \(\PageIndex{3}\). Certainly, we need \(x>0.\) Furthermore, the side length of the square cannot be greater than or equal to half the length of the shorter side, \(24\,\text{in.}\); otherwise, one of the flaps would be completely cut off. Therefore, we are trying to determine whether there is a maximum volume of the box for \(x\) over the open interval \((0,12).\) Since \(V\) is a continuous function over the closed interval \([0,12]\), we know \(V\) will have an absolute maximum over the closed interval. Therefore, we consider \(V\) over the closed interval \([0,12]\) and check whether the absolute maximum occurs at an interior point.

Step 6: Since \(V(x)\) is a continuous function over the closed, bounded interval \([0,12]\), \(V\) must have an absolute maximum (and an absolute minimum). Since \(V(x)=0\) at the endpoints and \(V(x)>0\) for \(0<x<12,\) the maximum must occur at a critical point. The derivative is

\(V′(x)=12x^2−240x+864.\)

To find the critical points, we need to solve the equation

\(12x^2−240x+864=0.\)

Dividing both sides of this equation by \(12\), the problem simplifies to solving the equation

\(x^2−20x+72=0.\)

Using the quadratic formula, we find that the critical points are

\[\begin{align*} x &=\dfrac{20±\sqrt{(−20)^2−4(1)(72)}}{2} \\[4pt] &=\dfrac{20±\sqrt{112}}{2} \\[4pt] &=\dfrac{20±4\sqrt{7}}{2} \\[4pt] &=10±2\sqrt{7} \end{align*}. \nonumber \]

Since \(10+2\sqrt{7}\) is not in the domain of consideration, the only critical point we need to consider is \(10−2\sqrt{7}\). Therefore, the volume is maximized if we let \(x=10−2\sqrt{7}\,\text{in.}\) The maximum volume is

\[V(10−2\sqrt{7})=640+448\sqrt{7}≈1825\,\text{in}^3. \nonumber \]

as shown in the following graph.

Exercise \(\PageIndex{2}\)

Suppose the dimensions of the cardboard in Example \(\PageIndex{2}\) are \(20\,\text{in.}\) by \(30\,\text{in.}\) Let \(x\) be the side length of each square and write the volume of the open-top box as a function of \(x\). Determine the domain of consideration for \(x\).

The volume of the box is \(L⋅W⋅H.\)

\(V(x)=x(20−2x)(30−2x).\) The domain is \([0,10]\).

Example \(\PageIndex{3}\): Minimizing Travel Time

An island is \(2\) mi due north of its closest point along a straight shoreline. A visitor is staying at a cabin on the shore that is \(6\) mi west of that point. The visitor is planning to go from the cabin to the island. Suppose the visitor runs at a rate of \(8\) mph and swims at a rate of \(3\) mph. How far should the visitor run before swimming to minimize the time it takes to reach the island?

Step 1: Let \(x\) be the distance running and let \(y\) be the distance swimming (Figure \(\PageIndex{5}\)). Let \(T\) be the time it takes to get from the cabin to the island.

Step 2: The problem is to minimize \(T\).

Step 3: To find the time spent traveling from the cabin to the island, add the time spent running and the time spent swimming. Since Distance = Rate × Time \((D=R×T),\) the time spent running is

\(T_{running}=\dfrac{D_{running}}{R_{running}}=\dfrac{x}{8}\),

and the time spent swimming is

\(T_{swimming}=\dfrac{D_{swimming}}{R_{swimming}}=\dfrac{y}{3}\).

Therefore, the total time spent traveling is

\(T=\dfrac{x}{8}+\dfrac{y}{3}\).

Step 4: From Figure \(\PageIndex{5}\), the line segment of \(y\) miles forms the hypotenuse of a right triangle with legs of length \(2\) mi and \(6−x\) mi. Therefore, by the Pythagorean theorem, \(2^2+(6−x)^2=y^2\), and we obtain \(y=\sqrt{(6−x)^2+4}\). Thus, the total time spent traveling is given by the function

\(T(x)=\dfrac{x}{8}+\dfrac{\sqrt{(6−x)^2+4}}{3}\).

Step 5: From Figure \(\PageIndex{5}\), we see that \(0≤x≤6\). Therefore, \([0,6]\) is the domain of consideration.

Step 6: Since \(T(x)\) is a continuous function over a closed, bounded interval, it has a maximum and a minimum. Let’s begin by looking for any critical points of \(T\) over the interval \([0,6].\) The derivative is

\[\begin{align*} T′(x) &=\dfrac{1}{8}−\dfrac{1}{2}\dfrac{[(6−x)^2+4]^{−1/2}}{3}⋅2(6−x) \\[4pt] &=\dfrac{1}{8}−\dfrac{(6−x)}{3\sqrt{(6−x)^2+4}} \end{align*}\]

If \(T′(x)=0,\), then

\[\dfrac{1}{8}=\dfrac{6−x}{3\sqrt{(6−x)^2+4}} \label{ex3eq1} \]

\[3\sqrt{(6−x)^2+4}=8(6−x). \label{ex3eq2} \]

Squaring both sides of this equation, we see that if \(x\) satisfies this equation, then \(x\) must satisfy

\[9[(6−x)^2+4]=64(6−x)^2,\nonumber \]

which implies

\[55(6−x)^2=36. \nonumber \]

We conclude that if \(x\) is a critical point, then \(x\) satisfies

\[(x−6)^2=\dfrac{36}{55}. \nonumber \]

[Note that since we are squaring, \( (x-6)^2 = (6-x)^2.\)]

Therefore, the possibilities for critical points are

\[x=6±\dfrac{6}{\sqrt{55}}.\nonumber \]

Since \(x=6+6/\sqrt{55}\) is not in the domain, it is not a possibility for a critical point. On the other hand, \(x=6−6/\sqrt{55}\) is in the domain. Since we squared both sides of Equation \ref{ex3eq2} to arrive at the possible critical points, it remains to verify that \(x=6−6/\sqrt{55}\) satisfies Equation \ref{ex3eq1}. Since \(x=6−6/\sqrt{55}\) does satisfy that equation, we conclude that \(x=6−6/\sqrt{55}\) is a critical point, and it is the only one. To justify that the time is minimized for this value of \(x\), we just need to check the values of \(T(x)\) at the endpoints \(x=0\) and \(x=6\), and compare them with the value of \(T(x)\) at the critical point \(x=6−6/\sqrt{55}\). We find that \(T(0)≈2.108\,\text{h}\) and \(T(6)≈1.417\,\text{h}\), whereas

\[T(6−6/\sqrt{55})≈1.368\,\text{h}. \nonumber \]

Therefore, we conclude that \(T\) has a local minimum at \(x≈5.19\) mi.

Exercise \(\PageIndex{3}\)

Suppose the island is \(1\) mi from shore, and the distance from the cabin to the point on the shore closest to the island is \(15\) mi. Suppose a visitor swims at the rate of \(2.5\) mph and runs at a rate of \(6\) mph. Let \(x\) denote the distance the visitor will run before swimming, and find a function for the time it takes the visitor to get from the cabin to the island.

The time \(T=T_{running}+T_{swimming}.\)

\(T(x)=\dfrac{x}{6}+\dfrac{\sqrt{(15−x)^2+1}}{2.5} \)

In business, companies are interested in maximizing revenue. In the following example, we consider a scenario in which a company has collected data on how many cars it is able to lease, depending on the price it charges its customers to rent a car. Let’s use these data to determine the price the company should charge to maximize the amount of money it brings in.

Example \(\PageIndex{4}\): Maximizing Revenue

Owners of a car rental company have determined that if they charge customers \(p\) dollars per day to rent a car, where \(50≤p≤200\), the number of cars \(n\) they rent per day can be modeled by the linear function \(n(p)=1000−5p\). If they charge \($50\) per day or less, they will rent all their cars. If they charge \($200\) per day or more, they will not rent any cars. Assuming the owners plan to charge customers between \($50\) per day and \($200\) per day to rent a car, how much should they charge to maximize their revenue?

Step 1: Let \(p\) be the price charged per car per day and let \(n\) be the number of cars rented per day. Let \(R\) be the revenue per day.

Step 2: The problem is to maximize \(R.\)

Step 3: The revenue (per day) is equal to the number of cars rented per day times the price charged per car per day—that is, \(R=n×p.\)

Step 4: Since the number of cars rented per day is modeled by the linear function \(n(p)=1000−5p,\) the revenue \(R\) can be represented by the function

\[ \begin{align*} R(p) &=n×p \\[4pt] &=(1000−5p)p \\[4pt] &=−5p^2+1000p.\end{align*}\]

Step 5: Since the owners plan to charge between \($50\) per car per day and \($200\) per car per day, the problem is to find the maximum revenue \(R(p)\) for \(p\) in the closed interval \([50,200]\).

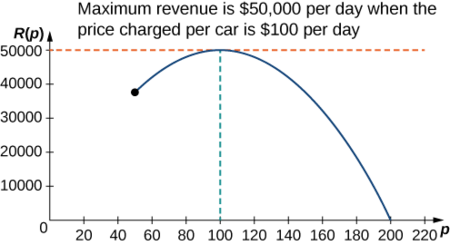
Step 6: Since \(R\) is a continuous function over the closed, bounded interval \([50,200]\), it has an absolute maximum (and an absolute minimum) in that interval. To find the maximum value, look for critical points. The derivative is \(R′(p)=−10p+1000.\) Therefore, the critical point is \(p=100\). When \(p=100, R(100)=$50,000.\) When \(p=50, R(p)=$37,500\). When \(p=200, R(p)=$0\).

Therefore, the absolute maximum occurs at \(p=$100\). The car rental company should charge \($100\) per day per car to maximize revenue as shown in the following figure.

Exercise \(\PageIndex{4}\)

A car rental company charges its customers \(p\) dollars per day, where \(60≤p≤150\). It has found that the number of cars rented per day can be modeled by the linear function \(n(p)=750−5p.\) How much should the company charge each customer to maximize revenue?

\(R(p)=n×p,\) where \(n\) is the number of cars rented and \(p\) is the price charged per car.

The company should charge \($75\) per car per day.

Example \(\PageIndex{5}\): Maximizing the Area of an Inscribed Rectangle

A rectangle is to be inscribed in the ellipse

\[\dfrac{x^2}{4}+y^2=1. \nonumber \]

What should the dimensions of the rectangle be to maximize its area? What is the maximum area?

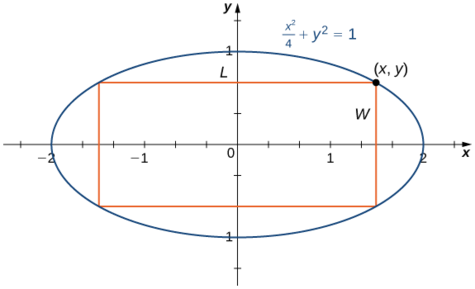
Step 1: For a rectangle to be inscribed in the ellipse, the sides of the rectangle must be parallel to the axes. Let \(L\) be the length of the rectangle and \(W\) be its width. Let \(A\) be the area of the rectangle.

Step 2: The problem is to maximize \(A\).

Step 3: The area of the rectangle is \(A=LW.\)

Step 4: Let \((x,y)\) be the corner of the rectangle that lies in the first quadrant, as shown in Figure \(\PageIndex{7}\). We can write length \(L=2x\) and width \(W=2y\). Since \(\dfrac{x^2}{4}+y^2=1\) and \(y>0\), we have \(y=\sqrt{1-\dfrac{x^2}{4}}\). Therefore, the area is

\(A=LW=(2x)(2y)=4x\sqrt{1-\dfrac{x^2}{4}}=2x\sqrt{4−x^2}\)

Step 5: From Figure \(\PageIndex{7}\), we see that to inscribe a rectangle in the ellipse, the \(x\)-coordinate of the corner in the first quadrant must satisfy \(0<x<2\). Therefore, the problem reduces to looking for the maximum value of \(A(x)\) over the open interval \((0,2)\). Since \(A(x)\) will have an absolute maximum (and absolute minimum) over the closed interval \([0,2]\), we consider \(A(x)=2x\sqrt{4−x^2}\) over the interval \([0,2]\). If the absolute maximum occurs at an interior point, then we have found an absolute maximum in the open interval.

Step 6: As mentioned earlier, \(A(x)\) is a continuous function over the closed, bounded interval \([0,2]\). Therefore, it has an absolute maximum (and absolute minimum). At the endpoints \(x=0\) and \(x=2\), \(A(x)=0.\) For \(0<x<2\), \(A(x)>0\).

Therefore, the maximum must occur at a critical point. Taking the derivative of \(A(x)\), we obtain

\[ \begin{align*} A'(x) &=2\sqrt{4−x^2}+2x⋅\dfrac{1}{2\sqrt{4−x^2}}(−2x) \\[4pt] &=2\sqrt{4−x^2}−\dfrac{2x^2}{\sqrt{4−x^2}} \\[4pt] &=\dfrac{8−4x^2}{\sqrt{4−x^2}} . \end{align*}\]

To find critical points, we need to find where \(A'(x)=0.\) We can see that if \(x\) is a solution of

\[\dfrac{8−4x^2}{\sqrt{4−x^2}}=0, \label{ex5eq1} \]

then \(x\) must satisfy

\[8−4x^2=0. \nonumber \]

Therefore, \(x^2=2.\) Thus, \(x=±\sqrt{2}\) are the possible solutions of Equation \ref{ex5eq1}. Since we are considering \(x\) over the interval \([0,2]\), \(x=\sqrt{2}\) is a possibility for a critical point, but \(x=−\sqrt{2}\) is not. Therefore, we check whether \(\sqrt{2}\) is a solution of Equation \ref{ex5eq1}. Since \(x=\sqrt{2}\) is a solution of Equation \ref{ex5eq1}, we conclude that \(\sqrt{2}\) is the only critical point of \(A(x)\) in the interval \([0,2]\).

Therefore, \(A(x)\) must have an absolute maximum at the critical point \(x=\sqrt{2}\). To determine the dimensions of the rectangle, we need to find the length \(L\) and the width \(W\). If \(x=\sqrt{2}\) then

\[y=\sqrt{1−\dfrac{(\sqrt{2})^2}{4}}=\sqrt{1−\dfrac{1}{2}}=\dfrac{1}{\sqrt{2}}.\nonumber \]

Therefore, the dimensions of the rectangle are \(L=2x=2\sqrt{2}\) and \(W=2y=\dfrac{2}{\sqrt{2}}=\sqrt{2}\). The area of this rectangle is \( A=LW=(2\sqrt{2})(\sqrt{2})=4.\)

Exercise \(\PageIndex{5}\)

Modify the area function \(A\) if the rectangle is to be inscribed in the unit circle \(x^2+y^2=1\). What is the domain of consideration?

If \((x,y)\) is the vertex of the square that lies in the first quadrant, then the area of the square is \(A=(2x)(2y)=4xy.\)

\(A(x)=4x\sqrt{1−x^2}.\) The domain of consideration is \([0,1]\).

Solving Optimization Problems when the Interval Is Not Closed or Is Unbounded

In the previous examples, we considered functions on closed, bounded domains. Consequently, by the extreme value theorem, we were guaranteed that the functions had absolute extrema. Let’s now consider functions for which the domain is neither closed nor bounded.

Many functions still have at least one absolute extrema, even if the domain is not closed or the domain is unbounded. For example, the function \(f(x)=x^2+4\) over \((−∞,∞)\) has an absolute minimum of \(4\) at \(x=0\). Therefore, we can still consider functions over unbounded domains or open intervals and determine whether they have any absolute extrema. In the next example, we try to minimize a function over an unbounded domain. We will see that, although the domain of consideration is \((0,∞),\) the function has an absolute minimum.

In the following example, we look at constructing a box of least surface area with a prescribed volume. It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the smallest surface area. Consequently, we consider the modified problem of determining which open-topped box with a specified volume has the smallest surface area.

Example \(\PageIndex{6}\): Minimizing Surface Area

A rectangular box with a square base, an open top, and a volume of \(216 \,\text{in}^3\) is to be constructed. What should the dimensions of the box be to minimize the surface area of the box? What is the minimum surface area?

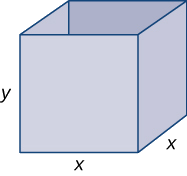
Step 1: Draw a rectangular box and introduce the variable \(x\) to represent the length of each side of the square base; let \(y\) represent the height of the box. Let \(S\) denote the surface area of the open-top box.

Step 2: We need to minimize the surface area. Therefore, we need to minimize \(S\).

Step 3: Since the box has an open top, we need only determine the area of the four vertical sides and the base. The area of each of the four vertical sides is \(x⋅y.\) The area of the base is \(x^2\). Therefore, the surface area of the box is

\(S=4xy+x^2\).

Step 4: Since the volume of this box is \(x^2y\) and the volume is given as \(216\,\text{in}^3\), the constraint equation is

\(x^2y=216\).

Solving the constraint equation for \(y\), we have \(y=\dfrac{216}{x^2}\). Therefore, we can write the surface area as a function of \(x\) only:

\[S(x)=4x\left(\dfrac{216}{x^2}\right)+x^2.\nonumber \]

Therefore, \(S(x)=\dfrac{864}{x}+x^2\).

Step 5: Since we are requiring that \(x^2y=216\), we cannot have \(x=0\). Therefore, we need \(x>0\). On the other hand, \(x\) is allowed to have any positive value. Note that as \(x\) becomes large, the height of the box \(y\) becomes correspondingly small so that \(x^2y=216\). Similarly, as \(x\) becomes small, the height of the box becomes correspondingly large. We conclude that the domain is the open, unbounded interval \((0,∞)\). Note that, unlike the previous examples, we cannot reduce our problem to looking for an absolute maximum or absolute minimum over a closed, bounded interval. However, in the next step, we discover why this function must have an absolute minimum over the interval \((0,∞).\)

Step 6: Note that as \(x→0^+,\, S(x)→∞.\) Also, as \(x→∞, \,S(x)→∞\). Since \(S\) is a continuous function that approaches infinity at the ends, it must have an absolute minimum at some \(x∈(0,∞)\). This minimum must occur at a critical point of \(S\). The derivative is

\[S′(x)=−\dfrac{864}{x^2}+2x.\nonumber \]

Therefore, \(S′(x)=0\) when \(2x=\dfrac{864}{x^2}\). Solving this equation for \(x\), we obtain \(x^3=432\), so \(x=\sqrt[3]{432}=6\sqrt[3]{2}.\) Since this is the only critical point of \(S\), the absolute minimum must occur at \(x=6\sqrt[3]{2}\) (see Figure \(\PageIndex{9}\)).

When \(x=6\sqrt[3]{2}\), \(y=\dfrac{216}{(6\sqrt[3]{2})^2}=3\sqrt[3]{2}\,\text{in.}\) Therefore, the dimensions of the box should be \(x=6\sqrt[3]{2}\,\text{in.}\) and \(y=3\sqrt[3]{2}\,\text{in.}\) With these dimensions, the surface area is

\[S(6\sqrt[3]{2})=\dfrac{864}{6\sqrt[3]{2}}+(6\sqrt[3]{2})^2=108\sqrt[3]{4}\,\text{in}^2\nonumber \]

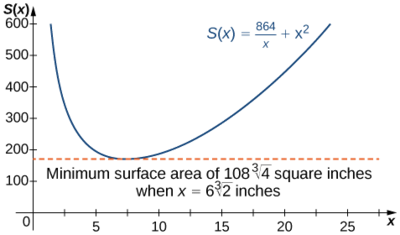
Exercise \(\PageIndex{6}\)

Consider the same open-top box, which is to have volume \(216\,\text{in}^3\). Suppose the cost of the material for the base is \(20¢/\text{in}^2\) and the cost of the material for the sides is \(30¢/\text{in}^2\) and we are trying to minimize the cost of this box. Write the cost as a function of the side lengths of the base. (Let \(x\) be the side length of the base and \(y\) be the height of the box.)

If the cost of one of the sides is \(30¢/\text{in}^2,\) the cost of that side is \(0.30xy\) dollars.

\(c(x)=\dfrac{259.2}{x}+0.2x^2\) dollars

Key Concepts

• To solve an optimization problem, begin by drawing a picture and introducing variables.
• Find an equation relating the variables.
• Find a function of one variable to describe the quantity that is to be minimized or maximized.
• Look for critical points to locate local extrema.