problem solving involving quadratic inequality

Solving Quadratic Inequalities

... and more ...

A Quadratic Equation (in Standard Form) looks like:

The above is an equation (=) but sometimes we need to solve inequalities like these:

Solving inequalities is very like solving equations ... we do most of the same things.

So this is what we do:

• find the "=0" points
• greater than zero (>0), or
• less than zero (<0)
• then pick a test value to find out which it is (>0 or <0)

Here is an example:

Example: x 2 − x − 6 < 0

x 2 − x − 6 has these simple factors (what luck!):

(x+2)(x−3) < 0

Firstly , let us find where it is equal to zero:

(x+2)(x−3) = 0

It is equal to zero when x = −2 or x = +3 because when x = −2, then (x+2) is zero or when x = +3, then (x−3) is zero

So between −2 and +3, the function will either be

• always greater than zero, or
• always less than zero

We don't know which ... yet!

Let's pick a value in-between (say x=0) and test it:

So between x=−2 and x=+3, the function is less than zero.

And that is the region we want, so...

x 2 − x − 6 < 0 in the interval (−2, 3)

Note: x 2 − x − 6 > 0   in the interval (−∞,−2) and (3, +∞)

Also try the Inequality Grapher .

What If It Doesn't Go Through Zero?

A "real world" example, a stuntman will jump off a 20 m building. a high-speed camera is ready to film him between 15 m and 10 m above the ground..

When should the camera film him?

We can use this formula for distance and time:

d = 20 − 5t 2

• d = distance above ground (m), and
• t = time from jump (seconds)

(Note: if you are curious about the formula, it is simplified from d = d 0 + v 0 t + ½a 0 t 2 , where d 0 =20 , v 0 =0 , and a 0 =−9.81 the acceleration due to gravity.)

OK, let's go.

First , let us sketch the question:

The distance we want is from 10 m to 15 m :

10 < d < 15

And we know the formula for d :

10 < 20 − 5t 2 < 15

Now let's solve it!

First, let's subtract 20 from both sides:

−10 < −5t 2 <−5

 Now multiply both sides by −(1/5). But because we are multiplying by a negative number, the inequalities will change direction ... read Solving Inequalities to see why.

2 > t 2 > 1

To be neat, the smaller number should be on the left, and the larger on the right. So let's swap them over (and make sure the inequalities still point correctly):

1 < t 2 < 2

 Lastly, we can safely take square roots, since all values are greater then zero:

√1 < t < √2

We can tell the film crew:

"Film from 1.0 to 1.4 seconds after jumping"

Higher Than Quadratic

The same ideas can help us solve more complicated inequalities:

Example: x 3 + 4 ≥ 3x 2 + x

First, let's put it in standard form:

x 3 − 3x 2 − x + 4 ≥ 0

This is a cubic equation (the highest exponent is a cube, i.e. x 3 ), and is hard to solve, so let us graph it instead:

The zero points are approximately :

And from the graph we can see the intervals where it is greater than (or equal to) zero:

• From −1.1 to 1.3, and
• From 2.9 on

In interval notation we can write:

Approximately: [−1.1, 1.3] U [2.9, +∞)

Quadratic Inequalities Practice Questions

Click here for questions, click here for answers.

quadratic inequality

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Quadratic Inequalities – Explanation & Examples

Solving Quadratic Inequalities – Explanation & Examples

A quadratic inequality is an equation of second degree that uses an inequality sign instead of an equal sign.

The solutions to quadratic inequality always give the two roots. The nature of the roots may differ and can be determined by discriminant (b 2 – 4ac).

The general forms of the quadratic inequalities are:

ax 2 + bx + c < 0

ax 2 + bx + c ≤ 0

ax 2 + bx + c > 0

ax 2 + bx + c ≥ 0

Examples of quadratic inequalities are:

x 2 – 6x – 16 ≤ 0, 2x 2  – 11x + 12 > 0, x 2  + 4 > 0, x 2  – 3x + 2 ≤ 0 etc.

How to Solve Quadratic Inequalities?

Examples of quadratic inequalities are: x 2 – 6x – 16 ≤ 0, 2x 2  – 11x + 12 > 0, x 2  + 4 > 0, x 2  – 3x + 2 ≤ 0 etc.

Solving a quadratic inequality in Algebra is similar to solving a quadratic equation. The only exception is that, with quadratic equations, you equate the expressions to zero, but with inequalities, you’re interested in knowing what’s on either side of the zero i.e. negatives and positives.

Quadratic equations can be solved by either the factorization method or by use of the quadratic formula . Before we can learn how to solve quadratic inequalities, let’s recall how quadratic equations are solved by handling a few examples.

How Quadratic Equations are Solved by Factorization Method?

Since we know we can similarly solve quadratic inequalities as quadratic equations, it is useful to understand how to factorize the given equation or inequality.

Let’s see a few examples here.

• 6x 2 – 7x + 2 = 0

⟹ 6x 2  – 4x – 3x + 2 = 0

Factorize the expression;

⟹ 2x (3x – 2) – 1(3x – 2) = 0

⟹ (3x – 2) (2x – 1) = 0

⟹ 3x – 2 = 0 or 2x – 1 = 0

⟹ 3x = 2 or 2x = 1

⟹ x = 2/3 or x = 1/2

Therefore, x = 2/3, ½

• Solve 3x 2 – 6x + 4x – 8 = 0

Factorize the expression on the left-hand side.

⟹ 3x 2  – 6x + 4x – 8 = 0

⟹ 3x (x – 2) + 4(x – 2) = 0

⟹ (x – 2) (3x + 4) = 0

⟹ x – 2 = 0 or 3x + 4 = 0

⟹ x = 2 or x = -4/3

Therefore, the roots of the quadratic equation are, x = 2, -4/3.

• Solve 2(x 2 + 1) = 5x

2x 2 + 2 = 5x

⟹ 2x 2  – 5x + 2 = 0

⟹ 2x 2  – 4x – x + 2 = 0

⟹ 2x (x – 2) – 1(x – 2) = 0

⟹ (x – 2) (2x – 1) = 0

⟹ x – 2 = 0 or 2x – 1 = 0

⟹ x = 2 or x = 1/2

Therefore, the solutions are x = 2, 1/2.

• (2x – 3) 2 = 25

Expand and factorize the expression.

(2x – 3) 2  = 25

⟹ 4x 2  – 12x + 9 – 25 = 0

⟹ 4x 2  – 12x – 16 = 0

⟹ x 2  – 3x – 4 = 0

⟹ (x – 4) (x + 1) = 0

⟹ x = 4 or x = -1

• Solve x 2 + (4 – 3y) x – 12y = 0

Expand the equation;

x 2  + 4x – 3xy – 12y = 0

⟹ x (x + 4) – 3y (x + 4) = 0

x + 4) (x – 3y) = 0

⟹ x + 4 = 0 or x – 3y = 0

⟹ x = -4 or x = 3y

Thus, x = -4 or x = 3y

To solve a quadratic inequality, we also apply the same method as illustrated in the procedure below:

• Write the quadratic inequality in standard form: ax 2  + bx + c where a, b and are coefficients and a ≠ 0
• Determine the roots of the inequality.
• Write the solution in inequality notation or interval notation.

Solve the inequality x 2  – 4x > –3

First, make one side one side of the inequality zero by adding both sides by 3.

x 2  – 4x > –3 ⟹ x 2  – 4x + 3 > 0

Factor the left side of the inequality.

x 2  – 4x + 3 > 0 ⟹ (x – 3) (x – 1) > 0

Solve for all the zeroes for the inequality;

For, (x – 1) > 0 ⟹ x > 1 and for, (x – 3) > 0 ⟹ x>3

Since y is positive, we therefore choose the values of x which the curve will be above the x-axis. x < 1 or x > 3

Solve the inequality x 2  – x > 12.

To write the inequality in standard form, subtract both sides of the inequality by 12.

x 2  – x > 12 ⟹ x 2  – x – 12 > 0.

Factorize the quadratic inequality to get to;

( x  – 4) ( x  + 3) > 0

For, (x + 3) > 0 ⟹ x > -3

For x – 4 > 0 ⟹ x > 4

The values x < –3 or x > 4 are therefore the solution of this quadratic inequality.

Solve 2x 2  < 9x + 5

Write the inequality in standard form by making one side of the inequality zero.

2x 2  < 9x + 5 ⟹ 2x 2  – 9x – 5 < 0

Factor the left side of the quadratic inequality.

2x 2  – 9x – 5 < 0 ⟹ (2x + 1) (x – 5) < 0

Solve for all the zeroes for the inequality

For, (x – 5) < 0 ⟹ x < 5 and for (2x + 1) < 0 ⟹ x < -1/2

Since y is negative for the equation 2x 2  – 9x – 5 < 0, we therefore choose the values of x which the curve will be below the x axis.

Therefore, the solution is   -1/2 < x < 5

Solve – x 2 + 4 < 0.

Since the inequality is already in standard form, we therefore factor the expression.

-x 2 + 4 < 0 ⟹ (x + 2) (x – 2) < 0

For, (x + 2) < 0 ⟹ x < -2 and for, (x – 2) < 0 ⟹ x < 2

The y for –x 2 + 4 < 0 is negative; therefore, we choose the values of x in which the curve will below the x- axis: –2 < x > 2

Solve 2x 2  + x − 15 ≤ 0.

Factor the quadratic equation.

2x 2  + x − 15 = 0

2x 2  + 6x – 5x− 15 = 0

2x (x + 3) – 5(x + 3) = 0

(2x – 5) (x + 3) = 0

For, 2x – 5 = 0 ⟹ x= 5/2 and for, x + 3= 0 ⟹ x = -3

Since the y for 2x 2  + x − 15 ≤ 0 is negative, the we choose the values of x in which the curve will be below the x axis. Therefore, x ≤ -3 or x ≥5/2 is the solution.

Solve – x 2  + 3x − 2 ≥ 0

Multiply the quadratic equation by -1 and remember to change the sign.

x 2  – 3x + 2 = 0

x 2  – 1x – 2x + 2 = 0

x (x – 1) – 2(x – 1) = 0

(x – 2) (x – 1) = 0

For, x – 2 = 0 ⟹ x = 2 and for, x – 1= 0 ⟹x=1

Therefore, the solution to the quadratic inequality is 1 ≤ x ≤ 2

Solve x 2 − 3x + 2 > 0

Factorize the expression to get;

x 2 − 3x + 2 > 0 ⟹ (x − 2) (x − 1) > 0

Now solve for the roots of the inequality as;

(x − 2) > 0 ⟹ x > 2

(x − 1) > 0 ⟹x > 1

The curve for x 2 − 3x + 2 > 0 has positive y, therefore which choose the values of x in which the curve will be above the x-axis. The solution is hence, x < 1 or x > 2.

Solve −2x 2 + 5x + 12 ≥ 0

Multiply the entire expression by -1 and change the inequality sign

−2x 2 + 5x + 12 ≥ 0 ⟹2x 2 − 5x − 12 ≤ 0

(2x + 3) (x − 4) ≤ 0.

Solve the roots;

(2x + 3) ≤ 0 ⟹ x ≤ -3/2.

(x − 4) ≤ 0 ⟹ x ≤ 4.

By applying the rule; (x – a) (x – b) ≥ 0, then a ≤ x ≤ b, we can comfortably write the solutions of this quadratic inequality as:

-3/2 ≤ x ≤ 4.

x 2  − x − 6 < 0

Factorize x 2  − x − 6 to get;

(x + 2) (x − 3) < 0

Find the roots of the equation as;

(x + 2) (x − 3) = 0

x = −2 or x = +3 Because y is negative for x 2  − x − 6 < 0, then we choose an interval in which the curve will be below the x axis. Therefore, -2 < x < 3 is the solution.

Practice Questions

Previous lesson  |  main page | next lesson.

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

In order to access this I need to be confident with:

This topic is relevant for:

Quadratic inequalities

Quadratic Inequalities

Here we will learn about quadratic inequalities including how to solve quadratic inequalities, identify solution sets using inequality notation and represent solutions on a number line.

There are also quadratic inequalities worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are quadratic inequalities?

Quadratic inequalities are similar to quadratic equations and when plotted they display a parabola. We can solve quadratic inequalities to give a range of solutions.

For example,

The quadratic equation x^{2}+ 6x +5 = 0 has two solutions .

This is shown on the graph below where the parabola crosses the x axis.  

We could solve this by factorising: (x + 1)(x + 5) = 0 .

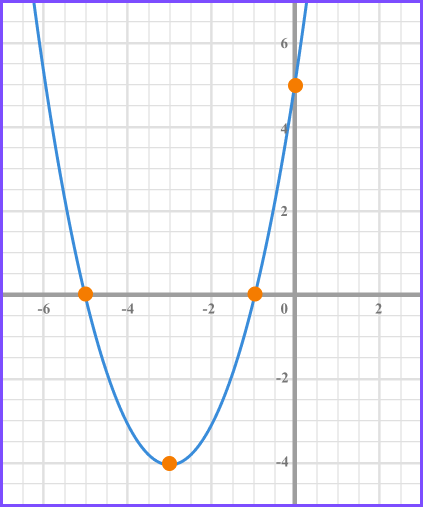
The two values of x that equate this equation to zero are x = - 1 and x = - 5 .

The quadratic inequality x^{2}+ 6x +5  \leq 0 can be solved by factorising but instead of two solutions, there are a range of solutions .

x^{2}+ 6x +5 \leq 0 means that the we need to know the x values that when the graph is less than 0 .

This corresponds to where the curve is below the x axis .

We can see the from the graph that the x values need to be between -1 and -5 .

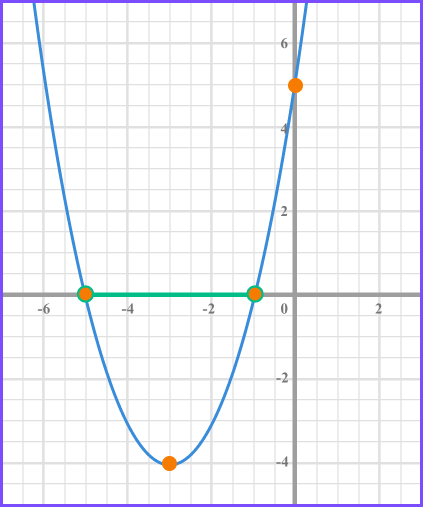
Therefore the solution to this inequality can be written using inequality notation,

-5\leq x \leq-1 .

The quadratic inequality x^{2} + 6x +5 > 0 is similar to the previous inequality and has a range of solutions.

x^{2}+ 6x +5 > 0 means that we need to know the x values when the graph is greater than 0 . 

This corresponds to where the curve is above the x axis .

We can see the from the graph that the x values need to be greater than -1 and less than -5 .

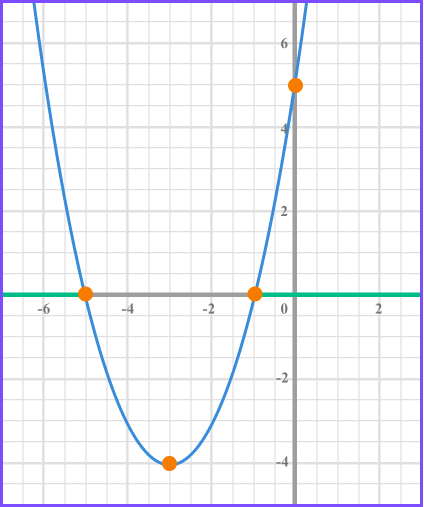
Therefore the solution to this inequality can be written using inequality notation as two inequalities  x > -1 or x < -5 .

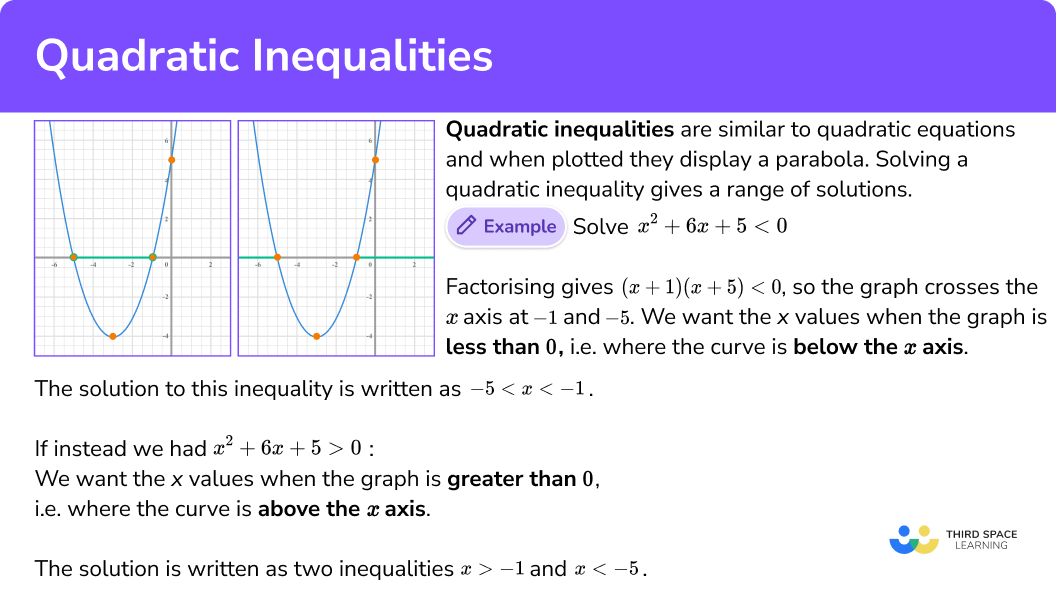
How to solve quadratic inequalities

In order to solve quadratic inequalities by factorising:

Factorise the quadratic expression.

Find the values of x that make each bracket equal zero.

Write the solution using inequality notation.

In order to solve quadratic inequalities by using the quadratic formula:

Identify values of a, b and c to substitute into the quadratic formula.

• Solve the quadratic inequality using the quadratic formula.

Simplify to calculate the solutions of the inequality.

How to solve quadratic inequalities by factorising

How to solve quadratic inequalities by using the quadratic formula

Quadratic inequalities worksheet

Get your free quadratic inequalities worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Related lessons on inequalities

Quadratic inequalities is part of our series of lessons to support revision on inequalities . You may find it helpful to start with the main inequalities lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• Inequalities
• Solving inequalities  
• Inequalities on a number line
• Inequalities on a graph
• Linear inequalities
• Greater than sign
• Less than sign

Quadratic inequalities examples

Example 1: solving by factorising.

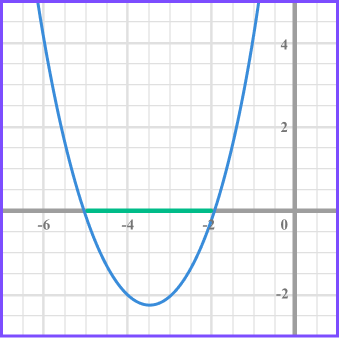
Solve x ^{2}+7x+10 < 0 .

2 Find the values of x that make each bracket equal zero.

(x + 2) = 0 when x = -2

(x + 5) = 0 when x = -5

3 Write the solution using inequality notation.

We need the values of x that produce a graph that is less than 0 and so below the x axis. 

The inequality is given by -5 < x < -2 .

4 Represent the solution set on a number line.

-5 and -2 are not included in the solution set so these values are indicated with open circles.

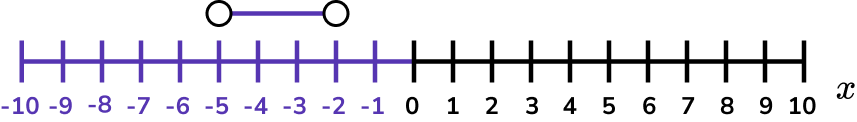
Example 2: solving by factorising

Solve x^{2}+3x+10\leq0 .

(x - 2) = 0 when x = 2

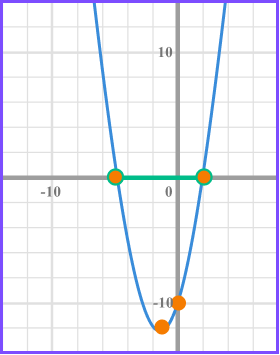
We need the values of x that produce a graph that is less than or equal to 0 and so below the x axis.

The inequality is given by -5\leq x \leq2 .

Represent the solution set on a number line.

-5 and 2 are included in the solution set so these values are indicated with closed circles.

Example 3: solving by factorising

Solve x^{2}-6x+8\geq0 .

Find the values of x that make each bracket equal zero .

(x -2) = 0 when x = 2

(x -4 ) = 0 when x = 4

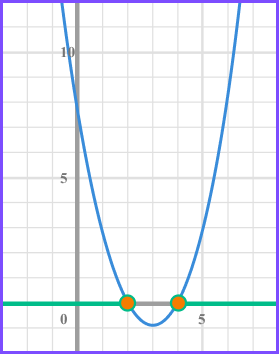
We need the values of x that produce a graph that is greater than or equal to 0 and so above the x axis.

There will be two separate inequalities as there are two separate regions indicated on the graph.

x \geq4 and x \leq2 .

2 and 4 are included in the solution set so these values are indicated with closed circles.

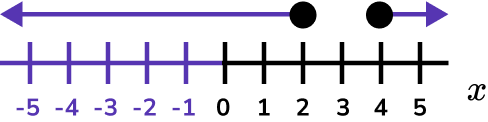
Example 4: solving by factorising

List the integers that satisfy 2x^{2} + 9x + 4\leq0

(2x + 1) = 0 when x = -\frac{1}{2}

(x +4 ) = 0 when x = -4

We need the values of x that produce a graph that is less than or equal to 0 and so below the x axis. 

The inequality is given by -4\leq x \leq-\frac{1}{2} .

List the integer values that are included in the solution set.

x is any value greater than or equal to  -4 and less than or equal to -\frac{1}{2} . The highest integer below -\frac{1}{2} is -1 .

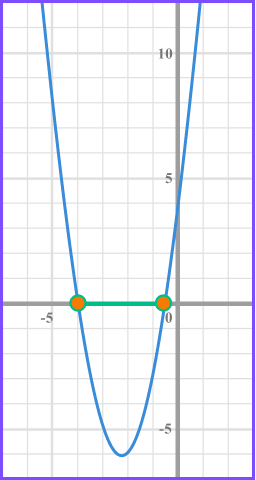
Example 5: solving by factorising

Solve x^{2}-9>0 .

(x +3) = 0 when x = -3

(x -3 ) = 0 when x = 3

We need the values of x that produce a graph that is greater than 0 and so above the x axis.

x>3 and x < -3 .

-3 and 3 are not included in the solution set so these values are indicated with closed circles.

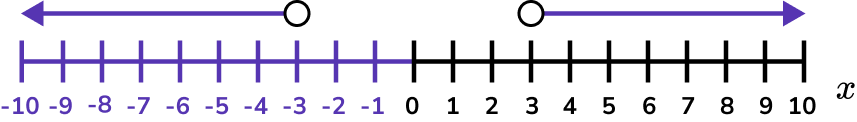
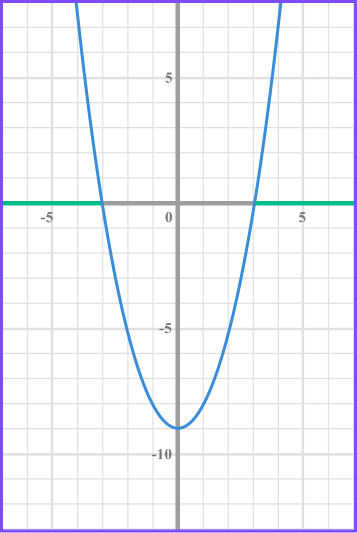
Example 6: solving by factorising and rearranging

List the integers that satisfy x^{2}<16 .

Rearrange the inequality.

Rearrange the inequality so that it is less than 0 by subtracting 16 from both sides.

Factorise the inequality.

(x +4) = 0 when x = -4

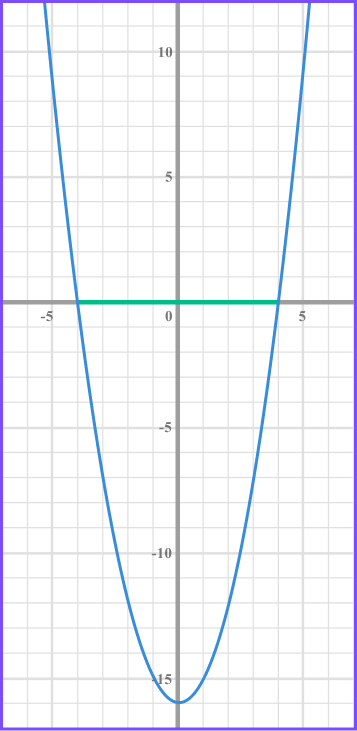
Write the solution using inequality notation .

The inequality is given by -4 < x < 4 .

x is any value greater than -4 and less than 4 .

Example 7: solving by using the quadratic formula

Solve 5x^{2}+6x-12\leq0 .

A quadratic expression is in the form ax^{2} + bx  + c .

In this inequality a = 5, b = 6 and c = -12 .

Substitute the values into the quadratic formula.

The quadratic formula is x = \frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} .

Substituting the values a = 5, b = 6 and c = -12 gives x = \frac{-6 \pm \sqrt{6^{2}-4 \times 5 \times-12}}{2 \times 5} .

We need to use the quadratic formula to solve rather than factorising as the discriminant is not a square number.

In this case the answer is given in surd form but you may be asked to leave the answers rounded to a degree of accuracy.

We need the values of x that produce a graph that is less than or equal 0 and so below the x axis.

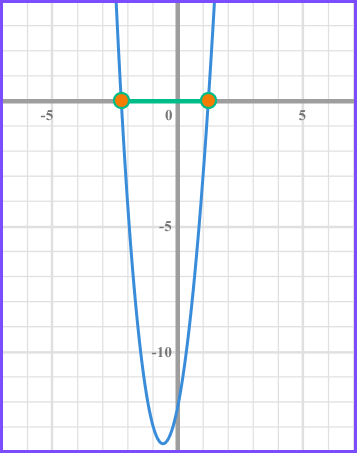
The inequality is given by \frac{-3- \sqrt{69}}{5} \leq x \leq \frac{-3+ \sqrt{69}}{5} .

Example 8: solving by using the quadratic formula

Solve 2x^{2}-3x- 4 < 0 .

A quadratic expression is in the form ax^{2}+bx+c .

In this inequality a = 2, b = -3 and c = -4 .

Substituting the values   a = 2, b =-36 and c = -4 gives

x=\frac{-(-3) \pm \sqrt{(-3)^{2}-4 \times 2 \times-4}}{2 \times 2} .

In this case the answer is being given to two decimal places but you could leave the solution in surd form.

We need the values of x that produce a graph that is less than 0 and so below the x axis.

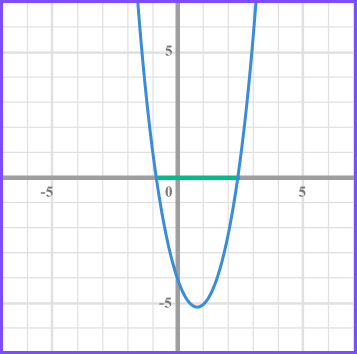
The inequality is given by -0.85 < x< 2.35 .

Rounded to two decimal places. 

Example 9: one solution

Solve x^{2}+6x+9\leq0 .

(x + 3)(x + 3) \leq 0 or (x+3)^{2}

As both brackets are equal, there is only one solution.

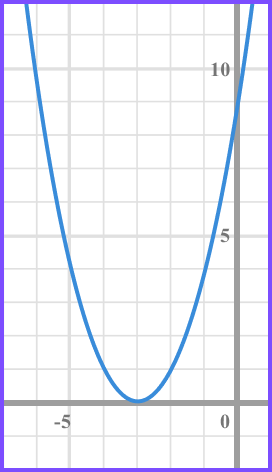
We need the values of x that produce a graph that is less than or equal to 0 and so below the x axis. This only happens when, x = -3 .

Common misconceptions

• Square root of a number has two solutions

A common error when calculating the square root of a number is only writing the positive solution. A negative number squared will also give a positive solution.

When solving x^2=16, x=\pm \sqrt{16} =\pm 4 .

• Not maintaining the original inequality sign

A common error is to accidentally change the direction of the inequality sign or not writing an inequality sign in the solution.

• Writing a double inequality when the solution set is split

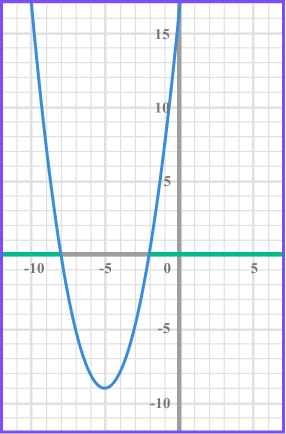
When solving  x^{2} + 10x +16  < 0 there is one solution set which is below the x axis. Therefore the solution is -8 < x < -2 .

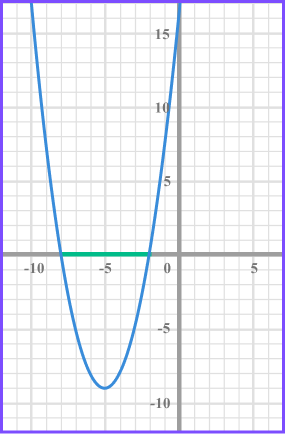
When solving  x^{2} + 10x +16  > 0 there is one solution set which is above the x axis. Therefore the solution is x<-8 and x > -2 .

Practice quadratic inequalities questions

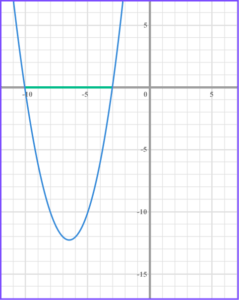
1. Solve x^{2}+13x+30<0 .

Factorise the quadratic, (x + 3)(x +10) < 0 .

Find the values of x that make the bracket equal zero, x = -10 and x = -3 .

Write the solution using interval notation, -10 < x < -3 .

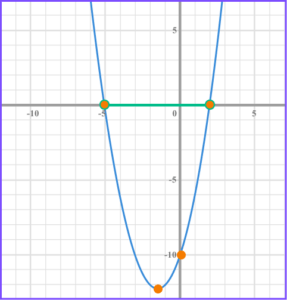
2. Solve x^{2}+3x-10\leq0 .

Factorise the quadratic, (x + 5)(x -2) \leq 0 .

Find the values of x that make the bracket equal zero, x = -5 and x = 2 .

Write the solution using interval notation, -5\leq x \leq2 .

3. Solve x^{2}-7x+6\geq0 .

x \leq 1 and x\geq 6

Factorise the quadratic, (x-6)(x-1)\geq 0 .

Find the values of x that make the bracket equal zero, x = 6 and x =1 .

Write the solution using interval notation, x \leq 1 and x\geq6 .

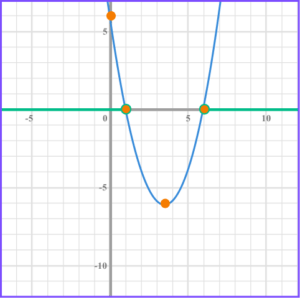
4. Solve 2x^{2}-11x+ 5 \leq 0 .

Factorise the quadratic, (2x-1)(x-5) \leq 0 .

Find the values of x that make the bracket equal zero, x =\frac{1}{2} and x =5 .

Write the solution using interval notation, \frac{1}{2} \leq x\leq 5 .

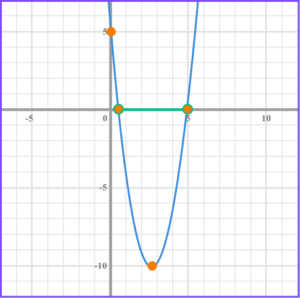
5. Solve x^{2}-25>0 .

x = -5 and x =5

Factorise the quadratic, (x + 5)(x -5) > 0 .

Find the values of x that make the bracket equal zero, x = -5 and x =5 .

Write the solution using interval notation, x < -5 and x > 5 .

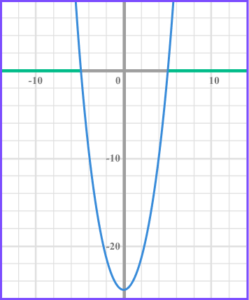
6. Solve   x^{2}<1 .

Rearrange to make the inequality less than zero, x^{2} – 1<0 .

Factorise the quadratic, (x + 1)(x -5) < 0 .

Find the values of x that make the bracket equal zero, x = -1 and x =1 .

Write the solution using interval notation, -1 < x < 1 .

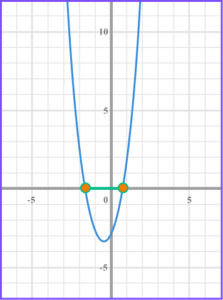
7. Solve 3x^{2}+4x-2\leq 0 .

3x^{2} + 4x – 2 \leq 0 .

Identify a, b and c from the form ax^{2} +bx + c \leq 0 , a = 3, b = 4, c = -2 .

Substitute the values in to the quadratic formula, x = \frac{-4 \pm \sqrt{4^{2}-4 \times 3 \times-2}}{2 \times 3} .

Simplify the inequality, x = \frac{-4 \pm \sqrt{16–24}}{6} .

Simplify further, x=\frac{-4 \pm \sqrt{40}}{6} .

You could simplify to surd form, x = \frac{-4 \pm 2 \sqrt{10}}{6} .

Simplify the fraction. You could leave in surd form, x = \frac{-2 \pm \sqrt{10}}{3} .

Correct to 2 decimal places, x \leq 0.39 and x \geq -1.72 .

Written in surd form written in interval notation, \frac{-2+\sqrt{10}}{3} \leq x \leq \frac{-2+\sqrt{10}}{3} .

Written as an inequality with values rounded to 2 decimal places, -1.72 \leq x \leq 0.39 .

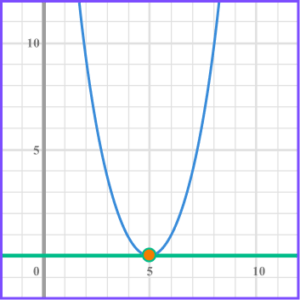
8. Solve x^{2}-10x+25 \leq 0 .

x^{2} -10x +25 \leq 0 .

Factorise the quadratic, (x – 5)(x -5) \leq 0 .

Find the values of x that make the bracket equal zero, x =5 .

The quadratic only has one root at 5, so is never less than zero but equal to zero at 5, x = 5 .

Quadratic inequalities GCSE questions

1. Solve the inequality x^{2}-8x+15\leq 0 .

Factorise the inequality. 1 mark if there are one or two errors.

Roots found x = 3 and x = 5

Correct answer.

2. (a) Find the interval for which x^{2}+3x – 10 < 0 .

(b) Represent your solution to part (a) on the number line below.

1 mark if there are one or two errors.

Roots found x =2 and x = -5

-5 and 2 indicated.

Correct solution with open circles.

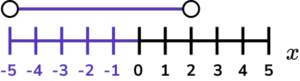
3. Here is a rectangle.

All measurements are in centimetres.

x is an integer.

The total area of the rectangle is less than 21cm^{2} .

Show that 4 <x < 7 .

x^{2} – 4x <21 .

x^{2} – 4x – 21< 0 .

(x – 7)(x + 3) < 0 .

4<x < 7 as you cannot have a negative value for distance.

Learning checklist

You have now learned how to:

• Solve quadratic inequalities
• Use inequality notation and represent solutions on a number line
• List integers that are in the solution set

The next lessons are

• Functions in algebra
• Laws of indices

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview