hypothesis testing two population means calculator

Two Population Calculator

Related: hypothesis testing calculator, confidence interval, hypothesis testing.

When computing confidence intervals for two population means, we are interested in the difference between the population means ($ \mu_1 - \mu_2 $). A confidence interval is made up of two parts, the point estimate and the margin of error. The point estimate of the difference between two population means is simply the difference between two sample means ($ \bar{x}_1 - \bar{x}_2 $). The standard error of $ \bar{x}_1 - \bar{x}_2 $, which is used in computing the margin of error, is given by the formula below.

The formula for the margin of error depends on whether the population standard deviations ($\sigma_1$ and $\sigma_2$) are known or unknown. If the population standard deviations are known, then they are used in the formula. If they are unknown, then the sample standard deviations ($s_1$ and $s_2$)are used in their place. To change from $\sigma$ known to $\sigma$ unknown, click on $\boxed{σ}$ and select $\boxed{s}$ in the Two Population Calculator.

While the formulas for the margin of error in the two population case are similar to those in the one population case, the formula for the degrees of freedom is quite a bit more complicated. Although this formula does seem intimidating at first sight, there is a shortcut to get the answer faster. Notice that the terms $\frac{s_1^2}{n_1}$ and $\frac{s_2^2}{n_2}$ each repeat twice. The terms are actually computed previously when finding the margin of error so they don't need to be calculated again.

If the two population variances are assumed to be equal, an alternative formula for computing the degrees of freedom is used. It's simply df = n1 + n2 - 2. This is a simple extension of the formula for the one population case. In the one population case the degrees of freedom is given by df = n - 1. If we add up the degrees of freedom for the two samples we would get df = (n1 - 1) + (n2 - 1) = n1 + n2 - 2. This formula gives a pretty good approximation of the more complicated formula above.

Just like in hypothesis tests about a single population mean, there are lower-tail, upper-tail and two tailed tests. However, the null and alternative are slightly different. First of all, instead of having mu on the left side of the equality, we have $\mu_1 - \mu_2$. On the right side of the equality, we don't have $\mu_0$, the hypothesized value of the population mean. Instead we have $D_0$, the hypothesized difference between the population means. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.

Again, hypothesis testing for a single population mean is very similar to hypothesis testing for two population means. For a single population mean, the test statistics is the difference between mu and mu0 dividied by the standard error. For two population means, the test statistic is the difference between $\bar{x}_1 - \bar{x}_2$ and $D_0$ divided by the standard error. The procedure after computing the test statistic is identical to the one population case. That is, you proceed with the p-value approach or critical value approach in the same exact way.

The calculator above computes confidence intervals and hypothesis tests for the difference between two population means. The simpler version of this is confidence intervals and hypothesis tests for a single population mean. For confidence intervals about a single population mean, visit the Confidence Interval Calculator . For hypothesis tests about a single population mean, visit the Hypothesis Testing Calculator .

Difference in Means Hypothesis Test Calculator

Use the calculator below to analyze the results of a difference in sample means hypothesis test. Enter your sample means, sample standard deviations, sample sizes, hypothesized difference in means, test type, and significance level to calculate your results.

You will find a description of how to conduct a two sample t-test below the calculator.

Define the Two Sample t-test

The difference between the sample means under the null distribution, conducting a hypothesis test for the difference in means.

When two populations are related, you can compare them by analyzing the difference between their means.

A hypothesis test for the difference in samples means can help you make inferences about the relationships between two population means.

Testing for a Difference in Means

For the results of a hypothesis test to be valid, you should follow these steps:

Check Your Conditions

State your hypothesis, determine your analysis plan, analyze your sample, interpret your results.

To use the testing procedure described below, you should check the following conditions:

• Independence of Samples - Your samples should be collected independently of one another.
• Simple Random Sampling - You should collect your samples with simple random sampling. This type of sampling requires that every occurrence of a value in a population has an equal chance of being selected when taking a sample.
• Normality of Sample Distributions - The sampling distributions for both samples should follow the Normal or a nearly Normal distribution. A sampling distribution will be nearly Normal when the samples are collected independently and when the population distribution is nearly Normal. Generally, the larger the sample size, the more normally distributed the sampling distribution. Additionally, outlier data points can make a distribution less Normal, so if your data contains many outliers, exercise caution when verifying this condition.

You must state a null hypothesis and an alternative hypothesis to conduct an hypothesis test of the difference in means.

The null hypothesis is a skeptical claim that you would like to test.

The alternative hypothesis represents the alternative claim to the null hypothesis.

Your null hypothesis and alternative hypothesis should be stated in one of three mutually exclusive ways listed in the table below.

D is the hypothesized difference between the populations' means that you would like to test.

Before conducting a hypothesis test, you must determine a reasonable significance level, α, or the probability of rejecting the null hypothesis assuming it is true. The lower your significance level, the more confident you can be of the conclusion of your hypothesis test. Common significance levels are 10%, 5%, and 1%.

To evaluate your hypothesis test at the significance level that you set, consider if you are conducting a one or two tail test:

• Two-tail tests divide the rejection region, or critical region, evenly above and below the null distribution, i.e. to the tails of the null sampling distribution. For example, in a two-tail test with a 5% significance level, your rejection region would be the upper and lower 2.5% of the null distribution. An alternative hypothesis of μ 1 - μ 2 ≠ D requires a two tail test.
• One-tail tests place the rejection region entirely on one side of the distribution i.e. to the right or left tail of the null distribution. For example, in a one-tail test evaluating if the actual difference in means, D, is above the null distribution with a 5% significance level, your rejection region would be the upper 5% of the null distribution. μ 1 - μ 2 > D and μ 1 - μ 2 < D alternative hypotheses require one-tail tests.

The graphical results section of the calculator above shades rejection regions blue.

After checking your conditions, stating your hypothesis, determining your significance level, and collecting your sample, you are ready to analyze your hypothesis.

Sample means follow the Normal distribution with the following parameters:

• The Difference in the Population Means, D - The true difference in the population means is unknown, but we use the hypothesized difference in the means, D, from the null hypothesis in the calculations.
• The Standard Error, SE - The standard error of the difference in the sample means can be computed as follows:      SE = (s 1 2 /n 1 + s 2 2 /n 2 ) (1/2) with s 1 being the standard deviation of sample one, n 1 being the sample size of sample one, s 2 being the standard deviation of sample one, and n 2 being the sample size of sample two. The standard error defines how differences in sample means are expected to vary around the null difference in means sampling distribution given the sample sizes and under the assumption that the null hypothesis is true.
• The Degrees of Freedom, DF - The degrees of freedom calculation can be estimated as the smaller of n 1 - 1 or n 2 - 1. For more accurate results, use the following formula for the degrees of freedom (DF):      DF = (s 1 2 /n 1 + s 2 2 /n 2 ) 2 / ((s 1 2 /n 1 ) 2 / (n 1 - 1) + (s 2 2 /n 2 ) 2 / (n 2 - 1))

In a difference in means hypothesis test, we calculate the probability that we would observe the difference in sample means (x̄ 1 - x̄ 2 ), assuming the null hypothesis is true, also known as the p-value . If the p-value is less than the significance level, then we can reject the null hypothesis.

You can determine a precise p-value using the calculator above, but we can find an estimate of the p-value manually by calculating the t-score, or t-statistic, as follows: t = (x̄ 1 - x̄ 2 - D) / SE

The t-score is a test statistic that tells you how far our observation is from the null hypothesis's difference in means under the null distribution. Using any t-score table, you can look up the probability of observing the results under the null distribution. You will need to look up the t-score for the type of test you are conducting, i.e. one or two tail. A hypothesis test for the difference in means is sometimes known as a two sample mean t-test because of the use of a t-score in analyzing results.

The conclusion of a hypothesis test for the difference in means is always either:

• Reject the null hypothesis
• Do not reject the null hypothesis

If you reject the null hypothesis, you cannot say that your sample difference in means is the true difference between the means. If you do not reject the null hypothesis, you cannot say that the hypothesized difference in means is true.

A hypothesis test is simply a way to look at evidence and conclude if it provides sufficient evidence to reject the null hypothesis.

Example: Hypothesis Test for the Difference in Two Means

Let’s say you are a manager at a company that designs batteries for smartphones. One of your engineers believes that she has developed a battery that will last more than two hours longer than your standard battery.

Before you can consider if you should replace your standard battery with the new one, you need to test the engineer’s claim. So, you decided to run a difference in means hypothesis test to see if her claim that the new battery will last two hours longer than the standard one is reasonable.

You direct your team to run a study. They will take a sample of 100 of the new batteries and compare their performance to 1,000 of the old standard batteries.

• Check the conditions - Your test consists of independent samples . Your team collects your samples using simple random sampling , and you have reason to believe that all your batteries' performances are always close to normally distributed . So, the conditions are met to conduct a two sample t-test.
• State Your Hypothesis - Your null hypothesis is that the charge of the new battery lasts at most two hours longer than your standard battery (i.e. μ 1 - μ 2 ≤ 2). Your alternative hypothesis is that the new battery lasts more than two hours longer than the standard battery (i.e. μ 1 - μ 2 > 2).
• Determine Your Analysis Plan - You believe that a 1% significance level is reasonable. As your test is a one-tail test, you will evaluate if the difference in mean charge between the samples would occur at the upper 1% of the null distribution.
• Analyze Your Sample - After collecting your samples (which you do after steps 1-3), you find the new battery sample had a mean charge of 10.4 hours, x̄ 1 , with a 0.8 hour standard deviation, s 1 . Your standard battery sample had a mean charge of 8.2 hours, x̄ 2 , with a standard deviation of 0.2 hours, s 2 . Using the calculator above, you find that a difference in sample means of 2.2 hours [2 = 10.4 – 8.2] would results in a t-score of 2.49 under the null distribution, which translates to a p-value of 0.72%.
• Interpret Your Results - Since your p-value of 0.72% is less than the significance level of 1%, you have sufficient evidence to reject the null hypothesis.

In this example, you found that you can reject your null hypothesis that the new battery design does not result in more than 2 hours of extra battery life. The test does not guarantee that your engineer’s new battery lasts two hours longer than your standard battery, but it does give you strong reason to believe her claim.

Statistics Made Easy

Two Sample t-test Calculator

t = -1.608761

p-value (one-tailed) = 0.060963

p-value (two-tailed) = 0.121926

Hey there. My name is Zach Bobbitt. I have a Master of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

One Reply to “Two Sample t-test Calculator”

good work zach

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

• Find Us On Facebook
• Follow on Twitter
• Subscribe using RSS

Two-Sample t-test

Use this calculator to test whether samples from two independent populations provide evidence that the populations have different means. For example, based on blood pressures measurements taken from a sample of women and a sample of men, can we conclude that women and men have different mean blood pressures?

This test is known as an a two sample (or unpaired) t-test. It produces a “p-value”, which can be used to decide whether there is evidence of a difference between the two population means.

The p-value is the probability that the difference between the sample means is at least as large as what has been observed, under the assumption that the population means are equal. The smaller the p-value, the more surprised we would be by the observed difference in sample means if there really was no difference between the population means. Therefore, the smaller the p-value, the stronger the evidence is that the two populations have different means.

Typically a threshold (known as the significance level) is chosen, and a p-value less than the threshold is interpreted as indicating evidence of a difference between the population means. The most common choice of significance level is 0.05, but other values, such as 0.1 or 0.01 are also used.

This calculator should be used when the sampling units (e.g. the sampled individuals) in the two groups are independent. If you are comparing two measurements taken on the same sampling unit (e.g. blood pressure of an individual before and after a drug is administered) then the appropriate test is the paired t-test.

More Information

Worked example.

A study compares the average capillary density in the feet of individuals with and without ulcers. A sample of 10 patients with ulcers has mean capillary density of 29, with standard deviation 7.5. A control sample of 10 individuals without ulcers has mean capillary density of 34, with standard deviation 8.0. (All measurements are in capillaries per square mm.) Using this information, the p-value is calculated as 0.167. Since this p-value is greater than 0.05, it would conventionally be interpreted as meaning that the data do not provide strong evidence of a difference in capillary density between individuals with and without ulcers.

If both sample sizes were increased to 20, the p-value would reduce to 0.048 (assuming the sample means and standard deviations remained the same), which we would interpret as strong evidence of a difference. Note that this result is not inconsistent with the previous result: with bigger samples we are able to detect smaller differences between populations.

Assumptions

This test assumes that the two populations follow normal distributions (otherwise known as Gaussian distributions). Normality of the distributions can be tested using, for example, a Q-Q plot . An alternative test that can be used if you suspect that the data are drawn from non-normal distributions is the Mann-Whitney U test .

The version of the test used here also assumes that the two populations have different variances. If you think the populations have the same variance, an alternative version of the two sample t-test (two sample t-test with a pooled variance estimator) can be used. The advantage of the alternative version is that if the populations have the same variance then it has greater statistical power – that is, there is a higher probability of detecting a difference between the population means if such a difference exists.

Performing this test assesses the extent to which the difference between the sample means provides evidence of a difference between the population means. The test puts forward a “null” hypothesis that the population means are equal, and measures the probability of observing a difference at least as big as that seen in the data under the null hypothesis (the p-value). If the p-value is large then the observed difference between the sample means is unsurprising and is interpreted as being consistent with hypothesis of equal population means. If on the other hand the p-value is small then we would be surprised about the observed difference if the null hypothesis really was true. Therefore, a small p-value is interpreted as evidence that the null hypothesis is false and that there really is a difference between the population means. Typically a threshold (known as the significance level) is chosen, and a p-value less than the threshold is interpreted as indicating evidence of a difference between the population means. The most common choice of significance level is 0.05, but other values, such as 0.1 or 0.01 are also used.

Note that a large p-value (say, larger than 0.05) cannot in itself be interpreted as evidence that the populations have equal means. It may just mean that the sample size is not large enough to detect a difference. To find out how large your sample needs to be in order to detect a difference (if a difference exists), see our sample size calculator .

If evidence of a difference in the population means is found, you may wish to quantify that difference. The difference between the sample means is a point estimate of the difference between the population means, but it can be useful to assess how reliable this estimate is using a confidence interval . A confidence interval provides you with a set of limits in which you expect the difference between the population means to lie. The p-value and the confidence interval are related and have a consistent interpretation: if the p-value is less than α then a (1-α)*100% confidence interval will not contain zero. For example, if the p-value is less than 0.05 then a 95% confidence interval will not contain zero.

If you wish to calculate a confidence interval, our confidence interval calculator will do the work for you.

Definitions

Sample mean.

The sample mean is your ‘best guess’ for what the true population mean is given your sample of data and is calcuated as:

μ = (1/n)* ∑ n i=1 x i ,

where n is the sample size and x 1 ,…,x n are the n sample observations.

Sample standard deviation

The sample standard deviation is calcuated as s=√ σ 2 , where:

σ 2 = (1/(n-1))* ∑ n i=1 (x i -μ) 2 ,

μ is the sample mean, n is the sample size and x 1 ,…,x n are the n sample observations.

Sample size

This is the total number of samples randomly drawn from you population.  The larger the sample size, the more certain you can be that the estimate reflects the population.  Choosing a sample size is an important aspect when desiging your study or survey.  For some further information, see our blog post on The Importance and Effect of Sample Size and for guidance on how to choose your sample size, see our sample size calculator .

Tell us what you want to achieve

• Data Collection & Management
• Data Mining
• Innovation & Research
• Qualitative Analysis
• Surveys & Sampling
• Visualisation
• Agriculture
• Environment
• Market Research
• Public Sector

Select Statistical Services Ltd

Oxygen House, Grenadier Road, Exeter Business Park,

Exeter EX1 3LH

t: 01392 440426

e: [email protected]

Sign up to our Newsletter

• Please tick this box to confirm that you are happy for us to store and process the information supplied above for the purpose of managing your subscription to our newsletter.
• Email This field is for validation purposes and should be left unchanged.
• Telephone Number

• By using this form you agree with the storage and handling of your data by this website.

Enquiry - Jobs

• Name This field is for validation purposes and should be left unchanged.

T-test for two Means – Unknown Population Standard Deviations

Instructions : Use this T-Test Calculator for two Independent Means calculator to conduct a t-test for two population means (\(\mu_1\) and \(\mu_2\)), with unknown population standard deviations. This test apply when you have two-independent samples, and the population standard deviations \(\sigma_1\) and \(\sigma_2\) and not known. Please select the null and alternative hypotheses, type the significance level, the sample means, the sample standard deviations, the sample sizes, and the results of the t-test for two independent samples will be displayed for you:

The T-test for Two Independent Samples

More about the t-test for two means so you can better interpret the output presented above: A t-test for two means with unknown population variances and two independent samples is a hypothesis test that attempts to make a claim about the population means (\(\mu_1\) and \(\mu_2\)).

More specifically, a t-test uses sample information to assess how plausible it is for the population means \(\mu_1\) and \(\mu_2\) to be equal. The test has two non-overlapping hypotheses, the null and the alternative hypothesis.

The null hypothesis is a statement about the population means, specifically the assumption of no effect, and the alternative hypothesis is the complementary hypothesis to the null hypothesis.

Properties of the two sample t-test

The main properties of a two sample t-test for two population means are:

• Depending on our knowledge about the "no effect" situation, the t-test can be two-tailed, left-tailed or right-tailed
• The main principle of hypothesis testing is that the null hypothesis is rejected if the test statistic obtained is sufficiently unlikely under the assumption that the null hypothesis is true
• The p-value is the probability of obtaining sample results as extreme or more extreme than the sample results obtained, under the assumption that the null hypothesis is true
• In a hypothesis tests there are two types of errors. Type I error occurs when we reject a true null hypothesis, and the Type II error occurs when we fail to reject a false null hypothesis

How do you compute the t-statistic for the t test for two independent samples?

The formula for a t-statistic for two population means (with two independent samples), with unknown population variances shows us how to calculate t-test with mean and standard deviation and it depends on whether the population variances are assumed to be equal or not. If the population variances are assumed to be unequal, then the formula is:

On the other hand, if the population variances are assumed to be equal, then the formula is:

Normally, the way of knowing whether the population variances must be assumed to be equal or unequal is by using an F-test for equality of variances.

With the above t-statistic, we can compute the corresponding p-value, which allows us to assess whether or not there is a statistically significant difference between two means.

Why is it called t-test for independent samples?

This is because the samples are not related with each other, in a way that the outcomes from one sample are unrelated from the other sample. If the samples are related (for example, you are comparing the answers of husbands and wives, or identical twins), you should use a t-test for paired samples instead .

What if the population standard deviations are known?

The main purpose of this calculator is for comparing two population mean when sigma is unknown for both populations. In case that the population standard deviations are known, then you should use instead this z-test for two means .

Related Calculators

log in to your account

Reset password.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Inference for Comparing 2 Population Means (HT for 2 Means, independent samples)

More of the good stuff! We will need to know how to label the null and alternative hypothesis, calculate the test statistic, and then reach our conclusion using the critical value method or the p-value method.

The Test Statistic for a Test of 2 Means from Independent Samples:

[latex]t = \displaystyle \frac{(\bar{x_1} - \bar{x_2}) - (\mu_1 - \mu_2)}{\sqrt{\displaystyle \frac{s_1^2}{n_1} + \displaystyle \frac{s_2^2}{n_2}}}[/latex]

What the different symbols mean:

[latex]n_1[/latex] is the sample size for the first group

[latex]n_2[/latex] is the sample size for the second group

[latex]df[/latex], the degrees of freedom, is the smaller of [latex]n_1 - 1[/latex] and [latex]n_2 - 1[/latex]

[latex]\mu_1[/latex] is the population mean from the first group

[latex]\mu_2[/latex] is the population mean from the second group

[latex]\bar{x_1}[/latex] is the sample mean for the first group

[latex]\bar{x_2}[/latex] is the sample mean for the second group

[latex]s_1[/latex] is the sample standard deviation for the first group

[latex]s_2[/latex] is the sample standard deviation for the second group

[latex]\alpha[/latex] is the significance level , usually given within the problem, or if not given, we assume it to be 5% or 0.05

Assumptions when conducting a Test for 2 Means from Independent Samples:

• We do not know the population standard deviations, and we do not assume they are equal
• The two samples or groups are independent
• Both samples are simple random samples
• Both populations are Normally distributed OR both samples are large ([latex]n_1 > 30[/latex] and [latex]n_2 > 30[/latex])

Steps to conduct the Test for 2 Means from Independent Samples:

• Identify all the symbols listed above (all the stuff that will go into the formulas). This includes [latex]n_1[/latex] and [latex]n_2[/latex], [latex]df[/latex], [latex]\mu_1[/latex] and [latex]\mu_2[/latex], [latex]\bar{x_1}[/latex] and [latex]\bar{x_2}[/latex], [latex]s_1[/latex] and [latex]s_2[/latex], and [latex]\alpha[/latex]
• Identify the null and alternative hypotheses
• Calculate the test statistic, [latex]t = \displaystyle \frac{(\bar{x_1} - \bar{x_2}) - (\mu_1 - \mu_2)}{\sqrt{\displaystyle \frac{s_1^2}{n_1} + \displaystyle \frac{s_2^2}{n_2}}}[/latex]
• Find the critical value(s) OR the p-value OR both
• Apply the Decision Rule
• Write up a conclusion for the test

Example 1: Study on the effectiveness of stents for stroke patients [1]

In this study , researchers randomly assigned stroke patients to two groups: one received the current standard care (control) and the other received a stent surgery in addition to the standard care (stent treatment). If the stents work, the treatment group should have a lower average disability score . Do the results give convincing statistical evidence that the stent treatment reduces the average disability from stroke?

Since we are being asked for convincing statistical evidence, a hypothesis test should be conducted. In this case, we are dealing with averages from two samples or groups (the patients with stent treatment and patients receiving the standard care), so we will conduct a Test of 2 Means.

• [latex]n_1 = 98[/latex] is the sample size for the first group
• [latex]n_2 = 93[/latex] is the sample size for the second group
• [latex]df[/latex], the degrees of freedom, is the smaller of [latex]98 - 1 = 97[/latex] and [latex]93 - 1 = 92[/latex], so [latex]df = 92[/latex]
• [latex]\bar{x_1} = 2.26[/latex] is the sample mean for the first group
• [latex]\bar{x_2} = 3.23[/latex] is the sample mean for the second group
• [latex]s_1 = 1.78[/latex] is the sample standard deviation for the first group
• [latex]s_2 = 1.78[/latex] is the sample standard deviation for the second group
• [latex]\alpha = 0.05[/latex] (we were not told a specific value in the problem, so we are assuming it is 5%)
• One additional assumption we extend from the null hypothesis is that [latex]\mu_1 - \mu_2 = 0[/latex]; this means that in our formula, those variables cancel out
• [latex]H_{0}: \mu_1 = \mu_2[/latex]
• [latex]H_{A}: \mu_1 < \mu_2[/latex]
• [latex]t = \displaystyle \frac{(\bar{x_1} - \bar{x_2}) - (\mu_1 - \mu_2)}{\sqrt{\displaystyle \frac{s_1^2}{n_1} + \displaystyle \frac{s_2^2}{n_2}}} = \displaystyle \frac{(2.26 - 3.23) - 0)}{\sqrt{\displaystyle \frac{1.78^2}{98} + \displaystyle \frac{1.78^2}{93}}} = -3.76[/latex]
• StatDisk : We can conduct this test using StatDisk. The nice thing about StatDisk is that it will also compute the test statistic. From the main menu above we click on Analysis, Hypothesis Testing, and then Mean Two Independent Samples. From there enter the 0.05 significance, along with the specific values as outlined in the picture below in Step 2. Notice the alternative hypothesis is the [latex]<[/latex] option. Enter the sample size, mean, and standard deviation for each group, and make sure that unequal variances is selected. Now we click on Evaluate. If you check the values, the test statistic is reported in the Step 3 display, as well as the P-Value of 0.00011.
• Applying the Decision Rule: We now compare this to our significance level, which is 0.05. If the p-value is smaller or equal to the alpha level, we have enough evidence for our claim, otherwise we do not. Here, [latex]p-value = 0.00011[/latex], which is definitely smaller than [latex]\alpha = 0.05[/latex], so we have enough evidence for the alternative hypothesis…but what does this mean?
• Conclusion: Because our p-value  of [latex]0.00011[/latex] is less than our [latex]\alpha[/latex] level of [latex]0.05[/latex], we reject [latex]H_{0}[/latex]. We have convincing statistical evidence that the stent treatment reduces the average disability from stroke.

Example 2: Home Run Distances

In 1998, Sammy Sosa and Mark McGwire (2 players in Major League Baseball) were on pace to set a new home run record. At the end of the season McGwire ended up with 70 home runs, and Sosa ended up with 66. The home run distances were recorded and compared (sometimes a player’s home run distance is used to measure their “power”). Do the results give convincing statistical evidence that the home run distances are different from each other? Who would you say “hit the ball farther” in this comparison?

Since we are being asked for convincing statistical evidence, a hypothesis test should be conducted. In this case, we are dealing with averages from two samples or groups (the home run distances), so we will conduct a Test of 2 Means.

• [latex]n_1 = 70[/latex] is the sample size for the first group
• [latex]n_2 = 66[/latex] is the sample size for the second group
• [latex]df[/latex], the degrees of freedom, is the smaller of [latex]70 - 1 = 69[/latex] and [latex]66 - 1 = 65[/latex], so [latex]df = 65[/latex]
• [latex]\bar{x_1} = 418.5[/latex] is the sample mean for the first group
• [latex]\bar{x_2} = 404.8[/latex] is the sample mean for the second group
• [latex]s_1 = 45.5[/latex] is the sample standard deviation for the first group
• [latex]s_2 = 35.7[/latex] is the sample standard deviation for the second group
• [latex]H_{A}: \mu_1 \neq \mu_2[/latex]
• [latex]t = \displaystyle \frac{(\bar{x_1} - \bar{x_2}) - (\mu_1 - \mu_2)}{\sqrt{\displaystyle \frac{s_1^2}{n_1} + \displaystyle \frac{s_2^2}{n_2}}} = \displaystyle \frac{(418.5 - 404.8) - 0)}{\sqrt{\displaystyle \frac{45.5^2}{70} + \displaystyle \frac{35.7^2}{65}}} = 1.95[/latex]
• StatDisk : We can conduct this test using StatDisk. The nice thing about StatDisk is that it will also compute the test statistic. From the main menu above we click on Analysis, Hypothesis Testing, and then Mean Two Independent Samples. From there enter the 0.05 significance, along with the specific values as outlined in the picture below in Step 2. Notice the alternative hypothesis is the [latex]\neq[/latex] option. Enter the sample size, mean, and standard deviation for each group, and make sure that unequal variances is selected. Now we click on Evaluate. If you check the values, the test statistic is reported in the Step 3 display, as well as the P-Value of 0.05221.
• Applying the Decision Rule: We now compare this to our significance level, which is 0.05. If the p-value is smaller or equal to the alpha level, we have enough evidence for our claim, otherwise we do not. Here, [latex]p-value = 0.05221[/latex], which is larger than [latex]\alpha = 0.05[/latex], so we do not have enough evidence for the alternative hypothesis…but what does this mean?
• Conclusion: Because our p-value  of [latex]0.05221[/latex] is larger than our [latex]\alpha[/latex] level of [latex]0.05[/latex], we fail to reject [latex]H_{0}[/latex]. We do not have convincing statistical evidence that the home run distances are different.
• Follow-up commentary: But what does this mean? There actually was a difference, right? If we take McGwire’s average and subtract Sosa’s average we get a difference of 13.7. What this result indicates is that the difference is not statistically significant; it could be due more to random chance than something meaningful. Other factors, such as sample size, could also be a determining factor (with a larger sample size, the difference may have been more meaningful).
• Adapted from the Skew The Script curriculum ( skewthescript.org ), licensed under CC BY-NC-Sa 4.0 ↵

Basic Statistics Copyright © by Allyn Leon is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

7.3 - Comparing Two Population Means

Introduction.

In this section, we are going to approach constructing the confidence interval and developing the hypothesis test similarly to how we approached those of the difference in two proportions.

There are a few extra steps we need to take, however. First, we need to consider whether the two populations are independent. When considering the sample mean, there were two parameters we had to consider, \(\mu\) the population mean, and \(\sigma\) the population standard deviation. Therefore, the second step is to determine if we are in a situation where the population standard deviations are the same or if they are different.

Independent and Dependent Samples

It is important to be able to distinguish between an independent sample or a dependent sample.

The following are examples to illustrate the two types of samples.

Example 7-3: Gas Mileage

We want to compare the gas mileage of two brands of gasoline. Describe how to design a study involving...

• independent sample Answer: Randomly assign 12 cars to use Brand A and another 12 cars to use Brand B.
• dependent samples Answer: Using 12 cars, have each car use Brand A and Brand B. Compare the differences in mileage for each car.
• Design involving independent samples
• Design involving dependent samples
• Answer: Randomly assign half of the subjects to taste Coke and the other half to taste Pepsi.

Answer: Allow all the subjects to rate both Coke and Pepsi. The drinks should be given in random order. The same subject's ratings of the Coke and the Pepsi form a paired data set.

• We randomly select 20 males and 20 females and compare the average time they spend watching TV. Is this an independent sample or paired sample?
• We randomly select 20 couples and compare the time the husbands and wives spend watching TV. Is this an independent sample or paired sample?
• Answer: Independent Sample

Answer: Paired sample

The two types of samples require a different theory to construct a confidence interval and develop a hypothesis test. We consider each case separately, beginning with independent samples.

7.3.1 - Inference for Independent Means

Two-cases for independent means.

As with comparing two population proportions, when we compare two population means from independent populations, the interest is in the difference of the two means. In other words, if \(\mu_1\) is the population mean from population 1 and \(\mu_2\) is the population mean from population 2, then the difference is \(\mu_1-\mu_2\). If \(\mu_1-\mu_2=0\) then there is no difference between the two population parameters.

If each population is normal, then the sampling distribution of \(\bar{x}_i\) is normal with mean \(\mu_i\), standard error \(\dfrac{\sigma_i}{\sqrt{n_i}}\), and the estimated standard error \(\dfrac{s_i}{\sqrt{n_i}}\), for \(i=1, 2\).

Using the Central Limit Theorem, if the population is not normal, then with a large sample, the sampling distribution is approximately normal.

The theorem presented in this Lesson says that if either of the above are true, then \(\bar{x}_1-\bar{x}_2\) is approximately normal with mean \(\mu_1-\mu_2\), and standard error \(\sqrt{\dfrac{\sigma^2_1}{n_1}+\dfrac{\sigma^2_2}{n_2}}\).

However, in most cases, \(\sigma_1\) and \(\sigma_2\) are unknown, and they have to be estimated. It seems natural to estimate \(\sigma_1\) by \(s_1\) and \(\sigma_2\) by \(s_2\). When the sample sizes are small, the estimates may not be that accurate and one may get a better estimate for the common standard deviation by pooling the data from both populations if the standard deviations for the two populations are not that different.

Given this, there are two options for estimating the variances for the independent samples:

• Using pooled variances
• Using unpooled (or unequal) variances

When to use which? When we are reasonably sure that the two populations have nearly equal variances, then we use the pooled variances test. Otherwise, we use the unpooled (or separate) variance test.

7.3.1.1 - Pooled Variances

Confidence intervals for \(\boldsymbol{\mu_1-\mu_2}\): pooled variances.

When we have good reason to believe that the variance for population 1 is equal to that of population 2, we can estimate the common variance by pooling information from samples from population 1 and population 2.

An informal check for this is to compare the ratio of the two sample standard deviations. If the two are equal , the ratio would be 1, i.e. \(\frac{s_1}{s_2}=1\). However, since these are samples and therefore involve error, we cannot expect the ratio to be exactly 1. When the sample sizes are nearly equal (admittedly "nearly equal" is somewhat ambiguous, so often if sample sizes are small one requires they be equal), then a good Rule of Thumb to use is to see if the ratio falls from 0.5 to 2. That is, neither sample standard deviation is more than twice the other.

If this rule of thumb is satisfied, we can assume the variances are equal. Later in this lesson, we will examine a more formal test for equality of variances.

• Let \(n_1\) be the sample size from population 1 and let \(s_1\) be the sample standard deviation of population 1.
• Let \(n_2\) be the sample size from population 2 and \(s_2\) be the sample standard deviation of population 2.

Then the common standard deviation can be estimated by the pooled standard deviation:

\(s_p=\sqrt{\dfrac{(n_1-1)s_1^2+(n_2-1)s^2_2}{n_1+n_2-2}}\)

If we can assume the populations are independent, that each population is normal or has a large sample size, and that the population variances are the same, then it can be shown that...

\(t=\dfrac{\bar{x}_1-\bar{x_2}-0}{s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\)

follows a t-distribution with \(n_1+n_2-2\) degrees of freedom.

Now, we can construct a confidence interval for the difference of two means, \(\mu_1-\mu_2\).

where \(t_{\alpha/2}\) comes from a t-distribution with \(n_1+n_2-2\) degrees of freedom.

Hypothesis Tests for \(\boldsymbol{\mu_1-\mu_2}\): The Pooled t-test

Now let's consider the hypothesis test for the mean differences with pooled variances.

\(H_0\colon\mu_1-\mu_2=0\)

\(H_a\colon \mu_1-\mu_2\ne0\)

\(H_a\colon \mu_1-\mu_2>0\)

\(H_a\colon \mu_1-\mu_2<0\)

The assumptions/conditions are:

• The populations are independent
• The population variances are equal
• Each population is either normal or the sample size is large.

The test statistic is...

\(t^*=\dfrac{\bar{x}_1-\bar{x}_2-0}{s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\)

And \(t^*\) follows a t-distribution with degrees of freedom equal to \(df=n_1+n_2-2\).

The p-value, critical value, rejection region, and conclusion are found similarly to what we have done before.

Example 7-4: Comparing Packing Machines

In a packing plant, a machine packs cartons with jars. It is supposed that a new machine will pack faster on the average than the machine currently used. To test that hypothesis, the times it takes each machine to pack ten cartons are recorded. The results, ( machine.txt ), in seconds, are shown in the tables.

\(\bar{x}_1=42.14, \text{s}_1= 0.683\)

\(\bar{x}_2=43.23, \text{s}_2= 0.750\)

Do the data provide sufficient evidence to conclude that, on the average, the new machine packs faster?

• Hypothesis Test
• Confidence Interval

Are these independent samples? Yes, since the samples from the two machines are not related.

Are these large samples or a normal population?

We have \(n_1\lt 30\) and \(n_2\lt 30\). We do not have large enough samples, and thus we need to check the normality assumption from both populations. Let's take a look at the normality plots for this data:

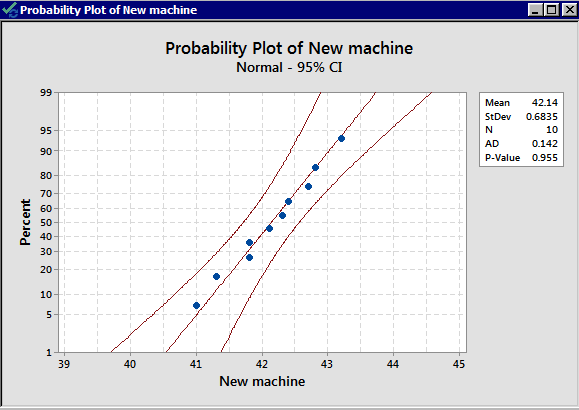
From the normal probability plots, we conclude that both populations may come from normal distributions. Remember the plots do not indicate that they DO come from a normal distribution. It only shows if there are clear violations. We should proceed with caution.

Do the populations have equal variance? No information allows us to assume they are equal. We can use our rule of thumb to see if they are “close.” They are not that different as \(\dfrac{s_1}{s_2}=\dfrac{0.683}{0.750}=0.91\) is quite close to 1. This assumption does not seem to be violated.

We can thus proceed with the pooled t -test.

Let \(\mu_1\) denote the mean for the new machine and \(\mu_2\) denote the mean for the old machine.

The null hypothesis is that there is no difference in the two population means, i.e.

\(H_0\colon \mu_1-\mu_2=0\)

The alternative is that the new machine is faster, i.e.

The significance level is 5%. Since we may assume the population variances are equal, we first have to calculate the pooled standard deviation:

\begin{align} s_p&=\sqrt{\frac{(n_1-1)s^2_1+(n_2-1)s^2_2}{n_1+n_2-2}}\\ &=\sqrt{\frac{(10-1)(0.683)^2+(10-1)(0.750)^2}{10+10-2}}\\ &=\sqrt{\dfrac{9.261}{18}}\\ &=0.7173 \end{align}

The test statistic is:

\begin{align} t^*&=\dfrac{\bar{x}_1-\bar{x}_2-0}{s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\\ &=\dfrac{42.14-43.23}{0.7173\sqrt{\frac{1}{10}+\frac{1}{10}}}\\&=-3.398 \end{align}

The alternative is left-tailed so the critical value is the value \(a\) such that \(P(T<a)=0.05\), with \(10+10-2=18\) degrees of freedom. The critical value is -1.7341. The rejection region is \(t^*<-1.7341\).

Our test statistic, -3.3978, is in our rejection region, therefore, we reject the null hypothesis. With a significance level of 5%, we reject the null hypothesis and conclude there is enough evidence to suggest that the new machine is faster than the old machine.

To find the interval, we need all of the pieces. We calculated all but one when we conducted the hypothesis test. We only need the multiplier. For a 99% confidence interval, the multiplier is \(t_{0.01/2}\) with degrees of freedom equal to 18. This value is 2.878.

The interval is:

\(\bar{x}_1-\bar{x}_2\pm t_{\alpha/2}s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}\)

\((42.14-43.23)\pm 2.878(0.7173)\sqrt{\frac{1}{10}+\frac{1}{10}}\)

\(-1.09\pm 0.9232\)

The 99% confidence interval is (-2.013, -0.167).

We are 99% confident that the difference between the two population mean times is between -2.012 and -0.167.

  Minitab: 2-Sample t-test - Pooled

The following steps are used to conduct a 2-sample t-test for pooled variances in Minitab.

• Choose Stat > Basic Statistics > 2-Sample t .

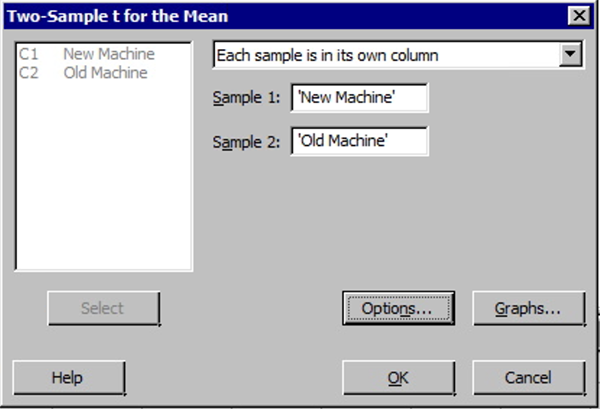
• Select the Options button and enter the desired 'confidence level', 'null hypothesis value' (again for our class this will be 0), and select the correct 'alternative hypothesis' from the drop-down menu. Finally, check the box for 'assume equal variances'. This latter selection should only be done when we have verified the two variances can be assumed equal.

The Minitab output for the packing time example:

Two-Sample T-Test and CI: New Machine, Old Machine

μ 1 : mean of New Machine

μ 2 : mean of Old Machine

Difference: μ 1 - μ 2

Equal variances are assumed for this analysis.

Descriptive Statistics

Estimation for difference.

Alternative hypothesis

H 1 : μ 1 - μ 2 < 0

7.3.1.2 - Unpooled Variances

When the assumption of equal variances is not valid, we need to use separate, or unpooled, variances. The mathematics and theory are complicated for this case and we intentionally leave out the details.

We still have the following assumptions:

If the assumptions are satisfied, then

\(t^*=\dfrac{\bar{x}_1-\bar{x_2}-0}{\sqrt{\frac{s^2_1}{n_1}+\frac{s^2_2}{n_2}}}\)

will have a t-distribution with degrees of freedom

\(df=\dfrac{(n_1-1)(n_2-1)}{(n_2-1)C^2+(1-C)^2(n_1-1)}\)

where \(C=\dfrac{\frac{s^2_1}{n_1}}{\frac{s^2_1}{n_1}+\frac{s^2_2}{n_2}}\).

Where \(t_{\alpha/2}\) comes from the t-distribution using the degrees of freedom above.

Minitab ®

Minitab: unpooled t-test.

To perform a separate variance 2-sample, t -procedure use the same commands as for the pooled procedure EXCEPT we do NOT check box for 'Use Equal Variances.'

• Choose Stat > Basic Statistics > 2-sample t
• Select the Options box and enter the desired 'Confidence level,' 'Null hypothesis value' (again for our class this will be 0), and select the correct 'Alternative hypothesis' from the drop-down menu.

For some examples, one can use both the pooled t-procedure and the separate variances (non-pooled) t -procedure and obtain results that are close to each other. However, when the sample standard deviations are very different from each other, and the sample sizes are different, the separate variances 2-sample t -procedure is more reliable.

Example 7-5: Grade Point Average

Independent random samples of 17 sophomores and 13 juniors attending a large university yield the following data on grade point averages ( student_gpa.txt ):

At the 5% significance level, do the data provide sufficient evidence to conclude that the mean GPAs of sophomores and juniors at the university differ?

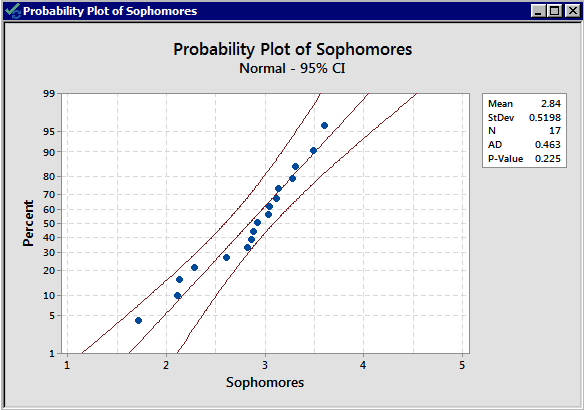
There is no indication that there is a violation of the normal assumption for both samples. As before, we should proceed with caution.

Now, we need to determine whether to use the pooled t-test or the non-pooled (separate variances) t -test. The summary statistics are:

The standard deviations are 0.520 and 0.3093 respectively; both the sample sizes are small, and the standard deviations are quite different from each other. We, therefore, decide to use an unpooled t -test.

The null and alternative hypotheses are:

\(H_0\colon \mu_1-\mu_2=0\) vs \(H_a\colon \mu_1-\mu_2\ne0\)

The significance level is 5%. Perform the 2-sample t -test in Minitab with the appropriate alternative hypothesis.

Remember, the default for the 2-sample t-test in Minitab is the non-pooled one. Minitab generates the following output.

Two sample T for sophomores vs juniors

95% CI for mu sophomore - mu juniors: (-0.45, 0.173)

T-Test mu sophomore = mu juniors (Vs no =): T = -0.92

P = 0.36 DF = 26

Since the p-value of 0.36 is larger than \(\alpha=0.05\), we fail to reject the null hypothesis.

At 5% level of significance, the data does not provide sufficient evidence that the mean GPAs of sophomores and juniors at the university are different.

95% CI for mu sophomore- mu juniors is;

(-0.45, 0.173)

We are 95% confident that the difference between the mean GPA of sophomores and juniors is between -0.45 and 0.173.

7.3.2 - Inference for Paired Means

When we developed the inference for the independent samples, we depended on the statistical theory to help us. The theory, however, required the samples to be independent. What can we do when the two samples are not independent, i.e., the data is paired?

Consider an example where we are interested in a person’s weight before implementing a diet plan and after. Since the interest is focusing on the difference, it makes sense to “condense” these two measurements into one and consider the difference between the two measurements. For example, if instead of considering the two measures, we take the before diet weight and subtract the after diet weight. The difference makes sense too! It is the weight lost on the diet.

When we take the two measurements to make one measurement (i.e., the difference), we are now back to the one sample case! Now we can apply all we learned for the one sample mean to the difference (Cool!)

The Confidence Interval for the Difference of Paired Means, \(\mu_d\)

When we consider the difference of two measurements, the parameter of interest is the mean difference, denoted \(\mu_d\). The mean difference is the mean of the differences. We are still interested in comparing this difference to zero.

Suppose we have two paired samples of size \(n\):

\(x_1, x_2, …., x_n\) and \(y_1, y_2, … , y_n\)

Their difference can be denoted as:

\(d_1=x_1-y_1, d_2=x_2-y_2, …., d_n=x_n-y_n\)

The sample mean of the differences is:

\(\bar{d}=\frac{1}{n}\sum_{i=1}^n d_i\)

Denote the sample standard deviation of the differences as \(s_d\).

If \(\bar{d}\) is normal (or the sample size is large), the sampling distribution of \(\bar{d}\) is (approximately) normal with mean \(\mu_d\), standard error \(\dfrac{\sigma_d}{\sqrt{n}}\), and estimated standard error \(\dfrac{s_d}{\sqrt{n}}\).

At this point, the confidence interval will be the same as that of one sample.

\(\bar{d}\pm t_{\alpha/2}\frac{s_d}{\sqrt{n}}\)

where \(t_{\alpha/2}\) comes from \(t\)-distribution with \(n-1\) degrees of freedom

Example 7-6: Zinc Concentrations

Trace metals in drinking water affect the flavor and an unusually high concentration can pose a health hazard. Ten pairs of data were taken measuring zinc concentration in bottom water and surface water ( zinc_conc.txt ).

Does the data suggest that the true average concentration in the bottom water is different than that of surface water? Construct a confidence interval to address this question.

Zinc concentrations

In this example, the response variable is concentration and is a quantitative measurement. The explanatory variable is location (bottom or surface) and is categorical. The two populations (bottom or surface) are not independent. Therefore, we are in the paired data setting. The parameter of interest is \(\mu_d\).

Find the difference as the concentration of the bottom water minus the concentration of the surface water.

Since the problem did not provide a confidence level, we should use 5%.

To use the methods we developed previously, we need to check the conditions. The problem does not indicate that the differences come from a normal distribution and the sample size is small (n=10). We should check, using the Normal Probability Plot to see if there is any violation. First, we need to find the differences.

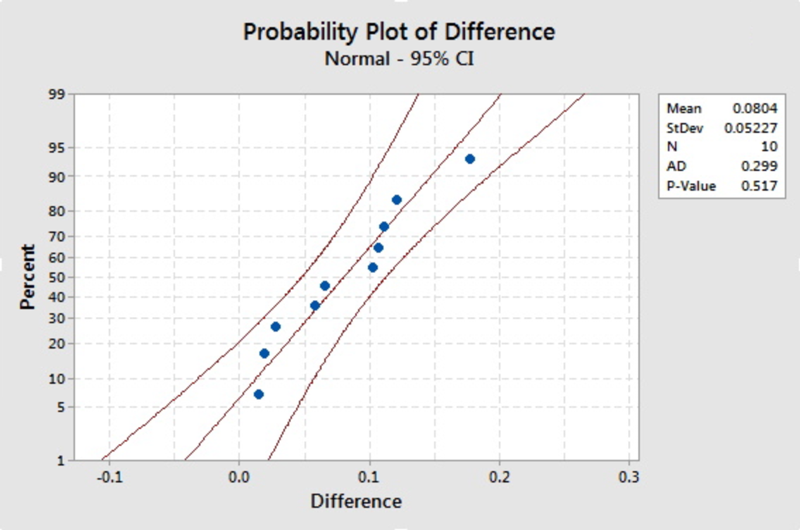
All of the differences fall within the boundaries, so there is no clear violation of the assumption. We can proceed with using our tools, but we should proceed with caution.

We need all of the pieces for the confidence interval. The sample mean difference is \(\bar{d}=0.0804\) and the standard deviation is \(s_d=0.0523\). For practice, you should find the sample mean of the differences and the standard deviation by hand. With \(n-1=10-1=9\) degrees of freedom, \(t_{0.05/2}=2.2622\).

The 95% confidence interval for the mean difference, \(\mu_d\) is:

\(\bar{d}\pm t_{\alpha/2}\dfrac{s_d}{\sqrt{n}}\)

\(0.0804\pm 2.2622\left( \dfrac{0.0523}{\sqrt{10}}\right)\)

(0.04299, 0.11781)

We are 95% confident that the population mean difference of bottom water and surface water zinc concentration is between 0.04299 and 0.11781.

If there is no difference between the means of the two measures, then the mean difference will be 0. Since 0 is not in our confidence interval, then the means are statistically different (or statistical significant or statistically different).

Note! Minitab will calculate the confidence interval and a hypothesis test simultaneously. We demonstrate how to find this interval using Minitab after presenting the hypothesis test.

Hypothesis Test for the Difference of Paired Means, \(\mu_d\)

In this section, we will develop the hypothesis test for the mean difference for paired samples. As we learned in the previous section, if we consider the difference rather than the two samples, then we are back in the one-sample mean scenario.

The possible null and alternative hypotheses are:

\(H_0\colon \mu_d=0\)

\(H_a\colon \mu_d\ne 0\)

\(H_a\colon \mu_d>0\)

\(H_a\colon \mu_d<0\)

We still need to check the conditions and at least one of the following need to be satisfied:

• The differences of the paired follow a normal distribution
• The sample size is large, \(n>30\).

If at least one is satisfied then...

\(t^*=\dfrac{\bar{d}-0}{\frac{s_d}{\sqrt{n}}}\)

Will follow a t-distribution with \(n-1\) degrees of freedom.

The same process for the hypothesis test for one mean can be applied. The test for the mean difference may be referred to as the paired t-test or the test for paired means.

Example 7-7: Zinc Concentrations - Hypothesis Test

Recall the zinc concentration example. Does the data suggest that the true average concentration in the bottom water exceeds that of surface water? Conduct this test using the rejection region approach. ( zinc_conc.txt ).

If we find the difference as the concentration of the bottom water minus the concentration of the surface water, then null and alternative hypotheses are:

\(H_0\colon \mu_d=0\) vs \(H_a\colon \mu_d>0\)

Note! If the difference was defined as surface - bottom, then the alternative would be left-tailed.

The desired significance level was not stated so we will use \(\alpha=0.05\).

The assumptions were discussed when we constructed the confidence interval for this example. Remember although the Normal Probability Plot for the differences showed no violation, we should still proceed with caution.

The next step is to find the critical value and the rejection region. The critical value is the value \(a\) such that \(P(T>a)=0.05\). Using the table or software, the value is 1.8331. For a right-tailed test, the rejection region is \(t^*>1.8331\).

Recall from the previous example, the sample mean difference is \(\bar{d}=0.0804\) and the sample standard deviation of the difference is \(s_d=0.0523\). Therefore, the test statistic is:

\(t^*=\dfrac{\bar{d}-0}{\frac{s_d}{\sqrt{n}}}=\dfrac{0.0804}{\frac{0.0523}{\sqrt{10}}}=4.86\)

The value of our test statistic falls in the rejection region. Therefore, we reject the null hypothesis. With a significance level of 5%, there is enough evidence in the data to suggest that the bottom water has higher concentrations of zinc than the surface level.

Minitab ®  – Paired t-Test

You can use a paired t -test in Minitab to perform the test. Alternatively, you can perform a 1-sample t -test on difference = bottom - surface.

• Choose Stat > Basic Statistics > Paired t
• Click Options to specify the confidence level for the interval and the alternative hypothesis you want to test. The default null hypothesis is 0.

Zinc Concentrations Example

The Minitab output for paired T for bottom - surface is as follows:

Paired T for bottom - surface

95% lower bound for mean difference: 0.0505

T-Test of mean difference = 0 (vs > 0): T-Value = 4.86 P-Value = 0.000

Note! In Minitab, if you choose a lower-tailed or an upper-tailed hypothesis test, an upper or lower confidence bound will be constructed, respectively, rather than a confidence interval.

Using the p -value to draw a conclusion about our example:

p -value = 0.000 < 0.05

Reject \(H_0\) and conclude that bottom zinc concentration is higher than surface zinc concentration.

Additional Notes

• For the zinc concentration problem, if you do not recognize the paired structure, but mistakenly use the 2-sample t -test treating them as independent samples, you will not be able to reject the null hypothesis. This demonstrates the importance of distinguishing the two types of samples. Also, it is wise to design an experiment efficiently whenever possible.
• What if the assumption of normality is not satisfied? Considering a nonparametric test would be wise.

Module 10: Inference for Means

Hypothesis test for a difference in two population means (1 of 2), learning outcomes.

• Under appropriate conditions, conduct a hypothesis test about a difference between two population means. State a conclusion in context.

Using the Hypothesis Test for a Difference in Two Population Means

The general steps of this hypothesis test are the same as always. As expected, the details of the conditions for use of the test and the test statistic are unique to this test (but similar in many ways to what we have seen before.)

Step 1: Determine the hypotheses.

The hypotheses for a difference in two population means are similar to those for a difference in two population proportions. The null hypothesis, H 0 , is again a statement of “no effect” or “no difference.”

• H 0 : μ 1 – μ 2 = 0, which is the same as H 0 : μ 1 = μ 2

The alternative hypothesis, H a , can be any one of the following.

• H a : μ 1 – μ 2 < 0, which is the same as H a : μ 1 < μ 2
• H a : μ 1 – μ 2 > 0, which is the same as H a : μ 1 > μ 2
• H a : μ 1 – μ 2 ≠ 0, which is the same as H a : μ 1 ≠ μ 2

Step 2: Collect the data.

As usual, how we collect the data determines whether we can use it in the inference procedure. We have our usual two requirements for data collection.

• Samples must be random to remove or minimize bias.
• Samples must be representative of the populations in question.

We use this hypothesis test when the data meets the following conditions.

• The two random samples are independent .
• The variable is normally distributed in both populations . If this variable is not known, samples of more than 30 will have a difference in sample means that can be modeled adequately by the t-distribution. As we discussed in “Hypothesis Test for a Population Mean,” t-procedures are robust even when the variable is not normally distributed in the population. If checking normality in the populations is impossible, then we look at the distribution in the samples. If a histogram or dotplot of the data does not show extreme skew or outliers, we take it as a sign that the variable is not heavily skewed in the populations, and we use the inference procedure. (Note: This is the same condition we used for the one-sample t-test in “Hypothesis Test for a Population Mean.”)

Step 3: Assess the evidence.

If the conditions are met, then we calculate the t-test statistic. The t-test statistic has a familiar form.

[latex]T\text{}=\text{}\frac{(\mathrm{Observed}\text{}\mathrm{difference}\text{}\mathrm{in}\text{}\mathrm{sample}\text{}\mathrm{means})-(\mathrm{Hypothesized}\text{}\mathrm{difference}\text{}\mathrm{in}\text{}\mathrm{population}\text{}\mathrm{means})}{\mathrm{Standard}\text{}\mathrm{error}}[/latex]

[latex]T\text{}=\text{}\frac{({\stackrel{¯}{x}}_{1}-{\stackrel{¯}{x}}_{2})-({μ}_{1}-{μ}_{2})}{\sqrt{\frac{{{s}_{1}}^{2}}{{n}_{1}}+\frac{{{s}_{2}}^{2}}{{n}_{2}}}}[/latex]

Since the null hypothesis assumes there is no difference in the population means, the expression (μ 1 – μ 2 ) is always zero.

As we learned in “Estimating a Population Mean,” the t-distribution depends on the degrees of freedom (df) . In the one-sample and matched-pair cases df = n – 1. For the two-sample t-test, determining the correct df is based on a complicated formula that we do not cover in this course. We will either give the df or use technology to find the df . With the t-test statistic and the degrees of freedom, we can use the appropriate t-model to find the P-value, just as we did in “Hypothesis Test for a Population Mean.” We can even use the same simulation.

Step 4: State a conclusion.

To state a conclusion, we follow what we have done with other hypothesis tests. We compare our P-value to a stated level of significance.

• If the P-value ≤ α, we reject the null hypothesis in favor of the alternative hypothesis.
• If the P-value > α, we fail to reject the null hypothesis. We do not have enough evidence to support the alternative hypothesis.

As always, we state our conclusion in context, usually by referring to the alternative hypothesis.

“Context and Calories”

Does the company you keep impact what you eat? This example comes from an article titled “Impact of Group Settings and Gender on Meals Purchased by College Students” (Allen-O’Donnell, M., T. C. Nowak, K. A. Snyder, and M. D. Cottingham, Journal of Applied Social Psychology 49(9), 2011, onlinelibrary.wiley.com/doi/10.1111/j.1559-1816.2011.00804.x/full) . In this study, researchers examined this issue in the context of gender-related theories in their field. For our purposes, we look at this research more narrowly.

Step 1: Stating the hypotheses.

In the article, the authors make the following hypothesis. “The attempt to appear feminine will be empirically demonstrated by the purchase of fewer calories by women in mixed-gender groups than by women in same-gender groups.” We translate this into a simpler and narrower research question: Do women purchase fewer calories when they eat with men compared to when they eat with women?

Here the two populations are “women eating with women” (population 1) and “women eating with men” (population 2). The variable is the calories in the meal. We test the following hypotheses at the 5% level of significance.

The null hypothesis is always H 0 : μ 1 – μ 2 = 0, which is the same as H 0 : μ 1 = μ 2 .

The alternative hypothesis H a : μ 1 – μ 2 > 0, which is the same as H a : μ 1 > μ 2 .

Here μ 1 represents the mean number of calories ordered by women when they were eating with other women, and μ 2 represents the mean number of calories ordered by women when they were eating with men.

Note: It does not matter which population we label as 1 or 2, but once we decide, we have to stay consistent throughout the hypothesis test. Since we expect the number of calories to be greater for the women eating with other women, the difference is positive if “women eating with women” is population 1. If you prefer to work with positive numbers, choose the group with the larger expected mean as population 1. This is a good general tip.

Step 2: Collect Data.

As usual, there are two major things to keep in mind when considering the collection of data.

• Samples need to be representative of the population in question.
• Samples need to be random in order to remove or minimize bias.

Representative Samples?

The researchers state their hypothesis in terms of “women.” We did the same. But the researchers gathered data by watching people eat at the HUB Rock Café II on the campus of Indiana University of Pennsylvania during the Spring semester of 2006. Almost all of the women in the data set were white undergraduates between the ages of 18 and 24, so there are some definite limitations on the scope of this study. These limitations will affect our conclusion (and the specific definition of the population means in our hypotheses.)

Random Samples?

The observations were collected on February 13, 2006, through February 22, 2006, between 11 a.m. and 7 p.m. We can see that the researchers included both lunch and dinner. They also made observations on all days of the week to ensure that weekly customer patterns did not confound their findings. The authors state that “since the time period for observations and the place where [they] observed students were limited, the sample was a convenience sample.” Despite these limitations, the researchers conducted inference procedures with the data, and the results were published in a reputable journal. We will also conduct inference with this data, but we also include a discussion of the limitations of the study with our conclusion. The authors did this, also.

Do the data met the conditions for use of a t-test?

The researchers reported the following sample statistics.

• In a sample of 45 women dining with other women, the average number of calories ordered was 850, and the standard deviation was 252.
• In a sample of 27 women dining with men, the average number of calories ordered was 719, and the standard deviation was 322.

One of the samples has fewer than 30 women. We need to make sure the distribution of calories in this sample is not heavily skewed and has no outliers, but we do not have access to a spreadsheet of the actual data. Since the researchers conducted a t-test with this data, we will assume that the conditions are met. This includes the assumption that the samples are independent.

As noted previously, the researchers reported the following sample statistics.

To compute the t-test statistic, make sure sample 1 corresponds to population 1. Here our population 1 is “women eating with other women.” So x 1 = 850, s 1 = 252, n 1 =45, and so on.

[latex]T\text{}=\text{}\frac{{\stackrel{¯}{x}}_{1}\text{}\text{−}\text{}{\stackrel{¯}{x}}_{2}}{\sqrt{\frac{{{s}_{1}}^{2}}{{n}_{1}}+\frac{{{s}_{2}}^{2}}{{n}_{2}}}}\text{}=\text{}\frac{850\text{}\text{−}\text{}719}{\sqrt{\frac{{252}^{2}}{45}+\frac{{322}^{2}}{27}}}\text{}\approx \text{}\frac{131}{72.47}\text{}\approx \text{}1.81[/latex]

Using technology, we determined that the degrees of freedom are about 45 for this data. To find the P-value, we use our familiar simulation of the t-distribution. Since the alternative hypothesis is a “greater than” statement, we look for the area to the right of T = 1.81. The P-value is 0.0385.

Generic Conclusion

The hypotheses for this test are H 0 : μ 1 – μ 2 = 0 and H a : μ 1 – μ 2 > 0. Since the P-value is less than the significance level (0.0385 < 0.05), we reject H 0 and accept H a .

Conclusion in context

At Indiana University of Pennsylvania, the mean number of calories ordered by undergraduate women eating with other women is greater than the mean number of calories ordered by undergraduate women eating with men (P-value = 0.0385).

Comment about Conclusions

In the conclusion above, we did not generalize the findings to all women. Since the samples included only undergraduate women at one university, we included this information in our conclusion. But our conclusion is a cautious statement of the findings. The authors see the results more broadly in the context of theories in the field of social psychology. In the context of these theories, they write, “Our findings support the assertion that meal size is a tool for influencing the impressions of others. For traditional-age, predominantly White college women, diminished meal size appears to be an attempt to assert femininity in groups that include men.” This viewpoint is echoed in the following summary of the study for the general public on National Public Radio (npr.org).

• Both men and women appear to choose larger portions when they eat with women, and both men and women choose smaller portions when they eat in the company of men, according to new research published in the Journal of Applied Social Psychology . The study, conducted among a sample of 127 college students, suggests that both men and women are influenced by unconscious scripts about how to behave in each other’s company. And these scripts change the way men and women eat when they eat together and when they eat apart.

Should we be concerned that the findings of this study are generalized in this way? Perhaps. But the authors of the article address this concern by including the following disclaimer with their findings: “While the results of our research are suggestive, they should be replicated with larger, representative samples. Studies should be done not only with primarily White, middle-class college students, but also with students who differ in terms of race/ethnicity, social class, age, sexual orientation, and so forth.” This is an example of good statistical practice. It is often very difficult to select truly random samples from the populations of interest. Researchers therefore discuss the limitations of their sampling design when they discuss their conclusions.

In the following activities, you will have the opportunity to practice parts of the hypothesis test for a difference in two population means. On the next page, the activities focus on the entire process and also incorporate technology.

National Health and Nutrition Survey

Contribute.

Improve this page Learn More

• Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

• Calculators
• Descriptive Statistics
• Merchandise
• Which Statistics Test?

T Test Calculator for 2 Dependent Means

The t -test for dependent means (also called a repeated-measures t -test, paired samples t -test, matched pairs t -test and matched samples t -test) is used to compare the means of two sets of scores that are directly related to each other. So, for example, it could be used to test whether subjects' galvanic skin responses are different under two conditions - first, on exposure to a photograph of a beach scene; second, on exposure to a photograph of a spider.

Requirements

• The data is normally distributed
• Scale of measurement should be interval or ratio
• The two sets of scores are paired or matched in some way

Null Hypothesis

H 0 : U D = U 1 - U 2 = 0, where U D equals the mean of the population of difference scores across the two measurements.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.2: Comparing Two Independent Population Means (Hypothesis test)

• Last updated
• Save as PDF
• Page ID 125735

• The two independent samples are simple random samples from two distinct populations.
• if the sample sizes are small, the distributions are important (should be normal)
• if the sample sizes are large, the distributions are not important (need not be normal)

The test comparing two independent population means with unknown and possibly unequal population standard deviations is called the Aspin-Welch \(t\)-test. The degrees of freedom formula was developed by Aspin-Welch.

The comparison of two population means is very common. A difference between the two samples depends on both the means and the standard deviations. Very different means can occur by chance if there is great variation among the individual samples. In order to account for the variation, we take the difference of the sample means, \(\bar{X}_{1} - \bar{X}_{2}\), and divide by the standard error in order to standardize the difference. The result is a t-score test statistic.

Because we do not know the population standard deviations, we estimate them using the two sample standard deviations from our independent samples. For the hypothesis test, we calculate the estimated standard deviation, or standard error , of the difference in sample means , \(\bar{X}_{1} - \bar{X}_{2}\).

The standard error is:

\[\sqrt{\dfrac{(s_{1})^{2}}{n_{1}} + \dfrac{(s_{2})^{2}}{n_{2}}}\]

The test statistic ( t -score) is calculated as follows:

\[\dfrac{(\bar{x}-\bar{x}) - (\mu_{1} - \mu_{2})}{\sqrt{\dfrac{(s_{1})^{2}}{n_{1}} + \dfrac{(s_{2})^{2}}{n_{2}}}}\]

• \(s_{1}\) and \(s_{2}\), the sample standard deviations, are estimates of \(\sigma_{1}\) and \(\sigma_{1}\), respectively.
• \(\sigma_{1}\) and \(\sigma_{2}\) are the unknown population standard deviations.
• \(\bar{x}_{1}\) and \(\bar{x}_{2}\) are the sample means. \(\mu_{1}\) and \(\mu_{2}\) are the population means.

The number of degrees of freedom (\(df\)) requires a somewhat complicated calculation. However, a computer or calculator calculates it easily. The \(df\) are not always a whole number. The test statistic calculated previously is approximated by the Student's t -distribution with \(df\) as follows:

Degrees of freedom

\[df = \dfrac{\left(\dfrac{(s_{1})^{2}}{n_{1}} + \dfrac{(s_{2})^{2}}{n_{2}}\right)^{2}}{\left(\dfrac{1}{n_{1}-1}\right)\left(\dfrac{(s_{1})^{2}}{n_{1}}\right)^{2} + \left(\dfrac{1}{n_{2}-1}\right)\left(\dfrac{(s_{2})^{2}}{n_{2}}\right)^{2}}\]

We can also use a conservative estimation of degree of freedom by taking DF to be the smallest of \(n_{1}-1\) and \(n_{2}-1\)

When both sample sizes \(n_{1}\) and \(n_{2}\) are five or larger, the Student's t approximation is very good. Notice that the sample variances \((s_{1})^{2}\) and \((s_{2})^{2}\) are not pooled. (If the question comes up, do not pool the variances.)

It is not necessary to compute the degrees of freedom by hand. A calculator or computer easily computes it.

Example \(\PageIndex{1}\): Independent groups

The average amount of time boys and girls aged seven to 11 spend playing sports each day is believed to be the same. A study is done and data are collected, resulting in the data in Table \(\PageIndex{1}\). Each populations has a normal distribution.

Is there a difference in the mean amount of time boys and girls aged seven to 11 play sports each day? Test at the 5% level of significance.

The population standard deviations are not known. Let g be the subscript for girls and b be the subscript for boys. Then, \(\mu_{g}\) is the population mean for girls and \(\mu_{b}\) is the population mean for boys. This is a test of two independent groups, two population means.

Random variable: \(\bar{X}_{g} - \bar{X}_{b} =\) difference in the sample mean amount of time girls and boys play sports each day.

• \(H_{0}: \mu_{g} = \mu_{b}\)  
• \(H_{0}: \mu_{g} - \mu_{b} = 0\)
• \(H_{a}: \mu_{g} \neq \mu_{b}\)  
• \(H_{a}: \mu_{g} - \mu_{b} \neq 0\)

The words "the same" tell you \(H_{0}\) has an "=". Since there are no other words to indicate \(H_{a}\), assume it says "is different." This is a two-tailed test.

Distribution for the test: Use \(t_{df}\) where \(df\) is calculated using the \(df\) formula for independent groups, two population means. Using a calculator, \(df\) is approximately 18.8462. Do not pool the variances.

Calculate the p -value using a Student's t -distribution: \(p\text{-value} = 0.0054\)

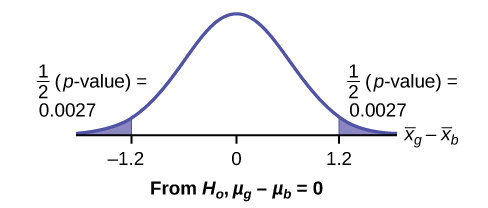
\[s_{g} = 0.866\]

\[s_{b} = 1\]

\[\bar{x}_{g} - \bar{x}_{b} = 2 - 3.2 = -1.2\]

Half the \(p\text{-value}\) is below –1.2 and half is above 1.2.

Make a decision: Since \(\alpha > p\text{-value}\), reject \(H_{0}\). This means you reject \(\mu_{g} = \mu_{b}\). The means are different.

Press STAT . Arrow over to TESTS and press 4:2-SampTTest . Arrow over to Stats and press ENTER . Arrow down and enter 2 for the first sample mean, \(\sqrt{0.866}\) for Sx1, 9 for n1, 3.2 for the second sample mean, 1 for Sx2, and 16 for n2. Arrow down to μ1: and arrow to does not equal μ2. Press ENTER . Arrow down to Pooled: and No . Press ENTER . Arrow down to Calculate and press ENTER . The \(p\text{-value}\) is \(p = 0.0054\), the dfs are approximately 18.8462, and the test statistic is -3.14. Do the procedure again but instead of Calculate do Draw.

Conclusion: At the 5% level of significance, the sample data show there is sufficient evidence to conclude that the mean number of hours that girls and boys aged seven to 11 play sports per day is different (mean number of hours boys aged seven to 11 play sports per day is greater than the mean number of hours played by girls OR the mean number of hours girls aged seven to 11 play sports per day is greater than the mean number of hours played by boys).

Exercise \(\PageIndex{1}\)

Two samples are shown in Table. Both have normal distributions. The means for the two populations are thought to be the same. Is there a difference in the means? Test at the 5% level of significance.

The \(p\text{-value}\) is \(0.4125\), which is much higher than 0.05, so we decline to reject the null hypothesis. There is not sufficient evidence to conclude that the means of the two populations are not the same.

When the sum of the sample sizes is larger than \(30 (n_{1} + n_{2} > 30)\) you can use the normal distribution to approximate the Student's \(t\).

Example \(\PageIndex{2}\)

A study is done by a community group in two neighboring colleges to determine which one graduates students with more math classes. College A samples 11 graduates. Their average is four math classes with a standard deviation of 1.5 math classes. College B samples nine graduates. Their average is 3.5 math classes with a standard deviation of one math class. The community group believes that a student who graduates from college A has taken more math classes, on the average. Both populations have a normal distribution. Test at a 1% significance level. Answer the following questions.

• Is this a test of two means or two proportions?
• Are the populations standard deviations known or unknown?
• Which distribution do you use to perform the test?
• What is the random variable?
• What are the null and alternate hypotheses? Write the null and alternate hypotheses in words and in symbols.
• Is this test right-, left-, or two-tailed?
• What is the \(p\text{-value}\)?
• Do you reject or not reject the null hypothesis?
• Student's t
• \(\bar{X}_{A} - \bar{X}_{B}\)
• \(H_{0}: \mu_{A} \leq \mu_{B}\) and \(H_{a}: \mu_{A} > \mu_{B}\)

• h. Do not reject.
• i. At the 1% level of significance, from the sample data, there is not sufficient evidence to conclude that a student who graduates from college A has taken more math classes, on the average, than a student who graduates from college B.

Exercise \(\PageIndex{2}\)

A study is done to determine if Company A retains its workers longer than Company B. Company A samples 15 workers, and their average time with the company is five years with a standard deviation of 1.2. Company B samples 20 workers, and their average time with the company is 4.5 years with a standard deviation of 0.8. The populations are normally distributed.

• Are the population standard deviations known?
• Conduct an appropriate hypothesis test. At the 5% significance level, what is your conclusion?
• They are unknown.
• The \(p\text{-value} = 0.0878\). At the 5% level of significance, there is insufficient evidence to conclude that the workers of Company A stay longer with the company.

Example \(\PageIndex{3}\)

A professor at a large community college wanted to determine whether there is a difference in the means of final exam scores between students who took his statistics course online and the students who took his face-to-face statistics class. He believed that the mean of the final exam scores for the online class would be lower than that of the face-to-face class. Was the professor correct? The randomly selected 30 final exam scores from each group are listed in Table \(\PageIndex{3}\) and Table \(\PageIndex{4}\).

Is the mean of the Final Exam scores of the online class lower than the mean of the Final Exam scores of the face-to-face class? Test at a 5% significance level. Answer the following questions:

• Are the population standard deviations known or unknown?
• What are the null and alternative hypotheses? Write the null and alternative hypotheses in words and in symbols.
• Is this test right, left, or two tailed?
• At the ___ level of significance, from the sample data, there ______ (is/is not) sufficient evidence to conclude that ______.

(See the conclusion in Example, and write yours in a similar fashion)

Be careful not to mix up the information for Group 1 and Group 2!

• Student's \(t\)
• \(\bar{X}_{1} - \bar{X}_{2}\)
• \(H_{0}: \mu_{1} = \mu_{2}\) Null hypothesis: the means of the final exam scores are equal for the online and face-to-face statistics classes.
• \(H_{a}: \mu_{1} < \mu_{2}\) Alternative hypothesis: the mean of the final exam scores of the online class is less than the mean of the final exam scores of the face-to-face class.
• left-tailed

Figure \(\PageIndex{3}\).

• Reject the null hypothesis

At the 5% level of significance, from the sample data, there is (is/is not) sufficient evidence to conclude that the mean of the final exam scores for the online class is less than the mean of final exam scores of the face-to-face class.

First put the data for each group into two lists (such as L1 and L2). Press STAT. Arrow over to TESTS and press 4:2SampTTest. Make sure Data is highlighted and press ENTER. Arrow down and enter L1 for the first list and L2 for the second list. Arrow down to \(\mu_{1}\): and arrow to \(\neq \mu_{1}\) (does not equal). Press ENTER. Arrow down to Pooled: No. Press ENTER. Arrow down to Calculate and press ENTER.

Cohen's Standards for Small, Medium, and Large Effect Sizes

Cohen's \(d\) is a measure of effect size based on the differences between two means. Cohen’s \(d\), named for United States statistician Jacob Cohen, measures the relative strength of the differences between the means of two populations based on sample data. The calculated value of effect size is then compared to Cohen’s standards of small, medium, and large effect sizes.

Cohen's \(d\) is the measure of the difference between two means divided by the pooled standard deviation: \(d = \dfrac{\bar{x}_{2}-\bar{x}_{2}}{s_{\text{pooled}}}\) where \(s_{pooled} = \sqrt{\dfrac{(n_{1}-1)s^{2}_{1} + (n_{2}-1)s^{2}_{2}}{n_{1}+n_{2}-2}}\)

Example \(\PageIndex{4}\)

Calculate Cohen’s d for Example. Is the size of the effect small, medium, or large? Explain what the size of the effect means for this problem.

\(\mu_{1} = 4 s_{1} = 1.5 n_{1} = 11\)

\(\mu_{2} = 3.5 s_{2} = 1 n_{2} = 9\)

\(d = 0.384\)

The effect is small because 0.384 is between Cohen’s value of 0.2 for small effect size and 0.5 for medium effect size. The size of the differences of the means for the two colleges is small indicating that there is not a significant difference between them.

Example \(\PageIndex{5}\)

Calculate Cohen’s \(d\) for Example. Is the size of the effect small, medium or large? Explain what the size of the effect means for this problem.

\(d = 0.834\); Large, because 0.834 is greater than Cohen’s 0.8 for a large effect size. The size of the differences between the means of the Final Exam scores of online students and students in a face-to-face class is large indicating a significant difference.

Example 10.2.6

Weighted alpha is a measure of risk-adjusted performance of stocks over a period of a year. A high positive weighted alpha signifies a stock whose price has risen while a small positive weighted alpha indicates an unchanged stock price during the time period. Weighted alpha is used to identify companies with strong upward or downward trends. The weighted alpha for the top 30 stocks of banks in the northeast and in the west as identified by Nasdaq on May 24, 2013 are listed in Table and Table, respectively.

Is there a difference in the weighted alpha of the top 30 stocks of banks in the northeast and in the west? Test at a 5% significance level. Answer the following questions:

• Calculate Cohen’s d and interpret it.
• Student’s-t
• \(H_{0}: \mu_{1} = \mu_{2}\) Null hypothesis: the means of the weighted alphas are equal.
• \(H_{a}: \mu_{1} \neq \mu_{2}\) Alternative hypothesis : the means of the weighted alphas are not equal.
• \(p\text{-value} = 0.8787\)
• Do not reject the null hypothesis

Figure \(\PageIndex{4}\).

• \(d = 0.040\), Very small, because 0.040 is less than Cohen’s value of 0.2 for small effect size. The size of the difference of the means of the weighted alphas for the two regions of banks is small indicating that there is not a significant difference between their trends in stocks.
• Data from Graduating Engineer + Computer Careers. Available online at www.graduatingengineer.com
• Data from Microsoft Bookshelf .
• Data from the United States Senate website, available online at www.Senate.gov (accessed June 17, 2013).
• “List of current United States Senators by Age.” Wikipedia. Available online at en.Wikipedia.org/wiki/List_of...enators_by_age (accessed June 17, 2013).
• “Sectoring by Industry Groups.” Nasdaq. Available online at www.nasdaq.com/markets/barcha...&base=industry (accessed June 17, 2013).
• “Strip Clubs: Where Prostitution and Trafficking Happen.” Prostitution Research and Education, 2013. Available online at www.prostitutionresearch.com/ProsViolPosttrauStress.html (accessed June 17, 2013).
• “World Series History.” Baseball-Almanac, 2013. Available online at http://www.baseball-almanac.com/ws/wsmenu.shtml (accessed June 17, 2013).

Two population means from independent samples where the population standard deviations are not known

• Random Variable: \(\bar{X}_{1} - \bar{X}_{2} =\) the difference of the sampling means
• Distribution: Student's t -distribution with degrees of freedom (variances not pooled)

Formula Review

Standard error: \[SE = \sqrt{\dfrac{(s_{1}^{2})}{n_{1}} + \dfrac{(s_{2}^{2})}{n_{2}}}\]

Test statistic ( t -score): \[t = \dfrac{(\bar{x}_{1}-\bar{x}_{2}) - (\mu_{1}-\mu_{2})}{\sqrt{\dfrac{(s_{1})^{2}}{n_{1}} + \dfrac{(s_{2})^{2}}{n_{2}}}}\]

Degrees of freedom:

\[df = \dfrac{\left(\dfrac{(s_{1})^{2}}{n_{1}} + \dfrac{(s_{2})^{2}}{n_{2}}\right)^{2}}{\left(\dfrac{1}{n_{1} - 1}\right)\left(\dfrac{(s_{1})^{2}}{n_{1}}\right)^{2}} + \left(\dfrac{1}{n_{2} - 1}\right)\left(\dfrac{(s_{2})^{2}}{n_{2}}\right)^{2}\]

• \(s_{1}\) and \(s_{2}\) are the sample standard deviations, and n 1 and n 2 are the sample sizes.
• \(x_{1}\) and \(x_{2}\) are the sample means.

OR use the   DF to be the smallest of \(n_{1}-1\) and \(n_{2}-1\)

Cohen’s \(d\) is the measure of effect size:

\[d = \dfrac{\bar{x}_{1} - \bar{x}_{2}}{s_{\text{pooled}}}\]

\[s_{\text{pooled}} = \sqrt{\dfrac{(n_{1} - 1)s^{2}_{1} + (n_{2} - 1)s^{2}_{2}}{n_{1} + n_{2} - 2}}\]

• The domain of the random variable (RV) is not necessarily a numerical set; the domain may be expressed in words; for example, if \(X =\) hair color, then the domain is {black, blond, gray, green, orange}.
• We can tell what specific value x of the random variable \(X\) takes only after performing the experiment.

Hypothesis Testing Calculator for Population Mean English Español

A free online hypothesis testing calculator for population mean to find the Hypothesis for the given population mean. Enter the sample mean, population mean, sample standard deviation, population size and the significance level to know the T score test value, P value and result of hypothesis.

Hypothesis Testing: Hypothesis Test, also known as Statistical Hypothesis Test is a method of statistical inference. Since it is a hypothesis that is testable on the basis of observing a process that is modeled via a set of random variables, it is also referred to as confirmatory data analysis. The hypothesis testing for population mean analyses the results of the null hypothesis and the alternative hypothesis of a population. Hypothesis testing is one of the final analysis of statistical data. Use this free sample and population statistics calculator to perform a statistical hypothesis test for the given population mean. This online hypothesis testing calculator for population mean helps you to perform the two-tailed and one-tailed statistical hypothesis testing.

If you are performing one-tailed test for the sample mean of 20, population mean of 15, the size of the population of 5, SD of 25 and the significance level of -10, then you will get the below values as result.

Solution 1 :

T-score is 0.44721

Solution 2 :

P-value is 0.6726

P-value > -10 ( Significance level). Hence, H0 is not rejected. H0 is Null Hypothesis.

Related Calculators:

• Standard Deviation Calculator
• Population Confidence Interval
• Sample Size Calculator
• Mean Squared Error, Sum Of Squared Error Calculator
• Hypothesis Test For Population Variance
• Probability (P) Value T Test Calculator
• Cumulative Sum Calculator

Calculators and Converters

• Calculators
• Sample And Population Statistics

Ask a Question

Top calculators, popular calculators.

• Derivative Calculator
• Inverse of Matrix Calculator
• Compound Interest Calculator
• Pregnancy Calculator Online

Top Categories

Critical Value Calculator

How to use critical value calculator, what is a critical value, critical value definition, how to calculate critical values, z critical values, t critical values, chi-square critical values (χ²), f critical values, behind the scenes of the critical value calculator.

Welcome to the critical value calculator! Here you can quickly determine the critical value(s) for two-tailed tests, as well as for one-tailed tests. It works for most common distributions in statistical testing: the standard normal distribution N(0,1) (that is when you have a Z-score), t-Student, chi-square, and F-distribution .

What is a critical value? And what is the critical value formula? Scroll down – we provide you with the critical value definition and explain how to calculate critical values in order to use them to construct rejection regions (also known as critical regions).

The critical value calculator is your go-to tool for swiftly determining critical values in statistical tests, be it one-tailed or two-tailed. To effectively use the calculator, follow these steps:

In the first field, input the distribution of your test statistic under the null hypothesis: is it a standard normal N (0,1), t-Student, chi-squared, or Snedecor's F? If you are not sure, check the sections below devoted to those distributions, and try to localize the test you need to perform.

In the field What type of test? choose the alternative hypothesis : two-tailed, right-tailed, or left-tailed.

If needed, specify the degrees of freedom of the test statistic's distribution. If you need more clarification, check the description of the test you are performing. You can learn more about the meaning of this quantity in statistics from the degrees of freedom calculator .

Set the significance level, α \alpha α . By default, we pre-set it to the most common value, 0.05, but you can adjust it to your needs.

The critical value calculator will display your critical value(s) and the rejection region(s).

Click the advanced mode if you need to increase the precision with which the critical values are computed.

For example, let's envision a scenario where you are conducting a one-tailed hypothesis test using a t-Student distribution with 15 degrees of freedom. You have opted for a right-tailed test and set a significance level (α) of 0.05. The results indicate that the critical value is 1.7531, and the critical region is (1.7531, ∞). This implies that if your test statistic exceeds 1.7531, you will reject the null hypothesis at the 0.05 significance level.

👩‍🏫 Want to learn more about critical values? Keep reading!

In hypothesis testing, critical values are one of the two approaches which allow you to decide whether to retain or reject the null hypothesis. The other approach is to calculate the p-value (for example, using the p-value calculator ).

The critical value approach consists of checking if the value of the test statistic generated by your sample belongs to the so-called rejection region , or critical region , which is the region where the test statistic is highly improbable to lie . A critical value is a cut-off value (or two cut-off values in the case of a two-tailed test) that constitutes the boundary of the rejection region(s). In other words, critical values divide the scale of your test statistic into the rejection region and the non-rejection region.

Once you have found the rejection region, check if the value of the test statistic generated by your sample belongs to it :

• If so, it means that you can reject the null hypothesis and accept the alternative hypothesis; and
• If not, then there is not enough evidence to reject H 0 .

But how to calculate critical values? First of all, you need to set a significance level , α \alpha α , which quantifies the probability of rejecting the null hypothesis when it is actually correct. The choice of α is arbitrary; in practice, we most often use a value of 0.05 or 0.01. Critical values also depend on the alternative hypothesis you choose for your test , elucidated in the next section .

To determine critical values, you need to know the distribution of your test statistic under the assumption that the null hypothesis holds. Critical values are then points with the property that the probability of your test statistic assuming values at least as extreme at those critical values is equal to the significance level α . Wow, quite a definition, isn't it? Don't worry, we'll explain what it all means.

First, let us point out it is the alternative hypothesis that determines what "extreme" means. In particular, if the test is one-sided, then there will be just one critical value; if it is two-sided, then there will be two of them: one to the left and the other to the right of the median value of the distribution.

Critical values can be conveniently depicted as the points with the property that the area under the density curve of the test statistic from those points to the tails is equal to α \alpha α :

Left-tailed test: the area under the density curve from the critical value to the left is equal to α \alpha α ;

Right-tailed test: the area under the density curve from the critical value to the right is equal to α \alpha α ; and

Two-tailed test: the area under the density curve from the left critical value to the left is equal to α / 2 \alpha/2 α /2 , and the area under the curve from the right critical value to the right is equal to α / 2 \alpha/2 α /2 as well; thus, total area equals α \alpha α .

As you can see, finding the critical values for a two-tailed test with significance α \alpha α boils down to finding both one-tailed critical values with a significance level of α / 2 \alpha/2 α /2 .

The formulae for the critical values involve the quantile function , Q Q Q , which is the inverse of the cumulative distribution function ( c d f \mathrm{cdf} cdf ) for the test statistic distribution (calculated under the assumption that H 0 holds!): Q = c d f − 1 Q = \mathrm{cdf}^{-1} Q = cdf − 1 .

Once we have agreed upon the value of α \alpha α , the critical value formulae are the following:

• Left-tailed test :
• Right-tailed test :
• Two-tailed test :

In the case of a distribution symmetric about 0 , the critical values for the two-tailed test are symmetric as well:

Unfortunately, the probability distributions that are the most widespread in hypothesis testing have somewhat complicated c d f \mathrm{cdf} cdf formulae. To find critical values by hand, you would need to use specialized software or statistical tables. In these cases, the best option is, of course, our critical value calculator! 😁

Use the Z (standard normal) option if your test statistic follows (at least approximately) the standard normal distribution N(0,1) .

In the formulae below, u u u denotes the quantile function of the standard normal distribution N(0,1):

Left-tailed Z critical value: u ( α ) u(\alpha) u ( α )

Right-tailed Z critical value: u ( 1 − α ) u(1-\alpha) u ( 1 − α )

Two-tailed Z critical value: ± u ( 1 − α / 2 ) \pm u(1- \alpha/2) ± u ( 1 − α /2 )

Check out Z-test calculator to learn more about the most common Z-test used on the population mean. There are also Z-tests for the difference between two population means, in particular, one between two proportions.

Use the t-Student option if your test statistic follows the t-Student distribution . This distribution is similar to N(0,1) , but its tails are fatter – the exact shape depends on the number of degrees of freedom . If this number is large (>30), which generically happens for large samples, then the t-Student distribution is practically indistinguishable from N(0,1). Check our t-statistic calculator to compute the related test statistic.

In the formulae below, Q t , d Q_{\text{t}, d} Q t , d ​ is the quantile function of the t-Student distribution with d d d degrees of freedom:

Left-tailed t critical value: Q t , d ( α ) Q_{\text{t}, d}(\alpha) Q t , d ​ ( α )

Right-tailed t critical value: Q t , d ( 1 − α ) Q_{\text{t}, d}(1 - \alpha) Q t , d ​ ( 1 − α )

Two-tailed t critical values: ± Q t , d ( 1 − α / 2 ) \pm Q_{\text{t}, d}(1 - \alpha/2) ± Q t , d ​ ( 1 − α /2 )

Visit the t-test calculator to learn more about various t-tests: the one for a population mean with an unknown population standard deviation , those for the difference between the means of two populations (with either equal or unequal population standard deviations), as well as about the t-test for paired samples .

Use the χ² (chi-square) option when performing a test in which the test statistic follows the χ²-distribution .

You need to determine the number of degrees of freedom of the χ²-distribution of your test statistic – below, we list them for the most commonly used χ²-tests.

Here we give the formulae for chi square critical values; Q χ 2 , d Q_{\chi^2, d} Q χ 2 , d ​ is the quantile function of the χ²-distribution with d d d degrees of freedom:

Left-tailed χ² critical value: Q χ 2 , d ( α ) Q_{\chi^2, d}(\alpha) Q χ 2 , d ​ ( α )

Right-tailed χ² critical value: Q χ 2 , d ( 1 − α ) Q_{\chi^2, d}(1 - \alpha) Q χ 2 , d ​ ( 1 − α )

Two-tailed χ² critical values: Q χ 2 , d ( α / 2 ) Q_{\chi^2, d}(\alpha/2) Q χ 2 , d ​ ( α /2 ) and Q χ 2 , d ( 1 − α / 2 ) Q_{\chi^2, d}(1 - \alpha/2) Q χ 2 , d ​ ( 1 − α /2 )

Several different tests lead to a χ²-score:

Goodness-of-fit test : does the empirical distribution agree with the expected distribution?

This test is right-tailed . Its test statistic follows the χ²-distribution with k − 1 k - 1 k − 1 degrees of freedom, where k k k is the number of classes into which the sample is divided.

Independence test : is there a statistically significant relationship between two variables?

This test is also right-tailed , and its test statistic is computed from the contingency table. There are ( r − 1 ) ( c − 1 ) (r - 1)(c - 1) ( r − 1 ) ( c − 1 ) degrees of freedom, where r r r is the number of rows, and c c c is the number of columns in the contingency table.

Test for the variance of normally distributed data : does this variance have some pre-determined value?

This test can be one- or two-tailed! Its test statistic has the χ²-distribution with n − 1 n - 1 n − 1 degrees of freedom, where n n n is the sample size.

Finally, choose F (Fisher-Snedecor) if your test statistic follows the F-distribution . This distribution has a pair of degrees of freedom .

Let us see how those degrees of freedom arise. Assume that you have two independent random variables, X X X and Y Y Y , that follow χ²-distributions with d 1 d_1 d 1 ​ and d 2 d_2 d 2 ​ degrees of freedom, respectively. If you now consider the ratio ( X d 1 ) : ( Y d 2 ) (\frac{X}{d_1}):(\frac{Y}{d_2}) ( d 1 ​ X ​ ) : ( d 2 ​ Y ​ ) , it turns out it follows the F-distribution with ( d 1 , d 2 ) (d_1, d_2) ( d 1 ​ , d 2 ​ ) degrees of freedom. That's the reason why we call d 1 d_1 d 1 ​ and d 2 d_2 d 2 ​ the numerator and denominator degrees of freedom , respectively.

In the formulae below, Q F , d 1 , d 2 Q_{\text{F}, d_1, d_2} Q F , d 1 ​ , d 2 ​ ​ stands for the quantile function of the F-distribution with ( d 1 , d 2 ) (d_1, d_2) ( d 1 ​ , d 2 ​ ) degrees of freedom:

Left-tailed F critical value: Q F , d 1 , d 2 ( α ) Q_{\text{F}, d_1, d_2}(\alpha) Q F , d 1 ​ , d 2 ​ ​ ( α )

Right-tailed F critical value: Q F , d 1 , d 2 ( 1 − α ) Q_{\text{F}, d_1, d_2}(1 - \alpha) Q F , d 1 ​ , d 2 ​ ​ ( 1 − α )

Two-tailed F critical values: Q F , d 1 , d 2 ( α / 2 ) Q_{\text{F}, d_1, d_2}(\alpha/2) Q F , d 1 ​ , d 2 ​ ​ ( α /2 ) and Q F , d 1 , d 2 ( 1 − α / 2 ) Q_{\text{F}, d_1, d_2}(1 -\alpha/2) Q F , d 1 ​ , d 2 ​ ​ ( 1 − α /2 )

Here we list the most important tests that produce F-scores: each of them is right-tailed .

ANOVA : tests the equality of means in three or more groups that come from normally distributed populations with equal variances. There are ( k − 1 , n − k ) (k - 1, n - k) ( k − 1 , n − k ) degrees of freedom, where k k k is the number of groups, and n n n is the total sample size (across every group).

Overall significance in regression analysis . The test statistic has ( k − 1 , n − k ) (k - 1, n - k) ( k − 1 , n − k ) degrees of freedom, where n n n is the sample size, and k k k is the number of variables (including the intercept).

Compare two nested regression models . The test statistic follows the F-distribution with ( k 2 − k 1 , n − k 2 ) (k_2 - k_1, n - k_2) ( k 2 ​ − k 1 ​ , n − k 2 ​ ) degrees of freedom, where k 1 k_1 k 1 ​ and k 2 k_2 k 2 ​ are the number of variables in the smaller and bigger models, respectively, and n n n is the sample size.

The equality of variances in two normally distributed populations . There are ( n − 1 , m − 1 ) (n - 1, m - 1) ( n − 1 , m − 1 ) degrees of freedom, where n n n and m m m are the respective sample sizes.

I'm Anna, the mastermind behind the critical value calculator and a PhD in mathematics from Jagiellonian University .

The idea for creating the tool originated from my experiences in teaching and research. Recognizing the need for a tool that simplifies the critical value determination process across various statistical distributions, I built a user-friendly calculator accessible to both students and professionals. After publishing the tool, I soon found myself using the calculator in my research and as a teaching aid.

Trust in this calculator is paramount to me. Each tool undergoes a rigorous review process , with peer-reviewed insights from experts and meticulous proofreading by native speakers. This commitment to accuracy and reliability ensures that users can be confident in the content. Please check the Editorial Policies page for more details on our standards.

What is a Z critical value?

A Z critical value is the value that defines the critical region in hypothesis testing when the test statistic follows the standard normal distribution . If the value of the test statistic falls into the critical region, you should reject the null hypothesis and accept the alternative hypothesis.

How do I calculate Z critical value?

To find a Z critical value for a given confidence level α :

Check if you perform a one- or two-tailed test .

For a one-tailed test:

Left -tailed: critical value is the α -th quantile of the standard normal distribution N(0,1).

Right -tailed: critical value is the (1-α) -th quantile.

Two-tailed test: critical value equals ±(1-α/2) -th quantile of N(0,1).

No quantile tables ? Use CDF tables! (The quantile function is the inverse of the CDF.)

Verify your answer with an online critical value calculator.

Is a t critical value the same as Z critical value?

In theory, no . In practice, very often, yes . The t-Student distribution is similar to the standard normal distribution, but it is not the same . However, if the number of degrees of freedom (which is, roughly speaking, the size of your sample) is large enough (>30), then the two distributions are practically indistinguishable , and so the t critical value has practically the same value as the Z critical value.

What is the Z critical value for 95% confidence?

The Z critical value for a 95% confidence interval is:

• 1.96 for a two-tailed test;
• 1.64 for a right-tailed test; and
• -1.64 for a left-tailed test.

Black Friday

Books vs e-books, order from least to greatest, third quartile.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (570)
• Health (440)
• Physics (510)
• Sports (105)
• Statistics (182)
• Other (182)
• Discover Omni (40)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants

Scientific Calculator

• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

29: Hypothesis Test for a Population Proportion Calculator

• Last updated
• Save as PDF
• Page ID 8351

• Larry Green
• Lake Tahoe Community College

hypothesis test for a population Proportion calculator

Fill in the sample size, n, the number of successes, x, the hypothesized population proportion \(p_0\), and indicate if the test is left tailed, <, right tailed, >, or two tailed, \(\neq\).  Then hit "Calculate" and the test statistic and p-Value will be calculated for you.